Вероятность — появление — событие
Вероятность — появление — событие
Cтраница 1
Вероятность появления события в каждом из независимых испытаний равна 0.8. Сколько необходимо произвести испытаний, чтобы с вероятностью 0.9 можно было ожидать, что событие появится не менее 75 раз. [1]
Вероятность появления события на интервале, следующем за интервалом, на котором событие не появлялось, является условной вероятностью. [3]
Вероятность появления события при одном испытании равна р, вероятность непоявления события 1 — р — При каком р результат испытания обладает наибольшей неопределенностью. [4]
Вероятность появления события А в / — м испытании равна pf, Р ( т) — вероятность / n — кратного появления события А в п испытаниях. [5]
Вероятность появления события А и / — м испытании равна р -; Рп ( т) — вероятность от-кратного появления события Л в п испытаниях. [7]
Какова вероятность появления события А при одном опыте, если при каждом опыте эта вероятность одинакова. [8]
При прогнозировании вероятность появления события эквивалентна степени истинности соответствующего высказывания. [9]
Так как вероятность Рт появления события т раз в этом случае зависит только от V ( R / T), то вычисление Рт может быть доведено до конца. [10]
Для вычисления вероятности появления события
А в том случае, когда результат опыта определяется случайным положением точек в некоторой области, используется определение геометрической вероятности. При этом любые положения точек в этой области считаются равновероятными. [11]Что называется вероятностью появления события. [12]
Закон Пуассона дает вероятность появления события и раз за время, если можно считать, что вероятность наступления события за интервал А / пропорциональна этому интервалу и события в различные моменты времени независимы. [13]
Обозначим через р вероятность появления событий А в N реализациях. [14]
Таким образом, вероятность появления события Л зависит от того, произошло событие В или нет. Это значит, что событие А зависит от события В. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
Повторение испытаний. Формула Бернулли, Интегральная теорма Лапласа, Локальная теорема Лапласа
| | Повторение испытаний. Формула Бернулли, интегральная и локальная теоремы Лапласа. | | | | | |3. Повторение испытаний
3.1. Формула Бернулли
Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события одинакова и равна p () , событие наступит ровно k раз (безразлично в какой последовательности), равна
— Формула Бернулли
, где
Также возможны случаи когда нас будет интересовать появление события А не ровно к раз, а :
· Событие А появится менее k раз
· Событие А появится более k раз
· Событие А появится не менее k раз
· Событие А появится не более k раз
Где каждое из слагаемых находится по формуле Бернулли
3.2. Локальная и интегральная теоремы Лапласа
При достаточно большом числе испытаний n (в литературе нет четкого значения этого достаточно большого значения, чаще всего встречается при n>30) вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события одинакова и равна p, событие А появится ровно k раз.
, где
Где — функция Лапласа
Данная функция является четной, т.е.
Данная функция табулирована, т.е. ее значения занесены в таблицу.
Вероятность того, что события А появится в диапазоне от до раз необходимо находить сложением каждой вероятности, то при большой разнице между и данная операция представляется достаточно ресурсоёмкой. В таком случае необходимо использовать интегральную теорему Лапласа:
Если вероятность p наступления события а в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что события А появится в n испытаниях от до раз, приближенно равна
, где ;
— функция Лапласа.
Интеграл не выражается через элементарные функции, т.е. является «не берущимся».
Функция является нечётной
Данная функция также табулирована.
3.3. Отклонение относительной частоты от постоянной вероятности в независимых испытаниях
Вероятность того, что в n испытаниях, в каждом из которых вероятность появления события равна p (), абсолютная величина отклонения относительной частоты появления события от вероятности появления события не превысит положительного числа , приближенно равна
Где:
— функция Лапласа.
Интеграл не выражается через элементарные функции, т.е. является «не берущимся».
Функция является нечётной
Данная функция табулирована.
3.4. Наивероятнейшее число появлений события в независимых испытаниях
Число , наступления события А в независимых испытаниях, в каждом из которых вероятность появления события А равна p, называют наивероятнейшим, если вероятность того, что событие А наступит в этих испытаниях ровно раз, не меньше вероятности остальных возможных исходов испытания. Наивероятнейшее число определяют по формуле
При вычислениях следует помнить, что — натуральное число или нуль.
primer.by
2.5. Вероятность появления хотя бы одного события
Теорема. Вероятность
появления хотя бы одного из событий А1 ,
А2,…,Аn, независимых
в совокупности, равна разности между
единицей и произведением вероятностей
противоположных событий 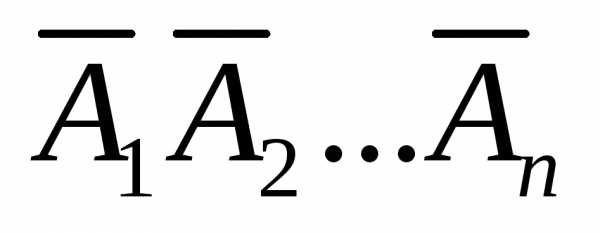 :
:
(2.7) |
Пример 2.5. Три стрелка делают по одному выстрелу в мишень. Вероятность попадания в мишень для первого стрелка равна 0,7, второго – 0,8 и третьего – 0,9. Найти вероятность того, что хотя бы один стрелок попадет в мишень.
Решение. Рассмотрим следующие события: А – хотя бы один стрелок попадет в мишень А1 – первый стрелок попадет в мишень, А2 – второй стрелок, А3 – третий стрелок. Вероятность попадания в мишень каждым из стрелков не зависит от результатов стрельбы других стрелков, поэтому события
Вероятности событий, противоположных событиям А1, А2 и А3 (т.е. вероятности промахов), соответственно равны:
= 1 – 0,7 = 0,3;
= 1 – 0,8 = 0,2;
= 1 – 0,9 = 0,1.
Искомая вероятность
= 1 – 0,3·0,2·0,1 = 0,994. ◄
Частный случай. Если события А1, А2,…,Аnимеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий
где q = 1 – p.
2.6. Условная вероятность
Пусть события А и В зависимые. Из определения зависимых событий следует, что вероятность одного из событий зависит от появления или непоявления другого события. Поэтому, если нас интересует вероятность события В, то важно знать, наступило событие А или нет.
Определение. Условной вероятностью РА(В) или Р(В|А) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
Например, в урне находится пять шаров. Два из них белого цвета, остальные три – черного. Наудачу один за другим берут два шара, не возвращая их обратно в урну. Рассмотрим событие А – «первый вынутый шар оказался белого цвета» и событие В – «второй вынутый шар оказался белого цвета». Найдем условную вероятность события В, при условии, что событие А уже наступило. Если в первый раз был вынут шар белого цвета, то в урне осталось четыре шара, из которых один белого цвета. Следовательно, Р(В | А) = 1/4.
Если же вынутый шар возвращается назад в урну, то условия второго испытания остаются неизменными после проведения первого испытания. Тогда
2.7. Теорема умножения вероятностей зависимых событий
Пусть события А и В зависимые, причем вероятности Р(А) и Р(В|А) известны. Как найти вероятность совмещения этих событий, т.е. вероятность того, что появится и событие А и событие В? Ответ на этот вопрос дает теорема умножения.
Теорема. Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Р(АВ) = Р(А)·Р(В|А). | (2.9) |
Следствие. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
Р(А1А2…Аn) = Р(А1)·Р(А2| А1) …·Р(Аn| А1 А2… Аn-1). | (2.10) |
Пример 2.6. В урне находится пять шаров. Один из них красного цвета, два – зеленого и два – синего. Наудачу один за другим извлекают три шара, не возвращая их обратно в урну. Найти вероятность того, что последовательно будут извлечены красный, зеленый и синий шар.
Решение. Рассмотрим события: A – первым извлечен шар красного цвета, B – вторым извлечен шар зеленого цвета, C – третьим извлечен шар синего цвета. Вероятность события А: Р(А) = 1/5. Условная вероятность события В при условии, что событие А уже наступило: Р(В|А) = 2/4. Условная вероятность события С при условии, что события А и В уже наступили: Р(С|АВ) = 2/3. Вероятность совместного появления трех зависимых событий А, В и С:
Р(АВС)
= Р(А)·Р(В/А)·Р(С/АВ)
= 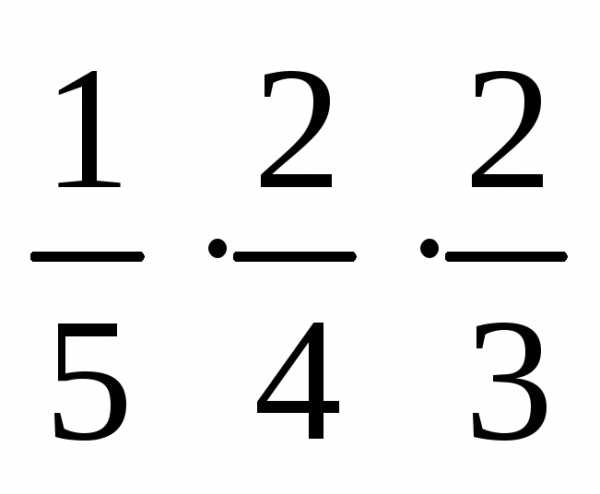 =
=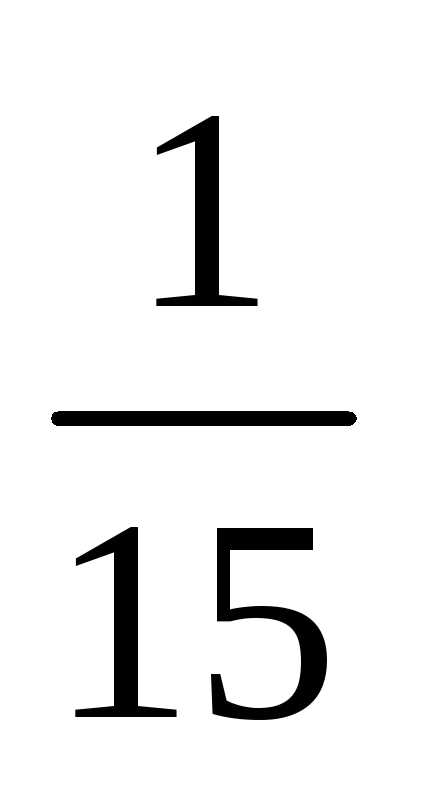 .
◄
.
◄
studfiles.net
Вероятность — появление — событие
Вероятность — появление — событие
Cтраница 3
Пусть р3 ( 1) есть вероятность появления события А ровно один раз в течение трех испытаний. [31]
Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А. В § 1 — 4 этой главы рассматриваются независимые испытания, в каждом из которых вероятность появления события одинакова. [32]
Известно, что в зависимости от вероятности появления события в каждом испытании имеют место асимптотические биномиальные распределения, либо распределения Гаусса при вероятности, стремящейся к 0 5, либо распределения Пуассона при вероятности, стремящейся к нулю. [33]
Если появление события А влияет на вероятность появления события В, то говорят, что данные события зависимы. [34]
Во многих технических задачах возникает вопрос относительно вероятности появления события Л точно г раз, если испытание повторяется и раз, где п г. Если результаты каждого испытания независимы, то эта вероятность дается биноминальным распределением. [35]
Для данного эксперимента часто бывает необходимо рассматривать вероятность появления события А в случае, когда имеется добавочная информация об исходе эксперимента после появления некоторого другого события В. Эта величина называется условной вероятностью А при заданном В. [36]
Типичное толкование, р ( х) есть вероятность появления события ( успеха) т-и раз после точно т — f — х — 1 испытаний по схеме Бернулли при вероятности успеха в. [38]
Часто обозначают Р ( А) Р — вероятность появления события; P ( A) q — вероятность непоявления события. [39]
В 360 испытаниях, в каждом из которых вероятность появления события одинакова и неизвестна, событие А появилось 270 раз. [40]
Испытания называются независимыми относительно события А, если вероятность появления события А в каждом из этих испытаний не зависит от результата, полученного в других испытания. [41]
В 360 испытаниях, в каждом из которых вероятность появления события одинакова и неизвестна, событие А появилось 270 раз. [42]
В 360 испытаниях, б каждом из которых вероятность появления события одинакова и неизвестна, событие А появилось 270 раз. [43]
Типичное толкование, р ( х) есть вероятность появления события ( успеха) в т-и раз после точно т — — х — 1 испытаний по схеме Бернулли при вероятности успеха и. А) есть вероятность того, что m — й успех наступит самое большее после т х — I испытаний. [45]
Страницы: 1 2 3 4
www.ngpedia.ru
