Лекция 8. Формула Муавра. Корни из к.ч
Лекции по алгебре и геометрии. Семестр 1.
Лекция 8. Формула Муавра. Корни из комплексных чисел.
Краткое содержание: формула Муавра, деление к.ч. в тригонометрической форме записи, корни из к.ч. и их расположение на комплексной плоскости, группа корней из 1, многочлен деления круга и его разложение на неприводимые множители с действительными коэффициентами.
Глава 8. Формула Муавра. Корни из комплексных чисел.
п.1.Формула Муавра.
Теорема. (Формула Муавра, 1707 г.)
Для
любого целого числа nи
любого действительного числа имеет место следующее равенство:
имеет место следующее равенство:
. (1)
Доказательство. Разобьем доказательство на 3 этапа.
1)
Пусть 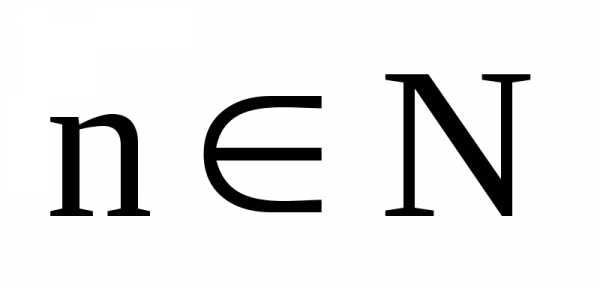
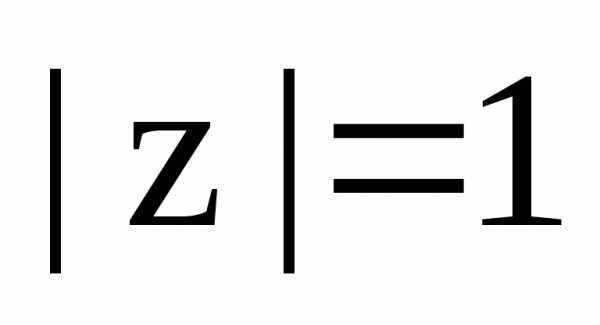 ,
то справедливость формулы Муавра в этом
случае следует из следствия 2 теоремы
об умножении комплексных чисел в
тригонометрической форме записи.
,
то справедливость формулы Муавра в этом
случае следует из следствия 2 теоремы
об умножении комплексных чисел в
тригонометрической форме записи.2)
Пусть теперь 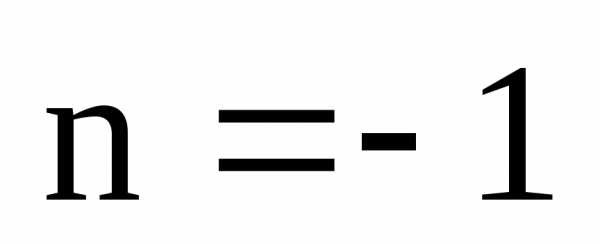 .
Тогда
.
Тогда
, ч.т.д.
3)
Пусть
,
где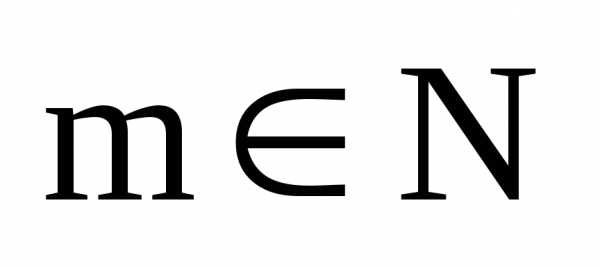 – натуральное число. Тогда по свойству
целых степеней, которые справедливы в
любом поле, в том числе и в поле комплексных
чисел, имеем:
– натуральное число. Тогда по свойству
целых степеней, которые справедливы в
любом поле, в том числе и в поле комплексных
чисел, имеем:
.
Здесь мы использовали уже доказанные случаи формулы Муавра возведения в натуральную степень и в степень, равную (–1).
Теорема доказана.
Следствие. (О целых степенях комплексного числа.)
Пусть
.
Тогда
.
Доказательство предоставляется читателю.
п.2. Деление комплексных чисел в тригонометрической форме записи.
Теорема. (О делении комплексных чисел в тригонометрической форме)
Пусть , гдеи, где– два произвольных комплексных числа записанных в тригонометрической форме. Тогда
. (2)
Доказательство. Воспользуемся следствием формулы Муавра и правилом умножения комплексных чисел в тригонометрической форме записи. Получаем:
, ч.т.д.
Пример
1. Запишите комплексные числа 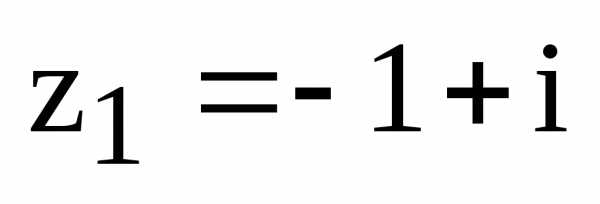 и
и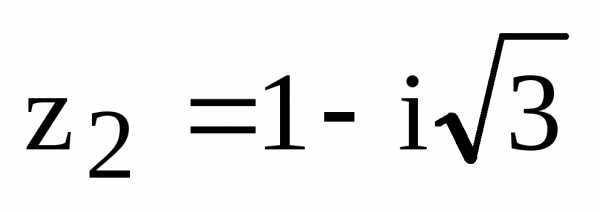 в тригонометрической форме и найдите
их произведение
в тригонометрической форме и найдите
их произведение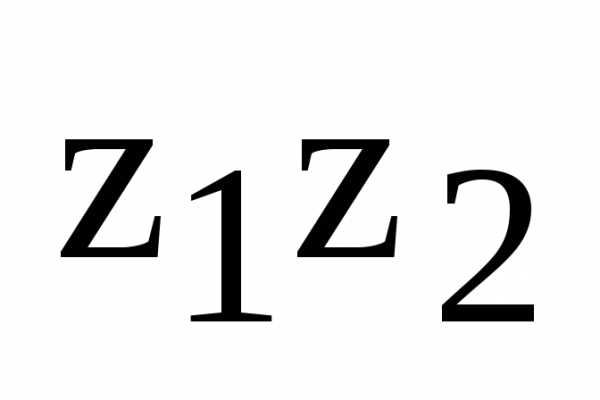
 .
.Решение.
1) Комплексное число  на комплексной плоскости находится во
второй четверти, поэтому
на комплексной плоскости находится во
второй четверти, поэтому
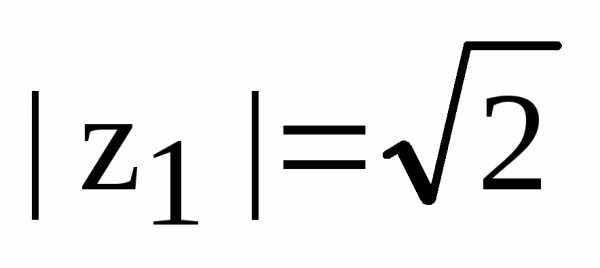 ,
.
,
.
2)
Комплексное число 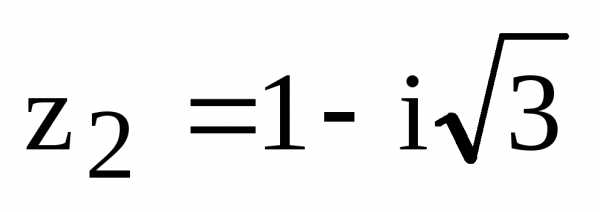 на комплексной плоскости находится во
четвертой четверти, поэтому
на комплексной плоскости находится во
четвертой четверти, поэтому
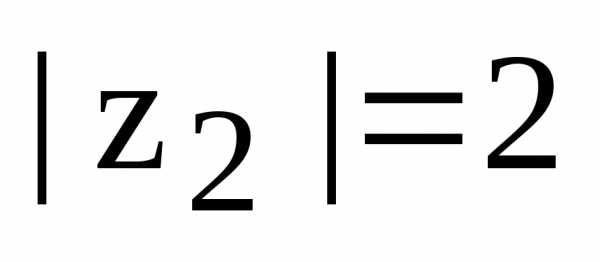 ,
.
,
.
3)
.
Ответ: ,.
Пример
2. Вычислить 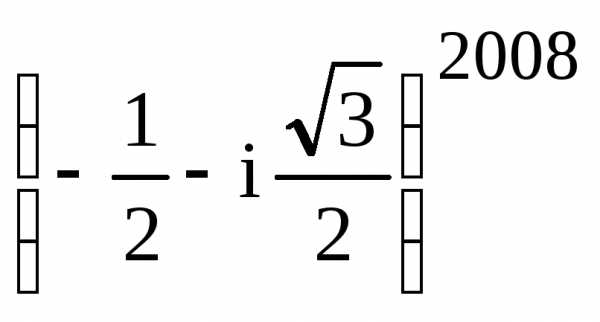
Решение.
Комплексное число 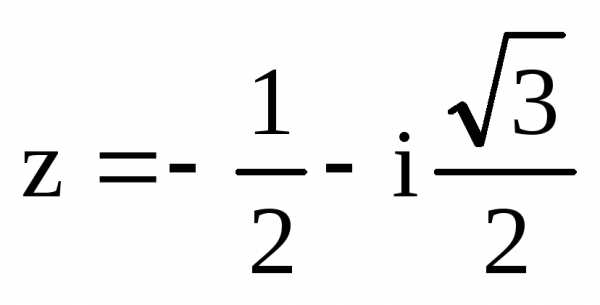 на комплексной плоскости находится в
третьей четверти, поэтому
на комплексной плоскости находится в
третьей четверти, поэтому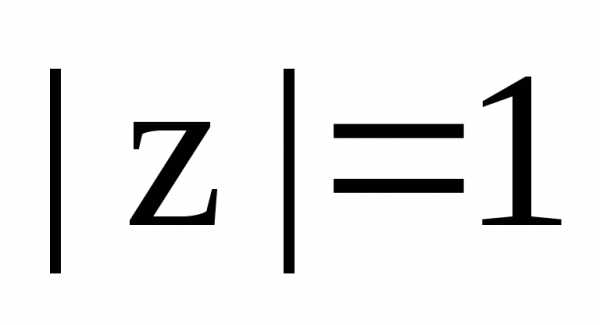 ,
,
Применим формулу Муавра:
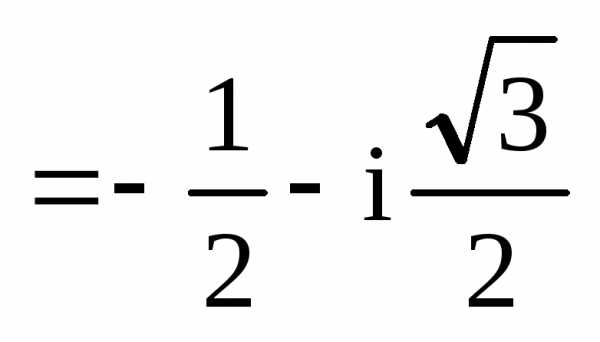 .
.
п.3. Корни из комплексных чисел.
Определение.
Пусть 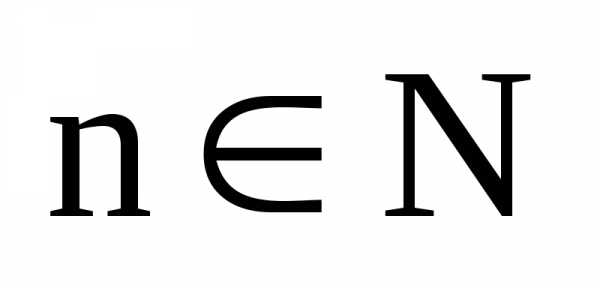 и
и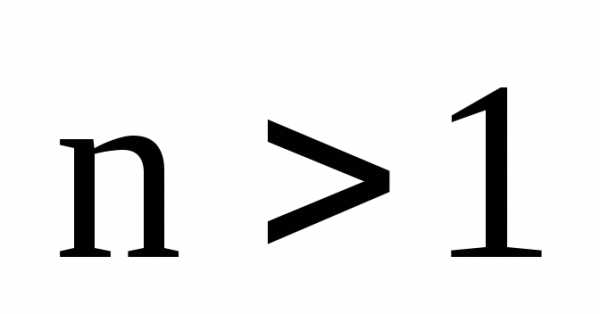 .
Корнемn-й степени из
комплексного числаzназывается комплексное число
.
Корнемn-й степени из
комплексного числаzназывается комплексное число
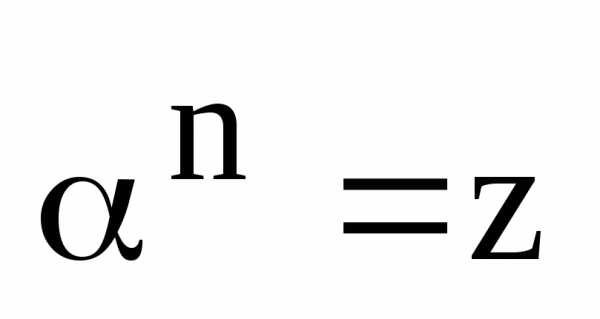 .
.Теорема. (Формула корней из комплексного числа.)
Для любого ненулевого комплексного числа
, где , существует ровноnкорнейn-й степени из комплексного числаzи все они могут быть найдены по формуле
, (3)
где
,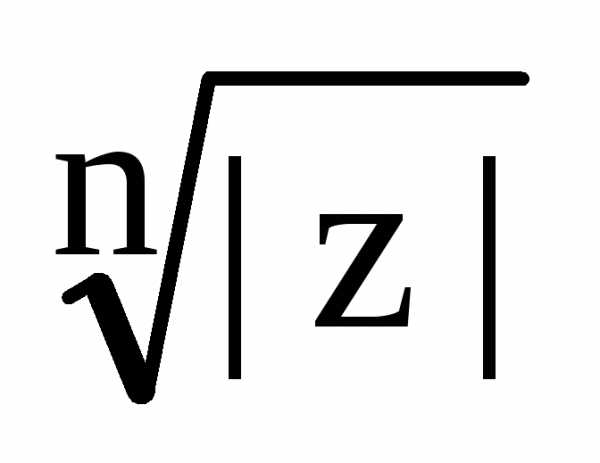 – арифметический кореньn-й
степени из положительного числа
– арифметический кореньn-й
степени из положительного числа .
.
Доказательство. Обозначим
(4)
и докажем, что данное множество исчерпывает все множество корней n-й степени из комплексного числаz.
Доказательство проведем в 3 этапа. Сначала мы докажем, что все элементы множества (4) являются корнями n-й степени из комплексного числаz. Затем мы покажем, что среди корней множества (4) нет равных. И, наконец, мы покажем, что любой кореньn-й степени из комплексного числаzявляется элементом множества (4).
1) По следствию 2 формулы Муавра
, ч.т.д.
2)
Допустим, что 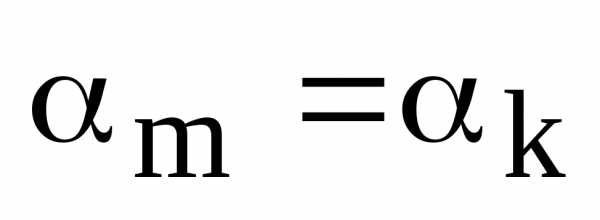 ,
гдеи
,
гдеи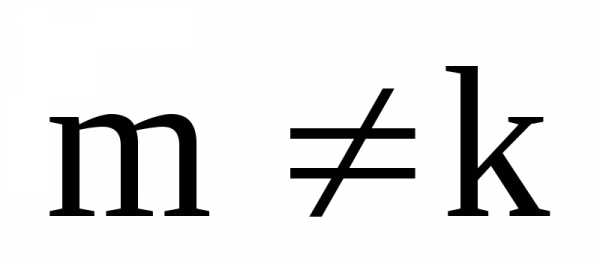 .
Тогда по теореме о равенстве двух
комплексных чисел в тригонометрической
форме записи следует, что равны их
аргументы.
.
Тогда по теореме о равенстве двух
комплексных чисел в тригонометрической
форме записи следует, что равны их
аргументы.
Но,
аргумент числа  может отличаться от числа
может отличаться от числа на число кратное числу
на число кратное числу
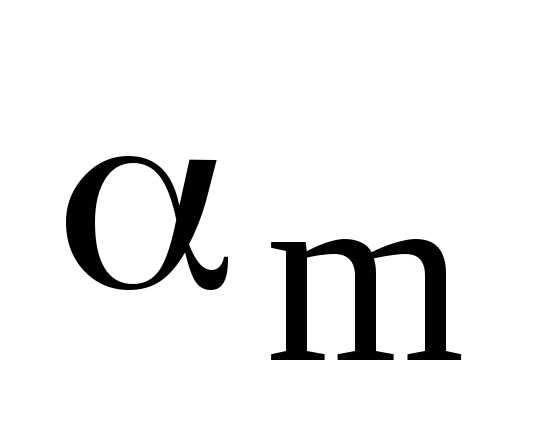 .
Отсюда следует, что,
где
.
Отсюда следует, что,
где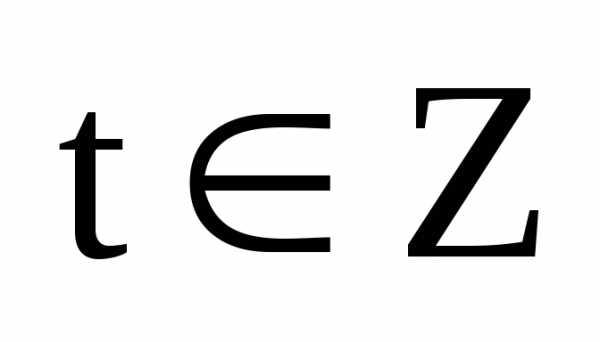 .
Умножим это равенство наn:.
Отсюда следует, чтои т.к. по нашему предположению
.
Умножим это равенство наn:.
Отсюда следует, чтои т.к. по нашему предположению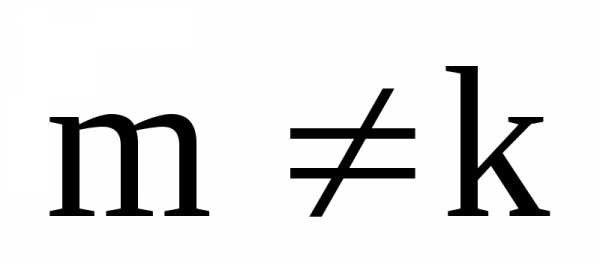 ,
то,
чего не может быть, т.к.и.
Получили противоречие. Следовательно,
среди корней в множестве (10) нет равных,
ч.т.д.
,
то,
чего не может быть, т.к.и.
Получили противоречие. Следовательно,
среди корней в множестве (10) нет равных,
ч.т.д.3)
Пусть теперь комплексное число
является корнемn-й степени
из комплексного числаz,
т.е.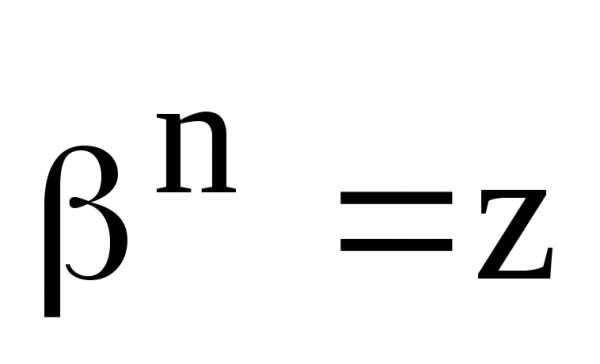 .
Так как.
Отсюда, из тех же соображений, что и во
второй части доказательства, следуют
равенства
.
Так как.
Отсюда, из тех же соображений, что и во
второй части доказательства, следуют
равенства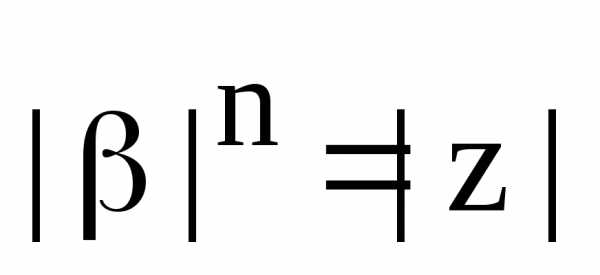
 .
Из первого равенства получаем, что
.
Из первого равенства получаем, что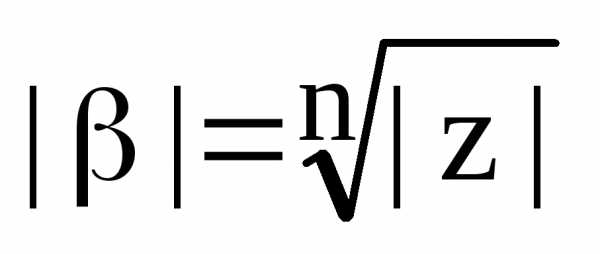 ,
а из второго следует
,
а из второго следует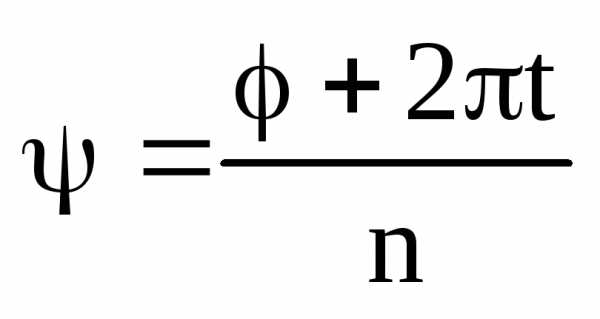 .
. Далее, разделим
целое число tнаnс возможным остатком:,
где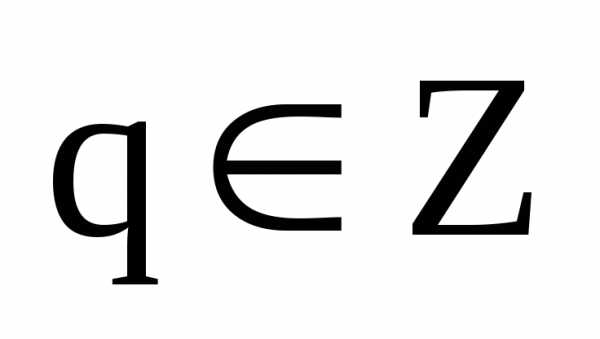 ,
а остатокrтакже является
целым числом, но.
Отсюда
,
а остатокrтакже является
целым числом, но.
Отсюда
и
.
Таким образом, корень 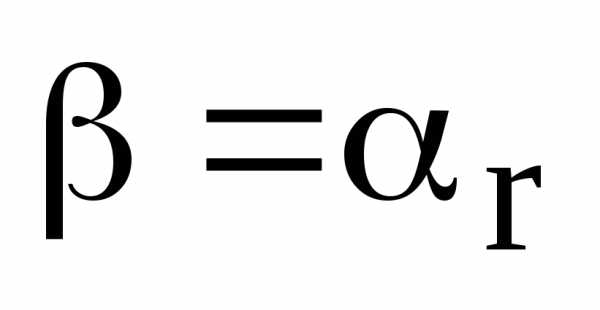 является корнем из множества корней
(4), ч.т.д.
является корнем из множества корней
(4), ч.т.д.
Теорема доказана.
Пример. Вычислить .
Решение. Запишем число в тригонометрической форме записи:. Тогда
, где
, 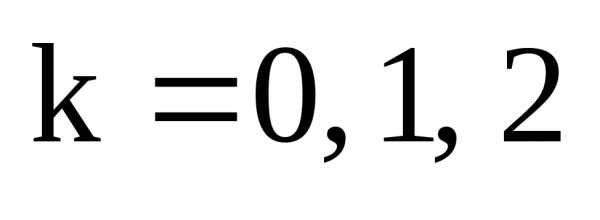 .
.
Ответ: , где
,
,
.
п.4. Расположение корней на комплексной плоскости.
Перепишем формулу (3) в виде
,
где 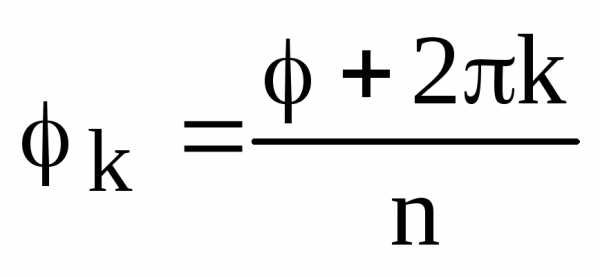 ,.
,.
Заметим, что
. (5)
Из этой формулы мы видим, что аргументы корней образуют арифметическую прогрессию.
Так
как модуль у всех корней одинаковый, то
на комплексной плоскости они удалены
от начала координат на одинаковое
расстояние. Отсюда делаем вывод, что
все корни на комплексной плоскости
изображаются точками, лежащими на
окружности радиуса 
рис.1.
При изображении корней на комплексной плоскости около точки, с которой отождествляется корень проставляется только его аргумент, поскольку модули у всех корней одинаковые.
Пример.
Изобразить все корни 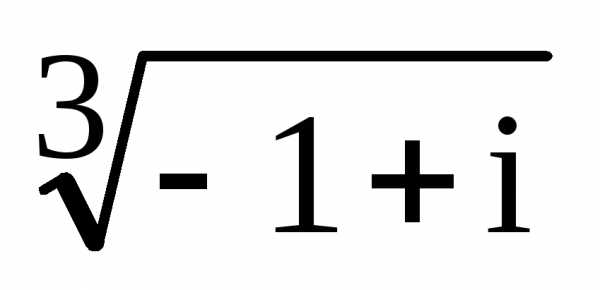 на комплексной плоскости.
на комплексной плоскости.
Решение.
Сами корни мы уже вычислили (см. предыдущий
пример). Изображаем координатные оси,
проводим окружность радиуса 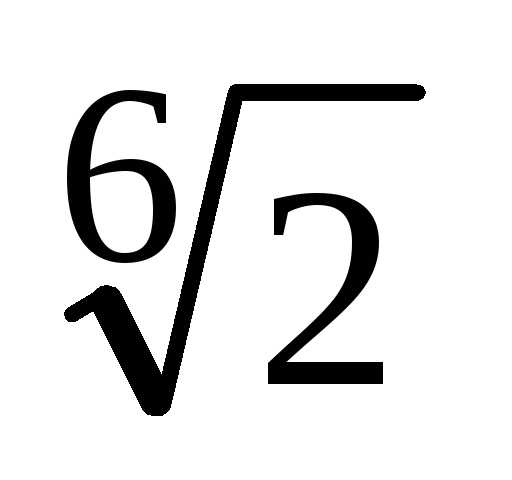
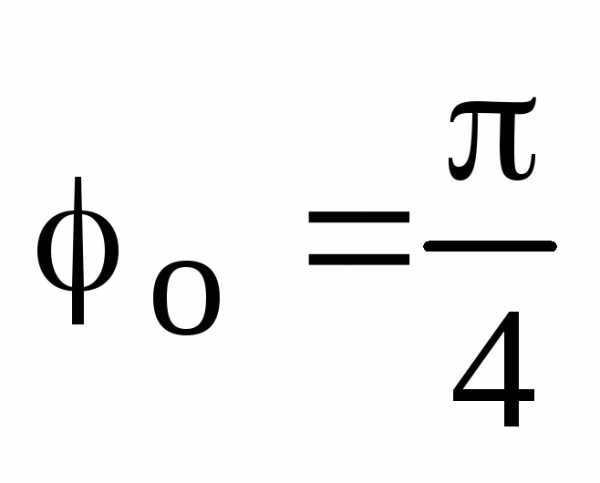 ,
, 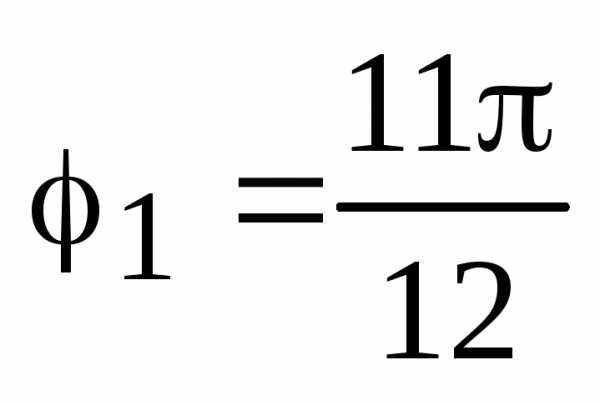 ,
,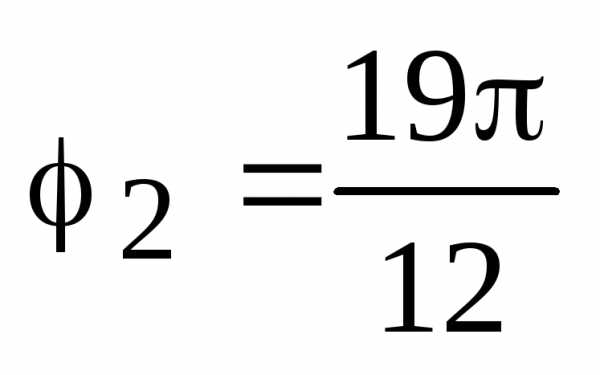 .
.
Соединим построенные точки отрезками прямых и получаем правильный треугольник.
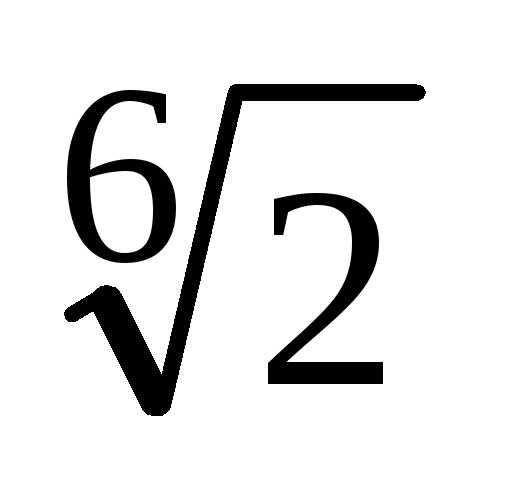
рис.2.
п.5*. Корни из единицы.
Пусть 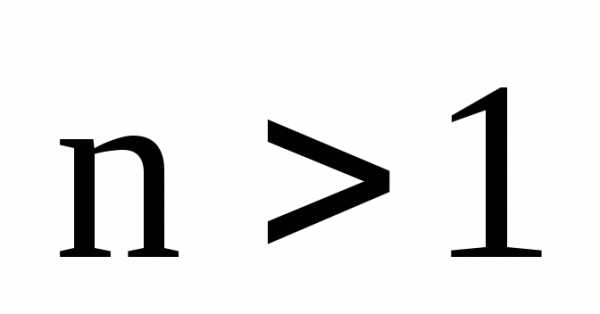 – натуральное число. По формуле корней
из комплексного числа, существует ровноnкорней из комплексного
числа.
Для вычисления этих корней запишем
единицу в тригонометрической форме:
– натуральное число. По формуле корней
из комплексного числа, существует ровноnкорней из комплексного
числа.
Для вычисления этих корней запишем
единицу в тригонометрической форме:
,
т.е. 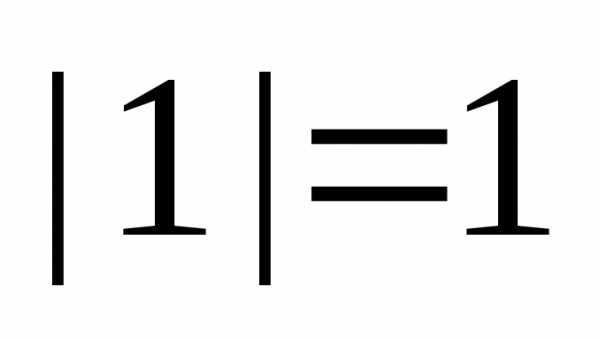 ,
, .
.
Обозначим все
множество корней через 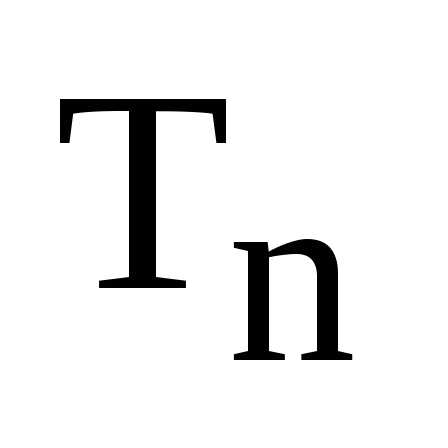 .
По формуле корней получаем:
.
По формуле корней получаем:
, (6)
где
, . (7)
В частности, ,
. (8)
Заметим, что верна формула:
 .
(9)
.
(9)
Действительно, равенство (9) сразу же получается по формуле Муавра:
.
Теперь
мы все множество корней 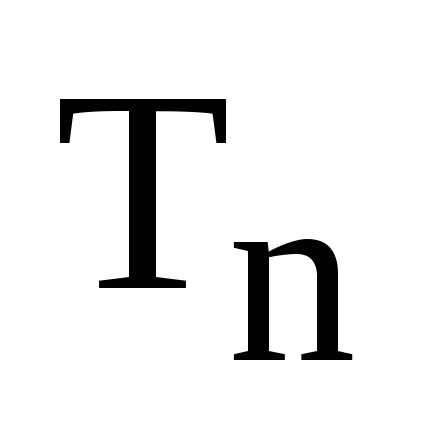 из 1 можем записать так:
из 1 можем записать так:
(10)
Теорема. Множество всех корней из 1 является коммутативной группой.
Доказательство.
Сначала мы должны показать, что множество  замкнуто относительно умножения. Пусть
замкнуто относительно умножения. Пусть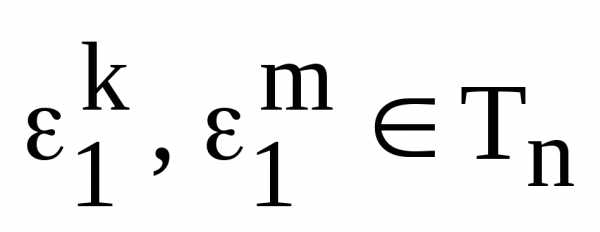 – два произвольных корня из 1, т.е..
Найдем их произведение:
– два произвольных корня из 1, т.е..
Найдем их произведение:
.
Замечаем, что
. (11)
Отсюда следует, что , если. В противном случае,. Обозначим черези. Тогда
, ч.т.д.
Таким образом, на
множестве 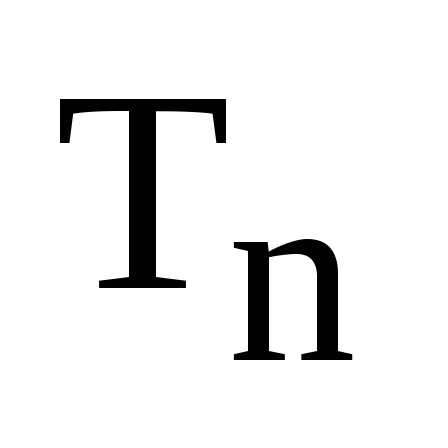 определена операция умножения и т.к.
она ассоциативна и коммутативна в поле
комплексных чисел, то она ассоциативна
и коммутативна и на множестве
определена операция умножения и т.к.
она ассоциативна и коммутативна в поле
комплексных чисел, то она ассоциативна
и коммутативна и на множестве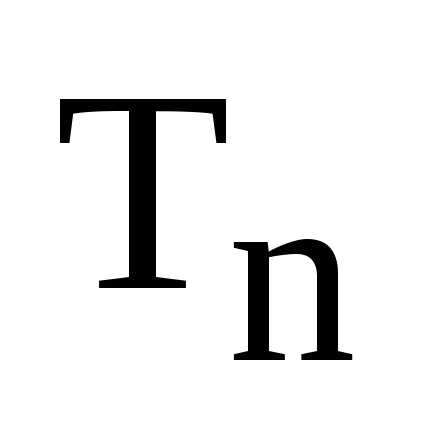 .
Далее,
.
Далее,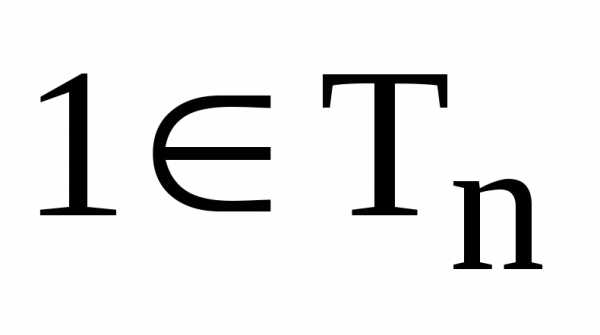 .
Покажем, что любой элемент из
.
Покажем, что любой элемент из имеет обратный элемент также принадлежащий
множеству
имеет обратный элемент также принадлежащий
множеству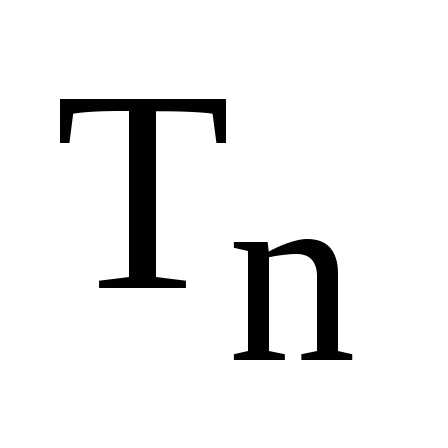 :
:
.
Действительно, по условию . Тогда
, т.е. .
Теорема доказана.
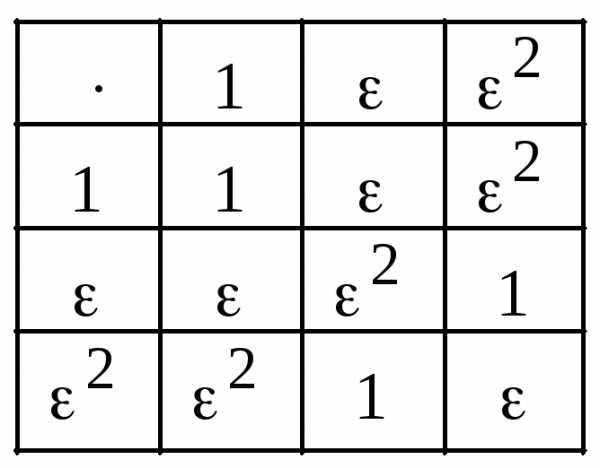
Пример.
Построить таблицу умножения для группы  .
.
Решение. Обозначим для простоты
.
Тогда,
где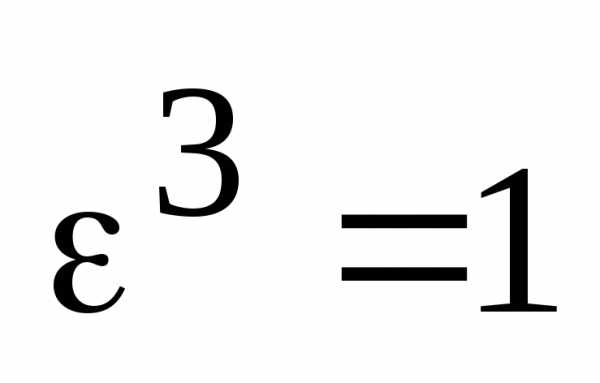 .
.
Заполняем таблицу Кэли (таблицу умножения):
Изобразим все корни третьей степени из 1 на комплексной плоскости. Т.к. их модуль равен 1, то все они лежат на тригонометрической (т.е. единичной) окружности:
рис.3.
Здесь, 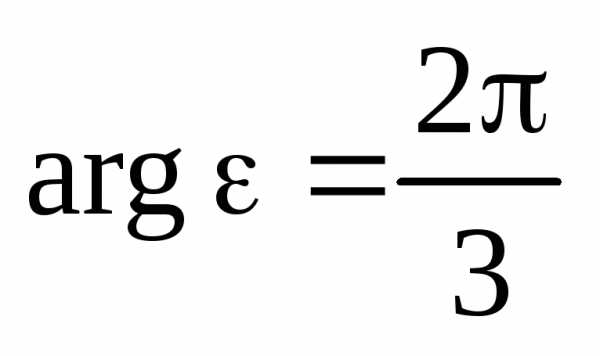 ,
,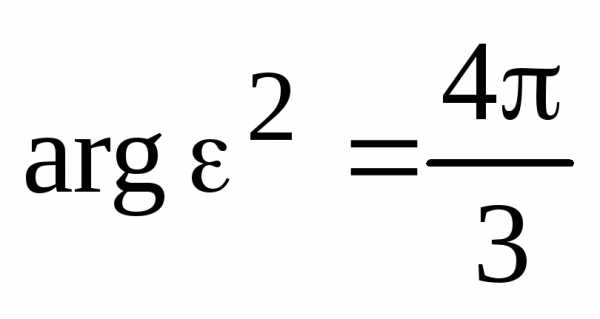 .
.
п.6*. Многочлен деления круга.
Определение. Многочлен
называется многочленом деления круга.
Теорема. Все корни многочлена
являются
корнями 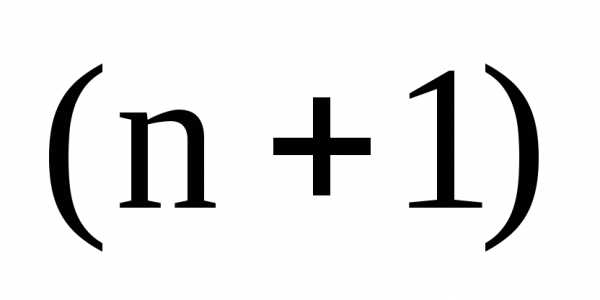 -й
степени из 1.
-й
степени из 1.
Доказательство. Рассмотрим многочлен деления круга как сумму членов геометрической прогрессии со знаменателем х. Тогда
.
Теорема доказана.
Так как корни из 1 делят единичную окружность на nравных дуг, то из теоремы следует, что все корни многочленавместе с 1 делят окружность на равные дуги, откуда и произошло название этого многочлена.
Поставим задачу разложить многочлен деления круга на неприводимые (неразложимые) множители с действительными коэффициентами.
Известно (см. Дополнение 6), что любой многочлен с действительными коэффициентами можно представить в виде:
, (12)
где
–
все различные действительные корни
многочлена ,m– их число,– их кратности,t– число
квадратных трехчленов с действительными
коэффициентамии отрицательными дискриминантами,– кратности соответствующих комплексных
корней,
,m– их число,– их кратности,t– число
квадратных трехчленов с действительными
коэффициентамии отрицательными дискриминантами,– кратности соответствующих комплексных
корней,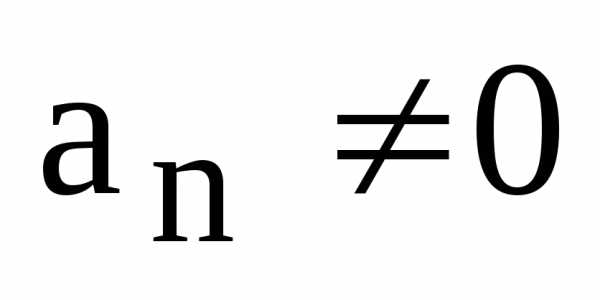 – старший коэффициент многочлена
– старший коэффициент многочлена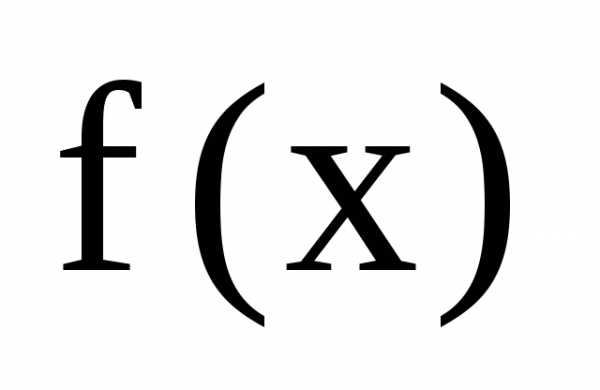 ,n– его степень.
,n– его степень.
Замечание. Линейных
множителей может и не быть. Тогда 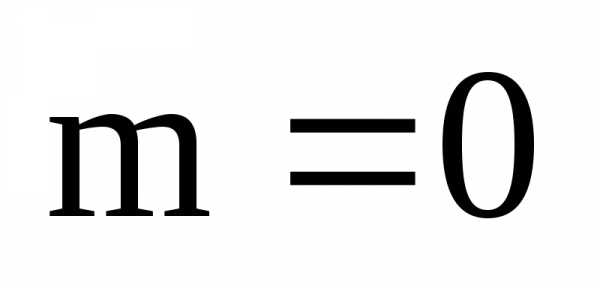 и многочлен не имеет действительных
корней. Аналогично, многочлен может не
иметь комплексных корней, тогда
и многочлен не имеет действительных
корней. Аналогично, многочлен может не
иметь комплексных корней, тогда .
Далее, очевидно, что степень многочлена
.
Далее, очевидно, что степень многочлена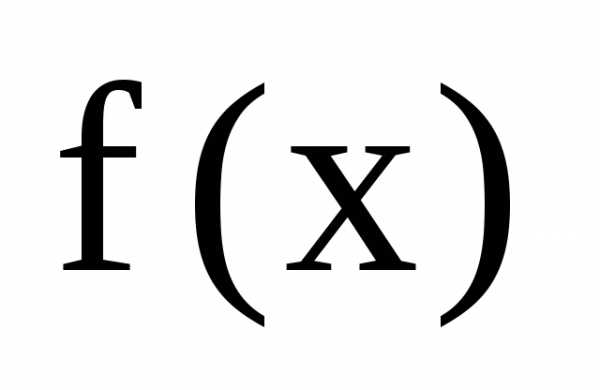
. (13)
Из последнего равенства вытекает следующее следствие.
Следствие. Любой многочлен нечетной степени с действительными коэффициентами имеет хотя бы один действительный корень.
Легко получить
разложение (12), если известны все корни
многочлена f(x).
Тогда многочлен раскладывается над
полем комплексных чисел на линейные
множители. Так как коэффициенты многочленаf(x)
предполагаются действительными, то
если многочлен имеет комплексный корень ,
то комплексно сопряженное ему число
,
то комплексно сопряженное ему число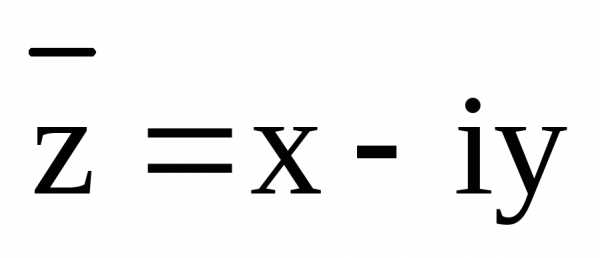 также является корнем этого многочлена.
Действительно, если
также является корнем этого многочлена.
Действительно, если ,
то.
,
то.
Разложение многочлена f(x) на линейные множители будет иметь вид:
, (14)
где
–
все различные действительные корни
многочлена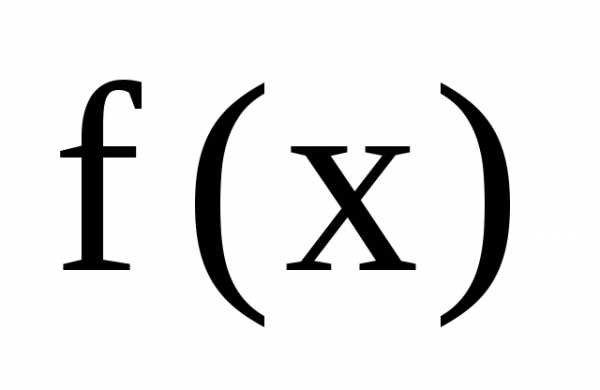 ,m– их число,– их кратности,– все различные комплексно сопряженные
корни многочлена
,m– их число,– их кратности,– все различные комплексно сопряженные
корни многочлена ,t– число пар всех различных
комплексно сопряженных корней,– их кратности,
,t– число пар всех различных
комплексно сопряженных корней,– их кратности,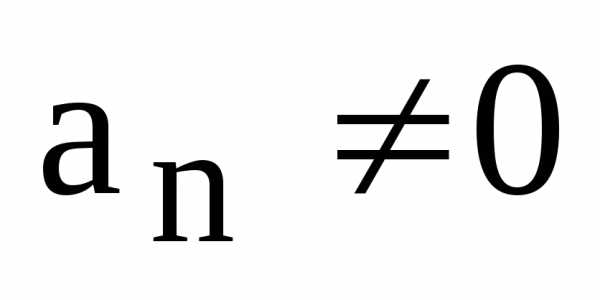 – старший коэффициент многочлена
– старший коэффициент многочлена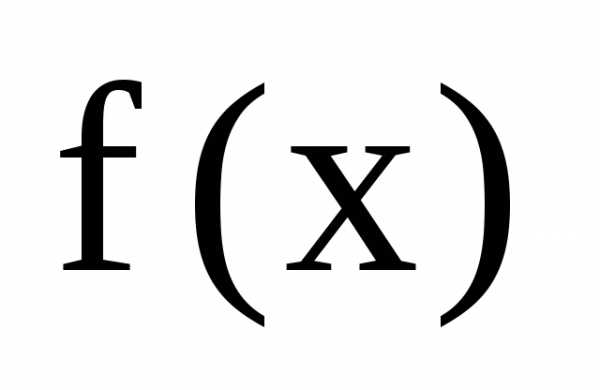 ,n– его степень.
,n– его степень.
Теперь, перемножим пару линейных множителей содержащие комплексно сопряженные корни. Пусть
.
Тогда , откуда и получаем:
.
Проделав то же самое со всеми парами комплексно сопряженных корней, из разложения (14) получим разложение (12).
Осталось заметить, что все корни многочлена деления круга различны и их легко вычислить и, следовательно, получить разложение на линейные множители.
Пример. Разложить на неприводимые множители с действительными коэффициентами (т.е. на полем R) многочлен.
Решение.
Решим уравнение 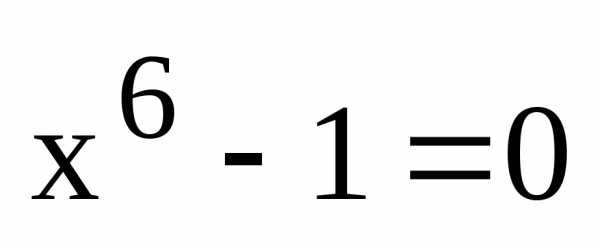 .
Так как
.
Так как
,
то найдя все корни уравнения 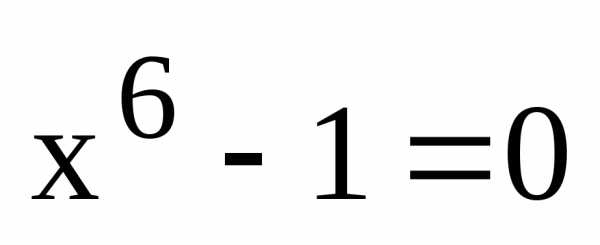 ,
мы найдем тем самым все корни многочлена.
,
мы найдем тем самым все корни многочлена.
Имеем, , где
.
рис.4.
Вычисляя остальные корни по формуле
,
, получаем (см. рис.4):
; ;
; 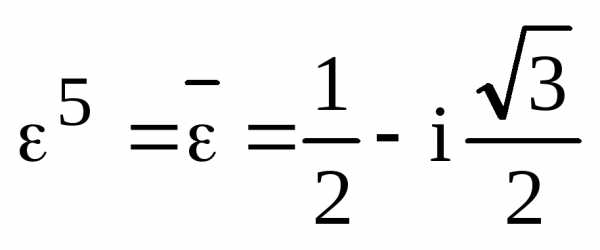 .
.
Отсюда, и
,
т.к. 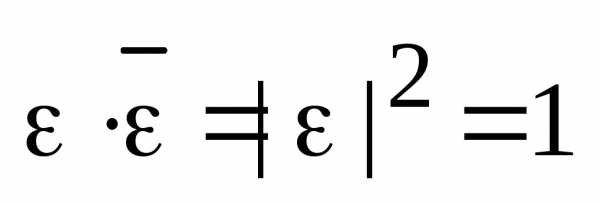 ,,,
,,,
.
Ответ: .
п.7*. Исторический экскурс к вопросу о построении правильного многоугольника с помощью циркуля и линейки.
(Виленкин Н.Я. и др. За страницами учебника математики.)
Геометрические задачи на построение с помощью циркуля и линейки зародились еще в древней Греции во времена Евклида и Платона. Еще в те времена, математики умели строить с помощью циркуля и линейки правильные треугольники, пятиугольники и квадраты.
Более того, они
умели с помощью циркуля и линейки делить
угол пополам, поэтому они умели строить
и правильные 6-ти, 10-ти и 15-ти угольники
и все правильные n-угольники,
где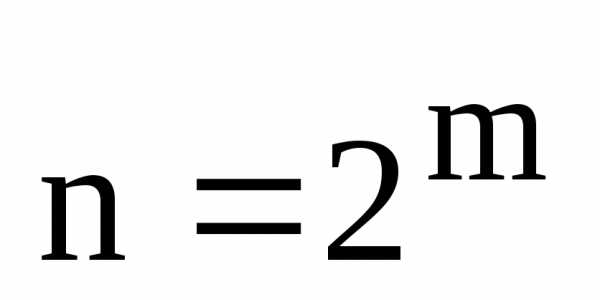 ,
, ,
,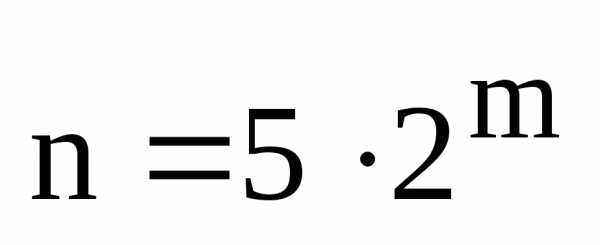 и
и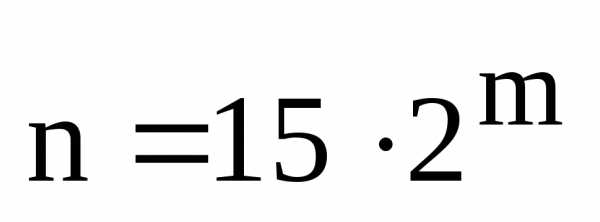 ,
, .
Очень важно, что с помощью линейки
проводятся только отрезки прямых, а
длины отрезков измеряются с помощью
циркуля, а не делений на линейке. Так,
используя эти инструменты можно построить
отрезок, длина которого выражается
числом, полученным из 1 с помощью четырех
арифметических действий (сложения,
вычитания, умножения, деления) и
извлечением квадратного корня. Т.е.
вначале есть только отрезок, длина
которого принимается за 1. Тогда можно
построить отрезок, длина которого равна
рациональному числу или квадратному
корню из рационального числа. Далее,
если отрезок длины а уже построен с
помощью циркуля и линейки, то можно
построить с помощью этих инструментов
отрезок длиныb, если
числоbвыражается через
а с помощью арифметических действий и
квадратного корня. Говорят, что такое
число выражается в квадратных радикалах.
.
Очень важно, что с помощью линейки
проводятся только отрезки прямых, а
длины отрезков измеряются с помощью
циркуля, а не делений на линейке. Так,
используя эти инструменты можно построить
отрезок, длина которого выражается
числом, полученным из 1 с помощью четырех
арифметических действий (сложения,
вычитания, умножения, деления) и
извлечением квадратного корня. Т.е.
вначале есть только отрезок, длина
которого принимается за 1. Тогда можно
построить отрезок, длина которого равна
рациональному числу или квадратному
корню из рационального числа. Далее,
если отрезок длины а уже построен с
помощью циркуля и линейки, то можно
построить с помощью этих инструментов
отрезок длиныb, если
числоbвыражается через
а с помощью арифметических действий и
квадратного корня. Говорят, что такое
число выражается в квадратных радикалах.
Таким образом, с помощью циркуля и линейки можно построить отрезок, длина которого выражается в квадратных радикалах. Все это знали еще математики древней Греции. Задачу построения других правильных многоугольников (или доказательство невозможности таких построений) не могли решить в течение двух последующих тысячелетий, а решена она была немецким студентом филологического факультета Гёттингенского университета Карлом Фридрихом Гауссом в 1796 году. В то время Гауссу было 18 лет и он разрывался между занятиями филологией и математикой и не мог сделать окончательного выбора. Решение древней задачи помогло ему сделать окончательный выбор в пользу (и на пользу) математики. Страшно даже подумать на сколько бы затормозилось развитие математики останься Гаусс филологом! До сих пор математики всего мира называют Гаусса королем математики.
studfiles.net
1) Выполнить действия в алгебраической, тригонометрической и показательной формах;
25
Контрольная работа №1
Задание 5
Даны три комплексных числа
2) Найти расстояние между точками ина комплексной плоскости.
Решение
1)
а) Найдем число  в
в алгебраической форме.
в
в алгебраической форме.
Найдем поэтапно:
z34 = [(-1-i)2]2 = ((-1)2 + 2(-1)(-i) + (-i)2)2 = (1 + 2i + i2)2 = (1 + 2i — 1)2 = (2i)2 = 4i2 = = — 4
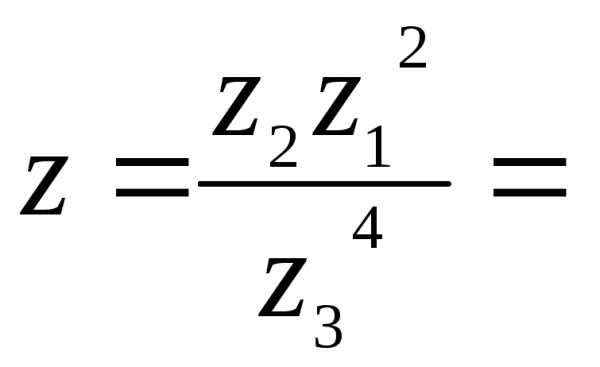
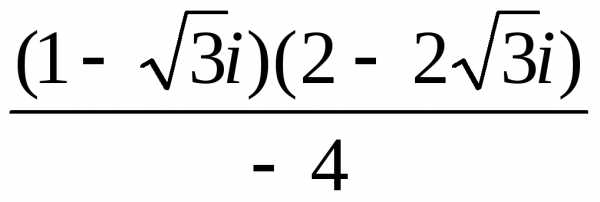
Найдем произведение двух комплексных чисел по формуле:
(а1 + b1 i) (а2 + b2 i) = (a1 a2 — b1 b2) + (b1 а2+ a1b2) i
Найдем
б) Тригонометрическая форма комплексного числа: w = r(cos + isin), где
— модуль комплексного числа,
=  аргумент комплексного числа
аргумент комплексного числа
Представим числа z1, z2, z3 в тригонометрической форме:
1 = (угол находится во 2-ой четверти).
z1 = r1(cos1 + isin1)
= 2(cos 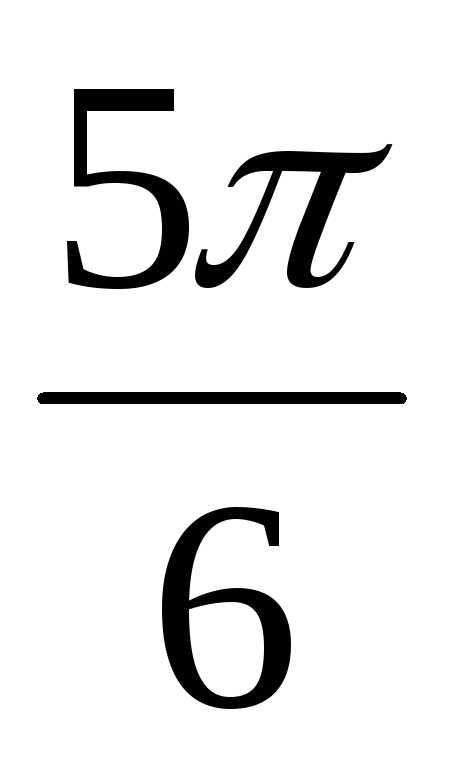 + isin )
+ isin )
2 = (угол находится в 4-ой четверти).
z2 = r2(cos2 + isin2)
= 2(cos 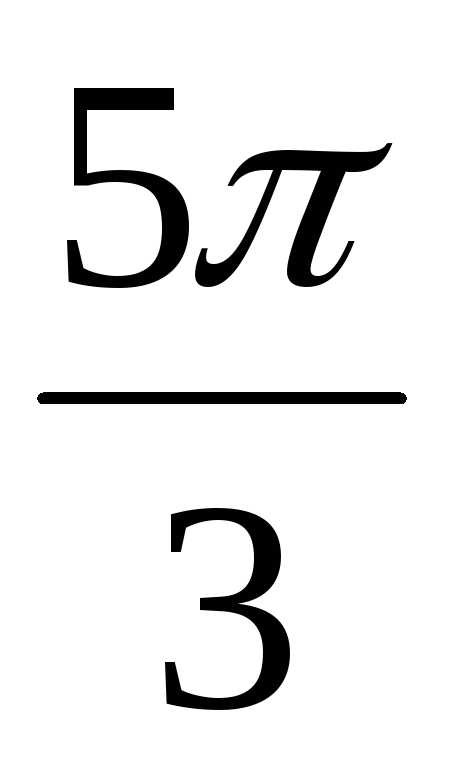 + isin
+ isin  )
)
3 = (угол находится в 3-ей четверти).
z3 = r3(cos3 + isin3)
= 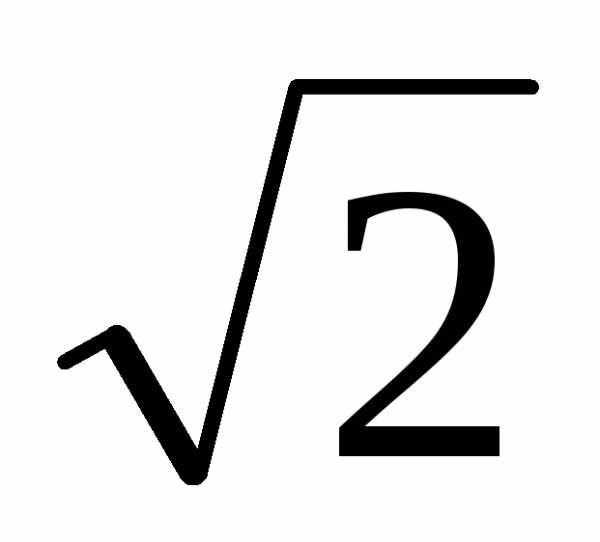 (cos
(cos 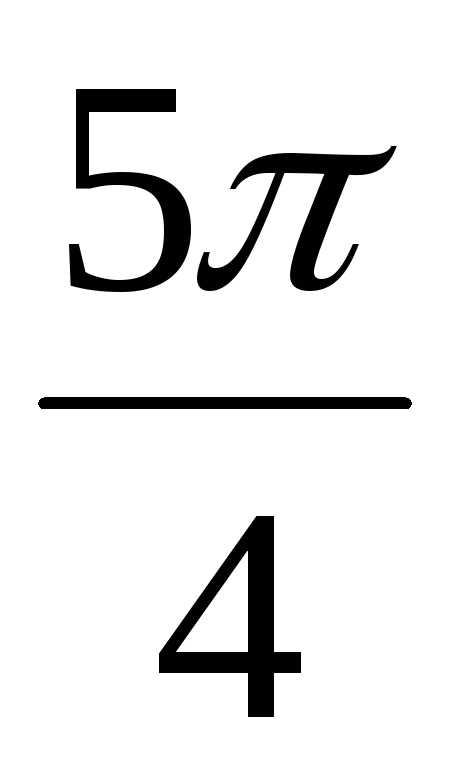 + isin
+ isin 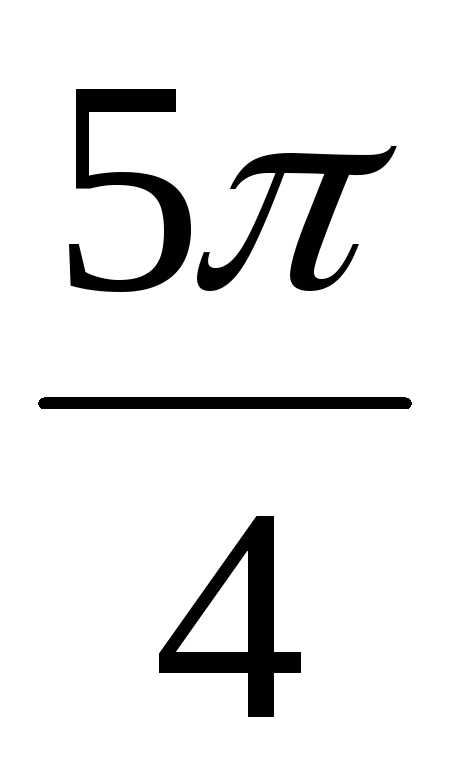 )
)
Для нахождения z12 воспользуемся формулой Муавра:
(r (cos + i sin)) n = rn (cos n + i sin n)
z12 = r12(cos21 + isin21)
= 22 (cos 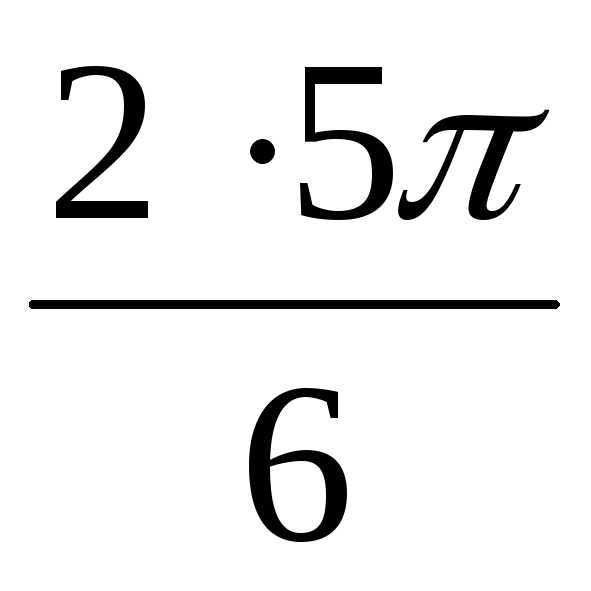 + isin
+ isin 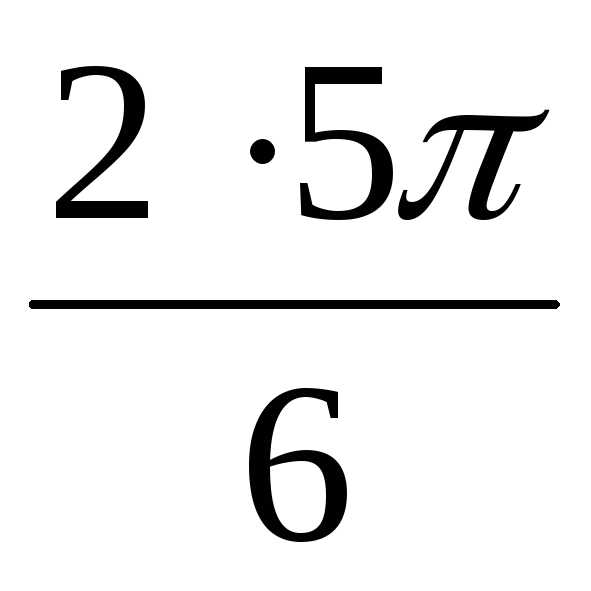 )
= =
)
= =
Аналогично находим z34 = r34(cos42 + isin42)
= ( )4 (cos
)4 (cos  + isin
+ isin 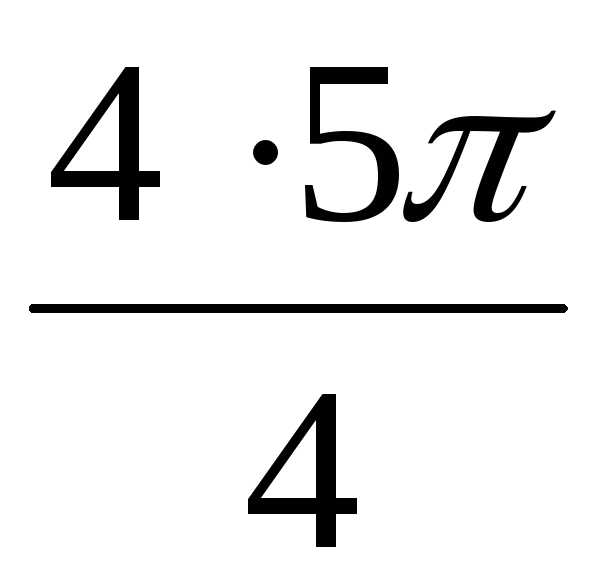 )=
= 4(cos 5 + isin 5)
= 4(cos (4 + )
+ isin (4 + ))
= 4(cos + i sin )
)=
= 4(cos 5 + isin 5)
= 4(cos (4 + )
+ isin (4 + ))
= 4(cos + i sin )
Находим
Произведение двух комплексных чисел в тригонометрической форме находи по формуле:
Тогда
Частное двух комплексных чисел в тригонометрической форме находят по формуле
Тогда
в) z = r e i φ — показательная форма комплексного числа.
z1 = r1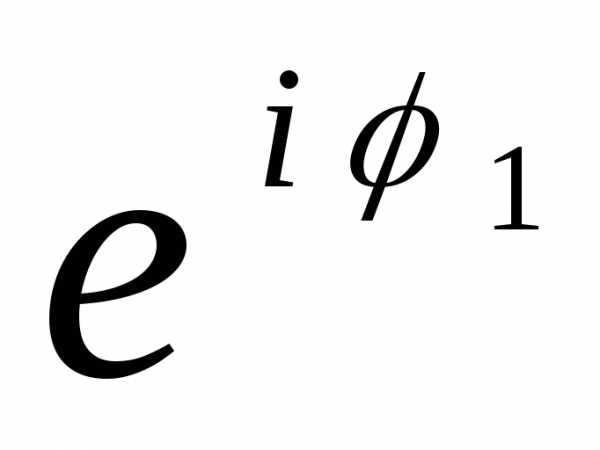 =2e
=2e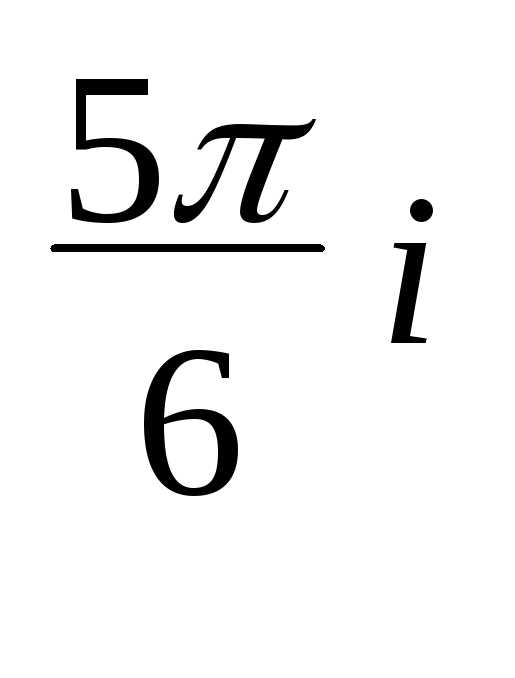
z2 = r2 = 2e
= 2e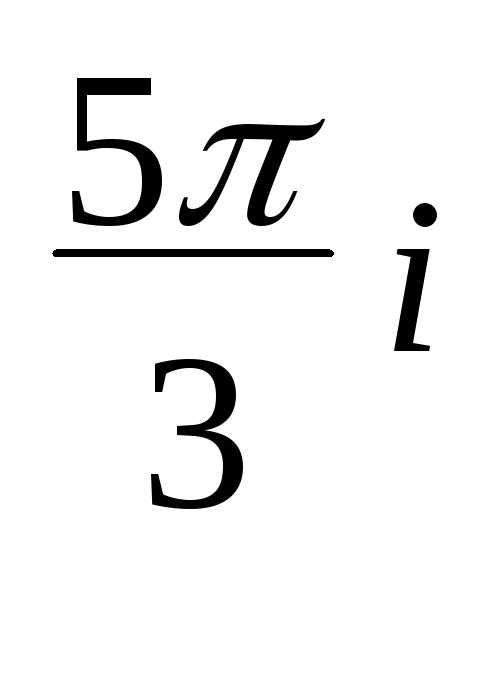
z3 = r3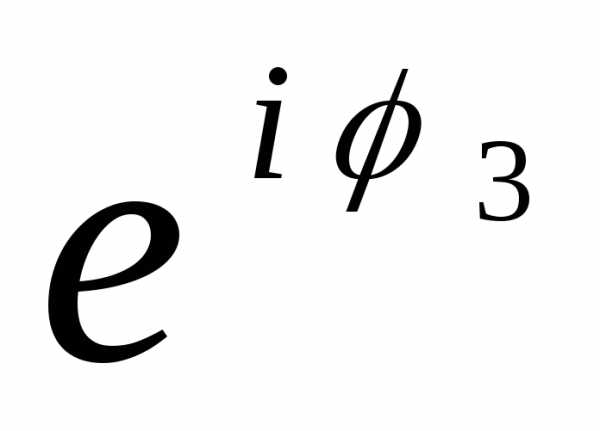 =
= e
e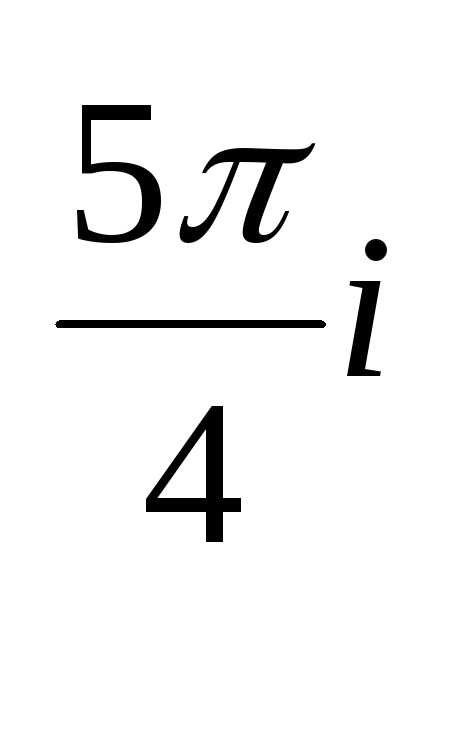
Далее воспользуемся формулой Муавра:
(r 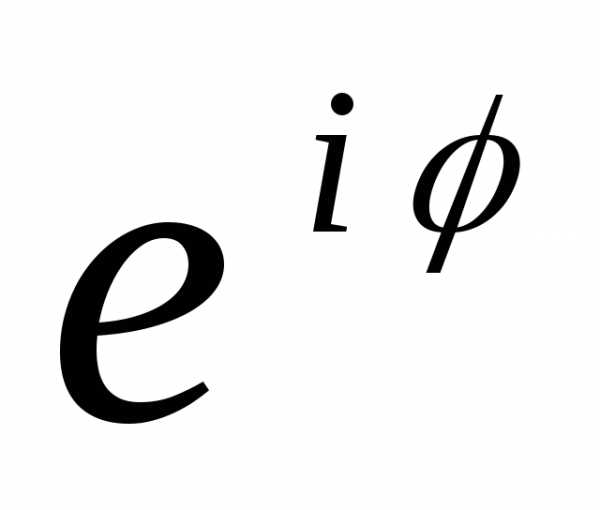 ) n = r n
) n = r n 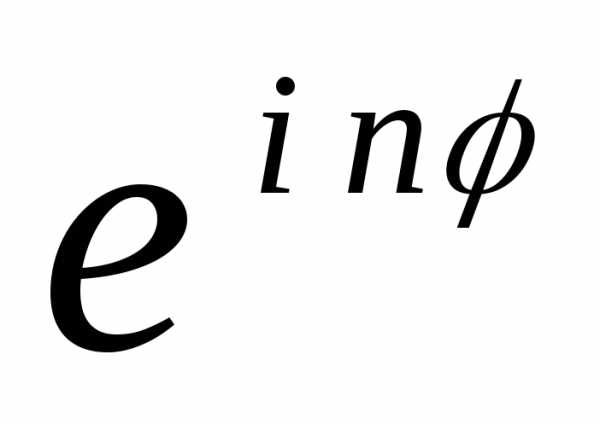
z12 = 22 e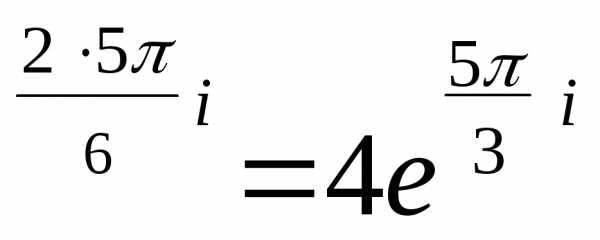
Аналогично
находим z34 = (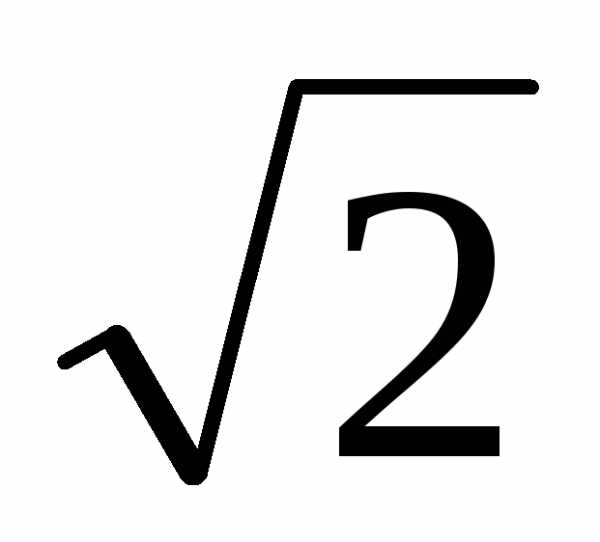 )4
)4 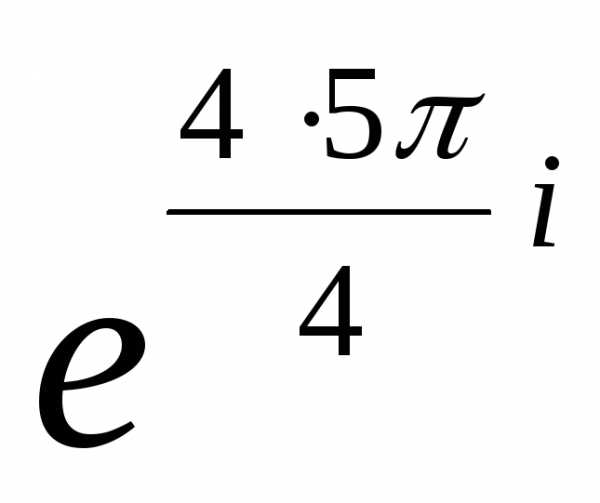 =
4
=
4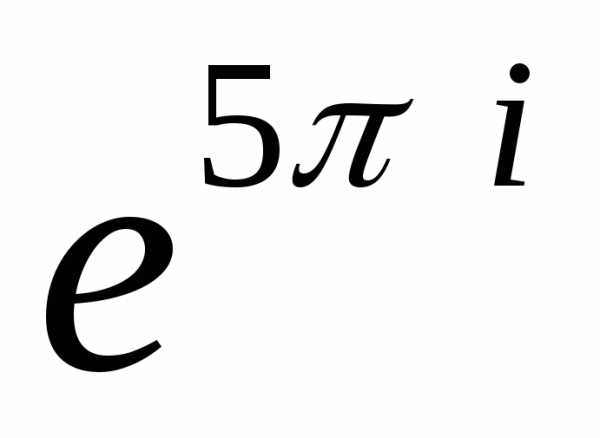
Находим
2)
Найдем расстояние d между точками 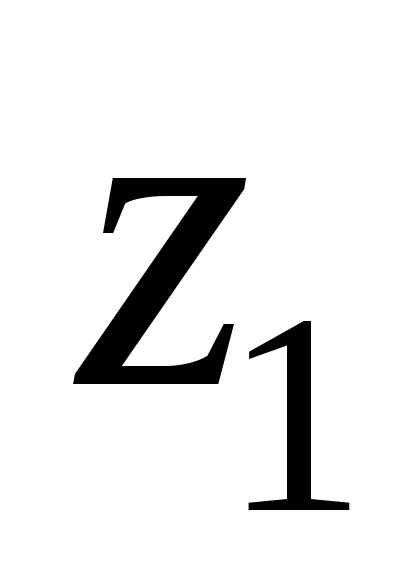 и
и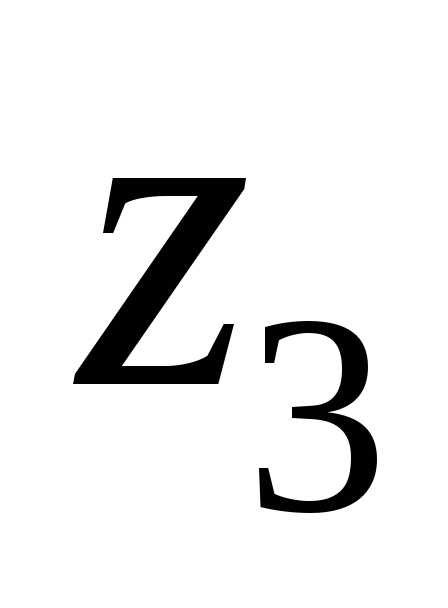 на комплексной плоскости, которое равно
модулю их разности.
на комплексной плоскости, которое равно
модулю их разности.
Разность двух комплексных чисел вычисляем по формуле:
(а1 + b1 i) — (а2 + b2 i) = (a1 — a2) + (b1 — b2) i
Тогда
расстояние d между точками 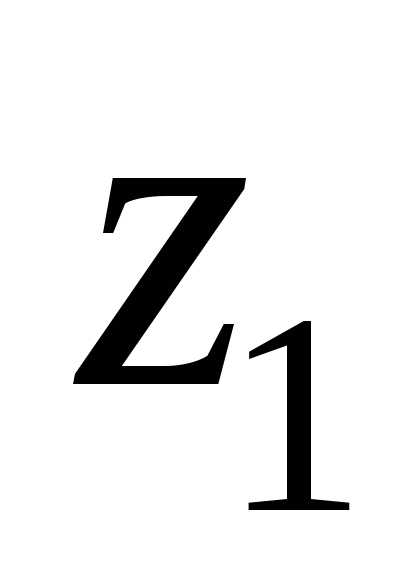 и
и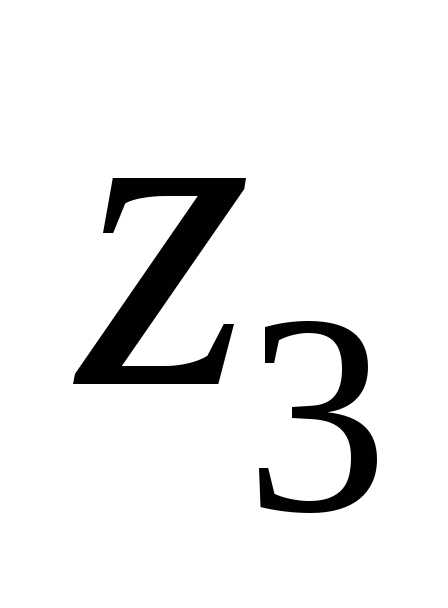 будет
будет
d =
Ответ:
1) 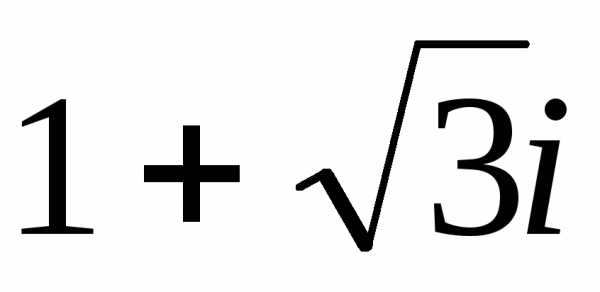 —
алгебраическая форма;
—
алгебраическая форма;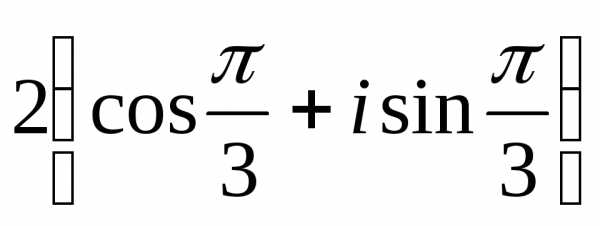 —
тригонометрическая форма;
—
тригонометрическая форма;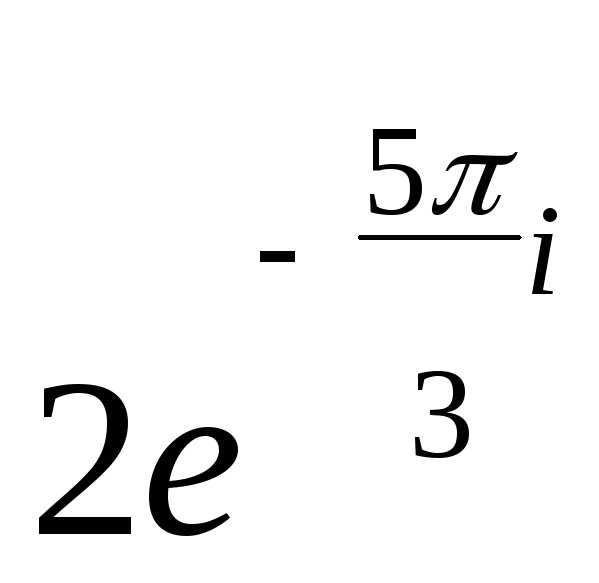 —
показательная форма; 2)
—
показательная форма; 2)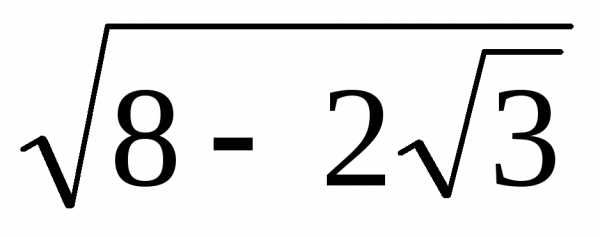
Задание 15
Решить уравнение на множестве комплексных чисел.
Решение
Решим заданное биквадратное уравнение относительноz2:
Это
уравнение относительно z2 не имеет решений на множестве действительных
чисел и имеет два решения (z12 = 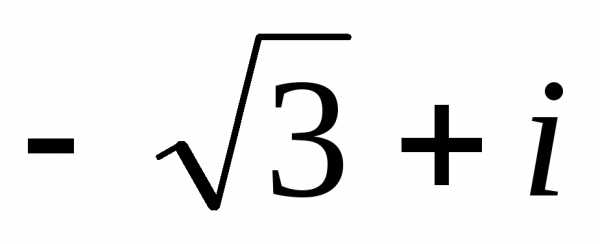 иz22 =
иz22 = 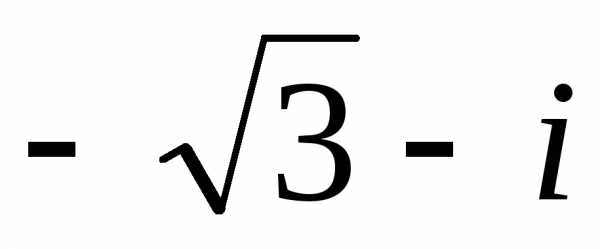 )
на множестве комплексных чисел.
)
на множестве комплексных чисел.
Тогда z1 = 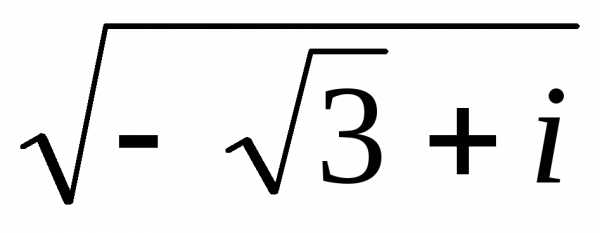 иz2 =
иz2 = 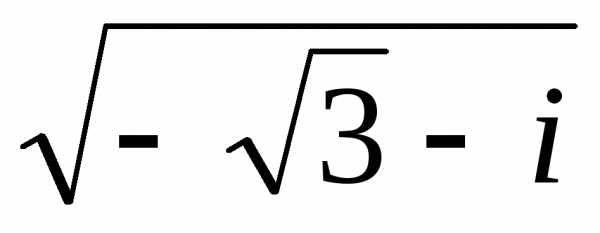
Квадратным корнем из комплексного числа будет комплексное число, квадрат которого равен данному комплексному числу.
.Числа u и vопределим из равенств
Обозначим z1 = 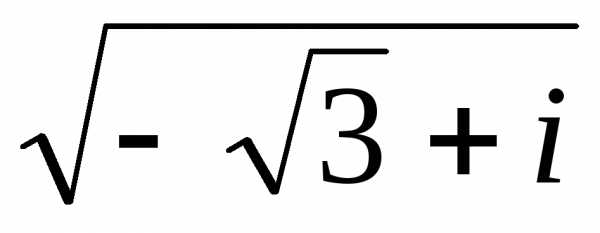 =u + iv.
Тогда
=u + iv.
Тогда
Соответственно
Получили два значения корней:
Аналогично
обозначим z2 = 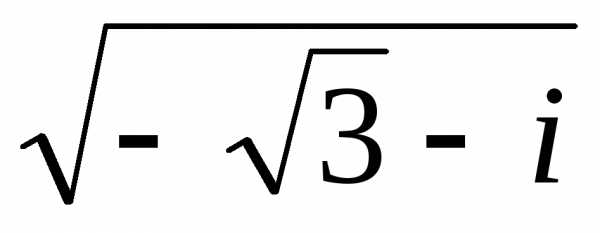 =w — it.
Тогда
=w — it.
Тогда
Соответственно
Получили два значения корней:
Как видим, корни λ1 и λ3, λ2 и λ4 являются соответственно сопряженными, т.к. чила z1 и z2 – сопряженные.
Ответ: ,
,
Задание 25
Решить
систему уравнений 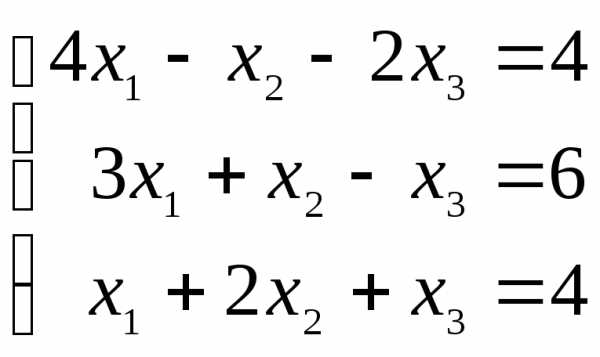 тремя
способами:
тремя
способами:
1) Методом Крамера;
2) Методом обратной матрицы;
3) Методом Гаусса.
Решение
а) Составим матрицу А системы из коэффициентов этой системы и найдем определитель матрицы:
А
= 
∆ =
= —
Т.к. ∆ ≠ 0, значит ранг r(A) матрицы системы и ранг расширенной матрицы
r (A) равны: r (A) = r (A) = 3. Значит, система уравнений совместна и имеет
единственное решение.
Решим заданную систему по формулам Крамера.
Решение системы найдем с помощью вспомогательных определителей ∆х1, ∆х2, ∆х3:
х1 = ∆х1 , х2 = ∆х2, х3 = ∆х3
∆ ∆ ∆
∆x1 =
=
∆x2 =
= —
∆x3 =
=
Найдем корни уравнения:
х1 = ∆х1 = 6 = 1
∆ 6
х2 = ∆х2 = 12 = 2
∆ 6
х3 = ∆х3 = — 6 = — 1
∆ 6
б) Решим данную систему методом Гаусса, для чего проведем последовательных элементарных преобразований строк расширенной матрицы, стремясь к тому, к тому, чтобы каждая строка, кроме первой, начиналась с нулей, и число нулей до первого ненулевого элемента в каждой следующей строке было больше, чем в предыдущей.
Представим систему в виде расширенной матрицы:

Поменяем 1-ую и 3-ю строки местами:
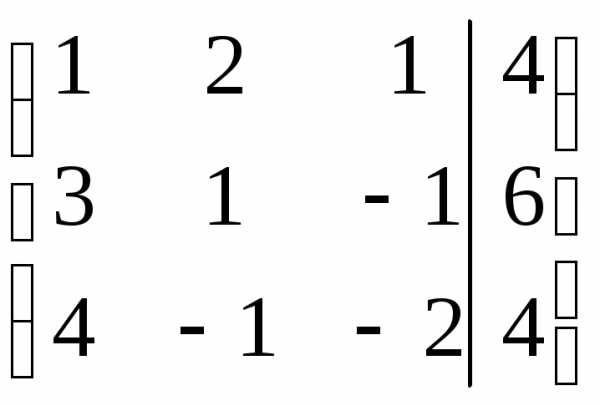
Из 2-ой строки вычтем 1-ую, умноженную на 3. Из 3-ей строки вычтем 1-ую, умноженную на 4:
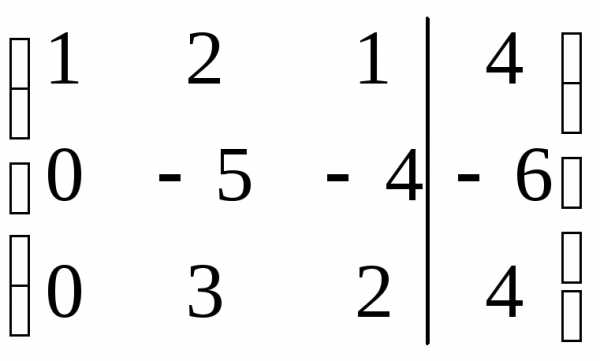
К 3-ей строке, умноженной на 5 прибавим 2-ую, умноженную на 3:
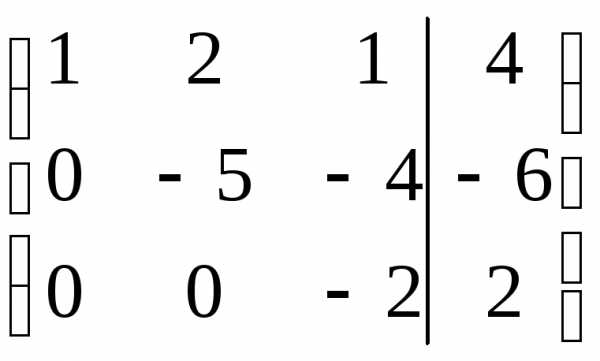
Разделим 2-ую строку на (-1), 3-ью — на (-2):
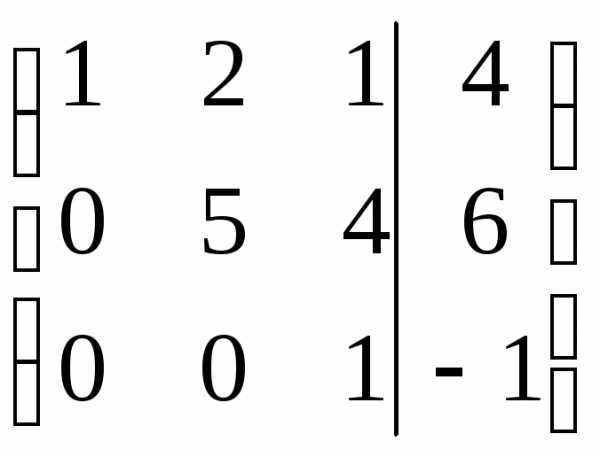
Получили эквивалентную исходной систему:
х1 + 2х2 + х3 = 4
5х2 + 4х3 = 6
х3 = — 1
Последовательно снизу вверх находим:
х3 = — 1,
5х2 + 4 (-1) = 6 5х2 = 10 х2 = 2
х1 + 2 2 + (-1) = 4 х1 = 1
в) Решим исходную систему матричным методом.
Рассмотрим три матрицы системы:
матрицу
системы А = 
матрицу-
столбец неизвестных В = 
матрицу-
столбец правых частей (свободных членов)
С = 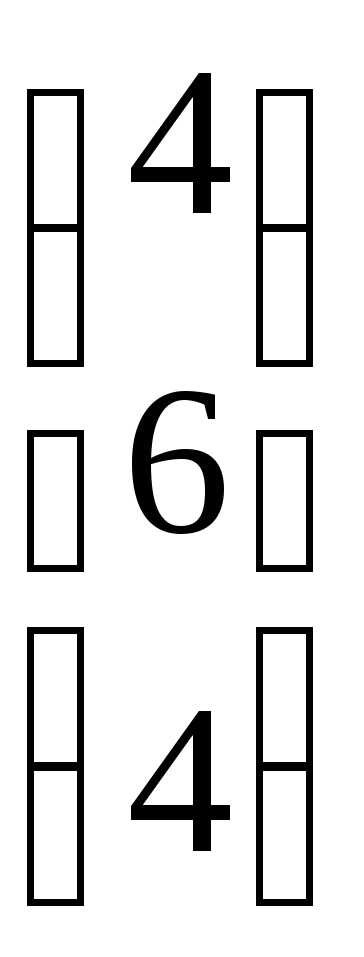
Тогда систему можно записать в матричном виде: АВ = С, а т.к. определитель матрицы А ∆ = detA = 6 ≠ 0, то ее решение можно записать в матричном виде: В = А-1С, где А-1 — матрица, обратная к матрице А.
Составим матрицу из алгебраических дополнений к элементам матрицы. А затем транспонируем ее, т.е. поменяем ее строки на столбцы, а столбцы на строки и найдем обратную матрицу А-1 по формуле:
А-1 = 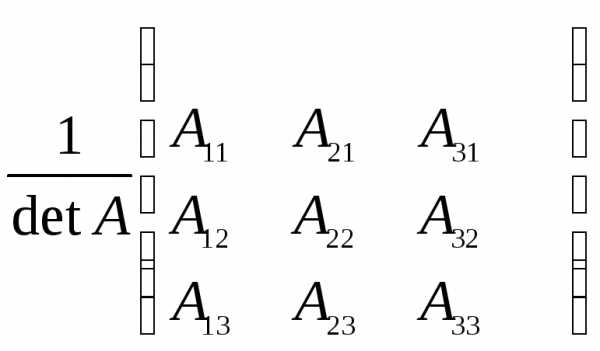 , где Аij — алгебраические дополнения соответствующих элементов.
, где Аij — алгебраические дополнения соответствующих элементов.
А11 = (-1)1+1 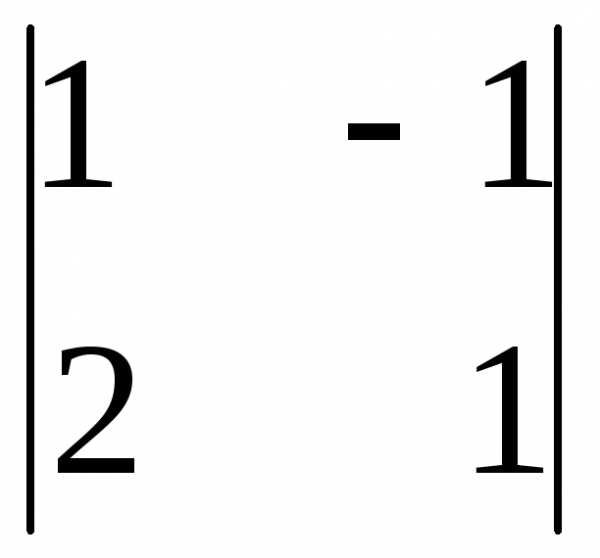 = 1 · 1 – 2 · (-1) = 3
= 1 · 1 – 2 · (-1) = 3
А12 = (-1)1+2 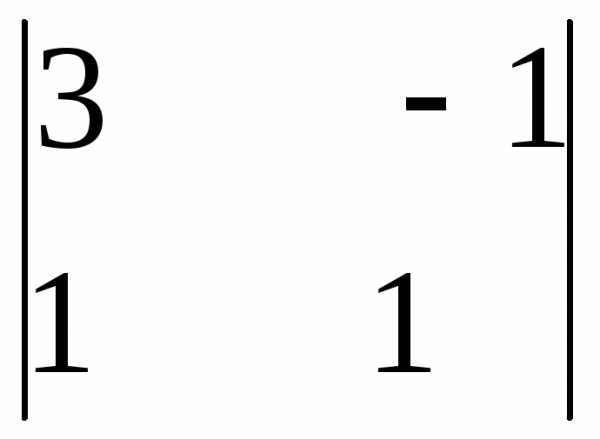 =
— (3 · 1 – 1 · (-1)) = — 4
=
— (3 · 1 – 1 · (-1)) = — 4
А13 = (-1)1+3 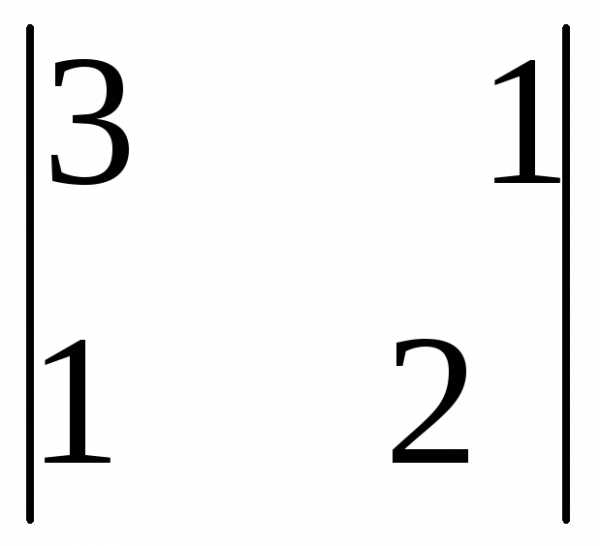 = 3 · 2 – 1 · 1 = 5
= 3 · 2 – 1 · 1 = 5
А21 = (-1)2+1 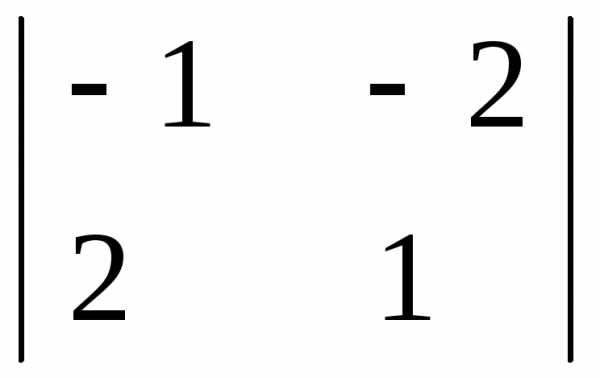 = — ((-1) · 1 – 2 · (-2) = — 3
= — ((-1) · 1 – 2 · (-2) = — 3
А22 = (-1)2+2 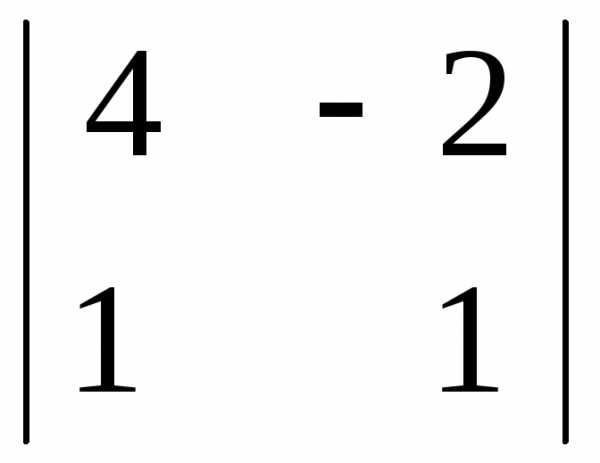 = 4 · 1 – 1 · (-2) = 6
= 4 · 1 – 1 · (-2) = 6
А23 = (-1)2+3 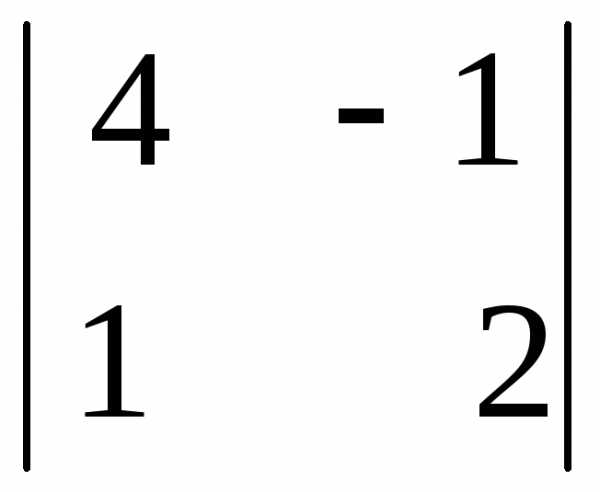 = — (4 · 2 – 1 · (-1)) = — 9
= — (4 · 2 – 1 · (-1)) = — 9
А31 = (-1)3+1 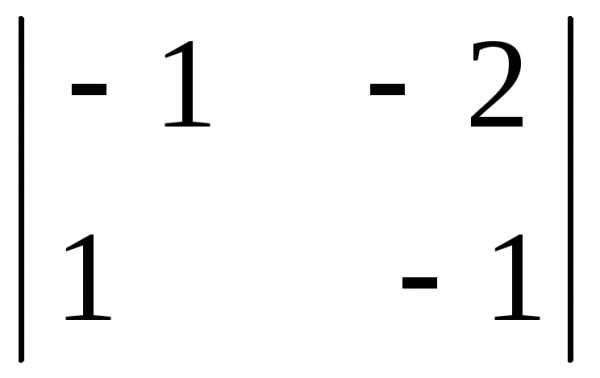 = (-1) · (-1) – (- 2) · 1 = 3
= (-1) · (-1) – (- 2) · 1 = 3
А32 = (-1)3+2 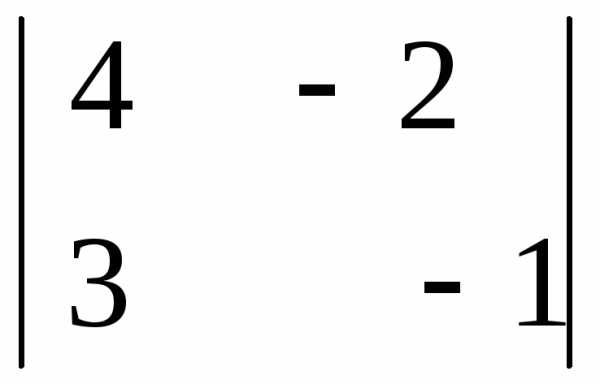 = — (4 · (-1) – 3 · (-2)) = — 2
= — (4 · (-1) – 3 · (-2)) = — 2
А33 = (-1)3+3 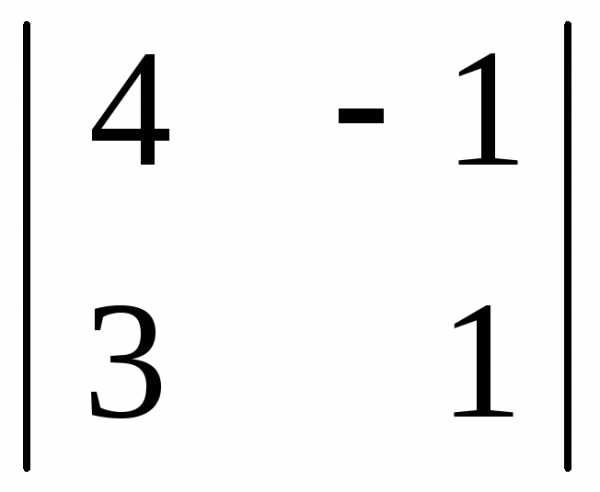 = 4 · 1 – 3 · (-1) = 7
= 4 · 1 – 3 · (-1) = 7
А-1 = 
Таким образом, х1 = 1; х2 = 2; х3 = — 1
Ответ: х1 = 1; х2 = 2; х3 = — 1
Задание 35
Даны три вектора
Доказать,
что векторы 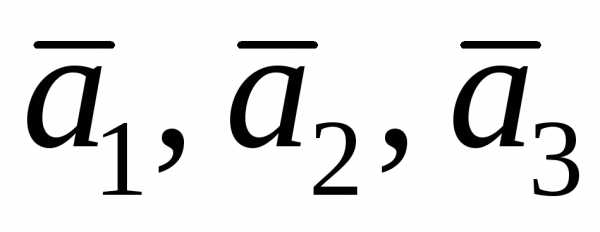 образуют базис, и определить, какая это
тройка векторов: правая или левая.
образуют базис, и определить, какая это
тройка векторов: правая или левая.
Решение
3)
Найдем смешанное произведение векторов 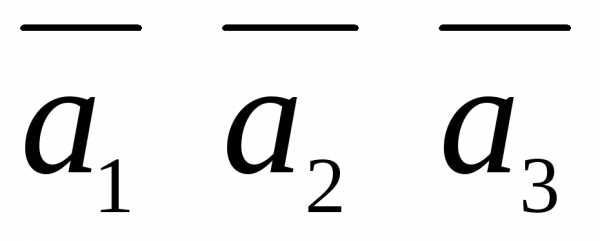 :
:
Т.к. 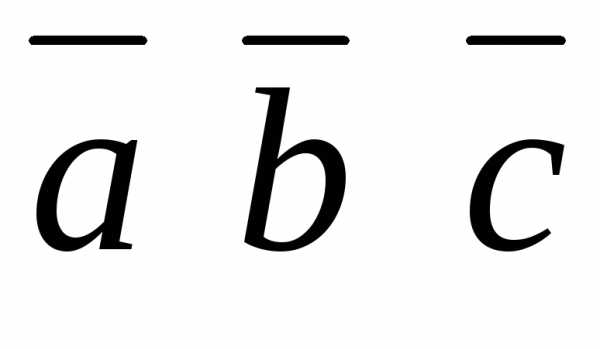 ≠
0, значит данные векторы не компланарны.
Таким образом, они линейно независимы
и образуют базис. При этом, они образуют
правую тройку векторов, т.к. их смешанное
произведение – число положительное:
≠
0, значит данные векторы не компланарны.
Таким образом, они линейно независимы
и образуют базис. При этом, они образуют
правую тройку векторов, т.к. их смешанное
произведение – число положительное:
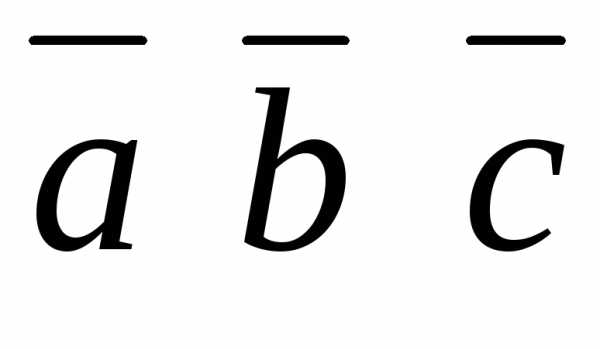 =
23 0.
=
23 0.
Ответ:
Векторы  образуют
базис, тройка векторов
образуют
базис, тройка векторов 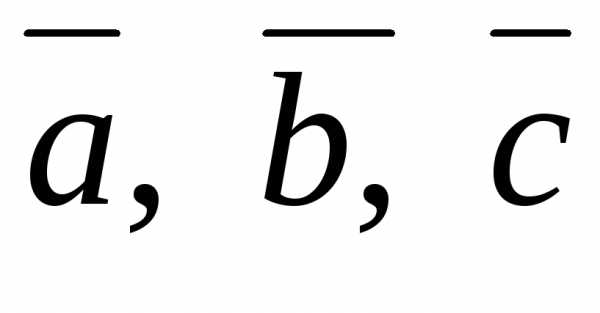 –
правая.
–
правая.
Задание 45
Даны координаты вершин треугольной пирамиды А1А2А3А4:
Найти:
studfiles.net
Формула Муавра. Комплексное число в степени
Рассмотрим случай, когда комплексное число необходимо возвести в степень. Как правило, комплексное число задано в алгебраической форме, к примеру:
Необходимо возвести во вторую степень комплексное число z.
Поэтому первым делом избавляемся от алгебраического представления и приводим наше число к тригонометрическому виду:
Формула Муавра утверждает, что степень
комплексного числа z равна
Применяем формулу Муавра:
По большому счету, что значит возвести комплексное число в степень? Это умножить комплексное число само на себя n раз. На мой взгляд, формулу Муавра целесообразно использовать в случае, когда степень n > 2. В ином случае, когда n = 2, можно поупражняться в умножении комплексных чисел как обычных алгебраических двучленов, рассмотренных в статье ранее. А в целом, эта формула работает для любой степени.
Пример 1. Возвести в четвертую степень комплексное число
Сначала разберем структуру исходного комплексного числа, которое необходимо возвести в степень. Запишем, чему равно значение его действительной и мнимой части:
.
Найдем модуль и аргумент комплексного числа:
Запишем тригонометрическое представление комплексного числа:
Теперь, используя формулу Муавра, найдем
matematyka.ru
Комплексные числа. Операции над комплексными числами
Лекция 6
Комплексные числа
1. Основные сведения
2. Операции над комплексными числами
3. Формула Муавра
4. Формула Эйлера
Основные сведения
Множество действительных чисел есть подмножество множества комплексных чисел.,т.е. R Ì C.
Алгебраическая форма комплексного числа записывается в виде z= x+ yi, где:
x = Re z — действительная часть, y = Im z — мнимая часть z, (x,y)Î R; i — мнимая единица, i2 = -1.
Геометрически каждое комплексное число z =х+ iу изображается точкой М (х; у) координатной плоскости х0у. В этом случае плоскость х0у называют комплексной числовой плоскостью, или плоскостью комплексного переменного z.
Тригонометрическая форма комплексного числа записывается в виде z = x+ yi =
= r×(cosj + i×sinj), где в полярных координатах: модуль zесть r = |z| = и
аргумент z есть j = arg z точки М, являющейся изображением комплексного числа z = x+ iy.
Аргумент z может быть определен из равенств cosj = или sinj =.
Аргумент z определяется с точностью до 2kp, kÎ Z.
Главным значением аргумента будем считать значение аргумента argz из промежутка [0,2p[.
Общее значение аргумента Arg z = arg z + 2pk, k Î Z.
Операции сложения и умножения комплексных чисел выполняют так же, как аналогичные операции с многочленами с учетом того, что i2 = -1.
Число называют сопряженным числу z = x + yi.
Отметим, что z — действительное число. Это используют при выполнении операции деления комплексных чисел.
Пример 1. Вычислить (2+i)×(1-i)= 2×1 + i×1 — 2×i — i2 = 2 + i — 2i +1 = 3 — i.
Пример 2. Вычислить
Операции над комплексными числами
Если даны два комплексных числа z = r×(cosj + i×sinj) и z1 = r1×(cosj1 + i×sinj1) то:
10. z ± z1=(x ± x1)+ i(y ± y1)
10. z× z1= (xx1 –yy1) + i(xy1+x1y) = r×r1×[cos(j+j1)+i×sin(j+j1)];
20. , если z1¹ 0;
30. — формула Муавра, nÎ N
Корень степени n из комплексного числа z имеет п различных значений, которые можно вычислить по формуле:
40. , k =0,1,2,…,n-1.
50. lnz = ln r + (j + 2kp)i, kÎZ.
Пример 3. Вычислить (1- i)15.
z = 1- i; x =1, y = -1, тогда: |z|=, , Þ (II -аячетверть) Þ применим 30, тогда по формуле Муавра:z15 = (1 — i)15 =
=27(-1+ i).
Формула Эйлера
vunivere.ru
формула Муавра — ПриМат
Любое комплексное число можно изобразить как точку на комплексной плоскости с координатами и , где ось абсцисс называется вещественной, а ось ординат — мнимой.
Определение 1:
Модулем комплексного числа называется корень суммы квадратов его действительной и мнимой частей. , ,
Определение 2:
Величина угла, который образует вектор изображающий данное число на комплексной плоскости с вещественной осью называется аргументом этого комплексного числа
Угол, отсчитываемый от оси против часовой стрелки — отрицательный, по — положительный.
Углы, отличающиеся на , соответствуют одному и тому же числу и записываются как:
, .
Определение 3:
У комплексного числа существует тригонометрическая форма записи
Примеры:
Найти геометрическое место точек (ГМТ):
Формула Муавра:
Лемма 1:
Для любых двух комлексных чисел справедливо неравенство
Доказательство:
Пусть ,
(*)
(*)=
Литература:
Геометрическая интерпретация комплексных чисел
Лимит времени: 0
Информация
Тест на тему «Геометрическая интерпретация комплексных чисел»:
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- С ответом
- С отметкой о просмотре
Поделиться ссылкой:
ib.mazurok.com
Линейная алгебра N 12
8
Занятие 12. Комплексные числа.
12.1. Определение комплексных чисел в алгебраической форме. Сравнение и изображение комплексных чисел на комплексной плоскости. Комплексное сопряжение. Сложение, умножение, деление комплексных чисел.
12.2. Модуль, аргумент комплексного числа.
12.3. Тригонометрическая и показательная формы записи комплексного числа.
12.4. Возведение в целую степень и извлечение корня из комплексного числа.
Определение комплексных чисел в алгебраической форме. Сравнение и изображение комплексных чисел на комплексной плоскости. Комплексное сопряжение. Сложение, умножение, деление комплексных чисел.
Комплексным числом в алгебраической форме называется число
, (1)
где 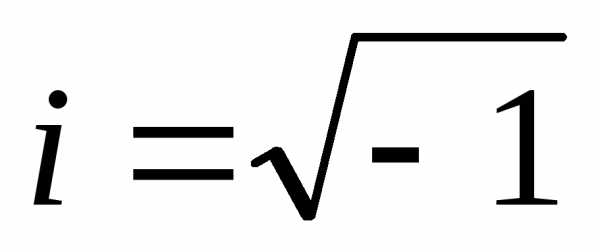 называетсямнимой единицейи
называетсямнимой единицейи — действительные числа:
— действительные числа: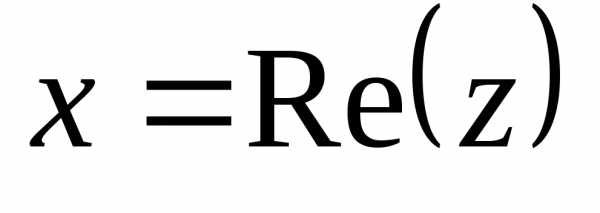 называетсядействительной (вещественной)
частью;
называетсядействительной (вещественной)
частью; —мнимой частьюкомплексного числа
—мнимой частьюкомплексного числа .
Комплексные числа виданазываютсячисто мнимыми числами.
Множество всех комплексных чисел
обозначается буквой
.
Комплексные числа виданазываютсячисто мнимыми числами.
Множество всех комплексных чисел
обозначается буквой .
.
По определению,
,
и т.д.
Множество всех действительных чисел  является частью множества
является частью множества
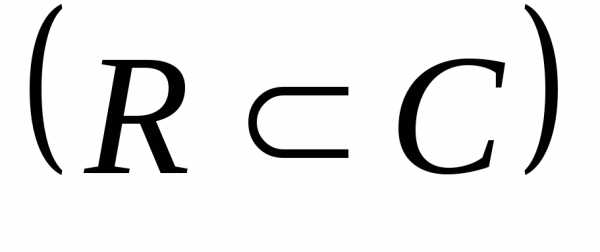 :.
С другой стороны, существуют комплексные
числа, не принадлежащие множеству
:.
С другой стороны, существуют комплексные
числа, не принадлежащие множеству .
Например,и
.
Например,и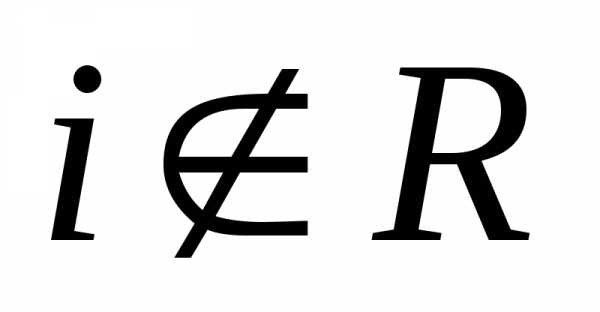 ,
т.к.
,
т.к. .
.
Комплексные числа в алгебраической форме естественным образом возникают при решении квадратных уравнений с отрицательным дискриминантом.
Пример 1. Решить уравнение.
Решение. ,
т.к. .
Следовательно, заданное квадратное уравнение имеет комплексные корни
,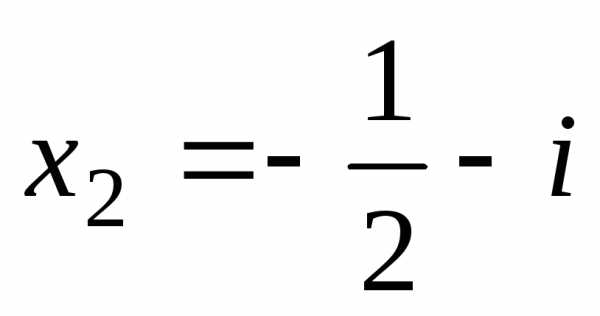 .
.
Пример 2. Найти действительную и мнимую части комплексных чисел
,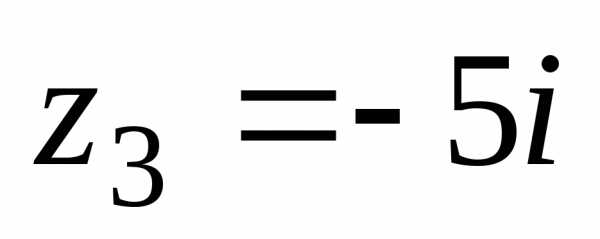 ,
,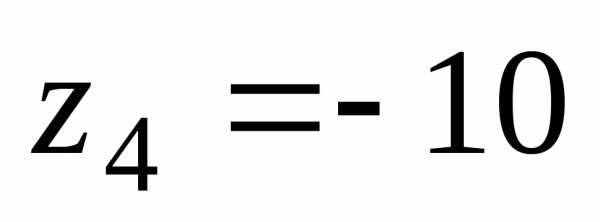 .
.
Решение.
— соответственно вещественная и мнимая
части числа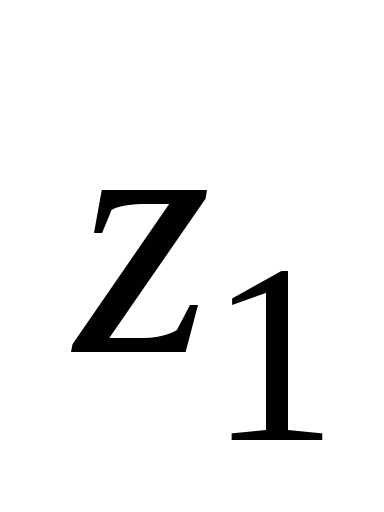 ,
,
.
.
.
Любое комплексное число
изображается вектором на комплексной
плоскости ,
представляющей плоскость с декартовой
системой координат
,
представляющей плоскость с декартовой
системой координат .
Начало вектора лежит в точке
.
Начало вектора лежит в точке ,
а конец — в точке с координатами
,
а конец — в точке с координатами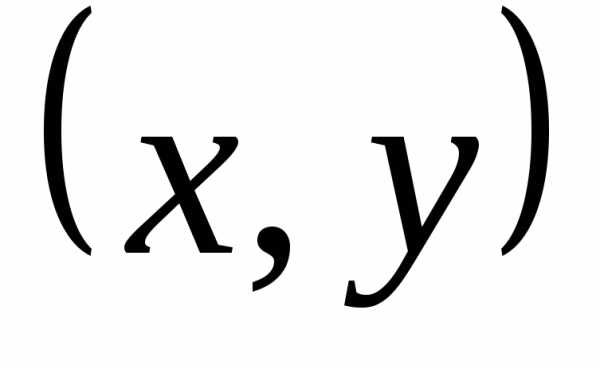 (рис
1.) Ось
(рис
1.) Ось называется
вещественной осью, а ось
называется
вещественной осью, а ось — мнимой осью комплексной плоскости
— мнимой осью комплексной плоскости .
.
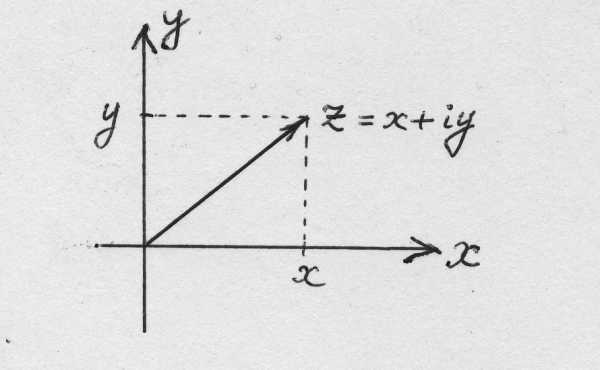
Рис. 1.
Комплексные числа
сравниваются между собой только знаками ..
Если же хотя бы одно из равенств:нарушено, то
..
Если же хотя бы одно из равенств:нарушено, то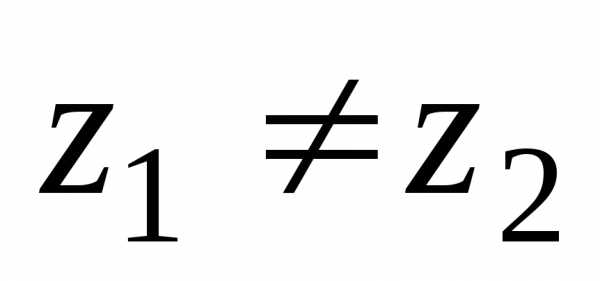 .Записи типа
не имеют смысла.
.Записи типа
не имеют смысла.
По определению, комплексное число
называется комплексно сопряженным
числу.
В этом случае пишут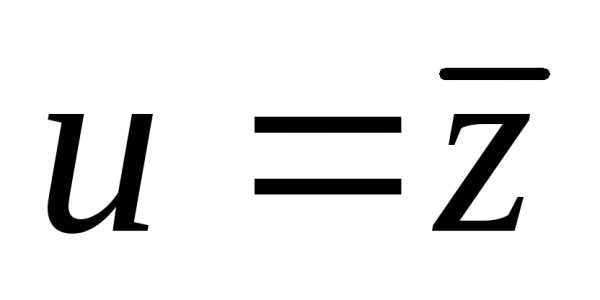 .
Очевидно, что
.
Очевидно, что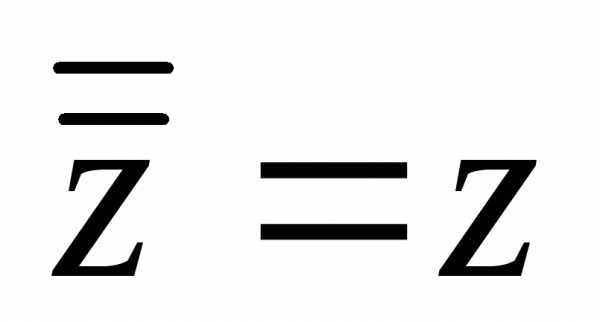 .
Везде далее черта сверху над комплексным
числом будет означать комплексное
сопряжение.
.
Везде далее черта сверху над комплексным
числом будет означать комплексное
сопряжение.
Например, .
Над комплексными числами можно выполнять такие операции, как сложение (вычитание), умножение, деление.
1. Сложение комплексных чиселпроизводится так:
.
Свойства операции сложения:
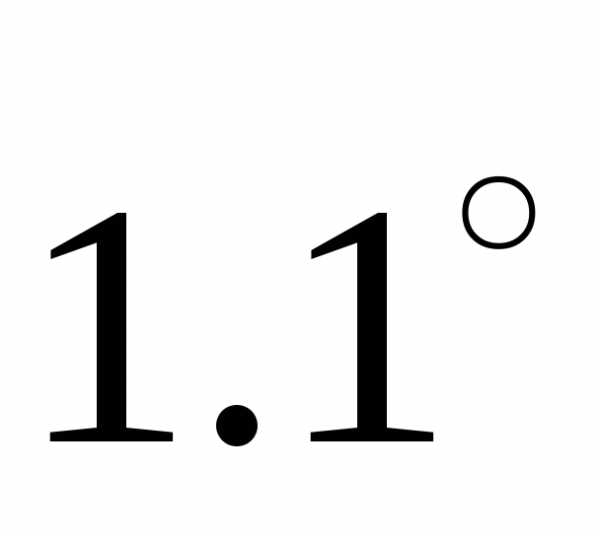 — свойство коммутативности;
— свойство коммутативности;
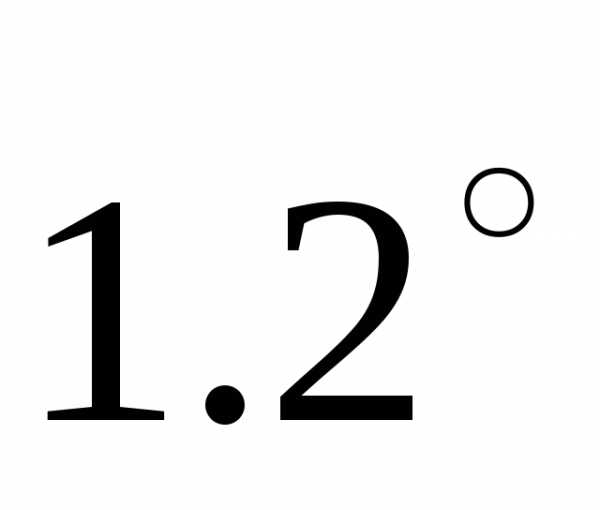 — свойство ассоциативности.
— свойство ассоциативности.
Нетрудно видеть, что геометрически
сложение комплексных чисел  означает сложение отвечающих им на
плоскости
означает сложение отвечающих им на
плоскости векторов по правилу параллелограмма.
векторов по правилу параллелограмма.
Операция вычитание числа  из числа
из числа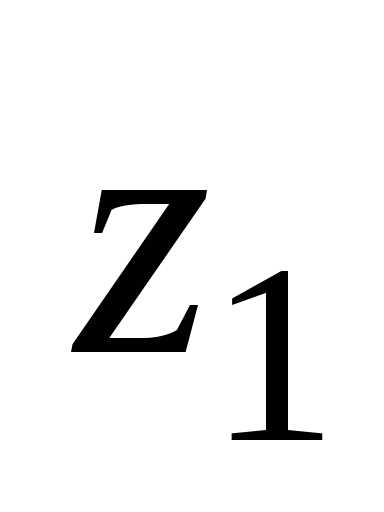 производится так:
производится так:
.
2. Умножение комплексных чисел производится так:
.
Свойства операции умножения:
 — свойство коммутативности;
— свойство коммутативности;
 — свойство ассоциативности;
— свойство ассоциативности;
 — закон дистрибутивности.
— закон дистрибутивности.
3. Деление комплексных чисел 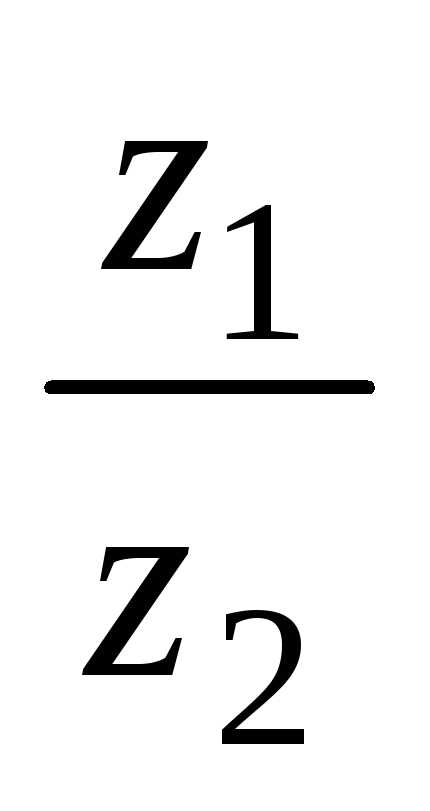 выполнимо только при
выполнимо только при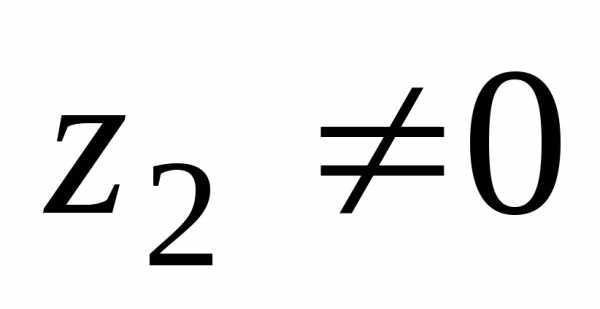 и производится так:
и производится так:
.
Пример 3. Найти, если.
Решение.
1) .(ош!)
2) .(ош!)
3) .(ош!)
4) .
5) .
Пример 4. Вычислить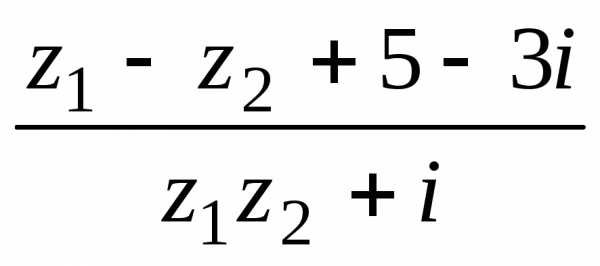 ,
если.
,
если.
Решение.
.
z, т.к.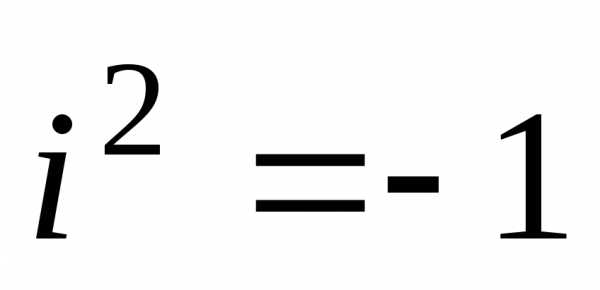 .
.
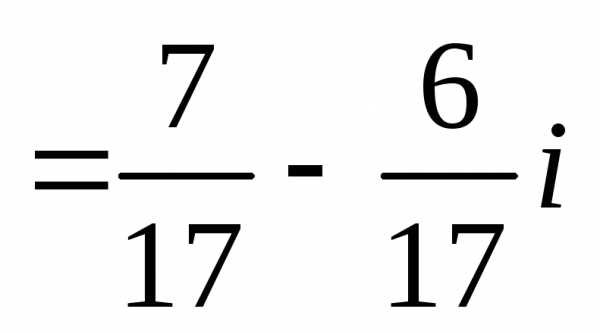 .(ош!)
.(ош!)
Нетрудно проверить (предлагается это сделать самостоятельно) справедливость следующих утверждений:
.
Модуль, аргумент комплексного числа.
Модуль комплексного числа (модуль обозначается
обозначается )
это — неотрицательное число
)
это — неотрицательное число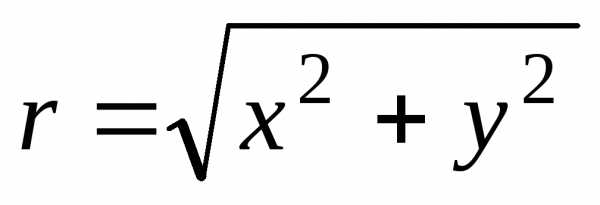 ,
т.е. .
,
т.е. .
Геометрический смысл 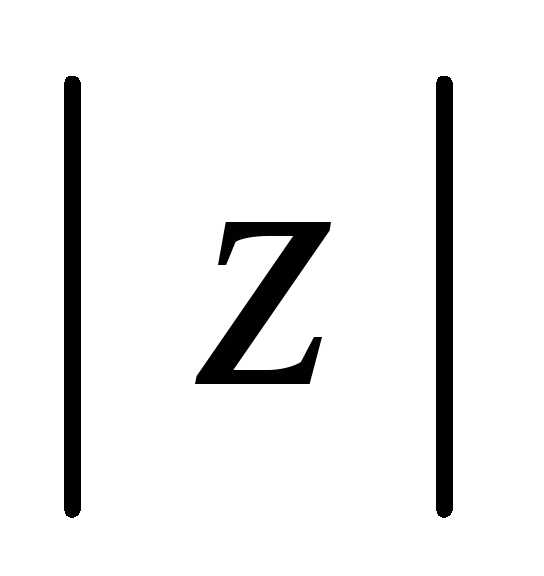 — длина вектора, представляющего число
— длина вектора, представляющего число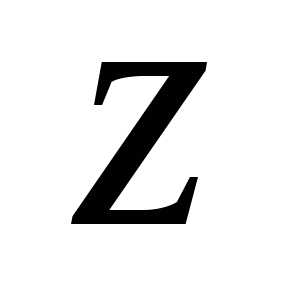 на комплексной плоскости
на комплексной плоскости .
Уравнение
.
Уравнение определяет множество всех чисел
определяет множество всех чисел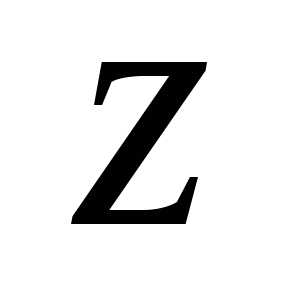 (векторов на
(векторов на ),
концы которых лежат на единичной
окружности
),
концы которых лежат на единичной
окружности .
.
Аргумент комплексного числа (аргумент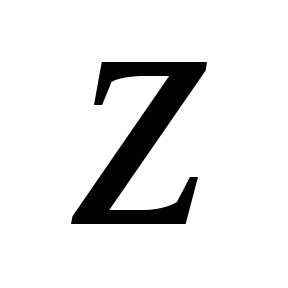 обозначается
обозначается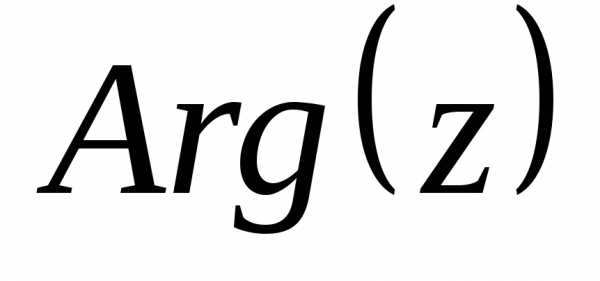 )
это – угол
)
это – угол в радианах между вещественной осью
в радианах между вещественной осью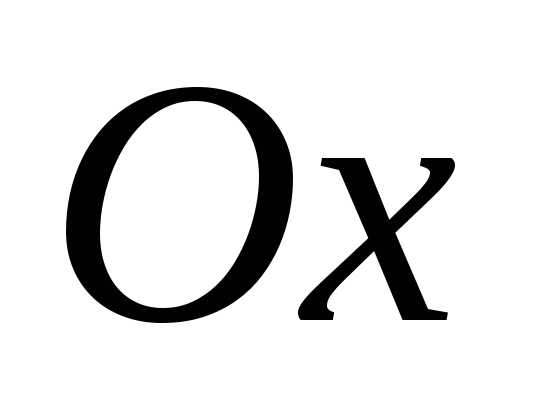 и числом
и числом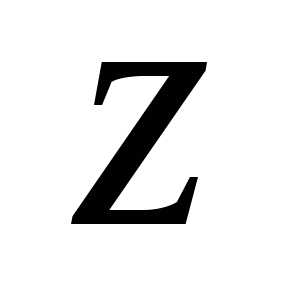 на комплексной плоскости
на комплексной плоскости ,
причем
,
причем  положителен, если он отсчитывается от
положителен, если он отсчитывается от до
до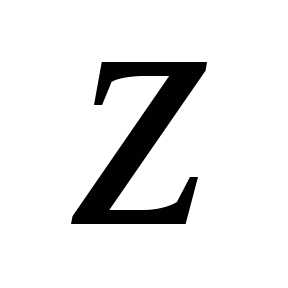 против часовой стрелки, и
против часовой стрелки, и отрицателен, если
отрицателен, если отсчитывается от оси
отсчитывается от оси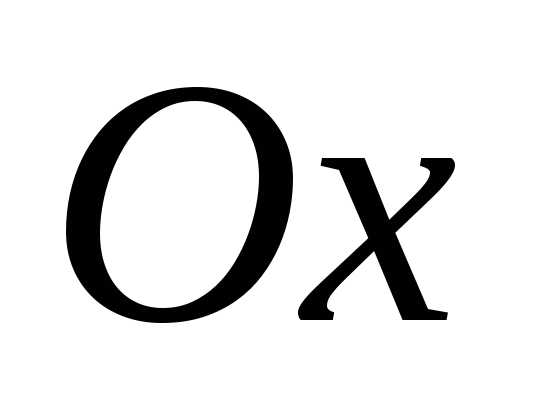 до
до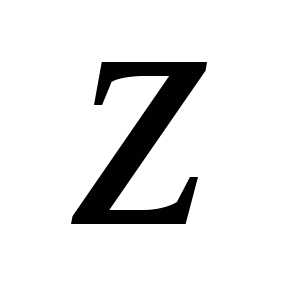 по часовой стрелке.
по часовой стрелке.
Таким образом, аргумент числа  определяется неоднозначно, с точностью
до слагаемого
определяется неоднозначно, с точностью
до слагаемого ,
где
,
где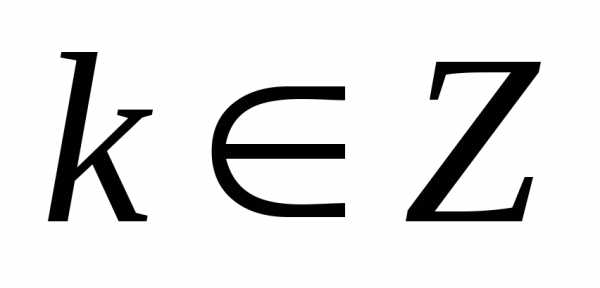 .
Однозначно аргумент числа
.
Однозначно аргумент числа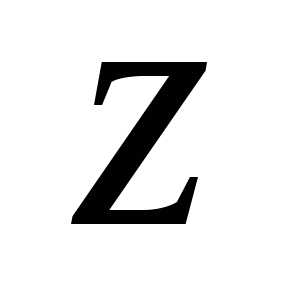 определяется в пределах одного обхода
единичной окружности
определяется в пределах одного обхода
единичной окружности на плоскости
на плоскости .Обычно требуется найти
.Обычно требуется найти 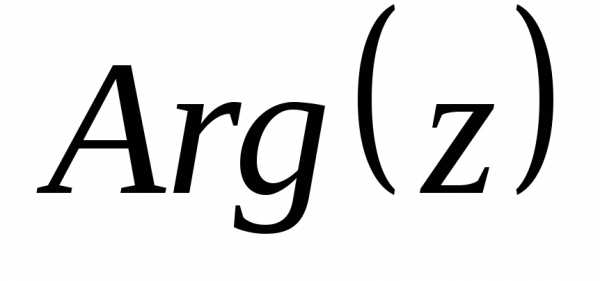 в пределах интервала
в пределах интервала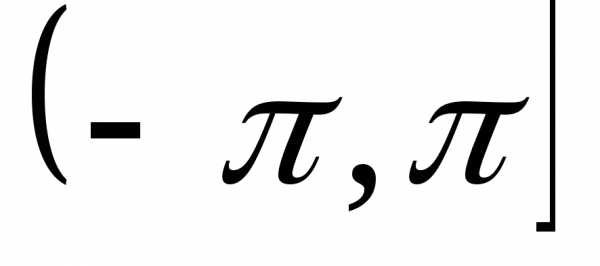 , такое значение называется главным
значением аргумента числа
, такое значение называется главным
значением аргумента числа 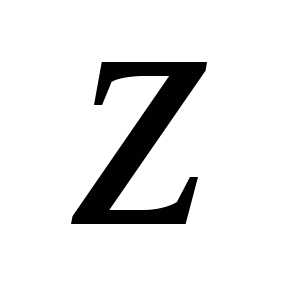 и обозначается
и обозначается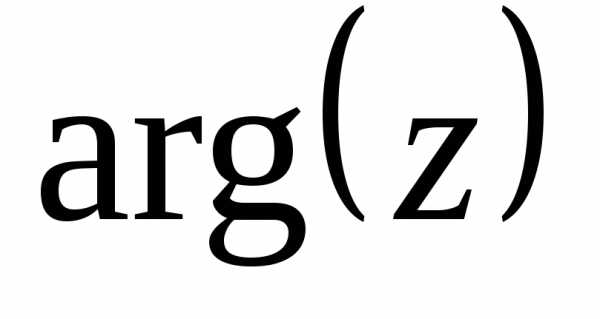 .
.
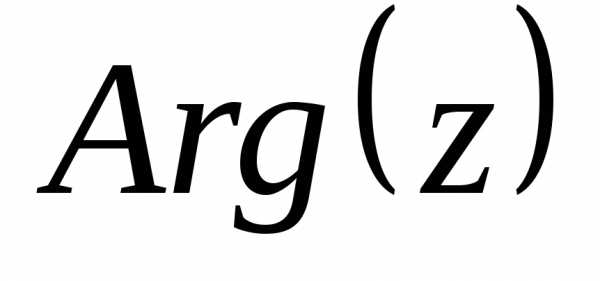 и
и числа
числа можно найти из уравнения
можно найти из уравнения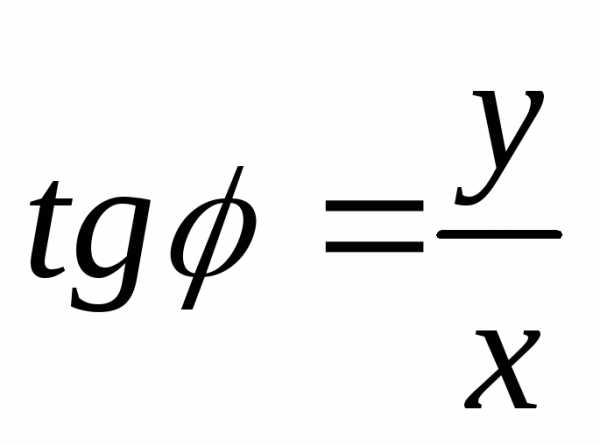 ,
при этомобязательнонужно
учитывать, в какой четверти плоскости
,
при этомобязательнонужно
учитывать, в какой четверти плоскости лежит конец вектора
лежит конец вектора — точка
— точка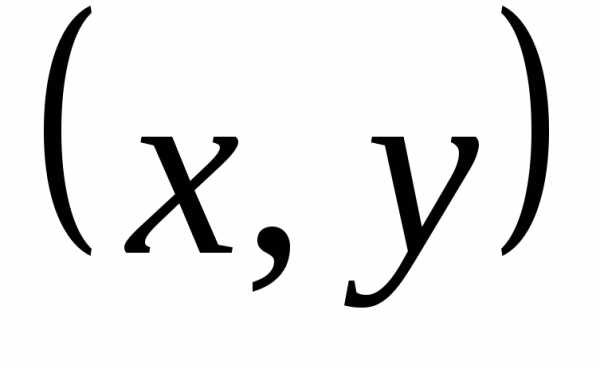 :
:
если
(1-я четверть плоскости ),
то;
),
то;
если
(2-я четверть плоскости ),
то;
),
то;
если
(3-я четверть плоскости ),
то;
),
то;
если
(4-я четверть плоскости ),
то.
),
то.
Фактически, модуль и аргумент числа ,
это полярные координаты точки
точки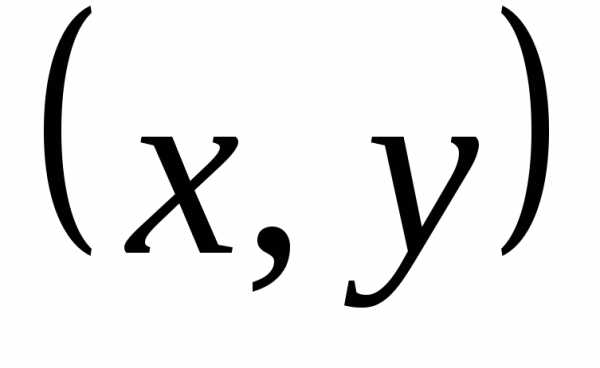 — конца вектора
— конца вектора на плоскости
на плоскости .
.
Пример 5. Найти модуль и главное значение аргумента чисел:
.
Решение.
1) .
2) .
3)
.
4) .
5)
.
6) .
7)
.
8) .
Аргументы чисел
,
лежащих осях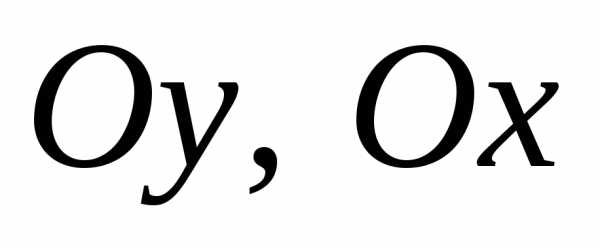 ,
разделяющих четверти 1,2,3,4 комплексной
плоскости
,
разделяющих четверти 1,2,3,4 комплексной
плоскости ,
находятся сразу же по графическим
изображениям этих чисел на плоскости
,
находятся сразу же по графическим
изображениям этих чисел на плоскости .
.
Тригонометрическая и показательная формы записи комплексного числа. Умножение и деление комплексных чисел в тригонометрической и показательной формах записи.
Тригонометрическая форма записикомплексного числаимеет вид:
, (2)
где 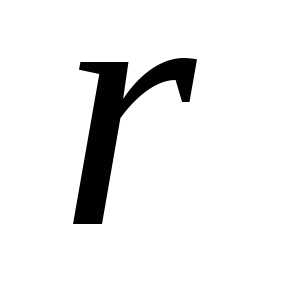 —
модуль,
—
модуль, —
аргумент комплексного числа
—
аргумент комплексного числа .
Такое представление комплексных чисел
вытекает из равенств.
.
Такое представление комплексных чисел
вытекает из равенств.
Показательная (экспоненциальная) форма записи комплексного числаимеет вид:
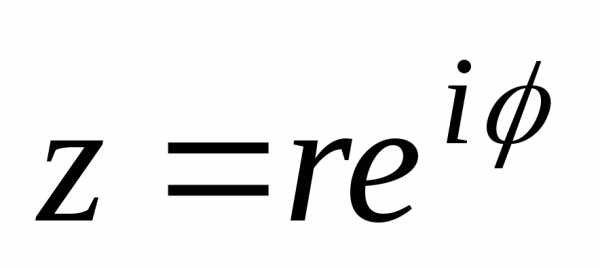 ,
(3)
,
(3)
где 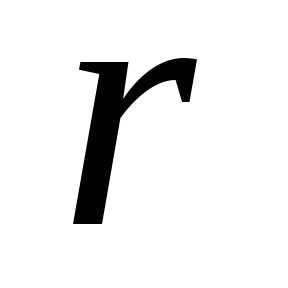 —
модуль,
—
модуль, —
аргумент числа
—
аргумент числа .
Возможность представления комплексных
чисел в показательной форме (3) вытекает
из тригонометрической формы (2) и формулы
Эйлера:
.
Возможность представления комплексных
чисел в показательной форме (3) вытекает
из тригонометрической формы (2) и формулы
Эйлера:
. (4)
Эта формула доказывается в курсе ТФКП (Теория функций комплексного переменного).
Пример 6. Найти тригонометрическую и экспоненциальную формы записи комплексных чисел:из примера 5.
Решение. Воспользуемся результатами примера 5, в котором найдены модули и аргументы всех указанных чисел.
1)
— тригонометрическая форма записи числа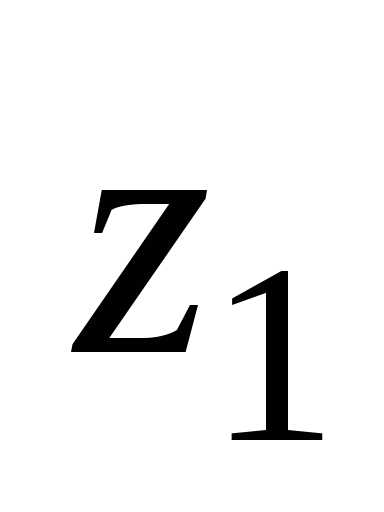 ,
,
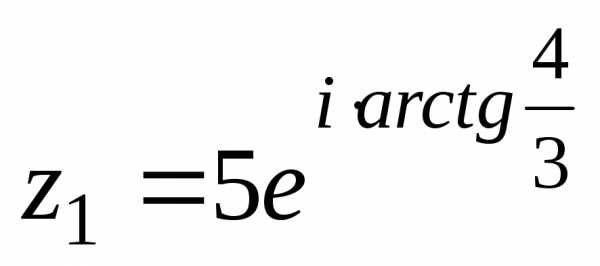 — показательная (экспоненциальная)
форма записи числа
— показательная (экспоненциальная)
форма записи числа .
.
2)
— тригонометрическая форма записи числа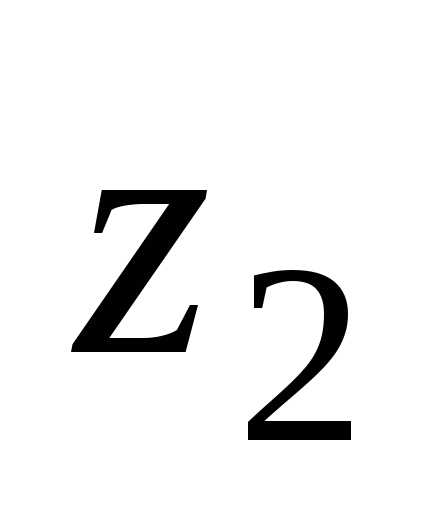 ,
,
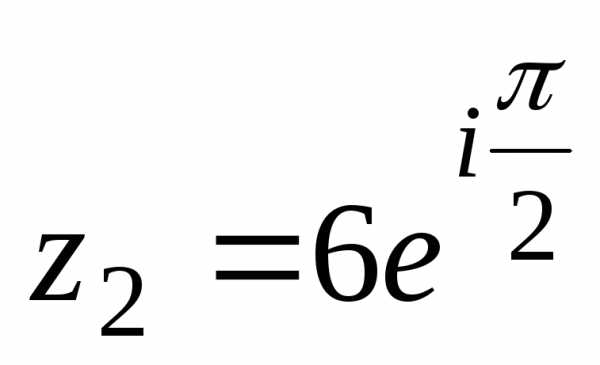 — показательная (экспоненциальная)
форма записи числа
— показательная (экспоненциальная)
форма записи числа .
.
3)
— тригонометрическая форма записи числа ,
,
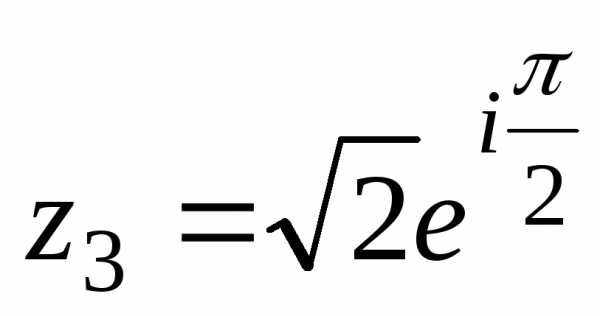 — показательная (экспоненциальная)
форма записи числа
— показательная (экспоненциальная)
форма записи числа .
.
4)
— тригонометрическая форма записи числа ,
,
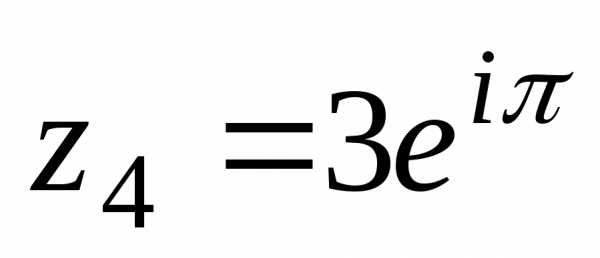 — показательная (экспоненциальная)
форма записи числа
— показательная (экспоненциальная)
форма записи числа .
.
5)
— тригонометрическая форма записи числа ,
,
— показательная (экспоненциальная)
форма записи числа .
.
6)
— тригонометрическая форма числа ,
,
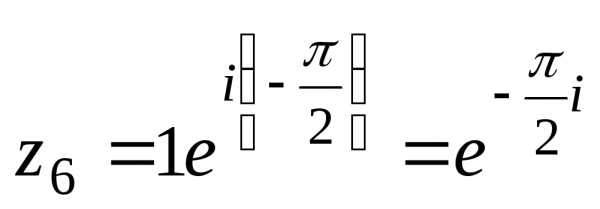 — показательная (экспоненциальная)
форма числа
— показательная (экспоненциальная)
форма числа .
.
7)
— тригонометрическая форма записи числа ,
,
— показательная (экспоненциальная)
форма числа .
.
8)
— тригонометрическая форма записи числа ,
,
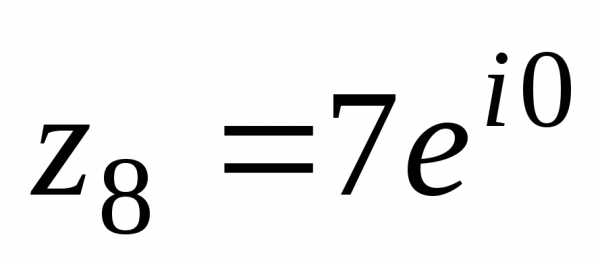 — показательная (экспоненциальная)
форма записи числа
— показательная (экспоненциальная)
форма записи числа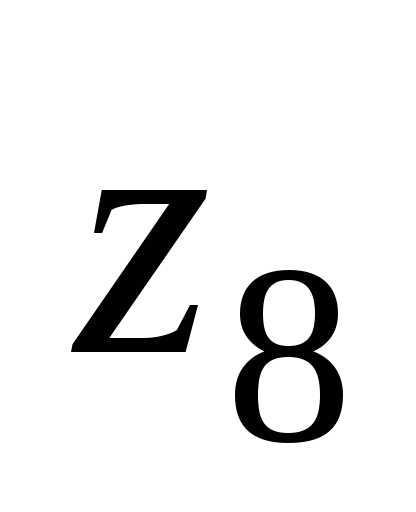 .
.
Показательная форма записи комплексных
чисел приводит к следующей геометрической
трактовке операций умножения и деления
комплексных чисел. Пусть
— показательные формы чисел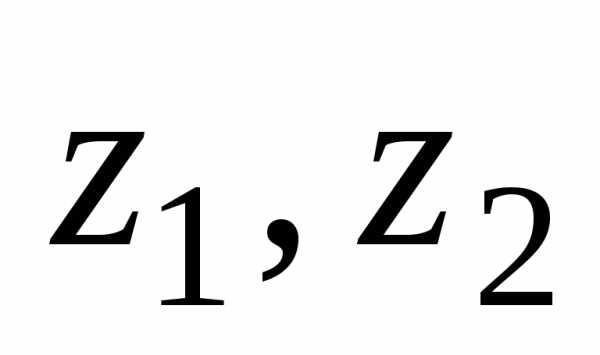 .
.
1.При перемножении комплексных чисел их модули перемножаются, а аргументы складываются.
2.При делении комплексного числа 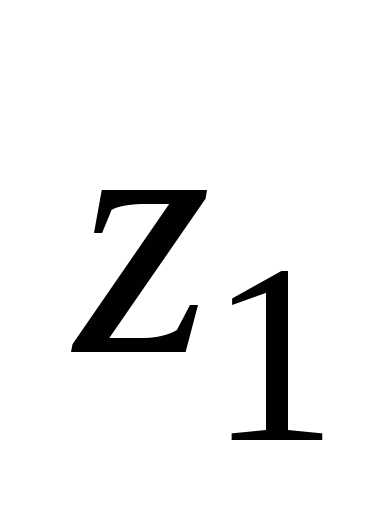 на число
на число получается комплексное число
получается комплексное число ,
модуль
,
модуль которого равен отношению модулей
которого равен отношению модулей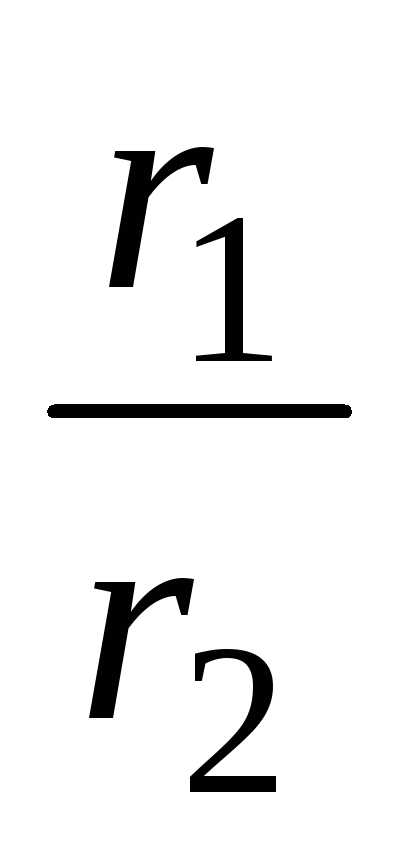 ,
а аргумент
,
а аргумент — разности
— разности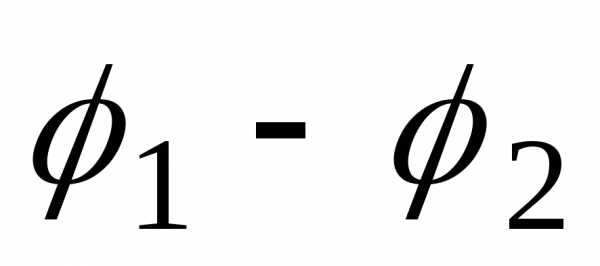 аргументов чисел
аргументов чисел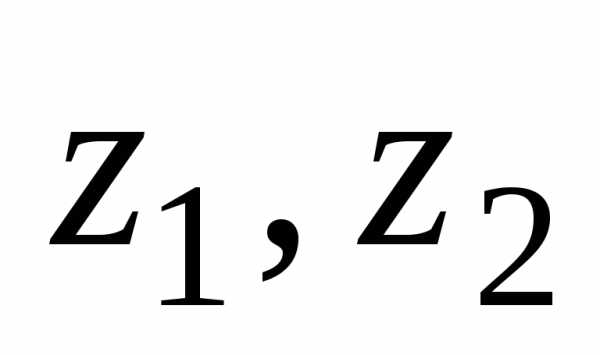 .
.
Возведение в целую степень и извлечение корня из комплексного числа.
По определению,
.
При возведении в целую степень  комплексного
числа,
следует действовать так: сначала найти
модуль
комплексного
числа,
следует действовать так: сначала найти
модуль и аргумент
и аргумент этого числа; представить
этого числа; представить в показательной форме
в показательной форме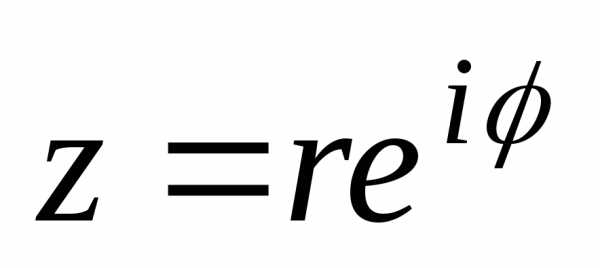 ;
найти
;
найти ,
выполнив следующую последовательность
действий
,
выполнив следующую последовательность
действий
, где. (5)
Замечание.Аргумент числа
числа может не принадлежать интервалу
может не принадлежать интервалу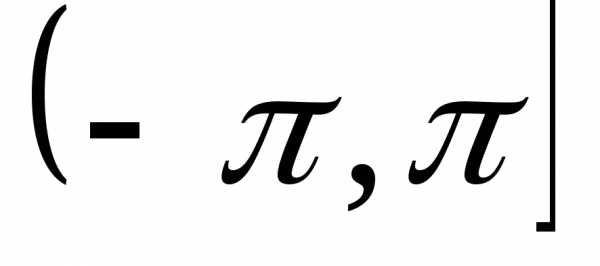 .
В этом случае следует по полученному
значению
.
В этом случае следует по полученному
значению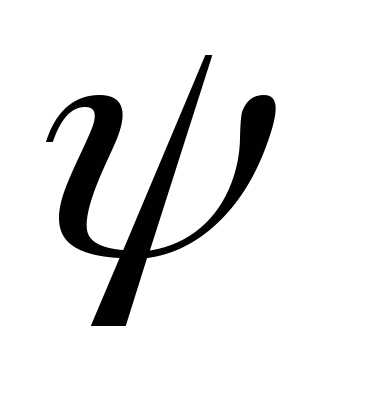 найти главное значениеаргумента
найти главное значениеаргумента
числа 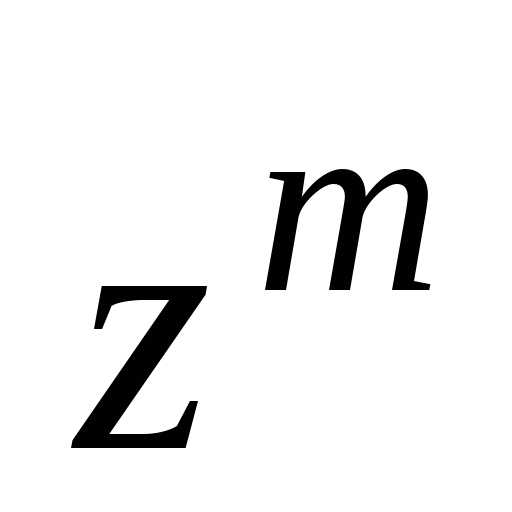 ,
прибавляя (или вычитая) число
,
прибавляя (или вычитая) число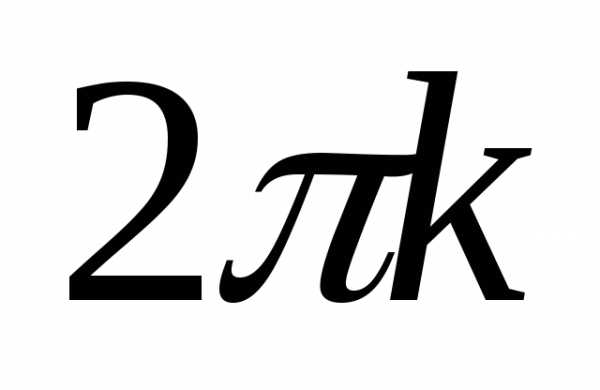 с таким значением
с таким значением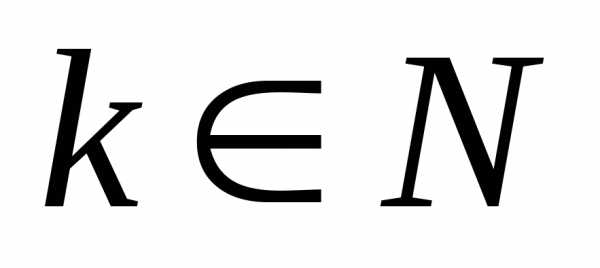 ,
чтобы
,
чтобы
принадлежало интервалу  .
После этого, нужно заменить в формулах
(5)
.
После этого, нужно заменить в формулах
(5)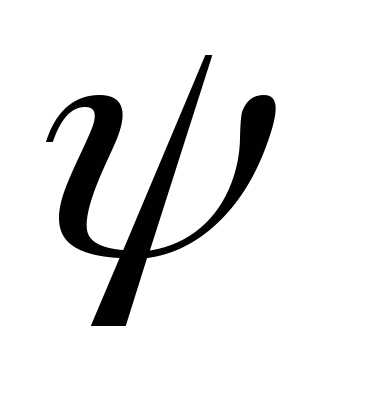 на
на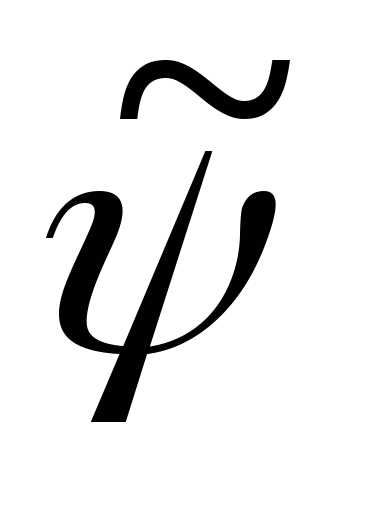 .
.
Пример 7. Найти и
и ,
если.
,
если.
Решение.
1)
=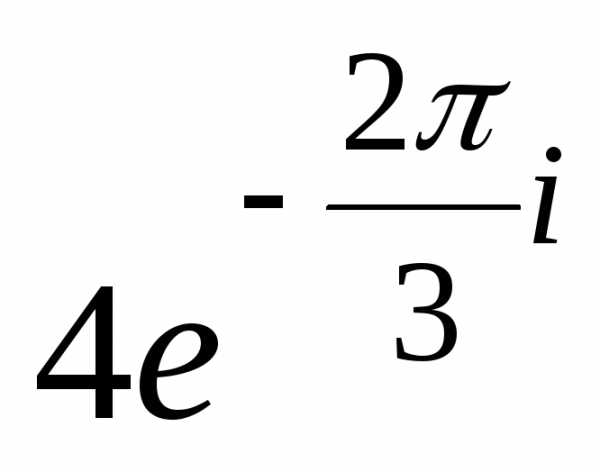 (см. число
(см. число из примера 6).
из примера 6).
2)
,
где..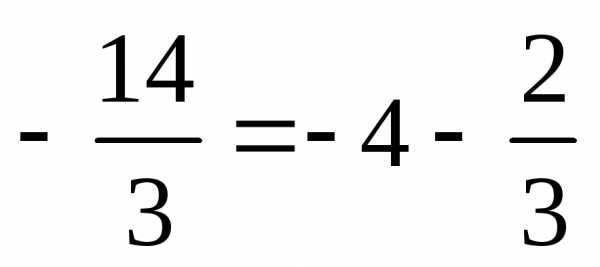 .
.
Следовательно, 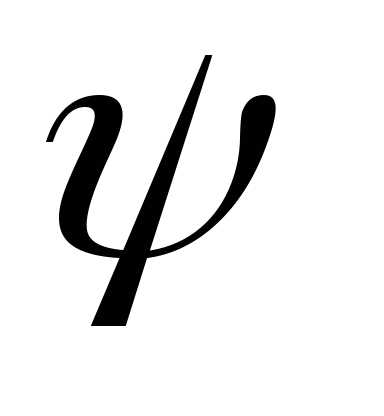 можно заменить наи, значит,
можно заменить наи, значит,
, где.
3) , где..
Заменим 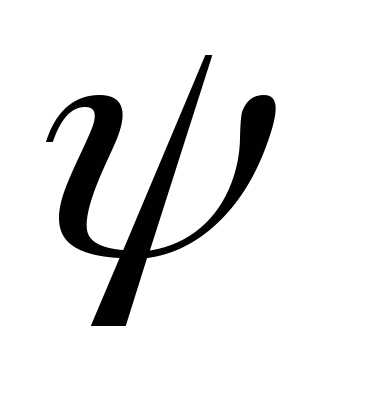 на.
Следовательно,
на.
Следовательно,
.
Извлечение корня 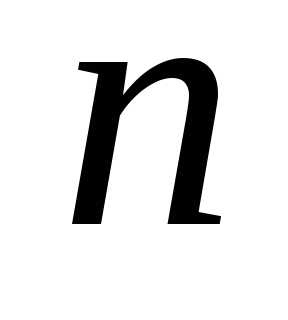 -й
степени
-й
степени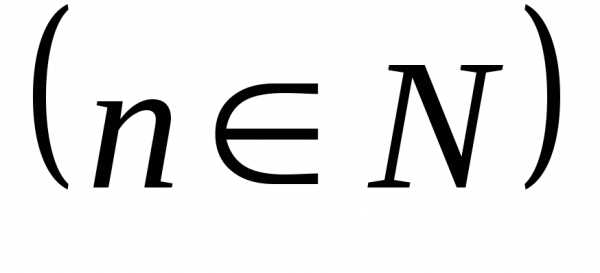 из комплексного числапроводится по формуле Муавра-Лапласа
из комплексного числапроводится по формуле Муавра-Лапласа
. (6)
Из формулы (6) видно, что  имеет ровно
имеет ровно различных значений.
различных значений.
studfiles.net
Деление комплексных чисел в алгебраической форме
Определение:
Комплексное число 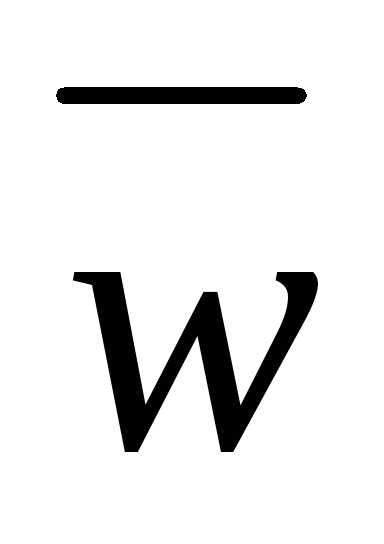 =x – yiназывается сопряженным числом по
отношению кw = x + yi.
=x – yiназывается сопряженным числом по
отношению кw = x + yi.
Примеры сопряженных комплексных чисел:
–1 + 5iи –1 – 5i, 2 – 3i и 2 + 3i.
Для деления двух комплексных чисел в алгебраической форме, как правило, удобно числитель и знаменатель дроби домножать на число, сопряженное знаменателю [1, с. 190-191].
Пример 4Выполнить деление: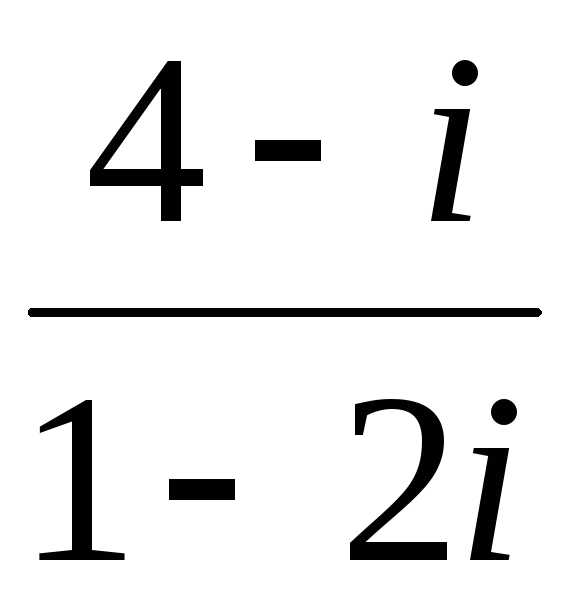 = [домножаем числитель и знаменатель
дроби на число, сопряженное знаменателю]
=
= [домножаем числитель и знаменатель
дроби на число, сопряженное знаменателю]
=
=
.
Заметим, что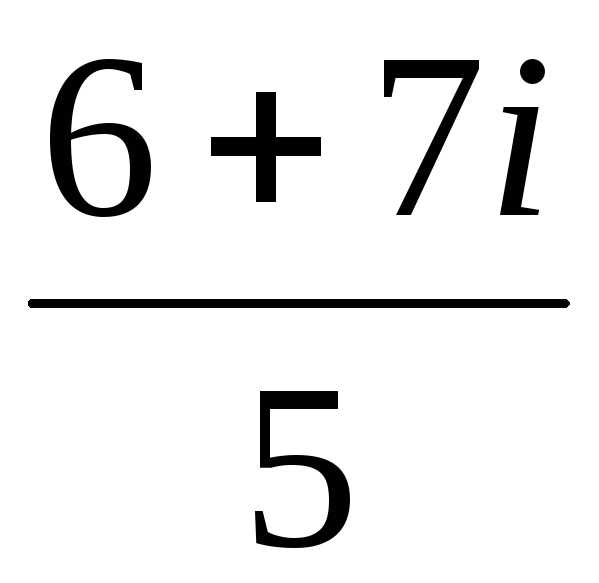 есть выражение, а не число, поэтому его
нельзя рассматривать как ответ.
есть выражение, а не число, поэтому его
нельзя рассматривать как ответ.
Пример 5Выполнить действия: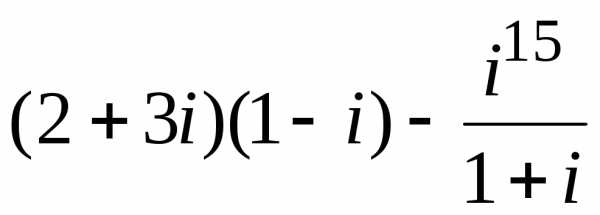 =
=
==.
Пример 6Выполнить действия: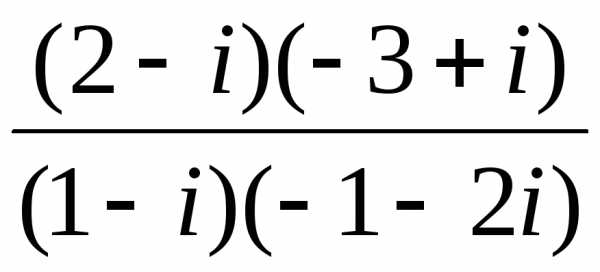 =
[домножаем числитель и знаменатель
дроби на числа, сопряженные обоим числам
знаменателя] =
=
[домножаем числитель и знаменатель
дроби на числа, сопряженные обоим числам
знаменателя] =
=
=.
Извлечение квадратного корня из комплексного числа в алгебраической форме
Определение. Комплексное число называется квадратным корнем из
комплексного числаz,
если
называется квадратным корнем из
комплексного числаz,
если [1, с. 191].
[1, с. 191].
Пример 7 Вычислить.
Решение.Пусть= x + yi, тогда
Составляем систему, приравнивая вещественные и мнимые части левой и правой частей равенства:
Решим отдельно биквадратное уравнение:
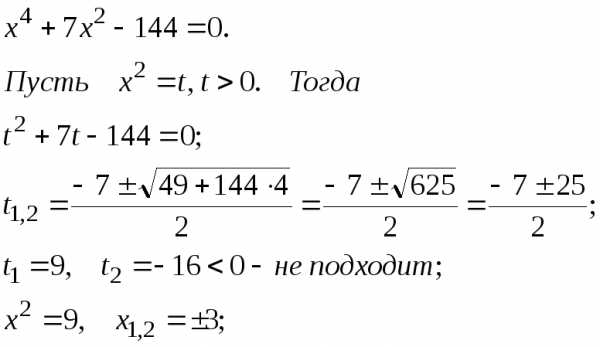 Ответ:{‑3 + 4i;
3 ‑ 4i}.
Ответ:{‑3 + 4i;
3 ‑ 4i}.
Другой способ решения возможен после введения тригонометрической формы записи комплексного числа (см. с. 14).
Решение линейных и квадратных уравнений для комплексных чисел
В области комплексных чисел верны те же формулы для решения линейных и квадратных уравнений, что и в области действительных чисел.
Пример 8 Решить уравнение: (‑2 ‑i)z = 3 +i.
Пример 9 Решить уравнение:.
Решение. Воспользуемся формулой для нахождения корней квадратного уравнения:
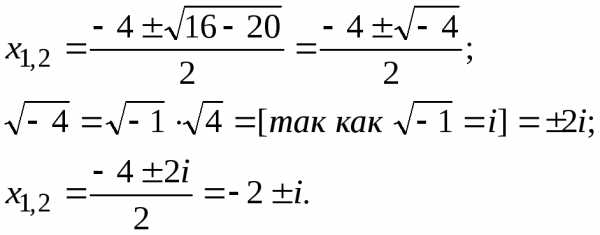 Ответ:{‑2 +i;
‑2 –i}.
Ответ:{‑2 +i;
‑2 –i}.
Пример 10 Решить уравнение:.
Решение:
Ответ:{1 ‑ 2i; 1 –i}.
Пример 11 Решить уравнение: .
.
Решение:
Вычислим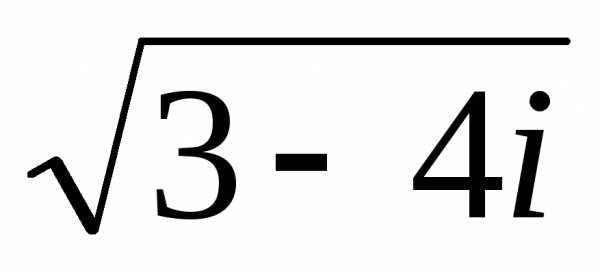 :
: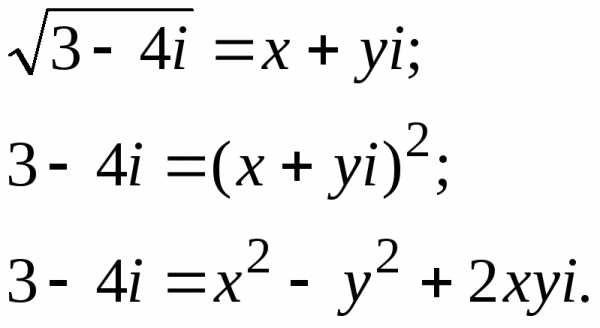
Составляем систему, приравнивая вещественные и мнимые части левой и правой частей равенства:
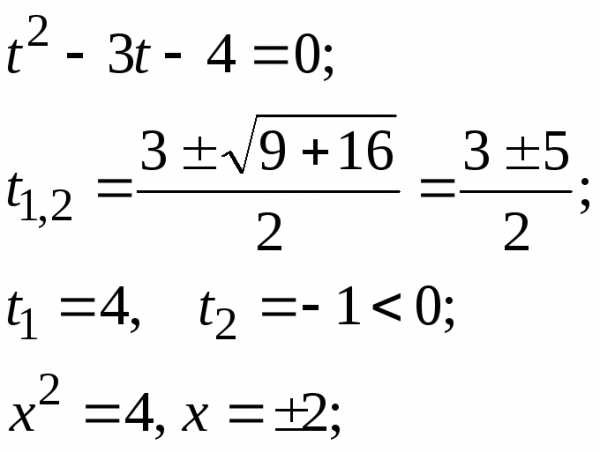
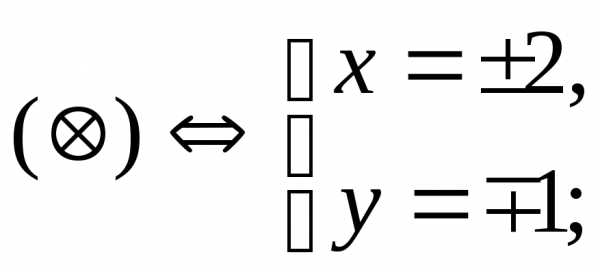
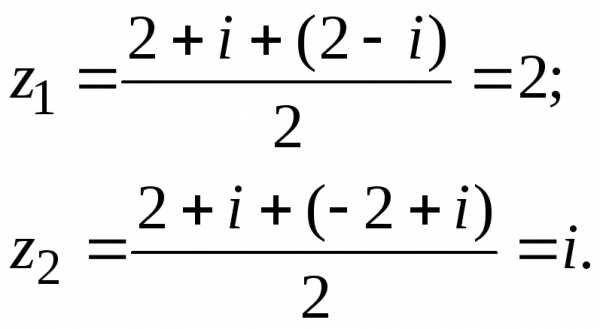 Ответ:{2;i}.
Ответ:{2;i}.
Пример 12 Решить систему уравнений:
Решение. Выражаем из первого уравнения системы переменнуюxчерез переменнуюy:
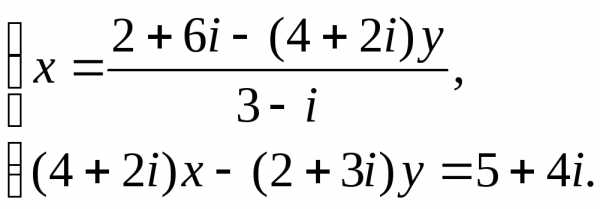
Домножаем числитель и знаменатель дроби на число, сопряженное знаменателю:
В числителе дроби раскрываем скобки и приводим подобные слагаемые:
Подставляем полученное значение переменной x во второе уравнение системы:
;

Ответ: {1 +i; i}.
Тригонометрическая форма записи комплексных чисел
Геометрическое изображение комплексных чисел
При изучении свойств комплексных чисел весьма удобной является их геометрическая интерпретация [1, с. 186-187]. Поскольку комплексное число определяется как пара действительных чисел, то каждое комплексное число z = a + biизображается точкой плоскости (x, y) с координатамиx = a и y = b. Такая плоскость называется комплексной плоскостью, ось абсцисс ‑ действительной (Rez), а ось ординат ‑ мнимой осью (Imz).
Пример 13 Изобразить на плоскости точки, соответствующие числам:
Р ешение.
У числаz1действительная часть равна ‑2, а
мнимая ‑ 0. Следовательно, изображением
числаz1служит
точка (‑2, 0) (рис. 1.1).
ешение.
У числаz1действительная часть равна ‑2, а
мнимая ‑ 0. Следовательно, изображением
числаz1служит
точка (‑2, 0) (рис. 1.1).
У числа z2действительная часть равна 0, а мнимая равна 3. Следовательно, изображением числаz2служит точка (0, 3). У числаz3действительная часть равна 1, а мнимая ‑4. Следовательно, изображением числаz3служит точка (1, ‑4).
У числа z4действительная часть равна 1 и мнимая 1. Следовательно, изображением числаz4служит точка (1, 1).
У числа z5действительная часть равна ‑3, а мнимая ‑2. Следовательно, изображением числаz5служит точка (‑3, ‑2).
Сопряженные числа изображаются точками на комплексной плоскости, симметричными относительно действительной оси Rez.
studfiles.net
