X cosx график – График y = cos x

alexxlab / / Школьная жизнь

Mathway | Популярные задачи

1 Найти точное значение sin(30)
2 Найти точное значение sin(45)
3 Найти точное значение sin(60)
4 Найти точное значение sin(30 град. )
5 Найти точное значение sin(60 град. )
6 Найти точное значение tan(30 град. )
7 Найти точное значение arcsin(-1)
8 Найти точное значение sin(pi/6)
9 Найти точное значение cos(pi/4)
10 Найти точное значение sin(45 град. )
11 Найти точное значение sin(pi/3)
12 Найти точное значение arctan(-1)
13 Найти точное значение cos(45 град. )
14 Найти точное значение cos(30 град. )
15 Найти точное значение tan(60)
16 Найти точное значение csc(45 град. )
17 Найти точное значение tan(60 град. )
18 Найти точное значение sec(30 град. )
19 Преобразовать из радианов в градусы (3pi)/4
20 График y=sin(x)
21 Преобразовать из радианов в градусы pi/6
22 Найти точное значение cos(60 град. )
23 Найти точное значение cos(150)
24 Найти точное значение tan(45)
25 Найти точное значение sin(30)
26 Найти точное значение sin(60)
27 Найти точное значение cos(pi/2)
28 Найти точное значение tan(45 град. )
29 График y=sin(x)
30 Найти точное значение arctan(- квадратный корень 3)
31 Найти точное значение csc(60 град. )
32 Найти точное значение sec(45 град. )
33 Найти точное значение csc(30 град. )
34 Найти точное значение sin(0)
35 Найти точное значение sin(120)
36 Найти точное значение cos(90)
37 Преобразовать из радианов в градусы pi/3
38 Найти точное значение sin(45)
39 Найти точное значение tan(30)
40 Преобразовать из градусов в радианы 45
41 Найти точное значение tan(60)
42 Упростить квадратный корень x^2
43 Найти точное значение cos(45)
44 Упростить sin(theta)^2+cos(theta)^2
45 Преобразовать из радианов в градусы pi/6
46 Найти точное значение cot(30 град. )
47 Найти точное значение arccos(-1)
48 Найти точное значение arctan(0)
49 График y=cos(x)
50 Найти точное значение cot(60 град. )
51 Преобразовать из градусов в радианы 30
52 Упростить ( квадратный корень x+ квадратный корень 2)^2
53 Преобразовать из радианов в градусы (2pi)/3
54 Найти точное значение sin((5pi)/3)
55 Упростить 1/( кубический корень от x^4)
56 Найти точное значение sin((3pi)/4)
57 Найти точное значение tan(pi/2)
58 Найти угол А tri{}{90}{}{}{}{}
59 Найти точное значение sin(300)
60 Найти точное значение cos(30)
61 Найти точное значение cos(60)
62 Найти точное значение cos(0)
63 Найти точное значение arctan( квадратный корень 3)
64 Найти точное значение cos(135)
65 Найти точное значение cos((5pi)/3)
66 Найти точное значение cos(210)
67 Найти точное значение sec(60 град. )
68 Найти точное значение sin(300 град. )
69 Преобразовать из градусов в радианы 135
70 Преобразовать из градусов в радианы 150
71 Преобразовать из радианов в градусы (5pi)/6
72 Преобразовать из радианов в градусы (5pi)/3
73 Преобразовать из градусов в радианы 89 град.
74 Преобразовать из градусов в радианы 60
75 Найти точное значение sin(135 град. )
76 Найти точное значение sin(150)
77 Найти точное значение sin(240 град. )
78 Найти точное значение cot(45 град. )
79 Преобразовать из радианов в градусы (5pi)/4
80 Упростить 1/( кубический корень от x^8)
81 Найти точное значение sin(225)
82 Найти точное значение sin(240)
83 Найти точное значение cos(150 град. )
84 Найти точное значение tan(45)
85 Вычислить sin(30 град. )
86 Найти точное значение sec(0)
87 Упростить arcsin(-( квадратный корень 2)/2)
88 Найти точное значение cos((5pi)/6)
89 Найти точное значение csc(30)
90 Найти точное значение arcsin(( квадратный корень 2)/2)
91 Найти точное значение tan((5pi)/3)
92 Найти точное значение tan(0)
93 Вычислить sin(60 град. )
94 Найти точное значение arctan(-( квадратный корень 3)/3)
95 Преобразовать из радианов в градусы (3pi)/4
96 Вычислить arcsin(-1)
97 Найти точное значение sin((7pi)/4)
98 Найти точное значение arcsin(-1/2)
99 Найти точное значение sin((4pi)/3)
100 Найти точное значение csc(45)

www.mathway.com

y = cos(x/2)

Дано

$$f{\left (x \right )} = \cos{\left (\frac{x}{2} \right )}$$

График функции

Точки пересечения с осью координат X

График функции пересекает ось X при f = 0
значит надо решить уравнение:
$$\cos{\left (\frac{x}{2} \right )} = 0$$
Решаем это уравнение
Точки пересечения с осью X:

Аналитическое решение
$$x_{1} = \pi$$
$$x_{2} = 3 \pi$$
Численное решение
$$x_{1} = 9.42477796077$$
$$x_{2} = 84.8230016469$$
$$x_{3} = -53.407075111$$
$$x_{4} = 65.9734457254$$
$$x_{5} = 3.14159265359$$
$$x_{6} = 15.7079632679$$
$$x_{7} = -3.14159265359$$
$$x_{8} = 40.8407044967$$
$$x_{9} = -59.6902604182$$
$$x_{10} = 97.3893722613$$
$$x_{11} = 78.5398163397$$
$$x_{12} = -34.5575191895$$
$$x_{13} = 28.2743338823$$
$$x_{14} = 7517042.68028$$
$$x_{15} = -91.1061869541$$
$$x_{16} = 72.2566310326$$
$$x_{17} = -9.42477796077$$
$$x_{18} = -65.9734457254$$
$$x_{19} = -72.2566310326$$
$$x_{20} = 47.1238898038$$
$$x_{21} = -84.8230016469$$
$$x_{22} = -9591.28237141$$
$$x_{23} = 91.1061869541$$
$$x_{24} = 59.6902604182$$
$$x_{25} = -47.1238898038$$
$$x_{26} = -21.9911485751$$
$$x_{27} = -97.3893722613$$
$$x_{28} = 34.5575191895$$
$$x_{29} = 21.9911485751$$
$$x_{30} = -160.221225333$$
$$x_{31} = 53.407075111$$
$$x_{32} = -78.5398163397$$
$$x_{33} = -40.8407044967$$
$$x_{34} = -15.7079632679$$
$$x_{35} = -28.2743338823$$

Точки пересечения с осью координат Y График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в cos(x/2).
$$\cos{\left (\frac{0}{2} \right )}$$
Результат:
$$f{\left (0 \right )} = 1$$
Точка:

(0, 1)

Экстремумы функции

Для того, чтобы найти экстремумы, нужно решить уравнение
$$\frac{d}{d x} f{\left (x \right )} = 0$$
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$\frac{d}{d x} f{\left (x \right )} = $$
Решаем это уравнение
Корни этого ур-ния
$$x_{1} = 0$$
$$x_{2} = 2 \pi$$
Зн. экстремумы в точках:

(0, 1)

(2*pi, -1)

Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумы функции в точках:
$$x_{2} = 2 \pi$$
Максимумы функции в точках:
$$x_{2} = 0$$

Убывает на промежутках

(-oo, 0] U [2*pi, oo)

Возрастает на промежутках

[0, 2*pi]

Точки перегибов Найдем точки перегибов, для этого надо решить уравнение
$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = 0$$
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = $$
Решаем это уравнение
Корни этого ур-ния
$$x_{1} = \pi$$
$$x_{2} = 3 \pi$$

Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках

[pi, 3*pi]

Выпуклая на промежутках

(-oo, pi] U [3*pi, oo)

Горизонтальные асимптоты

Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo
$$lim_{x to -\infty} \cos{\left (\frac{x}{2} \right )} = \langle -1, 1\rangle$$
Возьмём предел
значит,
уравнение горизонтальной асимптоты справа:
$$y = \langle -1, 1\rangle$$

Наклонные асимптоты

Наклонную асимптоту можно найти, подсчитав предел функции cos(x/2), делённой на x при x->+oo и x ->-oo
$$lim_{x to -\infty}\left(\frac{1}{x} \cos{\left (\frac{x}{2} \right )}\right) = 0$$
Возьмём предел
значит,
наклонная совпадает с горизонтальной асимптотой слева

Чётность и нечётность функции

Проверим функци чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
$$\cos{\left (\frac{x}{2} \right )} = \cos{\left (\frac{x}{2} \right )}$$
— Нет
$$\cos{\left (\frac{x}{2} \right )} = — \cos{\left (\frac{x}{2} \right )}$$
— Нет
значит, функция
не является
ни чётной ни нечётной

Загрузка… x*(1/30+1/30+1/40)-y*1/30=-10/3 y*(1/40+1/50+1/30)-x*1/20=5/4+8/3 2*x+1=9 >>

uchimatchast.ru

y = 1/cos(x)

Дано

$$f{\left (x \right )} = \frac{1}{\cos{\left (x \right )}}$$

График функции

Область определения функции

Точки, в которых функция точно неопределена:
$$x_{1} = 1.5707963267949$$
$$x_{2} = 4.71238898038469$$

Точки пересечения с осью координат X

График функции пересекает ось X при f = 0
значит надо решить уравнение:
$$\frac{1}{\cos{\left (x \right )}} = 0$$
Решаем это уравнение
Решения не найдено,
может быть, что график не пересекает ось X

Точки пересечения с осью координат Y

График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в 1/cos(x).
$$\frac{1}{\cos{\left (0 \right )}}$$
Результат:
$$f{\left (0 \right )} = 1$$
Точка:

(0, 1)

Экстремумы функции

Для того, чтобы найти экстремумы, нужно решить уравнение
$$\frac{d}{d x} f{\left (x \right )} = 0$$
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$\frac{d}{d x} f{\left (x \right )} = $$
Решаем это уравнение
Корни этого ур-ния
$$x_{1} = 0$$
$$x_{2} = \pi$$
Зн. экстремумы в точках:

(0, 1)

(pi, -1)

Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумы функции в точках:
$$x_{2} = 0$$
Максимумы функции в точках:
$$x_{2} = \pi$$
Убывает на промежутках

[0, pi]

Возрастает на промежутках

(-oo, 0] U [pi, oo)

Точки перегибов

Найдем точки перегибов, для этого надо решить уравнение
$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = 0$$
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = $$
Решаем это уравнение
Решения не найдены,
возможно перегибов у функции нет

Вертикальные асимптоты

Есть:
$$x_{1} = 1.5707963267949$$
$$x_{2} = 4.71238898038469$$

Горизонтальные асимптоты

Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo
$$lim_{x to -\infty} \frac{1}{\cos{\left (x \right )}} = \langle -\infty, \infty\rangle$$
Возьмём предел
значит,
уравнение горизонтальной асимптоты справа:
$$y = \langle -\infty, \infty\rangle$$

Наклонные асимптоты

Наклонную асимптоту можно найти, подсчитав предел функции 1/cos(x), делённой на x при x->+oo и x ->-oo

True

Возьмём предел
значит,
уравнение наклонной асимптоты справа:
$$y = x lim_{x to \infty}\left(\frac{1}{x \cos{\left (x \right )}}\right)$$

Чётность и нечётность функции

Проверим функци чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
$$\frac{1}{\cos{\left (x \right )}} = \frac{1}{\cos{\left (x \right )}}$$
— Да
$$\frac{1}{\cos{\left (x \right )}} = — \frac{1}{\cos{\left (x \right )}}$$
— Нет
значит, функция
является
чётной

Загрузка… x+y2=11 xy2=18 16^x+4^x-2>0 >>

uchimatchast.ru

Типовые задачи на производную с тригонометрическими функциями. Функция f(x)=cos2x-cosx

Тригонометрические функции имеют важную особенность – наличие периода. Всю методику, которую знаем для исследования функций без тригонометрических включений, используем, но надо учесть наличие периода.

Наличие периода дает возможность провести исследование функции и построение графика на отрезке длиной, равной периоду. Затем график функции периодически распространяется для всех значений аргумента из области определения функции.

Задача.

Построить график функции .

Преобразуем формулу: .

Найдем период данной функции. У функции  наименьший период . У функции , если понизить степень и выразить через  — период . Итак,

функция  имеет наименьший период . Это означает, что график функции сначала можно построить на промежутке длиной , а потом продолжить по периодичности.

Функция четная, так как  для всех  из . График симметричный относительно оси .

Учитывая периодичность функции, можно построить график этой функции на любом промежутке, длиной . Свойство четности функции дает возможность задачу упростить, а именно, построить график на участке , а на участке  — построить по симметрии.

Найдем  интервалы знакопостоянства функции.

:  .

, когда , отсюда 

Знак функции на каждом интервале удобно определить с помощью единичной окружности (см. рис.1). Точки , ,  — точки, которые формируют интервалы знакопостоянства функции.

Рис. 1. Интервалы знакопостоянства функции  на единичной окружности

Выясним знак функции на интервале . Для этого возьмем значение функции в какой-нибудь точке из этого интервала. Например,

 , значит, на этом интервале функция отрицательна. Дальше, на интервале  функция меняет знак. В силу симметрии, на интервале  — функция отрицательна, а на интервале  — функция положительна (см. рис.2).

Рис. 2 Интервалы знакопостоянства функции

Построим график функции в окрестности каждого корня.

Точка  — является точкой максимума, так как на промежутках  и  — функция отрицательна, кривая находится под осью , и только в точке  она равна нулю. Значит, функция в окрестности корней ведет себя следующим образом (см. рис.3):

Рис. 3. График функции в окрестности каждого корня

Понятно, что на интервалах  и  – функция будет иметь точки экстремума.

Исследуем функцию с помощью производной:

 Приравняем ее к нулю:

 , отсюда  .

Найдем критические точки:

   — это все критические точки, которые имеет функция. Но нам нужны те, которые попадают в выбранный промежуток: , , . Вычислим значение функции в точках , и определим – это точки максимума или минимума.

Найдем интервалы знакопостоянства производной на единичной окружности (см. рис.4).

Рис. 4. Интервалы знакопостоянства производной

Найдем знак производной, в какой- либо точке из интервала :

. Таким образом, точка  — точка минимума, а  — точка максимума. Вычислим:

; .

Построим график  функции  (см. рис.5-6).

Рис. 5. График функции  на

Рис. 6. График функции

Одна из типовых задач – нахождение множества значений функции.

Ответ:  .

На уроке рассмотрены особенности исследования и построения графика тригонометрической функции.  Все типовые задачи решаются аналогично  задачам из предыдущих уроков.

 

Список рекомендованной литературы

1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.

2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник  для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.

3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.

4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.

5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.

6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.

7. ЗвавичЛ.И., Шляпочник Л.Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).-М.: Дрофа, 2002.

8. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.

9. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.

10. Глейзер Г.И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983

 

Дополнительные веб-ресурсы

1. Интернет-портал Mathematics.ru (Источник).  

2. Интернет-портал Exponenta.ru (Источник).

 

Домашнее задание

№ 726(а), 739(а) (Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре

interneturok.ru

Свойства функции y = cosx и её график. Алгебра, 10 класс: уроки, тесты, задания.

1. Возрастание и убывание функции y = cosx

Сложность: лёгкое

1
2. Сравнение чисел с использованием свойств функции y = cosx

Сложность: лёгкое

2
3. Определение значений косинусов некоторых углов

Сложность: лёгкое

1
4. Преобразование выражения cos t и определение его значения

Сложность: лёгкое

1
5. Применение формул приведения к сравнению чисел

Сложность: среднее

2
6. Построение графика функции y = cosx + b или y = cos(x + а)

Сложность: среднее

1
7. Принадлежность точек графику функции y = k cos(x + a) + b

Сложность: среднее

1
8. Нахождение наибольшего и наименьшего значений функции y = cosx

Сложность: среднее

1
9. Область значений функции y = cosx

Сложность: среднее

1
10. Определение чётности функции

Сложность: среднее

1
11. Решение уравнения cosx = ax + b графически

Сложность: сложное

1
12. Определение наибольшего и наименьшего значений функции

Сложность: сложное

2
13. Построение графиков функций y = cos(x + a) + b

Сложность: сложное

4

www.yaklass.ru

Mathway | Популярные задачи

1 Найти точное значение sin(30)
2 Найти точное значение sin(45)
3 Найти точное значение sin(60)
4 Найти точное значение sin(30 град. )
5 Найти точное значение sin(60 град. )
6 Найти точное значение tan(30 град. )
7 Найти точное значение arcsin(-1)
8 Найти точное значение sin(pi/6)
9 Найти точное значение cos(pi/4)
10 Найти точное значение sin(45 град. )
11 Найти точное значение sin(pi/3)
12 Найти точное значение arctan(-1)
13 Найти точное значение cos(45 град. )
14 Найти точное значение cos(30 град. )
15 Найти точное значение tan(60)
16 Найти точное значение csc(45 град. )
17 Найти точное значение tan(60 град. )
18 Найти точное значение sec(30 град. )
19 Преобразовать из радианов в градусы (3pi)/4
20 График y=sin(x)
21 Преобразовать из радианов в градусы pi/6
22 Найти точное значение cos(60 град. )
23 Найти точное значение cos(150)
24 Найти точное значение tan(45)
25 Найти точное значение sin(30)
26 Найти точное значение sin(60)
27 Найти точное значение cos(pi/2)
28 Найти точное значение tan(45 град. )
29 График y=sin(x)
30 Найти точное значение arctan(- квадратный корень 3)
31 Найти точное значение csc(60 град. )
32 Найти точное значение sec(45 град. )
33 Найти точное значение csc(30 град. )
34 Найти точное значение sin(0)
35 Найти точное значение sin(120)
36 Найти точное значение cos(90)
37 Преобразовать из радианов в градусы pi/3
38 Найти точное значение sin(45)
39 Найти точное значение tan(30)
40 Преобразовать из градусов в радианы 45
41 Найти точное значение tan(60)
42 Упростить квадратный корень x^2
43 Найти точное значение cos(45)
44 Упростить sin(theta)^2+cos(theta)^2
45 Преобразовать из радианов в градусы pi/6
46 Найти точное значение cot(30 град. )
47 Найти точное значение arccos(-1)
48 Найти точное значение arctan(0)
49 График y=cos(x)
50 Найти точное значение cot(60 град. )
51 Преобразовать из градусов в радианы 30
52 Упростить ( квадратный корень x+ квадратный корень 2)^2
53 Преобразовать из радианов в градусы (2pi)/3
54 Найти точное значение sin((5pi)/3)
55 Упростить 1/( кубический корень от x^4)
56 Найти точное значение sin((3pi)/4)
57 Найти точное значение tan(pi/2)
58 Найти угол А tri{}{90}{}{}{}{}
59 Найти точное значение sin(300)
60 Найти точное значение cos(30)
61 Найти точное значение cos(60)
62 Найти точное значение cos(0)
63 Найти точное значение arctan( квадратный корень 3)
64 Найти точное значение cos(135)
65 Найти точное значение cos((5pi)/3)
66 Найти точное значение cos(210)
67 Найти точное значение sec(60 град. )
68 Найти точное значение sin(300 град. )
69 Преобразовать из градусов в радианы 135
70 Преобразовать из градусов в радианы 150
71 Преобразовать из радианов в градусы (5pi)/6
72 Преобразовать из радианов в градусы (5pi)/3
73 Преобразовать из градусов в радианы 89 град.
74 Преобразовать из градусов в радианы 60
75 Найти точное значение sin(135 град. )
76 Найти точное значение sin(150)
77 Найти точное значение sin(240 град. )
78 Найти точное значение cot(45 град. )
79 Преобразовать из радианов в градусы (5pi)/4
80 Упростить 1/( кубический корень от x^8)
81 Найти точное значение sin(225)
82 Найти точное значение sin(240)
83 Найти точное значение cos(150 град. )
84 Найти точное значение tan(45)
85 Вычислить sin(30 град. )
86 Найти точное значение sec(0)
87 Упростить arcsin(-( квадратный корень 2)/2)
88 Найти точное значение cos((5pi)/6)
89 Найти точное значение csc(30)
90 Найти точное значение arcsin(( квадратный корень 2)/2)
91 Найти точное значение tan((5pi)/3)
92 Найти точное значение tan(0)
93 Вычислить sin(60 град. )
94 Найти точное значение arctan(-( квадратный корень 3)/3)
95 Преобразовать из радианов в градусы (3pi)/4
96 Вычислить arcsin(-1)
97 Найти точное значение sin((7pi)/4)
98 Найти точное значение arcsin(-1/2)
99 Найти точное значение sin((4pi)/3)
100 Найти точное значение csc(45)

www.mathway.com

10 класс. Алгебра. Тригонометрические функции. Функции у=sinx, y=cosx, их свойства, графики, типовые задачи. — Функция y=cosx, ее основные свойства и график.

Комментарии преподавателя

Функ­ция y=cost, её ос­нов­ные свой­ства и гра­фик

Функ­ци­ей на­зы­ва­ет­ся закон, по ко­то­ро­му каж­до­му зна­че­нию неза­ви­си­мо­го ар­гу­мен­та ста­вит­ся в со­от­вет­ствие един­ствен­ное зна­че­ние функ­ции.

Вспом­ним опре­де­ле­ние функ­ции Пусть t – любое дей­стви­тель­ное число. Ему со­от­вет­ству­ет един­ствен­ная точка Mна чис­ло­вой окруж­но­сти. У точки M есть един­ствен­ная абс­цис­са. Она и на­зы­ва­ет­ся ко­си­ну­сом числа t. Каж­до­му зна­че­нию ар­гу­мен­та t со­от­вет­ству­ет толь­ко одно зна­че­ние функ­ции  (рис. 1).

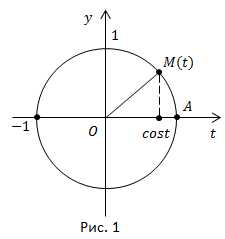
Цен­траль­ный угол чис­лен­но равен ве­ли­чине дуги в ра­ди­а­нах, т.е. числу  По­это­му ар­гу­мен­том может быть и дей­стви­тель­ное число, и угол в ра­ди­а­нах.

Если мы умеем для каж­до­го зна­че­ния  опре­де­лить  то можем по­стро­ить гра­фик функ­ции 

Можно по­лу­чить гра­фик функ­ции  и дру­гим спо­со­бом. По фор­му­лам при­ве­де­ния  по­это­му гра­фик ко­си­ну­са – это си­ну­со­и­да, сдви­ну­тая по оси x на  влево (рис.2).

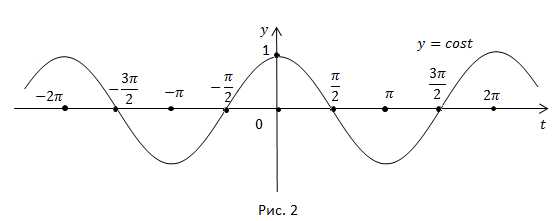
Свой­ства функ­ции 

1) Об­

www.kursoteka.ru

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *