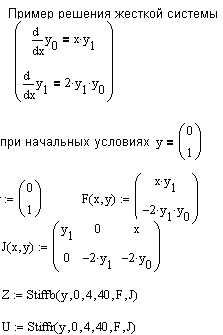6.02. Задача Коши для дифференциального уравнения первого порядка
Общее решение любого дифференциального уравнения первого порядка F(х; у; у’) = 0, как это следует из схемы его получения (1.3), содержит бесчисленное множество частных решений. Возникает естественный вопрос: как из этого множество частных решений выделить интересующее нас конкретное частное решение? Иначе говоря, как из множества интегральных кривых данного дифференциального уравнения выделить нужную интегральную кривую?
Ответ почти очевиден: для этого на плоскости Хоу нужно задать некоторую точку , через которую должна пройти искомая интегральная кривая. Тогда её уравнение и будет тем частным решением, которое выделяется из прочих (рис. 6.2).
Задание точки равносильно заданию условия для искомого, выделяемого из прочих, частного решения данного дифференциального уравнения. Это условие называется Начальным условием для дифференциального уравнения первого порядка F(х; у; у’) = 0. Начальным оно называется потому, что очень часто в реальных задачах по исследованию различного рода процессов роль независимой переменной
Если дифференциальное уравнение первого порядка F(х; у; у’) = 0 задано вместе с начальным для него условием , То говорят, что для этого уравнения задана Задача Коши:
(2.1)
Решить её — это значит найти те частные решения дифференциального уравнения F(х; у; у’) = 0 , которые еще удовлетворяют и заданному начальному условию . С точки зрения рисунка 6.2 решить задачу Коши (2.1) – это значит найти уравнения всех интегральных кривых дифференциального уравнения F(х; у; у’) = 0, проходящих через начальную точку .
Как правило, задача Коши (2.1) имеет единственное решение . То есть через заданную начальную точку проходит единственная интегральная кривая дифференциального уравнения F(х; у; у’) = 0 (как на рис. 6.2). Но бывает, что задача Коши не имеет решений. То есть бывает, что ни одна из интегральных кривых не проходит через заданную начальную точку . Тогда такая точка называется Особой точкой дифференциального уравнения. А бывает, что задача Коши имеет несколько решений. То есть бывает, что через начальную точку проходит несколько интегральных кривых. Сколько решений будет у задачи Коши (2.1) и каковы они, выясняется в процессе её решения. А Схема решения задачи Коши (2.1) такова:
1. Решаем дифференциальное уравнение F(х; у; у’) = 0 и находим все его решения. То есть находим общее решение (общий интеграл) и возможные особые решения .
2. Подставляем начальные значения Х = х0 И У = у0 в общее решение и находим соответствующее значение (значения) константы С:
(2.2)
3. Подставляем каждое из найденных значений С В общее решение и получаем частные решения
,
Являющиеся решением задачи Коши. Это те решения этой задачи, которые выделяются из общего решения дифференцированного уравнения F(х; у; у’) = 0.
4. Проверяем, нет ли среди особых решений Дифференциального уравнения F(х; у; у’) = 0 таких, которые удовлетворяют начальному условию У(х0) = у0. Если такие найдутся, они тоже будут решениями задачи Коши (2.1).
Пример1. Решить задачу Коши:
Решение.
1. Сначала решим дифференциальное уравнение . Оно уже решено ранее – его решение найдено в примере 3, §1:
— общее решение; – особое решение.
2. Подставим начальные значения В общее решение и найдем С:
3. Подставим в общее решение и получим частное решение
.
Эта функция является решением данной задачи Коши.
4. Обратим внимание на особое решение У=0. Начальному условию У(0)=1 оно не удовлетворяет, поэтому решением данной задачи Коши не является.
Ответ: — единственное решение поставленной задачи Коши.
Пример 2. Материальное тело поднято на высоту H и в начальный момент времени T=0 отпущено в свободное падение. Описать математически процесс падения тела. А именно, найти зависимость ν = ν(T) скорости ν падающего тела от времени T, и найти зависимость S = S(T) пути S, пройденного падающим телом, от времени T. Сопротивлением воздуха пренебречь.
Решение. Как известно, все свободно падающие тела падают с постоянным ускорением G ≈ 9,8 м/сек2 — с ускорением свободного падения. А так как ускорение – это производная от скорости, то получаем: . Это — дифференциальное уравнение первого порядка для искомой функции
Решим эту задачу.
1. Сначала решим дифференциальное уравнения:
Это – общее решение уравнения , содержащее все его решения. Особых решений у него нет.
2. Используем начальное условие и найдем С:
0 = G0+С => С = 0.
3. Подставим С=0 в общее решение V=Gt+C и получим окончательно: V=Gt. Это и есть решение поставленной задачи Коши (единственное). И заодно V=Gt — это искомая зависимость скорости V падающего тела от времени T.
А теперь займёмся поиском зависимости S=S(t) Пути S От времени T. Учтём, что и что . Тогда для определения этой зависимости получим следующую задачу Коши:
Решим эту задачу.
1. Сначала решим дифференциальное уравнение :
;
Это — общее решение уравнения , содержащее все его решения. Особых решений у него нет.
2. Используем начальное условие и найдём С:
.
3. Подставим С=0 в общее решение и получим окончательно: . Это и есть решение рассматриваемой задачи Коши. И заодно — это искомая зависимость пути S, проходимого свободно падающим телом, от времени T.
Ответ: — известные школьные формулы.
Пример3. Дать математическое описание демографического процесса (процесса изменение численности населения со временем) для достаточно крупного населённого региона, если в начальный момент времени численность населения региона составляла человек.
;
Здесь и – некоторые числовые коэффициенты, связанные соответственно с уровнем рождаемости и уровнем смертности в данном регионе. Тогда общее изменение численности населения за время найдется по формуле:
.
Здесь . Из получённого равенства следует: . Устремляя здесь (при этом, очевидно, и ), то есть переходя к бесконечно малым и , получим:
, или .
Это – дифференциальное уравнение первого порядка для искомой функции . Дополняя это заданным начальным условием , получим для этой функции задачу Коши:
Решим эту задачу.
1. Сначала решим дифференциальное уравнение . Функция является его очевидным частным решением. Но это, очевидно, не та функция, которую мы ищем – она не удовлетворяет начальному условию, да и вообще она означает, что население в регионе отсутствует.
Будем искать те решения уравнения для которых :
Итак, — общее решение дифференциального уравнения . В него, кстати, при С = 0 входит и отмеченное ранее нулевое решение . То есть в найденном общем решении содержатся все решения дифференциального уравнения.
2. Используем начальное условие и найдём С:
.
3. Подставим в общее решение и получим искомое решение задачи Коши:
.
Это и есть искомая зависимость Численности населения региона от времени .
Проанализируем эту зависимость.
а) Если , то численность населения экспоненциально растёт со временем (рис. 6.3(а)).
б) Если , то численность населения Экспоненциально убывает со временем (рис. 6.3(б)).
в) Если , то , то есть численность населения региона не меняется (рис. 6.3(в).
Какой именно будет величина для данного региона, можно выяснить опытным путём. Пусть, например, перепись населения показала, что в некоторый момент времени в регионе проживало человек. Подставляя эти данные в формулу , можем найти :
.
Примечание. Полученная формула будет верно описывать демографический процесс в регионе, если уровень рождаемости и уровень смертности в нем не меняются со временем. То есть если коэффициенты и рождаемости и смертности не меняются со временем. А значит, если не меняется со временем и итоговый коэффициент . Но это, как известно, не так: с течением времени, в силу разных причин, ситуация и со смертностью, и с рождаемостью может существенно измениться. Поэтому полученную формулу при конкретном числовом значении оправданно применять лишь на протяжении достаточно ограниченного периода времени. В другой период времени тоже можно применять эту формулу, но уже при другом значении .
Пример 4. Рассмотрим задачу о математической модели естественного роста выпуска продукции.
Пусть — объем продукции некоторого предприятия, реализованной моменту времени . Будем считать, что вся продукция реализуется по некоторой фиксированной цене за единицу продукции независимо от объема продаж . Это значит, что рынок данной продукции длительное время является насыщенным – удается продавать по фиксированной цене практически любые объемы этой продукции.
Доход от продаж составит: . Будем считать, что некоторая часть этого дохода используется в качестве инвестиций в производство выпускаемой продукции. То есть объем инвестиций составит:
(2.4)
Здесь – так называется Норма инвестиций. Она показывает, какая часть дохода возвращается в производство.
Чем больше объем инвестиций , тем быстрее растёт объем производства . В модели естественного роста это значит, что скорость роста объема производства (так называемая
. (2.5)
Здесь
(2.6)
— так называемая Норма акселерации, которая показывает, каким должен быть объём инвестиций , чтобы обеспечить единичную скорость роста объема производства (обеспечить рост на единицу продукции за единицу времени). Подставляя (2.4) в (2.5), получим
, (2.7)
Где – числовой коэффициент. Равенство (2.7) представляет собой дифференциальное уравнение первого порядка для функции . Дополняя его некоторым начальным условием , получим задачу Коши:
(2.8)
Эта задача полностью совпадает с задачей Коши для демографического процесса (см. пример 3). Значит, у них полностью совпадают и решения:
(2.9)
Заметим, что условие постоянства цены единицы продаваемой продукции, то есть условие насыщенности рынка, не может выполнятся всегда, при любых . С увеличением объема продаж на некотором этапе рынок насыщается, спрос на товар падает, и дальнейшее увеличении объема продаж возможно лишь при снижении цены на него – в соответствии с классической убывающей кривой спроса . Если учесть эту зависимость от , то выражение (2.4) для примет вид:
(2.10)
А вместо (2.7) из (2.5) получим:
, (2.11)
Где . Это дифференциальное уравнение вместе с начальным условием составит задачу Коши:
(2.12)
Для определения функции , характеризующей объем продаж при насыщенном спросе, когда рост объема продаж возможен лишь при снижении цены на продаваемую продукцию. Эта функция, естественно, будет отличаться от функции (2.9) (будет более сложной).
Упражнения
1. Сформулировать и решить задачу по определению скорости V=V(T) свободно падающего тела массой M при условии, что учитывается сопротивление воздуха, пропорциональное скорости падения тела.
Ответ: .
2. Сформулировать и решить задачу по определению объема У=y(t) реализованной продукции, если известно, что кривая спроса Р= р(у) задаётся уравнением Р=2-у; норма инвестиций M=0,5; норма акселерации ; У(0)=0,5 – начальное условие.
Ответ:
3. При условиях предыдущей задачи 2 найти эластичность объема продаж относительно цены Р и определить условия, при которых продажи продукции являются эластичными и неэластичными.
Ответ: .
Если 0,5<Y<1, то есть если , то , и продажи представляют собой эластичный процесс (продажи растут относительно быстрее снижения цены). Доход от продаж при снижении цены возрастает. А если 1<Y<2, то есть если , то , и продажи представляют собой неэластичный процесс (продажи растут относительно медленнее снижения цены). Доход от продаж растёт при увеличении цены товара (см. §7 главы 4).
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Решение неоднородных дифференциальных уравнений. Задача Коши
Неоднородные дифференциальные уравнения вычисляют немного больше времени чем однородные, кроме однородного решения необходимо установить частичное решение неоднородного ДУ. На практике это отражается в решении двух разных по схеме вычислений ДУ. Если еще есть условие Коши напоследок всех поисков решения дифференциального уравнения необходимо определить значение постоянных, входящие в функцию. Все это достаточно просто реализуется, поэтому переходим к анализу готовых ответов.
Пример 1. Найти решение задачи Коши для дифференциального уравнения
Решение: Имеем неоднородное дифференциальное уравнение первого порядка. Как поступать с такими уравнениями подробно рассмотрены на предыдущих уроках.
Найдем сначала решение однородного ДУ. Интегрируем для этого уравнения (левую часть), предварительно разделив переменные:
Далее считаем, что стала С(х) является функцией от переменной x
Все это делается для того, чтобы подобрать постоянную таким образом, чтобы удовлетворить неоднородную функцию — правая часть ДУ.
Найдем производную y’ с учетом выше сказанного
Подставляем функцию и ее производную в исходное дифференциальное уравнение
Видим, что двое слагаемых при суммировании дадут ноль и в результате получим зависимость для производной от постоянной
Из последнего уравнения методом интегрирования находим явный вид постоянной С(x)
После этого можем записать общее решение уравнения
Но это еще не финал вычислений, нам нужно найти частичный решение (задача Коши). Для этого удовлетворяем начальное условие на функцию и вычисляем постоянную
Итак, задача Коши решена и найдено частичное решение дифференциального уравнения в виде
На этом одно из уравнений вычислено. Схема нахождения функции не слишком запутана с одной стороны, с другой ее легко реализовать (постоянную принимаем за функцию). Рассмотрим еще несколько готовых примеров, а дальше учитесь вычислять самостоятельно.
Пример 2. Решить задачу Коши для уравнения
Решение:Имеем неоднородное дифференциальное уравнение первого порядка + условие Коши. Запишем и проинтегрируем соответствующее однородное уравнение, предварительно разделив переменные
Решение однородного уравнения найти в данном случае довольно легко. Изучите для практики внесения сталой в интегралах под логарифм — это значительно упростит дальнейшие преобразования с решением. Далее рассмотрим константу C как функцию от переменной x
Производная y’ по формуле примет выражение
Подставим функцию y и ее производную y’ в исходное дифференциальное уравнение и выразим производную постоянной
Интегрированием находим недостающую зависимость C(x)
Заменив постоянную полученным только что значением, получим общее решение дифференциального уравнения
Решим задачу Коши. С начального условия имеем
Определив сталую получим y=x2— частичное решение дифференциального уравнения.
Пример 3. Найти решение дифференциального уравнения и задачи Коши
Решение:Начнем с анализа левой части дифференциального уравнения. Интегрируем однородное дифференциальное уравнение, предварительно отделив в нем переменные
Для последнего перехода использовали свойство экспоненты — второе слагаемое записали как логарифм от экспоненты ln(exp(1/x)).
Теперь предположим, что константа C(x) — это функция от переменной x:
тогда ее производная равна
Подставляем постоянную и ее производную в исходное дифференциальное уравнение
которое после сокращения слагаемых превратится в зависимость
Из последнего уравнения функцию C(x) находим интегрированием
Итак, мы нашли общее решение дифференциального уравнения
Найдем частичное решение уравнения (задача Коши). Удовлетворим начальное условие на функцию и вычислим постоянную
Отсюда имеем y=x2— частичное решение уравнения. На вид простая запись, хотя на ее вычисления потрачено немало времени.
Частичное решения двух последних примеров совпадают, такое редко бывает на практике. Теперь Вы знаете, как решить неоднородное уравнение и выполнить условие Коши.
Если на экзамене или контрольной работе Вам нужна помощь — обращайтесь. Мы помогли не одной тысячи студентов, сможем помочь и Вам.
yukhym.com
5.2 Решение дифференциальных уравнений и систем. (Задача Коши и граничные задачи)
Решение одиночного дифференциального уравнения. |
Для численного решения одиночного дифференциального уравнения в MathCAD имеется функция Odesolve, с помощью которой может быть решена как задача Коши для обыкновенного дифференциального уравнения, так и граничная задача. Эта функция входит в состав блока решения и сявляется его заключительным ключевым словом.
Odesolve(x,b,[step]) — Возвращает функцию, которая является решением дифференциального уравнения. Используется в блоке с оператором Given.
x— переменная интегрирования, действительное число
b— конечная точка отрезка интегрирования
step— величина шага по переменной интегрирования (необязательный аргумент)
Замечания:
Уравнение должно быть линейным относительно старшей производной.
Число заданных начальных или граничных условий внутри блока должно быть равно порядку уравнения.
При записи уравнения для обозначения производных функции используйте специальные кнопки с панели Math или ‘ (штрих) — [Ctrl+F7], для знака равенства =[Ctrl+=](в том числе и для дополнительных условий).
Конечная точка должна быть больше начальной.
Не допускаются начальные и граничные условия смешанного типа (f ‘(a)+f(a)=5).
Искомая функция в блоке дложна быть обязательно с аргументом ( f(x))
|
| |||
Численное решение задачи Коши для дифференциальных уравнений и систем. |
Для численного решения задачи Коши для дифференциальных уравнений и систем могут быть использованы функции:
rkfixed(y,x1,x2,n,F)— возвращает матрицу решений системы уравнений методом Рунге-Кутта 4-го порядка при фиксированном шаге по x,
rkadapt(y,x1,x2,n,F)— ищет решение с переменным шагом ( там, где решение меняется медленнее, шаг увеличивается, а в области быстрого изменения решения шаг функции уменьшается). Возвращается решение с равным шагом. Функция работает быстрее, чем rkfixed,
Bulstoer(y,x1,x2,n,F)— дает более точное решение (методом Bulirsch-Stoer),
Агрументы вышеуказанных функций:
y— вектор начальных условий
x1,x2— границы интервала для поиска решения
n— количество точек на интервале
F(x,y)— вектор-функция первых производных.
При решении дифференциальных уравнений порядка выше первого (или систем уравнений, выше первого порядка) исходное уравнение (систему) необходимо преобразовать к системе дифференциальных уравнений первого порядка.
В результате работы укзанных функций рассчитывается матрица, количество стобцов которой равно порядку уравнения +1(или сумме порядков уравнений в системе +1), а количество строк равно параметру n. Первый столбец содержит значения независимой переменной, второй — значение функции, третий — для диф. уравнений 2-го порядка — значение производной искомой функции (если решается система двух уравнений 1-го порядка, то третий столбец будет содержать значения второй функции). Для выделения решений (функций или их производных) можно воспользоваться стандартным оператором вывода столбцов матрицы M< >.
Если матрица правых частей дифференциальных уравнений почти вырождена, то такие системы называются жесткими. В этом случае решения, возвращаемые функцией rkfixed будет неустойчивым и для решения таких систем необходимо применять функции Stiffb, Stiffr:
Stiffb(y,x1,x2,n,F,J)— ищет решение диф. уравнения или системы дифференциальных уравнений методом Bulirsch-Stoer.
Stiffr(y,x1,x2,n,F,J) — ищет решение диф. уравнения или системы дифференциальных уравнений методом Rosenbrock.
Первые пять аргументов такие же,как и при решении хорошо обусловленных систем дифференциальных уравнений . Дополнительный аргумент — матрица J размером nx(n+1), первый столбец которой содержит частные производные dF/dx, остальные столбцы и строки представляют собой матрицу Якоби dF/dy
Пример решения жесткой системы дифференциальных уравнений.
Для отыскания решения системы диф. уравнений только в конечной точке используются функции bulstoer,rkadapt, stiffb, stiffr (начинаются с прописной буквы).
Набор парамтров для этих функций: ¶bulstoer(y,x1,x2,acc,F,kmax,save) ¶rkadapt(y,x1,x2,acc,F,kmax,save) ¶stiffb(y,x1,x2,acc,F,J,kmax,save) ¶stiffr(y,x1,x2,acc,F,J,kmax,save)
Первые три параметра и пятый (F) этих функций те же, что идля функции Rkadapt. Дополнительные параметры:
acc— параметр, контролирующий точность решения (реком. асс=0.001)
kmax — максимальное число промежуточных точек в которых ищется решение save — минимально допустимый интервал между точками, в которых ищется решение.
Решение граничных задач для обыкновенных дифференциальных уравнений
Если для дифференциального уравнения n-го порядка k граничных условий заданы в начальной точке х1, а (n-k) граничных условий — в конечной точке х2, то такая задача называется краевой. В MathCAD реализованы две функции, позволяющие численно найти недостающие условия в точках х1 и х2.
Двухточечная краевая задача
Задача решается в два этапа. Сначала с помощью функции sbval находятся недостающие начальные значения, а затем применяется одна из выше описанных функций для решения стандартной задачи Коши на отрезке.
sbval(v,x1,x2,F,load,score) — ищет недостающие начальные условия в точке х1
v — вектор началных приближений для искомых начальных значений в точке х1,
х1,х2— граничные точки интервала
F(x,y)— вектор-столбец из n элементов, содержит правые части дифференциальных уравнений
load(x1,v) — вектор-столбец из n элементов, содержит начальные значения в точке х1; некоторые из значений- константы, другие неизвестны и будут найдены в процессе решения.
score(x2,y) — вектор-столбец размерности вектора v, содержащий разность между начальным условием в точке х2 и значеием искомого решения в этой точке.
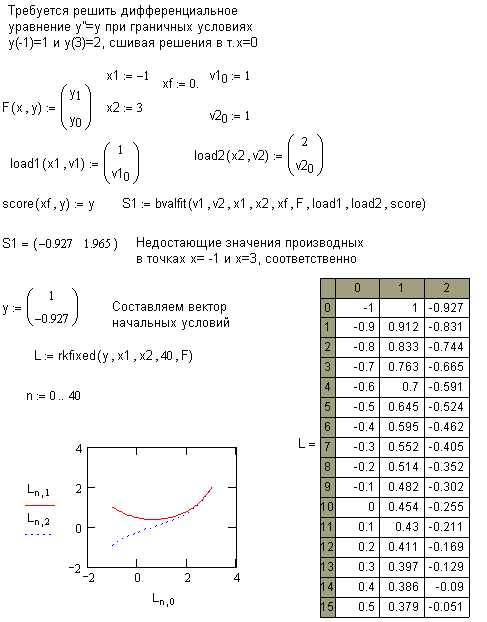
Краевая задача с условиями внутри интервала.
На первом этапе используется функция
balfit(V1,V2,x1,x2,xf,F,load1,load2,score) — ищет недостающие начальные условия в точках х1 и х2, сшивая решения, выходящие из этих точек, в точке xf
V1,V2 — вектора началных приближений для искомых начальных значений в точках х1 и х2
х1,х2— граничные точки интервала
load1(x1,V1) — вектор-столбец из n элементов, содержит начальные значения в точке х1; некоторые из значений- константы, другие неизвестны и будут найдены в процессе решения
load2(x2,V2) — вектор-столбец из n элементов, содержит начальные значения в точке х2; некоторые из значений- константы, другие неизвестны и будут найдены в процессе решения.
score(xf,y) — вектор-столбец размерности n, содержащий разность между решениями, начинающимися в точках х1 и х2, в точке xf
Лабораторная работа №5
Найдите решения систем уравнений (если они существуют !) с помощью блоков Given…Find, Given…Minner. Проверьте, все ли решения найдены. ¶
Решите на отрезке [0,3] задачу Коши используя:
а) функцию odersolve(в блоке сGiven)
b) функцию rkfixed.Выведите значение полученного решения в точке x=3.¶
Решите задачу Коши для дифференциального уравнения на отрезке [0,1], используя:
а) функцию odersolve(в блоке сGiven)
b) функцию rkadapt..¶
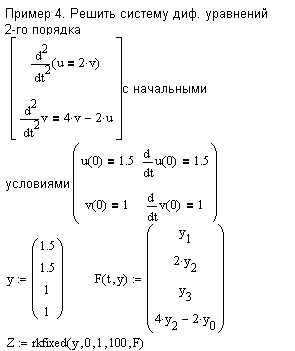
Решите систему дифференциальных уравнений на отрезке [0,3]. Выведите значения искомых функций и их производных в точке с координатой х=1.5¶
Решите краевую задачу для дифференциального уравнения на отрезке [0,8], выведите значение функции и ее производных в конечной точке отрезка.¶
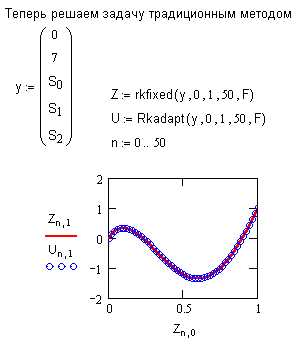
Для примера из п.4 вычислите значение функции только в конечной точке. (используйте специально предназначенные для этого формы функций bulstoer, rkadapt, stiffb, stiffr )
Найдите корни многочлена y(x) = 2x3+ 20 x2— 2x + 100 с помощью функций root и poltroots. (Обратите внимание на значение системной переменной TOL).
studfiles.net
2. Начальные условия и задача коши
Определение. Начальные
условия для дифференциального уравнения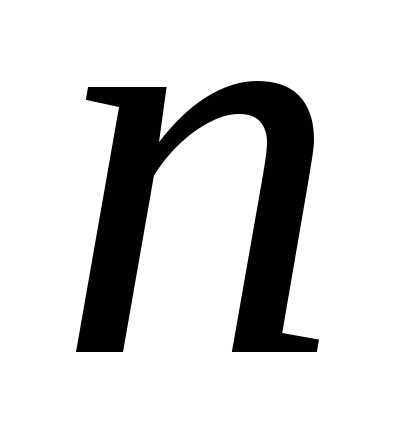 
-го
порядка — это набор чисел
, (2)
задающий
для фиксированного значения независимой
переменной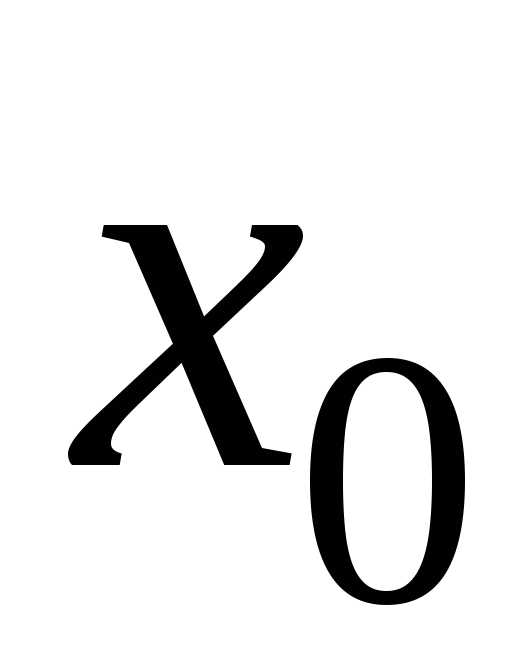 
значения неизвестной функциии ее производных вплоть до порядка, на
единицу меньшего порядка уравнения:
.
Определение. Задачей
Коши для дифференциального уравнения
называется задача отыскания решения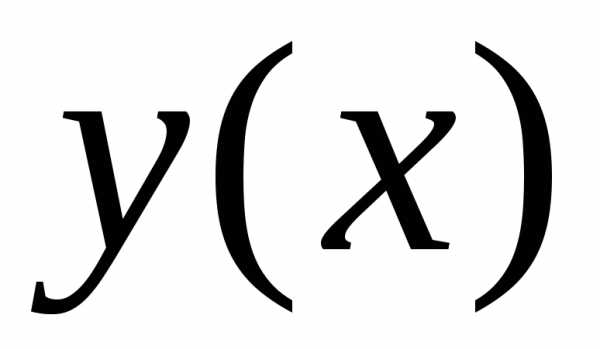 
,
отвечающего заданным начальным условиям.
Геометрический смысл задачи Коши для дифференциального уравнения 1-го порядка
Для
дифференциального уравнения 1-го порядка
(при 
)
начальные условия (2) имеют вид пары
чисел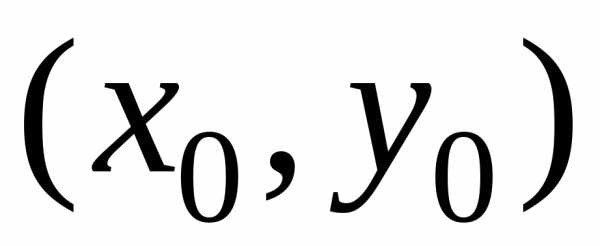
.
Тем самым ставится задача отыскания
решения
,
для которого.
Геометрически это означает выбор из
совокупности интегральных кривых той,
которая проходит через заданную точку
плоскости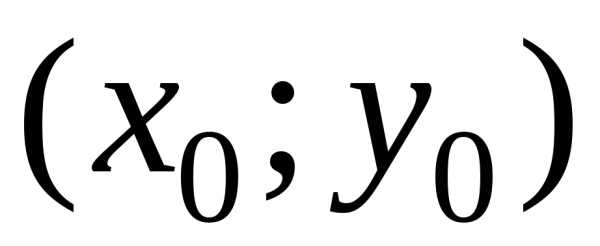
(рис. 1).
Рис. 1
Геометрический смысл задачи Коши для дифференциального уравнения 2-го порядка
Для
дифференциального уравнения 2-го порядка
(при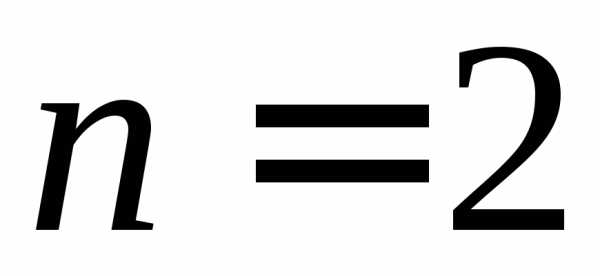 
)
начальные условия (2) имеют вид тройки
чисел,
и ставится задача отыскания решения
,
для которогои.
Геометрически это означает выбор из
совокупности интегральных кривых той,
которая, во-первых, проходит через
заданную точку плоскости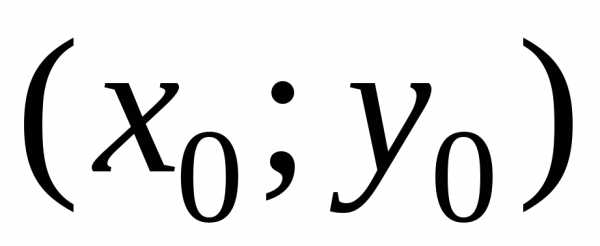
,
и, во-вторых, имеет в этой точке заданный
угловой коэффициент касательной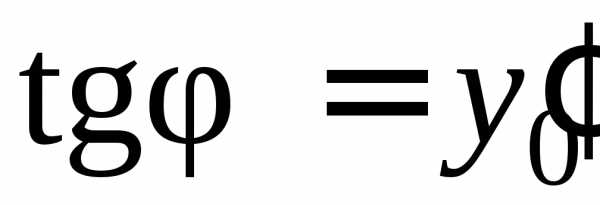
(рис. 2).
М0
Рис. 2
3. Общее решение и общий интеграл
Начальные
условия
,
будучи набором из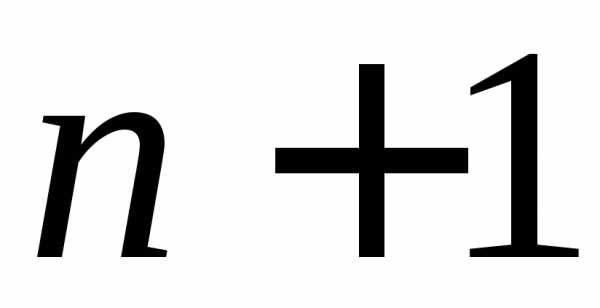 
чисел, задают точку пространства
.
Множество всех рассматриваемых вариантов
начальных условий образует некоторую
область.
Для
различных видов ограничений на функцию 
и на область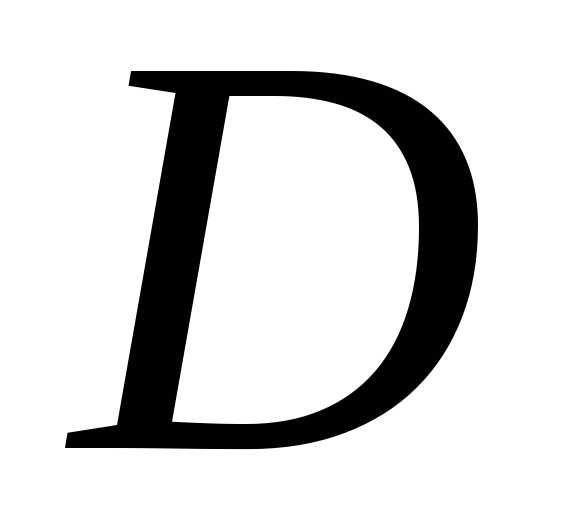
имеет место существование и единственность
решения задачи Коши для начальных
условий из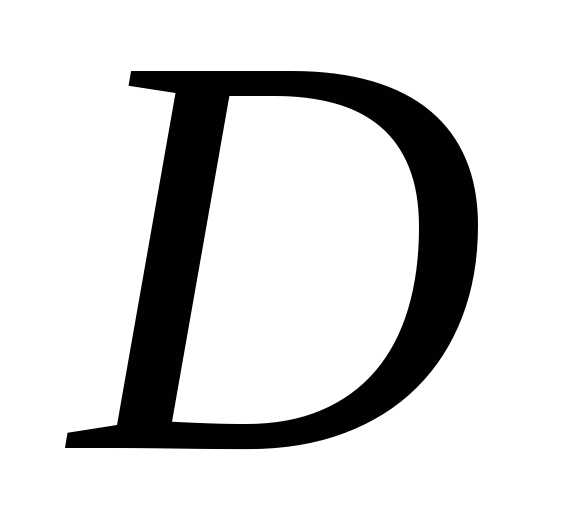
.
Приведем примеры соответствующих
теорем.
I.
Пусть уравнение 1-го порядка является
разрешённым относительно производной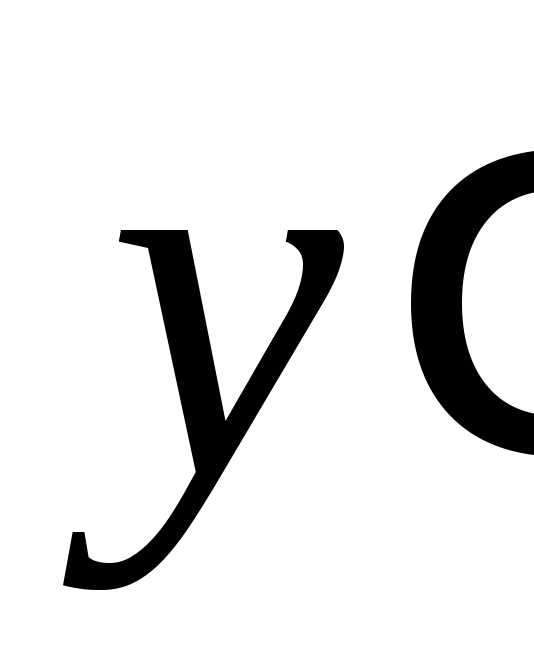 
:
.
Теорема 1. Если
функция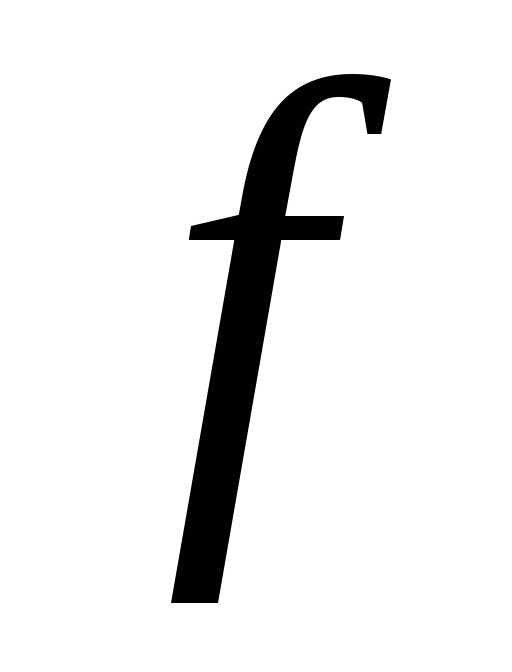 
и ее частная производная
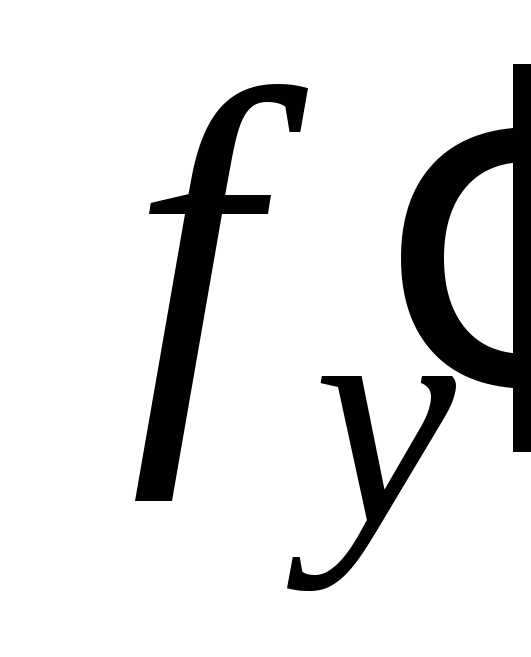непрерывны в области
плоскости
,
то решение задачи Коши для любых начальных
условийсуществует и единственно в некоторой
окрестности точки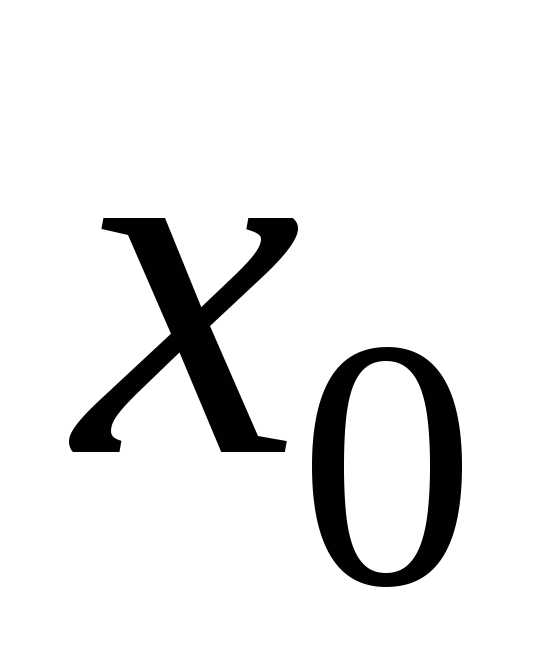
.
II. Пусть
уравнение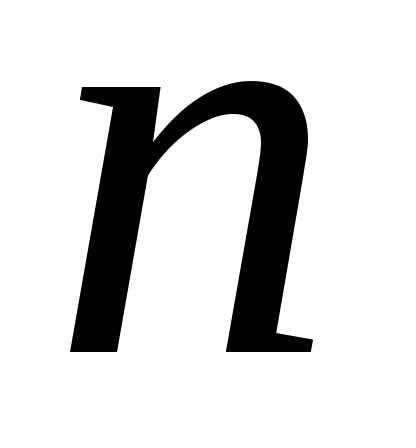 
-го
порядка является разрешённым относительно
старшей производной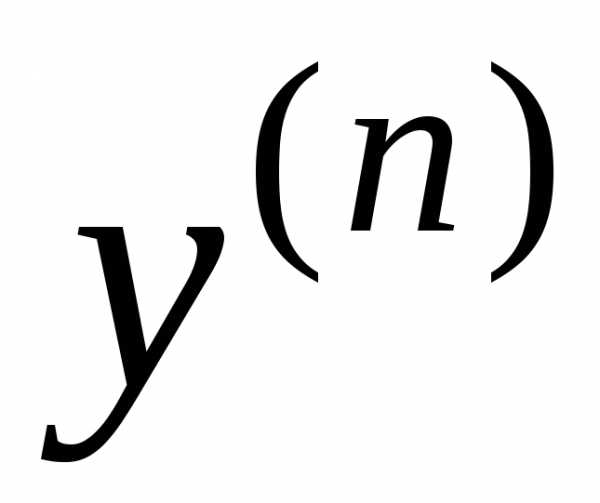 
:
.
Теорема 2. Если
функция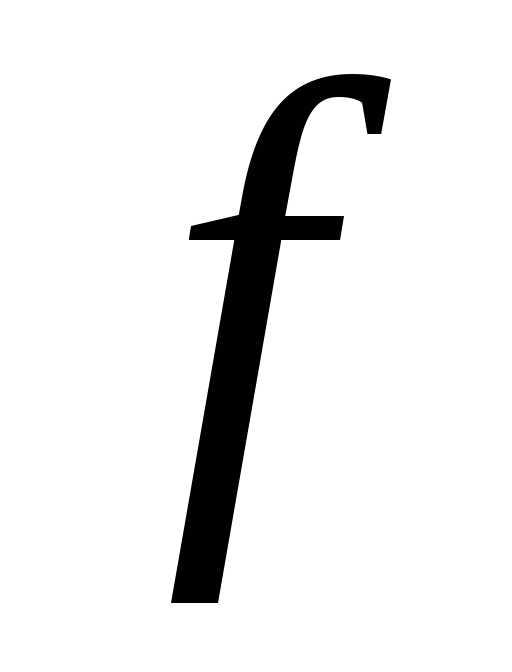 
и ее частные производныенепрерывны в области
-мерного
пространства,
то решение задачи Коши для любых начальных
условийсуществует и единственно в некоторой
окрестности точки.
В дальнейшем будем
предполагать, что дифференциальные
уравнения рассматриваются в области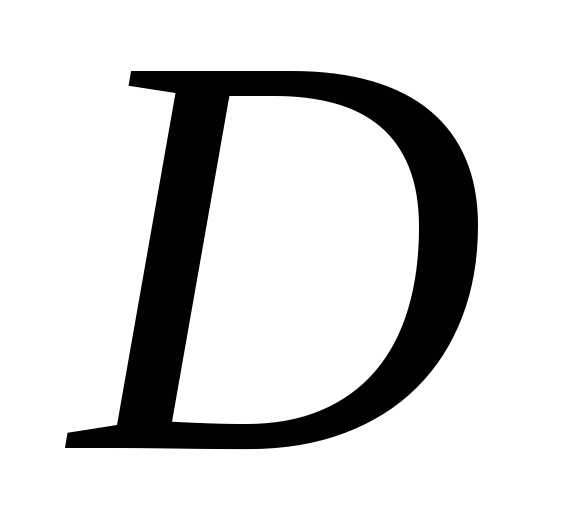 
существования и единственности решения.
Определение. Общим решением дифференциального уравнения 
-го
порядка называется функция
,
зависящая от аргумента
и от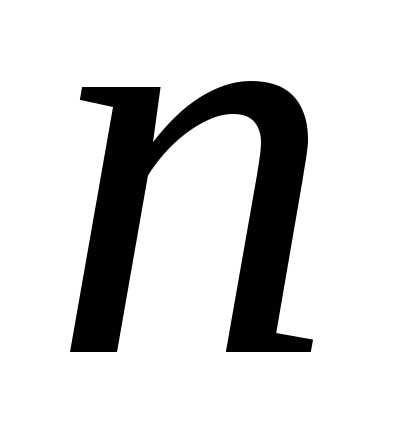
произвольных постоянных
,
которая удовлетворяет двум условиям:
1) при любых значениях произвольных постоянных эта функция является решением;
2) за счет выбора значений произвольных постоянных можно получить решение задачи Коши для любых начальных условий из области существования и единственности решения.
Заметим, что количество произвольных постоянных равно порядку уравнения.
Определение. Частным решением дифференциального уравнения называется функция, которая получается из общего решения, если произвольным постоянным придать определенные значения.
Напомним определение
неявной функции: функция
в окрестноститочки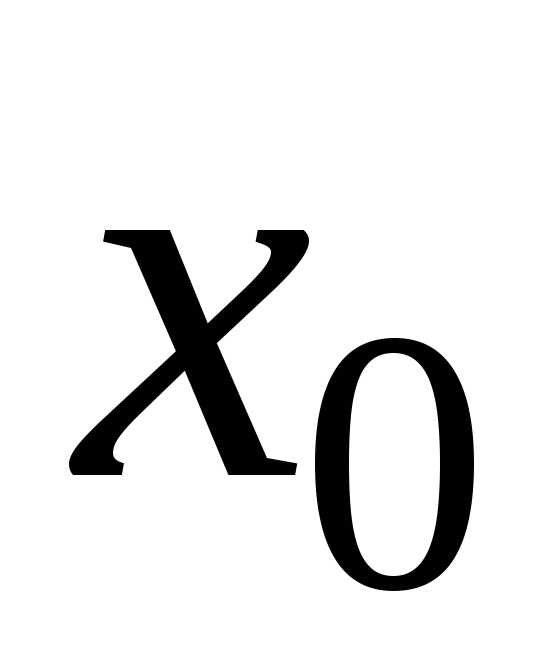
,задана неявно уравнением ,
если при всех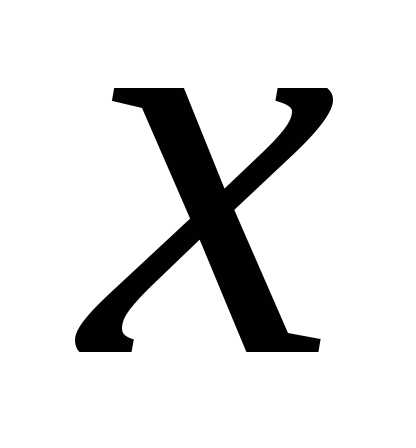
из этой окрестности справедливо равенство.
Обычное, «явное» задание функции можно рассматривать как частный случай неявного: ; здесь.
Определение. Общим
интегралом дифференциального уравнения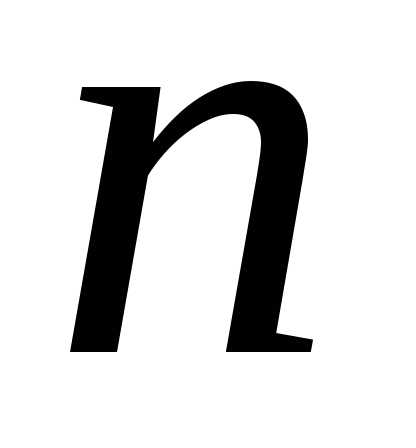 
-го
порядка называется уравнение
, (3)
зависящее от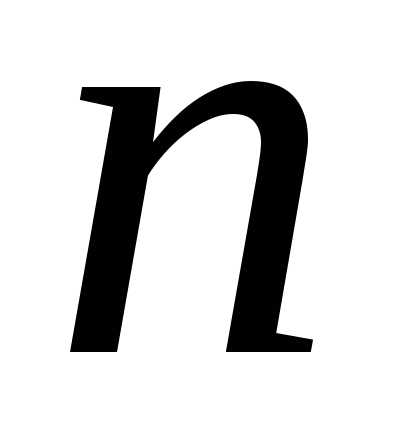 
произвольных постоянных
,
которое задает общее решениекак неявную функцию.
Определение. Частным интегралом называется уравнение, которое получается из общего интеграла (3), если произвольным постоянным придать определенные значения.
Замечание. В тех случаях, когда удается найти
решение дифференциального уравнения,
оно имеет, как правило, вид общего
интеграла (3). Если при этом можно 
явно выразить через(«разрешить уравнение относительно
»),
то приходим к общему решению.
studfiles.net
Задача Коши
Задача Коши, ,- начальные данные:
Решением задачи Коши является функция, определённая на интервале <a,b>, включающем , являющаяся решением уравнения (1) и удовлетворяющая начальному условию (2).
Определение. Решением интегрального уравнения:
является функция , которая определена на <a,b>и
(непрерывна)
<a,b>
подстановка превращает уравнение (3) в тождество.
Лемма. Функция является решением задачи Коши тогда и только тогда, когда она является решением интегрального уравнения.
Доказательство. Пусть — решение задачи Кошии
Проинтегрируем тождество от до:
Теперь пусть — решение интегрального уравнения, покажем, что она есть решение дифф. уравнения и удовлетворяет начальному условию. Для этого вначале подставим в (3):
Продифференцируем (3) и получим (1)
Определение. , заданная на , удовлетворяет условию Липшица, если
Заметим, что если функция удовлетворяет условию Липшица, то она является равномерно непрерывной на (для док-ва замечания надо взять)
Определение. Последовательность функций является равномерно ограниченной если
Определение. Последовательность функций называется равнестепенно непрерывной, если
Единственность решения задачи Коши
Определение. Функция f удовлетворяет локальному в области G условию Липшица по переменной y, если окрестностьи постоянная
Теорема. Если функция f удовлетворяет локальному условию Липшица, тогда решение задачи Коши единственное
Доказательство. От противного. Пусть существует два решения , определённые наи. В точкерешенияпо условию задачи Коши, но. Пусть.
Рассмотрим точку всех точек, таких что.
Множество точек непустое и ограниченное.
Поскольку непрерывны, супремум — максимум, значити{}
на (1)
на (2)
В силу условия теоремы удовлетворяет локальному условию Липшицанекоторая окрестностьверно как только
Вычтем (1) из (2): наПроинтегрируем неравенство на:
Заменим отрезок на меньший
. Выберем , чтобыоказалось. Получаем что, чего быть не может.
Определение. Функция удовлетворяет локальному в области G условию Осгуда по переменной, еслидиаметраи функциятакие что
Теорема. Если функция f удовлетворяет локальному условию Осгуда, тогда решение задачи Коши единственно.
Доказательство. Пусть у задачи Коши 2 решения: Повторяя доказательство предыдущего утверждения, приходим к тому, что функциияудовлетворяет на отрезкетождествуна.
Поделим обе части неравенства на :всюду на
на . Проинтегрируем на:
. Устремим ., второй интеграл- противоречие.
Метод Эйлера
Метод Эйлера— наиболее простойчисленный методрешения (систем)обыкновенных дифференциальных уравнений. Впервые описанЛеонардом Эйлеромв 1768 году в работе «Интегральное исчисление»[1]. Метод Эйлера является явным, одношаговым методом первого порядка точности, основанном на аппроксимацииинтегральной кривойкусочно линейной функцией, т. н. ломаной Эйлера.
[править] Описание метода
Пусть дана задача Кошидля уравнения первого порядка
где функция определена на некоторой области. Решение разыскивается на интервале. На этом интервале введем узлы
Приближенное решение в узлах , которое обозначим черезопределяется по формуле
Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.
[] Оценка погрешности
Метод Эйлера является методом первого порядка. Если функция непрерывна ви непрерывнодифференцируемапо переменнойв, то имеет место следующая оценка погрешности
где — средний шаг, то есть существуеттакая, что.
Заметим, что условия гладкости на правую часть, гарантирующие единственность решения задачи Коши, необходимы для обоснования сходимости метода Эйлера.
[] Значение метода Эйлера
Метод Эйлера являлся исторически первым методом численного решения задачи Коши. О. Кошииспользовал этот метод для доказательства существования решения задачи Коши. Ввиду невысокой точности и вычислительной неустойчивости для практического нахождения решений задачи Коши метод Эйлера применяется редко. Однако в виду своей простоты метод Эйлера находит свое применение в теоретических исследованиях дифференциальных уравнений, задачвариационного исчисленияи ряда других математических проблем.
[] Модифицированный метод Эйлера с пересчетом
Вычисления по методу Эйлера с пересчетом делаются в два этапа.
Прогноз:
.
Коррекция:
.
Модифицированный метод Эйлера с пересчетом имеет второй порядок точности, однако для его реализации необходимо дважды вычислять правую часть функции. Заметим, что метод Эйлера с пересчетом представляет собой разновидность методов Рунге-Кутты(предиктор-корректор).
Метод Рунге — Кутты
Ме́тоды Ру́нге — Ку́тты(распространено неправильное названиеМе́тоды Ру́нге — Ку́ттаили дажеМе́тоды Ру́нге — Кутта́) — важное семействочисленных алгоритмоврешенияобыкновенных дифференциальных уравненийи их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математикамиК. РунгеиМ. В. Куттой.
Формально, методом Рунге — Кутты является модифицированный и исправленный метод Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения. Наиболее часто используется и реализована в различных математических пакетах (Maple,MathCAD,Maxima) стандартная схема четвёртого порядка. Иногда при выполнении расчётов с повышенной точностью применяются схемы пятого и шестого порядков[1][2]. Построение схем более высокого порядка сопряжено с большими вычислительными трудностями[3]. Методы седьмого порядка должны иметь по меньшей мере девять стадий, в схему восьмого порядка входит 11 стадий. Хотя схемы девятого порядка не имеют большой практической значимости, неизвестно, сколько стадий необходимо для достижения этого порядка точности. Аналогичная задача существует для схем десятого и более высоких порядков[3].
studfiles.net
Найти решение задачи коши
Задача.
Найти решение задачи Коши для дифференциального уравнения при начальном условии у(1) = е.
Решение.
Заданное по условию диф. уравнение является линейным. Произведем в нем следующую замену — функцию у заменим произведением двух функций:
y = uv.
Найдем производную от функции у:
y’ = u’v + uv’.
Подставим новые переменные в заданное диф. уравнение:
Общий множитель, который видим в левой части уравнения, вынесем за скобки:
Составим следующую систему уравнений:
Найдем переменную v из первого уравнения системы. Для этого сначала перейдем к уравнению в дифференциалах:
Затем проинтегрируем и решим уравнение:
Теперь подставим найденное значение функцию во второе уравнение системы и вычислим функцию u:
Перейдем к уравнению в дифференциалах:
Интегрируем:
/
Внесем функцию под знак дифференциала:
Подставим теперь обе найденные функции в общее уравнение:
Не забываем, что С — это произвольная постоянная, которая на данный момент неизвестна.
И наконец, решим задачу Коши при условии, что у(1)=е.
Рассчитаем значение функции от 1 и приравняем его к е. Таким образом, мы найдем значение неизвестной постоянной С:
6e+C=e;
C = —5e.
В таком случае, решением задачи Коши будет функция .
Ответ. .
ru.solverbook.com
59.Задача Коши, начальные условия. Теорема существования и единственности решения задачи Коши для уравнения . Особые точки. Особые решения. Примеры.
http://www.nsc.ru/rus/textbooks/akhmerov/ode_unicode/m-21/m-21.html
НАЧАЛЬНЫЕ УСЛОВИЯ
— условия при постановке задачи Коши для дифференциальных уравнений. Для обыкновенного дифференциального уравнения, разрешенного относительно старшей производной:
Н. у. состоят в задании производных (данных Коши)
где — произвольная фиксированная точка области определения функции F;эта точка наз. начальной точкой искомого решения. Задачу Коши (1), (2) часто наз. также начальной задачей.
Для дифференциального уравнения с частными производными, записанного в нормальной форме относительно выделенной переменной V.
Н. у. состоят в задании производных (данные Коши):
от искомого решения и( х, t )этого уравнения на гиперплоскости t=0 (носителя начальных условий).
60.Уравнение 1-го порядка с разделяющимися переменными.
Уравнением с разделенными переменными называется дифференциальное уравнение вида
f(x)dx + g(y)dy = 0
с непрерывными функциями f(х) и g(y).
Равенство
где C — произвольная постоянная, определяет общий интеграл уравнения с разделёнными переменными.
Начальное условие для уравнения f(x)dx + g(y)dy = 0 можно задавать в виде y(x0) = y0 или в виде x(y0) = x0 .
Уравнением с разделяющимися переменными называется дифференциальное уравнение вида
f1(x)g1 (y)dx + f2(x) g2(y)dy =0 .
Функции f1(x), g1(y), f2(x), g2(y) непрерывны в cвоих областях определения и g1(y)f2(x) ≠ 0 .
Разделив обе части уравнения на отличное от нуля произведение g1(y)f2(x), получим уравнение с разделенными переменными
Общий интеграл этого уравнения имеет вид
Решение уравнения в области, где g1(y)f2(x) = 0 требует специального обсуждения.
61. Однородное уравнение 1-го порядка. Определение однородной функции
Определение однородного дифференциального уравнения
Дифференциальное уравнение первого порядка
называется однородным, если правая часть удовлетворяет соотношению
для всех значений t. Другими словами, правая часть должна являться однородной функцией нулевого порядка по отношению к переменным x и y:
Однородное дифференциальное уравнение можно также записать в виде
или через дифференциалы:
где P(x,y) и Q(x,y) − однородные функции одинакового порядка.
Определение однородной функции
Функция P(x,y) называется однородной функцией порядка n, если для всех t > 0 справедливо следующее соотношение:
Решение однородных дифференциальных уравнений
Однородное дифференциальное уравнение можно решить с помощью подстановки y = ux, которая преобразует однородное уравнение в уравнение с разделяющимися переменными. Дифференциальное уравнение вида
преобразуется в уравнение с разделяющимися переменными посредством переноса начала системы координат в точку пересечения прямых линий, заданных в уравнении. Если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными путем замены переменной:
62. Линейное уравнение 1-го порядка. Методы решения: метод Лагранжа, метод Бернулли. Структура решения линейного уравнения.
Линейным дифференциальным уравнением первого порядка называется уравнение вида
Здесь a(x) и b(x) — известные, непрерывные на [a;b] функции.
Доказано, что если функции a(x) и b(x) непрерывны на [a;b] , то для любой начальной точки (x0, y0) , x0∈ [a; b] , задача Коши
имеет единственное решение y = y(x) на [a;b].
Рассматривают однородные и неоднородные линейные уравнения первого порядка:
Общее решение линейного уравнения 1-го порядка можно найти с помощью замены y(x) = u(x) · v(x) .
studfiles.net