Задача №24. Расчёт показателей вариации по несгруппированным данным
По имеющимся данным о ценах товара в различных магазинах города определить:
1) среднюю цену,
2) моду и медиану,
3) размах вариации,
4) среднее линейное отклонение,
5) дисперсию,
6) среднее квадратическое отклонение,
7) коэффициент осцилляции,
8) коэффициент вариации.
| Магазин | Цена товара |
|---|---|
| 1 | 50,38 |
| 2 | 64,46 |
| 3 | 42,13 |
| 4 | 39,36 |
| 5 | 70,48 |
| 6 | 65,85 |
| 7 | 73,95 |
| 8 | 73,24 |
| 9 | 44,72 |
| 10 | 79,25 |
| 11 | 70,05 |
| 12 | 62,51 |
| 13 | 69,68 |
| 14 | 36,92 |
| 15 | 52,75 |
| 16 | 44,87 |
| 17 | 18,14 |
| 18 | 39,32 |
| 19 | 90,71 |
| 20 | 58,27 |
Решение:
1) Расчёт средней цены произведём по формуле средней арифметической простой:
ден. ед.
2) Найдём моду и медиану.
Мода — это величина признака наиболее часто встречающегося в совокупности.
В данной задаче все цены индивидуальны, и нельзя сказать какая из цен встречается наиболее часто. Поэтому мода в данном ряду распределения отсутствует.
Для нахождения медианы варианты дискретного ряда ранжируем, например, по возрастанию и выберем вариант, стоящий в середине полученного ряда.
18,14
26,92
39,32
39,36
42,13
44,72
44,87
50,38
52,75
58,27
62,51
64,46
65,85
69,68
70,05
70,48
73,24
73,95
79,25
90,71
Так как ряд распределения состоит из чётного числа вариантов, середина приходится на среднее значение 10-го и 11-го варианта.
3) Размах вариации определяется как разность между наибольшим и наименьшим значением признака:
ден. ед.
4) Среднее линейное отклонение вычиляется как средняя арифметическая из абсолютных значений отклонений вариант хi от среднего значения. Для удобства вычислений воспользуемся таблицей:
| Магазин | Цена товара, х | |||
|---|---|---|---|---|
| 1 | 50,38 | -6,472 | 6,472 | 41,886784 |
| 2 | 64,46 | 7,608 | 7,608 | 57,881664 |
| 3 | 42,13 | -14,722 | 14,722 | 216,737284 |
| 4 | 39,36 | -17,492 | 17,492 | 305,970064 |
| 5 | 70,48 | 13,628 | 13,628 | 185,722384 |
| 6 | 65,85 | 8,998 | 8,998 | 80,964004 |
| 7 | 73,95 | 17,098 | 17,098 | 292,341604 |
| 8 | 73,24 | 16,388 | 16,388 | 268,566544 |
| 9 | 44,72 | -12,132 | 12,132 | 147,185424 |
| 10 | 79,25 | 22,398 | 22,398 | 501,670404 |
| 11 | 70,05 | 13,198 | 13,198 | 174,187204 |
| 12 | 62,51 | 5,658 | 5,658 | 32,012964 |
| 13 | 69,68 | 12,828 | 12,828 | 164,557584 |
| 14 | 36,92 | -29,932 | 29,932 | 895,924624 |
| 15 | 52,75 | -4,102 | 4,102 | 16,826404 |
| 16 | 44,87 | -11,982 | 11,982 | 143,568324 |
| 17 | 18,14 | -38,712 | 38,712 | 1498,618944 |
| 18 | 39,32 | -17,532 | 17,532 | 307,371024 |
| 19 | 90,71 | 33,858 | 33,858 | 1146,364164 |
| 20 | 58,27 | 1,418 | 1,418 | 2,010724 |
| Итого | 1137,04 | — | 6480,36812 |
Варианты цен отклоняются от их средней величины в среднем на 15,3078 ден. ед.
5) Расчёт дисперсии произведём по формуле:
6) Извлекая из дисперсии корень второй степени получаем среднее квадратическое отклонение.
Значения цен в ряду распределения могут отличаться от среднего значения на 18,0005 ден. ед.
7) Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней и определяется по формуле:
8) Коэффициент вариации рассчитывается по формуле
Поскольку V < 33%, следовательно, вариация умеренная, а совокупность однородна.
ecson.ru
Правило сложения дисперсий — внутригрупповая, межгрупповая и общая дисперсии
Условие задачи
Имеются данные о фонде месячной заработной платы и средней зарплаты одного рабочего по трем цехам согласно табл. 10
Таблица 10
| Цех | Средняя месячная зарплата одного рабочего (у.е.) | Фонд зарплаты (у.е.) | СКО по зарплате (у.е.) |
| 1 | 148 | 41200.7 | 3000 |
| 2 | 150 | 51290.4 | 2100 |
| 3 | 151 | 41530.5 | 4900 |
Требуется:
- Определить среднюю зарплату одного рабочего по предприятию в целом.
- Общую дисперсию по зарплате.
Задали объемную контрольную работу? Скоро важный зачет/экзамен? Нет времени на выполнение работы или подготовку к зачету/экзамену, но есть деньги? На сайте 100task.ru можно заказать решение контрольной работы или онлайн-помощь на зачете/экзамене 〉〉
Решение задачи
Вычисление средней
Среднюю заработную плату вычислим по формуле средней гармонической:
где – фонд заработной платы в цехе
– средняя заработная плата в цехе
Вычисление средней внутригрупповой и межгрупповой дисперсий
Вычислим общую дисперсию, пользуясь правилом сложения дисперсий:
Внутригрупповые дисперсии найдем как квадрат среднего квадратического отклонения (СКО) по зарплате:
Вычислим количество рабочих в цеху, разделив фонд заработной платы на среднюю месячную заработную плату по цеху:
Средняя из внутригрупповых дисперсий:
Рассчитаем межгрупповую дисперсию:
Согласно правилу сложения дисперсий:
Выводы к задаче
Таким образом средняя заработная плата по трем цехам составила 149,685 у.е. при общей дисперсии заработной платы .
К оглавлению решебника по статистике 〉
100task.ru
Образцы решения типовых задач
2 | 7 | 9 | 10 | |
8 | 14 | 10 | 18 |
Решение. Объем выборки . Находим выборочное среднее по формуле (2.1):
Для вычисления несмещенной выборочной дисперсии используем формулу (2.4):
Несмещенное выборочное среднее квадратичное отклонение рассчитывается по формуле (2.6):
Пример 2. Найти выборочное среднее, исправленную выборочную дисперсию и исправленное выборочное среднее квадратическое отклонение для интервального статистического ряда:
Границы интервалов | ||||||
1 | 1 | 3 | 2 | 1 |
Решение. Объем выборки Выборка разбита на шесть интервалов (). Найдем середины интервалов и добавим их в исходную таблицу:
Границы интервалов | ||||||
Середины интервалов | 2 | 6 | 10 | 14 | 18 | 22 |
1 | 1 | 3 | 2 | 1 | 1 |
Выборочное среднее, находим по формуле (2.3):
Несмещенная выборочная дисперсия, определяется по формуле (2.5):
Несмещенное выборочное среднее квадратическое отклонение рассчитывается по формуле (2.6):
Пример 3. Найти выборочное среднее по выборке объема
2560 | 2600 | 2620 | 2650 | 2700 | |
2 | 3 | 10 | 4 | 1 |
Решение. Для упрощения расчетов перейдем к условным вариантам
иi = хi – 2620:
иi | – 60 | – 20 | 0 | 30 | 80 |
mi | 2 | 3 | 10 | 4 | 1 |
Тогда и
Замечание. В качестве числа, которое вычитается при переходе к условным вариантам (условный нуль), обычно выбирается варианта, стоящая в середине ряда, либо та, для которой частота максимальна (выборочная мода). В данном примере они совпадают.
Пример 4. Найти неисправленную выборочную дисперсию по выборке объема :
18,4 | 18,9 | 19,3 | 19,6 | |
5 | 10 | 20 | 15 |
Решение. Перейдем к условным вариантам иi = 10(хi – 19,3). Тогда
Dиi = D(10 — 193) = 100 Dхi
и
иi | – 9 | – 4 | 0 | 3 |
mi | 5 | 10 | 20 | 15 |
Найдем выборочную дисперсию для новой варианты иi:
Переходя к первоначальной варианте хi, получаем
Пример 5. По выборке объема найдена смещенная оценка теоретической дисперсии. Найти исправленную оценку дисперсии генеральной совокупности.
Решение. Несмещенная оценка дисперсии связана со смещенной следующей формулой:
Пример 6. Вычислите коэффициенты асимметрии и эксцесса распределения числа проданных цветных телевизоров по данным примера 5 подмодуля 1.1 (табл. 1.1).
Решение. и интервального вариационного ряда, приведенного в таблице 1.1 подмодуля 1.1, найдем по формулам
и
По аналогии, с приведенными выше примерами, найдем и
Для нахождения μ3 и μ4 составим вспомогательную расчетную таблицу 2.1.
Таблица 2.1
xi | mi | ximi | xi – | (xi –)mi | (xi –)2mi | (xi –)3mi | (xi –)4mi |
9 | 1 | 9 | –6,5 | –6,5 | 42,25 | –274,625 | 1785,0625 |
12 | 2 | 24 | –3,5 | –7 | 24,5 | –85,75 | 300,125 |
13 | 3 | 39 | –2,5 | –7,5 | 18,75 | –46,875 | 117,1875 |
14 | 6 | 84 | –1,5 | –9 | 13,5 | –20,25 | 30,375 |
15 | 5 | 75 | –0,5 | –2,5 | 1,25 | –0,625 | 0,3125 |
16 | 3 | 48 | 0,5 | 1,5 | 0,75 | 0,375 | 0,1875 |
17 | 2 | 34 | 1,5 | 3 | 4,5 | 6,75 | 10,125 |
19 | 1 | 19 | 3,5 | 3,5 | 12,25 | 42,875 | 150,0525 |
21 | 1 | 21 | 5,5 | 5,5 | 30,25 | 166,375 | 915,0625 |
23 | 1 | 23 | 7,5 | 7,5 | 56,25 | 421,875 | 3164,0625 |
27 | 1 | 27 | 11,5 | 11,5 | 132,25 | 1520,875 | 17490,0625 |
Σ | 26 | 403 | – | 0 | 336,5 | 1731 | 23962,63 |
= = = =
= 1,4299.
= – 3 = = 5,5022 – 3= = 2,5022.
Таким образом, рассматриваемое распределение числа проданных цветных телевизоров обнаруживает не только некоторую правостороннюю асимметрию, но и положительный эксцесс.
Пример 7. В течение недели регистрировались пропуски занятий студентами одной группы. В результате регистрации получили статистические данные:
2, 1, 3, 1, 2, 1, 2, 4, 3, 5, 3, 2, 2, 2, 1, 2, 3, 1, 0, 0, 0, 2, 3, 1, 4.
Вычислите числовые характеристики выборки: выборочное среднее, выборочную дисперсию, моду, медиану, коэффициенты асимметрии и эксцесса, коэффициент вариации.
Решение. Воспользуемся средствами MS Excel.
Сформируем таблицу исходных данных:
Для подсчета выборочного среднего выберем ячейку А5 и перейдем на вкладку Формулы – Другие функции – Статистические и выберем из раскрывающегося списка СРЗНАЧ. В появившемся окне в поле Число1 вводим диапазон исходных данных (А1:J3). После нажатия кнопки ОК, в ячейке А5 появится результат вычисления: 2.
Для подсчета выборочной дисперсии выберем ячейку А6 и перейдем на вкладку Формулы – Другие функции – Статистические и выберем из раскрывающегося списка ДИСП.В. В появившемся окне в поле Число1 вводим диапазон исходных данных (А1:J3). После нажатия кнопки ОК, в ячейке А6 появится результат вычисления: ≈1,67
Для подсчета моды выберем ячейку А7 и перейдем на вкладку Формулы – Другие функции – Статистические и выберем из раскрывающегося списка МОДА.ОДН. В появившемся окне в поле Число1 вводим диапазон исходных данных (А1:J3). После нажатия кнопки ОК, в ячейке А7 появится результат вычисления: 2.
Для подсчета медианы выберем ячейку А8 и перейдем на вкладку Формулы – Другие функции – Статистические и выберем из раскрывающегося списка МЕДИАНА. В появившемся окне в поле Число1 вводим диапазон исходных данных (А1:J3). После нажатия кнопки ОК, в ячейке А8 появится результат вычисления: 2.
Для подсчета коэффициента асимметрии выберем ячейку А9 и перейдем на вкладку Формулы – Другие функции – Статистические и выберем из раскрывающегося списка СКОС. В появившемся окне в поле Число1 вводим диапазон исходных данных (А1:J3). После нажатия кнопки ОК, в ячейке А9 появится результат вычисления: ≈0,38.
Для подсчета коэффициента эксцесса выберем ячейку А10 и перейдем на вкладку Формулы – Другие функции – Статистические и выберем из раскрывающегося списка ЭКСЦЕСС. В появившемся окне в поле Число1 вводим диапазон исходных данных (А1:J3). После нажатия кнопки ОК, в ячейке А10 появится результат вычисления: ≈-0,1.
Для подсчета коэффициента вариации сначала найдем значение среднего квадратического отклонения для выборки, так как коэффициент вариации представляет собой отношение среднего квадратического отклонения к среднему арифметическому. Для этого выберем ячейку А11 и перейдем на вкладку Формулы – Другие функции – Статистические и выберем из раскрывающегося списка СТАНДОТКЛОН.В. В появившемся окне в поле Число1 вводим диапазон исходных данных (А1:J3). После нажатия кнопки ОК, в ячейке А11 появится результат вычисления: ≈1,3.
Теперь для вычисления коэффициента вариации есть все необходимые величины. Выберем ячейку А12 и введем в неё формулу: =(A11/A5)*100 (Коэффициент вариации обычно выражается в процентах). После нажатия кнопки Enter в ячейке А12 появится результат вычисления: ≈ 64,55.
Пример 8. По данным выборки
1, 5, 2, 4, 3, 4, 6, 4, 5,1,2, 2, 3, 4, 5, 3, 4, 5, 2, 1,
4, 5, 5, 4, 3, 4, 6, 1, 2, 4,4, 3, 5, 6, 4, 3, 3, 1, 3, 4,
3, 4, 3, 1, 2, 4, 4, 5, 6, 1,3, 4, 5, 4, 4, 3, 2, 6, 1, 2,
4, 5, 3, 3, 2, 3, 6, 4, 3, 4,5, 4, 3, 3, 2, 6, 3, 3, 5, 4,
4, 3, 3, 2, 1, 2, 1, 6, 5, 4,3, 2, 3, 4, 4, 3, 5, 6, 1, 5.
Определить средний разряд рабочего, выборочную дисперсию и выборочное среднее квадратическое отклонение.
Решение. 1. Для начала сформируем таблицу исходных данных в программе MS Excel:
2. Для нахождения среднего разряда воспользуемся функцией МОДА.ОДН:
а) Необходимо выбрать ячейку, в которую будет помещен результат (А11)
б) Перейти на вкладку ФОРМУЛЫ – Другие функции – Статистические и из выпадающего списка выбрать МОДА.ОДН
в) В поле Число1 указать диапазон исходных данных (А1:К10)
г) Нажать кнопку ОК. В ячейке А11 появится результат вычисления = 4.
3. Для нахождения выборочной дисперсии воспользуемся функцией ДИСП.В:
а) Необходимо выбрать ячейку, в которую будет помещен результат (А12)
б) Перейти на вкладку ФОРМУЛЫ – Другие функции – Статистические и из выпадающего списка выбрать ДИСП.В
в) В поле Число1 указать диапазон исходных данных (А1:К10).
г) Нажать кнопку ОК. В ячейке А12 появится результат вычисления ≈ 2,03.
4. Чтобы найти выборочное среднее квадратическое отклонение будем использовать функцию СТАНДОТКЛОН.В:
а) Необходимо выбрать ячейку, в которую будет помещен результат (А13)
б) Перейти на вкладку ФОРМУЛЫ – Другие функции – Статистические и из выпадающего списка выбрать СТАНДОТКЛОН.В
в) В поле Число1 указать диапазон исходных данных (А1:К10)
г) Нажать кнопку ОК. В ячейке А13 появится результат вычисления ≈ 1,42.
studfiles.net
Решение задач на нахождение дисперсии дискретной случайной величины X
Задача 4
1)Случайная величина X может принимать два значения: x1 с вероятностью 0,3 и x2 с вероятностью 0,7. Найти значение выражения если дисперсия D(x)=3/5
Ответ 2.85714
2) Найти дисперсию дискретной
случайной величины X, имеющей закон распределения:
Ответ: 3.45
3) Найти дисперсию дискретной
случайной величины X, имеющей закон распределения:
Ответ 4.45
4) Случайная величина X может принимать два значения: x1с вероятностью 0,7 и x2 с вероятностью 0,3. Найти значение выражения если дисперсия D(x)=18/25
Ответ 3.4286
6) Случайная величина X может принимать два значения: x1 с вероятностью 0,2 и с вероятностью 0,8. Найти значение выражения если дисперсия D(x)= 9/20
Ответ:2.8125
7) Найти дисперсию дискретной
случайной величины X, имеющей закон распределения:
Ответ 3.21
8) Случайная величина X может принимать два значения: c x1 с вероятностью 0,2 и с вероятностью 0,8. Найти значение выражения если дисперсия D(x)=11/20
Ответ 3.4375
9) Случайная величина X может принимать два значения: x 1с вероятностью 0,8 и x2 с вероятностью 0,2. Найти значение выражения если дисперсия
Ответ 1.31578
10) Случайная величина X может принимать два значения: x1с вероятностью 0,6 и с вероятностью 0,4. Найти значение выражения если дисперсия D(x)= 6/11
Ответ 2.2727
11) Случайная величина X может принимать два значения: x1 с вероятностью 0,6 и x2 с вероятностью 0,4. Найти значение выражения если дисперсия
Ответ 3.88889
12) Найти дисперсию дискретной случайной величины X,
имеющей закон распределения:
Ответ 7.21
13) Случайная величина X может принимать два значения: x1 с вероятностью 0,4 и x2 с вероятностью 0,6. Найти значение выражения если дисперсия D(x)=7/20
Ответ 1.458333333
14) Случайная величина X может принимать два значения: x1 с вероятностью 0,8 и x2 с вероятностью 0,2. Найти значение выражения если дисперсия D(x)=3/8
Ответ 2.34375
15) Случайная величина X может принимать два значения: x1 с вероятностью 0,6 и x2 с вероятностью 0,4. Найти значение выражения если дисперсия D(x)=13/5
Ответ 10.833
16) Случайная величина X может принимать два значения: x1с вероятностью 0,8 и x2 с вероятностью 0,2. Найти значение выражения если дисперсия D(x)=4/19
Ответ 1.3157
17) Случайная величина X может принимать два значения: x1 с вероятностью 0,2 и x2 с вероятностью 0,8. Найти значение выражения если дисперсия D(x)=8/17
Ответ 2.9412
18) Найти дисперсию
дискретной случайной величины X, имеющей закон распределения:
Ответ 7.61
19) Случайная величина X может принимать два значения: x1 с вероятностью 0,7 и x2 с вероятностью 0,3. Найти значение выражения если дисперсия D(x)=17/20
Ответ 4.0476
vunivere.ru
Несмещенная оценка дисперсии — исправленная выборочная дисперсия
Условие задачи
Найти несмещенную выборочную дисперсию на основании данного распределения выборки.
| 16 | 20 | 22 | 30 | |
| 14 | 26 | 17 | 3 |
Решение задачи
Задали объемную контрольную? Скоро важный зачет/экзамен? Нет времени на выполнение работы или подготовку к зачету/экзамену, но есть деньги? На сайте 100task.ru можно заказать решение или онлайн-помощь на зачете/экзамене 〉〉
Выборочная дисперсия является смещенной оценкой генеральной дисперсии, поэтому в статистике применяют также исправленную выборочную дисперсию, которая является несмещенной оценкой генеральной дисперсии.
Сумма частот:
Вычислим среднюю:
Средняя квадратов:
Несмещенная выборочная дисперсия:
Ответ
Кроме этой задачи на другой странице сайта есть пример расчета исправленной выборочной дисперсии и среднего квадратического отклонения для интервального вариационного ряда
К оглавлению решебника по теории вероятностей и математической статистике 〉
100task.ru
Дисперсия дискретной случайной величины
Как уже говорилось выше, математическое ожидание является средней характеристикой случайной величины. Однако оно не характеризует случайную величину достаточно полно, и по этой причине рассматриваются и другие числовые характеристики. Пусть Х — случайная величина, а М(Х) — ее математическое ожидание.
Определение 2. Разность между случайной величиной и ее математическим ожиданием называется отклонением.
Пусть закон распределения случайной величины Х дается формулой (18.1), тогда отклонение X — M(X) имеет следующий закон распределения:
Отклонение имеет важное свойство, которое устанавливается непосредственно из свойств математического ожидания:
т.е. математическое ожидание отклонения равно нулю.
Пример 5. По данным примера 3 найти закон распределения отклонения числа проданных за день автомашин.
Решение. Как было подсчитано в примере 3, М(Х) = 2,675. Тогда, согласно (18.8), искомый закон определяется следующей таблицей:
На практике важной характеристикой является рассеяние возможных значений случайной величины вокруг ее среднего значения. Среднее значение отклонения, согласно (18.9), равно нулю, так как суммируются отрицательные и положительные отклонения (см. пример 5), поэтому целесообразно ввести в рассмотрение абсолютные значения отклонений или их квадраты.
Определение 3. Математическое ожидание квадрата отклонения называется дисперсией, или рассеянием:
Пусть случайная величина задана законом распределения (18.1), тогда квадрат отклонения этой случайной величины имеет следующий закон распределения:
Отсюда, согласно формуле (18.10), получаем формулу дисперсии в развернутом виде:
При вычислении дисперсии часто бывает удобно воспользоваться формулой, которая непосредственно выводится из формулы (18.10):
Пример 6. Найти дисперсию ежедневной продажи числа автомашин по данным примера 3.
Решение. Закон распределения случайной величины X2 имеет вид
Математическое ожидание М(Х2) подсчитывается из этой таблицы:
Математическое ожидание М(Х) = 2,675. Следовательно, согласно формуле (18.11), получаем искомую величину дисперсии:
Свойства дисперсии
Приведем здесь основные свойства дисперсии.
Свойство 1. Дисперсия постоянной величины С равна нулю:
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
Свойство 3. Дисперсия суммы независимых случайных величин равна сумме их дисперсий:
Перечисленные свойства дисперсии используются при вычислениях, когда мы имеем дело с несколькими случайными величинами. Из свойств 1 и 3 следует важный вывод: D(X + C) = D(X), где С — постоянная величина. Кроме того, справедлива следующая теорема.
ТЕОРЕМА 2. Дисперсия числа появления события А в п независимых испытаниях с вероятностью появления р в каждом из них этого события вычисляется по формуле
Приведем здесь еще два важных результата: для случайной величины, распределенной по закону Пуассона (18.4), математическое ожидание и дисперсия равны параметру данного распределения.
Пример 7. Найти дисперсию числа выигрышных лотерейных билетов по данным примера 4.
Решение. Имеем 200 независимых испытаний с вероятностью появления выигрышного билета р = 0,015. Стало быть, q = 1 — 0,015 = 0,985, откуда и получаем искомую дисперсию:
Пример 8. Банк выдал ссуды п разным заемщикам в размере S р. каждому под ставку ссудного процента r. Найти математическое ожидание и дисперсию прибыли банка, а также условие на ставку ссудного процента, если вероятность возврата ссуды заемщиком равна р.
Решение. Поскольку заемщики между собой не связаны, то можно полагать, что мы имеем п независимых испытаний. Вероятность утери ссуды для банка в каждом испытании равна q = 1 — р. Пусть Х — число заемщиков, возвративших ссуду с ссудным процентом, тогда прибыль банка определяется формулой
где Х является случайной величиной с биномиальным законом распределения. Тогда, согласно теореме 18.1, математическое ожидание прибыли определяется с использованием формулы (18.7):
Поскольку выдача ссуды имеет смысл лишь при положительном математическом ожидании прибыли (положительная средняя величина прибыли), то из условия М(П) > 0 вытекает условие на ставку ссудного процента:
Дисперсия прибыли банка находится, согласно теореме 18.2, с использованием формулы (18.14) и свойств 1-3:
studfiles.net
4.2.1. Дисперсия случайной величины
Дисперсией(рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
Для вычисления дисперсии можно использовать слегка преобразованную формулу
,
так как М(Х), 2 и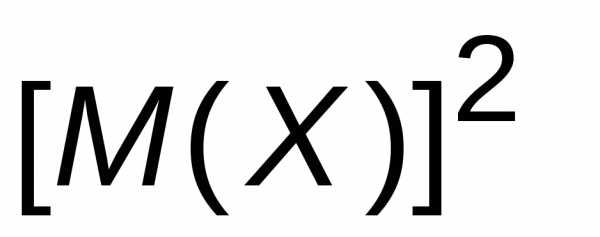
–
постоянные величины. Таким образом,
.
4.2.2. Свойства дисперсии
Свойство 1.Дисперсия постоянной величины равна нулю. Действительно, по определению
Свойство 2.Постоянный множитель можно выносить за знак дисперсии с возведением его в квадрат.
Доказательство
Центрированной случайной величиной называется отклонение случайной величины от ее математического ожидания:
Центрированная величина обладает двумя удобными для преобразования свойствами:
Свойство 3.Если случайные величины Х иYнезависимы, то
Доказательство. Обозначим. Тогдаи.
Поэтому
Во втором слагаемом в силу независимости случайных величин и свойств центрированных случайных величин
,
поэтому
.
Пример 4.5. Еслиaиb– постоянные, тоD(aХ+b)=D(aХ)+D(b)=.
4.2.3. Среднее квадратическое отклонение
Дисперсия, как
характеристика разброса случайной
величины, имеет один недостаток. Если,
например, Х – ошибка измерения имеет размерность ММ,
то дисперсия имеет размерность 
.
Поэтому часто предпочитают пользоваться
другой характеристикой разброса –средним
квадратическим отклонением,
которое равно корню квадратному из
дисперсии
Среднее квадратическое отклонение имеет ту же размерность, что и сама случайная величина.
Пример 4.6. Дисперсия числа появления события в схеме независимых испытаний
Производится nнезависимых испытаний и вероятность появления события в каждом испытании равнар. Выразим, как и прежде, число появления событияХчерез число появления события в отдельных опытах:
Так как опыты независимы, то и связанные
с опытами случайные величины 
независимы. А в силу независимости
имеем
Но каждая из случайных величин имеет закон распределения (пример 3.2)
| 0 | 1 |
Р | 1-р | р |
и (пример 4.4). Поэтому, по определению дисперсии:
,
где q=1-p.
В итоге имеем ,
Среднее квадратическое отклонение
числа появлений события в nнезависимых опытах равно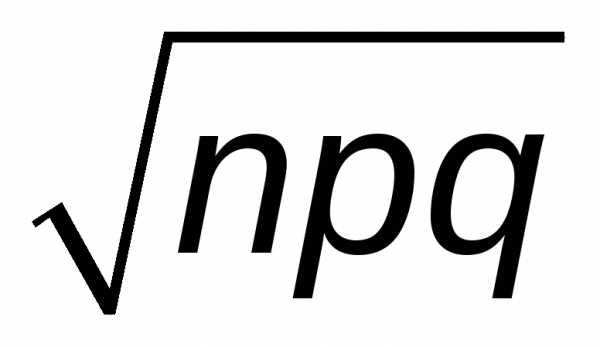
.
4.3. Моменты случайных величин
Помимо уже рассмотренных случайные величины имеют множество других числовых характеристик.
Начальным
моментом k-го
порядка случайной величины Х (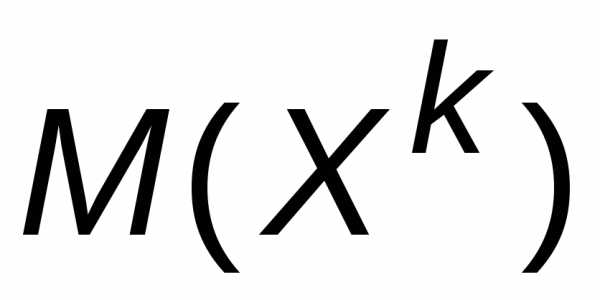
)
называется математическое ожиданиеk-й
степени этой случайной величины.
Центральным моментомk-го порядка случайной величиныХназывается математическое ожиданиеk-ой степени соответствующей центрированной величины.
Легко видеть, что центральный момент первого порядка всегда равен нулю, центральный момент второго порядка равен дисперсии, так как .
Центральный момент третьего порядка дает представление об асимметрии распределения случайной величины. Моменты порядка выше второго употребляются сравнительно редко, поэтому мы ограничимся только самими понятиями о них.
4.4. Примеры нахождения законов распределения
Рассмотрим примеры нахождения законов распределения случайных величин и их числовых характеристик.
Пример 4.7.
Составить закон распределения числа
попаданий в цель при трех выстрелах по
мишени, если вероятность попадания при
каждом выстреле равна 0,4. Найти интегральную
функцию F(х)для
полученного распределения дискретной
случайной величиныХи начертить
ее график. Найти математическое ожиданиеM(X),
дисперсиюD(X)и среднее квадратическое отклонение 
(Х)
случайной величиныX.
Решение
1) Дискретная случайная величина Х– число попаданий в цель при трех выстрелах – может принимать четыре значения:0, 1, 2, 3. Вероятность того, что она примет каждое из них, найдем по формуле Бернулли при:n=3,p=0,4,q=1-p=0,6 иm=0, 1, 2, 3:
.
Получим вероятности возможных значений Х:;
;
.
Составим искомый закон распределения случайной величины Х:
Х | 0 | 1 | 2 | 3 |
Р | 0,216 | 0,432 | 0,288 | 0,064 |
Контроль: 0,216+0,432+0,288+0,064=1.
Построим многоугольник распределения полученной случайной величины Х. Для этого в прямоугольной системе координат отметим точки (0; 0,216), (1; 0,432), (2; 0,288), (3; 0,064). Соединим эти точки отрезками прямых, полученная ломаная и есть искомый многоугольник распределения (рис. 4.1).
х
Рис. 4.1.
2) Если х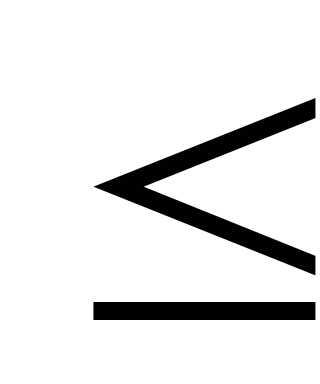
0,
то F(х)=0.
Действительно, значений, меньших нуля,
величина Х не принимает. Следовательно, при всех х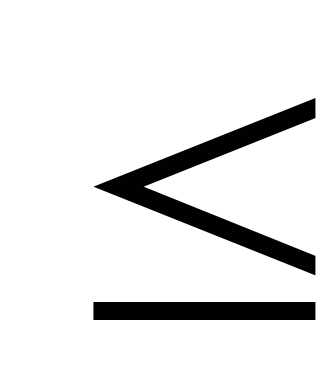
0
, пользуясь определениемF(х),
получим F(х)=P(X<x)=0
(как вероятность невозможного события).
Если 0<x
,
тоF(X)=0,216.
Действительно, в этом случаеF(х)=P(X<x)=
=P(-
<X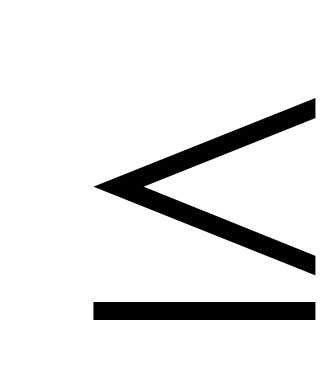
0)+P(
0<X<x)=0,216+0=0,216.
Если взять, например, х=0,2, тоF(0,2)=P(X<0,2). Но вероятность событияХ<0,2 равна 0,216, так как случайная величинаХлишь в одном случае принимает значение меньшее 0,2, а именно0с вероятностью 0,216.
Если 1<x
,
то
Действительно, Хможет принять значение 0 с вероятностью 0,216 и значение 1 с вероятностью 0,432; следовательно, одно из этих значений, безразлично какое,Хможет принять (по теореме сложения вероятностей несовместных событий) с вероятностью 0,648.
Если 2<x
,
то рассуждая аналогично, получимF(х)=0,216+0,432 +
+ 0,288=0,936. Действительно, пусть, например,х=3. ТогдаF(3)=P(X<3)выражает вероятность событияX<3 –
стрелок сделает меньше трех попаданий,
т.е. ноль, один или два. Применяя теорему
сложения вероятностей, получим указанное
значение функцииF(х).
Если x>3, тоF(х)=0,216+0,432+0,288+0,064=1.
Действительно, событиеX
является
достоверным и вероятность его равна
единице, аX>3 –
невозможным. Учитывая, что
F(х)=P(X<x)=P(X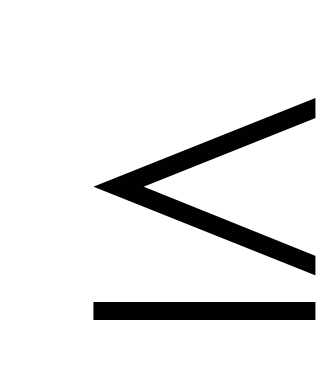
3)
+ P(3<X<x),
получим указанный результат.
Итак, получена искомая интегральная функция распределения случайной величины Х:
F(x)=
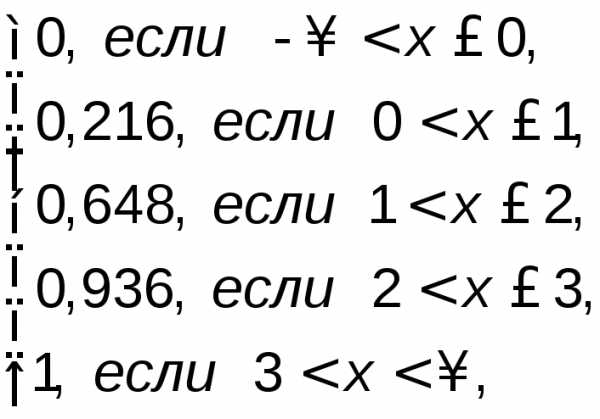
график которой изображен на рис. 4.2.
Рис. 4.2
3) Математическое ожидание дискретной случайной величины равно сумме произведений всех возможных значений Хна их вероятности:
М(Х)=0=1,2.
То есть, в среднем происходит одно попадание в цель при трех выстрелах.
Дисперсию можно вычислить, исходя из
определения дисперсии D(X)=M(X—M(X))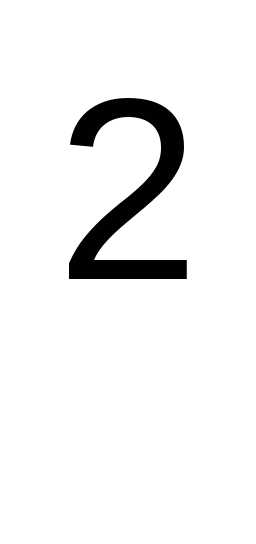
или воспользоваться формулойD(X)=M(X,
которая ведет к цели быстрее.
Напишем закон распределения случайной
величины Х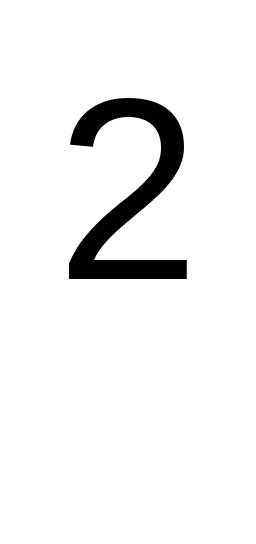
:
Х2 | 0 | 1 | 4 | 9 | . |
Р | 0,216 | 0,432 | 0,288 | 0,064 |
Найдем математическое ожидание для Х:
М(Х
)= 04= 2,16.
Вычислим искомую дисперсию:
D(X)
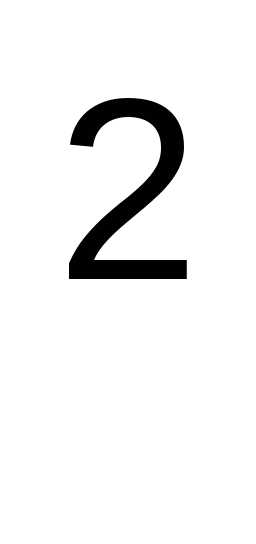= M(X
)
– (M(X))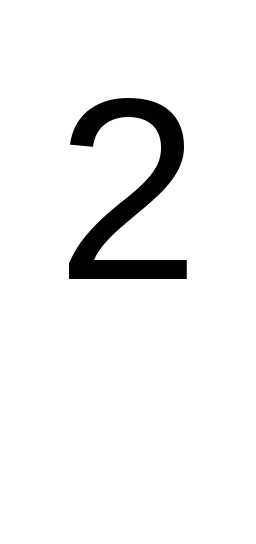
= 2,16 – (1,2)
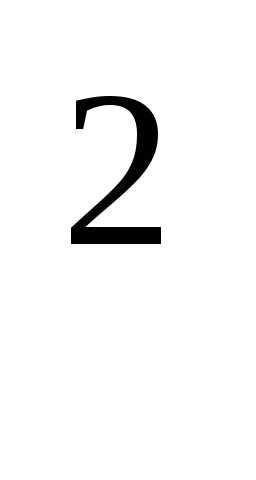= 0,72.
Среднее квадратическое отклонение найдем по формуле
(X)
=
= 0,848.
Интервал (M—
; M+
)
= (1,2-0,85; 1,2+0,85) = (0,35; 2,05) – интервал
наиболее вероятных значений случайной
величиныХ, в него попадают значения
1 и 2.
Пример 4.8.
Дана дифференциальная функция распределения (функция плотности) непрерывной случайной величины Х:
f(x)=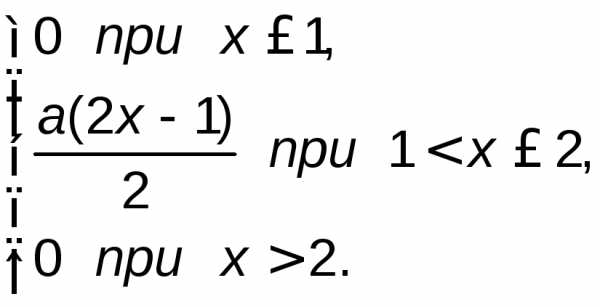
1) Определить постоянный параметр a.
2) Найти интегральную функцию F(x).
3) Построить графики функций f(x)иF(x).
4) Найти двумя способами вероятности Р(0,5<X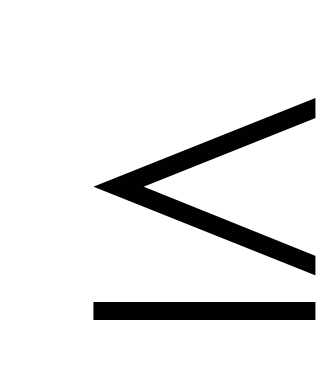
1,5)иP(1,5<X<3,5).
5). Найти математическое ожидание М(Х),
дисперсиюD(Х)и
среднее квадратическое отклонение 
случайной величиныХ.
Решение
1) Дифференциальная функция по свойству f(x)должна удовлетворять условию
.
Вычислим этот несобственный интеграл для данной функции f(x):
Подставляя этот результат в левую часть
равенства, получим, что а=1. В условии
дляf(x)заменим параметрана 1:
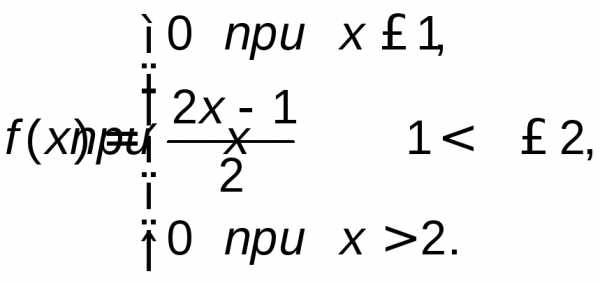
2) Для нахождения F(x)воспользуемся формулой
.
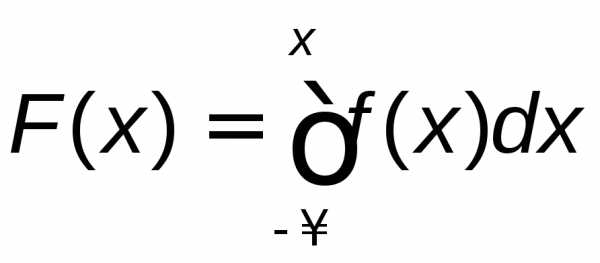Если х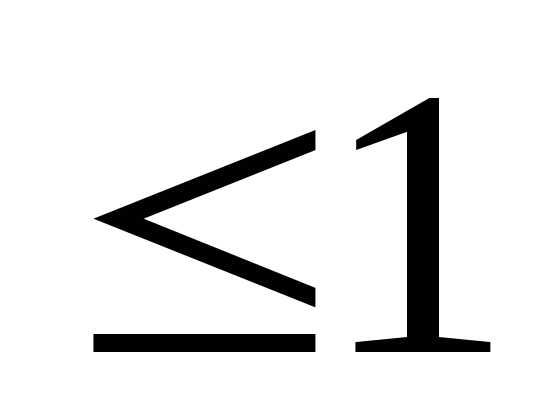
,
то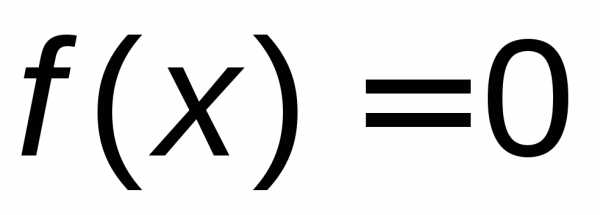
,
следовательно,
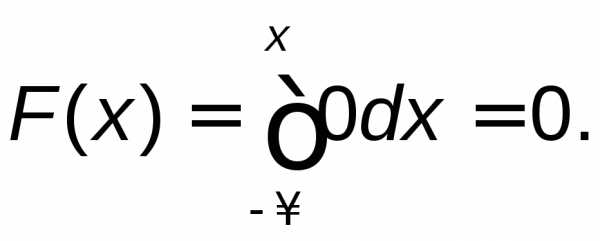
Если 1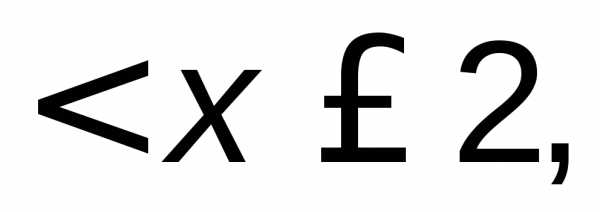
то
Если x>2, то
Итак, искомая интегральная функция F(x)имеет вид:
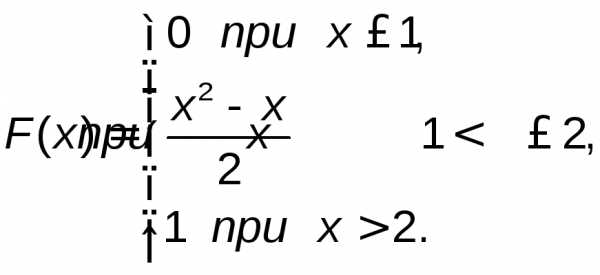
3) Построим графики функций f(x)иF(x) (рис. 4.3 и 4.4).
Рис. 4.3
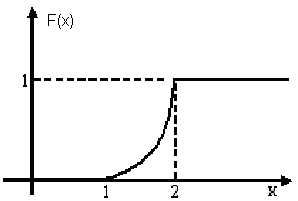
Рис. 4.4.
4) Вероятность попадания случайной величины в заданный интервал (а,b)вычисляется по формуле , если известнафункция f(x), и по формуле P(a < X <b) = F(b) – F(a), если известна функция F(x).
Найдем по двум формулам и сравним результаты. По условиюа=0,5; b=1,5; функцияf(X) задана в пункте 1). Следовательно, искомая вероятность по формуле равна:
Та же вероятность может быть вычислена по формуле b) через приращение полученной в п.2). интегральной функцииF(x)на этом интервале:
, так какF(0,5)=0.
Аналогично находим
,
или
,
так как F(3,5)=1.
5) Для нахождения математического
ожидания М(Х)воспользуемся формулой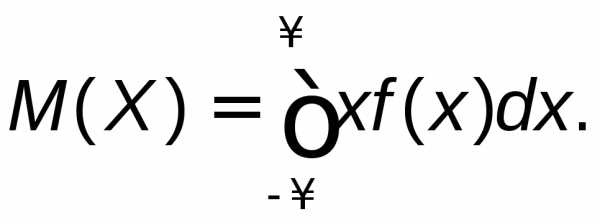 
Функцияf(x) задана в решении пункта 1), она равна
нулю вне интервала (1,2]:
Дисперсия
непрерывной случайной величиныD(Х)определяется равенством
, или равносильным равенством
.
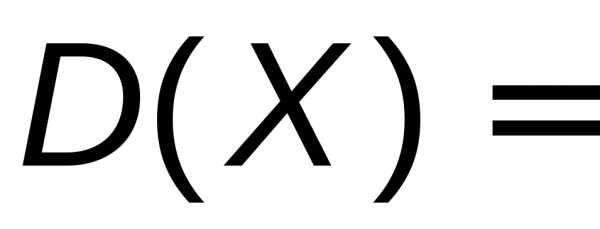Для
нахожденияD(X)воспользуемся последней формулой и
учтем, что все возможные значенияf(x)принадлежат интервалу (1,2]:
Среднее квадратическое отклонение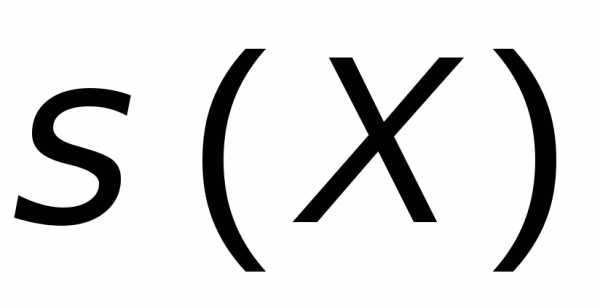 
=
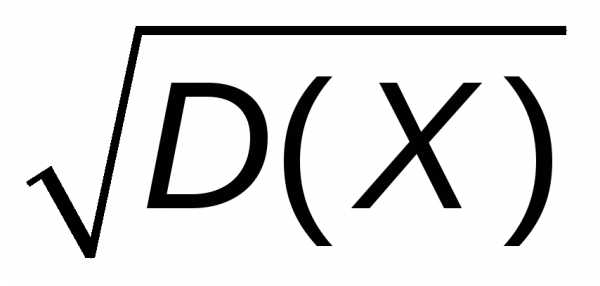=0,276.
Интервал наиболее вероятных значений случайной величины Хравен
(М-
,М+
)
= (1,58-0,28; 1,58+0,28) = (1,3; 1,86).
studfiles.net