Задачи на треугольники с решением – Задачи с треугольниками

zadachi-ru.com.ua

Решение задач на подобие. Подобные треугольники.

Рассмотрим задачи, при решении которых мы будем использовать подобие треугольников.  Уделим внимание как базовым задачам, так и задачам посложней. В конце статье вы найдете задачи для самостоятельной работы.

Задача 1. 

Через точки М и N, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МN, параллельная стороне АС. Найдите длину СN, если ВС = 6, МN = 4 и АС = 9.

Решение: + показать

Задача 2.

Прямая, параллельная основанию треугольника, делит его на треугольник и трапецию, площади которых относятся как 4:5. Периметр образовавшегося треугольника равен 20 см. Найдите периметр данного треугольника.

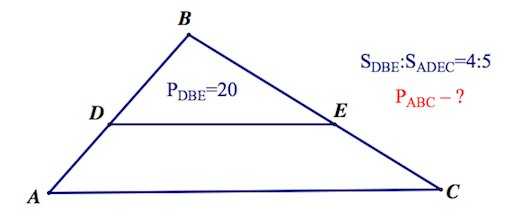
Решение: + показать

Задача 3.

Через вершину прямого угла прямоугольного треугольника с катетами 6 и 8 см проведен перпендикуляр к гипотенузе. Вычислите площади образовавшихся треугольников.

Решение: + показать

Задача 4.

Из одной точки проведены к кругу две касательные. Длина касательной равна 156, а расстояние между точками касания равно 120. Найдите радиус круга.

Решение: + показать

Задача 5.

В трапеции меньшая диагональ , равная 6, перпендикулярна основаниям и . Найдите сумму тупых углов и .

Решение:+ показать

Задача 6.

Основания трапеции равны a и b. Определите длину отрезка, параллельного основаниям и делящего трапецию на равновеликие части.

Решение: + показать

Задачи для самостоятельной работы

1. Через точки E и F, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая EF, параллельная стороне АС. Найдите длину BС, если EF = 10, AC = 15 и FC = 9. (Ответ: 27).

2. В прямоугольном треугольнике проведена высота к гипотенузе. , Найдите катет . (Ответ: 20/3).

3. Прямая, параллельная основанию треугольника, отсекает от него треугольник, площадь которого в 8 раз меньше площади оставшейся части. Периметр большего треугольника равен 27. Найдите периметр меньшего треугольника. (Ответ: 9).

4. Основание треугольника 15 см, а боковые стороны 13 и 14 см. Высота разделена в отношении 2:3 (считая от вершины) и через точку деления проведена прямая, параллельная основанию. Найдите площадь образовавшейся при этом трапеции. (Ответ: 70,56 (возможно, вам потребуется формула Герона)).

5. В трапеции с основаниями и диагонали пересекаются в точке . Площадь треугольника равна 4, площадь треугольника равна 9. Найдите площадь трапеции. (Ответ: 25).

6. Трапеция разделена диагоналями на четыре части. Определить ее площадь, если известны площади ее частей, прилежащих к основаниям и . (Ответ: ).

egemaximum.ru

Решение треугольников, все формулы и примеры

Определение и формулы для решения треугольников

Стороны треугольника обычно обозначают буквами , а противолежащие углы – .

Решение треугольников заключается в отыскании всех неизвестных сторон и всех неизвестных углов треугольника по известным данным.

При решении задач используют теорему косинусов или теорему синусов.

Теоремы для решения треугольников

Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной вокруг треугольника окружности:

Также используют условия, которым удовлетворяют стороны треугольника (неравенство треугольника):

и углы

Примеры решения задач

Решение треугольников | Геометрия 9 класс | Примеры решения задач

Содержание страницы:

• – задачи 76 — 77 представлены с примерами решений и ответами по теме «Решение треугольников»;
• – онлайн задания, как найти решение треугольника через синус и косинус угла, рассматриваются в тестах 78 — 81;
• – решения, как найти угол, сторону треугольника, объясняются в контрольных работах 82 — 85.

Задача 76.

Треугольник ΔABC,

стороны треугольника a=10, b=7

Угол A = 60°

Решить треугольник: Угол по сторонам треугольника B, C, сторону c

Решение:

Известно, что формула синуса

, получаем выражение

Sin B = = = = ≈ 0,6062

Используя Sin B ≈ 0,6062, находим из тригонометрической таблицы («Четырехзначные математические таблицы» Владимира Модестовича Брадиса)

B = 37°19’

Тогда C = 180° — (60° + 37°19’) = 82°41’

Используя теорему синусов

, получаем равенство

с=≈ 11

Ответ: B = 37°19’; C = 82°41’; c ≈ 11

***

Задача 77.

Дано:

Треугольник ΔABC, стороны треугольника

a=6,3

b=6,3

Найти: Угол по сторонам треугольника A, B, сторону c

Решение:

Т.к. a=b=6,3, то треугольник ΔABC — равнобедренный.

Тогда A =B = (180° — 54°): 2 = 63°

Используя теорему синусов

, получаем равенство

с = = ≈ 5,7

Ответ: A =B = 63°; с ≈ 5,7

***

Наверх

Решение треугольников через синус и косинус угла

Задача 78.

Дано:

Треугольник ΔABC

A = 60°

c=14

Найти: угол треугольника C, стороны a,b

Решение:

C = 180° — (40° + 60°) = 80°

Используя теорему синусов

, получаем выражение

b = ≈ 9

Ответ: C = 80°; a ≈ 12; b ≈ 9

***

Задача 79.

Треугольник ΔABC

BC=a=6

AC=b=7,3

AB=c=4,8

Найти: углы треугольника A, B, C по сторонам

Решение:

Известно, что формула косинуса

, находим косинус угла B

Cos B = = = = ≈ 0,0998263

Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим значение угла B

B = 84°16’

Используя формулу теоремы косинусов, находим косинус угла C

Cos C = = =

= ≈ 0,7562785

Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим значение угла C

C = 40°52’

Тогда угол A равен A =180° — (40°52’ + 84°16’) = 54°52’

Ответ: A = 54°52’ ; C = 40°52’ ; B = 84°16’

***

Задача 80.

Дано:

Треугольник ΔABC

A = 30°

C = 75°

b = 4,5

Найти: угол B, стороны треугольника a,c

Решение:

B = 180° — (30° + 75°) = 75°

Т.к. два угла в треугольнике равны B =C = 75°, тогда треугольник ΔABC — равнобедренный.

Значит, две стороны равны AC=AB=b=c=4,5

Используя теорему синусов

,

находим сторону BC=a

a = ≈ 2,3

Ответ: B = 75°; a ≈ 2,3 ; c = 4,5

***

Задача 81.

Дано:

Треугольник ΔABC, длины трех его сторон

Найти: является ли треугольник тупоугольным, прямоугольным, остроугольным

Решение:

1) Т.к. b=c=4, то треугольник ΔABC — равнобедренный, и, значит, остроугольный.

, находим косинус угла A

Cos A =

Тогда угол A равен A = 90°. Следовательно, треугольник ΔABC — прямоугольный.

3) Используя формулу теоремы косинусов

, находим косинус угла B

Cos B = == -< 0.

Т.к. значение косинуса угла B меньше нуля, следовательно, угол B — тупой, а треугольник ΔABC — тупоугольный.

***

Наверх

Решение треугольника через угол по сторонам

Задача 82.

Треугольник ΔABC, два угла и сторона

A = 45°

C = 30°

AD = 3 м

Найти: длину всех сторон треугольника ΔABC = ?

Решение:

Зная размер двух углов в треугольнике ΔABC, находим третий уголB = 180° — (30° + 45°) = 105°

Найдем угол DAB и рассмотрим ΔADC

Используя теорему синусов

, находим сторону AC

AC = (3 • 1) • 2 = 6 (м)

Используя теорему синусов

, находим сторону AB

AB = ≈ 3 (м)

Используя теорему синусов

, находим сторону BC

BC =≈ 4 (м)

Ответ: AB ≈ 3 м, AC = 6 м, BC ≈ 4 м.

***

Дано:

Треугольник ΔABC

Три стороны a = 14, b = 18,

c = 20

Найти:

все углы треугольника ΔABC = ?

Решение:

Т.к. против большего угла лежит большая сторона, то используя формулу теоремы косинусов

Cos C =, находим косинус угла C

Cos C = = ≈ 0,24

Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла C

C ≈ 76°07’

Используя формулу теоремы косинусов

Cos B =, находим косинус угла B

Cos B = ==≈ 0,4857

Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла B

B ≈ 60,941 ≈ 60°57’

Следовательно, A = 180° — (76°13’ + 60°57’) ≈ 42°56’

Ответ: A ≈ 42°56’ ; B ≈ 60°57’ ; C ≈ 76°07’

***

Задача 84.

Дано:

Треугольник ΔEKP, сторона и два угла

EP = 0,75

P = 40°

K = 25°

Найти: сторону треугольника PK = ?

Решение:

Используя теорему синусов

, находим сторону PK

Sin 115° = Sin (180° — 65°) = Sin 65°

Тогда

Ответ: PK ≈ 1,61.

***

Задача 85.

Дано:

Треугольник ΔABC, две стороны и угол

b = 18, c = 12

A = 50°

Найти: решить треугольник — определить значение стороны и двух углов

(a, B, C ) = ?

Решение:

Используя формулу теоремы косинусов

, получаем

a = = ≈ 13,8

Используя формулу теоремы косинусов

Cos C =, находим косинус угла C

Cos C == ≈ 0,7457

Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла C

C ≈ 41°47’

Следовательно, B = 180° — (50° + 41°47’) ≈ 88°13’

Ответ: a ≈ 13,8 ; B ≈ 88°13’ ; C ≈ 41°47’

***

www.petrovskov.ru

Решение задач по теме «Равнобедренный треугольник» . Видеоурок. Геометрия 7 Класс

Данный видеоурок предназначен для самостоятельного изучения темы «Решение задач по теме “Равнобедренный треугольник”». Вы вспомните определение равнобедренного треугольника и повторите его свойства. Разберете несколько задач на треугольники, для решения которых понадобятся полученные ранее знания.

Вспомним предварительно определение равнобедренного треугольника.     

Рис. 1. Равнобедренный треугольник

Определение: Треугольник называется равнобедренным, если у него две стороны равны.                                                                                                     

АВ = АС,  треугольник АВС – равнобедренный. АВ и АС – боковые стороны, ВС – основание.

Определение: Треугольник называется равносторонним, если у него все три стороны равны.

Рис. 2. Равносторонний треугольник

АВ = АС = ВС, треугольник АВС – равносторонний.

Следует повторить следующие свойства равнобедренного треугольника:

1. Углы при основании равнобедренного треугольника равны. ∠В = ∠С.

2. Пусть точка D – середина ВС. Отрезок AD является медианой, биссектрисой и высотой треугольника.

Рис. 3. Свойства равнобедренного треугольника

Рассмотрим следующие задачи:

Пример 1: На рисунке АВ = ВС, ∠1 = . Найдите ∠2.

Решение: Выполним пояснительный рисунок:

Рис. 4. Чертеж к примеру 1

1. ∠АСВ = – = (по свойству смежных углов). Значит, угол при основании равнобедренного треугольника равен .

2. ∠ВАС = ∠АСВ = (поскольку углы при основании равнобедренного треугольника равны).

3. ∠2 = ∠ВАС (как вертикальные), значит, ∠2 = ∠ВАС = .

Ответ:.

Пример 2: Периметр равнобедренного треугольника АВС с основанием ВС равен 40 см, а периметр равностороннего треугольника ВСD равен 45 см. Найдите стороны АВ и ВС.

Дано: АВ = АС, ВС = СD = DB. = 40 см. = 45 см.

Найти: АВ и ВС.

Решение: Выполним пояснительный рисунок:

Рис. 5. Чертеж к примеру 2

Решение: Пусть ВС = х, тогда все стороны равностороннего треугольника тоже равны х. Пусть АВ = у, тогда обе боковые стороны треугольника равны у. Следуя условию, 3х = 45. Найдем х. х = 45 : 3 = 15. Используем факт, что = 40 см. 15 + 2у = 40, 2у = 25, у = 25 : 2 = 12,5.

Ответ: АВ = 12,5 см, ВС = 15 см.

Пример 3: Медиана АМ в  треугольнике АВС равна отрезку ВМ. Докажите, что ∠ВАС = ∠В + ∠С.

Дано: ВМ = МС, АМ = ВМ.

Доказать: ∠ВАС = ∠В + ∠С.

Доказательство: Выполним пояснительный рисунок:

Рис. 6. Чертеж к примеру 3

Треугольник АМВ – равнобедренный, углы при основании равны, значит, ∠1 = ∠2.  треугольник АМС – равнобедренный, значит, углы при основании равны, ∠4 = ∠3.

∠1 + ∠4 = ∠2 + ∠3

∠ВАС = ∠В + ∠С

Ответ: Доказано.

На сегодняшнем уроке мы решили задачи по теме «Равнобедренный треугольник». На следующем уроке мы изучим второй и третий признаки равенства треугольников.

Список рекомендованной литературы

1. Александров  А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. – М.: Просвещение.
2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. – М.: Просвещение.
3. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.

Рекомендованные ссылки на интернет-ресурсы

1. Фестиваль педагогической идеи «Открытый урок» (Источник).
2. Кaknauchit.ru (Источник).

Рекомендованное домашнее задание

1. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А.  – М.: Просвещение, 2010.
2. Докажите, что в равнобедренном треугольнике медианы, проведенные к боковым сторонам, равны.
3. Точки А и В лежат по одну сторону от прямой . Перпендикуляры АС и ВЕ, проведенные к прямой , равны. Точка О – середина отрезка СЕ. Докажите, что углы ОАВ и ОВА равны.
4. Медиана равнобедренного треугольника делит его периметр на части, которые равны 12 см и 9 см. Найдите стороны треугольника.

interneturok.ru

Задачи на комбинацию окружности и треугольника

Продолжаем решать простейшие геометрические задачки.

Разбираем Задачи №6  ЕГЭ по математике.

Сегодня работаем с окружностью, вписанной в треугольник и описанной около треугольника. 

Вы можете пройти автотренинг «Планиметрия»

В категорию «Задачи №6» входят  также задачи следующих типов + показать

Окружность, вписанная в треугольник

Задача 1.

Площадь треугольника равна 800, а радиус вписанной окружности равен 16. Найдите периметр этого треугольника.

Решение: + показать

Задача 2.

Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 66.

Решение: + показать

Радиус вписанной окружности в правильный треугольник – есть высоты (), так в правильном треугольнике высоты совпадают с медианами, а медианы в точке пересечения делятся в отношении 2:1, считая от вершины.

Итак,

Ответ: 22. 

Задача 3.

Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.

Решение: + показать

Задача 4.

В треугольнике ABC  . Найдите радиус вписанной окружности.

Решение: + показать

Найдем гипотенузу по т. Пифагора:

Найдем площадь и периметр треугольника, чтобы воспользоваться затем формулой :

Тогда

Ответ: 1. 

Задача 5.

Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 11. Найдите гипотенузу c этого треугольника. В ответе укажите .

Решение: + показать

Задача 6.

Боковые стороны равнобедренного треугольника равны 181, основание равно 38. Найдите радиус вписанной окружности.

Решение: + показать

Задача 7.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 13 и 5, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

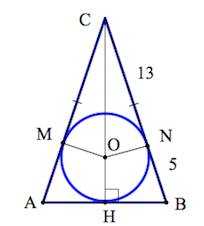
Решение: + показать

Задача 8.

К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 10, 18, 33. Найдите периметр данного треугольника.

Решение: + показать

Окружность, описанная около треугольника

Задача 1.

Найдите радиус окружности, описанной около прямоугольного треугольника , если стороны квадратных клеток равны 1.

Решение: + показать

Задача 2.

Боковые стороны равнобедренного треугольника равны 50, основание равно 60. Найдите радиус описанной окружности этого треугольника.

Решение: + показать

Воспользуемся следующей формулой:

Площадь будем искать по формуле Герона:

Тогда  

Ответ: 31,25. 

Задача 3.

Сторона AB треугольника ABC равна 28. Противолежащий ей угол C равен 150˚. Найдите радиус окружности, описанной около этого треугольника.

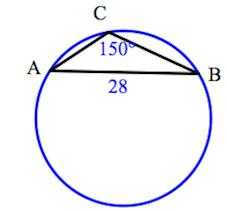
Решение: + показать

Согласно т. Синусов

Ответ: 28. 

Задача 4.

Угол C треугольника ABC, вписанного в окружность радиуса 47, равен 30˚. Найдите сторону AB этого треугольника.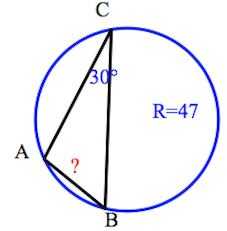

Решение: + показать

Задача 5.

В треугольнике ABC BC, угол C равен 90°. Радиус описанной окружности этого треугольника равен 17,5. Найдите AC.

Решение: + показать

В прямоугольном треугольнике гипотенуза – диаметр описанной окружности.

Значит,

По теореме Пифагора

Ответ: 30. 

Задача 6.

Радиус окружности, описанной около правильного треугольника, равен Найдите сторону этого треугольника.

Решение: + показать

Задача 7.

Точки A, B, C, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1:6:11. Найдите больший угол треугольника ABC. Ответ дайте в градусах.

Решение: + показать

Объемный раздел получился… Отдохнем немножко? –>+ показать

Вы может пройти тест «Окружность, описанная около треугольника. Окружность, вписанная в треугольник»

egemaximum.ru

Решение треугольников. Более сложная задача. Видеоурок. Геометрия 9 Класс

На этом уроке мы будем находить элементы треугольника, используя основные теоремы синусов и косинусов и теоремы о площади.

Рассмотрим задачу, в которой заданы две стороны треугольника и угол не между ними, в этом случае число решений зависит от конкретных числовых данных.

Число решений может быть два:

предположим, что . В треугольнике может быть угол  или  (рис. 1)

Рис. 1. Иллюстрация к задаче

Дано: треугольник ABC, a = 6, b =8,  (рис. 2)

Найти: углы , γ; сторону с

Решение:

Воспользуемся теоремой синусов

Рис. 2. Иллюстрация к задаче

Видим, что , следовательно, угол β существует и существует два угла.

Рисунок 3 иллюстрирует наличие двух углов β.

Рис. 3. Иллюстрация к задаче

Треугольник ABC (рис. 2) имеет определённый радиус описанной окружности.

По теореме синусов:

Рассмотрим два случая:

1.  (рис. 4) 

Тогда угол :

interneturok.ru