Треугольник геометрия – Геометрия треугольника

Треугольники. Видеоурок. Геометрия 7 Класс

Определение:  Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, соединенных отрезками.

                          

Рис. 1. Треугольник АВС

На данном рисунке изображен треугольник АВС. Обозначение выглядит так: .

Точка С не принадлежит отрезку АВ. Точки А, В, С называются вершинами треугольника, а отрезки АВ, АС, ВС называются его сторонами. Логично, что треугольник имеет три угла: ∠А, ∠В, ∠С, или ∠ВАС, ∠АВС, ∠ВСА. В геометрии принято, что угол А обозначается греческой буквой α, а сторона, лежащая напротив этого угла, обозначается а, поэтому ∠А = α, ВС = а. Аналогично, ∠В = β, АС = b, ∠С = γ, АВ = c.

Периметр треугольника – это сумма длин всех его сторон.

Вспомним, какие фигуры называются равными. Фигура F1 и фигура F2 называются равными, если их можно совместить наложением.

 

Рис. 2. Равные треугольники АВС и А

1В₁С₁

Треугольники АВС и А₁В₁С₁ являются равными, так как их можно совместить наложением. Из этого факта следует, что у равных фигур равны их соответствующие элементы. Таким образом, если стороны , то и углы .

Как же доказать равенство треугольников? Первый способ – по определению. Необходимо совместить наложением два треугольника. Если их элементы совпадают, треугольники равны. Однако данный процесс трудоемкий. Второй способ – сравнить части элементов, но с гарантией совмещения всех остальных элементов, то есть разработать признаки равенства.

Рассмотрим следующий пример:

Пример 1: Начертите треугольник DEF таким, чтобы угол Е был прямым. Назовите стороны, лежащие против соответствующих вершин.

Решение:

                                         

Рис. 3. Рисунок к примеру 1

Ответ: сторона DF лежит напротив угла Е, сторона EF лежит напротив угла D, сторона DE лежит напротив угла F.

Пример 2: Начертите треугольник DEF таким, чтобы угол Е был прямым. Назовите углы, лежащие против соответствующих сторон.

Решение:

                                         

Рис. 4. Рисунок к примеру 2

Ответ: Угол Е лежит напротив стороны DF, угол D лежит напротив стороны EF, угол F лежит напротив стороны DE.

Пример 3: Начертите треугольник DEF таким, чтобы угол Е был прямым. Укажите углы, которые прилежат к соответствующим сторонам.

Решение:

                                         

Рис. 5. Рисунок к примеру 3

Ответ: Углы D и F прилежат к стороне DF, углы Е и F прилежат к стороне EF, углы Е и D прилежат к стороне ED.

Пример 4: Периметр треугольника равен 48 см, а одна из сторон равна 18 см. Найдите две другие стороны, если их разность равна 4,6 см.

Решение:

Выполним пояснительный рисунок.

                           

Рис. 6. Рисунок к примеру 4

Известно, что периметр (сумма всех сторон треугольника) равен 48 см. Запишем это равенство: , также известно, что сторона a = 18 см, а . Выразим из соотношения периметра сумму .

. Выразим из соотношения разности двух сторон любую сторону:  и подставим в соотношение . Получим и решим уравнение.  Следовательно,

Ответ: 12,7 см и 17,3 см.

Пример 5: Сторона АВ треугольника АВС равна 17 см. Сторона АС вдвое больше стороны АВ, а сторона ВС на 10 меньше стороны АС. Найдите периметр треугольника.

Решение:

Выполним пояснительный рисунок:

                            

Рис. 7. Рисунок к примеру 5

Поскольку сторона АС вдвое больше стороны АВ, то АС = 2 · AB = 2 · 17 = 34 см. Далее найдем сторону ВС, по условию она меньше стороны АС на 10 см, то есть BC = AC – 10 = 34 – 10 = 24 см.

Периметр мы можем найти, сложив длины всех сторон треугольника Р = АС + ВС + АС = 34 + 24 + 17 = 75 см.

Ответ: 75 см.

Пример 6: Отрезок BD = DC. Сравните периметры треугольников АВС и ABD.

Решение:

Рис. 8. Рисунок к примеру 6

Выразим периметры соответствующих треугольников:

 Чтобы сравнить, какой периметр больше, мы воспользуемся стандартным методом в математике – методом вычитания. Вычтем периметры треугольников. Учитываем также, что BD = DC.

Таким образом, мы получили положительное число (длина стороны ВС), поэтому .

Ответ: .

           

Рекомендованные ссылки на интернет-ресурсы

1. Треугольник (Источник).
2. Треугольник. Справочник (Источник).
3. Прямая линия, отрезок (Источник).

 

Рекомендованное домашнее задание

1.  Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.

2.  Вычислите периметр треугольника со сторонами 1 дм, 12 см и 30 мм.

3.  Запишите прилежащие и противолежащие углы к сторонам треугольника КМР.

4.  *Периметр треугольника равен 27 см. Сторона АВ вдвое больше стороны ВС, а сторона АС втрое больше стороны АВ. Найдите длины сторон треугольника.

interneturok.ru

Все о треугольниках ГЕОМЕТРИЯ 7 КЛАСС Треугольник

Все о треугольниках ГЕОМЕТРИЯ 7 КЛАСС

Треугольник – геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, последовательно соединенных отрезками

Виды треугольников: l остроугольные l Тупоугольные l прямоугольные

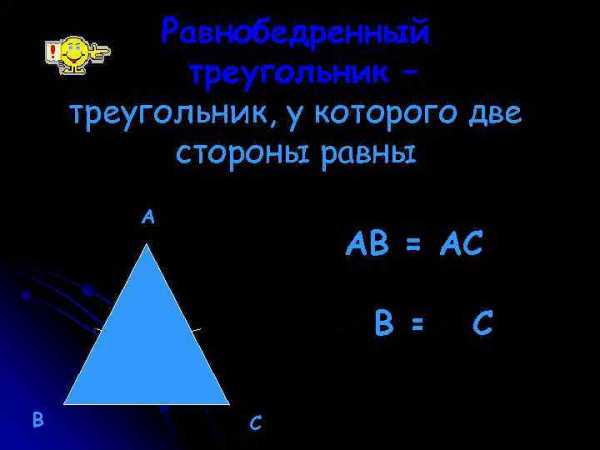Равнобедренный треугольник – треугольник, у которого две стороны равны А АВ = АС B = В С C

Если два треугольника равны, то элементы одного треугольника соответственно равны элементам другого треугольника. В равных треугольниках против соответственно равных сторон лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны.

Первый признак равенства треугольников: l Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Второй признак равенства треугольников: l Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Третий признак равенства треугольников: l Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

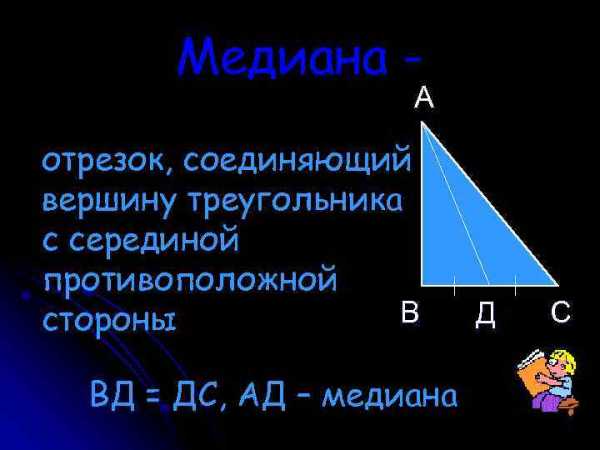Медиана — А отрезок, соединяющий вершину треугольника с серединой противоположной В стороны ВД = ДС, АД – медиана Д С

Биссектриса — отрезок биссектрисы А угла треугольника, соединяющий вершину треугольника с точкой противоположной В стороны ВАК = САК, АК — биссектриса К С

Высота перпендикуляр, В проведенный из вершины треугольника к прямой, содержащей противоположную А сторону ВД АС, ВД — высота С Д

В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты или их продолжения также пересекаются в одной точке

В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой

Внешним углом треугольника называется угол, смежный с каким – нибудь углом этого треугольника Внешний Угол Внешний угол треугольника равен сумме двух других углов треугольника, не смежных с ним

Прямоугольный треугольник к г и а п о т т е н е у з т к а т е т а

Некоторые свойства прямоугольных треугольников • сумма двух острых углов прямо- угольного треугольника равна 90° • катет 30 о • прямоугольного треуголь ника, лежащий против угла в 30°, равен половине гипотенузы если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°

Признаки равенства прямоугольных треугольников • Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны • Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны

Признаки равенства прямоугольных треугольников • если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны • если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны

Соотношение между сторонами и углами треугольника • В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона • В прямоугольном треугольнике гипотенуза больше катета • Если два угла треугольника равны, то треугольник равнобедренный

Неравенство треугольника Каждая сторона треугольника меньше суммы двух других сторон Для любых трех точек А, В и С, не лежащих на одной прямой, справедливы неравенства: АВ

Построение треугольника по трем сторонам C • A • • B

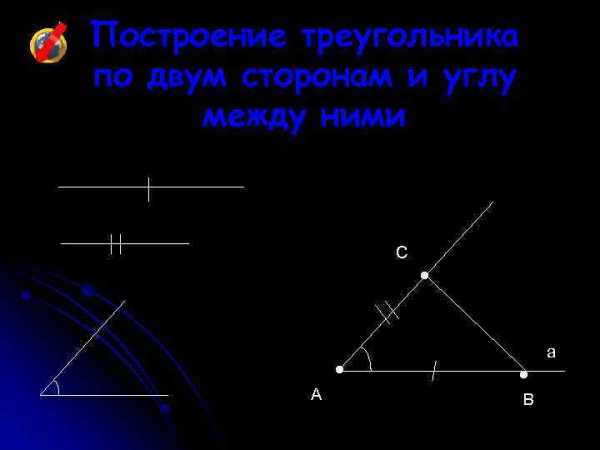Построение треугольника по двум сторонам и углу между ними C A • • • B a

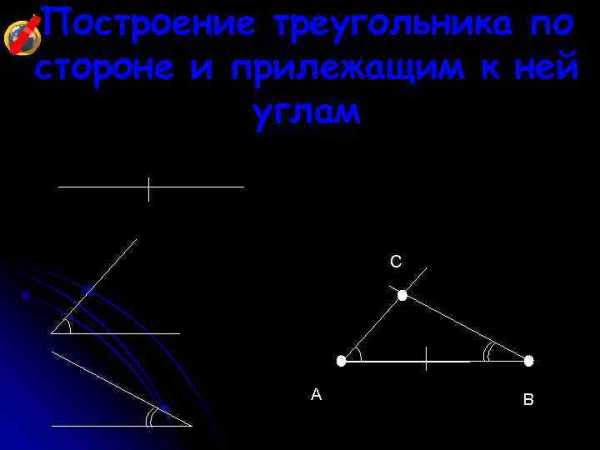Построение треугольника по стороне и прилежащим к ней углам C A B

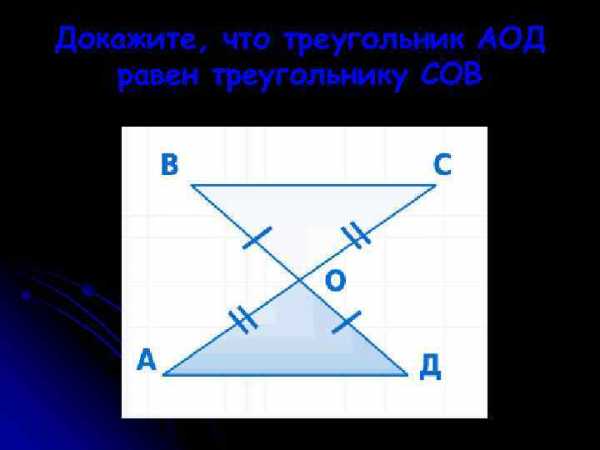Докажите, что треугольник АОД равен треугольнику СОВ

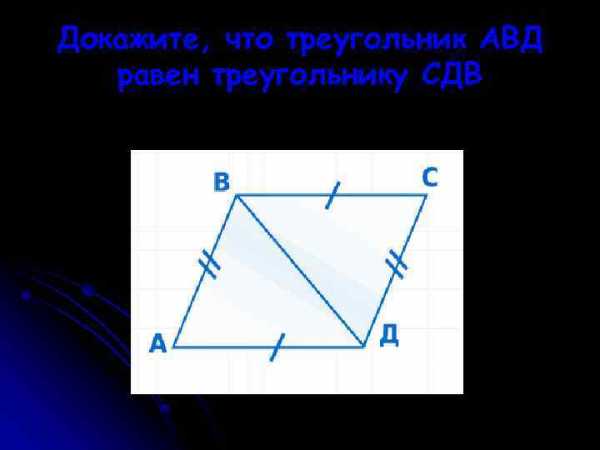Докажите, что треугольник АВД равен треугольнику СДВ

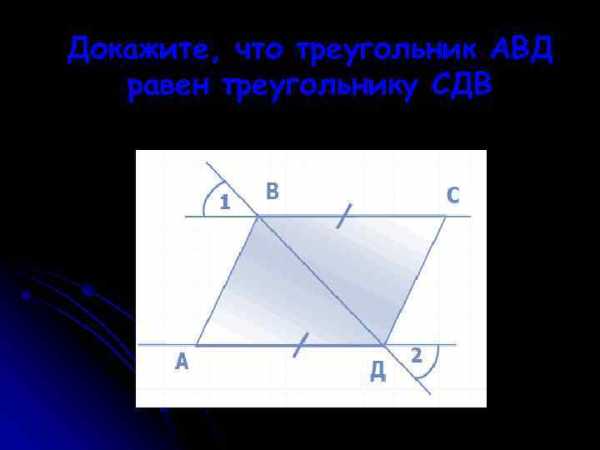Докажите, что треугольник АВД равен треугольнику СДВ

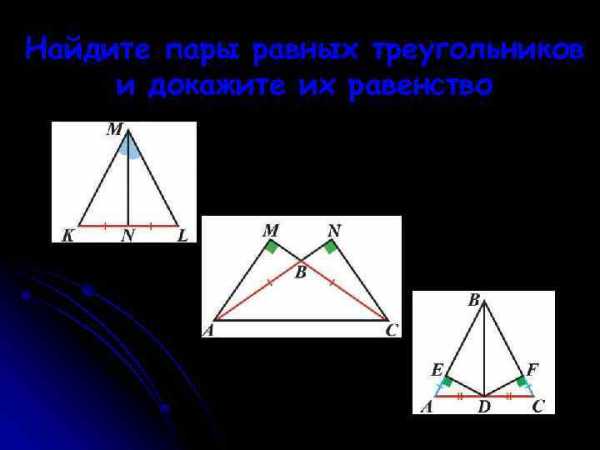Найдите пары равных треугольников и докажите их равенство

present5.com

Треугольники в геометрии. Равные треугольники. Высота треугольника. Медиана треугольника

Треугольник

Треугольник в геометрии

Треугольник в геометрии.

На рисунке показан треугольник ABC:

Отрезки AB, BC, CA называют сторонами треугольника. Точки A, B, C называют вершинами треугольника.

Периметр треугольника

Периметр треугольника:

Периметр треугольника – это сумма длин его сторон.

В нашем примере периметр треугольника ABC равен сумме длин сторон AB, BC, CA.

Биссектриса треугольника

Биссектриса треугольника:

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, связывающий вершину данного угла с точкой на противоположной стороне.

У треугольника три угла и, соответственно, три биссектрисы.

Свойство биссектрис треугольника

Свойством биссектрис треугольника является то, что все они пересекаются в одной точке.

Медиана треугольника

Медиана треугольника:

Медиана треугольника – это отрезок, связывающий вершину данного угла с серединой противоположной стороны.

У треугольника три угла и, соответственно, три медианы.

Свойство медиан треугольника

Свойством медиан треугольника является то, что все они пересекаются в одной точке.

Высота треугольника

Высота треугольника:

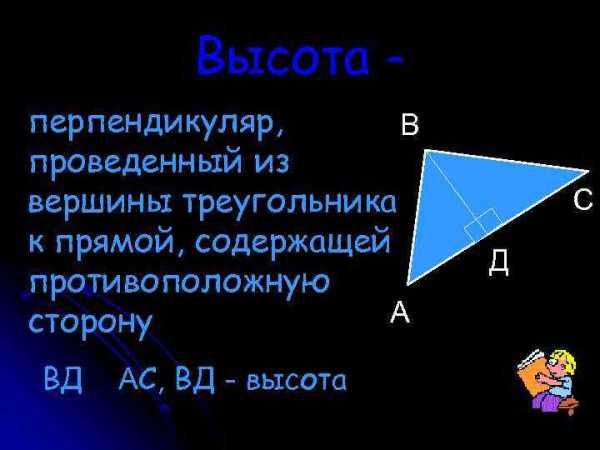
Высота треугольника – это перпендикуляр, опущенный из вершины треугольника на прямую, которой принадлежит противоположная сторона.

У треугольника три угла и, соответственно, три высоты.

Свойство высот треугольника

Свойством высот треугольника является то, что все они пересекаются в одной точке.

Признаки равенства треугольников

Для установления факта равенства двух треугольников используют признаки равенства треугольников:

www.sbp-program.ru

Геометрия треугольника | Lonskaya’s Blog

Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки попарно. Точки называются вершинами, а отрезки – сторонами треугольника.

A, B и С – вершины треугольника. AB, BC и CA — стороны треугольника.
Треугольник обозначается указанием его вершин: треугольник ABC.
Вместо слова треугольник употребляется символ Δ. т.е. Δ ABC.
Углом треугольника ABC при вершине A (или углом между сторонами AB и AC) называется угол, образованный лучами AB и AC; ∠A = ∠BAC = ∠CAB.

Треугольником также называют часть плоскости,  ограниченную отрезками АВ, ВС, АС (плоский треугольник). Точки А, В, С — вершины, отрезки АВ, ВС, АС — стороны треугольника. Сумма длин трех сторон треугольника  называется его периметром.

P = AB + BC + AC

Углом (или внутренним углом) треугольника ABC при вершине А называется угол, образованный лучами АВ и АС. Так же определяются углы треугольника при  вершинах В и С.

Углы CAB, ABC и ВСА треугольника ABC часто  обозначают одной буквой (А, В, С соответственно) или  греческими буквами α, β, γ (при этом внутри углов рисуют дуги).

Говорят, что угол А противолежит стороне ВС или сторона ВС противолежит углу А; так же угол В и сторона АС, угол С и сторона АВ противолежат (друг другу).

Угол, смежный с каким-нибудь углом треугольника,  называется внешним углом этого треугольника. Таков,  например, угол BCD (рис. 2). При каждом угле треугольника можно построить по два внешних угла (продолжив одну или другую сторону угла). Эти два угла равны как углы  вертикальные.

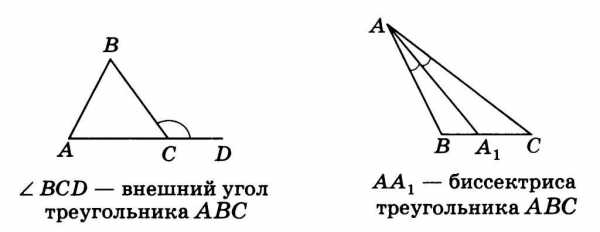
рисунок 2

Медиана и биссектриса треугольника

Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны, называется биссектрисой треугольника.

Определение 2: Биссектрисой треугольника, проведенной из данной вершины, называют отрезок, соединяющий эту вершину с точкой на противоположной стороне и делящий угол при данной вершине пополам.
Любой треугольник имеет три биссектрисы. Биссектрисы треугольника пересекаются в одной точке, и эта точка совпадает с центром вписанной окружности.

Отрезок, соединяющий вершину треугольника с  серединой противолежащей стороны, называется медианой треугольника (см. рис. ).

Любой треугольник имеет три медианы.

Точка пересечения медиан треугольника делит каждую медиану в отношении 2 : 1 (считая от вершины).

• Три медианы пересекаются в одной точке, которая всегда находится внутри треугольника (центр масс треугольника) и делят треугольник на 6 равновеликих треугольника.
• Каждая медиана делит треугольник на 2 равновеликих треугольника (одинаковой площади)

В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.

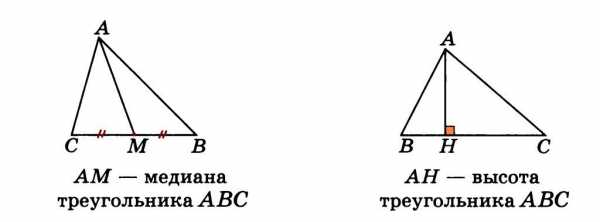
Перпендикуляр, проведенный из вершины  треугольника к прямой, содержащей противолежащую сторону,  называется высотой треугольника (см. рис. ).

Любой треугольник имеет три высоты.  Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.

 

Рассмотрим некоторые теоремы и свойства, связанные с медианой и биссектрисой

Скачать:  mediana_bissektrisa

Рассмотрим одно дополнительное построение, которое помогает при решении многих задач.

Пусть дан треугольник АВС и точка М находится на стороне ВС. Допустим дано, что АС = 20, АМ = 12 и ВМ : МС = 1 : 4, т.е. условия соответствуют следующему рисунку (рис.1).  Построим прямую , 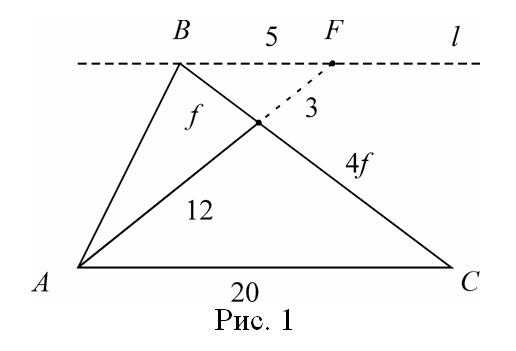проходящую через вершину В параллельно стороне АС и продолжим АМ до пересечения с прямой  в точке F. Ясно, что треугольники АМС и ВМF подобны (коэффициент подобия равен 4). Получаем, что BF = 5, MF = 3, т.е. появились новые данные, которые помогут решить задачу. Обратим внимание на два частных случая для прямой .  Если АМ – медиана (ВМ : МС = 1 : 1), то BF = AC и MF = AM (происходит продолжение медианы на свою длину) (рис.2).

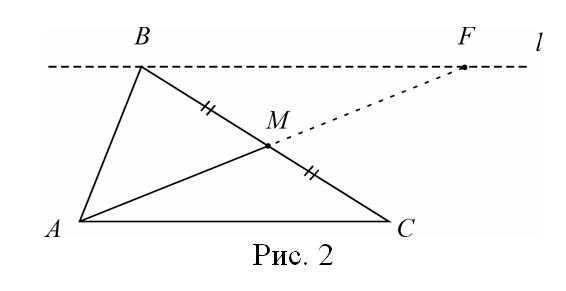
Если АМ – биссектриса, то треугольник АBF – равнобедренный(по углам). И «новый» отрезок ВF равен стороне AВ. Продолжение биссектрисы – отрезок MF равен (рис.3).   Прямую  будем называть «суперпрямой».

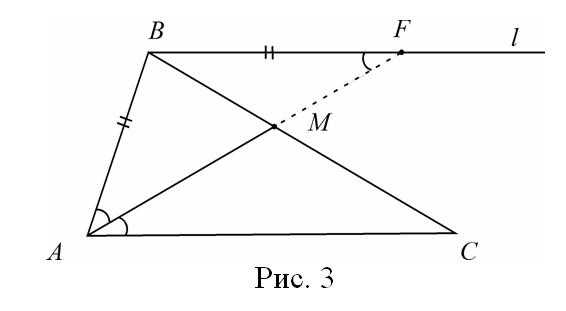
Задача 1. Доказать, что медиана треугольника меньше полусуммы двух сторон, между которыми она заключена.

Решение. Пусть AB = с, (рис.4)  АС = b и CM = m_c. Пусть F – точка пересечения прямой СМ и прямой, проходящей через А параллельно прямой ВС.  Ясно, что ΔMAF = ΔMBC  (по стороне c/2 и двум прилежащим углам)

Понравилось это:

Нравится Загрузка…

lonskaya.wordpress.com

СФЕРИЧЕСКАЯ ГЕОМЕТРИЯ | Энциклопедия Кругосвет

Содержание статьи

СФЕРИЧЕСКАЯ ГЕОМЕТРИЯ – математическая дисциплина, изучающая геометрические образы (точки, линии, фигуры), находящиеся на сфере, и соотношения между ними.

По-видимому, первым обращением человечества к тому, что потом получит название сферической геометрии, была планетарная теория греческого математика Евдокса (ок. 408–355), одного из участников Академии Платона. Это была попытка объяснить движение планет вокруг Земли с помощью четырех вращающихся концентрических сфер, каждая из которых имела особую ось вращения с концами, закрепленными на охватывающей сфере, к которой, в свою очередь, были «прибиты» звезды. Таким образом объяснялись замысловатые траектории планет (в переводе с греческого «планета» – блуждающая). Именно благодаря такой модели древнегреческие ученые умели достаточно точно описывать и предсказывать движения планет. Это было необходимо, например, в мореплавании, а так же во многих других «земных» задачах, где нужно было учитывать, что Земля – не плоский блин, покоящийся на трех китах. Значительный вклад в сферическую геометрию внес Менелай из Александрии (ок. 100 н.э.). Его труд Сферика стал вершиной достижений греков в этой области. В Сферике рассматриваются сферические треугольники – предмет, которого нет у Евклида. Менелай перенес на сферу евклидову теорию плоских треугольников и в числе прочего получил условие, при котором три точки на сторонах сферического треугольника или их продолжениях лежат на одной прямой. Соответствующая теорема для плоскости в то время была уже широко известна, однако в историю геометрии она вошла именно как теорема Менелая, причем, в отличие от Птолемея (ок. 150), у которого в работах немало вычислений, трактат Менелая геометричен строго в духе евклидовой традиции.

Основные положения сферической геометрии.

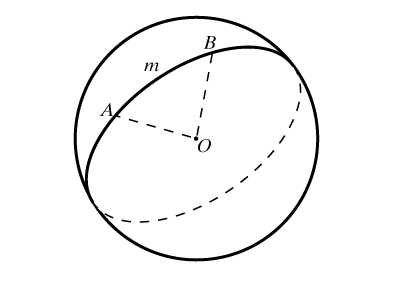
Всякая плоскость, пересекающая сферу, дает в сечении окружность. Если плоскость проходит через центр сферы, то в сечении получается так называемый большой круг. Через любые две точки на сфере, кроме диаметрально противоположных, можно провести единственный большой круг. (На глобусе примером большого круга служит экватор и все меридианы.) Через диаметрально противоположные точки проходит же бесконечное количество больших кругов. Меньшая дуга AmB (рис. 1) большого круга является кратчайшей из всех линий на сфере, соединяющих заданные точки. Такая линия называется геодезической. Геодезические линии играют на сфере ту же роль, что и прямые в планиметрии. Многие положения геометрии на плоскости справедливы и на сфере, но, в отличие от плоскости, две сферические прямые пересекаются в двух диаметрально противоположных точках. Таким образом, в сферической геометрии просто не существует понятия параллельности. Еще одно отличие – сферическая прямая замкнута, т.е. двигаясь по ней в одном и том же направлении, мы вернемся в исходную точку, точка не разбивает прямую на две части. И еще один удивительный с точки зрения планиметрии факт – треугольник на сфере может иметь все три прямых угла.

Прямые, отрезки, расстояния и углы на сфере.

Прямыми на сфере считаются большие окружности. Если две точки принадлежат большой окружности, то длина меньшей из дуг, соединяющих эти точки, определяется как сферическое расстояние между этими точками, а сама дуга – как сферический отрезок. Диаметрально противоположные точки соединены бесконечным числом сферических отрезков – больших полуокружностей. Длина сферического отрезка определяется через радианную меру центрального угла a и радиус сферы R (рис. 2), по формуле длины дуги она равна R a. Любая точка С сферического отрезка АВ разбивает его на два, и сумма их сферических длин, как и в планиметрии, равна длине всего отрезка, т.е. РАОС + РСОВ = РАОВ. Для любой же точки D вне отрезка АВ имеет место «сферическое неравенство треугольника»: сумма сферических расстояний от D до А и от D до В больше АВ, т.е. РAOD + РDOB > РAOB, – полное соответствие между сферической и плоской геометриями. Неравенство треугольника – одно из основополагающих в сферической геометрии, из него следует, что, как и в планиметрии, сферический отрезок короче любой сферической ломаной, а значит, и любой кривой на сфере, соединяющей его концы.

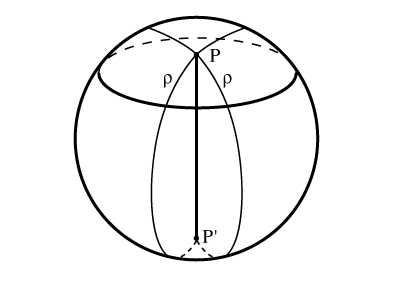
Таким же образом на сферу можно перенести и многие другие понятия планиметрии, в частности те, которые можно выразить через расстояния. Например, сферическая окружность – множество точек сферы, равноудаленных от заданной точки Р. Легко показать, что окружность лежит в плоскости, перпендикулярной диаметру сферы РР` (рис. 3), т.е. это обычная плоская окружность с центром на диаметре РР`. Но сферических центров у нее два: Р и Р`. Эти центры принято называть полюсами. Если обратиться к глобусу, то можно видеть, что идет речь именно о таких окружностях, как параллели, и сферическими центрами всех параллелей являются Северный и Южный полюса. Если диаметр r сферической окружности равен p/2, то сферическая окружность превращается в сферическую прямую. (На глобусе – экватор). В этом случае такую окружность называют полярой каждой из точек Р и P`.

Одним из важнейших понятий в геометрии является равенство фигур. Фигуры считаются равными, если одну на другую можно отобразить таким образом (поворотом и переносом), что сохранятся расстояния. Это верно и для сферической геометрии.

Углы на сфере определяются следующим образом. При пересечении двух сферических прямых a и b на сфере образуются четыре сферических двуугольника, подобно тому, как две пересекающиеся прямые на плоскости разбивают ее на четыре плоских угла (рис. 4). Каждому из двуугольников соответствует двугранный угол, образованный диаметральными плоскостями, содержащими a и b. А угол между сферическими прямыми равен меньшему из углов образуемых ими двуугольников.

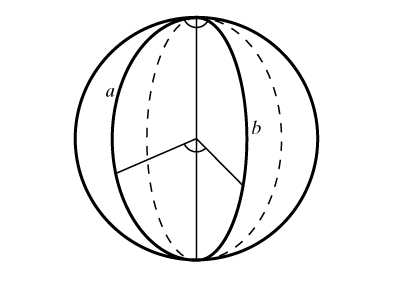
Отметим так же, что угол РABC, образованный на сфере двумя дугами большого круга, измеряют углом РA`BC` между касательными к соответствующим дугам в точке В (рис. 5) или двугранным углом, образованным диаметральными плоскостями, содержащими сферические отрезки АВ и ВС.

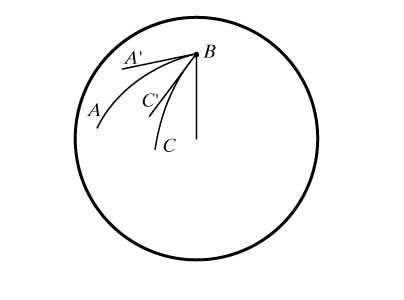
Точно так же, как и в стереометрии, каждой точке сферы сопоставляется луч, проведенный из центра сферы в эту точку, а любой фигуре на сфере – объединение всех пересекающих ее лучей. Так, сферической прямой соответствует содержащая ее диаметральная плоскость, сферическому отрезку – плоский угол, двуугольнику – двугранный угол, сферической окружности – коническая поверхность, ось которой проходит через полюсы окружности.

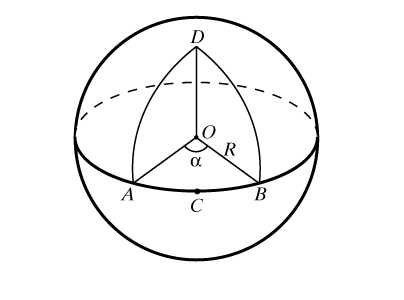
Многогранный угол с вершиной в центре сферы пересекает сферу по сферическому многоугольнику (рис. 6). Это область на сфере, ограниченная ломаной из сферических отрезков. Звенья ломаной – стороны сферического многоугольника. Их длины равны величинам соответствующих плоских углов многогранного угла, а величина угла при любой вершине А равна величине двугранного угла при ребре ОА.

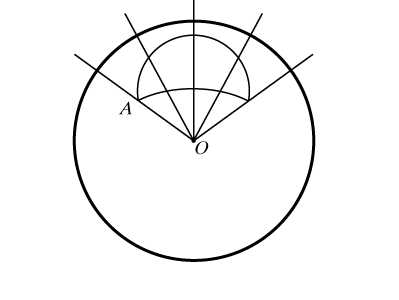
Сферический треугольник.

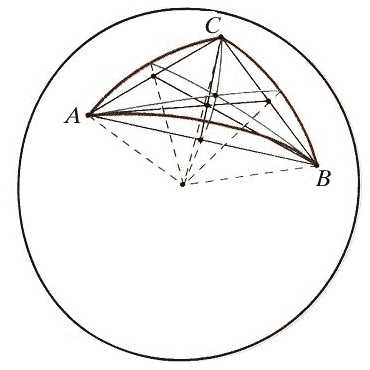
Среди всех сферических многоугольников наибольший интерес представляет сферический треугольник. Три больших окружности, пересекаясь попарно в двух точках, образуют на сфере восемь сферических треугольников. Зная элементы (стороны и углы) одного из них, можно определить элементы все остальных, поэтому рассматривают соотношения между элементами одного из них, того, у которого все стороны меньше половины большой окружности. Стороны треугольника измеряются плоскими углами трехгранного угла ОАВС, углы треугольника – двугранными углами того же трехгранного угла (рис. 7).

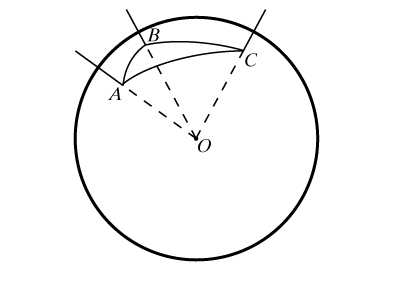
Многие свойства сферического треугольника (а они одновременно являются и свойствами трехгранных углов) почти полностью повторяют свойства обычного треугольника. Среди них – неравенство треугольника, которое на языке трехгранных углов гласит, что любой плоский угол трёхгранного угла меньше суммы двух других. Или, например, три признака равенства треугольников. Все планиметрические следствия упомянутых теорем вместе с их доказательствами остаются справедливыми на сфере. Так, множество точек, равноудаленных от концов отрезка, будет и на сфере перпендикулярной к нему прямой, проходящей через его середину, откуда следует, что серединные перпендикуляры к сторонам сферического треугольника AВС имеют общую точку, точнее, две диаметрально противоположные общие точки Р и Р`, являющиеся полюсами его единственной описанной окружности (рис. 8). В стереометрии это означает, что около любого трёхгранного угла можно описать конус. Легко перенести на сферу и теорему о том, что биссектрисы треугольника пересекаются в центре его вписанной окружности.

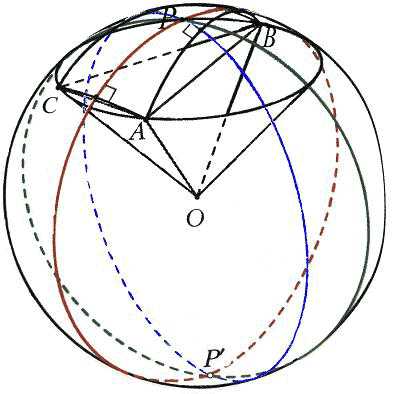
Теоремы о пересечении высот и медиан также остаются верными, но их обычные доказательства в планиметрии прямо или косвенно используют параллельность, которой, на сфере нет, и потому проще доказать их заново, на языке стереометрии. Рис. 9 иллюстрирует доказательство сферической теоремы о медианах: плоскости, содержащие медианы сферического треугольника АВС, пересекают плоский треугольник с теми же вершинами по его обычным медианам, следовательно, все они содержат радиус сферы, проходящий через точку пересечения плоских медиан. Конец радиуса и будет общей точкой трех «сферических» медиан.

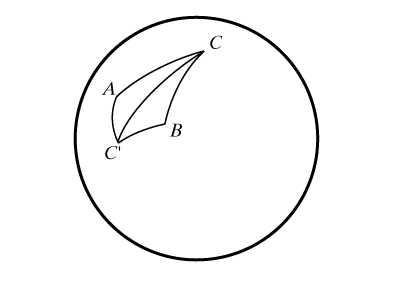
Свойства сферических треугольников во многом отличаются от свойств треугольников на плоскости. Так, к известным трем случаям равенства прямолинейных треугольников добавляется еще и четвертый: два треугольника АВС и А`В`С` равны, если равны соответственно три угла РА = РА`, РВ = РВ`, РС = РС`. Таким образом, на сфере не существует подобных треугольников, более того, в сферической геометрии нет самого понятия подобия, т.к. не существует преобразований, изменяющих все расстояния в одинаковое (не равное 1) число раз. Эти особенности связаны с нарушением евклидовой аксиомы о параллельных прямых и также присущи геометрии Лобачевского. Треугольники, имеющие равные элементы и различную ориентацию, называются симметричными, таковы, например, треугольники АС`С и ВСС` (рис. 10).

Сумма углов всякого сферического треугольника всегда больше 180°. Разность РА+РВ +РС – p = d (измеряемая в радианах) – величина положительная и называется сферическим избытком данного сферического треугольника. Площадь сферического треугольника: S = R2 d где R – радиус сферы, а d – сферический избыток. Эта формула впервые была опубликована голландцем А.Жираром в 1629 и названа его именем.

Если рассматривать двуугольник с углом a, то при 226 = 2p/n (n – целое число) сферу можно разрезать ровно на п копий такого двуугольника, а площадь сферы равна 4пR² = 4p при R = 1, поэтому площадь двуугольника равна 4p/n = 2a. Эта формула верна и при a = 2pт/п и, следовательно, верна для всех a. Если продолжить стороны сферического треугольника АВС и выразить площадь сферы через площади образующихся при этом двуугольников с углами А, В, С и его собственную площадь, то можно прийти к вышеприведенной формуле Жирара.

Координаты на сфере.

Каждая точка на сфере вполне определяется заданием двух чисел; эти числа (координаты) определяются следующим образом (рис. 11). Фиксируется некоторый большой круг QQ` (экватор), одна из двух точек пересечения диаметра сферы PP`, перпендикулярного к плоскости экватора, с поверхностью сферы, например Р (полюс), и один из больших полукругов PAP`, выходящих из полюса (первый меридиан). Большие полукруги, выходящие из P, называются меридианами, малые круги, параллельные экватору, такие, как LL`, – параллелями. В качестве одной из координат точки M на сфере принимается угол q = POM (высота точки), в качестве второй – угол j = AON между первым меридианом и меридианом, проходящим через точку M (долгота точки, отсчитываемая против часовой стрелки).

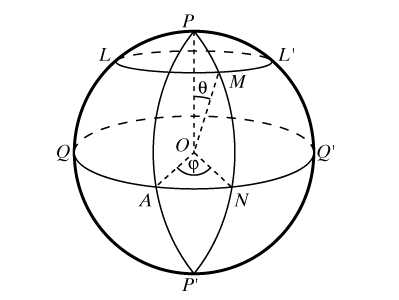
В географии (на глобусе) в качестве первого меридиана принято использовать Гринвичский меридиан, проходящий через главный зал Гринвичской обсерватории (Гринвич – городской округ Лондона), он разделяет Землю на Восточное и Западное полушария, соответственно и долгота бывает восточной либо западной и измеряется от 0 до 180° в обе стороны от Гринвича. А вместо высоты точки в географии принято использовать широту, т.е. угол NOM = 90° – q, отсчитываемый от экватора. Т.к. экватор делит Землю на Северное и Южное полушария, то и широта бывает северной либо южной и изменяется от 0 до 90°.

Марина Федосова

www.krugosvet.ru

Треугольник (в геометрии) — это… Что такое Треугольник (в геометрии)?



Треугольник (в геометрии)

Треугольник прямолинейный, часть плоскости, ограниченная тремя отрезками прямых (стороны Т.), имеющими попарно по одному общему концу (вершины Т.). Т., у которого длины всех сторон равны, называется равносторонним, или правильным (рис., 1), Т. с двумя равными сторонами ‒ равнобедренным (рис., 2). Т. называется остроугольным (рис., 3), если все углы его острые; прямоугольным (рис., 4) ‒ если один из его углов прямой; тупоугольным (рис., 5) ‒ если один из его углов тупой. Более одного прямого или тупого угла Т. иметь не может, так как сумма всех трёх углов равна двум прямым углам (180° или, в радианах, p). Площадь Т. равна ah/2, где а ‒ любая из сторон Т., принимаемая за его основание, a h ‒ соответствующая высота (рис., 6). Стороны Т. подчинены условию: длина каждой из них меньше суммы и больше разности длин двух других сторон. Два Т. конгруэнтны (равны), если они имеют равными (попарно) все стороны или две стороны и угол между ними, или сторону и два прилежащих угла. Числовые соотношения между углами и сторонами Т. изучаются в тригонометрии. О Т. на сфере см. Сферическая геометрия. Сферическая тригонометрия.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

• Третьяковы
• Треугольник (муз. инструмент)

Смотреть что такое «Треугольник (в геометрии)» в других словарях:

• ТРЕУГОЛЬНИК (в геометрии) — ТРЕУГОЛЬНИК, часть плоскости, ограниченная тремя отрезками прямых (сторонами треугольника), имеющими попарно по одному общему концу (вершины треугольника). Сумма всех углов треугольника равна двум прямым (180°). Площадь треугольника S=1/2 ah, где …   Энциклопедический словарь

• ТРЕУГОЛЬНИК — (1) простейшая плоская геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами Т., а отрезки его сторонами. Углами Т. (точнее, его внутренними углами)… …   Большая политехническая энциклопедия

• Треугольник — Предположим, что на какой нибудь поверхности даны триточки А, В и С, не лежащие на одной и той же кратчайшей (геодезической)линии. Соединив эти точки кратчайшими линиями, получим фигуру,называемую треугольником. Точки А, В и С наз. вершинами, а… …   Энциклопедия Брокгауза и Ефрона

• Треугольник — У этого термина существуют и другие значения, см. Треугольник (значения). Треугольник (в евклидовом пространстве)  это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки,… …   Википедия

• ТРЕУГОЛЬНИК — в евклидовой плоскости три точки (вершины) и три отрезка прямых (стороны) с концами в этих точках. Иногда при определении Т. к нему относят и выпуклую часть плоскости, к рая ограничена сторонами Т. Понятие Т. вводится и в многообразиях, отличных… …   Математическая энциклопедия

• Треугольник — Предположим, что на какой нибудь поверхности даны три точки А, В и С, не лежащие на одной и той же кратчайшей (геодезической) линии. Соединив эти точки кратчайшими линиями, получим фигуру, называемую треугольником. Точки А, В и С наз. вершинами,… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

• Пятая аксиома в евклидовой геометрии — Пересечения прямых (анимация) Аксиома параллельности Евклида, или пятый постулат одна из аксиом, лежащих в основании классической планиметрии. Впервые приведена в «Началах» Евклида [1]: И если прямая, падающая на две прямые, образует внутренние и …   Википедия

• Полярный треугольник — понятие сферической геометрии. Полярным для данного сферического треугольника называется такой сферический треугольник, по отношению к сторонам которого вершины данного треугольника являются полюсами. Полюсом называется одна из двух точек… …   Википедия

• ГЕОДЕЗИЧЕСКИЙ ТРЕУГОЛЬНИК — фигура, состоящая из трех различных точек и попарно соединяющих их геодезических линий. Точки наз. вершинами, геодезические сторонами. Г. т. может рассматриваться в любом пространстве, где есть геодезические. Если стороны Г. т., лежащего в… …   Математическая энциклопедия

• СФЕРИЧЕСКИЙ ТРЕУГОЛЬНИК — СФЕРИЧЕСКИЙ ТРЕУГОЛЬНИК, ТРЕУГОЛЬНИК, образованный пересечением на поверхности СФЕРЫ дуг трех больших ОКРУЖНОСТЕЙ (имеющих тот же РАДИУС, что и сфера). Стороны сферических треугольников измеряются в углах, которым эти дуги противолежат из центра… …   Научно-технический энциклопедический словарь

dic.academic.ru

Геометрия прямоугольного треугольника. | Геометрия

Геометрия прямоугольного треугольника. | Геометрия — просто!

Добрый день, друзья! Сегодня из «Сборника задач для поступающих во ВТУЗы» мы будем решать задачи по геометрии прямоугольного треугольника.
Такие треугольники примечательны тем, что у них присутствуют некоторые особенности,  которых нет у простых треугольников, а именно.
Катет прямоугольного треугольника, лежащий против угла в 30º равен половине гипотенузы.
Это правило вообще-то необходимо запомнить накрепко, особенно тем ученикам, которые собираются в 10-11 классы.
Поскольку с помощью него  будут рассчитаны  многие значения углов в тригонометрии.
Ещё правило — медиана прямоугольного треугольника, проведённая  из вершины прямого угла, равна половине гипотенузы.
Т.е. она образует два равнобедренных треугольника.
Пока на этом остановимся и перейдём к задачам.

Задача 1. Медиана гипотенузы прямоугольного треугольника равна m и делит прямой угол в отношении 1:2. Найти стороны треугольника.
Решение: Поскольку медиана делит прямой угол в отношении 2:1, то принимая  1 за Х, а 2 за 2Х получим 3Х=90, или Х=30.
Медиана разделила прямой угол на 2 угла: 60º и 30º.
 Так как ВЕ=ЕС=m, то треугольник АВЕ — равнобедренный с углом при основании 60º.
Но если один угол при основании  равнобедренного треугольника равен 60º, то и другой тоже будет 60º.
А так как сумма внутренних углов треугольника равна 180º, то на третий угол приходится 180-60-60=60º.
Т.е. треугольник АВЕ — равносторонний, а это значит, что АВ=m.
Нам осталось найти второй катет АС.
Из треугольника АЕС мы видим, что АЕ=ЕС=m.
Треугольник равнобедренный, а это значит, что угол при вершине С равен 30º.
Теперь рассмотрим треугольник EDC.
ED — перпендикуляр, а также медиана угла при вершине равнобедренного треугольника АЕС.
ED = m/2, как катет, лежащий против угла в 30º.
По теореме Пифагора из треугольника EDC находим DC.
DC² = m² — (m/2)² = 3m²/4.
Или DC = m√3/2.  А вся сторона треугольника АС = m√3.
Ответ: Стороны треугольника равны АВ = m, ВС = 2m, АС =m√3.

Задача 2. В прямоугольный треугольник с углом 60º вписан ромб со стороной, равной 6 см так, что угол 60° у них общий и все вершины ромба лежат на сторонах треугольника.
Найти стороны треугольника.
Решение: Нам дано, что в прямоугольном треугольнике один угол равен 60°. Значит, второй угол равен 30°.
Ведь сумма острых углов в прямоугольном треугольнике равна 90°.
Так как BDKM ромб, то его противоположные стороны параллельны.
BM параллельна DK. А это значит, что при пересечении двух параллельных секущей ВС, образуются соответственные углы MBD и KDC.
Так как прямые параллельны, то углы равны по 60°.
Получилось, что в треугольнике DKC два угла равны соответственно 60° и 30°.
А это значит, что третий угол равен 90°.
Т.е. треугольник DKC прямоугольный.
Поскольку в ромбе все стороны равны, то BD=BM,  равно 6 см.
Сторона DK в треугольнике DKC тоже равна 6 см.
Но она лежит против угла в 30°.
Значит, гипотенуза DC треугольника равна  12 см.
А вся гипотенуза треугольника АВС равна 6+12 = 18 см.
Из прямоугольного треугольника АМК, в котором острые углы так же равны 30° и 60°находим катет АМ.
Он равен половине гипотенузы МК или 6:2 = 3 см.
А всего катет АВ треугольника АВС равен 6+3 = 9 см.
Остаётся найти второй катет  треугольника АВС.
Его мы находим по теореме Пифагора.
АС² = ВС² — АВ² = 18² — 9² = 324 — 81 = 243.  Отсюда, АС = √243 = 9√3.
Ответ: Стороны треугольника равны 9 см, 9√3 см и 18 см.

Задача 3. Точка на гипотенузе, равноудалённая от обоих катетов, делит гипотенузу на отрезки длиной 3 и 4 см.
Найти катеты треугольника.
Решение: Так как как точка М равноудалена от катетов, а кратчайшее расстояние между точкой и прямой есть перпендикуляр,
то углы К и М — прямые.
Образовались прямоугольные треугольники ВКМ и MNC.
Эти треугольники подобны друг другу и треугольнику АВС.
Из подобия треугольников мы можем составить пропорцию:
МС так относится к  Х, как ВМ относится к ВК. Или 4/Х = 3/ВК.
Отсюда, ВК = 3Х/4.
Составляем другую пропорцию:
4/NC = 3/X, отсюда NC = 4Х/3.
Получается, что катет АВ равен Х + 3Х/4= 7Х/4,
а катет АС равен Х + 4Х/3 = 7Х/3.
По теореме Пифагора имеем:
(7Х/4)² + (7Х/3)² = 7²
49х²/16 + 49х²/9 = 49, или
Х²(1/16 + 1/9) = 1
25Х² = 16*9
Х = 4*3/5 = 12/5 = 2,4 см
АС = 2,4 + 2,4 * 4/3 = 2,4 + 3,2 = 5,6 см.
АВ = 2,4 + 2,4 * 3/4 = 2,4 + 1,8 = 4,2 см.
Ответ: 5,6 см; 4,2 см.

Задача 4. В прямоугольном треугольнике медианы катетов равны BE = √52 и CD =√73.
Найти гипотенузу треугольника.
Решение: Примем АЕ = АС = m.
BD = AD = k.
Из прямоугольного треугольника АВЕ имеем:
(2k)² + m² = (√52)²
Из прямоугольного треугольника ADC  имеем:
k² + (2m)² = (√73)².
Решаем совместно систему двух уравнений с двумя неизвестными:
4k² + m² = 52
k² + 4m² = 73
Домножаем второе уравнение на 4 и вычитаем из первого уравнения второе:
4k² + m² -4k² — 16m² = 52 — 292
-15m² = — 240
m² = 16
m=4 см   k² + 4*4² = 73   k² = 9  k = 3 см.
Катеты треугольника АВС равны 6 см и 8 см,
По теореме Пифагора гипотенуза равна 10 см.
Ответ: гипотенуза ВС = 10 см.

На сегодня всё. В следующий раз мы продолжим решение геометрических задач для подготовки к ОГЭ.

Вам так же будет интересно:

Оставить комментарий

geometriyaprosto.ru