Задачи по статистике с решениями и выводами
Кратко рассматривается статистическая сводка и группировка, виды группировок, а также формула Стерджесса. Приведен пример решения задачи на группировку статистической совокупности.
Рассматриваются относительные показатели планового задания, выполнения плана, динамики и их взаимосвязь между собой. Приведены примеры расчета рассматриваемых относительных величин.
На странице рассмотрен расчет относительных показателей структуры (ОВС) и координации (ОВК). Приведены примеры расчета рассматриваемых относительных величин.
На странице рассматриваются относительные показатели динамики (ОВД) и интенсивности (ОВИ). Приведены примеры расчета рассматриваемых относительных величин.
Решено несколько задач по статистике на использование средних величин. Приведены примеры вычислений средней арифметической простой, средней арифметической взвешенной, средней гармонической взвешенной. Решение задач предваряет краткая теория.
Рассматривается понятие средней хронологической величины в рядах динамики, виды средней хронологической. Приведены примеры расчета средней хронологической для моментных и интервальных рядов с равноотстоящими и неравноотстоящими интервалами.
Описание структурных средних дискретного и интервального рядов. На примерах решения задач показан расчет показателей — моды, медианы, квартилей, децилей.
В приведенной на странице задаче показано вычисление абсолютных и относительных показателей вариации интервального ряда — размах вариации, среднее линейное отклонение, дисперсия, коэффициент вариации.
На странице рассмотрена задача на правило сложения дисперсий и сопутствующий расчет средней внутригрупповой и межгрупповой дисперсий.
Вычисление числовых характеристик выборки. Рассчитаны такие характеристики как выборочная средняя, мода и медиана, средний квадрат отклонений (дисперсия), выборочное среднее квадратическое отклонение и коэффициент вариации. Приведен пример вычисления предельной ошибки выборочной средней и выборочной доли, а также границ генеральной средней и удельного веса.
Страница содежит описание методов выборочного наблюдения, приведены формулы для расчета средней и предельной ошибок выборки. Изложены сведения по методам собственно-случайного отбора, механической выборки, типической (районированной) выборки, серийной выборки. Привена таблица с формулами для определения численности выборки при различных методах отбора.
Приведена краткая теория и рассмотрен пример решения задачи на расчет коэффициента корреляции знаков Фехнера.
Формула и смысл коэффициента линейной корреляции Пирсона, значимость линейного коэффициента корреляции. Страница содержит краткую теорию и типовой пример по расчету коэффициента корреляции Пирсона и проверке его значимости.
Содержится краткая теория и пример решения задачи на ранговую корреляцию. Дано понятие ранговой корреляции, показан расчет коэффициента ранговой корреляции Спирмена.
На странице рассмотрено применение ранговой корреляции и коэффициента ранговой корреляции Кендалла в статистике. Приведена краткая теория, а также задача с примером расчета коэффициента Кендалла с проверкой гипотезы о его значимости.
Рассмотрено вычисление эмпирического корреляционного отношения и эмпирического коэффициента детерминации, на примере показан расчет внутригрупповой и межгрупповой дисперсии.
Дана краткая теория и на примере решения задачи показан расчет коэффициентов ассоциации и контингенции.
Страница содержит сведения по методам изучения взаимосвязей между качественными признаками с помощью коэффициентов взаимной сопряженности Чупрова и Пирсона.
На странице рассмотрены задачи на ряды динамики. Показано вычисление цепных, базисных и средних показателей динамики, а также недостающих уровней динамических рядов. Приведены формулы цепных, базисных и средних абсолютных приростов, темпов роста и темпов прироста.
Страница содержит последовательное и систематизированное изложение проверенных практикой методов обработки динамических рядов — метода скользящей средней и метода укрупнения интервалов.
Содержатся сведения по анализу рядов динамики — изучение тренда временного ряда с помощью аналитического выравнивания по прямой методом наименьших квадратов, построение точечного и интервального прогноза.
Представлены базовые методы индексного анализа. В решенных задачах рассчитаны индивидуальные и общие индексы цен, себестоимости, физического объема, стоимости товарооборота и затрат, а также показано разложение абсолютного прироста по факторам. Приведен расчет средних индексов — индексов цен и себестоимости переменного и постоянного составов, а также индекс структурных сдвигов. Показано разложение абсолютного прироста средней цены и себестоимости на факторы.
Приведен пример решения задачи на вычисление индексов цен Пааше, Ласпейреса, Фишера, а также индексов физического объема Ласпейреса и Пааше. Показана взаимосвязь между исчисленными индексами.
Изложена методика расчета календарного, табельного и максимально-возможного фондов рабочего времени, а также коэффициентов их использования. Содержатся сведения по составлению балансов рабочего времени на предприятии. Рассматриваются коэффициенты использования рабочего дня, рабочего периода, а также интегральный показатель использования рабочего времени.
Решена задача с вычислением уровня и динамики производительности труда. Рассчитаны индексы средней производительности труда — индекс переменного состава, постоянного состава и структурных сдвигов. Показано разложение на факторы прироста продукции, вычисление числа высвободившихся работников в связи с ростом производительности.
В представленной на странице задаче вычислены индексы средней заработной платы переменного состава, постоянного состава, структурных сдвигов, показано разложение на факторы изменения средней заработной платы и фонда заработной платы.
Страница содержит краткое описание показателей движения рабочей силы, также на примере показаны расчеты коэффициентов текучести кадров, оборота по приему и увольнению, общего оборота и постоянства кадров.
Рассмотрены основные показатели статистики основых фондов — полная и остаточная стоимость основных фондов, коэффициенты годности и износа, коэффициенты обновления и выбытия, показатели фондоотдачи и фондоемкости.
Рассмотрена краткая теория и решена задача по статистике оборотных средств предприятия. На примере показаны расчеты показателей эффективности использования оборотных средств — коэффициента оборачиваемости, закрепления, продолжительности одного оборота.
Страница содержит описание показателей естественного и механического движения населения. Рассмотрены общие коэффициенты рождаемости, смертности, механического движения, естественного и общего прироста населения.
Рассматриваются показатели статистики трудовых ресурсов — трудоспособное население, экономически активное население, коэффициенты замещения и воспроизводства трудовых ресурсов, коэффициент пенсионной нагрузки, коэффициент экономической активности населения, коэффициенты занятости и безработицы.
Краткое описание системы национальных счетов и основные показатели этой системы. Рассматривается пример решения задачи на составление консолидированных счетов СНС.
Приведены необходимые теоретические сведения и образцы решения задач для расчета валового внутреннего продукта (ВВП) тремя методами — производственным методом, распределительным методом и методом конечного использования.
На странице рассмотрены понятия номинальной и реальной стоимости ВВП — валового внутреннего продукта в текущих и постоянных ценах. Рассмотрена задача с применением индекса-дефлятора и индекса физической стоимости ВВП.
100task.ru
Задачи по статистике с решениями
Примеры решения задач по статистике
Задача Статистическая сводка и группировка.
Теория по решению задачи.
Статистическая сводка – научно обработанный материал статистического наблюдения в целях получения обобщенной характеристики изучаемого явления.
Группировка – распределение единиц изучаемого объекта на однородные типичные группы по существенным для них признакам.
Интервал – разница между максимальным и минимальным значением признака в каждой группе.
, где
i – величина интервала;
R – размах колебания (R=xmax-xmin)
n – принятое число групп;
xmax, xmin – наибольшее и наименьшее значение признака в изучаемой совокупности.
, где
N – число наблюдений
Типовая задача № 1
Распределите потребительские общества по размеру товарооборота на 3 группы с равными интервалами. В каждой группе подсчитайте количество потребительских обществ, сумму товарооборота, сумму издержек обращения. Результаты группировок представьте в табличной форме. К какому виду статистических таблиц относится составление вами таблица, и какой вид группировки она содержит?
Имеются основные экономические показатели потребительских обществ за отчетный период:
Таблица № 1
|
№ п/п |
Товарооборот в млн. грн. |
Издержки обращения, в млн. грн. |
Прибыль, в млн. грн. |
|
1 |
390 |
14 |
40 |
|
2 |
190 |
8 |
15 |
|
3 |
180 |
8 |
15 |
|
4 |
450 |
16 |
42 |
|
5 |
200 |
10 |
20 |
|
6 |
390 |
14 |
40 |
|
7 |
180 |
10 |
13 |
|
8 |
250 |
11 |
25 |
|
9 |
330 |
12 |
25 |
|
10 |
240 |
8 |
|
|
11 |
300 |
11 |
24 |
|
12 |
230 |
10 |
15 |
|
13 |
420 |
12 |
36 |
|
14 |
190 |
14 |
12 |
|
15 |
450 |
15 |
42 |
|
16 |
200 |
8 |
23 |
|
Итого |
4590 |
181 |
408 |
Ход решения задачи:
Т. к. нам известен группировочный признак, работу необходимо начать в определения величины интервала по формуле:
Образец 3 группы потребительских обществ по размеру товарооборота.
Определяем границы групп:
1 группа: 180+90=270 (180-270)
2 группа: 270+90=360 (270-360)
3 группа: 360+90+450 (360-450)
После того, как выбран группировочный признак, намечено число групп и образованы сами группы, необходимо отобрать показатели, которыми будут характеризоваться группы, и определить их величину по каждой группе.
В нашем примере каждую группу необходимо охарактеризовать следующими показателями:
а) количеством потребительских обществ;
б) суммой товарооборота;
в) суммой издержек обращения.
Для заполнения итоговой таблицы составим предварительно рабочие таблицы № 2, 3, 4.
Группа потребительских обществ с товарооборотом от 180 до 270 млн. грн.
Таблица № 2
|
№ п/п |
Номер потребительского общества |
Товарооборот, в млн. грн. |
Сумма издержек обращения, в млн. грн. |
|
1 |
2 |
190 |
8 |
|
2 |
3 |
180 |
8 |
|
3 |
5 |
200 |
10 |
|
4 |
7 |
180 |
10 |
|
5 |
8 |
250 |
11 |
|
6 |
10 |
240 |
8 |
|
7 |
12 |
230 |
10 |
|
8 |
14 |
190 |
14 |
|
9 |
16 |
200 |
8 |
|
Итого |
9 |
1860 |
87 |
Группа потребительских обществ с товарооборотом от 270 до 3660 млн. грн.
Таблица № 3
|
№ п/п |
Номер потребительского общества |
Товарооборот, в млн. грн. |
Сумма издержек обращения, в млн. грн. |
|
1 |
9 |
330 |
12 |
|
2 |
11 |
300 |
11 |
|
Итого |
2 |
630 |
23 |
Группа потребительских обществ с товарооборотом от 360 до 450 млн. грн.
Таблица № 4
|
№ п/п |
Номер потребительского общества |
Товарооборот, в млн. грн. |
Сумма издержек обращения, в млн. грн. |
|
1 |
1 |
390 |
14 |
|
2 |
4 |
450 |
16 |
|
3 |
6 |
390 |
14 |
|
4 |
13 |
420 |
12 |
|
5 |
15 |
450 |
15 |
|
Итого |
5 |
2100 |
71 |
Итоговые показатели рабочих таблиц занесем в окончательную итоговую таблицу и получим групповую таблицу № 5.
Группировка потребительских обществ, по размеру товарооборота:
Таблица № 5
|
Группы потребительских обществ по размеру товарооборота, млн. грн. |
Количество потребительских обществ |
Товарооборот, в млн. грн. |
Сумма издержек обращения, в млн. грн. |
|
180-270 |
9 |
1860 |
87 |
|
270-360 |
2 |
630 |
23 |
|
360-450 |
16 |
4590 |
181 |
Вывод: По результатам итоговой таблицы можно сделать вывод, что с увеличением объема товарооборота потребительских обществ, относительный показатель уровня издержек обращения снижается. Следовательно, между ними существует обратная связь. Составленная нами таблица является групповой таблицей, т. к. ее подлежащее содержит группы потребительских обществ по размеру товарооборота. Она содержит аналитический вид группировки.
Задача — Ряды распределения и статистические таблицы.
Теория по решению задачи.
Статистический ряд распределения – упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку.
Дискретный вариационный ряд – характеризует распределение единиц совокупности по дискретному (прерывному) признаку.
Интервальный вариационный ряд – характеризует распределение единиц совокупности по интервальному (непрерывному) признаку.
Для изображения дискретных вариационных рядов распределения используется «полигон распределения». Для графического изображения интервального вариационного ряда применяются «гистограмма» и «кумулята».
Задача 1.
На экзамене по истории студенты получили оценки:
3 4 4 4 3 4
3 4 3 5 4 4
5 5 2 3 2 3
3 4 4 5 3 3
5 4 5 4 4 4
Построить дискретный вариационный ряд распределения студентов по баллам и изобразить его графически.
Ход решения задачи:
Определяем элементы ряда распределения: варианты, частоты, частоты.
|
Оценка, баллы |
Кол-во студентов с такой оценкой, человек |
В процентах к итогу |
|
2 |
2 |
6,7 |
|
3 |
9 |
30 |
|
4 |
13 |
43,3 |
|
5 |
6 |
20 |
|
Итого |
30 |
100 |
Теперь графически изобразим дискретный ряд распределения в виде помпона распределения.
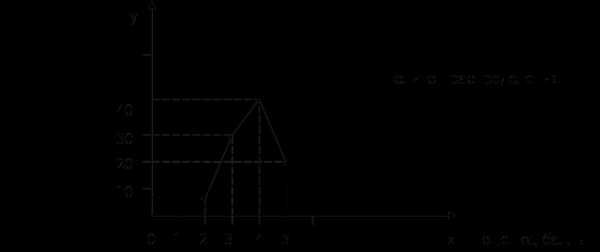
Можно сделать вывод о том, что преобладающее большинство студентов получило «4» (43,3 %).
Задача 2.
Во время выборочной проверки было установлено, что продолжительность одной покупки в кондитерском отделе магазина была такой: (секунды).
77 70 82 81 81
82 75 80 71 80
81 89 75 67 78
73 76 78 73 76
82 69 61 66 84
72 74 82 82 76
Построить интервальный вариационный ряд распределения покупок по продолжительности, создав 4 группы с одинаковыми интервалами. Обозначить элементы ряда. Изобразить его графически, сделать вывод.
Ход решения задачи по статистике:
Определяем элементы ряда распределения: варианты, частоты, частости, накопленные частоты.
Но прежде рассчитаем границы 4 заданных групп с одинаковыми интервалами:
Величину интервала определим по формуле .
В нашем случае
Границы групп соответственно равны:
I 61+7=68 (61-68)
II 68+7=75 (68-75)
III 75+7=82 (75-82)
IV 82+7=89 (82-89)
|
Группы покупок по продолжительности, сек. |
Число покупок |
В процентах к итогу |
Накопленные частоты |
|
61-68 |
3 |
10 |
3 |
|
68-75 |
9 |
30 |
12 |
|
75-82 |
16 |
53,3 |
28 |
|
82-89 |
2 |
6,7 |
30 |
|
Итого |
30 |
100 |
Теперь графически отобразим наш интервальный вариационный ряд в виде гистограммы и кумуляты.
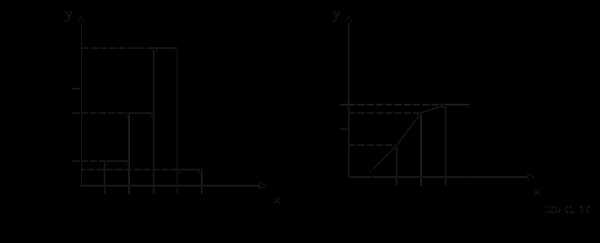
По таблице и графика можно сделать вывод о том, что преобладающее большинство покупок (16 или 53.3%) находится во временном интервале 75-82, сек.
Статистика задача — Абсолютные и относительные величины.
Теория по решению статистической задачи.
Абсолютные величины – показатели, которые выражают размеры общественных явлений и процессов числом единиц совокупности.
Относительные величины – показатели, выражающие количественные соотношения численностей или величин признаков изучаемых явлений.
Виды относительных величин:
1) Относительная величина выполнения плана:
2) Относительная величина планового задания:
3) Относительная величина динамики:
4) Относительная величина структуры:
5) Относительная величина сравнения отражает соотношение двух объемов или уровней в пространстве: соотношение производства автомобилей в Украине и России, соотношение уровней оплаты труда в разных хозяйствах, соотношение уровней производительности на разных предприятиях отрасли и т. д.
6) Относительная величина координации получается посредством деления друг на друга разноименных исходных показателей, она дает типичную характеристику соотношения одно-порядковых по значимости исходных показателей, во-первых, непосредственно связанных между собой, во-вторых, обладающих некоторой общностью.
7) Относительная величина интенсивности:
Типовая задача № 1
Два консервных завода выработали по 100 тыс. шт. банок виноградного сока. На первом заводе емкость каждой банки составляет 500 см3, а на втором – 200 см3. Можно ли сказать, что оба завода работали одинаково?
Ход решения задачи по статистике:
Для того, чтобы ответить на этот вопрос необходимо установить коэффициенты перевода фактического объема банок в условные банки и затем умножить количество выпущенных банок на эти коэффициенты. Представим расчет в таблице № 1.
Таблица № 1
|
Заводы |
Количество выпущенных банок, тыс. шт. |
Объем банки см3 |
Коэффициенты перевода |
Количество выпущенных условных банок, тыс. шт. |
|
№ 1 |
100 |
500 |
100*1,414=141,4 |
|
|
№ 2 |
100 |
200 |
100*0,566=56,6 |
Таким образом, завод № 1 по сравнению с заводом № 2 выпустил виноградного сока на 84,8 тыс. Банок больше (141,4-56,6).
Статистика — Типовая задача № 2
Имеются следующие данные розничного товарооборота:
Таблица № 2
|
Универмаги |
Розничный товарооборот (млн. грн.) |
||
|
Фактически за базисный год |
Отчетный год |
||
|
По плану |
Фактически |
||
|
«Крым» |
105 |
110 |
98 |
|
«Центральный» |
137 |
148 |
150 |
Определить:
1. Относительную величину выполнения плана.
2. Относительную величину планового задания.
3. Относительную величину динамики.
Ход решения задачи:
1. Определяем относительную величину выполнения плана по двум универмагам:
2. Определим относительную величину планового задания:
3. Определяем относительную величину динамики:
Статистическая задача — Средние и структурные средние величины.
Теория по решению статистической задачи:
Средние величины – это показатели. Выражающие типичные черты и дают обобщающую количественную характеристику уровня признака по совокупности однородных явлений.
1. Средняя арифметическая:
2. Средняя гармоническая:
3. Средняя квадратическая:
4. Средняя хронологическая:
5. Средняя геометрическая:
К1, К2, К3 и Кn – коэффициенты динамики по отношению к предыдущему периоду.
6. мода интервальных рядов распределения вычисляется по следующей формуле:
х0 – минимальная граница модального интервала;
i – величина интервала;
f2 – частота модального интервала;
f1 – частота интервала, предшествующего модальному;
f3 – частота интервала, следующего за модальным.
Мода для дискретных рядов распределения – это наиболее часто встречающаяся величина признака в данной совокупности.
7. Медиана для интервальных рядов распределения вычисляется по формуле:
x0 – нижняя граница медианного интервала;
i – величина медианного интервала;
∑f – сумма частот ряда;
SМЕ-1 – сумма накопленных частот, предшествующих медианному интервалу;
fМЕ – частота медианного интервала.
Чтобы определить медиану в дискретном вариационном ряду. Необходимо сумму частот разделить пополам и к полученному результату добавить ½.
Типовая задача № 1
Имеются следующие данные о заработной плате рабочих:
Таблица № 1
|
Месячная заработная плата (грн.) (х) |
Число рабочих (f) |
х*f |
|
х1=120 |
27 |
3240 |
|
х2=145 |
33 |
4785 |
|
х4=200 |
48 |
9600 |
|
х5=208 |
51 |
10608 |
|
х6=250 |
16 |
4000 |
|
х7=337 |
28 |
9436 |
|
Итого |
203 |
41669 |
Определите среднюю заработную плату одного рабочего.
Ход решения:
Среднюю заработную плату определим по формуле средней арифметической взвешенной:
Т. о. средняя заработная плата рабочего составила 205,27 грн.
Типовая задача (статистика) № 2
Имеются, следующие данные выпуска литья в литейном цехе завода за пятилетний период:
Таблица № 2
|
Годы |
1-й |
2-й |
3-й |
4-й |
5-й |
|
Выпуск литья, тонн |
528,34 |
336,98 |
439,24 |
297,55 |
672,17 |
|
В % к предыдущему году |
— |
63,8 |
130,3 |
67,7 |
225,9 |
Требуется определить средний темп выпуска литья.
Ход решения задачи:
Для определения среднего темпа выпуска литья используем формулу средней геометрической:
Типовая задача № 3
Имеются следующие данные:
Таблица № 3
|
Група рабочих по размеру заработной платы (в грн.) |
Число рабочих |
SМЕ |
|
150-200 |
28 |
28 |
|
200-250 |
54 |
82 |
|
250-300 |
30 |
112 |
|
300-350 |
47 |
159 |
|
350-400 |
63 |
222 |
|
400-450 |
18 |
240 |
|
450-500 |
22 |
262 |
|
Итого |
262 |
— |
Определить моду и медиану.
Ход решения задачи:
1. Определяем моду:
2. Определяем медиану:
Практические задачи по статистике для самостоятельного решения с ответами
Задача по статистике 1.
Имеются следующие данные об урожайности зерновых культур:
|
Урожайность зерновых культур |
Количество хозяйств |
|
До 20 |
30 |
|
20-30 |
40 |
|
30-40 |
60 |
|
40 и выше |
20 |
Определить среднюю урожайность зерновых культур, моду и медиану.
Ответ.
средняя урожайность: 30,3 ц/га
мода: 33,3
медиана: 30,8
Задача 2.
|
Годы |
97г. |
98г. |
99г. |
2000г. |
2001г. |
|
Производства зерна, тыс. тонн |
150 |
168 |
179 |
186 |
191 |
Требуется определить: (цепным и базисным способом):
1) абсолютный прирост;
2) темп роста и прироста;
3) средний абсолютный прирост;
4) средние темпы роста и прироста.
Ответ 2.
цепным способом базисным способом
абсолютный прирост 18 абсолютный прирост 18
11 29
7 36
5 41
темп роста 1,12 темп роста 1,12
1,07 1,19
1,04 1,24
1,03 1,27
темп прироста 0,12 темп прироста 0,12
0,07 0,19
0,04 0,24
0,03 0,27
средний абсолютный прирост: 31 средний абсолютный прирост: 31
средний темп роста 1,02 средний темп роста: 1,05
средний темп прироста 0,02 средний темп прироста: 0,05
Задача 3.
Методом случайной повторной выборки было взято для проверки на вес 200 шт. деталей. В результате проверки был установлен средний вес детали 30 г. при среднем квадратическом отклонении 4 г. С вероятностью 0,954 требуется определить предел в котором находится средний вес деталей в генеральной совокупности.
Ответ.
Средний вес детали колеблется в пределах 29,44 ‹ х ‹ 30,56.
Задача 4.
По имеющимся данным определить индивидуальные и общий индексы себестоимости и экономию (перерасход) от снижения (роста) себестоимости.
|
Вид товара |
Общие затраты, грн. |
Имеющие единицы себестоимость в отчетном году, % |
|
|
Базисный год |
Отчетный год |
||
|
Электробритва |
9500 |
10244 |
-1,5 |
|
Электрофен |
600 |
612 |
+2,0 |
Ответ.
Индивидуальный индекс себестоимости по электробритве 0,985
Индивидуальный индекс себестоимости электрофену 1,02
Общий индекс себестоимости 0,99.
Перерасход денежных средств от роста себестоимости 144 грн.
Задача 5.
Полная первоначальная стоимость оборудования 250,4 тыс. грн. Это оборудование может работать 20 лет при условии проведения в капитальных ремонтов на сумму 2,5 тыс. грн. каждый. После полного износа оборудования может быть реализовано как металлолом за 1 тыс. грн. Затраты на модернизацию в течении срока службы 62,6 тыс. грн. Определить сумму ежегодных амортизационных отчислений, общую норму амортизации.
Ответ.
Сумма ежегодных отчислений 16,6 тыс. грн.
Общая норма амортизации 6,6 %.
Задача по статистике 6.
Определить календарный, режимный, располагаемый (плановый) и фактический фонды станочного времени по 2 видам станков и коэффициенты использования станочного времени за апрель по таким данным:
|
Виды станков |
Количество установленных станков |
Фактически отработано станкочасов |
Запланировано на ремонт станков, станкочасов |
|
Токарные |
48 |
15127 |
60 |
|
Фрезерные |
52 |
16420 |
80 |
Число рабочих дней в апреле 22. Режим работы – 2 смены. Установленная продолжительность смены: 8 часов.
Ответ.
Календарный фонд 72000 станкочасов
Режимный фонд 35200 станкочасов
Плановый фонд 35060 станкочасов
Фактический фонд 31547 станкочасов
Коэффициент использования календарного фонда 43,8 %
Коэффициент использования режимного фонда 89,6 %
Коэффициент использования планового фонда 90 %
Задача 7.
В квартале 62 рабочих дня, отработало 136400 человеко-дней; целодневные простои 930 человеко-дней; неявок по различным причинам (включая праздничные и выходные) 69670 человеко-дней. Определить: коэффициенты использования среднесписочной и среднеявочной численности.
Ответ.
К использования среднесписочной численности 0,96 %
Коэффициент использования среднеявочной численности 0,99 %
Задача 8.
На заводе с численностью персонала 3000 человек производительность труда выросла на 25 %, а на заводе, где работают 5000 человек, снизилась на 5 %. Как изменилась производительность труда на 2-х заводах вместе.
Ответ.
Увеличилась на 6 % производительность на двух заводах.
Задача 9 по статистике
Объем продукции в натуральном выражении на предприятии вырос за отчетный период на 28 %, а производственные затраты в целом возросли на 19 %. Определить как изменилась себестоимость единицы продукции.
К задаче 9 ответ
Себестоимость единицы продукции снизилась на 7 %.
Задача 10.
Какой была численность населения в начале и конце года, если среднегодовой показатель ее за этот год составил 800 тыс. человек, сальдо миграции + 32 тысячи человек, коэффициент естественного прироста 30 % 0.
Ответ — Численность на начало года 772000 человек.
К задаче 10.
Численность на конец года 828000 человек.
zadachi-ru.com.ua
Задачи по статистике
Задача — Ряды распределения и статистические таблицы.
Теория по решению задачи.
Статистический ряд распределения – упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку.
Дискретный вариационный ряд – характеризует распределение единиц совокупности по дискретному (прерывному) признаку.
Интервальный вариационный ряд – характеризует распределение единиц совокупности по интервальному (непрерывному) признаку.
Для изображения дискретных вариационных рядов распределения используется «полигон распределения». Для графического изображения интервального вариационного ряда применяются «гистограмма» и «кумулята».
Задача 1.
На экзамене по истории студенты получили оценки:
3 4 4 4 3 4
3 4 3 5 4 4
5 5 2 3 2 3
3 4 4 5 3 3
5 4 5 4 4 4
Построить дискретный вариационный ряд распределения студентов по баллам и изобразить его графически.
Ход решения задачи:
Определяем элементы ряда распределения: варианты, частоты, частоты.
Оценка, баллы | Кол-во студентов с такой оценкой, человек | В процентах к итогу |
2 | 2 | 6,7 |
3 | 9 | 30 |
4 | 13 | 43,3 |
5 | 6 | 20 |
Итого | 30 | 100 |
Теперь графически изобразим дискретный ряд распределения в виде помпона распределения.
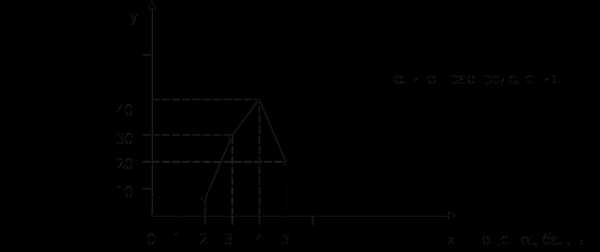
Можно сделать вывод о том, что преобладающее большинство студентов получило «4» (43,3 %).
Задача 2.
Во время выборочной проверки было установлено, что продолжительность одной покупки в кондитерском отделе магазина была такой: (секунды).
77 70 82 81 81
82 75 80 71 80
81 89 75 67 78
73 76 78 73 76
82 69 61 66 84
72 74 82 82 76
Построить интервальный вариационный ряд распределения покупок по продолжительности, создав 4 группы с одинаковыми интервалами. Обозначить элементы ряда. Изобразить его графически, сделать вывод.
Ход решения задачи по статистике:
Определяем элементы ряда распределения: варианты, частоты, частости, накопленные частоты.
Но прежде рассчитаем границы 4 заданных групп с одинаковыми интервалами:
Величину интервала определим по формуле .
В нашем случае
Границы групп соответственно равны:
I 61+7=68 (61-68)
II 68+7=75 (68-75)
III 75+7=82 (75-82)
IV 82+7=89 (82-89)
Группы покупок по продолжительности, сек. | Число покупок | В процентах к итогу | Накопленные частоты |
61-68 | 3 | 10 | 3 |
68-75 | 9 | 30 | 12 |
75-82 | 16 | 53,3 | 28 |
82-89 | 2 | 6,7 | 30 |
Итого | 30 | 100 |
|
Теперь графически отобразим наш интервальный вариационный ряд в виде гистограммы и кумуляты.

По таблице и графика можно сделать вывод о том, что преобладающее большинство покупок (16 или 53.3%) находится во временном интервале 75-82, сек.
Статистика задача — Абсолютные и относительные величины.
Теория по решению статистической задачи.
Абсолютные величины – показатели, которые выражают размеры общественных явлений и процессов числом единиц совокупности.
Относительные величины – показатели, выражающие количественные соотношения численностей или величин признаков изучаемых явлений.
Виды относительных величин:
1) Относительная величина выполнения плана:
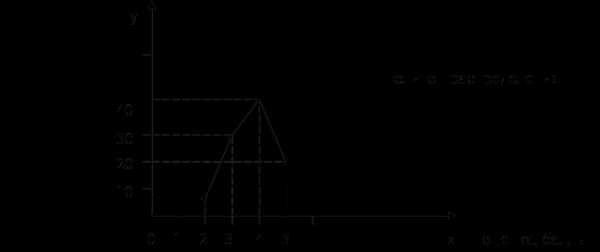
2) Относительная величина планового задания:
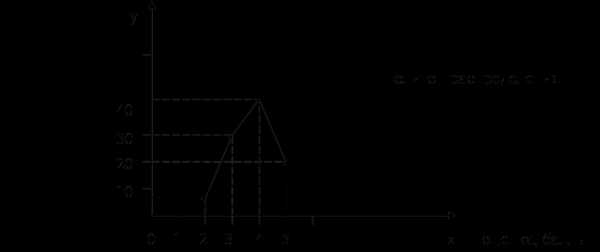
3) Относительная величина динамики:
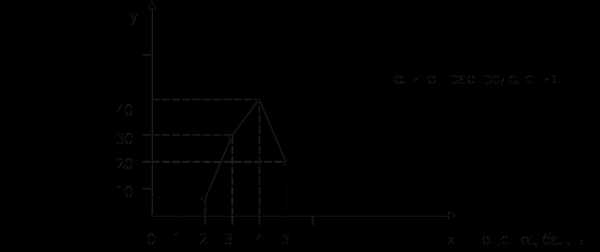
4) Относительная величина структуры:
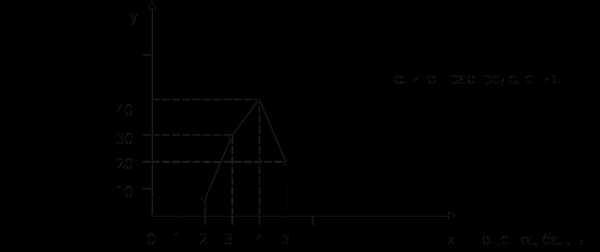
5) Относительная величина сравнения отражает соотношение двух объемов или уровней в пространстве: соотношение производства автомобилей в Украине и России, соотношение уровней оплаты труда в разных хозяйствах, соотношение уровней производительности на разных предприятиях отрасли и т. д.
6) Относительная величина координации получается посредством деления друг на друга разноименных исходных показателей, она дает типичную характеристику соотношения одно-порядковых по значимости исходных показателей, во-первых, непосредственно связанных между собой, во-вторых, обладающих некоторой общностью.
7) Относительная величина интенсивности:
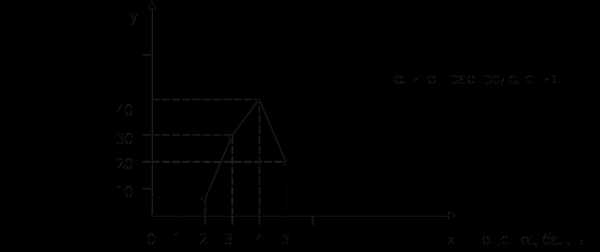
Типовая задача № 1
Два консервных завода выработали по 100 тыс. шт. банок виноградного сока. На первом заводе емкость каждой банки составляет 500 см3, а на втором – 200 см3. Можно ли сказать, что оба завода работали одинаково?
Ход решения задачи по статистике:
Для того, чтобы ответить на этот вопрос необходимо установить коэффициенты перевода фактического объема банок в условные банки и затем умножить количество выпущенных банок на эти коэффициенты. Представим расчет в таблице № 1.
Таблица № 1
Заводы | Количество выпущенных банок, тыс. шт. | Объем банки см3 | Коэффициенты перевода | Количество выпущенных условных банок, тыс. шт. |
№ 1 | 100 | 500 | 100*1,414=141,4 | |
№ 2 | 100 | 200 | 100*0,566=56,6 |
Таким образом, завод № 1 по сравнению с заводом № 2 выпустил виноградного сока на 84,8 тыс. Банок больше (141,4-56,6).
Статистика — Типовая задача № 2
Имеются следующие данные розничного товарооборота:
Таблица № 2
Универмаги | Розничный товарооборот (млн. грн.) | ||
Фактически за базисный год | Отчетный год | ||
По плану | Фактически | ||
«Крым» | 105 | 110 | 98 |
«Центральный» | 137 | 148 | 150 |
Определить:
1. Относительную величину выполнения плана.
2. Относительную величину планового задания.
3. Относительную величину динамики.
Ход решения задачи:
1. Определяем относительную величину выполнения плана по двум универмагам:
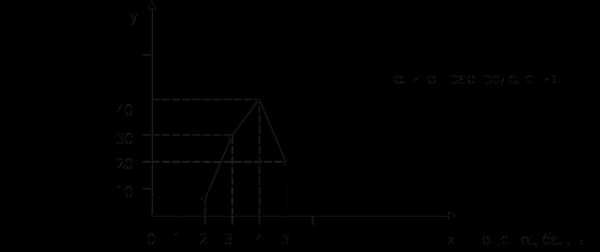
2. Определим относительную величину планового задания:
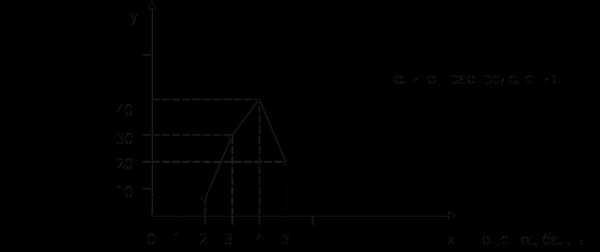
3. Определяем относительную величину динамики:

Статистическая задача — Средние и структурные средние величины.
Теория по решению статистической задачи:
Средние величины – это показатели. Выражающие типичные черты и дают обобщающую количественную характеристику уровня признака по совокупности однородных явлений.
1. Средняя арифметическая:
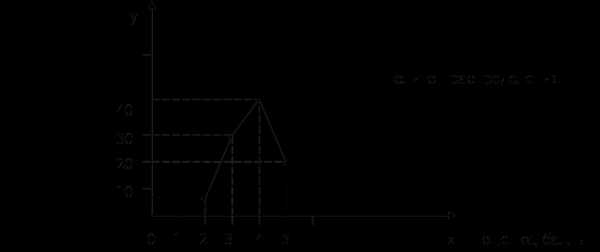
2. Средняя гармоническая:
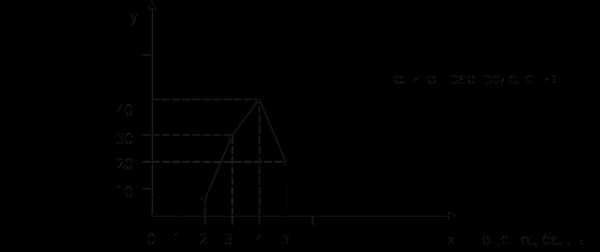
3. Средняя квадратическая:
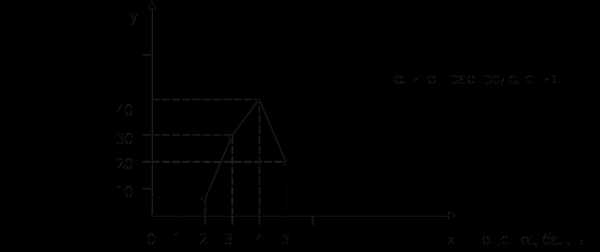
4. Средняя хронологическая:
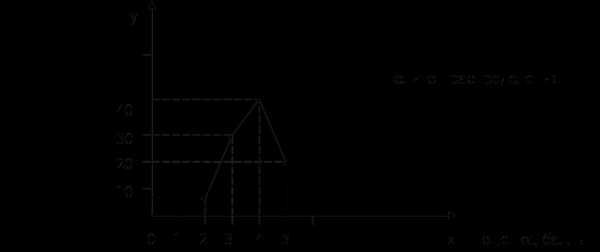
5. Средняя геометрическая:

К1, К2, К3 и Кn – коэффициенты динамики по отношению к предыдущему периоду.
6. мода интервальных рядов распределения вычисляется по следующей формуле:
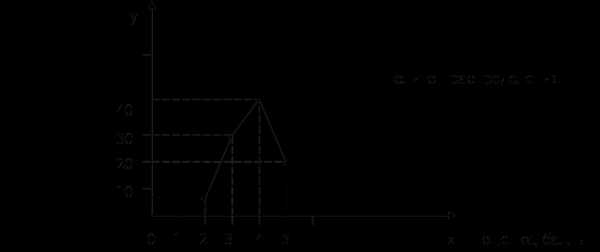
х0 – минимальная граница модального интервала;
i – величина интервала;
f2 – частота модального интервала;
f1 – частота интервала, предшествующего модальному;
f3 – частота интервала, следующего за модальным.
Мода для дискретных рядов распределения – это наиболее часто встречающаяся величина признака в данной совокупности.
7. Медиана для интервальных рядов распределения вычисляется по формуле:
x0 – нижняя граница медианного интервала;
i – величина медианного интервала;
∑f – сумма частот ряда;
SМЕ-1 – сумма накопленных частот, предшествующих медианному интервалу;
fМЕ – частота медианного интервала.
Чтобы определить медиану в дискретном вариационном ряду. Необходимо сумму частот разделить пополам и к полученному результату добавить ½.
Типовая задача № 1
Имеются следующие данные о заработной плате рабочих:
Таблица № 1
Месячная заработная плата (грн.) (х) | Число рабочих (f) | х*f |
х1=120 | 27 | 3240 |
х2=145 | 33 | 4785 |
х4=200 | 48 | 9600 |
х5=208 | 51 | 10608 |
х6=250 | 16 | 4000 |
х7=337 | 28 | 9436 |
Итого | 203 | 41669 |
Определите среднюю заработную плату одного рабочего.
Ход решения:
Среднюю заработную плату определим по формуле средней арифметической взвешенной:
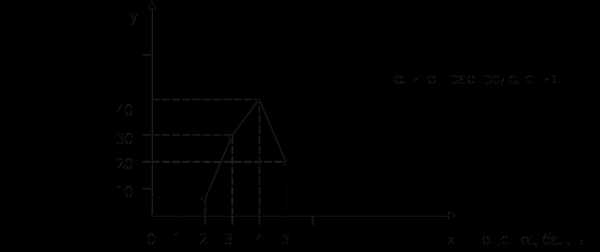
Т. о. средняя заработная плата рабочего составила 205,27 грн.
Типовая задача (статистика) № 2
Имеются, следующие данные выпуска литья в литейном цехе завода за пятилетний период:
Таблица № 2
Годы | 1-й | 2-й | 3-й | 4-й | 5-й |
Выпуск литья, тонн | 528,34 | 336,98 | 439,24 | 297,55 | 672,17 |
В % к предыдущему году | — | 63,8 | 130,3 | 67,7 | 225,9 |
Требуется определить средний темп выпуска литья.
Ход решения задачи:
Для определения среднего темпа выпуска литья используем формулу средней геометрической:
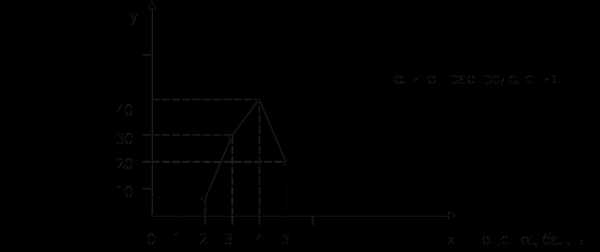
Типовая задача № 3
Имеются следующие данные:
Таблица № 3
Група рабочих по размеру заработной платы (в грн.) | Число рабочих | SМЕ |
150-200 | 28 | 28 |
200-250 | 54 | 82 |
250-300 | 30 | 112 |
300-350 | 47 | 159 |
350-400 | 63 | 222 |
400-450 | 18 | 240 |
450-500 | 22 | 262 |
Итого | 262 | — |
Определить моду и медиану.
Ход решения задачи:
1. Определяем моду:
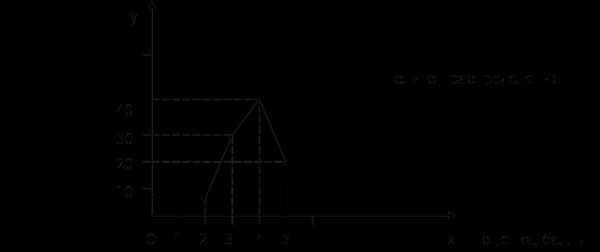
2. Определяем медиану:
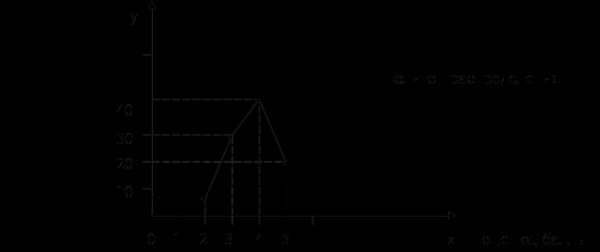
studfiles.net
Задача №5
По трем населенным пунктам имеются следующие данные:
Населенные пункты | Число жителей всего, тыс. чел. | % лиц, старше 18 лет | % лиц, старше 18 лет, занятых в общественном производстве |
a | b | c | |
1 2 3 | 100 60 85 | 60 69 54 | 70 75 83 |
Определить среднее значение каждого признака.
Решение.
1)
Используем формулу средней арифметической простой:
тыс. чел.
2)
Используем формулу средней арифметической взвешенной:
тыс. чел.
3)
Используем формулу средней арифметической взвешенной:
тыс. чел.
Ответ: г) 81,7; 60,1; 75,5.
www.ekonomstat.ru
Задача №3
Количество пряжи, выработанной поддельным цехом фабрики, увеличилось по сравнению с прошлым годом в полтора раза, а количество пряжи, вырабатывавшейся за 1 чел/час, возросло на 10%. Определить, как изменилось общее число отработанных чел/часов.
Решение.
Общее количество выработанной пряжи равно произведению количества пряжи, выработанной за один человеко-час , на общее число отработанных человеко-часов :
.
Следовательно, между соответствующими им индексами существует аналогичная взаимосвязь:
.
По условию,
;
.
или 136,4%,
то есть общее число отработанных человеко-часов увеличилось в 1,36 раза.
Ответ: г) увеличилось в 1,36 раза.
www.ekonomstat.ru
Задачи по статистике с решениями
Нужна ли статистика экономисту? Отвечу Вам — нужна. Эта отрасль знаний производит сбор, исследование, измерение первичных данных. В этой статье приведены задачи по статистике с решением и будет началом циклу задачи по статистике срешением, полный список которых Вы сможете найти, перейдя по ссылке Статистика.
Часть 1. Приведем исходное условие в таблица 1.
Табл. 1 Стоимость станков компании, млн. грн.
Руководство к решению задачи по статистике
1) Определим средние величины:
— арифметическая:
— гармоническая:
— квадратическая:
2) Размах вариации:
Rx = 59,5 – 8,8 = 50,7 млн. гривен
3) Среднее линейное отклонение:
4) Дисперсия:
5) Средне квадратическое отклонение:
6) Коэффициент вариации:
Как показывает последние расчеты, исходные данные являются не однородными.
Часть 2. Приведем исходное условие в таблица 2.
Табл. 2 Стоимость станков компании, млн. грн.
Руководство к решению задачи по статистике
1) Определим средние величины:
— арифметическая:
— гармоническая:
— квадратическая:
2) Размах вариации:
Rx = 72– 4,4 = 67,6 млн. гривен
3) Среднее линейное отклонение:
4) Дисперсия:
5) Средне квадратическое отклонение:
6) Коэффициент вариации:
Как показывает последние расчеты, исходные данные являются не однородными.
Задачи по статистике с решением помогают понять применимость теории статистика, изучаемую на лекциях. Так же на сайте Вы найдете как провести дисперсионный анализ, проанализироватья выборочное наблюдение, определить корреляционную взаимосвязь, найти показатели анализа рядов рядов динамики.
madgicbox.com
