1.2.1. Свойства пределов. Замечательные пределы
Бесконечно малые функции и их свойства
Функция У=α(х) называется бесконечно малой при , если |
Свойства бесконечно малых
1. Сумма двух бесконечно малых есть бесконечно малая. |
Доказательство.
Если A(х) и B(х) – бесконечно малые при , то существуют D1 и D2 такие,
Что |A(X)|<E/2 и |B(X)|<E/2 для выбранного значения E. Тогда |A(X)+B(X)|≤|A(X)|+|B(X)|<E, то есть |(A(X)+B(X))-0|<E. Следовательно,
То есть A(х)+B(х) – бесконечно малая.
Замечание. Отсюда следует, что сумма любого конечного числа бесконечно малых есть бесконечно малая.
2. Если A(Х) – бесконечно малая при , а F(X) – функция, ограниченная в некоторой окрестности Х0, То A(х)F(X) – бесконечно малая при . |
Доказательство.
Выберем число М такое, что |F(X)|<M при |X—X0|<D1, и найдем такое D2, что
Тогда, если выбрать в качестве D меньшее из чисел D1 и D2,
То есть A(х)·F(X) – бесконечно малая.
Следствие 1.
Произведение бесконечно малой на конечное число есть бесконечно малая.
Следствие 2.
Произведение двух или нескольких бесконечно малых есть бесконечно малая.
Следствие 3.
Линейная комбинация бесконечно малых есть бесконечно малая.
Теорема (Третье определение предела). Если То необходимым и достаточным условием этого является то, что функцию F(X) можно представить в виде F(X)=A+A(X), где A(х) – бесконечно малая при Х→х0. |
Доказательство.
1)Пусть A(х) – бесконечно малая при Х→х0. Следовательно, F(X)=A+A(X).
2)Пусть F(X)=A+A(X). Тогда
Значит,
Cледовательно,
Замечание. Тем самым получено еще одно определение предела, эквивалентное двум предыдущим.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Замечательные пределы
Математика Замечательные пределы
Количество просмотров публикации Замечательные пределы — 272
| Наименование параметра | Значение |
| Тема статьи: | Замечательные пределы |
| Рубрика (тематическая категория) | Математика |
В математике важную роль играют два специальных предела, которые ввиду их важности названы ʼʼзамечательнымиʼʼ:
— первый замечательный предел
— второй замечательный предел
Пример 1.
(здесь введена новая переменная ).
Пример 2. . Положим .
Получаем
.
Замечательные пределы — понятие и виды. Классификация и особенности категории «Замечательные пределы» 2017, 2018.
Читайте также
Терема lim (sin(x)/x)=1 x®0 Доказательство: S&… [читать подробнее].
, где P(x) = a0xn + a1xn-1 +…+an, Q(x) = b0xm + b1xm-1 +…+bm — многочлены. Итого: Первый замечательный предел Второй замечательный предел Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести… [читать подробнее].
Первый замечательный предел Первым замечательным пределом называется выражение . Отсюда . Следствия из первого замечательного предела: 1) ; 2) ; 3) . Например, вычислить . … [читать подробнее].
1) первым замечательным пределом называется следующий предел Lim sinx/x =1 Xстремится к 0 Доказательство геометрия-нереально написать 2. Второй замечательный предел Рассмотрим числовую последовательность Xn=(1+1/n)^n X1=(1+1/1)’=2 X2=(1+1/2)’2=2.25 Рисуем координатную прямую Можно… [читать подробнее].
1. Первый замечательный предел . Доказательство: Возьмем круг радиуса 1, обозначим радиальную меру угла MOB через t. Функция четная, т.к. По условию и отношениеположительно при любом знаке t, следовательно, достаточно рассмотреть значения t, удовлетворяющие неравенствам . … [читать подробнее].
referatwork.ru
Замечательные пределы
215. Используя замечательные пределы найти предельные значения выражений
;
8) 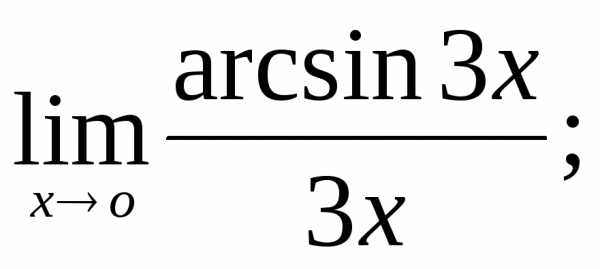 9)
9) 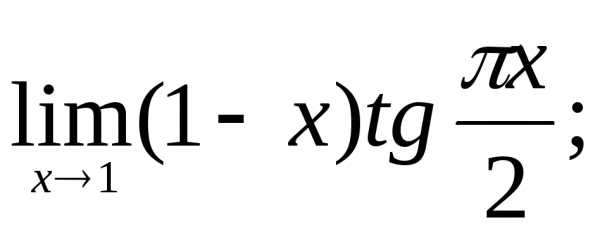 10)
10) 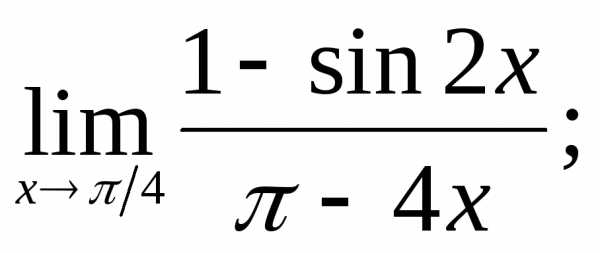
11) 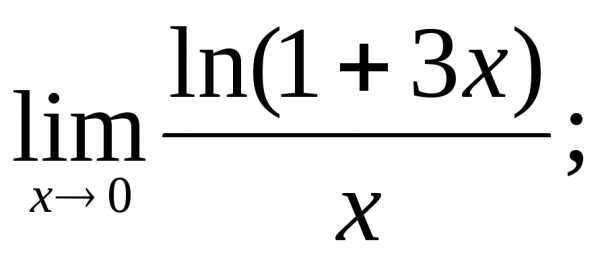 12)
12)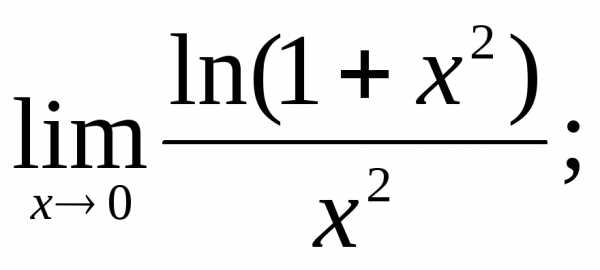 13)
13)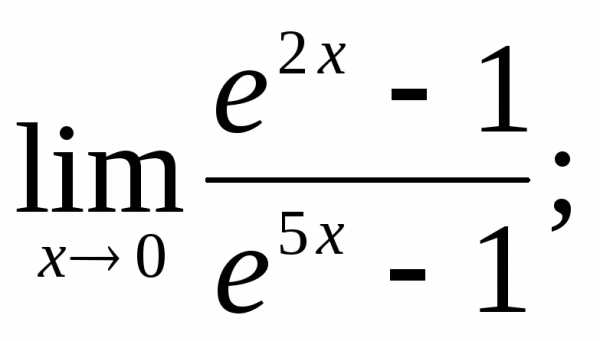 14)
14)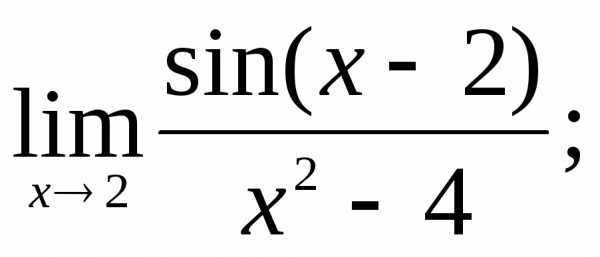
15) 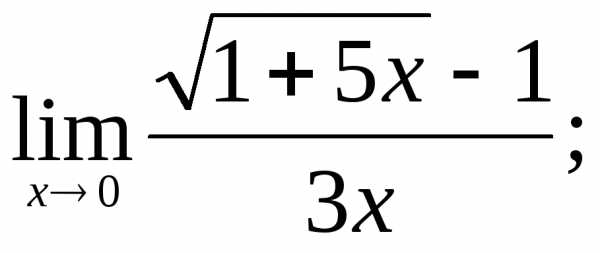 16)
16)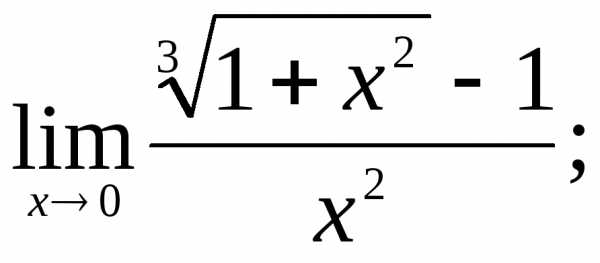 17)
17)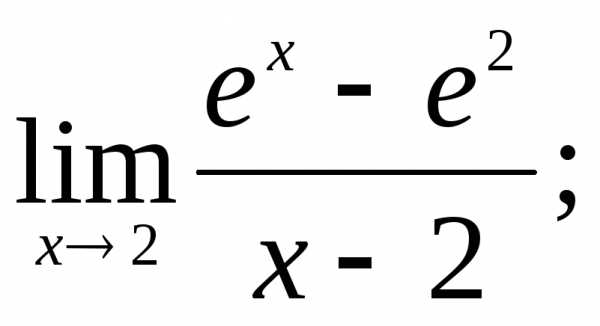
18) 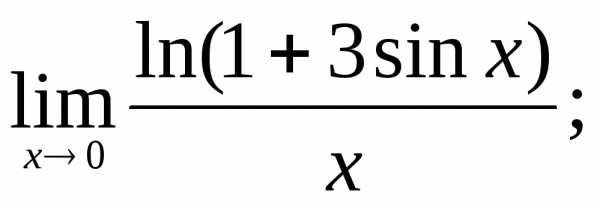 19)
19)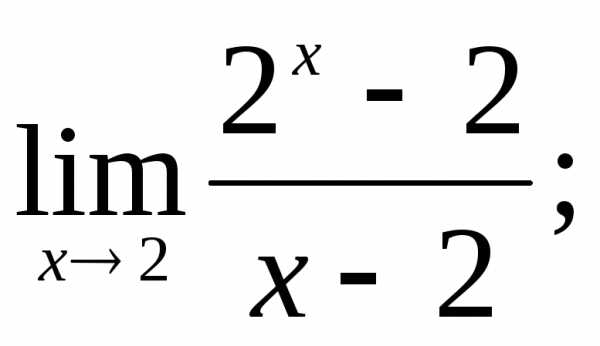 20)
20) 21)
21)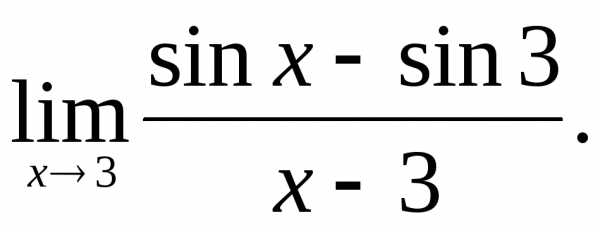
216. Используя второй замечательный предел найти предельные значения выражений
217. Вычислить указанные пределы
218. Вычислить указанные пределы:
1) 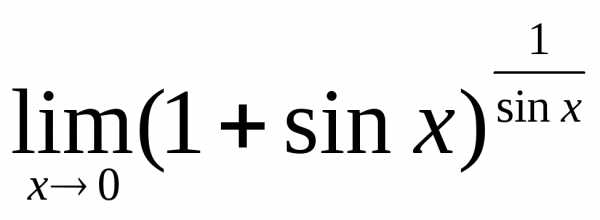 2)
2) 3)
3)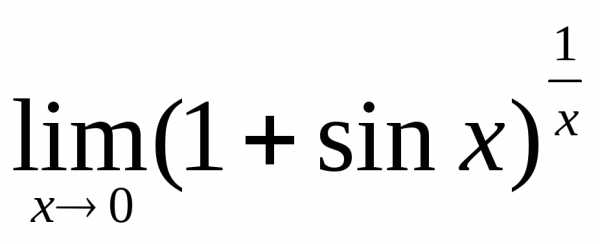
Дифференцирование. Определения. Основные правила.
219. Вычислить приращение функции 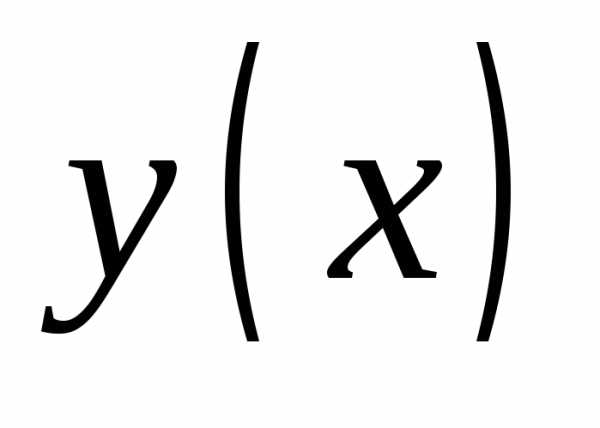 в
точке
в
точке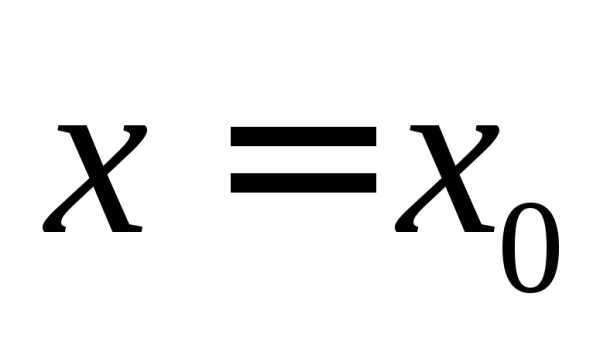
Используя определение производной функции и соответствующие замечательные пределы, вычислить производные данных функций в точке х=х0
1)
2)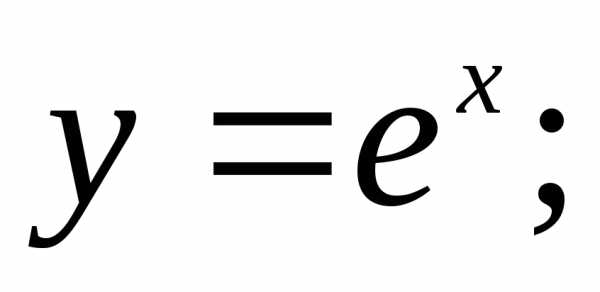 3)
3)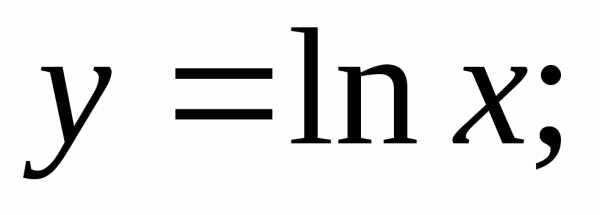 4)
4)
Написать уравнение касательной и нормальной прямой к функции

в точке 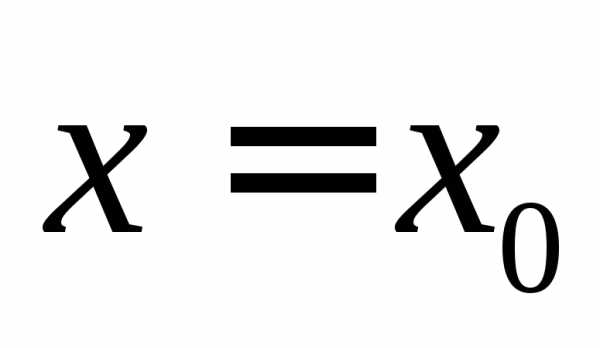 :
:
Найти точки пересечения полученных касательных с осями координат.
Найти точку, в которой касательная к графику функции параллельна
прямой
223. Найти угол между касательными, проведенными в точках
к графику функции
224. Найти точку, в которой касательная
к графику функции 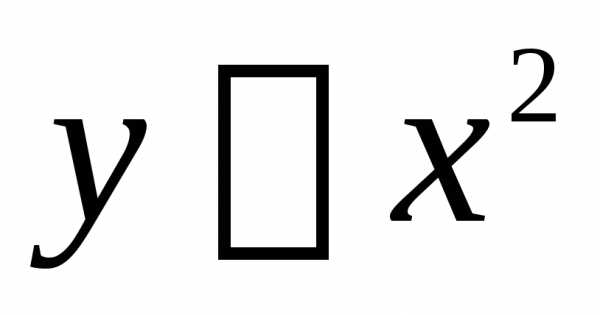
Перпендикулярна прямой
225 . Найти острый угол между графиками функций в точке
их пересечения
226. По оси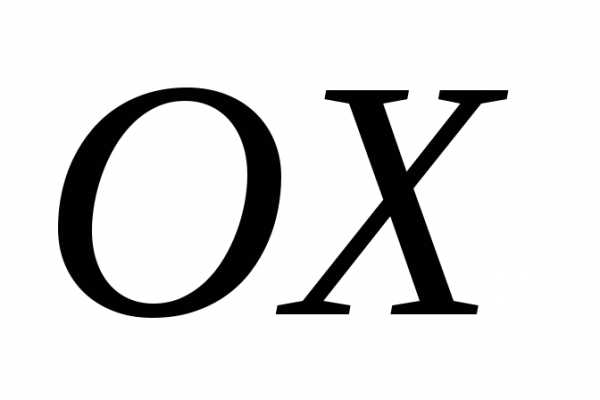 движется
точка, абсцисса которой с течением
движется
точка, абсцисса которой с течением
времени изменяется по закону +2. Определим абсциссу точки и её
скорость и ускорение в моменты времени: . Определить
моменты времени, когда усилие, действующее на точку равно: 1) нулю,
2) максимально.
227. Пусть материальная точка движется
вдоль оси ОХ по закону 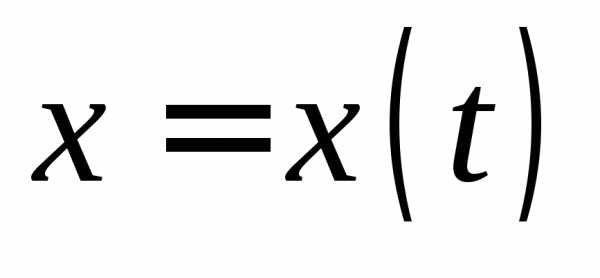 ,
где
,
где
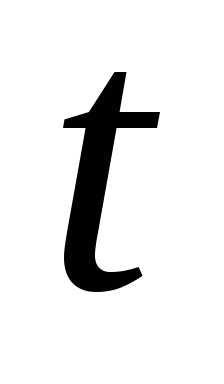 —
время:
—
время:
А. Вычислить среднюю
скорость за промежуток времени 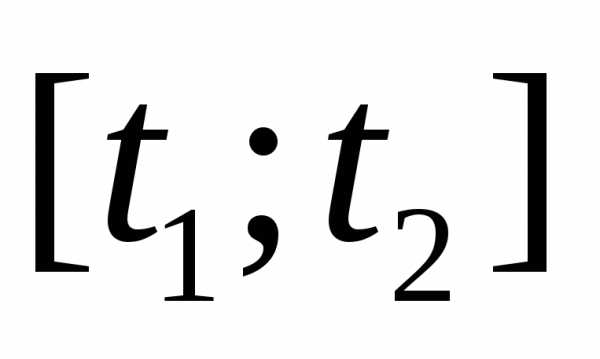 .
.
В.вычислить мгновенную
скорость точки в моменты времени 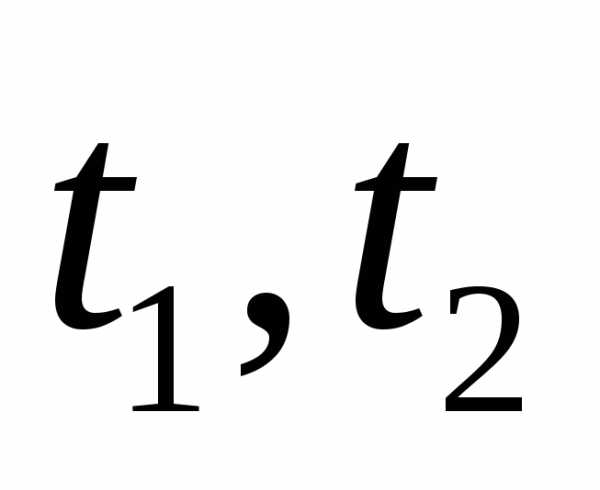
228. Найти координаты материальных точек, движущихся по закону
, в момент времени когда
их скорости совпадают.
229. Вычислить производные функций
1)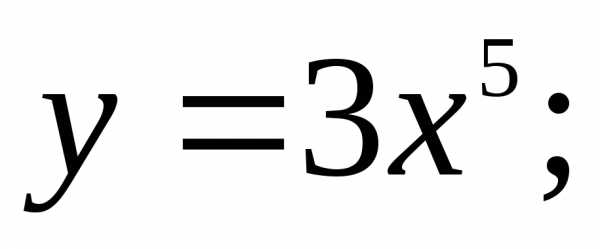 2)3)4)
2)3)4)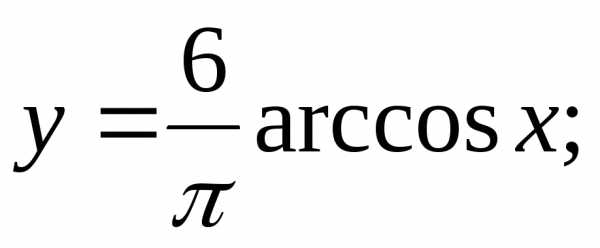
230. Вычислить производные функций
12)
13)
14)
15) 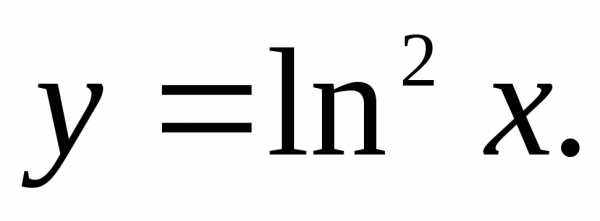
231. Вычислить производные функций
232 . Используя калькулятор,
вычислить производные функций в точке 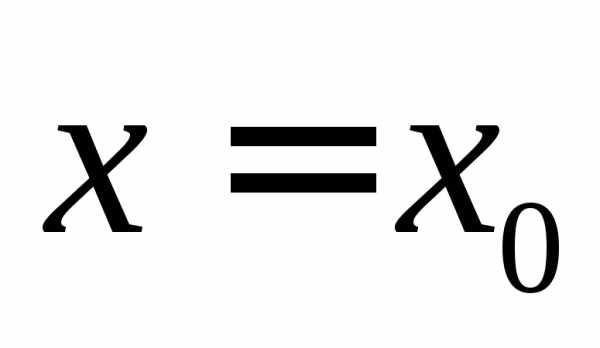
1) 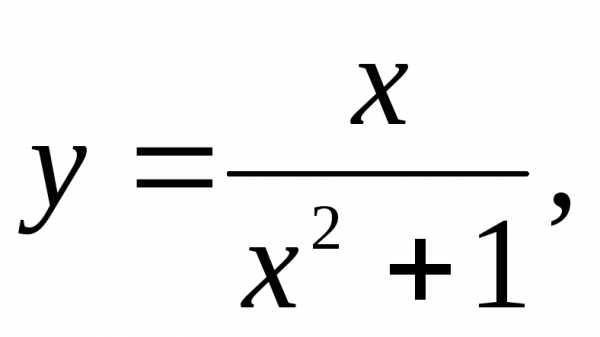
 2)
2) 3)
3)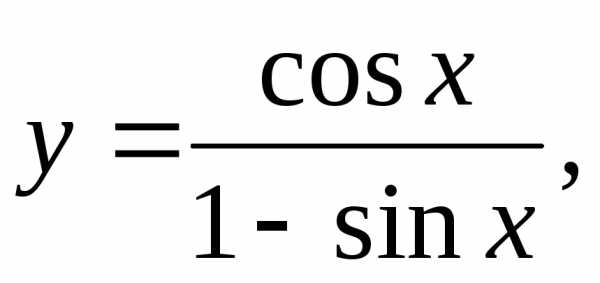
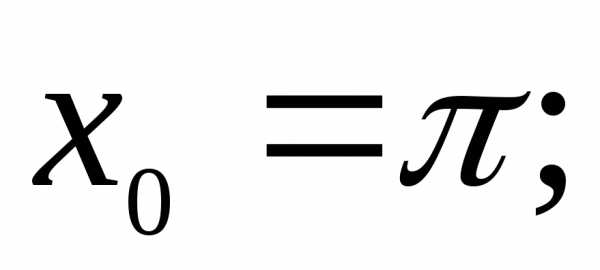
4) 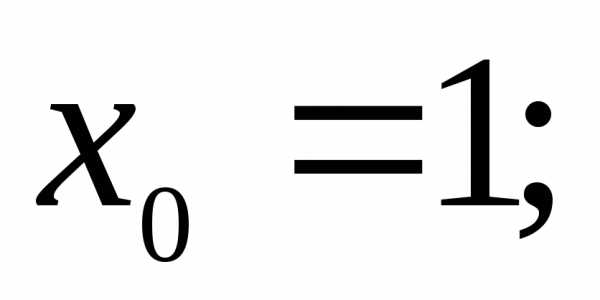 5)
5)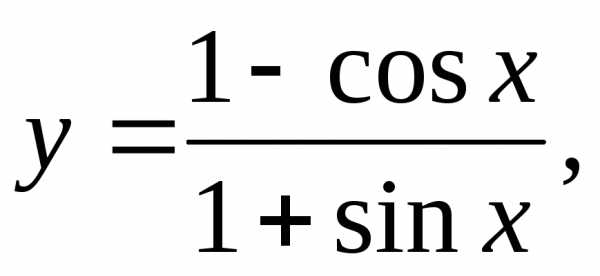
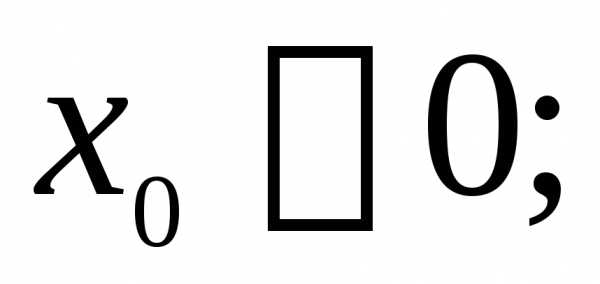 6)
6)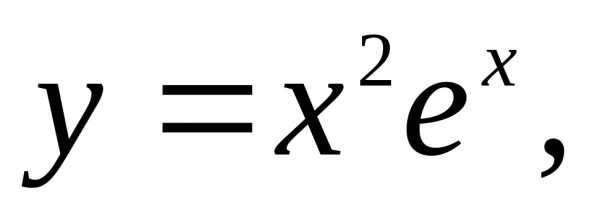

7)  8)
8)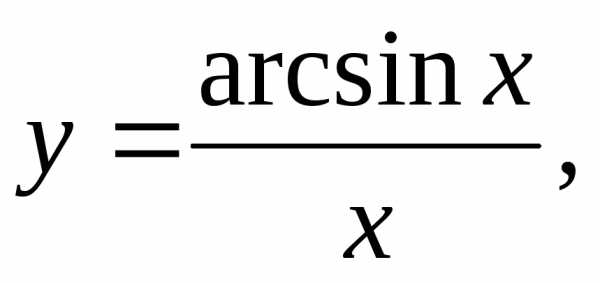
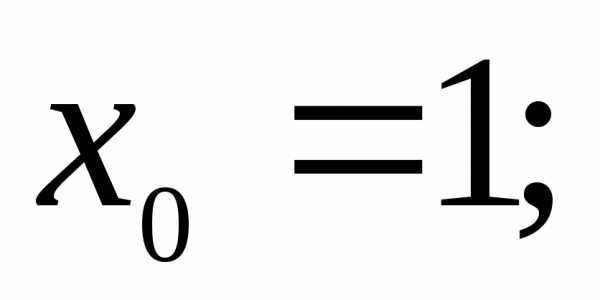 9)
9)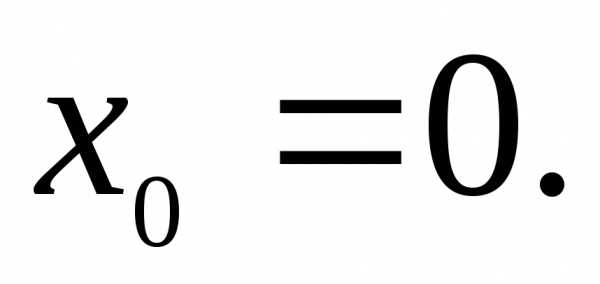
233. Найти функцию по заданной производной. Сделать проверку
234. Проверьте, что данная функция:
обращает соответствующее уравнение в тождество:
235. Найти вторые производные заданных функций
236. Проверьте, что функция 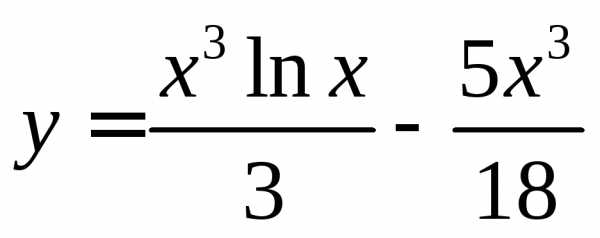 обращает уравнение
обращает уравнение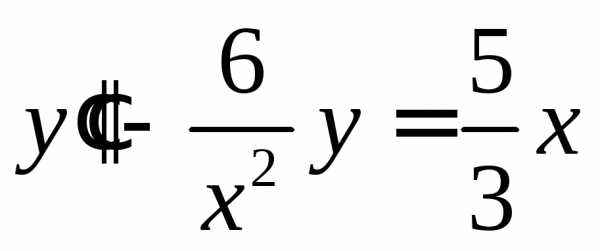
в тождество.
studfiles.net
Замечательные пределы. | Бесплатные курсовые, рефераты и дипломные работы
Первый замечательный предел: .
Второй замечательный предел: .
Пример 1. Вычислить пределы функции при
Решение.В задаче следует найти предел частного. С этой целью необходимо вычислить пределы числителя и знаменателя дроби, подставив в них предельное значение аргумента.
а) .
Здесь применима теорема о пределе частного.
б) .
При подстановке в числитель и знаменатель дроби убеждаемся, что их значения …
равны нулю, поэтому теорема о пределе частного здесь не применима. В данном случае говорят, что имеется неопределенность вида .
Неопределенность вида при может быть раскрыта сокращением дроби на множитель вида(х–х0), который обращает числитель и знаменатель дроби в нуль, в данном случае на(х+4). Поэтому, следует разложить на множители числитель и знаменатель дроби .
| 3х2+10х – | 4х2+15х– 4 = 0; |
| D= | D= |
| 3х2+10х–8 = 3(х+4)(х–2/3) = | 4х2+15х – 4 = 4(х+4)(х–1/4 ) = |
| = (х+4)(3х–2). | = (х+4)(4х–1). |
Таким образом,
в)
Здесь применима теорема о пределе частного, так как существуют конечные пределы числителя и знаменателя, и предел знаменателя не равен нулю.
г)
Здесь использована теорема о связи бесконечно малой и бесконечно большой функций.
д) .
Пределы числителя и знаменателя дроби равны . В этом случае говорят, что имеется неопределенность вида «бесконечность на бесконечность». Теорема о пределе частного здесь не применима.
Чтобы раскрыть неопределенность вида при , каждый член числителя и знаменателя дроби делят на x в наивысшей степени (в нашем примере на х2), отчего величина дроби не изменится, но исчезнет неопределенность.
так как
(по теореме о связи бесконечно большой и бесконечно малой функций).
Замечание. Полезно запомнить, что при предел отношения многочленов c одинаковыми наивысшими степенями равен отношению коэффициентов при этих степенях.
В нашем примере, коэффициенты при наивысшей степени х2многочленов равны 3 и 4, поэтому и предел дроби равен .
Ответы.
Пример 2.Найти предел .
Решение. Так как tg5x ~ 5x и sin7x ~ 7x при х ® 0, то, заменив функции эквивалентными бесконечно малыми, получим:
МЕТОДЫ ДИФФЕРЕНЦИАЛЬНОГО И ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
8. Дифференцирование функций одной переменной
8.1. Основные определения
8.1.1.Дифференциальное исчисление – раздел математики, в котором изучаются производные и дифференциалы функций, исследуются функции и решаются прикладные задачи (например, задачи на экстремум).
8.1.2.Дифференцирование– операции нахождения производных (частных производных) функций и их дифференциалов.
8.1.3.Дифференцируемая функция– функция одного или нескольких переменных называется дифференцируемой в некоторой точке, если в данной точке существует дифференциал этой функции. Для дифференцируемости функции необходимо и достаточно существование конечной производной для функции одной переменной или чтобы существовали в этой точке непрерывные частные производные для функции нескольких переменных.
8.1.4.Производная– основное понятие дифференциального исчисления, характеризующее скорость изменения функции при изменении аргумента x. Пусть функция определена в некоторой окрестности точки . Предел отношения приращения функции в этой точке (если он существует) к приращению аргумента, когда , называется производной функции в точке . Обозначения производной: или или или . Таким образом, . Численно производная равна угловому коэффициенту касательной, проведённой к кривой в данной точке (тангенсу угла наклона касательной к оси Ox). Если существует производная функции , её называют второй производной и пишут: . Аналогично определяется производная любого (целого) порядка n: . Производная называется первой производной или производной первого порядка, вторая, третья производная и т.д. – производными высших порядков. Вычисление производной называется дифференцированием функции.
8.1.5. Производной функции по аргументу x называется предел отношения ее приращения к приращению аргумента x, когда приращение аргумента стремится к нулю:
.
Если этот предел конечный, то функция y=f(x) называется дифференцируемой в точке x. Если же этот предел есть ∞, то говорят, что функция y=f(x) имеет в точке x бесконечную производную.
8.2. Механический смысл производной:скорость есть первая производная пути по времени, т.е. .
8.3. Геометрический смысл производной:тангенс угла наклона касательной к графику функции равен первой производной этой функции, вычисленной в точке касания, т.е.
Уравнение касательной к графику функции в точке :
Уравнение нормали к графику функции в точке :
Таблица производных
Рассмотрим примеры.
Найти производные функций:
Пример 1:
Решение:
+
Пример 2:
Решение:
Пример 3:
Решение:
refac.ru
Первый замечательные пределы.
Математика Первый замечательные пределы.
Количество просмотров публикации Первый замечательные пределы. — 68
| Наименование параметра | Значение |
| Тема статьи: | Первый замечательные пределы. |
| Рубрика (тематическая категория) | Математика |
Терема lim (sin(x)/x)=1
x®0
Доказательство:
S∆OMN=1/2 sin(x)
SсекOMN=1/2(x)
S∆OKN=1/2 tg(x)
S∆OMN<SсекOMN< S∆OKN
1/2sin(x)<1/2(x)<tg(x)
sin(x)<x<tg(x)
1<x/sin(x)<1/cos(x)
lim (1-cos(1/n))=0
n®+¥
lim (1-cos(x))=0 Þ lim (cos(x))=1
x®0 x®0
lim (x/sin(x))=0
x®0
x>0
lim (x/sin(x))=1
x®0
lim(1/(x/sin(x)))= lim(sin(x)/x)=1 что и требовалось доказать
x®0x®0
Определение бесконечного предела и пределов при х®+¥.
lim (f (x))=+¥ Û «ε>0 $d>0: » xÎO°d(x0)Þf(x)ÎOε(+¥)
x®x°
«(x): 0<|x-x0|<d
(////////// x
ε
lim (f (x))=-¥ Û «ε>0 $d>0: » xÎO°d(x0)Þf(x)ÎOε(-¥)
x®x°
«(x): 0<|x-x0|<d
lim (f (x))=¥ Û «ε>0 $d>0: » xÎO°d(x0)Þf(x)ÎOε(¥)
x®x°
|f(x)|>ε
lim (f (x))=b Û «ε>0 $∆>0: » xÎO∆(+¥)Þf(x)ÎOε(b)
x®+¥
» x: x>∆ |f(x)-b |<ε
lim (f (x))=b Û «ε>0 $∆>0: » xÎO∆(-¥)Þf(x)ÎOε(b)
x®—¥
» x: x<-∆ |f(x)-b |<ε
Односторонние пределы.
Первый замечательные пределы. — понятие и виды. Классификация и особенности категории «Первый замечательные пределы.» 2017, 2018.
referatwork.ru
Первый и второй замечательные пределы.
; — первый замечательный предел;
; — второй замечательный предел. Число е≈2,71828.
Пример 1. Вычислить предел
Решение. Если неопределенность представляют тригонометрические функции, то для ее раскрытия используют первый замечательный предел .
Преобразуем числитель дроби по формуле .
Пример 2. Вычислить предел
Решение.Используем второй замечательный предел .
Пример 3. Вычислить предел
В этом примере также используется второй замечательный предел <img …
src=»http://konspekta.net/studopediaru/baza18/388205111199.files/image429.png» /> . Преобразуем выражение, используя свойства логарифмов.
refac.ru
Замечательные пределы
Предел функции при 0 (Первый замечательный предел).
Для функции в точке имеет место неопределенность . Найдем предел этой функции при0. Будем использовать признак существования предела (а).
Рассмотрим окружность радиуса . Обозначим центральный уголMOB через ,при этом 0 < < .В результате получаем оценку для площадей:
C Площадь ∆MOA < площади сектора MOA < площади ∆COA.
M Площадь ∆MOA = OA MB = 1 MB = .
O B A Площадь сектора MOA = OA = 1.
Площадь ∆COA = OAAC = 1 =.
Из оценки для площадей следует оценка для функций: < < .
Разделим все последнего соотношения на :
1 < <или<< 1.
Это неравенство справедливо в предположении, что > 0. Но в силу четности:
= и =, заключаем, что оно верно и при< 0.
С учетом того, что ,, переменнаязаключена между двумя величинами, имеющими один и тот же предел, равный1. По признаку существования предела = 1.
Второй замечательный предел .
Для последовательности с общим членом приимеет место неопределенность , раскрывая которую получаем предел, заключенный между числами 2 и 3 .
Доказательство основано на признаке существования предела (б). Поэтому требуется установить, что члены последовательности монотонно возрастают, и последовательность ограничена сверху.
Для доказательства монотонности используем формулу бинома Ньютона, и получаем для общего члена последовательности выражение:
= 1 + ++ + +
+
= 1 + 1 + ++ +
+ .
Из последнего равенства видно, что каждый последующий член этой последовательности по сравнению с предыдущимсодержит еще одно положительное слагаемое. Кроме того, каждое слагаемое в выражении длябольше соответствующего слагаемого в выражении:. Следовательно,, то есть последовательность является возрастающей.
Для доказательства ограниченности сверху данной последовательности заметим, что каждое выражение в скобках в соотношении (*) меньше единицы:
; < 1 ….. . Поэтому для общего члена последовательности получаем оценку:
< 1 + 1 + +++;
< ,<,,<;
< 1 + 1 + +++.
Выражение 1 + +++представляет сумму членов геометрической прогрессии со знаменателем q = и первым членом 1. Используя формулу суммы геометрической прогрессии, приходим к неравенству:
< 1 + = 1 +< 3.
С учетом неравенства 2 ( следует из (*)) получаем оценку
2 < 3.
По признаку существования предела, если последовательность монотонно возрастает и ограничена, то она имеет предел. Этот предел обозначается буквой :
.
Число- иррациональное число, равное= 2,7182818284…
studfiles.net