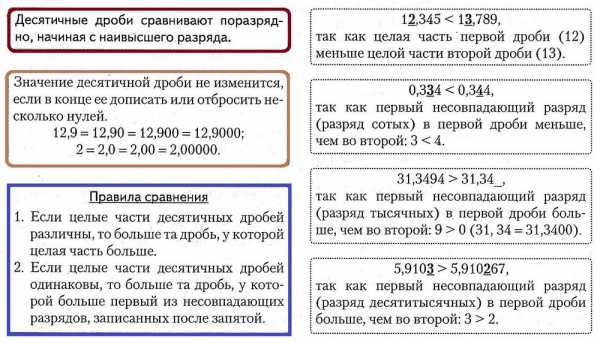
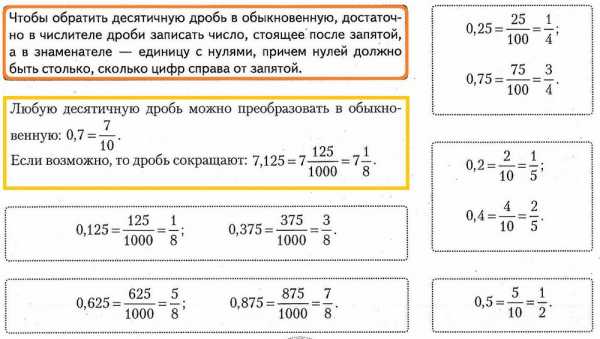
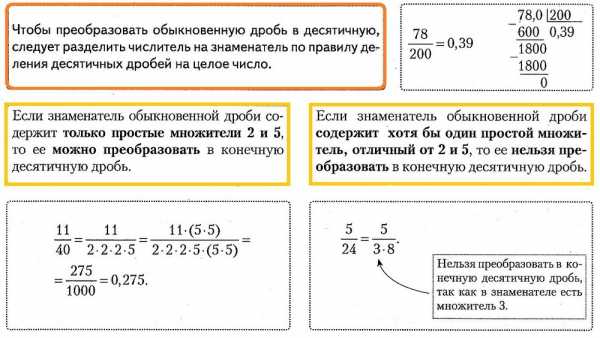
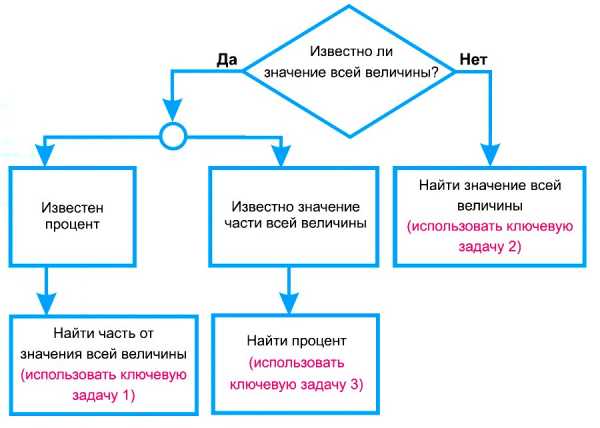
1.03. Некоторые сведения из комбинаторики
Комбинаторика — это часть так называемой Дискретной математики, изучающая разнообразные соединения элементов. Под элементами понимаются любые однотипные вещи: предметы, буквы, числа, живые существа и т. д. Различают 3 вида соединений элементов:
· Размещения;
· Перестановки;
· Сочетания.
1. Размещения. Пусть рассматривается совокупность из N упорядоченных, т. е. пронумерованных, элементов (A1; A2;…An). Будет составлять из этих N элементов всевозможные Упорядоченные группы По M элементов в каждой группе, где M – любое натуральное число, не превосходящее N. Эти группы будем считать различными, если они отличаются друг от друга хотя бы одним элементом или даже только порядком следования элементов в группе (у каждого элемента в упорядоченной группе есть свое учитываемое место). Такие группы называются Размещениями из N элементов по M элементов в каждом размещении. Их общее число обозначается символом , и находится оно по формуле:
= (2.1)
Напомним, что выражение N! Называется эн–факториал, и определяется оно так:
0!=1; 1!=1; 2!= 1·2=2; 3!=1·2·3=6; 4!=1·2·3·4=24;… N!= 1·2·3···N. (2.2)
Доказательство формулы (2.1).
1) Составим сначала все возможные размещения из N Элементов (A1; A2;…An) по одному элементу в каждом размещении и подсчитаем их число . Эти размещения – просто отдельно взятые элементы A1; A2;…An. Их количество равно N. То есть
=N (2.3)
2) Составим теперь все возможные размещения из N элементов по два элемента в каждом размещении и подсчитаем их число . Эти размещения тоже очевидны:
A1 a2 a2 a1 a3 a1 an a1
A1 a3 a2 a3 a3 a2 an a2
A1 a4 a2 a4 a3 a4 an a3 (2.4)
…… …… …… ……
A1 an a2 an a3 an an an-1
В каждом из столбцов (2.4) N —1 размещение, а всех столбцов N, поэтому
=N(N—1) (2.5)
3) Составим все возможные размещения из N элементов по три элемента в каждом размещении и подсчитаем их число . Эти размещения получим, если возьмем за основу все возможные размещения (2.4) по два элемента и добавим по очереди справа к каждому из них любой из оставшихся N-2 элементов. Таким образом, из каждого размещения (2.4) по два элемента можно образовать N-2 размещения по три элемента. Например, из одного размещение A1 A2 , содержащего два элемента, можно образовать следующее N-2 размещений по три элемента:
A1 a2 a3 ; a1 a2 a4; a1 a2 a5;……… a1 a2 an (2.6)
Следовательно,
=· (N-2)=N(N-1)(N-2) (2.7)
Аналогично:
= · (N-3)=N(N-1)(N-2)(N-3) (2.8)
= · (N-4)=N(N-1)(N-2)(N-3)(N-4)
………………………………………
То есть
= N(N-1)(N-2)(N-3)…..(N—M+1) (2.9)
Итак, мы получили формулу для при произвольном M (M=1,2,…N).
Преобразуем ее к более удобному виду. Для этого домножим и разделим выражение (2.9) на убывающие недостающие множители (N—M)(N—M-1)····3·2·1 так, чтобы последний множитель в (2.9) стал 1:
==
==
Формула (2.1) доказана.
Для примера подсчитаем общее количество всех возможныхРазмещений из трех элементов (A1; A2; A3) по одному, по два и по три элемента. Причем сделаем это и непосредственно, составив все эти размещения и пересчитав их, и по формуле (2.1):
=3; =6; =6 (2.11)
Эти же результаты дает и формула (2.1):
==; =; = (2.12)
2. Перестановки. Перестановками из данной совокупности N Элементов (A1; A2;…An) называются различным образом упорядоченные (по разному переставленные) комбинации всех этих элементов. Их общее количество обозначается символом . Так как перестановки – это по сути размещения из N элементов по N элементов в каждом размещении, то
(2.13)
3. Сочетания. Сочетаниями из N элементов по M Элементов в каждом сочетании называются (в отличие от размещений) всевозможные Неупорядоченные группы по M элементов в каждой группе. Неупорядоченные — это значит, что важно, какие элементы содержатся в каждом сочетании, а каком порядке они там находятся – это неважно. Различные размещения отличаются друг от друга хотя бы одним элементом. Общее их количество обозначается символом , и находится оно по формуле:
= (2.14)
Доказательство формулы (2.14)
Очевидно, что если взять все возможные сочетания из N элементов по M элементов и сделать в каждом из них все возможные перестановки, то в итоге получим все возможные размещения из N Элементов по M элементов в каждом размещении. Отсюда следует:
, и значит (2.15)
Для примера подсчитаем общее количество всех возможных сочетаний из трех элементов (A1; A2; A3) по одному, по два и по три элемента. Причем сделаем это и непосредственно, составив все эти сочетания и пересчитав их, и по формуле (2.14):
(2.16)
Эти же результаты дает и формула (2.14):
; (2.17)
Кстати, комбинации в (2.11) и в (2.16) наглядно демонстрируют разницу между размещениями и сочетаниями.
Выводя формулы (2.1), (2.13) и (2.14) для общего числа размещений, перестановок и сочетаний, мы полагали, что в каждом из указанных соединений любой из элементов совокупности (А1; а2; …..аN) может встретиться только один раз. То есть повторять в них элементы нельзя. Если же повторять их всё же можно, то мы придём к Размещениям, перестановкам и сочетаниям с повторениями.
4. Размещения с повторениями. Начнём с рассмотрения частного случая. Пусть исходная совокупность элементов составляет всего три элемента (А1; а2; а3). Составим из них все возможные размещения с повторениями по два элемента в каждом размещении и пересчитаем их. Очевидно, их будет 9 – те 6 , что представлены в (2.11) и в которых оба элемента разные, и ещё три размещения А1а1; а2а2; а3а3 с повторяющимися элементами. Если обозначить общее число всех возможных размещений из трёх элементов по два в каждом размещении символом , то получим: =9.
Впрочем, мы могли подсчитать это число и иначе. Составляя любое размещение из двух элементов, на первое место в таком размещении можно поставить любой из данных трёх элементов (три варианта). На второе место – тоже любой из трёх элементов (тоже три варианта). Комбинируя каждый элемент, стоящий на первом месте, с каждым элементом, стоящим на втором месте, получим 32=9 всех возможных комбинаций. То есть =32=9.
А теперь легко понять, что если всех элементов не три, а N, и из них составляются все возможные размещения с повторениями по M Элементов в каждом размещении, то их общее число найдётся по формуле:
=Nm (2.18)
5. Сочетания с повторениями. Опять начнём с частного случая. А именно, подсчитаем – общее число всех возможных сочетаний с повторениями из трёх элементов (А1; а2; а3) по два элемента в каждом сочетании. Этих сочетаний, очевидно, будет 6 – те 3, которые представлены в (2.16) и в которых оба элемента разные, и ещё три сочетания А1а1; а2а2; а3а3 с повторяющимися элементами. То есть =6=. И вообще, можно доказать, что
(2.19)
6. Перестановки с повторениями. Пусть среди элементов (А1; а2; …..аN) содержится лишь K различных элементов (K<N), причём первый из них повторяется N1 раз, второй N2 раз, …K-ый Nk раз. Очевидно, что N1+N2+… Nk=N. Тогда число всех возможных перестановок из таких N Элементов обозначается символом И находится по формуле:
(2/20)
В самом деле, если бы все N Элементов были разными, то число всех возможных перестановок из них, согласно (2.13), было бы равно Но среди них разных элементов лишь K, остальные N – K элементов повторяют эти K элементов. В частности, первый из этих K элементов повторяется раз. Сделав любую перестановку из этих Одинаковых элементов (не трогая остальных!) мы ничего не нарушим ни в какой перестановке из N элементов. А вот если бы все эти повторяющихся элементов были разными, то сделав любую их перестановку, мы получили бы другую перестановку из N элементов. Количество всех возможных перестановок из N1 Элементов равно . Значит, наличие этих одинаковых элементов уменьшает в раз общее количество всех возможных перестановок из N Элементов по сравнению с тем случаем, когда все N элементов были бы разными. Тот же эффект производит наличие второго повторяющегося раз элемента, третьего, … K-ого. В итоге и приходим к формуле (2.20).
А теперь рассмотрим примеры на применение полученных выше формул.
Пример 1. В посёлке устанавливается телефонная сеть с трёхзначными телефонными номерами. Сколько всего можно установить телефонных номеров? Сколько из них будет тех, которые содержат: 1) три разные цифры? 2) две одинаковые цифры? 3) три одинаковые цифры?
Решение. Всех возможных трёхзначных телефонных номеров будет, очевидно, 1000: это номера 000, 001, 002, … 999.
1) Номеров с тремя разными цифрами будет, очевидно, столько, сколько существует всех возможных соединений (комбинаций) из 10 цифр 0,1,2,…9 по три цифры в каждом соединении. Так как в этих соединениях важен порядок следования цифр (например, 137 и 173 – это разные номера), то этими соединениями будут размещения. А значит, их общее количество N1 можно найти по формуле (2.1):
3) Пропуская вопрос (2), ответим на вопрос (3). Номеров с тремя одинаковыми цифрами будет, очевидно, 10. Это номера 000, 111, 222, … 999. То есть N3 = 10.
2) Все остальные номера – с двумя одинаковыми цифрами. Следовательно, их общее количество
N2 = 1000 – (N1 + N3 ) = 1000 – (720 + 10) = 270.
Пример 2. Сколько всего диагоналей у выпуклого N – угольника?
Решение: Соединяя каждую пару вершин треугольника, получим либо диагональ, либо сторону многоугольника. Число всех различных пар вершин N-угольника равно числу всех возможных соединений из N элементов (вершин многоугольника) по два элемента (по две вершины) в каждом соединении. Так как порядок следования элементов в этих парах, очевидно, не важен (диагональ, соединяющая, например, 2-ю и 5-ю вершину – это та же диагональ, которая соединяет 5-ю и 2-ю вершину), то такими парными соединениями будут сочетания из N элементов по два элемента в каждом сочетании. Следовательно, их общее число равно . В это число входят и сами N сторон многоугольника. Поэтому искомое число N Диагоналей N-угольника найдётся по формуле:
Пример 3. В чемпионате области по футболу участвуют 20 команд, причём каждые две из них встречаются между собой два раза (игры идут в два круга). Сколько всего матчей играется в течение сезона?
Решение. В первом круге состоится столько матчей, сколько существует сочетаний из 20 команд по две в каждом сочетании. То есть их число равно:
Во втором круге играется столько же матчей, поэтому в течение сезона их состоится 190·2=380.
Пример 4. Сколькими различными способами можно рассадить N человек за круглым столом?
Решение. Общее число всех способов, с помощью которых N человек может занять N мест за любым (не только круглым) столом равно, очевидно, числу всех перестановок из N Элементов (из N человек), то есть равно Но если стол круглый, то любая циклическая перестановка (одновременная пересадка всех вправо или влево на одно или несколько мест) не нарушает порядка рассаживания людей за столом. А таких циклических пересаживаний всего N. Поэтому искомое число Nn рассаживания N человек за круглым столом равно:
В частности, N2=1; N3 = 2; N4 = 6; N5 = 24;…..
Пример 5. Автомобильные номера состоят из двух букв (всего используется 30 букв) и трёх цифр (используются все 10 цифр). Сколько всего автомобилей можно занумеровать таким образом, чтобы никакие два автомобиля не имели одинакового номера?
Решение: Различных пар букв будет столько, сколько можно составить размещений с повторениями из 30 букв по две в каждом размещении. То есть, согласно формуле (2.18), их будет:
=302=900.
Аналогично различных троек цифр будет:
=103=1000.
(впрочем, это и так очевидно). Комбинируя (соединяя) теперь каждую пару букв с каждой тройкой цифр, получим искомое общее число N различных автомобильных номеров:
N= 900 · 1000 = 900000.
Пример 6. Имеются две колоды по 36 карт. Из каждой колоды вынимаются по одной карте. Сколько различных пар карт может быть при этом образовано?
Решение. В образовываемых парах карт порядок их следования, очевидно, не важен. Поэтому эти пары – различные сочетания из 36 карт. По условию, среди этих пар могут оказаться n пары с одинаковыми картами. То есть образованные пары карт – это сочетания с повторениями. А значит, их общее число:
Пример 7. Сколько всех возможных перестановок букв можно сделать в слове «математика»?
Решение. В слове «математика» всего 10 букв, из которых буква А повторяется 3 раза, буква М – два раза, буква т – два раза. Поэтому искомое число N Перестановок в слове «математика» — это число перестановок с повторениями. Согласно формуле (2.20),
Пример 8. Сколькими различными способами могут занять места в президиуме 5 человек, если в президиуме 8 мест?
Решение. – число всех возможных способов выбора пяти различных мест из имеющихся восьми. На этих местах 5 человек можно рассадить числом способов = 5! В итоге искомое число способов
Пример 9. Из колоды в 36 карт наудачу вынимаются две карты. Какова вероятность того, что ими окажется два туза (любых)?
Решение. В данной задаче испытание – это вынимание из колоды наудачу двух карт, а событие А – вынимание двух тузов. Возможных исходов в испытании столько, сколько всего пар карт можно составить. Таких пар будет, очевидно, N = = 630. Все эти 630 возможных исходов испытания, очевидно, равновозможны. А число M исходов, благоприятствующих событию А – это, очевидно, число всех пар из четырёх тузов, то есть M = = 6. Поэтому по классической формуле (1.3) получаем:
Пример 10. Ребёнок играет двумя карточками с буквой «М» и двумя карточками с буквой «А», выкладывая их в линию. Какова вероятность того, что у него получится слово «МАМА»?
Решение. В данной задаче испытание — это выкладывание ребёнком наудачу в линию четырёх карточек, а событие А – выкладывание слова «МАМА». Возможные исходы испытания – это различные перестановки четырёх карточек, причём перестановки с повторениями, в которых и буква М, и буква А повторяются два раза. Число таких перестановок, согласно формуле (2.20), равно
Это – число N Всех возможных исходов испытания, причём исходов равновозможных. А число M исходов, благоприятствующих событию А, равно 1: M=1 (перестановка «МАМА»). В итоге по классической формуле (1.3) получаем:
Пример 11. Из десяти билетов выигрышными являются два. Определить вероятность того, что среди наудачу взятых пяти билетов: а) только один выигрышный; б) оба выигрышные.
Решение. Здесь испытание – выбор пяти билетов из десяти. Всего существует способов выбрать 5 билетов из 10. Следовательно, число N Всех возможных исходов испытания и в задаче а), и в задаче б) одинаково и равно . Причём все эти исходы равновозможны.
В задаче а) благоприятный исход испытания состоит в том, что из двух выигрышных билетов будет выбран один (это можно сделать двумя способами), а из восьми невыигрышных будут выбраны четыре (это можно сделать Способами). Таким образом, общее число всех благоприятных исходов равно 2·, а значит, вероятность события А, состоящего в том, что среди пяти отобранных билетов окажется лишь один выигрышный, по классической формуле (1.3) равна:
В задаче б) благоприятный исход испытания состоит в том, что из двух выигрышных билетов будут взяты оба (их можно взять одним способом) и ещё три билета будут взяты невыигрышных (их можно взять способами). Число благоприятных исходов, таким образом равно , а вероятность события В, состоящего в том, что среди пяти отобранных билетов окажется два выигрышных, по классической формуле равна
Пример 12. На книжную полку в произвольном порядке выставлены 5 книг. Какова вероятность того, что некоторые две из них, составляющие двухтомник, окажутся на полке рядом?
Решение. В данной задаче испытание – это установка на полку в произвольном порядке пяти книг. А событие А – то, что книги двухтомника окажутся рядом.
Всех возможных исходов испытания, очевидно, столько, сколько существует перестановок из пяти книг. То есть их = 5! = 120. Благоприятствующими событию А будут те из них, когда книги двухтомника стоят рядом.
Для начала подсчитаем число тех благоприятствующих исходов, когда книги двухтомника стоят на первых двух местах, причём первый том стоит на первом месте, а второй на втором. Так как последние три книги могут быть установлены произвольно, то таких исходов будет =3! = 6. Меняя местами книги двухтомника, получим ещё 6 благоприятствующих исходов. Таким образом, если книги двухтомника занимают на полке первые два места, то всего соответствующих благоприятствующих исходов (перестановок книг) оказывается 2· = 12. Но благоприятствующими событию А Исходами будут и те, при которых книги двухтомника стоят на 2-3, 3-4, 4-5 местах. Итого всех таких исходов оказывается 12·4=48. А тогда по классической формуле (1.3) получаем:
Упражнения.
1. В пятом классе изучается 12 предметов. Сколькими способами можно составить расписание занятий на понедельник, если в этот день должно быть 4 урока? Решить задачу в предположении, что:
А) порядок уроков важен;
Б) порядок уроков не важен.
Ответ: а) 11880; б) 495.
2. Сколько различных символов можно закодировать с помощью 8-значных двоичных чисел (чисел, содержащих в своей записи лишь нули и единицы общим числом 8)?
Ответ: 256.
3. Пять девушек и пять юношей разыграли 10 мест выделенного им на концерт зрительного ряда (места с 31 по 40). Какова вероятность того, что они будут сидеть строго вперемешку (никакие две девушки и два юноши не будут сидеть рядом)?
Ответ: 1/126.
4. Найти вероятность того, что в лотерее «Спортлото 5 из 36» можно угадать:
А) все 5 номеров; б) 4 номера; в) 3 номера.
Ответ: а) 1/324632; б) 150/324632; в) 4350/324632.
5. Доказать, что вероятность того, что у двенадцати случайно выбранных человек дни рождения приходятся на разные месяцы, меньше 0,0001.
6. Сколькими различными способами можно распределить 6 различных учебников между тремя студентами по два учебника каждому?
Ответ: 90 способами.
matica.org.ua
Элементы комбинаторики. Методы решения некоторых задач
Разделы: Математика
Класс:
1) Немного истории.
В математике и ее приложениях часто
приходится иметь дело с различного рода
множествами и подмножествами: устанавливать их
связь между элементами каждого, определять число
множеств или их подмножеств, обладающих заданным
свойством. Такие задачи приходится
рассматривать при определении наиболее выгодных
коммуникаций внутри города, при организации
автоматической телефонной связи, работы морских
портов, при выявлении связей внутри сложных
молекул, генетического кода, а также в
лингвистике, в автоматической системе
управления, значит и в теории вероятностей, и в
математической статистике со всеми их
многочисленными приложениями.
Поговорим об одном из разделов теории
вероятности – комбинаторике.
Комбинаторика — ветвь математики,
изучающая комбинации и перестановки предметов.
Еще комбинаторику можно понимать как перебор
возможных вариантов. Комбинаторика возникла в 17
веке. Долгое время она лежала вне основного русла
развития математики.
С задачами, в которых приходилось выбирать те или
иные предметы, располагать их в определенном
порядке и отыскивать среди разных расположений
наилучшие, люди столкнулись еще в доисторическую
эпоху, выбирая наилучшее положение охотников во
время охоты, воинов – во время битвы,
инструментов — во время работы.
Комбинаторные навыки оказались полезными и в
часы досуга. Нельзя точно сказать, когда наряду с
состязаниями в беге, метании диска, прыжках
появились игры, требовавшие, в первую очередь,
умения рассчитывать, составлять планы и
опровергать планы противника.
Со временем появились различные игры (нарды,
карты, шашки, шахматы и т.д.). В каждой из этих игр
приходилось рассматривать различные сочетания
фигур, и выигрывал тот, кто их лучше изучил, знал
выигрышные комбинации и умел избегать
проигрышных. Не только азартные игры давали пищу
для комбинаторных размышлений математиков. Еще с
давних пор дипломаты, стремясь к тайне переписки,
изобретали сложные шифры, а секретные службы
других государств пытались эти шифры разгадать.
Стали применять шифры, основанные на
комбинаторных принципах, например, на различных
перестановках букв, заменах букв с
использованием ключевых слов и т.д.
Комбинаторика как наука стала развиваться в 18
веке параллельно с возникновением теории
вероятностей, так как для решения вероятностных
задач необходимо было подсчитать число
различных комбинаций элементов. Первые научные
исследования по комбинаторике принадлежат
итальянским ученым Дж.Кардано, Н.Тарталье (1499-1557),
Г.Галилею (1564-1642) и французс- ким ученым Б.Паскалю
(1623-1662) и П.Ферма.
Комбинаторику как самостоятельный раздел
математики первым стал рассматривать немецкий
ученый Г.Лейбниц в своей работе “ Об искусстве
комбинаторики ”, опубликованной в 1666 году. Он
также впервые ввел термин “комбинаторика”.
Значительный вклад в развитие комбинаторики
внес Л.Эйлер. В современном обществе с развитием
вычислительной техники комбинаторика
“добилась” новых успехов. В настоящее время в
образовательный стандарт по математике включены
основы комбинаторики, решение комбинаторных
задач методом перебора, составлением дерева
вариантов (еще его называют “дерево
возможностей”) с применением правила умножения.
Так, например, “дерево возможностей” помогает
решать разнообразные задачи, касающиеся
перебора вариантов происходящих событий. Каждый
путь по этому “дереву” соответствует одному из
способов выбора, число способов выбора равно
числу точек в нижнем ряду “дерева”. Правило
умножения заключается в том, что для того, чтобы
найти число всех возможных исходов независимого
проведения двух испытаний А и В, следует
перемножить число всех исходов испытания А и
число всех исходов испытания В. В задачах по
комбинаторике часто применяется такое понятие
как факториал (в переводе с английского “factor” -
“множитель”).
Итак, произведение всех натуральных чисел от 1 до
n включительно называют n-факториалом и пишут: n!=1 2
3 … (n-1) n
В комбинаторике решаются задачи, связанные с
рассмотрением множеств и составлением различных
комбинаций из элементов этих множеств. В
зависимости от правил составления можно
выделить три типа комбинаций: перестановки,
размещения, сочетания.
2) ЗАДАЧИ
1. В школьной столовой на первое можно
заказать борщ, солянку, грибной суп, на второе -
мясо с макаронами, рыбу с картошкой, курицу с
рисом, а на третье — чай и компот. Сколько
различных обедов можно составить из указанных
блюд?
1 способ. Перечислим возможные
варианты
Чай(Ч)
Компот (К) |
Мясо с макаронами(М) |
Рыба с картошкой(Р) |
Курица с рисом(Кр) |
Борщ (Б) |
БМЧ/ БМК |
БРЧ/БРК |
БКрЧ/БКрК |
Солянка(С) |
СМЧ/ СМК |
СРЧ/СРК |
СКрЧ/СКрК |
Грибной суп(Г) |
ГМЧ/ГМК |
ГРЧ/ГРК |
ГКрЧ/ГКрК |
18 вариантов.
2 способ. Дерево возможностей.
3 способ. Используя правило
умножения, получаем: 3х3х2=1
2. Свете на день рождения подарили 4
плюшевых игрушки, 2 мяча и 5 кукол. Мама положила
все игрушки в большую коробку. Сколькими
способами Света сможет достать из коробки 1
плюшевую игрушку, 1 мяч и 1 куклу?
1 способ. Обозначим мячи — М1, М2,
игрушки- И1,И2,И3, И4, куклы- К1,К2, К3, К4, К5.
Перечислим возможные варианты:
М1-И1-К1, М1-И1-К2, М1-И1-К3, М1-И1-К4, М1-И1-К5,
М1-И2-К1, М1-И2-К2, М1-И2-К3, М1-И2-К4, М1-И2-К5,
М1-И3-К1, М1-И3-К2, М1-И3-К3, М1-И3-К4, М1-И3-К5,
М1-И4-К1, М1-И4-К2, М1-И4-К3, М1-И4-К4, М1-И4-К5
М2-И1-К1, М2-И1-К2, М2-И1-К3, М2-И1-К4, М2-И1-К5,
М2-И2-К1, М2-И2-К2, М2-И2-К3, М2-И2-К4, М2-И2-К5,
М2-И3-К1, М2-И3-К2, М2-И3-К3, М2-И3-К4, М2-И3-К5,
М2-И4-К1, М2-И4-К2, М2-И4-К3, М2-И4-К4, М2-И4-К5
Ответ: 40 вариантов.
2 способ. Используя правило умножения,
получаем: 2х4х5= 40
3. Сколько четных двузначных чисел
можно составить из цифр 0, 2, 3, 6, 7, 9?
1 способ.
Перечислим возможные варианты.
| |
0 |
2 |
6 |
2 |
20 |
22 |
26 |
3 |
30 |
32 |
36 |
6 |
60 |
62 |
66 |
7 |
70 |
72 |
76 |
9 |
90 |
92 |
96 |
2 способ. Дерево возможностей.
3 способ. Используя правило
умножения, получаем: 5х3=15 .
4. Мисс Марпл, расследуя убийство,
заметила отъезжающее от дома мистера Дэвидсона
такси. Она запомнила первую цифру “2”. В городке
номера машин были трехзначные и состояли из цифр
1,2,3,4 и 5. Скольких водителей, в худшем случае, ей
придется опросить, чтобы найти настоящего
убийцу?
1 способ. Перечислим возможные
варианты номеров такси:
| |
1 |
2 |
3 |
4 |
5 |
1 |
211 |
212 |
213 |
214 |
215 |
2 |
221 |
222 |
223 |
224 |
225 |
3 |
231 |
232 |
233 |
234 |
235 |
4 |
241 |
242 |
243 |
244 |
245 |
5 |
251 |
252 |
253 |
254 |
255 |
Ответ: 25 человек.
2 способ. Используя правило
умножения, получаем: 5х5=25
5. Саша, Петя, Денис, Оля, Настя часто
ходят в кафе. Каждый раз, обедая там, они
рассаживаются по-разному. Сколько дней друзья
смогут это сделать без повторения?
1 способ. Пронумеруем стулья, на
которых должен сесть каждый, и будем считать, что
они рассаживаются поочередно:
№1 — Саша — есть возможность выбрать из 5
вариантов (стульев)
№2 — Петя — 4 варианта
№3- Денис — 3 варианта
№4- Оля — 2 варианта
№5 — Настя- 1 вариант
Используя правило умножения, получаем:
5х4х3х2х1=120
2 способ. Решаем, используя понятие
факториала: 5!=120
6. Из учащихся пяти 11 классов нужно
выбрать двоих дежурных. Сколько пар дежурных
можно составить (ученики в паре не должны быть из
одного класса)?
1 способ. Перечислим возможные
варианты состава пары:
11А-11Б, 11А-11В, 11А-11Г, 11А-11Д,
11Б-11В, 11Б-11Г, 11Б-11Д, 11В-11Г, 11В-11Д, 11Г-11Д
Ответ: 10 пар.
2 способ. Из пяти классов нужно
выбрать 2 дежурных.
Число элементарных событий = = 10
7. В 8 “а” классе лучше всех
математику знают 5 учеников: Вася, Дима, Олег, Катя
и Аня. На олимпиаду по математике нужно отправить
пару, состоящую из 1 мальчика и 1 девочки.
Сколькими способами учительница может эту пару
выбрать?
1 способ. Обозначим имена детей
первыми заглавными буквами.
Получаем следующие пары:
В-К, В-А, Д-К, Д-А, О-К, О-А.
Ответ: 6 пар.
2 способ. Мальчиков 3, из них 1 можно
выбрать ,
девочек 2, из них можно 1 выбрать , используя
правило умножения, получаем:
х = 6
8. В соревнованиях по фигурному
катанию принимали участие россияне, итальянцы,
украинцы, немцы, китайцы и французы.
Сколькими способами могут
распределится места по окончании соревнований?
Обозначим участников по первой заглавной букве
страны и пронумеруем: Р1, И2, У3, Н4,К5, Ф6
Р1 — имеют возможность занять с1-6 места, т.е. 6
вариантов
И2 — 5 вариантов
У3- 4 варианта
Н4- 3 варианта
К5- 2 варианта
Ф6- 1 вариант
Используя правило умножения, получаем: 6х5х4х3х2х1=
720
2 способ. Используя понятие
факториала, получаем: 6!=720
9. В 9 “б” классе 6 человек (Галя,
Света, Катя, Оля, Максим, Витя) учатся на все
пятерки. Департамент образования премировал
лучших учащихся путевками в Анапу. Но, к
сожалению, путевок всего четыре. Сколько
возможно вариантов выбора учеников на отдых?
Обозначим первыми заглавными буквами
имен учащихся.
Возможны следующие тройки:
Г-С-К-О, Г-С-К-М, Г-С-К-В,
Г-С-О-М, Г-С-О-В, Г-С-М-В
С-К-О-М, С-К-О-В, С-К-М-В,
К-О-М-В, С-О-М-В, Г-К-О-В,
Г-К-О-В, Г-О-М-В, Г-К-М-В
2 способ. Из 6 человек нужно выбрать
4, число элементарных событий равно = 15
10. Пете на день рождения подарили 7
новых дисков с играми, а Вале папа привез 9 дисков
из командировки. Сколькими способами они могут
обменять 4 любых диска одного на 4 диска другого?
Вычислим, сколько четверок из 7 дисков
можно составить у Пети:
=35, число
четверок у Вали из 9 дисков -= 126
По правилу умножения находим число обменов 35х126=4410
11. Войсковое подразделение состоит
из 5 офицеров, 8 сержантов и 70 рядовых. Сколькими
способами можно выделить отряд из 2 офицеров, 4
сержантов и 15 рядовых?
Из 5 офицеров выбрать 2 можно с помощью
числа сочетаний =10 способами, из 8 сержантов 4 — =70, из 70 рядовых 15 -. По правилу
умножения находим число выбора отряда:
10х70х= 700х
12. В ювелирную мастерскую привезли 6
изумрудов, 9 алмазов и 7 сапфиров. Ювелиру
заказали браслет, в котором 3 изумруда, 5 алмазов и
2 сапфиров. Сколькими способами он может выбрать
камни на браслет?
Из 6 изумрудов 3 он может выбрать =20 способами, из 9
алмазов 5 -=126,
из 7 сапфиров 2 — =21.
По правилу умножения находим число вариантов
20х126х21=52920
13. На выборах победили 9 человек -
Сафонов, Николаев, Петров, Кулаков, Мишин, Гусев,
Володин, Афонин, Титов. Из них нужно выбрать
председателя, заместителя и профорга. Сколькими
способами это можно сделать?
Здесь речь идет о размещениях
Можно было решать по-другому. На должность
председателя выбираем из 9 человек, на
заместителя — из 8, на профорга — из 7
По правилу умножения получаем 9х8х7=504
14. В районе построили новую школу. Из
пришедших 25 человек нужно выбрать директора
школы, завуча начальной школы, завуча среднего
звена и завуча по воспитательной работе.
Сколькими способами это можно сделать?
На должность директора выбираем из 25
человек, на завуча начальной — из 24, завуча
среднего звена — из 23, завуча по воспитательной
работе — 22. По правилу умножения получаем:
25х24х23х22 = 303600
Или, зная формулу размещения, получаем
15. В студенческом общежитии в одной
комнате живут трое студентов Петя, Вася и Коля. У
них есть 6 чашек, 8 блюдец и 10 чайных ложек (все
принадлежности отличаются друг от друга).
Сколькими способами ребята могут накрыть стол
для чаепития (так, что каждый получит чашку,
блюдце и ложку)?
Для Пети набор можно набрать 6х8х10=480
способами, для Васи — 5х7х9=315, для Коли — 4х6х8=192. По
правилу умножения получаем
480х315х192=29030400 способами.
16. В кабинете заведующего ювелирного
магазина имеется код, состоящий из двух
различных гласных букв русского алфавита, за
которой следуют 3 различные цифры. Сколько
вариантов придется перебрать мошеннику, чтобы
раздобыть драгоценности, которые там хранятся?
В русском языке 9 гласных букв — а, е, е,
и, о, у, э, ю, я. Выбрать из них 2 можно =36 способами. Из 10
цифр выбрать 3 можно=120 способами. Применяя правило умножения,
получаем:
36х120=4320
17. Сколькими способами можно составить
трехцветный флаг из полос разной ширины, если
имеются материи из 8 тканей?
Эта задача на размещение
Другой способ решения.
1цвет выбирается из 8 тканей 8 способами
2цвет выбирается 7 способами
3 цвет — 6способами
Используя правило умножения, получаем 8х7х6=336
способов.
18. В 9 классе 15 предметов. Завучу школы
нужно составить расписание на субботу, если в
этот день 5 уроков. Сколько различных вариантов
расписания можно составить, если все уроки
различные?
Из 15 предметов 5 любых можно выбрать
19. В огороде у бабушки растут 3 белые, 2
алые и 4 чайных розы. Сколькими различными
способами можно составить букет из трех роз
разного цвета?
1 способ. Обозначим белые — Б1, Б2, Б3,
алые — А1,А2, чайные — Ч1, Ч2, Ч3,Ч4
Перечислим возможные варианты
Б1-А1-Ч1, Б1-А1-Ч2, Б1-А1-Ч3, Б1-А1-Ч4, Б1-А2-Ч1,Б1-А2-Ч2, Б1-А2-Ч3,
Б1-А2-Ч4
Б2- А1-Ч1, Б2-А1-Ч2, Б2-А1-Ч3, Б2-А1-Ч4, Б2-А2-Ч1,Б2-А2-Ч2, Б2-А2-Ч3,
Б2-А2-Ч4
Б3- А1-Ч1, Б3-А1-Ч2, Б3-А1-Ч3, Б3-А1-Ч4, Б3-А2-Ч1,Б3-А2-Ч2, Б3-А2-Ч3,
Б3-А2-Ч4
Ответ: 24 варианта.
2способ. Дерево возможностей
3 способ. Используя правило
умножения, получаем: 2х3х4=24
20. К 60-летию Победы группа школьников
отправилась по местам боевых действий в
Смоленской области. Они планировали осуществить
поход по маршруту деревни Сосновка-Быковка-
Масловка- Видово. Из С в Б можно проплыть по реке
или пройти пешком, из Б в М- пешком или на
автобусе, из М в В — по реке, пешком или автобусе.
Сколько вариантов похода есть у щкольников?
1 способ. Обозначим СБ — путь из
Сосновки в Бытовку, ВГ — путь из Быковки в
Масловку, МВ — путь из Масловки в Видово.
По реке -Р, пешком — П, на автобусе — А
Перечислим возможные варианты:
СБР- БМП-МВР, СБР- БМП-МВП, СБР- БМП-МВА
СБР-БМА-МВР, СБР-БМА-МВП, СБР-БМА-МВА
СБА- БМП-МВР, СБА- БМП-МВП, СБА- БМП-МВА
СБА-БМА-МВР, СБА-БМА-МВП, СБА-БМА-МВА
Ответ: 12 вариантов.
2 способ. Дерево возможностей
ЛИТЕРАТУРА
1) Еженедельное учебно-методическое
приложение “Математика” Изд. Пресса. Москва.1999 г
2) Ю.Н.Макарычев и др. Алгебра 9. Учебник
для класса с углубленным изучением математики.
Изд. Мнемозина, Москва.2005 год.
3) Л.Г. Петерсон. Математика 4 класс. Изд.
Баласс. Москва.1999 г.
4) Ю.Н. Тюрин и др. Теория вероятностей и
статистика. МЦНМО. Москва. 2004 год.
28.02.2007
urok.1sept.ru
Задание №10 ЕГЭ по математике базовый уровень
Вероятность и статистика
В задании №10 ЕГЭ по математике базового уровня нам предстоит решить задачу по теории вероятности. Задачи довольно простые и адаптированы под реальные жизненные ситуации, что делает их решение интересным для школьников. Разберем с Вами несколько подробных примеров.
Разбор типовых вариантов задания №10 ЕГЭ по математике базового уровня
Первый вариант задания (демонстрационный вариант 2018)
В чемпионате по прыжкам в воду участвуют 35 спортсменов: 7 из России, 12 из Китая, 9 из Японии и 7 из США. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из России.
Алгоритм выполнения:
- Вспомнить определение вероятности.
- Определить из условия задачи необходимые величины.
- Подставить значения и вычислить вероятность.
Решение:
Вспомним определение вероятности.
Вероятность – это отношение возможности происшествия одного или нескольких конкретных событий к общему числу возможных результатов.
Для того, чтобы определить вероятность происшествия конкретного события(в данном случае – что первым будет россиянин) нужно разделить число благоприятных исходов на общее число событий.
Определим из условия задачи необходимые величины.
Вариантов благоприятного исхода 7, так как россиян 7 и каждый из них имеет равные шансы выступать первым.
Всего общее число вариантов 35, так как спортсменов всего 35 и каждый из них может выступать первым.
Подставим значения и вычислим вероятность.
7/35 = 1/5 = 0,2
Ответ: 0,2.
Второй вариант задания
Олег, Петя, Миша и Дима бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет не Миша.
Алгоритм выполнения:
- Вспомнить определение вероятности.
- Определить из условия задачи необходимые величины.
- Подставить значения и вычислить вероятность.
Решение:
Вспомним определение вероятности.
Вероятность – это отношение возможности происшествия одного или нескольких конкретных событий к общему числу возможных результатов.
Для того, чтобы определить вероятность происшествия конкретного события(в данном случае – что игру должен будет начинать не Миша) нужно разделить число благоприятных исходов на общее число событий.
Определим из условия задачи необходимые величины.
Вариантов благоприятного исхода 3, так как «не Миш» трое и каждый из них имеет равные шансы начинать игру.
Всего общее число вариантов 4, так как мальчиков всего 4 и каждый из них может начинать игру.
Подставим значения и вычислим вероятность.
3/4 = 0,75
Вариант решения в общем виде:
При бросании жребия начинает игру один из 4 мальчиков. Вероятность этого события составляет P = 1/4 (для любого мальчика, в том числе и для Миши). Тогда обратная вероятность того, что Миша не будет начинать игру, равна:
Ответ: 0,75.
Третий вариант задания
Вася, Петя, Олег, Коля и Лёша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Вася или Петя.
Алгоритм выполнения:
- Вспомнить определение вероятности.
- Определить из условия задачи необходимые величины.
- Подставить значения и вычислить вероятность.
Решение:
Вспомним определение вероятности.
Вероятность – это отношение возможности происшествия одного или нескольких конкретных событий к общему числу возможных результатов.
Для того, чтобы определить вероятность происшествия конкретного события(в данном случае – что игру должен будет начинать Вася или Петя) нужно разделить число благоприятных исходов на общее число событий.
Определим из условия задачи необходимые величины.
Вариантов благоприятного исхода 2, так как Вася и Петя – это два мальчика, каждый из них имеет равные шансы начинать игру.
Всего общее число вариантов 4, так как мальчиков всего 5 и каждый из них может начинать игру.
Подставим значения и вычислим вероятность.
2/5 = 0,4
Решение в общем виде:
Всего при бросании жребия может быть n = 5 исходов (для 5 человек). Обозначим через событие А – жребий выпал Васе или Пете. Число благоприятных исходов для события A равно m = 2. Следовательно, искомая вероятность, равна:
Ответ: 0,4.
Четвертый вариант задания
Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,1. Найдите вероятность того, что в течение года обе лампы перегорят.
Алгоритм выполнения:
- Определить вероятность каждого события в отдельности.
- Перемножить вероятности событий. Это даст вероятность того, что события произойдут последовательно.
Решение:
Определим вероятность каждого события в отдельности.
Вероятность того, что перегорит первая лампа по условию 0,1. Вероятность того, что перегорит вторая лампа по условию 0,1.
Перемножим вероятности событий. Это даст вероятность того, что события произойдут последовательно.
Ответ: 0,01.
Пятый вариант задания
Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,15. Найдите вероятность того, что в течение года обе лампы перегорят.
Алгоритм выполнения:
- Определить вероятность каждого события в отдельности.
- Перемножить вероятности событий. Это даст вероятность того, что события произойдут последовательно.
Решение:
Определим вероятность каждого события в отдельности.
Вероятность того, что перегорит первая лампа по условию 0,15. Вероятность того, что перегорит вторая лампа по условию 0,15.
Перемножим вероятности событий. Это даст вероятность того, что события произойдут последовательно.
Ответ: 0,0225.
Вариант десятого задания 2017
Из каждых 100 лампочек, поступающих в продажу, в среднем 3 неисправны. Какова вероятность того, что случайно выбранная в магазине лампочка окажется исправной?
Данная задача даже проще, чем предыдущая. В начале, нам необходимо найти количество исправных лампочек:
100 — 3 = 97
После этого находим вероятность, она равна отношению количества исправных лампочек к общему количеству:
97 / 100 = 0,97
Ответ: 0,97
Вариант десятого задания 2019 года(1)
На семинар приехали 6 ученых из Норвегии, 5 из России и 9 из Испании. Каждый ученый подготовил один доклад. Порядок докладов определяется случайным образом. Найдите вероятность того, что восьмым окажется доклад ученого из России.
Алгоритм выполнения
- Поскольку событие, описанное в условии, является независимым, то вероятность того, что ученый из России выступит именно 8-м, такая же, как и вероятность выступления под любых другим номером. Поэтому для решения можем применить формулу-определение для вероятности P=Nб/N, где Nб – кол-во благоприятствующих данному событию исходов, N – общее кол-во исходов.
- Подсчитываем общее кол-во исходов. Оно равно сумме всех докладов.
- Определяем кол-во благоприятствующих исходов как число докладов от российских ученых.
- Подставляем полученные данные в формулу, вычисляем вероятность.
Решение:
P=Nб/N
N=6+5+9=20
Nб=5
P=5/20=0,25
Вариант десятого задания 2019 года(2)
В коробке вперемешку лежат чайные пакетики с черным и зеленым чаем, одинаковые на вид, причем пакетиков с черным чаем в 4 раза больше, чаем пакетиков с зеленым. Найдите вероятность того, что случайно выбранный из этой коробки пакетик окажется пакетиком с зеленым чаем.
Алгоритм выполнения
- Обозначаем через х кол-во пакетиков с зеленым чаем. Выражаем затем через х кол-во пакетиков с черным чаем.
- Записываем ф-лу для нахождения вероятности, имея в виду, что число благоприятствующих исходов равно кол-ву пакетиков зеленого чая, а общее число исходов – общему кол-ву пакетиков.
- Вычисляем вероятность.
Решение:
Пусть х – кол-во пакетиков зеленого чая. Тогда кол-во пакетиков черного составляет 4х.
Вероятность P=Nб/N. Здесь Nб=х, поскольку вероятность определяется именно для пакетиков с зеленым чаем. N=х+4х=5х.
Получаем: P=х/(5х)=1/5=0,2.
Вариант десятого задания 2019года(3)
В среднем из 1400 садовых насосов, поступивших в продажу, 14 подтекает. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Алгоритм выполнения
- Из 1400 вычитаем 14. Получаем кол-во исправных насосов.
- По ф-ле P=Nб/N (где Nб – кол-во исправных насосов, N – общее кол-во насосов) находим искомую вероятность.
Решение:
1400 – 14 = 1386 (шт.) – исправных насосов поступило в продажу.
1386 / 1400 = 0,99 – вероятность того, что случайно подобранный насос исправен (не подтекает).
Вариант десятого задания 2019 года(4)
В кармане у Дани было пять конфет – «Ласточка», «Взлетная», «Василек», «Грильяж» и «Гусиные лапки», а также ключи от квартиры. Вынимая ключи, Даня случайно выронил из кармана одну конфету. Найдите вероятность того, что упала конфета «Взлетная».
Алгоритм выполнения
- Определяем общее кол-во конфет. Фиксируем, что упала единственная конфета.
- Применяя ф-лу для вероятности P=Nб/N, находим искомую вероятность.
Решение:
В кармане у Дани находится 6 предметов – 5 конфет и ключи. Ключи для расчета не учитываем, поскольку их извлечение из кармана не является случайным событием. Тогда общее кол-во случайных событий N=5. Кол-во благоприятных исходов для этих событий в данном случае равно 1, т.к. падает 1 конфета. Отсюда Nб=1.
Вероятность находим по ф-ле P=Nб/N. Подставляем числовые данные, получаем: P=1/5=0,2.
Вариант десятого задания 2019 года(5)
На борту самолета 26 мест рядом с запасными выходами и 10 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир Д. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру Д. достанется удобное место, если всего в самолете 300 мест.
Алгоритм выполнения
- Суммируем 26 и 10, чтобы найти общее кол-во удобных для пассажира Д. мест.
- Используя ф-лу P=Nб/N, где Nб – кол-во удобных мест, N – общее кол-во мест, находим искомую вероятность.
Решение:
26 + 10 = 36 – кол-во мест, которые удобны для пассажира Д
Р = 36 / 300 = 0,1233 – вероятность того, что при случайном выборе пассажиру достанется удобное место
Вариант десятого задания 2019 года(6)
Вероятность того, что новая шариковая ручка пишет плохо или вовсе не пишет, равна 0,21. Покупатель не глядя берет одну шариковую ручку из коробки. Найдите вероятность того, что эта ручка пишет хорошо.
Алгоритм выполнения
- Анализируем ситуацию, описанную в условии. Определяем, что существует только 2 варианта возможных событий.
- Находим искомую вероятность как разность единицы и вероятности того, что ручка пишет плохо.
Решение:
Вариантов событий в данном случае имеется два – ручка пишет хорошо или она пишет плохо. При этом ручка в любом случае будет из коробки взята, т.е. событие состоится. Это означает, что его вероятность равна 1.
Поскольку вероятность того, что ручка пишет плохо, составляет 0,21, то вероятность того, ручка будет писать хорошо, равна:
1 – 0,21 = 0,79.
Вариант десятого задания 2019 года(7)
На олимпиаде по русскому языку участников рассаживают по трем аудиториям. В первых двух по 130 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчете выяснилось, что всего было 400 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
Алгоритм выполнения
- Умножаем 130 на 2, получаем кол-во участников в первых двух аудиториях.
- Из 400 вычитаем полученное произведение. Узнаем, сколько участников находилось в запасной аудитории.
- Делим полученную разность на 400. Находим искомую вероятность.
Решение:
130 · 2 = 260 – участников писали олимпиаду в первых 2-х аудиториях.
400 – 260 = 140 – участников находилось в запасной аудитории.
Вероятность P = Nб / N. Здесь Nб = 140, N = 400.
Получаем: Р = 140 / 400 = 0,35.
Вариант десятого задания 2019 года(8)
В группе туристов 8 человек. С помощью жребия они выбирают двух человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдет в магазин?
Алгоритм выполнения
- Записываем ф-лу P=Nб/N, где Nб – кол-во благоприятных исходов для ситуации, N – общее кол-во исходов.
- Благоприятным исходом в данном случае является попадание туриста Д. в группу из 2 человек, которым нужно идти в магазин. Т.е. Nб=2.
- Общее кол-во исходов – число туристов, составляющих полную группу.
- Подставляем определенные числовые величины в ф-лу, находим искомую вероятность.
Решение:
Вероятность равна: P = Nб / N.
Nб = 2, т.к. по условию для похода в магазин требуется 2 человека.
N = 8, т.к. всего в группе 8 туристов.
Р = 2 / 8 = 0,25.
Вариант десятого задания 2019 года(9)
На тарелке лежат одинаковые на вид пирожки: 1 с мясом, 12 с капустой и 3 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что этот пирожок окажется с капустой.
Алгоритм выполнения
- Для вычисления вероятности используем ф-лу P=Nб/N, где Nб – кол-во благоприятных исходов ситуации, N – общее кол-во исходов.
- Определяем кол-во благоприятных исходов. Здесь таковым является кол-во пирожков с капустой.
- Находим общее кол-во исходов. Это – кол-во всех (любых) пирожков.
- Подставляем числовые данные в формулы, определяем требуемую вероятность.
Решение:
Искомую вероятность найдем по ф-ле P=Nб/N.
В данном случае Nб = 12, поскольку именно столько на тарелке пирожков с капустой.
Общее число исходов N = 1 + 12 + 3 = 16 (пирожков).
Р = 12 / 16 = 0,75.
Вариант десятого задания 2019 года(10)
Конкурс исполнителей проводится в 5 дней. Всего заявлено 50 выступлений – по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 14 выступлений, остальные распределены поровну между оставшимися днями.
Алгоритм выполнения
- Из 50 вычитаем 14. Получаем кол-во незапланированных выступлений, которые приходятся на 2–5-й дни.
- Полученную разность делим на 4, т.е. на кол-во дней, в течение которых будет заслушано выступление российского исполнителя. Получим кол-во выступлений, которые приходятся на каждый из этих дней.
- По ф-ле P=Nб/N (где Nб – кол-во выступлений в каждый из дней, кроме первого; N – общее кол-во выступлений в эти дни) находим искомую вероятность.
Решение:
50 – 14 = 36 – кол-во незапланированных выступлений, в числе которых как раз и предполагается выступление россиянина.
5 – 1 = 4 – кол-во дней, в течение которых распределены поровну 36 выступлений.
36 : 4 = 9 – кол-во выступлений, приходящихся на каждый день, начиная со 2-го.
Поскольку выступление в 3-й день, равно как и в любой другой, начиная со 2-го, является независимым и равновероятным событием, то вероятность его положит.исхода можно определить по ф-ле P=Nб/N. Здесь Nб = 9, N = 36. Тогда: Р = 9 / 36 = 0,25.
spadilo.ru
С++. Задачи с решениями. Числа и циклы. Задачи 1-10
1. Составьте программу, выводящую на экран квадраты чисел от 10 до 20 включительно.
|
|
int main() { for (int i=10; i<=20; i++) cout<<i*i<<» «; cout<<endl; return 0; } |
2. Даны натуральные числа от 35 до 87. Вывести на консоль те из них, которые при делении на 7 дают остаток 1, 2 или 5.
|
|
int main() { for (int i=35; i<=87; i++) { if (i % 7 == 1 || i % 7 == 2 || i % 7 == 5) cout<<i<<» «; } cout<<endl; return 0; } |
3. Найдите сумму , где число вводится пользователем с клавиатуры.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
|
int main() { int n; cout<<«input n: «; cin>>n; if (n<1) cout<<«error»<<endl; else { int sum=0; for (int i=1; i<=n; i++) sum+=i; cout<<«sum = «<<sum<<endl; } return 0; } |
4. Найдите произведение цифр трехзначного числа.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
|
int main() { int n; cout<<«input n: «; cin>>n; if (n<100 || n>999) cout<<«error n»<<endl; else { int a,b,c; a=n%10; // первая цифра справа b=(n/10)%10; // вторая цифра справа c=n/100; // убрать две цифры справа int res; res=a*b*c; cout<<«answer: «<<res<<endl; } return 0; } |
5. Найдите количество четных цифр данного натурального числа.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
|
int main() { int n; cout<<«input n: «; cin>>n; if (n<=0) cout<<«error n»<<endl; else { int count=0; while (n>0) { if ((n%10)%2==0) count++; n/=10; } cout<<«answer: «<<count<<endl; } return 0; } |
6. Найдите наибольшую цифру данного натурального числа.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
|
int main() { int n; cout<<«input n: «; cin>>n; if (n<=0) cout<<«error n»<<endl; else { int max=0; while (n>0) { if ((n%10)>max) max=n%10; n/=10; } cout<<«answer: «<<max<<endl; } return 0; } |
7. Найдите все четырехзначные числа, сумма цифр каждого из которых равна 15.
|
|
int main() { for (int i=1000; i<10000; i++) if (i%10+(i/10)%10+(i/100)%10+i/1000==15) cout<<i<<endl; return 0; } |
Метки задачи, циклы. Смотреть запись.
www.itmathrepetitor.ru
Олимпиадные задачи по теме «Комбинаторика».
Задача 1:
В магазине «Все для чая» есть 5 разных чашек и 3 разных блюдца. Сколькими способами можно купить чашку с блюдцем?
Решение:
Выберем чашку. В комплект к ней можно выбрать любое из трех блюдец. Поэтому есть 3 разных комплекта, содержащих выбранную чашку. Поскольку чашек всего 5, то число различных комплектов равно 15 (15 = 5 • 3).
Задача 2:
В магазине «Все для чая» есть еще 4 чайные ложки. Сколькими способами можно купить комплект из чашки, блюдца и ложки?
Решение:
Выберем любой из 15 комплектов предыдущей задачи. Его можно дополнить ложкой четырьмя различными способами. Поэтому общее число возможных комплектов равно 60 (60 = 15 • 4 = 5 • 3 • 4).
Задача 3:
В Стране Чудес есть три города: А, Б и В. Из города А в город Б ведет 6 дорог, а из города Б в город В – 4 дороги. Сколькими способами можно проехать от А до В?
Решение:
Ответ: 24 = 6 • 4.
Задача 4:
В Стране Чудес есть четыре города: А, Б и В и Г. Из города А в город Б ведет 6 дорог, а из города Б в город В – 4 дороги, Из города А в город Г – две дороги, и из города Г в город В – тоже две дороги. Сколькими способами можно проехать от А до В?
Решение:
Выделим два случая: путь проходит через город Б или через город Г. В каждом из этих случаев легко сосчитать количество возможных маршрутов: в первом – 24, во втором – 6. Складывая, получаем общее количество маршрутов: 30.
Задача 5:
В магазине «Все для чая» по-прежнему продается 5 чашек, 3 блюдца и 4 чайные ложки. Сколькими способами можно купить два предмета с разными названиями?
Решение:
Возможны три разных случая: первый – покупаются чашка с блюдцем, второй – чашка с ложкой, третий – блюдце и ложка. В каждом из этих случаев легко сосчитать количество возможных вариантов (в первом – 15, во втором – 20, в третьем – 12). Складывая, получаем общее число возможных вариантов: 47.
Задача 6:
Назовем натуральное число «симпатичным» , если в его записи встречаются только нечетные цифры. Сколько существует 4-значных «симпатичных» чисел?
Решение:
Понятно, что однозначных «симпатичных» чисел ровно 5. К каждому однозначному «симпатичному» числу вторая нечетная цифра может быть дописана пятью различными способами. Таким образом, двузначных «симпатичных» чисел всего 5 • 5 = 25. Аналогично, трехзначных «симпатичных» чисел 5 • 5 • 5 = 125, и четырехзначных – 5 • 5 • 5 • 5 = 54 = 625.
Задача 7:
Монету бросают трижды. Сколько разных последовательностей орлов и решек можно при этом получить?
Решение:
Ответ: 2?.
Задача 8:
Каждую клетку квадратной таблицы 2 ? 2 можно покрасить в черный или белый цвет. Сколько существует различных раскрасок этой таблицы?
Решение:
Ответ: 24.
Задача 9:
Сколькими способами можно заполнить одну карточку в лотерее «Спорт-про-г-ноз»? (В этой лотерее нужно предсказать итог тринадцати спортивных матчей. Итог каждого матча – победа одной из команд либо ничья; счет роли не играет).
Решение:
Ответ: 3?3.
Задача 10:
Алфавит племени Мумбо-Юмбо состоит из трех букв А, Б и В. Словом является любая последовательность, состоящая не более, чем из 4 букв. Сколько слов в языке племени Мумбо-Юмбо? Указание. Сосчитайте отдельно количества одно-, двух-, трех- и четырехбуквенных слов.
Решение:
Ответ: 3 + 3? + 3? + 34 = 120.
Задача 11:
В футбольной команде (11 человек) нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?
Решение:
Капитаном может стать любой из 11 футболистов. После выбора капитана на роль его заместителя могут претендовать 10 оставшихся человек. Таким образом, всего есть 11 • 10 = 110 разных вариантов выборов.
Задача 12:
Сколькими способами можно сделать трехцветный флаг с горизонтальными полосами одинаковой ширины, если имеется материя шести различных цветов?
Решение:
Цвет для верхней полоски флага можно выбрать шестью разными способами. После этого для средней полоски флага остается пять возможных цветов, а затем для нижней полоски флага – четыре различных цвета. Таким образом, флаг можно сделать 6 • 5 • 4 = 120 способами.
Задача 13:
Сколькими способами можно поставить на шахматную доску белую и черную ладьи так, чтобы они не били друг друга?
Решение:
Белую ладью можно поставить на любую из 64 клеток. Независимо от своего расположения она бьет 15 полей (включая поле, на котором она стоит). Поэтому остается 49 полей, на которые можно поставить черную ладью. Таким образом, всего есть 64 • 49 = 3136 разных способов.
Задача 14:
Сколькими способами можно поставить на шахматную доску белого и черного королей так, чтобы получилась допустимая правилами игры позиция?
Решение:
Белого короля можно поставить на любое из 64 полей. Однако количество полей, которые он при этом будет бить, зависит от его расположения. Поэтому необходимо разобрать три случая:
а) если белый король стоит в углу (углов всего 4), то он бьет 4 поля (включая то, на котором стоит), и остается 60 полей, на которые можно поставить черного короля;
б) если белый король стоит на краю доски, но не в углу (таких полей – 24), то он бьет 6 полей, и для черного короля остается 58 возможных полей;
в) если же белый король стоит не на краю доски (таких полей – 36), то он бьет 9 полей, и для черного короля остается 55 возможных полей.
Таким образом, всего есть 4 • 60 + 24 • 58 + 36 • 55 = 3612 способов расстановки королей.
Задача 15:
Сколько существует трехзначных чисел, в записи которых цифры 1, 2, 3 встречаются ровно по одному разу?
Решение:
Будем рассуждать точно так же, как при решении задач предыдущего цикла. На первое место можно поставить любую из трех цифр, на второе – любую из двух оставшихся, а на третье – последнюю оставшуюся цифру. Таким образом, всего получается 3 • 2 • 1 = 3! чисел.
Задача 16:
Сколькими способами можно выложить в ряд красный, черный, синий и зеленый шарики?
Решение:
На первое место можно положить любой из четырех шариков, на второе – любой из трех оставшихся, на третье – любой из двух оставшихся, а на четвертое – последний оставшийся шарик. Итак, ответ: 4 • 3 • 2 • 1 = 4!.
Задача 17: Слово – любая конечная последовательность букв русского алфавита. Выясните, сколько различных слов сожно составить из слов
а) «ВЕКТОР»;
б) «ЛИНИЯ»;
в) «ПАРАБОЛА»;
г) «БИССЕКТРИСА»;
д) «МАТЕМАТИКА»;
Решение:
а) Так как все буквы слова различны, то всего можно получить 6! слов.
б) В этом слове две буквы И, а все остальные буквы разные. Временно будем считать разными и буквы И, обозначив их через И1 и И2. При этом предположении получится 5! = 120 разных слов. Однако те слова, которые получаются друг из друга только перестановкой букв И1 и И2, на самом деле одинаковы. Таким образом, полученные 120 слов разбиваются на пары одинаковых. Поэтому разных слов всего 120:2 = 60.
в) Считая три буквы А этого слова различными (А1, А2, А3), получим 8! разных слов. Однако слова, отличающиеся лишь перестановкой букв А, на самом деле одинаковы. Поскольку буквы А1, А2, А3 можно переставлять 3! способами, все 8! слов разбиваются на группы по 3! одинаковых. Поэтому разных слов всего 8!/3!.
г) В этом слове три буквы С и две буквы И. Считая все буквы различными, получаем 11! слов. Отождествляя слова, отличающиеся лишь перестановкой букв И, но не С, получаем 11!/2! различных слов. Отождествляя теперь слова, отличающиеся перестановкой букв С, получаем окончательный результат 11!/(2! • 3!).
д) Ответ: 10!/(3! • 2! • 2!).
Задача 22:
В стране 20 городов, каждые два из которых соединены авиалинией. Сколько авиалиний в этой стране?
Решение:
Каждая авиалиния соединяет два города. В качестве первого города можно взять любой из 20 городов (город А), а в качестве второго – любой из 19 оставшихся (город В). Перемножив эти числа, получаем 20 • 19 = 380. Однако при этом подсчете каждая авиалиния учтена дважды (первый раз, когда в качестве первого города был выбран город А, а второго – город В, а второй раз – наоборот). Таким образом, число авиалиний равно 380:2 = 190.
Задача 23:
Сколько диагоналей в выпуклом n-угольнике?
Решение:
Ответ: n(n – 3)/2.
Задача 24:
Бусы – это кольцо, на которое нанизаны бусины. Бусы можно поворачивать, но не переворачивать. Сколько различных бус можно сделать из 13 разноцветных бусин?
Решение:
Ответ: 13!/13 = 12!.
Задача 25:
Предположим теперь, что бусы можно и переворачивать. Сколько тогда различных бус можно сделать из 13 разноцветных бусин?
Решение:
Ответ: 12!/2.
Задача 26:
Сколько существует 6-значных чисел, в записи которых есть хотя бы одна четная цифра?
Решение:
Вместо того, чтобы подсчитывать количество требуемых 6-значных чисел, определим количество 6-значных чисел, не обладающих нужным свойством. Так как это в точности те числа, в записи которых встречаются только нечетные цифры, то их количество, очевидно, равно 56 = 15625. Всего 6-значных чисел 900000. Поэтому количество 6-значных чисел, обладающих указанным свойством, равно 900000 – 15625 = 884375.
Задача 27:
В алфавите племени Бум-Бум шесть букв. Словом является любая последовательность из шести букв, в которой есть хотя бы две одинаковые буквы. Сколько слов в языке племени Бум-Бум?
Решение:
Ответ: 66 – 6!.
Задача 28:
В киоске «Союзпечать» продаются 5 видов конвертов и 4 вида марок. Сколькими способами можно купить конверт с маркой?
Решение:
Ответ: 5 • 4 = 20
Задача 29:
Сколькими способами можно выбрать гласную и согласную буквы из слова «КРУЖОК»?
Решение:
Ответ: 2 • 3 = 6
Задача 30:
На доске написаны 7 существительных, 5 глаголов и 2 прилагательных. Для предложения нужно выбрать по одному слову каждой из этих частей речи. Сколькими способами это можно сделать?
Решение:
Ответ: 7 • 5 • 2 = 70
Задача 31:
У двух начинающих коллекционеров по 20 марок и по 10 значков. Честным обменом называется обмен одной марки на одну марку или одного значка на один значок. Сколькими способами коллекционеры могут осуществить честный обмен?
Решение:
Ответ: 20 • 20 + 10 • 10 = 500
Задача 32:
Сколько существует 6-значных чисел, все цифры которых имеют одинаковую четность?
Решение:
Ответ: 56 + 4 • 55
Задача 33:
Надо послать 6 срочных писем. Сколькими способами это можно сделать, если для передачи писем можно использовать трех курьеров и каждое письмо можно дать любому из курьеров?
Решение:
Ответ: 36
Задача 34:
Сколькими способами из полной колоды (52 карты) можно выбрать 4 карты разных мастей и достоинств?
Решение:
Ответ: 13 • 12 • 11 • 10
Задача 35:
На полке стоят 5 книг. Сколькими способами можно выложить в стопку несколько из них (стопка может состоять и из одной книги)?
Решение:
Ответ: 5 + 5 • 4 + 5 • 4 • 3 + 5 • 4 • 3 • 2 + 5 • 4 • 3 • 2 • 1 = 325
Задача 36:
Сколькими способами можно поставить 8 ладей на шахматную доску так, чтобы они не били друг друга?
Решение:
Ответ: 8!
Задача 37:
На танцплощадке собрались N юношей и N девушек. Сколькими способами они могут разбиться на пары для участия в очередном танце?
Решение:
Ответ: n!
Задача 38:
Чемпионат России по шахматам проводится в один круг. Сколько играется партий, если участвуют 18 шахматистов?
Решение:
Ответ: 18 • 17/2 = 153
Задача 39:
Сколькими способами можно поставить на шахматную доску так, чтобы они не били друг друга а) две ладьи; б) двух королей; в) двух слонов; г) двух коней; д) двух ферзей?
Решение:
Ответ: a) 64 • 49/2 = 1568 б) (4 • 60 + 24 • 58 + 36 • 55)/2 = 1806 в) (28 • 56 + 20 • 54 + 12 • 52 + 4 • 50)/2 = 1736 г) (4 • 61 + 8 • 60 + 20 • 59 + 16 • 57 + 16 • 55)/2 = 1848 д) (28 • 42 + 20 • 40 + 12 • 38 + 4 • 36)/2 = 1288
Задача 40:
У мамы два яблока, три груши и четыре апельсина. Каждый день в течение девяти дней подряд она дает сыну один из оставшихся фруктов. Сколькими способами это может быть сделано?
Решение:
Ответ: 9!/2!3!4!
Задача 41:
Сколькими способами можно поселить 7 студентов в три комнаты: одноместную, двухместную и четырехместную?
Решение:
Ответ: 7!/1!2!4!
Задача 42:
Сколькими способами можно расставить на первой горизонтали шахматной доски комплект белых фигур (король, ферзь, две ладьи, два слона и два коня)?
Решение:
Ответ: 8!/2!2!2!
Задача 43:
Сколько слов можно составить из пяти букв А и не более чем из трех букв Б?
Решение:
Ответ: 1 + 6!/5!1! + 7!/5!2! + 8!/5!3! = 84
Задача 44:
Сколько существует 10-значных чисел, в которых имеется хотя бы две одинакоые цифры?
Решение: 9 • 109 – 9 • 9!
Задача 45:
Каких 7-значных чисел больше: тех, в записи которых есть 1, или остальных?
Решение:
8 • 96
Задача 46:
Кубик бросают трижды. Среди всех возможных последовательностей результатов есть такие, в которых хотя бы один раз встречается шестерка. Сколько их?
Решение:
Ответ: 6? – 5?
Задача 47:
Сколькими способами можно разбить 14 человек на пары?
Решение:
Ответ: 13 • 11 • 9 • 7 • 5 • 3 • 1
Задача 48:
Сколько существует 9-значных чисел, сумма цифр которых четна?
Решение:
Ответ: 9 • 107 • 5
lib.repetitors.eu
 Каждому из нас ещё со школьной скамьи (а точнее с 1-го класса начальной школы) должны быть знакомы такие простые математические символы, как знак больше и знак меньше, а также знак равно.
Каждому из нас ещё со школьной скамьи (а точнее с 1-го класса начальной школы) должны быть знакомы такие простые математические символы, как знак больше и знак меньше, а также знак равно.

 Как писать знак меньше, пожалуй, повторно объяснять уже не стоит. Совершенно аналогично знаку больше. Если знак смотрит влево узкой стороной — меньшей, то перед вами знак меньше.
Как писать знак меньше, пожалуй, повторно объяснять уже не стоит. Совершенно аналогично знаку больше. Если знак смотрит влево узкой стороной — меньшей, то перед вами знак меньше.




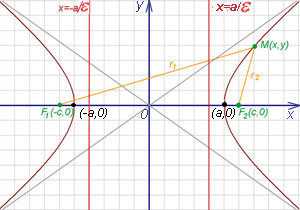
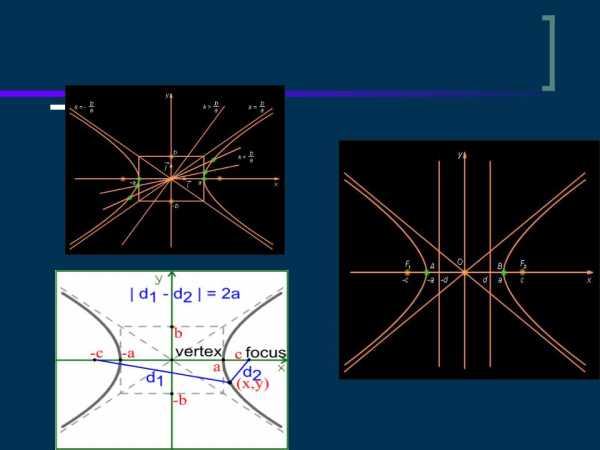
 Асимптоты гиперболы (красные кривые), показанные голубым пунктиром, пересекаются в центре гиперболы, C. Два фокуса гиперболы обозначены как F1 и F2. Директрисы гиперболы обозначены линиями двойной толщины и обозначены D1 и D2. Эксцентриситет ε равен отношению расстояний точки P на гиперболе до фокуса и до соответствующей директрисы (показаны зелёным). Вершины гиперболы обозначены как ±a. Параметры гиперболы обозначают следующее:
Асимптоты гиперболы (красные кривые), показанные голубым пунктиром, пересекаются в центре гиперболы, C. Два фокуса гиперболы обозначены как F1 и F2. Директрисы гиперболы обозначены линиями двойной толщины и обозначены D1 и D2. Эксцентриситет ε равен отношению расстояний точки P на гиперболе до фокуса и до соответствующей директрисы (показаны зелёным). Вершины гиперболы обозначены как ±a. Параметры гиперболы обозначают следующее: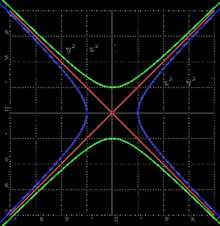 Две сопряженные гиперболы (голубая и зелёная) обладают совпадающими асимптотами (красные). Эти гиперболы единичные и равнобочные, так как a = b = 1
Две сопряженные гиперболы (голубая и зелёная) обладают совпадающими асимптотами (красные). Эти гиперболы единичные и равнобочные, так как a = b = 1 Графики математических функций. Гипербола
Графики математических функций. Гипербола ИСТОРИЯ ПРОИСХОЖДЕНИЯ ГИПЕРБОЛЫ Одним из первых, кто начал изучать конические сечения — эллипс, парабола, гипербола, был ученик знаменитого Платона, древнегреческий математик Менехм (IV в. до н. э. ). Решая задачу об удвоении куба, Менехм задумался: «А что случится, если разрезать конус плоскостью, перпендикулярной его образующей? »
ИСТОРИЯ ПРОИСХОЖДЕНИЯ ГИПЕРБОЛЫ Одним из первых, кто начал изучать конические сечения — эллипс, парабола, гипербола, был ученик знаменитого Платона, древнегреческий математик Менехм (IV в. до н. э. ). Решая задачу об удвоении куба, Менехм задумался: «А что случится, если разрезать конус плоскостью, перпендикулярной его образующей? » ИСТОРИЯ ПРОИСХОЖДЕНИЯ ГИПЕРБОЛЫ Так, изменяя угол при вершине прямого кругового конуса, Менехм получил три вида кривых: эллипс — если угол при вершине конуса острый; парабола — если угол прямой; одну ветвь гиперболы — если угол тупой. Название этих кривых придумал не Менехм.
ИСТОРИЯ ПРОИСХОЖДЕНИЯ ГИПЕРБОЛЫ Так, изменяя угол при вершине прямого кругового конуса, Менехм получил три вида кривых: эллипс — если угол при вершине конуса острый; парабола — если угол прямой; одну ветвь гиперболы — если угол тупой. Название этих кривых придумал не Менехм. ИСТОРИЯ ПРОИСХОЖДЕНИЯ ГИПЕРБОЛЫ Названия предложил один из крупнейших геометров древности Аполлоний Пергский, посвятивший замечательным кривым трактат из восьми книг «Конические сечения» ( «О кониках» ). Семь книг сохранились, три из них — в арабском переводе. Первые четыре книги содержат начало теории и основные свойства конических сечений. Это — трактат об эллипсе, параболе и гиперболе, определяемых как сечения кругового конуса, где изложение доведено до исследования эволют конического сечения.
ИСТОРИЯ ПРОИСХОЖДЕНИЯ ГИПЕРБОЛЫ Названия предложил один из крупнейших геометров древности Аполлоний Пергский, посвятивший замечательным кривым трактат из восьми книг «Конические сечения» ( «О кониках» ). Семь книг сохранились, три из них — в арабском переводе. Первые четыре книги содержат начало теории и основные свойства конических сечений. Это — трактат об эллипсе, параболе и гиперболе, определяемых как сечения кругового конуса, где изложение доведено до исследования эволют конического сечения. ИСТОРИЯ ПРОИСХОЖДЕНИЯ ГИПЕРБОЛЫ Аполлоний показал, что кривые можно получить, проводя различные сечения одного и того же кругового конуса, причем любого. При надлежащем наклоне секущей плоскости удается получить все типы конических сечений. Если считать, что конус не заканчивается в вершине, а проектируется на нее, тогда у некоторых сечений образуется две ветви.
ИСТОРИЯ ПРОИСХОЖДЕНИЯ ГИПЕРБОЛЫ Аполлоний показал, что кривые можно получить, проводя различные сечения одного и того же кругового конуса, причем любого. При надлежащем наклоне секущей плоскости удается получить все типы конических сечений. Если считать, что конус не заканчивается в вершине, а проектируется на нее, тогда у некоторых сечений образуется две ветви. МАТЕМАТИЧЕСКАЯ ГИПЕРБОЛА Из школьного курса математики известно, что кривая, задаваемая уравнением , называется гиперболой. Однако это —частный случай гиперболы (равносторонняя гипербола). Определение: гиперболой называется множество точек плоскости, абсолютная величина разности которых до двух данных точек (F 1 и F 2), называемых фокусами, есть величина постоянная (ее обозначают через 2 а), причем эта постоянная меньше расстояния между фокусами (2 c).
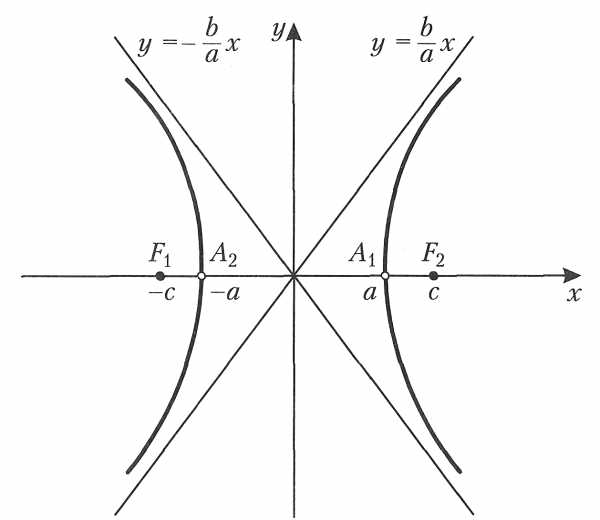
МАТЕМАТИЧЕСКАЯ ГИПЕРБОЛА Из школьного курса математики известно, что кривая, задаваемая уравнением , называется гиперболой. Однако это —частный случай гиперболы (равносторонняя гипербола). Определение: гиперболой называется множество точек плоскости, абсолютная величина разности которых до двух данных точек (F 1 и F 2), называемых фокусами, есть величина постоянная (ее обозначают через 2 а), причем эта постоянная меньше расстояния между фокусами (2 c). ЭЛЕМЕНТЫ ГИПЕРБОЛЫ Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью (2 а) гиперболы (ось Ох для канонического выбора координатной системы), а половина действительной оси – действительной полуосью (а). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (2 b) (в канонических координатах – ось Оу), а половина мнимой оси – мнимой полуосью (b). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси. Прямоугольник со сторонами 2 а и 2 b называется основным прямоугольником гиперболы.
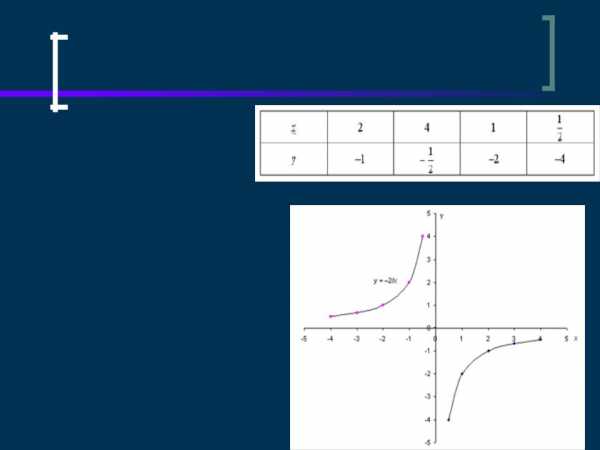
ЭЛЕМЕНТЫ ГИПЕРБОЛЫ Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью (2 а) гиперболы (ось Ох для канонического выбора координатной системы), а половина действительной оси – действительной полуосью (а). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (2 b) (в канонических координатах – ось Оу), а половина мнимой оси – мнимой полуосью (b). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси. Прямоугольник со сторонами 2 а и 2 b называется основным прямоугольником гиперболы.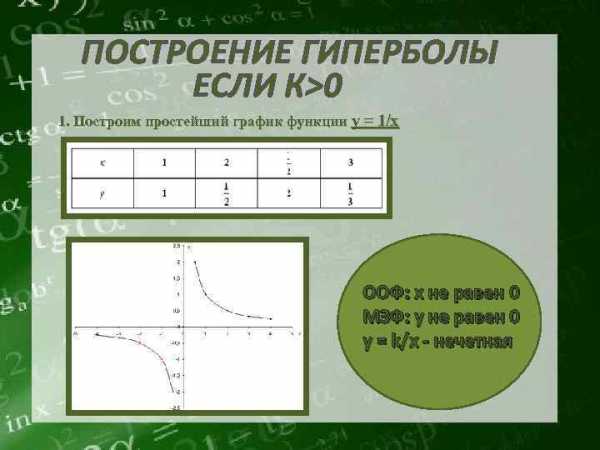 ПОСТРОЕНИЕ ГИПЕРБОЛЫ ЕСЛИ К>0 1. Построим простейший график функции y = 1/x ООФ: х не равен 0 МЗФ: у не равен 0 y = k/x — нечетная
ПОСТРОЕНИЕ ГИПЕРБОЛЫ ЕСЛИ К>0 1. Построим простейший график функции y = 1/x ООФ: х не равен 0 МЗФ: у не равен 0 y = k/x — нечетная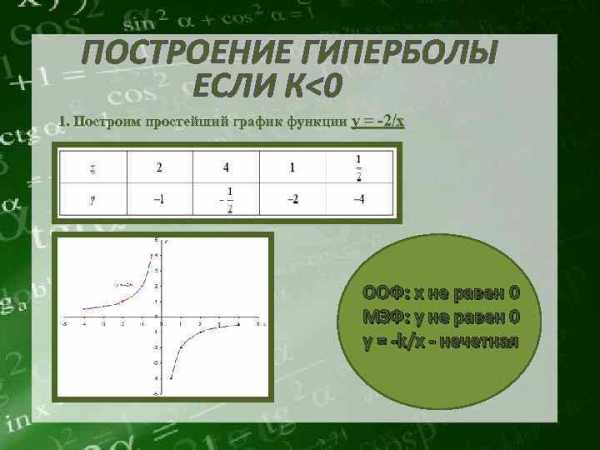 ПОСТРОЕНИЕ ГИПЕРБОЛЫ ЕСЛИ К
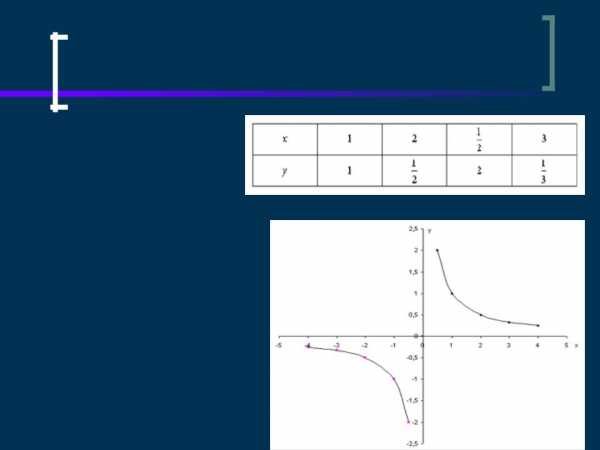
ПОСТРОЕНИЕ ГИПЕРБОЛЫ ЕСЛИ К
 АСИМПТОТА Прямая L называется асимптотой неограниченной кривой K, если расстояние d от точки M кривой K до этой прямой стремится к нулю при неограниченном удалении точки M вдоль кривой K от начала координат (см. рис. 1). Асимптота кривой, имеющая бесконечную ветвь — это прямая, которая обладает тем свойством, что когда точка по кривой удаляется в бесконечность, ее расстояние до этой прямой стремится к нулю.
АСИМПТОТА Прямая L называется асимптотой неограниченной кривой K, если расстояние d от точки M кривой K до этой прямой стремится к нулю при неограниченном удалении точки M вдоль кривой K от начала координат (см. рис. 1). Асимптота кривой, имеющая бесконечную ветвь — это прямая, которая обладает тем свойством, что когда точка по кривой удаляется в бесконечность, ее расстояние до этой прямой стремится к нулю. СВЯЗАННЫЕ ОПРЕДЕЛЕНИЯ Гипербола состоит из двух отдельных кривых, которые называют ветвями. Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами. Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы. Середина большой оси называется центром гиперболы. Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы. ◦Обычно обозначается a. Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием. ◦Обычно обозначается c.
СВЯЗАННЫЕ ОПРЕДЕЛЕНИЯ Гипербола состоит из двух отдельных кривых, которые называют ветвями. Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами. Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы. Середина большой оси называется центром гиперболы. Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы. ◦Обычно обозначается a. Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием. ◦Обычно обозначается c. СВЯЗАННЫЕ ОПРЕДЕЛЕНИЯ Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной или поперечной осью гиперболы. Прямая, перпендикулярная действительной оси и проходящая через её центр называется мнимой или сопряженной осью гиперболы. Отрезок между фокусом гиперболы и гиперболой, перпендикулярный её действительной оси, называется фокальным параметром: Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром. ◦Обычно обозначается b. • Уравнения директрис:
СВЯЗАННЫЕ ОПРЕДЕЛЕНИЯ Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной или поперечной осью гиперболы. Прямая, перпендикулярная действительной оси и проходящая через её центр называется мнимой или сопряженной осью гиперболы. Отрезок между фокусом гиперболы и гиперболой, перпендикулярный её действительной оси, называется фокальным параметром: Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром. ◦Обычно обозначается b. • Уравнения директрис: ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ Примером является зона слышимости звука пролетающего самолета. Если самолет движется со сверхзвуковой скоростью, то в воздухе зона слышимости образует конус. Поверхность Земли может приближенно считаться плоскостью, рассекающей этот конус. Если гиперболу вращать вокруг ее оси, проходящей через фокусы, то получающаяся поверхность будет называться двуполостным гиперболоидом, потому что состоит из двух полостей: одна – рассмотренная нами, а вторая получается от вращения второй ветви гиперболы. Если же вращать гиперболу вокруг второй ее оси, то получится поверхность, называемая однополостным гиперболоидом. Такую форму имеют секции Шаболовской радиобашни в Москве.
ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ Примером является зона слышимости звука пролетающего самолета. Если самолет движется со сверхзвуковой скоростью, то в воздухе зона слышимости образует конус. Поверхность Земли может приближенно считаться плоскостью, рассекающей этот конус. Если гиперболу вращать вокруг ее оси, проходящей через фокусы, то получающаяся поверхность будет называться двуполостным гиперболоидом, потому что состоит из двух полостей: одна – рассмотренная нами, а вторая получается от вращения второй ветви гиперболы. Если же вращать гиперболу вокруг второй ее оси, то получится поверхность, называемая однополостным гиперболоидом. Такую форму имеют секции Шаболовской радиобашни в Москве. ПРЕЗЕНТАЦИЮ ВЫПОЛНИЛИ: УЧЕНИЦЫ 10 «Б» КЛАССА ЯКУБОВСКАЯ КСЕНИЯ ЛЕПЕШКО ЕКАТЕРИНА
ПРЕЗЕНТАЦИЮ ВЫПОЛНИЛИ: УЧЕНИЦЫ 10 «Б» КЛАССА ЯКУБОВСКАЯ КСЕНИЯ ЛЕПЕШКО ЕКАТЕРИНА



















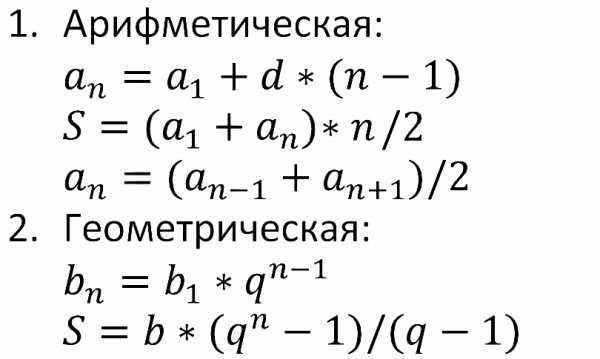
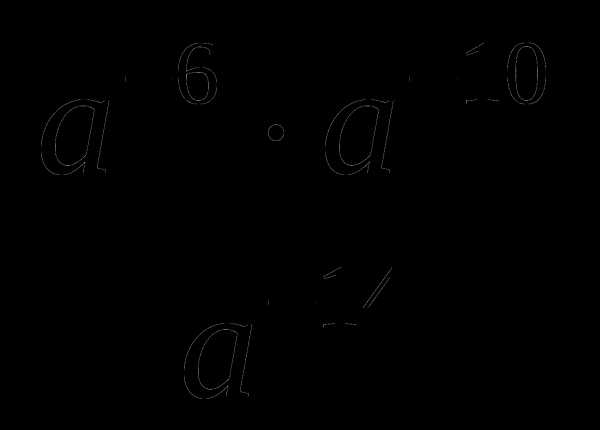 при a =
при a = 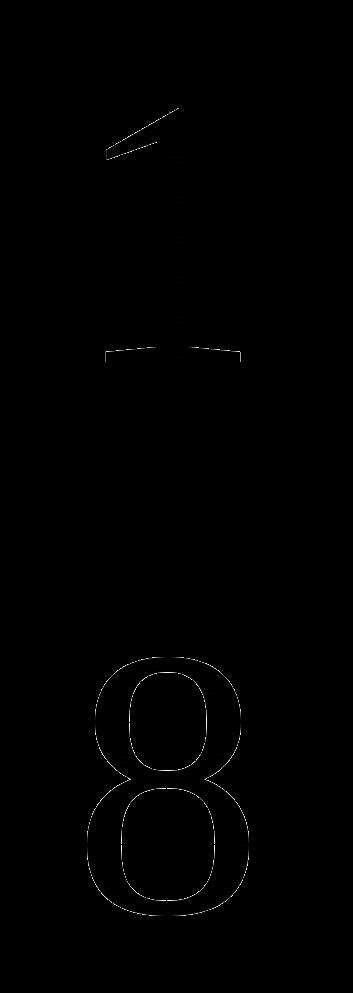 .
. Г. —
Г. —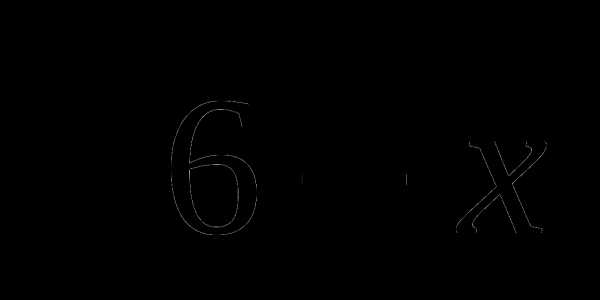 не имеет смысла?
не имеет смысла? А.
А. 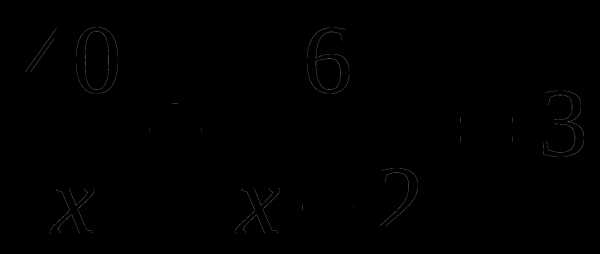 Б.
Б. 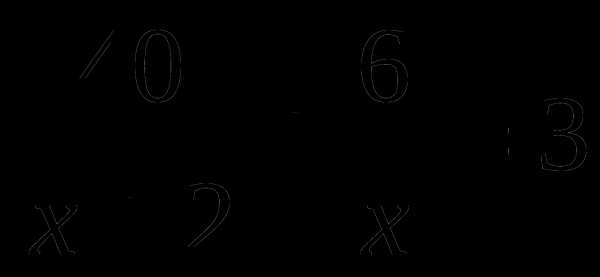
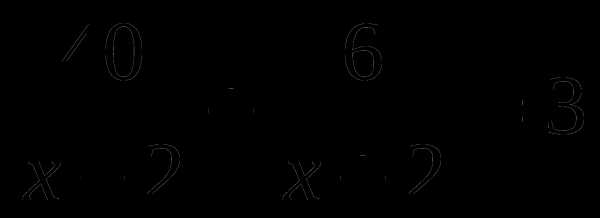 Г.
Г. 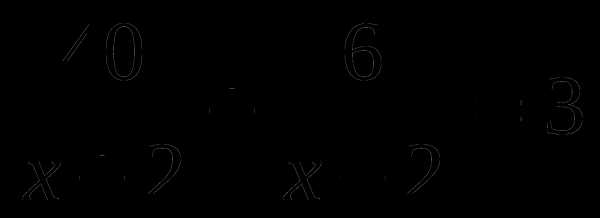
 Б.
Б.  В.
В.  Г.
Г. 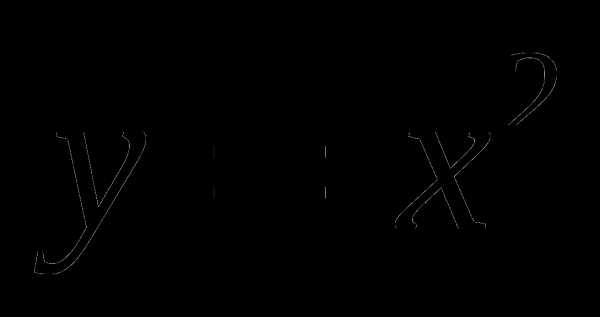
 при х = —
при х = — .
.
 Б.
Б. 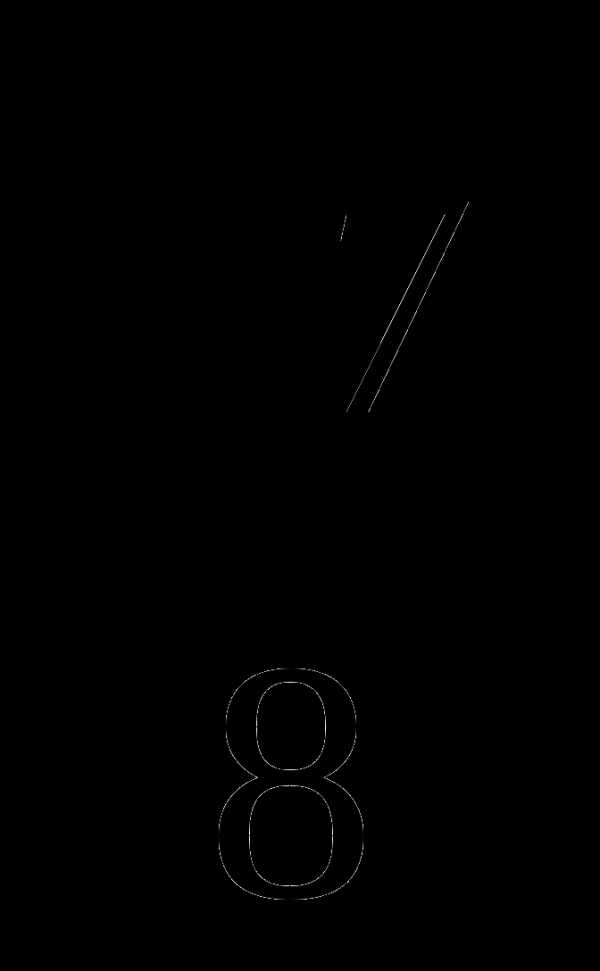 В.
В. 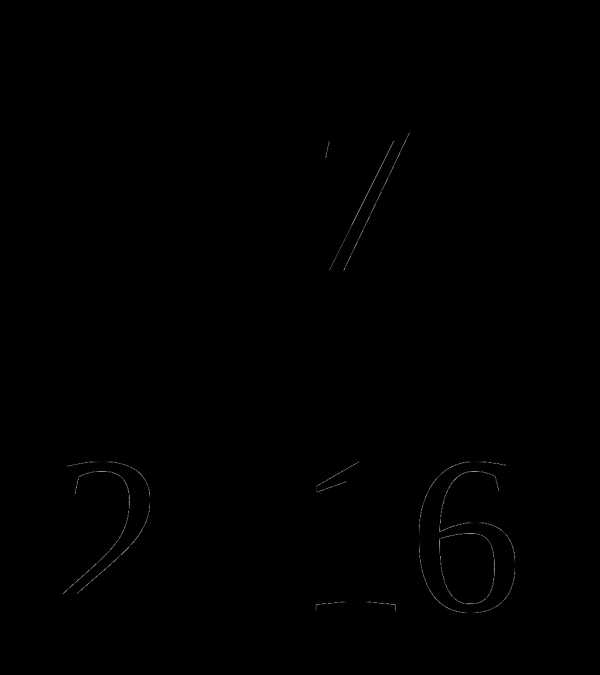 Г.
Г. 
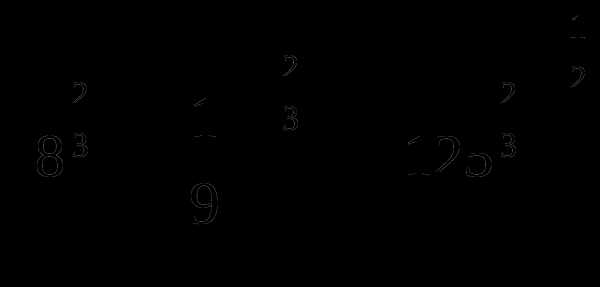

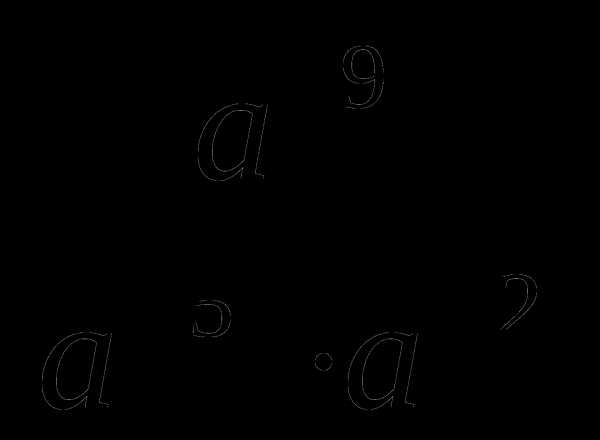 при
при 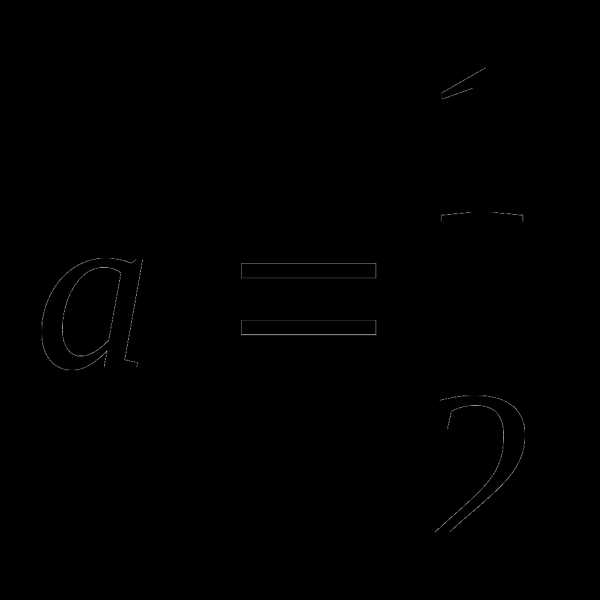
 В.
В.  Г. 4
Г. 4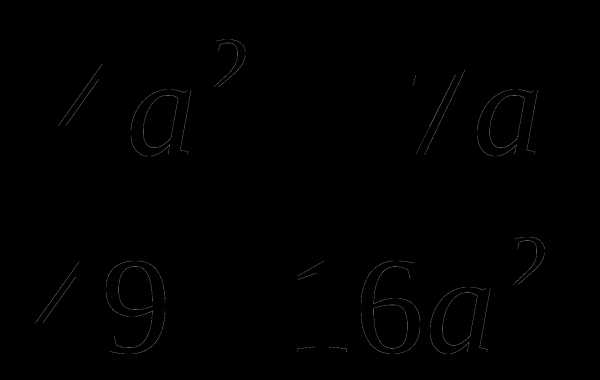
 Б.
Б.  В.
В.  Г.
Г. 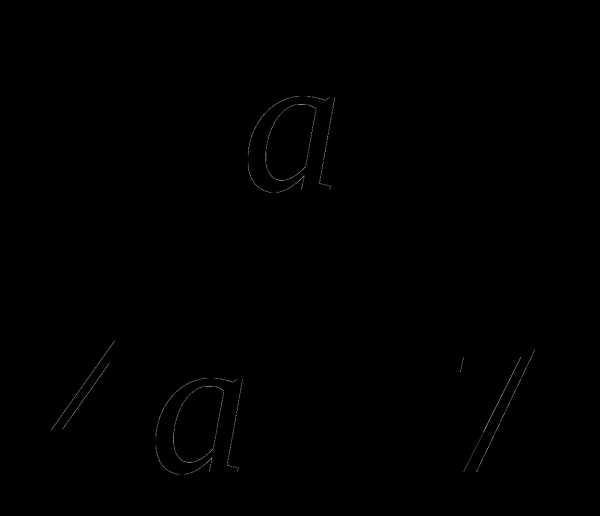
 В. 2. Г.
В. 2. Г. 
 В.
В.  Г. 14
Г. 14 = (2;3;-4),
= (2;3;-4),  =(-1;2;1) и
=(-1;2;1) и  =(3;0;2), найдите координаты векторов
=(3;0;2), найдите координаты векторов
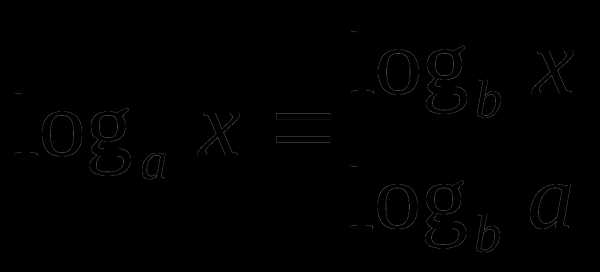
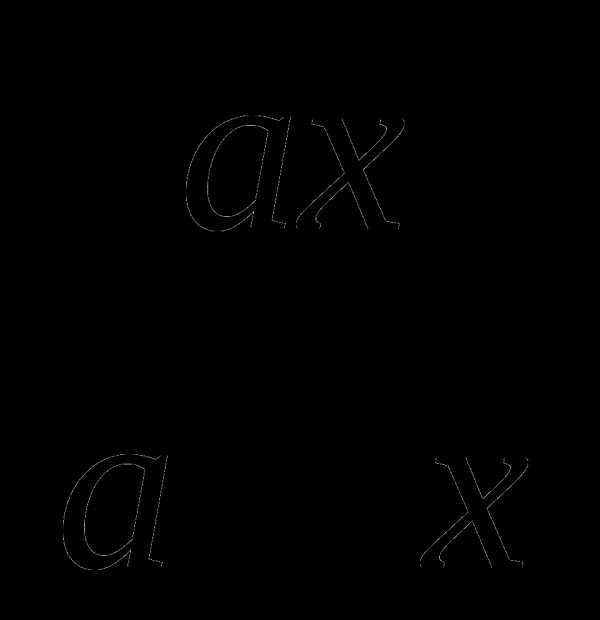 при
при 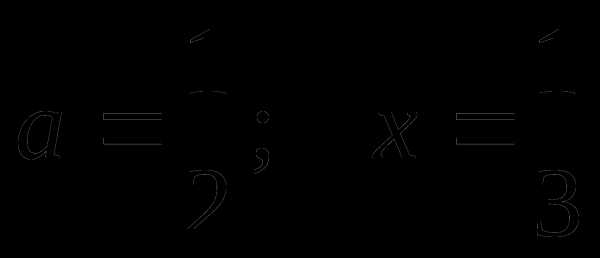
 -1 В. 5 Г. 0,5
-1 В. 5 Г. 0,5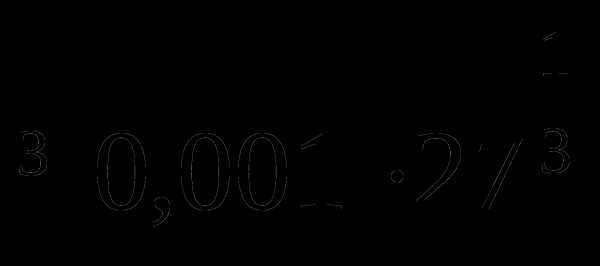
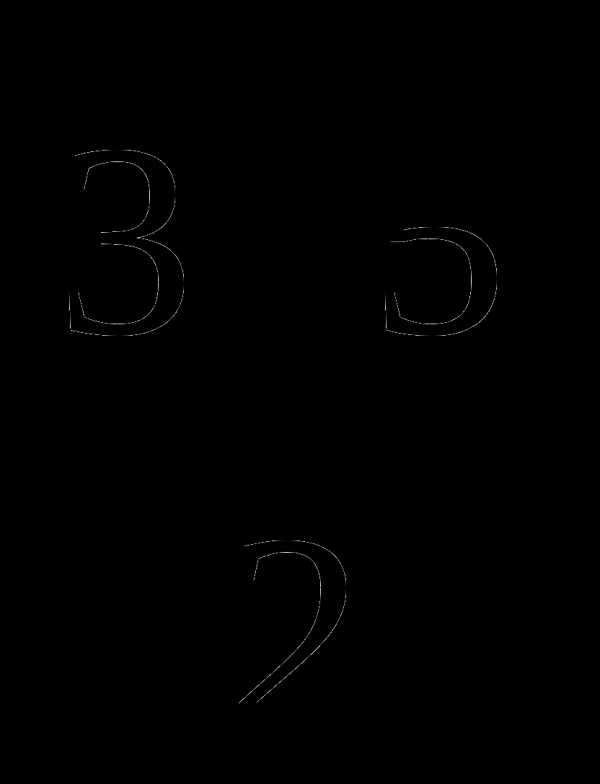
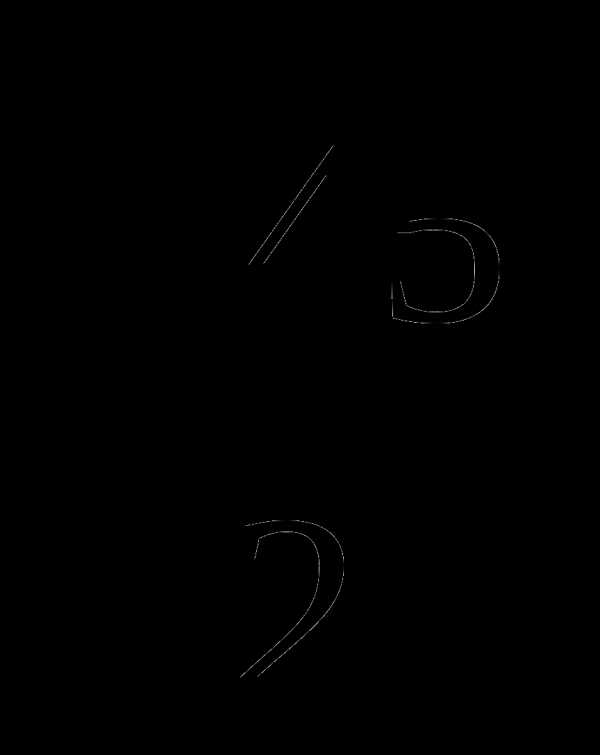 Б.
Б. 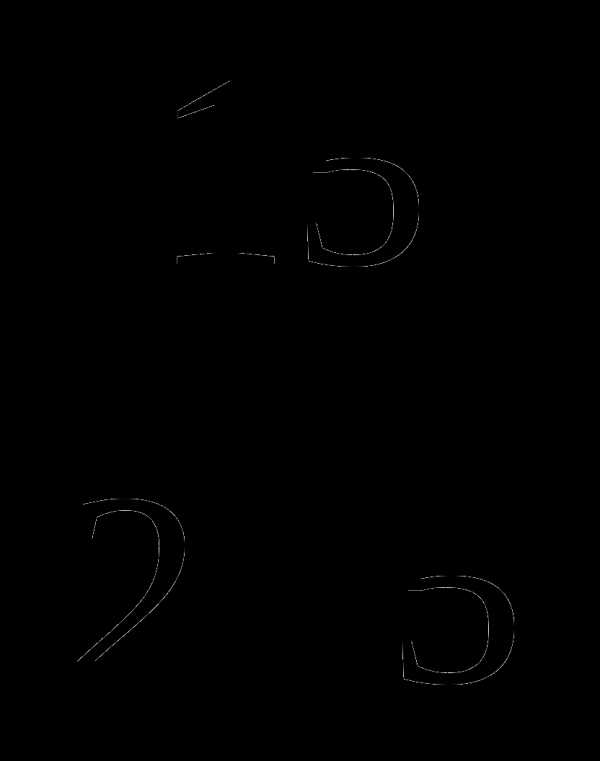 В.
В. 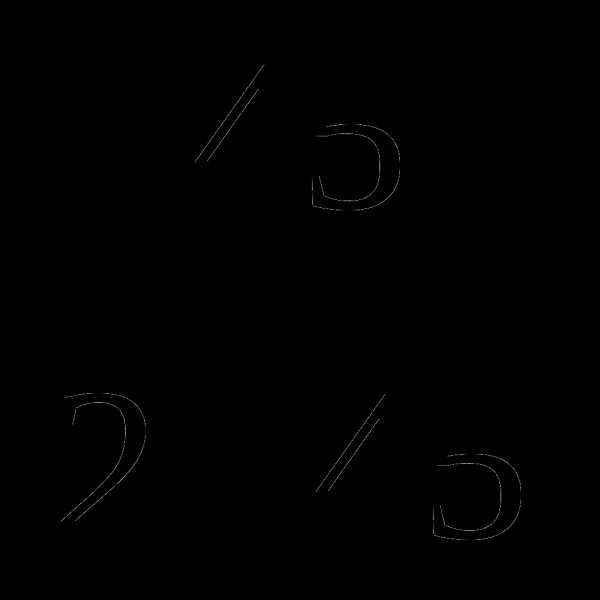 Г.
Г. 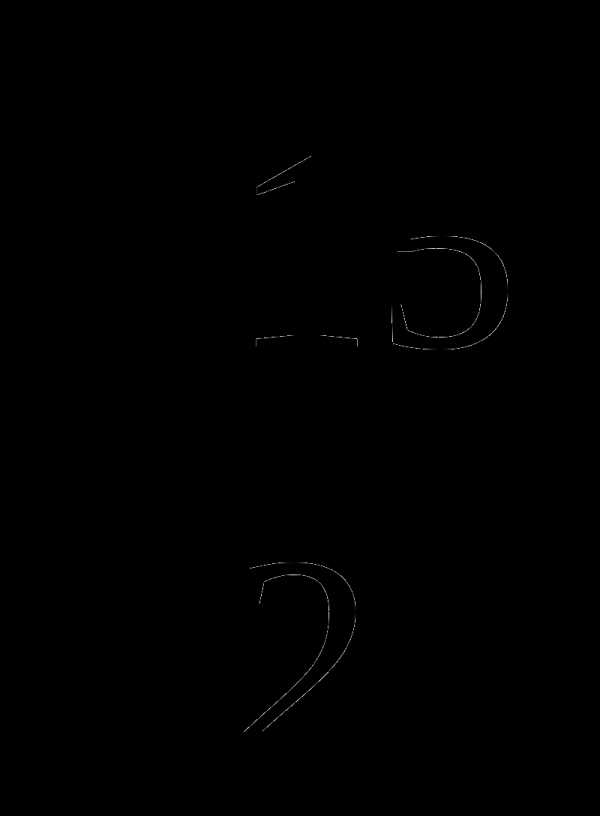
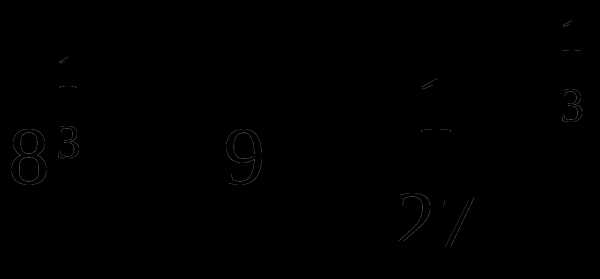
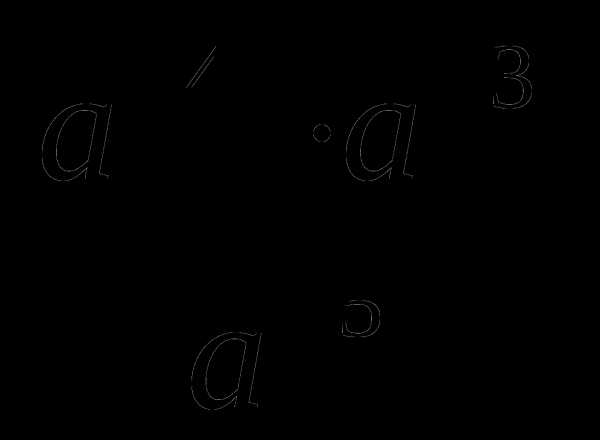 при
при 
 В.
В. 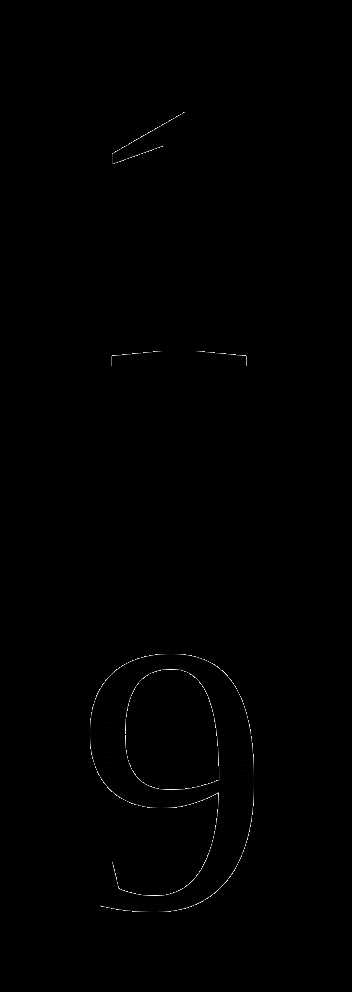 Г. 9
Г. 9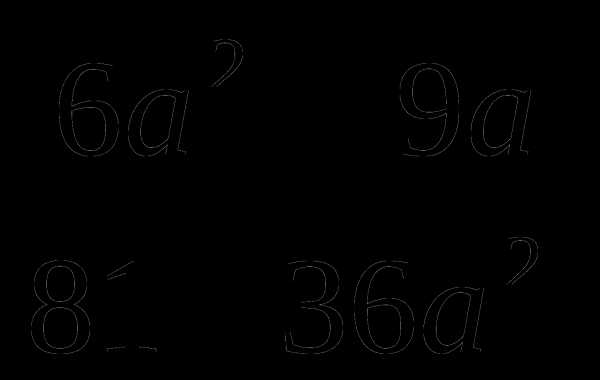
 Б.
Б.  В.
В.  Г.
Г. 
 если
если
 называется …….вектора
называется …….вектора