Теория, пособие для подготовки к ЕГЭ по математике
Факт 1.
\(\bullet\) Множество натуральных чисел \(\mathbb{N}\) – это числа \(1,
\ 2, \ 3, \ 4 \ \) и т.д.
\(\bullet\) Множество целых чисел \(\mathbb{Z}\) состоит из натуральных чисел, противоположных им (\(-1, \ -2, \ -3 \) и т.д.) и нуля \(0\).
\(\bullet\) Рациональные числа \(\mathbb{Q}\) – числа вида \(\dfrac ab\), где \(a\in \mathbb{Z}\), \(b\in \mathbb{N}\).
Таким образом, существует включение: \(\mathbb{N}\) содержится в \(\mathbb{Z}\), а \(\mathbb{Z}\) содержится в \(\mathbb{Q}\).
Факт 2.
\(\bullet\) Правила сложения дробей: \[\begin{aligned} &\dfrac ab+\dfrac cb=\dfrac{a+c}b\\[2ex]
&\dfrac ab+\dfrac cd=\dfrac{ad+bc}{bd}\end{aligned}\] Пример: \(\dfrac {31}6+\dfrac {67}6=\dfrac{31+67}6=\dfrac{98}6\)
\(\bullet\) Правила умножения дробей: \[\dfrac ab\cdot \dfrac cd=\dfrac{ac}{bd}\] Пример: \(\dfrac 47\cdot \dfrac{14}5=\dfrac{4\cdot 14}{7\cdot 5}\)
\(\bullet\) Правила деления дробей: \[\dfrac ab: \dfrac cd=\dfrac ab\cdot \dfrac dc\] Пример: \(\dfrac 45 :\dfrac 67=\dfrac 45\cdot \dfrac 76\)
Факт 2.
\(\bullet\) Сокращение дробей – деление числителя и знаменателя на одно и то же число, отличное от нуля.
Пример:
\(\begin{aligned} &\dfrac{98}6=\dfrac{49\cdot
2\llap{/}}{3\cdot
2\llap{/}}=\dfrac{49}3\\[2ex]
&\dfrac{4\cdot 14}{7\cdot 5}=\dfrac{4\cdot 2\cdot
7\llap{/}}{7\llap{/}\cdot
5}=\dfrac 85\\[2ex]
&\dfrac{4\cdot 7}{5\cdot 6}=\dfrac {2\llap{/}\cdot 2\cdot 7}{5\cdot
3\cdot
2\llap{/}}=\dfrac{14}{15}\end{aligned}\)
\(\bullet\) Если \(\dfrac ab\) – несократимая дробь, то ее можно представить в виде конечной десятичной дроби тогда и только тогда, когда знаменатель \(b\) делится только на числа \(2\) и \(5\).
Пример: дробь \(\dfrac2{65}\) нельзя представить в виде конечной десятичной дроби, так как \(65=5\cdot 13\), то есть \(\dfrac2{65}=0,0307…\)
дробь \(\dfrac3{160}\) можно представить в виде конечной десятичной дроби, так как \(160=2^5\cdot 5\), то есть \(\dfrac3{160}=0,01875\).
Факт 3.
\(\bullet\) Формулы сокращенного умножения:
\(\blacktriangleright\) Квадрат суммы и квадрат разности: \[(a+b)^2=a^2+2ab+b^2\] \[(a-b)^2=a^2-2ab+b^2\]
\(\blacktriangleright\) Куб суммы и куб разности: \[(a+b)^3=a^3+3a^2b+3ab^2+b^3\quad {\small{\text{или}}}\quad (a+b)^3=a^3+b^3+3ab(a+b)\] \[(a-b)^3=a^3-3a^2b+3ab^2-b^3\quad {\small{\text{или}}}\quad (a-b)^3=a^3-b^3-3ab(a-b)\]
Заметим, что применение данных формул справа налево часто помогает упростить вычисления:
\(13^3+3\cdot 13^2\cdot 7+3\cdot 13\cdot 49+7^3=(13+7)^3=20^3=8000\)
\(\blacktriangleright\) Разность квадратов: \[a^2-b^2=(a-b)(a+b)\]
\(\blacktriangleright\) Сумма кубов и разность кубов: \[a^3+b^3=(a+b)(a^2-ab+b^2)\] \[a^3-b^3=(a-b)(a^2+ab+b^2)\]
Заметим, что не существует формулы суммы квадратов \(a^2+b^2\).
Заметим, что применение данных формул слева направо часто помогает упростить вычисления:
\(\dfrac{7^6-2^6}{7^4+14^2+16}= \dfrac{(7^2-2^2)(7^4+7^2\cdot2^2+2^4)} {7^4+(7\cdot2)^2+2^4}=7^2-2^2=45\)
Факт 4.
\(\bullet\) Квадрат суммы нескольких слагаемых равен сумме квадратов этих слагаемых и удвоенных попарных произведений: \[\begin{aligned}
&(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc\\[2ex]
&(a+b+c+d)^2=a^2+b^2+c^2+d^2+2ab+2ac+2ad+2bc+2bd+2cd\\[2ex]
&{\small{\text{и т.д.}}}\end{aligned}\]
shkolkovo.net
Все формулы по математике — Формулы под рукой
Не решается задачка? Наш сайт поможет тебе в учебе, подготовке к сложным экзаменам, контрольным, олимпиадам, сессиям, ЕГЭ.
ФОРМУЛЫ ПО АЛГЕБРЕ
ФОРМУЛЫ ПО ГЕОМЕТРИИ
ФОРМУЛЫ ПО ТРИГОНОМЕТРИИ
Обладатель премии Эйнштейна, известнейший британский исследователь в области теоретический физики Стивен Хокинг однажды рассказал, что получил должность профессора математики в Оксфордском университете, не имея специального образования. На тот момент за его плечами были лишь изрядно подзабытые школьные знания по математике. Царицу наук постигал «на ходу», читая студенческий учебник с опережением программы на две недели. Впоследствии студенты Хокинга вспоминали его занятия как исключительно познавательные и захватывающие!
Такие примеры вдохновляют, вселяют уверенность, что и каждый из нас может с таким же успехом освежить «хорошо забытое». А там и новый вектор развития появится.
Чтобы вспомнить (или освоить!) школьный материал было легче, предлагаем листать не страницы учебников и справочной литературы, а воспользоваться нашим сайтом, где удобная навигация и система поиска позволят быстро отыскать нужную формулу по предметам:
- арифметика;
- алгебра;
- геометрия;
- физика;
- химия.
От теории к практике
Бывает, что и материал знаком, да и формулы, теоремы и аксиомы по нужной теме — вот они, а задачка не поддается. Педагогический «диагноз»: нет опыта. Приобретается этот опыт при помощи решения типовых уравнений и задач. Предлагаем наиболее удачные и интуитивно понятные методики, которые уже помогли не одному ученику овладеть инструментарием точных наук!
Быстрее, выше, сильнее!
Возможно, сейчас ты и считаешь, что выучить все школьные формулы невозможно. Но на самом деле формул, необходимых для решения задач школьного уровня по математике, не более двухсот, а по физике — и того меньше! А это значит, что, заглядывая в наши справочники и освоив принципы решения типовых задач, можно постепенно запомнить все базовые формулы!
Какими бы сложными ни казались тебе задания твоих преподавателей сейчас, через какое-то время школьные, да и институтские стены могут показаться тебе тесными.
На нашем сайте собраны как часто используемые, так и гораздо более сложные формулы. Если захочешь знать больше, чем написано в школьном учебнике, начни с аксиомы — слов Марка Твена, который «никогда не позволял, чтобы школьные занятия мешали образованию!».
megaformula.ru
Основные формулы для подготовки к ЕГЭ по математике
Формулы дифференцирования
Правила дифференцирования
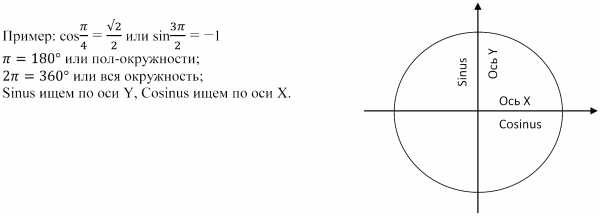
Таблица некоторых значений тригонометрических функций
Таблица первообразных и интегралов
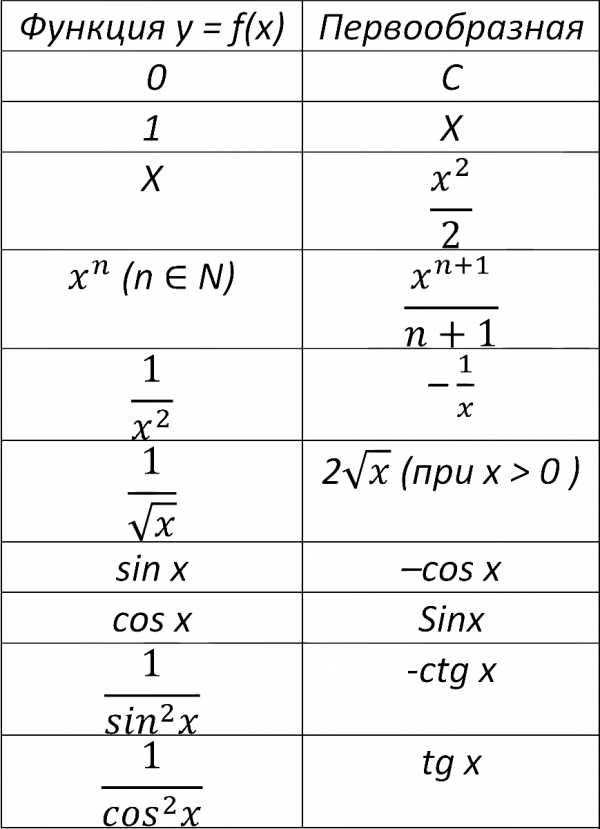

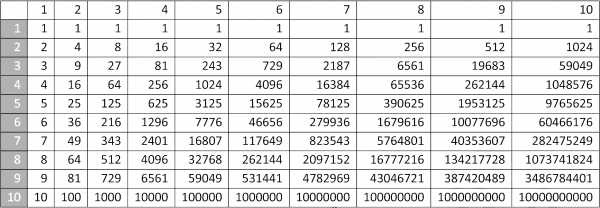
Таблица степеней чисел
Законы степеней чисел:
Свойства корня n-ой степени
Координаты точек
Координаты точек
Формулы приведения
Формулы сокращённого умножения:
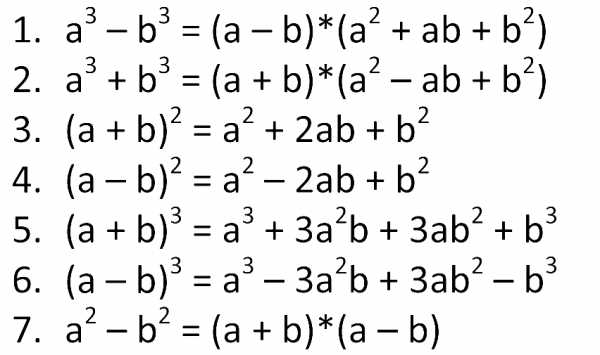
Применение производной:
Прогрессии:
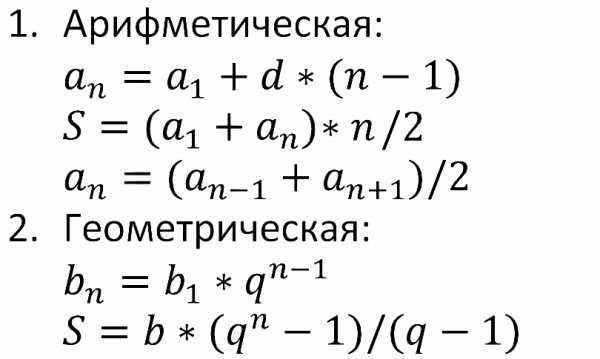
Вернуться в меню выбора предмета
www.examen.ru
Сборник формул по математике (карманный справочник) / 2003.
Некоторые математические обозначения
Греческий алфавит
Латинский алфавит
ШКОЛЬНЫЙ КУРС
Арифметика
Признаки делимости
Пропорции
Средние величины
Золотое сечение
Некоторые конечные числовые ряды
Формулы сокращенного умножения
Свойства степени
Свойства квадратного (арифметического) корня
Уравнения и системы уравнений
Неравенства
Прогрессии
Логарифмы (Сравнение логарифмов)
Теория соединений. Бином Ньютона
Начала анализа
Графики элементарных функций
Тригонометрия
Градусная и радианная мера углов
Тригонометрические функции
Тригонометрические функции в прямоугольном треугольнике
Тригонометрические тождества
Выражение одних тригонометрических функций через другие
Формулы сложения тригонометрических функций
Формулы приведения тригонометрических функций
Тригонометрические функции кратных углов
Тригонометрические функции половинного угла
Сумма тригонометрических функций
Понижение степени тригонометрических функций
Произведение тригонометрических функций
Формула дополнительного угла
Соотношения между обратными тригонометрическими функциями
Геометрия
Треугольники
Правильные n-угольники
Окружность и круг
Многогранники
Правильные многогранники
Тела вращения
Векторы
ВЫСШАЯ МАТЕМАТИКА
Аналитическая геометрия на плоскости
Координаты точки
Площадь треугольника
Уравнение прямой
Уравнение окружности
Эллипс
Гипербола
Парабола
Аналитическая геометрия в пространстве
Координаты точки
Уравнение плоскости
Уравнение прямой
Прямая и плоскость
Уравнение сферы
Поверхности второго порядка
Комплексные числа
Алгебра
Матрицы
Определители
Элементы векторной алгебры
Дифференциальное исчисление
Определение и свойства пределов
Производная и дифференциал
Дифференциальное исчисление функций двух переменных
Дифференциальное исчисление функций нескольких переменных
Интегральное исчисление
Неопределенный интеграл
Таблица неопределенных интегралов
Определенный интеграл
Кратные интегралы
Ряды
Числовые ряды
Степенные ряды
Ряды Фурье
Дифференциальные уравнения
Дифференциальные уравнения первого порядка
Дифференциальные уравнения второго порядка
Теория вероятностей
Некоторые замечательные кривые
istudy.su
