| Символ (TeX) | Символ (Unicode) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒ → ⊃ | Импликация, следование | означает «если верно, то также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.). | верно, но неверно (так как также является решением). | |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| ⇔ | Равносильность | означает « верно тогда и только тогда, когда верно». | ||
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧ | Конъюнкция | истинно тогда и только тогда, когда и оба истинны. | , если — натуральное число. | |
| «и» | ||||
| Математическая логика | ||||
| ∨ | Дизъюнкция | истинно, когда хотя бы одно из условий и истинно. | , если — натуральное число. | |
| «или» | ||||
| Математическая логика | ||||
| ¬ | Отрицание | истинно тогда и только тогда, когда ложно . | ||
| «не» | ||||
| Математическая логика | ||||
| ∀ | Квантор всеобщности | обозначает « верно для всех ». | ||
| «Для любых», «Для всех» | ||||
| Математическая логика | ||||
| ∃ | Квантор существования | означает «существует хотя бы один такой, что верно » | (подходит число 5) | |
| «существует» | ||||
| Математическая логика | ||||
| = | Равенство | обозначает « и обозначают одно и то же значение». | 1 + 2 = 6 − 3 | |
| «равно» | ||||
| везде | ||||
| := :⇔ | Определение | означает « по определению равен ». означает « по определению равносильно » | (Гиперболический косинус) (Исключающее или) | |
| «равно/равносильно по определению» | ||||
| везде | ||||
| { , } | Множество элементов | означает множество, элементами которого являются , и . | (множество натуральных чисел) | |
| «Множество…» | ||||
| Теория множеств | ||||
| { | } { : } | Множество элементов, удовлетворяющих условию | означает множество всех таких, что верно . | ||
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅ {} | Пустое множество | и означают множество, не содержащее ни одного элемента. | ||
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈ ∉ | Принадлежность/непринадлежность к множеству | означает « является элементом множества » означает « не является элементом множества » | ||
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| ⊆ ⊂ | Подмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇ ⊃ | Надмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊ | Собственное подмножество | означает и . | ||
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋ | Собственное надмножество | означает и . | ||
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| ∪ | Объединение | означает множество элементов, принадлежащих или (или обоим сразу). | ||
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ⋂ | Пересечение | означает множество элементов, принадлежащих и , и . | ||
| «Пересечение … и … », «…, пересечённое с …» | ||||
| Теория множеств | ||||
| \ | Разность множеств | означает множество элементов, принадлежащих , но не принадлежащих . | ||
| «разность … и … », «минус», «… без …» | ||||
| Теория множеств | ||||
| → | Функция | означает функцию с областью определения и областью прибытия (областью значений) . | Функция , определённая как | |
| «из … в», | ||||
| везде | ||||
| ↦ | Отображение | означает, что образом после применения функции будет . | Функцию, определённую как , можно записать так: | |
| «отображается в» | ||||
| везде | ||||
| N или ℕ | Натуральные числа | означает множество или реже (в зависимости от ситуации). | ||
| «Эн» | ||||
| Числа | ||||
| Z или ℤ | Целые числа | означает множество | ||
| «Зед» | ||||
| Числа | ||||
| Q или ℚ | Рациональные числа | означает | ||
| «Ку» | ||||
| Числа | ||||
| R или ℝ | Вещественные числа, или действительные числа | означает множество всех пределов последовательностей из | ( — комплексное число: ) | |
| «Эр» | ||||
| Числа | ||||
| C или ℂ | Комплексные числа | означает множество | ||
| «Це» | ||||
| Числа | ||||
| < > | Сравнение | обозначает, что строго меньше . означает, что строго больше . | ||
| «меньше чем», «больше чем» | ||||
| Отношение порядка | ||||
| ≤ или ⩽ ≥ или ⩾ | Сравнение | означает, что меньше или равен . означает, что больше или равен . | ||
| «меньше или равно»; «больше или равно» | ||||
| Отношение порядка | ||||
| ≈ | Приблизительное равенство | с точностью до означает, что 2,718 отличается от не больше чем на . | с точностью до . | |
| «приблизительно равно» | ||||
| Числа | ||||
| √ | Арифметический квадратный корень | означает неотрицательное действительное число, которое в квадрате даёт . | ||
| «Корень квадратный из …» | ||||
| Числа | ||||
| ∞ | Бесконечность | и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. | ||
| «Плюс/минус бесконечность» | ||||
| Числа | ||||
| | | | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества | обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов . | ||
| «Модуль»; «Мощность» | ||||
| Числа и Теория множеств | ||||
| ∑ | Сумма, сумма ряда | означает «сумма , где принимает значения от 1 до », то есть . означает сумму ряда, состоящего из . | ||
| «Сумма … по … от … до …» | ||||
| Арифметика, Математический анализ | ||||
| ∏ | Произведение | означает «произведение для всех от 1 до », то есть | ||
| «Произведение … по … от … до …» | ||||
| Арифметика | ||||
| ! | Факториал | означает «произведение всех натуральных чисел от 1 до включительно, то есть | ||
| « факториал» | ||||
| Комбинаторика | ||||
| ∫ | Интеграл | означает «интеграл от до функции от по переменной ». | ||
| «Интеграл (от … до …) функции … по (или d)…» | ||||
| Математический анализ | ||||
| df/dx f'(x) | Производная | или означает «(первая) производная функции от по переменной ». | ||
| «Производная … по …» | ||||
| Математический анализ | ||||
| Производная -го порядка | или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ». | |||
| «-я производная … по …» | ||||
| Математический анализ |
dic.academic.ru
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Алфавиты, номиналы, единицы / / Алфавиты, в т.ч. греческий и латинский. Символы. Коды. Альфа, бета, гамма, дельта, эпсилон… / / Таблица научных, математических, физических символов и сокращений. Скоропись физического, математического, химического и, в целом, научного текста, математические обозначения. Математический, Физический алфавит, Научный алфавит.
| ||||
dpva.ru
Математические знаки и символы: список, таблица, история возникновения
Когда люди долгое время взаимодействуют в рамках определенной сферы деятельности, они начинают искать способ оптимизировать процесс коммуникации. Система математических знаков и символов представляет собой искусственный язык, который был разработан, чтобы уменьшить объем графически передаваемой информации и при этом полностью сохранить заложенный в сообщение смысл.
Любой язык требует изучения, и язык математики в этом плане – не исключение. Чтобы понимать значение формул, уравнений и графиков, требуется заранее владеть определенной информацией, разбираться в терминах, системе обозначений и т. д. При отсутствии такого знания текст будет восприниматься как написанный на незнакомом иностранном языке.
В соответствии с запросами общества графические символы для более простых математических операций (например, обозначение сложения и вычитания) были выработаны раньше, чем для сложных понятий наподобие интеграла или дифференциала. Чем сложнее понятие, тем более сложным знаком оно обычно обозначается.
Модели образования графических обозначений
На ранних этапах развития цивилизации люди связывали простейшие математические операции с привычными для них понятиями на основе ассоциаций. Например, в Древнем Египте сложение и вычитание обозначались рисунком идущих ног: направленные по направлению чтения строки они обозначали «плюс», а в обратную сторону – «минус».
Цифры, пожалуй, во всех культурах изначально обозначались соответствующим количеством черточек. Позже для записи стали использоваться условные обозначения — это экономило время, а также место на материальных носителях. Часто в качестве символов использовались буквы: такая стратегия получила распространение в греческом, латинском и многих других языках мира.
 История возникновения математических символов и знаков знает два наиболее продуктивных способа образования графических элементов.
История возникновения математических символов и знаков знает два наиболее продуктивных способа образования графических элементов.Преобразование словесного представления
Изначально любое математическое понятие выражается некоторым словом или словосочетанием и не имеет собственного графического представления (помимо лексического). Однако выполнение расчетов и написание формул словами – процедура длительная и занимающая неоправданно много места на материальном носителе.
Распространенный способ создания математических символов – трансформация лексического представления понятия в графический элемент. Иначе говоря, слово, обозначающее понятие, с течением времени сокращается или преобразуется каким-либо другим способом.
 Например, основной гипотезой происхождения знака «плюс» является его сокращение от латинского et, аналогом которого в русском языке является союз «и». Постепенно в скорописи первая буква перестала писаться, а t сократилась до креста.
Например, основной гипотезой происхождения знака «плюс» является его сокращение от латинского et, аналогом которого в русском языке является союз «и». Постепенно в скорописи первая буква перестала писаться, а t сократилась до креста.Другой пример – знак «икс», обозначающий неизвестное, который изначально представлял собой сокращение от арабского слова «нечто». Сходным образом произошли знаки для обозначения квадратного корня, процента, интеграла, логарифма и др. В таблице математических символов и знаков можно встретить более десятка графических элементов, появившихся таким образом.
Назначение произвольного символа
Второй распространенный вариант образования математических знаков и символов – назначение символа произвольным образом. В этом случае слово и графическое обозначение между собой не связаны — знак обычно утверждается в результате рекомендации одного из членов научного сообщества.
Например, знаки умножения, деления, равенства были предложены математиками Уильямом Отредом, Иоганном Раном и Робертом Рекордом. В некоторых случаях несколько математических знаков могли быть введены в науку одним ученым. В частности, Готфрид Вильгельм Лейбниц предложил целый ряд символов, в том числе интеграла, дифференциала, производной.
Простейшие операции
Такие знаки, как «плюс» и «минус», а также символы, обозначающие умножение и деление, знает каждый школьник, несмотря на то, что для последних двух упомянутых операций существует несколько возможных графических знаков.
Можно с уверенностью говорить, что складывать и вычитать люди умели ещё за много тысячелетий до нашей эры, а вот стандартизованные математические знаки и символы, обозначающие данные действия и известные нам сегодня, появились лишь к XIV-XV столетию.
 Впрочем, несмотря на установление определенной договоренности в научном сообществе, умножение и в наше время может изображаться тремя различными знаками (диагональный крестик, точка, звёздочка), а деление – двумя (горизонтальная черта с точками сверху и снизу или наклонная черта).
Впрочем, несмотря на установление определенной договоренности в научном сообществе, умножение и в наше время может изображаться тремя различными знаками (диагональный крестик, точка, звёздочка), а деление – двумя (горизонтальная черта с точками сверху и снизу или наклонная черта).Латинские буквы
На протяжении многих столетий научное сообщество использовало для обмена информацией исключительно латынь, и многие математические термины и знаки обнаруживают свои истоки именно в этом языке. В некоторых случаях графические элементы стали результатом сокращения слов, реже – их намеренного или случайного преобразования (например, вследствие описки).
Обозначение процента («%»), вероятнее всего, происходит от ошибочного написания сокращения cto (cento, т. е. «сотая доля»). Сходным образом произошёл знак «плюс», история которого описана выше.
Гораздо большее количество символов было образовано путём намеренного сокращения слова, хотя это не всегда очевидно. Далеко не каждый человек узнает в знаке квадратного корня букву R, т. е. первый знак в слове Radix («корень»). Символ интеграла также представляет собой первую букву слова Summa, однако интуитивно она похожа на прописную f без горизонтальной черты. К слову, в первой публикации издатели совершили именно такую ошибку, напечатав f вместо данного символа.
Греческие буквы
В качестве графических обозначений для различных понятий используются не только латинские, но и греческие буквы. В таблице математических символов можно найти целый ряд примеров такого наименования.
Число Пи, представляющее собой отношение длины окружности к её диаметру, произошло от первой буквы греческого слова, обозначающего окружность. Существует ещё несколько менее известных иррациональных чисел, обозначаемых буквами греческого алфавита.
 Крайне распространенным знаком в математике является «дельта», отражающая величину изменения значения переменных. Ещё одним употребительным знаком является «сигма», выполняющая функцию знака суммы.
Крайне распространенным знаком в математике является «дельта», отражающая величину изменения значения переменных. Ещё одним употребительным знаком является «сигма», выполняющая функцию знака суммы.Более того, практически все греческие буквы так или иначе используются в математике. Однако данные математические знаки и символы и их значение знают только люди, занимающиеся наукой профессионально. В быту и повседневной жизни эти знания человеку не требуются.
Знаки логики
Как ни странно, многие интуитивно понятные символы были придуманы совсем недавно.
В частности, горизонтальная стрелка, заменяющая слово «следовательно», была предложена лишь в 1922 года Давидом Гильбертом. Кванторы существования и всеобщности, т. е. знаки, читающиеся как: «существует…» и «для любого…», были введены в 1897 и 1935 году соответственно.
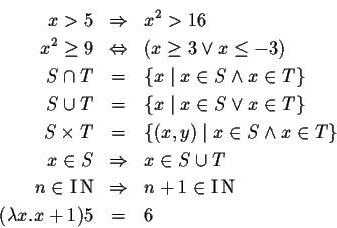 Символы из области теории множеств были придуманы в 1888-1889 гг. А перечеркнутый круг, который сегодня известен любому учащемуся средней школы как знак пустого множества, появился в 1939 году.
Символы из области теории множеств были придуманы в 1888-1889 гг. А перечеркнутый круг, который сегодня известен любому учащемуся средней школы как знак пустого множества, появился в 1939 году.Таким образом, знаки для столь непростых понятий, как интеграл или логарифм, были придуманы на столетия раньше, чем некоторые интуитивно понятные символы, легко воспринимаемые и усваиваемые даже без предварительной подготовки.
Математические символы на английском
Ввиду того, что значительная часть понятий была описана в научных трудах на латыни, ряд названий математических знаков и символов на английском и русском языке одинаковы. Например: Plus («плюс»), Integral («интеграл»), Delta function («дельта-функция»), Perpendicular («перпендикулярный»), Parallel («параллельный»), Null («нуль»).
Часть понятий в двух языках называются различным образом: так, деление – это Division, умножение – Multiplication. В редких случаях английское название для математического знака получает некоторое распространение в русском языке: например, косая черта в последние годы нередко именуется «слешем» (англ. Slash).
Таблица символов
Самый простой и удобный способ ознакомиться с перечнем математических знаков – посмотреть специальную таблицу, в которой содержатся знаки операций, символы математической логики, теории множеств, геометрии, комбинаторики, математического анализа, линейной алгебры. В данной таблице представлены основные математические знаки на английском языке.
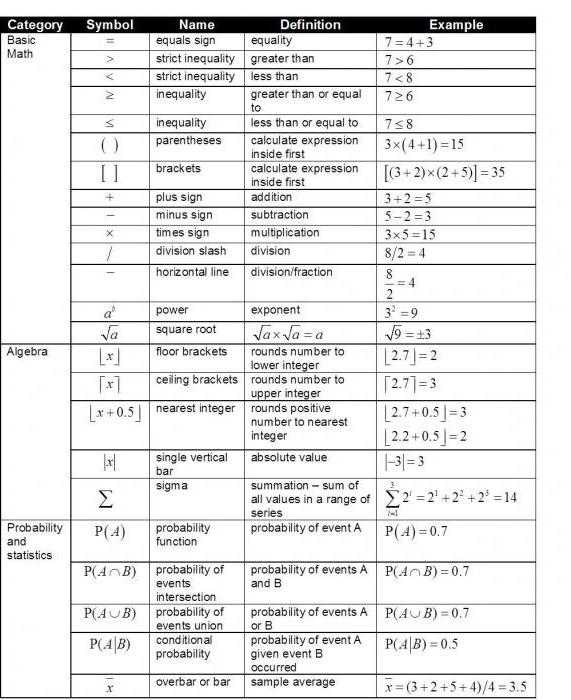
Математические знаки в текстовом редакторе
При выполнении различного рода работ зачастую требуется использовать формулы, где употребляются знаки, отсутствующие на клавиатуре компьютера.
Как и графические элементы из практически любой области знаний, математические знаки и символы в «Ворде» можно найти во вкладке «Вставка». В версиях программы 2003 или 2007 года существует опция «Вставка символа»: при нажатии на кнопку в правой части панели пользователь увидит таблицу, в которой представлены все необходимые математические знаки, греческие строчные и прописные буквы, различные виды скобок и многое другое.
В версиях программы, вышедших после 2010 года, разработана более удобная опция. При нажатии на кнопку «Формула» происходит переход в конструктор формул, где предусмотрено использование дробей, занесения данных под корень, смена регистра (для обозначения степеней или порядковых номеров переменных). Здесь же могут быть найдены все знаки из таблицы, представленной выше.
Стоит ли учить математические символы
Система математических обозначений представляет собой искусственный язык, который лишь упрощает процесс записи, но не может принести понимание предмета стороннему наблюдателю. Таким образом, запоминание знаков без изучения терминов, правил, логических связей между понятиями не приведет к овладению данной областью знаний.
 Человеческий мозг легко усваивает знаки, буквы и сокращения – математические обозначения запоминаются сами при изучении предмета. Понимание смысла каждого конкретного действия создает настолько прочные ассоциативные связи, что знаки, обозначающие термины, а зачастую и формулы, связанные с ними, остаются в памяти на многие годы и даже десятилетия.
Человеческий мозг легко усваивает знаки, буквы и сокращения – математические обозначения запоминаются сами при изучении предмета. Понимание смысла каждого конкретного действия создает настолько прочные ассоциативные связи, что знаки, обозначающие термины, а зачастую и формулы, связанные с ними, остаются в памяти на многие годы и даже десятилетия.В заключение
Поскольку любой язык, в том числе искусственный, является открытым к изменениям и дополнениям, число математических знаков и символов непременно будет расти с течением времени. Не исключено, что какие-то элементы будут заменены или скорректированы, а другие – стандартизованы в единственно возможном виде, что актуально, например, для знаков умножения или деления.
Умение пользоваться математическими символами на уровне полного школьного курса является в современном мире практически необходимым. В условиях бурного развития информационных технологий и науки, повсеместной алгоритмизации и автоматизации владение математическим аппаратом следует воспринимать как данность, а освоение математических символов – как неотъемлемую его часть.
Поскольку расчеты используются и в гуманитарной сфере, и в экономике, и в естественных науках, и, разумеется, в области техники и высоких технологий, понимание математических понятий и знание символов станет полезным для любого специалиста.
fb.ru
| N | множество натуральных чисел |
| Z | множество целых чисел |
| Q | множество рациональных чисел |
| I | множество иррациональных чисел |
| R | множество действительных (вещественных) чисел |
| ø | пустое множество |
| ∈ | знак принадлежности |
| ∩ | пересечение множеств |
| ∪ | объединение множеств |
| ⊂ и ⊃ | включение множеств (знак подмножеств) |
| \ | разность множеств |
| = | равно |
| ≠ | не равно |
| ≈ | приближённо (примерно) равно |
| > | больше |
| < | меньше |
| ≥ | больше или равно (не меньше) |
| ≤ | меньше или равно (не больше) |
| НОД (a, b) | наибольший общий делитель чисел a и b |
| НОК (a, b) | наименьшее общее кратное чисел a и b |
| |a| | модуль (абсолютная величина) числа а |
| [a] | целая часть числа а |
| {a} | дробная часть числа а |
| √a | арифметический квадратный корень из числа а |
| n√a | арифметический корень n-й степени из числа а |
| log a b | логарифм числа b с основанием а |
| lg b | десятичный логарифм числа b |
| ln b | натуральный логарифм числа b |
| π | число «пи» – отношение длины окружности к её диаметру |
| e | число «е» – основание натурального логарифма |
| f(x0) | значение функции f в точке х0 |
| sin x | функция синус х |
| cos x | функция косинус х |
| tg x | функция тангенс х |
| ctg x | функция котангенс х |
| arcsin x | функция арксинус х |
| arccos x | функция арккосинус х |
|
arctg x |
функция арктангенс х |
| arcctg x | функция арккотангенс х |
| [a; b] |
замкнутый промежуток (отрезок) с началом а и концом b |
| (a; b) | открытый промежуток (интервал) с началом а и концом b |
| [a; b) и (a; b] | полузамкнутые числовые промежутки с началом а и концом b |
| (– ∞; + ∞) | числовая прямая |
| (– ∞ ; a] и [b; + ∞) | полузамкнутые числовые лучи |
| (– ∞ ; a) и (b; + ∞) | открытые числовые лучи |
| a < x < b | двойное неравенство: х больше а и меньше b |
| a ≤ x < b | двойное неравенство: х не меньше а и меньше b |
| a < x ≤ b | двойное неравенство: х больше а и не больше b |
| a ≤ x ≤ b | двойное неравенство: х не меньше а и не больше b |
| (a; b) | упорядоченная пара чисел |
| (a; b; c) | упорядоченная тройка чисел |
| Ox, Oy, Oz | координатные оси: ось абсцисс, ось ординат, ось апликат |
| M(x) | точка М с координатой х на координатной прямой |
| M(x; y) | точка М с координатами х и у в координатной плоскости |
| M(x; y; z) | точка М с координатами х, у и z в координатном пространстве |
| lim x→a f(b) = b | b – предел функции f(b) при условии, что х стремится к а |
| Δx, Δy или Δf(x) | приращение аргумента и приращение функции |
| f'(x), f»(x), f»'(x), f(n)(x0) | производные функции: первая, вторая, третья и n-го прядка |
| F(x) | первообразная функция для функции f(x) |
| ∫ f(x) dx | неопределённый интеграл функции f(x) |
| a∫b f(x) dx | определённый интеграл функции f(x) от а до b |
| i | мнимая единица |
| z = a + bi | комплексное число с действительной частью а и мнимой – bi |
| Re z | действительная часть комплексного числа z |
| Im z | мнимая часть комплексного числа z |
| z | число, сопряжённое числу z |
| arg z | аргумент комплексного числа z |
| |z| | модуль комплексного числа z |
| n! | n-факториал |
| Pn | число перестановок из n элементов |
| Anm | число размещений из n элементов по m |
| Cnm | число сочетаний из n элементов по m |
| Σ, Π | сумма и произведение |
| A, B, C | случайные события |
| P(A) | вероятность случайного события А |
| A + B, A · B | сумма и произведение событий А и В |
| A | событие, противоположное событию А |
| { | знак системы |
| [ | знак совокупности |
| x° y’ z» | x градусов, y минут, z секунд |
| AB | отрезок или прямая АВ |
| ∪AB | дуга окружности с концами в точках А и В |
| ∠ ABC | угол с вершиной в точке В и сторонами ВА и ВС |
| ∠A | любой угол с вершиной в точке А |
| Δ ABC | треугольник с вершинами в точках А, В и С |
| PF | периметр многоугольника F |
| SF | площадь фигуры F |
| VF | объём тела F |
|
F ∼ G |
фигуры F и G подобны |
| F = G | фигуры F и G равны |
math4school.ru
Математические символы — Таблица символов Юникода®
На этой странице собраны математические знаки.
Знаки плюс, минус, плюс минус, равно, не равно, примерно равно, умножения, деления, сумма:
+ − ± ∓ = ≠ ≈ ≃ ÷ ∗ ∙ × ∑ ⩱ ⩲
Интегралы:
∫ ∬ ∭ ∮ ∯ ∰ ∱ ∲ ∳ ⨌ ⨍ ⨎ ⨏ ⨐ ⨑ ⨒ ⨓ ⨔ ⨕ ⨖ ⨗ ⨘ ⨙ ⨚ ⨛ ⨜
Сравнение — больше меньше или равно:
< > ≤ ≥ ≪ ≫ ≮ ≯
Геометрические — диаметр, угол, градус, перпендикуляр, параллельность, диаметр, пропорциональности, подобия, пересечения, объединения:
⌀ ∠ ∡ ∢ ⦛ ⦜ ⦝ ⦞ ⦟ ⦠ ⦡ ⦢ ⦣ ° ⟂ ⏊ ⊥ ∥ ∦ |∙ ~ ∝ ⋂ ⋃
Степени и корни:
99 ^ ⁰ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ⁺ ⁻ ⁼ ⁽ ⁾ √ ∛ ∜
Фигуры — треугольники, дуги, параллелограмм, ромб:
⌒ ◠ ◡ ⊿ △ ▷ ▽ ◁ □ ▭ ▱ ○ ◊
Логические — следовательно, и, или, отрицания, тождественный:
⇒ ⇔ ⇐ ⇍ ⇏ → ∧ ∨ ⋀ ⋁ ∴ ¬ ≡
Ещё знаки — существует, пустое множество, принадлежит, подмножество, бесконечность:
∃ ∀ ∅ ∈ ∉ ⊆ ∞
В разделе собраны математические символы, которые невозможно корректно отобразить с помощью ввода на клавиатуре. Весь представленный набор можно разделить на несколько групп:
- знаки операций – сложение, вычитание, деление, умножение, сумма, тождество;
- символы интегралов – двойные, тройные, интеграл по объему, поверхности, с правым и левым обходом;
- знаки сравнения – больше, меньше, равно;
- геометрические символы – отображение угла, пропорции, диаметра;
- геометрические фигуры;
- знак извлечения из корня, степень;
- иные символы – бесконечность, множество, квантор существования.
Использование данных иконок – единственный вариант корректного отображения ряда математических символов на сайте или в сообщении в любой операционной системе конечного пользователя. Достаточно лишь скопировать закодированный значок. Применение изображений для этих целей значительно усложняет процесс, требует подгонки при разработке и наполнении интернет-ресурса. Кроме того, медиа-контент занимает большой объем дискового пространства.
Математические символы подойдут для публикаций в социальных сетях, создания сообщений в чатах и форумах, разработки интернет-страниц.
Математика, как язык всех наук, не может обходиться без системы записи. Многочисленные понятия, и операторы обрели своё начертание по мере развития этой науки. Так как в стандартные алфавиты эти символы не входят, напечатать их с клавиатуры может оказаться проблематично. Отсюда можно скопировать и вставить.
Консорциуму Юникода не чужды проблемы учёных, поэтому в таблицу было включено множество различных знаков. Если тут нет того, что нужно, воспользуйтесь поиском по сайту или посмотрите в разделах математические символы, разнообразные математические символы-A, разнообразные математические символы-B, дополнительные математические операторы. Буквы для формул можно взять в наборе греческие буквы и блоке математические буквенно-цифровые символы.
Числа для степеней составляются из маленьких цифр. Там же собраны дроби.
Этот текст также доступен на следующих языках: English;
unicode-table.com
Основные математические понятия и обозначения
44
Одним из основных математических понятий является понятие множества.
Определение: Множеством называют совокупность каких-то объектов, объединенных по некоторому правилу или признаку.
Примерымножеств: — натуральные числа, целые числа, действительные числа.
Определение: Объекты, которые входят в состав множества, называют элементами данного множества.
Обычно множества обозначаются большими латинскими буквами (A, B, C), а их элементы – малыми (a, b, c).
Определение: Множество, которое имеет конечное число элементов – именуется конечным множеством; бесконечное — бесконечным.
Обычно любое множество задается некоторым свойством, т.е. таким свойством, которым обладают только элементы данного множества, например: M=a,b,c,d- некоторое множество.
Множество натуральных четных чисел: N2={2*n, где nN}
Определение:Множество, которое не содержит ни одного элемента, называется пустым множеством и обозначается 0
Множества чисел и их обозначения
N — множество натуральных чисел- {1,2,3,…, n,….}
Z — множество целых чисел {…-3,-2,-1,0,1,2,……….}
Q — множество рациональных чисел – это те числа, которые можно представить в виде дроби m/n, где m -принадлежит множеству целых чисел, а n — множеству натуральных чисел
Q={m/n, mZ, nN}
Иррациональные числа: J={ 2, 3, , e, …..}
Множество действительных чисел: R=Q U J
Множество комплексных чисел:
C={a+i*b; i=-1, a, bR}
Любое множество графически можно изобразить в виде круга (диаграммы Эйлера-Венна):
А
Определение: Множество В называется подмножеством множества А , (В А), если любой элемент множества В, является элементом множества А.
A
B В А
Основные операции над множествами
1. Сумма (Объединение) двух множеств А и В называется такое множество, которое состоит только из тех элементов, которые принадлежат хотя бы одному из множеств А или В.
В виде характеристического свойства — А U В={x, xA или xB}
Если изображают
ввиде круговA B А U В
Пример:
А={1,2,3} B={2,4,5} А U В={1,2,3,4,5}
2. Произведение (Пересечение) двух множеств А и В состоит из тех элементов, которые одновременно принадлежат и множеству А и множеству В: А В={x, xA и xB}
для рассмотренного
выше примера:A B А В
А В={2}
3. Разность двух множеств А и В (обозначается А\В) – называется множество, состоящее из элементов, которые принадлежат множеству А и не принадлежат множеству В
А\В={x, xA и x B} A B А\В
Для рассмотренного выше
примера:
А\В={1,3}
Логические символы
Для краткости записи, вместо слов: существует, найдется, будет использован символ ,
вместо слов любой, каждый, всякий .
Примеры: x, x+1N ; xX,X:2
Специальные математические символы
Для краткости записи произведения первых n-натуральных чисел вводят:
1*2*3*4*……..* n = n! , n –факториал.
1!=1 , 2!=1*2=2 , 5!=1*2*3*4*5=120,
0!=1 0-факториал.
Для краткости записи суммы и произведения будем использовать символы:
n
сумма ai = a1+a2+a3+….+an ; ai = a1+a2+…+an +…;
i=1 i=1
n
Произведение ai = a1*a2*a3*….*an
i=1
studfiles.net
| Символ (TeX) | Символ (Юникод) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒ → ⊃ | Импликация, следование | означает «если верно, то также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.). | верно, но неверно (так как также является решением). | |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| ⇔ | Равносильность | означает « верно тогда и только тогда, когда верно». | ||
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧ | Конъюнкция | истинно тогда и только тогда, когда и оба истинны. | , если — натуральное число. | |
| «и» | ||||
| Математическая логика | ||||
| ∨ | Дизъюнкция | истинно, когда хотя бы одно из условий и истинно. | , если — натуральное число. | |
| «или» | ||||
| Математическая логика | ||||
| ¬ | Отрицание | истинно тогда и только тогда, когда ложно . | ||
| «не» | ||||
| Математическая логика | ||||
| ∀ | Квантор всеобщности | обозначает « верно для всех ». | ||
| «Для любых», «Для всех», «Для всякого» | ||||
| Математическая логика | ||||
| ∃ | Квантор существования | означает «существует хотя бы один такой, что верно » | (подходит число 5) | |
| «существует» | ||||
| Математическая логика | ||||
| = | Равенство | обозначает « и обозначают одно и то же значение». | 1 + 2 = 6 − 3 | |
| «равно» | ||||
| везде | ||||
| := :⇔ | Определение | означает « по определению равен ». означает « по определению равносильно » | (определение гиперболического косинуса) (определение исключающего «ИЛИ») | |
| «равно/равносильно по определению» | ||||
| везде | ||||
| { } | Множество элементов | означает множество, элементами которого являются , и . | (множество натуральных чисел) | |
| «Множество…» | ||||
| Теория множеств | ||||
| {|} | Множество элементов, удовлетворяющих условию | означает множество всех таких, что верно . | ||
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅ {} | Пустое множество | и означают множество, не содержащее ни одного элемента. | ||
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈ ∉ | Принадлежность/непринадлежность к множеству | означает « является элементом множества » означает « не является элементом множества » | ||
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| ⊆ ⊂ | Подмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇ ⊃ | Надмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊ | Собственное подмножество | означает и . | ||
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋ | Собственное надмножество | означает и . | ||
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| ∪ | Объединение | означает множество элементов, принадлежащих и | ||
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ⋂ | Пересечение | означает множество одинаковых элементов, принадлежащих и , и . | ||
| «Пересечение … и … «, «…, пересечённое с …» | ||||
| Теория множеств | ||||
| \ | Разность множеств | означает множество элементов, принадлежащих , но не принадлежащих . | ||
| «разность … и …», «минус», «… без …» | ||||
| Теория множеств | ||||
| → | Функция (отображение) | означает функцию с областью определения и областью значений . | Функция , определённая как | |
| «из … в …», | ||||
| везде | ||||
| ↦ | Отображение | означает, что образом после применения функции будет . | Функцию, определённую как , можно записать так: | |
| «отображается в» | ||||
| везде | ||||
| N или ℕ | Натуральные числа | означает множество или реже (в зависимости от ситуации). | ||
| «Эн» | ||||
| Числа | ||||
| Z или ℤ | Целые числа | означает множество | ||
| «Зед» | ||||
| Числа | ||||
| Q или ℚ | Рациональные числа | означает | ||
| «Ку» или «Къю» | ||||
| Числа | ||||
| R или ℝ | Вещественные (действительные) числа | означает множество всех пределов последовательностей из | ( — мнимая единица: ) | |
| «Эр» | ||||
| Числа | ||||
| C или ℂ | Комплексные числа | означает множество | ||
| «Це» | ||||
| Числа | ||||
| H или | Кватернионы | означает множество | ||
| «Аш» | ||||
| Числа | ||||
| < > | Сравнение | обозначает, что строго меньше . означает, что строго больше . | ||
| «меньше чем», «больше чем» | ||||
| Отношение порядка | ||||
| или или | ⩽ или ≤ ⩾ или ≥ | Сравнение | означает, что меньше или равен . означает, что больше или равен . | |
| «меньше или равно»; «больше или равно» | ||||
| Отношение порядка | ||||
| ≈ | Приблизительное равенство | с точностью до 10−3 означает, что 2,718 отличается от не больше чем на 10−3. | с точностью до 10−7. | |
| «приблизительно равно» | ||||
| Числа | ||||
| √ | Арифметический квадратный корень | означает неотрицательное действительное число, которое в квадрате даёт . | ||
| «Корень квадратный из …» | ||||
| Числа | ||||
| ∞ | Бесконечность | и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. | ||
| «Плюс/минус бесконечность» | ||||
| Числа | ||||
| | | | Абсолютная величина (абсолютное значение, модуль) числа, или мощность множества | обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов . | ||
| «Модуль»; «Мощность» | ||||
| Числа и Теория множеств | ||||
| ∑ | Сумма (набора чисел), сумма ряда | означает «сумма , где принимает значения от 1 до », то есть . означает сумму ряда, состоящего из . | ||
| «Сумма … по … от … до …» | ||||
| Арифметика, Математический анализ | ||||
| ∏ | Произведение | означает «произведение для всех от 1 до », то есть | ||
| «Произведение … по … от … до …» | ||||
| Арифметика | ||||
| ! | Факториал | означает произведение всех натуральных чисел от 1 до включительно, то есть | ||
| « факториал» | ||||
| Комбинаторика | ||||
| ∫ | Интеграл | означает «интеграл от до функции от по переменной ». | ||
| «Интеграл (от … до …) функции … по (или d)…» | ||||
| Математический анализ | ||||
| df/dx f'(x) | Производная | или означает «(первая) производная функции от по переменной ». | ||
| «Производная … по …» | ||||
| Математический анализ | ||||
| ∂f/∂y | Частная производная | означает «(первая) частная производная функции от переменных по переменной ». | ||
| «Частная производная … по …» | ||||
| Математический анализ | ||||
| dnf/dxn f(n)(x) | Производная -го порядка | или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ». | ||
| «-я производная … по …» | ||||
| Математический анализ |
www.turkaramamotoru.com

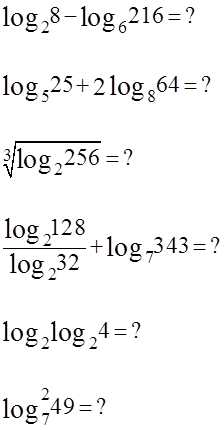
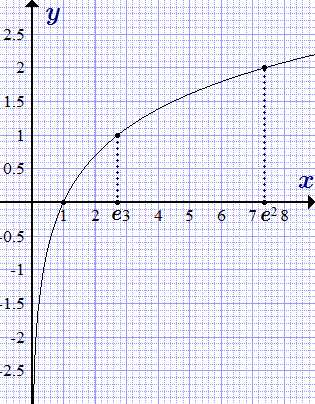
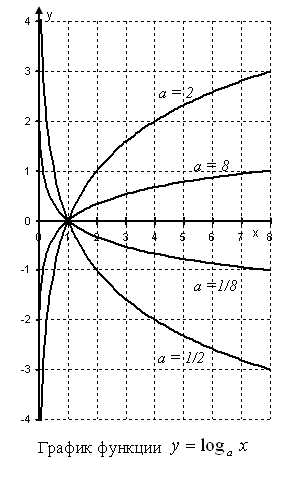 График логарифма получается из графика показательной функции зеркальным отражением относительно прямой y = x. Слева изображены графики функции y(x) = loga x для четырех значений основания логарифма: a = 2, a = 8, a = 1/2 и a = 1/8. На графике видно, что при a > 1 логарифм монотонно возрастает. С увеличением x рост существенно замедляется. При 0 < a < 1 логарифм монотонно убывает.
График логарифма получается из графика показательной функции зеркальным отражением относительно прямой y = x. Слева изображены графики функции y(x) = loga x для четырех значений основания логарифма: a = 2, a = 8, a = 1/2 и a = 1/8. На графике видно, что при a > 1 логарифм монотонно возрастает. С увеличением x рост существенно замедляется. При 0 < a < 1 логарифм монотонно убывает.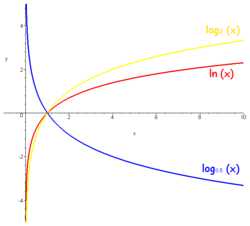
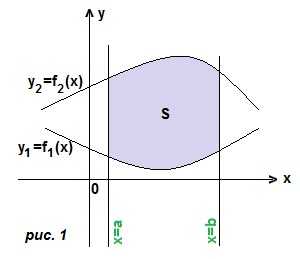 1) переменная интегрирования х. В этом случае трапеция ограничена сверху и снизу двумя кривыми, а слева и справа прямыми х=а, х=b. (рис. 1). Границы интегрирования a и b, а чтобы получить подынтегральную функцию, мы из уравнения верхней линии вычитаем уравнение нижней линии. Тогда площадь трапеции:
1) переменная интегрирования х. В этом случае трапеция ограничена сверху и снизу двумя кривыми, а слева и справа прямыми х=а, х=b. (рис. 1). Границы интегрирования a и b, а чтобы получить подынтегральную функцию, мы из уравнения верхней линии вычитаем уравнение нижней линии. Тогда площадь трапеции: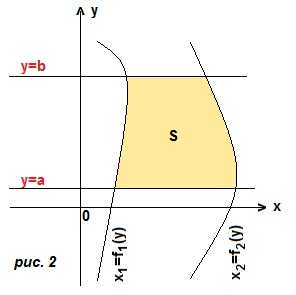 2) переменная интегрирования у. Криволинейная трапеция ограничена справа и слева двумя кривыми, а снизу и сверху прямыми y=a, y=b. (рис. 2). Границы интегрирования a и b. Чтобы получить подынтегральное выражение, мы из уравнения правой линии вычтем уравнение левой линии. Тогда площадь трапеции:
2) переменная интегрирования у. Криволинейная трапеция ограничена справа и слева двумя кривыми, а снизу и сверху прямыми y=a, y=b. (рис. 2). Границы интегрирования a и b. Чтобы получить подынтегральное выражение, мы из уравнения правой линии вычтем уравнение левой линии. Тогда площадь трапеции: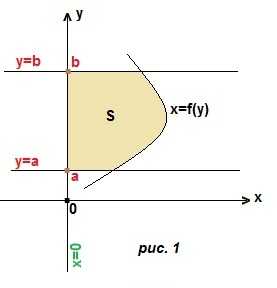 Если криволинейная трапеция прилегает к оси Оу (рис. 1) и ограничена непрерывной кривой x=f (y), осью ординат (прямой х=0) и прямыми y=a, y=b, то ее площадь вычисляется по той же формуле Ньютона-Лейбница (ф. Н-Л), только переменная интегрирования не х, а у:
Если криволинейная трапеция прилегает к оси Оу (рис. 1) и ограничена непрерывной кривой x=f (y), осью ординат (прямой х=0) и прямыми y=a, y=b, то ее площадь вычисляется по той же формуле Ньютона-Лейбница (ф. Н-Л), только переменная интегрирования не х, а у: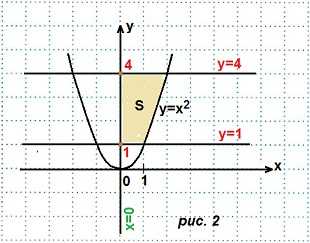 Пример 1. Найти площадь криволинейной трапеции, ограниченной линиями: y=x², y=1, y=4 и осью Оу.
Пример 1. Найти площадь криволинейной трапеции, ограниченной линиями: y=x², y=1, y=4 и осью Оу.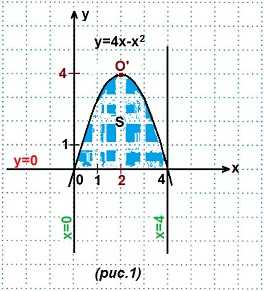 Пример 1. Найти площадь криволинейной трапеции, ограниченной линиями: y=4x-x²; y=0; x=0; x=4.
Пример 1. Найти площадь криволинейной трапеции, ограниченной линиями: y=4x-x²; y=0; x=0; x=4.
 Определенный интеграл (см. рисунок слева) представляет собой криволинейную трапецию, ограниченную сверху графиком функции y=f (x), снизу — осью Ох, а слева и справа прямыми x=a и х=b.
Определенный интеграл (см. рисунок слева) представляет собой криволинейную трапецию, ограниченную сверху графиком функции y=f (x), снизу — осью Ох, а слева и справа прямыми x=a и х=b. 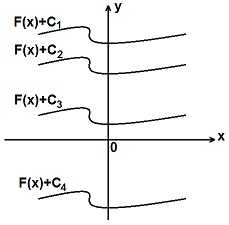 где F (x) — первообразная функции f (x), а С — некоторая постоянная величина?
где F (x) — первообразная функции f (x), а С — некоторая постоянная величина?
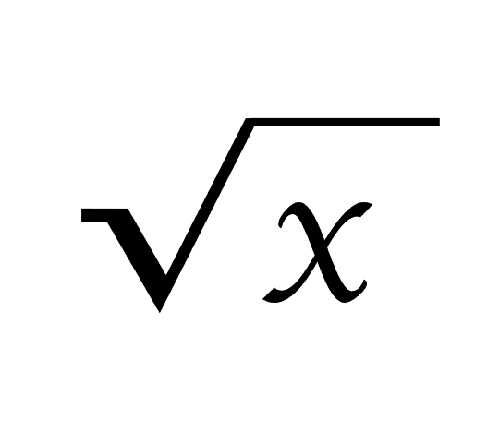
 Ермаков В.И.
Ермаков В.И.

 Под ред. Ермакова В.И.
Под ред. Ермакова В.И.







 Аннотация: Сборник задач по математике для втузов. В 4 частях. Ч. 2:
Учебное пособие для втузов / Под общ. ред. А. В. Ефимова и А. С.
Поспелова. — 4-е изд. перераб. и доп. —М.: Издательство
Физико-мате-матической литературы, 2001.—432 е.—ISBN 5-94052-035-9 (Ч.
2).
Аннотация: Сборник задач по математике для втузов. В 4 частях. Ч. 2:
Учебное пособие для втузов / Под общ. ред. А. В. Ефимова и А. С.
Поспелова. — 4-е изд. перераб. и доп. —М.: Издательство
Физико-мате-матической литературы, 2001.—432 е.—ISBN 5-94052-035-9 (Ч.
2). Аннотация: Ефимов А.В. (ред.), Поспелов А.С. (ред.) Сборник задач по математике для втузов. В 4-х ч. — М.: Физматлит. т.4 — 2004. -432с.
Аннотация: Ефимов А.В. (ред.), Поспелов А.С. (ред.) Сборник задач по математике для втузов. В 4-х ч. — М.: Физматлит. т.4 — 2004. -432с.