Вероятность, Теория вероятности, вычисление экспериментальной вероятности
Когда бросается монета, можно сказать, что она упадет орлом вверх, или вероятность этого составляет 1/2. Конечно, это не означает того, что если монета подбрасывается 10 раз, она обязательно упадет вверх орлом 5 раз. Если монета является «честной» и если она подбрасывается много раз, то орел выпадет очень близко в половине случаев. Таким образом, существует два вида вероятностей: экспериментальная и теоретическая.
Экспериментальная и теоретическая вероятность
Если бросить монетку большое количество раз — скажем, 1000 — и посчитать, сколько раз выпадет орел, мы можем определить вероятность того, что выпадет орел. Если орел выпадет 503 раза, мы можем посчитать вероятность его выпадения:
503/1000, или 0,503.
Это экспериментальное определение вероятности. Такое определение вероятности вытекает из наблюдения и изучения данных и является довольно распространенным и очень полезным. Вот, к примеру, некоторые вероятности которые были определены экспериментально:
1. Вероятность того, что у женщины разовьется рак молочной железы составляет 1/11.
2. Если вы целуетесь, с кем-то, кто болен простудой, то вероятность того, что вы тоже заболеете простудой, составляет 0,07.
3. Человек, который только что был освобожден из тюрьмы, имеет 80% вероятности возвращения назад в тюрьму.
Если мы рассматриваем бросание монеты и беря во внимание то, что столь же вероятно, что выпадет орел или решка, мы можем вычислить вероятность выпадение орла: 1 / 2. Это теоретическое определение вероятности. Вот некоторые другие вероятности, которые были определены теоретически, с помощью математики:
1. Если находится 30 человек в комнате, вероятность того, что двое из них имеют одинаковый день рождения (исключая год), составляет 0,706.
2. Во время поездки, Вы встречаете кого-то, и в течение разговора обнаруживаете,
www.math10.com
Основы теории вероятностей и математической статистики
Разделы: Математика
ВВЕДЕНИЕ
Многие вещи нам непонятны не потому, что наши понятия слабы;
но потому, что сии вещи не входят в круг наших понятий.
Козьма Прутков
Основная цель изучения математики в средних специальных учебных заведениях состоит в том, чтобы дать студентам набор математических знаний и навыков, необходимых для изучения других программных дисциплин, использующих в той или иной мере математику, для умения выполнять практические расчеты, для формирования и развития логического мышления.
В данной работе последовательно вводятся все базовые понятия раздела математики «Основы теории вероятностей и математической статистики», предусмотренные программой и Государственными образовательными стандартами среднего профессионального образования (Министерство образования Российской Федерации. М., 2002г.), формулируются основные теоремы, большая часть которых не доказывается. Рассматриваются основные задачи и методы их решения и технологии применения этих методов к решению практических задач. Изложение сопровождается подробными комментариями и многочисленными примерами.
Методические указания могут быть использованы для первичного ознакомления с изучаемым материалом, при конспектировании лекций, для подготовки к практическим занятиям, для закрепления полученных знаний, умений и навыков. Кроме того, пособие будет полезно и студентам- старшекурсникам как справочное пособие, позволяющее быстро восстановить в памяти то, что было изучено ранее.
В конце работы приведены примеры и задания, которые студенты могут выполнять в режиме самоконтроля.
Методические указания предназначены для студентов заочной и дневной форм обучения.
ОСНОВНЫЕ ПОНЯТИЯ
Теория вероятностей изучает объективные закономерности массовых случайных событий. Она является теоретической базой для математической статистики, занимающейся разработкой методов сбора, описания и обработки результатов наблюдений. Путем наблюдений (испытаний, экспериментов), т.е. опыта в широком смысле слова, происходит познание явлений действительного мира.
В своей практической деятельности мы часто встречаемся с явлениями, исход которых невозможно предсказать, результат которых зависит от случая.
Случайное явление можно охарактеризовать отношением числа его наступлений к числу испытаний, в каждом из которых при одинаковых условиях всех испытаний оно могло наступить или не наступить.
Теория вероятностей есть раздел математики, в котором изучаются случайные явления (события) и выявляются закономерности при массовом их повторении.
Математическая статистика — это раздел математики, который имеет своим предметом изучения методов сбора, систематизации, обработки и использования статистических данных для получения научно обоснованных выводов и принятия решений.
При этом под статистическими данными понимается совокупность чисел, которые представляют количественные характеристики интересующих нас признаков изучаемых объектов. Статистические данные получаются в результате специально поставленных опытов, наблюдений.
Статистические данные по своей сущности зависят от многих случайных факторов, поэтому математическая статистика тесно связана с теорией вероятностей, которая является ее теоретической основой.
I. ВЕРОЯТНОСТЬ. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
1.1. Основные понятия комбинаторики
В разделе математики, который называется комбинаторикой, решаются некоторые задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. Например, если взять 10 различных цифр 0, 1, 2, 3,: , 9 и составлять из них комбинации, то будем получать различные числа, например 143, 431, 5671, 1207, 43 и т.п.
Мы видим, что некоторые из таких комбинаций отличаются только порядком цифр (например, 143 и 431), другие — входящими в них цифрами (например, 5671 и 1207), третьи различаются и числом цифр (например, 143 и 43).
Таким образом, полученные комбинации удовлетворяют различным условиям.
В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.
Предварительно познакомимся с понятием факториала.
Произведение всех натуральных чисел от 1 до n включительно называют n-факториалом и пишут .
Пример 1.
Вычислить: а) ; б) ; в) .
Решение. а) .
б) Так как и , то можно вынести за скобки
Тогда получим
.
в) .
Перестановки.
Комбинация из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками.
Перестановки обозначаются символом Рn, где n- число элементов, входящих в каждую перестановку. (Р — первая буква французского слова permutation— перестановка).
Число перестановок можно вычислить по формуле
или с помощью факториала:
Запомним, что 0!=1 и 1!=1.
Пример 2. Сколькими способами можно расставлять на одной полке шесть различных книг?
Решение. Искомое число способов равно числ
xn--i1abbnckbmcl9fb.xn--p1ai
Как найти вероятность события 🚩 Математика
svyatoslav1997Эксперт + Математик
336
49 подписчиков
Спросить
Любые ситуации обладают набором исходов, каждый из которых имеет свою вероятность. Анализом таких ситуаций занимается наука под названием теория вероятностей, основной задачей которой и является поиск вероятностей каждого из исходов.

Статьи по теме:
Инструкция
Исходы бывают дискретные и непрерывные. Дискретные величины обладают собственными вероятностями. Например вероятность выпадения орла составляет 50%, как и решки — тоже 50 %. Вместе эти исходы образуют полную группу — совокупность всех возможных событий. Вероятность появления непрерывной величины стремится к нулю, так как она находится по принципу отношения площадей. При этом нам известно, что точка не имеет площади соответственно и вероятность попадания в точку равна 0.

При исследовании непрерывных исходов имеет смысл считать вероятность исходов, попадающих в какой-либо интервал значений. Тогда вероятность будет равна отношению площадей благоприятных исходов и полной группы исходов. Площадь полной группы исходов, как и сумма всех вероятностей должна равняться единице или 100%.
Для описания вероятностей всех возможных исходов используют ряд распределения для дискретных величин и закон распределения для непрерывных величин. Ряд распределения состоит из двух строк, причем в первой строке записываются все возможные исходы, а под ними — их вероятности. Сумма вероятностей должна удовлетворять условию полноты — их сумма равна единице.
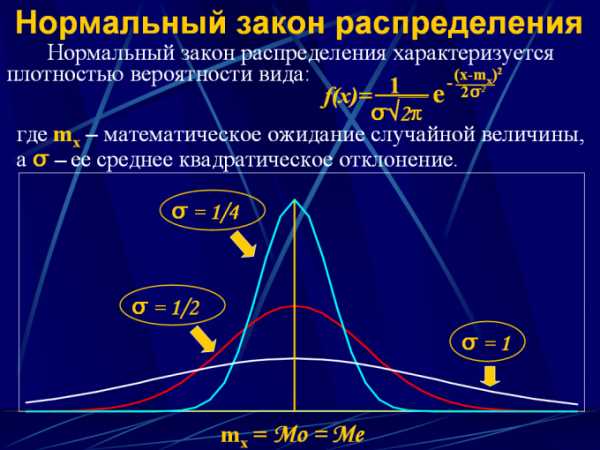
Для описания распределения вероятностей непрерывной величины используют законы распределения в виде аналитической функции y = F(x), где x — интервал непрерывных значений от 0 до x, а y — вероятность того, что случайная величина попадет в заданный интервал. Существует несколько таких законов распределения:
1. Равномерное распределение
2. Нормальное распределение
3. Распределение Пуассона
4. Распределение Стьюдента
5. Биноминальное распределение
Случайная величина может вести себя совершенно по-разному. Для описания ее поведения используют тот закон, который более всего согласуется с реальным распределением. Для того чтобы определить, подходит ли какой-либо из законов, нужно применить критерий согласия Пирсона. Эта величина характеризует отклонение реального распределения от теоретического распределения по данному закону. Если эта величина меньше 0,05, то такой теоретический закон нельзя применять.

www.kakprosto.ru
Как найти вероятность в математике формула
Please complete the security check to access znanija.com
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Cloudflare Ray ID: 407d9afc26aa9ab2 • Your IP : 5.189.134.229 • Performance & security by Cloudflare
Вероятность — это величина, которая измеряет возможность воплощения в реальности того или иного события. Отрицательные и положительные основания вероятности позволяют определить её степень. Чем больше отрицательных оснований, тем меньше вероятность, и наоборот.

Вероятность как систему впервые описали Б. Паскаль, Я. Бернулли и П. Лаплас в семнадцатом веке. Учёные анализировали возможность исхода азартных игр и сформулировали вероятность как отношение положительных факторов к числу всех возможных в равной степени. Чтобы находить вероятность того или иного события, необходимо знать соответствующие формулы.
Быстрая навигация по статье
Классическое вычисление вероятности
Для вычисления вероятности используется классическая формула: Р(А)=m/n, где:
- m-количество благоприятных исходов;
- n- количество равновероятных исходов (при этом m<n).
Можно привести несколько примеров вычисления вероятности согласно данной формуле:
В коробке находится 200 карандашей красного и зелёного цвета, при этом зелёных карандашей 10 штук. Следует рассчитать вероятность того, что карандаш, вытянутый наугад, будет зелёного цвета.
Количество равновероятных исходов в этой ситуации равно 200 (то есть, n=200). Количество исходов того, что карандаш окажется зелёным равно 10 (то есть, m=10).
Расчёт: Р(А)=10/200=0,05 (согласно формуле Р(А)=m/n). Следовательно, вероятность того, что карандаш окажется зелёным, равна 5% (результат 0,05 умножается на 100, чтобы получить значение в процентах).
В мешке лежат фишки красного, чёрного и белого цвета. Красных фишек — 20 штук, чёрных — 40 штук, а белых – 60 штук. Какова вероятность того, что первой попавшейся будет фишка:
А) Красного цвета; В) Чёрного цвета; С) Белого цвета
В этом случае три возможных исхода события: фишка окажется белого, красного или чёрного цвета. Общее количество возможных равновероятных исходов равно 120. Для вычисления вероятности каждого из событий используется стандартная формула Р=m/n:
В коробке находится десять карандашей: 6 красных и 4 зелёных. Какова вероятность того, что оба вытянутых карандаша окажутся красными?
Эта задача содержит элементы комбинаторики. В данном случае существует возможность смешения элементов и число способов вытянуть два карандаша из десяти высчитывается по формуле:
Следующим шагом будет вычисление количества случаев, когда два карандаша будут красными:
Вероятность того, что оба вытянутых карандаша окажутся красными, высчитывается по классической формуле:
У системы вероятностей есть несколько основных свойств:
- Достоверное событие имеет величину вероятности, равную единице;
- Вероятность невозможного события равна нулю;
- Вероятность любого события находится в числовом промежутке между нулём и единицей;
- Согласно теории сложения вероятностей, сумма вероятности двух несовместимых событий равна вероятности суммы этих событий.
Сайт не хранит личную информацию граждан Российской Федерации (регистрация закрыта, комментарии отключены). Некоторые опубликованные на сайте материалы могут содержать информацию, предназначеную для пользователей старше 16 лет (согласно №436-ФЗ от 29.12.2010 года «О защите детей от информации причиняющей вред их здоровью и развитию»). 16+. Использование данного сайта подразумевает принятие условий пользовательского соглашения.
© Google Inc., 2016. Все права защищены. Наименование Google и логотип Google являются товарными знаками компании Google Inc.
GoogleTM, Android™, Google Maps™, Google Play™, Google Docs™, Google Picasa™, Gmail™, Google Chrome™, Google Plus™, YouTube™ и соответствующие логотипы являются товарными знаками Google, Inc. в США и других странах.
Microsoft®, Windows®, Windows XP®, Windows Vista®, Xbox®, Zune®, SharePoint®, Internet Explorer®, Hotmail®, Bing®, Office®, Word®, PowerPoint®, Excel®, Outlook® и их логотипы являются товарными знаками Microsoft Corporation в США и других странах.
Mozilla®, Mozilla Firefox® и их логотипы являются товарными знаками Mozilla Foundation в США и других странах.
Skype® и соответствующий логотип являются товарными знаками Skype в США и других странах.
Понять формулу проще всего на примерах.
Пример 1. В корзине 9 красных шаров и 3 синих. Шары различаются только цветом. Наугад (не глядя) достаём один из них. Какова вероятность того, что выбранный таким образом шар окажется синего цвета?
Комментарий. В задачах по теории вероятности происходит нечто (в данном случае наше действие по вытаскиванию шара), что может иметь разный результат — исход. Нужно заметить, что на результат можно смотреть по-разному. «Мы вытащили какой-то шар» — тоже результат. «Мы вытащили синий шар» — результат. «Мы вытащили именно вот этот шар из всех возможных шаров» — такой наименее обобщенный взгляд на результат называется элементарным исходом. Именно элементарные исходы имеются в виду в формуле для вычисления вероятности.
Решение. Теперь вычислим вероятность выбора синего шара.
Событие А: «выбранный шар оказался синего цвета»
Общее число всех возможных исходов: 9+3=12 (количество всех шаров, которые мы могли бы вытащить)
Число благоприятных для события А исходов: 3 (количество таких исходов, при которых событие А произошло, — то есть, количество синих шаров)
Посчитаем для той же задачи вероятность выбора красного шара.
Общее число возможных исходов останется тем же, 12. Число благоприятных исходов: 9. Искомая вероятность: 9/12=3/4=0,75
Вероятность любого события всегда лежит в пределах от 0 до 1.
Иногда в повседневной речи (но не в теории вероятности!) вероятность событий оценивают в процентах. Переход между математической и разговорной оценкой осуществляется путем умножения (или деления) на 100%.
Итак,
При этом вероятность равна нулю у событий, которые не могут произойти — невероятны. Например, в нашем примере это была бы вероятность вытащить из корзины зеленый шар. (Число благоприятных исходов равно 0, Р(А)=0/12=0, если считать по формуле)
Вероятность 1 имеют события, которые абсолютно точно произойдут, без вариантов. Например, вероятность того, что «выбранный шар окажется или красным или синим» — для нашей задачи. (Число благоприятных исходов: 12, Р(А)=12/12=1)
Мы рассмотрели классический пример, иллюстрирующий определение вероятности. Все подобные задачи ЕГЭ по теории вероятности решаются применением данной формулы.
На месте красных и синих шаров могут быть яблоки и груши, мальчики и девочки, выученные и невыученные билеты, билеты, содержащие и не содержащие вопрос по какой-то теме (прототипы 285926, 285927), бракованные и качественные сумки или садовые насосы (прототипы 282857, 282856) – принцип остается тем же.
Немного отличаются формулировкой задачи теории вероятности ЕГЭ, где нужно вычислить вероятность выпадения какого-то события на определенный день. (285922, 285923) Как и в предыдущих задачах нужно определить, что является элементарным исходом, после чего применить ту же формулу.
Пример 2. Конференция длится три дня. В первый и второй день выступают по 15 докладчиков, в третий день – 20. Какова вероятность того, что доклад профессора М. выпадет на третий день, если порядок докладов определяется жеребьевкой?
Что здесь является элементарным исходом? – Присвоение докладу профессора какого-то одного из всех возможных порядковых номеров для выступления. В жеребьевке участвует 15+15+20=50 человек. Таким образом, доклад профессора М. может получить один из 50 номеров. Значит, и элементарных исходов всего 50.
А какие исходы благоприятные? – Те, при которых окажется, что профессор будет выступать в третий день. То есть, последние 20 номеров.
По формуле вероятность P(A)= 20/50=2/5=4/10=0,4
Жеребьевка здесь представляет собой установление случайного соответствия между людьми и упорядоченными местами. В примере 2 установление соответствия рассматривалось с точки зрения того, какое из мест мог бы занять конкретный человек. Можно к той же ситуации подходить с другой стороны: кто из людей с какой вероятностью мог бы попасть на конкретное место (прототипы 282855, 282858, 285924, 285928):
Пример 3. В жеребьевке участвуют 5 немцев, 8 французов и 3 эстонца. Какова вероятность того, что первым (/вторым/седьмым/последним – не важно) будет выступать француз.
Количество элементарных исходов – количество всех возможных людей, которые могли бы по жеребьевке попасть на данное место. 5+8+3=16 человек.
Благоприятные исходы – французы. 8 человек.
Искомая вероятность: 8/16=1/2=0,5
Немного отличается прототип 285925. Остались задачи про монеты (282854) и игральные кости (285853), несколько более творческие. Решение этих задач можно посмотреть на страницах прототипов.
Приведем несколько примеров на бросание монеты или кубика.
Пример 4. Когда подбрасываем монету, какова вероятность выпадения решки?
Исходов 2 – орел или решка. (считается, что монета никогда не падает на ребро) Благоприятный исход – решка, 1.
Пример 5. А если подбрасываем монету два раза? Какова вероятность того, что оба раза выпадет орел?
Главное определить, какие элементарные исходы будем рассматривать при подбрасывании двух монет. После подбрасывания двух монет может получиться один из следующих результатов:
1) PP – оба раза выпала решка
2) PO – первый раз решка, второй раз орел
3) OP – первый раз орел, второй раз решка
4) OO – оба раза выпал орел
Других вариантов нет. Значит, элементарных исходов 4. Благоприятный из них только первый, 1.
Какова вероятность того, что из двух подбрасываний монеты один раз выпадет решка?
Количество элементарных исходов то же, 4. Благоприятные исходы – второй и третий, 2.
Вероятность выпадения одной решки: 2/4=0,5
В таких задачах может пригодиться ещё одна формула.
Если при одном бросании монеты возможных вариантов результата у нас 2, то для двух бросаний результатов будет 2·2=2 2 =4 (как в примере 5), для трех бросаний 2·29middot;2=2 3 =8, для четырех: 2·29middot;29middot;2=2 4 =16, … для N бросаний возможных результатов будет 2·29middot;. ·2=2 N .
Так, можно найти вероятность выпадения 5 решек из 5 бросаний монеты.
Общее число элементарных исходов: 2 5 =32.
Благоприятных исходов: 1. (РРРРР – все 5 раз решка)
То же верно и для игральной кости. При одном бросании возможных результатов здесь 6. Значит, для двух бросаний: 6·6=36, для трех 6·69middot;6=216, и т. д.
Пример 6. Бросаем игральную кость. Какова вероятность, что выпадет четное число?
Всего исходов: 6, по числу граней.
Благоприятных: 3 исхода. (2, 4, 6)
Пример 7. Бросаем две игральные кости. Какова вероятность, что в сумме выпадет 10? (округлить до сотых)
Для одного кубика 6 возможных исходов. Значит, для двух, по вышеупомянутому правилу, 6·6=36.
Какие исходы будут благоприятными для того, чтоб в сумме выпало 10?
10 надо разложить на сумму двух чисел от 1 до 6. Это можно сделать двумя способами: 10=6+4 и 10=5+5. Значит, для кубиков возможны варианты:
(6 на первом и 4 на втором)
(4 на первом и 6 на втором)
(5 на первом и 5 на втором)
Итого, 3 варианта. Искомая вероятность: 3/36=1/12=0,08
Другие типы задач B6 будут рассмотрены в одной из следующих статей «Как решать».
Внимание, только СЕГОДНЯ! Загрузка…
amvtrade.ru











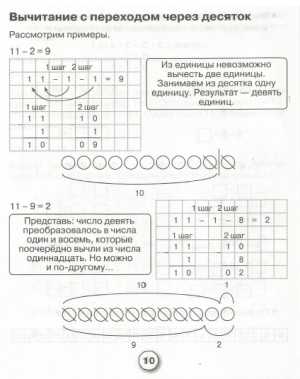





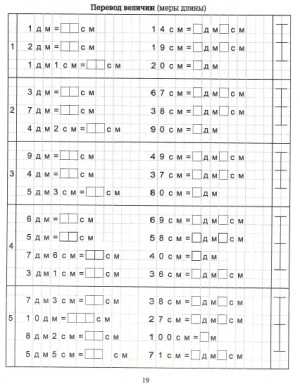






 Школьные программы все разные, а олимпиады для всех равны, и задания в них не из легких. Но все же, при правильном подходе, и олимпиадные задачки ребенка можно научить щелкать, как орешки. Наша подборка задач по математике выросла из задач разных современных международных олимпиад по математике: математические ступеньки, зеленая математика и других. В принципе, задания перекликаются, и поняв саму стратегию и тактику, дети с легкостью смогут решить и другие подобные задачи, поставленные перед ним.
Школьные программы все разные, а олимпиады для всех равны, и задания в них не из легких. Но все же, при правильном подходе, и олимпиадные задачки ребенка можно научить щелкать, как орешки. Наша подборка задач по математике выросла из задач разных современных международных олимпиад по математике: математические ступеньки, зеленая математика и других. В принципе, задания перекликаются, и поняв саму стратегию и тактику, дети с легкостью смогут решить и другие подобные задачи, поставленные перед ним.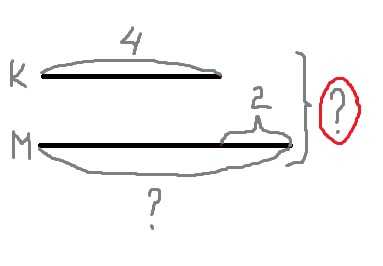
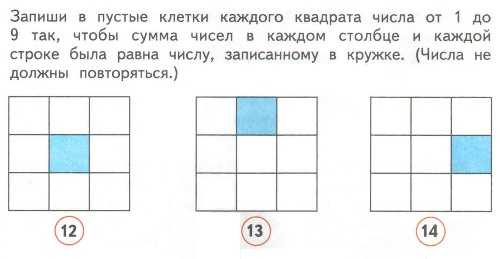






 Кстати, следует отметить, что упомянутое выше правило действенно как для умножения, так и для деления. Произведение отрицательного и положительного числа даст лишь «минус. Если речь идет о двух цифрах со знаком «-», то в результате получится положительное число. То же касается и деления. Если одно из чисел будет отрицательным, то частное тоже будет со знаком «-».
Кстати, следует отметить, что упомянутое выше правило действенно как для умножения, так и для деления. Произведение отрицательного и положительного числа даст лишь «минус. Если речь идет о двух цифрах со знаком «-», то в результате получится положительное число. То же касается и деления. Если одно из чисел будет отрицательным, то частное тоже будет со знаком «-».

 Кстати, следует отметить, что упомянутое выше правило действенно как для умножения, так и для деления. Произведение отрицательного и положительного числа даст лишь «минус. Если речь идет о двух цифрах со знаком «-», то в результате получится положительное число. То же касается и деления. Если одно из чисел будет отрицательным, то частное тоже будет со знаком «-».
Кстати, следует отметить, что упомянутое выше правило действенно как для умножения, так и для деления. Произведение отрицательного и положительного числа даст лишь «минус. Если речь идет о двух цифрах со знаком «-», то в результате получится положительное число. То же касается и деления. Если одно из чисел будет отрицательным, то частное тоже будет со знаком «-».
 1. Перед началом решения новых типов задач повторите основы.
1. Перед началом решения новых типов задач повторите основы.