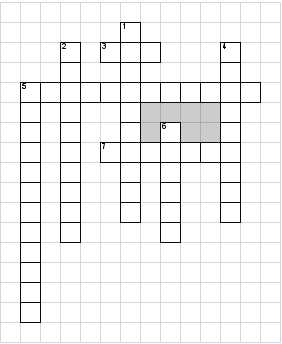
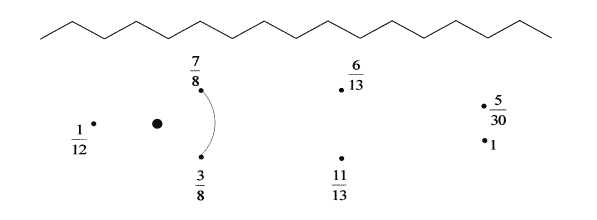
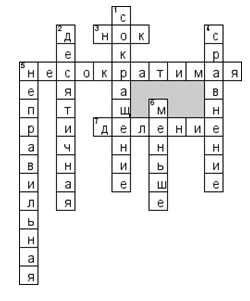
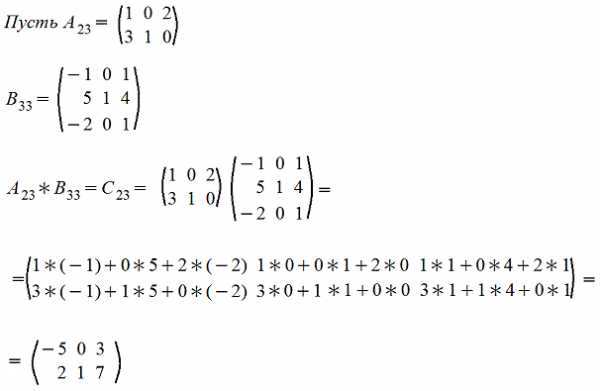Контрольная работа по математике 4 класс по теме «Дроби»
1) За три дня в магазине продали 240 кг картофеля. Первый день продали всего картофеля, а во второй день всего картофеля. Сколько кг картофеля продали в третий день?
2) Длина участка 270 м, а ширина составляет его длины. Чему равен периметр и площадь участка?
3) Сократить.
; ; ; ; ;
4) Превратить смешанное число в неправильную дробь.
5; 28; 15; 6; 3
5) Превратить неправильную дробь в смешанное число.
; ; ; ;
1) За три дня в магазине продали 240 кг картофеля. Первый день продали всего картофеля, а во второй день всего картофеля. Сколько кг картофеля продали в третий день?
2) Длина участка 270 м, а ширина составляет его длины. Чему равен периметр и площадь участка?
3) Сократить.
; ; ; ; ;
4) Превратить смешанное число в неправильную дробь.
5; 28; 15; 6; 3
5) Превратить неправильную дробь в смешанное число.
; ; ; ;
1) За три дня в магазине продали 240 кг картофеля. Первый день продали всего картофеля, а во второй день всего картофеля. Сколько кг картофеля продали в третий день?
2) Длина участка 270 м, а ширина составляет его длины. Чему равен периметр и площадь участка?
3) Сократить.
; ; ; ; ;
4) Превратить смешанное число в неправильную дробь.
5; 28; 15; 6; 3
5) Превратить неправильную дробь в смешанное число.
; ; ; ;
1) В ларьке продавалось 450 кг овощей. Помидоров было всего количества, картофеля всего количества, а остальное были баклажаны. Сколько кг баклажанов продавалось в ларьке?
2) Длина прямоугольника 490 дм, а ширина составляет длины. Чему равен периметр и площадь прямоугольника?
3) Сократить.
; ; ; ; ;
4) Превратить смешанное число в неправильную дробь.
6; 26; 14; 5; 5
5) Превратить неправильную дробь в смешанное число.
; ; ;
1) В ларьке продавалось 450 кг овощей. Помидоров было всего количества, картофеля всего количества, а остальное были баклажаны. Сколько кг баклажанов продавалось в ларьке?
2) Длина прямоугольника 490 дм, а ширина составляет длины. Чему равен периметр и площадь прямоугольника?
3) Сократить.
; ; ; ; ;
4) Превратить смешанное число в неправильную дробь.
6; 26; 14; 5; 5
5) Превратить неправильную дробь в смешанное число.
; ; ;
1) В ларьке продавалось 450 кг овощей. Помидоров было всего количества, картофеля всего количества, а остальное были баклажаны. Сколько кг баклажанов продавалось в ларьке?
2) Длина прямоугольника 490 дм, а ширина составляет длины. Чему равен периметр и площадь прямоугольника?
3) Сократить.
; ; ; ; ;
4) Превратить смешанное число в неправильную дробь.
6; 26; 14; 5; 5
5) Превратить неправильную дробь в смешанное число.
; ; ;
infourok.ru
Тест по математике (4 класс) на тему: Контрольный тест по теме «Дроби» 4 класс Школа «2100»
Контрольный тест по теме «Дроби»
I вариант
- Расположите дроби в порядке возрастания, запиши.
1/15; 1/9; 1/34; 1/100; 1/50.
2. Бумажная полоска имеет длину 12см. Для аппликации нужно отрезать ¾ этой полоски. Сколько сантиметров нужно отрезать?
А) 9см Б) 90 см В) 109 см
3. Найдите длину катушки ниток, если 7/10 составляют 63м.
А) 90см Б) 90 м В) 109 м
4. Три груши разделили на 9 человек. Какую часть груши получит каждый?
А) 9/3 Б) 3/ 9 В) 3/3
5. Пять мальчиков нашли несколько лесных яблок. Сколько было яблок, если каждый получил по 5/7 яблока?
А) 12 Б) 7 В) 5
6. Сколько секунд составляют 7/12 минуты?
А) 25сек Б) 35сек В) 40сек
7. Сколько килограммов составляют 6/10 тонны?
А) 60кг Б) 606кг В) 600кг
8. Сколько суток составляют 3/5 невисокосного года?
А) 219 сут Б) 109 сут В) 209 сут
9. Запиши и сравни.
15/45 * 21/45 5/7 * 5/15 6/6 * 1
10. Запиши и реши
73/96 – 46/96 + 18/96 = 1 – (38/130 + 79/130 – 48/130) =
11. Реши уравнение 2/18 + х = 1 – 12/18
12. Из Костромы Оля привезла три сувенира: деревянную медаль, льняное полотенце и фарфоровую чашку. На них изображены монастырь, герб Костромы и ваза с фруктами. На полотенце нет изображений монастыря и герба, а на чашке нарисован монастырь. Школьному музею Оля подарила деревянную медаль. Что изображено на этой медали?
А) монастырь Б) герб Костромы В) ваза с фруктами
Контрольный тест по теме «Дроби»
II вариант
- Расположите дроби в порядке убывания, запиши.
15/100; 9/100; 34/100; 100/100; 50/100.
2.От катушки ниток длиной 25м для изготовления воздушного змея отрезали 4/5 всей длины катушки. Сколько метров отрезали?
А) 20м Б) 22м В) 20 см
3. Найдите длину отрезка, 4/5 которого составляют 12см.
А) 25см Б) 15см В) 5см
4. Четыре шоколадки разделили на 7 человек. Какую часть груши получит каждый?
А) 7/4 Б) 4/7 4/4
5. Четверо туристов поделили между собой несколько коробок сока. Сколько было коробок сока, если каждый получил по ¾ коробки?
А) 4 Б) 3 В) 7
6. Сколько часов составляют 5/12 суток?
А) 5ч Б) 12ч В) 10ч
7. Сколько килограммов составляют 5/10 центнера?
А) 500кг Б) 50кг В) 5кг
8. Сколько суток составляют 6/7 недели?
А) 7 сут Б) 6 сут В) 1 сут
9. Запиши и сравни.
17/20 * 15/20 3/5 * 3/15 5/5 * 1
10. Запиши и реши
84/99 – 56/99 + 35/99 = 1 – (92/120 – 46/120 + 57/120) =
11. Реши уравнение 1 – х = 14/30 + 9/30
12. Из Костромы Оля привезла три сувенира: деревянную медаль, льняное полотенце и фарфоровую чашку. На них изображены монастырь, герб Костромы и ваза с фруктами. На полотенце нет изображений монастыря и герба, а на чашке нарисован монастырь. Школьному музею Оля подарила деревянную медаль. Что изображено на этой медали?
А) монастырь Б) герб Костромы В) ваза с фруктами
nsportal.ru
Контрольная работа по математике 4 класс по теме «Дроби»
Вариант 1.
№1.
Нужно сделать фруктовый салат. В корзине 20 фруктов. Из них 3 – яблоки, 9 – груши, а остальные – абрикосы. Какую часть составляет абрикосы от общего количества фруктов?
№2.
Для изготовления бумажного корабля нужно отрезать 5/9 от листа ватмана. Какая часть листа ватмана останется после отрезания?
№3. Вычислите.
5/15 + 8/15 = 45/57 – 23/57 =
1 – 38/60 = 105/350 + 205/350 =
208/400 – 108/400 = 120/250 + 40/250 =
№4. Сравните.
2/4 2/7 1/3 1/2
15/30 21/30 27/40 33/40
№5. Расположите дроби в порядке возрастания.
35/100, 40/100, 10/100, 3/100, 50/100, 90/100.
Вариант 2.
№1.
Рисунок нужно сделать цветными карандашами. В коробке 34 карандаша. 7 из них – красные, 9 – зеленые, а остальные – синие. Какую часть составляют карандаши синего цвета?
№2.
Для изготовления стрекозы нужно отрезать 3/8 от листа красной бумаги. Какая часть листа красной бумаги останется после отрезания?
№3. Вычислите.
7/18 + 6/18 = 58/65 – 25/65 =
1 – 41/70 = 141/250 + 61/250 =
305/700 – 105/700 = 130/170 + 30/170 =
№4. Сравните.
3/5 3/4 2/7 2/8
18/20 19/20 11/50 5/50
№5. Расположите дроби в порядке возрастания.
3/10, 3/50, 3/5, 3/80, 3/21, 3/100.
infourok.ru
4 кл. 3 четв. Дроби и величины. 1 вар. 1. Выполни вычисления величин столбиком: Уровень №1. 346759 м + 237432 м 803546 кг – 476327 кг 37245 км х 4 1072 см : 8 2. Уровень №2. 3465 см + 587 дм 48763 т – 32146 ц 3698 см х 34 631275 м : 15 2.Вычисли: Уровень №1. 4\5 от 30 7\8 =28 5\9 от 54 4\9=32 3\4= 24 4\6 от 36 Уровень №2. Найди треть от каждой величины: 456312 мм 73245 т Найди всю величину, если известна ее четверть: 86973 дм 56387 кг 3. Реши задачи: Уровень №1. Найди длину всей ленты, если 3\8 составляют 21 м? Найди 1\6 длины провода, если 5\6 этой длины составляют 36 м? Уровень №2. Туристы прошли за неделю 240 км. В первый день они прошли 3\4 этого пути. Сколько км им осталось пройти? | 4 кл. 3 четв. Дроби и величины. 2 вар. 1. Выполни вычисления величин столбиком: Уровень №1. 456239 м + 372481 м 906357 кг – 758439 кг 34625 км х 4 1088 см : 8 2. Уровень №2. 36545 см + 465 дм 56234 т – 32876 ц 3689 см х 34 229860 м : 15 2.Вычисли: Уровень №1. 4\6 от 30 7\8 =49 5\9 от 63 4\9=36 3\4= 27 4\6 от 18 Уровень №2. Найди треть от каждой величины: 456321 мм 73254 т Найди всю величину, если известна ее четверть: 86793 дм 56783 кг 3. Реши задачи: Уровень №1. Найди длину всей ленты, если 3\8 составляют 27 м? Найди 1\7 длины провода, если 5\7 этой длины составляют 30 м? Уровень №2. Туристы прошли за неделю 360 км. В первый день они прошли 4\ 9 этого пути. Сколько км им осталось пройти? | 4 кл. 3 четв. Дроби и величины. 1 вар. 1. Выполни вычисления величин столбиком: Уровень №1. 346759 м + 237432 м 803546 кг – 476327 кг 37245 км х 4 1072 см : 8 2. Уровень №2. 3465 см + 587 дм 48763 т – 32146 ц 3698 см х 34 631275 м : 15 2.Вычисли: Уровень №1. 4\5 от 30 7\8 =28 5\9 от 54 4\9=32 3\4= 24 4\6 от 36 Уровень №2. Найди треть от каждой величины: 456312 мм 73245 т Найди всю величину, если известна ее четверть: 86973 дм 56387 кг 3. Реши задачи: Уровень №1. Найди длину всей ленты, если 3\8 составляют 21 м? Найди 1\6 длины провода, если 5\6 этой длины составляют 36 м? Уровень №2. Туристы прошли за неделю 240 км. В первый день они прошли 3\4 этого пути. Сколько км им осталось пройти? 4 кл. 3 четв. Дроби и величины. 3 вар. 1. Выполни вычисления величин столбиком: Уровень №1. 45623 м + 37248 м 90635 кг – 75843 кг 3625 км х 2 328 см : 8 2.Вычисли: Уровень №1. Образец: 5\6 от 30 30 : 6 х 5 = 25 4\6 от 30 4\6 от 18 5\9 от 63 Образец: 3\5 = 30 30 : 3 х 5= 50 4\9=36 3\4= 27 4\6 от 18 7\8 =49 3. Реши задачи: Уровень №1. Найди длину всей ленты, если 3\5 составляют 24 м? Найди 1\7 длины провода, если 5\7 этой длины составляют 30 м? | 4 кл. 3 четв. Дроби и величины. 2 вар. 1. Выполни вычисления величин столбиком: Уровень №1. 456239 м + 372481 м 906357 кг – 758439 кг 34625 км х 4 1088 см : 8 2. Уровень №2. 36545 см + 465 дм 56234 т – 32876 ц 3689 см х 34 229860 м : 15 2.Вычисли: Уровень №1. 4\6 от 30 7\8 =49 5\9 от 63 4\9=36 3\4= 27 4\6 от 18 Уровень №2. Найди треть от каждой величины: 456321 мм 73254 т Найди всю величину, если известна ее четверть: 86793 дм 56783 кг 3. Реши задачи: Уровень №1. Найди длину всей ленты, если 3\8 составляют 27 м? Найди 1\7 длины провода, если 5\7 этой длины составляют 30 м? Уровень №2. Туристы прошли за неделю 360 км. В первый день они прошли 4\ 9 этого пути. Сколько км им осталось пройти? 4 кл. 3 четв. Дроби и величины. 3 вар. 1. Выполни вычисления величин столбиком: Уровень №1. 45623 м + 37248 м 90635 кг – 75843 кг 3625 км х 2 328 см : 8 2.Вычисли: Уровень №1. Образец: 5\6 от 30 30 : 6 х 5 = 25 4\6 от 30 4\6 от 18 5\9 от 63 Образец: 3\5 = 30 30 : 3 х 5= 50 4\9=36 3\4= 27 4\6 от 18 7\8 =49 3. Реши задачи: Уровень №1. Найди длину всей ленты, если 3\5 составляют 24 м? Найди 1\7 длины провода, если 5\7 этой длины составляют 30 м? | 4 кл. 3 четв. Дроби и величины. 3 вар. 1. Выполни вычисления величин столбиком: Уровень №1. 45623 м + 37248 м 90635 кг – 75843 кг 3625 км х 2 328 см : 8 2.Вычисли: Уровень №1. Образец: 5\6 от 30 30 : 6 х 5 = 25 4\6 от 30 4\6 от 18 5\9 от 63 Образец: 3\5 = 30 30 : 3 х 5= 50 4\9=36 3\4= 27 4\6 от 18 7\8 =49 3. Реши задачи: Уровень №1. Найди длину всей ленты, если 3\5 составляют 24 м? Найди 1\7 длины провода, если 5\7 этой длины составляют 30 м? | 4 кл. 3 четв. Дроби и величины. 3 вар. 1. Выполни вычисления величин столбиком: Уровень №1. 45623 м + 37248 м 90635 кг – 75843 кг 3625 км х 2 328 см : 8 2.Вычисли: Уровень №1. Образец: 5\6 от 30 30 : 6 х 5 = 25 4\6 от 30 4\6 от 18 5\9 от 63 Образец: 3\5 = 30 30 : 3 х 5= 50 4\9=36 3\4= 27 4\6 от 18 7\8 =49 3. Реши задачи: Уровень №1. Найди длину всей ленты, если 3\5 составляют 24 м? Найди 1\7 длины провода, если 5\7 этой длины составляют 30 м? |
xn--j1ahfl.xn--p1ai
Контрольные работы по математике (4 класс, ОС «Школа 2100»)
Контрольная работа по теме: «Величины»
I вариант.
1.Решите задачу:
Масса пачки чая 50г . Мама купила 4 пачки чая и немного колбасы. Масса всей покупки 700 граммов. Сколько граммов колбасы купила мама?
2. Вычислите:
403 — 654 : 3+ 398 · 2
(903769 — 769) : 1000 ·10
3.Выразите в указанных единицах измерения:
8004 м =….км….м 2 мин 15 с = ….сек.
5 кг 040 г =….г 1207 ц = ….т….ц
72 ч =….сут. 180 мин =….ч
4.Сравните (< > = ):
60 см² … 6 дм² 40 000 м² … 4 а
300 см³ … 3 дм³ 12 000 л … 11 м³
5. Начерти прямоугольник со сторонами 80 мм и 30 мм. Найдите его площадь. Вырази в квадратных сантиметрах. Проведи отрезок, который разделит прямоугольник на два прямоугольных треугольника. Найди площадь прямоугольного треугольника.
Контрольная работа по теме: «Величины»
II вариант.
1.Решите задачу:
Купили 400граммов чёрного кофе и 3 пачки чая по 50г . Найдите массу всей покупки.
2. Вычисли:
703 – 972 : 4 + 289 · 2
(709 485 — 485) : 1000 · 10
3.Выразите в указанных единицах измерения:
12 дм 80 мм = ….. мм 72 мес. = …. лет
3 кг 003 г = …. г 7856 м = ….км…м
1 сут 2 ч = ….ч 2108 ц = ….т….ц
4.Сравните ( < > = ):
200 см² … 2 дм² 9 000 м² … 9 а
5 000 см³ … 5 дм³ 17 000 л … 13 м³
5. Начерти прямоугольник со сторонами 70 мм и 40 мм.
1) Найдите его площадь. Вырази в квадратных сантиметрах.
2) Проведи отрезок, который разделит прямоугольник на два прямоугольных треугольника.
3)Найди площадь прямоугольного треугольника.
infourok.ru
Контрольная работа по математике 4 класс по теме: «Дроби»
I вариант
- Расположите дроби в порядке возрастания, запиши.
1/15; 1/9; 1/34; 1/100; 1/50.
2. Бумажная полоска имеет длину 12см. Для аппликации нужно отрезать ¾ этой полоски. Сколько сантиметров нужно отрезать?
А) 9см Б) 90 см В) 109 см
3. Найдите длину катушки ниток, если 7/10 составляют 63м.
А) 90см Б) 90 м В) 109 м
4. Три груши разделили на 9 человек. Какую часть груши получит каждый?
А) 9/3 Б) 3/ 9 В) 3/3
5. Пять мальчиков нашли несколько лесных яблок. Сколько было яблок, если каждый получил по 5/7 яблока?
А) 12 Б) 7 В) 5
6. Сколько секунд составляют 7/12 минуты?
А) 25сек Б) 35сек В) 40сек
7. Сколько килограммов составляют 6/10 тонны?
А) 60кг Б) 606кг В) 600кг
8. Сколько суток составляют 3/5 невисокосного года?
А) 219 сут Б) 109 сут В) 209 сут
9. Запиши и сравни.
15/45 * 21/45 5/7 * 5/15 6/6 * 1
10. Запиши и реши
73/96 – 46/96 + 18/96 = 1 – (38/130 + 79/130 – 48/130) =
11. Реши уравнение 2/18 + х = 1 – 12/18
12. Из Костромы Оля привезла три сувенира: деревянную медаль, льняное полотенце и фарфоровую чашку. На них изображены монастырь, герб Костромы и ваза с фруктами. На полотенце нет изображений монастыря и герба, а на чашке нарисован монастырь. Школьному музею Оля подарила деревянную медаль. Что изображено на этой медали?
А) монастырь Б) герб Костромы В) ваза с фруктами
II вариант
- Расположите дроби в порядке убывания, запиши.
15/100; 9/100; 34/100; 100/100; 50/100.
2.От катушки ниток длиной 25м для изготовления воздушного змея отрезали 4/5 всей длины катушки. Сколько метров отрезали?
А) 20м Б) 22м В) 20 см
3. Найдите длину отрезка, 4/5 которого составляют 12см.
А) 25см Б) 15см В) 5см
4. Четыре шоколадки разделили на 7 человек. Какую часть груши получит каждый?
А) 7/4 Б) 4/7 4/4
5. Четверо туристов поделили между собой несколько коробок сока. Сколько было коробок сока, если каждый получил по ¾ коробки?
А) 4 Б) 3 В) 7
6. Сколько часов составляют 5/12 суток?
А) 5ч Б) 12ч В) 10ч
7. Сколько килограммов составляют 5/10 центнера?
А) 500кг Б) 50кг В) 5кг
8. Сколько суток составляют 6/7 недели?
А) 7 сут Б) 6 сут В) 1 сут
9. Запиши и сравни.
17/20 * 15/20 3/5 * 3/15 5/5 * 1
10. Запиши и реши
84/99 – 56/99 + 35/99 = 1 – (92/120 – 46/120 + 57/120) =
11. Реши уравнение 1 – х = 14/30 + 9/30
12. Из Костромы Оля привезла три сувенира: деревянную медаль, льняное полотенце и фарфоровую чашку. На них изображены монастырь, герб Костромы и ваза с фруктами. На полотенце нет изображений монастыря и герба, а на чашке нарисован монастырь. Школьному музею Оля подарила деревянную медаль. Что изображено на этой медали?
А) монастырь Б) герб Костромы В) ваза с фруктами
konspekty-zanyatij.ru
Контрольные работы по математике (4 класс)
4 класс
КОНТРОЛЬНЫЕ РАБОТЫ ПО МАТЕМАТИКЕ (Автор Г.В. Дорофеев, Т.Н. Миракова, Т.Б. Бука)
УМК « ПЕРСПЕКТИВА»
Контрольная работа №1 (входная)
Вариант I
1. Реши задачу:
Из 32 метров ткани сшили 8 одинаковых платьев. Сколько потребуется метров ткани, чтобы сшить 12 таких платьев?
2. Найди значения выражений (запиши решение в столбик).
109 ∙ 7 486 ∙2 686 : 7 608 – 359
3 ∙ 251 436 : 4 92 : 3 328 + 296
3. Вычисли:
72 + 48: (3 ∙ 2) (1230 + 600) — (570 — 70)
4. Вычисли периметр и площадь прямоугольника со сторонами 8 см и 3 см.
5*. Продолжи ряд чисел, записав еще 3 числа: 608, 618, 628.
6*. Составь выражение, для вычисления которого надо выполнить (по порядку) вычитание, деление, сложение.
7*. Логическая задача.
Торговка, сидя на рынке, соображала: «Если к моим яблокам прибавить половину их, да ещё десяток, то у меня была бы целая сотня».
Сколько яблок у неё было?
Вариант II
1. Реши задачу.
Из 32 метров ткани сшили 8 одинаковых платьев. Сколько можно сшить таких платьев из 60 метров ткани?
2. Найди значения выражений (запиши решение в столбик).
407 ∙ 2 2 ∙ 462 278 ∙ 3 706 — 428
812 ∙ 2 536 : 8 774 : 2 246 + 479
3. Вычисли:
41 — 3 ∙ (63: 9) (980 — 800) + (320 — 20)
4. Найди периметр и площадь квадрата со стороной 7 см.
5*. Продолжи ряд чисел, записав ещё 3 числа: 995,985,975…
6*. Составь выражение, для вычисления которого надо выполнить (по порядку) деление, сложение, умножение.
7*. Логическая задача.
Зачерпнул Емеля 37 литров воды в два ведра. Пока влезал на печь, пролил 2 литра воды из первого ведра и 5 литров из второго. Зато воды стало поровну. Сколько литров воды было в каждом ведре?
Контрольная работа №2
Вариант I
1.Решить задачу:
За 6 часов автомобиль прошёл 480 км. Сколько километров пройдёт автомобиль при той же скорости за 10 часов?
2. Сравни и поставь знаки « >», «<» или «=»
2500мм … 25см 3км205м … 3250м 6т 800кг …68ц 10250кг … 10т 2ц
5249 … 5 ∙ 1000 + 2 ∙ 100 + 9 ∙ 10 + 4
3. Выполни вычисления:
25819 + 1 395000 : 100
309 ∙ 100 75800 — 10000
500000 – 1 130007 + 8000
4. Вычислите:
а) Периметр и площадь прямоугольника со сторонами 2 см и 4 см.
б) Длину стороны квадрата с таким же периметром и его площадь.
Вариант II
1. Реши задачу:
За 7 часов поезд прошёл 560 км. Сколько километров пройдёт поезд за 10 часов при той же скорости?
2.Сравни и поставь знаки « > », « < » или « = ».
12 дм 80 мм … 1280 мм 52 мм … 2 см 5 мм 2400 кг … 240 ц 6т 8 кг … 6080 кг
814129… 814100 + 2 ∙ 10 + 9
3. Выполни вычисления:
73549 + 1 84600 : 10
326000 — 1000 30000 – 1
268 ∙ 1000 206317 – 300
4. Вычисли:
а) Периметр и площадь прямоугольника со сторонами 7 см и 3 см.
б) Длину стороны квадрата с таким же периметром и его площадь.
Контрольная работа №3
1 вариант
1. Реши задачу.
Школьники с одного участка собрали 852 кг помидоров, а с другого участка в 3 раза меньше, чем с первого. Половину всех помидоров они разложили в ящики, по 8 кг в каждый. Сколько потребовалось ящиков?
2. Найди значение выражений.
16384 · 4 22м35см · 6
919884 ׃ 7 2км361м ׃ 3
(10283 + 16789) ׃ 9
(200496 – 134597) · 2
5 · (125 + 75) ׃ 20 + 80
3. Сравни.
6т 20кг… 6т2ц
3сут10час… 190час
20км300м…23000м
4. Реши уравнение.
3 · х = 87 -6
5. Найди площадь прямоугольника, если его длина 9см, а ширина на 5 см меньше.
2 вариант
1. Реши задачу.
На одной пасеке получено 567 кг меда, а на другой в 2 раза больше. Седьмую часть меда, полученного на второй пасеке, разложили в 9 одинаковых бидонов. Сколько килограммов меда наливали в каждый бидон?
2. Найди значение выражений.
36452 · 4 12м18см · 5
3546 ׃ 9 7т008кг ׃ 8
(18370 +23679) ׃ 7
(800035 – 784942) · 6
156 – 96 ׃ ( 12 ׃4) ׃ 2
3. Сравни.
5км4м…5км40дм
6т200кг… 62000кг
254ч…4сут5ч
4. Реши уравнение.
84 ׃ х = 6 · 7
5. Найди площадь прямоугольника, если его ширина 4 см, а длина в 2 раза больше.
Контрольная работа №4
Вариант I
1. Реши задачу:
На комбинате в декабре изготовили 7163 л сока, а в январе — на 678 литров меньше. Из всего сока 9789 литров разлили в пакеты, а остальной сок — в бутылки. Сколько литров сока разлили в бутылки?
2. Выполни вычисления и сделай проверку:
700000 – 24618 804608 + 96395 312879 – 179542
3.Вычисли, записывая вычисления в столбик:
28 км 640 м – 9 км 890 м
18 т 360 кг + 16 т 740 кг
ч 40 мин – 55 мин
4.Реши уравнение: 165 – х = 75 + 25
Вариант II
1. Реши задачу:
Зимой в магазине продали 3486 кукол, весной — на 697 кукол меньше. Из всех проданных кукол 4486 кукол были в платьях, а остальные — в спортивных костюмах. Сколько было кукол в спортивных костюмах?
2. Выполни вычисления и сделай проверку:
600600-24863 143807 + 57296 529631-181479
3. Вычисли, записывая вычисления в столбик:
16т230кг-9т750кг
32 км 560 м +19 км 540 м
2 ч 2 мин — 45 мин
4. Реши уравнение: 400 – х = 275 + 25
Контрольная работа №5 (1)
Вариант I
1. Решите задачу.
На комбинате в декабре изготовили 7 163 л сока, а в январе на 678 литров меньше. Из всего сока 9 789 литров разлили в пакеты, а остальной сок — в бутылки. Сколько литров сока разлили в бутылки?
В концертном зале 2 000 мест. В партере 1 200 мест. В амфитеатре мест в 3 раза меньше, чем в партере, а остальные места на балконе. Сколько мест на балконе?
2. Сравните и поставьте знаки «<», «>» или «=».
6т20кг…6т2ц 3сут 10ч…190ч 20км300м…23 000м
3. Выполните вычисления.
(10 283 + 16 789) : 9
4. Решите уравнение.
3 · Х = 87 – 6
5. Геометрическая задача.
Найти площадь прямоугольника, если его длина 9 см, а ширина на 5 см меньше.
6*. Решите задачу.
Внук, родившийся в 1992 году, на 65 лет моложе деда. В каком году родился дед?
Вариант II
1. Решите задачу.
На рынок привезли груши, яблоки и сливы, всего 4 тонны. Яблок было 2 240 кг, груш в 2 раза меньше, чем яблок, а остальные сливы. Сколько килограммов слив привезли на рынок?
2. Сравните и поставьте знаки «<», «>» или «=».
5км4м…5км40дм 6т200кг…62 000кг 245ч…4сут5ч
3. Выполните вычисления
(18 370 + 23 679) : 7 156 – 96 : (12 : 4) :2
4. Решите уравнение.
84 : Х = 6 · 7
5. Геометрическая задача.
Найти площадь прямоугольника, если его ширина 4 см, а длина в 2 раза больше.
6*. Решите задачу.
Бабушка родилась в 1934 году. В каком году родилась внучка, если она на 56 лет моложе бабушки?
Цель: проанализировать результаты усвоения тем «Сложение и вычитание многозначных чисел. Величины»; способствовать формированию навыка самоконтроля, самостоятельности; проверить умения действовать в изменённой ситуации
Контрольная работа №5(2)
Вариант I
1. Решите задачу.
На комбинате в декабре изготовили 7 163 л сока, а в январе на 678 литров меньше. Из всего сока 9 789 литров разлили в пакеты, а остальной сок — в бутылки. Сколько литров сока разлили в бутылки?
2.Запишите столбиком и выполните вычисления
700 000 – 24 618 804 608 + 96 395 312 879 – 179 542
3.Вычислите, записывая вычисления в столбик:
28 км 640м – 9 км 890 м
18т 360кг + 16 т 740 кг
4 ч 40 мин – 55 мин
4. Решите уравнение
290+ х = 640 – 260
5*. Вставьте пропущенные цифры:
3* 79
+ 43 *1
56 0 *
**5 6 8
6 * Укажите порядок действий:
a : b – c * d + k * m : n
Вариант II
1. Решите задачу.
Зимой в магазине продали 3 486 кукол, весной – на 697 кукол меньше. Из всех проданных кукол 4 486 были в платьях, а остальные – в спортивных костюмах. Сколько было кукол в спортивных костюмах?
2.Запишите столбиком и выполните вычисления
600 600 – 24 863 143 807 + 57 296 529 631 – 181 479
3.Вычислите, записывая вычисления в столбик:
16 т 230 кг – 9 т 750 кг
32 км 560 м + 19 км 540 м
2ч 2 мин – 45 мин
4. Решите уравнение
400 – х = 275 + 25
5*. Вставьте пропущенные цифры:
671*
+ 5 *83
7 6*9
** 626
6 * Укажите порядок действий:
a : (b – c) * d + k * (m : n)
Контрольная работа №6
Вариант I
1. Решите задачу:
На четырех полках было 500 книг. На первой полке 139 книг, на второй на 12 книг меньше чем на первой, на третьей — в 2 раза меньше чем на 1-й и 2— вместе. Сколько книг было на четвертой полке?
2. Решите задачу:
Из двух городов, расстояние между которыми 918 км, вышли одновременно навстречу друг другу два скорых поезда. Скорость одного поезда 65 км в час. Определи скорость другого поезда, если поезда встретились через 6 часов?
3. Геометрическая задача.
Длина поля 130 м, ширина 70 м. 2/5 участка засеяно картофелем. Сколько квадратных метров площади засеяно картофелем?
4. Найди значение выражения:
600200 – 123321 : 303 + 2458 • 26
5. Реши уравнение:
6х+2х+ 18 = 78
Вариант II
1. Решите задачу:
В зернохранилище 700 т пшеницы. За зиму с базы отправили 124 т зерна, а во второй — на 203 т больше. Сколько тонн зерна осталось на базе?
2. Решите задачу:
Из двух городов одновременно навстречу друг другу отправились скорый и товарный поезда. Они встретились через 13 часов. Определи расстояние между городами, если известно, сто скорость скорого поезда 95 км в час, а товарного 3/5 от скорости скорого.
3. Геометрическая задача:
Участок прямоугольной формы, ширина которого в 2 раза меньше длины засеяли овсом. Периметр участка 1140 м. 1/2 убрали комбайном. Сколько квадратных метров участка осталось убрать?
4. Найди значение выражения:
800010 – 11520 : 288 + 1879 – 79
5. Реши уравнение:
10b – 5b + 44 = 139
Контрольная работа №7
1 вариант
1. Реши задачу:
Путь от села до города почтальон проехал на мотоцикле за 2 часа, двигаясь со скоростью 60 км/ч. Сколько километров от села до города?
2. Реши задачу:
Автобус проехал 180км за 4 часа. С какой скоростью он ехал?
3. Реши задачу:
Собака увидела в 50 метрах от себя хозяина, и побежала к нему со скоростью 10м/сек. Через сколько секунд она добежала до хозяина?
4. Реши задачу:
За 3 часа Петя проехал на велосипеде 36 км, а Коля за тоже время проехал 45 км. У кого скорость движения была больше и на сколько?
5. Реши задачу:
На элеватор за два дня поступило 574 т зерна. В первый день зерно доставили на 43 грузовиках, а во второй день на 39 таких же грузовиках. Сколько тонн зерна поступало каждый день?
6. Выполни действия.
90000 — 21476׃ 7· 3
3208 – 142 · 3 + 318
7. Сравни.
35км900м…35090м 3мин15с…200с
2ч35мин…100мин 17т040кг…17400кг
2 вариант
1. Реши задачу:
Теплоход проплыл за 4 часа 120 км. С какой скоростью двигался теплоход?
2. Реши задачу:
Лыжник двигался со скоростью 200 м/мин в течение 8 мин. Какой путь прошел лыжник?
3. Реши задачу:
Товарный поезд прошел 160 км со скоростью 40 км/ч. За какое время поезд прошел этот путь?
4. Реши задачу:
В походе дети шли 15 км со скоростью 5 км/час и 12км со скоростью 4 км/час. Сколько часов были в пути дети?
5. Реши задачу:
Магазин продал утром 3 ящика яиц, а вечером 2 таких же ящика. Всего продано 500 штук яиц. Сколько продано яиц утром и вечером в отдельности?
6.Ваполни действия.
70000 – 16272 ׃ 8 · 4
867 – 477 ׃ 9 – 50
7. Сравни.
8т 3ц…8050кг 2мин 18с…140с
4м3дм…403дм 1ч48 мин…100мин
Самостоятельная работа (103)
1 вариант
1. Решите задачу.
Ученик читал книгу по 50 страниц в день в течении 5 дней, а за выходные он прочитал всего 150 страниц. Сколько страниц ему осталось прочитать, если в книге 580 страниц?
2. Вычисли.
62240: 40 238800: 600
4050 · 600 7320 · 40
3. Найди значение выражения.
563430: 70 + 9204 · 40
4. Реши уравнение.
Х – 390 = 204 · 500
5. Геометрическое задание.
Начерти квадрат со стороной 6 см. Закрась одну шестую площади данного квадрата. Сколько квадратных сантиметров ты закрасил?
2 вариант
1. Решите задачу.
Ира читала книгу по 40 страниц в день в течении 5 дней, а за выходные прочитала всего 135 страниц. Сколько страниц ей осталось прочитать, если в книге 495 страниц?
2. Вычисли.
75270: 30 205100: 700
2740 · 900 4080 · 50
3. Найди значение выражения.
432360: 60 + 7021 · 30
4. Реши уравнение.
Х – 920 = 701 · 200
5. Геометрическое задание.
Начерти квадрат со стороной 7 см. Закрась одну седьмую площади квадрата. Сколько квадратных сантиметров ты закрасил?
Контрольная работа №8
Вариант I
1. Реши задачу:
В концертном зале 2000 мест. В партере 1200 мест. В амфитеатре мест в 3 раза меньше, чем в партере, а остальные места на балконе. Сколько мест на балконе?
2. Найди значения выражений:
(10283 + 16789) : 9 5 ∙ (125 + 75): 20 + 80 (200496 – 134597) • 2
3. Сравни, поставь знаки «<»,«> », « = » :
6 т 20 кг… 6т2ц 20 км 300 м… 23000 м Зсут10ч… 190 ч
4. Реши уравнение: 3 • х = 87 – 6
5. Найди площадь прямоугольника, если его длина 9 см, а ширина на 5 см меньше.
Вариант II
1. Реши задачу:
На рынок привезли груши, яблоки и сливы, всего 4 т. Яблок было 2240 кг, груш в 2 раза меньше, чем яблок, а остальные сливы. Сколько килограммов слив привезли на рынок?
2. Найди значения выражений:
(18370 + 23679): 7 156 — 96 : (12 : 4): 2 (800035 — 784942) • 6
3. Сравни, поставь знаки « < », « > », « = » :
5 км 4 м … 5 км 40 дм 245 ч … 4 сут 5 ч00 6т 200 кг …62000 кг
4.Реши уравнение: 84: х = 6 • 7
5. Найди площадь прямоугольника, если его ширина 4 см, а длина в 2 раза больше.
Самостоятельная работа (125)
Вариант I
Решите задачу:
Ученик читал «Гарри Поттера и философский камень» по 55 страниц в день в течении 5 дней, а за субботу и воскресенье 150 страниц. Сколько страниц осталось ему прочитать, если в книге 580 страниц?
Вычисли:
62240 : 40 238800 : 600
4050 – 600 7320 – 40
Найдем значение выражения:
563430 : 70 + 9204 – 40
Реши уравнение:
204 • 500 – х = 390
Геометрическое задание.
Начерти квадрат со стороной 6 см. Закрась 1/6 площади данного квадрата. Сколько квадратных сантиметров ты закрасил?
Вариант II
Реши задачу:
Ира читала новую книгу про Таню Гроттер по 47 страниц в день в течение 5 дней, а за субботу и воскресенье прочитала 135 страниц. Сколько страниц ей осталось прочитать, если в книге 495 страниц.
Вычисли:
75270 : 30 205100 : 700
2700 • 900 4080 ∙ 50
Контрольная работа №9
Вариант I
1. Реши задачу:
Колумбийский фермер собрал 4 т кофейных зерен. Из них 940 кг он продал на шоколадную фабрику, а остальные огурцы поместил в 68 мешков поровну. Сколько килограммов кофейных зерен в каждом мешке?
2. Выполни действия:
7247 – 5 930760 – 845999
1305 : 9 ? 68754 + 224689
6098 – 83 16727 : 389
38744 : 58 189088 : 622
5289 • 9
3. Выполни действия:
2т 2ц 88кг + 7ц 86кг = …т … ц … кг
2 мин 52 сек + 43 сек = … мин … сек
8 сут 17 час — 5 сут 22 час 10 мин = … сут… час… мин
4. Реши уравнение: 112 : Х = 48:6
Вариант II
1. Реши задачу:
Фермер вырастил 6 т 2 ц 88 кг яблок. Их них 2590 кг яблок сдали на переработку для производства сока. Оставшееся количество разложили в 86 ящиков поровну. Сколько килограммов яблок в каждом ящике?
2. Выполни действия:
48909 + 298698
5289 • 9
13518 : 9
15698 : 47
240542 : 86
92800 – 217995
19151 : 684
41097 : 399
3. Выполни действия:
33 м 49 см + 22 м 68 см = … м … см
8 мин 10 сек — 7 мин 45 сек = … мин … сек
3т 2ц 75 кг —8 ц98 кг = …т … ц …кг
4.Реши уравнение: 126 : х=54: 6
infourok.ru


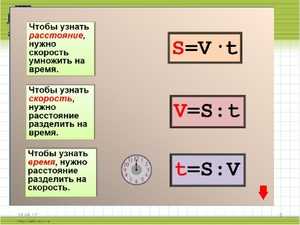
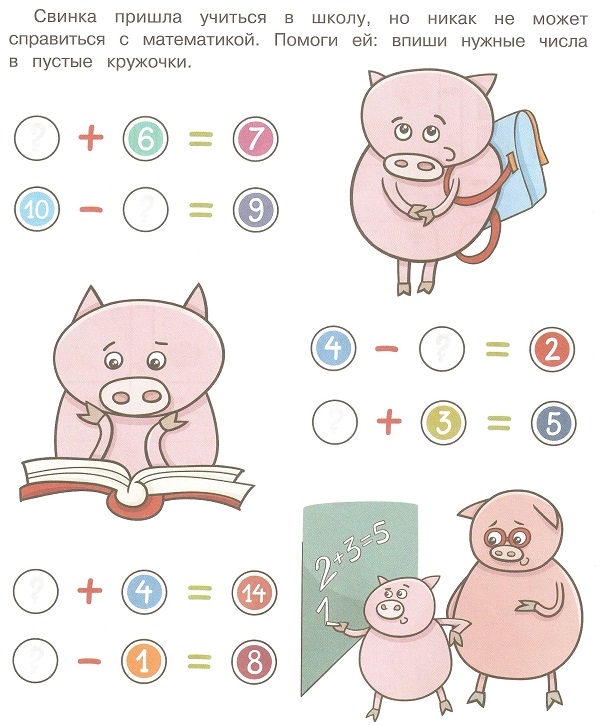

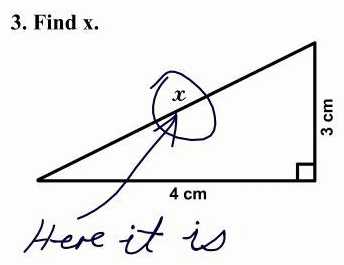
 Мы представляем вашему вниманию подборку логических задач для детей 6-7 лет. С ответами вы можете ознакомиться на этой же странице, прямо под логической задачей.
Мы представляем вашему вниманию подборку логических задач для детей 6-7 лет. С ответами вы можете ознакомиться на этой же странице, прямо под логической задачей. Старайтесь развивать ребенка в различных сферах и направлениях. В этом вам помогут материалы с нашего сайта, в том числе и статья с логическими задачами для детей 6-7 лет (с ответами).
Старайтесь развивать ребенка в различных сферах и направлениях. В этом вам помогут материалы с нашего сайта, в том числе и статья с логическими задачами для детей 6-7 лет (с ответами).

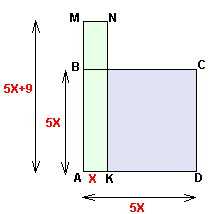 Итак, пусть AK=x, тогда AD=AB=5x. Поскольку сторону AB увеличили на 9 см, то длина полученного прямоугольника выражается как 5x+9. Принимая во внимание условие с периметром, получаем простенькое уравнение без дробей:
Итак, пусть AK=x, тогда AD=AB=5x. Поскольку сторону AB увеличили на 9 см, то длина полученного прямоугольника выражается как 5x+9. Принимая во внимание условие с периметром, получаем простенькое уравнение без дробей: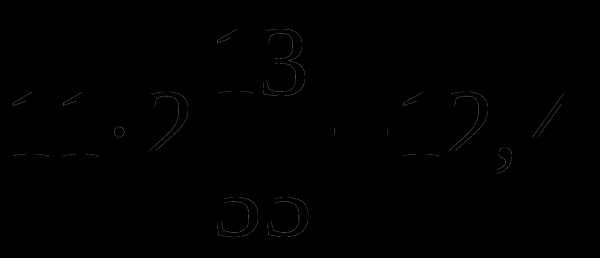 .
.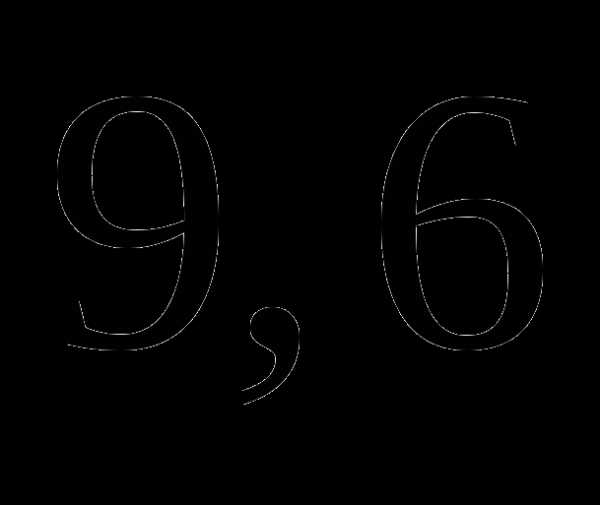 ;
;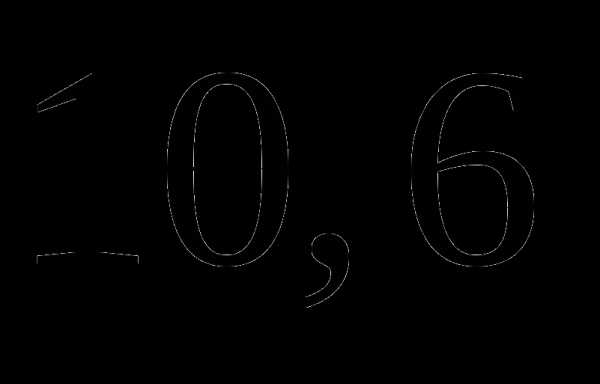 ;
;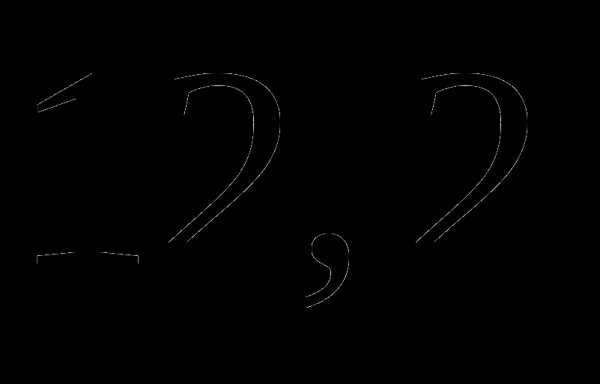 ;
;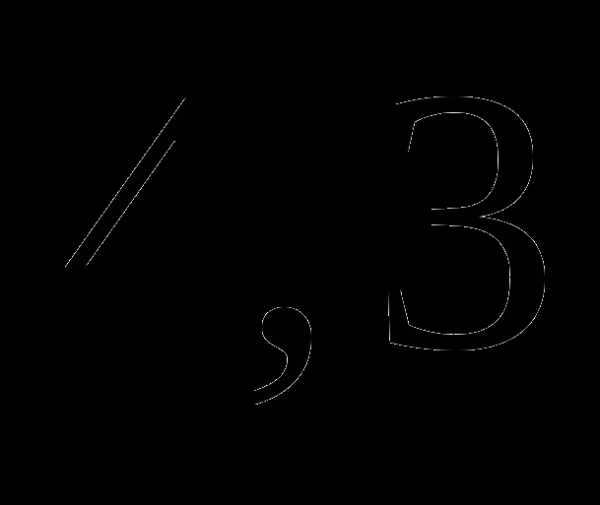 часа;
часа; часа;
часа;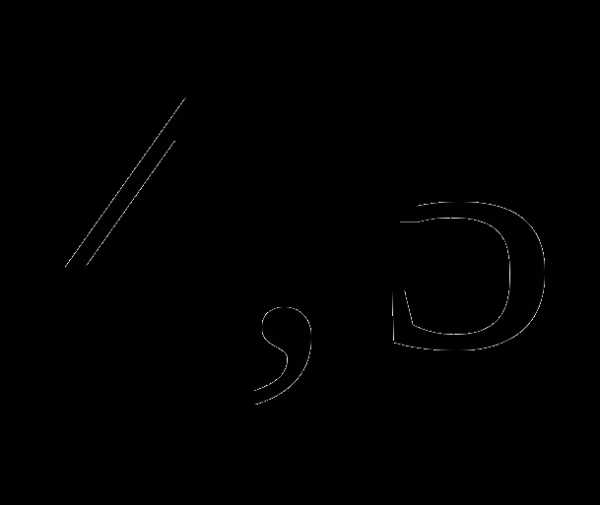 часа;
часа;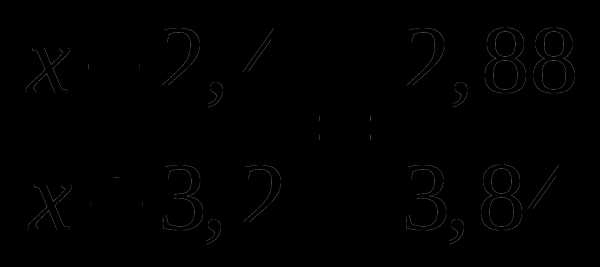 .
.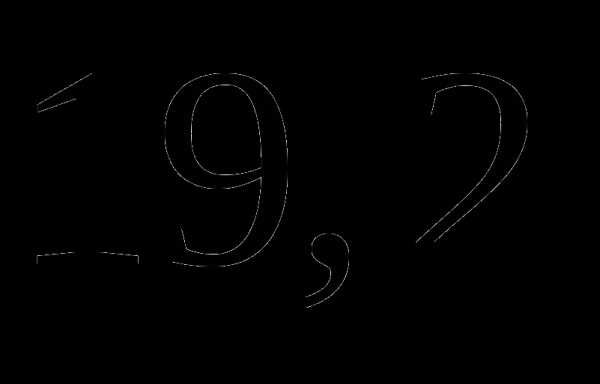 ;
;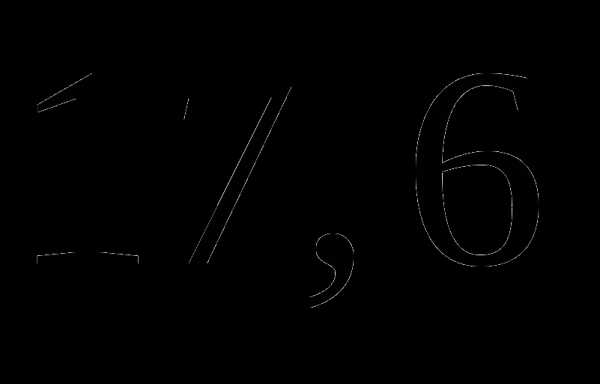 ;
;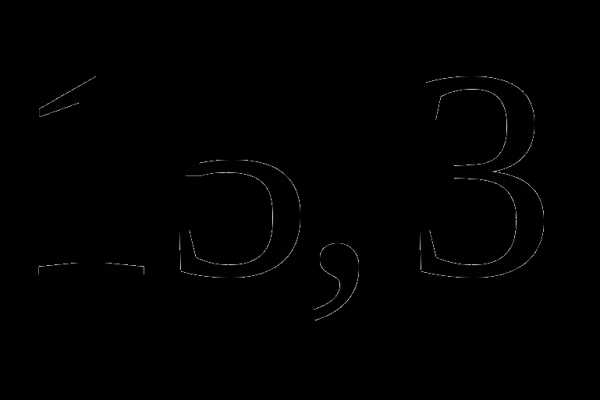 ;
; в число
в число 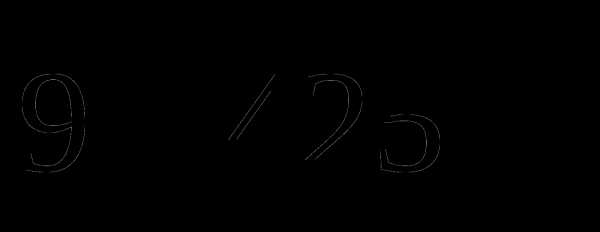 , чтобы полученное число делилось на
, чтобы полученное число делилось на  ?
?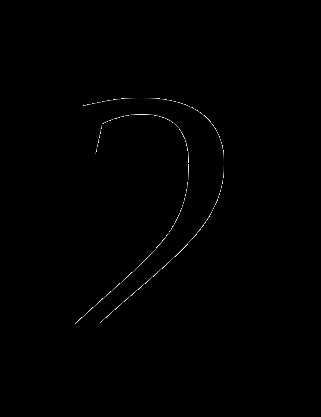 ;
;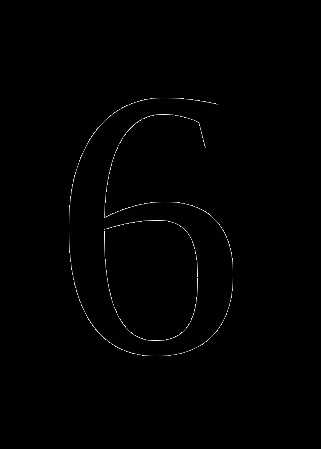 ;
; ;
;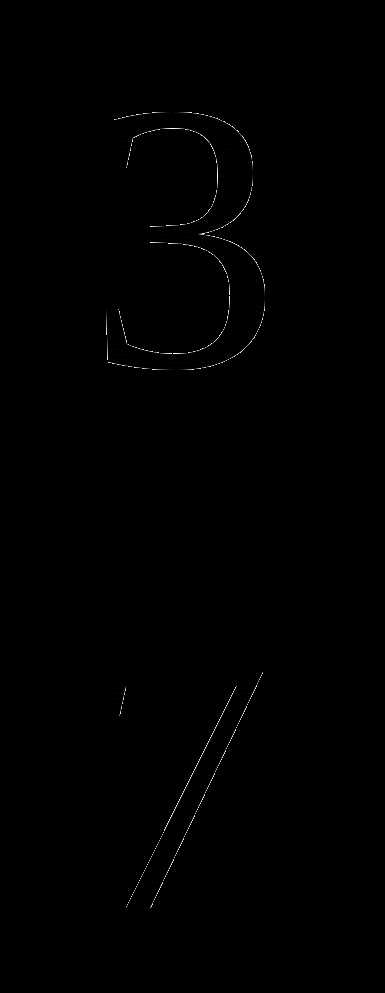 пути, а во второй –
пути, а во второй – 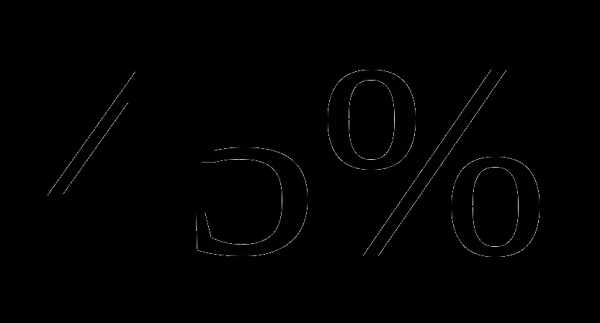 оставшегося пути. Какое расстояние он прошел за третий день?
оставшегося пути. Какое расстояние он прошел за третий день? км;
км;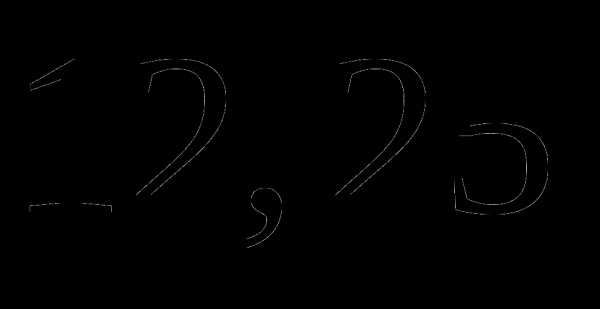 км;
км;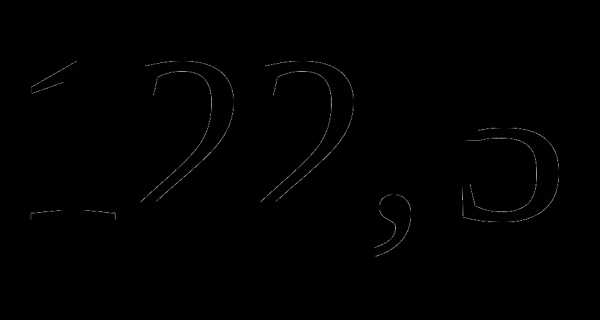 км;
км; которого равны
которого равны 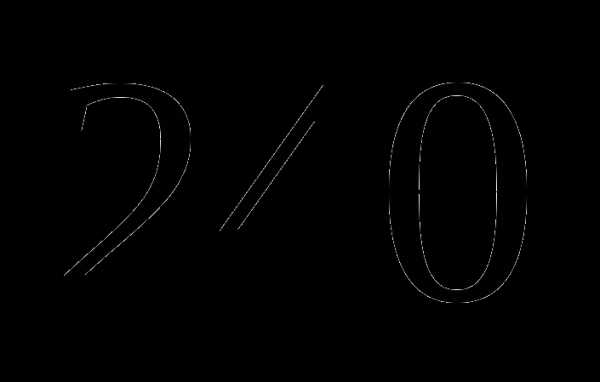 .
.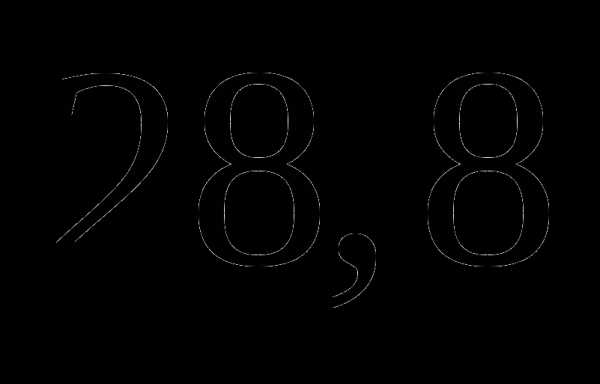 ;
;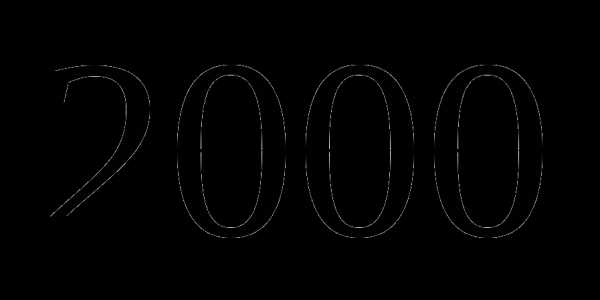 ;
; ;
;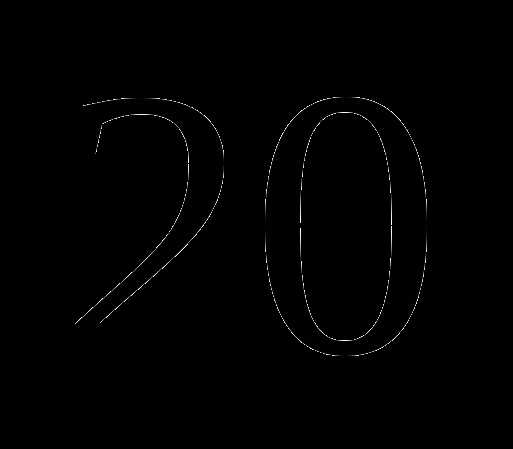 см. Найдите ее диаметр. Ответ округлите до сотых. Число
см. Найдите ее диаметр. Ответ округлите до сотых. Число 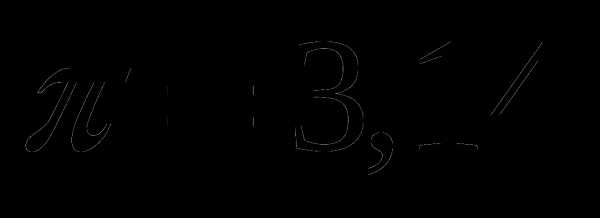 .
.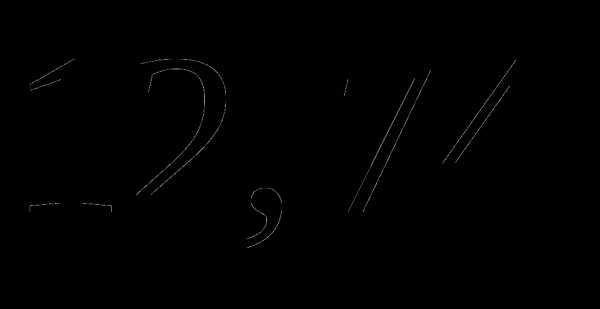 ;
;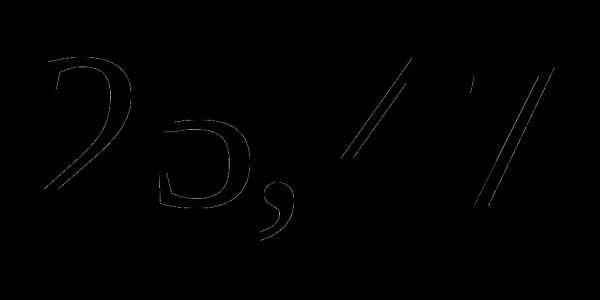 ;
;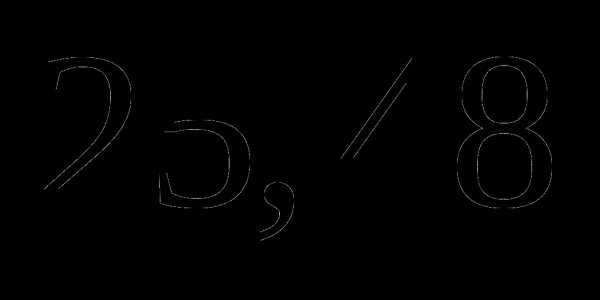 ;
; , если .
, если .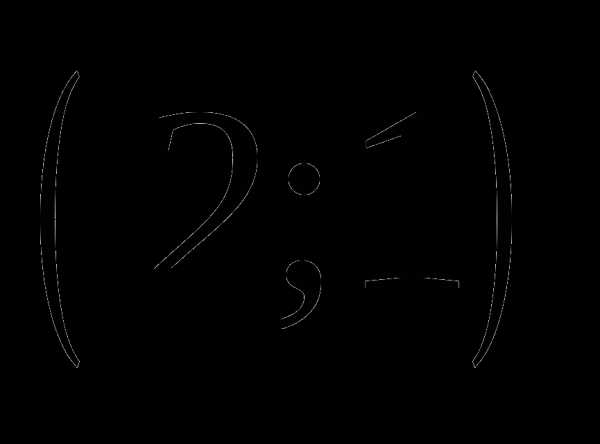 ;
; ;
;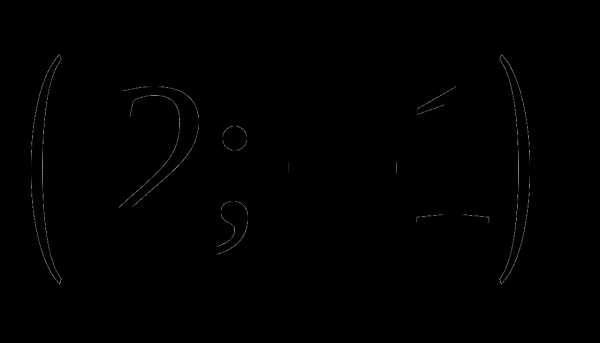 ;
; ;
;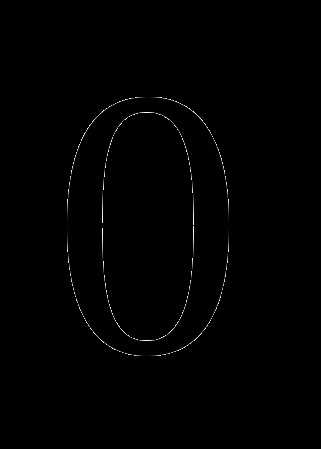 ;
; ;
; .
. ;
;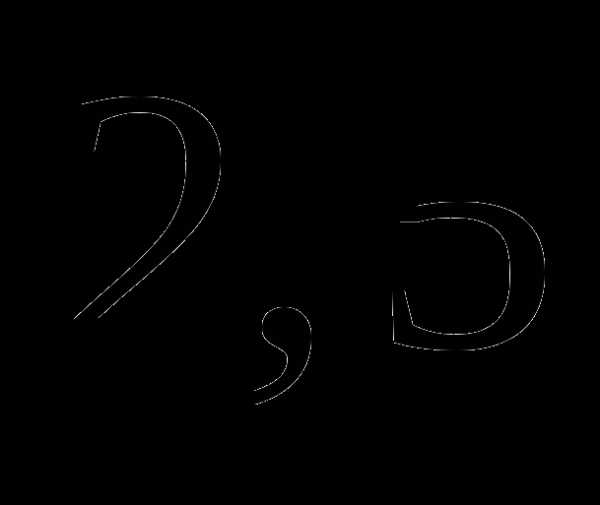 ;
;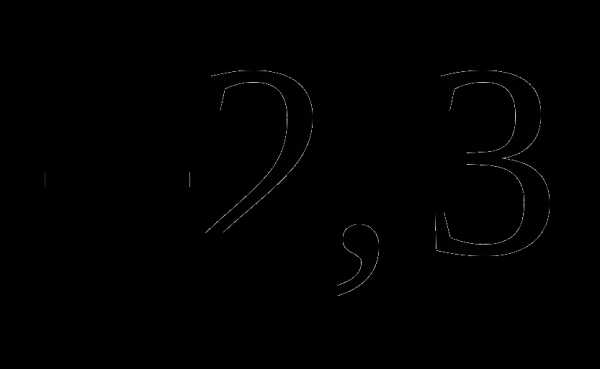 ;
;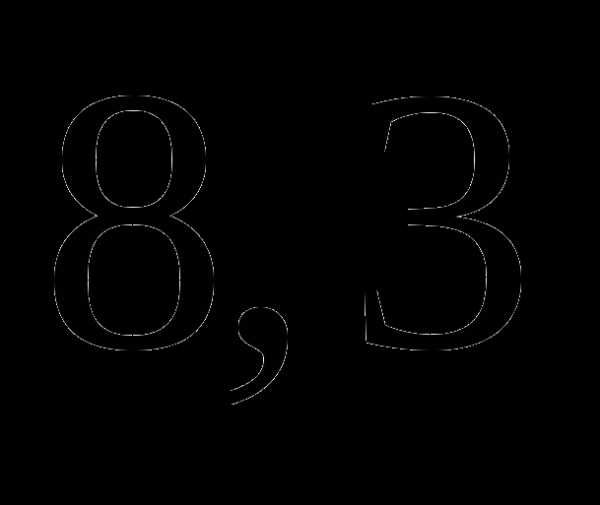 часа;
часа;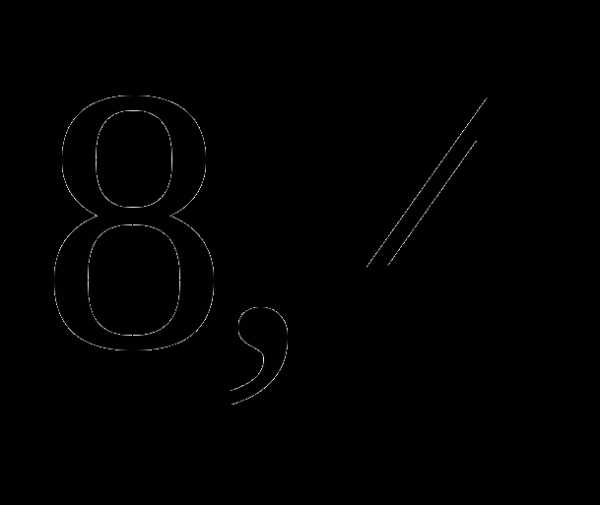 часа;
часа;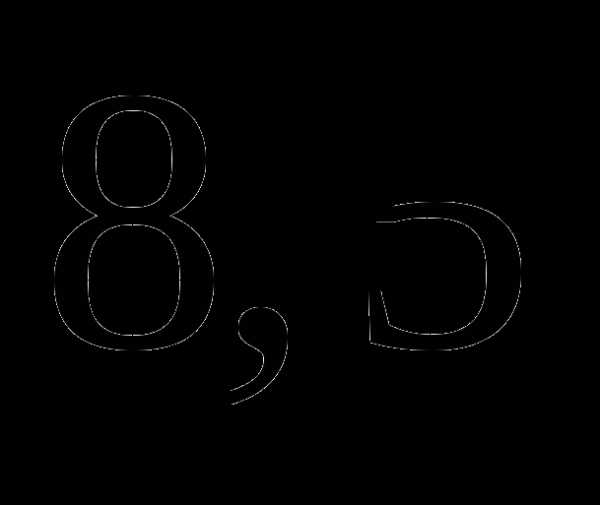 часа;
часа; ;
;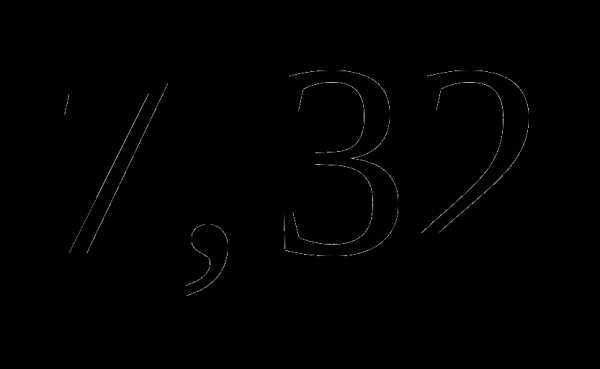 ;
; ;
;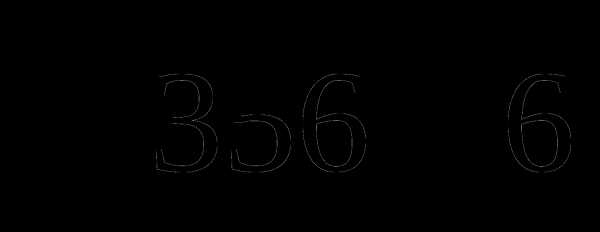 , чтобы полученное число делилось на
, чтобы полученное число делилось на  ?
?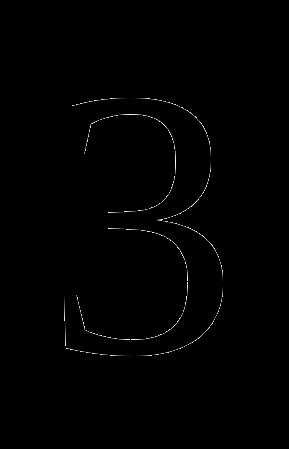 ;
;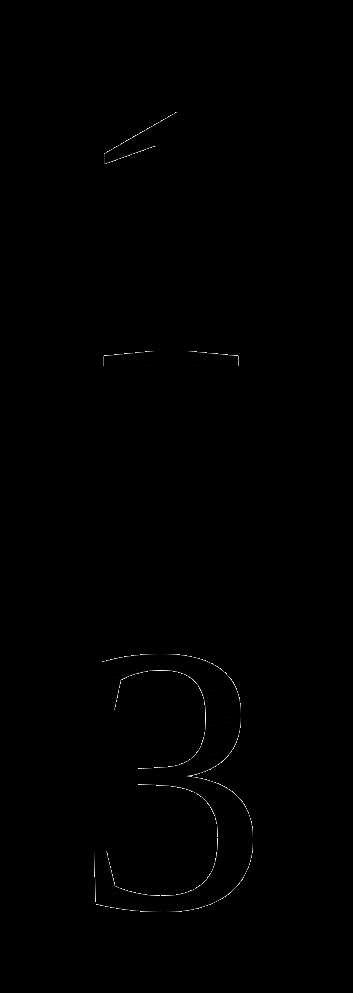 пути, а во второй –
пути, а во второй – 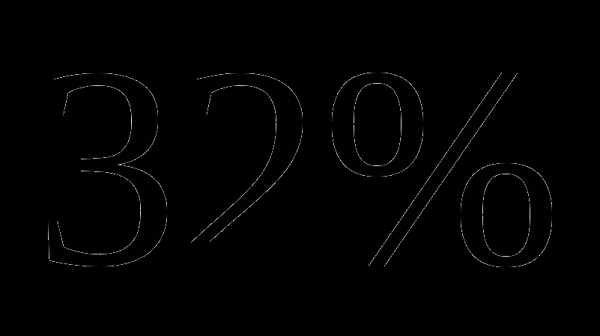 оставшегося пути. Какое расстояние он прошел за третий день?
оставшегося пути. Какое расстояние он прошел за третий день?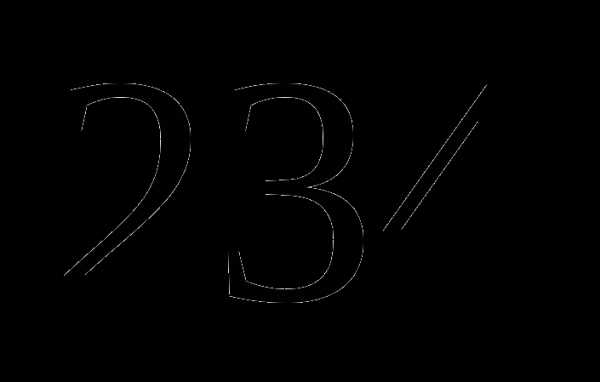 км;
км; км;
км;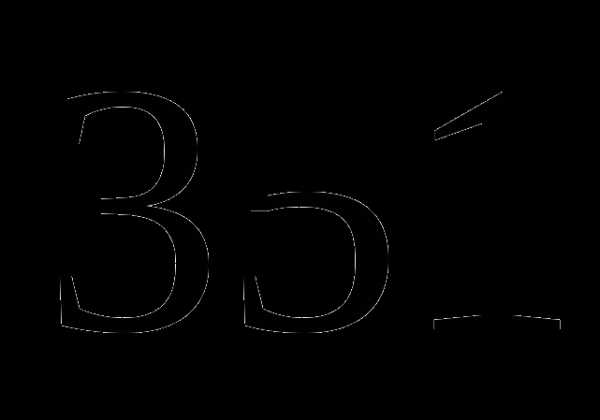 км;
км; которого равны
которого равны 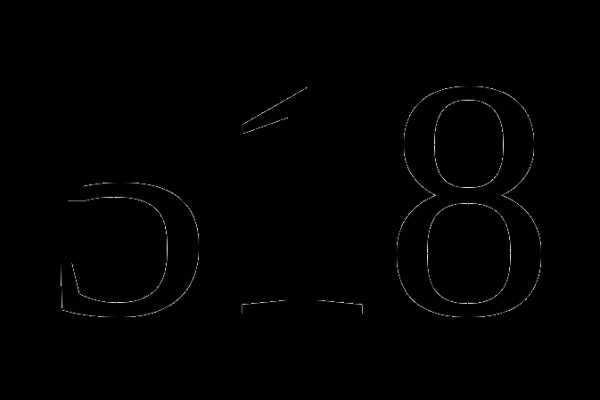 .
.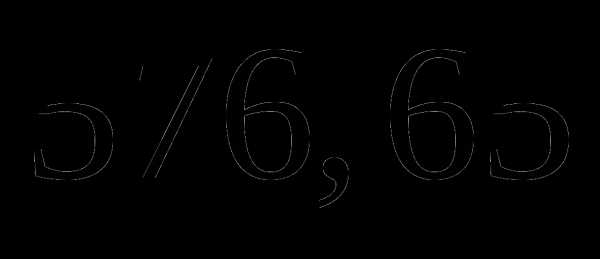 ;
;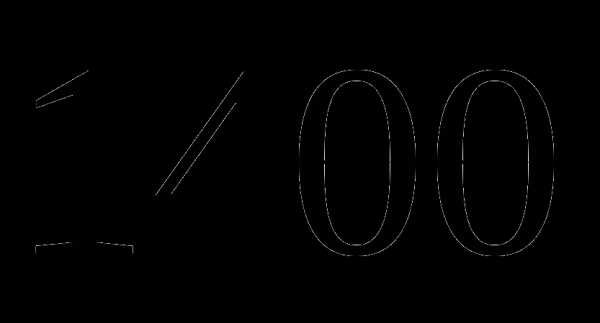 ;
; ;
; ;
; ;
;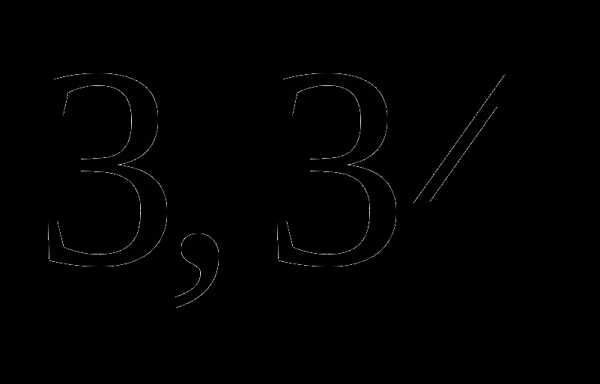 ;
;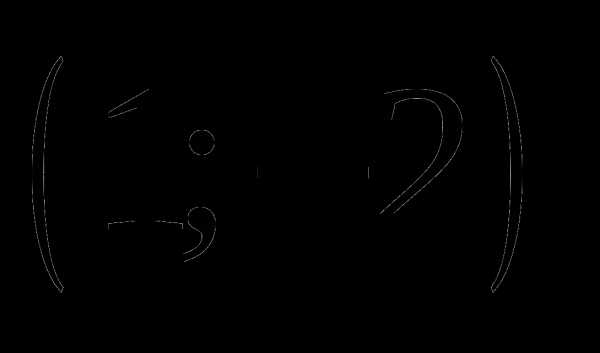 ;
;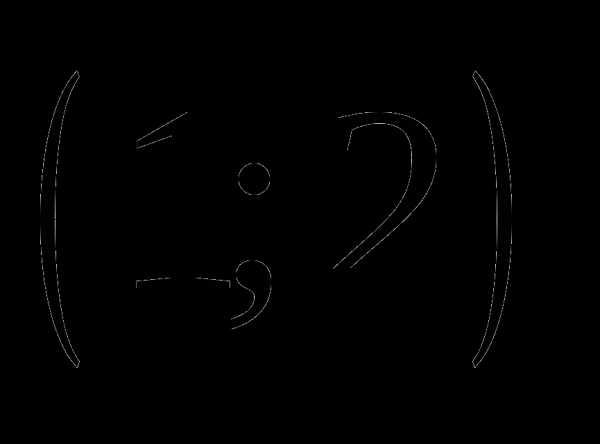 ;
;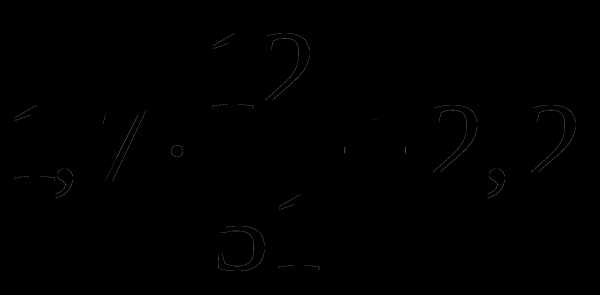 .
. ;
;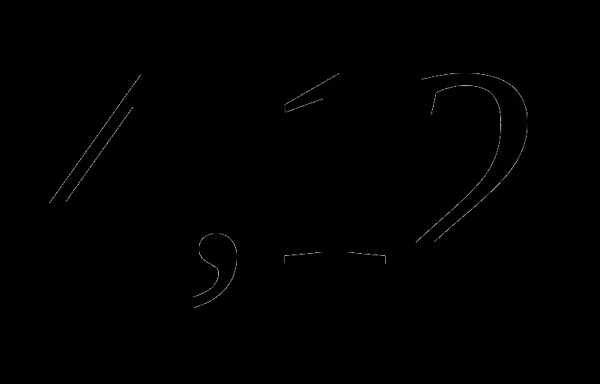 ;
;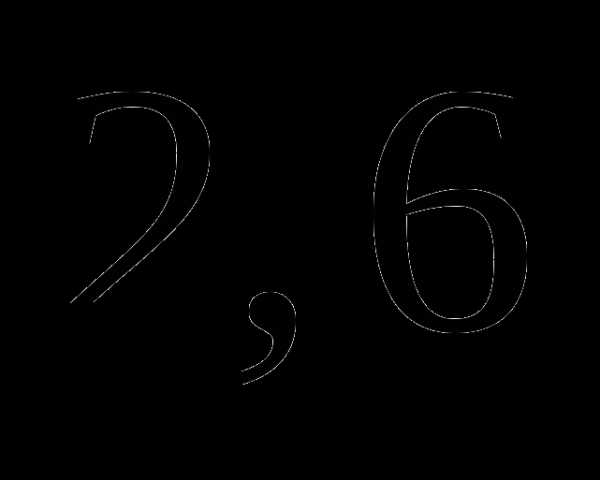 ;
;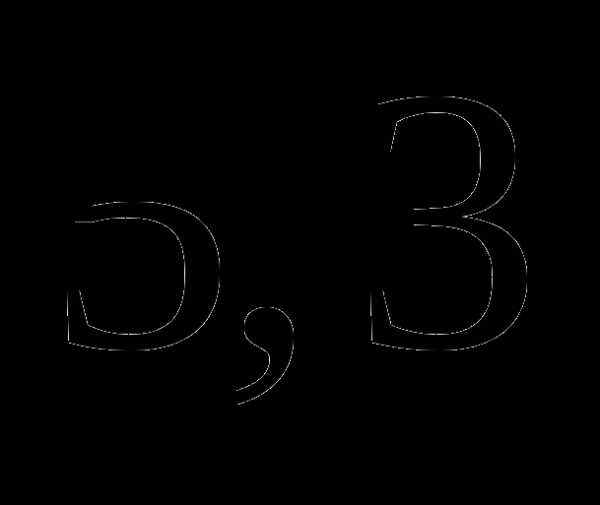 часа;
часа;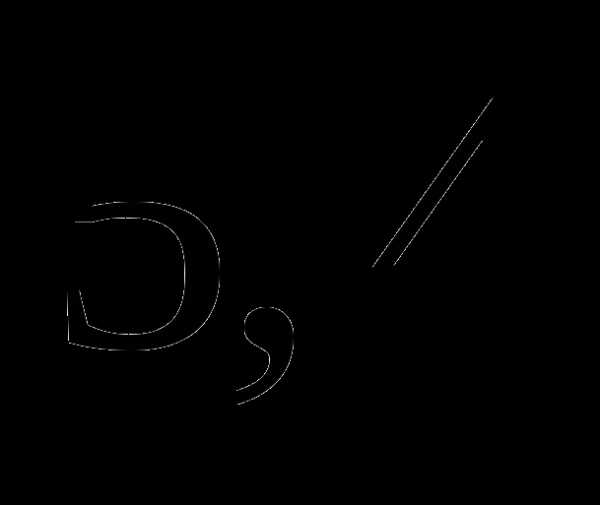 часа;
часа;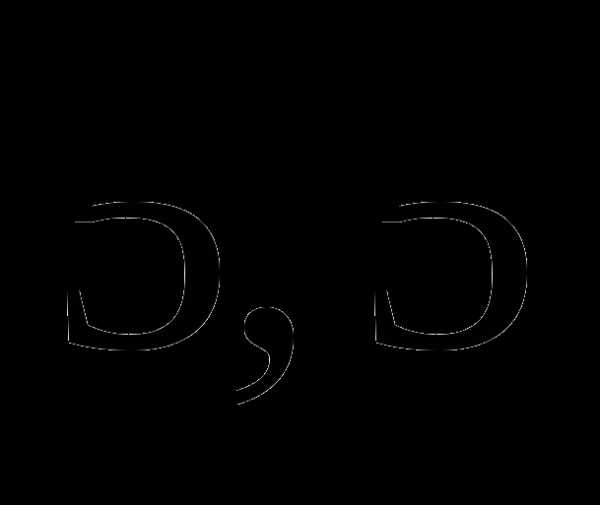 часа;
часа; .
.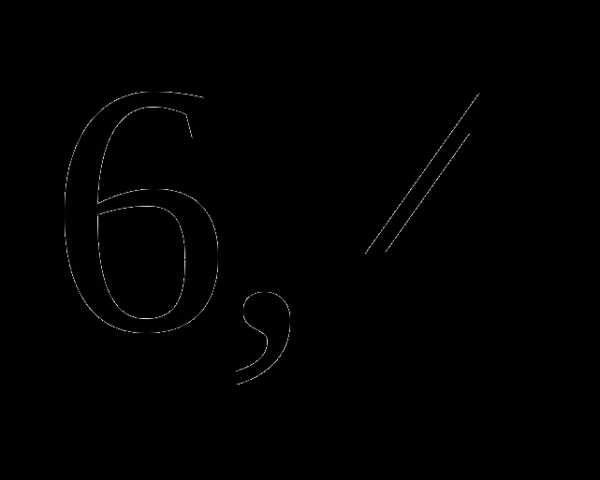 ;
;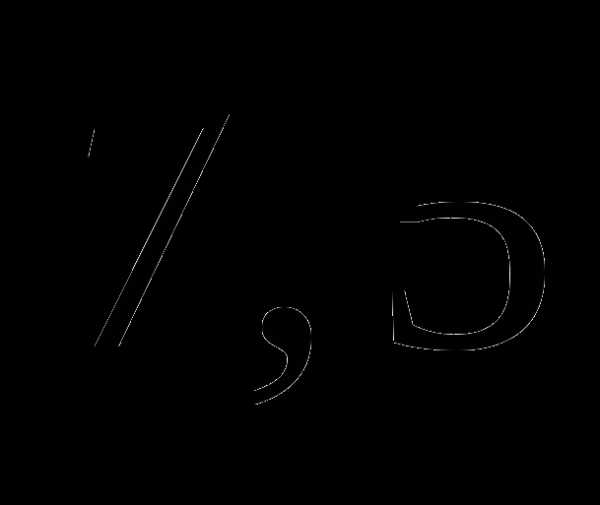 ;
;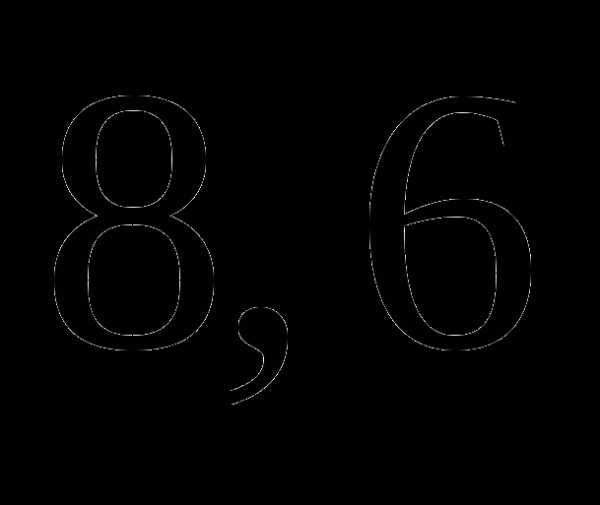 ;
; , чтобы полученное число делилось на
, чтобы полученное число делилось на  ;
;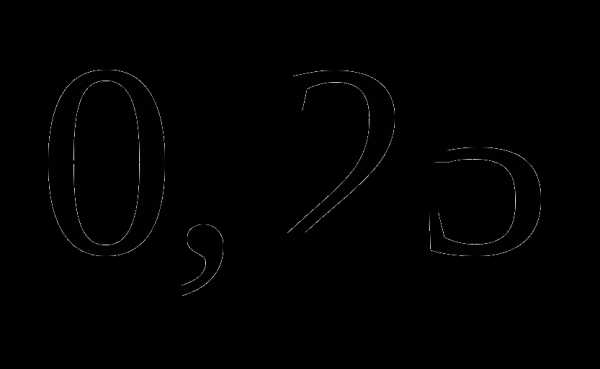 пути, а во второй –
пути, а во второй –  оставшегося пути. Какое расстояние он прошел за третий день?
оставшегося пути. Какое расстояние он прошел за третий день?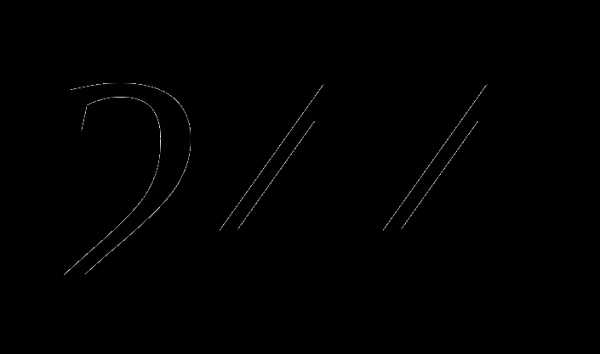 км;
км;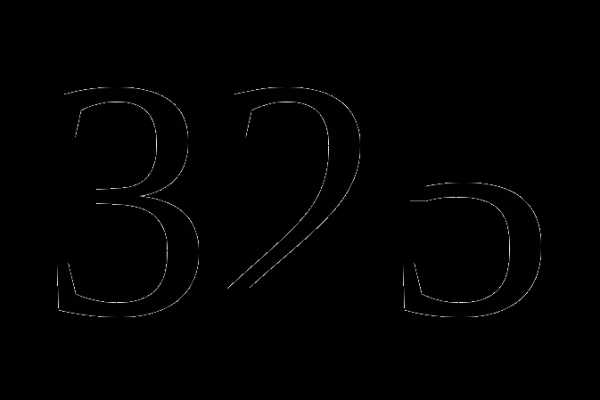 км;
км; км;
км; которого равны
которого равны 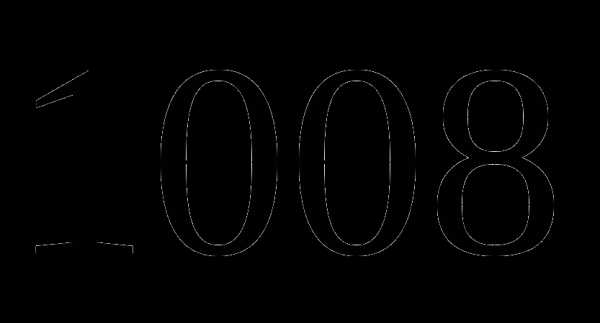 .
. ;
;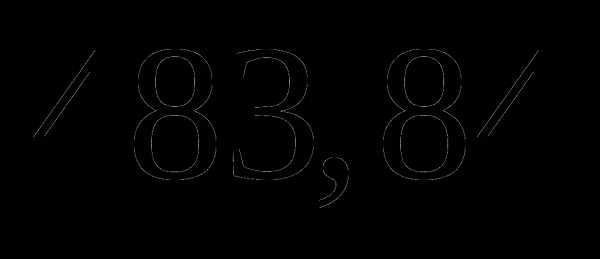 ;
;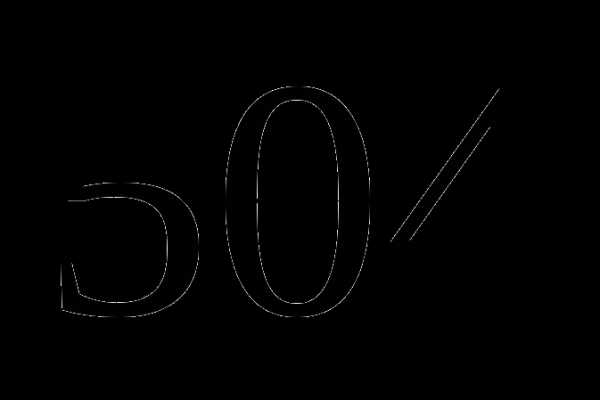 ;
;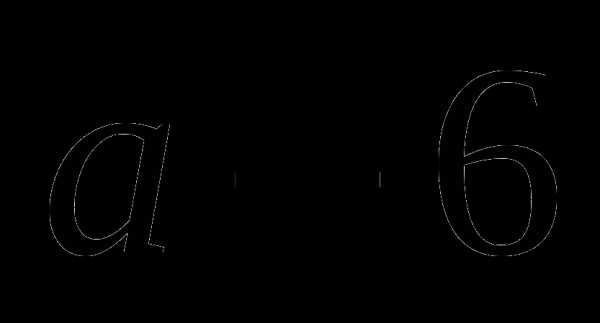 ;
;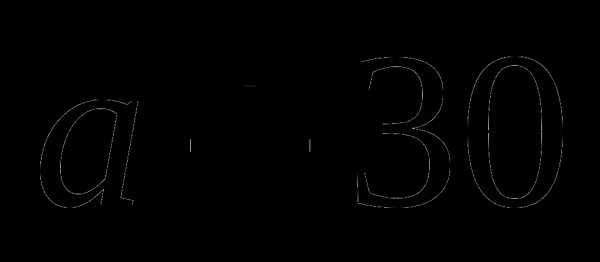 ;
;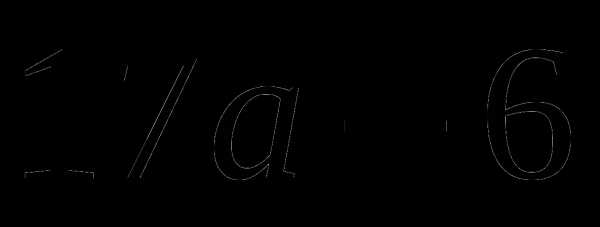 ;
;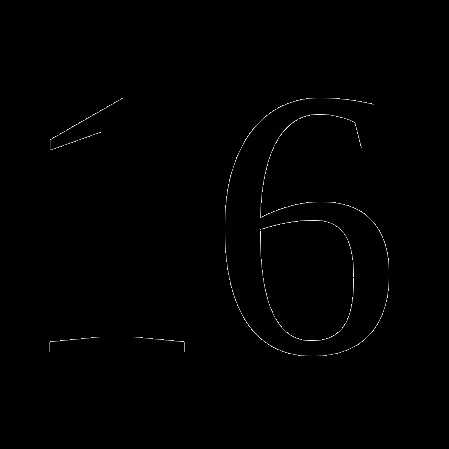 см. Найдите ее диаметр. Ответ округлите до сотых. Число
см. Найдите ее диаметр. Ответ округлите до сотых. Число 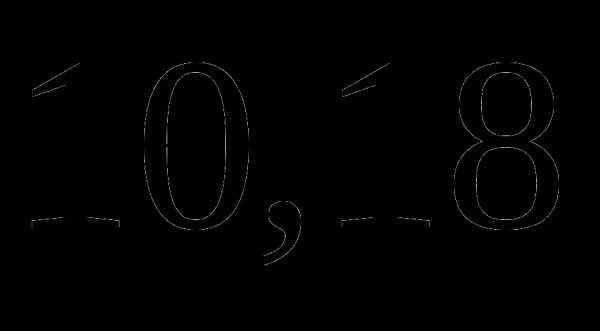 ;
;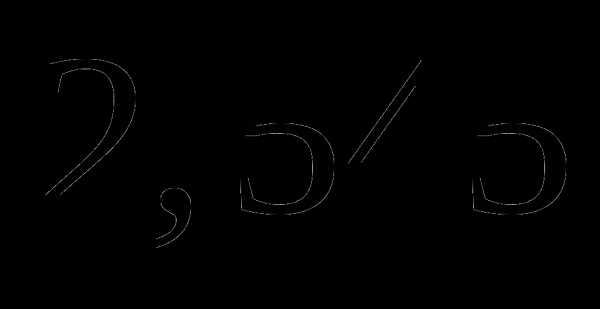 ;
; ;
;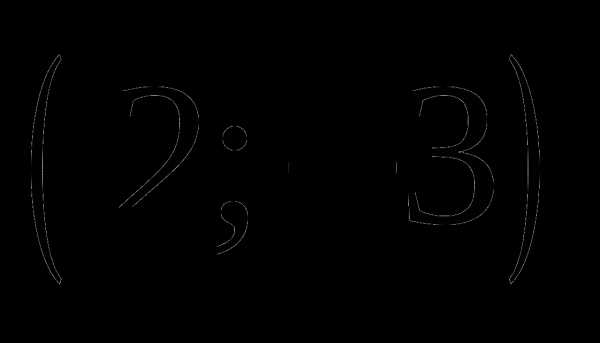 ;
; ;
;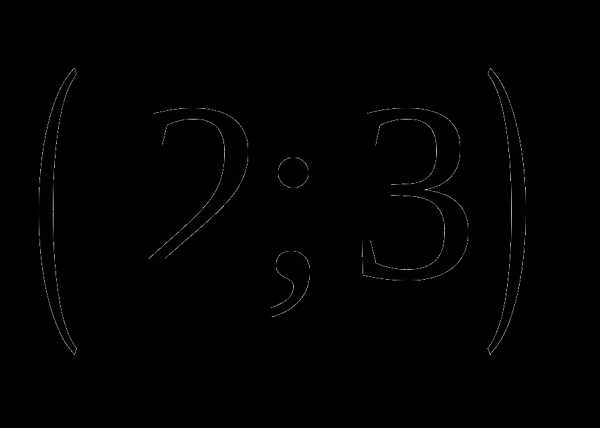 ;
;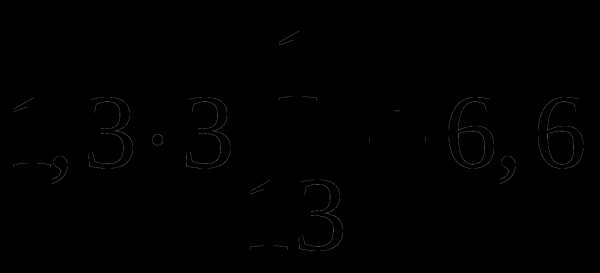 .
. ;
;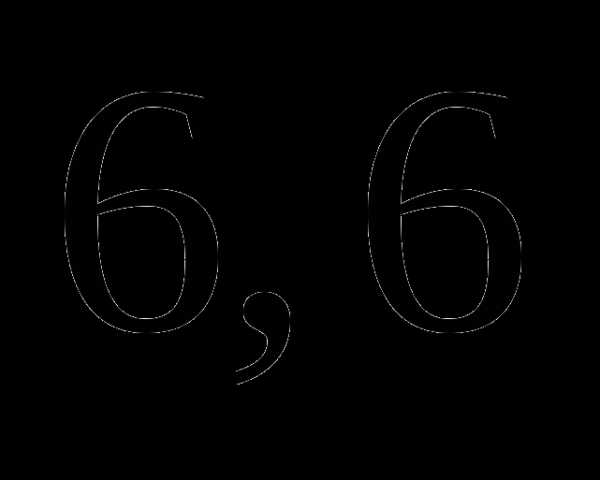 часа;
часа;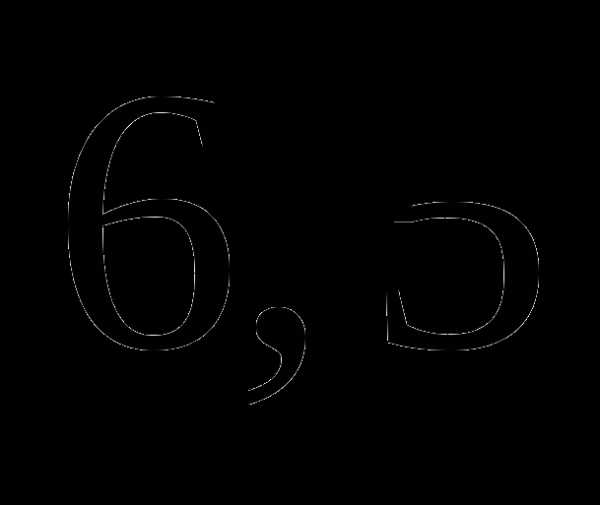 часа;
часа;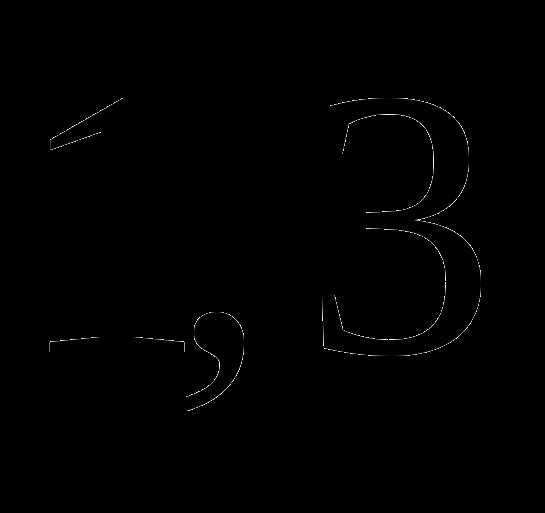 ;
; ;
;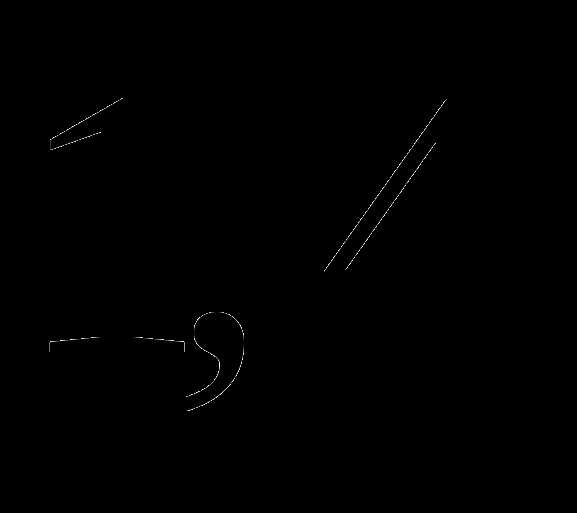 ;
;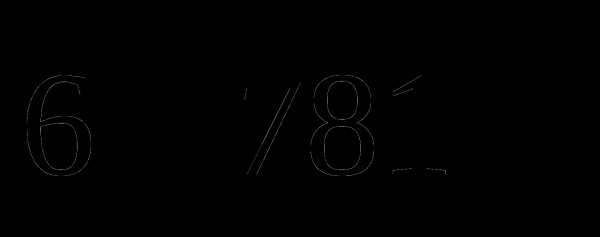 , чтобы полученное число делилось на
, чтобы полученное число делилось на 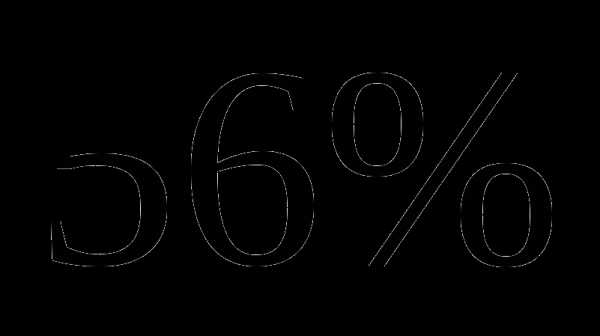 оставшегося пути. Какое расстояние он прошел за третий день?
оставшегося пути. Какое расстояние он прошел за третий день?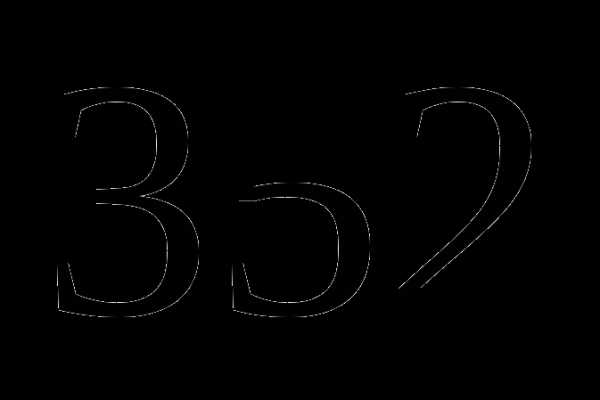 км;
км; км;
км;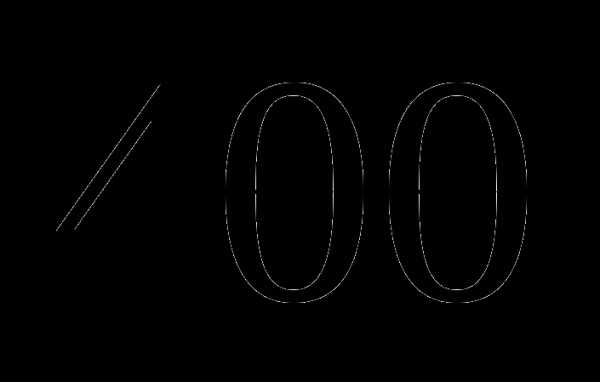 км;
км;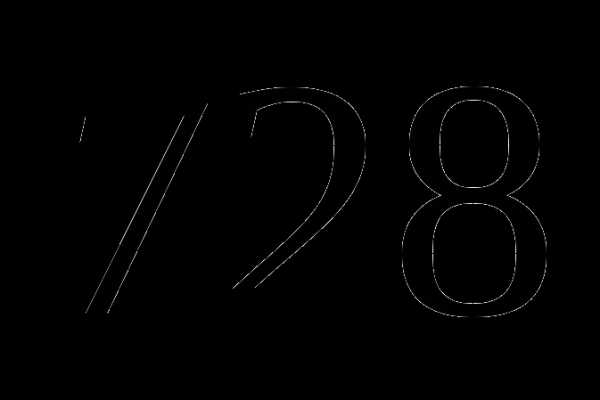 .
.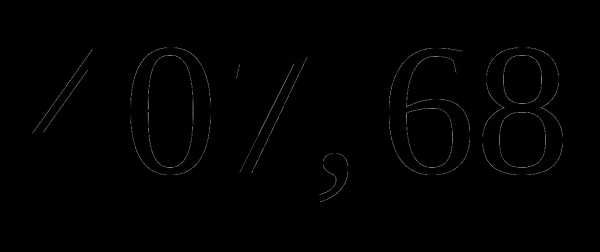 ;
;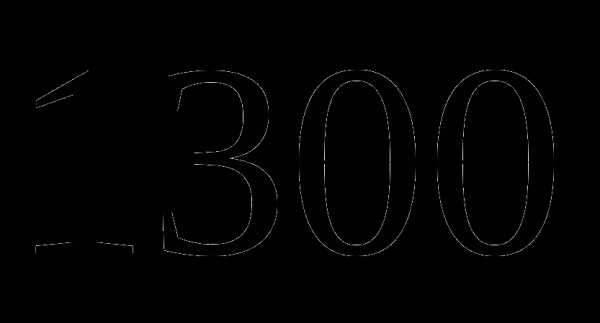 ;
;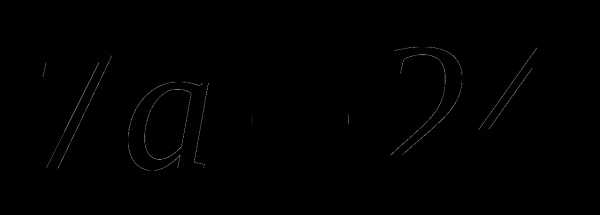 ;
; ;
; ;
;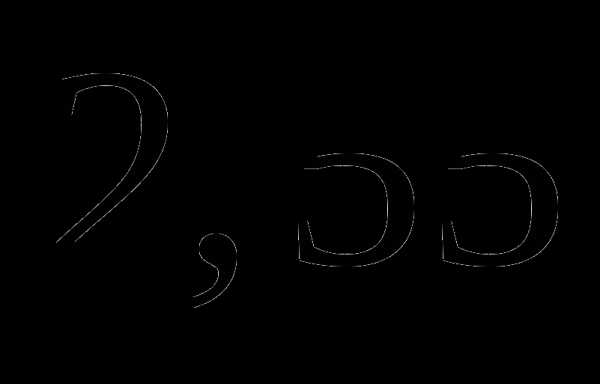 ;
;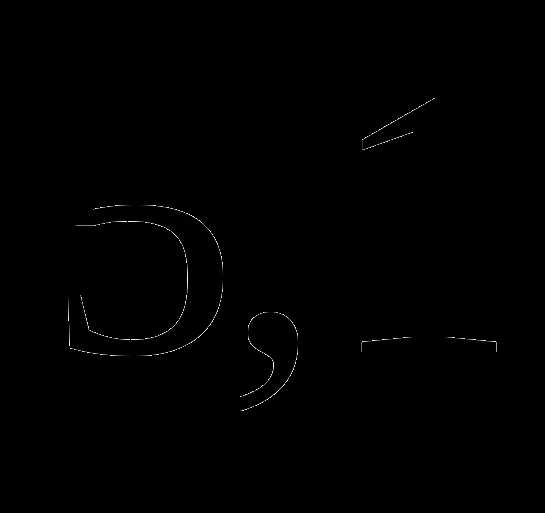 ;
;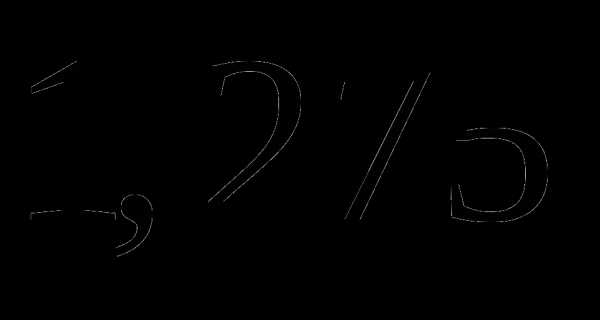 ;
;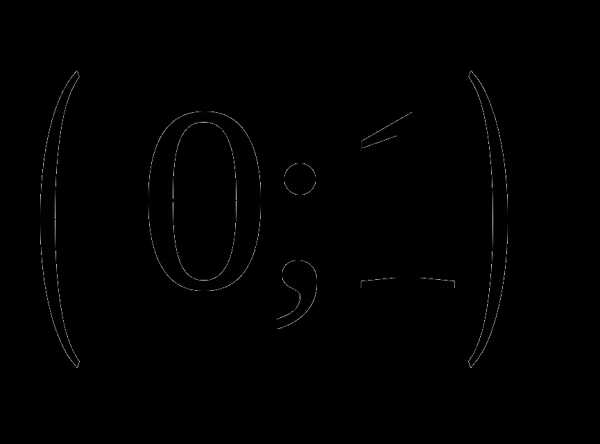 ;
;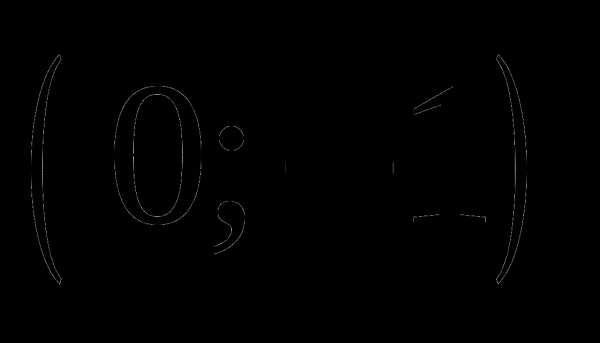 ;
;

 Авось
Авось Авось
Авось 0,5=
0,5= ; 2)
; 2)  =
= ; 3)
; 3)  =
=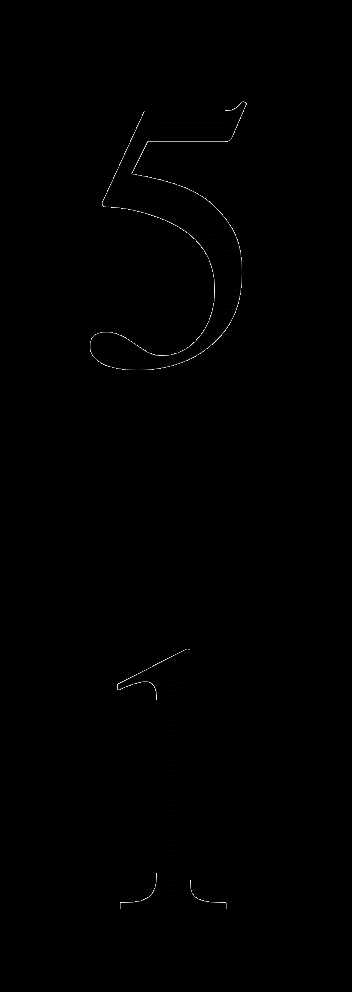 ; 4)
; 4)  =
= ; 5)
; 5) 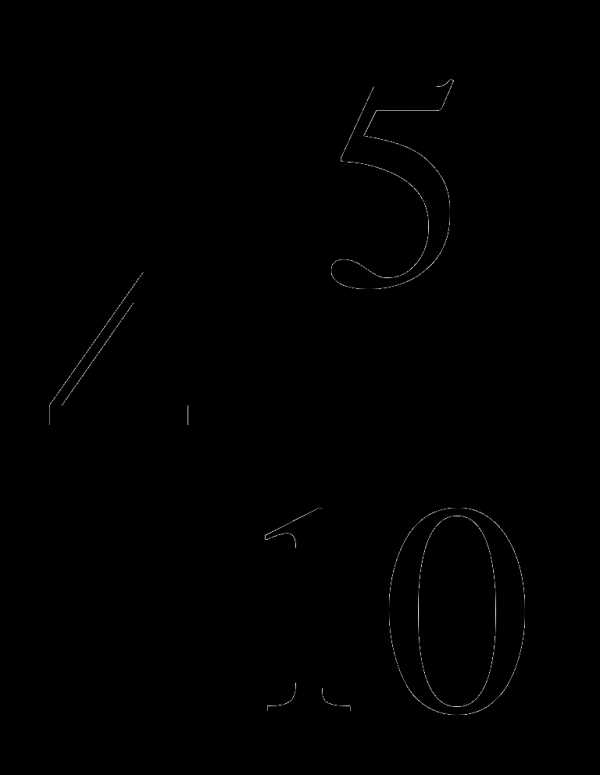 =
=


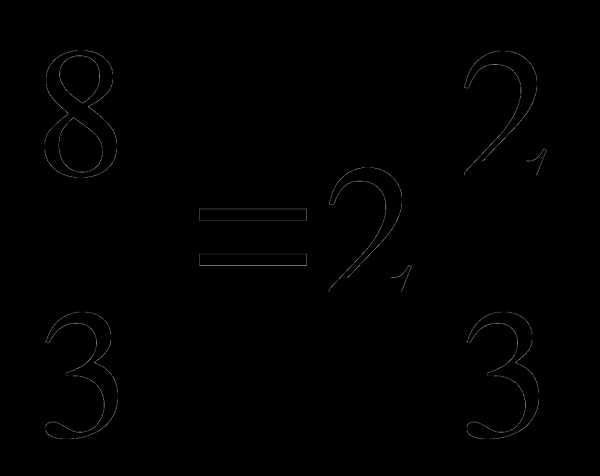
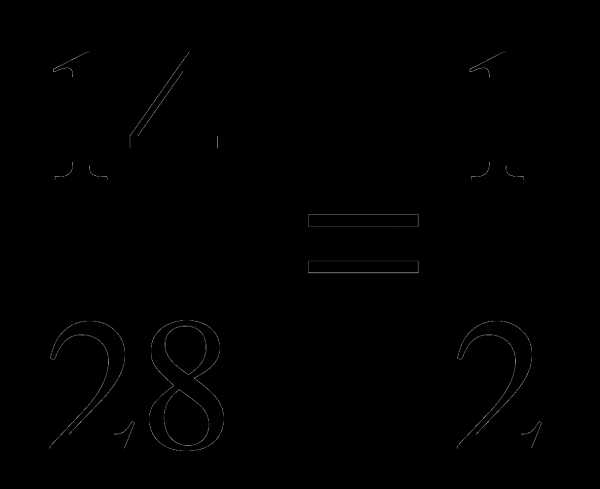




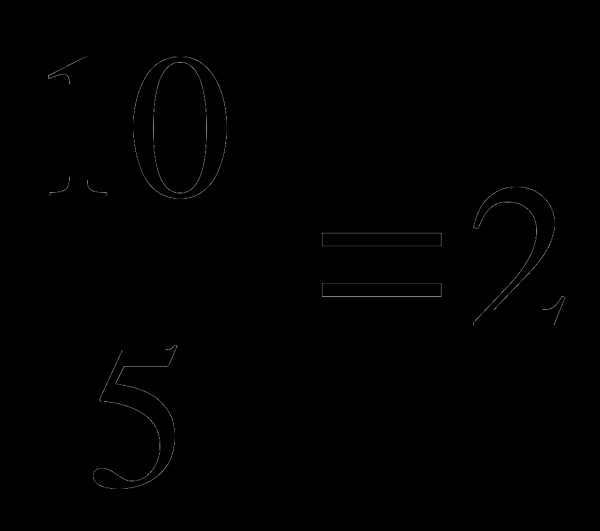

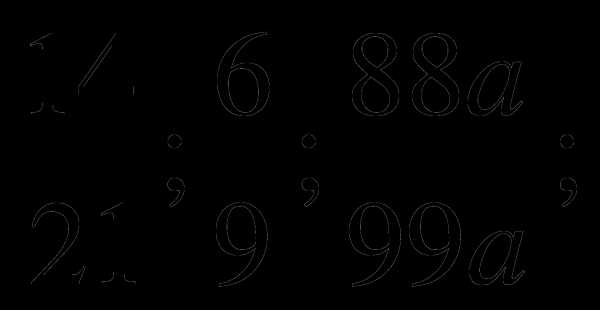
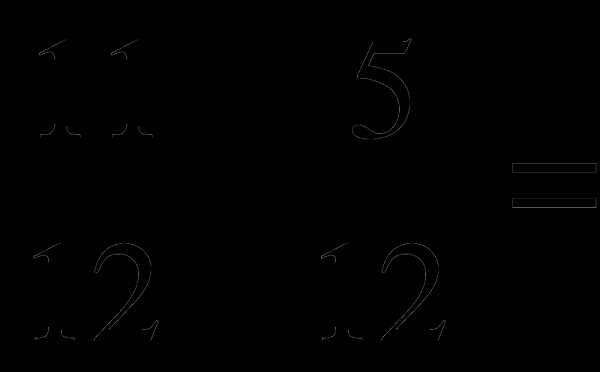 б)
б)
 ;
;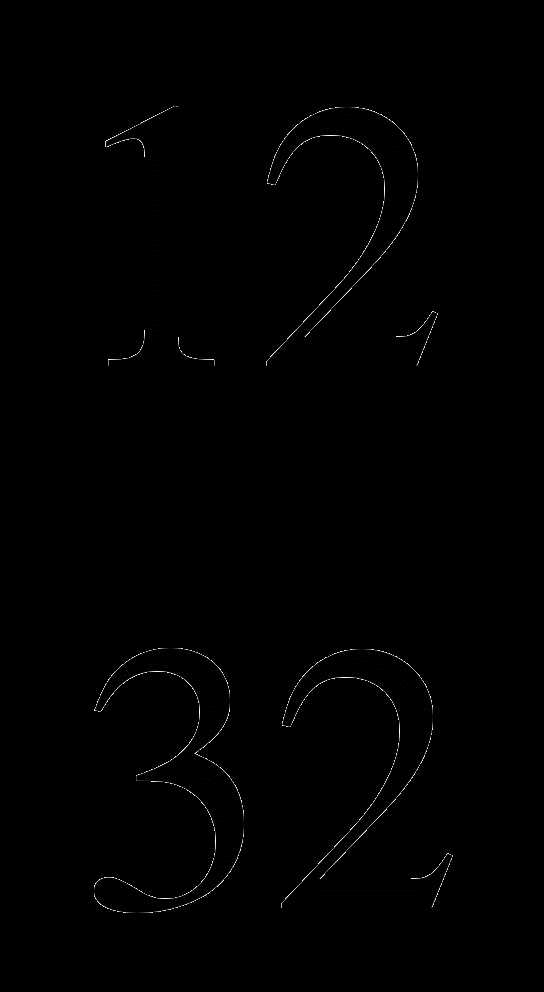 ;
; ;
; .
.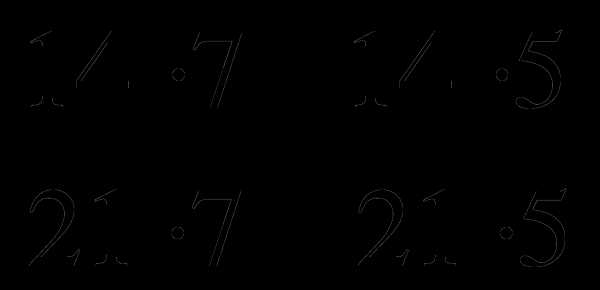
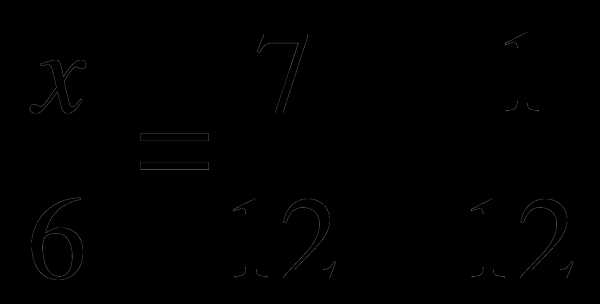 .
.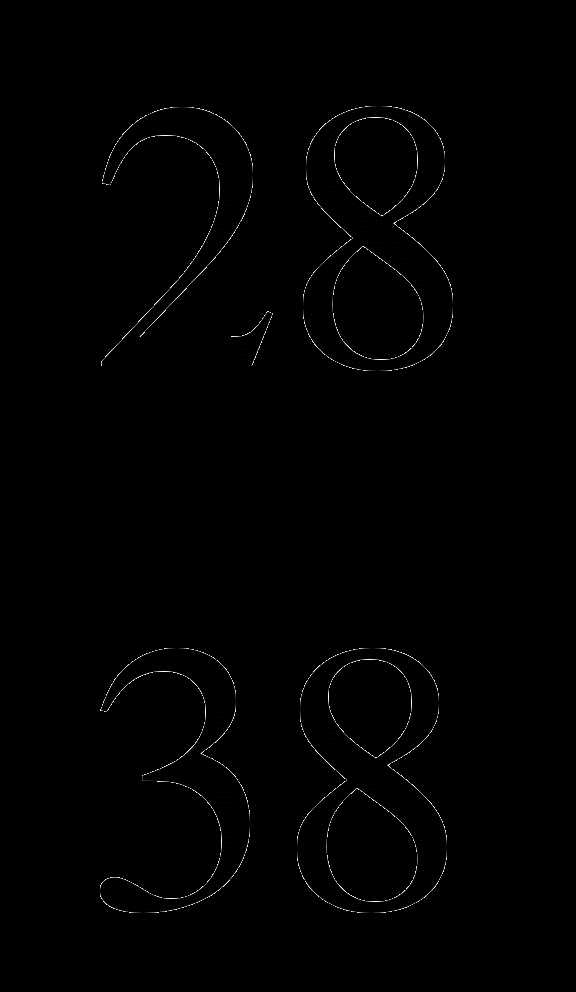 ;
; ;
;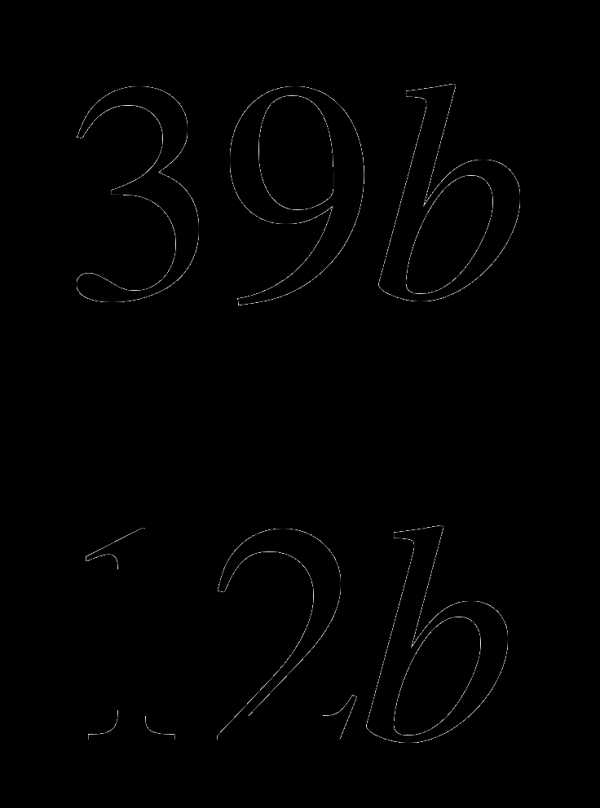 .
.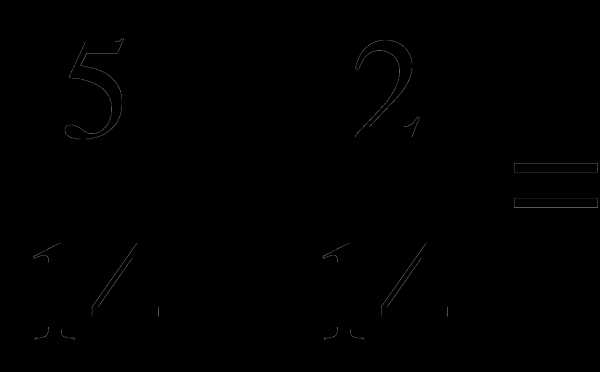 б)
б)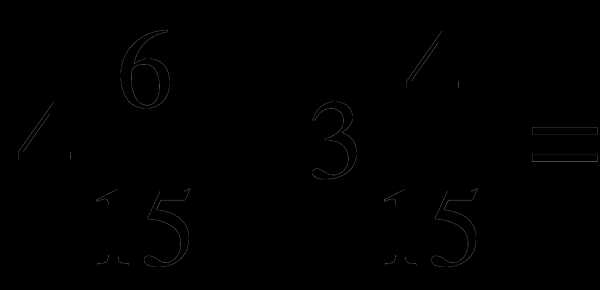
 ;
; ;
; .
.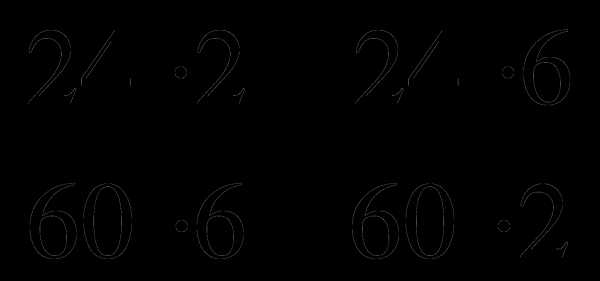
 .
.