Дроби по математике – Дроби

Дробь (математика) — Википедия

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Дробь.

8	/ 13		числитель
числитель	знаменатель		знаменатель
Две записи одной дроби

Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы^[1]. Дроби являются частью поля рациональных чисел. По способу записи дроби делятся на 2 формата: обыкновенные вида и десятичные.

[править] Обыкновенные дроби

Наглядное представление дроби

Обыкновенная (или простая) дробь — запись рационального числа в виде или где Горизонтальная или косая черта обозначает знак деления, в результате чего получается частное. Делимое называется числителем

дроби, а делитель — знаменателем.

[править] Обозначения обыкновенных дробей

Есть несколько видов записи обыкновенных дробей в печатном виде:

[править] Правильные и неправильные дроби

Правильной называется дробь, у которой модуль числителя меньше модуля знаменателя. Дробь, не являющаяся правильной, называется неправильной, и представляет рациональное число, по модулю большее или равное единице.

Например, дроби , и  — правильные дроби, в то время как , , и  — неправильные дроби. Всякое целое число можно представить в виде неправильной обыкновенной дроби со знаменателем 1.

[править] Смешанные дроби

Дробь, записанная в виде целого числа и правильной дроби, называется смешанной дробью и понимается как сумма этого числа и дроби. Любое рациональное число можно записать в виде смешанной дроби. В противоположность смешанной дроби, дробь, содержащая лишь числитель и знаменатель, называется простой.

Например, . В строгой математической литературе такую запись предпочитают не использовать из-за схожести обозначения смешанной дроби с обозначением произведения целого числа на дробь, а также из-за более громоздкой записи и менее удобных вычислений.

[править] Высота дроби

Высота обыкновенной дроби — модуль суммы числителя и знаменателя этой дроби. Высота рационального числа — модуль суммы числителя и знаменателя несократимой обыкновенной дроби, соответствующей этому числу.

Например, высота дроби равна . Высота же соответствующего рационального числа равна , так как дробь сокращается на .

[править] Составные дроби

Многоэтажной, или составной, дробью называется выражение, содержащее несколько горизонтальных (или реже — наклонных) черт:

или или

[править] Десятичные дроби

Десятичной дробью называют позиционную запись дроби. Она выглядит следующим образом:

Пример: .

Часть записи, которая стоит до позиционной запятой, является целой частью числа (дроби), а стоящая после запятой — дробной частью. Всякую обыкновенную дробь можно преобразовать в десятичную, которая в этом случае либо имеет конечное число знаков после запятой, либо является периодической дробью.

Вообще говоря, для позиционной записи числа́ можно использовать не только десятичную систему счисления, но и другие (в том числе и специфические, такие, как фибоначчиева).

[править] Значение дроби и основное свойство дроби

Дробь является всего лишь записью числа. Одному и тому же числу могут соответствовать разные дроби, как обыкновенные, так и десятичные.

Если умножить числитель и знаменатель дроби на одинаковую величину:

то значение дроби останется прежним, хотя дроби — разные. Например:

И обратно, если числитель и знаменатель заданной дроби имеют общий делитель, то обе части можно разделить на него; такая операция называется сокращением дроби. Пример:

 — здесь числитель и знаменатель дроби сократили на общий делитель 4.

Несократимой называется дробь, числитель и знаменатель которой взаимно просты, т. е. не имеют общих делителей, кроме

Для десятичной дроби запись почти всегда однозначна, однако имеются исключения. Пример:

 — две разные дроби соответствуют одному числу.

[править] Действия над дробями

В этом разделе рассматриваются действия над обыкновенными дробями. О действиях над десятичными дробями см. Десятичная дробь.

[править] Приведение к общему знаменателю

Для сравнения, сложения и вычитания дробей их следует преобразовать (привести) к виду с одним и тем же знаменателем. Пусть даны две дроби: и . Порядок действий:

• Находим наименьшее общее кратное знаменателей: .
• Умножаем числитель и знаменатель первой дроби на .
• Умножаем числитель и знаменатель второй дроби на .

После этого знаменатели обеих дробей совпадают (равны M). Вместо наименьшего общего кратного можно в простых случаях взять в качестве M любое другое общее кратное, например, произведение знаменателей. Пример см. ниже в разделе Сравнение.

[править] Сравнение

Чтобы сравнить две обыкновенные дроби, следует привести их к общему знаменателю и сравнить числители получившихся дробей. Дробь с бо́льшим числителем будет больше.

Пример. Сравниваем и . НОК(4, 5) = 20. Приводим дроби к знаменателю 20.

Следовательно,

[править] Сложение и вычитание

Чтобы сложить две обыкновенные дроби, следует привести их к общему знаменателю. Затем сложить числители, а знаменатель оставить без изменений:

+ = + =

НОК знаменателей (здесь 2 и 3) равно 6. Приводим дробь к знаменателю 6, для этого числитель и знаменатель надо умножить на 3.
Получилось . Приводим дробь к тому же знаменателю, для этого числитель и знаменатель надо умножить на 2. Получилось .
Чтобы получить разность дробей, их также надо привести к общему знаменателю, а затем вычесть числители, знаменатель при этом оставить без изменений:

 — =  — =

НОК знаменателей (здесь 2 и 4) равно 4. Приводим дробь к знаменателю 4, для этого надо числитель и знаменатель умножить на 2. Получаем .

[править] Умножение и деление

Чтобы умножить две обыкновенные дроби, нужно перемножить их числители и знаменатели:

В частности, чтобы умножить дробь на натуральное число, надо числитель умножить на число, а знаменатель оставить тем же:

В общем случае, числитель и знаменатель результирующей дроби могут не быть взаимно простыми, и может потребоваться сокращение дроби, например:

Чтобы поделить одну обыкновенную дробь на другую, нужно умножить первую на дробь, обратную второй:

Например,

[править] Преобразование между разными форматами записи

Чтобы преобразовать обыкновенную дробь в дробь десятичную, следует разделить числитель на знаменатель. Результат может иметь конечное число десятичных знаков, но может быть и бесконечной периодической дробью. Примеры:

 — бесконечно повторяющийся период принято записывать в круглых скобках.

Чтобы преобразовать десятичную дробь в дробь обыкновенную, следует представить её дробную часть в виде натурального числа, делённого на соответствующую степень 10. Затем к результату приписывается целая часть со знаком, формируя смешанную дробь. Пример:

[править] История и этимология термина

Русский термин дробь, как и его аналоги в других языках, происходит от лат. fractura, который, в свою очередь, является переводом арабского термина с тем же значением: ломать, раздроблять. Фундамент теории обыкновенных дробей заложили греческие и индийские математики.

Впервые в Европе данный термин употребил Леонардо Пизанский (1202). Поначалу европейские математики оперировали только с обыкновенными дробями, а в астрономии — с шестидесятеричными. Полноценная теория обыкновенных дробей и действий с ними сложилась в XVI веке (Тарталья, Клавиус).

В древней Руси дроби называли долями или ломаными числами. Термин

дробь, как аналог латинского fractura, используется в «Арифметике» Магницкого (1703) как для обыкновенных, так и для десятичных дробей.

Десятичные дроби впервые встречаются в Китае примерно с III века н. э. при вычислениях на счётной доске (суаньпань). В письменных источниках десятичные дроби ещё некоторое время изображали в традиционном (не позиционном) формате, но постепенно позиционная система вытеснила традиционную^[3]. Персидский математик и астроном Джамшид Гияс-ад-дин ал-Каши (1380—1429) в трактате «Ключ арифметики» объявил себя изобретателем десятичных дробей, хотя они встречались в трудах Ал-Уклидиси, жившего на 5 веков раньше^[4].

В Европе первые десятичные дроби ввёл Иммануил Бонфис около 1350 года, но широкое распространение они получили только после появления сочинения Симона Стевина «Десятая» (1585).

web.archive.org

Простые дроби, дробь, знаменатель дроби, числитель дроби | Формулы и расчеты онлайн

Простой дробью (или просто, дробью) называется часть единицы или несколько равных частей (долей) единицы.

простые дроби, числитель, знаменатель. Кольцо разделено на 5 секторов. 3 из них красные.

Знаменатель дроби — Число, показывающее на сколько долей разделена единица.

Числитель дроби — Число, показывающее количество взятых долей.

Запись:

\[ \frac{3}{5} \]

или 3/5 (три пятых), здесь 3 — числитель, 5 — знаменатель.

Если числитель меньше знаменателя, то дробь меньше единицы и называется правильной:

\[ \frac{3}{5} — правильная дробь. \]

Если числитель равен знаменателю, дробь равна единице.

Если числитель больше знаменателя, дробь больше единицы. В обоих последних случаях дробь называется неправильной.

Например:

\[ \frac{5}{5} , \frac{17}{5} — неправильные дроби. \]

Чтобы выделить наибольшее целое число, содержащееся в неправильной дроби, нужно разделить числитель на знаменатель. Если деление выполняется без остатка, то взятая неправильная дробь равна частному.

Например:

\[ \frac{45}{5} = 45 : 5 = 9 \]

Смешанные числа

Если деление выполняется с остатком, то (неполное) частное дает искомое целое число, остаток же становится числителем дробной части; знаменатель дробной части остается прежним.

Пример:

Дана дробь

\[ \frac{48}{5} \]

Делим 48 на 5. Получаем частное 9 и остаток 3.

\[ \frac{48}{5} = 9 \frac{3}{5} \]

Число, содержащее целую и дробную части

\[ 9 \frac{3}{5} \]

называется смешанным. Дробная часть смешанного числа может быть и неправильной дробью.

Например:

\[ 7 \frac{13}{5} \]

тогда можно из дробной части выделить наибольшее целое число и представить смешанное число в таком виде, чтобы дробная часть стала правильной дробью (или вовсе исчезла).

Например:

\[ 7 \frac{13}{5} = 7 + \frac{13}{5} = 7 + 2\frac{3}{5} = 9\frac{3}{5} \]

К подобному виду обычно и приводят смешанные числа.

Часто приходится (например, при умножении дробей) решать вопрос обратного характера:

Дается смешанное число,
требуется представить его в виде дроби (неправильной).
Для этого нужно:
1) целое число, входящее в смешанное, помножить на знаменатель дробной части;
2) к произведению прибавить числитель.
Полученное число будет числителем искомой дроби, знаменатель остается прежний.

Пример:

Дано смешанное число

\[ 9 \frac{3}{5} \]

\[ 9 · 5 = 45\]

\[ 45 + 3 = 48\]

\[ 9 \frac{3}{5} = \frac{48}{5} \]

В помощь студенту

Простые дроби, дробь, знаменатель дроби, числитель дроби	стр. 26

www.fxyz.ru

Обыкновенные дроби. Теория.

В математике дробь — это число, состоящее из одной или нескольких частей (долей) единицы. По форме записи дроби делятся на обыкновенные (пример \frac{5}{8}) и десятичные (например 123,45).

Определение. Обыкновенная дробь (или простая дробь)

Обыкновенной (простой) дробью называется число вида \pm\frac{m}{n} где m и n – натуральные числа. Число m называется числителем этой дроби, а число n – её знаменателем.

Горизонтальная или косая черта обозначает знак деления, то есть \frac{m}{n}={}^m/n=m:n

Обыкновенные дроби делятся на два вида: правильные и неправильные.

Определение. Правильная и неправильная дроби

Правильной называется дробь, у которой модуль числителя меньше модуля знаменателя. Например, \frac{9}{11}, ведь 9

Неправильной называется дробь, у которой модуль числителя больше или равен модулю знаменателя. Такая дробь представляет собой рациональное число, по модулю большее или равное единице. Примером будут дроби \frac{11}{2}, \frac{2}{1}, -\frac{7}{5}, \frac{1}{1}

Наряду с неправильной дробью существует иная запись числа, которая называется смешанной дробью (смешанным числом). Такая дробь не является обыкновенной.

Определение. Смешанная дробь (смешанное число)

Смешанной дробью называется дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби. Например, 2\frac{5}{7}

(запись в виде смешанного числа)2\frac{5}{7}=2+\frac{5}{7}=\frac{14}{7}+\frac{5}{7}=\frac{19}{7}(запись в виде неправильной дроби)

Дробь является всего лишь записью числа. Одному и тому же числу могут соответствовать разные дроби, как обыкновенные, так и десятичные. Сформируем признак равенства двух обыкновенных дробей.

Определение. Признак равенства дробей

Две дроби \frac{a}{b} и \frac{c}{d} являются равными, если a\cdot d=b\cdot c. Например, \frac{2}{3}=\frac{8}{12} так как 2\cdot12=3\cdot8

Из указанного признака следует основное свойство дроби.

Свойство. Основное свойство дроби

Если числитель и знаменатель данной дроби умножить или разделить на одно и то же число, неравное нулю, то получится дробь, равная данной.

\frac{A}{B}=\frac{A\cdot C}{B\cdot C}=\frac{A:K}{B:K};\quad C \ne 0,\quad K \ne 0

С помощью основного свойства дроби можно заменить данную дробь другой дробью, равной данной, но с меньшими числителем и знаменателем. Такая замена называется сокращением дроби. Например, \frac{12}{16}=\frac{6}{8}=\frac{3}{4} (здесь числитель и знаменатель разделили сначала на 2, а потом ещё на 2). Сокращение дроби можно провести тогда и только тогда, когда её числитель и знаменатель не являются взаимно простыми числами. Если же числитель и знаменатель данной дроби взаимно просты, то дробь сократить нельзя, например, \frac{3}{4} – несократимая дробь.

Правила для положительных дробей:

Из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше. Например, \frac{3}{15}.

Из двух дробей с одинаковыми числителями больше та дробь, знаменатель которой меньше. Например, \frac{4}{11}>\frac{4}{13}.

Чтобы сравнить две дроби с разными числителями и знаменателями, нужно преобразовать обе дроби так, чтобы их знаменатели стали одинаковыми. Такое преобразование называется приведением дробей к общему знаменателю.

onsolver.ru

Дроби

Раздел содержит учебные материалы для учащихся 5-6 классов.

Дроби. Введение

Введение
5 класс

Три различных вида дробей

Виды дробей
5 класс

Сокращение дробей, упрощение с помощью НОД

Сокращение дробей
6 класс

Сравнение дробей, нахождение наименьшего общего знаменателя

Сравнение дробей
6 класс

Сложение, вычитание, умножение, деление дробей

Операции с дробями
5-6 класс

Перевод дробей в проценты и десятичную дробь

Перевод дробей
6 класс

Дроби. Введение

Три различных вида дробей

Сокращение дробей, упрощение с помощью НОД

Сравнение дробей, нахождение наименьшего общего знаменателя

Сложение, вычитание, умножение, деление дробей

Перевод дробей в проценты и десятичную дробь

calcs.su

Урок по математике для 5 класса по теме «Что такое дробь»

Конспект урока по математике

Класс: 5

Тема урока: Что такое дробь

Тип урока: Урок открытия новых знаний

Цели урока:

Содержательная: повторить материал по теме «Доли», сформировать понятие обыкновенной дроби, числителя и знаменателя дроби, сформировать понятие правильных и неправильных дробей.

Деятельностная: сформировать умение читать, записывать и понимать значение обыкновенной дроби, сформировать умение понимать и различать правильные и неправильные дроби, сформировать умение решать задачи с использованием дробей.

Планируемые образовательные результаты:

Предметные: знать и оперировать понятиями обыкновенная дробь, числитель и знаменатель, правильная и неправильная дробь; уметь читать, понимать и записывать обыкновенные дроби; уметь применять и оперировать дробями в решении задач; уметь выполнять устно и письменно арифметические действия с числами.

Личностные: формирование познавательного интереса к предмету, формирование устойчивой мотивации к закреплению материала.

Метапредметные:

А) Регулятивные: осознает качество и уровень усвоения материала, самостоятельно обнаруживает и формулирует учебную проблему, самостоятельно планирует пути достижения целей.

Б) Познавательные: дает определение понятиям, строит логическое рассуждение, умозаключение и делает выводы.

В) Коммуникативные: грамотно и правильно описывает содержание совершаемых действий с целью ориентировки в предметно-практической деятельности, проявляет готовность к обсуждению разных точек зрения.

Формы организации учебной деятельности: фронтальная, индивидуальная.

Оборудование: презентация, мел, доска, учебник, наглядные пособия.

готовность к выполнению норм и требований учителя.

2. Актуа-лизация знаний

5 мин

— Все выполнили домашнее задание? Были какие-нибудь трудности при его выполнении?

Разобрать номера из домашнего задания, вызвавшие трудности, на доске.

— Давайте вспомним, что мы изучали на прошлом занятии.

— А что же называют долями?

— Если у нас есть большой торт и его нужно разделить на всех в классе, то какую долю торта получит каждый?

— А если я хочу поделить торт только на мальчиков? Или только на девочек?

— А теперь скажите, если мы будем делить торт только на мальчиков или только на девочек, то в каком случае доли (кусочки) торта будут больше? То есть что больше: седьмые или двенадцатые доли торта?

— Молодцы! Всё правильно!

Задают вопросы по домашнему заданию.

— Изучали доли.

— Равные части, на которые поделен какой-либо предмет.

— Торт поделим на 19 кусочка и каждый получит по одной девятнадцатой доли торта.

— То каждый мальчик получит по одной двенадцатой доли торта. Или каждая девочка по одной седьмой доли торта.

— Седьмые доли торта больше, потому что мы делим торт на меньшее количество частей, и поэтому у девочек будут кусочки торта больше.

Личностные:

умение вести диалог.

Коммуникативные:

адекватно использовать речевые средства для решения различных задач; владеть устной и письменной речью; аргументировать свою точку зрения.

Познавательные:

давать определение понятиям; строить логическое рассуждение, включающее установление причинно-следственных связей.

3. Изложе-ние нового матери-ала

15 мин

Цветная таблица по математике на тему дроби, Спектр.

Бумажные фигуры и предметы, разрезанные на равные части (торт, апельсин, яблоко).

Презентация на тему «Что такое дробь. Обыкновенные дроби».

— Теперь открываем тетради, записываем число и тему урока «Что такое дробь». На этом уроке мы познакомимся с понятием «дроби», узнаем, что же такое обыкновенная дробь, научимся читать и записывать обыкновенные дроби.

— Вы все, наверное, слышали песенку с такими словами:

Мы делили апельсин, 
Много нас, а он один! 
Эта долька для ежа, 
Эта долька для стрижа, 
Это долька для котят, 
Эта долька для утят…

— На сколько животных в этой песенке делят апельсин?

— Верно, на четверых, а, значит, по какой доле апельсина получит каждый?

— Верно, по одной четвертой доле или части апельсина. А записывают это так: ¼. Записи такого вида называют обыкновенными дробями.

— Теперь давайте посмотрим, что же показывает число, находящееся под чертой? 

— Верно. Итак, число, показывающее, на сколько долей делят, мы будем называть знаменателем.

— А что показывает число, находящееся над чертой? 

— Верно. Его называют числителем.

Итак, теперь сделаем запись в тетради: Запись вида a/b, где a и b натуральные числа, называется обыкновенной дробью. a — числитель дроби, b — знаменатель дроби, черта между ними – дробная черта.

— А теперь обратите внимание на экран. Мы видим апельсин, разделенный на шесть частей. Если мы возьмем все шесть его частей, то какую дробь мы получим? И какой вывод мы можем из этого сделать?

— Верно. На следующем слайде мы видим два одинаковых апельсина, так же разделенных на шесть частей. Если мы возьмем один апельсин целиком и еще две части другого, то получится 8/6 апельсина. А если мы возьмем один апельсин целиком и еще пять частей другого, то какая получится дробь?

— Верно, молодцы.

— Теперь запишем следующее определение в тетрадь: Дробь, в которой числитель меньше знаменателя, называется правильной. Дробь, в которой числитель равен ли больше знаменатель, называется неправильной.

Пишут в тетрадях число и тему урока.

— На четверых.

— По одной четвертой доле апельсина.

— На сколько одинаковых частей (долей) поделили апельсин.

— Сколько таких частей (долей) мы взяли.

Записывают определение в тетрадь.

— Шесть шестых 6/6 апельсина. Если числитель равен знаменателю, значит, мы взяли апельсин полностью, целый.

— Одиннадцать шестых 11/6 апельсина.

Записывают определение в тетрадь.

Личностные:

готовность и способность к выполнению норм и обязанностей ученика; умение вести диалог; устойчивый познавательный интерес и становление смыслообразующей функции познавательного мотива.

Регулятивные:

самостоятельно оценивать правильность выполнения действий, планировать пути достижения целей; уметь контролировать своѐ время и управлять им.

Коммуникативные: формулировать собственное мнение и позицию, аргументировать еѐ; задавать вопросы, необходимые для организации собственной деятельности; адекватно использовать речевые средства для решения различных задач; владеть устной и письменной речью.

Познавательные:

устанавливать причинно- следственные связи; строить логическое рассуждение; осуществлять логическую операцию перехода от видовых признаков к родовому понятию.

4. Физми-нутка 1мин

— Сделаем небольшой перерыв и проведем физминутку!

Одолела нас дремота, 
Шевельнуться неохота
Ну-ка делайте со мною 
Упражнение такое:
Раз – поднялись, потянулись,
Два – нагнулись, разогнулись,
Три – в ладоши три хлопка
Головою три кивка.

Выполняют упражнения.

5. Первич-ное закреп-ление

15 мин

Бумажные фигуры и предметы, разрезанные на равные части (торт, апельсин, яблоко, часы).

Презентация на тему «Что такое дробь. Обыкновенные дроби».

— А теперь давайте посмотрим на доску. Мы видим яблоко. Оно у нас поделено на 8 долек. Теперь, если мы разделим все дольки на четверых, какую часть получит каждый?

— Правильно! А чему будет равен числитель в этой дроби? А знаменатель?

— Откройте учебник на странице 164, давайте устно решим номер 620.

— А теперь давайте немного поиграем. Я буду называть дроби, а вы должны будете определить правильная она или неправильная. Если дробь правильная, то вы хлопаете в ладоши, если неправильная – нет. Начнем! (Дроби из №628)

— Какие все молодцы!

— А теперь давайте научимся правильно читать дроби. Называя числитель, мы отвечаем на вопрос «Сколько (частей)?» и, помним, что числитель будет иметь женский род. Одна (часть), две (части), восемь (частей), двадцать пять (частей) и т.д. А называя знаменатель, мы отвечаем на вопрос «Из каких (частей)?». Вторых, третьих, восьмых, сотых (частей).

— Давайте попробуем прочитать дроби, которые на слайде, по цепочке по одной дроби каждый.

— А вот скажите мне, как прочитать вот такую дробь: 3/0? И будет ли вообще это число дробью? И почему?

— Правильно, ребята! Теперь приступим к выполнению № 623 на странице 165. Кто желающий выйти к доске? Остальные записывайте решение в тетрадь.

Далее так же решаются №624 и 625. Учитель отвечает на уточняющие вопросы учащихся, корректирует и направляет выполнение заданий.

 

— Две восьмых.

— Двум.

— Восьми.

Учащиеся устно отвечают по картинкам, какая часть фигуры закрашена и не закрашена. Один желающий записывает соответствующие дроби на доске.

Учащиеся играют в игру.

Читают дроби.

— Не будет. Потому что числитель и знаменатель должны быть натуральными числами по определению, а 0 не является натуральным числом. И на 0 делить нельзя.

Желающий решает задачу у доски, остальные записывают в тетрадь.

Личностные:

готовность и способность к выполнению норм и обязанностей ученика; умение вести диалог; устойчивый познавательный интерес и становление смыслообразу-ющей функции познавательного мотива.

Регулятивные:

самостоятельно анализировать условия достижения цели; самостоятельно оценивать правильность выполнения действий и вносить необходимые коррективы.

Коммуникативные:

задавать вопросы, необходимые для организации собственной деятельности; адекватно использовать речевые средства для решения различных задач; владеть устной и письменной речью; отображать в речи содержание совершаемых действий.

Познавательные:

устанавливать причинно- следственные связи; строить логическое рассуждение; давать определение понятиям.

6. Поста-новка дом. задания 2 мин

— Итак, сегодня все хорошо поработали! А теперь достаем дневники и запишем домашнее задание. Дома вам предлагаю выполнить творческое задание: на квадрате со стороной 4 клетки различными способами закрасить 1/2. А также п. 8.2, выучить определения из тетради, № 627, 637, 639.

Учащиеся делают запись в дневнике, задают вопросы по домашнему заданию.

Личностные:

готовность и способность к выполнению норм и обязанностей ученика.

7. Рефлек-сия. Итог урока.

2 мин

— Теперь давайте подведём итог нашего урока. С какими важными понятиями мы сегодня познакомились на уроке?

— Все верно, молодцы! Спасибо всем за урок, все свободны. До свидания!

— Мы узнали, что такое обыкновенная дробь, числитель, знаменатель, дробная черта, правильная и неправильная дробь, научились читать и записывать обыкновенные дроби.

— До свидания.

Коммуникативные:

отображать в речи содержание совершаемых действий.

infourok.ru

Технологическая карта внеклассного мероприятия по математики по теме «Путешествие в страну дроби»

Озеро Ребусное

Здесь командам предлагается решить ребус и расшифровать анаграмму.

1. и т л и ь л е с ч

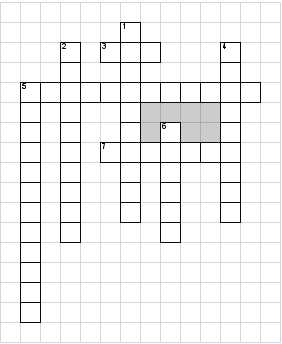
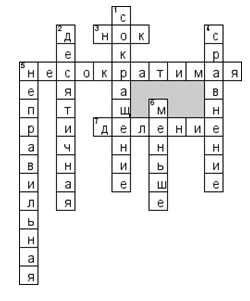
Замок Кроссвордный

По горизонтали

3. наименьшее натуральное число, которое кратно и a, и b.

5. Дробь у которой числитель и знаменатель взаимно простые числа

7. что означает дробная черта?

По вертикали

1. Деление числителя и знаменателя на одно и то же число.

2. дробь,в которой запятой, отделяем количество нулей в знаменателе

4. как называется действие, определяющее большую из двух дробей?

5. Название дроби, у которой числитель больше или равен знаменателю.

6. правильная дробь ….. единицы

Пролив правил

1. Какая дробь называется правильной?

2. Как из неправильной дроби выделить целую часть?

3. Сформулировать основное свойство дроби?

4. Правило сложения обыкновенных дробей с разными знаменателями?

5. Что называется сокращением дробей?

6. В каком случае дробь можно сократить?

Лес Сказочный

Чтобы продолжить наше путешествие, необходимо узнать имя хозяина леса. Расположите дроби в порядке возрастания и узнаете имя хозяина.

								1
и	е	к	с	о	л	в	о	ч

Мост Координатный

Для I команды: Изобразите на числовом луче, приняв за единичный отрезок 10 клеток, точки соответствующие дробям: 

Расположите дроби на числовом луче и вы расшифруете слово.

Для II команды: Изобразите на числовом луче, приняв за единичный отрезок 9 клеток, точки соответствующие дробям: 

Расположите дроби на числовом луче и вы расшифруете слово.

Горы Мозгодром

Готовятся карты игрового поля. Каждое поле содержит девять клеток с примерами. Каждой клетке соответствует карточка с ответом. На этой же карточке записывается слово или слова. При правильном наложении карточек на клетки игрового поля учащиеся получают фразу.

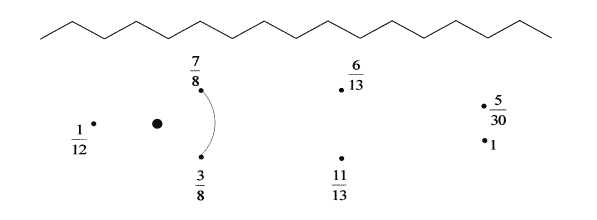
Избушка Художника

Командам выдается задание. Необходимо внимательно прочитать задание и приступить к его выполнению. Вам на выполнение отведено 5 – 6 минут.

Выполните действия.

Сравните результаты с указанными на рисунке ответами.

Соедините ответы карандашом в той последовательности, в которой они были получены и у вас получится рисунок.

Для I команды

Для II команды

Поселок Задачкино

Команды поочередно устно решают задачки:

1. В 2008 году 366 дней. В феврале – 29 дней, а в сентябре 30 день. Какую часть года составляет февраль, а какую – сентябрь?

2. Коля и Ира разделили апельсин пополам, каждому досталось 6 долек, однако к ним присоединились Таня и Вася. Коля и Ира отделил от своей доли апельсина половину и уступил ее ребятам. Какая часть апельсина досталась каждому из ребят.

Дробь

Числитель

1. У которой числитель меньше знаменателя

2. разделить с остатком числитель на знаменатель;

полученное неполное частное записываем в целую часть дроби;

остаток записываем в числитель дроби;

делитель записываем в знаменатель дроби.

3. если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

4. Нужно привести дроби к наименьшему общему знаменателю и выполнить сложение.

5. Деление числителя и знаменателя дроби на одно и то же число.

6. Если числитель и знаменатель не взаимно простые числа.

Лесовичок

ОСТАТОК

ОТРЕЗОК

I команды – две равные дроби обозначают одно и то же дробное число.

II команды – на координатном луче равные дроби соответствуют одной и той же точке

1.

2.

3.

4.

5.

6.

7.

8.

1.

2.

3.

4.

5.

6.

7.

8.

multiurok.ru

Дроби — это важно!

    Здравствуйте, Дорогие друзья! Эх, дроби, дроби, дроби… Кому-то из ребят эти самые дроби понятны и они с ними «работают» быстро и, как говорится, без затруднений. А у кого-то при этом слове возникает чувство горечи и невольно произносится: «Опять эти дроби :(».

А ведь эти самые дроби проходят сквозной нитью практически через все разделы математики –  уравнения и неравенства, задачи по геометрии, задачи на движение и работу, преобразование выражений, можно перечислять и перечислять.

Навык работы с дробями и понимание сути этой «дробной жизнедеятельности», я бы сказал – КРИТИЧЕСКИ необходимы! Не разберёшься с дробями – кранты!!! Экзамен если повезёт сдашь на 20 баллов. А если вдруг получите наследство от дяди из-за границы, например 13/63 от всего его состояния, тоже не сможете вычислить сколько вам причитается )))

Не секрет, что для некоторых учащиеся в старших классах дробь вообще некое непонятное полузабытое «создание». И для педагогов уже давно не удивителен факт, что в 9-11 классах ребята при сложении дробей складывают  числитель с числителем, а знаменатель со знаменателем.

При умножении теряются – что же делать-то? А при делении дроби на дробь вообще не понимают как быть – вроде бы что-то куда-то переворачивать нужно. И это при том, что всё ранее вроде бы было понятно и решали правильно. А в чём же дело тогда? Ответ прост – именно в понимании и систематичности практических занятий, закреплении навыков.

Надеюсь, что после изучения статей у вас с дробями всё заладится, по крайней мере, в этой теме больше не возникнет вопросов. Останется только лишь периодически практиковаться.

Содержание всей группы статей про дроби:

1. Вступление (уже было, смотрите выше).
2. Числитель и знаменатель. Виды дробей.
3. Что выражают дробью.
4. Основное свойство дроби.
5. Перевод дробей из одного вида в другой.
6. Сокращение дробей.
7. Действия с дробями.
8. Сравнение дробей.

*Кому будет полезна статья? ВСЕМ!!! С 5 по 11 класс, в том числе и родителям желающим помочь своим деткам в самом начале изучения темы. Учителям, надеюсь, тоже пригодится.

Рекомендация! Изучайте материал последовательно по пунктам.

С уважением, Александр Крутицких.

Делитесь информацией в социальных сетях.

matematikalegko.ru