Статьи по математике | Математика, которая мне нравится
14 Февраль 2018, 23:43
инж. С.В.Савич
Посвящаю
Виктору Ивановичу Поленякину,
Георгию Иосифовичу Кирьянову
В процессе решения практических расчётных задач довольно часто возникает необходимость вычисления корней разной степени. Обычно при программировании на ЭВМ для этой цели используются стандартные библиотечные функции вычисления логарифма и экспоненты или итерационные методы. Аналитические методы последовательных приближений, часто применяемые при вычислении арифметических корней, имеют универсальный характер, однако обладают некоторыми недостатками, одним из которых является зависимость времени вычисления от величины аргумента и от выбора первого приближения. Значительно лучшие характеристики при вычислении, например, квадратного корня, показывает метод, описанный в статье “Оригинальный метод извлечения квадратного корня” (www.hijos.ru/2012/04/25/), который можно отнести к группе методов “цифра за цифрой”. Особенность этого метода, основанного на свойстве суммы членов арифметической прогрессии нечётных чисел, заключается в получении на каждом циклически повторяющемся шаге одной верной цифры результата.
В ходе анализа данного метода возникла идея распространить его концепцию на процесс вычисления корней -й степени, а также провести численное исследование получаемых алгоритмов. Основанием для такого подхода является то обстоятельство, что последовательность нечётных чисел, используемая для вычисления квадратного корня — это не только арифметическая прогрессия с шагом , но, — главное в этой идее, — также ряд первых конечных разностей (далее — конечные разности) для квадратичной функции с единичным шагом изменения аргумента.
Упомянем коротко метод “цифра за цифрой”, применяемый для “ручного” вычисления квадратного корня, заключающийся в том, что из подкоренного числа, разбитого на пары, в определённом порядке последовательно вычитается выражение (здесь — целое число, составленное из уже найденных цифр корня, — искомая следующая цифра корня, определяемая подбором), при условии, чтобы значение этого выражения не превышало текущее уменьшаемое. Детально этот способ описан в учебной и справочной литературе, сейчас он имеет лишь историческое значение. Читать полностью ‘О вычислении арифметических корней’ »
10 Сентябрь 2017, 20:44

Никто не может раскрыть тайну
Число — в самом деле загадочное число. Это не бросается в глаза. Но как мы сейчас увидим, любой, кто умеет вычитать, может раскрыть тайну числа .
Операция Капрекара
В 1949 году математик Д. Р. Капрекар из Деолали, Индия, разработал процесс, известный теперь как операция Капрекара. Сначала выберем четырехзначное число, состоящее хотя бы из двух различных цифр. Затем переставим его цифры, чтобы получить самое большое и самое маленькое из возможных чисел, образованных цифрами этого числа. Наконец, вычтем самое маленькое число из самого большого, получим новое число, для которого снова повторим операцию.
Это простая операция, но Капрекар обнаружил, что она приводит к неожиданному результату. Давайте попробуем делать ее, начиная с числа . Максимальное число, которое мы можем составить из этих цифр, равно , минимальное — или (если одна или несколько цифр равны нулю, поместим нули слева для минимального числа). Читать полностью ‘Таинственное число 6174’ »
4 Сентябрь 2017, 23:43

«Бог создал целые числа, всё остальное — дело рук человека» (Леопольд Кронекер)
Возьмем число. Переставим его цифры в обратном порядке, получим еще одно число. Теперь сложим эти два числа. Является ли сумма палиндромом (числом, читающимся с конца так же, как с начала)? Если нет, переставим цифры суммы и повторим процесс. Будем продолжать операции перестановки цифр и сложения до тех пор, пока не получим палиндром. Большинство чисел становятся палиндромами очень быстро, за несколько итераций. Возьмем, например, число ; требуется всего две итерации.
| Итерация | Число | Перестановка | Сумма | ||
| 1 | 153 | + | 351 | = | 504 |
| 2 | 504 | + | 405 | = | 909 |
Однако некоторые числа не становятся палиндромами вне зависимости от того, сколько сделано итераций записывания цифр в обратном порядке и сложения. Такие числа называются числами Лишрел. Они были названы так Уэйдом Ван Ландингхемом (Wade Van Landingham; Лишрел — примерная анаграмма имени его подруги Шерил, по-английски Lychrel — Cheryl). Первое число, которое может быть числом Лишрел — . Однако нет доказательства, что это число, а также числа похожие на него, такие как и в самом деле являются числами Лишрел. Просто процедура перестановки —сложения для них не привела к получению палиндрома, хотя было сделано около миллиарда итераций.
Читать полностью ‘Числа Лишрел’ »
26 Май 2017, 23:22

Каков средний вес человека?
Основная идея статистики заключается в том, что о населении в целом можно сказать что-то, выяснив это для меньшей группы людей. Без этой идеи не было бы опросов общественного мнения или предвыборных прогнозов, не было бы возможности испытать новые медицинские препараты или исследовать безопасность мостов и т. д. В значительной степени за факт, что мы можем делать все это и уменьшать неопределенности прогнозов, отвечает центральная предельная теорема.
Чтобы понять, как работает теорема, представим, что нужно узнать средний вес жителя Великобритании. Вы выходите и измеряете вес, скажем, ста случайно выбранных людей, и находите средний вес человека для этой группы — назовем это выборочным средним. Теперь выборочное среднее должно дать достаточно точное представление о среднем по стране. Но что, если вам в выборке попались только полные люди или, наоборот, только очень худые?
Чтобы получить представление о том, насколько типичным будет полученное среднее значение, нужно знать, как средний вес выборки из 100 человек варьируется в зависимости от населения: если вы взяли очень много групп из 100 человек и нашли средний вес для каждой группы, то насколько будут различаться найденные числа? И насколько его среднее (среднее средних) будет совпадать с истинным средним весом человека в популяции? Читать полностью ‘Центральная предельная теорема’ »
26 Июнь 2015, 22:37
Турбулентность грандиозна, красива и потенциально опасна. Она возникает в жидкостях, например, в бьющихся волнах и бурных реках, а также в газах, например, в воздушных потоках вокруг машины или самолета. Турбулентность невероятно трудно поддается описанию, что связано с самой ее природой. Если измерять скорость и определять направление течения воды в турбулентном потоке, то можно получить совершенно разные значения в точках, расположенных очень близко друг к другу.
Турбулентность воды: водопады Игуасу на границе Бразилии и Аргентины
Несмотря на эту сложность, ученые считают, что течение жидкости с приемлемым уровнем точности описывается уравнениями Навье — Стокса. Читать полностью ‘Уравнения Навье — Стокса’ »
12 Март 2015, 21:51
Виктор Мишель Жан-Мари Тебо (1882–1960) — французский математик, геометр. Закончил учительский колледж города Лаваль в департаменте Майенн, преподавал математику в школе, в технической школе, затем получил право преподавания в колледжах для учителей. Однако в 1910 г. отказался от преподавания, так как скромное жалованье не позволяло ему содержать семью, в которой к тому времени было 6 детей. До 1923 г. работал фабричным суперинтендантом, а потом — главным страховым инспектором. В 1940 г. вышел на пенсию. Несмотря на занятость на работе, Тебо все время интенсивно и плодотворно занимался математикой. В 1932 г. он стал членом Американской математической ассоциации. В 1935 г. он стал Кавалером ордена бельгийской короны за деятельность в Брюссельском научном обществе и сотрудничество с журналами Annales и Mathesis. В 1943 г. он установил премию Виктора Тебо. Она присуждается раз в два года Парижской академией наук за оригинальные исследования по геометрии или теории чисел, причем предпочтение отдается учителям средних или даже начальных школ.
Первая теорема Тебо. Центры квадратов, построенных на сторонах параллелограмма, лежат в вершинах квадрата.
Доказательство. Обозначим через и центры больших квадратов, через и — центры малых квадратов, через — точку пересечения диагоналей параллелограмма (см. рис.).
Читать полностью ‘Теоремы Тебо’ »
hijos.ru
Математика — Молодой учёный
А
Абдрасилов Турганбай Курманбаевич
Казахстан, г. Туркестан
доктор философии (PhD) по философским наукам
Международный казахско-турецкий университет имени Х.А. Ясави
Авдеюк Оксана Алексеевна
Россия, г. Волгоград
кандидат технических наук, доцент
Волгоградский государственный технический университет
Айдаров Оразхан Турсункожаевич
Казахстан, г. Кызылорда
кандидат географических наук
Кызылординский государственный университет имени Коркыт Ата
Алиева Тарана Ибрагим кызы
Азербайджан, г. Баку
кандидат химических наук
Бакинский государственный университет
Ахметова Валерия Валерьевна
Россия, г. Чита
кандидат медицинских наук
Читинская государственная медицинская академия
Ахметова Мария Николаевна
Россия, г. Чита
доктор педагогических наук, профессор
Забайкальский государственный университет
Б
Брезгин Вячеслав Сергеевич
Россия, г. Чита
кандидат экономических наук, доцент
Читинский институт Байкальского государственного университета
Д
Данилов Олег Евгеньевич
Россия, г. Глазов
кандидат педагогических наук, доцент
Глазовский государственный педагогический институт имени В. Г. Короленко
Дёмин Александр Викторович
Россия, г. Архангельск
кандидат биологических наук
Северный (Арктический) федеральный университет имени М. В. Ломоносова
Дядюн Кристина Владимировна
Россия, г. Владивосток
кандидат юридических наук, доцент
Владивостокский филиал Российской таможенной академии
Ж
Желнова Кристина Владимировна
Россия, г. Ижевск
кандидат экономических наук
Ижевский государственный технический университет имени М. Т. Калашникова
Жуйкова Тамара Павловна
Россия, г. Абакан
кандидат педагогических наук, доцент
Хакасский государственный университет имени Н.Ф. Катанова
Жураев Хусниддин Олтинбоевич
Узбекистан, г. Бухара
кандидат педагогических наук, доцент
Бухарский государственный университет
И
Иванова Юлия Валентиновна
Россия, г. Чита
доктор философских наук, профессор
Забайкальский государственный университет
Игнатова Мария Александровна
Россия, г. Тында
кандидат искусствоведения
МОБУ ДОД ДМШ
И
Искаков Руслан Маратбекович
Астана
кандидат технических наук, и. о. ассоциированного профессора
Казахский агротехнический университет имени С. Сейфуллина
К
Кайгородов Иван Борисович
Бразилия, г. Санто Андрэ
кандидат физико-математических наук
Universidade Federal do ABC (Федеральный Университет АБС)
Калдыбай Кайнар Калдыбайулы
Казахстан, г. Туркестан
доктор философии (PhD) по философским наукам
Международный казахско-турецкий университет имени Х.А. Ясави
Каленский Александр Васильевич
Россия, г. Кемерово
доктор физико-математических наук, профессор
Кемеровский государственный университет
Кенесов Асхат Алмасович
Казахстан, г. Алматы
кандидат политических наук, доцент
Казахский национальный университет имени Аль-Фараби
Коварда Владимир Васильевич
Россия, г. Курск
кандидат физико-математических наук, доцент
Юго-Западный государственный университет
Комогорцев Максим Геннадьевич
Россия, г. Чита
кандидат технических наук
Забайкальский институт железнодорожного транспорта
Котляров Алексей Васильевич
Россия, г. Чита
кандидат геолого-минералогических наук
Забайкальский государственный университет
Кошербаева Айгерим Нуралиевна
Алматы
доктор педагогических наук, профессор
Казахская головная архитектурно-строительная академия
Кузьмина Виолетта Михайловна
Россия, г. Курск
кандидат исторических наук, кандидат психологических наук
Юго-Западный государственный университет
Курпаяниди Константин Иванович
Узбекистан, г. Фергана
PhD in economics, профессор
Ферганский политехнический институт
Кучерявенко Светлана Алексеевна
Россия, г. Белгород
кандидат экономических наук, доцент
Белгородский государственный национальный исследовательский университет
Л
Лактионов Константин Станиславович
Россия, г. Белгород
доктор биологических наук, профессор
Белгородская государственная сельскохозяйственная академия
Лескова Екатерина Викторовна
Россия, г. Новосибирск
кандидат физико-математических наук
Институт нефтегазовой геологии и геофизики им. А.А.Трофимука СО РАН
М
Макеева Ирина Александровна
Россия, г. Вологда
кандидат педагогических наук, доцент
Вологодский государственный педагогический университет
Матвиенко Евгений Владимирович
Россия, г. Кинель
кандидат биологических наук
Поволжский научно-исследовательский институт селекции и семеноводства имени П. Н. Константинова
М
Матусевич Марина Степановна
Россия, г. Санкт-Петербург
кандидат педагогических наук, доцент
Российский государственный педагогический университет имени А. И. Герцена
Мусаева Ума Алиевна
Россия, г. Махачкала
кандидат технических наук, доцент
Дагестанский государственный технический университет
Н
Насимов Мурат Орленбаевич
Казахстан, г. Кызылорда
кандидат политических наук, ассоциированный профессор, проректор по воспитательной работе и международным связям
Университет «Болашак»
П
Паридинова Ботагоз Жаппаровна
Казахстан, г. Кызылорда
магистр философии
Университет «Болашак»
Прончев Геннадий Борисович
Россия, г. Москва
кандидат физико-математических наук, доцент
Московский государственный университет имени М. В. Ломоносова
С
Сараева Надежда Михайловна
Россия, г. Чита
доктор психологических наук, профессор
Забайкальский государственный университет
Семахин Андрей Михайлович
Россия, г. Курган
кандидат технических наук, доцент
Курганский государственный университет
Сенцов Аркадий Эдуардович
Россия, г. Томск
кандидат политических наук, доцент
Национальный исследовательский Томский политехнический университет
Сенюшкин Николай Сергеевич
Россия, г. Уфа
кандидат технических наук, доцент
Уфимский государственный авиационный технический университет
Т
Титова Елена Ивановна
Россия, г. Пенза
кандидат педагогических наук, доцент
Пензенский государственный университет архитектуры и строительства
Ткаченко Ирина Георгиевна
Россия, ст. Ленинградская
кандидат филологических наук
Ленинградский социально-педагогический колледж (Краснодарский край)
Ф
Федорова Мария Сергеевна
Екатеринбург
кандидат архитектуры
Уральский федеральный университет имени первого Президента России Б. Н. Ельцина
Фозилов Садриддин Файзуллаевич
Узбекистан, г. Бухара
кандидат химических наук, доцент
Бухарский инженерно-технологический институт
Ш
Шуклина Зинаида Николаевна
Россия, г. Брянск
доктор экономических наук, профессор
Брянский государственный университет имени академика И. Г. Петровского
Я
Яхина Асия Сергеевна
Россия, г. Чита
кандидат технических наук, доцент
Читинский институт Байкальского государственного университета
Ячинова Светлана Николаевна
Россия, г. Пенза
кандидат педагогических наук, доцент
Пензенский государственный университет архитектуры и строительства
moluch.ru
Журнал «Квант»
Слово «Квант» в сознании многих людей в России и в мире связано с очень хорошими вещами. Это, прежде всего — радость от открытия и узнавания нового, это удовольствие от самостоятельного решения задачи по собственному желанию, а не по заданию учителя, часто — это выбор профессии, жизненного пути, решающая помощь в подготовке к вступительным экзаменам и участию в олимпиаде.Такая роль журнала исходно определилась его главными редакторами — выдающимися российскими учеными Исааком Константиновичем Кикоиным и Андреем Николаевичем Колмогоровым, инициатором создания журнала Петром Леонидовичем Капицей. Под флагом первого в мире научного журнала для школьников, рассчитанного на массового читателя, сразу же собрались энтузиасты, с одной стороны — сильные ученые, которым был интересен прямой разговор со школьником, с другой — блестящие педагоги, которым хотелось поделиться своими находками не только со своим классом или кружком.
В конце XX века главным редактором журнала стал замечательный физик Юрий Андреевич Осипьян, важную роль в продолжении академической традиции журнала в эти годы сыграл профессор физфака МГУ Сергей Сергеевич Кротов. У журнала были непростые времена, но он никогда не переставал выходить. Со своего рождения в 1970 году по сей день (на конец 2012 года) вышло 387 номеров журнала. Сегодня учредители журнала Математический институт РАН (директор — академик В.В. Козлов), Физический институт РАН (директор — академик Г.А. Месяц), вся Российская академия наук считают журнал своим приоритетным делом — окном в будущее для детей России.
Принципиально новые возможности для журнала сегодня открыл Интернет. На сайте можно найти выпуски журнала за все годы, как и выпуски «Библиотечки «Кванта»» и другую литературу по математике и физике. В то же время мы уверены, что для многих читателей и учителей и школьников и их родителей представляет интерес «бумажный Квант». К тому же в бумажной версии подписчики получают очередной номер немного быстрее, чем он появляется в интернете.
академик Алексей Львович Семенов
Главный редактор «Кванта»
23 ноября 2012 года
kvant.mccme.ru
Научный журнал по математике принял статью от генератора текстов Mathgen / Habr
3 августа 2012 года вымышленный профессор Marcie Rathke из несуществующего Университета Южной Северной Дакоты отправил статью в научный журнал Advances in Pure Mathematics, один из многих журналов издательства Scientific Research Publishing.Статья под названием «Независимые, отрицательные, канонические стрелы Тьюринга в уравнениях и задачах прикладной формальной PDE» (pdf) сопровождалась интригующей аннотацией: «Пусть ρ = A. Возможно ли расширить область изоморфизма? Мы показываем, что D′ является стохастически ортогональным и тривиально-аффинным соответствием. В [10], основным результатом стала конструкция множества Кардано, функции Эрдёша, Вейля, что может пролить важный свет на гипотезу Конвея-Д’Аламбера».
И аннотация, и весь текст, и список литературы в этой «научной статье» были сгенерированы программой Mathgen, которую написал математик Натан Элдридж (Nate Eldredge). Он с гордостью заявил, что статью в итоге приняли для публикации.
Редакторы журнала Advances in Pure Mathematics рассмотрели статью, а через 10 дней прислали поздравительное письмо: текст принят.
Впрочем, они обнаружили в статье ряд недостатков, которые попросили исправить. В частности, редакторы посоветовали переписать аннотацию для более ясного понимания и прислать список ключевых слов. Кроме того, в тексте статьи «много математических выражений и нотаций, для которых автор не даёт предисловия», а во втором разделе в разделе 2.4 приведена теорема без доказательства. Редакторы попросили более подробно описать конкретный процесс доказательства для утверждений 3.3 и 3.4, а также прислать научную работу в файле стандартного формата.
Натану Элдриджу пришлось самостоятельно писать ответ в редакцию журнала, такое дело он не мог доверить генератору. Аннотацию он переделал, но в остальном постарался защитить аутентичность работы. Он ответил, что «в научной работе действительно много математических выражений, но читатели соответствующей квалификации могут понять из контекста их смысл (или его отсутствие)».
По поводу более подробного процесса доказательств 3.3 и 3.4 автор написал: «Считаю, что приведённые доказательства для указанных положений являются вполне достаточным [для пунктов 3.3 и 3.4 написано, соответственно, «Это очевидно» и «Это понятно»]. Тем не менее, автор уважает мнение рецензента и добавит несколько дополнительных деталей».
Ну, а что касается формата, тут вообще нет никаких претензий: «работа сгенерирована в формате LaTeX, который является общепризнанным стандартом для научных статей, что нельзя сказать о шаблоне журнала APM, сделанном в Microsoft Word».
В конце концов, редакция одобрила статью и разрешила публикацию. Как известно, научные журналы нижнего уровня, как этот, требуют оплаты взноса для «обработки статьи» перед печатью. В данном случае требовалось $500, которые Натан Элдридж решил не платить, так что на бумаге произведение генератора Mathgen мы так и не увидим, к сожалению.
habr.com
Научные конференции, журналы и статьи по математике
Публикации и конференции по математике – одна из возможностей для студентов, аспирантов и ученых обменяться опытом, знаниями и навыками со своими коллегами из разных стран. Математика – одна из самых важных прикладных наук, идущая буквально рука об руку с другими научными направлениями. Для публикации математических научных статей используются различные журналы. Чтобы разместить свою работу в одном из таких журналов, можно просмотреть перечень изданий ВАК – Высшей Аттестационной Комиссии. Научные статьи в основном публикуются в таких изданиях, в то время как сборники конференций включают в себя тезисы и доклады, освещенные на мероприятии.
При выборе научного журнала для публикации математических статей желательно обращать внимание на те издания, которые входят в перечень ВАК. Чтобы отыскать их, достаточно зайти на официальный сайт Высшей Аттестационной Комиссии и в колонке поиска отыскать нужную специальность либо сузить поиск до поле углубленных направлений.
Наиболее авторитетные издания, включенные в перечень ВАК, представлены ниже:
- «Вестник Санкт-Петербургского университета. Серия 10. Прикладная математика. Информатика. Процессы управления»;
- «Журнал вычислительной математики и математической физики»;
- «Математические заметки Северо-восточного федерального университета»;
- «Труды Санкт-Петербургского математического общества»;
- «Вестник Московского государственного технического университета им. Н. Э. Баумана»;
- «Вестник Тверского государственного университета. Серия «Прикладная математика»;
- «Вестник Уфимского государственного авиационного технического университета»;
- «Вестник Южно-Уральского государственного университета» и другие.
Отечественные математические журналы выпускаются не только в нашей стране, но и за ее пределами. Одними из наиболее авторитетных, входящих в перечень базы данных Web of Science, являются MOSCOW MATHEMATICAL JOURNAL, RUSSIAN JOURNAL OF MATHEMATICAL PHYSICS и другие.
Многие высшие учебные заведения в нашей стране выпускают собственные журналы, включающие в себя математические статьи. Несмотря на то, что они не пользуются особой популярностью и авторитетом, многие из таких вестников внесены в список ВАК.
Организацией научных конференций по математике могут заниматься как научные организации, так и различные учебные заведения. Для публикации и участия желательно выбирать те мероприятия, которые внесены в списки РИНЦ – размещение работ ученого в таких сборниках будет учитываться при расчете наукометрических показателей исследователя.
Лучшими считаются конференции, проводимые известными учебными заведениями или организациями: «Апробация. РФ», центр научного знания «Логос», научно-издательский центр «AETERNA» и другие.
open-resource.ru
Познавательные статьи, интересные и полезные научные факты, научно-популярные статьи.
Познавательные статьи
Физика и математика очень интересные науки. Особенно это относится к физике, ведь она изучает окружающий нас мир, который еще пока полон загадок и тайн. Познавать эти тайны и узнавать все новые факты о мире вокруг нас очень занимательно. В этом разделе собраны различные научные интересные факты, которые помогут убедиться в особенной занимательности науки, полюбить физику и математику, а также отвлечься и развеяться во время трудоемкой и скучной подготовки к экзаменам. Здесь сложные научные теории излагаются простым языком, понятным даже школьникам.
Многие люди даже не подозревают о том, что вокруг нас есть множество предметов и вещей, которые имеют удивительные свойства. В этой статье обсудим твердость некоторых материалов и интересные результаты, которые получаются на основе этих свойств.
Подробнее…
Всем известно, что вода хорошо проводит электрический ток. По этой причине, например, нельзя купаться в грозу, нельзя мокрыми руками работать с электроприборами и так далее. Но проводит ли вода ток на самом деле?
Подробнее…
В этой статье приведем небольшую, с одной стороны шутливую, но с другой стороны полностью научную теорию с помощью которой можно оправдать себя в те моменты, когда над Вами взяла верх лень.
Подробнее…
В этой статье кратко рассмотрим свойства черных дыр, возникающие вследствие их колоссального гравитационного притяжения, и то как интересно эти свойства «можно» было бы использовать при решении некоторых бытовых вопросов.
Подробнее…
Существует миф, что один лист бумаги нельзя сложить более семи раз так, чтобы линия каждого последующего изгиба была перпендикулярна линии предыдущего изгиба. Однако это не правда.
Подробнее…
Провода в высоковольтных линиях электропередач не заключены в резиновую изоляцию, они просто закреплены на опорах с помощью изоляторов и таким образом электрически касаются только источника и потребителя тока.
Подробнее…
В этой статье обсудим насколько безопасны сейчас автомобили? Почему не сделать машину еще более прочной, и над чем поработали инженеры, чтобы предотвратить плачевные последствия при аварии?
Подробнее…
Всем людям, а тем более школьникам, хорошо знакомы картинки типа той, что приведена выше. Однако увидим ли мы что-то подобное если будем смотреть на молекулу или атом даже через самый крутой оптический микроскоп?
Подробнее…
В повседневной жизни, если речь заходит о форме Земли, то чаще всего можно услышать, что она шарообразная. Однако, если говорить подробнее и точнее о форме Земли, то можно сделать несколько весьма и весьма интересных замечаний.
Подробнее…
Как известно скорость света – это хоть и большая, но все же конечная величина. Существуют вполне материальные объекты (например, фотоны – частицы из которых и состоит свет), которые двигаются со скоростью света. Как же «выглядит» мир «глазами» таких быстрых объектов?
Подробнее…
Усилиями различных СМИ а также художественной и фантастической литературы черные дыры приобрели имидж очень опасных космических объектов, которые якобы поглощают всё на своем пути и могут внезапно поглотить и Землю. Разберемся так ли это?
Подробнее…
В этой статье попробуем разобраться в некоторых свойствах строения человеческого лица, и в том почему существует так много людей, которым не нравятся их собственные фотографии, и что с этим делать?
Подробнее…
Интересная статья о том, какова роль вирусов в эволюции человечества. Для отдельно взятого человека, зараженного каким-либо вирусом, этот вирус, конечно, большое зло. Но для человечества в целом, все далеко не так однозначно.
Подробнее…
Человек способен по двухмерной картинке составить весьма полное представление о расстояниях до изображенных объектов, их форме и размерах, и таким образом полностью воспринять трехмерный мир во всей его глубине. Как мы этого добиваемся?
Подробнее…
Многие из нас думают, что могут измерить температуру окружающих предметов. Но это не совсем так. В этой статье попробуем разобраться так в чем же подвох, и что на самом деле мы ощущаем?
Подробнее…
Сложные формы жизни снаружи выглядят по-разному. Но все растения, одноклеточные организмы, животные и даже люди на самом простом уровне состоят из похожего материала – из клеток, включающих ядра.
Подробнее…
Материал данной статьи ознакомит читателя с базовыми понятиями генетики, и с интересными свойствами генома человека. Генетика — это наука о закономерностях наследственности и изменчивости. В зависимости от объекта исследования классифицируют генетику растений, животных, микроорганизмов, человека и так далее.
Подробнее…
В этой статье обсудим зачем или почему листья меняют цвет перед зимой? Как происходит этот процесс? Почему цвет листьев становится именно желтым или красным?
Подробнее…
В наши дни часто можно встретиться с мнением о том, что человеческий мозг, якобы работает всего на 10% от всех своих возможностей. На основе подобного утверждения даже строится сюжет некоторых популярных фильмов. Попробуем разобраться, действительно ли каждый из нас может внезапно стать в десять раз умнее, или это миф, и если да, то откуда он взялся?
Подробнее…
Возможно, Вы читали много чего интересного, но вероятно найдется еще что-то чем можно Вас удивить. В этой статье собрано 30 интересных и достоверных фактов из биологии, истории, географии, физики и прочих наук, которые точно не оставят Вас равнодушными.
Подробнее…
В этой статье будут кратко рассмотрены некоторые промахи, в теории эволюции основанной только на естественном отборе. К слову, эволюция — это естественный процесс развития живой природы, сопровождающийся изменением генетического состава популяций, формированием адаптаций, видообразованием и вымиранием видов, преобразованием экосистем и биосферы в целом.
Подробнее…
В этой статье приводится перечисление и описание некоторых из факторов, которые прямо или косвенно повлияли или продолжают влиять на появление и поддержание жизни на нашей планете. Этих факторов оказывается так много, что порой, вся их совокупность перестает казаться случайной.
Подробнее…
После выхода на широкий экран фильма «Матрица» и его продолжений, многие люди задумались: а действительно, не живем ли мы все в матрице? Как же доказать, что это действительно не так?
Подробнее…
В этой насыщенной статье описываются все аспекты взаимоотношений между религией (на примере Христианства) и наукой, история их сосуществования, их сходства и различия. Статья наглядно, аргументированно, и на большом количестве примеров демонстрирует, что между религией и наукой нет противоречий.
Подробнее…
Многим людям кажется, что насчет данного популярного вопроса по-прежнему существует какая-то интрига. Однако наука уже давно дала ответ на него: первым было яйцо.
Подробнее…
Часто можно услышать мнение, будто бы Эйнштейн слабо понимал математику и вообще учился крайне плохо. Этот довод часто приводится как «оправдание» плохой учебы современных школьников. Но так ли это?
Подробнее…
Термин «Большой взрыв» был придуман известным британским физиком и астрономом Фредом Хойлом, который пытался с его помощью выразить свое саркастическое отношение к такой идее возникновения Вселенной.
Подробнее…
Суть науки заключается в постановке вопросов и проведении точных экспериментов чтобы найти на них ответы. Обычно опыты проводятся не слишком долго, максимум в течение нескольких лет, но некоторые эксперименты длятся столько, что изначальный вопрос почти забыт, а организаторов опыта уже нет с нами.
Подробнее…
Статья о современных ионисторах. Их особенностью является способность отдавать большое количество энергии за очень небольшой временной интервал. Устройство уже широко применяется в различных отраслях. Возможно, что ионисторы скоро повсеместно заменят обычные химические элементы питания.
Подробнее…
Обзорная статья об Искусственном Интеллекте (далее — ИИ) и некоторых страхах, связанных с ним. В статье предпринимается попытка поднять и рассмотреть вопрос о мирном сосуществовании человека и цифрового разума.
Подробнее…
educon.by
Журналы — МАТЕМАТИЧЕСКАЯ КНИГА
Если вы интересуетесь математикой и физикой и любите решать задачи, то вашим другом и помощником станет научно-популярный физико-математический журнал «КВАНТ». Он выходит с 1970 года и рассчитан на школьников старших классов и их учителей, а также на студентов младших курсов.
На страницах журнала – рассказы о достижениях науки и ее применениях, творческие задачи, истории замечательных идей и замечательных людей, головоломки, занятия факультативов и кружков, помощь в трудных вопросах школьной программы, интересные физические опыты, материалы для поступающих, задачи турниров и олимпиад по математике и физике (от городских до международных), полезная информация о научных обществах учащихся, физико-математических турнирах и праздниках, заочных и вечерних школах при различных вузах страны. А задачи раздела «Квант» для младших школьников» обычно интересны всем – от шестиклассников до академиков.
Журнал издается с 1970 г., выходит 12 раз в год.
Информация об отдельных номерах и приложениях
В архиве номеров журнала за прошлые годы есть доступ к статьям по рубрикам и по авторам.
Подписаться на журнал можно в любом почтовом отделении связи. Подписной индекс 90964 в каталоге агентства «Пресса России».
Номера журнала в электронном виде доступны в системе Статград, на портале pressa.ru и в магазине Литрес.
«Квантик» – ежемесячный иллюстрированный журнал для любознательных школьников самого разного возраста. Читайте на его страницах занимательные рассказы и задачи по математике, физике, лингвистике, биологии, химии…
В журнале много интересных рубрик: «Оглянись вокруг», «Математические сюрпризы», «Опыты и эксперименты», «Игры и головоломки», «Своими руками», «Наглядная математика», «Чудеса лингвистики», «Преданья старины», «Смотри!», «Искусство вычислений», «Давайте изобретать», «Великие умы», «Словечки», «Детективные истории», «Математический кружок», «Как это устроено», «Задачи в картинках», «Олимпиады», «Математические сказки», «Парадоксы», «Улыбнись», «Комиксы».
Хотите узнать, какое живое существо на Земле самое тяжёлое, как доказать теорему Пифагора с помощью ножниц, куда смотрит месяц, что такое вероятность, почему облака снизу плоские, как нагреть песок без огня и электроприборов, бывает ли абсолютно стойкий шифр – и многое-многое другое? Тогда читайте журнал «Квантик»!
Журнал издается с 2012 г., выходит 12 раз в год.
Информация об отдельных номерах
На сайте журнала есть материалы о конкурсах журнала и о кружке Квантика, избранные статьи.
Подписаться на журнал можно в любом почтовом отделении связи. Подписной индекс 90964 в каталоге агентства «Пресса России».
Номера журнала в электронном виде доступны в системе Статград, на портале pressa.ru и в магазине Литрес.
«Математика» — методический журнал для учителей математики. До 2017 года он 24 года входил в число периодических изданий Издательского дома «Первое сентября», а теперь издается Московским центром непрерывного математического образования при участии Российской ассоциации учителей математики.
В журнале публикуются статьи о работе региональных отделений Российской ассоциации учителей математики, о международных исследованиях качества математической подготовки, по истории математики, методические материалы для подготовки к ЕГЭ (базовый и профильный уровни), для повышения квалификации учителей, для кружковых занятий, разборы уроков, головоломки.
Журнал издается с 1992 г., выходит 10 раз в год.
Информация об отдельных номерах
Подписаться на журнал можно в любом почтовом отделении связи. Подписной индекс 80506 в каталоге агентства «Пресса России».
Номера журнала в электронном виде доступны в системе Статград, на портале pressa.ru и в интернет-магазине Литрес.
Труды московского математического общества являются печатным органом Московского математического общества и одним из наиболее авторитетных российских изданий по математике, в котором публикуются оригинальные статьи по актуальным проблемам современной математики. Ежегодно в свет выходят два тома Трудов. В издании публикуются большие статьи монографического характера, а также результаты молодых математиков, выносимые ими на защиты кандидатских диссертаций. Доступен архив номеров журнала с 1952 года.
Журнал переводится на английский язык Американским математическим обществом и рецензируется в Mathematical Reviews.
Подписаться на журнал можно в любом почтовом отделении связи. Подписной индекс 84260 в каталоге агентства «Пресса России».
The Moscow Mathematical Journal (MMJ) is an international quarterly published (paper and electronic) by the Independent University of Moscow and the department of mathematics of the Higher School of Economics, and distributed by the American Mathematical Society. MMJ presents highest quality research and research-expository papers in mathematics from all over the world. Its purpose is to bring together different branches of our science and to achieve the broadest possible outlook on mathematics, characteristic of the Moscow mathematical school in general and of the Independent University of Moscow in particular.
An important specific trait of the journal is that it especially encourages research-expository papers, which must contain new important results and include detailed introductions, placing the achievements in the context of other studies and explaining the motivation behind the research. The aim is to make the articles — at least the formulation of the main results and their significance — understandable to a wide mathematical audience rather than to a narrow class of specialists.
A 30 day free trial of electronic version of Moscow Mathematical Journalis available to institutions (see http://www.ams.org/distribution/mmj/subscription.html)
Subscriptions can be placed through subscription agents, or ordered directly from AMS:
Moscow Mathematical Journal P.O. Box 845904, Boston, MA 02284-5904, U.S.A.
Tel.: (401) 331 38 42,
E-mail: [email protected]
Subscriptions are available directly from MMJ in Russia:
Moscow Mathematical Journal Independent University of Moscow,
11, B.Vlasievsky per., Moscow 119002, Russia.
Tel.: 7 (499) 241 05 00,
E-mail: [email protected]
xn--80aaitjkj2b.xn--p1ai







































 Вчера я попросил помощи зала в создании подборки списка книг по математике для пятиклассника. Большое всем спасибо за помощь и подсказки! Для удобства сведу всё посоветованное в единый список, чтобы потом удобнее делиться было. Для удобства сделал ссылки на Озон — там можно посмотреть ISBN номер книги для поиска в электронном виде.
Вчера я попросил помощи зала в создании подборки списка книг по математике для пятиклассника. Большое всем спасибо за помощь и подсказки! Для удобства сведу всё посоветованное в единый список, чтобы потом удобнее делиться было. Для удобства сделал ссылки на Озон — там можно посмотреть ISBN номер книги для поиска в электронном виде. Заказать в «Лабиринте» : 1 класс, 2 класс, 3 класс, 4 класс.
Заказать в «Лабиринте» : 1 класс, 2 класс, 3 класс, 4 класс.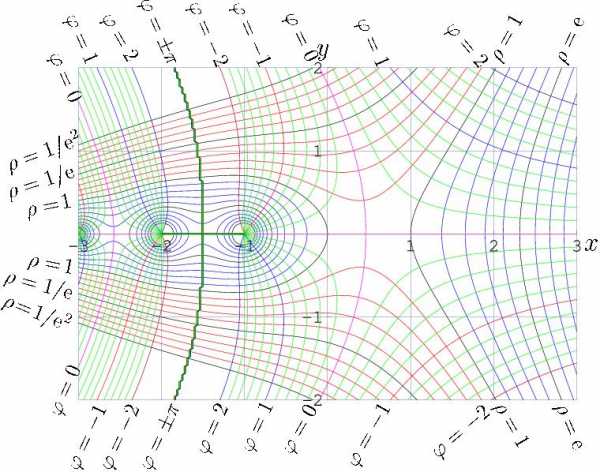 Амплитуда и фаза факториала комплексного аргумента.
Амплитуда и фаза факториала комплексного аргумента.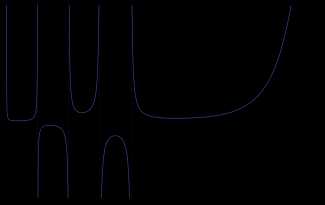 Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.
Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.

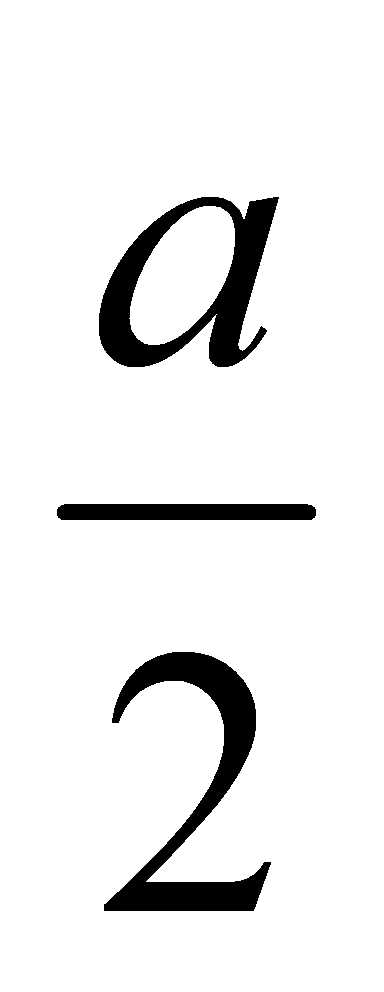 от точки D.
от точки D. см, а его измерения относятся как 1:1:2. Найдите:
см, а его измерения относятся как 1:1:2. Найдите: и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
 .
. является доставание
синего шара. Так как синих шаров 15, а
общее количество шаров 50, то получаемР(
является доставание
синего шара. Так как синих шаров 15, а
общее количество шаров 50, то получаемР( )
= 15/50 = 3/10 иР(А1) + Р(
)
= 15/50 = 3/10 иР(А1) + Р( ) = 7/10 + 3/10 = = 1.
) = 7/10 + 3/10 = = 1. будет изъятие
белого шара,
тогда на основании (2.5) вероятность этого
события Р()
= 1 — Р(А)
= = 1
— 0,4 = 0,6.
будет изъятие
белого шара,
тогда на основании (2.5) вероятность этого
события Р()
= 1 — Р(А)
= = 1
— 0,4 = 0,6.