Примеры по математике 11 класс с ответами – Олимпиада по математике 11 класс, задания, уравнения, задачи с ответами

Олимпиада по математике 11 класс, задания, уравнения, задачи с ответами

Курс математики в выпускном классе посвящен изучению степеней и корней, знакомству с показательной и логарифмической функцией, интегралами и элементами математической статистикой. Отдельное внимание в 11 классе посвящено повторению изученного за весь курс математики и подготовке к грядущему экзамену.

В связи с этим, для учеников 11 класса особенно важно участие в олимпиадах по математике и дополнительные занятия, посвященные решению заданий различной сложности.

На этой странице собраны задания для подготовки к олимпиаде по математике для 11 класса. Представлены уравнения, задачи и математические загадки с ответами и решениями. Этот материал может быть использован учителями или репетиторами для повышения уровня знания учеников.

Уравнения

1. Решите уравнение: = 3

2. Решите уравнение: ( − 8)² = ( + 9)²

3. Решите уравнение: log2 (5 + ) = log2 (1 − ) + 1

4. Решите уравнение: log5 ( + ) = log5 ( + 9)

5. Решите уравнение: log2 (4 − ) = 7

6. Решите уравнение: − + 72 = 0

7. Решите уравнение: ( + 7)² = ( − 1)²

8. Решите уравнение: ( − 8)² = ( − 2)²

9. Решите уравнение: ( − 6)² = −

10. Решите уравнение: + 9 = ( + 9)²

Задачи

Задача №1
Докажите, что уравнение  xy = 2006 (x + y) имеет решения в целых числах.

Задача №2
Докажите, что если α, β, γ — углы произвольного треугольника, то справедливо тождество cos2α + cos2β + cos2γ + 2 cosα cosβ cosγ = 1.

Задача №3
Три шара радиуса R касаются друг друга и плоскости α, четвертый шар радиуса R положен сверху так, что касается каждого из трех данных  шаров. Определите высоту «горки» из четырех шаров.

Задача №4
Докажите неравенство  −< 1/6 на луче [1/4; + ∞).

Задача №5
В прямоугольник 20 x 25 бросают 120 квадратов 1 x 1. Докажите, что в прямоугольник можно поместить круг с диаметром, равным 1, не имеющий общих точек ни с одним из квадратов.

Математические загадки

Загадка №1

Сколько лет человеку, если в 2012 году его возраст оказался равным сумме цифр года его рождения.

Загадка №2

Двадцать одна девочка и двадцать один мальчик принимали участие в математическом конкурсе. Каждый участник решил не более шести задач. Для любых девочки и мальчика найдётся хотя бы одна задача, решённая обоими. Докажите, что была задача, которую решили не менее трёх девочек и не менее трёх мальчиков.

Загадка №3

Существует ли многогранник с нечетным числом граней, каждая из которых есть многоугольник с нечетным числом сторон?

Загадка №4

В каждую клетку квадратной таблицы 25 x 25 вписано произвольным образом одно из чисел 1 или -1. Под каждым столбцом пишется произведение всех чисел, стоящих в этом столбце. Справа от каждой строки пишется произведение всех чисел, стоящих в этой строке. Докажите, что сумма 50 написанных произведений не может оказаться равной нулю.

Загадка №5

Сумма цифр в десятичной записи натурального числа n равна 100, а сумма цифр числа 44n равна 800.

Чему равна сумма цифр числа 3n?

Ответы к уравнениям

Уравнение	№ 1	№ 2	№ 3	№ 4	№ 5
Ответ	6	8,5 ∈ [8;9)	− 0,25	1,8	-124

Уравнение	№ 6	№ 7	№ 8	№ 9	№ 10
Ответ	9; 8	-1,5	1	-6	-4

Ответы к задачам

Задача 1
Преобразуем уравнение к следующему виду: (x – 2006)(y − 2006) = 20062. Уравнение имеет решения, например, x = y = 4012.

Задача 2
Преобразуем выражение в левой части равенства, учитывая, что α + β + γ = π, и применяя формулы: cos² x = (1 + cos 2x)/2, cos x = − cos (π − x), cos x + cos y = (2cos((x + y)/2)) cos((x − y)/2), получим справедливое тождество.

Задача 3
Пусть четыре шара радиуса R c центрами A, B, C, D касаются друг друга и первые три из них – плоскости a в точках A1, B1, C1 . Тогда точки A, B, C, D являются вершинами правильной пирамиды с ребром 2R. Вершина D этой пирамиды проектируется в центр основания О.

Высота «горки» из четырех шаров равна сумме OD + 2R = 2R  + 1

Задача 4
Пусть =  −. Тогда   =  − и с помощью метода интервалов получаем, что  < 0 при всех  >2/9. Но 1/4>2/9, следовательно, функция  убывает на луче [1/4; +∞]. Это значит, что  − < 1/16 − 3/64 = 1/64 < 1/64.

Задача 5
Окружим каждый квадрат полоской шириной 1/2. Образующие фигуры тоже квадраты со стороной 1 + 2 x 1/2 = 2, имеют площадь равную 4. Их общая площадь равна 4 x 120 = 480, в то время как искомая площадь равна 500. Следовательно, найдется точка, которая не покрыта построенными квадратами, но это значит, что она удалена от данных квадратов не меньше чем на по всем направлениям. Круг радиуса  с центром в этой точке не имеет общих точек  ни с одним из квадратов.

Ответ: 175 центов

Ответы на загадки

Загадка 1

1 вар. Человек родился в 19mn году, тогда

          2012 − 19mn= 1 + 9 + m + n

          2012 − 1900 − m − n = 10 + m + n

          102 = 11m + 2n

m = 8, n = 7, значит 1987 год, ему 25 лет.

2 вар. Человек родился в 200n году, тогда

          2012 − 200n = 2 + n

          2012 − 2000 − n = 2 + n

          12 − 2 = 2n

n = 5, значит 2005 год, ему 7 лет.

Загадка 2
Предположим, что нашлась задача, которую решили не более двух девочек или не более двух мальчиков.

Будем считать задачу «красной», если её решили не более двух девочек и «чёрной» в противоположном случае (тогда её решили не более двух мальчиков).

Представим шахматную доску с 21-й строкой, каждая из которых соответствует девочке, и 21-м столбцом, каждый из которых соответствует мальчику.

Тогда каждая клетка соответствует паре «мальчик–девочка». Каждую клетку покрасим в цвет какой-нибудь задачи, которую решили и мальчик-строка и девочка-столбец.

По принципу Дирихле в каком-нибудь столбце найдётся 11 чёрных клеток, или в какой-нибудь строке найдутся 11 красных клеток (потому что иначе получится, что всего клеток не более чем 21 × 10 + 21 × 10 < 21²).

Рассмотрим, например, девочку-строку, содержащую хотя бы 11 чёрных клеток.

Каждой из этих клеток соответствует задача, решённая максимум двумя мальчиками.

Тогда мы можем указать не менее 6 различных задач, решённых этой девочкой. В силу первого условия никаких других задач девочка не решала, но тогда максимум 12 мальчиков имеют общие решённые задачи с этой девочкой, что противоречит второму условию.

Точно также разбирается случай, если в каком-нибудь столбце найдутся 11 красных клеток.

Загадка 3

Пусть такой многогранник существует. Обозначим за 1, 2, …, число ребер на гранях, тогда 1 + 2 + … – удвоенная сумма всех ребер многогранника, она – четная. А в левой части стоит нечетная сумма слагаемых, каждое из которых – нечетно. Получили противоречие. Значит, такого многогранника не существует

Загадка 4
Найдем произведение всех 25 чисел, записанных под каждым столбцом и всех 25 чисел, записанных справа от строчек. Так как в этом произведении каждое из чисел квадратной таблицы входит по два раза, то произведение этих 50 произведений, в каждом из которых стоит по 25 множителей, будет положительным, т. е. равно 1. А так как произведение 50 чисел положительно, то отрицательных сомножителей будет четное число (2, 4, …, 50). Сумма же 50 произведений может быть нулем лишь в случае, когда 25 слагаемых равно 1, а 25 слагаемых равно — 1, т. е. слагаемых с — 1 должно быть нечетное число. А это значит, что сумма 50 написанных произведений не может равняться нулю.

Загадка 5
Заметим, что 44n есть сумма 4 экземпляров числа n и 4 экземпляров числа 10n.

Если складывать эти числа поразрядно, то в каждом разряде окажется сумма учетверённой цифры из этого же разряда числа n и учетверённой цифры из следующего разряда.

Если при этом не происходит никаких переносов, то каждая цифра числа n складывается 8 раз, и сумма цифр во всех разрядах оказывается равной 800. При переносах же сумма цифр, очевидно, уменьшается (так как из одного разряда вычитается 10, а к другому прибавляется только 1). Поэтому в ситуации условия задачи переносов не происходит. Это означает, в частности, что любая цифра числа n не превосходит 2. Тогда при умножении n на 3 просто умножается на 3 каждая его цифра, а, значит, и сумма цифр. Поэтому сумма цифр числа 3n равна 300.

Другие классы

Обновлено: 26/02/2015 , автор: Валерия Токарева

ruolimpiada.ru

Алгебра, 11 класс: уроки, тесты, задания

Степени и корни. Степенные функции

1. Понятие корня n-й степени из действительного числа

2. Функция корня n-й степени

3. Свойства корня n-ой степени

4. Преобразование выражений, содержащих радикалы

5. Понятие степени с любым рациональным показателем

6. Степенные функции, их свойства и графики

Показательная и логарифмическая функции

1. Показательная функция, её свойства и график

2. Показательные уравнения

3. Показательные неравенства

4. Понятие логарифма

5. Логарифмическая функция

6. Свойства логарифмов

7. Логарифмические уравнения

8. Логарифмические неравенства

9. Переход к новому основанию

10. Системы показательных и логарифмических уравнений

11. Системы логарифмических и показательных неравенств

12. Дифференцирование показательной и логарифмической функции

Первообразная и интеграл

1. Первообразная

2. Интеграл

3. Вычисление площадей с помощью интегралов

Комбинаторика

1. Правило суммы

2. Правило произведения

3. Перестановки

4. Размещения

5. Сочетания и их свойства

6. Бином Ньютона

Элементы теории вероятностей

1. События

2. Комбинации событий. Противоположные события

3. Вероятность события

4. Сложение вероятностей

5. Независимые события. Умножение вероятностей

6. Статистическая вероятность

Математическая статистика

1. Случайные величины

2. Центральные тенденции

3. Меры разброса

4. Гаусcова кривая. Закон больших чисел

Уравнения и неравенства

1. Равносильность уравнений

2. Общие методы решения уравнений

3. Решение неравенств с одной переменной

4. Уравнения и неравенства с двумя переменными

5. Системы уравнений

6. Уравнения и неравенства с параметрами

www.yaklass.ru

11 класс. Алгебра

Рубрика «11 класс. Алгебра»

В алгебре часто решаются задачи на нахождение площади криволинейной трапеции, заключенной между двумя кривыми. Различают два случая: 1) переменная интегрирования х; 2) переменная интегрирования у.

Рассмотрим оба этих случая.

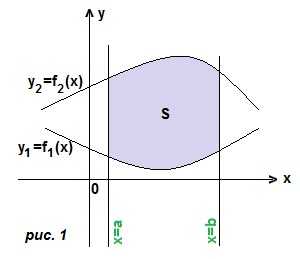1) переменная интегрирования х. В этом случае трапеция ограничена  сверху и снизу двумя кривыми, а слева и справа прямыми х=а, х=b. (рис. 1). Границы интегрирования a и b, а чтобы получить подынтегральную функцию, мы из уравнения верхней линии вычитаем уравнение нижней линии. Тогда площадь трапеции:

 

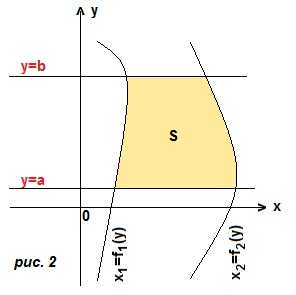2) переменная интегрирования у.  Криволинейная трапеция ограничена справа и слева двумя кривыми, а снизу и сверху прямыми y=a, y=b. (рис. 2). Границы интегрирования a и b. Чтобы получить подынтегральное выражение, мы из уравнения правой линии вычтем уравнение левой линии. Тогда площадь трапеции:

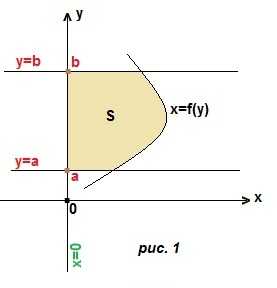Если криволинейная трапеция прилегает к оси Оу (рис. 1) и ограничена непрерывной кривой x=f (y), осью ординат (прямой х=0) и прямыми y=a, y=b, то ее площадь вычисляется по той же формуле Ньютона-Лейбница (ф. Н-Л), только переменная интегрирования не х, а у:

 

 

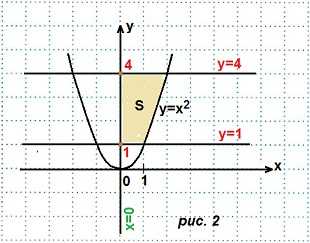Пример 1. Найти площадь криволинейной трапеции, ограниченной линиями: y=x², y=1, y=4 и осью Оу.

Решение.  Построим данную криволинейную трапецию (рис. 2).  Выразим х через у:

Искомую площадь S находим по формуле Ньютона-Лейбница (ф. Н-Л). У нас a=1, b=4.

 

Площадь криволинейной трапеции, ограниченной сверху графиком функции y=f (x), снизу — осью Ох, слева и справа прямыми х=a, x=b, находят по формуле Ньютона-Лейбница (ф. Н-Л):

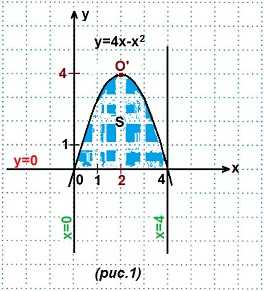Пример 1. Найти площадь криволинейной трапеции, ограниченной линиями: y=4x-x²; y=0; x=0; x=4.

Решение.  Строим графики данных линий.  (рис. 1).
1) y=4x-x² — парабола (вида y=ax²+bx+c). Запишем данное уравнение в общем виде: y=-x²+4x. Ветви этой параболы направлены вниз, так как первый коэффициент а=-1<0.

Вершина параболы находится

в точке O′(m; n), где

О′(2; 4). Нули функции (точки пересечения графика с осью Ох) найдем из уравнения:

4х-х²=0.

Выносим х за скобки, получаем:  х(4-х)=0. Отсюда, х=0 или х=4.  Абсциссы точек найдены, ордината равна нулю — искомые точки: (0; 0) и (4; 0).

2) y=0 — это ось Ох; 3) х=0 — это ось Оy; 4) х=4 — прямая, параллельная оси Оy и отстоящая от нее на 4 единичных отрезка вправо.

Площадь построенной криволинейной трапеции находим по (ф. Н-Л). У нас f (x)=4x-x², a=0, b=4.

Кстати, если Вы подсчитаете все целые заштрихованные клетки и добавите к ним половину всех остальных клеток заштрихованной фигуры, то получите приближенное значение искомой площади. Действительно, если единичный отрезок равен одной клетке, то площадь квадратика со стороной, равной 1 клетке, равна 1·1=1 (кв. ед.). Сколько квадратиков — столько квадратных единиц и составляет площадь фигуры.

Пример 2. Найти площадь криволинейной трапеции, ограниченной линиями:

Решение. Строим графики данных линий. (рис. 2).

Площадь данной криволинейной трапеции:

Пора познакомиться с мощнейшим средством исследования в математике, физике, механике и других точных дисциплинах. Это средство — определенный интеграл. В средней школе определенный интеграл применяют при вычислениях площадей криволинейных трапеций, объемов тел вращения, нахождении моментов инерции и т.д.

Что такое определенный интеграл? Чем он отличается от неопределенного, с которым мы уже достаточно знакомы.

Сравните:

 a и b — это границы, в которых изменяется переменная интегрирования х.

Сравниваем далее:

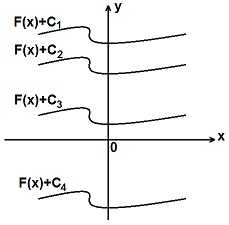
Неопределенный интеграл графически представляет собой семейство кривых, совмещаемых параллельным переносом (11.1.9).

Определенный интеграл (см. рисунок слева) представляет собой криволинейную трапецию, ограниченную сверху графиком функции y=f (x), снизу — осью Ох, а слева и справа прямыми x=a и х=b.

Значение определенного интеграла есть площадь S этой криволинейной трапеции:

Рассмотрим примеры на вычисление определенного интеграла.

Пример 1.

 

Найдем первообразную F (x) для подынтегральной функции f (x)=3x²-2x+1, а затем применим формулу Ньютона-Лейбница (ф. Н-Л).

Пример 2.

Возникает вопрос: раз определенный интеграл выражает собой площадь криволинейной трапеции, то нельзя ли увидеть эту криволинейную трапецию? А можно! Проиллюстрируем пример 2.

Полученный результат

выражает площадь криволинейной трапеции, ограниченной графиком функции y=(x+1)⁴, осью Ох и прямыми: х=0 (осью Оy) и х=1.

График функции y=(x+1)⁴ — парабола, ветви которой направлены вверх,

а вершина находится в точке О′(-1; 0).

Площадь этой криволинейной трапеции:

Вспомним определения:

1. Дифференцируемая функция F (x) называется первообразной для функции f (x) на заданном промежутке, если для всех х из этого промежутка справедливо равенство:

F′(x)=f (x).

2. Совокупность всех первообразных F (x)+C функции f (x) на рассматриваемом промежутке называется неопределенным интегралом.

Как можно представить себе неопределенный интеграл

где F (x) — первообразная функции f (x), а С — некоторая постоянная величина?

Если в данном примере или задаче не даются начальные условия для нахождения величины С, то мы получаем неоднозначную функцию F (x)+С — семейство интегральных кривых. Графики этих кривых можно совместить с помощью параллельного переноса. Из семейства этих кривых нам нужно уметь выделять ту, которая проходит через данную точку.

Пример 1. Найти для функции f (x)=1-2x первообразную, график которой проходит через точку М(3; 2).

Решение.

F (x)=∫(1-2x) dx=∫dx-2∫xdx=x-x²+C.

Так как F (3)=2 по условию, то получаем равенство:

2=3-3²+С;

2=3-9+С;

2=-6+С → С=8.

Тогда F (x)=x-x²+8.

Пример 2. Найти ∫(sinx-cosx) dx, если при π/2 первообразная равна 6.

Решение.

∫(sinx-cosx) dx=∫sinxdx-∫cosxdx=-cosx-sinx+C.

По условию F (π/2)=6. Получаем равенство: -cos (π/2) -sin (π/2)+C=6;

0-1+C=6 → C=6+1; C=7.

Искомая функция F (x)=-cosx-sinx+7.

Пример 3. Найти первообразную для функции

принимает значение, равное нулю.

Решение.

На предыдущем занятии (11.1.7.) мы рассмотрели простые примеры интегралов тригонометрических функций, когда подынтегральное выражение можно было упростить, используя подходящее тригонометрическое тождество, а затем применить соответствующую формулу интеграла тригонометрической функции. Кроме того, во всех примерах предыдущего занятия (11.1.7) мы интегрировали путем подведения под знак интеграла той линейной функции, которая являлась аргументом полученной тождественными преобразованиями тригонометрической функции.

Примеры этого занятия чуть сложнее, так как подынтегральное выражение нельзя будет упростить с помощью тригонометрического тождества. А как же будем решать? Мы продолжим применять тот же метод подведения под знак дифференциала, но уже подводить под знак дифференциала будем не просто линейную функцию, а тригонометрическую функцию, зависящую от линейной функции.

Пример 1. ∫sin⁷xcosxdx.

Подынтегральное выражение представляет собой произведение степени синуса на производную основания степени – синуса икс: (sinx)’ = cosx.

Воспользуемся способом подведения под знак дифференциала и формулой интеграла степенной функции (формула 1) лист Интегралы). Заменяем cosxdx на d (sinx).

∫sin⁷xcosxdx =∫sin⁷xd (sinx) =(1/8) sin⁸x  + C.

Пример 2. (аналогичный). ∫sin⁷(4x + 5) cos (4x + 5) dx =(¼)∫sin⁷(4x + 5) d (sin (4x + 5)) =

=(¼)·(1/8)·sin⁸(4x+5)+C=(1/32) sin⁸(4x+5)+C.

Пример 3. ∫sin3xcos⁴3xdx.  Воспользуемся способом подведения под знак дифференциала и формулой интеграла степени. Один множитель подынтегрального выражения cos⁴3x оставим, а sin3xdx запишем в виде: d (cos3x).

Проверка: d (cos3x) = — 3sin3x. Следовательно, перед знаком интеграла поставим коэффициент: — (1/3).

∫sin3xcos⁴3xdx= — (1/3)∫cos⁴3xd (cos3x) = — (1/3)·(1/5)·cos⁵3x+C = — (1/15) cos⁵3x+C.

Пример 4. 

Увидели формулу 4) (лист Интегралы):

В самом деле, u = sinx, du = d (sinx) = cosxdx. Тогда:

Пример 5. (такой же пример со сложным аргументом у тригонометрических функций).

А теперь пример на ту же формулу 4) (лист Интегралы), только в качестве u будет использована функция косинуса, а именно: u=cosx, отсюда du=-sinxdx.

Пример 6. 

Пример 7.

В следующих примерах мы также будем подводить функцию под знак интеграла, а затем применять формулу 2) (лист Интегралы):

Пример 8.

Пример 9.

И примеры чуть сложнее:

Пример 10.

Пример 11.

Продолжаем интегрировать тригонометрические функции по простейшим формулам 6) — 9) таблицы интегралов (лист «Интегралы«) Но вот незадача — у нас всего 4 формулы, и нужная формула не всегда сразу «видна»! Как же следует поступать в таких случаях? Нужно постараться упростить подынтегральное выражение, используя подходящие тригонометрические тождества.

Пример 1. ∫(cos²x-sin²x) dx. Такой формулы интегрирования у нас нет, но мы можем упростить подынтегральное выражение, используя тригонометрическую формулу для косинуса двойного аргумента: cos2α=cos²α-sin²α.

Решение.

∫(cos²x-sin²x) dx=∫cos2xdx=½∫cos2xd (2x)=1/2sin2x+C.

При решении мы применяем метод подведения под знак дифференциала (смотрите предыдущие занятия). Так как мы подвели под знак дифференциала 2х и получили выражение под знаком интеграла в 2 раза больше: d (2x)=2dx, то перед знаком интеграла ставим множитель ½. Сделаем проверку.

(F (x)+C)’=(1/2sin2x+C)’=½·cos2x·2=cos2x=cos²x-sin²x=f (x).

Пример 2. ∫(cos²4x-sin²4x) dx (аналогичный).

Решение.

∫(cos²4x-sin²4x) dx=∫cos8xdx=1/8∫cos8xd (8x)=1/8sin8x+C.

Пример 3. ∫(cos²x/2-sin²x/2) dx.

Решение.

∫(cos²x/2-sin²x/2) dx=∫сosxdx=sinx+C.

В примерах 2 и 3 мы так же, как и в примере 1, упрощали подынтегральное выражение по формуле для косинуса двойного аргумента,

а затем применяли формулу 6): ∫cosudu=sinu+C (лист Интегралы).

Пример 4. ∫(sin²x+cos²x) dx.

Решение.

Применяем основное тригонометрическое тождество: sin²α+cos²α=1. (*)

∫(sin²x+cos²x) dx=∫1·dx=∫dx=x+C.

Пример 5. ∫2sinxcosxdx.

Решение.

Используем формулу синуса двойного аргумента: sin2α=2sinαcosα (**) и упростим подынтегральное выражение.

∫2sinxcosxdx=∫sin2xdx=½∫sin2xd (2x)=-1/2cos2x+C.

Пример 6. ∫sin3xcos3xdx. Решаем аналогично примеру 5.

Решение.

∫sin3xcos3xdx=∫1/2sin6xdx=½∫sin6xdx=(½)·(1/6)∫sin6xd (6x)=- (1/12) cos6x+C.

В примерах 5 и 6 мы использовали формулу 7): ∫sinudu=-cosu+C (лист Интегралы), причем, интегрировали путем подведения под знак дифференциала.

Пример 7. ∫(sinx+cosx)²dx.

Решение.

Раскроем скобки, используя формулу квадрата суммы двух выражений: (a+b)²=a²+2ab+b².

∫(sinx+cosx)²dx=∫(sin²x+2sinxcosx+cos²x) dx. Теперь в подынтегральном выражении можно увидеть сразу 2 тригонометрические формулы (*) и  (**). 

∫(sinx+cosx)²dx=∫(sin²x+2sinxcosx+cos²x) dx=∫(1+sin2x) dx=

=∫dx+∫sin2xdx=∫dx+½∫sin2xd (2x)=x-1/2cos2x+C.

Пример 8. ∫2sin²xdx.

Решение.

Применим тригонометрическую формулу понижения степени для квадрата синуса данного аргумента: 2sin²α=1-cos2α.

∫2sin²xdx=∫(1-cos2x) dx=∫dx-∫cos2xdx=∫dx-½∫cos2xd (2x)=x-1/2sin2x+C.

Пример 9. ∫2cos²xdx.

Решение.

Применяем формулу понижения степени для квадрата косинуса аргумента: 2cos²α=1+cos2α. Тогда:

∫2cos²xdx=∫(1+cos2x) dx=∫dx+∫cos2xdx=∫dx+½∫cos2xd (2x)=x+1/2sin2x+C.

Пример 10 (аналогичный примеру 8). ∫2sin²5xdx.

Решение.

∫2sin²5xdx=∫(1-cos10x) dx=∫dx- (1/10)∫cos10xd (10x)=x- (1/10) sin10x+C.

Пример 11 (аналогичный примеру 9). ∫2cos²(x/2) dx.

Решение.

∫2cos²(x/2) dx=∫(1+cosx) dx=∫dx+∫cosxdx=x+sinx+C.

Пример 12. ∫8sinxcosxcos2xcos4xdx.

Решение.

Преобразуем подынтегральное выражение по формуле (**) — синуса двойного аргумента:

8sinxcosxcos2xcos4x=2·2·2·sinx·cosx·cos2x·cos4x=

=2sinxcosx·2·2·cos2x·cos4x=sin2x·2·2·cos2x·cos4x=

=2sin2xcos2x·2·cos4x=sin4x·2cos4x=sin8x.

Итак, ∫8sinxcosxcos2xcos4xdx=∫sin8xdx=1/8∫sin8xd (8x)=- (1/8) cos8x+C.

Пример 1. ∫sin3xdx.

У нас есть формула 7). Интегралы:  ∫sinudu= — cos u + C.

Из этой формулы следует, что какой аргумент у синуса – такой же должна быть и переменная интегрирования. Будем считать, что в нашем случае u = 3x, тогда du = 3dx. Подведем под знак дифференциала 3х, не забыв уравнять обе части равенства.

∫sin3xdx=(1/3)∫sin3xd (3x) = — (1/3) cos 3x + C.

Проверка.

(F (x)+C)’ = ( — 1/3 cos 3x + C)’ = — (1/3) · (cos 3x)’ = — (1/3) · (-3sin 3x) = sin 3x = f (x).

Пример 2. ∫cos (4x+3) dx.

Используем формулу 6). Интегралы:  ∫cosudu=sinu+C.

Подводим под знак дифференциала (4х + 3). Так как d (4x + 3) = 4dx, то

∫cos (4x+3) dx=(¼)∫cos (4x+3) d (4x+3) =(¼)  sin (4x + 3) + C.

Проверка.

(F (x)+C)’= ( (¼) sin (4x + 3) + C)’ = (¼) · 4 cos (4x + 3) = cos (4x + 3) = f (x).

Пример 3.

 

Какую формулу напоминает этот пример? Правильно, формулу 8). Интегралы.

Подводим под знак дифференциала (3х+π/4).  Тогда d (3x+π/4) = 3dx, значит, чтобы значение данного выражения не изменилось, поставим перед знаком интеграла 1/3.

Пример 4.  

Чтобы применить формулу 9). Интегралы, нужно подвести под знак дифференциала (4х- π/5). Отсюда следует: d (4х-π/5)=4dx. Перед знаком интеграла поставим множитель ¼.

При интегрировании путем подведения под знак дифференциала, в предыдущих занятиях, мы подводили под знак дифференциала линейную функцию. На самом деле, вместо переменной u мы каждый раз подразумевали выражение вида kx+b, т.е. полагали: u-kx+b, получали du=kdx, а затем перед знаком интеграла ставили коэффициент 1/k, чтобы не изменилось значение данного интеграла. При решении использовали свойства и таблицу интегралов — лист Интегралы.

А можно ли под знак дифференциала подводить нелинейную функцию? Да, если подынтегральное выражение представляет собой произведение двух множителей: один множитель — сложная функция от какой-то нелинейной функции, а другой множитель есть производная от этой нелинейной функции. Рассмотрим сказанное на примерах.

Найти неопределенные интегралы.

Пример 1. ∫(2x + 1)(x² + x + 2)⁵ dx = ∫(x² + x + 2)⁵ d (x² + x + 2) =(x²+x+2)⁶:6  + C.

Что представляет собой данное подынтегральное выражение? Произведение степенной функции от (х² + х + 2) и множителя (2х + 1), который равен производной от основания степени: (х² + х + 2)’ = 2х + 1.

Это и позволило нам подвести (2х + 1) под знак дифференциала:

(2x + 1) dx =  d (x² + x + 2). А далее мы применили формулу:

∫u⁵du=u⁶:6+ C.   (Формула 1). Интегралы)

Проверка. (F (x)+ C)’ =((x²+x+2)⁶:6  + C)′=1/6 · 6 (x² + x + 2)⁵ · (x² + x + 2)’ =

=(x² + x + 2)⁵ · (2x + 1) = (2x + 1)(x² + x + 2)⁵ = f (x).

Пример 2. ∫(3x² – 2x + 3)(x³ —  x² + 3x + 1)⁵ dx = ∫(x³ – x² + 3x + 1)⁵ d (x³ – x² + 3x + 1) =

=(x³- x²+3x+1)⁶:6  + C

И чем этот пример отличается от примера 1? Да ничем! Та же пятая степень с основанием  (х³ – х² + 3х + 1) умножается на трехчлен (3х² – 2х + 3), который является производной основания степени: (х³ – х² + 3х + 1)’ = 3х² – 2х + 3. Это основание степени мы и подвели под знак дифференциала, от чего значение подынтегрального выражения не изменилось, а затем применили ту же формулу 1). (Интегралы)

Пример 3.  

Здесь производная от (2х³ – 3х) даст (6х² – 3), а у нас

имеется (12х² – 6), то есть выражение в 2 раза большее, значит, подведем (2х³ – 3х) под знак дифференциала, а перед интегралом поставим множитель 2. Применим формулу 2) (лист Интегралы).

Вот что получится:

Сделаем проверку, учитывая, что:

Итак,

Что такое непосредственное интегрирование? Это интегрирование с использованием свойств и простейшей таблицы интегралов (Интегралы). Рассмотренный метод подведения под знак дифференциала (занятие 11.1.3) также относится к непосредственному интегрированию, так как нашей новой переменной служила линейная функция вида u=kx+b, но никаких новых букв мы не использовали, а просто применяли свойство VI (Интегралы), а именно:

 Это свойство значительно расширяет таблицу простейших интегралов, так как в силу этого свойства таблица интегралов оказывается справедливой независимо от того, является переменная интегрирования независимой переменной или дифференцируемой функцией. В занятии 11.1.3. мы учились применять метод подведения переменной под знак дифференциала, используя формулы 1) и 2) (Интегралы), причем, прежде чем использовать тот или иной табличный интеграл, мы приводили данный интеграл к виду:

∫f (φ(x))φ′(x) dx=∫f (u) du, где u=φ(x).     

Далее, продолжим непосредственное интегрирование с помощью остальных формул таблицы интегралов.

Рассмотрим пример на применение формулы 5) (Интегралы), а именно формулы:

В примере 1 неявно подразумевалось u=9x-2, что и позволило нам применить свойство VI и формулу 5), в результате чего под знак дифференциала мы подвели (9х-2). Перед знаком интеграла стоит множитель 1/9, так как d (9x-2)=9dx.

Рассмотрим пример на применение формулы 4) (Интегралы), а именно, формулы:

В примере 2 неявно подразумевается u=25x-1, поэтому, под знак дифференциала подвели 25х-1, отсюда du=25dx. Вот почему перед интегралом стоит множитель 1/25.

Страница 1 из 41234»

www.mathematics-repetition.com

Материалы школьной программы по математике за 11 класс

 

В 11 классе заканчивается школьный курс алгебры и основ анализа, а в заключении выпускники сдают экзамен в формате ЕГЭ. Программа 11 класса по математики включает в себя углубленное изучение понятий степени и корня. Кроме того рассматриваются степенная, показательная и логарифмическая функции. Исследуются их графики и выясняются основные свойства.

При изучении логарифмической функции вводится понятие логарифма и его свойства. Рассматриваются основные логарифмические уравнения и неравенства и методы их решения. Помимо этого школьники учатся решать системы уравнений и неравенств.

Курс анализа оканчивается изучением первообразной и определенного интеграла. Изучаются таблица простейших интегралов и применение их для вычисления площадей плоских фигур.

Ниже вы можете найти список материалов по математике для десятиклассников. Каждая отдельная тема написана репетитором и является уникальным образовательным материалом, который поможет ученику разобраться и понять сложные моменты. Данные материалы могут использоваться как учениками и их родителями, так и учителям и репетиторами для своих учеников.

Темы школьной программы 11 класс Математика:

Основное свойство первообразной: теорема и наглядные примерыТри правила нахождения первообразных: алгоритм нахождения и примерыФормула Ньютона — Лейбница: примеры вычисления интеграловПрименение интеграла: нахождение объема тела и вычисление центра масс телаИррациональные уравнения: алгоритм решения и примерыСтепень с рациональным показателем: их основные свойстваПоказательная функция: график и основные свойства функцииРешение показательных уравнений и неравенств: алгоритм решения и примерыЛогарифмы и их свойства: определение и алгоритм решенияЛогарифмическая функция: основные свойства и графикиПонятие об обратной функции: график функции и теоремаПроизводная и первообразная показательной функции: число е и примерыПроизводная и первообразная логарифмической функции: примеры и алгоритмПонятие о дифференциальных уравнениях: примеры использования уравнений

Нужна помощь в учебе?

Предыдущая тема: Материалы школьной программы по математике за 10 класс
Следующая тема:&nbsp&nbsp&nbspМатериалы школьной программы по русскому языку за 1 класс

Твитнуть

Нравится

Нравится

Все неприличные комментарии будут удаляться.

www.nado5.ru

Демонстрационные варианты ЕГЭ по математике (11 класс)

      Начиная с 2015 года, ЕГЭ по математике проводится в виде двух отдельных экзаменов – базового уровня и профильного уровня.

      Базовый ЕГЭ организуется для выпускников, изучающих математику для общего развития и успешной жизни в обществе, а также абитуриентов вузов, в которых не требуется высокий уровень владения математикой. Баллы, полученные на базовом ЕГЭ по математике, не переводятся в стобалльную шкалу и не дают возможности участия в конкурсе на поступление в вузы.

      Профильный ЕГЭ проводится для выпускников и абитуриентов, планирующих использовать математику и смежные дисциплины в будущей профессиональной деятельности. Результаты профильного ЕГЭ по математике переводятся в стобалльную шкалу и могут быть представлены абитуриентом на конкурс для поступления в вуз.

      Демонстрационный вариант для ЕГЭ базового уровня содержит только задания базового уровня сложности с кратким ответом (20 заданий). В демонстрационном варианте представлено по несколько примеров заданий на каждую позицию экзаменационной работы. В реальных вариантах экзаменационной работы базового уровня на каждую позицию предлагается только одно задание.

      При выполнении заданий экзаменационной работы ЕГЭ по математике базового уровня разрешено использовать справочные материалы, которые выдаются учащемуся вместе с вариантом ЕГЭ.

      Демонстрационный вариант профильного экзамена ЕГЭ состоит из двух частей: часть 1 содержит задания с кратким ответом, часть 2 — задания с кратким ответом и задания с развернутым ответом.

      Все демонстрационные варианты ЕГЭ по математике содержат ответы ко всем заданиям,а также критерии оценивания для заданий с развернутым ответом.

      В демонстрационных вариантах ЕГЭ по математике 2019 года как базового уровня, так и профильного уровня, по сравнению с демонстрационными вариантами ЕГЭ по математике 2018 года изменений не было.

      Приведенные материалы опубликованы на официальном информационном портале Единого Государственного Экзамена.

Демонстрационные варианты ЕГЭ по математике

      Отметим, что демонстрационные варианты за 2008 — 2019 годы представлены в формате pdf, и для их просмотра необходимо, чтобы на Вашем компьютере был установлен, например, свободно распространяемый программный пакет Adobe Reader.

Изменения в демонстрационных вариантах ЕГЭ по математике

      Демонстрационные варианты ЕГЭ по математике для 11 класса за 2002-2009 годы включали в себя три раздела: А (задачи с выбором ответа из нескольких предложенных), В (задачи с кратким ответом) и С (задания, для выполнения которых требовалось привести полное решение задачи).

      В 2010 году из демонстрационного варианта ЕГЭ по математике были исключены задачи с выбором ответа, ранее составлявшие раздел А. Таким образом, демонстрационный вариант ЕГЭ стал состоять уже только из двух разделов В и С.

      Демонстрационный вариант ЕГЭ 2011 года почти полностью совпадал с демонстрационным вариантом ЕГЭ 2010 года: были изменены лишь задания C1 и C5.

      В 2014 году в демонстрационном варианте ЕГЭ по математике тематических изменений по сравнению с предыдущим годом не было: задачи В3, В9, В14, С2 и С4 были заменены на другие задачи той же тематики. Кроме того, было добавлено задание базового уровня сложности с кратким ответом, проверяющее практические навыки применения математики в повседневной жизни и изменен порядок заданий.

      В 2015 году в порядке проведения ЕГЭ по математике произошли серьезные изменения: было решено проводить два отдельных экзамена – базового уровня и профильного уровня.

    В связи с этим в 2015 году было представлено 2 демонстрационных варианта: новая модель демонстрационного варианта для ЕГЭ базового уровня и модернизированная модель демонстрационного варианта 2014 года для проведения ЕГЭ профильного уровня.

      Демонстрационный вариант для ЕГЭ базового уровня содержал только задания базового уровня сложности с кратким ответом (20 заданий). В демонстрационном варианте было представлено по несколько примеров заданий на каждую позицию экзаменационной работы. В реальных вариантах экзаменационной работы на каждую позицию было предложено только одно задание.

      Демонстрационный вариант профильного экзамена 2015 года разработан на основе демонстрационного варианта ЕГЭ по математике 2014 года со следующими изменениями:

• Вариант стал состоять из двух частей (часть 1 — задания с кратким ответом, часть 2 — задания с кратким ответом и задания с развернутым ответом).
• Нумерация заданий стала сквозной по всему варианту без буквенных обозначений В, С.
• Во второй части добавлено 1 задание высокого уровня сложности с развёрнутым ответом, проверяющее практические навыки применения математики в повседневной жизни, навыки построения и исследования математических моделей.
• Из первой части исключено 1 задание базового уровня сложности.
• Произведены несущественные изменения формы и тематики заданий 16 и 17

      В демонстрационном варианте ЕГЭ по математике базового уровня 2016 года изменений не было .

      В демонстрационном варианте ЕГЭ по математике профильного уровня 2016 года произошли следующие изменения:

• Из первой части варианта были исключены два задания: задание практического содержания базового уровня сложности и задание по стереометрии повышенного уровня сложности.
• Максимальный первичный балл за выполнение всей работы был уменьшен с 34 до 32 баллов.

      В демонстрационных вариантах ЕГЭ по математике 2017 — 2019 годов как базового уровня, так и профильного уровня, по сравнению с демонстрационными вариантами ЕГЭ по математике 2016 года изменений не было.

      На нашем сайте можно также ознакомиться с подготовленными преподавателями нашего учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.

Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

      У нас также для школьников организованы

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»

www.resolventa.ru

ГДЗ по математике для 11 класса экзаменационные задания Т.А. Адамович

ГДЗ от Путина Найти

• • 1 класс
    • Математика
    • Английский язык
    • Русский язык
    • Немецкий язык
    • Информатика
    • Природоведение
    • Основы здоровья
    • Музыка
    • Литература
    • Окружающий мир
    • Человек и мир
  • 2 класс
    • Математика
    • Английский язык
    • Русский язык
    • Немецкий язык
    • Белорусский язык
    • Украинский язык
    • Информатика
    • Природоведение
    • Основы здоровья
    • Музыка
    • Литература
    • Окружающий мир
    • Человек и мир
    • Технология
  • 3 класс

  gdzputina.ru

  Примеры математических задач

  

  Добрый день, дорогие друзья! Сегодня мы приготовили для вас тест, в котором собраны простые математические примеры, которые можно щелкать как орешки, если в школе вы хотя бы бывали

  Добрый день, дорогие друзья! Сегодня мы приготовили для вас тест, в котором собраны простые математические примеры, которые можно щелкать как орешки, если в школе вы хотя бы бывали Решение математических примеров вам понравится

  В школе нам казалось, что решение математических примеров иногда очень даже сложное занятие, но сейчас, когда мы прошли огонь, воду и медные трубы, Вам уже ничего не страшно Обычные процедуры: вычитание, сложение, умножение, деление, ну и немного квадратных корней — вот всё, что сегодня Вы увидите в тесте По нашему мнению, тест получился достаточно простым, но в то же время интересным, потому что поможет расшевелить залежалый мозг, который не считает ничего более, чем скидку в магазине продуктов

  Кстати, ученые выяснили, что решая простые примеры с утра, мы помогаем головному мозгу проснуться и работать более активно, чем обычно. Поэтому, если вы проснулись недавно, мы поможем вам проснуться не хуже, чем чашка кофе. Математические примеры с ответами ждут Вас, вперед!

  Какой ответ верный?

  Далее >>

  Какой ответ верный?

  Далее >>

  Какой ответ верный?

  Далее >>

  Какой ответ верный?

  Далее >>

  Какой ответ верный?

  Далее >>

  Какой ответ верный?

  Далее >>

  Какой ответ верный?

  Далее >>

  Какой ответ верный?

  Далее >>

  Какой ответ верный?

  Далее >>

  Какой ответ верный?

  Далее >>

  Тест с математическими примерами

  Отлично, 5!

  Вы математический гений, поздравляем! Не забудьте поделиться результатом с друзьями, пусть завидуют

  Поделитесь результатом с друзьями:

  Facebook Twitter VK Тест с математическими примерами

  Хорошо, 4!

  Вы справились на 4+, поздравляем! Не забудьте поделиться результатом с друзьями, пусть завидуют

  Поделитесь результатом с друзьями:

  Facebook Twitter VK Тест с математическими примерами

  Хорошо, 4!

  Вы неплохо справились с поставленными задачами Не забудьте поделиться результатом с друзьями, пусть завидуют

  Поделитесь результатом с друзьями:

  Facebook Twitter VK Тест с математическими примерами

  Школа была давно?..)

  Не расстраивайтесь, не везет в математике — повезет в любви Не забудьте поделиться тестом с друзьями, пусть они тоже попробуют свои силы

  Поделитесь результатом с друзьями:

  Facebook Twitter VK

   PLAY AGAIN !

  Еще интересные тесты:

  smtimes.ru

  No related posts.