Дуга это в геометрии: Создание дуг окружностей—ArcGIS Pro | Документация

Создание дуг окружностей—ArcGIS Pro | Документация

На панели Создать объекты среди инструментов построения линейных и полигональных объектов есть метод создания дуг окружности. Они доступны на панели инструментов построения и в контекстном меню при создании объекта.

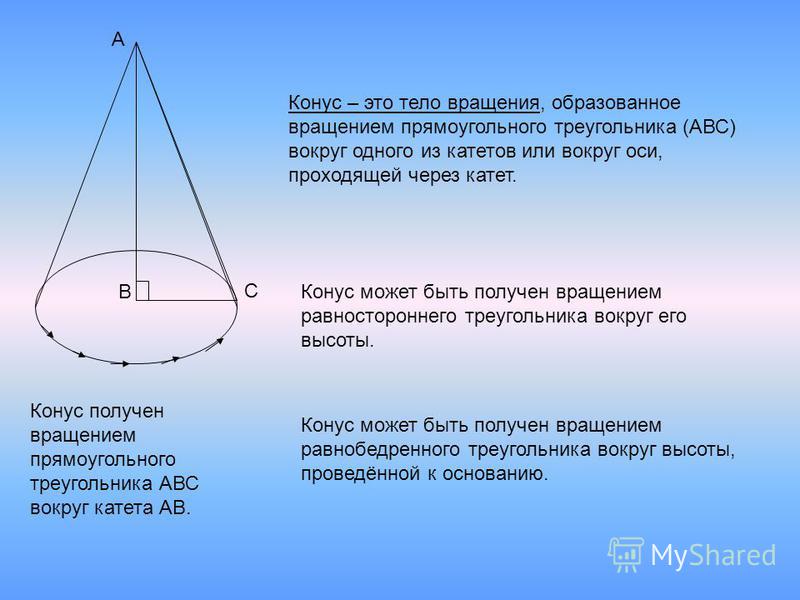
Дуга окружности — это часть линии круга. Геометрия задается радиусом и длиной хорды либо углом дельта. Вы можете создавать их в виде части непрерывной линии или контура полигона или как двухточечный дуговой элемент.

Шаги для получения линии или дуги из сегмента см. в разделе Изменение сегментов объектов.

Создание сегмента дуги

Сегмент дуги задается начальной точкой, точкой, через которую проходит дуга, и конечной точкой. Вы можете поставить все эти три точки, перетащить курсор либо указать радиус либо воспользоваться диалоговым окном дуги окружности, чтобы задать значения для геометрии.

1. На панели Каталог выполните следующие действия для добавления слоя полилиний к своей карте:
   • Разверните Базы данных , затем базу, содержащую ваши данные, и перетащите класс объектов на карту.
   • Щелкните правой кнопкой базу данных по умолчанию и создайте новый линейный или полигональный класс объектов.

   Перетаскивание на карту или создание класса объектов приводит к добавлению слоя на текущую карту и созданию шаблона объектов с настройками по умолчанию.

2. На закладке Редактирование в группе Замыкание задайте свои предпочтительные настройки замыкания.
3. Если вы работаете с объектами, имеющими z-значения, на вкладке Редактировать в группе Высота выберите способ добавления z-значений к объектам.

   Шаги для добавления z-значений при создании объектов с z-значениями см. в разделе Указание высоты для 3D-объектов.

4. На вкладке Редактировать в группе Объекты щелкните Создать .

   Появится панель Создать объекты.

5. На панели щелкните шаблон полилинейного или полигонального объекта.
   • Для создания вершины линии щелкните Линия .
   • Чтобы создать вершину полигона, щелкните Полигон.

   Внизу карты появляется панель инструментов Построение.

6. На панели инструментов построения щелкните инструмент Сегмент дуги .
7. Создайте начальную точку одним из следующих способов:
   • Щелкните карту.
   • Щелкните правой кнопкой мыши и используйте команды в контекстном меню, чтобы задать координаты x,y,z местоположения, а также расстояние и направление.
   • Начальной точкой является последняя точка предыдущего сегмента.
8. Создайте вторую точку, которая описывает путь дуги, одним из следующих способов:
   • Щелкните карту.
   • Щелкните правой кнопкой мыши и используйте команды в контекстном меню, чтобы задать координаты x,y,z местоположения, а также расстояние и направление.

   Путь дуги замкнется на эту новую точку.

9. Создайте конечную точку и задайте радиус, используя один из следующих способов:
   • Переместите указатель мыши, чтобы задать радиус, и снова щелкните на карте, чтобы создать конечную точку.
   • Нажмите клавишу R, введите радиус, нажмите Enter и щелкните карту, чтобы создать конечную точку.
   • Щелкните правой кнопкой, нажмите Дуга окружности , укажите радиус и другие значения геометрии и нажмите Enter, чтобы закрыть диалоговое окно и создать дугу.

     Значения геометрии по умолчанию для новой дуги основаны на расположении точек, которые вы нарисовали на карте.

10. Чтобы продолжить создание остальных сегментов дуги, используйте инструменты на панели инструментов построения.
11. На панели инструментов построения нажмите Готово или нажмите клавишу F2.

Создание дуги по конечным точкам

Сегмент дуги по конечным точкам задается начальной точкой, конечной точкой и радиусом. Вы можете поставить все эти три точки, перетащить курсор либо указать радиус, или воспользоваться диалоговым окном дуги окружности, чтобы задать значения ограничений для геометрии.

1. На панели Каталог выполните следующие действия для добавления слоя полилиний к своей карте:
   • Разверните Базы данных , затем разверните базу, содержащую ваши данные, и перетащите класс объектов на карту.
   • Щелкните правой кнопкой базу данных по умолчанию и создайте новый линейный или полигональный класс объектов.

   Перетаскивание на карту или создание класса объектов приводит к добавлению слоя на текущую карту и созданию шаблона объектов с настройками по умолчанию.

2. На закладке Редактирование в группе Замыкание задайте свои предпочтительные настройки замыкания.
3. На вкладке Редактировать в группе Объекты щелкните Создать .

   Появится панель Создать объекты.

4. На панели щелкните шаблон полилинейного или полигонального объекта.
   • Для создания вершины линии щелкните Линия .
   • Чтобы создать вершину полигона, щелкните Полигон.

   Внизу карты появляется панель инструментов Построение.

5. Если вы работаете с объектами, имеющими z-значения, на вкладке Редактировать в группе Высота выберите способ добавления z-значений к объектам.

   Шаги для добавления z-значений при создании объектов с z-значениями см. в разделе Указание высоты для 3D-объектов.

6. На панели инструментов построения щелкните инструмент Сегмент дуги конечной точки .

   Вы можете выбирать между прямыми и дуговыми сегментами в любой момент создания объекта.

7. Создайте начальную и конечную точки дуги одним из следующих способов:
   • Щелкните карту.
   • Щелкните правой кнопкой мыши и используйте команды в контекстном меню, чтобы задать координаты x,y,z местоположения, а также расстояние и направление.
   • Начальной точкой является последняя точка предыдущего сегмента.

   Между начальной и конечной точками будет создана дуга.

8. Создайте конечную точку и задайте радиус, используя один из следующих способов:
   • Переместите курсор, чтобы задать радиус, и щелкните на карте.
   • Нажмите клавишу R, введите радиус и нажмите Enter.
   • Щелкните правой кнопкой, нажмите Дуга окружности , укажите радиус и другие значения геометрии и нажмите Enter, чтобы закрыть диалоговое окно и создать дугу.
     Значения геометрии по умолчанию для новой дуги основаны на расположении точек, которые вы нарисовали на карте.

9. Чтобы продолжить создание остальных сегментов дуги, используйте инструменты на панели инструментов построения.
10. На панели инструментов построения нажмите Готово или нажмите клавишу F2.

Связанные разделы

---

Отзыв по этому разделу?

6 параметров для соблюдения геометрии электрода для орбитальной TIG-сварки

Электрод является основным элементом для орбитальной TIG-сварки. Именно электрод обеспечивает электрическую дугу, и качество сварки непосредственно зависит от его геометрии.

6 параметров, которые следует учитывать для соблюдения геометрии электрода при орбитальной TIG-сварке! 

 

№1 Длина вылета электрода (Stick out):

 

При очень большой длине вылета электрода эффект концентрации дуги не срабатывает, защита электрода и сварочной ванны станов

ится неэффективной.

Если же длина вылета слишком мала, дуга затухнет, а керамическая форсунка перегреется.

Следует отметить: 
Теоретически, когда глубина фасок это позволяет, длина вылета должна быть в 2 или 3 раза больше диаметра электрода.

 

 

№2 Влияние угла заточки

 

Это параметр, имеющий наибольшее влияние на характеристики дуги и геометрию шва. Поэтому он должен стать неотъемлемой частью процедуры сварки.

Этот угол влияет непосредственно на ширину проникновения.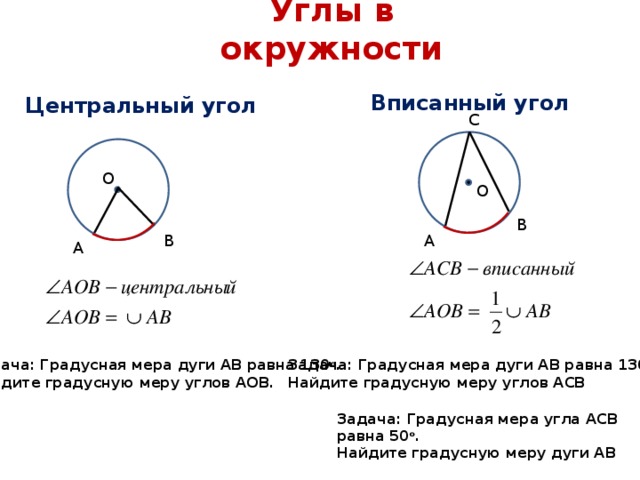

Если представить схематично, то с углом около 10° дуга имеет тенденцию к расширению (повышенное напряжение дуги), колонна дуги имеет форму конуса, а с углом около 45° колонна дуги становится более «цилиндрической» (напряжение дуги снижено).Влияние угла заточки становится заметным при превышении 50 ампер.

 

 

 

 

 

№3 Выступ кромки электрода 

Отметим важность выступа кромки на краю электрода, который определяется в зависимости от плотности сварочного тока.

Острозаточенный электрод облегчает зажигание дуги, но быстро разрушается, что приводит к риску попадания вольфрама в сварку. Большой выступ кромки помогает продлить срок службы электрода, но если этот выступ слишком велик для сварочного тока, дуга будет нестабильной, и ее сложно будет сфокусировать.

Настоятельно рекомендуется использовать оптимальный выступ кромки, чтобы обеспечить стабильность дуги и правильный перенос электронов, а также продлить срок службы электрода без риска попадания вольфрама в сварку.

 

 

Следует отметить:
Для труб диаметром более 50 мм концентричность становится менее очевидной, поэтому мы рекомендуем увеличить вышеуказанные значения, чтобы избежать контакта между трубой и электродом. При использовании припойной проволоки добавьте 0,5-1,5 мм к вышеуказанным значениям в зависимости от диаметра и скорости припоя.

 

№4 Расстояние между трубой и электродом

Это расстояние также является важнейшим параметром, так как оно влияет непосредственно на длину шва за счет увеличения напряжения дуги и, главным образом, на соотношение ширины внутреннего и наружного шва.

См. таблицу выше.

№5 Направление заточки электрода

Чтобы гарантировать оптимальную стабильность дуги, следует всегда проводить продольную заточку электрода. Электрод полируется для повышения срока его службы.

Не разрешается проводить заточку перпендикулярно оси, так как это приводит к нестабильной и непредсказуемой дуге, а, следовательно, и к неожиданным результатам.

 

 

 

№6 Срок службы электрода

Хотя вольфрамовый электрод считается неплавким, срок его службы не бесконечен, что напрямую связано с условиями эксплуатации.

Для оптимального срока службы следует соблюдать следующие рекомендации:

• вольфрамовый тип, адаптированный к типу сварочного тока и материала;
• соответствие диаметра и выступа кромки электрода сварочному току;
• соблюдение периодов перед и после продувки газа, а также расход газа и показатель его чистоты;
• качество очистки сборочных деталей (отсутствие масла, смазки, оксидов, краски, пр.).

Замена электрода требуется при окислении, деформации, разрушении, притуплении острия.

Первые признаки износа вольфрамового электрода: проблемы с зажиганием дуги, нестабильность дуги, плавающая колонна дуги, образование паразитной дуги и т.д.

НИКОГДА:

Не разламывайте электрод кусачками, чтобы получить нужную длину!
Не затачивайте электрод перпендикулярно его оси.  

 

Для более подробной информации об электродах для орбитальной TIG-сварки рекомендуем вам почитать этот справочник! 

 

Определение дуги в геометрии — примеры и как идентифицировать

, написанный

Малкольм Маккинси

11 января 2023

, проверенный на фактах

Пол Маззола

Круги и окружность

. есть запчасти. Одна часть — это дуга, отрезок круга, кусок его окружности. Сами дуги бывают разных типов, например, большие дуги, полуокружности и малые дуги.

Окружность — это множество всех точек, равноудаленных от данной точки. Окружность  – это расстояние по окружности.

Окружность круга

Окружности могут иметь углы, образованные двумя радиусами. Это центральных углов , и они почти всегда обозначаются либо их точным измерением угла (или радиана), либо греческой буквой тета, θ\thetaθ.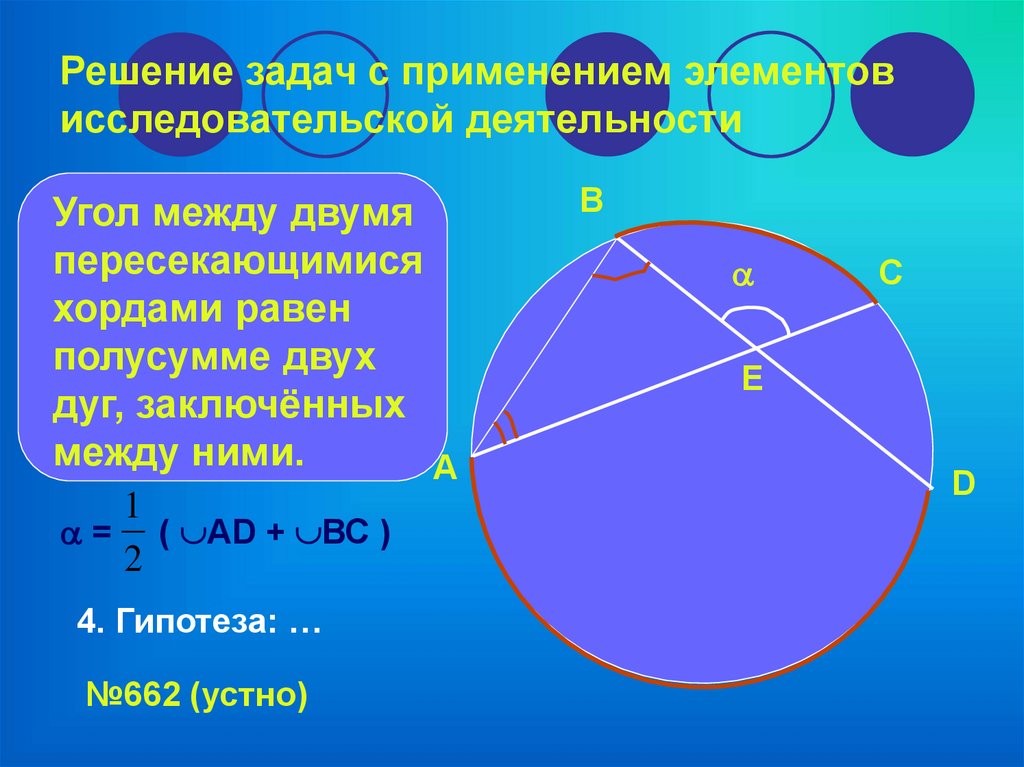

Центральные углы

Окружности также могут иметь углы, образованные двумя хордами (отрезками прямых с концами на окружности) с общей конечной точкой на окружности. Эти углы называются вписанными углами.

Вписанные углы

Как центральные, так и вписанные углы образуют большую и малую дуги.

Полуокружности и дуги

Дуга  – это часть окружности, которая меньше всей окружности. Так как это позволяет почти все возможные части, математики разбивают дуги следующим образом:

1. Малая дуга — Дуга, размер которой меньше или равен 180° или π\piπ радиан

2. 4

   Полуокружность дуга размером ровно 9

3. Большая дуга

Малая дуга, полуокружность и большая дуга

Идентификация дуг

В типичном рисунке круга читатель понимает, что речь идет о малой дуге. На этом рисунке нас интересует малая дуга, определяемая центральным углом θ\thetaθ.

Для маркировки малой дуги требуются только ее конечные точки на окружности. Вот второстепенная дуга GO :

Второстепенная дуга

Если вам нужна большая дуга, выберите и пометьте обе конечные точки дуги и случайную точку между ними. Здесь у нас есть большая дуга FUN :

Малая и большая дуги

Дуги обычно идентифицируются в письменной форме с помощью их точек (две для малой дуги, три для большой дуги), а затем рисуется крошечная короткая дуга, проведенная над буквы.

Измерение дуг

Дуги имеют два измерения:

1. Угол

2. Длина

Дугу можно измерить по центральному углу окружности. Это угол дуги . Вы помещаете букву m в нижнем регистре перед письменной формой дуги, например:

Угол дуги

Таким образом, вы можете написать mFUN⌢=45°m\overset\frown{FUN}=45°mFUN⌢=45°, и вы сказал бы: «Большая дуга FUN измеряет 45 градусов .»

Другой способ измерения дуг — их расстояние по окружности окружности. Это длина дуги .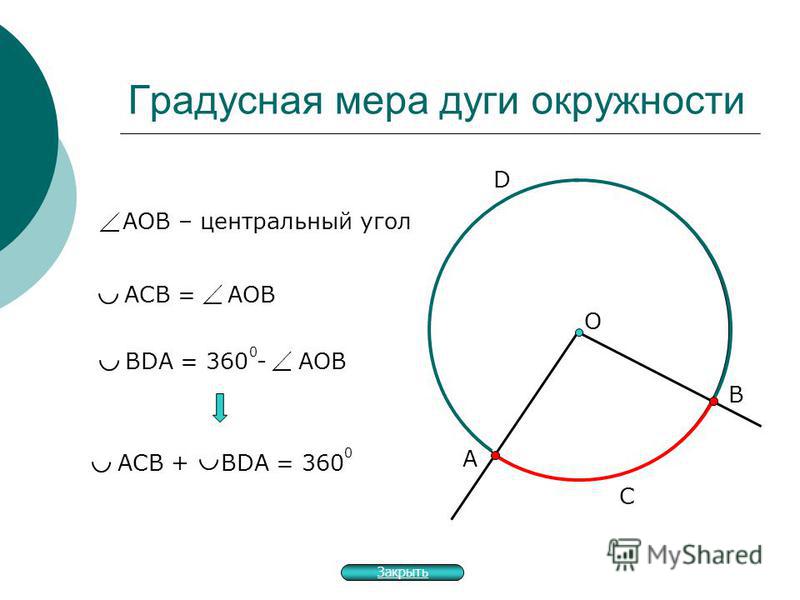 Чтобы записать длину дуги словами, вы ставите маленькую букву l перед письменной формой, например это:

Длина дуги

Таким образом, вы можете написать lGO⌢=13.4cml\overset\frown{GO}=13.4 cmlGO⌢=13.4cm и сказать: «Длина дуги GO равна 13,4 сантиметра . »

Дуга

Дуги часто изучаются в геометрии в контексте дуг окружности. На окружности вы можете думать о дуге как о части окружности окружности, как показано на рисунке ниже.

Дуги также существуют как часть кривых, но в большинстве случаев, когда люди говорят о дуге, они обычно имеют в виду дугу окружности, а не дугу кривой. Точно так же эта страница будет посвящена теме дуг окружности.

Дуга от A до B, обозначенная символически как , показана красным выше.

Дуги широко используются в машиностроении и других сферах быта. Показанный ниже мост имеет опоры в форме дуги.

Типы дуг

Полуокружность — это название дуги, охватывающей половину окружности круга (одно из значений слова «полукруг» — половина).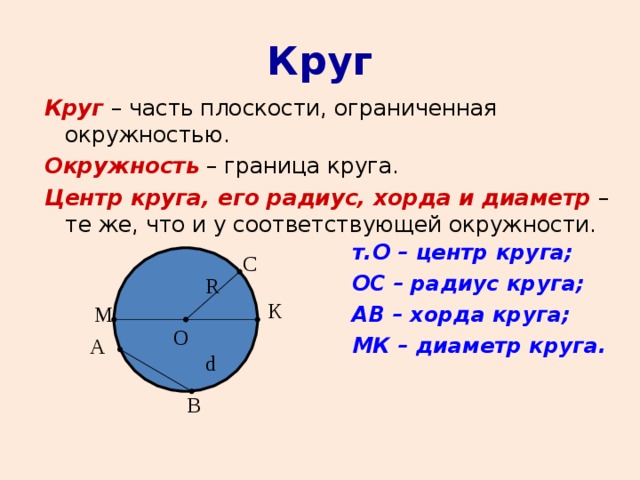

красным — полукруг для круга O.

Существует еще два типа дуг: малые дуги и большие дуги. Малая дуга — это дуга, длина которой меньше длины полуокружности. Большая дуга имеет длину дуги, которая больше, чем у полуокружности.

На рисунке ниже показана малая дуга. Второстепенные дуги обычно называют только их конечными точками. является большой дугой. Большие дуги называются по их конечным точкам и некоторым другим точкам, лежащим на дуге.

Центральный угол

Центральный угол — это угол, вершина которого находится в центре окружности. Когда концы дуги пересекают стороны центрального угла, говорят, что дуга стягивает угол. Мера дуги равна мере центрального угла, опирающегося на дугу.

стягивает ∠QPR, поэтому мера также равна θ.

Кроме того, поскольку длина окружности равна 360°, мы можем найти меру большой дуги, найдя разницу между 360° и мерой малой дуги. Итак,

Добавление дуги

Дуга, образованная двумя соседними дугами, имеет меру, являющуюся суммой двух соседних дуг.

Пример:

Найдите, если = 205° для круга O ниже.

205° = 45° +
= 160°

Другие углы и дуги

Вписанный угол — это угол, образованный внутри окружности при пересечении двух хорд или секущих на окружности. ∠RSQ на рисунке ниже является примером. Вписанный угол равен половине угла, опирающегося на дугу. На рисунке ниже

Мера каждого угла, образованного двумя пересекающимися хордами внутри окружности, равна половине суммы дуг, стягивающих углы. На рисунке ниже

Угол, образованный двумя секущими, пересекающимися вне круга, равен половине разности дуг, образующих угол, образованный секущими. На рисунке ниже

Длина дуги

Поскольку мера дуги равна величине ее центрального угла, мы можем определить длину дуги, используя отношение центрального угла дуги к 360°.

No related posts.