Периметром геометрической фигуры — называют длину границы геометрической фигуры. Навигация по странице: Формула периметра треугольника Формулы периметры квадрата Формула периметра прямоугольника Формула периметра параллелограмма Формула периметра ромба Формула периметра трапеции Формулы длины окружности (периметра круга) Онлайн калькуляторы для вычисления периметра Формула периметра треугольникаПериметр треугольника ∆ABC равен сумме длин его сторон P = a + b + c Смотрите также онлайн калькулятор для расчета периметра треугольника Формулы периметра квадратаПериметр квадрата равен произведению длины его стороны на четыре. P = 4a Периметр квадрата равен произведению длины его диагонали на два корня из двух. P = 2√2 d где P — периметр квадрата, Смотрите также онлайн калькулятор для расчета периметра квадрата Формула периметра прямоугольникаПериметр прямоугольника ABCD равен удвоенной сумме сторон, прилежащих к одному углу. P = 2(a + b) где P — периметр прямоугольника, Смотрите также онлайн калькулятор для расчета периметра прямоугольника Формула периметра параллелограммаПериметр параллелограмма ABCD равен удвоенной сумме сторон, прилежащих к одному углу P = 2(a + b) где P — периметр параллелограмма, Смотрите также онлайн калькулятор для расчета периметра параллелограмма Формула периметра ромбаПериметр ромба равен произведению длины его стороны на четыре. P = 4a где P — периметр ромба, Смотрите также онлайн калькулятор для расчета периметра ромба Формула периметра трапецииПериметр трапеции равен сумме длин ее сторон. P = a + b + c + d где P — периметр трапеции, Смотрите также онлайн калькулятор для расчета периметра трапеции. Формулы длины окружности.
где P — длина окружности, Смотрите также онлайн калькулятор для расчета длина окружности. Формулы по геометрии
Квадрат. Формулы и свойства квадрата
Прямоугольник. Формулы и свойства прямоугольника
Параллелограмм. Формулы и свойства параллелограмма
Ромб. Формулы и свойства ромба
Трапеция. Формулы и свойства трапеции
— Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции
— Прямоугольная трапеция. Все таблицы и формулы Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! |
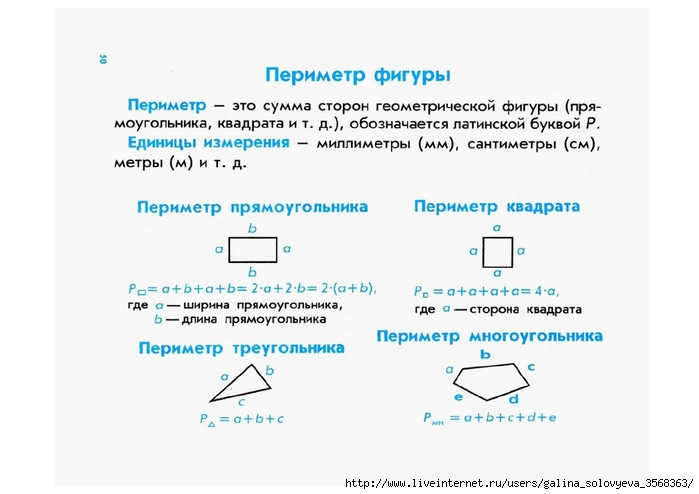
Формулы периметра.
Периметром геометрической фигуры — называют длину границы геометрической фигуры.
- Формула периметра треугольника
- Формулы периметры квадрата
- Формула периметра прямоугольника
- Формула периметра параллелограмма
- Формула периметра ромба
- Формула периметра трапеции
- Формулы периметра круга, длины окружности
Формула периметра треугольника
Периметр треугольника ∆ABC равен сумме длин его сторон
P =
a
+
b
+
c
Формулы периметра квадрата
Периметр квадрата равен произведению длины его стороны на четыре.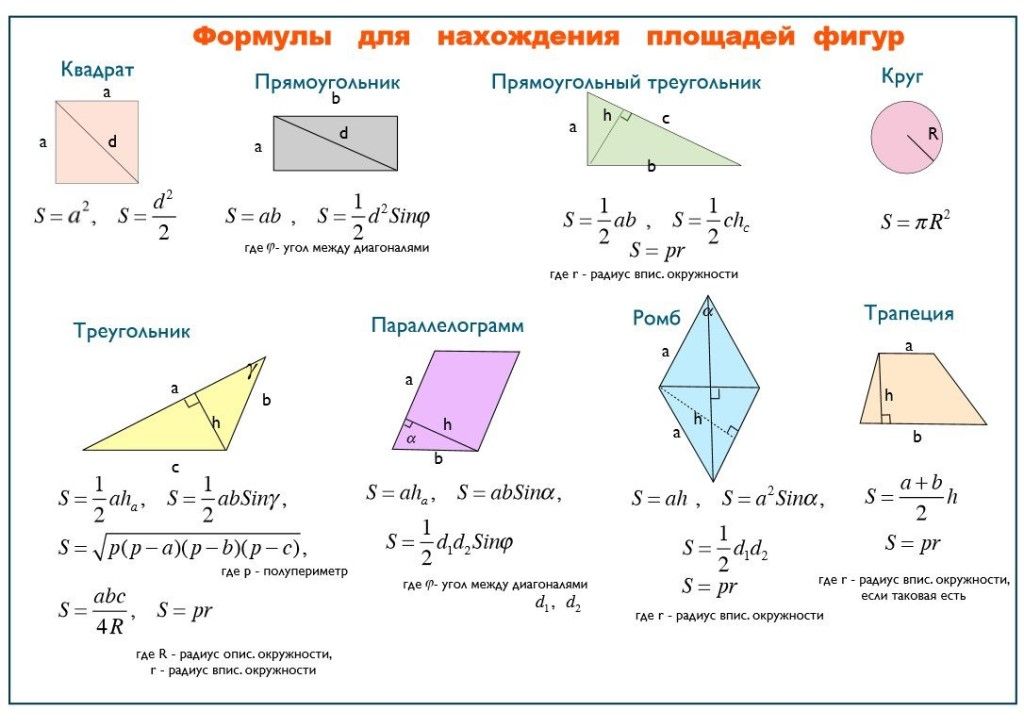
P = 4
a
Периметр квадрата равен произведению длины его диагонали на два корня из двух.
P = 2√2
d
где P — периметр квадрата,
a
— длина стороны квадрата,
d
— длина диагонали квадрата.
Формула периметра прямоугольника
Периметр прямоугольника ABCD равен удвоенной сумме сторон, прилежащих к одному углу.
P = 2(
a
+
b
)
где P — периметр прямоугольника,
a, b
— длины сторон прямоугольника.
Формула периметра параллелограмма
Периметр параллелограмма ABCD равен удвоенной сумме сторон, прилежащих к одному углу
P = 2(
a
+
b
)
где P — периметр параллелограмма,
a, b
— длины сторон параллелограмма.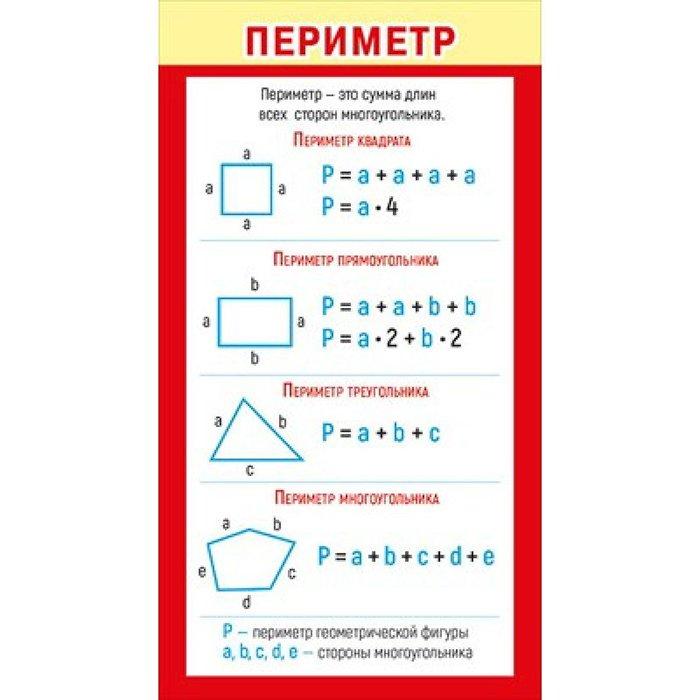
Формула периметра ромба
Периметр ромба равен произведению длины его стороны на четыре.
P = 4
a
где P — периметр ромба,
a
— длина стороны ромба.
Формула периметра трапеции
Периметр трапеции равен сумме длин ее сторон.
P =
a
+
b
+
c
+
d
где P — периметр трапеции,
a, c
— длины основ трапеции,
b, d
— длины боковых сторон трапеции.
Формулы периметра круга, длины окружности.
- P = 2
π r
- P =
π d
где P — периметр круга,
r
— радиус круга,
d
— диаметр круга,
π = 3.
141592
.
- Формулы по геометрии
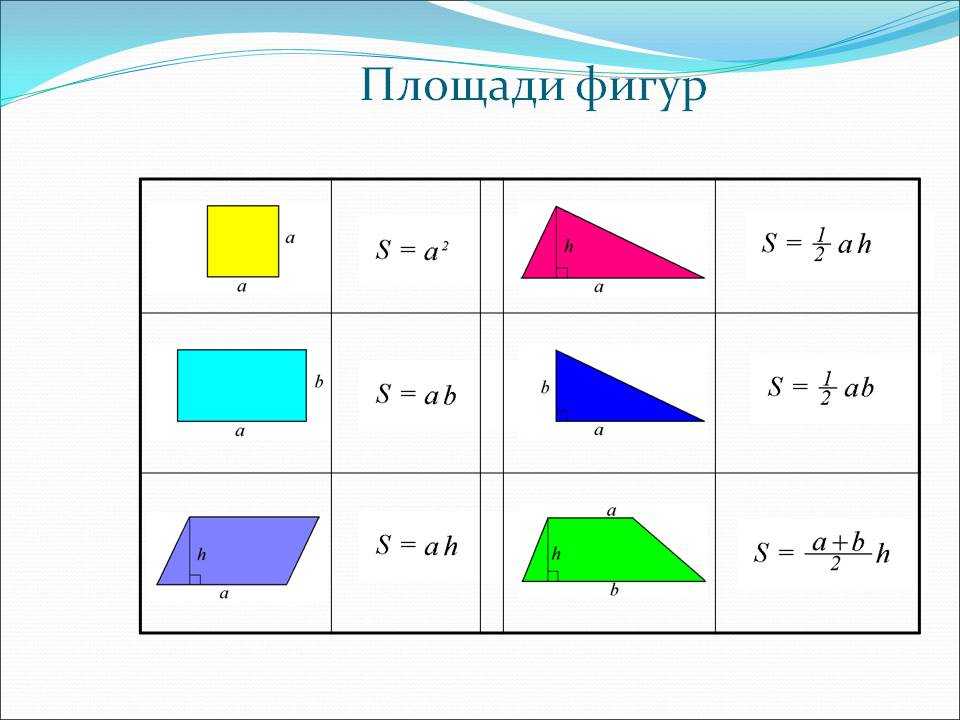
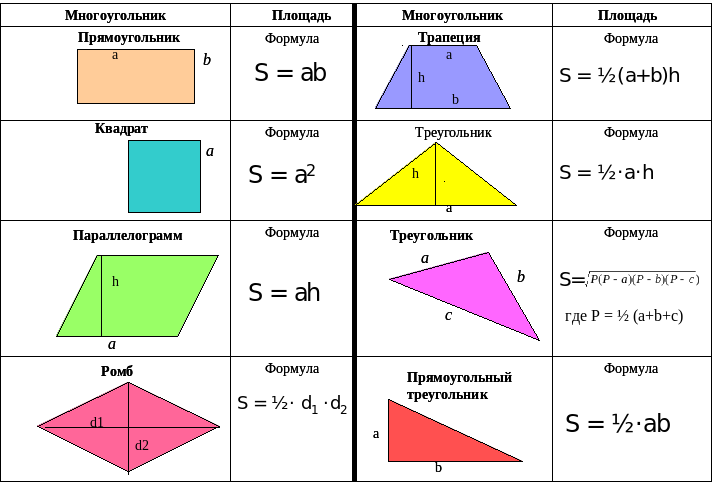
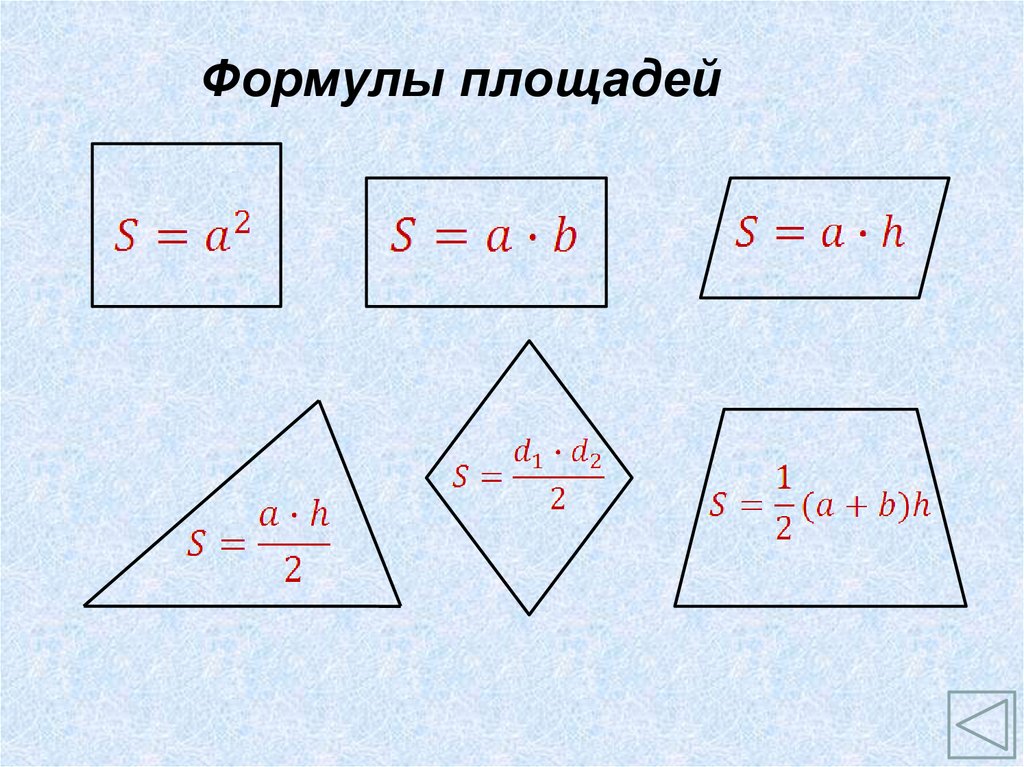
- Формулы площади геометрических фигур
- Формулы периметра геометрических фигур
- Формулы объема геометрических фигур
- Формулы площади поверхности геометрических фигур
| Twitt | Нравится |
Добавить комментарий
Формулы периметра для геометрических фигур
В математике или в повседневной жизни геометрия и геометрические формы всегда играют важную роль. Начиная от простого подноса и заканчивая большим зданием, нас всегда окружает геометрия разных форм и размеров. Форма и поверхность, которую должны занимать такие формы, должны быть рассчитаны таким образом, чтобы их можно было хранить без каких-либо затруднений или чтобы удовлетворить потребности людей, использующих их.
Такому исследованию или вычислению дается специальное название в области математики.
Всякий раз, когда вычисляются размеры различных геометрических фигур и измеряется их площадь или емкость в математике, это называется измерением. Измерение также помогает рассчитать размеры других форм по их площади поверхности и емкости.
Периметр можно определить как границу любой замкнутой фигуры. Периметр — это мера всех сторон любой замкнутой фигуры, скажем, треугольника, прямоугольника, квадрата, круга и т. д.
Общая формула периметра любой замкнутой фигуры = Сумма всех сторон
Теперь давайте найдем формулу периметра для различных фигур.
Периметр треугольника Треугольник — замкнутая фигура, образованная тремя прямыми линиями. Эти линии образуют стороны треугольника, поэтому у него три стороны, скажем, A, B, C. Эти три стороны могут быть одинаковыми или разными в зависимости от типа треугольника.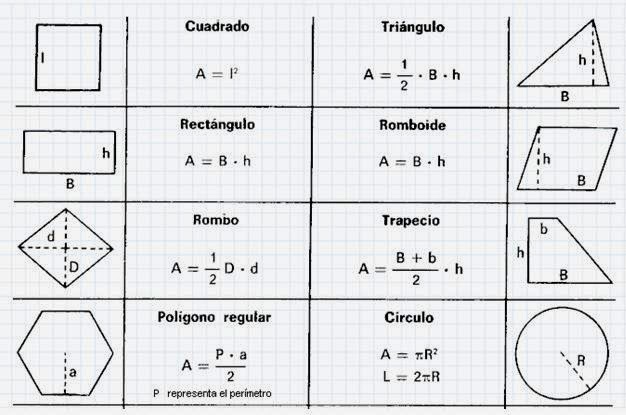
Типы треугольников
Существуют три типа треугольников: Разносторонний, Равнобедренный, Равносторонний.
Разносторонний треугольник: Треугольник, в котором все три стороны различны, называется разносторонним треугольником.
Периметр разностороннего треугольника = A + B + C
Равнобедренный треугольник: Треугольник, в котором две стороны равны, называется равнобедренным треугольником.
Здесь две стороны равны.
Периметр равнобедренного треугольника = A + A + B = 2 × A + B
Равносторонний треугольник: Треугольник, у которого все три стороны равны, называется равносторонним треугольником.
Здесь все три стороны равны.
КвадратПериметр равностороннего треугольника = A + A + A = 3×A
Квадрат — это замкнутая фигура, состоящая из четырех прямых линий.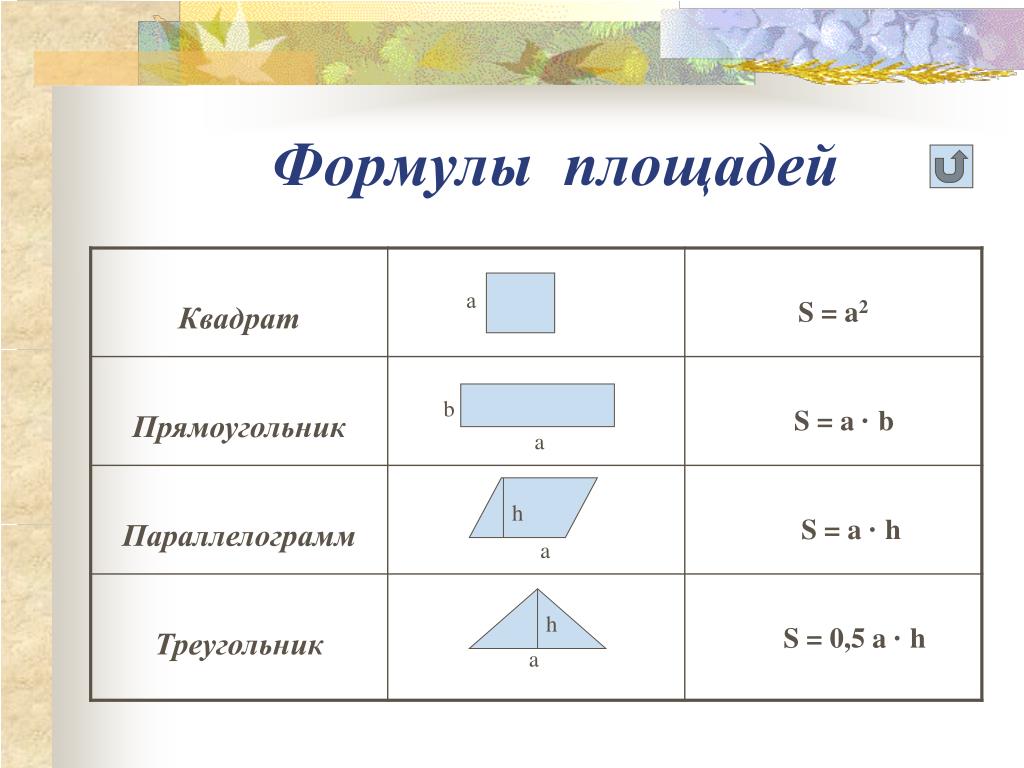
Все четыре прямые равны и все четыре угла квадрата равны 90 градусов.
Периметр прямоугольникаПериметр квадрата = сумма всех 4 сторон = 4×A
Прямоугольник — это замкнутая фигура, состоящая из четырех прямых линий. Обе пары противоположных прямых равны и все четыре угла прямоугольника равны 90 градусов.
Периметр кругаПериметр прямоугольника = сумма всех сторон = 2×A + 2×B = 2(A + B)
Окружность является границей замкнутой фигуры постоянное расстояние от центра окружности. Это постоянное расстояние от центра круга до границы называется радиусом круга.
Вопросы выборкиПериметр круга, также известный как окружность круга = 2 × π × R
Здесь R RADIUS
Вопрос 1: Что представляет имеет стороны a = 5 см, b = 8 см, c = 10 см?
Ответ:
Так как все стороны данного треугольника различны, то это разносторонний треугольник, поэтому периметр разностороннего треугольника равен сумме всех сторон.
Периметр = a + b + c = 5 + 8 + 10
Периметр = 23 см
Вопрос 2: Чему равен периметр круга, радиус которого равен 7 см?
Ответ:
Периметр круга определяется по формуле 2 × π × R
Таким образом, периметр = 2 × (22/7) × 7 Значение π — 22/7
= 44 см
Вопрос 3: Каков периметр квадрата, каждая сторона которого равна 10 см?
Ответ:
Периметр квадрата равен сумме всех сторон.
Периметр = 4 × сторона
= 4 × 10
= 40 см
Вопрос 4: Каков периметр Прямоугольник, чья длина = 5 см и ширина = 8 см??
Ответ:
Периметр прямоугольника находится по формуле = 2 × (A + B), где A — длина, а B — ширина.
Периметр = 2 × (a + b)
= 2 × (5 + 8)
= 2 × (13)
= 26 см
Вопрос 5: Что является периметром равных треугольник, сторона которого равна 8 см?
Ответ:
Поскольку все стороны равностороннего треугольника равны, формула для периметра равностороннего треугольника равна 3 × (сторона).
Периметр = 3 × 8
= 24 см
9.4: Периметр и окружность геометрических фигур
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 48888
- Денни Бурзински и Уэйд Эллис-младший
- Колледж Южной Невады через OpenStax CNX
Цели обучения
- знать, что такое многоугольник
- знать, что такое периметр и как его найти
- знать, что такое длина окружности, диаметр и радиус круга и как их найти
- знать значение символа ππ и его приближенное значение
- знать, что такое формула и четыре версии формулы окружности круга
Многоугольники
Мы можем использовать навыки преобразования с номиналами чисел для измерения геометрических фигур, таких как прямоугольники, треугольники и круги.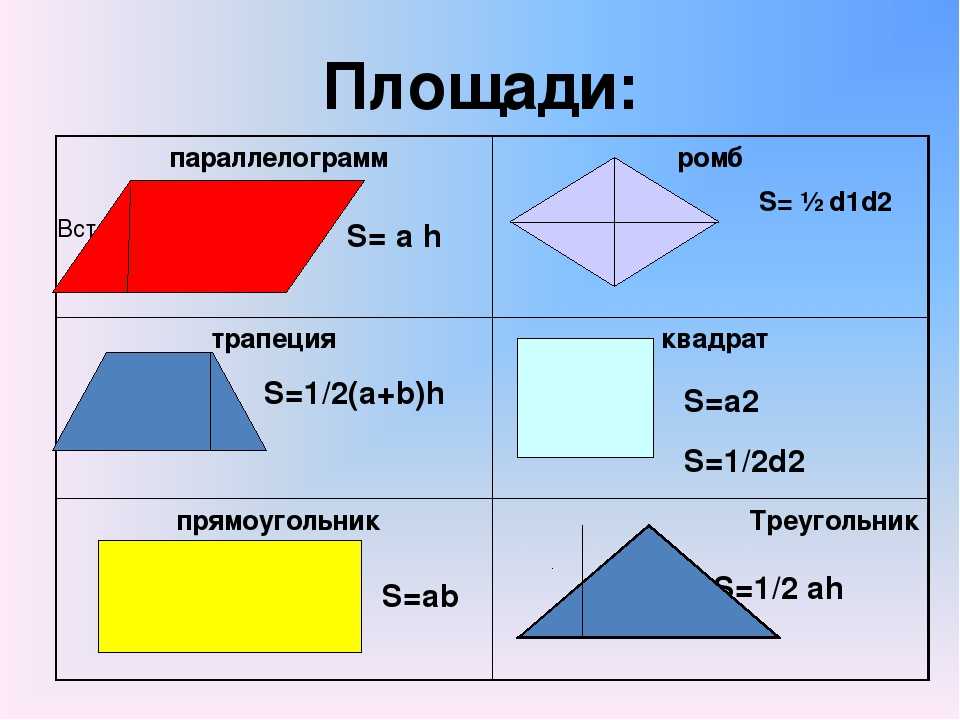
Для проведения этих измерений нам необходимо ознакомиться с несколькими определениями.
Определение: Многоугольник
Многоугольник представляет собой замкнутую плоскую (плоскую) фигуру, стороны которой являются отрезками (частями прямых).
Полигоны
Не полигоны
Периметр
Определение: периметр
периметр многоугольника — это расстояние вокруг многоугольника.
Чтобы найти периметр многоугольника, мы просто складываем длины всех сторон.
Sample Set A
Найдите периметр каждого многоугольника.
Решение
\(\begin{array} {rcl} {\text{Периметр}} & = & {\text{2 см + 5 см + 2 см + 5 см}} \\ {} & = & {\ text {14 см}} \ end {массив} \)
Набор образцов A
Решение
\(\begin{array} {rcr} {\text{Периметр}} & = & {\text{3,1 мм}} \\ {} & & {\text {4,2 мм}} \\ {} & & {\text{4,3 мм}} \\ {} & & {\text{1,52 мм}} \\ {} & & {\text{5,4 мм}} \\ { } & & {\ underline{\text{+ 9,2 мм}}} \\ {} & & {\text{27,72 мм}} \end{массив}\)
Sample Set A
Решение
Наше первое наблюдение состоит в том, что отсутствуют три измерения.
Однако мы можем определить недостающие измерения, используя следующий процесс. Пусть A, B и C представляют недостающие измерения. Визуализируйте
\(\text{A = 12м — 2м = 10м}\)
\(\text{B = 9м + 1м — 2м = 8м}\)
\(\text{C = 12м — 1м = 11м }\)
\(\begin{array} {rcr} {\text{Периметр}} & = & {\text{8 м}} \\ {} & & & {\text{10 м}} \\ { } & & {\ text {2 м}} \\ {} & & {\ text {2 м}} \\ {} & & {\ text {9 м}} \\ {} & & {\ text {11 м}} \\ {} & & {\text{1 м}} \\ {} & & {\underline{\text{+ 1 м}}} \\ {} & & {\text{44 м}} \конец{массив}\)
Тренировочный набор A
Найдите периметр каждого многоугольника.
- Ответить
20 футов
Тренировочный набор A
- Ответить
26,8 м
Тренировочный набор A
- Ответить
49,89 миль
Длина окружности/диаметр/радиус
Окружность
Окружность окружности – это расстояние по окружности.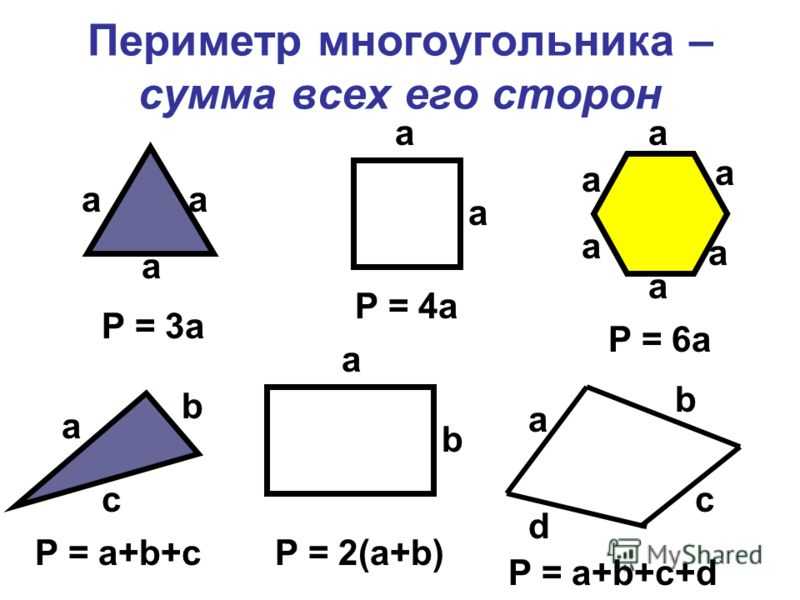
Диаметр
Диаметр окружности — это любой отрезок, который проходит через центр окружности и имеет конечные точки на окружности.
Радиус
Радиус окружности — это любой отрезок, конечными точками которого являются центр окружности и точка на окружности.
Радиус равен половине диаметра.
Число \(\pi\)
Символ \(\pi\), читаемый как «пи», представляет бесконечное, неповторяющееся десятичное число 3,14159 … . Это число было вычислено с точностью до миллионов знаков после запятой без появления повторяющегося блока цифр.
В вычислительных целях \(\pi\) часто аппроксимируется как 3,14. Мы будем писать \(\pi \приблизительно 3,14\), чтобы обозначить, что \(\pi\) приблизительно равно 3,14. Символ «≈» означает «приблизительно равно».
Формулы
Чтобы найти длину окружности, нам нужно знать только ее диаметр или радиус. Затем мы используем формулу для вычисления длины окружности.
Формула
Формула — это правило или метод выполнения задачи. В математике формула — это правило, которое направляет нас в вычислениях.
Формулы обычно состоят из букв, обозначающих важные, но, возможно, неизвестные величины.
Если \(C, d\) и \(r\) представляют соответственно длину окружности, диаметр и радиус окружности, то следующие две формулы дают нам указания для вычисления длины окружности.
Формулы длины окружности
- \(C = \pi d\) или \(C \приблизительно (3.14) d\)
- \(C = 2 \pi r\) или \(C \приблизительно 2 (3.14) r\)
Набор образцов B
Найдите точную длину окружности.
Решение
Используйте формулу \(C = \pi d\).
\(C = \pi \cdot 7\in.\)
По коммутативности умножения,
\(C = 7\in. \cdot \pi\)
\(C = 7 \pi in. \), ровно
Этот результат является точным, так как \(\pi\) не аппроксимировалось.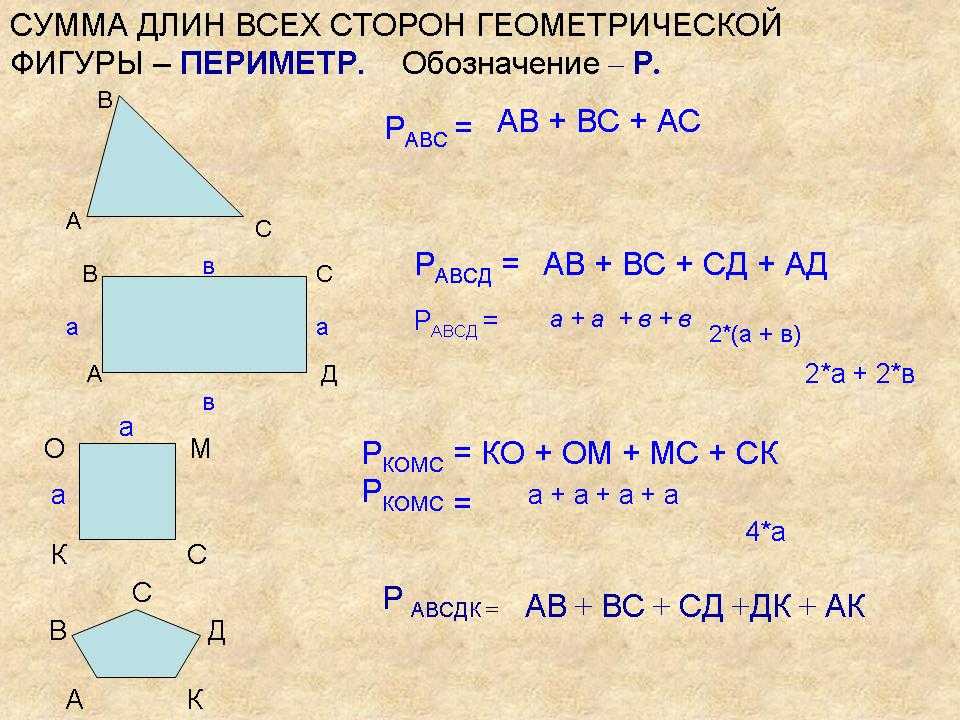
Набор образцов B
Найдите приблизительную длину окружности.
Решение
Используйте формулу \(C = \pi d\).
\(C \приблизительно (3.14)(6.2)\)
\(C \приблизительно 19,648 \text{мм}\)
Этот результат является приблизительным, так как ππ было приближено к 3.14.
Набор образцов B
Найдите приблизительную длину окружности с радиусом 18 дюймов.
Решение
Так как нам известно, что радиус \(r\) равен 18 дюймам, мы будем использовать формулу \(C = 2\pi r\).
\(C \приблизительно (2)(3,14)(18 \text{ дюймов})\)
\(C \приблизительно 113,04 \text{ дюймов}\)
Набор образцов B
Найдите приблизительное периметр фигуры.
Решение
Замечаем, что у нас есть два полукруга (полукруга).
Больший радиус 6,2 см.
Меньший радиус равен \(\text{6,2 см — 2,0 см = 4,2 см.}\)
Ширина нижней части прямоугольника 2,0 см.
\(\begin{array} {rcll} {\text{Периметр}} & = & {\text{2,0 см}} & {} \\ {} & & & {\text{5,1 см}} & {} \\ {} & & {\text{2,0 см}} & {} \\ {} & & {\text{5,1 см}} & {} \\ {} & & & {(0,5) \cdot (2) \ cdot (3.14) \cdot \text{(6.2 com)}} & {\text{Диаметр внешней полуокружности.}} \\ {} & \ \ + & {\underline{(0.5) \cdot (2) \cdot (3.14) \cdot \text{(4.2 com)}}} & {\text{Диаметр внутренней полуокружности.}} \\ {} & & {} & {\text{6,2 см — 2,0 см = 4,2 см}} \\ {} & & {} & {\text{0,5 появляется, потому что мы хотим}} \\ {} & & {} & {\text{периметр только половины круга.}} \end{массив}\ )
\(\begin{массив} {rcr} {\text{Периметр}} & \приблизительно & {\text{2,0 см}} \\ {} & & {\text{5,1 см}} \\ {} & & {\text{2,0 см}} \\ {} & & {\text{5,1 см}} \\ {} & & {\text{19,468 см}} \\ {} & & {\underline{\text{ +13,188 см}}} \\ {} & & {\text{48,856 см}} \end{массив}\)
Практический набор B
Найдите точную длину окружности.
- Ответить
\(9,1 \pi\) дюймов
Практический набор B
Найдите приблизительную длину окружности.
- Ответить
5,652 мм
Практический набор B
Найдите приблизительную длину окружности радиусом 20,1 м.
- Ответить
126,228 м
Практический набор B
Найдите приблизительный внешний периметр
- Ответить
41,634 мм
Упражнения
Найдите каждый периметр или примерную длину окружности. Используйте \(\pi = 3,14\).
Упражнение \(\PageIndex{1}\)
- Ответить
21,8 см
Упражнение \(\PageIndex{2}\)
Упражнение \(\PageIndex{3}\)
- Ответить
38,14 дюйма
Упражнение \(\PageIndex{4}\)
Упражнение \(\PageIndex{5}\)
- Ответить
0,86 м
Упражнение \(\PageIndex{6}\)
Упражнение \(\PageIndex{7}\)
- Ответить
87,92 м
Упражнение \(\PageIndex{8}\)
Упражнение \(\PageIndex{9}\)
- Ответить
16 328 см
Упражнение \(\PageIndex{10}\)
Упражнение \(\PageIndex{11}\)
- Ответить
0,0771 см
Упражнение \(\PageIndex{12}\)
Упражнение \(\PageIndex{13}\)
- Ответить
120,78 м
Упражнение \(\PageIndex{14}\)
Упражнение \(\PageIndex{15}\)
- Ответить
21,71 дюйма
Упражнение \(\PageIndex{16}\)
Упражнение \(\PageIndex{17}\)
- Ответить
43,7 мм
Упражнение \(\PageIndex{18}\)
Упражнение \(\PageIndex{19}\)
- Ответить
45,68 см
Упражнение \(\PageIndex{20}\)
Упражнения для обзора
Упражнение \(\PageIndex{19}\)
Найти значение \(2 \dfrac{8}{13} \cdot \sqrt{10 \dfrac{9{16}}\).