Zero To Hero
Содержание:
| 1. | Число e означает рост |
| 2. | Натуральный логарифм означает время |
| 3. | Этот нестандартный логарифмический счёт |
| 4. | Логарифмическое умножение — просто умора |
| 5. | Использование натурального логарифма при произвольном росте |
| 6. | Отпадный пример: Правило 72 |
| 7. | Дополнение: Натуральный логарифм от e |
Мы уже разобрались с экспоненциальной функцией в посвящённой ей статье, и нашей следующей целью становится натуральный логарифм.
В учебниках математики определение натурального логарифма такое, что ничего «натурального», естественного в нём нет: он определяется как действие, обратное функции ex, странной уже самой по себе.
Так что вот вам новое, упрощённое объяснение: Натуральный логарифм — это время, необходимое, чтобы вырасти до определённого уровня.
Представьте, что вы сделали инвестицию мишками Гамми (а кто так не делает?) с непрерывной доходностью 100% годовых. Если вы преследуете цель достичь десятикратного роста вклада, при условии «сложных процентов», вам пришлось бы ждать всего-то ln(10) = 2.3 года. Не можете понять, почему необходимо только пару лет, чтобы достичь 10х роста? Не понимаете, почему последовательность не 1, 2, 4, 8? Почитайте про число e.
Число e и натуральный логарифм — братья-близнецы:
- ex — уровень, достигнутый при непрерывном росте за определённый промежуток времени.
- натуральный логарифм (ln) — промежуток времени, необходимый для роста до определённого уровня.
Совсем неплохо, правда? Пока математики подбирают слова, чтобы дать вам длинное путанное определение, давайте поближе посмотрим на это простое и ясное.
Число e означает рост
Число e означает непрерывный рост. Как мы видели в прошлом примере, ex позволяет нам увязать процент и время: 3 года при росте 100% есть то же самое, что и 1 год при 300%, при условии «сложных процентов».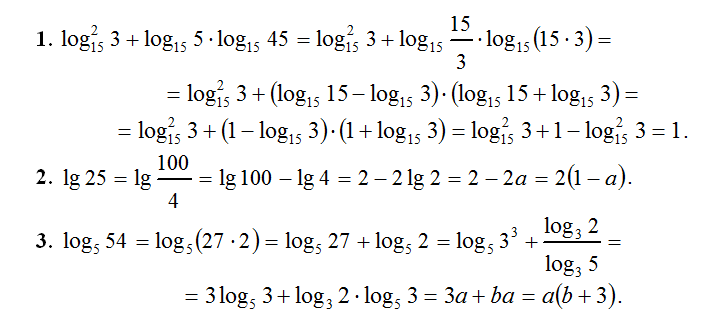
Можно подставлять любые значения процента и времени (50% на протяжении 4 лет), но лучше задать процент как 100% для удобства (получается 100% на протяжении 2 лет). За счёт перехода к 100% мы можем сфокусироваться исключительно на компоненте времени:
ex = eпроцент * время = e1.0 * время = eвремя
Очевидно, что ex означает:
- насколько вырастет мой вклад через x единиц времени (при условии 100%-го непрерывного роста).
- например, через 3 промежутка времени я получу в e3 = 20.08 раз больше «штуковин».
ex — это масштабирующий коэффициент, показывающий, до какого уровня мы вырастем за x отрезков времени.
Натуральный логарифм означает время
Натуральный логарифм — это инверсия числа e, такой причудливый термин для обозначения противоположности. Кстати, о причудах; по латыни он называется logarithmus naturali, отсюда и появилась аббревиатура ln.
И что эта инверсия или противоположность означает?
- ex позволяет нам подставить время и получить рост.

- ln(x) позволяет нам взять рост или доход и узнать время, необходимое для его получения.
Например:
- e3 равняется 20.08. Через три отрезка времени у нас будет в 20.08 раз больше того, с чего мы начали.
- ln(20.08) будет примерно 3. Если вас интересует рост в 20.08 раз, вам понадобится 3 промежутка времени (опять же, при условии стопроцентного непрерывного роста).
Всё ещё читаете? Натуральный логарифм показывает время, нужное, чтобы достичь желаемого уровня.
Этот нестандартный логарифмический счёт
Вы проходили логарифмы — это странные существа. Как им удалось превратить умножение в сложение? А деление в вычитание? Давайте посмотрим.
Чему равняется ln(1)? Интуитивно понятно, что вопрос стоит так: сколько нужно ждать, чтобы получить в 1 раз больше того, что у меня есть?
Ноль. Нуль. Нисколько. У вас уже это есть единожды. Не требуется нисколько времени, чтобы от уровня 1 дорости до уровня 1.
- ln(1) = 0
Хорошо, что насчёт дробного значения? Через сколько у нас останется 1/2 от имеющегося количества? Мы знаем, что при стопроцентном непрерывном росте ln(2) означает время, необходимое для удвоения. Если мы обратим время вспять (т.е. подождём отрицательное количество времени), то получим половину от того, что имеем.
Если мы обратим время вспять (т.е. подождём отрицательное количество времени), то получим половину от того, что имеем.
- ln(1/2) = —ln(2) = —0.693
Логично, правда? Если мы вернёмся назад (время вспять) на 0.693 секунды, то обнаружим половину имеющегося количества. Вообще можно переворачивать дробь и брать отрицательное значение: ln(1/3) = —ln(3) = —1.09. Это означает, что, если мы вернёмся в прошлое на 1.09 отрезков времени, то обнаружим только треть от нынешнего числа.
Ладно, а как насчёт логарифма отрицательного числа? Сколько времени нужно, чтобы «вырастить» колонию бактерий от 1 до —3?
Это невозможно! Нельзя получить отрицательное число бактерий, не так ли? Вы можете получить максимум (эээ… минимум) нуль, но вам никак не получить отрицательное число этих маленьких тварей. В отрицательном числе бактерий просто нет смысла.
- ln(отрицательное число) = неопределено
«Неопределено» означает, что нет такого промежутка времени, который надо было бы прождать, чтобы получить отрицательное значение.
Логарифмическое умножение — просто умора
Сколько времени займёт четырёхкратный рост? Конечно, можно просто взять ln(4). Но это слишком просто, мы пойдём другим путём.
Можно представить четырёхкратный рост как удвоение (требующее ln(2) единиц времени) и затем снова удвоение (требующее ещё ln(2) единиц времени):
- Время на 4х рост = ln(4) = Время на удвоится и затем ещё раз удвоится = ln(2) + ln(2)
Интересно. Любой показатель роста, скажем, 20, можно рассматривать как удвоение сразу после 10-кратного увеличения. Или роста в 4 раза, и затем в 5 раз. Либо же утроение и затем увеличение в 6.666 раз. Видите закономерность?
- ln(a*b) = ln(a) + ln(b)
Логарифм от A, умноженного на B, есть log(A) + log(B). Это отношение сразу обретает смысл, если оперировать в терминах роста.
Если вас интересует 30-кратный рост, вы можете подождать ln(30) за один присест, либо же подождать ln(3) Для утроения, и затем ещё ln(10) для удесятирения. Конечный результат тот же самый, так что конечно время должно оставаться постоянным (и остаётся).
Конечный результат тот же самый, так что конечно время должно оставаться постоянным (и остаётся).
Что на счёт деления? В частности, ln(5/3) означает: сколько времени понадобится для того, чтобы вырасти в 5 раз, и затем получить 1/3 от этого?
Отлично, рост в 5 раз есть ln(5). Рост в 1/3 раза займёт -ln(3) единиц времени. Итак,
- ln(5/3) = ln(5) – ln(3)
Сие означает: дайте вырасти в 5 раз, и затем «вернитесь во времени» к той отметке, где останется всего треть от того количества, так что у вас получится 5/3 рост. В общем получается
- ln(a/b) = ln(a) – ln(b)
Я надеюсь, что странная арифметика логарифмов начинает обретать для вас смысл: умножение показателей роста становится сложением единиц времени роста, а деление превращается в вычитание единиц времени. Не надо запоминать правила, попробуйте осознать их.
Использование натурального логарифма при произвольном росте
— Ну конечно, — скажете вы, — это всё хорошо, если рост 100%-ный, а что в случае 5%, которые я получаю?»
Нет проблем. «Время», которое мы рассчитываем с помощью ln(), на самом деле является комбинацией процентной ставки и времени, тот самый Х из уравнения ex. Мы всего лишь решили задать процент как 100% для простоты, но мы вольны использовать любые числа.
«Время», которое мы рассчитываем с помощью ln(), на самом деле является комбинацией процентной ставки и времени, тот самый Х из уравнения ex. Мы всего лишь решили задать процент как 100% для простоты, но мы вольны использовать любые числа.
Допустим, мы хотим достичь 30-кратного роста: берём ln(30) и получаем 3.4 Это означает:
- ex = рост
- e3.4 = 30
Очевидно, это уравнение означает «100%-ная доходность на протяжении 3.4 лет даёт рост в 30 раз». Мы можем записать это уравнение в таком виде:
- ex = eставка*время
- e100% * 3.4 года = 30
Мы можем менять значения «ставки» и «времени», лишь бы ставка * время оставалось 3.4. Например, если нас интересует 30-кратный рост — сколько нам придётся ждать при процентной ставке 5%?
- ln(30) = 3.4
- ставка * время = 3.4
- 0.05 * время = 3.4
- время = 3.4 / 0.05 = 68 лет
Я рассуждаю так: «ln(30) = 3. 4, значит, при 100%-ном росте это займёт 3.4 года. Если я удвою скорость роста, необходимое время уменьшится вдвое».
4, значит, при 100%-ном росте это займёт 3.4 года. Если я удвою скорость роста, необходимое время уменьшится вдвое».
- 100% за 3.4 года = 1.0 * 3.4 = 3.4
- 200% за 1.7 года = 2.0 * 1.7 = 3.4 [200%-ный рост означает уменьшение времени вдвое]
- 50% за 6.8 года = 0.5 * 6.8 = 3.4 [50%-ный рост означает, что понадобится в 2 раза больше времени]
- 5% за 68 года = .05 * 68 = 3.4 [5%-ный рост означает, что понадобится в 20 раз больше времени].
Здорово, правда? Натуральный логарифм может использоваться с любыми значениями процентной ставки и времени, поскольку их произведение остаётся постоянным. Можете перемещать значения переменных сколько душе угодно.
Отпадный пример: Правило семидесяти двух
Правило семидесяти двух — математический приём, позволяющий оценить, сколько времени понадобится, чтобы ваши деньги удвоились. Сейчас мы его выведем (да!), и более того, мы попробуем уяснить его суть.
Сколько времени понадобится, чтобы удвоить ваши деньги при 100% ставке, нарастающей ежегодно?
Оп-па. Мы использовали натуральный логарифм для случая с непрерывным ростом, а теперь ты ведёшь речь о ежегодном начислении? Не станет ли это формула непригодной для такого случая? Да, станет, однако для реальных процентных ставок вроде 5%, 6% или даже 15%, разница между ежегодным начислением процентов и непрерывным ростом будет невелика. Так что грубая оценка работает, мм, грубо, так что мы сделаем вид, что у нас полностью непрерывное начисление.
Мы использовали натуральный логарифм для случая с непрерывным ростом, а теперь ты ведёшь речь о ежегодном начислении? Не станет ли это формула непригодной для такого случая? Да, станет, однако для реальных процентных ставок вроде 5%, 6% или даже 15%, разница между ежегодным начислением процентов и непрерывным ростом будет невелика. Так что грубая оценка работает, мм, грубо, так что мы сделаем вид, что у нас полностью непрерывное начисление.
Теперь вопрос прост: Как быстро можно удвоиться при 100%-ном росте? ln(2) = 0.693. Нужно 0.693 единиц времени (лет — в нашем случае), чтобы удвоить нашу сумму с непрерывным ростом 100%.
Так, а что если процентная ставка — не 100%, а скажем, 5% или 10%?
Легко! Поскольку ставка * время = 0.693, мы удвоим сумму:
- ставка * время = 0.693
- время = 0.693 / ставка
Получается, если рост 10%-ный, это займёт 0.693 / 0.10 = 6.93 лет на удвоение.
Чтобы упростить вычисления, давайте домножим обе части на 100, тогда можно будет говорить «10», а не «0. 10″:
10″:
- время на удвоение = 69.3 / ставка, где ставка выражена в процентах.
Теперь черёд удваиваться при ставке 5%, 69.3 / 5 = 13.86 лет. Однако 69.3 — не самое удобное делимое. Давайте выберем близкое число, 72, которое удобно делить на 2, 3, 4, 6, 8 и другие числа.
- время на удвоение = 72 / ставка
что и является правилом семидесяти двух. Всё шито-крыто.
Если вам нужно найти время для утроения, можете использовать ln(3) ~ 109.8 и получить
- время на утроение = 110 / ставка
Что является ещё одним полезным правилом. «Правило 72» применимо росту по процентным ставкам, росту населения, культур бактерий, и всего, что растёт экспоненциально.
Что дальше?
Надеюсь, натуральный логарифм теперь приобрёл для вас смысл — он показывает время, необходимое для роста любого числа при экспоненциальном росте. Я думаю, натуральным он называется потому, что e — универсальная мера роста, так что ln можно считать универсальным способом определения, сколько времени нужно для роста.
Каждый раз, когда вы видите ln(x), вспоминайте «время, нужное, чтобы вырасти в Х раз». В предстоящей статье я опишу e и ln в связке, так что свежий аромат математики заполнит воздух.
Дополнение: Натуральный логарифм от e
Быстрая викторина: сколько будет ln(e)?
- математический робот скажет: поскольку они определены как инверсия одна другой, очевидно, что ln(e) = 1.
- понимающий человек: ln(e) это число времени, чтобы вырасти в «е» раз (около 2.718). Однако число e само по себе является мерой роста в 1 раз, так что ln(e) = 1.
Мыслите ясно.
Перевод статьи «Demystifying the Natural Logarithm (ln)»
11.4.4. Натуральный логарифм.
Главная » 11 класс. Алгебра. » 11.4.4. Натуральный логарифм
На чтение 2 мин. Просмотров 4.8k.
Логарифм по основанию е (Неперово число е≈2,7) называют натуральным логарифмом.
ln7=loge7, ln7 – натуральный логарифм числа 7.
Примеры.
Вычислить, используя определение логарифма.
1) lne². По определению натуральный логарифм числа e² — это показатель степени, в которую нужно возвести число е, чтобы получить число е². Очевидно, что это число 2.
lne²=2.
2) ln (1/e). По определению натуральный логарифм числа 1/е — это показатель степени, в которую нужно возвести число е, чтобы получить 1/е. Очевидно, что это число -1, так как е-1=1/е.
ln (1/e)=-1.
3) lne3+lne4=3+4=7.
4) lne-ln (1/e2)=1- (-2)=1+2=3.
Вычислить, применив основное логарифмическое тождество:
и формулу возведения степени в степень: (am)n=amn=(an)m.
1) eln24=24.
2) e2ln11=(eln11)2=112=121.
3) e-ln20=(eln20)-1=20-1=1/20=0,05.
4) (e4)ln5=(eln5)4=54=625.
Упростить, применив основное логарифмическое тождество:
формулу возведения степени в степень: (am)n=amn=(an)m ;
формулу произведения степеней с одинаковыми основаниями: am∙an=am+n и
формулу возведения в степень произведения: (a∙b)n=an∙bn.
1) eln4+2=eln4∙e2=4∙e2=4e2.
2) e1+ln3=e1∙eln3=e∙3=3e.
3) (e4+ln5)2=(e4∙eln5)2=(e4∙5)2=e4∙2∙52=e8∙25=25e8.
4) (eln2+3)4=(eln2∙e3)4=(2∙e3)4=24∙e3∙4=16e12.
Упростить, применив основное логарифмическое тождество:
формулу возведения степени в степень: (am)n=amn=(an)m ;
формулу частного степеней с одинаковыми основаниями: am:an=am-n и
формулу возведения в степень произведения: (a∙b)n=an∙bn.
1) e2-ln3=e2:eln3=e2:3=e2/3.
2) e1-ln5=e1:eln5=e:5=e/5=0,2e.
3) (e5-ln10)3=(e5:eln10)3=(e5:10)3=(0,1e5)3=0,13∙e5∙3=0,001e15.
4) (e3-ln2)4=(e3:eln2)4=(e3:2)4=(0,5e3)4=(0,5)4∙(e3)4=0,0625e12.
вычисление lna натуральный логарифм
( 1 оценка, среднее 5 из 5 )
8.7 Логарифмические функции. Основы бизнес-математики
Логарифмы обратны экспоненциальным функциям – они позволяют нам отменить экспоненциальные функции и найти показатель степени.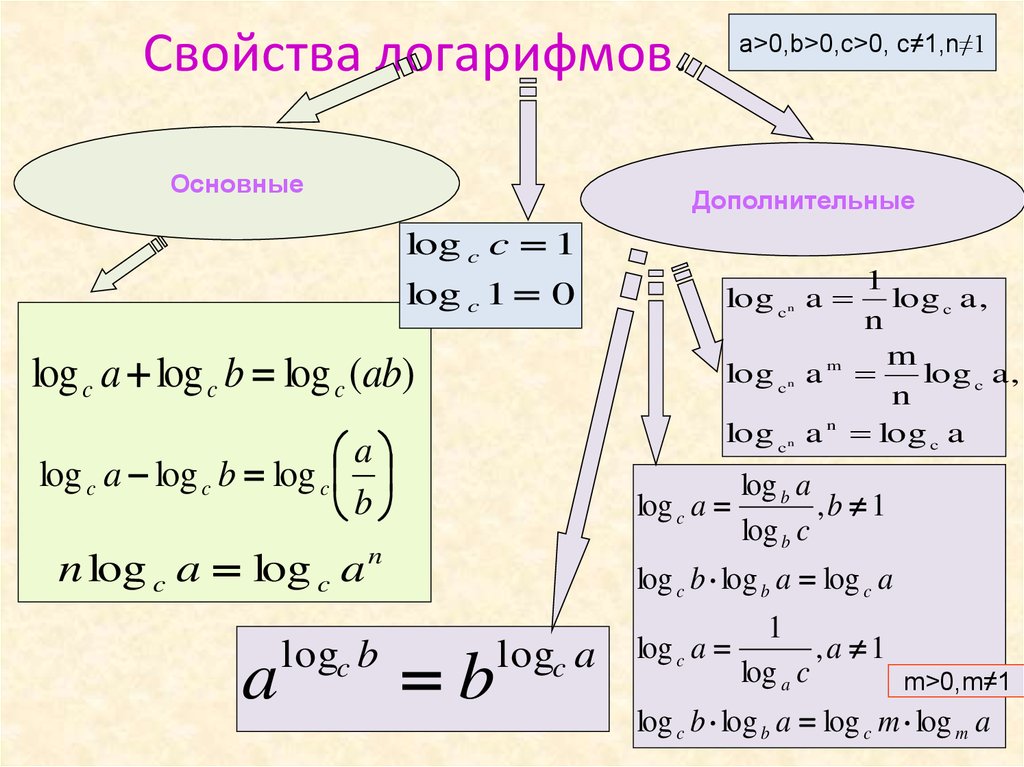 x[/латекс]. 9x=10[/латекс] для [латекс]х[/латекс].
x[/латекс]. 9x=10[/латекс] для [латекс]х[/латекс].
Ответ: Переписав это уравнение с помощью логарифма, мы получим [latex]x=\log_2(10)[/latex].
Хотя это и определяет решение, причем точное решение, оно может показаться вам несколько неудовлетворительным, поскольку трудно сравнить это выражение с десятичной оценкой, которую мы сделали ранее. Кроме того, давать точное выражение для решения не всегда полезно — часто нам действительно нужна десятичная аппроксимация решения. К счастью, с этой задачей хорошо справляются калькуляторы и компьютеры. К несчастью для нас, большинство калькуляторов и компьютеров вычисляют только логарифмы по двум основаниям: по основанию 10 и по основанию [латекс]е[/латекс]. К счастью, в конечном итоге это не проблема, как мы вскоре увидим.
Двойные и натуральные логарифмы
Общий журнал является логарифмом по основанию 10 и обычно записывается [латекс]\лог(х)[/латекс]. х=1000.[/латекс] 9{-3}[/латекс]
х=1000.[/латекс] 9{-3}[/латекс]
Оцените [латекс]\лог(500)[/латекс] с помощью калькулятора или компьютера.
Ответ: Используя компьютер или калькулятор, мы можем вычислить и найти, что [латекс]\лог(500)\приблизительно 2,69897[/латекс].
Поскольку логарифмы являются обратными функциями экспонент, мы можем, в частности, использовать их для решения экспоненциальных уравнений, где неизвестное находится в показателе степени, почти так же, как мы используем обратные свойства сложения и вычитания или умножения и умножения. деление при перестановке уравнений для решения относительно неизвестного значения. 9х=\фракция{17.2}{2}[/латекс]
Глядя на уравнение, мы видим, что единственное, что происходит с [latex]x[/latex] — это то, что [latex]x[/latex] помещается в показатель степени 1,8. Противоположной операцией было бы обратное свойство (1), поэтому мы могли бы применить [latex]log_{1. 8}[/latex], чтобы получить просто [latex]x[/latex]. Однако типичный научный калькулятор вычисляет только обычный и натуральный логарифм, поэтому [latex]log_{1.8}[/latex] бесполезен, когда применяется к другой стороне уравнения. Поэтому вместо этого мы применим либо [латекс]\лог[/латекс], либо [латекс]ln[/латекс] к обеим частям уравнения, а затем уменьшим показатель степени, используя свойство степени (3): 9x&=\ln\left(\frac{17.2}{2}\right)\Стрелка вправо x\ln(1.8)=\ln\left(\frac{17.2}{2}\right)\\ &\Стрелка вправо x= \frac{\ln\left(\frac{17.2}{2}\right)}{\ln(1.8)}\приблизительно 3,660788 \end{align*}[/latex]
8}[/latex], чтобы получить просто [latex]x[/latex]. Однако типичный научный калькулятор вычисляет только обычный и натуральный логарифм, поэтому [latex]log_{1.8}[/latex] бесполезен, когда применяется к другой стороне уравнения. Поэтому вместо этого мы применим либо [латекс]\лог[/латекс], либо [латекс]ln[/латекс] к обеим частям уравнения, а затем уменьшим показатель степени, используя свойство степени (3): 9x&=\ln\left(\frac{17.2}{2}\right)\Стрелка вправо x\ln(1.8)=\ln\left(\frac{17.2}{2}\right)\\ &\Стрелка вправо x= \frac{\ln\left(\frac{17.2}{2}\right)}{\ln(1.8)}\приблизительно 3,660788 \end{align*}[/latex]
Общий процесс решения показательных уравнений:
- По возможности изолируйте экспоненциальные выражения.
- Возьмем логарифм обеих частей.
- Используйте свойство экспоненты для логарифмов, чтобы вывести переменную из экспоненты вниз. 9t\right)=\ln\left(\dfrac{2}{1.14}\right)[/latex]
Примените свойство экспоненты справа. 
[латекс]t\cdot\ln(1.0134)=\ln\left(\dfrac{2}{1.14}\right)[/latex] Разделить обе части на [латекс]\ln(1.0134)[/латекс] [латекс] t = \dfrac{\ln\left(\dfrac{2}{1.14}\right)}{\ln(1.0134)}[/latex] Рассчитать. [латекс]т\около 42,23 \текст{ лет}[/латекс] Если такие темпы роста сохранятся, модель предсказывает, что население Индии достигнет 2 миллиардов примерно через 42 года после 2008 г., или примерно в 2050 г. 9{-0.3t}\right)=\ln\left(\dfrac{2}{5}\right)[/latex]
Используйте обратное свойство для бревен (2). [латекс]-0.3t=\ln\left(\dfrac{2}{5}\right)[/latex] Разделить на -0,3. [латекс] t = \dfrac{\ln\left(\dfrac{2}{5}\right)}{-0,3}[/latex] Рассчитать. [латекс]t\ок. 3,054[/латекс] Помимо решения экспоненциальных уравнений, логарифмические выражения очень полезны в вопросах на сложные проценты.
 {0,0189{0,0189t}\right)=\ln\left(\frac{2500}{2000}\right)\\ &\Стрелка вправо 0,0189t\ln(e)=\ln\left(\frac{2500}{2000} \right)\\ &\Стрелка вправо 0,0189t=\ln\left(\frac{2500}{2000}\right)\\ &\Стрелка вправо t=\frac{\ln\left(\frac{2500}{2000} \right)}{0,0189}\\ &\Rightarrow t\приблизительно 11,807 \end{align*}[/latex]
{0,0189{0,0189t}\right)=\ln\left(\frac{2500}{2000}\right)\\ &\Стрелка вправо 0,0189t\ln(e)=\ln\left(\frac{2500}{2000} \right)\\ &\Стрелка вправо 0,0189t=\ln\left(\frac{2500}{2000}\right)\\ &\Стрелка вправо t=\frac{\ln\left(\frac{2500}{2000} \right)}{0,0189}\\ &\Rightarrow t\приблизительно 11,807 \end{align*}[/latex]Поскольку 11,807 лет составляет примерно 11 лет и [latex]0,807(12)[/latex] месяцев, время, необходимое для того, чтобы инвестиции достигли 2500 долларов за счет непрерывного начисления сложных процентов, составляет 11 лет и 10 месяцев.
Хотя нам нечасто приходится рисовать график логарифма, полезно понимать его основную форму.
Графические особенности логарифма
Графически, учитывая функцию [latex]g(x)=\log_b(x)[/latex].
- График имеет горизонтальную точку пересечения в точках (1, 0).
- График имеет вертикальную асимптоту в точке [latex]x = 0[/latex].
- График увеличивается и вогнут вниз.

- Область определения функции: [latex]x \gt 0[/latex] или [latex](0, \infty)[/latex] в интервальной нотации.
- Областью действия функции являются все действительные числа или [латекс](-\infty, \infty)[/латекс] в интервальной нотации.
При построении общего логарифма по основанию [латекс]b[/латекс] полезно помнить, что график будет проходить через точки [латекс](1, 0)[/латекс] и [латекс](b, 1)[/латекс].
Чтобы понять, как основание влияет на форму графика, изучите приведенные ниже графики:
Другим важным наблюдением была область логарифмирования: [latex]x \gt 0[/latex]. Подобно функциям обратного и квадратного корня, логарифм имеет ограниченную область определения, которую необходимо учитывать при нахождении области определения композиции, включающей бревно.
Найдите область определения функции [latex]f(x)=\log(5-2x)[/latex].
Ответ: Логарифм определяется только при положительном входе, поэтому эта функция будет определена только тогда, когда [латекс]5-2x \gt 0[/латекс]. Решив это неравенство, [латекс]-2x \gt -5[/latex], поэтому [latex]x\lt \frac{5}{2}[/latex]. Областью определения этой функции является [latex]x\lt \frac{5}{2}[/latex ] или, в интервальных обозначениях, [латекс]\влево(-\infty, \frac{5}{2} \вправо)[/латекс].
Решив это неравенство, [латекс]-2x \gt -5[/latex], поэтому [latex]x\lt \frac{5}{2}[/latex]. Областью определения этой функции является [latex]x\lt \frac{5}{2}[/latex ] или, в интервальных обозначениях, [латекс]\влево(-\infty, \frac{5}{2} \вправо)[/латекс].Работайте над следующими упражнениями. Обсудите свои решения с коллегами и/или преподавателем курса.
Раздел 8.6 Упражнения — Логарифмические функции
5. Натуральные логарифмы (по основанию e)
М. Борна
Далее на этой странице
Изменение базы
Число и часто встречается в математике. (особенно исчисление) и является иррациональной константой (например, π ). Его значение e = 2,718 281 828 …
Помимо логарифмов по основанию 10, которые мы видели в предыдущем разделе, мы также можем иметь логарифмов по основанию e . Они называются натуральных логарифмов .
Мы обычно записываем натуральные логарифмы, используя `ln`, следующим образом:
`ln x` означает `log_e x` (то есть «`log x` по основанию `e`»)
Натуральные логарифмы широко используются в науке и технике.



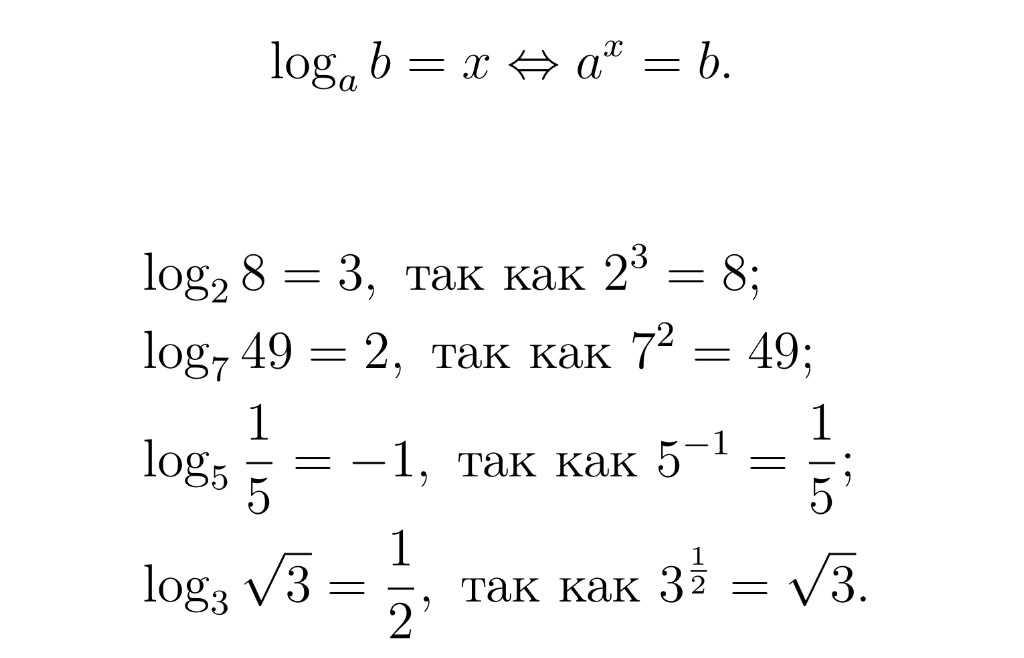
 {0,0189{0,0189t}\right)=\ln\left(\frac{2500}{2000}\right)\\ &\Стрелка вправо 0,0189t\ln(e)=\ln\left(\frac{2500}{2000} \right)\\ &\Стрелка вправо 0,0189t=\ln\left(\frac{2500}{2000}\right)\\ &\Стрелка вправо t=\frac{\ln\left(\frac{2500}{2000} \right)}{0,0189}\\ &\Rightarrow t\приблизительно 11,807 \end{align*}[/latex]
{0,0189{0,0189t}\right)=\ln\left(\frac{2500}{2000}\right)\\ &\Стрелка вправо 0,0189t\ln(e)=\ln\left(\frac{2500}{2000} \right)\\ &\Стрелка вправо 0,0189t=\ln\left(\frac{2500}{2000}\right)\\ &\Стрелка вправо t=\frac{\ln\left(\frac{2500}{2000} \right)}{0,0189}\\ &\Rightarrow t\приблизительно 11,807 \end{align*}[/latex]

