Дроби
Дроби это тема об которую спотыкается половина жителей нашей планеты. Если спросить у людей с какой темы у них начались проблемы с математикой, то большинство из них ответят — с дробей.
Этих людей нельзя упрекнуть. Дроби действительно тема не из простых. Тема дробей требует много терпения и внимания, особенно если человек изучает её впервые.
Но есть и хорошие новости. Если вы наберётесь терпения и освоите дроби, то уверяем, что дальнейшее изучение математики станет для вас простым и интересным.
А если вы ещё хорошо изучили предыдущий урок, который назывался деление, то можете быть уверены, что дроби вы освоили уже наполовину.
Что такое дробь?Если говорить простым языком, то дробь это часть чего-либо. Это «чего-либо» может быть чем угодно — едой, деньгами, числом. В народе дробь называют долей. Само слово «дробь» тоже говорит за себя — дробь означает дробление, деление, разделение.
Рассмотрим пример из жизни. Мы купили себе пиццу, чтобы съесть её в течении дня. Допустим мы решили разделить её на четыре части, чтобы съедать постепенно по одному кусочку.
Допустим мы решили разделить её на четыре части, чтобы съедать постепенно по одному кусочку.
Посмотрите на этот рисунок. Представьте, что это наша пицца, разделённая на четыре куска. Каждый кусок пиццы это и есть дробь, потому что каждый кусок по отдельности это часть пиццы.
Допустим мы съели один кусок. Как его записать? Очень просто. Сначала рисуется маленькая линия:
Внизу этой линии записывается на сколько кусков пицца была разделена. Пицца была разделена на четыре куска. Значит внизу линии записывается четвёрка:
А сверху этой линии записывается сколько кусков пиццы было съедено. Съеден был один кусок, значит сверху записываем единицу:
Такие записи называют дробями. Дробь состоит из числителя и знаменателя.
Число, которое записывается сверху, называется числителем дроби.
Число, которое записывается снизу, называется знаменателем дроби.
В нашем примере числитель дроби это единица, а знаменатель дроби — четвёрка. Эту дробь можно прочитать так: «одна четвёртая» либо «один кусок из четырёх» либо «одна четвёртая доля» либо «четверть» — всё это синонимы.
Эту дробь можно прочитать так: «одна четвёртая» либо «один кусок из четырёх» либо «одна четвёртая доля» либо «четверть» — всё это синонимы.
Теперь представьте, что мы съели ещё один кусок той же самой пиццы, которая была разделена на четыре куска. Как записать такую дробь?
Очень просто. Сверху записываем 2 (поскольку уже съедено два куска), а внизу записываем 4 (поскольку всего кусков было 4):
Эта дробь читается так: «две четвёртых» либо «два куска из четырёх» либо «две четвёртые доли».
Теперь представьте, что пиццу мы разделили не на четыре части, а на три.
Допустим мы съели один кусок этой пиццы. Как записать такую дробь?
Очень просто. Опять же рисуется маленькая линия. Внизу этой линии записывается число 3, поскольку пицца разделена на три части, а сверху этой линии записывается число 1, поскольку съеден один кусок:
Эта дробь читается так: «Одна третья» либо «Один кусок из трёх» либо «Одна третья доля» либо «Треть».
Если мы съедим два куска пиццы, то такая дробь будет называться «две третьих» и записываться следующим образом:
Теперь представьте, что пиццу мы разделили на две части, или как говорят в народе: «Пополам»:
Допустим, из этих двух кусков мы съели один кусок. Как записать такую дробь?
Опять же рисуем линию. Внизу этой линии записываем число 2, поскольку пицца разделена на две части, а вверху записываем число 1, поскольку съеден один кусок:
Эта дробь читается так: «одна вторая» либо «один кусок из двух» либо «одна вторая доля» либо «половина».
Дроби, которые мы сейчас рассмотрели, называют обыкновенными.
Вообще, дроби бывают двух видов: обыкновенные и десятичные. На данный момент мы рассматриваем обыкновенные дроби. Обыкновенная дробь это дробь, которая состоит из числителя и знаменателя. Десятичные дроби рассмотрим немного позже.
Знаменатель дроби — это число, которое показывает на сколько равных частей можно что-либо разделить. Вернёмся к нашей пицце. Поровну эта пицца может быть разделена и на 2 части и на 3, и на 4, и на 5, и на 6. В зависимости от того, на сколько частей мы будем делить пиццу, знаменатель будет меняться.
На следующем рисунке представлены три пиццы, которые разделены по разному. У первой пиццы знаменателем будет 2. У второй пиццы знаменателем будет 3. У третьей пиццы знаменателем будет 4.
Числитель же показывает сколько частей взято от чего-либо. К примеру, если разделить пиццу на две части, как на первом рисунке, и взять одну часть для трапезы, то получится что мы взяли (одну часть из двух), или как говорят в народе «половину» пиццы.
С помощью переменных дробь можно записать так:
где a — это числитель, b — знаменатель.
Следующая вещь, которую важно знать это то, что обыкновенные дроби бывают правильными и неправильными.
Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, следующие дроби являются правильными:
Почему такие дроби называют правильными? Вспомним, что дробь это часть чего-либо. Ведь будет логичнее, если эта часть будет меньше того, откуда эта часть была взята. Например, если пицца разделена на четыре части, и мы возьмём (одну четвёртую), то наш кусок будет меньше, чем все четыре куска вместе взятые (чем одна целая пицца). Поэтому такие дроби называют правильными.
С неправильной дробью всё с точностью наоборот. Неправильная дробь — это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными:
Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.
Теперь возьмём к примеру неправильную дробь и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.
В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.
Дробь, у которой числитель и знаменатель одинаковые, тоже называют неправильной. Например:
Вообще, такие дроби даже не должны называться дробями. И вот почему. Рассмотрим к примеру дробь . Применим её к нашей пицце.
Допустим, мы хотим съестьпиццы. В знаменателе стоит число 2, значит пицца разделена на две части. И в числителе стоит 2, значит взято две части. По сути, взята вся целая пицца, и если мы съедим этупиццы, то съедим не часть пиццы, а всю пиццу целиком. Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.
Дробь означает деление
Черта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель.
Она говорит, что числитель можно разделить на знаменатель.
Например, рассмотрим дробь . Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:
Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например:
Это простейшие примеры. Видно, что у них отсутствует остаток. С остатком немного сложнее, зато интереснее. Поговорим об этом в следующей теме, которая называется «выделение целой части дроби».
Выделение целой части дроби
Вычислим дробь . Пять разделить на два будет два и один в остатке:
5 : 2 = 2 (1 в остатке)
Проверка: (2 × 2) + 1 = 4 + 1 = 5
Но сейчас мы имеем дело с дробями, значит и отвечать надо в дробном виде. Чтобы хорошо понять, как это делается, рассмотрим пример из жизни.
Представьте, что у вас есть 5 яблок и вы решили поделиться ими со своим другом. Причём поделиться по-честному, чтобы каждому досталось поровну. Как разделить эти 5 яблок?
Причём поделиться по-честному, чтобы каждому досталось поровну. Как разделить эти 5 яблок?
Очевидно, что каждому из вас достанется по два яблока, а оставшееся одно яблоко вы разрежете ножом пополам и тоже разделите между собой:
Посмотрите внимательно на этот рисунок. На нём показано, как пять яблок разделены между вами и вашим другом. Очевидно, что каждому досталось по два целых яблока и по половинке яблока.
Теперь возвращаемся к дроби и отвечаем на её вопрос. Сколько будет пять разделить на два? Смотрим на наш рисунок и отвечаем: если пять яблок разделить на двоих, то каждому достанется два целых яблока и половинка яблока. Так и записываем:
Схематически это выглядит так:
Процедуру, которую мы сейчас провели, называют выделением целой части дроби.
В нашем примере мы выделили целую часть дроби и получили новую дробь . Такую дробь называют смешанной. Смешанная дробь — это дробь, у которой есть целая часть и дробная.
В нашем примере целая часть это 2, а дробная часть это
Обязательно запомните эти понятия! А лучше запишите в свою рабочую тетрадь.
Выделить целую часть можно только у неправильных дробей. Напомним, что неправильная дробь это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными, и у них выделена целая часть:
Чтобы выделить целую часть, достаточно знать, как делить числа уголком. Например, выделим целую часть у дроби . Записываем уголком данное выражение и решаем:
После того, как решение примера завершается, новую дробь собирают подобно детскому конструктору. Важно понимать, что куда относить. Частное относят к целой части, остаток относят в числитель дробной части, делитель относят в знаменатель дробной части.
В принципе, если вы хорошо знаете таблицу умножения, и можете быстро в уме выполнять элементарные вычисления, то можно обойтись без записей уголком. В школах кстати, именно этого и требуют — чтобы учащиеся не тратили время на простые операции, а сразу записывали ответы.
Но если вы только начинаете изучать математику, советуем записывать каждую мелочь.
Рассмотрим ещё один пример на выделение целой части. Пусть требуется выделить целую часть дроби
Записываем уголком данное выражение и решаем. Потом собираем смешанную дробь:
Получили:
Перевод смешанного числа в неправильную дробь
Любое смешанное число получается в результате выделения целой части в неправильной дроби. Например, рассмотрим неправильную дробь . Если выделить в ней целую часть, то получается
Но возможен и обратный процесс — любое смешанное число можно перевести в неправильную дробь. Для этого целую часть надо умножить на знаменатель дробной части и полученный результат прибавить к числителю дробной части. Полученный результат будет числителем новой дроби, а знаменатель останется без изменений.
Например, переведём смешанное число в неправильную дробь. Умножаем целую часть 2 на знаменатель дробной части:
2 × 3 = 6
Затем к 6 прибавляем числитель дробной части:
6 + 1 = 7
Полученная семёрка будет числителем новой дроби, а знаменатель 3 останется без изменений:
Подробное решение выглядит так:
А с помощью переменных перевод смешанного числа в неправильную дробь можно записать так:
Пример 2. Перевести смешанное число в неправильную дробь.
Перевести смешанное число в неправильную дробь.
Умножаем целую часть смешанного числа на знаменатель дробной части и прибавляем к числителю дробной части, а знаменатель оставляем без изменений:
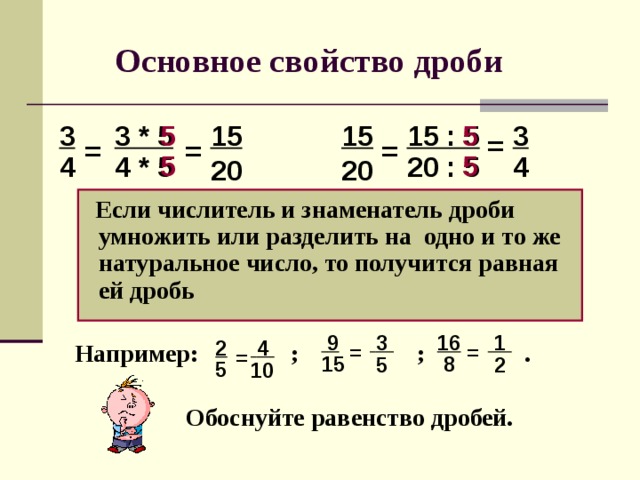
Основное свойство дроби
Основное свойство дроби говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь. Это означает, что значение дроби не изменится.
Например, рассмотрим дробь . Умножим её числитель и знаменатель на одно и то же число, например на число 2
Получили новую дробь . Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (один кусок из двух), а второй иллюстрирует дробь (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и с неё взяли один кусок. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и с неё взяли один кусок. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
Теперь испытаем основное свойство дроби, разделив числитель и знаменатель на одно и то же число.
Рассмотрим дробь . Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2
Получили новую дробь . Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (четыре куска из восьми), а второй иллюстрирует дробь (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на восемь кусков, и с неё взяли четыре куска. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Первая пицца была разделана на восемь кусков, и с неё взяли четыре куска. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
Теперь мы полностью проверили, как работает основное свойство дроби, и убедились, что работает оно замечательно.
Число, на которое умножается числитель и знаменатель, называется дополнительным множителем. Запомните это обязательно!
Сокращение дробей
Дроби можно сокращать. Сократить — значит сделать дробь короче и проще для восприятия. Например, дробь выглядит намного проще и красивее, чем дробь .
Если при решении примеров получается большая и некрасивая дробь, то нужно попытаться её сократить.
Сокращение дроби опирается на основное свойство дроби. Поэтому, прежде чем изучать сокращение дробей, обязательно изучите основное свойство дроби.
Деление числителя и знаменателя на их наибольший общий делитель называется сокращением дроби.
Пример 1. Сократить дробь
Итак, нужно разделить числитель и знаменатель дроби на наибольший общий делитель чисел 2 и 4.
В данном случае дробь простая и для неё НОД ищется легко. НОД чисел 2 и 4 это число 2. Значит, числитель и знаменатель дроби надо разделить на 2
В результате дробь обратилась в более простую дробь . Значение исходной дроби при этом не изменилось, поскольку сокращение подразумевает деление числителя и знаменателя на одно и то же число. А это действие, как было указано ранее, не меняет значение дроби.
На рисунке представлены дроби и в виде кусочков пиццы. До сокращения и после сокращения они имеют одинаковые размеры. Разница лишь в том, что раздéланы они по-разному.
Пример 2. Сократим дробь
Чтобы сократить дробь , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 20 и 40.
НОД чисел 20 и 40 это число 20. Поэтому делим числитель и знаменатель дроби на 20
Пример 3. Сократим дробь
Сократим дробь
Чтобы сократить дробь , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 32 и 36.
НОД чисел 32 и 36 это число 4. Поэтому делим числитель и знаменатель дроби на 4
Если в числителе и знаменателе располагаются простые числа, то такую дробь сократить нельзя — она не сокращается. Такие дроби называют несократимыми. Например, следующие дроби являются несократимыми:
Напомним, что простыми называются числа, которые делятся только на единицу и самих себя.
Второй способ сокращения дроби
Второй способ является короткой версией первого способа. Суть его заключается в том, что пропускается подробное разъяснение того, на что был разделён числитель и знаменатель.
К примеру, вернёмся к дроби . Эту дробь мы сократили на 4, то есть разделили числитель и знаменатель этой дроби на число 4
Теперь представьте, что в данном выражении отсутствует конструкция , и сразу записан ответ . Получится следующее выражение:
Получится следующее выражение:
Суть в том что число, на которое разделили числитель и знаменатель, хранят в уме. В нашем случае числитель и знаменатель делят на 4 — это число и будем хранить в уме.
Сначала делим числитель на число 4. Полученный ответ записываем рядом с числителем, предварительно зачеркнув его:
Затем таким же образом делим знаменатель на число 4. Полученный ответ записываем рядом со знаменателем, предварительно зачеркнув его:
Затем собираем новую дробь. В числитель отправляем новое число 8 вместо 32, а в знаменатель отправляем новое число 9 вместо 36
Происходит своего рода замена одной дроби на другую. Значение новой дроби равно значению предыдущей дроби, поскольку срабатывает основное свойство дроби, которое говорит о том что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.
Также, дроби можно сокращать, предварительно разложив на простые множители числитель и знаменатель.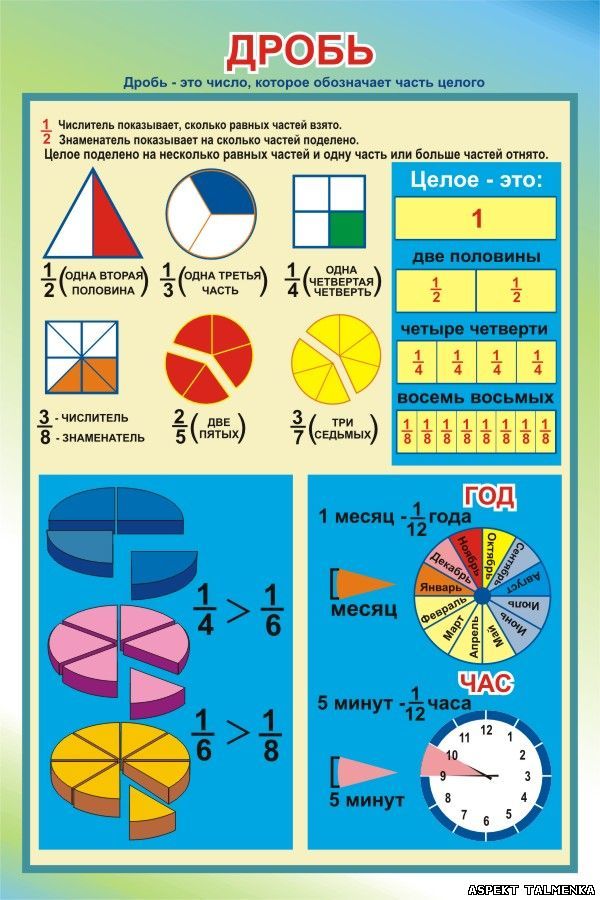
Например, сократим дробь , предварительно разложив на простые множители числитель и знаменатель:
Итак, мы разложили числитель и знаменатель дроби на множители. Теперь применяем второй способ сокращения. В числителе и в знаменателе выбираем по множителю и делим выбранные множители на НОД этих множителей.
Давайте сократим по тройке в числителе и в знаменателе. Для этого разделим эти тройки на 3 (на их наибольший общий делитель). Получим следующее выражение:
Сократить можно ещё по тройке в числителе и в знаменателе:
Дальше сокращать больше нéчего. Последнюю тройку в знаменателе просто так сократить нельзя, поскольку в числителе нет множителя, который можно было бы сократить вместе с этой тройкой.
Записываем новую дробь, в числителе и в знаменателе которой будут новые множители.
Получили ответ . Значит, при сокращении дроби получается новая дробь .
Не рекомендуется пользоваться вторым способом сокращения дроби и способом разложения на простые множители числителя и знаменателя, если человек только нáчал изучать математику. Практика показывает, что это оказывается сложным на первых этапах.
Практика показывает, что это оказывается сложным на первых этапах.
Поэтому, если испытываете затруднения при использовании второго способа, то пользуйтесь старым добрым способом сокращения: делите числитель и знаменатель дроби на их наибольший общий делитель. Выражение в таком случае получается простым, понятным и красивым. Так, предыдущий пример может быть решён старым способом и будет выглядеть так:
Сравните это выражение с выражением, которое мы получили, когда пользовались вторым способом:
Первое выражение намного понятнее, аккуратнее и короче. Не правда ли?
Задания для самостоятельного решения
Задание 1. Запишите в виде дроби следующий рисунок:
Показать решение
Задание 2. Запишите в виде дроби следующий рисунок:
Показать решение
Задание 3. Запишите в виде дроби следующий рисунок:
Показать решение
Задание 4. Запишите в виде дроби следующий рисунок:
Показать решение
Задание 5.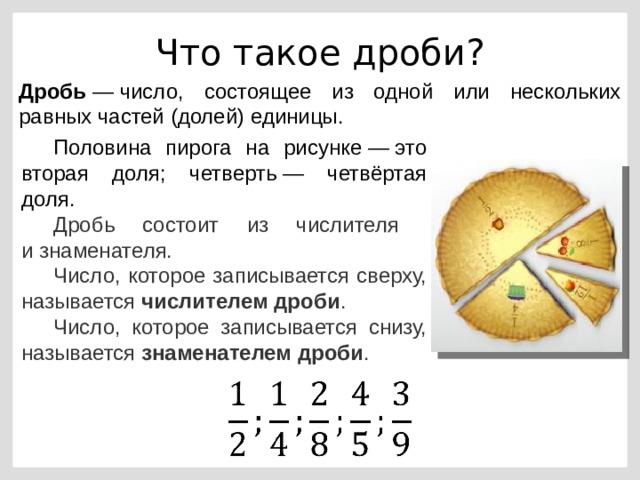 Запишите в виде дроби следующий рисунок:
Запишите в виде дроби следующий рисунок:
Показать решение
Задание 6. Выделите целые части в следующих дробях:
Показать решение
Задание 7. Выделите целые части в следующих дробях:
Показать решение
Задание 8. Переведите смешанные дроби в неправильные:
Показать решение
Задание 9. Переведите смешанные дроби в неправильные, не расписывая как целая часть умножается на знаменатель дробной части и полученный результат складывается с числителем дробной части
Показать решение
Задание 10. Сократите следующую дробь на 3
Показать решение
Задание 11. Сократите следующую дробь на 3 вторым способом
Показать решение
Задание 12. Сократите следующую дробь на 5
Показать решение
Задание 13. Сократите следующую дробь на 5 вторым способом
Показать решение
Задание 14. Сократите следующие дроби:
Показать решение
Задание 15. Сократите следующие дроби вторым способом:
Показать решение
Задание 16. Запишите в виде дроби следующий рисунок:
Запишите в виде дроби следующий рисунок:
Показать решение
Задание 17. Запишите в виде дроби следующий рисунок:
Показать решение
Задание 18. Запишите в виде дроби следующий рисунок:
Показать решение
Задание 19. Запишите в виде дроби следующий рисунок:
Показать решение
Задание 20. Запишите в виде дроби следующий рисунок:
Показать решение
Задание 21. Изобразите в виде рисунка следующую дробь:
Показать решение
Задание 22. Изобразите в виде рисунка следующую дробь:
Показать решение
Задание 23. Изобразите в виде рисунка следующую дробь:
Показать решение
Задание 24. Изобразите в виде рисунка следующую дробь:
Показать решение
Задание 25. Изобразите в виде рисунка следующую дробь:
Показать решение
Задание 26. Изобразите в виде рисунка следующую дробь:
Показать решение
Задание 27. Изобразите в виде рисунка следующую дробь:
Показать решение
Задание 28. Изобразите в виде рисунка следующую дробь:
Показать решение
Задание 29. Изобразите в виде рисунка следующую дробь:
Изобразите в виде рисунка следующую дробь:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже Опубликовано Автор
Дробь (математика) | это… Что такое Дробь (математика)?
У этого термина существуют и другие значения, см. Дробь.
| 8 | / 13 | числитель | |
| числитель | знаменатель | знаменатель | |
| Две записи одной дроби | |||
Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы[1]. Дроби являются частью поля рациональных чисел. По способу записи дроби делятся на 2 формата: обыкновенные вида и десятичные.
Дроби являются частью поля рациональных чисел. По способу записи дроби делятся на 2 формата: обыкновенные вида и десятичные.
Содержание
|
Виды дробей
Обыкновенные дроби
Обыкновенная (или простая) дробь — запись рационального числа в виде или где Горизонтальная или косая черта обозначает знак деления, в результате чего получается частное. Делимое называется числителем дроби, а делитель — знаменателем.
Делимое называется числителем дроби, а делитель — знаменателем.
Обозначения обыкновенных дробей
Есть несколько видов записи обыкновенных дробей в печатном виде:
- ½
- 1/2 или (наклонная черта называется «солидус»[2])
- выключная формула: (горизонтальная черта называется Винкулиум (англ.))
- строчная формула:
Правильные и неправильные дроби
Правильной называется дробь, у которой модуль числителя меньше модуля знаменателя. Дробь, не являющаяся правильной, называется неправильной, и представляет рациональное число, по модулю большее или равное единице.
Например, дроби , и — правильные дроби, в то время как , , и — неправильные дроби. Всякое целое число можно представить в виде неправильной обыкновенной дроби со знаменателем 1.
Смешанные дроби
Дробь, записанная в виде целого числа и правильной дроби, называется смешанной дробью и понимается как сумма этого числа и дроби. Любое рациональное число можно записать в виде смешанной дроби. В противоположность смешанной дроби, дробь, содержащая лишь числитель и знаменатель, называется простой.
Любое рациональное число можно записать в виде смешанной дроби. В противоположность смешанной дроби, дробь, содержащая лишь числитель и знаменатель, называется простой.
Например, . В строгой математической литературе такую запись предпочитают не использовать из-за схожести обозначения смешанной дроби с обозначением произведения целого числа на дробь, а также из-за более громоздкой записи и менее удобных вычислений.
Высота дроби
Высота обыкновенной дроби — модуль суммы числителя и знаменателя этой дроби. Высота рационального числа — модуль суммы числителя и знаменателя несократимой обыкновенной дроби, соответствующей этому числу.
Например, высота дроби равна . Высота же соответствующего рационального числа равна , так как дробь сокращается на .
Составные дроби
Многоэтажной, или составной, дробью называется выражение, содержащее несколько горизонтальных (или реже — наклонных) черт:
- или или
Десятичные дроби
Основная статья: Десятичная дробь
Десятичной дробью называют позиционную запись дроби. Она выглядит следующим образом:
Она выглядит следующим образом:
Пример: .
Часть записи, которая стоит до позиционной запятой, является целой частью числа (дроби), а стоящая после запятой — дробной частью. Всякую обыкновенную дробь можно преобразовать в десятичную, которая в этом случае либо имеет конечное число знаков после запятой, либо является периодической дробью.
Вообще говоря, для позиционной записи числа́ можно использовать не только десятичную систему счисления, но и другие (в том числе и специфические, такие, как фибоначчиева).
Значение дроби и основное свойство дроби
Дробь является всего лишь записью числа. Одному и тому же числу могут соответствовать разные дроби, как обыкновенные, так и десятичные.
Если умножить числитель и знаменатель дроби на одинаковую величину:
то значение дроби останется прежним, хотя дроби — разные. Например:
И обратно, если числитель и знаменатель заданной дроби имеют общий делитель, то обе части можно разделить на него; такая операция называется сокращением дроби.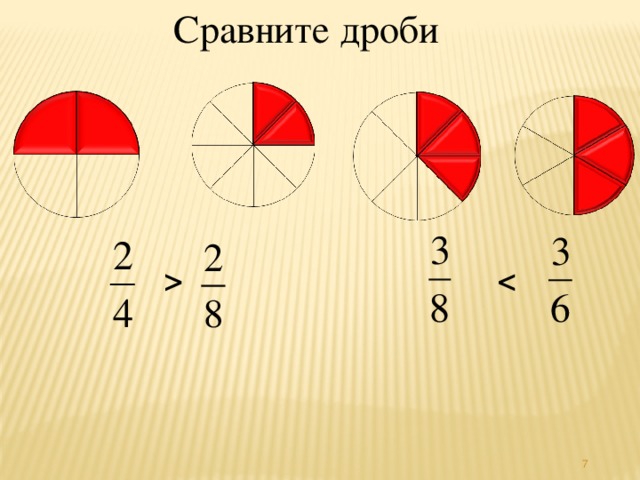 Пример:
Пример:
- — здесь числитель и знаменатель дроби сократили на общий делитель 4.
Несократимой называется дробь, числитель и знаменатель которой взаимно просты, т. е. не имеют общих делителей, кроме
Для десятичной дроби запись почти всегда однозначна, однако имеются исключения. Пример:
- — две разные дроби соответствуют одному числу.
Действия над дробями
В этом разделе рассматриваются действия над обыкновенными дробями. О действиях над десятичными дробями см. Десятичная дробь.
Приведение к общему знаменателю
Для сравнения, сложения и вычитания дробей их следует преобразовать (
- Находим наименьшее общее кратное знаменателей: .
- Умножаем числитель и знаменатель первой дроби на .
- Умножаем числитель и знаменатель второй дроби на .
После этого знаменатели обеих дробей совпадают (равны M). Вместо наименьшего общего кратного можно в простых случаях взять в качестве M любое другое общее кратное, например, произведение знаменателей. Пример см. ниже в разделе Сравнение.
Вместо наименьшего общего кратного можно в простых случаях взять в качестве M любое другое общее кратное, например, произведение знаменателей. Пример см. ниже в разделе Сравнение.
Сравнение
Чтобы сравнить две обыкновенные дроби, следует привести их к общему знаменателю и сравнить числители получившихся дробей. Дробь с бо́льшим числителем будет больше.
Пример. Сравниваем и . НОК(4, 5) = 20. Приводим дроби к знаменателю 20.
Следовательно,
Сложение и вычитание
Чтобы сложить две обыкновенные дроби, следует привести их к общему знаменателю. Затем сложить числители, а знаменатель оставить без изменений:
- + = + =
НОК знаменателей (здесь 2 и 3) равно 6. Приводим дробь к знаменателю 6, для этого числитель и знаменатель надо умножить на 3.
Получилось . Приводим дробь к тому же знаменателю, для этого числитель и знаменатель надо умножить на 2. Получилось .
Чтобы получить разность дробей, их также надо привести к общему знаменателю, а затем вычесть числители, знаменатель при этом оставить без изменений:
- — = — =
НОК знаменателей (здесь 2 и 4) равно 4. Приводим дробь к знаменателю 4, для этого надо числитель и знаменатель умножить на 2. Получаем .
Приводим дробь к знаменателю 4, для этого надо числитель и знаменатель умножить на 2. Получаем .
Умножение и деление
Чтобы умножить две обыкновенные дроби, нужно перемножить их числители и знаменатели:
В частности, чтобы умножить дробь на натуральное число, надо числитель умножить на число, а знаменатель оставить тем же:
В общем случае, числитель и знаменатель результирующей дроби могут не быть взаимно простыми, и может потребоваться сокращение дроби, например:
Чтобы поделить одну обыкновенную дробь на другую, нужно умножить первую на дробь, обратную второй:
Например,
Преобразование между разными форматами записи
Чтобы преобразовать обыкновенную дробь в дробь десятичную, следует разделить числитель на знаменатель. Результат может иметь конечное число десятичных знаков, но может быть и бесконечной периодической дробью. Примеры:
- — бесконечно повторяющийся период принято записывать в круглых скобках.

Чтобы преобразовать десятичную дробь в дробь обыкновенную, следует представить её дробную часть в виде натурального числа, делённого на соответствующую степень 10. Затем к результату приписывается целая часть со знаком, формируя смешанную дробь. Пример:
История и этимология
Русский термин дробь, как и его аналоги в других языках, происходит от лат. fractura, который, в свою очередь, является переводом арабского термина с тем же значением: ломать, раздроблять. Фундамент теории обыкновенных дробей заложили греческие и индийские математики.
Впервые в Европе данный термин употребил Леонардо Пизанский (1202). Поначалу европейские математики оперировали только с обыкновенными дробями, а в астрономии — с шестидесятеричными. Полноценная теория обыкновенных дробей и действий с ними сложилась в XVI веке (Тарталья, Клавиус).
В древней Руси дроби называли долями или ломаными числами. Термин дробь, как аналог латинского fractura, используется в «Арифметике» Магницкого (1703) как для обыкновенных, так и для десятичных дробей.
Десятичные дроби впервые встречаются в Китае примерно с III века н. э. при вычислениях на счётной доске (суаньпань). В письменных источниках десятичные дроби ещё некоторое время изображали в традиционном (не позиционном) формате, но постепенно позиционная система вытеснила традиционную[3]. Персидский математик и астроном Джамшид Гияс-ад-дин ал-Каши (1380—1429) в трактате «Ключ арифметики» объявил себя изобретателем десятичных дробей, хотя они встречались в трудах Ал-Уклидиси, жившего на 5 веков раньше[4].
В Европе первые десятичные дроби ввёл Иммануил Бонфис около 1350 года, но широкое распространение они получили только после появления сочинения Симона Стевина «Десятая» (1585).
Обобщения
- Кольцо частных
- Рациональная функция — дробь, составленная из многочленов.
См. также
- Дроби в Юникоде
- Цепная дробь
Литература
- Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982.
 — Т. 2.
— Т. 2.
Примечания
- ↑ Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 2.
- ↑ Дробная черта (Fraction bar, Solidus) — Справочник ПараТайп
- ↑ Jean-Claude Martzloff. A History of Chinese Mathematics. Springer. 1997. ISBN 3-540-33782-2.
- ↑ Berggren J. Lennart Mathematics in Medieval Islam // The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. — Princeton University Press, 2007. — P. 518. — ISBN 978-0-691-11485-9
определение и классификация, основные отличия и примеры
Математика
12.11.21
12 мин.
Не всегда числа выражаются целыми величинами. Понятие дроби в математике 5 класса рассматривается более подробно, поскольку каждый ученик должен понимать основные принципы работы с числами любого формата. Это позволит грамотно выполнять вычисления, используя свойства дробных выражений. Специалисты рекомендуют изучить теорию, а затем перейти к ее практическому применению.
Специалисты рекомендуют изучить теорию, а затем перейти к ее практическому применению.
Оглавление:
- Применение дробных величин
- Классификация дробей
- Смешанная форма
Общие сведения
Числа делятся на целые и дробные. К первым относится множество всех натуральных величин, используемых при устном счете. Однако не все значения можно записать, воспользовавшись первым типом. Например, может быть не целый торт, а его половина. Для этой цели были придуманы дроби, характеризующие некоторую часть от целого. Чтобы понять основную разницу между величинами, нужно разобрать объяснение дробей для 5 класса и примеры их применения.
Дробь — значение, которое применяется для точного представления числовой формы. Для иллюстрации определения на практике нужно рассмотреть такой пример: при расчетах ускорения свободного падения была получена величина «9,81».
Если использовать приближенное целое значение, получаются числа 9 и 10. Однако при решении задачи по физике необходимо брать точное выражение. При отказе от подробного представления появится большая погрешность при вычислениях. Далее необходимо разобрать дробные величины подробно, чтобы любой ребенок мог производить без особого труда действия над ними.
Однако при решении задачи по физике необходимо брать точное выражение. При отказе от подробного представления появится большая погрешность при вычислениях. Далее необходимо разобрать дробные величины подробно, чтобы любой ребенок мог производить без особого труда действия над ними.
Применение дробных величин
Для сравнения необходимо решить задачу по физике и рассчитать силу тяжести «Fт» физического тела, масса которого составляет 100 кг. Формула для расчета имеет такой вид: Fт=m*g, где m — масса тела и g — ускорение свободного падения. Далее следует разобрать два случая:
- Приближенный.
- Точный.
Для приближенного расчета соотношение будет выглядеть следующим образом: Fт = 9 * 100 = 900 (Н) и Fт = 10 * 100 = 1000 (Н). При точном вычислении: Fт = 9,81 * 100 = 981 (Н). Следует отметить, что в первом случае наблюдаются значительные погрешности, как в большую, так и в меньшую сторону, т. е. 981−900=81 и 1000−981=19. Этого допускать нельзя.
Для иллюстрации необходимости использования дробных величин была подобрана задача по физике, поскольку нужно было доказать ученикам, насколько она связана с математикой. Далее необходимо разобрать классификацию дробей.
Классификация дробей
Дробные величины математики делят на 3 вида. К ним относятся:
- Десятичные.
- Обыкновенные.
- Смешанные формы.
В первом случае любое дробное значение, состоящее из дробной части, отделенной от целого выражения точкой или запятой, называется десятичной дробью. Последняя бывает в двух формах, а именно: конечной и бесконечной. Первая характеризуется ограниченным количеством знаков после запятой (точки). Например, величина 0,2356 состоит из целой части (0) и дробной (2356).
Бесконечная дробь классифицируется на 2 типа. К ним относятся следующие:
- Периодическая.

- Непериодическая.
К первой относятся все бесконечные десятичные дробные выражения, знаки которых после запятой повторяются по определенному закону. Повторяющиеся символы необходимо брать в круглые скобки (указывать период). При этом запись выглядит более компактной, т. е. 0,(13). Однако не во всех случаях величину можно записать на листке бумаги. Эту операцию невозможно осуществить для бесконечной непериодической. Очень часто ее округляют до определенной величины, а именно: до десятых, сотых долей и т. д.
Кроме десятичных, бывают еще и обыкновенные дробные величины. Они состоят из верхней и нижней частей, разделенными между собой косой чертой «/». Примером является число, записанное в общем виде «W/V», где W — числитель и V — знаменатель. В зависимости от последних параметров, обыкновенные дроби классифицируются на 2 вида:
- Правильные.
- Неправильные.
У первых числитель меньше, чем знаменатель.
В этом случае справедливо условие W<V. Если последнее неравенство не выполняется, можно сделать вывод о принадлежности дробного значения ко второму виду. Существует еще одна форма представления дробных элементов, но ее необходимо разобрать отдельно.
Смешанная форма
Смешанным числом называется величина, включающая целую и дробную части. Такие формы образуются при помощи десятичных и обыкновенных дробей. Суть преобразований для каждого случая является различной.
Для смешанного выражения, образованного десятичной дробью, нужно разобрать пример самого числа «5,526». Оно состоит из целого (5) и дробного элемента (526). Его получают при делении одной величины на другую. В конкретном примере делимое равно 5526, а делитель — 1000, т. е. первая величина примерно в 5 раз больше второй. Для преобразования существует очень простой алгоритм, который легко объяснить, воспользовавшись следующими пунктами:
- Записать величину: 0,12.

- Обозначить числитель (соответствует дробной части после запятой): 12.
- Определить знаменатель (эквивалентен десяти в степени, равной количеству знаков в дробной части): 10 2 .
- Написать результат: 12/100.
Величина, полученная в пункте 4, может быть преобразована при помощи сокращения: 12/100=(4*3)/(4*25)=3/25. Ученикам требуется обратить внимание, как решать пример. Для начала нужно вынести общий множитель для числителя и знаменателя, разложив их на сомножители: 12=4*3 и 100=4*25. После этого нужно сократить на 4.
Смешанное число, состоящее из целого компонента и правильной дроби, образуется из неправильного дробного тождества. Операция позволяет выделить целый элемент. Алгоритм преобразования:
- Записывается искомая неправильная дробь: W/V.
- Выделяется целый компонент, при делении числителя на знаменатель (берется только целое число без учета дробной составляющей): R=W/V.
- Рассчитывается величина нового числителя: W’=W-RV.

- Записывается искомый результат: R[W’/V].
Если нужно выполнить обратную операцию по конвертации смешанного элемента в неправильную дробь, можно воспользоваться специальной методикой:
- Написать число в смешанной обыкновенной форме: R[W’/V].
- Вычислить значение нового числителя W по следующему соотношению: W=VR+W’.
- Записать искомый результат: W/V.
Методики расписаны во многих учебниках и позволяют решить дроби в 5 классе без ошибок. Специалисты рекомендуют выписать их на отдельный лист бумаги и положить «перед глазами». Однако со временем надобность в шпаргалке отпадет, поскольку действия при регулярных занятиях будут отточены до автоматизма. Далее необходимо затронуть тему об основных свойствах дробей.
Важные свойства
Каждая из дробей обладает определенными свойствами. Для десятичной они являются следующими:
- Десятичная дробная величина — частное, полученное в результате операции деления двух чисел.

- У дробной части можно дописать любое количество нулей, т. е. 0,5=0,500000000000. При этом величина конечной и начальной дробей не изменится.
- Любую десятичную дробную величину можно представить в виде обыкновенной.
Далее необходимо рассмотреть основные свойства обыкновенных дробей:
- При умножении числителя и знаменателя на одно и то же числовое значение величина дроби не изменится, т. е. 9/10=(8*9)/(8*10).
- Если к числителю прибавить одно значение, а затем его отнять, величина дробного выражения не изменится, т. е. (9+3−3)/10=9/10. Для знаменателя можно также воспользоваться аналогичным свойством: 9/(10+3−3).
- Произведение обратных обыкновенных дробей эквивалентно единице, т. е. (5/8) * (8/5) = 1.
- Если поделить одну обыкновенную дробную величину на обратную, получится исходное число в квадрате, т. е. (5/8): (8/5) = 25/64.
Следует отметить, что свойства необходимо применять при решении различных задач, доказательства теорем и выведения различных соотношений, поэтому нужно научиться производить различные действия над дробями.
Таким образом, дроби применяются в математике для вычислений точных значений, которые используются при расчетах различных величин, характеризующих процессы, явления и количественные характеристики.
Проект «Обыкновенные дроби в жизни людей»
Руководитель проекта:
Ганченкова Оксана Алексеевна
Учреждение:
МАОУ Средняя общеобразовательная школа № 10
В индивидуальной исследовательской работе по математике на тему «Обыкновенные дроби в жизни людей» автором работы была проанализирована научная литература по алгебре, и дано развернутое определение понятия «обыкновенная дробь», а также изучена важность обыкновенных дробей в повседневной жизни.
Подробнее о работе:
В исследовательском проекте по математике на тему «Обыкновенные дроби в жизни людей» рассматривается история возникновения дробей, а также приводятся красочные примеры использования обыкновенных дробей в профессиональной деятельности человека на примере профессии «Разметчик».
Учебная работа по математике «Обыкновенные дроби в жизни людей» в 5 классе школы рассматривает необходимость дробей в повседневной жизни человека. Автор акцентирует внимание на том, что каждый день нам приходится сталкиваться с проблемой деления целого на части, и даже в определенный момент кажется, что нас больше окружают не целые, а дробные числа. Поэтому тема проекта актуальна и интересна для изучения.
Оглавление
Введение
1. Понятие дроби.
2. История возникновения дробей.
3. Использование обыкновенных дробей в профессиональной деятельности человека.
3.1 Дроби для профессии «Разметчик».
4. Практическая часть.
4.1. Мои наблюдения.
Заключение
Список использованной литературы
Введение
Уважаемые друзья! Ответственно вам сообщаю, есть люди, которые считают, будто дробям нет места в нашей жизни. За примерами далеко ходить не надо. Когда я учился в начальных классах, думал: «Зачем математики придумали дроби?» Наверное, только для того, чтобы портить жизнь школьникам. Другого объяснения не знал, пока не начали изучать в 5 классе тему «Дроби»
Другого объяснения не знал, пока не начали изучать в 5 классе тему «Дроби»
С первого знакомства с дробями было понятно, что они очень необычные числа, начиная с их непривычной записи и заканчивая сложными правилами действий с ними.
В обычной жизни, и взрослым, и детям каждый день приходится сталкиваться с проблемой деления целого на части, и даже в определенный момент кажется, что нас больше окружают не целые, а дробные числа, что является актуальностью данной темы.
Мне стало интересно узнать: как и когда появились дроби? В какой сфере жизни больше всего практически их применяют? Хотелось в ходе исследования этого вопроса убедиться и убедить других в необходимости дробей в повседневной жизни.
Объект исследования: обыкновенные дроби
Предмет исследования: использование дробей в нашей повседневной жизни.
Цель: показать, что дроби нужны не только в математике, но и в повседневной жизни.
Задачи:
- Узнать, что такое дробь, какие виды дроби существуют
- Изучить историю возникновения дробей.

- Рассмотреть применение дробей в повседневной жизни.
- Оценить достижения науки в данной области.
Понятие дроби
Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы. Дробь выражается отношением двух целых чисел m/n, где n — показывает на сколько долей разделена единица, а m – показывает сколько таких долей содержится в дроби.
В математике применяются следующие виды дробей:
- обыкновенная дробь;
- правильная дробь;
- неправильная дробь;
- смешанная дробь;
- десятичная дробь.
Дроби разные нужны, дроби всякие важны
Обыкновенная дробь имеет вид n/m или m/n где m и n — натуральные числа. Делимое (m) — называют числителем дроби, делитель (n) — называют знаменателем данной дроби. Горизонтальная или косая линия в дроби обозначает деление. Черта наклонная называется — «солидус», а горизонтальная – «винкулум».
Если числитель дроби меньше знаменателя, то дробь называется правильной (например 3/7), если больше или равен — неправильной (например 7/3).
Числа, в состав которых входит целое число и правильная дробь, называются смешанными. Целое число называют целой частью смешанного числа, а правильная дробь называется дробной частью смешанного числа. Например, для смешанной дроби число 3 — целая часть, 2/5 — дробная.
Десятичная дробь, это дробь, которая записывается без знаменателя.
Выглядят они так: 5,6; 3,17; 0,17 и т.д. На самом деле это особая запись обыкновенных дробей, у которых знаменатель равен 10, 100, 1000 и т. д.
История возникновения дробей
Память человечества не сохранила для нас имя изобретателя колеса. Также невозможно назвать точно даже тот отрезок времени, когда появились дроби.
Можно предположить, что потребность делить целое на части возникала ещё в первобытном обществе. Могло быть и так…
Были у древнего человека жена и двое детей. Вот пошла однажды древняя женщина собирать плоды и нашла всего лишь 1 яблоко. Детей у неё двое, а яблоко одно. Наверное, она догадалась: взяла каменный нож да и разделила это яблоко на 2 половины.
Вот пошла однажды древняя женщина собирать плоды и нашла всего лишь 1 яблоко. Детей у неё двое, а яблоко одно. Наверное, она догадалась: взяла каменный нож да и разделила это яблоко на 2 половины.
А в это время самый — самый древний человек пошёл на охоту и убил самого — самого древнего кабана. Пришёл домой и разделил свою добычу на четыре равные части: себе, жене, сыну и дочке. Конечно, эти древние люди и не догадывались, что, разделив целое число на части, они занимались таким трудным разделом математики, который впоследствии назовут «дроби». Итак, дроби появились в тот период времени, когда в трудовой деятельности людей появилась потребность более точно измерять какие-то величины, хотя делением на части люди пользовались, наверное, с древнейших времён.
Дроби в Древнем Египте
На протяжении многих веков египтяне именовали дроби «ломаным числом», а первая дробь, с которой они познакомились, была 1/2 . За ней последовали 1/4, 1/8 , 1/16, … затем 1/3, 1/6, … т. е. самые простые дроби, называемые единичными или основными дробями.
е. самые простые дроби, называемые единичными или основными дробями.
У них числитель всегда единица. Лишь значительно позже у греков, затем у индийцев и других народов стали входить в употребление и дроби общего вида, называемые обыкновенными, у которых числитель и знаменатель могут быть любыми натуральными числами. В Древнем Египте архитектура достигла высокого развития. Чтобы строить грандиозные пирамиды и храмы, чтобы вычислять длины, площади и объемы фигур, необходимо было знать арифметику.
Из расшифрованных сведений на папирусах ученые узнали, что египтяне 4000 лет назад имели десятичную систему счисления, умели решать многие задачи, связанные с потребностями строительства, торговли и военного дела.
Одним из первых известных упоминаний о дробях является математический папирус Ринда. Три более древних текста, в которых упоминаются дроби — это Египетский математический кожаный свиток, Московский математический папирус и Деревянная табличка Ахмима. Папирус Ринда включает таблицу египетских дробей для рациональных чисел вида 1/n, а также 84 математических задачи, их решения и ответы, записанные в виде египетских дробей.
Папирус Ринда включает таблицу египетских дробей для рациональных чисел вида 1/n, а также 84 математических задачи, их решения и ответы, записанные в виде египетских дробей.
Египтяне ставили иероглиф (ер, «один из» или ре, рот) над числом для обозначения единичной дроби в обычной записи, а в священных текстах использовали линию. У них также были специальные символы для дробей 1/2, 2/3 и 3/4, которыми можно было записывать также другие дроби.
Остальные дроби они записывали в виде суммы долей. Дробь 7/8 они записывали в виде ½ ¼ 1/8, но знак «+» не указывали. А сумму 4+1/3 записывали в виде 41/3. Такая запись смешанных чисел (без знака «+») сохранилась до сих пор.
Вавилонские дроби
Жители древнего Вавилона примерно за 3000 лет до нашей эры создали систему мер аналогичную нашей метрической, только в основе её лежало не число 10, а число 60, в которой меньшая единица измерения составляла 1/60 часть высшей единицы. Полностью эта система выдерживалась у вавилонян для измерения времени и углов, и мы унаследовали от них деление часа и градуса на 60 минут, а минуты на 60 секунд.
Полностью эта система выдерживалась у вавилонян для измерения времени и углов, и мы унаследовали от них деление часа и градуса на 60 минут, а минуты на 60 секунд.
Исследователи по-разному объясняют появление у вавилонян шестидесятеричной системы. Число 60 прекрасно делится на 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 и 60, что значительно облегчает всякие расчеты. Шестидесятые доли были привычны в жизни вавилонян.
Вот почему они пользовались шестидесятеричными дробями, имеющими знаменателем всегда число 60 или его степени: 602, 603 и т.д. В этом отношении шестидесятеричные дроби можно сравнить с нашими десятичными дробями. Вавилонская математика оказала влияние на греческую математику. Следы вавилонской шестидесятеричной системы счисления удержались в современной науке при измерении времени и углов. До наших дней сохранилось деление часа на 60 мин., минуты на 60 с, окружности на 360˚, градуса на 60 мин., минуты на 60с.
Вавилоняне внесли ценный вклад в развитие астрономии. Шестидесятеричными дробями пользовались в астрономии ученые всех народов до XVII века, называя их астрономическимидробями. В отличие от них, дроби общего вида, которыми пользуемся мы, были названы обыкновенными.
Шестидесятеричными дробями пользовались в астрономии ученые всех народов до XVII века, называя их астрономическимидробями. В отличие от них, дроби общего вида, которыми пользуемся мы, были названы обыкновенными.
Дроби в Древней Греции
Греки работали с обыкновенными дробями не часто, поэтому использовали различные обозначения. Герон и Диофант, самые известные арифметики среди древнегреческих математиков, записывали дроби в алфавитной форме, причем числитель располагали под знаменателем. Но в принципе предпочтение отдавалось либо дробям с единичным числителем, либо шестидесятеричным дробям.
Недостатки греческой системы счисления относят к их любви к строгости, которое заметно увеличило трудности, связанные с анализом отношения несоизмеримых величин. Слово «число» греки понимали, как набор единиц, поэтому то, что мы теперь рассматриваем как единое число – дробь, – греки понимали, как отношение двух целых чисел. Именно этим объясняется, почему обыкновенные дроби редко встречались в греческой арифметике.
Именно этим объясняется, почему обыкновенные дроби редко встречались в греческой арифметике.
Дроби в Древнем Китае
В Древнем Китае уже пользовались десятичной системой мер, обозначали дробь словами, используя меры длины чи: цуни, доли, порядковые, шерстинки, тончайшие, паутинки. Дробь вида 2,135436 выглядела так: 2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок. Так записывались дроби на протяжении двух веков, а в V веке китайский ученый Цзу-Чун-Чжи принял за единицу не чи, а чжан = 10 чи, тогда эта дробь выглядела так: 2 чжана, 1 чи, 3 цуня, 5 долей, 4 порядковых, 3 шерстинки, 6 тончайших, 0 паутинок.
Дроби на Руси
В русском языке слово «дробь» появилось лишь в VIII веке. Происходит оно от слова «дробить, разбивать, ломать на части». В русских рукописных арифметиках XVII в. дроби называли долями, позднее «ломаными числами». В старых руководствах существуют следующие названия дробей на Руси:
| 1/2 — половина, полтина | 1/3 – треть |
| 1/4 – четь | 1/6 – полтреть |
| 1/8 — полчеть | 1/12 –полполтреть |
| 1/16 — полполчеть | 1/24 – полполполтреть (малая треть) |
| 1/32 – полполполчеть (малая четь) | 1/5 – пятина |
| 1/7 — седьмина | 1/10 — десятина |
Славянская нумерация употреблялась в России до XVI века, затем в страну начала постепенно проникать десятичная система счисления.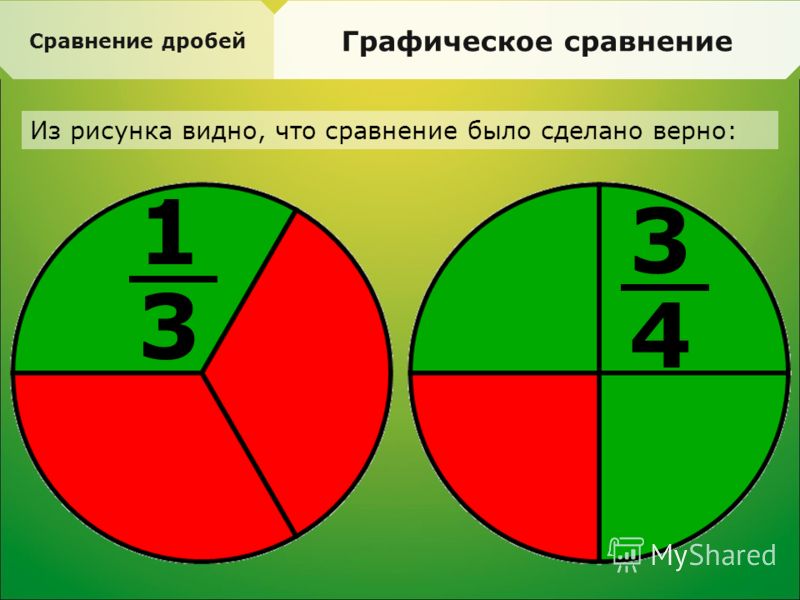 Она окончательно вытеснила славянскую нумерацию при Петре I.
Она окончательно вытеснила славянскую нумерацию при Петре I.
Дроби в других государствах древности
В китайской «Математике в девяти разделах» уже имеют место сокращения дробей и все действия с дробями. У индийского математика Брахмагупты найдена достаточно развитую систему дробей. У него встречаются разные дроби: и основные, и производные с любым числителем. Числитель и знаменатель записываются так же, как и у нас сейчас, но без горизонтальной черты, а просто размещаются один над другим.
Арабы первыми начали отделять чертой числитель от знаменателя.
Леонардо Пизанский уже записывает дроби, помещая в случае смешанного числа, целое число справа, но читает так, как принято у нас. В XV – XVI столетиях учение о дробях приобретает уже знакомый нам теперь вид и оформляется приблизительно в те самые разделы, которые встречаются в наших учебниках.
Следует отметить, что раздел арифметики о дробях долгое время был одним из наиболее трудных. Недаром у немцев сохранилась поговорка: «Попасть в дроби», что означало – зайти в безвыходное положение. Считалось, что тот, кто не знает дробей, не знает и арифметики.
Недаром у немцев сохранилась поговорка: «Попасть в дроби», что означало – зайти в безвыходное положение. Считалось, что тот, кто не знает дробей, не знает и арифметики.
Использование обыкновенных дробей в профессиональной деятельности человека
Живя в окружении дробей, мы не всегда их явно замечаем. И все же, мы сталкиваемся с ним очень часто: дома, на улице, в магазине, на работе и так далее. Покажу лишь малую часть того, где мы можно увидеть присутствие дробей.
В медицине. Чтобы приготовить необходимое лекарство нужно знать его состав, записанный с помощью дробей, или, когда врач назначает больному ½ таблетки.
Дроби в кулинарии. Поварам нужны дроби для соблюдения пропорции при приготовлении блюда. В рецептах очень часто используются такие фразы, например, как одна вторая стакана, четверть столовой ложки.
Дроби в музыке. Учащиеся музыкальной школы знакомятся с дробями раньше, чем в общеобразовательной школе. С первых дней занятий дети знакомятся с такими понятиями как размер и длительности нот. Древнегреческий философ Пифагор (570 г. до н. э.), один из самых первых установил связь музыки и математики. Он создал учение о звуке. Пифагор связал длительность звучания нот с дробями.
С первых дней занятий дети знакомятся с такими понятиями как размер и длительности нот. Древнегреческий философ Пифагор (570 г. до н. э.), один из самых первых установил связь музыки и математики. Он создал учение о звуке. Пифагор связал длительность звучания нот с дробями.
Счёт длительностей в музыке ведётся от целой ноты, которая считается до четырёх. В целой ноте 2 половинные, 4 четверти, 8 восьмых, 16 шестнадцатых. Так музыка живёт в согласии с математикой.
Дроби в географии: Материк Евразия занимает 1/3 часть суши;
Масштаб карты равен 1/50000
Участки земной поверхности изображаются на карте в уменьшенном виде, для этого используется понятие масштаба: отношение длины отрезка на карте к длине соответствующего отрезка на местности.
Например, масштаб карты 1/10000 означает, что 1см на карте соответствует 10000 см на местности.
Дроби в спорте. Когда смотрим ½ финала матча по футболу.
Дроби в пропорции человека тоже связаны с дробями. Голова маленького ребенка составляет 1/5 часть роста человека. Голова подростка – 1/6. А голова взрослого человека – 1/8 часть роста. Основываясь на этих данных, была создана кукла «Барби».
Голова маленького ребенка составляет 1/5 часть роста человека. Голова подростка – 1/6. А голова взрослого человека – 1/8 часть роста. Основываясь на этих данных, была создана кукла «Барби».
Дроби в юридической деятельности. Взрослые в жизни встречаются с такими ситуациями: в наследство каждый по завещанию получили, например А- 1/8 имущества наследодателя; Б. – 6/17; В. — завещано всё остальное . Какие доли достались каждому из наследников?
Дроби для портных. Портной при раскрое одежды использует дроби. (рукав длины три четверти — ¾ или брюки длины 7/8)
В настоящее время невозможно представить ни одну отрасль промышленности или сельского хозяйства, или строительства, где бы в расчётах не встречалось дробных чисел.
Дроби для профессии «Разметчик»
На машиностроительных заводах есть очень увлекательная профессия, называется она — разметчик. Разметчик намечает на заготовке линии, по которым эту заготовку следует обрабатывать, чтобы придать ей необходимую форму.
Разметчику приходится решать интересные и подчас нелегкие геометрические задачи, производить арифметические расчеты и т. д.
«Понадобилось как-то распределить 7 одинаковых прямоугольных пластинок равными долями между 12 деталями. Принесли эти 7 пластинок разметчику и попросили его, если можно, разметить пластинки так, чтобы не пришлось дробить ни одной из них на очень мелкие части. Значит, простейшее решение — резать каждую пластинку на 12 равных частей — не годилось, так как при этом получалось много мелких долей. Как же быть?
Возможно ли деление данных пластинок на более крупные доли? Разметчик подумал, произвел какие-то арифметические расчеты с дробями и нашел все-таки самый экономный способ деления данных пластинок.
Впоследствии он легко дробил 5 пластинок для распределения их равными долями между шестью деталями, 13 пластинок для 12 деталей, 13 пластинок для 36 деталей, 26 для 21 и т.п.
Оказывается, разметчик представил дробь 7\12 в виде суммы единичных дробей 1\3 + 1\4. Значит, если из 7 данных пластинок 4 разрезать на три равные части каждую, то получим 12 третей, то есть по одной трети для каждой детали. Остальные 3 пластинки разрежем 4 равные части каждую, получим 12 четвертей, то есть по одной четверти для каждой детали. Аналогично, используя представления дробей в виде суммы единичных дробей 5\6 = 1\2+1\3; 13\12 =1\3+3\4; 13\36 =1\4+1\9.
Значит, если из 7 данных пластинок 4 разрезать на три равные части каждую, то получим 12 третей, то есть по одной трети для каждой детали. Остальные 3 пластинки разрежем 4 равные части каждую, получим 12 четвертей, то есть по одной четверти для каждой детали. Аналогично, используя представления дробей в виде суммы единичных дробей 5\6 = 1\2+1\3; 13\12 =1\3+3\4; 13\36 =1\4+1\9.
Практическая часть. Мои наблюдения
Дроби в часах. «Встреча».
Мы часто отвечаем на вопрос «который час?» дробями. «Без четверти пять» без пятнадцати минут пять; «Сейчас три часа без четверти» -2 час 45 минут; «Половина второго» -1 час 30 минут.
Ситуация 1. В парке стоит молодой человек с букетом цветов:
Извините. Не подскажете который час? — спрашивает у прохожего.
«Без четверти пять», — отвечает прохожий.
Что опаздывает?
Да, на целых ¾ часа.
Сочувствую.
Спасибо.
Дроби в кулинарии. «Пряники».
Поварам нужны дроби для соблюдения пропорции при приготовлении блюда. В рецептах очень часто используются такие фразы, например, как одна вторая стакана, четверть столовой ложки.
Ситуация 2. Ученик в одежде повара. Готовит тесто для пряников.
— Для пряников понадобится 1 яйцо, один с четвертью стакана муки, две с половиною столовой ложки меда, треть чайной ложки соли, половина чайной ложки имбиря. Всё тщательно перемешиваем и печем пряники.
Дроби в кулинарии. «Пирожное».
Приготовленные блюда нужно умело делить на порции.
Ситуация 3. На столе стоит тарелка. В ней 5 пирожное.
— На день рождения пришли 6 друзей. Передо мной встал вопрос: «Как поровну разделить 5 пирожное между 6 человек»?
Решение было такое: нужно 5 пирожное разделить пополам каждый. Затем ещё 2 пирожное разделить на 3 части. Получается 6 абсолютно равных частей.
Получается 6 абсолютно равных частей.
Дроби в математике.
Учитель математики после изучения сокращения дробей задал домашнее задание. Найти значение выражения рациональным способом.
65 : (407 : 9) 22 (37 : 26) — (2911 : 213) 6 (35: 287) : 45
На первый взгляд, обыкновенные натуральные числа. Сначала надо решить действия в скобках, потом делить и умножать. Но, здесь должна быть какая-то хитрость?! Надо найти рациональный способ. Я решил данное выражение так:
1) Записал выражение в виде дроби.
2) Преобразовал каждое натуральное число в виде произведения двух множителей.
3) В полученных дробях получились числа, которых можно сократить.
4) Получил ответ
Заключение
При выполнении своего проекта, я узнал много нового и интересного о дробях. Думаю, что эти знания пригодятся в учебе. Прочитал много книг и разделов из энциклопедий. Познакомился с первыми дробями, которыми оперировали люди, узнал новые для меня имена ученых, внесших свой вклад в развитие учения о дробях. А особенно то, что дроби используются почти во всех сферах деятельности человека, а это значит, что людям всех профессий нужно обязательно изучать дроби! Уметь решать задачи на дроби, знать правила сложения и вычитания, умножения и деления дробей.
А особенно то, что дроби используются почти во всех сферах деятельности человека, а это значит, что людям всех профессий нужно обязательно изучать дроби! Уметь решать задачи на дроби, знать правила сложения и вычитания, умножения и деления дробей.
Без знания математики, особенно знания дробей вся современная жизнь была бы невозможна. Например, у нас не было бы хороших домов, потому что строители должны уметь измерять, считать, сооружать. Наша одежда была бы очень грубой, так как ее нужно хорошо скроить, то есть точно все измерить, Не было бы ни какой большой промышленности, ни какой коммерции.
И конечно, не было бы радио, телевидения, кино, телефона и тысяч других вещей, составляющих часть нашей цивилизации. Использование дробей, измерения «на сколько?», «как долго?» являются жизненно необходимой частью мира, в котором мы живем.
В заключении можно сказать, что дроби бывают разные, дроби бывают важные. Знание понятия математическая дробь очень важно!
Считаю, что материалы моей работы будут интересными для других учащихся. Они могут быть использованы как на уроке, так и для проведения учителями внеклассных мероприятий по математике.
Они могут быть использованы как на уроке, так и для проведения учителями внеклассных мероприятий по математике.
Список использованной литературы
- Анищенко Е. А. Число как основное понятие математики. Мариуполь, 2002.
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика. 5 класс: учеб.для общеобразовательных учреждений/- 26-е изд., стер. – М.: Мнемозина, 2009. — 280 с.
- Гейзер Г.И. История математики в школе. Пособие для учителей. – М.: Просвещение, 1981. – 239 с.
- Математика. 5 класс: учеб.для общеобразоват. учреждений. [СМ. Никольский, М.К.Потапов, Н.Н.Решетников, А.В. Шевкин]. — 11-е изд, дораб. — М.: Просвещение, 2016. — 272 с. — (МГУ — школе).
- Математический энциклопедический словарь. – М., 1988.
Если страница Вам понравилась, поделитесь в социальных сетях:
Как понять, что такое дроби?
“Человек подобен дроби: в знаменателе — то, что он о себе думает, в числителе — то, что он есть на самом деле.
Чем больше знаменатель, тем меньше дробь.” — Лев Толстой
Если так сказал сам Толстой, то скорее всего это правда! Тем не менее также общеизвестно, что для большинства людей такие разделы математики, как дроби, скорее сложны и запутаны, чем поэтичны. Неслучайно для большинства школьников самый сложный предмет — это бесспорно математика, причём заметно опережая другие предметы.
Поколению Z намного больше по душе русский язык, история, география и ИЗО. И все же математика очень важна! Такие темы, как дроби, уравнения и проценты, могут пригодиться нам в работе и выручить во многих жизненных ситуациях. Вот почему в сегодняшней статье мы узнаем о том, как же понять дроби раз и навсегда и научиться применять их в нужный момент.
Вы можете также узнать, как выучить другие разделы математики на нашем сайте.
Лучшие преподаватели по математике доступны для занятий
Поехали!
О важности дробей
Дроби могут очень пригодиться нам в повседневной жизни | Unsplash
Испокон веков школьники жалуются своим родителям на то, как сложны дроби. По разным оценкам больше половины всех детей сталкиваются со сложностями при их изучении в начальной школе. Но самое главное — не сдаваться! Дроби — очень полезное изобретение, и у нынешних школьников будет немало случаев в этом убедиться.
По разным оценкам больше половины всех детей сталкиваются со сложностями при их изучении в начальной школе. Но самое главное — не сдаваться! Дроби — очень полезное изобретение, и у нынешних школьников будет немало случаев в этом убедиться.
Вот несколько примеров того, как дроби могут пригодиться обычным людям в обычное время:
- Приготовить блюдо по рецепту: если вы когда-нибудь листали поваренную книгу, вы там точно видели множество рецептов с пропорциями в виде дробей. Чтобы блюдо удалось, их нужно четко соблюсти, и для этого в первую очередь придется понять, что они означают.
- Сказать (и понять) сколько времени: в начальной школе мы учимся говорить время с помощью таких долей, как полчаса, четверть часа, треть часа и т.д. Конечно, в эпоху смартфонов мы все реже спрашиваем время на улице, но всякое может случиться!
- Сходить за покупками: кто откажется посвятить выходной день шопинг-терапии? Что может быть лучше, чем пробежаться по бутикам и узнать обо всех новинках? Так вот знайте, что, освоив дроби, вы получите намного больше удовольствия в любом торговом центре.
 Как это так? Сейчас объясню. Представьте, что вы заходите в какой-нибудь магазин и замечаете роскошные туфли или сумку, и к тому же на ценнике написано, что действует скидка 75%. Чтобы понять, сколько денег вы можете сэкономить, необходимы знание дробей!
Как это так? Сейчас объясню. Представьте, что вы заходите в какой-нибудь магазин и замечаете роскошные туфли или сумку, и к тому же на ценнике написано, что действует скидка 75%. Чтобы понять, сколько денег вы можете сэкономить, необходимы знание дробей!
Дроби могут пригодиться в этих и множестве других ситуаций в повседневной жизни, поэтому давайте не будем терять время и наконец разберемся, что же они такое и с чем их едят.
Из истории дробей
Многим школьникам порой хотелось бы, чтобы дроби просто исчезли, и их жизнь стала легче, но этого не произойдёт. Дроби существуют уже много-много лет, и как ни странно лучший способ действительно упростить себе существование — это их понять. Так что давайте начнем.
Изначально слово дробь происходит от глагола “дробить”, то есть разбивать на мелкие кусочки, и это неспроста! В математике дроби обозначают равные доли от целого и их количество. То есть каждый раз мы делим наше число на части и потом считаем сколько их! Например, одна вторая (½) — это одна из двух половин нашего “раздробленного” предмета.
Как мы сказали, дроби появились очень давно. Ими столетиями пользовались древние цивилизации, например: египтяне и шумеры. Однако, происхождение десятичных дробей восходит к одному человеку, жившему в 1500-х годах, по имени Симон Стевин. Он был фламандским математиком и посвятил много времени стандартизации использования десятичных дробей или, говоря простым языком, сделал так, чтобы люди “дробили” все числа на одно и то же количество частей.
Благодаря Симону Стевину использовать дроби стало проще, и со временем их освоило огромное количество людей. Скоро это сделаем и мы с вами.
Для успешного изучения дробей самая важная тема — это обыкновенные дроби. Их особенность в том, что они состоят из целых чисел, таких как 1, 2, 3 и т.д. Это значит, что понять их намного проще, чем другие разновидности дробей, и они могут пригодиться в большем количестве ситуаций. Ведь когда мы считаем разные предметы, мы пользуемся именно целыми числами.
Тем не менее даже обыкновенные дроби делятся на подвиды, и сейчас мы разберемся в самых главных из них, которых всего 3.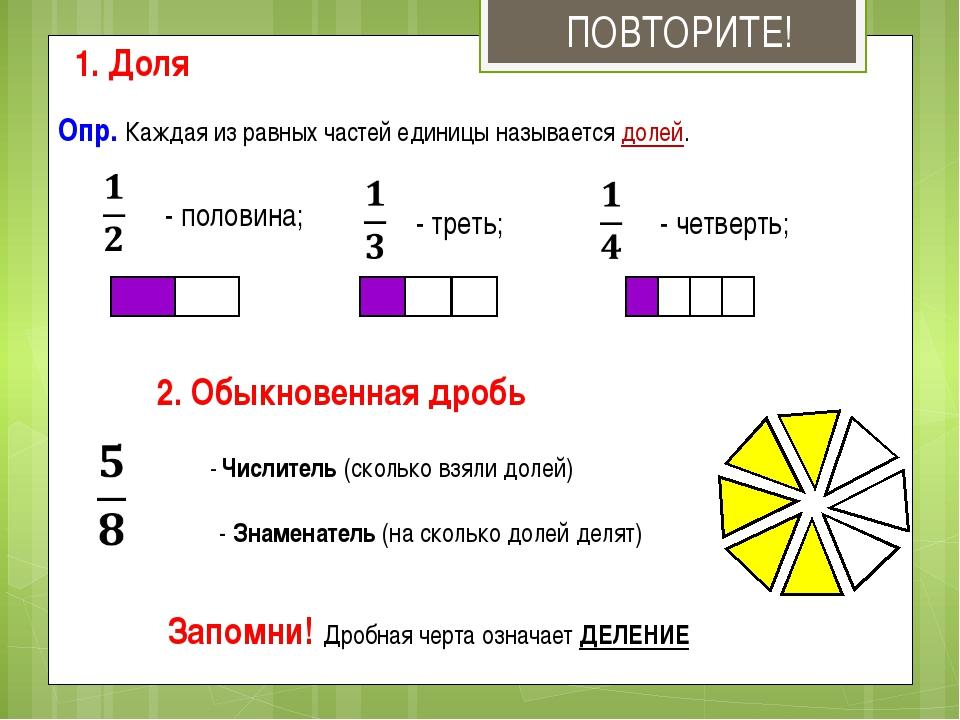
Также при изучении дробей вам может пригодится таблица умножения. Узнайте о том, как выучить таблицу умножения на нашем сайте.
К какому из трёх подвидов относится дробь?
Чтобы лучше понять правила использования дробей, в первую очередь необходимо знать три группы, на которые их разделяют. К ним относятся: правильные, неправильные и смешанные дроби. Вот краткое описание каждого из этих подвидов:
- Правильные дроби: чтобы распознать правильную дробь, школьникам нужно лишь знать, что знаменатели в правильных дробях больше, чем числители.
- Неправильные дроби: дроби, в которых числитель равен или больше знаменателя, называются неправильными дробями.
- Смешанные дроби: в действительности смешанные дроби — это разновидность неправильных дробей. Просто их записывают в виде целого и дробной части.
Подвиды дробей — это непростая тема, но, поверьте, очень скоро вы во всем разберетесь. А помогут вам в этом наши хитрые советы!
Лучшие преподаватели по математике доступны для занятий
Поехали!
О разных способах выучить дроби
Поняв дроби, вы сможете решить множество примеров | Unsplash
Каждый из нас мыслит и запоминает информацию по-своему. У кого-то хорошо развита зрительная память, поэтому им нужно увидеть конкретные примеры. А кто-то имеет развитое абстрактное мышление и легче понимает теоретические объяснения. Существует огромное количество различных подходов к изучению дробей. Самое главное — это выбрать методику, которая подойдет именно вам и тренироваться, решая задачи. Вы можете найти огромное количество математических задач в интернете.
У кого-то хорошо развита зрительная память, поэтому им нужно увидеть конкретные примеры. А кто-то имеет развитое абстрактное мышление и легче понимает теоретические объяснения. Существует огромное количество различных подходов к изучению дробей. Самое главное — это выбрать методику, которая подойдет именно вам и тренироваться, решая задачи. Вы можете найти огромное количество математических задач в интернете.
Вот несколько основных подходов к изучению дробей, которые могут помочь вам найти самый действенный способ для вас.
Определить важные составляющие
Прежде чем начать оперировать дробями, нужно разобраться, из чего состоит каждая обыкновенная дробь. Вот основные понятия с их определениями:
- Числитель — это крайне важная цифра, расположенная над чертой в обыкновенной дроби. Она обозначает количество частей.
- Знаменатель находится под чертой и жизненно необходим, потому что он показывает на сколько частей целое было разделено.

Поняв функции числителя и знаменателя, вы с легкостью разберетесь в правильных, неправильных и смешанных дробях. Вы сможете переходить к более сложным темам и использовать дроби в разных областях.
Числитель и знаменатель необходимы, чтобы понять, что такое дробь и что она обозначает. Если школьник увидит, что дроби — это не просто непонятные математические символы, а что они основаны на реальных предметах, то он легче осознает всю их важность. А когда мы осознаем важность какого-то понятия, мы стараемся всеми силами в нём разобраться.
Используйте рисунки и зрительную память
Наше первое знакомство с дробями обычно происходит в 3-4 классе начальной школы. Поскольку у детей хорошая зрительная память, и их нужно заинтересовать — им нужно много рисунков.
Мы очень рекомендуем начинать с основ: например, нарисовать круг и разделить его на равные части. Тогда дети поймут, что такое дроби и что они обозначают. Это в свою очередь позволит разжечь их интерес, чтобы двигаться дальше.
При наличии правильного подхода изучение дробей может показаться не таким уж и сложным процессом!
Хитрые советы, которые помогут при анализе дробей
Мы обычно начинаем изучать дроби в конце начальной школы | Unsplash
Какой бы раздел или тему мы не проходили на математике, нам нужно время, чтобы все хорошо понять и начать быстро решать задачи. Дроби — не исключение. Простые дроби специально проходят в конце начальной школы, чтобы ученики могли хорошо их освоить и использовать при решении более сложных примеров. Также дроби тесно связаны с математической операцией деления. Узнать больше о делении вы можете на нашем сайте.
Учитывая важность дробей, школьникам просто необходимо с ними разобраться. К счастью, для этого есть множество приёмов. В интернете легко можно найти хорошие образовательный материалы, а репетиторы по математике на Superprof могут все объяснить быстро и понятно. Они также могут поделиться хитрыми советами, которые помогут ученикам в решении задач.
Вот несколько особенно полезных советов от опытных математиков, которые уже выручили не одного школьника:
- Поиск наименьшего общего знаменателя: общий знаменатель необходим для сложения или вычитания дробей. Почему это полезная хитрость? Школьник научится оперировать дробями и глубже поймет, как они работают. К тому же поиск общего знаменателя — это хорошая умственная гимнастика.
- Использование круговых диаграмм: как и любой другой подход, основанный на рисунках, метод круговых диаграмм поможет в изучении дробей любому школьнику. Чем он полезен? Ученики будут представлять дроби в виде картинок и легче научатся применять их в разных ситуациях.
- Хорошо выучить таблицу умножения: как известно, в математике все взаимосвязано. Мы постоянно движемся от простого к сложному, и очень важно это простое не забывать. Таблица умножения поможет школьникам как при делении, так и при поиске общего знаменателя. Они будут быстрее решать примеры с дробями и почувствуют себя увереннее благодаря этому.
 Таблица умножения — это действительно основа основ, и ей следует уделить должное внимание.
Таблица умножения — это действительно основа основ, и ей следует уделить должное внимание.
После ознакомления с этими хитрыми и полезными советами школьникам станет намного легче решать примеры и задачи с дробями, и это будет огромным шагом к пониманию математики.
Также при изучении дробей вам могут помочь приложения и занимательные игры. Узнайте о том, как выучить математику с помощью интернета на нашем сайте.
Дело Superprof — помочь вам в этом! Просто начните свой поиск с фразы: «репетитор по математике».
Определения из сегодняшней статьи
Поскольку в сегодняшней статье было довольно много технических терминов, и использовались слова, которые нечасто встретишь в повседневном общении, мы решили добавить несколько определений. Они будут полезны всем читателям, включая даже тех, кто уже с ними знаком. Как известно, повторение — мать учения.
Что такое наименьший общий знаменатель?
С математической точки зрения, наименьший общей знаменатель — это самое маленькое положительное число, которое можно разделить на a и b.
Что такое целое число?
При изучении различных разделов математики периодически употребляется термин “целое число”. Определение целого числа довольно простое — это любое положительное, отрицательное число или ноль, не являющееся дробью!
Надеемся, что чтение сегодняшней статьи доставило вам удовольствие и вдохновило вас и дальше открывать для себя чудесный мир математики!
Ищете преподавателя, который поможет вам разобрать в дробях? Тогда просто вбейте в поисковике: «репетитор по математике», «репетитор по математике москва» или «репетитор по математике спб».
дроби
- Главная
- Ключевые слова
- дроби
Проектирование учебного занятия на основании ПРП, математика 5-й класс по теме «Правильные и неправильные дроби» 2022
Автор: Львова Елена Николаевна
Это урок «открытия нового» знания спроектированный с учётом введения обновлённых ФГОС ООО 2022, направленный на создание условий для развития мыслительной деятельности учащихся, умения анализировать, сравнивать, обобщать и делать выводы.
 Данный урок призван развивать логическое мышление, внимание, интерес к предмету, математическую речь учащихся; развивать навыки самоконтроля и самооценки учащихся. Целью данного урока (занятия) является формирование понятий «правильная дробь» и «неправильная дробь», а также формирование умения применять полученные знания для решения практических задач.
Данный урок призван развивать логическое мышление, внимание, интерес к предмету, математическую речь учащихся; развивать навыки самоконтроля и самооценки учащихся. Целью данного урока (занятия) является формирование понятий «правильная дробь» и «неправильная дробь», а также формирование умения применять полученные знания для решения практических задач.дроби, правильные и неправильные дроби
Духовно-нравственное и патриотическое воспитание на уроках математики 2022
Автор: Жукова Светлана Владимировна
В обучении математике с точки зрения патриотического воспитания огромную роль играет подбор математических задач для уроков с учётом дидактических и методических требований.
 Решение задач, включающих исторические сведения, способствует развитию кругозора учащихся и познавательного интереса к предмету. Тогда урок математики становится для них не просто уроком, на котором нужно решать, вычислять и заучивать формулы, а пробуждает чувства сопричастности к величию своей страны, собственных предков. Решение задач с практическим содержанием дает возможность учащимся задуматься о тяготах военных лет.
Решение задач, включающих исторические сведения, способствует развитию кругозора учащихся и познавательного интереса к предмету. Тогда урок математики становится для них не просто уроком, на котором нужно решать, вычислять и заучивать формулы, а пробуждает чувства сопричастности к величию своей страны, собственных предков. Решение задач с практическим содержанием дает возможность учащимся задуматься о тяготах военных лет.дроби, Решение задач с практическим содержанием
Интегрированный урок «Салат и дроби». 5-й класс 2022
Автор: Осинцева Оксана Николаевна
Цель урока: показать практическое применение математики в жизни людей.

Формирование функциональной грамотности на уроках математики 2022
Автор: Горина Ксения Александровна
На уроках математики возможна дифференциация заданий, то есть, все задания должны иметь разные уровни сложности. При решении и составлении задач учащимся могут предлагаться различные картинки, по которым им нужно составить и решить задачу. Оформлением дети занимаются самостоятельно, однако учителю необходимо тщательно следить за работой учеников. При затруднении выполнить данное действие предполагается, что учитель будет задавать наводящие вопросы.
дроби, инклюзивное образование, ЗПР, инклюзивный подход
Путешествие в страну дроби 2021
Автор: Сейфетдинова Хамдия Вагдятовна
Цели урока: повторить и обобщить знания и умения учащихся по теме «Дроби»; формировать умение анализировать, обобщать, развивать математическое мышление.

Проведение уроков математике в условиях инклюзивного обучения 2021
Автор: Горина Ксения Александровна
На уроках математики возможна дифференциация заданий, то есть, все задания должны иметь разные уровни сложности. При решении и составлении задач учащимся могут предлагаться различные картинки, по которым им нужно составить и решить задачу. Оформлением дети занимаются самостоятельно, однако учителю необходимо тщательно следить за работой учеников. При затруднении выполнить данное действие предполагается, что учитель будет задавать наводящие вопросы.
дроби, инклюзивное образование, ЗПР, доли
Презентация к уроку математики по теме «Умножение дробей».
 6-й класс
2020
6-й класс
2020Автор: Жилис Елена Валерьевна
Представлена презентация к уроку математики по теме «Умножение дробей»в 6-м классе.
дроби, умножение дробей
Сложение и вычитание обыкновенных дробей 2020
Автор: Лихачева Елена Николаевна
Занятие с целью закрепления и систематизации знаний по теме сложения и вычитания обыкновенных дробей.
 Ради повышения интереса к математике урок построен как путешествие в страну дробей.
Ради повышения интереса к математике урок построен как путешествие в страну дробей.дроби, сложение, вычитание
Технологическая карта урока математики в 5-м классе «Сложение и вычитание дробей с одинаковыми знаменателями» 2020
Автор: Нарейко Евгения Генадьевна
Цель урока: ввести правила сложения и вычитания дробей с одинаковыми знаменателями; развивать умение анализировать, сравнивать, обобщать, делать выводы, развивать внимание; развивать познавательный интерес через игровые моменты взаимоконтроля, взаимопроверки.

дроби, Сложение и вычитание дробей с одинаковыми знаменателями
Методическая разработка урока математики в 5-м классе «Равенство дробей» 2019
Автор: Черняева Леся Васильевна
Цели урока: познакомить с понятием равные, с основным свойством дроби и научить применять его в преобразовании дробей; способствовать формированию самооценки учащихся; формировать навыки взаимодействия друг с другом при работе в парах и группах.
дроби, математика, обыкновенные дроби
Технологическая карта урока по математике.
 Тема урока: «Приведение дробей к новому знаменателю»
2019
Тема урока: «Приведение дробей к новому знаменателю»
2019Автор: Исманова Рания Файзрахмановна
Цели урока: познакомить учащихся с основным свойством дроби; сформировать умения использовать основное свойство дроби для приведения дробей к новому знаменателю; развитие логики рассуждений, умения формулировать гипотезы, предложения, анализировать ситуации; способствовать развитию математической речи, оперативной памяти, произвольного внимания, наглядно-действенного мышлении; воспитывать культуру поведения при фронтальной работе, индивидуальной, парной работе.
дроби, математика, приведение дробей к новому знаменателю
Не нашли интересующий материал? Воспользуйтесь поиском по сайту.
Что такое дробь? Определение, части, примеры
Дробь показывает часть целого. Это целое может быть регионом или коллекцией. Слово «фракция» происходит от латинского слова «fractio», что означает «ломать». Египтяне, будучи первой цивилизацией, изучавшей дроби, использовали дроби для решения своих математических задач, которые включали в себя деление продуктов питания, припасов и отсутствие валюты в слитках.
В Древнем Риме дроби записывались только словами, обозначающими часть целого. В Индии дроби сначала записывались с одним числом над другим (числитель и знаменатель), но без черты. Только арабы добавили линию, которая используется для разделения числителя и знаменателя.
| 1. | Что такое дроби? |
| 2. | Части дроби |
| 3. | Типы фракций |
| 4. | Дроби в числовой строке |
5.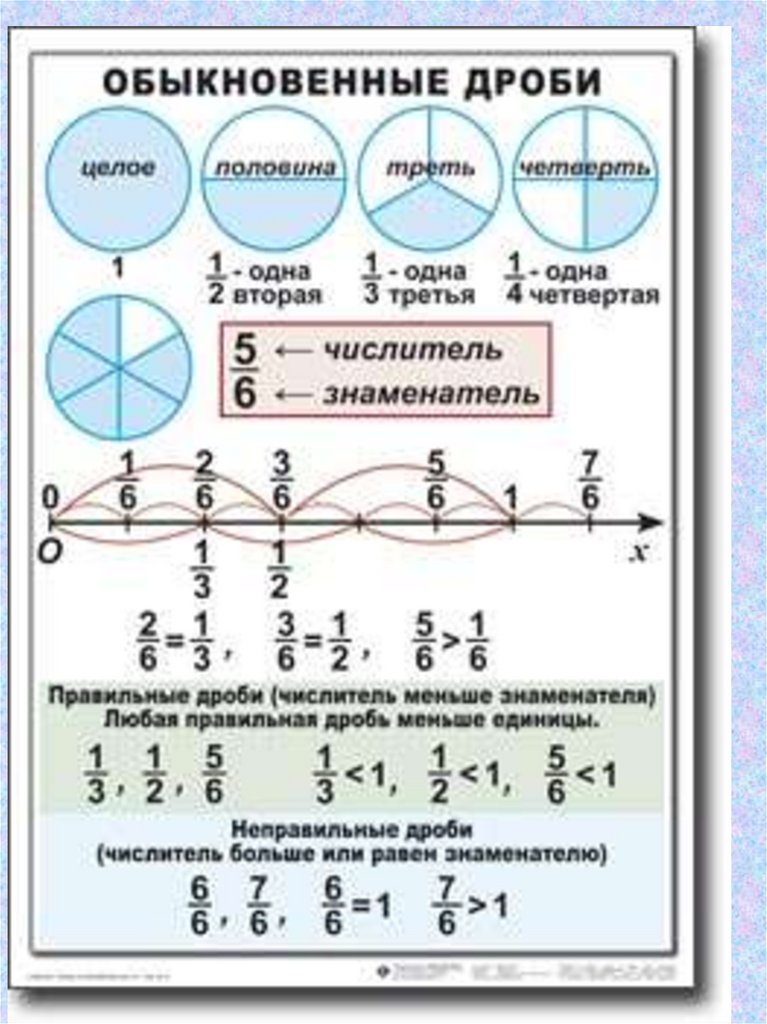 | Часто задаваемые вопросы о дробях |
Что такое дроби?
В математике дроби представлены числовым значением, которое определяет часть целого. Дробь может быть частью или частью любого количества из целого, где целым может быть любое число, определенное значение или вещь. Давайте разберемся с этой концепцией на примере. На следующем рисунке показана пицца, разделенная на 8 равных частей. Теперь, если мы хотим выразить одну выбранную часть пиццы, мы можем выразить ее как 1/8, что показывает, что из 8 равных частей мы имеем в виду 1 часть.
Означает одну из восьми равных частей. Его также можно прочитать как:
- Одна восьмая или .
- 1 на 8
Если мы выберем 2 части пиццы, это будет выражено как 2/8. Точно так же, если мы имеем в виду 6 частей этой пиццы, мы запишем это как 6/8 как дробь.
Части дроби
Все дроби состоят из числителя и знаменателя и разделены горизонтальной чертой, известной как дробная черта.
- Знаменатель указывает количество частей, на которые было разделено целое. Он помещается в нижнюю часть дроби под дробной чертой.
- Числитель указывает, сколько разделов дроби представлено или выбрано. Он ставится в верхней части дроби над дробной чертой.
Типы фракций
На основании числителя и знаменателя, которые являются частями дроби, существуют различные типы дробей, перечисленные ниже:
Правильная дробь
Правильные дроби — это дроби, у которых числитель меньше знаменателя. Например, 5/7, 3/8, 2/5 и т. д. — правильные дроби.
Неправильная дробь
Неправильная дробь — это дробь, в которой числитель больше или равен знаменателю. Оно всегда такое же или больше, чем целое. Например , 4/3, 5/2, 8/5 и так далее.
Дробная единица
Дроби, в которых числитель равен 1, называются единичными дробями. Например , 1/4, 1/7, 1/9 и так далее.
Смешанная дробь
Смешанная дробь представляет собой смесь целого числа и правильной дроби. Например, \(5\frac{1}{3}\), где 5 – целое число, а 1/3 – правильная дробь, или \(2\frac{2}{5}\), \( 7\frac{9}{11}\) и так далее.
Эквивалентная дробь
Эквивалентные дроби — это дроби, представляющие одно и то же значение после их упрощения. Чтобы получить эквивалентные дроби любой заданной дроби:
- Мы можем умножить и числитель, и знаменатель данной дроби на одно и то же число.
- Мы можем разделить и числитель, и знаменатель данной дроби на одно и то же число.
Пример: Найдите две дроби, равные 5/7.
Решение:
Эквивалентная дробь 1: Умножим числитель и знаменатель на одно и то же число 2. Это означает, что 5/7= (5 × 2)/(7 × 2) = 10/14
Эквивалентная дробь 2: Умножим числитель и знаменатель на одно и то же число 3. Это означает, что 5/7 = (5 × 3)/(7 × 3) = 15/21
Следовательно, 10/14, 15/21 и 5/7 — эквивалентные дроби.
Подобные и разные дроби
Подобные дроби — это дроби, имеющие одинаковые знаменатели. Например, 5/15, 3/15, 17/15 и 31/15 похожи на дроби.
В отличие от дробей, дроби имеют разные знаменатели. Например, 2/7, 9/11, 3/13 и 39/46 — разные дроби.
Дробь в числовой строке
Представление дробей на числовой прямой демонстрирует интервалы между двумя целыми числами, что также показывает нам фундаментальный принцип построения дробных чисел. Дроби на числовой прямой можно представить, составив равные части целого, то есть от 0 до 1. Знаменатель дроби будет представлять количество равных частей, на которые числовая линия будет разделена и отмечена. Например, если нам нужно представить 1/8 на числовой прямой, нам нужно отметить 0 и 1 на двух концах и разделить числовую прямую на 8 равных частей. Тогда первый интервал можно обозначить как 1/8. Точно так же следующий интервал можно пометить как 2/8, следующий — как 3/8 и так далее. Следует отметить, что последний интервал представляет 8/8, что означает 1. Обратите внимание на следующую числовую строку, которая представляет эти дроби в числовой строке.
Обратите внимание на следующую числовую строку, которая представляет эти дроби в числовой строке.
☛Статьи по теме
- Умножение дробей
- Деление дробей
- Сложение и вычитание дробей
Примеры дробей
Пример 1: Запишите две эквивалентные дроби для 5/15
Решение:
Давайте запишем эквивалентные дроби для 5/15, используя умножение и деление.
а.) Умножим числитель и знаменатель на одно и то же число 2. Это означает, что (5 × 2)/(15 × 2) = 10/30
б.) Разделим числитель и знаменатель с тем же числом 5. Это означает, что (5 ÷ 5)/(15 ÷ 5) = 1/3
Следовательно, 10/30 и 1/3 эквивалентны 5/15. Другими словами, 10/30, 1/3 и 5/15 являются эквивалентными дробями.
Пример 2: В классе 48 учеников, 1/4 из них смотрят мультфильмы. Сколько школьников не смотрят мультфильмы?
Решение:
Общее количество учеников = 48, доля учеников, смотрящих мультфильмы = 1/4
Количество учеников, которые смотрят мультфильмы = 1/4 × 48 = 12
Таким образом, количество учеников которые не смотрят мультики = 48 — 12 = 36
Следовательно, число школьников, которые не смотрят мультики, равно 36.

Пример 3: Укажите истинное или ложное значение.
а.) Правильные дроби – это дроби, у которых числитель меньше знаменателя.
б.) 9/2 — правильная дробь.
в.) 3/4 и 2/4 подобны дробям.
Решение:
а.) Правильными дробями называются дроби, у которых числитель меньше знаменателя.
b.) Неверно, 9/2 — неправильная дробь, потому что числитель больше знаменателя.
в.) Верно, что 3/4 и 2/4 подобны дробям, потому что у них одинаковые знаменатели.
перейти к слайдуперейти к слайдуперейти к слайду
Хотите построить прочную основу в математике?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Забронировать бесплатный пробный урок
Практические вопросы по дробям
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о дробях
Что такое дроби в математике?
Дроби в математике представляют числовое значение, выражающее часть целого. Целое может быть любым числом, определенным значением или вещью. Фракции представлены в виде p/q. Например, ¼, ½, ¾ и так далее.
Целое может быть любым числом, определенным значением или вещью. Фракции представлены в виде p/q. Например, ¼, ½, ¾ и так далее.
Какие существуют типы дробей?
Дроби классифицируются по следующему признаку:
- На основании числителя и знаменателя они подразделяются на правильные дроби, неправильные дроби, смешанные дроби.
- На основе групп они классифицируются как похожие дроби, непохожие дроби и эквивалентные дроби.
Сколько частей в дроби?
Дробь состоит из двух частей: числителя и знаменателя.
- Числитель: Числитель представляет собой число, расположенное над дробной чертой. Например, в 6/7 числитель 6.
- Знаменатель: Знаменатель указывает число, расположенное под дробной чертой. Например, в 6/7 7 является знаменателем.
Что такое 0,125 в виде дроби?
0,125, поскольку дробь может быть записана как 1/8. Мы можем преобразовать десятичную дробь в дробь следующим образом. 0,125 = 125/1000 = 5/40 = 1/8
0,125 = 125/1000 = 5/40 = 1/8
Как связаны дроби и десятичные числа?
Дроби и десятичные дроби — это разные способы представления чисел. Дроби записывают в виде p/q, где q≠0, например, 3/5; а в десятичных числах целая часть числа и дробная часть связаны с запятой, например, 3,56. Дробь можно преобразовать в десятичную, если разделить данный числитель на знаменатель. Точно так же, чтобы преобразовать десятичную дробь в дробь, мы записываем данную десятичную дробь в качестве числителя, а под ней ставим дробную черту. Затем мы помещаем 1 прямо под десятичной точкой, за которой следует необходимое количество нулей. Затем эту дробь можно упростить. Например, если нам нужно преобразовать 0,5 в дробь, мы помещаем 10 в знаменатель и удаляем десятичную точку, что дает 5/10. После сокращения дроби получаем (5 ÷ 5) / (10 ÷ 5) = 1/2.
Как упростить дроби?
Чтобы упростить дробь, мы сначала запишем множители для числителя и знаменателя. Затем определите наибольший общий множитель между ними и разделите числитель и знаменатель на наибольший общий множитель (GCF). Приведенная дробь, которую мы получаем, является простейшей формой данной дроби. Например, чтобы упростить 36/45, мы найдем НОД 36 и 45. НОД 36 и 45 = 9. Теперь разделим числитель и знаменатель на 9., то есть (36 ÷ 9)/(45 ÷ 9) = 4/5
Приведенная дробь, которую мы получаем, является простейшей формой данной дроби. Например, чтобы упростить 36/45, мы найдем НОД 36 и 45. НОД 36 и 45 = 9. Теперь разделим числитель и знаменатель на 9., то есть (36 ÷ 9)/(45 ÷ 9) = 4/5
Как умножать дроби?
Чтобы умножить любые две дроби, мы сначала умножаем числители, затем умножаем знаменатели. Затем упростите полученную дробь. Например, 3/5 × 15/18 = 45/90 = 1/2.
Как делить дроби?
Чтобы разделить одну дробь на другую, мы сначала записываем обратную величину второй дроби, а затем умножаем дроби. Другими словами, мы умножаем первую дробь на обратную величину второй дроби. Написав обратную величину второй дроби, умножаем дроби обычным способом. Мы умножаем числители, а затем умножаем знаменатели. Затем упростите полученную дробь, если требуется. Например, 5/6 ÷ 1/5 = 5/6 × 5/1 = 25/6 = \(4\frac{1}{6}\)
Как называются дроби с одинаковым знаменателем?
Дроби с одинаковым знаменателем называются подобными дробями.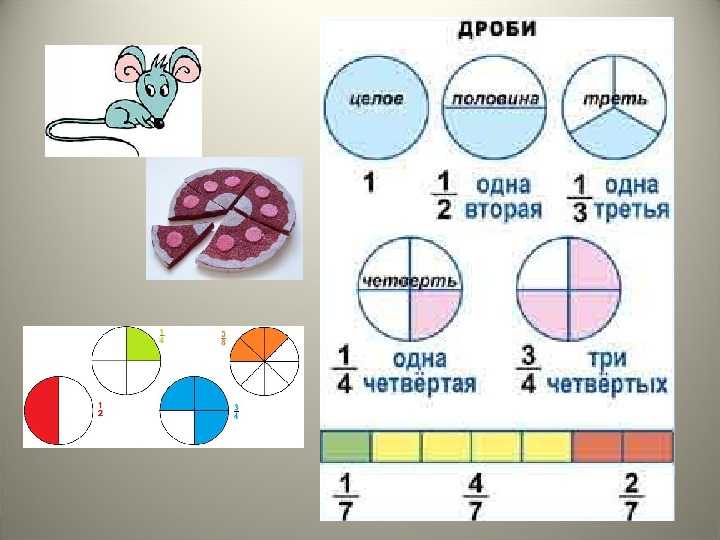 Например, 4/7, 3/7, 5/7 похожи на дроби, потому что у них один и тот же знаменатель.
Например, 4/7, 3/7, 5/7 похожи на дроби, потому что у них один и тот же знаменатель.
Как определить, какая дробь больше?
Чтобы определить большую дробь, нам сначала нужно проверить, являются ли данные дроби похожими на дроби. Для этого нам нужно сравнить знаменатели.
- При одинаковых знаменателях больше будет та дробь, у которой числитель больше. Например, чтобы сравнить 3/4 и 2/4, мы можем легко проверить числители и сказать, что 3/4 > 2/4 .
- В случае разных знаменателей мы переводим данные дроби в подобные дроби, записывая для них общий знаменатель, а затем сравниваем числители. Например, чтобы сравнить 2/3 и 4/5, мы найдем наименьшее общее кратное (НОК) знаменателей. Как только знаменатели станут одинаковыми, мы сможем легко сравнивать дроби. НОК чисел 3 и 5 равно 15. Теперь переведем их так, чтобы знаменатели стали одинаковыми. Умножим первую дробь 2/3 на 5/5, то есть 2/3 × 5/5 = 10/15. Теперь умножим вторую дробь 4/5 на 3/3, то есть 4/5 × 3/3 = 12/15.
 Сравните дроби: 10/15 и 12/15. Поскольку знаменатели одинаковы, мы сравним числители и увидим, что 12 > 10 . Дробь с большим числителем является большей дробью, то есть 10/15 < 12/15. Следовательно, 2/3 < 4/5.
Сравните дроби: 10/15 и 12/15. Поскольку знаменатели одинаковы, мы сравним числители и увидим, что 12 > 10 . Дробь с большим числителем является большей дробью, то есть 10/15 < 12/15. Следовательно, 2/3 < 4/5.
Все ли дроби меньше 1?
Нет, все дроби не меньше 1.
- Правильные дроби больше 0, но меньше 1. (Числитель меньше знаменателя).
- Неправильные дроби всегда равны 1 или больше 1. (Числитель больше или равен знаменателю)
Как складывать дроби с разными знаменателями?
Чтобы сложить дроби с разными знаменателями, нам нужно выполнить следующие шаги. Сложим дроби 4/5 + 6/7
- Шаг 1: Поскольку знаменатели в данных дробях разные, мы найдем НОК 5 и 7, чтобы сделать их одинаковыми. НОК 5 и 7 = 35,
- Шаг 2: После этого шага мы умножим 4/5 на 7/7, то есть (4/5) × (7/7) = 28/35, а 6/7 на 5/5, ( 6/7) × (5/5) = 30/35. Этот шаг преобразует их в похожие дроби с одинаковыми знаменателями.

- Шаг 3: Теперь знаменатели совпадают, поэтому мы можем сложить числители и сохранить общий знаменатель. Новые дроби с общими знаменателями — 28/35 и 30/35. Итак, 28/35 + 30/35 = (28 + 30)/35 = 58/35 = \(1\frac{23}{35}\).
Как умножать дроби на целые числа?
Чтобы умножить дроби на целые числа, мы записываем целое число в виде дроби, помещая 1 в знаменатель, а затем следуем обычной процедуре умножения дробей. Например, давайте умножим 5/8 × 3. Здесь 3 — целое число, и мы запишем его как 3/1. Теперь умножим 5/8 × 3/1 = 15/8 = \(1\frac{7}{8}\)
Что такое сравнение дробей?
Сравнение дробей означает нахождение большей и меньшей дроби между любыми двумя или более дробями. Например, давайте сравним 3/16 и 7/16. Сначала рассмотрим знаменатели данных дробей: 3/16 и 7/16. Поскольку знаменатели одинаковы, мы можем сравнить числители. Мы видим, что 3 < 7. Дробь с большим числителем является большей дробью. Следовательно, 3/16 < 7/16. В случае, если дроби имеют разные знаменатели, мы преобразуем их в подобные дроби, найдя НОК знаменателей и записав соответствующие эквивалентные дроби. Как только знаменатели станут одинаковыми, мы можем легко сравнить числители и определить большую дробь.
В случае, если дроби имеют разные знаменатели, мы преобразуем их в подобные дроби, найдя НОК знаменателей и записав соответствующие эквивалентные дроби. Как только знаменатели станут одинаковыми, мы можем легко сравнить числители и определить большую дробь.
Руководство по дробям из 10 простых фактов | Бретт Берри | Математические приемы
Без шуток, просто
Математики любят дроби, а остальной мир их ненавидит . Я не знаю, какие травмирующие события вы пережили в детстве, но мне жаль, что они были такими болезненными.
В ДЕСЯТИ ФАКТАХ я объясню все, что вам нужно знать о дробях, как можно яснее.
Да, один урок, десять основных идей, менее десяти минут чтения.
Готов?
факт первый
Каждая дробь имеет числитель , который равен количеству частей, у нас есть , и знаменатель , равный общему количеству частей в целом.
Как и в случае с тортом, у вас может быть 2 маленьких кусочка или 1 кусок в два раза больше, и это будет столько же. Следовательно, многие дроби эквивалентны, например, 2/5 и 4/10.
4/102/5факт два
Напишите любое целое число, превышающее 1 , чтобы оно стало дробью, поскольку общее количество частей в любом неделимом целом равно единице.
факт три
Умножение дробей легко , просто умножить прямо.
3 x 7 = 21 и 5 x 8 = 40Примечание. Сначала нужно преобразовать смешанные числа в неправильные дроби. Подробнее об этом читайте дальше.
факт четыре
Число 1 называется мультипликативное тождество , потому что мы можем умножить его на любое число, и число останется прежним. Это важно для дробей, потому что часто нам нужно изменить внешний вид дроби без фактического изменения ее значения.
Например, я могу преобразовать 1/3 в эквивалентную дробь 3/9, умножив на 3/3.
Факт пять
При сложении и вычитании дробей знаменатели должны быть одинаковыми . Это имеет смысл. Если мы хотим объединить или убрать части, мы должны говорить о частях одинакового размера, иначе это приведет к путанице.
Так что же делать, если ваши дроби не имеют одинаковых размеров?
Умножьте на единицу, чтобы привести знаменатели к общему размеру. По сути, мы делим дроби на части меньшего размера, пока они не станут одинакового размера. Это называется найти общий знаменатель.
По правде говоря, подойдет любой общий знаменатель, но люди предпочитают находить наименьший. В этом случае наименьшее число, в которое входят и 7, и 3 без остатка, равно 21. Итак, умножьте первую дробь на 3/3, а вторую на 7/7.
Умножьте на формы 1, чтобы получить общий знаменатель 21. Если вы не можете придумать наименьший общий знаменатель, вы всегда можете умножить каждую дробь на противоположный номинал . Иногда, как в данном случае, это оказывается наименьшим общим знаменателем. Если это не так, просто сократите свой ответ в конце.
Иногда, как в данном случае, это оказывается наименьшим общим знаменателем. Если это не так, просто сократите свой ответ в конце.
Когда знаменатели совпадут, вычтите числители, чтобы получить 8/21.
15–7 = 8Это работает, как и следовало ожидать. Графически начните с 15 штук из 21 всего.
Обратите внимание: у меня 5/7 повторяются 3 раза, это напрямую связано с умножением 5/7 на 3/3 для получения 15/21.Удалите краску с 7 из 15 синих блоков.
Что оставляет 21 августа, как и ожидалось.
факт шесть
смешанное число представляет собой комбинацию целого числа и дроби.
Пример смешанного числаСмешанные числа плохо сочетаются с другими дробями. Рекомендуется сначала преобразовать их в неправильные дроби.
Примечание: неправильная дробь — это дробь, числитель которой больше знаменателя, следовательно, ее значение больше единицы.
факт семь
Чтобы преобразовать 2 и 4/5 в неправильную дробь , прибавьте 2 + 4/5.
Шаг 1: Начните с перезаписи 2 как 2/1.
Шаг 2: Умножьте 2/1 на 5/5, чтобы получить эквивалентную дробь 10/5, которая имеет желаемый общий знаменатель 5.
5/5 = 1, мультипликативное тождествоШаг 3 : Сложение 10/5 + 4/5.
Наш результат — эквивалент неправильной дроби 14/5.
Чтобы преобразовать обратно в смешанное число, выполните деление. Например, 5 входит в число 14 два раза (поскольку 5 x 2 = 10), и остается 4 части.
Равные дроби в неправильной (слева) и смешанной форме (справа)факт восемь
Предположим, мы хотим определить, что больше: 5/12 или 6/13.
Сначала убедитесь, что они не в форме смешанных чисел!Шаг первый: Умножьте диагональ и запишите произведение над числителем.
Шаг второй: Умножьте другую диагональ и запишите ее произведение над числителем.
Шаг третий: Сравните продукты. Сторона с , чем больше произведение, тем больше дробь. Итак, в данном случае 5/12 меньше, чем 6/13.
Сторона с , чем больше произведение, тем больше дробь. Итак, в данном случае 5/12 меньше, чем 6/13.
Мы также можем определить, равны ли дроби, используя векторные произведения.
Перекрестное произведение 3/7 и 12/28 равно 84, поэтому 3/7 = 12/28.
факт девять
Самое лучшее в дробях заключается в том, что вы можете найти множество возможностей отменить. Что делает их быстрыми и легкими в управлении.
Допустим, у меня есть дробь 8/10. И 8, и 10 можно переписать с множителем 2.
Поскольку 2/2 = 1, я могу сократить двойки, оставив 4/5 в виде сокращенной дроби.
Вычеркните двойки, так как 2/2 = 1Используйте эту стратегию, чтобы упростить умножение дробей.
Начните с перезаписи каждого числа в множителях.
Отменить все пары чисел, которые делятся на 1. Например, 5/5 = 1.
У меня есть еще одна пара пятерок, а также пара троек, которые тоже делятся на 1.
Ой! Я мог бы переписать 6 как 2 x 3 и отменить пару двоек. Ничего страшного, если вы пропустите какой-то фактор, просто продолжайте, пока не получите их все.
Примечание: я переписал 2 как 2 x 1, так что, когда я исключаю двойки, в числителе остается единица.Если бы умножить 15/25 на 10/18 напрямую, то пришлось бы много арифметических действий, используя отмену I , чтобы предварительно уменьшить дроби и упростить умножение.
факт десять
Принцип деления дробей прост на простых примерах, таких как:
В целом есть две половины, поэтому в 5 целых 10 половинок.
Но с более сложными дробями эта концепция усложняется.
Чтобы решить эту задачу, мы будем использовать два факта:
- Мы можем умножать на любую форму единицы (т.е. на что угодно над самим собой)
- Умножая на обратную величину 3/2, которая равна 2/3, приводит к 1 через отмену
Шаг первый: Начните с умножения на обратную величину над собой.
Теперь нам нужно решить две меньшие задачи (синяя и зеленая).
Шаг второй: Отменить все, что делится на 1 в нижней (зеленой) дроби. Это должно всегда приводить к 1.
Теперь нам осталось решить основную проблему.
Шаг третий: Используйте отмену для предварительного уменьшения дроби. Сделав эти сокращения, умножьте, чтобы получить 4/3.
Ярлык
Это механика длинной руки » флип и умножение. ”
Мы можем пропустить умножение на обратную величину внизу, так как она всегда сокращается до 1. Поэтому все, что вам нужно сделать, это умножьте числитель на обратную величину знаменателя.
Почему работает трюк с перекрестным произведением?
Отличный вопрос! Чтобы обобщить, составьте две дроби, используя буквы a, b, c и d, чтобы представить четыре разных числа.
Умножьте обе дроби на b•d (это позволит нам сократить знаменатели).
Теперь сократите b слева и d справа, так как они делятся на 1. У нас больше нет дробей, только произведения d•a и c•b.
Посмотрите на исходные дроби. Это те же произведения, как если бы мы перемножили диагонали. Поэтому проще всего сравнить перекрестный продукт.
❤ ОСТАВАЙТЕСЬ НА СВЯЗИ ❤
Будьте в курсе всех новостей Math Hacks!
Инстаграм | Фейсбук | Twitter
Далее: Головоломка с числами 8, 8, 3, 3
Спасибо за чтение!
Math Hacks уже на YouTube!
Присоединяйтесь ко мне, пока мы вместе решим математику, по одной задаче за раз. Распространение любви к математике + расширение прав и возможностей. Подпишитесь на новые…
www.youtube.com
Распространенная математическая ошибка, которую я заметил в последнее время
Вы случайно сделали это с домашним заданием вашего ребенка?
medium. com
com
Комбинации и перестановки
Мы используем термин «комбинация» вольно и обычно неправильно. Мы говорим что-то вроде: «Эй, что у тебя…
medium.com
Понимание логарифмов и корней
Бревна и корни — нет, я не говорю о деревьях. Я говорю о математическом роде. Бьюсь об заклад, вы думаете,
medium.com
4: Дроби — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4997
- OpenStax
- OpenStax
Часто в жизни целые суммы — это не совсем то, что нам нужно. Пекарь должен использовать чуть больше чашки молока или части чайной ложки сахара. Точно так же плотнику может понадобиться меньше фута дерева, а маляру может понадобиться часть галлона краски. В этой главе мы узнаем о числах, которые описывают части целого. Эти числа, называемые дробями, очень полезны как в алгебре, так и в повседневной жизни. Вы обнаружите, что уже знакомы со многими примерами дробей!
Точно так же плотнику может понадобиться меньше фута дерева, а маляру может понадобиться часть галлона краски. В этой главе мы узнаем о числах, которые описывают части целого. Эти числа, называемые дробями, очень полезны как в алгебре, так и в повседневной жизни. Вы обнаружите, что уже знакомы со многими примерами дробей!
- 4.1: Визуализация дробей (часть 1)
- Дробь — это способ представления частей целого. Знаменатель b представляет собой количество равных частей, на которые было разделено целое, а числитель a представляет, сколько частей включено. Знаменатель b не может быть равен нулю, потому что деление на ноль не определено. Смешанное число состоит из целого числа и дроби. Когда дробь имеет числитель меньше знаменателя, она называется правильной дробью, и ее значение меньше единицы.
- 4.2: Визуализация дробей (часть 2)
- Эквивалентные дроби — это дроби, имеющие одинаковое значение.
 При работе с дробями часто бывает необходимо выразить одну и ту же дробь в разных формах. Чтобы найти эквивалентные формы дроби, мы можем использовать свойство эквивалентных дробей. Мы можем использовать символы неравенства для упорядочивания дробей. Помните, что a > b означает, что a находится справа от b на числовой прямой. По мере того, как мы движемся слева направо по числовой прямой, значения увеличиваются.
При работе с дробями часто бывает необходимо выразить одну и ту же дробь в разных формах. Чтобы найти эквивалентные формы дроби, мы можем использовать свойство эквивалентных дробей. Мы можем использовать символы неравенства для упорядочивания дробей. Помните, что a > b означает, что a находится справа от b на числовой прямой. По мере того, как мы движемся слева направо по числовой прямой, значения увеличиваются.
- 4.3: Умножение и деление дробей (часть 1)
- Дробь считается упрощенной, если в числителе и знаменателе нет общих множителей, кроме 1. Если дробь имеет общие делители в числителе и знаменателе, мы можем привести дробь к ее упрощенной форме, удалив общие делители. Чтобы умножить дроби, мы умножаем числители и умножаем знаменатели. Тогда запишем дробь в упрощенной форме.
- 4.4: Умножение и деление дробей (Часть 2)
- Обратная дробь a/b равна b/a, где a ≠ 0 и b ≠ 0.
 Произведение числа и его обратной величины равно 1. Чтобы найти обратную дробь, мы инвертируем дробь. Это означает, что мы помещаем числитель в знаменатель, а знаменатель в числитель. Чтобы разделить дроби, умножьте первую дробь на обратную вторую.
Произведение числа и его обратной величины равно 1. Чтобы найти обратную дробь, мы инвертируем дробь. Это означает, что мы помещаем числитель в знаменатель, а знаменатель в числитель. Чтобы разделить дроби, умножьте первую дробь на обратную вторую.
- 4.5: Умножение и деление смешанных чисел и комплексных дробей (часть 1)
- Чтобы умножить или разделить смешанные числа, преобразуйте смешанные числа в неправильные дроби. Затем следуйте правилам умножения или деления дробей, а затем упростите, если это возможно. Сложная дробь – это дробь, в которой число и/или знаменатель содержит дробь. Чтобы упростить сложную дробь, перепишите сложную дробь в виде задачи на деление. Затем следуйте правилам деления дробей и затем упростите, если это возможно.
- 4.6: Умножение и деление смешанных чисел и комплексных дробей (Часть 2)
- Обычно перед дробью ставится знак минус, но иногда встречаются дроби с отрицательным числителем или знаменателем.
 Когда числитель и знаменатель имеют разные знаки, частное отрицательно. Если и числитель, и знаменатель отрицательны, то дробь положительна, потому что мы делим отрицательное число на отрицательное. Полосы дробей действуют как символы группировки. Выражения над и под разделительной чертой следует рассматривать так, как если бы они были заключены в круглые скобки.
Когда числитель и знаменатель имеют разные знаки, частное отрицательно. Если и числитель, и знаменатель отрицательны, то дробь положительна, потому что мы делим отрицательное число на отрицательное. Полосы дробей действуют как символы группировки. Выражения над и под разделительной чертой следует рассматривать так, как если бы они были заключены в круглые скобки.
- 4.7: Сложение и вычитание дробей с общим знаменателем
- Чтобы сложить дроби, сложите числители и поместите сумму над общим знаменателем. Чтобы вычесть дроби, вычтите числители и поместите разницу над общим знаменателем.
- 4.8: Сложение и вычитание дробей с разными знаменателями (часть 1)
- Наименьший общий знаменатель (НОД) двух дробей — это наименьшее общее кратное (НОК) их знаменателей. Чтобы найти LCD двух дробей, разложите каждый знаменатель на его простые числа. Затем перечислите простые числа, по возможности совпадая с простыми числами в столбцах, и сократите столбцы.
 Наконец, умножьте множители вместе, произведение будет LCM знаменателей, который также является LCD дробей.
Наконец, умножьте множители вместе, произведение будет LCM знаменателей, который также является LCD дробей.
- 4.9: Сложение и вычитание дробей с разными знаменателями (Часть 2)
- При умножении дробей вы умножаете числители и знаменатели вместе соответственно. Чтобы разделить дроби, нужно умножить первую дробь на обратную вторую. Для сложения дробей сложите числители и поместите сумму над общим знаменателем. Если дроби имеют разные знаменатели, сначала преобразуйте их в эквивалентные формы с помощью ЖК-дисплея. Аналогично, для вычитания дроби вычтите числители и поместите разницу над общим знаменателем.
- 4.E: Fractions (Exercises)
- 4.S: Fractions (Summary)
- 4.10: Add and Subtract Mixed Numbers (Part 1)
- To сложите смешанные числа с общим знаменателем, сначала перепишите задачу в вертикальной форме.
 Затем сложите целые числа и дроби вместе. Наконец, упростите сумму, если это возможно. Альтернативный метод сложения смешанных чисел состоит в том, чтобы преобразовать смешанные числа в неправильные дроби, а затем сложить неправильные дроби. Этот метод обычно пишется горизонтально.
Затем сложите целые числа и дроби вместе. Наконец, упростите сумму, если это возможно. Альтернативный метод сложения смешанных чисел состоит в том, чтобы преобразовать смешанные числа в неправильные дроби, а затем сложить неправильные дроби. Этот метод обычно пишется горизонтально.
- 4.11: Сложение и вычитание смешанных чисел (Часть 2)
- Чтобы вычесть смешанные числа с общими знаменателями, сначала перепишите задачу в вертикальной форме и сравните две дроби. Если верхняя дробь больше нижней, вычтите дроби, а затем целые числа. Если верхняя дробь не больше нижней дроби, то в верхнем смешанном числе взять одно целое и прибавить его к дробной части, получив смешанное число с неправильной дробью. Затем вычтите дроби, а затем целые числа. Наконец, упростите, если это возможно.
- 4.12: Решение уравнений с дробями (часть 1)
- Шаги, которые мы предпринимаем, чтобы определить, является ли число решением уравнения, одинаковы, независимо от того, является ли решение целым числом, целым числом или дробью .
 Чтобы определить, является ли число решением уравнения, сначала подставьте число вместо переменной в уравнении. Затем упростите выражения в обеих частях уравнения и определите, верно ли полученное уравнение. Если это правда, число является решением. Если это не так, число не является решением.
Чтобы определить, является ли число решением уравнения, сначала подставьте число вместо переменной в уравнении. Затем упростите выражения в обеих частях уравнения и определите, верно ли полученное уравнение. Если это правда, число является решением. Если это не так, число не является решением.
- 4.13: Решение уравнений с дробями (Часть 2)
- Чтобы решить реальные задачи, нам сначала нужно прочитать задачу, чтобы определить, что мы ищем. Затем мы пишем словосочетание, которое дает информацию, чтобы найти его. Затем мы переводим словосочетание в математическую запись, а затем упрощаем. Наконец, мы переводим математическую запись в предложение, чтобы ответить на вопрос.
Рис. 4.1. Пекари комбинируют ингредиенты для приготовления вкусного хлеба и выпечки. (кредит: Агустин Руис, Flickr)
Эта страница под названием 4: Fractions распространяется по незаявленной лицензии и была создана, изменена и/или курирована OpenStax.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Глава
- Автор
- ОпенСтакс
- Версия лицензии
- 4,0
- Показать страницу Содержание
- нет
- Теги
Основы дробей – Математика для торговли: Том 1
Дроби
Что такое дробь? Вы когда-нибудь имели дело с дробями в школе или на работе? Итак, дробь — это часть (или часть) целого.
Допустим, вы заказали пиццу, и в ней было 8 кусков. В тот день вы были голодны и съели 5 ломтиков, поэтому съели 5 из 8 ломтиков. Это можно представить в виде дроби.
Наша история о фракциях начинается с Эбигейл, Ханны и Наоми, учениц-электриков, которые одновременно учатся в школе и надеются вместе открыть компанию, как только получат билеты на электричество с красной печатью.
Начнем с пары определений. Каждая дробь состоит из двух частей: числителя и знаменателя. Давайте посмотрим на дробь, чтобы определить каждую.
Числитель : Число над чертой в дроби. Он показывает, сколько частей целого подсчитывается.
Знаменатель : Число под чертой в дроби. Он показывает, сколько всего частей в целом.
Если Эбигейл, Ханна и Наоми в конечном итоге станут владельцами компании, каждая из них будет владеть ⅓ этой компании. Каждый человек представляет 1 владельца, а вместе в компании 3 владельца.
Вот еще несколько примеров дробей:
[латекс]\БОЛЬШОЙ\dfrac{1}{2}\ \dfrac{3}{8}\ \dfrac{5}{16}\ \dfrac{4}{9}\ \dfrac{7}{15} \\dfrac{77}{145}[/латекс]
Приведенные выше примеры представляют собой типичные дроби, но мы не всегда видим дроби в такой форме. Есть еще два типа дробей, с которыми мы имеем дело: смешанные числа и неправильные дроби .
Есть еще два типа дробей, с которыми мы имеем дело: смешанные числа и неправильные дроби .
Смешанные номера
Допустим, трое учеников собираются однажды вечером, чтобы поговорить о будущем, и заказывают 2 пиццы, по 8 штук в каждой.
(Я знаю, что пиццы выглядят совершенно одинаково, но в этом вам придется мне поверить. Одно можно сказать наверняка: каждая пицца состоит из 8 ломтиков, и кто-то пошел дальше и попробовал обе пиццы на вкус.)
Нам нужно разбить это на части: всего у нас есть 2 пиццы, каждая из которых состоит из 8 ломтиков. Всего получается 16 ломтиков. Если ученики съедят 1 пиццу целиком, они съедят 8 из 8 кусков.
[латекс]\БОЛЬШОЙ\dfrac{8}{8}=1[/латекс]
Теперь предположим, что у одного из них есть еще один кусок второй пиццы. Теперь они съедят 1 целую пиццу плюс 1 кусочек.
[латекс]\БОЛЬШОЙ1+\dfrac{1}{8}=1\dfrac{1}{8}\longleftarrow\text{Смешанное число}[/latex]
Это так называемое смешанное число. Смешанное число можно определить следующим образом:
Смешанное число можно определить следующим образом:
Смешанное число : Сочетание целого числа и дроби.
Далее рассмотрим неправильные дроби.
Неправильные дроби
Неправильная дробь : Дробь, в которой числитель больше знаменателя.
Это означает, что число в верхней части дроби больше числа в нижней части. Мы вернемся к нашему примеру с пиццей. Вместе ученики съели в общей сложности 9ломтики. Это составляет 1 целую пиццу плюс 1 кусок второй пиццы. В виде неправильной дроби количество съеденных пицц будет выглядеть так:
.[латекс]\БОЛЬШОЙ\dfrac{9}{8}[/латекс]
Теперь мы хотим преобразовать смешанное число в неправильную дробь, а затем сделать обратное, взять неправильную дробь и преобразовать ее обратно в смешанное число.
Замените следующее смешанное число неправильной дробью:
[латекс]\НАИБОЛЬШИЙ1\dfrac{3}{4}[/latex]
Шаг 1 : Превратите целое число в дробь со знаменателем 4.
[latex]\LARGE1=\dfrac{4}{4}[/latex]
Шаг 2 две дроби вместе. Теперь нам придется немного забежать вперед, так как мы еще не рассмотрели добавление дробей. Я дам вам дешевую и простую версию здесь. Пока знаменатели одинаковы, у нас все хорошо. При сложении дробей мы просто сохраняем знаменатели одинаковыми и добавляем числители. (Мы подробно рассмотрим сложение дробей в следующей главе.)
[латекс]\БОЛЬШОЙ\dfrac{4}{4}+\dfrac{3}{4}=\dfrac{7}{4}[/latex]
Итак:
[латекс]\БОЛЬШОЙ1\dfrac {3}{4}=\dfrac{7}{4}[/latex]
Еще один способ найти ответ:
Это может показаться немного запутанным, но следуйте за мной. Со смешанным числом 1 ¾ возьмите 4 и умножьте его на 1. Затем прибавьте 3, и вы получите 7. Это тот же ответ, просто другой способ его получения.
Попробуйте самостоятельно перейти от смешанного числа к неправильной дроби.
Измените следующую дробь на неправильную. Посмотрите видео ответ, чтобы увидеть, как вы это сделали.
[латекс]\БОЛЬШОЙ3\dfrac{3}{8}[/латекс]
Хорошо: надеюсь, вы справились с вычислением смешанных чисел и неправильных дробей. Но как насчет обратного? Мы также должны рассмотреть пример этого, а затем дать вам возможность проработать его самостоятельно.
Превратите следующую неправильную дробь в смешанное число:
[латекс]\БОЛЬШОЙ\dfrac{27}{6}[/латекс]
Шаг 1 : Узнайте, сколько раз 6 входит в число 27. Мы можем сделать это, используя деление в большую сторону. Хорошей новостью здесь является то, что мы уже прошли длинное деление в первой главе. Если вам нужно пересмотреть его, оглянитесь назад, чтобы увидеть, как это делается (см. Разделение целых чисел).
В итоге мы получаем, что 6 входит в число 27 четыре раза, а 3 остается. Таким образом, наше смешанное число становится следующим:
[латекс]\БОЛЬШОЙ4\dfrac{3}{6}[/латекс]
Попробуйте еще один тренировочный вопрос.
Замените следующую неправильную дробь смешанным числом. Посмотрите видео-ответ, чтобы узнать, как вы это сделали.
Посмотрите видео-ответ, чтобы узнать, как вы это сделали.
[латекс]\БОЛЬШОЙ\dfrac{17}{3}[/латекс]
Прежде чем мы перейдем к сложению и вычитанию дробей, мы должны коснуться другого понятия, известного как сокращение дробей. Уменьшение — это то, что мы делаем, когда хотим сделать уменьшенную версию дроби, которая по-прежнему имеет то же математическое значение, что и оригинал.
Вернемся к нашей пицце. Еще раз, у нас есть 8 кусочков на пиццу. Теперь, скажем, мы съедаем 4 таких ломтика. Мы съели:
Если бы вас спросили, сколько у вас пиццы, что бы вы ответили? Скажете ли вы: «Я съел 4 из 8 возможных кусочков» или «Я съел половину пиццы»? Думаю, мы все согласимся, что просто скажем, что съели половину пиццы, поскольку 4 куска составляют половину пиццы. Если бы мы записали половину как дробь, это выглядело бы так:
.[латекс]\БОЛЬШОЙ\dfrac{1}{2}[/латекс]
Тогда мы могли бы заключить, что две дроби математически представляют одно и то же, и это всего лишь два разных способа представления одного и того же. Вы можете посмотреть на это так: я вырезал два куска дерева. Один из них имеет длину 12 дюймов, а другой — 1 фут. Они одинаковой длины — просто их длины выражаются по-разному. В итоге имеем вот это:
Вы можете посмотреть на это так: я вырезал два куска дерева. Один из них имеет длину 12 дюймов, а другой — 1 фут. Они одинаковой длины — просто их длины выражаются по-разному. В итоге имеем вот это:
[латекс]\БОЛЬШОЙ\dfrac{4}{8}=\dfrac{1}{2}[/латекс]
Что мы сделали, так это уменьшили дробь с 4 на 8 до 1 на 2 без изменения фактического представленного значения. Математически это было сделано следующим образом: мы взяли исходный числитель 4 и разделили его на 4. То, что делается с одной частью дроби, должно быть сделано и с другой, поэтому мы также разделили знаменатель 8 на 4, в результате чего дробь от 1 к 2.
Выполнение одного и того же действия с числителем и знаменателем гарантирует, что исходная дробь и конечная дробь равны по значению.
Мы сокращаем дроби, когда можем разделить одно и то же число без остатка как на числитель, так и на знаменатель. В нашем примере 4 можно разделить на оба. Обратите внимание, что число 2 также можно разделить как на числитель, так и на знаменатель. Если мы разделим оба на 2, мы получим:
Если мы разделим оба на 2, мы получим:
Хотя с математической точки зрения это по-прежнему работает, мы часто хотим привести дробь к ее наименьшему выражению, то есть к точке, в которой ее уже нельзя уменьшить. Доля 2 к 4 может быть еще больше уменьшена до 1 к 2, так что мы могли бы проделать дополнительную работу, если бы захотели.
Давайте пройдемся по мыслительной схеме при сокращении дробей. Возьмите следующую дробь и уменьшите ее до наименьшего значения:
[латекс]\БОЛЬШОЙ\dfrac{8}{12}[/латекс]
Шаг 1 : Здесь мы хотим взглянуть на оба числитель и знаменатель и определить, есть ли число, которое может войти в них обоих. Возможно, будет проще, если вы запишете числа, начиная с 1, а затем решите, какие числа могут входить как в 8, так и в 12.
Из этого мы можем сделать вывод, что наибольшее число, которое может входить как в 8, так и в 12, равно 4.
Шаг 2 : Разделите числитель и знаменатель на 4.
Вот и все: теперь дробь приведена к наименьшему значению. Когда вы закончите, всегда смотрите на ответ, просто чтобы убедиться, что определенно нет другого числа, которое могло бы войти в числитель и знаменатель, так как это означало бы, что дробь может быть уменьшена еще больше.
Когда вы закончите, всегда смотрите на ответ, просто чтобы убедиться, что определенно нет другого числа, которое могло бы войти в числитель и знаменатель, так как это означало бы, что дробь может быть уменьшена еще больше.
Приведенный выше пример довольно прост. Когда речь идет о больших числах, иногда проще решить вопрос за пару шагов, чтобы медленно уменьшить дробь. Взгляните на следующий пример, чтобы понять, что я имею в виду.
Сократите следующую дробь до наименьшего члена:
[латекс]\НАИБОЛЬШИЙ\dfrac{24}{168}[/латекс]
Шаг 1 : Определите, существует ли число, которое может войти как в числитель, так и в числитель. знаменатель. Если имеется более одного числа, используйте большее число.
Это немного сложнее, чем первый вопрос, так как числа намного больше и с ними сложнее работать. Возвращаясь к нашим таблицам умножения, мы видим, что 6, 8 и 12 составляют 24. Мы также можем сказать, что 24 составляет 24. Но как насчет 168? Что входит в это?
Одна вещь, которую мы знаем наверняка, это то, что 2 входит в обе части, так почему бы нам не начать с того, что мы возьмем каждую часть дроби и разделим ее на 2. Если у вас возникли проблемы с делением 168 на 2 в уме, продолжайте и воспользуйся своим калькулятором.
Если у вас возникли проблемы с делением 168 на 2 в уме, продолжайте и воспользуйся своим калькулятором.
Шаг 2 : Определите, можно ли еще уменьшить дробь. Мы видим, что снова можно разделить оба числа на 2.
Шаг 3 : Повторите шаг 2 и определите, можно ли еще уменьшить дробь. На этот раз мы отмечаем, что 6 может входить как в 6, так и в 42, поэтому мы делим и числитель, и знаменатель на 6.
Вот и все: мы сократили эту крупную дробь до минимального значения всего за несколько шагов. Я признаю, что если бы мы использовали калькулятор для всей этой процедуры, мы могли бы получить ответ с меньшими усилиями, но это не главное. Делая это в долгосрочной перспективе, вы начинаете тренировать свой мозг в отношениях между числами. Когда вы лучше познакомитесь с числами, вы сможете различать закономерности и понимать отношения, формирующиеся в математике. Хотя поначалу это может занять немного больше времени, со временем отдача будет велика.
Попробуйте задать себе пару вопросов и посмотрите ответы в видео, чтобы узнать, как вы справились.
Приведите следующие дроби к наименьшему виду.
[латекс]\БОЛЬШОЙ\dfrac{15}{18}[/латекс]
[латекс]\БОЛЬШОЙ\dfrac{24}{36}[/латекс]
Brilliant Math & Science Wiki
Хеманг Агарвал, Даниэль Майя, Мира Б, а также
способствовал
Содержимое
- Визуальное представление
- Классификация
- Умножение дробей
- Добавление дробей
- Арифметика дробей
- Сложные дроби
- Дроби — Проблемы со словами
- Дроби — решение задач
- Смотрите также
Часть, заштрихованная синим цветом ниже, является визуальным представлением двух третей:
две трети заполнены
Продолжая шаг за шагом, мы можем понять, почему 23 \frac{2}{3} 32 выглядит так, как показано на рисунке выше:
Начните с целого объекта или единицы: 111.

единицаРазделите его в соответствии со знаменателем (((здесь мы делим на 3):133): \frac{1}{3}3):31.
разделитьУмножьте этот результат в соответствии с числителем (((здесь мы умножаем на 2):232): \frac{2}{3}2):32.
результат
Правильная дробь – это дробь, у которой числитель меньше знаменателя, например 45. \фракция{4}{5}. 54.
Неправильная дробь — это дробь, у которой числитель больше знаменателя, например. 74. \фракция{7}{4}. 47.
Смешанное число записывается как целая часть числа, за которой следует дробная часть. Дробная часть смешанного числа всегда является правильной дробью, например. 413. 4\фракция{1}{3}. 431.
Чтобы умножить дроби, выполните следующие действия:
- Умножьте числители.
- Умножьте знаменатели.

- Упростите дробь, разделив ее на их НОД.
Вычислите 23×94 \frac{ 2}{3} \times \frac{ 9}{ 4 } 32×49.
Перемножая числители и знаменатели, получаем
23×94=2×93×4=1812. \dfrac{2}{3} \times \dfrac{9}{4} = \dfrac{ 2 \times 9 } { 3 \times 4} = \dfrac{ 18 } { 12 } . 32×49=3×42×9=1218.
Так как gcd(12,18)=6 \gcd(12,18) = 6 gcd(12,18)=6, упрощенная дробь равна
1812=18÷612÷6=32. \dfrac{18}{12} = \dfrac{ 18 \div 6 } { 12 \div 6 } = \dfrac{3}{2}. 1218=12÷618÷6=23.
Таким образом, 23×94=32 \frac{2}{3} \times \frac{9}{4} = \frac{3}{2} 32×49=23. □ _\квадрат □
Если дробь смешанная, то перед умножением ее нужно сначала преобразовать в неправильную дробь.
Вычислить 123×234 1 \frac{2}{3} \times 2 \frac{ 3}{4} 132×243.
Преобразовав смешанные дроби в неправильные дроби, мы получим
123=1×3+23=53,234=2×4+34=114. 1 \dfrac{2}{3} = \dfrac{ 1 \times 3 + 2 } { 3} = \dfrac{5}{3}, \quad 2 \dfrac{3}{4} = \dfrac{ 2 \ умножить на 4 + 3} {4} = \dfrac{11}{4}.
132=31×3+2=35, 243=42×4+3=411.
Следовательно,
123×234=53×114=5×113×4=5512. 1 \dfrac{2}{3} \times 2 \dfrac{3}{4} = \dfrac{5}{3} \times \dfrac{ 11}{4} = \dfrac{5 \times 11 } { 3 \times 4 } = \dfrac{55}{12} . 132×243=35×411=3×45×11=1255.
Поскольку наибольший общий делитель чисел 555555 и 121212 равен 1,1,1, окончательный ответ равен 5512\frac{55}{12} 1255. □ _\квадрат□
Обратите внимание, что
123×234≠(1×2)2×33×4=212. 1 \dfrac{2}{3} \times 2 \dfrac{3} {4} \neq ( 1 \times 2) \dfrac{ 2 \times 3 } { 3 \times 4} = 2 \dfrac{1}{ 2}.132×243=(1×2)3×42×3=221.
Упростить 45×332.\dfrac{4}{5} \times 3 \dfrac{3}{2}. 54×323.
Преобразовав смешанную дробь в неправильную, получим 332=3×2+32=92. 3 \frac{3}{2} = \frac{3 \times 2 + 3}{2} = \frac{9}{2},323=23×2+3=29. Следовательно,
45×332=45×92=4×95×2=3610=185, \dfrac{4}{5} \times 3 \dfrac{3}{2} = \dfrac{4}{5} \times \ dfrac{9}{2} =\dfrac{4 \times 9}{5 \times 2}= \dfrac{36}{10}= \dfrac{18}{5},54×323=54× 29=5×24×9=1036=518,
, где мы упростили дробь, разделив числитель и знаменатель на gcd(36,10)=2.
\gcd(36, 10) = 2 .gcd(36,10)=2. □ _\квадрат □
Оцените 23×134×65. \frac{2}{3} \times 1 \frac{3}{4} \times \frac{6}{5} .32×143×56.
Преобразовав смешанную дробь в неправильную, мы получим 134=74. 1 \ гидроразрыв {3} {4} = \ гидроразрыв {7} {4}. 143=47. Следовательно,
23×74×65=2×7×63×4×5=8460=75, \dfrac{2}{3} \times \dfrac{7}{4} \times \dfrac{6}{5} = \dfrac{2 \times 7 \times 6}{3 \times 4 \times 5} = \dfrac{84}{60} = \dfrac{7}{5} ,32×47×56=3× 4×52×7×6=6084=57,
, где мы упростили дробь, разделив числитель и знаменатель на gcd(84,60)=12. \gcd(84, 60) =12 .gcd(84,60)=12. □ _\квадрат □
Чтобы сложить дроби, выполните следующие действия:
- Преобразуйте к общему знаменателю, используя наименьшее общее кратное.
- Добавьте числители.
- Упростите дробь, разделив ее на наибольший общий делитель.
Вычислите 23+45 \frac{2}{3} + \frac{4}{5} 32+54.
Поскольку знаменатели разные, надо найти общий знаменатель. Наименьшее общее кратное 3 и 5 равно 15, поэтому мы имеем 23=2×53×5=1015 \frac{2}{3} = \frac{ 2 \times 5 } { 3 \times 5 } = \frac{ 10}{15} 32=3×52×5=1510 и 45=4×35×3=1215 \frac{4}{5} = \frac{4 \times 3 } { 5 \times 3 } = \frac{ 12}{15} 54=5×34×3=1512.
Затем мы складываем числители, чтобы получить
1015+1215=2215. \frac{10}{15} + \frac{12}{15} = \frac{22}{15} . 1510+1512=1522.
Так как gcd(22,15)=1 \gcd(22,15) = 1 gcd(22,15)=1, эта дробь уже упрощена.
Таким образом, 23+45=2215=1715 \frac{2}{3} + \frac{4}{5} = \frac{22}{15} = 1 \frac{7}{15} 32+54 =1522=1157. □_\квадрат□
Процедура аналогична для смешанных дробей, но сначала мы должны преобразовать их в неправильную дробь.
В качестве альтернативы может быть проще складывать целые и дробные части по отдельности.
Оцените 123+256 1 \frac{2}{3} + 2 \frac{5}{6} 132+265.
Преобразуя в неправильные дроби, мы имеем 123=1×3+23=53 1 \frac{2}{3} = \frac{1 \times 3 + 2 } { 3} = \frac{5}{3} 132=31×3+2=35 и 256=2×6+56=176 2 \frac{5}{6} = \frac{2 \times 6 + 5} { 6} = \frac{17 {6} 265=62×6+5=617.
Поскольку знаменатели разные, мы приводим к общему знаменателю 666. Это дает нам
53+176=5×23×2+176=276 \frac{5}{3} + \frac{17}{6} = \frac{ 5 \times 2 } { 3 \times 2 } + \frac{ 17}{6} = \frac{27} { 6} 35+617=3×25×2+617=627
Наконец, упростим дробь. Поскольку gcd(27,6)=3 \gcd(27,6) = 3 gcd(27,6)=3, следовательно, мы делим все на 3, чтобы получить 27÷36÷3=92 \frac{27 \div 3 } { 6 \div 3} = \frac{9}{2} 6÷327÷3=29.
Таким образом, 123+256=92=412 1 \frac{2}{3} + 2 \frac{5}{6} = \frac{9}{2} = 4 \frac{1}{2} 132 +265=29=421. □_\квадрат□
Вычислите 234+112,2 \frac{3}{4} + 1\frac{1}{2},243+121.
Преобразуя каждое слагаемое в неправильные дроби, мы имеем 234=2×4+34=113 2 \frac{3}{4} = \frac{2 \times 4 + 3}{4} = \frac{11}{ 3} 243=42×4+3=311 и 112=1×2+12=32.
1\frac{1}{2} = \frac{1\times2+1}{2}=\frac{3}{2}.121=21×2+1=23.
Поскольку знаменатели разные, приводим к общему знаменателю 6.6.6. Это дает нам
234+112=113+32=11×23×2+3×32×3=22+96=316. □ 2 \frac{3}{4} + 1\frac{1}{2} = \frac{11}{3} + \frac{3}{2} = \frac{11 \times 2}{3 \ умножить на 2} + \frac{3 \times 3} {2 \times 3} = \frac{22 + 9{6} = \frac{31}{6} . \ _\квадрат 243+121=311+23=3×211×2+2×33×3=622+9=631. □
Оцените 312+223+134. 3\frac{1}{2} + 2\frac{2}{3} + 1\frac{3}{4}.321+232+143.
Преобразуя каждое слагаемое в неправильные дроби, мы имеем 312=3×2+12=72,223=2×3+23=83 3\frac{1}{2} = \frac{3\times2+1}{2} = \frac{7}{2}, 2\frac{2}{3} = \frac{2\times3 + 2}{3} = \frac{8}{3}321=23×2+1 =27, 232=32×3+2=38 и 134=1×4+34=74. 1\frac{3}{4} = \frac{1\times4+3}{4}=\frac{7}{4}.143=41×4+3=47.
Поскольку знаменатели разные, приводим к общему знаменателю 12.12.12. Это дает нам
312+223+134=72+83+74=7×62×6+8×43×4+7×34×3=42+32+2112=9512.
\begin{выровнено} 3\frac{1}{2} + 2\frac{2}{3} + 1\frac{3}{4} &= \frac{7}{2} + \frac{8}{3} + \ гидроразрыв{7}{4} \\ &= \frac{7\times6}{2\times6} + \frac{8\times4}{3\times4}+\frac{7\times3}{4\times3} \\ &= \фракция{42+32+21}{12} \\ &= \фракция{95}{12}. \end{выровнено} 321+232+143=27+38+47=2×67×6+3×48×4+4×37×3=1242+32+21 = 1295.
Так как gcd(95,12)=1, \gcd(95,12) = 1 ,gcd(95,12)=1, эта дробь уже упрощена.
Таким образом, 312+223+134=9512=71112. 3\frac{1}{2} + 2\frac{2}{3} + 1\frac{3}{4} = \frac{95}{12} = 7\frac{11}{12},321 +232+143=1295=71211. □ _ \квадрат□
160\dfrac{1}{60}601 760\dfrac{7}{60}607 5160\dfrac{51}{60}6051 5360\dfrac{53}{60}6053
Какая из следующих дробей при добавлении к сумме приведенных выше чисел дает в результате целое число?
Учитывая последовательность операций над правильными дробями, возможно, включая умножение, деление, сложение и вычитание, мы сначала определяем порядок выполнения последовательности операций, следуя обычным правилам порядка операций.
Что такое 14+23−35?\frac{1}{4} + \frac{2}{3} — \frac{3}{5}?41+32−53?
Собирая дроби, используя наименьшее общее кратное знаменателей, мы имеем
14+23−35=1560+4060−3660=15+40−3660=1960.\begin{выровнено} \frac{1}{4} + \frac{2}{3} — \frac{3}{5} &= \frac{15}{60} + \frac{40}{60} — \frac{36 {60}\\\\ &= \фракция{15 + 40 — 36}{60}\\ & = \фракция{19}{60}. \end{align}41+32−53=6015+6040−6036=6015+40−36=6019.
Поскольку наибольший общий делитель чисел 191919 и 606060 равен 1, окончательный ответ равен 1960\frac{19{60} 6019. □ _\квадрат□
Что такое 13+25÷65? \frac{1}{3} + \frac{2}{5} \div \frac{6}{5}?31+52÷56?
Следуя порядку операций, мы должны сначала разделить, поэтому мы имеем 13+(25÷65)=13+13=23 \frac{1}{3} + \left( \frac{2}{5} \div \frac{6}{5} \right) = \frac{1}{3} + \frac{1}{3} = \frac{2}{3} 31+(52÷56)=31 +31=32. Таким образом, ответ равен 23 \frac{2}{3} 32. □ _\квадрат □
Что такое 203−19÷[37×(−14)×(−23)2]? \frac{20}{3} -\frac{1}{92 \right] &= \frac{20}{3} -\frac{1}{9} \div \left[ \frac{3}{7} \times \left( — \frac{1}{4} \right) \times \left( \frac{4}{9} \right) \right]\\ &= \frac{20}{3} -\frac{1}{9} \div \left[ \frac{3}{7} \times \left( — \frac{1}{9} \right) \ Правильно]\\ &= \frac{20}{3} + \frac{1}{9} \div \left[ \frac{3}{63} \right]\\ &= \frac{20}{3} + \left( \frac{1}{9} \times \frac{63}{3} \right)\\ &= \frac{20}{3} + \left( \frac{7}{3} \right)\\ &= \фракция{27}{3}\\ & = 9.
\ _\квадрат \end{выровнено}320−91÷[73×(−41)×(−32)2]=320−91÷[73×(-41)×(94)]=320−91÷ [73×(−91)]=320+91÷[633]=320+(91×363)=320+(37)=327=9. □
Найдите значение a+b a + b a+b в приведенном ниже выражении, где a a a и b b b — положительные целые числа без общих делителей:
16+110=ab. \frac{1}{6} + \frac{1}{10} = \frac{a}{b}. 61+101=ба.
Основная статья: Сложные дроби
Сложная дробь — это дробь, в которой другая дробь стоит в числителе или знаменателе (или в обоих). Ниже приведен пример сложной дроби:
1−1×1+1x. \frac{1-\frac{1}{x}}{1+\frac{1}{x}}. 1+x11−x1.
Сложные дроби не следует путать с дробями, содержащими комплексные числа.
Упростить
2327. \frac{\hspace{2мм} \frac23 \hspace{2мм} }{\hspace{2мм} \frac27\hspace{2мм} }.7232.
Мы можем умножить и числитель, и знаменатель на 21, что является НОК 333 и 7.
7.7. Затем
23×2127×21=2×72×3=146=73=213. □ \ frac {\ frac {2} {3} \ times 21} {\ frac {2} {7} \ times 21} = \ frac {2 \ times 7} {2 \ times 3} = \ frac {14} {6} = \ гидроразрыва {7} {3} = 2 \ гидроразрыва {1} {3}. \ _ \квадрат 72×2132×21=2×32×7=614=37=231. □
Чтобы иметь возможность решать текстовые задачи с дробями, вы должны сначала уметь решать обычные текстовые задачи, переводя обычный язык в математику. Вики SAT Translating Word Problems дает отличное представление о том, как это можно сделать. Посмотрите, если вы не знакомы с текстовыми задачами.
Дроби могут быть очень полезны в более реалистичных сценариях, в которых необходимо вычислить часть суммы. Химические растворы, например, используют большое количество дробей для вычисления частей общего числа, и точно так же, как задачи, связанные с решениями, любая другая задача, которая должна дифференцировать или выполнять любой другой процесс с частями общего числа, обычно может быть решена и упрощена. правильное употребление дробей.
правильное употребление дробей.
Дроби могут быть заданы непосредственно в словесной задаче (\big((например, 710 \frac{7}{10} 107 человеческого тела состоит из воды)\big)) или обычным языком, без чисел, представляющих Это. В этом случае вы должны иметь возможность искать и идентифицировать ключевые слова , которые относятся к дробям, которые обычно являются теми же самыми, которые относятся к делению, поскольку технически это одна и та же операция.
Финальный экзамен по математике будет длиться 1 час. Учитель сказал, что весь тест можно прочитать за 5 минут, ответить на каждый вопрос за 2 минуты, а работу проверить за оставшееся время. Если в тесте 20 вопросов, то какую часть времени теста можно использовать для его повторения?
Учитывая, что задача прочитана, мы должны определить, о чем она спрашивала. Проблема заключается в том, чтобы получить долю времени, которое можно использовать для проверки, из общего времени, необходимого для выполнения теста.
Итак, здесь нам нужны две вещи: время на просмотр теста (числитель) от общего времени тестирования (знаменатель):
Время пересмотреть тестВремя теста. \frac{\text{Время просмотреть тест}}{\text{Время теста}}. Время тестированияВремя для просмотра теста.
Время на просмотр теста не дано, поэтому надо разобраться. Общее время теста 1 час. В каждом часе 60 минут. Поскольку все остальное, что делается в тесте, дается в минутах, мы должны иметь обе единицы измерения в одной и той же мере, чтобы иметь возможность правильно их сравнивать. Итак, часы нужно перевести в минуты:
Время тестирования = 1 час 1 час = 60 минут Время тестирования = 60 минут Время просмотра теста Время тестирования = Время просмотра теста 60 минут. \begin {aligned} \text{Время тестирования} &= 1 \text{час} \\\\ 1 \text{ час} &= 60 \text{ минут} \\\\ \text{Время тестирования} &= 60 \text{ минут} \\\\ \frac{\text{Время просмотра теста}}{\text{Время теста}} &= \frac{\text{Время просмотра теста}}{60 \text{минут}}.
\end{aligned} Время тестирования1 часВремя тестированияВремя тестированияВремя просмотра теста=1час=60 минут=60 минут=60 минутВремя просмотра теста.
Теперь надо найти время, чтобы просмотреть тест. Время проверки — это время, оставшееся после завершения всего остального, поскольку, согласно задаче, «работа [просматривается] в оставшееся время». Чтобы найти оставшееся время, мы должны найти время, которое было использовано. 5 минут теста будут использованы для его чтения и 2 минуты для чтения каждого вопроса. Есть 20 вопросов, поэтому 2 минуты × 20 2 \text{ минуты} \times 20 2 минуты × 20 минут будут использованы для ответов на вопросы. Из общего количества 1 часа, это время, которое останется:
Время на просмотр теста = 60 минут – 5 минут – 2 минуты × 20 = 55 минут – 40 минут = 15 минут.\begin{aligned} \text{Пора пересмотреть тест} &= 60 \text{ минут} — 5 \text{ минут} — 2 \text{ минут} \times 20 \\\\ &= 55 \text{ минут} — 40 \text{ минут} \\\\ &= 15 \text{ минут}.
\end{align}Время на проверку теста = 60 минут – 5 минут – 2 минуты × 20 = 55 минут – 40 минут = 15 минут.
Теперь у нас есть числитель и знаменатель:
Время просмотра тестаВремя теста=15 минут60 минут=14. \frac{\text{Время просмотра теста}}{\text{Время теста}}= \frac{15 \text{минут}}{60 \text{минут}} = \frac{1}{4}. Время тестаВремя просмотра теста=60 минут15 минут=41.
Таким образом, ответ равен 14 \frac{1}{4} 41. □_\квадрат□
Задачи с базовыми задачами на сложение и вычитание относительно просты для анализа и определения основных процедур для их решения. Однако другие проблемы могут потребовать более глубокого понимания контекста, чтобы можно было выявить дальнейшие корреляции между данными.
Джед покупает апельсины. Он продает 35\frac{3}{5}53 этих апельсинов. Из оставшихся у него апельсинов 14\frac{1}{4}41 плохие. Джед выбрасывает их. Теперь у него осталось 24 апельсина. Сколько апельсинов купил Джед?
Сколько 17 \frac{1}{7}71 в числе 1025? 10 \frac{2}{5}?1052?
Измерение одного числа другим — это просто деление, поэтому вопрос эквивалентен запросу 1025÷17 10\frac{2}{5} \div \frac{1}{7} 1052÷71.
Преобразовав смешанное число в неправильную дробь и проделав операцию, получим
1025÷17=525÷17=525×7=3645. □ \begin{выровнено} 10\frac{2}{5} \div \frac{1}{7} &= \frac{52}{5} \div \frac{1}{7} \\ &= \frac{52}{5} \times 7 \\ &= \frac{364}{5}.\ _\квадрат \end{выровнено} 1052÷71=552÷71=552×7=5364. □ 92к2.
- Преобразование десятичных и дробных чисел
- Обратные связи
- Иррациональные числа
Цитировать как: Фракции. Brilliant.org . Извлекаются из https://brilliant.org/wiki/fractions/
Как делать дроби для начинающих
Мы имеем дело с дробями каждый день. Но что такое дробь? Как нам узнать их лучше? В этом уроке мы изучим основы и попрактикуемся вместе, чтобы дроби могли стать ценными помощниками в повседневной жизни и за ее пределами.
Часть 1. Дробь в виде доли
Представим себе целый пирог, разделенный на 4 равные части.
изображение круга с одной четвертью, закрашенной краснымОдна часть окрашена в красный цвет.
Одна красная часть из четырех равных частей означает 1/4 целого закрашено. Если мы подумаем о равных частях целого как о долях, одна доля пирога здесь заштрихована красным.
рисунок дроби 1/4. 1 — числитель, 4 — знаменательЧисло 1 выше линия называется Числитель . Он показывает, сколько акций заштриховано. Число 4 ниже линии называется знаменателем . Он показывает, на сколько равных долей делится целое. Давайте посмотрим на другой пример.
изображение круга с тремя шестыми, заштрихованными краснымНовый круг вверху разделен на 6 равных частей. Следовательно, знаменатель будет равен 6. Из этих 6 равных долей 3 заштрихованы красным цветом. Следовательно, числитель будет равен 3. Другими словами, 3/6 круга заштриховано.
Теперь давайте проверим то, что мы уже узнали. Как известно, в сутках 24 часа. Если вы потратили на обучение 6 часов, какую часть дня вы потратили на обучение?
РЕКЛАМА
Какая часть суток составляет 6 часов?
Выберите 1 ответ
6/24
6
1/3
1/6
День делится на 24 равных долей, называемых часами. Таким образом, знаменатель будет равен 24. Подумайте о 6 часах, потраченных на учебу, как о 6 заштрихованных долях пирога. Это сделает числитель равным 6. Искомая дробь 6/24 .
Часть 2. Упрощение дробей
Помните круговую диаграмму из предыдущего примера? У него было 3/6 его заштриховано красным. Давайте добавим два новых пирога и посмотрим на них вместе.
изображение 3 кругов, половина каждого из которых окрашена в красный цветПервый круг разделен на 4 доли, две из которых закрашены красным.
Но, как мы видим, это половина пирога. Второй круг разделен на 6 долей, три из которых закрашены красным. Снова половина пирога. Наконец, третий круг разделен на две половины, и одна половина закрашена красным.
Так как половина круга заштрихована в любом случае, мы можем заключить, что дроби равны: 2/4 = 3/6 = 1/2 .
изображение 3 кругов, половина каждого из которых окрашена в красный цвет. 2/4 = 3/6 = 1/2Наконец, при умножении или делении числителя и знаменателя на одно и то же число дробь останется прежней (кроме случая деления на ноль, что выходит за рамки данной статьи и здесь рассматриваться не будет). ).
Это правило помогает упростить дроби и облегчает их использование. В качестве примера рассмотрим 4/12. Деление числителя и знаменателя на 4 дает нам (4 : 4 ) / (12 : 4 ) = 1 / 3. Пришло время проверить свои знания.
РЕКЛАМА
Какая дробь равна 2/5?
Выберите 1 ответ
4/25
5/2
8/20
6/10
Часть 3.
Сравнение дробей
Когда мы видим два куска пирога, мы обычно можем сказать, какой из них больше. Как и в случае с дробями, существует простой способ сравнения их друг с другом.
Допустим, нам нужно сравнить 1/3 и 2/7. Поскольку у них разные знаменатели, они имеют разное количество частей. Таким образом, Первый шаг должен состоять в том, чтобы найти точки соприкосновения . Мы делаем это, находя общий знаменатель .
Одним из способов нахождения общего знаменателя двух или более дробей является умножение знаменателей друг на друга. 3 умножить на 7 = 21 .
Теперь, когда мы нашли общий знаменатель, нам нужно заменить собственный знаменатель каждой дроби на общий знаменатель.
приведение 1/3 и 2/7 к общему знаменателюПервая дробь равна 1/3, поэтому мы делим 21 на 3 и получаем 7 умножаем на числитель этой дроби. Поскольку числитель равен 1, мы получаем 7 умножить на 1 = 7 .
Вторая дробь равна 2/7, поэтому 21 разделить на 7 дает 3. Умножив этот числитель дробей в 3 раза, мы получим 3 умножить на 2 = 6 .
Теперь, когда дроби имеют одинаковый знаменатель, мы наконец можем их сравнить. 7 долей больше, чем 6 долей, поэтому 7/21 больше, чем 6/21.
Математический символ, обозначающий наш результат, — это знак > . 21/7 > 21/6 . Читается как « больше «. Символ, обозначающий меньше , выглядит так: < . Мы можем переписать наш результат следующим образом: 6/21 < 7/21 .
РЕКЛАМА
Сравните 3/4 и 5/7
Выберите 1 ответ
3/4 меньше 5/7
3/4 больше 5/7
3/4 равно 5/7
Их нельзя сравнивать
Часть 4. Сложение дробей
Чтобы сложить дроби, нам снова нужно найти общий знаменатель.
Давайте посмотрим на следующий пример.
Нам нужно сложить 2/7 и 3/9 . Общий знаменатель равен 7 умножить на 9 = 63 . Следующим шагом будет замена собственного знаменателя каждой дроби на общий.
Для первой дроби 63 разделить на 7 = 9 и 9 умножить на 2 = 18 . Результат 18/63 . Для второго 63 разделить на 9 = 7 и 7 умножить на 3 = 21 . Результат 21/63 .
Далее добавляем числители. 18 плюс 21 = 39, , что дает нам сумму 39/63 .
В качестве полезной привычки всегда проверяйте, можно ли еще больше упростить полученную дробь.
Мы знаем, что 39делится на 3 без остатка. 63 также делится без остатка на 3. Поскольку и числитель, и знаменатель делятся на одно и то же число, дробь останется прежней. 39 разделить на 3 = 13 и 63 разделить на 3 = 21 .
Вычисление сложения дробей 2/7 + 3/9 = 39/63 = 13/21Наш окончательный результат: 13/21 .
Что, если нам нужно сложить смешанные числа? Чтобы сложить смешанные числа, мы сначала складываем целые числа, а затем дроби.
Например, чтобы добавить 1 с половиной до 2 с половиной , добавьте 1 и 2 = 3 , затем добавьте 1/2 и 1/2 = 1 . Наконец, добавить 3 и 1 = 4 . Давайте немного потренируемся и вспомним, как упростить результаты.
РЕКЛАМА
Какой результат 4/6 + 2/9?
Выберите 1 ответ
8/9
9/8
1/2
7/18
Часть 5. Вычитание дробей
Начнем с двух простых дробей. Вычтите 1/3 из 3/5. Как и в случае сложения, нам нужно найти общий знаменатель. Итак, если мы умножим наши знаменатели, то равно 3 умножить на 5 = 15 .
Далее заменяем старые знаменатели на общие.
изображение 3/5 — 1/3 = 4/15Затем нам нужно найти наши числители. Для первой дроби 15 разделить на 5 = 3 и 3 умножить на 3 = 9 . Результат 15 сентября . Для второго 15 разделить на 3 = 5 и 5 умножить на 1 = 5 . Результат 5/15 .
Последним шагом является вычитание скорректированных числителей: 9 минус 5 = 4. Полученная дробь равна 4/15 .
Теперь рассмотрим случай, когда нам нужно вычесть из дробь целого числа . Начнем с 1 — 2/7 .
Вы помните из предыдущих разделов, что целое число похоже на полностью закрашенный круг. Таким образом, если круг разделить на 3 детали , все 3 детали заштрихованы. Если его разделить на 7 частей, то 7 частей будут заштрихованы.
Итак, 1 = 3/3 = 7/7 и т. д.
Поскольку нам нужно вычесть 2/7 , мы превратим 1 целое в 7/7 , чтобы упростить нашу задачу. 7/7 минус 2/7 = 5/7 . Если целое число отличается от 1 , мы записываем его как смешанное число и следуем шагам из последнего примера.
Итак, давайте вычтем 2/7 из 3 .
изображение 3 — 2/7 = 19/7Часто в результате вычислений может получиться дробь, у которой числитель больше или равен знаменателю. Такие дроби называются неправильными дробями. Например, 5/3 (пять третей), 7/2 (семь половинок) и так далее. Их можно преобразовать в смешанные числа и наоборот.
Преобразование неправильных дробей в смешанные числа и наоборотВсе рассмотренные до сих пор правила применимы и к неправильным дробям.
РЕКЛАМА
Каков результат 9/11 — 3/4?
Выберите 1 ответ
6/7
6/44
3/44
6/11
Часть 6.
Умножение дробей
Допустим, нам нужно умножить две дроби, 2/5 умножить на 3/7 . Числитель произведения будет произведением числителей 9.0067 этих дробей: 2 умножить на 3 = 6. Знаменатель произведения будет произведением знаменателей этих дробей: 5 умножить на 7 = 35 . Таким образом, 2/5 умножить на 3/7 = 6/35 .
Если нам нужно умножить дробь на целое число , то числитель произведения будет произведением числителя дроби на целое число . Знаменатель произведения останется таким же, как знаменатель дроби .
Например, 3/10 умножить на 5 = 15/10 . Для упрощения делим числитель и знаменатель на 5 и получаем 3/2.
Наконец, если нам нужно умножить смешанные числа, сначала мы преобразуем их в неправильные дроби, а затем умножим их, как мы сделали выше.
изображение 3/2 умножить на 11/5 равно 33/10В приведенном ниже примере показаны шаги.
РЕКЛАМА
Часть 7. Деление дробей
Чтобы разделить дроби, переверните делитель так, чтобы его числитель стал новый знаменатель и знаменатель становится новым числителем . Затем просто перемножьте дроби, как мы это делали раньше.
Например, разделите 3/7 на 2/5. После переворачивания 2/5 становится 5/2 , и в итоге мы умножаем 3/7 на 5/2 = 15/14 .
Чтобы разделить дробь на целое число , мы инвертируем это число, и оно станет 1 деленным на это число .
Например, 2 становится 1/2 , 9 становится 1/9 и т. д. Затем мы умножаем, как указано выше. Как вы, наверное, уже догадались, деление смешанных чисел работает точно так же. Давайте посмотрим на пример ниже.
разделить 11/6 на 17/8 = 44/51Давайте проверим ваши знания.
Каков результат деления 11/3 на 11/7?
Выберите 1 ответ
3/7
3
7
7/3
РЕКЛАМА
Часть 8. Некоторые практические примеры
Чтобы найти дробь некоторого числа, нам нужно умножить данное число на эту дробь .
Представьте, в вашем школьном учебнике 200 страниц. Если вы прочитали 3/5 учебника, сколько страниц вы прочитали? Нам дано число, равное 200. Чтобы найти 3/5 от 200, мы умножаем 200 на 3/5 и получаем 120 страниц.
Следующий вопрос решите самостоятельно. В моем праздничном торте было 12 штук. Несколько друзей пришли и съели 2/3 торта. Сколько штук было у моих друзей?
Сколько штук было у моих друзей?
Выберите 1 ответ
2/3
4
9
8
Наконец, есть еще одно дело, которое я хочу изучить.
Что, если мы знаем, чему равна данная дробь некоторого числа , и нам нужно найти это число?
Например, мы знаем, что у моих друзей было 8 кусочков праздничного торта, а это 2/3 из целого торта . Сколько кусочков было в торте вначале? Чтобы найти это целое число , нам нужно разделить 8 на 2/3 , что равно 12 .
Следующий вопрос решите самостоятельно. Гоночная машина проехала по трассе 900 метров, что составляет 3/5 всей дистанции. Какова длина гоночной трассы?
РЕКЛАМА
Какова длина гоночной трассы?
Выберите 1 ответ
1200 метров
1500 метров
2700 метров
540 метров
Научитесь программировать бесплатно. Учебная программа freeCodeCamp с открытым исходным кодом помогла более чем 40 000 человек получить работу в качестве разработчиков.


 — Т. 2.
— Т. 2.
 В этом случае справедливо условие W<V. Если последнее неравенство не выполняется, можно сделать вывод о принадлежности дробного значения ко второму виду. Существует еще одна форма представления дробных элементов, но ее необходимо разобрать отдельно.
В этом случае справедливо условие W<V. Если последнее неравенство не выполняется, можно сделать вывод о принадлежности дробного значения ко второму виду. Существует еще одна форма представления дробных элементов, но ее необходимо разобрать отдельно.



 Чем больше знаменатель, тем меньше дробь.” — Лев Толстой
Чем больше знаменатель, тем меньше дробь.” — Лев Толстой Как это так? Сейчас объясню. Представьте, что вы заходите в какой-нибудь магазин и замечаете роскошные туфли или сумку, и к тому же на ценнике написано, что действует скидка 75%. Чтобы понять, сколько денег вы можете сэкономить, необходимы знание дробей!
Как это так? Сейчас объясню. Представьте, что вы заходите в какой-нибудь магазин и замечаете роскошные туфли или сумку, и к тому же на ценнике написано, что действует скидка 75%. Чтобы понять, сколько денег вы можете сэкономить, необходимы знание дробей!
 Таблица умножения — это действительно основа основ, и ей следует уделить должное внимание.
Таблица умножения — это действительно основа основ, и ей следует уделить должное внимание.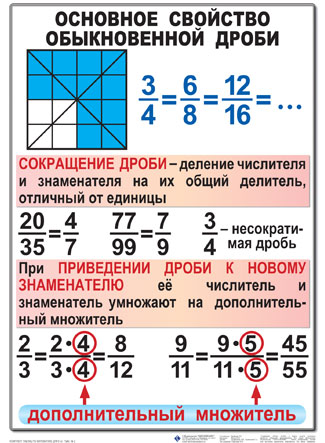 Данный урок призван развивать логическое мышление, внимание, интерес к предмету, математическую речь учащихся; развивать навыки самоконтроля и самооценки учащихся. Целью данного урока (занятия) является формирование понятий «правильная дробь» и «неправильная дробь», а также формирование умения применять полученные знания для решения практических задач.
Данный урок призван развивать логическое мышление, внимание, интерес к предмету, математическую речь учащихся; развивать навыки самоконтроля и самооценки учащихся. Целью данного урока (занятия) является формирование понятий «правильная дробь» и «неправильная дробь», а также формирование умения применять полученные знания для решения практических задач. Решение задач, включающих исторические сведения, способствует развитию кругозора учащихся и познавательного интереса к предмету. Тогда урок математики становится для них не просто уроком, на котором нужно решать, вычислять и заучивать формулы, а пробуждает чувства сопричастности к величию своей страны, собственных предков. Решение задач с практическим содержанием дает возможность учащимся задуматься о тяготах военных лет.
Решение задач, включающих исторические сведения, способствует развитию кругозора учащихся и познавательного интереса к предмету. Тогда урок математики становится для них не просто уроком, на котором нужно решать, вычислять и заучивать формулы, а пробуждает чувства сопричастности к величию своей страны, собственных предков. Решение задач с практическим содержанием дает возможность учащимся задуматься о тяготах военных лет.

 6-й класс
2020
6-й класс
2020 Ради повышения интереса к математике урок построен как путешествие в страну дробей.
Ради повышения интереса к математике урок построен как путешествие в страну дробей.
 Тема урока: «Приведение дробей к новому знаменателю»
2019
Тема урока: «Приведение дробей к новому знаменателю»
2019