Дроби правила по математике: Сложение и вычитание дробей – правила (5 класс, математика)

Сложение и вычитание дробей – правила (5 класс, математика)

4.1

Средняя оценка: 4.1

Всего получено оценок: 81.

4.1

Средняя оценка: 4.1

Всего получено оценок: 81.

Сложение и вычитание дробей процесс не сложный, но специфический. Поэтому, чтобы в курсе математики 5 класса не возникло проблем с той темой, стоит подробнее разобраться во всех ее аспектах.

Дробь

Что такое дробь? Дробь – это деление, недовведенное до конца. То есть, чтобы получить дробь ${7\over{15}}$ нужно взять число, поделить его на 15 частей и из них оставить только 7 .

Именно дроби лежат в основе многих процессов. Без них невозможно было бы посчитать процент по кредиту, определить, какая часть тепла проходит через окно, даже посчитать, сколько кусочков пиццы причитается каждому из друзей, не получилось бы без дробей.

Но иногда приходится дроби складывать и вычитать согласно сочетательному свойству деления:

а:в+с:в=(а+с):в

В большинстве различных формул стоит знак «+».

Почему? Да потому, что существует определение математического сложения, которое включает в себя как сложение, так и вычитание. Просто вычитание считается сложением положительного и отрицательного числа.

Виды дробей

Перед тем, как преступить к рассмотрению сложения и вычитания дробей, нужно обратить внимание на тот факт, что дроби бывают разные, и в зависимости от вида дробей будет немного меняться и сам процесс сложения.

Виды дробей:

• Правильные и неправильные. Неправильные дроби могут превращаться в смешанные, т.е. дроби, у которых есть целая и дробная часть. Правильными дробями называются дроби, у которых числитель меньше знаменателя.
• Обыкновенные и десятичные. В зависимости от знаменателя выделяют десятичные и обыкновенные дроби. Десятичные дроби имеют знаменатель кратный 10, при этом такая дробь должна быть записана в строку, иначе она считается обыкновенной.

Отдельной строкой идут смешанные числа, то есть неправильные дроби, в которых выделили целую часть.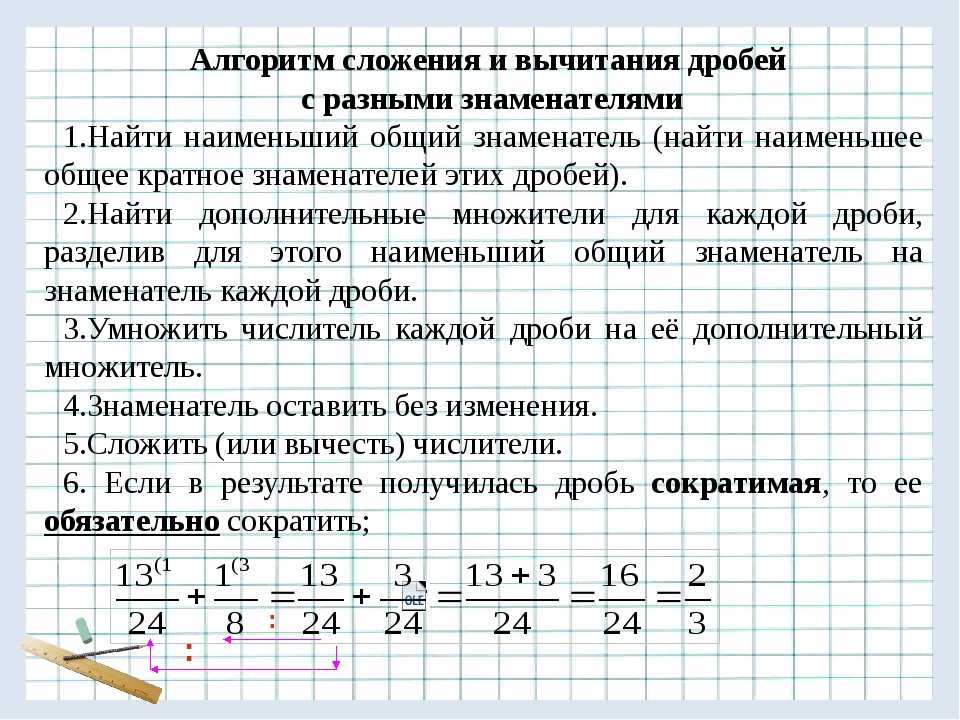

Эти числа так же условно относятся к дробям.

Сложение и вычитание дробей

Правило сложения и вычитания дробей:

• Сравнение знаменателей. Обратите внимание, что сочетательного свойство, благодаря которому возможны операции над дробями, работает только если у дробей одинаковые числители.
• Если знаменатели различны, то необходимо привести дроби к одинаковому знаменателю. Для этого выписываются оба знаменателя, для них находится наибольшее общее кратное НОК, которое и будет являться знаменателем дроби-результата. Числитель и знаменатель домножаются на одно и то же число так, чтобы дроби приобрели одинаковые знаменатели. Если знаменатели дробей одинаковы, то этот пункт можно пропустить.
• После этого дроби подводят под один знаменатель. Под чертой остается тот самый НОК, который мы нашли, а в числителе записывается сумма или разность, где в качестве первого слагаемого или уменьшаемого выступает числитель первой дроби, а в качестве второго слагаемого или вычитаемого выступает числитель второй дроби.
• Выполняется действие в числителе.
• При необходимости выделяется целая часть дроби.

Десятичные дроби складываются по тому же принципу, что и обычные числа. К числам дописываются разряды так, чтобы получились числа с одинаковым количеством знаков после запятой. Приведем небольшой пример:

3,65-2,6=3,65-2,60=1,05

Что мы узнали?

Мы поговорили о том, что такое дробь. Обговорили порядок действий при сложении и вычитании дробей. Обсудили, как выполнить необходимое условие сложение и привести дроби к одному знаменателю. Выделили виды дробей и поговорили о каждом из них.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка статьи

4.1

Средняя оценка: 4.1

Всего получено оценок: 81.

---

А какая ваша оценка?

правила с разными и одинаковыми знаменателями, как происходит, примеры с решениями

Вычитание дробей является важной темой при изучении арифметических операций.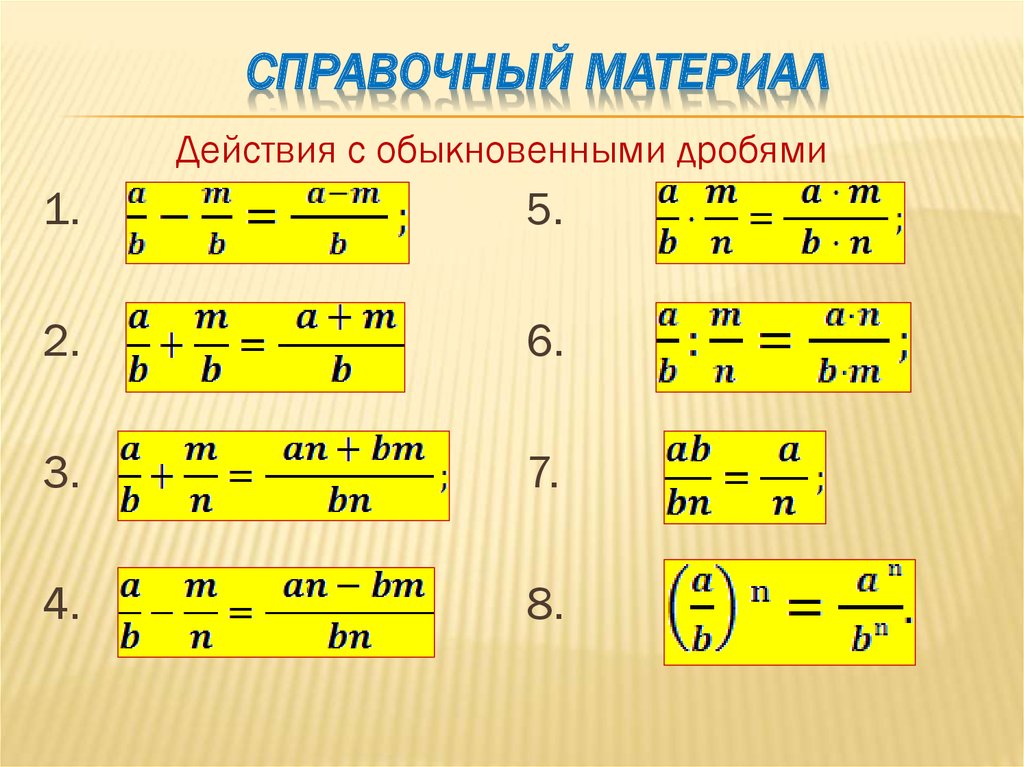 Чтобы его выполнять, нужно понять и изучить несколько простых правил, которые изложены далее. Знания о вычитании дробей могут пригодиться не только на уроке математики, но и в повседневной жизни. Например, при расчете процента за кредит или при разделении объекта на несколько частей.

Особенности темы дробей в программе обучения

Вычитание – действие в арифметике, когда от одного числа (не обязательно большего) отнимают второе. Его на практике применяют очень часто, и не только в отношении дробей, но и простых цифр. Проводить подобную операцию учат еще в младших классах школы, постепенно совершенствуя навыки. Но с вычитанием дробей не все так просто. Мало просто понять одно число от другого. Нужно понять принципы этого процесса и выучить правила.

Дробь – термин, который обозначает количество, определяемое как доля от некоторого числа. Дробное число состоит из числителя и знаменателя. Его можно выразить несколькими способами: 1/2 = 2/4 = 3/6. Если оба умножить на одно и то же, то изменений не произойдет. Для этого может быть использован десятичный вид – 0,5 = 1/2.

В некоторых случаях для выражения потребуется десятичная форма с бесконечным количеством цифр после запятой.

Если необходимо вычитать дроби с разными знаменателями, вместо них используют эквивалентные, но с одинаковыми нижними показателями.

Как происходит вычитание

Эта операция обратна по отношению к сложению. Проще всего осуществлять вычитание обыкновенных дробей, нижние значения которых равны. Для решения подобных уравнений достаточно от первого числителя отнять второй. Можно рассмотреть это на примере:

7/15 — 3/15 = 4/15

Отнимая 3 из 7 получают числитель.

Если нижние части различаются, следует сделать так, чтобы свести вычисления к первому случаю. Для этого используют тот факт, что для каждой ситуации существуют эквивалентные варианты. Умножая верхнюю и нижнюю часть на одно и то же число, значение изменить нельзя. Вычитание дробей с разными знаменателями основано на правильном выполнении эквивалентных преобразований уменьшаемого и вычитаемого.

Воспользовавшись этим правилом, можно привести дробные числа к виду, когда нижние показатели у них равны. После этого осуществляют действие обычным образом. Сказанное можно лучше понять, решив простое задание – сколько будет из 2/3 вычесть 4/7?

Для того, чтобы привести их к эквивалентному виду, оба числа умножают одинаковым образом. Вот несколько возможных вариантов:

2/3 = 4/6 = 6/9 = 8/12 = 10/15= 12/18 = 14/21

Теперь проводят аналогичные действия со вторым операндом. Здесь получают:

4/7= 8/14 = 12/21

Сравнивая полученные показатели видно, что в обоих случаях есть величины с использованием 21. После эквивалентного преобразования ранее сформулированное задание получило следующую формулировку – сколько будет из 14/21 вычесть 12/21?

Чтобы получить числитель, надо от первого отнять второй: 14 — 12 = 2. Результат равен 2/21.

Можно решать такие уравнения и не обязательно искать эквивалентные значения до тех пор, пока не получиться наткнуться на подходящее. Нужный цифры получают перемножением.

Для решения предложено задание – сколько будет из 15/17 вычесть 5/7?

Нужный ответ получается при умножении 17 на 7. Он равен 119. Таким образом, выражение преобразуется:

15/17 — 5/7 = 15х7/17х7 — 5х17/7х17 = 105/119 — 85/119 = (105 — 85)/119 = 20/119

Если делается вычитание десятичных дробей, то действия происходят аналогичным способом. У них знаменатель равен 10, 100, 1000 или аналогичным значениям. Работа с ними будет рассмотрена в задании – чему равно 0,56 — 0,32?

Здесь речь идет о 56/100и 32/100. В этом случае выполняют вычитание величин, у которых одинаковая нижняя часть. Осуществляется это так:

0,56 — 0,32 = 56/100 — 32/100 = (56 — 32)/100 = 24/100 = 0,24

Иногда используется различное количество цифр после запятой. Вот пример – сколько будет из 0,71 вычесть 0,335 ?

Для начала надо преобразовать десятичные величины в обычные. При этом будет результат такой: 0,71 = 71/100, 0,335 = 335/1000. Здесь поступают в соответствии с правилами работы с величинами с различными знаменателями. Однако нужное значение определяется более легким способом. Если первый операнд умножить на 10, то будет использована 1000.

Теперь делают подсчеты так:

0,71 — 0,335 = 71х10/100х10 — 335/1000 = 710 — 335/1000 = 375/1000 = 0,375

С десятичными дробными величинами работают обычным способом. При этом ту, в которой меньше знаков после запятой, дополняют нужным количеством нулей, чтобы уравнять количество цифр после запятой. Операцию выполняют приведенным ранее способом.

В рассмотренном выше примере решение будет выглядеть та:

0,71 — 0,335 = 0,710 — 0,335 = 0,375

Если в результате подсчета требуется получить положительное значение, необходимо сделать так, чтобы уменьшаемое было больше вычитаемого. Это проверяют, приведя обе цифры к обычной форме. У уменьшаемого числитель должен быть больше.

При выполнении операций при наличии целого и дробного значения, их сначала преобразуют в неправильную дробь, затем поступают так, как указано выше. Чтобы их вычитать, нужно сначала привести к общему знаменателю. Затем от одного числителя отнимают второй.

Вычитание дробей – не слишком легкая и доступная тема в математике. Чтобы понять, как проводить подобные подсчеты, следует потренироваться сначала на более простых примерах и обязательно изучить правила. Тогда никаких проблем точно не возникнет. Случаются ли у вас проблемы при вычитании? С чем они были связаны? Напишите в комментариях. Поделитесь статьей в социальных сетях и сохраните ее в закладках, чтобы не потерять полезную информацию и основные правила.

Также рекомендуем посмотреть подобранные видео по нашей теме.

Вычитание дробей с разными знаменателями

Сложение и вычитание дробей с одинаковыми знаменателями.

Дроби — Математика: Базовые уроки

Виртуальная помощь

• Пообщайтесь с сотрудниками библиотеки прямо сейчас
• Свяжитесь с вашей библиотекой

Перейти к основному содержанию

Учебный портал — Библиотеки колледжей Онтарио

Дроби — это нецелые числа; они представляют части целого числа. Вы, вероятно, сталкивались с несколькими примерами дробей в своей повседневной жизни. Например, рецепт может потребовать 3 четверти стакана муки. Если пиццу разделить на восемь равных кусков, это дробь: каждый кусочек составляет одну восьмую всей пиццы. Этот модуль поможет вам понять дроби и ознакомиться с ключевыми понятиями, чтобы вы чувствовали себя комфортно при работе с дробями.

 

Лучшие советы

• Не бойтесь работать с дробями! Вы столкнетесь с дробями в математике и в повседневной жизни, так что освойтесь с ними.
• Чтобы складывать и вычитать дроби, сначала нужен общий знаменатель. После этого вы можете складывать или вычитать числители и помещать их над общим знаменателем.
• Чтобы умножить дроби, умножьте числители и знаменатели по отдельности. Перемножьте числители дробей, а затем умножьте знаменатели, чтобы получить результат.
• Чтобы разделить дроби, умножьте первую дробь на обратную величину второй дроби.
  Чтобы получить обратную дробь, переверните вторую дробь так, чтобы числитель стал знаменателем, и наоборот. Умножьте это на первую дробь.
• Всегда переводите смешанные числа в неправильные дроби перед умножением или делением дробей. Вместо целого числа с дробью (например, 5 ⅔) вам нужна дробь, в которой числитель больше знаменателя (например, 17/3). Вы также можете сделать это для сложения и вычитания, если вы предпочитаете этот метод.
• В окончательном ответе не забывайте упрощать дроби до минимума. Если числитель и знаменатель имеют общий множитель, отличный от 1 (т. е. они могут делиться на одно и то же число), упростите их.
• Любое целое число можно записать в виде дроби, поместив его над 1. Если у вас есть целое число и дробь для работы, это позволит вам работать с двумя дробями вместо этого.

Ресурсы

Темы

Фракции 8 подмодулей

• << Предыдущая: Главная
• Следующая: Знакомство с фракциями >>

О нас и Условия использования | Карта сайта | Свяжитесь с нами

Примечание. Этот материал предназначен в качестве общего руководства, если инструкции вашего преподавателя отличаются от предоставленной нами информации, всегда следуйте инструкциям вашего преподавателя. Также обратите внимание, что значки на этом сайте используются по лицензии Noun Project Pro. Пожалуйста, не забудьте указать надлежащую авторство, если вы используете их повторно.

Раскройте секрет дробей с помощью этих 3 странных правил

Должен сказать: дроби — это тема номер один, которую я преподаю повторно на всех уровнях

. Неважно, учатся ли они в начальной школе, старшей школе или колледже. Люди просто запутались в дробях. Мои ученики будут прыгать, решая математические задачи, а затем остановят из-за того, что выпадет дробь.

Одно время я думал, что у меня плохо с математикой. Да, дроби меня тоже пугали, пока я, наконец, не освоил эти 3 правила дробей. Теперь я похож на волшебника-математика, когда применяю эти правила вместо оленя в свете фар.

Я хочу это для вам . Я хочу это для твоего малыша . Я хочу этого для каждого человека на планете! Потому что дроби супер крутые и мега полезные.

 

Любое число, написанное поверх самого себя, равно единице.

АКА:  Copycat ONE

Я ВЛЮБЛЕН в номер один, потому что могу написать его бесконечно по-разному.

Последняя фракция может заставить вас биться головой о стену. В знаменателе замаскировано количество единиц. Это факторизованная версия числителя. Я взял коэффициент 2 и разделил его на каждое из условий.  То же количество , только написано по-другому.

Мы используем это правило, чтобы создавать эквивалентные дроби, упрощать дроби и находить скрытые количества единицы, такие как дурацкая дробь, которую я только что показал вам.

Любое число, написанное над 1, не меняет своего значения.

Также известное как Phat Cat

Это правило позволяет мне превращать любое целое число в дробь, чтобы я мог использовать подражатель для получения общих знаменателей, умножения дроби на целое число и многого другого. Я называю этот тип дроби

жирным котом.

 

 

 

Мое количество не меняется.  Неправильный числитель означает, что он больше знаменателя.  Мне нравится называть этот тип жирным котом.  С помощью этого простого правила можно преобразовать любое обычное старое число в дробь.

Мы используем это правило, чтобы умножать целые числа на дробь, делить целые числа на дробь и даже делать эквивалентные дроби. Все это вы можете узнать, посмотрев мой урок дробей, но давайте перейдем к последнему правилу.

 

Если произведение двух дробей равно единице, то они обратны друг другу.

АКА: Cool Cat

Произведение означает, что мы умножаем дроби. Обратное позволяет нам «отменить» фракцию и выйти из дробной земли.

Я называю этот тип дроби фракцией крутого кота . Вы знаете, потому что это очень круто — иметь возможность уйти от дробей и сделать некоторые основные математические вещи правильно?

Когда мы умножаем дроби, мы умножаем числители (число вверху) друг на друга и записываем это в новую дробь. Затем делаем то же самое со знаменателем (число внизу). Это создает копию единицы (правило дроби № 1), и мы знаем, что это означает, что у нас есть количество единиц.

Это правило часто используется на более высоких уровнях математики. Мы видим это с уравнениями, факторинговыми полиномами, графиками и многим другим. В этом примере вы можете увидеть, как cool cat используется для изоляции переменной, чтобы мы могли узнать ее значение.

Я стремлюсь помочь ученикам средней школы освоить дроби, чтобы с этого момента они могли почувствовать себя математическим волшебником, а не оленем в свете фар.