С++. Математические функции
Программирование, С/C++
Для всех математических функций необходим заголовок <cmath>. В программах на языке C используется заголовок <math.h>
| 1 | acos | Функция double acos(double arg) возвращает арккосинус аргумента arg. Значение аргумента функции должно лежать в интервале от -1 до 1, иначе произойдет ошибка. |
| 2 | asin | Функция double asin(double arg) возвращает арккосинус аргумента arg. Значение аргумента функции должно лежать в интервале от -1 до 1, иначе произойдет ошибка. |
| 3 | atan | Функция double atan(double arg) возвращает арктангенс аргумента arg. |
| 4 | atan2 | Функция double atan2(double x, double  |
| 5 | ceil | Функция double ceil(double num) возвращает ближайшее целое число (представленное как действительное число с плавающей точкой), которое не меньше значения аргумента num. Например, ceil(1.02) вернет 2.0. Такое преобразование называется округлением с избытком. |
| 6 | cos | Функция double cos(double arg) возвращает косинус аргумента arg. Значение аргумента должно быть выражено в радианах. |
| 7 | cosh | Функция double cosh(double arg) возвращает гиперболический косинус аргумента arg. |
| 8 | exp | Функция double exp(double arg) возвращает основание натурального логарифма e, возведенное в степень arg. |
| 9 | fabs | Функция double fabs(double num) возвращает абсолютное значение (значение по модулю) аргумента num. |
| 10 | floor | Функция double floor(double num) возвращает наибольшее целое число (представленное как действительное число с плавающей точкой), не превышающее значения аргумента num. Например, floor(1.02) вернет число 1.0. Такое преобразование называется округлением с недостатком. |
| 11 | fmod | Функция double fmod(double x, double y) возвращает остаток от деления x/y. |
| 12 | frexp | Функция double frexp(double num, int *exp) раскладывает число num на мантиссу, изменяющуюся в диапазоне от 0.1 до 1, не включая 1, и целый показатель степени, так что |
| 13 | log | Функция double log(double num) возвращает натуральный логарифм числа num. Если аргумент num отрицателен или равен нулю, возникает ошибка. |
| 14 | log10 | Функция double log10(double num) возвращает десятичный логарифм числа num. Если аргумент num отрицателен или равен нулю, возникает ошибка. |
| 15 | pow | Функция double pow(double base, double exp) возвращает число base, возведенное в степени exp. Если основание степени base равно нулю, а показатель степени exp меньше или равен нулю, может произойти ошибка, связанная с выходом аргумента из области определения функции (domain error). Это ошибка возникает также, если аргумент base отрицателен, а аргумент exp не является целым числом. |
| 16 | sin | Функция double sin(double arg) возвращает синус аргумента arg. Значение аргумента должно быть выражено в радианах. |
| 17 | sinh | Функция double sinh(double arg) возвращает гиперболический синус аргумента arg. |
| 18 | sqrt | Функция double sqrt(double num) возвращает квадратный корень аргумента num. Если значение аргумента отрицательно, возникает ошибка, связанная с выходом из области определения функции. |
| 19 | tan | Функция double tan(double arg) возвращает тангенс аргумента arg. Значение аргумента должно быть выражено в радианах. |
| 20 | tanh | Функция double tanh(double arg) возвращает гиперболический тангенс аргумента arg. |
Метки функции. Смотреть запись.
«Как пришли к выводу, что 0 в степени 0 равно 1? Это что-то дало математике?» — Яндекс Кью
На самом деле, это не всегда так.
n)/(factorial(n))]
Как видим, на одно слагаемое меньше.
Но для разложений в ряд специально хочу обратить особое внимание, что в данном конкретном случае мы работаем с ординалами (т.е. с обобщением натуральных чисел), которые на компьютере мы будем передавать типом integer.
Аргумент, как видим, опять же, формалистский и, исключительно, из области эстетики. И, как и в предыдущих случаях, он касается только натуральных / целых / ординалов, но не действительных чисел.
Решение спора пришло вместе с развитием computer science. IEEE приняли решение, что под возведением в степень мы понимаем, на самом деле, как минимум, три разные функции, а именно:
pow(a,b)
pown(a,b)
powr(a,b)
Где pown() — строго типизированная функция, определенная для аргументов типа integer, и для случая pown(0,0) возвращает единицу.
powr() — строго типизированная функция, определенная для аргументов типа real, и при подстановке «нулей» вернет NaN — Not-A-Number (букв.
log(a)) , а натуральный логарифм от нуля, как мы помним, принципиально не может быть определен.
Отдельно хотелось бы остановиться на «наивной» «эмпирической» конвенции до Огюстена Луи Коши: когда значение показательно-степенной функции приближалось «справа». Обычно, такую наивную операцию сторонники Кнутовского ригоризма («должно быть определено!») предлагают проверить на калькуляторе, опытным т.с., путём предлагая возводить число в степень себя самого, постепенно уменьшая аргумент к нулю, минуя минимум функции в точке 1/e. Однако, это приближение не является равномерным и не проводится приближение слева. Потому что слева комплексная показательно-степенная функция приближается к комплексному же значению, а не к целочисленной единице.
В настоящий момент, советский подход— то есть восприятие выражения как неопределенного— практически изжит и наиболее популярен кнутовский ригоризм, фундаментализм и, не побоюсь этого слова, фанатизм, благодаря распространению опус магнум Дональда Кнута «Искусство Программирования».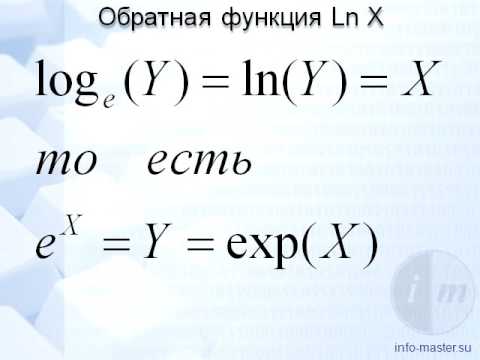
Так что основная аргументация сторонников определенности иногда сводится вообще к аргументу ad verecundiam: «так у Дональда Кнута написано». Но иногда бывает небесполезно читать бюллетени IEEE и ставить все радикальные assertio под сомнение.
Это если совсем кратенечко и по верхам.
От себя лично отмечу, что по моему личному мнению, радикальные «кнутовцы» находятся в состоянии тяжкого греха и не могут получать Святого Причастия.
Я буду за них молиться.
PS: в бухгалтерии выражение не встречается никогда и в этой прикладной дисциплине не имеет смысла, вне зависимости от локальной конвенции по его значению.
Обозначение— Что означает $\exp(f)$?
спросил
Изменено 4 года назад
Просмотрено 6к раз
$\begingroup$
В нескольких сообщениях на этом сайте я встречал выражение $\exp(x)$, где $x$ — произвольное выражение.
$\endgroup$
Зарегистрируйтесь или войдите
Зарегистрироваться через Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
n\\
4. & f(x+y) = f(x) \cdot f(y) \text{ где }f(x) >0 \text{ непрерывно в одной точке и } f(1) = e
\end{выравнивание}
Если вы начнете с любого из них, вы сможете вывести/доказать и другие. 9х$. Когда определения эквивалентны, мы можем выбрать любое из них для получения остальных. Таким образом, мы вольны выбирать, какое из эквивалентных определений будет лучше всего служить нашей цели, в зависимости от того, когда и как нам нужно его использовать. Это справедливо для многих математических объектов: например, существует нет * ОДНО * верное определение $\pi$: есть много способов определить уникальное число $\pi$.
$\endgroup$
1
$\begingroup$
Еще одна актуальная статья в Википедии — «Характеристики экспоненциальной функции».
Какая характеристика наиболее подходит для определения, зависит от контекста.