Урок математики в 3-м классе по теме «Формула пути. Закрепление. Решение творческих задач»
Цели:
- Установить взаимосвязь между скоростью, временем и расстоянием, учиться анализировать задачи, применяя знания о взаимосвязи между величинами;
- Совершенствовать умения решать задачи на движение по данным, записанным в таблице;
- Способствовать развитию творчества детей, логики.
Оборудование:
- тетради, ручки;
- карточки с заданиями по вариантам;
- мультимедийный проектор;
- экран.
Ход урока
1. Организационный момент.
– Сегодня на уроке нас с вами ожидает интересная и разноплановая работа.
Математика пришла,
Занимай свои места!
Математика сложна,
Но скажу с почтеньем:
Математика нужна
Всем без исключения!
2. Актуализация знаний о формуле пути:
Актуализация знаний о формуле пути:
– Напомните, пожалуйста, формулу пути
S = u * t
– Запишите ее в тетрадь.
– Что обозначает буква S? (Расстояние.)
– Что обозначает буква t? (Время.)
– Как найти скорость, зная расстояние и время?
u = S : t
– Запишите в тетрадь.
– Как найти время, зная расстояние и скорость?
t = S : u
– Запишите в тетрадь. Сегодня вам эти формулы будут очень нужны.
1. Решение задач, составленных детьми:
– Решаем задачи, которые вы составляли на прошлом уроке.
– Задачу для I ряда читает Валерия.
(Задачи появляются друг за другом на экране.)
- Задача:
Кит проплыл 14 км за 2 часа. Сколько км он проплывет за 1 час, за 3 часа, за 8 часов?
– Записывайте в тетради только ответы в столбик.
– Задачу для II ряда читает Олег:
- Задача:
Сорока летит со скоростью 52 км/ч. Какое расстояние пролетит сорока за два
часа, за 3 часа, за 5 часов?
Какое расстояние пролетит сорока за два
часа, за 3 часа, за 5 часов?
– Записывайте в тетради только ответы в столбик.
– Задачу для III ряда читает Даша.
- Задача:
Уж проплыл 50 дм за 5 секунд. Сколько дм он проплывает за 1 секунду, за 12 секунд, за 30 секунд?
– Записывайте в тетради только ответы в столбик.
– Проверим ваши ответы. Зачитайте их, пожалуйста (фронтальный опрос).
I ряд
7
21
42
II ряд
104
156
260
III ряд
10
120
300
(После зачитывания ответов на экране появляется запись.)
– А теперь каждый сложите ваши числа в столбиках и найдите результаты.
(На экране появляется запись.)
– Молодцы! Оцените свою работу значком + или – на полях.
– Найдите значение выражения.
(На экране появляется запись. )
)
– Какой получится результат? (Пять.)
(На экране появляется красная пятерка.)
– Я желаю всем сегодня работать с радостью, с удовольствием, тогда и результат вашей работы будет оценен высоким балом.
3. Исправление задач с недостающими данными и их решение.
– Я прочла все ваши задачи очень внимательно, были среди них и такие:
1 задача:
Орел пролетел 320 км. Сколько часов он летел?
– Это задача? (Еще нет.)
– Что не верно? (Не хватает данных.)
– Каких? (Скорости.)
– Исправьте задачу, используя таблицу.
(На экране появляется таблица “Скорости полета птиц”.)
Ученики: “Орел пролетел 320 км. Скорость полета птицы 160 км. Сколько часов он летел?
– Что нужно найти? (Время.)
– Запишите решение и ответ: 320 : 160 = 2 часа.
– Прочтите решение.
2 задача:
“Стриж летит со скоростью 108 км/ч. Сколько км он пролетит за 1 час?”
Сколько км он пролетит за 1 час?”
– Это задача? (Нет.)
– Что не так? (Время.)
– Составьте правильную задачу.
Ученики: “Стриж летит со скоростью 108 км/ч. Сколько км он пролетит за 5 часов?”
– Что нужно найти? (Расстояние.)
– Запишите решение и ответ: 105 * 5 = 540км
– Прочтите решение.
3 задача:
“Утка летела 10 часов. С какой скоростью летела утка?”
– Получилась задача? (Нет)
– Чего не хватает? (Расстояния)
СКОРОСТЬ ПОЛЕТА ПТИЦ
| Вальдшнеп | 26 км/ч | Стриж | 108 км/ч |
| Ворон | 38 км/ч | Голубь | 62 км/ч |
| Зимородок | 57 км/ч | Лебедь | 88 км/ч |
| Щегол | 28 км/ч | Сокол | 99 км/ч |
| Чайка | 49 км/ч | Орел | 160 км/ч |
| Сорока | 56 км/ч | Ястреб-перепелятник | 40 км/ч |
| Грач | 72 км/ч | Утка | 96 км/ч |
– Скорость утки 96 км. Сколько пролетит утка за 10 часов? (960км)
Сколько пролетит утка за 10 часов? (960км)
Ученики: “Утка пролетела 960 км за 10 часов. С какой скоростью летела утка?
– Что надо найти? (Скорость.)
– Напишите решение и ответ: 960 : 10 = 96 км/ч.
– Прочтите решение.
– Если вы записали это задание чисто, аккуратно и правильно поставьте на полях
+, если нет –.
4. Физкультминутка.
5. Самостоятельная работа.
– А теперь зная взаимосвязь между расстоянием, скоростью и временем заполните таблицы, которые у вас на партах.
I вариант
| S | U | t |
| 60 км | ? | 3 ч |
| ? | 9 м/мин | 40 мин |
| 75 дм | 3 дм/с | ? |
| ? | 5 м/с | 9 с |
| 48 км | ? | 6 ч |
| 21 км | 7 м/мин | ? |
II вариант
| S | U | t |
| 48 м | 8 м/мин | ? |
| 540 дм | ? | 18 с |
| ? | 64 км | 4 с |
| 320 | ? | 80 ч |
| 180 м | 9 м/мин | ? |
| ? | 60 м/с | 50 с |
– Поменяйтесь карточками и проверьте работу своего товарища.
(На экране запись со вставленными числами.)
| S | U | t |
| 60 км | 20 км/ч | 3 ч |
| 360 м | 9 м/мин | 40 мин |
| 75 дм | 3 дм/с | 25 с |
| 45 м | 5 м/с | 9 с |
| 48 км | 8 км/ч | 6 ч |
| 21 км | 7 м/мин | 3 мин |
| S | U | t |
| 48 м | 8 м/мин | 6 мин |
| 540 дм | 30 дм/с | 18 с |
| 256 км | 64 км/ч | 4 ч |
| 320 км | 4 км/ч | 80 ч |
| 180 м | 9 м/мин | 20 мин |
| 3000 м | 60 м/с |
5. Подведение итогов урока.
Подведение итогов урока.
– Чем заинтересовал вас урок? Что новое вы узнали?
– Выполнение каких заданий вызывало у вас затруднение? Почему? С чем это
связано?
– Достигли мы целей нашего урока?
6. Домашнее задание:
- с. 61, № 9, 13;
- Творческого характера – по желанию составить задачу на движение применяя знания о взаимосвязи между величинами.
7. Оценивание обучающихся:
– А теперь еще раз посмотрите оценки на полях.
– Какая поговорка для вас больше подходит?
На доске поговорки:
- Терпение дает умение!
- Это успех!
- Не будь тороплив, а будь терпелив!
- Нерадивый дважды дело делает.
- Перо пишет, а ум водит.
- Захотел – сделал!
– Отметьте на полях тетради цифру поговорки.
Спасибо за урок. До свидания.
Приложение.
Урок математики 3 класс. Л.Г.
 Петерсон. Тема «Формула работы»
Петерсон. Тема «Формула работы»I. Организационный момент.
— Сейчас урок математики.
II. Мотивация к учебной деятельности.
— Давайте прочитаем хором высказывание
Человек лишь тогда чего-то добивается, когда он верит в свои силы. (немецкий философ Андреас Фейербах)
— О каких качествах идет речь?
— Как эти качества могут нам пригодиться?
III. Актуализация знаний.
— В математике часто используются формулы.
— Какие формулы вы знаете?
— А зачем они нужны? (Чтобы решать похожие и обратные задачи)
– Рассмотрите таблицу. О каких величинах можно составить задачи.
— Составьте задачи по данным таблицы.
s | v | t |
? | 60 км/ч | 4ч |
540 км | ? | 6ч |
57км | 19км/ч | ? |
S=v•t t=s:v v=a•b•c s= a•b v=s:t
— Какие формулы вы будете использовать для решения этих задач? Подчеркнем их и прочитаем.
— Запишите в тетради только ответы этих задач.
— Давайте проверим с помощью сигнальных кругов.
-Те, кто не ошибся в решении задач, поставьте на полях +.
IV. Пробное действие.
— Запишите формулу, для решения следующей задачи.
«Одна швея за 5ч сшила 20 фартуков, другая за 4ч сшила 16 таких же фартуков. Какая швея работает быстрее?»
— Какие формулы записали? А кто не записал никакой формулы?
— В чем трудность? (Не могу записать формулу для такой задачи)
— Почему возникло затруднение? (Не знаем такой формулы)
— О чем эта задача? (о работе)
— Какие величины есть в задаче? (время работы, скорость работы)
— Какая новая величина? (работа)
— Как же можно назвать эту формулу? (формула работы)
V. Сообщение темы урока и постановка целей.
— Итак тема урока «Формула работы»
— Какие же цели мы поставим на сегодняшний урок?
Цели урока:
1. Узнать формулу работы.
2. Научиться решать задачи по формуле работы.
VI. Решение учебной задачи. Открытие нового знания.
— Заполним таблицу к задаче.
— О каких величинах идет речь в этой задаче?
(о времени, количестве выполненной работы)
— Если сказано «быстрей», то о какой величине идет речь?
— Какие задачи напоминает? (задачи на движение)
— Как же найти скорость работы? (всю работу разделить на время)
— В математике скорость работы принято обозначать v, так же, как и в задачах на движение.
Вся выполненная работа – А,
Время, затраченное на работу – t, так же, как и в задачах на движение.
— Попробуйте сами записать формулу, по которой можно найти скорость работы. v=A: t
— А теперь выведем формулу работы.
— Чем является А? (А – делимое, чтобы найти делимое, нужно частное умножить на делитель)
— Прочитайте получившуюся формулу. A=v•t
— Какую еще формулу можно вывести? t= A: v
— А теперь сверим с текстом на доске.
— Что нового узнали, почитав текст?
(Скорость еще называют производительностью)
— Что же мы подразумеваем под словом работа?
VII. Физминутка.
Физминутка.
— Объясните, как вы понимаете смысл следующих высказываний? (с. 44 № 1)
— Давайте еще раз озвучим цели урока.
— Узнали формулу работы? Прочитайте ее.
— Какие формулы вывели? Прочитайте их.
VIII. Первичное закрепление.
— Какой была вторая цель?
(Научиться решать задачи по формуле работы.)
— Предлагаю выполнить следующие задания:
1. Составить и решить задачи по таблице.
A | v | t |
? | 4 детали/мин | 5 мин |
160 скворечников | ? | 8 дней |
120 шт. | 60 шт/ч | ? |
A=v•t v=A: t t= A: v
— Запишите решение этих задач.
-Проверим решение задач через документ-камеру.
— Какую формулы выбрали для решения задач?
— Покажите, какую формулу использовали для нахождения неизвестной величины.
— Те, кто не ошибся в решении задач, поставьте на полях +.
2. Практическая работа (индивидуальные карточки с примерами)
— А сейчас вы попробуете вычислить производительность своего умственного труда.
— Будем решать на время примеры, а данные заносить в таблицу.
Вся работа A | Производительность V | Время работы t |
… | ? | 2мин |
3. Взаимопроверка
— Давайте проверим правильность решения.
— Запишите количество правильных ответов в таблицу.
— Если количество правильных ответов не меньше 10 – поставьте себе +
— Как узнать производительность? Какой формулой воспользуемся? (v=A: t)
— Вычислите свою производительность.
(количество правильных примеров разделить на 2 мин)
-Где в жизни может пригодиться умение находить производительность, объем работы, время работы?
IX. Контроль достижения целей.
Контроль достижения целей.
— А теперь вернемся к задаче, которая вызвала затруднение.
— Какую же формулу выберем?
— Запишите самостоятельно решение этой задачи в тетрадь.
— Проверим решение.
— Те, кто правильно решил задачу, поставьте на полях +.
X. Рефлексия.
— Итак, какой была тема урока?
— Какие цели мы поставили на урок? Прочитайте формулу работы.
— Достигли этих целей?
— Помогли ли нам в достижении поставленных целей те качества, о которых мы говорили в начале урока.?
XI. Д/з с. 44 № 4, № 5.
Уравнения — Математика 3 класса
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерия
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Мы открыты в субботу и воскресенье!
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все материалы по математике для 3-го класса
7 практических тестов Вопрос дня Карточки Learn by Concept
Справка по математике для 3-го класса » Уравнения
В корзине для игрушек у Спота есть мячи.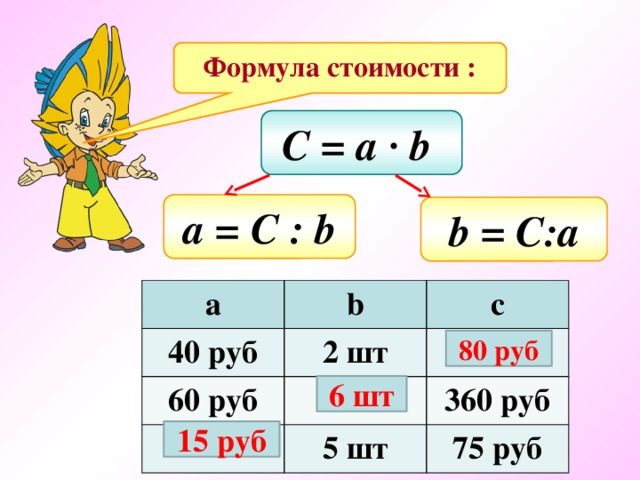 Мягких игрушек больше, чем мячей, а веревок вдвое больше, чем мячей. Сколько игрушек у Спота в корзине?
Мягких игрушек больше, чем мячей, а веревок вдвое больше, чем мячей. Сколько игрушек у Спота в корзине?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы решить эту задачу, нам сначала нужно найти неизвестные. Наши неизвестные — это количество веревок и мягких игрушек, которые есть у Спота. Мы можем составить уравнения для этих неизвестных, представляя веревки и мягкие игрушки.
потому что у него больше мягких игрушек, чем мячей.
потому что удвоение означает в разы больше.
Теперь нам нужно сложить количество мячей, мягких игрушек и веревок, чтобы найти общее количество.
Сообщить об ошибке.
Посмотреть репетиторов
Стивен
Сертифицированный репетитор
SUNY в Олбани, бакалавр искусств, русский язык. SUNY в Олбани, бакалавр искусств, испанский язык.
Посмотреть репетиторов
Изабель
Сертифицированный репетитор
Государственный университет Остина Пей, бакалавр наук, политологии и государственного управления.
Все материалы по математике для 3-го класса
7 практических тестов Вопрос дня Карточки Learn by Concept
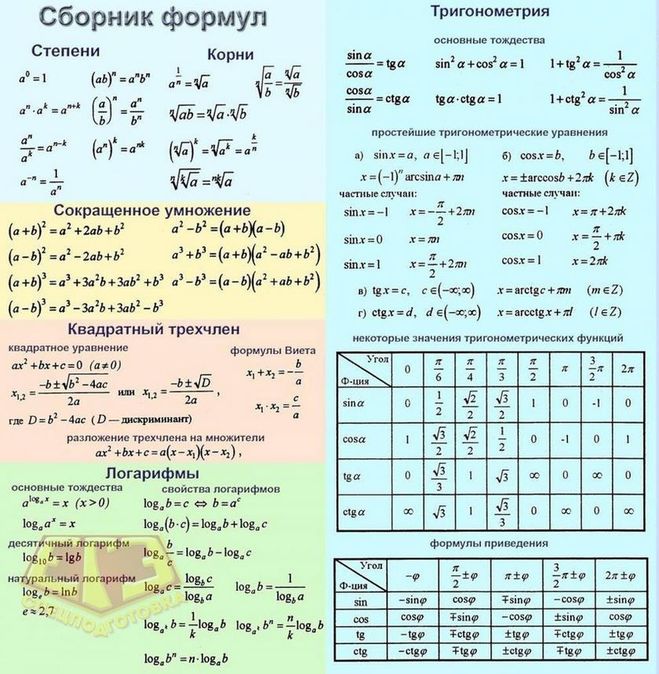
CBSE Class 8 Math Formulas: Проверьте формулы по главам
- Автор Акаш_Ананд
- Последнее изменение 27-01-2023
Математические формулы CBSE Class 8: Математические формулы CBSE Class 8 являются хорошей отправной точкой для подготовки к экзаменам. Поэтому важно знать и изучать их досконально. Понятно, что дети испытывают тревогу, потому что изучение арифметических понятий может быть сложной задачей. Чтобы получить высокий уровень знаний, учащиеся должны сначала выучить математические формулы 8-го класса, а затем перейти к решению вопросов.
Чтобы облегчить задачу ученикам, в этой статье представлен обзор всех арифметических формул для восьмого класса. Это позволит учащимся преодолеть свой учебный барьер и сохранять самообладание на протяжении всего экзамена. Важные математические формулы для 8-го класса, обсуждаемые в этой статье, не только облегчат учащимся понимание их значения, но и познакомят их с несколькими полезными стратегиями обучения, которые можно быстро включить в свои занятия.
Это позволит учащимся преодолеть свой учебный барьер и сохранять самообладание на протяжении всего экзамена. Важные математические формулы для 8-го класса, обсуждаемые в этой статье, не только облегчат учащимся понимание их значения, но и познакомят их с несколькими полезными стратегиями обучения, которые можно быстро включить в свои занятия.
Математические формулы NCERT для 8-го класса
Многие ученики спорят о том, что математические формулы трудно понять. Однако, если вы понимаете смысл формул, регулярно их практикуете и решаете достаточное количество вопросов, все формулы будут у вас под рукой. Теперь учащимся не понадобятся формулы по математике для CBSE класса 8 в формате PDF, так как мы перечислили все формулы для вас.
Математика класса 8 CBSE состоит из следующих глав:
- 9019Глава 1: . Рациональные числа Обработка
- Глава 6: Квадратные и квадратные корни
- Глава 7: Куб и кубические корни0006
- Chapter-10: Mensuration
- Chapter-11: Exponents and Power
- Chapter-12: Direct and Inverse Proportion
- Chapter-13: Factorization
- Chapter-14: Introduction к графикам
- Глава 15: Игра с числами
Математические формулы CBSE Class 8: рациональные числа
Любое число, которое можно записать в виде p ⁄ q, где q ≠ 0 — рациональные числа. Обладает свойствами:
Обладает свойствами:
- Аддитивная идентичность: (a ⁄ b + 0) = (a ⁄ b)
- Мультипликативная идентичность: (a ⁄ b) × 1 = (a/b)
- Мультипликативная обратная:
- ⁄ b) × (b/a) = 1
- Свойство замыкания – сложение: Для любых двух рациональных чисел a и b a + b также является рациональным числом.
- Свойство замыкания – вычитание: Для любых двух рациональных чисел a и b a – b также является рациональным числом.
- Свойство замыкания — умножение: Для любых двух рациональных чисел a и b a × b также является рациональным числом.
- Свойство замыкания – Деление: Рациональные числа не замыкаются при делении.
- Переместительное свойство – Дополнение: Для любых рациональных чисел a и b, a + b = b + a.
- Коммутативное свойство – вычитание: Для любых рациональных чисел a и b, a – b ≠ b – a.

- Коммутативное свойство – Умножение: Для любых рациональных чисел a и b (a x b) = (b x a).
- Коммутативное свойство – Деление: Для любых рациональных чисел a и b (a/b) ≠ (b/a).
- Ассоциативное свойство – Дополнение: Для любых рациональных чисел a, b и c: (a + b) + c = a + (b + c) .
- Ассоциативное свойство – вычитание: Для любых рациональных чисел a, b и c, (a – b) – c ≠ a – (b – c)
- Ассоциативное свойство — умножение: Для любого рационального числа a, b и c: (a x b) x c = a x (b x c).
- Ассоциативное свойство — деление: Для любых рациональных чисел a, b и c (a/b) /c ≠ a/(b/c) .
- Распределительное свойство: Для любых трех рациональных чисел a, b и c , a × ( b + c ) = (a × b) + (a × c) .

Формирование числа
- Двузначное число «ab» можно записать в виде: ab = 10a + b
- Трехзначное число «abc» можно записать в виде: abc = 100a+10b+c
- Можно составить четырехзначное число ‘abcd’: abcd = 1000a+100b+10c+d
Математические формулы 8 класса CBSE: законы экспоненты
- a 0 = 1
- а -м = 1/а м
- (а м ) н = а мн
- а м / а н = а м-н
- a м x b м = (ab) м
- a м / b м = (a/b) м
- (а/б) -м =(б/а) м
- (1) n = 1 для бесконечных значений n .
Математические формулы CBSE класса 8: алгебраическое тождество
Алгебраическое тождество состоит из нескольких уравнений равенства, которые состоят из разных переменных.
- Линейные уравнения с одной переменной: Линейное уравнение с одной переменной имеет максимальную одну переменную первого порядка. Оно изображается в виде ax + b = 0, где x — переменная.
- Линейные уравнения с двумя переменными: Линейное уравнение с двумя переменными имеет максимум двух переменных 2-го порядка. Оно изображается в виде + б) 2 = а 2 + 2аб + б 2
- (а – б) 2 = а 2 – 2аб + б 2
- (а + б) (а – б) = а 2 – б 2
- (х + а) (х + Ь) = х 2 + (а + Ь)х + аб
- (х + а) (х – б) = х 2 + (а – б)х – аб
- (х – а) (х + б) = х 2 + (б – а)х – аб
- (х – а) (х – б) = х 2 – (а + б)х + аб
- (а + b) 3 = а 3 + b 3 + 3ab(a + b)
- (а – б) 3 = а 3 – б 3 – 3аб(а – б)
- Каждое квадратное число обязательно заканчивается на 0, 1, 4, 5, 6 и 9 на месте своих единиц.
- Квадрат — это операция, обратная квадрату.
- Если каждое число в простой факторизации встречается три раза, то число является совершенным кубом.
- Символ куба ∛.
- Куб и куб mysqladmin: ∛27 = 3 и 3 3 = 27.
- Скидка = указанная цена – цена продажи
- Скидка = скидка в % от указанной цены
- CP = Цена покупки + Накладные расходы
- Налог = Налог % от суммы счета 9{2t}\)
R/2 = полугодовая ставка,
2t = количество полугодийМатематические формулы CBSE класса 8: обработка данных и вероятность
Любая полезная информация, которая может быть использована для некоторых конкретных целей известен как данные. Эти данные могут быть представлены либо графически (пиктограмма/гистограмма/круговая диаграмма), либо симметрично (табличная форма). Найдите важные математические формулы класса 8 для обработки данных и вероятности.
- Интервал класса — это определенный диапазон чисел, например 10–20, 20–30, 30–40 и т. д.
- Для интервала классов 10-20 нижний предел класса = 10 и верхний предел класса = 20
- Частота — это количество раз, когда определенное значение встречается.
Вероятность = количество благоприятных исходов/общее число исходов
Математика 8 класса CBSE Все формулы: геометрия для удобства:
- LSA – боковая/криволинейная поверхность
- TSA – Total Surface Area
Name of the Solid Figure Formulas Cuboid LSA: 2h(l + b)
TSA: 2(lb + BH + HL)
Том: L × B × HL = длина,
B = ширина,
H = высотаLSA: LSA: LSA: LSA: LSA.  6а 2
6а 2
Том: A 3A = стороны куба
Правая пирамида LSA: ½ × L
TSA: ½ × L
TSA: ½ × L
: × L.
: × L.
. × Площадь основания × hp = периметр основания,
2πr (r + h)
l = наклонная высота, h = высота
Объем: π × r 2 × hr = радиус,
H = высотаПравый круговой конус LSA: π
TSA: π
TSA: π
TSA: ×
: π
: π
: π
: . (πr 2 H)R = радиус,
L = высота наклона,
H = высотаПравой Призма LSA: P × H LSA: P × H . 
LSA: P × H
9.LSA: P × H 9. LSA: P × H LSA: P × LS: . B × h p = периметр основания,
B = площадь основания, h = высотаSphere LSA: 4 × π × r 2
TSA: 4 × π × r 2
Volume: 4/3 × (πr 3 )r = radius
Hemisphere LSA: 2 × π × r 2
TSA: 3 × π × r 2
Volume: ⅔ × (πr 3 )r = радиус
Список важных математических формул класса 8
Постоянная практика необходима для успеха в математике. Студентам предлагается решить как можно больше задач, так как это познакомит их с различными формулами.
 Это фантастическая техника для запоминания формул без необходимости их бормотать. Вот краткий список математических формул класса 8, которые можно использовать.
Это фантастическая техника для запоминания формул без необходимости их бормотать. Вот краткий список математических формул класса 8, которые можно использовать.- Аддитивное значение, обратное рациональному числу: a/b = -b/a
- Мультипликативная инверсия a/b = c/d , если a/b × c/d = 1
- Распределимость a(b – c) = ab – ac
- Вероятность возникновения события = количество исходов, составляющих событие/общее количество исходов
- Формула сложных процентов = Сумма — Основная сумма, Сумма в случае, если проценты должны рассчитываться ежегодно = Основная сумма (1 + Ставка/100) n , где «n» — период времени.
- (а – б) 2 = а 2 – 2аб + б 2
- (a + b) (a – b) = a 2 – b 2
- Формула Эйлера: для любого многогранника количество граней + количество вершин – количество ребер = 2·
- Объем конуса = (1/3)πr 2 ч
- Объем сферы = (4/3) π r 3
Часто задаваемые вопросы по математическим формулам CBSE для 8-го класса
Q.

Математические формулы CBSE класса 8: квадратные и квадратные корни
Если натуральное число m = n 2 и n — натуральное число, то говорят, что m — квадратное число.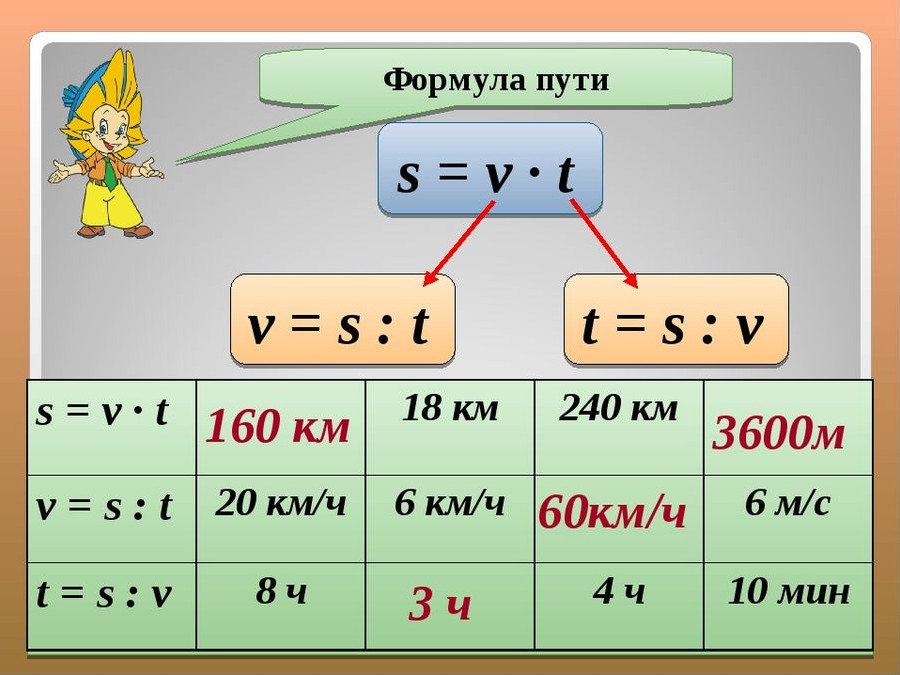
Математические формулы CBSE Class 8: куб и кубические корни
Числа, полученные при трехкратном умножении сами на себя, называются кубическими числами.
Математические формулы CBSE класса 8: сравнение количеств
Накладные расходы – это дополнительные расходы, понесенные после покупки товара. Они включены в себестоимость (CP) этого конкретного товара.
GST (налог на товары и услуги) рассчитывается при поставке товаров.



 6а 2
6а 2 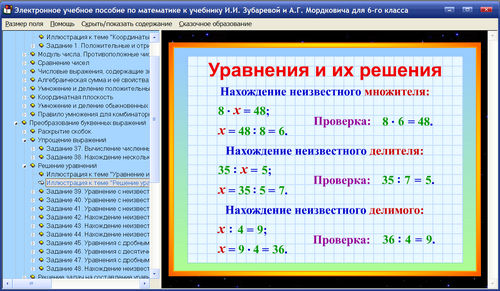
 Это фантастическая техника для запоминания формул без необходимости их бормотать. Вот краткий список математических формул класса 8, которые можно использовать.
Это фантастическая техника для запоминания формул без необходимости их бормотать. Вот краткий список математических формул класса 8, которые можно использовать.