Периметр определение в математике: Периметр — урок. Математика, 2 класс.

Что такое прямоугольник и что такое периметр

Прямоугольник – это геометрическая фигура, которая представляет собой четырехугольник, а конкретно параллелограмм (фигура, у которой противоположные стороны равны и параллельны). Но параллелограмм не обычный, а с особенностями. У него все стороны пересекаются друг с другом под прямым углом.

Выглядит прямоугольник соответственно:

А частным случаем прямоугольника является квадрат:

У такого прямоугольника стороны не только пересекаются под прямым углом, но и равны между собой.

Как и многие термины в математике, слово «периметр» пришло к нам из Древней Греции. Дословно оно означает «περιμετρέο» — «окружность» или «измерять вокруг». Таким образом,

Периметр – это совокупная длина границ любой геометрической фигуры. Этим словом обозначают как сами границы, так и их математическое значение.

С этим словом мы часто встречаемся в повседневной жизни. Например, когда нужно поставить забор на дачном участке, то его устанавливают по периметру участка. И мы понимаем, что речь идет о границах.

Также, солдаты или полицейские часто стоят в оцеплении «по периметру» какой-то территории. А кулинары часто украшают торт фруктами или кремовыми цветами также «по периметру».

Как найти периметр прямоугольника

Возьмем для примера такой прямоугольник:

Исходя из общего определения, чтобы посчитать периметр прямоугольника, надо просто сложить все его стороны.

Периметр в математике обозначается латинской буквой «Р». И соответственно формула выглядит так:

С учетом равенства сторон, формулы можно существенно упростить:

или

Предположим, что у нас длина прямоугольника равна 4 сантиметрам, а ширина 2. Тогда периметр этой геометрической фигуры составит:

И тут появляется важное замечание. Периметр измеряется в тех же величинах, что и длины сторон прямоугольника. Это могут быть миллиметры, сантиметры, метры, километры и так далее.

В случае с квадратом, который, напомним, является частным случаем прямоугольника, посчитать периметр еще проще. Благодаря тому, что у него все стороны равны (назовем их условно «а»), формула выглядит так:

или

Опять же приведем конкретный пример. Если возьмем квадрат со стороной 4 сантиметра, то его периметр составит P = 4 * 4 = 16 сантиметров.

Другие формулы для расчета периметра прямоугольника

Иногда школьникам предлагают такую задачу – нужно вычислить периметр прямоугольника, зная его площадь и длину одной стороны.

Тут надо знать, как вычисляется сама площадь. Для этого надо просто перемножить длины двух сторон:

Соответственно, мы можем определить длину недостающей нам стороны. Для этого надо просто разделить площадь на другую сторону:

Таким образом, мы у нас будут значения обеих сторон прямоугольника. А уже после периметр вычисляется по стандартной формуле.

Бывают и более сложные задачи по нахождению периметра прямоугольники, например, как в приведенном ниже видео:

Вместо заключения

Зная длины сторон, можно вычислять и периметры более сложных прямоугольных фигур. Вот таких:

Страшно выглядят они только на первый взгляд. А на деле, надо просто провести недостающую линию и разделить каждую из фигур на два прямоугольника. Далее вычисляем их периметры по отдельности и складываем друг с другом.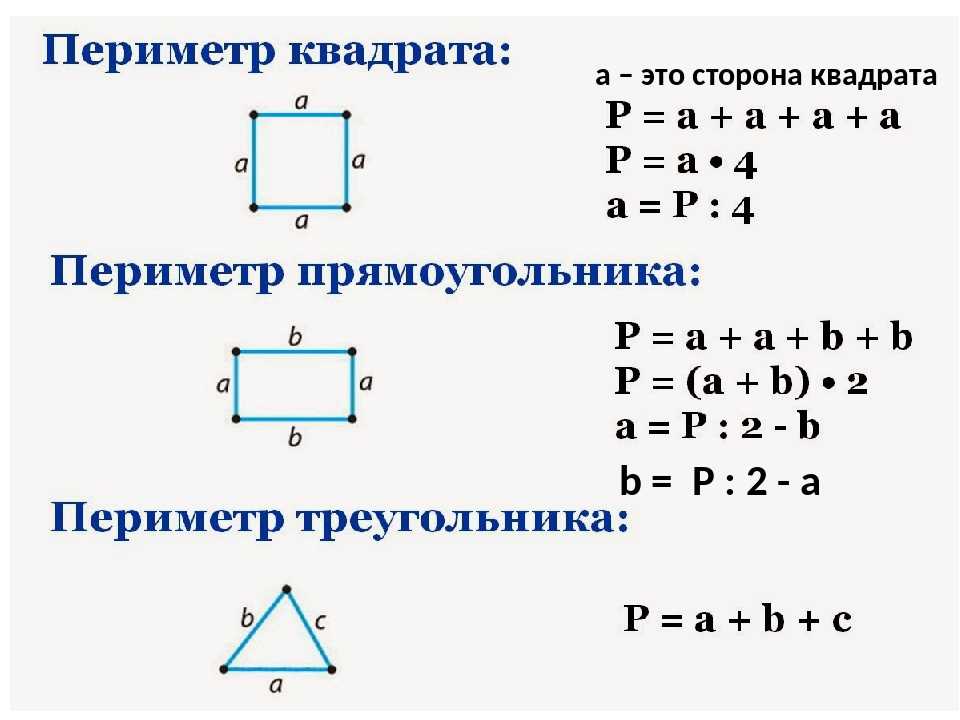 Как результат – общий периметр фигуры.

Вот и все, что мы хотели сегодня рассказать.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

• Математика

Периметр прямоугольника – формула нахождения

4.5

Средняя оценка: 4.5

Всего получено оценок: 680.

4.5

Средняя оценка: 4.5

Всего получено оценок: 680.

Одним из базовых понятий математики является периметр прямоугольника. На эту тему существует множество задач, при решении которых не обойтись без формулы периметра и навыков его вычисления.

Материал подготовлен совместно с учителем первой категории Камушковой Натальей Владимировной.

Опыт работы учителем математики — 27 лет.

Основные понятия

Прямоугольник – это четырехугольник, у которого все углы прямые, а противоположные стороны попарно равны и параллельны. В нашей жизни многие фигуры имеют форму прямоугольника.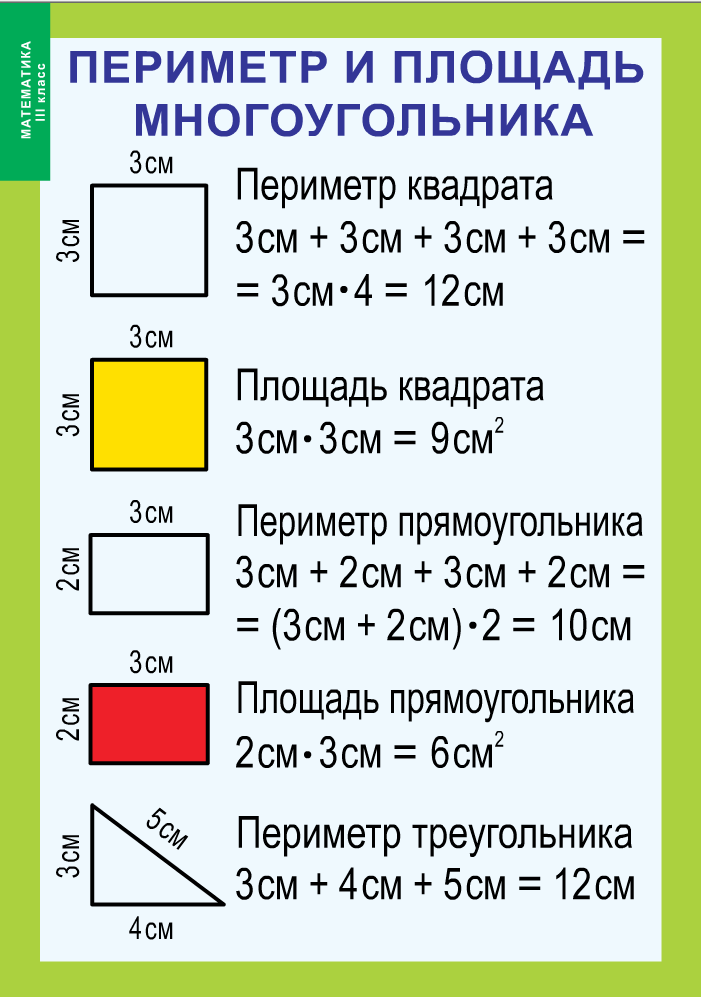 Например, поверхность стола, тетрадь и другие.

Рассмотрим пример: по границам земельного участка необходимо поставить забор. Для того чтобы узнать длину каждой из сторон необходимо их измерить.

Земельный участок имеет стороны длиной 2 м, 4 м, 2 м, 4 м. Поэтому чтобы узнать общую длину забора необходимо сложить длины всех его сторон:

2+2+4+4= 2·2+4·2 =(2+4)·2 =12 м.

Именно эта величина в общем случае и называется периметром. Таким образом, для нахождения периметра необходимо сложить все стороны фигуры. Для обозначения периметра используют латинскую букву P.

Для вычисления периметра произвольной фигуры не нужно разделять её на прямоугольники, нужно измерить линейкой (рулеткой) лишь все стороны данной фигуры и найти их сумму.

Периметр прямоугольника измеряется в различных единицах длины: мм, см, м, км и так далее. При необходимости, данные в задании, переводят в одинаковые единицы измерения.

Формула периметра фигуры

Если принять во внимание тот факт, что противоположные стороны прямоугольника равны, то можно вывести формулу периметра прямоугольника:

$P = (a+b) * 2$, где а, b – стороны фигуры.

Задание: Вычислить периметр прямоугольника, если его стороны равны 4 см и 6 см.

Решение:

Используем формулу $P = (a+b)*2$

$P = (4+6)*2=20 см$

Таким образом, периметр фигуры $P = 20 см$.

Так как периметр – это сумма всех сторон четырёхугольника, то полупериметр это сумма только одной длины и ширины. Чтобы получить периметр необходимо полупериметр умножить на 2.

Площадь и периметр – это два основных понятия измерения любой фигуры. Их нельзя путать, хоть они и связаны между собой. Если увеличить, либо уменьшить площадь, то, соответственно, увеличится либо уменьшится его периметр.

Что мы узнали?

Мы узнали, как найти периметр прямоугольника. А также ознакомились с формулой его вычисления. С этой темой можно столкнуться не только при решении математических задач, но и в реальной жизни.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Лев Макровский

  5/5

• Аня Мороз

  5/5

• Максим Андреев

  5/5

• Любовь Корелина

  5/5

• Мадия Аманджолова

  5/5

• Кристиночка Кристинка

  4/5

• Мария Дмитриева

  5/5

• Светлана Кравченко

  4/5

• Румия Семененко (фахреева)

  5/5

• Дмитрий Степанов

  5/5

Оценка статьи

4.5

Средняя оценка: 4.5

Всего получено оценок: 680.

А какая ваша оценка?

Что такое площадь и периметр? Определение, формула, примеры, факты

Периметр двумерной фигуры – это общее расстояние вокруг соответствующей фигуры. Для фигур с прямыми сторонами, таких как треугольник, прямоугольник, квадрат или многоугольник; периметр это сумма длин всех сторон.

Площадь двумерной фигуры — это пространство, ограниченное периметром данной фигуры.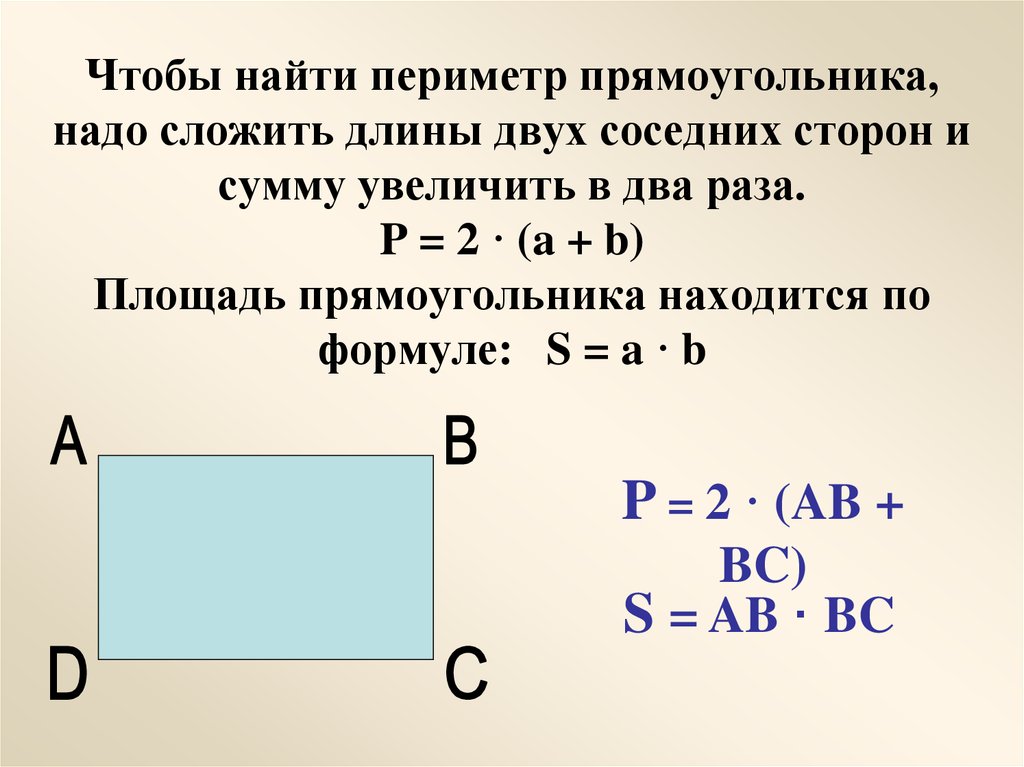 Чтобы вычислить площадь различных фигур, используйте разные формулы, основанные на количестве сторон и других характеристиках, таких как углы между сторонами.

Если все измерения выражены в сантиметрах, единицы измерения периметра и площади различных форм:

Понятия площади и периметра являются основой для понимания евклидовой геометрии и вычисления объема объемных фигур в трехмерном пространстве. пространство, такое как конусы, призма, сфера и цилиндр. Кроме того, мы используем эти формулы для вычисления площади и периметра четырехугольников и многоугольников, состоящих из сторон и кривых. Реальная полезность этой концепции в нескольких областях, таких как картографирование, архитектура и геодезия. Геометрическое представление фигур делается путем зарисовки расстояний и площадей для ясности понимания.

Трехмерные объекты, полученные из двухмерных форм и топографической съемки полей.

Как объяснить ребенку разницу между площадью и периметром?

Во-первых, площадь фигуры — это поверхность или плоское пространство, которое она покрывает, тогда как периметр формы представляет собой расстояние вокруг ее границы. Во-вторых, площадь измеряется в квадратных единицах, тогда как периметр измеряется в линейных единицах. Например, площадь квадрата длиной 3 см будет равна (3 см × 3 см) = 9квадратный см. Его периметр будет 4 × 3 см = 12 см.

Где мы используем площадь и периметр в реальной жизни?

Мы используем площадь и периметр для различных целей в нашей повседневной жизни. Например, покупая дом, мы должны знать его площадь, а покупая проволоку для ограждения сада, мы должны знать его периметр.

Периметр добавляет или умножает стороны фигуры?

Периметр — это мера границы формы. Чтобы найти периметр, нужно сложить длины всех сторон.

Дан набор фигур с одинаковой площадью, какая из фигур будет иметь самый короткий периметр?

Окружность будет иметь самый короткий периметр.

Периметр и окружность | SkillsYouNeed

Как и многие математические термины, слово периметр берет свое начало в работах древних греческих математиков.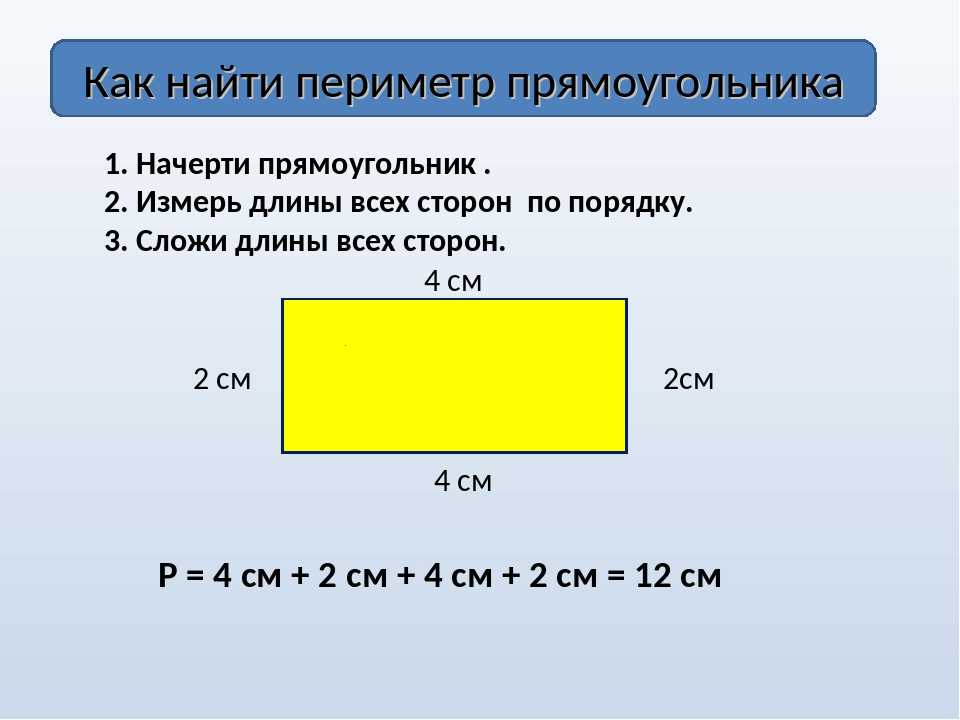 Оно происходит от греческих слов «пери», что означает «вокруг», и «метрон», что означает «измерение». Периметр буквально а измерение около .

В повседневном использовании вы могли встретить такие фразы, как забор по периметру , периметр поместья или охрана периметра . Это означает, что забор или меры безопасности расположены по краям, внешним границам или краям измеряемого участка земли или собственности.

Понимание того, как рассчитать периметр, является полезным математическим навыком как для учебы, так и для реальной жизни, будь то выполнение геометрических вычислений, разметка игрового поля или замена забора.

Периметр или граница?

Определение границы — это разделительная линия между двумя областями. В крикете граница — это линия, обозначающая край поля.

Периметр – это измеренная длина такой границы. В геометрии он определяется как сумма расстояний всех длин сторон объекта. Периметр измеряется в любой единице длины, т.е. метры, сантиметры, мили или дюймы. Подробнее об этом читайте на нашей странице измерительные системы .

Таким образом, в обычном языке эти два слова часто используются взаимозаменяемо. Однако в математическом контексте мы используем только периметр .

Окружность — это очень специфический тип периметра, относящийся только к круглым формам и формам. Подробнее об этом позже.

Измерение периметра правильных многоугольников

Периметр двумерной фигуры представляет собой общую длину всех сторон, сложенных вместе.

Например, периметр квадрата со стороной 6 м — это просто четыре участка по 6 м, т. е. 4 × 6 м = 24 м. Квадрат имеет четыре стороны одинаковой длины, которые складываются вместе.

Квадрат со стороной любой длины s поэтому имеет периметр, равный 4 × s, или просто 4 s .

Периметр против площади

Не путайте периметр и площадь .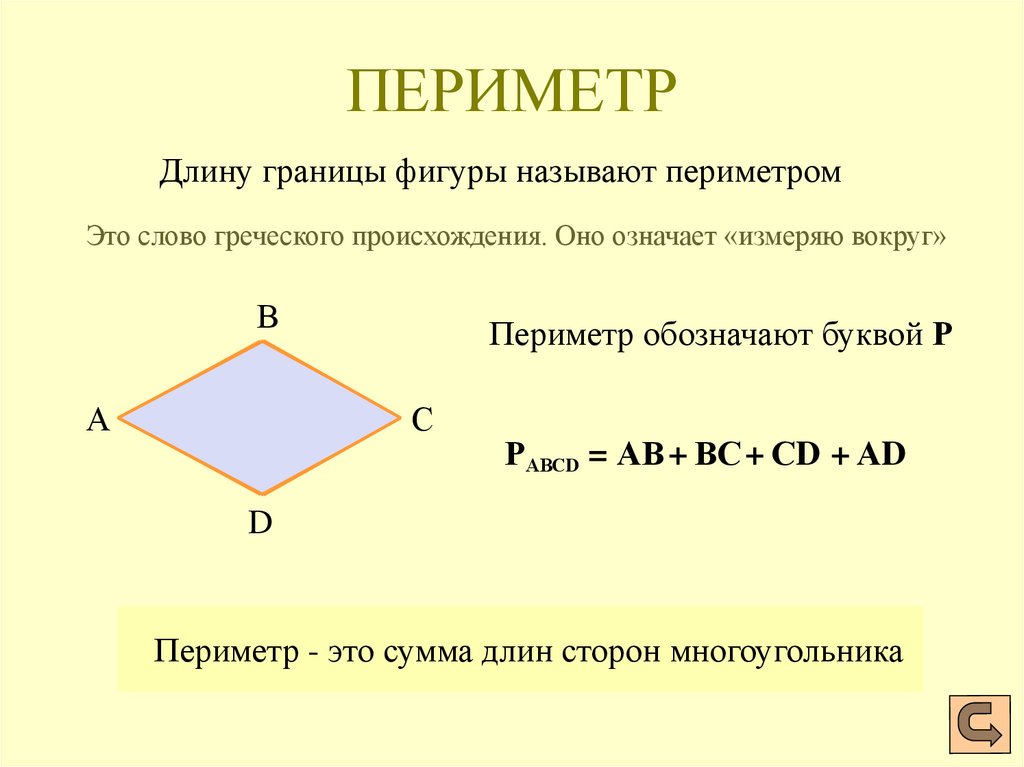 В то время как периметр является измерением контура формы, площадь — это измерение пространства, заключенного в пределах периметра.

Таким образом, в то время как периметр измеряется в единицах длины, площадь измеряется в квадратных единицах, например. м ² , см ² или дюймы ² .

Подробнее об измерении площади см. на нашей странице Вычисление площади .

По тому же принципу можно вычислить периметр любого правильного многоугольника , имеющего любое количество сторон одинаковой длины:

Если ваш многоугольник имеет n количество сторон, все длины s , то его периметр всегда равен n × s , или просто ns .

Например, если у вас есть семиугольник (7 сторон) со стороной 15 см, то длина периметра 7 × 15 = 105 см.

Дополнительную информацию о правильных, неправильных и других многоугольниках (прямолинейных формах), включая полезную таблицу с иллюстрациями, см.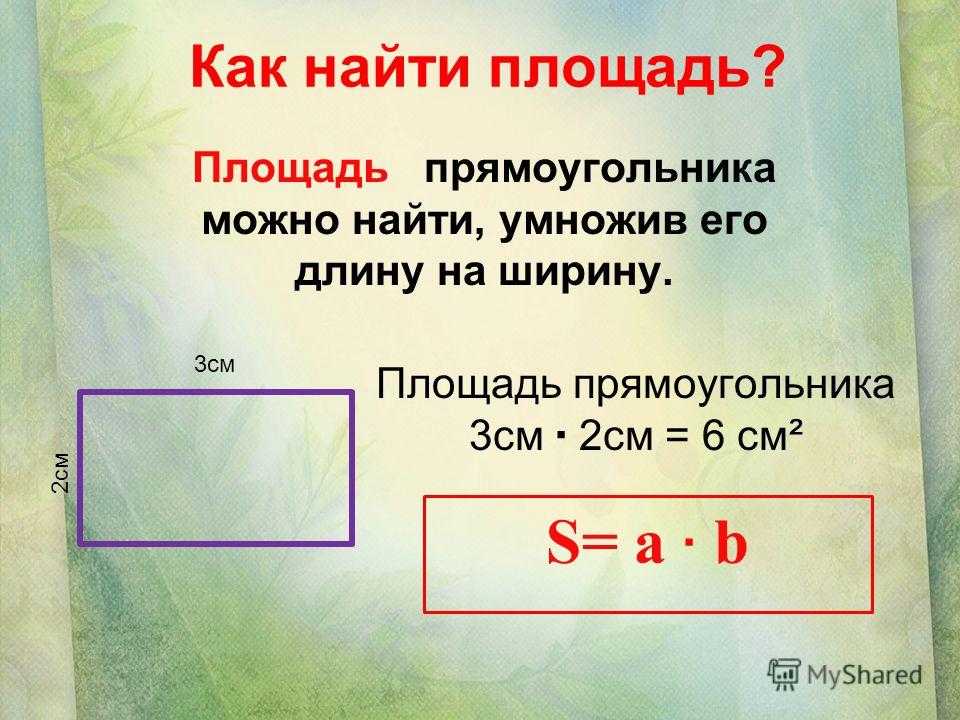 на нашей странице свойств многоугольников .

Измерение периметра неправильных многоугольников
У правильного многоугольника все стороны и внутренние углы равны, а у неправильного многоугольника — нет.

Например, прямоугольник, который не является точным квадратом, имеет две пары сторон одинаковой длины, но все четыре стороны имеют разную длину.

Пример

Найдите периметр прямоугольного футбольного поля размером 105 × 68 м.

Длины противоположных сторон равны между собой, поэтому нужно сложить два участка по 105м и два участка по 68м.

2 × 105 = 210 м
2 × 68 = 136 м
210 + 136 = 346 м

Периметр поля равен 346 м .

Неправильные многоугольники могут быть образованы любой комбинацией прямых линий, которые соединяются, чтобы ограничить область. Какой бы сложной ни была форма, периметр всегда будет суммой длин сторон .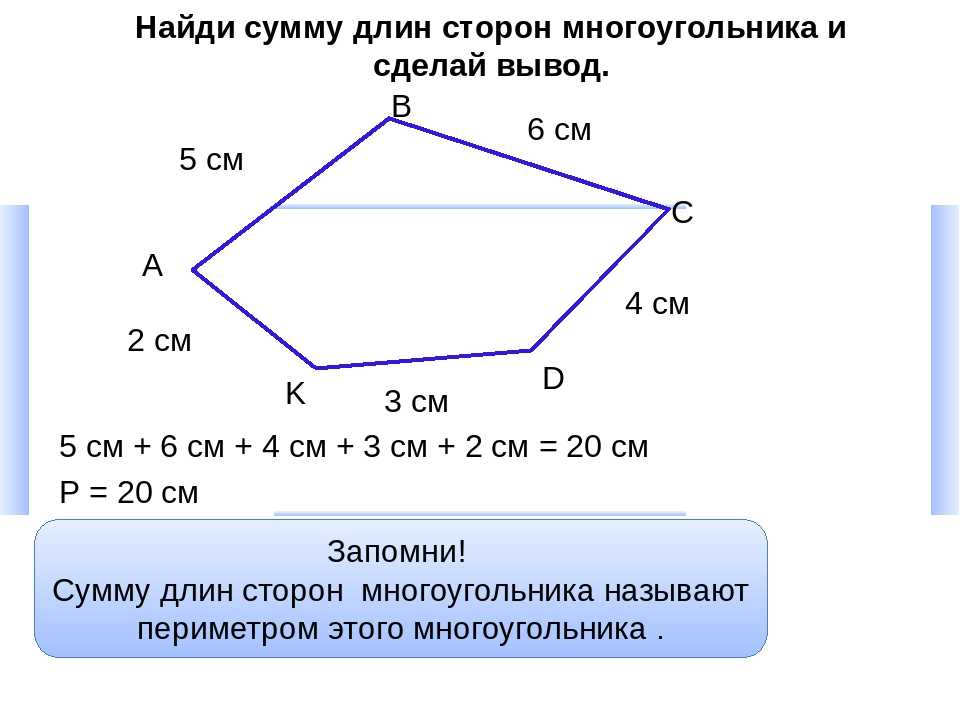

Фигура внизу может быть садовым участком или чем-то еще, что вы можете придумать. С геометрической точки зрения, это восьмигранная замкнутая двумерная фигура, у которой нет сторон одинаковой длины и внутренних углов одинакового размера.

Это неправильный восьмиугольник (8 сторон), периметр которого равен a + b + c + d + e + f + g + h.

Пример

Рассчитайте периметр шаблона ниже, размеры указаны в дюймах.

Начиная с нижнего левого угла и двигаясь вокруг фигуры по часовой стрелке, сложите длины сторон:

5 + 2 + 3 + 4 + 2 + 3 + 4 + 9 = 32 дюйма.

Периметр фигуры 32 дюйма.

Окружность

Окружность — это особый тип периметра, который применяется исключительно к круглым формам.

Измерение длины окружности

Математическое выражение для вычисления длины окружности:

2 × π × радиус  или просто 2πr

Диаметр окружности равен удвоенному радиусу, поэтому выражение для длины окружности также можно записать как πD .

Пи π

π (пи) — греческая буква, которая используется в математике для обозначения константы с приблизительным значением 3,142 (это иррациональное число с бесконечным числом десятичных знаков). Подробнее об этом читайте на наших страницах о кругах и изогнутых формах и со специальными номерами .

Измерение длины окружности эллипса

Не все изогнутые формы идеально круглые, и иногда может возникнуть необходимость найти периметр 92}{2}}\), где a и b составляют половину длины малой и большой осей соответственно. (Подробнее об эллипсах см. нашу страницу о кругах и изогнутых формах ).

Это уравнение обеспечивает только приближение (≈). Чем более вытянутым становится эллипс, тем неточнее ответ. Математики придумали несколько сложных формул для решения этой задачи. Ни один из них не достиг 100% точности в математическом смысле, но маловероятно, что вам понадобится такой высокий уровень точности, если вы не работаете в области проектирования или проектирования.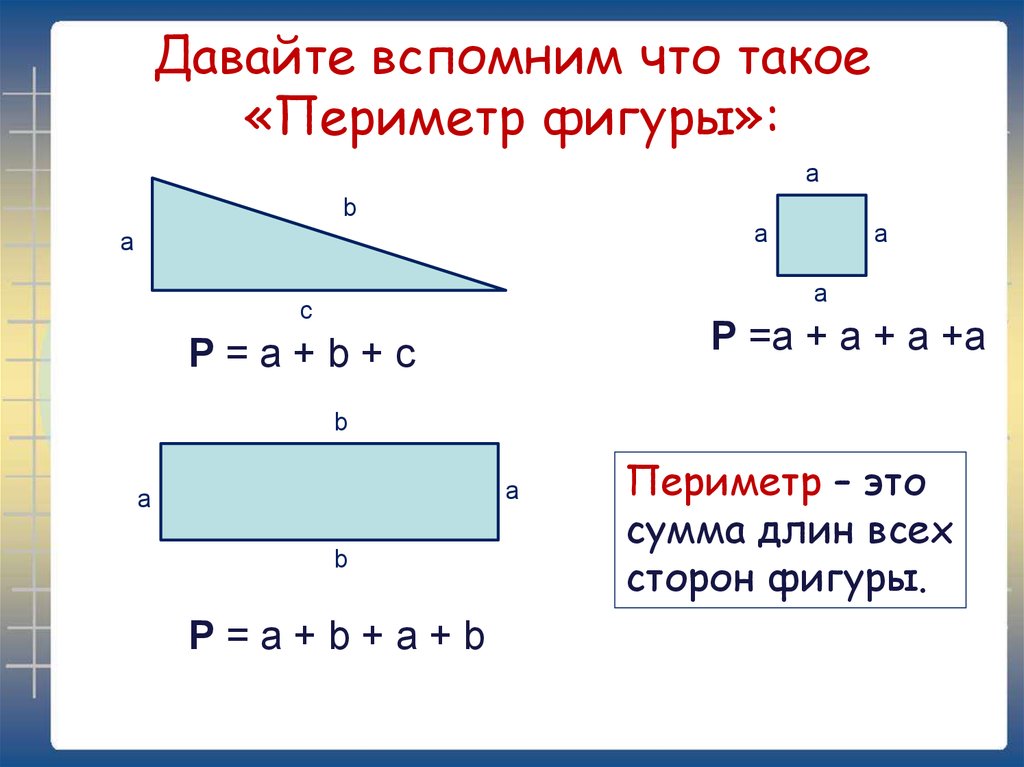

Ремесленные инструменты

Существует множество профессий и профессий, требующих физических измерений периметров и границ, таких как гражданское строительство, геодезия, ландшафтная архитектура, садовый дизайн и уход за спортивными площадками.

Необходимо не только понимать основные математические принципы, описанные выше, но и более сложные инструменты счета, такие как тригонометрия . Важны не только длины линий, но и точное измерение углов между этими линиями.

Помимо математических знаний, для таких занятий нужен интересный и разнообразный инструментарий. Относительно короткие расстояния можно измерять с помощью стальных рулеток или мерных колес. Устройства электронного измерения расстояния (EDM), которые используют электромагнитные волны, чаще используются землемерами. Они используются в сочетании с другими инструментами, такими как нивелиры и теодолиты, которые обеспечивают точность и точность угловых измерений с использованием математической техники, называемой 9. 0100 триангуляция .

Однако, если вам просто нужно заменить садовый забор, вам, вероятно, хватит рулетки и клубка веревки!

Дальнейшее чтение из книги «Навыки, которые вам нужны»

Понимание геометрии
Часть руководства «Навыки, которые вам необходимы для счета»

В этой электронной книге рассматриваются основы геометрии и рассматриваются свойства форм, линий и твердых тел. Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.

Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.

Заключение

Многие профессии требуют этих математических навыков, часто используемых в сочетании с гораздо более сложной геометрией и тригонометрией.