Группы чисел в математике 2: Конспект урока «ГРУППЫ ЧИСЕЛ» 2 класс скачать

ГРУПП ТЕОРИЯ • Большая российская энциклопедия

ГРУПП ТЕО́РИЯ, раз­дел ал­геб­ры, изу­чаю­щий в са­мой об­щей фор­ме свой­ст­ва дей­ст­вий (опе­ра­ций), наи­бо­лее час­то встре­чаю­щих­ся в ма­те­ма­ти­ке и её при­ло­же­ни­ях. При­ме­ра­ми та­ких дей­ст­вий яв­ля­ют­ся ум­но­же­ние и сло­же­ние чи­сел, сло­же­ние век­то­ров, по­сле­до­ва­тель­ное вы­пол­не­ние пре­об­ра­зо­ва­ний и т. п. При этом Г. т. изу­ча­ет не про­из­воль­ные опе­ра­ции, а лишь те, ко­то­рые об­ла­да­ют ря­дом свойств, пе­ре­чис­ляе­мых в оп­ре­де­ле­нии груп­пы.

Об­щее (фор­маль­ное) оп­ре­де­ле­ние груп­пы та­ко­во. Пусть $G$ – про­из­воль­ное мно­же­ст­во, на ко­то­ром за­да­на би­нар­ная опе­ра­ция, т. е. для лю­бых двух эле­мен­тов $a$, $b$ из $G$ оп­ре­де­лён не­ко­то­рый эле­мент (обо­зна­чае­мый, напр., $a \circ b$), ко­то­рый так­же при­над­ле­жит $G$. Ес­ли при этом вы­пол­ня­ют­ся ус­ло­вия: 1) $(a \circ b) \circ c=a \circ (b \circ c)$ для лю­бых $a$,$b$,$c$ из $G$; 2) в $G$ су­ще­ст­ву­ет та­кой эле­мент $e$ (на­зы­вае­мый еди­ни­цей, ино­гда – ней­траль­ным эле­мен­том), что $a \circ e=e \circ a=a$ для лю­бо­го $a$ из $G$; 3) для лю­бо­го $a$ из $G$ су­ще­ству­ет та­кой эле­мент $a^{-1}$ (об­рат­ный к $a$ эле­мент), что $a \circ a^{-1}=a^{-1} \circ a=e$, то множе­ст­во $G$ с за­дан­ной на нём опе­ра­ци­ей (ком­по­зи­ци­ей) $\circ$ на­зы­ва­ет­ся груп­пой.

При­ме­ры групп. 1. Мно­же­ст­во $G$ разл. дви­же­ний евк­ли­до­вой плос­ко­сти, са­мо­со­вме­щаю­щих дан­ную фи­гу­ру, т. е. пе­ре­во­дя­щих её са­му в се­бя, опе­ра­ци­ей на ко­то­ром слу­жит ком­по­зи­ция дви­же­ний (ес­ли $\varphi$, $\psi$ – два дви­же­ния из $G$, то ре­зуль­та­том их ком­по­зи­ции на­зы­ва­ет­ся дви­же­ние $\varphi \circ \psi$ , рав­но­силь­ное по­сле­до­ва­тель­но­му вы­пол­не­нию сна­ча­ла дви­же­ния $\varphi$, а за­тем дви­же­ния $\psi$), об­ра­зу­ет т. н. груп­пу сим­мет­рий фи­гу­ры. Еди­ни­цей в этой груп­пе яв­ля­ет­ся то­ж­де­ст­вен­ное пре­об­ра­зо­ва­ние плос­ко­сти, а об­рат­ным к $\varphi$ эле­мен­том – об­рат­ное к $\varphi$ пре­об­ра­зо­ва­ние. Груп­па $G$ яв­ля­ет­ся ха­рак­те­ри­сти­кой боль­шей или мень­шей сим­мет­рич­но­сти фи­гу­ры: чем ши­ре мно­же­ст­во $G$, тем сим­мет­рич­нее фи­гу­ра. Напр., груп­па сим­мет­рий квад­ра­та (рис., а) со­сто­ит из вось­ми дви­же­ний (че­ты­ре по­во­ро­та во­круг цен­тра квад­ра­та и че­ты­ре от­ра­же­ния: два – от­но­си­тель­но диа­го­на­лей и два – от­но­си­тель­но пря­мых, со­еди­няю­щих се­ре­ди­ны про­ти­во­по­лож­ных сто­рон). Для кру­га (рис., б) груп­па сим­мет­рий со­дер­жит бес­ко­неч­но мно­го эле­мен­тов (напр., все по­во­ро­ты во­круг цен­тра), а для фи­гу­ры, изо­бра­жён­ной на рис. (в), груп­па сим­мет­рий со­сто­ит из од­но­го то­ж­де­ст­вен­но­го пре­об­ра­зо­ва­ния.

2. Ес­ли $\boldsymbol Z$ – мно­же­ст­во це­лых чи­сел, а опе­ра­ция на $\boldsymbol Z$ – их обыч­ное сло­же­ние +, то $\boldsymbol Z$ – груп­па. Роль $e$ иг­ра­ет чис­ло 0, а роль об­рат­но­го к $z$ эле­мен­та – чис­ло $-z$. Часть $H$ мно­же­ст­ва $\boldsymbol Z$, со­стоя­щая из чёт­ных чи­сел, са­ма яв­ля­ет­ся груп­пой от­но­си­тель­но той же опе­ра­ции. В та­ком слу­чае го­во­рят, что $H$ – под­груп­па груп­пы $\boldsymbol Z$. Обе груп­пы $\boldsymbol Z$ и $H$ удов­ле­тво­ря­ют сле­дую­ще­му до­пол­нит. ус­ло­вию: 4) $a+b=b+a$ для лю­бых $a$ и $b$ из груп­пы. Вся­кая груп­па, в ко­то­рой вы­пол­ня­ет­ся по­след­нее ус­ло­вие, на­зы­ва­ет­ся ком­му­та­тив­ной или абе­ле­вой.

3. Мно­же­ст­во всех под­ста­но­вок (пе­ре­ста­но­вок) $n$ сим­во­лов об­ра­зу­ет груп­пу от­но­си­тель­но ком­по­зи­ции под­ста­но­вок, на­зы­вае­мую сим­мет­рич. груп­пой сте­пе­ни $n$. При $n \geq3$ сим­мет­рич. груп­па не­ком­му­та­тив­на. По­ря­док (чис­ло эле­мен­тов) сим­мет­рич. груп­пы ра­вен $n!$ (см. Ком­би­на­тор­ный ана­лиз).

Историческая справка

Г. т. по­слу­жи­ла во мно­гих от­но­ше­ни­ях об­раз­цом при пе­ре­строй­ке ал­геб­ры и ма­те­ма­ти­ки во­об­ще на ру­бе­же 19–20 вв. Ис­то­ки по­ня­тия груп­пы об­на­ру­жи­ва­ют­ся в не­сколь­ких дис­ци­п­ли­нах, глав­ная из ко­то­рых – тео­рия ре­ше­ний ал­геб­ра­ич. урав­не­ний в ра­ди­ка­лах. В 1771 франц. ма­те­ма­ти­ки Ж. Ла­гранж и А. Ван­дер­монд впер­вые для нужд этой тео­рии при­ме­ни­ли под­ста­нов­ки. За­тем в ря­де ра­бот итал. ма­те­ма­ти­ка П. Руф­фи­ни (1799 и в по­сле­дую­щих), по­свя­щён­ных до­ка­за­тель­ст­ву не­раз­ре­ши­мо­сти урав­не­ний 5-й сте­пе­ни в ра­ди­ка­лах, сис­те­ма­ти­че­ски ис­поль­зо­ва­лась замк­ну­тость мно­же­ст­ва под­ста­но­вок от­но­си­тель­но их ком­по­зи­ции и по су­ще­ст­ву опи­са­ны под­груп­пы груп­пы всех под­ста­но­вок пя­ти сим­во­лов. Глу­бо­кие свя­зи ме­ж­ду свой­ст­ва­ми групп под­ста­но­вок и свой­ст­ва­ми урав­не­ний бы­ли об­на­ру­же­ны Н. Абе­лем (1824) и Э. Га­луа (1830). Га­луа при­над­ле­жат мн. дос­ти­же­ния в Г. т., та­кие как от­кры­тие ро­ли т. н. нор­маль­ных под­групп в свя­зи с за­да­чей о раз­ре­ши­мо­сти урав­не­ний в ра­ди­ка­лах, до­ка­за­тель­ст­во про­сто­ты зна­ко­пе­ре­мен­ных групп сте­пе­ни $n \geq 5$; он же ввёл тер­мин «груп­па», хо­тя и не дал его стро­го­го оп­ре­де­ле­ния. Важ­ную роль в сис­те­ма­ти­за­ции и раз­ви­тии Г. т. сыг­рал трак­тат М. Э. К. Жор­да­на о груп­пе под­ста­но­вок (1870).

Не­за­ви­си­мо (и из дру­гих со­об­ра­же­ний) по­ня­тие груп­пы воз­ник­ло в гео­мет­рии, ко­гда в сер. 19 в. на сме­ну ан­тич­ной гео­мет­рии при­шли др. «гео­мет­рии» и встал во­прос об ус­та­нов­ле­нии свя­зей и род­ст­ва ме­ж­ду ни­ми. Вы­ход из соз­дав­ше­го­ся по­ло­же­ния был на­ме­чен ис­сле­до­ва­ния­ми по про­ек­тив­ной гео­мет­рии, по­свя­щён­ны­ми изу­че­нию по­ве­де­ния фи­гур при разл. пре­об­ра­зо­ва­ни­ях. По­сте­пен­но ин­те­рес в этих ис­сле­до­ва­ни­ях пе­ре­шёл на изу­че­ние са­мих пре­об­ра­зо­ва­ний и по­иск их клас­си­фи­ка­ции. Та­ким «изу­че­ни­ем гео­мет­ри­че­ско­го род­ст­ва» за­ни­мал­ся А. Мё­би­ус. За­клю­чит. эта­пом на этом пу­ти яви­лась «Эр­лан­ген­ская про­грам­ма» Ф. Клей­на (1872), по­ло­жив­шая в ос­но­ву клас­си­фи­ка­ции гео­мет­рий по­ня­тие груп­пы пре­об­ра­зо­ва­ний: ка­ж­дая гео­мет­рия оп­ре­де­ле­на не­ко­то­рой груп­пой пре­об­ра­зо­ва­ний про­стран­ст­ва, и толь­ко те свой­ст­ва фи­гур при­над­ле­жат дан­ной гео­мет­рии, ко­то­рые ин­ва­ри­ант­ны от­но­си­тель­но пре­об­ра­зо­ва­ний со­от­вет­ст­вую­щей груп­пы.

Тре­тий ис­точ­ник про­ис­хо­ж­де­ния по­ня­тия груп­пы – чи­сел тео­рия. Л. Эй­лер (1761), изу­чая «вы­че­ты, ос­таю­щие­ся при де­ле­нии сте­пе­ней», по су­ще­ст­ву поль­зовал­ся срав­не­ния­ми и раз­бие­ния­ми на клас­сы вы­че­тов, что на тео­ре­ти­ко-груп­по­вом язы­ке оз­на­ча­ет раз­ло­же­ние груп­пы на смеж­ные клас­сы по под­груп­пе. К. Га­усс в «Ариф­ме­ти­че­ских ис­сле­до­ва­ни­ях» (1801), за­ни­ма­ясь урав­не­ни­ем де­ле­ния кру­га, фак­ти­че­ски оп­ре­де­лил под­груп­пы его груп­пы Га­луа (см. Га­луа тео­рия). Там же, изу­чая «ком­по­зи­цию дво­ич­ных квад­ра­тич­ных форм», Га­усс по су­ще­ст­ву до­ка­зал, что клас­сы эк­ви­ва­лент­ных форм об­ра­зу­ют ко­неч­ную абе­ле­ву груп­пу от­но­си­тель­но ком­по­зи­ции.

Един­ст­во тео­ре­ти­ко-груп­по­вых форм мыш­ле­ния, су­ще­ст­во­вав­ших к кон. 19 в. в разл. об­лас­тях ма­те­ма­ти­ки, при­ве­ло к вы­ра­бот­ке совр. аб­ст­ракт­но­го по­ня­тия груп­пы (С. Ли, Ф. Г. Фро­бе­ни­ус и др.). Так, уже в 1895 Ли оп­ре­де­лял груп­пу как со­во­куп­ность пре­об­ра­зо­ва­ний, замк­ну­тую от­но­си­тель­но их ком­по­зи­ции, удов­ле­тво­ряю­щей ус­ло­ви­ям 1), 2), 3). Изу­че­ние групп без пред­по­ло­же­ния их ко­неч­но­сти и без ка­ких бы то ни бы­ло пред­по­ло­же­ний о при­ро­де эле­мен­тов впер­вые офор­ми­лось в са­мо­сто­ят. раз­дел ма­те­ма­ти­ки с вы­хо­дом кни­ги О.  Ю. Шмид­та «Аб­ст­ракт­ная тео­рия групп» (1916).

Основные разделы теории групп

Ко­неч­ной целью соб­ст­вен­но Г. т. яв­ля­ет­ся опи­са­ние всех воз­мож­ных груп­по­вых ком­по­зи­ций. В Г. т. вы­де­ля­ет­ся ряд раз­де­лов, оп­ре­де­ляе­мых ча­ще все­го до­пол­нит. ус­ло­вия­ми на груп­по­вую ком­по­зицию или вне­се­ни­ем в груп­пу до­пол­нит. струк­тур, свя­зан­ных с груп­по­вой ком­по­зи­ци­ей. Важ­ней­ши­ми в Г. т. счи­та­ют­ся сле­дую­щие раз­де­лы.

а) Тео­рия ко­неч­ных групп. Осн. про­бле­ма этой ста­рей­шей вет­ви Г. т. – клас­си­фи­ка­ция т. н. про­стых ко­неч­ных групп, иг­раю­щих роль бло­ков при по­строе­нии про­из­воль­ной ко­неч­ной груп­пы. С тео­ри­ей ко­неч­ных групп тес­но свя­за­на ком­би­на­тор­ная тео­рия групп, где ис­поль­зу­ют­ся идеи и ме­то­ды ком­би­на­тор­но­го ана­ли­за.

б) Тео­рия абе­ле­вых групп. От­прав­ной точ­кой мн. ис­сле­до­ва­ний в этой об­лас­ти слу­жит осн. тео­ре­ма о ко­неч­но по­ро­ж­дён­ных абе­ле­вых груп­пах, пол­но­стью вы­яс­няю­щая их строе­ние.

в) Тео­рия раз­ре­ши­мых групп. По­ня­тие раз­ре­ши­мой груп­пы яв­ля­ет­ся обоб­ще­ни­ем по­ня­тия абе­ле­вой груп­пы. Оно по су­ще­ст­ву идёт от идей Э. Га­луа и тес­но свя­за­но с раз­ре­ши­мо­стью урав­не­ний в ра­ди­ка­лах. Для ко­неч­ных групп это по­ня­тие мо­жет быть оп­ре­де­ле­но мн. рав­но­силь­ны­ми спо­со­ба­ми, ко­то­рые пе­ре­ста­ют быть рав­но­силь­ны­ми при от­казе от ко­неч­но­сти груп­пы. Изу­че­ние воз­ни­каю­щих при этом клас­сов групп со­став­ля­ет пред­мет тео­рии обоб­щён­но раз­ре­ши­мых групп.

г) Теория групп пре­об­ра­зо­ва­ний. По­ня­тие груп­пы воз­ник­ло ис­то­ри­че­ски имен­но как по­ня­тие груп­пы пре­об­ра­зо­ва­ний, но в даль­ней­шем бы­ло обоб­ще­но, при этом Г. т. пре­об­ра­зо­ва­ний ос­та­лась важ­ной ча­стью об­щей тео­рии. Ти­пич­ным в этой тео­рии яв­ля­ет­ся во­прос о том, ка­ки­ми свой­ст­ва­ми об­ла­да­ет груп­па, за­дан­ная как груп­па пре­об­ра­зо­ва­ний не­ко­то­ро­го мно­же­ст­ва. К Г. т. пре­об­ра­зо­ва­ний от­но­сят­ся, в ча­ст­но­сти, груп­па под­ста­но­вок и груп­па мат­риц.

д) Тео­рия пред­став­ле­ний групп. Эта тео­рия – од­но из средств изу­че­ния аб­ст­ракт­ных групп. Пред­став­ле­ние аб­ст­ракт­ной груп­пы в ви­де не­ко­то­рой кон­крет­ной груп­пы (напр., в ви­де груп­пы под­ста­но­вок или груп­пы мат­риц) по­зво­ля­ет об­на­ру­жи­вать важ­ные свой­ст­ва этой груп­пы. В тео­рии ко­неч­ных групп с по­мо­щью тео­рии пред­став­ле­ний по­лу­чен ряд важ­ных ре­зуль­та­тов.

е) Из раз­де­лов Г. т., вы­де­ляе­мых вне­се­ни­ем в груп­пу до­пол­нит. струк­тур, со­гла­со­ван­ных с груп­по­вой ком­по­зи­ци­ей, осо­бен­но важ­на тео­рия то­по­ло­гич. групп, в ко­то­рых груп­по­вая ком­по­зи­ция в не­ко­то­ром смыс­ле не­пре­рыв­на. Ста­рей­шая ветвь это­го раз­де­ла Г. т. – Ли групп тео­рия.

Г. т. яв­ля­ет­ся од­ной из са­мых раз­ви­тых об­лас­тей ал­геб­ры и име­ет мно­го­числ. при­ме­не­ния как в са­мой ма­те­ма­ти­ке, так и в её при­ло­же­ни­ях. Напр., Е. С. Фё­до­ров (1890) с по­мо­щью Г. т. ре­шил за­дачу клас­си­фи­ка­ции пра­виль­ных про­стран­ст­вен­ных сис­тем то­чек, яв­ляю­щую­ся од­ной из осн. за­дач кри­стал­ло­гра­фии. Это был ис­то­ри­че­ски пер­вый слу­чай при­ме­не­ния Г. т. не­по­сред­ст­вен­но в ес­те­ст­во­зна­нии. Боль­шую роль Г. т. иг­ра­ет в фи­зи­ке, напр. в кван­то­вой ме­ха­ни­ке, где ши­ро­ко ис­поль­зу­ют­ся со­об­ра­же­ния сим­мет­рии и тео­рия пред­став­ле­ния групп ли­ней­ны­ми пре­об­ра­зо­ва­ния­ми.

Конспект по математике для детей старшей группы «Путешествие чисел». | План-конспект занятия по математике (старшая группа) на тему:

Конспект занятия по математике детей шестого года жизни «Путешествие чисел».

Задачи:

1.1Продолжать формировать понятие о натуральном ряде чисел, соотносить число с количеством используя субитацию ,выполнять сложную инструкцию.

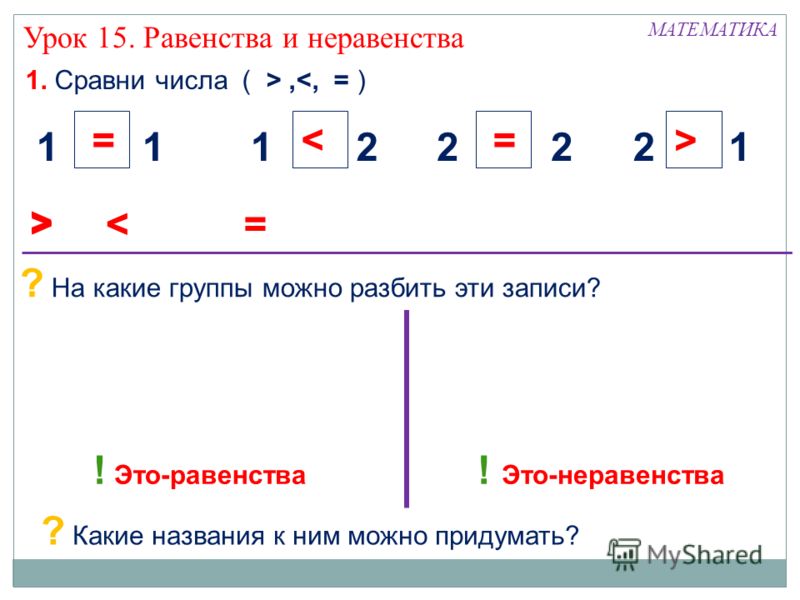
2.Учить читать равенства и неравенства, пользоваться линейкой.

3.Формировать умение на основе наглядного материала, сравнивать числа, учить читать математические записи и доказывать правильное написание.

2.1. Развивать внимание , усидчивость ,мышление ,умение анализировать постановку вопроса ,умение решать задачи.

2.Развивать мелкую моторику рук.

3.1. Воспитывать умение выслушивать вопрос до конца и отвечать полным ответом самостоятельно.

Материал: рабочие тетради, набор цифр, карандаши, ручка, линейка, знаки больше, меньше, наборное полотно.

Словарь: знаки ,цифры, числа, короче, длиннее, числовой ряд , по-порядку , друг за другом ,ельник , отрезок.

      1. Дети проходят в группу.

• Дети, приходил Петрушка и составил натуральный ряд чисел. Правильно он составил? Почему?

1 3 4 6 5 7 9 10.

• Какое число пропущено?
• Где оно должно стоять в натуральном ряду чисел?
• Какое число пропущено?
• Что получилось? (натуральный ряд чисел)
• Что можно сказать про числа натурального ряда? (каждое число в натуральном ряду занимает свое место, числа идут по — порядку, и каждое число больше предыдущего на одну единицу.)

2.Проходим за столы. Открыли тетради, нашли сегодняшнее число.

• Посмотрите, что у вас написано в тетради? (числа)
• Соедините числа по — порядку.
• Что получилось? (звезда)

• Звезда что украшает? (елку).
• А как называется лес, в котором растут одни ели?
• Ельник.

     3. — Давайте с вами отправимся в путешествие по еловому лесу. — Посмотрите, в этом ельнике, сколько елок? (субитация)

• Что нужно сделать? (пересчитать)

• Как мы будем считать? (каждый предмет один раз)
• Какой цифрой обозначим число предметов?
• А теперь давайте сравним эти числа. (Например: 5 > 4, 6
• Покажи мне число 8 при помощи пальчиков.
• Почему ты показал 8 пальцев? (так как число 8 состоит из 8 единиц).

4.-Физкульминутка  

  Посчитаем.

Раз, два, три, четыре, пять.   

Можно все пересчитать.           Ходьба с выставлением указательного пальца вперед.

Сколько в комнате углов?        Показать на углы с поворотами туловища.

Сколько ног у воробьев?          Приподнимать  поочередно ноги.

Сколько пальцев на руках?      Раскрыть пальцы рук.

Сколько пальцев на ногах?      Присесть, коснуться носков ног.

Сколько в садике скамеек?     Полуприседания.

Сколько в пятачке копеек?      Попрыгать легко или приподнимать пятки.

     

   5.- Проходим за столы, открываем опять тетради.

• Найдите натуральный ряд чисел от 1 — 8.
• Какое число стоит первым? (один).
• Сколько единиц в числе 1? (одна)
• Поставь одну единицу.

(Воспитатель на доске вместе с детьми выполняет задание).

• Какое число следует за числом 1 ? (два)
• Сколько единиц в числе 2? (две)
• Поставьте 2 единицы.
• А теперь напишите самостоятельно.

( Сколько единиц в каждом числе — разобрать).

   6. -Ребята, скоро Новый год и к нам спешат Дед Мороз и Снегурочка. По одной дороге едет Снегурочка, по другой Дед Мороз.

Установка: что нужно сделать, чтобы начертить отрезок? (Взять линейку и совместить О с точкой. )

• От красной точки начертите отрезок длиной 7 см.
• Что ты делаешь? (совмещаю 0 с точкой, нахожу число7 на линейке, ставлю точку и соединяю две точки прямой линией.)
• А от синей точки начертите отрезок на один см длиннее, чем первый.
• Какой он будет длины? (8 см)
• От синей точки начерти отрезок длиной 8 см.
• По первой дорожке спешит Снегурочка, а по второй — Дед Мороз. Кто приедет первым, почему? (путь Снегурочки на один см короче, поэтому она приедет первой) Сравнить путь числом: 7

7. Дед Мороз едет с подарками. Задача:

Было 9 конфет, одну съели. Сколько осталось конфет?

• Что я сказала? (задачу)
• Что есть у задачи? (выставить правила)

1. Условие (назови Слава условие)
2. Вопрос (назови Таня вопрос)
3. Решение (Катя назови решение)
4. Ответ (назови Лера ответ)

Задача:

Было 7 шаров, надули еще один шар. Сколько шаров стало?

(Решаем аналогично первой)

Дети самостоятельно составляют свои задачи.

8. Подведение итогов.

—

групп цифр

Все предметы

• Предварительные
  • Умножение и деление с использованием нуля
  • Общие математические символы
  • Викторина: способы показать умножение и деление, умножение и деление на ноль и общие математические символы
  • Свойства основных математических операций
  • Тест: свойства основных математических операций
  • Группировка символов и порядок операций
  • Группы чисел
  • Викторина: Группы чисел
  • Способы показать умножение и деление
  • Порядок операций
  • Викторина: группировка символов и порядок действий
• Целые числа
  • Оценка сумм, разностей, произведений и частных
  • Викторина: оценка сумм, разностей, произведений и частных
  • Правила делимости
  • Викторина: правила делимости
  • Факторы, простые числа, композиты и деревья факторов
  • Место Значение
  • Викторина: Факторы, простые числа, композиты и факторные деревья
  • Викторина: Значение места
• Десятичные
  • Использование таблицы стоимости места
  • Викторина: использование таблицы значений мест
  • Десятичные вычисления
  • Викторина: Десятичные вычисления
  • Оценка сумм, разностей, произведений и частных
  • Викторина: оценка сумм, разностей, произведений и частных
  • Что такое десятичные дроби?
  • Повторяющиеся десятичные дроби
• Фракции
  • Правильные и неправильные дроби
  • Смешанные номера
  • Переименование дробей
  • Викторина: правильные и неправильные дроби, смешанные числа и переименование дробей
  • Факторы
  • Мультипликаторы
  • Что такое дроби?
  • Викторина: Факторы и множители
  • Сложение и вычитание дробей
  • Сложение и вычитание смешанных чисел
  • Тест: сложение и вычитание дробей и смешанных чисел
  • Умножение дробей и смешанных чисел
  • Деление дробей и смешанных чисел
  • Тест: умножение и деление дробей и смешанных чисел
  • Упрощение дробей и сложных дробей
  • Викторина: Упрощение дробей и сложных дробей
  • Преобразование дробей в десятичные
  • Преобразование десятичных дробей в дроби
  • Преобразование бесконечных повторяющихся десятичных дробей в дроби
  • Викторина: Преобразование дробей в десятичные дроби, Преобразование завершающих десятичных дробей в дроби и Преобразование бесконечных повторяющихся десятичных дробей в дроби
• Проценты
  • Применение процентов
  • Викторина: Применение процентов
  • Изменение процентов, десятичных знаков и дробей
  • Важные эквиваленты
  • Викторина: изменение процентов, десятичных знаков и дробей, а также важные эквиваленты
• Целые числа и рациональные числа
  • Викторина: Рациональные числа (числа со знаком, включая дроби)
  • Целые числа
  • Викторина: Целые числа
  • Рациональные числа (числа со знаком, включая дроби)
• Экспоненты и корни в степенях
  • Викторина: Квадратные корни и кубические корни
  • Полномочия и показатели
  • Викторина: Полномочия и показатели
  • Квадратные корни и кубические корни
• Степени десяти и научная нотация
  • Викторина: Научная нотация
  • Силы десяти
  • Викторина: Силы десяти
  • Научная нотация
• Измерения
  • Метрическая система
  • Преобразование единиц измерения
  • Викторина: обычная система США, метрическая система и перевод единиц измерения
  • Точность
  • Значащие цифры
  • Викторина: точность и значащие цифры
  • Традиционная система США
  • Расчет измерений базовых фигур
  • Викторина: Расчет размеров базовых фигур
• Графики
  • Гистограммы
  • Викторина: гистограммы
  • Линейные графики
  • Викторина: линейные графики
  • Круговые диаграммы или круговые диаграммы
  • Введение в графики
  • Викторина: круговые диаграммы или круговые диаграммы
  • Графики координат
  • Викторина: Графики координат
• Вероятности и статистика
  • Викторина: Статистика
  • Вероятность
  • Викторина: Вероятность
  • Статистика
• Серия номеров
  • Арифметические прогрессии
  • Геометрические прогрессии
  • Викторина: арифметические прогрессии и геометрические прогрессии
• Переменные Алгебраические выражения и простые уравнения
  • Викторина: переменные и алгебраические выражения
  • Решение простых уравнений
  • Викторина: Решение простых уравнений
  • Переменные и алгебраические выражения
• Текстовые задачи
  • Ключевые слова
  • Викторина: Процесс решения и ключевые слова
  • Процесс решения
• Базовые тесты по математике

Группы чисел

При выполнении основных математических операций вы работаете с множеством различных групп чисел. Чем больше вы знаете об этих группах, тем легче их понять и с ними работать.

• Натуральные или счетные числа: 1, 2, 3, 4, …

• Целые числа: 0, 1, 2, 3, 4, …

• Целые числа: … –3, –2, –1, 0, 1, 2, 3, …

• Отрицательные целые числа: … –3, –2, –1

• Целые положительные числа: 1, 2, 3, … (натуральные числа)

Примечание:   Ноль не является ни положительным, ни отрицательным. Это нейтрально.

• Нечетные числа; целые числа, не делящиеся на 2:

• … – 5, – 3, – 1, 1, 3, 5, …

• Четные числа: Целые числа, делящиеся на 2:

• … – 6, – 4, – 2, 2, 4, 6, …

• Рациональные числа: Дроби, такие как  или . Все целых чисел являются рациональными числами;  например, цифра 5 может быть записана как . Все рациональные числа можно записать в виде дробей, где a — целое число, а b — натуральное число. И конечные десятичные дроби (например, 0,5), и повторяющиеся десятичные дроби (например, 0,333…) также являются рациональными числами, поскольку в этой форме их можно записать в виде дробей.

• Иррациональные числа:  Числа, которые нельзя  записать в виде дробей, где a  – целое число, а  b  – натуральное число. (греческая буква пи) являются примерами иррациональных чисел.

Предыдущий Группировка символов и порядок операций

Следующий Викторина: Группы чисел

Вернуться к началу

Адам Беде

был добавлен в ваш список для чтения

!

OkUndo
   Управление моим списком чтения×

Адам Беде

добавлен в ваш список чтения

!

Хорошо    Управление списком чтения×

Удаление #книги# из вашего списка для чтения также удалит все закладки страниц, связанных с этим заголовком.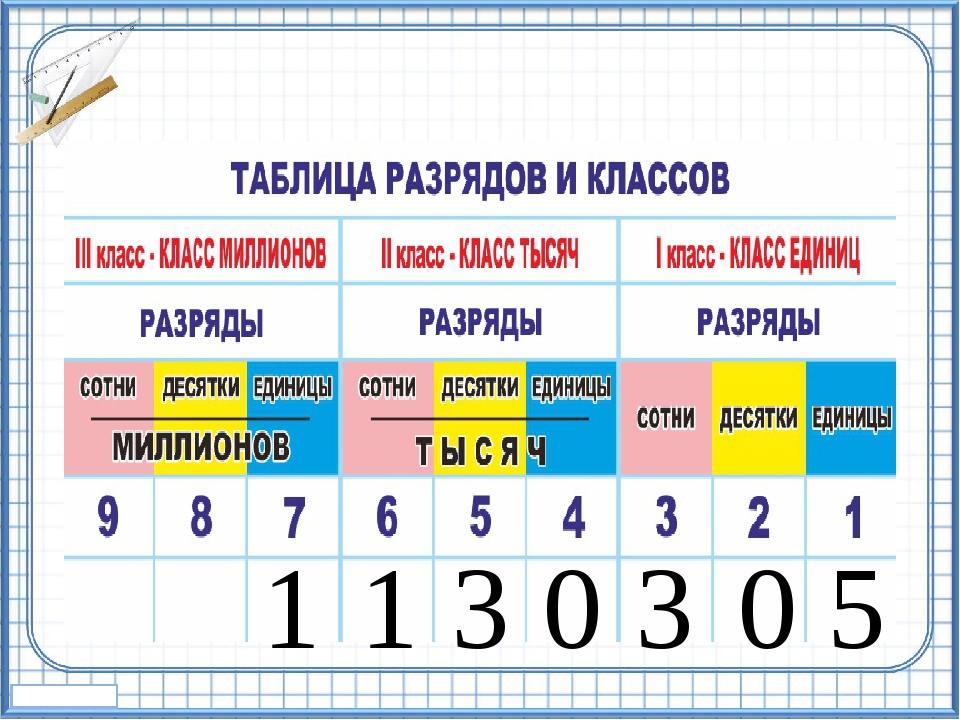

Вы уверены, что хотите удалить #bookConfirmation# и любые соответствующие закладки?

Удалить

Отменить

×

УДАЛЕННЫЙ

Базовая математика | Раздел Объяснение

Поиск по моему сайту:

Поделись этой страницей!

Деление как многократное вычитание

Деление является обратным умножению.

При умножении мы хотим узнать сумму групп чисел .

В приведенном ниже примере мы хотим узнать сумму 4 групп по 8 .

При делении мы хотим разделить сумму на несколько групп и узнать, сколько человек в каждой группе.

В приведенном ниже примере мы хотим узнать, сколько человек в каждой группе, если мы разделим 72 на 4 равные группы?

(Часть 2) Подробнее о разделе

Словарь раздела

Раздел с остатком

Длинный раздел

Посмотрите видео с обзором отдела.

Деление также можно объяснить следующим образом: мы хотим разделить сумму на группы определенного числа и хотим знать, сколько имеется групп.

В приведенном ниже примере мы хотим узнать, сколько групп по 4 можно получить из 36?

Распечатайте и вырежьте эти карточки.

Содержание

Разделить на равные группы

Вот как вы научите своего ребенка делить число на равные группы.

Разделим 12 на 3 равные группы. Сколько в каждой группе?

Дайте ребенку 12 жетонов (для иллюстрации я буду использовать морские ракушки) и разделите их следующим образом:

1. Начните с 12.

(Не обязательно ставить их в ряд.)

2. Возьмите один кусок и отложить в сторону.

3. Возьмите еще один кусок и положите его во вторую стопку.

4. Возьмите следующий кусок и положите его в третью стопку.

Теперь у нас есть 3 стопки или группы.

5. Положите четвертую часть обратно в первую стопку.

Продолжайте помещать фишку в каждую группу, пока не будут израсходованы все 12 жетонов.

В каждой группе будет по 4 счетчика, поэтому 12 разделить на 3 равно 4.

Запишите это так: 12 ÷ 3 = 4

Содержание

Разделите число на группы

Здесь это еще один способ разделить.

Разделите 12 на группы по 3 человека. Сколько групп я получу? Другими словами, сколько троек входит в число 12?

Дайте ребенку 12 фишек, затем разделите их следующим образом:

1. Начните с 12.

2. Сгруппируйте их по три.

Вы получите 4 группы.

Еще раз, 12 разделить на 3 равно 4. Или 4 группы троек образуют 12.

Запишите это так: 12 ÷ 3 = 4

Деление как многократное вычитание

повторное вычитание.

Например, 12 ÷ 4 означает, сколько раз можно вычесть 4 из 12?

Резюме

Подробнее о дивизионе

Словарь от дивизии

Дивизион с оставшимся

Длинной дивизион

Факторы, наибольший общий фактор

Факторы.