Правила знаков в математике: Правила знаков

Содержание

Вся элементарная математика — Средняя математическая интернет-школа

Действия с отрицательными и положительными числами

Абсолютная величина (модуль). Сложение.

Вычитание. Умножение. Деление.

Абсолютная величина ( модуль ). Для отрицательного числа – это положительное число, получаемое от перемены его знака с « – » на « + »; для положительного числа и нуля – само это число. Для обозначения абсолютной величины (модуля) числа используются две прямые черты, внутри которых записывается это число.

П р и м е р ы : | – 5 | = 5, | 7 | = 7, | 0 | = 0.

Сложение :

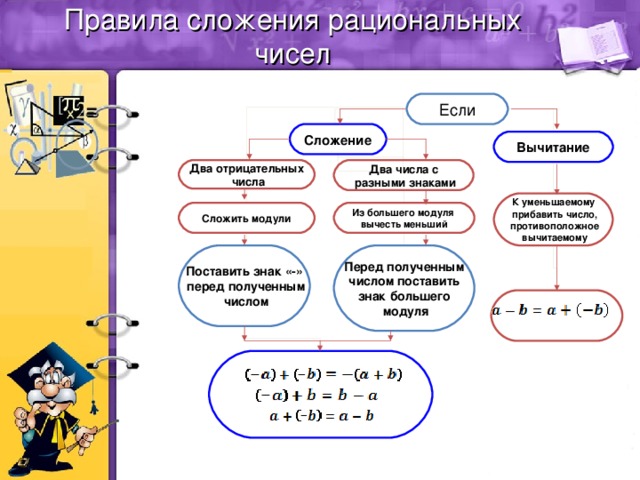
при сложении двух чисел с одинаковыми знаками складываются

их абсолютные величины и перед суммой ставится общий знак.

П р и м е р ы :

( + 6 ) + ( + 5 ) = 11 ;

( – 6 ) + ( – 5 ) = – 11 .

2) при сложении двух чисел с разными знаками их абсолютные

величины вычитаются ( из большей меньшая ) и ставится знак

числа с большей абсолютной величиной.

П р и м е р ы :

( – 6 ) + ( + 9 ) = 3 ;

( – 6 ) + ( + 3 ) = – 3 .

Вычитание. Можно заменить вычитание двух чисел сложением, при этом уменьшаемое сохраняет свой знак, а вычитаемое берётся с обратным знаком.

П р и м е р ы :

( + 8 ) – ( + 5 ) = ( + 8 ) + ( – 5 ) = 3;

( + 8 ) – ( – 5 ) = ( + 8 ) + ( + 5 ) = 13;

( – 8 ) – ( – 5 ) = ( – 8 ) + ( + 5 ) = – 3;

( – 8 ) – ( + 5 ) = ( – 8 ) + ( – 5 ) = – 13;

Умножение. При умножении двух чисел их абсолютные величины умножаются, а произведение принимает знак « + » , если знаки сомножителей одинаковы, и знак « – » , если знаки сомножителей разные.

Полезна следующая схема ( правила знаков при умножении ):

+ · + = +

+ · – = –

– · + = –

– · – = +

При умножении нескольких чисел ( двух и более ) произведение имеет знак « + » , если число отрицательных сомножителей чётно, и знак « – » , если их число нечётно.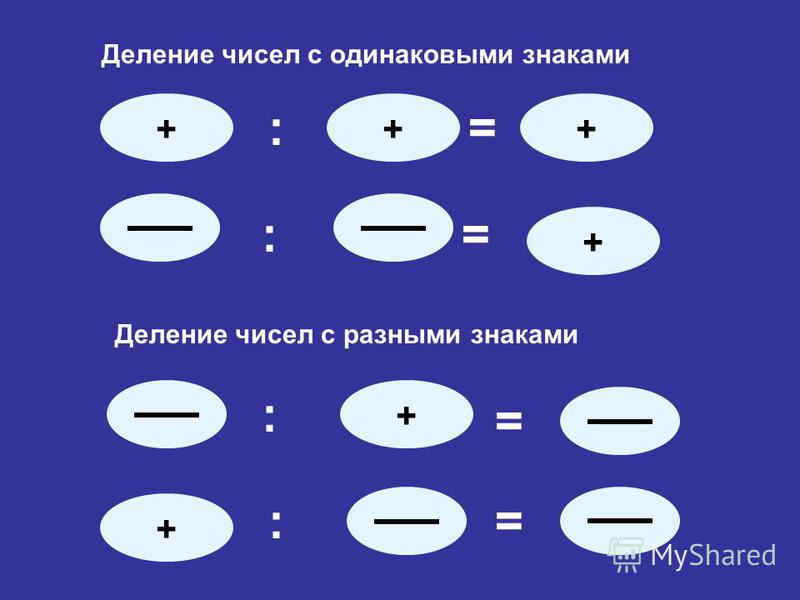

П р и м е р :

Деление.

При делении двух чисел абсолютная величина делимого делится на абсолютную величину делителя, а частное принимает знак « + » , если знаки делимого и делителя одинаковы, и знак « – » , если знаки делимого и делителя разные.

Здесь действуют те же правила знаков, что и при умножении :

+ : + = +

+ : – = –

– : + = –

– : – = +

П р и м е р : ( – 12 ) : ( + 4 ) = – 3 .

Символы математики | -matematika

Бесконечность. Дж.Валлис (1655).

Впервые встречается в трактате английского математика Джон Валиса «О конических сечениях».

Сложение, вычитание. Я.Видман (1489).

Знаки плюса и минуса придумали, по-видимому, в немецкой математической школе «коссистов» (то есть алгебраистов). Они используются в учебнике Яна (Йоханнеса) Видмана «Быстрый и приятный счёт для всех торговцев», изданном в 1489 году. До этого сложение обозначалось буквой p (от латинского plus «больше») или латинским словом et (союз «и»), а вычитание – буквой m (от латинского minus «менее, меньше»). У Видмана символ плюса заменяет не только сложение, но и союз «и». Происхождение этих символов неясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа вскоре получили общее распространение в Европе — за исключением Италии, которая ещё около века использовала старые обозначения.

Деление. И.Ран (1659), Г.Лейбниц (1684).

Уильям Оутред в качестве знака деления использовал косую черту /. Двоеточием деление стал обозначать Готфрид Лейбниц. До них часто использовали также букву D. Начиная с Фибоначчи, используется также горизонтальная черта дроби, употреблявшаяся ещё у Герона, Диофанта и в арабских сочинениях. В Англии и США распространение получил символ ÷ (обелюс), который предложил Иоганн Ран (возможно, при участии Джона Пелла) в 1659 году. Попытка Американского национального комитета по математическим стандартам (National Committee on Mathematical Requirements) вывести обелюс из практики (1923) оказалась безрезультатной.

Факториал. К.Крамп (1808).

Факториал числа n (обозначается n!, произносится «эн факториал») – произведение всех натуральных чисел до n включительно: n! = 1·2·3·…·n. Например, 5! = 1·2·3·4·5 = 120. По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел. Факториал числа n равен числу перестановок из n элементов. Например, 3! = 6, действительно,

♣ ♥ ♦

♣ ♦ ♥

♥ ♣ ♦

♥ ♦ ♣

♦ ♣ ♥

♦ ♥ ♣

– все шесть и только шесть вариантов перестановок из трёх элементов.

Термин «факториал» ввёл французский математик и политический деятель Луи Франсуа Антуан Арбогаст (1800), обозначение n! – французский математик Кристиан Крамп (1808).

Равенство. Р.Рекорд (1557).

Знак равенства предложил уэльский врач и математик Роберт Рекорд в 1557 году; начертание символа было намного длиннее нынешнего, так как имитировало изображение двух параллельных отрезков. Автор пояснил, что нет в мире ничего более равного, чем два параллельных отрезка одинаковой длины. До этого в античной и средневековой математике равенство обозначалось словесно (например est egale). Рене Декарт в XVII веке при записи стал использовать æ (от лат. aequalis), а современный знак равенства он использовал чтобы указать, что коэффициент может быть отрицательным. Франсуа Виет знаком равенства обозначал вычитание. Символ Рекорда получил распространение далеко не сразу. Распространению символа Рекорда мешало то обстоятельство, что с античных времён такой же символ использовался для обозначения параллельности прямых; в конце концов было решено символ параллельности сделать вертикальным.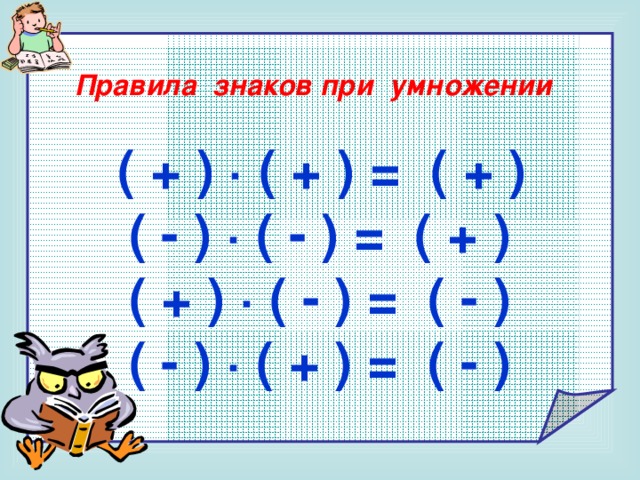 В континентальной Европе знак «=» был введён Готфридом Лейбницем только на рубеже XVII–XVIII веков, то есть более чем через 100 лет, после смерти впервые использовавшего его для этого Роберта Рекорда.

Перпендикулярность. П.Эригон (1634).

Перпендикулярность – взаимное расположение двух прямых, плоскостей или прямой и плоскости, при котором указанные фигуры составляют прямой угол. Знак ⊥ для обозначения перпендикулярности ввёл в 1634 году французский математик и астроном Пьер Эригон. Понятие перпендикулярности имеет ряд обобщений, но всем им, как правило, сопутствует знак ⊥.

Пересечение, объединение. Дж.Пеано (1888).

Пересечение множеств – это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам. Объединение множеств – множество, содержащее в себе все элементы исходных множеств. Пересечением и объединением называются и операции над множествами, ставящие в соответствие некоторым множествам новые по указанным выше правилам. Обозначаются ∩ и ∪, соответственно. Например, если

А={♠ ♣ ♥} и В={♣ ♥ ♦},

то

А∩В={♣ ♥}

А∪В={♠ ♣ ♥ ♦}.

Автором знаков ∩ и ∪ является итальянский математик Джузеппе Пеано. Впервые они были использованы в 1888 году.

Квантор всеобщности, квантор существования. Г.Генцен (1935), Ч.Пирс (1885).

Квантор – общее название для логических операций, указывающих область истинности какого-либо предиката (математического высказывания). Философы давно обращали внимание на логические операции, ограничивающие область истинности предиката, однако не выделяли их в отдельный класс операций. Хотя кванторно-логические конструкции широко используются как в научной, так и в обыденной речи, их формализация произошла только в 1879 году, в книге немецкого логика, математика и философа Фридриха Людвига Готлоба Фреге «Исчисление понятий». Обозначения Фреге имели вид громоздких графических конструкций и не были приняты. Впоследствии было предложено множество более удачных символов, но общепринятыми стали обозначения ∃ для квантора существования (читается «существует», «найдётся»), предложенное американским философом, логиком и математиком Чарльзом Пирсом в 1885 году, и ∀ для квантора всеобщности (читается «любой», «каждый», «всякий»), образованное немецким математиком и логиком Герхардом Карлом Эрихом Генценом в 1935 году по аналогии с символом квантора существования (перевёрнутые первые буквы английских слов Existence (существование) и Any (любой)). Например, запись

(∀ε>0) (∃δ>0) (∀x≠x0, |x–x0|<δ) (|f(x)–A|<ε)

читается так: «для любого ε>0 существует δ>0 такое, что для всех х, не равных х0 и удовлетворяющих неравенству |x–x0|<δ, выполняется неравенство |f(x)–A|<ε».

Еще символы

Источник: http://math5school.ru/

Отношение длины окружности к диаметру. У.Джонс (1706), Л.Эйлер (1736).

Математическая константа, иррациональное число. Число «пи», старое название – лудольфово число. Как и всякое иррациональное число, π представляется бесконечной непереодической десятичной дробью:

π=3,141592653589793…

Впервые обозначением этого числа греческой буквой π воспользовался британский математик Уильям Джонс в книге «Новое введение в математику», а общепринятым оно стало после работ Леонарда Эйлера. Это обозначение происходит от начальной буквы греческих слов περιφερεια – окружность, периферия и περιμετρος – периметр. Иоганн Генрих Ламберт доказал иррациональность π в 1761 году, а Адриен Мари Лежандр в 1774 году доказал иррациональность π2. Лежандр, и Эйлер предполагали, чтоπ может быть трансцендентным, т.е. не может удовлетворять никакому алгебраическому уравнению с целыми коэффициентами, что было в конечном итоге доказано в 1882 году Фердинандом фон Линдеманом.

Умножение. У.Оутред (1631), Г.Лейбниц (1698).

Знак умножения в виде косого крестика ввёл в 1631 году англичанин Уильям Оутред. До него использовали чаще всего букву M, хотя предлагались и другие обозначения: символ прямоугольника (французский математик Эригон, 1634), звёздочка (швейцарский математик Иоганн Ран, 1659). Позднее Готфрид Вильгельм Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у немецкого астронома и математика Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560 –1621).

Процент. М. де ла Порт (1685).

Сотая доля целого, принимаемого за единицу. Само слово «процент» происходит от латинского «pro centum», что означает в переводе «на сто». В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращённо от cento). Однако наборщик принял это «cto» за дробь и напечатал «%». Так из-за опечатки этот знак вошёл в обиход.

Модуль, абсолютная величина. К.Вейерштрасс (1841).

Модуль, абсолютная величина действительного числа х – неотрицательное число, определяемое следующим образом: |х| = х при х ≥ 0, и |х| = –х при х ≤ 0. Например, |7| = 7, |– 0,23| = –(–0,23) = 0,23. Модуль комплексного числа z = a + ib – действительное число, равное √(a2 + b2).

Считают, что термин «модуль» предложил использовать английский математик и философ, ученик Ньютона, Роджер Котс. Готфрид Лейбниц тоже использовал эту функцию, которую называл «модулем» и обозначал: mol x. Общепринятое обозначение абсолютной величины введено в 1841 году немецким математиком Карлом Вейерштрассом. Для комплексных чисел это понятие ввели французские математики Огюстен Коши и Жан Робер Арган в начале XIX века. В 1903 году австрийский учёный Конрад Лоренц использовал эту же символику для длины вектора.

Примерно равно, приблизительно равно. А.Гюнтер (1882).

Знак «≈» ввёл в использование как символ отношения «примерно равно» немецкий математик и физик Адам Вильгельм Зигмунд Гюнтер в 1882 году.

Больше, меньше. Т.Гарриот (1631).

Эти два знака ввёл в использование английский астроном, математик, этнограф и переводчик Томас Гарриот в 1631 году, до этого использовали слова «больше» и «меньше».

Параллельность. У.Оутред (посмертное издание 1677 года).

Параллельность – отношение между некоторыми геометрическими фигурами; например, прямыми. Определяется по-разному в зависимости от различных геометрий; например, в геометрии Евклида и в геометрии Лобачевского. Знак параллельности известен с античных времён, его использовали Герон и Папп Александрийский. Сначала символ был похож на нынешний знак равенства (только более протяжённый), но с появлением последнего, во избежание путаницы, символ был повёрнут вертикально ||. В таком виде он появился впервые в посмертном издании работ английского математика Уильяма Оутреда в 1677 году.

Содержится, содержит. Э.Шрёдер (1890).

Если А и В – два множества и в А нет элементов, не принадлежащих В, то говорят что А содержится в В. Пишут А⊂В или В⊃А (В содержит А). Например,

{♠}⊂{♠ ♣}⊂{♠ ♣ ♥ ♦}

{♠ ♣ ♥ ♦}⊃{♥ ♦}⊃{♦}

Символы «содержится» и «содержит» появились в 1890 году у немецкого математика логика Эрнста Шрёдера.

Принадлежность. Дж.Пеано (1895).

Если а – элемент множества А, то пишут а∈А и читают «а принадлежит А». Если а не является элементом множества А, пишут а∉А и читают «а не принадлежит А». Вначале отношения «содержится» и «принадлежит» («является элементом») не различали, но со временем эти понятия потребовали разграничения. Знак принадлежности ∈ впервые стал использовать итальянский математик Джузеппе Пеано в 1895 году. Символ ∈ происходит от первой буквы греческого слова εστι – быть.

Пустое множество. Н.Бурбаки (1939).

Множество, не содержащее ни одного элемента. Знак пустого множества был введён в книгах Николя Бурбаки в 1939 году. Бурбаки – коллективный псевдоним группы французских математиков, созданной в 1935 году. Одним из участников группы Бурбаки был Андре Вейль – автор символа Ø.

Что и требовалось доказать. Д.Кнут (1978).

В математике под доказательством понимается последовательность рассуждений, построеных на определённых правилах, показывающая, что верно некоторое утверждение. Со времён эпохи Возрождения окончание доказательства обозначалось математиками сокращением «Q.E.D.», от латинского выражения «Quod Erat Demonstrandum» – «Что и требовалось доказать». При создании системы компьютерной вёрстки ΤΕΧ в 1978 году американский профессор информатики Дональд Эдвин Кнут использовал символ: заполненный квадрат, так называемый «символ Халмоша», по имени американского математика венгерского происхождения Пола Ричарда Халмоша. Сегодня завершение доказательства как правило обозначают Символом Халмоша. В качестве альтернативы используют и другие знаки: пустой квадрат, правый треугольник, // (две косых черты), а также русскую аббревиатуру «ч.т.д.».

Бесплатная онлайн-игра для решения смешанных операций на время для детей

Добавить игру в избранное

Это онлайн-игра для решения смешанных операций на время для детей. Каждый вопрос представляет собой уравнение с ответом и недостающим математическим символом. Вы должны выбрать правильный математический символ из «+», «-», «x» или «÷». Игра отрабатывает решение задач на сложение, вычитание, умножение и деление. Каждый правильный ответ будет увеличивать ваш счет. Если вы получите неправильный ответ, он будет вычтен из ваших баллов. У игроков есть 1 минута, чтобы решить как можно больше математических уравнений. По истечении времени результаты показывают ваш общий балл.

Решите как можно больше вопросов за отведенное время. У вас есть 1 минута, чтобы правильно ответить на вопросы.
Выберите правильный математический символ для уравнения. Выберите «+», «-», «x» или «÷».
Правильный ответ добавляет очки. Между тем, неправильные ответы будут вычитать баллы из вашего счета.
Отвечайте как можно быстрее. Ответ на вопрос автоматически перенаправит вас к следующему вопросу.

Игра заканчивается, когда время истекает. Ваш счет отображается в конце игры.

Общая сумма

Дизайн

Сложность

Повтор

Играть в математические знаки Онлайн игра для решения арифметических задач

Дети и школьники могут играть в эту математическую онлайн-игру на скорость, щелкнув в окне ниже.

Кроме того, дети и студенты могут играть в эту бесплатную онлайн-игру для решения уравнений и смешанных операций в качестве веб-приложения здесь.

Математические знаки Игра Бесплатные онлайн игры с расчетом чисел на время Инструкции по игре

Запуск игры
- Нажмите зеленую кнопку Play, расположенную внизу экрана. Это приведет вас прямо к игре.
- Будьте готовы, так как таймер запускается, как только появляется слово «Готов?» исчезает, а «Go» уменьшается.
- Игрокам дается 1 минута, чтобы решить как можно больше математических задач.
Управление игрой
- Выберите правильный математический символ из вариантов внизу игры.
- Мышь
  - Щелкните левой кнопкой мыши правильный математический символ для уравнения. Выберите «+», «-», «x» или «÷».
  - Щелкнув по ответу, вы сразу же увидите, правильный или неправильный выбранный вами ответ.
  - Следующий вопрос отображается, как только вы выбираете ответ.
- Сенсорный экран
  - Нажмите на правильный математический символ для уравнения. Выберите «+», «-», «x» или «÷».
  - Нажатие на ответ сразу же покажет, правильный или неправильный выбранный вами ответ.
  - Следующий вопрос отображается сразу после выбора ответа.
Другие кнопки открытия экрана
- В верхнем левом углу экрана есть 2 кнопки социальных сетей:
  - Значок «F» — это кнопка Facebook. Выберите его, чтобы посетить учетную запись разработчика в Facebook.
  - Значок птицы — это кнопка Twitter. Выберите его, чтобы посетить учетную запись разработчика в Twitter.
- В правом верхнем углу экрана есть 2 кнопки:
  - Значок контроллера — это кнопка игры. Выберите его, чтобы посетить другие игры.
  - Значок мегафона — это кнопка «Аудио». Выберите его, чтобы включить или выключить игровую музыку.
- Внизу находится кнопка КРЕДИТЫ. Выберите его, чтобы просмотреть команду Math Signs Game.
Экран результатов игры
- Страница результатов появляется по истечении 1-минутного таймера.
- Показывает ваш текущий счет и лучший результат.
- Ваш веб-браузер сохраняет ваш рекорд каждый раз, когда вы побиваете свой предыдущий рекорд.
- В левом нижнем углу экрана есть 2 кнопки:.
  - Первая кнопка — это кнопка «Домой». Выберите его, чтобы вернуться к экрану приветствия.
  - Вторая кнопка — это кнопка повтора. Выберите его, чтобы сбросить настройки и снова начать игру.
Стратегия
- Эта обучающая математическая игра представляет собой 1-минутную игру для решения уравнений на время для детей.
- Это бросает вызов вашим навыкам быстрого счета. Вам нужно выбрать правильный символ, чтобы завершить уравнение. Выберите из «+», «-», «x» или «÷».
- Следующий вопрос появится, как только вы выберете ответ. Это также покажет вам, если вы выбрали правильный или неправильный ответ сразу.
  - Постарайтесь получить как можно больше правильных ответов за отведенное время. Правильные ответы принесут более высокие баллы, а неправильные ответы вычтут баллы из вашего счета.
  - Как и в случае с обычным тестом или текстом, вы не можете получить отрицательную оценку. Но вы должны работать над получением более высоких баллов.
  - Вы можете приостановить игру, выбрав другую вкладку. Но гораздо лучше постоянно играть в игру, чтобы бросить себе вызов.
  - Вопросы генерируются случайным образом, поэтому нет смысла запоминать порядок для каждой игры.
  - Тем не менее, стоит продолжать играть, чтобы тренировать свои арифметические навыки. Знание правильного ответа каждый раз, когда уравнение мигает, также помогает.
  - Чем чаще вы играете в игру, тем лучше вы будете помнить ответы на определенные математические уравнения. Это поможет вам быстрее отвечать на вопросы.
- Уравнения состоят из простых математических вопросов. С ним должны справиться учащиеся, имеющие базовые знания о сложении, вычитании, умножении и делении.
- Играйте с друзьями или одноклассниками и сравнивайте результаты. Это отличная головоломка, которая поможет учащимся отточить свои математические навыки с помощью различных операций.