Решения задачи по математике: Решебник по математике, решение примеров и задач

Урок 28. решение задач. проверка решения задачи — Математика — 2 класс

Математика, 2 класс

Урок №28. Решение задач. Проверка решения задачи

Перечень вопросов, рассматриваемых в теме:

— Как проверить решение задачи?

— Как моделировать текст задачи табличным способом?

Глоссарий по теме:

Задача – это упражнение, которое выполняется посредством умозаключения, вычисления.

Выражение – формула, выражающая какие–либо математические отношения.

Обратные задачи – это задачи, в которых число и результат меняются местами (известное становится неизвестным, а неизвестное известным).

Основная и дополнительная литература по теме урока:

1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. – 8-е изд. – М.: Просвещение, 2017. – с88, 89.
2. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.1/М. И. Моро, М.А.Бантова – 6-е изд., дораб. – М.: Просвещение, 2016. – с.62.
3. Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. М. И. Моро, С. И. Волкова – 9-е изд. – М.: Просвещение, 2014. – с.23, 24.
4. Математика. Тетрадь учебных достижений. Учебное пособие для общеобразовательных организаций. С. И. Волкова – М.: Просвещение, 2017. – с.34, 35.

Теоретический материал для самостоятельного изучения

Действия сложение и вычитание связаны друг с другом, являются взаимно обратными действиями.

СЛОЖЕНИЕ

ВЫЧИТАНИЕ

Вы помните, что в математике существуют обратные задачи. Они нам помогут при проверке решения. Обратные задачи должны обладать следующими признаками: сходный сюжет задач, число и результат меняются местами (известное становится неизвестным, а неизвестное известным).

Вы уже умеете выполнять проверку сложения и вычитания двумя способами. Вспомним эти правила.

Для проверки сложения надо из значения суммы вычесть одно из слагаемых. Если в результате вычитания получается другое слагаемое, значит, сложение выполнено верно

Для проверки вычитания, надо к значению разности прибавить вычитаемое. Если в результате сложения получается уменьшаемое, значит, вычитание выполнено верно.

Для проверки вычитания, надо из уменьшаемого вычесть разность. Если в результате получается вычитаемое, значит, вычитание выполнено верно.

Решим задачу и на её примере выполним проверку решения.

Папа поймал на рыбалке 6 окуней и 8 лещей. Сколько всего рыб поймал папа?

Чтобы узнать, сколько всего рыбы поймал папа, сложим количество окуней и лещей.

8 + 6 = 14 (р.) всего поймал папа.

Выполним проверку обратным действием.

Проверка: 14 – 6 = 8 (р.)

8 – это количество лещей, которых поймал папа. Значит, задачу решили верно.

Это действие является решением обратной задачи:

Папа поймал на рыбалке 14 окуней и лещей. Окуней было 6. Сколько лещей поймал папа?

Значит, чтобы проверить решение задачи, можно решить обратную задачу.

Теперь рассмотрим, как представить текст задачи в таблице. Прочитайте задачу.

Выделим главные слова в этой задаче, которые показывают действия, совершаемые с карандашами. Это слова: было, взяли, положили, стало.

Начертим таблицу из четырёх столбиков и двух строк. Запишем главные слова и вставим данные и вопрос.

БЫЛО	ВЗЯЛИ	ПОЛОЖИЛИ	СТАЛО
24 к.	? к.	3 к.	17 к.

Решим задачу. Сначала узнаем, сколько стало карандашей, когда их положила сестра.

24 + 3 = 27 (к.)

Теперь узнаем, сколько карандашей взял брат, если их осталось только семнадцать.

27 – 17 = 10 (к.)

Выполним проверку другим способом. Подставим в таблицу все данные и запишем выражение к задаче.

БЫЛО	ВЗЯЛИ	ПОЛОЖИЛИ	СТАЛО
24 к.	10 к.	3 к.	17 к.

Проверка: 24 – 10 + 3 = 17 (к.)

Получили верное равенство, значит, задачу решили верно.

Вывод: Чтобы выполнить проверку решения задачи можно подставить полученные данные в условие или проверить правильность вычислений обратным действием. Текст задачи можно моделировать разными способами: в виде схематического чертежа, таблицы, диаграммы.

Тренировочные задания.

1.Подберите обратные задачи к задаче: «В книге 48 страниц. Таня прочитала 30 страниц. Сколько страниц этой книги осталось прочитать Тане?»

Правильные ответы:

1 задача и 3 задача

2. Выберите для каждой задачи все выражения для её решения.

13 – (7 + 5)

13 – 5 + 7

7 – 5 + 13

13 – 7 – 5

(13 + 7) – 5

Правильные ответы:

13 – 5 + 7

7 – 5 + 13

13 – 7 – 5

13 – (7 + 5)

(13 + 7) – 5

Пример оформления задач по математике *

Умение решать задачи по математике – обязательное условие для студентов физмата, поэтому большинство обучающихся успешно с ними справляется. Проблемы, чаще всего, возникают именно из-за неправильного оформления условия, решения, записи слов, числовых значений и т.д. Чтобы избежать таких ситуаций, необходимо вспомнить, как записываются задачи.

Общие требования

Преподаватели вуза нередко снижают оценки своим студентам за помарки, описки, неполную запись, отступление от общепринятых международных сокращений. Работа, в ряде случаев, вообще может быть не зачтена, что чревато задолженностью и обострением отношений. Чтобы этого не произошло, нужно учесть ряд таких нюансов:

1. Слова, числовые значения аккуратно и разборчиво записываются синей (или черной, по требованию вуза) пастой.

2. Графические элементы (к примеру, для краткой записи в виде рисунков, таблиц, чертежей, схем, графиков) – только простым хорошо заточенным карандашом. Если нужно получить ровные линии, обязательно используется линейка. Для построения окружностей применяют циркуль, элипсообразных фигур – шаблон. От руки делать этого не стоит.

3. Чтобы записать решение, нужно отступить одну клетку от условия (краткой записи). Если предстоит решить задачу на доказательство или построение, нередко употребляются слова «следовательно», «значит», «параллельно». Они должны записываться только буквами, замена математическим знаком не допускается.

4. Все действия нумеруются, результаты записываются как числом, так и словами (в скобках, сокращенно, не забывая о международных сокращениях: кг, дм, см и т.д.). Отступы между ними также обязательны (1 клетка).

5. После каждого действия (за исключением последнего) нужно письменно давать пояснения. Если необходимо сократить слово, следует учесть, что последним должен быть согласный звук. После гласного точку ставить нельзя.

6. Необходимо правильно располагать математические знаки в строке. Перенести формулу или выражение (при необходимости) можно только, если делается это на сложении, вычитании, умножении, равенстве. На следующей строке эти же знаки снова дублируются. Учтите, что нельзя разрывать дробь.

7. Запись ответа (вывода) производится без сокращений, но максимально лаконично и понятно.ошибки в оформлении задач

Распространенные ошибки при оформлении задач по математике

Решение задачи должно быть правильным, без математических и логических ошибок, и это даже не обсуждается. Однако на практике не всегда получается идеальный результат. Допускаются как грубые (из-за которых существенно снижется оценка), так и несущественные ошибки (не мешают учащемуся получить правильный ответ). Как их различают?

К существенной ошибке преподаватель отнесет незнание формулы, правила, математического понятия, утверждения или неумение применить на практике полученные в рамках программы знания. К примеру, ошибочное построение графика элементарной функции, выбор неактуальных для конкретной задачи методов, способов и приемов решения.

Не грубыми называют ошибки, которые несущественно влияют на ход решения: некоторые неправильно произведенные вычисления, механическая описка, недостаточно полная формулировка вопроса, математического утверждения. Сюда же относят небрежность в словесном и графическом оформлении, наличие грамматических ошибок.

Следует избегать логических ошибок, характерных для рассуждений и доказательств. Они вызваны непониманием условия, неумением доказывать «от противного» и рядом других причин.

Обратите внимание!

1. Точные изображения. При решении геометрических задач в большинстве случаев обязателен рисунок. Если изображение выполнено небрежно, не дает полного представления о фигуре и возможности провести дополнительные действия (построения), оно верным не считается. А это, практически, 1/3 задания!

2. Обоснованность решения. Если решение задачи сопровождается пояснительным текстом, в нем должны прозвучать отсылки к необходимым аксиомам, теоремам. В то же время, важно указывать существенные данные, те, которые не очевидны по ходу выполнения задания. При отсутствии обоснования конечный результат может быть неверным.

3. Полнота. Учащиеся нередко стараются как можно короче и лаконичнее написать ход решения задачи. В ряде случаев такая «экономия» негативно сказывается на конечном результате – оценке. Если в задаче необходимо более подробно расписать полученный итог, это нужно сделать. В противном случае отсутствие полноты решения будет зачтено как существенный недостаток.

4. Рациональное решение. При выполнении задания может оказаться, что оно выполняется несколькими способами. Ученику необходимо выбрать наиболее рациональный вариант.

5. Грамотность. Многие ошибочно полагают, что для математики грамотность – это не главное. На самом деле преподаватель, увидев орфографические или пунктуационные ошибки, должен их исправить, что, несомненно испортит общую картину, даже если задача решена идеально.

Как подготовиться к решению задач с параметром на ЕГЭ

Личный кабинет

8 800 551-50-78 (бесплатно)

Онлайн подготовка к ЕГЭ-2023 по профильной математике

Подготовьтесь к ЕГЭ на 80+ баллов. Смотрите видео, читайте теорию, занимайтесь на онлайн-тренажерах

1С:Репетитор

8 800 551-50-78

Личный кабинет

1С:Репетитор – подготовка к ЕГЭ по математике

© ООО «1С-Софт» | ЧОУ ДПО «1С-ОБРАЗОВАНИЕ» | 2016–2022

8 800 551-50-78

Связаться с нами:

Главная

Задача с параметром – для обычного школьника одна из самых сложных задач варианта КИМ ЕГЭ: в программах по математике для общеобразовательных школ (за исключением профильных и специализированных классов, школ и лицеев) таким задачам либо не уделяется должного внимания, либо они не рассматриваются вовсе. Несмотря на это, знание набора методов и подходов к решению таких задач и определенная практика их решения позволяют продвинуться в решении задачи с параметром достаточно далеко и если уж не решить ее полностью, то хотя бы получить за нее некоторое количество баллов на экзамене.

Ранее, до появления единого государственного экзамена, задачи с параметрами входили в варианты вступительных экзаменов по математике в ведущие вузы, а сегодня входят в вариант КИМ ЕГЭ профильного уровня. Дело в том, что эти задачи обладают высокой диагностической ценностью: они позволяют не только определить, насколько хорошо выпускник знает основные разделы школьного курса математики, но и проверить, насколько высок уровень его математического и логического мышления, насколько сильны первоначальные навыки математической исследовательской деятельности, а главное – насколько успешно он сможет овладеть курсом математики в вузе.

«Научите меня решать задачи с параметром», – такую просьбу я часто слышу от своих учеников. Что ж, эта задача потребует от выпускника немало интеллектуальных усилий. С чего начать изучение? С освоения методов решения задач с параметром. Собственно, если вы внимательно читали наши рекомендации, как подготовиться к решению сложных задач варианта КИМ ЕГЭ, то заметили, что это универсальный совет. Именно так построен наш курс «1С:Репетитор»: изучаем как можно более широкий спектр методов и приемов решения задач и тренируемся в применении этих методов на практике.

Чему нужно научиться, решая задачи с параметром

В первую очередь – правильно применять равносильные преобразования уравнений, неравенств и их систем. То есть понять, при каких ограничениях, накладываемых на параметр, можно выполнять то или иное преобразование. Лучше всего начать с заданий вида: «Для каждого значения параметра решить…» и рассмотреть по возможности все основные элементарные функции, встречающиеся в школьном курсе математики.

Если с несложными задачами такого вида школьник справляется неплохо, то можно переходить к изучению аналитических методов решения задач, содержательно усложняя и классифицируя задачи с точки зрения применения к ним этих методов исследования. Имеется в виду знакомство с подходами к решению задач, содержащих формулировки типа: «При каких значениях параметра уравнение (неравенство, система) имеет одно (два, три, бесконечно много и т. д.) решений», «При каких значениях параметра решением уравнения (неравенства, системы) является некоторое подмножество множества действительных чисел» и т.д.

Следующий шаг, который мы рекомендуем, – тщательно изучить схему исследования квадратичной функции. Поскольку квадратичная функция является одной из самых хорошо изученных в школьном курсе математики, на ее основе можно предложить большое количество исследовательских задач, разнообразных по форме и содержанию, чем и пользуются составители вариантов КИМ ЕГЭ.

Мы рекомендуем подойти к рассмотрению данных задач по следующей схеме:

задачи, основанные на свойствах дискриминанта и старшего коэффициента квадратного трехчлена;

применение теоремы Виета в задачах с параметром;

расположение корней квадратного трехчлена относительно заданных точек;

более сложные задачи, сводящиеся к исследованию квадратного трехчлена.

Следующая тема курса – графические методы решения задач с параметром

Существует два принципиально различных подхода – построение графиков функций или уравнений в плоскости (x; y) или в плоскости (x; a). Кроме того, для графического метода решения задач с параметром в плоскости (x; y) необходимо рассмотреть различные виды преобразования графиков – обычно это параллельный перенос, поворот прямой и гомотетия. Есть класс задач, решение которых основано на аналитических свойствах функций (области определения, области значений, четности, периодичности и т.д.), эти свойства и приемы их использования тоже нужно знать.

На этом перечень методов решения задач с параметрами, разумеется, не заканчивается, но анализ вариантов КИМ ЕГЭ профильного уровня и практика показывают, что в настоящее время этого достаточно для успешного решения задачи № 18 на экзамене.

В заключение отметим, что выстроить подобный курс самостоятельно, без преподавателя, обычный школьник не сможет, даже имея под рукой хорошие учебные пособия по методам решения задач с параметром. Здесь необходима помощь опытного наставника, который сможет подобрать нужные задачи и выстроить траекторию движения школьника по ним.

Заметим, кстати, что весьма эффективным инструментом для изучения именно методов решения задач с параметром являются интерактивные тренажеры с пошаговым разбором решения.

Работая с таким тренажером, школьник одновременно учится выстраивать логику решения задачи с параметром и контролирует правильность выполнения каждого шага решения. Это очень важное умение, так как одна из основных сложностей в решении задачи с параметром состоит в том, что необходимо на каждом шаге решения понимать, что означают уже полученные результаты и что (в зависимости от этих результатов) еще остается сделать, чтобы довести решение до конца.

Регулярно тренируйтесь в решении задач

Чтобы начать заниматься на портале «1С:Репетитор», достаточно Зарегистрироваться.
Вы можете:

• Начать заниматься бесплатно.
• Купить доступ к этой задаче в составе экспресс-курса «Алгебра» и научиться решать задачи №13, №15, №17, №18 и №19 на максимальный балл.

Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Включают теорию в форме текстов, слайдов и видео, задачи с решениями, интерактивные тренажеры, модели, и тесты.

Остались вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.

Здесь ключевые фразы, чтобы поисковые роботы лучше находили наши советы:
Разбор задач с параметрами из ЕГЭ по математике, по теме задачи с параметром ЕГЭ, как решать задание 18 в экзамене ЕГЭ, задачи с параметром ЕГЭ, задания с параметром ЕГЭ, задача 18 ЕГЭ, модуль и окружности, решение параметров ЕГЭ, решение задачи 18, система уравнений с параметром, научиться решать задачи с параметрами, сложных задач варианта КИМ ЕГЭ, начертить графики функций, ЕГЭ по математике профильного уровня, методы решения уравнений и неравенств, выпускникам 11 класса в 2018 году, поступающим в технический вуз.

Алгоритм решения задач по физике — 4ЕГЭ

18 декабря 2015

В закладки

Обсудить

Жалоба

Физика

Pеклaмa Бесплатные уроки для подготовки к ЕГЭ каждый день от MAXIMUM Education →
Готовим к ЕГЭ бесплатно и проводим более 300 уроков в месяц по всем предметам. Начни учиться прямо сейчас!

Советы по основным типам заданий.

Алгоритм решения задач по физике
1. Внимательно прочти условие задачи.
2. Произведи краткую запись условия задачи с помощью общепринятых буквенных обозначений (СИ).
3. Выполни рисунки или чертежи задачи.
4. Определи, каким методом будет решаться задача.
5. Запиши основные уравнения, описывающие процессы, предложенные задачной системой.
6. Найди решение в общем виде, выразив искомые величины, через заданные.

7. Проверь правильность решения задачи в общем виде, произведя действия с наименованием величин.
8. Произведи вычисления.
9. Произведи оценку реальности полученного решения.
10. Запиши ответ.

Алгоритм решения задач по кинематике
1. Проанализировать условие задачи: определить движение тела и характер этого движения.
2. Записать краткое условие задачи в единицах СИ.
3. Сделать чертёж. Записать кинематические законы движения для тела в векторной форме.
4. Спроецировать векторные величины на оси х и у.
5. Вывести формулу для расчёта искомой величины.
6. Вычислить значение искомой величины.
7. Проконтролировать размерность и ответ.

Алгоритм решения задач по динамике
1. Проанализировать условие задачи: выяснить характер движения.
2. Записать краткое условие задачи в единицах СИ.

3. Сделать чертеж с указанием все сил, действующих на тело, векторы ускорений и системы координат.
4. Записать уравнение второго закона Ньютона в векторной форме.
5. Записать уравнение второго закона Ньютона в проекциях на оси координат с учетом направления осей координат и векторов.
6. Вывести формулу для расчёта искомой величины.
7. Вычислить значение искомой величины.
8. Проконтролировать размерность и ответ.

Алгоритм решения задач на применение закона сохранения импульса.
1. Проанализировать условие задачи: проверить систему взаимодействующих тел на замкнутость.
2. Записать краткое условие задачи в единицах СИ.
3. Изобразить на чертеже векторы импульсов тел системы до и после взаимодействия.
4. Записать закон сохранения импульса в векторной форме.
5. Спроецировать векторные величины на оси х и у; записать закон сохранения импульса в скалярной форме.

6. Вывести формулу для расчёта искомой величины.
7. Вычислить значение искомой величины.
8. Проконтролировать размерность и ответ.

Алгоритм решения задач на закон сохранения и превращения энергии
1. Проанализировать условие задачи: проверить систему взаимодействующих тел на замкнутость.
2. Записать краткое условие задачи в единицах СИ.
3.Сделать чертёж с указанием положения системы для различных моментов времени.
4. Записать формулы для определения полной механической энергии в начальный и конечный момент времени.
5. Вывести формулу для расчёта искомой величины.
6. Вычислить значение искомой величины.
7. Проконтролировать размерность и ответ.

Алгоритм решения задач на «Газовые законы»
1. Проанализировать условие задачи: выяснить, сколько состояний газа рассматривается в задаче.
2. Записать краткое условие задачи в единицах СИ.
3. Записать параметры p,V и T, характеризующие каждое состояние газа. Определить какой процесс произошёл.
4. Записать уравнение закон Клапейрона — Менделеева для данных состояний.
5. Вывести формулу для расчёта искомой величины.
6. Вычислить значение искомой величины.
7. Проконтролировать размерность и ответ.

Алгоритм решения задач на «Основы термодинамики»
1. Проанализировать условие задачи: проверить систему тел на замкнутость; определить, какие тела участвуют в теплообмене.
2. Записать краткое условие задачи в единицах СИ.
3. Определить для каждого тела, какие процессы с ним происходят при теплообмене.
4. Записать для каждого процесса формулу для вычисления количества теплоты, выделенной или поглощённой.
4. Составить уравнение теплового баланса.
5. Вывести формулу для расчёта искомой величины.
5. Вычислить значение искомой величины.
6. Проконтролировать размерность и ответ.

Алгоритм решения задач на тему «Электростатика»
1. Проанализировать условие задачи: выяснить, какая система зарядов создаёт электростатическое поле.
2. Записать краткое условие задачи в единицах СИ.
3. Сделать чертёж; определить направление векторов напряжённости, которые создаются в данной точке, каждым из зарядов.
4. Рассчитать модули векторов напряжённости.
5. Вывести формулу для расчёта искомой величины, используя принцип суперпозиции для напряжённости.
6. Вычислить значение искомой величины.
7. Проконтролировать размерность и ответ.

Способы проверки решения арифметических задач и вычислений | Методическая разработка по математике на тему:

Акимова Ольга Ивановна,

учитель ГБОУ школы №115 Выборгского района г. Санкт-Петербурга

Способы проверки решения арифметических  задач и вычислений

Методическая разработка

 Основное содержание начального курса математики составляют устные и письменные вычисления и решение арифметических задач. Умения вычислять и решать задачи имеют не только большое практическое значение, но и являются прекрасным средством углубления приобретённых детьми на уроках математики теоретических  знаний, служат  для развития творческого мышления учащихся, способствуют развитию у них сообразительности, внимания, гибкости и умственной самостоятельности.

 При выполнении вычислений и решении задач школьники допускают большое количество ошибок, исправление которых часто бывает, затруднено не только и не столько непониманием учеником природы ошибок, сколько неумением их обнаружить.

 Программа обучения математике в начальной школе предполагает знакомство с некоторыми видами проверки вычислений и арифметических задач, но проверка выполняется , если такое задание сформулировано в учебнике или данный вопрос в это время изучается специально.           Систематическая проверка ,как правило,  в школе не проводится. Решение задач и примеров заканчивается получением результата. Следствием этого является то, что дети не в состоянии проконтролировать свою деятельность, часто не замечают ошибок в ходе и результате решения.

Организуя проверку решения задачи, учитель должен помнить, что не все способы применимы к любой  задаче. В методической литературе выделяются следующие способы проверки арифметических задач:

• Составление и решение обратной задачи
• Решение задачи другим способом
• Прикидка результата

Из перечисленных способов особое внимание уделяется составлению и решению обратной задачи. Этот приём достаточно универсален, так как составить обратную задачу можно к любой исходной. Лучше этот приём использовать, начиная со 2 класса, так как при составлении обратной задачи  может получиться задача труднее, чем исходная.

Решение задачи другим способом — приём достаточно сложный, так как является творческим видом работы и не все учащиеся могут найти даже один способ решения задачи. Существуют приёмы, которые позволяют отыскать иной способ решения задачи:  построение иной модели задачи, чем та, которая была использована; дополнение условия задачи сведениями, не влияющими на результат решения; представление практического разрешения ситуации, описанной в задаче.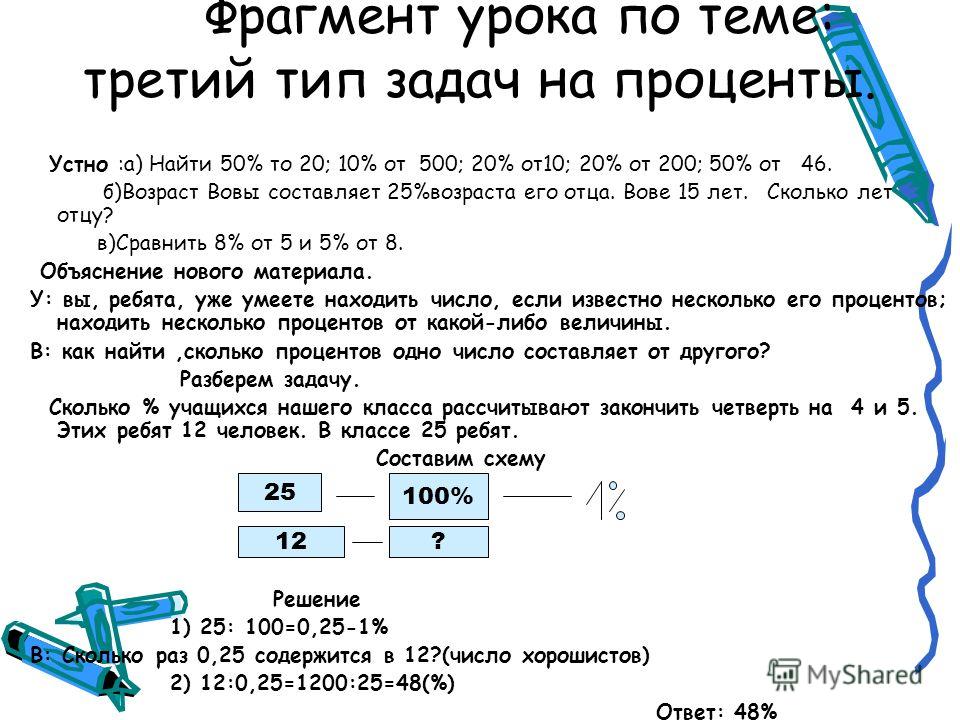 Эти приёмы представляются ученику в виде учебной задачи.

Самым элементарным способом проверки является прикидка – установление границ искомого числа. Предполагается вводить его уже в первом классе. Прикидка обычно проводится перед решением задачи, устанавливаются границы значений искомого числа. После получения ответа проверяют, удовлетворяет ли он выбранным границам. В случае несоответствия делают вывод о неправильности результата.

Применять этот способ можно как для простых, так и для составных задач. Данный способ является необходимой частью анализа задач в косвенной форме, в связи с тем, что еще до решения задачи нужно выяснить, какое число получится в ответе – больше или меньше данного.

Приёмы проверки решения арифметических задач легко переносятся на вычисления и выполняются с использованием тех же алгоритмов.

Умение проверять решение задач и вычисления способствует выработке потребности самоконтроля у младших школьников, оно не только порождает уверенность в правильности решения, но и позволяет глубже понять математическое содержание данных видов упражнений, осознать связи между этими упражнениями, формирует умение рассуждать, активизирует мыслительную деятельность детей.

Для эффективности усвоения приёмов проверки решения задач и вычислений созданы памятки, содержащие систему операций.

Памятка для проверки решения задачи способом составления и решения обратной задачи.

1. Решить прямую задачу
2. Подставить в текст задачи полученное число
3. Выбрать из данных задачи новое неизвестное число
4. Сформулировать новую задачу
5. Решить её
6. Сравнить полученное число с тем, которое было выбрано в качестве неизвестного
7. Сделать вывод о правильности решения задачи

Памятка для проверки вычислений способом составления и решения обратного примера

1. Реши исходный пример
2. Подставь в пример найденное число
3. Выбрать из данных примера новое неизвестное число
4. Запиши новый пример
5. Реши пример
6. Сравнить полученное число с тем, которое было выбрано в качестве неизвестного
7. Сделать вывод о правильности решения примера

Памятка для проверки решения задачи способом прикидки результата

1. Прочитай задачу
2. Выдели данное и искомое
3. Подумай, с каким  из чисел можно сравнить искомое
4. Подумай, какое число должно получиться в ответе, больше или меньше, чем данные
5. Реши задачу
6. Сравни полученный ответ с данным задачи
7. Сделать вывод о правильности решения задачи

Памятка для проверки вычислений способом прикидки результата

1. Прочитай исходный пример
2. Выдели данные и искомое
3. Подумай, с каким  из чисел можно сравнить искомое
4. Подумай, какое число должно получиться в ответе, больше или меньше, чем данные
5. Реши пример
6. Сравни полученный ответ с  данным  примера
7. Сделать вывод о правильности вычисления

Как с помощью Android решать задачи по математике и не только

Думаю, всем доводилось слышать, что компьютеры – это машины, которые способны решать самые сложные задачи. Но это теперь я знаю, о каких задачах шла речь, а в детстве мне казалось, что можно подсунуть компьютеру задачку по математике и заставить его решать именно её. Правда, как это сделать, я не понимал и всячески пытался выяснить, чтобы не делать домашнее задание самому. Но, как вы поняли, сделать этого мне не удалось, а вот у современных детей такая возможность есть, и им для этого будет достаточного одного смартфона.

Ваш смартфон может решать задачи за вас

Зачем нужен Google Объектив

Google начала распространение обновления для «Google Объектива», добавив поддержку нового режима под названием «Домашняя работа». В этом режиме сервис распознаёт и решает математические задачи. Достаточно просто навести объектив камеры на пример, отсканировать его и получить готовое решение одним из нескольких способов. Само собой, задачи на логику «Google Объектив» вам не решит, потому что не ищет готовый результате в интернете, а вот квадратное уравнение – запросто. При этом сервис выдаст не только ответ, но и распишет решение.

Как решить квадратное уравнение

• Запустите «Google Объектив» и включите режим Homework;
• Наведите объектив камеры на задачу и дождитесь распознавания;

Google Объектив реально сам решает задачи

• Выберите способ решения: по общей формуле или факторинг;
• Перепишите готовое решение в тетрадку и сдайте на проверку.

Десять скрытых возможностей Google Фото

Как видите, всё очень просто. Другое дело, что спектр задач, которые может решать «Google Объектив», пока сильно ограничен. Например, с задачками по химии он не справляется, а также плохо понимает, как выстраивать решения детских задач, условия в которых задаются текстом. То есть задачу формата «у Вани было 3 яблока» сервис не решит, хотя, казалось бы, что может быть проще? А вот квадратные уравнения – это конёк «Объектива». Он решает их несколькими способами и по каждому предлагает свой вариант решения.

Как искать ответы на задачи

Но, если вы ещё не дошли до квадратных уравнений или, наоборот, уже превзошли их, а делать домашку самостоятельно не хочется, вы можете воспользоваться более универсальным приложением от Google, которое всё сделает за вас. Оно называется Socratic и позволяет сфотографировать задание по любым предметам (ну, почти) и найти на них ответ. В отличие от «Объектива», Socratic просто ищет ответ в интернете, а не подбирает решение самостоятельно. Это позволяет серьёзно расширить спектр задач, с решением которых он может помочь, но от возможных ошибок он не застрахован.

• Скачайте Socratic из Google Play себе на смартфон;
• Разрешите ему доступ к камере и сфотографируйте задачу;

Socratic ищет ответы на поставленные вопросы, но, как правило, находит верные

• Дождитесь, пока сервис найдёт ответы;
• Выберите веб-ресурс, на котором даются объяснения по решению, и перепишите ответ себе в тетрадку.

Как настроить горячие клавиши для расширений Google Chrome

Учитывайте, что Socratic не переведён на русский язык, поэтому лучше всего ему будут даваться задачи с вычислениями. Несмотря на это он может решать задачки и по биологии, и по физике, и по химии, находя ответы на вопросы из тестов и контрольных работ. В принципе, мне удавалось найти ответы и для задач по литературе, но оценить их релевантность я смог только благодаря собственным познаниям. А вот если у вас с литературой всё совсем плохо, не исключено, что вы просто наткнётесь на ошибочный ответ и получите заслуженную двойку.

Теги

• Компания Google
• Образование
• Операционная система Android
• Приложения для Андроид

Лонгриды для вас

В России снова хотят заблокировать YouTube. Теперь назвали даже сроки

Несмотря на то что российские власти как будто отказались от блокировки YouTube, опасность такого исхода по-прежнему не миновала. Судя по всему, видеохостингу Google позволили продолжить работу банально из-за отсутствия альтернатив. Ведь если людям будет негде скоротать время, ничем хорошим это явно не обернётся. Но к моменту, когда VK Видео и RuTube доведут до ума, и они смогут принять большой наплыв новых авторов и зрителей, не исключено, что в дальнейшем присутствии YouTube в России смысла больше не будет.

Читать далее

Как установить приложения для Андроид на Windows

Последнее время крупные компании, такие как Apple и Microsoft, пытаются всячески стандартизировать свои операционные системы. Дальше всех в этом вопросе продвинулась именно яблочная компания. Так, их компьютеры и ноутбуки переведены на собственные ARM-процессоры, аналогичные по архитектуре тем, которые используются в смартфонах и планшетах. И появилась возможность без всяких танцев с бубнами использовать мобильные приложениях даже на настольных компьютерах. Microsoft пошла обратной дорогой. Она дала возможность устанавливать на свою систему для процессоров на архитектуре x86 приложения от операционной системы Android.

Читать далее

Общаться в WhatsApp можно будет не добавляя номер в контакты

Пользуетесь WhatsApp? Если да, то согласитесь, что при всей его простоте, доступности и распространенности, у него есть несколько существенных минусов. Я сейчас говорю даже не об отсутствии нормальной возможности одновременно работать на нескольких устройствах, которая тестируется уже несколько месяцев, а о другой важной проблеме. Вспомните, как вам давали чей-то номер телефона и вы хотели ему написать, но не могли этого сделать, пока не вносили номер в свою телефонную книгу. Только после этого можно было создать с ним чат. Это очень неудобно и однозначно надо что-то с этим делать. И вот, судя по всему, сделали.

Читать далее

Новый комментарий

Новости партнеров

• Приложение Фитнес в iOS 16. Зачем оно нужно и как работает

• Как работает авторизация без пароля в iOS 16

• Мнение: Зачем MacBook вырез от iPhone 14 Pro

• Каким будет iPad Pro 2022

Решение математических задач через совместное обучение. Важность взаимного признания и дружеских отношений

Введение

Исследования по обучению решению математических задач значительно продвинулись за последние десятилетия. Тем не менее, по-прежнему необходимо расширять наши знания о том, как учителя могут поддерживать своих учеников в выполнении этой сложной деятельности (Lester and Cai, 2016). Результаты Программы международной оценки учащихся (PISA) показывают, что только 53% учащихся из стран-участниц смогли решить задачи, требующие большего, чем прямое умозаключение и использование представлений из различных источников информации (OECD, 2019).). Кроме того, ОЭСР (2019 г.) сообщила о больших различиях в успеваемости в зависимости от происхождения учащихся. Таким образом, существует потребность в учебных подходах для поощрения решения учащимися задач по математике, особенно в неоднородных классах, в которых учащиеся с разным опытом и потребностями учатся вместе. Подходы к обучению в малых группах были предложены как важные для содействия обучению слабоуспевающих учащихся и учащихся с особыми потребностями (Kunsch et al., 2007). Одним из таких подходов является совместное обучение (CL), которое включает структурированное сотрудничество в разнородных группах, руководствуясь пятью принципами для повышения групповой сплоченности (Johnson et al. , 19).93; Джонсон и др., 2009 г.; Гиллис, 2016). В то время как ДО было хорошо изучено в подходах для всего класса (Capar and Tarim, 2015), существует несколько исследований этого подхода в отношении учащихся с особыми образовательными потребностями (SEN; McMaster and Fuchs, 2002). Это исследование вносит вклад в предыдущие исследования, изучая влияние подхода CL на решение математических задач учащимися в разнородных классах, в которых учащиеся с особыми потребностями учатся вместе со своими сверстниками.

Групповое сотрудничество посредством подхода CL построено в соответствии с пятью принципами сотрудничества: позитивная взаимозависимость, индивидуальная ответственность, четкое обучение социальным навыкам, стимулирующее взаимодействие и групповая обработка (Johnson et al., 19).93). Во-первых, групповые задания должны быть структурированы так, чтобы все члены группы чувствовали себя зависимыми друг от друга в выполнении задачи, тем самым способствуя положительной взаимозависимости. Во-вторых, для индивидуальной ответственности учитель должен гарантировать, что каждый член группы чувствует ответственность за свою долю работы, предоставляя возможности для индивидуальных отчетов или оценок. В-третьих, учащиеся нуждаются в четком обучении социальным навыкам, необходимым для совместной работы. В-четвертых, задания и рассадка должны быть разработаны таким образом, чтобы способствовать взаимодействию между членами группы. В-пятых, необходимо выделить время для групповой обработки, с помощью которой члены группы могут оценить свою совместную работу для планирования будущих действий. Согласно Capar and Tarim (2015), использование этих принципов для сотрудничества приводит к прогрессу в математике, которые провели метаанализ исследований совместного обучения и математики и обнаружили увеличение на 0,59.на успеваемость учащихся по математике в целом. Однако количество рассмотренных исследований было ограниченным, и исследователи предположили, что необходимо провести дополнительные исследования. В текущем исследовании мы сосредоточились на эффекте подхода CL в конкретной области математики: решении задач.

Решение математических задач является центральной областью обучения математике и составляет важную часть подготовки учащихся к работе в современном обществе (Gravemeijer et al., 2017). На самом деле, обучение решению задач дает учащимся возможность применить свои знания математических концепций, интегрировать и соединить разрозненные математические знания и достичь более глубокого концептуального понимания математики как предмета (Lester and Cai, 2016). Некоторые исследователи предполагают, что математика сама по себе является наукой о решении задач и разработке теорий и методов решения задач (Hamilton, 2007; Давыдов, 2008).

Процессы решения проблем изучались с разных точек зрения (Леш и Завоевски, 2007). Эвристика решения проблем Полиа (1948) в значительной степени повлияла на наше восприятие решения проблем, включая четыре принципа: понимание проблемы, разработка плана, выполнение плана, оглядывание назад и размышление над предложенным решением. Schoenfield (2016) предложил использовать определенные стратегии решения проблем для различных типов проблем, которые учитывают метакогнитивные процессы и убеждения учащихся в отношении решения проблем. Кроме того, модели и перспективы моделирования в математике (Lesh and Doerr, 2003; Lesh and Zawojewski, 2007) подчеркивают важность вовлечения учащихся в деятельность по выявлению моделей, в которой проблемные ситуации интерпретируются математически, поскольку учащиеся устанавливают связи между информацией о проблеме и знаниями о ней. математические операции, закономерности и правила (Mousoulides et al., 2010; Stohlmann and Albarracín, 2016).

Однако не всем учащимся легко решать сложные математические задачи. Учащиеся могут испытывать трудности с определением важных для решения элементов проблемы или визуализацией подходящего решения проблемной ситуации. Кроме того, учащимся может понадобиться помощь в распознавании базовой модели в задачах. Например, в двух исследованиях Degrande et al. (2016) учащимся четвертого-шестого классов были предложены математические задачи в контексте пропорционального мышления. Авторы обнаружили, что учащиеся, когда им предлагали словесную задачу, не могли определить основную модель, а скорее сосредоточивались на поверхностных характеристиках проблемы. Хотя учащиеся в исследовании продемонстрировали больший успех, когда им представили проблему, сформулированную в символах, авторы указали на необходимость занятий, которые помогают учащимся различать разные типы пропорциональных задач. Кроме того, учащимся, испытывающим определенные трудности в обучении, может потребоваться дополнительная поддержка как в общих стратегиях решения проблем (Lein et al., 2020; Montague et al., 2014), так и в конкретных стратегиях, относящихся к базовым моделям проблем. Вмешательство CL в настоящем исследовании было сосредоточено на поддержке учащихся в решении проблем посредством обучения принципам решения проблем (Полиа, 19 лет).48), специально примененный к трем моделям решения математических задач — умножению/делению, геометрии и пропорциональности.

Способность учащихся решать проблемы может быть улучшена за счет участия в обсуждениях в малых группах. В условиях небольшой группы все учащиеся имеют возможность объяснить свои решения, прояснить свое мышление и улучшить понимание рассматриваемой проблемы (Yackel et al., 1991; Webb and Mastergeorge, 2003). Фактически, обучение в малых группах способствует обучению учащихся математике, предоставляя учащимся возможность использовать язык для рассуждений и концептуального понимания (Mercer and Sams, 2006), обмениваться различными представлениями о рассматриваемой проблеме (Fujita et al., 2019).), а также узнавать и понимать точки зрения одногруппников на мышление (Kazak et al., 2015). Эти возможности для обучения создаются через диалогические пространства, характеризующиеся открытостью взглядам друг друга и решениям математических задач (Wegerif, 2011).

Однако групповое сотрудничество связано не только с положительным опытом. Фактически, исследования показывают, что некоторым учащимся могут не предоставляться равные возможности для выражения своего мнения из-за различий в академическом статусе (Langer-Osuna, 2016). Действительно, лица, решающие проблемы, борющиеся со сложными задачами, могут испытывать негативные эмоции, что приводит к неуверенности в том, что они не знают точного ответа, что требует поддержки со стороны сверстников (Jordan and McDaniel, 2014; Hannula, 2015). Таким образом, особенно в разнородных группах, учащимся может потребоваться дополнительная поддержка для развития группового взаимодействия. Поэтому в этом исследовании мы использовали подход к совместному обучению, который, в отличие от подходов к совместному обучению, уделяет больше внимания поддержке групповой сплоченности посредством обучения социальным навыкам и времени для размышлений о групповой работе (Davidson and Major, 2014).

Хотя совместный подход к обучению призван способствовать сплоченности и принятию сверстников в разнородных группах (Rzoska and Ward, 1991), предыдущие исследования показывают, что проблемы в групповой динамике могут привести к неравному участию (Mulryan, 1992; Cohen, 1994). Поведение сверстников может повлиять на решение задач учащимися (Hwang and Hu, 2013), а работа в группах со сверстниками, которых считают друзьями, может повысить мотивацию учащихся к изучению математики (Deacon and Edwards, 2012). Принимая во внимание важность поддержки сверстников, это исследование было направлено на изучение того, связаны ли результаты вмешательства с использованием подхода CL с принятием и дружбой учащихся со сверстниками.

Текущее исследование

В предыдущих исследованиях подход CL показал себя многообещающим подходом в преподавании и изучении математики (Capar and Tarim, 2015), но было проведено меньше исследований, посвященных подходам всего класса в целом и учащимся с В частности, SEN (McMaster and Fuchs, 2002). Это исследование направлено на то, чтобы внести свой вклад в предыдущие исследования, исследуя влияние вмешательства CL на решение математических задач учащимися 5-го класса. Что касается сложности решения математических задач (Lesh and Zawojewski, 2007; Degrande et al., 2016; Stohlmann and Albarracín, 2016), подход CL в этом исследовании был объединен с принципами решения задач, относящимися к трем основным моделям решения задач — умножению/делению, геометрии и пропорциональности. Кроме того, учитывая важность поддержки сверстников при решении проблем в малых группах (Mulryan, 1992; Коэн, 1994; Hwang and Hu, 2013), в исследовании изучалось, как принятие сверстников и дружба были связаны с влиянием подхода CL на способности учащихся решать проблемы. Исследование было направлено на поиск ответов на следующие исследовательские вопросы:

а) Каково влияние подхода CL на решение задач учащимися по математике?

b) Связаны ли общественное признание и дружба с влиянием НН на решение задач по математике учащимися?

Методы

Участники

Участниками стали 958 учащихся 5-х классов и их учителя. Согласно анализу мощности до начала исследования требовалось 1020 учащихся и 51 класс с ожидаемым размером эффекта 0,30 и мощностью 80% при условии, что в классе 20 учеников и внутриклассовая корреляция составляет 0,10. Приглашение к участию в проекте было разослано учителям пяти муниципалитетов по электронной почте. Кроме того, информация была размещена на сайте Упсальского университета и распространена через группы интересов Facebook. Как показано на рис. 1, учителя 1165 учащихся согласились принять участие в исследовании, однако информированное согласие было получено только у 9 учащихся.58 студентов (463 в интервенционной и 495 в контрольной группе). Дальнейшее отсеивание произошло до и после измерения, в результате чего в качестве основы для анализа был взят тест 581 учащегося (269 в группе вмешательства и 312 в контрольной группе). Меньшее количество студентов (n = 493) было, наконец, включено в анализ ассоциации социального принятия и дружбы студентов и влияния CL на решение математических задач студентами (219 в группе вмешательства и 274 в контрольной группе). Причины отсева включали увольнение учителей из-за отпуска по болезни или личных обстоятельств (два учителя в контрольной группе и пять учителей в группе вмешательства). Кроме того, некоторые ученики болели в день сбора данных, а некоторые учителя не отправили исследователям результаты анализов.

РИСУНОК 1 . Блок-схема для участников, включенных в сбор данных и анализ данных.

Как видно из Таблицы 1, в классах как интервенционной, так и контрольной групп в среднем было 27 учащихся. На 75 % классов приходилось 33–36 % учащихся с ООП. В Швеции не требуется формального медицинского диагноза для выявления учащихся с СОП. Именно учителя и школьные социальные группы решают, нуждаются ли учащиеся в дополнительной адаптации или специальной поддержке (Шведское национальное агентство по образованию, 2014). Информацию о типе СЕН отдельных учащихся получить не удалось из-за положений о защите информации о физических лицах (SFS 2009).). Таким образом, информация о количестве учащихся с ООП на уровне класса была получена из отчетов учителей.

ТАБЛИЦА 1 . Фоновые характеристики классов и учителей в интервенционной и контрольной группах.

Вмешательство

Вмешательство с использованием подхода CL длилось 15 недель, и учителя работали с подходом CL от трех до четырех уроков в неделю. Во-первых, учителя приняли участие в двухдневном тренинге по подходу CL, используя специально разработанное руководство по CL (Klang et al. , 2018). Обучение было сосредоточено на пяти принципах подхода CL (позитивная взаимозависимость, индивидуальная ответственность, четкое обучение социальным навыкам, стимулирующее взаимодействие и групповая обработка). После тренинга учителя представили подход CL в своих классах и в течение 7 недель сосредоточились на групповых мероприятиях. Затем учителям было предоставлено 2 дня обучения, в ходе которого подход CL был встроен в действия по решению математических задач и пониманию прочитанного. Учителям были розданы учебные материалы, содержащие математические задачи в области умножения и деления, геометрии и пропорциональности (Karlsson and Kilborn, 2018a). В дополнение к конкретным задачам, адаптированным для подхода ГО, учебные материалы содержали руководство для учителей, в котором излагались принципы решения задач (Поля, 1948) были представлены как шаги в решении проблемы. После обучения учителя применяли подход CL на уроках решения математических задач в течение 8 недель.

Решение проблемы — это вопрос целенаправленного рассуждения, начиная с понимания проблемы и заканчивая поиском ее решения с использованием известных математических моделей. Это предполагает, что текущая проблема выбирается из известного контекста (Stillman et al., 2008; Zawojewski, 2010). Это отличается от решения задач в учебниках, которое основано на обучении уже известным формулам и процедурам (Hamilton, 2007). Более того, важно, чтобы учащиеся изучали моделирование в соответствии со своими текущими способностями и условиями (Рассел, 19 лет).91).

Для создания сходных условий в экспериментальной и контрольной группах преподаватели должны были использовать один и тот же учебный материал (Карлссон, Килборн, 2018а; Карлссон, Килборн, 2018б), написанный с учетом указанного взгляда на проблему -решение. Учебный материал разделен на три области — умножение/деление, геометрия и пропорциональность — и начинается с краткого пособия для учителя, где представлен взгляд на решение задач, основанный на работе Поля (19).48) и Лестер и Кай (2016). Задания построены таким образом, чтобы в центре внимания были концептуальные знания, а не формулы и процедурные знания.

Внедрение вмешательства

Чтобы обеспечить выполнение вмешательства, исследователи посетили класс каждого учителя дважды в течение двух фаз периода вмешательства, как описано выше. Во время каждого визита исследователи наблюдали за уроком, используя контрольный список, включающий пять принципов подхода CL. После урока исследователи дали письменную и устную обратную связь каждому учителю. Как видно из таблицы 1, в 18 из 23 классов учителя реализовали вмешательство в соответствии с принципами CL. Кроме того, учителей попросили сообщить об использовании подхода ДО в их обучении и использовании заданий по решению проблем, включающих ДО в период вмешательства. Как показано в Таблице 1, учителя только 11 из 23 классов сообщили об использовании подхода ДО и действий по решению проблем, встроенных в подход ДО, по крайней мере, один раз в неделю.

Контрольная группа

Учителя из контрольной группы в течение 2 дней обучались улучшению навыков решения задач и понимания прочитанного учащимися. Учителя также получили учебные материалы, включая математические задачи Карлссона и Килборна (2018b) и принципы решения задач (Полиа, 1948). Однако ни одно из действий во время обучения или в учебных материалах не включало подход CL. Как видно из таблицы 1, только 10 из 25 учителей сообщили, что посвящают хотя бы один урок в неделю решению математических задач.

Меры

Тесты решения математических задач

Тесты решения математических задач проводились до и после вмешательства, которое длилось 15 недель. Тесты были сосредоточены на моделях умножения/деления, геометрии и пропорциональности. Три модели были выбраны на основе учебного плана по предмету математика для 4–6 классов Шведской национальной учебной программы (Шведское национальное агентство по образованию, 2018 г.). Кроме того, намерение состояло в том, чтобы создать разнообразие типов задач для решения. Для каждой из этих трех моделей было проведено два теста: предварительный тест и посттест. Каждый тест содержал три задания с возрастающей сложностью (дополнительное приложение SA).

Тесты на умножение и деление (Ma1) были выбраны из разных контекстов и начинались с одношаговой задачи, а следующие две задачи были многоэтапными. Что касается умножения, то многие учащиеся 5-го класса до сих пор понимают умножение как многократное сложение, вызывая серьезные проблемы, поскольку эта концепция неприменима к умножению за пределами натуральных чисел (Verschaffel et al., 2007). Это может быть препятствием для развития мультипликативных рассуждений (Barmby et al., 2009).). Многошаговые задачи в этом исследовании были построены, чтобы помочь учащимся в мультипликативных рассуждениях.

Что касается тестов по геометрии (Ma2), важно учитывать сдвиг парадигмы в отношении геометрии в образовании, который произошел в середине 20-го века, когда строгая евклидова геометрия уступила место другим аспектам геометрии, таким как симметрия, преобразование и закономерности. ван Хиле (1986) подготовил новую таксономию геометрии в пять шагов, от визуального до логического уровня. Поэтому в тестах основное внимание уделялось свойствам четырехугольников и треугольников, а также тому, как определять площади путем реорганизации фигур в новые узоры. Это означает, что структура была важнее формул.

Построение тестов на пропорциональность (М3) было более сложным. Во-первых, задачи на пропорциональность можно встретить во многих различных контекстах, таких как предписания, шкалы, скорости, скидки, проценты и т. д. Во-вторых, математическая модель сложна и требует хорошего знания рациональных чисел и отношений (Леш и др., 1988). ). Это также требует развитого взгляда на умножение, полезного в операциях с действительными числами, а не только в виде многократного сложения, операции, ограниченной натуральными числами (Lybeck, 19).81; Дегранд и др., 2016). Линейная структура умножения как многократного сложения приводит к ограничениям в плане обобщения и развития понятия умножения. Это стало очевидным в исследовании, проведенном в шведском контексте (Karlsson and Kilborn, 2018c). Пропорциональность может быть выражена как a/b = c/d или как a/b = k. Последнее также может быть выражено как a = b∙k, где k — константа, определяющая связь между a и b. Типичными примерами k являются скорость (км/ч), масштаб и процент (%). Важным предварительным знанием для работы с пропорциями является освоение дробей как классов эквивалентности, таких как 1/3 = 2/6 = 3/9.= 4/12 = 5/15 = 6/18 = 7/21 = 8/24… (Карлссон и Килборн, 2020). Все эти аспекты было важно учитывать при построении и оценке решений задач.

Тесты оценивались опытным учителем математики (4 ^th автор) и двумя студентами последнего года обучения учителей. До выставления оценок приемлемые уровни межоценочной надежности были достигнуты за счет независимой оценки решений учащихся и обсуждений, в ходе которых разрешались разногласия между оценщиками. Каждому ответу учащегося присваивался один балл, если он содержал правильный ответ, и два балла, когда учащийся аргументировал правильный ответ и подробно объяснял свое решение. Таким образом, оценка основывалась на аспектах качества с упором на концептуальные знания. Поскольку каждый субтест содержал три вопроса, он генерировал три решения учащихся. Так, баллы по каждому субтесту варьировались от 0 до 6 баллов, а по сумме баллов — от 0 до 18 баллов. Чтобы удостовериться, что пре- и пост-тесты были эквивалентны по степени сложности, тесты были проведены на дополнительной выборке из 169 человек.учащиеся 5 класса. Тестирование для каждой модели проводилось отдельно, так как учащиеся участвовали в пре- и пост-тестировании для каждой модели на одном уроке. Порядок тестов был изменен для половины студентов, чтобы избежать влияния порядка, в котором предъявлялись пре- и пост-тесты. Корреляция между успеваемостью учащихся на пре- и посттесте составила 0,39 ( p < 0,000) для тестов на умножение/деление; 0,48 ( p < 0,000) для тестов по геометрии; и 0,56 ( p < 0,000) для тестов на пропорциональность. Таким образом, степень сложности могла различаться до и после теста.

Показатели принятия сверстников и дружбы

Для изучения отношения учащихся к сверстникам и дружбы использовались номинации сверстников, оцененные до и после вмешательства. Студентов попросили назвать сверстников, с которыми они предпочли бы работать в группах и с кем предпочли бы дружить. Отрицательных номинаций сверстников избегали из-за этических соображений, выдвинутых учителями и родителями (Child and Nind, 2013). Было использовано неограниченное количество номинаций, поскольку считается, что они имеют высокую экологическую обоснованность (Cillessen and Marks, 2017). Номинации сверстников использовались как мера общественного признания, а взаимные номинации использовались как мера дружбы. Количество номинаций для каждого учащегося было суммировано и разделено на количество номинантов, чтобы создать долю номинаций для каждого учащегося (Velásquez et al., 2013).

Статистический анализ

Многоуровневый регрессионный анализ был проведен в пакете R, lme4 Bates et al. (2015) для учета вложенности данных. Принадлежность учащихся к классу рассматривалась как переменная уровня 2. Во-первых, мы использовали модель, в которой результаты студентов на тестах решения задач изучались в зависимости от времени (до и после) и принадлежности к группе (интервенционная и контрольная группа). Во-вторых, та же модель была применена к подгруппам учащихся, которые на предварительном тесте показали результаты выше и ниже среднего, чтобы выяснить, оказало ли вмешательство CL дифференциальное влияние на успеваемость учащихся. В этой второй модели результаты для подгрупп студентов не могли быть получены для тестов по геометрии для подгруппы ниже медианы и для тестов пропорциональности для подгруппы выше медианы. Возможной причиной этого должно быть асимметричное распределение студентов в этих подгруппах. Поэтому была применена другая модель, которая исследовала успеваемость учащихся по математике как до, так и после теста в зависимости от принадлежности к группе. В-третьих, баллы учащихся по социальному принятию и дружбе были добавлены в качестве условия взаимодействия к первой модели. В нашем предыдущем исследовании социальное признание студентов изменилось в результате того же вмешательства CL (Klang et al., 2020).

Предположения для многоуровневой регрессии были подтверждены в ходе анализа (Snijders and Bosker, 2012). Предположение о нормальности остатков было выполнено, что контролировалось визуальным осмотром квантиль-квантильных графиков. Однако для подгрупп нанесенные на графике остатки несколько отклонялись от прямой линии. Количество выбросов, студенческое остаточное значение которых превышало ±3, варьировалось от 0 до 5, но ни один из выбросов не имел значение расстояния Кука больше 1. Допущение о мультиколлинеарности было выполнено, поскольку коэффициенты инфляции дисперсии (VIF ) не превышала значения 10. Перед анализом случаи с отсутствующими данными удалялись по списку.

Результаты

Каково влияние подхода CL на решение задач учащимися по математике?

Как видно из коэффициентов регрессии в таблице 2, вмешательство CL оказало значительное влияние на общие баллы учащихся за решение математических задач и баллы учащихся за решение задач по геометрии (Ma2). Судя по средним значениям, учащиеся интервенционной группы имели низкие баллы по решению задач по геометрии, но к концу интервенции достигли уровня решения задач контрольной группы. Вмешательство не оказало существенного влияния на успеваемость учащихся в решении задач, связанных с моделями умножения/деления и пропорциональности.

ТАБЛИЦА 2 . Средние баллы (стандартное отклонение в скобках) и нестандартизированные оценки многоуровневой регрессии для тестов на решение математических задач.

Вопрос, однако, заключается в том, по-разному ли вмешательство CL повлияло на учащихся с разными оценками перед тестом. Таблица 2 включает коэффициенты регрессии для подгрупп студентов, которые на предварительном тесте показали результаты ниже и выше медианы. Как видно из таблицы, подход CL не оказал существенного влияния на решение задач студентами, когда выборка была разделена на эти подгруппы. Небольшой отрицательный эффект был обнаружен для группы вмешательства по сравнению с контрольной группой, но доверительные интервалы (ДИ) для эффекта указывают на то, что он не был значительным.

Связано ли социальное признание и дружба с влиянием CL на решение задач учащимися по математике?

Как видно из Таблицы 3, признание учащихся сверстниками и их дружба во время предварительного тестирования были в значительной степени связаны с влиянием подхода CL на результаты учащихся по решению математических задач. Изменения в восприятии учащимися сверстников и дружеских отношениях не были существенно связаны с влиянием подхода CL на решение математических задач учащимися. Следовательно, можно сделать вывод, что номинация со стороны сверстников и наличие друзей в начале вмешательства могут быть важным фактором, когда участие в групповой работе, структурированной в соответствии с подходом CL, приводит к успеху в решении математических задач.

ТАБЛИЦА 3 . Средние баллы (стандартное отклонение в скобках) и нестандартизированные многоуровневые регрессионные оценки для тестов решения математических задач, включая баллы социального принятия и дружбы в модели.

Обсуждение

В свете ограниченного количества исследований влияния ДО на решение задач учащимися во всех классах (Capar and Tarim, 2015) и, в частности, на учащихся с СОП (McMaster and Fuchs, 2002), это исследование было направлено на изучение того, влияет ли подход CL, встроенный в деятельность по решению проблем, на решение задач учащимися в разнородных классах. Необходимость исследования была оправдана задачей обеспечения равноправного обучения математике разнородным студенческим контингентам (ОЭСР, 2019 г.).). Подходы к обучению в малых группах, такие как CL, считаются многообещающими подходами в этом отношении (Kunsch et al., 2007). Результаты показали значительное влияние подхода CL на решение задач учащимися по геометрии и общий балл за решение задач. Кроме того, что касается важности поддержки сверстников в решении проблем (Deacon and Edwards, 2012; Hwang and Hu, 2013), в исследовании изучалось, связано ли влияние CL на решение проблем учащихся с их социальным признанием. и дружба. Результаты показали, что принятие учащимися сверстников и дружба во время предварительного тестирования были в значительной степени связаны с эффектом подхода CL, в то время как изменение в принятии учащимися сверстников и дружбе от предварительного к послетестовому не было.

Результаты исследования подтверждают предыдущие исследования влияния подхода CL на математические достижения учащихся (Capar and Tarim, 2015). Особый вклад исследования заключается в том, что оно проводилось в классах, 75% которых состояло из 33–36% учащихся с СОП. Таким образом, в то время как в предыдущем обзоре были обнаружены неубедительные выводы о влиянии ДО на успеваемость учащихся (McMaster and Fuchs, 2002), настоящее исследование дополняет доказательства влияния подхода ДО в неоднородных классах, в которых учащиеся с особыми потребностями обучались вместе со своими сверстниками. В условиях небольшой группы учащиеся имеют возможность обсудить свои идеи решения имеющейся проблемы, давая объяснения и разъяснения, тем самым улучшая свое понимание решения проблем (Yackel et al. , 19).91; Уэбб и Мастерджордж, 2003 г.).

В этом исследовании, в соответствии с предыдущими исследованиями по решению математических задач (Lesh and Zawojewski, 2007; Degrande et al., 2016; Stohlmann and Albarracín, 2016), подход CL сочетался с обучением принципам решения задач Pólya (1948) и учебные материалы, помогающие в обучении основным математическим моделям. Намерение исследования состояло в том, чтобы предоставить доказательства эффективности подхода CL выше обучения решению задач, поскольку материалы для решения задач были доступны учителям как в экспериментальной, так и в контрольной группах. Однако из-за проблем с реализацией не все учителя в экспериментальной и контрольной группах сообщили об использовании учебных материалов и обучении, как ожидалось. Таким образом, невозможно сделать выводы об эффективности одного только КЛ-подхода. Однако в повседневном обучении в классе может быть трудно отделить содержание обучения от действий, которые используются для опосредования этого содержания (Doerr and Tripp, 19). 99; Гравемейер, 1999).

Кроме того, для успешного обучения решению математических задач создание подмостков для содержания необходимо сочетать с подмостками для диалога (Kazak et al., 2015). С диалогической точки зрения (Wegerif, 2011) учащимся может понадобиться опора на новые способы мышления, включающие в себя сомнение в своем понимании и предоставление аргументов в пользу своих решений, чтобы создать диалогические пространства, в которых озвучиваются и обсуждаются различные решения. В этом исследовании обучение в малых группах с использованием подхода CL направлено на поддержку дискуссий в малых группах, но исследование опирается исключительно на количественные показатели математических способностей учащихся. Видеозаписи студенческих дискуссий могли дать важную информацию о диалогических отношениях, возникающих в групповых дискуссиях.

Несмотря на положительные результаты подхода CL к решению задач учащимися, важно отметить, что вмешательство не повлияло на решение учащимися задач, связанных с моделями умножения/деления и пропорциональности. Хотя CL считается многообещающим учебным подходом, количество исследований его влияния на математические достижения учащихся все еще ограничено (Capar and Tarim, 2015). Таким образом, необходимы дальнейшие исследования того, как вмешательство CL может быть разработано для содействия решению задач учащимися в других областях математики.

Результаты этого исследования показывают, что эффект вмешательства CL на решение проблем учащихся был связан с первоначальными оценками учащихся в отношении социального признания и дружбы. Таким образом, можно предположить, что студенты, которые были популярны среди своих одноклассников и имели друзей в начале вмешательства, также добились больших успехов в решении математических задач в результате вмешательства CL. Этот вывод согласуется с исследованием Дикона и Эдвардса о важности дружеских отношений для мотивации учащихся к изучению математики в небольших группах (Дикон и Эдвардс, 2012). Однако эффект вмешательства CL не был связан с изменением показателей социального принятия и дружбы учащихся. Эти результаты показывают, что учащиеся, которые были номинированы большим количеством студентов и которые получили большее количество друзей, не получили значительной пользы от вмешательства CL. Что касается ранее отмеченного неравенства в сотрудничестве в разнородных группах (Коэн, 1994; Малриан, 1992; Langer Osuna, 2016) и важность поведения сверстников для решения проблем (Hwang and Hu, 2013), учителям следует рассмотреть возможность создания инклюзивных норм и поддерживающих отношений со сверстниками при использовании подхода CL. Требования решения сложных проблем могут вызывать негативные эмоции и неуверенность (Ханнула, 2015; Джордан и МакДэниел, 2014), и в таких ситуациях может быть необходима поддержка сверстников.

Ограничения

Выводы исследования следует интерпретировать с осторожностью из-за ряда ограничений. Во-первых, благодаря положению о защите физических лиц (SFS 2009), исследователи не могли получить информацию о типе SEN для отдельных студентов, что ограничивало возможности исследования для изучения эффектов подхода CL для этих студентов. Во-вторых, не все учителя в группе вмешательства внедрили подход ОП, встроенный в деятельность по решению проблем, и не все учителя в контрольной группе сообщили об использовании учебных материалов по решению проблем. Недостаточный уровень реализации представляет собой серьезную проблему для внутренней валидности исследования. В-третьих, дополнительное исследование для изучения эквивалентности сложности до и после теста, в том числе 169студенты, выявили слабую или умеренную корреляцию в оценках успеваемости студентов, что может указывать на проблемы с внутренней валидностью исследования.

Последствия

Результаты исследования имеют некоторые последствия для практики. Основываясь на результатах значительного влияния вмешательства CL на решение проблем учащихся, подход CL кажется многообещающим учебным подходом в поощрении решения проблем учащимися. Однако, поскольку результаты подхода CL не были значимыми для всех субтестов решения задач и из-за недостаточного уровня реализации, невозможно сделать вывод о важности вмешательства CL для решения задач учащимися. Кроме того, кажется важным создавать возможности для контактов со сверстниками и дружбы, когда подход CL используется в деятельности по решению математических задач.

Заявление о доступности данных

Необработанные данные, подтверждающие выводы этой статьи, будут предоставлены авторами без неоправданных оговорок.

Заявление об этике

Исследования с участием людей были рассмотрены и одобрены Региональным комитетом по этике Уппсалы, Dnr. 2017/372. Письменное информированное согласие на участие в этом исследовании было предоставлено законным опекуном/ближайшим родственником участников.

Вклад авторов

NiK отвечал за проект и участвовал в сборе и анализе данных. NaK и WK отвечали за вмешательство, уделяя особое внимание учебным материалам и тестам по решению математических задач. PE участвовал в планировании исследования и анализе данных, включая координацию анализа тестов студентов. МК участвовал в разработке и планировании исследования, а также в сборе и анализе данных.

Финансирование

Проект финансировался Шведским исследовательским советом в рамках гранта 2016-04,679.

Конфликт интересов

Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.

Примечание издателя

Все утверждения, изложенные в этой статье, принадлежат исключительно авторам и не обязательно представляют претензии их дочерних организаций или издателя, редакторов и рецензентов. Любой продукт, который может быть оценен в этой статье, или претензии, которые могут быть сделаны его производителем, не гарантируются и не поддерживаются издателем.

Благодарности

Мы хотели бы выразить благодарность учителям, которые приняли участие в проекте.

Дополнительный материал

Дополнительный материал к этой статье можно найти в Интернете по адресу: https://www.frontiersin.org/articles/10. 3389/feduc.2021.710296/full#supplementary-material

Ссылки

Barmby, P. , Харрис Т., Хиггинс С. и Саггейт Дж. (2009). Представление массива и начальное понимание детей и рассуждения в умножении. Учеб. Стад. Мат. 70 (3), 217–241. doi:10.1007/s10649-008-0.1007/s10649-008-9145-1

CrossRef Полный текст | Google Scholar

Бейтс Д., Махлер М., Болкер Б. и Уокер С. (2015). Подгонка линейных моделей смешанных эффектов с использованием lme4. Дж. Стат. Мягкий. 67 (1), 1–48. doi:10.18637/jss.v067.i01

Полный текст перекрестной ссылки | Google Scholar

Капар Г. и Тарим К. (2015). Эффективность метода совместного обучения в отношении успеваемости и отношения к математике: метаанализ. Учеб. научн-теор. 15 (2), 553–559. doi:10.12738/estp.2015.2.2098

CrossRef Полный текст | Google Scholar

Чайлд С. и Нинд М. (2013). Социометрические методы и отличие: Сила добра — или еще больше вреда. Инвалид. соц. 28 (7), 1012–1023. doi:10.1080/09687599.2012.741517

CrossRef Full Text | Google Scholar

Силлессен, А. Х. Н., и Маркс, П. Е. Л. (2017). Методологический выбор в исследовании номинации равных. Новый реж. Ребенок-подросток. Дев. 2017, 21–44. doi:10.1002/cad.20206

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Кларк Б., Чизман Дж. и Кларк Д. (2006). Математические знания и понимание маленькие дети привносят в школу. Матем. Эд. Рез. J. 18 (1), 78–102. doi:10.1007/bf03217430

Полный текст CrossRef | Google Scholar

Коэн, Э. Г. (1994). Реструктуризация класса: условия для продуктивных малых групп. Ред. Образование. Рез. 64 (1), 1–35. дои: 10.3102/00346543064001001

Полнотекстовая перекрестная ссылка | Google Scholar

Дэвидсон Н. и Мейджор С. Х. (2014). Пересечение границ: совместное обучение, совместное обучение и проблемно-ориентированное обучение. Дж. Excell. Сб. Учить. 25 (3-4), 7.

Google Scholar

Давыдов В.В. (2008). Задачи развивающих инструкций. Теоретическое и экспериментальное психологическое исследование . Нью-Йорк: Nova Science Publishers, Inc.

Дикон, Д., и Эдвардс, Дж. (2012). Влияние групп дружбы на мотивацию изучения математики в средних классах. Проц. бр. соц. Рез. в Учиться. Мат. 32 (2), 22–27.

Google Scholar

Дегранд Т., Вершаффель Л. и ван Доурен В. (2016). «Решение задач на пропорциональные слова с помощью моделирующей линзы: стакан наполовину пуст или наполовину полон?», в Постановка и решение математических задач, Исследования в области математического образования . Редактор П. Фельмер.

Google Scholar

Доерр, Х.М., и Трипп, Дж.С. (1999). Понимание того, как учащиеся разрабатывают математические модели. Мат. Думая Учись. 1 (3), 231–254. doi:10.1207/s15327833mtl0103_3

CrossRef Полный текст | Google Scholar

Фуджита Т. , Дони Дж. и Вегериф Р. (2019). Процессы совместного принятия решений студентами при определении и классификации четырехугольников: семиотический/диалогический подход. Учеб. Стад. Мат. 101 (3), 341–356. doi:10.1007/s10649-019-09892-9

CrossRef Full Text | Google Scholar

Гиллис, Р. (2016). Совместное обучение: обзор исследований и практики. Айте 41 (3), 39–54. doi:10.14221/ajte.2016v41n3.3

CrossRef Full Text | Google Scholar

Gravemeijer, K. (1999). Как возникающие модели могут способствовать формированию конституции формальной математики. Матем. Думая Учись. 1 (2), 155–177. doi:10.1207/s15327833mtl0102_4

CrossRef Полный текст | Google Scholar

Gravemeijer, K., Stephan, M., Julie, C., Lin, F.-L., and Ohtani, M. (2017). Какое математическое образование может подготовить учащихся к жизни в обществе будущего? Междунар. J. Sci. Мат. Образовательный 15 (С1), 105–123. doi:10.1007/s10763-017-9814-6

CrossRef Full Text | Google Scholar

Гамильтон, Э. (2007). «Какие изменения необходимы в ситуациях решения задач, когда математическое мышление необходимо вне школы?», в «Основы будущего в математическом образовании» . Редакторы Р. Леш, Э. Гамильтон и Капут (Махва, Нью-Джерси: Лоуренс Эрлбаум), 1–6.

Google Scholar

Hannula, MS (2015). «Эмоции в решении проблем», в Избранные регулярные лекции 12 ^th Международного конгресса по математическому образованию . Редактор SJ Cho. doi:10.1007/978-3-319-17187-6_16

CrossRef Full Text | Google Scholar

Хванг В.-Ю. и Ху С.-С. (2013). Анализ поведения при взаимном обучении с использованием нескольких представлений в виртуальной реальности и их влияние на решение геометрических задач. Вычисл. Эду. 62, 308–319. doi:10.1016/j.compedu.2012.10.005

Полнотекстовая перекрестная ссылка | Google Scholar

Джонсон, Д. В., Джонсон, Р. Т., и Джонсон Холубек, Э. (2009). Круг обучения: сотрудничество в классе . Гургаон: Interaction Book Company.

Джонсон, Д. В., Джонсон, Р. Т., и Джонсон Холубек, Э. (1993). Сотрудничество в классе . Гургаон: Interaction Book Company.

Джордан, М.Е., и Макдэниел, Р.Р. (2014). Управление неопределенностью во время совместного решения проблем в командах начальной школы: роль влияния сверстников в деятельности по разработке робототехники. Дж. Учись. науч. 23 (4), 490–536. doi:10.1080/10508406.2014.896254

CrossRef Full Text | Google Scholar

Карлссон Н. и Килборн В. (2018a). Инклюзия через обучение в группе: задания на решение проблем. [Включая геном lärande i grupp: uppgifter for Problemlösning] . Уппсала: Упсальский университет.

Карлссон Н. и Килборн В. (2018c). Достаточно, если они это понимают. Исследование восприятия учителями и учениками умножения и таблицы умножения [Det räcker om de förstår den. En studie av lärares och elevers uppfattningar om multiplikation och multiplikationstabellen]. Седерторнский конный завод. Высшее образование. , 175.

Google Scholar

Карлссон Н. и Килборн В. (2018b). Задачи на решение задач по математике. [Подарок для задач по математике] . Уппсала: Упсальский университет.

Карлссон, Н., и Килборн, В. (2020). «Восприятие рациональных чисел учителем и учеником», в Interim Proceedings of the 44 ^th Conference of the International Group for the Psychology of Mathematics Education , Interim Vol., Отчеты об исследованиях . Редакторы М. Инпрасита, Н. Чангри и Н. Бунсена (Хон Каен, Таиланд: PME), 291–297.

Google Scholar

Казак С., Вегериф Р. и Фуджита Т. (2015). Сочетание каркасов для контента и каркасов для диалога для поддержки концептуальных прорывов в понимании вероятности. ZDM Матем. Эду. 47 (7), 1269–1283. doi:10.1007/s11858-015-0720-5

CrossRef Full Text | Google Scholar

Кланг Н., Олссон И., Уайлдер Дж. , Линдквист Г., Фолин Н. и Нилхольм К. (2020). Совместное учебное вмешательство для содействия социальной интеграции в разнородных классах. Фронт. Психол. 11, 586489. doi:10.3389/fpsyg.2020.586489

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Кланг Н., Фолин Н. и Стоддард М. (2018). Инклюзия через обучение в группе: совместное обучение [Включая геномные группы и группы: кооперативные группы] . Уппсала: Упсальский университет.

Кунш, К.А., Джитендра, А.К., и Суд, С. (2007). Эффекты обучения математике при посредничестве сверстников для учащихся с проблемами обучения: синтез исследований. Учиться. Disabil Res Pract 22 (1), 1–12. doi:10.1111/j.1540-5826.2007.00226.x

CrossRef Full Text | Google Scholar

Лангер-Осуна, Дж. М. (2016). Социальное построение авторитета среди сверстников и его последствия для совместного решения математических задач. Матем. Думая Учись. 18 (2), 107–124. doi:10. 1080/10986065.2016.1148529

CrossRef Full Text | Google Scholar

Лейн, А. Э., Джитендра, А. К., и Харвелл, М. Р. (2020). Эффективность мер по решению математических задач для учащихся с трудностями в обучении и/или математическими трудностями: метаанализ. Дж. Образование. Психол. 112 (7), 1388–1408. doi:10.1037/edu0000453

Полный текст CrossRef | Google Scholar

Леш Р. и Дорр Х. (2003). За пределами конструктивизма: модели и перспективы моделирования решения математических задач, обучения и преподавания . Махва, Нью-Джерси: Эрлбаум.

Леш Р., Пост Т. и Бер М. (1988). «Рассуждение о пропорциях», в «Понятия чисел и операции с числами в средних классах ». Редакторы Дж. Хиберт и М. Бер (Хиллсдейл, Нью-Джерси: Lawrence Erlbaum Associates), 93–118.

Google Scholar

Леш Р. и Завоевский (2007). «Решение задач и моделирование», в Второй справочник по исследованиям в области преподавания и обучения математике: проект Национального совета учителей математики . Редактор LFK Lester (Charlotte, NC: Information Age Pub), vol. 2.

Google Scholar

Лестер Ф.К. и Кай Дж. (2016). «Можно ли научить решать математические задачи? Предварительные ответы за 30 лет исследований», в Постановка и решение математических задач. Исследования в области математического образования .

Google Scholar

Либек, Л. (1981). «Архимед в классе. [Arkimedes i klassen]», в Göteborg Studies in Educational Sciences (Göteborg: Acta Universitatis Gotoburgensis), 37.

Google Scholar

Макмастер, К. Н., и Фукс, Д. (2002). Влияние совместного обучения на академическую успеваемость учащихся с ограниченными возможностями обучения: обновление обзора Татеямы-Снезека. Учиться. Disabil Res Pract 17 (2), 107–117. doi:10.1111/1540-5826.00037

CrossRef Full Text | Google Scholar

Мерсер, Н., и Сэмс, К. (2006). Обучение детей тому, как использовать язык для решения математических задач. Ланг. Эду. 20 (6), 507–528. doi:10.2167/le678.0

CrossRef Полный текст | Google Scholar

Монтегю М., Кравец Дж., Эндерс К. и Дитц С. (2014). Влияние обучения когнитивной стратегии на решение математических задач учащихся средней школы с разными способностями. Дж. Образование. Психол. 106 (2), 469–481. doi:10.1037/a0035176

CrossRef Полный текст | Google Scholar

Мусулидес Н., Питталис М., Христу К. и Стираман Б. (2010). «Отслеживание процессов моделирования учащихся в школе», в Моделирование навыков математического моделирования учащихся . Редактор Р. Леш (Берлин, Германия: Springer Science+Business Media). doi:10.1007/978-1-4419-0561-1_10

Полный текст CrossRef | Google Scholar

Малриан, К. М. (1992). Пассивность учащихся при совместной работе малых групп по математике. Дж. Образование. Рез. 85 (5), 261–273. doi:10.1080/00220671.1992.9941126

CrossRef Full Text | Google Scholar

ОЭСР (2019). Результаты PISA 2018 (Том I): что знают и умеют учащиеся . Париж: Издательство ОЭСР. doi:10.1787/5f07c754-en

Полный текст CrossRef

Полиа, Г. (1948). Как решить: новый аспект математического метода . Принстон, Нью-Джерси: Издательство Принстонского университета.

Рассел, С.Дж. (1991). «Считая носы и страшные вещи: дети строят свои представления о данных», в материалах Proceedings of the Third International Conference on the Teaching of Statistics . Редактор И. Д. Вер-Джонс (Данедин, Новая Зеландия: Университет Отаго), 141–164, с.

Google Scholar

Рзоска К.М. и Уорд К. (1991). Влияние совместных и конкурентных методов обучения на успеваемость по математике, отношение к школе, самооценку и выбор дружбы детей маори, пакеха и самоа. Новая Зеландия J. Psychol. 20 (1), 17–24.

Google Scholar

Schoenfeld, AH (2016). Учимся мыслить математически: решение проблем, метапознание и осмысление математики (перепечатка). Дж. Эду. 196 (2), 1–38. doi:10.1177/002205741619600202

CrossRef Полный текст | Google Scholar

SFS 2009:400. Оффентлайгетс- оч секретеслаг. [Закон о публичности и конфиденциальности] . Получено с https://www.riksdagen.se/sv/dokument-lagar/dokument/svensk-forfattningssamling/offentlighets—och-sekretesslag-2009.400_sfs-2009-400 от 14 октября.

Google Scholar

Снайдерс Т.А.Б. и Боскер Р.Дж. (2012). Многоуровневый анализ. Введение в базовое и расширенное многоуровневое моделирование . 2-е изд. Лондон: SAGE.

Стиллман Г., Браун Дж. и Гэлбрейт П. (2008). Исследования в области преподавания и изучения приложений и моделирования в Австралазии. In H. Forgasz, A. Barkatas, A. Bishop, B. Clarke, S. Keast, W. Seah и P. Sullivan (red.), Research in Mathematics Education in Australasiae , 2004-2007 , стр.141–164. Rotterdam: Sense Publishers.doi:10.1163/9789087

9_009

CrossRef Полный текст | Google Scholar

Столман М. С. и Альбаррасин Л. (2016). Что известно о математическом моделировании в начальных классах. Эду. Рез. Междунар. 2016, 1–9. doi:10.1155/2016/5240683

CrossRef Полный текст | Google Scholar

Шведское национальное агентство по образованию (2014 г.). Меры поддержки в образовании – по лидерству и поощрению, дополнительной адаптации и специальной поддержке [Stödinsatser I utbildningen – om ledning och stimulans, extra anpassningar och särskilt stöd] . Стокгольм: Национальное агентство образования Швеции.

Шведское национальное агентство по образованию (2018 г.). Программа по предмету математика в обязательной школе . Получено с https://www.skolverket.se/undervisning/grundskolan/laroplan-och-kursplaner-for-grundskolan/laroplan-lgr11-for-grundskolan-samt-for-forskoleklassen-och-fritidshemmet?url=-996270488%2Fcompulsorycw %2Fjsp%2Fsubject.htm%3FsubjectCode%3DGRGRMAT01%26tos%3Dgr&sv.url=12.5dfee44715d35a5cdfa219f ( 32 июля 2021 г.).

ван Хиле, П. (1986). Структура и понимание. Теория математического образования . Лондон: Академическая пресса.

Веласкес, А.М., Буковски, В.М., и Салдарриага, Л.М. (2013). Корректировка влияния размера группы в данных о номинации коллег. Соц. Дев. 22 (4), а–н. doi:10.1111/sode.12029

Полный текст CrossRef | Google Scholar

Вершаффель Л., Грир Б. и Де Корте Э. (2007). «Понятия и операции с целыми числами», в Второе руководство по исследованиям в области преподавания и обучения математике: проект Национального совета учителей математики . Редактор Ф. К. Лестер (Шарлотта, Северная Каролина: паб Information Age), 557–628.

Google Scholar

Уэбб, Н. М., и Мастерджордж, А. (2003). Содействие эффективному помогающему поведению в группах, ориентированных на сверстников. Междунар. Дж. Образ. Рез. 39 (1), 73–97. doi:10.1016/S0883-0355(03)00074-0

Полный текст CrossRef | Google Scholar

Wegerif, R. (2011). «Теории обучения и исследования учебной практики», в Теории обучения и исследования учебной практики. Исследования в области наук об обучении, учебных систем и исполнительских технологий . Редактор Т. Кошманн (Берлин, Германия: Springer). doi:10.1007/978-1-4419-7582-9

CrossRef Full Text | Google Scholar

Якель Э., Кобб П. и Вуд Т. (1991). Взаимодействия в малых группах как источник возможностей обучения математике во втором классе. Дж. Рез. Мат. Эду. 22 (5), 390–408. doi:10.2307/749187

CrossRef Полный текст | Google Scholar

Zawojewski, J. (2010). Решение проблем против моделирования. В Р. Леш, П. Гэлбрейт, К. Р. Хейнс и А. Херфорд (ред.), Моделирование Компетенции математического моделирования студента: ICTMA , с. 237–243. Нью-Йорк, штат Нью-Йорк: Springer.doi:10.1007/978-1-4419-0561-1_20

Полный текст CrossRef | Google Scholar

Стратегии решения математических задач — Маневрирование посередине

Автор: Тайн Брэк

19 сентября

706 акции

• Поделиться

Сколько раз вы преподавали концепцию, в которой ученики чувствовали себя уверенно, только для того, чтобы они полностью отключились, столкнувшись с проблемой со словом? Для меня ответов слишком много, чтобы сосчитать. Словесные задачи требуют стратегий решения проблем. И больше всего на свете текстовые задачи требуют декодирования, исключения дополнительной информации и возможности для учащихся решить то, о чем вопрос не просит. Есть так много мест, где ученики могут ошибаться! Давайте поговорим о некоторых стратегиях решения проблем, которые могут помочь учащимся и воодушевить их!

Получите бесплатную стратегию решения проблем здесь!

Обновление на 2020 год: прокрутите вниз, чтобы узнать, как мы решаем проблему демонстрации вашей работы во время дистанционного обучения.

1. КУБЫ.

C.U.B.E.S означает обвести важные числа, подчеркнуть вопрос, выделить слова, являющиеся ключевыми словами, исключить лишнюю информацию и решить, показав работу.

• Почему мне это нравится: Дает учащимся очень конкретное «что делать».
• Почему мне это не нравится: При всех аннотациях задачи я не уверен, что учащиеся действительно читают задачу. Ни один из шагов не акцентирует внимание на чтении проблемы, но, возможно, это данность.

2. Р.У.Н.С.

Р.У.Н.С. расшифровывается как «прочитай задачу», подчеркни вопрос, назови тип проблемы и напиши стратегическое предложение.

• Почему мне это нравится: Студенты вынуждены думать о том, что это за задача (разложение на множители, деление и т. д.), а затем придумывать план ее решения с помощью предложения о стратегии. Это отличная стратегия для обучения, когда вы решаете различные типы проблем.
• Почему мне это не нравится: Хотя мне нравится, когда студенты могут писать по математике, написание формулировки стратегии для каждой задачи может отнять много времени.

3. ИБП ЧЕК

ИБП «Проверить» означает «понимать», «планировать», «решать» и «проверять».

• Почему мне это нравится: Мне нравится, что в этой стратегии решения проблем есть шаг проверки. Учащиеся должны защищать разумность своего ответа, что важно для их чувства числа.
• Почему мне это не нравится: Это может быть немного расплывчато и не дает конкретного «что делать». Проверка того, что учащиеся выполнили шаг «понять», может быть трудно увидеть.

4. Маневрирование средней стратегии AKA K.N.O.W.S.

Вот стратегия, которую я принял несколько лет назад. У него пока нет ни названия, ни аббревиатуры (так можно ли его вообще считать стратегией…?)

ОБНОВЛЕНИЕ: У НЕГО ЕСТЬ НАЗВАНИЕ! Спасибо нашим прекрасным читателям, Венди и Натали!

• Знать: Это поможет учащимся найти важную информацию.
• Необходимо знать: Это заставит учащихся перечитать вопрос и записать то, что они пытаются решить.
• Организовать:   Я думаю, что это было бы отличным местом для учителей, чтобы подчеркнуть рисунок модели или изображения.
• Работа: Здесь учащиеся показывают свои расчеты.
• Решение: Здесь учащиеся спросят себя, разумен ли ответ и отвечает ли он на вопрос.

Я развернул эту стратегию решения задач для студентов, и она прошла достойно. Когда я предоставил им поля (см. ниже) для заполнения, я не получил тяжелых вздохов о том, что заставляю их показывать свою работу. #mathteacherwin
Я думаю, коробки ясно дали понять, что это часть необходимой работы, а не что-то «лишнее», на что я тратил время.

Вот где я обычно борюсь со стратегиями решения проблем: 1) моделирование стратегии в течение нескольких недель моего обучения после того, как я научил студентов использовать стратегию, и 2) принуждение студентов к ее выполнению. Итак… в общем все. Возможно, поэтому я не мог придерживаться стратегии из года в год.

5. Борьба за цифровое обучение

Многие учителя сталкиваются с тем, как заставить учащихся демонстрировать свою работу или стратегию решения проблем, когда им поручают отправить работу онлайн. Такие платформы, как Kami, делают это возможным. В Go Formative есть функция, с помощью которой учащиеся могут использовать мышь, чтобы «рисовать» свою работу. Если у ваших учеников нет доступа к сенсорному экрану, то лучше всего попросить их отправить изображения своей работы. Чтобы упростить этот процесс, я бы порекомендовал учащимся присылать изображения всех своих работ, а не отдельных задач. Мы не хотим создавать дополнительные барьеры для студентов.

Если вы хотите потратить свою энергию на обучение студентов решению задач, а не писать и находить математические задачи, не ищите ничего, кроме нашей подписки All Access. Нажмите кнопку, чтобы узнать больше.

Учащиеся, которые планируют, достигают большего успеха, чем учащиеся, которые не планируют. Есть ли у вас стратегия решения проблем, которой вы обучаете своих студентов?

Примечание редактора: Maneuvering the Middle публикует сообщения в блоге уже почти 6 лет! Этот пост был первоначально опубликован в сентябре 2017 года. Он был обновлен для обеспечения актуальности и точности.

706 акции

• Поделиться

Планирование урока, математические концепции

Распечатанные и цифровые математические задания

Адрес электронной почты

Проверьте эти сопутствующие товары в моем магазине

Посмотреть все продукты

Предыдущий пост Как преподавать уклон

Следующий пост Ошибки новичков: оценка всех работ учащихся

Взаимодействие с читателем

Анализ стратегий решения математических задач

Некоторое время назад я писал в блоге об использовании анекдотических записей в решении математических задач. И у меня было несколько вопросов о том, как выглядят эти стратегии, особенно о том, какие различия мы видим в реляционных стратегиях.

Итак, давайте обсудим стратегии решения математических задач: как они выглядят, что они говорят нам о детском мышлении и что мы можем сделать, чтобы помочь детям в каждой стратегии. #longpostalert

Прямое моделирование

Ребенок, который занимается непосредственным моделированием, — это тот, кто буквально напрямую моделирует сюжетную проблему. Они делают все, что велит им сюжетная задача, в том порядке, в котором она говорит им это делать. Люди, не связанные с компьютерной графикой, могли бы назвать это «рисованием картинки». Для этого поста давайте воспользуемся простой задачей на сложение:

Уитни собрала 42 моркови и 29 зеленых бобов со своего огорода. Сколько всего овощей она собрала?

Как это выглядит?  Наш непосредственный модельер нарисует все 42 морковки (которые выглядят как морковки или просто выглядят как круги или точки. .. не имеет значения). Затем он вытащит все 19 зеленых бобов. А затем сосчитайте их все, начиная с 1 и считая по единицам до 71.  Это мои дети, которым требуется 30 минут, чтобы решить одну задачу!

Что это говорит нам о детском мышлении?  Прямые моделисты говорят нам, что они не могут мыслить за пределами проблемы истории. Они не способны видеть группы десятков. Они не умеют складывать числа в десятки и единицы (по крайней мере, без подсказок). Они не способны сохранять число и рассчитывать на него. Иногда , они могут делать эти вещи, но застревают на прямом моделировании, потому что думают, что это проще, что им удобно, или что цифры слишком высоки для них, чтобы продемонстрировать эти навыки. Например, ребенок, который рассчитывает в задаче 13 + 14, может не решить эту, потому что цифры намного выше.

Чем мы можем помочь непосредственному моделисту?  Прямой моделист, который все еще рисует картинки только потому, что это проще, просто нуждается в простом толчке: «Покажите мне другой способ решить эту задачу, помимо рисования изображения каждого овоща». Я всегда узнаю, кто мои непосредственные моделисты по выбору детей, во время Math Talks. Во время математических бесед эти дети видят группы десятков, считают десятками, рассчитывают… но они борются или не хотят переходить к самостоятельному показу этих стратегий на бумаге. Еще одна процедура, которую я использую, — это заставлять моих детей маркировать свой счет. Это означает, что если они моделировали и считали от 1 до 71, они ДОЛЖНЫ писать все числа от 1 до 71. Хотя это может показаться чрезмерным… это работает. Во-первых, это помогает в написании чисел. Но также утомительно писать 71 число. Когда я слышу жалобы, я просто отвечаю: «Тогда найдите более быстрый путь!»

Разработчикам прямого моделирования, которые застряли в этой стратегии — и не по своему выбору — нужно много опыта в счете, пропуске счета, нахождении групп десятков в больших числах! Я делаю это с помощью Math Talks (об этом читайте здесь), где мы можем моделировать другие стратегии всей группой, Counting Collections (об этом читайте здесь), где они могут работать с партнерами, чтобы подсчитывать большие числа, используя группы десятков, и с помощью вмешательства малых групп. Во время наших дней работы с партнерами по сбору счетов или беглости фактов я собираю небольшие группы, где мы проводим некоторые управляемые математические вмешательства … Я часто привлекаю своих непосредственных специалистов по моделированию и работаю над подсчетом и поиском групп из десятков.

Еще один способ, которым я помогаю разработчикам моделей, — это совместное время. Если я разделю стратегию прямой модели Уитни со стратегией прямой модели по десяткам после нее, я могу спросить: «Значит, у Уитни тоже были группы десятков в ее стратегии? Может ли кто-нибудь подойти и найти группу десятков в мышлении Уитни?» И тогда мы выделяем группы десятков. После того, как один человек легко нашел один, я обращаюсь к своим непосредственным моделистам, чтобы заставить их найти десятки. Это помогает оттолкнуть их от прямого моделирования!

Прямое моделирование от Tens

Ребенок, который моделирует по десяткам, может решать задачи с помощью кубиков с основанием 10 (или кубиков unifix, если вы выбросили кубики с основанием 10, как это сделал я!) Они либо используют инструменты, либо рисуют изображение десятков и единиц.

Как это выглядит? Непосредственный создатель моделей по десяткам будет использовать инструменты для построения 42 и 29 с десятками и единицами. Затем она будет считать десятками и единицами, чтобы получить ответ. Важное различие между этим и реляционным мыслителем заключается в том, что разработчику прямого моделирования десятки ДОЛЖНЫ сначала нарисовать картинку или использовать инструменты, а реляционному мыслителю картинка не нужна.

Что это говорит нам о детском мышлении?  Прямой моделлер говорит нам, что она зависит от инструментов и изображений. Она умеет считать по 10 и по единицам. Она может разложить двузначное число на десятки и единицы, но ей нужны изображения/инструменты — она не может все сделать в уме.

Чем мы можем помочь прямому моделисту десятками? Важно не отвлекать детей от этой стратегии. Логичным следующим шагом является реляционное мышление с пониманием по основанию 10. Это сверхабстрактная стратегия, которая требует времени с конкретными инструментами и картинками, чтобы закрепить ее. В этой стратегии я фокусируюсь на детях в двух направлениях: нотация и гибкость. Я работаю над тем, чтобы заставить этих детей гибко переходить от прямого моделирования по 10 к счету по мере необходимости. Чем гибче их мышление, тем больше они будут думать о других стратегиях и начнут расширять свое мышление. Я работаю над нотацией, потому что, на мой взгляд, это мост к реляционному мышлению. Я учу этих детей стрелочной системе обозначений и выхожу за рамки простого написания 42+29.=71. В конце концов, когда они будут готовы, картинки отпадут, и они поймут, что нотации достаточно, и смогут следовать абстрактным шагам в нотации. Так что только не торопитесь с этим!

Подсчет

Ребенок, использующий стратегию счета, может считать с любого числа, а не только с единицы. Они могут начинаться с меньшего или большего числа и по-прежнему считаться счетчиком, хотя запуск с наибольшего числа более эффективен.

Как это выглядит?   Счетчик начнется с 42 и будет считать еще 29. Она также может начать с 29 и насчитать еще 42. Когда я моделирую эту стратегию, я обвожу число, чтобы показать, что я придумал это число в своей голове. И да, я заставляю их выписывать все числа так, как они считали.

Что это говорит нам о детском мышлении?   Счетчики говорят нам, что они могут сохранять числа (держать число в голове и считать). Если они рассчитывают на эффективность, они говорят нам, что могут найти большее двузначное число. Они не могут пропустить счет с любого числа. Они могут или не могут видеть группы десятков. Некоторые дети могут видеть группы десятков, но все равно предпочитают считать, потому что считают, что так быстрее. (А иногда и так, как в 42+5.)

Чем мы можем помочь прилавку?  Счетчикам нужна наша помощь только в том случае, если они застряли и не могут использовать десятичную систему счисления для решения проблем. Если они не могут решить задачу, используя стратегию с основанием 10, то я иногда стягиваю их с моими непосредственными моделистами в небольшие группы, чтобы обсудить поиск групп из десятков. Подсчет коллекций также поможет развить у этих детей «десятилетие». Важно помнить, что счет — это ОТЛИЧНАЯ основа для приращения (стратегия относительного мышления), поэтому я всегда стараюсь не навязывать этим детям десятичную систему счисления. Если они понимают основание 10, могут находить группы десятков, у них все будет хорошо!

Реляционное мышление

Реляционные мыслители не полагаются на картинки или инструменты. Они могут решать задачи в уме или только с помощью уравнений или обозначений. Они должны быть в состоянии объяснить или показать больше, чем просто уравнение для сюжетной задачи — подробнее об этом чуть позже! В их мышлении нет картинок…. Все абстрактно, никакой конкретики. Есть 3 различных типа реляционных мыслителей, и каждый из них выглядит немного по-разному, но абстрактность этих стратегий может затруднить их дифференциацию. Давайте подробнее рассмотрим каждый.

База 10:  Эти милашки, скорее всего, были непосредственными моделистами в 10-х годах назад, и они только начали сбрасывать картинку. Однако мы можем легко выделить их, потому что мы все еще можем видеть десятки и единицы в их записи. То, как они записывают свои мысли, будет зависеть от того, что вы моделируете в своем классе, но вот несколько вариантов, которые я видел, как первоклассники записывали с помощью и без помощи.

Компенсаторы: Эти малыши редко появляются в моем первом классе. Может быть, это потому, что я изо всех сил стараюсь думать компенсирующим образом, но время от времени я слышу, как эта стратегия всплывает в устной форме в математическом выступлении. Эти дети хотят работать с понятными числами, поэтому они компенсируют это, чтобы упростить уравнение. Вместо 42+29, они изменят уравнение на 41+30, чтобы сделать уравнение более удобным. У них должно быть фантастическое понимание равенства, чтобы использовать эту стратегию!

Инкрементеры:  Вероятнее всего, раньше эти младенцы были счетчиками. Я часто вижу, как счетчики переходят в режим увеличения, как только они понимают основание 10 и считают на 10 и единицы от любого числа. В отличие от детей с основанием 10, которые разлагают оба числа, инкрементаторы сохраняют первое число и разлагают только второе число. Они рассчитывают на 10 с и единицы (или на самом деле любое увеличение … это только то, что я нажимаю, чтобы помочь с пониманием базы 10), чтобы найти ответ. Это выглядит иначе, чем другие стратегии, потому что одно из чисел не меняется и не разлагается. И приращения такие же (все 10, а потом единицы, не больше 5, потом еще 3, потом еще 10, потом еще 2…)

Что мы можем сделать, чтобы помочь тем, кто мыслит отношениями?  Могут быть три разных типа реляционных мыслителей, но я одинаково помогаю каждому из них… Мое внимание к этим первоклассникам сосредоточено на гибкости. Многие реляционные мыслители уже легко переключаются между стратегиями, но если они этого не делают, я сосредотачиваюсь на этом, попросив их показать мне более чем один способ или объединив их с другими учениками с другими стратегиями — например, с ребенком с основанием 10 и инкрементером. поделиться и опробовать стратегии друг друга. Я также сосредотачиваюсь на оттачивании их навыков нотной записи… что занимает больше времени, чем в первом классе! *подмигнул* 🙂

Какие из этих стратегий вы видите в своем классе и как вы помогаете детям развивать их стратегии?

‎Photomath в App Store

Описание

Получите математическое приложение, которое поможет вам! Photomath — самая полезная в мире платформа для изучения математики, на которой миллионы учащихся всех уровней ежемесячно проверяют домашние задания, готовятся к тестам и совершают новые математические открытия.

Основные этапы решения и объяснения абсолютно БЕСПЛАТНЫ, но если вы готовы к совершенно новому миру обучения, Photomath Plus предоставляет вам доступ к:

ЭКСПЕРТНОЕ ПОНИМАНИЕ
С доступом к полной библиотеке пояснений к выбранным учебникам, включая задачи со словами и геометрией! Учитесь в своем собственном темпе с материалами, одобренными одними из лучших учителей математики в мире.

МУЛЬТИМЕДИЙНОЕ ОБУЧЕНИЕ
С подробными анимациями искусственного интеллекта и словесными пояснениями, которые помогут вам визуализировать и понять математику в соответствии с вашим стилем обучения.

MATH INSIGHTS
Повысьте уровень своего обучения, понимая, «как» и «почему» решаются математические задачи, или получайте напоминания о забытых терминах и понятиях с помощью нашего встроенного глоссария.

Итак, изучаете ли вы основы арифметики или занимаетесь сложной геометрией, мы поможем вам в этом вместе. Один шаг за раз.

ОСНОВНЫЕ ХАРАКТЕРИСТИКИ
• Бесплатные пошаговые объяснения
• Инструкции по задачам Word
• Интерактивные графики
• Видеообучение
• Несколько методов решения
• Расширенный научный калькулятор Вещественные и комплексные числа
— Сравнение действительных чисел
— Определение чисел
ФУНКЦИИ
— Графики функций (линейные, квадратичные, экспоненциальные и т. д.)
— Свойства функций (область определения, асимптоты и т. д.) Разложение на неполные дроби
— Решение уравнений и неравенств (линейных, квадратичных, экспоненциальных и т. д.)
— Системы уравнений
— Полиномиальное деление
— Биномиальная теорема, факториалы
— Комбинации, перестановки и вариации
— Матрицы и матричные уравнения
— Детерминанты
— Математическая индукция
ТРИГОНОМЕТРИЯ И УГЛЫ
— Преобразование углов между градусами и радианами
— Преобразование углов между десятичной и DMS формой
— Период тригонометрических функций
— Проверка тригонометрических тождеств
ПОСЛЕДОВАТЕЛЬНОСТИ
— Идентификация последовательностей
— Серия
— Рекурсивная и явная форма
— Тесты на сходимость
ВЫЧИСЛЕНИЕ
— Пределы
— Производные
— Интегралы
— Площадь под кривой
— Идентификация коник
— Вращение коник
— Параметризация кривых
— Идентификация квадратичных поверхностей
— Дифференциальные уравнения
— Касательные линии
— Преобразование между координатами

Ответ — это еще не все, что вы получите от этого бесплатного приложения. Photomath также предоставляет пошаговое руководство по решению каждой проблемы». — Huffington Post

«Пошаговое руководство полезно для учащихся, у которых нет доступа к репетитору и у которых возникают проблемы с решением математических задач». — Форбс

«Вирусное видео о новом приложении похоже на сбывшуюся мечту для всех, у кого проблемы с математикой». — Время
___________________________________________

• Оплата будет снята с вашей учетной записи Apple ID при подтверждении покупки.
• Подписка продлевается автоматически, если она не будет отменена по крайней мере за 24 часа до окончания текущего расчетного периода.
• С вашего аккаунта будет взиматься плата за продление в течение 24 часов до окончания текущего периода.
• Управляйте подпиской или отмените ее в настройках своей учетной записи в App Store после покупки.
• Предложения и цены могут быть изменены без предварительного уведомления.

Предложения или вопросы? Напишите нам по адресу support@photomath. com

Веб-сайт: www.photomath.com
TikTok: @photomath
Instagram: @photomath
Facebook: @Photomathapp
Twitter: @Photomath

Условия использования: https://photomath.com /en/termsofuse
Политика конфиденциальности: https://photomath.com/en/privacypolicy

4 сентября 2022 г.

Версия 8.11.0

Уже сентябрь?! Как ты себя чувствуешь? Увлажненный? Готовы на все? Если вы чувствуете, что работа продолжается, не волнуйтесь — мы тоже! Мы полны решимости ВСЕГДА помочь вам, поэтому, если у вас возникла проблема, отсканируйте ее, чтобы мы могли отправить ее нашим экспертам по математике и добавить в приложение! (Глядя на вас, проблемы со словами…) Это довольно интересно, когда работа продолжается, не так ли? Продолжаем двигаться вперед вместе 🙂

Рейтинги и обзоры

574,8 тыс. оценок

Выбор редакции

Время от времени появляется приложение, которое откинет вам волосы назад и заставит вас поверить, что вы живете в научно-фантастическом будущем. Photomath позволяет навести камеру на проблему, и на экране мгновенно появится пошаговое объяснение (и ответ!) Трехзначное умножение? Фотомат получил это. Линейные и квадратные неравенства? Без проблем.

ОЧЕНЬ хороший инструмент для математики.

Хотя есть еще 1 или 2 математических темы, с которыми это приложение пока не может помочь, это ЗАМЕЧАТЕЛЬНОЕ приложение, которое может решить около 90% математических задач, будь то общая алгебра или уравнения высшего и самого сложного уровня в колледже. Тем не менее, вы хотите, чтобы это приложение было на вашей стороне, когда вы занимаетесь математикой в ​​значительной степени и всеми видами. Его основная функция позволяет вам фотографировать математические уравнения, и, если на снимке случайно оказались части других уравнений, вы можете обрезать их, как только сделаете снимок, и он решит уравнение за вас, как только вы нажимаете кнопку «ОК». В нем также есть калькулятор, где вы можете вручную вводить уравнения и решать их. Это полезно, если вы поняли, что написали уравнение неправильно, потому что вы можете просто перейти прямо к части калькулятора и исправить его, так как все части уравнения, которые приложение увидело на фотографии, сразу же помещаются в калькулятор. Лучшая часть, на мой взгляд, — это последняя функция, где она точно сообщает вам, как она решила уравнение, и даже позволяет вам просматривать каждый шаг и дает вам краткое, но хорошее объяснение того, что происходит на шаге. Если вы также прокрутите вниз, находясь в той же функции, если вы сфотографировали уравнение, которое нужно изобразить в виде графика, вы действительно сможете увидеть уравнение, построенное для вас. Это очень хорошее приложение, и я НАСТОЯТЕЛЬНО рекомендую.

Здравствуйте! Большое спасибо за то, что поделились с нами своими отзывами, мы ценим это! В настоящее время мы формируем пул пользователей, которые считают наше приложение особенно полезным, поскольку мы часто получаем запросы на отзывы от СМИ. Хотели бы вы присоединиться к этому пулу и в конечном итоге получить шанс дать показания для прессы? Напишите нам по адресу [email protected], если у вас есть какие-либо вопросы или если вы рады принять участие.

Идея приложения!!!!Хотите сделать ваше приложение ЛУЧШЕ, прочитайте ЭТО!!

Отлично, это приложение творит чудеса! БАТТТ: Я должен заплатить за это, чтобы научить меня делать это, как Бру. Я думал, вы все зарабатываете на рекламе? Вместо этого у меня есть идея для вас всех. Вместо того, чтобы заставлять людей платить за обучение, но у вас должен быть вариант обучения, но не такой, как тот, который у вас есть сейчас, вариант обучения должен быть вариантом, который учит вас, как это делать, но вместо этого вам действительно нужно решать проблемы. а скорее вы проходите по нему тест и пересдаете его столько раз, сколько хотите! И вы можете заставить людей платить за это, так как это будет «премиум». Вы также можете включить флэш-карты и игры, чтобы помочь понять математический тип!! Люди определенно были бы готовы платить за приложение, которое учит добру!! То, что у вас есть сейчас, мало поможет в обучении, но вместо этого вы можете создать новый, улучшенный и УВЛЕКАТЕЛЬНЫЙ способ изучения математики, тогда вы можете попросить их добавлять баллы к уравнению всякий раз, когда вы правильно отвечаете на вопрос! А затем добавьте аватар, который вы можете настроить, но вам понадобятся монеты, чтобы купить все, что вы хотите, вы можете заработать эти монеты, правильно ответив на математику. Или, по крайней мере, получить 7/10 или больше прав!!! Опять же, это будет основным вашим приложением, как Funner, и учителя могут использовать его как способ обучения и будут платить за программу! Таким образом, добавление этого будет означать БОЛЬШЕ ДЕНЕГ для вашей компании !!! Дайте мне знать, если вы, ребята, используете эту идею, и спасибо за чтение 🥺❤️💕

Привет и спасибо за положительный отзыв! Мы постоянно работаем над улучшением Photomath, поэтому обязательно поделимся вашими предложениями с командой. Не стесняйтесь, напишите нам по адресу [email protected], если у вас есть идеи по улучшению приложения. Ваше здоровье!

Разработчик, Photomath, Inc., указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.

Данные, не связанные с вами

Следующие данные могут быть собраны, но они не связаны с вашей личностью:

• Покупки
• Расположение
• Контактная информация
• Пользовательский контент
• Идентификаторы
• Данные об использовании
• Диагностика
• Другие данные

Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста. Узнать больше

Информация

Продавец

Фотомат, ООО

Размер

32,5 МБ

Категория

Образование

Возрастной рейтинг

4+

Авторское право

© 2022 Photomath, Inc.

Цена

Бесплатно

• Сайт разработчика
• Тех. поддержка
• Политика конфиденциальности

Вам также может понравиться

Улучшение решения математических задач в классах с 4 по 8

• Опубликовано

Практическое руководство

Улучшение решения математических задач в 4–8 классах

• Рекомендации
• Детали
• Панель
• Связанные ресурсы

Это практическое руководство содержит пять рекомендаций по улучшению решения математических задач учащимися 4–8 классов. Это руководство предназначено для учителей, тренеров по математике, других педагогов и разработчиков учебных программ, которые хотят улучшить решение математических задач учащимися.

1

Подготовьте задачи и используйте их в обучении всего класса.

Показать больше Показывай меньше

2

Помочь учащимся контролировать процесс решения задач и размышлять над ним.

Показать больше Показывай меньше

3

Научите учащихся использовать визуальные представления.

Показать больше Показывай меньше

4

Предложите учащимся несколько стратегий решения проблем.

Показать больше Показывай меньше

5

Помогите учащимся распознавать и формулировать математические понятия и обозначения.

Показать больше Показывай меньше

Стенограмма PDF (588 КБ)

Видео (5:17 минут)

Узнайте больше об этой рекомендации (5,8 МБ)

Стенограмма PDF (541 КБ)

Видео (4:58 минут)

Узнайте больше об этой рекомендации (5,8 МБ)

Стенограмма PDF (558 КБ)

Видео (4:51 минут)

Узнайте больше об этой рекомендации (5,8 МБ)

Стенограмма PDF (598 КБ)

Видео (2:18 минут)

Узнайте больше об этой рекомендации (5,8 МБ)

Стенограмма PDF (922 КБ)

Видео (2:23 минуты)

Узнайте больше об этой рекомендации (5,8 МБ)

Веб-семинар

What Works Clearinghouse Веб-семинар по научно-обоснованным практикам и программам STEM

1 августа 2021 г.

What Works Clearinghouse выпустила вебинар для преподавателей, посвященный научно обоснованным ресурсам для улучшения навыков STEM для учащихся начальной, средней и старшей школы. Эксперты и педагоги обсудили пример…

Вебинар

Что работает: доказательная математика, советы по чтению и письму для личного и дистанционного обучения

1 июля 2021 г.

What Works Clearinghouse выпустила вебинар для преподавателей, посвященный научно обоснованным методам обучения математике, чтению и письму, а также учебные ресурсы, которыми можно поделиться с родителями и детьми.

Справочник

Что работает: доказательная математика, советы по чтению и письму для личного и дистанционного обучения

1 июля 2021 г.

What Works Clearinghouse выпустила вебинар для преподавателей, посвященный научно обоснованным методам обучения математике, чтению и письму, а также учебные ресурсы, которыми можно поделиться с родителями и детьми.

Видео

Использование практического руководства для улучшения решения математических задач в 4-8 классах

8 декабря 2020 г.

На этом вебинаре было рассмотрено, как книга «Улучшение решения математических задач в 4–8 классах: практическое руководство» способствует профессиональному развитию учителей математики в 4–8 классах.

Инфографика

Научно обоснованные рекомендации по дистанционному обучению математике в средних классах

1 октября 2020 г.

Эта инфографика содержит примеры из трех практических руководств по обучению математике в средней школе, которые можно внедрить бесплатно или по низкой цене в условиях дистанционного обучения.

Инфографика

Научно обоснованные рекомендации по дистанционному обучению математике в начальных классах

1 октября 2020 г.

Эта инфографика содержит примеры из трех практических руководств по обучению математике в начальной школе, которые можно использовать бесплатно или по низкой цене в условиях дистанционного обучения.

Руководство

Учебные советы на основе Практического руководства для преподавателей Улучшение решения математических задач в 4–8 классах

1 октября 2018 г.

Этот восьмистраничный набор учебных советов превращает рекомендации практического руководства в действенные подходы, которые преподаватели могут опробовать в своих классах.

Руководство

Краткое изложение фактических данных для учебных советов на основе Практического руководства для преподавателей

1 октября 2018 г.

В этом кратком обзоре данных описываются данные исследований, подтверждающие использование учебных советов в классах.

Видео

Интервью с председателем комиссии Джоном Вудвордом

11 апреля 2017 г.

Воспроизведение интервью председателя группы, Джона Вудворда: компоненты решения проблем (5:47 минут)

Протокол проверки практического руководства по решению математических задач

В соответствии с этим протоколом был проведен обзор исследований, на основе которых были составлены рекомендации, содержащиеся в практическом руководстве What Works Clearinghouse (WWC) «Улучшение решения математических задач в классах с 4 по 8», опубликованном в мае 2012 г.

Связанные ресурсы

Нажмите здесь, чтобы получить дополнительные ресурсы, связанные с этим практическим руководством.

Связь с WWC

loading

Ответ на вмешательство | Математика

Самостоятельное решение сложной математической задачи требует координации ряда сложных навыков. Студент должен иметь возможность надежно реализовать определенные шаги конкретного процесса решения проблем или когнитивной стратегии. Не менее важно, однако, то, что учащийся должен также обладать необходимыми метакогнитивными навыками для анализа проблемы, выбора подходящей стратегии для решения этой проблемы из множества возможных альтернатив и наблюдения за процессом решения проблемы, чтобы убедиться, что он проведен правильно.

 

Следующие стратегии сочетают в себе как когнитивные, так и метакогнитивные элементы (Montague, 1992; Montague & Dietz, 2009). Во-первых, учащегося учат 7-ступенчатому процессу решения математической задачи (когнитивная стратегия). Во-вторых, инструктор обучает студента использовать программу самокоучинга, состоящую из трех частей, для каждого из семи шагов решения проблем (метакогнитивная стратегия).

 

В когнитивной части этого мультистратегического вмешательства учащийся изучает последовательность шагов для анализа и решения математической задачи. Эти шаги включают в себя:

1. Чтение задачи. Учащийся внимательно читает задачу, отмечая и пытаясь прояснить любые неясные или непонятные области (например, неизвестные словарные термины).
2. Перефразируя проблему. Учащийся формулирует задачу своими словами.
3. «Рисование» задачи. Учащийся рисует задачу, создавая визуальное представление словесной задачи.
4. Создание плана решения проблемы. Учащийся выбирает наилучший способ решения проблемы и разрабатывает для этого план.
5. Прогнозирование/оценка ответа. Учащийся оценивает или предсказывает, каким будет ответ на задачу. Учащийся может вычислить быстрое приближение к ответу, используя округление или другие сокращения.
6. C подсчет ответа. Учащийся следует плану, разработанному ранее, чтобы вычислить ответ на задачу.
7. Проверка ответа. Учащийся методично проверяет расчеты для каждого шага задачи. Учащийся также сравнивает фактический ответ с предполагаемым ответом, рассчитанным на предыдущем шаге, чтобы убедиться, что между двумя значениями существует общее соответствие.

Метакогнитивный компонент вмешательства представляет собой процедуру, состоящую из трех частей, которая следует последовательности «Говорить», «Спрашивать», «Проверять». Для каждого из 7 шагов решения задач, рассмотренных выше:

• Учащийся сначала дает самостоятельный инструктаж, формулируя или «произнося» цель шага (« Скажи ’).
• Затем учащийся задает себе вопросы, «спрашивая», что он или она намеревается сделать, чтобы завершить шаг (« Спросить »).
• Учащийся завершает шаг самоконтролем или «проверкой» успешного завершения шага (« Проверить »).

 

В то время как последовательность «скажи-спроси-проверь» повторяется на всех 7 этапах решения проблемы, фактическое содержание комментариев учащегося при самообучении меняется на каждом этапе.

 

В таблице 1 (а также во вложении внизу страницы) показано, как каждый из шагов когнитивной стратегии решения текстовых задач соответствует последовательности, состоящей из трех частей:

 

Метакогнитивные подсказки «скажи-спроси-проверь», связанные с когнитивной стратегией словесной задачи (Montague, 1992)
Шаг когнитивной стратегии	Цели метакогнитивной подсказки «Скажи-спроси-проверь»	Образцы метакогнитивных подсказок «Скажи-спроси-проверь»
1. Прочитайте задачу.	«Произнеси» (самостоятельное обучение) Цель: Учащийся внимательно читает и изучает задачу, прежде чем продолжить. «Спросить» (самостоятельный вопрос) Цель: Полностью ли учащийся понимает проблему?	Скажи: «Я прочитаю задачу. Я перечитаю задачу, если не пойму». Спросите: « Теперь, когда я прочитал проблему, полностью ли я ее понимаю‌» Проверьте: «Я понимаю проблему и буду двигаться дальше».
2. Перефразируйте задачу.	«Произнеси» (самостоятельное обучение) Цель: Ученик переформулирует задачу, чтобы продемонстрировать понимание. «Спросить» (самостоятельный вопрос) Цель: Может ли учащийся перефразировать проблему‌ «Проверить» (самоконтроль) Цель: Убедитесь, что все выделенные ключевые слова относятся к вопросу.	Скажи: «Я выделю ключевые слова и фразы, относящиеся к проблемному вопросу». «Я переформулирую проблему своими словами». Спросите: « Выделил ли я самые важные слова или фразы в задаче‌» Проверьте: «Я нашел ключевые слова или фразы, которые помогут решить проблему».
3. «Нарисуй» задачу.	«Произнеси» (самоучитель) Цель: Учащийся рисует задачу, чтобы закрепить понимание. «Спросить» (само-вопрос) Цель: Есть ли соответствие между рисунком и задачей? основные элементы математической задачи.	Скажи: «Я нарисую схему задачи». Спросите: « Представляет ли мой рисунок проблему‌» Проверьте: «Рисунок содержит основные части проблемы».
4. Составьте план решения проблемы.	«Скажи» (самостоятельное обучение) Цель: Учащийся составляет план решения задачи. «Спросить» (самовопрос) Цель: Какой план поможет учащемуся решить эту проблему?	Скажи: «Я составлю план решения проблемы». Спросите: «Каков первый шаг этого плана‌ Каков следующий шаг плана‌» Проверьте: «В моем плане есть правильные шаги для решения проблемы».
5. Прогноз/ оценка Ответ.	«Говорить» (самостоятельное обучение) Цель: Учащийся использует оценку или другие стратегии, чтобы предсказать или оценить ответ. «Спросить» (самостоятельный вопрос) Цель: Какой метод оценки будет использовать учащийся, чтобы предсказать ответ‌ «Проверить» (самоконтроль) Цель: / Прогнозируемый ответ использована вся необходимая информация о проблеме.	Скажи: «Я прикину ответ». Спросить: «Какие числа в задаче следует использовать для моей оценки‌» Проверить: «Я не упустил никакой важной информации в своей оценке».
6. Вычислите ответ.	«Произнеси» (самостоятельное обучение) Цель: Учащийся следует плану, чтобы вычислить решение задачи. «Спросить» (самовопрос) Цель: Соответствует ли ответ оценке?	Скажи: «Я вычислю ответ на задачу». Спросите: «Мой ответ звучит правильно‌» «Мой ответ близок к моей оценке‌» Проверьте: «Я выполнил все операции в правильном порядке, чтобы решить эту проблему».
7. Проверьте ответ.	«Произнеси» (самоучитель) Цель: Ученик просматривает этапы вычисления, чтобы проверить ответ. «Спросить» (самостоятельный вопрос) Цель: Проверил ли учащийся все шаги решения задачи и все ли вычисления верны‌ «Проверить» (самоконтроль) Цель: 6 Решение проблемы, кажется, было сделано правильно.	Скажите: «Я проверю шаги своего ответа». Спросить: «Прошел ли я каждый шаг в своем ответе и проверил свою работу‌» Проверить: «»

 

Учащимся будет полезна непосредственная поддержка учителя при обучении сочетанию 7-этапной когнитивной стратегии решения математических задач с итеративной 3-этапной метакогнитивной последовательностью «Скажи-Спроси-Проверь». Учителя могут повысить вероятность того, что учащийся успешно приобретет эти навыки, используя методы обучения, основанные на исследованиях (Burns, VanDerHeyden, & Boice, 2008), в том числе:

• Проверка наличия у учащегося необходимых базовых навыков для решения математических задач
• Использование методов явного обучения для обучения когнитивным и метакогнитивным стратегиям
• Обеспечение того, чтобы все учебные задания позволяли учащемуся достичь адекватного уровня успеха
• Предоставление учащимся регулярных возможностей участвовать в активных и точных академических ответах
• Предлагайте частые отзывы об успеваемости, чтобы мотивировать учащегося и формировать его или ее обучение.

  No related posts.