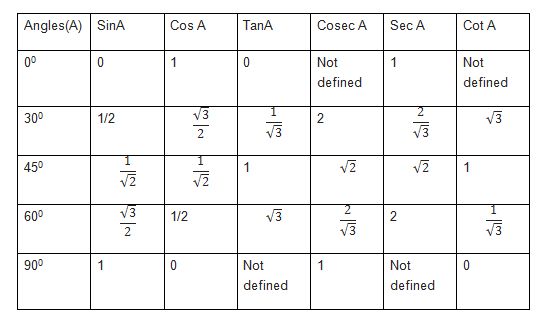
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | sin(120 град. ) ) | ||
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Что будет если cos умножить на sin
Обновлено: 24.09.2022
Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α — β 2 . Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Формулы понижения степени
sin 2 α = 1 — cos 2 α 2 cos 2 α = 1 + cos 2 α 2 sin 3 α = 3 sin α — sin 3 α 4 cos 3 α = 3 cos α + cos 3 α 4 sin 4 α = 3 — 4 cos 2 α + cos 4 α 8 cos 4 α = 3 + 4 cos 2 α + cos 4 α 8
Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
Общий вид формул понижения степени
sin n α = C n 2 n 2 n + 1 2 n — 1 ∑ k = 0 n 2 — 1 ( — 1 ) n 2 — k · C k n · cos ( ( n — 2 k ) α ) cos n α = C n 2 n 2 n + 1 2 n — 1 ∑ k = 0 n 2 — 1 C k n · cos ( ( n — 2 k ) α )
sin n α = 1 2 n — 1 ∑ k = 0 n — 1 2 ( — 1 ) n — 1 2 — k · C k n · sin ( ( n — 2 k ) α ) cos n α = 1 2 n — 1 ∑ k = 0 n — 1 2 C k n · cos ( ( n — 2 k ) α )
Примеры решения практических задач
Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов.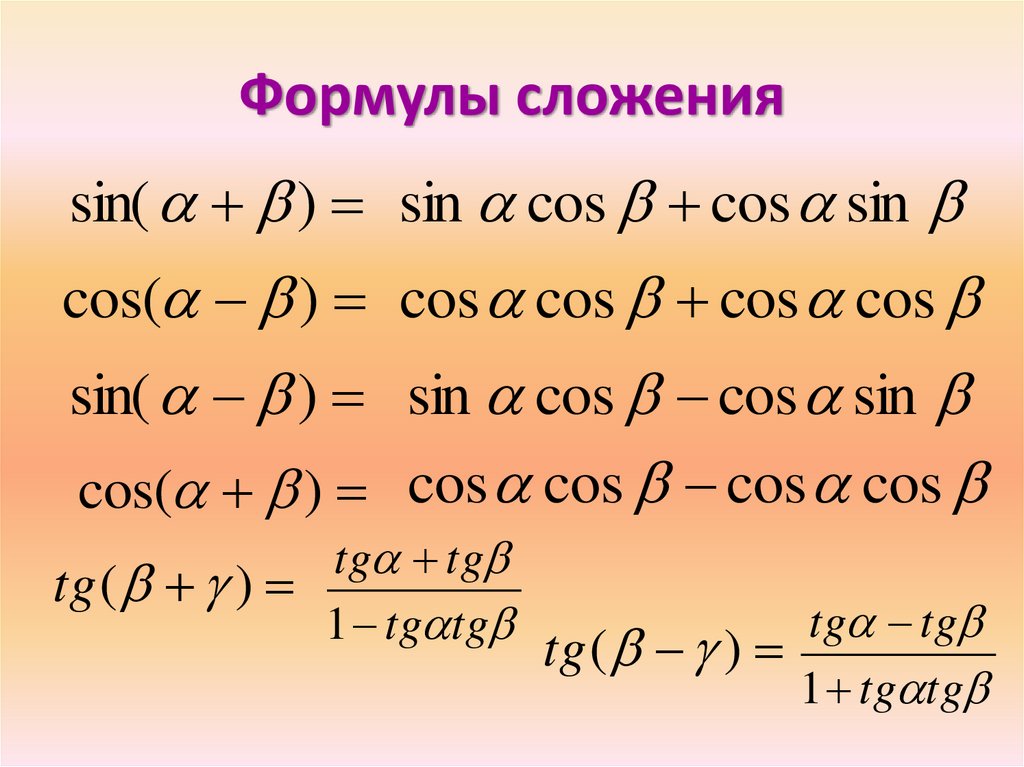 Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пример 1. Проверка формулы суммы синусов двух углов
α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 — π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2
Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.
Пример 2. Применение формулы разности синусов
α = 165 ° , β = 75 ° sin α — sin β = sin 165 ° — sin 75 ° sin 165 — sin 75 = 2 · sin 165 ° — 75 ° 2 cos 165 ° + 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · — 1 2 = 2 2
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Формулы приведения
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.
sin α + 2 π z = sin α , cos α + 2 π z = cos α t g α + 2 π z = t g α , c t g α + 2 π z = c t g α sin — α + 2 π z = — sin α , cos — α + 2 π z = cos α t g — α + 2 π z = — t g α , c t g — α + 2 π z = — c t g α sin π 2 + α + 2 π z = cos α , cos π 2 + α + 2 π z = — sin α t g π 2 + α + 2 π z = — c t g α , c t g π 2 + α + 2 π z = — t g α sin π 2 — α + 2 π z = cos α , cos π 2 — α + 2 π z = sin α t g π 2 — α + 2 π z = c t g α , c t g π 2 — α + 2 π z = t g α sin π + α + 2 π z = — sin α , cos π + α + 2 π z = — cos α t g π + α + 2 π z = t g α , c t g π + α + 2 π z = c t g α sin π — α + 2 π z = sin α , cos π — α + 2 π z = — cos α t g π — α + 2 π z = — t g α , c t g π — α + 2 π z = — c t g α sin 3 π 2 + α + 2 π z = — cos α , cos 3 π 2 + α + 2 π z = sin α t g 3 π 2 + α + 2 π z = — c t g α , c t g 3 π 2 + α + 2 π z = — t g α sin 3 π 2 — α + 2 π z = — cos α , cos 3 π 2 — α + 2 π z = — sin α t g 3 π 2 — α + 2 π z = c t g α , c t g 3 π 2 — α + 2 π z = t g α
Формулы приведения являются следствием периодичности тригонометрических функций.
Синус альфа умножить на косинус альфа
Sin(a)*cos(a) = 1/2 * 2*sin(a)*cos(a) = 1/2 * sin(2a)
При a из Re это принимает значения от -1/2 до +1/2.
Но если взять комплексные значения а, то можно получить любое значение.
Новые вопросы в Геометрия
даю 80 баллов лучше решить на листочке и расписать, если не сложно спасибо
даю 85 баллов лучше решить на листочке и расписать, если не сложно спасибо
трикутник ABC кут A=70°кут ACK=30°CK- бісектриса знайти кут ВДАЮ ВСЕ 100 ЮАЛЛОВ ПОМОГИТЕ СРОЧНО
График функции y=3x−5 пересекает ось Oy в точке с координатами? ПОМОГИТЕ ПЖ
геометрия(задача на тетраедр) с рисунком и объяснением.спасибо
довжини сторін трикутника дорівнюють 6, 10 і 12 см. обчислити площу квадрата стороною якого є бісектриса проведена до більшої сторони
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
sin ( α + β ) = sin α · cos β + cos α · sin β sin ( α — β ) = sin α · cos β — cos α · sin β cos ( α + β ) = cos α · cos β — sin α · sin β cos ( α — β ) = cos α · cos β + sin α · sin β
Также представим сами углы в виде суммы полусумм и полуразностей.
α = α + β 2 + α — β 2 = α 2 + β 2 + α 2 — β 2 β = α + β 2 — α — β 2 = α 2 + β 2 — α 2 + β 2
Переходим непосредственно к выводу формул суммы и разности для sin и cos.
Вывод формулы суммы синусов
В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим
sin α + sin β = sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2
Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)
sin α + β 2 + α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу
sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α + β 2 cos α — β 2
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
sin α — sin β = sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 — sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α — β 2 cos α + β 2
Вывод формулы суммы косинусов
cos α + cos β = cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 + cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = 2 cos α + β 2 cos α — β 2Вывод формулы разности косинусов
cos α — cos β = cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 — cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = — 2 sin α + β 2 sin α — β 2
Произведение синусов и косинусов: формулы, примеры
В данной статье рассмотрены формулы произведения синусов, косинусов, а также формулы произведения синуса на косинус. Допустим, есть необходимость вычислить произведение синусов или косинусов углов α и β . Формулы произведения позволяют перейти от произведения к сумме или разности синусов и косинусов углов α + β и α — β .
Допустим, есть необходимость вычислить произведение синусов или косинусов углов α и β . Формулы произведения позволяют перейти от произведения к сумме или разности синусов и косинусов углов α + β и α — β .
Приведем формулы произведения синуса на синус, косинуса на косинус и синуса на косинус.
Универсальная тригонометрическая подстановка
Все основные тригонометрические функции — синус, косинус, тангенс и котангенс, — могут быть выражены через тангенс половинного угла.
Универсальная тригонометрическая подстановка
sin α = 2 t g α 2 1 + t g 2 α 2 cos α = 1 — t g 2 α 2 1 + t g 2 α 2 t g α = 2 t g α 2 1 — t g 2 α 2 c t g α = 1 — t g 2 α 2 2 t g α 2
Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.
sin 2 a + cos 2 a = 1 t g α = sin α cos α , c t g α = cos α sin α t g α · c t g α = 1 t g 2 α + 1 = 1 cos 2 α , c t g 2 α + 1 = 1 sin 2 α
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Формулы кратного угла: двойного, тройного и т.д.
sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α — sin 2 α , cos 2 α = 1 — 2 sin 2 α , cos 2 α = 2 cos 2 α — 1 t g 2 α = 2 · t g α 1 — t g 2 α с t g 2 α = с t g 2 α — 1 2 · с t g α sin 3 α = 3 sin α · cos 2 α — sin 3 α , sin 3 α = 3 sin α — 4 sin 3 α cos 3 α = cos 3 α — 3 sin 2 α · cos α , cos 3 α = — 3 cos α + 4 cos 3 α t g 3 α = 3 t g α — t g 3 α 1 — 3 t g 2 α c t g 3 α = c t g 3 α — 3 c t g α 3 c t g 2 α — 1
Основные тригонометрические формулы и тождества sin, cos, tg, ctg
Основные формулы тригонометрии — это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.
Формулы произведения. Список
Приведем формулировки, а затем и сами формулы.
- Произведение синусов углов α и β равно полуразности косинуса угла α — β и косинуса угла α + β .
- Произведение косинусов углов α и β равно полусумме косинуса угла α — β и косинуса угла α + β .
- Произведение синуса угла α на косинус угла β равно полусумме синуса угла α — β и синуса угла α + β .
Для любых α и β справедливы формулы
- sin α · sin β = 1 2 cos α — β — cos α + β ;
- cos α · cos β = 1 2 cos α — β + cos α + β ;
- sin α · cos β = 1 2 sin α — β + sin α + β .
Формулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
Формулы половинного угла
sin 2 α 2 = 1 — cos α 2 cos 2 α 2 = 1 + cos α 2 t g 2 α 2 = 1 — cos α 1 + cos α c t g 2 α 2 = 1 + cos α 1 — cos α
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусов
sin α + sin β = 2 sin α + β 2 cos α — β 2 sin α — sin β = 2 sin α — β 2 cos α + β 2
cos α + cos β = 2 cos α + β 2 cos α — β 2 cos α — cos β = — 2 sin α + β 2 cos α — β 2 , cos α — cos β = 2 sin α + β 2 · β — α 2
Данные формулы справедливы для любых углов α и β .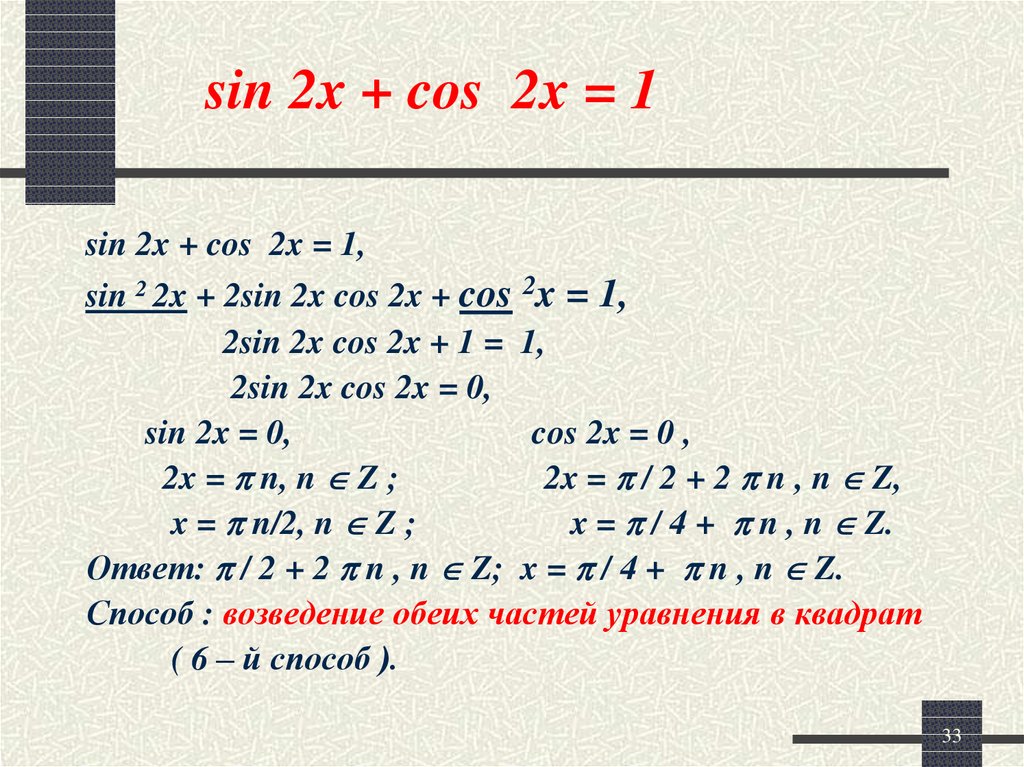 Углы α + β 2 и α — β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.
Углы α + β 2 и α — β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.
Определения формул сумм и разности синусов и косинусов
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.
Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.
Произведение тригонометрических функций
Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход — от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.
Формулы произведения тригонометрических функций
sin α · sin β = 1 2 · ( cos ( α — β ) — cos ( α + β ) ) cos α · cos β = 1 2 · ( cos ( α — β ) + cos ( α + β ) ) sin α · cos β = 1 2 · ( sin ( α — β ) + sin ( α + β ) )
Примеры использования
Приведем примеры использования формул произведения синусов, косинусов и синусов на косинус при решении задач.
Пусть α = 60 ° , β = 30 ° . Возьмем формулу произведения синусов и подставим в нее конкретные значения.
sin α · sin β = 1 2 ( cos α — β — cos α + β ) sin 60 ° · sin 30 ° = 1 2 ( cos 60 ° — 30 ° — cos 60 ° + 30 ° ) sin 60 ° · sin 30 ° = 1 2 ( cos 30 ° — cos 90 ° ) sin 60 ° · sin 30 ° = 1 2 ( 3 2 — 0 ) = 3 4
Теперь вычислим значение выражения, обратившись к таблице основных значений тригонометрических функций.
sin 60 ° · sin 30 ° = 3 2 · 1 2 = 3 4 .
Таким образом, мы проверили формулу на практике и убедились, что формула справедлива.
Пример. Формулы произведения
Нужно sin 75 ° умножить на cos 15 ° и вычислить точное значение произведения.
Мы не располагаем точными значениями синуса и косинуса данных углов, однако можем вычислить точное значение произведения sin 75 ° · cos 15 ° c помощью формулы произведения синуса на косинус.
sin 75 ° · cos 15 ° = 1 2 sin ( 75 ° — 15 ° + sin ( 75 ° + 15 ° ) ) sin 75 ° · cos 15 ° = 1 2 sin 60 ° + sin 90 ° = 1 2 3 2 + 1 = 3 + 2 4
Также формулы произведения используются преобразования тригонометрических выражений.
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Сумма и разность тригонометрических функций
sin α + sin β = 2 sin α + β 2 · cos α — β 2 sin α — sin β = 2 sin α — β 2 · cos α + β 2 cos α + cos β = 2 cos α + β 2 · cos α — β 2 cos α — cos β = — 2 sin α + β 2 · sin α — β 2 , cos α — cos β = 2 sin α + β 2 · sin β — α 2
Вывод формул
Вывод описанных выше формул проводится с помощью формул сложения и на основе свойства равенства. Согласно этому свойству, если левую и правую части верного равенства сложить соответственно с левой и правой частями другого верного равенста, то в результате получится еще одно верное равенство. Покажем вывод формул произведения.
Согласно этому свойству, если левую и правую части верного равенства сложить соответственно с левой и правой частями другого верного равенста, то в результате получится еще одно верное равенство. Покажем вывод формул произведения.
Сначала запишем формулы косинуса суммы и косинуса разности:
cos α + β = cos α · cos β — sin α · sin β cos α — β = cos α · cos β + sin α · sin β
Сложим эти равенства и получим:
cos α + β + cos α — β = cos α · cos β — sin α · sin β + cos α · cos β + sin α · sin β cos α + β + cos α — β = 2 · cos α · cos β
cos α · cos β = 1 2 cos α + β + cos α — β
Формула произведения косинусов доказана.
Перепишем формулу косинуса суммы следующим образом:
— cos ( α + β ) = — cos α · cos β + sin α · sin β
Добавим к равенству формулу cos α — β = cos α · cos β + sin α · sin β .
— cos ( α + β ) + cos α — β = — cos α · cos β + sin α · sin β + cos α · cos β + sin α · sin β — cos ( α + β ) + cos α — β = 2 · sin α · sin β sin α · sin β = 1 2 ( cos α — β — cos ( α + β ) )
Таким образом, выведена формула произведения синусов.
Теперь возьмем формулу синуса суммы, формулу синуса разности, и сложим их левые и правые части
sin α + β = sin α · cos β + cos α · sin β sin α — β = sin α · cos β — cos α · sin β sin α + β + sin α — β = sin α · cos β + cos α · sin β + sin α · cos β — cos α · sin β sin α + β + sin α — β = 2 sin α · cos β sin α · cos β = 1 2 ( sin α + β + sin α — β )
Формула произведения синуса на косинус выведена.
Тригонометрические формулы сложения
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
Тригонометрические формулы сложения
sin α ± β = sin α · cos β ± cos α · sin β cos α + β = cos α · cos β — sin α · sin β cos α — β = cos α · cos β + sin α · sin β t g α ± β = t g α ± t g β 1 ± t g α · t g β c t g α ± β = — 1 ± c t g α · c t g β c t g α ± c t g β
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Читайте также:
- Жить и любить fallout 4 где найти журналы
- Far cry 3 не сохраняется игра что делать
- Black ops как снять бан
- Cs go когда турниры
- Dark souls 2 бинокль где взять
Как найти угол зная значение косинуса
Значения косинуса графически могут быть отображены в виде тригонометрической окружности, на которой угол α образует с осью прямоугольный треугольник. Из этого треугольника, спроецировав точку пересечения угла α с окружностью на ось синуса или косинуса, можно получить его приближенное значение.
Из этого треугольника, спроецировав точку пересечения угла α с окружностью на ось синуса или косинуса, можно получить его приближенное значение.
Также тригонометрическая окружность показывает знак синуса и косинуса для каждого раскрытия угла α . Поскольку угол начинает раскрываться с правой стороны по оси косинусов, то значения косинуса угла α от 0° до 90° – положительны, так находятся правее нулевой точки отсчета. Угол α от 90° до 270° дает отрицательные значения косинусу, так как точка пересечения его с окружностью расположена левее оси синуса, то есть нуля. Косинус углов от 270° до 360° вновь становится положительным. Точные значения косинусов всех углов от 0° до 360° можно узнать из таблицы косинусов, приведенной ниже.
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30 ° , 45 ° , 60 ° . Если угол выходит за пределы 90 ° , то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α , можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу.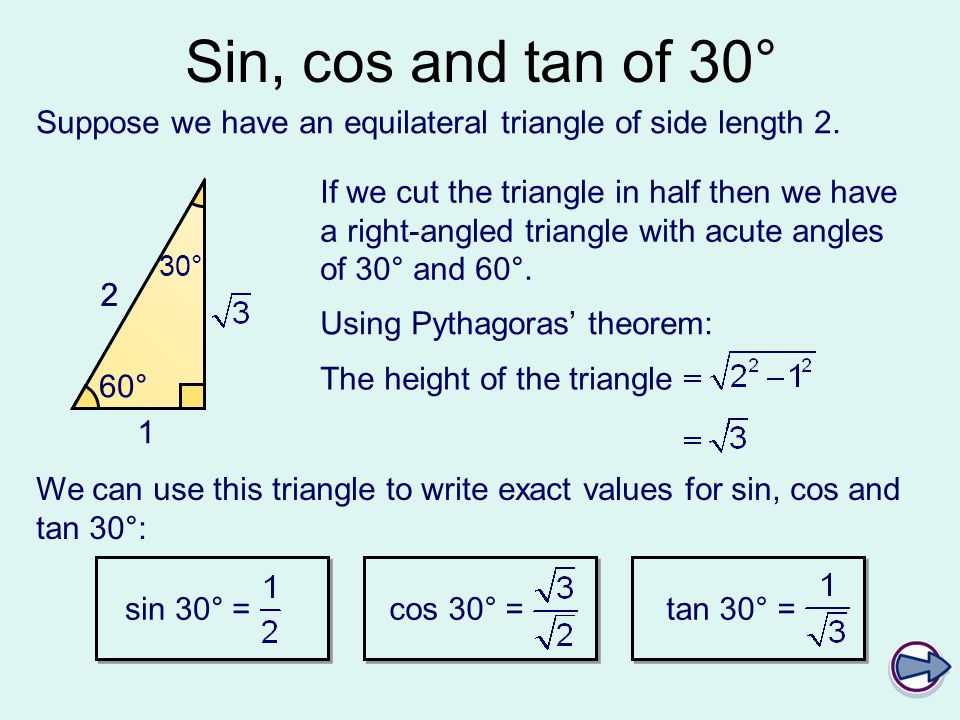 Например, по известному значению синуса 45 ° , мы сможем определить значение синуса 30 ° , воспользовавшись правилом из тригонометрии.
Например, по известному значению синуса 45 ° , мы сможем определить значение синуса 30 ° , воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α . Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0 ° , 90 ° , 180 ° , 270 ° , 360 ° .
Разобьем эти углы на четыре группы: 360 · z градусов ( 2 π · z рад), 90 + 360 · z градусов ( π 2 + 2 π · z рад), 180 + 360 · z градусов ( π + 2 π · z рад) и 270 + 360 · z градусов ( 3 π 2 + 2 π · z рад), где z – любое целое число.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
При повороте из точки A на 360 · z ° , она переходит в себя. А 1 ( 1 , 0 ) . Синус 0 ° , 360 ° , 720 ° равен 0 , а косинус равен 1 . Представим это в виде формулы: sin ( 360 ° · z ) = 0 и cos ( 360 ° · z ) = 1 .
А 1 ( 1 , 0 ) . Синус 0 ° , 360 ° , 720 ° равен 0 , а косинус равен 1 . Представим это в виде формулы: sin ( 360 ° · z ) = 0 и cos ( 360 ° · z ) = 1 .
Можно определить, что t g ( 360 ° · z ) = 0 1 = 0 , а котангенс не определен.
Если А ( 1 , 0 ) повернуть на 90 + 360 · z ° , то она перейдет в А 1 ( 0 , 1 ) . По определению: sin ( 90 ° + 360 ° · z ) = 1 и cos ( 90 ° + 360 ° · z ) = 0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: c t g ( 90 ° + 360 ° · z ) = 0 1 = 0 .
Рассмотрим особенности для третьей группы углов. После поворота точки А ( 1 , 0 ) на любой из углов 180 + 360 · z ° , она перейдет в A 1 ( − 1 , 0 ) . Мы находим значения функций кроме тангенса.
Рассмотрим правила для четвертой группы углов. При повороте точки на 270 + 360 · z ° мы попадем в A 1 ( 0 , − 1 ) . Мы находим значения всех функций кроме тангенса.
Для углов, которые не относятся к перечню от 0 ° , 90 ° , 180 ° , 270 ° , 360 ° … , точных значений нет.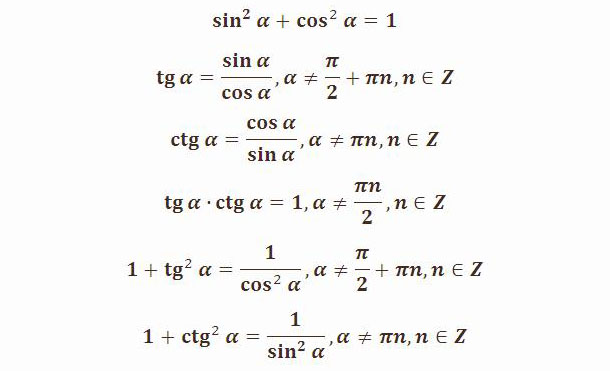 Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла − 52 ° . Выполним построения.
Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла − 52 ° . Выполним построения.
Согласно рисунку, абсцисса А 1 ≈ 0 , 62 , а ордината ≈ − 0 , 78 . Соответственно, sin ( – 52 ° ) ≈ – 0 , 78 и cos ( – 52 ° ) ≈ 0 , 62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: t g ( – 52 ° ) ≈ – 0 , 78 0 , 62 ≈ – 1 , 26 и c t g ( – 52 ° ) ≈ 0 , 62 – 0 , 78 ≈ – 0 , 79 .
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Как найти sin α , cos α , t g α , c t g α
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1 . Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 1 2 – 1 2 2 = 3 2 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30 ° = 1 2 1 = 1 2 и sin 60 ° = 3 2 1 = 3 2 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30 ° = 3 2 1 = 3 2 и cos 60 ° = 1 2 1 = 1 2 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: t g 30 ° = 1 2 3 2 = 1 3 = 3 3 и t g 60 ° = 3 2 1 2 = 3 .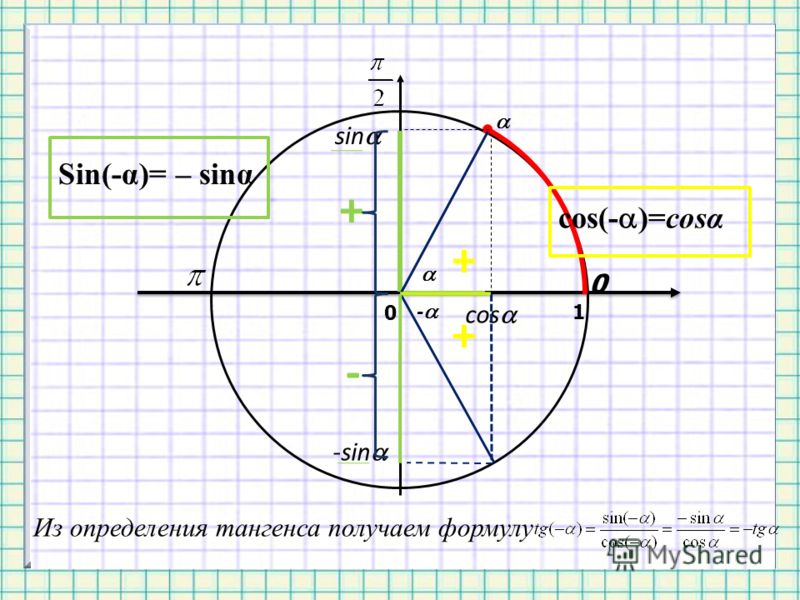 Находим котангенс по подобной схеме: с t g 30 ° = 3 2 1 2 = 3 и с t g 60 ° = 1 2 3 2 = 1 3 = 3 3 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45 ° и гипотенузой, которая равна 1 . Используем теорему Пифагора. Согласно формуле, длины катетов равны 2 2 . Т
Находим котангенс по подобной схеме: с t g 30 ° = 3 2 1 2 = 3 и с t g 60 ° = 1 2 3 2 = 1 3 = 3 3 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45 ° и гипотенузой, которая равна 1 . Используем теорему Пифагора. Согласно формуле, длины катетов равны 2 2 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: c t g 45 ° = 2 2 2 2 = 1 .
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α , cos α , t g α , c t g α для определенного угла. С помощью одной функции вы легко сможете найти другую.
С помощью одной функции вы легко сможете найти другую.
Для того, чтобы найти синус по известному косинусу, sin 2 α + cos 2 α = 1 .
Тангенс по известному косинусу t g 2 α + 1 = 1 cos 2 α .
Котангенс по известному синусу или наоборот 1 + c t g 2 α = 1 sin 2 α .
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: t g α · c t g α = 1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Необходимо найти значение синуса угла π 8 , если t g π 8 = 2 – 1 .
Сначала найдем котангенс угла: c t g π 8 = 1 t g π 8 = 1 2 – 1 = 2 + 1 ( 2 – 1 ) · ( 2 + 1 ) = 2 + 1 ( 2 ) 2 – 1 2 = 2 + 1 Воспользуемся формулой 1 + c t g 2 α = 1 sin 2 α . Благодаря этому мы вычисляем значение синуса. Имеем
sin 2 π 8 = 1 1 + c t g 2 π 8 = 1 1 + ( 2 + 1 ) 2 = 1 4 + 2 2 = 1 2 · ( 2 + 2 ) = 2 – 2 2 · ( 2 + 2 ) · ( 2 – 2 ) = = 2 – 2 2 · ( 2 2 – ( 2 ) 2 ) = 2 – 2 4
Для завершения необходимо определить значение синуса. Угол π 8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π 8 = sin 2 π 8 = 2 – 2 4 = 2 – 2 2 . sin π 8 = 2 – 2 2 .
Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π 8 = sin 2 π 8 = 2 – 2 4 = 2 – 2 2 . sin π 8 = 2 – 2 2 .
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 ° . Сведение к углу из интервала от 0 до 90 ° . Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Задача заключается в том, чтобы найти синус 210 ° . Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30 ° : sin 210 ° = sin ( 180 ° + 30 ° ) = – sin 30 ° = – 1 2 , или косинуса 60 ° sin 210 ° = sin ( 270 ° – 60 ° ) = – cos 60 ° = – 1 2 .
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90 ° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π 8 , который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Найдите значение t g π 8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства t g 2 π 8 = 1 – cos π 4 1 + cos π 4 . Значения косинуса угла π 4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
t g 2 π 8 = 1 – cos π 4 1 + cos π 4 = 1 – 2 2 1 + 2 2 = 2 – 2 2 + 2 = = ( 2 – 2 ) 2 ( 2 + 2 ) · ( 2 – 2 ) = ( 2 – 2 ) 2 2 2 – ( 2 ) 2 = ( 2 – 2 ) 2 2
Угол π 8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: t g π 8 = t g 2 π 8 = ( 2 – 2 ) 2 2 = 2 – 2 2 = 2 – 1
Продолжаем вычисления для дальнейшего решения: t g π 8 = t g 2 π 8 = ( 2 – 2 ) 2 2 = 2 – 2 2 = 2 – 1
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Косинус угла представляет собой одну из тригонометрических функций. Является соотношением ближнего к углу прямоугольного треугольника катета к гипотенузе. Записывается следующим образом: cos (А) = АС/АВ, где АС – ближний катет угла (А), АВ – гипотенуза.
Зачем необходимо производить такие сложные на первый взгляд вычисления? Еще с древних времен известна аксиома: знаю угол – знаю его тригонометрическую функцию. Соответственно, если известен cos любого угла, в таблице Брадиса можно найти этот угол. И наоборот – зная угол, не сложно вычислить косинус. Отсюда можно найти следующие данные: длина катетов и гипотенузы.
Эти данные используются не только в голых математических вычислениях. Невозможно составить даже элементарный план местности, не зная тригонометрических функций. Посредством онлайн калькулятора можно облегчить задачу и получать требуемые данные за доли секунды.
тригонометрия — Как получить значение синуса/косинуса из тангенсов
Вопрос задан
Изменено 4 года, 8 месяцев назад
Просмотрено 72k раз
$\begingroup$
Я знаю, что: $\tan(\alpha) = 1/2$.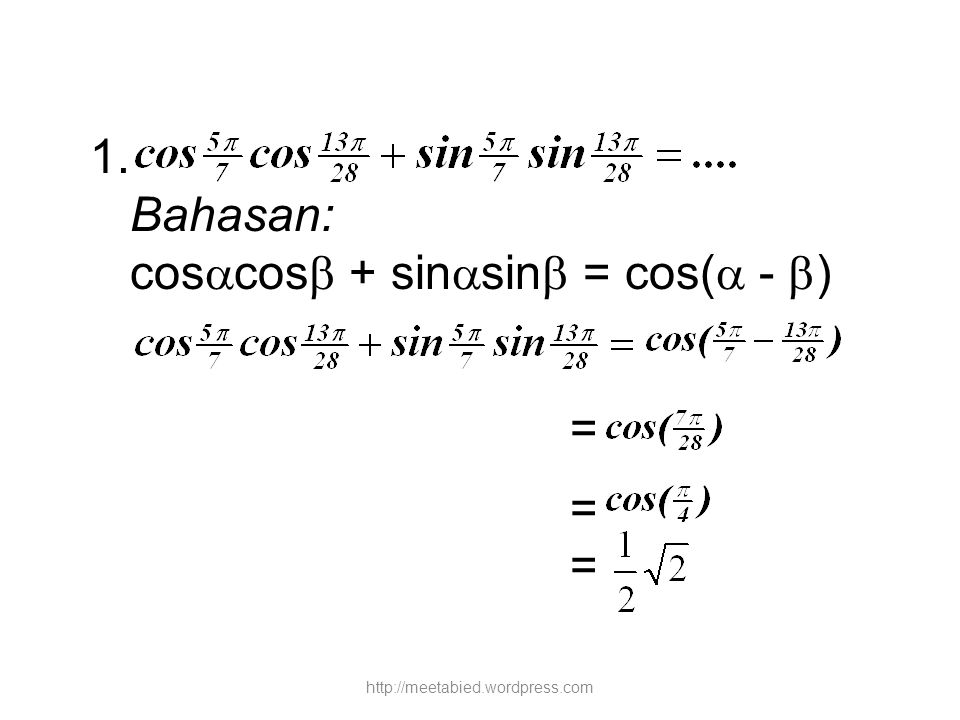
Как получить чистые значения синуса/косинуса без калькулятора ?
Есть ли связь?
Я знаю, что $\sin(\arctan(1/2))$ — это способ… Но я надеюсь, вы поняли суть. 9\circ$) углы $\alpha$.
2) Вы знаете, что тангенс $\alpha$ равен ${1\over2}$. Поскольку $\tan={\text{противоположный}\over \text{прилегающий}}$, вы можете обозначить сторону треугольника, примыкающую к $\alpha$, «1», а противоположную сторону — «2».
3) По теореме Пифагора можно найти длину гипотенузы треугольника.
4) Теперь вы можете прочитать $\sin(\alpha)$ из завершенного треугольника. И помните, что грех от угла противоположен/гипотенуза — 1/радикал 5 92 \alpha = \frac{4}{5}.$$
Таким образом, возможно $$\sin \alpha = \pm \frac{1}{\sqrt{5}}, \quad \cos \alpha = \pm \frac{2}{\sqrt{5}}.$$
Нам еще нужно показать, что эти возможности возможны. Мы знаем, что существует $\alpha$, такое что $\tan \alpha = \frac{1}{2}$. т. е. исходное уравнение имеет решение. Теперь, если $\alpha$ — решение, то $\alpha + \pi$ — тоже. Отсюда мы можем сделать вывод, что и $\sin \alpha = \frac{1}{\sqrt{5}}$, и $\sin \alpha = -\frac{1}{\sqrt{5}}$ достижимы и так и $\cos \alpha = \pm \frac{1}{\sqrt{5}}$. Причем знаки должны быть одинаковыми для обоих. Таким образом, решения
$$(\cos\alpha,\sin\alpha)\in\{(\frac{1}{\sqrt{5}}, \frac{1}{\sqrt{5}}), (-\frac{ 1}{\sqrt{5}}, -\frac{1}{\sqrt{5}})\}.$$
е. исходное уравнение имеет решение. Теперь, если $\alpha$ — решение, то $\alpha + \pi$ — тоже. Отсюда мы можем сделать вывод, что и $\sin \alpha = \frac{1}{\sqrt{5}}$, и $\sin \alpha = -\frac{1}{\sqrt{5}}$ достижимы и так и $\cos \alpha = \pm \frac{1}{\sqrt{5}}$. Причем знаки должны быть одинаковыми для обоих. Таким образом, решения
$$(\cos\alpha,\sin\alpha)\in\{(\frac{1}{\sqrt{5}}, \frac{1}{\sqrt{5}}), (-\frac{ 1}{\sqrt{5}}, -\frac{1}{\sqrt{5}})\}.$$
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.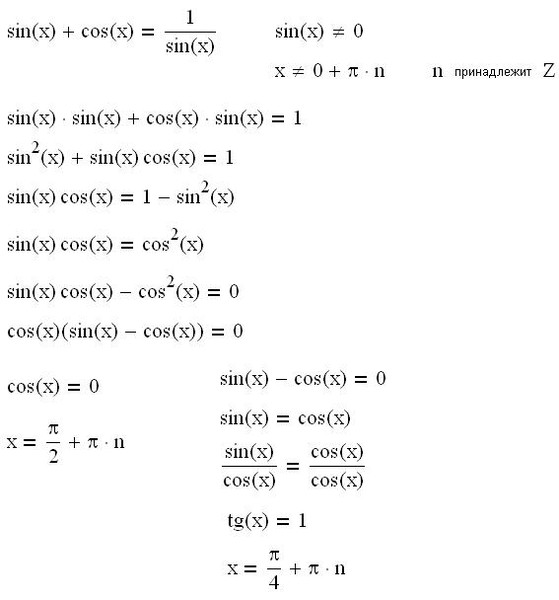
формул Sin Cos в тригонометрии с примерами
Тригонометрия, как следует из названия, изучает треугольники. Это важный раздел математики, изучающий взаимосвязь между длинами сторон и углами прямоугольного треугольника, а также помогающий определить недостающие длины сторон или углы треугольника. Существует шесть тригонометрических отношений или функций: синус, косинус, тангенс, косеканс, секанс и котангенс, где косеканс, секанс и котангенс являются обратными функциями трех других функций, то есть синуса, косинуса и тангенса соответственно. Тригонометрическое отношение определяется как отношение длин сторон прямоугольного треугольника. Тригонометрия используется в различных областях нашей повседневной жизни. Это помогает определить высоту холмов или зданий. Он также используется в таких областях, как криминология, строительство, физика, археология, разработка морских двигателей и т. д.
Формулы шести тригонометрических соотношений/функций
Рассмотрим прямоугольный треугольник XYZ, где ∠Y = 90°.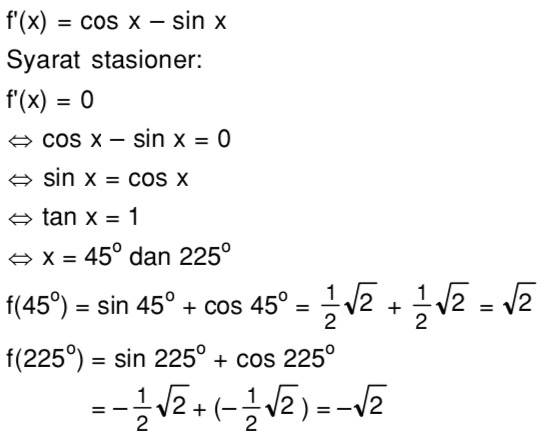 Пусть угол при вершине Z равен θ. Сторона, примыкающая к «θ», называется смежной стороной, а сторона, противоположная «θ», называется противоположной стороной. Гипотенуза — это сторона, противоположная прямому углу или самая длинная сторона прямого угла.
Пусть угол при вершине Z равен θ. Сторона, примыкающая к «θ», называется смежной стороной, а сторона, противоположная «θ», называется противоположной стороной. Гипотенуза — это сторона, противоположная прямому углу или самая длинная сторона прямого угла.
- sin θ = Противоположная сторона/Гипотенуза
- cos θ = Прилегающая сторона/Гипотенуза
- tan θ = Противоположная сторона/Прилегающая сторона
- cosec θ = 1/sin θ = гипотенуза/противоположная сторона
- sec θ = 1/cos θ = гипотенуза/прилегающая сторона
- cot θ = 1/tan θ = примыкающая сторона/противоположная сторона
5 9015 Формула
5 9015
Синус угла в прямоугольном треугольнике равен отношению длины противолежащего катета к длине гипотенузы к данному углу. Функция синуса представлена как «sin».
sin θ = противолежащая сторона/гипотенуза
Формула косинуса
Косинусом угла прямоугольного треугольника называется отношение длины прилежащего катета к длине гипотенузы данного угла.
Функция косинуса представлена как «cos».
cos θ = смежная сторона/гипотенуза
Некоторые основные формулы синуса и косинуса
Функции синуса и косинуса в квадрантах четвертые квадранты.
- Функция косинуса положительна в первом и четвертом квадрантах и отрицательна во втором и третьем квадрантах.
Degrees
Quadrant
Sign of Sine function
Sign of Cosine function
0° to 90°
1st quadrant
+ (положительный)
+ (положительный)
90° to 180°
2nd quadrant
+ (positive)
– (negative)
180° to 270°
3rd quadrant
– (negative)
– (negative)
270° to 360°
4th quadrant
– (negative)
+ (положительный)
Идентичность отрицательного угла функций синуса и косинуса
- Синус отрицательного угла всегда равен отрицательному синусу угла.
sin (– θ) = – sin θ
- Косинус отрицательного угла всегда равен косинусу угла.
cos (– θ) = cos θ
Связь между функцией синуса и косинуса
sin θ = cos (90° – θ)
Функции, обратные функциям синуса и косинуса
sin 3 θ – 4 sin 3 θcosec θ = 1/sin θ
- Функция секущей является обратной функцией функции косинуса.
сек θ = 1/cos θ
Тождество Пифагора
sin 2 θ + cos 2 θ = 1
Periodic identities of the sine and cosine functions
sin (θ + 2nπ) = sin θ
cos ( θ + 2nπ) = cos θ
Формулы с двойным углом для функций синуса и косинуса
sin 2θ = 2 sin θ cos θ
cos 2θ = cos 2 № 9015 COS 2θ = COS 2 –θ θ θ θ θ θ θ θ
.
θ = 2 потому что 2 θ – 1 = 1 – 2 sin 2 θ
Тождества половин углов для функций синуса и косинуса
sin (θ/2) = ±√ 2]
cos (θ/2) = ±√[(1 + cos θ)/2]
Тройные тождества углов для функций синуса и косинуса
cos 3θ = 4cos 3 θ – 3 cos θ
Формулы суммы и разности
- Функция синуса
sin (A + B) = sin A cos B + cos A sin B
sin A cos B (A cos B – 9001) – cos A sin B
- Функция косинуса
cos (A + B) = cos A cos B – sin A sin B
900 cos + sin A sin B
Закон синусов или правило синусов
Закон синусов по правилу синусов — это тригонометрический закон, определяющий соотношение между длинами сторон и углами треугольника.
a/sin A = b/sin B = c/sin C
Где a, b и c — длины трех сторон треугольника ABC, а A, B и C — углы.
Закон косинусов
Закон косинусов используется для определения отсутствующих или неизвестных углов или длин сторон треугольника.
A 2 = B 2 + C 2 — 2BC COS A
+ B 2 = C 2 + B 2 = C 2 + B 2 = C 2 + B 2 . c 2 = a 2 + b 2 – 2ab cos C
Где a, b и c — длины трех сторон треугольника ABC, а A, B и C — углы .
Таблица значений функций синуса и косинуса
Angle (in degrees) | Angle (in radians) | sin θ | cos θ |
|---|---|---|---|
0° | 0 | 0 | 1 |
30° | π/6 | 1/2 | _3/2 |
45° | π/4 | 1/√2 | 1/√2 |
60° | π/3 | √3/2 | 1/2 |
90° | π/2 | 1 | 0 |
120° | 2π/3 | √3/ 2 | -1/2 |
150° | 5π/6 | 1/2 | -√3/2 |
180° | π | 0 | -1 |
Задачи на формулы синуса и косинуса
Задача 1: Если cos α = 24/25, то найти значение sin α.
Решение:
Дано,
cos α = 24/25
Из пифагорейских тождеств мы имеем;
COS 2 θ + SIN 2 θ = 1
(24/25) 2 + SIN 2 α = 1
SIN 2 α = 1 — (24/25) 2 α = 1 — (24/25) 2 α = 1 — (24/25) 2.
sin 2 α = 1 – (576/625) = (625 – 576)/625
sin 2 α = (625 – 576)/625 = 49/626
9 sin 4 = 9000†2 /625 = ±7/25Следовательно, sin α = ±7/25.
Задача 2: Докажите формулы sin 2A и cos 2A, если ∠A= 30°.
Решение:
Дано, ∠A= 30°
Мы знаем, что
1) sin 2A = 2 sin A cos A
sin 2 cos 2(30°3)0 = °
sin 60° = 2 × (1/2) × (√3/2) {Поскольку sin 30° = 1/2, cos 30° = √3/2 и sin 60° = √3/2}
√3/2 = √3/2
Л.В.С. = ПРАВ.В.С.
0005
cos 60° = 2(√3/2) 2 – 1 = 3/2 – 1 {Поскольку, cos 60° = 1/2 и cos 30° = √3/2}
1/2 = 1/2
L.H.S = R.H.S
Отсюда доказано.
Задача 3: Найдите значение cos x, если tan x = 3/4.
Решение:
Учитывая, что tan x = 3/4
Мы знаем, что
tan x = противоположная сторона/прилежащая сторона = 3/4
гипотенуза 2 = противоположность 2 + прилегающий 2
H 2 = 3 2 + 4 2
H 2 =
9000 2 9000 2 9000 2
9000 2 9000 2
9000 2 9000 2 9000 2
9000 2 9000 2 9000 2
9000 2
9000 2 9000 2 9000 2
9000 2 9000 2 9000 2 9000 2
9000 2 9000 2 9000 2 9000 2
9000 2 9000 2 9000 2 9000 2
9000 2 9000 2
9000 2 =
2 =
Теперь cos x = смежная сторона/гипотенуза
cos x = 4/5
Таким образом, значение cos x равно 4/5.
Задача 4. Найдите ∠C (в градусах) и ∠A (в градусах), если ∠B = 45°, BC = 15 дюймов и AC = 12 дюймов.0005 Дано: ∠B = 45°, BC = a = 15 дюймов и AC = b = 12 дюймов. Из закона синусов имеем a/sin A = b/sin B = c/ sin C ⇒ a/sin A = b/sin B ⇒ 15/sin A = 12/sin 45° ⇒ 15/sin A = 12/(1/√2) ⇒ 15/sin A = 12√2 = 16,97 ⇒ sin A = 15/16,97 = 0,8839 ⇒ ∠A = sin -1 (0,8839) = 62,11° Мы знаем, что сумма внутренних углов треугольника равна 1° 8 . Итак, ∠A + ∠B + ∠C = 180° ⇒ 62,11° + 45° + ∠C = 180° ⇒ ∠C = 180° – (62,11° + 45°) = 72,89° Следовательно, ∠A = 62,11° и ∠9 = .8,89 Задача 5. Докажите тождество полууглов функции косинуса. Решение: Тождество полуугла функции косинуса: cos (θ/2) = ±√[(1 + cos θ)/2] have, cos 2A = 2 cos 2 A – 1 Теперь замените A на θ/2 с обеих сторон ⇒ cos 2(θ/2) = 2 cos 2 (θ/2) – 1 ⇒ cos θ = 2 cos 2 (θ/2) – 1 ⇒ 2 1 9035 /2) = cos θ + 1 ⇒ cos 2 (θ/2) = (cos θ + 1)/2 ⇒ cos (θ/2) = ±√[(1 + cos θ)/2 ] Отсюда доказано. 12 диагностических тестов
380 практических тестов
Вопрос дня
Карточки
Учитесь по концепции Справка по предварительному исчислению »
Графики и обратные тригонометрические функции »
График функций синуса и косинуса »
Найдите период функции синуса или косинуса Учитывая , каков период функции? Возможные ответы: Правильный ответ: Объяснение: Формула для периода функции синуса/косинуса . При стандартной форме: Так как формула принимает вид . Упрощенный, период . Сообщить об ошибке Каков период этого графика? Возможные ответы: Правильный ответ: Объяснение: Одна волна графика проходит точно от 0 до до повторения. Сообщить об ошибке Пожалуйста, выберите лучший ответ из следующих вариантов. Найдите период следующей функции в радианах: Возможные ответы: Правильный ответ: 5
Объяснение: Если вы посмотрите на график, то увидите, что период (длина одной волны) равен . Без графика вы можете разделить на частоту, которая в данном случае равна 1. Сообщить об ошибке Пожалуйста, выберите лучший ответ из следующих вариантов. Найдите период следующей функции. Возможные ответы: Правильный ответ: Объяснение: Период определяется как длина одной волны функции. Сообщить об ошибке Каков период этой синусоиды? Возможные ответы: Правильный ответ: Объяснение: На графике есть 3 волны между 0 и , что означает, что длина каждой из волн делится на 3, или . Сообщить об ошибке Напишите уравнение косинуса с минимумом в и максимумом в . Возможные ответы: Правильный ответ: Объяснение: Уравнение для этого графика будет иметь вид, где A — амплитуда, f — частота, h — сдвиг по горизонтали, а k — сдвиг по вертикали. Чтобы написать это уравнение, полезно начертить график: Нарисовав максимум и минимум, мы можем видеть, что график находится в центре и имеет амплитуду 2. Расстояние между максимумом а минимум составляет половину длины волны. Вот . Это означает, что полная длина волны равна , поэтому частота равна 1,9.0005 Минимум находится в середине графика, поэтому, чтобы выяснить, где он начинается, вычтите из координаты x минимума: Уравнение этого графика: . Сообщить об ошибке Задайте период и частоту для уравнения. Возможные ответы: Период: , Частота: Период: , Частота: Период: , Частота: Период: , Частота: Период: , Частота: Правильный ответ: Период: , Частота: Объяснение: Наше уравнение имеет форму , где A — амплитуда, f — частота, h — сдвиг по горизонтали, а k — сдвиг по вертикали. Мы можем посмотреть на уравнение и увидеть, что частота , равна . Период , поэтому в данном случае . Сообщить об ошибке Каков период графика? Возможные ответы: Правильный ответ: Объяснение: Уравнение для этой функции имеет вид , где A — амплитуда, f — частота, h — сдвиг по горизонтали, а k — сдвиг по вертикали. Глядя на уравнение, мы видим, что частота , равна . Период , поэтому в данном случае . Сообщить об ошибке Какую функцию может выполнять следующий график? Возможные ответы: Правильный ответ: Объяснение: Какой может быть функция для следующего графика? Для начала поймите, что мы имеем дело с периодической функцией, поэтому синус и косинус — лучший выбор. Далее обратите внимание, что диапазон функции и что функция проходит через точку . Из этой информации мы можем найти амплитуду: Итак, наша функция должна иметь выход впереди. Кроме того, из точки мы можем сделать вывод, что функция имеет вертикальный сдвиг положительной двойки. Единственным оставшимся препятствием является то, является ли функция синусоидальной или косинусоидальной. Напомним, что синус проходит через , а косинус проходит через . это означает, что наша функция должна быть синусоидальной, потому что для того, чтобы быть графиком косиенов, нам также потребуется горизонтальный перенос. Таким образом, наш ответ: Сообщить об ошибке Уведомление об авторских правах 12 Диагностических тестов
380 практических тестов
Вопрос дня
Карточки
Learn by Concept На графике видно, что четыре угла: x , x 2 , x 3 и x 4 ,
все имеют одинаковое значение функции синуса (за исключением
− знак.) Таким образом, вместо вычисления синуса x 2 , x 3 или x 4 мы можем вычислить синус x (красный в квадранте 1)
и просто прикрепите к ответу знак −, если угол был в
квадрант 3 или 4. Вот несколько примеров. На графике видно, что четыре угла: x , x 2 , x 3 и x 4 ,
все имеют одинаковое значение функции косинуса (за исключением
− знак.) Таким образом, вместо вычисления косинуса x 2 , x 3 или x 4 мы можем вычислить косинус x (красный в квадранте 1)
и просто прикрепите к ответу знак −, если угол был в
квадрант 2 или 3. Вот несколько примеров. В каждом случае квадрант 1
угол находится с помощью симметрии функции косинуса: Квадрант 1
угол находится с помощью функции симметрии касательной. Например
загар (110°) = — загар (70°). арксинус: Рассмотрим треугольник, показанный справа. Обратите внимание, что оба следующих
утверждения описывают угол θ: арккосинус: Посмотрите еще раз на треугольник. Обратите внимание, что оба следующих
утверждения описывают угол φ: Пример: Рассмотрим показанный здесь прямоугольный треугольник. Мы можем вычислить угол θ, используя арксинус: Основная идея такова: если мы хотим вычислить квадратный корень из некоторого числа м то рисуем график функции х = х 2 − м ,
как показано на рисунке справа, и найдите точку, где график
пересекает ось x . Это красная точка x =
. Метод Ньютона для нахождения этой точки начинается с любой начальной оценки квадратного корня, обозначенного точкой x 1 на рисунке.
Он использует высоту и наклон кривой при x 1 (синяя точка и красная пунктирная линия), чтобы получить лучшее
оценка, x 2 , из квадратного корня. Затем эта лучшая оценка используется для получения
еще лучшая оценка, x 3 и так далее.
Каждая итерация (цикл) удваивает число
цифр точности квадратного корня. При любой оценке x 1 из квадратного корня из м мы можем
получить улучшенную оценку x 2 по формуле: Если вы нашли эту страницу в веб-поиске, вы не увидите #116 апреля 2019 г. 21:52:44 Я вижу много в проекте, и я хочу знать, как использовать их в своих интересах #216 апреля 2019 г. Найдите в Google «sin, cos, and tan» среди нас ::red stack #316 апреля 2019 22:19:56 Синус числа (sin), косинус числа (cos) и тангенс числа (tan) используются в тригонометрии. Последний раз редактировалось codeman1044 (16 апреля 2019 г. 22:24: 01) 
Определение периода функции синуса или косинуса
Все ресурсы для предварительного исчисления
 Это означает, что период .
Это означает, что период . В этом случае одна полная волна составляет 180 градусов или радиан. Вы можете понять это, не глядя на график, разделив на частоту, которая в данном случае равна 2.
В этом случае одна полная волна составляет 180 градусов или радиан. Вы можете понять это, не глядя на график, разделив на частоту, которая в данном случае равна 2.


Все ресурсы Precalculus
Mathway | Популярные проблемы
1 Найти точное значение грех(30) 2 Найдите точное значение грех(45) 3 Найти точное значение грех(30 градусов) 4 Найти точное значение грех(60 градусов) 5 Найдите точное значение загар (30 градусов) 6 Найти точное значение угловой синус(-1) 7 Найти точное значение грех(пи/6) 8 Найти точное значение cos(pi/4) 9 Найти точное значение грех(45 градусов) 10 Найти точное значение грех(пи/3) 11 Найти точное значение арктический(-1) 12 Найти точное значение cos(45 градусов) 13 Найти точное значение cos(30 градусов) 14 Найти точное значение желтовато-коричневый(60) 15 Найти точное значение csc(45 градусов) 16 Найти точное значение загар (60 градусов) 17 Найти точное значение сек(30 градусов) 18 Найти точное значение cos(60 градусов) 19 Найти точное значение соз(150) 20 Найти точное значение грех(60) 21 Найдите точное значение cos(pi/2) 22 Найти точное значение загар (45 градусов) 23 Найти точное значение arctan(- квадратный корень из 3) 24 Найдите точное значение csc(60 градусов) 25 Найти точное значение сек(45 градусов) 26 Найти точное значение csc(30 градусов) 27 Найти точное значение грех(0) 28 Найти точное значение грех(120) 29 Найти точное значение соз(90) 30 Преобразовать из радианов в градусы пи/3 31 Найти точное значение желтовато-коричневый(30) 32 Преобразование градусов в радианы 45 33 Найти точное значение соз(45) 35 Преобразовать из радианов в градусы пи/6 36 Найти точное значение детская кроватка(30 градусов) 37 Найти точное значение арккос(-1) 38 Найти точное значение арктический(0) 39 Найти точное значение детская кроватка(60 градусов) 40 Преобразование градусов в радианы 30 41 Преобразовать из радианов в градусы (2 шт.  )/3
)/3 42 Найти точное значение sin((5pi)/3) 43 Найти точное значение sin((3pi)/4) 44 Найти точное значение желтовато-коричневый (пи/2) 45 Найти точное значение грех(300) 46 Найти точное значение соз(30) 47 Найдите точное значение соз(60) 48 Найти точное значение соз(0) 49 Найти точное значение соз(135) 50 Найти точное значение cos((5pi)/3) 51 Найти точное значение соз(210) 52 Найти точное значение сек (60 градусов) 53 Найти точное значение грех(300 градусов) 54 Преобразование градусов в радианы 135 55 Преобразование градусов в радианы 150 56 Преобразовать из радианов в градусы (5 дюймов)/6 57 Преобразовать из радианов в градусы (5 дюймов)/3 58 Преобразование градусов в радианы 89 градусов 59 Преобразование градусов в радианы 60 60 Найти точное значение грех(135 градусов) 61 Найти точное значение грех(150) 62 Найти точное значение грех(240 градусов) 63 Найти точное значение детская кроватка(45 градусов) 64 Преобразовать из радианов в градусы (5 дюймов)/4 65 Найти точное значение грех(225) 66 Найдите точное значение грех(240) 67 Найти точное значение cos(150 градусов) 68 Найти точное значение желтовато-коричневый(45) 69 Оценить грех(30 градусов) 70 Найти точное значение сек(0) 71 Найти точное значение cos((5pi)/6) 72 Найти точное значение КСК(30) 73 Найти точное значение arcsin(( квадратный корень из 2)/2) 74 Найти точное значение желтовато-коричневый ((5pi)/3) 75 Найти точное значение желтовато-коричневый(0) 76 Оценить грех(60 градусов) 77 Найти точное значение arctan(-(квадратный корень из 3)/3) 78 Преобразовать из радианов в градусы (3 шт.  )/4
)/4 79 Найти точное значение sin((7pi)/4) 80 Найти точное значение угловой синус(-1/2) 81 Найти точное значение sin((4pi)/3) 82 Найдите точное значение КСК(45) 83 Упростить арктан( квадратный корень из 3) 84 Найти точное значение грех(135) 85 Найдите точное значение грех(105) 86 Найти точное значение грех(150 градусов) 87 Найти точное значение sin((2pi)/3) 88 Найти точное значение желтовато-коричневый ((2pi)/3) 89 Преобразовать из радианов в градусы пи/4 90 Найти точное значение sin(pi/2) 91 Найти точное значение сек(45) 92 Найти точное значение cos((5pi)/4) 93 Найти точное значение cos((7pi)/6) 94 Найти точное значение угловой синус(0) 95 Найти точное значение грех(120 градусов) 96 Найти точное значение желтовато-коричневый ((7pi)/6) 97 Найти точное значение соз(270) 98 Найдите точное значение sin((7pi)/6) 99 Найти точное значение arcsin(-( квадратный корень из 2)/2) 100 Преобразование градусов в радианы 88 градусов Алгоритмы
Алгоритмы Алгоритмы расчета встроенных функций
Алгоритмы вычисления следующих одиннадцати функций построены в для
компьютерные чипы, используемые большинством научных калькуляторов и тренером по алгебре:
В этом разделе объясняются алгоритмы. синус (sin) косинус (косинус) тангенс (тангенс) арксинус (арксинус) арккосинус (arccos) арктангенс (арктангенс) логарифм по основанию 10 (логарифм) натуральный логарифм (ln) экспоненциальный с основанием e (exp or e x ) квадратный корень (sqrt) мощность ( y x )  Изучение алгоритмов
образовательным, потому что вы узнаете много нового о симметриях, тождествах и
другие свойства функций и то, как они используются для точного
оценки функций.
Изучение алгоритмов
образовательным, потому что вы узнаете много нового о симметриях, тождествах и
другие свойства функций и то, как они используются для точного
оценки функций.
Алгоритм вычисления sin (
x ) Этот алгоритм позволяет вычислить синус любого угла, используя только операции
сложения, вычитания, умножения и деления.
Основная идея заключается в использовании полиномиальной аппроксимации (шаг 4) для вычисления
синус угла x . Но поскольку это приближение верно только для
маленький x мы должны предпринять шаги (от 1 до 3), чтобы уменьшить x до самого маленького
угол, который по-прежнему имеет то же значение функции синуса.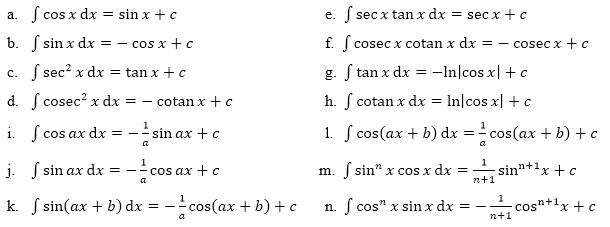 Это новое разрешение x имеет то же значение функции синуса, что и исходное разрешение x .
Это новое разрешение x имеет то же значение функции синуса, что и исходное разрешение x . В каждом случае квадрант 1
угол определяется с помощью симметрии функции синуса:
В каждом случае квадрант 1
угол определяется с помощью симметрии функции синуса:
Пример: вычислить sin (565°). Вот шаги
Пример: вычислить sin (1,830 радиан). Вот шаги
Алгоритм расчета cos (
x ) Этот алгоритм позволяет вычислить косинус любого угла, используя только операции
сложения, вычитания, умножения и деления. Основная идея заключается в использовании полиномиальной аппроксимации (шаг 4) для вычисления
косинус угла х . Но поскольку это приближение верно только для
маленький x мы должны предпринять шаги (от 1 до 3), чтобы уменьшить x до самого маленького
угол, который по-прежнему имеет то же значение функции косинуса.
Основная идея заключается в использовании полиномиальной аппроксимации (шаг 4) для вычисления
косинус угла х . Но поскольку это приближение верно только для
маленький x мы должны предпринять шаги (от 1 до 3), чтобы уменьшить x до самого маленького
угол, который по-прежнему имеет то же значение функции косинуса.
 Это изображение показывает
почему мы можем заменить косинус большого угла B синусом малого
угол, S : Установите x для малого угла S . Угол x теперь достаточно мал, чтобы применить
полиномиальное приближение. Нажмите здесь, чтобы использовать
синусоидальный полином или перейдите к шагу 4, чтобы использовать косинусный полином.
Это изображение показывает
почему мы можем заменить косинус большого угла B синусом малого
угол, S : Установите x для малого угла S . Угол x теперь достаточно мал, чтобы применить
полиномиальное приближение. Нажмите здесь, чтобы использовать
синусоидальный полином или перейдите к шагу 4, чтобы использовать косинусный полином.
Пример: вычислить cos (565°). Вот шаги
Пример: вычислить cos (1,830 радиан). Вот шаги
Вот шаги
Алгоритм расчета тангенса (
x ) Этот алгоритм позволяет вычислить тангенс любого угла, используя только операции
сложения, вычитания, умножения и деления.
Основная идея заключается в использовании полиномиальной аппроксимации (шаг 5) для вычисления
тангенс угла х . Но поскольку это приближение верно только для
маленький x мы должны предпринять шаги (от 1 до 4), чтобы уменьшить x до самого маленького
угол, который по-прежнему имеет то же значение функции тангенса. В противном случае уменьшите x , чтобы оно лежало в диапазоне
0≤ x ≤180° путем добавления или вычитания подходящего кратного
180° от него (мы предполагаем, что угол x измеряется в градусах).
Это новое x имеет то же значение функции тангенса, что и исходное x .
В противном случае уменьшите x , чтобы оно лежало в диапазоне
0≤ x ≤180° путем добавления или вычитания подходящего кратного
180° от него (мы предполагаем, что угол x измеряется в градусах).
Это новое x имеет то же значение функции тангенса, что и исходное x . Если он меньше 45°
затем перейдите к шагу 4. В противном случае
его можно сделать еще меньше, используя следующий прием:
вместо вычисления tan( x ) мы
вычислить тангенс (90 ° — x ) и взять обратное значение.
Это изображение показывает
почему мы можем заменить тангенс большого угла, B ,
обратной величиной тангенса малого угла, S : Установите x для малого угла S . x теперь меньше 45°.
Если он меньше 45°
затем перейдите к шагу 4. В противном случае
его можно сделать еще меньше, используя следующий прием:
вместо вычисления tan( x ) мы
вычислить тангенс (90 ° — x ) и взять обратное значение.
Это изображение показывает
почему мы можем заменить тангенс большого угла, B ,
обратной величиной тангенса малого угла, S : Установите x для малого угла S . x теперь меньше 45°. Затем подставьте x в формулу: Для x ≤ π/8 радиан (т.е. 22,5°) этот полином точен.
в пределах ±0,000006.
Затем подставьте x в формулу: Для x ≤ π/8 радиан (т.е. 22,5°) этот полином точен.
в пределах ±0,000006.
Пример: вычислить тангенс (194°). Вот шаги
Пример: вычислить тангенс (110°). Вот шаги
Пример: вычислить тангенс (40°). Вот шаги
Вот шаги
Алгоритмы расчета
arcsin (
x ) и
Arccos ( x ) Эти алгоритмы используют алгоритм для функции арктангенса.
Нажмите здесь, чтобы увидеть этот алгоритм. Нажмите здесь, чтобы увидеть алгоритм арктангенса.
Нажмите здесь, чтобы увидеть алгоритм арктангенса.
Алгоритм расчета арктангенса (
х ) Этот алгоритм позволяет вычислить арктангенс любого числа, используя только операции
сложения, вычитания, умножения и деления.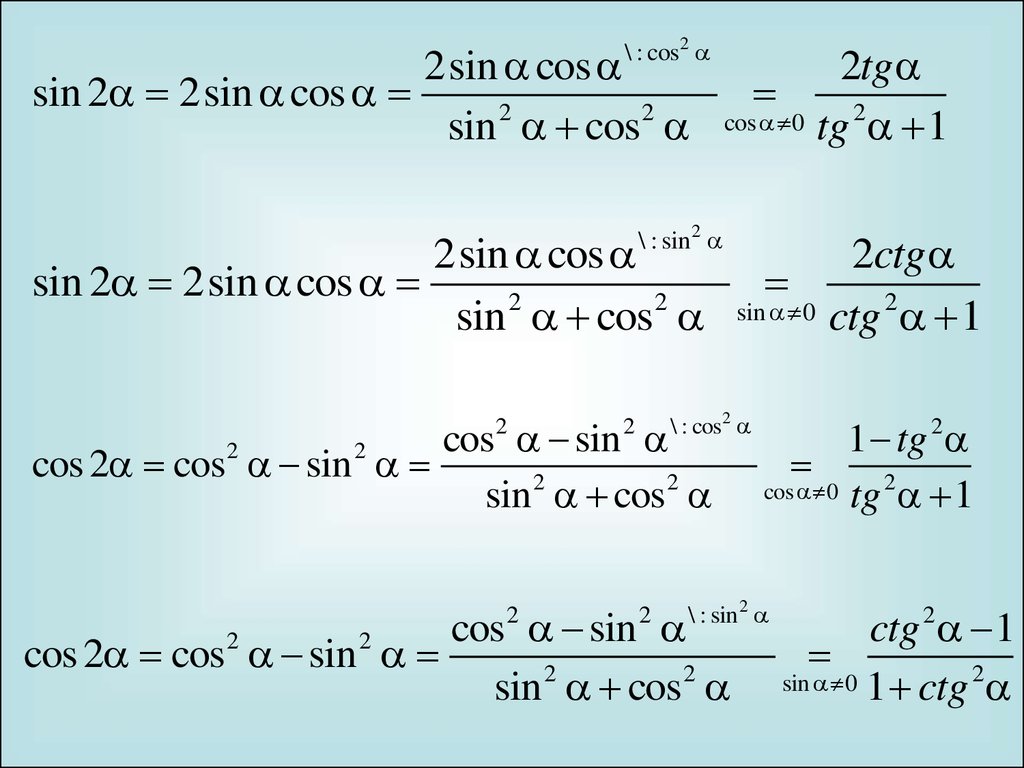 Основная идея состоит в том, чтобы использовать полиномиальную аппроксимацию (шаг 4) для вычисления
арктанг ( x ). Но поскольку это приближение верно только для
небольшие аргументы x мы должны сделать несколько шагов (от 1 до 3), чтобы уменьшить x на меньшее значение. Мы предполагаем, что искомый выход арктангенса
функция представляет собой угол в радианах.
Основная идея состоит в том, чтобы использовать полиномиальную аппроксимацию (шаг 4) для вычисления
арктанг ( x ). Но поскольку это приближение верно только для
небольшие аргументы x мы должны сделать несколько шагов (от 1 до 3), чтобы уменьшить x на меньшее значение. Мы предполагаем, что искомый выход арктангенса
функция представляет собой угол в радианах.
и это .
Пример: Рассчитайте арктангенс (0,7813) и выразите ответ в градусах.
Вот шаги:
Алгоритм расчета лог(
х ) Этот алгоритм позволяет вычислить логарифм (логарифм) по основанию 10 любого положительного числа. вычисляется только с помощью операций
сложения, вычитания, умножения и деления.
Основная идея состоит в том, чтобы использовать полиномиальную аппроксимацию (шаг 4) для вычисления
журнал ( x ). Но поскольку это приближение верно только для
небольшие аргументы x мы должны сделать несколько шагов (от 1 до 3), чтобы уменьшить x на меньшее значение.
вычисляется только с помощью операций
сложения, вычитания, умножения и деления.
Основная идея состоит в том, чтобы использовать полиномиальную аппроксимацию (шаг 4) для вычисления
журнал ( x ). Но поскольку это приближение верно только для
небольшие аргументы x мы должны сделать несколько шагов (от 1 до 3), чтобы уменьшить x на меньшее значение. бревно ( х ) = бревно ( м ) + р ,
где p — целое число и m (новый аргумент функции логарифмирования по основанию 10) — число от 1 до 10. log ( x ) = 0,43429448 ln ( x )
(Это следует из того, что 1/ln (10) = 0,43429448). Объединение шагов 1, 2 и 3 дает:
Объединение шагов 1, 2 и 3 дает:
Пример: Вычислить log (900).
Вот шаги:
x = 3 дает y = 2/4 = 0,5, поэтому полином принимает вид: Подставьте это обратно в результат шага 3: log (900) = 0,86858896 · 1,098 + 2 = 2,954
Алгоритм расчета ln (
х ) Этот алгоритм позволяет вычислить натуральный логарифм (ln) любого положительного числа. вычисляется только с помощью операций
сложения, вычитания, умножения и деления.
Основная идея состоит в том, чтобы использовать полиномиальную аппроксимацию на шаге 3 для вычисления
ln ( x ). Но поскольку это приближение верно только для
небольшие аргументы x мы должны выполнить шаги 1 и 2, чтобы уменьшить x на меньшее значение.
вычисляется только с помощью операций
сложения, вычитания, умножения и деления.
Основная идея состоит в том, чтобы использовать полиномиальную аппроксимацию на шаге 3 для вычисления
ln ( x ). Но поскольку это приближение верно только для
небольшие аргументы x мы должны выполнить шаги 1 и 2, чтобы уменьшить x на меньшее значение. ln ( x ) = ln ( m ) + 2,3025851 p ,
где p — целое число и m (новый аргумент функции натурального логарифма) — число от 1 до 10.
(Обратите внимание, что ln (10) = 2,3025851)
Объединение шагов 1 и 2 дает:
Пример: Вычислить ln (9000).
Вот шаги:
x = 3 дает y = 2/4 = 0,5, поэтому полином принимает вид: Подставьте это обратно в результат шага 2: ln (9000) = 2 · 1,098 + 3 · 2,3025851 = 9,104
Алгоритм расчета
exp (
x ) или e x Этот алгоритм позволяет вычислить exp ( x ) или e x . используя только операции сложения, вычитания, умножения и деления.
Основная идея состоит в том, чтобы использовать полиномиальную аппроксимацию на шаге 3 для вычисления e x . Но поскольку это приближение верно только для
небольшие аргументы x мы должны выполнить шаги 1 и 2, чтобы уменьшить x на меньшее значение.
используя только операции сложения, вычитания, умножения и деления.
Основная идея состоит в том, чтобы использовать полиномиальную аппроксимацию на шаге 3 для вычисления e x . Но поскольку это приближение верно только для
небольшие аргументы x мы должны выполнить шаги 1 и 2, чтобы уменьшить x на меньшее значение.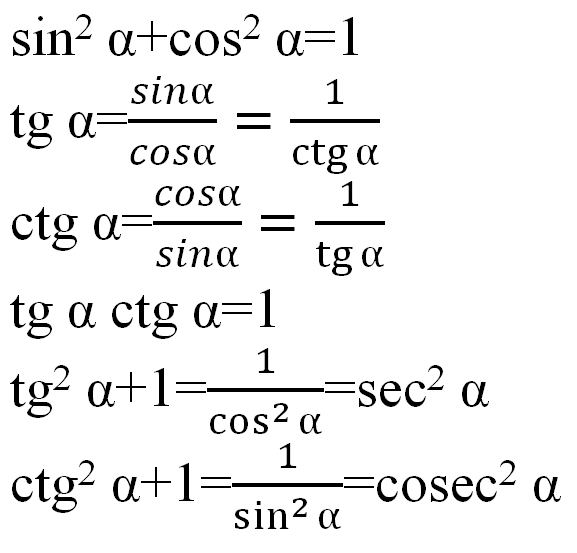 если так написано
((( e ) 2 ) 2 ) 2 .
Для дальнейшего повышения эффективности можно рассчитать различные целочисленные степени и .
один раз и сохраняется в таблице поиска.
если так написано
((( e ) 2 ) 2 ) 2 .
Для дальнейшего повышения эффективности можно рассчитать различные целочисленные степени и .
один раз и сохраняется в таблице поиска.
Пример: Рассчитать exp (−3,8) или e -3,8 :
Алгоритм вычисления квадратного корня
Этот алгоритм использует метод Ньютона. Это позволяет извлекать квадратный корень
любого положительного числа, которое нужно вычислить, используя только операции
сложения, вычитания, умножения и деления.
Это позволяет извлекать квадратный корень
любого положительного числа, которое нужно вычислить, используя только операции
сложения, вычитания, умножения и деления. Когда две последовательные оценки квадрата
root отличаются меньше, чем на какое-то маленькое значение, скажем, 0,0001, тогда алгоритм
останавливается, и мы получаем квадратный корень с точностью до ±0,0001.
Когда две последовательные оценки квадрата
root отличаются меньше, чем на какое-то маленькое значение, скажем, 0,0001, тогда алгоритм
останавливается, и мы получаем квадратный корень с точностью до ±0,0001.
Пример: Вычисление квадратного корня из 900 с точностью ±0,000001.
Начиная с начального предположения 50, вот результаты первых 6
итерации:
Мы показали расчет для x 2 в деталях.
Мы также показали красным цветом шестой десятичный разряд. На 6-й итерации нет
измените этот десятичный знак, чтобы мы могли остановиться и дать x 6 как ответ. Поскольку мы знаем, что точный ответ равен 30, мы можем увидеть
как количество правильных цифр примерно удваивается с каждой итерацией. x 1 50 x 2 x 3 30.  2352941176471
2352941176471 x 4 30.000 13138 x 5 30.0000000139698 x 6 30.0000000000000
Алгоритм расчета степенной функции
Мы можем использовать следующее уравнение, чтобы заменить вычисление
степенная функция с вычислением
натурального логарифма и e x Функция: Это уравнение следует из тождества e ln ( x ) = x и
показательное свойство показателей.
Пример: Оценка 5,2 3,6
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его. Как использовать (sin) (cos) и (tan)
Имя пользователя и пароль Нужна помощь?
15 сообщений Как мне использовать (sin) (cos) и (tan)
([sin v] of (something))
установить [уровень пушистости v] на (10)
 22:01:50
22:01:50
100+ сообщений Как использовать (sin) (cos) и (tan)
независимо от того, что проходит через эти ворота, ::grey hat
[you v] будет стоять на своем. ::grey stack
pick random () to () ::operators hat
RUN ::grey stack
1000+ сообщений Как использовать (sin) (cos) и (tan)
 для вычисления радиан окружностей и углов многоугольников (в основном треугольников).
для вычисления радиан окружностей и углов многоугольников (в основном треугольников).
Вероятно, вы еще не изучали тригонометрию в школе, поэтому термины кажутся вам незнакомыми.
Обычно в нулях эти функции используются для поиска угла поворота или изменения чего-либо (вы можете увидеть «Изменить», «Дельта» или «Δ»)
Это моя подпись, которая появляется каждый раз, когда я публикую сообщения, и является автоматической. Чтобы сделать собственную подпись, найдите параметр «Изменить подпись» в левом нижнем углу домашней страницы обсуждений.
Я не что иное, как постоянно непоследовательный.
Потенциально полезные уроки и охват тем
Если вы хотите увидеть новый урок, добавленный к этому, не стесняйтесь оставлять предложения в моем профиле.
#416 апреля 2019 г. 22:22:51
- codeman1044 Скретчер
1000+ сообщений
Как использовать (sin) (cos) и (tan)
Кроме того, вики хорошо объясняет это:
https://en. scratch-wiki.info/wiki/()_of_() _(Operators_block)
scratch-wiki.info/wiki/()_of_() _(Operators_block)
Надеюсь, это поможет!
Последний раз редактировалось codeman1044 (16 апреля 2019 22:24:35)
Это моя подпись, которая появляется каждый раз, когда я публикую сообщения, и является автоматической. Чтобы сделать собственную подпись, найдите параметр «Изменить подпись» в левом нижнем углу домашней страницы обсуждений. 909:14 Я не что иное, как постоянно непоследовательный.
Потенциально полезные уроки и охват тем
Если вы хотите увидеть новый урок, добавленный к этому, не стесняйтесь оставлять предложения в моем профиле.
#517 апреля 2019 г. 23:54:03
- -Рекс- Скретчер
500+ постов
Как использовать (sin) (cos) и (tan)
Они позволяют вычислять координаты точки на основе угла: Обратите внимание, что радиус окружности равен единице. В Scratch угол t указывается в градусах. Тангенс (tan) равен синусу (sin), деленному на косинус (cos). Арксинус (asin), арккосинус (acos) и арктангенс (atan) позволяют вам перейти «назад» от значения к исходному углу.
В Scratch угол t указывается в градусах. Тангенс (tan) равен синусу (sin), деленному на косинус (cos). Арксинус (asin), арккосинус (acos) и арктангенс (atan) позволяют вам перейти «назад» от значения к исходному углу.
Последний раз редактировалось -Rex- (17 апреля 2019 23:56:33)
#620 мая 2019 02:13:55
- —Взрыв— Скретчер
1000+ сообщений
Как использовать (sin) (cos) и (tan)
cs9999999999 написал:
поиск «sin»… -snip-
Поиск «sine» вместо
Последний раз редактировалось kaj (Завтра 00:00:00)
✰✩✭✴★—Взрыв—★✴✭✩✰
Форум помощник | мальчик | платформеры | 14 лет | гитара | сайт
#720 мая 2019 06:58:41
- 098765432154321 Скретчер
500+ постов
Как использовать (sin) (cos) и (tan)
Sin, Cos и Tan используются для продвинутых калькуляторов, а Scratch реализовал это для продвинутых средств проверки калькулятора.
(извините, если что-то не так)
Выделите что-нибудь и нажмите Shift+Down, чтобы пролистать мою подпись!
Я решил вашу проблему? Вы можете поддержать меня здесь в любое время здесь!
Профиль | Страница Scratch Wiki
Цель поста: 750 | Сообщений: 620 (осталось 130) | Прогресс: 82,6%
Имейте в виду, что это не обновляется автоматически, поэтому может быть немного не так.
Последнее обновление: 16.02.22
#820 мая 2019 г. 10:10:52
Скретчер1000+ сообщений
Как использовать (sin) (cos) и (tan)
098765432154321 написал:
Sin, Cos и Tan используются для продвинутых калькуляторов, а Scratch реализовал это для продвинутых средств проверки калькулятора.
(извините, если что-то не так)
Нет, эти функции можно использовать по-разному — они существуют не только для того, чтобы люди могли делать калькуляторы.
#926 мая 2019 г. 03:19:30
- 15-MinuteGaming Скретчер
100+ сообщений
Как использовать (sin) (cos) и (tan)
Я также использую их для перьевых проектов, связанных с кругами, такими как полярные координаты.
Мои кумкваты и форумные подписи съели друг друга. К счастью, ни один из них мне не понравился.
Злой кумкват должен быть как-то связан с котом Таносом. Злой кумкват — 2.0, а кот-танос — 3.0
1 апреля — эта суббота. Подробности здесь.
#10нояб. 9, 2019 11:18:27
- Wiz03A Скретчер
1 сообщение
Как использовать (sin) (cos) и (tan)
Sin и Cos полезны, если вы вращаете объект, а затем хотите переместить объект на основе ориентации, используя переменные для представления положения и скорости.
Scratch делает это в значительной степени ненужным, но может быть полезным в некоторых случаях.
Я использую переменные скорости и положения, чтобы точнее контролировать «отскоки». Я хочу увеличить скорость «ракеты» в зависимости от направления, в котором она смотрит. Sin и Cos позволяют мне получить компоненты x и y для скорости, которые я могу добавить или вычесть из существующей скорости. Это позволяет мне контролировать свойства x- и y-скорости при возникновении столкновений.
#11нояб. 10, 2019 21:53:01
- codeman1044 Скретчер
1000+ сообщений
Как использовать (sin) (cos) и (tan)
Wiz03A написал:
Sin и Cos полезны, если вы вращаете объект, а затем хотите переместить объект на основе ориентации, используя переменные для представления положения и скорости .
Scratch делает это в значительной степени ненужным, но может быть полезным в некоторых случаях.Я использую переменные скорости и положения, чтобы точнее контролировать «отскоки». Я хочу увеличить скорость «ракеты» в зависимости от направления, в котором она смотрит. Sin и Cos позволяют мне получить компоненты x и y для скорости, которые я могу добавить или вычесть из существующей скорости. Это позволяет мне контролировать свойства x- и y-скорости при возникновении столкновений.
Пожалуйста, проверьте дату темы перед публикацией.
Это моя подпись, которая появляется каждый раз, когда я публикую сообщения, и является автоматической. Чтобы сделать собственную подпись, найдите параметр «Изменить подпись» в левом нижнем углу домашней страницы обсуждений.
Я не что иное, как постоянно непоследовательный.
Потенциально полезные уроки и охват тем
Если вы хотите увидеть новый урок, добавленный к этому, не стесняйтесь оставлять предложения в моем профиле.

#1211 мая 2020 г. 08:53:33
- Security_hacker Скретчер
2 сообщения
Как использовать (sin) (cos) и (tan)
Но что они делают ( +2 ) ?????????????????????????? ???
также подписывайтесь на меня, так как я не новичок, это мой третий аккаунт!!! поэтому, пожалуйста, следуйте за мной здесь.
#1311 мая 2020 г. 10:48:06
- аззукар Скретчер
31 сообщение
Как использовать (sin) (cos) и (tan)
Security_hacker написал:
Но что они делают ( +2 ) ????????????????????? ?????????также подписывайтесь на меня, так как я не новичок, это мой третий аккаунт!!! поэтому, пожалуйста, следуйте за мной здесь.

 Функция косинуса представлена как «cos».
Функция косинуса представлена как «cos».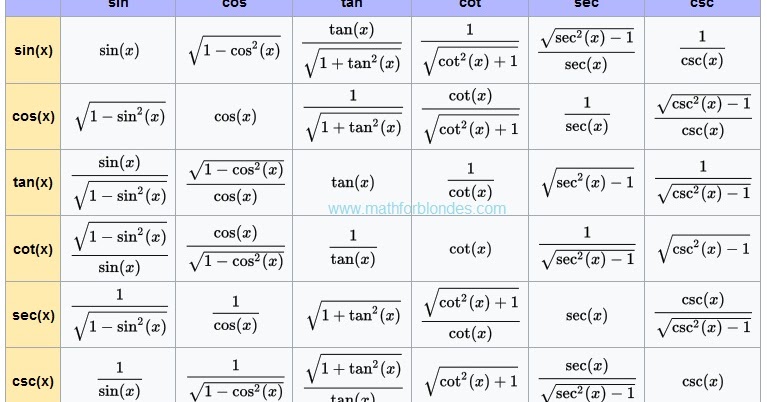
 θ = 2 потому что 2 θ – 1 = 1 – 2 sin 2 θ
θ = 2 потому что 2 θ – 1 = 1 – 2 sin 2 θ 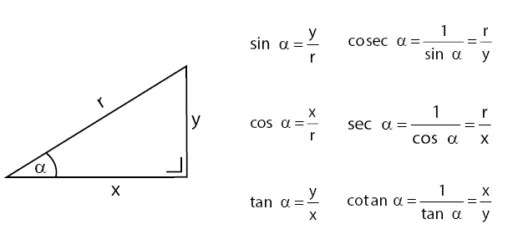 0005
0005