Как понять, почему «плюс» на «минус» дает «минус»
Минус на минус математика
Слушая учителя математики, большинство учеников воспринимают материал как аксиому. При этом мало кто пытается добраться до сути и разобраться, почему «минус» на «плюс» дает знак «минус», а при умножении двух отрицательных чисел выходит положительное.
Законы математики
Большинство взрослых не в силах объяснить ни себе, ни своим детям, почему так получается. Они твердо усвоили этот материал в школе, но при этом даже не попытались выяснить, откуда взялись такие правила. А зря. Зачастую современные дети не столь доверчивы, им необходимо докопаться до самой сути и понять, скажем, почему «плюс» на «минус» дает «минус». А иногда сорванцы специально задают каверзные вопросы, дабы насладиться моментом, когда взрослые не могут дать вразумительного ответа. И совсем уж беда, если впросак попадает молодой учитель.
Кстати, следует отметить, что упомянутое выше правило действенно как для умножения, так и для деления. Произведение отрицательного и положительного числа даст лишь «минус. Если речь идет о двух цифрах со знаком «-», то в результате получится положительное число. То же касается и деления. Если одно из чисел будет отрицательным, то частное тоже будет со знаком «-».
Произведение отрицательного и положительного числа даст лишь «минус. Если речь идет о двух цифрах со знаком «-», то в результате получится положительное число. То же касается и деления. Если одно из чисел будет отрицательным, то частное тоже будет со знаком «-».
Для объяснения правильности этого закона математики, необходимо сформулировать аксиомы кольца. Но для начала следует понять, что это такое. В математике кольцом принято называть множество, в котором задействованы две операции с двумя элементами. Но разбираться с этим лучше на примере.
Аксиома кольца
Существует несколько математических законов.
- Первый из них переместительный, согласно ему, C + V = V + C. Второй называется сочетательным (V + C) + D = V + (C + D).
Им же подчиняется и умножение (V х C) х D = V х (C х D).
Никто не отменял и правил, по которым открываются скобки (V + C) х D = V х D + C х D, также верно, что C х (V + D) = C х V + C х D.
Кроме того, установлено, что в кольцо можно ввести специальный, нейтральный по сложению элемент, при использовании которого будет верно следующее: C + 0 = C. Кроме того, для каждого C есть противоположный элемент, который можно обозначить, как (-C). При этом C + (-C) = 0.
Кроме того, для каждого C есть противоположный элемент, который можно обозначить, как (-C). При этом C + (-C) = 0.
Выведение аксиом для отрицательных чисел
Приняв приведенные выше утверждения, можно ответить на вопрос: «»Плюс» на «минус» дает какой знак?» Зная аксиому про умножение отрицательных чисел, необходимо подтвердить, что действительно (-C) х V = -(C х V). А также, что верно такое равенство: (-(-C)) = C.
Для этого придется вначале доказать, что у каждого из элементов существует лишь один ему противоположный «собрат». Рассмотрим следующий пример доказательства. Давайте попробуем представить, что для C противоположными являются два числа — V и D. Из этого следует, что C + V = 0 и C + D = 0, то есть C + V = 0 = C + D. Вспоминая о переместительных законах и о свойствах числа 0, можно рассмотреть сумму всех трех чисел: C, V и D. Попробуем выяснить значение V. Логично, что V = V + 0 = V + (C + D) = V + C + D, ведь значение C + D, как было принято выше, равняется 0. Значит, V = V + C + D.
Значит, V = V + C + D.
Точно так же выводится и значение для D: D = V + C + D = (V + C) + D = 0 + D = D. Исходя из этого, становится ясно, что V = D.
Для того чтобы понять, почему все же «плюс» на «минус» дает «минус», необходимо разобраться со следующим. Так, для элемента (-C) противоположными являются C и (-(-C)), то есть между собой они равны.
Тогда очевидно, что 0 х V = (C + (-C)) х V = C х V + (-C) х V. Из этого следует, что C х V противоположно (-)C х V, значит, (-C) х V = -(C х V).
Для полной математической строгости необходимо еще подтвердить, что 0 х V = 0 для любого элемента. Если следовать логике, то 0 х V = (0 + 0) х V = 0 х V + 0 х V. А это значит, что прибавление произведения 0 х V никак не меняет установленную сумму. Ведь это произведение равняется нулю.
Зная все эти аксиомы, можно вывести не только, сколько «плюс» на «минус» дает, но и что получается при умножении отрицательных чисел.
Умножение и деление двух чисел со знаком «-»
Если не углубляться в математические нюансы, то можно попробовать более простым способом объяснить правила действий с отрицательными числами.
Допустим, что C — (-V) = D, исходя из этого, C = D + (-V), то есть C = D — V. Переносим V и получаем, что C + V = D. То есть C + V = C — (-V). Этот пример объясняет, почему в выражении, где идут два «минуса» подряд, упомянутые знаки следует поменять на «плюс». Теперь разберемся с умножением.
(-C) х (-V) = D, в выражение можно добавить и вычесть два одинаковых произведения, которые не поменяют его значения: (-C) х (-V) + (C х V) — (C х V) = D.
Вспомная о правилах работы со скобками, получаем:
1) (-C) х (-V) + (C х V) + (-C) х V = D;
2) (-C) х ((-V) + V) + C х V = D;
3) (-C) х 0 + C х V = D;
Из этого следует, что C х V = (-C) х (-V).
Аналогично можно доказать, что и в результате деления двух отрицательных чисел выйдет положительное.
Общие математические правила
Конечно, такое объяснение не подойдет для школьников младших классов, которые только начинают учить абстрактные отрицательные числа. Им лучше объяснять на видимых предметах, манипулируя знакомым им термином зазеркалья.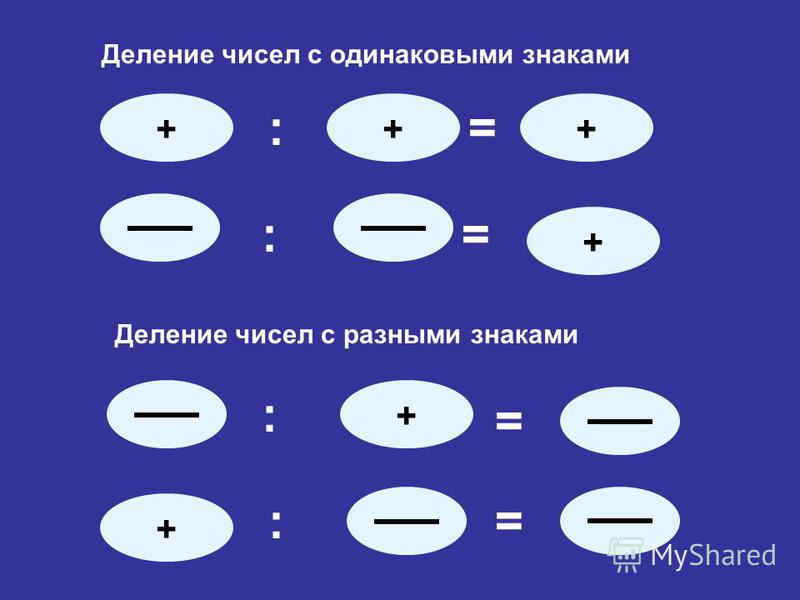 Например, придуманные, но не существующие игрушки находятся именно там. Их и можно отобразить со знаком «-». Умножение двух зазеркальных объектов переносит их в еще один мир, который приравнивается к настоящему, то есть в результате мы имеем положительные числа. А вот умножение абстрактного отрицательного числа на положительное лишь дает знакомый всем результат. Ведь «плюс» умножить на «минус» дает «минус». Правда, в младшем школьном возрасте дети не слишком-то пытаются вникнуть во все математические нюансы.
Например, придуманные, но не существующие игрушки находятся именно там. Их и можно отобразить со знаком «-». Умножение двух зазеркальных объектов переносит их в еще один мир, который приравнивается к настоящему, то есть в результате мы имеем положительные числа. А вот умножение абстрактного отрицательного числа на положительное лишь дает знакомый всем результат. Ведь «плюс» умножить на «минус» дает «минус». Правда, в младшем школьном возрасте дети не слишком-то пытаются вникнуть во все математические нюансы.
Хотя, если смотреть правде в глаза, для многих людей даже с высшим образованием так и остаются загадкой многие правила. Все принимают как данность то, что преподают им учителя, не затрудняясь вникать во все сложности, которые таит в себе математика. «Минус» на «минус» дает «плюс» – об этом знают все без исключения. Это верно как для целых, так и для дробных чисел.
Слушая учителя математики, большинство учеников воспринимают материал как аксиому. При этом мало кто пытается добраться до сути и разобраться, почему «минус» на «плюс» дает знак «минус», а при умножении двух отрицательных чисел выходит положительное.
Большинство взрослых не в силах объяснить ни себе, ни своим детям, почему так получается. Они твердо усвоили этот материал в школе, но при этом даже не попытались выяснить, откуда взялись такие правила. А зря. Зачастую современные дети не столь доверчивы, им необходимо докопаться до самой сути и понять, скажем, почему «плюс» на «минус» дает «минус». А иногда сорванцы специально задают каверзные вопросы, дабы насладиться моментом, когда взрослые не могут дать вразумительного ответа. И совсем уж беда, если впросак попадает молодой учитель.
Кстати, следует отметить, что упомянутое выше правило действенно как для умножения, так и для деления. Произведение отрицательного и положительного числа даст лишь «минус. Если речь идет о двух цифрах со знаком «-», то в результате получится положительное число. То же касается и деления. Если одно из чисел будет отрицательным, то частное тоже будет со знаком «-».
Для объяснения правильности этого закона математики, необходимо сформулировать аксиомы кольца. Но для начала следует понять, что это такое. В математике кольцом принято называть множество, в котором задействованы две операции с двумя элементами. Но разбираться с этим лучше на примере.
Но для начала следует понять, что это такое. В математике кольцом принято называть множество, в котором задействованы две операции с двумя элементами. Но разбираться с этим лучше на примере.
Но разбираться с этим лучше на примере.
Fb. ru
05.08.2018 20:00:45
2018-08-05 20:00:45
Источники:
Https://fb. ru/article/135051/kak-ponyat-pochemu-plyus-na-minus-daet-minus
Математика для блондинок: Минус на плюс что дает? » /> » /> .keyword { color: red; }
Минус на минус математика
Математикой должны заниматься блондинки — они врать не умеют.
Страницы
- Главная страница Новая математика Словарик
Четверг, 31 декабря 2020 г.
Минус на плюс что дает?
Положительные и отрицательные числа придумали математики. Делать им было нечего, вот они и придумали. Правила умножения и деления положительных и отрицательных чисел придумали всё те же математики. Специально для того, чтобы нам жизнь мёдом не казалась. Как же нам быть? Нужно выучить эти правила, чтобы говорить математикам то, что они хотят от нас слышать.
Как же нам быть? Нужно выучить эти правила, чтобы говорить математикам то, что они хотят от нас слышать.
Запомнить правила умножения или деления положительных и отрицательных чисел очень просто. Если два числа имеют разные знаки, в результате всегда будет знак минус.
Рассмотрим все возможные варианты. Что дает минус на плюс? При умножении и делении минус на плюс дает минус. Что дает плюс на минус? При умножении и делении в результате мы тоже получаем знак минус.
| Минус на плюс, плюс на минус. |
Как вы видите, все варианты умножения и деления положительных и отрицательных чисел исчерпаны, но знак плюс у нас так и не появился. Это мы сформулировали правило для себя, чтобы запомнить. Что говорить математикам? При умножении или делении положительных и отрицательных чисел в результате получается отрицательное число. Всегда.
Всегда.
Что дает минус на минус? Всегда будет получаться плюс, если мы выполняем умножение или деление. Что дает плюс на плюс?
Здесь совсем просто. Умножение или деление плюса на плюс дает всегда плюс.| Минус на минус, плюс на плюс. |
Надеюсь, это вы запомнили: минус на минус дает плюс, плюс на плюс дает минус. Что говорить математикам? При умножении и делении положительных или отрицательных чисел в результате получается положительное число.
Если с умножением и делением двух плюсов всё понятно (в результате получается такой же плюс), то с двумя минусами ничего не понятно. По логике, если два плюса дают плюс, то два минуса должны давать минус. Такой большой, жирный минус. Но не тут-то было. Математики думают иначе. Так почему минус и минус превращаются в плюс?
Могу вас заверить, что интуитивно математики правильно решили задачу на умножение и деление плюсов и минусов. Они записали правила в учебники, не особо вдаваясь в подробности. Для правильного ответа на вопрос, нам нужно разобраться, что же означают знаки плюс и минус в математике.
Они записали правила в учебники, не особо вдаваясь в подробности. Для правильного ответа на вопрос, нам нужно разобраться, что же означают знаки плюс и минус в математике.
Давайте попробуем применить правило умножениея и деления положительных и отрицательных чисел на практике. Придумаем какой-нибудь пример из нашей жизни. Думаю, вы слышали про бочку мёда и ложку дёгтя, которая может испортить весь мёд. Пусть мёд — это положительные числа, а дёготь — это числа отрицательные. Пробуем. Смотрим на картинки и описываем правила.
Если в бочку дёгтя добавить ложку мёда, получится бочка дёгтя.
Если в бочку мёда добавить ложку дёгтя, получится бочка дёгтя.
Если в бочку дёгтя добавить ложку дёгтя, получится бочка мёда.
Если в бочку мёда добавить ложку мёда, получится бочка мёда.
Первых два примера с натяжкой можно принять. Последний пример вообще не вызывает вопросов. А вот с предпоследним примером возникают очень большие проблемы — в жизни такого не бывает.
Здесь возможны два варианта:
 Математики не правильно записали свое правило.
Математики не правильно записали свое правило. 2. Мы не правильно применяем математическое правило.
Лично я за второй вариант. Объясню почему. Математику не только нужно знать, но нею ещё нужно уметь пользоваться.
Приведу пример из собственного опыта. Один учитель математики на уроках нам говорил: «математика – это точная наука, два раза соври – получится правда». Это утверждение однажды мне очень пригодилось. Как-то я решал сложную задачу с длинным решением. Я точно знал, какой результат должен быть. Но результат был другим. Я долго искал ошибку в расчетах, но не смог ее найти. Тогда, за несколько действий до итогового результата, я изменил одно число так, чтобы результат получился правильным. Я в расчетах соврал два раза и получил правильный результат. Математические вычисления в тот раз никто не проверял и я получил хорошую оценку. Это очень похоже на правило «минус на минус дает плюс», не так ли?
Но вернемся к нашим бочкам. Кстати, говорят, именно с бочек с вином математики срисовали знак «минус». Виноделы этим знаком обозначали пустые бочки. После наполнения бочек вином они перечеркивали знак «минус» и получался знак «плюс». По сути, знак «минус» заменял виноделам обычный ноль, ведь он обозначал отсутствие вина в бочке. Но математики ловко присобачили знак «минус» к числам и назвали их «отрицательными».
Виноделы этим знаком обозначали пустые бочки. После наполнения бочек вином они перечеркивали знак «минус» и получался знак «плюс». По сути, знак «минус» заменял виноделам обычный ноль, ведь он обозначал отсутствие вина в бочке. Но математики ловко присобачили знак «минус» к числам и назвали их «отрицательными».
Так что же не так с мёдом и дёгтем в бочках? Мои четыре примера описывают действие сложения — ведь мы прибавляем одно к другому, а математические правила мы рассматриваем для деления и умножения. Это абсолютно разные вещи, сколько бы математики не повторяли, что умножение это и есть сложение. Сложение — это изменение количества. Умножение — это изменение качества. При добавлении ложки дёгтя в бочку мёда, мёд не превращается в дёготь. Мы просто получаем бочку испорченного мёда. Точно так же и дёготь, добавленный в бочку дёгтя, не превращает всё в мёд. При сложении и вычитании положительных и отрицательных чисел действуют совсем другие правила знаков.
В чем же отличие качественных изменений от количественных? В единицах измерения, которые в математике предпочитают игнорировать. Вот смотрите. Если мы к метрам длины прибавим метры ширины, мы получим метры периметра. А если мы умножим метры длины на метры ширины, то в результате будут метры квадратные площади. Теперь вопрос к математикам: сколько метров длины или ширины нужно сложить, чтобы получить один метр квадратный площади? Или вопрос к вам: сколько метров ниток вам нужно намотать на себя, чтобы одеться? Ведь ткань — это те же самые нитки, только в совершенно другом качестве. Ну и наглядный пример из алгебры:
Вот смотрите. Если мы к метрам длины прибавим метры ширины, мы получим метры периметра. А если мы умножим метры длины на метры ширины, то в результате будут метры квадратные площади. Теперь вопрос к математикам: сколько метров длины или ширины нужно сложить, чтобы получить один метр квадратный площади? Или вопрос к вам: сколько метров ниток вам нужно намотать на себя, чтобы одеться? Ведь ткань — это те же самые нитки, только в совершенно другом качестве. Ну и наглядный пример из алгебры:
В этом примере буква а выполняет роль единицы измерения. Кстати, правило умножения отрицательных чисел наводит на ещё один вопрос математикам: сколько отрицательных чисел нужно сложить, чтобы получилось одно положительное число?
Так что же такое знаки «плюс» и «минус» в математике? Существуют ли отрицательные числа? Об этом мы поговорим как-нибудь в другой раз.
Четверг, 31 декабря 2020 г.
Если два числа имеют одинаковые знаки, в результате всегда будет плюс.
Www. webstaratel. ru
ru
09.08.2017 3:26:38
2017-08-09 03:26:38
Источники:
Https://www. webstaratel. ru/2020/12/minus-na-pljus-chto-daet. html
Что дает плюс на минус в математике » /> » /> .keyword { color: red; }
Минус на минус математика
Как понять, почему «плюс» на «минус» дает «минус» ?
Слушая учителя математики, большинство учеников воспринимают материал как аксиому. При этом мало кто пытается добраться до сути и разобраться, почему «минус» на «плюс» дает знак «минус», а при умножении двух отрицательных чисел выходит положительное.
Законы математики
Большинство взрослых не в силах объяснить ни себе, ни своим детям, почему так получается. Они твердо усвоили этот материал в школе, но при этом даже не попытались выяснить, откуда взялись такие правила. А зря. Зачастую современные дети не столь доверчивы, им необходимо докопаться до самой сути и понять, скажем, почему «плюс» на «минус» дает «минус». А иногда сорванцы специально задают каверзные вопросы, дабы насладиться моментом, когда взрослые не могут дать вразумительного ответа. И совсем уж беда, если впросак попадает молодой учитель.
И совсем уж беда, если впросак попадает молодой учитель.
Для объяснения правильности этого закона математики, необходимо сформулировать аксиомы кольца. Но для начала следует понять, что это такое. В математике кольцом принято называть множество, в котором задействованы две операции с двумя элементами. Но разбираться с этим лучше на примере.
Аксиома кольца
Существует несколько математических законов.
- Первый из них переместительный, согласно ему, C + V = V + C. Второй называется сочетательным (V + C) + D = V + (C + D).
Им же подчиняется и умножение (V х C) х D = V х (C х D).
Никто не отменял и правил, по которым открываются скобки (V + C) х D = V х D + C х D, также верно, что C х (V + D) = C х V + C х D.
Кроме того, установлено, что в кольцо можно ввести специальный, нейтральный по сложению элемент, при использовании которого будет верно следующее: C + 0 = C. Кроме того, для каждого C есть противоположный элемент, который можно обозначить, как (-C). При этом C + (-C) = 0.
При этом C + (-C) = 0.
Выведение аксиом для отрицательных чисел
Приняв приведенные выше утверждения, можно ответить на вопрос: «»Плюс» на «минус» дает какой знак?» Зная аксиому про умножение отрицательных чисел, необходимо подтвердить, что действительно (-C) х V = -(C х V). А также, что верно такое равенство: (-(-C)) = C.
Для этого придется вначале доказать, что у каждого из элементов существует лишь один ему противоположный «собрат». Рассмотрим следующий пример доказательства. Давайте попробуем представить, что для C противоположными являются два числа — V и D. Из этого следует, что C + V = 0 и C + D = 0, то есть C + V = 0 = C + D. Вспоминая о переместительных законах и о свойствах числа 0, можно рассмотреть сумму всех трех чисел: C, V и D. Попробуем выяснить значение V. Логично, что V = V + 0 = V + (C + D) = V + C + D, ведь значение C + D, как было принято выше, равняется 0. Значит, V = V + C + D.
Точно так же выводится и значение для D: D = V + C + D = (V + C) + D = 0 + D = D. Исходя из этого, становится ясно, что V = D.
Исходя из этого, становится ясно, что V = D.
Для того чтобы понять, почему все же «плюс» на «минус» дает «минус», необходимо разобраться со следующим. Так, для элемента (-C) противоположными являются C и (-(-C)), то есть между собой они равны.
Тогда очевидно, что 0 х V = (C + (-C)) х V = C х V + (-C) х V. Из этого следует, что C х V противоположно (-)C х V, значит, (-C) х V = -(C х V).
Для полной математической строгости необходимо еще подтвердить, что 0 х V = 0 для любого элемента. Если следовать логике, то 0 х V = (0 + 0) х V = 0 х V + 0 х V. А это значит, что прибавление произведения 0 х V никак не меняет установленную сумму. Ведь это произведение равняется нулю.
Зная все эти аксиомы, можно вывести не только, сколько «плюс» на «минус» дает, но и что получается при умножении отрицательных чисел.
Умножение и деление двух чисел со знаком «-»
Если не углубляться в математические нюансы, то можно попробовать более простым способом объяснить правила действий с отрицательными числами.
Допустим, что C — (-V) = D, исходя из этого, C = D + (-V), то есть C = D — V. Переносим V и получаем, что C + V = D. То есть C + V = C — (-V). Этот пример объясняет, почему в выражении, где идут два «минуса» подряд, упомянутые знаки следует поменять на «плюс». Теперь разберемся с умножением.
(-C) х (-V) = D, в выражение можно добавить и вычесть два одинаковых произведения, которые не поменяют его значения: (-C) х (-V) + (C х V) — (C х V) = D.
Вспомная о правилах работы со скобками, получаем:
1) (-C) х (-V) + (C х V) + (-C) х V = D;
2) (-C) х ((-V) + V) + C х V = D;
3) (-C) х 0 + C х V = D;
Из этого следует, что C х V = (-C) х (-V).
Аналогично можно доказать, что и в результате деления двух отрицательных чисел выйдет положительное.
Общие математические правила
Конечно, такое объяснение не подойдет для школьников младших классов, которые только начинают учить абстрактные отрицательные числа. Им лучше объяснять на видимых предметах, манипулируя знакомым им термином зазеркалья. Например, придуманные, но не существующие игрушки находятся именно там. Их и можно отобразить со знаком «-». Умножение двух зазеркальных объектов переносит их в еще один мир, который приравнивается к настоящему, то есть в результате мы имеем положительные числа. А вот умножение абстрактного отрицательного числа на положительное лишь дает знакомый всем результат. Ведь «плюс» умножить на «минус» дает «минус». Правда, в младшем школьном возрасте дети не слишком-то пытаются вникнуть во все математические нюансы.
Например, придуманные, но не существующие игрушки находятся именно там. Их и можно отобразить со знаком «-». Умножение двух зазеркальных объектов переносит их в еще один мир, который приравнивается к настоящему, то есть в результате мы имеем положительные числа. А вот умножение абстрактного отрицательного числа на положительное лишь дает знакомый всем результат. Ведь «плюс» умножить на «минус» дает «минус». Правда, в младшем школьном возрасте дети не слишком-то пытаются вникнуть во все математические нюансы.
Хотя, если смотреть правде в глаза, для многих людей даже с высшим образованием так и остаются загадкой многие правила. Все принимают как данность то, что преподают им учителя, не затрудняясь вникать во все сложности, которые таит в себе математика. «Минус» на «минус» дает «плюс» – об этом знают все без исключения. Это верно как для целых, так и для дробных чисел.
ПЛЮС МИНУС
Плюс и минус — это признаки положительных и отрицательных чисел в математике. Какой результат получается при умножении и делении положительных и отрицательных чисел? Эта простая таблица наглядно показывает результаты умножения и деления двух чисел с разными знаками.
Приведенные в таблице результаты применимы как при умножении и делении целых чисел, так и при умножении и делении дробей. Для определения числовых значений результата умножения или деления воспользуйтесь таблицами умножения и деления, которые можно скачать бесплатно.
При умножении или делении двух положительных чисел в результате получается положительное число. Плюс умноженный на плюс дает плюс, плюс деленный на плюс будет плюс. Это правило математики. Произведение двух положительных чисел — число положительное, частное двух положительных чисел — положительное число.
В математике умножение или деление положительного числа на отрицательное дает в результате отрицательное число. Плюс умноженный на минус дает минус. Плюс деленный на минус будет минус. Если положительную дробь умножить или разделить на отрицательную дробь получится отрицательное число. Это число может быть целым или дробным. Произведение положительного числа на отрицательное — число отрицательное, частное положительного числа на отрицательное число — отрицательное число. Если числитель дроби положительный, а знаменатель отрицательный — дробь (или целое число) будет отрицательной.
Если числитель дроби положительный, а знаменатель отрицательный — дробь (или целое число) будет отрицательной.
При делении или умножении отрицательного числа на положительное в результате получается отрицательное число. Минус умноженный на плюс будет минус. Минус деленный на плюс в математике будет минус. Когда числитель дроби отрицательный, а знаменатель положительный — дробь (или целое число) будет отрицательной. Если отрицательную дробь умножить или разделить на положительную дробь получится отрицательное число. Это число может быть целым или дробным, что определяется другими правилами математики. Произведение отрицательного числа на положительное — число отрицательное, частное отрицательного числа на положительное число — отрицательное число.
Когда умножаются или делятся два отрицательных числа, результатом будет положительное число. Минус умноженный на минус дает плюс, минус деленный на минус будет плюс. Произведение двух отрицательного чисел — положительное число, частное двух отрицательного чисел — число положительное. При делении или умножении двух отрицательных чисел получается положительное число. Правила знаков в математике распространяются как на целые, так и на дробные числа. При делении двух отрицательных дробей результат будет положительным. При умножении двух отрицательных дробей результат так же будет положительным, то есть со знаком плюс.
При делении или умножении двух отрицательных чисел получается положительное число. Правила знаков в математике распространяются как на целые, так и на дробные числа. При делении двух отрицательных дробей результат будет положительным. При умножении двух отрицательных дробей результат так же будет положительным, то есть со знаком плюс.
ВОПРОС — ОТВЕТ
«Кто ввел знаки сложения и вычитания в математику?» — первое употребление слов plus (больше) и minus (меньше) как обозначения действия сложения было найдено историком математики Энестремом в итальянской алгебре четырнадцатого века. Вначале действия сложения и вычитания обозначали перввыми буквами слов «p» и «m». Современные знаки плюс «+» и минус «-» появились в Германии в последнее десятилетие пятнадцатого века в книге Видмана, которая была руководством по счету для купцов (“Behende und ubsche Rechenung auf allen Kaufmannschaft”, 1498). Существует предположение, что знаки плюс «+» и минус «-» появились из торговой практики: проданные меры вина отмечались на бочке черточкой «-«, а при восстановлении запаса их перечеркивали, откуда получился знак «+». Здесь я хочу особо подчеркнуть, что знаком «минус» отмечалась не мера (бочка) с «отрицательным» вином, а пустая мера (бочка), что гораздо больше соответствует понятию «ноль». Когда вам математики будут рассказывать об отрицательных числах, всегда помните о пустой бочке, которая по воле математиков превратилась в бочку со знаком «минус».
Здесь я хочу особо подчеркнуть, что знаком «минус» отмечалась не мера (бочка) с «отрицательным» вином, а пустая мера (бочка), что гораздо больше соответствует понятию «ноль». Когда вам математики будут рассказывать об отрицательных числах, всегда помните о пустой бочке, которая по воле математиков превратилась в бочку со знаком «минус».
«Минус 6 делить на минус 3 как быть?» — сперва отбрасываем знаки минус и делим просто 6 (шесть) на 3 (три) при помощи таблицы деления и получаем в результате 2 (два). Потом по табличке вверху странички делим минус на минус и получаем плюс. Теперь прилепливаем полученный плюс к ранее полученной двойке
Впрочем, знак «+» перед числами писать не принято, поэтому красивее и правильнее будет так:
«Если число со знаком минус спереди умножаем на такое же число?» — решение смотри выше.
Математика для блондинок
Математикой должны заниматься блондинки — они врать не умеют.
Страницы
- Главная страница Новая математика Словарик
Четверг, 31 декабря 2020 г.

Минус на плюс что дает?
Положительные и отрицательные числа придумали математики. Делать им было нечего, вот они и придумали. Правила умножения и деления положительных и отрицательных чисел придумали всё те же математики. Специально для того, чтобы нам жизнь мёдом не казалась. Как же нам быть? Нужно выучить эти правила, чтобы говорить математикам то, что они хотят от нас слышать.
Запомнить правила умножения или деления положительных и отрицательных чисел очень просто. Если два числа имеют разные знаки, в результате всегда будет знак минус.
Если два числа имеют одинаковые знаки, в результате всегда будет плюс.
Рассмотрим все возможные варианты. Что дает минус на плюс? При умножении и делении минус на плюс дает минус. Что дает плюс на минус? При умножении и делении в результате мы тоже получаем знак минус.
| Минус на плюс, плюс на минус. |
Как вы видите, все варианты умножения и деления положительных и отрицательных чисел исчерпаны, но знак плюс у нас так и не появился.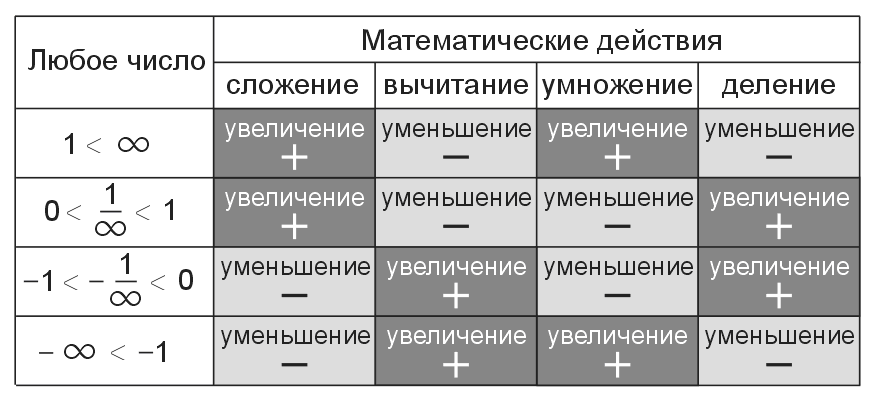
Что дает минус на минус? Всегда будет получаться плюс, если мы выполняем умножение или деление. Что дает плюс на плюс? Здесь совсем просто. Умножение или деление плюса на плюс дает всегда плюс.
| Alt=»Минус на минус, плюс на плюс. Умножение и деление отрицательных или положительных чисел в результате дает положительное число. Математика для блондинок. или» width=»654″ height=»848″ /> |
| Минус на минус, плюс на плюс. |
Надеюсь, это вы запомнили: минус на минус дает плюс, плюс на плюс дает минус. Что говорить математикам? При умножении и делении положительных или отрицательных чисел в результате получается положительное число.
Если с умножением и делением двух плюсов всё понятно (в результате получается такой же плюс), то с двумя минусами ничего не понятно. По логике, если два плюса дают плюс, то два минуса должны давать минус. Такой большой, жирный минус. Но не тут-то было. Математики думают иначе. Так почему минус и минус превращаются в плюс?
По логике, если два плюса дают плюс, то два минуса должны давать минус. Такой большой, жирный минус. Но не тут-то было. Математики думают иначе. Так почему минус и минус превращаются в плюс?
Могу вас заверить, что интуитивно математики правильно решили задачу на умножение и деление плюсов и минусов. Они записали правила в учебники, не особо вдаваясь в подробности. Для правильного ответа на вопрос, нам нужно разобраться, что же означают знаки плюс и минус в математике.
Давайте попробуем применить правило умножениея и деления положительных и отрицательных чисел на практике. Придумаем какой-нибудь пример из нашей жизни. Думаю, вы слышали про бочку мёда и ложку дёгтя, которая может испортить весь мёд. Пусть мёд — это положительные числа, а дёготь — это числа отрицательные. Пробуем. Смотрим на картинки и описываем правила.
Если в бочку дёгтя добавить ложку мёда, получится бочка дёгтя.
Если в бочку мёда добавить ложку дёгтя, получится бочка дёгтя.
Если в бочку дёгтя добавить ложку дёгтя, получится бочка мёда.
Если в бочку мёда добавить ложку мёда, получится бочка мёда.
Первых два примера с натяжкой можно принять. Последний пример вообще не вызывает вопросов. А вот с предпоследним примером возникают очень большие проблемы — в жизни такого не бывает.
Здесь возможны два варианта:
1. Математики не правильно записали свое правило.
2. Мы не правильно применяем математическое правило.
Лично я за второй вариант. Объясню почему. Математику не только нужно знать, но нею ещё нужно уметь пользоваться.
Приведу пример из собственного опыта. Один учитель математики на уроках нам говорил: «математика – это точная наука, два раза соври – получится правда». Это утверждение однажды мне очень пригодилось. Как-то я решал сложную задачу с длинным решением. Я точно знал, какой результат должен быть. Но результат был другим. Я долго искал ошибку в расчетах, но не смог ее найти. Тогда, за несколько действий до итогового результата, я изменил одно число так, чтобы результат получился правильным. Я в расчетах соврал два раза и получил правильный результат. Математические вычисления в тот раз никто не проверял и я получил хорошую оценку. Это очень похоже на правило «минус на минус дает плюс», не так ли?
Я в расчетах соврал два раза и получил правильный результат. Математические вычисления в тот раз никто не проверял и я получил хорошую оценку. Это очень похоже на правило «минус на минус дает плюс», не так ли?
Но вернемся к нашим бочкам. Кстати, говорят, именно с бочек с вином математики срисовали знак «минус». Виноделы этим знаком обозначали пустые бочки. После наполнения бочек вином они перечеркивали знак «минус» и получался знак «плюс». По сути, знак «минус» заменял виноделам обычный ноль, ведь он обозначал отсутствие вина в бочке. Но математики ловко присобачили знак «минус» к числам и назвали их «отрицательными».
Так что же не так с мёдом и дёгтем в бочках? Мои четыре примера описывают действие сложения — ведь мы прибавляем одно к другому, а математические правила мы рассматриваем для деления и умножения. Это абсолютно разные вещи, сколько бы математики не повторяли, что умножение это и есть сложение. Сложение — это изменение количества. Умножение — это изменение качества. При добавлении ложки дёгтя в бочку мёда, мёд не превращается в дёготь. Мы просто получаем бочку испорченного мёда. Точно так же и дёготь, добавленный в бочку дёгтя, не превращает всё в мёд. При сложении и вычитании положительных и отрицательных чисел действуют совсем другие правила знаков.
При добавлении ложки дёгтя в бочку мёда, мёд не превращается в дёготь. Мы просто получаем бочку испорченного мёда. Точно так же и дёготь, добавленный в бочку дёгтя, не превращает всё в мёд. При сложении и вычитании положительных и отрицательных чисел действуют совсем другие правила знаков.
В чем же отличие качественных изменений от количественных? В единицах измерения, которые в математике предпочитают игнорировать. Вот смотрите. Если мы к метрам длины прибавим метры ширины, мы получим метры периметра. А если мы умножим метры длины на метры ширины, то в результате будут метры квадратные площади. Теперь вопрос к математикам: сколько метров длины или ширины нужно сложить, чтобы получить один метр квадратный площади? Или вопрос к вам: сколько метров ниток вам нужно намотать на себя, чтобы одеться? Ведь ткань — это те же самые нитки, только в совершенно другом качестве. Ну и наглядный пример из алгебры:
В этом примере буква а выполняет роль единицы измерения. Кстати, правило умножения отрицательных чисел наводит на ещё один вопрос математикам: сколько отрицательных чисел нужно сложить, чтобы получилось одно положительное число?
Так что же такое знаки «плюс» и «минус» в математике? Существуют ли отрицательные числа? Об этом мы поговорим как-нибудь в другой раз.
Слушая учителя математики, большинство учеников воспринимают материал как аксиому. При этом мало кто пытается добраться до сути и разобраться, почему «минус» на «плюс» дает знак «минус», а при умножении двух отрицательных чисел выходит положительное.
Законы математики
Большинство взрослых не в силах объяснить ни себе, ни своим детям, почему так получается. Они твердо усвоили этот материал в школе, но при этом даже не попытались выяснить, откуда взялись такие правила. А зря. Зачастую современные дети не столь доверчивы, им необходимо докопаться до самой сути и понять, скажем, почему «плюс» на «минус» дает «минус». А иногда сорванцы специально задают каверзные вопросы, дабы насладиться моментом, когда взрослые не могут дать вразумительного ответа. И совсем уж беда, если впросак попадает молодой учитель.
Для объяснения правильности этого закона математики, необходимо сформулировать аксиомы кольца. Но для начала следует понять, что это такое. В математике кольцом принято называть множество, в котором задействованы две операции с двумя элементами. Но разбираться с этим лучше на примере.
Но разбираться с этим лучше на примере.
Аксиома кольца
Существует несколько математических законов.
- Первый из них переместительный, согласно ему, C + V = V + C. Второй называется сочетательным (V + C) + D = V + (C + D).
Им же подчиняется и умножение (V х C) х D = V х (C х D).
Никто не отменял и правил, по которым открываются скобки (V + C) х D = V х D + C х D, также верно, что C х (V + D) = C х V + C х D.
Кроме того, установлено, что в кольцо можно ввести специальный, нейтральный по сложению элемент, при использовании которого будет верно следующее: C + 0 = C. Кроме того, для каждого C есть противоположный элемент, который можно обозначить, как (-C). При этом C + (-C) = 0.
Выведение аксиом для отрицательных чисел
Приняв приведенные выше утверждения, можно ответить на вопрос: «»Плюс» на «минус» дает какой знак?» Зная аксиому про умножение отрицательных чисел, необходимо подтвердить, что действительно (-C) х V = -(C х V). А также, что верно такое равенство: (-(-C)) = C.
Для этого придется вначале доказать, что у каждого из элементов существует лишь один ему противоположный «собрат». Рассмотрим следующий пример доказательства. Давайте попробуем представить, что для C противоположными являются два числа — V и D. Из этого следует, что C + V = 0 и C + D = 0, то есть C + V = 0 = C + D. Вспоминая о переместительных законах и о свойствах числа 0, можно рассмотреть сумму всех трех чисел: C, V и D. Попробуем выяснить значение V. Логично, что V = V + 0 = V + (C + D) = V + C + D, ведь значение C + D, как было принято выше, равняется 0. Значит, V = V + C + D.
Точно так же выводится и значение для D: D = V + C + D = (V + C) + D = 0 + D = D. Исходя из этого, становится ясно, что V = D.
Для того чтобы понять, почему все же «плюс» на «минус» дает «минус», необходимо разобраться со следующим. Так, для элемента (-C) противоположными являются C и (-(-C)), то есть между собой они равны.
Тогда очевидно, что 0 х V = (C + (-C)) х V = C х V + (-C) х V.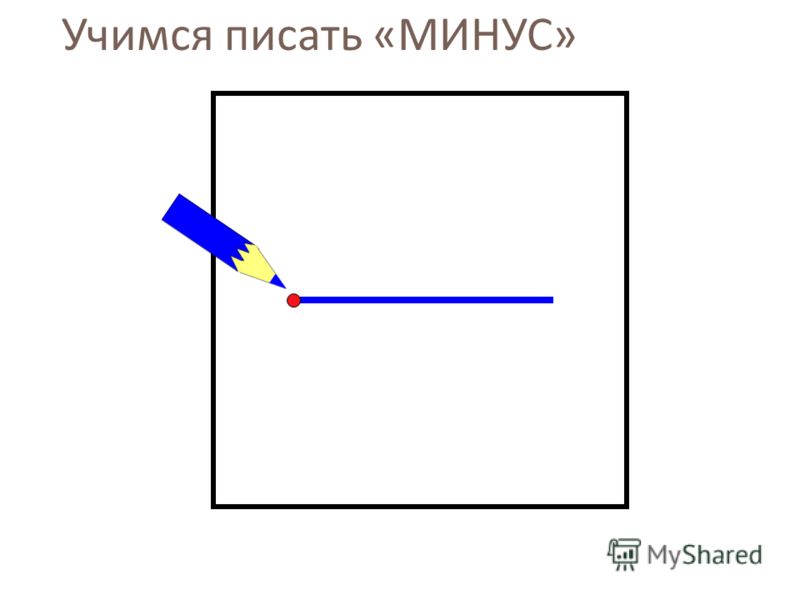 Из этого следует, что C х V противоположно (-)C х V, значит, (-C) х V = -(C х V).
Из этого следует, что C х V противоположно (-)C х V, значит, (-C) х V = -(C х V).
Для полной математической строгости необходимо еще подтвердить, что 0 х V = 0 для любого элемента. Если следовать логике, то 0 х V = (0 + 0) х V = 0 х V + 0 х V. А это значит, что прибавление произведения 0 х V никак не меняет установленную сумму. Ведь это произведение равняется нулю.
Зная все эти аксиомы, можно вывести не только, сколько «плюс» на «минус» дает, но и что получается при умножении отрицательных чисел.
Умножение и деление двух чисел со знаком «-»
Если не углубляться в математические нюансы, то можно попробовать более простым способом объяснить правила действий с отрицательными числами.
Допустим, что C — (-V) = D, исходя из этого, C = D + (-V), то есть C = D — V. Переносим V и получаем, что C + V = D. То есть C + V = C — (-V). Этот пример объясняет, почему в выражении, где идут два «минуса» подряд, упомянутые знаки следует поменять на «плюс». Теперь разберемся с умножением.
(-C) х (-V) = D, в выражение можно добавить и вычесть два одинаковых произведения, которые не поменяют его значения: (-C) х (-V) + (C х V) — (C х V) = D.
Вспомная о правилах работы со скобками, получаем:
1) (-C) х (-V) + (C х V) + (-C) х V = D;
2) (-C) х ((-V) + V) + C х V = D;
3) (-C) х 0 + C х V = D;
Из этого следует, что C х V = (-C) х (-V).
Аналогично можно доказать, что и в результате деления двух отрицательных чисел выйдет положительное.
Общие математические правила
Конечно, такое объяснение не подойдет для школьников младших классов, которые только начинают учить абстрактные отрицательные числа. Им лучше объяснять на видимых предметах, манипулируя знакомым им термином зазеркалья. Например, придуманные, но не существующие игрушки находятся именно там. Их и можно отобразить со знаком «-». Умножение двух зазеркальных объектов переносит их в еще один мир, который приравнивается к настоящему, то есть в результате мы имеем положительные числа. А вот умножение абстрактного отрицательного числа на положительное лишь дает знакомый всем результат. Ведь «плюс» умножить на «минус» дает «минус». Правда, в младшем школьном возрасте дети не слишком-то пытаются вникнуть во все математические нюансы.
А вот умножение абстрактного отрицательного числа на положительное лишь дает знакомый всем результат. Ведь «плюс» умножить на «минус» дает «минус». Правда, в младшем школьном возрасте дети не слишком-то пытаются вникнуть во все математические нюансы.
Хотя, если смотреть правде в глаза, для многих людей даже с высшим образованием так и остаются загадкой многие правила. Все принимают как данность то, что преподают им учителя, не затрудняясь вникать во все сложности, которые таит в себе математика. «Минус» на «минус» дает «плюс» – об этом знают все без исключения. Это верно как для целых, так и для дробных чисел.
Четверг, 31 декабря 2020 г.
Общие математические правила.
Zahidknyha. com. ua
20.05.2017 21:49:43
2017-05-20 21:49:43
Источники:
Https://zahidknyha. com. ua/dokument/urok/chto-daet-pljus-na-minus-v-matematike/
Как называется минус в математике
ТАБЛИЦЫ СЛОЖЕНИЯ, ВЫЧИТАНИЯ, УМНОЖЕНИЯ, ДЕЛЕНИЯ
Сложение, вычитание, умножение и деление относятся к математическим действиям, точнее, к арифметическим действиям. Таблица сложения, таблица вычитания, таблица умножения и таблица деления наглядно демонстрируют результаты этих математических действий.
Таблица сложения, таблица вычитания, таблица умножения и таблица деления наглядно демонстрируют результаты этих математических действий.
При сложении чисел получается новое число. Числа, которые складываются, называются «слагаемые», результат сложения называется «сумма». Обозначают сложение чисел знаком «плюс» +. При сложении сумма всегда больше любого из слагаемых. Результаты сложения можно записать в виде таблицы сложения.
Математическим действием, обратным сложению, является вычитание. Вычитание также называют отниманием чисел. Число, из которого вычитают, называется «уменьшаемое». Число, которое вычитают, называется «вычитаемое». Результат вычитания называется «разность». Обозначают вычитание чисел знаком «минус» -. При вычитании уменьшаемое всегда больше разности. Для проверки правильности полученного результата при вычитании нужно сложить разность и вычитаемое. В результате сложения должно получиться уменьшаемое. Результаты вычитания можно записать в виде таблицы вычитания. Эта таблица не является арифметической таблицей вычитания, поскольку в ней представлены отрицательные числа. Отрицательные числа не являются натуральными числами и изучаются алгеброй, а не арифметикой. Перед отрицательными числами ставится знак минус.
Эта таблица не является арифметической таблицей вычитания, поскольку в ней представлены отрицательные числа. Отрицательные числа не являются натуральными числами и изучаются алгеброй, а не арифметикой. Перед отрицательными числами ставится знак минус.
После небольшой рекламной паузы, во время которой вы можете насладиться всеми прелестями Интернета, мы продолжим изучение математических действий и рассмотрим другую «сладкую парочку» – умножение и деление. Там вас ожидает совершенно бесплатный, умопомрачительный бонус — целых ДВЕ упаковки таблицы деления!
Числа, которые умножаются, называются «сомножители», результат умножения называется «произведение». Обозначают умножение чисел знаком «умножение» х. При умножении положительных чисел произведение всегда положительное и больше любого из сомножителей. При умножении положительного числа на отрицательное результат получается отрицательным – плюс на минус дает минус, минус на плюс дает минус. При умножении двух отрицательных чисел результат получается положительным – минус на минус дает плюс. Результаты умножения можно записать в виде таблицы умножения.
Результаты умножения можно записать в виде таблицы умножения.
Математическим действием, обратным умножению, является деление. Иногда при обозначении деления употребляется выражение «частное двух чисел». Обозначают деление знаком «деление» : или дробной чертой. Число, которое делится, называется «делимое». Если число записывается в виде дроби, делимое всегда находится в числителе дроби – над дробной чертой. Число, на которое делят, называется «делитель». Делитель всегда находится в знаменателе дроби – под дробной чертой. Результат деления называется «частное». При делении положительных чисел частное всегда положительно. Если одно из двух чисел, делимое или делитель, отрицательно, результат получается отрицательным – плюс на минус дает минус, минус на плюс дает минус. При делении отрицательного числа на отрицательное получается положительное число – минус на минус дает плюс. Результаты деления можно записать в виде таблицы деления. Таблицу деления можно представить правильными дробями или десятичными дробями.
Немного от себя.
Иметь калькулятор — это хорошо, но знать таблицу умножения — это выгодно! Тогда в любой ситуации продавцам будет гораздо труднее вас обсчитывать. «Пять у два — пятнадцать, плюс двенадцать — сорок семь, а всего с вас семьдесят!» — бойко лопочет продавщица, клацая по клавишам калькулятора. Я тупо смотрю на приготовленные три десятки в руках и прикидываю, могли ли так резко подскочить цены на товары. «А почём же у вас . » — удивленно спрашиваю я. «Ой, я, наверное, ошиблась. » — продавщица снова клацает по калькулятору, берет у меня приготовленную сумму и дает мне сдачи.
В помощь посетителям добавлю маленькую рубрику вопрос-ответ . Все вопросы взяты из поисковых запросов посетителей этого сайта, ответы на вопросы — мои.
Как Петр 1 называл сложение, вычитание, умножение и деление? — Петр 1 называл их адиция (по-английски сложение будет addition), субстракция (в английском языке пишется substraction и переводится как фундамент, основание; вычитание в английском языке пишется deduction) мультипликация (на английском языке multiplication означает умножение) и дивизия (по-английски деление будет division; моё любимое «деление на ноль» будет division by zero).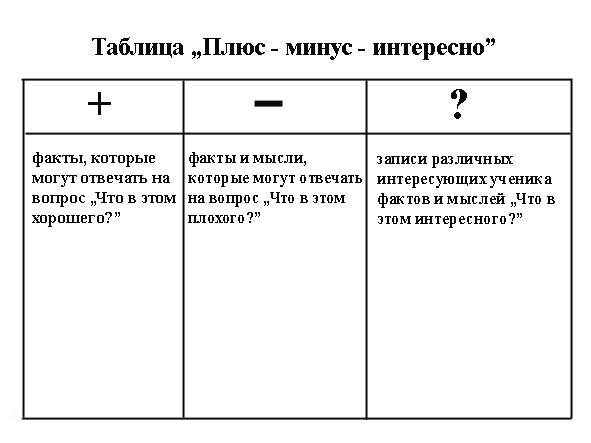 Так было сказано в одной из книг о Петре 1, что он должен был знать адицию, субстракцию, мультипликацию и дивизию. То ли кто-то что-то напутал (в смысле спутал основы знаний с банальным вычитанием), то ли царь Петр не шибко вникал в то, что он говорил. Оно и понятно, это подданным нельзя ошибаться, а царям — всё можно.
Так было сказано в одной из книг о Петре 1, что он должен был знать адицию, субстракцию, мультипликацию и дивизию. То ли кто-то что-то напутал (в смысле спутал основы знаний с банальным вычитанием), то ли царь Петр не шибко вникал в то, что он говорил. Оно и понятно, это подданным нельзя ошибаться, а царям — всё можно.
Умножение и деление на 1 — при умножении или делении числа на единицу это число не изменяется. Например, восемнадцать умноженное (или деленное) на один равняется восемнадцать. Если отрицательное число умножить или разделить на один, в результате получится точно такое же отрицательное число.
Как называются числа при сложении? — при сложении числа называются слагаемыми. Слагаемых может быть два или больше.
Частное — это деление или умножение? — частное — так называется результат деления.
Как делить отрицательные числа? — точно так же, как и положительные. Только не забывайте ставить знак минус перед результатом деления. Если отрицательное число разделить на положительное — в результате будет отрицательное число.
Минус умножить на минус — при умножении минуса на минус будет плюс.
Деление минус на минус — при делении минуса на минус будет плюс.
Деление отрицательных дробей, деление отрицательной дроби на отрицательную — при делении двух отрицательных дробей результат будет положительным. Результат деления может быть как дробным, так и целым числом.
Деление на минус, деление на отрицательное число — при делении положительного числа (плюс) в результате получается отрицательное число (минус), при делении отрицательного числа (минус) в результате будет положительное число (плюс).
Деление положительного числа на отрицательное — дает в результате отрицательное число.
Если вам понравилась публикация и вы хотите знать больше, помогите мне в работе над другими материалами.
Почему минус на минус дает плюс объяснение?
Минус умноженный на минус дает плюс, минус деленный на минус будет плюс. Произведение двух отрицательного чисел — положительное число, частное двух отрицательного чисел — число положительное.
Как умножить минус на минус?
Правила знаков для умножения
Запомнить правило знаков для умножения очень просто. Данное правило совпадает с правилом раскрытия скобок. Минус на минус даёт плюс, Плюс на минус даёт минус.
Что дает плюс на минус?
«+»·«+» = «+» — плюс на плюс дает плюс; «–»·«+» = «–» — минус на плюс дает минус; «+»·«–» = «–» — плюс на минус дает минус; «–»·«–» = «+» — минус на минус дает плюс.
Как называется минус в математике?
Знак минус (−) имеет три основных применения в математике: Оператор вычитания: бинарный оператор, указывающий на операцию вычитания, например 36 − 5 = 31; Как указатель отрицательных величин, например −5; Унарный оператор, который действует в качестве инструкции для замены операнда на противоположное число.
Что получается при делении минус на минус?
«−−»− при умножении минус на минус результат становится положительным; «−+»− при умножении минуса на плюс результат становится отрицательным; «+−»− при умножении плюса на минус результат становится отрицательным; «++»− при умножении плюса на плюс результат становится положительным.
Можно ли разделить на минус?
Правило знаков при делении
Поэтому в конце результат получится со знаком «минус». Частное от деления нуля на число, отличное от нуля, равно нулю. Делить на ноль НЕЛЬЗЯ!
Когда минус на минус дает плюс?
При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.
Как умножить на отрицательное число?
Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел –a, −b данное равенство считается верным. (−а)⋅(−b)=a⋅b.
Как умножить дробь на отрицательное число?
Чтобы найти произведение двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем перемножить дроби по правилу умножения дробей. Пример. При умножении отрицательной дроби на положительную результат будет отрицательным.![]()
Как вычитать положительные и отрицательные числа?
Как видим, чтобы вычесть из положительного числа отрицательное число, нужно просто сложить их модули. Таким образом, при вычитании отрицательного числа из отрицательного мы действуем по правилу сложения чисел с разными знаками, и у нас может получиться как положительное, так и отрицательное число.
Для чего нужны отрицательные числа?
Отрицательные числа нужны для измерения значений величин относительно нуля. А также служат для описания величин. Отрицательное число с древних времен ассоциируется со словом «долг», тогда как положительное число можно ассоциировать со словом «доход». Эти числа нужны для того чтобы измерять величины и т.
Что такое Что такое произведение?
Смотреть что такое «произведение чисел» в других словарях:
ПРОИЗВЕДЕНИЕ — (product) Результат умножения. Произведение чисел, алгебраических выражений, векторов или матриц; может быть показано точкой, косой крестик или же просто написанием их последовательно один за другим, т.
Как называется выражение со знаком минус?
Знак, обозначающий вычитание — минус; … Выражение, в котором числа соединены знаком вычитания — разность; Сумма: 5 + 20 = 25, 10 + 2 = 12; Разность: 5- 3 = 2, 10 — 5 = 5.10 мая 2020 г.
Как называется минус?
Минусовая фонограмма («минус», «минусовка»; от «запись минус один голос») — запись музыкального произведения, в котором отсутствует одна или более партий, обычно вокал или солирующий инструмент. … Под такую запись музыкант (профессионал или любитель) имеет возможность сам исполнять отсутствующую партию.
Презентация — Математические знаки «Плюс — Минус — Равно»
Lusana.ru — сервис хранения презентаций, докладов, шаблонов, фонов в формате ppt-pptx. Ищете слайды для PowerPoint — мы поможем! Скачивайте, загружайте, делитесь и оценивайте работу других. Наши учебные презентации помогут не только студентам, но и школьникам!
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.
Как понять, почему «плюс» на «минус» дает «минус» ?
Слушая учителя математики, большинство учеников воспринимают материал как аксиому. При этом мало кто пытается добраться до сути и разобраться, почему «минус» на «плюс» дает знак «минус», а при умножении двух отрицательных чисел выходит положительное.
Законы математики
Большинство взрослых не в силах объяснить ни себе, ни своим детям, почему так получается. Они твердо усвоили этот материал в школе, но при этом даже не попытались выяснить, откуда взялись такие правила. А зря. Зачастую современные дети не столь доверчивы, им необходимо докопаться до самой сути и понять, скажем, почему «плюс» на «минус» дает «минус». А иногда сорванцы специально задают каверзные вопросы, дабы насладиться моментом, когда взрослые не могут дать вразумительного ответа. И совсем уж беда, если впросак попадает молодой учитель…
Кстати, следует отметить, что упомянутое выше правило действенно как для умножения, так и для деления. Произведение отрицательного и положительного числа даст лишь «минус. Если речь идет о двух цифрах со знаком «-», то в результате получится положительное число. То же касается и деления. Если одно из чисел будет отрицательным, то частное тоже будет со знаком «-».
Произведение отрицательного и положительного числа даст лишь «минус. Если речь идет о двух цифрах со знаком «-», то в результате получится положительное число. То же касается и деления. Если одно из чисел будет отрицательным, то частное тоже будет со знаком «-».
Для объяснения правильности этого закона математики, необходимо сформулировать аксиомы кольца. Но для начала следует понять, что это такое. В математике кольцом принято называть множество, в котором задействованы две операции с двумя элементами. Но разбираться с этим лучше на примере.
Аксиома кольца
Существует несколько математических законов.
- Первый из них переместительный, согласно ему, C + V = V + C.
- Второй называется сочетательным (V + C) + D = V + (C + D).
Им же подчиняется и умножение (V х C) х D = V х (C х D).
Никто не отменял и правил, по которым открываются скобки (V + C) х D = V х D + C х D, также верно, что C х (V + D) = C х V + C х D.
Кроме того, установлено, что в кольцо можно ввести специальный, нейтральный по сложению элемент, при использовании которого будет верно следующее: C + 0 = C. Кроме того, для каждого C есть противоположный элемент, который можно обозначить, как (-C). При этом C + (-C) = 0.
Кроме того, для каждого C есть противоположный элемент, который можно обозначить, как (-C). При этом C + (-C) = 0.
Выведение аксиом для отрицательных чисел
Приняв приведенные выше утверждения, можно ответить на вопрос: «»Плюс» на «минус» дает какой знак?» Зная аксиому про умножение отрицательных чисел, необходимо подтвердить, что действительно (-C) х V = -(C х V). А также, что верно такое равенство: (-(-C)) = C.
Для этого придется вначале доказать, что у каждого из элементов существует лишь один ему противоположный «собрат». Рассмотрим следующий пример доказательства. Давайте попробуем представить, что для C противоположными являются два числа — V и D. Из этого следует, что C + V = 0 и C + D = 0, то есть C + V = 0 = C + D. Вспоминая о переместительных законах и о свойствах числа 0, можно рассмотреть сумму всех трех чисел: C, V и D. Попробуем выяснить значение V. Логично, что V = V + 0 = V + (C + D) = V + C + D, ведь значение C + D, как было принято выше, равняется 0. Значит, V = V + C + D.
Значит, V = V + C + D.
Точно так же выводится и значение для D: D = V + C + D = (V + C) + D = 0 + D = D. Исходя из этого, становится ясно, что V = D.
Для того чтобы понять, почему все же «плюс» на «минус» дает «минус», необходимо разобраться со следующим. Так, для элемента (-C) противоположными являются C и (-(-C)), то есть между собой они равны.
Тогда очевидно, что 0 х V = (C + (-C)) х V = C х V + (-C) х V. Из этого следует, что C х V противоположно (-)C х V, значит, (-C) х V = -(C х V).
Для полной математической строгости необходимо еще подтвердить, что 0 х V = 0 для любого элемента. Если следовать логике, то 0 х V = (0 + 0) х V = 0 х V + 0 х V. А это значит, что прибавление произведения 0 х V никак не меняет установленную сумму. Ведь это произведение равняется нулю.
Зная все эти аксиомы, можно вывести не только, сколько «плюс» на «минус» дает, но и что получается при умножении отрицательных чисел.
Умножение и деление двух чисел со знаком «-»
Если не углубляться в математические нюансы, то можно попробовать более простым способом объяснить правила действий с отрицательными числами.
Допустим, что C — (-V) = D, исходя из этого, C = D + (-V), то есть C = D — V. Переносим V и получаем, что C + V = D. То есть C + V = C — (-V). Этот пример объясняет, почему в выражении, где идут два «минуса» подряд, упомянутые знаки следует поменять на «плюс». Теперь разберемся с умножением.
(-C) х (-V) = D, в выражение можно добавить и вычесть два одинаковых произведения, которые не поменяют его значения: (-C) х (-V) + (C х V) — (C х V) = D.
Вспомная о правилах работы со скобками, получаем:
1) (-C) х (-V) + (C х V) + (-C) х V = D;
2) (-C) х ((-V) + V) + C х V = D;
3) (-C) х 0 + C х V = D;
4) C х V = D.
Из этого следует, что C х V = (-C) х (-V).
Аналогично можно доказать, что и в результате деления двух отрицательных чисел выйдет положительное.
Общие математические правила
Конечно, такое объяснение не подойдет для школьников младших классов, которые только начинают учить абстрактные отрицательные числа. Им лучше объяснять на видимых предметах, манипулируя знакомым им термином зазеркалья. Например, придуманные, но не существующие игрушки находятся именно там. Их и можно отобразить со знаком «-». Умножение двух зазеркальных объектов переносит их в еще один мир, который приравнивается к настоящему, то есть в результате мы имеем положительные числа. А вот умножение абстрактного отрицательного числа на положительное лишь дает знакомый всем результат. Ведь «плюс» умножить на «минус» дает «минус». Правда, в младшем школьном возрасте дети не слишком-то пытаются вникнуть во все математические нюансы.
Например, придуманные, но не существующие игрушки находятся именно там. Их и можно отобразить со знаком «-». Умножение двух зазеркальных объектов переносит их в еще один мир, который приравнивается к настоящему, то есть в результате мы имеем положительные числа. А вот умножение абстрактного отрицательного числа на положительное лишь дает знакомый всем результат. Ведь «плюс» умножить на «минус» дает «минус». Правда, в младшем школьном возрасте дети не слишком-то пытаются вникнуть во все математические нюансы.
Хотя, если смотреть правде в глаза, для многих людей даже с высшим образованием так и остаются загадкой многие правила. Все принимают как данность то, что преподают им учителя, не затрудняясь вникать во все сложности, которые таит в себе математика. «Минус» на «минус» дает «плюс» – об этом знают все без исключения. Это верно как для целых, так и для дробных чисел.
Минус на минус, Минус на минус — ориджинал, автор Эйприл, Лето в городе – горячее и знойное – полностью восполнило их общую больную потребность в тепле и .
 ..
..2 сентября 2021, 00:00
Настройки текста
Лапке всегда было плевать на сплетни у себя за спиной и змеиное перешептывание ее одноклассников.
Она прекрасно знала, как ее за глазки называли в этом показательно-прилизанном физико-математическом гадюшнике. Ей плевать на лицемерное осуждение: у каждого свое понимание романтики и морали.
Открыто в лицо ей никогда никто ничего не высказывал. Да и зачем, что она могла сказать в ответ? Все равно никто не поверит, что почти все сплетни про нее – выдумка и преувеличенные больные фантазии, передающиеся сломанным телефоном от одного к другому с постепенно нарастающей градацией грязи.
Кажется, сплетни в социуме так и работали – по принципу сломанного телефона.
Лапке было плевать, правда.
В подобных стерильных лучших по городу физико-математических гимназиях, где всего две проблемы: заваленный срез по алгебре и скандальный залет к концу 11 класса, черт знает от кого, главной умницы и отличницы школы – еще всегда должны быть свои обсасываемые всеми, кому не лень, Лапки. Свои «родные» девочки с грязными надуманными слухами про бешеный недотрах нынешних малолеток и порченную мораль в коридорах и классах, а еще с воем из каждой учительской: «А вот в наше время, в святом и непогрешимом СССР, девочки в таком возрасте еще в куколки играли!».
Иначе, наверно, от скуки можно повеситься.
Из всех развлечений у Лапки в этой гимназии только перешептывания и назойливые, липкие взгляды в коридорах.
Не считая разве что того, чтобы в очередной раз довести до сорванных голосовых связок психованную историчку. Да нечастых уроков русского и литературы у единственной по-настоящему доброй и любящей детей учительницы.
Но это все быстро приелось и стало неинтересным, тогда в ее жизни и появился он.
Ее невыносимо красивый холодный мальчик, что не умеет улыбаться.
При первом взгляде на холодного мальчика – красивого, будто выточенного изо льда, высокомерно-нелюдимого и со взглядом острым, ледяным, отточено-плавно разрезающим пространство и людей, как лезвием ножа – Лапка чувствовала что-то очень похожее на восхищение.
Свои «родные» девочки с грязными надуманными слухами про бешеный недотрах нынешних малолеток и порченную мораль в коридорах и классах, а еще с воем из каждой учительской: «А вот в наше время, в святом и непогрешимом СССР, девочки в таком возрасте еще в куколки играли!».
Иначе, наверно, от скуки можно повеситься.
Из всех развлечений у Лапки в этой гимназии только перешептывания и назойливые, липкие взгляды в коридорах.
Не считая разве что того, чтобы в очередной раз довести до сорванных голосовых связок психованную историчку. Да нечастых уроков русского и литературы у единственной по-настоящему доброй и любящей детей учительницы.
Но это все быстро приелось и стало неинтересным, тогда в ее жизни и появился он.
Ее невыносимо красивый холодный мальчик, что не умеет улыбаться.
При первом взгляде на холодного мальчика – красивого, будто выточенного изо льда, высокомерно-нелюдимого и со взглядом острым, ледяным, отточено-плавно разрезающим пространство и людей, как лезвием ножа – Лапка чувствовала что-то очень похожее на восхищение. Она была невероятно падка всю свою жизнь на красивое и недоступное на первый взгляд.
А еще было в этом холодном мальчике что-то… больное. Темное. Жуткое. Оно скрывалось за слоями белоснежных рубашек, кожи и костей, растворялось в идеальности холодных черт его лица, ледяной дьявольской зелени глаз и полной отмороженной безэмоциональности.
Это сразу и привлекло ее внимание. Ее мгновенный интерес сравним разве что с ироничной тягой суицидников к высоким этажам и острым предметам. Не наигранно мрачное и пугающее в людях заводило, заставляло ее дрожать изнутри от многообещающего сочетания: холодной внешней идеальности и темной неидеальной внутренней сути.
«Хочу» – было ее первой мыслью при виде него.
«Мудак» – второе, что она подумала, когда он в самом начале их знакомства сразу же показал презрительное пренебрежение к ней.
Лапка показала ему средний палец на открытое оскорбление.
И от его взгляда: полуприщуренного, темного и уже совсем не символично «разрезающего» ее по оси, которым он ответил ей на это, внутри Лапки все панически – и не очень – отмерло и разгорячилось от гортани до низа живота.
Она была невероятно падка всю свою жизнь на красивое и недоступное на первый взгляд.
А еще было в этом холодном мальчике что-то… больное. Темное. Жуткое. Оно скрывалось за слоями белоснежных рубашек, кожи и костей, растворялось в идеальности холодных черт его лица, ледяной дьявольской зелени глаз и полной отмороженной безэмоциональности.
Это сразу и привлекло ее внимание. Ее мгновенный интерес сравним разве что с ироничной тягой суицидников к высоким этажам и острым предметам. Не наигранно мрачное и пугающее в людях заводило, заставляло ее дрожать изнутри от многообещающего сочетания: холодной внешней идеальности и темной неидеальной внутренней сути.
«Хочу» – было ее первой мыслью при виде него.
«Мудак» – второе, что она подумала, когда он в самом начале их знакомства сразу же показал презрительное пренебрежение к ней.
Лапка показала ему средний палец на открытое оскорбление.
И от его взгляда: полуприщуренного, темного и уже совсем не символично «разрезающего» ее по оси, которым он ответил ей на это, внутри Лапки все панически – и не очень – отмерло и разгорячилось от гортани до низа живота. Крайне многообещающе. Интуиция на такие вещи ее еще ни разу не подводила.
Их последующая игра в «игнорирование» существования друг друга была интересной, но недолгой. Холодный мальчик – невероятно упертый и почти не поддающийся на ее манипуляции. Она же необычайно терпелива и изобретательна, особенно когда чего-то так сильно хотела.
«На коленях еще ползать за мной будешь» – мстительно думала она, через пару недель скалясь в приторно-сахарной улыбке его однокласснику.
Умение обращать на себя взгляды даже особо отмороженных – один из ее бесспорных талантов. Для этого любые средства были хороши.
И холодный мальчик, конечно же, заметил ее провокацию. И был зол. Проиграл. Но и сахарная кривовато-насмешливая улыбка на губах Лапки, слишком натянутая – трещала по швам (можно услышать, если вслушаться и стоять близко), из-под кукольной маски девочки без моральных принципов щерилось безумное довольство от удачной провокации.
Крайне многообещающе. Интуиция на такие вещи ее еще ни разу не подводила.
Их последующая игра в «игнорирование» существования друг друга была интересной, но недолгой. Холодный мальчик – невероятно упертый и почти не поддающийся на ее манипуляции. Она же необычайно терпелива и изобретательна, особенно когда чего-то так сильно хотела.
«На коленях еще ползать за мной будешь» – мстительно думала она, через пару недель скалясь в приторно-сахарной улыбке его однокласснику.
Умение обращать на себя взгляды даже особо отмороженных – один из ее бесспорных талантов. Для этого любые средства были хороши.
И холодный мальчик, конечно же, заметил ее провокацию. И был зол. Проиграл. Но и сахарная кривовато-насмешливая улыбка на губах Лапки, слишком натянутая – трещала по швам (можно услышать, если вслушаться и стоять близко), из-под кукольной маски девочки без моральных принципов щерилось безумное довольство от удачной провокации. (Заметил все-таки, и ему не все равно!) Нитки, которыми была пришита наигранно-невинная улыбочка (ах, как же неловко получилось: поцеловалась с твоим одноклассником у тебя на глазах), лопались, швы сочились сукровицей, полный триумфа смех уже в прерывистом вздохе заполнял ее легкие и чужие барабанные перепонки. В эмоциональном плане она больна намного больше холодного мальчика.
Тогда все и закрутилось в разноцветной карусели.
Ее холодному мальчику не нужны были подачки и урванные куски ее внимания.
– Все или ничего, – предложил он ей.
И она повелась. Конечно же, повелась!
«Все или ничего» – это так красиво и драматично, почти фатально, кто бы на это не повелся в свои шестнадцать? Явно не она.
Лапка пьяная, наивно верящая в любовь на всю жизнь, и внутри полностью разбитая, нуждающаяся в чем-то постоянном и неизменном в своей жизни. В чем-то теплом и хорошем.
«Хорошо» ей давно не было.
(Заметил все-таки, и ему не все равно!) Нитки, которыми была пришита наигранно-невинная улыбочка (ах, как же неловко получилось: поцеловалась с твоим одноклассником у тебя на глазах), лопались, швы сочились сукровицей, полный триумфа смех уже в прерывистом вздохе заполнял ее легкие и чужие барабанные перепонки. В эмоциональном плане она больна намного больше холодного мальчика.
Тогда все и закрутилось в разноцветной карусели.
Ее холодному мальчику не нужны были подачки и урванные куски ее внимания.
– Все или ничего, – предложил он ей.
И она повелась. Конечно же, повелась!
«Все или ничего» – это так красиво и драматично, почти фатально, кто бы на это не повелся в свои шестнадцать? Явно не она.
Лапка пьяная, наивно верящая в любовь на всю жизнь, и внутри полностью разбитая, нуждающаяся в чем-то постоянном и неизменном в своей жизни. В чем-то теплом и хорошем.
«Хорошо» ей давно не было. С начала седьмого класса включительно.
У Лапки к нему интерес клинический, намешанный на фундаменте собственного непростого прошлого и подросткового максимализма. Ей никогда и не нужно было много: пары секунд для разгона вполне достаточно, чтобы понять: чертов холодный мальчик тянет ее, как в омут.
Он безбожно сорвал с нее все предохранители (это не сложно), сложнее было сорвать их с него.
Лапка целовала своего холодного мальчика голодно и смазанно, будто пытаясь оставить под собственной кожей его запах. Откровенно тонула в нем, забывая напрочь о том, что из общего у них разве что нужда в теплоте извне и общий друг Федотов.
– Как же я тебя обожаю, – хрипло в чужие губы. – Хочу…
Ее холодный мальчик маячил абсентовым бликом перед глазами, обжигал кожу голодными поцелуями и руками расщеплял на молекулярном уровне все ее внутренности, разум плыл, затмеваясь похлеще, чем от высокоградусного алкоголя.
С начала седьмого класса включительно.
У Лапки к нему интерес клинический, намешанный на фундаменте собственного непростого прошлого и подросткового максимализма. Ей никогда и не нужно было много: пары секунд для разгона вполне достаточно, чтобы понять: чертов холодный мальчик тянет ее, как в омут.
Он безбожно сорвал с нее все предохранители (это не сложно), сложнее было сорвать их с него.
Лапка целовала своего холодного мальчика голодно и смазанно, будто пытаясь оставить под собственной кожей его запах. Откровенно тонула в нем, забывая напрочь о том, что из общего у них разве что нужда в теплоте извне и общий друг Федотов.
– Как же я тебя обожаю, – хрипло в чужие губы. – Хочу…
Ее холодный мальчик маячил абсентовым бликом перед глазами, обжигал кожу голодными поцелуями и руками расщеплял на молекулярном уровне все ее внутренности, разум плыл, затмеваясь похлеще, чем от высокоградусного алкоголя. Она повелась… Как же она на него повелась, но по-настоящему тепло так и не стало.
Ее красивый мальчик бесконечно холодный, рядом с ним никогда не тепло, да вот только Лапке на это плевать. Над головой у них палящий, слепящий круг разогретого солнца. Лето в городе – горячее и знойное – полностью восполнило их общую больную потребность в тепле и неспособность согреваться друг в друге. Это только в нереалистичной, оторванной от мира математике минус на минус дает плюс, в реальности же холод на холод – дает холод в кубе.
Мальчик совсем не улыбался, и Лапке плевать. Она улыбалась за них двоих, ей совсем это не сложно. Ей было гораздо важнее, что мальчик давал себя обнимать чересчур крепко, а еще позволял цепляться/впиваться ногтями в свою кожу слишком сильно, практически до хруста и ржавых царапин на изнанке его ребер и спины.
Он первый, кто ей это все позволял – она обожала его за одно лишь это.
Выражение острых чувств у всех тоже разное – у нее оно вот такое больное.
Она повелась… Как же она на него повелась, но по-настоящему тепло так и не стало.
Ее красивый мальчик бесконечно холодный, рядом с ним никогда не тепло, да вот только Лапке на это плевать. Над головой у них палящий, слепящий круг разогретого солнца. Лето в городе – горячее и знойное – полностью восполнило их общую больную потребность в тепле и неспособность согреваться друг в друге. Это только в нереалистичной, оторванной от мира математике минус на минус дает плюс, в реальности же холод на холод – дает холод в кубе.
Мальчик совсем не улыбался, и Лапке плевать. Она улыбалась за них двоих, ей совсем это не сложно. Ей было гораздо важнее, что мальчик давал себя обнимать чересчур крепко, а еще позволял цепляться/впиваться ногтями в свою кожу слишком сильно, практически до хруста и ржавых царапин на изнанке его ребер и спины.
Он первый, кто ей это все позволял – она обожала его за одно лишь это.
Выражение острых чувств у всех тоже разное – у нее оно вот такое больное. Но вот только к приятному шло и неприятное. Ведь еще мальчик жестокий и грубый; иногда Лапка рвано дышала и с трудом сдерживалась – настолько нестерпимо ей хотелось ударить мальчика по лицу, когда он начинал себя вести с ней, как полный конченный мудак – то есть почти всегда.
После Федотов беззлобно шутил на эту тему:
– Я тоже постоянно хочу ему врезать, Лапка. Он реально мудак. Ну, это же Саня… Он всегда такой. Просто забей.
А после все начало рушиться. Как всегда, впрочем.
Лапка знала, что счастливые концы едва ли бывают надолго. И у их поломанных отношений был срок годности в одно лето, а дальше в отсутствие жары и солнца нечем было их греть. И все же, вопреки всему, они продолжились дальше.
Ее мальчик же пообещал ей «все или ничего», и это должно было быть надолго. Это обещание Лапка запомнила навсегда, потому что оно определило ее жизнь, как бы потом ни отвращало быть зависимой. У ее холодного мальчика было много проблем и типичных, и редких, но он всегда со всем справлялся.
Но вот только к приятному шло и неприятное. Ведь еще мальчик жестокий и грубый; иногда Лапка рвано дышала и с трудом сдерживалась – настолько нестерпимо ей хотелось ударить мальчика по лицу, когда он начинал себя вести с ней, как полный конченный мудак – то есть почти всегда.
После Федотов беззлобно шутил на эту тему:
– Я тоже постоянно хочу ему врезать, Лапка. Он реально мудак. Ну, это же Саня… Он всегда такой. Просто забей.
А после все начало рушиться. Как всегда, впрочем.
Лапка знала, что счастливые концы едва ли бывают надолго. И у их поломанных отношений был срок годности в одно лето, а дальше в отсутствие жары и солнца нечем было их греть. И все же, вопреки всему, они продолжились дальше.
Ее мальчик же пообещал ей «все или ничего», и это должно было быть надолго. Это обещание Лапка запомнила навсегда, потому что оно определило ее жизнь, как бы потом ни отвращало быть зависимой. У ее холодного мальчика было много проблем и типичных, и редких, но он всегда со всем справлялся. Лапка инфантильно чувствовала себя рядом с ним, как за этой «мифической» каменой стеной, будто нет на свете такой стихии, которая сможет его согнуть.
Это ощущение «безопасности» было приятным. Непривычным в ее жизни.
Все начало скатываться именно осенью. Когда началась бытовая драматургия разъебанного дома, отсутствия человеческого отопления, холодной, никогда не прогретой, воды по трубам и ярких осенних красок за окном под аккомпанемент затяжных ливней. В самом начале этой жизни Лапка прогуливала учебу через день, грела холодные пальцы, забираясь своему красивому мальчику под рубашки, пила длинными вечерами паршивый глинтвейн и искренне верила в то, что любовь искупает множество грехов.
С ее холодным мальчиком у них на двоих обшарпанная холодная комната с выцветшими обоями (с выведенным синими чернилами тройным «LLL» над кроватью), раздолбанными деревянными рамами окон и черный теплый плед.
Лапка попеременно куталась то в него, то в собственный черный свитер с растянутыми рукавами, но все равно постоянно мерзла.
Лапка инфантильно чувствовала себя рядом с ним, как за этой «мифической» каменой стеной, будто нет на свете такой стихии, которая сможет его согнуть.
Это ощущение «безопасности» было приятным. Непривычным в ее жизни.
Все начало скатываться именно осенью. Когда началась бытовая драматургия разъебанного дома, отсутствия человеческого отопления, холодной, никогда не прогретой, воды по трубам и ярких осенних красок за окном под аккомпанемент затяжных ливней. В самом начале этой жизни Лапка прогуливала учебу через день, грела холодные пальцы, забираясь своему красивому мальчику под рубашки, пила длинными вечерами паршивый глинтвейн и искренне верила в то, что любовь искупает множество грехов.
С ее холодным мальчиком у них на двоих обшарпанная холодная комната с выцветшими обоями (с выведенным синими чернилами тройным «LLL» над кроватью), раздолбанными деревянными рамами окон и черный теплый плед.
Лапка попеременно куталась то в него, то в собственный черный свитер с растянутыми рукавами, но все равно постоянно мерзла. У нее перманентно ледяные пальцы то ли от того, что окно в их комнате всегда раскрыто нараспашку, то ли из-за откровенно хренового нечастого питания, состоящего на 70% из алкоголя и на остальные тридцать из того, что найдет на обшарпанной кухне (алкоголь там просто находился завидно чаще чего-то съедобного).
– В октябре должны дать отопление, а пока закрывай окна в комнате раз тебе так холодно, – бросал небрежно Федотов на ее капризно тянущееся:
– Почему так холодно, Олежа? Сделай с этим что-нибудь, ну.
Но теплее в октябре не стало и с отоплением. Пришел слякотный холод с порывистым ветром. За окном их комнаты рос пугающий и злой дуб – он протягивал кривые старые ветки, бился по ночам по деревянной раме под заунывные колыбельные ветра и пугал ее.
Лапка стала закрывать окна на ночь.
Теплее все равно не становилось.
Иногда ее красивый холодный мальчик говорил что-то красиво-сложное и не до конца понятное ей:
– На свете все двоично: либо удалось, либо нет.
У нее перманентно ледяные пальцы то ли от того, что окно в их комнате всегда раскрыто нараспашку, то ли из-за откровенно хренового нечастого питания, состоящего на 70% из алкоголя и на остальные тридцать из того, что найдет на обшарпанной кухне (алкоголь там просто находился завидно чаще чего-то съедобного).
– В октябре должны дать отопление, а пока закрывай окна в комнате раз тебе так холодно, – бросал небрежно Федотов на ее капризно тянущееся:
– Почему так холодно, Олежа? Сделай с этим что-нибудь, ну.
Но теплее в октябре не стало и с отоплением. Пришел слякотный холод с порывистым ветром. За окном их комнаты рос пугающий и злой дуб – он протягивал кривые старые ветки, бился по ночам по деревянной раме под заунывные колыбельные ветра и пугал ее.
Лапка стала закрывать окна на ночь.
Теплее все равно не становилось.
Иногда ее красивый холодный мальчик говорил что-то красиво-сложное и не до конца понятное ей:
– На свете все двоично: либо удалось, либо нет. Вселенная говорит на языке математики, понимаешь?
– Да.
Но на самом деле нет. Не понимала.
«Надеюсь, что мы двоичны» – инфантильно во вселенную (которую не могла даже абстрактно представить в голове) отпускала «молитву» она, скрещивая пальцы у него за спиной.
Вселенная – это всегда неприятно. Это что-то про космос (космос темный, бесконечный, не имеющий начала и конца), а значит и про звезды.
«Триста тринадцать, и чтоб вы все сдохли!».
И плевать даже, что солнце – тоже звезда.
А еще ее мальчик рассказывал ей, что такое ответственность (и между строк открыто сквозило: это то, что не ты, Лапка), она лишь хрипло смеялась и тянулась к его губам.
Каждый раз растягивая уголки рта в очередной сахарной улыбке, она насмешливо тянула:
– Все когда-нибудь умрем. Я умру – и ты умрешь.
– Ты такая оптимистка.
Лапка хрипло смеялась.
Вселенная говорит на языке математики, понимаешь?
– Да.
Но на самом деле нет. Не понимала.
«Надеюсь, что мы двоичны» – инфантильно во вселенную (которую не могла даже абстрактно представить в голове) отпускала «молитву» она, скрещивая пальцы у него за спиной.
Вселенная – это всегда неприятно. Это что-то про космос (космос темный, бесконечный, не имеющий начала и конца), а значит и про звезды.
«Триста тринадцать, и чтоб вы все сдохли!».
И плевать даже, что солнце – тоже звезда.
А еще ее мальчик рассказывал ей, что такое ответственность (и между строк открыто сквозило: это то, что не ты, Лапка), она лишь хрипло смеялась и тянулась к его губам.
Каждый раз растягивая уголки рта в очередной сахарной улыбке, она насмешливо тянула:
– Все когда-нибудь умрем. Я умру – и ты умрешь.
– Ты такая оптимистка.
Лапка хрипло смеялась. Ее до крайней степени веселила и своя и чужая смерть, потому что всегда казалась чем-то абстрактным и игрушечным. Ненастоящим. Она любила выискивать в газетах пометки о неизбежном конце света (по прогнозам майя в 2012 году – в текущем 1994 году это казалось через целую вечность) и вслух их зачитывать всем, кому не лень.
«Ну подумаешь умрем, что из-за этого драму разводить?».
Конец августа для нее всегда неприятный удар, лето кончилось, а смерть… Смерть, особенно всех людей на планете сразу без разбора, пока только веселила.
У нее с холодным мальчиком с каждым новым днем все отчетливее чувствовалось что-то вроде вынужденного соседства с натянутостью чувств, что забавно совпадало с постепенным понижением градусов за окном.
Растворять себя друг в друге и трахаться после каждой ссоры, не доводя ее до логического конца – намного легче, чем нудно разбирать, что и когда у них в отношениях пошло не так (правильный ответ: всё и с самого начала).
Ее до крайней степени веселила и своя и чужая смерть, потому что всегда казалась чем-то абстрактным и игрушечным. Ненастоящим. Она любила выискивать в газетах пометки о неизбежном конце света (по прогнозам майя в 2012 году – в текущем 1994 году это казалось через целую вечность) и вслух их зачитывать всем, кому не лень.
«Ну подумаешь умрем, что из-за этого драму разводить?».
Конец августа для нее всегда неприятный удар, лето кончилось, а смерть… Смерть, особенно всех людей на планете сразу без разбора, пока только веселила.
У нее с холодным мальчиком с каждым новым днем все отчетливее чувствовалось что-то вроде вынужденного соседства с натянутостью чувств, что забавно совпадало с постепенным понижением градусов за окном.
Растворять себя друг в друге и трахаться после каждой ссоры, не доводя ее до логического конца – намного легче, чем нудно разбирать, что и когда у них в отношениях пошло не так (правильный ответ: всё и с самого начала). У них из связующего: постепенно уходящий жар минувшего лета и все еще на привычке больная привязанность друг к другу.
И этого становилось критически мало до прокушенной губы и трех дней без сна в бесконечном ожидании своего холодного мальчика.
Лапке казалось день за днем, что еще чуть-чуть и она либо отключится (потому что организму плевать на всю ее драму, холод, самокопания и ноющую боль за ребрами от неоправдавших себя отношений), либо сойдет с ума от недосыпа. Лапка еще не решила, какой из вариантов ей нравится больше. Ее скандальное, склонное к истерикам и вниманию нутро было всеми руками за тот, что с сумасшествием, криками, битой посудой и пафосным «я всегда знала, какой ты мудак!» и «до чего ты меня довел!».
Было бы еще кому это все слушать.
Дверь в их комнату, наконец, скрипнула.
Пришел!
Она даже и головой не повела в его сторону, показательно обиженно сгорбившись на подоконнике.
У них из связующего: постепенно уходящий жар минувшего лета и все еще на привычке больная привязанность друг к другу.
И этого становилось критически мало до прокушенной губы и трех дней без сна в бесконечном ожидании своего холодного мальчика.
Лапке казалось день за днем, что еще чуть-чуть и она либо отключится (потому что организму плевать на всю ее драму, холод, самокопания и ноющую боль за ребрами от неоправдавших себя отношений), либо сойдет с ума от недосыпа. Лапка еще не решила, какой из вариантов ей нравится больше. Ее скандальное, склонное к истерикам и вниманию нутро было всеми руками за тот, что с сумасшествием, криками, битой посудой и пафосным «я всегда знала, какой ты мудак!» и «до чего ты меня довел!».
Было бы еще кому это все слушать.
Дверь в их комнату, наконец, скрипнула.
Пришел!
Она даже и головой не повела в его сторону, показательно обиженно сгорбившись на подоконнике. Воздух с его появлением отчего-то начал пахнуть холодным дождем, хотя его сегодня не было.
Его пальцы – неизменно горячие (обманчиво, потому что ни черта они не грели) – легли ей на предплечье, привлекая внимание:
– И что ты здесь сидишь? – с ноткой бесконечной усталости в голосе спросил он. – Холодно. Пойдем уже спать.
И она оттаивала мгновенно, замирая в его руках. Обнимала его до духоты и трещания собственных костей, шла, покорно шла за ним. Послушно и безропотно. Чтобы проснуться через пару часов от того, что он опять уходил.
Как у него получалось жить, учиться, работать с постоянным недосыпом – ей искренне непонятно. При точно таком же графике сна, она находила в себе силы лишь на существование.
У нее внутри мерзлое бездушное одиночество, и это хуже всего остального. Он всегда уходил. Его никогда нет. И рядом никого. После ее отчисления из гимназии не осталось даже прилипчивых назойливых взглядов – не с кем больше поиграть и, насытившись чужим «неравнодушием», пренебрежительно отмахнуться, словно от приставших бездомных щенков.
Воздух с его появлением отчего-то начал пахнуть холодным дождем, хотя его сегодня не было.
Его пальцы – неизменно горячие (обманчиво, потому что ни черта они не грели) – легли ей на предплечье, привлекая внимание:
– И что ты здесь сидишь? – с ноткой бесконечной усталости в голосе спросил он. – Холодно. Пойдем уже спать.
И она оттаивала мгновенно, замирая в его руках. Обнимала его до духоты и трещания собственных костей, шла, покорно шла за ним. Послушно и безропотно. Чтобы проснуться через пару часов от того, что он опять уходил.
Как у него получалось жить, учиться, работать с постоянным недосыпом – ей искренне непонятно. При точно таком же графике сна, она находила в себе силы лишь на существование.
У нее внутри мерзлое бездушное одиночество, и это хуже всего остального. Он всегда уходил. Его никогда нет. И рядом никого. После ее отчисления из гимназии не осталось даже прилипчивых назойливых взглядов – не с кем больше поиграть и, насытившись чужим «неравнодушием», пренебрежительно отмахнуться, словно от приставших бездомных щенков. – Ты можешь хотя бы сегодня побыть со мной? – у Лапки дрожащий голос и воспаленные глаза, у Лапки очередная бессонная ночь в ожидании его; она сама чувствует себя тем самым пристающим щенком, той собакой на коротком поводке, которой день за днем приказывают «ждать». – Сдохнешь, если один день не пойдешь на свою ебанную учебу?
Это все унизительно, жалко и нестерпимо. Это выламывало ее и пригибало к полу, вдребезги сносило старые установки, приводя к настоящему отчаянию.
У мальчика привычная ледяная радужка цвета дьявольской зелени; и ему плевать, плевать, плевать.
– А ты можешь хоть на один день прекратить свой скулеж? Найди себе уже какое-то занятие. Перебей опять всю посуду в доме, как ты любишь, и прекрати ебать мне мозг.
Да вот только она давно перебила все стеклянное в доме. И осталось нечего больше разбивать, кроме себя.
– Ну и катись! – шипела она. – Какой же ты ублюдок!
Их взгляды скрестились, и Лапку заполнило острым тошнотворным чувством собственной ненужности.
– Ты можешь хотя бы сегодня побыть со мной? – у Лапки дрожащий голос и воспаленные глаза, у Лапки очередная бессонная ночь в ожидании его; она сама чувствует себя тем самым пристающим щенком, той собакой на коротком поводке, которой день за днем приказывают «ждать». – Сдохнешь, если один день не пойдешь на свою ебанную учебу?
Это все унизительно, жалко и нестерпимо. Это выламывало ее и пригибало к полу, вдребезги сносило старые установки, приводя к настоящему отчаянию.
У мальчика привычная ледяная радужка цвета дьявольской зелени; и ему плевать, плевать, плевать.
– А ты можешь хоть на один день прекратить свой скулеж? Найди себе уже какое-то занятие. Перебей опять всю посуду в доме, как ты любишь, и прекрати ебать мне мозг.
Да вот только она давно перебила все стеклянное в доме. И осталось нечего больше разбивать, кроме себя.
– Ну и катись! – шипела она. – Какой же ты ублюдок!
Их взгляды скрестились, и Лапку заполнило острым тошнотворным чувством собственной ненужности. Когда ноль шансов привычно забраться под чужие ребра – это обычно сразу очевидно читаемо, если не быть совсем уж инфантильной и на своей особой волне. И для Лапки такое случается далеко не впервые, но впервые так горько, фатально и бессильно.
Ее холодному мальчику и на это откровенно плевать. На нее. На них. На все.
Он бросал ее одну разбитую, продрогшую в холодной непрогретой квартире, с несобранными глянцевыми осколками былого гонора, гордости и уставшим, давно совсем севшим «останься со мной, не оставляй меня здесь одну». Ее красивый холодный мальчик никогда не оставался с ней, никогда ее не слышал, даже когда она срывала голос в попытках докричаться. У ее мальчика лед вместо того горячего четырехкамерного, что должно биться в грудной клетке.
Он не умел жалеть. Он всегда уходил.
Она смотрела ему вслед несчастно с затушенной до искр яростью – словно весь ее мир разваливался на части, и именно он в этом виноват. Ненавидеть же всегда проще – не так энергозатратно, потому что не нужно стараться видеть лучшее.
Когда ноль шансов привычно забраться под чужие ребра – это обычно сразу очевидно читаемо, если не быть совсем уж инфантильной и на своей особой волне. И для Лапки такое случается далеко не впервые, но впервые так горько, фатально и бессильно.
Ее холодному мальчику и на это откровенно плевать. На нее. На них. На все.
Он бросал ее одну разбитую, продрогшую в холодной непрогретой квартире, с несобранными глянцевыми осколками былого гонора, гордости и уставшим, давно совсем севшим «останься со мной, не оставляй меня здесь одну». Ее красивый холодный мальчик никогда не оставался с ней, никогда ее не слышал, даже когда она срывала голос в попытках докричаться. У ее мальчика лед вместо того горячего четырехкамерного, что должно биться в грудной клетке.
Он не умел жалеть. Он всегда уходил.
Она смотрела ему вслед несчастно с затушенной до искр яростью – словно весь ее мир разваливался на части, и именно он в этом виноват. Ненавидеть же всегда проще – не так энергозатратно, потому что не нужно стараться видеть лучшее. Лапина каждый раз ждала его. Ждала. Ждала. Ждала. Лапка так и не научилась не нуждаться в нем, Лапка ему себя полностью отдала, как и договаривались:
«Все или ничего».
Да вот только из них двоих именно она почему-то и осталась с этим холодным полным «ничем».
Всё скатилось к чертям; у нее горькое разочарование трансформировалось в константу обновленной жизни.
Она устала мерзнуть. Она устала быть одна. Ей не хватало тепла. Ей не хватало хоть чего-нибудь, кроме долбанного холода.
Очередной вечер плавно перетек в ночь – холодную и пустую. Ее мальчика снова не будет до утра. А она послушная преданная псина, которой дали команду «ждать».
Ледяная дрожь раз за разом проходила по ее телу под мягкой тканью ее свитера. Лапина нервно повела плечами, потерла ладони друг о дружку в отчаянной попытке согреться хотя бы внешне, раз уж внутренне все намертво промерзло.
«Какой же ты муда-ак!»
«Не хочу так жить!»
Ее отчаянно трясло в очередной истерике.
Лапина каждый раз ждала его. Ждала. Ждала. Ждала. Лапка так и не научилась не нуждаться в нем, Лапка ему себя полностью отдала, как и договаривались:
«Все или ничего».
Да вот только из них двоих именно она почему-то и осталась с этим холодным полным «ничем».
Всё скатилось к чертям; у нее горькое разочарование трансформировалось в константу обновленной жизни.
Она устала мерзнуть. Она устала быть одна. Ей не хватало тепла. Ей не хватало хоть чего-нибудь, кроме долбанного холода.
Очередной вечер плавно перетек в ночь – холодную и пустую. Ее мальчика снова не будет до утра. А она послушная преданная псина, которой дали команду «ждать».
Ледяная дрожь раз за разом проходила по ее телу под мягкой тканью ее свитера. Лапина нервно повела плечами, потерла ладони друг о дружку в отчаянной попытке согреться хотя бы внешне, раз уж внутренне все намертво промерзло.
«Какой же ты муда-ак!»
«Не хочу так жить!»
Ее отчаянно трясло в очередной истерике. Она стягивала плед с кровати, и, укутавшись в него, ложилась прямо на пол, не мигая, смотрела в темноту бесцветно-серого потолка, игнорируя стук по стеклу окна веток дуба, и представляла на уровне визуальных галлюцинаций: оранжевые летние закаты, слепящее глаза солнце, нагретый асфальт, тепло, голодные красные всполохи костра.
Ей так мало было надо. Она лишь хотела тепла и не быть одной, а получила холодного красивого мальчика, нервные срывы, промерзшее нутро и одиночество. А приятным «дополнением» еще, кажется, начинающееся безумие (будто и без этого хуйни в жизни не хватало), потому что раз за разом возвращалась в своих воспоминаниях в минувший август.
В самое лучшее пережитое ей время.
Когда осень, этот чертов переезд в эту убогую квартиру и очередной новый учебный год (где ее еще не исключили) еще не скоро, даже и близко не на горизонте, она об этом еще и не думала, потому что пока…
Пока в нагретой раскаленным летним солнцем электричке до Москвы было до одури жарко и не хватало кислорода.
Она стягивала плед с кровати, и, укутавшись в него, ложилась прямо на пол, не мигая, смотрела в темноту бесцветно-серого потолка, игнорируя стук по стеклу окна веток дуба, и представляла на уровне визуальных галлюцинаций: оранжевые летние закаты, слепящее глаза солнце, нагретый асфальт, тепло, голодные красные всполохи костра.
Ей так мало было надо. Она лишь хотела тепла и не быть одной, а получила холодного красивого мальчика, нервные срывы, промерзшее нутро и одиночество. А приятным «дополнением» еще, кажется, начинающееся безумие (будто и без этого хуйни в жизни не хватало), потому что раз за разом возвращалась в своих воспоминаниях в минувший август.
В самое лучшее пережитое ей время.
Когда осень, этот чертов переезд в эту убогую квартиру и очередной новый учебный год (где ее еще не исключили) еще не скоро, даже и близко не на горизонте, она об этом еще и не думала, потому что пока…
Пока в нагретой раскаленным летним солнцем электричке до Москвы было до одури жарко и не хватало кислорода. Пока они ехали в идеальное место. Пока все ее тело приятно ломило после непрерывных часов пьяных танцев на обжигающем голые ступни нагретом асфальте. Пока она наваливалась всем корпусом на своего красивого холодного мальчика, не обращая внимания на острые осуждающие взгляды прочих пассажиров. Жалась к нему всем телом, переплетала их пальцы, водила носом по его горячей шее, жадно вбирая в легкие его запах: от него пахло костром, лесом, совсем выветрившимися нотками грубого парфюма и летом.
И она не думала о том, что будет дальше, что будет потом…
Потому что сейчас в реальности Лапина лежа на ветхом полу в холодной непрогретой квартире, закрыв ладонями лицо, в своих воспоминаниях — крепко жмурила глаза под палящим солнцем и горячо дышала в шею своего красивого мальчика (пока еще не полного мудака), пока ей было хорошо и светло, будто и это лето, и солнце над их головами вечно и никогда не кончится.
Пока они ехали в идеальное место. Пока все ее тело приятно ломило после непрерывных часов пьяных танцев на обжигающем голые ступни нагретом асфальте. Пока она наваливалась всем корпусом на своего красивого холодного мальчика, не обращая внимания на острые осуждающие взгляды прочих пассажиров. Жалась к нему всем телом, переплетала их пальцы, водила носом по его горячей шее, жадно вбирая в легкие его запах: от него пахло костром, лесом, совсем выветрившимися нотками грубого парфюма и летом.
И она не думала о том, что будет дальше, что будет потом…
Потому что сейчас в реальности Лапина лежа на ветхом полу в холодной непрогретой квартире, закрыв ладонями лицо, в своих воспоминаниях — крепко жмурила глаза под палящим солнцем и горячо дышала в шею своего красивого мальчика (пока еще не полного мудака), пока ей было хорошо и светло, будто и это лето, и солнце над их головами вечно и никогда не кончится.
Вычитание отрицательного числа, правило, примеры, как вычесть два отрицательных числа, как из отрицательного числа вычесть положительное
Данная статья посвящена разбору такой темы, как выполнение вычитания отрицательных чисел. Материал представляет собой полезную информацию о правиле вычитания отрицательных чисел и других определениях. Для закрепления сути параграфа мы детально разберем примеры типичных упражнений и задач.
Материал представляет собой полезную информацию о правиле вычитания отрицательных чисел и других определениях. Для закрепления сути параграфа мы детально разберем примеры типичных упражнений и задач.
Правило вычитания отрицательных чисел
Для того, чтобы разобраться в данной теме, следует узнать основные определения и понятия.
Определение 1Правило вычитания отрицательных чисел формулируется так: чтобы из числа a вычесть число b со знаком минус, необходимо к уменьшаемому a прибавить число −b, которое является противоположным вычитаемому b.
Если представить данное правило вычитания отрицательного числа b из произвольного числа a в буквенном виде, то оно будет выглядеть так: a−b=a+(−b).
Для того, чтобы использовать данное правило, необходимо доказать его справедливость.
Возьмем числа a и b. Чтобы вычесть из числа a число b, необходимо найти такое число с, которое в сумме с числом b будет равняться числу a. Другими словами, если найдено такое число c, что c+b=a, то разность a−b равна c.
Другими словами, если найдено такое число c, что c+b=a, то разность a−b равна c.
Для того, чтобы доказать правило вычитания, необходимо показать, что сложение суммы a+(−b) с числом b – это есть число a. Необходимо вспомнить о свойствах действий с действительными числами. Так как в этом случае работает сочетательное свойство сложения, то равенство (a+(−b)) +b=a+((−b) +b) будет верным.
Так, как сумма чисел с противоположными знаками равняется нулю, то a+((−b) +b) =a+0, а сумма a+0= а (если к числу прибавить нуль, то оно не изменится). Равенство a−b=a+(−b)считается доказанным, значит, доказана и справедливость приведенного правила вычитания чисел со знаком минус.
Мы рассмотрели, как работает данное правило для действительных чисел a и b. Но оно также считается справедливым для любых рациональных и целых чисел a и b. Действия с рациональными и целыми числами также обладают свойствами, использованными при доказательстве. Следует добавить, что с помощью разобранного правила можно выполнять действия числа со знаком минус как из положительного числа, так и из отрицательного или нуля.
Следует добавить, что с помощью разобранного правила можно выполнять действия числа со знаком минус как из положительного числа, так и из отрицательного или нуля.
Рассмотрим разобранное правило на типичных примерах.
Примеры использования правила вычитания
Рассмотрим примеры с вычитанием чисел. Для начала рассмотрим простой пример, который поможет легко разобраться со всеми тонкостями процесса.
Пример 1Необходимо отнять от числа −13 число −7.
Возьмем число, противоположное вычитаемому −7. Это число 7. Тогда по правилу вычитания отрицательных чисел имеем (−13) −(−7) =(−13) +7. Выполняем сложение. Теперь получаем: (−13) +7=−(13−7) =−6.
Вот все решение: (−13) −(−7) =(−13) +7=−(13−7) =−6. (−13)−(−7)=−6. Вычитание дробных отрицательных чисел также можно выполнять. Необходимо перейти к обыкновенным дробям, смешанным числам или десятичным дробям. Выбор числа зависит от того, с каким вариантом вам удобнее работать.
Пример 2Необходимо выполнить вычитание из числа 3,4 числа -2323.
Применяем описанное выше правило вычитания, получаем 3,4—2323=3,4+2323. Заменяем дробь на десятичное число: 3,4=3410=175=325 (как переводить дроби, можно посмотреть в материале по теме), получаем 3,4+2323=325+2323. Выполняем сложение. На этом вычитание отрицательного числа -2323 из числа 3,4 завершено.
Приведем краткую запись решения: 3,4—2323=27115.
Пример 3Необходимо выполнить вычитание числа −0,(326) от нуля.
По правилу вычитания, которое мы изучили выше, 0−(−0,(326))=0+0,(326)=0,(326).
Последний переход верен, так как здесь работает свойство сложения числа с нулем: 0−(−0,(326))=0,(326).
Из рассмотренных примеров видно, что при вычитании отрицательного числа может получиться как положительное, так и отрицательное число. Вычитание отрицательного числа может в результате дать и число 0, это происходит, когда уменьшаемое равно вычитаемому.
Пример 4Необходимо вычислить разность отрицательных чисел -5—5.
По правилу вычитания мы получаем -5—5=-5+5.
Мы пришли к сумме противоположных чисел, которая всегда равна нулю: -5—5=-5+5=0
Итак,-5—5=0.
В некоторых случаях результат вычитания необходимо записать в виде числового выражения. Это справедливо в тех случаях, когда уменьшаемое или вычитаемое является иррациональным числом. К примеру, вычитание из отрицательного числа −2 отрицательного числа –π проводится так: (−2)−(−π)=(−2)+π=π−2. Значение полученного выражения может быть вычислено максимально точно только в том случае, если это необходимо. Для подробной информации можно изучить другие разделы, связанные с данной темой.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
какие так называют, что такое в математике, чем отличаются
Содержание:
- Какие числа называются положительными и отрицательными
- Сравнение положительных и отрицательных чисел
- Правила действий с отрицательными и положительными числами
- Примеры задач с решением
Содержание
- Какие числа называются положительными и отрицательными
- Сравнение положительных и отрицательных чисел
- Правила действий с отрицательными и положительными числами
- Примеры задач с решением
Какие числа называются положительными и отрицательными
Отрицательными числами в алгебре являются числа со знаком минус (-). Например, к таким числам относят -1, -2, -3. Прочитать запись можно, как минус один, минус два, минус три.
Например, к таким числам относят -1, -2, -3. Прочитать запись можно, как минус один, минус два, минус три.
Отрицательное число — это какое-либо число меньше нуля, перед которым ставится знак минус.
Положительные числа — числа, состоящее в множестве положительных чисел, являются числами без знака минус в обозначении и не являются нулем.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В системе отрицательных чисел так же, как и среди положительных есть дроби: обыкновенные и десятичные, целые числа, корни и так далее. Почти все подвиды чисел, которые встречаются среди положительных чисел, есть и среди отрицательных. Стоит отметить, что, согласно понятию, число 0 не является ни положительным, ни отрицательным числом.
Положительные числа — это числа, соответствующие точкам в той части координатной прямой, которая лежит с правой стороны относительно начала отсчета.
Отрицательные числа — являются числами, соотносящимися с точками в части координатной прямой, которая расположена с левой стороны относительно начала отсчета (нуля).
Наглядным примером использования отрицательных чисел является термометр. Прибор демонстрирует температуру тела, воздуха, почвы, воды. Зимой при холодной погоде температура воздуха снижается до отрицательных значений. К примеру, -10 градусов мороза:
Обычные числа, в том числе, 1, 2, 3 называют положительными. Данные числа имеют знак (+). Обычно, его не записывают.
Координатная прямая — является прямой линией, на которой размещены все числа, включая отрицательные и положительные.
Координатная прямая имеет следующий вид:
В данном случае отмечены только числа от −5 до 5. В действительности координатная прямая бесконечна. На изображении можно увидеть только фрагмент этой прямой. Для того чтобы отметить на координатной прямой числа, использую точки. Началом отсчета является нуль. С левой стороны от нуля отмечают отрицательные числа, а с правой — положительные.
С левой стороны от нуля отмечают отрицательные числа, а с правой — положительные.
Координатная прямая продолжается бесконечно по обе стороны. Бесконечность в математике обозначается символом \(\infty\). Отрицательное направление будет обозначаться символом −\(\infty\), а положительное — символом +\(\infty\). Таким образом, координатная прямая содержит все числа от минус бесконечности до плюс бесконечности:
\((−\infty; +\infty)\)
Каждая точка на координатной прямой обладает определенным именем и координатой. Именем является какая-либо латинская буква. Координата представляет собой число, указывающее на положение точки на прямой. Таким образом, координатой является то число, которое требуется отметить на координатной прямой. К примеру, точка А(2) читается, как «точка А с координатой 2» и обозначается на координатной прямой таким образом:
При рассмотрении изображения координатной прямой можно заметить, что отрицательные числа лежат левее относительно начала отсчета, а положительные числа — правее. С каждым шагом в левую сторону число будет уменьшаться в меньшую сторону. При каждом шаге в правом направлении число будет увеличиваться.
С каждым шагом в левую сторону число будет уменьшаться в меньшую сторону. При каждом шаге в правом направлении число будет увеличиваться.
Сравнение положительных и отрицательных чисел
Положительные числа, то есть те, которые больше 0, можно рассматривать в качестве прибыли, прибавки, увеличения количества чего-либо. Отрицательные числа можно представить, как недостаток, убыток, расход, долг. Предположим, что имеется 55 неких предметов, например, яблок. Цифра 55 является положительной. В том случае, когда требуется отдать кому-то 5 яблок, данной действие можно обозначить, как -5. На градуснике рост температуры на 4,5 значений можно описать как +4,5, а снижение, в свою очередь, как −4,5. В приборах, которые используют для измерений, часто применяют положительные и отрицательные числа. Это объясняется удобством отображения изменения величин.
Любое отрицательное число меньше, чем любое положительное число. К примеру, если сравнить -5 и 3, то минус пять меньше трех. Это объясняется тем, что -5 представляет собой отрицательное число, а 3 является положительным числом. С помощью координатной прямой достаточно просто определить положение данных чисел.
Это объясняется тем, что -5 представляет собой отрицательное число, а 3 является положительным числом. С помощью координатной прямой достаточно просто определить положение данных чисел.
На прямой -5 расположено левее относительно числа 3. Согласно правилу, любое отрицательное число меньше любого положительного числа. Отсюда следует, что:
−5 < 3
Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. К примеру, при сравнении чисел -4 и -1 можно сделать вывод, что минус четыре меньше, чем минус единица. Причина заключается в том, что на координатной прямой -4 располагается левее, чем -1.
Видно, что -4 лежит левее, а -1 правее. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. Таким образом:
-4 < -1
Ноль больше, чем любое отрицательное число. К примеру, при сравнении 0 и -3 можно сделать вывод, что ноль больше, чем минус три. Это объясняется тем, что на координатной прямой 0 располагается правее, чем -3.
При рассмотрении координатной прямой можно заметить, что 0 лежит правее, а -3 левее. Согласно правилу, нуль больше любого отрицательного числа. Таким образом:
0 > -3
Нуль меньше любого положительного числа. К примеру, можно сравнить 0 и 4. Ноль меньше, чем 4.
На координатной прямой 0 располагается левее, а 4 правее. Исходя из правила, ноль меньше, чем какое-либо положительное число. Таким образом:
0 < 4
Правила действий с отрицательными и положительными числами
Существуют следующие правила знаков при умножении и делении отрицательных чисел:
- Умножение или деление отрицательного числа на отрицательное приводит в результате к получению положительного числа.
- При умножении или делении положительного числа на отрицательное число результатом является отрицательное число.
- Если требуется умножить или разделить отрицательное число на положительное, то получится отрицательное число.

В процессе сложения отрицательных чисел следует руководствоваться аналогичными правилами знаков в несколько ином виде. По общей формулировке правило знаков звучит так: «Плюс на минус дает минус, минус на минус дает плюс и плюс на плюс дает плюс». В таком случае, при сложении отрицательного числа с другим, получится:
-а+(-в)=-а-в — то есть из отрицательного числа вычитается положительное.
Аналогичное правило применимо для примеров с вычитанием отрицательных чисел:
-а-(-в)=-а+в — к отрицательному числу в итоге прибавляется положительное.
В том случае, когда требуется сложить два отрицательных числа, следует сложить два числа и поставить знак минус. К примеру:
(−2)+(−3)=−5(−2)+(−3)=−5
Если первое число положительное, а второе отрицательное, требуется определить, какое число по модулю больше. Далее нужно отнять от большего меньшее число и поставим знак большего числа. Например:
(−8)+4=4−8=−4
9+(−4)=9−4=5
Каждое число, за исключением 0, соответствует противоположному элементу. В сумме с ним число дает 0. Например:
В сумме с ним число дает 0. Например:
−9+9=0
7,1+(−7,1)=0
При вычитании двух отрицательных чисел следует руководствоваться правилом: минус на минус дает плюс. Таким образом, когда стоят рядом два минуса, в сумме получается плюс. К примеру:
(−7)−(−6)=(−7)+6=(−1)
В том случае, когда первое число положительное, а второе число является отрицательным, вычитание выполняют по тому же принципу, что и сложение. Нужно определить, какое число по модулю больше. Далее следует отнять от большего меньшее число и поставить знак большего числа.
7−9=−2
так как 9>7
Одним из ключевых свойств является то, что минус на минус дает плюс:
7−(−9)=7+9=16
Примеры задач с решением
Задача 1
Задача
Нужно решить: (+3) + (+4)
Решение:
(+3) + (+4) = +7
Ответ: 7
Задача 2
Задача
Требуется решить: (-4) + (-3)
Решение:
(-4) + (-3) = -7
Ответ: -7
Задача 3
Задача
Необходимо выполнить сложение: (+15) + (-7)
Решение:
(+15) + (-7) = 15 — 7 = 8
Ответ: 8
Задача 4
Задача
Нужно выполнить вычитание: (+7) — (+4)
Решение:
(+7) — (+4) = +3
Ответ: 3
Задача 5
Задача
Требуется найти разность чисел: -17 — (-14)
Решение:
-17 — (-14) = -17 + 14 = -3
Ответ: -3
Задача 6
Задача
Необходимо решить пример: (+5) ⋅ (-8)
Решение:
(+5) ⋅ (-8) = -40
Ответ: -40
Задача 7
Задача
Нужно найти произведение двух чисел: -9 ⋅ (-9)
Решение:
-9 ⋅ (-9) = 81
Ответ: 81
Задача 8
Задача
Требуется решить пример: -6 ⋅ 5
Решение:
-6 ⋅ 5 = -30
Ответ: -30
Задача 9
Задача
Нужно выполнить деление двух чисел: 40 : (-8)
Решение:
40 : (-8) = -5
Ответ: -5
Задача 10
Задача
Требуется найти разность: (-6) — (+6) — (-8)
Решение:
(-6) — (+6) — (-8) = -12 — (-8) = -12 + 8 = -4
Ответ: -4
Задача 11
Задача
Необходимо решить пример: (-5) ⋅ (-4) + (+3) ⋅ (-2)
Решение:
(-5) ⋅ (-4) + (+3) ⋅ (-2) = 20 + (-6) = 14
Ответ: 14
Задача 12
Задача
Нужно найти ответ: (-15) ⋅ [-3 + (-15)] : (+5)
Решение:
(-15) ⋅ [-3 + (-15)] : (+5) = -15 ⋅ (-18) : 5 = (-15 : 5) ⋅ (-18) = -3 ⋅ (-18) = 54
Ответ: 54
Задача 13
Задача
Требуется выполнить деление: -18 : [-20 — (30 — 56)]
Решение:
-18 : [-20 — (30 — 56)] = -18 : [-20 — (-26)] = -18 : (-20 + 26) = -18 : 6 = -3
Ответ: -3
Задача 14
Задача
Нужно найти значение выражения:
(−1)−(−512)⋅(+411)=(−1)−(−521)⋅(+114)
Решение:
(−1)−(−512)⋅411=−1−(−112)⋅411=(−1)−(−521)⋅114=−1−(−211)⋅114=−1−(−2)=−1+2=1−1−(−2)=−1+2=1
Ответ: 1
Задача 15
Задача
Необходимо вычислить:
Вычислить |a| — |b| + |c|
при a = -8, b = -5, c = 1
Решение:
|-8| — |-5| + |1| = 8 — 5 + 1 = 4
Ответ: 4
Задача 16
Задача
Требуется решить пример:
[2,4−(0,3−0,21)⋅2+0,44:(−2)]:45=[2,4−(0,3−0,21)⋅2+0,44:(−2)]:54
Решение:
[2,4−(0,3−0,21)⋅2+0,44:(−2)]:45=[2,4−(0,3−0,21)⋅2+0,44:(−2)]:54=
[2,4−0,09⋅2+(−0,22)]:45=[2,4−0,09⋅2+(−0,22)]:54= (2,4−0,18−0,22):25=
2:45=52=2,5(2,4−0,18−0,22):52=2:54=25=2,5
Ответ: 2,5
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Отрицательная математика | Издательство Принстонского университета
Отрицательная математика
Мягкая обложка ISBN: 9780691133911 22,95 доллара США / 17,99 фунтов стерлингов электронная книга ISBN: 9780691187822
электронные книги
Многие из наших электронных книг можно приобрести в этих интернет-магазины:
- Амазонка разжечь
- Гугл игры
- Ракутен Кобо
- Барнс и Благородный Уголок
- Apple Книги
Многие из наших электронных книг доступны в электронной библиотеке ресурсов, включая эти платформы:
- Книги в JSTOR
- Электронные книги EBSCO
- Эбрари
- Моя библиотека
- Библиотека электронных книг
Shipping to:
Choose CountryUnited StatesCanadaUnited KingdomAfghanistanAland IslandsAlbaniaAlgeriaAmerican SamoaAndorraAngolaAnguillaAntarcticaAntigua And BarbudaArgentinaArmeniaArubaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelarusBelgiumBelizeBeninBermudaBhutanBoliviaBonaire, Sint Eustatius and SabaBosnia And HerzegovinaBotswanaBouvet IslandBrazilBritish Indian Ocean TerritoryBrunei DarussalamBulgariaBurkina FasoBurundiCabo VerdeCambodiaCameroonCayman IslandsCentral African RepublicChadChileChinaChristmas IslandCocos (Keeling) IslandsColombiaComorosCongoCongo, Democratic RepublicCook IslandsCosta RicaCote D’IvoireCroatiaCubaCuraçao CyprusCzech RepublicDenmarkDjiboutiDominicaDominican RepublicEcuadorEgyptEl SalvadorEquatorial GuineaEritreaEstoniaEthiopiaFalkland Мальвинские островаФарерские островаФиджиФинляндияФранцияФранцузская ГвианаФранцузская ПолинезияФранцузские Южные ТерриторииГабонГамбияГрузияГерманияГанаГибралтарГрецияГренландияГренадаГваделупаГуамГуата malaGuernseyGuineaGuinea-BissauGuyanaHaitiHeard Island & Mcdonald IslandsHoly See (Vatican City State)HondurasHong KongHungaryIcelandIndiaIndonesiaIran, Islamic Republic OfIraqIrelandIsle Of ManIsraelItalyJamaicaJapanJerseyJordanKazakhstanKenyaKiribatiKoreaKorea People’ Republic OfKuwaitKyrgyzstanLao People’s Democratic RepublicLatviaLebanonLesothoLiberiaLibyan Arab JamahiriyaLiechtenstein LithuaniaLuxembourgMacaoMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMexicoMicronesia, Federated States OfMoldovaMonacoMongoliaMontenegroMontserratMoroccoMozambiqueMyanmarNamibiaNauruNepalNetherlandsNew CaledoniaNew ZealandNicaraguaNigerNigeriaNiueNorfolk IslandNorthern Mariana IslandsNorwayOmanPakistanPalauPalestinian Territory, OccupiedPanamaPapua New GuineaParaguayPeruPhilippinesPitcairnPolandPortugalPuerto RicoQatarReunionRomaniaRussian FederationRwandaSaint BarthelemySaint HelenaSaint Китс и НевисСент-ЛюсияСент-МартинСент-Пьер и MiquelonSaint Vincent And GrenadinesSamoaSan MarinoSao Tome And PrincipeSaudi ArabiaSenegalSerbiaSeychellesSierra LeoneSingaporeSint Maarten (Dutch part) SlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Georgia And Sandwich Isl. South SudanSpainSri LankaSudanSurinameSvalbard And Jan MayenSwazilandSwedenSwitzerlandSyrian Arab RepublicTaiwanTajikistanTanzaniaThailandTimor-LesteTogoTokelauTongaTrinidad And TobagoTunisiaTurkeyTurkmenistanTurks And Caicos IslandsTuvaluUgandaUkraineUnited Arab EmiratesUnited States Outlying IslandsUruguayUzbekistanVanuatuVenezuelaViet NamVirgin Islands, BritishVirgin Islands, U.S. Уоллис и ФутунаЗападная СахараЙеменЗамбияЗимбабве
South SudanSpainSri LankaSudanSurinameSvalbard And Jan MayenSwazilandSwedenSwitzerlandSyrian Arab RepublicTaiwanTajikistanTanzaniaThailandTimor-LesteTogoTokelauTongaTrinidad And TobagoTunisiaTurkeyTurkmenistanTurks And Caicos IslandsTuvaluUgandaUkraineUnited Arab EmiratesUnited States Outlying IslandsUruguayUzbekistanVanuatuVenezuelaViet NamVirgin Islands, BritishVirgin Islands, U.S. Уоллис и ФутунаЗападная СахараЙеменЗамбияЗимбабве
Поддержите свой местный независимый книжный магазин.
- США
- Канада
- Великобритания
- Европа
Математика
- Альберто А. Мартинес
Мягкая обложка
электронная книга
Купить это- Скачать обложку
Ученик в классе спрашивает учителя математики: «Разве минус, умноженный на минус, не должен давать минус?» Учителя вскоре убеждают большинство учеников, что это не так. И все же невинный вопрос несет в себе зародыш математического творчества. Что произойдет, если мы будем поощрять эту мысль, какой бы странной и необоснованной она ни казалась?
И все же невинный вопрос несет в себе зародыш математического творчества. Что произойдет, если мы будем поощрять эту мысль, какой бы странной и необоснованной она ни казалась?
Немногие книги по математике поощряют такое творческое мышление. Еще меньше из них увлекательно написано и интересно читать. Эта книга преуспевает в обоих случаях. Альберто Мартинес показывает нам, как многие из математических концепций, которые мы считаем само собой разумеющимися, когда-то считались надуманными, воображаемыми, абсурдными или просто ошибочными. Даже сегодня, пишет он, не все части математики соответствуют вещам, отношениям или операциям, которые мы можем реально наблюдать или выполнять в повседневной жизни.
Negative Math размышляет над этими проблемами, исследуя противоречия в истории чисел, особенно так называемые отрицательные и «невозможные» числа. Он использует историю, загадки и оживленные дебаты, чтобы продемонстрировать, как все еще возможно разрабатывать новые искусственные системы математических правил.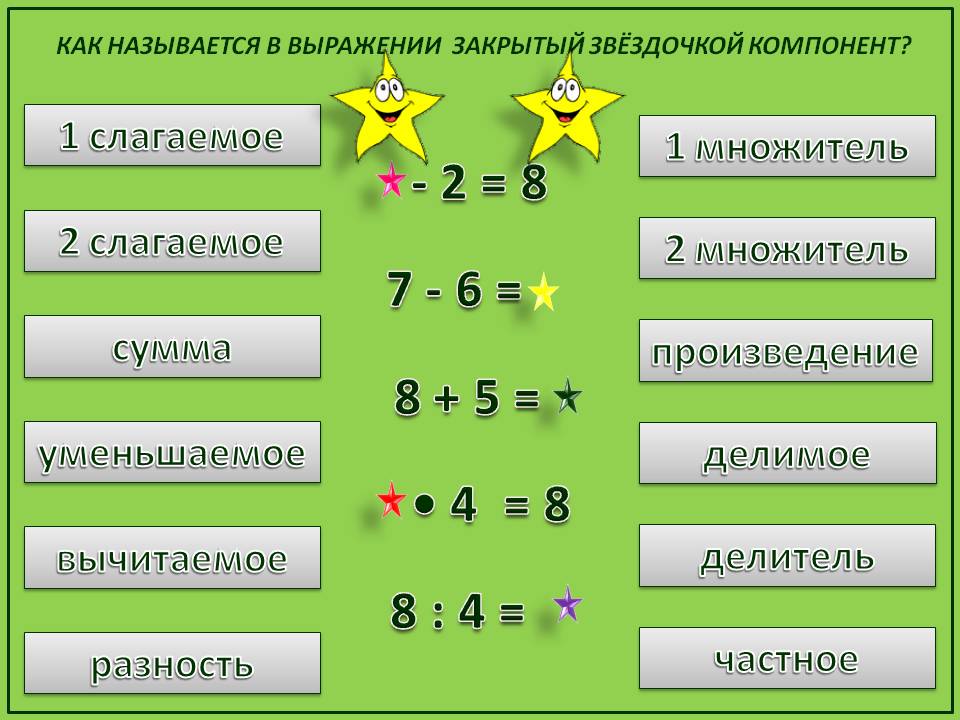 На самом деле, утверждается в книге, отклонения от традиционных правил могут даже стать основой для новых приложений. Например, используя алгебру, в которой минус, умноженный на минус, дает минус, математики могут описывать кривые или траектории, которые не представлены традиционной координатной геометрией.
На самом деле, утверждается в книге, отклонения от традиционных правил могут даже стать основой для новых приложений. Например, используя алгебру, в которой минус, умноженный на минус, дает минус, математики могут описывать кривые или траектории, которые не представлены традиционной координатной геометрией.
Ясно и доступно, Negative Math ожидает от своих читателей лишь мимолетного знакомства с основами алгебры средней школы. Это окажется приятным чтением не только для тех, кто любит популярную математику, но и для историков, философов и педагогов.
Основные характеристики?
- Использует историю, головоломки и оживленные дебаты для разработки новых математических систем
- Показывает, как отклонения от правил могут лежать в основе новых практических приложений
- Понятно и доступно
- Требуется только базовая алгебра средней школы
Альберто А. Мартинес преподает историю естественных наук и математики в Техасском университете в Остине. Он изучает историю, чтобы лучше понять научное творчество и прояснить неясности в элементах физики и алгебры.
Он изучает историю, чтобы лучше понять научное творчество и прояснить неясности в элементах физики и алгебры.
«Альберто А. Мартинес… показывает, что концепция отрицательных чисел приводила в замешательство не только молодых студентов, но и немало известных математиков… и непреложный закон природы. Мартинес показывает, что можно построить полностью непротиворечивую систему арифметики, в которой минус, умноженный на минус, дает минус. — Грег Росс, Американский ученый
«Альберто Мартинес… написал целую книгу о том факте, что произведение двух отрицательных чисел считается положительным. Он начинает с того, что напоминает своим читателям, что это не обязательно так. … Книга написана в непринужденной, разговорной манере… Ее можно рекомендовать всем, кто интересуется тем, как алгебра развивалась за кулисами, в то время, когда исчисление и аналитическая геометрия были основным направлением математических исследований. интерес.» —James Case, SIAM News
«[ Negative Math ] очень удобочитаемый и интересный стиль. Многое делается с помощью примеров, а не формальных доказательств. Автор избегает формальной математической логики и более эзотерических абстрактных алгебр. например, теория групп». — Mathematics Magazine
Многое делается с помощью примеров, а не формальных доказательств. Автор избегает формальной математической логики и более эзотерических абстрактных алгебр. например, теория групп». — Mathematics Magazine
«Отличная книга, по-настоящему удобочитаемая и точная. Меня неоднократно интриговали и вдохновляли примеры и подходы Мартинеса, которым удалось превратить компетентный исторический анализ в информативное и наводящее на размышления размышление о математическом смысле. .» — Джоан Л. Ричардс, Университет Брауна
«Красиво написано. Точно и надежно. Утверждение автора о том, что математика построена в соответствии с нашим суждением о том, что нам нужно, очень важно и малопонятно». — Рубен Херш, Университет Нью-Мексико
«Мартинес пишет с доступный и разговорный стиль. Его обсуждение отношения математики к физике и ее роли в конкретных особенностях мира делает эту книгу привлекательной как для обычных читателей, так и для ученых ». — Рональд Андерсон, Бостонский колледж
- Структура групп с квазивыпуклой иерархией
Дэниел Т. Уайз
Уайз - Теория групп
Предраг Цвитанович - Скалярная, векторная и матричная математика
Деннис С. Бернштейн - Часы работы с теоретиком геометрических групп
Под редакцией Мэтта Клэя и Дэна Маргалита - Асимптотическая дифференциальная алгебра и теория моделей трансрядов
Матиас Ашенбреннер, Лу ван ден Дрис и Йорис ван дер Хувен
Оставайтесь на связи, чтобы быть в курсе последних книг, идей и специальных предложений.

Будьте в курсе последних книжных новостей.
Отрицательные числа – Объяснение и примеры
Некоторым людям изучение отрицательных чисел может показаться немного скучным.
У этих людей возникают вопросы, например, зачем изучать отрицательные числа?
Как отрицательные числа связаны с их повседневной жизнью?
Итак, в этой статье мы узнаем, что такое отрицательные числа, их действия и как числа связаны в реальной жизни.
История отрицательных чисел началась тысячу лет назад, когда их начали использовать математики с Индийского субконтинента. Позже европейцы проявили интерес к отрицательным числам, но очень неохотно их принимали.
Египтяне также пренебрежительно относились к отрицательному числу и в какой-то момент считали отрицательное число смешным. Это потому, что математика, которую они использовали в то время, основывалась только на геометрических понятиях, таких как длина окружности и площадь. Позже европейцы начали догонять отрицательные числа, когда ученые начали переводить арабские тексты, полученные из Северной Африки.
Из этой краткой истории мы узнали, что этим поколениям выдающихся и умных людей изначально было трудно принять концепцию отрицательных чисел.
Они, наконец, приняли эту идею после того, как открыли значение отрицательных чисел.
Что такое отрицательное число?
Отрицательное число — это число, значение которого меньше нуля. Отрицательные числа обозначаются знаком минус или тире (-) перед числом.
Они представлены на числовой строке слева от начала координат. Отрицательные числа могут быть целыми, дробными или десятичными. Например, – 2, – 3, – 4, – 5, -2/3, -5/7, -3/4, -0,5, -0,7. и т. д. являются примерами отрицательных чисел. В этом случае эти числа произносятся как минус два, минус три, минус четыре и так далее.
Отрицательное число имеет несколько различных интерпретаций. А это:
- Отрицательное число — это число меньше нуля
- Числа слева от нуля на числовой прямой
- Число, противоположное положительному числу
- Отрицательное число означает потерю или отсутствие чего-либо.

- Величина, имеющая направление
Что такое отрицательное целое число?
Отрицательное целое число — это целое число, значение которого меньше нуля. Отрицательные целые числа обычно представляют собой целые числа, например, -3, -5, -8, -10 и т. д.
Операции с отрицательными целыми числами
Отрицательные целые числа имеют правила для выполнения различных вычислений. Это:
- Сложение отрицательного и положительного целых чисел
При сложении отрицательного и положительного целых чисел вычтите целые числа и запишите знак большего абсолютного значения. Другими словами, когда небольшое отрицательное целое число прибавляется к большему положительному целому, целые числа вычитаются и получают положительный знак. Например,
8 + (- 2) = 6. Точно так же при сложении небольшого положительного и большого отрицательного целых чисел сумма всегда будет отрицательной. Например, – 5 + 3 = – 2.
- Добавление отрицательных целых чисел
При добавлении отрицательных целых чисел числа складываются, и сумма принимает знак исходных целых чисел. Например, – 5 + (-1) = – 6.
- Вычитание целых чисел со знаком
Вычитание положительного целого числа из отрицательного числа эквивалентно прибавлению отрицательного числа этого целого числа. Например, -10 – 15 = -10 + (-15) = -25.
Вычитание отрицательного целого числа из другого отрицательного числа равносильно сложению положительного числа этого целого числа. Например, 13 – (-14) = 13 + 14 = 27.
- Умножение и деление отрицательных целых чисел
Когда отрицательное целое число умножается на другое отрицательное целое число, произведение положительное. Пример: -4 x -4 = 16. Точно так же деление отрицательного целого числа на другое отрицательное целое число дает положительное частное.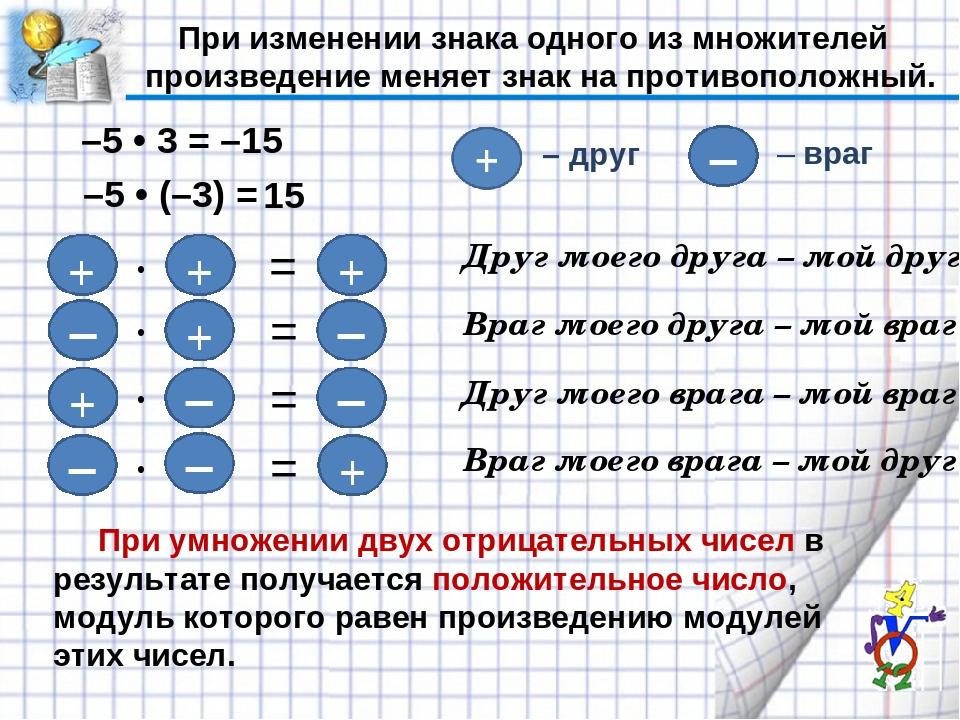
Умножение положительного целого числа на другое отрицательное число дает отрицательное произведение. Например, -2 х 5 = -10. А деление положительного целого числа на отрицательное дает отрицательное частное.
Применение отрицательных целых чисел в реальной жизни
Независимо от их значения, отрицательные целые числа широко применяются в различных сферах жизни. Следующие примеры применения отрицательных чисел в реальной жизни побудят вас увидеть преимущества их изучения.
- Банковско-финансовый сектор.
Банки и финансовые учреждения связаны с дебетом, кредитом и деньгами. По этой причине необходимо иметь номера, которые различают кредитную и дебетовую транзакцию. Прибыли и убытки также определяются положительным и отрицательным числом соответственно. Еще одна область, где используются отрицательные числа, — это фондовый рынок. Положительные и отрицательные числа используются для обозначения взлетов и падений цены акций.
Депозиты обычно обозначаются положительным знаком, тогда как снятие средств обозначается отрицательным знаком.
- Наука, техника и медицина
Отрицательные числа используются в прогнозировании погоды для отображения температуры в регионе. Отрицательные целые числа используются для отображения температуры по шкале Фаренгейта и Цельсия.
В технике, например, в таких приборах, как котлы и паровые двигатели, используются манометры и термометры, калиброванные от отрицательных до положительных целых чисел.
Приборы для измерения артериального давления, массы тела и тестирования на наркотики работают на отрицательной или положительной шкале.
- Другие применения отрицательных целых чисел в реальной жизни
Разница голов в таких видах спорта, как футбол, хоккей и баскетбол, обозначается отрицательными целыми числами.
Лифты, спидометры и Alco-blow используют отрицательные и положительные значения.
Нотация и моделирование Вычитание целых чисел
Результаты обучения
- Модель вычитания целых чисел со счетчиками цветов
В детстве вы учитесь вычитать числа с помощью повседневного опыта. Например, если у вас есть 10 печений животных и вы съели 6 из них, у вас останется 4 печенья животных.
Реальный жизненный опыт служит моделями для вычитания положительных чисел, а в некоторых случаях, таких как температура, для сложения как положительных, так и отрицательных чисел. Но трудно связать вычитание отрицательных чисел с обычным жизненным опытом. Большинство людей не имеют интуитивного понимания вычитания, когда речь идет об отрицательных числах. Учителя математики используют несколько разных моделей для объяснения вычитания отрицательных чисел.
Мы продолжим использовать счетчики для моделирования вычитания. Помните, что синие счетчики представляют положительные числа, а красные счетчики — отрицательные числа.
Возможно, когда вы были моложе, вы читали [латекс]5 — 3[/латекс] как пять отнять три . Когда мы используем счетчики, мы можем думать о вычитании таким же образом.
Мы смоделируем четыре сценария вычитания с использованием чисел [латекс]5[/латекс] и [латекс]3[/латекс].
- [латекс]5 — 3[/латекс]
- [латекс]- 5-\влево(-3\вправо)[/латекс]
- [латекс]-5 — 3[/латекс]
- [латекс]5-\влево(-3\вправо)[/латекс]
пример
Модель: [латекс]5 — 3[/латекс].
Решение:
Разница между [latex]5[/latex] и [latex]3[/latex] составляет [latex]2[/latex] .
Теперь вы можете попробовать аналогичную задачу.
попробуйте
Смоделируйте выражение:
[латекс]6 — 4[/латекс]
Показать решение
Смоделируйте выражение:
[латекс]7 — 4[/латекс]
Показать решение
В предыдущем примере мы вычли [латекс]3[/латекс] положительных результатов из положительных [латекс]5[/латекс]. Теперь мы вычтем [латекс]3[/латекс] негативы из минусов [латекс]5[/латекс]. Сравните результаты этого примера с предыдущим после прочтения.
Теперь мы вычтем [латекс]3[/латекс] негативы из минусов [латекс]5[/латекс]. Сравните результаты этого примера с предыдущим после прочтения.
пример
Модель: [латекс]-5-\влево(-3\вправо)[/латекс]
Показать решение
Вы можете попробовать аналогичную проблему.
попробуйте
Смоделируйте выражение:
[латекс]-6-\влево(-4\вправо)[/латекс]
Показать решение
Смоделируйте выражение:
[латекс]-7-\влево(-4\вправо)[/латекс]
Показать решение
Обратите внимание, что два предыдущих примера очень похожи.
- Сначала мы вычли [латекс]3[/латекс] положительных результатов из [латекс]5[/латекс] положительных результатов, чтобы получить [латекс]2[/латекс] положительных результатов.
- Затем мы вычли [латекс]3[/латекс] негативы из [латекс]5[/латекс] негативов, чтобы получить [латекс]2[/латекс] негативы.

В каждом примере использовались фишки только одного цвета, и модель вычитания «на вынос» была легко применима.
Теперь посмотрим, что получится, если вычесть одно положительное и одно отрицательное число. Нам нужно будет использовать как положительные, так и отрицательные счетчики, а иногда и некоторые нейтральные пары. Добавление нейтральной пары не меняет значение.
пример
Модель: [латекс]-5 — 3[/латекс]
Решение:
Итак, нам нужно убрать [латекс]3[/латекс] позитива.
Добавляйте нейтральные пары, пока у вас не будет [latex]3[/latex] положительных результатов.

Разница [латекс]-5[/латекс] и [латекс]3[/латекс] составляет [латекс]-8[/латекс] .
Теперь вы можете решить аналогичную задачу.
попробуйте
Смоделируйте выражение:
[латекс]-6 — 4[/латекс]
Показать решение
Смоделируйте выражение:
[латекс]-7 — 4[/латекс]
Показать решение
Теперь мы будем вычитать отрицательное число из положительного числа. Думайте об этом как о снятии негатива.
пример
Модель: [латекс]5-\влево(-3\вправо)[/латекс]
Показать решение
Теперь вы можете попробовать аналогичную задачу.
попробуйте
Смоделируйте выражение:
[латекс]6-\влево(-4\вправо)[/латекс]
Показать решение
Смоделируйте выражение:
[латекс]7-\влево(-4\вправо)[/латекс]
Показать решение
Теперь мы сделаем пример, который обобщает ситуации, описанные выше, с разными номерами. Вспомните различные сценарии:
Вспомните различные сценарии:
- вычитание положительного числа из положительного числа
- вычитание положительного числа из отрицательного числа
- вычитание отрицательного числа из положительного числа
- вычитание отрицательного числа из отрицательного числа
пример
Смоделируйте каждое вычитание.
- [латекс]8 − 2[/латекс]
- [латекс]−5 − 4[/латекс]
- [латекс]6 — (-6)[/латекс]
- [латекс]−8 − (−3)[/латекс]
Показать решение
Теперь вы можете попробовать аналогичную задачу.
попробуй
Моделирование каждого вычитания.
1. [латекс]7 — (-8)[/латекс]
2. [латекс]-7 — (-2)[/латекс]
3. [латекс]4 — 1[/латекс]
4. [латекс]-6 — 8[/латекс]
Показать решение
Смоделируйте каждое вычитание.
1. [латекс]4 — (-6)[/латекс]
2. [латекс]-8 — (-1)[/латекс]
3. [латекс]7 — 3[/латекс]
[латекс]7 — 3[/латекс]
4. [латекс]-4 — 2[/латекс]
Показать решение
Каждый из примеров до сих пор был тщательно построен так, чтобы знак ответа соответствовал знаку первого числа в выражении. Например, в [латекс]−5 – 4[/латекс] результатом будет [латекс]-9[/латекс], что имеет тот же знак, что и [латекс]-5[/латекс]. Теперь мы увидим вычитание, где знак результата отличается от начального числа.
пример
Смоделируйте каждое выражение вычитания:
- [латекс]2 — 8[/латекс]
- [латекс]-3-\влево(-8\вправо)[/латекс]
Показать решение
Теперь вы можете попробовать аналогичную задачу.
попробуй
Моделирование каждого выражения вычитания.
- [латекс]7 — 9[/латекс]
- [латекс]-5-9[/латекс]
Показать решение
Смоделируйте каждое выражение вычитания.
- [латекс]5 — 8[/латекс]
- [латекс]-7-\влево(-10\вправо)[/латекс]
Показать решение
Когда вы вычитаете два целых числа, есть две возможности: либо результат будет иметь знак, отличный от начального числа, либо тот же знак.
Посмотрите видео ниже, чтобы увидеть больше примеров моделирования целочисленного вычитания с помощью счетчиков цветов.
Что говорят исследования?
FutureLearn использует куки-файлы для повышения удобства использования веб-сайта. Все файлы cookie, кроме строго необходимых, в настоящее время отключены для этого браузера. Включите JavaScript, чтобы применить настройки файлов cookie для всех необязательных файлов cookie. Вы можете ознакомиться с политикой FutureLearn в отношении файлов cookie здесь.
Артикул. Краткое изложение некоторых исследований отрицательных чисел.
Вы наверняка слышали, как многие из ваших учеников читают числовое выражение «7 – -4» как «7 минус минус 4», и задавались вопросом, какой смысл они вкладывают в вычисления и символы.
- Что для них значит «минус минус»?
- Первый минус считают операцией или нет?
- Заметили ли они знаки минуса разного размера, которые вы написали на доске?
- Что они написали в своих книгах?
- Знак минус отличается от знака минус?
- Минус минус 4 равен 4 или (+4)?
- Почему пишут +4, а не просто 4?
Эти вопросы помогают понять, почему работа с отрицательными числами сбивает учащихся с толку и затрудняет освоение. На этом шаге представлен краткий обзор некоторой литературы, в которой основное внимание уделяется значениям языка и системы обозначений при работе с отрицательными числами.
Влассис (2008) утверждает, что отрицательный знак может иметь как минимум три значения в математике, и поэтому существует три основных категории трудностей учащихся, связанных с числовой системой: значение математических операций и значение знак минус. Эти трудности возникают из-за незнания учащимися функций знака минус, а именно унарной, бинарной и симметричной функций.
- В унарной функции знак минус указывает читателю, что число действительно отрицательное, например -10 означает «отрицательное 10».
- Двоичная функция относится к любой ситуации, когда знак минус показывает, что операция является вычитанием (знак операции). Это, пожалуй, наиболее распространенная интерпретация у школьников, т.е. отрицательный знак, трактуемый как действие типа отнятия или вычитания.
- Благодаря своей симметричной функции знак минус указывает на то, что число противоположно родственному ему числу, как в примере 5 и -5. Для примера это означает, что для выражения -(-8) первый знак минус будет означать операцию взятия, противоположную -8, а в 2а – (4а – 3б) первый минус в выражении указывает на противоположное 4а-3б.

Рекомендация
Учащиеся должны понимать знак минус в трех смыслах: унарном, бинарном и симметричном.
Однако исследователи также показали, что применение учащимися этих различных и часто неоднозначных концепций может привести к неверным рассуждениям в расчетах. Они также предполагают, что учащимся должна быть предоставлена возможность обсуждать и развивать чувство различных значений знака минус, чтобы быть гибкими, развивать надежное концептуальное изображение знака и продвигать чувство символа.
В соответствии с тремя концептуальными аспектами отрицательного числа, упомянутыми выше, Боффердинг (2014) рекомендует следующее:
- Использование термина «минус» в общем случае должно относиться к символу «-»;
- Знак вычитания относится к двоичному значению знака минус; и
- Знак минус относится к унарному значению знака минус.
Рекомендация
Учителям следует внимательно изучить значение языка и обозначений отрицательных чисел! Они должны моделировать полезный язык, особенно с младшими учениками, например:
- Читать -3 как «минус 3», а не «минус 3»;
- Читать 6–5 как «6 вычесть/убрать 5», а не как «6 минус 5».

Это очень большая педагогическая и концептуальная задача. Обращение к -5 как к минус 5, а не к минус 5, может помочь в контексте класса (Beswick 2011). Однако учащиеся слышали, что отрицательная температура читается как «минус 5», поэтому остается вопрос, полезны ли рекомендации и в какой степени.
В следующем упражнении вам представлен ряд сценариев, связанных с работой учащихся, связанных с отрицательными числами. Мы приглашаем вас принять участие в рассмотренном здесь исследовании, чтобы понять, почему учащиеся совершают такие ошибки и как вы можете им помочь.
Ссылки
Бесвик, К. (2011). Положительный опыт работы с отрицательными числами: опираясь на опыт учащихся в школе и за ее пределами. Австралийский учитель математики, Vol. 67 (2), 31-40.
Боффердинг, Л. (2014). Отрицательное целочисленное понимание: характеристика ментальных моделей первоклассников. Журнал исследований в области математического образования, 45 (2), 194-245.
Влассис, Дж. (2008 г.). Роль математических символов в развитии концептуализации чисел: случай со знаком минус. Философская психология, 21(4), 555-570.
Эта статья из бесплатного онлайн-ресурса
Ключевые идеи в наставничестве учителей математики
Автор:
Присоединяйся сейчас
Наша цель — изменить доступ к образованию.
Мы предлагаем широкий выбор курсов от ведущих университетов и учреждений культуры со всего мира. Они предоставляются поэтапно и доступны на мобильных устройствах, планшетах и компьютерах, поэтому вы можете приспособить обучение к своей жизни.
Мы считаем, что обучение должно быть приятным, социальным опытом, поэтому наши курсы дают возможность обсудить то, что вы изучаете, с другими, помогая вам делать новые открытия и формировать новые идеи.
Вы можете разблокировать новые возможности с неограниченным доступом к сотням коротких онлайн-курсов в течение года, подписавшись на наш безлимитный пакет. Развивайте свои знания в ведущих университетах и организациях.
Развивайте свои знания в ведущих университетах и организациях.
Узнайте больше о том, как FutureLearn меняет доступ к образованию
Вычитание против минуса — язык математики
Вот уравнение: 8-2=6
Обычно мы бы сказали: «Восемь минус два равно шести».
Неправильно ли сказать «Восемь вычесть два будет шесть?»
Мой сын сказал последнее в школе, как и я, работая с ним, и учитель сказал ему, что это неверно.
Это? Также неправильно говорить: «Восемь прибавить два равно десять»? Являются ли слова «минус/вычитание» или «добавление/плюс» взаимозаменяемыми, когда мы читаем уравнения, или неправильно говорить что-либо, кроме «плюс» или «минус»?
Я задал этот вопрос математической дискуссионной группе и получил множество ответов. Некоторые люди говорили, что грамматически неправильно говорить «вычесть», потому что это глагол, а минус — нет, а в предложении уже есть один глагол «равно».
Другие сказали, что либо правильно, но вычесть точнее, и что математические выражения не должны соответствовать английской грамматической структуре. Это была довольно оживленная дискуссия.
Самый четкий и лаконичный ответ, который я получил, пришел от Элисон Коутс из Института математики средней школы. Вот что она сказала:
Возможно, это придирка, но математику нелегко обсуждать на обычном языке. Вот почему мы используем символы для математики: символы математики — это «язык» математики, и наше коллективное нежелание в США готовить учащихся к манипуляциям с символами — основная причина того, что у них появляется все больше и больше ошибок, пока их ошибки в рассуждениях болотная правда.
Без всякой вербализации 8 — 2 = 6 точно, лаконично и правильно. Оно отличается от 2 — 8 = -6.
Только когда мы пытаемся выразить это словами, у нас возникают проблемы.
Здесь есть пара взаимосвязанных моментов, на которые стоит обратить внимание:
1. Мы должны научить детей «читать» приведенное выше уравнение как транслитерацию символов, чтобы кто-нибудь, услышав словесное выражение уравнения, записал его. правильный.
Мы должны научить детей «читать» приведенное выше уравнение как транслитерацию символов, чтобы кто-нибудь, услышав словесное выражение уравнения, записал его. правильный.
В английском языке мы озвучиваем вышеизложенное как «восемь минус 2 равно 6». Хотя мы можем захотеть обсудить или объяснить суммы, различия и т. д., в конце концов, учащийся должен знать, как правильно называть эти символы, чтобы он мог правильно записать соответствующее выражение без путаницы. Этот символ — минус (знак), а + — плюс (знак). Мы читаем 3 x 4 = 12 как «трижды четыре равно 12». Это отличается от того, как мы говорим об этих понятиях.
2. Точность имеет значение. Проблема с различными английскими выражениями и их неточностью в качестве замены математической точности часто проявляется только со временем, слишком поздно, чтобы исправлять неправильные представления.
Я встречал многих семиклассников, которые не знали, что десятичные дроби — это дроби. Им никогда не говорили, что «десятичная дробь — это дробь со степенью десяти в знаменателе». Они почти всегда с точностью до единицы озвучивают символ 4,56 как «четыре целых пять десятых». Они понятия не имеют, что 0,56 — это дробь пятьдесят шесть сотых. Быть вынужденным говорить это должным образом до тех пор, пока абсолютная демонстрация владения разрядным значением в десятичных дробях и распознавание десятичной дроби не станет критической.
Они почти всегда с точностью до единицы озвучивают символ 4,56 как «четыре целых пять десятых». Они понятия не имеют, что 0,56 — это дробь пятьдесят шесть сотых. Быть вынужденным говорить это должным образом до тех пор, пока абсолютная демонстрация владения разрядным значением в десятичных дробях и распознавание десятичной дроби не станет критической.
Точно так же я встречал многих второклассников, которые не могли решить: «У Анны на две машины больше, чем у ее брата Чарли. У Анны 8. Сколько у Чарли? потому что их учили, что вычитание — это «отнять». Но с их точки зрения здесь ничего не отнимается.
Я уверен, что большинство присутствующих здесь тщательно разобрались с ошибками в выражении «дробь является частью целого» — и вы можете подумать, что это другой тип языковой ошибки, но для большинства учителей это не так. ‘т. Если вы, как учитель, боитесь вводить определения равенства или коммутативных свойств, вам будет неудобно точно определять дробь на числовой прямой. (Для тех, кто не знает, что не так с фразой «дробь является частью целого», невероятно короткий ответ: это заставляет студента думать, что все дроби меньше 1. Потому что как может больше, чем целое, быть частью целого. Что такое 9/8 — что за часть, что за целое? Большинство учеников ответят: «На самом деле это 1 1/8», и они думают, что только 1/8 — это дробь.)
(Для тех, кто не знает, что не так с фразой «дробь является частью целого», невероятно короткий ответ: это заставляет студента думать, что все дроби меньше 1. Потому что как может больше, чем целое, быть частью целого. Что такое 9/8 — что за часть, что за целое? Большинство учеников ответят: «На самом деле это 1 1/8», и они думают, что только 1/8 — это дробь.)
Мой «любимый» пример того, как неправильное использование языка полностью разрушает понимание математики ребенком, относится к 6 летняя девочка в (номинально?) Монтессори-программе, которая приносила домашнюю страницу за страницей задач на сложение вертикального алгоритма 3 на 3 цифры и делала их правильно. Но потом мать попросила ее решить (по горизонтали) 9 + 2 = ?
, и она сказала (да, прямая цитата): «Одиннадцать, но ответ не может быть больше 9».
Она могла объяснить обмен местами в «магазине бисера» и могла правильно считать с переносом, но когда учитель научил ее складывать, учитель не смог различить «у нас есть только 10 цифр для записи» и «общее количество разрешенных объектов никогда не может быть больше девяти».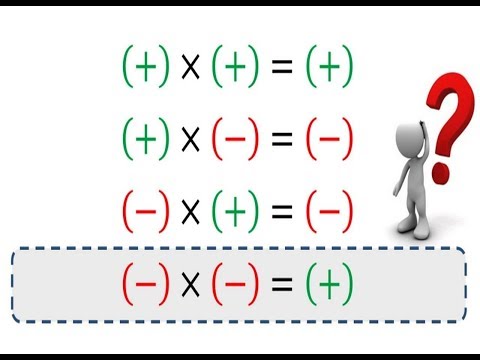 0147
0147
372
+159
правильно
и одновременно думал, что 9 + 2 = 11 было незаконным.
Уточнить эти детали для ребенка сложно, но они очень важны.
Allison Coates
Институт математики средней школы
WWW.MDSMI -MN.ORG
WWW.MDSMI -MN.ORGСАМОСТО0001
Все, что вам нужно знать, чтобы научить вашего ребенка вычитанию без часов механического заучивания, счета на пальцах или карточек.
Ошибка моего учителя-новичка
Когда я был совершенно новым учителем, я посвятил недели тому, чтобы убедиться, что все мои пятиклассники полностью усвоили факты сложения.
Я знал, что сложение фактов является важной основой и что без них мои ученики никогда не будут чувствовать себя уверенно в математике.
Но я не потратил ни одного дня на изучение фактов вычитания. Я полагал, что как только мои ученики узнают факты сложения, они смогут понять и вычитание.
Я полагал, что как только мои ученики узнают факты сложения, они смогут понять и вычитание.
Я ошибся.
Весь год у борцов за вычитание возникали проблемы каждый раз, когда мы касались темы, связанной с вычитанием. Длинное деление. Десятичные дроби. Фракции. По каждой из этих тем мои ученики тратили столько усилий на изучение базовых вычитаний, что у них не оставалось много умственной энергии для изучения новых понятий.
Так почему же мои ученики не могли легко применить свои знания о сложении фактов, чтобы вычислить факты вычитания. В конце концов, если бы они знали, что 9 + 5 = 14, разве они не должны были бы также знать, что 14 — 9 = 5?
Чему я научился
Я делал две ошибки: одну о вычитании, а другую о том, как думают дети.
Во-первых, я предполагал, что связанные факты сложения всегда являются лучшим способом выяснить факты вычитания. Это верно для некоторых фактов вычитания, но часто другая стратегия мышления работает лучше.
Во-вторых, я предполагал, что дети думают, как взрослые. (Любой родитель знает, что это не так!) Мы, взрослые, можем рассуждать абстрактно: поскольку вычитание противоположно сложению, мы знаем, что можем использовать факты сложения, чтобы выяснить связанные факты вычитания.
Но дети мыслят конкретно. Им нужно видеть связь между сложением и вычитанием снова и снова, используя практические материалы и много практики, прежде чем они смогут использовать факты сложения в качестве ступенек к фактам вычитания.
Но это не значит, что пора начинать делать стопки карточек или печатать стопки листов с упражнениями на вычитание. В этой статье вы узнаете все, что вам нужно знать, чтобы научить вашего ребенка фактам вычитания — без недель механического заучивания.
Какие факты вычитания? Почему они так важны?
Факты вычитания — это все разности от 2 — 1 до 18 — 9. Вот полная таблица фактов вычитания:
Точно так же, как факты сложения, факты вычитания закладывают основу для остальной части элементарной арифметики.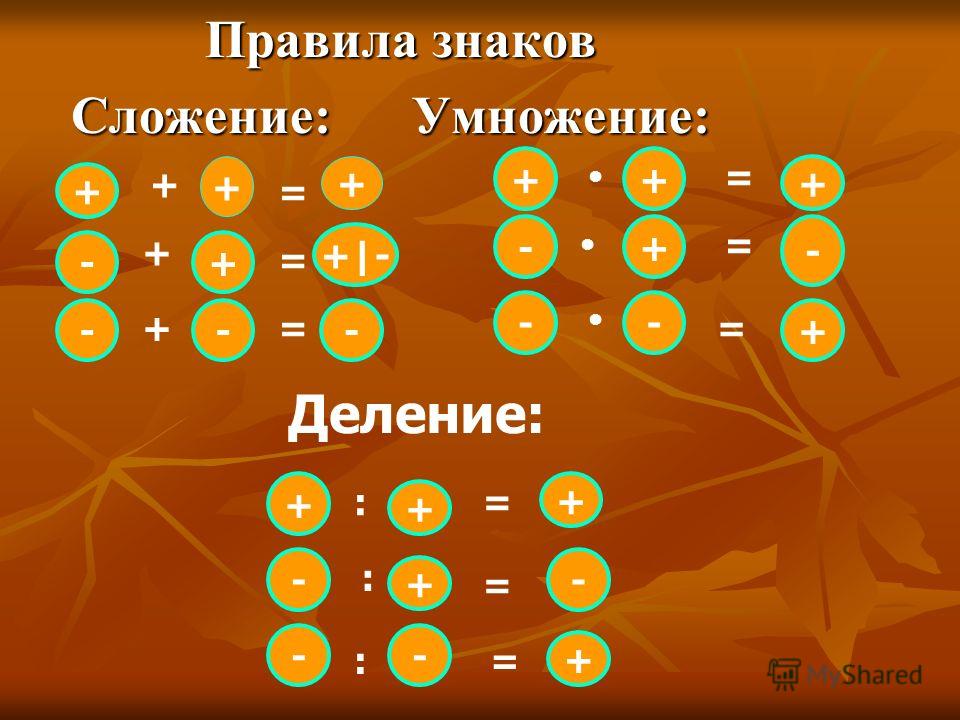 Без полного овладения фактами вычитания дети борются с , поскольку они решают задачи со словами и вычитание с большими числами. Это приводит к более медленному решению задач, большему количеству ошибок и общему недоверию к математике.
Без полного овладения фактами вычитания дети борются с , поскольку они решают задачи со словами и вычитание с большими числами. Это приводит к более медленному решению задач, большему количеству ошибок и общему недоверию к математике.
В каком классе дети должны изучать факты вычитания?
В идеале дети должны освоить вычитание к началу второго класса. Как только они запишут факты вычитания, они будут готовы работать над более сложными математическими темами для второго класса, такими как вычитание многозначных чисел. Но, если ваш старший ребенок не освоил факты вычитания, еще не поздно — изучение фактов вычитания сделает его более уверенным и успешным в математике.
Не уверены, что ваш ребенок усвоил факты вычитания? Загрузите этот бесплатный тест на вычитание, который можно распечатать, и узнайте!
Что нужно знать детям, прежде чем запоминать факты вычитания?
Прежде чем приступить к освоению фактов вычитания, ваш ребенок должен хорошо овладеть следующими навыками:
- Поймите, что вычитание может означать удаление или нахождение разницы.
 Например, 13 – 8 может означать: «Сколько останется, если от 13 отнять 8?» Или 13–8 можно интерпретировать как «Насколько больше 13, чем 8?»
Например, 13 – 8 может означать: «Сколько останется, если от 13 отнять 8?» Или 13–8 можно интерпретировать как «Насколько больше 13, чем 8?» - Поймите, что вычитание противоположно сложению.
- Знайте факты сложения до 9 + 9. Многие стратегии вычитания основаны на возможности использовать «обратное сложение», поэтому это очень важно. (Если ваш ребенок еще не освоил сложение фактов, сначала поработайте над сложением фактов, а затем займитесь вычитанием.)
Вы знаете своего ребенка лучше всех, но большинство детей в возрасте от 7 лет и старше уже готовы к усвоению фактов. Можно работать над основами вычитания с младшим ребенком, но не ждите полного мастерства, пока ваш ребенок немного не подрастет.
Как быстро дети должны знать факты вычитания?
Стремитесь не более 3 секунд на факт и меньше, если возможно. Но многое зависит от вашего ребенка. Дети, которые очень быстро обрабатывают информацию, вполне способны усвоить каждый факт менее чем за 1 секунду, но детям с более медленным процессором всегда может понадобиться несколько секунд. Вы родитель и знаете своего ребенка лучше всех, поэтому адаптируйте свои ожидания к каждому отдельному ребенку.
Вы родитель и знаете своего ребенка лучше всех, поэтому адаптируйте свои ожидания к каждому отдельному ребенку.
Неважно, сколько лет вашему ребенку, старайтесь, чтобы время занятий было расслабленным и позитивным. Тесты и упражнения на время не нужны, если только ваш ребенок не чувствует цейтнота и не находит удовлетворение в том, чтобы бить часы.
Шаг 1: Разбейте его.
Не перегружайте ребенка всеми фактами вычитания сразу. Вместо этого сначала разбейте факты на более мелкие группы.
Есть много способов сделать это, но я обнаружил, что лучше всего работать с фактами в следующем порядке: )
Такое разбиение фактов на вычитание делает их освоение более выполнимым (для детей и родителей). Кроме того, ваш ребенок станет увереннее, поскольку начнет с более простых фактов -1 и -2, а затем перейдет к более сложным фактам.
Кроме того, ваш ребенок станет увереннее, поскольку начнет с более простых фактов -1 и -2, а затем перейдет к более сложным фактам.
Шаг 2: Визуализируйте и разработайте стратегию.
Так же, как и в случае сложения фактов, этот шаг является недостающим элементом , который позволяет детям освоить факты вычитания с пониманием, а не просто заучиванием наизусть.
Вы выбрали одну небольшую группу фактов, чтобы сосредоточиться. Теперь пришло время научить вашего ребенка визуализировать числа и использовать эффективную стратегию для поиска ответов.
Почему визуализация так важна
Возможно, вы удивитесь, узнав, что визуализация величин — это важный шаг. Но подумайте об этом с точки зрения ребенка. Когда большинство детей думают о числах, они, как правило, видят в своем воображении груды неорганизованных счетчиков.
Итак, ребенок, пытающийся вычесть 12 – 4, представляет, что убирает 4 фишки из стопки из 12 фишек. Он знает, что ему нужно найти, сколько осталось, но единственная стратегия, которая у него есть, чтобы сложить их вместе, — это считать каждый счетчик один за другим или считать на пальцах.
Он знает, что ему нужно найти, сколько осталось, но единственная стратегия, которая у него есть, чтобы сложить их вместе, — это считать каждый счетчик один за другим или считать на пальцах.
Но когда дети визуализируют числа как организованные группы, они могут отказаться от счета и запоминания рут .
Как визуализация помогает
Вместо этого представьте себе ребенка, который научился визуализировать числа в виде организованных групп на десяти кадрах. Вот те самые 12 счетчиков, организованные по десятикадрам.
Организация 12 счетчиков на десятичной рамке облегчает визуализацию чисел (Десятичная рамка представляет собой простую сетку из 10 квадратов с линией, разделяющей две группы по 5. Темная линия обеспечивает точка отсчета, чтобы было легко увидеть числа больше 5 как комбинацию «5 и еще немного». )
)
Теперь, чтобы вычесть 4 из 12, ребенок может использовать простую конкретную стратегию, чтобы найти ответ.
Сначала он убирает 2 фишки из нижнего ряда. Затем он убирает еще 2 фишки из верхнего ряда. Теперь он сразу видит, что осталось 8 жетонов, поэтому 12 – 4 должно равняться 8.
Удаление 4 жетонов показывает, что 12 – 4 равно 8.Немного потренировавшись, он научится визуализировать числа. и даже манипулировать ими мысленно . Поскольку числа расположены в десятичной рамке, он может вспомнить их и представить, как перемещает счетчики, чтобы найти различия.
Теперь у него есть надежный и эффективный метод, который послужит ступенькой , чтобы помочь ему освоить одну группу фактов вычитания. С помощью всего нескольких стратегий, подобных этой, он выучит все факты вычитания.
См. также: Руководство для родителей по стратегиям вычитания фактов
Шаг 3. Практикуйте эти факты, пока не освоите их.
После того, как ваш ребенок освоил одну конкретную стратегию для одной конкретной группы фактов вычитания, ему все равно потребуется некоторая практика, прежде чем он сможет свободно использовать эту стратегию.
Итак, попросите вашего ребенка сосредоточиться только на этом конкретном наборе фактов в течение нескольких дней. Например, если вы научили ее описанной выше стратегии (которая хорошо работает для вычитания 3, 4 и 5 из чисел больше 10), пусть она попрактикуется в течение нескольких дней только на этих фактах: 14 – 5, 13 – 5. , 12 – 5, 11 – 5, 13 – 4, 12 – 4, 11 – 4, 12 – 3, 11 – 3 и 11 – 2.
Вы можете адаптировать практику вычитания фактов вашего ребенка так, чтобы она лучше всего подходила вам и вашему ребенку. Многие дети процветают на сочетании игр и рабочих листов. Игры делают изучение фактов вычитания увлекательным и интерактивным. Кроме того, они также дают вам возможность следить за тем, насколько хорошо ваш ребенок использует стратегию (и исправлять любые ошибки до того, как они укоренятся). чтобы иметь возможность свободно использовать факты в своей письменной школьной работе.
Шаг 4: Смешайте эти факты с другими фактами.
Как только ваш ребенок усвоил один набор фактов, пришло время смешать их с фактами, которые он уже усвоил.


 Уайз
Уайз 



 Например, 13 – 8 может означать: «Сколько останется, если от 13 отнять 8?» Или 13–8 можно интерпретировать как «Насколько больше 13, чем 8?»
Например, 13 – 8 может означать: «Сколько останется, если от 13 отнять 8?» Или 13–8 можно интерпретировать как «Насколько больше 13, чем 8?»