Секанс онлайн калькулятор
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
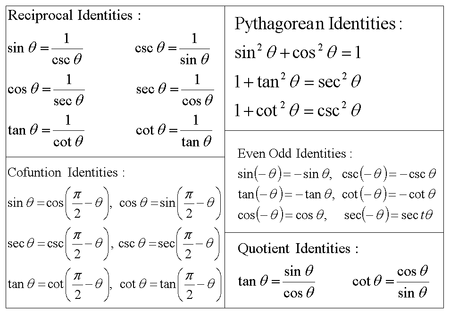
Данный калькулятор вычислит синус, косинус, тангенс, котангенс, секанс, косеканс угла как в градусной, так и в радианной мере.
Введите число
синус (sin)косинус (cos)тангенс (tg)котангенс (ctg)секанс (sec)косеканс (cosec)градусырадианы
Что такое секанс угла
Пусть задан прямоугольный треугольник ABC с острым углом α, тогда косинусом угла α будет отношение гипотенузы к прилежащему катету sec α = AC/AB.
Так же для определения секанса угла можно воспользоваться окружностью, построенной в декартовой системе координат, радиуса R и центром в начале координат O.
На окружности отметим точку P с координатами (1;0), теперь повернем луч OP на некоторый угол α. Направление против часовой стрелки считается положительным, по часовой стрелки – отрицательным.
Секансом угла α будет отношение радиуса окружности к абсциссе точки XPsec α = R/XP, в случае, если окружность единичная (радиус окружности = 1), формула примет вид sec α = 1/XP и так как косинус угла равен абсциссе точки XP, можно записать sec α = 1/cos α.
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Функция Sec(X) 6 Букв — ответ на кроссворд и сканворд
Решение этого кроссворда состоит из 6 букв длиной и начинается с буквы С
Ниже вы найдете правильный ответ на Функция sec(x) 6 букв, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.
ответ на кроссворд и сканворд
Четверг, 31 Октября 2019 Г.
СЕКАНС
предыдущий следующий
ты знаешь ответ ?
ответ:
связанные кроссворды
- Секанс
- Три и более карт одной масти, следующие друг за другом в порядке их достоинства (карточный термин)
- Функция угла
- Секанс
- Тригонометрическая функция угла 6 букв
- Отношение гипотенузы к прилежащему катету 6 букв
- Одна из тригонометрич.
 функций 6 букв
функций 6 букв - Тригонометрическая функция 6 букв
похожие кроссворды
- В математике: линейная функция 12 букв
- Математическая функция 12 букв
- Тригонометрическая функция угла 7 букв
- Тригонометрическая функция, равная отношению косинуса к синусу 9 букв
- (философия) обязанность, круг деятельности.
 «функция 7 букв
«функция 7 букв - Функция состояния термодинамической системы 8 букв
- Математическая тригонометрическая функция 7 букв
- Тригонометрическая функция 10 букв
- Функция секьюрити 6 букв
- Тригонометрическая функция угла 5 букв
- Тригонометрическая функция, равная отношению синуса к косинусу 7 букв
- Матем.
 функция 9 букв
функция 9 букв - Функция высшей математики 12 букв
- Функция от силы 5 букв
- Числовая функция 9 букв
- Простейшая периодическая функция 9 букв
- Унарная функция 9 букв
- Функция угла 9 букв
- Тригонометрическая функция угла 6 букв
- Функция научного исследования 8 букв
— формула, график, область и диапазон, свойства, примеры Итак, у нас есть косеканс
, который является обратным значением синуса, секанс является обратным значением косинуса, а котангенс является обратным значением функции тангенса.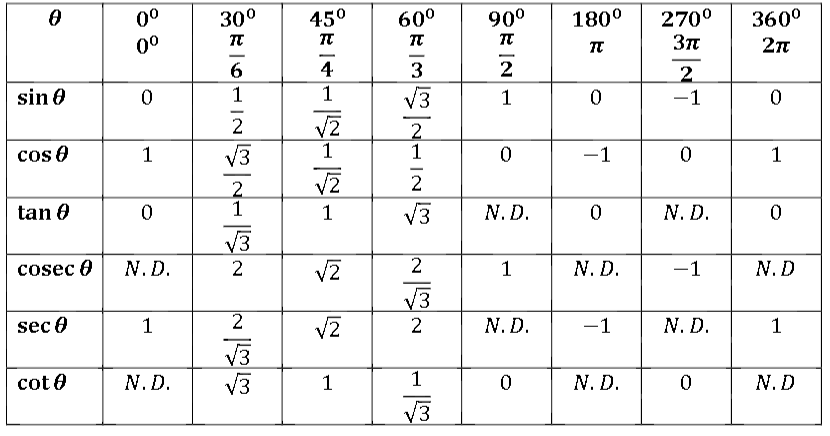 Значение функции секущей можно определить, взяв отношение гипотенузы к основанию прямоугольного треугольника.
Значение функции секущей можно определить, взяв отношение гипотенузы к основанию прямоугольного треугольника.В этой статье мы рассмотрим концепцию функции секущей и поймем ее формулу с использованием единичной окружности и углов, как использовать формулу, а также их различные применения и свойства. Также построим график функции секущей и определим ее значение под разными углами.
| 1. | Что такое секущая функция? |
| 2. | Формула секущей функции |
| 3. | Значения функции секанса |
| 4. | График функции секущей |
| 5. | Домен и диапазон функции секущей |
| 6. | Свойства функции секущей |
| 7. | Часто задаваемые вопросы о функции секущей |
Что такое секущая функция?
Функция секанса — это периодическая функция в тригонометрии.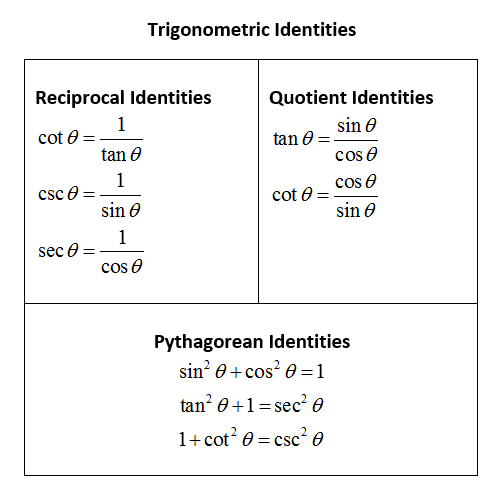 Функция секанса или сек функция может быть определена как отношение длины гипотенузы к длине основания в прямоугольном треугольнике. Это обратная функция косинуса и, следовательно, также записывается как sec x = 1 / cos x. Давайте попробуем понять концепцию функции секущей, анализируя единичный круг с центром в начале координат плоскости.
Функция секанса или сек функция может быть определена как отношение длины гипотенузы к длине основания в прямоугольном треугольнике. Это обратная функция косинуса и, следовательно, также записывается как sec x = 1 / cos x. Давайте попробуем понять концепцию функции секущей, анализируя единичный круг с центром в начале координат плоскости.
На окружности взята переменная точка P и она продолжает двигаться по окружности этой окружности. Из рисунка видно, что P находится в первом квадранте, а OP образует острый угол x радиан с положительной осью x. PQ — это перпендикуляр, опущенный из P (точка на окружности) на ось x. Таким образом, треугольник образуется путем соединения точек O, P и Q, как показано на рисунке, где OQ — основание, а PQ — высота треугольника. Следовательно, функция sec для приведенного выше случая может быть математически записана как:
сек x = OP / OQ
Здесь x — острый угол, образованный гипотенузой и основанием прямоугольного треугольника.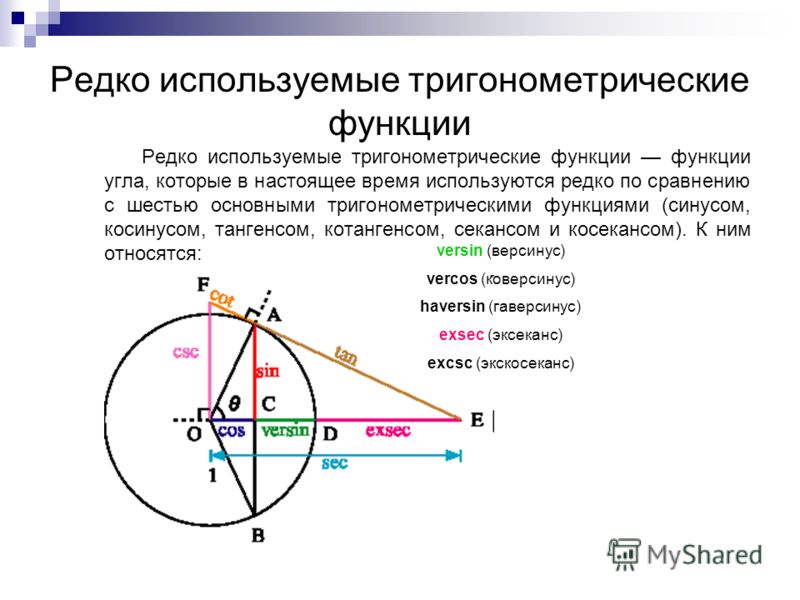
Формула секущей функции
Как обсуждалось выше, формула секущей определяется отношением гипотенузы к основанию прямоугольного треугольника. То есть мы можем записать это математически как sec θ = гипотенуза / основание. Кроме того, мы знаем, что функция секанса является обратной функцией косинуса. Следовательно, мы также можем записать его формулу в виде sec θ = 1/cos θ.
Значения функции секанса
Изучая тригонометрическую таблицу, мы наблюдаем значения тригонометрических функций под разными углами. В этом разделе мы рассмотрим значение функции секущей для стандартных углов, таких как 0°, 30°, 45°, 60° и 90°, а также других углов, таких как 180°, 270° и 360°. Лучше всего запомнить значения тригонометрических отношений этих стандартных углов, которые помогают в различных вычислениях.
| Функция секанса | Значение |
|---|---|
| сек 0° | 0 |
| сек 30° | 2/√3 |
| сек 45° | √2 |
| сек 60° | 2 |
| сек 90° | Не определено |
| сек 120° | -2 |
| сек 150° | -2/√3 |
| сек 180° | -1 |
| сек 270° | Не определено |
| сек 360° | 1 |
График функции секущей
Как мы наблюдали единичную окружность в первом сечении с центром O в начале координат и точкой P, движущейся по окружности этой окружности. Угол, который OP образует с положительным направлением оси x, равен x (радианы). PQ — перпендикуляр, опущенный из точки P на горизонтальную ось. Функция секанса является обратной функцией косинуса, то есть sec x = 1 / cos x. Это также рассматривается как формула секущей функции. Заметим, что: sec x = OP/OQ = 1/OQ. При изменении x заметим, что значение sec x изменяется при изменении длины OQ.
Угол, который OP образует с положительным направлением оси x, равен x (радианы). PQ — перпендикуляр, опущенный из точки P на горизонтальную ось. Функция секанса является обратной функцией косинуса, то есть sec x = 1 / cos x. Это также рассматривается как формула секущей функции. Заметим, что: sec x = OP/OQ = 1/OQ. При изменении x заметим, что значение sec x изменяется при изменении длины OQ.
Построение графика секанса становится очень простым, поскольку мы уже знаем график косинуса, поэтому мы можем легко построить график для sec x, найдя обратную величину каждого значения косинуса. Когда значение cos x очень мало, значение sec x становится очень большим. То есть нахождение 1/y для каждого значения y на кривой y=cosx. В таблице ниже показаны некоторые углы в радианах:
| x (радианы) | соз х | сек х |
|---|---|---|
| 0 | 1 | 1 |
| №/6 | √3/2 | 2/√3 |
| №/4 | 1/√2 | √2 |
| №/3 | 1/2 | 2 |
| π/2 | 0 | Не определено |
Также мы наблюдаем, что всякий раз, когда значение функции косинуса равно нулю, функция секанса стремится к бесконечности, что означает, что когда значение косинуса равно 0, секанс не определен. Таким образом, мы получаем следующий график sec x:
Таким образом, мы получаем следующий график sec x:
Домен и диапазон секущей функции
Глядя на функцию секущей в области с центром на оси Y, мы можем выявить ее симметрию. Таким образом, как мы можем видеть на графике функции секущей выше, функция секущей симметрична относительно начала координат. Таким образом, областью секущей являются все действительные числа, кроме точек (2n + 1)π/2. Диапазон секанса — это множество всех действительных чисел с величиной, большей или равной 1. Таким образом, мы имеем:
- Область определения функции секущей: R — (2n + 1)π/2
- Диапазон функции секанса: (-∞,-1] U [1, ∞)
Свойства функции секущей
Свойства функции секущей зависят от квадранта, в котором находится угол. Из приведенного выше графика секущей и окружности видно, что значение функции секущей положительно в первом и четвертом квадранте, тогда как во втором и третьем квадранте оно имеет отрицательное значение. Перечислим некоторые основные свойства функции секущей:
Перечислим некоторые основные свойства функции секущей:
- Функция секанса является периодической функцией.
Периодическая функция – это функция, которая при определенном сдвиге по горизонтали P приводит к функции, равной исходной функции, т. е. f(x + P) = f(x), для всех значений x в пределах области ф. График секущих повторяется через 2π, что предполагает периодичность функции с периодом 2π.
Итак, мы можем сказать, что: sec(x+2nπ) = sec x, для каждого x
- Функция секущей является четной функцией, поскольку sec(-x) = sec x для всех x.
- сек x имеет вертикальные асимптоты при всех значениях x = π/2 + nπ, где n — целое число.
- График функции секущей симметричен относительно оси Y.
Важные примечания о функции секанса
- Функция секанса может быть математически записана как: сек x = гипотенуза / основание
- Это периодическая функция с периодом 2π.

- Область определения секущей равна R — (2n + 1)π/2, а диапазон равен (-∞,-1] U [1, ∞).
☛ Похожие темы
- Cos Sec Tan
- Тригонометрические функции
- Наклон секущей линии Формула
Часто задаваемые вопросы о функции секущей
Что такое секущая функция в тригонометрии?
Секущая функция — одна из важных тригонометрических функций в тригонометрии. Он равен отношению гипотенузы к основанию прямоугольного треугольника. Функция секанса также известна как функция, обратная функции косинуса.
Как вы
Напишите функцию секущей?Мы можем записать формулу секущей как sec x = Hypotenuse / Base. Его также можно записать как sec x = 1 / cos x, поскольку он является обратной величиной cos x.
Что такое определение секущей?
Функция секанса или функция сек может быть определена как отношение длины гипотенузы к длине основания в прямоугольном треугольнике.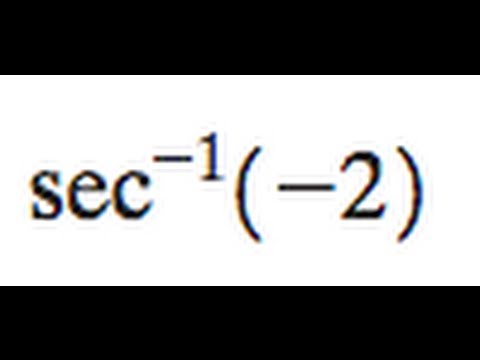
Что такое секанс относительно Cos?
Функция секущей относительно cos записывается как sec x = 1 / cos x.
Где секанс
Функция не определена?Функция секущей не определена в точках, где значение функции косинуса равно 0. Значение cos x равно нулю во всех действительных числах, кроме (2n + 1)π/2. Итак, функция секущей не определена в точках (2n + 1)π/2, где n — целое число.
В каком квадранте секанс отрицателен?
Функция секущей отрицательна во втором и третьем квадранте.
Чему равна функция, обратная секущей?
Используя взаимные тождества, мы знаем, что функция, обратная секущей, является функцией косинуса.
Является ли секущая функция четной функцией?
Функция секущей является четной функцией, поскольку sec (-x) = sec x для всех x.
Что такое домен и диапазон функции секущей?
Область определения секущей равна R — (2n + 1)π/2, а диапазон равен (-∞,-1] U [1, ∞).
Что такое период секущей функции?
Период секущей равен 2π.
Где находятся вертикальные асимптоты на графике секущей функции?
Функция секущей имеет вертикальные асимптоты в точках, где функция косинуса равна нулю. Поскольку sec x является обратной величиной cos x, поэтому sec x не определен в точках, где cos x равен 0. Таким образом, функция секанса имеет вертикальные асимптоты в точках (2n + 1) π/2, где n — целое число.
Функция секанса (сек) — Тригонометрия
Функция секанса (сек) — Тригонометрия — Открытый справочник по математикеОткрытый справочник по математике
Главная Контакт О Тематический указатель
В прямоугольном треугольнике секанс угла равен длине гипотенузы, деленной на длина соседней стороны. В формуле это сокращается до «сек».
Из шести возможных тригонометрических функций
секанс,
котангенс и
косеканс, используются редко.
На самом деле, у большинства калькуляторов нет кнопки для них, и библиотеки функций программного обеспечения не включают их.
Их можно легко заменить производными от более распространенных трех: sin, cos и tan.
Секанс можно получить как обратную величину косинуса:
Функция арксеканса — arcsec
Для каждой тригонометрической функции, такой как sec, существует обратная функция, которая работает в обратном порядке. Эти обратные функции имеют то же имя, но с «дугой» впереди. Таким образом, обратным значением sec является угловая секунда и т. д. Когда мы видим «угловую секунду A», мы интерпретируем ее как «угол, секанс которого равен A».
| сек 60 = 2.000 | Означает: секанс 60 градусов равен 2.000 |
| угловых секунд 2,0 = 60 | Означает: угол, секанс которого равен 2,0, равен 60 градусам. |
Иногда пишется как asec или sec -1
Большие и отрицательные углы
В прямоугольном треугольнике два переменных угла всегда меньше 90°.

 функций 6 букв
функций 6 букв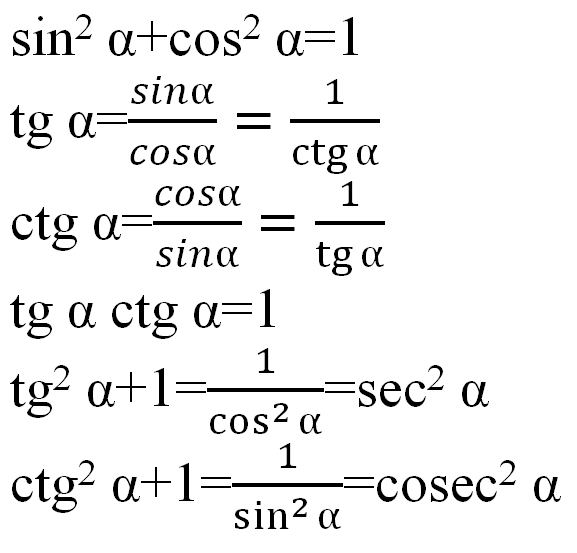 «функция 7 букв
«функция 7 букв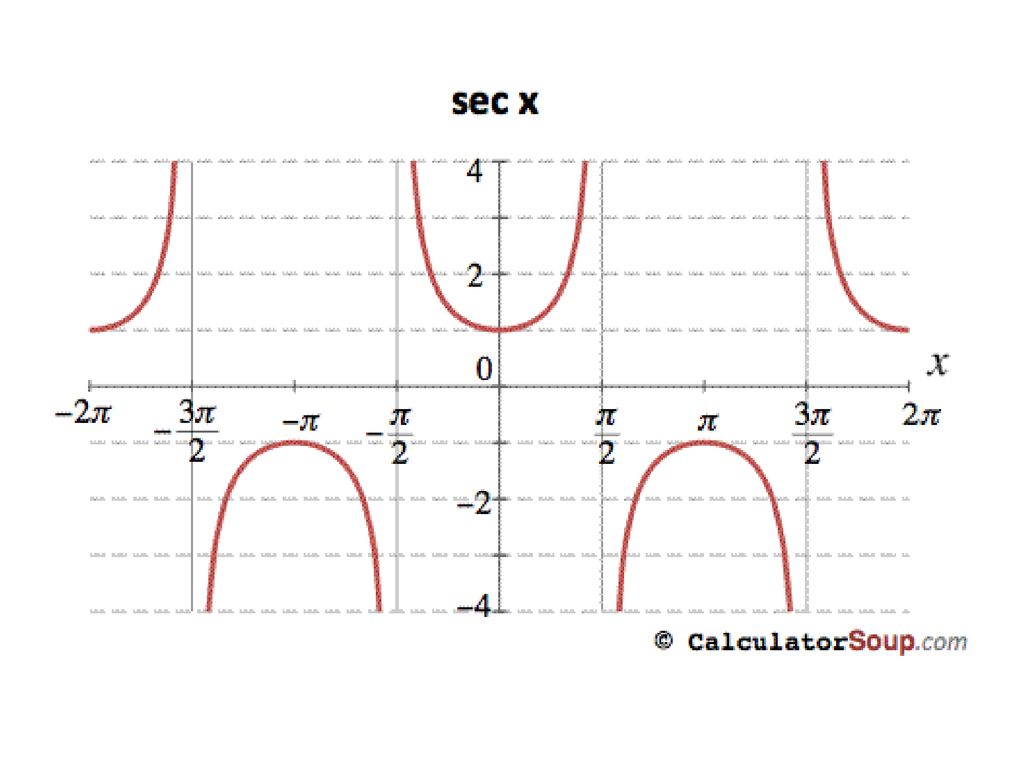 функция 9 букв
функция 9 букв