Учебник по высшей математике письменный онлайн: Письменный Д.Т. Конспект лекций по высшей математике

Д.Т. Письменный — Конспект лекции по высшей математике (2006) — PDF

PDF-файл из архива «Д.Т. Письменный — Конспект лекции по высшей математике (2006)», который расположен в категории «». Всё это находится в предмете «математический анализ» из раздела «», которые можно найти в файловом архиве НИУ «МЭИ» . Не смотря на прямую связь этого архива с НИУ «МЭИ» , его также можно найти и в других разделах. .

Дмитрий ПисьменныйКонспектvлекцииvпо вышеииматематикеПолный курс4-е изданиеМОСКВА~~ АЙРИС ПРЕСС2006УДКББК517(075.8)22.1я73-2П34Все права защищены.Никакая часть данной книги не может переиздаватьсяили распространяться в любой форме и любыми средствами,электронными или механическими, включая фотокопирование,звукозапись, любые запоминающие устройстваи системы поиска информации,без письменного разрешения правообладателя.Серийное оформление А.

М. ДраговоuПисьменный, Д. Т.П34/2006.-Конспект лекций по высшей математике: полный курсД. Т. Письменный.608с.: ил.—4-е изд. -М.: Айрис-пресс,(Высшее образование).ISBN 5·8112·1778-1Настоящий курс лекций предназначен для всех категорий студентоввысших у ч ебных заведений, изучающих в том или ином объеме высшуюматематику.Книга содержит необходимый материал по всем разделам курса выс­шей математики (линейная и векторная алгебра, аналитическая геомет­рия, основы м а тематического анализа), которые обычно изучаются сту­дентами на п е рвом и втором курсах вуза, а также дополнительные главы ,необходимые при’ изучении специальных курсов (двойные, тройные, криво­линейные и повер х ностные интегралы, дифференциальные уравнения, эле­менты теории поля и теории функций комплексного переменного, основыоперационного исчисления).Изложение теоретического материала по всем темам сопровождаетсярассмотрением большого количества примеров и задач, ведется на доступ­ном, по возможности строгом языке.Пособие поможет студентам освоить курс высшей математики, подго­товиться к сдаче зачетов и экзаменов по математическим дисциплинам.ББК 22.

1л73-2ISBN 5-8112-1778-1©УДК517(075.8)Айрис-пресс ,2005, 2006ОГЛАВЛЕНИЕПредисловие……………………………………………..15Глава 1.

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ§ 1.Матрицы………………………………………………1.1.1.2.§ 2.Основные понятия…………………………………Действия над матрицами…………………………..Определители………………………………………….2.1.2.2.Основные понятия………………. . . .

…………………..§ 3. Невырожденные матрицы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3.1. Основные понятия… ………………………………3.2. Обратная матрица. . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . .3.3. Ранг матрицы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .§ 4. Системы линейных уравнений. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4.1. Основные понятия. . . . . . .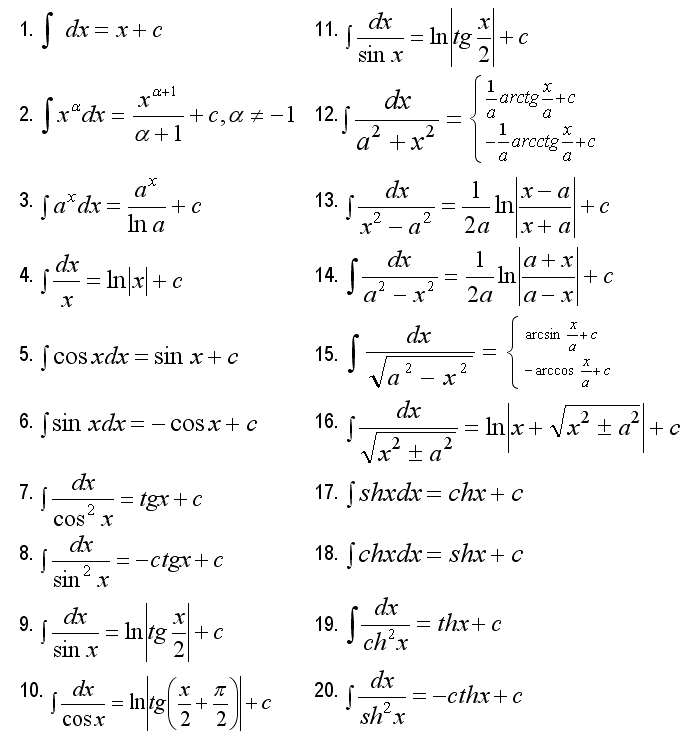

. . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . .4.2. Решение систем линейных уравнений.Свойства определителей………………………Теорема Кронекера-Капелли……………………….4.3.Решение невырожденных линейных систем.4.4.4.5.Решение систем линейных уравнений методом Гаусса.Формулы КрамераСистемы………………………………….линейных однородных уравнений. . . . . . . . .

. . . . .16161720202224242527292930323437Глава 11. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ§ 5.Векторы……………………………………………….5.1.5.2.5.3.5.4.Основные понятия…………………….. . …. . …….5.5.Действия над векторами, заданными проекциямиЛинейные операции над векторами……….Проекция вектора на ось…………………………………….Разложение вектора по ортам координатных осей.Модуль вектора. Направляющие косинусы.§ 6………………..Скалярное произведение векторов и его свойства…………6.1.6.2.6.3.Определение скалярного произведенияСвойства скалярного произведения.

. ………………………………..4445474748Выражение скалярного произведения………………………………………§ 7.

Векторное произведение векторов и его свойства. . . . . . . . . . . .7.1. Определение векторного произведения ……….. …….через координаты.6.4.39394042Некоторые приложения скалярного произведения3495051517.2.7.3.Свойства векторного произведения……………………………………………………..

.. . ..произведение векторов.. . . . . . . . . . . . . . . . . . . . . . . . . .через координаты .7.4.§ 8.Некоторые приложения векторного произведения .Смешанное8.1…………………………….. .. .. ….. … .. . ..Свойства смешанного произведения5555Выражение смешанного произведениячерез координаты.8.4.535455Определение смешанного произведения,его геометрический смысл.8.2 .8.3.52Выражение векторного произведения… .. ….

… …. …. .. …. .. .. … …. …. .. ..Некоторые приложения смешанного произведенияГлава111. 5657АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯНА ПЛОСКОСТИ§ 9.Система координат на плоскости.9.1 .9.2………………………..Основные понятия . .. .. ……………… . ……………Основные приложения метода координатна плоскости.9.3.§ 10.. ….

.. .. …. … .. .. .. …… ….. .. … .. .. ……. .. .. … … . .. ..плоскости. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Преобразовани е с истемы координат.Линии на10.1. Основные понятия .. …….. . … . .. . . .. .. . .. . . . .. .

. .. . …10.2. Уравнения прямой на плоскости. . …. .. … . …………10.3. Прямая линия на плоскости. Основные задачи. . . . . . . . .§ 11.5858Линии второго порядка на плоскости….. ….. …………..11 .1. Основные понятия….. .

……………. … …………..11 .2. Окружность . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11 .3. Эллипс… . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . .. . . .. . . . . . . . .11.4. Гипербола .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11 .5. Парабола…… . .. …. . . ……. .. . . .. … . . . . . . . . . .. . ……11 .6. Общее уравнение линий второго порядка . …………..ГлаваIV.60616464687374747576798486АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯВ ПРОСТРАНСТВЕ§ 12.Уравнения поверхности и линии в простран стве ………….12.1. Основные понятия . ….

… ….. . . .. . . . . . .. .. . …………12.2. Уравнения плоскости в пространстве . .. . …. .. … . .. .. .12.3. Плоскость. Основные задачи. . . . . . . . . . . . . . . . . . . . . . . . . . . .12.4. Уравнения прямой в пространстве …… . . .. . …. … .. ..12.5. Прямая линия в пространстве. Основные задачи. . . . . . .12.6. Прямая и плоскость в пространстве.Основные задачи. …

. . …………… .. . . .. …………..12.7. Цилиндрическиеповерхности.49090929698101103. . . . . . . . . . . . . . . . . . . . . . . . . .. 10412.8. Поверхности вращения. Конические поверхности. . . . . . .12.9. Канонические уравнения поверхностей106второго порядка……………………. . ……. .. … . ..109Глава У. ВВЕДЕНИЕ В АНАЛИЗ§ 13.Множества. Действительные числа… …

…. .. .. …. … …. .13.1.0сновные понятия……… . ……….. . .. . ………… . .13.2. Числовыемножества.Множество действительных чисел…. ….. .. .. .. ……..13.3. Числовые промежутки . Окрестность точки. . . . . . . . . . . . .§ 14. Функция. . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . .14.1. Понятие фуНКции….. .. ……. .. ……. . . .. . . . . … . .. .. .14.2. Числовые функции . График функции .Способы задания функций. . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . .14.3. Основные характеристики функции……… . .. … . … . .14.4. Обратная функция. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..14.5. Сложная функция. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..14.6. Основные элементарные функции и их графики.. . .

. . . .§ 15. Последовательности…………………………….. …… .15.1. Числовая последовательность………….. . …… . . . . ..15.2. Предел числовой последовательности……….. . .. . . .. .15.3. Предельный переход внеравенствах. . . . . . . . . . . .

. . . . . . . .15.4. Предел монотонной ограниченной последовательности .Число е. Натуральные логарифмы. . . . . . . . . . . . . . . . . . . . . .§ 16. Предел функции. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . .16.1. Предел функции в точке. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .16.2. Односторонние пределы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .16.3. Предел функции при х ~ 00 . . . . . . . . . . . . . . . . . . . . . . . . . . . «16.4. Бесконечно большая функция (б. б.ф.). . . . . . . . . . . .

Конспект лекций по высшей математике, Полный курс, Письменный Д. Т, 2009

Высшая математика конспекты

Конспект лекций по высшей математике, Полный курс, Письменный Д. Т., 2009.

Настоящий курс лекций предназначен для студентов, изучающих высшую математику в том или ином объеме в различных учебных заведениях.
Книга содержит необходимый материал по всем разделам курса высшей математики (линейная и векторная алгебра, аналитическая геометрия, основы математического анализа), которые обычно изучаются студентами на первом и втором курсах вуза, а также дополнительные главы, необходимые при изучении специальных курсов (двойные, тройные, криволинейные и поверхностные интегралы, дифференциальные уравнения, элементы теории поля и теории функций комплексного переменного, основы операционного исчисления).
Доступный, но строгий с научной точки зрения язык изложения, а также большое количество примеров и задач позволят студентам освоить курс высшей математики и эффективно подготовиться к сдаче зачетов и экзаменов.

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.

Решить систему — это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.

Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.

Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы.

ОГЛАВЛЕНИЕ.
Предисловие.
Глава I. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ.
Глава II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ.
Глава III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ.
Глава IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ.
Глава V. ВВЕДЕНИЕ В АНАЛИЗ.
Глава VI. КОМПЛЕКСНЫЕ ЧИСЛА.
Глава VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
Глава VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
Глава IX. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.
Глава X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
Глава XI. ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ.
Глава XII. КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ.
Глава XIII. ЧИСЛОВЫЕ РЯДЫ.
Глава XIV. СТЕПЕННЫЕ РЯДЫ.
Глава XV. РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ.
Глава XVI. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ.
Глава XVII. ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО.
Глава XVIII. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ.
Приложения.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Конспект лекций по высшей математике, Полный курс, Письменный Д. Т., 2009 — fileskachat. com, быстрое и бесплатное скачивание.

Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгу

КОМПЛЕКСНЫЕ ЧИСЛА.

Obuchalka. org

11.03.2019 5:48:42

2019-03-11 05:48:42

Источники:

Https://obuchalka. org/20201117126953/konspekt-lekcii-po-visshei-matematike-polnii-kurs-pismennii-d-t-2009.html

Конспект лекций и задачи по курсу Высшая математика: Учебное пособие. Скачать бесплатно онлайн в электронном виде | Единое окно » /> » /> .keyword { color: red; }

Высшая математика конспекты

Библиографическая ссылка:: Пучков Н. П. Конспект лекций и задачи по курсу «Высшая математика»: учебное пособие. — Тамбов: Изд-во Тамб. гос. техн. ун-та, 2008. — Ч. 1. — 80 с.

Представлены конспекты лекций по курсу «Высшая математика», содержащие основные понятия разделов «Элементы линейной алгебры и аналитической геометрии» и «Дифференциальное исчисление функции одной переменной». Приведены задачи, а также образцы экзаменационных билетов по названным разделам учебной программы. Рекомендуется студентам вузов экономических специальностей.

Конспект лекций и задачи по курсу Высшая математика Учебное пособие.

Window. edu. ru

30.10.2020 11:40:46

2020-10-30 11:40:46

Источники:

Http://window. edu. ru/resource/151/64151

2 курс | Кафедра Высшей Математики и Математической Физики » /> » /> .keyword { color: red; }

Высшая математика конспекты

Санкт-Петербургский Государственный Университет, Физический Факультет

Общие лекции

1 семестр

Высшая математика
Основной поток — лектор А. М.Будылин Усиленный поток — лектор А. А.Федотов Базовый поток — лектор С. Б.Левин

2 семестр

Основной поток — лектор А. М.Будылин Усиленный поток — лектор А. А.Федотов Базовый поток — лектор С. Б.Левин

Лекции

Усиленный поток

Основной поток

Базовый поток

Семинары

Появились результаты экзамена по Высшей математике 2 курса (18. 06.2018), усиленный поток, лектор А. А. Федотов.

Появились результаты экзамена на втором курсе в общем потоке. Апелляция — во вторник, 14-го июня.

Появились результаты экзамена на втором курсе в теоретическом потоке. Апелляция — во вторник, 14-го июня, 13:00, встреча в фойе физического факультета.

Появились результаты коллоквиума по высшей математике, второй курс, теоретический поток.

Апелляция у теоретического потока будет на первой лекции (или после нее).

У практического потока специальной апелляции по коллоквиуму нет, но в течение двух-трех недель после коллоквиума желающие могут персонально договориться с А. М. Будылиным об апелляции.

Апелляция и оформление зачёток на втором курсе в усиленном потоке (Федотов А. А.) состоится 19-го января (вторник) в 15-00 на факультете (встреча у расписания).

Появились результаты экзамена по Высшей математике. Второй курс, теоретический поток. Весенний семестр 14-15.

Появились результаты коллоквиума по Высшей математике. Второй курс, теоретический поток. Весенний семестр 14-15.

Появились результаты экзамена по Высшей математике. Второй курс, теоретический поток. Осенний семестр 14-15

1 семестр

бесплатных учебников по математике | Открытая культура

Бесплатные учебники (также известные как открытые учебники), написанные знающими учеными, — относительно новое явление. Ниже вы найдете мета-список бесплатных учебников по математике, которые являются частью нашей большой коллекции «200 бесплатных учебников: мета-коллекция». Также см. нашу онлайн-коллекцию , 1700 бесплатных онлайн-курсов от лучших университетов.

• Абстрактная алгебра: базовый выпускной год Роберт Б. Эш, Иллинойский университет
• Абстрактная алгебра: теория и приложения, Томас В. Джадсон, Государственный университет Стивена Ф. Остина
• Продвинутая алгебра II, Кенни Фелдер, Чартерная средняя школа Роли
• Расширенное исчисление Штернберг Шломо и Линн Лумис, Гарвардский университет
• Алгебра 1 (9 и 10 классы), Эндрю и Энн Глоаг, Высшая школа высоких технологий в Сан-Диего, Калифорния
• Алгебра и анализ для компьютерных наук, Жан Галье, Пенсильванский университет.
• Прикладная вероятность, Пол Пфайффер, Университет Райса
• Базовый анализ, Иржи Лебл, Университет Иллинойса в Урбана-Шампейн
• Основные понятия математики, Элиас Закон, Виндзорский университет
• Базовая теория вероятностей Роберта Б. Эша, Иллинойский университет
• Основы вероятности и статистики, Бренда Мири, учитель математики средней школы в Глейс-Бей, Новая Шотландия
• Книга доказательств доктора Ричарда Хаммака, Университет Содружества Вирджинии
• Исчисление для начинающих и художников от Массачусетского технологического института
• Онлайн-учебник по исчислению, Гилберт Странг, Массачусетский технологический институт
• Исчисление (PDF) Дэвида Гишара, Колледж Уитмена.
Исчисление
•  (PDF) Гилберта Странга, Массачусетский технологический институт
• Исчисление 1 Пола Докинза, Ламарский университет
• Исчисление 2 Пола Докинза, Ламарский университет
• Исчисление 3 Пола Докинза, Ламарский университет
• Исчисление с приложениями, Даниэль Клейтман, Массачусетский технологический институт
• CK-12 Геометрия (10–12 классы) от нескольких авторов. Охватывает учебную программу Калифорнии.
• CK-12 Исчисление одной переменной (11–12 классы) от нескольких авторов. Охватывает учебную программу Калифорнии.
• CK-12 Тригонометрия — второе издание (10–12 классы) от нескольких авторов. Охватывает учебную программу Калифорнии.
• Совместная статистика Барбары Илловски, доктора философии, и Сьюзен Дин, Колледж Де Анза
• Колледж алгебры Пола Докинза, Ламарский университет
• Комплексный анализ Джорджа Кейна, Технологический институт Джорджии
• Комплексные переменные Роберт Б. Эш, Университет Иллинойса
• Вычислительная геометрия Николаса М. Патрикалакиса, Такаси Маекава, Массачусетский технологический институт
• Вычислительное введение в теорию чисел и алгебру Виктора Шоупа, NYU
• Курс алгебраической теории чисел Роберта Б. Эша, Иллинойский университет
• Курс коммутативной алгебры Роберта Б. Эша, Иллинойский университет
• Дизайн сравнительных экспериментов Р. А. Бейли, Лондонский университет
• Разностные уравнения для дифференциальных уравнений: введение в исчисление, Дэн Слоутер, Университет Фурмана
• Дифференциальные уравнения Пола Докинза, Ламарский университет
• Дискретная математика: открытое введение Оскара Левина, Университет Северного Колорадо
• Динамические системы С. Штернберга, Гарвардский университет
• Учебник по электронной статистике Т. Хилла и П. Левицки.
• Элементарная абстрактная алгебра У. Эдвина Кларка, Университет Южной Флориды
• Элементарное исчисление: подход к бесконечно малым, Г. Джером Кейслер, Университет Висконсин-Мэдисон
• Элементарные дифференциальные уравнения (PDF) Уильяма Ф. Тренча, Тринити-университет
• Элементарные дифференциальные уравнения с краевыми задачами (PDF) Уильяма Ф. Тренча, Университет Тринити,
• Руководство по решениям для учащихся элементарных дифференциальных уравнений и элементарных дифференциальных уравнений с краевыми задачами (PDF) Уильяма Ф. Тренча, Университет Тринити
• Элементарная линейная алгебра Кит Мэтьюз, Университет Квинсленда
• Элементарная теория чисел, В. Эдвин Кларк, Университет Южной Флориды
• Элементы абстрактной и линейной алгебры, Эдвин Х. Коннелл, Университет Майами
• Первый курс комплексного анализа Матиаса Бека, Джеральда Маркези и Денниса Пикстона, SUNY — Бингемтон
• Первый курс линейной алгебры доктора Роберта Бизера, Университет Пьюджет-Саунд
• функций, определяемых несобственными интегралами (PDF) Уильяма Ф. Тренча, Университет Тринити,
• Генерирующая функционалология Герберта Уилфа, Пенсильванский университет
• Введение в матричную алгебру Аутар К. Кау, Университет Южной Флориды
• Введение в теорию вероятности, статистику и случайные процессы Хоссейн Пишро-Ник, UMass Amherst
• Введение в теорию вероятности (PDF) Чарльза Гринстеда и Дж. Лори Снелл, Swarthmore & Dartmouth Colleges
• Введение в реальный анализ (PDF) Уильяма Ф. Тренча, Университет Тринити
• Введение в статистическое обучение (PDF) Гарета Джеймса, Даниэлы Виттен, Тревора Хасти и Роберта Тибширани
• Введение в методы социальных сетей Роберт А. Ханнеман и Марк Риддл, Калифорнийский университет в Риверсайде
• Введение в статистическую мысль, Майкл Лавин, UMASS
• Введение в теорию чисел Лео Мозер, Макгилл
• Вводная статистика: концепции, модели и приложения , Дэвид В. Стокбургер, штат Миссури,
• Лекции по теории вероятностей, статистике и эконометрике, Марко Табога, экономист, Банк Италии
• Лекции по статистике Роберта Б. Эша, Иллинойский университет
• Линейная алгебра (PDF) Джима Хефферона, Колледж Святого Михаила
• Линейная алгебра Пола Докинза, Ламарский университет
• Math Alive, Ингрид Добеши, Принстонский университет
• Математика в обществе, Дэвид Липманн, Колледж Пирса
• Математика, числа и программирование (для инженеров-механиков), Масаюки Яно, Массачусетский технологический институт
• Математические методы инженерного анализа (PDF) Эрхана Чинлара и Роберта Дж. Вандербей, Принстонский университет
• Многомерное исчисление Джорджа Кейна и Джеймса Ирода, Технологический институт Джорджии
• Доказательства и концепции: основы абстрактной математики, Дэйв Витте Моррис и Джой Моррис, Университет Летбриджа
• Вещественные переменные с базовой топологией метрического пространства Роберт Б. Эш, Университет Иллинойса
• Статистика Филипа Б. Старка, Калифорнийский университет — Калифорнийский университет в Беркли
• Краткий обзор исчисления Карла Хайнца Доверманна, Гавайский университет
• Книга «A = B» Марко Петковсека, Герберта Уилфа и Дорона Зейлбергера, Univ. Пенсильвании и Рутгерса
• Элементы статистического обучения Тревора Хасти, Роберта Тибширани и Джерома Фридмана
• Метод множителей Лагранжа (PDF) Уильяма Тренча, Университет Тринити,
• Исчисление функций нескольких переменных, Дэн Слоутер, Университет Фурмана
• Еще один текст по исчислению Дэна Слоутера, Университет Фурмана

Онлайн-книги по математике

Общие
Элементарная алгебра и тригонометрия
Абстрактная алгебра
Математический анализ и вычисления
Дифференциальные уравнения
Линейная алгебра
Геометрия и топология
Математическая логика
Теория категорий
Теория чисел
Вероятность и статистика
Вычислительная математика
Прикладная математика и математическая физика
История математики и популярные книги

Алгебраические и геометрические методы в перечислительной комбинаторике
Федерико Ардила, 2014 г. , 143 стр., 1,8 МБ, PDF

Аналитическая комбинаторика
, Филипп Флажоле, Роберт Седжвик, 2008 г., 822 страницы, 9,8 МБ

Прикладные дискретные конструкции
Эл Дорр, Кен Левассер, 2013 г., 496 стр., Несколько файлов PDF

Assessing Mathematical Proficiency
Алана Х. Шенфельда, 2007 г., 391 страница, PDF

Комбинаторная теория: расположение гиперплоскостей
Ричарда Стэнли, 2004 г., PDF

Комбинаторика через управляемое открытие
Кеннета П. Богарта, 2004 г., 202 стр., 1,2 МБ, PDF

Современные проблемы математического образования
под редакцией Эстелы А. Гавосто, Стивена Г. Кранца, Уильяма МакКаллума, 1999 г.

Теория несоответствия
, Уильям Чен, 2012 г., 99 стр., 960 КБ, PDF

Дискретная математика
Викиучебник, 2012 г.

Дискретные структуры
, Владлен Колтун, 2008 г., 89 стр., 420 КБ, PDF

Элементарная компьютерная математика
Кеннет Р. Келер, 2002

Перечислительная комбинаторика: том 1
Ричарда П. Стэнли, 2011 г., 725 стр., 4,4 МБ, PDF

Изучение дискретной математики с помощью Maple
, Кеннет Х. Розен, 1996 г., 400 стр., Несколько файлов PDF

Теория дробных графов: рациональный подход к теории графов
, Дэниел Ульман, Эдвард Шейнерман, 2008 г., 167 страниц, 1,2 МБ, PDF

Теория графов
, Кейо Руохонен, 2008 г., 114 стр., 930 КБ, PDF

Теория графов
Рейнхарда Дистеля, 2005 г., 422 страницы, 2,9 МБ, PDF

Теория графов: расширенные алгоритмы и приложения
, Берил Сирмачек (ред.), 2018 г., 196 стр., Несколько файлов PDF

Уроки теории графов
, Кристофер П. Мавата, 2018 г., 384 стр., Онлайн-чтение

Справочник по рисованию и визуализации графиков
, Роберто Тамассиа (редактор), 2013 г., 862 стр., Несколько файлов PDF

Графики пересечений: введение
, Мадхумангал Пал, 2014 г., 49 стр., 470 КБ, PDF

Введение в комбинаторику и теорию графов
Дэвида Гишара, 2017 г., 153 стр. , 1,1 МБ, PDF

Введение в математическую философию
Бертрана Рассела

Лекции по философии математики
Джеймс Бирни Шоу, 19 лет18, 222 стр., несколько форматов

Математическая подготовка для всех учащихся
, Дебора Ловенберг Болл, 2003 г., PDF

Matroid Decomposition
Клауса Трумпера, 2009 г., PS

Тайна РЕАЛЬНОГО, трехмерный фрактал Мандельброта
Дэниела Уайта, 2008 г.

New Frontiers in Graph Theory
, Яган Чжан (ред.), 2012 г., 526 стр., 18 МБ, PDF

Новые перспективы в алгебраической комбинаторике
под редакцией Л. Биллеры, А. Бьорнера, К. Грина, Р. Симиона, Р. Стэнли, 1999, PS/PDF

Заметки по комбинаторике
Питера Дж. Кэмерона, 2007 г., 130 стр., 440 КБ, PDF

Философия математики
Альберта Тейлора Бледсо, 1886 г., 248 страниц, 16 МБ, PDF

Философия математики
Огюста Конта, 1851 г.

A Primer of Mathematical Writing
Стивен Г. Кранц, 2016 г.