Угол в математике это: Угол — урок. Математика, 2 класс.

Углы | Математика

Две прямые линии BA и BC (черт. 13), пересекающиеся в одной и той же точке B, образуют при точке B угол.

Определение угла. Углом называется неопределенная часть плоскости, ограниченная двумя пересекающимися прямыми линиями. Угол есть величина, определяющая наклонение одной прямой линии к другой.

Стороны угла. Пересекающиеся линии называются сторонами угла.

Вершина угла. Точка пересечения двух прямых называется вершиной угла. Величина угла не зависит от длины сторон, поэтому стороны угла можно неопределенно продолжать.

Название угла. a) Углы называют буквой, стоящей при вершине; так угол на черт. 13 называют углом B. b) Если при вершине несколько углов, то углы называют тремя буквами, стоящими при вершине и двух его сторонах. При этом буква при вершине произносится и пишется в середине.

На черт. 13 угол B называют угол ABC. Линии BA и BC — две стороны, а точка B — вершина угла.

Таким образом угол ABC есть угол B или

угол ABC = углу B.

Знак угла. Слово угол заменяют иногда знаком ∠.

Таким образом предыдущее равенство изображают письменно:

∠ABC = ∠B

В том случае, когда из точки выходит несколько линий, при точке B имеется несколько углов.

На черт. 14 из точки B выходят прямые линии BA, BC, BD и при вершине B имеются углы ABC, CBD, ABD.

Прилежащие углы. Два угла называются прилежащими, когда они имеют общею вершину, по одной общей стороне, а две другие лежат по обе стороны общей стороны.

Углы ABC и CBD (черт. 14) суть прилежащие углы. Они имеют общую вершину B, общую сторону BC, а две другие стороны BA и BD лежат одна сверху, а другая снизу общей стороны BC.

Углы изменяют свою величину, если изменяется наклонение одной стороны к другой. Из двух углов, имеющих общую вершину, тот угол, внутри которого помещается другой угол, называется большим углом. На чертеже 14

уг. ABD > уг. ABC и уг. CBD < уг. ABD.

Чтобы иметь понятие о взаимной величине двух углов, имеющих разные вершины, накладывают один угол на другой. При наложении совмещают их вершины и по одной стороне, тогда направление другой стороны даст возможность сравнивать их величину. Чтобы сравнить два угла ABC и DEF (черт. 15), накладывают угол DEF на угол ABC так, чтобы сторона EF пошла по стороне BC, точка E совмещалась с точкой B; тогда сторона ED может занять три положения: она может совпасть со стороной BA, упасть внутри и вне угла ABC.

a) Если линия ED совпадет с линией BA, углы называются равными

уг. ABC = уг. DEF.

b) Если линия ED упадет внутри угла ABC и займет положение BG, угол ABC будет больше угла DEF

уг. ABC > уг. DEF.

c) Если же линия ED упадет вне угла ABC по направлению BH, угол ABC меньше угла DEF

уг. ABC < уг. DEF.

Сложение, вычитание, умножение и деление углов.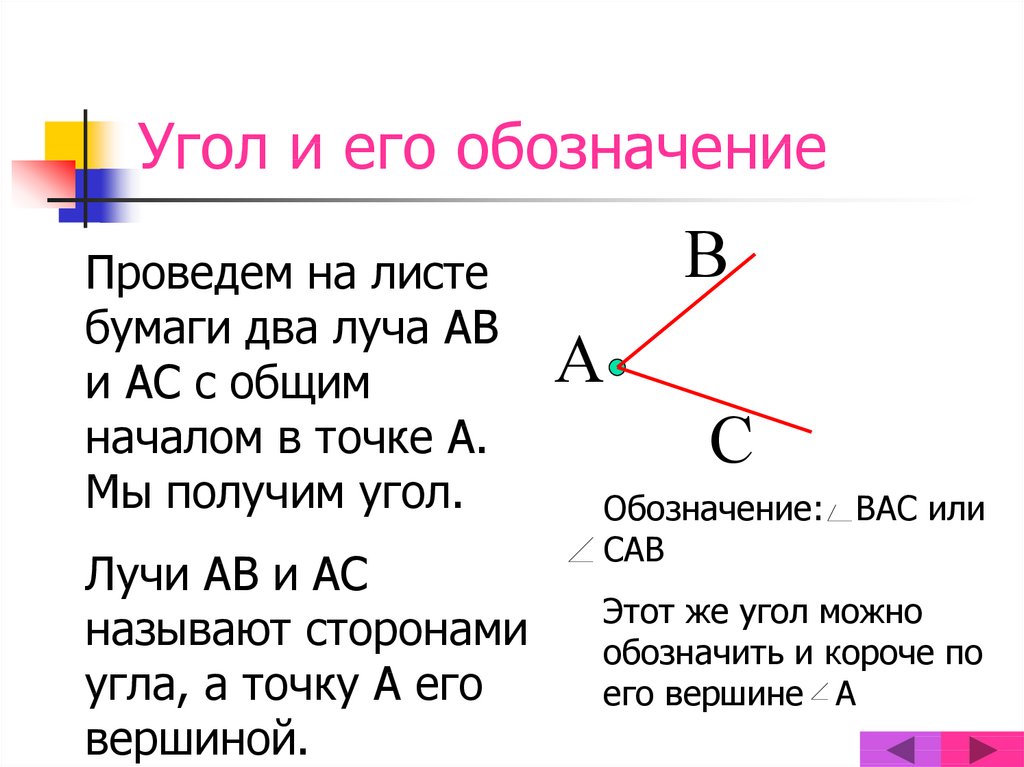 Два прилежащих угла ABC и CBD (чер. 14) образуют один угол ABC. Угол ABD называется суммой углов ABC и CBD. Это выражают письменно равенством:

∠ABD = ∠ABC + ∠CBD (a)

Из равенства (а) вытекает равенство:

∠ABC = ∠ABD — ∠CBD

∠CBD = ∠ABD — ∠ABC,

т. е. угол ABC есть разность углов ABD и CBD, и угол CBD есть разность углов ABD и ABC.

Углы можно складывать и вычитать.

Если при точке O (черт. 16) находится несколько равных прилежащих углов, т. е. если

∠AOB = ∠BOC = ∠COD = ∠DOE,

то угол AOC, равный сумме углов AOB и BOC равен двум углам AOB,

∠AOC = ∠AOB + ∠BOC, след. ∠AOC = 2AOB.

Угол AOD равен трем углам AOB

AOD = 3AOB.

Обратно, угол AOB составляет половину угла AOC, треть угла AOD, четверть угла AOE.

AOB = ½ AOC = 1/3 AOD = ¼ AOE.

Отсюда выводим, что углы как величины можно не только складывать и вычитать, но также умножать и делить на отвлеченное число.

Если из двух прилежащих углов ACD и DCB (чер. 17) две стороны CA и CB лежат на одной прямой, их называют смежными.

Смежные углы. Смежными называются такие углы, у которых одна сторона общая, а две другие лежат на одной прямой.

Если линия CD, поворачиваясь около точки C, займет положение CE, то угол ACD уменьшаясь обратится в угол ACE, а угол BCD увеличиваясь обратится в угол BCE. Линия CD, продолжая поворачиваться, может принять такое положение, что два смежных угла сделаются равными. Когда два смежных угла ACD и DCB равны (чер. 18), их называют прямыми углами.

В этом случае линия CD называется перпендикулярной к линии AB или просто перпендикуляром к линии AB.

На чертеже 19 начерчен один прямой угол без другого смежного с ним.

Прямой угол есть один из равных смежных углов.

Перпендикуляр есть прямая линия, образующая с другой линией прямой угол.

На чертеже 18 углы ACD и DCB, оставаясь смежными и равными, получают название прямых углов. Линия DC будет перпендикулярной к линии AB. Такое взаимное отношение двух линий выражают иногда письменно: CD ⊥ AB.

Так как линия AB будет также перпендикулярна к линии CD, то линия AB и CD будут взаимно-перпендикулярны, т. е. если CD ⊥ AB, то и AB ⊥ CD.

Подошва перпендикуляра. Точка взаимной встречи двух перпендикулярных линий называется подошвою перпендикуляра.

Точка C (чер. 18) есть подошва перпендикуляра CD.

В каждой точке линии AB можно провести перпендикуляр к линии AB.

Провести перпендикуляр к линии (AB) из точки, лежащей на линии, значит восставить перпендикуляр. Провести же перпендикуляр (DC) к линии (AB) из точки (D), лежащей вне прямой, значит опустить перпендикуляр (черт.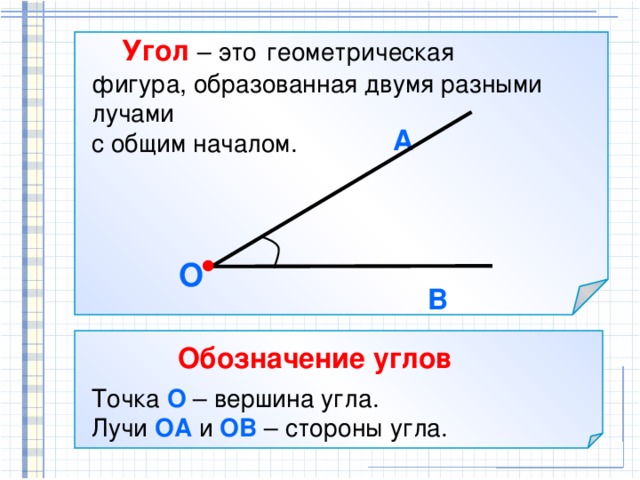 18).

Наклонная линия. Всякая линия неперпендикулярная к другой называется линией наклонною к ней.

На чертеже 20 линия CE будет наклона к линии AB, а линия CD перпендикулярна к линии AB.

Угол ECB меньше прямого, а угол ACE больше прямого. Угол ECB называется острым, а угол ACE тупым.

Острый угол есть всякий угол меньше прямого, а тупой угол есть угол больший прямого.

Одноименные и разноименные углы. Два острых или два тупых угла называются одноименными, а два угла, из которых один острый, а другой тупой, называются разноименными.

Наклонная линия CE образует (черт. 20) с прямою AB два смежных угла, из которых один меньше, а другой больше прямого, т. е. один острый, а другой тупой.

Теорема 3. Из точки, взятой на прямой линии, можно восставить к ней только один перпендикуляр.

Дана прямая AB и на ней точка C (черт. 20).

Требуется доказать, что можно к ней восставить только один перпендикуляр.

Доказательство. Положим, что можно из точки C к линии AB восставить два перпендикуляра (черт. 20) CD и CE. По свойству перпендикуляра

уг. DCB = уг. ACD (a)
уг. BCE = уг. ACE.

Если приложить к первой части последнего неравенства угол ECD, получим неравенство

уг. BCE + уг. ECD > уг. ACE, или уг. BCD > уг. ACE.

Заменяя в этом неравенстве уг. BCD равным ему углом ACD (a), получим

уг. DCA > уг. ACE,

неравенство очевидно нелепое, ибо часть не может быть более своего целого, следовательно предположение, что можно восставить два перпендикуляра, ведет к нелепости, поэтому оно ложно. Ложность предположения основана на том соображении, что из верного положения нельзя вывести неверного заключения, следовательно, наша теорема верна.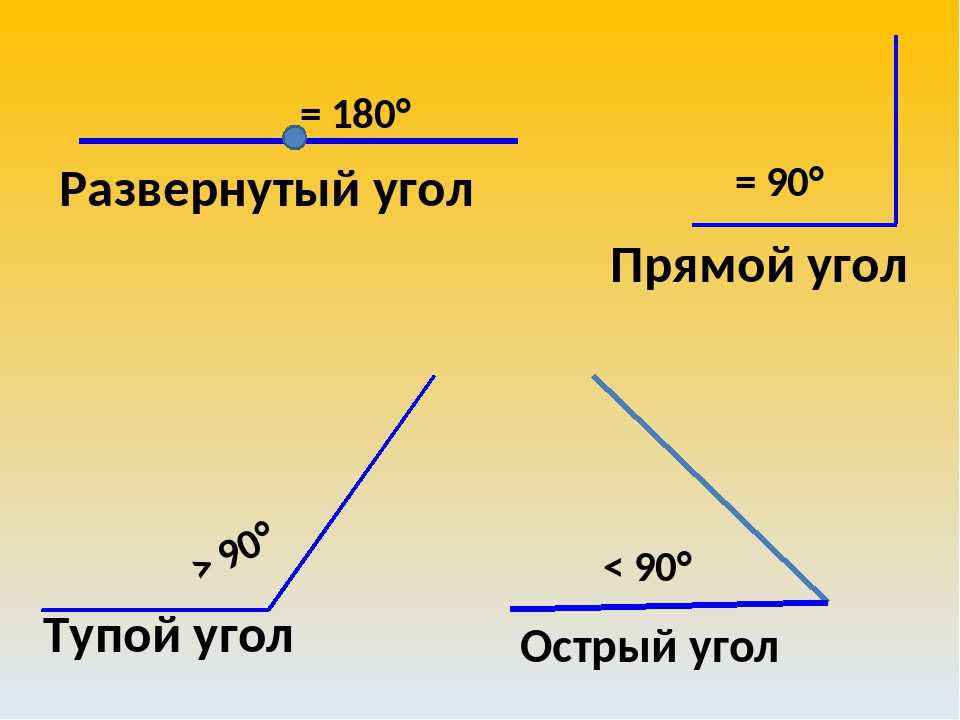

Способ доказывать справедливость данной теоремы указанием на невозможность и нелепость всякого другого предположения называется способом доказательства от противного или способом приведения к нелепости.

Теорема 4. Все прямые углы равны.

Предположим, мы имеем две пары прямых углов: одну пару составляют углы ACD и DCB, а другую углы EGH и HGF, следовательно, CD ⊥ AB и HG ⊥ EF (черт. 21).

Требуется доказать, что прямые углы равны.

Доказательство. Наложим линию EF на линию AB точкой G на точку C, тогда линия GH пойдет по линии CD, ибо из точки C можно восставить только один перпендикуляр, следовательно, прямой угол DCB = прямому углу HGF.

Заключение. Прямой угол есть величина постоянная.

Мера углов. При измерении углов прямой угол, как величину постоянную, принимают за единицу сравнения. Величину его обозначают буквою d.

В таком случае
всякий острый угол < d,
всякий тупой угол > d.

Все углы выражаются при помощи прямого. Так, например, говорят: данный угол равен ½ d, 2/3 d и т. д.

Теорема 5. Сумма двух смежных углов равна двум прямым.

Даны смежные углы ACD и DCB (черт. 22).

Требуется доказать, что ACD + DCB = 2d.

Доказательство. Из точки C восставим перпендикуляр CE, тогда

ACD = ACE + ECD = d + ECD
DCB = ECB — ECD = d — ECD

Сложив эти равенства, имеем:

ACD + DCB = ACE + ECB = 2d (что и требовалось доказать).

Два смежных угла пополняют один другой до двух прямых и потому называются углами дополнительными.

Из теоремы 5 вытекает следствие. Одна пара смежных углов равна другой паре смежных углов.

Теорема 6 (обратная теореме 5).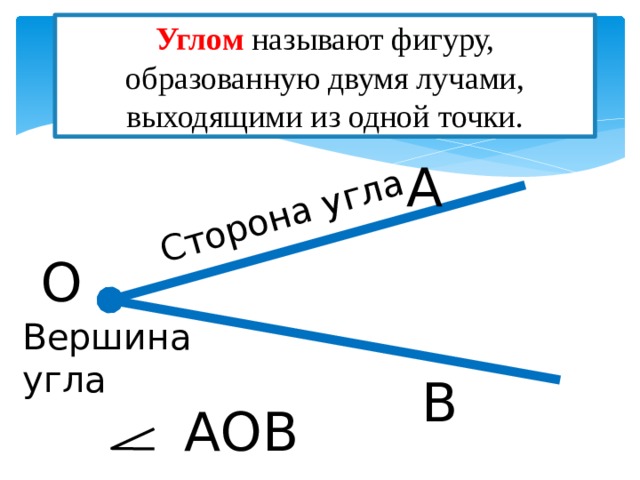 Если сумма двух прилежащих углов равна двум прямым, то две другие стороны лежат на одной прямой.

Пусть сумма двух прилежащих углов ACD и DCB равна двум прямым (черт. 23).

ACD + DCB = 2d.

Требуется доказать, что ACB прямая линия.

Доказательство. Допустим, что ACB есть ломаная линия и что продолжение линии AC будет линия CE, тогда

ACD + DCE = 2d

Две величины равные одной и той же третьей равны (аксиома 3), следовательно

ACD + DCB = ACD + DCE

откуда выходит при сокращении

DCB = DCE

заключение нелепое (часть равна целому, см. акс. 1), следовательно линия ACB есть прямая линия (что и требовалось доказать).

Теорема 7. Сумма углов, имеющих вершину в одной точке и расположенных по одну сторону прямой линии, равна двум прямым.

Даны углы ACD, DCE, ECF, FCG, GCB, имеющие общую вершину в точке C и расположенные по одну сторону прямой AB (черт.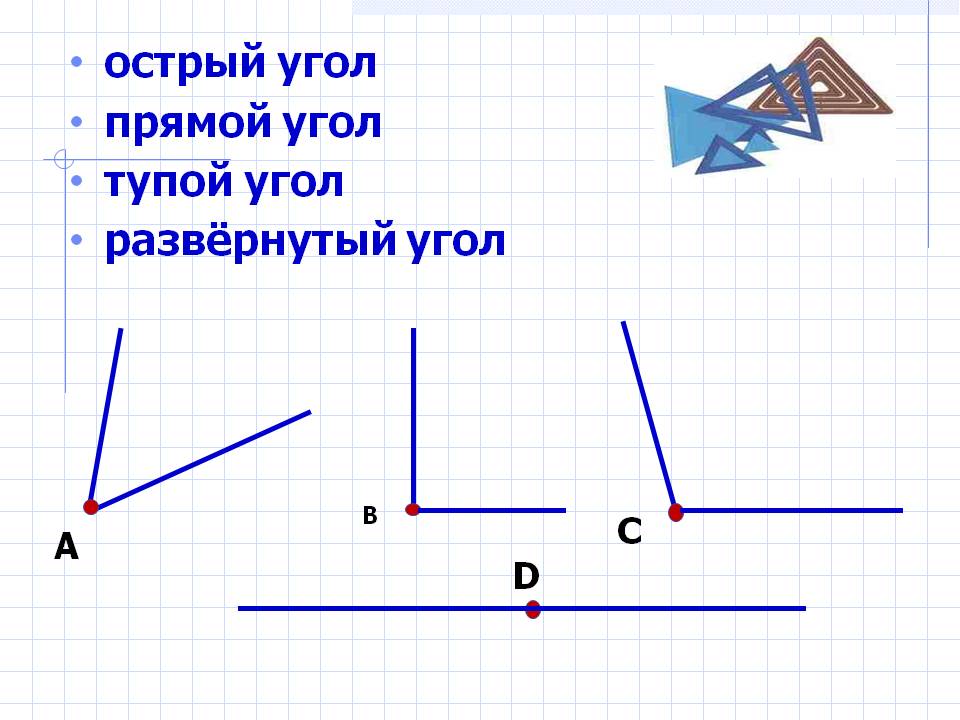 24).

Требуется доказать, что

ACD + DCE + ECF + FCG + GCB = 2d.

Доказательство. МЫ знаем, что сумма двух смежных углов ACF и FCB равна двум прямым (т. 5).

ACF + FCB = 2d.

Так как ACF = ACD + DCE + ECF и FCB = FCG + GCB, то заменяя углы ACF и FCB их величинами, находим:

ACD + DCE + ECF + FCG + GCB = 2d (что и требовалось доказать).

Теорема 8. Сумма всех углов, расположенных вокруг одной точки, равна четырем прямым.

Даны углы AOB, BOC, COD, DOE, EOA, имеющие общую вершину O и расположенные вокруг точки O (черт. 25).

Требуется доказать, что

AOB + BOC + COD + DOE + EOA = 4d.

Доказательство. Продолжим сторону EO по направлению OG (чер. 25), тогда

EOA + AOG = 2d.

Точно также

GOB + BOC + COD + DOE = 2d.

Сложив эти равенства, имеем:

EOA + AOG + GOB + BOC + COD + DOE = 4d.

Так как AOG + GOB = AOB, то

EOA + AOB + BOC + COD + DOE = 4d (ЧТД).

Угол ACB с углом DCE и угол BCD с углом ACE называются вертикальными (чер. 26).

Вертикальные углы. Вертикальными называются такие углы, у которых стороны одного составлены из продолжения сторон другого угла.

Теорема 9. Вертикальные углы равны между собой.

Даны вертикальные углы (чер. 26) ACB и DCE, точно также BCD и ACE.

Требуется доказать, что ACB = DCE и BCD = ACE.

Доказательство. На основании теоремы 5 имеют место равенства:

ACB + BCD = 2d (как сумма двух смежных углов)
BCD + DCE = 2d

следовательно,

ACB + BCD = BCD + DCE

откуда, отняв по равному углу BCD, находим

ACB = DCE.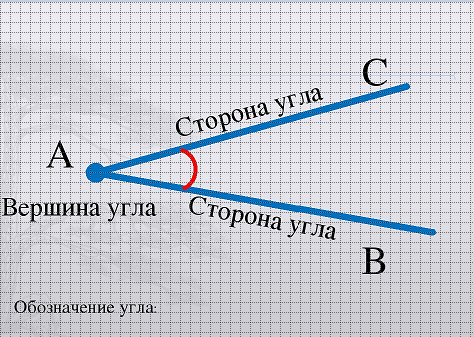

Подобным же образом доказывают, что

∠BCD = ∠ACE.

Равносекущая (биссектриса) есть линия, делящая угол пополам.

На чертеже 27 BD есть биссектриса, если ∠ABD = ∠DBC.

Теорема 10. Биссектрисы двух смежных углов взаимно перпендикулярны.

Даны смежные углы ACB и BCD (чер. 28). Их биссектрисы линии CF и CE делят смежные углы BCD и BCA пополам, следовательно BCF = FCD, ACE = ECB.

Требуется доказать, что EC ⊥ CF.

Доказательство. По условию

ECB = ½ ACB, BCF = ½ BCD

Сложив эти равенства, имеем:

ECB + BCF = ½ ACB + ½ BCD = ½ (ACB + BCD).

Так как ACB + BCD = 2d, то

ECB + BCF = ½ · 2d = d.

Так как ECB + BCF = ECF, то

ECF = d

Угол ECF прямой, т.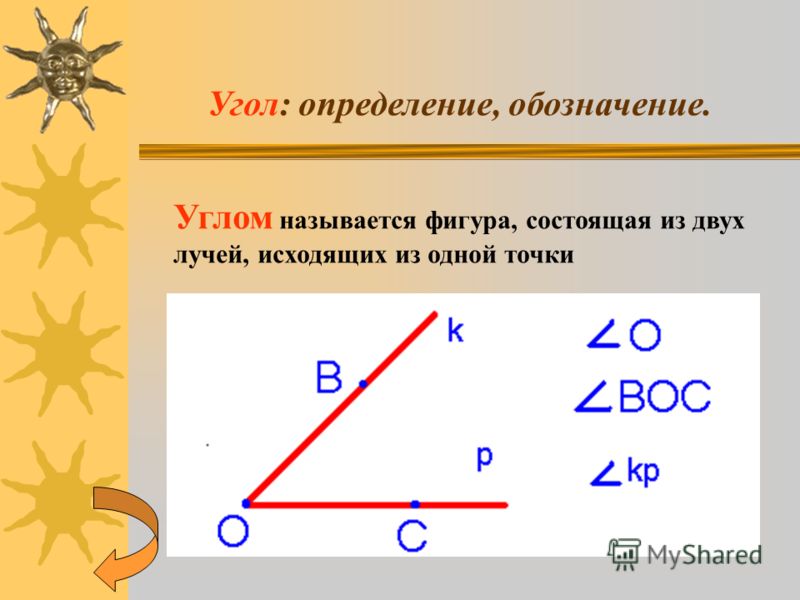 е. линии CE и CF взаимно перпендикулярны (ЧТД).

Геометрия. Урок 2. Углы — ЁП

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Углы

Понятие угла

Виды углов

Биссектриса угла

Углы, образованные при пересечении двух прямых

Углы, образованные при пересечени двух прямых секущей

Углы, образованные при пересечении двух параллельных прямых секущей

• Сумма углов многоугольника

Правильный многоугольник

• Примеры решений заданий из ОГЭ

 

Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.

Стороны угла – лучи, которые образуют угол.

Вершина угла – точка, из которой выходят лучи.

Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.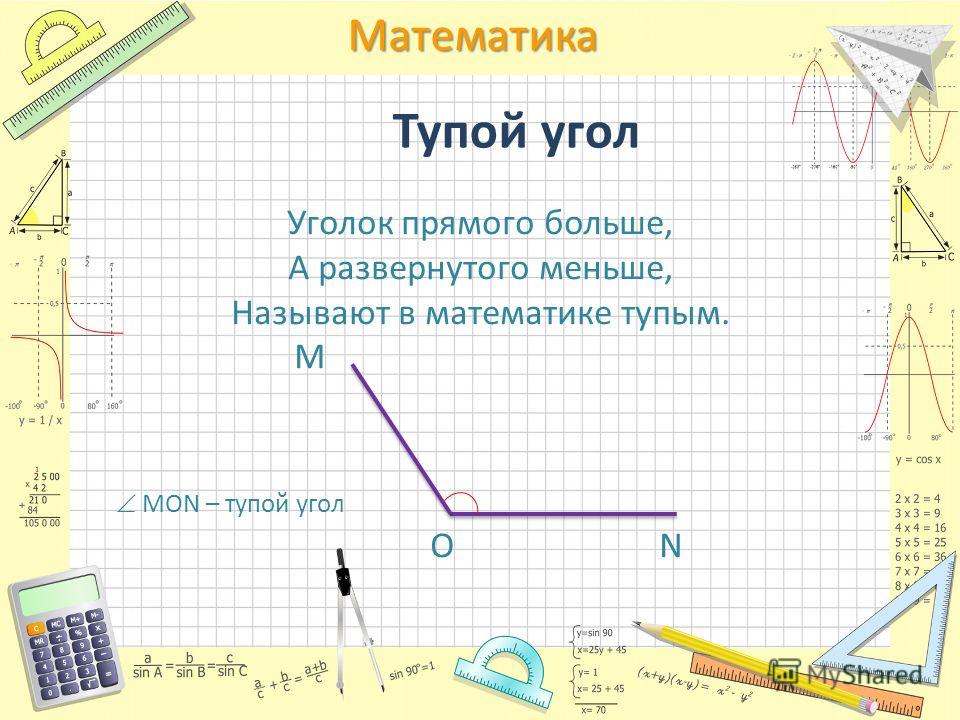

Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠AOB  или ∠BOA,  но ни в коем случае не ∠OAB,∠OBA,∠ABO,∠BAO.

Величину угла измеряют в градусах. ∠AOB=24°.

 

Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.

Или

Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.

OD – биссектриса угла ∠AOB. Она делит этот угол на два равных угла.

∠AOD=∠BOD=∠AOB2

Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон OA и OB угла ∠AOB.

Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.

Свойство: вертикальные углы равны.

Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.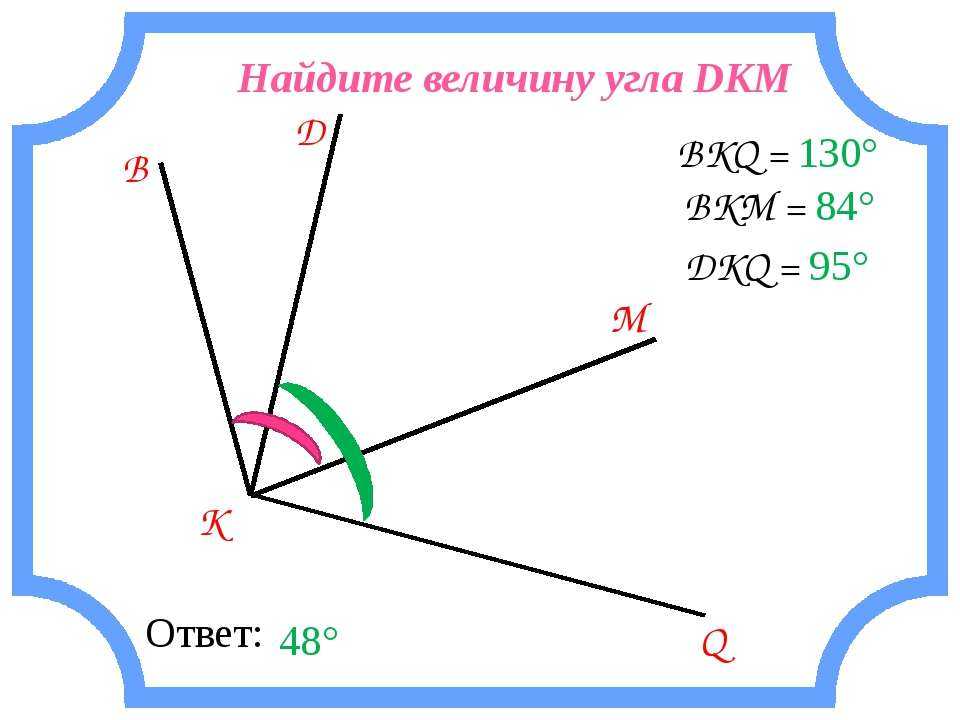

Свойство: сумма смежных углов равна 180°.

Пример:

Пары углов

(1) и (3)
(2) и (4)

называются вертикальными.

По свойству вертикальных углов:

∠COD=∠AOB
∠BOD=∠AOC

Пары углов

(1) и (2)
(2) и (3)
(3) и (4)
(4) и (1)

называются смежными.

По свойству смежных углов:

∠COD+∠DOB=180°∠DOB+∠BOA=180°∠BOA+∠AOC=180°∠AOC+∠COD=180°

 

Прямая, пересекающая две заданные прямые, называется секущей этих прямых.

Существует пять видов углов, которые образуются при пересечении двух прямых секущей.

Пары углов:

(1) и (5)
(2) и (6)
(3) и (7)
(4) и (8)

называются соответственными.
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).

Пары углов:

(3) и (5)
(4) и (6)

называются внутренними односторонними.
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).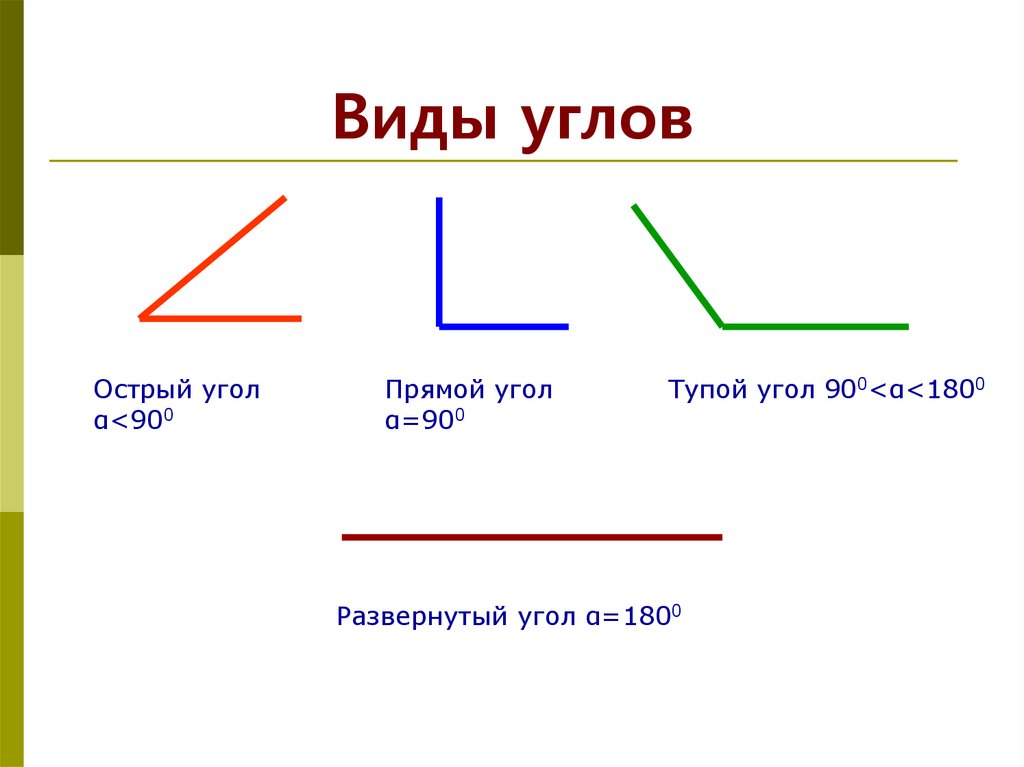

Пары углов:

(1) и (7)
(2) и (8)

называются внешними односторонними.
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).

Пары углов:

(3) и (6)
(4) и (5)

называются внутренними накрест лежащими.
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).

Пары углов:

(1) и (8)
(2) и (7)

называются внешними накрест лежащими.
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).

Если прямые, которые пересекает секущая, параллельны, то углы имеют следующие свойства:

• Соответственные углы равны.
• Внутренние накрест лежащие углы равны.
• Внешние накрест лежащие углы равны.
• Сумма внутренних односторонних углов равна 180°.
• Сумма внешних односторонних углов равна 180°.

 

Сумма углов произвольного n-угольника вычисляется по формуле:

Sn=180°⋅(n−2)

где n – это количество углов в n-угольнике.

Пользуясь этой формулой, можно вычислить сумму углов для произвольного n-угольника.

Сумма углов треугольника: S3=180°⋅(3−2)=180°

Сумма углов четырехугольника: S4=180°⋅(4−2)=360°

Сумма углов пятиугольника: S5=180°⋅(5−2)=540°

Так можно продолжать до бесконечности.

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.

На рисунках изображены примеры правильных многоугольников:

Чтобы найти величину угла правильного n-угольника, необходимо сумму углов этого многоугольника разделить на количество углов.

αn=180°⋅(n−2)n

 

Модуль геометрия: задания, связанные с углами

 

Скачать домашнее задание к уроку 2.

 

Геометрическая фигура угол

Угол — это геометрическая фигура, образованная из двух лучей, у которых начальная точка совпадает. Эта точка называется вершиной угла, а лучи называются сторонами угла. Стороны угла разбивают плоскость на 2 области, называемые плоскими углами или просто углами. Меньший угол называют внутренним, а больший — внешним углом.

Углы также можно обозначать в виде трех точек. Например, ABC. В такой записи B — это вершина, а A и C — это точки, лежащие на разных лучах угла. Для упрощения и быстрой записи, углы принято обозначать строчными греческими буквами: α — альфа,β — бета, γ — гамма, θ — тета, φ — фи и др. Угол обозначается символом в виде двух отрезков, символизирующий угол.

На рисунке изображены два луча AB и AC с вершиной в точке A, образующие два угла: α — внутренний угол, β — внешний угол.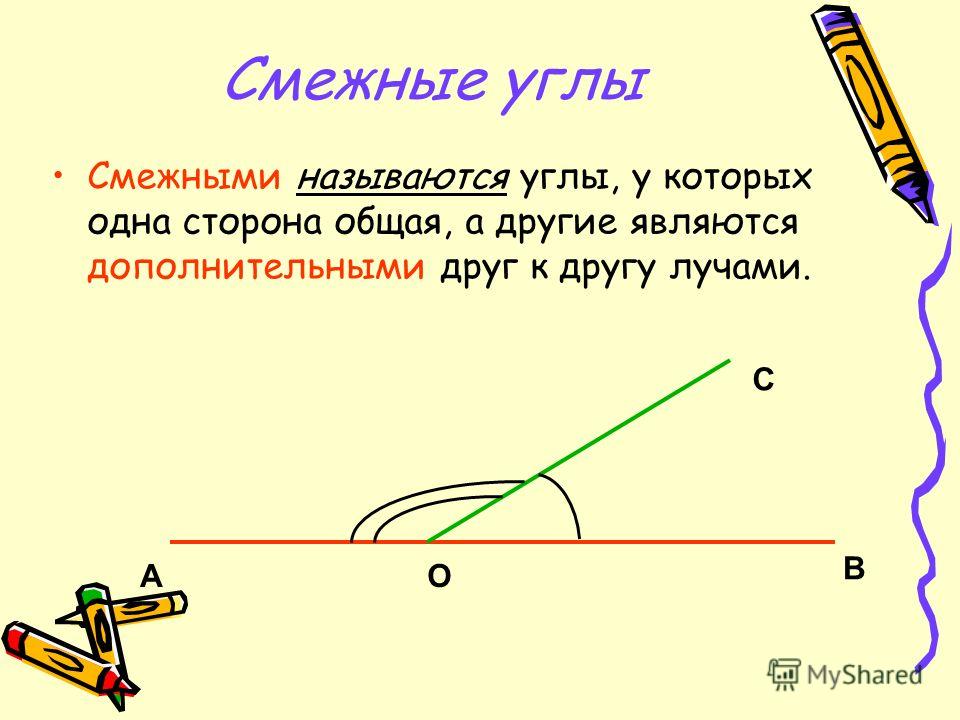

Угловая мера

Мера угла позволяет сравнивать углы между собой, то есть, зная меру угла, можно сказать, что этот угол или больше другого, или меньше, или они равны. Существует несколько мер углов:

• в градусах, минутах, секундах;
• в радианах;
• в оборотах;
• в градах, минутах, секундах.

В математике наиболее распространен первый вид меры угла — градусы, минуты, секунды. Остановимся на нем более подробно. Взгляни на циферблат часов, который изображен ниже.

Если приглядеться на часы, то мы можем представить стрелки часов как лучи, у которых начальная точка совпадает с центром циферблата. За полный оборот стрелки было принято 360 градусов. Градус обозначается символом °. Если стрелка пройдет половину оборота, то переместиться на 180 градусов или 180°, а если на четверть, то переместиться на 90°. На примере ниже, ты можешь увидеть, какое время соответствует углу в разное время. Например, 15:00 соответствует углу 90°, 18:00 соответствует углу 180°, 21:00 — 270° и 24:00 — 360°. Сумма внешнего и внутреннего угла всегда составляет 360°

Угловую меру ты будешь изучать подробно в других разделах математики: геометрия и тригонометрия.

Типы Углов

В зависимости от угловой меры существуют такие типы углов:

Нулевой угол

Нулевой угол — это угол, у которого две стороны совпадают. Из вершины выходят два равно направленных луча. Нулевой угол равен 0°.

Острый угол

Острый угол — это угол лежащий в рамках от 0° до 90°, где 0 и 90 не входят в эти рамки.

Острый угол легко запомнить. Все острые предметы имеют острый угол, например, клюв у птицы, шило, кухонный нож. На рисунке указана желтая граница, показывающая максимальную меру прямого угла.

Прямой угол

Прямой угол — угол, стороны которого перпендикулярны друг другу и равны 90°.

Прямой угол обозначают в виде маленького квадрата у основания угла, как на примере ниже.

Тупой угол

Тупой угол — это угол лежащий в рамках от 90° до 180°, где 90° и 180° не входят в эти рамки.

Косой угол

Косой угол — это все углы, которые не равны 0°, 90°, 180° или 270°.

Развёрнутый угол

Развёрнутый угол — угол равен 180°, лучи противоположно направлены.

Выпуклый угол

Выпуклый угол — это угол от 0° до 180° включительно.

Невыпуклый или вогнутый угол

Невыпуклый угол или вогнутый угол — это угол лежащий в рамках от 180° до 360°, не включая граничные значения.

Полный угол

Полный угол — это угол, у которого две стороны совпадают. Противоположность нулевого угла. Полный угол равен 360°.

У нулевого и полного угла совпадают стороны, нулевой угол — это внутренний угол, равен 0°, а полный — это внешний угол, равен 360°.

Посмотри на рисунок и сосчитай количество углов каждого типа?

• Нулевой угол — 2;
• Острый угол — 3;
• Прямой угол — 2;
• Тупой угол — 2;
• Косой угол — 6;
• Развёрнутый угол — 1;
• Выпуклый угол — 10;
• Вогнутый угол — 1;
• Полный угол — 1;

Тебе нравится этот урок?

thumb_upthumb_down

49

10

Поделись с Друзьями:

Основные Геометрические Фигуры

• 1.Простейшие геометрические фигуры
• 2.Геометрическая фигура угол
• 3.Все о треугольниках
• 4.Четырехугольники

определение, примеры решения и свойства

Угол — это геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла). Плоскость, содержащая обе стороны угла, делится углом на две области.

Содержание:

1. Луч
2. Понятие угла
3. Измерение углов
4. Равенство углов. Биссектриса угла
5. Смежные углы
6. Вертикальные углы

Луч

На рисунке 2.47 изображена прямая , на ней отмечена точка В, которая разделяет прямую на три части:

1)    первая состоит из точек, лежащих левее точки В;

2)    вторая состоит из самой точки В;

3)    третья состоит из точек, лежащих правее точки В.

Объединение первого или третьего множеств с точкой В называется лучом или полупрямой. Таким образом, точка В определила на прямой два луча.

Точка В называется началом каждого из этих лучей или начальной точкой полупрямой.

Луч обозначается латинскими буквами: одной строчной (например, на рис. 2.48) или двумя заглавными, одна из которых обозначает начало луча, а вторая — какую-либо точку на луче (например, луч ВС на рис. 2.49).

Полупрямые прямой , на которые она разбивается точкой В, называются дополнительными.

В повседневной жизни мы часто употребляем понятие направления: направление движения пешехода или автомобиля, направление удара мяча в

футбольном матче, направление полета самолета или ракеты и т. д.

При задании направления используют понятие луча. В геометрии считают, что направление задается лучом, а определить понятие «направление» можно как множество лучей, сонаправлен-ных (одинаково направленных) с данным (рис. 2.50).

1.    Если два луча лежат на одной прямой, то будем считать их одинаково направленными, если один из них содержится в другом, и противоположно направленными, если один из них не содержится в другом.

2.    Если два луча параллельны, но не лежат на одной прямой, то проведем через их начала плоскость, которая разделит пространство на два полупространства. Если лучи лежат в одном из этих полупространств, то они сонаправлены (рис. 2.51). Если же лучи лежат в разных полупространствах, то они противоположно направлены (рис. 2.52).

Понятие угла

На рисунке 2.53 два луча OA и ОВ имеют общее начало. Эти два луча с общим началом всегда лежат в одной плоскости.

При таком расположении лучи разбивают плоскость, которую они образуют, на две части (рис. 2.54). Эти части плоскости вместе с образовавшими их лучами в геометрии называются углами.

Определение. Углом называется фигура, состоящая из двух различных лучей с общим началом и ограниченной ими части плоскости.

На рисунке 2.54 лучи OA и ОВ имеют общее начало — точку О и разбивают плоскость на две части. Исходя из определения угла, получили два различных угла.

Точка, из которой выходят ограничивающие угол лучи, называется вершиной угла, а сами лучи — сторонами угла (рис. 2.55). Лучи OA и ОС на этом рисунке определяют два угла.

Весь угол изобразить на рисунке нельзя, как нельзя на рисунке изобразить весь луч. Каждый угол в действительности продолжается бесконечно. На рисунке 2.56 выделены только части изображенных углов.

Слово «угол» иногда заменяют знаком . Часто при изображении угла чертят только выходящие из вершины начальные участки его сторон, а ту часть, которую хотят указать, обозначают дужкой (рис. 2.57)

Угол обозначается или одной заглавной буквой, поставленной у вершины угла, например: (рис. 2.57), или тремя буквами, из которых одна ставится при вершине угла, а две другие — у каких-нибудь точек сторон, например: (рис. 2.57). Буква, стоящая при вершине угла, всегда записывается между двумя другими буквами. Иногда угол обозначают цифрой, поставленной внутри угла (рис. 2.58).

Для изучения свойств углов используется понятие луча, проходящего между сторонами угла.

Определение. Луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла.

На рисунке 2.59 луч ОВ проходит между сторонами угла АОС, так как он исходит из вершины угла АОС и пересекает отрезок MP. Концы отрезка MP лежат на сторонах угла АОС.

Возьмем луч АС (рис. 2.60) и будем поворачивать его вокруг точки А против часовой стрелки, например, до положения АВ, тогда его последовательные положения «заметут» угол со сторонами АС и АВ.

Продолжая вращать луч в том же направлении, мы будем получать все новые и новые углы. В определенный момент оба луча составят прямую линию (рис. 2.61). Такой угол называется развернутым углом.

Развернутый угол есть часть плоскости, ограниченная прямой, т. е. полуплоскость (рис. 2.62). Сторонами развернутого угла являются две дополнительные полупрямые.

Определение. Развернутым углом называют угол, стороны которого являются дополнительными полупрямыми одной прямой.

Если продолжить вращение луча дальше, чем показано на рисунке 2.62, то будут получаться новые углы (рис. 2.63), пока луч не вернется в свое первоначальное положение (рис. 2.64).

Самый большой возможный угол, полученный в ходе вращения луча, называется полным углом. Полный угол, в сущности, есть вся плоскость (рис. 2.65), а не ее часть, ограниченная двумя лучами.

Измерение углов

Каждый угол характеризуется его величиной, которая называется градусной мерой угла. Измерение углов осуществляется аналогично измерению отрезков — оно основано на сравнении их с углом, принятым за единицу измерения. Обычно за единицу измерения углов принимают градус — угол, равный части развернутого угла. Градус обозначают знаком .

Градусную меру часто называют просто величиной угла. Величина угла, равного  части градуса, называется минутой и обозначается знаком , часть минуты называется секундой и обозначается знаком . Например, угол в 60 градусов 32 минуты 17 секунд записывается так: 60°32’17».

Так как градус составляет часть развернутого угла, развернутый угол равен 180°.

Определение. Положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле, называют градусной мерой угла.

В зависимости от градусной меры углы бывают трех видов: острые, прямые и тупые.

Определение. Угол, равный 90°, называют прямым углом. Прямой угол обозначается буквой d. Угол, меньший 90°, называют острым углом. Угол, больший 90°, называют тупым углом.

Градусные меры угла обозначаются или так же, как сами углы, или буквами греческого алфавита. Например, запись читается: величина (или градусная мера) угла АОВ равна 45 градусам. На рисунке 2.66 величина острого угла записана: , читаем: величина угла меньше 90 градусов. Аналогично записываются и читаются величины прямого и тупого углов (рис. 2.67, 2.68).

Основные свойства измерения углов

Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

Например, на рисунке 2.69 луч ОС проходит между сторонами угла АОВ, градусная мера угла АОВ равна сумме градусных мер углов АОС и СОВ, то есть

Для измерения градусных мер углов (величин углов) на уроках геометрии применяется транспортир (рис. 2.70). На рисунке 2.71 показано, как с помощью транспортира можно измерять угол в 30°, 90°, 120°. На рисунке 2.72 показано, как с помощью транспортира можно отложить от полупрямой OA в верхнюю полуплоскость угол с данной градусной мерой 60°.

Пример: 

Между сторонами угла COD, равного 120°, проходит луч OA. Найдите углы СОА и AOD, если их градусные меры относятся как 4:2.

Решение: 

Из условия задачи имеем:

1.    

2.    Луч OA проходит между сторонами угла COD.

3.    

Найдите градусные меры углов СОА и AOD.

4.     (2, свойства измерения углов).

5.    Так как градусные меры углов СОА и AOD относятся как 4:2, то можно считать, что состоит из 6 частей (1, 2, 3, 4).

6.    

Равенство углов. Биссектриса угла

Как и при определении равенства отрезков, рассматриваются два определения равенства углов.

Определение. Углы равны, если равны их градусные меры.

На рисунке 2.73 изображены два угла ABC и DEM, величины которых равны, а значит, по определению, эти углы равны. Равенство углов обозначается так:

Определение. Углы называются равными, если их можно совместить наложением друг на друга.

Развернутые углы при наложении всегда могут быть совмещены. Отсюда следует, что все развернутые углы равны между собой. Полные углы равны между собой.

Пусть есть два угла: (рис. 2.74). Если угол 1 наложить на угол 2 так, чтобы их вершины совпали, одна из сторон угла 1 совместится со стороной угла 2, но при этом угол 1 составит только часть угла 2 (рис. 2.75). В этом случае говорят, что величина угла 1 меньше величины угла 2. Можно сформулировать по-другому: угол 1 меньше угла 2.

Используя понятие равенства углов, можно дать определение одному из важных понятий геометрии — биссектрисе угла.

Определение. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.

На рисунке 2.76 луч ОМ — биссектриса угла АОВ, при этом

Смежные углы

Определение. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.

На рисунке 2.77 являются смежными, так как лучи OA и ОС — дополнительные полупрямые, а луч ОВ — общая сторона этих углов.

Теорема 4.

Сумма смежных углов равна 180°.

Из теоремы 4 вытекают следующие следствия — свойства смежных углов.

Следствие 1. Если два угла равны, то смежные с ними углы равны.

Следствие 2. Угол, смежный с прямым углом, есть прямой угол.

Следствие 3. Угол, смежный с острым, является тупым, а смежный с тупым — острым.

Вертикальные углы

На рисунке 2.78 изображены две пересекающиеся в точке О прямые АВ и CD. При пересечении этих прямых образовалось четыре угла:

Определение. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.

На рисунке 2.78 углы 1 и 3, 2 и 4 вертикальные.

Теорема 5.

Вертикальные углы равны.

Очевидно, что две пересекающиеся прямые образуют смежные и вертикальные углы. Смежные углы дополняют друг друга до 180°. Угловая мера меньшего из них называется углом между прямыми.

Пример:

На рисунке 2.79 угол COD равен 30°. Чему равны углы АОК и DOK?

Решение: 

Из условия задачи имеем:

1.    Прямые СК и AD пересекаются в точке О.

2.    (рис. 2.79)

3.    Найдите углы АОК и DOK.

4.    Углы COD и АОК вертикальные (1, определение вертикальных углов).

5.     (2, свойство вертикальных углов).

6.    Угол DOK смежный с углом COD (1, определение смежных углов).

7.     (6, свойство смежных углов).

 

 

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

• Математика решение заданий и задач

Смотрите также дополнительные лекции по предмету «Математика»:

Угол.

Градусная мера угла.

• Альфашкола
• Статьи
• Угол

Понятие угла является одним из наиболее важных определений в геометрии.  У́гол  — геометрическая фигура, образованная двумя лучами, сторонами угла, выходящими из одной точки, которая называется вершиной угла. Понятия равенства и суммы углов часто используется в  тригонометрии. Например, углы \(15,30,45\) градусов.

Наиболее распространенными единицами измерения угла являются градус и радиан. Один градус —  это «\(\frac{1}{360}\)» полного круга. \(90\) градусов — это четверть круга, \(180\) – половина круга, \(270\) — три четверти круга и \(360\) это целый круг. Прямой угол равен \(90\) градусов, острый угол больше \(0\) и меньше \(90\) градусов и тупой угол  больше \(90\) градусов и  меньше \(180\) градусов.

Развернутый угол равен  \(180\) градусам.

Мы изучаем углы от \(0\)° до \(360\)°, но есть углы больше \(360\)° и отрицательные углы.

Градусы могут быть разделены на минуты и секунды. Каждый градус делится на \(60\) равных частей, которые называются минутами. Так семь с половиной градусов можно сказать \(7\) градусов и \(30\) минут и записать \(7\) ° \(30\)’. Каждая минута делится на \(60\) равных частей, каждая из которых равна одной секунде. Например, \(2\) градуса \(5\) минут \(30\) секунд записывается \(2\)° \(5\)’ \(30\)». Деление градуса на минуты и секунды  аналогично делению часа на минуты и секунды времени.

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Анна Фёдоровна Ринкман

Репетитор по математике

Стаж (лет)

Образование:

Коми государственный педагогический институт

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике 1-4 классов и русскому языку 1-6 классов. Помогаю дошкольникам и ученикам младшей школы легко и доступно понять учебный материал. Работала по программе Л. Г. Петерсон. Терпеливо и творчески нахожу подход к каждому ученику.

Мария Николаевна Тимоня

Репетитор по математике

Стаж (лет)

Образование:

ФГБОУ ВО Марийский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике для 5-9 классов. Готовлю к ОГЭ. Вместе разберемся со всеми сложностями, вам стоит лишь поверить в себя. Я обожаю моменты, когда даже самые трудные задачи решаются! Эмоциональное удовлетворение, духовный подъем — вот что дарит математика

Валерия Сергеевна Архипова

Репетитор по математике

Стаж (лет)

Образование:

МГУ им. А.Кулешова

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике 5-8 классов и по физике 5-7 классов. «Числа управляют миром», – говорили пифагорейцы. Но числа дают возможность человеку управлять миром, и в этом нас убеждает весь ход развития науки и техники наших дней. Цель моих занятий — объяснить, а не заучить, поэтому даже после прохождения курса у ученика остаются знания, ведь понимание — ключ к дальнейшему развитию.

Похожие статьи

• Геометрическая прогрессия
• Что такое процент?
• Как решать показательные уравнения?
• ЕГЭ по математике, профильный уровень. Неравенства
• Как найти точку пересечения плоскости и прямой
• Как вести себя преподавателю со «сложными» детьми
• Полезные упражнения для тех, кто долго сидит за учебниками: зарядка для глаз
• Тупики памяти или почему мы легко запоминаем песни, но не помним даты?

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Справочник по математике

Геометрия (Планиметрия)

Углы

      Углом называют часть плоскости, ограниченную двумя лучами, выходящими из одной точки. Лучи,ограничивающие угол, называют сторонами угла. Точку, из которой выходят лучи, называют вершиной угла.

      Схему обозначения углов рассмотрим на примере угла, изображенного на рисунке 1.

Рис.1

      Изображенный на рисунке 1 угол можно обозначить тремя способами:

      Углы называют равными углами, если их можно совместить.

      Если при пересечении двух прямых образуются четыре равных угла, то такие углы называют прямыми углами (рис.2). Пересекающиеся прямые линии, образующие прямые углы, называют перпендикулярными прямыми.

Рис.2

      Если через точку A, не лежащую на прямой l, проведена прямая, перпендикулярная к прямой l и пересекающая прямую l точке B, то говорят, что из точки B опущен перпендикупяр AB на прямую l (рис.3). Точку B называют основанием перпендикуляра AB.

Рис.3

      Замечание. Длину отрезка AB называют расстоянием от точки A до прямой l.

      Углом в 1° (один градус) называют угол, составляющий одну девяностую часть прямого угла.

      Угол, в k раз больший угла в 1°, называют углом в k° ( k градусов).

      Углы измеряют также и в радианах. О радианах можно прочитать в разделе нашего справочника «Измерение углов. Градусы и радианы».

Таблица 1 – Типы углов в зависимости от величины в градусах

Рисунок	Типы углов	Свойства углов
	Прямой угол	Прямой угол равен 90°
	Острый угол	Острый угол меньше 90°
	Тупой угол	Тупой угол больше 90°, но меньше 180°
	Развернутый угол	Развернутый угол равен 180°
	Угол больший, чем развернутый	Такой угол больше 180°, но меньше 360°
	Полный угол	Полный угол равен 360°
	Угол, равный нулю	Такой угол равен 0°

Прямой угол

Свойство: Прямой угол равен 90°

Острый угол

Свойство: Острый угол меньше 90°

Тупой угол

Свойство: Тупой угол больше 90°, но меньше 180°

Развернутый угол

Свойство: Развернутый угол равен 180°

Угол больший, чем развернутый

Свойство: Такой угол больше 180°, но меньше 360°

Полный угол

Свойство: Полный угол равен 360°

Угол, равный нулю

Свойство: Такой угол равен 0°

Таблица 2 – Типы углов в зависимости расположения сторон

Рисунок	Типы углов	Свойства углов
	Вертикальные углы	Вертикальные углы равны
	Смежные углы	Сумма смежных углов равна 180°
	Углы с соответственно параллельными сторонами	Углы с соответственно параллельными сторонами равны, если оба являются острыми или оба являются тупыми
		Сумма  углов с соответственно параллельными сторонами равна 180°, если один из них острый, а другой тупой
	Углы с соответственно перпендикулярными сторонами	Углы с соответственно перпендикулярными сторонами равны, если оба являются острыми или оба являются тупыми
		Сумма углов с соответственно перпендикулярными сторонами равна 180°, если один из них острый, а другой тупой

Вертикальные углы

Свойство вертикальных углов: Вертикальные углы равны

Смежные углы

Свойство смежных углов: Сумма смежных углов равна 180°

Углы с соответственно параллельными сторонами

Свойство углов с соответственно параллельными сторонами: Углы с соответственно параллельными сторонами равны, если оба являются острыми или оба являются тупыми

Свойство углов с соответственно параллельными сторонами: Сумма  углов с соответственно параллельными сторонами равна 180°, если один из них острый, а другой тупой

Углы с соответственно перпендикулярными сторонами

Свойство углов с соответственно перпендикулярными сторонами: Углы с соответственно перпендикулярными сторонами равны, если оба являются острыми или оба являются тупыми

Свойство углов с соответственно перпендикулярными сторонами: Сумма углов с соответственно перпендикулярными сторонами равна 180°, если один из них острый, а другой тупой

      Определение. Биссектрисой угла называют луч, делящий угол пополам.

      Задача. Доказать, что биссектрисы смежных углов перпендикулярны.

      Решение. Рассмотрим рисунок 4.

Рис.4

      На этом рисунке углы AOB и BOC – смежные, а лучи OE и OD – биссектрисы этих углов. Поскольку

2α + 2β = 180°.

то

α + β = 90°,

что и требовалось доказать.

   На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Что такое углы? Определение, свойства, типы, части, примеры

Что такое угол?

Угол образуется, когда две прямые линии или лучи пересекаются в общей конечной точке. Общая точка касания называется вершиной угла. Слово «угол» происходит от латинского слова «angulus», что означает «угол».

Углы вокруг нас:

Существует множество примеров использования углов в повседневной жизни, таких как вешалки для одежды, наконечники стрел, ножницы, частично открытые двери, пирамиды, край стола, край линейки и т. д.

Символ угла

Символ ∠ обозначает угол. Углы измеряются в градусах (°) с помощью транспортира.

Например, 45 градусов представляют как 45°

Части углов

• Вершина: Вершина — это угол угла, точка, где встречаются две линии/стороны. O — вершина на данной фигуре.
• Плечи: Две стороны угла, соединенные в общем конце. ОА и ОВ — стороны угла.
• Исходная сторона: Также известная как опорная линия, прямая линия, от которой строится угол. OB – это опорная линия.
• Сторона клеммы: Сторона, до которой выполняется измерение угла. На приведенной ниже диаграмме OA является конечной стороной.

Типы углов

Основываясь на их измерениях, вот различные типы углов:

• Острый угол меньше 90° при вершине.
• Тупой угол составляет от 90° до 180°.
• Прямой угол точно измеряет 90° в вершине.
• Угол, равный 180°, является прямым углом .
• A Угол рефлекса измеряется в пределах 180°-360°.
• A в сборе угол измеряет 360°.

Внутренние и внешние углы:

Внутренние углы: Внутренние углы — это углы, образованные внутри или внутри формы.

Здесь ∠ABC, ∠BCA и ∠CAB — внутренние углы.

Внешние углы: Внешние углы — это углы, образованные вне формы, между любой стороной фигуры и продолженной смежной стороной. Здесь ∠ACD — внешний угол.

Дополнительные и дополнительные углы:

Дополнительные углы: Углы, сумма которых составляет 90° (прямой угол), называются дополнительными углами.

Здесь ∠BXC и ∠CXD — дополнительные углы.

Дополнительные углы: Углы, сумма которых составляет 180° (прямой угол), называются дополнительными углами.

Здесь ∠AXD и ∠CXD — дополнительные углы.

Применение углов в реальной жизни

• Инженеры строят здания, мосты, дома, памятники и т. д., используя измерение углов.
• Спортсмены используют его концепцию в спорте для повышения своих результатов.
• Плотники используют его для изготовления такого оборудования, как двери, стулья, диваны, столы и т. д. 
• Художники используют свои знания в области измерений для создания эскизов или создания произведений искусства.
• Настенные часы используют концепцию углов для отображения времени с помощью часовой и минутной стрелок.

Как построить угол (с помощью транспортира)

1. Нарисуйте луч OA любой длины.
2. Теперь поместите транспортир в эту точку так, чтобы его середина касалась отмеченной точки O.
3. Теперь отметьте точку B на верхней круглой части транспортира в соответствии с предпочтительным углом, например, 40°.
4. Нарисуйте прямую линию, соединяющую эти две точки, O и B.
5. Отметьте градус угла, образованного при пересечении двух сторон прямой линии.

Видение Splashlearn состоит в том, чтобы изменить образование для учащихся K-5-х классов. Он обеспечивает индивидуальное обучение для каждого учащегося в соответствии с требованиями 21 века. SplashLearn позволяет учащимся изучать математику с помощью увлекательной индивидуальной программы. SplashLearn доступен на всех цифровых платформах, и им воспользовались более 40 миллионов студентов по всему миру.

Чтобы узнать больше об углах, нажмите здесь.

Решенные примеры

Пример 1

Найдите недостающий угол x на рисунке.

Решение:

Мы видим a ∠x + 35° = 90°

∠x = (90 – 35)° = 55°

Пример 2

Решите для x.

Решение:

5x — 70 = 105 (альтернативные углы)

5x = 175

Следовательно, x = 35 °

Пример 3

в треугольнике ABC, ♂ = 90 и omb = 30. Найдите ∠C?

Решение:

Сумма всех трех внутренних углов треугольника равна 180°. Следовательно, 90° + 30° + х = 180°.

Найдите x

x = 180 – (90 + 30) = 60°.

Практические задачи

360 ° 180 ° 270 ° 90 ° Правильный ответ: 360 ° Сумма всех углов. дополнительные углы углы отражения дополнительные углы Правильный ответ: дополнительные углы Углы, сумма которых равна 90° называются дополнительными углами. вертикальных угла дополнительных угла угла отражения дополнительных угла Правильный ответ: вертикальные углы Углы, противоположные друг другу, называются вертикальными углами.

Часто задаваемые вопросы

Укажите типы углов в зависимости от направления цикла?

         Углы ​​бывают двух типов в зависимости от направления цикла:

• Положительные углы: Положительные углы измеряются против или против часовой стрелки от базовой линии. Положительные углы записываются со знаком плюс или без него перед углами. Он рисуется из плоскости (+x, +y).
• Отрицательные углы: Отрицательные углы измеряются по часовой стрелке от базовой линии. Он рисуется из начала координат в плоскости (+x, -y).

Всегда ли сумма углов на прямой составляет 180°?

• Углы, имеющие общую вершину и одну сторону прямой, в сумме дают 180°.
• Углы с общей вершиной, занимающей пространство вокруг точки, в сумме дают 360°.

Какие бывают углы?

Типы углов, основанные на измерении:

• Прямой угол
• Прямой угол
• Угол отражения
• Тупой угол
• Острый угол

4 Каково применение углов в математике?

Инженеры и архитекторы используют углы для строительства, измерения, проектирования и т. д. Архитекторы и инженеры используют их для проектирования дорог, зданий и спортивных сооружений.

Типы углов, определение, свойства, примеры

Углы образуются при пересечении двух прямых в одной точке. Мера «расстояния» между этими двумя лучами называется «углом». Обозначается символом ∠. Углы обычно измеряются в градусах и радианах, что является мерой округлости или вращения. Углы являются частью нашей повседневной жизни. Инженеры и архитекторы используют углы для проектирования дорог, зданий и спортивных сооружений.

1.	Что такое углы?
2.	Типы углов и их свойства
3.	Углы на основе поворота
4.	Как измерить угол?
5.	Как построить углы?
6.	Часто задаваемые вопросы об углах

Что такое углы?

В геометрии угол образуется при соединении двух лучей в их концах. Эти лучи называются сторонами или плечами угла. Давайте прочитаем о различных частях угла.

Части угла

С углом связаны две основные части — стороны и вершина.

Плечи угла

Два луча, которые соединяются в одной точке, образуя угол, называются плечами угла . Обратите внимание на приведенный ниже рисунок, на котором показано, что ОА и ОВ являются сторонами угла АОВ.

Вершина угла

Вершина является общей конечной точкой, общей для двух лучей. Обратите внимание на рисунок, на котором вершина O отмечена как точка соединения двух плеч.

Мера угла

Угол измеряется в градусах. Один полный оборот вокруг точки образует полный угол в 360°.

Лучший способ измерить угол — использовать транспортир. Транспортир представляет собой измерительный инструмент, имеющий форму полукруга. Это полупрозрачный инструмент, который помогает нам измерять углы в градусах. Он имеет градусы, отмеченные по часовой стрелке от 0° до 180° на внешней шкале и против часовой стрелки от 0° до 180° на внутренней шкале.

Типы углов и их свойства

Существует шесть типов углов. Каждый тип угла имеет уникальную идентификацию на основе измерения угла. Давайте прочитаем о каждом типе угла в отдельности вместе с их свойствами.

Острый угол

Острый угол — это угол, градусная мера которого больше 0° и меньше 90°.

Прямой угол

Когда угол равен 90°, он называется прямым углом. Прямой угол легко заметить, так как он образует форму буквы L.

Тупой угол

Когда угол меньше 180°, но больше 90°, это тупой угол.

Прямой угол

Угол, образованный прямой линией, называется прямым углом. Другими словами, прямой угол — это прямая линия, а угол, образованный между двумя лучами, равен 180°. Под прямым углом два луча противоположны друг другу. Два прямых угла составляют прямой угол. Поскольку мера прямого угла равна 180°, он составляет половину полного оборота окружности.

Угол рефлекса

Угол рефлекса — это угол, величина которого больше 180°, но меньше 360°.

Полный угол

Когда измерение угла равно 360°, это полный угол.

Угол, основанный на вращении

В зависимости от направления измерения или направления вращения углы могут быть двух типов:

• Положительные углы
• Отрицательные углы

Положительные углы
Угол, измеренный в направлении против часовой стрелки (против часовой стрелки), является положительным углом. Другими словами, положительные углы — это те углы, которые повернуты от основания в направлении против часовой стрелки.

Отрицательные углы
Отрицательные углы — это те углы, которые измеряются по часовой стрелке от основания. Другими словами, отрицательные углы — это те углы, которые представляют собой углы, повернутые от основания по часовой стрелке.

Как измерить угол?

Мы используем транспортиры для измерения углов. Обратите внимание на приведенный ниже рисунок, на котором показано ∠AOB. Давайте попробуем и посмотрим, сможем ли мы выяснить, к какому типу относится угол ∠AOB. Разве это не похоже на острый угол? Это означает, что его мера больше 0° и меньше 90°. Давайте научимся измерять этот угол с помощью транспортира.

Как измерить острый угол?

Попробуем измерить заданный ∠AOB.

• Шаг 1: Совместите транспортир с лучом OB, как показано ниже. Начните считывать внутреннюю шкалу с отметки 0 ° в правом нижнем углу транспортира.

• Шаг 2: Число на транспортире, которое совпадает со вторым лучом , является мерой угла. Измерьте угол, используя внутреннюю шкалу транспортира. Таким образом, ∠AOB = 37°

Как измерить тупой угол?

Теперь попробуем измерить заданный ∠AOC.

• Шаг 1: Измерьте угол по внешней шкале транспортира от отметки 0° в нижнем левом углу .

• Шаг 2: Число на внешней шкале транспортира, совпадающее с OA, является мерой ∠AOC. Таким образом, ∠AOC = 143°

Как построить углы?

Транспортиром строим углы. Начертим угол 50°.

• Шаг 1: Сначала нарисуйте луч OB и совместите транспортир с OB , как показано.

• Шаг 2: Используя внутреннюю шкалу транспортира, отметьте точку A над отметкой на транспортире, которая соответствует 50°.

• Шаг 3: Снимите транспортир и проведите луч, начинающийся в точке O и проходящий через эту точку A. Таким образом, ∠AOB — искомый угол, то есть ∠AOB = 50°.

Примечание. Если луч идет в другом направлении, мы измеряем угол по внешней шкале от отметки 0° внизу слева.

На приведенном ниже рисунке показано, как нарисовать угол 50°, когда луч направлен в другую сторону.

После установки транспортира на OB мы используем внешнюю шкалу и отмечаем 50°, как показано. Затем мы отмечаем эту точку как A и соединяем ее с точкой O. Это образует угол AOB = 50°

Важные замечания по углам

• 0°< Острый угол < 90°
• 90°< Тупой угол < 180°
• 180° < угол отражения < 360°
• Прямой угол равен 90°
• Прямой угол равен 180°.

☛ Связанные статьи

• Пары уголков
• Секущие и смежные углы
• Внутренние уголки

 

Углы Примеры

1. Пример 1: Обратите внимание на размеры углов и определите тип углов для каждой фигуры.

   Решение:

   а) Данный угол равен 40°. Это острый угол, потому что его градусная мера меньше 90°.
   б) данный угол равен 117°. Это тупой угол, потому что его градусная мера больше 90°, но меньше 180°.
   в) данный угол равен 121°. Это тупой угол, потому что его градусная мера больше 90°, но менее 180°.
   г) данный угол равен 185°. Это рефлекторный угол, потому что его величина больше 180°, но меньше 360°.

2. Пример 2:

   Классифицируйте следующие углы на острые, тупые, прямые и отраженные.
   а) 24°
   б) 150°
   в) 90°
   г) 270°

   Решение:

   (а) 24° лежит между 0° и 90°, значит угол острый.
   (b) 154° лежит между 90° и 180°, поэтому это тупой угол.
   (c) 90° известен как прямой угол.
   (d) 270° находится между 180° и 360°, поэтому это рефлекторный угол.

3. Пример 3: Запишите верно или неверно следующие утверждения:

   a.) 180° < угол отражения < 360°

   b. ) 0°< тупой угол < 90°

   7 c. ) Два луча, соединяющиеся в одной точке и образующие угол, называются сторонами угла.

   Решение:

   a.) Верно, 180° < угол отражения < 360°

   b.) Неверно, 0°< острый угол < 90°

   c.) Верно, два луча, которые соединяются в общие точки, образующие угол, называются плечами угла.

перейти к слайду перейти к слайду перейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатный пробный урок

Практические вопросы по углам

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об углах

Что такое угол в математике?

Углы образуются при пересечении двух лучей в одной точке. «Отверстие» между этими двумя лучами называется «углом», который обозначается символом ∠. Углы обычно измеряются в градусах и выражаются как 60°, 90° и так далее.

Какие бывают 6 типов углов?

6 типов углов: прямые углы, острые углы, тупые углы, прямые углы, рефлекторные углы и полные углы.

Как вы описываете углы?

Угол можно описать как фигуру, образованную двумя лучами, встречающимися в общей конечной точке, называемой вершиной угла.

☛ Также проверьте:

• Рабочие листы углов
• Углы в четырехугольнике Рабочие листы
• Геометрические углы Рабочие листы

Какие бывают типы углов, основанные на вращении?

В зависимости от направления измерения или направления вращения углы можно разделить на два типа:

• Положительные углы: Положительные углы — это углы, которые измеряются и поворачиваются от основания в направлении против часовой стрелки.
• Отрицательные углы: отрицательные углы — это те углы, которые измеряются и поворачиваются от основания по часовой стрелке.

В чем разница между прямым углом и рефлекторным углом?

Прямой угол – это прямая линия, а угол между двумя лучами равен 180°. Его можно образовать путем совмещения двух смежных прямых углов. Другими словами, два прямых угла составляют прямой угол. Принимая во внимание, что угол рефлекса больше 180°, но меньше 360°.

Какие бывают виды углов, образованных при прохождении секущей через параллельные прямые?

Когда секущая проходит через параллельные прямые, образуется много пар углов, таких как соответствующие углы, вертикально противоположные углы, чередующиеся внутренние углы и чередующиеся внешние углы.

Какие типы углов меньше 180°?

Существует два типа углов, мера которых меньше 180°, т. е. острые и тупые углы. Мера острых углов всегда меньше 90°, а тупых углов больше 90°, но всегда меньше 180°. Примеры острых углов: 50°, 60°, тупые углы: 170°, 165°.

Какова сумма всех трех углов треугольника?

Сумма трех углов треугольника равна 180°.

☛ Проверить сейчас:

• Углы треугольника Рабочие листы
• Калькулятор углов треугольника

Сколько углов по 90 градусов в прямом угле?

В 180-градусном или прямом угле есть два угла 90°. Так как 90° + 90° = 180°, то в прямом углу два угла по 90°.

Перечислите типы парных углов.

Типы уголков попарно перечислены ниже:

• Смежные углы
• Дополнительные уголки
• Дополнительные уголки
• Альтернативные внутренние углы
• Альтернативные внешние углы
• Соответствующие углы
• Вертикальные уголки
• Последовательные внутренние углы

Что такое полный угол?

Когда угол завершает полный оборот, начиная с 0° и заканчивая 360°, он называется полным углом. Другими словами, полный угол равен 360°.

Угол (математика) — Энциклопедия Нового Света

Эта статья об углах в геометрии.

«∠», символ угла.

В геометрии и тригонометрии угол (или плоский угол ) — это фигура, образованная двумя лучами, имеющими общий конец. Конечная точка называется вершиной угла. Величина угла представляет собой «величину поворота», разделяющую два луча, и может быть измерена путем рассмотрения длины дуги окружности, выметаемой, когда один луч поворачивается вокруг вершины, чтобы совпасть с другим (см. «Измерение углов, » ниже).

Содержание

• 1 История
• 2 Измерение углов
  • 2.1 Единицы
  • 2.2 Положительные и отрицательные углы
  • 2.3 Приблизительно
• 3 типа уголка
• 4 Формальное определение
  • 4.1 Использование тригонометрических функций
  • 4.2 Использование вращения
• 5 Углы между кривыми
• 6 Скалярное произведение и обобщение
• 7 Углы в римановой геометрии
• 8 углов в географии и астрономии
• 9 См. также
• 10 Примечания
• 11 Каталожные номера
• 12 Внешние ссылки
• 13 кредитов

Слово угол происходит от латинского слова angulus, означает «угол». Слово angulus является уменьшительным, примитивная форма которого angus, не встречается в латыни. Родственными словами являются латинское angere, , означающее «сжимать в изгиб» или «задушить», и греческое ἀγκύλος 9.0723 (ankyοs), означает «кривой, искривленный»; оба связаны с корнем PIE *ank-, , означающим «сгибаться» или «поклоняться». ^[1]

История

Евклид определяет плоский угол как наклон друг к другу в плоскости двух линий, которые встречаются друг с другом и не лежат прямо по отношению друг к другу. Согласно Проклу, угол должен быть либо качеством, либо количеством, либо отношением. Первое понятие использовал Евдем, рассматривавший угол как отклонение от прямой линии; второй — Карпом Антиохийским, который рассматривал его как промежуток или пространство между пересекающимися линиями; Евклид принял третью концепцию, хотя и свои определения прямых, острых и тупых углов.

Измерение углов

Угол θ является частным s и r .

Для измерения угла θ дуга окружности с центром в вершине угла рисуется, например, с помощью циркуля. Затем длина дуги s делится на радиус окружности r и, возможно, умножается на константу масштабирования k (которая зависит от выбранных единиц измерения):

θ = sr (k) {\ displaystyle \ theta = {\ frac {s} {r}} (k)}

Определенное таким образом значение θ не зависит от размера круга: изменяется длина радиуса, то в той же пропорции изменяется и длина дуги, так что соотношение s / r не меняется.

Во многих геометрических ситуациях углы, которые отличаются на точное число, кратное полному кругу, фактически эквивалентны (не имеет значения, сколько раз линия проходит полный круг, потому что она всегда заканчивается в одном и том же месте). Тем не менее, это не всегда так. Например, при отслеживании кривой, такой как спираль, с использованием полярных координат дополнительный полный оборот приводит к совершенно другой точке кривой.

Единицы измерения

Углы считаются безразмерными, так как они определяются как отношение длин. Однако есть несколько единиц, используемых для измерения углов, в зависимости от выбора константы k в приведенной выше формуле.

За заметным исключением радиана, большинство единиц углового измерения определяются таким образом, что один полный круг (т. е. один оборот) равен n единиц, для некоторого целого числа n (например, в случае градусов, н = 360). Это эквивалентно установке k = n /2 π в приведенной выше формуле. (Чтобы понять почему, обратите внимание, что один полный круг соответствует дуге, равной длине окружности, которая равна 2 πr , поэтому s = 2 πr . Подставляя, мы получаем θ = ks / r = 2 πk . Но если один полный круг должен иметь числовое угловое значение n , то нам нужно θ = n . Это достигается установкой k = n /2 π .)

• градусов , обозначенные маленьким кругом в верхнем индексе (°), составляют 1/360 полного круга, поэтому один полный круг равен 360°. Одним из преимуществ этой старой шестидесятеричной единицы измерения является то, что многие углы, распространенные в простой геометрии, измеряются целым числом градусов. (Проблема измерения 90 723 всех 90 724 «интересных» углов в виде целых чисел, конечно, неразрешима.) Доли градуса можно записать в обычном десятичном представлении (например, 3,5 ° для трех с половиной градусов), но следующие шестидесятеричные единицы системы «градус-минута-секунда» также используются, особенно для географических координат, а также в астрономии и баллистике:
  • угловых минут (или МОА , угловых минут или просто минут ) составляет 1/60 градуса. Он обозначается одним штрихом ( ′ ). Например, 3° 30′ равно 3 + 30/60 градусам или 3,5 градусам. Также иногда используется смешанный формат с десятичными дробями, например, 3° 5,72′ = 3 + 5,72/60 градусов. Морская миля исторически определялась как минута дуги вдоль большого круга Земли.
  • угловых секунд (или угловых секунд , или просто секунд ) составляет 1/60 угловой минуты и 1/3600 градуса. Он обозначается двойным штрихом ( ″ ). Например, 3° 7′ 30″ равно 3 + 7/60 + 30/3600 градусов или 3,125 градуса.

θ = с / r рад = 1 рад.

• радиан — это угол, образуемый дугой окружности, длина которой равна радиусу окружности ( k = 1 в приведенной выше формуле). Один полный круг равен 2 π радиана, а один радиан равен 180/ π градуса, или примерно 57,2958 градуса. Радиан обозначается аббревиатурой рад, , хотя этот символ часто опускается в математических текстах, где предполагается радиан, если не указано иное. Радиан используется практически во всех математических работах, помимо простой практической геометрии, благодаря, например, приятным и «естественным» свойствам, которые демонстрируют тригонометрические функции, когда их аргументы выражены в радианах. Радиан — это (производная) единица измерения угла в системе СИ.

• мил равно приблизительно , равному миллирадиану. Есть несколько определений.

• Полный оборот (или оборот , оборот , полный оборот или цикл ) является одним полным оборотом. Оборот и вращение обозначаются rev и rot, соответственно, а просто r в об/мин (оборотов в минуту). 1 полный круг = 360° = 2 π рад = 400 гон = 4 прямых угла.

• Прямой угол составляет 1/4 полного круга. Это единица измерения, используемая в «Элементах» Евклида. 1 прямой угол = 90° = π /2 рад = 100 гон.

• Угол равностороннего треугольника составляет 1/6 часть полной окружности. Это устройство использовали вавилоняне, и его особенно легко построить с помощью линейки и циркуля. Градус, угловая минута и угловая секунда являются шестидесятеричными единицами вавилонской единицы измерения. Одна вавилонская единица = 60° = π /3 рад ≈ 1,047197551 рад.

• град , также называемый град , град или град составляет 1/400 полного круга, поэтому один полный круг равен 400 градам, а прямой угол равен 100 градам. Это десятичная единица прямого угла. Километр исторически определялся как сантиметр дуги вдоль большого круга Земли, поэтому километр является десятичным аналогом шестидесятеричной морской мили. Гон используется в основном в триангуляции.

• Точка , используемая в навигации, составляет 1/32 полного круга. Это бинарная субъединица полного круга. Назвать все 32 точки на розе ветров называется «боксирование компаса». 1 точка = 1/8 прямого угла = 11,25° = 12,5 угольника.

• Астрономический часовой угол составляет 1/24 полного круга. Шестидесятеричные единицы назывались минут времени и секунд времени (хотя они и являются угловыми единицами). 1 час = 15° = π /12 рад = 1/6 прямого угла ≈ 16,667 гон.

• Двоичный градус , также известный как двоичный радиан (или брэд ), составляет 1/256 полного круга. Двоичная степень используется в вычислениях, чтобы угол можно было эффективно представить одним байтом.

• уклон уклона или уклон не является на самом деле мерой угла (если только он явно не указан в градусах, как это иногда бывает). Вместо этого он равен тангенсу угла, а иногда и синусу. Градиенты часто выражаются в процентах. Для обычно встречающихся небольших значений (менее 5%) уклон уклона приблизительно равен углу в радианах.

Положительные и отрицательные углы

Общепринятое соглашение в математической письменной форме состоит в том, что углы со знаком составляют положительных углов при измерении против часовой стрелки и отрицательных углов при измерении по часовой стрелке от данной линии. Если линия не указана, можно предположить, что это ось x в декартовой плоскости. Во многих геометрических ситуациях отрицательный угол — θ фактически эквивалентен положительному углу «один полный оборот меньше θ ». Например, поворот по часовой стрелке на 45° (то есть угол -45°) часто фактически эквивалентен повороту против часовой стрелки на 360° — 45° (то есть угол 315°).

В трехмерной геометрии «по часовой стрелке» и «против часовой стрелки» не имеют абсолютного значения, поэтому направление положительных и отрицательных углов должно быть определено относительно некоторой точки отсчета, которая обычно представляет собой вектор, проходящий через вершину угла и перпендикулярный плоскости в котором лежат лучи угла.

В навигации азимут измеряется с севера, увеличиваясь по часовой стрелке, поэтому азимут 45 градусов соответствует северо-востоку. Отрицательные азимуты не используются в навигации, поэтому северо-запад составляет 315 градусов.

Приблизительно

• 1° примерно соответствует ширине мизинца на расстоянии вытянутой руки
• 10° примерно соответствует ширине сжатого кулака на расстоянии вытянутой руки.
• 20° примерно соответствует ширине размаха рук на расстоянии вытянутой руки.

Типы уголков

Прямой угол.

Острые ( a ), тупые ( b ) и прямые ( c ) углы. Здесь a и b — дополнительные углы.

Угол рефлекса.

Дополнительные углы a и b ( b является дополнением a , а a является дополнением b ).

• Угол 90° ( π /2 радиана, или четверть полного круга) называется прямым углом .

  Две линии, образующие прямой угол, называются перпендикулярными или ортогональными .

• Углы меньше прямого угла (менее 90°) называются острыми углами («острый» означает «острый»).
• Углы больше прямого угла и меньше двух прямых углов (между 90° и 180°) называются тупыми углами («тупой» означает «тупой»).
• Углы, равные двум прямым углам (180°), называются прямыми углами .
• Углы больше двух прямых, но меньше полной окружности (от 180° до 360°) называются рефлекторными углами .
• Углы, имеющие одинаковую меру, называются -конгруэнтными .
• Два противоположных угла, образованные двумя пересекающимися прямыми линиями, образующими форму, подобную букве «X», называются 9.0730 вертикальные углы или противоположные углы . Эти углы равны.
• Углы, имеющие общую вершину и ребро, но не имеющие общих внутренних точек, называются смежными углами .
• Два угла, сумма которых составляет один прямой угол (90°), называются дополнительными углами .

  Разность между углом и прямым углом называется дополнением угла.

• Два угла, которые в сумме составляют прямой угол (180°), называются дополнительные уголки .

  Разница между углом и прямым углом называется дополнением угла.

• Два угла, сумма которых составляет один полный круг (360°), называются дополнительными углами или сопряженными углами .
• Меньший угол в точке соединения двух отрезков называется внутренним углом .

  В евклидовой геометрии сумма внутренних углов треугольника равна π радиана или 180°; меры внутренних углов простого четырехугольника составляют в сумме 2 90 723 π 90 724 радиана, или 360°. В общем, меры внутренних углов простого многоугольника с n сторонами в сумме составляют [( n  — 2) × π ] радиан, или [( n  — 2) × 180]°.

• Угол, дополнительный к внутреннему углу, называется внешним углом .
• Угол между двумя плоскостями (например, двумя соседними гранями многогранника) называется двугранный угол . Его можно определить как острый угол между двумя прямыми, перпендикулярными плоскостям. {2}}}}} = {\ frac {y} {x}} = {\ frac {-y} {-x}} = {\ frac {\ sin (\ theta + \ pi)} {\ cos (\тета +\пи )}}} 9{2}}. Угол между двумя векторами будет просто углом поворота, который отображает один на другой. У нас пока нет численного способа определения угла. Для этого мы выбираем вектор (1,0) {\ displaystyle (1,0)}, затем для любой точки M на T {\ displaystyle \ mathbb {T}} на расстоянии θ {\ displaystyle \ theta} от ( 1,0){\displaystyle (1,0)} (на окружности), пусть u→=OM→{\displaystyle {\vec {u}}={\overrightarrow {OM}}}. Если мы назовем rθ{\displaystyle r_{\theta}} вращение, которое преобразует (1,0){\displaystyle (1,0)} в u→{\displaystyle {\vec {u}}}, то [rθ] ↦θ{\displaystyle \left[r _{\theta}\right]\mapsto \theta} — это биекция, что означает, что мы можем идентифицировать любой угол с числом от 0 до 2π{\displaystyle 2\pi}.

  Углы между кривыми

  Угол между двумя кривыми определяется как угол между касательными A и B на P

  Угол между прямой и кривой (смешанный угол) или между двумя пересекающимися кривых (криволинейный угол) определяется как угол между касательными в точке пересечения. Частным случаям давались различные названия (теперь редко, если вообще когда-либо) давались: амфикиртический (греч. ἀμφί , с обеих сторон, κυρτόσ , выпуклый) или циссоидальный (гр. κισσόσ , плющ), двояковыпуклый; ксистроидальный или систроидальный (гр. ξυστρίσ , инструмент для шабрения), вогнуто-выпуклый; амфицельный (гр. κοίλη , дупло) или angulus lunularis , двояковогнутый.

  Скалярное произведение и обобщение

  В евклидовой плоскости угол θ между двумя векторами u и v связан с их скалярным произведением и их длинами по формуле

  ты⋅v=cos⁡(θ) ‖u‖ ‖v‖.{\ displaystyle \ mathbf {u} \ cdot \ mathbf {v} = \ cos (\ theta) \ \|\ mathbf {u} \ |\ \|\mathbf {v} \|.}

  Это позволяет определить углы в любом вещественном пространстве внутреннего произведения, заменив евклидово скалярное произведение · внутренним произведением гильбертова пространства <·,·>.

  Углы в римановой геометрии

  В римановой геометрии метрический тензор используется для определения угла между двумя касательными. Где U и V — касательные векторы, а 9{j}\right|}}}.}

  Углы в географии и астрономии

  В географии мы указываем положение любой точки на Земле, используя Географическую систему координат . Эта система определяет широту и долготу любого местоположения с точки зрения углов, лежащих в центре Земли, с использованием экватора и (обычно) меридиана Гринвича в качестве ориентиров.

  В астрономии мы аналогичным образом задаем данную точку на небесной сфере, используя любой из нескольких Астрономические системы координат , где ссылки варьируются в зависимости от конкретной системы.

  Астрономы также могут измерить угловое расстояние двух звезд, вообразив две линии, проходящие через центр Земли, каждая из которых пересекает одну из звезд. Угол между этими линиями можно измерить, и он представляет собой угловое расстояние между двумя звездами.

  Астрономы также измеряют видимый размер объектов. Например, полная луна имеет угловое измерение примерно 0,5 °, если смотреть с Земли. Можно сказать: «Луна образует угол в полградуса». Формула малого угла может использоваться для преобразования такого углового измерения в отношение расстояния к размеру.

  См. также

  • Круг
  • Квадрат (геометрия)
  • Треугольник

  Примечания

  1. ↑ Джонатан Слокум. 2007. Предварительный индоевропейский лексикон: данные Pokorny PIE. Центр лингвистических исследований Техасского университета в Остине . Проверено 13 ноября 2007 г.

  Ссылки

  Ссылки ISBN поддерживают NWE за счет реферальных сборов

  • Coxeter, HSM 1989. Introduction to Geometry. Библиотека классики Wiley. Нью-Йорк: Уайли. ISBN 0471504580.
  • Эрнисс, Кэтлин и Дон О’Коннор. 1999. Простая геометрия. Торранс, Калифорния: Публикации Фрэнка Шаффера. ISBN 0768202620 .
  • Гибсон, К.Г. 2004. Элементарная евклидова геометрия: введение для студентов. Кембридж, Великобритания: Издательство Кембриджского университета. ISBN 0521834481.

  Внешние ссылки

  Все ссылки получены 19 июня 2021 г.

  • Биссектрисы четырехугольника в точке пересечения узла.
  • Построение треугольника по биссектрисам его углов в точке пересечения узла.
  • Страницы определения угла с интерактивными апплетами.
  • Различные угловые конструкции с компасом и линейкой Анимированные демонстрации.

  Авторы

  Энциклопедия Нового Света автора и редактора переписали и дополнили статью Википедии в соответствии со стандартами New World Encyclopedia . Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства. Кредит должен соответствовать условиям этой лицензии, которая может ссылаться как на Энциклопедия Нового Света участников и самоотверженных добровольных участников Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:

  • Угол  ^{история}

  История этой статьи с момента ее импорта в New World Encyclopedia :

  • История «Угла (математика)»

  Примечание. На использование отдельных изображений, которые лицензируются отдельно, могут распространяться некоторые ограничения.

  Блестящая вики по математике и естественным наукам

  Сандип Бхардвадж, Хаммад Джамиль, Джордан Калмс, а также

  способствовал

  Содержимое

  • Типы углов
  • Дополнительные и дополнительные углы
  • Вертикальные углы
  • Погоня за углом
  • Смотрите также

  Углы можно разделить на пять групп в зависимости от их измерения в градусах.

  9\ ок. .23∘. □_\квадрат□​

  Какой из углов на рисунке выше является острым?

  A) AOD\quad \text{A) } AODA) AOD
  B) COA\quad \text{B) } COAB) COA
  C) BOC\quad \text{C) } BOCC) BOC
  D) DOB\ quad \text{D) } DOBD) DOB

  Ответ C.\text{C}.C. AOD AOD AOD – прямой угол. И COA COACOA, и DOBDOBDOB тупые. Только BOCBOCBOC меньше 9\circ Z−X=(Z+Y)−(X+Y)=180∘−90∘=90∘. □_\квадрат□​

  Модуль дополнительного угла равен квадрату модуля угла.

  Найдите угол в градусах.

  Два противоположных угла, образованные парой пересекающихся прямых, называются вертикальными углами . Эти углы имеют равные меры.

  \hspace{5cm}

  На приведенной выше диаграмме ∠ABC \угол ABC ∠ABC и ∠DBE \угол DBE ∠DBE являются вертикальными углами и поэтому равны.

  Если прямые PQ PQPQ и XYXYXY пересекаются в ООО, какой угол по вертикали противоположен ∠POX? \угол POX?∠POX?

  Вертикально противоположный угол ∠POX \угол POX∠POX будет равен ∠QOY \углу QOY∠QOY (((который также равен ∠YOQ). \угол YOQ). ∠YOQ). □_\квадрат□​

  На следующем рисунке какая пара углов противоположна по вертикали?

  A) \quad \text{A) }A)  ABC,CBI ABC, CBIABC,CBI
  B) \quad \text{B) }B)  ABH,HBJ ABH, HBJ ABH,HBJ
  C) \quad \text{C) }C)  HBJ,JBI HBJ, JBI HBJ,JBI
  D) \quad \text{D) }D)  ABC,HBI ABC, HBI ABC,HBI
  E) \quad \ текст{E) }E)  ABH,JBI ABH, JBI ABH,JBI

  \hspace{5cm}

  Прорабатывая эти пары, мы видим, что единственная пара противоположных углов — это ABCABCABC и HBIHBI HBI. Следовательно, ответ D)\text{D)}D). □_\квадрат□​

  Примечание : Другая пара вертикальных углов — ABHABHABH и CBICBICBI.

  Учитывая, что ABEABE ABE и CBDCBDCBD являются прямыми линиями, пересекающими друг друга, если ∠ABD=75∘ \угол ABD = 75 ^ \circ ∠ABD=75∘, какова мера ∠CBE? \угол CBE?∠CBE? 9\circ,∠BAC=40∘, какова мера ∠ABC \угла ABC ∠ABC (в градусах)?

  
  Пояснение: HFAC,DFG,EDCB,IHGJHFAC, DFG, EDCB, IHGJHFAC,DFG,EDCB,IHGJ являются прямыми линиями.

  180 270 360 540

  Три отрезка AD,BE,CFAD,BE,CFAD,BE,CF пересекаются в одной точке на диаграмме справа. 9\ циркуляр . \ _\квадрат ∠CAB=180∘−∠ABC−∠BCA=180∘−40∘−60∘=80∘. □​

  360 480 540 600

  Найдите сумму (в градусах) четырех цветных углов на диаграмме.

  На рисунке четыре отрезка AB,CD,EF,GHAB, CD, EF, GHAB,CD,EF,GH пересекаются в одной точке. 9\circ∠GHF=85∘.

  • Удивительные углы и формы — базовая версия

  • Удивительные углы и формы — средний уровень

  • Параллельные линии

  • Перпендикулярные линии

  Процитировать как: Углы. Brilliant.org . Извлекаются из https://brilliant.org/wiki/angles/

  Типы углов — Острые, прямые, тупые, прямые и рефлекторные Углы

  Углы — одна из фундаментальных единиц геометрии, встречающаяся даже в природе. Для человека углы являются важным аспектом архитектуры и инженерии. Без него невозможно строить здания, производить машины, строить дороги и плотины и многие другие сооружения. Углы можно найти везде, от кусочка пиццы до плотницких эскизов и дизайна одежды.

  Типы углов — острые, прямые, тупые, прямые и обратные углы

  Знание углов очень важно, так как они составляют основу геометрии. В следующей статье мы рассмотрим различные типы и важность углов применительно к задачам геометрии. Простой способ начать с концепции состоит в том, что при пересечении двух прямых в точке их пересечения образуется угол. Два луча, образующие угол, называются сторонами угла. Необязательно, чтобы угол образовывался при пересечении двух прямых; он также может быть образован пересечением двух изогнутых линий. Прежде чем понять типы углов, давайте сначала сосредоточимся на том, как их измерять.

  Части угла

  (Изображение скоро будет загружено)

  Угол образуется при пересечении двух лучей в одной точке. При измерении угла одна рука фиксируется в качестве основания, а другая движется по часовой стрелке или против часовой стрелки, образуя угол между ними. Следовательно, все углы имеют две «стороны» или «плеча» и одну «вершину».

  Как маркировать углы?

  Существует два основных способа обозначения угла: 

  • Как показано на рисунке, углу присваивается греческий алфавит, например альфа (α) или тета (θ). Вы также можете пометить их строчными буквами.

  • При работе над геометрическими задачами со сложными фигурами углы можно обозначать с помощью маркировки фигуры. Рассмотрим приведенный выше рисунок; например, угол α также можно назвать углом PQR.

  Положительные и отрицательные углы 

  В зависимости от направления вращения можно классифицировать углы как положительные и отрицательные.

  (Изображение скоро будет загружено)

  Положительные углы: Углы измеряются в направлении против часовой стрелки (противоположном направлению вращения часов), начиная с основания угла.

  Отрицательные углы: Эти углы измеряются по часовой стрелке, начиная с основания угла.

  Величина угла 

  Величина угла — это вращение вокруг вершины, при котором одно из плеч образует угол. Говорят, что чем больше вращение или раскрытие между плечами, тем большую величину оно имеет. Например-

  (Изображение скоро будет загружено)

  Существуют различные типы углов в зависимости от их меры угла. Типы:

  1. Острый угол

  2. Прямой угол

  3. Тупой угол

  4. Прямой угол

  5. Рефлекторный угол

  Как измерить различные типы углов?

  1. Острый угол

  Угол, величина которого меньше 90°, называется острым углом. Измерение от 0° до 90°. На рисунке ниже угол, образованный пересечением PQ и QR в точке Q, образует угол PQR, равный 45°. Таким образом, PQR называется острым углом.

  (Изображение скоро будет загружено)

  2. Прямой угол

  Угол, равный ровно 90°, называется прямым. Обычно он образуется, когда две линии перпендикулярны друг другу. На рисунке ниже линия AB пересекает линию BC в точке B и образует угол ABC, равный 90°.

  (Изображение скоро будет загружено)

  3. Тупой угол

  Угол, величина которого превышает 90°, называется тупым углом. Диапазон измерения угла составляет от 90° до 180°. Тупой угол также можно найти, если у нас есть мера острого угла.

  Мера тупого угла = (180 — мера острого угла)

  На рисунке выше отрезок DO пересекает отрезок OQ в точке O и образует угол DOQ размером 120°. Таким образом, это тупой угол.

  (Изображение скоро будет загружено)

  Кроме того, если мы продолжим линию OQ до OP, то сможем найти меру острого угла.

  DOP = 180° — DOQ = 180° — 120° = 60°

  4. Прямой угол

  Угол, который составляет ровно 180°, называется прямым углом. Это похоже на прямую линию, отсюда и название прямого угла.

  Прямой угол — это не что иное, как смесь тупого и острого углов на прямой.

  5. Угол рефлекса

  Угол, величина которого больше 180° и меньше 360°, называется углом рефлекса. Угол рефлекса можно рассчитать, если указана мера острого угла, поскольку он дополняет острый угол на другой стороне линии.

  (Изображение скоро будет загружено)

  Используя угол отражения, мы можем найти меру острого угла.

  Мера острого угла = 360° – мера угла рефлекса

  6. Дополнительные и дополнительные углы

  Дополнительный угол

  Если сумма двух углов составляет 90°, то они называются дополнительными углами. Углы не обязательно должны быть смежными друг с другом, чтобы считаться дополнительными. Если в сумме они составляют 90°, их называют дополнительными углами.

  (Изображение скоро будет загружено)

  На приведенном выше рисунке углы расположены рядом друг с другом и в сумме составляют 90° и поэтому известны как дополнительные углы. На рисунках c и d углы не примыкают друг к другу, но в сумме дают 90° и поэтому называются дополнительными углами.

  Дополнительные углы

  Когда два угла в сумме составляют 180°, они называются дополнительными углами. Существуют различные типы дополнительных углов.

  • Смежные углы

  Эти углы имеют общую сторону и вершину, т.е. вершину угла. Однако эти точки никак не пересекаются. Проще говоря, смежные углы — это два угла рядом друг с другом.

  (изображение скоро будет загружено)

  • Несмежные углы

  Эти углы не имеют общего конца, т. е. обычно не имеют общей вершины.

  (Изображение скоро будет загружено)

  Типы несмежных углов-

  • Вертикальные углы

  Углы, имеющие общую вершину и стороны угла, образованные одними и теми же линиями, называются вертикальными углами. Вертикальные углы равны между собой.

  (Изображение скоро будет загружено)

  На приведенном выше рисунке 1 и 3, 2 и 4, 6 и 8, 5 и 7 являются вертикальными углами. Кроме того, 3, 4, 5, 6 известны как внутренние углы, а 1, 2, 7, 8 известны как внешние углы.

  Это пара внутренних углов на противоположной стороне поперечной. Самый простой способ обнаружить чередующиеся внутренние углы — определить букву «Z» на внутренней стороне.

  На приведенном выше рисунке 3 и 5, 4 и 6 — внутренние углы. Внутренние углы равны друг другу.

  Это похоже на альтернативные внутренние углы; только то, что он присутствует на внешней стороне. На приведенном выше рисунке 1 и 7, 2 и 8 — это пара чередующихся внешних углов. Подобно альтернативным внутренним углам, даже альтернативные внешние углы равны друг другу.

  Углы, находящиеся в одинаковом положении, называются соответствующими углами. На приведенном выше рисунке 1 и 5 — соответствующие углы, и они равны друг другу.

  Резюме

  1818

  Angle Type	Angle measure
  Acute angle	Greater than 0 °, Less than 90°
  Right angle	90 °
  Огромный угол	больше 90 °, менее 180 °
  Прямой угол
  Прямой угол
  9000
  9000
  9000
  5
  0005
  Угол рефлекса	Больше 180°, меньше 360°

  Основой геометрии являются углы. Углы находят свое применение практически во всех типах вопросов, будь то тригонометрия или замкнутые фигуры. Понимание углов и типов углов поможет в решении многих каверзных вопросов. Таким образом, убедитесь, что вы понимаете это хорошо.

  Угол – определение и типы с примерами

  После того, как вы узнали о точках, прямых, отрезках и плоскости, вам нужно узнать, что происходит, когда две прямые пересекаются в одной точке. То есть когда образуется угол.

  Углы — одно из основных понятий геометрии. Мы не можем думать об определении какой-либо формы, будь то треугольники, четырехугольники или многоугольники, без их углов. Таким образом, угол образует часть каждой геометрической формы.

  Что такое угол

  Математически угол определяется как фигура, которая образуется, когда два луча встречаются в одной точке. Обозначается символом ∠. Угол обычно измеряется в градусах, обозначаемых знаком «°». Термин «угол» происходит от латинского слова «angulus», что означает «угол».

  Угол

  Градус — это мера поворота. Полный оборот вокруг точки дает нам полный круг, равный 360°, половинный оборот дает нам полукруг, равный 180°, а четверть оборота дает нам прямой угол, равный 90°.

  Части угла

  Части угла
  1. Плечи : Две прямые или изогнутые стороны, соединяющиеся в угол, называются плечами. Здесь OX и OY — стороны угла ∠XOY.
  2. Вершина : Общая конечная точка, где два луча встречаются, образуя угол. Здесь точка «О» является вершиной.
  Присвоение имени углу

  Угол может быть назван двумя способами:

  Метод – 1 : Символ угла, за которым следуют три точки, определяющие угол. Средняя буква — вершина. Таким образом, приведенную выше цифру можно записать как ∠XOY или ∠YOX.

  Метод – 2 : Просто запишите вершину. Пишется как ∠O.

  Иногда греческие буквы, такие как α, β, γ, θ и φ, или строчные латинские буквы, такие как a, b, c, x, y и z, также используются для обозначения угла или его размера.

  Как найти угол

  Величина угла измеряется с помощью транспортира, который обычно имеет полукруглую форму и прозрачен.

  Измерение углов с помощью транспортира

  Типы углов

  Все углы обычно классифицируются в зависимости от их величины или степени вращения на шесть основных типов:

  Типы углов
  1. Острый угол : Угол, размер которого меньше 90° называется острым углом. Другими словами, он лежит в пределах от 0° до 9°.0°.
  2. Прямой угол : Угол, равный ровно 90°, называется прямым углом. Он образуется, когда две стороны угла перпендикулярны друг другу. Знак прямого угла также можно показать с помощью четверти круга вместе со стандартным знаком, как показано на рисунке.
  3. Тупой угол : Тупой угол называется угол, величина которого больше 90° и меньше 180°.
  4. Прямой угол : Угол, который составляет ровно 180°, называется прямым углом. Он похож на прямую линию, отсюда и название прямого угла.
  5. Угол рефлекса : Угол, величина которого больше 180° и меньше 360°, называется углом рефлекса.
  6. Полный угол : Угол, градусная мера которого равна 360°, называется полным углом. Он образован одним полным оборотом одного из его рычагов.

  Другие типы углов

  Углы также иногда классифицируют на основе их положения, направления вращения, суммы их пар или их поперечной на следующие типы:

  • Interior Angles
  • Exterior Angles
  • Positive Angles
  • Negative Angles
  • Complementary Angles
  • Supplementary Angles
  • Vertically Opposite Angles
  • Adjacent Angles
  • Alternate Interior Angles
  • Alternate Exterior Angles
  • Corresponding Angles
  • Последовательные внутренние углы

  Примеры из реальной жизни

  В нашей повседневной жизни мы видим углы почти повсюду вокруг нас. Некоторые из примеров приведены ниже:

  • Углы, образованные стрелками часов.

    No related posts.