Асимптоты графика функции с примерами решения
Содержание:
Понятие асимптоты:
Асимптота кривой — это прямая, к которой неограниченно приближается кривая при ее удалении в бесконечность.
Вертикальные асимптоты
— вертикальная асимптота, если при
Вертикальная асимптота может быть в точке если точка ограничивает открытые (или полуоткрытые) промежутки области определения данной функции и вблизи точки значения функции стремятся к бесконечности.
Примеры вертикальных асимптот графиков функций
— вертикальная асимптота ( — также асимптота, но горизонтальная)
— вертикальная асимптота
Наклонные и горизонтальные асимптоты
I. Если — дробно рациональная функция, у которой степень числителя на единицу больше степени знаменателя (или равна ей), то выделяем целую часть дроби и используем определение асимптоты.
Примеры:
При тогда Следовательно, — наклонная асимптота (также — вертикальная асимптота)
При тогда Следовательно, — горизонтальная асимптота (также — вертикальная асимптота)
II. В общем случае уравнения наклонных и горизонтальных асимптотможно получить с использованием формул
Понятие асимптоты
Если кривая имеет бесконечную ветвь, то асимптотой такой кривой называют прямую, к которой эта ветвь неограниченно приближается. Другими словами, асимптота кривой — это прямая, к которой неограниченно приближается кривая при ее удалении в бесконечность.
Асимптоты могут быть вертикальными, горизонтальными или наклонными.
Например, для графика функции (рис. 7.1) асимптотами будут оси координат, поскольку при и при график функции приближается к прямой ось — горизонтальная асимптота. Когда функция стремится к (или ), то кривая приближается к прямой ось — вертикальная асимптота.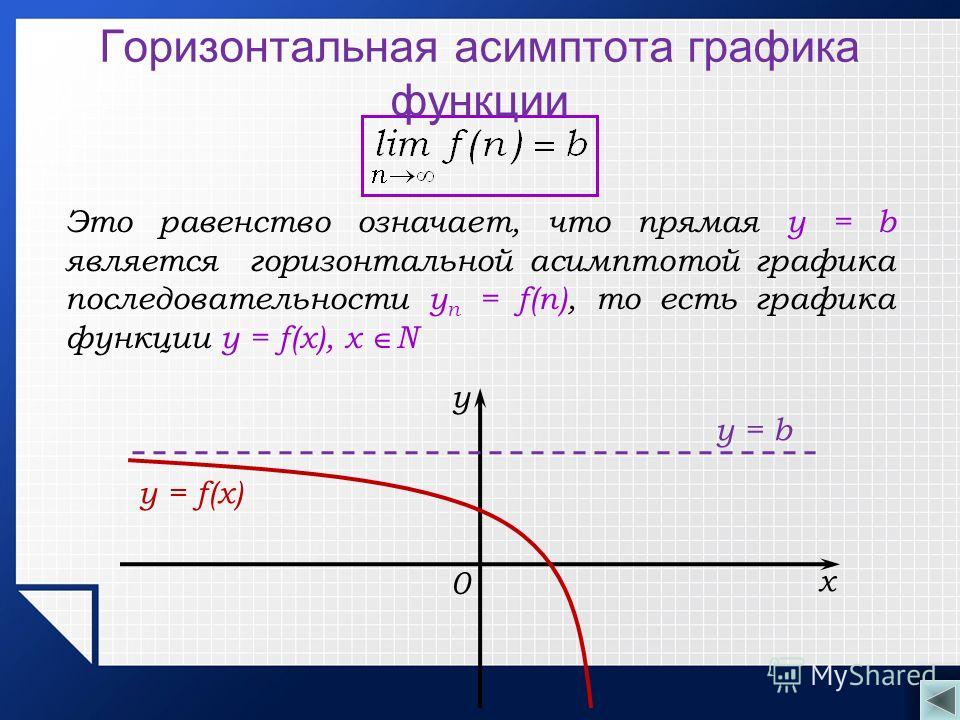
Если рассмотреть функцию то при выражение Вследствие этого график функции приближается к прямой поэтому эта прямая будет наклонной асимптотой графика функции(рис. 7.2) (график этой функции имеет также и вертикальную асимптоту ).
Следует отметить, что не любая кривая имеет асимптоту, поэтому не у каждого графика функции будет асимптота. Но исследование функции на наличие у ее графика асимптот позволяет уточнить свойства функции и поведение ее графика.
Вертикальные асимптоты
Если прямая — вертикальная асимптота, то по определению около точки кривая должна иметь бесконечную ветвь, то есть предел данной функции при (слева или справа) должен равняться бесконечности (). Исходя из непрерывности элементарных функций, которые рассматривались в школьном курсе математики, такими точками могут быть только точки, ограничивающие открытые (или полуоткрытые) промежутки области определения данной функции.
Например, у функции область определения имеет разрыв в точке (область определения: и точка 1 ограничивает открытые промежутки области определения). Можно предположить, что прямая будет вертикальной асимптотой. Для того чтобы убедиться в этом, необходимо проверить, будет ли функция стремиться к бесконечности около точки 1 (слева или справа). Для этого рассмотрим
Можно предположить, что прямая будет вертикальной асимптотой. Для того чтобы убедиться в этом, необходимо проверить, будет ли функция стремиться к бесконечности около точки 1 (слева или справа). Для этого рассмотрим
Аналогично
Таким образом, прямая является вертикальной асимптотой, поскольку при стремлении функции к бесконечности ее график неограниченно приближается к прямой (рис. 7.3).
Отметим, что не всегда в точке разрыва области определения функция будет иметь вертикальную асимптоту. Например, функция имеет область определения поэтому прямая «подозрительна» на вертикальную асимптоту. Но Аналогично Следовательно, около прямой функция не стремится к бесконечности, и поэтому прямая не является асимптотой графика данной функции (рис. 7.4).
Наклонные и горизонтальные асимптоты
Наклонные и горизонтальные асимптоты довольно просто находятся для графиков дробно-рациональных функций, у которых степень числителя на единицу больше степени знаменателя (или равна степени знаменателя). Для этого достаточно выделить целую часть заданной дроби и использовать определение асимптоты.
Для этого достаточно выделить целую часть заданной дроби и использовать определение асимптоты.
Например, еще раз рассмотрим функцию Выделим целую часть:
При выражение то есть график нашей функции будет х -1 неограниченно приближаться к прямой при Из этого следует, что наклонной асимптотой графика данной функции* будет прямая (рис. 7.3).
Рассмотрим, как находятся наклонные и горизонтальные асимптоты в общем случае.
Пусть наклонной (или горизонтальной) асимптотой графика функции является прямая По определению асимптоты при график функции неограниченно приближается к прямой Другими словами, при с любой точностью будет выполняться равенство
(1)
Эта равенство не нарушится, если обе его части разделить на Получим: При отношение поэтому отношение при , то есть
(2)
Возвращаясь к формуле (1), получаем, что при то есть
(3)
Формулы (2) и (3) дают возможность находить наклонные и горизонтальные асимптоты для графика любой функции (при условии, что они существуют).
Отметим, что если у графика функции есть горизонтальная асимптота, то ее уравнение будет (в этом случае ). Но при из формулы (3) получаем Следовательно, если существует число то график функции имеет горизонтальную асимптоту
- Заказать решение задач по высшей математике
Пример:
Пользуясь общими формулами, найдите наклонную асимптоту графика функции
Решение:
Будем искать наклонную асимптоту в виде где и находятся по формулам (2) и (3):
Асимптотой графика данной функции будет прямая то есть прямая
Пример:
Найдите асимптоты графика функции
Решение:
Область определения функции: — любое действительное число, то есть На всей области определения эта функция непрерывна, поэтому вертикальных асимптот график функции не имеет. Будем искать наклонные и горизонтальные асимптоты в виде Тогда
Таким образом, заданная функция имеет только горизонтальную асимптоту (рис.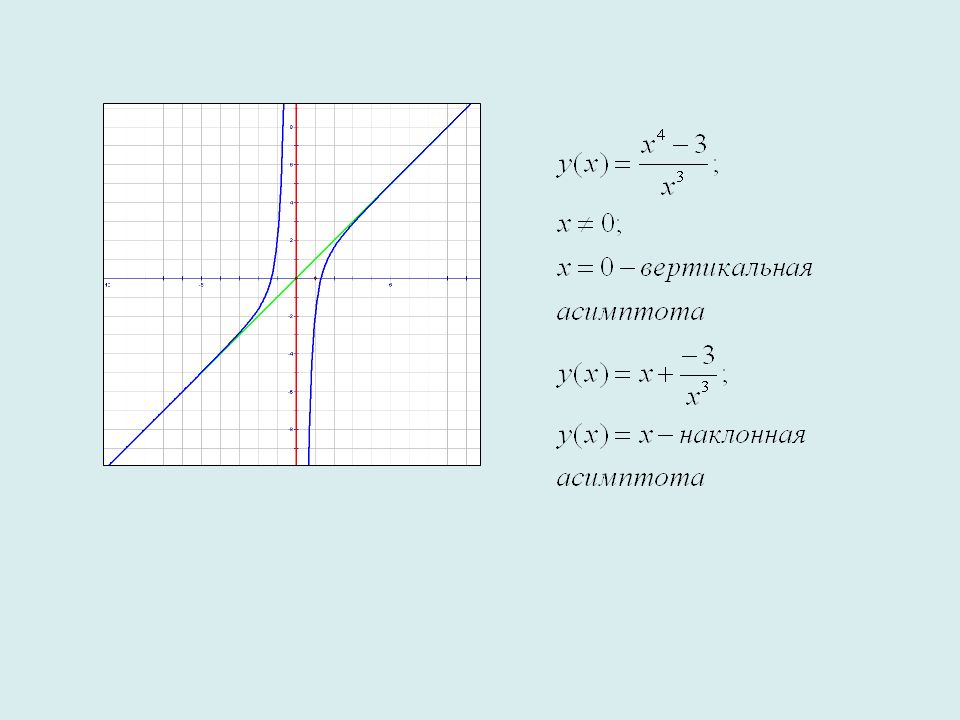 7.5).
7.5).
Иногда график функции может иметь разные асимптоты при и при в этом случае при использовании формул (2) и (3) приходится отдельно находить значения и при и при
Как найти асимптоты графика функцииПри исследовании поведения функции на бесконечности или вблизи точек разрыва часто оказывается, что расстояние между точками графика функции и точками некоторой прямой стремится к нулю при неограниченном удалении точек графика от начала координат. Прямая, к которой стремится кривая в бесконечно удаленной точке, называется асимптотой графика. Различают вертикальные и наклонные асимптоты. Прямая называется вертикальной асимптотой графика функции y=f(x), если хотя бы один из односторонних пределов в точке равен бесконечности: Такие асимптоты существуют только в точках разрыва второго рода.
Внимание! Непрерывные на множестве действительных чисел функции вертикальных асимптот на имеют.
Для того чтобы график функции y=f(x) имел наклонную асимптоту y=kx+b, необходимо и достаточно, чтобы существовали конечные пределы
Частным случаем наклонной асимптоты (k=0) является горизонтальная асимптота.
Пример:
Найти асимптоты графика функции
Решение:
Функция непрерывна в области определения как элементарная. Следовательно, вертикальных асимптот нет. Найдем наклонные асимптоты y=kx+b:
Получаем горизонтальную асимптоту y=0.
Общее исследование функции и построение графикаС помощью производной функции можно провести ее полное исследование и построить график этой функции. При этом рекомендуется использовать следующую схему.
- Найти область определения функции D(f).
- Исследовать функцию на четность нечетность периодичность
- Исследовать функцию на непрерывность, найти точки разрыва.
- Найти асимптоты графика функции.
- Исследовать функцию на монотонность, найти точки экстремума.
- Найти интервалы выпуклости и вогнутости, точки перегиба функции.
- Используя результаты проведенного исследования, построить график функции (можно вычислить координаты точек пересечения с осями координат).

Пример:
Провести полное исследование функции и построить ее график.
Решение:
Область определения функции — вся числовая прямая:
Функция непериодическая. Она нечетная, т.к. область определения симметрична относительно начала координат и
Следовательно, график функции симметричен относительно начала координат и достаточно исследовать функцию для
Функция непрерывна в области определения как композиция основных элементарных функций. Поскольку точек разрыва нет.
Строим график функции, используя результаты исследования.
Как найти асимптоты функции. Как найти асимптоты графика функции? И в точке
Ни одной, одна, две, три,… или бесконечно много. За примерами далеко ходить не будем, вспомним элементарные функции. Парабола, кубическая парабола, синусоида вовсе не имеют асимптот. График экспоненциальной, логарифмической функции обладает единственной асимптотой. У арктангенса, арккотангенса их две, а у тангенса, котангенса — бесконечно много. Не редкость, когда график укомплектован и горизонтальными и вертикальными асимптотами. Гипербола, will always love you.
Не редкость, когда график укомплектован и горизонтальными и вертикальными асимптотами. Гипербола, will always love you.
Что значит найти асимптоты графика функции?
Это значит выяснить их уравнения, ну и начертить прямые линии, если того требует условие задачи. Процесс предполагает нахождение пределов функции.
Вертикальная асимптота графика, как правило, находится в точке бесконечного разрыва функции. Всё просто: если в точке функция терпит бесконечный разрыв, то прямая, заданная уравнением является вертикальной асимптотой графика.
Примечание: обратите внимание, что запись используется для обозначения двух совершенно разных понятий. Точка подразумевается или уравнение прямой — зависит от контекста.
Таким образом, чтобы установить наличие вертикальной асимптоты в точке достаточно показать, что хотя бы один из односторонних пределов бесконечен. Чаще всего это точка, где знаменатель функции равен нулю. По существу, мы уже находили вертикальные асимптоты в последних примерах урока о непрерывности функции. Но в ряде случаев существует только один односторонний предел, и, если он бесконечен, то снова — любите и жалуйте вертикальную асимптоту. Простейшая иллюстрация: и ось ординат.
Но в ряде случаев существует только один односторонний предел, и, если он бесконечен, то снова — любите и жалуйте вертикальную асимптоту. Простейшая иллюстрация: и ось ординат.
Из вышесказанного также следует очевидный факт: если функция непрерывна на, то вертикальные асимптоты отсутствуют. На ум почему-то пришла парабола. Действительно, где тут «воткнёшь» прямую? …да… понимаю… последователи дядюшки Фрейда забились в истерике =)
Обратное утверждение в общем случае неверно: так, функция не определена на всей числовой прямой, однако совершенно обделена асимптотами.
Наклонные асимптоты графика функции
Наклонные (как частный случай — горизонтальные) асимптоты могут нарисоваться, если аргумент функции стремится к «плюс бесконечности» или к «минус бесконечности». Поэтому график функции не может иметь больше 2-х наклонных асимптот. Например, график экспоненциальной функции обладает единственной горизонтальной асимптотой при, а график арктангенса при — двумя такими асимптотами, причём различными.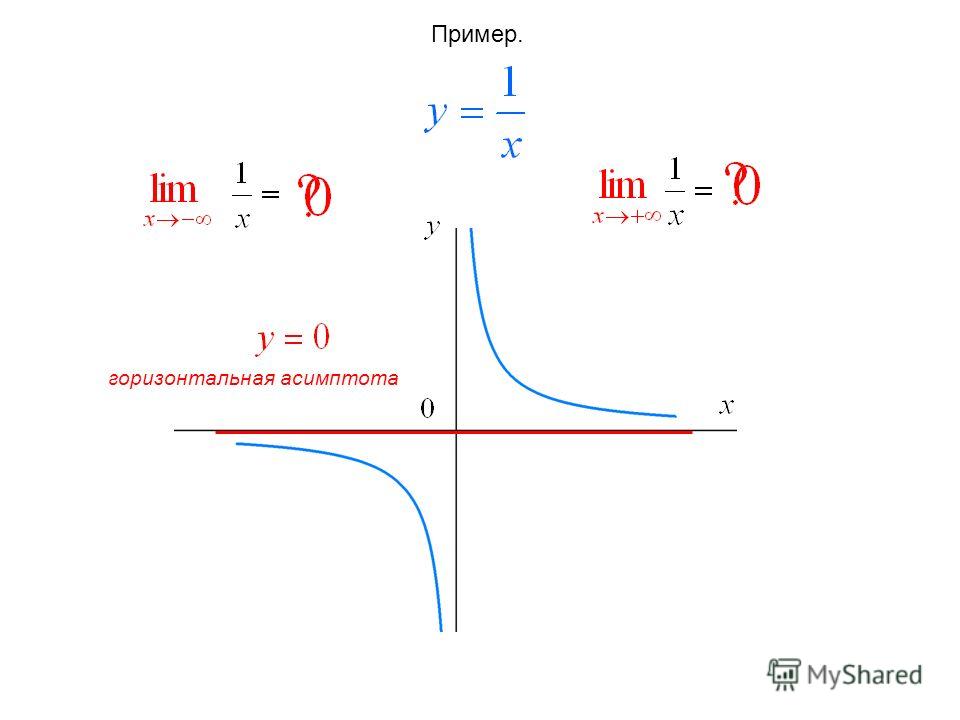
Когда график и там и там сближается с единственной наклонной асимптотой, то «бесконечности» принято объединять под единой записью. Например, …правильно догадались: .
Именно так формулируется типовое задание, и оно предполагает нахождение ВСЕХ асимптот графика (вертикальных, наклонных/горизонтальных). Хотя, если быть более точным в постановке вопроса — речь идёт об исследовании на наличие асимптот (ведь таковых может и вовсе не оказаться).
Начнём с чего-нибудь простого:
Пример 1
Решение удобно разбить на два пункта:
1) Сначала проверяем, есть ли вертикальные асимптоты. Знаменатель обращается в ноль при , и сразу понятно, что в данной точке функция терпит бесконечный разрыв , а прямая, заданная уравнением , является вертикальной асимптотой графика функции . Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:
Напоминаю технику вычислений, на которой я подобно останавливался в статье непрерывность функции. Точки разрыва . В выражение под знаком предела вместо «икса» подставляем . В числителе ничего интересного:
Точки разрыва . В выражение под знаком предела вместо «икса» подставляем . В числителе ничего интересного:
.
А вот в знаменателе получается бесконечно малое отрицательное число :
, оно и определяет судьбу предела.
Левосторонний предел бесконечный, и, в принципе уже можно вынести вердикт о наличии вертикальной асимптоты. Но односторонние пределы нужны не только для этого — они ПОМОГАЮТ ПОНЯТЬ, КАК расположен график функции и построить его КОРРЕКТНО . Поэтому обязательно вычислим и правосторонний предел:
Вывод : односторонние пределы бесконечны, значит, прямая является вертикальной асимптотой графика функции при .
Первый предел конечен , значит, необходимо «продолжить разговор» и найти второй предел:
Второй предел тоже конечен .
Таким образом, наша асимптота:
Вывод : прямая, заданная уравнением является горизонтальной асимптотой графика функции при .
Для нахождения горизонтальной асимптоты можно пользоваться упрощенной формулой :
Если существует конечный
предел , то прямая является горизонтальной асимптотой графика функции при .
Нетрудно заметить, что числитель и знаменатель функции одного порядка роста , а значит, искомый предел будет конечным:
Ответ :
По условию не нужно выполнять чертёж, но если в самом разгаре исследование функции , то на черновике сразу же делаем набросок:
Исходя из трёх найденных пределов , попытайтесь самостоятельно прикинуть, как может располагаться график функции . Совсем трудно? Найдите 5-6-7-8 точек и отметьте их на чертеже. Впрочем, график данной функции строится с помощью преобразований графика элементарной функции , и читатели, внимательно рассмотревшие Пример 21 указанной статьи легко догадаются, что это за кривая.
Пример 2
Найти асимптоты графика функции
Это пример для самостоятельного решения. Процесс, напоминаю, удобно разбить на два пункта — вертикальные асимптоты и наклонные асимптоты. В образце решения горизонтальная асимптота найдёна по упрощенной схеме.
На практике чаще всего встречаются дробно-рациональные функции, и после тренировки на гиперболах усложним задание:
Пример 3
Найти асимптоты графика функции
Решение : Раз, два и готово:
1) Вертикальные асимптоты находятся в точках бесконечного разрыва , поэтому нужно проверить, обращается ли знаменатель в ноль.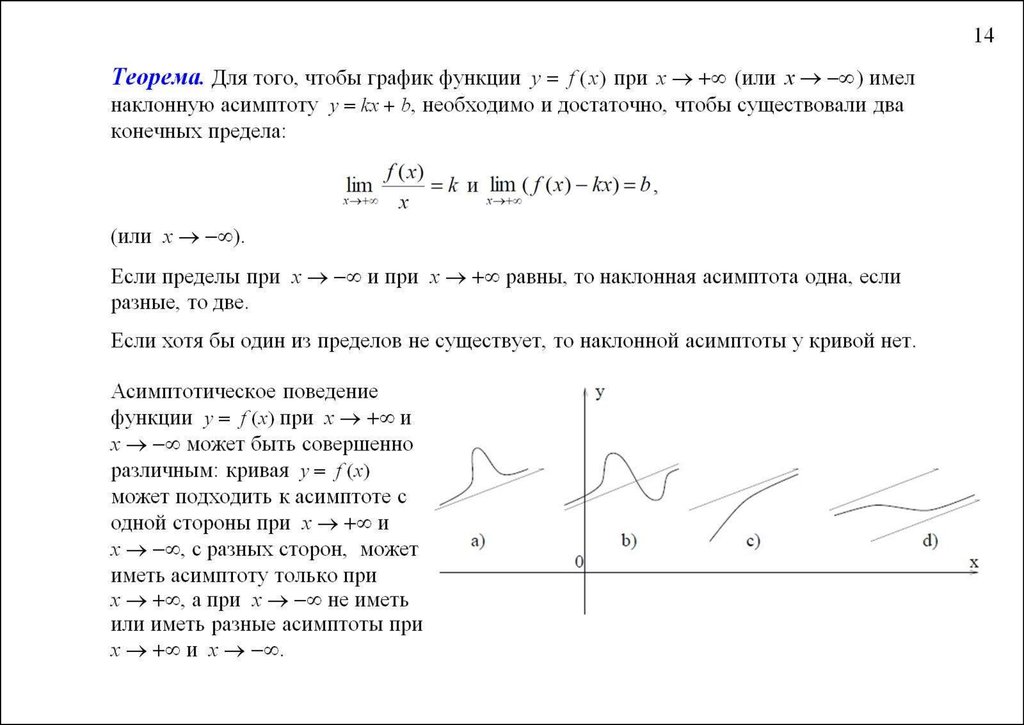 Решим квадратное уравнение :
Решим квадратное уравнение :
Дискриминант положителен, поэтому уравнение имеет два действительных корня, и работы значительно прибавляется =)
В целях дальнейшего нахождения односторонних пределов квадратный трёхчлен удобно разложить на множители :
(для компактной записи «минус» внесли в первую скобку). Для подстраховки выполним проверку, мысленно либо на черновике раскрыв скобки.
Перепишем функцию в виде
Найдём односторонние пределы в точке :
И в точке :
Таким образом, прямые являются вертикальными асимптотами графика рассматриваемой функции.
2) Если посмотреть на функцию , то совершенно очевидно, что предел будет конечным и у нас горизонтальная асимптота. Покажем её наличие коротким способом:
Таким образом, прямая (ось абсцисс) является горизонтальной асимптотой графика данной функции.
Ответ :
Найденные пределы и асимптоты дают немало информации о графике функции. Постарайтесь мысленно представить чертёж с учётом следующих фактов:
Схематично изобразите вашу версию графика на черновике.
Конечно, найденные пределы однозначно не определяют вид графика, и возможно, вы допустите ошибку, но само упражнение окажет неоценимую помощь в ходе полного исследования функции . Правильная картинка — в конце урока.
Пример 4
Найти асимптоты графика функции
Пример 5
Найти асимптоты графика функции
Это задания для самостоятельного решения. Оба графика снова обладают горизонтальными асимптотами, которые немедленно детектируются по следующим признакам: в Примере 4 порядок роста знаменателя больше , чем порядок роста числителя, а в Примере 5 числитель и знаменатель одного порядка роста . В образце решения первая функция исследована на наличие наклонных асимптот полным путём, а вторая — через предел .
Горизонтальные асимптоты, по моему субъективному впечатлению, встречаются заметно чаще, чем те, которые «по-настоящему наклонены». Долгожданный общий случай:
Пример 6
Найти асимптоты графика функции
Решение : классика жанра:
1) Поскольку знаменатель положителен, то функция непрерывна на всей числовой прямой, и вертикальные асимптоты отсутствуют.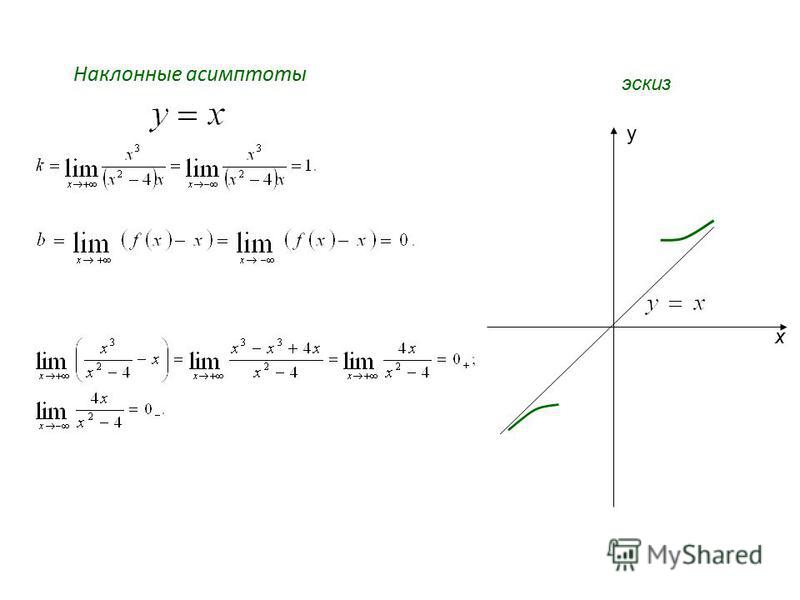 …Хорошо ли это? Не то слово — отлично! Пункт №1 закрыт.
…Хорошо ли это? Не то слово — отлично! Пункт №1 закрыт.
2) Проверим наличие наклонных асимптот:
Первый предел конечен , поэтому едем дальше. В ходе вычисления второго предела для устранения неопределённости «бесконечность минус бесконечность» приводим выражение к общему знаменателю:
Второй предел тоже конечен , следовательно, у графика рассматриваемой функции существует наклонная асимптота:
Вывод :
Таким образом, при график функции бесконечно близко приближается к прямой :
Заметьте, что он пересекает свою наклонную асимптоту в начале координат, и такие точки пересечения вполне допустимы — важно, чтобы «всё было нормально» на бесконечности (собственно, речь об асимптотах и заходит именно там).
Пример 7
Найти асимптоты графика функции
Решение : комментировать особо нечего, поэтому оформлю примерный образец чистового решения:
1) Вертикальные асимптоты. Исследуем точку .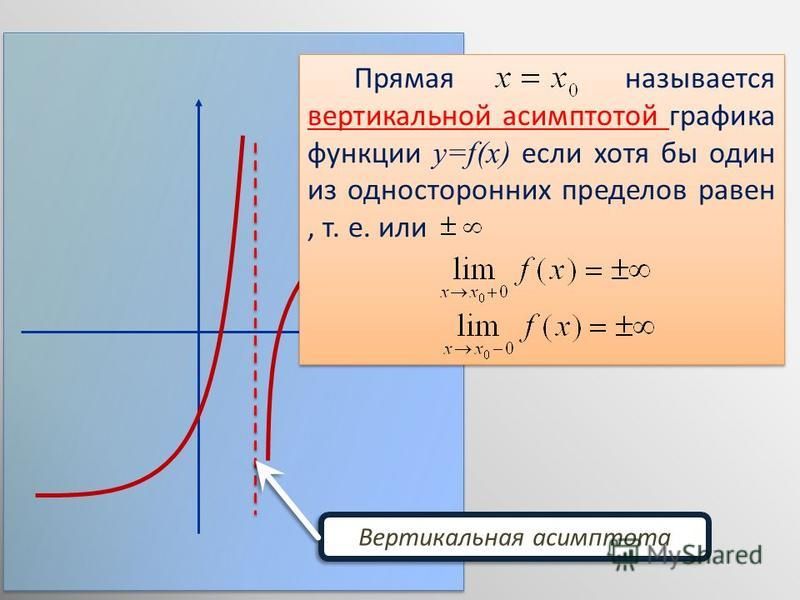
Прямая является вертикальной асимптотой для графика при .
2) Наклонные асимптоты:
Прямая является наклонной асимптотой для графика при .
Ответ :
Найдённые односторонние пределы и асимптоты с высокой достоверностью позволяют предположить, как выглядит график данной функции. Корректный чертёж в конце урока.
Пример 8
Найти асимптоты графика функции
Это пример для самостоятельного решения, для удобства вычисления некоторых пределов можно почленно разделить числитель на знаменатель. И снова, анализируя полученные результаты, постарайтесь начертить график данной функции.
Очевидно, что обладателями «настоящих» наклонных асимптот являются графики тех дробно-рациональных функций, у которых старшая степень числителя на единицу больше старшей степени знаменателя. Если больше — наклонной асимптоты уже не будет (например, ).
Но в жизни происходят и другие чудеса:
Пример 9
Решение : функция непрерывна на всей числовой прямой, значит, вертикальные асимптоты отсутствует. Но вот наклонные вполне могут быть. Проверяем:
Но вот наклонные вполне могут быть. Проверяем:
Вспоминаю, как ещё в ВУЗе столкнулся с похожей функцией и просто не мог поверить, что у неё есть наклонная асимптота. До тех пор, пока не вычислил второй предел:
Строго говоря, здесь две неопределённости: и , но так или иначе, нужно использовать метод решения, который разобран в Примерах 5-6 статьи о пределах повышенной сложности . Умножаем и делим на сопряженное выражение, чтобы воспользоваться формулой :
Ответ :
Пожалуй, самая популярная наклонная асимптота.
До сих пор бесконечности удавалось «стричь под одну гребёнку», но бывает, что у графика функции две разные наклонные асимптоты при и при :
Пример 10
Исследовать график функции на наличие асимптот
Решение : подкоренное выражение положительно, значит, область определения — любое действительно число, и вертикальных палок быть не может.
Проверим, существуют ли наклонные асимптоты.
Если «икс» стремится к «минус бесконечности», то:
(при внесении «икса» под квадратный корень необходимо добавить знак «минус», чтобы не потерять отрицательность знаменателя)
Выглядит необычно, но здесь неопределённость «бесконечность минус бесконечность». Умножаем числитель и знаменатель на сопряженное выражение:
Таким образом, прямая является наклонной асимптотой графика при .
С «плюс бесконечностью» всё тривиальнее:
А прямая — при .
Ответ :
Если ;
, если .
Не удержусь от графического изображения:
Это одна из ветвей гиперболы .
Не редкость, когда потенциальное наличие асимптот изначально ограничено областью определения функции :
Пример 11
Исследовать график функции на наличие асимптот
Решение : очевидно, что , поэтому рассматриваем только правую полуплоскость, где есть график функции.
1) Функция непрерывна на интервале , а значит, если вертикальная асимптота и существует, то это может быть только ось ординат.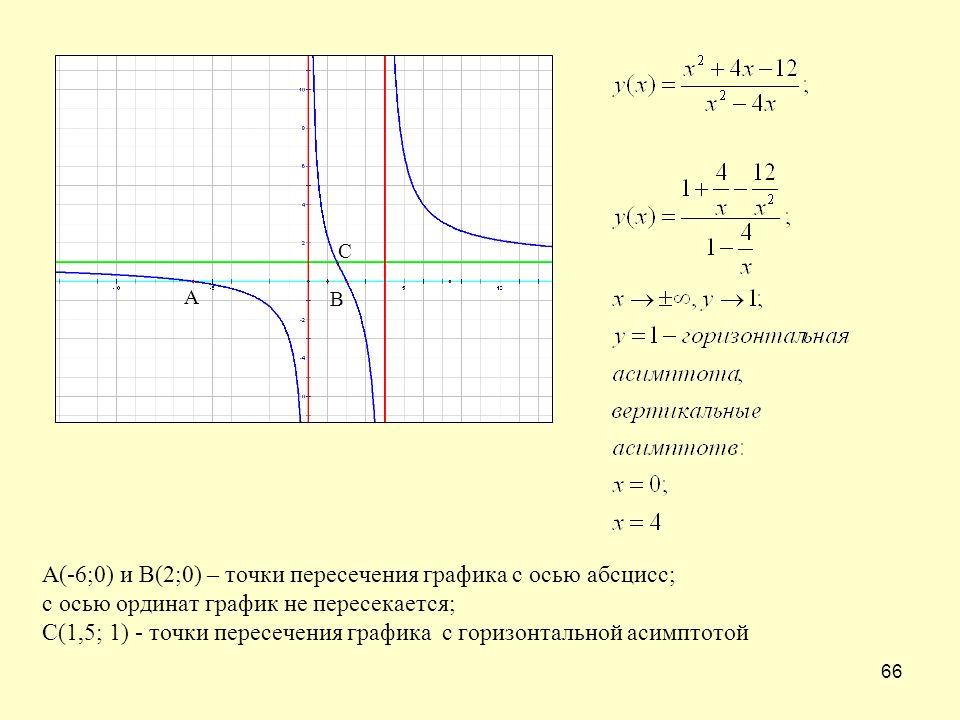 Исследуем поведение функции вблизи точки справа :
Исследуем поведение функции вблизи точки справа :
Обратите внимание, здесь НЕТ неопределённости (на таких случаях акцентировалось внимание в начале статьи Методы решения пределов) .
Таким образом, прямая (ось ординат) является вертикальной асимптотой для графика функции при .
2) Исследование на наклонную асимптоту можно провести по полной схеме, но в статье Правила Лопитал мы выяснили, что линейная функция более высокого порядка роста, чем логарифмическая, следовательно: (см. Пример 1 того же урока).
Вывод: ось абсцисс является горизонтальной асимптотой графика функции при .
Ответ :
Если ;
, если .
Чертёж для наглядности:
Интересно, что у вроде бы похожей функции асимптот нет вообще (желающие могут это проверить).
Два заключительных примера для самостоятельного изучения:
Пример 12
Исследовать график функции на наличие асимптот
Для проверки на вертикальные асимптоты сначала нужно найти область определения функции , а затем вычислить пару односторонних пределов в «подозрительных» точках. Наклонные асимптоты тоже не исключены, поскольку функция определена на «плюс» и «минус» бесконечности.
Наклонные асимптоты тоже не исключены, поскольку функция определена на «плюс» и «минус» бесконечности.
Пример 13
Исследовать график функции на наличие асимптот
А здесь могут быть только наклонные асимптоты, причём направления , следует рассмотреть отдельно.
Надеюсь, вы отыскали нужную асимптоту =)
Желаю успехов!
Решения и ответы:
Пример 2: Решение :
. Найдём односторонние пределы:
Прямая является вертикальной асимптотой графика функции при .
2) Наклонные асимптоты.
Прямая .
Ответ :
Чертёж к Примеру 3:
Пример 4: Решение :
1) Вертикальные асимптоты. Функция терпит бесконечный разрыв в точке . Вычислим односторонние пределы:
Примечание : бесконечно малое отрицательное число в чётной степени равно бесконечно малому положительному числу: .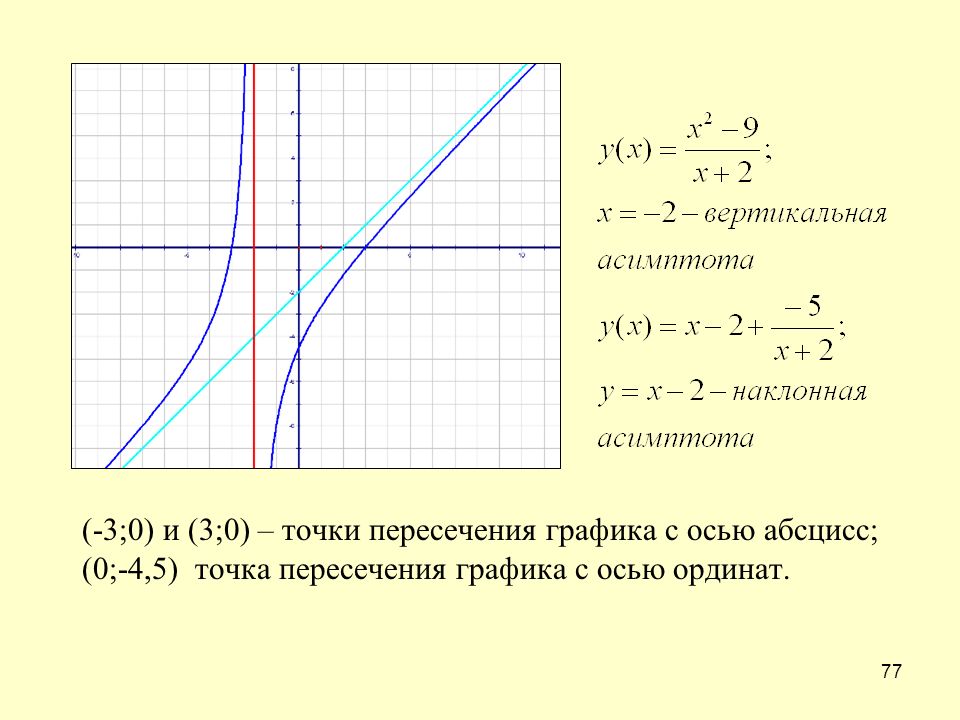
Прямая является вертикальной асимптотой графика функции.
2) Наклонные асимптоты.
Прямая (ось абсцисс) является горизонтальной асимптотой графика функции при .
Ответ :
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Понятие асимптоты
Если предварительно построить асимптоты кривой, то многих случаях построение графика функции облегчается.
Судьба асимптоты полна трагизма. Представьте себе, каково это: всю жизнь двигаться
по прямой к заветной цели, подойти к ней максимально близко, но так и не достигнуть её. Например, стремиться
соединить свой жизненный путь с путём желанного человека, в какой-то момент приблизиться к нему почти
вплотную, но даже не коснуться его. Или стремиться заработать миллиард, но до достижения этой цели
и записи в книгу рекордов Гиннеса для своего случая не достаёт сотых долей цента. И тому подобное. Так
и с асимптотой: она постоянно стремится достигнуть кривой графика функции, приближается к нему на минимальное
возможное расстояние, но так и не касается его.
И тому подобное. Так
и с асимптотой: она постоянно стремится достигнуть кривой графика функции, приближается к нему на минимальное
возможное расстояние, но так и не касается его.
Определение 1. Асимптотами называются такие прямые , к которым сколь угодно близко приближается график функции, когда переменная стремится к плюс бесконечности или к минус бесконечности.
Определение 2. Прямая называется асимптотой графика функции, если расстояние от переменной точки М графика функции до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-либо ветви графика функции.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Вертикальные асимптоты
Первое, что нужно узнать о вертикальных асимптотах: они параллельны оси Oy .
Определение . Прямая x = a является вертикальной асимптотой графика функции , если точка x = a является точкой разрыва второго рода для этой функции.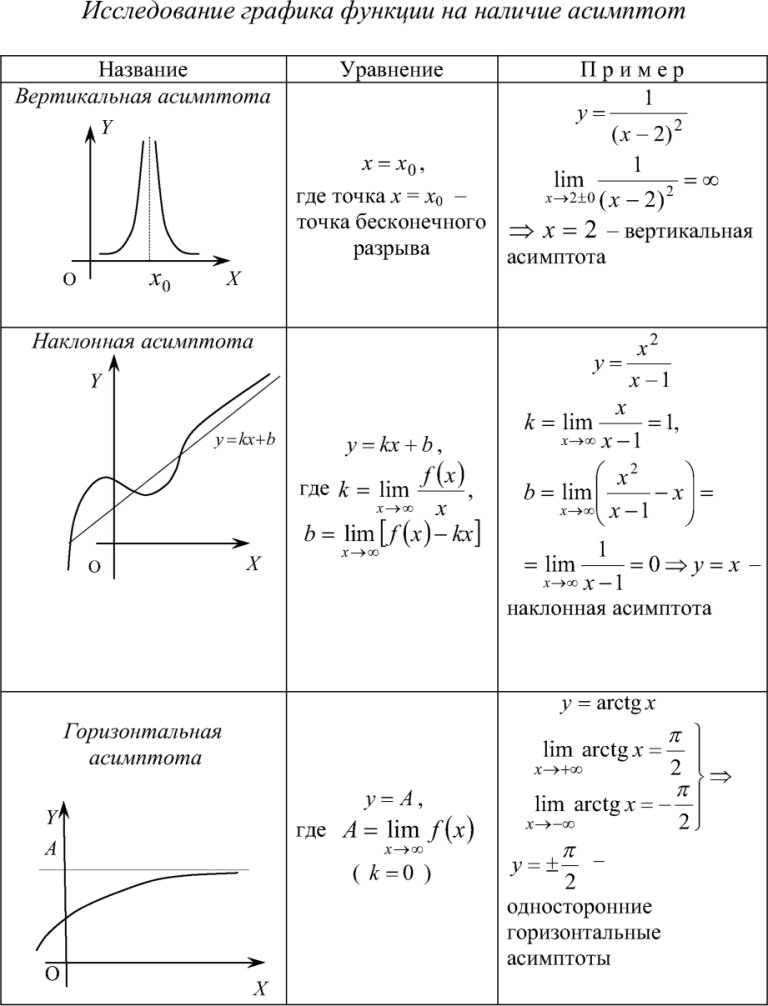
Из определения следует, что прямая x = a является вертикальной асимптотой графика функции f (x ) , если выполняется хотя бы одно из условий:
При этом функция f (x ) может быть вообще не определена соответственно при x ≥ a и x ≤ a .
Замечание:
Пример 1. График функции y =lnx имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy ) на границе области определения, так как предел функции при стремлении икса к нулю справа равен минус бесконечности:
(рис. сверху).
самостоятельно, а затем посмотреть решения
Пример 2. Найти асимптоты графика функции .
Пример 3. Найти асимптоты графика функции
Горизонтальные асимптоты
Первое, что нужно узнать о горизонтальных асимптотах: они параллельны оси Ox .
Если
(предел функции при стремлении аргумента к плюс или минус бесконечности равен некоторому значению b ),
то y = b – горизонтальная асимптота кривой y = f (x )
(правая при иксе, стремящимся к плюс бесконечности, левая при иксе, стремящимся к минус бесконечности,
и двусторонняя, если пределы при стремлении икса к плюс или минус бесконечности равны).
Пример 5. График функции
при a > 1 имеет левую горизонтальную асимпототу y = 0 (т.е. совпадающую с осью Ox ), так как предел функции при стремлении «икса» к минус бесконечности равен нулю:
Правой горизонтальной асимптоты у кривой нет, поскольку предел функции при стремлении «икса» к плюс бесконечности равен бесконечности:
Наклонные асимптоты
Вертикальные и горизонтальные асимптоты, которые мы рассмотрели выше, параллельны
осям координат, поэтому для их построения нам требовалось лишь определённое число — точка на оси
абсцисс или ординат, через которую проходит асимптота. Для наклонной асимптоты необходимо больше —
угловой коэффициент k , который показывает угол наклона прямой, и свободный член b , который показывает,
насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию,
а из неё — уравнения прямой, заметят, что для наклонной асимптоты находят уравнение
прямой с угловым коэффициентом . Существование наклонной асимптоты определяется следующей теоремой,
на основании которой и находят названные только что коэффициенты.
Существование наклонной асимптоты определяется следующей теоремой,
на основании которой и находят названные только что коэффициенты.
Теорема. Для того, чтобы кривая y = f (x ) имела асимптоту y = kx + b , необходимо и достаточно, чтобы существовали конечные пределы k и b рассматриваемой функции при стремлении переменной x к плюс бесконечности и минус бесконечности:
(1)
(2)
Найденные таким образом числа k и b и являются коэффициентами наклонной асимптоты.
В первом случае (при стремлении икса к плюс бесконечности) получается правая наклонная асимптота, во втором (при стремлении икса к минус бесконечности) – левая. Правая наклонная асимптота изображена на рис. снизу.
При нахождении уравнения наклонной асимптоты необходимо учитывать стремление икса
и к плюс бесконечности, и к минус бесконечности. У некоторых функций, например, у дробно-рациональных,
эти пределы совпадают, однако у многих функций эти пределы различны а также может существовать только
один из них.
При совпадении пределов при иксе, стремящемся к плюс бесконечности и к минус бесконечности прямая y = kx + b является двусторонней асимптотой кривой.
Если хотя бы один из пределов, определяющих асимптоту y = kx + b , не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).
Нетрудно видеть, что горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0 .
Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.
Пример 6. Найти асимптоты графика функции
Решение. Функция определена на всей числовой прямой, кроме x = 0 , т.е.
Поэтому в точке разрыва x = 0 кривая может иметь вертикальную асимптоту. Действительно, предел функции при стремлении икса к нулю слева равен плюс бесконечности:
Следовательно, x = 0
– вертикальная асимптота
графика данной функции.
Горизонтальной асимптоты график данной функции не имеет, так как предел функции при стремлении икса к плюс бесконечности равен плюс бесконечности:
Выясним наличие наклонной асимптоты:
Получили конечные пределы k = 2 и b = 0 . Прямая y = 2x является двусторонней наклонной асимптотой графика данной функции (рис. внутри примера).
Пример 7. Найти асимптоты графика функции
Решение. Функция имеет одну точку разрыва x = −1 . Вычислим односторонние пределы и определим вид разрыва:
Заключение: x = −1 — точка разрыва второго рода, поэтому прямая x = −1 является вертикальной асимптотой графика данной функции.
Ищем наклонные асимптоты. Так как данная функция — дробно-рациональная, пределы при и при будут совпадать. Таким образом, находим коэффициенты для подстановки в уравнение прямой — наклонной асимптоты:
Подставляя найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты:
y = −3x + 5
.
На рисунке график функции обозначен бордовым цветом, а асимптоты — чёрным.
Пример 8. Найти асимптоты графика функции
Решение. Так как данная функция непрерывна, её график не имеет вертикальных асимптот. Ищем наклонные асимптоты:
.
Таким образом, график данной функции имеет асимптоту y = 0 при и не имеет асиптоты при .
Пример 9. Найти асимптоты графика функции
Решение. Сначала ищем вертикальные асимптоты. Для этого найдём область определения функции. Функция определена, когда выполняется неравенство и при этом . Знак переменной x совпадает со знаком . Поэтому рассмотрим эквивалентное неравенство . Из этого получаем область определения функции: . Вертикальная асимптота может быть только на границе области определения функции. Но x = 0 не может быть вертикальной асимптотой, так как функция определена при x = 0 .
Рассмотрим правосторонний предел при (левосторонний предел не существует):
.
Точка x = 2 — точка разрыва второго рода, поэтому прямая x = 2 — вертикальная асимптота графика данной функции.
Ищем наклонные асимптоты:
Итак, y = x + 1 — наклонная асимптота графика данной функции при . Ищем наклонную асимптоту при :
Итак, y = −x − 1 — наклонная асимптота при .
Пример 10. Найти асимптоты графика функции
Решение. Функция имеет область определения . Так как вертикальная асимптота графика этой функции может быть только на границе области определения, найдём односторонние пределы функции при .
Призрак асимптоты давно бродил по сайту чтобы, наконец, материализоваться в отдельно взятой статье и привести в особый восторг читателей, озадаченных полным исследованием функции . Нахождение асимптот графика – одна из немногих частей указанного задания, которая освещается в школьном курсе лишь в обзорном порядке, поскольку события вращаются вокруг вычисления пределов функций , а они относятся всё-таки к высшей математике. Посетители, слабо разбирающиеся в математическом анализе, намёк, думаю, понятен;-) …стоп-стоп, вы куда? Пределы – это легко!
Посетители, слабо разбирающиеся в математическом анализе, намёк, думаю, понятен;-) …стоп-стоп, вы куда? Пределы – это легко!
Примеры асимптот встретились сразу же на первом уроке о графиках элементарных функций , и сейчас тема получает детальное рассмотрение.
Итак, что такое асимптота?Представьте переменную точку , которая «ездит» по графику функции. Асимптота – это прямая , к которой неограниченно близко приближается график функции при удалении его переменной точки в бесконечность.
Примечание : определение содержательно, если вам необходима формулировка в обозначениях математического анализа, пожалуйста, обратитесь к учебнику.
На плоскости асимптоты классифицируют по их естественному расположению:
1) Вертикальные асимптоты , которые задаются уравнением вида , где «альфа» – действительное число. Популярная представительница определяет саму ось ординат,
с приступом лёгкой тошноты вспоминаем гиперболу .
2) Наклонные асимптоты традиционно записываются уравнением прямой с угловым коэффициентом . Иногда отдельной группой выделяют частный случай – горизонтальные асимптоты . Например, та же гипербола с асимптотой .
Резво пошло-поехало, ударим по теме короткой автоматной очередью:
Сколько асимптот может быть у графика функции?Ни одной, одна, две, три,… или бесконечно много. За примерами далеко ходить не будем, вспомним элементарные функции . Парабола, кубическая парабола, синусоида вовсе не имеют асимптот. График экспоненциальной, логарифмической функции обладает единственной асимптотой. У арктангенса, арккотангенса их две, а у тангенса, котангенса – бесконечно много. Не редкость, когда график укомплектован и горизонтальными и вертикальными асимптотами. Гипербола, will always love you.
Что значит ? Вертикальные асимптоты графика функцииВертикальная асимптота графика, как правило, находится в точке бесконечного разрыва функции.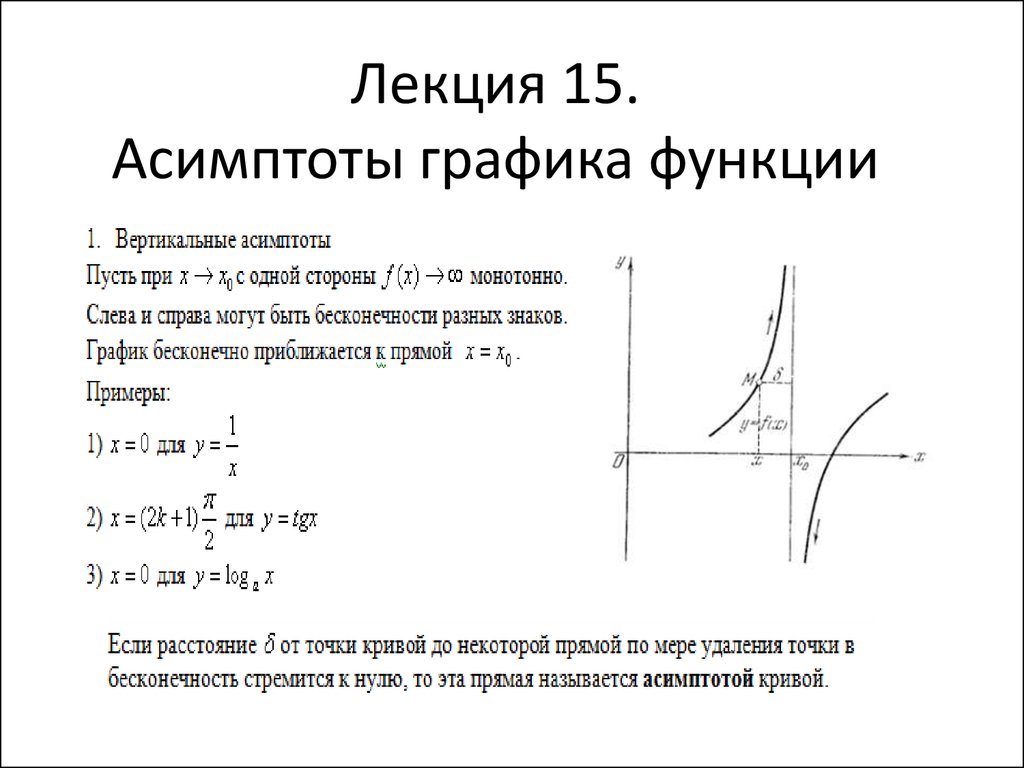 Всё просто: если в точке функция терпит бесконечный разрыв, то прямая, заданная уравнением является вертикальной асимптотой графика.
Всё просто: если в точке функция терпит бесконечный разрыв, то прямая, заданная уравнением является вертикальной асимптотой графика.
Примечание : обратите внимание, что запись используется для обозначения двух совершенно разных понятий. Точка подразумевается или уравнение прямой – зависит от контекста.
Таким образом, чтобы установить наличие вертикальной асимптоты в точке достаточно показать, что хотя бы один из односторонних пределов бесконечен. Чаще всего это точка, где знаменатель функции равен нулю. По существу, мы уже находили вертикальные асимптоты в последних примерах урока о непрерывности функции . Но в ряде случаев существует только один односторонний предел, и, если он бесконечен, то снова – любите и жалуйте вертикальную асимптоту. Простейшая иллюстрация: и ось ординат (см. Графики и свойства элементарных функций ).
Из вышесказанного также следует очевидный факт: если функция непрерывна на , то вертикальные асимптоты отсутствуют . На ум почему-то пришла парабола. Действительно, где тут «воткнёшь» прямую? …да… понимаю… последователи дядюшки Фрейда забились в истерике =)
На ум почему-то пришла парабола. Действительно, где тут «воткнёшь» прямую? …да… понимаю… последователи дядюшки Фрейда забились в истерике =)
Обратное утверждение в общем случае неверно: так, функция не определена на всей числовой прямой, однако совершенно обделена асимптотами.
Наклонные асимптоты графика функцииНаклонные (как частный случай – горизонтальные) асимптоты могут нарисоваться, если аргумент функции стремится к «плюс бесконечности» или к «минус бесконечности». Поэтому график функции не может иметь больше двух наклонных асимптот . Например, график экспоненциальной функции обладает единственной горизонтальной асимптотой при , а график арктангенса при – двумя такими асимптотами, причём различными.
Когда график и там и там сближается с единственной наклонной асимптотой, то «бесконечности» принято объединять под единой записью . Например, …правильно догадались: .
Общее практическое правило :
Если существуют два конечных предела , то прямая является наклонной асимптотой графика функции при .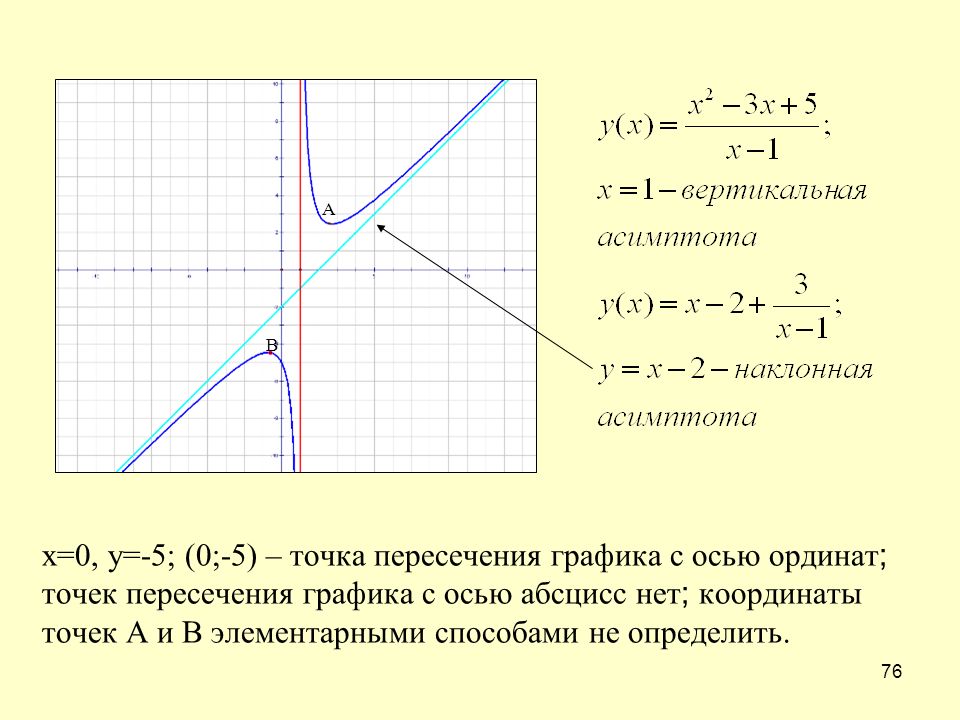 Если хотя бы один из перечисленных пределов бесконечен, то наклонная асимптота отсутствует.
Если хотя бы один из перечисленных пределов бесконечен, то наклонная асимптота отсутствует.
Примечание : формулы остаются справедливыми, если «икс» стремится только к «плюс бесконечности» или только к «минус бесконечности».
Покажем, что у параболы нет наклонных асимптот:
Предел бесконечен, значит, наклонная асимптота отсутствует. Заметьте, что в нахождении предела необходимость отпала, поскольку ответ уже получен.
Примечание : если у вас возникли (или возникнут) трудности с пониманием знаков «плюс-минус», «минус-плюс», пожалуйста, посмотрите справку в начале урока
о бесконечно малых функциях , где я рассказал, как правильно интерпретировать данные знаки.
Очевидно, что у любой квадратичной, кубической функции, многочлена 4-й и высших степеней также нет наклонных асимптот.
А теперь убедимся, что при у графика тоже нет наклонной асимптоты. Для раскрытия неопределённости используем правило Лопиталя :
, что и требовалось проверить.
При функция неограниченно растёт, однако не существует такой прямой, к которой бы её график приближался бесконечно близко .
Переходим к практической части урока:
Как найти асимптоты графика функции?Именно так формулируется типовое задание, и оно предполагает нахождение ВСЕХ асимптот графика (вертикальных, наклонных/горизонтальных). Хотя, если быть более точным в постановке вопроса – речь идёт об исследовании на наличие асимптот (ведь таковых может и вовсе не оказаться). Начнём с чего-нибудь простого:
Пример 1
Найти асимптоты графика функции
Решение удобно разбить на два пункта:
1) Сначала проверяем, есть ли вертикальные асимптоты. Знаменатель обращается в ноль при , и сразу понятно, что в данной точке функция терпит бесконечный разрыв , а прямая, заданная уравнением , является вертикальной асимптотой графика функции . Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:
Напоминаю технику вычислений, на которой я подобно останавливался в статье Непрерывность функции. Точки разрыва . В выражение под знаком предела вместо «икса» подставляем . В числителе ничего интересного:
Точки разрыва . В выражение под знаком предела вместо «икса» подставляем . В числителе ничего интересного:
.
А вот в знаменателе получается бесконечно малое отрицательное число :
, оно и определяет судьбу предела.
Левосторонний предел бесконечный, и, в принципе уже можно вынести вердикт о наличии вертикальной асимптоты. Но односторонние пределы нужны не только для этого – они ПОМОГАЮТ ПОНЯТЬ, КАК расположен график функции и построить его КОРРЕКТНО . Поэтому обязательно вычислим и правосторонний предел:
Вывод : односторонние пределы бесконечны, значит, прямая является вертикальной асимптотой графика функции при .
Первый предел конечен , значит, необходимо «продолжить разговор» и найти второй предел:
Второй предел тоже конечен .
Таким образом, наша асимптота:
Вывод : прямая, заданная уравнением является горизонтальной асимптотой графика функции при .
Для нахождения горизонтальной асимптотыможно пользоваться упрощенной формулой :
Если существует конечный предел , то прямая является горизонтальной асимптотой графика функции при .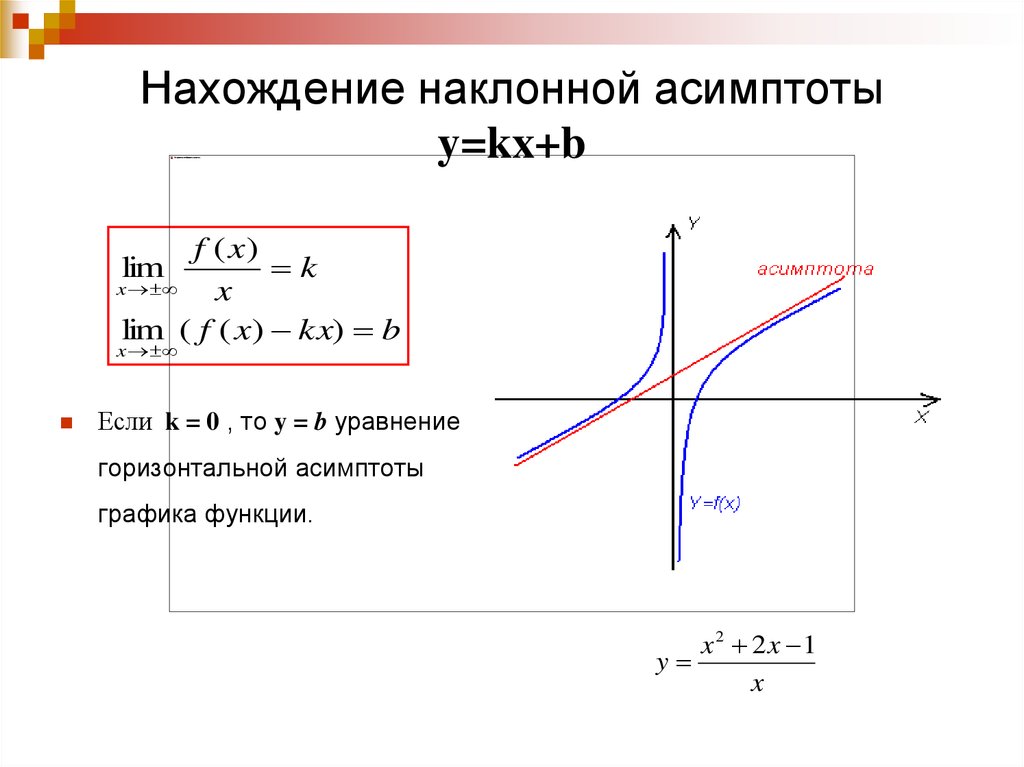
Нетрудно заметить, что числитель и знаменатель функции одного порядка роста , а значит, искомый предел будет конечным:
Ответ :
По условию не нужно выполнять чертёж, но если в самом разгаре исследование функции , то на черновике сразу же делаем набросок:
Исходя из трёх найденных пределов , попытайтесь самостоятельно прикинуть, как может располагаться график функции . Совсем трудно? Найдите 5-6-7-8 точек и отметьте их на чертеже. Впрочем, график данной функции строится с помощью преобразований графика элементарной функции , и читатели, внимательно рассмотревшие Пример 21 указанной статьи легко догадаются, что это за кривая.
Пример 2
Найти асимптоты графика функции
Это пример для самостоятельного решения. Процесс, напоминаю, удобно разбить на два пункта – вертикальные асимптоты и наклонные асимптоты. В образце решения горизонтальная асимптота найдена по упрощенной схеме.
На практике чаще всего встречаются дробно-рациональные функции, и после тренировки на гиперболах усложним задание:
Пример 3
Найти асимптоты графика функции
Решение : Раз, два и готово:
1) Вертикальные асимптоты находятся в точках бесконечного разрыва , поэтому нужно проверить, обращается ли знаменатель в ноль. Решим квадратное уравнение :
Решим квадратное уравнение :
Дискриминант положителен, поэтому уравнение имеет два действительных корня, и работы значительно прибавляется =)
В целях дальнейшего нахождения односторонних пределов квадратный трёхчлен удобно разложить на множители :
(для компактной записи «минус» внесли в первую скобку). Для подстраховки выполним проверку, мысленно либо на черновике раскрыв скобки.
Перепишем функцию в виде
Найдём односторонние пределы в точке :
И в точке :
Таким образом, прямые являются вертикальными асимптотами графика рассматриваемой функции.
2) Если посмотреть на функцию , то совершенно очевидно, что предел будет конечным и у нас горизонтальная асимптота. Покажем её наличие коротким способом:
Таким образом, прямая (ось абсцисс) является горизонтальной асимптотой графика данной функции.
Ответ :
Найденные пределы и асимптоты дают немало информации о графике функции. Постарайтесь мысленно представить чертёж с учётом следующих фактов:
Схематично изобразите вашу версию графика на черновике.
Конечно, найденные пределы однозначно не определяют вид графика, и возможно, вы допустите ошибку, но само упражнение окажет неоценимую помощь в ходе полного исследования функции . Правильная картинка – в конце урока.
Пример 4
Найти асимптоты графика функции
Пример 5
Найти асимптоты графика функции
Это задания для самостоятельного решения. Оба графика снова обладают горизонтальными асимптотами, которые немедленно детектируются по следующим признакам: в Примере 4 порядок роста знаменателя больше , чем порядок роста числителя, а в Примере 5 числитель и знаменатель одного порядка роста . В образце решения первая функция исследована на наличие наклонных асимптот полным путём, а вторая – через предел .
Горизонтальные асимптоты, по моему субъективному впечатлению, встречаются заметно чаще, чем те, которые «по-настоящему наклонены». Долгожданный общий случай:
Пример 6
Найти асимптоты графика функции
Решение : классика жанра:
1) Поскольку знаменатель положителен, то функция непрерывна на всей числовой прямой, и вертикальные асимптоты отсутствуют. …Хорошо ли это? Не то слово – отлично! Пункт №1 закрыт.
…Хорошо ли это? Не то слово – отлично! Пункт №1 закрыт.
2) Проверим наличие наклонных асимптот:
Первый предел конечен , поэтому едем дальше. В ходе вычисления второго предела для устранения неопределённости «бесконечность минус бесконечность» приводим выражение к общему знаменателю:
Второй предел тоже конечен , следовательно, у графика рассматриваемой функции существует наклонная асимптота:
Вывод :
Таким образом, при график функции бесконечно близко приближается к прямой :
Заметьте, что он пересекает свою наклонную асимптоту в начале координат, и такие точки пересечения вполне допустимы – важно, чтобы «всё было нормально» на бесконечности (собственно, речь об асимптотах и заходит именно там).
Пример 7
Найти асимптоты графика функции
Решение : комментировать особо нечего, поэтому оформлю примерный образец чистового решения:
1) Вертикальные асимптоты. Исследуем точку .
Прямая является вертикальной асимптотой для графика при .
2) Наклонные асимптоты:
Прямая является наклонной асимптотой для графика при .
Ответ :
Найдённые односторонние пределы и асимптоты с высокой достоверностью позволяют предположить, как выглядит график данной функции. Корректный чертёж в конце урока.
Пример 8
Найти асимптоты графика функции
Это пример для самостоятельного решения, для удобства вычисления некоторых пределов можно почленно разделить числитель на знаменатель. И снова, анализируя полученные результаты, постарайтесь начертить график данной функции.
Очевидно, что обладателями «настоящих» наклонных асимптот являются графики тех дробно-рациональных функций, у которых старшая степень числителя на единицу больше старшей степени знаменателя. Если больше – наклонной асимптоты уже не будет (например, ).
Но в жизни происходят и другие чудеса:
Пример 9
Пример 11
Исследовать график функции на наличие асимптот
Решение : очевидно, что , поэтому рассматриваем только правую полуплоскость, где есть график функции.
Таким образом, прямая (ось ординат) является вертикальной асимптотой для графика функции при .
2) Исследование на наклонную асимптоту можно провести по полной схеме, но в статье Правила Лопиталя мы выяснили, что линейная функция более высокого порядка роста, чем логарифмическая, следовательно: (см. Пример 1 того же урока).
Вывод: ось абсцисс является горизонтальной асимптотой графика функции при .
Ответ :
, если ;
, если .
Чертёж для наглядности:
Интересно, что у вроде бы похожей функции асимптот нет вообще (желающие могут это проверить).
Два заключительных примера для самостоятельного изучения:
Пример 12
Исследовать график функции на наличие асимптот
Решение удобно разбить на два пункта:
1) Сначала проверяем, есть ли вертикальные асимптоты. Знаменатель обращается в ноль при, и сразу понятно, что в данной точке функция терпит бесконечный разрыв, а прямая, заданная уравнением, является вертикальной асимптотой графика функции. Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:
Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:
Напоминаю технику вычислений, на которой я подобно останавливался в статье Непрерывность функции. Точки разрыва. В выражение под знаком предела вместо «икса» подставляем. В числителе ничего интересного:
А вот в знаменателе получается бесконечно малое отрицательное число:
Оно и определяет судьбу предела.
Левосторонний предел бесконечный, и, в принципе уже можно вынести вердикт о наличии вертикальной асимптоты. Но односторонние пределы нужны не только для этого — они ПОМОГАЮТ ПОНЯТЬ, КАК расположен график функции и построить его КОРРЕКТНО. Поэтому обязательно вычислим и правосторонний предел:
Вывод: односторонние пределы бесконечны, значит, прямая является вертикальной асимптотой графика функции при.
Первый предел конечен, значит, необходимо «продолжить разговор» и найти второй предел:
Второй предел тоже конечен.
Таким образом, наша асимптота:
Вывод: прямая, заданная уравнением является горизонтальной асимптотой графика функции при.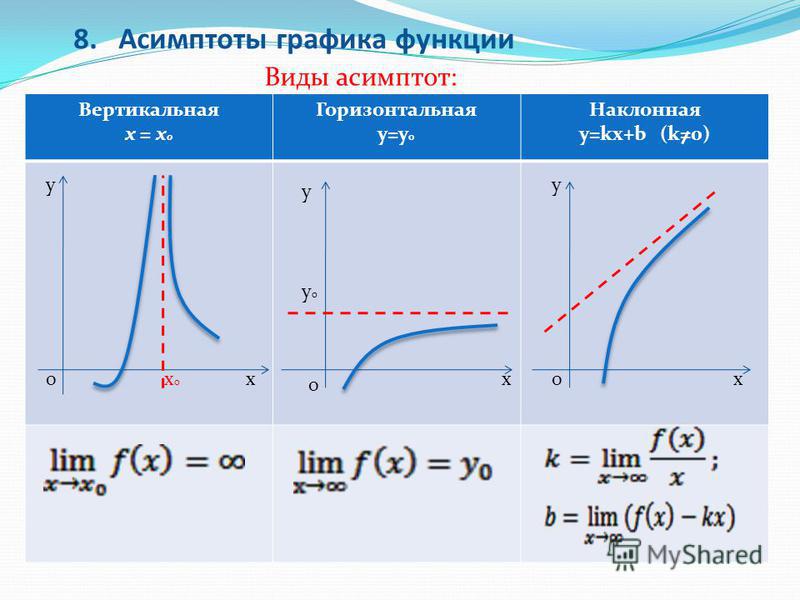
Для нахождения горизонтальной асимптоты можно пользоваться упрощенной формулой:
Если существует конечный предел, то прямая является горизонтальной асимптотой графика функции при.
Нетрудно заметить, что числитель и знаменатель функции одного порядка роста, а значит, искомый предел будет конечным:
По условию не нужно выполнять чертёж, но если в самом разгаре исследование функции, то на черновике сразу же делаем набросок:
Исходя из трёх найденных пределов, попытайтесь самостоятельно прикинуть, как может располагаться график функции. Совсем трудно? Найдите 5-6-7-8 точек и отметьте их на чертеже. Впрочем, график данной функции строится с помощью преобразований графика элементарной функции, и читатели, внимательно рассмотревшие Пример 21 указанной статьи легко догадаются, что это за кривая.
Это пример для самостоятельного решения. Процесс, напоминаю, удобно разбить на два пункта — вертикальные асимптоты и наклонные асимптоты. В образце решения горизонтальная асимптота найдёна по упрощенной схеме.
На практике чаще всего встречаются дробно-рациональные функции, и после тренировки на гиперболах усложним задание:
Найти асимптоты графика функции
Решение: Раз, два и готово:
1) Вертикальные асимптоты находятся в точках бесконечного разрыва, поэтому нужно проверить, обращается ли знаменатель в ноль. Решим квадратное уравнение:
Дискриминант положителен, поэтому уравнение имеет два действительных корня, и работы значительно прибавляется
В целях дальнейшего нахождения односторонних пределов квадратный трёхчлен удобно разложить на множители:
(для компактной записи «минус» внесли в первую скобку). Для подстраховки выполним проверку, мысленно либо на черновике раскрыв скобки.
Перепишем функцию в виде
Найдём односторонние пределы в точке:
асимптота график функция предел
И в точке:
Таким образом, прямые являются вертикальными асимптотами графика рассматриваемой функции.
2) Если посмотреть на функцию, то совершенно очевидно, что предел будет конечным и у нас горизонтальная асимптота. Покажем её наличие коротким способом:
Покажем её наличие коротким способом:
Таким образом, прямая (ось абсцисс) является горизонтальной асимптотой графика данной функции.
Найденные пределы и асимптоты дают немало информации о графике функции. Постарайтесь мысленно представить чертёж с учётом следующих фактов:
Схематично изобразите вашу версию графика на черновике.
Конечно, найденные пределы однозначно не определяют вид графика, и возможно, вы допустите ошибку, но само упражнение окажет неоценимую помощь в ходе полного исследования функции. Правильная картинка — в конце урока.
Найти асимптоты графика функции
Найти асимптоты графика функции
Это задания для самостоятельного решения. Оба графика снова обладают горизонтальными асимптотами, которые немедленно детектируются по следующим признакам: в Примере 4порядок роста знаменателя больше, чем порядок роста числителя, а в Примере 5 числитель и знаменатель одного порядка роста. В образце решения первая функция исследована на наличие наклонных асимптот полным путём, а вторая — через предел.
Горизонтальные асимптоты, по моему субъективному впечатлению, встречаются заметно чаще, чем те, которые «по-настоящему наклонены». Долгожданный общий случай:
Найти асимптоты графика функции
Решение: классика жанра:
- 1) Поскольку знаменатель положителен, то функция непрерывна на всей числовой прямой, и вертикальные асимптоты отсутствуют. …Хорошо ли это? Не то слово — отлично! Пункт №1 закрыт.
- 2) Проверим наличие наклонных асимптот:
Второй предел тоже конечен, следовательно, у графика рассматриваемой функции существует наклонная асимптота:
Таким образом, при график функции бесконечно близко приближается к прямой.
Заметьте, что он пересекает свою наклонную асимптоту в начале координат, и такие точки пересечения вполне допустимы — важно, чтобы «всё было нормально» на бесконечности (собственно, речь об асимптотах и заходит именно там).
Найти асимптоты графика функции
Решение: комментировать особо нечего, поэтому оформлю примерный образец чистового решения:
1) Вертикальные асимптоты.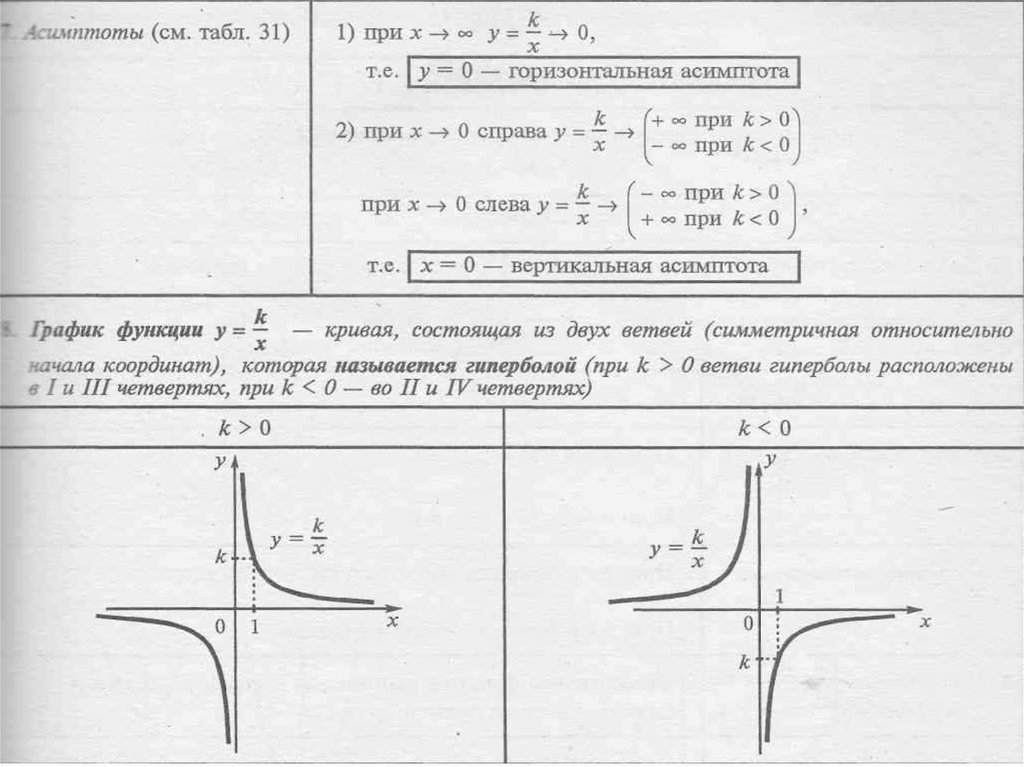 Исследуем точку.
Исследуем точку.
Прямая является вертикальной асимптотой для графика при.
2) Наклонные асимптоты:
Прямая является наклонной асимптотой для графика при.
Найдённые односторонние пределы и асимптоты с высокой достоверностью позволяют предположить, как выглядит график данной функции.
Найти асимптоты графика функции
Это пример для самостоятельного решения, для удобства вычисления некоторых пределов можно почленно разделить числитель на знаменатель. И снова, анализируя полученные результаты, постарайтесь начертить график данной функции.
Очевидно, что обладателями «настоящих» наклонных асимптот являются графики тех дробно-рациональных функций, у которых старшая степень числителя на единицу больше старшей степени знаменателя. Если больше — наклонной асимптоты уже не будет (например,).
Но в жизни происходят и другие чудеса.
Как найти наклонную асимптоту
- Как найти наклонную асимптоту
- Как находить область определения функции
- Как построить график функции
Наклонная асимптота — прямая, к которой неограниченно стремится график функции f(x) по мере того, как x неограниченно возрастает или убывает.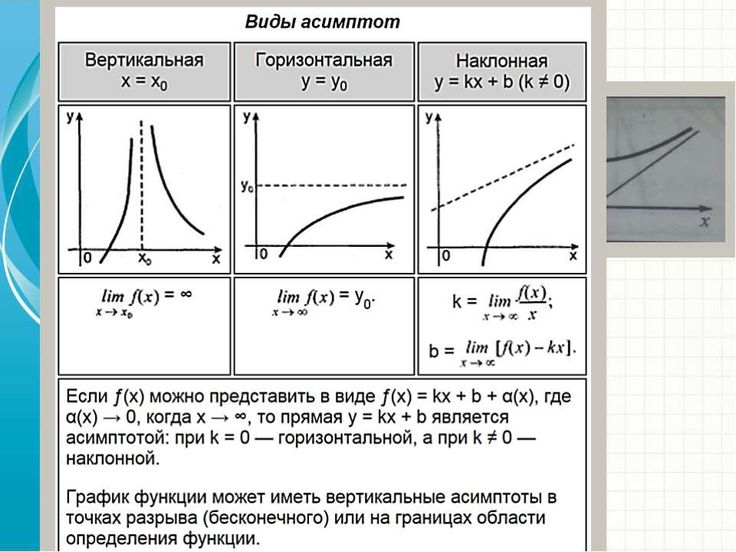 Функция может иметь и вертикальные, и наклонные асимптоты.
Функция может иметь и вертикальные, и наклонные асимптоты.
В практических целях различают наклонные асимптоты при x → ∞ и при x → -∞. В ряде случаев функция может стремиться к одной и той же асимптоте в обе стороны, но, вообще говоря, они не обязаны совпадать.
Асимптота, как и всякая наклонная прямая, имеет уравнение вида y = kx + b, где k и b — константы.
Прямая будет наклонной асимптотой функции при x → ∞, если по мере стремления x к бесконечности разность f(x) — (kx+b) стремится к нулю. Аналогично, если эта разность стремится к нулю при x → -∞, то прямая kx + b будет наклонной асимптотой функции в этом направлении.
Чтобы понять, имеет ли заданная функция наклонную асимптоту, и если имеет — найти ее уравнение, нужно вычислить константы k и b. Метод вычисления не меняется от того, в каком направлении вы ищете асимптоту.
Константа k, также называемая угловым коэффициентом наклонной асимптоты, является пределом отношения f(x)/x при x → ∞.
Например, путь задана функция f(x) = 1/x + x. 2). Его предел при x → ∞ равен 1. Следовательно, заданная функция имеет наклонную асимптоту с угловым коэффициентом 1.
2). Его предел при x → ∞ равен 1. Следовательно, заданная функция имеет наклонную асимптоту с угловым коэффициентом 1.
Если коэффициент k получается нулевым, это значит, что наклонная асимптота заданной функции горизонтальна, и ее уравнение y = b.
Понятие асимптоты
Если предварительно построить асимптоты кривой, то многих случаях построение графика функции облегчается.
Судьба асимптоты полна трагизма. Представьте себе, каково это: всю жизнь двигаться по прямой к заветной цели, подойти к ней максимально близко, но так и не достигнуть её. Например, стремиться соединить свой жизненный путь с путём желанного человека, в какой-то момент приблизиться к нему почти вплотную, но даже не коснуться его. Или стремиться заработать миллиард, но до достижения этой цели и записи в книгу рекордов Гиннеса для своего случая не достаёт сотых долей цента. И тому подобное. Так и с асимптотой: она постоянно стремится достигнуть кривой графика функции, приближается к нему на минимальное возможное расстояние, но так и не касается его.
Определение 1. Асимптотами называются такие прямые, к которым сколь угодно близко приближается график функции, когда переменная стремится к плюс бесконечности или к минус бесконечности.
Определение 2. Прямая называется асимптотой графика функции, если расстояние от переменной точки М графика функции до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-либо ветви графика функции.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Вертикальные асимптоты
Первое, что нужно узнать о вертикальных асимптотах: они параллельны оси Oy .
Определение. Прямая x = a является вертикальной асимптотой графика функции, если точка x = a является точкой разрыва второго рода для этой функции.
Из определения следует, что прямая x = a является вертикальной асимптотой графика функции f(x) , если выполняется хотя бы одно из условий:
- (предел функции при значении аргумента, стремящимся к некоторому значению a слева, равен плюс или минус бесконечности)
- (предел функции при значении аргумента, стремящимся к некоторому значению a справа, равен плюс или минус бесконечности).

При этом функция f(x) может быть вообще не определена соответственно при x ≥ a и x ≤ a .
- символом обозначается стремление x к a справа, причём x остаётся больше a;
- символом обозначается стремление x к a слева, причём x остаётся меньше a.
Из сказанного следует, что вертикальные асимптоты графика функции можно искать не только в точках разрыва, но и на границах области определения. График функции, непрерывной на всей числовой прямой, вертикальных асимптот не имеет.
Пример 1. График функции y=lnx имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy ) на границе области определения, так как предел функции при стремлении икса к нулю справа равен минус бесконечности:
Найти асимптоты графика функции самостоятельно, а затем посмотреть решения
Пример 2. Найти асимптоты графика функции .
Найти асимптоты графика функции .
Пример 3. Найти асимптоты графика функции
Пример 4. Найти асимптоты график функции .
Горизонтальные асимптоты
Первое, что нужно узнать о горизонтальных асимптотах: они параллельны оси Ox .
Если (предел функции при стремлении аргумента к плюс или минус бесконечности равен некоторому значению b), то y = b – горизонтальная асимптота кривой y = f(x ) (правая при иксе, стремящимся к плюс бесконечности, левая при иксе, стремящимся к минус бесконечности, и двусторонняя, если пределы при стремлении икса к плюс или минус бесконечности равны).
Пример 5. График функции
при a > 1 имеет левую горизонтальную асимпототу y = 0 (т.е. совпадающую с осью Ox ), так как предел функции при стремлении «икса» к минус бесконечности равен нулю:
Правой горизонтальной асимптоты у кривой нет, поскольку предел функции при стремлении «икса» к плюс бесконечности равен бесконечности:
Наклонные асимптоты
Вертикальные и горизонтальные асимптоты, которые мы рассмотрели выше, параллельны осям координат, поэтому для их построения нам требовалось лишь определённое число — точка на оси абсцисс или ординат, через которую проходит асимптота.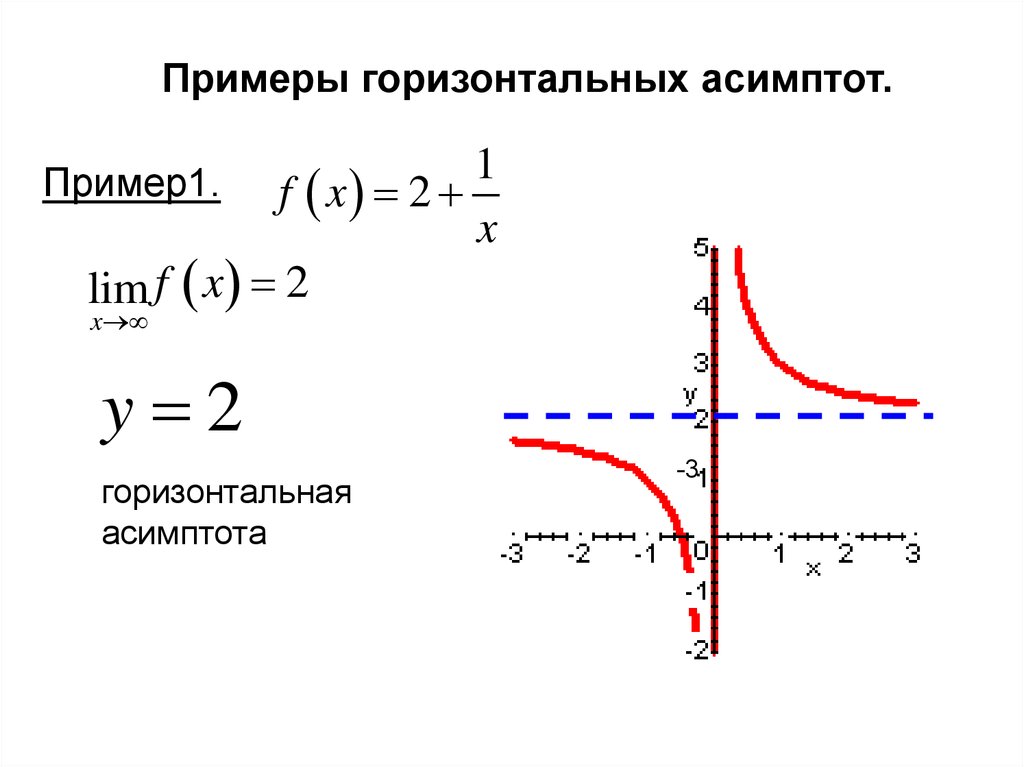 Для наклонной асимптоты необходимо больше — угловой коэффициент k, который показывает угол наклона прямой, и свободный член b, который показывает, насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию, а из неё — уравнения прямой, заметят, что для наклонной асимптоты находят уравнение прямой с угловым коэффициентом. Существование наклонной асимптоты определяется следующей теоремой, на основании которой и находят названные только что коэффициенты.
Для наклонной асимптоты необходимо больше — угловой коэффициент k, который показывает угол наклона прямой, и свободный член b, который показывает, насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию, а из неё — уравнения прямой, заметят, что для наклонной асимптоты находят уравнение прямой с угловым коэффициентом. Существование наклонной асимптоты определяется следующей теоремой, на основании которой и находят названные только что коэффициенты.
Теорема. Для того, чтобы кривая y = f(x) имела асимптоту y = kx + b , необходимо и достаточно, чтобы существовали конечные пределы k и b рассматриваемой функции при стремлении переменной x к плюс бесконечности и минус бесконечности:
(1)
(2)
Найденные таким образом числа k и b и являются коэффициентами наклонной асимптоты.
В первом случае (при стремлении икса к плюс бесконечности) получается правая наклонная асимптота, во втором (при стремлении икса к минус бесконечности) – левая.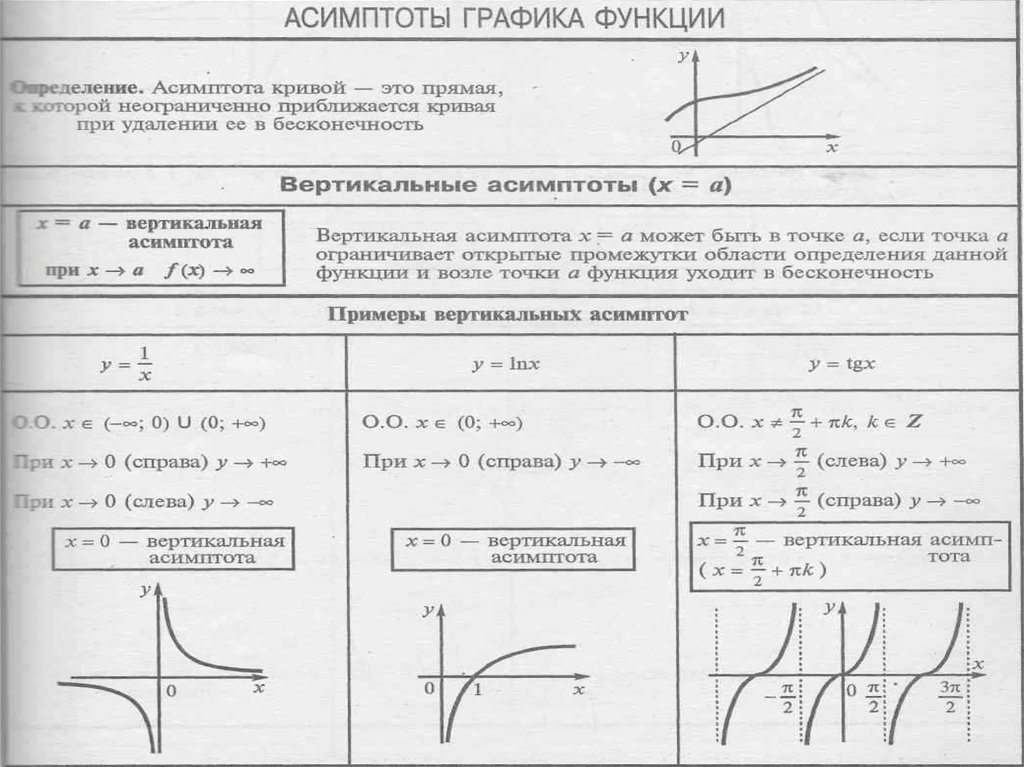 Правая наклонная асимптота изображена на рис. снизу.
Правая наклонная асимптота изображена на рис. снизу.
При нахождении уравнения наклонной асимптоты необходимо учитывать стремление икса и к плюс бесконечности, и к минус бесконечности. У некоторых функций, например, у дробно-рациональных, эти пределы совпадают, однако у многих функций эти пределы различны а также может существовать только один из них.
При совпадении пределов при иксе, стремящемся к плюс бесконечности и к минус бесконечности прямая y = kx + b является двусторонней асимптотой кривой.
Если хотя бы один из пределов, определяющих асимптоту y = kx + b , не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).
Нетрудно видеть, что горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0 .
Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.
Пример 6. Найти асимптоты графика функции
Решение. Функция определена на всей числовой прямой, кроме x = 0 , т.е.
Поэтому в точке разрыва x = 0 кривая может иметь вертикальную асимптоту. Действительно, предел функции при стремлении икса к нулю слева равен плюс бесконечности:
Следовательно, x = 0 – вертикальная асимптота графика данной функции.
Горизонтальной асимптоты график данной функции не имеет, так как предел функции при стремлении икса к плюс бесконечности равен плюс бесконечности:
Выясним наличие наклонной асимптоты:
Получили конечные пределы k = 2 и b = 0 . Прямая y = 2x является двусторонней наклонной асимптотой графика данной функции (рис. внутри примера).
Пример 7. Найти асимптоты графика функции
Решение. Функция имеет одну точку разрыва x = −1 . Вычислим односторонние пределы и определим вид разрыва:
,
.
Заключение: x = −1 — точка разрыва второго рода, поэтому прямая x = −1 является вертикальной асимптотой графика данной функции.
Ищем наклонные асимптоты. Так как данная функция — дробно-рациональная, пределы при и при будут совпадать. Таким образом, находим коэффициенты для подстановки в уравнение прямой — наклонной асимптоты:
Подставляя найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты:
На рисунке график функции обозначен бордовым цветом, а асимптоты — чёрным.
Пример 8. Найти асимптоты графика функции
.
Решение. Так как данная функция непрерывна, её график не имеет вертикальных асимптот. Ищем наклонные асимптоты:
.
Таким образом, график данной функции имеет асимптоту y = 0 при и не имеет асиптоты при .
Пример 9. Найти асимптоты графика функции
.
Решение. Сначала ищем вертикальные асимптоты. Для этого найдём область определения функции. Функция определена, когда выполняется неравенство и при этом . Знак переменной x совпадает со знаком . Поэтому рассмотрим эквивалентное неравенство . Из этого получаем область определения функции: . Вертикальная асимптота может быть только на границе области определения функции. Но x = 0 не может быть вертикальной асимптотой, так как функция определена при x = 0 .
Для этого найдём область определения функции. Функция определена, когда выполняется неравенство и при этом . Знак переменной x совпадает со знаком . Поэтому рассмотрим эквивалентное неравенство . Из этого получаем область определения функции: . Вертикальная асимптота может быть только на границе области определения функции. Но x = 0 не может быть вертикальной асимптотой, так как функция определена при x = 0 .
Рассмотрим правосторонний предел при (левосторонний предел не существует):
.
Точка x = 2 — точка разрыва второго рода, поэтому прямая x = 2 — вертикальная асимптота графика данной функции.
Ищем наклонные асимптоты:
Итак, y = x + 1 — наклонная асимптота графика данной функции при . Ищем наклонную асимптоту при :
Итак, y = −x − 1 — наклонная асимптота при .
Пример 10. Найти асимптоты графика функции
Решение. Функция имеет область определения . Так как вертикальная асимптота графика этой функции может быть только на границе области определения, найдём односторонние пределы функции при :
Так как вертикальная асимптота графика этой функции может быть только на границе области определения, найдём односторонние пределы функции при :
,
.
Оба предела нашли, используя первый замечательный предел. Заключение: x = 0 — точка устранимого разрыва, поэтому у графика функции нет вертикальных асимптот.
Ищем наклонные асимптоты:
Таким образом, при наклонной асимптотой графика данной функции является прямая y = x . Но при найденные пределы не изменяются. Поэтому при наклонной асимптотой графика данной функции также является y = x .
Пример 11. Найти асимптоты графика функции
.
Решение. Сначала найдём вертикальные асимптоты. Для этого найдём точки разрыва функции и их виды. Знаменатель не может быть равным нулю, поэтому должно соблюдаться условие . Функция имеет две точки разрыва: , . Чтобы установить вид разрыва, найдём односторонние пределы:
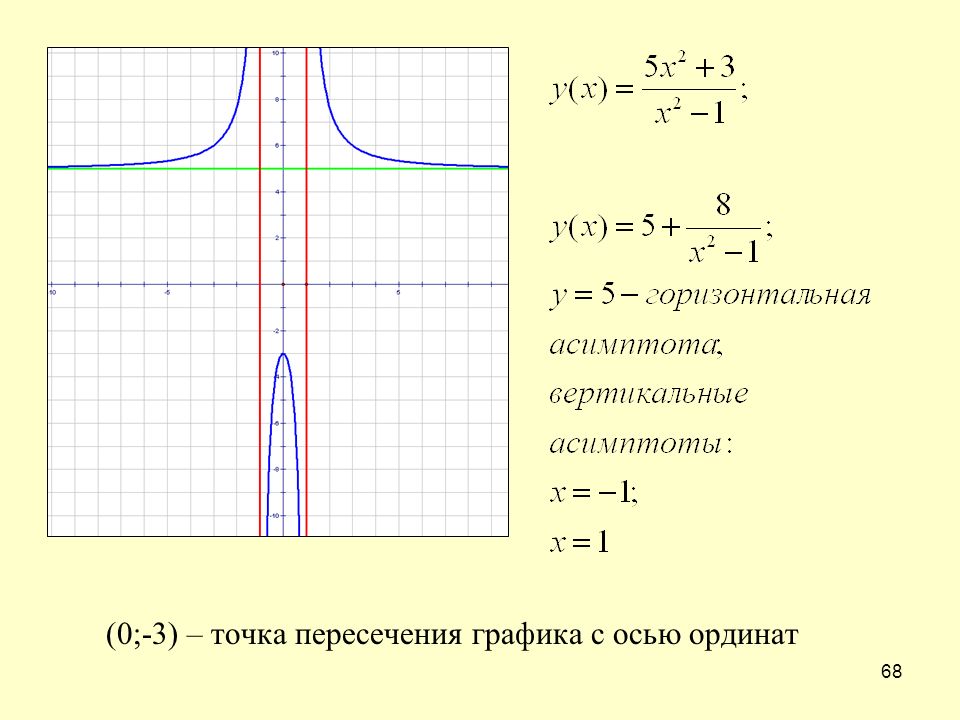
Так как все пределы равны бесконечности, обе точки разрыва — второго рода.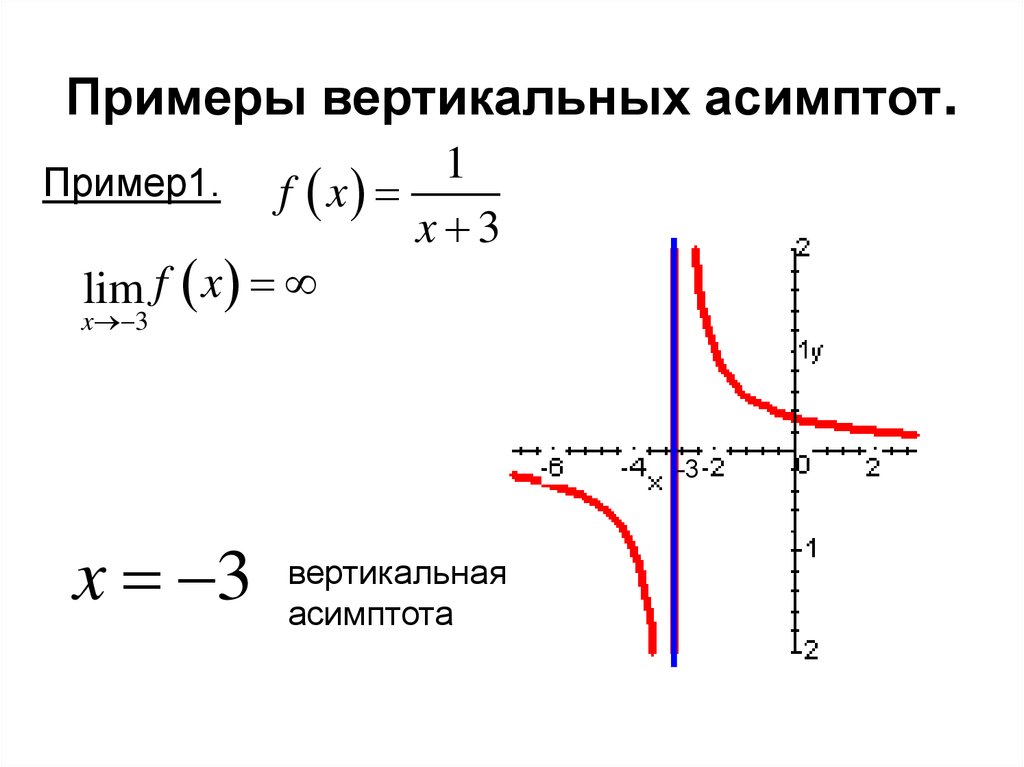 Поэтому график данной функции имеет две вертикальные асимптоты: x = 2 и x = −2 .
Поэтому график данной функции имеет две вертикальные асимптоты: x = 2 и x = −2 .
Ищем наклонные асимптоты. Так как данная функция является дробно-рациональной, пределы при и при совпадают. Поэтому, определяя коэффициенты прямой, ищем просто пределы:
Подставляем найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты y = 2x . Таким образом, график данной функции имеет три асимптоты: x = 2 , x = −2 и y = 2x .
Часто задание на нахождение асимптот функции встречается в курсе математического анализа, в частности при решении задач на тему исследования функции. Для того, чтобы успешно ответить на вопрос: как найти асимптоты функции? необходимо уметь вычислять пределы, понимать что они собой представляют, знать основные методы решения пределов. Если всё это вы умеете на должном уровне, тогда найти асимптоты для вас не будет проблемой. Итак, что такое асимптота? Асимптота это линия, к которой бесконечно приближается ветвь графика функции. Чтобы было наглядно, посмотрите на изображения представленные ниже.
Чтобы было наглядно, посмотрите на изображения представленные ниже.
Обратите внимание, что соприкосновения между асимптотой и графиками нет, и не должно быть. Асимптота бесконечно приближается к графику функции. Давайте рассмотрим какие виды асимптоты функции бывают и как их находить, но о последнем будет рассказано далее.
Из таблицы узнаем, что асимптоты у функции бывают трех видов: вертикальные, горизонтальные, наклонные. Каждую найти асимптоту функции нужно по своему. Для этого нужны лимиты. Сколько бывает асимптот всего у функции? Ответ: ни одной, одна, две, три. и бесконечно много. У каждой функции по разному.
Вертикальные асимптоты
Чтобы найти данный вид асимптот необходимо найти область определения заданной функции и отметить точки разрыва. В этих точках предел функции будет равен бесконечности, а это значит, что функция в этой точке бесконечно приближается к линии асимптоты.
Горизонтальные асимптоты
Необходимо устремить аргумент лимита функции к бесконечности. Если предел существует и равен числу, то горизонтальная асимптота будет найдена и равна $ y=y_0 $ как показано во втором столбце таблицы
Если предел существует и равен числу, то горизонтальная асимптота будет найдена и равна $ y=y_0 $ как показано во втором столбце таблицы
Наклонные асимптоты
Наклонная асимптота представляется в виде $ y = kx+b $. Где $ k $ — это коэффициент наклона асимптоты. Сначала находится коэффициент $ k $, затем $ b $. Если какой либо из них равен $ infty $, тогда наклонной асимптоты нет. А если $ b = 0 $, то получаем горизонтальную асимптоту. Так что для экономии времени лучше сразу находить наклонную асимптоту, а горизонтальная проявится сама собой в случае её существования.
Примеры решений
| Пример 1 |
| Найти все асимптоты графика функции $$ f(x) = frac<5x> <3x+2>$$ |
| Решение |
| Ответ |
| $$ y = frac<5> <3>$$ |
| Пример 2 |
| Найти все асимптоты графика функции $ f(x) = frac<1> <1-x>$ |
| Решение |
| Решение |
| Ответ |
| $$ y = 0 $$ |
Если в задачах даются элементарные функции, то заранее известно сколько и есть ли асимптоты. Например, у параболы, кубической параболы, синусоиды вообще нет никаких. У графиков функций таких как логарифмическая или экспоненциальная есть по одной. А у функций тангенса и котангенса бесчисленное множество асимптот, но арктангенс и арккатангенс имеет по две штуки.
Во всех приведенных примерах пределы вычислялись с помощью правило Лопиталя, которое очень ускоряет процесс вычисления и создает меньше ошибок.
Асимптоты графика функции — основные понятия и определения с примерами решения и образцами выполнения
Содержание:
- Асимптоты графика функции
- Асимптоты и функция
- Схема исследования графика функции
При исследовании функций часто бывает, что их графики сколь угодно близко приближаются к той или иной прямой. С такими линиями вы встречались при изучении гиперболы.
С такими линиями вы встречались при изучении гиперболы.
Определение 1. Прямую линию называют асимптотой графика функции y = f (x), если расстояние точки M графика от этой прямой стремится к нулю при удалении точки M в бесконечность.
Асимптоты бывают вертикальными, наклонными и горизонтальными. Вертикальные асимптоты существуют тогда, когда функция имеет разрывы второго рода.
Определение 2. Если в точке хоть один из односторонних пределов или то прямая является вертикальной асимптотой.
Например, для функции
и
Итак, x = 0 — вертикальная асимптота (рис. 17).
Рис. 17.
Определение 3. Если существует конечный предел то прямая y = b называется горизонтальной асимптотой.
Поскольку для функции имеем то прямая y = 0 —горизонтальная асимптота.
Уравнение наклонной асимптоты ищут в виде прямой с угловым коэффициентом y = kx + b. Расстояние точки M (x, y) графика функции y = f (x) примерно можно выразить через разность ординат при одном и том же значении x: d = f (x) – (kx + b).
По определению асимптоты d → 0 при , то есть
(4.9)
Разделив это равенство на x, имеем:
Поскольку то (4.10)
Если предел (4.10) не существует, то наклонной асимптоты не будет.
Если k — конечное число, то из (4.9) найдем:
Таким образом, получим уравнение наклонной асимптоты y = kx + b. При k = 0 имеем уравнение горизонтальной асимптоты y = b.
Пример. Найти асимптоты графика функции
Найти асимптоты графика функции
Решение. Область определения функции ( ; 0) (0; ).
Итак, x = 0 — вертикальная асимптота.
Находим наклонные асимптоты y = kx + b
Следовательно, y = x + 2 — наклонная асимптота (рис. 18).
Рис. 18.
Горизонтальных асимптот нет, поскольку
Асимптоты и функция
Определение 1.
Говорят, что прямая является вертикальной асимптотой графика функции если хотя бы один из пределов равен
Пример 1:
График функции имеет вертикальную асимптоту
ибо (рис. 11.10).
Пусть, далее, функция определена для сколь угодно больших значений аргумента (ради определенности будем рассматривать сколь угодно большие значения положительного знака).
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Определение 2.
Говорят, что прямая
является наклонной асимптотой графика если функция представима в виде наклонной где
Теорема 19. Для того чтобы график функции имел при наклонную асимптоту (11.58), необходимо и достаточно, чтобы существовали два предела
Доказательство.
1. Необходимость.
Пусть график функции имеет при асимптоту (11.58), т. е. для справедливо представление (11.59). Тогда
2. Достаточность.
Пусть существуют пределы (11.60). Тогда второй из этих пределов дает право утверждать, что разность является
бесконечно малой при Обозначив эту бесконечно малую через получим для представления (11.59). Теорема доказана.
Замечание. Аналогично определяется наклонная асимптота и доказывается теорема 19 и для случая
Возможно вам будут полезны данные страницы:
Преобразование графиков функций |
Элементарные преобразования графиков функций |
Найдите координаты точки пересечения прямых |
Найдите координаты точки пересечения графиков |
Пример 2:
График функции имеет наклонную асимптоту и при и при и, кроме того, имеет вертикальную асимптоту (рис. 11.11). Действительно,
11.11). Действительно,
Схема исследования графика функции
В этом параграфе мы изложим схему, по которой целесообразно исследовать график функции, и приведем пример, иллюстрирующий эту схему.
Итак, целесообразно провести следующие исследования:
- Уточнить область задания функции.
- Выяснить вопрос о существовании асимптот (вертикальных и наклонных).
- Найти области возрастания и убывания функции и точки экстремума.
- Найти области сохранения направления выпуклости и точки перегиба.
- Найти точки пересечения графика функции с осью Ох.
По полученным данным легко строится эскиз графика функции.
В качестве примера построим график функции
Будем следовать изложенной выше схеме:
1. Поскольку функция (11.61) представляет собой рациональную дробь, то она определена и непрерывна всюду на бесконечной прямой, кроме точки х = 0, в которой обращается в нуль ее знаменатель.
2. Выясним вопрос о существовании асимптот. Очевидно, что
Очевидно, что
поэтому график функции имеет вертикальную асимптоту х = 0. Далее, из существования пределов вытекает, что и при и при график функции имеет наклонную асимптоту 3. Для нахождения областей возрастания и убывания функции (11.61) вычислим ее первую производную
Имея в виду, кроме того, что сама функция и первая производная не существуют при , мы получим следующие области сохранения знака ;
Из приведенной таблицы очевидно, что функция имеет следующие точки экстремума:
- максимум при х = -3, причем
- максимум при х= 1, причем
- минимум при х = 2, причем
Для нахождения областей сохранения направления выпуклости вычислим вторую производную
Имея в виду, что сама функция и ее производные не существуют в точке , мы получим следующие области сохранения знака :
Из приведенной таблицы очевидно, что график функции имеет перегиб в точке Легко подсчитать, что
Остается найти точки пересечения графика с осью Эти точки соответствуют вещественным корням уравнения
Легко видеть, что Поскольку квадратный трехчлен имеет комплексные корни, то рассматриваемое уравнение имеет только один вещественный корень так что граф
ик функции пересекает ось в точке (1/2, 0). По полученным данным строим эскиз графика рассматриваемой функции (рис. 11.12). Асимптоты графика функции.
По полученным данным строим эскиз графика рассматриваемой функции (рис. 11.12). Асимптоты графика функции.
Прямая линия называется асимптотой графика функции , если расстояние от точки А/, лежащей на графике, до этой прямой стремится к нулю при движении точки по графику в бесконечность.
Существует три вида асимптот: вертикальные, горизонтальные и наклонные.
Прямая называется вертикальной асимптотой графика функции , если хотя бы одно из предельных значений или равно
Прямая называется горизонтальной асимптотой графика функции
Прямая называется наклонной асимптотой графика функции если функцию можно представить в виде при
Теорема 7. Для того чтобы график функции имел при наклонную асимптоту необходимо и достаточно, чтобы существовали два предела:
Пример 3:
Найти асимптоты графика функции
Решение:
Точка — точка разрыва второго рода данной функции, причем
— вертикальная асимптота. Так как то
Так как то
график функции наклонных асимптот не имеет.
Находим горизонтальную асимптоту: Таким образом, график данной функции имеет вертикальную асимптоту х=3 и горизонтальную асимптоту
Пример 4:
Найти асимптоты графика функции
Решение:
Так как функция непрерывна на всей числовой прямой, то вертикальных асимптот нет. Нет и горизонтальных асимптот, так как Будем искать наклонные асимптоты. Пределы при будут различными, поэтому надо рассмотреть отдельно два случая.
Находим правую асимптоту (при ):
Находим левую асимптоту (при ):
Таким образом, получаем, что график функции ные наклонные асимптоты: при
19. Асимптоты, их нахождение. Асимптоты оэф. Схема исследования функции и построения ее графика по характерным точкам. Примеры
Определение. Асимптотой
графика функции
называется прямая, обладающая тем
свойством, что расстояние от точкиграфика функции до этой прямой стремится
к нулю при неограниченном удалении
точки графика от начала координат.
По способам их отыскания выделяют три вида асимптот: вертикальные , горизонтальные, наклонные.
Очевидно, горизонтальные являются частными случаями наклонных (при ).
Нахождение асимптот графика функции основано на следующих утверждениях.
Теорема 1. Пусть функция определена хотя бы в некоторой полуокрестности точкии хотя бы один из ее односторонних пределов в этой точке бесконечен, т.е. равенили. Тогда прямаяявляется вертикальной асимптотой графика функции.
Таким образом, вертикальные асимптоты графика функции следует искать в точках разрыва функции или на концах ее области определения (если это конечные числа).
Теорема
2. Пусть
функция
определена при значениях аргумента,
достаточно больших по абсолютной
величине, и существует конечный предел
функции.
Тогда прямаяесть горизонтальная асимптота графика
функции.
Может случиться, что , а, причеми- конечные числа, тогда график имеет две различные горизонтальные асимптоты: левостороннюю и правостороннюю. Если же существует лишь один из конечных пределов или, то график имеет либо одну левостороннюю, либо одну правостороннюю горизонтальную асимптоту.
Теорема 3. Пусть функция определена при значениях аргумента, достаточно больших по абсолютной величине, и существуют конечные пределыи. Тогда прямаяявляется наклонной асимптотой графика функции.
Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет.
Наклонная асимптота так же, как и горизонтальная, может быть односторонней.
Пример. Найдите все асимптоты графика функции .
Решение.
Функция определена при . Найдем ее односторонние пределы в точках.
Так
как
и(два других односторонних предела можно
уже не находить), то прямыеиявляются вертикальными асимптотами
графика функции.
Вычислим
(применим правило Лопиталя) =.
Значит, прямая — горизонтальная асимптота.
Так как горизонтальная асимптота существует, то наклонные уже не ищем (их нет).
Ответ: график имеет две вертикальные асимптоты и одну горизонтальную.
Общие исследование функции y = f(x).
Область определения функции. Найти ее область определения D(f) . Если это не слишком сложно, то полезно найти также область значений E(f) . (Однако, во многих случаях, вопрос нахождения E(f) откладывается до нахождения экстремумов функции.)
Особые свойства функции. Выяснить общие свойства функции: четность, нечетность, периодичность и т.п. Не любая функция обладает такими свойствами, как четность либо нечетность. Функция заведомо не является ни четной, ни нечетной, если ее область определения несимметрична относительно точки 0 на оси Ox.
 Точно так же, у любой периодической
функции область определения состоит
либо из всей вещественной оси, либо из
объединения периодически повторяющихся
систем промежутков.
Точно так же, у любой периодической
функции область определения состоит
либо из всей вещественной оси, либо из
объединения периодически повторяющихся
систем промежутков.Вертикальные асимптоты. Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определенияD(f), если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она не определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.
Наклонные и горизонтальные асимптоты. Если область определения D(f) вклоючает в себя лучи вида (a;+) или (−;b), то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) при x+или x−соответственно, т.е. найти limxf(x).Наклонные асимптоты: y = kx + b, где k=limx+xf(x) и b=limx+(f(x)−x).Горизонтальны асимптоты: y = b, где limxf(x)=b.

Нахождение точек пересечения графика с осями. Нахождение точки пересечения графика с осью Oy. Для этого нужно вычислить значение f(0). Найти также точки пересечения графика с осью Ox, для чего найти корни уравнения f(x) = 0 (или убедиться в отсутствии корней). Уравнение часто удается решить лишь приближунно, но уже отделение корней помогает лучше уяснить строение графика. Далее, нужно определить знак функции на промежутках между корнями и точками разрыва.
Нахождение точек пересечения графика с асимптотой. В некоторых случаях бывает нужно найти характерные точки графика, которые не были упомянуты в предыдущих пунктах. Например, если функция имеет наклонную асимптоту, то можно попытаться выяснить, нет ли точек пересечения графика с этой асимптотой.
Нахождение интервалов выпуклости и вогнутости. Это делается с помощью исследования знака второй производной f(x). Найти точки перегиба на стыках интервалов выпуклости и вогнутости.
 Вычислить
значение функции в точках перегиба.
Если функция имеет другие точки
непрерывности (кроме точек перегиба),
в которых вторая производная равна 0
либо не существует, то в этих точках
также полезно вычислить значение
функции. Найдя f(x)
, мы решаем неравенство f(x)0.
На каждом из интервалов решения функция
будет выпуклой вниз. Решая обратное
неравенство f(x)0,
мы находим интервалы, на которых функция
выпукла вверх (то есть вогнута). Определяем
точки перегиба как те точки, в которых
функция меняет направление выпуклости
(и непрерывна).
Вычислить
значение функции в точках перегиба.
Если функция имеет другие точки
непрерывности (кроме точек перегиба),
в которых вторая производная равна 0
либо не существует, то в этих точках
также полезно вычислить значение
функции. Найдя f(x)
, мы решаем неравенство f(x)0.
На каждом из интервалов решения функция
будет выпуклой вниз. Решая обратное
неравенство f(x)0,
мы находим интервалы, на которых функция
выпукла вверх (то есть вогнута). Определяем
точки перегиба как те точки, в которых
функция меняет направление выпуклости
(и непрерывна).
Асимптоты графика. Найти асимптоты графика функции
Ни одной, одна, две, три,… или бесконечно много. За примерами далеко ходить не будем, вспомним элементарные функции. Парабола, кубическая парабола, синусоида вовсе не имеют асимптот. График экспоненциальной, логарифмической функции обладает единственной асимптотой. У арктангенса, арккотангенса их две, а у тангенса, котангенса — бесконечно много. Не редкость, когда график укомплектован и горизонтальными и вертикальными асимптотами. Гипербола, will always love you.
Гипербола, will always love you.
Что значит найти асимптоты графика функции?
Это значит выяснить их уравнения, ну и начертить прямые линии, если того требует условие задачи. Процесс предполагает нахождение пределов функции.
Вертикальная асимптота графика, как правило, находится в точке бесконечного разрыва функции. Всё просто: если в точке функция терпит бесконечный разрыв, то прямая, заданная уравнением является вертикальной асимптотой графика.
Примечание: обратите внимание, что запись используется для обозначения двух совершенно разных понятий. Точка подразумевается или уравнение прямой — зависит от контекста.
Таким образом, чтобы установить наличие вертикальной асимптоты в точке достаточно показать, что хотя бы один из односторонних пределов бесконечен. Чаще всего это точка, где знаменатель функции равен нулю. По существу, мы уже находили вертикальные асимптоты в последних примерах урока о непрерывности функции. Но в ряде случаев существует только один односторонний предел, и, если он бесконечен, то снова — любите и жалуйте вертикальную асимптоту. Простейшая иллюстрация: и ось ординат.
Простейшая иллюстрация: и ось ординат.
Из вышесказанного также следует очевидный факт: если функция непрерывна на, то вертикальные асимптоты отсутствуют. На ум почему-то пришла парабола. Действительно, где тут «воткнёшь» прямую? …да… понимаю… последователи дядюшки Фрейда забились в истерике =)
Обратное утверждение в общем случае неверно: так, функция не определена на всей числовой прямой, однако совершенно обделена асимптотами.
Наклонные асимптоты графика функции
Наклонные (как частный случай — горизонтальные) асимптоты могут нарисоваться, если аргумент функции стремится к «плюс бесконечности» или к «минус бесконечности». Поэтому график функции не может иметь больше 2-х наклонных асимптот. Например, график экспоненциальной функции обладает единственной горизонтальной асимптотой при, а график арктангенса при — двумя такими асимптотами, причём различными.
Когда график и там и там сближается с единственной наклонной асимптотой, то «бесконечности» принято объединять под единой записью. Например, …правильно догадались: .
Например, …правильно догадались: .
Решение удобно разбить на два пункта:
1) Сначала проверяем, есть ли вертикальные асимптоты. Знаменатель обращается в ноль при, и сразу понятно, что в данной точке функция терпит бесконечный разрыв, а прямая, заданная уравнением, является вертикальной асимптотой графика функции. Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:
Напоминаю технику вычислений, на которой я подобно останавливался в статье Непрерывность функции. Точки разрыва. В выражение под знаком предела вместо «икса» подставляем. В числителе ничего интересного:
А вот в знаменателе получается бесконечно малое отрицательное число:
Оно и определяет судьбу предела.
Левосторонний предел бесконечный, и, в принципе уже можно вынести вердикт о наличии вертикальной асимптоты. Но односторонние пределы нужны не только для этого — они ПОМОГАЮТ ПОНЯТЬ, КАК расположен график функции и построить его КОРРЕКТНО. Поэтому обязательно вычислим и правосторонний предел:
Вывод: односторонние пределы бесконечны, значит, прямая является вертикальной асимптотой графика функции при.
Первый предел конечен, значит, необходимо «продолжить разговор» и найти второй предел:
Второй предел тоже конечен.
Таким образом, наша асимптота:
Вывод: прямая, заданная уравнением является горизонтальной асимптотой графика функции при.
Для нахождения горизонтальной асимптоты можно пользоваться упрощенной формулой:
Если существует конечный предел, то прямая является горизонтальной асимптотой графика функции при.
Нетрудно заметить, что числитель и знаменатель функции одного порядка роста, а значит, искомый предел будет конечным:
По условию не нужно выполнять чертёж, но если в самом разгаре исследование функции, то на черновике сразу же делаем набросок:
Исходя из трёх найденных пределов, попытайтесь самостоятельно прикинуть, как может располагаться график функции. Совсем трудно? Найдите 5-6-7-8 точек и отметьте их на чертеже. Впрочем, график данной функции строится с помощью преобразований графика элементарной функции, и читатели, внимательно рассмотревшие Пример 21 указанной статьи легко догадаются, что это за кривая.
Это пример для самостоятельного решения. Процесс, напоминаю, удобно разбить на два пункта — вертикальные асимптоты и наклонные асимптоты. В образце решения горизонтальная асимптота найдёна по упрощенной схеме.
На практике чаще всего встречаются дробно-рациональные функции, и после тренировки на гиперболах усложним задание:
Найти асимптоты графика функции
Решение: Раз, два и готово:
1) Вертикальные асимптоты находятся в точках бесконечного разрыва, поэтому нужно проверить, обращается ли знаменатель в ноль. Решим квадратное уравнение:
Дискриминант положителен, поэтому уравнение имеет два действительных корня, и работы значительно прибавляется
В целях дальнейшего нахождения односторонних пределов квадратный трёхчлен удобно разложить на множители:
(для компактной записи «минус» внесли в первую скобку). Для подстраховки выполним проверку, мысленно либо на черновике раскрыв скобки.
Перепишем функцию в виде
Найдём односторонние пределы в точке:
асимптота график функция предел
И в точке:
Таким образом, прямые являются вертикальными асимптотами графика рассматриваемой функции.
2) Если посмотреть на функцию, то совершенно очевидно, что предел будет конечным и у нас горизонтальная асимптота. Покажем её наличие коротким способом:
Таким образом, прямая (ось абсцисс) является горизонтальной асимптотой графика данной функции.
Найденные пределы и асимптоты дают немало информации о графике функции. Постарайтесь мысленно представить чертёж с учётом следующих фактов:
Схематично изобразите вашу версию графика на черновике.
Конечно, найденные пределы однозначно не определяют вид графика, и возможно, вы допустите ошибку, но само упражнение окажет неоценимую помощь в ходе полного исследования функции. Правильная картинка — в конце урока.
Найти асимптоты графика функции
Найти асимптоты графика функции
Это задания для самостоятельного решения. Оба графика снова обладают горизонтальными асимптотами, которые немедленно детектируются по следующим признакам: в Примере 4порядок роста знаменателя больше, чем порядок роста числителя, а в Примере 5 числитель и знаменатель одного порядка роста. В образце решения первая функция исследована на наличие наклонных асимптот полным путём, а вторая — через предел.
В образце решения первая функция исследована на наличие наклонных асимптот полным путём, а вторая — через предел.
Горизонтальные асимптоты, по моему субъективному впечатлению, встречаются заметно чаще, чем те, которые «по-настоящему наклонены». Долгожданный общий случай:
Найти асимптоты графика функции
Решение: классика жанра:
- 1) Поскольку знаменатель положителен, то функция непрерывна на всей числовой прямой, и вертикальные асимптоты отсутствуют. …Хорошо ли это? Не то слово — отлично! Пункт №1 закрыт.
- 2) Проверим наличие наклонных асимптот:
Второй предел тоже конечен, следовательно, у графика рассматриваемой функции существует наклонная асимптота:
Таким образом, при график функции бесконечно близко приближается к прямой.
Заметьте, что он пересекает свою наклонную асимптоту в начале координат, и такие точки пересечения вполне допустимы — важно, чтобы «всё было нормально» на бесконечности (собственно, речь об асимптотах и заходит именно там).
Найти асимптоты графика функции
Решение: комментировать особо нечего, поэтому оформлю примерный образец чистового решения:
1) Вертикальные асимптоты. Исследуем точку.
Прямая является вертикальной асимптотой для графика при.
2) Наклонные асимптоты:
Прямая является наклонной асимптотой для графика при.
Найдённые односторонние пределы и асимптоты с высокой достоверностью позволяют предположить, как выглядит график данной функции.
Найти асимптоты графика функции
Это пример для самостоятельного решения, для удобства вычисления некоторых пределов можно почленно разделить числитель на знаменатель. И снова, анализируя полученные результаты, постарайтесь начертить график данной функции.
Очевидно, что обладателями «настоящих» наклонных асимптот являются графики тех дробно-рациональных функций, у которых старшая степень числителя на единицу больше старшей степени знаменателя. Если больше — наклонной асимптоты уже не будет (например,).
Но в жизни происходят и другие чудеса.
Определение . Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от точкиграфика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат .
По способам их отыскания выделяют три вида асимптот: вертикальные , горизонтальные, наклонные.
Очевидно, горизонтальные являются частными случаями наклонных (при ).
Нахождение асимптот графика функции основано на следующих утверждениях.
Теорема 1 . Пусть функция определена хотя бы в некоторой полуокрестности точкии хотя бы один из ее односторонних пределов в этой точке бесконечен, т.е. равенили. Тогда прямаяявляется вертикальной асимптотой графика функции .
Таким образом, вертикальные асимптоты графика функции следует искать в точках разрыва функции или на концах ее области определения (если это конечные числа).
Теорема
2 . Пусть
функция
определена при значениях аргумента,
достаточно больших по абсолютной
величине, и существует конечный предел
функции.
Тогда прямаяесть горизонтальная асимптота графика
функции.
Пусть
функция
определена при значениях аргумента,
достаточно больших по абсолютной
величине, и существует конечный предел
функции.
Тогда прямаяесть горизонтальная асимптота графика
функции.
Может случиться, что , а, причеми- конечные числа, тогда график имеет две различные горизонтальные асимптоты: левостороннюю и правостороннюю. Если же существует лишь один из конечных пределов или, то график имеет либо одну левостороннюю, либо одну правостороннюю горизонтальную асимптоту.
Теорема 3 . Пусть функция определена при значениях аргумента, достаточно больших по абсолютной величине, и существуют конечные пределыи. Тогда прямаяявляется наклонной асимптотой графика функции .
Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет.
Наклонная асимптота так же, как и горизонтальная, может быть односторонней.
Пример . Найдите все асимптоты графика функции .
Решение .
Функция
определена при
. Найдем ее односторонние пределы в точках.
Найдем ее односторонние пределы в точках.
Так как и(два других односторонних предела можно уже не находить), то прямыеиявляются вертикальными асимптотами графика функции.
Вычислим
(применим правило Лопиталя) =.
Значит, прямая — горизонтальная асимптота.
Так как горизонтальная асимптота существует, то наклонные уже не ищем (их нет).
Ответ : график имеет две вертикальные асимптоты и одну горизонтальную.
Общие исследование функции y = f (x ).
Область определения функции. Найти ее область определения D (f ) . Если это не слишком сложно, то полезно найти также область значений E (f ) . (Однако, во многих случаях, вопрос нахождения E (f ) откладывается до нахождения экстремумов функции.)
Особые
свойства функции. Выяснить
общие свойства функции: четность,
нечетность, периодичность и т.п. Не
любая функция обладает такими свойствами,
как четность либо нечетность. Функция
заведомо не является ни четной, ни
нечетной, если ее область определения
несимметрична относительно точки 0 на
оси Ox .
Точно так же, у любой периодической
функции область определения состоит
либо из всей вещественной оси, либо из
объединения периодически повторяющихся
систем промежутков.
Функция
заведомо не является ни четной, ни
нечетной, если ее область определения
несимметрична относительно точки 0 на
оси Ox .
Точно так же, у любой периодической
функции область определения состоит
либо из всей вещественной оси, либо из
объединения периодически повторяющихся
систем промежутков.
Вертикальные асимптоты. Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определенияD (f ), если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она не определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.
Наклонные
и горизонтальные асимптоты. Если область определения D (f )
вклоючает в себя лучи вида (a;+)
или (−;b),
то можно попытаться найти наклонные
асимптоты (или горизонтальные асимптоты)
при x+или x−соответственно, т.е. найти limxf(x).Наклонные
асимптоты : y = kx + b, где
k=limx+xf(x)
и b=limx+(f(x)−x). Горизонтальны
асимптоты : y = b, где
limxf(x)=b.
Горизонтальны
асимптоты : y = b, где
limxf(x)=b.
Нахождение точек пересечения графика с осями . Нахождение точки пересечения графика с осью Oy . Для этого нужно вычислить значение f (0). Найти также точки пересечения графика с осью Ox , для чего найти корни уравнения f (x ) = 0 (или убедиться в отсутствии корней). Уравнение часто удается решить лишь приближунно, но уже отделение корней помогает лучше уяснить строение графика. Далее, нужно определить знак функции на промежутках между корнями и точками разрыва.
Нахождение точек пересечения графика с асимптотой. В некоторых случаях бывает нужно найти характерные точки графика, которые не были упомянуты в предыдущих пунктах. Например, если функция имеет наклонную асимптоту, то можно попытаться выяснить, нет ли точек пересечения графика с этой асимптотой.
Нахождение
интервалов выпуклости и вогнутости .
Это делается с помощью исследования
знака второй производной f(x). Найти точки перегиба на стыках интервалов
выпуклости и вогнутости. Вычислить
значение функции в точках перегиба.
Если функция имеет другие точки
непрерывности (кроме точек перегиба),
в которых вторая производная равна 0
либо не существует, то в этих точках
также полезно вычислить значение
функции. Найдя f(x)
, мы решаем неравенство f(x)0.
На каждом из интервалов решения функция
будет выпуклой вниз. Решая обратное
неравенство f(x)0,
мы находим интервалы, на которых функция
выпукла вверх (то есть вогнута). Определяем
точки перегиба как те точки, в которых
функция меняет направление выпуклости
(и непрерывна).
Найти точки перегиба на стыках интервалов
выпуклости и вогнутости. Вычислить
значение функции в точках перегиба.
Если функция имеет другие точки
непрерывности (кроме точек перегиба),
в которых вторая производная равна 0
либо не существует, то в этих точках
также полезно вычислить значение
функции. Найдя f(x)
, мы решаем неравенство f(x)0.
На каждом из интервалов решения функция
будет выпуклой вниз. Решая обратное
неравенство f(x)0,
мы находим интервалы, на которых функция
выпукла вверх (то есть вогнута). Определяем
точки перегиба как те точки, в которых
функция меняет направление выпуклости
(и непрерывна).
Именно так формулируется типовое задание, и оно предполагает нахождение ВСЕХ асимптот графика (вертикальных, наклонных/горизонтальных). Хотя, если быть более точным в постановке вопроса — речь идёт об исследовании на наличие асимптот (ведь таковых может и вовсе не оказаться).
Начнём с чего-нибудь простого:
Пример 1
Решение удобно разбить на два пункта:
1) Сначала проверяем, есть ли вертикальные асимптоты. Знаменатель обращается в ноль при , и сразу понятно, что в данной точке функция терпит бесконечный разрыв , а прямая, заданная уравнением , является вертикальной асимптотой графика функции . Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:
Знаменатель обращается в ноль при , и сразу понятно, что в данной точке функция терпит бесконечный разрыв , а прямая, заданная уравнением , является вертикальной асимптотой графика функции . Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:
Напоминаю технику вычислений, на которой я подобно останавливался в статье непрерывность функции. Точки разрыва . В выражение под знаком предела вместо «икса» подставляем . В числителе ничего интересного:
.
А вот в знаменателе получается бесконечно малое отрицательное число :
, оно и определяет судьбу предела.
Левосторонний предел бесконечный, и, в принципе уже можно вынести вердикт о наличии вертикальной асимптоты. Но односторонние пределы нужны не только для этого — они ПОМОГАЮТ ПОНЯТЬ, КАК расположен график функции и построить его КОРРЕКТНО . Поэтому обязательно вычислим и правосторонний предел:
Вывод : односторонние пределы бесконечны, значит, прямая является вертикальной асимптотой графика функции при .
Первый предел конечен , значит, необходимо «продолжить разговор» и найти второй предел:
Второй предел тоже конечен .
Таким образом, наша асимптота:
Вывод : прямая, заданная уравнением является горизонтальной асимптотой графика функции при .
Для нахождения горизонтальной асимптоты можно пользоваться упрощенной формулой :
Если существует конечный предел , то прямая является горизонтальной асимптотой графика функции при .
Нетрудно заметить, что числитель и знаменатель функции одного порядка роста , а значит, искомый предел будет конечным:
Ответ :
По условию не нужно выполнять чертёж, но если в самом разгаре исследование функции , то на черновике сразу же делаем набросок:
Исходя из трёх найденных пределов , попытайтесь самостоятельно прикинуть, как может располагаться график функции . Совсем трудно? Найдите 5-6-7-8 точек и отметьте их на чертеже. Впрочем, график данной функции строится с помощью преобразований графика элементарной функции , и читатели, внимательно рассмотревшие Пример 21 указанной статьи легко догадаются, что это за кривая.
Пример 2
Найти асимптоты графика функции
Это пример для самостоятельного решения. Процесс, напоминаю, удобно разбить на два пункта — вертикальные асимптоты и наклонные асимптоты. В образце решения горизонтальная асимптота найдёна по упрощенной схеме.
На практике чаще всего встречаются дробно-рациональные функции, и после тренировки на гиперболах усложним задание:
Пример 3
Найти асимптоты графика функции
Решение : Раз, два и готово:
1) Вертикальные асимптоты находятся в точках бесконечного разрыва , поэтому нужно проверить, обращается ли знаменатель в ноль. Решим квадратное уравнение :
Дискриминант положителен, поэтому уравнение имеет два действительных корня, и работы значительно прибавляется =)
В целях дальнейшего нахождения односторонних пределов квадратный трёхчлен удобно разложить на множители :
(для компактной записи «минус» внесли в первую скобку). Для подстраховки выполним проверку, мысленно либо на черновике раскрыв скобки.
Перепишем функцию в виде
Найдём односторонние пределы в точке :
И в точке :
Таким образом, прямые являются вертикальными асимптотами графика рассматриваемой функции.
2) Если посмотреть на функцию , то совершенно очевидно, что предел будет конечным и у нас горизонтальная асимптота. Покажем её наличие коротким способом:
Таким образом, прямая (ось абсцисс) является горизонтальной асимптотой графика данной функции.
Ответ :
Найденные пределы и асимптоты дают немало информации о графике функции. Постарайтесь мысленно представить чертёж с учётом следующих фактов:
Схематично изобразите вашу версию графика на черновике.
Конечно, найденные пределы однозначно не определяют вид графика, и возможно, вы допустите ошибку, но само упражнение окажет неоценимую помощь в ходе полного исследования функции . Правильная картинка — в конце урока.
Пример 4
Найти асимптоты графика функции
Пример 5
Найти асимптоты графика функции
Это задания для самостоятельного решения. Оба графика снова обладают горизонтальными асимптотами, которые немедленно детектируются по следующим признакам: в Примере 4 порядок роста знаменателя больше
, чем порядок роста числителя, а в Примере 5 числитель и знаменатель одного порядка роста . В образце решения первая функция исследована на наличие наклонных асимптот полным путём, а вторая — через предел .
Оба графика снова обладают горизонтальными асимптотами, которые немедленно детектируются по следующим признакам: в Примере 4 порядок роста знаменателя больше
, чем порядок роста числителя, а в Примере 5 числитель и знаменатель одного порядка роста . В образце решения первая функция исследована на наличие наклонных асимптот полным путём, а вторая — через предел .
Горизонтальные асимптоты, по моему субъективному впечатлению, встречаются заметно чаще, чем те, которые «по-настоящему наклонены». Долгожданный общий случай:
Пример 6
Найти асимптоты графика функции
Решение : классика жанра:
1) Поскольку знаменатель положителен, то функция непрерывна на всей числовой прямой, и вертикальные асимптоты отсутствуют. …Хорошо ли это? Не то слово — отлично! Пункт №1 закрыт.
2) Проверим наличие наклонных асимптот:
Первый предел конечен , поэтому едем дальше. В ходе вычисления второго предела для устранения неопределённости «бесконечность минус бесконечность» приводим выражение к общему знаменателю:
Второй предел тоже конечен , следовательно, у графика рассматриваемой функции существует наклонная асимптота:
Вывод :
Таким образом, при график функции бесконечно близко приближается к прямой :
Заметьте, что он пересекает свою наклонную асимптоту в начале координат, и такие точки пересечения вполне допустимы — важно, чтобы «всё было нормально» на бесконечности (собственно, речь об асимптотах и заходит именно там).
Пример 7
Найти асимптоты графика функции
Решение : комментировать особо нечего, поэтому оформлю примерный образец чистового решения:
1) Вертикальные асимптоты. Исследуем точку .
Прямая является вертикальной асимптотой для графика при .
2) Наклонные асимптоты:
Прямая является наклонной асимптотой для графика при .
Ответ :
Найдённые односторонние пределы и асимптоты с высокой достоверностью позволяют предположить, как выглядит график данной функции. Корректный чертёж в конце урока.
Пример 8
Найти асимптоты графика функции
Это пример для самостоятельного решения, для удобства вычисления некоторых пределов можно почленно разделить числитель на знаменатель. И снова, анализируя полученные результаты, постарайтесь начертить график данной функции.
Очевидно, что обладателями «настоящих» наклонных асимптот являются графики тех дробно-рациональных функций, у которых старшая степень числителя на единицу больше старшей степени знаменателя. Если больше — наклонной асимптоты уже не будет (например, ).
Если больше — наклонной асимптоты уже не будет (например, ).
Но в жизни происходят и другие чудеса:
Пример 9
Решение : функция непрерывна на всей числовой прямой, значит, вертикальные асимптоты отсутствует. Но вот наклонные вполне могут быть. Проверяем:
Вспоминаю, как ещё в ВУЗе столкнулся с похожей функцией и просто не мог поверить, что у неё есть наклонная асимптота. До тех пор, пока не вычислил второй предел:
Строго говоря, здесь две неопределённости: и , но так или иначе, нужно использовать метод решения, который разобран в Примерах 5-6 статьи о пределах повышенной сложности . Умножаем и делим на сопряженное выражение, чтобы воспользоваться формулой :
Ответ :
Пожалуй, самая популярная наклонная асимптота.
До сих пор бесконечности удавалось «стричь под одну гребёнку», но бывает, что у графика функции две разные наклонные асимптоты при и при :
Пример 10
Исследовать график функции на наличие асимптот
Решение : подкоренное выражение положительно, значит, область определения — любое действительно число, и вертикальных палок быть не может.
Проверим, существуют ли наклонные асимптоты.
Если «икс» стремится к «минус бесконечности», то:
(при внесении «икса» под квадратный корень необходимо добавить знак «минус», чтобы не потерять отрицательность знаменателя)
Выглядит необычно, но здесь неопределённость «бесконечность минус бесконечность». Умножаем числитель и знаменатель на сопряженное выражение:
Таким образом, прямая является наклонной асимптотой графика при .
С «плюс бесконечностью» всё тривиальнее:
А прямая — при .
Ответ :
Если ;
, если .
Не удержусь от графического изображения:
Это одна из ветвей гиперболы .
Не редкость, когда потенциальное наличие асимптот изначально ограничено областью определения функции :
Пример 11
Исследовать график функции на наличие асимптот
Решение : очевидно, что , поэтому рассматриваем только правую полуплоскость, где есть график функции.
1) Функция непрерывна на интервале , а значит, если вертикальная асимптота и существует, то это может быть только ось ординат. Исследуем поведение функции вблизи точки справа :
Исследуем поведение функции вблизи точки справа :
Обратите внимание, здесь НЕТ неопределённости (на таких случаях акцентировалось внимание в начале статьи Методы решения пределов) .
Таким образом, прямая (ось ординат) является вертикальной асимптотой для графика функции при .
2) Исследование на наклонную асимптоту можно провести по полной схеме, но в статье Правила Лопитал мы выяснили, что линейная функция более высокого порядка роста, чем логарифмическая, следовательно: (см. Пример 1 того же урока).
Вывод: ось абсцисс является горизонтальной асимптотой графика функции при .
Ответ :
Если ;
, если .
Чертёж для наглядности:
Интересно, что у вроде бы похожей функции асимптот нет вообще (желающие могут это проверить).
Два заключительных примера для самостоятельного изучения:
Пример 12
Исследовать график функции на наличие асимптот
Для проверки на вертикальные асимптоты сначала нужно найти область определения функции , а затем вычислить пару односторонних пределов в «подозрительных» точках. Наклонные асимптоты тоже не исключены, поскольку функция определена на «плюс» и «минус» бесконечности.
Наклонные асимптоты тоже не исключены, поскольку функция определена на «плюс» и «минус» бесконечности.
Пример 13
Исследовать график функции на наличие асимптот
А здесь могут быть только наклонные асимптоты, причём направления , следует рассмотреть отдельно.
Надеюсь, вы отыскали нужную асимптоту =)
Желаю успехов!
Решения и ответы:
Пример 2: Решение :
. Найдём односторонние пределы:
Прямая является вертикальной асимптотой графика функции при .
2) Наклонные асимптоты.
Прямая .
Ответ :
Чертёж к Примеру 3:
Пример 4: Решение :
1) Вертикальные асимптоты. Функция терпит бесконечный разрыв в точке . Вычислим односторонние пределы:
Примечание : бесконечно малое отрицательное число в чётной степени равно бесконечно малому положительному числу: .
Прямая является вертикальной асимптотой графика функции.
2) Наклонные асимптоты.
Прямая (ось абсцисс) является горизонтальной асимптотой графика функции при .
Ответ : .
.
Значит, при у графика нет наклонной асимптоты.
Таким образом, прямая является горизонтальной асимптотой графика данной функции при .
Ответ : ось абсцисс при .
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Нули функции. Интервалы знакопостоянства функции.
Метод интервалов
Значительная доля материала, касающегося производных и исследования функций, традиционно относится к школьной программе, и данная статья не является исключением из правила. Сегодня мы потренируемся в нахождении нулей и интервалов знакопостоянства функции, а также подробно разберём метод интервалов, который можно сравнить с надёжной арматурой в стенах рассматриваемой темы.
Если же проект вашего здания находится на стадии котлована, пожалуйста, начните с вводного урока о графиках функций. Кроме того, желательно ознакомиться со статьями Область определения функции, Асимптоты графика, и, по существу, информация этой странички — логическое продолжение. Материал, естественно, будет полезен и старшеклассникам.
Если расстояние d от точки кривой у = f (х), имеющей бесконечную ветвь, до некоторой определенной прямой по мере удаления точки по этой кривой в бесконечность стремится к нулю, то прямая называется асимптотой кривой.
Различают асимптоты: 1) горизонтальные, 2) вертикальные и 3) наклонные.
1. Кривая у = f (х) имеет горизонтальную асимптоту у =b только в том случае, когда существует конечный предел функции f (х) при , и этот предел равен b , т. е. если
2.
Кривая у = f (х) имеет вертикальную
асимптоту х = а, если при
.
Для определения вертикальных асимптот
надо отыскать те значения аргумента,
вблизи которых f (х) неограниченно
возрастает по абсолютной величине. Если
такими значениями аргумента являются
а1, а2, …, то уравнения вертикальных
асимптот будут
Если
такими значениями аргумента являются
а1, а2, …, то уравнения вертикальных
асимптот будут
х = а1, х =а2…
3. Для определения наклонной асимптоты у = kx + b кривой у = f (х) надо найти числа k и b из формул
(следует отдельно рассматривать случаи ). Наклонные асимптоты у кривой у = f (х) существуют в том и только в том случае, когда эти пределы имеют конечное значение. При определении этих пределов удобно пользоваться правилом Лопиталя.
Пример.
Найти асимптоты кривой
Решение. Горизонтальных асимптот нет. Вертикальную асимптоту находим из условия
2х
+ 3 = 0 => х = — 3/2, при этом у
,
когда
,
у
,
когда
.
Определим наклонные асимптоты, уравнение
которых имеет вид: у = kx + b
Так
как k и b имеют конечные значения и равны
между собой при х
и при х
,
то имеется единственная наклонная
асимптота, уравнение которой
Под полным исследованием функции обычно понимается решение таких вопросов:
Определение
области существования функции.
Выявление вопроса о четности и нечетности функции.
Определение точек разрыва функции.
Определение асимптот графика функции.
Определение интервалов возрастания и убывания функции.
Определение экстремума функции.
Определение интервалов выпуклости и вогнутости графика функции.
Определение точек перегиба.
Нахождение пересечения с осями координат.
Построение графика функции.
Пример.
Исследуем функцию
D
(y) = (
).
Функция непрерывна на всей области
определения. Точек разрыва нет.
Функция не является ни четной, ни нечетной, ни периодической.
Точек разрыва нет.
Вертикальных
асимптот нет;
,
наклонных асимптот нет.
5,
6.
.
Критические точки х = -2, х = 0.
( | ( | ||||
Знак | = 0 | ||||
Поведение функции | Возрастает | 3 | Возрастает |
7,
8.
,
при
х = 1,
не существует при х = 0.
( | ( | ||||
Знак | = | = 0 | |||
Поведение функции | Выпукла верх | Не является точкой перегиба | Выпукла верх | Точка перегиба | Выпукла вниз |
9.
х
=0 и х = -5.
Задание 1
Вычислить определитель матрицы А второго порядка
Вычислить определитель матрицы В третьего порядка
Вычислить определитель матрицы В, разложив его по какой-либо строке и какому либо столбцу
Вычислить определитель матрицы В, пользуясь свойствами определителей. Свести вычисление определителя третьего порядка к вычислению одного определителя второго порядка
Вариант 1 | ||||||||||||||||||
Вариант 2 | ||||||||||||||||||
Вариант 3 | ||||||||||||||||||
Вариант 4 | ||||||||||||||||||
Вариант 5 | ||||||||||||||||||
Вариант 6 | ||||||||||||||||||
Вариант 7 | ||||||||||||||||||
Вариант 8 | |||||||||||
Вариант 9 | |||||||||||
Вариант 10 | |||||||||||
Задание 2
1. Решить методом Крамера систему уравнений Ах = а
Решить методом Крамера систему уравнений Ах = а
Решить методом Крамера систему уравнений В x = b
Решить методом Гаусса систему уравнений В x = b
Задание 3.
Ах = а
Решить матричным методом систему уравнений В x = b
Задание 4.
Вычислить ранг матрицы.
1.,
2.
;
3.
4.
5.
6.
7.
8
9.
10.
Задание 5
Даны две вершины треугольника Δ АВС: А (х 1 ,у 1 ), В (х 2 ,у 2 ) и точка D (x 3 , y 3 )пересечения высот:
а) составить уравнение высот, медиан, биссектрис треугольника Δ АВС .
б) найти уравнения прямых, проходящих через вершины треугольника и параллельных сторонам.
в)
определить длины высот треугольника и
расстояние от точки М (х 4 ,
у 4 )
до сторон треугольника.
x 1 | y 1 | x 2 | y 2 | x 3 | y 3 | x 4 | y 4 | |
Задание 6.
Даны координаты вершин пирамиды АВС D : А (х 1 ,у 1 , z 1 ), В (х 2 ,у 2 , z 3 ) ,C (x 2 , y 2 , z 2 ) ,D (х 4 , у 4 , z 3 )
1) длину ребра АВ; .
2) угол между ребрами АВ и А D ;
3) угол меду ребром AD и гранью ABC ;
4) площадь грани ABC ;
5) объем пирамиды;
6) уравнение прямой AB ;
7) уравнение плоскости ABC ;
8) уравнение высоты, опущенной из вершиныD на грань ABC .
n | x 1 | y 1 | z 1 | x 2 | y 2 | z 2 | x 3 | y 3 | z 3 | x 4 | y 4 | z 4 |
Задание 7.
Задание 8. Найти область определения функции
5.
7.
8.
9.
10.
Задание 9.Построить график функции
1.
2.
3.
4
5.
6.
7.
8.
9.
10.
Задание 10 .Найти пределы функции
1.а)
,
б)
,
в)
,
г)
,
д)
2.а)
,
б)
,
в)
,
г)
,
д)
3.а)
,
б)
,
в)
,
г)
,
д)
4.
а)
,
б)
,
в)
,
г)
,
д)
5.а)
,
б)
,
в)
,
г)
,
д)
6.а)
,
б)
,
в)
,
г)
,
д)
7.
а)
,
б)
,
в)
,
г)
,
д)
8.а)
,
б)
,
в)
,
г)
,
д)
9.а)
,
б)
,
в)
,
г)
,
д)
10.а)
,
б)
,
в)
,
г)
,
д)
Задание 11. Найти производную
1.
,
б),
в)
,
г)
,
д)
,
е)
2. а)
а)
,
б)
,
в)
,
г)
,
д)
,е)
3.
а),
б)
,
в)
,
г)
,
д)
,
e)
4.
а)
,
б)
,
в)
,
г)
,
д)
,
e)
5.
а)
,
б)
,
в)
,
г)
,
д)
,
е)
6.
а)
,
б)
,
в)
,
г)
,
д)
,
е)
7.
а)
,
б),
в)
,
г)
,
д)
,
е)
8.
а)
,
б)
,
в)
,
г)
,
д)
,
е)
9.
а)
,
б)
,
в)
,
г)
,
д)
,
е)
10.
а)
,
б)
,
в)
,
г)
,
д)
,
е)
Задание 12. Показать, что функция удовлетворяет равенству
Задание 13. Найти вторую производную функции, заданной параметрически.
1 .
6.
2.
7
3.
8
4.
9.
5.
10.
Задание 14. Найти пределы, пользуясь правилом Лопиталя
Задание 15. Найти экстремумы заданных функций.
1.
6.
2.
7.
3.
8.
4.
9.
5.
10.
Задание 16. Найти наибольшее и наименьшее значение на указанных отрезках и на указанных интервалах.
Задание 17. Провести полное исследование данных функций и начертить их графики.
1.
6.
2.
7.
3.
8.
4.
9.
5.
10.
Литература:
Баврин И.И. Курс высшей математики.-М.:Просвящение,1992.-400 с.
Бронштейн И.Н., Семендяев К.А. Справочник по математике. М, 1967г,608 с
Общий курс высшей математики для экономистов, под ред В.И.Ермакова-М. «Инфра-М».1999 г.-655 с.
Теуш В.Л. Курс высшей математики. — М.: Советская наука, 1958г, 270 с.
Шипачев В.С. Высшая математика: Учебное пособие М. Высшая школа,1990.-479с.
Высшая математика для экономистов: Учебник для вузов/Н.Ш.Кремер, Б.А.Путко и др.; М: ЮНИТИ, 2002. – 461 с.
Валєєв К.Г, Джалладова І.А Вища математика: Навч. Посібник.
Асимптоты — горизонтальные, вертикальные, наклонные (наклонные)
Асимптоты — это воображаемые линии, к которым очень близок общий график функции или часть графика. Асимптоты очень полезны при построении графика функции, поскольку они помогают подумать о том, каких линий кривая не должна касаться.
Асимптоты очень полезны при построении графика функции, поскольку они помогают подумать о том, каких линий кривая не должна касаться.
Давайте узнаем об асимптотах и их типах, а также о процессе их нахождения на дополнительных примерах.
| 1. | Что такое асимптота? |
| 2. | Типы асимптот |
| 3. | Как найти асимптоты? |
| 4. | Как найти вертикальные и горизонтальные асимптоты? |
| 5. | Разница между горизонтальной и вертикальной асимптотами |
| 6. | Наклонная асимптота (Наклонная асимптота) |
| 7. | Как найти наклонную асимптоту? |
| 8. | Часто задаваемые вопросы по асимптотам |
Что такое асимптота?
Асимптота — это линия, к которой приближается кривая, но никогда не касается кривой. т. е. асимптота — это прямая, к которой сходится график функции. Обычно нам не нужно рисовать асимптоты при построении графиков функций. Но нанесение их пунктирными линиями (воображаемыми линиями) заставляет нас позаботиться о том, чтобы кривая не касалась асимптоты. Следовательно, асимптоты — это просто воображаемые линии. Расстояние между асимптотой функции y = f(x) и ее графиком приблизительно равно 0, когда либо значение x, либо y стремится к ∞ или -∞.
т. е. асимптота — это прямая, к которой сходится график функции. Обычно нам не нужно рисовать асимптоты при построении графиков функций. Но нанесение их пунктирными линиями (воображаемыми линиями) заставляет нас позаботиться о том, чтобы кривая не касалась асимптоты. Следовательно, асимптоты — это просто воображаемые линии. Расстояние между асимптотой функции y = f(x) и ее графиком приблизительно равно 0, когда либо значение x, либо y стремится к ∞ или -∞.
Типы асимптот
Существует 3 типа асимптот.
- Горизонтальная асимптота (ГА) — это горизонтальная линия, поэтому ее уравнение имеет форму y = k.
- Вертикальная асимптота (VA) — это вертикальная линия, поэтому ее уравнение имеет форму x = k.
- Косая асимптота (Наклонная асимптота) — это наклонная линия и, следовательно, ее уравнение имеет вид y = mx + b.
Вот рисунок, иллюстрирующий все типы асимптот.
Как найти асимптоты?
Поскольку асимптота представляет собой горизонтальную, вертикальную или наклонную линию, ее уравнение имеет вид x = a, y = a или y = ax + b. Вот правила нахождения всех типов асимптот функции y = f(x).
Вот правила нахождения всех типов асимптот функции y = f(x).
- Горизонтальная асимптота имеет вид y = k, где x→∞ или x→ -∞. т. е. это значение одного/обоих пределов lim ₓ→∞ f(x) и lim ₓ→ -∞ f(x). Чтобы узнать, как найти горизонтальную асимптоту, нажмите здесь.
- Вертикальная асимптота имеет вид x = k, где y→∞ или y→ -∞. Чтобы узнать, как легко находить вертикальные асимптоты, нажмите здесь.
- Наклонная асимптота имеет вид y = mx + b, где m ≠ 0. Другое название наклонной асимптоты — наклонная асимптота. Обычно он существует для рациональных функций, и mx + b — это частное, полученное путем деления числителя рациональной функции на ее знаменатель.
Давайте подробнее изучим процесс нахождения каждой из этих асимптот в следующих разделах.
Как найти вертикальную и горизонтальную асимптоты?
Обычно мы изучаем асимптоты рациональной функции. Конечно, мы можем найти вертикальную и горизонтальную асимптоты рациональной функции, используя приведенные выше правила. Но вот несколько приемов для нахождения горизонтальной и вертикальной асимптот рациональной функции. Также найдем вертикальную и горизонтальную асимптоты функции f(x) = (3x 2 + 6x) / (x 2 + x).
Но вот несколько приемов для нахождения горизонтальной и вертикальной асимптот рациональной функции. Также найдем вертикальную и горизонтальную асимптоты функции f(x) = (3x 2 + 6x) / (x 2 + x).
Нахождение горизонтальных асимптот рациональной функции
Метод нахождения изменений горизонтальной асимптоты на основе степеней многочленов в числителе и знаменателе функции.
- Если оба многочлена имеют одинаковую степень, разделить коэффициенты при старших членах. Это ваша асимптота!
- Если степень числителя меньше знаменателя, то асимптота расположена на y = 0 (это ось x).
- Если степень числителя больше знаменателя, то горизонтальной асимптоты нет!
Пример: В функции f(x) = (3x 2 + 6x) / (x 2 + x) степень числителя = степени знаменателя (= 2). Таким образом, ее горизонтальная асимптота равна
y = (старший коэффициент числителя) / (старший коэффициент знаменателя) = 3/1 = 3.
Следовательно, ее HA равна y = 3.
Нахождение вертикальных асимптот рациональной функции
Чтобы найти вертикальную асимптоту рациональной функции, мы сначала упрощаем ее до наименьших членов, приравниваем ее знаменатель к нулю, а затем находим значения x.
Пример: Упростим функцию f(x) = (3x 2 + 6x) / (x 2 + x).
f(x) = 3x (x + 2) / x (x + 1) = 3(x+2) / (x+1).
Когда мы устанавливаем знаменатель = 0, x + 1 = 0. Отсюда x = -1.
Значит, его ВА равен x = -1.
Обратите внимание, что, поскольку x отменяется при упрощении, x = 0 является дырой на графике. Это означает, что ни одна точка на графиках не соответствует x = 0.
Мы можем видеть как HA, так и VA этой функции на графике ниже. Кроме того, обратите внимание на отверстие в точке x = 0,9.0003
Разница между горизонтальной и вертикальной асимптотами
Вот несколько различий между горизонтальной и вертикальной асимптотами:
| Горизонтальная асимптота | Вертикальная асимптота |
|---|---|
Он имеет форму y = k. | Он имеет форму x = k. |
| Получается, если взять предел как x→∞ или x→ -∞. | Получается, если принять предел как y→∞ или y→ -∞. |
| Иногда может пересекать кривую. | Он никогда не пересечет кривую. |
Наклонная асимптота (Наклонная асимптота)
Как следует из названия, наклонная асимптота не параллельна ни оси x, ни оси y, и, следовательно, ее наклон не равен 0 и не равен нулю. Она также известна как наклонная асимптота. Его уравнение имеет вид y = mx + b, где m — ненулевое действительное число. Рациональная функция имеет наклонную асимптоту только тогда, когда ее числитель ровно на 1 больше знаменателя, и, следовательно, функция с наклонной асимптотой никогда не может иметь горизонтальной асимптоты.
Как найти наклонную асимптоту?
Наклонная асимптота рациональной функции получается делением ее числителя на знаменатель с использованием длинного деления. Частное от деления (независимо от остатка), которому предшествует «у =», дает уравнение наклонной асимптоты. Вот пример.
Частное от деления (независимо от остатка), которому предшествует «у =», дает уравнение наклонной асимптоты. Вот пример.
Пример: Найдите наклонную асимптоту y = (3x 3 — 1) / (x 2 + 2x).
Разделим 3х 3 — 1 на х 2 + 2x с использованием длинного деления.
Следовательно, y = 3x — 6 является наклонной/наклонной асимптотой данной функции.
Важные замечания по асимптотам:
- Если функция имеет горизонтальную асимптоту, то она не может иметь наклонную асимптоту и наоборот.
- Полиномиальные функции, функции синуса и косинуса не имеют горизонтальных или вертикальных асимптот.
- Тригонометрические функции csc, sec, tan и cot имеют вертикальные асимптоты, но не имеют горизонтальных асимптот.
- Экспоненциальные функции имеют горизонтальные асимптоты, но не имеют вертикальных асимптот.
- Наклонная асимптота получается делением многочленов в длину.

☛ Похожие темы:
- Калькулятор асимптот
- Калькулятор графических функций
- Графический калькулятор
Часто задаваемые вопросы по асимптотам
Что означают асимптоты?
Асимптоты — это воображаемые линии на графике функции, к которым часть кривой очень близка, но асимптота никогда не касается графика. Функция может иметь 3 типа асимптот:
- Горизонтальная асимптота (HA)
- Вертикальная асимптота (ВА)
- Наклонная асимптота (Наклонная асимптота)
Как найти горизонтальную и вертикальную асимптоты показательной функции?
Показательная функция имеет вид y = a х + б. Вот правила нахождения горизонтальной и вертикальной асимптот экспоненциальной функции.
- Поскольку экспоненциальная функция определена везде, она не имеет вертикальных асимптот.
- При x→∞ или x→ -∞, y → b.
 Следовательно, горизонтальная асимптота y = a 90 105 x 90 106 + b равна y = b.
Следовательно, горизонтальная асимптота y = a 90 105 x 90 106 + b равна y = b.
Мы также можем нарисовать экспоненциальный график, чтобы определить асимптоты.
Что такое асимптота простыми словами?
Асимптота – это горизонтальная/вертикальная/наклонная линия, к которой кривая очень близка, но не касается асимптоты.
Каковы правила нахождения асимптот?
Вот правила нахождения асимптот функции y = f(x).
- Для нахождения горизонтальных асимптот применим предел x→∞ или x→ -∞.
- Чтобы найти вертикальные асимптоты, примените предел y→∞ или y→ -∞.
- Чтобы найти наклонную асимптоту (если есть), разделите числитель на знаменатель.
Как найти горизонтальную и вертикальную асимптоты логарифмической функции?
Логарифмическая функция имеет форму y = log (ax + b).
- Его вертикальная асимптота получается путем решения уравнения ax + b = 0 (что дает x = -b/a).
- При x→∞ или x→ -∞ y не стремится ни к какому конечному значению.
 Следовательно, она не имеет горизонтальной асимптоты.
Следовательно, она не имеет горизонтальной асимптоты.
Как найти наклонную асимптоту?
Рациональная функция имеет наклонную асимптоту только тогда, когда ее числитель имеет степень всего на одну больше, чем степень знаменателя. Он получается путем деления числителя на его знаменатель с использованием длинного деления многочленов.
Как асимптоты помогают в графическом построении рациональных функций?
Асимптоты очень полезны при графическом отображении функций, поскольку они определяют, должна ли кривая разбиваться по горизонтали и по вертикали. При построении графика кривая никогда не должна касаться асимптот.
Каждая ли рациональная функция имеет наклонную асимптоту?
Нет, не каждая рациональная функция имеет наклонную асимптоту. Рациональная функция имеет наклонную асимптоту только тогда, когда степень ее числителя больше степени знаменателя.
Математическая сцена — Функции 2 — Урок 3
Математическая сцена — Функции 2 — Урок 3 — Рациональные функции и асимптоты| 2009 Расмус Эф ог Джанн Сак | Функции 2 |
Урок 3
Рациональный
функции и асимптоты
Функция вида
где t(x) и n(x) — многочлены, называется рациональной функцией.
Графики рациональных функций можно узнаваемы по тому факту, что они часто распадаются на две или более частей. Эти части выходят за пределы системы координат по воображаемой прямой линии, называемой асимптота.
Давайте посмотрим на функцию
Этот график следует горизонтальной линии (красная на
диаграмме) по мере его перемещения из системы влево или вправо. Это
горизонтальная асимптота с уравнением y = 1. При приближении x к значениям 1 и
1 график построен по вертикальным линиям (синие). Эти вертикальные асимптоты
происходят, когда знаменатель функции n(x) равен нулю (не
числитель).
Чтобы найти уравнения вертикальных асимптот, мы должны решить уравнение:
x 2 1 = 0
х 2 = 1
х = 1 или х = 1
Рядом с значения х = 1 и x = 1 график идет почти вертикально вверх или вниз, а функция стремится либо к +∞, либо к ∞.
Получаем
горизонтальная асимптота, потому что
числитель и знаменатель, t(x) = x 2 и n(x) = x 2 1 почти равны, поскольку x становится все больше и больше.
Если, например, x = 100, то x 2 = 10000 и x 2 1 = 9999, так что, разделив одно на другое, мы получим почти 1.
Чем больше значение x, тем ближе мы к 1.
Вертикальные асимптоты можно найти, решив уравнение n(x) = 0, где n(x) — знаменатель функции (примечание: это применимо только в том случае, если числитель t (x) не равен нулю для одного и того же x ценность). Горизонтальные асимптоты можно найти, найдя предел |
Пример 1
Найдите асимптоты для функция .
Чтобы найти вертикаль асимптотой решаем уравнение
х 1 = 0
х = 1
График имеет вертикальную асимптота с уравнением х = 1,
Чтобы найти горизонталь асимптота, которую мы вычисляем .
Числитель всегда занимает
значение 1, поэтому чем больше x становится, тем меньше становится дробь. Например
если x = 1000, то f(x) = 001. По мере увеличения x f(x) становится все ближе и ближе
до нуля.
Например
если x = 1000, то f(x) = 001. По мере увеличения x f(x) становится все ближе и ближе
до нуля.
Это говорит нам о том, что у = 0 (которая является осью x) является горизонтальной асимптотой.
Наконец нарисуйте график в ваш калькулятор, чтобы подтвердить то, что вы нашли.
|
| Пример выше
предлагает следующее простое правило: Рациональная функция, у которой степень знаменателя выше чем степень числителя имеет ось x как горизонтальную асимптота. |
Пример 2
Найдите асимптоты для .
Сразу видно, что вертикальных асимптот нет, так как знаменатель никогда не может быть равен нулю.
x 2 + 1 = 0
x 2 = 1 не имеет вещественных раствор
Теперь посмотрим, что происходит, когда x становится бесконечно большим:
Метод, который мы использовали ранее для решения этого типа
Проблема состоит в том, чтобы разделить на наибольшую степень x.
| Разделить все на x 2 и затем отменить | |
| дроби, где х стоит в знаменателе а не числитель стремится к 0 . |
График имеет горизонтальную асимптота г = 2 .
Теперь нарисуем график с помощью калькулятора
Сначала выберите ГРАФИК в меню.
Затем введите формулу будьте осторожны, чтобы включить скобки, как показано
Вот что такое калькулятор показывает нам. График фактически пересекает свою асимптоту в одной точке. (Это никогда не может происходит с вертикальной асимптотой).
Пример 3
Теперь пример, где числитель на одну ступень выше знаменателя.
. Числитель является полиномом второй степени, а знаменатель – полиномом второй степени. первая степень.
первая степень.
Сначала вертикаль асимптоты:
х 1 = 0
x = 1
Одна вертикальная асимптота с уравнением x = 1 .
Мы используем длинное деление и разделить числитель на знаменатель
Теперь мы можем переписать ф(х):
Мы знаем, что это означает, что f(x) ≈ x + 1 по мере увеличения x.
говорит нам, что прямая линия у = х + 1 есть наклонная асимптота
График показан ниже.
Если мы хотим спекулировать на дальнейшие возможности, мы можем видеть, что если степень числителя равна 2 степени больше, чем у знаменателя, то график выходит за пределы система координат по параболической кривой и так далее.
Пример 4
Найдите асимптоты функция .
В этом примере деление
уже сделано, так что мы можем видеть, что есть наклонная асимптота с
уравнение y
= х .
Чтобы найти вертикаль асимптоты решаем уравнение п(х) = 0,
x 2 1 = 0
x 2 = 1
х = 1 или х = 1
Вертикальные асимптоты х = 1 и х = 1.
Вот график
1) Вертикальные асимптоты
может произойти, когда знаменатель n(x) 2) Если степень
знаменатель n(x) больше, чем у 3) Если степень
знаменатель n(x) такой же, как у 4) Если степень
знаменатель n(x) на единицу меньше, чем у |
Попрактикуйтесь в этих методах, затем попробуйте
Тест 3 по функциям 2.
Не забывайте использовать контрольный список, чтобы отслеживать свою работу.
Нахождение асимптот функции — горизонтальная, вертикальная и наклонная
Асимптоты функции можно вычислить, исследуя поведение графика функции. Однако определить, имеет ли функция асимптоты или нет, можно и без использования графика функции. Метод вычисления асимптот варьируется в зависимости от того, является ли асимптота вертикальной, горизонтальной или наклонной.
В этой статье мы увидим, как научиться вычислять асимптоты функции с примерами.
АЛГЕБРА
Актуально для …
Учимся находить три типа асимптот.
См. метод
Содержание
АЛГЕБРА
Актуально для …
Учимся находить три типа асимптот.
См. метод
Как найти вертикальную асимптоту функции?
Вертикальные асимптоты функции можно найти, исследуя множители знаменателя, которые не являются общими с множителями числителя. Вертикальные асимптоты лежат в нулях этих факторов.
Учитывая рациональную функцию, мы можем определить вертикальные асимптоты, выполнив следующие шаги:
Шаг 1: Умножьте числитель и знаменатель на множители.
Шаг 2: Соблюдайте все ограничения на домен функции. 92}-5x-6}$.
Решение: Начнем с факторизации числителя и знаменателя:
$latex f(x)=\frac{(x+3)(x-1)}{(x-6)(x+1) }$
Эту функцию больше нельзя упростить. Тогда x не может быть ни 6, ни -1, так как мы будем делить на ноль. Посмотрим на график этой рациональной функции:
Мы видим, что на графике отсутствуют вертикальные линии $latex x=6$ и $latex x=-1$. Это происходит потому, что x не может быть равно 6 или -1. Поэтому нарисуем вертикальные асимптоты штриховыми линиями: 92}+2x-8}$.
Это происходит потому, что x не может быть равно 6 или -1. Поэтому нарисуем вертикальные асимптоты штриховыми линиями: 92}+2x-8}$.
Решение: Числитель уже разложен на множители, поэтому множим на знаменатель:
$latex f(x)=\frac{x+2}{(x+4)(x-2)}$
Мы не можем упростить эту функцию и знаем, что у нас не может быть нуля в знаменателе, поэтому x не может быть равно $latex x=-4$ или $latex x=2$. Это говорит нам о том, что вертикальные асимптоты функции расположены в точках $latex x=-4$ и $latex x=2$:
Начните сейчас: изучите наши дополнительные ресурсы по математике 92}+5x+6}$.
Выберите ответ
$латекс x=3$, $латекс x=2$
$латекс x=-3$, $латекс x=-2$
$латекс x=-2$, $латекс x=3$
$latex x=1$, $latex x=-2$
Как найти горизонтальную асимптоту функции?
Метод определения горизонтальных асимптот изменяется на основе сравнения степеней полинома в числителе и знаменателе функции. 2}+2}$. 93}}$.
2}+2}$. 93}}$.
Выберите ответ
$латекс y=-\frac{4}{5}$
$латекс y=\frac{4}{5}$
$латекс y=\frac{4}{3}$
$latex y=-\frac{4}{3}$
Как найти наклонную асимптоту функции?
Чтобы найти наклонную или наклонную асимптоту функции, мы должны сравнить степень числителя и степень знаменателя.
Если степень числителя ровно на единицу больше степени знаменателя, то график рациональной функции будет примерно представлять собой наклонную линию с некоторыми сложными участками посередине. Асимптота этого типа функции называется наклонной или наклонной асимптотой. 92}+2}{x-1}$.
Решение: Начнем с деления этого рационального выражения в длинное:
Наверху у нас есть частное, линейное выражение $latex -3x-3$. Внизу у нас есть остаток. Это означает, что путем деления мы преобразуем функцию в смешанное выражение:
$latex f(x)=-3x-3+\frac{-1}{x-1}$
Это та же самая функция, мы просто переставляем его. При построении графика функции вместе с линией $latex y=-3x-3$ видно, что эта линия является наклонной асимптотой функции: 92}+3x+2}{x-2}$.
При построении графика функции вместе с линией $latex y=-3x-3$ видно, что эта линия является наклонной асимптотой функции: 92}+3x+2}{x-2}$.
Выберите ответ
$латекс y=x+5$
$латекс y=x-1$
$латекс y=x-5$
$latex y=x+3$
См. также
Хотите узнать больше о функциях? Взгляните на эти страницы:
- Кусочные функции – как решить и построить график
- Функции пола и потолка
Изучайте математику с помощью наших дополнительных ресурсов по различным темам
УЗНАТЬ БОЛЬШЕ
асимптот: рабочие примеры | Purplemath
VerticalHorizontalSlant
Purplemath
До сих пор мы рассматривали каждый тип асимптоты отдельно, примерно как в вашем учебнике, отводя каждому типу отдельный раздел в главе. Но в тесте вопросы не будут указывать, какой тип вам нужно найти.
В общем случае вам будет задана рациональная (дробная) функция, и вам нужно будет найти область определения и любые асимптоты. Вам нужно будет найти вертикальные асимптоты, если они есть, а затем выяснить, есть ли у вас горизонтальная или наклонная асимптота, и что это такое. Чтобы убедиться, что вы пришли к правильному (и полному) ответу, вам нужно знать, какие шаги предпринять и как распознать различные типы асимптот.
Вам нужно будет найти вертикальные асимптоты, если они есть, а затем выяснить, есть ли у вас горизонтальная или наклонная асимптота, и что это такое. Чтобы убедиться, что вы пришли к правильному (и полному) ответу, вам нужно знать, какие шаги предпринять и как распознать различные типы асимптот.
Давайте попрактикуемся:
Содержание продолжается ниже
MathHelp.com
Я начну с вертикальных асимптот.
Они (и любые ограничения по домену) будут генерироваться нулями знаменателя, поэтому приравняю знаменатель к нулю и решу.
4 x 2 − 9 = 00748 2 = / 4
x = ± 3 / 2
Тогда. Доктор All x 9076
. Затем Domain — x 9076
. , а две вертикальные асимптоты равны x = ± 3 / 2 .
Далее я перейду к вопросу о горизонтальных или наклонных асимптотах.
Так как степени числителя и знаменателя одинаковы (каждый равен 2), то это рациональное число имеет ненулевое (то есть не- x -ось) горизонтальная асимптота и не имеет наклонной асимптоты. The horizontal asymptote is found by dividing the leading terms:
Then the full answer is:
domain: x ≠ ± 3 / 2
vertical asymptotes: x = ± 3 / 2
горизонтальная асимптота: y = 1 / 4
наклонная асимптота: нет
Данная рациональная функция может иметь или не иметь вертикальную асимптоту (в зависимости от того, равен ли знаменатель когда-либо нулю), но (на этом уровне изучения) она всегда будет иметь либо горизонтальную, либо наклонную асимптоту.
Обратите внимание, однако, что функция будет иметь только один из этих двух; у вас будет либо горизонтальная асимптота, либо наклонная асимптота, , но не обе . Как только вы увидите, что у вас есть один из них, не утруждайте себя поиском другого.
Как только вы увидите, что у вас есть один из них, не утруждайте себя поиском другого.
Вертикальные асимптоты исходят из нулей знаменателя, поэтому я приравняю знаменатель к нулю и решу.
x 2 + 9 = 0
x 2 = −9
Ой! Это не имеет решения. (Да! Знаменатель — это сумма квадратов, а не разница. Таким образом, , конечно, не делят на множители, и не может иметь настоящих нулей. Я должен помнить об этом и спасать себя. когда-нибудь в будущем)
Так как в знаменателе нет нулей, то нет и вертикальных асимптот и областью определения является «все x «.
Поскольку степень в знаменателе больше, чем в числителе, значения y будут перетаскиваться вниз по оси x , и поэтому горизонтальная асимптота будет « y = 0″. Поскольку я нашел горизонтальную асимптоту, мне не нужно искать наклонную асимптоту.
Мой полный ответ:
домен: все x
Вертикальные асимптоты: нет
Горизонтальная асимптота: y = 0 ( x -оси)
Уловка Асимптота: None
Специальная корпуса с «Hope» 9006. с различными видами рациональных функций. Когда вы впервые познакомились с рациональными выражениями, вы, вероятно, научились их упрощать. Если бы вы могли, вы бы разложили полиномы на верхние и нижние множители, а затем увидели бы, сокращаются ли какие-либо значения.
Что делать, если вы нашли нули знаменателя рациональной функции (значит, вы нашли недопустимые точки в области определения), но тот или иной из множителей аннулируется? Давайте рассмотрим пример именно такой ситуации:
Так получилось, что эту функцию можно упростить как:
Таким образом, вся рациональная функция упрощается до линейной функции. Ясно, что исходная рациональная функция по крайней мере почти равна y = x + 1 — хотя мне нужно иметь в виду, что в исходной функции x не могло принимать значение 2. Но как насчет вертикальной асимптоты? Есть такой на x = 2 или нет?
Но как насчет вертикальной асимптоты? Есть такой на x = 2 или нет?
Если есть вертикальная асимптота, то график должен подниматься или опускаться по ней, когда я использую значения x , близкие к ограниченному значению x = 2. Я попробую несколько значений x , чтобы посмотреть, если это то, что происходит.
х = 1,5, y = 2,5
x = 1,9, Y = 2,9
x = 1,95, y = 2,95
x = 1,998 = 2,95
x = 1,999, 9074, 9074, 9074,
= = = = = = = = = = = = = = = = = = =. , а не , стреляющее куда угодно, на самом деле оно действует точно так же, как линия y = x + 1. Таким образом, очевидно, что ноль исходного знаменателя , а не генерирует вертикальную асимптоту, если этот нулевой множитель сокращается.
Хотя график исходной функции будет очень похож на график х = х + 1, это будет не совсем то же самое. И независимо от того, строю я график или нет, мне нужно помнить о домене с ограниченным доступом.
Поскольку степень числителя на единицу больше степени знаменателя, у меня будет наклонная асимптота (не горизонтальная), и я найду эту наклонную асимптоту путем деления в длину.
Хмм… Когда я делил, остатка не было. На самом деле это имеет смысл: поскольку x − 2 — это множитель числителя, а я делю на 9.0747 x
− 2, при делении должно получиться ровно . И, как я и ожидал, наклонная асимптота представляет собой прямую y = x + 1,Тогда полный ответ:
домен: x ≠ 2
вертикальные асимптоты: нет
горизонтальная асимптота: нет
наклонная асимптота: y = x + 1
Последний случай («с отверстием») не является нормой для наклонных асимптот, но вы должны ожидать увидеть хотя бы одну задача такого типа, в том числе возможно и на тесте.
Кстати, когда вы идете к графику функции в этом последнем примере, вы можете провести линию прямо на наклонной асимптоте. Но вам нужно будет оставить красивую открытую точку (то есть «дырку») там, где x = 2, чтобы указать, что эта точка на самом деле не включена в график, потому что она не является частью области определения исходной рациональной функции. .
Подводя итог, процесс работы с асимптотами выглядит следующим образом:
- приравнять знаменатель к нулю и решить (если возможно)
- нули (если есть) являются вертикальными асимптотами (при условии отсутствия сокращений)
- все остальное в домене
- сравнить степени числителя и знаменателя
- , если степени одинаковы, то у вас есть горизонтальная асимптота при y = (старший коэффициент числителя) / (старший коэффициент знаменателя)
- , если степень знаменателя больше (с любым запасом), то у вас есть горизонтальная асимптота в y = 0 (ось x )
- , если степень числителя больше (с запасом в 1), то у вас есть наклонная асимптота, которую вы найдете, выполнив деление в длинное число
Единственная трудность состоит в том, чтобы помнить, что иногда множитель из знаменателя может сокращаться, тем самым удаляя вертикальную асимптоту, но не изменяя ограничения на домен. Возможно, вы даже захотите на всякий случай проверить, являются ли полиномы в числителе и знаменателе факторами.
Возможно, вы даже захотите на всякий случай проверить, являются ли полиномы в числителе и знаменателе факторами.
В любом случае, когда вы решаете эти задачи, старайтесь выполнять шаги по порядку, чтобы вы могли запомнить весь процесс теста. Эти упражнения не так уж сложны, как только вы их освоите, поэтому обязательно выполняйте много практических упражнений.
URL: https://www.purplemath.com/modules/asymtote4.htm
Страница 1Страница 2Страница 3
Как найти вертикальные и горизонтальные асимптоты?
Функция — это тип оператора, который принимает входную переменную и предоставляет результат. Когда одна величина зависит от другой, создается функция. Интересное свойство функций состоит в том, что каждому входу соответствует один выход. Другими словами, такой оператор между двумя множествами, скажем, множеством A и множеством B, называется функцией тогда и только тогда, когда он сопоставляет каждому элементу множества B ровно один элемент множества A. Когда все входные и выходные значения нанесены на график декартова плоскость называется графиком функции.
Когда все входные и выходные значения нанесены на график декартова плоскость называется графиком функции.
Такие воображаемые линии, которые очень близки ко всему графику функции или сегменту графика, называются асимптотами. При построении графика функции асимптоты очень полезны, поскольку они помогают вам подумать о том, какие линии кривая не должна пересекать. Другими словами, асимптота — это точка, в которой график функции сходится. При графическом отображении функций нам редко приходится рисовать асимптоты.
Типы асимптот- Горизонтальные асимптоты: Горизонтальная асимптота — это горизонтальная линия, которая показывает поведение функции на крайних краях графика. Однако вполне возможно, что функция может пересечь асимптоту и даже коснуться ее. Для функций с полиномиальными числителем и знаменателем существуют горизонтальные асимптоты. Эти функции называются рациональными выражениями.
 Горизонтальная форма функции задается как y = k.
Горизонтальная форма функции задается как y = k.
- Вертикальные асимптоты: Вертикальная асимптота – это вертикальная линия, которая направляет, но не является частью графика функции. График никогда не пересечет его, поскольку это происходит при значении x, которое находится за пределами области определения функции. У функции может быть более одной вертикальной асимптоты.
Нахождение горизонтальных асимптот
Для вычисления горизонтальных асимптот необходимо учитывать степени числителя и знаменателя данной функции. Критерии определения горизонтальных асимптот функции следующие:
- Когда числитель и знаменатель имеют одинаковую степень: Разделите коэффициенты ведущих переменных, чтобы найти горизонтальную асимптоту.
- Если степень числителя меньше степени знаменателя: Горизонтальная асимптота находится при y = 0, т. е. по оси x.
- Если степень числителя больше степени знаменателя: Для данной рациональной функции нет горизонтальной асимптоты.

Нахождение вертикальных асимптот
Чтобы определить вертикальные асимптоты рациональных функций, необходимо выполнить два шага. Это:
Шаг I: Максимально уменьшите заданную рациональную функцию, убрав все общие множители и упростив числитель и знаменатель посредством факторизации.
Шаг II: Приравняйте знаменатель к нулю и найдите x. Значение(я) x является вертикальной асимптотой функции.
Примеры задачЗадача 1. Найти горизонтальную и вертикальную асимптоты функции: f(x) = .
Решение:
Горизонтальная асимптота:
Степень числителя = 2
Степень знаменателя = 1
Степень знаменателя = 1
не имеет горизонтальной асимптоты.
Вертикальная асимптота:
Поскольку функция уже имеет простейшую форму, просто приравняйте знаменатель к нулю, чтобы определить вертикальную асимптоту(ы).
⇒ x + 5 = 0
⇒ x = −5
Задача 2. Может ли квадратичная функция иметь асимптоты?
Решение:
Квадратичная функция является многочленом, поэтому она не может иметь никаких асимптот. Поскольку полиномиальные функции определены для всех действительных значений x, квадратичная функция не может иметь никаких вертикальных асимптот. Кроме того, поскольку функция стремится к бесконечности, как и x, горизонтальной асимптоты также не существует.
Задача 3. Найти горизонтальную и вертикальную асимптоты функции: f(x) = .
Solution:
Horizontal Asymptote:
Degree of the numerator = 2
Degree of the denominator = 2
Since the degree of the numerator is equal to that of the denominator, the horizontal asymptote определяется делением старших коэффициентов.
⇒ ГК = 2/2 = 1
Вертикальная асимптота:
Сначала необходимо упростить функцию.
Теперь, когда функция представлена в простейшей форме, приравняйте знаменатель к нулю, чтобы определить вертикальную асимптоту.
⇒ x + 1 = 0
⇒ x = −1
Задача 4. Найти горизонтальную и вертикальную асимптоты функции: f(x) = 10x 2 + 6x + 8,
2 Решение:Данная функция является квадратичной. Квадратичная функция является многочленом, поэтому она не может иметь никаких асимптот. Поскольку полиномиальные функции определены для всех действительных значений x, квадратичная функция не может иметь никаких вертикальных асимптот. Кроме того, поскольку функция стремится к бесконечности, как и x, горизонтальной асимптоты также не существует.
Задача 5. Найти горизонтальную асимптоту функции: f(x) = 9x/x 2 +2.
Решение:
Степень числителя = 1
Степень знаменателя = 2
Так как степень числителя меньше степени знаменателя, горизонтальная асимптота определяется выражением: 900 = 03.
Задача 6. Найти горизонтальную и вертикальную асимптоты функции: f(x) = x+1/3x-2.
Решение:
Горизонтальная асимптота:
Степень числителя = 1
Степень знаменателя = 1
Степень знаменателя = 1
определяется делением старших коэффициентов.
⇒ HA = 1/3
Вертикальная асимптота:
Функция имеет простейшую форму: приравняйте знаменатель к нулю, чтобы определить вертикальную асимптоту.
⇒ 3x – 2 = 0
⇒ x = 2/3
Задача 7. Найти горизонтальную и вертикальную асимптоты функции: f(x) = x 2 +1/3x+2.
Решение:
Горизонтальная асимптота:
Степень числителя = 2
Степень знаменателя = 1
Степень знаменателя = 1
не имеет горизонтальной асимптоты.
Вертикальная асимптота:
Поскольку функция уже имеет простейшую форму, просто приравняйте знаменатель к нулю, чтобы определить вертикальную асимптоту(ы).
⇒ 3x + 2 = 0
⇒ x = −2/3
Нахождение асимптот – Математика для старших классов
Нахождение асимптот – Математика для старших классов—>
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- MCAT Репетиторство
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство по ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительное исчисление
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский язык
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все ресурсы по математике для старших классов
8 диагностических тестов 613 практических тестов Вопрос дня Карточки Learn by Concept
Справка по математике для старших классов » Предварительный расчет » Функции и графики » Свойства функции » Нахождение асимптот
Функция определяется следующим рациональным уравнением:
Каковы горизонтальная и вертикальная асимптоты графика этой функции?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти горизонтальную асимптоту, сравните степени верхнего и нижнего многочленов. В этом случае две степени совпадают (1), а это означает, что уравнение горизонтальной асимптоты равно отношению старших коэффициентов (верхний: нижний). Поскольку старший коэффициент числителя равен 1, а старший коэффициент знаменателя равен 2, уравнение горизонтальной асимптоты имеет вид .
В этом случае две степени совпадают (1), а это означает, что уравнение горизонтальной асимптоты равно отношению старших коэффициентов (верхний: нижний). Поскольку старший коэффициент числителя равен 1, а старший коэффициент знаменателя равен 2, уравнение горизонтальной асимптоты имеет вид .
Чтобы найти вертикальную асимптоту, установите знаменатель равным нулю, чтобы найти случай, когда вся функция не определена:
Какая линия приближается к бесконечности?
Возможные ответы:
Правильный ответ:
Объяснение:
Этот вопрос касается наклонной асимптоты уравнения. Чтобы найти наклонную асимптоту, разделите числитель на знаменатель. Длинное деление дает нам следующее:
Однако, поскольку мы рассматриваем приближение к бесконечности, влияние последнего члена на общее линейное уравнение быстро становится незначительным (стремится к нулю).



 Получили точку разрыва $ x = -frac<2> <3>$. Вычислим в ней предел функции и убедимся окончательно, что вертикальная асимптота это $ x = -frac<2> <3>$.
Получили точку разрыва $ x = -frac<2> <3>$. Вычислим в ней предел функции и убедимся окончательно, что вертикальная асимптота это $ x = -frac<2> <3>$. <-x>$
<-x>$