sin — Викисловарь
sin
Семантические свойства
Значение
- синус, тригонометрическая функция, безразмерная ◆ sin α
См. также
- cos, tg, tan, ctg
- arcsin, arccos, arctg, arcctg
- sec, csc
Для улучшения этой статьи желательно:
|
sin (существительное)
Морфологические и синтаксические свойства
| ед. ч. | мн. ч. |
|---|---|
| sin | sins |
sin
Существительное.
Корень: -sin-.
Произношение
- МФА (Великобритания): ед. ч. [sɪn], мн. ч. [sɪnz]
- МФА (США): ед. ч. [sɪn]
мн. ч. [sɪnz](файл) (файл)
Семантические свойства
Значение
- религ. грех ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
- —
Антонимы
- —
Гиперонимы
- ?
Гипонимы
- ?
Родственные слова
| Ближайшее родство | |
| |
Этимология
От прагерм. формы *sundiō, от которой в числе прочего произошли: др.-англ. synn, англ. sin, др. -сакс. sundia, др.-фризск. sende, ср.-нидерл. sonde, нидерл. zonde, др.-в.-нем. sunta, ср.-в.-нем. sünde, нем. Sünde, др.-сканд. synd, исл., фарерск., шведск., датск., норв. synd и др.; восходит к праиндоевр. *h₁s-ónt-ih₂ от праиндоевр. *h₁sónts «суть, правда», само прич. наст. вр. от праиндоевр. *h₁es- «есть (быть)». Первоначальное значение подразумевало суждение «действительно виновен» (т. е. действительно быть тем, кто виновен). Использованы материалы Online Etymology Dictionary Дугласа Харпера. См. Список литературы.
-сакс. sundia, др.-фризск. sende, ср.-нидерл. sonde, нидерл. zonde, др.-в.-нем. sunta, ср.-в.-нем. sünde, нем. Sünde, др.-сканд. synd, исл., фарерск., шведск., датск., норв. synd и др.; восходит к праиндоевр. *h₁s-ónt-ih₂ от праиндоевр. *h₁sónts «суть, правда», само прич. наст. вр. от праиндоевр. *h₁es- «есть (быть)». Первоначальное значение подразумевало суждение «действительно виновен» (т. е. действительно быть тем, кто виновен). Использованы материалы Online Etymology Dictionary Дугласа Харпера. См. Список литературы.
Фразеологизмы и устойчивые сочетания
- mortal sin
- original sin
- seven deadly sins
- venial sin
Для улучшения этой статьи желательно:
|
sin (глагол)
Морфологические и синтаксические свойства
| Инфинитив | sin |
3-е л.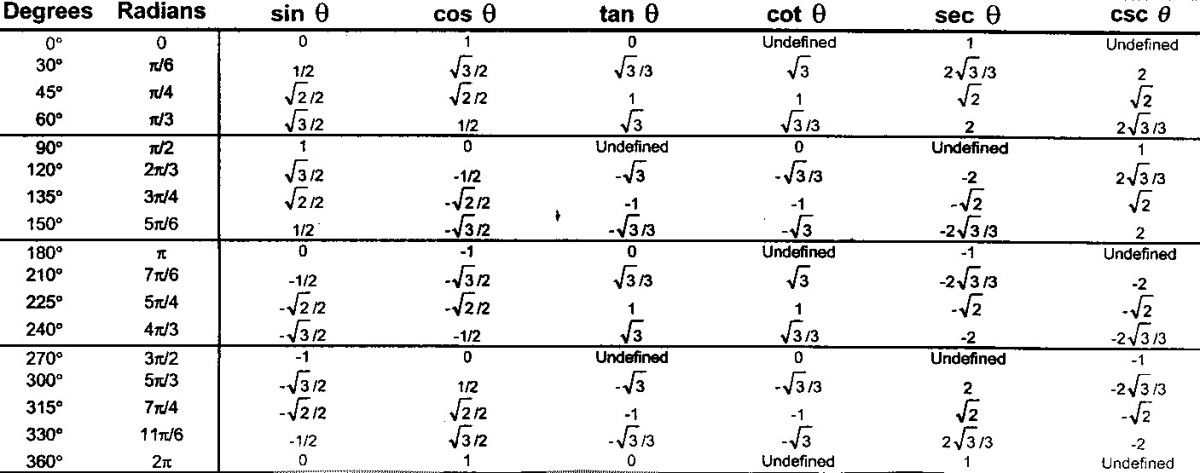 ед. ч. ед. ч. | sins |
| Прош. вр. | sinned |
| Прич. прош. вр. | sinned |
| Герундий | sinning |
sin
Глагол, правильный.
Корень: —.
Произношение
- МФА: [sɪn]
(файл)
Семантические свойства
Значение
- грешить ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
- ?
Антонимы
- ?
Гиперонимы
- ?
Гипонимы
- ?
Родственные слова
| Ближайшее родство | |
Этимология
Происходит от ??
Фразеологизмы и устойчивые сочетания
Библиография
Для улучшения этой статьи желательно:
|
sin (сокращение)
- Графическое сокращение от sine.

Морфологические и синтаксические свойства
sin
Существительное, мужской род.
Корень: -sin-.
Произношение
Семантические свойства
Значение
- сын ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
- —
Антонимы
- —
Гиперонимы
- ?
Гипонимы
- ?
Родственные слова
| Ближайшее родство | |
Этимология
Происходит от праслав. *synъ, от кот. в числе прочего произошли: др.-русск., ст.-слав. сꙑнъ (др.-греч. υἱός; Остром., Супр.), укр. син, белор. сын, болг. синъ́т, сербохорв. си̑н (род. п. си̑на), им. мн. си̏нови, словенск. sȋn (род. п. sȋna, sinȗ), чешск., словацк. syn, польск., в.-луж., н.-луж. syn. Древняя основа на -u. Родственно лит. sūnùs «сын», др.-прусск. souns (вин. ед. sunun), др.-инд. sūnúṣ, авест. hūnu-, готск. sunus, др.-в.-нем. sunu «сын», греч. гомер., лаконск., критск., аркадск. атт. (стар.) υἱύς (род. п. υἱέος) «сын», тохарск. А sе, В sоуä «сын», далее связано с др.-инд. sū́tē (sāuti), sūуаtē (sūyati), savati «рождает, производит», авест. hunāmi «рождаю», ирл. suth «рождение, плод», др.-инд. sū́tiṣ ж. «рождение», sū́tuṣ ж. «беременность». Использованы данные словаря М. Фасмера. См. Список литературы.
Родственно лит. sūnùs «сын», др.-прусск. souns (вин. ед. sunun), др.-инд. sūnúṣ, авест. hūnu-, готск. sunus, др.-в.-нем. sunu «сын», греч. гомер., лаконск., критск., аркадск. атт. (стар.) υἱύς (род. п. υἱέος) «сын», тохарск. А sе, В sоуä «сын», далее связано с др.-инд. sū́tē (sāuti), sūуаtē (sūyati), savati «рождает, производит», авест. hunāmi «рождаю», ирл. suth «рождение, плод», др.-инд. sū́tiṣ ж. «рождение», sū́tuṣ ж. «беременность». Использованы данные словаря М. Фасмера. См. Список литературы.
Фразеологизмы и устойчивые сочетания
Библиография
| Статья нуждается в доработке. Это незаконченная статья. Вы можете помочь проекту, исправив и дополнив её.
|
Морфологические и синтаксические свойства
sin
Существительное.
Корень: -sin-.
Произношение
Семантические свойства
Значение
- знак ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
- ?
Антонимы
- —
Гиперонимы
- ?
Гипонимы
- ?
Родственные слова
| Ближайшее родство | |
Этимология
Происходит от лат. signum.
Фразеологизмы и устойчивые сочетания
Библиография
Для улучшения этой статьи желательно:
|
Морфологические и синтаксические свойства
Глагол.
Корень: —.
Произношение
Семантические свойства
Значение
- быть ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
- ?
Антонимы
- ?
Гиперонимы
- —
Гипонимы
- ?
Родственные слова
| Ближайшее родство | |
Этимология
Из ??
Фразеологизмы и устойчивые сочетания
Библиография
| Статья нуждается в доработке. Это незаконченная статья. Вы можете помочь проекту, исправив и дополнив её.
|
Морфологические и синтаксические свойства
sin
Предлог
Корень: -sin-.
Произношение
- МФА: [sin]
Семантические свойства
Значение
- без ◆ No podré hacerlo sin ti. — Я не смогу это сделать без тебя.
- перед инфинитивом не ◆ Combate contra el mal sin vacilar. — Сражайся со злом, не колеблясь.
Синонимы
- —
- —
Антонимы
- con
Гиперонимы
- —
- —
Гипонимы
- —
- —
Родственные слова
| Ближайшее родство | |
Этимология
От лат. sine «без», далее из праиндоевр. *san- «отдельно, особо, без».
Фразеологизмы и устойчивые сочетания
- sin embargo = однако
- sin falta = обязательно
- sin más ni más = ни с того, ни с сего
Библиография
Для улучшения этой статьи желательно:
|
Морфологические и синтаксические свойства
sin
Числительное. , м.р. (Жен. род — snat)
, м.р. (Жен. род — snat)
Произношение
- МФА: [sin]
Семантические свойства
Значение
- два ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
- ?
Антонимы
- —
Гиперонимы
- ?
Гипонимы
- —
Родственные слова
| Ближайшее родство | |
Этимология
Происходит от ??
Фразеологизмы и устойчивые сочетания
Библиография
| Статья нуждается в доработке. Это незаконченная статья. Вы можете помочь проекту, исправив и дополнив её.
 |
Морфологические и синтаксические свойства
sin
Существительное.
Произношение
Семантические свойства
Значение
- грех ◆ Di Ju Lɔ ticha dɛn bin stil de aks Jizɔs kwɛshɔn, na in Jizɔs tinap ɛn se, «If ɛni wan pan una de we nɔ sin yet, mek da pɔsin de sɛn di fɔs ston pan dis uman.» — Когда же продолжали спрашивать Его, Он, восклонившись, сказал им: кто из вас без греха, первый брось на нее камень. «Ин 8.7»
Синонимы
- ?
Антонимы
- ?
Гиперонимы
- ?
Гипонимы
- ?
Родственные слова
| Ближайшее родство | |
Этимология
Происходит от ??
Фразеологизмы и устойчивые сочетания
Библиография
Статья нуждается в доработке. Это незаконченная статья. Вы можете помочь проекту, исправив и дополнив её.
|
Морфологические и синтаксические свойства
sin
(син)
Существительное, мужской род.
Корень: -sin-.
Произношение
Семантические свойства
Значение
- сын ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
- —
Антонимы
- —
Гиперонимы
- ?
Гипонимы
- ?
Родственные слова
| Ближайшее родство | |
Этимология
Происходит от праслав. *synъ, от кот. в числе прочего произошли: др. -русск., ст.-слав. сꙑнъ (др.-греч. υἱός; Остром., Супр.), укр. син, белор. сын, болг. синъ́т, сербохорв. си̑н (род. п. си̑на), им. мн. си̏нови, словенск. sȋn (род. п. sȋna, sinȗ), чешск., словацк. syn, польск., в.-луж., н.-луж. syn. Древняя основа на -u. Родственно лит. sūnùs «сын», др.-прусск. souns (вин. ед. sunun), др.-инд. sūnúṣ, авест. hūnu-, готск. sunus, др.-в.-нем. sunu «сын», греч. гомер., лаконск., критск., аркадск. атт. (стар.) υἱύς (род. п. υἱέος) «сын», тохарск. А sе, В sоуä «сын», далее связано с др.-инд. sū́tē (sāuti), sūуаtē (sūyati), savati «рождает, производит», авест. hunāmi «рождаю», ирл. suth «рождение, плод», др.-инд. sū́tiṣ ж. «рождение», sū́tuṣ ж. «беременность». Использованы данные словаря М. Фасмера. См. Список литературы.
-русск., ст.-слав. сꙑнъ (др.-греч. υἱός; Остром., Супр.), укр. син, белор. сын, болг. синъ́т, сербохорв. си̑н (род. п. си̑на), им. мн. си̏нови, словенск. sȋn (род. п. sȋna, sinȗ), чешск., словацк. syn, польск., в.-луж., н.-луж. syn. Древняя основа на -u. Родственно лит. sūnùs «сын», др.-прусск. souns (вин. ед. sunun), др.-инд. sūnúṣ, авест. hūnu-, готск. sunus, др.-в.-нем. sunu «сын», греч. гомер., лаконск., критск., аркадск. атт. (стар.) υἱύς (род. п. υἱέος) «сын», тохарск. А sе, В sоуä «сын», далее связано с др.-инд. sū́tē (sāuti), sūуаtē (sūyati), savati «рождает, производит», авест. hunāmi «рождаю», ирл. suth «рождение, плод», др.-инд. sū́tiṣ ж. «рождение», sū́tuṣ ж. «беременность». Использованы данные словаря М. Фасмера. См. Список литературы.
Фразеологизмы и устойчивые сочетания
Библиография
Для улучшения этой статьи желательно:
|
Морфологические и синтаксические свойства
sin
Местоимение.
| падеж | ед. ч. | мн. ч. |
|---|---|---|
| Им. | ||
| Прит. | ||
| Д. | ||
| В. | ||
| М. | ||
| Исх. |
Корень: -sin-.
Произношение
- МФА: [sin]
Семантические свойства
Значение
- ты ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
- ?
Антонимы
- —
Гиперонимы
- —
Гипонимы
- —
Родственные слова
| Ближайшее родство | |
Этимология
Общетюркское
Для улучшения этой статьи желательно:
|
Морфологические и синтаксические свойства
sin
Существительное, мужской род.
Корень: -sin-.
Произношение
Семантические свойства
Значение
- сын ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
- —
Антонимы
- —
Гиперонимы
- ?
Гипонимы
- ?
Родственные слова
| Ближайшее родство | |
Этимология
Происходит от праслав. *synъ, от кот. в числе прочего произошли: др.-русск., ст.-слав. сꙑнъ (др.-греч. υἱός; Остром., Супр.), укр. син, белор. сын, болг. синъ́т, сербохорв. си̑н (род. п. си̑на), им. мн. си̏нови, словенск. sȋn (род. п. sȋna, sinȗ), чешск., словацк. syn, польск., в.-луж., н.-луж. syn. Древняя основа на -u. Родственно лит. sūnùs «сын», др.-прусск. souns (вин. ед. sunun), др.-инд. sūnúṣ, авест. hūnu-, готск. sunus, др. -в.-нем. sunu «сын», греч. гомер., лаконск., критск., аркадск. атт. (стар.) υἱύς (род. п. υἱέος) «сын», тохарск. А sе, В sоуä «сын», далее связано с др.-инд. sū́tē (sāuti), sūуаtē (sūyati), savati «рождает, производит», авест. hunāmi «рождаю», ирл. suth «рождение, плод», др.-инд. sū́tiṣ ж. «рождение», sū́tuṣ ж. «беременность». Использованы данные словаря М. Фасмера. См. Список литературы.
-в.-нем. sunu «сын», греч. гомер., лаконск., критск., аркадск. атт. (стар.) υἱύς (род. п. υἱέος) «сын», тохарск. А sе, В sоуä «сын», далее связано с др.-инд. sū́tē (sāuti), sūуаtē (sūyati), savati «рождает, производит», авест. hunāmi «рождаю», ирл. suth «рождение, плод», др.-инд. sū́tiṣ ж. «рождение», sū́tuṣ ж. «беременность». Использованы данные словаря М. Фасмера. См. Список литературы.
Фразеологизмы и устойчивые сочетания
Библиография
Для улучшения этой статьи желательно:
|
Морфологические и синтаксические свойства
sin
Существительное.
Корень: -sin-.
Произношение
Семантические свойства
Значение
- сын ◆ Отсутствует пример употребления (см.
 рекомендации).
рекомендации).
Синонимы
- —
Антонимы
- —
Гиперонимы
- ?
Гипонимы
- ?
Родственные слова
| Ближайшее родство | |
Этимология
От праслав. *synъ, от кот. в числе прочего произошли: др.-русск., ст.-слав. сꙑнъ (др.-греч. υἱός; Остром., Супр.), укр. син, белор. сын, болг. синъ́т, сербохорв. си̑н (род. п. си̑на), им. мн. си̏нови, словенск. sȋn (род. п. sȋna, sinȗ), чешск., словацк. syn, польск., в.-луж., н.-луж. syn. Древняя основа на -u. Родственно лит. sūnùs «сын», др.-прусск. souns (вин. ед. sunun), др.-инд. sūnúṣ, авест. hūnu-, готск. sunus, др.-в.-нем. sunu «сын», греч. гомер., лаконск., критск., аркадск. атт. (стар.) υἱύς (род. п. υἱέος) «сын», тохарск. А sе, В sоуä «сын», далее связано с др.-инд. sū́tē (sāuti), sūуаtē (sūyati), savati «рождает, производит», авест. hunāmi «рождаю», ирл. suth «рождение, плод», др.-инд. sū́tiṣ ж. «рождение», sū́tuṣ ж. «беременность». Использованы данные словаря М. Фасмера. См. Список литературы.
sū́tē (sāuti), sūуаtē (sūyati), savati «рождает, производит», авест. hunāmi «рождаю», ирл. suth «рождение, плод», др.-инд. sū́tiṣ ж. «рождение», sū́tuṣ ж. «беременность». Использованы данные словаря М. Фасмера. См. Список литературы.
Фразеологизмы и устойчивые сочетания
Библиография
Для улучшения этой статьи желательно:
|
sin I
Морфологические и синтаксические свойства
sin
Основное слово, глагол.
Корень: —.
Произношение
- МФА: [ˈsin]
(файл)
Семантические свойства
Значение
- обновлять, освежать ◆ Отсутствует пример употребления (см. рекомендации).

Синонимы
- —
Антонимы
- ?
Гиперонимы
- ?
Гипонимы
- ?
Этимология
От китайск. 新 [xīn] — новый
Для улучшения этой статьи желательно:
|
sin II
Морфологические и синтаксические свойства
sin
Прилагательное.
Корень: —.
Произношение
- МФА: [ˈsin]
(файл)
Семантические свойства
Значение
- новый, свежий, обновлённый ◆ Отсутствует пример употребления (см. рекомендации).
- другой ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
- ?
- —
Антонимы
- ?
- ?
Гиперонимы
- ?
- ?
Гипонимы
- ?
- —
Фразеологизмы и устойчивые сочетания
- toki sin
Пословицы и поговорки
- sin en ante li sin e lawa li pana e sona
Этимология
От китайск.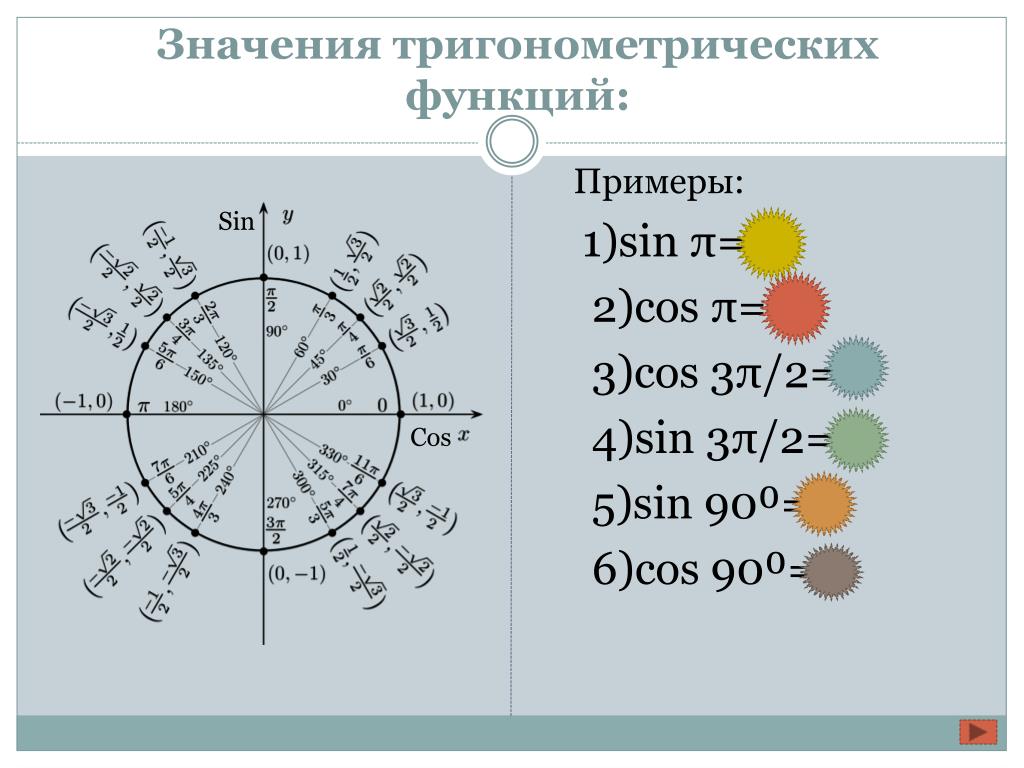 新 [xīn] — новый
新 [xīn] — новый
Для улучшения этой статьи желательно:
|
Морфологические и синтаксические свойства
sin
Существительное, мужской род.
Корень: -sin-.
Произношение
Семантические свойства
Значение
- сын ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
- —
Антонимы
- —
Гиперонимы
- ?
Гипонимы
- ?
Родственные слова
| Ближайшее родство | |
Этимология
Происходит от праслав. *synъ, от кот. в числе прочего произошли: др.-русск., ст.-слав. сꙑнъ (др.-греч. υἱός; Остром., Супр.), укр. син, белор. сын, болг. синъ́т, сербохорв. си̑н (род. п. си̑на), им. мн. си̏нови, словенск. sȋn (род. п. sȋna, sinȗ), чешск., словацк. syn, польск., в.-луж., н.-луж. syn. Древняя основа на -u. Родственно лит. sūnùs «сын», др.-прусск. souns (вин. ед. sunun), др.-инд. sūnúṣ, авест. hūnu-, готск. sunus, др.-в.-нем. sunu «сын», греч. гомер., лаконск., критск., аркадск. атт. (стар.) υἱύς (род. п. υἱέος) «сын», тохарск. А sе, В sоуä «сын», далее связано с др.-инд. sū́tē (sāuti), sūуаtē (sūyati), savati «рождает, производит», авест. hunāmi «рождаю», ирл. suth «рождение, плод», др.-инд. sū́tiṣ ж. «рождение», sū́tuṣ ж. «беременность». Использованы данные словаря М. Фасмера. См. Список литературы.
*synъ, от кот. в числе прочего произошли: др.-русск., ст.-слав. сꙑнъ (др.-греч. υἱός; Остром., Супр.), укр. син, белор. сын, болг. синъ́т, сербохорв. си̑н (род. п. си̑на), им. мн. си̏нови, словенск. sȋn (род. п. sȋna, sinȗ), чешск., словацк. syn, польск., в.-луж., н.-луж. syn. Древняя основа на -u. Родственно лит. sūnùs «сын», др.-прусск. souns (вин. ед. sunun), др.-инд. sūnúṣ, авест. hūnu-, готск. sunus, др.-в.-нем. sunu «сын», греч. гомер., лаконск., критск., аркадск. атт. (стар.) υἱύς (род. п. υἱέος) «сын», тохарск. А sе, В sоуä «сын», далее связано с др.-инд. sū́tē (sāuti), sūуаtē (sūyati), savati «рождает, производит», авест. hunāmi «рождаю», ирл. suth «рождение, плод», др.-инд. sū́tiṣ ж. «рождение», sū́tuṣ ж. «беременность». Использованы данные словаря М. Фасмера. См. Список литературы.
Фразеологизмы и устойчивые сочетания
Библиография
Для улучшения этой статьи желательно:
|
Морфологические и синтаксические свойства
sin
Местоимение.
Форма винительного падежа местоимения si
Произношение
- МФА: [sin]
Семантические свойства
Значение
- себя ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
- ?
Антонимы
- ?
Гиперонимы
- —
Гипонимы
- ?
Родственные слова
| Ближайшее родство | |
Этимология
Фразеологизмы и устойчивые сочетания
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град.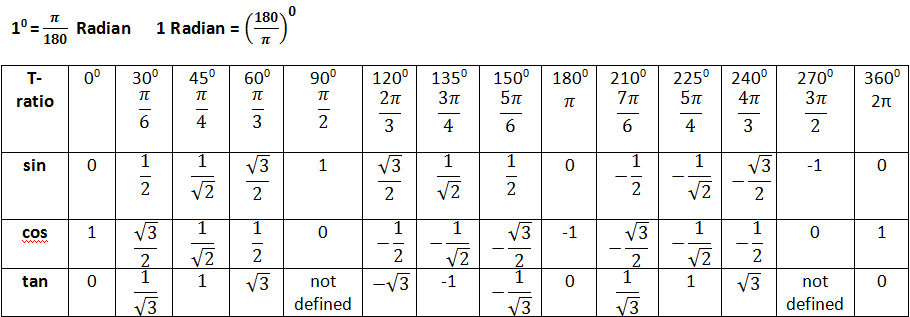 ) ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
|
Примечание.
Как были вычислены значения синуса, косинуса и тангенса 30 градусов?Далее приведено пошаговое пояснение логики расчета данных значений для угла тридцать градусов. 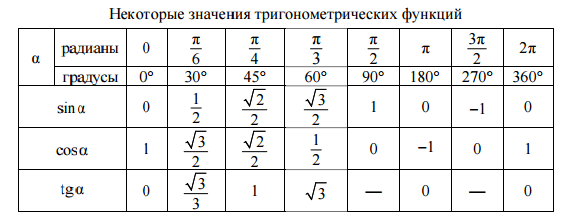 Для этого производится построение произвольного прямоугольного треугольника с соответствующими углами и вычисляется значение синуса, косинуса и тангенса 30 градусов. Для этого производится построение произвольного прямоугольного треугольника с соответствующими углами и вычисляется значение синуса, косинуса и тангенса 30 градусов.
Табличные значения sin 30, cos 30 и tg 30 градусов:Якорь: #sin30
То есть:
0 Синус, ко синус, тангенс угла 15 градусов (sin 15 cos 15 tg 15) | Описание курса | Синус, косинус, тангенс угла 45 градусов (sin 45, cos 45, tg 45)
|
Значения основных углов тригонометрических функций. Синус 30, 60
Значения основных углов тригонометрических функций. Синус 30, 60Перейти к содержанию
ПОИСК
Страница Вконтакте открывается в новом окне
Вы здесь:
Значения синусов в градусах
sin 0 = 0 (синус 0 градусов равен 0)
sin 30 = 1/2 (синус 30 градусов равен 1/2)
sin 45 = √2/2 (синус 45 градусов равен √2/2)
sin 60 = √3/2 (синус 60 градусов равен √3/2)
sin 90 = 1 (синус 90 градусов равен 1)
sin 180 = 0 (синус 180 градусов равен 0)
sin 270 = -1 (синус 270 градусов равен -1)
sin 360 = 0 (синус 360 градусов равен 0)
Значения синусов в радианах
sin 0 = 0
sin π/6 = 1/2
sin π/4 = √2/2
sin π/3 = √3/2
sin π/2 = 1
sin π = 0
sin 3π/2 = -1
sin 2π = 0
Значения косинусов в градусах
cos 0 = 1 (косинус 0 градусов равен 1)
cos 30 = √3/2 (косинус 30 градусов равен √3/2)
cos 45 = √2/2 (косинус 45 градусов равен √2/2)
cos 60 = ½ (косинус 60 градусов равен 1/2)
cos 90 = 0 (косинус 90 градусов равен 0)
cos 180 = -1 (косинус 180 градусов равен -1)
cos 270 = 0 (косинус 270 градусов равен 0)
cos 360 = 1 (косинус 360 градусов равен 1)
Значения косинусов в радианах
cos 0 = 1
cos π/6 = √3/2
cos π/4 = √2/2
cos π/3 = 1/2
cos π/2 = 0
cos π =- 1
cos 3π/2 = 0
cos 2π = 0
Значения тангенсов в градусах
tg 0 = 0 (тангенс 0 градусов равен 0)
tg 30 = √3/3 (тангенс 30 градусов равен √3/3)
tg 45 = 1 (тангенс 45 градусов равен 1)
tg 60 = √3 (тангенс 60 градусов равен √3)
tg 90 не существует (тангенс 90 градусов не существует)
tg 180 = 0 (тангенс 180 градусов равен 0)
tg 270 = не существует (тангенс 270 градусов не существует)
tg 360 = 0 (тангенс 360 градусов равен 0)
Значения тангенсов в радианах
tg 0 = 0
tg π/6 = √3/3
tg π/4 = 1
tg π/3 = √3
tg π/2 — не существует
tg π = 0
tg 3π/2 – не существует
tg 2π = 0
Значения котангенсов в градусах
ctg 0 – не существует (котангенс 0 градусов не существует)
ctg 30 = √3 (котангенс 30 градусов равен √3)
ctg 45 = 1 (котангенс 45 градусов равен 1)
ctg 60 = √3/3 (котангенс 60 градусов равен √3/3)
ctg 90 = 0 (котангенс 90 градусов равен 0)
ctg 180 = не существует
ctg 270 = 0 (котангенс 270 градусов равен 0)
ctg 360 – не существует — (котангенс 360 градусов не существует)
Значения котангенсов в радианах
ctg 0 = не существует
ctg π/6 = √3
ctg π/4 = 1
ctg π/3 = √3/3
ctg π/2 = 0
ctg π – не существует
ctg 3π/2 = 0
ctg 2π – не существует
Значения секансов в градусах
sec 0 = 1
sec 30 = 2√3/3
sec 45 = √2
sec 60 = 2
sec 90 – не существует
sec 180 = -1
sec 270 — не существует
sec 360 = 1
Значения секансов в радианах
sec 0 = 1
sec π/6 = 2√3/3
sec π/4 = √2
sec π/3 = 2
sec π/2 — не существует
sec π = -1
sec 3π/2 — не существует
sec 2π = 1
Значения косекансов в градусах
cosec 0 — не существует
cosec 30 = 2
cosec 45 = √2
cosec 60 = 2√3/3
cosec 90 = 1
cosec 180 — не существует
cosec 270 = -1
cosec 360 — не существует
Значения косекансов в радианах
cosec 0 — не существует
cosec π/6 = 2
cosec π/4 = √2
cosec π/3 = 2√3/3
cosec π/2 = 1
cosec π — не существует
cosec 3π/2 = -1
cosec 2π — не существует
Значения синуса и косинуса, тангенса и котангенса можно узнавать из тригонометрического круга, который является прекрасным источником информации о тригонометрических функциях.
Ссылки по теме
Тригонометрические функции. Понятие
Определение синуса, косинуса, тангенса, котангенса, секанса и косеканса
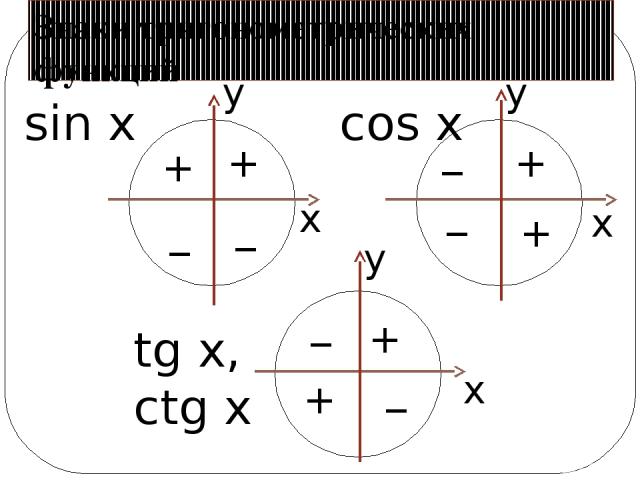
Знаки тригонометрических функций
Таблицы значений синусов и косинусов, тангенсов и котангенсов, секансов и косекансов
Как пользоваться таблицей синуса, косинуса, тангенса и котангенса
Как запомнить значения тригонометрических функций
Вывод значений для тригонометрических функций некоторых углов
Связь между радианами и градусами. Таблица
Номограмма, позволяющая осуществлять перевод градусов в радианы и радиан в градусы
9E09BEAE0A118E93DED3D74128EA2C147A65428915829EB11235F7758F7B38C3
MATHVOX
Вверх
Этот сайт использует файлы cookies для более комфортной работы пользователя. Продолжая просмотр страниц сайта, вы соглашаетесь с использованием файлов cookies. Если вам нужна дополнительная информация , пожалуйста, посетите страницу Политика Конфиденциальности Принять
Privacy & Cookies Policy
Don`t copy text!
§ 14.
 Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Свойства функций синуса, косинуса, тангенса и котангенса и их графики14. Свойства функций синуса, косинуса, тангенса
и котангенса и их графики
14.1. СВОЙСТВА ФУНКЦИИ y = sin x И ЕЕ ГРАФИК
Т а б л и ц а 21
|
График функции y = sin x (синусоида) |
|
Свойства функции y = sin x |
Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики:
1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями
координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания * ;8) наибольшее и наименьшее
значения функции.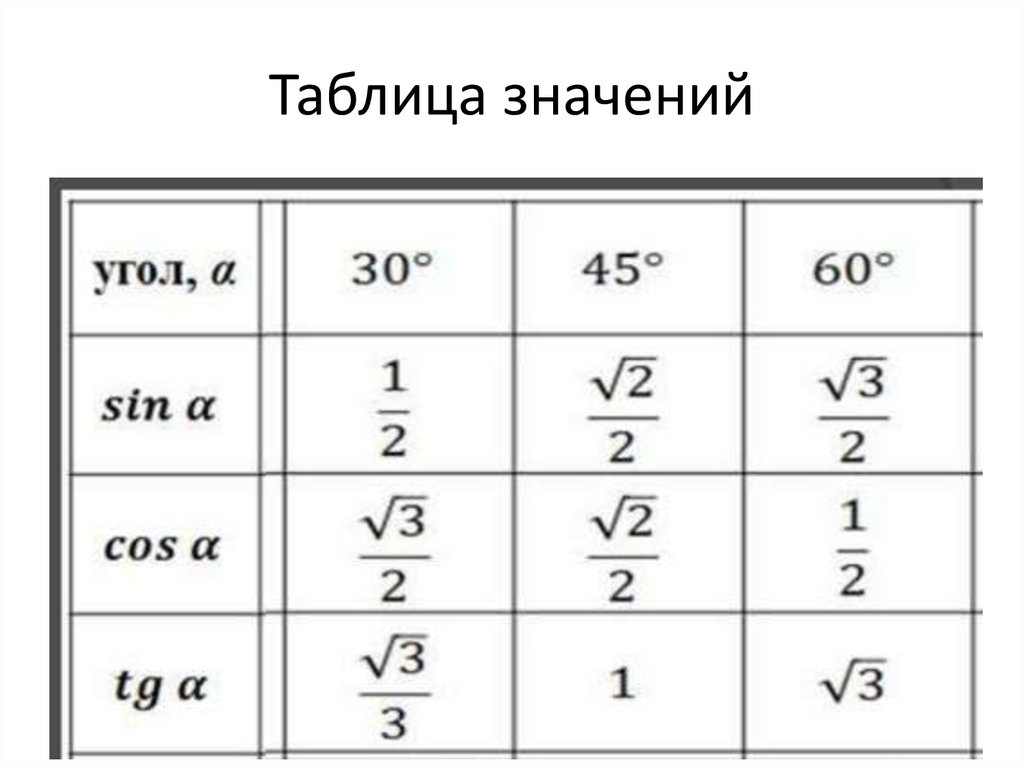
З а м е ч а н и е. Абсциссы точек пересечения графика функции с осью Ох
(то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.
Напомним, что значение синуса — это ордина-
та соответствующей точки единичной окружности
(рис. 79). Поскольку ординату можно найти для
любой точки единичной окружности (в силу того,
что через любую точку окружности всегда можно
провести единственную прямую, перпендикуляр-
ную оси ординат), то область определения функции
y = sin x — все действительные числа. Это можно за-
писать так: D (sin x) = R.
Для точек единичной окружности ординаты нахо-
дятся в промежутке [–1; 1] и принимают все значения
от –1 до 1, поскольку через любую точку отрезка [–1; 1]
Рис. 79
79
оси ординат (который является диаметром единичной
окружности) всегда можно провести прямую, перпендикулярную оси орди-
нат, и получить точку окружности, которая имеет рассматриваемую орди-
нату. Таким образом, для функции y = sin x область значений: y ∈ [–1; 1].
Это можно записать так: E (sin x) = [–1; 1].
Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда
соответствующей точкой единичной окружности является точка A, то есть при
Наименьшее значение функции sin x равно минус единице. Это значение
достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть
при
Как было показано в § 13, синус — нечетная функция: sin(-x)= — sin x,
поэтому ее график симметричен относительно начала координат.
В § 13 было обосновано также, что синус — периодическая функция с наименьшим положительным периодом
T = 2π: sin (x + 2π) = sin x, таким образом, через промежутки длиной 2π вид графика функции sin x повторя-
ется. Поэтому при построении графика этой функции достаточно построить график на любом промежутке длиной 2π, а
потом полученную линию параллельно перенести вправо и влево вдоль оси Ox на расстояние kT = 2πk, где
k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат,
напомним, что на оси Oy значение x = 0. Тогда соответствующее значение
y = sin 0 = 0, то есть график функции y = sin x проходит через начало координат.
На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при
которых sin x, то есть ордината соответствующей точки единичной окруж
ности, равна нулю.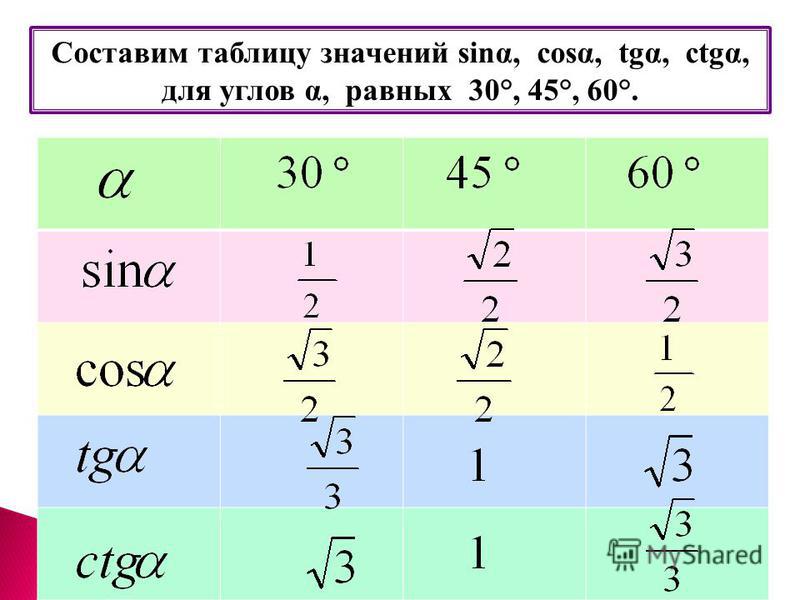 Это будет тогда и только тогда, когда на единичной окруж-
Это будет тогда и только тогда, когда на единичной окруж-
ности будут выбраны точки C или D, то есть при x = πk, k ∈ Z (см. рис. 79).
Промежутки знакопостоянства. Как было обосновано в § 13, значения
функции синус положительны (то есть ордината соответствующей точки
единичной окружности положительна) в I и II четвертях (рис. 80). Таким
образом, sin x > 0 при всех x ∈ (0; π), а также, учитывая период, при всех
x ∈ (2πk; π + 2πk), k ∈ Z.
Значения функции синус отрицательны (то есть ордината соответствую-
щей точки единичной окружности отрицательна) в III и IV четвертях, поэто-
му sin x < 0 при x ∈ (π + 2πk; 2π + 2πk), k ∈ Z.
Промежутки возрастания и убывания
Доказательство теоремы
Учитывая периодичность функции sin x с периодом T = 2π, достаточно
исследовать ее на возрастание и убывание на любом промежутке длиной
2π, например на промежутке
то при увеличении аргумента x (x2> x1) ордината соответствующей точки единичной окружности увеличивается (то есть
sin x 2 > sin x 1 ), следовательно, на этом промежутке функция sin x возрастает. Учитывая периодичность функции sin x,
Учитывая периодичность функции sin x,
делаем вывод, что она также возрастает на каждом из промежутков
Если x ∈ (рис. 81, б), то при увеличении аргумента x (x 2 > x 1 ) ордината соответствующей точки единичной
окружности уменьшается (то есть sin x 2 < sin x 1 ), таким образом, на этом промежутке функция sin x убывает. Учитывая
периодичность функции sin x, делаем вывод, что она также убывает на каждом из промежутков
Проведенное исследование позволяет обоснованно построить график функции y = sin x. Учитывая периодичность этой
функции (с периодом 2π), достаточно сначала построить график на любом промежутке длиной 2π, например на
промежутке [–π; π]. Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината
соответствующей точки единичной окружности. На рисунке 82 показано построение графика функции y = sin x на
На рисунке 82 показано построение графика функции y = sin x на
промежутке [0; π]. Учитывая нечетность функции sin x (ее график симметричен относительно начала координат), для
построения графика на промежутке [–π; 0] отображаем полученную кривую симметрично относительно начала координат
(рис. 83).
Поскольку мы построили график на
промежутке длиной 2π, то, учитывая
периодичность синуса (с периодом 2π),
повторяем вид графика на каждом про-
межутке длиной 2π (то есть переносим па-
раллельно график вдоль оси Ох на 2πk,
где k — целое число).
Получаем график, который называется
синусоидой (рис. 84).
З а м е ч а н и е. Тригонометрические функции широко применяются в математике, физике и технике. Например,
Например,
множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п.,
описываются функцией, которая задается формулой y = A sin (ωх + φ). Такие процессы называют гармоническими
колебаниями. График функции y = A sin (ωx + φ) можно получить из синусоиды y = sin х сжатием или растяжением ее вдоль
координатных осей и параллельным переносом вдоль оси Ох. Чаще всего гармоническое колебание является функцией
времени t. Тогда оно задается формулой y = A sin (ωt + φ), где А — амплитуда колебания, ω — частота, φ — начальная
фаза,
14.2. СВОЙСТВА ФУНКЦИИ y = cos x И ЕЕ ГРАФИК
Объяснение и обоснование
Напомним, что значение косинуса — это абсцис-
са соответствующей точки единичной окружности
(рис. 85). Поскольку абсциссу можно найти для лю-
85). Поскольку абсциссу можно найти для лю-
бой точки единичной окружности (в силу того, что
через любую точку окружности, всегда можно про-
вести единственную прямую, перпендикулярную оси
абсцисс), то область определения функции y = cos x —
все действительные числа. Это можно записать так:
D (cos x) = R.
Для точек единичной окружности абсциссы нахо-
дятся в промежутке [–1; 1] и принимают все значе-
ния от –1 до 1, поскольку через любую точку отрезка [–1; 1] оси абсцисс (который является диаметром единичной
окружности)
всегда можно провести прямую, перпендикулярную оси абсцисс, и получить
точку окружности, которая имеет рассматриваемую абсциссу. Следовательно, область значений функции y = cos x:
y ∈ [–1; 1]. Это можно записать так: E (cos x) = [–1; 1].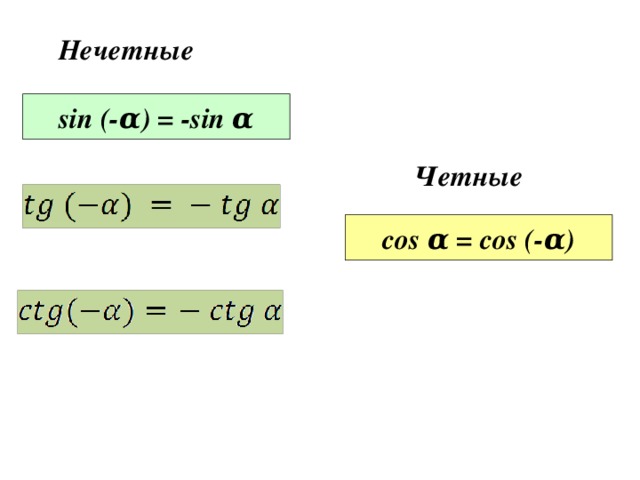 Как видим, наибольшее значение функции cos x равно единице. Это
Как видим, наибольшее значение функции cos x равно единице. Это
значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при
x = 2πk, k ∈ Z. Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда
соответствующей точкой единичной окружности является точка B, то есть при x = π + 2πk, k ∈ Z.
Как было показано в § 13, косинус — четная функция: cos (–x) = cos x, поэтому ее график симметричен относительно оси
Оу. В § 13 было обосновано также, что косинус — периодическая функция с наименьшим положительным периодом
T = 2π: cos (x + 2π) = cos x. Таким образом, через промежутки длиной 2π вид графика функции cos x повторяется.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси Oy значение x = 0.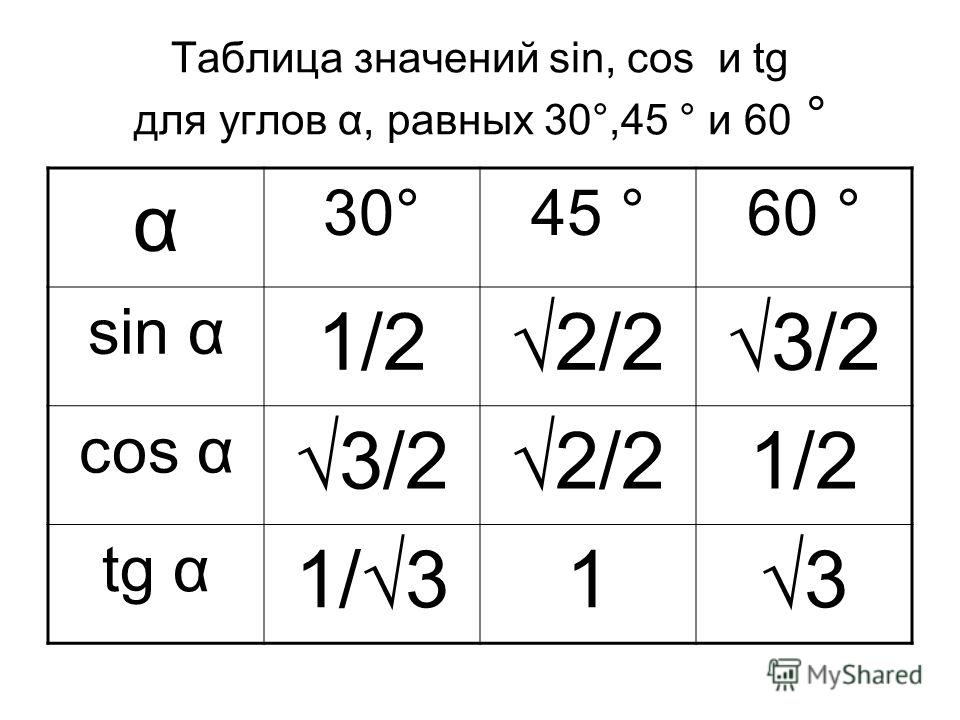 Тогда
Тогда
соответствующее значение y = cos 0 = 1. На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при
которых cos x, то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только
тогда, когда на единичной окружности будут выбраны точки C или D, то есть при
Промежутки знакопостоянства. Как было обосновано в § 13, значения
функции косинус положительны (то есть абсцисса соответствующей точки
единичной окружности положительна) в I и IV четвертях (рис. 86). Следова-
тельно, cos x > 0 при x ∈ (-П/2; П/2) а также, учитывая период, при всех
Значения функции косинус отрицательны (то есть абсцисса соответству-
ющей точки единичной окружности отрицательна) во ІІ и ІІІ четвертях,
поэтому cos x < 0 при x ∈
Промежутки возрастания и убывания
Учитывая периодичность функции cos x (T = 2π), достаточно исследовать
ее на возрастание и убывание на любом промежутке длиной 2π, например
на промежутке [0; 2π].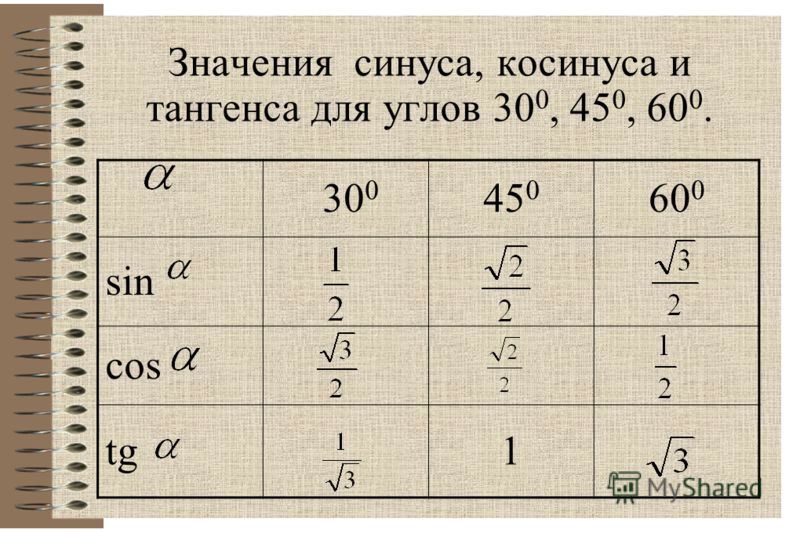
Если x ∈ [0; π] (рис. 87, а), то при увеличении аргумента x (x 2 > x 1 ) абсцисса соответствующей точки единичной
окружности уменьшается (то есть cos x 2<cos x 1 ), следовательно, на этом промежутке функция cos x убывает. Учитывая
периодичность функции cos x, делаем вывод, что она также убывает на каждом из промежутков [2πk; π + 2πk], k ∈ Z.
Если x ∈ [π; 2π] (рис. 87, б), то при увеличении аргумента x (x 2 > x 1 ) аб-
сцисса соответствующей точки единичной окружности увеличивается (то
есть cos x 2 >cos x 1 ), таким образом, на этом промежутке функция cos x
возрастает. Учитывая периодичность функции cos x, делаем вывод, что
она возрастает также на каждом из промежутков [π + 2πk; 2π + 2πk], k ∈ Z.
Проведенное исследование позволяет построить график функции y = cos x
аналогично тому, как был построен график функ-
ции y = sin x.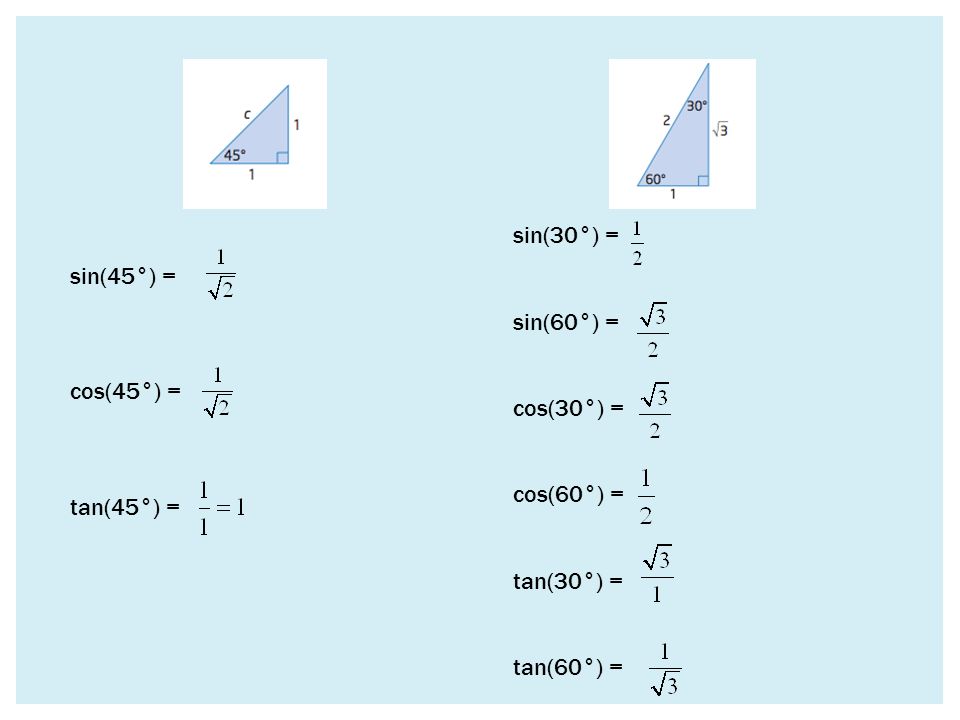 Но график функции у = cos x можно
Но график функции у = cos x можно
также получить с помощью геометрических преоб-
разований графика функции у = sin х, используя
формулу
Эту формулу можно обосновать, например, так.
Рассмотрим единичную окружность (рис. 88), отметим на ней точки
У sin х график. График функции y = sin x
|BD| — длина дуги окружности с центром в точке A .
α — угол, выраженный в радианах.
Синус (sin
α
) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos
α
) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin
x
и y = cos
x
периодичны с периодом 2
π
.
Четность
Функция синус — нечетная. Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
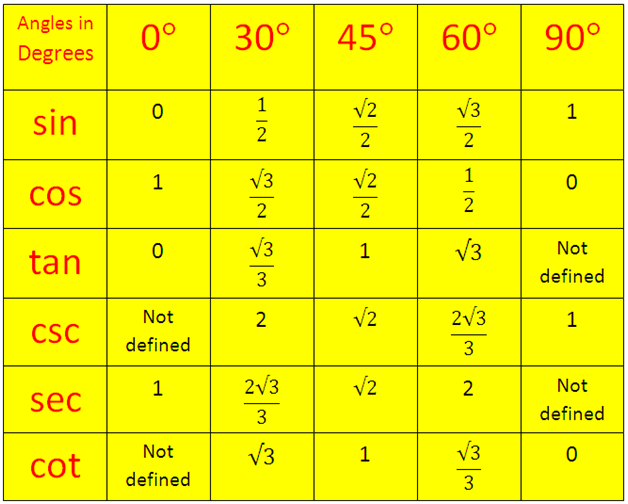
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
См. также:
На этом уроке мы подробно рассмотрим функцию у = sin х, ее основные свойства и график.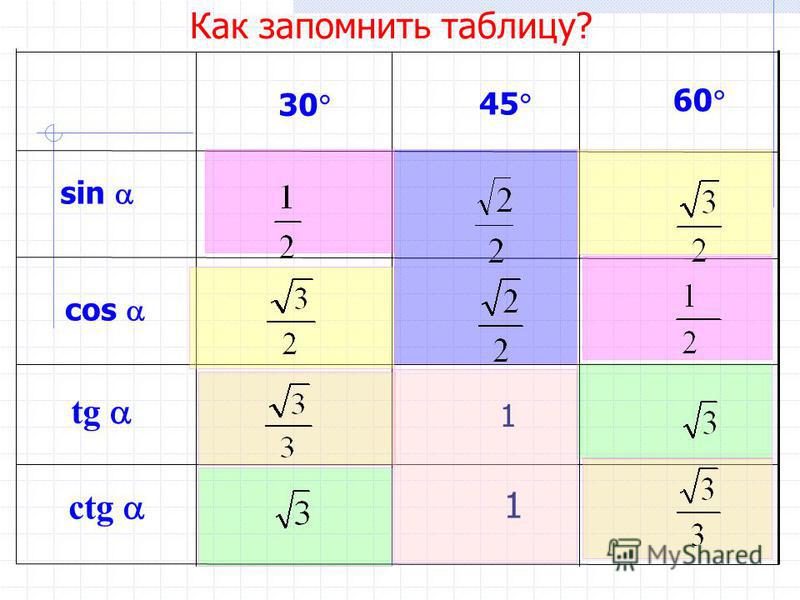 В начале урока дадим определение тригонометрической функции у = sin t на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.
В начале урока дадим определение тригонометрической функции у = sin t на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.
Тема: Тригонометрические функции
Урок: Функция y=sinx, её основные свойства и график
При рассмотрении функции важно каждому значению аргумента поставить в соответствие единственное значение функции. Этот закон соответствия и называется функцией.
Определим закон соответствия для .
Любому действительному числу соответствует единственная точка на единичной окружности У точки есть единственная ордината, которая и называется синусом числа (рис. 1).
Каждому значению аргумента ставится в соответствие единственное значение функции.
Из определения синуса вытекают очевидные свойства.
На рисунке видно, что т.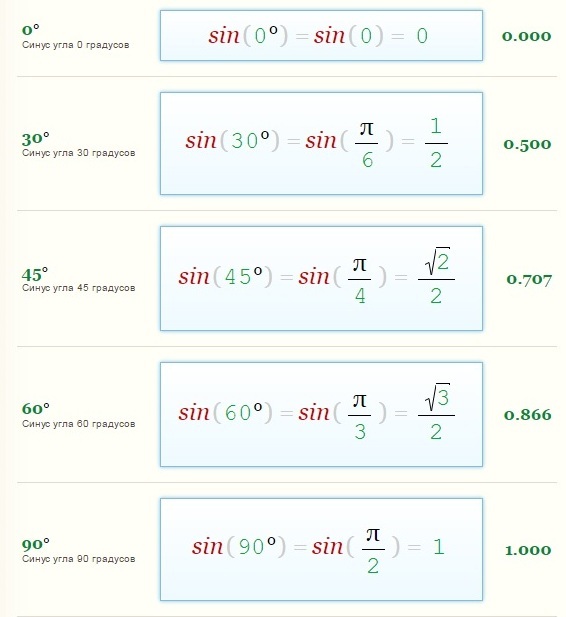 к. это ордината точки единичной окружности.
к. это ордината точки единичной окружности.
Рассмотрим график функции . Вспомним геометрическую интерпретацию аргумента. Аргумент — это центральный угол, измеряемый в радианах. По оси мы будем откладывать действительные числа или углы в радианах, по оси соответствующие значения функции.
Например, угол на единичной окружности соответствует точке на графике (рис. 2)
Мы получили график функции на участке Но зная период синуса мы можем изобразить график функции на всей области определения (рис. 3).
Основным периодом функции является Это значит, что график можно получить на отрезке а затем продолжить на всю область определения.
Рассмотрим свойства функции :
1) Область определения:
2) Область значений:
3) Функция нечетная:
4) Наименьший положительный период:
5) Координаты точек пересечения графика с осью абсцисс:
6) Координаты точки пересечения графика с осью ординат:
7) Промежутки, на которых функция принимает положительные значения:
8) Промежутки, на которых функция принимает отрицательные значения:
9) Промежутки возрастания:
10) Промежутки убывания:
11) Точки минимума:
12) Минимум функции:
13) Точки максимума:
14) Максимум функции:
Мы рассмотрели свойства функции и её график.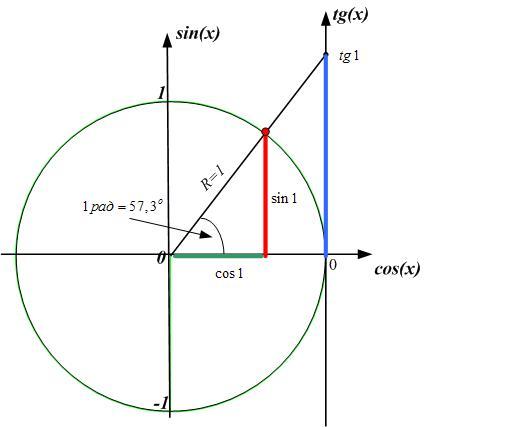 Свойства неоднократно будут использоваться при решении задач.
Свойства неоднократно будут использоваться при решении задач.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С. М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа: учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред.
А. Г. Мордковича. -М.: Мнемозина, 2007.
№№ 16.4, 16.5, 16.8.
Дополнительные веб-ресурсы
3. Образовательный портал для подготовки к экзаменам ().
На этом уроке мы подробно рассмотрим функцию у = sin х, ее основные свойства и график. В начале урока дадим определение тригонометрической функции у = sin t на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.
Тема: Тригонометрические функции
Урок: Функция y=sinx, её основные свойства и график
При рассмотрении функции важно каждому значению аргумента поставить в соответствие единственное значение функции. Этот закон соответствия и называется функцией.
Определим закон соответствия для .
Любому действительному числу соответствует единственная точка на единичной окружности У точки есть единственная ордината, которая и называется синусом числа (рис. 1).
Каждому значению аргумента ставится в соответствие единственное значение функции.
Из определения синуса вытекают очевидные свойства.
На рисунке видно, что т.к. это ордината точки единичной окружности.
Рассмотрим график функции . Вспомним геометрическую интерпретацию аргумента. Аргумент — это центральный угол, измеряемый в радианах. По оси мы будем откладывать действительные числа или углы в радианах, по оси соответствующие значения функции.
Например, угол на единичной окружности соответствует точке на графике (рис.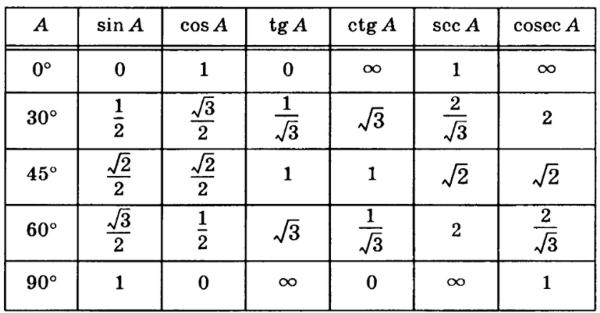 2)
2)
Мы получили график функции на участке Но зная период синуса мы можем изобразить график функции на всей области определения (рис. 3).
Основным периодом функции является Это значит, что график можно получить на отрезке а затем продолжить на всю область определения.
Рассмотрим свойства функции :
1) Область определения:
2) Область значений:
3) Функция нечетная:
4) Наименьший положительный период:
5) Координаты точек пересечения графика с осью абсцисс:
6) Координаты точки пересечения графика с осью ординат:
7) Промежутки, на которых функция принимает положительные значения:
8) Промежутки, на которых функция принимает отрицательные значения:
9) Промежутки возрастания:
10) Промежутки убывания:
11) Точки минимума:
12) Минимум функции:
13) Точки максимума:
14) Максимум функции:
Мы рассмотрели свойства функции и её график. Свойства неоднократно будут использоваться при решении задач.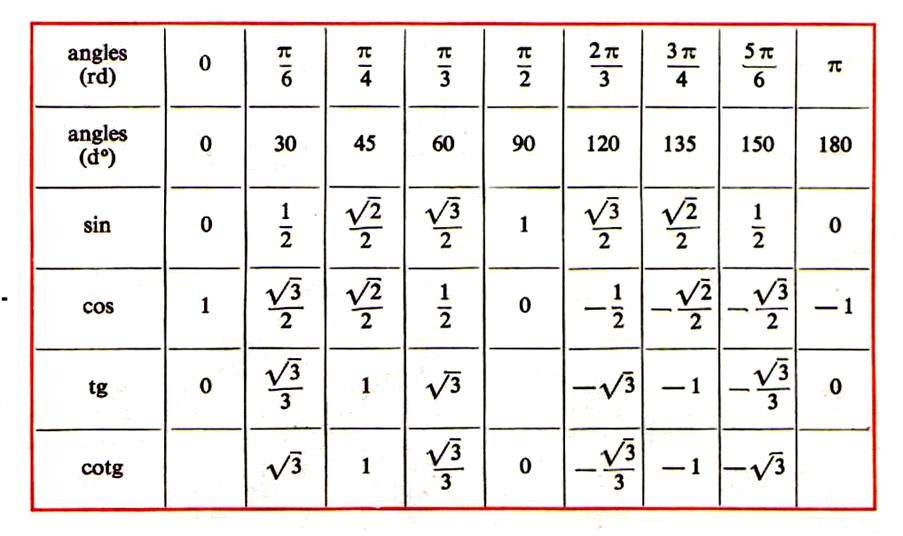
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа: учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред.
А. Г. Мордковича. -М.: Мнемозина, 2007.
№№ 16.4, 16.5, 16.8.
Дополнительные веб-ресурсы
3. Образовательный портал для подготовки к экзаменам ().
, Конкурс «Презентация к уроку»
Презентация к уроку
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Железо ржавеет, не находя себе применения,
стоячая вода гниет или на холоде замерзает,
а ум человека, не находя себе применения, чахнет.
Леонардо да Винчи
Используемые технологии: проблемного обучения, критического мышления, коммуникативного общения.
Цели:
- Развитие познавательного интереса к обучению.
- Изучение свойств функции у = sin x.
- Формирование практических навыков построения графика функции у = sin x на основе изученного теоретического материала.
Задачи:
1. Использовать имеющийся потенциал знаний о свойствах функции у = sin x в конкретных ситуациях.
2. Применять осознанное установление связей между аналитической и геометрической моделями функции у = sin x.
Развивать инициативу, определенную готовность и интерес к поиску решения; умение принимать решения, не останавливаться на достигнутом, отстаивать свою точку зрения.
Воспитывать у учащихся познавательную
активность, чувство ответственности, уважения
друг к другу, взаимопонимания, взаимоподдержки,
уверенности в себе; культуру общения.
Ход урока
1 этап. Актуализация опорных знаний, мотивация изучения нового материала
«Вход в урок».
На доске написаны 3 утверждения:
- Тригонометрическое уравнение sin t = a всегда имеет решения.
- График нечетной функции можно построить с помощью преобразования симметрии относительно оси Оу.
- График тригонометрической функции можно построить, используя одну главную полуволну.
Учащиеся обсуждают в парах: верны ли утверждения? (1 минута). Затем результаты первоначального обсуждения (да, нет) вносятся в таблицу в столбец «До».
Учитель ставит цели и задачи урока.
2. Актуализация знаний (фронтально на модели тригонометрического круга ).
Мы уже познакомились с функцией s = sin t.
1) Какие значения может принимать переменная t. Какова область определения этой функции?
2) В каком промежутке заключены значения
выражения sin t. Найти наибольшее и наименьшее
значения функции s = sin t.
3) Решите уравнение sin t = 0.
4) Что происходит с ординатой точки при ее движении по первой четверти? (ордината увеличивается). Что происходит с ординатой точки при ее движении по второй четверти? (ордината постепенно уменьшается). Как это связано с монотонностью функции? (функция s = sin t возрастает на отрезке и убывает на отрезке ).
5) Запишем функцию s = sin t в привычном для нас виде у = sin x (строить будем в привычной системе координат хОу) и составим таблицу значений этой функции.
| х | 0 | ||||||
| у | 0 | 1 | 0 |
2 этап. Восприятие, осмысление, первичное
закрепление, непроизвольное запоминание
Восприятие, осмысление, первичное
закрепление, непроизвольное запоминание
4 этап. Первичная систематизация знаний и способов деятельности, их перенос и применение в новых ситуациях
6. № 10.18 (б,в)
5 этап. Итоговый контроль, коррекция, оценка и самооценка
7. Возвращаемся к утверждениям (начало урока), обсуждаем, используя свойства тригонометрической функции у = sin x, и заполняем в таблице столбец «После».
8. Д/з: п.10, №№ 10.7(а), 10.8(б), 10.11(б), 10.16(а)
На этом уроке мы подробно рассмотрим функцию у = sin х, ее основные свойства и график. В начале урока дадим определение тригонометрической функции у = sin t на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.
Тема: Тригонометрические функции
Урок: Функция y=sinx, её основные свойства и график
При рассмотрении функции важно каждому значению аргумента поставить в соответствие единственное значение функции. Этот закон соответствия и называется функцией.
Этот закон соответствия и называется функцией.
Определим закон соответствия для .
Любому действительному числу соответствует единственная точка на единичной окружности У точки есть единственная ордината, которая и называется синусом числа (рис. 1).
Каждому значению аргумента ставится в соответствие единственное значение функции.
Из определения синуса вытекают очевидные свойства.
На рисунке видно, что т.к. это ордината точки единичной окружности.
Рассмотрим график функции . Вспомним геометрическую интерпретацию аргумента. Аргумент — это центральный угол, измеряемый в радианах. По оси мы будем откладывать действительные числа или углы в радианах, по оси соответствующие значения функции.
Например, угол на единичной окружности соответствует точке на графике (рис. 2)
Мы получили график функции на участке Но зная период синуса мы можем изобразить график функции на всей области определения (рис. 3).
Основным периодом функции является Это значит, что график можно получить на отрезке а затем продолжить на всю область определения.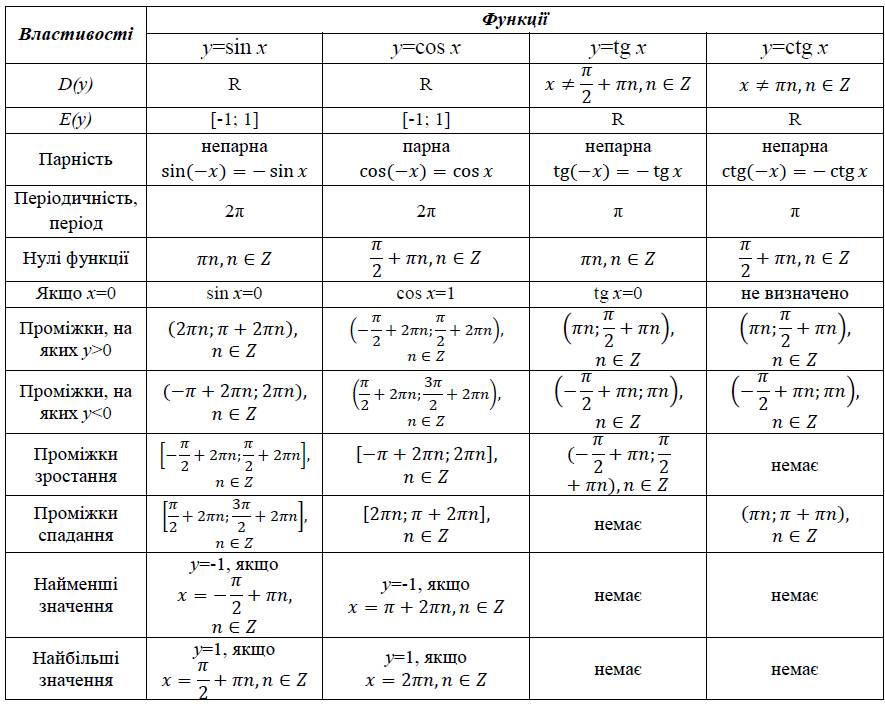
Рассмотрим свойства функции :
1) Область определения:
2) Область значений:
3) Функция нечетная:
4) Наименьший положительный период:
5) Координаты точек пересечения графика с осью абсцисс:
6) Координаты точки пересечения графика с осью ординат:
7) Промежутки, на которых функция принимает положительные значения:
8) Промежутки, на которых функция принимает отрицательные значения:
9) Промежутки возрастания:
10) Промежутки убывания:
11) Точки минимума:
12) Минимум функции:
13) Точки максимума:
14) Максимум функции:
Мы рассмотрели свойства функции и её график. Свойства неоднократно будут использоваться при решении задач.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.
Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа: учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред.
Задачник для общеобразовательных учреждений (профильный уровень) под ред.
А. Г. Мордковича. -М.: Мнемозина, 2007.
№№ 16.4, 16.5, 16.8.
Дополнительные веб-ресурсы
3. Образовательный портал для подготовки к экзаменам ().
Синус
Синус, записываемый как sin(θ), является одной из шести основных тригонометрических функций.
Определения синусов
Обычно тригонометрические функции обсуждаются двумя способами: в терминах прямоугольных треугольников и в терминах единичной окружности. Чаще всего вводится определение тригонометрических функций в виде прямоугольного треугольника, за которым следуют их определения в терминах единичного круга.
Определение прямоугольного треугольника
Для прямоугольного треугольника с острым углом θ значение синуса этого угла определяется как отношение длины противоположной стороны к длине гипотенузы.
Стороны прямоугольного треугольника обозначаются следующим образом:
- Смежный: сторона, следующая за θ, которая не является гипотенузой
- Напротив: сторона, противоположная θ.

- Гипотенуза: самая длинная сторона треугольника, лежащая напротив прямого угла.
Пример:
Найдите sin(θ) для прямоугольного треугольника ниже.
Мы также можем использовать функцию синуса при решении реальных задач, связанных с прямоугольными треугольниками.
Пример:
Пандус для инвалидных колясок должен иметь угол наклона 10° и высоту 3 фута. Какова длина пандуса?
Определение единичной окружности
Тригонометрические функции также могут быть определены как значения координат на единичной окружности. Единичная окружность — это окружность радиусом 1 с центром в начале координат. Определение тригонометрических функций прямоугольным треугольником допускает углы от 0° до 9°.0° (0 и в радианах). Определение единичного круга позволяет нам расширить область применения тригонометрических функций на все действительные числа. См. рисунок ниже.
Имея точку (x, y) на окружности единичного круга, мы можем сформировать прямоугольный треугольник, как показано на рисунке.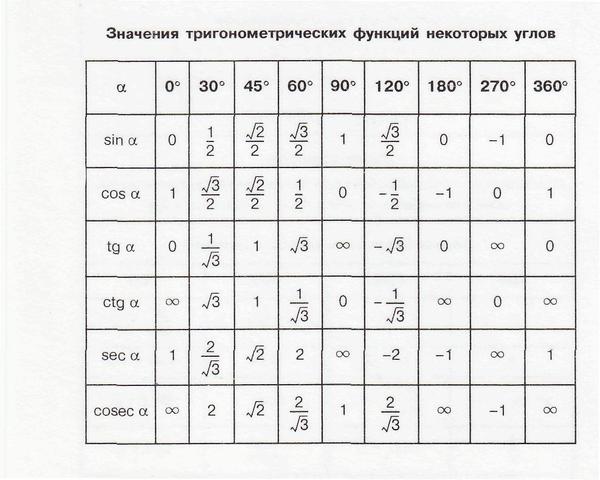 В таком треугольнике гипотенуза — это радиус единичной окружности, или 1. θ — это угол, образованный между начальной стороной угла вдоль оси x и конечной стороной угла, образованного вращением луча по часовой стрелке или против часовой стрелки. Конечная сторона угла является гипотенузой прямоугольного треугольника и является радиусом единичной окружности. Поэтому его длина всегда равна 1. Таким образом, мы можем использовать определение синуса прямоугольного треугольника, чтобы определить, что
В таком треугольнике гипотенуза — это радиус единичной окружности, или 1. θ — это угол, образованный между начальной стороной угла вдоль оси x и конечной стороной угла, образованного вращением луча по часовой стрелке или против часовой стрелки. Конечная сторона угла является гипотенузой прямоугольного треугольника и является радиусом единичной окружности. Поэтому его длина всегда равна 1. Таким образом, мы можем использовать определение синуса прямоугольного треугольника, чтобы определить, что
означает, что значение y любой точки на окружности единичного круга равно sin(θ).
В отличие от определений тригонометрических функций, основанных на прямоугольных треугольниках, это определение работает для любого угла, а не только для острого угла прямоугольного треугольника, если он находится в области определения sin(θ). Область определения синуса равна (-∞,∞), а ее диапазон равен [-1,1].
Значения функции синуса
Существует множество методов, которые можно использовать для определения значения синуса, например, обращение к таблице косинусов, использование калькулятора и аппроксимация с использованием ряда Тейлора для синуса. В большинстве практических случаев нет необходимости вычислять значение синуса вручную, и будет предоставлена таблица, калькулятор или какой-либо другой справочник.
В большинстве практических случаев нет необходимости вычислять значение синуса вручную, и будет предоставлена таблица, калькулятор или какой-либо другой справочник.
Калькулятор синуса
Ниже приведен калькулятор для нахождения значения синуса угла или угла по значению синуса.
| грех | деградировать | = | ||
Обычно используемые углы
Хотя мы можем найти значение синуса для любого угла, есть некоторые углы, которые чаще используются в тригонометрии. Ниже приведены 16 часто используемых углов как в радианах, так и в градусах, а также координаты соответствующих им точек на единичной окружности.
Рисунок выше служит ориентиром для быстрого определения синусов (значение y) и косинусов (значение x) углов, которые обычно используются в тригонометрии. Как видно из рисунка, синус имеет значение 0 при 0° и значение 1 при 90°. Косинус следует противоположной схеме; это потому, что синус и косинус являются кофункциями (описаны позже). Другими часто используемыми углами являются 30° (), 45° (), 60° () и их соответствующие кратные. Значения косинуса и синуса этих углов стоит запомнить в контексте тригонометрии, так как они очень часто используются.
Косинус следует противоположной схеме; это потому, что синус и косинус являются кофункциями (описаны позже). Другими часто используемыми углами являются 30° (), 45° (), 60° () и их соответствующие кратные. Значения косинуса и синуса этих углов стоит запомнить в контексте тригонометрии, так как они очень часто используются.
Один из методов, который может помочь в запоминании этих значений, состоит в том, чтобы выразить все значения sin(θ) в виде дробей, содержащих квадратный корень. Начиная с 0° и продвигаясь через 90°, sin(0°) = 0 = . Последующие значения sin(30°), sin(45°), sin(60°) и sin(90°) следуют шаблону, так что, используя значение sin(0°) в качестве эталона, найти значения синуса для последующих углов, мы просто увеличиваем число под знаком радикала в числителе на 1, как показано ниже.
Значения синуса от 0° до -90° следуют той же схеме, за исключением того, что значения являются отрицательными, а не положительными, поскольку синус отрицателен в квадранте IV.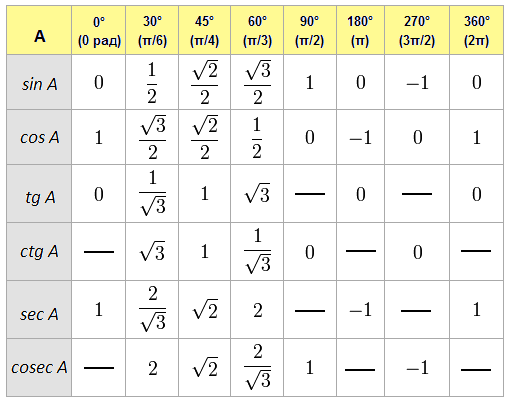 Этот шаблон периодически повторяется для соответствующих угловых измерений, и мы можем определить значения sin(θ) на основе положения θ в единичной окружности, принимая во внимание знак синуса: синус положительный в квадрантах I и II и отрицательный в квадрантах III и IV. Аналогичный метод запоминания можно использовать и для косинуса. При необходимости обратитесь к странице косинуса.
Этот шаблон периодически повторяется для соответствующих угловых измерений, и мы можем определить значения sin(θ) на основе положения θ в единичной окружности, принимая во внимание знак синуса: синус положительный в квадрантах I и II и отрицательный в квадрантах III и IV. Аналогичный метод запоминания можно использовать и для косинуса. При необходимости обратитесь к странице косинуса.
Зная значения косинуса и синуса для углов в первом квадранте, мы можем определить их значения для соответствующих углов в остальных квадрантах координатной плоскости с помощью опорных углов.
Опорные углы
Опорный угол — это острый угол (<90°), который может использоваться для представления угла любой величины. Любой угол в координатной плоскости имеет опорный угол в диапазоне от 0° до 90°. Это всегда наименьший угол (относительно оси абсцисс), который можно составить из конечной стороны угла. На рисунке ниже показан угол θ и его опорный угол θ'.
Поскольку θ’ является опорным углом θ, значения sin(θ) и sin(θ’) совпадают.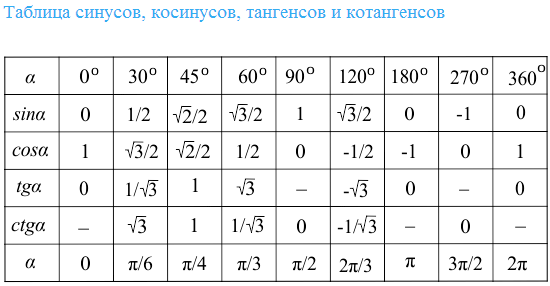 Например, 30° — это базовый угол 210°, и если мы обратимся к единичному кругу, то увидим, что значения синусов обоих имеют величину 1/2, хотя и имеют разные знаки. Поскольку у всех углов есть опорный угол, нам действительно нужно знать только значения sin(θ) (а также значения других тригонометрических функций) в квадранте I. Все другие соответствующие углы будут иметь значения одинаковой величины, и мы просто нужно обратить внимание на их знаки в зависимости от квадранта, в котором лежит конечная сторона угла. Ниже приведена таблица, показывающая знаки косинуса, синуса и тангенса в каждом квадранте.
Например, 30° — это базовый угол 210°, и если мы обратимся к единичному кругу, то увидим, что значения синусов обоих имеют величину 1/2, хотя и имеют разные знаки. Поскольку у всех углов есть опорный угол, нам действительно нужно знать только значения sin(θ) (а также значения других тригонометрических функций) в квадранте I. Все другие соответствующие углы будут иметь значения одинаковой величины, и мы просто нужно обратить внимание на их знаки в зависимости от квадранта, в котором лежит конечная сторона угла. Ниже приведена таблица, показывающая знаки косинуса, синуса и тангенса в каждом квадранте.
| Sine | Cosine | Tangent | |
| Quadrant I | + | + | + |
| Quadrant II | + | — | — |
| Quadrant III | — | — | + |
| Квадрат IV | — | + | — |
. Как только мы определим контрольный угла, мы можем определить стоимость тригонометрических функций. применяя соответствующий знак к их значению для эталонного угла. Следующие шаги могут быть использованы для нахождения исходного угла заданного угла θ:
Как только мы определим контрольный угла, мы можем определить стоимость тригонометрических функций. применяя соответствующий знак к их значению для эталонного угла. Следующие шаги могут быть использованы для нахождения исходного угла заданного угла θ:
- Вычтите 360° или 2π из угла столько раз, сколько необходимо (угол должен быть в пределах от 0° до 360° или от 0 до 2π). Если результирующий угол находится в диапазоне от 0° до 90°, это опорный угол.
- Определить, в каком квадранте лежит конечная сторона угла (начальная сторона угла проходит вдоль положительной оси абсцисс)
- В зависимости от того, в каком квадранте находится конечная сторона угла, используйте уравнения в таблице ниже, чтобы найти опорный угол. В квадранте I θ’=θ.
| Квадрант II | Квадрант III | Квадрант IV |
|---|---|---|
| θ’= 180° — θ | θ’= θ — 180° | θ’= 360° — θ |
Пример:
Найти sin(120°).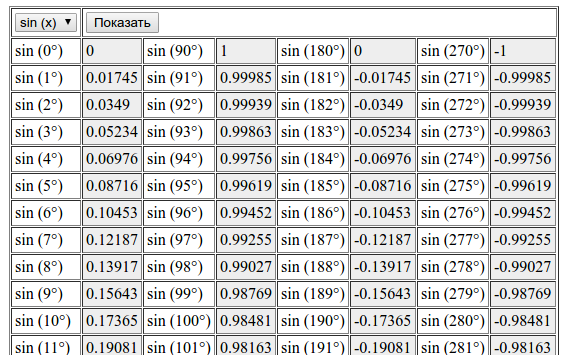
- θ уже находится в диапазоне от 0° до 360°
- 120° лежит в квадранте II
- 180° — 120° = 60°, поэтому опорный угол равен 60°
sin(60°)=. 120 ° находится в квадранте II, а синус положителен в квадранте II, поэтому:
Пример:
Найти sin(690°).
- 690° — 360° = 330°
- 330° лежит в квадранте IV
- 360° — 330° = 30°, поэтому опорный угол равен 30°
sin(30°)=. 330° находится в квадранте IV, где синус отрицательный, поэтому:
Свойства функции синуса
Ниже приведены некоторые свойства функции синуса, которые могут быть полезны при работе с тригонометрическими функциями.
Синус является функцией косинуса
Кофункция – это функция, в которой f(A) = g(B) при условии, что A и B являются дополнительными углами. В контексте косинуса и синуса:
sin(θ) = cos(90° — θ)
cos(θ) = sin(90° — θ)
Пример:
sin(60 °) = cos(90° — 60°) = cos(30°)
Ссылаясь на единичный круг, показанный выше, мы можем подставить значения для cos(30°) и sin(60°) и увидеть, что :
Синус — нечетная функция
Нечетная функция — это функция, в которой -f(x)=f(-x). Он имеет симметрию относительно начала координат. Таким образом,
Он имеет симметрию относительно начала координат. Таким образом,
-sin(θ) = sin(-θ)
Пример:
| -sin(60°) = sin(-60°) |
| -sin(60°) = sin (300°) |
Ссылаясь на единичный круг, мы видим, что sin(60°)=, поэтому -sin(60°)=, а sin(-60°) эквивалентно к sin(-60° + 360°) = sin(300°), что равно . Это только один пример, но это свойство верно для всех углов.
Синус — периодическая функция
Периодическая функция — это функция f, в которой существует некоторое положительное значение p такое, что
f(x+p) = f(x)
для всех x в области определения f p — наименьшее положительное число, для которого f является периодическим, и называется периодом f.
Тригонометрические функции обычно используются для моделирования периодических явлений из-за их периодичности; независимо от того, с какой точки мы начинаем на единичной окружности, если мы пройдем расстояние 2π (360 °) по единичной окружности от этой точки, мы вернемся в исходную точку. Если мы посмотрим на синусоидальную функцию, мы обнаружим, что она повторяется каждые 2π, поэтому 2π — это период синусоидальной функции. Мы можем записать это как:
Если мы посмотрим на синусоидальную функцию, мы обнаружим, что она повторяется каждые 2π, поэтому 2π — это период синусоидальной функции. Мы можем записать это как:
sin(θ+2π) = sin(θ)
Для учета нескольких полных оборотов это также можно записать как
sin(θ+2πn) = sin(θ)
, где n равно целое число.
На рисунке ниже показан пример такой периодичности.
Синим цветом мы видим, что . . Если мы добавим 2π к , мы получим угол, показанный красным цветом, . Как видно из рисунка, несмотря на разную степень поворота в обоих углах, их конечные стороны совершенно одинаковы, а это означает, что . Мы могли бы добавить еще 2π и все равно увидели бы, что имеет то же синусоидальное значение, что и . Такова природа периодических функций. называются котерминальными углами; это углы с одинаковыми начальными и конечными сторонами, но с разными поворотами.
Примеры:
1.
2.
График функции синуса
График синуса является периодическим, т. Повторение этой части y=sin(x) бесконечно слева и справа приведет к полному графику синуса. Ниже приведен график, показывающий четыре периода синусоидальной функции в интервале [-4π,4π]. На этом графике видно, что y=sin(x) демонстрирует симметрию относительно начала координат; если график отражается относительно начала координат, он создает зеркальное отражение. Это подтверждает, что синус является нечетной функцией, поскольку -sin(x)=sin(-x). Общая форма функции синуса: y = A·sin(B(x – C)) + D , где A, B, C и D — константы. Чтобы построить график синусоидального уравнения в общем виде, нам нужно сначала понять, как каждая из констант влияет на исходный график y=sin(x), как показано выше. A — амплитуда функции; высота от центра графика до максимума или минимума. В y=sin(x) центром является ось x, а амплитуда равна 1, или A=1, поэтому самая высокая и самая низкая точки, которых достигает график, равны 1 и -1, диапазон sin(x ). По сравнению с y=sin(x), показанной ниже фиолетовым, функция y=2 sin(x) (красная) имеет амплитуду, вдвое превышающую амплитуду исходного графика синуса. B — используется для определения периода функции; период функции — это расстояние от пика до пика (или любой точки на графике до следующей точки соответствия) и может быть найден как . В y=sin(x) период равен 2π. Мы можем убедиться в этом, посмотрев на график синусоиды. Ссылаясь на рисунок выше, мы можем видеть, что форма синусоидального графика между [-2π, 0] эквивалентна форме из [0, 2π], что означает, что он повторяется в течение интервала 2π; т. По сравнению с y=sin(x), показанным ниже фиолетовым цветом и имеющим период 2π, y=sin(2x) (красный) имеет период
. Это означает, что график повторяется через каждые π, а не через каждые 2π. C — фазовый сдвиг функции; фазовый сдвиг определяет, как функция сдвигается по горизонтали. Если C отрицательно, функция сдвигается влево. Если C положительно, функция сдвигается вправо. Будьте осторожны со знаком; если у нас есть уравнение, то C не является , потому что это уравнение в стандартной форме есть . Таким образом, мы бы сместили единицы графика влево. На рисунке ниже показаны y=sin(x) (фиолетовый) и (красный). Используя один из пиков синусоидального графика в качестве эталона, мы можем видеть, что пик at сместился влево от своего исходного положения и теперь находится в точке (0,1). D — вертикальное смещение функции; если D положительно, график сдвигается вверх на D единиц, а если отрицательно, то график сдвигается вниз. По сравнению с y=sin(x), показанным ниже фиолетовым цветом и центрированным по оси x (y=0), y=sin(x)+5 (красный) центрируется по линии y=5 (синий). Объединяя все приведенные выше примеры, на рисунке ниже показан график (красный) по сравнению с графиком y=sin(x) (фиолетовый). См. также косинус, тангенс, единичная окружность, тригонометрические функции, тригонометрия. спросил Изменено
11 месяцев назад Просмотрено
14 тысяч раз $\begingroup$ В старших классах меня учили, что я могу получить любое значение синуса с помощью некоторой базовой арифметики для значений следующего изображения: Но я так и не понял, откуда берутся эти значения, несколько дней назад изучить его, но я не мог обнаружить его. $$\sin=\frac{\text{напротив}}{\text{гипотенуза}}$$ Тогда я подумал, что мне просто нужно вычислить $\frac{1}{x}$, где $0 \leq x \leq 1$, но это не дало мне хороших результатов, тогда я подумал, что, возможно, я мог бы выразить это не как пропорцию противоположного и гипотенузы, я думал, что я мог бы выразить это как отношение между отрезками окружности, например: длина окружности $=\pi$, затем разделил его на $4$ (чтобы получить срез от $0$ до $90$ градусов), затем я получил: $x/ \frac{\pi}{4}$, где $0\leq x \leq \frac{\pi}{4} $, но это также не сработало, лучшее предположение, которое я мог сделать, было $\sqrt{x/ \frac{\pi}{4}}$, результат на следующем графике : Последняя догадка, которую я сделал, кажется (по крайней мере, визуально) очень похожей на исходную функцию синуса, кажется, ее нужно только повернуть, но отсюда у меня нет идей. Вы можете помочь мне? $\endgroup$ 4 $\begingroup$ Все значения на вашей картинке можно вывести из двух теорем: $\endgroup$ 4 $\begingroup$ Как и в ответе Альфонсо Фернандеса, замечательные значения на вашей диаграмме можно рассчитать с помощью базовой геометрии плоскости. Исторически сложилось так, что значения триггерных функций были выведены из значений с использованием формул сложения половинного угла и угла. Так как вы знаете 30°, вы можете использовать формулу половинного угла для вычисления 15, 7,5, 3,25, 1,125 и 0,5625 градусов. Теперь используйте формулу сложения углов, чтобы вычислить 0,5625° + 0,5625° = 2*0,5625°, и так далее для 3*0,5625°, 4*0,5625°… Их рассчитывали вручную в течение длительных периодов времени, а затем распечатывали в длинных таблицах, которые заполняли целые книги. Когда инженеру или моряку нужно было узнать конкретное значение триггера, он искал ближайшее значение, доступное в своей книге таблиц триггеров, и использовал его. Доминик Михаэлис указывает, что в высшей математике тригонометрические функции определяются без привязки к геометрии, и это позволяет придумывать для них явные формулы. Вы можете отвергнуть это как простую формалистскую чепуху, но концептуально я считаю, что определения триггерных функций университетского уровня делают гораздо больше смысла в , чем в геометрических, поскольку проясняет тайну того, почему эти функции появляются в ситуациях, которые не имеют ничего общего с углами или окружностями. Так что в конце концов вы можете потерять желание вычислять значения из геометрического определения. Конечно, если вы все равно собираетесь использовать геометрическое определение, вы также можете просто взять линейку и транспортир и измерить всю ночь, и таким образом вычислить таблицу триггерных значений. И последнее замечание: вы все еще используете определение «отношение сторон треугольника» для триггерных функций. Я настоятельно рекомендую вам отказаться от этого определения в пользу кругового определения: $sin(\theta)$ — это высота угла $\theta$, деленная на длину стороны угла, $cos$ то же самое для ширина угла, а $tan$ — наклон стороны угла. $\endgroup$ 10 $\begingroup$ [Изображения из Википедии.
]
$$\sin x = \frac ah\quad \cos x = \frac bh \quad \tan x = \frac ab$$ $\qquad\qquad\qquad\qquad\qquad\qquad$ И посмотрите, как это соотносится с единичным кругом, где $$\sin\theta = \frac{\text{противоположный}}{\text{гипотенуза}} = \frac y1 = y$$ $$ \cos\theta = \frac{\text{смежный}}{\text{гипотенуза}} = \frac х 1 = x$$ 92(30) = 3/4 \ подразумевает \cos(30) = \sqrt 3/2$$ $\endgroup$ 0 $\begingroup$ Для меня это действительно классический вопрос. Вот как вы читаете этот круг. $\endgroup$ 2 $\begingroup$ Если мы перейдем к незначительным деталям того, как мы получаем значения sin, cos, tan, то это функция численного анализа, в которой у нас есть разные методы для получения значений этих важных методов, я помню, это Ньютон Ральфсон. Я изучал численный анализ 2 года назад. однако, если вам нужно действительно узнать, вы можете искать в этой области, потому что это источник. См. метод Ньютона (Википедия) $\endgroup$ $\begingroup$ $cos(\phi)$ — значение $x$ точки под углом $\phi$, а $sin(\phi)$ — значение $y$ точки под углом $\phi$; на единичной окружности (на радиусе 1). $\endgroup$ Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя адрес электронной почты и пароль Электронная почта Обязательно, но не отображается Электронная почта Требуется, но не отображается е. повторяется бесконечно и имеет область значений -∞
е. повторяется бесконечно и имеет область значений -∞ Общее уравнение синуса
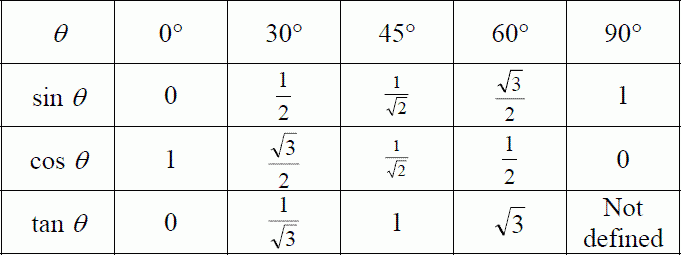 Чтобы применить что-либо, написанное ниже, уравнение должно иметь форму, указанную выше; будьте осторожны со знаками.
Чтобы применить что-либо, написанное ниже, уравнение должно иметь форму, указанную выше; будьте осторожны со знаками. е. имеет период 2π.
е. имеет период 2π.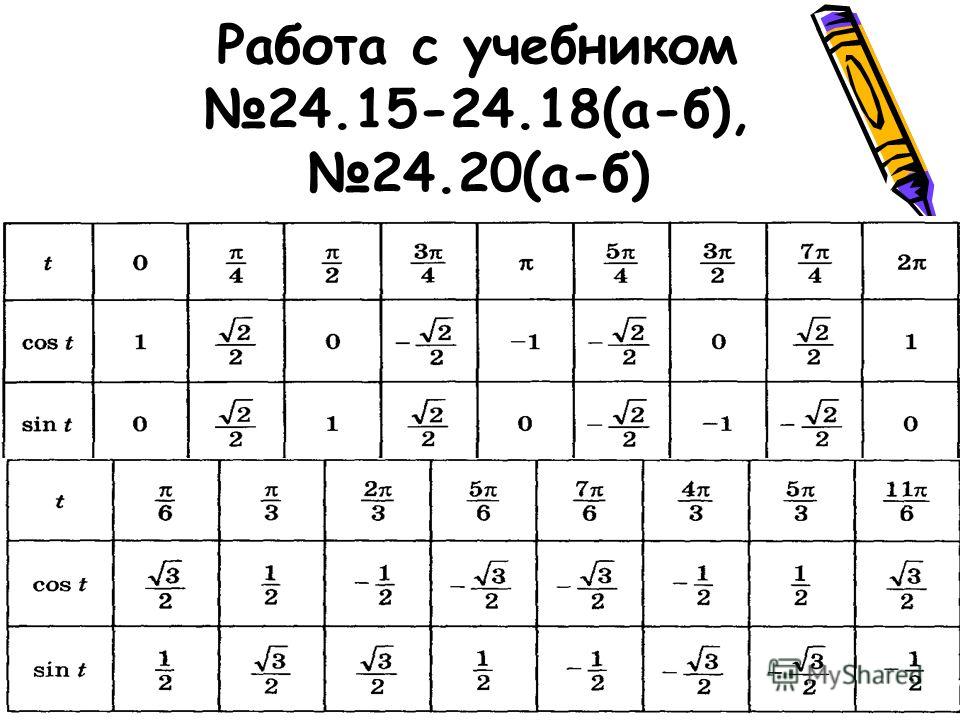
тригонометрия — Откуда берутся значения функции синуса?
 Почитав некоторое время, я вспомнил, что функция синуса:
Почитав некоторое время, я вспомнил, что функция синуса: 9\circ = \frac{\sqrt{3}}{2}$.

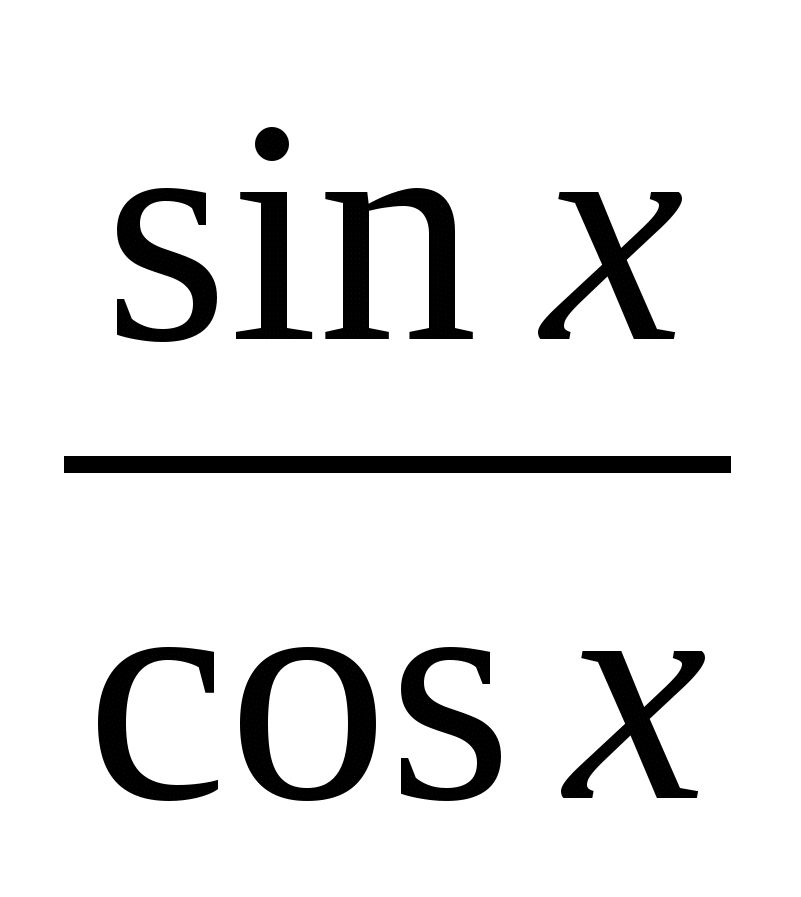
 Причина, по которой я рекомендую вам использовать это определение, заключается в том, что, хотя оно столь же концептуально, как и треугольное (если вы задумаетесь об этом на секунду), оно позволяет вам легко увидеть, где значения углов больше 9{i \varphi}$$, где $$\varphi= \arctan\left(\frac{\Im(z)}{\Re(z)}\right)$$ и $\Im(z)$ — мнимое часть $z$, а $\Re(z)$ — действительная часть $z$.
Причина, по которой я рекомендую вам использовать это определение, заключается в том, что, хотя оно столь же концептуально, как и треугольное (если вы задумаетесь об этом на секунду), оно позволяет вам легко увидеть, где значения углов больше 9{i \varphi}$$, где $$\varphi= \arctan\left(\frac{\Im(z)}{\Re(z)}\right)$$ и $\Im(z)$ — мнимое часть $z$, а $\Re(z)$ — действительная часть $z$.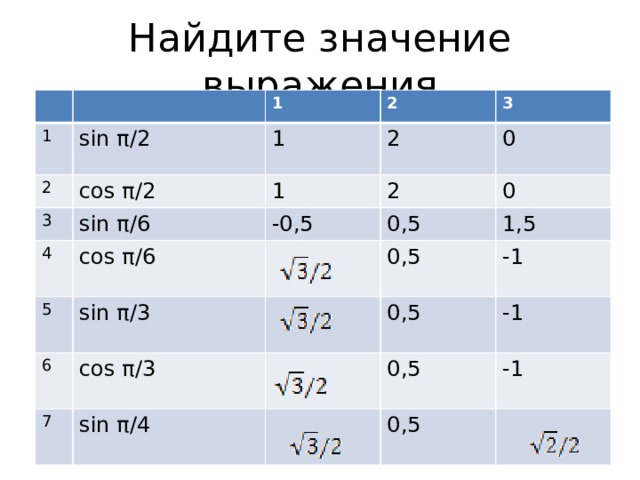 \circ$. Чтобы подняться на несколько градусов, перейдите на 9\circ$ достигнут.
\circ$. Чтобы подняться на несколько градусов, перейдите на 9\circ$ достигнут.
Твой ответ
Зарегистрируйтесь или войдите в систему
Опубликовать как гость
Опубликовать как гость
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
тригонометрия — Для каких углов мы знаем значение $\sin$ алгебраически (точно)?
спросил
9п=1$.Но известно, например, что не существует выражения для $\sin(\pi/9)$, которое начинается с целых чисел и использует только обычные арифметические операции и корни, в которых каждая компонента вещественна.
Следующая более узкая задача имеет долгую историю из-за ее тесной связи с проблемой построения углов с помощью линейки и циркуля.
Пусть $\theta=\frac{m}{n}\pi$, где $m$ и $n$ взаимно просты. Ограничьте наши алгебраические операции обычными арифметическими операциями плюс 92(х)}}\тег{3} $$ мы можем построить синус и косинус всех рациональных чисел, кратных $\pi$, где знаменатель является степенью 2$ или 3$, умноженной на степень 2$.
Например, $x=\pi/4$ с $(1)$ дает $$ \tan(\pi/8)=\sqrt{2}-1\тег{4} $$ тогда $(2)$ и $(4)$ дают $$ \начать{выравнивать} \загар(3\пи/8) &=\загар(\пи/4+\пи/8)\\ &=\frac{1+\tan(\pi/8)}{1-\tan(\pi/8)}\\ &=\sqrt{2}+1\тег{5} \end{выравнивание} $$ Тогда $(3)$ и $(5)$ дают $$ (\cos(3\pi/8),\sin(3\pi/8))=\frac{(1,\sqrt{2}+1)}{\sqrt{4+2\sqrt{2}} }\тег{6} $$
$\endgroup$
$\begingroup$
В январе 2008 года я разместил несколько ссылок, опубликованных в 1800-х годах, на таблицы, которые дают точные значения синуса и косинуса углов в градусах $3$, $6$, $9$, …, $90$.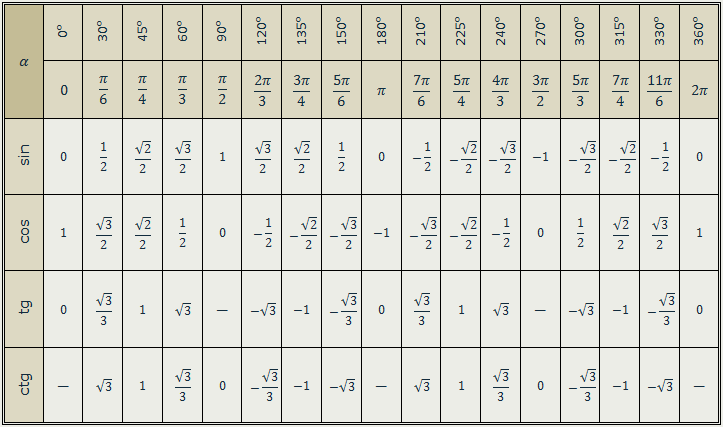 (Среди углов в целых градусах только те, которые кратны $3$, могут быть выражены в действительно-радикальной форме.) См. архив google-groups для 1-го поста и архив google-groups для 2-го поста.
(Среди углов в целых градусах только те, которые кратны $3$, могут быть выражены в действительно-радикальной форме.) См. архив google-groups для 1-го поста и архив google-groups для 2-го поста.
Лучшая из известных мне таблиц была составлена бельгийским математиком Э. Гелином в 1880-х годах. В его таблице приведен список значений с рационализированными знаменателями для всех шести триггеров. функции оценены в $3$, $6$, $9Углы $, …, $90$ градусов. Я знаю три места, где была опубликована его таблица:
Mathesis Recueil Mathematique (1) 8 (1888), Supplement 3. [См. стр. 327-333 загруженного файла .pdf.] ) 6 (1906 г.), Приложение 3. [См. стр. 338–348 загруженного файла в формате .pdf.]
Э. Гелен, Элементы тригонометрии, плоскости и сферы (1888 г.). [См. стр. 59-62, что эквивалентно стр. 66-69 загруженного файла .pdf.]
Я считаю, что Иоганн Генрих Ламберт был первым, кто опубликовал точные радикальные значения для синуса $3$, $6$ , $9$ и т. д. градусные углы. Таблица значений находится в Томе 1 его Собрания сочинений . Таблица находится в статье, опубликованной в 1770 году. Таблица Ламберта переиздавалась два или три раза в первой половине 1800-х годов (например, одна была в Crelle’s Journal [= Journal für die reine und angewandte Mathematik]), но я не знаю Точные рекомендации сейчас со мной.
Таблица значений находится в Томе 1 его Собрания сочинений . Таблица находится в статье, опубликованной в 1770 году. Таблица Ламберта переиздавалась два или три раза в первой половине 1800-х годов (например, одна была в Crelle’s Journal [= Journal für die reine und angewandte Mathematik]), но я не знаю Точные рекомендации сейчас со мной.
$\endgroup$
$\begingroup$
Возможно алгебраически точное значение синуса для всех целых углов. Пожалуйста, посетите https://archive.org/details/ExactTrigonometryTableForAllAnglesFinal для получения списка точных значений для синуса целых углов в градусах.
$\endgroup$
4
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
тригонометрия — Запоминание/вычисление значений синуса и косинуса 18 градусов, 36 градусов, 54 градусов, 72 градусов
спросил
Изменено 2 года, 3 месяца назад
Просмотрено 2к раз
$\begingroup$
Мне нужно запомнить значения синуса и косинуса 18 градусов, 36 градусов, 54 градуса, 72 градуса. Это кратно, если 18 градусов. Можно ли получить их примерно за минуту или около того? Используете ли вы какой-либо особый метод, чтобы запомнить их?
Это кратно, если 18 градусов. Можно ли получить их примерно за минуту или около того? Используете ли вы какой-либо особый метод, чтобы запомнить их?
Да, я знаю, что мы можем решить уравнение $\sin{5\theta}=\pi/2$ и подобные, но это слишком долго (во время экзаменов).
- тригонометрия
$\endgroup$ 9\circ — x) = \sin x$$
$\endgroup$
$\begingroup$
Путем механического запоминания вам нужно запомнить только два выражения, как указано ниже. Представьте отрицательные знаки, составляющие одну «строку» текста, и положительные знаки, составляющие следующую строку. $$\dfrac{\sqrt{5}\mp 1}{4}, \sqrt{\dfrac{5\mp \sqrt{5}}{8}}.$$ Читая как на простом английском языке (т.е. слева направо и сверху вниз), мы получаем синусы по порядку: $\sin 18°,\sin 36°,\sin 54°,\sin 72°$ .
Двигаясь в обратном направлении (снизу вверх и справа налево), аналогично получаем косинусы по порядку: $\cos 18°,\cos 36°,\cos 54°,\cos 72°$.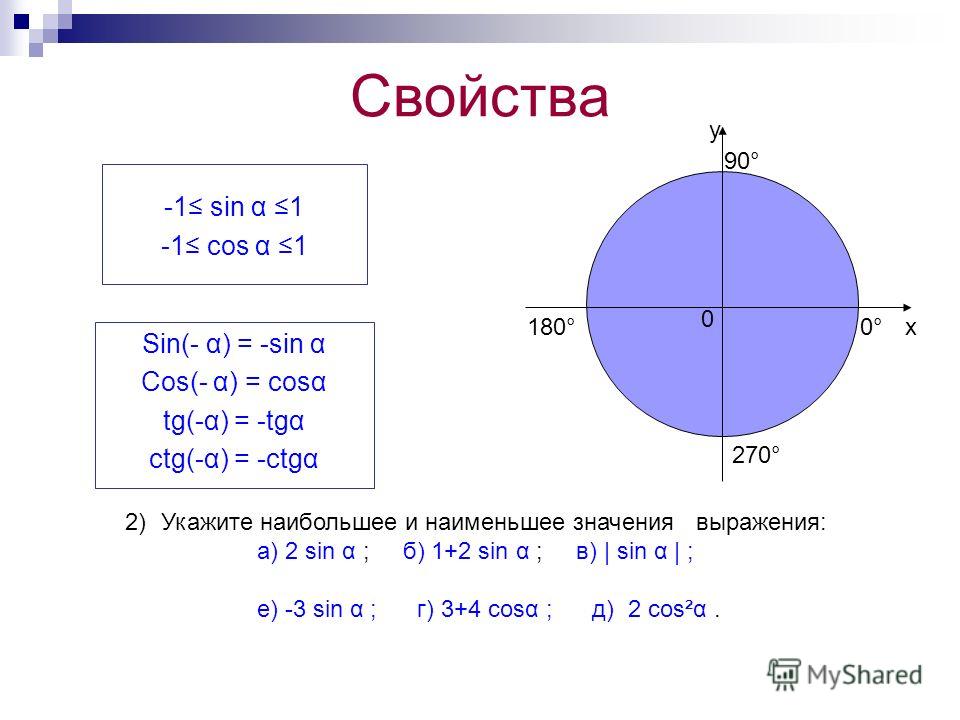
Независимо от того, как получить эти значения ради эффективности, лежащие в их основе понятия и интуиция всегда должны быть сохранены в памяти или, по крайней мере, оценены.
$\endgroup$
$\begingroup$
Я думаю, этот вывод хорошо запомнился:
Пусть $x=\pi/10$. Затем 92+2\sin(x)-1=0.$$
Отсюда
$$\sin(x)=\frac{-2+\sqrt{20}}{8}=\frac{-2+ 2\sqrt{5}}{8}=\frac{\sqrt{5}-1}{4}.$$
Затем используйте Pythagoras, чтобы получить $\cos(x)$. Затем используйте deMoivre, чтобы получить остальные.
Это слишком долго, чтобы переделывать?
$\endgroup$
$\begingroup$
Самый простой способ получить эти результаты — начать с правильного пятиугольника ABCDE. Добавьте диагонали AC и AD. Тогда треугольник ABC имеет углы 36, 36 и 108 градусов с $AB:BC:AC = 1:1:(1+\sqrt{5})/2$, а ACD имеет углы 72, 72 и 36 градусов с $ AC:AD:CD=(1+\sqrt{5})/2:(1+\sqrt{5})/2:1$.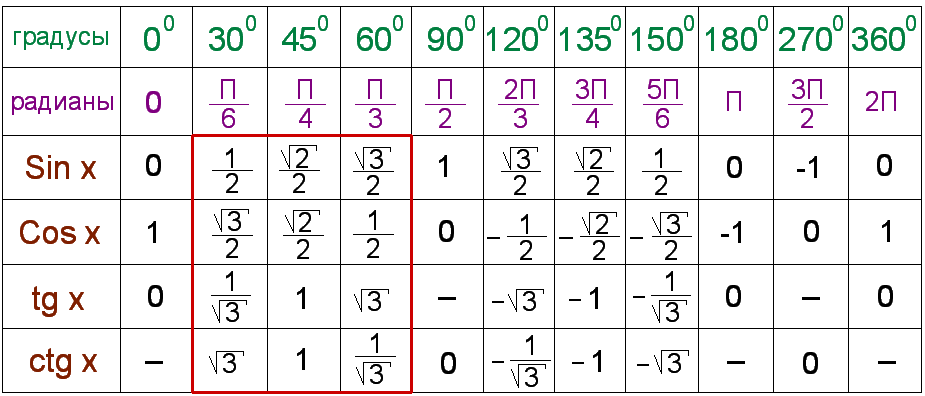 2 + х — 1 = 0$$ 92}}{2} = \sqrt{\frac{5-\sqrt5}{8}}$$
2 + х — 1 = 0$$ 92}}{2} = \sqrt{\frac{5-\sqrt5}{8}}$$
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.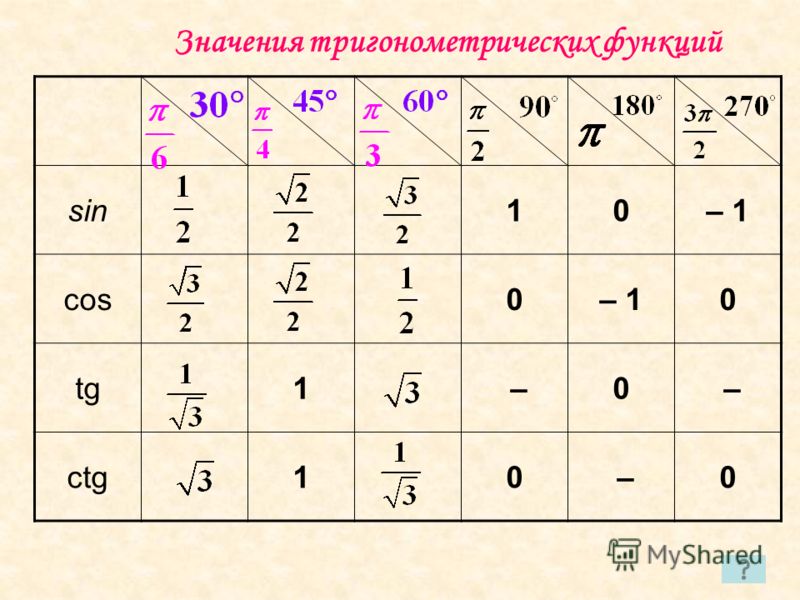
Найти значение функции синуса или косинуса угла по точке на его конечной стороне
Все ресурсы предварительного исчисления
12 Диагностические тесты 380 практических тестов Вопрос дня Карточки Learn by Concept
Precalculus Помощь » Тригонометрические функции » Круговые функции » Найдите значение функции синуса или косинуса угла по точке на его конечной стороне
Чему равен синус угла, если точка на конечной стороне угла ?
Возможные ответы:
Правильный ответ:
Объяснение:
Учитывая точку на координатной плоскости , начало этой точки можно вычислить по теореме Пифагора.
Гипотенуза прямоугольного треугольника, образованного началом и точкой.
Длина треугольника равна 1 единице, а высота треугольника равна 5.
Синус угла равен противолежащему катету, деленному на гипотенузу.
Рационализируйте знаменатель.
Сообщить об ошибке
Пожалуйста, выберите лучший ответ из следующих вариантов.
Найдите значение секанса , если это точка на конечной стороне угла в стандартном положении.
Возможные ответы:
Правильный ответ:
Пояснение:
Во-первых, используйте теорему Пифагора, чтобы найти все стороны треугольника. Вы знаете, что прилежащая сторона имеет длину 4 единицы, а противолежащая -9.единицы длины.
Используя теорему Пифагора, вы должны получить гипотенузу .
Секанс определяется как гипотенуза/противоположная.
Таким образом, давая вам ответ .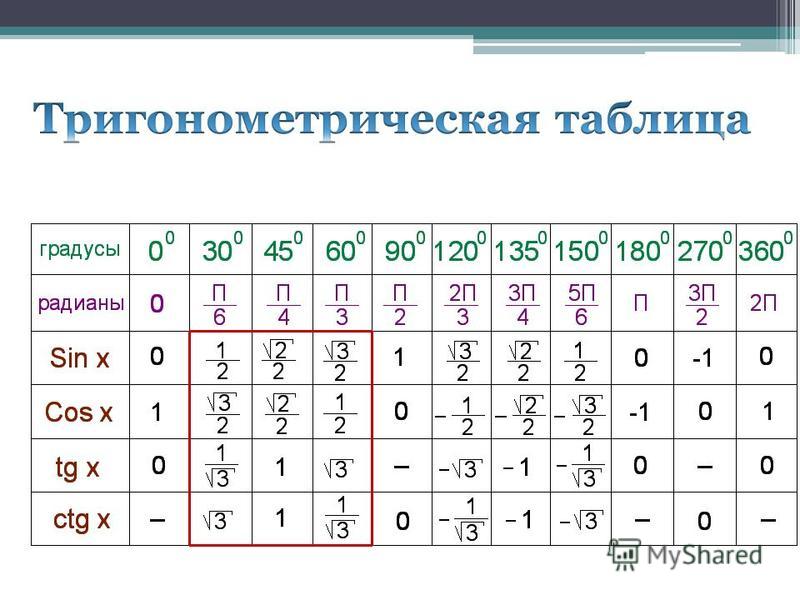
Сообщить об ошибке
Найдите значение синуса , если это точка на конечной стороне угла в стандартном положении.
Возможные ответы:
Правильный ответ:
Объяснение:
Это 30-60-90 треугольник. Треугольник 30-60-90 будет иметь длину катета и 1 и гипотенузу 2. Чтобы найти значение sin, вам нужно разделить длину противоположного катета на гипотенузу (противоположную/гипотенузу). Таким образом, давая вам .
Сообщить об ошибке
Если вы можете найти синус и косинус угла для точки на его конечной стороне, у вас есть достаточно информации, чтобы также найти его тангенс.
Что из следующего лучше всего описывает правильность приведенного выше утверждения?
Возможные ответы:
Утверждение неверно во всех случаях.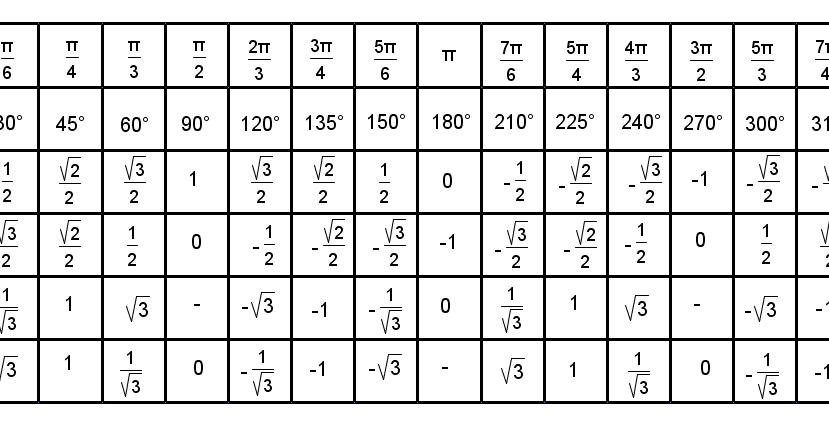
Утверждение верно во всех случаях.
Утверждение верно в некоторых случаях, но не во всех.
Правильный ответ:
Утверждение верно во всех случаях.
Объяснение:
Вспомните формулу тангенса. Если у нас достаточно информации для нахождения синуса и косинуса, то у нас есть значения противоположного и прилежащего угла.
Сообщить об ошибке
Метод решения тригонометрических функций угла по точке на его конечной стороне работает только для острых углов.
Какое из следующих утверждений лучше всего описывает правильность приведенного выше утверждения?
Возможные ответы:
Утверждение неверно
Утверждение верно
Правильный ответ:
Утверждение неверно
Объяснение:
Рассмотрим рисунок ниже.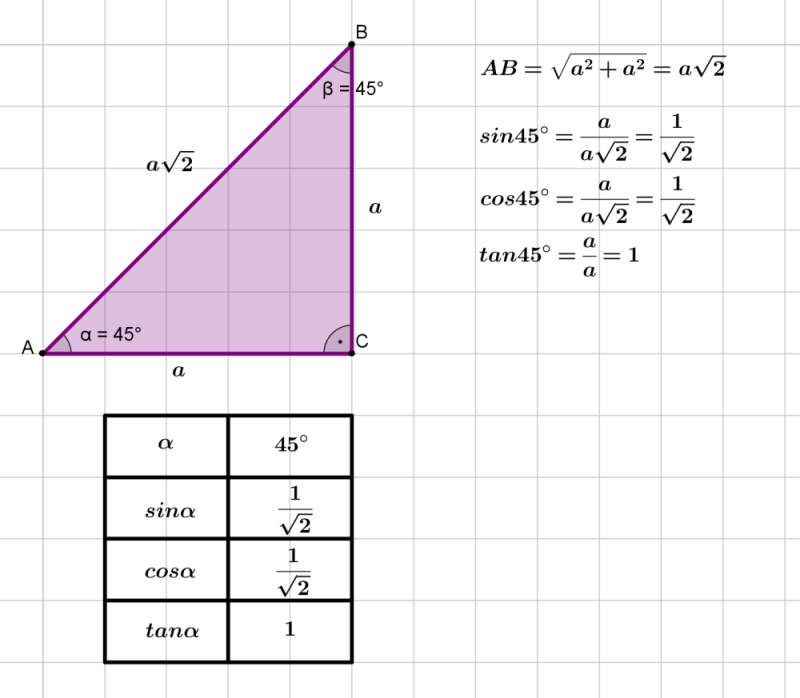
Мы можем сформировать треугольник, опустив вниз линию из точки (-2,3), перпендикулярную оси
x. Теперь у нас есть прямоугольный треугольник с катетом высотой 3 единицы и длиной основания 2
единиц. Теперь мы можем использовать теорему Пифагора, чтобы найти гипотенузу.
Теперь мы можем найти синус и косинус. Используйте тот факт, что . Противоположная сторона угла в данном случае является катетом высотой 3 единицы.
И мы будем использовать тот факт, что . Сторона, прилежащая к углу, является основанием, длина которого равна 2 единицам. Мы должны отметить, что мы используем, а не .
Таким образом, несмотря на то, что наш угол был тупым, мы все равно можем использовать тот же метод.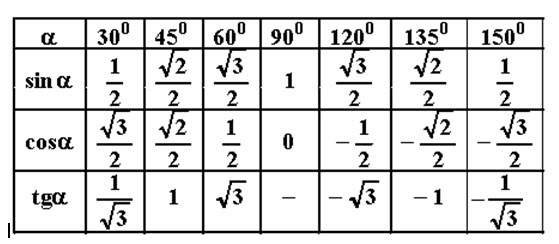
Сообщить об ошибке
Учитывая, что косинус угла равен , какова высота образованного этим треугольника? (т. е. конечная точка для этого угла равна (1, y), найдите y).
Возможные ответы:
Правильный ответ:
Объяснение:
Начнем с размышлений о том, что означает косинус при работе с прямоугольными треугольниками. Отзывать . Итак, если
Тогда прилежащая сторона или основание треугольника равна 1, а гипотенуза равна 2. Теперь мы можем использовать теорему Пифагора, чтобы найти недостающую сторону.
Сообщить об ошибке
Найдите значение косинуса угла, если точка на конце угла равна (3,4).
Возможные ответы:
Правильный ответ:
Объяснение:
Используя точку (3,4), мы можем увидеть, что это образует прямоугольный треугольник, длина основания которого составляет 3 единицы, а высота примыкающего катета — 4 единицы.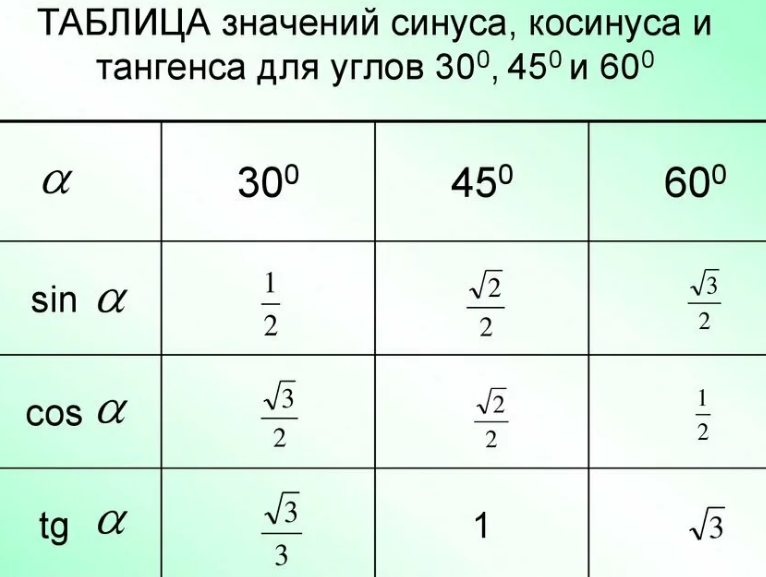 Мы можем найти гипотенузу этого треугольника, используя теорему Пифагора. Это даст нам расстояние от точки (3,4) до начала координат.
Мы можем найти гипотенузу этого треугольника, используя теорему Пифагора. Это даст нам расстояние от точки (3,4) до начала координат.
Таким образом, гипотенуза этого треугольника (расстояние от нашей точки, с которой мы работаем, до начала координат) составляет 5 единиц длины. Напомним, что при использовании косинуса для прямоугольных треугольников косинус представляет собой следующие
Итак, если мы рассматриваем угол, образованный осью x и нашей гипотенузой, примыкающая сторона будет основанием нашего треугольника; 3 единицы.
Сообщить об ошибке
Найдите синус и косинус следующего угла.
Возможные ответы:
Правильный ответ:
,
Пояснение:
Мы видим, что точка на концевой стороне равна (5,6). Итак, мы знаем, что с этой точкой образован прямоугольный треугольник с основанием длиной 5 единиц и высотой катета 6 единиц. Мы можем использовать теорему Пифагора, чтобы найти гипотенузу, образованную этим треугольником, и это скажет нам расстояние от точки до начала координат.
Итак, мы знаем, что с этой точкой образован прямоугольный треугольник с основанием длиной 5 единиц и высотой катета 6 единиц. Мы можем использовать теорему Пифагора, чтобы найти гипотенузу, образованную этим треугольником, и это скажет нам расстояние от точки до начала координат.
Сначала найдем синус. При работе с прямоугольными треугольниками помните, что и мы рассматриваем угол, образованный осью x и гипотенузой. Таким образом, противоположная сторона — это нога высотой 6 единиц.
Мы можем найти косинус, если вспомним, что . Наша соседняя сторона будет основанием длиной 5 единиц.
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы Precalculus
12 Диагностические тесты 380 практических тестов Вопрос дня Карточки Learn by Concept
Значения Sin Cos Tan — тригонометрические соотношения и часто задаваемые вопросы
Тригонометрия — это раздел математики, изучающий отношения между углами и сторонами треугольников или изучающий углы, длины и высоты треугольников и отношения между различными частями треугольников. круги и другие геометрические фигуры. Понятия тригонометрии очень полезны в практической жизни, а также находят применение в области техники, астрономии, физики и архитектурного проектирования.
круги и другие геометрические фигуры. Понятия тригонометрии очень полезны в практической жизни, а также находят применение в области техники, астрономии, физики и архитектурного проектирования.
В общей сложности это 6 соотношений, которые мы изучаем в тригонометрии, которые говорят нам о треугольнике, и Синус и Кос — два из них. Мы подробно обсудим соотношение Sin Cos, формулу и другие понятия.
Тригонометрические отношения
В математике определены шесть тригонометрических отношений для прямоугольного треугольника, то есть синус, косеканс, тангенс, косеканс, секанс соответственно. Эти тригонометрические отношения являются реальными функциями, которые связывают угол прямоугольного треугольника с отношением двух длин его сторон. Sin и Cos являются основными тригонометрическими функциями, которые говорят о форме прямоугольного треугольника. Существует шесть тригонометрических отношений: синус, косинус, тангенс, косеканс, секанс и котангенс, которые обозначаются как Sin, Cos, Tan, Csc, Sec, Cot. Их называют отношениями, потому что они могут быть выражены в терминах сторон прямоугольного треугольника для определенного угла \[\theta\].
Их называют отношениями, потому что они могут быть выражены в терминах сторон прямоугольного треугольника для определенного угла \[\theta\].
Смежный: это сторона, примыкающая к рассматриваемому углу.
Противоположная: это сторона, противоположная рассматриваемому углу.
Гипотенуза: это сторона, противоположная прямому углу треугольника или наибольшая сторона треугольника.
(Изображение будет загружено в ближайшее время)
Sin θ = \[\frac{Перпендикуляр}{Гипотенуза}\] = \[\frac{Противоположность}{Гипотенуза}\]
Cos θ = \[\frac{Base}{Гипотенуза}\] = \[\frac{Adjacent}{Hypotenuse}\]
Tan θ = \[\frac{Perpendicular}{Base}\ ] = \[\frac{Противоположный}{Смежный}\]
Cosec θ =\[\frac{Гипотенуза}{Перпендикуляр}\] = \[\frac{Гипотенуза}{Противоположный}\]
Sec θ = \[\frac{Hypotenuse}{Base}\] = \[\frac{Hypotenuse}{Adjacent}\]
Cot θ = \[\frac{Base}{Perpendicular}\] = \[ \frac{Смежный}{Напротив}\]
9{2} A = \frac{(1 + Cos2A)}{2} \]
Сумма и разность углов
Отношение Sin и Cos суммы и разности двух углов можно преобразовать в два произведения, используя следующие тождества:
Sin(A + B) = Sin(A) Cos( B) + Cos(A) Sin(B)
Sin(A − B) = Sin(A) Cos(B) − Cos(A) Sin(B)
Cos(A + B) = Cos(A) Cos(B) − Sin(A) Sin(B)
Cos(A − B) = Cos(A) Cos(B) + Sin(A) Sin(B)
Sin(A + B + C) = SinACosBCosC + CosASinBCosC + CosACosBSinC − SinASinBSinC
Cos(A + B + C) = CosACosBCosC − SinASinBCosC − SinACosBSinC − SinACosBSinC − CosASinBSinC
\[SinA + SinB = 2Sin \frac{(A + B)}{2}.
 Cos\frac{A — B}{2}\]
Cos\frac{A — B}{2}\]\[SinA — SinB = 2Sin\frac{A — B}{2} .Cos\frac{A + B}{2}\]
\[CosA + CosB = 2Cos \frac{(A + B)}{2}.Cos\frac{A − B}{2}\ ]
\[CosA + CosB = −2 Sin \frac{(A + B)}{2}.Sin\frac{A − B}{2}\] 9{\circ} \]
Углы (в радианах)
0
{4}\]
\[\frac{\pi}{3}\]
\[\frac{\pi}{2}\]
\[sin \ тета\]
0
\[ \frac{1}{2}\]
\[ \frac{1}{\sqrt{2}}\]
\[ 90 \ гидроразрыва {\ sqrt {3}} {2} \] 1
\ [cos \ theta \]
1
\ [\ frac {\ sqrt {3} {2 ra rably \ rably raim8968 \ [\ 2968 \
\ [\ frac {\ sqrt {3} {2 rather \] \
\ [\ frac {\ sqrt {3}} {2 raister \].
 frac{1}{\sqrt{2}}\]
frac{1}{\sqrt{2}}\]\[ \frac{1}{2}\]
0
\[tan \theta\]
3
3
0
\[ \frac{1}{\sqrt{3}}\]
1
\[\sqrt{3}\]
\ [\ infty \]
\ [cosec \ theta \]
\ [\ infty \]
2
2 9009 9008
2
.
\[\frac{2}{\sqrt{3}} \]
1
\[sec \theta\]
1
\[\ frac{2}{\sqrt{3}} \]
\[\sqrt{2}\]
2
\[\infty\]
\[cot \theta\]
\[\infty\]
\[\sqrt{3}\]
1
\[\frac{1}{\sqrt{3}} \]
0
Тригонометрия — раздел математики и подраздел алгебры, связанный с измерением конкретных функций углов и их применение в расчетах.
 Примером тригонометрии, который легко понять, является то, что архитекторы используют для расчета любых конкретных расстояний.
Примером тригонометрии, который легко понять, является то, что архитекторы используют для расчета любых конкретных расстояний.Алгебра и тригонометрия — две основные области математики. Алгебра включает в себя изучение математики с использованием определенных формул, правил, уравнений и других переменных. Тригонометрия имеет дело только с треугольниками и их измерениями.
Шесть основных функций угла, который обычно используется в тригонометрии, —
SINE (SIN),
косинус (COS),
(TAN),
0
(TAN),
0600.TANGENT (COT),
06060.TANGENGENT (TAN),
0060.
 TANGENGENT (TAN). ),
TANGENGENT (TAN). ),секанс (сек) и
косеканс (csc).
Легкий и простой способ изучить и понять тригонометрию — изучить все основы тригонометрических углов и формул, записав их в отдельную тетрадь, которая будет очень полезна для повторения перед экзаменами. Убедитесь, что вы хорошо понимаете и изучаете все концепции прямоугольного треугольника, чтобы вы могли сравнить любые проблемы с треугольником, прежде чем пытаться их решить. Основное эмпирическое правило, позволяющее добиться высоких результатов в тригонометрии, состоит в том, чтобы выучить теорему Пифагора всем сердцем. Имея под рукой правило синуса и правило косинуса, вы сможете решить любую задачу на экзамене. Наконец, перечислите все важные тождества и формулы тригонометрии в уме, а также в примечаниях к пересмотру, и будьте внимательны. Не забудьте научиться пользоваться таблицей тригонометрии в нужном месте.



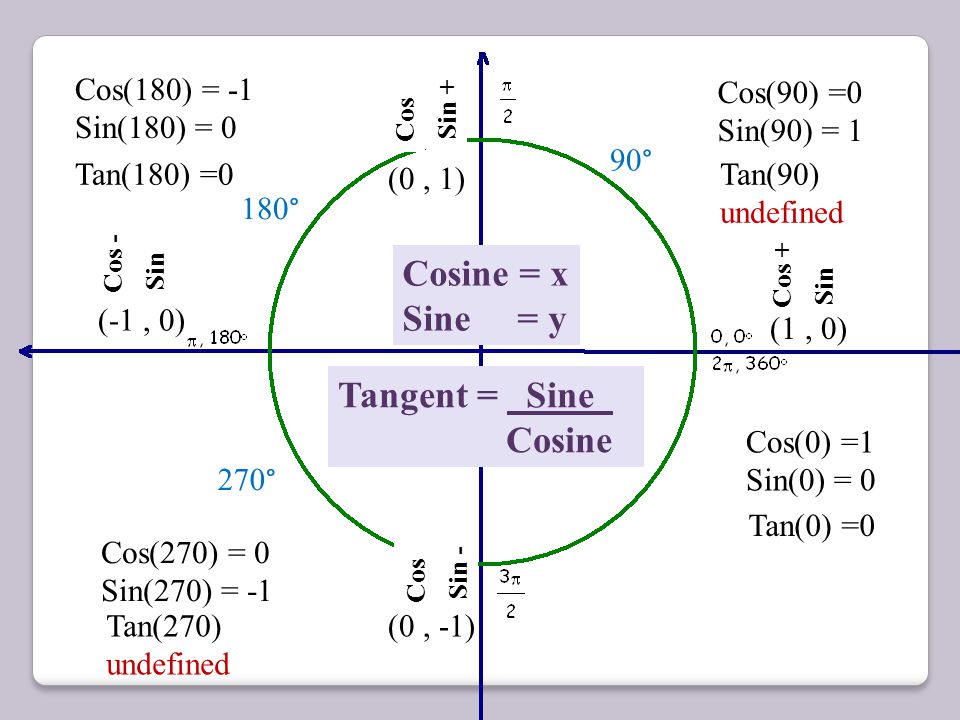 рекомендации).
рекомендации). 
 Метод геометрических мест
Метод геометрических мест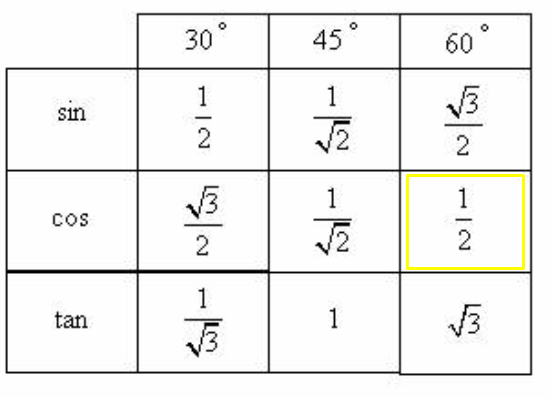 Первый признак подобия
Первый признак подобия Правильний чотирикутник (квадрат)
Правильний чотирикутник (квадрат)
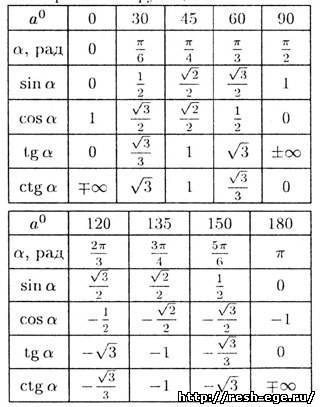 Свойства и признаки параллельности.
Свойства и признаки параллельности.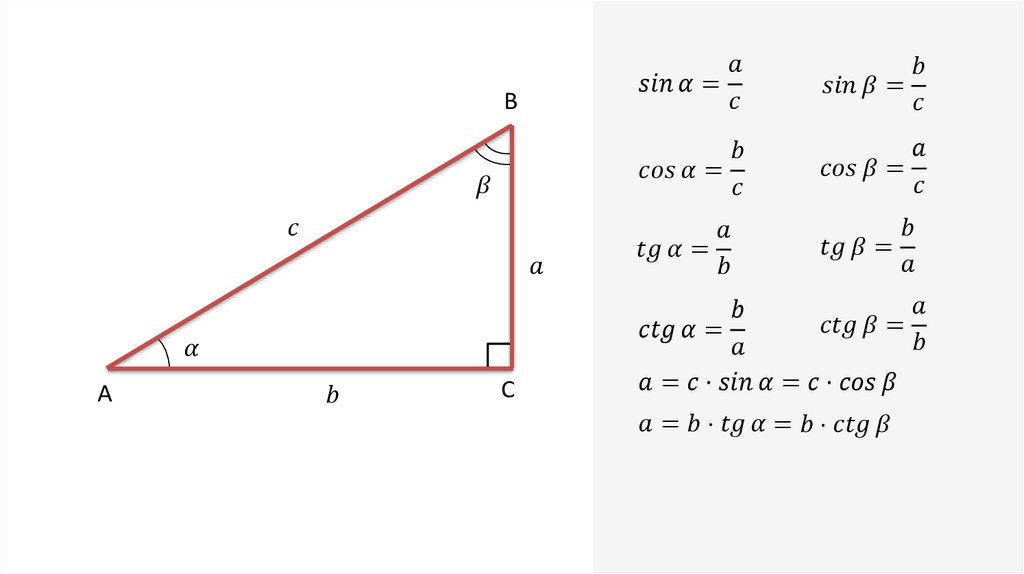 Решение задач
Решение задач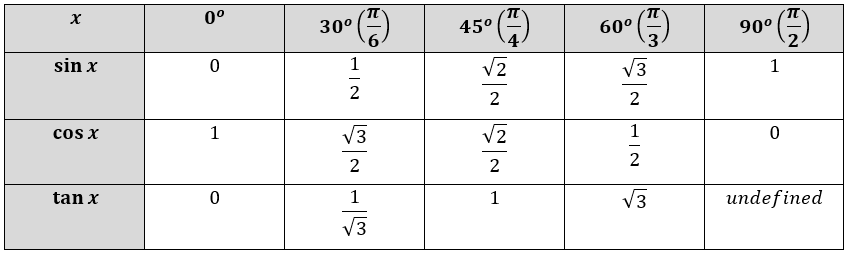 Шар. Куля
Шар. Куля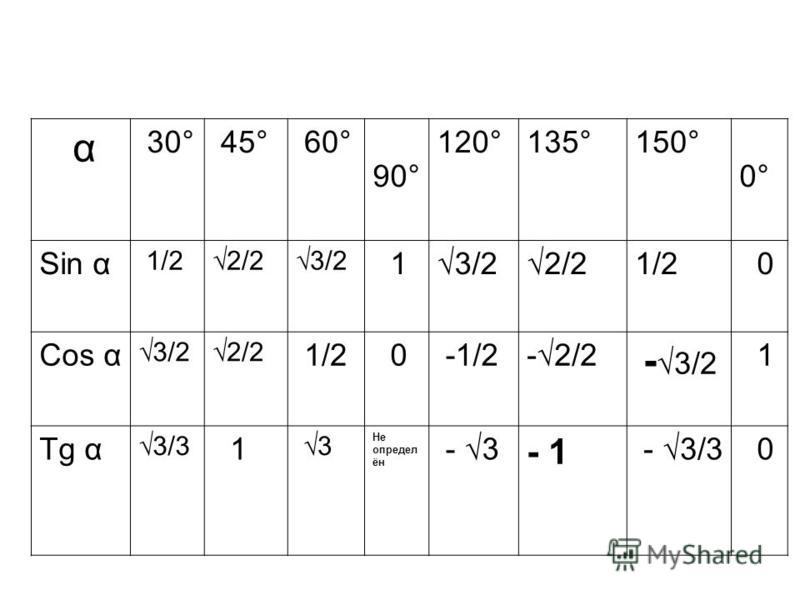 См. также полную таблицу значений тригонометрических функций для всех углов.
См. также полную таблицу значений тригонометрических функций для всех углов.
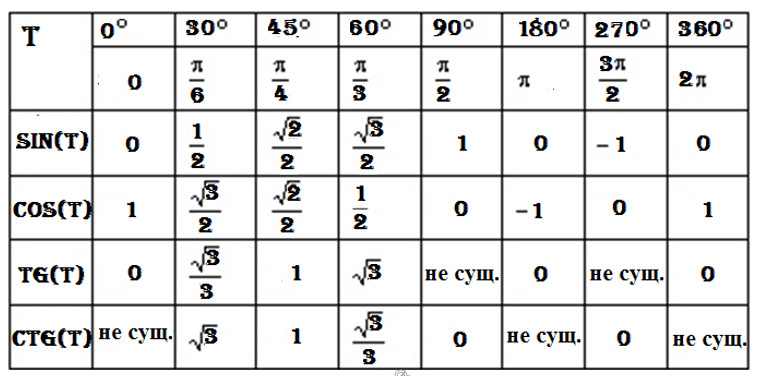

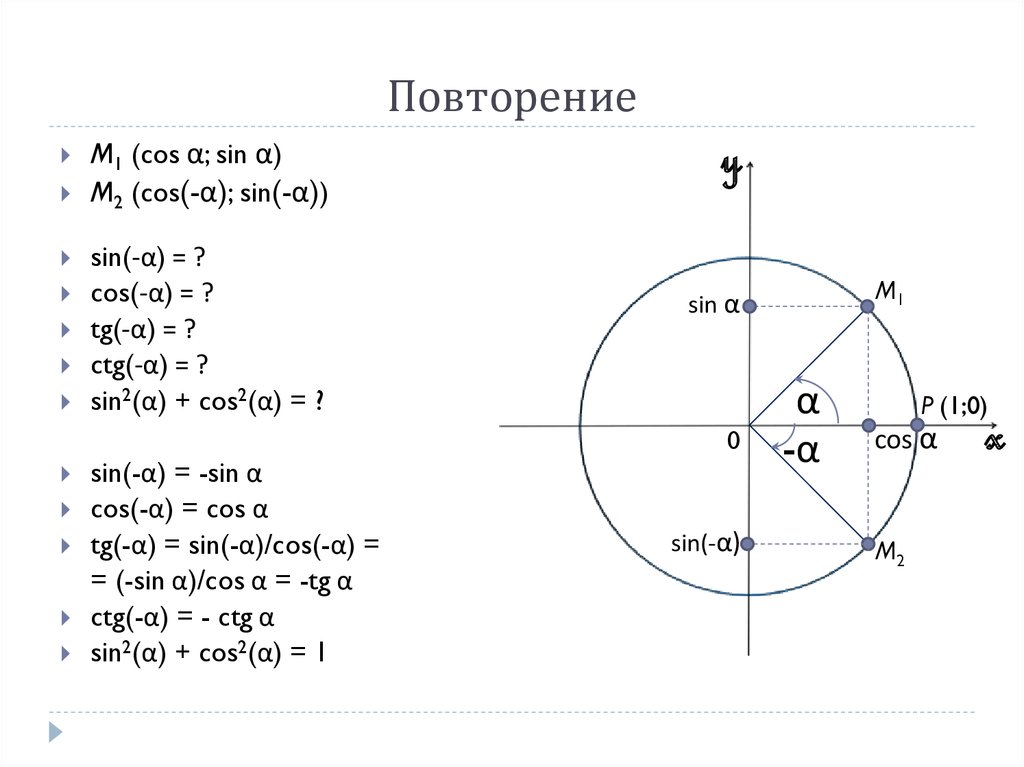 Учитывая, что AB = a, OB = a/2, AO = a√3/2, из соотношений сторон прямоугольного треугольника рассчитаем полученные значения. Согласно определению синуса, косинуса и тангенса:
Учитывая, что AB = a, OB = a/2, AO = a√3/2, из соотношений сторон прямоугольного треугольника рассчитаем полученные значения. Согласно определению синуса, косинуса и тангенса:
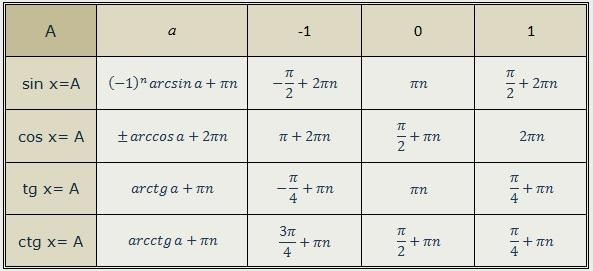 Катет OB рівний a/2, оскільки АO — медіана трикутника ABC. Знайдемо катет АТ.
Катет OB рівний a/2, оскільки АO — медіана трикутника ABC. Знайдемо катет АТ.
 В результатi одержуємо табличнi значення sin 30, cos 30 и tg 30 градусiв
В результатi одержуємо табличнi значення sin 30, cos 30 и tg 30 градусiв
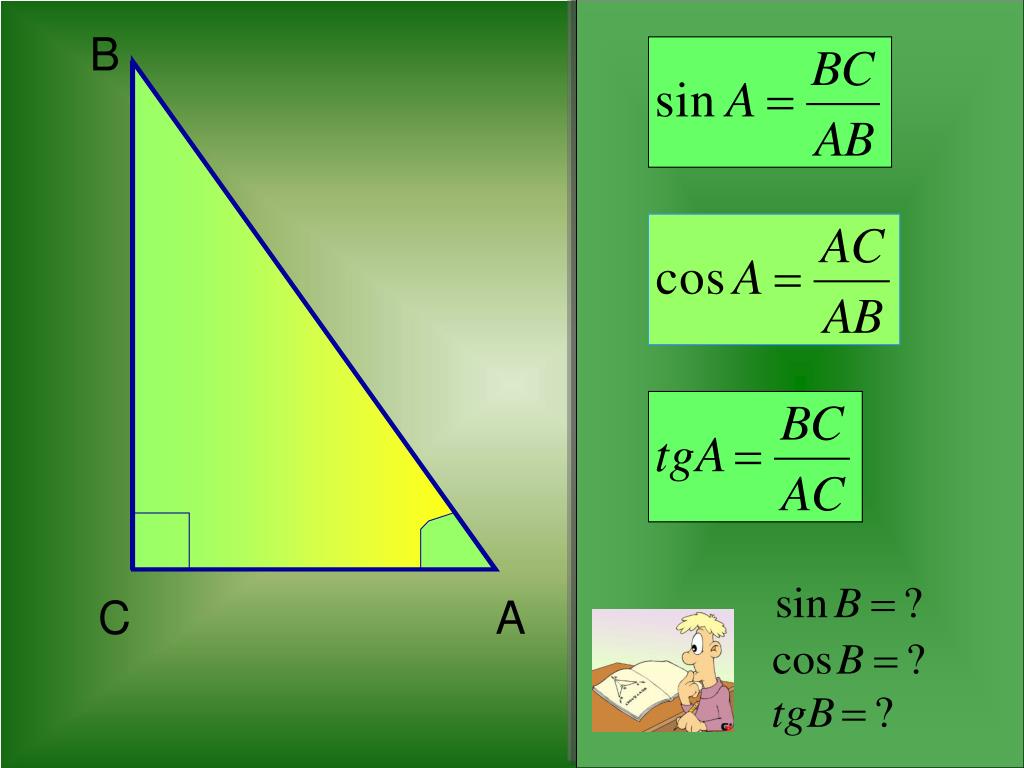

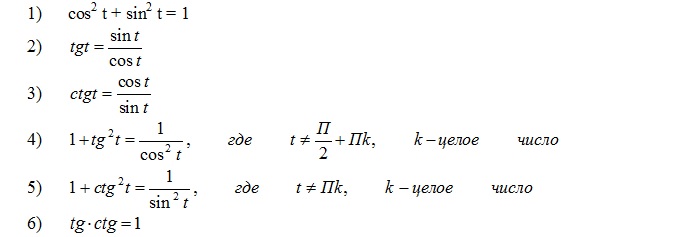
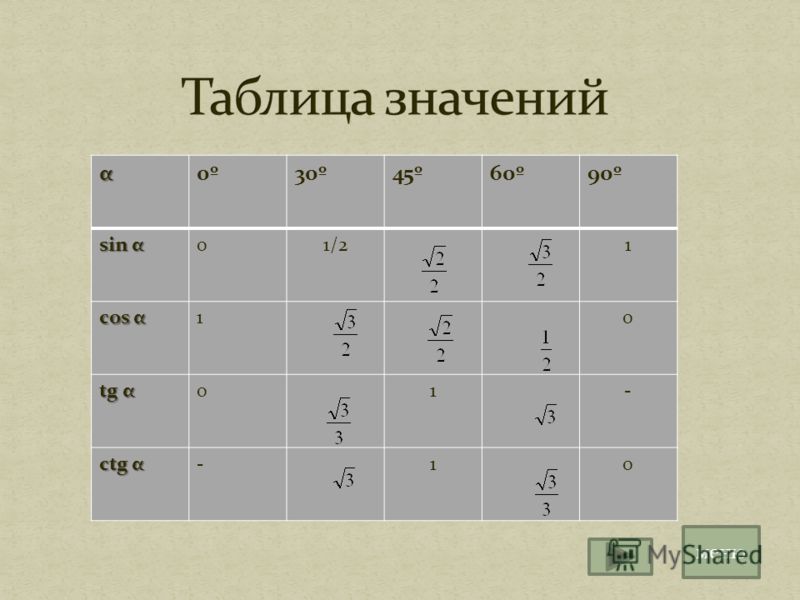 Cos\frac{A — B}{2}\]
Cos\frac{A — B}{2}\] frac{1}{\sqrt{2}}\]
frac{1}{\sqrt{2}}\]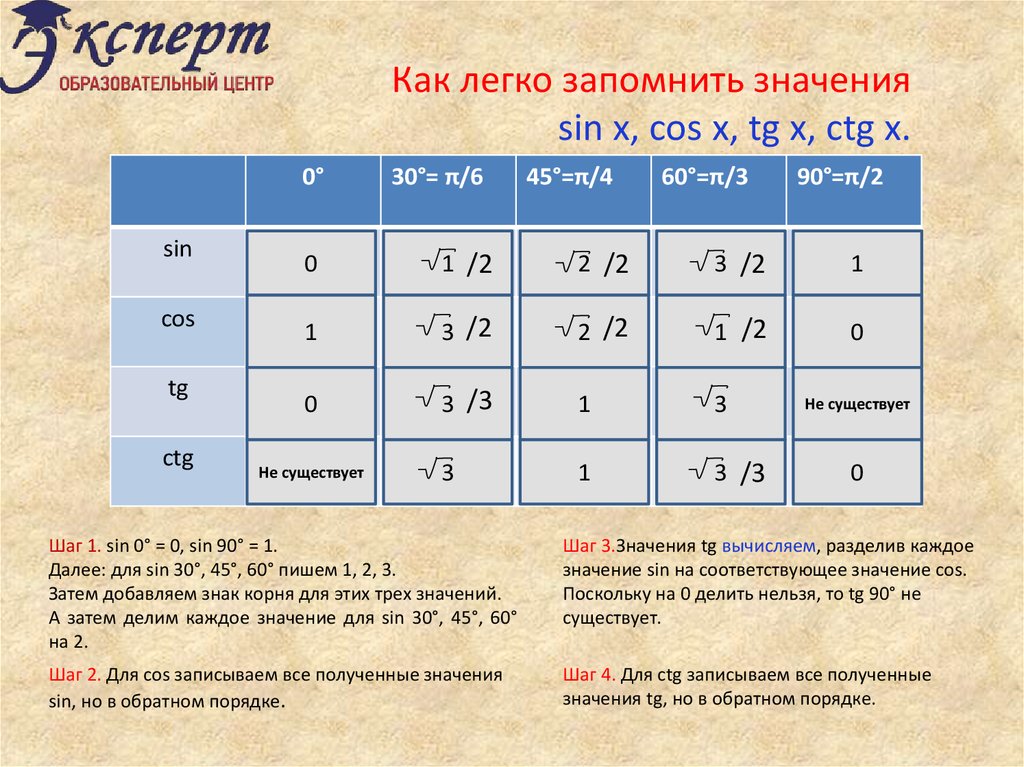 Примером тригонометрии, который легко понять, является то, что архитекторы используют для расчета любых конкретных расстояний.
Примером тригонометрии, который легко понять, является то, что архитекторы используют для расчета любых конкретных расстояний.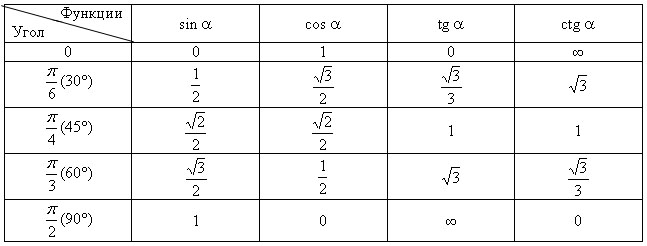 TANGENGENT (TAN). ),
TANGENGENT (TAN). ),