Перемножение матриц с: c# — Перемножение матриц — Stack Overflow на русском

Содержание

Перемножение матриц | это… Что такое Перемножение матриц?

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами.

Правила выполнения операций над матрицами сделаны такими, чтобы было удобно записывать системы линейных уравнений.

Обычно матрицу обозначают заглавной буквой латинского алфавита и выделяют круглыми скобками «(…)» (встречается также выделение квадратными скобками «[…]», двойными прямыми линиями «||…||»).

Числа, составляющие матрицу (элементы матрицы), часто обозначают той же буквой, что и саму матрицу, но строчной.

У каждого элемента матрицы есть 2 нижних индекса (a_ij) — первый «i» обозначает номер строки, в которой находится элемент, а второй «j» — номер столбца. Говорят «матрица размерности », подразумевая, что в матрице m строк и n столбцов.

Содержание

1 История
2 Матрица как запись коэффициентов системы линейных уравнений
3 Операции над матрицами
4 Квадратная матрица и смежные определения
5 Свойства матриц
6 Элементарные преобразования матриц
7 Типы матриц
8 Матрица линейного оператора
9 См. также
10 Литература
11 Ссылки

История

Понятие матрицы впервые появилось в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу.

Матрица как запись коэффициентов системы линейных уравнений

Систему из m уравнений с n неизвестными

можно представить в матричном виде

и тогда всю систему можно записать так:

AX = B,

где A имеет смысл таблицы коэффициентов a_i

j системы уравнений.

Если m = n и матрица A невырожденная, то решение этого уравнения состоит в нахождении обратной матрицы A ^{— 1}, поскольку умножив обе части уравнения на эту матрицу слева

A ^{— 1}AX = A ^{— 1}B

A ^{− 1}A — превращается в E (единичную матрицу). И это даёт возможность получить столбец корней уравнений

X = A ^{— 1}B.

Все правила, по которым проводятся операции над матрицами выводятся из операций над системами уравнений.

Операции над матрицами

Пусть a_ij — элементы матрицы A, а b_ij — элементы матрицы B.

Линейные операции:

Умножение матрицы A на число

λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен

b_ij = λa_ij

Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен

c_ij = a_ij + b_ij

Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой

c_ij = a_ij — b_ij

Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть

A + Θ = A

Все элементы нулевой матрицы равны нулю.

Нелинейные операции:

Умножение матриц (обозначение: AB, реже со знаком умножения ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

c_ij =	∑	a_ikb_kj
	k

В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность , B — , то размерность их произведения

AB = C есть . Умножение матриц не коммутативно.

Умножение матриц ассоциативно. Возводить в степень можно только квадратные матрицы.

Транспонирование матрицы (обозначение: A^T) — операция, при которой матрица отражается относительно главной диагонали, то есть

Если A — матрица размера , то A^T — матрица размера

Квадратная матрица и смежные определения

Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.

Для квадратных матриц существует единичная матрица E (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно

EA = AE = A

У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю

Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица A ^{— 1} такова, что если умножить матрицу на неё, то получится единичная матрица:

AA ^{− 1} = E

Обратная матрица существует не всегда. Матрицы, для которых обратная существует, называются невырожденными (или регулярными), а для которых нет — вырожденными (или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности на столбцах матрицы. Квадратная матрица над числовым полем вырождена тогда и только тогда, когда ее определитель равен нулю.

Свойства матриц

A + (B + C) = (A + B) + C
A + B = B + A
A(BC) = (AB)C
A(B + C) = AB + AC
(B + C)A = BA + CA
(A^T)^T = A
(A * B)^T = B^T * A^T

Элементарные преобразования матриц

Основная статья: Элементарные преобразования матрицы

Элементарными преобразованиями строк матрицы называются следующие преобразования:

Умножение строки на число отличное от нуля
Прибавление одной строки к другой строке

Элементарные преобразование столбцов матрицы определяются аналогично.

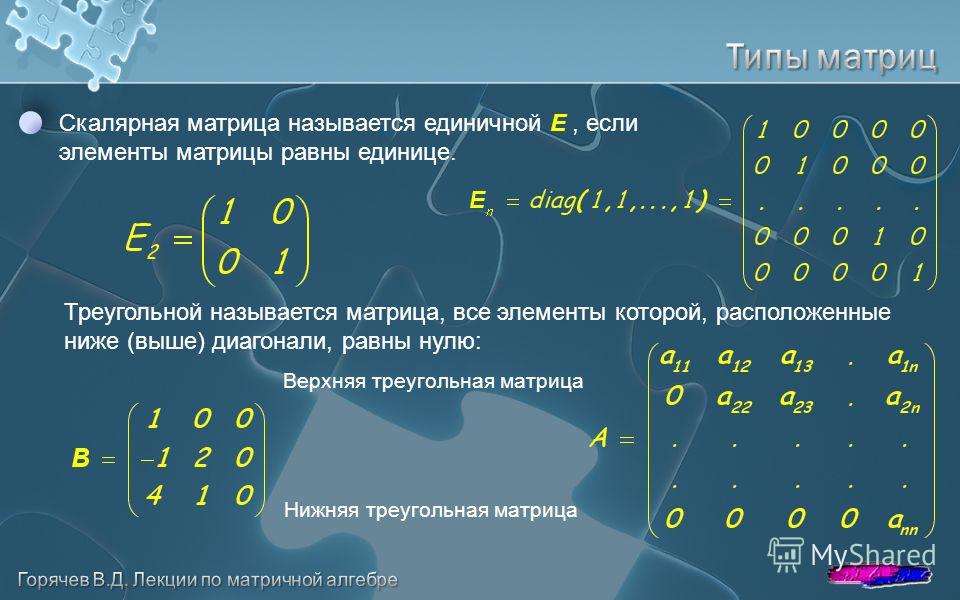
Типы матриц

Антиперестановочная: AB = − BA
Единичная
Блочно-диагональная
Ганкелева
Верхнетреугольная
Вырожденная
Диагональная
- Трёхдиагональная
Заполненная — в вычислительной математике матрица, которая практически не содержит нулей. Такую матрицу приходится хранить в памяти целиком. Антоним: разреженная.
Квадратной называют матрицу, количество строк в которой равно количеству столбцов. Для квадратных матриц существует определитель.
Кососимметрическая
Нижнетреугольная
Нормальная
Нулевая
Ортогональная
Перестановочная: AB = BA
Разреженная — в вычислительной математике матрица, содержащая много нулей. Организовав подходящую структуру данных, вычисления с разреженными матрицами можно проводить очень быстро. Частные случаи: диагональная, трёхдиагональная, жорданова. Антоним: заполненная.
Симметричная
1. Симметричная матрица A положительно определена (A > 0), если значения у всех ее главных угловых миноров A_k > 0
2. Симметричная матрица A отрицательно определена (A < 0), если матрица ( − A) положительно определена, то есть если для любого k главный минор k-го порядка A_k имеет знак ( − 1)^k
Теплицева
Треугольная
Эрмитова
Циркулянт
Унитарная
Унимодулярная

Матрица линейного оператора

Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать оператором на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы.

Матрица оператора аналогична координатам вектора. При этом действие оператора на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.

Выберем базис . Пусть — произвольный вектор. Тогда его можно разложить по этому базису:

где x^k — координаты вектора в выбранном базисе.

Здесь и далее предполагается суммирование по немым индексам.

Пусть — произвольный линейный оператор. Подействуем им на обе стороны предыдущего равенства, получим

Вектора также разложим в выбранном базисе, получим

где — j-я координата k-го вектора из .

Подставим разложение в предыдущую формулу, получим

Выражение , заключённое в скобки, есть ни что иное, как формула умножения матрицы на столбец, и, таким образом, матрица при умножении на столбец x^k даёт в результате координаты вектора , возникшего от действия оператора на вектор , что и требовалось получить.

См. также

Норма матрицы
Определитель матрицы
Массив — тип данных в программировании, соответствующий многомерной матрице.
Разрежённый массив — компьютерная форма представления матриц со множеством нулей.
Линейные матричные неравенства — аппарат для решения задач синтеза законов управления.

Литература

Дж. Голуб, Ч.Ван Лоун Матричные вычисления. — М.: Мир, 1999 (djvu).
Беллман Р. Введение в теорию матриц. — М.: Мир, 1969 (djvu).
Гантмахер Ф. Р. Теория матриц (2-е издание). — М.: Наука, 1966 (djvu).
Ланкастер П. Теория матриц. — М.: Наука, 1973 (djvu).
Соколов Н. П. Пространственные матрицы и их приложения. — М.: ГИФМЛ, 1960 (djvu).

Ссылки

Операции над матрицами онлайн

Как перемножать матрицы в экселе

Одной из частых операций, которую выполняют при работе с матрицами, является перемножение одной из них на другую. Программа Excel является мощным табличным процессором, который предназначен, в том числе и для работы над матрицами. Поэтому у него имеются инструменты, которые позволяют перемножить их между собой. Давайте узнаем, как это можно выполнить различными способами.

Процедура перемножения матриц

Сразу нужно сказать, что перемножить между собой можно далеко не все матрицы, а только те, которые соответствуют определенному условию: число столбцов одной матрицы должно быть равным числу строк другой и наоборот. Кроме того, исключается наличие в составе матриц пустых элементов. В этом случае тоже выполнить требуемую операцию не получится.

Способов перемножить матрицы в Экселе все-таки не так уж и много — всего два. И оба они связаны с применением встроенных функций Excel. Разберем в деталях каждый из данных вариантов.

Способ 1: функция МУМНОЖ

Наиболее простым и популярным вариантом среди пользователей является применение функции МУМНОЖ. Оператор МУМНОЖ относится к математической группе функций. Как раз его непосредственной задачей и является нахождение произведения двух матричных массивов. Синтаксис МУМНОЖ имеет такой вид:

Таким образом этот оператор имеет два аргумента, которые представляют собой ссылки на диапазоны двух перемножаемых матриц.

Теперь давайте посмотрим, как используется функция МУМНОЖ на конкретном примере. Имеется две матрицы, число строк одной из которых, соответствует количеству столбцов в другой и наоборот. Нам нужно перемножить два этих элемента.

«Вставить функцию»

Активируется Мастер функций. Перемещаемся в блок «Математические», кликаем по наименованию «МУМНОЖ» и клацаем по кнопке «OK» в нижней части окна.

После того, как оба аргумента внесены, не спешим жать на кнопку «OK», так как мы имеем дело с функцией массива, а это значит, что для получения корректного результата обычный вариант завершения работы с оператором не подойдет. Данный оператор предназначен не для того, чтобы выводить результат в одну ячейку, так как выводит его в целый диапазон на листе. Итак, вместо нажатия кнопки «OK» жмем комбинацию кнопок Ctrl+Shift+Enter.

Как видим, после этого предварительно выделенный диапазон был заполнен данными. Это и есть результат умножения матричных массивов. Если взглянуть на строку формул, после выделения любого из элементов данного диапазона, то мы увидим, что сама формула обернута в фигурные скобки. Это и есть признак функции массива, который добавляется после нажатия сочетания клавиш Ctrl+Shift+Enter перед выводом результат на лист.

Способ 2: использование составной формулы

Кроме того, существует ещё один способ умножения двух матриц. Он более сложный, чем предыдущий, но тоже заслуживает упоминания, как альтернативный вариант. Данный способ предполагает использование составной формулы массива, которая будет состоять из функции СУММПРОИЗВ и вложенного в неё в качестве аргумента оператора ТРАНСП.

«Вставить функцию»

Мастер функций запускается. Перемещаемся в блок операторов «Математические», но на этот раз выбираем наименование СУММПРОИЗВ. Клацаем по кнопке «OK».

Происходит открытие окна аргументов вышеуказанной функции. Данный оператор предназначен для перемножения различных массивов между собой. Его синтаксис следующий:

В качестве аргументов из группы «Массив» используется ссылка на конкретный диапазон, который нужно перемножить. Всего может быть использовано от двух до 255 таких аргументов. Но в нашем случае, так как мы имеем дело с двумя матрицами, нам понадобится как раз два аргумента.

Ставим курсор в поле «Массив1». Тут нам нужно будет ввести адрес первой строки первой матрицы. Для этого, зажав левую кнопку мыши, нужно просто выделить её на листе курсором. Тут же координаты данного диапазона будут отображены в соответствующем поле окна аргументов. После этого следует зафиксировать координаты полученной ссылки по столбцам, то есть, эти координаты нужно сделать абсолютными. Для этого перед буквами в выражении, которое вписано в поле, устанавливаем знак доллара ($). Перед координатами, отображенными в цифрах (строки), это делать не следует. Также, можно вместо этого выделить всё выражение в поле и трижды нажать на функциональную клавишу F4. В данном случае абсолютными тоже станут лишь координаты столбцов.

После этого устанавливаем курсор в поле «Массив2». С этим аргументом будет посложнее, так как по правилам умножения матриц, вторую матрицу нужно «перевернуть». Для этого используем вложенную функцию ТРАНСП.

Чтобы перейти к ней, клацаем по значку в виде треугольника, направленного острым углом вниз, который размещен слева от строки формул. Открывается список недавно используемых формул. Если вы в нем найдете наименование «ТРАНСП», то щелкайте по нему. Если же вы давно использовали данный оператор или вообще никогда не применяли его, то в этом списке указанное наименование вы не отыщите. В этом случае требуется нажать по пункту «Другие функции…».

Открывается уже хорошо знакомое нам окно Мастера функций. На этот раз перемещаемся в категорию «Ссылки и массивы» и выбираем наименование «ТРАНСП». Щелкаем по кнопке «OK».

Производится запуск окна аргументов функции ТРАНСП. Данный оператор предназначен для транспонирования таблиц. То есть, попросту говоря, он меняет местами столбцы и строки. Это нам и нужно сделать для второго аргумента оператора СУММПРОИЗВ. Синтаксис функции ТРАНСП предельно простой:

То есть, единственным аргументом данного оператора является ссылка на тот массив, который следует «перевернуть». Вернее, в нашем случае даже не на весь массив, а только на его первый столбец.

Итак, устанавливаем курсор в поле «Массив» и выделяем первый столбец второй матрицы на листе с зажатой левой кнопкой мыши. Адрес отобразится в поле. Как и в предыдущем случае, тут тоже нужно сделать определенные координаты абсолютными, но на этот раз не координаты столбцов, а адреса строк. Поэтому ставим знак доллара перед цифрами в ссылке, которая отображается в поле. Можно также выделить всё выражение и дважды кликнуть по клавише F4. После того, как нужные элементы стали иметь абсолютные свойства, не жмем на кнопку «OK», а так же, как и в предыдущем способе, применяем нажатие комбинации клавиш Ctrl+Shift+Enter.

Но на этот раз у нас заполнился не массив, а только одна ячейка, которую мы ранее выделили при вызове Мастера функций.

Нам нужно заполнить данными такой же по размеру массив, как и в первом способе. Для этого следует скопировать формулу, полученную в ячейке, на равнозначный диапазон, который будет равен количеству строк первой матрицы и количеству столбцов второй. В конкретно нашем случае получается три строки и три столбца.

Для копирования прибегнем к использованию маркера заполнения. Наводим курсор на нижний правый угол ячейки, в которой расположена формула. Курсор преобразуется в черный крестик. Это и есть маркер заполнения. Зажимаем левую кнопку мыши и протягиваем курсор по всему вышеуказанному диапазону. Сама начальная ячейка с формулой должна стать левым верхним элементом данного массива.

Как видим, выделенный диапазон заполнен данными. Если их сравнить с тем результатом, который мы получили благодаря применению оператора МУМНОЖ, то увидим, что значения полностью идентичны. Это означает, что умножение двух матриц выполнено верно.

Как видим, несмотря на то, что был получен равнозначный результат, использовать функцию для умножения матриц МУМНОЖ значительно проще, чем применять для этих же целей составную формулу из операторов СУММПРОИЗВ и ТРАНСП. Но все-таки данный альтернативный вариант тоже нельзя оставить без внимания при изучении всех возможностей перемножения матриц в Microsoft Excel.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Функционал программы Microsoft Excel позволяет рассчитывать сложные математические операции. В том числе и перемножение матриц. Сделать это можно произведя несколько шагов.

Как пример возьмёт матрицу :

Для начала элементы матриц запишем в ячейки и оставим курсор там где в конце должен появиться результат.

После этого выбираем в основном меню раздел «Формулы», в нем нажимаем «Математические» и в списке кликаем на пункт «МУМНОЖ».

Откроется специальное окно. В нём нужно ввести адреса ячеек наиболее удобным для себя способом в поля «Массив1» и «Массив 2». В них нужно ввести координаты элементов матриц.

После подтверждения действия в рабочем окне можно увидеть результат в обычном матричном виде и выделяем два столбца и две строки.

Далее на клавиатуре нажимаем клавишу F2 и одновременно нажимаем комбинацию клавиш Ctrl+Shift+Enter. После этого будет показан полный результат перемножения матриц.

Программа Microsoft Office Excel позволяет выполнять операции с матрицами с помощью встроенных функций и формул. Рассмотрим основные операции над матрицами:

умножение и деление матрицы на число;
сложение, вычитание и умножение матриц;
транспонирование матрицы;
нахождение обратной матрицы;
вычисление определителя.

Введем условные обозначения. Матрица А размерностью i x j — это прямоугольная таблица чисел, состоящая из i строк и j столбцов, а_ij — элемент матрицы.

Умножение и деление матрицы на число в Excel

Способ 1

Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.

Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а₁₁ матрицы А.

Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.

С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.

Таким образом, мы умножили матрицу А в Excel и получим матрицу В.

Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.

Способ 2

Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.

Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/h5, т.е. знак «*» меняем на «/».

Сложение и вычитание матриц в Excel

Способ 1

Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т. е. с_ij = а_ij + b_ij.

Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+h4, где B3 и h4 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.

С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.

Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — h4 и скопируем её на весь диапазон матрицы С.

Способ 2

Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.

Умножение матриц в Excel

Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.

Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.

Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.

В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.

В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.

Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.

Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.

Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.

В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.

Мы получим результат умножения матриц А и В.

Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.

Транспонирование матрицы в Excel

Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т .

Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3.

Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.

На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.

В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А Т .

Нажмите для увеличения

Мы получили транспонированную матрицу.

Нахождение обратной матрицы в Excel

Матрица А -1 называется обратной для матрицы А, если АА -1 =А -1 А=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).

Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().

Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.

В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.

В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А -1 .

Нажмите для увеличения

Мы получили обратную матрицу.

Нахождение определителя матрицы в Excel

Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.

Как найти определить матрицы в Excel

Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().

Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.

В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.

В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.

Нажмите для увеличения

Мы вычислили определитель матрицы А.

В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.

Нажмите для увеличения

Мы можем удалить только все элементы этой матрицы.

Видеоурок

Кратко об авторе:

Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Есть мнение?
Оставьте комментарий

Понравился материал?
Хотите прочитать позже?
Сохраните на своей стене и
поделитесь с друзьями

Вы можете разместить на своём сайте анонс статьи со ссылкой на её полный текст

2.2. Умножение матрицы на число

Матрицу любой размерности можно умножить на число . Это значит – умножить на число все элементы матрицы: , т.е.

если , то .

Примеры выполнения заданий:

Задача 1. Даны матрицы: .

Выполните действия: .

Решение:

;

Ответ: .

Задача 2. Найдите значение линейной комбинации матриц .

Решение:

Ответ: .

Для самостоятельного решения:

Найдите линейные комбинации заданных матриц:

1) .

2) .

3) .

2.3. Умножение матриц

Матрицу A можно умножить на матрицу B только в том случае, когда число столбцов матрицы A равно числу строк матрицы B.

В результате умножения получится матрица C, у которой столько же строк, сколько их в матрице A, и столько же столбцов, сколько их в матрице B, а элементы матрицы C вычисляются по формуле: .

Другими словами: для получения элемента , расположенного в i-ой строке и j-ом столбце матрицы C надо элементы i-ой строки матрицы A умножить на соответствующие элементы j-го столбца матрицы B и полученные произведения сложить.

Алгоритм вычисления произведения матрицы на матрицу :

1) Проверить, совпадает ли число столбцов матрицы с числом строк матрицы , («согласованы» ли порядки множителей). Только в этом случае можно умножить A на B. В противном случае вычислить C нельзя.

2) Определить порядок матрицы произведения: имеет порядок , где m – число строк первого множителя A, k – число столбцов второго множителя B.

3) Вычислить каждый элемент матрицы произведения C по формулам:

4) Выписать полученную матрицу C.

Примеры выполнения заданий:

Задача 1. Найдите произведение матриц , если .

Решение:

1. Проверим, совпадает ли число столбцов матрицы А с числом строк матрицы B – совпадают, порядки множителей «согласованы».

2. Определим порядок матрицы произведения: имеет порядок , где 2 – число строк первого множителя A, 2 – число столбцов второго множителя B.

3. Вычислим каждый элемент матрицы произведения C по формулам:

4. Выписать полученную матрицу C.

Ответ: .

Задача 2. Пусть . Найдите произведения и (если это возможно).

Решение:

Произведение не существует, так как число столбцов матрицы B не совпадает с числом строк матрицы .

Задача 3. Найдите произведение матриц , если ;

Решение:

Ответ: .

Задача 4. Найдите произведение матриц , если .

Решение: .

Ответ: 2.

Задача 5. Найдите произведение матриц , если .

Решение:

Ответ: .

Задача 6. Найдите произведение матриц , если .

Решение:

Ответ: .

Задача 7. Найдите произведение матриц , если

Решение:

Ответ: .

Задача 8. Найдите произведение матриц , если

Решение:

Ответ: .

Для самостоятельного решения:

Даны матрицы .

Найти и . Докажите, что .

Свойства операции умножения матриц

1. Умножение матриц не коммутативно, т.е. , даже если определены оба произведения. Однако если для каких-либо матриц соотношение выполняется, то такие матрицы называются еще перестановочными.

Самым характерным примером может служить единичная матрица E, которая является перестановочной с любой другой матрицей того же размера. Перестановочными могут быть только квадратные матрицы одного и того же порядка . Очевидно, что для любых матриц выполняется следующее свойство: , где O – нулевая матрица.

2. Операция перемножения матриц ассоциативна, т.е. если определены произведения и , то определены и , и выполняется равенство: .

3. Операция умножения матриц дистрибутивна по отношению к сложению, т. е. если имеют смысл выражения и , то соответственно:

4. Если произведение определено, то для любого числа k верно соотношение: .

Замечание 1.1. Произведение матриц определено только в том случае, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведение матриц содержит столько строк, сколько имеет первая матрица, и столько столбцов, сколько имеет вторая матрица.

Замечание 1.2. В общем случае , даже если оба произведения матриц, и , определены. Матрицы, для которых выполняется условие , называются коммутативными.

5. Как и умножение чисел, произведение матриц подчиняется сочетательному закону: .

Для самостоятельного решения:

Проверьте, коммутируют ли матрицы

1. ; 2. ;

3. ; 4. .

Умножение матриц NumPy: начните за 5 минут

NumPy — популярная библиотека Python, которая предлагает ряд мощных математических функций. Библиотека широко используется в количественных областях, таких как наука о данных, машинное обучение и глубокое обучение. Мы можем использовать NumPy для выполнения сложных математических вычислений, таких как умножение матриц.

Умножение матриц может помочь нам быстро приблизиться к очень сложным вычислениям. Он может помочь нам в теории сетей, линейных системах уравнений, моделировании населения и многом другом. В этом руководстве мы рассмотрим некоторые основные вычисления с умножением матриц NumPy.

Содержание

Что такое NumPy?
Установка и импорт NumPy
Что такое матрица NumPy?
Методы умножения матриц NumPy
Скалярное умножение или скалярное произведение с numpy.dot
Матричный продукт с numpy.matmul
Поэлементное умножение матриц с помощью numpy.multiply
Подведение итогов и следующие шаги

Что такое NumPy?

NumPy — это библиотека Python с открытым исходным кодом, которую мы можем использовать для выполнения высокоуровневых математических операций с массивами, матрицами, линейной алгеброй, анализом Фурье и т. Д. Библиотека NumPy очень популярна в научных вычислениях, науках о данных и машинном обучении. NumPy совместим с популярными библиотеками данных, такими как pandas, matplotlib и Scikit-learn. Это намного быстрее, чем списки Python, потому что он объединяет более быстрые коды, такие как C и C ++, в Python. Он также разбивает наши задачи на несколько частей и обрабатывает каждую часть одновременно.

Установка и импорт NumPy

Прежде чем мы начнем, убедитесь, что у нас установлен NumPy. Если у вас уже есть Python, вы можете установить NumPy с помощью одной из следующих команд:

conda install numpy

или

pip install numpy

Чтобы импортировать NumPy в наш код Python, мы можем использовать следующую команду:

import numpy as np

Что такое матрица NumPy?

Матрица — это двумерный массив. Каждый элемент в массиве имеет два индекса. Давайте посмотрим на пример в NumPy:

import numpy as np
A = [[6, 7],
[8, 9]]
print(np. array(A) [0,0])

В приведенном выше коде, мы имеем матрицу A [[6, 7], [8, 9]]. Мы запрашиваем элемент, указанный в (0,0), и наш результат возвращается 6. Когда мы хотим определить форму нашей матрицы, мы используем количество строк по количеству столбцов. Это означает, что матрица A имеет форму 2×2.

Теперь давайте взглянем на несколько различных методов умножения матриц NumPy.

Методы умножения матриц NumPy

Есть три основных способа выполнить умножение матрицы NumPy:

np.dot(array a, array b): возвращает скалярное произведение или скалярное произведение двух массивов
np.matmul(array a, array b): возвращает матричное произведение двух массивов
np.multiply(array a, array b): возвращает поэлементное матричное умножение двух массивов

Давайте подробнее рассмотрим каждый из трех методов:

Скалярное умножение или скалярное произведение с numpy.dot

Скалярное умножение — это простая форма умножения матриц, это просто число, как 1, 2или 3. При скалярном умножении мы умножаем скаляр на матрицу. Каждый элемент в матрице умножается на скаляр, в результате чего выходные данные имеют ту же форму, что и исходная матрица.

При скалярном умножении порядок не имеет значения. Мы получим один и тот же результат независимо от того, умножаем ли мы скаляр на матрицу или матрицу на скаляр.

Давайте посмотрим на пример:

import numpy as np
A = 5
B = [[6, 7],
[8, 9]]
print(np.dot(A,B))

Теперь давайте умножим двумерную матрицу на другую двумерную матрицу. При умножении двух матриц порядок имеет значение. Это означает, что матрица A, умноженная на матрицу B, не то же самое, что матрица B, умноженная на матрицу A.

Прежде чем мы начнем, давайте посмотрим на визуальное представление того, как выполняется умножение.

import numpy as np
A = [[6, 7],
[8, 9]]
B = [[1, 3],
[5, 7]]
print(np.dot(A,B))
print(«———-«)
print(np. dot(B,A))

Примечание. Важно отметить, что мы можем перемножить две матрицы только в том случае, если количество столбцов в первой матрице равно количеству строк во второй матрице.

Матричный продукт с numpy.matmul

matmul()Функция дает нам матрицу произведение двух 2-й массивов. С помощью этого метода мы не можем использовать скалярные значения для нашего ввода. Если один из наших аргументов представляет собой одномерный массив, функция преобразует его в матрицу, добавляя 1 к его измерению. Он удаляется после завершения умножения.

Если один из наших аргументов больше 2-d, функция рассматривает его как стек матриц в последних двух индексах. Этот matmul()метод отлично подходит для случаев, когда мы не уверены в размерах наших матриц.

Давайте посмотрим на несколько примеров:

Умножение двумерного массива на другой двумерный массив

import numpy as np
A = [[2, 4],
[6, 8]]
B = [[1, 3],
[5, 7]]
print(np. matmul(A,B))

Умножение двумерного массива на одномерный массив

import numpy as np
A = [[5, 0],
[0, 5]]
B = [5, 2]
print(np.matmul(A,B))

Один массив с размерами больше 2-х

import numpy as np
A = np.arange(8).reshape(2, 2, 2)
B = np.arange(4).reshape(2, 2)
print(np.matmul(A,B))

Поэлементное умножение матриц с помощью numpy.multiply

numpy.multiply()Метод принимает две матрицы в качестве входных данных и выполняет поэлементное умножение на них. Поэлементное умножение, или произведение Адамара, умножает каждый элемент первой матрицы на эквивалентный элемент во второй матрице. При использовании этого метода обе матрицы должны иметь одинаковые размеры.

Давайте посмотрим на пример:

import numpy as np
A = np.array([[1, 3, 5, 7, 9], [2, 4, 6, 8, 10]])
B = np.array([[1, 2, 3, 4, 5], [5, 4, 3, 2, 1]])
print(np. multiply(A,B))

Мы можем передать в numpy.multiply()метод определенные строки, столбцы или подматрицы. Размеры строк, столбцов или подматриц, которые мы передаем в качестве наших операндов, должны быть одинаковыми. Давайте посмотрим на пример:

import numpy as np
A = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]])
B = np.array([[11, 12, 13, 14, 15], [16, 17, 18, 19, 20]])
print(np.multiply(A[ 0,:], B[ 1,: ]))
print(«———-«)
print(np.multiply(A[ 1,:], B[ 0,:]))

Подведение итогов и следующие шаги

Поздравляем с вашими первыми шагами в умножении матриц NumPy! Это сложная, но важная часть линейной алгебры. Это помогает нам лучше понять различные аспекты науки о данных, машинного обучения, глубокого обучения и других распространенных областей. Еще многое предстоит узнать о NumPy и матрицах. Вот некоторые рекомендуемые темы для обсуждения:

Транспонирование матрицы NumPy
Массивы NumPy (ndarray)
NumPy векторизация

Умножение матриц — 2×2, 3×3

Умножение матриц или умножение матриц — одна из операций, которые можно выполнять над матрицами в линейной алгебре. Умножение матрицы A на матрицу B возможно, когда обе заданные матрицы A и B совместимы. Умножение матриц — это бинарная операция, которая дает матрицу из двух заданных матриц.

Умножение матриц было впервые введено в 1812 году французским математиком Жаком Филиппом Мари Бине для представления линейных карт с использованием матриц. Давайте разберемся с правилом умножения матриц в следующих разделах.

1.	Что такое умножение матриц?
2.	Как умножать матрицы?
3.	Правила умножения матриц
4.	Формула умножения матриц 2×2
5.	Формула умножения матриц 3×3
6.	Свойства умножения матриц
7.	Часто задаваемые вопросы по умножению матриц

Что такое умножение матриц?

Умножение матриц — это бинарная операция, результатом которой также является матрица при умножении двух матриц. В линейной алгебре умножение матриц возможно только тогда, когда матрицы совместимы. В общем случае умножение матриц, в отличие от арифметического, не является коммутативным, а это означает, что умножение матриц A и B, заданных как AB, не может быть равно BA, т. е. AB ≠ BA. Поэтому порядок умножения для умножения матриц важен.

Две матрицы A и B называются совместимыми, если количество столбцов в A равно количеству строк в B. Это означает, что если A — матрица порядка m×n, а B — матрица порядка n× p, то можно сказать, что матрицы A и B совместимы.

Предположим, у нас есть две матрицы A и B, произведение матрицы A на матрицу B можно представить как (AB). Это означает, что результирующая матрица для умножения любой матрицы m × n «A» на матрицу «B» размера n × p может быть представлена как матрица «C» порядка m × p. Давайте разберемся с этой концепцией подробно в следующем разделе.

Как умножать матрицы?

Мы можем понять общий процесс умножения матриц с помощью метода: «Первые строки умножаются на столбцы (элемент за элементом), а затем строки заполняются. Умножение матриц можно выполнить, используя следующие шаги:

Шаг 1: Убедитесь, что количество столбцов в матрице 1 ^st равно количеству строк в матрице 2 ^nd (совместимость матриц).
Шаг 2: Умножьте элементы строки i ^th первой матрицы на элементы столбца j ^th второй матрицы и сложите произведения. Это будет элемент, который находится в i ^-й-й строке и j ^-м-м столбце результирующей матрицы.
Шаг 3: Разместите добавленные товары на соответствующих позициях.

Давайте лучше разберемся с этими шагами умножения матриц на примере.

Пример: Умножьте приведенные ниже матрицы, чтобы найти их произведение $ \begin{pmatrix}
1 и 2 \
3 и 4 \ 5 и 1 \
\end{pmatrix} \text{and}\begin{pmatrix}
2\\
4\
\end{pmatrix}
$.

Решение: Данные матрицы имеют порядок 3×2 и 2×1 . Таким образом, t заданные матрицы совместимы, мы можем выполнить умножение матриц, и матрица произведения будет иметь порядок 3×1.

$\begin{pmatrix}
1 и 2 \
3 и 4 \ 5 и 1 \
\end{pmatrix}.\begin{pmatrix}
2\\
4\
\end{pmatrix}\\\\
= \begin{pmatrix}
(1\times2)+(2\times4) \\
(3\times2)+(4\times4) \\ (5\times2)+(1\times4) \\
\end{pmatrix} \\\\ = \begin{pmatrix}
2+8 \\
6+16\10+4\
\end{pmatrix}
\\\\
= \begin{pmatrix}
10\
22\14\
\end{pmatrix}$

Следовательно, матрица произведения равна $\begin{pmatrix}
10\
22\14\
\end{pmatrix}
$

В результирующей матрице видно, что первый элемент первой строки получается умножением элементов первой строки первой матрицы на соответствующие элементы первого столбца второй матрицы и последующим сложением. т. е., вообще говоря, найти элемент в i ^-я-я строка и j ^-й-й столбец в матрице произведения,

Возьмите элементы i ^-й-й строки первой матрицы.
Возьмем элементы j ^-го-го столбца второй матрицы.
Умножьте соответствующие элементы.
Добавить все продукты.

Правила умножения матриц

Как мы изучили, две матрицы можно перемножать только тогда, когда они совместимы, а это означает, что для существования умножения матриц количество столбцов в первой матрице должно быть равно количеству строк во второй матрице, в приведенном выше случай ‘н’. Если A — матрица порядка m×n, а B — матрица порядка n×p, то порядок произведения матриц равен m×p.

Примеры:

а) Умножение матрицы 4 × 3 на матрицу 3 × 4 верно и дает матрицу порядка 4 × 4

б) Матрица 7 × 1 и матрицы 1 × 2 совместимый; произведение дает матрицу 7 × 2.

c) Умножение матрицы 4 × 3 на матрицу 2 × 3 НЕВОЗМОЖНО.

Формула умножения матриц 2×2

Процесс одинаков для матрицы любого порядка. Умножаем элементы каждой строки первой матрицы на элементы каждого столбца второй матрицы (поэлементно), как показано на рисунке. Наконец, мы добавляем продукты. Результатом произведения двух матриц 2×2 снова является матрица 2×2.

Формула умножения матриц 3×3

Матрица 3×3 Умножение можно выполнить с помощью формулы умножения матриц, так как любые две матрицы 3×3 совместимы. Процесс точно такой же для матрицы любого порядка. Результатом произведения двух матриц 3×3 снова является матрица 3×3.

Здесь матрицы имеют одинаковые размеры, поэтому результирующая матрица также имеет одинаковую размерность 3×3.

Пример:

$\left(\begin{array}{rrr}
1&2&-1\
3 & 2 & 0 \
-4 и 0 и 2
\end{массив}\right)$ $\left(\begin{массив}{rrr}
3 и 4 и 2 \
0&1&0\
-2 и 0 и 1
\end{массив}\right)$

= $\left(\begin{массив}{rrr}
1(3)+2(0)+(-1)(-2) и 1(4)+2(1)+(-1)0 и 1(2)+2(0)+(-1)( 1)\
3(3)+2(0)+(0)(-2) и 3(4)+2(1)+(0)0 и 3(2)+2(0)+(0)(1) \ \
-4(3)+0(0)+(2)(-2) и -4(4)+0(1)+(2)0 и -4(2)+0(0)+(2)( 1)\
\end{массив}\right)$

= $\left(\begin{массив}{rrr}
5 и 6 и 1 \
9 и 14 и 6 \
-16&-16&-6\
\конец{массив}\справа)$

Свойства умножения матриц

Существуют определенные свойства операции умножения матриц в линейной алгебре в математике. Эти свойства приведены ниже,

Некоммутативный: Умножение матриц является некоммутативным, т. е. для умножения двух матриц A и B AB ≠ BA.
Дистрибутивность: Свойство дистрибутивности можно применять при перемножении матриц, т. е. A(B + C) = AB + BC, учитывая, что A, B и C совместимы.
Произведение со скаляром: Если произведение матриц A и B, AB определено, то c(AB) = (cA)B = A(Bc), так что c является скаляром.
Транспонирование: Транспонирование произведения матриц A и B может быть задано как (AB) ^T = B ^T A ^T , где ^T обозначает транспонирование.
Комплексное сопряжение: Если A и B являются комплексными элементами, то (AB) ^* = B ^* A ^*
Ассоциативность: Умножение матриц является ассоциативным. Для трех матриц A, B и C, произведения (AB)C и A(BC) определены, тогда (AB)C = A(BC).
Определитель: Определитель произведения матриц есть не что иное, как произведение определителей отдельных матриц. т. е. det (AB) = det A × det B,

Нестандартное мышление:

Используя приведенные ниже матрицы, проверьте, является ли умножение матриц коммутативным или нет.
$ \begin{pmatrix}
1 & 0 \\\
2 и 4 \
\end{pmatrix} \text{and}\begin{pmatrix}
6 и 8 \\\
4 и 3 \
\end{pmatrix}
$
Является ли умножение матриц ассоциативным?

Важные замечания по умножению матриц:

Для умножения матриц данные матрицы должны быть совместимы.
Порядок матрицы произведения можно получить по следующему правилу:
Если A — матрица порядка m×n, а B — матрица порядка n×p, то порядок матрицы произведения равен m×p.
Умножение матриц указывает на умножение строк на столбцы.

☛ Похожие темы:

Калькулятор умножения матриц
Матричный калькулятор
Калькулятор сложения матриц

Часто задаваемые вопросы по умножению матриц

Что такое умножение матриц в линейной алгебре?

Умножение матриц — одна из бинарных операций, которые можно применять к матрицам в линейной алгебре. Чтобы умножить две матрицы A и B, количество столбцов в матрице A должно быть равно количеству строк в матрице B. ⇒AB существует.

Как перемножать матрицы 3×3?

Матрицы 3×3 в математике можно умножать путем умножения строк первой матрицы на столбцы второй матрицы для получения соответствующих элементов матрицы произведения.

Что такое формула умножения матриц?

Формула умножения матриц используется для выполнения умножения матриц в целом. Например, для матриц 3×3 формула выглядит следующим образом:

Можно ли перемножать матрицы порядка 2×3 и 2×2?

Нет, мы не можем умножать матрицы 2×3 и 2×2, потому что для умножая матрицы, две матрицы должны быть совместимы. Поскольку количество столбцов в первой матрице (3) не равно количеству строк во второй матрице (2), мы не можем выполнить умножение матриц для этого случая.

Какова цель умножения матриц?

Умножение матриц важно для облегчения вычислений в линейной алгебре и используется для представления линейных карт. Это важный инструмент во многих областях математики, а также в прикладной математике, статистике, физике, экономике и технике.

Чему равно произведение матриц порядков 2×1 и 2×2?

Нет, их нельзя перемножить, так как эти матрицы несовместимы. Количество столбцов первой матрицы не равно количеству строк второй матрицы.

Когда возможно умножение матриц?

Умножение матриц возможно, только если матрицы совместимы, т. е. умножение матриц допустимо только в том случае, если количество столбцов первой матрицы равно количеству строк второй матрицы.

Всегда ли умножение матриц является коммутативным?

Умножение матриц, в отличие от арифметического умножения, не является коммутативным. Это означает, что порядок умножения матриц имеет значение.

Всегда ли определено умножение матриц?

Умножение матриц возможно только в том случае, если матрицы совместимы. Чтобы существовало умножение матриц, количество столбцов в первой матрице должно быть равно количеству строк во второй матрице

Умножение матриц — ChiliMath

Поиск

Умножение матриц — это «беспорядочный тип», потому что вам нужно будет выполнить определенный набор процедур, чтобы сделать это правильно. Это «грязный тип», потому что процесс более сложный. Однако позже, после прохождения процедуры и некоторых примеров, вы поймете, что необходимые шаги выполнимы. Не волнуйся, я помогу тебе в этом!

Но сначала нам нужно убедиться, что две матрицы «разрешено» перемножать. В противном случае данные две матрицы «несовместимы» для перемножения. В этом случае говорят, что решение не определено.

Всегда помните об этом!

Чтобы умножение матриц работало, количество столбцов левой матрицы ДОЛЖНО РАВНО количеству строк правой матрицы.

Предположим, нам даны матрицы A и B, найдите AB (выполните умножение матриц, если применимо). Определите, какая из них является левой и правой матрицами, исходя из их расположения. Это очень важный шаг.

Чтобы определить, могу ли я умножить две заданные матрицы, мне нужно обратить внимание на количество столбцов матрицы A и количество строк матрицы B. Если они равны, то я могу приступить к умножению матриц. В противном случае я сделаю вывод, что ответ не определен!

Поскольку матрица A имеет количество столбцов 2 , а матрица B имеет количество строк 3 , и они не равны (2 ≠ 3) , я заключаю, что AB = undefined . Это означает, что их продукт не может быть найден.

Примеры умножения матриц, также известного как «беспорядочный тип»

Указания : Имея следующие матрицы, выполните указанную операцию.

Пример 1 : Рассчитайте, если возможно, произведение В и Е.

Чтобы матрицы B и E имели произведение, количество столбцов левой матрицы B должно равняться количеству строк правой матрицы E.

Матрица B (левая) столбцы = 3
Матрица E (справа)
количество строк = 3
Поскольку это так, то можно перемножить их вместе. Вот шаги:
Шаг 1: Поместите их рядом.
Шаг 2: Умножьте строки B на столбцы E путем умножения соответствующих элементов каждой строки на каждый элемент столбца, а затем сложите их вместе.
Пожалуйста, внимательно посмотрите анимированное решение.
Если у вас не хватает терпения смотреть анимированное решение выше о том, как выполнить умножение матриц, вы можете просмотреть обычное решение, которое я включил ниже.
Пример 2 : Рассчитайте, если возможно, произведение E и F.
Сначала проверьте, существует ли произведение двух матриц, убедившись, что количество столбцов левой матрицы E равно количеству строк правой матрицы F.
Матрица E (левая)
число столбцов = 2
Матрица F (справа)
количество строк = 2
Это замечательно, поскольку количество столбцов матрицы E равно количеству строк матрицы F. Это означает произведение EF определено, поэтому мы можем продолжить и выполнить матричное умножение. Ниже показано анимированное пошаговое решение умножения матриц.
Пример 3 : Рассчитайте, если возможно, произведение F и E.
В нашем предыдущем примере мы успешно получили произведение EF. На этот раз мы хотим выяснить, сможем ли мы найти произведение E[латекс] и [латекс]F в таком порядке.
Напомню, что действительные числа коммутативны при умножении, что означает, что порядок умножения не влияет на конечный продукт. Например…
Таким образом, возникает большой вопрос, работает ли это также при умножении матриц?
Проверим, равно ли количество столбцов матрицы F количеству строк матрицы E.
Матрица F (слева)
количество столбцов = 2
Матрица E (справа) 80
количество строк = 3
Очевидно, что количество столбцов матрицы F не равно количеству строк матрицы E. Отсюда следует, что произведение КЭ не может быть вычислено, а значит, не определено!
В общем случае умножение матриц не является коммутативным.
Пример 4 : Рассчитайте, если возможно, произведение AE.
Стандартный способ описания размера или размерности матрицы:…
(указать количество строк) x (указать количество столбцов)
…читается как «количество строк в Число столбцов».
3 x 3 (матрица три на три)
3 x 2 (матрица три на два)
Так как количество столбцов матрицы A равно количество строк матрицы E , то делаем вывод, что произведение AE определено.
Давайте разберемся. См. анимированное решение ниже.
Пример 5 : Вычислите, если возможно, произведение E и A. количество столбцов матрицы E не равно количеству столбцов матрицы A. Следовательно, произведение EA не может быть вычислено или не определено. 92}. Другими словами, мы возводим в квадрат матрицу C.
Здесь нужно быть осторожным. Обратите внимание, что возвести в квадрат можно только квадратную матрицу. Напомним, что квадратная матрица — это матрица, в которой номер строки равен номеру столбца.
Я предоставляю вам возможность проверить правильность приведенного ниже решения. Для подобных математических задач, хотя и утомительных, я всегда рекомендую решать их вручную с помощью карандаша и бумаги.
Вас также может заинтересовать:
Сложение и вычитание матриц
Скалярное умножение
Скалярное и матричное умножение
Вернуться к Указатель уроков | Делайте уроки в заказе | Подходит для печати страница
Скаляр и умножение матриц (стр. 1 из 3)
Существует два типа умножение матриц: скалярное умножение и умножение матриц. Скалярное умножение легко. Вы просто берете обычный номер (называется «скаляр») и умножить его на каждую запись в матрице.
Для следующей матрицы А , найти 2 А и 1 А .
Сделать первый скаляр умножение, чтобы найти 2 А , я просто умножаю на 2 на каждую запись в матрице:
Другое скалярное умножение, найти 1 A , работает так же:
Итак, окончательный ответ: Авторские права Элизабет Стапель 2003-2011 Все права защищены
Скалярное умножение легкий. Однако умножение матриц — это совсем другая история. Фактически, это королевская боль. Ваш текст, вероятно, дал вам сложную формулу для процесс, и эта формула, вероятно, не имела для вас никакого смысла. Это хорошо. Процесс запутанный, и эта сложная формула — лучшее, что они могут сделать. может подойти для объяснения в формальной обстановке, как учебник. Вот как работает процесс:
Найти продукт AB для следующих матриц:
Для расчета AB , Я записываю А и В рядом друг с другом вот так:
Теперь мне нужно умножить РЯД А КОЛОННАМИ B . Под этим я подразумеваю, что сначала беру первый ряд А и первый столбец B , и я умножаю первые записи, затем вторые записи, а затем третьи записи, а затем я добавляю три продукта. Сумма одна запись в матрице продуктов AB ; на самом деле, будучи продуктом строки 1 и столбец 1, результат — 1,1-вход из АБ . Затем продолжаю в том же духе. Например, сумма произведений со 2 ряда из А и столбец 1 из В 2,1-вход AB .
Когда я перемножаю матрицы, Я использую свои пальцы, чтобы следить за тем, что я делаю. Следующая анимация моя попытка проиллюстрировать этот процесс. (Не смейтесь, я не художник!)
(Ну, класс, что я сделал сказать о смехе?)
Окончательный ответ:
Как вы видели в приведенном выше примере, общее правило состоит в том, что продукт и -го ряд А и j -й колонна B это я ,j -й ввод матрицы продуктов AB . Это общее правило в значительной степени состоит в том, что та сложная формула в весь ваш текст был об этом.
Например, когда я в приведенный выше пример сначала умножил ряд (из А ) и второй столбец (из B ), это дало мне в первом ряду — во втором столбце запись в матрице продуктов AB .
Топ | 1 | 2 | 3 | Вернуться к индексу Далее >>
Процитировать эту статью как:
Стапель, Элизабет. «Скалярное и матричное умножение». Пурпурная математика . Доступно с
https://www.purplemath.com/modules/mtrxmult.htm . Доступ [Дата] [Месяц] 2016

«Домашнее задание
» Руководство»
Опрос по обучению
Репетиторство от Purplemath
Найдите местного репетитора по математике
2.
2: Умножение матриц — Mathematics LibreTexts
Последнее обновление
Сохранить как PDF

Идентификатор страницы
14506

Кен Каттлер
Университет Бригама Янга через Lyryx

Следующей важной операцией с матрицами, которую мы рассмотрим, является умножение матриц. Операция умножения матриц — одна из самых важных и полезных из матричных операций. В этом разделе мы также покажем, как умножение матриц связано с линейными системами уравнений.

Во-первых, мы даем формальное определение векторов строк и столбцов. 9{th}\) столбец матрицы-строки.

Матрица $n\times 1$ \[X=\left[ \begin{array}{c} x_{1} \\ \vdots \\ x_{n} \end{array} \right]\ nonumber \] называется вектор-столбцом . Матрица $1\times n$ \[X = \left[ \begin{array}{ccc} x_{1} & \cdots & x_{n} \end{array} \right]\nonumber \] называется вектором-строкой .

В этом тексте мы можем просто использовать термин вектор для обозначения либо столбца, либо вектора-строки. Если мы это сделаем, то из контекста будет ясно, о чем мы говорим.

В этой главе мы снова будем использовать понятие линейной комбинации векторов, как в определении 9.2.2. В этом контексте линейная комбинация представляет собой сумму, состоящую из векторов, умноженных на скаляры. Например, \[\left[ \begin{array}{r} 50 \\ 122 \end{array} \right] = 7\left[ \begin{array}{r} 1 \\ 4 \end{array} \right] +8\left[ \begin{array}{r} 2 \\ 5 \end{array} \right] +9\left[ \begin{array}{r} 3 \\ 6 \end{array} \right]\nonumber \] представляет собой линейную комбинацию трех векторов.

Оказывается, любую систему линейных уравнений можно представить в виде линейной комбинации векторов. На самом деле векторы, которые мы будем использовать, — это всего лишь столбцы соответствующей расширенной матрицы!

Определение $\PageIndex{2}$: векторная форма системы линейных уравнений

Предположим, что у нас есть система уравнений, заданная \[\begin{array}{c} a_{11}x_{1} +\cdots +a_{1n}x_{n}=b_{1} \\ \vdots \\ a_{m1}x_{1}+\cdots +a_{mn}x_{n}=b_{m} \end {array}\nonumber \] Мы можем выразить эту систему в векторной форме , которая выглядит следующим образом: \[x_1 \left[ \begin{array}{c} a_{11}\\ a_{21}\\ \vdots \\ a_{m1} \end{массив} \right] + x_2 \left[ \begin{array}{c} a_{12}\\ a_{22}\\ \vdots \\ a_{m2} \end{ array} \right] + \cdots + x_n \left[ \begin{array}{c} a_{1n}\\ a_{2n}\\ \vdots \\ a_{mn} \end{array} \right] = \left[ \begin{array}{c} b_1\\ b_2\\ \vdots \\ b_m \end{array} \right]\nonumber \]

Обратите внимание, что каждый используемый здесь вектор представляет собой один столбец соответствующей расширенной матрицы. Существует один вектор для каждой переменной в системе вместе с постоянным вектором.

Первая важная форма матричного умножения — умножение матрицы на вектор. Рассмотрим произведение, заданное \[\left[ \begin{array}{rrr} 1 & 2 & 3 \\ 4 & 5 & 6 \end{array} \right] \left[ \begin{array}{r} 7 \\ 8 \\ 9 \end{array} \right]\nonumber \] Вскоре мы увидим, что это равно \[7\left[ \begin{array}{c} 1 \\ 4 \end{array} \right ] +8\left[ \begin{array}{c} 2 \\ 5 \end{array} \right] +9\left[ \begin{array}{c} 3 \\ 6 \end{array} \right] =\left[ \begin{array}{c} 50 \\ 122 \end{array} \right]\nonumber \ ]

В общих чертах, \[\begin{aligned} \left[ \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_ {23} \end{массив} \right] \left[ \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{массив} \right] &= \ x_ {1}\left[ \begin{array}{c} a_{11} \\ a_{21} \end{array} \right] +x_{2}\left[ \begin{array}{c} a_{ 12} \\ a_{22} \end{массив} \right] +x_{3}\left[ \begin{array}{c} a_{13} \\ a_{23} \end{массив} \right] \\ &=\left[ \begin{array}{c} a_{11}x_{1}+a_{12}x_{2}+a_{13}x_{3} \\ a_{21}x_{1 }+a_{22}x_{2}+a_{23}x_{3} \end{array} \right] \end{aligned}\] Таким образом, вы берете $x_{1}$ раз первый столбец, добавьте к $x_{2}$ раз второй столбец и, наконец, $x_{3}$ раз третий столбец. {n}x_{j}A_{j}\номер \]

Если мы запишем столбцы $A$ с точки зрения их записей, они будут иметь вид \[A_{j} = \left[ \begin{array}{c} a_{1j} \\ a_{ 2j} \\ \vdots \\ a_{mj} \end{array} \right]\nonumber \] Тогда мы можем записать произведение $AX$ как \[AX = x_{1}\left[ \begin {array}{c} a_{11} \\ a_{21} \\ \vdots \\ a_{m1} \end{array} \right] + x_{2}\left[ \begin{array}{c} a_{12} \\ a_{22} \\ \vdots \\ a_{m2} \end{array} \right] +\cdots + x_{n}\left[ \begin{array}{c} a_{1n } \\ a_{2n} \\ \vdots \\ a_{mn} \end{массив} \right]\nonumber \]

Обратите внимание, что умножение матрицы $m \times n$ на вектор $n \times 1$ дает вектор $m \times 1$.

Вот пример.

Пример $\PageIndex{1}$: вектор, умноженный на матрицу

Вычислить произведение $AX$ для \[A = \left[ \begin{array}{rrrr} 1 & 2 & 1 & 3 \\ 0 & 2 & 1 & -2 \\ 2 & 1 & 4 & 1 \end{array} \right], X = \left[ \begin{array}{r} 1 \\ 2 \\ 0 \ \ 1 \end{массив} \right]\nonumber \]

Решение

Мы будем использовать определение $\PageIndex{3}$ для вычисления произведения. Поэтому мы вычисляем произведение $AX$ следующим образом. \[\begin{align} & 1\left[ \begin{array}{r} 1 \\ 0 \\ 2 \end{array} \right] + 2\left[ \begin{array}{r} 2 \ \ 2 \\ 1 \end{array} \right] + 0\left[ \begin{array}{r} 1 \\ 1 \\ 4 \end{array} \right] + 1 \left[ \begin{array }{r} 3 \\ -2\\ 1 \end{массив} \right] \\ &= \left[ \begin{array}{r} 1 \\ 0 \\ 2 \end{массив} \right] + \left[ \begin{array}{r} 4 \\ 4 \\ 2 \end{array} \right] + \left[ \begin{array}{r} 0 \\ 0 \\ 0 \end{array } \right] + \left[ \begin{array}{r} 3 \\ -2\\ 1 \end{array} \right] \\ &= \left[ \begin{array}{r} 8 \\ 2 \\ 5 \конец{массив} \справа]\конец{выровнено}\]

Используя описанную выше операцию, мы также можем написать систему линейных уравнений в матричной форме . В этой форме мы выражаем систему как матрицу, умноженную на вектор. Рассмотрим следующее определение.

Определение $\PageIndex{4}$: матричная форма системы линейных уравнений

Предположим, у нас есть система уравнений, заданная \[\begin{array}{c} a_{11}x_{1} +\cdots +a_{1n}x_{n}=b_{1} \\ a_{21}x_{1}+ \cdots + a_{2n}x_{n} = b_{2} \\ \vdots \\ a_{m1}x_{1}+\cdots +a_{mn}x_{n}=b_{m} \end{array}\nonumber \] Тогда мы можем выразить эту систему в 9Матрица 0057 формы выглядит следующим образом. \[\left[ \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \ \ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right] \left[ \begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{массив} \right] = \left[ \begin{массив}{c} b_{1}\\ b_{2} \\ \vdots \\ b_{m} \end{array} \right]\nonumber \]

Выражение $AX=B$ также известно как Матрица Форма соответствующей системы линейных уравнений. Матрица $A$ — это просто матрица коэффициентов системы, вектор $X$ — вектор-столбец, построенный из переменных системы, и, наконец, вектор $B$ — это вектор-столбец, построенный из константы системы. Важно отметить, что в таком виде можно записать любую систему линейных уравнений.

Обратите внимание, что если мы запишем однородную систему уравнений в матричной форме, она будет иметь вид $AX=0$ для нулевого вектора $0$.

Из этого определения видно, что вектор \[X = \left[ \begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array} \right]\nonumber \] будет удовлетворять уравнению $AX=B$ только тогда, когда элементы $x_{1}, x_{2}, \cdots, x_{n}$ вектора \(X\ ) являются решениями исходной системы.

Теперь, когда мы рассмотрели, как умножать матрицу на вектор, мы хотим рассмотреть случай, когда мы умножаем две матрицы более общих размеров, хотя, как мы увидим, эти размеры все еще должны быть подходящими. Например, в примере $\PageIndex{1}$ мы умножили матрицу $3 \times 4$ на вектор $4 \times 1$. Мы хотим исследовать, как умножать другие размеры матриц.

Мы еще не дали никаких условий, когда возможно умножение матриц! Для матриц $A$ и $B$, чтобы образовать произведение $AB$, количество столбцов $A$ должно равняться количеству строк $B.$ Рассмотрим произведение $AB$, где $A$ имеет размер $m\times n$, а $B$ имеет размер $n \times p$. Затем произведение с точки зрения размера матриц определяется как \[(m\times\overset{\text{они должны совпадать!}}{\widehat{n)\;(n}\times p})=m\ раз p\номер \]

Обратите внимание, что две внешние цифры обозначают размер продукта. Одно из важнейших правил умножения матриц заключается в следующем. Если два средних числа не совпадают, вы не можете умножать матрицы!

Когда количество столбцов $A$ равно количеству строк $B$, говорят, что две матрицы созвучны , а произведение $AB$ получается следующим образом. {th}\) столбец $AB$.

Рассмотрим следующий пример.

Пример $\PageIndex{2}$: умножение двух матриц

Найдите $AB$, если возможно. \[A = \left[ \begin{array}{rrr} 1 & 2 & 1 \\ 0 & 2 & 1 \end{array} \right], B = \left[ \begin{array}{rrr} 1 & 2 & 0 \\ 0 & 3 & 1 \\ -2 & 1 & 1 \end{array} \right]\nonumber \]

Решение

Первое, что вам нужно проверить при вычислении произведения, это то, возможно умножение. Первая матрица имеет размер $2\times 3$, а вторая матрица имеет размер $3\times 3$. Внутренние числа равны, поэтому матрицы $A$ и $B$ созвучны. Согласно приведенному выше обсуждению, $AB$ будет матрицей $2\times 3$. Определение $\PageIndex{5}$ дает нам способ вычислить каждый столбец $AB$ следующим образом.

\[\left[ \overset{ \text{Первый столбец}}{\overbrace{\left[ \begin{array}{rrr} 1 & 2 & 1 \\ 0 & 2 & 1 \end{array} \ right] \left[ \begin{array}{r} 1 \\ 0 \\ -2 \end{array} \right] }},\overset{\text{Второй столбец}}{\overbrace{\left[ \ begin{array}{rrr} 1 & 2 & 1 \\ 0 & 2 & 1 \end{array} \right] \left[ \begin{array}{r} 2 \\ 3 \\ 1 \end{array} \right] }},\overset{\text{Третий столбец}}{\overbrace{\left[ \begin{array}{rrr} 1 & 2 & 1 \\ 0 & 2 & 1 \end{массив} \right ] \left[ \begin{array}{r} 0 \\ 1 \\ 1 \end{array} \right] }}\right]\nonumber \] Вы знаете, как умножить матрицу на вектор, используя Определение \ (\PageIndex{3}\) для каждого из трех столбцов. Таким образом, \[\left[ \begin{array}{rrr} 1 & 2 & 1 \\ 0 & 2 & 1 \end{array} \right] \left[ \begin{array}{rrr} 1 & 2 & 0 \\ 0 & 3 & 1 \\ -2 & 1 & 1 \end{массив} \right] = \ \left[ \begin{массив}{rrr} -1 & 9& 3 \\ -2 & 7 & 3 \end{array} \right]\nonumber \]

Поскольку векторы представляют собой просто $n \times 1$ или $1 \times m$ матрицы, мы также можем умножить вектор на другой вектор.

Пример $\PageIndex{3}$: умножение вектора на вектор

Умножить, если возможно $\left[ \begin{array}{r} 1 \\ 2 \\ 1 \end{array} \right] \ left[ \begin{array}{rrrr} 1 & 2 & 1 & 0 \end{array} \right] .$

Решение

В этом случае мы умножаем матрицу размера $3 \times 1\ ) матрицей размера \(1 \times 4.$ Внутренние числа совпадают, поэтому произведение определено. Обратите внимание, что произведение будет матрицей размера $3 x 4$. Используя определение $\PageIndex{5}$, мы можем вычислить это произведение следующим образом $\: $ \[\left[ \begin{array}{r} 1 \\ 2 \\ 1 \end{array} \right] \left[ \begin{array}{rrrr} 1 & 2 & 1 & 0 \end{array} \right] = \left[ \overset{ \text{Первый столбец}}{\overbrace{\left[ \begin{array}{r} 1 \\ 2 \\ 1 \end{массив} \right] \left[ \begin{array}{r} 1 \end{массив} \right] }},\overset{\ text{Второй столбец}}{\overbrace{\left[ \begin{array}{r} 1 \\ 2\\ 1 \end{массив} \right] \left[ \begin{array}{r} 2 \end {массив} \right] }},\overset{\text{Третий столбец}}{\overbrace{\left[ \begin{array}{r} 1 \\ 2 \\ 1 \end{массив} \right] \ left[ \begin{array}{r} 1 \end{array} \right] }}, \overset {\text{Четвертый столбец}}{\overbrace{\left[ \begin{array}{r} 1\\ 2\\ 1 \end{массив} \right] \left[ \begin{array}{r} 0 \end{массив} \right]}} \right]\nonumber \]

Вы можете использовать определение $\PageIndex{3}$, чтобы убедиться, что этот продукт является \[\left[ \begin{array}{cccc} 1 & 2 & 1 & 0 \\ 2 & 4 & 2 & 0 \\ 1 & 2 & 1 & 0 \end{массив} \right]\nonumber \]

Пример $\PageIndex{4}$: умножение, которое не определено

Найдите $BA$, если возможно. \[B = \left[ \begin{array}{ccc} 1 & 2 & 0 \\ 0 & 3 & 1 \\ -2 & 1 & 1 \end{array} \right], A = \left[ \ begin{массив}{ccc} 1 & 2 & 1 \\ 0 & 2 & 1 \end{массив} \right]\nonumber \]

Решение

Сначала проверьте, возможно ли это. Это произведение имеет вид $\влево( 3\умножить на 3\вправо) \влево( 2\умножить на 3\вправо).$ Внутренние числа не совпадают, поэтому вы не можете выполнить это умножение.

В этом случае мы говорим, что умножение не определено. Обратите внимание, что это те же матрицы, которые мы использовали в примере $\PageIndex{2}$. В этом примере мы попытались вычислить $BA$ вместо $AB$. Это демонстрирует еще одно свойство матричного умножения. Хотя произведение $AB$ может быть определено, мы не можем предполагать, что произведение $BA$ будет возможно. Поэтому важно всегда проверять, определено ли произведение, прежде чем выполнять какие-либо расчеты.

Ранее мы определили нулевую матрицу $0$ как матрицу (соответствующего размера), содержащую нули во всех элементах. Рассмотрим следующий пример умножения на нулевую матрицу.

Пример $\PageIndex{5}$: умножение на нулевую матрицу

Вычислить произведение $A0$ для матрицы \[A= \left[ \begin{array}{rr} 1 & 2 \\ 3 & 4 \end{array} \right]\nonumber \] и $2 \times 2$ нулевая матрица, заданная как \[0= \left[ \begin{array}{rr} 0 & 0 \\ 0 & 0 \end{массив} \right]\nonumber \]

Решение

В этом продукте мы вычисляем \[\left[ \begin{array}{rr} 1 & 2 \\ 3 & 4 \end{array} \right] \left[ \begin{array}{rr } 0 & 0 \\ 0 & 0 \end{массив} \right] = \left[ \begin{array}{rr} 0 & 0 \\ 0 & 0 \end{массив} \right]\nonumber \]

Следовательно, $A0=0$.

Обратите внимание, что мы также можем умножить $A$ на $2 \times 1$ нулевой вектор, заданный выражением $\left[ \begin{array}{r} 0 \\ 0 \end{array} \ Правильно]$. Результатом будет $2 \times 1$ нулевой вектор. Поэтому всегда имеет место $A0=0$ для нулевой матрицы или вектора соответствующего размера.

Эта страница под названием 2. 2: Умножение матриц распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Кеном Каттлером (Lyryx) с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или страница
Автор
Кен Каттлер
Лицензия
СС BY
Версия лицензии
4,0
Показать страницу Содержание
нет
Теги
1. источник@https://lyryx. com/first-course-linear-алгебра

Начните работу через 5 минут

03 сентября 2021 г. — 5 мин чтения

Эрин Шаффер

NumPy — популярная библиотека Python, предлагающая ряд мощных математических функций. Библиотека широко используется в количественных областях, таких как наука о данных, машинное обучение и глубокое обучение. Мы можем использовать NumPy для выполнения сложных математических вычислений, таких как умножение матриц.

Умножение матриц может помочь нам быстро приблизиться к очень сложным вычислениям. Это может помочь нам с теорией сетей, линейными системами уравнений, моделированием населения и многим другим. В этом уроке мы рассмотрим некоторые базовые вычисления с умножением матриц NumPy.

Начнем!

Мы рассмотрим :

Что такое NumPy?
Что такое матрица NumPy?
Методы умножения матриц NumPy
Подведение итогов и последующие шаги

Что такое NumPy?

NumPy — это библиотека Python с открытым исходным кодом, которую мы можем использовать для выполнения высокоуровневых математических операций с массивами, матрицами, линейной алгеброй, анализом Фурье и многим другим. Библиотека NumPy очень популярна в научных вычислениях, науке о данных и машинном обучении. NumPy совместим с популярными библиотеками данных, такими как pandas, matplotlib и Scikit-learn. Это намного быстрее, чем Python перечисляет , потому что он интегрирует более быстрые коды, такие как C и C++, в Python. Он также разбивает наши задачи на несколько частей и обрабатывает каждую часть одновременно.

Установка и импорт NumPy

 conda install numpy

 pip install numpy

Чтобы импортировать NumPy в наш код Python, мы можем использовать следующую команду:

 импортировать numpy как np

Что такое матрица NumPy?
Матрица — это двумерный массив. Каждый элемент массива имеет два индекса. Давайте рассмотрим пример в NumPy:
импортировать numpy как np А = [[6, 7], [8, 9]] print(np. array(A) [0,0])
В приведенном выше коде у нас есть матрица A [[6, 7], [8, 9]] . Мы запрашиваем элемент, заданный по адресу (0,0) , и наш вывод возвращает 6 . Когда мы хотим определить форму нашей матрицы, мы используем количество строк по количеству столбцов. Это означает, что матрица A имеет форму 2×2.
Теперь давайте рассмотрим несколько различных методов умножения матриц NumPy.
Методы умножения матриц NumPy
Существует три основных способа выполнения умножения матриц NumPy:
np.dot(массив a, массив b) : возвращает скалярное произведение двух массивов
.
np.matmul(массив a, массив b) : возвращает матричное произведение двух массивов
np.multiply(array a, array b) : возвращает поэлементное матричное умножение двух массивов
Давайте подробнее рассмотрим каждый из трех методов:
Скалярное умножение или скалярное произведение с numpy.
dot
Скалярное умножение — это простая форма матричного умножения. Скаляр — это просто число, например 1 , 2 или 3 . При скалярном умножении мы умножаем скаляр на матрицу . Каждый элемент в матрице умножается на скаляр, в результате чего на выходе получается та же форма, что и у исходной матрицы.
При скалярном умножении порядок не имеет значения . Мы получим один и тот же результат, умножим ли мы скаляр на матрицу или матрицу на скаляр.
Давайте рассмотрим пример:
импортировать numpy как np А = 5 В = [[6, 7], [8, 9]] print(np.dot(A,B))
Теперь давайте умножим двумерную матрицу на другую двумерную матрицу. При умножении двух матриц порядок имеет значение . Это означает, что матрица A, умноженная на матрицу B, не совпадает с матрицей B, умноженной на матрицу A.
Прежде чем мы начнем, давайте посмотрим на визуализацию того, как выполняется умножение.
импортировать numpy как np А = [[6, 7], [8, 9]] В = [[1, 3], [5, 7]] печать (np.dot (A, B)) Распечатать("----------") печать (np.dot (B, A))
Примечание . Важно отметить, что мы можем умножать две матрицы только в том случае, если количество столбцов в первой матрице равно количеству строк во второй матрице.

Продолжайте изучать NumPy бесплатно.
Начните бесплатно анализировать данные Python с помощью нашей 1-недельной образовательной неограниченной пробной версии. Текстовые схемы обучения Educative легко просматриваются и включают живую среду кодирования, что делает обучение быстрым и эффективным.
Анализ и визуализация данных Python

Произведение матриц с numpy.matmul
Функция matmul() дает нам матричное произведение двух двумерных массивов. С помощью этого метода мы не можем использовать скалярные значения для нашего ввода. Если один из наших аргументов является одномерным массивом, функция преобразует его в матрицу, добавляя 1 к его размерности. Это удаляется после выполнения умножения.
Если один из наших аргументов больше 2-d, функция рассматривает его как стек матриц по двум последним индексам. Метод matmul() отлично подходит для случаев, когда мы не уверены в том, какими будут размеры наших матриц.
Давайте рассмотрим несколько примеров:
Умножение двумерного массива на другой двумерный массив
import numpy as np А = [[2, 4], [6, 8]] В = [[1, 3], [5, 7]] print(np.matmul(A,B))
Умножение двумерного массива на одномерный массив
импортировать numpy как np А = [[5, 0], [0, 5]] В = [5, 2] print(np.matmul(A,B))
Один массив с размерами больше 2-d
импортировать numpy как np A = np.arange(8).reshape(2, 2, 2) B = np.arange(4).reshape(2, 2) print(np. matmul(A,B))
Поэлементное умножение матриц с помощью numpy.multiply
Метод numpy.multiply() принимает две матрицы в качестве входных данных и выполняет поэлементное умножение на них. Поэлементное умножение, или произведение Адамара, умножает каждый элемент первой матрицы на эквивалентный элемент второй матрицы. При использовании этого метода обе матрицы должны иметь одинаковые размеры.
Давайте рассмотрим пример:
импортировать numpy как np A = np.array([[1, 3, 5, 7, 9], [2, 4, 6, 8, 10]]) B = np.array([[1, 2, 3, 4, 5], [5, 4, 3, 2, 1]]) print(np.multiply(A,B))
Мы можем передать определенные строки, столбцы или подматрицы методу numpy.multiply() . Размеры строк, столбцов или подматриц, которые мы передаем в качестве наших операндов, должны быть одинаковыми. Давайте рассмотрим пример:
импортировать numpy как np A = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]]) B = np.array([[11, 12, 13, 14, 15], [16, 17, 18, 19, 20]]) печать (np. multiply (A [0,:], B[1,:])) Распечатать("----------") печать (np.multiply (A [1,:], B[0,:]))
Завершение и следующие шаги
Поздравляем с первыми шагами в умножении матриц NumPy! Это сложная, но важная часть линейной алгебры. Это помогает нам углубить наше понимание различных аспектов науки о данных, машинного обучения, глубокого обучения и других распространенных областей. Нам еще многое предстоит узнать о NumPy и матрицах. Некоторые рекомендуемые темы для следующего обсуждения:
Транспонирование матрицы NumPy
Массивы NumPy (ndarray)
Векторизация NumPy
Чтобы начать изучение этих и других концепций, ознакомьтесь с планом обучения Educative Анализ и визуализация данных Python . Этот практический путь обучения поможет вам овладеть навыками извлечения информации из данных с использованием мощного ассортимента популярных библиотек Python.
Приятного обучения!
Продолжить изучение Python
50 вопросов и ответов на собеседовании по Python
Наука о данных стала проще: 5 основных приемов обучения Scikit
Шпаргалка Pandas: 35 лучших команд и операций
НАПИСАЛ BYErin Schaffer
Присоединяйтесь к сообществу, насчитывающему более 1,4 миллиона читателей. Бесплатное электронное письмо раз в два месяца с обзором лучших статей и советов по программированию на сайте Educative.
Умножение матриц — MathBootCamps
Хотя сложение или вычитание матриц относительно просто, умножение матриц сильно отличается от большинства математических операций, которые вы изучали ранее. Здесь мы рассмотрим хороший способ умножения двух матриц и некоторые важные свойства, связанные с ним. Вы также узнаете, как узнать, когда умножение не определено.
реклама
Содержание:
Умножение двух матриц: «строки попали в столбцы» (анимация этого)
Умножение матриц не всегда определено
Умножение матриц не является коммутативным
Примеры умножения матриц
Краткое описание свойств
Умножение двух матриц: «строки попадают в столбцы»
Чтобы понять общую схему умножения двух матриц, подумайте «строки попадают в столбцы и заполняют строки». Рассмотрим следующий пример.
Первая строка «соответствует» первому столбцу, что дает нам первую запись продукта. Обратите внимание, что поскольку это произведение двух матриц 2 x 2 (количество строк и столбцов), результатом также будет матрица 2 x 2. Мы рассмотрим, как размер матрицы влияет на это позже в статье.
Теперь первая строка «соприкасается» со второй колонкой, заполняя строку продукта.
Закончив столбцы для «попадания», теперь работаем со второй строкой.
Осталась последняя запись для вычисления. Вторая строка теперь «поразит» второй столбец.
Наконец, нам просто нужно выполнить арифметические действия, чтобы получить окончательный ответ.
Анимация этого процесса
Вы можете увидеть анимацию этого процесса здесь. Звука нет — так что не беспокойтесь о поиске наушников!

Вскоре мы увидим еще пару примеров, но сначала нам нужно обсудить, как размер матрицы влияет на результат умножения. На самом деле бывают случаи, когда из-за размера матрицы умножение не определено.
Умножение матриц не всегда определено
При умножении матриц размер двух задействованных матриц определяет, будет ли определено произведение. Вы также можете использовать размеры, чтобы определить результат умножения двух матриц. Напомним, что размер матрицы — это количество строк на количество столбцов. Приведенные выше матрицы были 2 x 2, поскольку каждая из них имела 2 строки и 2 столбца.
Как видите, размеры матриц не обязательно должны быть одинаковыми, вам просто нужно, чтобы совпадали средние два числа, когда вы записываете размеры рядом. В противном случае продукт не определен.
Подумайте вот о чем: если, например, матрица A имеет размер 3 x 4, то произведение A на себя не будет определено, так как внутренние числа не будут совпадать. Это всего лишь один пример того, как умножение матриц ведет себя не так, как вы могли бы ожидать.
Умножение матриц не коммутативно
Из начальной школы вы знаете, что произведение (2)(3) = (3)(2). Неважно, в каком порядке вы умножаете числа, результат один и тот же. Это не работает вообще для матриц. Только в особых случаях можно сказать, что АВ = ВА. Так что в целом следует считать, что они не равны. Может быть даже так, что AB определено, а BA не определено!
Даже если произведение определено, маловероятно, что результаты для AB и BA будут одинаковыми.
Примеры умножения матриц
Теперь, когда мы рассмотрели некоторые важные свойства умножения матриц, давайте рассмотрим пару примеров.
Пример
Найдите произведение AB, где:
$A = \left[\begin{array}{cc} -5 & 3\\ -4 & -1\\ \end{array}\right]$
и
$ B = \left[\begin{массив}{cc} 1 & -1\\ 2 & 6\\ \end{массив}\right]$
Решение
Помните, что строки пересекаются со столбцами и заполняют строки. Здесь каждая матрица имеет размер 2 x 2, поэтому результатом будет матрица 2 x 2.
$\begin{align} AB &= \left[\begin{array}{cc} -5 & 3\\ -4 & -1\\ \end{array}\right] \left[\begin{array} {cc} 1 & -1\\ 2 & 6\\ \end{массив}\right]\\ &= \left[\begin{массив}{cc} -5(1) + 3(2) & -5 (-1) + 3(6)\\ -4(1) +(-1)(2) & (-4)(-1)+(-1)(6)\\ \end{массив}\right ]\\ &= \boxed{\left[\begin{array}{cc} 1 & 23\\ -6 & -2\\ \end{массив}\right]}\end{align}$
Пример
Найдите произведение AB, где:
$A = \left[\begin{array}{cccc} -2 & -1 & 0 & 0 \\ 1 & 2 & 1 & 1\\ \end{array}\right ]$
и
$B = \left[\begin{array}{cccc} 3 & 1 & 1 & 2 \\ -1 & -1 & 0 & 1\\ \end{массив}\right]\ )
Решение
Здесь у нас есть матрица 2 x 4, умноженная на матрицу 2 x 4. Внутренние номера этих размеров не совпадают, поэтому:
\(\boxed{AB \text{не определено}}$
Пример
Найдите произведение AB, где:
$A = \left[\begin{array}{cc} 1 & 2\\ -2 & 0\\ 3 & 1\\\end{array}\right]$
и
$B = \left[\begin{array}{cc} 4 & 0\\ 0 & 1\\ \end{array}\right]$
Решение
Произведение матрицы 3 x 2 и матрицы 2 x 2. Внутренние числа совпадают, поэтому продукт определен. В результате получится матрица 3 х 2.
$\begin{align} AB &= \left[\begin{array}{cc} 1 & 2\\ -2 & 0\\ 3 & 1\\\end{array}\right]\left[\begin {array}{cc} 4 & 0\\ 0 & 1\\ \end{array}\right]\\ &= \left[\begin{array}{cc} 1(4) + 2(0) & 1 (0) + 2(1)\\ -2(4) + 0(0) & -2(0) + 0(1)\\ 3(4) + 1(0) & 3(0) + 1( 1)\\\end{массив}\right]\\ &= \boxed{\left[\begin{array}{cc} 4 & 2\\ -8 & 0\\ 12 & 1\\\end{массив }\right]}\end{выравнивание}$
реклама
Резюме
Всегда помните следующее при перемножении двух или более матриц.
No related posts.

Перемножение матриц | это… Что такое Перемножение матриц?

Содержание

История

Матрица как запись коэффициентов системы линейных уравнений

Операции над матрицами

Квадратная матрица и смежные определения

Свойства матриц

Элементарные преобразования матриц

Типы матриц

Матрица линейного оператора

См. также

Литература

Ссылки

Как перемножать матрицы в экселе

Процедура перемножения матриц

Способ 1: функция МУМНОЖ

Способ 2: использование составной формулы

Умножение и деление матрицы на число в Excel

Способ 1

Способ 2

Сложение и вычитание матриц в Excel

Способ 1

Способ 2

Умножение матриц в Excel

Транспонирование матрицы в Excel

Нахождение обратной матрицы в Excel

Нахождение определителя матрицы в Excel

Как найти определить матрицы в Excel

Видеоурок

2.2. Умножение матрицы на число

2.3. Умножение матриц

Алгоритм вычисления произведения матрицы на матрицу :

Свойства операции умножения матриц

Умножение матриц NumPy: начните за 5 минут

Что такое NumPy?

Установка и импорт NumPy

Что такое матрица NumPy?

Методы умножения матриц NumPy

Скалярное умножение или скалярное произведение с numpy.dot

Матричный продукт с numpy.matmul

Поэлементное умножение матриц с помощью numpy.multiply

Подведение итогов и следующие шаги

Умножение матриц — 2×2, 3×3

Что такое умножение матриц?

Как умножать матрицы?

Правила умножения матриц

Формула умножения матриц 2×2

Формула умножения матриц 3×3

Свойства умножения матриц

Часто задаваемые вопросы по умножению матриц

Что такое умножение матриц в линейной алгебре?

Как перемножать матрицы 3×3?

Что такое формула умножения матриц?

Можно ли перемножать матрицы порядка 2×3 и 2×2?

Какова цель умножения матриц?

Чему равно произведение матриц порядков 2×1 и 2×2?

Когда возможно умножение матриц?

Всегда ли умножение матриц является коммутативным?

Всегда ли определено умножение матриц?

Умножение матриц — ChiliMath

Примеры умножения матриц, также известного как «беспорядочный тип»

Скалярное и матричное умножение

2.

Определение \(\PageIndex{2}\): векторная форма системы линейных уравнений

Пример \(\PageIndex{1}\): вектор, умноженный на матрицу

Решение

Определение \(\PageIndex{4}\): матричная форма системы линейных уравнений

Пример \(\PageIndex{2}\): умножение двух матриц

Решение

Пример \(\PageIndex{3}\): умножение вектора на вектор

Решение

Пример \(\PageIndex{4}\): умножение, которое не определено

Решение

Пример \(\PageIndex{5}\): умножение на нулевую матрицу

Решение

Начните работу через 5 минут

Что такое NumPy?

Установка и импорт NumPy

Что такое матрица NumPy?

Методы умножения матриц NumPy