| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град.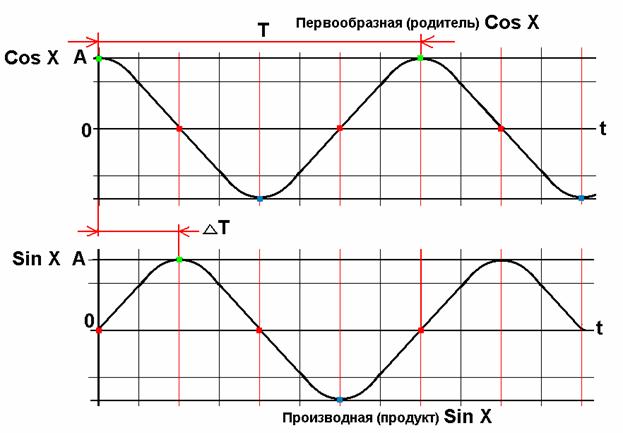 ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.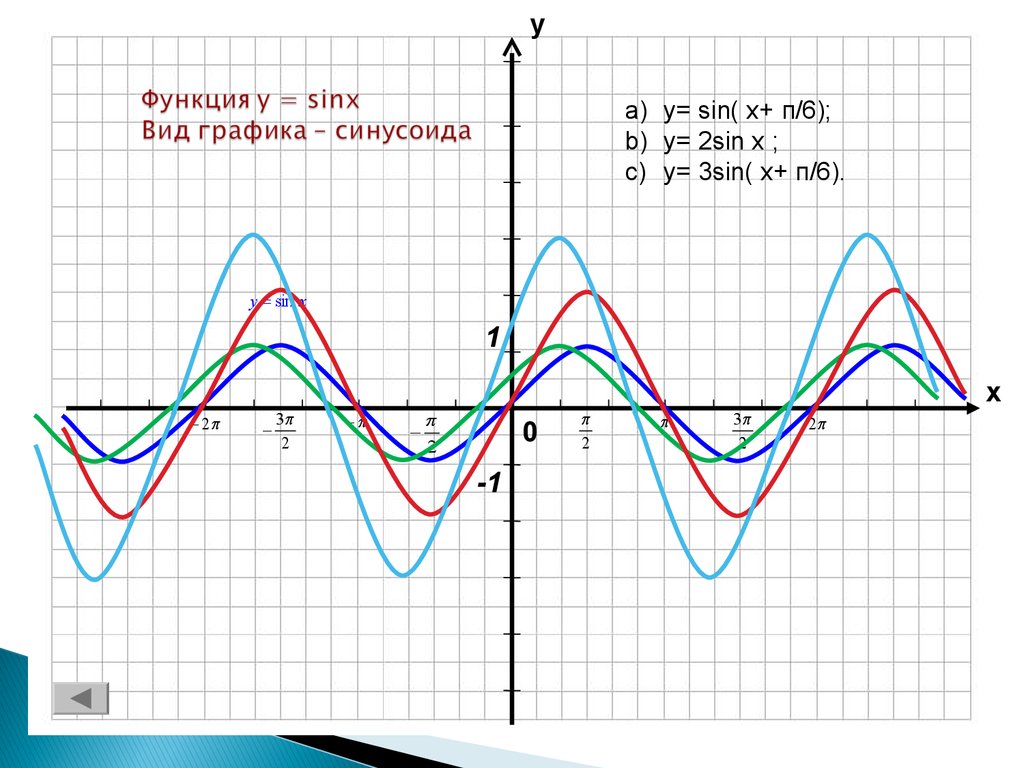 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.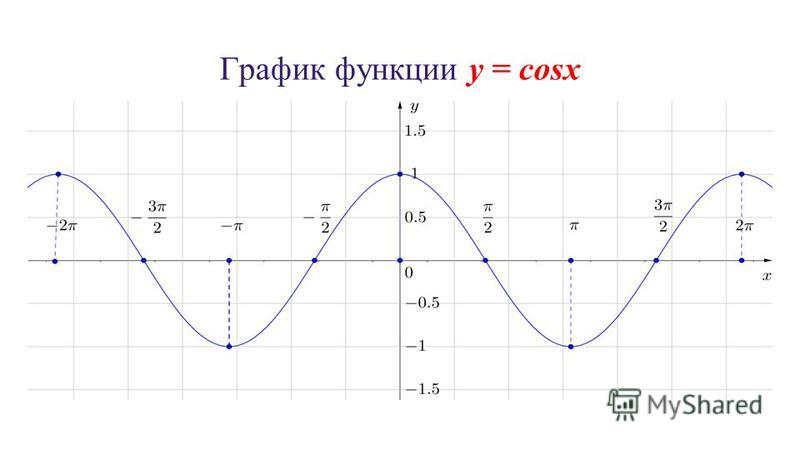 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.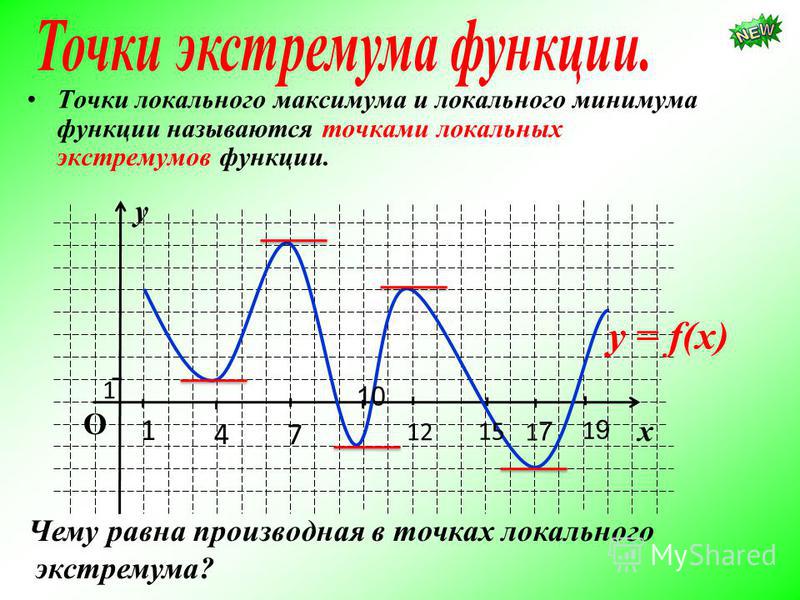 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.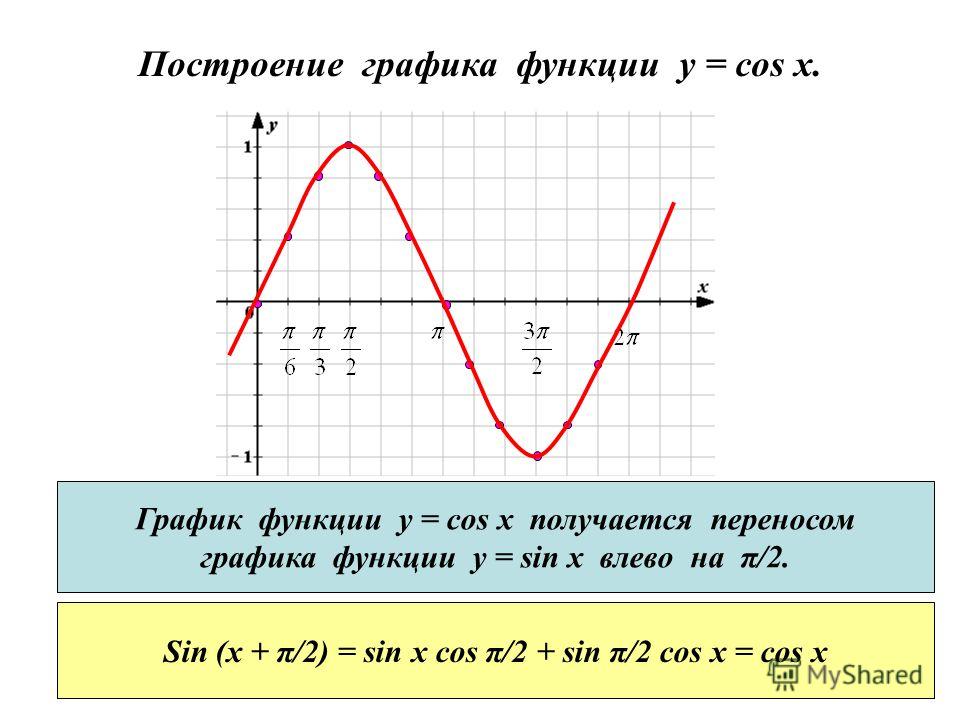 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
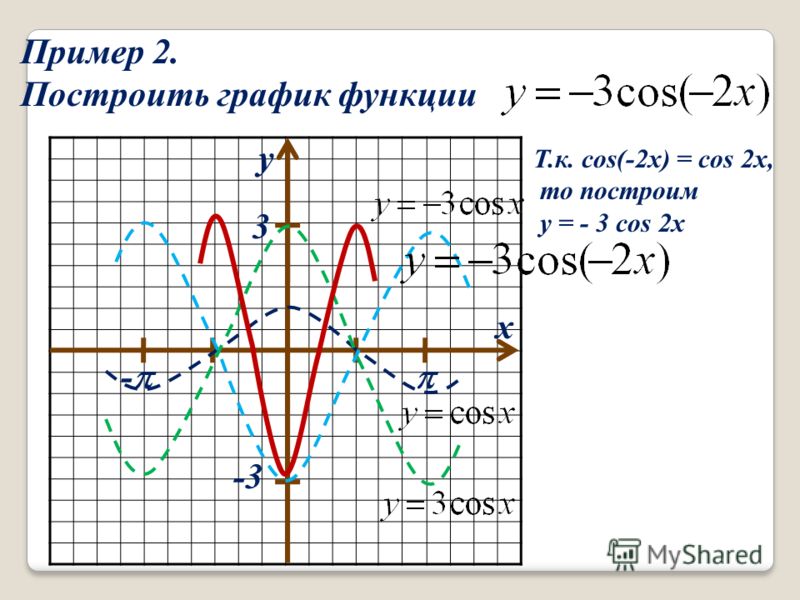
График функции cos x 2. Графики тригонометрических функций кратных углов
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
4. Примеры.
Определение функции косинуса у=cos(x)
Ребята, мы уже познакомились с функцией Y=sin(X).
Давайте вспомним одну из формул привидения : sin(X + π/2) = cos(X).
Благодаря этой формуле, мы можем утверждать, что функции sin(X + π/2) и cos(X) тождественны, и их графики функций совпадают.
График функции sin(X + π/2) получается из графика функции sin(X) параллельным переносом на π/2 единиц влево. Это и будет график функции Y=cos(X).
График функции Y=cos(X) так же называют синусоидой.
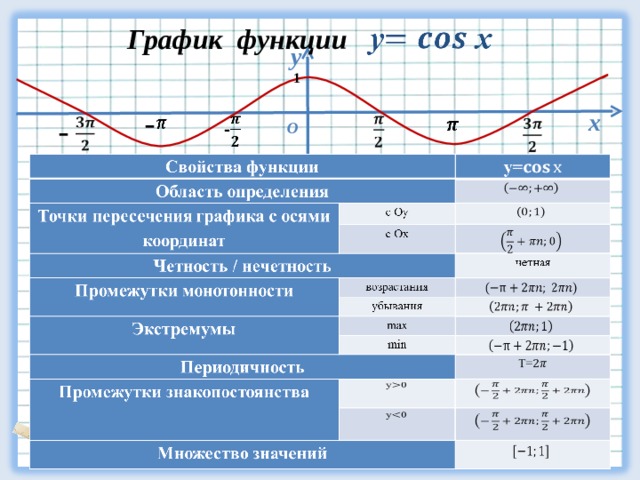
Свойства функции cos(x)
- Запишем свойства нашей функции:
- Область определения – множество действительных чисел.
- Функция четная.
 Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция. - Функция Y=cos(X) убывает на отрезке и возрастает на отрезке [π; 2π]. В этом мы можем убедиться на графике нашей функции.
- Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ cos(X) ≤ 1 - Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
- Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.
- Область значений отрезок [- 1; 1]. Это также хорошо видно из графика.
- Функция Y=cos(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.
Примеры с функцией cos(x)
1. Решить уравнение cos(X)=(x — 2π) 2 + 1
Решить уравнение cos(X)=(x — 2π) 2 + 1
Решение: Построим 2 графика функции: y=cos(x) и y=(x — 2π) 2 + 1 (см. рисунок).
y=(x — 2π) 2 + 1 — это парабола, смещенная вправо на 2π и вверх на 1. Наши графики пересекаются в одной точке А(2π;1), это и есть ответ: x = 2π.
2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0
Решение: Чтобы построить требуемый график, давайте построим два графика функции по «кусочкам». Первый кусочек: y=cos(x) при х ≤ 0. Второй кусочек: y=sin(x)
при x ≥ 0. Изобразим оба «кусочка» на одном
графике.
3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]
Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4]. На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.
Ответ: cos(π) = -1 – наименьшее значение, cos(7π/4) = наибольшее значение.
4. Построить график функции y=cos(π/3 — x) + 1
Решение: cos(-x)= cos(x), тогда искомый график получится путем переноса графика функции y=cos(x) на π/3 единиц вправо и 1 единицу вверх.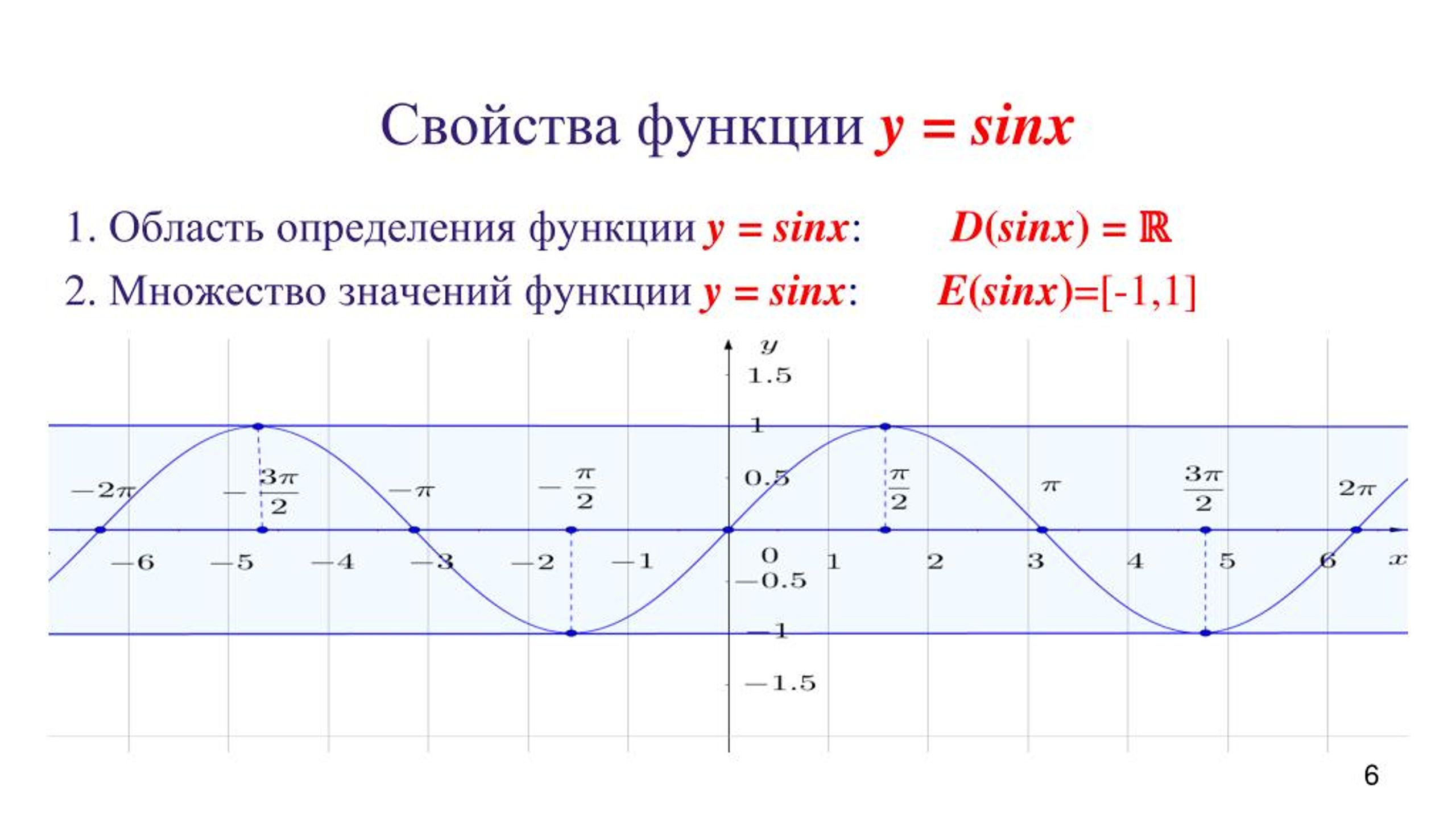
Задачи для самостоятельного решения
1)Решить уравнение: cos(x)= x – π/2.
2) Решить уравнение: cos(x)= — (x – π) 2 — 1.
3) Построить график функции y=cos(π/4 + x) — 2.
4) Построить график функции y=cos(-2π/3 + x) + 1.
5) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке .
6) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке [- π/6; 5π/4].
«Графики функций и их свойства» — y = ctg x. 4) Ограниченность функции. 3) Нечётная функция. (График функции симметричен относительно начала координат). y = tg x. 7) Функция непрерывна на любом интервале вида (?k; ? + ?k). Функция y = tg x непрерывна на любом интервале вида. 4) Функция убывает на любом интервале вида (?k; ? + ?k). График функции y = tg x называется тангенсоидой.
«График функции Y X» — Шаблон параболы у = х2. Чтобы увидеть графики, щелкни мышкой. Пример 2. Построим график функции y = x2 + 1, опираясь на график функции y=x2 (щелчок мышкой).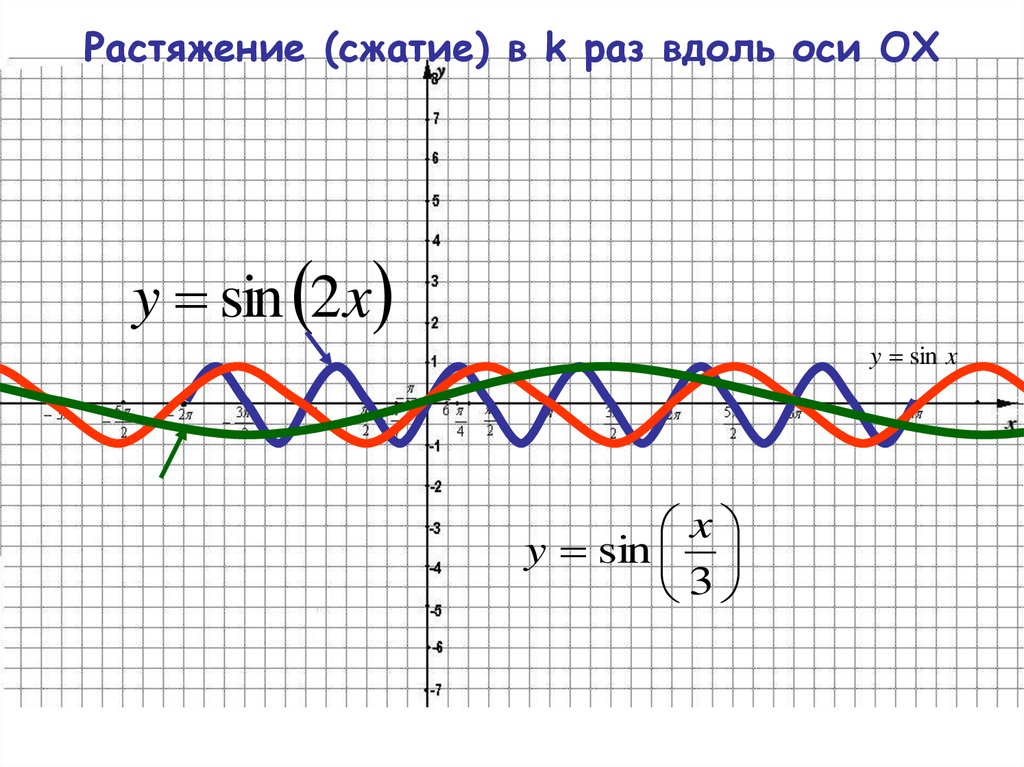 Пример 3. Докажем, что графиком функции у = х2 + 6х + 8 является парабола, и построим график. График функции y=(x — m)2 является параболой с вершиной в точке (m; 0).
Пример 3. Докажем, что графиком функции у = х2 + 6х + 8 является парабола, и построим график. График функции y=(x — m)2 является параболой с вершиной в точке (m; 0).
«Математика графики» — Как можно строить графики? Наиболее естественно функциональные зависимости отражаются с помощью графиков. Интересное применение: рисунки,… Зачем мы изучаем графики? Графики элементарных функций. Что вы можете нарисовать с помощью графиков? Рассматриваем применение графиков в учебных предметах: математике, физике,…
«Построение графиков с помощью производной» — Обобщение. Построить эскиз графика функции. Найти асимптоты графика функции. График производной функции. Дополнительное задание. Исследовать функцию. Назвать промежутки убывания функции. Самостоятельная работа учащихся. Расширить знания. Урок закрепления изученного материала. Оцените свои умения. Точки максимума функции.
«Графики с модулем» — Отобрази «нижнюю» часть в верхнюю полуплоскость. Модуль действительного числа. Свойства функции y = |x|. |x|. Числа. Алгоритм построения графика функции. Алгоритм построения. Функция y= lхl. Свойства. Самостоятельная работа. Нули функции. Советы великих. Решение самостоятельной работы.
|x|. Числа. Алгоритм построения графика функции. Алгоритм построения. Функция y= lхl. Свойства. Самостоятельная работа. Нули функции. Советы великих. Решение самостоятельной работы.
«Уравнение касательной» — Уравнение касательной. Уравнение нормали. Если,то и кривые пересекаются под прямым углом. Условия параллельности и перпендикулярности двух прямых. Угол между графиками функций. Уравнение касательной к графику функции в точке. Пусть функция дифференцируема в точке. Пусть прямые заданы уравнениями и.
Всего в теме 25 презентаций
Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx , где ω — некоторое положительное число.
Для построения графика функции у = sin ωx сравним эту функцию с уже изученной нами функцией у = sin x . Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда
у 0 = sin x 0 .
Преобразуем это соотношение следующим образом:
Следовательно, функция у = sin ωx при х = x 0 / ω принимает то же самое значение у 0 , что и функция у = sin х при х = x 0 . А это означает, что функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция у
= sin x . Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.
А это означает, что функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция у
= sin x . Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.
Например, график функции у = sin 2х получается путем «сжатия» синусоиды у = sin x вдвое вдоль оси абсцисс.
График функции у = sin x / 2 получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 / 2 раза) вдоль оси х.
Поскольку функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция
у = sin x , то период ее в ω раз меньше периода функции у = sin x . Например, период функции у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π
/ x / 2 = 4π .
Интересно провести исследование поведения функции у = sin аx на примере анимации, которую очень просто можно создать в программе Maple :
Аналогично строятся графики и других тригонометрических функций кратных углов. На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
График функции у = cos x / 2 получается путем «растяжения» косинусоиды у = cos х вдвое вдоль оси х.
На рисунке вы видите график функции у = tg 2x , полученный «сжатием» тангенсоиды у = tg x вдвое вдоль оси абсцисс.
График функции у = tg x / 2 , полученный «растяжением» тангенсоиды у = tg x вдвое вдоль оси х.
И, наконец, анимация, выполненная программой Maple:
Упражнения
1. Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.
а). y = sin 4x / 3 г). y = tg 5x / 6 ж). y = cos 2x / 3
б). у= cos 5x / 3 д). у = ctg 5x / 3 з).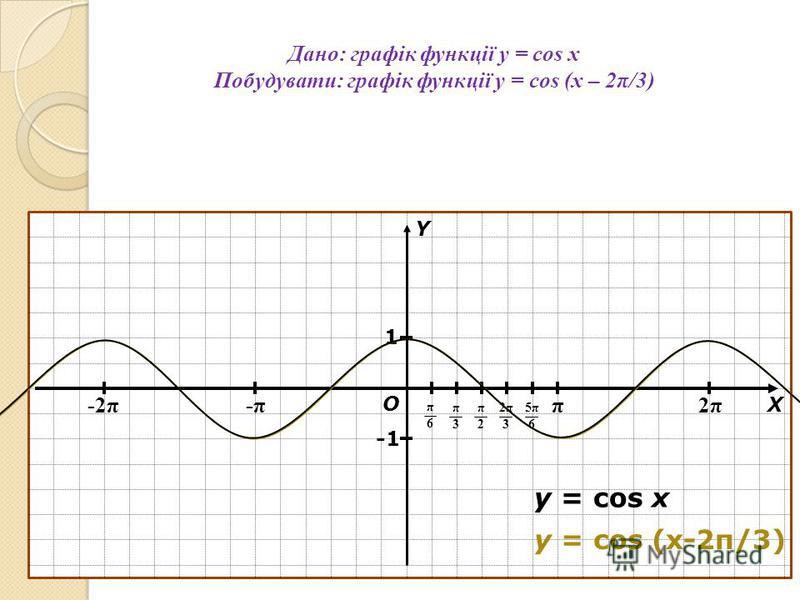 у= ctg x / 3
у= ctg x / 3
в). y = tg 4x / 3 е). у = sin 2x / 3
2. Определить периоды функций у = sin (πх) и у = tg ( πх / 2 ).
3. Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.
4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .
5. Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.
6 *. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.
Функция y=cos t, её свойства и график 9 класс онлайн-подготовка на Ростелеком Лицей
Определение косинуса
Вспомним определение косинуса:
– любое действительное число, ему соответствует единственная точка на числовой окружности.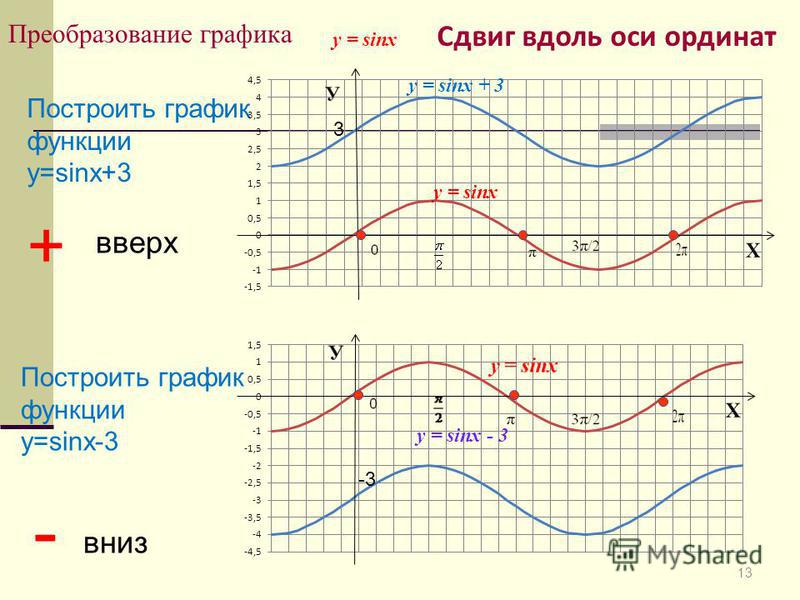 Как эта точка получается: начало отсчета – точка , дуга откладывается против часовой стрелки, если – положительное число и по часовой стрелке, если отрицательное. Длина дуги равняется модулю числа . Задали произвольное и получили единственную точку , у которой есть единственная пара координат . Первую координату назвали косинусом (), а вторую – синусом () (рис. 1).
Как эта точка получается: начало отсчета – точка , дуга откладывается против часовой стрелки, если – положительное число и по часовой стрелке, если отрицательное. Длина дуги равняется модулю числа . Задали произвольное и получили единственную точку , у которой есть единственная пара координат . Первую координату назвали косинусом (), а вторую – синусом () (рис. 1).
В соответствии с данным правилом, мы дали определение двум функциям: и .
Рис. 1. Иллюстрация для определения косинуса
Построение графика
Построим график функции из определения по точкам.
Если мы захотим узнать значение косинуса в иных точках, то используем формулу .
Например:
Получается, зная значения косинуса при и данную формулу, вполне можно узнать значения косинуса для любых значений . Для этого используется симметрия функции косинуса (благодаря ее четности) и периодичность, учитывая, что период у косинуса равен .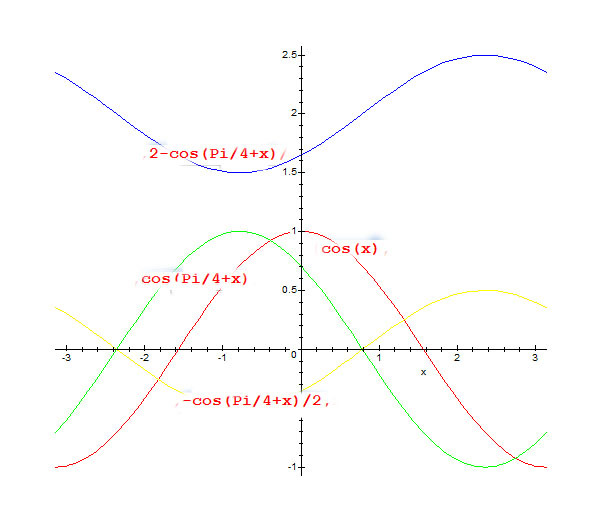
Построим график косинуса по точкам (рис. 2):
На отрезке отметим точки, кратные , , как показано на рисунке, это значения аргумента.
Рис. 2. График функции косинуса по точкам
Для начала необходимо нарисовать график лишь на отрезке . Так как функция четная, график симметричен относительно оси ординат – получим и график на отрезке . В результате имеем график на отрезке . Так как этот промежуток длиной в период (, то этого достаточно, чтобы впоследствии нарисовать весь график.
Изучим функцию и построим график косинуса, используя график синуса и связь между синусом и косинусом:
Эта формула позволяет, зная график синуса, сдвинуть его на в нужную сторону и получить график косинуса.
Докажем данную формулу.
Произвольному числу соответствует единственная точка , тогда числу будет соответствовать тоже единственная точка . Мы знаем, как получились точки и , причем или длина дуги (рис. 3).
Рис. 3. Иллюстрация к доказательству формулы связи синуса и косинуса
Итак, имеется две точки и . Косинус – это отрезок . Синус – это отрезок . Докажем, что эти отрезки равны.
Косинус – это отрезок . Синус – это отрезок . Докажем, что эти отрезки равны.
Исходя из графика, можно сделать вывод, что эти отрезки равны по знаку. Оба отрезка входят в соответствующие треугольники в качестве сторон, значит, нам можно доказать равенство треугольников, чтобы доказать равенство сторон.
Докажем, что дуга равна дуге .
Дуга получается, если отнять от дуги дугу : .
Дуга получается, если отнять от дуги дугу : .
Из этих двух равенств следует, что дуги и равны. А значит, центральный угол равен центральному углу . Получается, что накрест лежащие углы также равны, а значит, . В результате получаем, что по углу и гипотенузе, так как они прямоугольные, и гипотенузы являются радиусами в одной и той же окружности. Из равенства треугольников получаем равенство отрезков , значит, .
Построим теперь график (здесь заменена буква на более привычную ), или, что то же самое, график . Этот график можно построить, если синусоиду сдвинуть влево на . Итак, строится график , сдвигаем каждую точку на влево, получаем кривую (рис. 4).
Итак, строится график , сдвигаем каждую точку на влево, получаем кривую (рис. 4).
Рис. 4. Построение графика косинуса, сдвигом графика синуса
Свойства функции y=cost
Свойства функции :
1. Областью определения (областью допустимых значений) данной функции является множество всех действительных чисел (). Каждому действительному числу сопоставляется единственное число .
2. Множество значений данной функции – отрезок от минус одного, до одного (). Один из способов получения данного промежутка – это спроецировать график косинуса на ось ординат, тогда мы и получим отрезок . Здесь заключены два утверждения: при задании любого мы получим , который будет лежать в данном диапазоне; задав любое значение из этого отрезка, знаем, что оно достигается хотя бы при одном значении .
3. Функция периодична. Наименьший положительный период . Это означает, что для любого .
4. Четность функции. Это означает, что для всех значений аргумента из области определения: . Также из этого следует, что график функции симметричен относительно оси ординат.
Также из этого следует, что график функции симметричен относительно оси ординат.
На основании свойств 3 и 4, можно сделать вывод, что функцию достаточно изучить на промежутке , а далее, используя симметрию относительно оси , получить функцию на участке в период () и далее использовать периодичность (рис. 5).
Приведем пример данного метода.
Рис. 5. Пример построения графика косинуса используя его свойства четности и периодичности
Отрезок , на нем функция убывает от до . В силу четности, симметрично оси отражаем часть графика и получаем график функции на отрезке . На нем функция возрастает от до . В результате мы получили график функции на отрезке длиной в период, этого достаточно, далее используем периодичность и строим график на любом заданном участке.
5. Наибольшее и наименьшее значения функции достигаются в точках и . Причем достигается в точках , – любое целое число, а достигается в точках , – любое целое число.
6. Интервалы монотонности функции: рассмотрим интервал, равный периоду функции.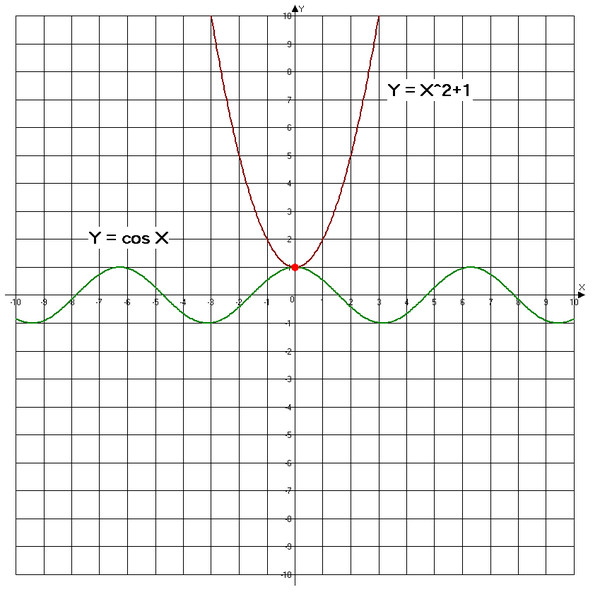 Если аргумент возрастает от до , то функция возрастает от до . Через период это повторяется: если аргумент возрастает от до , то функция возрастает от до и так далее. Значит, функция монотонно возрастает при , где . Аналогично, функция монотонно убывает при , где (рис. 6).
Если аргумент возрастает от до , то функция возрастает от до . Через период это повторяется: если аргумент возрастает от до , то функция возрастает от до и так далее. Значит, функция монотонно возрастает при , где . Аналогично, функция монотонно убывает при , где (рис. 6).
Рис. 6. Иллюстрация интервалов монотонности функции косинуса
Рассмотренные свойства функции используются в разных задачах, в том числе в задачах с параметрами.
Решение задач
Задача на смысл множества значений функции.
Найти все значения параметра , при каждом из которых уравнение имеет хотя бы одно решение.
Решение
Перепишем функцию следующим образом: .
Построим в одной системе координат графики функций из левой и правой частей уравнения, а именно: и , учитывая, что – это семейство параллельных прямых (рис. 7):
Рис. 7. Графики функций и в одной системе координат
Если или – никакого пересечения нет и уравнение корней не имеет.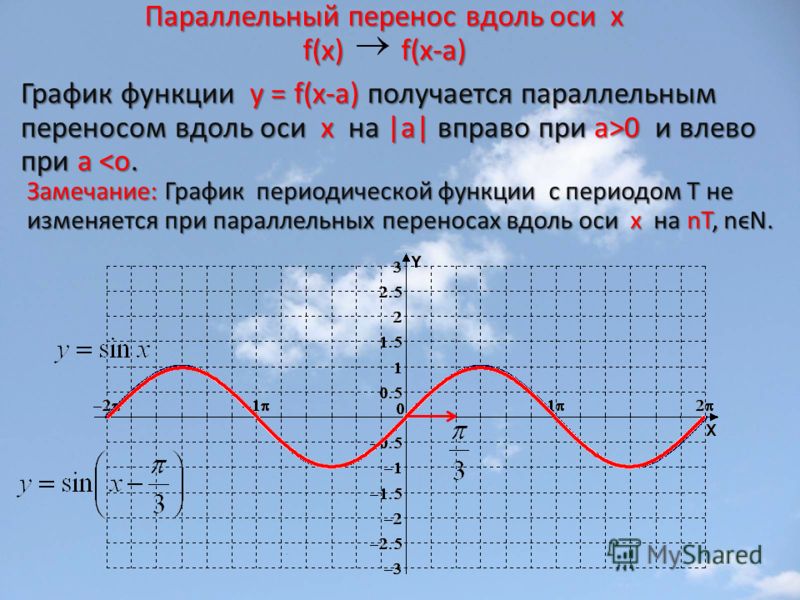
Если , то есть лежит в пределах области значений функции, то есть пересечение с хотя бы одним .
Ответ: .
Задача
Найти число корней уравнения с параметром .
Решение
Решить уравнение с параметром – это «перебрать» все значения параметра и для каждого дать ответ.
Построим график функции косинуса, рассекаем его семейством прямых (рис. 8).
Рис. 8. Графики функций и в одной системе координат, для нахождения числа корней уравнения
Находим точки пересечения, если они есть.
При – уравнение корней не имеет.
При – уравнение имеет бесчисленное множество решений.
Ответ: при – уравнение имеет бесчисленное множество корней.
Выводы
На данном уроке мы рассмотрели функцию , изучили ее свойства и построили график.
Список литературы
- Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др.
 Алгебра 8. – изд. 5. – М.: Просвещение, 2010.
Алгебра 8. – изд. 5. – М.: Просвещение, 2010. - Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Домашнее задание
- Можно ли построить график косинуса по основным точкам?
- Охарактеризуйте связь между синусом и косинусом.
- Верно ли равенство ?
- Чем отличается монотонно убывающий участок функции от монотонно возрастающего?
- Имеет ли функция косинуса точки пересечения с функцией синуса? Если да, то выпишите все точки пересечения.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Yaklass.ru (Источник).
- Интернет-портал Mathematics-tests.com (Источник).
- Интернет-портал Festival.1september.ru (Источник).
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Имеется два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации.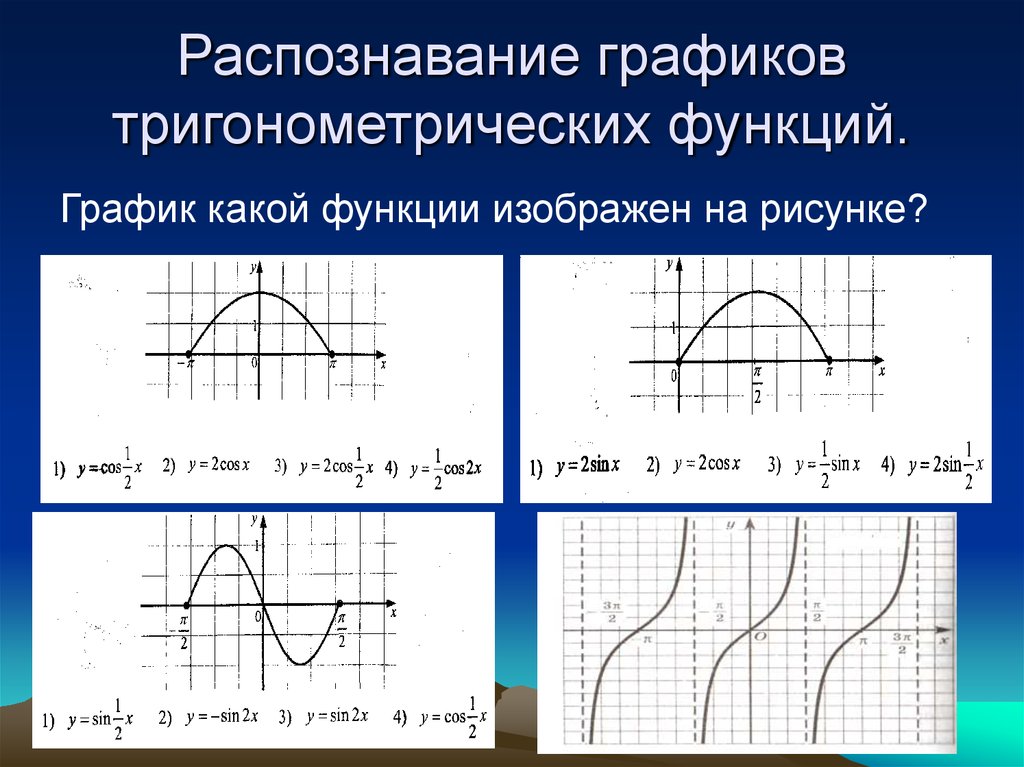 ln7
ln7
Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площад
Пользуйтесь нашим приложением
Тригонометрические функции
В школьной программе изучаются четыре тригонометрических функции — синус, косинус, тангенс и котангенс. В этой статье мы рассмотрим графики и основные свойства этих функций.
1. Начнем с построения графика функции y = sin x.
Выберем подходящий масштаб. По оси X: три клетки примем за (это примерно полтора). Тогда — одна клеточка, — две клетки.
По оси Y : две клетки примем за единицу.
Область определения функции y = sin x — все действительные числа, поскольку значение sin α можно посчитать для любого угла α.
Вспомним, что у нас есть тригонометрический круг, на котором обозначены синусы и косинусы основных углов.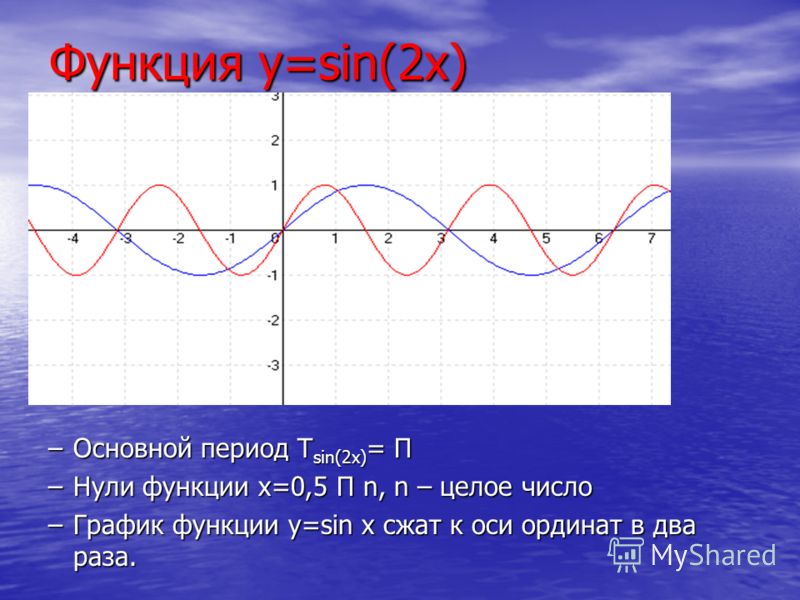 Удобнее всего отметить на будущем графике точки, в которых значение синуса является рациональным числом.
Удобнее всего отметить на будущем графике точки, в которых значение синуса является рациональным числом.
| x | 0 | ||||
| sin x | 0 |
Можем добавить, для большей плавности графика, точки и . В них значение синуса равно
Соединим полученные точки плавной кривой.
Мы помним, что . Это значит, что
Получается часть графика, симметричная той, которую нарисовали раньше.
Кроме того, значения синуса повторяются через полный круг или через целое число кругов, то есть
Это значит, что функция y = sin x является периодической. Мы уже построили уча-сток графика длиной 2π. А теперь мы как будто «копируем» этот участок и повторяем его с периодом 2π:
Синусоида построена.
Перечислим основные свойства функции y = sin x.
1) D(y): x ∈ R, то есть область определения — все действительные числа.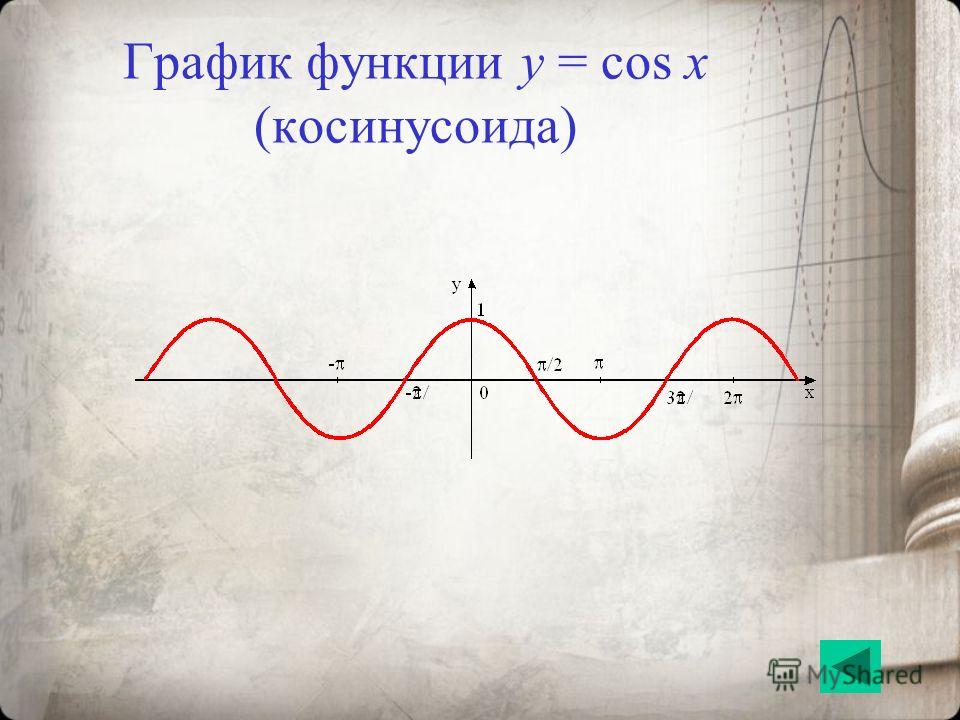
2) E(y): y ∈ [−1; 1]. Это означает, что наибольшее значение функции y = sin x равно единице, а наименьшее — минус единице.
3) Функция y = sin x — нечетная. Ее график симметричен относительно нуля.
4) Функция y = sin x — периодическая. Ее наименьший положительный период равен 2π.
2. Следующий график: y = cos x. Масштаб — тот же. Отметим на графике точки, в которых косинус является рациональным числом:
| x | 0 | ||||
| cos x | 1 | 0 |
Поскольку cos (−x) = cos x, график будет симметричен относительно оси Y , то есть левая его часть будет зеркальным отражением правой.
Функция y = cos x — тоже периодическая. Так же, как и для синуса, ее значения повторяются через 2πn. «Копируем» участок графика, который уже построили, и повторяем периодически.
Перечислим основные свойства функции y = cos x.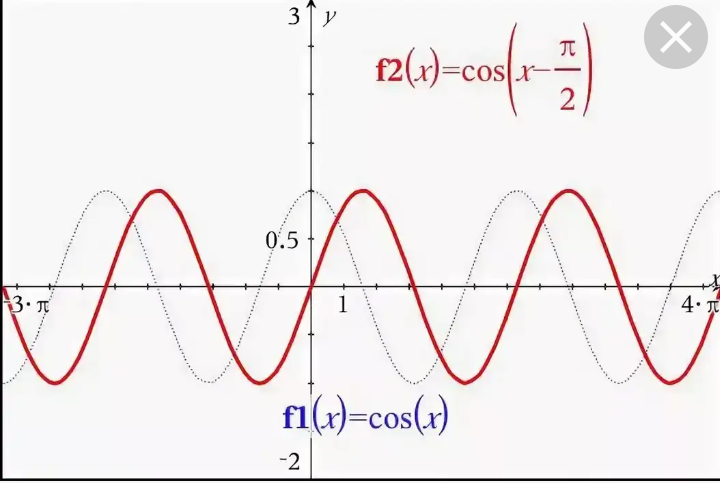
1) D(y): x ∈ R, то есть область определения — все действительные числа.
2) E(y): y ∈ [−1; 1]. Это означает, что наибольшее значение функции y = cos x равно единице, а наименьшее — минус единице.
3) Функция y = cos x — четная. Ее график симметричен относительно оси Y .
4) Функция y = cos x — периодическая. Ее наименьший положительный период равен 2π.
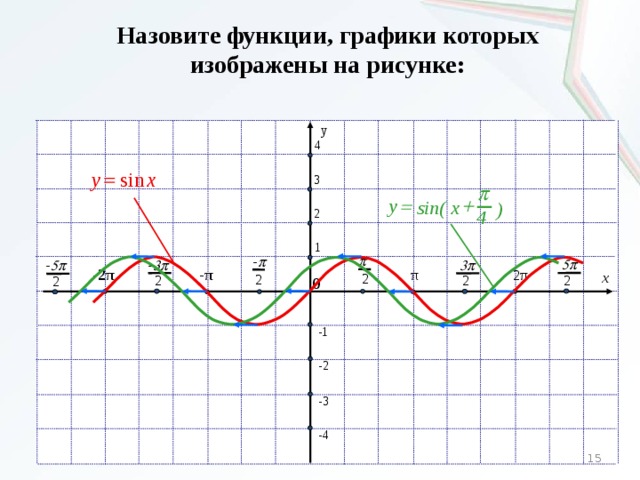
Отметим еще одно свойство. Графики функций y = sin x и y = cos x весьма похожи друг на друга. Можно даже сказать, что график косинуса получится, если график синуса сдвинуть на влево. Так оно и есть — по одной из формул приведения,.
Форма графиков функций синус и косинус, которые мы построили, очень характерна и хорошо знакома нам. Такой линией дети рисуют волны. Да, это и есть волны!
Функции синус и косинус идеально подходят для описания колебаний и волн — то есть процессов, повторяющихся во времени.
По закону синуса (или косинуса) происходят колебания маятника или груза на пружине. Переменный ток (тот, который в розетке) выражается формулой I(t) = I cos(ωt+α).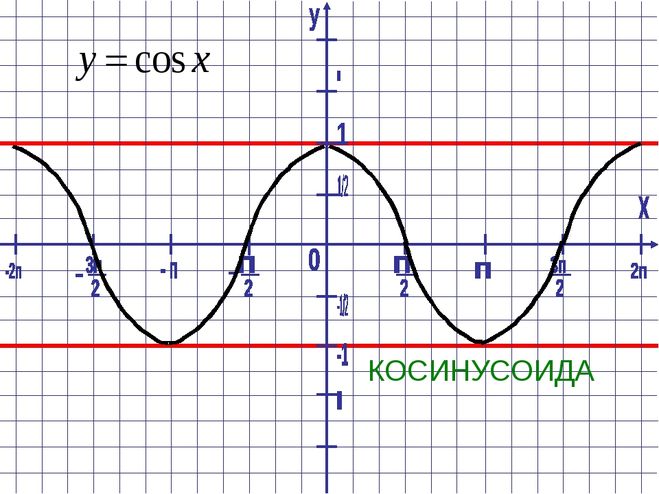 Но и это не все. Функции синус и косинус описывают звуковые, инфра– и ультразвуковые волны, а также весь спектр электромагнитных колебаний. Ведь то, что наш глаз воспринимает как свет и цвет, на самом деле представляет собой электромагнитные колебания. Разные длины волн света воспринимается нами как разные цвета. Наши глаза видят лишь небольшую часть спектра электромагнитных волн. Кроме видимого цвета, в нем присутствуют радиоволны, тепловое (инфракрасное) излучение, ультрафиолетовое, рентгеновское и гамма–излучение. Более того — объекты микромира (например, электрон) проявляют волновые свойства.
Но и это не все. Функции синус и косинус описывают звуковые, инфра– и ультразвуковые волны, а также весь спектр электромагнитных колебаний. Ведь то, что наш глаз воспринимает как свет и цвет, на самом деле представляет собой электромагнитные колебания. Разные длины волн света воспринимается нами как разные цвета. Наши глаза видят лишь небольшую часть спектра электромагнитных волн. Кроме видимого цвета, в нем присутствуют радиоволны, тепловое (инфракрасное) излучение, ультрафиолетовое, рентгеновское и гамма–излучение. Более того — объекты микромира (например, электрон) проявляют волновые свойства.
3. Перейдем к графику функции y = tg x.
Чтобы построить его, воспользуемся таблицей значений тангенса. Масштаб возьмем тот же — три клетки по оси X соответствуют , две клетки по Y — единице. График будем строить на отрезке от 0 до π. Поскольку tg (x + πn) = tg x, функ-ция тангенс также является периодической. Мы нарисуем участок длиной π, а затем периодически его повторим.
Непонятно только, как быть с точкой . Ведь в этой точке значение тангенса не определено. А как же будет вести себя график функции y = tg x при x, близких к , то есть к 90 градусам?
Ведь в этой точке значение тангенса не определено. А как же будет вести себя график функции y = tg x при x, близких к , то есть к 90 градусам?
Чтобы ответить на этот вопрос, возьмем значение x, близкое к , и посчитаем на калькуляторе значения синуса и косинуса этого угла. Пусть .
Синус угла — это почти 1. Точнее, sin = 0,9998. Косинус этого угла близок к нулю. Точнее, cos = 0,0175.
Тогда
график уйдет на 59 единиц (то есть на 118 клеток) вверх. Можно сказать, что если x стремится к (то есть к , значение функции y = tg x стремится к бесконечности.
Аналогично, при x, близких к , график тангенса уходит вниз, то есть стремится к минус бесконечности.
Осталось только «скопировать» этот участок графика и повторить его с периодом π.
Перечислим свойства функции y = tg x.
1) .
Другими словами, тангенс не определен для где n ∈ Z.
2) Область значений E(y) — все действительные числа.
3) Функция y = tg x — нечетная.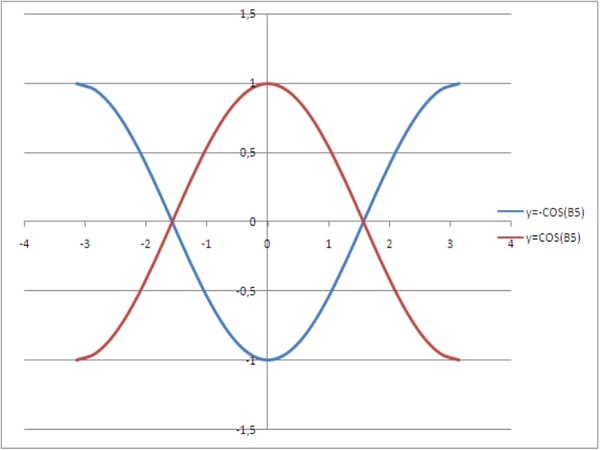 Ее график симметричен относительно начала координат.
Ее график симметричен относительно начала координат.
4) Функция y = tg x — периодическая. Ее наименьший положительный период равен π.
5) Функция y = tg x возрастает при то есть на каждом участке, на котором она непрерывна.
4. График функции y = ctg x строится аналогично. Вот он:
1) .
Другими словами, котангенс не определен для где n ∈ Z.
2) Область значений E(y) — все действительные числа.
3) Функция y = сtg x — нечетная. Ее график симметричен относительно начала координат.
4) Функция y = сtg x — периодическая. Ее наименьший положительный период равен π.
5) Функция y = сtg x убывает при то есть на каждом участке, на котором она непрерывна.
«Тригонометрические функции» с использованием интерактивных методов)
Глава 1. Тригонометрические функции.
Урок изучения нового материала
«Свойства функции у=cos(x)
и график ».
(Третий урок по теме: «Тригонометрические функции» с использованием интерактивных методов)
Сумина Елена Васильевна,
учитель математики
МБОУ «Левженская СОШ»
Рузаевского муниципального района
Саранск 2012
Урок№1 по
теме: «Свойства
функции у=cos(x) и график.
11 класс. (3 час) по учебнику Колягина Ю.М.
Учебная цель- изучение свойств функции у=cos(x), обучение построению графика функции и применение свойств функции при решении уравнений .
Учебно-воспитательные задачи:
1. Образовательные – изучение свойств функции y=cosx,обучение построению графика функции и применение свойств функции, обеспечить повторение и систематизацию материала темы.
2. Развивающие – способствовать формированию умений применять приемы: сравнения, обобщения, выявления главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти.
3. Воспитательные
– содействовать воспитанию интереса к математике и ее приложениям, любовь
к родному краю на примерах регионального компонента, активности,
мобильности, умения общаться, общей культуры, формирование точности и
аккуратности при выполнении чертежей.
Методы обучения: словесный, практический, групповая работа, выступления учащихся, интерактивные методы, самопроверка, восприятие нового материала, взаимопроверка.
Формы организации урока: индивидуальная, групповая, фронтальная.
Оборудование и источники информации: Экран; мультимедийный проектор; компьютер. Программное обеспечение: Microsoft Power Point, Microsoft Excel
У учащихся на партах оценочные листы учета знаний; раздаточный материал с построенными ранее синусоидами (заготовки, заготовки координатной плоскости..
Ход урока:
1. Орг. момент. Цитата Гете. Тема урока. Задачи урока.
2. Диктант. Проверка на экране.
3. Подготовка к ЕГЭ
4. Изучение нового
материала.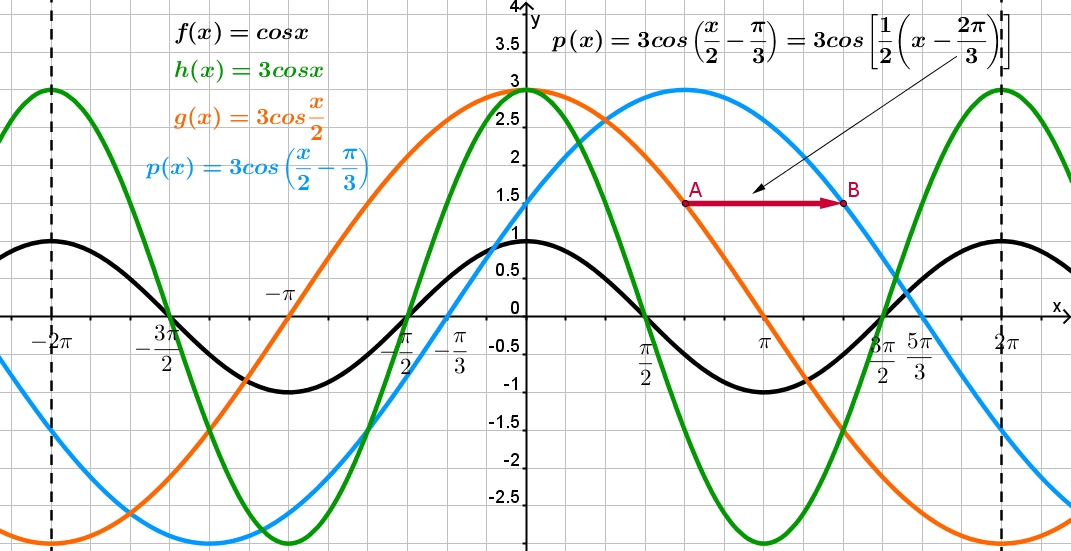
5. Историческая справка – регионального характера
6. Физкультминутка для глаз.
7. Изобразить эскиз графика функции y=cosx.
8. Решение упражнений из учебника
9. Тест
10. Выступление учащихся по преобразованиям графиков функций. Как выполнить преобразования синусоиды. Примеры. Совместное обсуждение.
11. Практическая работа.
12. Итог урока. Выводы.
13. Домашнее задание.
14. Рефлексия урока.
1. Организационный момент. СЛАЙДЫ 1-2
Немецкий гений Гете однажды заметил: «Недостаточно только
получить знания, надо найти им приложение. Недостаточно только желать; надо
делать». Так вот, давайте сегодня на уроке будем следовать этому
совету писателя, будем активны, внимательны, будем поглощать знания с
большим желанием, ведь они пригодятся вам в вашей дальнейшей жизни.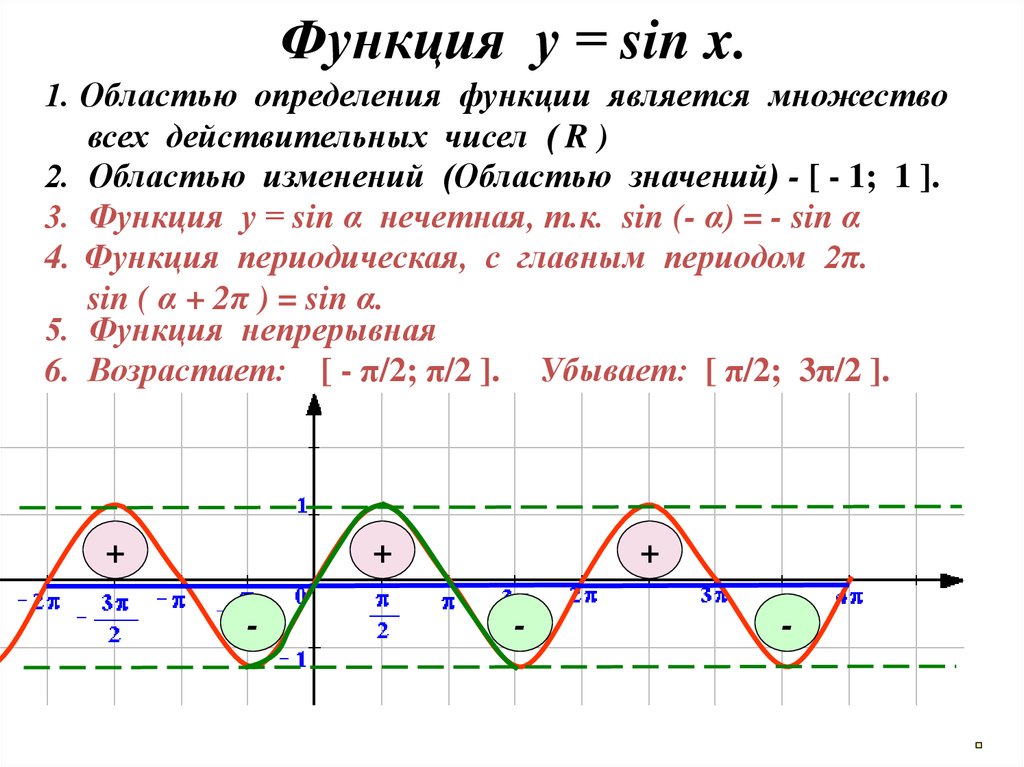
Сегодня у нас 1 урок по теме «Свойства и график функции y=cosx». (Тему записываем в тетрадях). Также мы будем повторять изученные ранее вопросы тригонометрии. Перед нами стоит задача – познакомиться со свойствами функции, поработать с графиком функции y=cos x. Для каждого я приготовила оценочные листы, на которых показаны все этапы нашего урока. Вам необходимо проставлять в эту таблицу себе баллы за правильные ответы. В конце урока мы подведем итоги, посмотрим результаты и оценим их.
2. Диктант. СЛАЙДЫ 3
Перед вами знакомая вам тригонометрическая окружность, с которой мы много работали последние уроки: учились находить значения синуса, косинуса, тангенса, котангенса табличных углов по этой окружности. А также находить все углы, заданные точками тригонометрической окружности, записывать их формулами. Сейчас проведем небольшой диктант. Записать формулами все углы, для которых…
Работа окончена, один человек читает ответы, которые он
записал, проверка на экране. Все учащиеся ставят себе + за правильные ответы
или – за неправильные ответы. Соответствующие баллы – в листы оценивания.
Все учащиеся ставят себе + за правильные ответы
или – за неправильные ответы. Соответствующие баллы – в листы оценивания.
3.Подготовка к ЕГЭ СЛАЙД 4
Объяснение задания В7
Решение задания типа В7 из материалов теста ЕГЭ 2012, со взаимной проверкой
• Найдите значение выражения
• 13 sin 2x, если cos х= 2/ √13 , -П<x<0
• Решение.
• По формуле синуса двойного аргумента имеем 13 sin 2x= 13 sinх cosx
• Найдем sinх. Так как , -П<x<0, то sinх<o, поэтому sinх=-√1-cos2 x
• 13 sinх cosx = -6
• В7 вариат 1, ЕГЭ 2012- самостоятельно
4.Изучение нового материала. СЛАЙДЫ 5-8
Теоретический материал параграфа четко разделен на логические блоки
1. Исследование функции у= соsх
Исследование функции у= соsх
2. Построение графика функции
3. Наблюдение свойств функции у= соsх по графику
Изучение нового материала 1 Исследование функции. Функция y = cos x определена на всей числовой прямой и множеством её значений является отрезок [-1; 1]. Функция ограничена и график её расположен в полосе между прямыми y = -1 и y = 1.
Функция y = cos x периодическая с периодом 2π, то достаточно построить её график на каком-нибудь промежутке длиной 2π. Тогда на промежутках, получаемых сдвигами выбранного отрезка на 2πn, где n€z график будет таким же.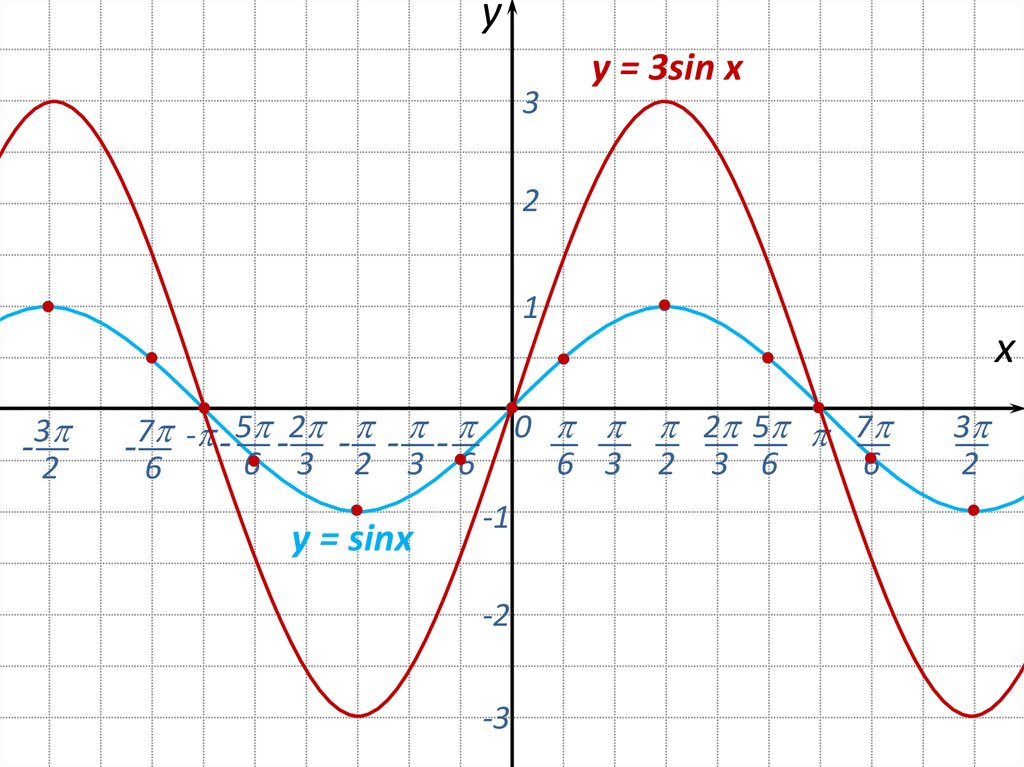
Функция y = cos x является чётной. Поэтому её график симметричен относительно оси Oy.
При повороте точки P (1; 0) вокруг начала координат против часовой стрелки на угол от 0 до π, абсцисса точки, т.е. cos x, уменьшается от 1 до – 1. cos x1 > cos x2то (рис. 2) Это и означает, что функция y = cos x убывает на отрезке [0; π].
Пользуясь свойством чётности функции y = cos x, отразим построенный на отрезке [0;П ] график симметрично относительно оси Oy. Получим график этой функции на отрезке [-π;π] (рис. 4).
3.Наблюдение свойств функции
Так как y = cos x – периодическая функция с периодом 2π и её
график построен на отрезке [-π;π] , длина которого равна периоду, распространим
его по всей числовой прямой с помощью сдвигов на 2π, 4π
и т.д. вправо, на -2π, -4π и т.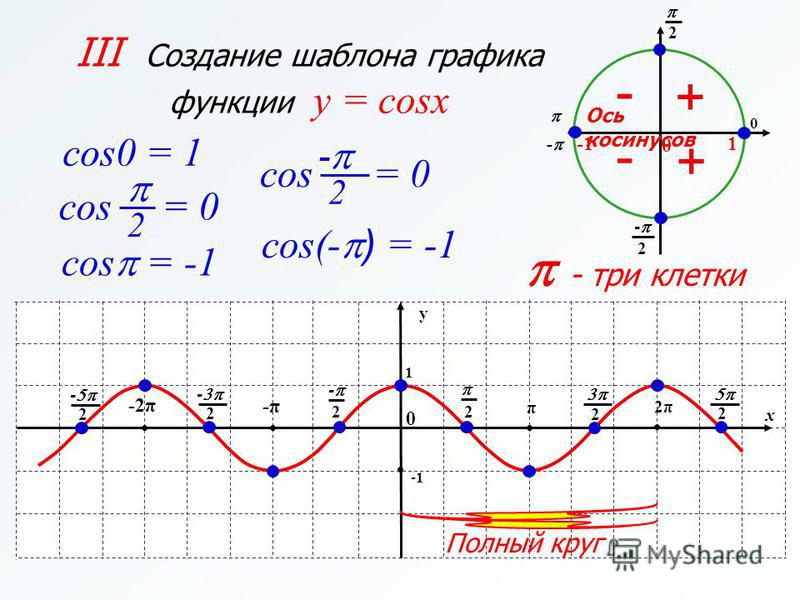 д. влево, (рис. 5)
д. влево, (рис. 5)
5.Историческая справка – регионального характера. СЛАЙД 9
График звуковой волны представляет собой синусоиду. Слушая и, главное, воспринимая звуки колоколов, человек настраивается на светлое, духовное, возвышенное. В уневерсальных лечебных целях особенно ценны кононические колокольные звоны.
Кафедральный Собор св. праведного воина Феодора Ушакова в Г Саранске построен в стиле ампир крестовокупольного типа. Он был открыт 6 августа 2006 года и освящен Патриархом Московским и всея Руси Алексием II.
Центральный крест собора возвышается на 62 метра, одновременно присутствовать в соборе на богослужении могут 3000 человек.
По периметру храма в 4 звонницах расположены 12 колоколов, самый большой из которых весит 6 тонн.
6.Физкультминутка для глаз. СЛАЙДЫ 10
Составленная по материалам офтальмолога В.Ф. Базарного.
1. Сделайте 15
колебательных движений глазами по горизонтали справа-на лево, затем слева на
право
Сделайте 15
колебательных движений глазами по горизонтали справа-на лево, затем слева на
право
2. 15 колебательных движений глазами по вертикале –вверз -вниз.
3. Круговые вращательные движения глазами слева- направо.
4. То же самое, но справа- налево
5. Вычертите глазами уложенную набок цифру 8.
7.Изобразить эскиз графика функции y=cosx.
Изобразить эскиз графика функции у =cos x по точкам (0;1),(П/2; 0), (П;-1), (3п/2;0), (2g$1)/ Выбирая соответствующий единичный отрезок на осях координат. Прочитать свойства функции по графику.
8.Решение упражнений.
§3. № 29-31, №28 –самостоятельно, дополнительно №42
№34 – провести рассуждения разными путями.
1 способ- выяснить как ведет себя функция
2 способ – рассмотреть промежутки
9. Тест
Тест
2 варианта (Приложения к уроку —pril2)
Тест по теме функция у = cosx | |
Вариант II | |
Вопрос № 1 | |
Период функции у=3cos(3x+2) равен: | |
a)π | c) π/2 |
b)2π/3 | d) 2π |
Вопрос № 2 | |
Множество значений функции у = 3cos (x-3) | |
a) [0;3] | c)[-3;0] |
b)[1/3;3] | d) [-3;3] |
Вопрос №3 | |
Корень уравнения cos2х=1/2: | |
a) ±π/6+πn,n∊Z | c)2πn,n∊Z |
b)πn,n∊Z | d) ±π/3+2πn,n∊Z |
Вопрос № 4 | |
Число 3cos(-π/3) является: | |
a) иррациональным | c)положительным |
b)отрицательным | d)равно нулю |
Вопрос № 5 | |
Сравнить числа cosπ/6 и cosπ/3 | |
a) = | c) < |
b) ≥ | d) > |
8. Преобразования графиков функции.
Преобразования графиков функции.
Выступления учащихся.
Сегодня мы будем выполнять преобразования синусоиды. Запишем в тетрадь: «Преобразование графика y=sinx». Вспомним, как выполняются основные преобразования графиков функций, поговорим о том, как можно выполнять преобразования с синусоидой. Я заранее давала задание некоторым учащимся подготовить сообщения по преобразованиям (сдвиг вдоль осей, растяжение – сжатие вдоль оси ординат). Напомнить нам о них. Эти преобразования выполняются с синусоидой на экране.
10. Практическая работа. Преобразования графика . Работа в группах.
А сейчас перейдем к практической работе. Работаем на заготовленных листах. (Раздаточный материал Эскизов)
11.Итог урока. Выводы.
Давайте подведем итоги урока.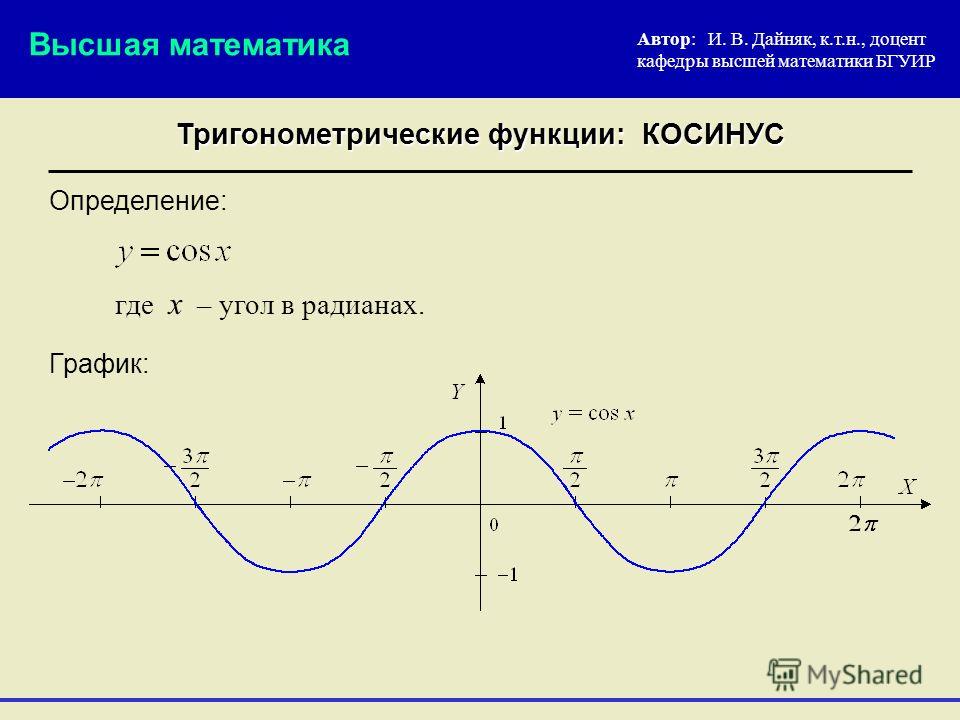 Сегодня на уроке мы выполняли
преобразования функции, с помощью этих преобразований мы выполняли построение
графиков сложных тригонометрических функций. А где нам пригодится умение
строить такие графики?
Сегодня на уроке мы выполняли
преобразования функции, с помощью этих преобразований мы выполняли построение
графиков сложных тригонометрических функций. А где нам пригодится умение
строить такие графики?
Умение строить графики тригонометрических функций нужны нам при решении уравнений, неравенств, для выполнения заданий, связанных с исследованием свойств функций. (Ребята сами делают эти выводы).
А теперь посчитайте свои баллы. Назовите наибольшие баллы. У кого сегодня неудачно прошла работа, не расстраивайтесь, мы обязательно еще будем отрабатывать преобразование графиков других тригонометрических функций Оценки за урок: лидеры команд, за диктант, активным учащимся.
12.Домашнее задание.
§3. До задачи №1№ 29-31, четные, Тестовые задания В7 –вариант 3, 4.
13. Рефлексия урока.
Продолжите фразу:
• Самым сложным на уроке было…
• Самым интересным при работе для меня было…
• Самым неожиданным для меня было…
Литература
· Учебник Колягина Ю.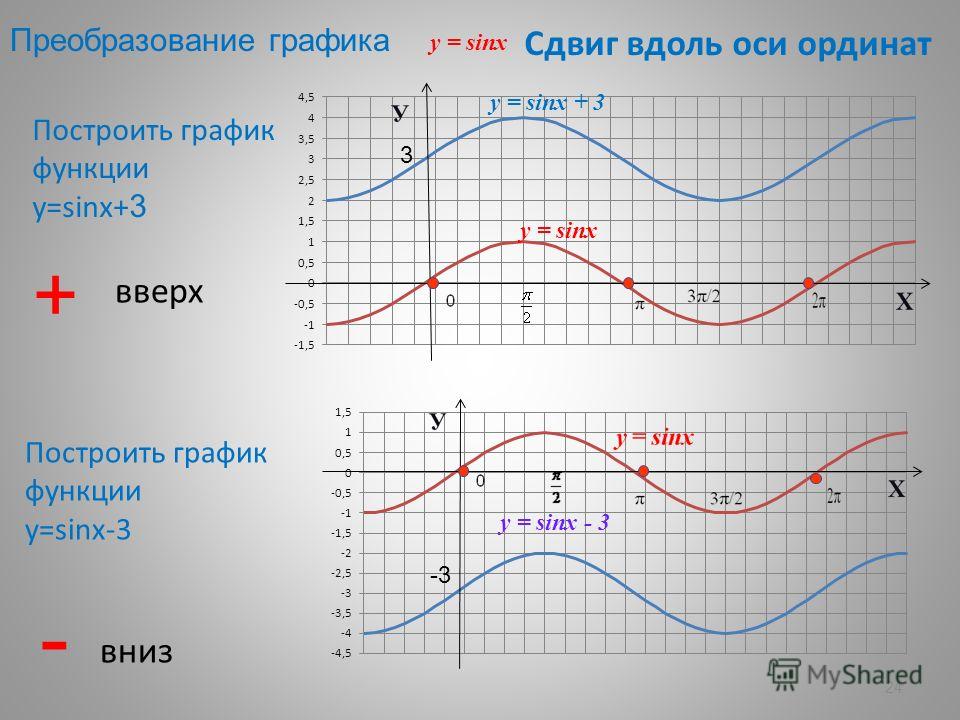 М..
Алгебра и начала анализа. 11 класс. Москва, Издательство Просвещение, 2010 год.
М..
Алгебра и начала анализа. 11 класс. Москва, Издательство Просвещение, 2010 год.
· Математический энциклопедический словарь. М. «Советская энциклопедия», 1988 г
· Интернет ресурсы: http://teoria.nath-portal.ru Математическая энциклопедия; http://WWW.prosv.ru .
· Тестовые задания ЕГЭ по математике 2012 год.
· Пособие для учителя Н.Е.Федорова «Изучение алгебры и начала анализа» 11 класс. Москва, Издательство Просвещение, 2010 год.
·
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.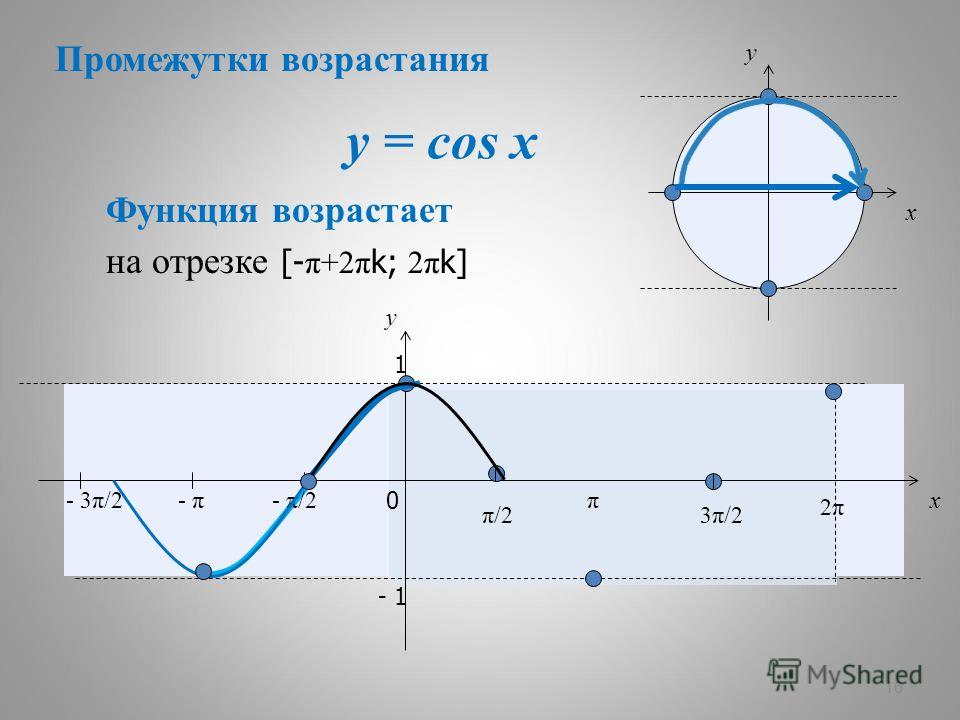 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Как нарисовать f(x)=cos^3(x)?
Тригонометрия
Наука
- Анатомия и физиология
- астрономия
- Астрофизика
- Биология
- Химия
- науки о Земле
- Наука об окружающей среде
- Органическая химия
- Физика
Математика
- Алгебра
- Исчисление
- Геометрия
- Преалгебра
- Предварительный расчет
- Статистика
- Тригонометрия
Гуманитарные науки
- Английская грамматика
- История США
- Всемирная история
- Сократическая мета
- Избранные ответы
.
 .. и не только
.. и не толькоТемы
Влияние этого вопроса
7490 просмотров по всему миру
Вы можете повторно использовать этот ответ
Лицензия Creative Commons
Cos3x — формула, вывод, примеры, тождество
Cos3x — тождество тройного угла в тригонометрии. Это частный случай идентичности составных углов функции косинуса. Cos3x дает значение тригонометрической функции косинуса для тройного угла. Расширение cos3x может быть получено с использованием идентичности сложения углов косинуса, и оно включает термин cos куб x (cos ^ 3x). 3x помогают решать различные тригонометрические задачи. 93x, их вывод и применение вместе с решенными примерами для лучшего понимания. Мы также изучим график функции cos3x, чтобы понять ее поведение.
3x помогают решать различные тригонометрические задачи. 93x, их вывод и применение вместе с решенными примерами для лучшего понимания. Мы также изучим график функции cos3x, чтобы понять ее поведение.
| 1. | Что такое Cos3x в тригонометрии? |
| 2. | Формула Cos3x |
| 3. | Получение формулы Cos3x |
| 4. | График Cos3x 93x Формула |
| 7. | Как применять формулу Cos3x? |
| 8. | Часто задаваемые вопросы по Cos3x |
Что такое Cos3x в тригонометрии?
Cos3x — важное тождество в тригонометрии, которое используется для определения значения функции косинуса для угла, который в три раза больше угла x. Его можно выразить через cos x. Поведение функции cos3x аналогично поведению cos x. Поскольку период cos x равен 2π, период cos3x равен 2π/3, то есть цикл cos3x повторяется через каждые 2π/3 радиана.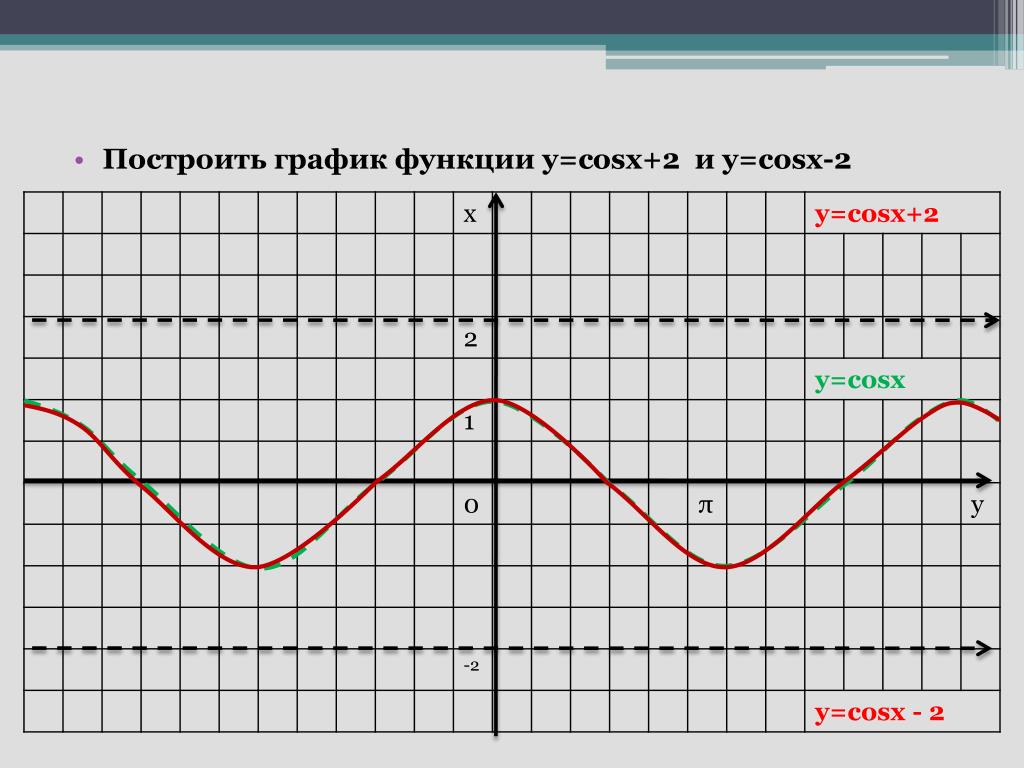 Теперь давайте посмотрим на формулу для cos3x. 93x — 3 cos x = 4 cos 3 x — 3 cos x . Теперь мы рассмотрим вывод формулы cos3x в следующем разделе, используя формулу суммы углов функции косинуса.
Теперь давайте посмотрим на формулу для cos3x. 93x — 3 cos x = 4 cos 3 x — 3 cos x . Теперь мы рассмотрим вывод формулы cos3x в следующем разделе, используя формулу суммы углов функции косинуса.
Получение формулы Cos3x
Мы будем использовать формулу сложения углов функции косинуса, чтобы вывести формулу cos3x. Мы знаем, что угол 3x можно записать как 3x = 2x + x. Мы будем использовать следующие тригонометрические тождества для вывода cos3x:
- cos (a + b) = cos a cos b — sin a sin b
- sin 2x = 2 sin x cos x
- cos 2x = 1 — 2sin 2 x
- sin 2 х + cos 2 х = 1
Мы будем использовать приведенные выше тождества для доказательства тождества cos3x. Используя формулу сложения углов для функции косинуса, мы имеем
cos3x = cos (2x + x)
= cos 2x cos x — sin 2x sin x [Потому что cos (a + b) = cos a cos b — sin a sin б] 9093x — 3cosx
Следовательно, мы получили cos3x = 4 cos 3 x — 3 cos x , используя тождество сложения углов для функции косинуса.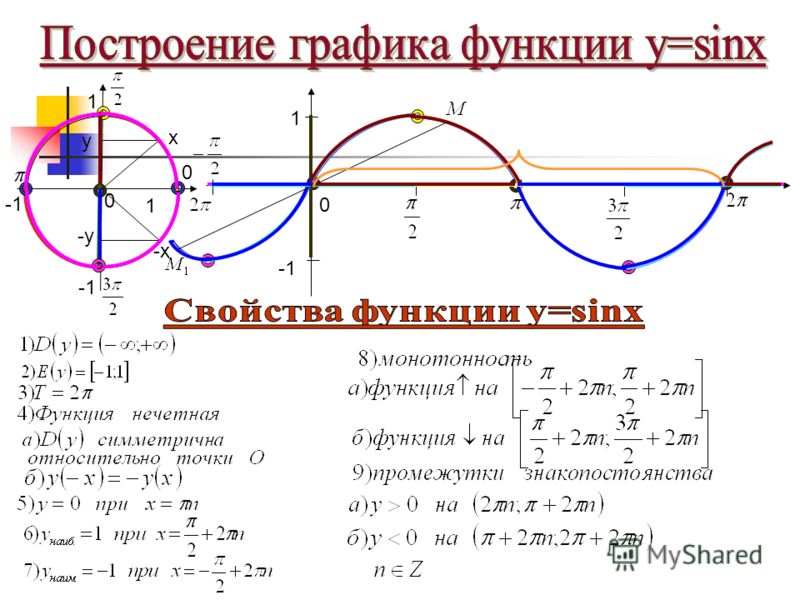
График Cos3x
График cos3x подобен графику cos x. Поскольку угол в cos3x в три раза больше угла в cos x, график cos3x уже, чем cos x, и, следовательно, период cos3x также составляет одну треть периода функции cos x. Кроме того, для функции cos bx период равен 2π/|b|. Следовательно, период cos3x равен 2π/3. Мы можем построить график cos 3x, взяв несколько точек на графике и соединив их. Рассмотрим несколько точек для y = cos3x и y = cos x и нанесем их на график. 93x ⇒ cos 3 x = 1/сек 3 x
Как применять формулу Cos3x?
Чтобы понять применение cos3x, рассмотрим пример. Изучаем и запоминаем значение функции косинуса для некоторых конкретных углов, таких как 0°, 30°, 45°, 60°, 90° и т. д. Теперь определим значение cos 135° по формуле cos3x. Если 3x = 135°, x = 135°/3 = 45°. Следовательно, используя формулу cos3x, мы имеем
cos 135° = cos (3 × 45°) = 4 cos 93x = (1/4) cos3x + (3/4) cosx, который используется для упрощения сложных задач интеграции.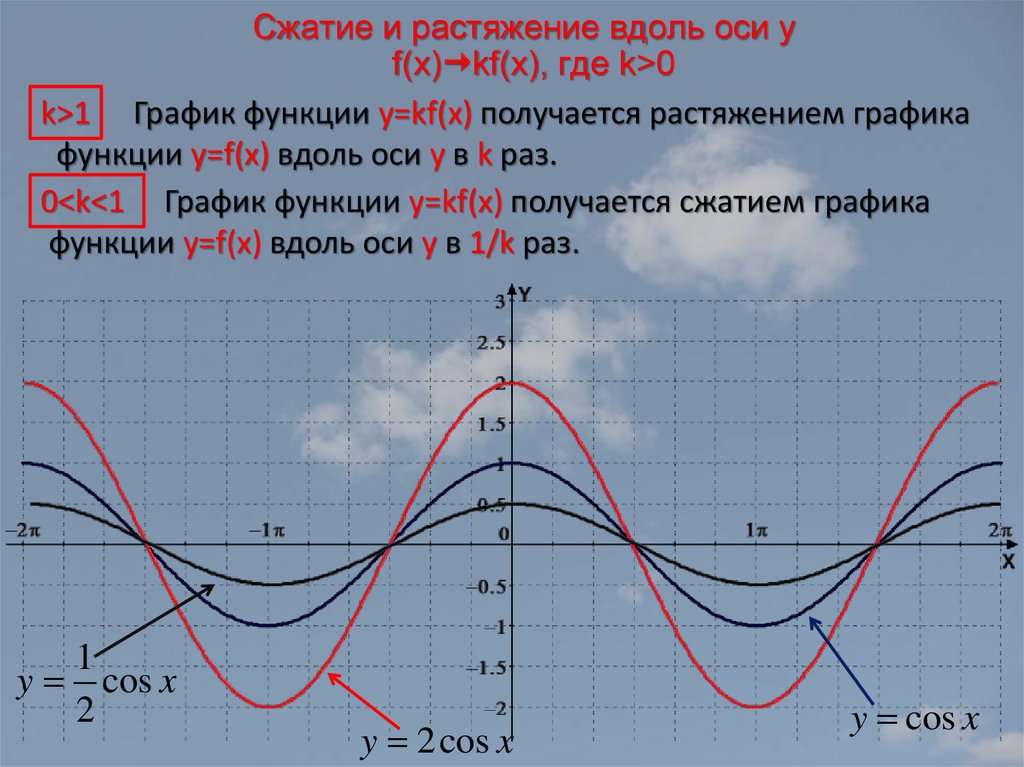
☛ Статьи по теме:
- Грех греха Инверсия
- грех 2 пи
- соз а сос б
- sin3x
Часто задаваемые вопросы по Cos3x
Что такое Cos3x в тригонометрии?
Cos3x — тождество тройного угла в тригонометрии. Его можно получить, используя тождество сложения углов функции косинуса. Идентичность cos3x задается как cos3x = 4 cos 3 х — 3 cos х.
Что такое Период cos3x?
Поскольку угол в cos3x в три раза больше угла в cos x, период cos3x также составляет одну треть периода функции cos x. Для функции cos bx период равен 2π/|b|. Следовательно, период cos3x равен 2π/3.
Как построить график cos3x?
Поскольку угол в cos3x в три раза больше угла в cos x, график cos3x уже, чем cos x. Мы можем рассмотреть несколько точек для y = cos3x и y = cos x и соединить их, чтобы построить график.
- Когда x = 0, 3x = 0 ⇒ cos x = 1, cos3x = 1
- Когда x = -π/3, 3x = -π ⇒ cos x = 1/2, cos3x = -1
- Когда x = π/3, 3x = π ⇒ cos x = 1/2, cos3x = -1
- Когда x = 2π/3, 3x = 2π ⇒ cos x = -1/2, cos3x = 1
- Когда x = -2π/3, 3x = -2π ⇒ cos x = -1/2, cos3x = 1
Какая формула для Cos3x?
Тригонометрическая формула для cos3x: cos3x = 4 cos 3 x — 3 cos x. Мы можем вывести эту формулу cos3x, используя формулу cos a плюс b. 93x = (1/4)(cos3x + 3 cosx).
Мы можем вывести эту формулу cos3x, используя формулу cos a плюс b. 93x = (1/4)(cos3x + 3 cosx).
Построение синуса и косинуса с помощью Matplotlib и Python
- Заговор
- Построение синуса и косинуса с помощью Matplotlib и Python
Составление чертежей — важный навык для инженеров. Графики могут отображать тенденции в данных и выбросы. Графики — это способ визуального представления результатов вашей команде инженеров, руководителям и клиентам. В этом посте мы собираемся построить пару триггерных функций, используя Python и matplotlib . Matplotlib — это библиотека построения графиков, которая может создавать линейные графики, гистограммы, гистограммы и многие другие типы графиков с использованием Python.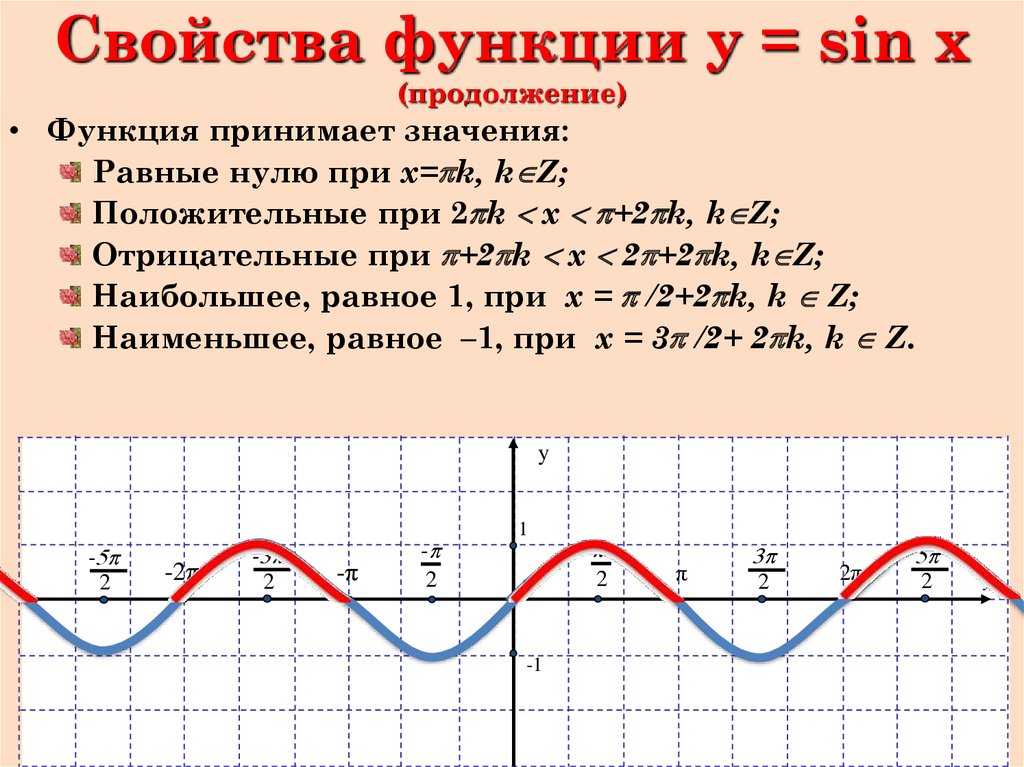 Matplotlib не входит в стандартную библиотеку. Если вы загрузили Python с сайта python.org, вам потребуется установить matplotlib и numpy с pip в командной строке.
Matplotlib не входит в стандартную библиотеку. Если вы загрузили Python с сайта python.org, вам потребуется установить matplotlib и numpy с pip в командной строке.
> pip установить matplotlib > пип установить numpy
Если вы используете дистрибутив Python Anaconda (это дистрибутив Python, который я рекомендую для инженеров-студентов), включены matplotlib и numpy (плюс множество других библиотек, полезных для инженеров). Если вы используете Anaconda , вам не нужно устанавливать какие-либо дополнительные пакеты для использования матплотлиб .
В этом посте мы собираемся построить пару графиков, которые показывают триггерные функции синуса и косинуса . Мы начнем с импорта matplotlib и numpy , используя стандартные строки import matplotlib. и  pyplot as plt
pyplot as plt import numpy as np . Это означает, что мы можем использовать короткие псевдонимы plt и np при вызове этих двух библиотек. Вы можете импортировать numpy как Wonderburger и использовать Wonderburger.sin() для вызова функции numpy sine, но другим инженерам это покажется забавным. Строка import numpy as np стала общепринятой и будет знакома другим инженерам, использующим Python. Если вы работаете в блокноте Juypiter, команда %matplotlib inline также необходима для просмотра графиков непосредственно в блокноте.
В [1]:
импортировать matplotlib.pyplot как plt импортировать numpy как np # при использовании блокнота Jupyter %matplotlib встроенный
Далее мы создадим набор значений x от нуля до 4π с шагом 0,1 радиана для использования на нашем графике. Значения x хранятся в массиве numpy. Функция Numpy arange() имеет три аргумента: start , stop , step . Мы начинаем с нуля, останавливаем на 4π и шагаем на 0,1 радиана. Затем мы определяем переменную
Мы начинаем с нуля, останавливаем на 4π и шагаем на 0,1 радиана. Затем мы определяем переменную y как синус x, используя функцию numpy sin() .
В [2]:
x = np.arange(0,4*np.pi,0.1) # старт,стоп,шаг у = np.sin (х)
Чтобы создать график, мы используем функцию matplotlib plt.plot() . Два аргумента — это наши пустые массивы x и y . Строка plt.show() покажет готовый график.
В [3]:
plt.plot(x,y) plt.show()
Далее давайте построим график, который показывает две триггерные функции, синус и косинус. Мы создадим те же два массива numpy x и y , как и раньше, и добавьте третий массив numpy z , который является косинусом x .
В [4]:
x = np.arange(0,4*np.pi,0.1) # start,stop,step у = np.sin (х) г = np.cos (х)
Чтобы построить синус и косинус на одном и том же наборе осей, нам нужно включить две пары значений x,y в наши аргументы plt.. Первая пара 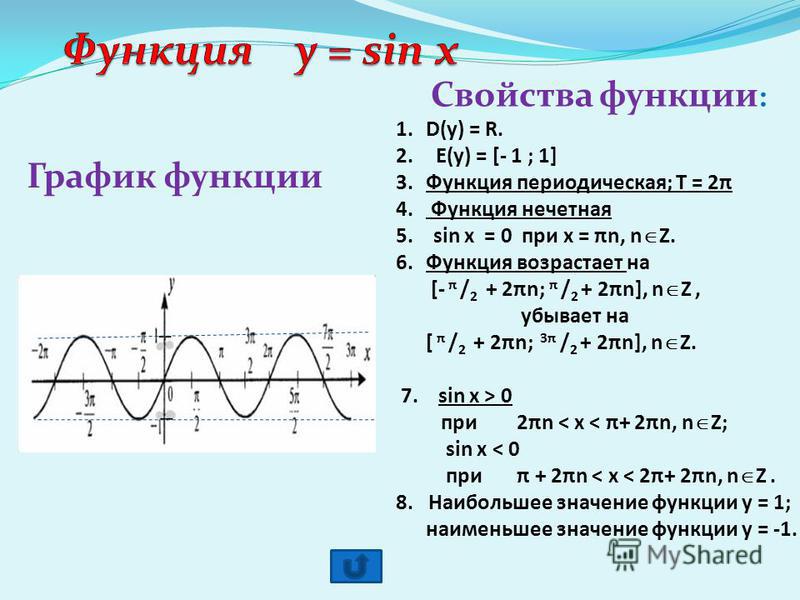 plot()
plot() x,y . Это соответствует синусоидальной функции. Вторая пара х,з . Это соответствует функции косинуса. Если вы попытаетесь добавить только три аргумента, как в plt.plot(x,y,z) , ваш график не будет отображать синус и косинус на одном и том же наборе осей.
В [5]:
plt.plot(x,y,x,z) plt.show()
Давайте построим еще один график, график, который показывает синус и косинус x, а также включает метки осей, заголовок и легенду. Мы строим массивы numpy, используя триггерные функции, как и раньше:
В [6]:
x = np.arange(0,4*np.pi-1,0.1) # старт, стоп, шаг у = np.sin (х) г = np.cos (х)
Вызов plt.plot() такой же, как и раньше, с использованием двух пар значений x и y. Чтобы добавить метки осей, мы будем использовать следующие методы:
| метод matplotlib | описание | пример |
|---|---|---|
plt. xlabel() xlabel() | метка оси x | plt.xlabel('значения x от 0 до 4pi') |
| plt.ylabel() | метка оси Y | plt.ylabel('sin(x) и cos(x)') |
| табл.название() | название сюжета | plt.title('График sin и cos от 0 до 4pi') |
| табл.легенда([ ]) | легенда | plt.legend(['sin(x)', 'cos(x)']) |
Обратите внимание, что plt.legend() требуется список строк ( ['string1', 'string2'] ), где отдельные строки заключены в кавычки, затем разделены запятыми и, наконец, заключены в квадратные скобки, чтобы составить список. Первая строка в списке соответствует первой паре x-y, когда мы вызывали plt.plot() , вторая строка в списке соответствует второй паре x,y в строке plt.plot() .
В [7]:
plt.plot(x,y,x,z) plt.xlabel('значения x от 0 до 4pi') # строка должна быть заключена в кавычки ' ' plt.ylabel('sin(x) и cos(x)') plt.title('График sin и cos от 0 до 4pi') plt.legend(['sin(x)', 'cos(x)']) # записи легенды в виде отдельных строк в списке plt.show()
Серия Фурье
Синусоидальные и косинусоидальные волны могут выполнять другие функции!
Здесь две разные синусоидальные волны складываются вместе, образуя новую волну:
Попробуйте «sin(x)+sin(2x)» на графике функций.
(Вы также можете послушать на Sound Beats.)
Прямоугольная волна
Можем ли мы использовать синусоидальные волны для создания прямоугольной волны ?
Наша цель — прямоугольная волна:
Начните с sin(x) :
Затем возьмите sin(3x)/3 :
И добавьте его, чтобы получить sin(x)+sin(3x)/3 :
Вы видите, как это начинает немного походить на прямоугольную волну?
Теперь возьмите sin(5x)/5 :
Добавьте его также, чтобы получить sin(x)+sin(3x)/3+sin(5x)/5 :
Поправляйся! Давайте добавим намного больше синусоид.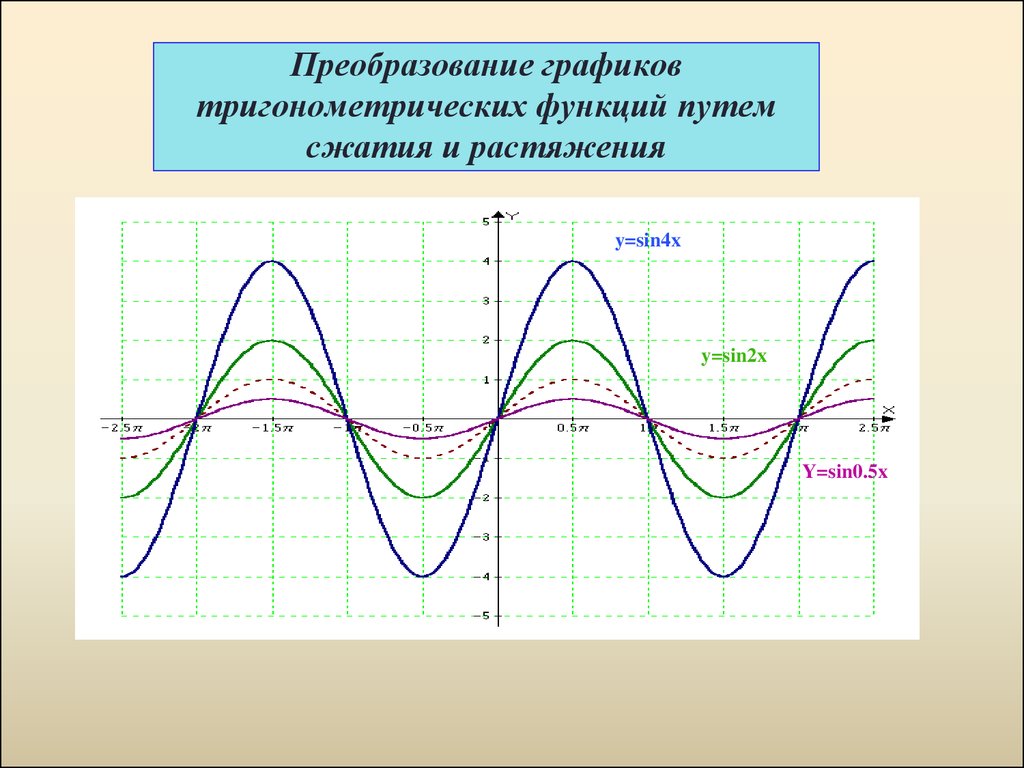
Используя 20 синусоид, мы получаем sin(x)+sin(3x)/3+sin(5x)/5 + … + sin(39x)/39 :
Используя 100 синусоид, мы получаем sin(x)+sin(3x)/3+sin(5x)/5 + … + sin(199x)/199 :
И если бы мы могли добавить бесконечные синусоидальные волны в этот узор, мы бы получили прямоугольную волну!
Итак, мы можем сказать, что:
прямоугольная волна = sin(x) + sin(3x)/3 + sin(5x)/5 + … (бесконечно)
В этом заключается идея ряда Фурье.
Добавляя бесконечные синусоидальные (и/или косинусоидальные) волны, мы можем создавать другие функции, даже если они немного странные.
Возможно, вам захочется немного поиграть с:
Графом серии Фурье
Также интересно использовать Spiral Artist и наблюдать, как круги создают волны.
Они предназначены для экспериментов, так что поиграйте и прочувствуйте предмет.
Нахождение коэффициентов
Откуда мы узнали, что нужно использовать sin(3x)/3, sin(5x)/5 и т. д.?
д.?
Есть формулы!
Сначала запишем полный ряд синусов и косинусов, назвав все коэффициенты:
f(x) = а 0 +
a n cos(nx π L ) +
b n sin(nx π L )
9Где:
- f(x) — функция, которую мы хотим (например, прямоугольная волна)
- L это половина периода функции
- a 0 , a n и b n — это коэффициенты , которые нам нужно рассчитать!
Что означает
a n cos(nx π L ) означает?
Используется сигма-нотация для обозначения суммы вверх по ряду значений, начиная с n=1:
- a 1 cos(1x π/L)
- a 2 cos(2x π/L)
- и т.
 д.
д.
Мы (пока) не знаем значения числа 1 , 2 и т. д.
Чтобы найти коэффициенты a 0 , a n и b n , мы используем следующие формулы:
a 0 = 1 2L
f(x) dx
a n = 1 L
f(x) cos(nx π L ) dx
b n = 1 L
f(x) sin(nx π L ) dx
Что означает
f(x) sin(nx π L ) dx среднее?
Это интеграл, но на практике он просто означает нахождение чистой площади
f(x) sin(nx π L )
между −L и L
7 9 часто находим эту область, просто делая наброски и используя базовые вычисления, но в других случаях нам может понадобиться использовать правила интеграции.
Вот что мы делаем:
- Возьмем нашу целевую функцию , умножим ее на синус (или косинус) и проинтегрируем (найдем площадь)
- Сделайте это для n=0, n=1 и т. д., чтобы вычислить каждый коэффициент
- И после того, как мы рассчитаем все коэффициенты, подставим их в приведенную выше формулу ряда.
Давайте посмотрим, как выполнить каждый шаг, а затем соберем результат в конце!
Пример: прямоугольная волна:
- L = π (Период 2π)
- Прямоугольная волна от −h до +h
Now our job is to calculate a 0 , a n and b n
a 0 is the net area between −L and L, then divided по 2л. Это в основном 9 1052 в среднем 9 1053 f (x) в этом диапазоне.
Глядя на этот эскиз:
Чистая площадь прямоугольной волны от −L до L равна ноль .
Таким образом, мы знаем, что:
A 0 = 0
для A 1 Мы знаем, что n = 1 и L = π, SO:
A 4154541541541541541541541541541541544154154154154154154154154154154154154154154154154101584. π
f(x) cos(1x π π ) dx
Which simplifies to:
a 1 = 1 π
f(x) cos(x) dx
Теперь, поскольку прямоугольная волна резко меняется при x=0, нам нужно разбить вычисление на −π до 0 и 0 до π ,
От −π до 0 мы знаем, что f(x) просто равно −h :
1 7 − 9h 9097 π (x) DX
Мы можем перемещать постоянную −h за пределами интеграла:
-H π
Cos (x) DX
707105. 101505.
101505.
- 5 Cos (x) DX
- a n = 0 (все!),
- b n = 0 , когда n равно
- б п = 4ч nπ когда n нечетное
- Подумайте о каждом коэффициенте, зарисуйте функции и посмотрите, сможете ли вы найти закономерность,
- объединил все это в формулу ряда в конце
- функция
- функция умножает на синус
- функция, умноженная на косинус
- Это периодические функции с периодом [latex]\,2\pi .
 [/latex]
[/latex] - Домен каждой функции: [латекс]\,\left(-\infty ,\infty \right)\,[/latex], а диапазон — [латекс]\,\left[-1,1\right]. [/латекс]
- График [latex]\,y=\mathrm{sin}\text{ }x\,[/latex] симметричен относительно начала координат, потому что это нечетная функция.
- График [latex]\,y=\mathrm{cos}\text{ }x\,[/latex]симметричен относительно оси [latex]\,y\text{-}[/latex], поскольку он является четной функцией.
- Определите амплитуду как [латекс]\,|А|.[/латекс]
- Определите период как [латекс]\,P=\frac{2\pi }{|B|}.[/latex]
- Определить фазовый сдвиг как[latex]\,\frac{C}{B}.[/latex]
- Определите среднюю линию как [латекс]\,у=D.[/латекс]
- Определить амплитуду,[латекс]\,|А|.[/латекс]
- Определить период,[латекс]\,P=\frac{2\pi }{|B|}.[/latex]
- Начните с исходной точки, при этом функция увеличивается вправо, если [латекс]\,А\,[/латекс] положительна, или уменьшается, если [латекс]\,А\,[/латекс]отрицательна.

- При[латекс]\,х=\frac{\pi }{2|B|}\,[/latex]есть локальный максимум для[латекс]\,А>0\,[/латекс]или минимум для[латекс]\,А<0,\,[/латекс]с[латекс]\,у=А.[/латекс]
- Кривая возвращается к оси x в точке [латекс]\,x=\frac{\pi }{|B|}.[/latex]
- Существует локальный минимум для[латекс]\,А>0\,[/латекс](максимум для[латекс]\,А<0[/латекс]) в [латекс]\,х=\фрак{3\ pi }{2|B|}\,[/latex]с [латексом]\,y=–A.[/latex]
- Кривая снова возвращается к оси x в точке [latex]\,x=\frac{2\pi }{|B|}.[/latex]
- Выразите функцию в общем виде [латекс]\,y=A\mathrm{sin}\left(Bx-C\right)+D\text{ или }y=A\mathrm{cos}\left (Bx-C\справа)+D.[/латекс]
- Определить амплитуду,[латекс]\,|А|.[/латекс]
- Определить период,[латекс]\,P=\frac{2\pi }{|B|}.[/latex]
- Определение фазового сдвига,[латекс]\,\фракция{С}{В}.[/латекс]
- Нарисуйте график [латекс]\,f\left(x\right)=A\mathrm{sin}\left(Bx\right)\,[/latex] сдвинут вправо или влево на [латекс]\, \frac{C}{B}\,[/latex]и вверх или вниз на[latex]\,D.[/latex]
- Амплитуда и период синуса и косинуса
- Переводы синуса и косинуса
- Графические преобразования синуса и косинуса
- График функции синуса
- Периодические функции повторяются после заданного значения. Наименьшей такой величиной является период. Основные функции синуса и косинуса имеют период[latex]\,2\pi .[/latex]
- Функция [latex]\mathrm{sin}\,x\,[/latex] нечетна, поэтому ее график симметричен относительно начала координат. Функция [latex]\,\mathrm{cos}\,x\,[/latex] является четной, поэтому ее график симметричен относительно оси y .
- График синусоидальной функции имеет ту же общую форму, что и синусоидальная или косинусоидальная функция.
- В общей формуле для синусоидальной функции период равен[latex]\,P=\frac{2\pi }{|B|}.\,[/latex]См. (рисунок).
- В общей формуле для синусоидальной функции [латекс]\,|А|\,[/латекс] представляет собой амплитуду.
 Если [латекс]\,|A|>1,\,[/латекс] функция растягивается, тогда как если [латекс]\,|А|<1,\,[/латекс] функция сжимается. См. (Рисунок).
Если [латекс]\,|A|>1,\,[/латекс] функция растягивается, тогда как если [латекс]\,|А|<1,\,[/латекс] функция сжимается. См. (Рисунок). - Значение[latex]\,\frac{C}{B}\,[/latex]в общей формуле для синусоидальной функции указывает на фазовый сдвиг. См. (Рисунок).
- Значение[latex]\,D\,[/latex]в общей формуле для синусоидальной функции указывает вертикальное смещение от средней линии. См. (Рисунок).
- Комбинации вариаций синусоидальных функций могут быть обнаружены из уравнения. См. (Рисунок).
- Уравнение синусоидальной функции можно определить по графику. См. (Рисунок) и (Рисунок).
- Функцию можно изобразить в виде графика, определив ее амплитуду и период. См. (Рисунок) и (Рисунок).
- Функцию также можно изобразить в виде графика, указав ее амплитуду, период, фазовый сдвиг и сдвиг по горизонтали. См. (Рисунок).
- Синусоидальные функции можно использовать для решения реальных задач. См. (Рисунок), (Рисунок) и (Рисунок).
707107.107107.107107.103107. чистая площадь cos(x) от -π до 0 равна нулю .
Таким образом, чистая площадь должна быть 0:
-H π
COS (x) DX = 0
Такая же идея применяется от 0 до π 9053,
. ноль .
и, таким образом, мы можем заключить, что:
a 1 = 0
Теперь давайте посмотрим на 2
Аааа… происходит то же самое!
Чистая площадь cos(2x) от -π до 0 равна нулю .
And:
Чистая площадь cos(2x) от 0 до π также равна нулю .
So we know that:
a 2 = 0
In fact we can extend this idea to every value of a and conclude that:
a n = 0
So far не было необходимости в каких-либо серьезных расчетах! Нескольких набросков и небольшого размышления было достаточно.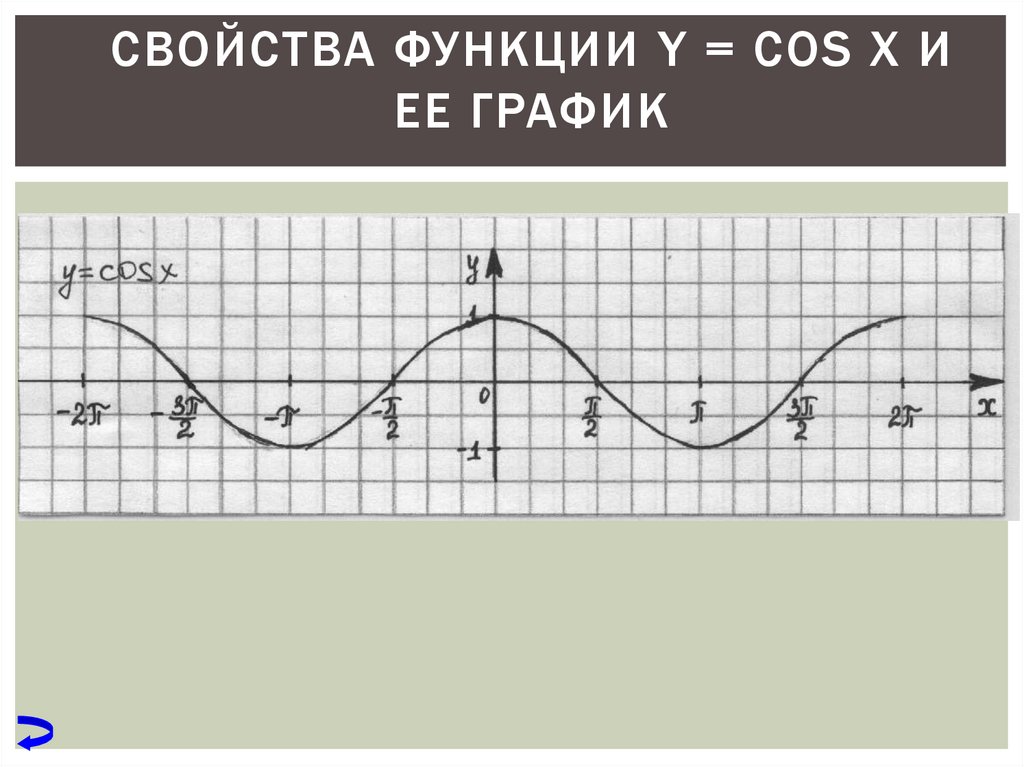
А теперь к синусу функция!
для B 1 Мы знаем, что n = 1 и L = π, SO:
B 1 = 1
Что упрощает до:
b 1 = 1 π
sin(x) dx
и, как и прежде, из-за резкого изменения при x=0, нам нужно разбить вычисление на -π до 0 и 0 до π ,
Итак, просто взглянув на интеграл от −π до 0 , мы знаем, что f(x) = −h:
Мы можем вынести константу −h за пределы интеграла:
−h π
sin(x) dx
И sin(x) выглядит так:
Откуда мы знаем, что площадь равна −2?
Сначала мы используем правила интегрирования, чтобы найти интеграл от sin(x) is − cos(x) :
Затем мы вычисляем определенный интеграл между −π и 0, вычисляя значение −cos( х) на 0 , а для −π , а затем вычитание:
[−cos(0)] − [−cos(−π)] = −1 − 1 = −2
Итак, между −π и 0 we get
−h π (−2)
Next we look at the integral from 0 to π :
h π
sin(x) dx
And его интеграл:
[−cos(π)] − [−cos(0)] = 1 − [−1] = 2
Теперь, объединив обе части, мы получим:
b 1 = 1 π [ (−h) × (−2) + (h) × (2) ] = 4h π
For b 2 у нас есть этот интеграл:
−h π
sin(2x) dx
От −π до 0 это выглядит так:
Чистая площадь sin(2x) от −π до 0 это ноль .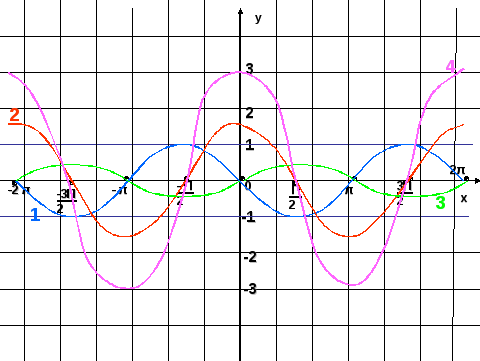
И мы уже видели подобное раньше, поэтому мы заключаем, что:
B 2 = 0
для B 3 Мы имеем этот интеграл:
-H π
(3X). :
Два направления отменяются, но важно третье!
Это похоже на интеграл b 1 , но только с одной третью площади.
Для от 0 до π имеем:
Опять две области сокращаются, но не третья
And we can conclude:
b 3 = b 1 3 = 4h 3π
The pattern continues:
When n is even the areas cancel for a результат ноль.
Когда n нечетно, все области, кроме одной, сокращаются, что дает результат 1/n.
Таким образом, мы можем сказать
b n = 4h nπ , когда n нечетно, и 0 в противном случае
И мы подходим к последнему шагу: подставляем коэффициенты в основную формулу:
f(x) = a 0 +
A N COS (NX π L ) +
B N SIN (NX π L )
π L ) π L ) π L ) π L ) π L )Итак:
f(x) = 4h π [ sin(x) + sin(3x) 3 + sin(5x) 90 + 7 7 9 .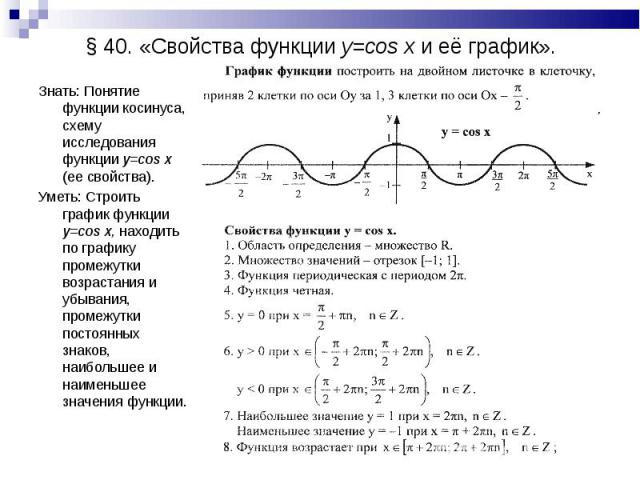 .. 909]
.. 909]
В заключение:
И когда вы закончите, перейдите к:
Графический прибор серии Фурье
и проверьте, правильно ли вы поняли!
Почему бы не попробовать это с «sin((2n-1)*x)/(2n-1)», 2n−1 аккуратно дает нечетные значения и посмотреть, получится ли прямоугольная волна.
Прочие функции
Конечно, мы можем использовать это для многих других функций!
Но мы должны уметь вычислять все коэффициенты, что на практике означает, что мы вычисляем площадь из:
Но, как мы видели выше, мы можем использовать такие приемы, как разбиение функции на части, используя здравый смысл, геометрию и исчисление, чтобы помочь нам.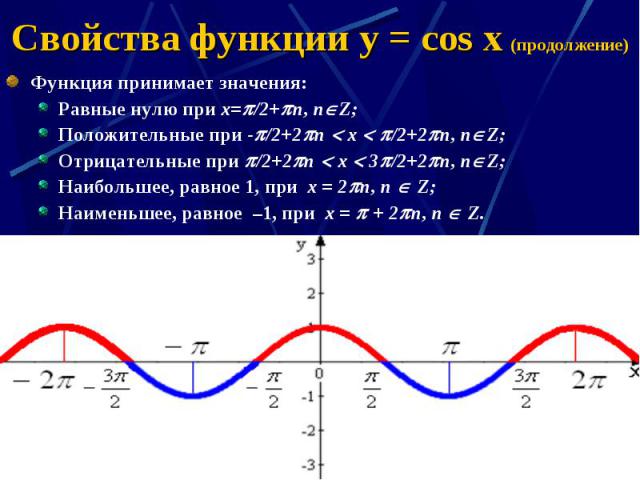
Вот несколько известных:
| Волна | Серия | Графическое устройство серии Фурье |
|---|---|---|
| Прямоугольная волна | sin(x) + sin(3x)/3 + sin(5x)/5 + … | sin((2n−1)*x)/(2n−1) 92 |
Сноска. Различные версии формулы!
На этой странице мы использовали общую формулу:
f(x) = a 0 +
A N COS (NX π L ) +
B n SIN (NX π L )
π L ) π мы можем использовать упрощенную версию:f(x) = a 0 +
a n cos(nx) +
b n sin(nx)
Или вот этот, где 0 скатывается в первую сумму (теперь n= 0 ) :
f(x) =
a n cos(nx) +
b n sin(nx)
Но я предпочитаю тот, который мы используем здесь, так как он более практичен с учетом разных периодов.
Графики функций синуса и косинуса
Белый свет, такой как солнечный свет, на самом деле вовсе не белый. Вместо этого это композиция всех цветов радуги в виде волн. Отдельные цвета можно увидеть, только когда белый свет проходит через оптическую призму, которая разделяет волны в соответствии с их длинами волн, образуя радугу.
Световые волны графически могут быть представлены синусоидальной функцией. В главе о тригонометрических функциях мы рассмотрели тригонометрические функции, такие как функция синуса. В этом разделе мы будем интерпретировать и создавать графики функций синуса и косинуса.
Графические функции синуса и косинуса
Напомним, что функции синуса и косинуса связывают вещественные значения с координатами x и y точки на единичной окружности. Так как же они выглядят на графике в координатной плоскости? Начнем с функции синуса. Мы можем создать таблицу значений и использовать их для построения графика. (Рисунок) перечисляет некоторые значения функции синуса на единичном круге.
(Рисунок) перечисляет некоторые значения функции синуса на единичном круге.
| [латекс]x[/латекс] | [латекс]0[/латекс] | [латекс]\frac{\pi }{6}[/латекс] | [латекс]\frac{\pi }{4}[/латекс] | [латекс]\frac{\pi }{3}[/латекс] | [латекс]\frac{\pi }{2}[/латекс] | [латекс]\frac{2\pi }{3}[/латекс] | [латекс]\frac{3\pi }{4}[/латекс] | [латекс]\frac{5\pi }{6}[/латекс] | [латекс]\pi [/латекс] |
| [латекс]\mathrm{sin}\left(x\right)[/latex] | [латекс]0[/латекс] | [латекс]\фракция{1}{2}[/латекс] | [латекс]\frac{\sqrt{2}}{2}[/латекс] | [латекс]\frac{\sqrt{3}}{2}[/латекс] | [латекс]1[/латекс] | [латекс]\frac{\sqrt{3}}{2}[/латекс] | [латекс]\frac{\sqrt{2}}{2}[/латекс] | [латекс]\фракция{1}{2}[/латекс] | [латекс]0[/латекс] |
Нанесение точек из таблицы и продолжение вдоль оси x дает форму функции синуса. См. (Рисунок).
См. (Рисунок).
Рисунок 2. Синусоидальная функция
Обратите внимание, что значения синуса положительны между 0 и [latex]\,\pi ,\,[/latex], что соответствует значениям синусоидальной функции в квадрантах I и II на единичной окружности, а значения синуса отрицательны между [латекс]\,\пи \,[/латекс] и [латекс]\,2\пи ,\,[/латекс], которые соответствуют значениям функции синуса в четвертях III и IV на единичной окружности. См. (Рисунок).
Рис. 3. График значений функции синуса
Теперь давайте аналогично рассмотрим функцию косинуса. Опять же, мы можем создать таблицу значений и использовать их для построения графика. (Рисунок) перечисляет некоторые значения функции косинуса на единичном круге.
| [латекс]\mathbf{x}[/латекс] | [латекс]0[/латекс] | [латекс]\frac{\pi }{6}[/латекс] | [латекс]\frac{\pi }{4}[/латекс] | [латекс]\frac{\pi }{3}[/латекс] | [латекс]\frac{\pi }{2}[/латекс] | [латекс]\frac{2\pi }{3}[/латекс] | [латекс]\frac{3\pi }{4}[/латекс] | [латекс]\frac{5\pi }{6}[/латекс] | [латекс]\pi [/латекс] |
| [латекс]\mathbf{cos}\влево(\mathbf{x}\вправо)[/латекс] | [латекс]1[/латекс] | [латекс]\frac{\sqrt{3}}{2}[/латекс] | [латекс]\frac{\sqrt{2}}{2}[/латекс] | [латекс]\фракция{1}{2}[/латекс] | [латекс]0[/латекс] | [латекс]-\frac{1}{2}[/латекс] | [латекс]-\frac{\sqrt{2}}{2}[/латекс] | [латекс]-\frac{\sqrt{3}}{2}[/латекс] | [латекс]-1[/латекс] |
Как и в случае функции синуса, мы можем нанести точки на график функции косинуса, как показано на рисунке.
Рис. 4. Функция косинуса
Поскольку мы можем вычислить синус и косинус любого действительного числа, обе эти функции определены для всех действительных чисел. Думая о значениях синуса и косинуса как о координатах точек на единичной окружности, становится ясно, что диапазон обеих функций должен быть интервалом [латекс]\,\влево[-1,1\вправо].[/латекс]
На обоих графиках форма графика повторяется после [латекс]\,2\пи ,\,[/латекс], что означает периодичность функций с периодом [латекс]\,2\пи .\,[ /latex]Периодическая функция — это функция, для которой определенный сдвиг по горизонтали, P , приводит к функции, равной исходной функции:[latex]\,f\left(x+P\right)=f\left( x\right)\,[/latex]для всех значений [latex]\,x\,[/latex]в домене [latex]\,f.\,[/latex]Когда это происходит, мы вызываем наименьший такой сдвиг по горизонтали с [латекс]\,Р>0\,[/латекс] периодом функции. (Рисунок) показывает несколько периодов функций синуса и косинуса.
Рис.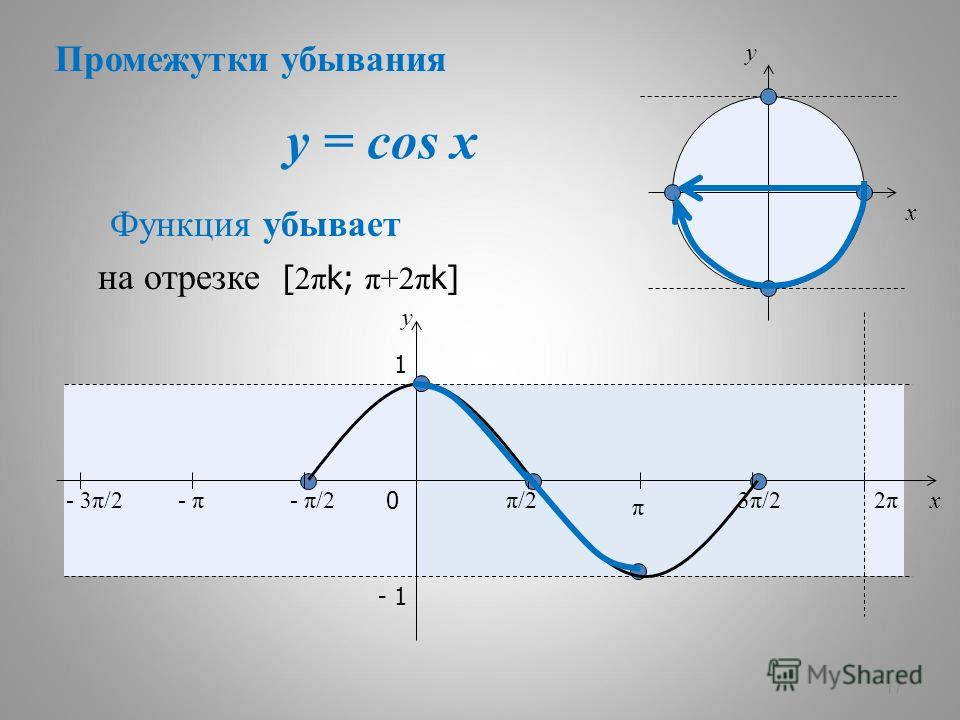 5.
5.
Повторный взгляд на функции синуса и косинуса в области с центром на оси y помогает выявить симметрию. Как мы видим на (Рисунок), синусоидальная функция симметрична относительно начала координат. Вспомните из книги «Другие тригонометрические функции», которую мы определили по единичному кругу, что синусоидальная функция является нечетной функцией, потому что [латекс]\,\mathrm{sin}\left(-x\right)=-\mathrm{sin}\,x .\,[/latex]
Теперь мы можем ясно увидеть это свойство на графике.
Рисунок 6. Нечетная симметрия функции синуса
(рисунок) показывает, что функция косинуса симметрична относительно оси y . Опять же, мы определили, что функция косинуса является четной функцией. Теперь из графика видно, что [латекс]\mathrm{cos}\left(-x\right)=\mathrm{cos}\text{ }x.[/latex]
Рис. 7. Четная симметрия функция косинуса
Характеристики функций синуса и косинуса
Функции синуса и косинуса имеют несколько отличительных характеристик:
Исследование синусоидальных функций
Как мы видим, синусоидальные и косинусоидальные функции имеют регулярный период и диапазон. Если мы понаблюдаем за океанскими волнами или рябью на пруду, мы увидим, что они напоминают функции синуса или косинуса. Однако они не обязательно идентичны. Некоторые выше или длиннее других. Функция, которая имеет ту же общую форму, что и функция синуса или косинуса, известна как синусоидальная функция. Общие формы синусоидальных функций:
[латекс]\begin{array}{l}y=A\mathrm{sin}\left(Bx-C\right)+D\hfill \\ \text{ and}\hfill \\ y=A\mathrm{cos}\left(Bx-C\right)+D\hfill \end{массив}[/latex]
Определение периода синусоидальных функций
Глядя на формы синусоидальных функций, мы можем видеть, что они являются преобразованиями функций синуса и косинуса.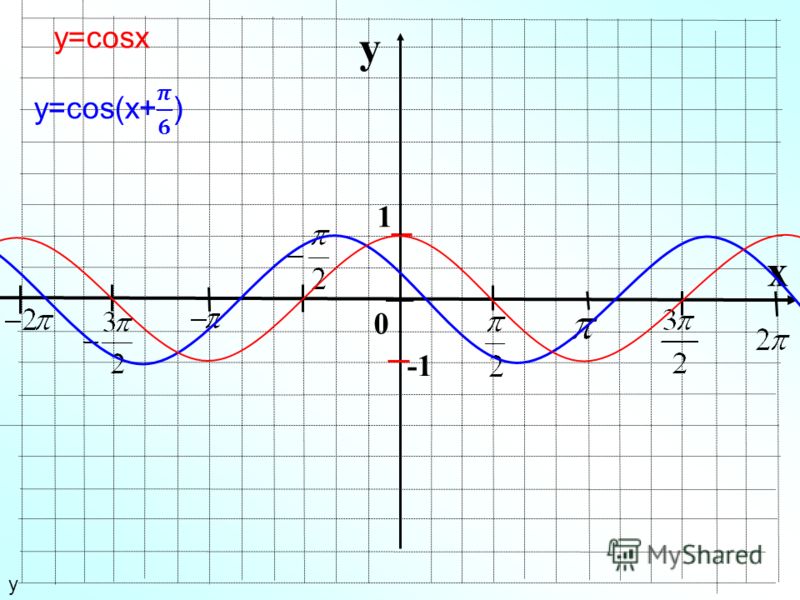 Мы можем использовать то, что мы знаем о преобразованиях, для определения периода.
Мы можем использовать то, что мы знаем о преобразованиях, для определения периода.
В общей формуле [латекс]\,В\,[/латекс]связан с периодом соотношением[латекс]\,P=\frac{2\pi }{|B|}.\,[/латекс ]If[latex]\,|B|>1,\,[/latex]то период меньше, чем[latex]\,2\pi \,[/latex]и функция подвергается горизонтальному сжатию, тогда как если[ латекс]\,|B|<1,\,[/латекс], то период больше, чем[латекс]\,2\пи \,[/латекс], и функция подвергается горизонтальному растяжению. Например, [латекс]\,f\влево(х\вправо)=\mathrm{sin}\влево(х\вправо),\,[/латекс][латекс]B=1,\,[/латекс] так период [латекс]\,2\пи ,\текст{}[/латекс], который мы знали. Если[латекс]\,f\влево(х\вправо)=\mathrm{sin}\влево(2x\вправо),\,[/латекс],то[латекс]\,В=2,\,[/латекс] поэтому период равен [латекс]\,\пи \,[/латекс], а график сжат. Если [латекс]\,f\left(x\right)=\mathrm{sin}\left(\frac{x}{2}\right),\,[/latex],то[латекс]\,B=\ frac{1}{2},\,[/latex], поэтому период равен [latex]\,4\pi \,[/latex], а график растянут. Обратите внимание на (рисунок), как период косвенно связан с [латекс]\,|В|.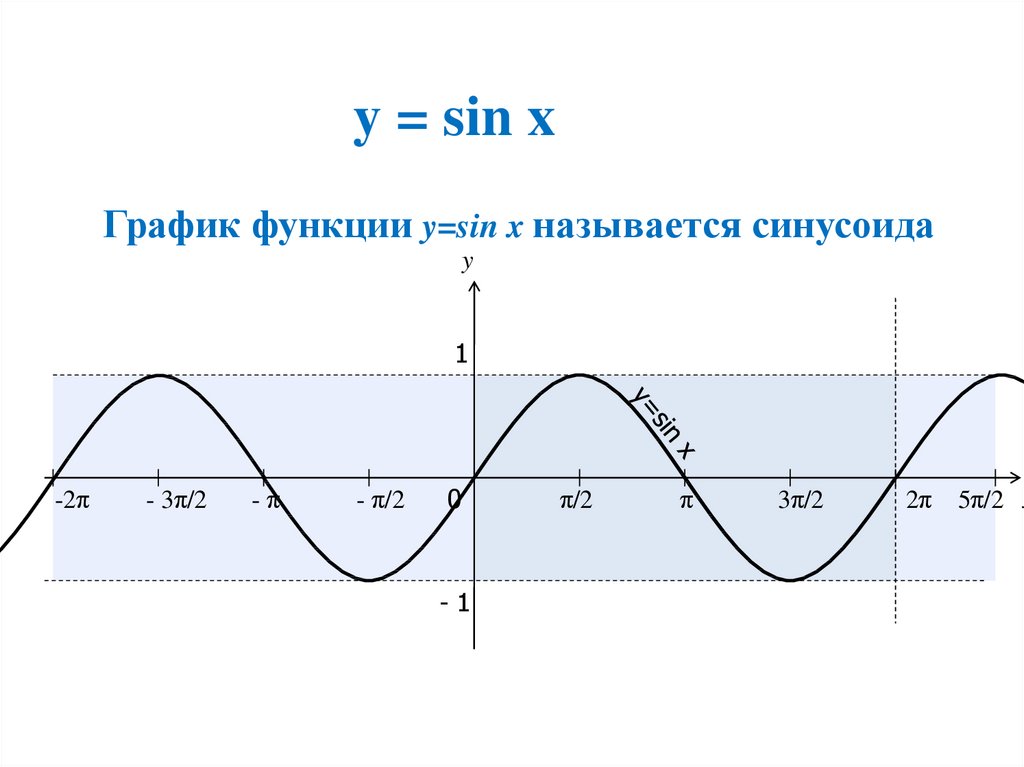 [/латекс]
[/латекс]
Рис. 8.
Период синусоидальных функций
Если принять [латекс]\,С=0\,[/латекс]и[латекс]\,D=0\,[/латекс]в общем из уравнений синуса и косинуса получаем формы
[latex]y=A\mathrm{sin}\left(Bx\right)[/latex]
[latex]y=A\mathrm{cos} \left(Bx\right)[/latex]
Период равен [latex]\,\frac{2\pi }{|B|}.[/latex]
Определение периода функции синуса или косинуса
Определите период функции [латекс]\,f\left(x\right)=\mathrm{sin}\left(\frac{\pi }{6}x\right).[/latex]
Показать решение
Попробуйте
Определите период функции[latex]\,g\left(x\right)=\mathrm{cos}\left(\frac{x}{3}\right).[/latex]
Показать решение
Определение амплитуды
Возвращаясь к общей формуле для синусоидальной функции, мы проанализировали, как переменная [латекс]\,В\,[/латекс] относится к периоду. Теперь давайте обратимся к переменной [латекс]\,А\,[/латекс], чтобы мы могли проанализировать, как она связана с амплитудой или наибольшим расстоянием от покоя. [латекс]\,А\,[/латекс] представляет коэффициент вертикального растяжения, а его абсолютное значение[latex]\,|A|\,[/latex]является амплитудой. Локальные максимумы будут на расстоянии [латекс]\,|А|\,[/латекс] выше горизонтали средняя линия графика, которая является линией[латекс]\,y=D;\,[/latex],потому что[латекс]\,D=0\,[/латекс]в данном случае средней линией является х -ось. Локальные минимумы будут на таком же расстоянии ниже средней линии. Если[latex]\,|A|>1,\,[/latex] функция растягивается. Например, амплитуда [латекс]\,f\left(x\right)=4\,\mathrm{sin}\,x\,[/latex] в два раза больше амплитуды [латекс]\,f\left (x\right)=2\,\mathrm{sin}\,x.\,[/latex]Если[latex]\,|A|<1,\,[/latex] функция сжимается. (Рисунок) сравнивает несколько синусоидальных функций с разными амплитудами.
[латекс]\,А\,[/латекс] представляет коэффициент вертикального растяжения, а его абсолютное значение[latex]\,|A|\,[/latex]является амплитудой. Локальные максимумы будут на расстоянии [латекс]\,|А|\,[/латекс] выше горизонтали средняя линия графика, которая является линией[латекс]\,y=D;\,[/latex],потому что[латекс]\,D=0\,[/латекс]в данном случае средней линией является х -ось. Локальные минимумы будут на таком же расстоянии ниже средней линии. Если[latex]\,|A|>1,\,[/latex] функция растягивается. Например, амплитуда [латекс]\,f\left(x\right)=4\,\mathrm{sin}\,x\,[/latex] в два раза больше амплитуды [латекс]\,f\left (x\right)=2\,\mathrm{sin}\,x.\,[/latex]Если[latex]\,|A|<1,\,[/latex] функция сжимается. (Рисунок) сравнивает несколько синусоидальных функций с разными амплитудами.
Рис. 9.
Амплитуда синусоидальной функции
из уравнений синуса и косинуса получаем формы
[latex]y=A\mathrm{sin}\left(Bx\right)\text{ и }y=A\mathrm{cos}\left(Bx \right)[/latex]
Амплитуда равна[latex]\,A,\,[/latex], а высота по вертикали от средней линии равна[latex]\,|A|. \,[/latex]Кроме того , обратите внимание, что в примере
\,[/latex]Кроме того , обратите внимание, что в примере
[latex]|A|\text{ = амплитуда = }\frac{1}{2}|\text{максимум }-\text{минимум}|[/latex]
Определение амплитуды функции синуса или косинуса
Какова амплитуда синусоидальной функции[латекс]\,f\влево(х\вправо)=-4\mathrm{sin}\влево(х\вправо)?\,[/латекс]Является ли функция растянутой или сжато по вертикали?
Показать раствор
Анализ
Отрицательное значение [латекс]\,А\,[/латекс] приводит к отражению синусоидальной функции по оси x , как показано на (рис.).
. (x\right)?\,[/latex]Функция растянута или сжата по вертикали?
[latex]\frac{1}{2}\,[/latex]compressed
Анализ графиков вариаций
y = sin x и y = cos x Теперь мы понимаем как[латекс]\,А\,[/латекс]и[латекс]\,В\,[/латекс]относятся к общему уравнению формы для функций синуса и косинуса, мы исследуем переменные[латекс]\,С \,[/latex]и[латекс]\,D. \,[/latex]Напомним общую форму:
\,[/latex]Напомним общую форму:
[латекс]\begin{array}{c}y=A\mathrm{sin}\left(Bx-C\right)+D\text{и}y=A\mathrm{cos}\left(Bx- C\right)+D\\ or\\ y=A\mathrm{sin}\left(B\left(x-\frac{C}{B}\right)\right)+D\text{ и }y =A\mathrm{cos}\left(B\left(x-\frac{C}{B}\right)\right)+D\end{array}[/latex]
Значение[latex]\, \frac{C}{B}\,[/latex] для синусоидальной функции называется фазовым сдвигом или горизонтальным смещением основной функции синуса или косинуса. Если[latex]\,C>0,\,[/latex]график сдвигается вправо. Если[latex]\,C<0,\,[/latex]граф сдвинется влево. Чем больше значение[latex]\,|C|,\,[/latex], тем больше сдвигается график. (Рисунок) показывает, что график [латекс]\,f\left(x\right)=\mathrm{sin}\left(x-\pi \right)\,[/latex]смещается вправо на[латекс ]\,\pi \,[/latex]единиц, что больше, чем мы видим на графике [latex]\,f\left(x\right)=\mathrm{sin}\left(x-\frac{ \pi }{4}\right),\,[/latex], которая сдвигается вправо на [latex]\,\frac{\pi }{4}\,[/latex]единицы.
Рисунок 11.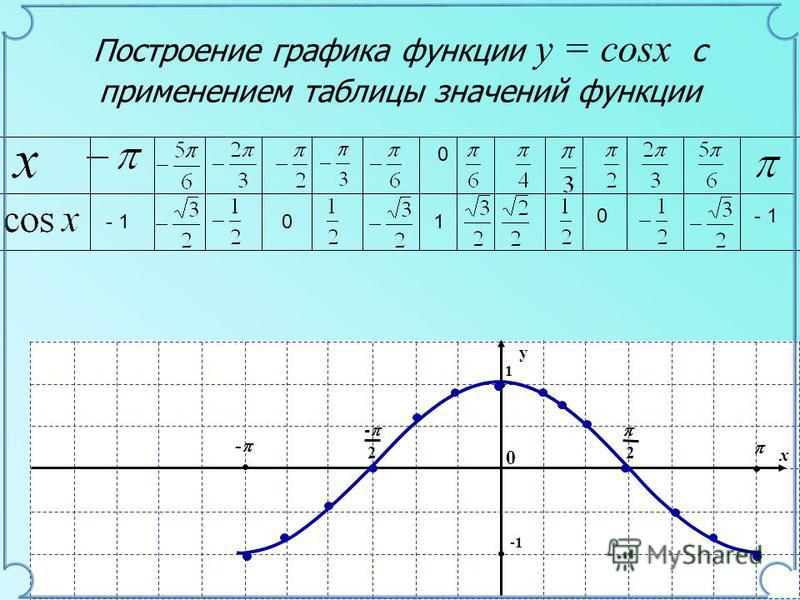
В то время как [латекс]\,С\,[/латекс] относится к горизонтальному смещению, [латекс]\,D\,[/латекс]обозначает вертикальное смещение от средней линии в целом Формула синусоидальной функции. См. (Рисунок). Средняя линия функции [латекс]\,y=\mathrm{cos}\left(x\right)+D\,[/latex] проходит через [латекс]\,y=D.[/latex]
Рисунок 12.
Любое значение [latex]\,D\,[/latex], отличное от нуля, сдвигает график вверх или вниз. (Рисунок) сравнивает [латекс]\,f\left(x\right)=\mathrm{sin}\,x\,[/latex]с[латекс]\,f\left(x\right)=\mathrm{ sin}\,x+2,\,[/latex], который сдвигается на 2 единицы вверх на графике.
. справа)+D\,[/латекс]или[латекс]\,f\влево(х\вправо)=А\mathrm{cos}\влево(Bx-C\вправо)+D,\,[/латекс][ латекс]\frac{C}{B}\,[/latex] — фазовый сдвиг, а [latex]\,D\,[/latex] — вертикальный сдвиг.
Определение фазового сдвига функции
Определение направления и величины фазового сдвига для [латекс]\,f\left(x\right)=\mathrm{sin}\left(x+\frac{\pi } {6}\справа)-2.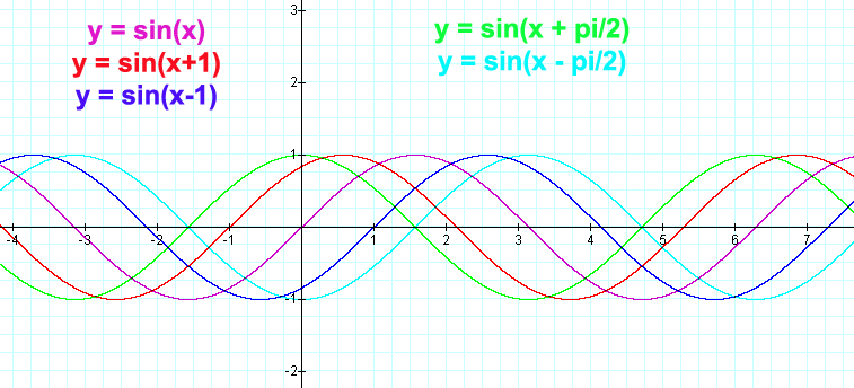 [/латекс]
[/латекс]
Показать решение
Анализ
Мы должны обратить внимание на знак в уравнении для общего вида синусоидальной функции. В уравнении перед [латексом]\,С.\,[/латекс] стоит знак минус {6}\right)-2\,[/latex] можно переписать как [латекс]\,f\left(x\right)=\mathrm{sin}\left(x-\left(-\frac{\ pi }{6}\right)\right)-2.\,[/latex]Если значение [latex]\,C\,[/latex]отрицательно, сдвиг происходит влево.
Попробуйте
Определите направление и величину фазового сдвига для [латекс]\,f\влево(х\вправо)=3\mathrm{cos}\влево(х-\фракция{\пи}}{2}\вправо). [/latex]
Показать решение
Определение вертикального сдвига функции
Определите направление и величину вертикального сдвига для [латекс]\,f\влево(х\вправо)=\mathrm{cos}\влево(х\вправо)-3. [/latex]
Показать решение
Попробуйте
Определите направление и величину вертикального смещения для [латекс]\,f\влево(х\вправо)=3\mathrm{sin}\влево(х\вправо)+2.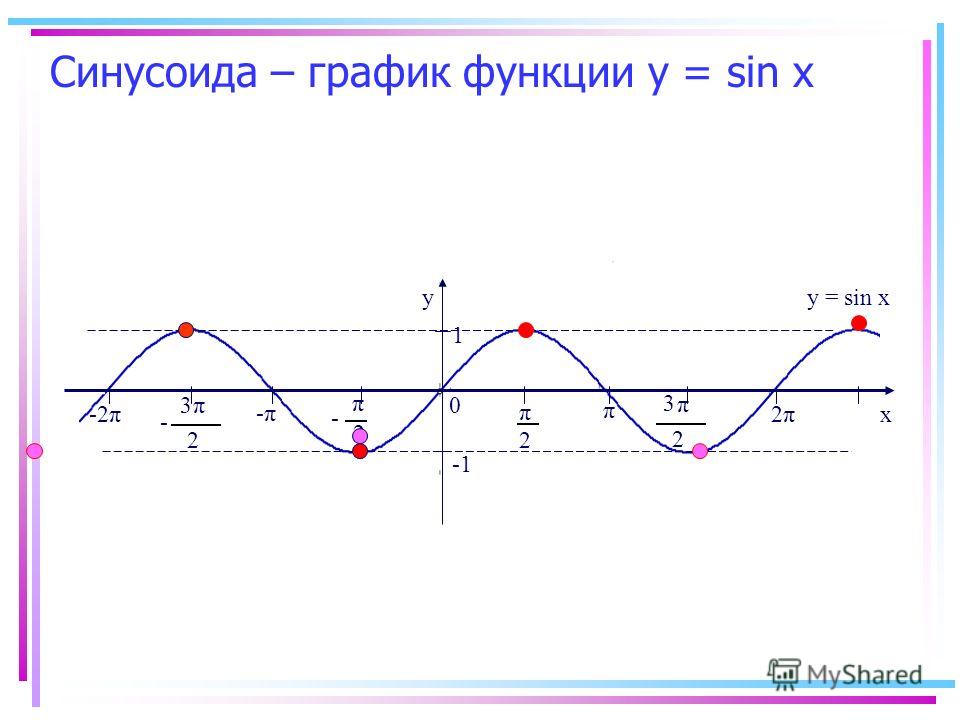 [/латекс]
[/латекс]
Показать решение
Дана синусоидальная функция в виде [латекс]\,f\left(x\right)=A\mathrm{sin}\left(Bx-C\right)+D,\,[/latex] определите срединную линию, амплитуду, период и фазовый сдвиг.
Идентификация вариаций синусоидальной функции из уравнения
Определение средней линии, амплитуды, периода и фазового сдвига функции[latex]\,y=3\mathrm{sin}\left(2x\right)+1 .[/latex]
Показать решение
Анализ
Изучая график, мы можем определить, что период равен [латекс]\,\pi ,\,[/латекс], средняя линия — [латекс]\,у=1,\,[/латекс], а амплитуда 3 см. (рисунок).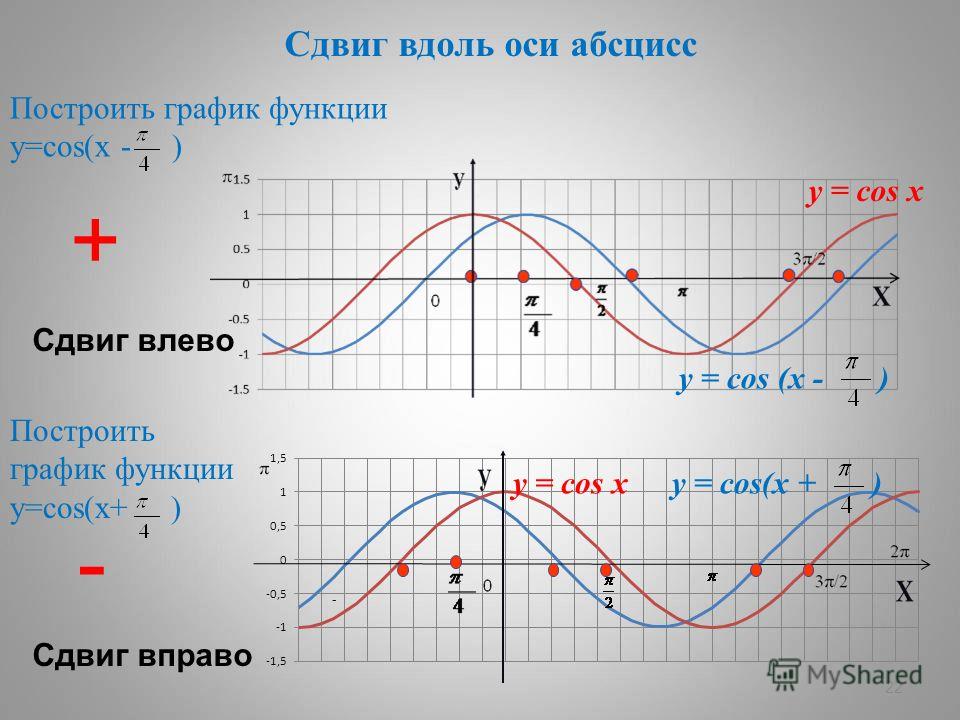
Рис. 14.
Попробуйте
Определение средней линии, амплитуды, периода и фазового сдвига функции[latex]\,y=\frac{1}{2}\mathrm{cos}\left(\frac{x}{3}-\frac {\pi }{3}\right).[/latex]
Показать решение
Определение уравнения для синусоидальной функции на графике
Определите формулу для функции косинуса на (рис.).
Рис. 15.
Показать решение
Попробуйте
Определите формулу синуса на (рис.).
Рис. 16.
Показать решение
Определение уравнения для синусоидальной функции на графике
Определите уравнение для синусоидальной функции на (рис.).
Рис. 17.
Показать решение
Попробуйте
Напишите формулу для функции, изображенной на (рис.).
Рис.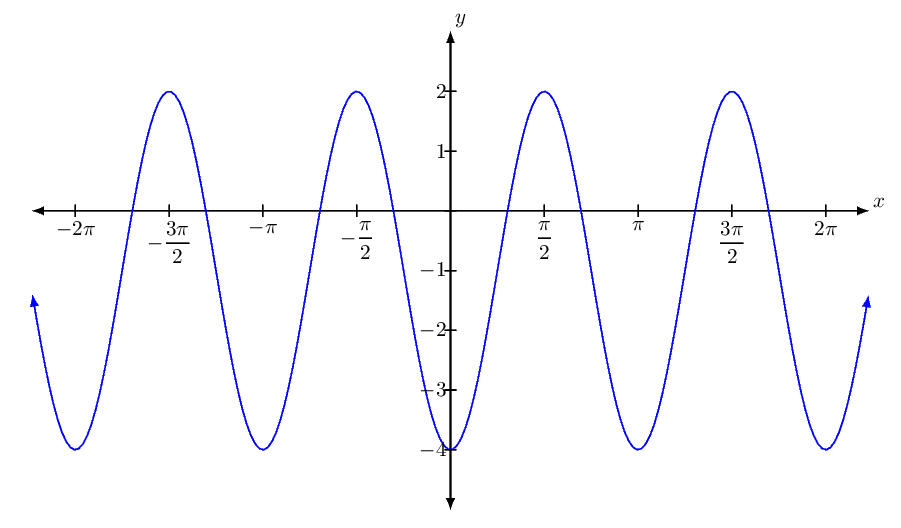 18.
18.
Показать решение
Графические варианты
y = sin x и y = cos xВ этом разделе мы узнали о типах вариаций функций синуса и косинуса и использовали эту информацию для написания уравнений из графиков. Теперь мы можем использовать ту же информацию для создания графиков из уравнений.
Вместо того, чтобы сосредоточиться на уравнениях общей формы
[латекс]y=A\mathrm{sin}\left(Bx-C\right)+D\text{ и }y=A\mathrm{cos}\left( Bx-C\right)+D,[/latex]
допустим [latex]\,C=0\,[/latex]и [latex]\,D=0\,[/latex]и работаем с упрощенная форма уравнений в следующих примерах.
Для данной функции[латекс]\,у=А\mathrm{sin}\left(Bx\right),\,[/латекс] нарисуйте ее график.
График функции и определение амплитуды и периода
Нарисуйте график [латекс]\,f\left(x\right)=-2\mathrm{sin}\left(\frac{\pi x}{2 }\справа).[/латекс]
Показать решение
Попробуйте
Нарисуйте график [латекс]\,g\влево(х\вправо)=-0,8\mathrm{cos}\влево(2x\вправо).\,[/латекс]Определите срединную линию, амплитуду , период и фазовый сдвиг.
Показать раствор
Дана синусоидальная функция со сдвигом по фазе и по вертикали, нарисуйте ее график.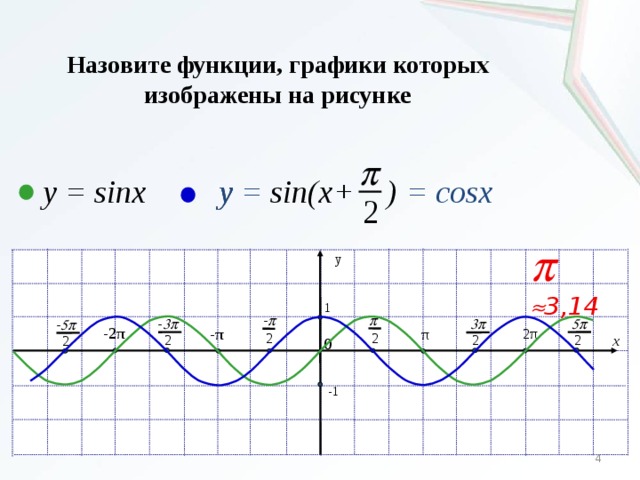
Построение преобразованной синусоиды
Нарисуйте график [латекс]\,f\left(x\right)=3\mathrm{sin}\left(\frac{\pi}{4}x-\frac{\ пи }{4}\справа).[/латекс]
Показать решение
Попробуйте
Нарисуйте график [латекс]\,g\left(x\right)=-2\mathrm{cos}\left(\frac{\pi }{3}x+\frac{\pi } {6}\right).\,[/latex]Определить срединную линию, амплитуду, период и фазовый сдвиг.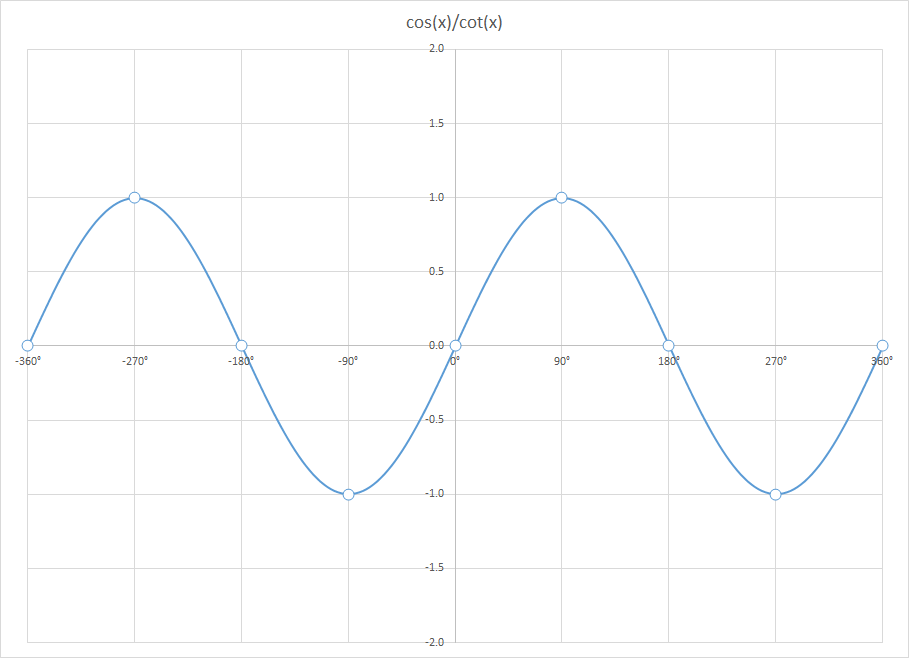
Показать раствор
Определение свойств синусоидальной функции
Дано[латекс]\,y=-2\mathrm{cos}\left(\frac{\pi }{2}x+\pi \right)+3,\,[ /latex] определяют амплитуду, период, фазовый сдвиг и сдвиг по горизонтали. Затем постройте график функции.
Показать решение
Использование преобразований функций синуса и косинуса
Мы можем использовать преобразования функций синуса и косинуса во многих приложениях. Как упоминалось в начале главы, круговое движение можно моделировать с помощью функции синуса или косинуса.
Нахождение вертикальной составляющей кругового движения
Точка вращается вокруг окружности радиусом 3 с центром в начале координат. Нарисуйте график зависимости координаты y точки от угла поворота.
Показать решение
Анализ
Обратите внимание, что период функции по-прежнему равен[latex]\,2\pi ;\,[/latex], когда мы движемся по кругу, мы возвращаемся в точку[latex]\,\left(3 ,0\right)\,[/latex]for[latex]\,x=2\pi ,4\pi ,6\pi ,….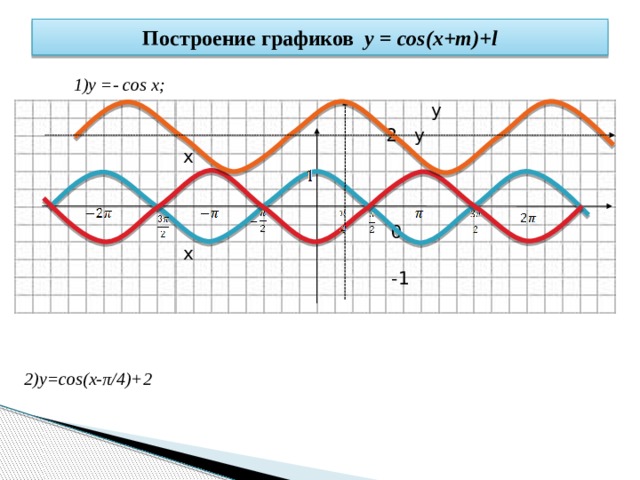 [/latex]Поскольку выходные данные графика теперь будут колебаться между[latex] \,–3\,[/latex]и[латекс]\,3,\,[/латекс]амплитуда синусоиды равна[латекс]\,3.[/латекс]
[/latex]Поскольку выходные данные графика теперь будут колебаться между[latex] \,–3\,[/latex]и[латекс]\,3,\,[/латекс]амплитуда синусоиды равна[латекс]\,3.[/латекс]
Попробуйте
Что такое амплитуда функции[латекс]\,f\влево(х\вправо)=7\mathrm{cos}\влево(х\вправо)?\,[/латекс]Нарисуйте график этой функции.
Показать решение
Нахождение вертикальной составляющей кругового движения
Круг радиусом 3 фута установлен с центром на расстоянии 4 фута от земли. Ближайшая к земле точка помечена P , как показано на (Рисунок). Нарисуйте график высоты над землей точки [латекс]\,Р\,[/латекс] при вращении круга; затем найдите функцию, которая дает высоту через угол поворота.
Рис. 23.
Показать решение
Попробуйте
Груз прикрепляется к пружине, которую затем подвешивают к доске, как показано на (Рисунок). Когда пружина колеблется вверх и вниз, положение [латекс]\,y\,[/латекс] груза относительно доски находится в диапазоне от[латекс]\,–1\,[/латекс]дюйм.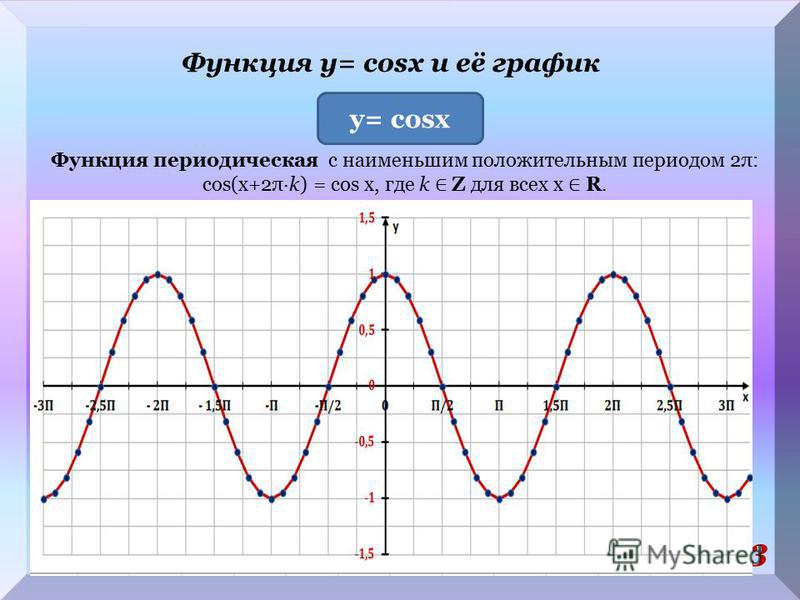 (в момент времени[латекс]\,х=0)\,[/латекс]в[латекс]\,–7\,[/латекс]в. (в момент времени[латекс]\,х=\пи )\,[/латекс]под доской. Предположим, что положение [латекс]\,у\,[/латекс] задано как синусоидальная функция [латекс]\,х.\,[/латекс] Нарисуйте график функции, а затем найдите функцию косинуса, которая дает позицию[латекс]\,у\,[/латекс]в терминах[латекс]\,х.[/латекс]
(в момент времени[латекс]\,х=0)\,[/латекс]в[латекс]\,–7\,[/латекс]в. (в момент времени[латекс]\,х=\пи )\,[/латекс]под доской. Предположим, что положение [латекс]\,у\,[/латекс] задано как синусоидальная функция [латекс]\,х.\,[/латекс] Нарисуйте график функции, а затем найдите функцию косинуса, которая дает позицию[латекс]\,у\,[/латекс]в терминах[латекс]\,х.[/латекс]
Рис. 25.
Показать решение
Определение роста всадника на колесе обозрения
Лондонский глаз — это огромное колесо обозрения диаметром 135 метров (443 фута). Он совершает один оборот каждые 30 минут. Всадники садятся с платформы на высоте 2 метра над землей. Выразите высоту всадника над землей как функцию времени в минутах.
Показать раствор
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с графиками функций синуса и косинуса.
Ключевые уравнения
Ключевые понятия
Раздел Упражнения
Вербальные
Почему функции синуса и косинуса называются периодическими функциями?
Показать раствор
Как график [латекс]\,y=\mathrm{sin}\,x\,[/latex]
сравнивается с графиком [латекс]\,y=\mathrm{cos}\,x? \,[/latex]
Объясните, как можно горизонтально перевести график [latex]\,y=\mathrm{sin}\,x\,[/latex]
для получения [латекс]\,y=\mathrm{cos}\,x. [/latex]
[/latex]
Для уравнения[латекс]\,A\,\mathrm{cos}\left(Bx+C\right) +D,[/latex]какие константы влияют на диапазон функции и как они влияют на диапазон?
Показать раствор
Как диапазон преобразованной синусоидальной функции связан с уравнением[латекс]\,у=А\,\mathrm{sin}\left(Bx+C\right)+D?[/latex]
Как можно единичный круг можно использовать для построения графика [латекс]\,f\left(t\right)=\mathrm{sin}\,t?[/latex]
Показать решение
Графический
Для следующих упражнений постройте график двух полных периодов каждой функции и укажите амплитуду, период и среднюю линию. Укажите максимальное и минимальное значения y и соответствующие им значения x на одном периоде для [latex]\,x>0.\,[/latex]При необходимости округлите ответы до двух знаков после запятой.
[латекс]f\left(x\right)=2\mathrm{sin}\,x[/latex]
[латекс]f\left(x\right)=\frac{2}{3}\ mathrm{cos}\,x[/латекс]
Показать решение
[латекс]f\left(x\right)=-3\mathrm{sin}\,x[/latex]
[латекс]f\left(x\right)=4\mathrm{sin}\, x[/latex]
Показать решение
[латекс]f\влево(х\вправо)=2\mathrm{cos}\,x[/латекс]
[латекс]f\влево(x\вправо)=\mathrm{cos}\влево(2x \right)[/latex]
Показать решение
[латекс]f\left(x\right)=2\,\mathrm{sin}\left(\frac{1}{2}x\right)[/latex]
[латекс]f\left( x\right)=4\,\mathrm{cos}\left(\pi x\right)[/latex]
Показать решение
[латекс]f\влево(х\вправо)=3\,\mathrm{cos}\влево(\frac{6}{5}x\вправо)[/латекс]
[латекс]y=3\ ,\mathrm{sin}\left(8\left(x+4\right)\right)+5[/latex]
Показать решение
[латекс]y=2\,\mathrm{sin}\left(3x-21\right)+4[/latex]
[латекс]y=5\,\mathrm{sin}\left(5x+ 20\right)-2[/latex]
Показать решение
Для следующих упражнений нарисуйте один полный период каждой функции, начиная с [latex]\,x=0. \,[/latex]Для каждой функции укажите амплитуду, период и среднюю линию. Укажите максимум и минимум y -значения и соответствующие им x -значения на одном периоде для [latex]\,x>0.\,[/latex]Укажите фазовый сдвиг и вертикальное смещение, если применимо. При необходимости округлить ответы до двух знаков после запятой.
\,[/latex]Для каждой функции укажите амплитуду, период и среднюю линию. Укажите максимум и минимум y -значения и соответствующие им x -значения на одном периоде для [latex]\,x>0.\,[/latex]Укажите фазовый сдвиг и вертикальное смещение, если применимо. При необходимости округлить ответы до двух знаков после запятой.
[латекс]f\left(t\right)=2\mathrm{sin}\left(t-\frac{5\pi }{6}\right)[/latex]
[латекс]f\left (t\right)=-\mathrm{cos}\left(t+\frac{\pi }{3}\right)+1[/latex]
Показать решение
[латекс] f \ влево (t \ вправо) = 4 \ mathrm {cos} \ влево (2 \ влево (t + \ frac {\ pi} {4} \ вправо) \ вправо) -3 [/латекс]
[латекс]f\left(t\right)=-\mathrm{sin}\left(\frac{1}{2}t+\frac{5\pi }{3}\right)[/latex]
Показать решение
[латекс] f \ влево (х \ вправо) = 4 \ mathrm {sin} \ влево (\ гидроразрыва {\ pi} {2} \ влево (х-3 \ вправо) \ вправо) + 7 [/латекс]
Определите амплитуду, среднюю линию, период и уравнение, включающее функцию синуса, для графика, показанного на (рис. ).
).
Рис. 26.
Показать решение
Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на (рис.).
Рисунок 27.
Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на (Рисунок).
Рис. 28.
Показать решение
Определите амплитуду, период, среднюю линию и уравнение, включающее синус, для графика, показанного на (рис.).
Рисунок 29.
Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на (Рисунок).
Рисунок 30.
Показать решение
Определите амплитуду, период, среднюю линию и уравнение, включающее синус, для графика, показанного на (рис.).
Рис. 31.
Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на (рис. ).
).
Рис. 32.
Показать решение
Определите амплитуду, период, среднюю линию и уравнение, включающее синус, для графика, показанного на (рис.).
Рисунок 33.
Алгебраический
Для следующих упражнений пусть [латекс]\,f\left(x\right)=\mathrm{sin}\,x.[/latex]
On[latex ]\,\left[0,2\pi \right),[/latex]solve[latex]\,f\left(x\right)=0.[/latex]
On[latex]\,\left [0,2\pi \right),[/latex]solve[latex]\,f\left(x\right)=\frac{1}{2}.[/latex]
Показать решение
Вычислить [латекс]\,f\left(\frac{\pi }{2}\right).[/latex]
On[латекс]\,\left[0,2\pi \right),f \left(x\right)=\frac{\sqrt{2}}{2}.\,[/latex]Найти все значения [latex]\,x.[/latex]
Показать решение
В [латексе]\,\слева[0,2\пи \справа),[/латекс] максимальное значение(я) функции происходит(я) при каком x -значении?
On[latex]\,\left[0,2\pi \right),[/latex]минимальное значение(я) функции встречается(я) при каком x -значении?
Показать раствор
Покажите, что [латекс]\,f\left(-x\right)=-f\left(x\right). \,[/latex]Это означает, что [латекс]\,f\left(x\right) )=\mathrm{sin}\,x\,[/latex]является нечетной функцией и обладает симметрией относительно ________________.
\,[/latex]Это означает, что [латекс]\,f\left(x\right) )=\mathrm{sin}\,x\,[/latex]является нечетной функцией и обладает симметрией относительно ________________.
Для следующих упражнений пусть [латекс]\,f\left(x\right)=\mathrm{cos}\,x.[/latex]
On[латекс]\,\left[0,2\ pi \right),[/latex]решите уравнение[latex]\,f\left(x\right)=\mathrm{cos}\,x=0.[/latex]
Показать решение
On[латекс]\,\влево[0,2\pi \вправо),[/латекс]решить[латекс]\,f\влево(х\вправо)=\frac{1}{2}.[/ латекс]
В [латекс]\,\слева[0,2\пи \справа),[/латекс] найдите x -перехваты [латекс]\,f\слева(х\справа)=\mathrm {cos}\,x.[/latex]
Показать решение
On[latex]\,\left[0,2\pi \right),[/latex] найдите x -значения, при которых функция имеет максимальное или минимальное значение.
На[латекс]\,\влево[0,2\пи\вправо),[/латекс]решите уравнение[латекс]\,f\влево(х\вправо)=\frac{\sqrt{3}} {2}.[/latex]
Показать решение
Технология
График[латекс]\,h\влево(х\вправо)=x+\mathrm{sin}\,x\,[/латекс]на[латекс]\,\влево[0,2\pi \ right]. \,[/latex]Объясните, почему график выглядит именно так.
\,[/latex]Объясните, почему график выглядит именно так.
График[латекс]\,ч\влево(х\вправо)=х+\mathrm{sin}\,х\,[/латекс]на[латекс]\,\влево[-100,100\вправо].\,[ /latex]Показался ли график так, как предполагалось в предыдущем упражнении?
Показать решение
График[латекс]\,f\влево(х\вправо)=x\,\mathrm{sin}\,x\,[/латекс]на[латекс]\,\влево[0,2\pi \вправо ]\,[/latex] и опишите, как график отличается от графика [latex]\,f\left(x\right)=\mathrm{sin}\,x.[/latex]
График[latex] \,f\left(x\right)=x\,\mathrm{sin}\,x\,[/latex]на окне[латекс]\,\left[-10,10\right]\,[/ латекс] и объясните, что изображено на графике.
Показать раствор
График[латекс]\,f\left(x\right)=\frac{\mathrm{sin}\,x}{x}\,[/latex]на окне[латекс]\,\left[- 5\pi ,5\pi \right]\,[/latex] и объясните, что изображено на графике.
Реальные приложения
Колесо обозрения имеет диаметр 25 метров и садится на платформу, которая находится на высоте 1 метр над землей.

 Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция. Алгебра 8. – изд. 5. – М.: Просвещение, 2010.
Алгебра 8. – изд. 5. – М.: Просвещение, 2010.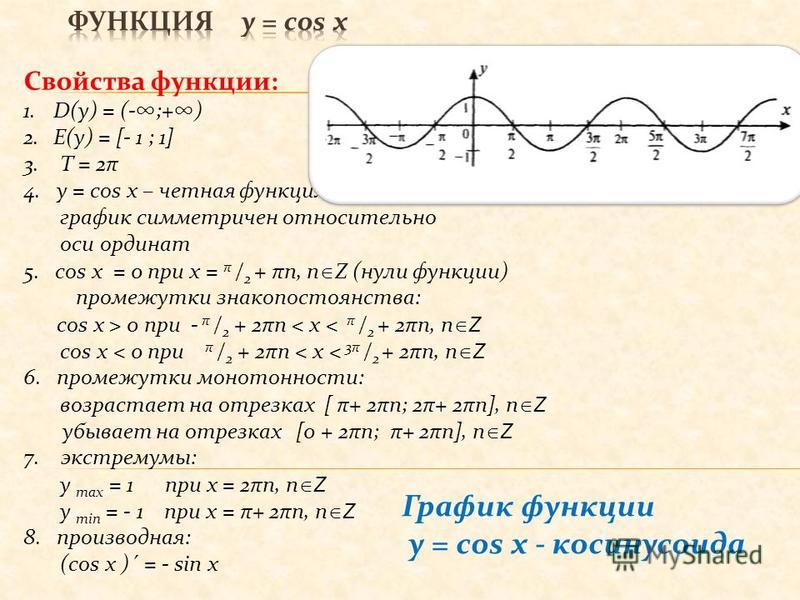 06.17
06.17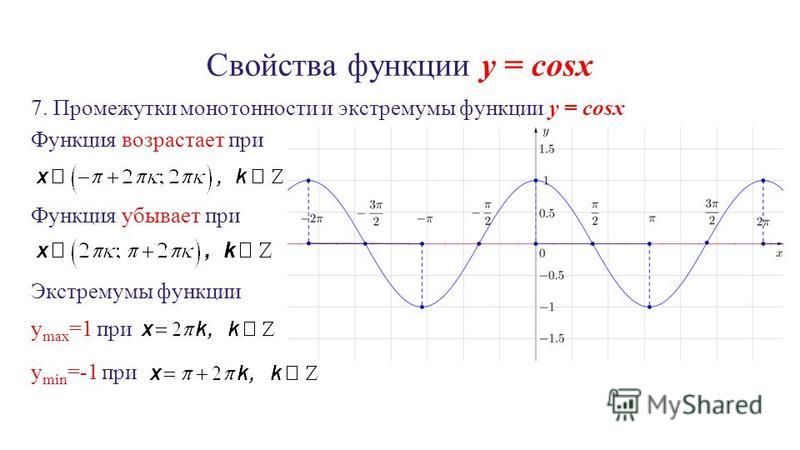 xlabel('значения x от 0 до 4pi') # строка должна быть заключена в кавычки ' '
plt.ylabel('sin(x) и cos(x)')
plt.title('График sin и cos от 0 до 4pi')
plt.legend(['sin(x)', 'cos(x)']) # записи легенды в виде отдельных строк в списке
plt.show()
xlabel('значения x от 0 до 4pi') # строка должна быть заключена в кавычки ' '
plt.ylabel('sin(x) и cos(x)')
plt.title('График sin и cos от 0 до 4pi')
plt.legend(['sin(x)', 'cos(x)']) # записи легенды в виде отдельных строк в списке
plt.show()
 д.
д. [/latex]
[/latex]