Логические задачи для 3 класса с ответами и решениями, задания на логику для детей 9-10 лет
Занимательная математика / 3 класс / Задачи на логику
Задания на логику для 3 класса от ЛогикЛайк — это более 300 видов занимательных задач и упражнений. Подсказки, решения и пояснения помогут научиться решать любые задачи.
Попробуйте развивающий курс ЛогикЛайк!
Выберите возраст для старта
3 класс
4+ класс
Рекомендуем тематические курсы
онлайн для 3 класса
Подготовка к олимпиаде Начать
Почему дети и родители выбирают ЛогикЛайк?
2 варианта занятий, выбор сложности
-
Пройдите 3 стартовые главы курса логики
– и откройте доступ к разным категориям.
 Попробуйте
«Логические задачи», «Закономерности», «Истина и ложь», «Умный
счёт».
Попробуйте
«Логические задачи», «Закономерности», «Истина и ложь», «Умный
счёт».
- Попробуйте задания разного уровня сложности: «Новичок», «Опытный», «Эксперт».
На LogicLike.com дети учатся рассуждать, развивают логику, способности к математике и познавательный интерес.
У нас есть всё, что вы искали!
Попробуйте задания от ЛогикЛайкВопросы и загадки на логику
Задания на 2D- и 3D‑мышление
Простые высказывания
Математические ребусы
Графические и числовые закономерности
Начать курс! Начать курс!
Решение логических задач по математике — один из самых полезных способов тренировки ума,
развития мышления и сообразительности у младших школьников. Смотрите подробный материал о развитии логики у детей.
Смотрите подробный материал о развитии логики у детей.
Задачи на логику 2-3 уровня сложности
Подборка из обучающего курса ЛогикЛайк
Для ознакомления предлагаем несколько задач из раздела «Классические логические задачи». У нас ещё очень много (более 3500) интересных задач: логические, математические, пространственные головоломки от простых к сложным.
Задача 1. На разделение предметов
Условие: Для
проведения очередного опыта Профессор купил 9 металлических стержней.
Некоторые из них он распилил на 5 частей. Всего стало 33 стержня.
Всего стало 33 стержня.
Вопрос: Сколько стержней распилил Профессор?
Cмотреть решение
Ответ:
6 стержней.
Решение
Если распилить один стержень на 5 частей, то
количественно добавляется 4 куска.
Всего добавилось 33 – 9 = 24 куска.
Значит, ученый распилил 24 : 4 = 6 стержней.
Решать задачи онлайн!
ВСЯ ЛОГИКА В ИГРОВОЙ ФОРМЕ!
- Гибкий ум и уверенность Когда дети решают задачи и головоломки на LogicLike, они тренируют «извилины» и развивают смекалку.
- Фундамент
для IT
Учим работать с информацией, тренируем память и развиваем
логико-математический интеллект.

- Свобода родителю Потратьте 20-30 минут на себя, пока ребёнок занят полезным делом.
Начать занятия!
Задача 2. Разрезание на части
Условие: Юра
разрезал огромную пиццу на 10 кусков. Затем он взял один из кусков и
разрезал его еще на 10.
Вопрос: Сколько в результате кусков пиццы у него получилось?
Показать решение
Ответ:
37 кусков.
Решение
После того, как Юра разрезает один кусок пиццы на 10
кусков, общее количество кусков увеличивается на 9
Изначально был один кусок (целая пицца), а всего, по условию задачи, указанную операцию Юра проделал 4 раза.

Всего стало 1 + 36 = 37 кусков.
Научиться решать задачи!
Задача 3. Сосчитай количество попаданий в цель
Условие: В
компьютерной игре нужно победить монстра.
Изначально у Юры было только 9 выстрелов. Но за каждое попадание он получал
дополнительно еще 3 выстрела.
Вопрос: Сколько раз Юра попал в цель, если всего он выстрелил 30 раз, израсходовав все выстрелы?
Узнать ответ
Ответ:
7.
Комментарий:
30 — 9 = 21 — столько дополнительных выстрелов Юра
заработал за попадания.
За каждое попадание давалось 3 выстрела:
21 ÷ 3 = 7 попаданий.
Начать интерактивные занятия!
Взять подсказку
Подсказка
Решить эту задачу можно методом последовательных рассуждений, а можно еще быстрее и проще.
Занятия на ЛогикЛайк помогут научиться с легкостью
решать любые задачи на логику и сообразительность.
Решайте 10-15 разных задач в день: математические ребусы, текстовые логические, пространственные, закономерности, алгоритмы и другие.
Понравился материал? Поделитесь с друзьями!
Научим решать любые логические задачи
Более 150 000 детей и родителей со всего мира уже занимаются на сайте ЛогикЛайк. Подключайтесь и развивайте логику и мышление.
Начать обучение! Начать обучение
Другие категории заданий
по возрасту и по темам
5-6 лет
6-7 лет
1 класс
2 класс
4 класс
Логические задачи
Тест: Логические задачи — Математика 3 класс
Английский язык
Астрономия
Белорусский язык
Биология
География
ИЗО
Информатика
История
Итальянский язык
Краеведение
Литература
Математика
Музыка
Немецкий язык
ОБЖ
Обществознание
Окружающий мир
ОРКСЭ
Русский язык
Технология
Физика
Физкультура
Химия
Черчение
Для учителей
Дошкольникам
VIP — доступ
- Предметы »
- Математика »
- 3 класс »
- Логические задачи
Логические задачи
Проверка логического , алгоритмического мышления
Математика 3 класс | Автор: Ливанова Ирина Георгиевна | ID: 2153 | Дата: 29. 4.2014
4.2014
Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться
«;} else {document.getElementById(«torf1″).innerHTML=»
«;}; if (answ.charAt(1)==»1») {document.getElementById(«torf2″).innerHTML=»
«;} else {document.getElementById(«torf2″).innerHTML=»
«;}; if (answ.charAt(2)==»1») {document.getElementById(«torf3″).innerHTML=»
«;} else {document.getElementById(«torf3″).innerHTML=»
«;}; if (answ.charAt(3)==»1») {document.getElementById(«torf4″).innerHTML=»
«;} else {document.getElementById(«torf4″).innerHTML=»
«;};
if (answ.charAt(4)==»1») {document.getElementById(«torf5»). innerHTML=»
innerHTML=»
«;} else {document.getElementById(«torf5″).innerHTML=»
«;}; if (answ.charAt(5)==»1») {document.getElementById(«torf6″).innerHTML=»
«;} else {document.getElementById(«torf6″).innerHTML=»
«;}; if (answ.charAt(6)==»1») {document.getElementById(«torf7″).innerHTML=»
«;} else {document.getElementById(«torf7″).innerHTML=»
«;}; if (answ.charAt(7)==»1») {document.getElementById(«torf8″).innerHTML=»
«;} else {document.getElementById(«torf8″).innerHTML=»
«;}; if (answ.charAt(8)==»1») {document.getElementById(«torf9″).innerHTML=»
«;} else {document.getElementById(«torf9″).innerHTML=»
«;}; } }
Вопрос №
1
Серёжа покрасил каждую грань кубика разными красками. Сколько красок для этого потребовалось ?
Сколько красок для этого потребовалось ?
4
3
6
Вопрос №
2
У Алины несколько кукол. Папа подарил ей не день рождения столько же кукол, сколько у неё было. Теперь у Алины 12 кукол. Сколько кукол подарил ей папа ?
12
5
6
Вопрос №
3
Сумма двух чисел равна семи, а их разность равна трём. Найдите эти числа.
3 и 4
2 и 5
7 и 9
Вопрос №
4
Володя, Дима и Петя устроили соревнование. Один из мальчиков решил 12 примеров, второй — 13, а третий — 14. Сколько примеров решил каждый мальчик, если Петя решил примеров меньше, чем Дима, а Дима меньше чем Володя ?
Дима -13, Петя — 12, Володя — 14
Дима — 14, Петя — 13, Володя — 12
Дима — 12, Петя — 14, Володя — 13
Вопрос №
5
У Вити сегодня день рождения. Он моложе своей сестры, которой исполнилось 6 лет. Сколько лет может быть Вите ?
Он моложе своей сестры, которой исполнилось 6 лет. Сколько лет может быть Вите ?
7 лет
1 годик
8 лет
Вопрос №
6
Витя, Саша и Андрей смастерили из бумаги кораблик, змея и аиста. Какую игрушку сделал каждый мальчик, если Витя не сделал кораблика и змея, а Саша не делал кораблик?
Витя — змея, Саша — кораблик. Андрей — аиста
Витя — кораблик, Саша — аиста, Андрей — змея
Витя — аиста, Саша — змея, Андрей — кораблик
Вопрос №
7
Маша загадала число. Чтобы его разгадать, возьми число 81, уменьши его в 3 раза, прибавь 6, прибавь 3 сотни. У тебя получилось число, которое задумала Лена.
433
333
233
Вопрос №
8
Восьмого марта в кино пришло 100 ребят. На приключенческий фильм было продано 87 билетов, а на комедию — 63. Сколько ребят посмотрели и тот фильм, и другой? (Каждый посмотрел по меньшей мере один из фильмов.)
На приключенческий фильм было продано 87 билетов, а на комедию — 63. Сколько ребят посмотрели и тот фильм, и другой? (Каждый посмотрел по меньшей мере один из фильмов.)
40
37
50
Вопрос №
9
На доске нарисованы два круга, внутри которых отмечено несколько точек. Внутри первого из них всего 190 отмеченных точек. Внутри второго — всего 230 отмеченные точки. Внутри обоих кругов одновременно находится ровно 70 точек. А сколько отмеченных точек всего?
300
350
400
Показать ответы
Получение сертификата
о прохождении теста
Доступно только зарегистрированным пользователям
© TestEdu.ru 2013-2022
E-mail администратора: [email protected]
Задачи на логику, ответы, 1 класс | Материал по математике (1 класс) по теме:
Ответы А
| Ответы А
| Ответы А
|
Задачи на логику. 1 класс А
- Бабушка связала Нине две пары носков.
 Сколько носков связала бабушка Нине?
Сколько носков связала бабушка Нине? - По двору ходят куры. У всех кур Петя насчитал 6 ног. Сколько кур?
- У Толи 2 пары варежек. Сколько варежек на левую руку?
- Какое число самое маленькое?
- В семье четверо детей: сестёр столько же, сколько братьев и сестёр. Сколько сестёр?
- Из бочки взяли 2 раза по 2 полных ведра воды. Сколько вёдер воды взяли?
- В корзине сидят котята. У всех котят 3 пары ушек. Сколько котят в корзине?
- На горке катались 6 ребят. Двое ушли обедать, но после обеда вернулись на горку. Сколько ребят стало на горке?
- У паука 4 пары ног. Сколько всего ног у паука?
- У Юры 3 кубика, а у Серёжи 2 кубика. На столе стоит коробка, в которой умещается 4 кубика. Смогут ли мальчики уложить в эту коробку все свои кубики?
- У жука 3 пары ног. Сколько всего ног у жука?
- На кусте утром было 8 бутонов. К середине дня все бутоны распустились и стали красивыми розами. Сколько бутонов осталось на этом кусте нераскрытыми?
- В пакете лежат красные и жёлтые яблоки.
 Из пакета взяли 4 красных и 5 жёлтых яблок, и пакет опустел. Сколько яблок было в пакете?
Из пакета взяли 4 красных и 5 жёлтых яблок, и пакет опустел. Сколько яблок было в пакете? - Дима выиграл у Алёши 2 партии в шахматы, а Алёша выиграл 3 партии. Сколько партий сыграли мальчики?
- Каждый из троих взрослых ведёт за руку двоих детей. Сколько детей идут со всеми взрослыми?
- Сколько целых батонов можно хлеба можно составить из шести половинок?
- По дороге один за другим идут 5 детей. За каждым мальчиком, кроме последнего, идёт девочка. Сколько девочек идут по дороге?
- Я придумала два числа. Когда я их сложила, то получила 6. Когда же из одного вычла другое, то снова получила 6. Что же это за числа?
- В коробке 8 пирожных. Сколько пирожных надо взять из коробки, чтобы в ней осталось 5 пирожных?
- Катя задумала число, прибавила к нему 5 и получила 15. Какое число задумала Катя?
- В семье двое детей. Саша – брат Жени, но Женя Саше не брат. Может ли так быть? Кто Женя?
- На яблоне было 10 яблок, Садовник разрешил детям сорвать с яблони по 1 яблоку.
 На яблоне осталось 6 яблок. Сколько было детей?
На яблоне осталось 6 яблок. Сколько было детей? - Поезд состоит из 10 вагонов. Петя сел в пятый вагон от начала поезда, а Федя – в пятый вагон от конца. В одном ли вагоне они едут?
- Плитка шоколада состоит из 6 квадратных долек. Сколько разломов нужно сделать, чтобы разломить эту плитку на отдельные дольки?
- Пётр сын Сергея, а Сергей – сын Фёдора. Кем приходится Пётр Фёдору?
- В саду яблонь на 3 больше, чем груш. Яблонь 7. Сколько груш?
- Из книги выпало несколько листов. На первой выпавшей странице стоит номер 5, а на последней номер 10. Сколько листов выпало из книги?
- У Зины на 4 открытки меньше, чем у Гали. У Зины 6 открыток. Сколько открыток у Гали?
- Меня зовут Иваном Сергеевичем, а моего деда (отца моего отца) – Петром Николаевичем. Запишите имя и отчество моего отца.
- Красный шнур на 1м длиннее зелёного и на 2м длиннее синего. Длина зелёного шнура 5м. Найди длину зелёного шнура.
- На вешалке висят головные уборы; шляп на 1 больше, чем беретов.
 Шляп 8. Сколько шапок и сколько беретов?
Шляп 8. Сколько шапок и сколько беретов? - Уменьшаемое больше вычитаемого на 2. Чему равна разность?
- Угадайте, сколько лет моему дедушке, если через 15 лет мы будем отмечать его семидесятилетие.
- Разность двух чисел равна вычитаемому. Придумайте такие числа и запишите пример.
- Разность двух чисел равна 0. Придумайте и запишите пример.
- Бабушка положила в тарелку 12 груш. После того как внуки взяли с тарелки по 1 груше, осталось 8 груш. Сколько у бабушки внуков?
- На уроке математики Ольга Петровна попросила Гошу назвать все числа, меньше 7, а Витю – все числа, которые больше 3 и меньше 9. Какие одинаковые числа назвали мальчики?
Б
1.Мама купила детям 3 пары варежек. Сколько всего левых варежек и сколько правых варежек?
2. В парке было 7 скамеек. 3скамейки заменили новыми. Сколько скамеек стало в парке?
3.В квартире 2 комнаты. Из одной комнаты сделали две. Сколько комнат стало в квартире?
4. Юра попросил в библиотеке журналы «Нафаня» со второго по шестой номер. Сколько журналов выдал ему библиотекарь?
Сколько журналов выдал ему библиотекарь?
5. В квартире 4 комнаты. Две комнаты соединили вместе и сделали из них одну большую комнату. Сколько комнат стало в квартире?
6. У всех цыплят, которые сидели в корзине, Юля насчитала 10 ног. Сколько цыплят было в корзине?
7. Таня сказала, что у неё кукол больше 4 и меньше 7. Сколько кукол могло быть у Тани?
8. Коля старше Серёжи, а Серёжа старше Миши. Запиши имя мальчика, который моложе всех.
9. На подоконнике лежали 8 зелёных помидоров. Через 3 дня они покраснели. Сколько зелёных помидоров осталось?
10. Кролики сидят в клетке так, что видны их уши. Вова насчитал 5 пар ушей. Сколько кроликов в клетке?
11. Кузнец подковал двух лошадей. Сколько подков ему потребовалось?
12. Алёшу угостили конфетами. Он решил дать своей сестрёнке 4 конфеты, а себе взять 3. Сколько конфет дали Алёше?
13. У Маши и Вани по 9 леденцов. Маша съела 4 леденца, и Ваня сделал тоже самое. Сколько леденцов осталось у Вани?
14. Нина задумала число. Это число она сначала прибавила к 7, а потом отняла его от 7. Ответ оказался одним и тем же – 7. Какое число задумала Нина?
Нина задумала число. Это число она сначала прибавила к 7, а потом отняла его от 7. Ответ оказался одним и тем же – 7. Какое число задумала Нина?
15. Роме подарили столько значков сколько у него уже было. Рома пересчитал все значки, их оказалось 8. Сколько значков было у Ромы сначала?
16. Чтобы рассадить 7 детей в комнате, не хватает 2 стульев. Сколько стульев в комнате?
17. У паука 4 пары ног, а у жука 3 пары ног. На сколько ног больше у паука, чем у жука?
18. В коробке 6 ячеек. В каждой ячейке умещается только одна ёлочная игрушка. Можно ли в эту коробку положить 4 шарика и 3 шишки?
19. Сестра старше брата на 1 год. На сколько лет сестра будет старше брата через 5 лет?
20. Может ли сумма двух чисел быть равной слагаемому?
21. Может ли разность двух чисел быть равной уменьшаемому?
22. Запиши число меньшее 20, в котором число десятков на 4 меньше числа единиц.
23. На каждую страницу альбома я наклеил 4 переводных картинки. Сколько страниц заняли 8 картинок?
24. Сумма двух чисел равна 8, а их разность 4. Угадайте, какие это числа?
Сумма двух чисел равна 8, а их разность 4. Угадайте, какие это числа?
25. Меня зовут Нина Александровна, а моего дедушку(отца моего отца) – Иван Николаевич. Как зовут моего отца?
26. На левой чашке весов стоят пакет с мукой и гиря в 1 кг. На правой чашке весов гиря в 3 кг. Весы в равновесии. Найдите массу пакеты с мукой.
27. в обувном отделе универмага висит указатель: «Обувь 37 – 42 размеров». Можно ли в этом отделе купить обувь 39 размера?
28.Какие двузначные числа можно записать, используя цифры 5 и 6?
29.Сахар-песок продают расфасованным в пакеты по 1 кг, 2кг, 3кг. Мама выбила в кассе чек на покупку 7 кг сахара. Продавщица дала ей 3 пакета с сахаром. Сколько сахара было в каждом из пакетов? Рассмотри возможные случаи.
30. Сравни числа *2 и 95 Сделай запись с помощью одного из знаков .
31. Юля и Марина нашли в лесу поровну грибов. У Юли 4 гриба оказались червивыми, и по дороге домой она их выбросила. А Марина нашла ещё 5 грибов. На сколько грибов у Марины стало больше, чем у Юли?
32. В ящике стола лежат деньги. На эти деньги можно купить 2 одинаковых по цене стула или одно кресло. Что дороже кресло или стул?
В ящике стола лежат деньги. На эти деньги можно купить 2 одинаковых по цене стула или одно кресло. Что дороже кресло или стул?
33.На верхней полке книг столько же, сколько на нижней. На верхнюю полку поставили 3 книги, а с нижней 3 книги сняли. На какой полке стало больше книг и на сколько?
34. В коробке 12 красных и зелёных шаров. Из коробки взяли 3 красных и 4 зелёных шара. После этого в коробке зелёных шаров не осталось. Сколько красных шаров осталось в коробке?
35. В корзине на 5 яблок больше, чем в пакете. Из корзины взяли 7 яблок. Где осталось яблок больше: в корзине или в пакете, и на сколько?
36. К трём замкам волшебник сделал 3 ключа: медный, серебряный и золотой. К каждому замку подходит только один ключ. Медный ключ не подходит к ни к первому, ни ко второму замку. Серебряный ключ не подходит ко второму замку. К какому замку подходит каждый из ключей?
37. У Пети на 4 конфеты меньше, чем у Серёжи. Мама дала Пете ещё 5 конфет. У кого конфет больше и на сколько?
38. Зелёная лента на 3 м длиннее красной. От зелёной ленты отрезали 5 м, а от красной 2м. Сравните длины оставшихся кусков лент.
Зелёная лента на 3 м длиннее красной. От зелёной ленты отрезали 5 м, а от красной 2м. Сравните длины оставшихся кусков лент.
39. У Юры денег ровно столько, чтобы купить 4 вафли или 2 конфеты. Сможет ли он на свои деньги купить 1 конфету и 4 вафли?
40. Запишите 6 чисел по такому правилу: первое 1, второе 2, а каждое следующее равно сумме двух предыдущих.
41. Оля может купить на свои деньги 4 карандаша и 3 тетради. Хватит ли у неё денег, чтобы купить 3 карандаша или 3 тетради?
42. Каждой из трёх внучек дедушка разрешил сорвать с четырёх кустов по одной розе. Сколько роз сорвали все внучки?
43. Запишите 5 чисел по такому правилу: первое 18, второе 10, а каждое следующее равно разности двух предыдущих.
44. Половину числа яблок, лежащих на тарелке, взяли для компота. Сколько яблок осталось на тарелке, если компот сварили из 6 яблок?
45. Купили пакет кефира. Половину всего кефира, который был в пакете, выпили Маша и Даша. В пакете осталось 2 стакана кефира. Сколько стаканов кефира было в пакете?
Сколько стаканов кефира было в пакете?
46. Дыня тяжелее арбуза и легче тыквы. Что самое тяжелое?
47. На столе лежат овощи: репок на 1 меньше, чем огурцов, а огурцов на 1 меньше, чем помидоров. На сколько репок меньше, чем помидоров?
48. Красная лента короче синей ленты и длиннее зелёной. Какая лента самая короткая?
49. Дима на 1 год старше Серёжи, а Серёжа на 1 год старше Ромы. На сколько лет Дима старше Ромы?
50. За каждую минуту в ванну из крана наливается 10 л воды. За то же время через неплотно прикрытое пробкой отверстие в дне ванны 2 л воды выливается. Увеличивается или уменьшается количество воды в ванне и на сколько литров каждую минуту?
51. Петя взял 3кубика и поставил их один на один так, что получилась «башня». Красный кубик оказался ниже синего, а синий ниже зелёного. Какой кубик Петя поставил выше всех?
52. Из трёх кубиков построили башню. Жёлтый кубик поставили выше синего и ниже красного. Какой кубик оказался выше всех?
53. Торт разрезали на 4 одинаковые части, а потом каждую часть разрезали на 2 одинаковые части. На сколько человек хватит торта, если каждому положить на блюдце один кусок?
Торт разрезали на 4 одинаковые части, а потом каждую часть разрезали на 2 одинаковые части. На сколько человек хватит торта, если каждому положить на блюдце один кусок?
54. В коробке лежат пряники и вафли: пряников на 2 меньше, чем вафель. Сколько вафель, если пряников 6?
55. Митя на 2 года старше Гены. Мите 10 лет. Сколько лет Гене?
56. Сумма двух чисел 9. Сумма больше первого слагаемого на 5.Чему равно второе слагаемое?
57. На катке катались на коньках 6 девочек и 2 мальчика. Вскоре троих детей позвали обедать, и они ушли домой. Осталась ли на катке хоть одна девочка?
58. Купили банку виноградного сока. Четверым детям налили из банки по полному стакану сока. После этого в банке осталось ровно столько, сколько выпили дети. Сколько стаканов сока было в банке?
60. Дыня на 3 кг легче арбуза. От дыни отрезали кусок массой 1 кг, а от арбуза – кусок массой
3 кг. Чего осталось больше: дыни или арбуза, и на сколько килограммов?
Ответы Б
7-0=7
2 способ: 3+4=7. 12-7=5
| Ответы Б
7-0=7
2 способ: 3+4=7. 12-7=5
| Ответы Б
7-0=7
2 способ: 3+4=7. 12-7=5
|
Лучшие упражнения для логического математического интеллекта —
Одним из восьми интеллектов или способностей, определенных Говардом Гарднером в его книге Структуры разума: теория множественного интеллекта , является логический математический интеллект.
В традиционной системе образования особое внимание уделяется использованию и развитию логических математических навыков наряду с вербальными навыками. Однако как педагоги и родители, обучающиеся на дому, мы должны осознавать, что все восемь видов интеллекта одинаково важны для продуктивного функционирования в обществе. Таким образом, несмотря на то, что в этом посте в первую очередь будет обсуждаться тема логического математического интеллекта, вы заметите, что эти действия также коснутся нескольких видов интеллекта.
Когда говорят, что кто-то «разбирается в математике», что приходит на ум? Этот человек, конечно, хорошо разбирается в цифрах. Но логический математический интеллект означает гораздо больше. Логические математические люди могут легко выявлять и анализировать закономерности, рассуждать дедуктивно, анализировать проблемы логически, критически задавать вопросы и делать выводы, объединяя имеющуюся информацию.
Во всех классах и в большинстве семей мы найдем детей, явно предпочитающих логический математический стиль обучения. Этот пост предназначен для тех педагогов или родителей, которые занимаются домашним обучением, которые хотят предоставить проверенные учителями задания для учащихся с логическим математическим интеллектом.
Этот пост предназначен для тех педагогов или родителей, которые занимаются домашним обучением, которые хотят предоставить проверенные учителями задания для учащихся с логическим математическим интеллектом.
Как я писал в других статьях о множественном интеллекте, ни у кого нет только одного типа интеллекта. Мы все приходим к пониманию мира благодаря сочетанию 8 видов интеллекта, определенных Гарднером. Это правда, что у людей обычно есть одна или две более сильные способности, которые помогают им легко учиться.
Прежде чем мы перейдем к некоторым замечательным занятиям для «умных в математике» детей, давайте сначала рассмотрим некоторые характеристики логического математического интеллекта.
Этот пост может содержать партнерские ссылки, и я могу получать небольшую комиссию, когда вы нажимаете на ссылки без каких-либо дополнительных затрат для вас. Являясь партнером Amazon, я зарабатываю на соответствующих покупках. Вы можете прочитать мое полное раскрытие здесь.
Существует несколько характеристик логического математического интеллекта, на которые следует обращать внимание при попытке определить доминирующие способности учащихся или детей. Некоторые из этих характеристик включают в себя:
- Они обладают хорошими навыками решения проблем
- Они поглощают информацию лучше всего через Рассуждение и логическое секвенирование
- им нравится Организованные
- У них хороших математических навыков и Great At At At At At At At At At At At At At At At 4444244.
- Им нравятся схемы, классификация и классификация вещей
- Нравится проводить научных эксперимента
- Работать с абстрактные идеи это то, что они любят
- Им нравится исследовать проблемы с помощью логики и фактов
- Их решения также основаны на фактах и здравом смысле .
 Они редко принимают решения, основанные на чувствах
Они редко принимают решения, основанные на чувствах - Им нравится разгадывать головоломки и загадки
- Они ориентированы на достижение цели
- Когда дело доходит до письма, они предпочитают прямолинейный стиль, а не творческий. письмо
- Им нравятся четко определенные правила
Теперь, когда вы знаете наиболее важные характеристики логического математического интеллекта, вы можете начать наблюдать за своими учащимися и определить, сколько из них «сообразительны в математике». Согласно Sage Journals, дети в возрасте 4 или 5 лет могут проявлять предпочтения в отношении того или иного типа интеллекта. В случае с маленькими детьми вы можете просто наблюдать за ними и на основе этого формировать «профиль интеллекта». Для детей старшего возраста, которые умеют читать и писать, помимо наблюдения за ними, вы можете дать им этот тест, который поможет вам определить их сильные и слабые стороны.
1.
Загадки и загадкиТе, кто изучает логику и математику, несомненно, полюбят сложные головоломки. Хорошая новость заключается в том, что существует так много вариантов (бесплатных и платных) как для физических, так и для онлайн-материалов. Вот некоторые из наших рекомендаций (для детей от 4 до 8 лет):
Рабочие тетради и рабочие тетради для печати :
- Логические головоломки для детей от 4 до 8 лет Рабочая тетрадь
- Идеальная логическая рабочая тетрадь
- Учебник с легковыми и грузовыми автомобилями
- Учебник Numbers Busy для дошкольников
Ознакомьтесь с нашей фантастической тетрадью Numbers Busy. 50 забавных страниц для детей, чтобы попрактиковаться в распознавании чисел, счете и основных математических операциях.
Получить сейчас
Игры
- Игра-головоломка «Час пик»
- Mental Blox
- Магнитная игра-головоломка «Лабиринт» (также отлично подходит для зрительно-пространственных способностей)
- Игры для мозга – многоразовые/стираемые коврики для занятий
2.
 Загадки
Загадки Ничто так не тренирует мозг, как хорошая загадка. Не говоря уже о том, что они забавны, особенно для «умного в математике» ребенка. Если вы ищете отличные загадки для маленьких детей, посмотрите здесь. Что мне нравится в этом посте, так это то, что он также дает подсказки к загадкам.
3.
Настольные игрыНастольные игры — это фантастические забавные инструменты для обучения. Они развивают навыки сотрудничества, терпение, учатся выигрывать или проигрывать изящно и в зависимости от настольной игры, математические и логические навыки. Вот несколько отличных настольных игр для маленьких детей, которые вы, возможно, захотите попробовать:
- Sum Swamp Board Game
- Математика лягуша увлекаются стратегическими играми, такими как шахматы, Крестики-нолики, Connect 4, домино и т. д.
5.
Исследовательские проектыУчащиеся логических математических наук любят логически организовывать информацию, исследуя факты.
6. Научные эксперименты Так почему бы не бросить детям увлекательный исследовательский проект? Просто выберите интересующую тему, например определенного динозавра, насекомое, солнечную систему, вулканы и т. д., и позвольте вашему малышу узнать как можно больше информации по этой теме. Дети постарше могут организовать и структурировать информацию самостоятельно, однако для детей помладше вы можете создать рабочие листы, чтобы направлять их исследования. Мне нравятся материалы Wifeteachermommy.com.
Так почему бы не бросить детям увлекательный исследовательский проект? Просто выберите интересующую тему, например определенного динозавра, насекомое, солнечную систему, вулканы и т. д., и позвольте вашему малышу узнать как можно больше информации по этой теме. Дети постарше могут организовать и структурировать информацию самостоятельно, однако для детей помладше вы можете создать рабочие листы, чтобы направлять их исследования. Мне нравятся материалы Wifeteachermommy.com.Одной из характеристик логического математического интеллекта является любопытство. Людям с такими способностями нравится знать, как все устроено, и понимать мир с помощью логики и рассуждений.
Вот почему такие занятия, как проведение научных экспериментов, будут очень приятными. Если вы не знаете, какие эксперименты провести со своим ребенком, взгляните на этот классный ресурс: 10 бесплатных сайтов для детей, которые любят науку.
7. Программирование
Программирование Мы живем в эпоху цифровых технологий, поэтому дети должны осваивать кодирование. Программирование помогает с навыками решения проблем, языком и общением, творчеством, математическими навыками и многим другим. Детей в возрасте от 2 лет можно познакомить с миром программирования с помощью простых упражнений и игр для предварительного программирования. Взгляните на эти практические игры для детей и этот список приложений для детей.
8. Проведение опросаПроведение опроса требует множества навыков, таких как умение слушать, говорить, хорошая организация, категоризация, математика и т. д.
Это отличное занятие для логически изучающих математику, так как они могут организовать вопросы в виде маркеров или в виде таблицы, они могут делать логические предположения, суммируя результаты и используя графики данных, такие как круговые диаграммы, столбцы или линии, для организовать результаты.
9. Математические игрыПонятно, что детям, занимающимся логикой и математикой, понравятся математические игры.
10. Создание временных шкал В Интернете можно найти как платные, так и бесплатные игры, которые понравятся вашему ребенку и помогут ему практиковать математику. Например, Math Games — это бесплатный веб-сайт, который содержит множество аркадных игр, рабочих листов, игр типа «Вопросы и ответы» и многое другое, все организовано по навыкам или оценкам.
В Интернете можно найти как платные, так и бесплатные игры, которые понравятся вашему ребенку и помогут ему практиковать математику. Например, Math Games — это бесплатный веб-сайт, который содержит множество аркадных игр, рабочих листов, игр типа «Вопросы и ответы» и многое другое, все организовано по навыкам или оценкам.Хороший способ для изучающих логику и математику усвоить информацию по такому предмету, как история, например, — создать временные шкалы. Организация информации в ясной, логичной форме поможет ребенку учиться намного легче, чем чтение страниц прозы.
11. Определение закономерностейОбразцы помогают детям находить логический порядок в окружающем их мире. Паттерны также дают возможность делать прогнозы, потому что они понимают, что будет дальше. Выявление закономерностей — важный навык, которым должны овладеть дети младшего возраста и который включает в себя нахождение взаимосвязей между различными элементами, алгебраическое мышление, наблюдение математических особенностей и закономерностей.
 Так что никогда не рано начинать знакомить вашего ребенка с шаблонными действиями. Не говоря уже о том, что когда дело доходит до логических математических действий, шаблоны очень популярны.
Так что никогда не рано начинать знакомить вашего ребенка с шаблонными действиями. Не говоря уже о том, что когда дело доходит до логических математических действий, шаблоны очень популярны.В дополнение к логическим математическим упражнениям, упомянутым выше, я хотел бы предложить некоторые дополнительные практические занятия и игры, в которые я играю со своим маленьким мальчиком, и многие другие игры, которые я использовал в классе.
Эти занятия подходят для детей от 3 лет и старше, что ж, можно с уверенностью сказать, что некоторым взрослым до сих пор нравятся эти игры, хе-хе. Поэтому обязательно адаптируйте игры в соответствии с возрастом и способностями вашего ребенка.
Практические занятия для логического математического интеллекта 1. Угадай животноеЭта игра позволит ребенку делать логические выводы на основе полученной информации.
Один игрок думает о животном и дает другим игрокам подсказки о нем.
 Вы можете определить количество подсказок. По подсказкам игрок должен угадать животное.
Вы можете определить количество подсказок. По подсказкам игрок должен угадать животное.Например, «Обитает в океане», «Питается планктоном», «Это самое большое животное на Земле» — кит.
2. Игра «Связь»Простая игра для тренировки мозга. Один игрок говорит 3 (видимо) случайных предмета. Другие игроки должны найти что-то общее, что есть у всех объектов. Если ваш ребенок также является визуальным учеником, то может помочь увидеть объекты, и в этом случае вы можете использовать реалии.
3. Разгадай загадку ЭйнштейнаЭто задание для детей постарше и потребует ручку, бумагу и их (воображаемые) детективные шляпы.
Из городского аквариума украли самую редкую в мире рыбу. Полицейские собаки пошли по следу в район с пятью одинаковыми домами. Вы должны следовать подсказкам (есть список из 15 подсказок, так что будьте готовы) и раскрыть дело.
Посмотрите видео и давайте посмотрим, сможете ли вы использовать свои навыки решения проблем, использовать логику, систематизировать информацию и решить проблему, используя факты.
4. Сборка из Lego Удачи!
Удачи!Я люблю Лего. Помимо того, что это весело, он предлагает так много возможностей для тренировки таких навыков, как мелкая моторика, зрительно-пространственное восприятие, общение, творчество, терпение, сосредоточенность и логический математический интеллект. Lego — это золотая жила.
Вы можете практиковать математические операции, создавать узоры, практиковать навыки геометрии, тренировать навыки решения задач и т. д.
Вы вполне можете просто бросить кусочки Lego на пол и позволить вашему ребенку свободно играть, он будет практиковать многие из навыки, упомянутые выше, сами по себе, или вы можете направить их игру в определенном направлении, если хотите усовершенствовать определенные способности.

Вот некоторые ресурсы, если вы ищете вдохновение для того, как играть с Lego:
- 10 забавных математических идей с Lego
- 30 Lego Math Ideas
- 50 способов научить Lego Math
- 25 Lego Упражнения
- 30 Lego Math Ideas
- 5. Различия и сходства (с использованием диаграмм Венна)
На диаграмме Венна используются перекрывающиеся круги, чтобы показать различия и сходства между набором из двух или более элементов. Таким образом, перекрывающаяся часть показывает общие элементы, в то время как отдельные части кругов показывают элементы, отличающие их друг от друга.
Игра с диаграммой Венна — отличное занятие для изучающих логику и математику, поскольку они могут логически организовать информацию, классифицировать и категоризировать элементы, используя факты.
Some suggestions that you can use:
- Dogs vs dolphins
- Bananas vs oranges
- Earth vs Mars
- Crocodile vs alligator
 The Intruder (Odd one out )
The Intruder (Odd one out ) Одно из самых простых логических математических заданий, которое вы можете выполнить с ребенком, — «Выпадение нечетного». Просто покажите ребенку набор из 4-5 предметов, один из которых будет злоумышленником, так как не имеет ничего общего с остальными. Ребенок должен идентифицировать этот объект и привести аргументы, почему он может быть лишним. Помимо того, что это хорошая игра для детей с логическим математическим стилем обучения, она также хороша для развития вербально-лингвистического интеллекта.
7. 4 в рядЭто игра для всех возрастов. Игра 4 в ряд подтолкнет детей к разработке стратегии для победы, планирования наперед, выявления закономерностей, решения проблем, прогнозирования результатов и т. д. Это фантастическая игра, которая должна быть у каждой семьи. Вы можете выбрать маленькую настольную игру или пройти все 9 ярдов и получить гигантскую версию.
Заключительные мыслиМы используем логический математический интеллект в повседневной жизни независимо от того, считаем ли мы себя «умными в математике» или нет.
 Мы не должны забывать, что мы рождаемся обладающими всеми восемью видами интеллекта, однако в силу биологических и культурных аспектов все мы имеем разные сильные и слабые стороны. В идеальной образовательной системе преподаватели должны представлять материалы таким образом, чтобы задействовать большинство из восьми видов интеллекта, давая своим ученикам возможность усвоить информацию удобным и легким для них способом.
Мы не должны забывать, что мы рождаемся обладающими всеми восемью видами интеллекта, однако в силу биологических и культурных аспектов все мы имеем разные сильные и слабые стороны. В идеальной образовательной системе преподаватели должны представлять материалы таким образом, чтобы задействовать большинство из восьми видов интеллекта, давая своим ученикам возможность усвоить информацию удобным и легким для них способом.Еще один аспект, о котором мы должны помнить, это то, что таланты и способности, с которыми мы рождаемся, не высечены в камне. На протяжении всей жизни мы можем развивать любой интеллект посредством практики.
Итак, этот пост предназначен как для учащихся, у которых есть логический математический стиль обучения, так и для тех, кто хочет его развить.
Читайте также:
Безумно увлекательные занятия для вербально-лингвистических учащихся
Занятия для аудиалов
Упражнения для детей с внутриличностным интеллектом
Лучшие занятия для тех, кто учатся телесно-кинестетически
Лучшие упражнения для тех, кто развивает визуально-пространственное мышление
Как теория множественного интеллекта может помочь вашему ребенку?
Кристина
Мама двоих замечательных детей, преданный учитель и любитель книг.

Логические головоломки | Brilliant Math & Science Wiki
Энди Хейс, Хуа Чжи Ви, Чимин Хим, а также
способствовал
Содержимое
- Силлогизмы
- Сетки исключения
- Правдивцы и лжецы
- Криптограммы
- Арифметические головоломки
- Головоломка с переходом через реку
- Тур Пазлы
- Нонограммы
- Морские головоломки
- Судоку
- Шахматные головоломки
- K-уровень мышления
- Другие головоломки
Основная статья: Логика высказываний
См.
 также: Логика предикатов
также: Логика предикатовОдин из простейших типов логических головоломок — силлогизм . В этом типе головоломки вам дается набор утверждений, и вы должны определить некоторую истину из этих утверждений. Эти типы головоломок часто можно решить, применяя принципы логики высказываний и логики предикатов. Следующий силлогизм принадлежит Чарльзу Лютвиджу Доджсону, более известному под псевдонимом Льюис Кэрролл.
У меня есть блюдо из картофеля. Верны следующие утверждения:
- Моя картошка, новая, не вареная.
- Весь мой картофель в этом блюде можно есть.
- Мой невареный картофель нельзя есть.
В этом блюде есть молодой картофель?
Первое и третье утверждения могут быть связаны транзитивным аргументом. Весь молодой картофель невареный, а невареный картофель непригоден для еды, поэтому молодой картофель не годится для еды.
Второе утверждение может быть выражено как эквивалентное противопоставление.
 Весь картофель в блюде годен для еды; если есть картофель, который нельзя есть, значит, его нет в блюде.
Весь картофель в блюде годен для еды; если есть картофель, который нельзя есть, значит, его нет в блюде.Затем снова применяется транзитивный аргумент. Молодой картофель не годится для еды, а несъедобного картофеля в тарелке нет. Таким образом, молодой картошки в блюде нет. □_\квадрат□
а) б) в) г)
Ниже приведены три утверждения, за которыми следуют три вывода. Примите три утверждения за истину, даже если они отличаются от общеизвестных фактов. Прочитайте утверждения и решите, какие выводы логически следуют из утверждений.
Заявления:
1. Все актеры — музыканты.
2. Ни один музыкант не является певцом.
3. Некоторые певцы умеют танцевать.Выводы:
1. Некоторые актеры поют.
2. Некоторые танцоры — актеры.
3. Ни один актер не является певцом.
Варианты ответов:
а) Далее следует только вывод 1.
б) Отсюда следует только вывод 2.
в) Далее следует только вывод 3.
г) следует хотя бы 2 вывода.Основная статья: Сетки на выбывание
Некоторые логические головоломки требуют, чтобы вы определили правильные пары для наборов объектов. Эти головоломки часто можно решить с помощью процесса исключения, и сетка исключения является эффективным инструментом для применения этого процесса.
Пример сетки исключений
Сетки исключений выровнены таким образом, что каждая строка представляет объект в наборе, а каждый столбец представляет объект, который должен быть соединен с объектом из этого набора. Флажки и метки X используются, чтобы показать, какие объекты являются парными, а какие нет.
младший ребенок третий ребенок второй ребенок старший ребенок
У мистера и миссис Тан четверо детей — три мальчика и девочка —
, каждому из которых нравится один из цветов — синий, зеленый, красный, желтый —
и одна из букв — P, Q , R, S.
- Старшему ребенку нравится буква Q.
- Младший ребенок любит зеленый цвет.
- Альфреду нравится буква S.
- У Бренды есть старший брат, который любит Р.
- Тот, кто любит синий, не самый старый.
- Тому, кто любит красный цвет, нравится буква П.
- Чарльз любит желтый цвет.
Исходя из вышеизложенного, Дариус является __________.\text{\_\_\_\_\_\_\_\_\_\_}.__________.
Основная статья: Правдивцы и лжецы
Разновидностью головоломок на выбывание является головоломка о правде и лжеце , также известная как головоломка о рыцарях и лжецах . В этом типе головоломки вам дается набор людей и их соответствующие утверждения, и вам также говорят, что некоторые люди всегда говорят правду, а некоторые всегда лгут. Цель головоломки состоит в том, чтобы вывести истину из данных утверждений. 9\text{101}математик 20-го века Рэймонд Смаллян популяризировал эти типы головоломок.

Только у А есть сокровище A и C имеют сокровище Только у B есть сокровище B и C имеют сокровище Только у C есть сокровище Во всех сундуках есть сокровища A и B имеют сокровище
Вы находитесь в комнате с тремя сундуками. Вы знаете, что по крайней мере в одном из них есть сокровища, а если в сундуке нет сокровищ, значит, он содержит смертельный яд.
В каждом сундуке есть сообщение, но все сообщения врут .
- Левый сундук: «В среднем сундуке сокровища».
- Средний сундук: «Во всех этих сундуках есть сокровища.»
- Правый сундук: «Только в одном из этих сундуков есть сокровища.»
В каких сундуках есть сокровища?
A — рыцарь, B — лжец А — лжец, а Б — рыцарь Оба они лжецы Оба они рыцари
Есть два человека, A и B , каждый из которых либо рыцарь, либо лжец.

А говорит: «По крайней мере, один из нас — лжец».
Что такое A и B ?
Детали и предположения:- Рыцарь всегда говорит правду.
- Мошенник всегда лжет.
Основная статья: Криптограммы
Криптограмма — это головоломка, в которой числовые цифры в числовом предложении заменены символами, и цель головоломки — определить значения этих символов.
PPQPQQ+QQQ876 \begin{массив} { л л л л } &&П&П&В\\ & &P & Q & Q \\ + && Q & Q & Q \\ \hline & & 8 & 7 & 6 \\ \end{массив} +PPQ8PQQ7QQQ6
В сумме, показанной выше, каждый из PPP и QQQ представляет цифру. Какова ценность P+QP+QP+Q?
EVE‾÷DID‾=0.TALKTALKTALKTALK…‾ \overline{EVE} \div \overline{DID} = 0. \overline{TALKTALKTALKTALK\ldots} EVE÷DID=0.TALKTALKTALKTALK…
Учитывая, что E,V ,D,I,T,A,LE,V,D,I,T,A,LE,V,D,I,T,A,L и KK K — различные одиночные цифры, пусть EVE‾\overline{EVE} EVE и DID‾ \overline{DID} DID — два взаимно простых 3-значных положительных целых числа, а TALK‾\overline{TALK} TALK — 4-значное целое число, такое что приведенное выше уравнение верно, где правая часть повторяющееся десятичное число.

Найдите значение суммы EVE‾+DID‾+TALK‾ \overline{EVE} + \overline{DID} + \overline{TALK} EVE+DID+TALK.
Основные статьи: заполнение пробелов и поиск оператора
Арифметические головоломки содержат ряд чисел, операций и пробелов по порядку, и цель головоломки состоит в том, чтобы заполнить пробелы для получения желаемого результата.
□×□□=□□□\огромный{\Box \times \Box \Box = \Box \Box \Box}□×□□=□□□
Заполните поля выше цифрами 1,2, 3,4,5,61,2,3,4,5,61,2,3,4,5,6 без повторяющихся цифр, так что уравнение верно.
Введите ответ, соединив все цифры в порядке их появления. Например, если ответ 1 × 23 = 4561 \ умножить на 23 = 4561 × 23 = 456, введите 123456123456123456 в качестве окончательного ответа.
Также попробуйте родственную задачу.
0 + 0 = 00 − 0 = 00 × 0 = 00 ÷ 0 = 00 ÷ 0 = 00 ÷ 0 = \ в коробке {\ phantom0} \; + \; \ в коробке {\ phantom0} \; знак равно \ в коробке {\ phantom0} \\ \ в коробке {\ phantom0} \; — \; \ в коробке {\ phantom0} \; знак равно \ в коробке {\ phantom0} \\ \ в коробке {\ phantom0} \; \раз\; \ в коробке {\ фантом0} \; знак равно \ в коробке {\ phantom0} \\ \ в коробке {\ phantom0} \; \дел\; \ в коробке {\ phantom0} \; знак равно \ в коробке {\ phantom0} \\ \end{выровнено}} 0+00−00×00÷0====0000
Поместите одно из целых чисел 1,2,…,131, 2, \ldots , 131,2,…,13 в каждую из ячеек так, чтобы двенадцать из этих чисел использовались один раз для каждого (и одно число не используется вообще) и все четыре уравнения верны.

Какова сумма всех возможных значений отсутствующего (неиспользованного) числа?
Основная статья: Головоломки с переходом через реку
В головоломке о пересечении реки цель состоит в том, чтобы найти способ переместить группу людей или объектов через реку (или какое-либо другое препятствие) и сделать это за наименьшее количество шагов или как минимум количество времени.
Известная задача о переходе через реку — это задача Ричарда Ховассе о мосте и факеле , описанная ниже.
Ночью к реке приходят четыре человека. Есть узкий мост, но он может вместить только двух человек одновременно. У них есть один фонарик, а так как сейчас ночь, фонарик приходится использовать при пересечении моста. Человек A может пересечь мост за одну минуту, B за две минуты, C за пять минут и D за восемь минут. Когда два человека пересекают мост вместе, они должны двигаться со скоростью более медленного человека.
 Вопрос в том, смогут ли они все перейти мост за 15 минут или меньше?
Вопрос в том, смогут ли они все перейти мост за 15 минут или меньше?Предположим, что решение минимизирует общее количество крестиков. Это дает в общей сложности пять скрещиваний — три парных скрещивания и два одиночных скрещивания. Кроме того, предположим, что мы всегда выбираем самых быстрых для одиночного кросса.
Во-первых, мы показываем, что если два самых медленных человека (C и D) пересекают дорогу по отдельности, их общее время перехода равно 15. Для этого нужно взять людей A, C, D: D+A+C+A = 8+ 1+5+1=15. (Здесь мы используем A, потому что мы знаем, что использование A для пересечения C и D по отдельности является наиболее эффективным.) Но время истекло, а люди A и B все еще находятся на начальной стороне моста и должны перейти. Таким образом, два самых медленных (C и D) не могут пересекаться по отдельности.
Во-вторых, мы показываем, что для того, чтобы C и D пересеклись вместе, они должны пересечься во второй паре перекрестков: то есть не C или D, поэтому A и B должны пересечься вместе первыми.
 Помните наше первоначальное предположение о том, что мы должны свести к минимуму пересечения, поэтому у нас есть пять пересечений — 3 парных пересечения и 2 одиночных пересечения. Предположим, что C и D пересекаются первыми. Но затем C или D должны вернуться, чтобы переместить факел на другую сторону, поэтому тот, кто пересек дорогу в одиночку, должен пересечь снова. Следовательно, они будут пересекаться отдельно. Кроме того, они не могут пересечься вместе последними, поскольку это означает, что один из них должен был пересечь дорогу раньше, иначе на стартовой стороне было бы всего три человека. Таким образом, поскольку есть только три варианта парного пересечения, а C и D не могут пересечься первым или последним, они должны пересечься вместе во втором, или среднем, парном пересечении.
Помните наше первоначальное предположение о том, что мы должны свести к минимуму пересечения, поэтому у нас есть пять пересечений — 3 парных пересечения и 2 одиночных пересечения. Предположим, что C и D пересекаются первыми. Но затем C или D должны вернуться, чтобы переместить факел на другую сторону, поэтому тот, кто пересек дорогу в одиночку, должен пересечь снова. Следовательно, они будут пересекаться отдельно. Кроме того, они не могут пересечься вместе последними, поскольку это означает, что один из них должен был пересечь дорогу раньше, иначе на стартовой стороне было бы всего три человека. Таким образом, поскольку есть только три варианта парного пересечения, а C и D не могут пересечься первым или последним, они должны пересечься вместе во втором, или среднем, парном пересечении.Собирая все это вместе, A и B должны пересечься первыми, поскольку мы знаем, что C и D не могут, и мы минимизируем пересечения. Затем A должен пересечься следующим, так как мы предполагаем, что должны выбрать самого быстрого, чтобы совершить одиночное пересечение.
. Тогда мы находимся на втором, или среднем, парном пересечении, поэтому C и D должны уйти. Затем мы решаем отправить назад самого быстрого, то есть B. Теперь A и B находятся на стартовой стороне и должны пересечься последней парой. Это дает нам B+A+D+B+B = 2+1+8+2+2 = 15,
Тогда мы находимся на втором, или среднем, парном пересечении, поэтому C и D должны уйти. Затем мы решаем отправить назад самого быстрого, то есть B. Теперь A и B находятся на стартовой стороне и должны пересечься последней парой. Это дает нам B+A+D+B+B = 2+1+8+2+2 = 15,Все четыре человека могут пересечь границу за 15 минут. □_\квадрат□
Основная статья: Тур Пазлы
См. также: Путь Эйлера
В головоломке Tour цель состоит в том, чтобы определить правильный путь для объекта, чтобы пересечь график. Эти виды головоломок могут принимать несколько форм: шахматные туры, обходы лабиринта, эйлеровы пути и другие.
Найдите путь, ведущий от звезды в центре обратно к звезде в центре. Пути могут идти только в направлении стрелки.
Изображение предоставлено: Эрик Фиск
Путь решения обведен красным ниже.

Определите путь через приведенный ниже граф так, чтобы каждое ребро было пройдено ровно один раз .
Есть несколько возможных решений. Одно из возможных решений показано ниже, где ребра отмечены в порядке их пересечения.
Шахматный тур — интересная головоломка сама по себе, подробное описание которой приведено ниже.
Основная статья: Нонограммы
нонограмма — это головоломка на основе сетки, в которой рядом с прямоугольной сеткой дается ряд числовых подсказок. Когда головоломка собрана, в сетке формируется картинка.
Головоломка начинается с ряда чисел слева и над сеткой. Каждое из этих чисел представляет собой последовательную серию заштрихованных пробелов в соответствующей строке или столбце.
 Каждый последующий запуск отделяется от других запусков хотя бы одним пустым пространством. Головоломка завершена, когда все числа были удовлетворены. Основным методом решения этих головоломок является процесс исключения. Если головоломка составлена правильно, никаких догадок не требуется.
Каждый последующий запуск отделяется от других запусков хотя бы одним пустым пространством. Головоломка завершена, когда все числа были удовлетворены. Основным методом решения этих головоломок является процесс исключения. Если головоломка составлена правильно, никаких догадок не требуется.Заполните кроссворд:
Одной из многих логических головоломок является головоломка «Морской бой» (иногда называемая «Бимару», «Юботу», «Морские корабли-пасьянсы» или «Солитер-морской бой»). Головоломка основана на игре Морской бой.
Морской пасьянс Solitaire был изобретен Хайме Пониачиком в Аргентине и впервые был опубликован в журнале Humor & Juegos.
Это пример решенной головоломки Морской бой. Головоломка состоит из маленьких квадратов 10 × 10, которые содержат следующее:
- 1 линкор 4 квадрата длиной
- 2 крейсера 3 квадрата каждый
- 3 эсминцы 2 квадрата каждый
- 4 подводные лодки по 1 квадрату каждая.

Их можно поставить горизонтально или вертикально, но никогда по диагонали. Лодки размещены так, чтобы ни одна из лодок не касалась друг друга даже вертикально. Цифры рядом со строкой/столбцом обозначают количество клеток, занятых в строке/столбце соответственно. ⬤ указывает на подводную лодку, а ⬛ указывает на корпус корабля, а полукруги указывают на начало/конец корабля.
Цель игры — заполнить сетку водой или кораблями.
Основная статья: Судоку
A судоку головоломка на 9×99\times 99×9 сетка, в которой каждая строка, столбец и меньшая квадратная часть содержат каждую из цифр от 1 до 9, каждая не более одного раза. Каждая головоломка начинается с заполнения некоторых мест в сетке. Цель состоит в том, чтобы заполнить оставшиеся места в головоломке. Головоломка решается в основном через процесс исключения. Для решения не требуется никаких догадок, и для любой заданной головоломки должно быть только одно решение.

Решите головоломку судоку:
Головоломка, созданная генератором судоку Open Sky
Каждая строка должна содержать каждую из цифр от 1 до 9 ровно один раз. То же самое верно для столбцов и меньших квадратов 3×33\x 33×3.
Основная статья: Шахматные головоломки
См. также: Сокращенные партии, дебютные стратегии и ладейные стратегии
Шахматные головоломки основаны на правилах игры в шахматы и требуют от вас выполнения определенных действий или определения состояний доски.
Одним из видов шахматной головоломки является шахматный тур , связанный с головоломками тура, упомянутыми в разделе выше. Этот тип головоломки предлагает вам совершить путешествие по шахматной фигуре по доске, применяя правила движения этой фигуры.

Дэн Сэм Ни у одного из них нет выигрышной стратегии
Дэн и Сэм играют в игру на доске 5×35\×35×3. Дэн ставит Белого рыцаря в угол, а Сэм ставит Черного рыцаря в ближайший угол. Каждый в свой ход перемещает своего рыцаря на клетки с , а не уже посещал любой из рыцарей в любой момент матча.
Например, ходит Дэн, затем Сэм, и Дэн хочет пройти на исходную клетку Черного рыцаря, но не может, так как эта клетка была занята ранее.
Когда кто-то не может двигаться, он проигрывает. Если начнет Дэн, кто выиграет, если оба игрока будут играть оптимально?
Это семнадцатая задача из набора «Стратегии выигрыша».
Благодаря четко определенному набору правил игра в шахматы позволяет решать множество различных типов головоломок. Приведенная ниже задача показывает, что вы даже можете определить, чей сейчас ход, из определенного состояния доски (или, возможно, вы не можете).

Ход белых Черный, чтобы двигаться Невозможно определить Это невозможная позиция
Чей теперь ход?
Основная статья: Мышление K-уровня
См. также: Индукция — Введение
Мышление К-уровня — это название своего рода предположения в некоторых логических головоломках. В подобных головоломках в ситуации участвует несколько действующих лиц, и каждый из них совершенно логичен в принятии решений. Более того, каждый из этих действующих лиц осознает, что все остальные действующие лица в данной ситуации совершенно логичны в своих решениях.
Кальвин, Зандра и Эли учатся в математическом классе мистера Сильвермана. Мистер Сильверман вручает каждому из них запечатанный конверт с номером внутри.
Он говорит им, что у каждого из них есть положительное целое число, а сумма трех чисел равна 14.
 Каждый открывает свой конверт и проверяет свое число, не видя других чисел.
Каждый открывает свой конверт и проверяет свое число, не видя других чисел.Кальвин говорит: «Я знаю, что у Зандры и Илая разные числа».
Зандра отвечает: «Я уже знала, что все три наших номера разные». 904:12 После короткой паузы Эли наконец говорит: «А, теперь я знаю, какой у каждого номер!»Какое число получил каждый ученик?
Отформатируйте свой ответ, написав сначала номер Кальвина, затем номер Зандры и, наконец, номер Эли. Например, если у Кальвина 8, у Зандры 12, а у Эли 8, ответ будет 8128.
Два логика должны найти два различных целых числа AAA и BBB так, чтобы оба они были между 2 и 100 включительно, а AAA делит BBB . Первый логик знает сумму A+B A + B A+B, а второй логик знает разность B−AB-AB−A.
Далее происходит следующее обсуждение:
Логик 1: Я их не знаю.
Логик 2: Я это уже знал.Логик 1: Я уже знаю, что вы должны это знать.
Логик 2: Я думаю, что. .. я знаю… что ты собирался это сказать!
.. я знаю… что ты собирался это сказать!Логик 1: Я до сих пор не могу понять, что это за два числа.
Логик 2: Ой! Плохо… мой предыдущий вывод был необоснованным. Я этого еще не знал!Какие два числа?
Введите ответ в виде десятичного числа A.BA.BA.B.
(((Например, если A=23A=23A=23 и B=92B=92B=92, напишите 23,92.)23,92.)23,92.)Примечание: В этой задаче участники не участвуют в соревнование, кто первым найдет числа. Если у одного из них достаточно информации для определения чисел, он может промолчать. Поэтому ничего нельзя вывести из молчания. Единственная используемая информация — это явные объявления в диалоге.
Конечно, головоломки, описанные выше, не единственные типы головоломок, с которыми можно столкнуться. Ниже приведены еще несколько логических головоломок, не связанных с типами, описанными выше.
Вам предлагается угадать целое число от 111 до NNN включительно.
 \text{rd}3-е предположение слишком мало, вы вышли.
\text{rd}3-е предположение слишком мало, вы вышли.При каком максимальном NNN вы гарантированно выполните это задание?
Пояснение : Например, если вам было позволено угадать один раз слишком много и один раз слишком мало, вы могли бы гарантировать правильный ответ, если N=5N=5N=5, но не для N>5N>5N> 5. Итак, в этом случае ответ будет 555.Вы играете в игру с кучей золотых монет NNN.
Вы и ваш друг по очереди берете 1, 3 или 6 монет из стопки.
Выигрывает тот, кто возьмет последнюю монету.Сколько существует выигрышных стратегий для того, кто ходит первым, для N<1000?N < 1000?N<1000?
Уточнение: Для 1≤N≤9991 \leq N \leq 9991≤N≤999, для скольких значений NNN первый игрок может разработать выигрышную стратегию?Процитировать как: Логические головоломки. Brilliant.org . Извлекаются из https://brilliant.
 org/wiki/логические-пазлы/
org/wiki/логические-пазлы/Superb Logical Math Вопросы с ответами
Вы хотите решать головоломки, где вы можете применить как логику, так и математику, чтобы получить ответ? Начните здесь.
- Логическая математическая головоломка
Посмотреть Ответ
Ответ 1: 177 — 77 = 100; 100; Ответ 2: (7+7) * (7 + (1/7)) = 100;- Логические математические задачки
Учитель поставил 13 баллов одному ученику и 12 баллов другому ученику за один экзамен.
Можете ли вы определить ВРЕМЯ, используя приведенное выше предложение????
Просмотреть ответ
Ответ : 1,45
Учитель поставил двум ученикам 25 баллов.
 25 — это
25 — это
квартал.Итак, учитель дал «без четверти два».
Формат времени «без четверти два» — 1,45.
- Логические математические задачки
Позавчера мне было 25.
В следующем году мне будет 28.
Это правда только один день в году.
В какой день у меня День Рождения?Посмотреть ответ
Мой день рождения 31 декабря. Я говорю это 1 января.
Позавчера (30 декабря) = Мне 25 лет
Сегодня (1 января) мне будет 27.В следующем году 31 декабря = I будет 28.
- Логические головоломки математики
У вас есть 3 -литровая бутылка и 5 -литровая бутылка.
 Как вы можете отмерить 4 литра воды, используя 3-литровые и 5-литровые бутылки???
Как вы можете отмерить 4 литра воды, используя 3-литровые и 5-литровые бутылки???Посмотреть ответ
Решение 1 :
1. Сначала полностью заполните 3-литровую бутыль и перелейте 3 литра в 5-литровую бутыль.
2. Снова полностью заполните 3-литровую бутыль. Теперь налейте 2 литра в 5-литровую бутылку, пока она не наполнится.
3. Пустая 5-литровая бутылка.
4. Перелейте оставшийся 1 литр из 3-литровой бутылки в 5-литровую бутыль.
5. Теперь снова полностью заполните 3-литровую бутыль и перелейте 3 литра в 5-литровую бутыль.
6. Теперь у вас есть 4 литра в 5-литровой бутыли. Вот и все.Раствор 2 :
1. Сначала полностью заполните 5-литровую бутыль и перелейте 3 литра в 3-литровую бутыль.
2. Пустая 3-литровая бутылка.
3. Перелейте оставшиеся 2 литра из 5-литровой бутылки в 3-литровую бутыль.
4. Снова полностью наполните 5-литровую бутыль и перелейте 1 литр в 3-литровую бутылку, пока она не наполнится.
5. Теперь у вас есть 4 литра в 5-литровой бутыли. Вот и все.
Теперь у вас есть 4 литра в 5-литровой бутыли. Вот и все.- Логические математические задачки
3 Друзья пошли в магазин и купили 3 игрушки. Каждый человек заплатил 10 рупий, что составляет стоимость одной игрушки. Итак, они заплатили 30 рупий, т.е. общую сумму. Владелец магазина предоставил скидку в размере 5 рупий на общую покупку 3 игрушек за 30 рупий. Затем среди 5 рупий каждый человек взял 1 рупию, а оставшиеся 2 рупии отдали нищему возле магазина.
Теперь фактическая сумма, выплачиваемая каждым человеком, составляет 9 рупий, а сумма, отдаваемая нищему, составляет 2 рупии. Таким образом, общая эффективная выплаченная сумма составляет 9 * 3 = 27, а сумма, отданная нищему, составляет 2 рупии, таким образом, общая сумма составляет 29 рупий. Куда делся другой Rs.1 от оригинальных Rs.
 30 ?????
30 ?????Посмотреть ответ
Логика такова, что платежи должны быть равны поступлениям. мы не можем сложить сумму, уплаченную людьми, и сумму, отданную нищему, и сравнить ее с 30 рупиями.
Общая выплаченная сумма составляет 27 рупий. Таким образом, из 27 рупий владелец магазина получил 25 рупий, а нищий получил рупий. 2. Таким образом, платежи равны поступлениям.- Логические математические задачи
Человек взбирается на наклонную гору. Ему нужно проехать 100 км, чтобы добраться до вершины горы. Каждый день днем он поднимается на 2 км вперед. Измученный, он отдыхает там ночью. Ночью, пока он спит, он соскальзывает на 1 км назад, потому что гора наклонена.
Тогда за сколько дней он доберется до вершины горы ????
Просмотреть ответ
Ответ: 99 дней
Каждый день общий прогресс = 2 км – 1 км = 1 км
Итак, 98 дней = 98 км.
На 99-й день он может достичь вершины горы, пройдя 2 км в дневное время.
Итак, ответ 99 дней- Логические математические задачки
За 1 банан вы получите 40 рупий.
За 3 рупии вы получите 1 манго.
За 5 рупий вы получаете 1 яблоко. Теперь вы хотите получить 100 фруктов за 100 рупий. Итак, сколько бананов, манго и яблок вы купите ??Просмотреть ответ
Ответ : 100
95 рупий — 19 яблок
3 рупии — 1 манго
2 рупии — 80 бананов
Всего 100 фруктов за 100 рупий.
- Логическая математическая головоломка
Узнайте нечетное письмо из следующего набора
Ответ
.


 Попробуйте
«Логические задачи», «Закономерности», «Истина и ложь», «Умный
счёт».
Попробуйте
«Логические задачи», «Закономерности», «Истина и ложь», «Умный
счёт».
 к.
к. д.
д. Сколько носков связала бабушка Нине?
Сколько носков связала бабушка Нине? Из пакета взяли 4 красных и 5 жёлтых яблок, и пакет опустел. Сколько яблок было в пакете?
Из пакета взяли 4 красных и 5 жёлтых яблок, и пакет опустел. Сколько яблок было в пакете? На яблоне осталось 6 яблок. Сколько было детей?
На яблоне осталось 6 яблок. Сколько было детей? Шляп 8. Сколько шапок и сколько беретов?
Шляп 8. Сколько шапок и сколько беретов?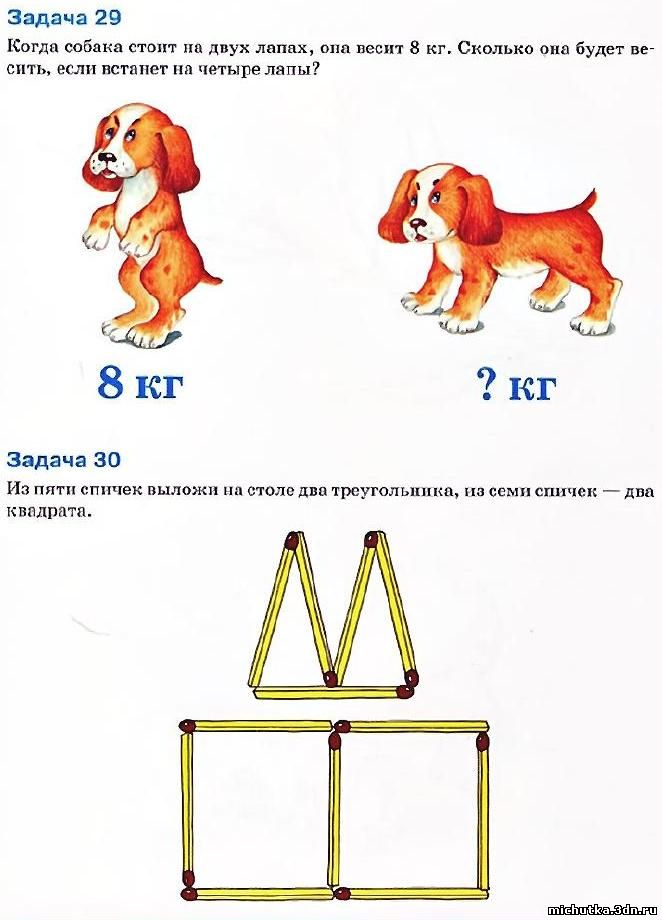 Если одно из слагаемых равно нулю. Например: 5+0=5
Если одно из слагаемых равно нулю. Например: 5+0=5 Если одно из слагаемых равно нулю. Например: 5+0=5
Если одно из слагаемых равно нулю. Например: 5+0=5 Если одно из слагаемых равно нулю. Например: 5+0=5
Если одно из слагаемых равно нулю. Например: 5+0=5 Они редко принимают решения, основанные на чувствах
Они редко принимают решения, основанные на чувствах Так почему бы не бросить детям увлекательный исследовательский проект? Просто выберите интересующую тему, например определенного динозавра, насекомое, солнечную систему, вулканы и т. д., и позвольте вашему малышу узнать как можно больше информации по этой теме. Дети постарше могут организовать и структурировать информацию самостоятельно, однако для детей помладше вы можете создать рабочие листы, чтобы направлять их исследования. Мне нравятся материалы Wifeteachermommy.com.
Так почему бы не бросить детям увлекательный исследовательский проект? Просто выберите интересующую тему, например определенного динозавра, насекомое, солнечную систему, вулканы и т. д., и позвольте вашему малышу узнать как можно больше информации по этой теме. Дети постарше могут организовать и структурировать информацию самостоятельно, однако для детей помладше вы можете создать рабочие листы, чтобы направлять их исследования. Мне нравятся материалы Wifeteachermommy.com. Программирование
Программирование  В Интернете можно найти как платные, так и бесплатные игры, которые понравятся вашему ребенку и помогут ему практиковать математику. Например, Math Games — это бесплатный веб-сайт, который содержит множество аркадных игр, рабочих листов, игр типа «Вопросы и ответы» и многое другое, все организовано по навыкам или оценкам.
В Интернете можно найти как платные, так и бесплатные игры, которые понравятся вашему ребенку и помогут ему практиковать математику. Например, Math Games — это бесплатный веб-сайт, который содержит множество аркадных игр, рабочих листов, игр типа «Вопросы и ответы» и многое другое, все организовано по навыкам или оценкам. Так что никогда не рано начинать знакомить вашего ребенка с шаблонными действиями. Не говоря уже о том, что когда дело доходит до логических математических действий, шаблоны очень популярны.
Так что никогда не рано начинать знакомить вашего ребенка с шаблонными действиями. Не говоря уже о том, что когда дело доходит до логических математических действий, шаблоны очень популярны. Вы можете определить количество подсказок. По подсказкам игрок должен угадать животное.
Вы можете определить количество подсказок. По подсказкам игрок должен угадать животное. Удачи!
Удачи!
 The Intruder (Odd one out )
The Intruder (Odd one out )  Мы не должны забывать, что мы рождаемся обладающими всеми восемью видами интеллекта, однако в силу биологических и культурных аспектов все мы имеем разные сильные и слабые стороны. В идеальной образовательной системе преподаватели должны представлять материалы таким образом, чтобы задействовать большинство из восьми видов интеллекта, давая своим ученикам возможность усвоить информацию удобным и легким для них способом.
Мы не должны забывать, что мы рождаемся обладающими всеми восемью видами интеллекта, однако в силу биологических и культурных аспектов все мы имеем разные сильные и слабые стороны. В идеальной образовательной системе преподаватели должны представлять материалы таким образом, чтобы задействовать большинство из восьми видов интеллекта, давая своим ученикам возможность усвоить информацию удобным и легким для них способом.
 также: Логика предикатов
также: Логика предикатов Весь картофель в блюде годен для еды; если есть картофель, который нельзя есть, значит, его нет в блюде.
Весь картофель в блюде годен для еды; если есть картофель, который нельзя есть, значит, его нет в блюде.





 Вопрос в том, смогут ли они все перейти мост за 15 минут или меньше?
Вопрос в том, смогут ли они все перейти мост за 15 минут или меньше? Помните наше первоначальное предположение о том, что мы должны свести к минимуму пересечения, поэтому у нас есть пять пересечений — 3 парных пересечения и 2 одиночных пересечения. Предположим, что C и D пересекаются первыми. Но затем C или D должны вернуться, чтобы переместить факел на другую сторону, поэтому тот, кто пересек дорогу в одиночку, должен пересечь снова. Следовательно, они будут пересекаться отдельно. Кроме того, они не могут пересечься вместе последними, поскольку это означает, что один из них должен был пересечь дорогу раньше, иначе на стартовой стороне было бы всего три человека. Таким образом, поскольку есть только три варианта парного пересечения, а C и D не могут пересечься первым или последним, они должны пересечься вместе во втором, или среднем, парном пересечении.
Помните наше первоначальное предположение о том, что мы должны свести к минимуму пересечения, поэтому у нас есть пять пересечений — 3 парных пересечения и 2 одиночных пересечения. Предположим, что C и D пересекаются первыми. Но затем C или D должны вернуться, чтобы переместить факел на другую сторону, поэтому тот, кто пересек дорогу в одиночку, должен пересечь снова. Следовательно, они будут пересекаться отдельно. Кроме того, они не могут пересечься вместе последними, поскольку это означает, что один из них должен был пересечь дорогу раньше, иначе на стартовой стороне было бы всего три человека. Таким образом, поскольку есть только три варианта парного пересечения, а C и D не могут пересечься первым или последним, они должны пересечься вместе во втором, или среднем, парном пересечении. Тогда мы находимся на втором, или среднем, парном пересечении, поэтому C и D должны уйти. Затем мы решаем отправить назад самого быстрого, то есть B. Теперь A и B находятся на стартовой стороне и должны пересечься последней парой. Это дает нам B+A+D+B+B = 2+1+8+2+2 = 15,
Тогда мы находимся на втором, или среднем, парном пересечении, поэтому C и D должны уйти. Затем мы решаем отправить назад самого быстрого, то есть B. Теперь A и B находятся на стартовой стороне и должны пересечься последней парой. Это дает нам B+A+D+B+B = 2+1+8+2+2 = 15,
 Каждый последующий запуск отделяется от других запусков хотя бы одним пустым пространством. Головоломка завершена, когда все числа были удовлетворены. Основным методом решения этих головоломок является процесс исключения. Если головоломка составлена правильно, никаких догадок не требуется.
Каждый последующий запуск отделяется от других запусков хотя бы одним пустым пространством. Головоломка завершена, когда все числа были удовлетворены. Основным методом решения этих головоломок является процесс исключения. Если головоломка составлена правильно, никаких догадок не требуется.



 Каждый открывает свой конверт и проверяет свое число, не видя других чисел.
Каждый открывает свой конверт и проверяет свое число, не видя других чисел. .. я знаю… что ты собирался это сказать!
.. я знаю… что ты собирался это сказать! \text{rd}3-е предположение слишком мало, вы вышли.
\text{rd}3-е предположение слишком мало, вы вышли. org/wiki/логические-пазлы/
org/wiki/логические-пазлы/ 25 — это
25 — это  Как вы можете отмерить 4 литра воды, используя 3-литровые и 5-литровые бутылки???
Как вы можете отмерить 4 литра воды, используя 3-литровые и 5-литровые бутылки??? Теперь у вас есть 4 литра в 5-литровой бутыли. Вот и все.
Теперь у вас есть 4 литра в 5-литровой бутыли. Вот и все. 30 ?????
30 ?????
