Нахождение НОД по алгоритму Евклида и с помощью разложения на простые множители
Рассмотрим два основных метода нахождения НОД двумя основными способами: с использованием алгоритма Евклида и путем разложения на простые множители. Применим оба метода для двух, трех и большего количества чисел.
Алгоритм Евклида для нахождения НОД
Алгоритм Евклида позволяет с легкостью вычислить наибольший общий делитель для двух положительных чисел. Формулировки и доказательство алгоритма Евклида мы привели в разделе «Наибольший общий делитель: определитель, примеры».
Суть алгоритма заключается в том, чтобы последовательно проводить деление с остатком, в ходе которого получается ряд равенств вида:
a=b·q1+r1, 0<r1<bb=r1·q2+r2, 0<r2<r1r1=r2·q3+r3, 0<r3<r2r2=r3·q4+r4, 0<r4<r3⋮rk-2=rk-1·qk+rk, 0<rk<rk-1rk-1=rk·qk+1
Мы можем закончить деление тогда, когда rk+1=0, при этом rk=НОД(a, b).
Найдите наибольший общий делитель чисел 64 и 48.
Решение
Введем обозначения: a=64, b=48.
На основе алгоритма Евклида проведем деление 64 на 48.
Получим 1 и остаток 16. Получается, что q1=1, r1=16.
Вторым шагом разделим
Ответ: НОД(64, 48)=16.
Пример 2Чему равен НОД чисел 111 и 432?
Решение
Делим 432 на 111. Согласно алгоритму Евклида получаем цепочку равенств 432=111·3+99, 111=99·1+12, 99=12·8+3, 12=3·4.
Таким образом, наибольший общий делитель чисел 111 и 432 – это 3.
Ответ: НОД(111, 432)=3.
Пример 3Найдите наибольший общий делитель чисел 661 и 113.
Решение
Проведем последовательно деление чисел и получим НОД(661, 113)=1. Это значит, что 661 и 113 – это взаимно простые числа. Мы могли выяснить это до начала вычислений, если бы обратились к таблице простых чисел.
Это значит, что 661 и 113 – это взаимно простые числа. Мы могли выяснить это до начала вычислений, если бы обратились к таблице простых чисел.
Ответ: НОД(661, 113)=1.
Нахождение НОД с помощью разложения чисел на простые множители
Для того, чтобы найти наибольший общий делитель двух чисел методом разложения на множители, необходимо перемножить все простые множители, которые получаются при разложении этих двух чисел и являются для них общими.
Пример 4Если мы разложим числа 220 и 600 на простые множители, то получим два произведения: 220=2·2·5·11 и 600=2·2·2·3·5·5. Общими в этих двух произведениях будут множители 2,2 и 5. Это значит, что НОД(220, 600)=2·2·5=20.
Пример 5Найдите наибольший общий делитель чисел 72 и 96.
Решение
Найдем все простые множители чисел 72 и 96:
72361893122233
96482412631222223
Общими для двух чисел простые множители: 2, 2, 2 и 3. Это значит, что НОД(72, 96)=2·2·2·3=24.
Это значит, что НОД(72, 96)=2·2·2·3=24.
Ответ: НОД(72, 96)=24.
Правило нахождения наибольшего общего делителя двух чисел основано на свойствах наибольшего общего делителя, согласно которому НОД(m·a1, m·b1)=m·НОД(a1, b1), где m– любое целое положительное число.
Нахождение НОД трех и большего количества чисел
Независимо от количества чисел, для которых нам нужно найти НОД, мы будем действовать по одному и тому же алгоритму, который заключается в последовательном нахождении НОД двух чисел. Основан этот алгоритм на применении следующей теоремы: НОД нескольких чисел a1, a2, …, ak равен числу dk, которое находится при последовательном вычислении НОД(a1, a2)=d2, НОД(d2, a3)=d3, НОД(d3, a4)=d4, …, НОД(dk-1, ak)=dk.
Пример 6Найдите наибольший общий делитель четырех чисел 78, 294, 570 и 36.
Решение
Введем обозначения: a1=78, a2=294, a3=570, a4=36.
Начнем с того, что найдем НОД чисел 78 и 294: d2=НОД(78, 294)=6.
Теперь приступим к нахождению d3=НОД(d2, a3)=НОД(6, 570). Согласно алгоритму Евклида 570=6·95. Это значит, что d3=НОД(6, 570)=6.
Найдем d4=НОД(d3, a4)=НОД(6, 36). 36 делится на 6 без остатка. Это позволяет нам получить d4=НОД(6, 36)=6.
d4=6, то есть, НОД(78, 294, 570, 36)=6.
Ответ: НОД(78, 294, 570, 36)=6.
А теперь давайте рассмотрим еще один способ вычисления НОД для тех и большего количества чисел. Мы можем найти НОД, перемножив все общие простые множители чисел.
Пример 7Вычислите НОД чисел 78, 294, 570 и 36.
Решение
Произведем разложение данных чисел на простые множители: 78=2·3·13, 294=2·3·7·7, 570=2·3·5·19, 36=2·2·3·3.
Для всех четырех чисел общими простыми множителями будут числа 2 и 3.
Получается, что НОД(78, 294, 570, 36)=2·3=6.
Ответ: НОД(78, 294, 570, 36)=6.
Нахождение НОД отрицательных чисел
Если нам приходится иметь дело с отрицательными числами, то для нахождения наибольшего общего делителя мы можем воспользоваться модулями этих чисел. Мы можем так поступить, зная свойство чисел с противоположными знаками: числа n и -n имеют одинаковые делители.
Мы можем так поступить, зная свойство чисел с противоположными знаками: числа n и -n имеют одинаковые делители.
Найдите НОД отрицательных целых чисел −231 и −140.
Решение
Для выполнения вычислений возьмем модули чисел, данных в условии. Это будут числа 231 и 140. Запишем это кратко: НОД(−231, −140)=НОД(231, 140). Теперь применим алгоритм Евклида для нахождения простых множителей двух чисел: 231=140·1+91; 140=91·1+49; 91=49·1+42; 49=42·1+7 и 42=7·6. Получаем, что НОД(231, 140)=7.
А так как НОД(−231, −140)=НОД(231, 140), то НОД чисел −231 и −140 равен 7.
Ответ: НОД(−231, −140)=7.
Пример 9Определите НОД трех чисел −585, 81 и −189.
Решение
Заменим отрицательные числа в приведенном перечне на их абсолютные величины, получим НОД(−585, 81, −189)=НОД(585, 81, 189). Затем разложим все данные числа на простые множители: 585=3·3·5·13, 81=3·3·3·3 и 189=3·3·3·7. Общими для трех чисел являются простые множители 3 и 3. Получается , что НОД(585, 81, 189)=НОД(−585, 81, −189)=9.
Общими для трех чисел являются простые множители 3 и 3. Получается , что НОД(585, 81, 189)=НОД(−585, 81, −189)=9.
Ответ: НОД(−585, 81, −189)=9.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
разлагать на множители — итальянский перевод
Разложение на множители | Fattorizzazione |
разложение на множители | Fattorizza |
Это называется разложением на множители. В результате получим простые множители. | In questo caso, moltiplicate semplicemente ciascun fattore una volta per fare 30. |
Так что мы разложем это на множители. | Quindi quello che faremo e’ scomporlo in fattori. |
Давайте рассмотрим множители 15. | Il cui prodotto è 15? Quindi se semplicemente scomponiamo 15 abbiamo 1 e 15. |
То есть, мы можем разложить это на множители. | Questo si fattorizza in questo piu’ questo. |
Здесь мы видим наглядные примеры разложения многочленов на множители. | Ora possiamo usare questa identica proprieta’ abbiamo questo schema qualcosa al quadrato meno qualcosaltro al quadrato. |
Сможем ли мы разложить на простые множители этот корень. | La radice di 1080. |
Давайте вернёмся к первой задаче сложности разложения на простые множители. | Torniamo al punto precedente la difficoltà di fattorizzare numeri primi Torniamo al punto precedente |
Это показывает, что разложение на простые множители фундаментально сложная задача. | La fattorizzazione è un problema difficle |
Добро пожаловать в решение квадратных уравнений путем разложения на множители. | Benvenuto alla fattorizzazione di polinomi. |
Но всецело полагаться на стимулы означает морально разлагать профессиональную деятельность в обоих смыслах этого слова. | Ma affidarsi eccessivamente agli incentivi demoralizza l’attività professionale in due sensi della parola. |
В этом упражнении вам нужно разложить указанное число на простые множители. | In questo esercizio devi convertire un numero in frazione. |
В этом упражнении вам будет нужно разложить указанное число на множители. | In questo esercizio dei ridurre in fattori un numero dato. |
Конечно, это нужно разложить на множители и все это под корнем. | Quindi c 2 su 4 per tutto questo. E poi dobbiamo chiudere la radice quadrata. Fammi distribuire la c 2 4. |
Например, разложение на множители квадратного трёхчлена со старшим коэффициентом выше единицы. | Per esempio, fattorizzare un polinomio di secondo grado con il coefficiente del termine quadrato maggiore di uno. |
RSA основывается на двух вещах 1) Факте, что разложение на простые множители сложно выполнить. | Abbiamo conosciuto la codifica RSA e abbiamo appreso che dipende da due elementi 1) che la fattorizzazione di un numero primo è un problema difficile da risolvere |
Итак, вспомним, что любое число N имеет разложение на простые множители. Правильно? | Ogni N è fattorizzabile in numeri primi |
Применив некоторые усилия вы выясните, что 19×31 это разложение на простые множители. | Alfine troverete che la fattorizzazione di 589 è 19×31 |
Я просто разложил 168 на множители. b может быть равно минус 14. | Ho appena fattorizzato. Quindi b potrebbe essere uguale a meno 14. |
Множители числа 8 один, два, четыре и восемь. | I fattori di 8 sono 1, 2, 4, e 8. |
Таким образом это легко выполнить. Теперь сравним это с разложением на простые множители. | Si dice che è un’operazione ‘facile’ Ora confrontatela con la fattorizzazione |
Нам нужно разложить на множители трехчлен t в квадрате плюс 8t плюс 15. | Scomponiamo t al quadrato più 8t più 15 |
Целлюлоза это тип углеводов, образующийся в растениях, которые наш организм не способен разлагать. | La cellulosa è un tipo di carboidrato che si trova nelle piante e che il nostro corpo non è in grado di scomporre. |
Ага, похоже они хотят чтобы мы разложили на множители каждое из этих квадратных уравнений, и проверить, не сократятся ли какие нибудь множители. Давайте попытаемся сделать это. | Ci viene chiesto probabilmente di scomporre in fattori ognuno di questi numeri al quadrato e vedere se qualcuno di questi termini si annulla proviamo a farlo |
Ну давайте попытаемся разложить на множители верхнее и нижнее уравнения и посмотрим, что получится. | Quindi semplicemente proviamo a scomporre in fattori i numeri sopra e quelli sotto e vedere cosa succede |
Вы должны помнить из разложения многочленов на множители, что х² у² можно разложить на (х у)(х у). | E useremo questa cosa piu’ e piu’ volte. Ora se chiami ca 2 x e chiami tutta questa grossa cosa qui |
Затем она запросто вычисляет Фи(n), так как знает разложение n на простые множители. | Poi calcola Phi(n) 3016, cosa facile per chi conosca la fattorizzazione di ‘n’, che è 3016 |
Если вас попросят найти разложение на простые множители для 589, вы поймете, что задача кажется сложной. | Fattorizzare 589 è molto più difficile |
Так учатся раскладывать на множители и решать квадратные уравнения. Всё сделано зримо, с информативной обратной связью. | Qui gli studenti imparano a svolgere e risolvere equazioni di secondo grado, tutto visivamente e con feedback. |
Но единственные множители, между которыми разница один, это пять и шесть | Ma gli unici che hanno una differenza di uno sono 5 e 6. |
Очевидно, если множители равны нулю, то и все выражение равно 0. | Ovviamente se si può rendere uno di questi termini 0, si rende tutto ciò 0. |
Например, 77 раскладывается на простые множители 7 и 11. Так что Фи(77) это 6 10 60. | Ad esempio, la fattorizzazione di 77 è 7×11, quindi Phi di 77 è 6×10 60 |
Мы поставили цель найти в близлежащей реке Фрейзер бактерии, которые могут разлагать вредный пластификатор под названием фталат. | Eravamo intenzionate a trovare batteri nel fiume locale, il Fraser, che potessero decomporre un dannoso plastificante chiamato ftalato. |
В нашем случае 2, 3 и 5 это простые множители 30 ти. | 2 volte 3 volte 5 è la riduzione in fattori primi di 30. |
Итак, что такого особенного в разложении на простые множители, или в самих простых числах, что делает задачу трудной? | la difficoltà di fattorizzare numeri primi Cosa rende difficile risolvere questo problema ? Cosa rende difficile risolvere questo problema ? |
Его стойкость зависит от трудоемкости разложения на простые множители. | La sua forza è dovuta alla difficoltà della fattorizzazione dei numeri primi difficoltà che affonda le proprie radici nel mistero della distribuzione dei numeri primi |
Что от нас хотят в этой задаче, это сократить выражения разложить выражения на множители и затем сократить повторяющиеся. | Quindi, in sostanza vogliono che fattorizziamo e fattorizzarlo e renderlo come prodotto di fattori e poi annullare. |
2000 лет назад Эвклид показал, что каждое число единственным образом раскладывается на простые множители, которые можно считать секретным ключом. | Oltre 2000 anni fa Euclide mostrò che ogni numero è fattorizzabile in numeri primi in modo unico, una specie di chiave segreta |
Если вас попросят найти разложение на простые множители для 437 231, вы, возможно, сдадитесь и используете компьютер для помощи. | Se doveste trovare la fattorizzazione di 437.231 vi arrendereste e ricorrereste all’aiuto d’un computer |
Вот и все. Мы справились с заданием. В принципе нам можно было и не раскладывать на множители способом группировки. | In realtà non abbiamo |
Вот если бы мы говорили о переходе в Шаге 1, где мы раскладываем на множители, там используется дистрибутивное свойство… | Se siamo arrivati da questo passo a questo passo dove noi lo stavamo moltiplicando, può essere stato, perchè tu stai veramente facendo la proprietà distributiva ma io non voglio confonderti. |
Вместо того, чтобы ждать, пока этот мусор будет накапливаться, нужно найти способ, как можно разлагать пластики с помощью бактерий. | Invece di aspettare che i rifiuti si accumulino, cerchiamo un modo per disintegrarli con i batteri. |
Ну давайте подумаем, какие множители у тридцати. | Beh pensiamo semplicemente a tutti i fattori di 30. 1, 2, 3, 5, 6, 10, 15, 30. |
Эвклид понял, что можно перемножить эти простые множители определенное число раз, чтобы получить исходное число. | Pensatela come una conbinazione speciale. Non c’è altro modo di fare 30 con un altro gruppo di numeri primi moltiplicati tra loro. |
Факторы числа 231 — Найти простые факторизации/множители числа 231 33, 77, 231. Простые множители числа 231 равны 3 × 7 × 11, а его парные множители — (1, 231), (3, 77), (7, 33), (11, 21).
- Все коэффициенты 231: 1, 3, 7, 11, 21, 33, 77 и 231
- Отрицательные коэффициенты 231: -1, -3, -7, -11, -21, -33, -77 и -231
- Простые множители числа 231: 3, 7, 11
- Факторизация числа 231: 3 1 × 7 1 × 11 1
- Сумма коэффициентов 231: 384
1. | Какие множители числа 231? |
| 2. | Коэффициенты числа 231 с помощью простой факторизации |
| 3. | Коэффициенты 231 в парах |
| 4. | Часто задаваемые вопросы о факторах 231 |
Что такое множители числа 231?
Множители 231 — это пары тех чисел, произведения которых дают 231. Эти множители являются либо простыми, либо составными числами.
Как найти делители числа 231?
Чтобы найти делители числа 231, нам нужно найти список чисел, на которые число 231 делится без остатка.
- 231/231 = 1; следовательно, 231 — это множитель 231.
- 231/77 = 3; поэтому 77 является коэффициентом 231.
Точно так же мы можем найти и другие факторы. Следовательно, делители числа 231 равны 1, 3, 7, 11, 21, 33, 77, 231.
☛ Также проверьте:
- Коэффициенты 70 — Коэффициенты 70 равны 1, 2, 5, 7, 10, 14, 35, 70
- Коэффициенты 55 — Коэффициенты 55 равны 1, 5, 11, 55
- Множители 26 — Множители 26 равны 1, 2, 13, 26
- Коэффициенты 100 — Коэффициенты 100 равны 1, 2, 4, 5, 10, 20, 25, 50, 100
- Коэффициенты 15 — Коэффициенты 15 равны 1, 3, 5, 15
Коэффициенты числа 231 с помощью простой факторизации
Число 231 составное, поэтому оно имеет простые делители. Теперь давайте научимся вычислять простые делители числа 231.
Первый шаг — разделить число 231 на наименьший простой множитель, здесь это 3. Продолжаем делить, пока не получится ненулевой остаток.
Теперь давайте научимся вычислять простые делители числа 231.
Первый шаг — разделить число 231 на наименьший простой множитель, здесь это 3. Продолжаем делить, пока не получится ненулевой остаток.
- 231 ÷ 3 = 77
Дальнейшее деление 77 на 3 дает ненулевой остаток. Поэтому мы останавливаем процесс и продолжаем делить число 77 на следующий наименьший простой множитель. В конце концов мы останавливаемся, если следующего простого множителя не существует или когда мы не можем дальше делить.
Итак, разложение числа 231 на простые множители можно записать как 3 1 × 7 1 × 11 1 , где 3, 7, 11 — простые числа.
Парные множители числа 231
Парные множители числа 231 — это пары чисел, которые при умножении дают произведение 231. Множители числа 231 в парах:
- 1 × 231 = (1, 231)
- 3 × 77 = (3, 77)
- 7 × 33 = (7, 33)
- 11 × 21 = (11, 21)
Отрицательные парные множители числа 231:
- -1 × -231 = (-1, -231)
- -3 × -77 = (-3, -77)
- -7 × -33 = (-7, -33)
- -11 × -21 = (-11, -21)
ПРИМЕЧАНИЕ: Если (a, b) является парным множителем числа, то (b, a) также является парным множителем этого числа.
Коэффициенты 231 решенного примера
Пример 1: Сколько множителей существует для числа 231?
Решение:
Делители числа 231 равны 1, 3, 7, 11, 21, 33, 77, 231. Следовательно, число 231 имеет 8 делителей.
Пример 2. Найдите НОК и наибольший общий делитель (НОД) чисел 231 и 102.
Решение:
Делители 102 равны 1, 2, 3, 6, 17, 34, 51, 102.
Следовательно, LCM 231 и 102 равен 7854, а наибольший общий делитель (GCF) 231 и 102 равен 3.
Пример 3. Найдите, являются ли 1, 3, 7, 51 и 77 делителями 231.
Решение:
При делении 231 на 51 остается остаток. Следовательно, число 51 не является делителем 231. Все числа, кроме 51, являются делителями 231.
Пример 4. Найдите произведение всех простых множителей числа 231.
Решение:
Поскольку простые делители числа 231 равны 3, 7, 11.
 Следовательно, произведение простых делителей = 3 × 7 × 11 = 231.
Следовательно, произведение простых делителей = 3 × 7 × 11 = 231.
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Забронировать бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о множителях числа 231
Что такое множители числа 231?
Множители числа 231 равны 1, 3, 7, 11, 21, 33, 77, 231, а его отрицательные множители равны -1, -3, -7, -11, -21, -33, -77, -231 .
Какова сумма множителей числа 231?
Сумма всех делителей числа 231 = (3 1 + 1 — 1)/(3 — 1) × (7 1 + 1 — 1)/(7 — 1) × (11 1 + 1 9)0023 — 1)/(11 — 1) = 384
Какие числа являются парными множителями числа 231?
Парные множители числа 231: (1, 231), (3, 77), (7, 33), (11, 21).
Какой наибольший общий делитель чисел 231 и 31?
Делители числа 231 равны 1, 3, 7, 11, 21, 33, 77, 231, а делители числа 31 равны 1, 31. являются взаимно простыми.
Следовательно, наибольший общий делитель (GCF) чисел 231 и 31 равен 1.
93-8Найдите разложение числа 231 на простые множители, используя показатели степени
| Введите целое число, которое вы хотите получить, его простые делители: Пример: 2, 3, 4, 11, 10225 и т.  д. д. |
Результат простой факторизации:Число 231 является составным числом, поэтому его можно разложить на множители. Другими словами, 231 можно разделить на 1, само по себе и по крайней мере на 3, 7 и 11. Составное число — это натуральное число, имеющее хотя бы один положительный делитель, отличный от единицы или самого числа. Другими словами, составное число — это любое целое число, большее единицы, которое не является простым числом. Разложение числа 231 на простые множители = 3•7•11. Простые делители числа 231 равны 3, 7 и 11. Факторное дерево или простое разложение для 231Поскольку 231 является составным числом, мы можем нарисовать его факторное дерево: |
Вот ответ на такие вопросы, как: Найдите разложение числа 231 на простые множители с использованием показателей степени или является ли 231 простым или составным числом?
Используйте приведенный выше инструмент факторизации простых чисел, чтобы определить, является ли данное число простым или составным, и в этом случае вычислите его простые множители. См. также на этой веб-странице диаграмму факторизации простых чисел со всеми простыми числами от 1 до 1000.
См. также на этой веб-странице диаграмму факторизации простых чисел со всеми простыми числами от 1 до 1000.
Что такое первичная факторизация?
Определение простой факторизации
Простой факторизации — это разложение составного числа на произведение простых множителей, которые при умножении воссоздают исходное число. Факторы по определению — это числа, которые умножаются, чтобы создать другое число. Простое число — это целое число больше единицы, которое делится только на единицу и само на себя. Например, единственные делители 7 — это 1 и 7, поэтому 7 — простое число, а число 72 имеет делители, полученные из 2·9.0022 3 •3 2 подобно 2, 3, 4, 6, 8, 12, 24 … и самому 72, что делает 72 не простым числом. Обратите внимание, что единственными «простыми» делителями числа 72 являются 2 и 3, которые являются простыми числами.
Пример 1 простой факторизации
Давайте найдем простую факторизацию числа 72.
Решение 1
Начните с наименьшего простого числа, которое делится на 72, в данном случае 2. Мы можем записать 72 как:
Мы можем записать 72 как:
72 = 2 x 36
Теперь найдите наименьшее простое число, которое делится на 36. Снова мы можем использовать 2 и записать 36 как 2 х 18, чтобы дать.
72 = 2 x 2 x 18
18 также делится на 2 (18 = 2 x 9), поэтому мы имеем:
72 = 2 x 2 x 2 x 9
9 делится на 3 (9 = 3 x 3), поэтому у нас есть:
72 = 2 x 2 x 2 x 3 x 3
2, 2, 2, 3 и 3 — все простые числа, поэтому у нас есть ответ.
Короче говоря, решение можно записать так:
72 = 2 x 36
72 = 2 x 2 x 18
72 = 2 x 2 x 2 x 9
72 = 2 x 2 x 2 x 3 x 3
72 = 2 3 x 3 2 (экспоненциальная форма простой факторизации)
Раствор 2
Использование дерева факторов:
- Процедура:
- Найти 2 множителя числа;
- Посмотрите на 2 множителя и определите, не является ли хотя бы один из них простым;
- Если это не простой множитель это;
- Повторяйте этот процесс, пока все делители не станут простыми.

Посмотрите, как разложить число 72 на множители:
| 18 / \ 3 3 | 72 не простое —> разделить на 2 36 не простое —> разделить на 2 18 не простое —> разделить на 2 9 не простое —> разделить на 3 3 и 3 простые —> стоп |
Умножив левые числа и крайнее правое число последней строки (делители), мы получим
72 = 2 x 2 x 2 x 3 x 3
72 = 2 3 x 3 2 (экспоненциальная форма простой факторизации)
Обратите внимание, что эти делители являются простыми множителями. Их также называют листьями факторного дерева.
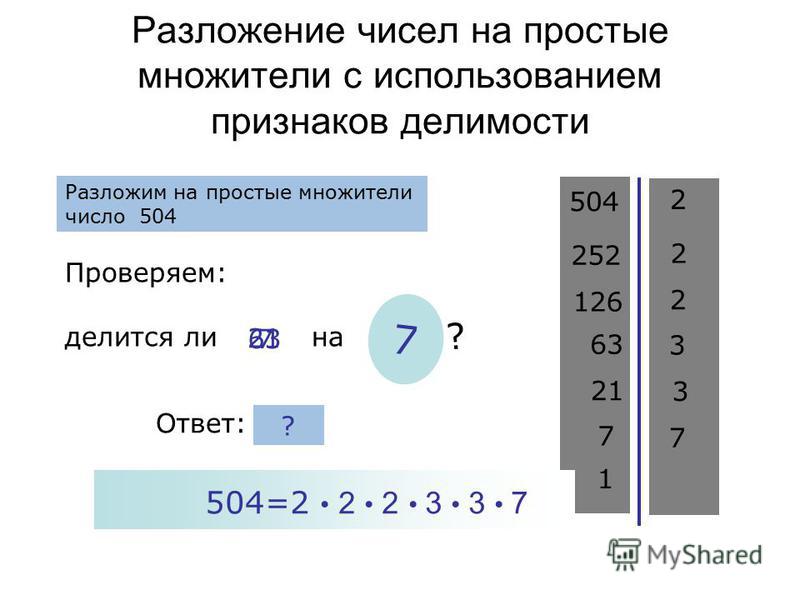
Пример факторизации простых чисел 2
Посмотрите, как разложить число 588 на множители:
| 588 /\ 2 294 /\ 2 147 /\ 3 49 /\ 7 7 | 588 не простое —> разделить на 2 294 не простое —> разделить на 2 147 не простое —> разделить на 3 49 не простое —> разделить на 7 7 и 7 простые —> стоп |
Взяв левые числа и крайнее правое число последней строки (делители), умножив их, мы получим
588 = 2 x 2 x 3 x 7 x 7
588 = 2 2 x 3 x 7 2 (экспоненциальная форма простой факторизации)
Таблица факторизации простых чисел 1-1000
| n | Prime Factorization | |||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 = | 2 | |||||||||||||||||||||||||||||||
| 3 = | 3 | |||||||||||||||||||||||||||||||
| 4 = | 2•2 | |||||||||||||||||||||||||||||||
| 5 = | 5 | |||||||||||||||||||||||||||||||
| 6 = | 2•3 | |||||||||||||||||||||||||||||||
| 7 = | 7 | |||||||||||||||||||||||||||||||
| 8 = | 2•2•2 | |||||||||||||||||||||||||||||||
| 9 = | 3•3 | |||||||||||||||||||||||||||||||
| 10 = | 2 • 5 | |||||||||||||||||||||||||||||||
. •7 •7 | ||||||||||||||||||||||||||||||||
| 15 = | 3•5 | |||||||||||||||||||||||||||||||
| 16 = | 2•2•2•2 | |||||||||||||||||||||||||||||||
| 17 = | 17 | |||||||||||||||||||||||||||||||
| 18 = | 2•3•3 | |||||||||||||||||||||||||||||||
| 19 = | 19 | |||||||||||||||||||||||||||||||
| 20 = | 2•2•5 | |||||||||||||||||||||||||||||||
| 21 = | 3•7 | |||||||||||||||||||||||||||||||
| 22 = | 2•11 | |||||||||||||||||||||||||||||||
| 23 = | 23 | |||||||||||||||||||||||||||||||
| 24 = | 2•2•2•3 | |||||||||||||||||||||||||||||||
| 25 = | 5•5 | |||||||||||||||||||||||||||||||
| 26 = | 2•13 | |||||||||||||||||||||||||||||||
| 27 = | 3•3•3 | |||||||||||||||||||||||||||||||
| 28 = | 2•2•7 | |||||||||||||||||||||||||||||||
| 29 = | 29 | |||||||||||||||||||||||||||||||
| 30 = | 2•3•5 | |||||||||||||||||||||||||||||||
| 31 = | 31 | |||||||||||||||||||||||||||||||
| 32 = | 2•2•2•2•2 | |||||||||||||||||||||||||||||||
| 33 = | 3•11 | |||||||||||||||||||||||||||||||
| 34 = | 2 • 17 | |||||||||||||||||||||||||||||||
| 35 = | 5 • 7 | |||||||||||||||||||||||||||||||
| 36 = | 2 • 2 • 3 • 3 | |||||||||||||||||||||||||||||||
| 37 = | 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 3 | |||||||||||||||||||||||||||||||
37. | 2•19 | |||||||||||||||||||||||||||||||
| 39 = | 3•13 | |||||||||||||||||||||||||||||||
| 40 = | 2•2•2•5 | |||||||||||||||||||||||||||||||
| 41 = | 41 | |||||||||||||||||||||||||||||||
| 42 = | 2•3•7 | |||||||||||||||||||||||||||||||
| 43 = | 43 | |||||||||||||||||||||||||||||||
| 44 = | 2•2•11 | |||||||||||||||||||||||||||||||
| 45 = | 3•3•5 | |||||||||||||||||||||||||||||||
| 46 = | 2•23 | |||||||||||||||||||||||||||||||
| 47 = | 47 | |||||||||||||||||||||||||||||||
| 48 = | 2•2 •2•2•3 | |||||||||||||||||||||||||||||||
| 49 = | 7•7 | |||||||||||||||||||||||||||||||
| 50 = | 2•5•5 | |||||||||||||||||||||||||||||||
| 51 = | 3•17 | |||||||||||||||||||||||||||||||
| 52 = | 2•2•13 | |||||||||||||||||||||||||||||||
| 53 = | 53 | |||||||||||||||||||||||||||||||
| 54 = | 2•3•3•3 | |||||||||||||||||||||||||||||||
| 55 = | 5•11 | |||||||||||||||||||||||||||||||
| 56 = | 2•2•2•7 | |||||||||||||||||||||||||||||||
| 57 = | 3•19 | |||||||||||||||||||||||||||||||
| 58 = | 2•29 | |||||||||||||||||||||||||||||||
| 59 = | 59 | |||||||||||||||||||||||||||||||
| 60 = | 2 • 2 • 3 • 5 | |||||||||||||||||||||||||||||||
| 61 = | 61 | |||||||||||||||||||||||||||||||
| 62 = | 2 • 31 | |||||||||||||||||||||||||||||||
| 63 = | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 70037 3 70037 3 70037 3 70037 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | ||||||||||||
. = = | 2 • 2 • 2 • 2 • 2 • 2 | |||||||||||||||||||||||||||||||
| 65 = | 5 • 13 | |||||||||||||||||||||||||||||||
| 66 = | 2 • 3 • 11 | |||||||||||||||||||||||||||||||
| 67 = | 7777777778 | |||||||||||||||||||||||||||||||
| 77777778 | ||||||||||||||||||||||||||||||||
| . | 68 = | 2•2•17 | ||||||||||||||||||||||||||||||
| 69 = | 3•23 | |||||||||||||||||||||||||||||||
| 70 = | 2•5•7 | |||||||||||||||||||||||||||||||
| 71 = | 71 | |||||||||||||||||||||||||||||||
| 72 = | 2•2•2•3•3 | |||||||||||||||||||||||||||||||
| 73 = | 73 | |||||||||||||||||||||||||||||||
| 74 = | 2•37 | |||||||||||||||||||||||||||||||
| 75 = | 3•5•5 | |||||||||||||||||||||||||||||||
| 76 = | 2•2•19 | |||||||||||||||||||||||||||||||
| 77 = | 7•11 | |||||||||||||||||||||||||||||||
| 78 = | 2•3•13 | |||||||||||||||||||||||||||||||
| 79 = | 79 | |||||||||||||||||||||||||||||||
| 80 = | 2 • 2 • 2 • 2 • 5 | |||||||||||||||||||||||||||||||
| 81 = | 3 • 3 • 3 • 3 | |||||||||||||||||||||||||||||||
| 82 = | 2. | |||||||||||||||||||||||||||||||
| 84 = | 2•2•3•7 | |||||||||||||||||||||||||||||||
| 85 = | 5•17 | |||||||||||||||||||||||||||||||
| 86 = | 2•43 | |||||||||||||||||||||||||||||||
| 87 = | 3•29 | |||||||||||||||||||||||||||||||
| 88 = | 2•2•2•11 | |||||||||||||||||||||||||||||||
| 89 = | 89 | |||||||||||||||||||||||||||||||
| 90 = | 2•3•3•5 | |||||||||||||||||||||||||||||||
| 91 = | 7•13 | |||||||||||||||||||||||||||||||
| 92 = | 2•2•23 | |||||||||||||||||||||||||||||||
| 93 = | 3•31 | |||||||||||||||||||||||||||||||
| 94 = | 2 • 47 | |||||||||||||||||||||||||||||||
| 95 = | 5 • 19 | |||||||||||||||||||||||||||||||
| 96 = | 2 • 2 • 2 • 2 • 3 | |||||||||||||||||||||||||||||||
| 2 • 2 • 2 • 2 | ||||||||||||||||||||||||||||||||
| 7 | 7777777777777777777777777777777777777777777777777778 | 2 | ||||||||||||||||||||||||||||||
| 98 = | 2•7•7 | |||||||||||||||||||||||||||||||
| 99 = | 3•3•11 | |||||||||||||||||||||||||||||||
| 100 = | 2•2•5•5 | |||||||||||||||||||||||||||||||
| 101 = | 101 | |||||||||||||||||||||||||||||||
| 102 = | 2•3•17 | |||||||||||||||||||||||||||||||
| 103 = | 103 | |||||||||||||||||||||||||||||||
| 104 = | 2•2•2•13 | |||||||||||||||||||||||||||||||
| 105 = | 3•5•7 | |||||||||||||||||||||||||||||||
| 106 = | 2•53 | |||||||||||||||||||||||||||||||
| 107 = | 107 | |||||||||||||||||||||||||||||||
| 108 = | 2•2•3•3•3 | |||||||||||||||||||||||||||||||
| 109 = | 109 | |||||||||||||||||||||||||||||||
| 110 = | 2 • 5 • 11 | |||||||||||||||||||||||||||||||
| 111 = | 3 • 37 | |||||||||||||||||||||||||||||||
| 112 = | 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • | 112 = | 2 • 2 • 2 • | |||||||||||||||||||||||||||||
| 113 | ||||||||||||||||||||||||||||||||
| 114 = | 2•3•19 | |||||||||||||||||||||||||||||||
| 115 = | 5•23 | |||||||||||||||||||||||||||||||
| 116 = | 2•2•29 | |||||||||||||||||||||||||||||||
| 117 = | 3• 3•13 | |||||||||||||||||||||||||||||||
| 118 = | 2•59 | |||||||||||||||||||||||||||||||
| 119 = | 7•17 | |||||||||||||||||||||||||||||||
| 120 = | 2•2•2•3•5 | |||||||||||||||||||||||||||||||
| 121 = | 11•11 | |||||||||||||||||||||||||||||||
| 122 = | 2•61 | |||||||||||||||||||||||||||||||
| 123 = | 3 • 41 | |||||||||||||||||||||||||||||||
| . | ||||||||||||||||||||||||||||||||
| 127 = | 127 | |||||||||||||||||||||||||||||||
| 128 = | 2•2•2•2•2•2•2 | |||||||||||||||||||||||||||||||
| 129 = | 3•43 | |||||||||||||||||||||||||||||||
| 130 = | 2•5•13 | |||||||||||||||||||||||||||||||
| 131 = | 131 | |||||||||||||||||||||||||||||||
| 132 = | 2•2•3•11 | |||||||||||||||||||||||||||||||
| 133 = | 7•19 | |||||||||||||||||||||||||||||||
| 134 = | 2•67 | |||||||||||||||||||||||||||||||
| 135 = | 3•3•3•5 | |||||||||||||||||||||||||||||||
| 136 = | 2•2•2•17 | |||||||||||||||||||||||||||||||
| 137 = | 137 | |||||||||||||||||||||||||||||||
| 138 = | 2•3•23 | |||||||||||||||||||||||||||||||
| 139 = | 139 | |||||||||||||||||||||||||||||||
| 140 = | 2•2•5•7 | |||||||||||||||||||||||||||||||
| 141 = | 3•47 | |||||||||||||||||||||||||||||||
| 142 = | 2 • 71 | |||||||||||||||||||||||||||||||
| 143 = | 11 • 13 | |||||||||||||||||||||||||||||||
| 144 = | 2 • 2 • 2 • 3 • 3 | |||||||||||||||||||||||||||||||
| 145 = | 5 | |||||||||||||||||||||||||||||||
. | 2•73 | |||||||||||||||||||||||||||||||
| 147 = | 3•7•7 | |||||||||||||||||||||||||||||||
| 148 = | 2 • 2 • 37 | |||||||||||||||||||||||||||||||
| 149 = | 149 | |||||||||||||||||||||||||||||||
| 150 = | 2 • 3 • 5 | |||||||||||||||||||||||||||||||
| 151137 2 • 5 • 5 | ||||||||||||||||||||||||||||||||
| 151 151 = | = | = | = | = | = | = | = | = | = | = | = | = | = | = | = | = | = | = | = | = | = | = | . | 2 • 2 • 2 • 19 | ||||||||
| 153 = | 3 • 3 • 17 | |||||||||||||||||||||||||||||||
| 154 = | 2 • 7 • 11 | |||||||||||||||||||||||||||||||
| 155 = | 57 57 57 57 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 577 5 7 | |||||||||||||||||||||||||||||||
| . 156 = | 2•2•3•13 | |||||||||||||||||||||||||||||||
| 157 = | 157 | |||||||||||||||||||||||||||||||
| 158 = | 2 • 79 | |||||||||||||||||||||||||||||||
| 159 = | 3 • 53 | |||||||||||||||||||||||||||||||
| 160 = | 2 • 2 • 2 • 2 • 5 | |||||||||||||||||||||||||||||||
| 2 • 2 • 2 • 2 • 5 | ||||||||||||||||||||||||||||||||
| 2 • 2 • 2 • 2 • 5 | ||||||||||||||||||||||||||||||||
| 2 • 2 • 2 • 2 • 5 | 9036 | 2. • 23 • 23 | ||||||||||||||||||||||||||||||
| 162 = | 2 • 3 • 3 • 3 • 3 | |||||||||||||||||||||||||||||||
| 163 = | 163 | |||||||||||||||||||||||||||||||
| 164 = | 2 • 2 • 410038 | 9136 3 | ||||||||||||||||||||||||||||||
| 2 | ||||||||||||||||||||||||||||||||
| . •5•11 | ||||||||||||||||||||||||||||||||
| 166 = | 2•83 | |||||||||||||||||||||||||||||||
| 167 = | 167 | |||||||||||||||||||||||||||||||
| 168 = | 2•2•2•3•7 | |||||||||||||||||||||||||||||||
| 169 = | 13•13 | |||||||||||||||||||||||||||||||
| 170 = | 2•5•17 | |||||||||||||||||||||||||||||||
| 171 = | 3•3•19 | |||||||||||||||||||||||||||||||
| 172 = | 2•2•43 | |||||||||||||||||||||||||||||||
| 173 = | 173 | |||||||||||||||||||||||||||||||
| 174 = | 2•3•29 | |||||||||||||||||||||||||||||||
| 175 = | 5•5•7 | |||||||||||||||||||||||||||||||
| 176 = | 2•2•2•2•11 | |||||||||||||||||||||||||||||||
| 177 = | 3•59 | |||||||||||||||||||||||||||||||
| 178 = | 2•89 | |||||||||||||||||||||||||||||||
| 179 = | 179 | |||||||||||||||||||||||||||||||
| 180 = | 2•2•3•3•5 | |||||||||||||||||||||||||||||||
| 181 = | 181 | |||||||||||||||||||||||||||||||
| 182 = | 2•7•13 | |||||||||||||||||||||||||||||||
| 183 = | 3•61 | |||||||||||||||||||||||||||||||
| 184 = | 2•2•2•23 | |||||||||||||||||||||||||||||||
| 185 = | 5•37 | |||||||||||||||||||||||||||||||
| 186 = | 2•3•31 | |||||||||||||||||||||||||||||||
| 187 = | 11•17 | |||||||||||||||||||||||||||||||
| 188 = | 2•2•47 | |||||||||||||||||||||||||||||||
| 189 = | 3•3•3•7 | |||||||||||||||||||||||||||||||
| 190 = | 2•5•19 | |||||||||||||||||||||||||||||||
| 191 = | 191 | |||||||||||||||||||||||||||||||
| 192 = | 2•2•2•2•2•2•3 | |||||||||||||||||||||||||||||||
| 193 = | 193 | |||||||||||||||||||||||||||||||
| 194 = | 2•97 | |||||||||||||||||||||||||||||||
| 195 = | 3•5•13 | |||||||||||||||||||||||||||||||
| 196 = | 2•2•7•7 | |||||||||||||||||||||||||||||||
| 197 = | 197 | |||||||||||||||||||||||||||||||
| 198 = | 2•3•3•11 | |||||||||||||||||||||||||||||||
| 199 = | 199 | |||||||||||||||||||||||||||||||
| 200 = | 2•2•2•5•5 | |||||||||||||||||||||||||||||||
| 201 = | 3•67 | |||||||||||||||||||||||||||||||
| 202 = | 2•101 | |||||||||||||||||||||||||||||||
| 203 = | 7•29 | |||||||||||||||||||||||||||||||
| 204 = | 2•2•3•17 | |||||||||||||||||||||||||||||||
| 205 = | 5•41 | |||||||||||||||||||||||||||||||
| 206 = | 2 • 103 | |||||||||||||||||||||||||||||||
. • 19 • 19 | ||||||||||||||||||||||||||||||||
| 210 = | 2 • 3 • 5 • 7 | |||||||||||||||||||||||||||||||
| 211 = | 211 | |||||||||||||||||||||||||||||||
| 212 = | 2 • 2 • 53978 | 2 • 2 • 53 | 37 212 =2. | |||||||||||||||||||||||||||||
| 214 = | 2•107 | |||||||||||||||||||||||||||||||
| 215 = | 5 • 43 | |||||||||||||||||||||||||||||||
| 216 = | 2 • 2 • 2 • 3 • 3 • 3 | |||||||||||||||||||||||||||||||
| 217 = | 7 • 31 | |||||||||||||||||||||||||||||||
| 218 = | 2 | 2 2 2 2 2 2 2 2 2 2 2 2 2 2|||||||||||||||||||||||||||||||
| 218 = | 2 | |||||||||||||||||||||||||||||||
| . 219 = | 3•73 | |||||||||||||||||||||||||||||||
| 220 = | 2•2•5•11 | |||||||||||||||||||||||||||||||
| 221 = | 13•17 | |||||||||||||||||||||||||||||||
| 222 = | 2•3•37 | |||||||||||||||||||||||||||||||
| 223 = | 223 | |||||||||||||||||||||||||||||||
| 224 = | 2•2•2•2•2•7 | |||||||||||||||||||||||||||||||
| 225 = | 3•3•5•5 | |||||||||||||||||||||||||||||||
| 226 = | 2•113 | |||||||||||||||||||||||||||||||
| 227 = | 227 | |||||||||||||||||||||||||||||||
| 228 = | 2•2•3•19 | |||||||||||||||||||||||||||||||
| 229 = | 229 | |||||||||||||||||||||||||||||||
| 230 = | 2•5•23 | |||||||||||||||||||||||||||||||
| 231 = | 3•7•11 | |||||||||||||||||||||||||||||||
| 232 = | 2•2•2•29 | |||||||||||||||||||||||||||||||
| 233 = | 233 | |||||||||||||||||||||||||||||||
| 234 = | 2•3•3•13 | |||||||||||||||||||||||||||||||
| 235 = | 5•47 | |||||||||||||||||||||||||||||||
| 236 = | 2•2•59 | |||||||||||||||||||||||||||||||
| 237 = | 3•79 | |||||||||||||||||||||||||||||||
| 238 = | 2•7•17 | |||||||||||||||||||||||||||||||
| 239 = | 239 | |||||||||||||||||||||||||||||||
| 240 = | 2•2•2•2•3•5 | |||||||||||||||||||||||||||||||
| 241 = | 241 | |||||||||||||||||||||||||||||||
| 242 = | 2•11•11 | |||||||||||||||||||||||||||||||
| 243 = | 3•3•3•3•3 | |||||||||||||||||||||||||||||||
| 244 = | 2 • 2 • 61 | |||||||||||||||||||||||||||||||
| 245 = | 5 • 7 • 7 | |||||||||||||||||||||||||||||||
| 246 = | 2 • 3 • 41 | |||||||||||||||||||||||||||||||
| 7 | 2 • 3 • 41 | |||||||||||||||||||||||||||||||
7777 24. | = = = = = = = = = = = = = = = = =.||||||||||||||||||||||||||||||||
| 248 = | 2 • 2 • 2 • 31 | |||||||||||||||||||||||||||||||
| 249 = | 3 • 83 | |||||||||||||||||||||||||||||||
| 250 = | 2 • 5 • 5 |
| n | Простое число Факторизация | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 251 = | 251 | ||||||||||||
| 252 = | 2 • 2 • 3 • 3 • 7 | ||||||||||||
| 253 = | 11 • 23 | ||||||||||||
| 254 = | 2 • 127 | ||||||||||||
| 254 = | 2 • 127 | ||||||||||||
| 7777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777. | |||||||||||||
| 254 = | . •17 | ||||||||||||
| 256 = | 2•2•2•2•2•2•2•2 | ||||||||||||
| 257 = | 257 | ||||||||||||
| 258 = | 2•3•43 | ||||||||||||
| 259 = | 7•37 | ||||||||||||
| 260 = | 2•2•5•13 | ||||||||||||
| 261 = | 3 • 3 • 29 | ||||||||||||
| 262 = | 2 • 131 | ||||||||||||
| 263 = | 263 | ||||||||||||
| 264 = | 2.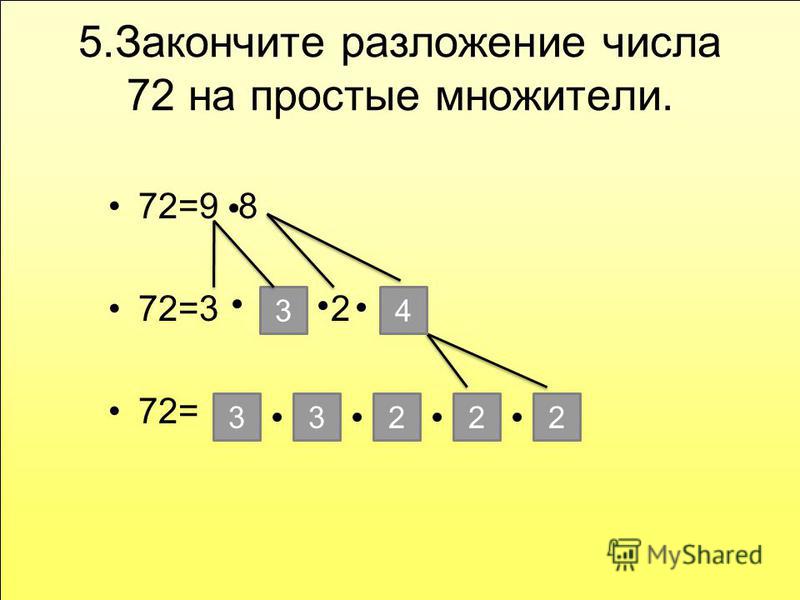 2,9003. 2,9003 2. 2,9003 2 2 2637 2. 2 2,9003. 2,9003 2. 2,9003 2 2 2637 2. 2 | 2,0037 2 2 2637 2 | .265 = | 5•53 | |||||||||
| 266 = | 2•7•19 | ||||||||||||
| 267 = | 3•89 | ||||||||||||
| 268 = | 2•2•67 | ||||||||||||
| 269 = | 269 | ||||||||||||
| 270 = | 2•3•3•3•5 | ||||||||||||
| 271 = | 271 | ||||||||||||
| 272 = | 2•2•2•2•17 | ||||||||||||
| 273 = | 3•7•13 | ||||||||||||
| 274 = | 2•137 | ||||||||||||
| 275 = | 5•5•11 | ||||||||||||
| 276 = | 2•2•3•23 | ||||||||||||
| 277 = | 277 | ||||||||||||
| 278 = | 2•139 | ||||||||||||
| 279 = | 3•3•31 | ||||||||||||
| 280 = | 2 • 2 • 2 • 5 • 7 | ||||||||||||
| 281 = | 281 | ||||||||||||
| 282 = | 2 • 3 • 47 | ||||||||||||
| 283 = | 78 | ||||||||||||
| 283 = | 778 | ||||||||||||
| 283 = | 778 | ||||||||||||
| 283 = | 778 | ||||||||||||
| 283 = | 7878 | ||||||||||||
| 283 = | 28778 | ||||||||||||
. 2•2•71 2•2•71 | |||||||||||||
| 285 = | 3•5•19 | ||||||||||||
| 286 = | 2•11•13 | ||||||||||||
| 287 = | 7•41 | ||||||||||||
| 288 = | 2•2•2•2•2•3•3 | ||||||||||||
| 289 = | 17•17 | ||||||||||||
| 290 = | 2 • 5 • 29 | ||||||||||||
| 291 = | 3 • 97 | ||||||||||||
| 292 = | 2 • 2 • 73 | ||||||||||||
| 2 • 2 • 73 | 2. = | 2•3•7•7 | |||||||||||
| 295 = | 5•59 | ||||||||||||
| 296 = | 2•2•2•37 | ||||||||||||
| 297 = | 3•3•3• 11 | ||||||||||||
| 298 = | 2•149 | ||||||||||||
| 299 = | 13•23 | ||||||||||||
| 300 = | 2•2•3•5•5 | ||||||||||||
| 301 = | 7•43 | ||||||||||||
| 302 = | 2•151 | ||||||||||||
| 303 = | 3 • 101 | ||||||||||||
| 304 = | 2 • 2 • 2 • 2 • 19 | ||||||||||||
| 305 = | 5 • 61 | ||||||||||||
| 306 = | 2 • 3 • 3 • 3 • 3 • 7. 3,1 3,1 | ||||||||||||
| 306 = | 277 2 • 3 • 3 • 3 • 3 • 3 • 3 • 7. 3,1 | ||||||||||||
| 306 = | 2 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3,1 | ||||||||||||
| 306. | 307 = | 307 | |||||||||||
| 308 = | 2•2•7•11 | ||||||||||||
| 309 = | 3 • 103 | ||||||||||||
| 310 = | 2 • 5) | ||||||||||||
| 313 = | 313 | ||||||||||||
| 314 = | 2 • 157 | ||||||||||||
| 315 = | 3 • 3 • 5 • 7 | ||||||||||||
| 3137 = | ......938 =... 3,. 317 =317 | ||||||||||||
| 318 = | 2•3•53 | ||||||||||||
| 319 = | 11•29 | ||||||||||||
| 320 = | 2•2•2•2•2•2•5 | ||||||||||||
| 321 = | 3•107 | ||||||||||||
| 322 = | 2 • 7 • 23 | ||||||||||||
| 323 = | 17 • 19 | ||||||||||||
| 324 = | 2 • 2 • 3 • 3 • 3 • 3 | ||||||||||||
| 325 = | 57 577 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 577 577 577 577 577 57. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 577 577 577 577 577 57. | ||||||||||||
| 326 = | 2•163 | ||||||||||||
| 327 = | 3•109 | ||||||||||||
| 328 = | 2•2•2•41 | ||||||||||||
| 329 = | 7•47 | ||||||||||||
| 330 = | 2•3•5•11 | ||||||||||||
| 331 = | 331 | ||||||||||||
| 332 = | 2•2•83 | ||||||||||||
| 333 = | 3•3•37 | ||||||||||||
| 334 = | 2•167 | ||||||||||||
| 335 = | 5•67 | ||||||||||||
| 336 = | 2•2•2•2•3•7 | ||||||||||||
| 337 = | 337 | ||||||||||||
| 338 = | 2 • 13 • 13 | ||||||||||||
| 339 = | 3 • 113 | ||||||||||||
| 340 = | 2 • 2 • 17. | 340 = | 2 • 2 • 17 | 340 = | . | ||||||||
| 342 = | 2•3•3•19 | ||||||||||||
| 343 = | 7•7•7 | ||||||||||||
| 344 = | 2•2•2•43 | ||||||||||||
| 345 = | 3•5•23 | ||||||||||||
| 346 = | 2•173 | ||||||||||||
| 347 = | 347 | ||||||||||||
| 348 = | 2•2•3•29 | ||||||||||||
| 349 = | 349 | ||||||||||||
| 350 = | 2•5•5•7 | ||||||||||||
| 351 = | 3•3•3•13 | ||||||||||||
| 352 = | 2•2•2•2•2•11 | ||||||||||||
| 353 = | 353 | ||||||||||||
| 354 = | 2•3• 59 | ||||||||||||
| 355 = | 5•71 | ||||||||||||
| 356 = | 2•2•89 | ||||||||||||
| 357 = | 3•7•17 | ||||||||||||
| 358 = | 2•179 | ||||||||||||
| 359 = | 359 | ||||||||||||
| 360 = | 2•2•2•3•3 •5 | ||||||||||||
| 361 = | 19•19 | ||||||||||||
| 362 = | 2•181 | ||||||||||||
| 363 = | 3•11•11 | ||||||||||||
| 364 = | 2•2•7 •13 | ||||||||||||
| 365 = | 5•73 | ||||||||||||
| 366 = | 2•3•61 | ||||||||||||
| 367 = | 367 | ||||||||||||
| 368 = | 2•2•2•2•23 | ||||||||||||
| 369 = | 3•3•41 | ||||||||||||
| 370 = | 2•5•37 | ||||||||||||
| 371 = | 7•53 | ||||||||||||
| 372 = | 2•2•3•31 | ||||||||||||
| 373 = | 373 | ||||||||||||
| 374 = | 2•11•17 | ||||||||||||
| 375 = | 3•5•5•5 | ||||||||||||
| 376 = | 2 • 2 • 2 • 47 | ||||||||||||
| 377 = | 13 • 29 | ||||||||||||
| 378 = | 2 • 3 • 3 • 7. | ||||||||||||
| 2 | |||||||||||||
| 2. 379 | |||||||||||||
| 380 = | 2•2•5•19 | ||||||||||||
| 381 = | 3•127 | ||||||||||||
| 382 = | 2•191 | ||||||||||||
| 383 = | 383 | ||||||||||||
| 384 = | 2•2•2•2•2•2•2•3 | ||||||||||||
| 385 = | 5•7•11 | ||||||||||||
| 386 = | 2•193 | ||||||||||||
| 387 = | 3•3•43 | ||||||||||||
| 388 = | 2•2•97 | ||||||||||||
| 389 = | 389 | ||||||||||||
| 390 = | 2 • 3 • 5 • 13 | ||||||||||||
| 391 = | 17 • 23 | ||||||||||||
| 392 = | 2 2,9003. 2,9003. 2 | • | • | • | • | • | • | • | • | • | • | • | • | 2 2
| . | 2 2|||||||||||||
| 392 = | 2|||||||||||||
392. 393 = 393 = | 3•131 | ||||||||||||
| 394 = | 2•197 | ||||||||||||
| 395 = | 5•79 | ||||||||||||
| 396 = | 2•2•3•3•11 | ||||||||||||
| 397 = | 397 | ||||||||||||
| 398 = | 2•199 | ||||||||||||
| 399 = | 3 • 7 • 19 | ||||||||||||
| 400 = | 2 • 2 • 2 • 2 • 5 • 5 | ||||||||||||
| 401 = | 401 | ||||||||||||
| 403 4038 = | 401 | ||||||||||||
| 402 = | 401 2 40038|||||||||||||
| 402 = | |||||||||||||
| 402 = | |||||||||||||
| 402 = | 401 2 40038401 403 403. 67 | ||||||||||||
| 403 = | 13•31 | ||||||||||||
| 404 = | 2•2•101 | ||||||||||||
| 405 = | 3•3•3•3•5 | ||||||||||||
| 406 = | 2•7•29 | ||||||||||||
| 407 = | 11•37 | ||||||||||||
| 408 = | 2•2•2•3•17 | ||||||||||||
| 409 = | 409 | ||||||||||||
| 410 = | 2•5•41 | ||||||||||||
| 411 = | 3•137 | ||||||||||||
| 412 = | 2•2•103 | ||||||||||||
| 413 = | 7•59 | ||||||||||||
| 414 = | 2 • 3 • 3 • 23 | ||||||||||||
| 415 = | 5 • 83 | ||||||||||||
| 416 = | 2 • 2 • 2 • 2 • 13 | 2 • 2 • 2 • 2 • 13 | 9.2. | 3•139 | |||||||||
| 418 = | 2•11•19 | ||||||||||||
| 419 = | 419 | ||||||||||||
| 420 = | 2•2•3•5•7 | ||||||||||||
| 421 = | 421 | ||||||||||||
| 422 = | 2•211 | ||||||||||||
| 423 = | 3•3•47 | ||||||||||||
| 424 = | 2•2•2•53 | ||||||||||||
| 425 = | 5•5•17 | ||||||||||||
| 426 = | 2•3•71 | ||||||||||||
| 427 = | 7•61 | ||||||||||||
| 428 = | 2•2•107 | ||||||||||||
| 429 = | 3•11•13 | ||||||||||||
| 430 = | 2•5•43 | ||||||||||||
| 431 = | 431 | ||||||||||||
| 432 = | 2•2•2•2•3•3•3 | ||||||||||||
| 433 = | 433 | ||||||||||||
| 434 = | 2•7•31 | ||||||||||||
| 435 = | 3•5•29 | ||||||||||||
| 436 = | 2•2•109 | ||||||||||||
| 437 = | 19•23 | ||||||||||||
| 438 = | 2•3•73 | ||||||||||||
| 439 = | 439 | ||||||||||||
| 440 = | 2•2•2•5•11 | ||||||||||||
| 441 = | 3•3•7•7 | ||||||||||||
| 442 = | 2•13•17 | ||||||||||||
| 443 = | 443 | ||||||||||||
| 444 = | 2•2•3•37 | ||||||||||||
| 445 = | 5•89 | ||||||||||||
| 446 = | 2•223 | ||||||||||||
| 447 = | 3•149 | ||||||||||||
| 448 = | 2•2•2•2•2•2•7 | ||||||||||||
| 449 = | 449 | ||||||||||||
| 450 = | 2•3•3•5•5 | ||||||||||||
| 451 = | 11•41 | ||||||||||||
| 452 = | 2•2•113 | ||||||||||||
| 453 = | 3•151 | ||||||||||||
| 454 = | 2•227 | ||||||||||||
| 455 = | 5•7•13 | ||||||||||||
| 456 = | 2 • 2 • 2 • 3 • 19 | ||||||||||||
| 457 = | 457 | ||||||||||||
| 458 = | 2 • 229 | ||||||||||||
| 457 4 | . | ||||||||||||
| 460 = | 2•2•5•23 | ||||||||||||
| 461 = | 461 | ||||||||||||
| 462 = | 2•3•7•11 | ||||||||||||
| 463 = | 463 | ||||||||||||
| 464 = | 2•2•2•2•29 | ||||||||||||
| 465 = | 3 • 5 • 31 | ||||||||||||
| 466 = | 2 • 233 | ||||||||||||
| 467 = | 467 | ||||||||||||
| 468 = | 2 • 3. 3900 3900 2 | ||||||||||||
| 7•67 | |||||||||||||
| 470 = | 2•5•47 | ||||||||||||
| 471 = | 3•157 | ||||||||||||
| 472 = | 2•2•2•59 | ||||||||||||
| 473 = | 11•43 | ||||||||||||
| 474 = | 2•3•79 | ||||||||||||
| 475 = | 5 • 5 • 19 | ||||||||||||
| 476 = | 2 • 2 • 7 • 17 | ||||||||||||
| 477 = | 3 • 3 • 53 | 477 = | . 239 | ||||||||||
| 479 = | 479 | ||||||||||||
| 480 = | 2 • 2 • 2 • 2 • 2 • 3 • 5 | ||||||||||||
| 481 = | 13 • 37 | ||||||||||||
| 482 = | 2 • 241 | ||||||||||||
| 483 = | 2 241|||||||||||||
| 483 = | 8778 8777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3777 3 241 3. | ||||||||||||
| 484 = | 2•2•11•11 | ||||||||||||
| 485 = | 5•97 | ||||||||||||
| 486 = | 2•3•3•3•3•3 | ||||||||||||
| 487 = | 487 | ||||||||||||
| 488 = | 2•2•2•61 | ||||||||||||
| 489 = | 3•163 | ||||||||||||
| 490 = | 2•5•7•7 | ||||||||||||
| 491 = | 491 | ||||||||||||
| 492 = | 2•2•3•41 | ||||||||||||
| 493 = | 17•29 | ||||||||||||
| 494 = | 2•13•19 | ||||||||||||
| 495 = | 3•3•5•11 | ||||||||||||
| 496 = | 2•2•2•2•31 | ||||||||||||
| 497 = | 7•71 | ||||||||||||
| 498 = | 2•3•83 | ||||||||||||
| 499 = | 499 | ||||||||||||
| 500 = | 2•2•5•5•5 |
| n | Prime Factorization | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 501 = | 3•167 | ||||||||||||
| 502 = | 2•251 | ||||||||||||
| 503 = | 503 | ||||||||||||
| 504 = | 2 •2•2•3•3•7 | ||||||||||||
| 505 = | 5•101 | ||||||||||||
| 506 = | 2•11•23 | ||||||||||||
| 507 = | 3 • 13 • 13 | ||||||||||||
. | |||||||||||||
| 511 = | 7•73 | ||||||||||||
| 512 = | 2•2•2•2•2•2•2•2•2 | ||||||||||||
| 513 = | 3•3•3• 19 | ||||||||||||
| 514 = | 2•257 | ||||||||||||
| 515 = | 5•103 | ||||||||||||
| 516 = | 2•2•3•43 | ||||||||||||
| 517 = | 11•47 | ||||||||||||
| 518 = | 2•7•37 | ||||||||||||
| 519 = | 3•173 | ||||||||||||
| 520 = | 2•2•2•5•13 | ||||||||||||
| 521 = | 521 | ||||||||||||
| 522 = | 2•3•3•29 | ||||||||||||
| 523 = | 523 | ||||||||||||
| 524 = | 2•2•131 | ||||||||||||
| 525 = | 3 • 5 • 5 • 7 | ||||||||||||
| 526 = | 2 • 263 | ||||||||||||
| 527 = | 17 • 31 | ||||||||||||
| 528 = | 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2. | ||||||||||||
| 529 = | 23•23 | ||||||||||||
| 530 = | 2•5•53 | ||||||||||||
| 531 = | 3•3•59 | ||||||||||||
| 532 = | 2•2•7• 19 | ||||||||||||
| 533 = | 13•41 | ||||||||||||
| 534 = | 2•3•89 | ||||||||||||
| 535 = | 5 • 107 | ||||||||||||
| . | 539 = | 7•7•11 | |||||||||||
| 540 = | 2•2•3•3•3•5 | ||||||||||||
| 541 = | 541 | ||||||||||||
| 542 = | 2•271 | ||||||||||||
| 543 = | 3•181 | ||||||||||||
| 544 = | 2 • 2 • 2 • 2 • 2 • 17 | ||||||||||||
| 545 = | 5 • 109 | ||||||||||||
| 546 = | 2 • 3 • 7 • 13 | ||||||||||||
| 547 = | 7789138...... =. =. =. =..|||||||||||||
| 548 = | 2•2•137 | ||||||||||||
| 549 = | 3•3•61 | ||||||||||||
| 550 = | 2•5•5•11 | ||||||||||||
| 551 = | 19•29 | ||||||||||||
| 552 = | 2•2•2•3•23 | ||||||||||||
| 553 = | 7•79 | ||||||||||||
| 554 = | 2 • 277 | ||||||||||||
| 555 = | 3 • 5 • 37 | ||||||||||||
| 556 = | 2 • 2 • 13 | 5566 = | . 558 = 558 = | 2 • 3 • 3 • 31 | |||||||||
| 559 = | . •11•17 | ||||||||||||
| 562 = | 2•281 | ||||||||||||
| 563 = | 563 | ||||||||||||
| 564 = | 2 • 2 • 3 • 47 | ||||||||||||
| 565 = | 5 • 113 | ||||||||||||
| 56666637 • | |||||||||||||
| 566666637. | 5666666637. | ||||||||||||
| 566 66666. | . | 3 • 3 • 3 • 3 • 7 | |||||||||||
| 568 = | 2 • 2 • 2 • 71 | ||||||||||||
| 569 = | 569 | ||||||||||||
| 5770 = | 2. 3 | ||||||||||||
| 570 = | 2. 57877 2. 5777 2 | • 5777 2 | 2 | ||||||||||
| 571 = | 571 | ||||||||||||
| 572 = | 2•2•11•13 | ||||||||||||
| 573 = | 3 • 191 | ||||||||||||
| 574 = | 2 • 7 • 41 | ||||||||||||
| 575 = | 5. • 5. 2388 | 5 70038 | |||||||||||
| 5 | |||||||||||||
5. •2•2•2•3•3 •2•2•2•3•3 | |||||||||||||
| 577 = | 577 | ||||||||||||
| 578 = | 2•17•17 | ||||||||||||
| 579 = | 3•193 | ||||||||||||
| 580 = | 2•2•5•29 | ||||||||||||
| 581 = | 7•83 | ||||||||||||
| 582 = | 2•3•97 | ||||||||||||
| 583 = | 11•53 | ||||||||||||
| 584 = | 2•2•2•73 | ||||||||||||
| 585 = | 3•3•5• 13 | ||||||||||||
| 586 = | 2 • 293 | ||||||||||||
| 587 = | 587 | ||||||||||||
| 588 = | 2 • 2 • 3 • 7. 7 | ||||||||||||
| 2. | |||||||||||||
| 590 = | 2•5•59 | ||||||||||||
| 591 = | 3•197 | ||||||||||||
| 592 = | 2•2•2•2•37 | ||||||||||||
| 593 = | 593 | ||||||||||||
| 594 = | 2•3•3•3•11 | ||||||||||||
| 595 = | 5 • 7 • 17 | ||||||||||||
| 596 = | 2 • 2 • 149 | ||||||||||||
| 597 = | 3 • 199 | ||||||||||||
| 598 = | 2 • | 2900 3 | 2 | 2 237. 2 2 | 2900 3 | 2 | 2 | 2 | 2 | 2900 3 | 2 | 2 2377 2 2377 2 2377 2 2377 2 2377 2 2377 2 2377 2 2377 2 2377 2 2377 2 2377 2 2377 2 2377 2 | |
| 5989 | |||||||||||||
| . | 599 | ||||||||||||
| 600 = | 2•2•2•3•5•5 | ||||||||||||
| 601 = | 601 | ||||||||||||
| 602 = | 2 • 7 • 43 | ||||||||||||
| 603 = | 3 • 3 • 67 | ||||||||||||
| 6037 = | .. 70037637. 70038. = = = =. | = | . 605 =5•11•11 | ||||||||||
| 606 = | 2•3•101 | ||||||||||||
| 607 = | 607 | ||||||||||||
| 608 = | 2•2•2•2•2•19 | ||||||||||||
| 609 = | 3•7•29 | ||||||||||||
| 610 = | 2 • 5 • 61 | ||||||||||||
| 611 = | 13 • 47 | ||||||||||||
| 612 = | 2 • 2 • 3 • 17 | ||||||||||||
| 613 = | 7778 | ||||||||||||
| 613 = | 7777778 | ||||||||||||
| 613 = | 777777778 | ||||||||||||
| 613 = | 7777778 | ||||||||||||
613. | 2 • 307 | ||||||||||||
| 615 = | 3 • 5 • 41 | ||||||||||||
| 616 = | 2 • 2 • 2 • 7 • 11 | ||||||||||||
| 617 = | 778 | 7777777777777777777777777888 | |||||||||||
| 617. | 2•3•103 | ||||||||||||
| 619 = | 619 | ||||||||||||
| 620 = | 2•2•5•31 | ||||||||||||
| 621 = | 3•3•3•23 | ||||||||||||
| 622 = | 2•311 | ||||||||||||
| 623 = | 7•89 | ||||||||||||
| 624 = | 2•2•2•2•3•13 | ||||||||||||
| 625 = | 5•5•5•5 | ||||||||||||
| 626 = | 2•313 | ||||||||||||
| 627 = | 3•11•19 | ||||||||||||
| 628 = | 2•2•157 | ||||||||||||
| 629= | 17•37 | ||||||||||||
| 630 = | 2•3•3•5•7 | ||||||||||||
| 631 = | 631 | ||||||||||||
| 632 = | 2•2•2•79 | ||||||||||||
| 633 = | 3•211 | ||||||||||||
| 634 = | 2•317 | ||||||||||||
| 635 = | 5•127 | ||||||||||||
| 636 = | 2•2•3•53 | ||||||||||||
| 637 = | 7•7•13 | ||||||||||||
| 638 = | 2•11•29 | ||||||||||||
| 639 = | 3 • 3 • 71 | ||||||||||||
| 640 = | 2 • 2 • 2 • 2 • 2 • 2 • 5 | ||||||||||||
| 641 = | 7777888888 | ||||||||||||
| 641 = | 77777777778888888 | ||||||||||||
641. = = | 2•3•107 | ||||||||||||
| 643 = | 643 | ||||||||||||
| 644 = | 2•2•7•23 | ||||||||||||
| 645 = | 3•5•43 | ||||||||||||
| 646 = | 2•17•19 | ||||||||||||
| 647 = | 647 | ||||||||||||
| 648 = | 2 • 2 • 2 • 3 • 3 • 3 • 3 | ||||||||||||
| 649 = | 11 • 59 | ||||||||||||
| 650 = | 2 • 5 • 5 • 13 | ||||||||||||
| . | 3 • 7 • 31 | ||||||||||||
| 652 = | 2 • 2 • 163 | ||||||||||||
| 653 = | 653 | ||||||||||||
| 654 = | 2 • 3 | 2. | 2. 2. 2. 2. 2 2 2|||||||||||
| . 5•131 | |||||||||||||
| 656 = | 2•2•2•2•41 | ||||||||||||
| 657 = | 3 • 3 • 73 | ||||||||||||
| 658 = | 2 • 7 • 47 | ||||||||||||
| 659 = | 659 | ||||||||||||
| 660 = | 2 • 2 • 5. 7003. 7003. | . | . | ||||||||||
| 661 | |||||||||||||
| 662 = | 2•331 | ||||||||||||
| 663 = | 3•13•17 | ||||||||||||
| 664 = | 2•2•2•83 | ||||||||||||
| 665 = | 5•7•19 | ||||||||||||
| 666 = | 2•3•3•37 | ||||||||||||
| 667 = | 23 • 29 | ||||||||||||
| 668 = | 2 • 2 • 167 | ||||||||||||
| 669 = | 3 • 223 | ||||||||||||
| 6 67878 | . 671 = | 11•61 | |||||||||||
| 672 = | 2•2•2•2•2•3•7 | ||||||||||||
| 673 = | 673 | ||||||||||||
| 674 = | 2•337 | ||||||||||||
| 675 = | 3•3•3•5•5 | ||||||||||||
| 676 = | 2 • 2 • 13 • 13 | ||||||||||||
| 677 = | 677 | ||||||||||||
| 678 = | 2 • 3 • 113 | ||||||||||||
| 679 = | |||||||||||||
| 679 = | 7777 7. | ||||||||||||
| 679 = | |||||||||||||
| 679. • 2 • 2 • 5 • 17 | |||||||||||||
| 681 = | 3 • 227 | ||||||||||||
| 682 = | 2 • 11 • 310038 | ||||||||||||
| 683 = | 78 | ||||||||||||
| . •2•3•3•19 | |||||||||||||
| 685 = | 5•137 | ||||||||||||
| 686 = | 2 • 7 • 7 • 7 | ||||||||||||
| 687 = | 3 • 229 | ||||||||||||
| 688 = | 2 • 2 • 2 • 43 | ||||||||||||
| 690 = | 2 • 3 • 5 • 23 | ||||||||||||
| 691 = | 691 | ||||||||||||
| 692 = | 2 • 173 | ||||||||||||
| 692 = | 2 • 173 | ||||||||||||
| . •7•11 | |||||||||||||
| 694 = | 2•347 | ||||||||||||
| 695 = | 5 • 139 | ||||||||||||
| 696 = | 2 • 2 • 2 • 3 • 29 | ||||||||||||
| 697 = | 17 • 41 | ||||||||||||
| 698 = | 2. 34999999989878 2. 349999998 2. 349999998 2. 3499999998 2. 3499999998 2. 349999999778 2. 34999999978 2. 34999999978 2. 34999999978 2. 3499999978 2 40038 3499999998 2. 3499999998 2. 349999999778 2. 34999999978 2. 34999999978 2. 34999999978 2. 3499999978 2 40038 | ||||||||||||
| 698 = | 2|||||||||||||
| . | 3 • 233 | ||||||||||||
| 700 = | 2 • 2 • 5 • 5 • 7 | ||||||||||||
| 701 = | 701 | ||||||||||||
| 702 = | 2 • 3 • 3. 3. 3 | 70037. 3. 3. 3. 3. 3. 3. 3. 3 | 7.10037. 3 | 7. 3 | . 3 | 7. 3. 3. 3. 3. 3. 3. 3 | 702 = | ||||||
| 702 = | |||||||||||||
| 702 = | |||||||||||||
| 703 = | 19•37 | ||||||||||||
| 704 = | 2•2•2•2•2•2•11 | ||||||||||||
| 705 = | 3 • 5 • 47 | ||||||||||||
| 706 = | 2 • 353 | ||||||||||||
| 707 = | 7. 70038 | ||||||||||||
| 707 = | 7. 70038 | ||||||||||||
| 7 7. 70038 | |||||||||||||
| 77777777777777777777777777777777777777777. | |||||||||||||
| 709 = | 709 | ||||||||||||
| 710 = | 2•5•71 | ||||||||||||
| 711 = | 3•3•79 | ||||||||||||
| 712 = | 2•2•2•89 | ||||||||||||
| 713 = | 23•31 | ||||||||||||
| 714 = | 2•3•7•17 | ||||||||||||
| 715 = | 5•11•13 | ||||||||||||
| 716 = | 2•2•179 | ||||||||||||
| 717 = | 3•239 | ||||||||||||
| 718 = | 2 • 359 | ||||||||||||
| 719 = | 719 | ||||||||||||
| 720 = | 2 • 2 • 2 • 2 • 3 • 5 | ||||||||||||
77777777777777777777777777777777777777777777777777777777777 7. 900 = 900 = | 77777777777777777777777777777777777777777777777777 7. | .||||||||||||
| 722 = | 2•19•19 | ||||||||||||
| 723 = | 3•241 | ||||||||||||
| 724 = | 2•2•181 | ||||||||||||
| 725 = | 5•5•29 | ||||||||||||
| 726 = | 2•3•11•11 | ||||||||||||
| 727 = | 727 | ||||||||||||
| 728 = | 2•2•2•7•13 | ||||||||||||
| 729 = | 3•3•3•3•3•3 | ||||||||||||
| 730 = | 2•5•73 | ||||||||||||
| 731 = | 17•43 | ||||||||||||
| 732 = | 2•2•3•61 | ||||||||||||
| 733 = | 733 | ||||||||||||
| 734 = | 2 • 367 | ||||||||||||
| 735 = | 3 • 5 • 7. 7 | ||||||||||||
| 737777 21 • | |||||||||||||
| 776 736 786 386 7876 = | |||||||||||||
| 737 = | 11•67 | ||||||||||||
| 738 = | 2•3•3•41 | ||||||||||||
| 739 = | 739 | ||||||||||||
| 740 = | 2•2•5 •37 | ||||||||||||
| 741 = | 3•13•19 | ||||||||||||
| 742 = | 2 • 7 • 53 | ||||||||||||
| 743 = | 743 | ||||||||||||
| 744 = | 2 • 2 • 3 • 31 | ||||||||||||
| 745 = | 57 57 57 57 57 577 57 577 577 577 577 577 577 577 577 577 57 577 577 577 577 5777. | ||||||||||||
| 745 = | 577 57 57 57 57 577 57 577 5 | ||||||||||||
| 745 = | |||||||||||||
| . | 2•373 | ||||||||||||
| 747 = | 3•3•83 | ||||||||||||
| 748 = | 2•2•11•17 | ||||||||||||
| 749 = | 7•107 | ||||||||||||
| 750 = | 2•3•5•5•5 |
| нет | Prime Factorization | |||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 751 = | 751 | |||||||||||||||||||||||||||||||
| 752 = | 2•2•2•2•47 | |||||||||||||||||||||||||||||||
| 753 = | 3•251 | |||||||||||||||||||||||||||||||
| 754 = | 2 • 13 • 29 | |||||||||||||||||||||||||||||||
| 755 = | 5 • 151 | |||||||||||||||||||||||||||||||
| 756 = | 2 • 2 • 3 • 3 • 7 | |||||||||||||||||||||||||||||||
| 757 = | 7778 | |||||||||||||||||||||||||||||||
| 757 = | 77777 | |||||||||||||||||||||||||||||||
| 757. | 2•379 | |||||||||||||||||||||||||||||||
| 759 = | 3•11•23 | |||||||||||||||||||||||||||||||
| 760 = | 2•2•2•5•19 | |||||||||||||||||||||||||||||||
| 761 = | 761 | |||||||||||||||||||||||||||||||
| 762 = | 2•3•127 | |||||||||||||||||||||||||||||||
| 763 = | 7•109 | |||||||||||||||||||||||||||||||
| 764 = | 2•2•191 | |||||||||||||||||||||||||||||||
| 765 = | 3•3•5•17 | |||||||||||||||||||||||||||||||
| 766 = | 2•383 | |||||||||||||||||||||||||||||||
| 767 = | 13•59 | |||||||||||||||||||||||||||||||
| 768 = | 2•2•2•2•2•2•2•2•3 | |||||||||||||||||||||||||||||||
| 769 = | 769 | |||||||||||||||||||||||||||||||
| 770 = | 2 • 5 • 7 • 11 | |||||||||||||||||||||||||||||||
| 771 = | 3 • 257 | |||||||||||||||||||||||||||||||
| 778 | 3 • 257 | |||||||||||||||||||||||||||||||
| 7778 | 3 • 257 | |||||||||||||||||||||||||||||||
| 7777778 | . 773 = 773 = | 773 | ||||||||||||||||||||||||||||||
| 774 = | 2•3•3•43 | |||||||||||||||||||||||||||||||
| 775 = | 5•5•31 | |||||||||||||||||||||||||||||||
| 776 = | 2•2•2•97 | |||||||||||||||||||||||||||||||
| 777 = | 3•7•37 | |||||||||||||||||||||||||||||||
| 778 = | 2 • 389 | |||||||||||||||||||||||||||||||
| 779 = | 19 • 41 | |||||||||||||||||||||||||||||||
| 780 = | 2 • 2 • 5 • 13 | |||||||||||||||||||||||||||||||
| 781 = | 778 | |||||||||||||||||||||||||||||||
| 781 = | 777 | |||||||||||||||||||||||||||||||
| 781 = | 777 | |||||||||||||||||||||||||||||||
| 781. | 2 • 17 • 23 | |||||||||||||||||||||||||||||||
| 783 = | 3 • 3 • 3 • 29 | |||||||||||||||||||||||||||||||
| 784 = | 2 • 2 • 2 • 7 • 7 | |||||||||||||||||||||||||||||||
| 785 = | 577777777777777788888888888888888887878 7. 157 | |||||||||||||||||||||||||||||||
| 786 = | 2•3•131 | |||||||||||||||||||||||||||||||
| 787 = | 787 | |||||||||||||||||||||||||||||||
| 788 = | 2•2•197 | |||||||||||||||||||||||||||||||
| 789 = | 3•263 | |||||||||||||||||||||||||||||||
| 790 = | 2•5•79 | |||||||||||||||||||||||||||||||
| 791 = | 7•113 | |||||||||||||||||||||||||||||||
| 792 = | 2•2•2•3•3•11 | |||||||||||||||||||||||||||||||
| 793 = | 13•61 | |||||||||||||||||||||||||||||||
| 794 = | 2•397 | |||||||||||||||||||||||||||||||
| 795 = | 3•5• 53 | |||||||||||||||||||||||||||||||
| 796 = | 2•2•199 | |||||||||||||||||||||||||||||||
| 797 = | 797 | |||||||||||||||||||||||||||||||
| 798 = | 2•3•7•19 | |||||||||||||||||||||||||||||||
| 799 = | 17•47 | |||||||||||||||||||||||||||||||
| 800 = | 2•2•2•2•2•5 • 5 | |||||||||||||||||||||||||||||||
| 801 = | 3 • 3 • 89 | |||||||||||||||||||||||||||||||
| 802 = | . •67 •67 | |||||||||||||||||||||||||||||||
| 805 = | 5•7•23 | |||||||||||||||||||||||||||||||
| 806 = | 2•13•31 | |||||||||||||||||||||||||||||||
| 807 = | 3•269 | |||||||||||||||||||||||||||||||
| 808 = | 2•2•2•101 | |||||||||||||||||||||||||||||||
| 809 = | 809 | |||||||||||||||||||||||||||||||
| 810 = | 2•3•3•3 •3•5 | |||||||||||||||||||||||||||||||
| 811 = | 811 | |||||||||||||||||||||||||||||||
| 812 = | 2•2•7•29 | |||||||||||||||||||||||||||||||
| 813 = | 3•271 | |||||||||||||||||||||||||||||||
| 814 = | 2•11 •37 | |||||||||||||||||||||||||||||||
| 815 = | 5•163 | |||||||||||||||||||||||||||||||
| 816 = | 2 • 2 • 2 • 2 • 3 • 17 | |||||||||||||||||||||||||||||||
| 817 = | 19 • 43 | |||||||||||||||||||||||||||||||
| 818 = | 2 • 409 | |||||||||||||||||||||||||||||||
| 819 = | 83,3377 3 70037 3 | 3 | 37777777777777777777777777 3 | 3 | 3 | . 30037 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | . | ||||||
| 820 = | 2•2•5•41 | |||||||||||||||||||||||||||||||
| 821 = | 821 | |||||||||||||||||||||||||||||||
| 822 = | 2•3•137 | |||||||||||||||||||||||||||||||
| 823 = | 823 | |||||||||||||||||||||||||||||||
| 824 = | 2•2•2•103 | |||||||||||||||||||||||||||||||
| 825 = | 3•5•5•11 | |||||||||||||||||||||||||||||||
| 826 = | 2 • 7 • 59 | |||||||||||||||||||||||||||||||
| 827 = | 827 | |||||||||||||||||||||||||||||||
| 828 = | 2 • 2 • 3 • • 23 | 828 =2 • 2 • 3 23 | ||||||||||||||||||||||||||||||
2. • 2 • 3 23 • 2 • 3 23 | 828 = | 2. | ||||||||||||||||||||||||||||||
| 830 = | 2 • 5 • 83 | |||||||||||||||||||||||||||||||
| 831 = | 3 • 277 | |||||||||||||||||||||||||||||||
| 832 = | 2 • 2 • 2 • 2 • 2 • 13 | 2 • 2 • 2 • 2 • 2 • | 36||||||||||||||||||||||||||||||
| 2 • 2 • 2 • 2 • 2 • 13 | ||||||||||||||||||||||||||||||||
| 2 • 2 • 2 • 2 • 2 • 13 | 2 • 2 • 2 • 2 • 2 • 1378 | 2 • 2 • 2 • 2 • 2 • 2 | 2. | 7•7•17 | ||||||||||||||||||||||||||||
| 834 = | 2•3•139 | |||||||||||||||||||||||||||||||
| 835 = | 5 • 167 | |||||||||||||||||||||||||||||||
| 836 = | 2 • 2 • 11 • 19 | |||||||||||||||||||||||||||||||
| 837 = | 3 • 3 • 31 | |||||||||||||||||||||||||||||||
| 8378 838 8388 8388 838 83878 83878 83878 83878 8378 83878 8378 8378 8378 83878 83878 83878 83878 83878 83878 83878. | ||||||||||||||||||||||||||||||||
| 839 = | 839 | |||||||||||||||||||||||||||||||
| 840 = | 2•2•2•3•5•7 | |||||||||||||||||||||||||||||||
| 841 = | 29•29 | |||||||||||||||||||||||||||||||
| 842 = | 2•421 | |||||||||||||||||||||||||||||||
| 843 = | 3•281 | |||||||||||||||||||||||||||||||
| 844 = | 2•2•211 | |||||||||||||||||||||||||||||||
| 845 = | 5 • 13 • 13 | |||||||||||||||||||||||||||||||
| 846 = | 2 • 3 • 3 • 47 | |||||||||||||||||||||||||||||||
| 847 = | 7 • 110038 | |||||||||||||||||||||||||||||||
| . •2•2•2•53 | ||||||||||||||||||||||||||||||||
| 849 = | 3•283 | |||||||||||||||||||||||||||||||
| 850 = | 2•5•5•17 | |||||||||||||||||||||||||||||||
| 851 = | 23•37 | |||||||||||||||||||||||||||||||
| 852 = | 2•2•3•71 | |||||||||||||||||||||||||||||||
| 853 = | 853 | |||||||||||||||||||||||||||||||
| 854 = | 2 • 7 • 61 | |||||||||||||||||||||||||||||||
| 855 = | 3 • 3 • 5 • 19 | |||||||||||||||||||||||||||||||
| 856 = | 2 • 2 • 2 • 107 | 877878788888888888888888888888878888888887888888888788888878888888888888888888888888888888887 | ||||||||||||||||||||||||||||||
| 858 = | 2•3•11•13 | |||||||||||||||||||||||||||||||
| 859 = | 859 | |||||||||||||||||||||||||||||||
| 860 = | 2•2•5•43 | |||||||||||||||||||||||||||||||
| 861 = | 3•7• 41 | |||||||||||||||||||||||||||||||
| 862 = | 2•431 | |||||||||||||||||||||||||||||||
| 863 = | 863 | |||||||||||||||||||||||||||||||
| 864 = | 2 • 2 • 2 • 2 • 2 • 3 • 3 • 3 | |||||||||||||||||||||||||||||||
| 865 = | 5 • 173 | |||||||||||||||||||||||||||||||
| 866 = | 2. 433333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333тели | |||||||||||||||||||||||||||||||
866. = = | 3 • 17 • 17 | |||||||||||||||||||||||||||||||
| 868 = | 2 • 2 • 7 • 31 | |||||||||||||||||||||||||||||||
| 869 = | 11 • 79 | |||||||||||||||||||||||||||||||
| 870 = | 777 2• 3 | • 3 | • 3 | • 3 | • 3 | • 3 | • 3 | • 3 | • 3 | • 3 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | . |
| 871 = | 13•67 | |||||||||||||||||||||||||||||||
| 872 = | 2•2•2•109 | |||||||||||||||||||||||||||||||
| 873 = | 3 • 3 • 97 | |||||||||||||||||||||||||||||||
| 874 = | 2 • 19 • 23 | |||||||||||||||||||||||||||||||
| 875 = | 5 • 5 • 5 • 7 | 77777777777777777777777777777777777777777777878787878787 8777 8777 8777 8 | 877777877 8 | 877777878 7. | 8 | 8777777878 7. | 8 | 8 | 8 | 7 8777 8 | 8 | 8 | 8 | 8 | 8 | 877778787878787 •3•73 | ||||||||||||||||
| 877 = | 877 | |||||||||||||||||||||||||||||||
| 878 = | 2•439 | |||||||||||||||||||||||||||||||
| 879 = | 3•293 | |||||||||||||||||||||||||||||||
| 880 = | 2•2•2•2 •5•11 | |||||||||||||||||||||||||||||||
| 881 = | 881 | |||||||||||||||||||||||||||||||
| 882 = | 2 • 3 • 3 • 7 • 7 | |||||||||||||||||||||||||||||||
| 883 = | 883 | |||||||||||||||||||||||||||||||
| 884 = | 2 • 2 • 13 • 17 | |||||||||||||||||||||||||||||||
| 885 = | 377. 5900 3900 3900 3900 377. 5937 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 3 5900 3900 3900 3900 377. 5937 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 3 | |||||||||||||||||||||||||||||||
| 885. | 886 = | 2•443 | ||||||||||||||||||||||||||||||
| 887 = | 887 | |||||||||||||||||||||||||||||||
| 888 = | 2•2•2•3•37 | |||||||||||||||||||||||||||||||
| 889 = | 7•127 | |||||||||||||||||||||||||||||||
| 890 = | 2•5•89 | |||||||||||||||||||||||||||||||
| 891 = | 3•3•3•3•11 | |||||||||||||||||||||||||||||||
| 892 = | 2•2•223 | |||||||||||||||||||||||||||||||
| 893 = | 19•47 | |||||||||||||||||||||||||||||||
| 894 = | 2•3•149 | |||||||||||||||||||||||||||||||
| 895 = | 5•179 | |||||||||||||||||||||||||||||||
| 896 = | 2 • 2 • 2 • 2 • 2 • 2 • 2 • 7 | |||||||||||||||||||||||||||||||
| 897 = | 3 • 13 • 23 | |||||||||||||||||||||||||||||||
| 898 = | 2 • 449 | 7 7999 89999999999999999999999937 8999999999999999999999999999999999999937 | 2. | 29•31 | ||||||||||||||||||||||||||||
| 900 = | 2•2•3•3•5•5 | |||||||||||||||||||||||||||||||
| 901 = | 17 • 53 | |||||||||||||||||||||||||||||||
| 902 = | 2 • 11 • 41 | |||||||||||||||||||||||||||||||
| 903 = | 3 • 7 • 43 | |||||||||||||||||||||||||||||||
| 3 • 43 | ||||||||||||||||||||||||||||||||
| = | =. | 2 | 2 | . | . | |||||||||||||||||||||||||||
| 905 = | 5•181 | |||||||||||||||||||||||||||||||
| 906 = | 2•3•151 | |||||||||||||||||||||||||||||||
| 907 = | 907 | |||||||||||||||||||||||||||||||
| 908 = | 2•2•227 | |||||||||||||||||||||||||||||||
| 909 = | 3•3•101 | |||||||||||||||||||||||||||||||
| 910 = | 2•5•7•13 | |||||||||||||||||||||||||||||||
| 911 = | 911 | |||||||||||||||||||||||||||||||
| 912 = | 2•2•2•2•3•19 | |||||||||||||||||||||||||||||||
| 913 = | 11•83 | |||||||||||||||||||||||||||||||
| 914 = | 2•457 | |||||||||||||||||||||||||||||||
| 915 = | 3•5•61 | |||||||||||||||||||||||||||||||
| 916 = | 2•2•229 | |||||||||||||||||||||||||||||||
| 917 = | 7•131 | |||||||||||||||||||||||||||||||
| 918 = | 2•3•3 •3•17 | |||||||||||||||||||||||||||||||
| 919 = | 919 | |||||||||||||||||||||||||||||||
| 920 = | 2•2•2•5•23 | |||||||||||||||||||||||||||||||
| 921 = | 3•307 | |||||||||||||||||||||||||||||||
| 922 = | 2•461 | |||||||||||||||||||||||||||||||
| 923 = | 13•71 | |||||||||||||||||||||||||||||||
| 924 = | 2•2•3•7•11 | |||||||||||||||||||||||||||||||
| 925 = | 5•5•37 | |||||||||||||||||||||||||||||||
| 926 = | 2•463 | |||||||||||||||||||||||||||||||
| 927 = | 3•3•103 | |||||||||||||||||||||||||||||||
| 928 = | 2•2•2•2•2•29 | |||||||||||||||||||||||||||||||
| 929 = | 929 | |||||||||||||||||||||||||||||||
| 930 = | 2•3•5•31 | |||||||||||||||||||||||||||||||
| 931 = | 7•7•19 | |||||||||||||||||||||||||||||||
| 932 = | 2•2•233 | |||||||||||||||||||||||||||||||
| 933 = | 3 • 311 | |||||||||||||||||||||||||||||||
| 934 = | 2 • 467 | |||||||||||||||||||||||||||||||
| 935 = | 5 • 11 • 17 | |||||||||||||||||||||||||||||||
| 936 = | 2 • 2 • 2 • 3 • 3 • 3. 3. 3900 3 3. 3900 3 | |||||||||||||||||||||||||||||||
| . | 937 = | 937 | ||||||||||||||||||||||||||||||
| 938 = | 2•7•67 | |||||||||||||||||||||||||||||||
| 939 = | 3•313 | |||||||||||||||||||||||||||||||
| 940 = | 2•2•5•47 | |||||||||||||||||||||||||||||||
| 941 = | 941 | |||||||||||||||||||||||||||||||
| 942 = | 2•3•157 | |||||||||||||||||||||||||||||||
| 943 = | 23 • 41 | |||||||||||||||||||||||||||||||
| 944 = | 2 • 2 • 2 • 2 • 59 | |||||||||||||||||||||||||||||||
| 945 = | 3 • 3 • 5 • 7 | |||||||||||||||||||||||||||||||
| 946 946 3789 2 | 9. 3 • | 9. 3 • | 9. 3 • | 9. •11•43 | ||||||||||||||||||||||||||||
| 947 = | 947 | |||||||||||||||||||||||||||||||
| 948 = | 2 • 2 • 3 • 79 | |||||||||||||||||||||||||||||||
| 949 = | 13 • 73 | |||||||||||||||||||||||||||||||
| 950 = | 2 • 5 • 5 • 1 | |||||||||||||||||||||||||||||||
| = | 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 377 3 310038 | |||||||||||||||||||||||||||||||
| = 5 • 5 • 1 | ||||||||||||||||||||||||||||||||
. = = | 2 • 2 • 2 • 7 • 17 | |||||||||||||||||||||||||||||||
| 953 = | 953 | |||||||||||||||||||||||||||||||
| 954 = | 2 • 3 • 3 • 53 | |||||||||||||||||||||||||||||||
| 955 = | 77777777777777777777777777777777778888888 | |||||||||||||||||||||||||||||||
| . | 956 = | 2•2•239 | ||||||||||||||||||||||||||||||
| 957 = | 3•11•29 | |||||||||||||||||||||||||||||||
| 958 = | 2•479 | |||||||||||||||||||||||||||||||
| 959 = | 7•137 | |||||||||||||||||||||||||||||||
| 960 = | 2•2•2•2•2•2•3•5 | |||||||||||||||||||||||||||||||
| 961 = | 31•31 | |||||||||||||||||||||||||||||||
| 962 = | 2•13•37 | |||||||||||||||||||||||||||||||
| 963 = | 3•3•107 | |||||||||||||||||||||||||||||||
| 964 = | 2•2•241 | |||||||||||||||||||||||||||||||
| 965 = | 5•193 | |||||||||||||||||||||||||||||||
| 966 = | 2•3•7•23 | |||||||||||||||||||||||||||||||
| 967 = | 967 | |||||||||||||||||||||||||||||||
| 968 = | 2•2•2•11•11 | |||||||||||||||||||||||||||||||
| 969 = | 3•17•19 | |||||||||||||||||||||||||||||||
| 970 = | 2•5•97 | |||||||||||||||||||||||||||||||
| 971 = | 971 | |||||||||||||||||||||||||||||||
| 972 = | 2•2•3•3•3•3•3 | |||||||||||||||||||||||||||||||
| 973 = | 7•139 | |||||||||||||||||||||||||||||||
| 974 = | 2• 487 | |||||||||||||||||||||||||||||||
| 975 = | 3•5•5•13 | |||||||||||||||||||||||||||||||
| 976 = | 2•2•2•2•61 | |||||||||||||||||||||||||||||||
| 977 = | 977 | |||||||||||||||||||||||||||||||
| 978 = | 2•3•163 | |||||||||||||||||||||||||||||||
| 979 = | 11•89 | |||||||||||||||||||||||||||||||
| 980 = | 2•2•5•7•7 | |||||||||||||||||||||||||||||||
| 981 = | 3•3•109 | |||||||||||||||||||||||||||||||
| 982 = | 2•491 | |||||||||||||||||||||||||||||||
| 983 = | 983 | |||||||||||||||||||||||||||||||
| 984 = | 2•2•2•3•41 | |||||||||||||||||||||||||||||||
| 985 = | 5•197 | |||||||||||||||||||||||||||||||
| 986 = | 2•17•29 | |||||||||||||||||||||||||||||||
| 987 = | 3•7•47 | |||||||||||||||||||||||||||||||
| 988 = | 2•2•13•19 | |||||||||||||||||||||||||||||||
| 989 = | 23• 43 | |||||||||||||||||||||||||||||||
| 990 = | 2•3•3•5•11 | |||||||||||||||||||||||||||||||
| 991 = | 991 | |||||||||||||||||||||||||||||||
| 992 = | 2•2•2•2•2•31 | |||||||||||||||||||||||||||||||
| 993 = | 3•331 | |||||||||||||||||||||||||||||||
| 994 = | 2•7•71 | |||||||||||||||||||||||||||||||
| 995 = | 5•199 | |||||||||||||||||||||||||||||||
| 996 = | 2•2•3•83 | |||||||||||||||||||||||||||||||
| 997 = | 997 | |||||||||||||||||||||||||||||||
| 998 = | 2•499 | |||||||||||||||||||||||||||||||
| 999 = | 3•3•3•37 | |||||||||||||||||||||||||||||||
| 1000 = | 2•2•2•5•5•5 |
Калькулятор факторизации простых чисел
Пожалуйста, дайте ссылку на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.






 Получается 3016.
Получается 3016.
 Это результат широкого круга вопросов о распределении простых чисел.
Это результат широкого круга вопросов о распределении простых чисел.
 один, два, три, пять, шесть, десять, пятнадцать, тридцать.
один, два, три, пять, шесть, десять, пятнадцать, тридцать. Следовательно, произведение простых делителей = 3 × 7 × 11 = 231.
Следовательно, произведение простых делителей = 3 × 7 × 11 = 231.


