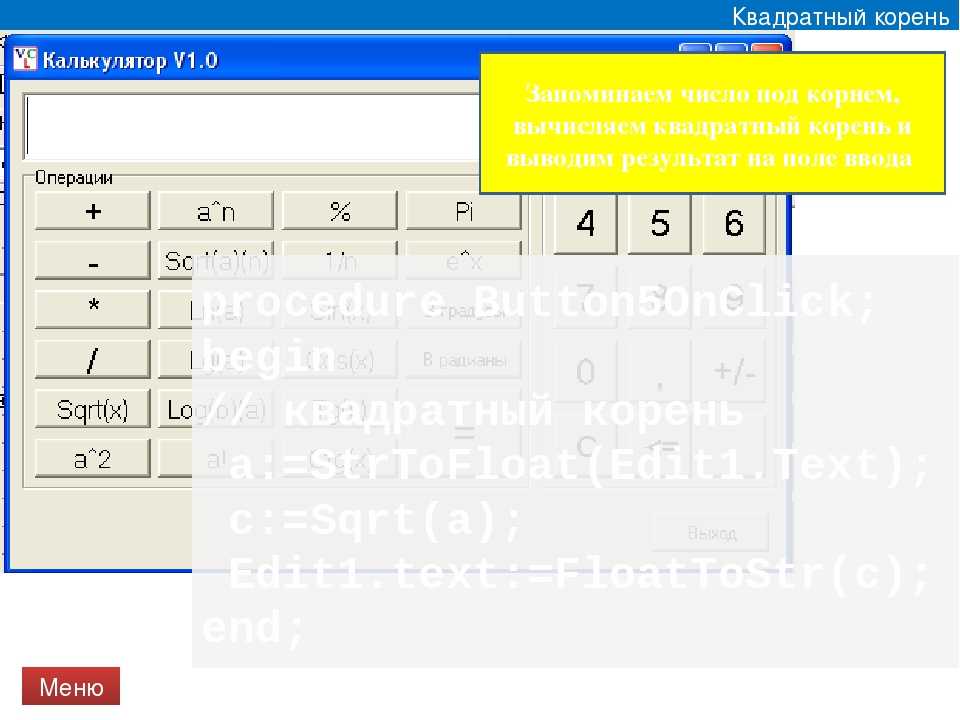
Как извлечь квадратный корень без калькулятора
‘).insertAfter(«#intro»),$(‘
‘).insertBefore(«.youmightalsolike»),$(‘
‘).insertBefore(«#quiz_container»),$(‘
‘).insertBefore(«#newsletter_block_main»),fa(! 0),b=document.getElementsByClassName(«scrolltomarker»),a=0;a
В этой статье:
Извлечение квадратного корня из целых чисел
Извлечение квадратного корня из других чисел
Возведение в квадрат отрицательных чисел
Дополнительные статьи
Источники
Извлечь квадратный корень довольно легко, если под знаком корня стоит целое число (полный квадрат). В противном случае квадратный корень (из любого числа) можно извлечь вручную, то есть без калькулятора. Чтобы пользоваться описанным методом, нужно знать основные математические операции: умножение, сложение и деление.
Шаги
1
 Квадратный корень из исходного числа – это число, которое при умножении на себя дает исходное число. То есть нужно найти такое число, чтобы при его умножении на себя получить данное в задаче число.
Квадратный корень из исходного числа – это число, которое при умножении на себя дает исходное число. То есть нужно найти такое число, чтобы при его умножении на себя получить данное в задаче число.- Например, квадратный корень из 1 равен 1, потому что 1 умножить на 1 равно 1 (1×1 = 1). Квадратный корень из 4 равен 2, потому что 2 умножить на 2 равно 4 (2х2 = 4). Представьте дуб. Дуб вырастает из желудя. Таким образом, дуб намного больше желудя, но связан с ним, потому что именно желудь пускает первые корни. В приведенном выше примере 4 – это дерево, а 2 – желудь.
- Таким образом, квадратный корень из 9 равен 3 (3х3 = 9), из 16 равен 4 (4х4 = 16), из 25 равен 5 (5х5 = 25), из 36 равен 6 (6х6 = 36), из 49 равен 7 (7х7 = 49), из 64 равен 8 (8х8 = 64), из 81 равен 9 (9х9 = 81), из 100 равен 10 (10х10 = 100). [1] X Источник информации
2
Чтобы извлечь квадратный корень из целого числа, воспользуйтесь делением в столбик.
 Для этого разделите целое число (делимое) на некоторое число (делитель) так, чтобы результат (частное) совпал с делителем.
Для этого разделите целое число (делимое) на некоторое число (делитель) так, чтобы результат (частное) совпал с делителем.- Например: 16 делить на 4 равно 4; 4 делить на 2 равно 2 и так далее. Таким образом, 4 – это квадратный корень из 16, а 2 – квадратный корень из 4.
- Корнями из полных квадратов являются целые числа, а не обыкновенные и десятичные дроби.
3
Правильно обозначайте квадратный корень. В научной и учебной литературе квадратный корень обозначается специальным символом, который называется радикалом и имеет вид галочки с верхней горизонтальной линией: √N.[2] X Источник информации
- где N – это подкоренное выражение, то есть число, из которого нужно извлечь корень. Такое число записывается под знаком корня.[3] X Источник информации
- Таким образом, если нужно извлечь квадратный корень из 9, то 9 записывается под знаком корня (радикала), затем пишется знак равенства, а потом 3.
 Это означает, что квадратный корень из 9 равен 3.
Это означает, что квадратный корень из 9 равен 3.
Реклама
1
Воспользуйтесь методом проб и ошибок. Сложнее извлечь корень из числа, которое не является полным квадратом, но это возможно.
- Например, извлеките квадратный корень из 20. Вспомните, что 16 – это полный квадрат, корень из которого равен 4 (4X4 = 16). Число 25 так же является полным квадратом, корень из которого равен 5 (5х5 = 25), поэтому корень из 20 должен быть равен числу, которое находится между 4 и 5.
- В качестве квадратного корня из 20 попробуйте рассмотреть число 4,5. Это число возведите в квадрат, то есть умножьте его на себя: 4,5х4,5. Если результат больше или меньше 20, попробуйте рассмотреть другое число, например, 4,6 или 4,4. Делайте так до тех пор, пока результат не приблизится к 20.[4] X Источник информации
- 4,5х4,5 = 20,25, поэтому рассмотрите меньшее число, например, 4,4: 4,4х4,4 = 19,36.
 Таким образом, квадратный корень из 20 равен числу, которое находится между 4,4 и 4,5. Рассмотрите 4,445: 4,445х4,445 = 19,758. Это уже довольно близко к 20. Продолжайте в том же духе и в конце концов вы придете к: 4,475х4,475 = 20,03 ≈ 20.
Таким образом, квадратный корень из 20 равен числу, которое находится между 4,4 и 4,5. Рассмотрите 4,445: 4,445х4,445 = 19,758. Это уже довольно близко к 20. Продолжайте в том же духе и в конце концов вы придете к: 4,475х4,475 = 20,03 ≈ 20.
2
Воспользуйтесь процессом усреднения. Он также начинается с поиска двух полных квадратов, между которыми находится данное число.
- Затем разделите данное число на квадратный корень из одного из чисел. Потом найдите среднее арифметическое данного числа и результата деления (в данном случае среднее арифметическое – это сумма двух чисел, деленная на два). Затем данное число разделите на среднее арифметическое. Наконец, найдите среднее арифметическое последнего результата и первого среднего арифметического.
- Сложно? Не очень, если рассмотреть пример. Дано число 10. Оно находится между двумя полными квадратами 9 (3х3 = 9) и 16 (4х4 = 16).
 Квадратные корни из этих чисел равны 3 и 4. Итак, разделите 10 на первое число: 10/3 = 3,33. Теперь найдите среднее арифметическое 3 и 3,33: (3+3,33)/2 = 3,1667. Теперь 10 разделите на среднее арифметическое: 10/3,1667 = 3,1579. Теперь найдите среднее арифметическое 3,1579 и 3,1667: (3,1579+3,1667)/2 = 3,1623.
Квадратные корни из этих чисел равны 3 и 4. Итак, разделите 10 на первое число: 10/3 = 3,33. Теперь найдите среднее арифметическое 3 и 3,33: (3+3,33)/2 = 3,1667. Теперь 10 разделите на среднее арифметическое: 10/3,1667 = 3,1579. Теперь найдите среднее арифметическое 3,1579 и 3,1667: (3,1579+3,1667)/2 = 3,1623. - Проверьте ответ, умножив его на себя. 3,1623х3,1623 = 10,001 ≈ 10.
Реклама
1
Возведите в квадрат отрицательное число при помощи одного и того же процесса. Помните, что при перемножении двух отрицательных чисел получается положительное число. Таким образом, при возведении в квадрат отрицательного числа получится положительное число.
- Например, -5х-5 = 25. Также 5х5 = 25. Таким образом, квадратный корень из 25 равен -5 и 5. То есть в результате извлечения квадратного корня получаются два числа.
- Например, 3×3 = 9 и -3x-3 = 9, поэтому квадратный корень из 9 равен 3 и -3 (записывается как ±3).
 Положительный результат называется арифметическим значением корня, и на данном этапе можно рассматривать только это значение.[6] X Источник информации [7] X Источник информации
Положительный результат называется арифметическим значением корня, и на данном этапе можно рассматривать только это значение.[6] X Источник информации [7] X Источник информации
2
Воспользуйтесь калькулятором. Отлично, если вы умеете извлекать корни вручную, но существует множество онлайн-калькуляторов, при помощи которых можно извлечь корень из любого числа.
- В обыкновенном калькуляторе тоже есть клавиша со значком радикала.
- В случае онлайн-калькулятора просто введите число, из которого нужно извлечь квадратный корень, и нажмите соответствующую кнопку. Компьютер вычислит квадратный корень из этого числа.[8] X Источник информации
Реклама
Советы
- Обязательно запомните следующие полные квадраты:
- 02 = 0, 12 = 1, 32 = 9, 42 = 16, 52 = 25, 62 = 36, 7 2 = 49, 82 = 64, 92 = 81, 102 = 100
- Также рекомендуется запомнить такие полные квадраты: 112 = 121, 122 = 144, 132 169, 142 = 196, 152 = 225, 162 = 256, 172 = 289
- А эти полные квадраты запомнить совсем легко: 102 = 100, 202 = 400, 302 = 900, 402 = 1600, 502 = 2500
Реклама
Источники
Об этой статье
На других языках
Как извлечь квадратный корень без калькулятора — Wiki How Русский
Извлечь квадратный корень довольно легко, если под знаком корня стоит целое число (полный квадрат). В противном случае квадратный корень (из любого числа) можно извлечь вручную, то есть без калькулятора. Чтобы пользоваться описанным методом, нужно знать основные математические операции: умножение, сложение и деление.
В противном случае квадратный корень (из любого числа) можно извлечь вручную, то есть без калькулятора. Чтобы пользоваться описанным методом, нужно знать основные математические операции: умножение, сложение и деление.
Реклама
Что сумма корней. Правила вычитания корней
Корень из числа проще всего вычесть с помощью калькулятора. Но, если у вас нет калькулятора, тогда надо знать алгоритм вычисления квадратного корня. Дело в том, что под корнем сидит число в квадрате. Например, 4 в квадрате — это 16. То есть корень квадратный из 16 будет равен четырем. Так же 5 в квадрате — это 25. Поэтому корень из 25 будет 5. И так далее.
Если число небольшое, то его можно легко вычесть устно, к примеру, корень из 25 будет равен 5, а корень из 144-12. Также на калькуляторе можно посчитать, есть специальный значок корня, нужно вбить число и нажать на значок.
Поможет также таблица квадратных корней:
Есть еще способы, которые более сложные, однако очень эффективные:
Корень из какого либо числа можно вычесть с помощью калькулятора, тем более они есть в каждом телефоне на сегодняшний день.
Можно попробовать примерно прикинуть как может получится данное число, умножив одно число само на себя.
Вычислить корень квадратный из числа не сложно, особенно, если есть специальная таблица. Всем хорошо известная таблица еще с уроков алгебры. Такая операция называется извлечение квадратного корня из числа quot;aquot;, другими словами решение уравнения. Почти все калькуляторы, в смартфонах имеют функцию определения квадратного корня.
Результатом извлечения квадратного корня из известного числа будет другое число, которое, при возведении во вторую степень (квадрат), даст то самое число, которое нам известно. Рассмотрим одно из описаний расчтов, которое представляется кратким и понятным:
Вот видео по теме:
Вычеслить корень квадратный из числа можно несколькими способами.
Самым популярным способом — является использование специальной таблицы кореня (смотрите ниже).
Также на каждом калькуляторе есть функция при помощи которой можно узнать корень.
Или при помощи специальной формулы.
Извлечь квадратный корень из числа можно несколькими способами. Один из них — самый быстрый, с помощью калькулятора.
Но если нет калькулятора, то можно это сделать вручную.
Результат получится точным.
Принцип практически такой же как деление столбиком:
Попробуем без калькулятора найти значение квадратного корняот числа, к примеру, 190969.
Таким образом, вс предельно просто. В вычислениях главное придерживаться определнных простых правил и логически размышлять.
Для этого нужна таблица квадратов
Вот например, корень из 100 = 10, из 20 = 400 из 43 = 1849
Сейчас практически все калькуляторы, в том числе и на смартфонах умеют высчитывать квадратный корень из числа. НО если калькулятора у вас нет, то можно найти корень из числа несколькими простыми способами:
Разложение на простые множители
Разложите подкоренное число на множители, являющиеся квадратными числами.
В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа числа, из которых можно извлечь целый квадратный корень. Множители числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как 25 = 5, 36 = 6, 49 = 7. Квадратные множители это множители, являющиеся квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 это квадратное число. Разделив 400 на 25, вы получите 16, которое также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
Запишите это как: 400 = (25 х 16).
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть (а х b) = a x b .
Воспользовавшись этим правилом, извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
В нашем примере извлеките корень из 25 и из 16.
Если подкоренное число не раскладывается на два квадратных множителя (а это происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
Теперь вы можете оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу.
Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (1 = 1) и 4 (4 = 2). Таким образом, значение 3 расположено между 1 и 2. Та как значение 3, вероятно, ближе к 2, чем к 1, то наша оценка: 3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
Этот метод также работает с большими числами. Например, рассмотрим 35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (25 = 5) и 36 (36 = 6). Таким образом, значение 35 расположено между 5 и 6. Та как значение 35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что 35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
Еще один способ разложите подкоренное число на простые множители.
Простые множители числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, 45 = (3 х 3 х 5). 3 можно вынести за знак корня: 45 = 35. Теперь можно оценить 5.
Рассмотрим другой пример: 88.
= (2 х 4 х 11)
= (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
2(2 х 11) = 22 х 11. Теперь можно оценить 2 и 11 и найти приблизительный ответ.
Может быть полезным будет еще это обучающее видео:
Чтобы извлечь корень из числа следует воспользоваться калькулятором, либо если нет подходящего, советую зайти вот на этот сайт и решить задачу с помощью онлайн калькулятора, который за секунды выдаст правильное значение.
Квадратным корнем из числа X называется число A , которое в процессе умножения самого на себя (A * A ) может дать число X .
Т.е. A * A = A 2 = X , и √X = A .
Над квадратными корнями (√x ), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение. Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.
Шаг 1. Извлечение квадратных корней
Во-первых, для сложения квадратных корней сначала нужно эти корни извлечь. Это можно будет сделать в том случае, если числа под знаком корня будут полными квадратами. Для примера возьмем заданное выражение √4 + √9 . Первое число 4 является квадратом числа 2 . Второе число 9 является квадратом числа 3 . Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5 .
Второе число 9 является квадратом числа 3 . Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5 .
Все, пример решен. Но так просто бывает далеко не всегда.
Шаг 2. Вынесение множителя числа из-под корня
Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54 .
Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3 ,
54 = 2 * 3 * 3 * 3 .
В числе 24 мы имеем множитель 4 , его можно вынести из-под знака квадратного корня. В числе 54 мы имеем множитель 9 .
Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6 .
Рассматривая данный пример, мы получаем вынос множителя из-под знака корня, тем самым упрощая заданное выражение.
Шаг 3. Сокращение знаменателя
Рассмотрим следующую ситуацию: сумма двух квадратных корней — это знаменатель дроби, например, A / (√a + √b) .
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b .
Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a — b .
Аналогично, если в знаменателе имеется разность корней: √a — √b , числитель и знаменатель дроби умножаем на выражение √a + √b .
Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3) .
Пример сложного сокращения знаменателя
Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.
Для примера берём дробь: 12 / (√2 + √3 + √5) .
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5 .
Получаем:
12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.
Шаг 4. Вычисление приблизительного значения на калькуляторе
Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней. Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.
Пример вычисления приблизительного значения
Необходимо вычислить приблизительное значение данного выражения √7 + √5 .
В итоге получаем:
√7 + √5 ≈ 2,65 + 2,24 = 4,89 .
Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо. То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.
Полезный совет: если вы решили разложить число на множители, для того, чтобы вывести квадрат из-под знака корня, вам необходимо сделать обратную проверку, то есть перемножить все множители, которые получились в результате вычислений, и в конечном результате этого математического расчёта должно получиться число, которое нам было задано первоначально.
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Содержимое:
В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня. Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
Шаги
Часть 1 Определение корней
- 1 Обозначение корней. Выражение под знаком корня (√) означает, что из этого выражения необходимо извлечь корень определенной степени.
- Корень обозначают знаком √.
- Показатель (степень) корня пишется слева над знаком корня. Например, кубический корень из 27 записывается так: 3 √(27)
- Если показатель (степень) корня отсутствует, то показатель считается равным 2, то есть это квадратный корень (или корень второй степени).
- Число, записанное перед знаком корня, называется множителем (то есть это число умножается на корень), например 5√(2)
- Если множителя перед корнем нет, то он равен 1 (напомним, что любое число, умноженное на 1, равняется самому себе).

- Если вы впервые работаете с корнями, сделайте соответствующие пометки над множителем и показателем корня, чтобы не запутаться и лучше понять их назначение.
- 2 Запомните, какие корни можно складывать, а какие нельзя. Также, как нельзя складывать разные члены выражения, например, 2а + 2b ≠ 4ab, вы не можете складывать разные корни.
- Нельзя складывать корни с разными подкоренными выражениями, например, √(2) + √(3) ≠ √(5). Но вы можете сложить числа, стоящие под одним корнем, например, √(2 + 3) = √(5) (квадратный корень из 2 примерно равен 1,414, квадратный корень из 3 примерно равен 1,732, а квадратный корень из 5 примерно равен 2,236).
- Нельзя складывать корни с одинаковыми подкоренными выражениями, но разными показателями, например, √(64) + 3 √(64) (эта сумма не равна 5 √(64), так как квадратный корень из 64 равен 8, кубический корень из 64 равен 4, 8 + 4 = 12, что гораздо больше, чем корень пятой степени из 64, который примерно равен 2,297).

Часть 2 Упрощение и сложение корней
- 1 Определите и сгруппируйте подобные корни. Подобные корни – корни, у которых одинаковые показатели и одинаковые подкоренные выражения. Например, рассмотрим выражение:
2√(3) + 3 √(81) + 2√(50) + √(32) + 6√(3)- Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
2√(3) + 2√(50) + √(32) + 6√(3) + 3 √(81) - Затем перепишите выражение так, чтобы корни с одинаковым показателем и с одинаковым подкоренным выражением располагались последовательно.
2√(50) + √(32) + 2√(3) + 6√(3) + 3 √(81)
- Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
- 2 Упростите корни. Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.
- В приведенном выше примере разложите число 50 на 2*25, а число 32 – на 2*16. Из 25 и 16 можно извлечь квадратные корни (соответственно 5 и 4) и вынести 5 и 4 из-под корня, соответственно умножив их на множители 2 и 1.
 Таким образом, вы получите упрощенное выражение: 10√(2) + 4√(2) + 2√(3) + 6√(3) + 3 √(81)
Таким образом, вы получите упрощенное выражение: 10√(2) + 4√(2) + 2√(3) + 6√(3) + 3 √(81) - Число 81 можно разложить на множители 3*27, а из числа 27 можно извлечь кубический корень, равный 3. Это число 3 можно вынести из-под корня. Таким образом, вы получите еще более упрощенное выражение: 10√(2) + 4√(2) + 2√(3)+ 6√(3) + 3 3 √(3)
- В приведенном выше примере разложите число 50 на 2*25, а число 32 – на 2*16. Из 25 и 16 можно извлечь квадратные корни (соответственно 5 и 4) и вынести 5 и 4 из-под корня, соответственно умножив их на множители 2 и 1.
- 3 Сложите множители подобных корней. В нашем примере есть подобные квадратные корни из 2 (их можно сложить) и подобные квадратные корни из 3 (их тоже можно сложить). У кубического корня из 3 подобных корней нет.
- 10√(2) + 4√(2) = 14√(2).
- 2√(3)+ 6√(3) = 8√(3).
- Окончательное упрощенное выражение: 14√(2) + 8√(3) + 3 3 √(3)
- Не существует общепринятых правил порядка записи корней в выражении. Потому вы можете записывать корни в порядке возрастания их показателей и в порядке возрастания подкоренных выражений.
Приветствую, котаны! В прошлый раз мы подробно разобрали, что такое корни (если не помните, рекомендую почитать). Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.
Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.
Сегодня мы идём дальше. Будем учиться умножать корни, изучим некоторые проблемы, связанные с умножением (если эти проблемы не решить, то на экзамене они могут стать фатальными) и как следует потренируемся. Поэтому запасайтесь попкорном, устраивайтесь поудобнее — и мы начинаем.:)
Вы ведь тоже ещё не вкурили?
Урок получился довольно большим, поэтому я разделил его на две части:
- Сначала мы разберём правила умножения. Кэп как бы намекает: это когда есть два корня, между ними стоит знак «умножить» — и мы хотим что-то с этим сделать.
- Затем разберём обратную ситуацию: есть один большой корень, а нам приспичило представить его в виде произведения двух корней попроще. С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.
Тем, кому не терпится сразу перейти ко второй части — милости прошу. С остальными начнём по порядку.
С остальными начнём по порядку.
Основное правило умножения
Начнём с самого простого — классических квадратных корней. Тех самых, которые обозначаются $\sqrt{a}$ и $\sqrt{b}$. Для них всё вообще очевидно:
Правило умножения. Чтобы умножить один квадратный корень на другой, нужно просто перемножить их подкоренные выражения, а результат записать под общим радикалом:
\[\sqrt{a}\cdot \sqrt{b}=\sqrt{a\cdot b}\]
Никаких дополнительных ограничений на числа, стоящие справа или слева, не накладывается: если корни-множители существуют, то и произведение тоже существует.
Примеры. Рассмотрим сразу четыре примера с числами:
\[\begin{align} & \sqrt{25}\cdot \sqrt{4}=\sqrt{25\cdot 4}=\sqrt{100}=10; \\ & \sqrt{32}\cdot \sqrt{2}=\sqrt{32\cdot 2}=\sqrt{64}=8; \\ & \sqrt{54}\cdot \sqrt{6}=\sqrt{54\cdot 6}=\sqrt{324}=18; \\ & \sqrt{\frac{3}{17}}\cdot \sqrt{\frac{17}{27}}=\sqrt{\frac{3}{17}\cdot \frac{17}{27}}=\sqrt{\frac{1}{9}}=\frac{1}{3}.
\\ \end{align}\]
Как видите, основной смысл этого правила — упрощение иррациональных выражений. И если в первом примере мы бы и сами извлекли корни из 25 и 4 без всяких новых правил, то дальше начинается жесть: $\sqrt{32}$ и $\sqrt{2}$ сами по себе не считаются, но их произведение оказывается точным квадратом, поэтому корень из него равен рациональному числу .
Отдельно хотел бы отметить последнюю строчку. Там оба подкоренных выражения представляют собой дроби. Благодаря произведению многие множители сокращаются, а всё выражение превращается в адекватное число.
Конечно, не всегда всё будет так красиво. Иногда под корнями будет стоять полная лажа — непонятно, что с ней делать и как преобразовывать после умножения. Чуть позже, когда начнёте изучать иррациональные уравнения и неравенства, там вообще будут всякие переменные и функции. И очень часто составители задач как раз и рассчитывают на то, что вы обнаружите какие-то сокращающиеся слагаемые или множители, после чего задача многократно упростится.
Кроме того, совсем необязательно перемножать именно два корня. Можно умножить сразу три, четыре — да хоть десять! Правило от этого не поменяется. Взгляните:
\[\begin{align} & \sqrt{2}\cdot \sqrt{3}\cdot \sqrt{6}=\sqrt{2\cdot 3\cdot 6}=\sqrt{36}=6; \\ & \sqrt{5}\cdot \sqrt{2}\cdot \sqrt{0,001}=\sqrt{5\cdot 2\cdot 0,001}= \\ & =\sqrt{10\cdot \frac{1}{1000}}=\sqrt{\frac{1}{100}}=\frac{1}{10}. \\ \end{align}\]
И опять небольшое замечание по второму примеру. Как видите, в третьем множителе под корнем стоит десятичная дробь — в процессе вычислений мы заменяем её обычной, после чего всё легко сокращается. Так вот: очень рекомендую избавляться от десятичных дробей в любых иррациональных выражениях (т.е. содержащих хотя бы один значок радикала). В будущем это сэкономит вам кучу времени и нервов.
Но это было лирическое отступление. Теперь рассмотрим более общий случай — когда в показателе корня стоит произвольное число $n$, а не только «классическая» двойка. {2n}}}=\left| a \right|. \\ \end{align}\]
{2n}}}=\left| a \right|. \\ \end{align}\]
Подобные «махинации» могут здорово сэкономить вам время на экзамене или контрольной работе, поэтому запомните:
Не спешите перемножать числа в подкоренном выражении. Сначала проверьте: вдруг там «зашифрована» точная степень какого-либо выражения?
При всей очевидности этого замечания должен признать, что большинство неподготовленных учеников в упор не видят точные степени. Вместо этого они перемножают всё напролом, а затем удивляются: почему это получились такие зверские числа?:)
Впрочем, всё это детский лепет по сравнению с тем, что мы изучим сейчас.
Умножение корней с разными показателями
Ну хорошо, теперь мы умеем перемножать корни с одинаковыми показателями. А что, если показатели разные? Скажем, как умножить обычный $\sqrt{2}$ на какую-нибудь хрень типа $\sqrt{23}$? Можно ли вообще это делать?
Да конечно можно. Всё делается вот по этой формуле:
Правило умножения корней.
{2}}}=\sqrt{5}. \\ \end{align}\]
Но тогда получается какая-то хрень:
\[\sqrt{-5}=\sqrt{5}\]
Этого не может быть, потому что $\sqrt{-5} \lt 0$, а $\sqrt{5} \gt 0$. Значит, для чётных степеней и отрицательных чисел наша формула уже не работает. После чего у нас есть два варианта:
- Убиться об стену констатировать, что математика — это дурацкая наука, где «есть какие-то правила, но это неточно»;
- Ввести дополнительные ограничения, при которых формула станет рабочей на 100%.
В первом варианте нам придётся постоянно вылавливать «неработающие» случаи — это трудно, долго и вообще фу. Поэтому математики предпочли второй вариант.:)
Но не переживайте! На практике это ограничение никак не влияет на вычисления, потому что все описанные проблемы касаются лишь корней нечётной степени, а из них можно выносить минусы.
Поэтому сформулируем ещё одно правило, которое распространяется вообще на все действия с корнями:
Прежде чем перемножать корни, сделайте так, чтобы подкоренные выражения были неотрицательны.
{2}}}=\sqrt{75}. \end{align}\]
Ну что ж, с умножением корней разобрались. Теперь рассмотрим обратную операцию: что делать, когда под корнем стоит произведение?
Значения кнопок на калькуляторе
Skip to content
Содержание:
- 1 Простейшие калькуляторы
- 2 Дополнительные кнопки
- 2.1 Бухгалтерские калькуляторы
- 2.2 Что означают кнопки инженерного калькулятора
Такие простые с первого взгляда устройства, как калькуляторы, могут оказаться сложными в обращении.
Всеми возможностями этих «счетных машинок» не пользуются даже опытные бухгалтеры, финансисты и программисты, уже не говоря о школьниках или студентах.
В первой части нашего материала рассмотрим функции самых простых калькуляторов (в качестве примера возьмем кнопки калькулятора Citizen), во второй – бухгалтерских, и в заключительной — инженерных (с поддержкой вычисления функций и т.п.).
За что отвечают кнопки на калькуляторе
Простейшие калькуляторы
Неотъемлемая часть любой вычислительной техники, работающей с числами – клавиши для ввода цифр.
Поэтому кнопки от «0» до «9» в представлении не нуждаются.
Операторы основных математических операций, такие как умножение («*» или «×»), деление («/» или «÷»), сложение («+»), вычитание («-») и сравнение («=») знакомы по урокам математики.
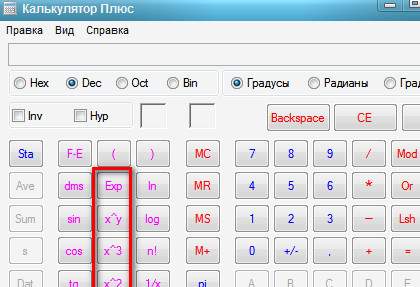
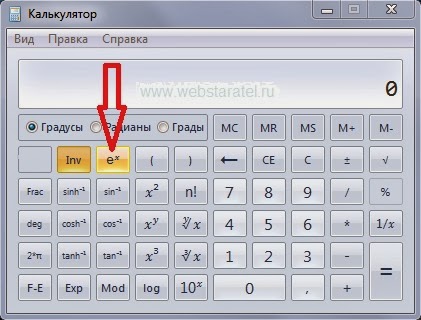
Не должны вызвать проблем и операторы «квадратный корень от числа» («√»), квадрат числа («x2»), а также часть целого («1/x», единица делится на отображаемое значение).
Однако, с виду простой оператор % оказывается на деле сложен в использовании.
Если набрать любое число и нажать %, значение обнулится. И верно, ведь 1% — это одна сотая доля от какого-либо числа, а значит, требуемую к вычислению долю/часть необходимо дополнительно задать.
100+10%=110, ведь 10% от предыдущего числа (от 100) – это 10, а 100+10=110.
Аналогичные процедуры можно производить и с другими математическими операциями («-«, «/», «*»).Дополнительные кнопки
- ± — позволяет сменить текущее положительное число на отрицательное или наоборот (очень полезно в качестве модуля отрицательного числа, нет необходимости вводить полученную разницу без минуса).
- . – разделитель разрядов (десятичный разделитель).
- C / AC – сокращение от англ. «Clean» — «очистить» (AC – «All Clean» — «очистить все»), стирает все введенные ранее данные, в том числе и из памяти.
- CE – сокращение от англ. «Clean Entry» — «очистить запись», нажатие на эту кнопку очищает только текущее поле ввода (все, что было в памяти, сохраняется).
- Если кнопка C совмещена с CE (C/CE) , то для очистки ввода необходимо нажать 1 раз на указанную клавишу, а для полной очистки – 2 раза.
- Если на устройстве клавиши ON, C, CE и AC разнесены отдельно, то кнопка C сбрасывает только последнее выражение, CE – очищает дисплей, включая последний операнд, а AC – очищает все данные.
- Sqrt — означает квадратный корень.
Кнопки памяти на калькуляторе выносятся отдельным блоком и требуют определенных последовательностей работы с ними.
- MS – от англ. «Memory Save» («Сохранить в памяти») – нажатие записывает текущее значение на дисплее в буфер памяти для последующего использования.
- MC – от англ. «Memory Clean» («Очистить память») – удаляет все данные в памяти (обнуляет).
- MR — от англ. «Memory Read» («Прочитать память») – отображает текущее содержимое буфера.
- M- — вычитает значение в буфере из текущего значения на дисплее и сохраняет в буфер памяти, итоговое значение можно увидеть только после нажатия MR.
- M+ — аналогично M-, только значение прибавляется и сохраняет обратно в буфер.
В качестве примера.
- Если написать на дисплее число 555 и нажать MS (или M+, что равноценно при нулевом/исходном состоянии буфера памяти, так как текущее значение прибавится к нулю в буфере и сохранится как 555), затем CE, то значение на дисплее обнулится, но в памяти сохранится 555.
- Узнать это можно, выведя буфер клавишей MR. Отобразится 555. Нажав M-, мы вычтем из текущего значения буфер (555) и запишем его вместо старого значения (555-555=0). На дисплее ничего не изменится. Узнать новое значение памяти можно, нажав снова MR – отобразится 0.
- Вторая ячейка памяти будет обозначаться «MII» (не на всех моделях калькуляторов).
Бухгалтерские калькуляторы
Бухгалтерские модели устройств имеют дополнительные функции, такие как GT, MU, EX (не путать с EXP), TAX и другие (быстрый ввод нулей «00», «000», округление до заданного знака и в требуемую сторону, и т.п.). Ниже рассмотрим наиболее популярные клавиши.
- GT («Grand Total» — «общая сумма») позволяет суммировать результаты всех произведенных вычислений с момента обнуления («CA»).
То есть после трех следующих вычислений:
2*3=6 (нажатие CE)
5-3=2 (нажатие CE)
5/2=2,5Нажатие GT отобразит результат 10,5 (6+2+2,5). Повторное нажатие GT обнулит регистр суммы.
- MU (от англ. «Mark Up» — «наценка») – позволяет рассчитать надбавки в зависимости от исходных задач.
Нагляднее всего операции с кнопкой MU демонстрируют равнозначные математические формулы ниже:
X+Y (MU) = 100 * (X+Y)/Y
X-Y (MU) = 100 * (X-Y)/Y
X*Y (MU) = X * (1 + Y/100)
X/Y (MU) = X / (1 — Y/100)
- EX – функция замены введенных операторов местами, очень полезна при ошибках ввода.
Например:
9 / 10 = 0,9
А если ввод был перепутан:
10/9 EX = 0,9
- TAX+ и TAX — помогают работать с налогами (чаще всего у бухгалтеров это НДС), они работают вкупе с кнопкой SET, устанавливающей требуемую ставку.
Таким образом, первым делом устанавливается ставка (кнопкой SET), например, в 20%, и далее производятся вычисления с использованием TAX:
400 «TAX+» = 480 (при ставке 20%),
400 «TAX-» = 320.Очень полезными будут функции округления, которые часто реализуются специальными переключателями.
- Стрелка вверх – в этом положении калькулятор принудительно будет округлять все получаемые результаты в сторону увеличения (при любом знаке после заданного разряда больше нуля).
- Стрелка вниз – в этом положении устройство будет действовать аналогично, но округлять в меньшую сторону.
- «4/5» — это не простая дробь, как может показаться. В этом положении счетное устройство будет работать в соответствии с логикой рациональных вычислений (при следующем знаке после требуемого разряда меньшем 5 округление производится в сторону уменьшения, а при 5 и более – в сторону увеличения).
- Флажок со шкалой «0,1,2,3,4,5» позволяет быстро задать разряд округления после целого числа (0 – до целых, 1 – до десятичных и т.д.).
Что означают кнопки инженерного калькулятора
Инженерные калькуляторы могут быть весьма сложными в обиходе ввиду того, что позволяют реализовывать множество стандартных функций высшей математики и поддерживают ввод сложносоставных выражений.
На некоторых моделях можно составлять полноценные программы (в сети даже есть видео с запуском 3D игр на таких устройствах).
Описание стандартных возможностей в оригинальных инструкциях занимает несколько десятков страниц.
Лучше всего значение кнопок на инженерном калькуляторе уточнять именно в официальной инструкции или на сайте производителя.
Почему? Очень часто функции требуют соблюдения определенного синтаксиса, а большинство тригонометрических функций может работать только с заданными единицами измерения углов (одни работают только с градусами, одни только с радианами, есть универсальные модели и т.
п.).
Во всем остальном обозначения и логика расчета полностью совпадают с требованиями высшей математики. То есть достаточно знать, как пишется функция и для чего она нужна, и тогда результат и процесс вычисления станет понятен («tg», «ctg», «sin», «cos», «acos», «actg», «atg», «logyx» и др.).
Единственная рекомендация – ставьте больше скобок, чтобы правильно распределить приоритеты в порядке действий по вычислениям. И тогда результат не станет для вас неожиданностью.
[ OFF ] – выключение. Если в течение 8–11 мин. не нажималась ни одна клавиша, калькулятор автоматически отключается.
[+][-][ x ][ ¸ ] – арифметические операции
[ CE / C ] – сброс последнего набранного числа/сброс
[ AC ] – общий сброс
[ M +] – занесение числа в память с плюсом
[ M -] – занесение числа в память с минусом
[ MRC ] – извлечение из памяти. После второго нажатия память обнуляется. В некоторых моделях данные функции разделены (клавиши [ MR ][ MC ])
[ MII +][ MII -][ MIIRC ] – работа со второй ячейкой памяти
[ MU ] – операция «Повышение цены» (может не работать)
[ GT ] – автоматическое суммирование операций
[ √ ] – извлечение квадратного корня
[♪] – звуковое подтверждение нажатия клавиш вкл.
/выкл.
[→] – стирание последней введенной цифры
A 0 2 3 F – переключатель положения знака
в десятичной дроби
0,2,3 – число знаков после запятой, А – режим расчета денежных единиц, F – фиксированная запятая
— переключатель режима округления
ИНСТРУКЦИЯ ПО ПРИМЕНЕНИЮ КАЛЬКУЛЯТОРА
Вычисление квадратного корня
= 7
[(6 + 4) ´ 2 — 8]/5 = 2.4
6 + 4 ´ 2 — 8 / 5 = 2.4
Вычисления с константами
4 ´ 3 =12, 4 ´ 5 = 20
6 / 2 = 3, 8 / 2 = 4
Вычисления с памятью
(5 ´ 0.25)+(6 ´ 0.75)-(2 ´ 0.15)=5.45
Питание от батареи G10*2
Примечание. В данной модели калькулятора возможно отсутствие, объединение или дополнение некоторых операционных клавиш.
Продавец: «Первый Оптовый» (купить калькуляторы оптом можно именно у нас)
Питание калькулятора – от источника питания 1.5 в типа G13.
Рабочая температура от 0 до +40 о С
Средний срок эксплуатации – 5 лет.
Гарантия — 1 месяц.
Гарантия не распространяется на элементы питания.
Калькулятор не подлежит гарантийному ремонту, возврату или замене при отсутствии упаковки; при наличии механических повреждений.
А теперь внимательно посмотрите на свой настольный калькулятор.
Возможно, вы до сих пор не раскрыли весь его потенциал!
В нашем цикле статей мы подробно расскажем о всех возможностях вашего калькулятора, о которых вы даже не догадывались!
Расчет налогов [+TAX] [-TAX] [RATE] Функция, позволяющая автоматически вычислять цену товара с учетом налога или без учета налога (например цена товара с НДС или без НДС).
Используется в моделях калькуляторов:
Как это работает? [+TAX] [-TAX] [RATE] 1-й шаг
Ввести число процентов в память калькулятора.
Для этого нажать последовательно 18 [RATE] [+TAX]
(налог в данном случае равен 18%).Введенное значение налога будет использоваться в дальнейшем при вычислениях и не сотрется, пока вы не замените его на новое.
Чтобы посмотреть записанное число процентов, нажмите [RATE] [-TAX].
Калькулятор CITIZEN настольный CDC-80VRD BP, 8 разр., двойное питание.
2-й шаг [+TAX]
Если вы имеете цену без НДС, и хотите узнать цену с НДС.
Введите цену товара без налога — [100], нажмите[+TAX] и цена с НДС будет указана на дисплее => [118]
Нажмите[+TAX] ещё раз чтобы увидеть суму НДС: [18]
(на индикаторе высветится значок TAX).3-й шаг [-TAX]
Если вы имеете цену с НДС, и хотите узнать цену без НДС.
lВведите цену товара с налогом — [147,50] и нажмите [-TAX] — цена без НДС будет указана на дисплее => [125]
lНажмите кнопку [-TAX] чтобы узнать сумму НДС – [22,50]
(на индикаторе высветится значок TAX).
Калькулятор CITIZEN настольный SDC-760N, 16 разр., двойное питание.
Переключатель запятой – F – плавающая запятая — отсутствие фиксации запятой (выключение режима округления). Если вам не нужно округлять числа всегда ставьте переключатель в положение F.
– 0– 2– 3– 4–определяют, сколько знаков после запятой будет показывать индикатор.
– A – ADD–mode — режим «Автоматической запятой«. Этот режим удобен для тех, кто постоянно работает с деньгами, вводя целые и сотые доли единиц (рубли/копейки, доллары/центы и т. п.). В этом режиме при сложении и вычитании не нужно вводить десятичную точку. Она вводится автоматически.
Рубрики
- Без рубрики
- Дримкаст аксессуары
- Дримкаст игры
- Дримкаст прохождения
- Дримкаст эмуляторы
- История
- Компьютеры
- Помощь
- Приставки
Adblock
detectorтеория чисел — Вычисление n-го корня в простом калькуляторе?
Задавать вопрос
Спросил
Изменено 6 лет, 11 месяцев назад
Просмотрено 70 тысяч раз
$\begingroup$
Недавно во время моего урока физики, как извлечь кубический корень в простом калькуляторе.
Выполните шаги, указанные ниже
Шаг 1. Нажмите кнопку квадратного корня 13 раз 9{\frac 1r}}=\sqrt[r]x$$
Чтобы получить наилучшую точность для этого метода, нужно извлечь квадратный корень (а затем снова возвести его в квадрат) достаточное количество раз, чтобы приблизиться к пределу, без потеря точности из-за отбрасывания слишком большого количества значащих цифр.
$\endgroup$
$\begingroup$
Для чисел, очень близких к 1, функция корня $n$ имеет наклон $1/n$, то есть корень $n$ из $1+x$ приблизительно равен $1+x/n$, когда x очень маленький. Ваш учитель использовал повторяющиеся корни, чтобы получить число в диапазоне, где это верно, а затем повторил возведение в квадрат, чтобы вернуть результат в его правильный диапазон. Эти функции (квадратный корень и квадрат) не влияют на вычисление кубического корня, если они совпадают. 9{\ln(\sqrt[3]{x})}=\sqrt[3]{x}$.
Тот же аргумент работает, когда вы заменяете $3$ другими числами.
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Квадратный корень в калькуляторе вашего компьютера
Квадратный корень в калькуляторе вашего компьютера
Ваш компьютерный калькулятор       У этой страницы две цели — объяснить математику квадрата корни и объяснить, как использовать калькулятор для получения точного корня или приближенного значения корня.
    Два набора справочных материалов подготовят вас к этой задаче — математические определения и словарный запас и другие функции или кнопки калькулятора.
Чтобы подготовиться к работе с калькулятором, сначала посетите:
- постоянная функция
- обратное число
- Включает калькулятор вашего компьютера
    силы десяти, полномочия, главный корень, площадь, квадратный корень, радикальный, знак радикала и подкоренное.
Оставить оба заметки открыты и ваш калькулятор открытый.
    Используйте кнопку КАЛЬКУЛЯТОР для просмотра изображения калькулятора компьютера.
Квадратный корень       Вычислите в уме квадратные корни в первых двух примерах. Затем используйте калькулятор на своем компьютере, чтобы завершить каждый пример, чтобы увидеть как работает калькулятор.
Чтобы извлечь квадратный корень, вы должны:
- Введите начальный номер
- Нажмите []
Пример #1: Квадратный корень из 25
- [25] []
- 5 это главный квадратный корень из 25
«Лошадь другого цвета»       «Лошадь другого цвета» — это выражение, используемое в ситуации в которой, хотя человек много знает об одной ситуации, текущая ситуация достаточно отличается, чтобы рассматривать его как совершенно другую ситуацию.
Пример №3: Упрощение:
- [4], для начала писать -4
- [+/-], поменять знак и написать -4,
- [], чтобы извлечь квадратный корень
- на калькуляторе появляется сообщение об ошибке — «недопустимый ввод для функции»
- 2 и , воображаемый и сложный число является правильным главным квадратным корнем из -4
      Это означает, что этот калькулятор не может «говорить» на всех языках людей использовать, когда они делают математику.
Этот калькулятор не может выполнить требуемую работу — это не сделано для этой цели. Научный или графический калькулятор, использующий комплексные числа. требуется для.
Другой пример: «Кто-то использует Джона наверху»       Вы знаете… «Кто-то использует наверху, Джон» — высокий котел в использовании — гипотенуза — та штука с Теорема Пифагора.
    Возможно, вы сможете завершить этот пример в уме. Посмотрите, насколько больше требуется работа, когда калькулятор выполняет арифметические действия.
Пример 4. Найдите гипотенуза или прямоугольный треугольник, у которого стороны 3 единицы и 4 единицы.
- Вызов: a² + b² = c²
- Переформулировать текущую информацию:   3² + 4² = c²
- Итак, с помощью калькулятора находим: c = +
- [3][x][3][=], чтобы получить 9
- [МС], для хранения 9
- [4][x][4][=], чтобы получить 16
- [M+], чтобы добавить это в память
- [MR], чтобы вызвать сохраненную сумму, 25
- [], чтобы извлечь квадратный корень
- 5 это главный квадратный корень из 25
- Гипотенуза имеет длину 5 единиц.
Половинная мощность     площадь и квадратный корень обратный операций — одно отменяет другое. Экспоненциальное обозначение, или силы, привыкшие к указать, что каждый преднамеренно взаимные друг другу.
- Чтобы возвести в квадрат, возведите во вторую степень — во вторую степень.
- Чтобы получить квадратный корень, возведите в половинную степень — в 1/2 степени.
- Чтобы сделать куб, возведите в третью степень — в третью степень.
- Чтобы получить кубический корень, возведите в степень 1/3 — степень 1/3.
- Чтобы «отменить» четвертую степень, используйте одну четвертую степень —
- Сила 1/4 «отменяет» силу 4.
- Чтобы «отменить» пятый корень, используйте пятую степень —
- сила 5 «отменяет» силу 1/5.
- Пример №5. Возведение квадратного корня в квадрат для получения
- исходного числа
- Выберите любое положительное число, включая десятичные дроби.
- — и введите его в калькулятор.
- Нажмите [], клавишу квадратного корня
- — для извлечения квадратного корня.
- Нажмите [MS], клавиша сохранения в памяти
- — для сохранения десятичной аппроксимации числа.
- Теперь вы знаете оба:
- — ОРИГИНАЛЬНЫЙ НОМЕР и
- — ПРИБЛИЗИТЕЛЬНЫЙ КВАДРАТНЫЙ КОРЕНЬ КВАДРАТНОГО КАЛЬКУЛЯТОРА.
- Нажмите [x], затем [MR], затем [=]
- — умножить отображаемый корень сам на себя.
- РЕЗУЛЬТАТ ИСХОДНЫЙ НОМЕР
- — Квадрат квадратного корня является исходным числом.
    Далее расширяем список некоторых сил два, так что половинные мощности также включены.
Пример #6: Еще больше степеней двойки
- , 2 до нуля
- есть , квадратный корень из 2
- это 2 к первому
- есть , 2 раза больше квадратного корня из 2
- есть , 2 в квадрате
- есть , 2 в квадрате, умноженный на квадратный корень из 2
- это
2 в кубе- есть , 2 в кубе, умноженный на квадратный корень из 2
- есть , 2 к четвертому
    Итак, возведение числа в половинную степень означает квадратный корень.
    Следующий, вернуться к стр. 7 из ПОЖАЛУЙСТА, ИЗВИНИТЕ МОЮ ДОРОГУЮ ТЕТУ САЛЛИ!, Порядок действий.
    Эта страница предоставлена вам MATHEMATICAL CONCEPTS, Inc., издателями МАТЕМАТИКА ГОВОРЯТ ЗДЕСЬ! , ISBN: 0-9623593-5-1.
    Настоящим вам предоставляется разрешение сделать ОДНУ печатную копию этой страницы и его изображения для вашего ЛИЧНОГО и некоммерческого использования.
ВЫ МОЖЕТЕ НЕ СДЕЛАТЬ ЛЮБЫЕ ДОПОЛНИТЕЛЬНЫЕ КОПИИ ЭТОЙ СТРАНИЦЫ, ЕЕ ИЗОБРАЖЕНИЙ, ЕЕ ЗВУКОВЫХ КЛИПОВ ИЛИ ЕЕ АНИМИРОВАННЫХ ГИФКИ БЕЗ РАЗРЕШЕНИЯ ОТ: [email protected] или по почте на адрес адрес ниже.
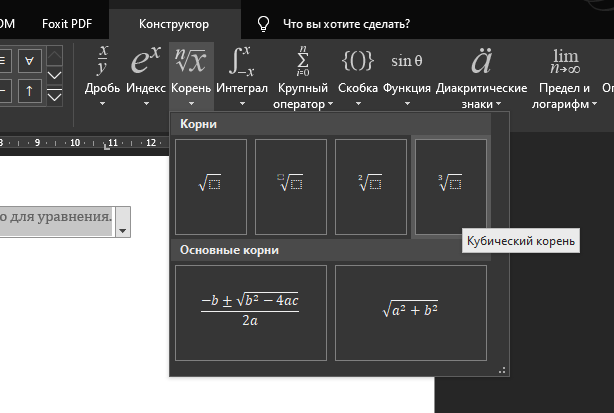
Как вычислить КВАДРАТНЫЙ КОРЕНЬ в Excel [5 лучших методов] + добавить символ
Главная ➜ Формулы Excel ➜ Как вычислить КВАДРАТНЫЙ КОРЕНЬ в Excel + вставить символ
Что такое КВАДРАТНЫЙ КОРЕНЬ?
Метод-1: Используйте функцию SQRT, чтобы найти КВАДРАТНЫЙ корень числа
Метод-2: Вычислите КВАДРАТНЫЙ корень числа, используя функцию POWER
Метод-3: Примените формулу экспоненты, чтобы получить КВАДРАТНЫЙ корень числа
Метод-4: Код VBA для отображения КВАДРАТНОГО корня числа
Метод-5: Использование Power Query для преобразования чисел в КВАДРАТНЫЕ корни
[Дополнительный совет] Как добавить символ квадратного корня в Excel
Образец файла
Заключение
Дополнительные формулы
Excel подобен швейцарскому армейскому ножу для расчетов.
От математических до финансовых, это для каждой вещи, которую вам нужно рассчитать. Вы можете вычислять простые и самые сложные вещи в Excel.
Возьмем, к примеру, КВАДРАТНЫЙ КОРЕНЬ . Квадратный корень — это довольно распространенный расчет, который мы делаем в нашей повседневной работе, и в Excel вы можете легко его вычислить.
Знаешь что?
Я обнаружил, что существует пять различных способов вычисления квадратного корня в Excel. Да, пять разных методов, которые можно использовать в разных ситуациях.
И сегодня в этом посте я хотел бы поделиться с вами этими пятью простыми методами нахождения квадратного корня числа в Excel. Итак, давайте изучим это дело.
Что такое КВАДРАТНЫЙ КОРЕНЬ?
Прежде чем мы научимся его вычислять, важно понять, что он на самом деле означает, как мы обычно его вычисляем.
Вычисление квадратного корня является обратным вычислением для возврата к корню из квадрата.
Итак, когда вы вычисляете квадрат 10, умножая его на себя, это (10 * 10 = 100).
Тогда квадратный корень означает возвращение от 100 к 10.
Подробнее об этом можно узнать из Википедии. Но теперь давайте узнаем, как мы можем сделать это в Excel.
Как я уже сказал, мы можем использовать 5 различных способов вычисления квадратного корня в соответствии с необходимостью или личными предпочтениями.
Не все методы одинаковы, но полезны.
Метод-1: Используйте функцию КОРЕНЬ, чтобы найти КВАДРАТНЫЙ корень числа
Если вам нужно использовать только один метод для вычисления квадратного корня, используйте функцию КОРЕНЬ. Для этого есть специальная функция.
Вам просто нужно обратиться к ячейке или указать номер.
Синтаксис SQRT: Где число — это число или ссылка на ячейку, которая содержит число, для которого вы хотите найти квадратный корень.
SQRT(число)
Примеры:
В приведенном ниже примере у нас есть число 625 в ячейке A1. Итак, чтобы вычислить квадратный корень для этого, мы можем вставить приведенную ниже формулу (Панель формул) в B1.
=SQRT(A1)
Возвращаемое значение равно 25, что является квадратным корнем из 625. Как видите, SQRT прост в использовании и прост в применении.
Если у вас есть отрицательное число, как показано ниже, оно вернет #ЧИСЛО!.
Таким образом, решение этой проблемы заключается в использовании функции ABS вместе с SQRT. Вот пример:
=SQRT(ABS(A1))
Когда мы используем ABS, он преобразует число в абсолютное число. Это означает, что a преобразует отрицательное число в положительное.
Метод 2: вычисление квадратного корня из числа с помощью функции СТЕПЕНЬ
Другой способ вычисления квадратного корня — использование функции СТЕПЕНЬ. Функция POWER имеет большую мощность, чем SQRT, поскольку она возвращает результат возведения числа N в заданную степень.
Синтаксис POWER:
POWER(число, мощность)
Где номер — это число или ссылка на ячейку, которая содержит число, для которого вы хотите найти квадратный корень, а мощность — это показатель степени для увеличения мощности.
Допустим, нам нужно найти квадратный корень числа из ячейки A1 (это 625), тогда мы можем использовать 1/2 в качестве мощного аргумента в этой функции.
И формула будет такой:
=СТЕПЕНЬ(A1,1/2)
Как видите, в результате возвращается 25, что является квадратным корнем из 625. 9(1/2)
В приведенной выше формуле A1 — это ячейка, в которой у нас есть число, для которого нам нужно найти квадратный корень, а затем мы использовали оператор экспоненты, а затем (1/2) для возведения в степень .
Наилучшим преимуществом этой формулы является ее применение. Помимо квадратного корня, мы можем использовать его для вычисления кубического корня или любого корня n-й степени.
Метод-4: Код VBA для отображения КВАДРАТНОГО корня числа
Позвольте мне рассказать вам о другом сценарии, в котором нам нужно проверить квадратный корень числа, а не вычислять его в ячейке. 9(1 / 2) MsgBox «Квадратный корень из » & rng & » is » & sqr, vbOKOnly, «Значение квадратного корня» Еще MsgBox «Выберите числовое значение», vbOKOnly, «Ошибка» Конец, если End Sub
Как работает этот код
Когда мы запускаем этот код, он проверяет значение в выбранной ячейке, и если это значение является числом, он вычисляет квадратный корень этого числа и показывает его в окне сообщения.
Обратите внимание, что если вы выберете более одной ячейки, этот код не будет работать. 9(1 / 2) MsgBox «Квадратный корень из » & sq & » is » & sqr, vbOKOnly, «Значение квадратного корня» Еще MsgBox «Пожалуйста, введите число.», vbOKOnly, «Ошибка» Конец, если End Sub
как работает этот код
Когда мы запускаем этот код, он показывает нам поле ввода, запрашивающее число, для которого нам нужно получить квадратный корень.
И когда мы вводим это число, он вычисляет квадратный корень для этого числа и показывает окно сообщения с квадратным корнем. Вы можете использовать любой из приведенных выше кодов, которые идеально подходят для вас.
Метод 5: использование Power Query для преобразования чисел в квадратные корни
Вот еще один способ, который мы можем использовать, если вам нужно преобразовать несколько чисел в их квадратные корни.
Это Power Query.
Ниже у нас есть таблица, в которой у нас есть несколько чисел, и здесь мы хотим получить квадратный корень из этих чисел за один раз.
Примечание: Использование расширенного запроса для квадратного корня — это динамический метод, каждый раз, когда вы вводите новое значение в таблицу, он возвращает квадратный корень из этого числа.
Теперь выполните следующие простые шаги.
- Прежде всего, выберите любую ячейку в таблице и перейдите на вкладку «Данные» ➜ «Получить и преобразовать данные» и нажмите «Из таблицы/диапазона».
- После того, как вы щелкнете по нему, Excel откроет редактор запросов Power и добавит в него эту таблицу.
- Отсюда нам нужно создать новый столбец со значениями квадратного корня, для этого перейдите на вкладку «Добавить столбец» и нажмите «Пользовательский столбец».
- На данный момент у нас открыто окно Custom Column, и в этом окне нам нужно добавить следующее:
- Прежде всего, введите имя столбца «Квадратный корень» в поле ввода имени столбца.
- После этого введите (=Number.Sqrt([Numbers])) в поле ввода формулы пользовательского столбца и нажмите OK.
- Теперь у нас есть новый столбец с квадратными корнями из числа в первом столбце.
- Отсюда вам нужно удалить первый столбец исходных значений. Итак, щелкните правой кнопкой мыши по нему и нажмите «Удалить».
- После этого перейдите на главную вкладку и нажмите закрыть и тоже загрузить.
- Здесь открывается окно для загрузки данных. Прежде всего, выберите существующий рабочий лист и добавьте диапазон B1. Во-вторых, отметьте «Добавить в модель данных».
Как я уже сказал, эта таблица динамическая. Когда вы вводите новое значение в исходную таблицу данных, оно автоматически вычисляет его квадратный корень в вашей новой таблице при ее обновлении.
И здесь мы не используем никаких формул.
[Дополнительный совет] Как добавить символ квадратного корня в Excel
После того, как вы вычислите квадратный корень из числа, следующее, что вы можете сделать, это добавить символ квадратного корня.
И для этого у нас есть два разных способа, которые мы можем использовать.
1. Использование сочетания клавиш
Простой способ добавить символ квадратного корня — это сочетание клавиш Alt + 251. Вам нужно удерживать клавишу Alt, когда вы набираете 251 на цифровой клавиатуре. и как только вы отпустите клавишу Alt, появится символ.
2. Добавьте символ КВАДРАТНОГО корня, применив пользовательское форматирование
Это наиболее эффективный способ добавления символа. Все, что вам нужно сделать, это выбрать все ячейки, открыть параметр пользовательского форматирования и добавить форматирование на панель ввода форматирования.
√Общие
3. VBA для добавления квадратного символа
Вы также можете использовать приведенный ниже код VBA для применения пользовательского форматирования ко всем ячейкам в выделении.
Подпрограмма add_squareroot() Selection.NumberFormat = ChrW(8730) & «Общие» End SubПримечание: Преимущество использования методов № 2 и № 3 заключается в том, что вам не нужно добавлять символ во все ячейки один за другим, а когда вы добавляете символ в ячейку, значение в ячейке становится текстом и больше не может использоваться как число.

 Квадратный корень из исходного числа – это число, которое при умножении на себя дает исходное число. То есть нужно найти такое число, чтобы при его умножении на себя получить данное в задаче число.
Квадратный корень из исходного числа – это число, которое при умножении на себя дает исходное число. То есть нужно найти такое число, чтобы при его умножении на себя получить данное в задаче число. Для этого разделите целое число (делимое) на некоторое число (делитель) так, чтобы результат (частное) совпал с делителем.
Для этого разделите целое число (делимое) на некоторое число (делитель) так, чтобы результат (частное) совпал с делителем. Это означает, что квадратный корень из 9 равен 3.
Это означает, что квадратный корень из 9 равен 3. Таким образом, квадратный корень из 20 равен числу, которое находится между 4,4 и 4,5. Рассмотрите 4,445: 4,445х4,445 = 19,758. Это уже довольно близко к 20. Продолжайте в том же духе и в конце концов вы придете к: 4,475х4,475 = 20,03 ≈ 20.
Таким образом, квадратный корень из 20 равен числу, которое находится между 4,4 и 4,5. Рассмотрите 4,445: 4,445х4,445 = 19,758. Это уже довольно близко к 20. Продолжайте в том же духе и в конце концов вы придете к: 4,475х4,475 = 20,03 ≈ 20. Квадратные корни из этих чисел равны 3 и 4. Итак, разделите 10 на первое число: 10/3 = 3,33. Теперь найдите среднее арифметическое 3 и 3,33: (3+3,33)/2 = 3,1667. Теперь 10 разделите на среднее арифметическое: 10/3,1667 = 3,1579. Теперь найдите среднее арифметическое 3,1579 и 3,1667: (3,1579+3,1667)/2 = 3,1623.
Квадратные корни из этих чисел равны 3 и 4. Итак, разделите 10 на первое число: 10/3 = 3,33. Теперь найдите среднее арифметическое 3 и 3,33: (3+3,33)/2 = 3,1667. Теперь 10 разделите на среднее арифметическое: 10/3,1667 = 3,1579. Теперь найдите среднее арифметическое 3,1579 и 3,1667: (3,1579+3,1667)/2 = 3,1623. Положительный результат называется арифметическим значением корня, и на данном этапе можно рассматривать только это значение.
Положительный результат называется арифметическим значением корня, и на данном этапе можно рассматривать только это значение. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа числа, из которых можно извлечь целый квадратный корень. Множители числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как 25 = 5, 36 = 6, 49 = 7. Квадратные множители это множители, являющиеся квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа числа, из которых можно извлечь целый квадратный корень. Множители числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как 25 = 5, 36 = 6, 49 = 7. Квадратные множители это множители, являющиеся квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители. Воспользовавшись этим правилом, извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
Воспользовавшись этим правилом, извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня. Простые множители числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
Простые множители числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.

 Таким образом, вы получите упрощенное выражение: 10√(2) + 4√(2) + 2√(3) + 6√(3) + 3 √(81)
Таким образом, вы получите упрощенное выражение: 10√(2) + 4√(2) + 2√(3) + 6√(3) + 3 √(81) \\ \end{align}\]
\\ \end{align}\]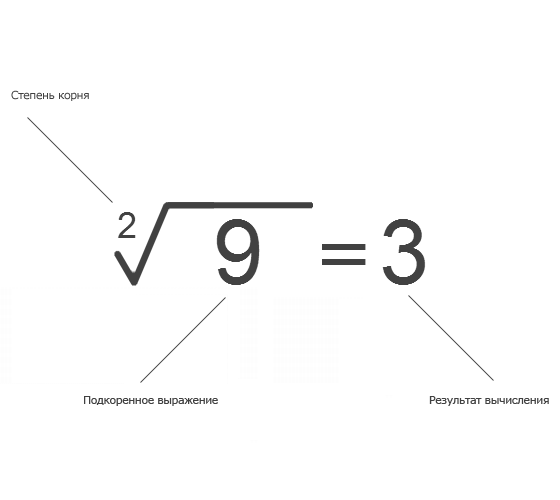 {2}}}=\sqrt{5}. \\ \end{align}\]
{2}}}=\sqrt{5}. \\ \end{align}\] {2}}}=\sqrt{75}. \end{align}\]
{2}}}=\sqrt{75}. \end{align}\] Поэтому кнопки от «0» до «9» в представлении не нуждаются.
Поэтому кнопки от «0» до «9» в представлении не нуждаются.




 п.).
п.). /выкл.
/выкл. Гарантия не распространяется на элементы питания.
Гарантия не распространяется на элементы питания.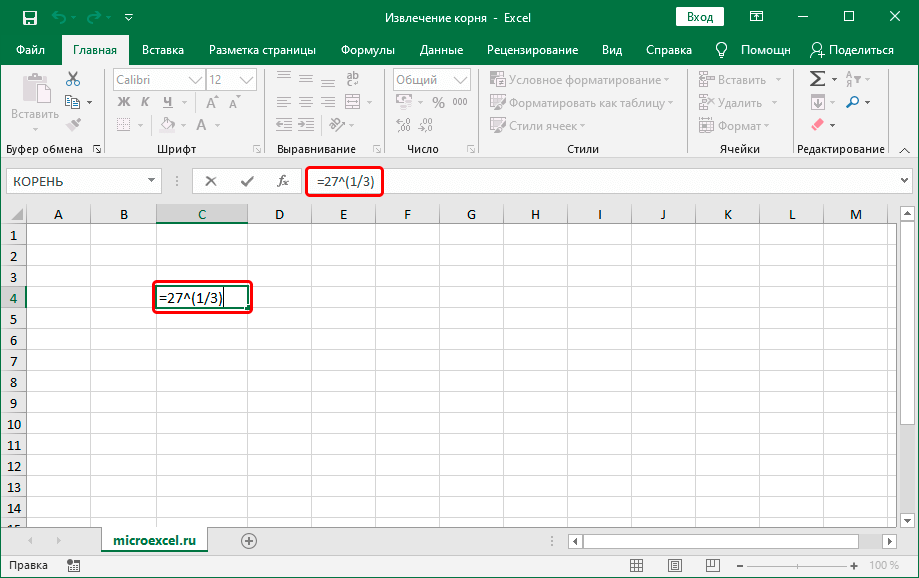 Для этого нажать последовательно 18 [RATE] [+TAX]
Для этого нажать последовательно 18 [RATE] [+TAX] 


 Этот калькулятор не может выполнить требуемую работу — это не
сделано для этой цели. Научный или графический калькулятор, использующий комплексные числа.
требуется для.
Этот калькулятор не может выполнить требуемую работу — это не
сделано для этой цели. Научный или графический калькулятор, использующий комплексные числа.
требуется для.
 ВЫ МОЖЕТЕ НЕ СДЕЛАТЬ
ЛЮБЫЕ ДОПОЛНИТЕЛЬНЫЕ КОПИИ ЭТОЙ СТРАНИЦЫ, ЕЕ ИЗОБРАЖЕНИЙ, ЕЕ ЗВУКОВЫХ КЛИПОВ ИЛИ ЕЕ АНИМИРОВАННЫХ
ГИФКИ БЕЗ РАЗРЕШЕНИЯ ОТ:
ВЫ МОЖЕТЕ НЕ СДЕЛАТЬ
ЛЮБЫЕ ДОПОЛНИТЕЛЬНЫЕ КОПИИ ЭТОЙ СТРАНИЦЫ, ЕЕ ИЗОБРАЖЕНИЙ, ЕЕ ЗВУКОВЫХ КЛИПОВ ИЛИ ЕЕ АНИМИРОВАННЫХ
ГИФКИ БЕЗ РАЗРЕШЕНИЯ ОТ:
 От математических до финансовых, это для каждой вещи, которую вам нужно рассчитать. Вы можете вычислять простые и самые сложные вещи в Excel.
От математических до финансовых, это для каждой вещи, которую вам нужно рассчитать. Вы можете вычислять простые и самые сложные вещи в Excel.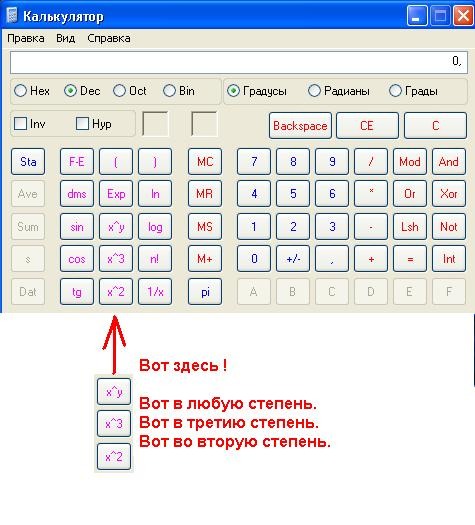 Тогда квадратный корень означает возвращение от 100 к 10.
Тогда квадратный корень означает возвращение от 100 к 10.
 И для этого у нас есть два разных способа, которые мы можем использовать.
И для этого у нас есть два разных способа, которые мы можем использовать.