Элемент (математика) — это… Что такое Элемент (математика)?
Мно́жество — один из ключевых объектов математики, в частности, теории множеств. «Под множеством мы понимаем объединение в одно целое определенных, вполне различимых объектов нашей интуиции или нашей мысли» (Г. Кантор). Это не является в полном смысле логическим определением понятия множество, а всего лишь пояснением (ибо определить понятие — значит найти такое родовое понятие, в которое данное понятие входит в качестве вида, но множество — это, пожалуй, самое широкое понятие математики и логики).
В математической логике и дискретной математике часто употребляемый синоним множества — алфавит.
Теории
Существует два основных подхода к понятию множества — наивная и аксиоматическая теория множеств.
«Наивная теория множеств»
Дать определение какому-нибудь понятию — это значит описать это понятие через понятия, определённые ранее. Если число определений в теории конечно, то первое определение должно быть основано на понятиях, которые являются аксиоматическими, то есть изначально неопределёнными. Множество — как раз одно из таких аксиоматических понятий. В рамках наивной теории множеств множеством считается любой чётко определённый набор объектов (
Наивная теория множеств была создана Кантором в конце XIX века.
История определения
До XIX века считалось, что точного определения множества нет. Множеством считалось любое скопление предметов.
В конце XIX века Георг Кантор определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством». Эти объекты называются элементами множества. Множество объектов, обладающих свойством A(x), обозначается . Если некое множество , то A(x) называется характеристическим свойством множества Y.
Эта концепция привела к парадоксам, в частности, к парадоксу Рассела.
После этого теория множеств была аксиоматизирована.
Аксиоматическая теория множеств
На сегодняшний день множество определяется как модель, удовлетворяющая аксиомам ZFC (аксиомы Цермело — Френкеля с аксиомой выбора). При таком подходе в некоторых математических теориях возникают совокупности объектов, которые не являются множествами. Такие совокупности называются классами (различных порядков).
Элемент множества
Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают большими буквами латинского алфавита, его элементы — маленькими. Если а — элемент множества А, то записывают а ∈ А (а принадлежит А). Если а не является элементом множества А, то записывают а∉А(а не принадлежит А).
Некоторые виды множеств
По иерархии:
- Множество множеств
- Подмножество
- Надмножество
По ограничению:
Литература
- Столл Р. Р. Множества. Логика. Аксиоматические теории. — М.: Просвещение, 1968. — 232 с.
См. также
Wikimedia Foundation. 2010.
dic.academic.ru
Элементы статистики
Продолжаем изучать элементарные задачи по математике. Сегодня мы поговорим о статистике.
Статистика — это раздел математики в котором изучаются вопросы сбора, измерения и анализа информации, представленной в числовой форме. Происходит слово статистика от латинского слова status (состояние или положение дел).
Так, с помощью статистики мы можем узнать свое положение дел, касающихся финансов. С начала месяца можно вести дневник расходов и по окончании месяца, воспользовавшись статистикой, узнать сколько денег в среднем мы тратили каждый день или какая потраченная сумма была наибольшей в этом месяце либо узнать какую сумму мы тратили наиболее часто.
На основе этой информации можно провести анализ и сделать определенные выводы: следует ли в следующем месяце немного сбавить аппетит, чтобы тратить меньше денег, либо наоборот позволить себе не только хлеб с водой, но и колбасу.
Выборка. Объем. Размах
Что такое выборка? Если говорить простым языком, то это отобранная нами информация для исследования. Например, мы можем сформировать следующую выборку — суммы денег, потраченных в каждый из шести дней. Давайте нарисуем таблицу в которую занесем расходы за шесть дней
Выборка состоит из n-элементов. Вместо переменной n может стоять любое число. У нас имеется шесть элементов, поэтому переменная n равна 6
n = 6
Элементы выборки обозначаются с помощью переменных с индексами . Последний элемент является шестым элементом выборки, поэтому вместо
Обозначим элементы нашей выборки через переменные
Количество элементов выборки называют объемом выборки. В нашем случае объем равен шести.
Размахом выборки называют разницу между самым большим и маленьким элементом выборки.
В нашем случае, самым большим элементом выборки является элемент 250, а самым маленьким — элемент 150. Разница между ними равна 100
Среднее арифметическое
Понятие среднего значения часто используется в повседневной жизни.
Примеры:
- средняя зарплата жителей страны;
- средний балл учащихся;
- средняя скорость движения;
- средняя производительность труда.
Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.
Среднее арифметическое — это результат деления суммы элементов выборки на их количество.
Вернемся к нашему примеру
Узнаем сколько в среднем мы тратили в каждом из шести дней:
Средняя скорость движения
При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.
В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.
Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.
Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.
Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)
Значит автомобиль ехал со средней скоростью 71,08 км/ч.
Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:
66,2 × 3 = 198,6 км.
Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:
78,4 × 2 = 156,8 км.
Сложим эти расстояния и результат разделим на 5
Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.
Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:
Мода и медиана
Модой называют элемент, который встречается в выборке чаще других.
Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров
Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.
Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат
Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.
Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:
Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 183, 184, 185, 188, 190
В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.
Медианой упорядоченной выборки называют элемент, располагающийся посередине.
Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.
В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану
Но возможны случаи, когда количество элементов выборки чётно.
К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:
Построим этих шестерых спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 184, 186, 188, 190
В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.
Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186
Найдем среднее арифметическое элементов 184 и 186
Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.
Поэтому более точное определение медианы зависит от количества элементов в выборке.
Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.
Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.
Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190
Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:
Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:
0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1
Определим среднее арифметическое для данной выборки — получим значение 2,2
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка
Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:
0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6
В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.
Частота
Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.
Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.
По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.
Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:
Такие таблицы называют таблицами частот.
Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.
Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:
4 + 5 + 10 + 8 + 6 + 3 = 36
Относительная частота
Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.
Относительная частота равна отношению частоты на общее число элементов выборки.
Вернемся к нашей таблице:
Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:
Выполним деление в этих дробях:
Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:
Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Навигация по записям
spacemath.xyz
Кодификатор элементов содержания по МАТЕМАТИКЕ
Проект
Единый государственный экзамен по МАТЕМАТИКЕ
Кодификатор
элементов содержания по МАТЕМАТИКЕ
для составления контрольных измерительных материалов для
проведения единого государственного экзамена
подготовлен Федеральным государственным бюджетным
научным учреждением
«ФЕДЕРАЛЬНЫЙ ИНСТИТУТ ПЕДАГОГИЧЕСКИХ ИЗМЕРЕНИЙ»
Кодификатор элементов содержания для составления контрольных измерительных материалов ЕГЭ по математике составлен на основе Обязательного минимума содержания основных образовательных программ и Требований к уровню подготовки выпускников средней школы (приказ Минобразования России от 05.03.2004 № 1089 «Об утверждении федерального компонента Государственных стандартов начального общего, основного общего и среднего (полного) общего образования»).
Кодификатор элементов содержания по всем разделам включает в себя элементы содержания за курс средней школы (базовый уровень) и необходимые элементы содержания за курс основной школы.
1 Алгебра
Числа, корни и степени
1.1.1 Целые числа
1.1.2 Степень с натуральным показателем
1.1.3 Дроби, проценты, рациональные числа
1.1.4 Степень с целым показателем
1.1.5 Корень степени n > 1 и его свойства
1.1.6 Степень с рациональным показателем и её свойства
1.1.7 Свойства степени с действительным показателем
Основы тригонометрии
1.2.1 Синус, косинус, тангенс, котангенс произвольного угла
1.2.2 Радианная мера угла
1.2.3 Синус, косинус, тангенс и котангенс числа
1.2.4 Основные тригонометрические тождества
1.2.5 Формулы приведения
1.2.6 Синус, косинус и тангенс суммы и разности двух углов
1.2.7 Синус и косинус двойного угла
Логарифмы
1.3.1 Логарифм числа
1.3.2 Логарифм произведения, частного, степени
1.3.3 Десятичный и натуральный логарифмы, число е
1.4 Преобразования выражений
1.4.1 Преобразования выражений, включающих арифметические
1.4.2 Преобразования выражений, включающих операцию возведения в степень
1.4.3 Преобразования выражений, включающих корни натуральной степени
1.4.4 Преобразования тригонометрических выражений
1.4.5 Преобразование выражений, включающих операцию логарифмирования
1.4.6 Модуль (абсолютная величина) числа
2 Уравнения и неравенства
Уравнения
2.1.1 Квадратные уравнения
2.1.2 Рациональные уравнения
2.1.3 Иррациональные уравнения
2.1.4 Тригонометрические уравнения
2.1.5 Показательные уравнения
2.1.6 Логарифмические уравнения
2.1.7 Равносильность уравнений, систем уравнений
2.1.8 Простейшие системы уравнений с двумя неизвестными
2.1.9 Основные приёмы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных
2.1.10 Использование свойств и графиков функций при решении уравнений
2.1.11 Изображение на координатной плоскости множества решений уравнений с двумя переменными и их систем
2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учёт реальных ограничений
Неравенства
2.2.1 Квадратные неравенства
2.2.2 Рациональные неравенства
2.2.3 Показательные неравенства
2.2.4 Логарифмические неравенства
2.2.5 Системы линейных неравенств
2.2.6 Системы неравенств с одной переменной
2.2.7 Равносильность неравенств, систем неравенств
2.2.8 Использование свойств и графиков функций при решении неравенств
2.2.9 Метод интервалов
2.2.10 Изображение на координатной плоскости множества решений неравенств с двумя переменными и их систем
3 Функции
Определение и график функции
3.1.1 Функция, область определения функции
3.1.2 Множество значений функции
3.1.3 График функции. Примеры функциональных зависимостей в реальных процессах и явлениях
3.1.4 Обратная функция. График обратной функции
3.1.5 Преобразования графиков: параллельный перенос, симметрия относительно осей координат
Элементарное исследование функций
3.2.1 Монотонность функции. Промежутки возрастания и убывания
3.2.2 Чётность и нечётность функции
3.2.3 Периодичность функции
3.2.4 Ограниченность функции
3.2.5 Точки экстремума (локального максимума и минимума) функции
3.2.6 Наибольшее и наименьшее значения функции
Основные элементарные функции
3.3.1 Линейная функция, её график
3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график
3.3.3 Квадратичная функция, её график
3.3.4 Степенная функция с натуральным показателем, её график
3.3.5 Тригонометрические функции, их графики
3.3.6 Показательная функция, её график
3.3.7 Логарифмическая функция, её график
4 Начала математического анализа
Производная
4.1.1 Понятие о производной функции, геометрический смысл производной
4.1.2 Физический смысл производной, нахождение скорости для процесса, заданного формулой или графиком
4.1.3 Уравнение касательной к графику функции
4.1.4 Производные суммы, разности, произведения, частного
4.1.5 Производные основных элементарных функций
4.1.6 Вторая производная и её физический смысл
Исследование функций
4.2.1 Применение производной к исследованию функций и построению графиков
4.2.2 Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально- экономических, задачах
Первообразная и интеграл
4.3.1 Первообразные элементарных функций
4.3.2 Примеры применения интеграла в физике и геометрии
5 Геометрия
Планиметрия
5.1.1 Треугольник
5.1.2 Параллелограмм, прямоугольник, ромб, квадрат
5.1.3 Трапеция
5.1.4 Окружность и круг
5.1.5 Окружность, вписанная в треугольник, и окружность, описанная около треугольника
5.1.6 Многоугольник. Сумма углов выпуклого многоугольника
5.1.7 Правильные многоугольники. Вписанная окружность и описанная окружность правильного многоугольника
Прямые и плоскости в пространстве
5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых
5.2.2 Параллельность прямой и плоскости, признаки и свойства
5.2.3 Параллельность плоскостей, признаки и свойства
5.2.4 Перпендикулярность прямой и плоскости, признаки и свойства; перпендикуляр и наклонная; теорема о трёх перпендикулярах
5.2.5 Перпендикулярность плоскостей, признаки и свойства
5.2.6 Параллельное проектирование. Изображение пространственных фигур
Многогранники
5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма
5.3.2 Параллелепипед; куб; симметрии в кубе, в параллелепипеде
5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида
5.3.4 Сечения куба, призмы, пирамиды
5.3.5 Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр)
Тела и поверхности вращения
5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развертка
5.4.2 Конус. Основание, высота, боковая поверхность, образующая, развертка
5.4.3 Шар и сфера, их сечения
Измерение геометрических величин
5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
5.5.2 Угол между прямыми в пространстве; угол между прямой и плоскостью, угол между плоскостями
5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
5.5.4 Расстояние от точки до прямой, от точки до плоскости; расстояние между параллельными и скрещивающимися прямыми, расстояние между параллельными плоскостями
5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
5.5.6 Площадь поверхности конуса, цилиндра, сферы
5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
5.6 Координаты и векторы
5.6.1 Координаты на прямой, декартовы координаты на плоскости и в пространстве
5.6.2 Формула расстояния между двумя точками; уравнение сферы
5.6.3 Вектор, модуль вектора, равенство векторов; сложение векторов и умножение вектора на число
5.6.4 Коллинеарные векторы. Разложение вектора по двум неколлинеарным векторам
5.6.5 Компланарные векторы. Разложение по трём некомпланарным векторам
5.6.6 Координаты вектора; скалярное произведение векторов; угол между векторами
6 Элементы комбинаторики, статистики и теории вероятностей
Элементы комбинаторики
6.1.1 Поочередный и одновременный выбор
6.1.2 Формулы числа сочетаний и перестановок. Бином Ньютона
Элементы статистики
6.2.1 Табличное и графическое представление данных
6.2.2 Числовые характеристики рядов данных
Элементы теории вероятностей
6.3.1 Вероятности событий
6.3.2 Примеры использования вероятностей и статистики при решении прикладных задач
xn--j1ahfl.xn--p1ai
Конспект урока по математике «Элементы математической статистики и теории вероятности»
Тема урока: Элементы математической статистики и теории вероятности.
Основные цели и задачи урока: Повторить основные понятия изучаемого предмета: числовые характеристики числового ряда, вероятность. Развивать умения решать задачи по теме, логическое мышление, математический кругозор. Воспитывать культуру письменной и устной математической речи.
Ход урока
Организационный момент.
Вводная беседа. Слайд 1
В повседневной жизни, в практической и научной деятельности часто наблюдаются те или иные явления, проводят определенные эксперименты.
Проблема выбора наилучшего из нескольких вариантов решения, оценка степени риска и шансов на успех, находится в сфере реальных интересов личности. Подготовку человека к таким проблемам во всем мире осуществляет школьный курс математики, и в частности ее раздел »математическая статистика».
В наши дни результаты наблюдений используют для статистической оценки качества изготовляемой продукции и для управления качеством в процессе производства. И на производстве и в научных экспериментах очень важно бывает проверить, насколько неизменны условия наблюдения. Для этого вводятся числовые характеристики.
Давайте вспомним какие числовые характеристики статистических данных или числового ряда мы знаем.
Определение моды, медианы, размаха, среднего числового ряда. Слайд 2

Задание на нахождение размаха, мода и медианы Слайд 3

Задание на нахождение среднего числового ряда Слайд 4
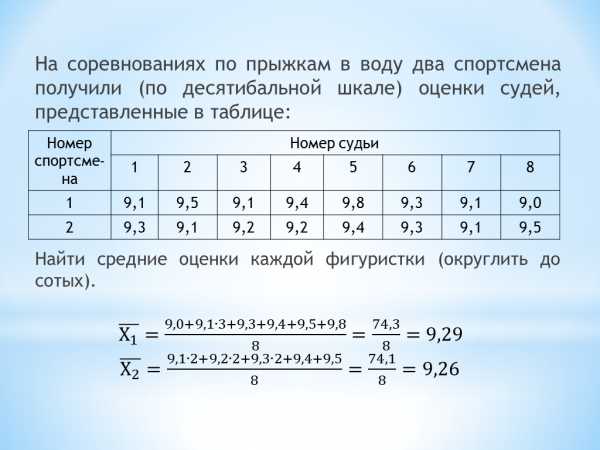
Работа в парах (Найти ошибку) Слайд 5
1. Дан числовой ряд 1, 4, 2, 6, 4, 5, 1, 8, 9, 7. Взяты не максимальное и минимальное зн.
R = 7 – 1 = 6
2. Мода числового ряда 1, 3, 3, 2, 3, -1, 5, -1 не абсолютное значение числа, которое
равна 1. Встречается чаще других
3. Дан числовой ряд 3, 4, 2, 6, 3, 5, 1, 8, 9, 5. Не упорядочили ряд
Ме= (3+5)/2=4
4.Дан числовой ряд 1,2; 1,2; 1,5; 1,8; 2; 2,6 четный ряд полусумма средних ч.
Ме= 1,5
5. Среднее числового ряда 2, 5, 1, 4, 3, 6, 2 равно вычислительная ошибка
(2+5+1+4+3+6+2)/7=3
6. Среднее числового ряда 2, 2, 3, 4, 4, 5, 7 равно суммировали не все числа
(2+3+4+5+7)/7=3
7. Размах числового ряда -1; -3; 2; 4; 5; 2; 6 равен R = 6 – 1 = 5 неверно отняли
1. Дан числовой ряд 1, 4, 2, 6, 4, 5, 1, 8, 9, 7.
R = 7 – 1 = 6
В нашу жизнь властно вошли выборы и референдумы, банковские кредиты и страховые полисы, таблицы занятости и диаграммы социологических опросов. И даже в газете читаем: вероятность долговременного прогноза погоды на неделю – 0.8.
А что же такое вероятность?.
Еще первобытный вождь понимал, что у десятка охотников вероятность поразить копьем зверя гораздо больше, чем у одного. Поэтому охотились тогда коллективно. Необоснованно было бы думать. Что такие древние полководцы, как Александр Македонский или Дмитрий Донской, готовясь к сражению, уповали только на доблесть и искусство воинов. Несомненно, они на основании наблюдений и опыта военного руководства умели как-то оценить вероятность своего возвращения со щитом или на щите, знали, когда принимать бой, когда уклониться от него. Они не были рабами случая, но вместе с тем они были еще очень далеки от теории вероятностей.
Давайте дадим классическое определение понятия вероятности случайного события. Слайд 6
Задачи на нахождение вероятности Слайд 7

Оценивая возможность наступления какого-либо события, мы часто говорим: «Это очень возможно», «Это непременно произойдет», «Это маловероятно», «Это никогда не случится
Так в каких же пределах изменяется вероятность от 0 до 1
Вероятность какого события равна 0
Вероятность какого события равна 1
Самостоятельная работа.
I вариант
№ 1. Провели несколько измерений случайной величины:
38; 34: 30; 6 ; 30; 30.
Найти моду, размах, медиану, среднее данного ряда.
№ 2. Магазин продает 8 видов хлеба по следующим ценам:
3,1; 2,2; 2,4; 2,7; 3,0; 3,6; 1,9; 2,7.
Найдите разность среднего арифметического и медианы этого набора
чисел.
№ 3. В корзине лежат 3 красных, 2 белых, 5 черных шара. Найти вероятность
того, что будет выбран:
А) красный шар
Б) не белый шар
№ 4. Из цифр 0,5,4,1 составили трехзначное число. Какова вероятность того,
что составят четное число?
II вариант
№ 1. Провели несколько измерений случайной величины:
19; 27; 24; 24; 28.
Найти моду, размах, медиану, среднее данного ряда.
№ 2. Провели несколько измерений случайной величины:
6,4; 5,8; 7,2; 4,6; 4,8; 7; 8,2; 8,4; 7.
Найти разность среднего и медианы данного ряда.
№ 3. В корзине лежат 4 красных, 6 белых, 5 черных шара. Найти вероятность
того, что будет выбран:
А) черный шар
Б) не белый шар
№ 4. Из цифр 0,5,4,1 составили трехзначное число. Какова вероятность того, что составят нечетное число?
Итог урока.
doc4web.ru
Элемент (математика) Википедия
Мно́жество — одно из ключевых понятий математики; это математический объект, сам являющийся набором, совокупностью, собранием каких-либо объектов, которые называются элементами этого множества и обладают общим для всех их характеристическим свойством[1]. Изучением общих свойств множеств занимаются теория множеств, а также смежные разделы математики и математической логики.
Примеры: множество жителей заданного города, множество непрерывных функций, множество решений заданного уравнения.
Множество может быть пустым и непустым, упорядоченным и неупорядоченным, конечным и бесконечным, бесконечное множество может быть счётным или несчётным. Более того, как в наивной, так и в аксиоматической теориях множеств любой объект обычно считается множеством. Понятие множества позволяет практически всем разделам математики использовать общую идеологию и терминологию.
История понятия
Основы теории конечных и бесконечных множеств были заложены Бернардом Больцано, который сформулировал некоторые из её принципов.
С 1872 года по 1897 год (главным образом в 1872—1884 годы) Георг Кантор опубликовал ряд работ, в которых были систематически изложены основные разделы теории множеств, включая теорию точечных множеств и теорию трансфинитных чисел (кардинальных и порядковых). В этих работах он не только ввёл основные понятия теории множеств, но и обогатил математику рассуждениями нового типа, которые применил для доказательства теорем теории множеств, в частности впервые к бесконечным множествам. Поэтому общепризнано, что теорию множеств создал Георг Кантор. В частности определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством». Эти объекты назвал элементами множества. Множество объектов, обладающих свойством A(x){\displaystyle A(x)}, обозначил {x∣A(x)}{\displaystyle \{x\mid A(x)\}}. Если некоторое множество Y={x∣A(x)}{\displaystyle Y=\{x\mid A(x)\}}, то A(x){\displaystyle A(x)} назвал характеристическим свойством множества Y{\displaystyle Y}.
Эта концепция привела к парадоксам, в частности, к парадоксу Рассела.
Так как теория множеств фактически используется как основание и язык всех современных математических теорий в 1908 году теория множеств была аксиоматизирована независимо Бертраном Расселом и Эрнстом Цермело. В дальнейшем многие исследователи пересматривали и изменяли обе системы, в основном сохранив их характер. До сих пор они всё ещё известны как теория типов Рассела и теория множеств Цермело. Впоследствии теорию множеств Кантора стало принято называть наивной теорией множеств, а вновь построенную — аксиоматической теорией множеств.
В практике, сложившейся с середины XX века множество определяется как модель, удовлетворяющая аксиомам ZFC (аксиомы Цермело — Френкеля с аксиомой выбора). При таком подходе в некоторых математических теориях возникают совокупности объектов, которые не являются множествами. Такие совокупности называются классами (различных порядков).
Элемент множества
Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают заглавными буквами латинского алфавита, его элементы — строчными. Если a{\displaystyle a} — элемент множества A{\displaystyle A}, то записывают a∈A{\displaystyle a\in A} («a{\displaystyle a} принадлежит A{\displaystyle A}»). Если a{\displaystyle a} не является элементом множества A{\displaystyle A}, то записывают a∉A{\displaystyle a\notin A} («a{\displaystyle a} не принадлежит A{\displaystyle A}»). В отличие от мультимножества каждый элемент множества уникален, и во множестве не может быть двух идентичных элементов. Иначе говоря, добавление к множеству элементов, идентичных уже принадлежащим множеству, не меняет его:
- {6,11}={11,6}={11,11,6,11,6}{\displaystyle \{6,11\}=\{11,6\}=\{11,11,6,11,6\}}.
Равенство A=B{\displaystyle A=B} двух множеств означает
- x∈A⟺x∈B.{\displaystyle x\in A\iff x\in B.}
Задание множества
Существуют два основных способа задания множеств: перечисление и описание.
Первый способ состоит в том, что задаётся и перечисляется полный список элементов, входящих в множество. Например, множество Y{\displaystyle Y} неотрицательных чётных чисел, меньших 10 можно задать в виде списка: Y={0,2,4,6,8}{\displaystyle Y=\left\{0,2,4,6,8\right\}}. Данный способ удобно применять лишь к ограниченному числу конечных множеств.
Второй способ применяется, когда множество нельзя или затруднительно задать с помощью списка. В таком случае множества определяются свойствами их элементов. Множество Y{\displaystyle Y} задано, если указано условие A(x){\displaystyle A(x)}, которому удовлетворяют все элементы, принадлежащие множеству Y{\displaystyle Y} и которому не удовлетворяют элементы, не принадлежащие множеству Y{\displaystyle Y}.
Обозначение
- Y={x∈X∣A(x)},{\displaystyle Y=\{\,x\in X\mid A(x)\,\},}
используется для задания множества Y{\displaystyle Y}; оно означает, что множество Y{\displaystyle Y} состоит из тех и только тех элементов x{\displaystyle x} множества X{\displaystyle X}, для которых выполнено условие A(x){\displaystyle A(x)}.
Например, график функции f:X→Y{\displaystyle f\colon X\to Y} можно задать следующим образом:
- Γ={(x,y)∈X×Y∣f(x)=y},{\displaystyle \Gamma =\{\,(x,y)\in X\times Y\mid f(x)=y\,\},}
Некоторые виды множеств и сходных объектов
Специальные множества
Сходные объекты
- Кортеж (в частности, упорядоченная пара) — упорядоченная совокупность конечного числа именованных объектов. Записывается внутри круглых или угловых скобок, а элементы могут повторяться.
- Мультимножество (в теории сетей Петри называется «комплект») — множество с кратными элементами.
- Пространство — множество с некоторой дополнительной структурой.
- Вектор — элемент линейного пространства, содержащий конечное число элементов некоторого поля в качестве координат. Порядок имеет значение, элементы могут повторяться.
- Последовательность — функция одного натурального переменного. Представляется как бесконечный набор элементов (не обязательно различных), порядок которых имеет значение.
- Нечёткое множество — математический объект, подобный множеству, принадлежность которому задаётся не отношением, а функцией. Иными словами, относительно элементов нечёткого множества можно говорить «в какой мере» они в него входят, а не просто, входят они в него или нет.
По иерархии
- Множество множеств (в частности, булеан — множество всех подмножеств данного множества).
- Подмножество
- Надмножество
Отношения между множествами
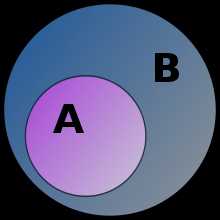
Два множества A{\displaystyle A} и B{\displaystyle B} могут вступать друг с другом в различные отношения.
- A{\displaystyle A} включено в B{\displaystyle B}, если каждый элемент множества A{\displaystyle A} принадлежит также и множеству B{\displaystyle B}:
- A⊆B⇔∀a∈A:a∈B{\displaystyle A\subseteq B\Leftrightarrow \forall a\in A\colon a\in B}
- A{\displaystyle A} включает B{\displaystyle B}, если B{\displaystyle B} включено в A{\displaystyle A}:
- A⊇B⇔B⊆A{\displaystyle A\supseteq B\Leftrightarrow B\subseteq A}
- A{\displaystyle A} равно B{\displaystyle B}, если A{\displaystyle A} и B{\displaystyle B} включены друг в друга:
- A=B⇔(A⊆B)∧(B⊆A){\displaystyle A=B\Leftrightarrow (A\subseteq B)\land (B\subseteq A)}
- A{\displaystyle A} строго включено в B{\displaystyle B}, если A{\displaystyle A} включено в B{\displaystyle B}, но не равно ему:
- A⊂B⇔(A⊆B)∧(A≠B){\displaystyle A\subset B\Leftrightarrow (A\subseteq B)\land (A\neq B)}
- A{\displaystyle A} строго включает B{\displaystyle B}, если B{\displaystyle B} строго включено в A{\displaystyle A}:
- A⊃B⇔B⊂A{\displaystyle A\supset B\Leftrightarrow B\subset A}
- A{\displaystyle A} и B{\displaystyle B} не пересекаются, если у них нет общих элементов:
- A{\displaystyle A} и B{\displaystyle B} не пересекаются ⇔∀a∈A:a∉B{\displaystyle \Leftrightarrow \forall a\in A\colon a\notin B}
- A{\displaystyle A} и B{\displaystyle B} находятся в общем положении, если существует элемент, принадлежащий исключительно множеству A{\displaystyle A}, элемент, принадлежащий исключительно множеству B{\displaystyle B}, а также элемент, принадлежащий обоим множествам:
- A{\displaystyle A} и B{\displaystyle B} находятся в общем положении ⇔{\displaystyle \Leftrightarrow } ∃a,b,c:(a∈A)∧(a∉B)∧(b∈B)∧(b∉A)∧(c∈A)∧(c∈B){\displaystyle \exists a,b,c\colon (a\in A)\land (a\notin B)\land (b\in B)\land (b\notin A)\land (c\in A)\land (c\in B)}
Операции над множествами
Бинарные операции
Основные бинарные операции, определяемые над множествами:
- Если множества A{\displaystyle A} и B{\displaystyle B} не пересекаются, то A∩B=∅{\displaystyle A\cap B=\varnothing }. Их объединение обозначают также: A+B=A∪B{\displaystyle A+B=A\cup B}.
Для объяснения смысла операций часто используются диаграммы Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек.
Всякая система множеств, замкнутая относительно операций объединения и пересечения, образует относительно объединения и пересечения дистрибутивную решётку.
Унарные операции
Дополнение определяется следующим образом:
- A¯≡A∁:={x∣x∉A}{\displaystyle {\overline {A}}\equiv A^{\complement }:=\{x\mid x\notin A\}}.
Операция дополнения подразумевает некоторый зафиксированный универсум (универсальное множество U{\displaystyle U}, которое содержит A{\displaystyle A}), и сводится к разности множеств с этим универсумом:
- A¯=U∖A{\displaystyle {\overline {A}}=U\setminus A}.
Система множеств с фиксированным универсумом, замкнутая относительно операций объединения, пересечения с введённым таким образом дополнением образует булеву алгебру.
Булеан — множество всех подмножеств:
- 2X≡PX:={A∣A⊂X}{\displaystyle 2^{X}\equiv {\mathcal {P}}X:=\{A\mid A\subset X\}}.
Обозначение 2X{\displaystyle 2^{X}} происходит из свойства мощности множества всех подмножеств конечного множества:
- |2X|=2|X|{\displaystyle \left|2^{X}\right|=2^{|X|}}.
Булеан 2X{\displaystyle 2^{X}} порождает систему множеств с фиксированным универсумом X{\displaystyle X}, замкнутую относительно операций объединения и пересечения, то есть, образует булеву алгебру.
Приоритет операций
Последовательность выполнения операций над множествами, как и обычно, может быть задана скобками. При отсутствии скобок сначала выполняются унарные операции (дополнение), затем — пересечения, затем — объединения и разности, которые имеют одинаковый приоритет. Операции одного приоритета выполняются слева направо. При этом надо иметь в виду, что в отличие от арифметических сложения и вычитания, для которых верно, что (a+b)−c=a+(b−c){\displaystyle (a+b)-c=a+(b-c)}, для аналогичных операций над множествами это неверно. Например, если A={1,3},B={1,2},C={2,3},{\displaystyle A=\{1,3\},B=\{1,2\},C=\{2,3\},} то (A∪B)∖C={1},{\displaystyle (A\cup B)\setminus C=\{1\},} но, в то же время, A∪(B∖C)={1,3}{\displaystyle A\cup (B\setminus C)=\{1,3\}}.
Мощность
Мощность множества — характеристика множества, обобщающая понятие о количестве элементов для конечного множества таким образом, чтобы множества, между которыми возможно установление биекции были равномощны. Обозначается |A|{\displaystyle |A|} или ♯A{\displaystyle \sharp A}. Мощность пустого множества равна нулю, для конечных множеств мощность совпадает с числом элементов, для бесконечных множеств вводятся специальные кардинальные числа, соотносящиеся друг с другом по принципу включения (если A⊆B{\displaystyle A\subseteq B}, то |A|⩽|B|{\displaystyle |A|\leqslant |B|}) и распространением свойства мощности булеана конечного множества: |2A|=2|A|{\displaystyle |2^{A}|=2^{|A|}} на случай бесконечных множеств (само обозначение 2A{\displaystyle 2^{A}} мотивировано этим свойством).
Наименьшая бесконечная мощность обозначается ℵ0{\displaystyle \aleph _{0}}, это мощность счётного множества. Мощность континуума, биективного булеану счётного множества обозначается c{\displaystyle {\mathfrak {c}}} или 2ℵ0{\displaystyle 2^{\aleph _{0}}}. Континуум-гипотеза — предположение о том, что между счётной мощностью и мощностью континуума нет промежуточных мощностей.
Примечания
Литература
- К. Куратовский, А. Мостовский. Теория множеств / Перевод с английского М. И. Кратко под редакцией А. Д. Тайманова. — М.: Мир, 1970. — 416 с.
- Столл Р. Р. Множества. Логика. Аксиоматические теории. / Перевод с английского Ю. А. Гастева и И. Х. Шмаина под редакцией Ю. А. Шихановича. — М.: Просвещение, 1968. — 232 с.
wikiredia.ru
Элементы математики. Свойства операций и отношений
Удалитеиз текста все лишние пробелы: любые пары пробелов должны замениться одним. По возможности выполните это за меньшее число операций замены.
Замените формат всех английских букв: они должны быть Times New Roman 16 курсив. Для поиска английских букв используйте флажок Подстановочные символы. Тогда среди специальных появится Знак в диапазоне. Укажите английскими буквами [a-z], а при повторной команде – [A-Z].
Привключенном флажке Подстановочные символы ввести маску ввода т*т, попробовать несколько раз Найти далее и объяснить, какие тексты находятся. Проверить, какие будут находиться при маске <т*т>? Объяснить, что разного произойдет, если в поле Найти ввести маски «ра» и «<ра*>», а в поле Заменить на – формат: курсив?
Удалитьиз текста графические объекты. Находятся только те рисунки, формулы, стрелки, кружки и другие объекты, которые включены в текст. По шагам посмотрите, как будет проходить удаление.
Любой раздел математики определяется, если для него указаны его элементы:
Элементы: | Числовая алгебра | Право |
1. система объектов | Числа | Человек, государство, собственность, … |
2. отношения между объектами | >, <, =, … | родства, гражданство, к собственности (собственник, владелец,…), … |
3. операции над объектами | + – */ … | купли-продажи,… |
Часто абстрактные объекты в математике обозначаются именами. Например, в геометрии точки обозначаются прописными латинскими буквами A, B, C,…; имена отрезков образуются из имен концов отрезков – AB, CD,…., числовые значения длин отрезков представляются строчными латинскими буквами – a, b, c,… в числовой алгебре числа также могут заменяться именами: Вес = Рост – 100, a2 + b2 = c2, y < x2. Имена могут содержать и цифры, например, индексы: A1, x12..
В математике операции могут удовлетворять свойствам (на примере сложения и умножения чисел, для абстрактных сложения и умножения эти операции могут и называться не так):
a + b = b + a коммутативность
a(bc) = (ab)c ассоциативность
a(b + c) = ab + ac дистрибутивность (двух операций).
В числовой алгебре некоммутативными являются операции «/» и «–», они же не ассоциативны.
Важно! Чаще всего математика имеет дело с алгеброй, для нее наложено ограничение: результат любой операции ▫ всегда входит в систему объектов:
Число ▫ Число = Число в числовой алгебре
Высказывание ▫ Высказывание = Высказывание в алгебре логики
Множество ▫ Множество = Множество в теории множеств
Событие ▫ Событие = Событие в теории вероятностей
и т.д.
Отношения между объектами также могут обладать определенными свойствами.
Из a ▪ b и b ▪ c следует a ▪ c свойство транзитивности.
Например, в числовой алгебре:
из a < b и b < c следует a < c;
из a = b и b = c следует a = c
Свойство справедливо не для всех отношений. Например, отношение «является противоположным» не транзитивно. на множестве людей отношения «старше чем», «выше» обладают свойством транзитивности, а «является отцом» – нет.
Состояние | Команда | Рассмотрим систему строевых команд: Смирно, наЛево, наПраво, Кругом. | |||
С | Л | К | П | ||
С | С | Л | К | П | |
Л | Л | К | П | С | |
К | К | П | С | Л | |
П | П | С | Л | К | |
Заметим, что последовательность команд налево, кругом равносильна одной команде направо. Этот факт можно записать символически, введя операцию «+» и отношение «=»: Л + К = П. То, что записано слева и справа от знака равенства, вообще говоря, различно. Одинаковы только положения, которые получаются в результате применения команд. Вообще, каждое из возможных положений можно определить как получаемое в результате одной команды, следовательно, сумма команд является командой и мы имеем дело с алгеброй. Легко заметить в этой алгебре, что команда С выполняет роль нуля в числовой алгебре:
Команда + С = Команда.
В любой алгебре противоположные элементы вводятся как удовлетворяющие соотношению: a + b = 0. И в алгебре команд можно указать противоположные, подтвердить коммутативность, ассоциативность сложения и т.д.
Как правило, объекты математики являются абстракциями реально существующих явлений и разделы математики изучают общие свойства объектов как абстрактных. Знакомство с различными разделами математики традиционно заключается в описании ее элементов: объектов, которыми этот раздел оперирует, операций и отношений, которые на этих объектах определены.
Пример различных разделов математики и их элементов.
Раздел математики | Объекты | Операции | Отношения |
Числовая алгебра | Числа | 3 + 4 3 x | 3 < 4 3 ≠ 4 3 ≤ x |
Теория множеств | Множества, Элементы | A B A B | A B, B C –подмножество; =, ≠ |
Теория вероятностей | Случайные события; Случайные величины | A+ B, AB x + y,… | Совместные,.. Зависимые,… |
Алгебра логики | Высказывания, Предикаты | A & B,… | Равнозначные |
studfiles.net
элементы математики — это… Что такое элементы математики?
- элементы математики
- the elements of mathematics
Большой англо-русский и русско-английский словарь. 2001.
- элементы
- элементы одного уровня
Смотреть что такое «элементы математики» в других словарях:
История математики — История науки … Википедия
Институт прикладной математики им. М. В. Келдыша РАН — (ИПМ РАН) … Википедия
Институт прикладной математики — им. М. В. Келдыша РАН (ИПМ РАН) . Международное название Keldysh Institute of Applied Mathematics, KIAM Основан … Википедия
Институт прикладной математики АН СССР — Институт прикладной математики им. М. В. Келдыша РАН (ИПМ РАН) . Международное название Keldysh Institute of Applied Mathematics, KIAM Основан … Википедия
Институт прикладной математики им. акад. М.В. Келдыша — Институт прикладной математики им. М. В. Келдыша РАН (ИПМ РАН) . Международное название Keldysh Institute of Applied Mathematics, KIAM Основан … Википедия
Разделы математики — Существует три официальных способа подразделения математики. Содержание 1 Математика как специальность 2 Математика как учебная дисциплина … Википедия
Принципы математики — «ПРИНЦИПЫ МАТЕМАТИКИ» («PRINCIPIA MATHEMATICA») трехтомный труд о логике и основаниях математики, написанный А.Н. Уайтхедом и Б. Расселом и опубликованный в 1910, 1912 и 1913 (около 2000 с). Целью этой работы было показать, что, используя … Энциклопедия эпистемологии и философии науки
Бесконечно удалённые элементы — в математике, элементы (называемые точками, прямыми, плоскостями), которыми пополняется евклидова плоскость или евклидово пространство для интерпретации некоторых разделов математики (проективная геометрия, теория функций комплексного… … Большая советская энциклопедия
Математика гармонии — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/22 ноября 2012. Пока процесс обсуждени … Википедия
Николя Бурбаки — Шарль Дени Бурбаки, французский генерал, фамилия которого была взята в качестве псевдонима Николя Бурбаки (фр. Nicolas Bourbaki) коллективный псевдоним группы французских математиков (позднее в неё вошли несколько иностранцев),… … Википедия
Бурбаки — Николя Бурбаки (фр. Nicolas Bourbaki) коллективный псевдоним группы французских математиков (позднее в нее вошли несколько иностранцев), созданной в 1935 году. Шарль Дени Бурбаки, французский генерал, фамилия которого была взята в качестве… … Википедия
Книги
- Элементы математики для физиков. Часть 1. Векторы в физике, С. С. Кокарев, В пособии систематически излагаются основы векторного исчисления и на большом числе примеров иллюстрируются его приложения к различным физическим и геометрическим задачам. Пособие… Издатель: Логос, Подробнее Купить за 471 руб
- Элементы математики в задачах с решениями и комментариями. Часть 1, Татьяна Голенищева-Кутузова, Александр Казанцев, Андрей Кустарев, Юрий Кудряшов, Григорий Мерзон, Книга содержит один из курсов математики в задачах, на протяжении ряда лет используемых в 57 школе города Москвы. В представленном виде курс преподавался классу В 2008 года выпуска. Данная… Издатель: МЦНМО, Производитель: МЦНМО, Подробнее Купить за 303 грн (только Украина)
- Элементы математики в задачах (с решениями и комментариями). Часть 2, Т. И. Голенищева-Кутузова, А. Д. Казанцев, Ю. Г. Кудряшов, А. А. Кустарев, Г. А. Мерзон, И. В. Ящен, Книга содержит один из курсов математики в задачах, на протяжении ряда лет используемых в 57 школе города Москвы. В представленном виде курс преподавался классу В 2008 года выпуска. Часть 2… Издатель: МЦНМО, Производитель: МЦНМО, Подробнее Купить за 277 грн (только Украина)
dic.academic.ru
