Примеры с дробями для 6 класса по математике – Сайт vpr-klass.com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации.

Дробные выражения. Математика, 6 класс: уроки, тесты, задания.

1.	Числитель и знаменатель числового дробного выражения Сложность: лёгкое	1
2.	Две десятичные дроби (десятые) Сложность: лёгкое	1
3.	Две обыкновенные дроби Сложность: лёгкое	2
4.	Смешанное число и целое (отрицательные числа) Сложность: среднее	4
5.	Десятичные дроби и целые числа Сложность: среднее	3
6.	Натуральные числа Сложность: среднее	3
7.	Обыкновенные и десятичные дроби Сложность: среднее	4
8.	Дробное выражение (1) Сложность: среднее	3
9.	Дробное выражение (2) Сложность: среднее	6
10.	Буквенное выражение (разность) Сложность: сложное	6
11.	Буквенное выражение (сумма) Сложность: сложное	7

www.yaklass.ru

Сложение и вычитание дробей с разными знаменателями. Сравнение дробей

Вспомним, что мы уже знаем об обыкновенных дробях.

1. Любая дробь обозначает количество, часть от какого-то числа. Эту часть мы умеем находить. Например, от это : .

2. Одно и то же количество, одну и ту же часть можно выразить разными дробями. Такие дроби называются эквивалентными (Рис. 1).

Рис. 1. Пример эквивалентных дробей

3. При сложении/вычитании дробей с одинаковыми знаменателями складываем/вычитаем числители.

4. При сравнении двух дробей с одинаковыми знаменателями большей является та, у которой числитель больше (Рис. 2).

Рис. 2. Пример сравнения дробей с одинаковым знаменателем

Теперь перейдем к вопросу о том, что делать, если у дробей будут разные знаменатели. Например, как нам сложить и (Рис. 3)?

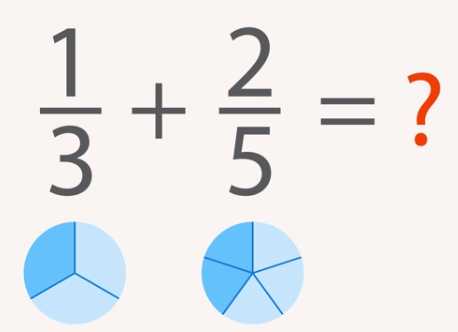
Рис. 3. Иллюстрация к примеру

Если мы заменим одну из дробей на эквивалентную (равную ей), то сумма, очевидно, не изменится.

Для дроби существует бесконечное множество дробей, которые ей эквивалентны. Чтобы их получить, нужно одновременно умножать и числитель, и знаменатель на одно и то же число (, , и т.д.). Тем самым мы получим цепочку эквивалентных дробей:

Аналогично поступим и со второй дробью:

Мы можем заменить исходные дроби эквивалентными. Но выбирать нужно так, чтобы новые дроби имели одинаковые знаменатели, ведь мы уже умеем их складывать. Одинаковый знаменатель у дробей и , заменим исходные дроби на них:

То есть идея оказался очень простой. Если нам нужно сложить две дроби, то смотрим на их знаменатели.

1) Если знаменатели одинаковые, то складываем сразу.

2) Если знаменатели разные, то заменяем исходные дроби эквивалентными, чтобы новые дроби имели одинаковые знаменатели. И складываем эти новые дроби.

Выполните вычисление:

1) 2) 3) 4) 5)

Решение:

1) Несложно заметить, что дробь легко превращается в ей эквивалентную дробь со знаменателем . Для этого нам нужно домножить ее числитель и знаменатель на :

2) Несложно увидеть, что мы вторую дробь можем превратить в дробь со знаменателем , для этого умножим ее числитель и знаменатель на : .

3) Обе дроби мы можем заменить эквивалентными дробями со знаменателем . Числитель и знаменатель первой дроби домножим на , а второй – на :

Таким образом, если знаменатели разные, то нужно заменить исходные дроби равными так, чтобы у новых дробей были одинаковые знаменатели. Такое преобразование называют приведением дробей к одному знаменателю (или к общему знаменателю).

4) Приведем дроби к общему знаменателю. Видно, что первую дробь можно привести к знаменателю . А у второй дроби он уже . Общий знаменатель .

5) Общим знаменателем для этих дробей является число . Числитель и знаменатель первой дроби домножим на , а второй – на : .

Ответим теперь сами себе на следующий вопрос: Все ли мы умеем, чтобы сложить две дроби?

Если у них одинаковые знаменатели, то да, несомненно.

Если у них разные знаменатели, то мы начнем заменять дроби равными им, чтобы у новых дробей были одинаковые знаменатели. Иными словами, будем приводить их к общему знаменателю. Всегда ли это легко сделать? Нет, не всегда.

Пример . Сложите две дроби: .

Решение. Очевидно, что в знаменателе будет такое число, которое получается и из домножением на что-то, и из 18 домножением на что-то. Но такое число найти нетрудно.

Это .

Числитель и знаменатель первой дроби умножим на . Числитель и знаменатель второй дроби умножим на . Дроби, конечно, стали более громоздкими, но зато теперь у них одинаковый знаменатель: .

Теперь мы можем решить задачу и на сравнение этих дробей: .

Следовательно, первое слагаемое меньше второго: .

Пример . Сравните две дроби и. После этого от большей дроби отнимите меньшую.

Решение. Чтобы сравнить две эти дроби, приведем их к общему знаменателю. Общий знаменатель найдем как произведение .

Чтобы в первой дроби получить знаменатель , умножим ее числитель и знаменатель на : .

Чтобы у второй дроби получить знаменатель , умножим ее числитель и знаменатель на : .

Итак, мы видим, что первая дробь больше: . Значит, .

Вычтем из большей дроби меньшую: .

На этом уроке мы научились складывать, вычитать, сравнивать дроби с разными знаменателями. Существуют способы упрощения сложения громоздких дробей. Не всегда общий знаменатель ищут как произведение имеющихся знаменателей. Для этого в шестом классе вы будете изучать такое понятие, как наименьшее общее кратное.

Список рекомендованной литературы

1) Виленкин Н.Я. Математика. 6 класс: учеб. для учащихся общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 30-е изд., стер. – М.: Мнемозина, 2013. – 288 с. : ил.

2) Зубарева И.И., Мордкович А.Г. Математика. 6 класс. – М.: Мнемозина.

3) Истомина И.Б. Математика, 6 класс. – М.: Ассоциация ХХI век.

Рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Ru.onlinemschool.com (Источник).

2. Интернет-портал Cleverstudents.ru (Источник).

3. Интернет-портал Calc.ru (Источник).

Домашнее задание

2) Сложите дроби:

а) б)

3) Укажите разность:

а) б)

4) ^* Сравните дроби и из большей вычтите меньшую:

а) и б) и в) и

interneturok.ru

Умножение и деление обыкновенных дробей. Математика, 6 класс: уроки, тесты, задания.

1.	Умножение дробей, правильная дробь Сложность: лёгкое	2
2.	Деление обыкновенных дробей (одинаковые знаменатели) Сложность: лёгкое	2
3.	Число, обратное обыкновенной дроби Сложность: среднее	2
4.	Число, обратное смешанному Сложность: среднее	1
5.	Число, обратное целому числу Сложность: среднее	1
6.	Обыкновенная дробь в квадрате Сложность: среднее	2
7.	Обыкновенная дробь в кубе Сложность: среднее	2
8.	Произведение смешанного числа и обыкновенной дроби Сложность: среднее	2
9.	Произведение двух смешанных чисел (разные знаменатели) Сложность: среднее	3
10.	Текстовая задача (два смешанных числа) Сложность: среднее	4
11.	Произведение десятичной дроби и обыкновенной Сложность: среднее	2
12.	Произведение двух отрицательных дробей Сложность: среднее	1
13.	Деление целого числа на смешанное число Сложность: среднее	2
14.	Деление смешанного числа на обыкновенную дробь Сложность: среднее	2
15.	Деление смешанного числа на обыкновенную дробь Сложность: среднее	4
16.	Частное десятичной дроби и обыкновенной Сложность: среднее	2
17.	Частное обыкновенных дробей с разными знаками Сложность: среднее	2
18.	Частное двух отрицательных дробей Сложность: среднее	2
19.	Текстовая задача Сложность: среднее	3
20.	Произведение трёх дробей Сложность: среднее	2
21.	Деление дроби на три другие дроби Сложность: среднее	4
22.	Неизвестное число Сложность: сложное	4
23.	Уравнение (произведение) Сложность: сложное	7
24.	Уравнение (сумма) Сложность: сложное	5
25.	Значение буквенного выражения Сложность: сложное	4

Дробные выражения. Математика, 6 класс: уроки, тесты, задания.

Сложение и вычитание дробей с разными знаменателями. Сравнение дробей

Умножение и деление обыкновенных дробей. Математика, 6 класс: уроки, тесты, задания.

Добавить комментарий Отменить ответ