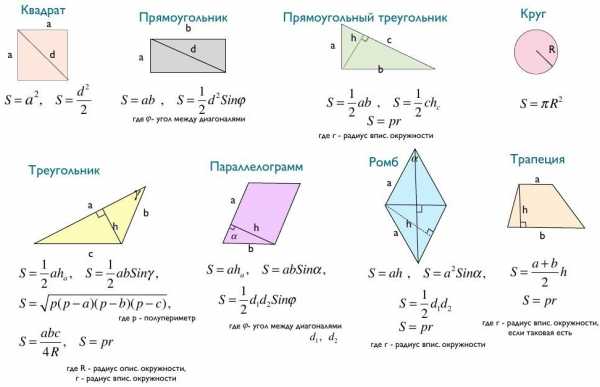
Площади различных фигур
Площади различных фигур (площади квадрата и многоугольника были уроком ранее)
Площадь параллелограмма
Одна из сторон параллелограмма называется основанием, а перпендикуляр из точки противоположной стороны к основанию называется высотой.
Площадь параллелограмма = произведению основания на высоту.
Площадь треугольника
Одна из сторон треугольника будет основанием, а проведенный к этой стороне перпендикуляр будет высотой.
Площадь треугольника = половине произведения основания на высоту.
Соответственно, в прямоугольном треугольнике мы найдем площадь по половине произведения катетов.
Еще один способ посчитать площадь треугольника через половину его периметра.
Выразим:
площадь — S;
стороны — a, b, c;
полупериметр треугольника: p = 1/2(a + b + c)
Тогда S =
Площадь трапеции
Высота в трапеции проводится также в виде перпендикуляра от противоположной стороны к основанию.
Площадь трапеции = половине суммы оснований умноженной на высоту.
Т.е. S = 1/2 * (BC + AD) * BH
Площадь правильного многоугольника
S — площадь n-угольника
P — периметр
r — радиус вписанной окружности
По формуле:
S = 1/2 * Pr
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
uchilegko.info
Внеклассный урок — Площади различных геометрических фигур
1) Площадь ромба равна половине произведений его диагоналей:
d1 · d2
S = ————
2
2) Так как ромб является также параллелограммом, то его площадь равна произведению стороны на высоту:
S = ah
3) Площадь ромба равна произведению квадрата стороны на синус угла между двумя смежными сторонами:
S = a2 · sin α
S = a2 · sin β
4) Площадь ромба можно вычислить, соотнеся диагонали (D или d) и тангенс углов:
1
S = — D2tg(α/2)
2
1
S = — d2tg(β/2)
2
где D – большая диагональ, d – меньшая диагональ, α – острый угол, β – тупой угол.
4) Площадь ромба можно также вычислить по радиусу вписанной окружности и углу α:
4r2
S = ———
sin α
S = 2a · r
raal100.narod.ru
Как найти площадь фигуры?
Как найти площадь фигуры?
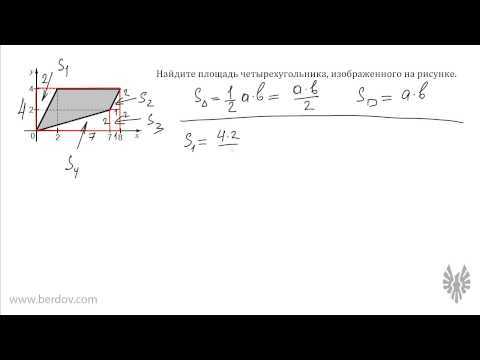

Площадь
Часть плоскости, заключенная внутри замкнутого контура, называется площадью этой плоскости. Выражается площадь количеством заключенных в ней квадратных единиц.
Чтобы вычислить площадь основных геометрических фигур, необходимо использовать правильную формулу.
Площадь треугольника
Обозначения:
- S — искомая площадь,
- a, b, c — длины сторон треугольника,
- h — высота искомого треугольника,
- γ — угол, находящийся между стороной a и стороной b,
- r — радиус окружности (вписанной в треугольник),
 R — радиус окружности (описанной вокруг треугольника),
R — радиус окружности (описанной вокруг треугольника),- p — половина периметра треугольника.
- Если известны h, a, то площадь искомого треугольника определяется как произведение длин стороны и высоты треугольника, опущенной к этой стороне, разделенное пополам: S=(a·h)/2
- Ес
elhow.ru
Площадь фигуры — Википедия
Материал из Википедии — свободной энциклопедии
Площадь плоской фигуры — аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.
Об определении[ | ]
Формальное введение понятия площадь и объём можно найти в статье мера Жордана, здесь мы приводим лишь намётки определения с комментариями.
Площадь — это вещественнозначная функция, определённая на определённом классе
- Положительность — площадь неотрицательна;
- Нормировка — квадрат со стороной единица имеет площадь 1;
- Конгруэнтность — конгруэнтные фигуры имеют равную площадь;
- Аддитивность — площадь объединения двух фигур без общих внутренних точек равна сумме площадей.
При этом определённый класс должен быть замкнут относительно пересечения и объединения, а также относительно движений плоскости и включать в себя все многоугольники. Из этих аксиом следует монотонность площади, то есть
- Если одна фигура принадлежит другой фигуре, то площадь первой не превосходит площади второй:
Чаще всего за «определённый класс» берут множество квадрируемых фигур. Фигура F{\displaystyle F} называется квадрируемой, если для любого ε>0{\displaystyle \varepsilon >0} существует пара многоугольников P{\displaystyle P} и Q{\displaystyle Q}, такие что P⊂F⊂Q{\displaystyle P\subset F\subset Q} и S(Q)−S(P)<ε{\displaystyle S(Q)-S(P)<\varepsilon }, где S(P){\displaystyle S(P)} обозначает площадь P{\displaystyle P}.
- Примеры квадрируемых фигур
Связанные определения[ | ]
- Две фигуры называются равновеликими, если они имеют равную площадь.
Комментарии[ | ]
- Существует математически строгий, но неоднозначный способ определить площадь для всех ограниченных подмножеств плоскости. То есть на множестве всех ограниченных подмножеств плоскости существуют различные функции площади, удовлетворяющие вышеприведённым аксиомам, а множество квадрируемых фигур является максимальным множеством фигур, на которых площадь определяется однозначно.
Формулы[ | ]
encyclopaedia.bid
Площадь фигуры — это… Что такое Площадь фигуры?
Пло́щадь плоской фигуры
Об определении
Формальное введение понятия площадь и объём можно найти в статье мера Жордана, здесь мы приводим лишь намётки определения с комментариями.
Площадь — это вещественнозначная функция, определённая на определённом классе фигур евклидовой плоскости, такая что:
- (положительность) площадь неотрицательна;
- (нормировка) квадрат со стороной единица имеет площадь 1;
- конгруэнтные фигуры имеют равную площадь;
- (аддитивность) площадь объединения двух фигур без общих внутренних точек равна сумме площадей.
Определённый класс должен быть замкнут относительно пересечения и объединения, а также относительно движений плоскости и включать в себя все многоугольники. Из этих аксиом следует монотонность площади, то есть
- Если одна фигура принадлежит другой фигуре, то площадь первой не превосходит площади второй:
Чаще всего за «определённый класс» берут множество квадрируемых фигур. Фигура называется квадрируемой, если для любого существует пара многоугольников и , такие что и , где обозначает площадь .
Связанные определения
- Две фигуры называются равновеликими, если они имеют равную площадь.
Комментарии
На самом деле, есть довольно неестественный и неоднозначный способ определить площадь для всех ограниченных подмножеств плоскости. На множестве всех ограниченных подмножеств плоскости существуют различные функции площади, т. е. не равные функции, удовлетворяющие вышеприведённым аксиомам, а множество квадрируемых фигур является максимальным множеством фигур, на которых функционал площади определяется однозначно.
То же самое можно сделать для длины на прямой, но нельзя для объёма в евклидовом пространстве и также нельзя для площади на единичной сфере в евклидовом пространстве, (смотри соответственно парадокс Банаха — Тарского и парадокс Хаусдорфа).
Площади некоторых фигур
Формулы для нахождения площадей различных фигур
| Фигура | Формула | Комментарий |
|---|---|---|
| Правильный треугольник | — длина стороны треугольника. | |
| Треугольник | Формула Герона. — полупериметр, , и — длины сторон треугольника. | |
| Треугольник | и — две стороны треугольника, а — угол между ними. | |
| Треугольник | и — сторона треугольника и высота, проведённая к этой стороне. | |
| Квадрат | — длина стороны квадрата. | |
| Прямоугольник | и — длины сторон прямоугольника. | |
| Ромб | и — длины диагоналей ромба. | |
| Параллелограмм | — длина одной из сторон параллелограмма, а — высота, проведённая к этой стороне. | |
| Трапеция | и — длины параллельных сторон, а — расстояние между ними (высота). | |
| Правильный шестиугольник | — длина стороны шестиугольника. | |
| Правильный восьмиугольник | — длина стороны восьмиугольника. | |
| Правильный многоугольник | — длина стороны многоугольника, а — количество сторон многоугольника. | |
| — апофема (или радиус вписанной в многоугольник окружности), а — периметр многоугольника. | ||
| Круг | или | — радиус окружности, а — её диаметр. |
| Сектор круга | и — соответственно радиус и угол сектора (в радианах). | |
| Эллипс | и — большая и малая полуоси эллипса. | |
| Поверхность Цилиндра | и — радиус и высота цилиндра соответственно. | |
| Боковая поверхность цилиндра | и — радиус и высота цилиндра соответственно. | |
| Поверхность конуса | и — радиус и длина образующей соответственно. | |
| Боковая поверхность конуса | и — радиус и длина образующей соответственно. | |
| Поверхность сферы | и — радиус и диаметр соответственно. | |
| Поверхность эллипсоида | См. статью. |
- Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне:
- Площадь прямоугольника равна произведению его смежных сторон:
- Площадь произвольного четырехугольника ABCD равна половине произведения диагоналей и синуса угла между ними:
- ,
- где — угол между диагоналями.
- Площадь ромба ABCD равна половине произведения диагоналей:
- Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне:
- Площадь трапеции равна произведению полусуммы оснований на высоту:
См. также
Ссылки
- В.Болтянский, О понятиях площади и объёма. Квант, № 5, 1977
- Б. П. Гейдман, Площади многоугольников, Библиотека «Математическое просвещение», выпуск 16, (2002).
- В. А. Рохлин, Площадь и объём, Энциклопедия элементарной математики, Книга 5, Геометрия, под редакцией П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина.
brokgauz.academic.ru
Равенство геометрических фигур и площадь фигуры
Определение. Фигуры, которые можно наложить одна на другую так, чтобы они совместились, называются равными фигурами.
Для обозначения равенства фигур используется знак равенства в кратком наименовании фигур.
Пример. Два треугольника равны, но один по отношению к другому смещен но плоскости листа и повернут на 180°. ΔABC = ΔA1B1C1.
Два треугольника равны, если у них соответствующие стороны и соответствующие углы равны.
Тогда ΔABC = ΔA1B1C1 если:
1) AB = A1B1 BC = B1C1 AC = A1C1
2)∠A = ∠A1 ∠B = ∠B1 ∠C = ∠C1
Равные фигуры имеют равные площади.
Существуют формулы площади для всех простейших многоугольников и круга. Для составных фигур площадь определяется как сумма площадей простых фигур. Так, шестиугольник можно разбить па 2 треугольника и четырехугольник, определить площади каждого из них, а потом сложить.
Единицами площади служат единицы измерения длинны (мм, дм, см, м, км) в квадрате (перемноженные дважды: мм2, см2, дм2, м2, км2) или специальные единицы площади (ар, или «сотка»; гектар).
Единицы площади — величины взаимосвязанные:
1 см2 = 100 мм2
1 дм2 = 100 см2
1 м2 = 100 дм2 = 10 000 см2
1 км2 = 1 000 000 м2
1а = 100 м2
1 га = 100 а = 10 000 м2.
Формулы для вычисления площади простых геометрических фигур
S = a 2
Площадь квадрата, где а — сторона квадрата.
S = a * b
Площадь прямоугольника, где а — длина; Ь — ширина прямоугольника.
S = ½ * a * h
Площадь треугольника, где а — сторона треугольника; Н — высота треугольника, проведенная к этой стороне.
Если фигура сложной конфигурации состоит из нескольких простых фигур, то необходимо посчитать по формулам площади простых фигур, а потом эти площади сложить.
Примеры.
Вычислить площадь квадрата со стороной 5 см.
Решение: Формула площади квадрата:S=a2. Подставим значение его стороны в формулу: S = 5 * 5 = 25 (см2).
Ответ: 25см2.
Вычислить площадь прямоугольника со сторонами 5 см и 30 мм.
Решение: Формула площади прямоугольника: S = a * b. Так как длины сторон заданы в разных единицах измерения, то приведем обе стороны к измерению в сантиметрах: 30 мм = 3 см.
Подставим значения сторон в формулу:
S = 5 * 3 = 15 (см2)
Ответ: 15 см2
shkolo.ru

 R — радиус окружности (описанной вокруг треугольника),
R — радиус окружности (описанной вокруг треугольника),