Ответы@Mail.Ru: как упростить выражение? (любое)
Научитесь вычислять степени с натуральными показателями. При умножении степеней с одинаковыми основаниями получают степень числа, основание которого остается прежним, а показатели степеней складываются в^м+в^н=в^(м+н) . При делении степеней с одинаковыми основаниями получают степень числа, основание которого остается прежним, а показатели степеней вычитаются, причем из показателя делимого вычитается показатель делителя в^м: б^н=в^(м-н) . При возведении степени в степень получается степень числа, основание которого остается прежним, а показатели перемножаются (в^м) ^н=в^(мн) При возведении в степень произведения чисел в эту степень возводится каждый множитель. (авс) ^м=а^м*в^м*с^м 2 Раскладывайте многочлены на множители, т. е. представляйте их в виде произведения нескольких сомножителей – многочленов и одночленов. Выносите общий множитель за скобки. Выучите основные формулы сокращенного умножения: разность квадратов, квадрат суммы, квадрат разности, сумму кубов, разность кубов, куб суммы и разности. Например, м^8+2*м^4*н^4+н^8=(м^4)^2+2*м4*н^4+(н^4)^2. Именно эти формулы являются основными в упрощении выражений. Используйте способ выделения полного квадрата в трехчлене вида ах^2+вх+с 3 Как можно чаще сокращайте дроби. Например, (2*а^2*в) /(а^2*в*с) =2/(а*с) . Но помните, что сокращать можно только множители. Если числитель и знаменатель алгебраической дроби умножать на одно и то же число, отличное от нуля, то при этом значение дроби не изменится. Преобразовывать рациональные выражения можно двумя способами: цепочкой и по действиям. Предпочтительней второй способ, т. к. легче проверить результаты промежуточных действий. 4 Нередко в выражениях необходимо извлекать корни. Корни четной степени извлекаются только из неотрицательных выражений или чисел. Корни нечетной степени извлекаются из любых выражений.
вынесением за скобки, сведением общих.
Научитесь вычислять степени с натуральными показателями. При умножении степеней с одинаковыми основаниями получают степень числа, основание которого остается прежним, а показатели степеней складываются в^м+в^н=в^(м+н) . При делении степеней с одинаковыми основаниями получают степень числа, основание которого остается прежним, а показатели степеней вычитаются, причем из показателя делимого вычитается показатель делителя в^м: б^н=в^(м-н) . При возведении степени в степень получается степень числа, основание которого остается прежним, а показатели перемножаются (в^м) ^н=в^(мн) При возведении в степень произведения чисел в эту степень возводится каждый множитель. (авс) ^м=а^м*в^м*с^м 2 Раскладывайте многочлены на множители, т. е. представляйте их в виде произведения нескольких сомножителей – многочленов и одночленов. Выносите общий множитель за скобки. Выучите основные формулы сокращенного умножения: разность квадратов, квадрат суммы, квадрат разности, сумму кубов, разность кубов, куб суммы и разности. Например, м^8+2*м^4*н^4+н^8=(м^4)^2+2*м4*н^4+(н^4)^2. Именно эти формулы являются основными в упрощении выражений. Используйте способ выделения полного квадрата в трехчлене вида ах^2+вх+с 3 Как можно чаще сокращайте дроби. Например, (2*а^2*в) /(а^2*в*с) =2/(а*с) . Но помните, что сокращать можно только множители. Если числитель и знаменатель алгебраической дроби умножать на одно и то же число, отличное от нуля, то при этом значение дроби не изменится. Преобразовывать рациональные выражения можно двумя способами: цепочкой и по действиям. Предпочтительней второй способ, т. к. легче проверить результаты промежуточных действий. 4 Нередко в выражениях необходимо извлекать корни. Корни четной степени извлекаются только из неотрицательных выражений или чисел. Корни нечетной степени извлекаются из любых выражений.
Научитесь вычислять степени с натуральными показателями. При умножении степеней с одинаковыми основаниями получают степень числа, основание которого остается прежним, а показатели степеней складываются в^м+в^н=в^(м+н) . При делении степеней с одинаковыми основаниями получают степень числа, основание которого остается прежним, а показатели степеней вычитаются, причем из показателя делимого вычитается показатель делителя в^м: б^н=в^(м-н) . При возведении степени в степень получается степень числа, основание которого остается прежним, а показатели перемножаются (в^м) ^н=в^(мн) При возведении в степень произведения чисел в эту степень возводится каждый множитель. (авс) ^м=а^м*в^м*с^м 2 Раскладывайте многочлены на множители, т. е. представляйте их в виде произведения нескольких сомножителей – многочленов и одночленов. Выносите общий множитель за скобки. Выучите основные формулы сокращенного умножения: разность квадратов, квадрат суммы, квадрат разности, сумму кубов, разность кубов, куб суммы и разности. Например, м^8+2*м^4*н^4+н^8=(м^4)^2+2*м4*н^4+(н^4)^2. Именно эти формулы являются основными в упрощении выражений. Используйте способ выделения полного квадрата в трехчлене вида ах^2+вх+с 3 Как можно чаще сокращайте дроби. Например, (2*а^2*в) /(а^2*в*с) =2/(а*с) . Но помните, что сокращать можно только множители. Если числитель и знаменатель алгебраической дроби умножать на одно и то же число, отличное от нуля, то при этом значение дроби не изменится. Преобразовывать рациональные выражения можно двумя способами: цепочкой и по действиям. Предпочтительней второй способ, т. к. легче проверить результаты промежуточных действий. 4 Нередко в выражениях необходимо извлекать корни. Корни четной степени извлекаются только из неотрицательных выражений или чисел. Корни нечетной степени извлекаются из любых выражений.
Упростить выражение — это значит раскрыть все скобки (если это возможно), совершить все возможные действие и в результате должно получится маленькое выражение, решаемое всего несколькими действиями или даже одним. Например: х+(2*3+7) Упрощаем: х+(6+7) И еще: х+13 Все. Это уже максимально упрощенное выражение. Решить его можно, только зная значение х (это именно выражение, а не равенство или уравнение) удачи 🙂
touch.otvet.mail.ru
Как упростить выражение | Сделай все сам
Дабы стремительно и результативно изготавливать расчеты, упрощайте математические выражения. Для этого используйте математические соотношения, дозволяющие сделать выражение короче, а расчеты упростить.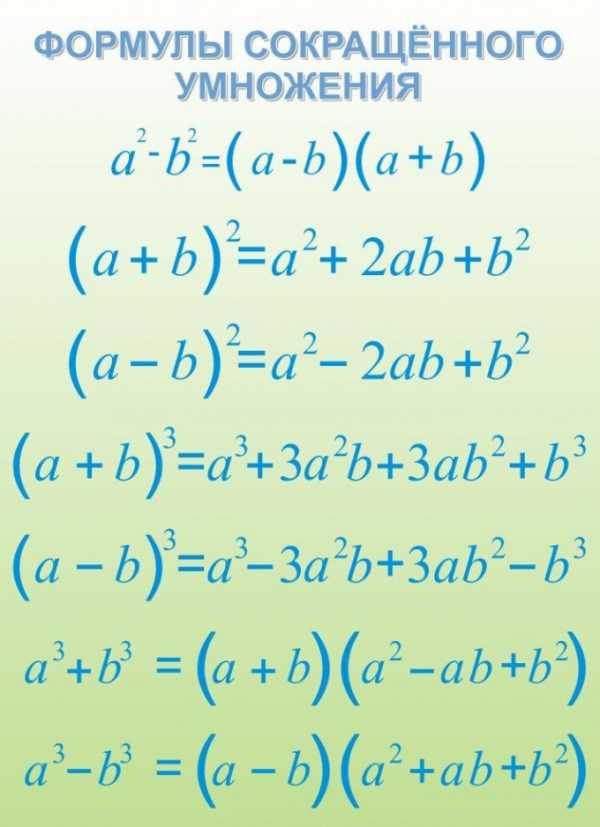
Вам понадобится
- – представление одночлена многочлена;
- – формулы сокращенного умножения;
- – действия с дробями;
- – основные тригонометрические тождества.
Инструкция
1. Если в выражении имеются одночлены с идентичными множителями, обнаружьте сумму показателей при них и умножьте на цельный для них множитель. Скажем, если есть выражение 2•а-4•а+5•а+а=(2-4+5+1)?а=4?а.
2. Для облегчения выражения используйте формулы сокращенного умножения. К особенно знаменитым относятся квадрат разности, разность квадратов, разность и сумма кубов. Скажем, если есть выражение 256-384+144, представьте его как 16?-2•16•12+12?=(16-12)?=4?=16.
3. В том случае, если выражение представляет собой естественную дробь, выделите из числителя и знаменателя всеобщий множитель и сократите дробь на него. Скажем, если необходимо сократить дробь (3•a?-6•a•b+3•b?)/(6?a?-6?b?), вынесите из числителя и знаменателя всеобщие множители в числителе это будет 3, в знаменателе 6. Получите выражение (3•(a?-2•a•b+b?))/(6?(a?-b?)). Сократите числитель и знаменатель на 3 и примените к оставшимся выражениям формулы сокращенного умножения. Для числителя это квадрат разности, а для знаменателя разность квадратов. Получите выражение (a-b)?/(2? (a+b)?(a-b)) сократив его на всеобщий множитель a-b, получите выражение (a-b)/(2? (a+b)), которое при определенных значениях переменных значительно легче посчитать.
4. Если одночлены имеют идентичные множители, возведенные в степень, то при их суммировании следите, дабы степени были равны, напротив сводить сходственные невозможно. Скажем, если есть выражение 2?m?+6•m?-m?-4•m?+7, то при сведении сходственных получится m?+2•m?+7.
5. При облегчении тригонометрических тождеств используйте формулы для их реформирования. Основное тригонометрическое тождество sin?(x)+cos?(x)=1, sin(x)/cos(x)=tg(x), 1/ tg(x)= ctg(x), формулы суммы и разности доводов, двойного, тройного довода и другие. Скажем, (sin(2?x)- cos(x))/ ctg(x). Распишите формулу двойного довода и котангенса, как отношения косинуса на синус. Получите (2? sin(x)• cos(x)- cos(x))• sin(x)/cos(x). Вынесите всеобщий множитель, cos(x) и сократите дробь cos(x)•(2? sin(x) – 1)• sin(x)/cos(x)= (2? sin(x) – 1) • sin(x).
Краткость, как говорится, – сестра дара. Всякому хочется блеснуть даром, но вот его сестра – штука трудная. Феноменальные мысли отчего-то сами собой облекаются в сложноподчинённые предложения со большинством деепричастных циклов. Впрочем в ваших силах упростить свои предложения и сделать их внятными и доступными каждым.
Инструкция
1. Дабы облегчить адресату (будь то слушатель либо читатель) жизнь, постарайтесь заменять причастные и деепричастные циклы короткими придаточными предложениями, исключительно если вышеуказанных циклов слишком много в одном предложении. “Пришедший домой кот, только что съевший мышь, громко мурлыча, ласкался к владельцу, пытаясь заглянуть ему в глаза, веря выпросить рыбу, принесённую из магазина” – такое не пойдёт. Разбейте сходственную конструкцию на несколько частей, не спешите и не пытайтесь сказать всё одним предложением, и будет вам блаженство.
2. Если вы замыслили феноменальное высказывание, но в нём оказалось слишком много придаточных предложений (тем больше с одним союзом), то отличнее разбить высказывание на несколько отдельных предложений либо опустить какой-то элемент. “Мы решили, что он расскажет Марине Васильевне, что Катя скажет Вите, что…” – дозволено продолжать беспредельно. Своевременно остановитесь и припомните о том человеке, кто будет это читать либо выслушивать.
3. Впрочем подводные камни кроются не только в структуре предложения. Обратите внимание на лексику. Иноязычные слова, длинные термины, слова, почерпнутые из художественной литературы 19 столетия – всё это только осложнит воспринятие. Нужно уточнить для себя, для какой аудитории вы составляете текст: технари, безусловно, осознают и трудные термины, и специфические слова; но если вы те же слова предложите учительнице литературы, вряд ли она вас поймёт.
4. Дар – великая вещь. Если вы гениальны (а людей без способностей не бывает), перед вами открывается уйма дорог. Но дар состоит не в трудности, а простоте, как ни необычно. Будьте проще, и ваши дары будут внятны и доступны каждым.
Видео по теме
«Выражением » в математике обыкновенно называют комплект арифметических и алгебраических действий с числами и переменными значениями. По аналогии с форматом записи чисел такой комплект называют «дробным» в том случае, когда он содержит операцию деления. К дробным выражениям, как и к числам в формате обычной дроби, применимы операции облегчения.
Инструкция
1. Начните с нахождения всеобщего множителя для выражений, стоящих в числителе и знаменателе дроби – это правило идентично как для численных соотношений, так и для содержащих неведомые переменные. Скажем, если в числителе стоит выражение 45*X, а в знаменателе 18*Y, то наибольшим всеобщим множителем будет число 9. Позже выполнения этого шага числитель дозволено записать как 9*5*X, а знаменатель – как 9*2*Y.
2. Если выражения в числителе и знаменателе содержат комбинацию основных математических операций (умножение, деление, сложение и вычитание), то вначале придется перенести за скобки всеобщий множитель для всякого из них в отдельности, а после этого вычленить из этих чисел крупнейший всеобщий делитель. Скажем, для выражения 45*X+180, стоящего в числителе, за скобки следует перенести множитель 45: 45*X+180 = 45*(X+4). А выражение 18+54*Y в знаменателе нужно привести к виду 18*(1+3*Y). После этого, как в предыдущем, шаге обнаружьте крупнейший всеобщий делитель вынесенных за скобки множителей: 45*X+180 / 18+54*Y = 45*(X+4) / 18*(1+3*Y) = 9*5*(X+4) / 9*2*(1+3*Y). В этом примере он тоже равен девятке.
3. Сократите обнаруженный на предыдущих шагах всеобщий множитель выражений в числителе и знаменателе дроби. Для примера из первого шага всю операцию облегчения дозволено записать так: 45*X / 18*Y = 9*5*X / 9*2*Y = 5*X / 2*Y.
4. Не неукоснительно при облегчении уменьшаемым всеобщим делителем должно быть число, это может быть и выражение, содержащее переменную. Скажем, если в числителе дроби стоит (4*X + X*Y + 12 + 3*Y), а в знаменателе (X*Y + 3*Y – 7*X – 21), то наибольшим всеобщим делителем будет выражение X+3, которое и следует сократить для облегчения выражения: (4*X + X*Y + 12 + 3*Y) / (X*Y + 3*Y – 7*X – 21) = (X+3)*(4+Y) / (X+3)*(Y-7) = (4+Y) / (Y-7).
Видео по теме
jprosto.ru
Упростить выражение № 1
- Подробности
- Категория: Рациональные дроби
Упростить выражение
Решение:
Упростим выражение по действиям.
1. Выполним вычитание дробей:
Для этого приведем дроби к общему знаменателю.
Общий знаменатель:
Расставим дополнительные множители для первой (2m + 1) и второй (2m — 1) дроби:
Умножим числители на дополнительные множители:
Раскроем скобки в числители с помощью формулы квадрата суммы:
2. Вторым действием, преобразуем дробь
В знаменателе вынесем общий множитель 5 получим:
3. Третьим действием выполним деление:
Для этого первую дробь умножим на дробь, обратную второй:
Выполним сокращение:
В итоге получим:
Ответ:
