| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Урок 13.
 многочлены от нескольких переменных — Алгебра и начала математического анализа — 10 класс
многочлены от нескольких переменных — Алгебра и начала математического анализа — 10 классАлгебра и начала математического анализа, 10 класс
Урок №13. Многочлены от нескольких переменных.
Перечень вопросов, рассматриваемых в теме
1) определение многочлена от нескольких переменных;
2) понятие симметрических многочленов;
3) формулы сокращенного умножения для старших степеней;
4) бином Ньютона;
5) метод неопределенных коэффициентов.
Глоссарий по теме
Многочлен Р(х;у) называют однородным многочленом n-й степени, если сумма показателей степеней переменных в каждом члене многочлена равна n. Если Р(х;у) — однородный многочлен, то уравнение Р(х;у) = 0 называют однородным уравнением.
Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х.
Уравнение Р(x;y) = а, где , называютсимметрическим, если Р(х;y) — симметрический многочлен.
Треугольник Паскаля —бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Многочлены от нескольких переменных можно складывать, вычитать, перемножать, возводить в натуральную степень, разлагать на множители — это вам известно из курса алгебры 7—9-го классов. Этот урок позволит нам несколько расширить знания о многочленах.
Этот урок позволит нам несколько расширить знания о многочленах.
Пример 1. Разложить на множители многочлен: 2x2-5xy+2y2.
Воспользуемся методом группировки
2x2-5xy+2y2= 2x2-4xy-xy+2y2= 2x(x-2y) –y(x-2y)=
(x-2y)(2x+2y).
Пример 2. Выведем формулу сокращенного умножения для «квадрата суммы» (x+y+z+u)2.
(x+y+z+u)2=((x+y)+(z+u))2= (x+y)2+2(x+y)(z+u)+(z+u)2= x2+y2+z2+u2+2(xy+xz+xu+yz+yu+zu).
Итак, мы получили (x+y+z+u)2= x2+y2+z2+u2+2(xy+xz+xu+yz+yu+zu).
Среди многочленов от двух переменных выделяют однородные и симметрические многочлены.
Многочлен Р(х;у) называют однородным многочленом n-й степени, если сумма показателей степеней переменных в каждом члене многочлена равна n. Если Р(х;у) — однородный многочлен, то уравнение Р(х;у) = 0 называют однородным уравнением.
Приведем примеры.
1) р(х; у)=2х+3у – однородный многочлен первой степени; соответственно 2х+3у=0 – однородное уравнение первой степени.
2) р(х; у)=3х2+5ху-7у2 — однородный многочлен второй степени; соответственно 3х2+5ху-7у2 =0 — однородное уравнение второй степени.
3) p(x; y)= x3+4xy2-5y3 — однородный многочлен третьей степени; x3+4xy2-5y3 =0 соответственно — однородное уравнение третьей степени.
4) p(x; y)= anxn+an-1xn-1y+an-2xn-2y2+…+a1xyn-1+a0yn — общий вид однородного многочлена n-й степени.
Рассмотрим еще один метод разложения многочленов на множители-
метод неопределенных коэффициентов. Суть метода неопределённых коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определятся путём перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной. Теоретической основой метода являются следующие утверждения
Теоретической основой метода являются следующие утверждения
- Два многочлена равны тогда и только тогда, когда равны их коэффициенты.
- Любой многочлен третьей степени имеет хотя бы один действительный корень, а потому разлагается в произведение линейного и квадратичного сомножителя.
- Любой многочлен четвёртой степени разлагается в произведение многочленов второй степени.
Пример 3. Разложить на множители многочлен
3 x 3 – x 2 – 3 x + 1.
Решение. Поскольку многочлен третьей степени разлагается в произведение линейного и квадратичного сомножителей, то будем искать многочлены x – p и ax 2 + bx + c такие, что справедливо равенство 3 x 3 – x 2 – 3 x + 1 = ( x – p )( ax 2+ bx + c ) = ax 3 + ( b – ap ) x 2 + ( c – bp ) x – pc . Приравнивая коэффициенты при одинаковых степенях в левой и правой частях этого равенства, получаем систему четырех уравнений для определения четырех неизвестных коэффициентов:
Решая эту систему, получаем: a = 3, p = –1, b = 2, c = –1. Итак, многочлен 3 x 3 – x 2 – 3 x + 1 разлагается на множители: 3 x 3 – x 2 – 3 x + 1 = ( x – 1)(3 x 2 + 2 x – 1).
Итак, многочлен 3 x 3 – x 2 – 3 x + 1 разлагается на множители: 3 x 3 – x 2 – 3 x + 1 = ( x – 1)(3 x 2 + 2 x – 1).
Стоит отметить, что существует достаточно изящный способ решения однородных уравнений. Поясним его суть на примере.
Пример 4. Решим уравнение x3+4xy2-5y3 =0
Заметим, что если в заданном уравнении взять х=0, то получится у=0; это означает, что пара (0; 0) является решением однородного уравнения. Пусть теперь х. Разделим почленно обе части заданного однородного уравнения на х3, получим:
Введем новую переменную . Тогда уравнение примет вид 1+4z2-5z3=0.
Далее последовательно находим:
5z3-4z2-1=0
(5z3-5z2)+(z2-1)=0
5z2(z-1)+(z-1)(z+1)=0
(z-1)(5z2+z+1)=0
Из уравнения z-1=0 находим z=1, уравнение 5z3-4z2-1=0 действительных корней не имеет.
Если z=1, то , т.е. у=х. Это значит, что любая пара вида (t; t) является решением заданного однородного уравнения. Между прочим, и отмеченная нами ранее пара (0; 0) также входит в указанный перечень решений.
Ответ: (t; t), где t- любое действительное число.
Теперь поговорим о симметрических многочленах. Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х. Например, симметрическим является двучлен x2y+xy2. В самом деле, при одновременной замене х на у и у на х получится двучлен y2x+yx2, но это то же самое, что x2y+xy2 . Другие примеры симметрических многочленов: xy, x+y, x2+y2, x3+y3, x4+y4 и т.д. Первые два из записанных многочленов считаются основными в том смысле, что любые другие симметрические многочлены можно представить в виде некоторой комбинации многочленов х + у и ху.
Теорема. Любой симметрический многочлен Р(х;у) можно представить в виде многочлена от ху и х+у.
Например,
x2+y2=(x+y)2-2xy
x3+y3=(x+y)3-3xy(x+y)
x4+y4= 2xy(x2+y2)-(x4+y4)+3(xy)2 и т.д.
Уравнение Р(x;y) = а, где , называют симметрическим, если Р(х;y) — симметрический многочлен. Мы с вами рассматривали его на предыдущем уроке.
А теперь перейдем к такому понятию как бином Ньютона.
Слово бином означает «Два числа». В математике биномом называют «формулу для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных». Бином Ньютона — название формулы, выражающей степень двучлена в виде суммы одночленов.
Давайте вслед за Ньютоном попробуем ее вывести, чтобы затем применять.
Вы наверняка помните (или, по крайней мере, должны помнить), формулы сокращенного умножения для квадрата и куба суммы двух слагаемых (такая сумма называется «бином», по-русски – двучлен.
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
Если вы забыли эти формулы, можно их получить напрямую, раскрыв скобки в очевидных равенствах
(a+b)2=(a+b)(a+b)
(a+b)3=(a+b)(a+b)(a+b)
Может быть, вам приходил в голову вопрос: можно ли (без компьютера) получить формулы типа для биномов четвертой степени, пятой, десятой – какой угодно?
Давайте попробуем дойти напрямую хотя бы до пятой степени, а там, может быть, окажется «рояль в кустах» (для порядка будем размещать слагаемые в правой части по убыванию степени а, она убывает от максимума до нуля):
(a+b)4=(a+b)3(a+b)=(a3+3a2b+3ab2+b3)(a+b)=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=(a+b)4(a+b)=(a4+4a3b+6a2b2+4ab3+b4)(a+b)=a5+5a4b+10a3b2+10a2b3+5ab4+b5
Теперь отдельно выпишем численные коэффициенты в правых частях формул при возведении бинома в заданную степень:
n=2 1,2,1
n=3 1,3,3,1
n=4 1,4,6,4,1
n=5 1,5,10,5,1
Легко проверить, что выписанные на численные коэффициенты – это строчки треугольника Паскаля, начиная с третьей. Этот «усеченный треугольник», в котором не хватает первых двух строк, легко сделать полным (получить строчки при n=0 и n=1):
Этот «усеченный треугольник», в котором не хватает первых двух строк, легко сделать полным (получить строчки при n=0 и n=1):
n=0, (a+b)0=1
n=1, (a+b)1=a+b
Окончательно получим:
n=0 1
n=1 1,1
n=2 1,2,1
n=3 1,3,3,1
n=4 1,4,6,4,1
n=5 1,5,10,5,1
Общая формула бинома Ньютона:
.
Правая часть формулы называется разложением степени бинома.
— называется биномиальными коэффициентами, а все слагаемые — членами бинома.
Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля.
На самом деле, о треугольнике Паскаля было известно задолго до Паскаля — его знал живший в XI-XII вв. среднеазиатский математик и поэт Омар Хайям (к сожалению, его сочинение об этом до нас не дошло). Первое, дошедшее до нас описание формулы бинома Ньютона содержится в появившейся в 1265 г. книге среднеазиатского математика ат-Туси, где дана таблица чисел (биномиальных коэффициентов) до n=12 включительно.
Первое, дошедшее до нас описание формулы бинома Ньютона содержится в появившейся в 1265 г. книге среднеазиатского математика ат-Туси, где дана таблица чисел (биномиальных коэффициентов) до n=12 включительно.
Европейские ученые познакомились с формулой бинома Ньютона, по-видимому, через восточных математиков. Детальное изучение свойств биномиальных коэффициентов провел французский математик и философ Б. Паскаль в 1654 г.
В заключении рассмотрим пример, в котором использование бинома Ньютона позволяет доказать делимость выражения на заданное число.
Пример 5.
Доказать, что значение выражения 5n+28n-1, где n – натуральное число, делится на 16 без остатка.
Решение: представим первое слагаемое выражение как 5n= (4+1)n и воспользуемся формулой бинома Ньютона:
Полученное произведение доказывает делимость исходного выражения на 16.
Бином Ньютона применяется при доказательстве Теоремы Ферма, в теории бесконечных рядов и выводе формулы Ньютона-Лейбница
Примеры и разборы решения заданий тренировочного модуля
№1.
Из данных многочленов выделите симметрические:
- 2х2-5ху+2у2-6
- 6x⁴-16xy²-6y3+19
- -3ху+6х²-5у²+8
- 16x4y²+16x²y4-x⁴-y⁴
Решение: к данному заданию применим определение симметрических многочленов (Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х). Получим, что нам подходят 1 и 4 пункты.
Верный ответ:
- 2х2-5ху+2у2-6
- 6x⁴-16xy²-6y3+19
- -3ху+6х²-5у²+8
- 16x4y²+16x²y4-x⁴-y⁴
№2.
(а+b)5= __a5 +___a4b+___a3b2+___a2b3+___ab4+__b5
Решение: для решения данного задания воспользуемся треугольником Паскаля
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
Нас интересует последняя строчка.
Применив ее, получим ответ:
(а+b)5= 1a5 +5a4b+10a3b2+10a2b3+5ab4+1b5
Степени сколиоза по градусам | Какие есть искривление позвоночника?
15.10.2021
Степени сколиоза
Сколиозом называют боковое искривление позвоночника. Без лечения он деформируется еще и в передне-заднем направлении, а тела позвонков скручиваются. Независимо от локализации кривизны в патологический процесс вовлекаются все позвоночные отделы, что приводит к нарушению работы органов грудной клетки и малого таза.
Откуда берется сколиоз
В большинстве случаев сколиоз обнаруживается у детей и подростков. Он является болезнью роста, так как быстро прогрессирует именно в период активного развития скелета. Искривление позвоночника – это очень распространенное заболевание, которым страдают порядка 30% школьников.
Для справки! 8–9 пациентам из 10 ставится диагноз «идиопатический сколиоз», так как причину его появления выяснить не удается.
Наибольшую опасность представляют этапы, когда организм ребенка быстро растет: с 4-х до 6-ти лет и с 10 до 14. Но особенно быстрый, «взрывной» рост скелета отмечается в пубертатном периоде, который у мальчиков начинается в 10-11 лет, а у девочек – в 8–9. Завершается половое созревание к 19–20 и 16–17 годам соответственно.
Фактором повышенного риска являются уже имеющиеся сколиотические изменения, рентгенологически подтвержденные до начала пубертата. Даже небольшой сколиоз 4 градуса может буквально за 2–3 месяца увеличиться в несколько раз, достигнув угла искривления 30˚ и больше.
Форсированный рост – не единственная причина деформаций. Позвоночник может искривляться из-за болезней соединительных тканей, эндокринных расстройств, а также после тяжелых травм и ампутации конечностей.
Перекос спины возможен при разной длине ног и врожденных дефектах позвонков. Виновником патологического изгиба бывают патологии нервной и мышечной систем.
Сколько степеней сколиоза
В зависимости от угла кривизны патология классифицируется на 4 степени:
- 1 степень — 1–10°;
- 2 степень — 11–25˚;
- 3 степень — 26–40°;
- 4 степень — больше 40°.
Для определения угла наклона позвоночника делают рентген в 3-х проекциях: в положении стоя, лежа на горизонтальной и наклонной поверхности. Степени представляют собой стадии деформации, каждая из которых характеризуется типичными признаками и симптомами.
Для справки! Сколиоз можно считать женской болезнью, так как он поражает девочек примерно в 5 раз чаще, чем мальчиков.
Как понять степень сколиоза
Для определения стадии деформации следует обращать внимание на внешние признаки и жалобы самого больного.
1 степень
Сколиотическая дуга образует угол до 10°, что почти не отражается на самочувствии. Боль в спине возникает лишь при значительных физических нагрузках и после долгого пребывания в статичной позе.
Внешние признаки:
- когда человек стоит, одно его плечо располагается ниже другого;
- расстояние от позвоночника до каждой из лопаток разнится;
- в наклоне видно, что позвоночный столб отклонен от своей оси влево или вправо в одном или нескольких местах;
- осанка сохраняется, но небольшая сутулость уже есть.
2 степень
Угол сколиотической дуги составляет 11–25°. То есть сколиоз 12 градусов – это уже 2 стадия деформации.
Симптомы:
- выраженная сутулость, в особенности при S-образном искривлении;
- наличие межреберного горба с одной стороны спины, заметного в наклоненном положении;
- мышечный валик на уровне поясницы, состоящий из спазмированных мышц;
- болевой синдром в разных частях спины, который беспокоит сильнее и чаще, чем при 1 степени кривизны;
- спина быстро устает даже после незначительных нагрузок.

3 степень
Сколиоз, угол искривления которого 26–40°, имеет 3 степень и характеризуется:
- выраженным позвоночным изгибом в форме буквы С, S или Z;
- сильной асимметрией всего тела и сутулостью;
- деформацией грудной клетки;
- значительной разницей высоты положения плеч и лопаток;
- интенсивными и почти постоянными болями в спине;
- нарушением функции органов дыхания и сердца, что проявляется быстрой усталостью от двигательной активности, одышкой и частыми простудами;
- сдавливанием спинного мозга, приводящим к расстройству чувствительности, мышечной слабости в спине и/или конечностях.
4 степень
Угол сколиотической дуги больше 40° – это уже инвалидность и существенное снижение качества жизни. Помимо выраженной асимметрии туловища, искажения формы позвоночника и грудины, отмечается смещение внутренних органов с нарушением их работы.
Спина болит очень сильно, а компрессия спинномозгового канала может вызывать тяжелые осложнения. В числе последних так называемый «синдром конского хвоста», при котором наступает паралич нижних конечностей.
Методы лечения
Подход к лечению при разных углах кривизны отличается. Сколиоз 50 градусов нередко требует оперативного вмешательства. Вопрос о его целесообразности решается в индивидуальном порядке, с учетом таких факторов, как:
- возраст больного;
- причина деформации;
- локализация патологического изгиба;
- эффективность консервативных методик лечения;
- общее состояние здоровья и имеющиеся симптомы;
1 степень
На первой стадии искривления достаточно выполнять лечебную гимнастику и посещать массажные сеансы. Врачи также рекомендуют заниматься плаванием и регулярно проходить обследование. Для укрепления мышечного корсета могут назначаться физиотерапевтические процедуры электрофореза и электромиостимуляции.
Для справки! Сколиоз 8 градусов и меньше нельзя оставлять без внимания. Необходимо обязательно принять меры по профилактике его усиления и выполнять все врачебные назначения.
2 степень
Корректировать 2 степень деформации сложнее, чем первую. Выпрямить позвоночник вряд ли получится, но уменьшить градус кривизны и предупредить дальнейшее ухудшение состояния по силам каждому.
В комплексную терапию входит ЛФК, – лечебная физическая культура – массаж и физиолечение. Детям назначаются ортопедические корсеты, если они продолжают расти и имеют искривление от 15°. У пациентов с завершенным ростом корсетирование не применяется.
Хорошие результаты дает тракционное вытяжение, которое проводится на специальных кроватях с наклоном, и мануальная терапия.
Важно, чтобы процедуры были регулярными:
- ЛФК – ежедневно;
- массаж – 1 раз в полгода-год;
- плавание – 2–3 раза в неделю.

Детям и подросткам со 2-й степенью заболевания нежелательно ходить на физкультуру, поскольку командные игры могут обернуться травмой.
Если консервативное лечение результатов не дает, ставится вопрос об операции.
3 степень
Справиться с искривлением позвоночника 3-й степени консервативно возможно лишь в детском возрасте, не позднее 11 лет. После 11 позвонки окостеневают полностью, и результатом лечения будет только замедление сколиотического процесса и небольшое уменьшение угла кривизны.
На 3 стадии деформации широко применяются физиопроцедуры – электрофорез, импульсные токи, магнитотерапия.
В тяжелых случаях, когда пациент жалуется на сильные боли, прибегают к оперативному вмешательству.
4 степень
Угол сколиотической дуги больше 40° является прямым показанием к операции, если консервативные методы неэффективны. Комплекс лечебных мероприятий не отличается от такового при позвоночном искривлении 3 степени.
Комплекс лечебных мероприятий не отличается от такового при позвоночном искривлении 3 степени.
Для справки! С целью повышения подвижности деформированного участка проводятся сеансы мануальной терапии. Они входят в список подготовительных процедур перед операцией.
Хирургическое лечение заключается в выпрямлении позвоночно-двигательного сегмента до «нормального» угла. Фиксация позвонков производится с помощью металлоконструкций – пластин, стержней, винтов и крючков.
Прооперированная зона становится неподвижной. Чтобы скорректировать форму позвонков и расширить их, а также для укрепления всей конструкции применяются костные трансплантаты-вкладыши.
Если вы или ваш ребенок страдаете сколиозом, не затягивайте с лечением. Вы можете избавиться от деформации при своевременном обращении к грамотному врачу – именно такие специалисты работают у нас.
Наши доктора проводят консультации и лечебные процедуры с максимальным комфортом для пациентов. Вам не придется терпеть боль и неудобства, ведь все манипуляции выполняются на современном и эргономичном оборудовании.
Вам не придется терпеть боль и неудобства, ведь все манипуляции выполняются на современном и эргономичном оборудовании.
Для каждого пациента разрабатывается индивидуальный план лечения, по окончании которого выдаются рекомендации по поддержанию достигнутого эффекта.
Записаться на прием вы можете по телефону +375 29 628 85 82 или оставить свои контакты в форме обратной связи .
Записаться на прием
Наши услуги
Иглоукалывание при остеохондрозе Лечебный массаж спины Уколы при болях в тазобедренном суставе
Возврат к списку
Диагностика 0, 1, 2, 3, 4 стадии рака груди
Рак молочной железы. Симптомы и признаки
Причины возникновения рака молочной железы
Стадии рака молочной железы
Диагностика рака молочной железы
Лечение рака молочной железы
Лечение рака молочной железы на различных стадиях
Хирургическое лечение рака молочной железы
Лучевая терапия при раке молочной железы
Химиотерапия при раке молочной железы
Гормонотерапия при раке молочной железы
Таргетная терапия рака молочной железы
Паллиативное лечение рака молочной железы
Прогнозируемые результаты и профилактика
Выявление рака молочной железы на ранних стадиях дает больше шансов пациентке на полное выздоровление. Обнаружить рак молочной железы на 0 и 1 стадиях самостоятельно довольно сложно из-за небольших размеров новообразования, потому так важны регулярные обследования у специалистов и скрининговые методы обследования.
Обнаружить рак молочной железы на 0 и 1 стадиях самостоятельно довольно сложно из-за небольших размеров новообразования, потому так важны регулярные обследования у специалистов и скрининговые методы обследования.
Диагностика 0 и 1 стадии
Основным методом ранней диагностики является УЗИ молочных желез и маммография (рентгенография молочных желез c помощью специального аппарата), кроме того в качестве скриннингового исследования используется магнитно-резонансная томография. Окончательный диагноз устанавливается на основании аспирационной биопсии опухоли, сторожевых или перифирических лимфоузлов с дальнейшим гистологическим и иммуногистохимическим анализом. После постановки диагноза для разработки схемы лечения определяется уровень экспрессии рецепторов гормонов, проводится FISH-тест для выявления HER2-позитивных опухолей (HER2 — белок, способный влиять на рост раковых клеток).
Признаки 1 стадии рака груди:
- Размер опухоли менее 2 см.
- Прилегающие к опухоли ткани и органы не затронуты, метастазы в лимфоузлы отсутствуют.

Диагностика 2 стадии рака молочной железы
Характерными признаками 2 стадии заболевания являются:размер опухоли до 5 см., отмечается вовлечение в патологический процесс лимфатических узлов подмышечной зоны с пораженной стороны. Данную стадию рака считают ранней, за исключением случаев, когда метастазы уже поразили множество лимфоузлов. Тогда ее относят к более поздним формам заболевания. Когда лимфоузлы начинают образовывать спайки между собой и с прилегающими тканями, теряя подвижность, можно говорить о вступлении в 3-ю стадию заболевания.
2 стадия подразделяется на категории А и В.
На стадии 2А размер опухоли не превышает 2 см, отмечается метастатическое поражение от 1 до 3-х лимфоузлов подмышечной зоны. Еще один вариант — размер опухоли от 2 до 5 см., но лимфоузлы не поражены.
При стадии 2В опухоль не больше 5 см в диаметре, в процесс вовлечены 1-3 подмышечных лимфоузла, либо размер опухоли превышает 5 см., но поражения лимфоузлов нет.
Опухоль, размер которой превышает 2 см, может быть обнаружена при прощупывании.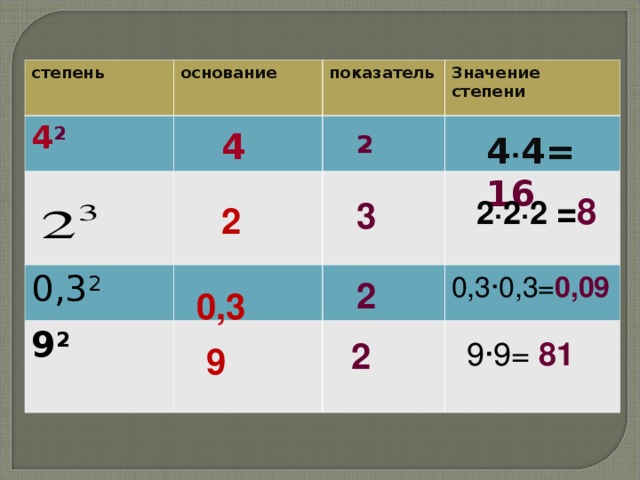 Потому так важно ежемесячное самообследование женщины. Регулярное посещение врача-маммолога и проведение контрольных обследований может способствовать выявлению злокачественного образования на еще более раннем этапе.
Потому так важно ежемесячное самообследование женщины. Регулярное посещение врача-маммолога и проведение контрольных обследований может способствовать выявлению злокачественного образования на еще более раннем этапе.
Если первичный диагноз рак молочной железы установлен, проводится расширенная комплексная диагностика, включая компьютерную томографию. Выясняется распространенность процесса в молочной железе и за ее пределами. Устанавливается окончательный диагноз и стадия заболевания, чувствительность опухоли к гормонам, химиотерапевтическим и таргетным препаратам.
3 стадия рака молочной железы
На 3 стадии может отмечаться поражение сразу нескольких лимфоузлов подмышечной области, сливающихся между собой и с прилегающими тканями в малоподвижные конгломераты. Метастазы в отдаленные органы еще отсутствуют. Третью стадию также принято называть местно-распространенным раком молочной железы.
Согласно международной системе ТNM выделяют 3 подкатегории данной стадии:
- Стадия 3А.
 Размер опухоли превышает 5 см в диаметре, поражены 1-3 подмышечных лимфоузла. Еще один вариант — опухоль меньшего размера, но при этом пораженные метастазами лимфоузлы спаянны между собой и с окружающими тканями;
Размер опухоли превышает 5 см в диаметре, поражены 1-3 подмышечных лимфоузла. Еще один вариант — опухоль меньшего размера, но при этом пораженные метастазами лимфоузлы спаянны между собой и с окружающими тканями; - Стадия 3В. Опухоль проросла в близлежащие ткани (грудные мышцы, кожные покровы). Размер образования на этом этапе может быть любым. Метастазы в лимфоузлы подмышечной зоны могут отсутствовать, либо могут быть поражены несколько из них. К стадии 3В причисляют и довольно редкую форму заболевания — воспалительный рак молочной железы. Он характеризуется крайне агрессивным течением.
- Стадия 3С. Опухоль может быть любого размера, но злокачественный процесс уже затронул большое количество лимфоузлов. На данной стадии заболевания могут быть поражены более 10 подмышечных лимфоузлов, затронуты надключичные и подключичные лимфоузлы, а также узлы, расположенные в толще груди и в области шеи.
Чаще всего третья стадия выявляется у женщин, которые уже проходят лечение рака молочной железы 1 или 2 стадии. Степень распространенности заболевания и его стадия определяются с помощью рентгенографии грудной клетки, магнитно-резонансной и компьютерной томографии, позитронно-эмиссионной томографии (ПЭТ, ПЭТ/КТ), сцинтиграфии костной системы и пр.
Степень распространенности заболевания и его стадия определяются с помощью рентгенографии грудной клетки, магнитно-резонансной и компьютерной томографии, позитронно-эмиссионной томографии (ПЭТ, ПЭТ/КТ), сцинтиграфии костной системы и пр.
4 стадия рака груди
На 4 стадии происходит метастазирование опухоли в отдаленные органы и ткани. Чаще всего метастазы поражают легкие, печень, надпочечники, кости, головной мозг.
Несмотря на это, при условии активной борьбы с заболеванием, женщина имеет шанс продлить свою жизнь на годы. Современные методы лечения способны добиться значительного улучшения качества жизни пациента даже на поздних стадиях рака.
Цены
Маммолог, заведующая отделением, первичный прием
2600 i
Маммолог Пивенштейн Л.В., первичный прием
2600 i
Онколог, заведующая отделением, первичный прием
2700 i
Онколог Пивенштейн Л. В., первичный прием
В., первичный прием
2700 i
Остеохондроз 1, 2, 3 и 4 степени поясничного отдела
Врачи выделяют четыре степени остеохондроза поясничного отдела. Самым уязвимым отделом позвоночника является поясница (ПОП), поэтому в этом отделе остеохондроз встречается намного чаще, чем в грудном и шейном.
Факторы, приводящие к повреждениям
Самая большая нагрузка верхней части тела во время ходьбы, при сидении, беге и любой иной физической нагрузке попадает именно на этот отдел. Поясничный отдел состоит из 5 позвонков, которые в верхней части соединяются с грудным отделом, а в нижней — с крестцом и копчиком.
Повреждение и деформация межпозвонковых дисков и есть остеохондроз поясничного отдела позвоночника. При развитии этой патологии теряется эластичность, уменьшается высота и происходит постепенное разрушение дисков, которое влечет за собой выпячивание фиброзного кольца.
Часто пациент приходит к врачу с жалобой на боли в пояснице, считая, что не болен, а просто поднял что-то тяжелое или сделал неловкое движение, поэтому и прихватило спину. Человек порой не осознает всей серьезности положения.
Человек порой не осознает всей серьезности положения.
Поскольку разрушительный процесс происходит не за 1 день, различают четыре степени остеохондроза.
Проявления остеохондроза поясничного отдела первой степени
Остеохондроз 1 степени поясничного отдела — это начальная стадия, когда происходят изменения в дисках. Первая стадия дает о себе знать слабыми (терпимыми) болями, которые периодически возникают при:
- движениях;
- наклонах;
- поворотах;
- поднятии тяжестей.
Происходит постепенное уменьшение высоты дисков, а это значит, что зазоры между позвонками становятся узкими, и основную амортизирующую функцию позвоночник полноценно выполнять не может.
На начальной стадии деформацию дисков можно приостановить. Для этого пациенту нужно пройти курс лечебного массажа, в результате которого снимаются мышечные спазмы и восстанавливается кровообращение. Но одного курса массажа недостаточно для полного восстановления поясницы.
Начальная стадия — это сигнал тревоги, который является предвестником протрузий и грыж. Поэтому очень важно выполнять простые упражнения, не набирать лишний вес и стараться вести подвижный образ жизни.
Первую степень заболевания называют еще болезнью люмбаго. Боль на этой стадии не вызывает беспокойства. На этом этапе помогает отдых в положении лежа. Полезно под ноги подкладывать высокий валик, чтобы разгружать поясничный отдел.
Как проявляется остеохондроз поясницы второй степени?
Диагностируется остеохондроз 2 степени поясничного отдела, если боль из поясницы отдает в ягодичную мышцу и голень, ограничивая движения. Боль становится все интенсивнее и сильнее, связано это с ущемлением нерва, который возникает из-за сужения просвета между позвонками.
На 2 стадии происходит изменение формы диска. Он расплющивается и выпячивается. Подобная деформация называется протрузией, в результате которой происходит сдавливание нервного корешка. В зависимости от того, с какой стороны произойдет выпячивание, и будут происходить неврологические боли.
Остеохондроз 1 степени отличается от 2 степени тем, что одним только расслабляющим массажем и упражнениями больной не обходится. Если при 1 степени еще помогает ортопедическая постель, то для коррекции позвонков и дисков нужна помощь мануального терапевта. Многим помогает иглоукалывание и точечный массаж.
Нужно приложить огромные усилия, чтобы остановить дегеративно-дистрофический процесс, чтобы не дать разорваться фиброзному кольцу, которое становится причиной образования грыжи. Остеохондроз поясничного отдела 2 степени опасен тем, что для ликвидации болевых симптомов применяется лечение медикаментами. Подобным образом купируется боль и снимается воспалительный процесс, но проблема остается не решенной, и болезнь продолжает прогрессировать дальше.
Деформацию поясничного отдела позвоночника 2 степени очень важно корректировать специально разработанными упражнениями, поскольку только движениями тела можно укрепить мышцы и связки, которые поддерживают позвонки.
Остеохондроз поясничного отдела второй степени проявляется выраженными болями. В болезненном участке может ощущаться жар или холод. Вторая степень недуга связана с деформацией диска и образованием протрузий.
В болезненном участке может ощущаться жар или холод. Вторая степень недуга связана с деформацией диска и образованием протрузий.
При остеохондрозе 1 и 2 степени поясничного отдела следует с осторожностью нагибаться вперед. Надевая обувь, нужно садиться на стул или ставить ногу на табурет. Про сильные физические нагрузки следует на время забыть. Сидя на стуле, нужно подкладывать за поясницу небольшую подушку или валик, чтобы искусственно создать правильный изгиб позвонков.
Читайте также: Какой матрас выбрать при остеохондрозе?
Остеохондроз поясницы третьей степени
Остеохондроз 3 степени поясничного отдела характеризуется тем, что происходит разрыв фиброзного кольца и вытекание его содержимого в межпозвонковую область. При образовании грыж и протрузий человек ощущает постоянную боль и дискомфорт. Движения становятся ограниченными и появляются проблемы с внутренними органами, потому что поясничный отдел позвоночника связан со следующими частями организма:
- мочевой пузырь;
- половые органы;
- аппендикс;
- слепая кишка;
- голени;
- стопы;
- ягодицы;
- прямая кишка и задний проход.

На третьей стадии деформации позвоночника медикаменты, упражнения и вмешательства мануальных терапевтов помогают мало. Занимаясь самолечением или игнорируя заболевание, больной в конечном итоге попадает к хирургу, когда единственным способом избавления от инвалидности является оперативное вмешательство. Остеохондроз позвоночника 3 степени отличается разрывом фиброзного кольца и образованием грыж.
Четвертая степень остеохондроза поясницы
Остеохондроз 4 степени поясничного отдела характеризуется следующими необратимыми изменениями: происходит атрофия хрящей, в результате которой позвонки начинают разрастаться. Это приводит к проблемам при передвижении, а в тяжелых случаях к полному ограничению движений и инвалидности. Происходит пережатие спинномозговых нервов и канала, что становится причиной пареза и паралича.
Когда страдает поясничный отдел позвоночника, то захватывается и крестцовый отдел. Поэтому диагностируется пояснично-крестцовый остеохондроз.
Как поставить точный диагноз? Остеохондроз может сопровождаться артрозом — изнашиванием суставов поясницы. Во время артроза суставной хрящ разрушаается, что приводит к тем же проблемам, что и при остеохондрозе. Причиной развития артроза является нарушение обмена веществ, из-за которого сустав, не получив питательных веществ, теряет свою эластичность.
Симптомы остеохондроза и артроза очень похожи, но подход к лечению может несколько отличаться. Обычно артроз развивается в пожилом возрасте, когда по утрам возникает чувство скованности в пояснице, из-за чего порой бывает очень сложно подняться с постели. Отличить самостоятельно остеохондроз от артроза может только специалист после проведения соответствующих обследований.
Остеохондроз поясницы является серьезной патологией, которую нельзя оставлять без внимания. Это касается всех этапов развития болезни. Нужно все усилия направлять на восстановление тканей, улучшение кровообращения в них, снятие отека, спазмов и восстановление обмена веществ.
Очень важно пересмотреть свой образ жизни и рацион. Для восстановления пояснично-крестцового отдела лечение должно проводиться комплексно, нужно использовать все методы. Важно после снятия болевых синдромов ежедневно выполнять лечебные упражнения, которые поддержат нормальные процессы в тканях.
Watch this video on YouTube
При лечении позвоночника, следует помнить, что он состоит не только из позвонков и дисков, но и мышц, связок, сосудов и нервов. Выполнять лечебно-профилактические упражнения на любой стадии заболевания следует лежа на полу. Главное — не количество выполненных упражнений, а правильное растягивание и укрепление нужных связок. Неправильно сделанное движение во время упражнений, может усугубить ситуацию, поэтому при их выполнении нужно прислушиваться к своему организму.
Опьянение и отрезвление — Alkoinfo.ee
Посоветуй
Степени опьянения и время вытрезвления
От чего зависит опьянение?
То, насколько повышается содержание алкоголя в крови, зависит от множества факторов. Однако общее правило заключается в том, что чем больше алкоголя, тем выше его содержание в крови. В то же время многое зависит от темпа употребления: если пить быстро, содержание алкоголя в крови увеличивается сильнее, чем при медленном употреблении. При пустом желудке алкоголь всасывается полностью и быстрее, чем у сытого человека. Крепкие напитки всасываются быстрее, чем легкие, создавая большую концентрацию алкоголя в крови. Важна и масса тела: на худощавых людей то же количество алкоголя оказывает больший эффект. Кроме того, алкоголь по-разному действует на женщин и мужчин. Поскольку в организме женщин обычно содержится меньше воды, при том же количестве выпитого алкоголя его содержание в крови женщины будет выше даже при одинаковой с мужчиной массе тела.
Однако общее правило заключается в том, что чем больше алкоголя, тем выше его содержание в крови. В то же время многое зависит от темпа употребления: если пить быстро, содержание алкоголя в крови увеличивается сильнее, чем при медленном употреблении. При пустом желудке алкоголь всасывается полностью и быстрее, чем у сытого человека. Крепкие напитки всасываются быстрее, чем легкие, создавая большую концентрацию алкоголя в крови. Важна и масса тела: на худощавых людей то же количество алкоголя оказывает больший эффект. Кроме того, алкоголь по-разному действует на женщин и мужчин. Поскольку в организме женщин обычно содержится меньше воды, при том же количестве выпитого алкоголя его содержание в крови женщины будет выше даже при одинаковой с мужчиной массе тела.
Измерение степени опьянения
Степень опьянения измеряется в промилле. Промилле показывает массу алкоголя в 1000 мл крови. Например, 0,5-процентное опьянение означает, что в 1000 мл циркулирующей в организме крови содержится 0,5 г чистого алкоголя.
Степень опьянения оценивается как по выдыхаемому воздуху, так и с помощью анализа крови. Содержание алкоголя в выдыхаемом воздухе измеряется в миллиграммах на литр. Однако чаще используется понятие промилле. Для того, чтобы миллиграммы на литр выразить в промилле, нужно полученное число умножить на 2,1. Например, опьянение с 0,5 мл/л в выдыхаемом воздухе соответствует около 1,05 процента.
Согласно законодательству Эстонии, различаются следующие степени опьянения:
признаки употребления алкоголя – содержание алкоголя от 0,10 до 0,24 миллиграмма в литре выдыхаемого воздуха, либо от 0,20 до 0,49 промилле в крови;
легкое алкогольное опьянение – содержание алкоголя от 0,1 до 0,75 миллиграмма в литре выдыхаемого воздуха, либо от 0,20 до 1,50 промилле в крови;
умеренное алкогольное опьянение – содержание алкоголя от 0,76 до 1,25 миллиграмма в литре выдыхаемого воздуха, либо от 1,51 до 2,5 промилле в крови;
тяжелое алкогольное опьянение – содержание алкоголя свыше 1,25 миллиграмма в литре выдыхаемого воздуха, либо свыше 2,5 промилле в крови.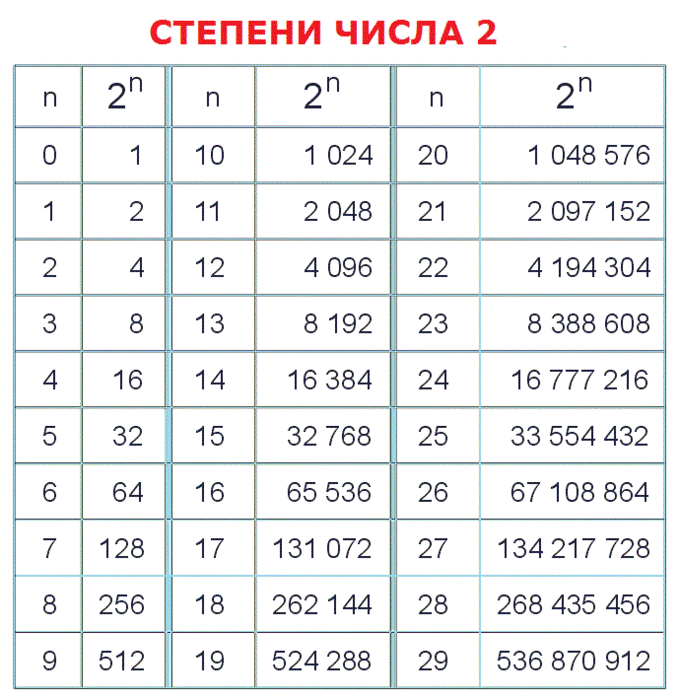
Управление транспортным средством в состоянии опьянения – это преступление! Производство о правонарушении проводится в случае, если содержание алкоголя в одном грамме крови водителя составляет 0,20 мг и больше, либо если в одном литре выдыхаемого им воздуха содержится 0,10 мг или больше алкоголя.
Воздействие опьянения на восприятие и поведение
У некоторых людей симптомы опьянения наступают быстрее и легче, чем у других. Есть и люди, у которых уже образовалась толерантность, из-за чего они не способны почувствовать, насколько пьяны.
В общих чертах все же можно определить, как меняется настроение и поведение при разных степенях опьянения.
0,2–0,3 промилле Вы можете чувствовать себя слегка расслабленным, внутренние ограничения несколько ослабляются. После приема алкоголя настроение начинает подниматься.
0,4–0,6 промилле Вы чувствуете тепло и расслабленность. Ваше поведение может быть более вызывающим: речь становится смелее и быстрее, а голос громче, чем обычно. Усиливаются эмоции – хорошее настроение становится еще лучше и точно так же усиливаются отрицательные эмоции. Вы можете ощущать легкую эйфорию. Мыслительные способности и память могут слегка нарушиться, делая вас неосмотрительным.
Усиливаются эмоции – хорошее настроение становится еще лучше и точно так же усиливаются отрицательные эмоции. Вы можете ощущать легкую эйфорию. Мыслительные способности и память могут слегка нарушиться, делая вас неосмотрительным.
0,7–0,9 промилле При этой степени опьянения начинаются нарушения равновесия, двигательных функций, четкости речи, скорости реакции, зрения и слуха. Нарушается самоконтроль и способность рассуждать, вы считаете, что действуете лучше обычного и вам трудно не продолжить пить. Вы можете чувствовать эйфорию.
1,0–1,2 промилле У вас эйфория, хотя моторные функции, координация, скорость реакции и равновесие уже сильно нарушены. То же со способностью рассуждать и с памятью. В действительности вы не помните, сколько порций уже выпили. Ваши эмоции усиливаются. Некоторые люди становятся очень шумными и агрессивными.
1,3–1,5 промилле Отсутствует равновесие, зрение затуманено, возникают трудности с передвижением и с речью. Мышление, восприятие и способность к принятию решений сильно нарушены. Эйфория понемногу проходит и сменяется неприятными чувствами, такими как тревожность, беспокойство, гнев и подавленность.
Мышление, восприятие и способность к принятию решений сильно нарушены. Эйфория понемногу проходит и сменяется неприятными чувствами, такими как тревожность, беспокойство, гнев и подавленность.
1,6–1,9 промилле Вас наполняют сильные отрицательные эмоции, в результате вы можете стать агрессивным – и ненамеренно причинить вред себе или другим. На этой стадии могут образоваться т.н. провалы памяти – мозг больше не фиксирует происходящее. Моторные функции сильно нарушены.
более 2 промилле Вам не скрыть спутанности сознания, бестолковости и неспособности понимать происходящее. Вам нужна помощь, чтобы встать или ходить. Если вы нанесете себе травму, то скорее всего не осознаете этого, поскольку не чувствуете боли. Вас тошнит или рвет (у некоторых эти симптомы могут возникнуть раньше). Поскольку рвотный рефлекс нарушен, есть опасность захлебнуться собственной рвотой. На этой стадии часты провалы памяти, поэтому вы, очевидно, на следующее утро ничего не вспомните.
более 2,5 промилле Сильно нарушены все психические и физические функции, в том числе восприятие. Наступает эмоциональная бесчувственность. Повышен риск захлебнуться собственной рвотой, упасть и нанести себе серьезную травму или стать жертвой другого несчастного случая.
более 3 промилле Вы в полубессознательном состоянии. Вы не понимаете, где находитесь. Вы можете внезапно потерять сознание, вас трудно привести в чувство.
более 3,5 промилле Такая доза алкоголя действует как наркоз, используемый при операциях. Возможно, вы впадете в кому. Дыхание может стать прерывистым.
более 4 промилле Нарушается работа сердца и дыхание. Фактически, вы в коме или уже мертвы.
Время на вытрезвление
В среднем алкоголь выводится из организма человека со скоростью 0,1 промилле в час. Скорость процесса зависит от пола, массы тела, роста и того, сколько было съедено до приема алкоголя. Поэтому следующие таблицы, показывающие время отрезвления, являются информативными и не должны использоваться для расчета, когда можно будет сесть за руль.Проверяйте трезвость алкометром!
Женщина
Здоровая женщина весом 60 кг
| Количество выпитых алкогольных напитков | Приблизительное время, необходимое для полного вытрезвления |
| 1 бокал (0,125 л) вина (12%) | 0,36 промилле (красный 3, оранжевый 1) |
| 1 бутылка (0,33 л) сидра (4,5%) | 0,35 промилле (красный 3, оранжевый 1) |
| 2 бокала (0,3 л) игристого вина (7,5%) | 0,53 промилле (красный 5, оранжевый 1,5) |
| 2 стопки (0,08 л) водки (40%) | 0,77 промилле (красный 7, оранжевый 1,5) |
| 3 бутылки (0,5 л) пива (4,5%) | 1,6 промилле (красный 15, оранжевый 1,5) |
Мужчина
Здоровый мужчина весом 80 кг
| Количество выпитых алкогольных напитков | Приблизительное время, необходимое для полного вытрезвления |
| 1 бокал (0,125 л) вина (12%) | 0,22 промилле (красный 2, оранжевый 1) |
| 1 бутылка (0,5 л) пива (4,5%) | 0,32 промилле (красный 3, оранжевый 1) |
| 2 стопки (0,08 л) водки (40%) | 0,46 промилле (красный 4, оранжевый 1,5) |
| 4 стопки (0,16 л) ликера (35%) | 0,81 промилле (красный 8, оранжевый 1,5) |
| 5 бутылок (2 л) пива (4,5%) | 1,6 промилле (красный 16, оранжевый 2) |
(При калькуляции использована формула Видмарка)
Мифы об алкоголе и действительность
Можно ли ускорить процесс расщепления алкоголя?
95% алкоголя выводится из организма благодаря работе печени. Небольшое количество выделяется с выдыхаемым воздухом, с мочой и через кожу. Единственный способ протрезветь – выждать время.
Небольшое количество выделяется с выдыхаемым воздухом, с мочой и через кожу. Единственный способ протрезветь – выждать время.
Как влияет на отрезвление сауна?
Поскольку менее 5% алкоголя покидает организм с потом и мочой, процесс сжигания алкоголя не ускоряет ни сауна, ни потение в жаркий летний день. Под действием алкоголя ускоряется частота сердцебиения, повышается потребление сердцем кислорода. Одной из причин ускорения сердечной деятельности является расширение кровеносных сосудов. Кровь приливает к коже, давление крови падает, и потому сердце начинает биться сильнее, чтобы снабжать кровью другие органы. Поэтому сауна и у здорового человека может вызвать опасные изменения кровообращения. В состоянии опьянения человек недостаточно хорошо переносит жар сауны и возникающую в ней потерю жидкости.
Как влияют на отрезвление кофе, энергетические напитки или холодный душ?
Содержащийся в кофе кофеин обладает стимулирующим действием, но в действительности лишь бодрит человека, а не снимает опьянение. Аналогично кофе действует и душ: процесс сжигания алкоголя происходит прежде всего в печени, и его скорость изменить невозможно. Совместное употребление алкоголя и энергетических напитков повышает вероятность алкогольного отравления. Оно также может вызвать обезвоживание, сопровождающееся диареей, тошнотой или рвотой, мышечными судорогами, усталостью и головной болью.
Аналогично кофе действует и душ: процесс сжигания алкоголя происходит прежде всего в печени, и его скорость изменить невозможно. Совместное употребление алкоголя и энергетических напитков повышает вероятность алкогольного отравления. Оно также может вызвать обезвоживание, сопровождающееся диареей, тошнотой или рвотой, мышечными судорогами, усталостью и головной болью.
Можно ли быстрее протрезветь за счет тренировки?
Все-таки нельзя. В результате физической нагрузки в мышцах скапливается молочная кислота, которая вызывает боль. Печень не может одновременно выводить алкоголь и молочную кислоту. Поэтому работоспособность мышц будет низкой, а концентрация молочной кислоты – выше нормы. Алкоголь опустошает в печени запасы гликогена, являющегося для организма источником энергии именно при физических нагрузках.
Алкоголь вызывает обезвоживание, снижает уровень энергии, лишает организм витаминов и минералов и понижает уровень тестостерона. Большая физическая нагрузка в состоянии опьянения скорее опасна для здоровья.
Можно ли опьянеть от кефира и конфет?
В кефире и некоторых конфетах в действительности содержится минимум алкоголя (1–2% от общей массы), но столь малое количество не вызывает алкогольного опьянения.
элементарная теория чисел — Последняя цифра четвертой степени
$\begingroup$
Я работаю над «Теорией элементарных чисел» Андервуда Дадли, и это задача 13 в разделе 4.
Вопрос: «Какой может быть последняя цифра четвертой степени?» Я получил правильный ответ, но мне интересно, есть ли другой более элегантный способ сделать это. Мне также интересно, обоснован ли мой аргумент или я просто случайно получил правильный ответ. Мой аргумент таков: 94 \экв 1\pmod{10}$.
Таким образом, четвертая степень любого целого числа должна заканчиваться либо на 0,1,5, либо на 6.
Мне повезло или это нормально? Есть ли другие более элегантные способы?
Спасибо!
- элементарная теория чисел
- модульная арифметика
$\endgroup$
2
$\begingroup$
Выглядит неплохо, хотя вы могли бы сократить аргумент, заметив, что последняя цифра произведения зависит только от последней цифры каждого множителя, и, следовательно, то же самое относится и к степеням.
Вы могли бы сократить его еще больше, рассмотрев четвертые степени по модулю 2 и по модулю 5. Вы можете получить либо 0, либо 1 по модулю 2 (очевидно), и то же самое можно получить по модулю 5 (чуть менее очевидно, но вы могли бы использовать маленькую теорему Ферма если вы чувствовали себя очень ленивым).
Объединение двух результатов дает 0, 1, 5, 6 по модулю 10, как вы нашли.
$\endgroup$
2
$\begingroup$ 94\эквив1\пмод{10}$. Это сужает дела с 10 до 6 долларов.
$\endgroup$
$\begingroup$
Последними одной, двумя или тремя конечными цифрами совершенной 4-й степени должны быть:
конечной цифрой: 0,1,5,6 25,16,36,56,76,96
последние 3 цифры: 000, 001, 201, 401, 601, 801, 121, 321, 521, 721, 921, 041, 241, 441, 641, 841, 161, 361, 561, 761, 961, 081, 281, 481, 681, 881, 625, 016, 216, 416, 616, 816, 136, 336, 536, 736, 936, 056, 256, 456, 656, 856, 176, 376, 576, 776, 976, 096, 296, 496, 696, 896.
Список продолжается…………. ….
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie 90$ равно $1$: потому что $1$ — это количество способов не делать выбор из отсутствия выбора. 0=1$ полезно и естественно, поэтому мы определяем его таким образом в этом контексте. Для других контекстов (таких, как упомянутый на mathforum, когда вы имеете дело исключительно с аналитическими функциями, где проблем с пределами не возникает) могут быть как естественные, так и полезные определения.
0=1$ полезно и естественно, поэтому мы определяем его таким образом в этом контексте. Для других контекстов (таких, как упомянутый на mathforum, когда вы имеете дело исключительно с аналитическими функциями, где проблем с пределами не возникает) могут быть как естественные, так и полезные определения.
В основном мы определяем его (или не определяем его) в зависимости от того, каким образом это наиболее полезно и естественно для рассматриваемого контекста. Для дискретной математики не возникает вопроса, каким «полезным и естественным» образом должно быть , поэтому мы определяем его таким образом.
$\endgroup$
43
$\begingroup$
Это всего лишь определение, и его нельзя доказать с помощью стандартной алгебры. Однако два примера мест, где это удобно предположить: 90=1$ из-за этого. Это не математический ответ сам по себе, но на него стоит обратить внимание из-за все более вычислительного характера современной математики, чтобы ни с чем не столкнуться. 0=1$ — хорошее определение. 90$ определенно равен 1, за исключением случаев, когда приближается от $y=0$, когда кажется равным нулю.
0=1$ — хорошее определение. 90$ определенно равен 1, за исключением случаев, когда приближается от $y=0$, когда кажется равным нулю.
$\endgroup$
$\begingroup$
Ответ Кнута не хуже любого ответа, который вы получите здесь: http://arxiv.org/pdf/math/9205211v1.pdf См. стр. 4-6, начиная с нижней части стр. 4.
$\endgroup$
0
$\begingroup$ 90$. Математический журнал, Vol. 50, № 1 (январь 1977 г.), стр. 41-42.
Л. Дж. Пейдж. Замечание о неопределенных формах. American Mathematical Monthly, 61 (1954), 189–190; перепечатано в томе Математической ассоциации Америки 1969 г., Избранные статьи по математическому анализу, стр. 210–211.
Бэксли и Хаяши. Замечание о неопределенных формах. American Mathematical Monthly, 85 (1978), стр. 0$ 90$, но когда я это делаю, я определяю его как $1$.
0$ 90$, но когда я это делаю, я определяю его как $1$.
$\endgroup$
11
$\begingroup$
Еще один подход и еще один результат!
Определим экспоненциальную функцию на $\mathbb{R}$ как функцию $E:\mathbb{R}\rightarrow \mathbb{R}$ такую, что $$ E(x+y)=E(x)E(y) \qquad \forall x,y \in \mathbb{R} $$ Это очень общее и мощное определение, и мне оно нравится, потому что оно фиксирует связь между алгебрами Ли и группами Ли.
Из этого определения сразу получаем, что если $\существует a\in \mathbb{R}$ такое, что $E(a)=0$, то $E(x)=0 \; \forall x \in \mathbb{R}$. Для этого не нужны ни непрерывность, ни другие топологические свойства. В экспоненциальной теории полей такая функция называется тривиальной экспоненциальной функцией.
Если $E$ не является этой тривиальной функцией, то легко видеть, что мы должны иметь $E(0)=1$ и, если $E(x)=1$ для некоторого $x \ne 0$, то $E (x)=1 \forall x \in \mathbb{R}$, т. е. является константой (еще одна тривиальная эксп. функция). 90=1 не всегда самое полезное или актуальное значение.
е. является константой (еще одна тривиальная эксп. функция). 90=1 не всегда самое полезное или актуальное значение.
Использование пределов, исчисления или биномиальных теорем на самом деле не дает вам интуитивного понимания того, почему это так, но я надеюсь, что этот пост помог вам понять , почему это так, и заставить вас почувствовать это своей селезенкой.
$\endgroup$
0
$\begingroup$
На Scribd опубликован документ для широкой публики: «От нуля до нулевой степени» (стр. 7–11): http://www.scribd.com/JJJacquelin/documents 9{х}=0$$
См. http://en.wikipedia.org/wiki/Indeterminate_form
$\endgroup$
10
$\begingroup$
Взгляните на обсуждение WolframMathWorld [1]. {ab}$ до 9{a\ln x}$, и можно доказать, что это переопределение дает те же результаты, что и все приведенные выше соглашения, но оно работает только потому, что $\ln x$ корректно определено для положительного $x$. Как только вы попытаетесь разрешить отрицательное значение $x$, у вас возникнут проблемы, поскольку в этом случае $\ln x$ определено некорректно. Один может определять логарифмы отрицательных и комплексных чисел, но они не являются однозначными, и есть всевозможные технические тонкости выбора «ветви» функции логарифма.
{ab}$ до 9{a\ln x}$, и можно доказать, что это переопределение дает те же результаты, что и все приведенные выше соглашения, но оно работает только потому, что $\ln x$ корректно определено для положительного $x$. Как только вы попытаетесь разрешить отрицательное значение $x$, у вас возникнут проблемы, поскольку в этом случае $\ln x$ определено некорректно. Один может определять логарифмы отрицательных и комплексных чисел, но они не являются однозначными, и есть всевозможные технические тонкости выбора «ветви» функции логарифма.
7.5 — Биномиальная теорема
7.5 — Биномиальная теоремаБиномы, возведенные в степень
Биномиал — это многочлен с двумя членами. Мы рассмотрим биномиальное расширение. Теорема, быстрый способ возведения двучлена в степень.
(х+у) 0 = 1 Есть несколько вещей, которые вы, надеюсь, заметили после просмотра дополнения. Треугольник Паскаля, названный в честь французского математика Блеза Паскаля, позволяет легко найти
коэффициенты расширения. Каждая строка в треугольнике начинается и заканчивается 1. Каждый элемент в треугольнике является суммой
два элемента непосредственно над ним. будут более подробно обсуждаться в разделе 7.6, но
вот краткое изложение, чтобы вы начали с биномиала
Теорема расширения. Комбинация – это расположение предметов без
повторение и порядок не важен. Другим определением комбинации является количество
такие договоренности, которые возможны. n и r в формуле означают общее количество объектов для выбора и количество
объекты в аранжировке соответственно. Самый быстрый способ, хотя и лишенный воображения, — использовать функцию комбинирования на
ваш калькулятор. На TI-82 и TI-83 он находится в меню «Математика», «Вероятность».
подменю, выбор 3. Сначала введите значение n, затем n C r обозначение, то значение для r. Каждый элемент треугольника Паскаля представляет собой комбинацию n элементов. Рассмотрим n=4 ряд треугольника. 4 С 0 = 1, 4С 1 = 4, 4С 2 = 6, 4С 3 = 4, 4С 4 = 1 Обратите внимание, что термин 3 rd является термином с r=2. То есть начинаем считать с 0. Это будет
вступать в игру позже. Хорошо, теперь мы готовы собрать все воедино. Теорема о биномиальном разложении может быть записана на
нотация суммирования, где она очень компактна и
управляемый. Помните, что поскольку нижний предел суммирования начинается с 0, 7 -й -й член последовательности
на самом деле термин, когда k = 6. Когда вы собираетесь использовать теорему о биномиальном разложении, на самом деле проще
применять рекомендации из верхней части этой страницы на практике. Расширение (3x — 2y) 5 Начните с расчета коэффициентов. Помните, что это комбинации
из 5 вещей, по k за раз, где k — это либо мощность x, либо мощность
на y (комбинации симметричны, так что это не имеет значения). С(5,0) = 1; С(5,1) = 5; С(5,2) = 10; С(5,3) = 10; С(5,4) = 5; С(5,5) = 1 Теперь добавим условия 3x и -2y. 1(3x) 5 (-2y) 0 + 5(3x) 4 (-2y) 1 + 10(3x) 3 (-2y) 24x() 2 (-2y) 3 + 5(3x) 1 (-2y) 4 + 1(3x) 0 (-2y) 5 Поднимите отдельные факторы до их надлежащего уровня. 1(243x 5 )(1) + 5(81x 4 )(-2y) + 10(27x 3 )(4y 2 ) + 10(9x 2 )(-8y 3 x ) + 5(x) )(16 лет 4 ) +
1(1)(-32 года 5 ) Упростите каждый термин, чтобы получить окончательный ответ. 243x 5 — 810x 4 y + 1080x 3 y 2 — 720x 2 y 3 + 240xy 4 — 32y 5 Найдите 9-й член разложения (x-2y) 13 Поскольку мы начинаем считать с 0, 9-й член на самом деле будет, когда
к=8. То есть мощность x будет 13-8=5, а мощность -2y будет
быть 8. Коэффициент либо C(13,8), либо C(13,5), комбинации симметричны,
так что это не имеет значения. C(13,8) * (x) 5 (-2y) 8 = 1287 (x 5 ) (256y 8 )
= 329472x 5 у 8 Пожалуйста, объясните, каков ответ на каждую из этих математических задач. +3 голоса 0 голосов 4 в четвертой степени будет 256, потому что 4×4=16, 16×4=64, 64×4=256. Мы только что сделали модуль по степеням и показателям! прокомментировал по
Кекс Это действительно круто Каков ответ на эту математическую задачу? спросил
5 марта 2014 г. Что означает «в силу»? спросил
17 апр. 2013 г.
по математике
по
Нетбол
(2,4 тыс. баллов) ПРОБЛЕМА СООТНОШЕНИЯ спросил
2 декабря 2015 г.
по математике
по
Джазлинни
(43,0 тыс. баллов) Математические упражнения для начинающих спросил
19 ноября 2015 г.
по математике
по
оранжевая федора
(3,5 тыс. баллов) FOR ALL DEM MATH WEIZES OUT DER… спросил
25 августа 2015 г.
по математике
по
Рэй
(107 тыс. баллов) Как умножать дроби на целые числа? (например, 3 3/4 умножить на 3 3/4) спросил
1 марта 2016 г. что означает число 3 в степени 4? спросил
20 февраля 2015 г.
по математике
по
Эндрю ДЛЯ СОХРАНЕНИЯ МАТЕМАТИЧЕСКИХ КАРАНДАШЕЙ… спросил
30 августа 2015 г.
по математике
по
Рэй
(107 тыс. баллов) Почему я так долго не могу заснуть? спросил
18 августа 2020 г.
в других
по
Джейн Так вы пропускаете счет (кстати, он увеличивается до 9, а может быть до 12) спросил
21 декабря 2016 г.
по математике
по
(Телец) SweetieGem
(24,2 тыс. баллов) Как упростить дроби спросил
2 июля 2016 г. Как округлить числа? спросил
19 октября 2013 г.
по математике
по
быстрый
(23,6 тыс. баллов) что за # после 2 спросил
10 июля 2015 г.
по математике
по
калем Можете ли вы угадать номер? спросил
2 февраля 2015 г.
по математике
по
Техарена Почему перимитер прямоугольника и квадрата не меняется? спросил
6 марта 2016 г.
в Шутки и загадки
по
Лу Лу Это математика для меня спросил
2 сентября
по математике
по
Эзи
(24,9 тыс. Сколько 0 разделить на 0? спросил
15 января 2018 г.
по математике
по
НАТАН
(78,2 тыс. баллов) что такое 1054548695673957367367358*76 спросил
3 ноября 2017 г.
по математике
по
аркзо помогите мне с углами треугольника спросил
12 октября 2017 г.
по математике
по
Друзья приходят и уходят
(3,7 тыс. баллов) Как умножать двузначные числа на двузначные?!?! спросил
17 апр. 2017 г.
по математике
по
командаКитнисс
(3,1 тыс. баллов) Определение математики спросил
15 октября 2016 г. Какой твой любимый предмет в школе? спросил
16 мая 2016 г.
по математике
по
аркзо
(441 тыс. баллов) Математические задачи спросил
9 апр. 2016 г.
по математике
по
Джек123
(440 баллов) Квадратные корни спросил
29 марта 2016 г.
по математике
по
❤️ГриффиндорГаль❤️
(132 тыс. баллов) Как делить целые числа на дроби? пр.-6 разделить на 2/3 спросил
27 января 2016 г.
по математике
по
Лу Лу Примечательный вопрос Отличный вопрос Отличный вопрос Хороший вопрос Хороший вопрос .
(х+у) 1 = х + у
(x + y) 2 = x 2 + 2xy + y 2
(x + y) 3 = x 3 + 3x 2 y + 3xy 2 3 2 2 2 2 2 2 2 3 2 2 2 2 2 + 3x 2 .
(x+y) 4 = x 4 + 4x 3 y + 6x 2 y 2 + 4xy 3 + y 4
(x+y) 5 = x 5 + 5x 4 y + 10x 3 y 2 +10x 2 y 3 + 5xy 4 9 5 + 3 y0003 Треугольник Паскаля

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
Комбинации
Комбинации Значение r начинается с нуля
и работает до n. Или, из-за симметрии, вы могли бы сказать, что оно начинается с n и работает
вплоть до 0.
Значение r начинается с нуля
и работает до n. Или, из-за симметрии, вы могли бы сказать, что оно начинается с n и работает
вплоть до 0. Теорема биномиального разложения
 Х начинается
до n -й степени и каждый раз уменьшается на единицу, y начинается с 0--й степени (не там) и каждый раз увеличивается на единицу. Коэффициенты являются комбинациями.
Х начинается
до n -й степени и каждый раз уменьшается на единицу, y начинается с 0--й степени (не там) и каждый раз увеличивается на единицу. Коэффициенты являются комбинациями. Биномиальное расширение Пример:
Нахождение k
-го термина 4 умножить на 4 = 4 в четвертой степени?
спросил по математике
по
улыбка828
(34,4 тыс. баллов) Затем скажите, равны ли они или больше и меньше.
Затем скажите, равны ли они или больше и меньше. 2 ответа
Категории
 ..
(257)
..
(257) Похожие вопросы
 по математике
по
улыбка828
(34,4 тыс. баллов)
по математике
по
улыбка828
(34,4 тыс. баллов) по математике
по
шоколад в изобилии
по математике
по
шоколад в изобилии по математике
по
Ээээ, не мое настоящее имя?
по математике
по
Ээээ, не мое настоящее имя? баллов)
баллов) по математике
по
#Синдистронг-Скай
(16,9к баллов)
по математике
по
#Синдистронг-Скай
(16,9к баллов) Последние значки
Заданный вопрос получил 50 просмотров
— Queen Bee —
Вопрос получил +8 голосов
— im kanye —
Вопрос получен +8 голосов
— ler81602 —
Получен вопрос +3 голоса
— Даллас —
Получен вопрос +3 голоса
— YayDay ..
.. НАУЧНАЯ НОТА
4
Вернуться к научной нотации
Проблемы преобразования
Преобразование научной записи в действительное число:
5,14 × 10 5 = 514000,0
Научное представление состоит из коэффициента (здесь 5.14) умножить на 10, возведя в степень (здесь 5). Конвертировать к действительному числу, начните с основания и умножьте на 5 десятков, как это: 5,14 × 10 × 10 × 10 × 10 × 10 = 514000.0. Умножать на десятки легко: нужно просто передвинуть десятичную дробь. точка в базе (5.14) 5 мест вправо , прибавляя доп. нули по необходимости.
5,14 × 10 5
= 51,4 × 10 4
= 514,0 × 10 3
= 5140,0 × 10 4
0695 = 51400,0 × 10 1
= 514000.0 × 10 0
= 514000.0
Преобразование из реального числа в научную нотацию:
0,000345 = 3,45 × 10 -4 0000345 = 3,45 × 10 -4 .
 коэффициент умножить на 10, возведя в степень . Превратить в научный
обозначения, начните с перемещения десятичного разряда в числе до тех пор, пока не
иметь коэффициент от 1 до 10; здесь 3,45.
количество мест до оставил , что нужно было переместить десятичную дробь
точка — показатель степени. Здесь нам пришлось переместить десятичные 4 разряда в
справа, поэтому показатель степени равен -4.
коэффициент умножить на 10, возведя в степень . Превратить в научный
обозначения, начните с перемещения десятичного разряда в числе до тех пор, пока не
иметь коэффициент от 1 до 10; здесь 3,45.
количество мест до оставил , что нужно было переместить десятичную дробь
точка — показатель степени. Здесь нам пришлось переместить десятичные 4 разряда в
справа, поэтому показатель степени равен -4. 0,000345
= 0,00345 / 10
= 0,0345 / (10 х 10)
= 0,345 / (10 х 10 х 10)
= 3,45 / (10 х 10 х 10 х 10) )
= 3,45 × 10 -4
Вернуться к научной нотации
Задачи на умножение/деление
Умножение двух чисел, записанных в экспоненциальной записи:
(9 × 10 -1 ) × (3 × 10 10 ) = 2,7 × 10 10
Умножение и деление можно производить в любом порядке — взять
преимущество в этом! Сначала умножьте два коэффициента, а затем
умножьте две степени десяти, добавив их показатели степени: так как -1 +
10 = 9, тогда 10 -1 × 10 10 =
10 9 . Наконец, объедините два ваших ответа и преобразуйте в
экспоненциальное представление: 27 × 10 9 = 2,7 ×
10 10 . В символах:
Наконец, объедините два ваших ответа и преобразуйте в
экспоненциальное представление: 27 × 10 9 = 2,7 ×
10 10 . В символах:
(9 × 10 -1 ) × (3 × 10 10 )
= (9 × 3) × (10 -1 × 10 10 )
= (27) × ( 10 9 )
= 2,7 × 10 10
Разделить два числа, записанные в экспоненциальной записи:
(3,5 × 10 -6 ) / (5 × 10 -6 ) / (5 × 10 -2 )
Распределить деление как по коэффициентам, так и по степеням 10. Далее делим два коэффициента: 3,5/5 = (35/10)/5 = (35/5)/10 = 7/10 = 0,7. Затем разделите две степени десяти, вычитая их показатели степени: так как -6 — (-2) = -6 + 2 = -4, то 10 -6 / 10 -2 = 10 -4 . Наконец, объедините два ваших ответа и перевести в научную запись. В символах:
(3,5 × 10 -6 ) / (5 × 10 -2 )
= (3,5 / 5) × (10 -6 / 10 -2 )
= (0,7) × (10 -4 )
= 7 × 10 -5
Вернуться к научной нотации
Задачи на сложение/вычитание
Сложение двух чисел, записанных в экспоненциальном представлении:
4,9 × 10 2 + 7,9 × 10 3 = 8,39 × 10 3
Сначала вынесите одну из степеней десяти; либо будет работать, но
меньший может быть проще.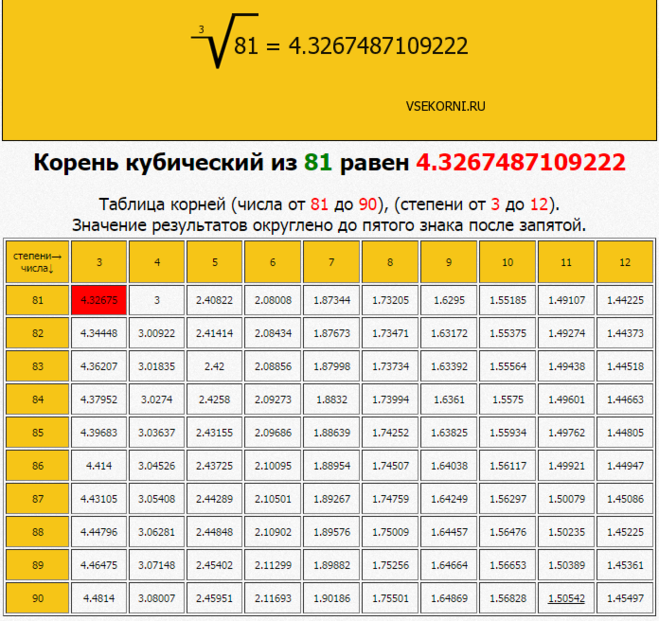 Для этого нужно разделить оба числа на
степени десяти и умножив все количество на ту же степень
10. Чтобы разделить одну степень десяти на другую, просто вычтите два
степени (см. Умножение/Деление). Затем преобразуйте два числа
от научной записи к действительным числам. Теперь сложите два числа
обычно. Наконец, преобразуйте в экспоненциальное представление, если коэффициент
меньше 1 или больше 10,
Для этого нужно разделить оба числа на
степени десяти и умножив все количество на ту же степень
10. Чтобы разделить одну степень десяти на другую, просто вычтите два
степени (см. Умножение/Деление). Затем преобразуйте два числа
от научной записи к действительным числам. Теперь сложите два числа
обычно. Наконец, преобразуйте в экспоненциальное представление, если коэффициент
меньше 1 или больше 10,
4,9 × 10 2 + 7,9 × 10 3
= (4,9 × 10 2 /10 2 + 7,9 × 10 3 /10 2 ) × 10 3 /10 2 ) × 10 3 /10 2 ) × 10 3 /10 2 ) × 10 3 /10 2 ) × 10 3 /10 2 ) × 10 . 4.9 × 10 0 + 7.9 × 10 1 ) × 10 2
= (4.9 + 79) × 10 2
= 83.9 × 10 2
= 8.39 × 10 3
Another способ выполнить любую операцию над двумя экспоненциальными обозначениями
числа состоит в том, чтобы преобразовать оба числа в обычные числа, а затем выполнить
операцию и, наконец, преобразовать результат обратно в научный
обозначение.



 Размер опухоли превышает 5 см в диаметре, поражены 1-3 подмышечных лимфоузла. Еще один вариант — опухоль меньшего размера, но при этом пораженные метастазами лимфоузлы спаянны между собой и с окружающими тканями;
Размер опухоли превышает 5 см в диаметре, поражены 1-3 подмышечных лимфоузла. Еще один вариант — опухоль меньшего размера, но при этом пораженные метастазами лимфоузлы спаянны между собой и с окружающими тканями;

 Проверяйте трезвость алкометром!
Проверяйте трезвость алкометром!