Раціональним або ірраціональним є число. Що таке раціональні та ірраціональні числа
раціональне число — число, що представляється звичайної дробом m / n, де чисельник m — ціле число, а знаменник n — натуральне число. Будь-яке раціональне число можна подати у вигляді періодичної нескінченного десяткового дробу. Безліч раціональних чисел позначається Q.
Якщо дійсне число не є раціональним, то воно ірраціональне число. Десяткові дроби, що виражають ірраціональні числа нескінченні і не періодичні. Безліч ірраціональних чисел зазвичай позначається великою латинською літерою I.
Дійсне число називається алгебраїчним, Якщо воно є коренем деякого многочлена (ненульовий ступеня) з раціональними коефіцієнтами. Будь-яке неалгебраїчні число називається трансцендентним.
Деякі властивості:
Безліч раціональних чисел розташовується на числової осі всюди щільно: між будь-якими двома різними раціональними числами розташоване хоча б одне раціональне число (а значить, і безліч раціональних чисел).
Безліч Q раціональних чисел є замкнутим щодо додавання, віднімання, множення і ділення, тобто сума, різниця, добуток і частку двох раціональних чисел також є раціональними числами.
Всі раціональні числа є алгебраїчними (зворотне твердження — невірне).
Кожне речовий трансцендентне число є ірраціональним.
Кожне ірраціональне число є або алгебраїчним, або трансцендентним.
Безліч ірраціональних чисел усюди щільно на числовій прямій: між будь-якими двома числами є ірраціональне число (а значить, і безліч ірраціональних чисел).
Безліч ірраціональних чисел незліченну.
При вирішенні завдань буває зручно разом з ірраціональним числом a + b√ c (де a, b — раціональні числа, з — ціле, що не є квадратом натурального числа) розглянути «поєднане» з ним число a — b√ c: його сума і твір з вихідним — раціональні числа.
Завдання з рішеннями
1. Доведіть, що
а) число √ 7;
б) число lg 80;
в) число √ 2 + 3 √ 3;
є ірраціональним.
а) Припустимо, що число √ 7 раціональне. Тоді, існують такі взаємно прості p і q, що √ 7 \u003d p / q, звідки отримуємо p 2 \u003d 7q 2. Так як p і q взаємно прості, то p 2, а значить і p ділиться на 7. Тоді р \u003d 7k, де k — деяке натуральне число. Звідси q 2 \u003d 7k 2 \u003d pk, що суперечить тому, що p і q взаємно прості.
Отже, припущення помилково, значить, число √ 7 ірраціональне.
б) Припустимо, що число lg 80 раціональне. Тоді існують такі натуральні p і q, що lg 80 \u003d p / q, або 10 p \u003d 80 q, звідки отримуємо 2 p-4q \u003d 5 q-p. З огляду на, що числа 2 і 5 взаємно прості, отримуємо, що остання рівність можливо тільки при p-4q \u003d 0 і q-p \u003d 0. Звідки p \u003d q \u003d 0, що неможливо, так як p і q обрані натуральними.
Отже, припущення помилково, значить, число lg 80 ірраціональне.
в) Позначимо дане число через х.
Тоді (х — √ 2) 3 \u003d 3, або х 3 + 6х — 3 \u003d √ 2 · (3х 2 + 2). Після зведення цього рівняння в квадрат отримуємо, що х повинен задовольняти рівняння
х 6 — 6х 4 — 6х 3 + 12х 2 — 36х + 1 \u003d 0.
Його раціональними коренями можуть бути тільки числа 1 і -1. Перевірка ж показує, що 1 і -1 не є корінням.
Отже, дане число √ 2 + 3 √ 3 \u200b\u200bє ірраціональним.
2. Відомо, що числа a, b, √ a -√ b, — раціональні. Доведіть, що √ a і √ b- теж раціональні числа.
Розглянемо твір
(√ a — √ b) · (√ a + √ b) \u003d a — b.
число √ a + √ b, що дорівнює відношенню чисел a — b і √ a -√ b, є раціональним, так як частка від ділення двох раціональних чисел — число раціональне. Сума двох раціональних чисел
½ (√ a + √ b) + ½ (√ a — √ b) \u003d √ a
— число раціональне, їх різниця,
½ (√ a + √ b) — ½ (√ a — √ b) \u003d √ b,
теж раціональне число, що й треба було довести.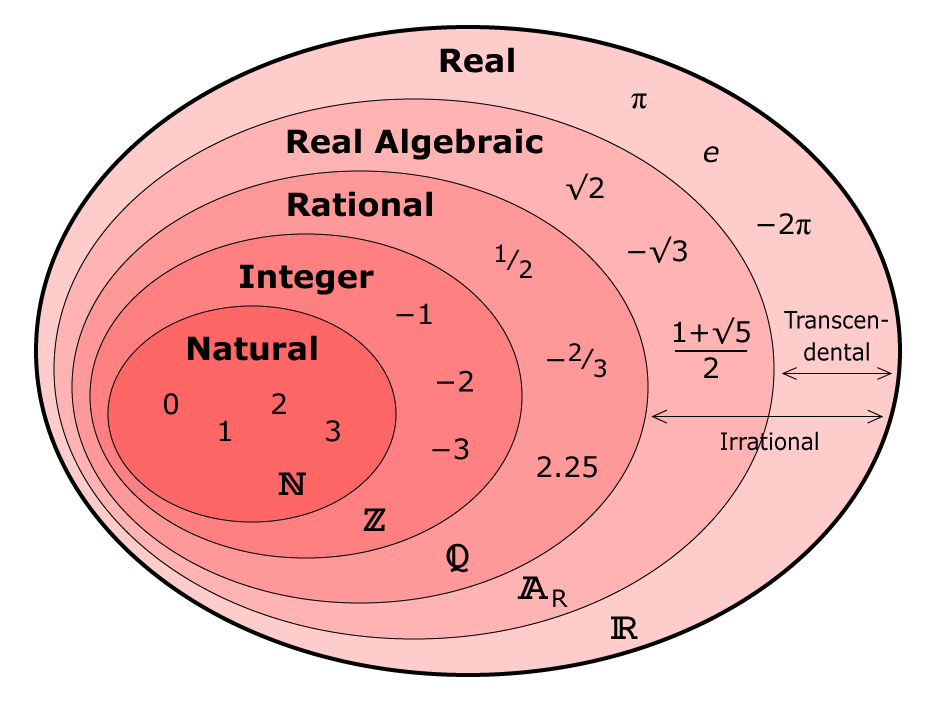
3. Доведіть, що існують позитивні ірраціональні числа a і b, для яких число a b є натуральним.
4. Чи існують раціональні числа a, b, c, d, що задовольняють рівності
(A + b √ 2) 2n + (c + d√ 2) 2n \u003d 5 + 4√ 2,
де n — натуральне число?
Якщо виконано рівність, дане в умові, а числа a, b, c, d — раціональні, то виконано і рівність:
(A — b √ 2) 2n + (c — d√ 2) 2n \u003d 5 — 4√ 2.
Але 5 — 4√ 2 (a — b√ 2) 2n + (c — d√ 2) 2n\u003e 0. Отримане протиріччя доводить те, що вихідне рівність неможливо.
Відповідь: не існує.
5. Якщо відрізки з довжинами a, b, c утворюють трикутник, то для всіх n \u003d 2, 3, 4,. . . відрізки з довжинами n √ a, n √ b, n √ c так само утворюють трикутник. Доведіть це.
Якщо відрізки з довжинами a, b, c утворюють трикутник, то нерівність трикутника дає
Тому ми маємо
(N √ a + n √ b) n\u003e a + b\u003e c \u003d (n √ c) n,
N √ a + n √ b\u003e n √ c.
Решта випадків перевірки нерівності трикутника розглядаються аналогічно, звідки і треба зробити висновок.
6. Доведіть, що нескінченна десяткова дріб +0,1234567891011121314 … (після коми поспіль виписані всі натуральні числа по порядку) являє собою ірраціональне число.
Як відомо, раціональні числа виражаються десятковими дробами, які мають період починаючи з деякого знака. Тому досить довести, що дана дріб не є періодичною ні з якого знака. Припустимо, що це не так, і деяка послідовність T, що складається з n цифр, є періодом дробу, починаючи з m-го знака після коми. Ясно, що серед цифр після m-го знака зустрічаються ненульові, тому в послідовності цифр T є ненульова цифра. Це означає, що починаючи з m-ой цифри після коми, серед будь-яких n цифр поспіль є ненульова цифра. Однак в десяткового запису даної дробу має бути присутня десяткова запис числа 100 … 0 \u003d 10 k, де k\u003e m і k\u003e n. Зрозуміло, що цей запис зустрінеться правіше m-ой цифри і містить більш n нулів підряд. Тим самим, отримуємо протиріччя, яким завершує доказ.
7. Дана нескінченна десяткова дріб 0, a 1 a 2 .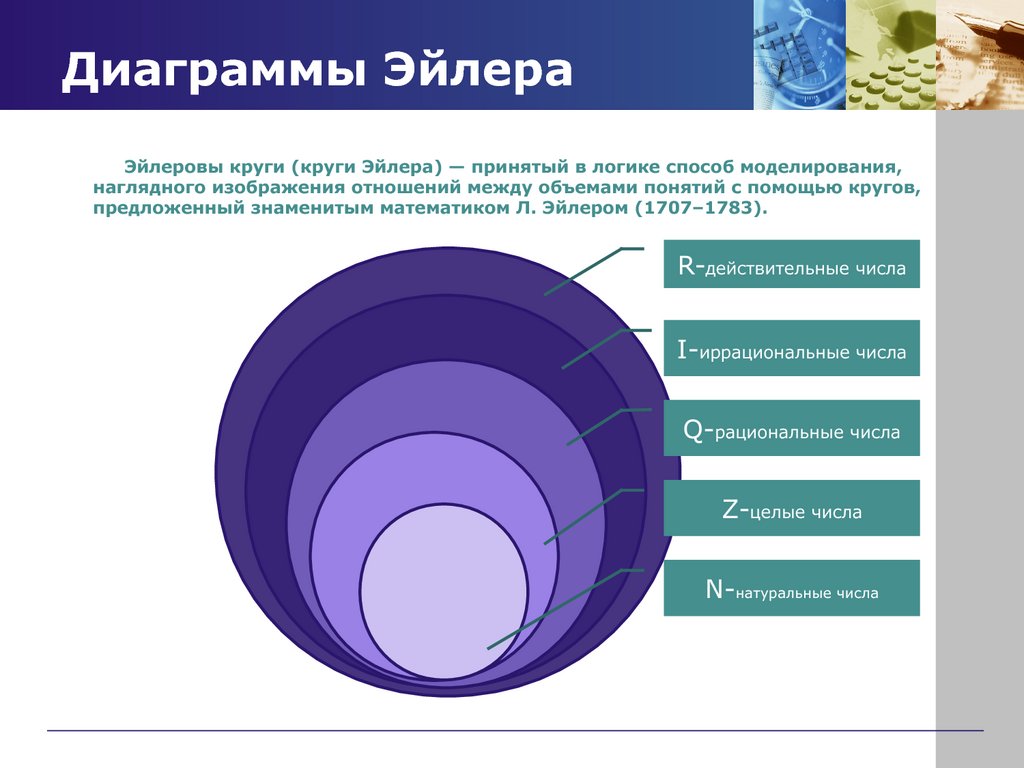 … Доведіть, що цифри в її десяткового запису можна переставити так, щоб отримана дріб висловлювала раціональне число.
… Доведіть, що цифри в її десяткового запису можна переставити так, щоб отримана дріб висловлювала раціональне число.
Нагадаємо, що дріб висловлює раціональне число в тому і тільки тому випадку, коли вона періодична, починаючи з деякого знака. Цифри від 0 до 9 розділимо на два класи: до першого класу включимо ті цифри, які зустрічаються у вихідній дробу кінцеве число раз, до другого класу — ті, які зустрічаються у вихідній дробу нескінченну кількість разів. Почнемо виписувати періодичну дріб, яка може бути отримана з вихідної перестановкою цифр. Спочатку після нуля і коми напишемо в довільному порядку всі цифри з першого класу — кожну стільки раз, скільки вона зустрічається в запису вихідної дробу. Записані цифри першого класу будуть передувати періоду в дробової частини десяткового дробу. Далі, запишемо в деякому порядку по одному разу цифри з другого класу. Цю комбінацію оголосимо періодом і будемо повторювати її нескінченне число разів. Таким чином, ми виписали шукану періодичну дріб, яка має деяке раціональне число.
8. Довести, що в кожної нескінченного десяткового дробу існує послідовність десяткових знаків довільної довжини, яка в розкладанні дробу зустрічається нескінченно багато разів.
Нехай m — довільно задане натуральне число. Розіб’ємо цю нескінченну десяткову дріб на відрізки, по m чисел в кожному. Таких відрізків буде нескінченно багато. З іншого боку, різних систем, що складаються з m чисел, існує тільки 10 m, т. Е. Кінцеве число. Отже, хоча б одна з цих систем повинна повторюватися тут нескінченно багато разів.
Зауваження. Для ірраціональних чисел √ 2, π або е ми навіть не знаємо, яка цифра повторюється нескінченно багато разів в відповідних їм нескінченних десяткових дробах, хоча кожне з цих чисел, як легко можна довести, містить принаймні дві різні такі цифри.
9. Доведіть елементарним шляхом, що позитивний корінь рівняння
є ірраціональним.
Для х\u003e 0 ліва частина рівняння збільшується зі зростанням х, і легко помітити, що при х \u003d 1,5 вона менше 10, а при х \u003d 1,6 — більше 10.
Запишемо корінь як нескоротний дріб p / q, де p і q — деякі взаємно прості натуральні числа. Тоді при х \u003d p / q рівняння прийме наступний вигляд:
p 5 + pq 4 \u003d 10q 5,
звідки випливає, що р — дільник 10, отже, р дорівнює одному з чисел 1, 2, 5, 10. Однак виписуючи дроби з числителями 1, 2, 5, 10, відразу ж помічаємо, що жодна з них не потрапляє всередину інтервалу (1,5; 1,6).
Отже, позитивний корінь вихідного рівняння не може бути представлений у вигляді звичайного дробу, а значить є ірраціональним числом.
10. а) Чи існують на площині три такі точки A, B і C, що для будь-якої точки X довжина хоча б одного з відрізків XA, XB і XC ірраціональна?
б) Координати вершин трикутника раціональні. Доведіть, що координати центру його описаного кола також раціональні.
в) Чи існує така сфера, на якій є рівно одна раціональна точка? (Раціональна точка — точка, у якій всі три декартові координати — раціональні числа.
а) Так, існують. Нехай C — середина відрізка AB. Тоді XC 2 \u003d (2XA 2 + 2XB 2 — AB 2) / 2. Якщо число AB 2 ірраціонально, то числа XA, XB і XC не можуть одночасно бути раціональними.
б) Нехай (a 1; b 1), (a 2; b 2) і (a 3; b 3) — координати вершин трикутника. Координати центру його описаного кола задаються системою рівнянь:
(X — a 1) 2 + (y — b 1) 2 \u003d (x — a 2) 2 + (y — b 2) 2,
(X — a 1) 2 + (y — b 1) 2 \u003d (x — a 3) 2 + (y — b 3) 2.
Легко перевірити, що ці рівняння лінійні, а значить, рішення даної системи рівнянь раціонально.
в) Така сфера існує. Наприклад, сфера з рівнянням
(X — √ 2) 2 + y 2 + z 2 \u003d 2.
Точка O з координатами (0; 0; 0) — раціональна точка, що лежить на цій сфері. Решта точки сфери ірраціональні. Доведемо це.
Припустимо гидке: нехай (x; y; z) — раціональна точка сфери, відмінна від точки O. Зрозуміло, що х відмінний від 0, так як при x \u003d 0 є єдине рішення (0; 0; 0), яке нас зараз не цікавить. Розкриємо дужки і висловимо √ 2:
x 2 — 2√ 2 x + 2 + y 2 + z 2 \u003d 2
√ 2 \u003d (x 2 + y 2 + z 2) / (2x),
чого не може бути при раціональних x, y, z і ірраціональному √ 2. Отже, О (0; 0; 0) — єдина раціональна точка на даній сфері.
Отже, О (0; 0; 0) — єдина раціональна точка на даній сфері.
Завдання без рішень
1. Доведіть, що число
\\ [\\ Sqrt (10+ \\ sqrt (24) + \\ sqrt (40) + \\ sqrt (60)) \\]
є ірраціональним.
2. За яких цілих m і n виконується рівність (5 + 3√ 2) m \u003d (3 + 5√ 2) n?
3. Чи існує таке число а, щоб числа а — √ 3 і 1 / а + √ 3 були цілими?
4. Чи можуть числа 1, √ 2, 4 бути членами (не обов’язково сусідніми) арифметичної прогресії?
5. Доведіть, що при будь-якому натуральному n рівняння (х + у√ 3) 2n \u003d 1 + √ 3 не має рішень в раціональних числах (х; у).
Безліч ірраціональних чисел зазвичай позначається великою латинською літерою I (\\ displaystyle \\ mathbb (I)) в напівжирному зображенні без заливки. Таким чином: I \u003d R ∖ Q (\\ displaystyle \\ mathbb (I) \u003d \\ mathbb (R) \\ backslash \\ mathbb (Q)), Тобто безліч ірраціональних чисел є різниця множин речових і раціональних чисел.
Про існування ірраціональних чисел, точніше відрізків, непорівнянних із відрізком одиничної довжини, знали вже стародавні математики: їм була відома, наприклад, несумісність діагоналі і сторони квадрата, що рівносильно ірраціональності числа. (2)).
(2)).
Історія
античність
Концепція ірраціональних чисел була неявним чином сприйнята індійськими математиками в VII столітті до нашої ери, коли Манава (бл. 750 р. До н.е.. — бл. 690 р. До н.е..) З’ясував, що квадратний корінь деяких натуральних чисел, таких як 2 і 61, не можуть бути явно виражені [ ] .
Перший доказ існування ірраціональних чисел зазвичай приписується Гіппаса з Метапонта (бл. 500 рр. До н. Е.), Піфагорійці. За часів піфагорійців вважалося, що існує єдина одиниця довжини, досить мала і неподільна, яка ціле число раз входить в будь-який відрізок [ ] .
Немає точних даних про те, ірраціональність якого числа було доведено Гіппаса. Згідно з легендою він знайшов його вивчаючи довжини сторін пентаграми. Тому розумно припустити, що це було золотий перетин [ ] .
Грецькі математики назвали це відношення несумірних величин алогос (Невимовним), проте згідно з легендами не віддати Гіппаса належної поваги. Існує легенда, що Гиппас зробив відкриття, перебуваючи в морському поході, і був викинутий за борт іншими піфагорійцями «за створення елементи всесвіту, який заперечує доктрину, що все суті у всесвіті можуть бути зведені до цілих чисел і їх відносин». Відкриття Гіппаса поставило перед піфагорейської математикою серйозну проблему, зруйнувавши яке лежало в основі всієї теорії припущення, що числа і геометричні об’єкти єдині і нероздільні.
Відкриття Гіппаса поставило перед піфагорейської математикою серйозну проблему, зруйнувавши яке лежало в основі всієї теорії припущення, що числа і геометричні об’єкти єдині і нероздільні.
Визначення ірраціонального числа
Ірраціональними називають такі числа, які в десяткового запису є нескінченні неперіодичні десяткові дроби.
Так, наприклад, числа, отримані шляхом вилучення квадратного кореня з натуральних чисел, є ірраціональними і не є квадратами натуральних чисел. Але не всі ірраціональні числа отримують шляхом вилучення квадратних коренів, адже отримане шляхом розподілу, число «пі», також є ірраціональним, і його ви навряд чи отримаєте, намагаючись витягти квадратний корінь з натурального числа.
Властивості ірраціональних чисел
На відміну від чисел, записаних нескінченної десятковим дробом, тільки ірраціональні числа записуються непериодическими нескінченними десятковими дробами.
Сума двох невід’ємних ірраціональних чисел в результаті може бути раціональним числом.
Ірраціональні числа визначають дедекіндових перетину в безлічі раціональних чисел, в нижньому класі у яких немає найбільшого числа, а в верхньому немає меншого.
Будь-яке дійсне трансцендентне число є ірраціональним.
Все ірраціональні числа є або алгебраїчними, або трансцендентними.
Безліч ірраціональних чисел на прямій розташовуються щільно, і між його будь-якими двома числами обов’язково знайдеться ірраціональне число.
Безліч ірраціональних чисел нескінченно, незліченно і є безліччю 2-ї категорії.
При виконанні будь-якої арифметичної операції з раціональними числами, крім поділу на 0, його результатом буде раціональне число.
При додаванні оптимальної кількості з ірраціональним, в результаті завжди виходить ірраціональне число.
При додаванні ірраціональних чисел в результаті ми можемо отримати раціональне число.
Безліч ірраціональних чисел не є парним.
Числа, не є ірраціональними
Іноді досить складно відповісти на питання, чи є число ірраціональним, особливо у випадках, коли число має вигляд десяткового дробу або у вигляді числового виразу, кореня або логарифма.
Тому не зайвим буде знати, які числа не належать до ірраціональним. Якщо слідувати визначення ірраціональних чисел, то нам вже відомо, що раціональні числа не можуть бути ірраціональними.
Ірраціональними числами не є:
По-перше, всі натуральні числа;
По-друге, цілі числа;
По-третє, звичайні дроби;
По-четверте, різні змішані числа;
По-п’яте, це нескінченні періодичні десяткові дроби.
Крім усього перерахованого, ірраціональним числом не може бути будь-яка комбінація раціональних чисел, яка виконується знаками арифметичних операцій, як +, -,,:, так як при цьому підсумком двох раціональних чисел буде також раціональне число.
А тепер подивимося, які ж з чисел є ірраціональними:
А чи відомо вам про існування фан-клубу, де шанувальники цього загадкового математичного феномена шукають все нові відомості про Пі, намагаючись розгадати його таємницю. Членом цього клубу може сталь будь-яка людина, яка знає напам’ять певну кількість чисел Пі після коми;
А чи знаєте ви, що в Німеччині під охороною ЮНЕСКО знаходиться палац Кастадель Монте, завдяки пропорціям якого можна обчислити Пі. Цілий палац присвятив цьому числу король Фрідріх II.
Цілий палац присвятив цьому числу король Фрідріх II.
Виявляється, число Пі намагалися використовувати при будівництві Вавилонської вежі. Але на превеликий жаль, це призвело до краху проекту, так як на той момент було недостатньо вивчено точне обчислення значення Пі.
Співачка Кейт Буш у своєму новому диску записала пісню під назвою «Пі», в якій прозвучало сто двадцять чотири числа з знаменитого числового ряду 3, 141 … ..
Раніше ми вже показали, що $ 1 \\ frac25 $ — близько до $ \\ sqrt2 $. Якби воно точно дорівнювало $ \\ sqrt2 $,. Тоді співвідношення — $ \\ frac (1 \\ frac25) (1) $, яке можна перетворити в співвідношення цілих чисел $ \\ frac75 $, помноживши верхню і нижню частини дробу на 5, і було б шуканої величиною.
Але, на жаль, $ 1 \\ frac25 $ не є точною величиною $ \\ sqrt2 $. Більш точну відповідь $ 1 \\ frac (41) (100) $, дає нам співвідношення $ \\ frac (141) (100) $. Ще більшої точності ми досягаємо, коли прирівнюємо $ \\ sqrt2 $ до $ 1 \\ frac (207) (500) $. У цьому випадку співвідношення в цілих числах дорівнюватиме $ \\ frac (707) (500) $. Але і $ 1 \\ frac (207) (500) $ не є точним значенням кореня квадратного з 2. Грецькі математики витратили масу часу і сил, щоб обчислити точне значення $ \\ sqrt2 $, але це їм так і не вдалося. Вони не змогли представити співвідношення $ \\ frac (\\ sqrt2) (1) $ в вигляді співвідношення цілих чисел.
У цьому випадку співвідношення в цілих числах дорівнюватиме $ \\ frac (707) (500) $. Але і $ 1 \\ frac (207) (500) $ не є точним значенням кореня квадратного з 2. Грецькі математики витратили масу часу і сил, щоб обчислити точне значення $ \\ sqrt2 $, але це їм так і не вдалося. Вони не змогли представити співвідношення $ \\ frac (\\ sqrt2) (1) $ в вигляді співвідношення цілих чисел.
Нарешті, великий грецький математик Евклід довів, що, як би не збільшувалася точність підрахунків, отримати точне значення $ \\ sqrt2 $ неможливо. Не існує такої дробу, яка, будучи зведена в квадрат, дасть в результаті 2. Кажуть, що першим до цього висновку прийшов Піфагор, але цей незрозумілий факт настільки вразив вченого, що він поклявся сам і взяв зі своїх учнів клятву зберігати це відкриття в таємниці . Однак, можливо, ці відомості не відповідають дійсності.
Але якщо число $ \\ frac (\\ sqrt2) (1) $ не може бути представлено у вигляді співвідношення цілих чисел, то і ніяка, що містить $ \\ sqrt2 $, наприклад $ \\ frac (\\ sqrt2) (2) $ або $ \\ frac (4) (\\ sqrt2) $ також не може бути представлена \u200b\u200bу вигляді співвідношення цілих чисел, оскільки всі такі дроби можуть бути перетворені в $ \\ frac (\\ sqrt2) (1) $, помножене на яке-небудь число. Так $ \\ frac (\\ sqrt2) (2) \u003d \\ frac (\\ sqrt2) (1) \\ times \\ frac12 $. Або $ \\ frac (\\ sqrt2) (1) \\ times 2 \u003d 2 \\ frac (\\ sqrt2) (1) $, що можна перетворити, помноживши верхню і нижню частини на $ \\ sqrt2 $, і отримати $ \\ frac (4) (\\ sqrt2) $. (Не слід забувати, що незалежно від того, що являє собою число $ \\ sqrt2 $, якщо ми помножимо його на $ \\ sqrt2 $, то отримаємо 2.)
Так $ \\ frac (\\ sqrt2) (2) \u003d \\ frac (\\ sqrt2) (1) \\ times \\ frac12 $. Або $ \\ frac (\\ sqrt2) (1) \\ times 2 \u003d 2 \\ frac (\\ sqrt2) (1) $, що можна перетворити, помноживши верхню і нижню частини на $ \\ sqrt2 $, і отримати $ \\ frac (4) (\\ sqrt2) $. (Не слід забувати, що незалежно від того, що являє собою число $ \\ sqrt2 $, якщо ми помножимо його на $ \\ sqrt2 $, то отримаємо 2.)
Оскільки число $ \\ sqrt2 $ можна представити у вигляді співвідношення цілих чисел, воно отримало назву ірраціонального числа. З іншого боку, все числа, які можна представити у вигляді співвідношення цілих чисел, називаються раціональними.
Раціональними є всі цілі і дробові числа, як позитивні, так і негативні.
Як виявилося, більшість квадратних коренів є ірраціональними числами. Раціональні квадратного кореня є тільки у чисел, що входять в ряд квадратних чисел. Ці числа називаються також ідеальними квадратами. Раціональними числами є також дробу, складені з цих ідеальних квадратів. Наприклад, $ \\ sqrt (1 \\ frac79) $ є раціональним числом, так як $ \\ sqrt (1 \\ frac79) \u003d \\ frac (\\ sqrt16) (\\ sqrt9) \u003d \\ frac43 $ або $ 1 \\ frac13 $ (4 — це корінь квадратний з 16, а 3 — корінь квадратний з 9).
Наприклад, $ \\ sqrt (1 \\ frac79) $ є раціональним числом, так як $ \\ sqrt (1 \\ frac79) \u003d \\ frac (\\ sqrt16) (\\ sqrt9) \u003d \\ frac43 $ або $ 1 \\ frac13 $ (4 — це корінь квадратний з 16, а 3 — корінь квадратний з 9).
Розуміння чисел, особливо натуральних чисел, є одним з найстаріших математичних «умінь». Багато цивілізації, навіть сучасні, приписували числам якісь містичні властивості через їх величезної важливості в описі природи. Хоча сучасна наука і математика не підтверджують ці «чарівні» властивості, значення теорії чисел незаперечно.
Історично спочатку з’явилося безліч натуральних чисел, потім досить скоро до них додалися дроби і позитивні ірраціональні числа. Нуль і негативні числа були введені після цих підмножин безлічі дійсних чисел. Останнє безліч, безліч комплексних чисел, з’явилося тільки з розвитком сучасної науки.
У сучасній математиці числа вводять не в історичному порядку, хоча і в досить близькому до нього.
Натуральні числа $ \\ mathbb (N) $
Безліч натуральних чисел часто позначається як $ \\ mathbb (N) \u003d \\ lbrace 1,2,3,4 . .. \\ rbrace $, і часто його доповнюють нулем, позначаючи $ \\ mathbb (N) _0 $.
.. \\ rbrace $, і часто його доповнюють нулем, позначаючи $ \\ mathbb (N) _0 $.
В $ \\ mathbb (N) $ визначені операції додавання (+) і множення ($ \\ cdot $) з наступними властивостями для будь-яких $ a, b, c \\ in \\ mathbb (N) $:
1. $ a + b \\ in \\ mathbb (N) $, $ a \\ cdot b \\ in \\ mathbb (N) $ безліч $ \\ mathbb (N) $ замкнуто щодо операцій додавання і множення
2. $ a + b \u003d b + a $, $ a \\ cdot b \u003d b \\ cdot a $ коммутативность
3. $ (a + b) + c \u003d a + (b + c) $, $ (a \\ cdot b) \\ cdot c \u003d a \\ cdot (b \\ cdot c) $ асоціативність
4. $ a \\ cdot (b + c) \u003d a \\ cdot b + a \\ cdot c $ дистрибутивность
5. $ a \\ cdot 1 \u003d a $ є нейтральним елементом для множення
Оскільки безліч $ \\ mathbb (N) $ містить нейтральний елемент для множення, але не для складання, додавання нуля до цього безлічі забезпечує включення в нього нейтрального елемента для складання.
Крім цих двох операцій, на безлічі $ \\ mathbb (N) $ визначені відносини «менше» ($
1. $ a b $ трихотомія
$ a b $ трихотомія
2. якщо $ a \\ leq b $ і $ b \\ leq a $, то $ a \u003d b $ антисимметрия
3. якщо $ a \\ leq b $ і $ b \\ leq c $, то $ a \\ leq c $ транзитивність
4. якщо $ a \\ leq b $, то $ a + c \\ leq b + c $
5. якщо $ a \\ leq b $, то $ a \\ cdot c \\ leq b \\ cdot c $
Цілі числа $ \\ mathbb (Z) $
Приклади цілих чисел:
$1, -20, -100, 30, -40, 120…$
Рішення рівняння $ a + x \u003d b $, де $ a $ і $ b $ — відомі натуральні числа, а $ x $ — невідоме натуральне число, вимагає введення нової операції — віднімання (-). Якщо існує натуральне число $ x $, що задовольняє цьому рівнянню, то $ x \u003d b-a $. Однак, це конкретне рівняння не обов’язково має рішення на безлічі $ \\ mathbb (N) $, тому практичні міркування вимагають розширення безлічі натуральних чисел таким чином, щоб включити рішення такого рівняння. Це призводить до введення безлічі цілих чисел: $ \\ mathbb (Z) \u003d \\ lbrace 0,1, -1,2, -2,3, -3 … \\ rbrace $.
Оскільки $ \\ mathbb (N) \\ subset \\ mathbb (Z) $, логічно припустити, що введені раніше операції $ + $ і $ \\ cdot $ і відносини $ 1. $ 0 + a \u003d a + 0 \u003d a $ існує нейтральний елемент для складання
$ 0 + a \u003d a + 0 \u003d a $ існує нейтральний елемент для складання
2. $ a + (- a) \u003d (- a) + a \u003d 0 $ існує протилежне число $ -a $ для $ a $
Властивість 5 .:
5. якщо $ 0 \\ leq a $ і $ 0 \\ leq b $, то $ 0 \\ leq a \\ cdot b $
Безліч $ \\ mathbb (Z) $ замкнуто також і щодо операції віднімання, тобто $ (\\ forall a, b \\ in \\ mathbb (Z)) (a-b \\ in \\ mathbb (Z)) $.
Раціональні числа $ \\ mathbb (Q) $
Приклади раціональних чисел:
$ \\ Frac (1) (2), \\ frac (4) (7), — \\ frac (5) (8), \\ frac (10) (20) … $
Тепер розглянемо рівняння виду $ a \\ cdot x \u003d b $, де $ a $ і $ b $ — відомі цілі числа, а $ x $ — невідоме. Щоб рішення було можливим, необхідно ввести операцію ділення ($: $), і рішення набуває вигляду $ x \u003d b: a $, тобто $ x \u003d \\ frac (b) (a) $. Знову виникає проблема, що $ x $ не завжди належить $ \\ mathbb (Z) $, тому безліч цілих чисел необхідно розширити. Таким чином вводиться безліч раціональних чисел $ \\ mathbb (Q) $ з елементами $ \\ frac (p) (q) $, де $ p \\ in \\ mathbb (Z) $ і $ q \\ in \\ mathbb (N) $.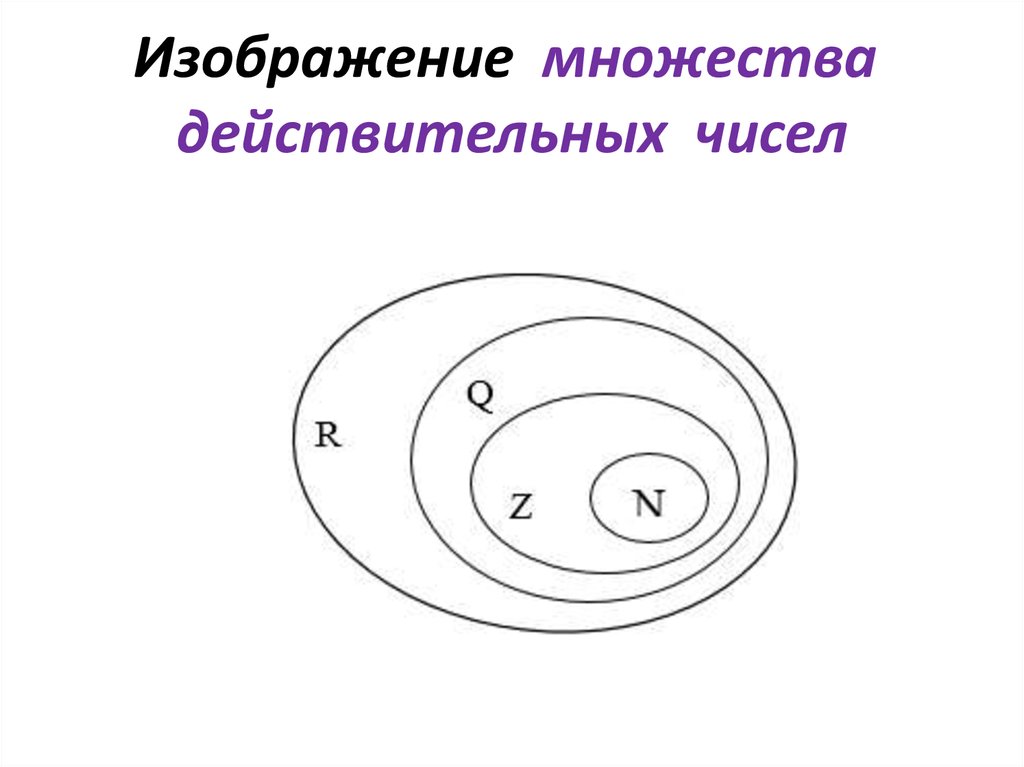 (- 1) $:
(- 1) $:
$ (\\ Forall a \\ in \\ mathbb (Q) \\ setminus \\ lbrace 0 \\ rbrace) (\\ exists \\ frac (1) (a)) (a \\ cdot \\ frac (1) (a) \u003d \\ frac (1) (a) \\ cdot a \u003d a) $
Порядок безлічі $ \\ mathbb (Q) $ можна розширити таким чином:
$ \\ Frac (p_1) (q_1)
Безліч $ \\ mathbb (Q) $ має одну важливу властивість: між будь-якими двома раціональними числами знаходиться нескінченно багато інших раціональних чисел, отже, не існує двох сусідніх раціональних чисел, на відміну від безлічі натуральних і цілих чисел.
Ірраціональні числа $ \\ mathbb (I) $
Приклади ірраціональних чисел:
$0.333333…$
$ \\ Sqrt (2) \\ approx 1.41422135 … $
$ \\ Pi \\ approx 3.1415926535 … $
З огляду на те, що між будь-якими двома раціональними числами знаходиться нескінченно багато інших раціональних чисел, легко можна зробити помилковий висновок, що безліч раціональних чисел настільки щільне, що немає необхідності в його подальше розширення. Навіть Піфагор свого часу зробив таку помилку.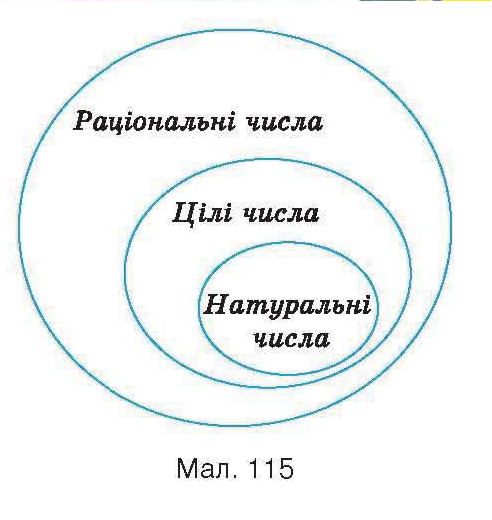 2 \u003d a $, де $ a $ — відоме раціональне число, а $ x $ — невідоме, не завжди має рішення на безлічі раціональних чисел, і знову виникає необхідність в розширенні множини. Виникає безліч ірраціональних чисел, і такі числа як $ \\ sqrt (2) $, $ \\ sqrt (3) $, $ \\ pi $ … належать цій множині.
2 \u003d a $, де $ a $ — відоме раціональне число, а $ x $ — невідоме, не завжди має рішення на безлічі раціональних чисел, і знову виникає необхідність в розширенні множини. Виникає безліч ірраціональних чисел, і такі числа як $ \\ sqrt (2) $, $ \\ sqrt (3) $, $ \\ pi $ … належать цій множині.
Дійсні числа $ \\ mathbb (R) $
Об’єднанням множин раціональних і ірраціональних чисел є безліч дійсних чисел. Оскільки $ \\ mathbb (Q) \\ subset \\ mathbb (R) $, знову логічно припустити, що введені арифметичні операції і відносини зберігають свої властивості на новому безлічі. Формальне доказ цього досить складно, тому вищезгадані властивості арифметичних операцій і відносини на множині дійсних чисел вводяться як аксіоми. В алгебрі такий об’єкт називається полем, тому говорять, що безліч дійсних чисел є впорядкованим полем.
Для того, щоб визначення безлічі дійсних чисел було повним, необхідно ввести додаткову аксіому, розрізняють безлічі $ \\ mathbb (Q) $ і $ \\ mathbb (R) $. 2 \u003d -1 $. Розширення безлічі $ \\ mathbb (R) $ на безліч $ \\ mathbb (C) $ дозволяє визначити квадратний корінь з від’ємних чисел, що і послужило причиною введення безлічі комплексних чисел. Також легко показати, що підмножина безлічі $ \\ mathbb (C) $, задане як $ \\ mathbb (C) _0 \u003d \\ lbrace (a, 0) | a \\ in \\ mathbb (R) \\ rbrace $, задовольняє всім аксіомам для дійсних чисел, отже $ \\ mathbb (C) _0 \u003d \\ mathbb (R) $, або $ R \\ subset \\ mathbb (C) $.
2 \u003d -1 $. Розширення безлічі $ \\ mathbb (R) $ на безліч $ \\ mathbb (C) $ дозволяє визначити квадратний корінь з від’ємних чисел, що і послужило причиною введення безлічі комплексних чисел. Також легко показати, що підмножина безлічі $ \\ mathbb (C) $, задане як $ \\ mathbb (C) _0 \u003d \\ lbrace (a, 0) | a \\ in \\ mathbb (R) \\ rbrace $, задовольняє всім аксіомам для дійсних чисел, отже $ \\ mathbb (C) _0 \u003d \\ mathbb (R) $, або $ R \\ subset \\ mathbb (C) $.
Алгебраїчна структура безлічі $ \\ mathbb (C) $ щодо операцій додавання і множення має такі властивості:
1. коммутативность додавання і множення
2. асоціативність додавання і множення
3. $ 0 + i0 $ — нейтральний елемент для складання
4. $ 1 + i0 $ — нейтральний елемент для множення
5. множення дистрибутивно по відношенню до складання
6. існує єдиний зворотний елемент як для складання, так і для множення.
| 1 | Множитель | x^2-4 | |
| 2 | Множитель | 4x^2+20x+16 | |
| 3 | График | y=-x^2 | |
| 4 | Вычислить | 2+2 | |
| 5 | Множитель | x^2-25 | |
| 6 | Множитель | x^2+5x+6 | |
| 7 | Множитель | x^2-9 | |
| 8 | Множитель | x^3-8 | |
| 9 | Вычислить | квадратный корень из 12 | |
| 10 | Вычислить | квадратный корень из 20 | |
| 11 | Вычислить | квадратный корень из 50 | |
| 12 | Множитель | x^2-16 | |
| 13 | Вычислить | квадратный корень из 75 | |
| 14 | Множитель | x^2-1 | |
| 15 | Множитель | x^3+8 | |
| 16 | Вычислить | -2^2 | |
| 17 | Вычислить | квадратный корень из (-3)^4 | |
| 18 | Вычислить | квадратный корень из 45 | |
| 19 | Вычислить | квадратный корень из 32 | |
| 20 | Вычислить | квадратный корень из 18 | |
| 21 | Множитель | x^4-16 | |
| 22 | Вычислить | квадратный корень из 48 | |
| 23 | Вычислить | квадратный корень из 72 | |
| 24 | Вычислить | квадратный корень из (-2)^4 | |
| 25 | Множитель | x^3-27 | |
| 26 | Вычислить | -3^2 | |
| 27 | Множитель | x^4-1 | |
| 28 | Множитель | x^2+x-6 | |
| 29 | Множитель | x^3+27 | |
| 30 | Множитель | x^2-5x+6 | |
| 31 | Вычислить | квадратный корень из 24 | |
| 32 | Множитель | x^2-36 | |
| 33 | Множитель | x^2-4x+4 | |
| 34 | Вычислить | -4^2 | |
| 35 | Множитель | x^2-x-6 | |
| 36 | Множитель | x^4-81 | |
| 37 | Множитель | x^3-64 | |
| 38 | Вычислить | 4^3 | |
| 39 | Множитель | x^3-1 | |
| 40 | График | y=x^2 | |
| 41 | Вычислить | 2^3 | |
| 42 | Вычислить | (-12+ квадратный корень из -18)/60 | |
| 43 | Множитель | x^2-6x+9 | |
| 44 | Множитель | x^2-64 | |
| 45 | График | y=2x | |
| 46 | Множитель | x^3+64 | |
| 47 | Вычислить | (-8+ квадратный корень из -12)/40 | |
| 48 | Множитель | x^2-8x+16 | |
| 49 | Вычислить | 3^4 | |
| 50 | Вычислить | -5^2 | |
| 51 | Множитель | x^2-49 | |
| 52 | Вычислить | (-20+ квадратный корень из -75)/40 | |
| 53 | Множитель | x^2+6x+9 | |
| 54 | Множитель | 4x^2-25 | |
| 55 | Вычислить | квадратный корень из 28 | |
| 56 | Множитель | x^2-81 | |
| 57 | Вычислить | 2^5 | |
| 58 | Вычислить | -8^2 | |
| 59 | Вычислить | 2^4 | |
| 60 | Множитель | 4x^2-9 | |
| 61 | Вычислить | (-20+ квадратный корень из -50)/60 | |
| 62 | Вычислить | (-8+ квадратный корень из -20)/24 | |
| 63 | Множитель | x^2+4x+4 | |
| 64 | Множитель | x^2-10x+25 | |
| 65 | Вычислить | квадратный корень из -16 | |
| 66 | Множитель | x^2-2x+1 | |
| 67 | Вычислить | -7^2 | |
| 68 | График | f(x)=2^x | |
| 69 | Вычислить | 2^-2 | |
| 70 | Вычислить | квадратный корень из 27 | |
| 71 | Вычислить | квадратный корень из 80 | |
| 72 | Множитель | x^3+125 | |
| 73 | Вычислить | -9^2 | |
| 74 | Множитель | 2x^2-5x-3 | |
| 75 | Вычислить | квадратный корень из 40 | |
| 76 | Множитель | x^2+2x+1 | |
| 77 | Множитель | x^2+8x+16 | |
| 78 | График | y=3x | |
| 79 | Множитель | x^2+10x+25 | |
| 80 | Вычислить | 3^3 | |
| 81 | Вычислить | 5^-2 | |
| 82 | График | f(x)=x^2 | |
| 83 | Вычислить | квадратный корень из 54 | |
| 84 | Вычислить | (-12+ квадратный корень из -45)/24 | |
| 85 | Множитель | x^2+x-2 | |
| 86 | Вычислить | (-3)^3 | |
| 87 | Множитель | x^2-12x+36 | |
| 88 | Множитель | x^2+4 | |
| 89 | Вычислить | квадратный корень из (-8)^2 | |
| 90 | Множитель | x^2+7x+12 | |
| 91 | Вычислить | квадратный корень из -25 | |
| 92 | Множитель | x^2-x-20 | |
| 93 | Вычислить | 5^3 | |
| 94 | Множитель | x^2+8x+15 | |
| 95 | Множитель | x^2+7x+10 | |
| 96 | Множитель | 2x^2+5x-3 | |
| 97 | Вычислить квадратный корень | квадратный корень из 116 | |
| 98 | Множитель | x^2-x-12 | |
| 99 | Множитель | x^2-x-2 | |
| 100 | Вычислить | 2^2 |
Ірраціональні числа вікі
Ірраціональне число — це дійсне число. яке не є раціональним. тобто не може бути представлено у вигляді дробу m n >>. де m — ціле число. n — натуральне число. Ірраціональне число може бути представлено у вигляді нескінченної неперіодичної десяткового дробу.
яке не є раціональним. тобто не може бути представлено у вигляді дробу m n >>. де m — ціле число. n — натуральне число. Ірраціональне число може бути представлено у вигляді нескінченної неперіодичної десяткового дробу.
Безліч ірраціональних чисел зазвичай позначається великою латинською літерою I> в напівжирному зображенні без заливки. Таким чином: I = R # X2216; Q = \ mathbb \ backslash \ mathbb>. тобто безліч ірраціональних чисел є різниця множин речових і раціональних чисел.
Про існування ірраціональних чисел, точніше відрізків. несумірних з відрізком одиничної довжини, знали вже стародавні математики: їм була відома, наприклад, несумісність діагоналі і сторони квадрата, що рівносильно ірраціональності числа 2 >>.
Властивості [| ]
Приклади [| ]
Приклади докази ірраціональності [| ]
Зведено передбачуване рівність в квадрат:
У канонічний розклад лівій частині рівності число 2 входить в парному ступеня, а в розкладання 2n 2 — в непарній. >
>
Але 2 m> парно, а права частина отриманого рівності непарна. Отримуємо протиріччя.
Історія [| ]
Античність [| ]
Концепція ірраціональних чисел була неявним чином сприйнята індійськими математиками в VII столітті до нашої ери, коли Манава (бл. 750 р. До н.е.. — бл. 690 р. До н.е..) З’ясував, що квадратний корінь деяких натуральних чисел, таких як 2 і 61, не можуть бути явно виражені [джерело не вказано 672 дня].
Перший доказ існування ірраціональних чисел зазвичай приписується Гіппаса з Метапонта (бл. 500 рр. До н. Е.), Піфагорійці. За часів піфагорійців вважалося, що існує єдина одиниця довжини, досить мала і неподільна, яка ціле число раз входить в будь-який відрізок [джерело не вказано 672 дня].
Немає точних даних про те, ірраціональність якого числа було доведено Гіппаса. Згідно з легендою він знайшов його вивчаючи довжини сторін пентаграми. Тому розумно припустити, що це було золотий перетин [джерело не вказано 643 дня].
Грецькі математики назвали це відношення несумірних величин алогос (невимовним), проте згідно з легендами не віддати Гіппаса належної поваги.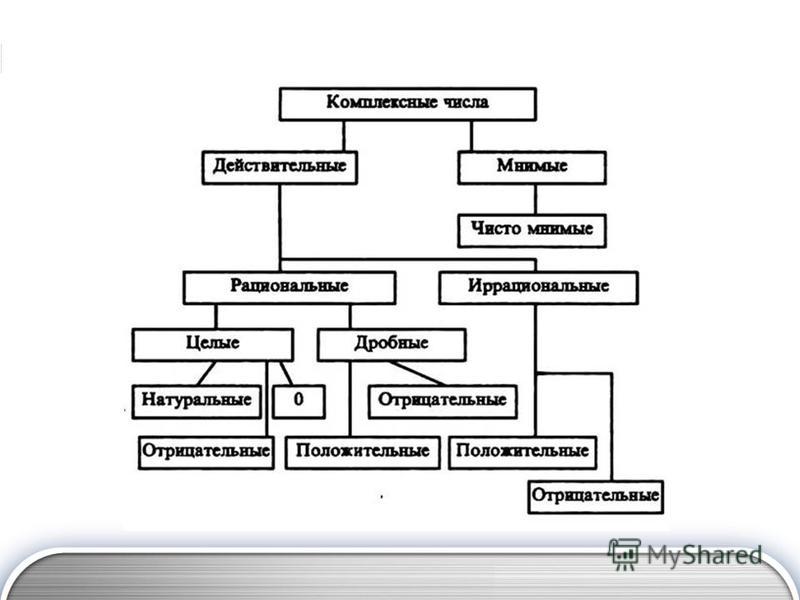 Існує легенда, що Гиппас зробив відкриття, перебуваючи в морському поході, і був викинутий за борт іншими піфагорійцями «за створення елементи всесвіту, який заперечує доктрину, що все суті у всесвіті можуть бути зведені до цілих чисел і їх відносин». Відкриття Гіппаса поставило перед піфагорейської математикою серйозну проблему, зруйнувавши яке лежало в основі всієї теорії припущення, що числа і геометричні об’єкти єдині і нероздільні.
Існує легенда, що Гиппас зробив відкриття, перебуваючи в морському поході, і був викинутий за борт іншими піфагорійцями «за створення елементи всесвіту, який заперечує доктрину, що все суті у всесвіті можуть бути зведені до цілих чисел і їх відносин». Відкриття Гіппаса поставило перед піфагорейської математикою серйозну проблему, зруйнувавши яке лежало в основі всієї теорії припущення, що числа і геометричні об’єкти єдині і нероздільні.
Феодор Киренский довів ірраціональність коренів натуральних чисел до 17 (виключаючи, природно, точні квадрати — 1, 4, 9 та 16), але зупинився на цьому, тому що имевшаяся в його інструментарії алгебра не дозволяла довести ірраціональність квадратного кореня з 17. З приводу того , яким могло бути це доказ, істориками математики було висловлено кілька різних припущень. Згідно найбільш правдоподібного [2] припущенням Жана ІТАР [fr]. воно було засноване на теоремі про те, що непарне квадратне число ділиться на вісім із залишком один [3].
Пізніше Евдокс Кнідський (410 або 408 р. До н.е.. — 355 або 347 р. До н.е..) Розвинув теорію пропорцій, яка брала до уваги як раціональні, так і ірраціональні відносини. Це послужило підставою для розуміння фундаментальної суті ірраціональних чисел. Величина стала вважатися не числом, але позначенням сутностей, таких як відрізки прямих, кути, площі, обсяги, проміжки часу — сутностей, які можуть змінюватися безперервно (в сучасному розумінні цього слова). Величини були протиставлені числах, які можуть змінюватися лише «стрибками» від одного числа до сусіднього, наприклад, з 4 на 5. Числа складаються з найменшою неподільною величини, в той час як величини можна зменшувати нескінченно.
До н.е.. — 355 або 347 р. До н.е..) Розвинув теорію пропорцій, яка брала до уваги як раціональні, так і ірраціональні відносини. Це послужило підставою для розуміння фундаментальної суті ірраціональних чисел. Величина стала вважатися не числом, але позначенням сутностей, таких як відрізки прямих, кути, площі, обсяги, проміжки часу — сутностей, які можуть змінюватися безперервно (в сучасному розумінні цього слова). Величини були протиставлені числах, які можуть змінюватися лише «стрибками» від одного числа до сусіднього, наприклад, з 4 на 5. Числа складаються з найменшою неподільною величини, в той час як величини можна зменшувати нескінченно.
Оскільки жодне кількісне значення не пов’язана із величиною, Евдокс зміг охопити і співмірні, і несумірні величини при визначенні дробу як відносини двох величин, і пропорції як рівності двох дробів. Прибравши з рівнянь кількісні значення (числа), він уникнув пастки, що складається в необхідності назвати ірраціональну величину числом. Теорія Евдокса дозволила грецьким математикам зробити неймовірний прогрес в геометрії, надавши їм необхідне логічне обгрунтування для роботи з непомірними величинами. «Книга 10 Елементів» Евкліда присвячена класифікації ірраціональних величин.
«Книга 10 Елементів» Евкліда присвячена класифікації ірраціональних величин.
Середні століття [| ]
Середні століття ознаменувалися прийняттям таких понять як нуль, негативні числа, цілі і дробові числа, спершу індійськими, потім китайськими математиками. Пізніше приєдналися арабські математики, які першими стали вважати негативні числа алгебраїчними об’єктами (поряд і на рівних правах з позитивними числами), що дозволило розвинути дисципліну, нині звану алгеброю.
Раціональної [величиною] є, наприклад, 10, 12, 3%, 6% і так далі, оскільки ці величини вимовлені і виражені кількісно. Що не раціонально, то ірраціонально, і неможливо вимовити або надати відповідну величину кількісно. Наприклад, квадратний корінь чисел таких так 10, 15, 20 — не є квадратами.
На противагу концепції Евкліда, що величини суть в першу чергу відрізки прямих, Аль Махане вважав цілі числа і дроби раціональними величинами, а квадратні і кубічні корені — ірраціональними. Він також ввів арифметичний підхід до безлічі ірраціональних чисел, оскільки саме він показав ірраціональність наступних величин:
результат складання ірраціональної величини і раціональної, результат віднімання раціональної величини з ірраціональної, результат віднімання ірраціональної величини з раціональної.
Єгипетський математик Абу Каміл (бл. 850 р. Н.е.. — бл. 930 р. Н.е..) Був першим, хто визнав прийнятним визнати ірраціональні числа рішенням квадратних рівнянь або коефіцієнтами в рівняннях — в основному, у вигляді квадратних або кубічних коренів, а також коренів четвертого ступеня. У X столітті іракський математик Аль Хашимі вивів загальні докази (а не наочні геометричні демонстрації) ірраціональності твори, приватного і результатів інших математичних перетворень над ірраціональними і раціональними числами. Ал Хазін (900 р. Н.е.. — 971 р. Н.е..) Подає таке визначення раціональної та ірраціональної величини:
Нехай одинична величина міститься в даній величині один або кілька разів, тоді ця [дана] величина відповідає цілому числу … Кожна величина, яка становить половину, або третину, або чверть одиничної величини, або, порівняно з одиничною величиною становить три п’ятих від неї, це раціональна величина. І в цілому, будь-яка величина, яка відноситься до одиничної як одне число до іншого, є раціональною. Якщо ж величина не може бути представлена як кілька або частина (l / n), або кілька частин (m / n) одиничної довжини, вона ірраціональна, тобто невимовна інакше як за допомогою коренів.
Якщо ж величина не може бути представлена як кілька або частина (l / n), або кілька частин (m / n) одиничної довжини, вона ірраціональна, тобто невимовна інакше як за допомогою коренів.
Багато з цих ідей були пізніше перейняті європейськими математиками після перекладу на латину арабських текстів в XII столітті. Аль Хассар, арабська математик з Магрибу, який спеціалізувався на ісламських законах про спадщину, в XII столітті ввів сучасну символьну математичну нотацію для дробів, розділивши чисельник і знаменник горизонтальною лінією. Та ж нотація з’явилася потім в роботах Фібоначчі в XIII столітті. Протягом XIV-XVI ст. Мадхава з Сангамаграми і представники Керальской школи астрономії та математики досліджували нескінченні ряди, що сходяться до деяких ірраціональним числам, наприклад, до π, а також показали ірраціональність деяких тригонометричних функцій. Джестадева привів ці результати в книзі «Йуктібхаза».
Новий час [| ]
Ланцюгові дроби. тісно пов’язані з ірраціональними числами (ланцюговий дріб, що представляє дане число, нескінченна тоді і тільки тоді, коли число є ірраціональним), були вперше досліджені Катальді в 1613 році, потім знову привернули до себе увагу в роботах Ейлера, а на початку XIX століття — в роботах Лагранжа. Діріхле також вніс значний вклад в розвиток теорії ланцюгових дробів. У 1761 року Ламберт з помощю ланцюгових дробів показав, що # X03C0; не є раціональним числом, а також що e x> і tg # X2061; x x> ірраціональні при будь-якому ненулевом раціональному x. Хоча доказ Ламберта можна назвати незавершеним, прийнято вважати його досить суворим, особливо з огляду на час його написання. Лежандр в 1794 році, після введення функції Бесселя — Кліффорда. показав, що # X03C0; 2> ірраціонально, звідки ірраціональність # X03C0; слід тривіально (раціональне число в квадраті дало б раціональне).
Діріхле також вніс значний вклад в розвиток теорії ланцюгових дробів. У 1761 року Ламберт з помощю ланцюгових дробів показав, що # X03C0; не є раціональним числом, а також що e x> і tg # X2061; x x> ірраціональні при будь-якому ненулевом раціональному x. Хоча доказ Ламберта можна назвати незавершеним, прийнято вважати його досить суворим, особливо з огляду на час його написання. Лежандр в 1794 році, після введення функції Бесселя — Кліффорда. показав, що # X03C0; 2> ірраціонально, звідки ірраціональність # X03C0; слід тривіально (раціональне число в квадраті дало б раціональне).
Існування трансцендентних чисел було доведено Ліувілль в 1844-1851 роках. Пізніше Георг Кантор (1873) показав їх існування, використовуючи інший метод, і обгрунтував, що будь-який інтервал речового ряду містить нескінченно багато трансцендентних чисел. Шарль Ерміта довів в 1873 році, що e трансцендентно, а Фердинанд Ліндеман в 1882 році, грунтуючись на цьому результаті, показав трансцендентність # X03C0; . Доказ Ліндеманна було потім спрощено Вейерштрассом в 1885 році, ще більш спрощено Давидом Гільбертом в 1893 році і, нарешті, доведено до майже елементарного Адольфом Гурвіцем і Паулем Горданом.
Доказ Ліндеманна було потім спрощено Вейерштрассом в 1885 році, ще більш спрощено Давидом Гільбертом в 1893 році і, нарешті, доведено до майже елементарного Адольфом Гурвіцем і Паулем Горданом.
Див. Також [| ]
Примітки [| ]
Схожі статті
-
Довести, що корінь з 3 ірраціональне число
-
Схиляння слова час за відмінками в однині та множині
-
Як називається число, з якого віднімають інше число — презентація 73157-10
Ірраціональні числа. Вложені корені, розкриття модулів
Продовжуємо вивчати, як правильно позбуватися ірраціональності та спрощувати такі вирази. Завдання, що далі розв’язані взяті із програми підготовки до ЗНО тестування, тому Ви добре знаєте де їх можете використати. Методи та схеми, що тут будуть наведені є загальновідомими, систематизованими та без вагань можуть бути застосовані Вами до аналогічних прикладів на ірраціональні вирази. Уважно розбирайте відповіді та вчіться красиво оформляти розв’язки.
Приклад 5.11 Звільнитися від ірраціональності в знаменнику дробу .
Обчислення:В цьому і всіх подібних прикладах для розкриття ірраціональності в знаменнику слід домножити і поділити дріб на вираз спряжений до знаменника. За формулою різниці квадратів в знаменнику дістанемо різницю чисел.
Для цього завдання рівносильні перетворення наведені формулою
Бувають складніші приклади, коли для розкриття ірраціональності слід звести знаменник під різницю кубів, але про них піде мова пізніше.
Ми в свою чергу стараємося подавати матеріал від простого до складнішого, щоб Ви все засвоїли з першого разу.
Відповідь: (√7+1)/2 – А.
Приклад 5.12 Внести множники під знаки коренів: a√(-a)+b√b.
ОДЗ: a≤0; b≥0.
Обчислення: Уважно переглянь те переходи в обчисленнях. Перевірте, чи самостійно Ви могли б прийти до наведеної відповіді
Вона в нас точно правильна, тому добре запам’ятайте як вносити від’ємні значення під корінь квадратний.
Відповідь: – Д.
Приклад 5.13 Спростити ірраціональний вираз
Обчислення: Переходимо до завдань на вкладені корені.
Вони вимагають добрих знань показникових функцій та послідовного розкриття коренів від внутрішнього вложеного до головного над усіма.
Скористаємося правилами та спростимо вираз
(при a≥0).
Уважно розберіть це завдання, далі підуть тільки важчі умови.
Відповідь: – Г.
Приклад 5.14Спростити вираз
А | Б | В | Г | Д |
-a2b | -ab | a2b | a2b2 | ab2 |
Обчислення:Пригадуємо властивості показників та розписуємо вложені корені, аж поки не прийдемо до компактної відповіді
.
Відповідь: a2b – В.
Приклад 5.15 Спростити вираз .
Обчислення: По аналогії з попереднім завданням позбуваємося кореня кубічного від частки добутків показникових виразів.
Після нескладних перетворень прийдемо до формули x3y2z/4, яка відповідає варіанту В тестових завдань.
Відповідь:x3y2z/4 – В.
Приклад 5.16 Знайти x, якщо
А | Б | В | Г | Д |
-1,125 | -0,875 | -0,625 | -0,375 | -0,125 |
Обчислення: Спочатку спростимо вложені корені, що стоять у лівій частині рівняння:
Прирівнюючи до правої частини, знаходимо невідоме значення:
, тобто x=-7/8, x=-0,875.
Відповідь: -0,875 – Б.
Приклад 5.17 Спростити вираз
А | Б | В | Г | Д |
0 | 4 | -4 | 4+2√5 | 2√5 |
Обчислення: При розкритті коренів від квадратів виразів отримаємо вирази за модулем. Далі оцінюємо чи підмодульний вираз додатний чи від’ємний. Якщо додатний то просто опускаємо модульні дужки, якщо приймає від’ємне значення то при розкритті модуля міняємо знак на протилежний.
Для наведеного прикладу відповідь можна сформулювати в наступному вигляді
Відповідь: 2√5 – Д.
Приклад 5.18 Знайти значення виразу , якщо x=√10.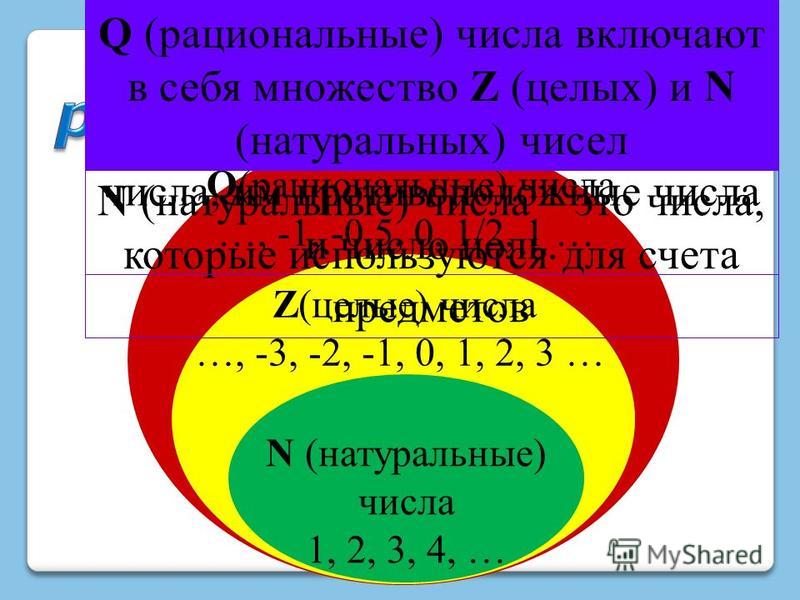
А | Б | В | Г | Д |
-4,5 | 2√10-10,5 | 2x-10,5 | 4,5 | 3,5 |
Обчислення: Мамо суму коренів четвертого порядку від виразу в у 4 степені. Для розкриття коренів поступаємо як і у попередньому прикладі, записуємо модулі таі після аналізу підмодульних виразів записуємо кінцеві значення.
тут мали x-3=√10-3>0 і x-7,5=√10-7,5<0
Чим більше Ви самостійно розв’яжете ідентичних за змістом прикладів, тим краще Вам запам’ятаються правила розкриття коренів та модулів.
Одних переглядів готових відповідей до ірраціональних виразів замало, щоб швидко обчислювати такі приклади самостійно, тому практикуйте побільше і почастіше.
Відповідь: 4,5 – Г.
Приклад 5.19Спростити вираз
А | Б | В | Г | Д |
√10 | 3,5+√10 | √3+2 | √2+√5 | 1+√6 |
Обчислення:Якщо маєте два вкладених корені і не бачите явної схеми як їх спростити то спробуйте розписати підкореневий вираз та подати його у вигляді квадрату виразу, що містить ірраціональність. Спершу Вам це буде важко вдаватися, але далі все легше зможете працювати з коренями.
В цьому завданні корінь з 10 розпишемо як корінь з 2 помножити на 5, а далі перегрупуємо доданки так як у випадку суми коренів з 2 та 5 в квадраті.
Запам’ятайте цю схему розкриття коренів, вона вимагає уваги до деталей та деякої практики.
Відповідь: √2+√5 – Г.
Приклад 5.20 Звільнитись від ірраціональності в знаменнику дробу
Обчислення: В знаменнику маємо різницю коренів кубічних з 7 та 2. Щоб позбутися ірраціональності в знаменнику необхідно отримати формулу різниці кубів, а для цього весь дріб необхідно розділити та помножити на вираз, що це забезпечує.
За формулою різниці кубів записуємо відповідний множник та виконуємо перетворення
Формули різниці кубів та квадратів варто мати під рукою, щоб не наробити помилок в подібних завданнях та прийти до правильного результату.
Відповідь: – В.
Далі підуть складніші в плані обчислень приклади із розкриття ірраціональності та знаходження значення ірраціонального виразу. Уважно перегляньте наведені завдання та вивчіть схему зведення під формулу квадрату виразу. Наступні 20 прикладів із ЗНО підготовки будуть розв’язані в наступних трьох публікаціях.
Після цього перейдемо до ірраціональних рівнянь та нерівностей.
- Вас може зацікавити:
- Обчислення ірраціональних виразів. Готові відповіді
- Методи розв’язування ірраціональних рівнянь
- Ірраціональні рівняння. Приклади
- Знайти область визначення. Ірраціональні рівняння
Що таке ірраціональне число визначення. Раціональні і ірраціональні числа
Головна > Ідеї > Що таке ірраціональне число визначення. Раціональні і ірраціональні числа
ірраціональне число — це дійсне число, Яке не є раціональним, тобто не може бути представлено у вигляді дробу, де — цілі числа,. Ірраціональне число може бути представлено у вигляді нескінченної неперіодичної десяткового дробу.
Безліч ірраціональних чисел зазвичай позначається великою латинською літерою в напівжирному зображенні без заливки. Таким чином:, тобто безліч ірраціональних чисел є різницю множин речових і раціональних чисел.
Про існування ірраціональних чисел, точніше відрізків, непорівнянних із відрізком одиничної довжини, знали вже стародавні математики: їм була відома, наприклад, несумісність діагоналі і сторони квадрата, що рівносильно ірраціональності числа.
властивості
- Будь-яке дійсне число може бути записано у вигляді нескінченного десяткового дробу, при цьому ірраціональні числа і тільки вони записуються непериодическими нескінченними десятковими дробами.
- Ірраціональні числа визначають дедекіндових перетину в безлічі раціональних чисел, у яких в нижньому класі немає найбільшого, а в верхньому немає найменшого числа.
- Кожне речовий трансцендентне число є ірраціональним.
- Кожне ірраціональне число є або алгебраїчним, або трансцендентним.
- Безліч ірраціональних чисел усюди щільно на числовій прямій: між будь-якими двома числами є ірраціональне число.
- Порядок на безлічі ірраціональних чисел ізоморфний порядку на безлічі речових трансцендентних чисел.
- Безліч ірраціональних чисел незліченну, є безліччю другої категорії.
приклади
| ірраціональні числа — ζ (3) — √2 — √3 — √5 — — — — — |
Ірраціональними є:
Приклади докази ірраціональності
Корінь з 2
Припустимо гидке: раціональний, тобто представляється у вигляді нескоротного дробу, де — ціле число, а — натуральне число. Зведено передбачуване рівність в квадрат:
Зведено передбачуване рівність в квадрат:
.
Звідси випливає, що парне, значить, парне і. Нехай, де ціле. тоді
Отже, парно, значить, парне і. Ми отримали, що і парні, що суперечить нескоротного дробу. Значить, вихідне припущення було невірним, і — ірраціональне число.
Двійковий логарифм числа 3
Припустимо гидке: раціональний, тобто представляється у вигляді дробу, де і — цілі числа. Оскільки, і можуть бути обрані позитивними. тоді
Але парно, а непарній. Отримуємо протиріччя.
eІсторія
Концепція ірраціональних чисел була неявним чином сприйнята індійськими математиками в VII столітті до нашої ери, коли Манава (бл. 750 р. До н.е.. — бл. 690 р. До н.е..) З’ясував, що квадратний корінь деяких натуральних чисел, таких як 2 і 61, не можуть бути явно виражені.
Перший доказ існування ірраціональних чисел зазвичай приписується Гіппаса з Метапонта (бл. 500 рр. До н. Е.), Піфагорійці, який знайшов цей доказ, вивчаючи довжини сторін пентаграми. За часів піфагорійців вважалося, що існує єдина одиниця довжини, досить мала і неподільна, яка ціле число раз входить в будь-який відрізок. Однак Гиппас обгрунтував, що не існує єдиної одиниці довжини, оскільки припущення про її існування призводить до протиріччя. Він показав, що якщо гіпотенуза рівнобедреного прямокутного трикутника містить ціле число одиничних відрізків, то це число повинне бути одночасно і парних, і непарних. Доказ виглядало наступним чином:
За часів піфагорійців вважалося, що існує єдина одиниця довжини, досить мала і неподільна, яка ціле число раз входить в будь-який відрізок. Однак Гиппас обгрунтував, що не існує єдиної одиниці довжини, оскільки припущення про її існування призводить до протиріччя. Він показав, що якщо гіпотенуза рівнобедреного прямокутного трикутника містить ціле число одиничних відрізків, то це число повинне бути одночасно і парних, і непарних. Доказ виглядало наступним чином:
- Відношення довжини гіпотенузи до довжини катета рівнобедреного прямокутного трикутника може бути виражено як a:b, де a і b обрані найменшими з можливих.
- По теоремі Піфагора: a² \u003d 2 b².
- Так як a² парне, a має бути парним (так як квадрат непарного числа був би непарних).
- оскільки a:b нескоротних, b має бути непарною.
- Так як a парне, позначимо a = 2y.
- тоді a² \u003d 4 y² \u003d 2 b².

- b² \u003d 2 y², отже b² парне, тоді і b парне.
- Однак було доведено, що b непарне. Протиріччя.
Грецькі математики назвали це відношення несумірних величин алогос (Невимовним), проте згідно з легендами не віддати Гіппаса належної поваги. Існує легенда, що Гиппас зробив відкриття, перебуваючи в морському поході, і був викинутий за борт іншими піфагорійцями «за створення елементи всесвіту, який заперечує доктрину, що все суті у всесвіті можуть бути зведені до цілих чисел і їх відносин». Відкриття Гіппаса поставило перед піфагорейської математикою серйозну проблему, зруйнувавши яке лежало в основі всієї теорії припущення, що числа і геометричні об’єкти єдині і нероздільні.
Матеріал цієї статті є початкову інформацію про ірраціональні числа. Спочатку ми дамо визначення ірраціональних чисел і роз’яснимо його. Далі наведемо приклади ірраціональних чисел. Нарешті, розглянемо деякі підходи до з’ясування, чи є задане число ірраціональним чи ні.
Навігація по сторінці.
Визначення і приклади ірраціональних чисел
При вивченні десяткових дробів ми окремо розглянули нескінченні неперіодичні десяткові дроби. Такі дробу виникають при десятковому вимірі довжин відрізків, непорівнянних із одиничним відрізком. Також ми відзначили, що нескінченні неперіодичні десяткові дроби не можуть бути переведені в звичайні дроби (дивіться переклад звичайних дробів на десяткові і назад), отже, ці цифри не є раціональними числами, вони представляють так звані ірраціональні числа.
Так ми підійшли до визначенню ірраціональних чисел.
Визначення.
Числа, які в десяткового запису є нескінченні неперіодичні десяткові дроби, називаються ірраціональними числами.
Озвучене визначення дозволяє привести приклади ірраціональних чисел. Наприклад, нескінченна неперіодичних десяткова дріб +4,10110011100011110000 … (кількість одиниць і нулів кожен раз збільшується на одну) є ірраціональним числом. Наведемо ще приклад ірраціонального числа: -22,353335333335 . .. (число трійок, які поділяють вісімки, кожен раз збільшується на дві).
.. (число трійок, які поділяють вісімки, кожен раз збільшується на дві).
Слід зазначити, що ірраціональні числа досить рідко зустрічаються саме у вигляді нескінченних неперіодичних десяткових дробів. Зазвичай вони зустрічаються у вигляді, і т.п., а також у вигляді спеціально введених букв. Найвідомішими прикладами ірраціональних чисел в такому записі є арифметичний квадратний корінь з двох, число «пі» π \u003d 3,141592 …, число e \u003d 2,718281 … і золоте число.
Ірраціональні числа також можна визначити через дійсні числа, які об’єднують раціональні та ірраціональні числа.
Визначення.
ірраціональні числа — це дійсні числа, які не є раціональними.
Чи є дане число ірраціональним?
Коли число задано не в вигляді десяткового дробу, а в вигляді деякого, кореня, логарифма і т.п., то відповісти на питання, чи є воно ірраціональним, у багатьох випадках досить складно.
Безсумнівно, при відповіді на поставлене запитання дуже корисно знати, які числа не є ірраціональними. З визначення ірраціональних чисел слід, що ірраціональними числами не є раціональні числа. Таким чином, ірраціональними числами НЕ є:
З визначення ірраціональних чисел слід, що ірраціональними числами не є раціональні числа. Таким чином, ірраціональними числами НЕ є:
- кінцеві і нескінченні періодичні десяткові дроби.
Також не є ірраціональним числом будь-яка композиція раціональних чисел, пов’язаних знаками арифметичних операцій (+, -, ·, :). Це пояснюється тим, що сума, різниця, добуток і частку двох раціональних чисел є раціональним числом. Наприклад, значення виразів і є раціональними числами. Тут же зауважимо, що якщо в подібних виразах серед раціональних чисел міститься одне єдине ірраціональне число, то значення всього виразу буде ірраціональним числом. Наприклад, у виразі число — ірраціональне, а решта числа раціональні, отже — ірраціональне число. Якби було раціональним числом, то з цього слідувала б раціональність числа, а воно не є раціональним.
Якщо ж вираз, яким задано число, містить кілька ірраціональних чисел, знаки кореня, логарифми, тригонометричні функції, числа π, e і т. п., то потрібно проводити доказ ірраціональності або раціональності заданого числа в кожному конкретному випадку. Однак існує ряд вже отриманих результатів, якими можна користуватися. Перелічимо основні з них.
п., то потрібно проводити доказ ірраціональності або раціональності заданого числа в кожному конкретному випадку. Однак існує ряд вже отриманих результатів, якими можна користуватися. Перелічимо основні з них.
Доведено, що корінь ступеня k з цілого числа є раціональним числом тільки тоді, коли число під коренем є k-ой ступенем іншого цілого числа, в інших випадках такий корінь задає ірраціональне число. Наприклад, числа і — ірраціональні, так як не існує цілого числа, квадрат якого дорівнює 7, і не існує цілого числа, зведення якого в п’яту ступінь дає число 15. А числа і не є ірраціональними, оскільки і.
Що стосується логарифмів, то довести їх ірраціональність іноді вдається методом від противного. Для прикладу доведемо, що log 2 3 є ірраціональним числом.
Припустимо, що log 2 3 раціональне число, а не ірраціональне, тобто його можна представити у вигляді звичайного дробу m / n. і дозволяють записати наступний ланцюжок рівностей:. Остання рівність неможливо, так як в його лівій частині непарне число, А в правій частині — парне. Так ми прийшли до протиріччя, значить, наше припущення виявилося невірним, і цим доведено, що log 2 3 — ірраціональне число.
Так ми прийшли до протиріччя, значить, наше припущення виявилося невірним, і цим доведено, що log 2 3 — ірраціональне число.
Зауважимо, що lna при будь-якому позитивному і відмінному від одиниці раціональному a є ірраціональним числом. Наприклад, і — ірраціональні числа.
Також доведено, що число e a при будь-якому відмінному від нуля раціональному a є ірраціональним, і що число π z при будь-якому відмінному від нуля цілому z є ірраціональним. Наприклад, числа — ірраціональні.
Ірраціональними числами також є тригонометричні функції sin, cos, tg і ctg при будь-якому раціональному і відмінному від нуля значенні аргументу. Наприклад, sin1, tg (-4), cos5,7, є ірраціональними числами.
Існують і інші доведені результати, на ми обмежимося вже перерахованими. Слід також сказати, що при доказі озвучених вище результатів застосовується теорія, пов’язана з алгебраїчними числами і трансцендентними числами.
На закінчення відзначимо, що не варто робити поспішних висновків щодо ірраціональності заданих чисел. Наприклад, здається очевидним, що ірраціональне число в ірраціонального рівня є ірраціональне число. Однак це не завжди так. В якості підтвердження озвученого факту наведемо ступінь. Відомо, що — ірраціональне число, а також доведено, що — ірраціональне число, але — раціональне число. Також можна навести приклади ірраціональних чисел, сума, різниця, добуток і частку яких є раціональні числа. Більш того, раціональність або ірраціональність чисел π + e, π-e, π · e, π π, π e і багатьох інших до сих пір не доведена.
Наприклад, здається очевидним, що ірраціональне число в ірраціонального рівня є ірраціональне число. Однак це не завжди так. В якості підтвердження озвученого факту наведемо ступінь. Відомо, що — ірраціональне число, а також доведено, що — ірраціональне число, але — раціональне число. Також можна навести приклади ірраціональних чисел, сума, різниця, добуток і частку яких є раціональні числа. Більш того, раціональність або ірраціональність чисел π + e, π-e, π · e, π π, π e і багатьох інших до сих пір не доведена.
Список літератури.
- Математика. 6 клас: навч. для загальноосвіт. установ / [Н. Я. Виленкин и др.]. — 22-е изд., Испр. — М .: Мнемозина, 2008. — 288 с .: іл. ISBN 978-5-346-00897-2.
- алгебра: навч. для 8 кл. загальноосвіт. установ / [Ю. Н. Макаричєв, Н. Г. Миндюк, К. І. Нешков, С. Б. Суворова]; під ред. С. А. Теляковского. — 16-е изд. — М.: Просвещение, 2008. — 271 с. : Ил. — ISBN 978-5-09-019243-9.
- Гусєв В. А., Мордкович А. Г.
 Математика (посібник для вступників до технікумів): Учеб. посібник.- М .; Вища. шк., 1984.-351 с., іл.
Математика (посібник для вступників до технікумів): Учеб. посібник.- М .; Вища. шк., 1984.-351 с., іл.
З відрізком одиничної довжини, знали вже стародавні математики: їм була відома, наприклад, несумісність діагоналі і сторони квадрата, що рівносильно ірраціональності числа.
Ірраціональними є:
Приклади докази ірраціональності
Корінь з 2
Припустимо гидке: раціональний, тобто представляється у вигляді нескоротного дробу, де і — цілі числа. Зведено передбачуване рівність в квадрат:
.
Звідси випливає, що парне, значить, парне і. Нехай, де ціле. тоді
Отже, парно, значить, парне і. Ми отримали, що і парні, що суперечить нескоротного дробу. Значить, вихідне припущення було невірним, і — ірраціональне число.
Двійковий логарифм числа 3
Припустимо гидке: раціональний, тобто представляється у вигляді дробу, де і — цілі числа. Оскільки, і можуть бути обрані позитивними. тоді
Але парно, а непарній. Отримуємо протиріччя.
Отримуємо протиріччя.
Історія
Концепція ірраціональних чисел була неявним чином сприйнята індійськими математиками в VII столітті до нашої ери, коли Манава (бл. 750 р. До н.е.. — бл. 690 р. До н.е..) З’ясував, що квадратний корінь деяких натуральних чисел, таких як 2 і 61, не можуть бути явно виражені.
Перший доказ існування ірраціональних чисел зазвичай приписується Гіппаса з Метапонта (бл. 500 рр. До н. Е.), Піфагорійці, який знайшов цей доказ, вивчаючи довжини сторін пентаграми. За часів піфагорійців вважалося, що існує єдина одиниця довжини, досить мала і неподільна, яка ціле число раз входить в будь-який відрізок. Однак Гиппас обгрунтував, що не існує єдиної одиниці довжини, оскільки припущення про її існування призводить до протиріччя. Він показав, що якщо гіпотенуза рівнобедреного прямокутного трикутника містить ціле число одиничних відрізків, то це число повинне бути одночасно і парних, і непарних. Доказ виглядало наступним чином:
- Відношення довжини гіпотенузи до довжини катета рівнобедреного прямокутного трикутника може бути виражено як a:b, де a і b обрані найменшими з можливих.

- По теоремі Піфагора: a² \u003d 2 b².
- Так як a² парне, a має бути парним (так як квадрат непарного числа був би непарних).
- оскільки a:b нескоротних, b має бути непарною.
- Так як a парне, позначимо a = 2y.
- тоді a² \u003d 4 y² \u003d 2 b².
- b² \u003d 2 y², отже b² парне, тоді і b парне.
- Однак було доведено, що b непарне. Протиріччя.
Грецькі математики назвали це відношення несумірних величин алогос (Невимовним), проте згідно з легендами не віддати Гіппаса належної поваги. Існує легенда, що Гиппас зробив відкриття, перебуваючи в морському поході, і був викинутий за борт іншими піфагорійцями «за створення елементи всесвіту, який заперечує доктрину, що все суті у всесвіті можуть бути зведені до цілих чисел і їх відносин». Відкриття Гіппаса поставило перед піфагорейської математикою серйозну проблему, зруйнувавши яке лежало в основі всієї теорії припущення, що числа і геометричні об’єкти єдині і нероздільні.
Див. також
Примітки
Розуміння чисел, особливо натуральних чисел, є одним з найстаріших математичних «умінь». Багато цивілізації, навіть сучасні, приписували числам якісь містичні властивості через їх величезної важливості в описі природи. Хоча сучасна наука і математика не підтверджують ці «чарівні» властивості, значення теорії чисел незаперечно.
Історично спочатку з’явилося безліч натуральних чисел, потім досить скоро до них додалися дроби і позитивні ірраціональні числа. Нуль і негативні числа були введені після цих підмножин безлічі дійсних чисел. Останнє безліч, безліч комплексних чисел, з’явилося тільки з розвитком сучасної науки.
У сучасній математиці числа вводять не в історичному порядку, хоча і в досить близькому до нього.
Натуральні числа $ \\ mathbb (N) $
Безліч натуральних чисел часто позначається як $ \\ mathbb (N) \u003d \\ lbrace 1,2,3,4 … \\ rbrace $, і часто його доповнюють нулем, позначаючи $ \\ mathbb (N) _0 $.
В $ \\ mathbb (N) $ визначені операції додавання (+) і множення ($ \\ cdot $) з наступними властивостями для будь-яких $ a, b, c \\ in \\ mathbb (N) $:
1. $ a + b \\ in \\ mathbb (N) $, $ a \\ cdot b \\ in \\ mathbb (N) $ безліч $ \\ mathbb (N) $ замкнуто щодо операцій додавання і множення
$ a + b \\ in \\ mathbb (N) $, $ a \\ cdot b \\ in \\ mathbb (N) $ безліч $ \\ mathbb (N) $ замкнуто щодо операцій додавання і множення
2. $ a + b \u003d b + a $, $ a \\ cdot b \u003d b \\ cdot a $ коммутативность
3. $ (a + b) + c \u003d a + (b + c) $, $ (a \\ cdot b) \\ cdot c \u003d a \\ cdot (b \\ cdot c) $ асоціативність
4. $ a \\ cdot (b + c) \u003d a \\ cdot b + a \\ cdot c $ дистрибутивность
5. $ a \\ cdot 1 \u003d a $ є нейтральним елементом для множення
Оскільки безліч $ \\ mathbb (N) $ містить нейтральний елемент для множення, але не для складання, додавання нуля до цього безлічі забезпечує включення в нього нейтрального елемента для складання.
Крім цих двох операцій, на безлічі $ \\ mathbb (N) $ визначені відносини «менше» ($
1. $ a b $ трихотомія
2. якщо $ a \\ leq b $ і $ b \\ leq a $, то $ a \u003d b $ антисимметрия
3. якщо $ a \\ leq b $ і $ b \\ leq c $, то $ a \\ leq c $ транзитивність
4. якщо $ a \\ leq b $, то $ a + c \\ leq b + c $
5. якщо $ a \\ leq b $, то $ a \\ cdot c \\ leq b \\ cdot c $
якщо $ a \\ leq b $, то $ a \\ cdot c \\ leq b \\ cdot c $
Цілі числа $ \\ mathbb (Z) $
Приклади цілих чисел:
$1, -20, -100, 30, -40, 120…$
Рішення рівняння $ a + x \u003d b $, де $ a $ і $ b $ — відомі натуральні числа, а $ x $ — невідоме натуральне число, вимагає введення нової операції — віднімання (-). Якщо існує натуральне число $ x $, що задовольняє цьому рівнянню, то $ x \u003d b-a $. Однак, це конкретне рівняння не обов’язково має рішення на безлічі $ \\ mathbb (N) $, тому практичні міркування вимагають розширення безлічі натуральних чисел таким чином, щоб включити рішення такого рівняння. Це призводить до введення безлічі цілих чисел: $ \\ mathbb (Z) \u003d \\ lbrace 0,1, -1,2, -2,3, -3 … \\ rbrace $.
Оскільки $ \\ mathbb (N) \\ subset \\ mathbb (Z) $, логічно припустити, що введені раніше операції $ + $ і $ \\ cdot $ і відносини $ 1. $ 0 + a \u003d a + 0 \u003d a $ існує нейтральний елемент для складання
2. $ a + (- a) \u003d (- a) + a \u003d 0 $ існує протилежне число $ -a $ для $ a $
Властивість 5 . :
:
5. якщо $ 0 \\ leq a $ і $ 0 \\ leq b $, то $ 0 \\ leq a \\ cdot b $
Безліч $ \\ mathbb (Z) $ замкнуто також і щодо операції віднімання, тобто $ (\\ forall a, b \\ in \\ mathbb (Z)) (a-b \\ in \\ mathbb (Z)) $.
Раціональні числа $ \\ mathbb (Q) $
Приклади раціональних чисел:
$ \\ Frac (1) (2), \\ frac (4) (7), — \\ frac (5) (8), \\ frac (10) (20) … $
Тепер розглянемо рівняння виду $ a \\ cdot x \u003d b $, де $ a $ і $ b $ — відомі цілі числа, а $ x $ — невідоме. Щоб рішення було можливим, необхідно ввести операцію ділення ($: $), і рішення набуває вигляду $ x \u003d b: a $, тобто $ x \u003d \\ frac (b) (a) $. Знову виникає проблема, що $ x $ не завжди належить $ \\ mathbb (Z) $, тому безліч цілих чисел необхідно розширити. Таким чином вводиться безліч раціональних чисел $ \\ mathbb (Q) $ з елементами $ \\ frac (p) (q) $, де $ p \\ in \\ mathbb (Z) $ і $ q \\ in \\ mathbb (N) $. Безліч $ \\ mathbb (Z) $ є підмножиною, в якому кожен елемент $ q \u003d 1 $, отже $ \\ mathbb (Z) \\ subset \\ mathbb (Q) $ і операції додавання і множення поширюються і на це безліч за такими правилами, які зберігають всі перераховані вище властивості і на безлічі $ \\ mathbb (Q) $:
$ \\ Frac (p_1) (q_1) + \\ frac (p_2) (q_2) \u003d \\ frac (p_1 \\ cdot q_2 + p_2 \\ cdot q_1) (q_1 \\ cdot q_2) $
$ \\ Frac (p-1) (q_1) \\ cdot \\ frac (p_2) (q_2) \u003d \\ frac (p_1 \\ cdot p_2) (q_1 \\ cdot q_2) $
Розподіл вводиться таким чином:
$ \\ Frac (p_1) (q_1): \\ frac (p_2) (q_2) \u003d \\ frac (p_1) (q_1) \\ cdot \\ frac (q_2) (p_2) $
На безлічі $ \\ mathbb (Q) $ рівняння $ a \\ cdot x \u003d b $ має єдине рішення для кожного $ a \\ neq 0 $ (поділ на нуль не визначене). (- 1) $:
(- 1) $:
$ (\\ Forall a \\ in \\ mathbb (Q) \\ setminus \\ lbrace 0 \\ rbrace) (\\ exists \\ frac (1) (a)) (a \\ cdot \\ frac (1) (a) \u003d \\ frac (1) (a) \\ cdot a \u003d a) $
Порядок безлічі $ \\ mathbb (Q) $ можна розширити таким чином:
$ \\ Frac (p_1) (q_1)
Безліч $ \\ mathbb (Q) $ має одну важливу властивість: між будь-якими двома раціональними числами знаходиться нескінченно багато інших раціональних чисел, отже, не існує двох сусідніх раціональних чисел, на відміну від безлічі натуральних і цілих чисел.
Ірраціональні числа $ \\ mathbb (I) $
Приклади ірраціональних чисел:
$0.333333…$
$ \\ Sqrt (2) \\ approx 1.41422135 … $
$ \\ Pi \\ approx 3.1415926535 … $
З огляду на те, що між будь-якими двома раціональними числами знаходиться нескінченно багато інших раціональних чисел, легко можна зробити помилковий висновок, що безліч раціональних чисел настільки щільне, що немає необхідності в його подальше розширення. Навіть Піфагор свого часу зробив таку помилку. 2 \u003d a $, де $ a $ — відоме раціональне число, а $ x $ — невідоме, не завжди має рішення на безлічі раціональних чисел, і знову виникає необхідність в розширенні множини. Виникає безліч ірраціональних чисел, і такі числа як $ \\ sqrt (2) $, $ \\ sqrt (3) $, $ \\ pi $ … належать цій множині.
2 \u003d a $, де $ a $ — відоме раціональне число, а $ x $ — невідоме, не завжди має рішення на безлічі раціональних чисел, і знову виникає необхідність в розширенні множини. Виникає безліч ірраціональних чисел, і такі числа як $ \\ sqrt (2) $, $ \\ sqrt (3) $, $ \\ pi $ … належать цій множині.
Дійсні числа $ \\ mathbb (R) $
Об’єднанням множин раціональних і ірраціональних чисел є безліч дійсних чисел. Оскільки $ \\ mathbb (Q) \\ subset \\ mathbb (R) $, знову логічно припустити, що введені арифметичні операції і відносини зберігають свої властивості на новому безлічі. Формальне доказ цього досить складно, тому вищезгадані властивості арифметичних операцій і відносини на множині дійсних чисел вводяться як аксіоми. В алгебрі такий об’єкт називається полем, тому говорять, що безліч дійсних чисел є впорядкованим полем.
Для того, щоб визначення безлічі дійсних чисел було повним, необхідно ввести додаткову аксіому, розрізняють безлічі $ \\ mathbb (Q) $ і $ \\ mathbb (R) $. 2 \u003d -1 $. Розширення безлічі $ \\ mathbb (R) $ на безліч $ \\ mathbb (C) $ дозволяє визначити квадратний корінь з від’ємних чисел, що і послужило причиною введення безлічі комплексних чисел. Також легко показати, що підмножина безлічі $ \\ mathbb (C) $, задане як $ \\ mathbb (C) _0 \u003d \\ lbrace (a, 0) | a \\ in \\ mathbb (R) \\ rbrace $, задовольняє всім аксіомам для дійсних чисел, отже $ \\ mathbb (C) _0 \u003d \\ mathbb (R) $, або $ R \\ subset \\ mathbb (C) $.
2 \u003d -1 $. Розширення безлічі $ \\ mathbb (R) $ на безліч $ \\ mathbb (C) $ дозволяє визначити квадратний корінь з від’ємних чисел, що і послужило причиною введення безлічі комплексних чисел. Також легко показати, що підмножина безлічі $ \\ mathbb (C) $, задане як $ \\ mathbb (C) _0 \u003d \\ lbrace (a, 0) | a \\ in \\ mathbb (R) \\ rbrace $, задовольняє всім аксіомам для дійсних чисел, отже $ \\ mathbb (C) _0 \u003d \\ mathbb (R) $, або $ R \\ subset \\ mathbb (C) $.
Алгебраїчна структура безлічі $ \\ mathbb (C) $ щодо операцій додавання і множення має такі властивості:
1. коммутативность додавання і множення
2. асоціативність додавання і множення
3. $ 0 + i0 $ — нейтральний елемент для складання
4. $ 1 + i0 $ — нейтральний елемент для множення
5. множення дистрибутивно по відношенню до складання
6. існує єдиний зворотний елемент як для складання, так і для множення.
— π
Таким чином, безліч ірраціональних чисел є різниця I \u003d R ∖ Q (\\ displaystyle \\ mathbb (I) \u003d \\ mathbb (R) \\ backslash \\ mathbb (Q)) множин речових і раціональних чисел.
Про існування ірраціональних чисел, точніше відрізків, непорівнянних із відрізком одиничної довжини, знали вже стародавні математики: їм була відома, наприклад, несумісність діагоналі і сторони квадрата, що рівносильно ірраціональності числа 2 (\\ displaystyle (\\ sqrt (2))).
властивості
- Сума двох позитивних ірраціональних чисел може бути раціональним числом.
- Ірраціональні числа визначають дедекіндових перетину в безлічі раціональних чисел, у яких в нижньому класі немає найбільшого, а в верхньому немає найменшого числа.
- Безліч ірраціональних чисел усюди щільно на числовій прямій: між будь-якими двома різними числами є ірраціональне число.
- Порядок на безлічі ірраціональних чисел ізоморфний порядку на безлічі речових трансцендентних чисел. [ ]
Алгебраїчні і трансцендентні числа
Кожне ірраціональне число є або алгебраїчним, або трансцендентним. Безліч алгебраїчних чисел є рахунковим безліччю. Так як безліч дійсних чисел незліченну, то безліч ірраціональних чисел незліченну. (2)).
(2)).
Історія
античність
Концепція ірраціональних чисел була неявним чином сприйнята індійськими математиками в VII столітті до нашої ери, коли Манава (приблизно 750-690 роки до нашої ери) з’ясував, що квадратний корінь деяких натуральних чисел, таких як 2 і 61, не можуть бути явно виражені [ ] .
Перший доказ існування ірраціональних чисел, а точніше існування несумірних відрізків, зазвичай приписується піфагорійців Гіппаса з Метапонта (приблизно 470 рік до нашої ери). За часів піфагорійців вважалося, що існує єдина одиниця довжини, досить мала і неподільна, яка ціле число раз входить в будь-який відрізок [ ] .
Немає точних даних про те, ірраціональність якого числа було доведено Гіппаса. Згідно з легендою він знайшов його, вивчаючи довжини сторін пентаграми. Тому розумно припустити, що це було золотий перетин так як це і є ставлення діагоналі до сторони в правильному п’ятикутнику.
Грецькі математики назвали це відношення несумірних величин алогос (Невимовним), проте згідно з легендами не віддати Гіппаса належної поваги. Існує легенда, що Гиппас зробив відкриття, перебуваючи в морському поході, і був викинутий за борт іншими піфагорійцями «за створення елементи всесвіту, який заперечує доктрину, що все суті у всесвіті можуть бути зведені до цілих чисел і їх відносин». Відкриття Гіппаса поставило перед піфагорейської математикою серйозну проблему, зруйнувавши яке лежало в основі всієї теорії припущення, що числа і геометричні об’єкти єдині і нероздільні.
Існує легенда, що Гиппас зробив відкриття, перебуваючи в морському поході, і був викинутий за борт іншими піфагорійцями «за створення елементи всесвіту, який заперечує доктрину, що все суті у всесвіті можуть бути зведені до цілих чисел і їх відносин». Відкриття Гіппаса поставило перед піфагорейської математикою серйозну проблему, зруйнувавши яке лежало в основі всієї теорії припущення, що числа і геометричні об’єкти єдині і нероздільні.
Пізніше Евдокс Кнідський (410 або 408 р. До н.е.. — 355 або 347 р. До н.е..) Розвинув теорію пропорцій, яка брала до уваги як раціональні, так і ірраціональні відносини. Це послужило підставою для розуміння фундаментальної суті ірраціональних чисел. Величина стала вважатися не числом, але позначенням сутностей, таких як відрізки прямих, кути, площі, обсяги, проміжки часу — сутностей, які можуть змінюватися безперервно (в сучасному розумінні цього слова). Величини були протиставлені числах, які можуть змінюватися лише «стрибками» від одного числа до сусіднього, наприклад, з 4 на 5. Числа складаються з найменшою неподільною величини, в той час як величини можна зменшувати нескінченно.
Числа складаються з найменшою неподільною величини, в той час як величини можна зменшувати нескінченно.
Оскільки жодне кількісне значення не пов’язана із величиною, Евдокс зміг охопити і співмірні, і несумірні величини при визначенні дробу як відносини двох величин, і пропорції як рівності двох дробів. Прибравши з рівнянь кількісні значення (числа), він уникнув пастки, що складається в необхідності назвати ірраціональну величину числом. Теорія Евдокса дозволила грецьким математикам зробити неймовірний прогрес в геометрії, надавши їм необхідне логічне обгрунтування для роботи з непомірними величинами. Десята книга «Почав» Евкліда присвячена класифікації ірраціональних величин.
Середньовіччя
Середні століття ознаменувалися прийняттям таких понять як нуль, негативні числа, цілі і дробові числа, спершу індійськими, потім китайськими математиками. Пізніше приєдналися арабські математики, які першими стали вважати негативні числа алгебраїчними об’єктами (поряд і на рівних правах з позитивними числами), що дозволило розвинути дисципліну, нині звану алгеброю.
Арабські математики з’єднали давньогрецькі поняття «числа» і «величини» в єдину, більш загальну ідею дійсних чисел. Вони критично ставилися до уявленням Евкліда про відносини, на противагу їй вони розвинули теорію відносин довільних величин і розширили поняття числа до відносин безперервних величин. У своїх коментарях на Книгу 10 Елементів Евкліда, перський математик Аль Махане (ок 800 рр. Н. Е.) Досліджував і класифікував квадратичні ірраціональні числа (числа виду) і більш загальні кубічні ірраціональні числа. Він дав визначення раціональним і ірраціональним величинам, які він і називав ірраціональними числами. Він легко оперував цими об’єктами, але міркував як про відокремлені об’єктах, наприклад:
На противагу концепції Евкліда, що величини суть в першу чергу відрізки прямих, Аль Махане вважав цілі числа і дроби раціональними величинами, а квадратні і кубічні корені — ірраціональними. Він також ввів арифметичний підхід до безлічі ірраціональних чисел, оскільки саме він показав ірраціональність наступних величин:
Єгипетський математик Абу Каміл (бл. 850 р. Н.е.. — бл. 930 р. Н.е..) Був першим, хто визнав прийнятним визнати ірраціональні числа рішенням квадратних рівнянь або коефіцієнтами в рівняннях — в основному, у вигляді квадратних або кубічних коренів, а також коренів четвертого ступеня. У X столітті іракський математик Аль Хашимі вивів загальні докази (а не наочні геометричні демонстрації) ірраціональності твори, приватного і результатів інших математичних перетворень над ірраціональними і раціональними числами. Ал Хазін (900 р. Н.е.. — 971 р. Н.е..) Подає таке визначення раціональної та ірраціональної величини:
850 р. Н.е.. — бл. 930 р. Н.е..) Був першим, хто визнав прийнятним визнати ірраціональні числа рішенням квадратних рівнянь або коефіцієнтами в рівняннях — в основному, у вигляді квадратних або кубічних коренів, а також коренів четвертого ступеня. У X столітті іракський математик Аль Хашимі вивів загальні докази (а не наочні геометричні демонстрації) ірраціональності твори, приватного і результатів інших математичних перетворень над ірраціональними і раціональними числами. Ал Хазін (900 р. Н.е.. — 971 р. Н.е..) Подає таке визначення раціональної та ірраціональної величини:
Нехай одинична величина міститься в даній величині один або кілька разів, тоді ця [дана] величина відповідає цілому числу … Кожна величина, яка становить половину, або третину, або чверть одиничної величини, або, порівняно з одиничною величиною становить три п’ятих від неї, це раціональна величина. І в цілому, будь-яка величина, яка відноситься до одиничної як одне число до іншого, є раціональною. Якщо ж величина не може бути представлена \u200b\u200bяк кілька або частина (l / n), або кілька частин (m / n) одиничної довжини, вона ірраціональна, тобто невимовна інакше як за допомогою коренів. Якщо ж величина не може бути представлена \u200b\u200bяк кілька або частина (l / n), або кілька частин (m / n) одиничної довжини, вона ірраціональна, тобто невимовна інакше як за допомогою коренів. |
Багато з цих ідей були пізніше перейняті європейськими математиками після перекладу на латину арабських текстів в XII столітті. Аль Хассар, арабська математик з Магрибу, який спеціалізувався на ісламських законах про спадщину, в XII столітті ввів сучасну символьну математичну нотацію для дробів, розділивши чисельник і знаменник горизонтальною лінією. Та ж нотація з’явилася потім в роботах Фібоначчі в XIII столітті. Протягом XIV-XVI ст. Мадхава з Сангамаграми і представники Керальской школи астрономії та математики досліджували нескінченні ряди, що сходяться до деяких ірраціональним числам, наприклад, до π, а також показали ірраціональність деяких тригонометричних функцій. Джестадева привів ці результати в книзі «Йуктібхаза». (Довівши при цьому існування трансцендентних чисел), тим самим переосмисливши роботи Евкліда за класифікацією ірраціональних чисел. (2)) ірраціонально, звідки ірраціональність π (\\ displaystyle \\ pi) слід тривіально (раціональне число в квадраті дало б раціональне).
(2)) ірраціонально, звідки ірраціональність π (\\ displaystyle \\ pi) слід тривіально (раціональне число в квадраті дало б раціональне).
Існування трансцендентних чисел було доведено Ліувілль в 1844-1851 роках. Пізніше Георг Кантор (1873) показав їх існування, використовуючи інший метод, і обгрунтував, що будь-який інтервал речового ряду містить нескінченно багато трансцендентних чисел. Шарль Ерміта довів в 1873 році, що e трансцендентно, а Фердинанд Ліндеман в 1882 році, грунтуючись на цьому результаті, показав трансцендентність π (\\ displaystyle \\ pi) література
Що таке ірраціональні числа
Рубрикатор
What Are You Looking For?
Popular Tags
Навчання
Какой язык программирования выбрать новичку
Додати
в обране
Навчання
Як початківцям вивчати англійську
Додати
в обране
Навчання
Навіщо потрібно вивчати англійську мову
Додати
в обране
Навчання
Оформлення інклюзивних класів
Додати
в обране
Навчання
Витамин Д
Додати
в обране
Навчання
Универсальность изопропилового спирта
Додати
в обране
Навчання
Буклетка – книжковий інтернет-магазин навчальної літератури
Додати
в обране
Навчання
15 неймовірних фактів про вовків
Додати
в обране
Навчання
Підготовка до ЗНО з математики: книги та підручники які стануть в нагоді
Додати
в обране
Навчання
Занятия с логопедом для детей в Equides Club
Додати
в обране
.
.
01
Навчання
Какой язык программирования выбрать новичку
02
Навчання
Як початківцям вивчати англійську
03
Навчання
Навіщо потрібно вивчати англійську мову
04
Навчання
Оформлення інклюзивних класів
05
Навчання
Витамин Д
06
Навчання
Универсальность изопропилового спирта
07
Навчання
Буклетка – книжковий інтернет-магазин навчальної літератури
08
Навчання
15 неймовірних фактів про вовків
09
Навчання
Підготовка до ЗНО з математики: книги та підручники які стануть в нагоді
10
Навчання
Занятия с логопедом для детей в Equides Club
Навчання Перегляди: 847
Навчання Перегляди: 847
Навчання Перегляди: 847
Ірраціональні числа належать до речових, але не є раціональними, тобто їх точне значення невідоме. Але якщо є опис способу, яким було отримано ірраціональне число, то воно вважається відомим. Іншими словами, його значення можна обчислити з необхідною точністю.
Але якщо є опис способу, яким було отримано ірраціональне число, то воно вважається відомим. Іншими словами, його значення можна обчислити з необхідною точністю.
Згідно з поняттями геометрії, якщо у двох відрізках міститься якась кількість однакових значень, то вони співмірні. Наприклад, різні сторони прямокутника співмірні. Але ось сторона квадрата і його діагональ не є співмірними. Вони не мають спільного заходу, в якому їх можна було б висловити. Ірраціональні числа стосуються неявно виражених. Вони неспівмірні з раціональними числами. До раціональних належать цілі, дробові, а також кінцеві та періодичні десяткові числа. Вони є співмірними одиниці. Нескінченні десяткові неперіодичні дроби називають ірраціональними, з одиницею вони неспівмірні. Але може бути вказаний спосіб отримання такого числа, тоді воно вважається заданим точно. За допомогою такого способу можна знайти будь-яку кількість знаків після коми у ірраціонального числа, це називається обчислити число з певною точністю, яка якраз і задається кількістю необхідних до обчислення знаків. Властивості ірраціональних чисел багато в чому схожі з властивостями раціональних. Наприклад, порівнюються вони однаково, над ними можливо робити ті ж самі арифметичні дії, вони можуть бути позитивними або негативними. Множення ірраціонального числа на нуль, точно так само як і раціонального, дає нуль. Якщо операція проводиться над двома числами, одне з яких раціональне, а інше ірраціональне, то прийнято за можливості не використовувати наближене значення, а брати точним чином задане число (наприклад, у вигляді недесятичної дробу) .Зрахується, що першим концепцію ірраціональних чисел відкрив Гіппас з Метапонта, що жив приблизно в VI ст. до н. Своє відкриття Гіппас здійснив під час морського походу, перебуваючи на кораблі. Згідно з легендою, коли він розповів іншим піфагорейцям про ірраціональні числа, надавши доказ їхнього існування, ті вислухали його і визнали його викладки правильними. Тим не менш, відкриття Гіппаса настільки шокувало їх, що він був викинутий за борт за те, що створив щось, що спростовує центральну піфагорейську доктрину про те, що все у всесвіті може бути зведено до цілих числах і їх відносин.
Властивості ірраціональних чисел багато в чому схожі з властивостями раціональних. Наприклад, порівнюються вони однаково, над ними можливо робити ті ж самі арифметичні дії, вони можуть бути позитивними або негативними. Множення ірраціонального числа на нуль, точно так само як і раціонального, дає нуль. Якщо операція проводиться над двома числами, одне з яких раціональне, а інше ірраціональне, то прийнято за можливості не використовувати наближене значення, а брати точним чином задане число (наприклад, у вигляді недесятичної дробу) .Зрахується, що першим концепцію ірраціональних чисел відкрив Гіппас з Метапонта, що жив приблизно в VI ст. до н. Своє відкриття Гіппас здійснив під час морського походу, перебуваючи на кораблі. Згідно з легендою, коли він розповів іншим піфагорейцям про ірраціональні числа, надавши доказ їхнього існування, ті вислухали його і визнали його викладки правильними. Тим не менш, відкриття Гіппаса настільки шокувало їх, що він був викинутий за борт за те, що створив щось, що спростовує центральну піфагорейську доктрину про те, що все у всесвіті може бути зведено до цілих числах і їх відносин.
- Попередня
- Наступна
Останні публікації
Преимущества и недостатки автомобильных грузоперевозок
вер. 21, 2022
Хотите знать, какой iPhone 14 купить? Представляем руководство по покупке для сомневающихся
вер. 21, 2022
Преимущества кофе в зернах
вер. 21, 2022
Найважливіші переваги впровадження системи CRM CRMIUM
вер. 21, 2022
Возбудители для женщин или «волшебная таблетка» для женского оргазма
вер. 20, 2022
Тематичні матеріали
Як одружувати на собі чоловіка?
Мама і тато. Шукаємо компроміс у вихованні дитини
Яєчня з копченою ковбаскою і сиром
Як створити посилання на сайт
Як приготувати баклажани
Без причини з ‘являються синці на ногах, що робити?
Як зробити блакитні очі яскравішими
Як спланувати передпокій
Як повернути дружину сім’ю — ради психолога
Як приховати вагітність від інших
Як приготувати рулетики з солоного оселедця
Як підібрати колір олівця для доль
Иррациональные числа
Раздел 1. 1 дает доказательство основной теоремы арифметики и использует
чтобы показать, что различные действительные числа иррациональны. Доказательство
Основная теорема не важна для этого курса, да и сама теорема
используется только для доказательства существования иррациональных чисел. Упражнения в
В разделе 1.1 исследуются некоторые другие факты об иррациональных числах.
(Обратите внимание, что историческая справочная информация в этом разделе и в других местах
в учебнике, для этого курса не требуются. Но они могут быть интересными,
поэтому вам рекомендуется их прочитать.)
1 дает доказательство основной теоремы арифметики и использует
чтобы показать, что различные действительные числа иррациональны. Доказательство
Основная теорема не важна для этого курса, да и сама теорема
используется только для доказательства существования иррациональных чисел. Упражнения в
В разделе 1.1 исследуются некоторые другие факты об иррациональных числах.
(Обратите внимание, что историческая справочная информация в этом разделе и в других местах
в учебнике, для этого курса не требуются. Но они могут быть интересными,
поэтому вам рекомендуется их прочитать.)
Математики работают с различными «системами счисления». множество натуральных чисел,
$\N$, является самым основным. Этот набор содержит положительные целые числа:
$\N=\{1,2,3,\dots\}$. С отрицательными целыми числами и нулем мы получаем набор
целых чисел: $\Z=\{\dots,-2,-1,0,1,2,\dots\}$.
Два натуральных числа можно складывать, но не всегда вычитать.
В каком-то смысле $\Z$ изобретено, чтобы сделать возможным вычитание; когда ты
вычесть натуральное число из меньшего натурального числа, в результате получится не натуральное число, а
отрицательное целое число. Мы говорим, что натуральные числа замкнуты
при сложении, но не замыкается при вычитании.
Мы говорим, что натуральные числа замкнуты
при сложении, но не замыкается при вычитании.
Аналогично, множество целых чисел не замыкается при делении. Рациональные числа придуманы, чтобы деление возможно (кроме, конечно, деления на ноль). Множество рациональных чисел $\Q$ содержит все частные, $\frac{n}{m}$, целых чисел, где знаменатель $m$ не равен нулю. Конечно, такое же рациональное число может быть представлено множеством различных дробей; Например $\frac{15}{3}=\frac{5}{1}=\frac{-30}{-6}=\frac{105}{21}=\cdots$. Если ты хочешь быть причудливым, рациональное число может быть определено как класс эквивалентности дробей где $\frac{a}{b}$ эквивалентно $\frac{c}{d}$ тогда и только тогда, когда $ad=bc$. Каждое ненулевое рациональное число можно однозначно представить в виде дроби $\frac{p}{q}$ где $q$ — натуральное число, а $p$ и $q$ не имеют общих делителей.
Набор действительных чисел $\R$ отличается.
Если мотивация изобретения $\Z$ и $\Q$ арифметическая, то мотивация
для изобретения $\R$ является более геометрическим. 2}$ или $\sqrt 2$. Но $\sqrt 2$ не может быть рациональным числом.
В учебнике дано известное доказательство иррациональности $\sqrt 2$. На самом деле, мы можем использовать Фундаментальную
Теорема арифметики, чтобы получить большой запас иррациональных чисел: 92$ не являются целыми числами.
Число $\pi$ можно определить
геометрически как длина окружности, диаметр которой равен 1.
Число $e$ является основанием натурального логарифма, и для его определения требуется
исчисление.
2}$ или $\sqrt 2$. Но $\sqrt 2$ не может быть рациональным числом.
В учебнике дано известное доказательство иррациональности $\sqrt 2$. На самом деле, мы можем использовать Фундаментальную
Теорема арифметики, чтобы получить большой запас иррациональных чисел: 92$ не являются целыми числами.
Число $\pi$ можно определить
геометрически как длина окружности, диаметр которой равен 1.
Число $e$ является основанием натурального логарифма, и для его определения требуется
исчисление.
Для множества других иррациональных чисел мы можем обратиться к неповторяющимся десятичным дробям.
(См. упражнения с 17 по 21 в разделе 1.1.)
Действительные числа часто представляются в десятичной форме, $a.d_1d_2d_3\dots$,
где $a$ — целое число, а $d_1,d_2,d_3,\dots$ — цифры, то есть целые числа в диапазоне
от 0 до 9n}$.) Число в десятичной форме
рационально тогда и только тогда, когда оно повторяется. В повторяющемся десятичном числе после некоторого
точка, существует конечный блок из одной или нескольких цифр, который просто
повторяется снова и снова навсегда. Например,
$\frac 13=0,3333333\dots=0.\overline{3}$ или $\frac{223}{165}=1,351515151\dots=1,3\overline{51}$
или $\frac12=0,500000\dots = 0,5\overline{0}$. Линия над 3 или 51 или 0 указывает на то, что
эта цифра или блок цифр повторяются вечно.
Например,
$\frac 13=0,3333333\dots=0.\overline{3}$ или $\frac{223}{165}=1,351515151\dots=1,3\overline{51}$
или $\frac12=0,500000\dots = 0,5\overline{0}$. Линия над 3 или 51 или 0 указывает на то, что
эта цифра или блок цифр повторяются вечно.
Но это означает, что любое неповторяющееся десятичное число представляет собой иррациональное количество. Например:
0,101001000100001000001000000100000001000000001000000000...
В этой десятичной дроби количество нулей между единицами увеличивается на единицу от каждой группы нулей к следующей, что делает невозможным десятичную дробь заканчиваются конечным повторяющимся блоком. Единицы можно заменить другими цифрами дать другие иррациональные числа. Например, мы можем заменить некоторые с двойками:
0.102002000100002000001000000100000002000000001000000000...
Мы можем выбрать любое подмножество единиц для замены на двойки.
Поскольку существует счетное количество единиц, существует несчетное количество
подмножества единиц, так что мы можем получить несчетное количество различных иррациональных
числа из этого примера. (Это предполагает, что
вы знаете о счетных и несчетных бесконечностях и о том, что
множество подмножеств бесконечного множества несчетно. Если это так, вы
вероятно, известно, что множество рациональных чисел счетно (т. е. может
поставить во взаимно однозначное соответствие с множеством натуральных чисел),
а множество действительных чисел несчетно. Но приятно иметь
конкретный пример несчетного множества иррациональных чисел.)
(Это предполагает, что
вы знаете о счетных и несчетных бесконечностях и о том, что
множество подмножеств бесконечного множества несчетно. Если это так, вы
вероятно, известно, что множество рациональных чисел счетно (т. е. может
поставить во взаимно однозначное соответствие с множеством натуральных чисел),
а множество действительных чисел несчетно. Но приятно иметь
конкретный пример несчетного множества иррациональных чисел.)
Тот факт, что десятичная дробь представляет рациональное число тогда и только тогда, когда десятичная дробь повторяется доказать не сложно. Если вам интересно, вот 22-минутная видео-презентация Некоторые примеры. (Это видео не является обязательной частью курса.)
Видео: Повторение десятичных дробей
Остается вопрос, можем ли мы как-то воспроизвести все числа иррациональные числа? Это и есть тема следующее чтение.
(назад к содержанию)
Увлекательные иррациональные числа: пи и квадратные корни
Большинство детей узнают о числах Пи и квадратных корнях где-то в средней школе. Они могут слышать термин «иррациональное число», а некоторые даже помнят его, но очень немногие действительно понимают, что оно означает. Что ж, иррациональные числа труднее понять, чем рациональные, но я считаю, что это стоит потраченного времени и усилий, потому что они обладают некоторыми удивительными свойствами. Я просто должен удивляться в благоговении, когда вижу факты, лежащие передо мной, потому что все это звучит невероятно, но все же доказано.
Они могут слышать термин «иррациональное число», а некоторые даже помнят его, но очень немногие действительно понимают, что оно означает. Что ж, иррациональные числа труднее понять, чем рациональные, но я считаю, что это стоит потраченного времени и усилий, потому что они обладают некоторыми удивительными свойствами. Я просто должен удивляться в благоговении, когда вижу факты, лежащие передо мной, потому что все это звучит невероятно, но все же доказано.
Чтобы изучать иррациональные числа, нужно сначала понять, что такое рациональных чисел. Короче говоря, рациональные числа — это целых числа, дроби и десятичных дроби — числа, которые мы используем в повседневной жизни.
В математике число является рациональным, если его можно записать как отношение двух целых чисел , другими словами, в виде a/b , где a и b являются целыми числами, а b не являются целыми числами. нуль. Ясно, что все дроби имеют такой вид. Завершающие десятичные числа могут быть легко записаны в этой форме, а также все неконечные повторяющиеся десятичные числа (десятичные числа, которые повторяют последовательность цифр) являются рациональными.
Иррациональные числа: неповторяющиеся неконечные десятичные числа
После обсуждения с учащимися рациональности завершающих и повторяющихся десятичных дробей вы можете объявить, что НЕПОВТОРЯЮЩИЕСЯ НЕКОНЧАЮЩИЕСЯ десятичные числа — это ИРРАЦИОНАЛЬНЫЕ ЧИСЛА .
Можете ли вы представить линию, проходящую через начало координат, которая НЕ касается НИ ОДНОЙ из точек с целочисленными координатами ????? Это сложно, но такие линии существуют. Они просто избегают касания любой из точек с целыми координатами, а их наклон является иррациональным числом. Трудно понять. Конечно, когда вы рисуете линии на бумаге или на компьютере, точность рисования ограничена, и даже линия y = π x , вероятно, проходит через точку с целочисленными координатами, а именно через точку (7,22), потому что 22/7 является довольно близким приближением к Pi. Если бы вы могли рисовать очень точно, линия на самом деле не проходила бы через (7, 22) — она просто проходила бы рядом.
Линия y = Pi * x действительно выглядит так, как будто она проходит через точку (7,22), так как графическая программа не может рисовать достаточно точно.
Что это означает на практике? Если вы можете составить последовательность цифр, которая никогда не заканчивается и никогда не переходит в закономерность, то у вас есть иррациональное число. Звучит легко? Ну, давай, попробуй. Вы не можете взять несколько маленьких паттернов и просто сдвинуть их, потому что это просто создаст более длинный паттерн. И если вы просто делаете это случайным образом, как вы можете быть уверены, что это не создает очень длинный шаблон длиной, может быть, в миллион цифр?
Ты помнишь Пи? В школе нам говорят, что число Пи равно примерно 3,14. На самом деле Пи — это бесконечная, никогда не повторяющаяся десятичная дробь, а значит, это иррациональное число. Вот первые цифры: 3.1415926535897932384626433832795
Другим примером иррационального числа является квадратный корень из 2, первые десятичные знаки которого равны 1,4142135623730950488016887242097. Большинство квадратных корней иррациональны. Еще один пример — синус большинства углов. Подробнее о синусе можно прочитать здесь.
Большинство квадратных корней иррациональны. Еще один пример — синус большинства углов. Подробнее о синусе можно прочитать здесь.
Немного потренируйтесь: Угадайте, какие из приведенных ниже квадратных корней иррациональны, а какие нет. Затем узнать с помощью калькулятора. Если вы видите длинное десятичное число, этот квадратный корень иррационален.
√7 , √8, √49 , √65 , √121 , √100, √101
Вы можете задаться вопросом, откуда мы знаем, что √2 не имеет шаблона в десятичной последовательности? Может быть, шаблон очень хорошо спрятан и действительно длинный, миллиарды цифр? Даже если вы проверите первый миллион цифр, может быть, шаблон длиннее этого?
Вот здесь и приходит на помощь математическое доказательство. Доказательство того, что √2 действительно иррационально, вовсе не опирается на компьютеры, а вместо этого является доказательством от противного: если бы √2 БЫЛО рациональным числом, то мы получили бы противоречие. Я призываю вас дать вашим старшеклассникам изучить это доказательство, так как оно очень иллюстрирует типичное доказательство в математике и не очень сложно следовать: Доказательство того, что квадратный корень из 2 является иррациональным числом.
Где найти особые иррациональные числа?
Ответ на этот вопрос зависит от того, что вы считаете «особенным». Математики доказали, что некоторые специальные числа иррациональны, например Пи и e . Число e является основанием натуральных логарифмов. Оно иррационально, как и Пи, и имеет приблизительное значение 2,7182818284535306….
.Не просто «придумать» такие специальные номера. Но вы можете легко найти больше иррациональных чисел, используя большинство квадратных корней. Например, что вы думаете о √2 + 1? Является ли результат сложения рациональным или иррациональным числом? Как ты можешь знать? А как насчет других сумм, в которых вы добавляете одно иррациональное и одно рациональное число, например √5 + 1/4?
Можно также сложить два иррациональных числа, и сумма будет многократно иррациональна. Однако не всегда; например, e + (- e ) = 0, и 0 рационально, хотя и e , и — e иррациональны. Или возьмите 1 + √3 и 1 − √3 и сложите эти два иррациональных числа — что вы получите?
Или возьмите 1 + √3 и 1 − √3 и сложите эти два иррациональных числа — что вы получите?
Если вы умножите или разделите иррациональное число на рациональное число, вы получите иррациональное число. Например, √7/10000 — иррациональное число. Еще одна возможность нахождения иррациональных чисел — умножение квадратных корней и других иррациональных чисел. Однако иногда это приводит к рациональному числу (когда?). Математики также изучали, что происходит, если возвести иррациональное число в рациональную или иррациональную степень.
Еще больше иррациональных чисел возникает, когда вы логарифмируете или вычисляете синусы, косинусы и тангенсы. У них нет специальных названий, а просто называются «синус 70 градусов» или «логарифм по основанию 10 от 5», и т. д. . Ваш калькулятор даст вам десятичные приближения к ним.
Чего больше: рациональных или иррациональных чисел?
А теперь еще одна удивительная вещь: существует множество конечных десятичных чисел и множество некончающихся повторяющихся десятичных знаков, но есть ЕЩЕ БОЛЬШЕ некончающихся неповторяющихся десятичных знаков, или, другими словами, иррациональных чисел. Обычно это показывают на курсах математики на уровне колледжа. В математических терминах мы говорим, что рациональные числа — это счетный набор , тогда как иррациональные числа представляют собой несчетный набор .
Обычно это показывают на курсах математики на уровне колледжа. В математических терминах мы говорим, что рациональные числа — это счетный набор , тогда как иррациональные числа представляют собой несчетный набор .
Другими словами, иррациональных чисел больше, чем рациональных. Вы можете понять это? Это похоже на то, что я принимаю как доказанный факт, но это невозможно осязать или легко проиллюстрировать в конкретных терминах — что часто бывает с иррациональными числами. Кажется, что они ускользают от нас, но думать о них интересно.
Дополнительная информация
Эволюция действительных чисел
Отличный учебник о различии рациональных и иррациональных чисел и о том, как мышление об этом «эволюционировало» в истории; охватывает такие темы, как соотношение натуральных чисел, непрерывные и дискретные, единичные дроби, измерения, обычная мера, квадраты и их стороны и т. д.
Все ли строки цифр в числе Пи?
Все ли возможные комбинации цифр встречаются в числе «пи»? Например, возможно ли, что где-то в десятичном представлении есть миллион двойок подряд?
Значение иррациональных показателей 9n, где n может быть целым, дробным, десятичным или иррациональным числом?
Комментарии
БЛЕСТЯЩИЙ. Мне особенно нравится чувствительность к визуальному представлению идеи. Поистине жемчужина в мире объяснения необъяснимого.
Мне особенно нравится чувствительность к визуальному представлению идеи. Поистине жемчужина в мире объяснения необъяснимого.
Элиза
Каковы другие названия линии квадратного корня и косой черты в дроби? Не сурд, косая черта или делитель.
Пэт Уилмор
Сурд может называться либо «радикальным знаком», либо «сурд-символом», либо «радикальным символом». Косая черта дроби также называется солидусом.
Какая самая длинная повторяющаяся десятичная дробь?
Лу Саймон
Я полагаю, вы имеете в виду самый длинный цикл. Ну, нет ограничений на длину цикла. Допустим, я делаю повторяющееся десятичное число с огромным количеством 4 подряд, за которыми следует одна 7. Вы всегда можете сделать цикл всего на одно число длиннее, добавив в него еще одну 4. И вы можете продолжать делать это бесконечно. Другими словами, если бы существовала такая вещь, как самый длинный цикл, его всегда можно было бы сделать длиннее, добавив в него одну четверку, так что он в конце концов не был бы самым длинным.
Как извлечь квадратный корень из числа, например 10, на числовой прямой с помощью циркуля и линейки?
Доктор Математика объясняет один метод: построить отрезок длины квадратного корня из X.
Все эти разговоры о том, насколько фантастично число пи, столь же иррационально и неповторяемо в своей структуре, но никогда не ссылаясь на тот факт, что это константа, согласно которой 2 пи R = длина окружности. Он никогда не повторяется, как круг бесконечен и совершенно круглый. Возможно, есть что-то, что нужно понять о такой константе, которая приводит к совершенству. Вы никогда не сможете достичь этого… или это всегда свежо — как будто ничто не повторяется дважды во времени одним и тем же путем. Имеет ли круг какое-либо отношение ко времени? Интересно, как мы измеряем время вещами, которые круглые, как вращающиеся стрелки часов по кругу. Что-то думать о. А также сама геометрическая форма.
Керр
Меню уроков математики
Иррациональные числа | Brilliant Math & Science Wiki
Эндрю Эллинор, Мэй Ли, Виктор Паес Плинио, а также
способствовал
Содержимое
- История
- Примеры иррациональных чисел
- Свойства иррациональных чисел
- Иррациональность 2\sqrt{2}2
- Смотрите также
Основная статья: История иррациональных чисел
Первый человек, признавший существование 9{2}a2+b2=c2, чтобы найти длину диагонали единичного квадрата. Это показало, что стороны квадрата несоизмеримы с его диагональю, и что эта длина не может быть выражена как отношение двух целых чисел. Другие пифагорейцы догматически считали, что могут существовать только положительные рациональные числа. Они были настолько напуганы идеей несоизмеримости, что выбросили Гиппаса за борт во время морского путешествия и поклялись хранить существование иррациональных чисел в официальной тайне своей секты. Однако есть веские основания полагать, что кончина Гиппаса — всего лишь апокрифический миф. Исторические документы, касающиеся этого инцидента, немногочисленны и написаны через 800 лет после времен Пифагора и Гиппаса. Лишь примерно через 300 лет после Гиппаса Евклид представил свое доказательство иррациональности 2.\sqrt{2}.2.
Это показало, что стороны квадрата несоизмеримы с его диагональю, и что эта длина не может быть выражена как отношение двух целых чисел. Другие пифагорейцы догматически считали, что могут существовать только положительные рациональные числа. Они были настолько напуганы идеей несоизмеримости, что выбросили Гиппаса за борт во время морского путешествия и поклялись хранить существование иррациональных чисел в официальной тайне своей секты. Однако есть веские основания полагать, что кончина Гиппаса — всего лишь апокрифический миф. Исторические документы, касающиеся этого инцидента, немногочисленны и написаны через 800 лет после времен Пифагора и Гиппаса. Лишь примерно через 300 лет после Гиппаса Евклид представил свое доказательство иррациональности 2.\sqrt{2}.2.
Вероятно, пифагорейцы вручную измерили диагональ единичного квадрата. Однако они расценили бы такое измерение как приближение, близкое к точному рациональному числу, которое дает истинную длину диагонали. До Гиппасса у пифагорейцев не было оснований подозревать, что существуют действительные числа, которые в принципе, а не только на практике, нельзя было измерить или сосчитать. Числа были для пифагорейцев духовной основой их философии и религии. Космология, физика, этика и духовность основывались на предпосылке, что «все есть число». Они верили, что все вещи — количество звезд на небе, высота музыкальных гамм и качества добродетели — все можно описать и постичь с помощью рациональных чисел.
Числа были для пифагорейцев духовной основой их философии и религии. Космология, физика, этика и духовность основывались на предпосылке, что «все есть число». Они верили, что все вещи — количество звезд на небе, высота музыкальных гамм и качества добродетели — все можно описать и постичь с помощью рациональных чисел.
Иррациональные числа возникают в математике во многих случаях. Примеры включают следующее:
- Гипотенуза прямоугольного треугольника с основаниями длины 1 имеет длину 2 \sqrt{2}2, что иррационально.
- В более общем смысле, D \sqrt{D}D является иррациональным для любого целого числа D DD, которое не является полным квадратом. Для демонстрации мы докажем, что 2\sqrt 22 является иррациональным числом в следующем разделе «Иррациональность 2\sqrt 22».
- Отношение π\piπ длины окружности к ее диаметру иррационально.
- Основание eee натурального логарифма иррационально.
Посмотрите следующий пример для лучшего понимания:
72+42 \frac{ 7 \sqrt{2+4} }{\sqrt{2} } 272+4 рационально или иррационально?
У нас есть
72+42=762=73.
\frac{ 7 \sqrt{2+4} }{\sqrt{2} } = \frac{ 7 \sqrt{6} }{\sqrt{2} } = 7 \sqrt{3}. 272+4=276=73.
По свойству 2 выше, 3\sqrt{3}3 является иррациональным числом, поскольку 3 не является полным квадратом. Следовательно, 73 7 \sqrt{3} 73 — иррациональное число. □_\квадрат□
Попробуйте решить следующую задачу:
Это рациональное число. Это иррациональное число.
Что вы можете сказать о 2+7×7?\sqrt{2+7}\times \sqrt 7?2+7×7?
- Если сложить иррациональное и рациональное числа, получится иррациональное число. Чтобы понять, почему это так, предположим, что xxx иррационально, yyy рационально, а сумма x+yx+yx+y является рациональным числом zzz. Тогда мы имеем x=z−yx = z-yx=z−y, и, поскольку разность двух рациональных чисел рациональна, отсюда следует, что xxx рационально. Это противоречие, поскольку xxx иррационально. Следовательно, сумма x+yx+yx+y должна быть иррациональной.
- Умножение иррационального числа на любое ненулевое рациональное число дает иррациональное число.
 Мы рассуждаем, как и выше, чтобы показать, что если xy=zxy = zxy=z рационально, то x=zy{x = \frac{z}{y}}x=yz рационально, что противоречит предположению, что xxx иррационально. Следовательно, произведение xyxyxy должно быть иррациональным.
Мы рассуждаем, как и выше, чтобы показать, что если xy=zxy = zxy=z рационально, то x=zy{x = \frac{z}{y}}x=yz рационально, что противоречит предположению, что xxx иррационально. Следовательно, произведение xyxyxy должно быть иррациональным. - Наименьшее общее кратное (НОК) двух иррациональных чисел может существовать, а может и не существовать.
- Сумма или произведение двух иррациональных чисел может быть рациональным; например,
2⋅2=2. \sqrt{2} \cdot \sqrt{2} = 2,2⋅2=2.
Следовательно, в отличие от множества рациональных чисел, множество иррациональных чисел не замкнуто относительно умножения.
Вот несколько примеров, основанных на вышеуказанных свойствах:
Является ли 36 \sqrt{36} 36 рациональным или иррациональным?
Поскольку 36=6, \sqrt{36} =6, 36=6, это рациональное число. □_\квадрат□
Покажите, что 2+3 \sqrt{2} + \sqrt{3}2+3 нерационально.
Докажем от противного.
Если 2+3 \sqrt{2}+\sqrt{3}2+3 рационально, то (3−2)×13+2=3−2 (3-2) \times \frac {1}{ \sqrt{3} + \sqrt{2}} = \sqrt{3}-\sqrt{2}(3−2)×3+21=3−2, что означает 3−2 \sqrt {3} — \sqrt{2}3−2 также рационально. Поскольку (3+2)−(3−2)=22 \big(\sqrt{3} + \sqrt{2}\big) — \big(\sqrt{3}-\sqrt{2}\big) = 2 \sqrt{2}(3+2)−(3−2)=22, получаем 22 2 \sqrt{2}22 рационально. Таким образом, 22×12=2 2 \sqrt{2} \times \frac {1}{2} = \sqrt{2}22×21=2 также рационально, что является противоречием. □_\квадрат□ 9{\frac {1}{m}} = anm1=a — целое число. □ _\квадрат□
Вот несколько задач, которые стоит попробовать:
Верно Ложь
Верно или неверно?
Сумма двух иррациональных чисел всегда является иррациональным числом.
1
1,5
2
2,5
3
Человек пока не может ответить. Ни один из них не соответствует действительности.
Ни один из них не соответствует действительности.
Прочтите следующие утверждения:
1) eπ\frac { e }{ \pi } πe — рациональное число.
2) πe\frac { \pi }{ e } eπ — иррациональное число.
3) π+ee\frac { \pi+e }{ e } eπ+e — рациональное число.
Дайте ответ как среднее значение порядковых номеров утверждений, которые верны.
(\big((Например, если все утверждения верны, то ответ будет 1+2+33=2.)\frac { 1+2+3 }{ 3 } =2.\big)31+2+3 =2.)
Детали и предположения:
- eee не обязательно может быть экспоненциальной константой, а π\pi π не обязательно может быть равно 3,14159…
0
1
е+πе+\пирог+π
eπe\pieπ
22e7\frac { 22e }{ 7 } 722e
Трансцендентное число, которое нельзя показать с помощью стандартных математических констант и функций. Не существует.
Не существует.
e, π\Large \color{#3D99F6}{e},~~ \color{#20A900}{\pi}e, π
Найдите наименьшее общее кратное (НОК) двух приведенных выше чисел.
Детали и предположения :
- Если вы считаете, что существование этого LCM неизвестно людям, укажите «Не существует» в качестве ответа.
- Если вы считаете, что он очень близок к нулю, но не равен нулю, то вы можете нажать «0».
- Если вы считаете, что это очень близко к единице, но не к единице, то можете нажать «1».
−6π-6\pi−6π −π-\pi−π π\piπ 6π6\pi6π Не существует. Ничего из вышеперечисленного
−6π, π\large \color{#EC7300}{-6\pi} \color{#333333},~~ \color{#20A900}{\pi}−6π, π
Найти наименьшее общее кратное (НОК) двух указанных выше чисел.
Для пояснения: НОК двух иррациональных чисел существует тогда и только тогда, когда их отношение рационально.
Вдохновение
Ниже вы можете увидеть доказательство иррациональности 2.\sqrt{2}.2.
Воспользуемся методом, известным как доказательство от противного.
Допустим, 2\sqrt{2}2 — рациональное число:
2=ab,\sqrt { 2 } =\frac { a }{ b},2=ba,
, где aaa и bbb — взаимно простые целые числа, т. е. aaa и bbb не имеют общих простых делителей и gcd(a,b)=1\gcd\left( a,b \right) =1gcd(a,b)=1 . Другими словами, ab\frac { a }{ b }ba — несократимая дробь. 9{ 2 }. \end{выровнено}2b2⇒b2=a2=(2c)2=4c2=2c2.
Как видите, bbb также является четным по той же причине, что и aaa. Ждать! У нас тут противоречие. Мы говорим, что aaa и bbb — взаимно простые целые числа, т. е. ab\frac{a}{b}ba неприводимо, но aaa и bbb — оба четные числа, которые не могут образовывать неприводимую дробь. Таким образом, это невозможная дробь, поэтому 2\sqrt{2}2 нельзя записать как отношение двух целых чисел.
□_\квадрат□
Трансцендентные Числа
Реальные числа
Цитировать как: Иррациональные числа. Brilliant.org . Извлекаются из https://brilliant.org/wiki/irrational-numbers/
1.2: Рациональные и иррациональные числа
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 60295
- JJP Veerman
- Портлендский государственный университет через PDXOpen: Open Educational Resources
Мы начнем с нескольких результатов, которые нам понадобятся в оставшейся части этого подраздела.
Теорема 1.7: принцип правильного порядка
Любое непустое множество \(S\) в \(\mathbb{N} \cup \{0\}\) имеет наименьший элемент.
- Доказательство
Предположим, что это неверно. Выберите \(s_{1} \in S\). Тогда существует другое натуральное число \(s_{2}\) в \(S\) такое, что \(s_{2} \le s_{1}-1\). После конечного числа шагов мы переходим к нулю, что означает, что в \(S\) меньше 0 элементов. Это противоречие.
Обратите внимание, что любое непустое множество \(S\) целых чисел с нижней границей может быть преобразовано добавлением целого числа \(b \in N_{0}\) в непустое \(S+b\) в \(N_{0}\). Тогда \(S + b\) имеет нижнюю границу, а значит, и \(S\). Кроме того, непустое множество \(S\) целых чисел с верхней гранью также может быть преобразовано в непустое \(-S+b\) в N0. Здесь \(-S\) обозначает набор элементов S, умноженный на \(-1\). Таким образом, мы имеем следующее следствие принципа упорядоченности.
Следствие 1.8
Пусть есть непустое множество \(S\) в \(\mathbb{Z}\) с нижней (верхней) границей. Тогда \(S\) имеет наименьший (самый большой) элемент.
Определение 1.9
Элемент \(x \in \mathbb{R}\) называется рациональным, если он удовлетворяет условию \(qx-p = 0\), где \(p\) и \(q \ne 0\) равны целые числа. В противном случае оно называется иррациональным числом. Множество рациональных чисел обозначается \(\mathbb{Q}\).
Обычный способ выразить это состоит в том, что рациональное число может быть записано как \(\frac{p}{q}\). Однако преимущество выражения рационального числа в виде решения многочлена степени 1 состоит в том, что это естественным образом приводит к определению 1.12.
Теорема 1.10
Любой интервал в \(\mathbb{R}\) содержит элемент \(\mathbb{Q}\). Мы говорим, что \(\mathbb{Q}\) плотно в \(\mathbb{R}\).
- Доказательство
Пусть \(I = (a, b)\) с \(b > a\) любым интервалом в \(\mathbb{R}\).
 Из следствия 1.8 мы видим, что существует n такое, что \(n > \frac{1}{b-a}\). В самом деле, если бы это было не так, то \(\mathbb{N}\) было бы ограничено сверху и, следовательно, имело бы наибольший элемент \(n_{0}\). Но если \(n_{0} \in \mathbb{N}\), то и \(n_{0}+1\). Это приводит к противоречию, поэтому указанное выше неравенство должно выполняться.
Из следствия 1.8 мы видим, что существует n такое, что \(n > \frac{1}{b-a}\). В самом деле, если бы это было не так, то \(\mathbb{N}\) было бы ограничено сверху и, следовательно, имело бы наибольший элемент \(n_{0}\). Но если \(n_{0} \in \mathbb{N}\), то и \(n_{0}+1\). Это приводит к противоречию, поэтому указанное выше неравенство должно выполняться.Отсюда следует, что \(nb-na > 1\). Таким образом, интервал \((na, nb)\) содержит целое число, скажем, \(p\). Итак, мы имеем это \(na
Суть следующего доказательства заключается в том, что мы берем интервал и увеличиваем его до тех пор, пока не узнаем, что в нем есть целое число, а затем снова уменьшаем его.
Теорема 1.11
\(\sqrt{2}\) иррационально.
- Доказательство
- 92\) кратно 4. Таким образом, \(s\) должно быть четным. Это противоречит предположению, что \(\gcd (r, s) = 1\).
Совершенно ясно, кто такие рациональные числа. Но кто или где остальные? Мы только что видели, что \(\sqrt{2}\) иррационально. Нетрудно заметить, что сумма любого рационального числа плюс \(\sqrt{2}\) также иррациональна. Или что любое рациональное ненулевое кратное \(\sqrt{2}\) иррационально. То же самое верно для \(\sqrt{2}, \sqrt{3}, \sqrt{5}\) и так далее. Мы рассмотрим это в упражнении 1.7. Отсюда нетрудно увидеть, что иррациональные числа тоже плотны (упражнение 1.8). В упражнении 1.15 мы докажем, что число \(e\) иррационально. Доказательство того, что \(\pi\) иррационально, немного сложнее, и его можно найти в [9].0227 1 ][раздел 11.17]. В главе 2 мы будем использовать основную теорему арифметики, теорему 2.14, для построения других иррациональных чисел. В заключение, в то время как рациональность рассматривается за чистую монету, для доказательства иррациональности числа могут потребоваться некоторые усилия, даже если их гораздо больше, как мы увидим в разделе 1.4.
Но кто или где остальные? Мы только что видели, что \(\sqrt{2}\) иррационально. Нетрудно заметить, что сумма любого рационального числа плюс \(\sqrt{2}\) также иррациональна. Или что любое рациональное ненулевое кратное \(\sqrt{2}\) иррационально. То же самое верно для \(\sqrt{2}, \sqrt{3}, \sqrt{5}\) и так далее. Мы рассмотрим это в упражнении 1.7. Отсюда нетрудно увидеть, что иррациональные числа тоже плотны (упражнение 1.8). В упражнении 1.15 мы докажем, что число \(e\) иррационально. Доказательство того, что \(\pi\) иррационально, немного сложнее, и его можно найти в [9].0227 1 ][раздел 11.17]. В главе 2 мы будем использовать основную теорему арифметики, теорему 2.14, для построения других иррациональных чисел. В заключение, в то время как рациональность рассматривается за чистую монету, для доказательства иррациональности числа могут потребоваться некоторые усилия, даже если их гораздо больше, как мы увидим в разделе 1.4.
Эта страница под названием 1. 2: Рациональные и иррациональные числа распространяется в соответствии с лицензией CC BY-NC, автором, ремиком и/или куратором которой является Дж. Дж. П. Вирман (PDXOpen: Открытые образовательные ресурсы).
2: Рациональные и иррациональные числа распространяется в соответствии с лицензией CC BY-NC, автором, ремиком и/или куратором которой является Дж. Дж. П. Вирман (PDXOpen: Открытые образовательные ресурсы).
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Дж. Дж. П. Вирман
- Лицензия
- СС BY-NC
- Программа ООР или издатель
- PDXOpen
- Показать страницу TOC
- нет
- Метки
- иррациональные числа
- рациональные числа
- Принцип упорядочения
Иррациональные числа « Блог на дне моря
Иррациональное число — это число, которое нельзя представить в виде дроби, используя целые числа в качестве числителя и знаменателя.
Я большой поклонник иррациональных чисел, и одна из главных причин этого заключается в том, что они отлично подходят для создания последовательностей с низким расхождением, которые дают потрясающие результаты при использовании в стохастических (рандомизированных) алгоритмах по сравнению с обычными случайными числами. Последовательности с низким расхождением являются двоюродными братьями синего шума, потому что обе они нацелены на то, чтобы сэмплы были хорошо распределены, но случай использования отличается, поэтому использование синего шума или LDS зависит от ситуации. Это означает, что, к счастью, в мире достаточно места как для LDS, так и для синего шума.
Этот пост представляет собой случайный набор вещей, связанных с иррациональными числами.
Пифагорейские культисты предположительно убили кого-то, чтобы сохранить иррациональные числа в секрете, так что, я думаю, это технически запрещенное знание.
Непрерывные дроби — это способ записи чисел, который может быть полезен при анализе иррациональных чисел и рациональных приближений к конкретным числам — независимо от того, рациональны они или иррациональны.
Если непрерывная дробь бесконечно длинная, это означает, что она представляет собой иррациональное число, а все иррациональные числа имеют непрерывные дроби бесконечной длины. Если непрерывная дробь не бесконечно длинна, значит, это рациональное число.
Вот начало непрерывной дроби для числа пи.
Другой способ записи непрерывных дробей состоит в том, чтобы избавиться от всех лишних «1 разделить на…» и просто написать целые числа, которые вы видите слева. Непрерывная дробь для пи выше будет выглядеть так, что намного компактнее:
[3;7,15,1,292,1,1,1,2,1,3,1]
Давайте поговорим о том, как вы составьте непрерывную дробь, пройдясь по тому, как сделать ее для пи, или, по крайней мере, 3,14159265359 в любом случае, так как пи идет вечно.
Сначала вы берете целую часть и используете ее как первую цифру. Вычитание этой целой части дает остаток:
[3]
остаток: 0,14159265359
Берем 1/остаток, чтобы получить 7,06251330592. Целая часть этого числа будет нашим следующим числом. Вычитание целой части дает нам следующий остаток:
Целая часть этого числа будет нашим следующим числом. Вычитание целой части дает нам следующий остаток:
[3;7]
остаток: 0,06251330592
1/остаток равен 15,9965944095, что превращает наше следующее целое число и остаток в:
[3; 7,15]
Остаток: 0,9965944095
1/Остальная часть 1,00341722818, так что теперь мы находимся в…
[3; 7,15,1]
Остальная теперь мы находимся в:
[3;7,15,1,292]
остаток: 0.63483365
1/остаток 1.57521580653 и мы остановимся на следующем шаге:
[3;7,15,1,292, 1]
остаток: 0,57521580653
Везде, где у вас есть большое число в непрерывной дроби, это потому, что вы только что разделили единицу на небольшое число. Чем больше целое число, тем меньше остаток, необходимый для получения этого целого числа.
Чем меньше остаток, тем лучше аппроксимируется число на этом шаге цепной дроби.
Это означает, что если вы видите большое число в непрерывной дроби, то если вы урежете непрерывную дробь прямо перед этим большим числом, вы получите довольно хорошее приближение к фактическому числу, которое представляет непрерывная дробь.
Чем больше число, тем точнее приближение.
Из-за этого, глядя на непрерывную дробь числа пи ниже, вы можете увидеть, что она имеет довольно большое число (292) довольно рано в последовательности.
[3;7,15,1,292,1,1,1,2,1,3,1]
Это означает, что следующая непрерывная дробь «довольно хорошо» аппроксимирует число пи.
[3;7,15,1]
Мы расскажем, как вычислить это далее в посте, но на самом деле эта дробь равна 355/113 и имеет специальное имя «Милю», найденное китайским математиком и астроном Цзо Чунчжи, родился в 429 году нашей эры. Он находится в пределах 0,000009% от значения числа пи.
Дополнительная информация из Википедии: https://en.wikipedia.org/wiki/Mil%C3%BC
Итак, хотя число пи, вероятно, самое известное иррациональное число, оно точно не самое иррациональное число из всех существующих, так как оно легко аппроксимируется небольшими целыми числами при делении.
Небольшое примечание, если вы пишете программу для преобразования числа с плавающей запятой в непрерывную дробь: если вы попытаетесь составить непрерывную дробь для числа, которое не может быть точно представлено с плавающей запятой, например, 4. 1, вы получите очень крошечный остаток, который затем дает очень большое целое число, когда вы его переворачиваете. В моем случае при использовании двойных чисел получилось такое большое число, что преобразование его в целое число привело к переполнению целого числа. Один из способов решить эту проблему — просто рассматривать любой остаток, меньший некоторого порога, как ноль. Например, любой остаток меньше 0,00001 можно считать нулем.
1, вы получите очень крошечный остаток, который затем дает очень большое целое число, когда вы его переворачиваете. В моем случае при использовании двойных чисел получилось такое большое число, что преобразование его в целое число привело к переполнению целого числа. Один из способов решить эту проблему — просто рассматривать любой остаток, меньший некоторого порога, как ноль. Например, любой остаток меньше 0,00001 можно считать нулем.
Таким образом, несмотря на то, что число пи не самое иррациональное, число фи есть (произносится как «плата», также известное как золотое сечение). Да, это самое иррациональное число!
Мы будем использовать значение 1,61803398875 и составим непрерывную дробь.
[1]
Остаток: 0,61803398875
1/Остаток: 1,61803398875
[1; 1]
Остаток: 0,61803398875
1/Остальная 1.61803398875
Подожди секунду… ты видишь закономерность? остаток всегда является одним и тем же значением, а затем, когда мы делаем 1/остаток, мы всегда снова получаем золотое сечение. Это означает, что эта непрерывная дробь равна 1 вплоть до бесконечности.
Это означает, что эта непрерывная дробь равна 1 вплоть до бесконечности.
В предыдущем разделе мы видели, как наличие большого числа в непрерывной дроби означает, что число в этой точке хорошо приближено в непрерывной дроби.
Золотое сечение имеет 1 для каждого числа в непрерывной дроби, что является наименьшим значением, которое вы можете иметь. Это означает, что на каждом этапе непрерывной дроби оно является наименее приближенным, насколько это возможно.
Вот что подразумевается под золотым сечением как самым иррациональным числом. Это наименее хорошо аппроксимируется рациональными числами (делением одного целого числа на другое).
Когда я сказал, что мне нравятся иррациональные числа, я в основном имел в виду золотое сечение, но и другие весьма иррациональные числа, такие как квадратный корень из 2, тоже хороши. Сильно иррациональные числа обладают свойствами, которые мне нравятся — свойствами, которые делают их полезными для использования в качестве последовательностей с низким расхождением.
Интересная вещь, которую вы могли заметить выше, это то, что когда вы делите 1 на золотое сечение, вы получаете золотое сечение минус 1. То есть:
1 / 1,61803398875 = 0,61803398875
Если вы замените золотое сечение на «x», вы получите следующее уравнение:
1/x = x-1
Если вы решите это уравнение, вы получите золотое сечение. Это единственное число, обладающее этим свойством! На самом деле, -0,61803398875 тоже имеет значение и относится к тому факту, что у этого квадратного уравнения есть решение с корнями + и -, но, возможно, это не так уж удивительно. 1/-0,61803398875 равно -1,61803398875. Поведение такое же, просто это происходит по другую сторону нуля.
Еще одна интересная вещь о золотом сечении заключается в том, что если вы возведете его в квадрат, это будет то же самое, что добавить 1. вы решаете это, вы снова получаете золотое сечение как единственное решение (ну и отрицательное золотое сечение минус 1, как и раньше). Вероятно, это не слишком удивительно, если вы посмотрите на формулы, поскольку вы можете использовать простую алгебру, чтобы изменить одну формулу на другую.
Если у вас есть непрерывная дробь и вы хотите превратить ее в правильную дробь (или действительное число), вы можете запустить процесс в обратном порядке.
Однако это означает, что вы начинаете с самой правой цифры непрерывной дроби и работаете влево, пока не дойдете до начала. Как это сделать с бесконечно длинной непрерывной дробью, как это было бы с иррациональным числом?
К счастью, есть способ начать слева и работать справа, так что вы можете получить приближения к бесконечно длинным непрерывным дробям (иррациональным числам).
Давайте сделаем это с числом пи, со следующей частью цепной дроби:
[3;7,15,1,292,1,1]
Что вы делаете, так это составляете таблицу, в которой есть строка для числителя и знаменателя. Первый числитель равен 1, а первый знаменатель равен 0. Второй числитель — это первое число в последовательности непрерывных дробей, а второй знаменатель — это 1.
Формула для остальных числителей и знаменателей:…
- числитель[индекс] = CF[индекс] * числитель[индекс-1] + числитель[индекс-2]
- знаменатель[индекс] = CF[индекс] * знаменатель[индекс-1] + знаменатель[индекс-2]
Делая это слева направо, вы получаете это:
Ниже мы делаем это с пи, золотым сечением, sqrt (2) и иррациональным числом, которое я придумал, которое не очень иррационально, и хорошо аппроксимируется 1. 01.
01.
Забавный тангенс заключается в том, что вы можете заметить, что для золотого сечения и числители, и знаменатели являются числами Фибоначчи. Это связь между золотым сечением и числами Фибоначчи.
Ниже показана процентная ошибка каждого числа по мере добавления новых членов непрерывной дроби.
Ошибка золотого сечения уменьшается медленнее всего, что показывает, что золотое сечение наименее хорошо аппроксимируется дробями. У выдуманного иррационального числа, равного примерно 1,01, ошибка уменьшается быстрее всего, потому что оно является наименее иррациональным из этих чисел. Пи показывает, что имеет довольно низкую иррациональность, а квадратный корень из 2 довольно иррационален.
Вот ошибка на логарифмической оси Y, чтобы лучше показать разницу в ошибках.
Стоит отметить, что соотношение 1/goldenRatio, также известное как 0,61803398875, столь же иррационально, как и само золотое сечение. Причина этого в том, что мы переворачиваем числитель и знаменатель этой несуществующей дроби. Переворачивание не делает его более представимым в виде дроби.
Переворачивание не делает его более представимым в виде дроби.
Когда я использую золотое сечение для последовательностей с низким расхождением, я обычно использую это значение 1/goldenRatio, также известное как «сопряженное золотое сечение», потому что меньшее значение означает, что у него будет меньше числовых проблем и больше точности, когда работа с небольшими значениями (например, между 0 и 1).
Кроме того, существует бесконечное количество чисел, столь же иррациональных, как и золотое сечение. Вы можете вычислить их, вычислив:
где p,q,r,s — целые числа, а абсолютное значение p*s-q*r равно 1.
Это преобразование Мёбиуса.
Если вам интересно, каково наименьшее иррациональное число, похоже, что их несколько (бесконечно), и это просто числа, которые очень, очень, очень хорошо аппроксимируются рациональными числами. Они называются числами Лиувилля и являются трансцендентными, то есть их нельзя вычислить с помощью полиномов. Доказательство существования этих чисел также исследовало существование самих трансцендентных чисел. (https://en.wikipedia.org/wiki/Liouville_number)
(https://en.wikipedia.org/wiki/Liouville_number)
Существует также нечто, называемое измерением иррациональности, но я не нашел его полезным. Не похоже, что это можно рассчитать с помощью программы и сравнить два числа, чтобы увидеть, какое из них более иррационально. https://mathworld.wolfram.com/IrrationalityMeasure.html
Если все 1 в непрерывной дроби составляют золотое сечение, то что дадут все 2 или все 3? Это составляет соотношение серебра и бронзы соответственно, и все три из них являются первыми тремя «металлическими средствами». Вы можете увидеть подробности о них ниже, вместе с pi. Википедия также говорит о них больше на https://en.wikipedia.org/wiki/Metallic_mean 9.3 = х+1.
Взаимопростые числа — это 2 или более целых чисел, делитель которых равен только 1.
Например, 7 и 11 — взаимно простые числа. Они также бывают простыми числами, но взаимно простые числа не обязательно должны быть простыми. 8 и 15 также взаимно простые числа, хотя ни одно из них не является простым. Можно даже свалить все четыре вместе и сказать, что 7, 8, 11, 15 — взаимно простые числа. Объединение списков взаимно простых чисел обычно не приводит к списку чисел, которые по-прежнему взаимно просты. Это просто сработало, потому что мы добавили только простые числа в другой список взаимно простых чисел, а добавление простых чисел всегда будет поддерживать список взаимно простых чисел.
Можно даже свалить все четыре вместе и сказать, что 7, 8, 11, 15 — взаимно простые числа. Объединение списков взаимно простых чисел обычно не приводит к списку чисел, которые по-прежнему взаимно просты. Это просто сработало, потому что мы добавили только простые числа в другой список взаимно простых чисел, а добавление простых чисел всегда будет поддерживать список взаимно простых чисел.
Вы можете задаться вопросом, почему вас должны волновать взаимно простые числа.
Я больше всего люблю использовать взаимно простые числа, когда мне нужно дешево перетасовать числа.
Например, предположим, что у вас есть 8 чисел, и вы хотите, чтобы они были перетасованы в случайном порядке, но это не должно быть очень качественное перемешивание.
Сначала вы выбираете любое число, взаимно простое с 8… скажем, 5. Затем вы считаете индекс от 1 до 8 и делаете это…
Out = (index * 5) % 8
Взяв индекс от 1 до 8, вы получите следующий результат:
5, 2, 7, 4, 1, 6, 3, 0
числа есть, и они довольно перепутаны, не так ли? Случайный наблюдатель, вероятно, не заметит никаких закономерностей, если вы использовали это в настройках игры для сброса сокровищ или чего-то еще.
Однако не все варианты coprime дают одинаковые качественные результаты. Вот что произойдет, если мы используем 7 как взаимно простое число вместо 5:
Out = (index * 7) % 8
7, 6, 5, 4, 3, 2, 1, 0
Просто перевернул список! Это не очень запутано.
Также давайте посмотрим, что произойдет, если вы не используете взаимно простые числа. Мы будем использовать 2 вместо 7.
Out = (index * 2) % 8
2, 4, 6, 0, 2, 4, 6, 0
Если числа не взаимно просты, t генерировать все числа в списке. Другой способ взглянуть на это состоит в том, что длина цикла числовой последовательности максимально длинна, когда числа взаимно просты, но не будет такой длинной (и будет повторяться), если числа не взаимно просты.
Обратите внимание, что вам не обязательно использовать значения индекса от 1 до 8. Вместо этого вы можете использовать от 0 до 7 или любые другие последовательные 8 значений, например от 127 до 134. В этом случае все числа относятся к модулю 8, поэтому от 127 до 134 эквивалентен числам от 7 до 14.
Аддитивная рекуррентная последовательность — это в основном та же концепция, что и в предыдущем разделе, но она перенесена в непрерывный мир, а не привязана к дискретным целым числам. Вы используете приведенную ниже формулу, где A — любое действительное число:
Out = (index * A) % 1
Как и раньше с взаимно простыми числами, значение, на которое умножается индекс, может улучшить или ухудшить результаты.
Если вы выберете 1/2 (0,5) для A, последовательность, которую вы получите, будет следующей:
0,5, 0,0, 0,5, 0,0, 0,5, …
Если вы выберете 1/4 (0,25) для A, вы получите это:
0.25, 0.5, 0.75, 0.0, 0.25, 0.5, 0.75, 0.0, …
1/3 получите это:
0.333, 0.666, 0.0, 0.333, 0.666, 0.04, … 9000 2/3 даст вам это:
0,666, 0,333, 0,0, 0,666, 0,333, 0,0, …
Вы также можете сделать что-то более сложное, например 5/8:
0,625, 0,25, 0,875, 0,5, 0,125, 0,75, 0,375, 0,0, …
(затем оно повторяется)
Если мы выбрали 2/4, мы d заканчивается 0,5, как мы делали, когда использовали 1/2. Думая о дробях, которые можно использовать в этой настройке, вы должны уменьшить дробь, потому что нередуцированные дроби дают то же значение, что и сокращенные дроби. Готовы к кикеру? Числитель и знаменатель сокращенной дроби всегда будут взаимно простыми целыми числами — по определению, это сокращенная дробь! Кроме того, знаменатель сокращенной дроби сообщит вам длину последовательности, которую он генерирует.
Думая о дробях, которые можно использовать в этой настройке, вы должны уменьшить дробь, потому что нередуцированные дроби дают то же значение, что и сокращенные дроби. Готовы к кикеру? Числитель и знаменатель сокращенной дроби всегда будут взаимно простыми целыми числами — по определению, это сокращенная дробь! Кроме того, знаменатель сокращенной дроби сообщит вам длину последовательности, которую он генерирует.
В примерах я уловил небольшой трюк, вы его уловили?
Давайте снова посмотрим на эту последовательность, используя 5/8, но давайте запишем результаты в виде дробей.
5/8, 2/8, 7/8, 4/8, 1/8, 6/8, 3/8, 0/8, …
Теперь давайте вернемся к последовательности, которую мы сделали в последнем разделе, где мы did (index*5)%8
5, 2, 7, 4, 1, 6, 3, 0
Числитель в дробях тот же, что и в целочисленных с использованием взаимно простых чисел. Вы можете умножить дробные результаты на 8 и получить точно такие же числа. На самом деле возьмите формулу, которую мы используем в этом разделе:
Out = (index * 5/8) % 1
И умножьте это на 8, чтобы получить формулу, использованную в последнем разделе!
Out = (index * 5) % 8
Итак, хотя мы, казалось, ушли от целых чисел к непрерывной области, на самом деле мы не… мы все еще находимся в стране последовательностей взаимно простых чисел. Мы всегда будем в стране последовательностей взаимно простых чисел, пока мы используем рациональные числа, потому что всегда будет пара взаимно простых числителя и знаменателя в упрощенной дроби, которая определяет длину последовательности, которая получается, когда мы подаем индексные числа. в.
Мы всегда будем в стране последовательностей взаимно простых чисел, пока мы используем рациональные числа, потому что всегда будет пара взаимно простых числителя и знаменателя в упрощенной дроби, которая определяет длину последовательности, которая получается, когда мы подаем индексные числа. в.
А что, если отказаться от рациональных чисел и перейти к иррациональным числам? Что ж, использование иррационального числа означает, что последовательность никогда не повторится. Хотя это само по себе звучит потрясающе, давайте представим, что мы используем иррациональное число, которое хорошо приближается к 1/4. Это означает, что последовательность никогда не будет повторяться, но будет ПОЧТИ повторяться каждые 4 значения.
Покажем последовательность, используя золотое сечение, где индекс идет от 1 до 8.
0,618034, 0,236068, 0,854102, 0,472136, 0,0
, 0,708204, 0,326238, 0,944272
Вот то же самое для не очень иррационального числа, которое мы собираемся аппроксимировать 0,24.
0,249000, 0,498000, 0,747000, 0,996000, 0,245000, 0,494001, 0,743001, 0,992001
Вы можете видеть, что последовательность с иррациональным ~0,25 не ТОЧНО повторяется, но она точно повторяется. Золотое сечение дает очень уникальные числа по сравнению с
. Так что, по сути, если вы используете иррациональное число, которое может быть близко аппроксимировано рациональным числом, оно будет вести себя очень похоже на это рациональное число и не будет действительно хорошим.
Вот чем хороша золотая пропорция и другие весьма иррациональные числа. Не существует рационального числа, которое бы их хорошо аппроксимировало, поэтому они не только не имеют фактических повторов, но и не имеют БЛИЖАЙШИХ повторений.
Используя в высшей степени иррациональные числа в этой аддитивной рекуррентной формуле, вы получите последовательность с низким расхождением.
Каждый раз, когда вы используете иррациональную LDS, вы будете получать одну и ту же последовательность, что иногда может быть проблемой.
Это можно обойти, каждый раз начиная с другого индекса или добавляя в последовательность другое начальное значение.
Вариант № 1: рандомизированный начальный индекс:
Исход = ((индекс + начальный индекс) * иррациональный) % 1 Как вы получите этот начальный индекс или начальное значение, зависит от вас. Честно говоря, я использую случайные числа белого шума, и это работает нормально, поэтому я буду продолжать делать это, пока не проанализирую это и не узнаю, насколько лучше использование LDS.
В любом случае, если вы помните из предыдущего поста, этот LDS не будет повторяться, пока вы используете иррациональное число. Это означает, что бесконечное количество поступающих целочисленных значений индекса означает, что вы получаете бесконечное количество уникальных действительных чисел. Это означает, что LDS может вывести любое возможное число, просто изменив индекс, в котором вы находитесь. Таким образом, смещение по индексу эквивалентно смещению по начальному значению, поскольку существует некоторый индекс, который должен давать тот же результат, что и любое конкретное начальное значение.
Я думал, что это правда, но оказалось, что это не так, потому что целые числа счетно бесконечны, а иррациональные числа представляют собой большую бесконечность.
Оказывается, это почти правда, и что всегда существует индекс, который даст вам значение, сколь угодно близкое к любому конкретному начальному значению.
Хотя это верно только математически. Компьютеры имеют конечное хранилище для целых чисел и чисел с плавающей запятой.
В любом случае, это сложно, но либо индекс смещения, либо начальное значение должны отлично работать для получения другой последовательности. Я сам иду по пути начального значения.
Подробнее об этой математической теме здесь: https://twitter.com/Atrix256/status/1285646721561899010?s=20
Кстати, хотя я показываю формулу для иррационального LDS как индекс, умноженный на иррациональное число, это будет иметь проблемы с числовой точностью по мере увеличения индекса. Вам лучше просто добавить иррациональное и выполнить модуль, когда вам нужно значение для следующего индекса. Разница огромна, как ни странно!
Разница огромна, как ни странно!
Существует концепция прогрессивной последовательности с низким расхождением, которая означает, что любое подмножество последовательности, начиная с индекса 0, будет иметь те же свойства, что и вся последовательность.
Например, если у вас есть прогрессивная последовательность синего шума со 100 семплами, использование только первых 10 сэмплов будет синим шумом, или использование первых 47 семплов, или первых 73, или всех 100.
Если вы имеет непрогрессивную последовательность синего шума, последовательность семплов не будет синим шумом, пока не будут использованы все 100 сэмплов (или когда вы приблизитесь к этому числу).
Иррациональные последовательности с низким расхождением имеют хорошее свойство: они прогрессивны, и они прогрессивны, начиная с ЛЮБОГО индекса, а не только с индекса 0. Это связано с тем, что смещения в индексе примерно эквивалентны смещениям в начальном значении, поэтому начиная с середины последовательности так же, как если бы вы только начали со значения этого образца в качестве начального значения.
Для этого идеально подходит золотое сечение. Каждый новый образец из LDS золотого сечения попадает в самую большую дыру, оставленную образцами до сих пор, поэтому он так хорош для численного интегрирования (и тому подобного). Он имеет большой охват в области выборки. Сумасшедшая вещь, однако, заключается в том, что вы можете начать с любого индекса в LDS, и это по-прежнему верно для этого начального индекса, хотя это также верно, если начинать с индекса 0.
Посмотрите на гифку ниже, чтобы увидеть, что я говоря о. Всего 16 образцов. Все 16 показаны слева, но только последние 8 показаны справа. Я показываю выборки на числовой прямой, поскольку они являются скалярными значениями от 0 до 1, но я также показываю их на круге, чтобы убедиться, что то, что я сказал о попадании в самый большой разрыв, верно даже с закруглением.
Вот та же установка для анимации с использованием вместо этого квадратного корня из 2.
Наконец, то же самое с числом пи. Пи хорошо аппроксимируется 22/7, и поскольку мы ходим по кругу, целые части не имеют значения. Поскольку 22/7 равно 3 1/7, это заставляет число пи вести себя почти как 1/7, и вы можете убедиться, что оно действительно почти повторяется каждые 7 отсчетов и действует очень похоже на 1/7. Вы можете видеть, как у pi есть сэмплы, которые слипаются, и он не дает очень хорошего покрытия по выборочной области для количества используемых сэмплов (сравните покрытие с золотым сечением!). Это показывает, как менее иррациональное число не так хорошо, как последовательность с низким расхождением.
Пи хорошо аппроксимируется 22/7, и поскольку мы ходим по кругу, целые части не имеют значения. Поскольку 22/7 равно 3 1/7, это заставляет число пи вести себя почти как 1/7, и вы можете убедиться, что оно действительно почти повторяется каждые 7 отсчетов и действует очень похоже на 1/7. Вы можете видеть, как у pi есть сэмплы, которые слипаются, и он не дает очень хорошего покрытия по выборочной области для количества используемых сэмплов (сравните покрытие с золотым сечением!). Это показывает, как менее иррациональное число не так хорошо, как последовательность с низким расхождением.
Если вы слышали, что у растений листья растут по схеме золотого сечения, сейчас самое время объяснить, почему. Вот последний кадр gif с золотым сечением, когда есть 16 сэмплов.
Одной из целей жизни растения является получение как можно большего количества солнца. Представьте, что солнце находится прямо над головой, и вы смотрите на растение сверху. На пути к этой цели максимизации солнечного света всякий раз, когда свету позволено падать на землю в радиусе круга тени растения, это упущенная возможность. Солнечный свет тратится впустую, попадая в грязь.
Солнечный свет тратится впустую, попадая в грязь.
Также могут быть временные или полупостоянные тени, которые существуют или возникают в любой момент жизни растения, и если оно поместит все свои листья так, что они слипнутся в одном направлении, все эти листья могут оказаться в тени и растение может голодать.
Решением этих проблем является выращивание листьев, равномерно распределенных по всему растению. Таким образом, при просмотре сверху нет перекрытий, а риск затенения сводится к минимуму благодаря хорошему распределению во всех направлениях.
На этом все и закончилось бы, если бы растение родилось со всеми своими листьями и знало бы, сколько листьев ему понадобится для роста, и что ни один лист не будет съеден.
Однако растения являются динамичными формами жизни в динамичной среде, поэтому листья должны быть расположены как можно более равномерно в радиальном направлении, когда это сеянец всего с парой листьев, а также когда он намного старше с большим количеством листьев, возможно, с некоторыми из них съедены животными, и все такое прочее.
Хороший способ сделать это — использовать золотое сечение, чтобы выяснить, где растет следующий лист.
При этом он будет иметь хороший охват по всему кругу возможного роста, это нормально, если старые листья отмирают и уходят, так как он все еще будет хорошо распределен, листья могут расти больше, потому что перекрытие будет сведено к минимуму.
Посмотрите еще раз на гифку и подумайте о каждой строке, как о листе, растущем вокруг центрального стебля по мере того, как растение становится выше. Круг справа показывает, что происходит, когда первые 8 листьев стареют, отмирают и опадают, заменяясь 8 новыми листьями.
Если этот разговор о растениях был интересен, почитайте здесь о «Phyllotaxis»
https://en.wikipedia.org/wiki/Phyllotaxis
Итак, когда у нас есть эта функция, где Out, A, B и индекс являются целыми числами :
Out = (index * A) % B
Мы получим неповторяющуюся последовательность чисел B длиной от 0 до B-1, если A и B взаимно просты. Поскольку простые числа взаимно просты со всеми другими числами, мы могли бы также сказать, что если A простое число, последовательность будет обладать этими свойствами. Оно не обязательно должно быть простым (просто взаимно простым), но давайте сделаем утверждение для простых чисел прямо сейчас.
Поскольку простые числа взаимно просты со всеми другими числами, мы могли бы также сказать, что если A простое число, последовательность будет обладать этими свойствами. Оно не обязательно должно быть простым (просто взаимно простым), но давайте сделаем утверждение для простых чисел прямо сейчас.
Если мы переместим это в мир действительных чисел, где index — целое число, а A и out — действительные числа:
Out = (index * A) % 1
Если A иррационально, мы получим неповторяющееся бесконечно длинная последовательность чисел. Таким образом, иррациональные числа подобны простым числам в том смысле, что при использовании они образуют неповторяющуюся последовательность максимально возможной длины.
Более того, поскольку A более иррационален, вы также получаете меньше «почти повторов», пока не доберетесь до золотого сечения, где вы получите доказуемо минимальное количество почти повторов.
Итак, простые и иррациональные числа (особенно золотое сечение) связаны тем, что при использовании над полем они образуют неповторяющиеся последовательности максимальной длины.
Мы говорили о взаимно простых числах и о том, как они составляют последовательность, которая «идет на всю длину», то есть они создают последовательность, которая не повторяется во всей последовательности. Если вы умножите индекс на 5 и сделаете модуль на 8, вы получите последовательность из 8 элементов, а затем повторите.
Мы также говорили об иррациональных числах и о том, как они образуют последовательности, которые НИКОГДА не повторяются, и говорили о том, как крайне иррациональные числа могут образовывать последовательности, в которых также почти нет повторов.
Это замечательно, если вам нужны одномерные последовательности, но что, если вам нужны двухмерные последовательности или выше?
Один из способов создания многомерных последовательностей с низким расхождением — просто использовать разные иррациональные числа для каждой оси.
Это здорово, но теперь вам приходится придумывать кучу высококачественных иррациональных чисел, поскольку вам нужно по одному для каждой оси. К сожалению, на самом деле существует только одно «золотое сечение» (преобразование Мёбиуса и сопряжение не дают разного поведения). Если бы вы использовали золотое сечение на каждой оси, у вас была бы корреляция между осями, и это было бы не очень хорошо. По сути, каждая ось будет иметь один и тот же шаблон, даже если вы начнете с другого индекса или начального значения.
К сожалению, на самом деле существует только одно «золотое сечение» (преобразование Мёбиуса и сопряжение не дают разного поведения). Если бы вы использовали золотое сечение на каждой оси, у вас была бы корреляция между осями, и это было бы не очень хорошо. По сути, каждая ось будет иметь один и тот же шаблон, даже если вы начнете с другого индекса или начального значения.
Есть концепция, о которой, я уверен, кто-то уже думал, возможно, под другим названием, которую я называю «коиррациональность».
Взаимно простые числа не имеют общих делителей, отличных от 1, и, следовательно, «нет общей длины цикла», что делает их выходные последовательности максимальной длины.
Точно так же коиррациональные числа должны минимизировать, насколько близко они подходят друг к другу с их рациональными приближениями. Там, где не взаимно простые числа, используемые для создания последовательности, будут повторяться, два числа, которые не очень коиррациональны, образуют последовательность, которая будет почти повторяться, что почти так же плохо.
Точно так же, как взаимно простое число не обязательно должно быть простым, коиррациональное число не обязательно должно быть очень хорошим иррациональным числом само по себе, и фактически, рациональное число и иррациональное число могут вместе быть “ коиррациональны» друг другу (как золотое сечение и 2). Кроме того, в наборе может быть более двух чисел, коиррациональных друг другу.
На вопрос, являются ли два или более числа взаимно простыми, следует однозначный ответ: да или нет.
На вопрос о том, являются ли два или более числа коиррациональными, дается серый ответ. Числа могут варьироваться от некоиррациональных вообще (если одно кратно другому) до коиррациональных разного уровня, вплоть до максимально коиррациональных (опять же, пример золотого сечения и 2).
Так как же определить, коиррациональны ли два числа или, точнее, насколько они коиррациональны?
В общем, разделите одно число на другое (неважно, где числитель, а где знаменатель) и посмотрите на иррациональность получившегося числа. Если результатом является рациональное число, числа не коиррациональны. Если результатом является иррациональное число, которое хорошо аппроксимируется путем деления относительно небольших целых чисел, числа не являются очень иррациональными. Если результатом является золотое сечение, числа максимально иррациональны.
Если результатом является рациональное число, числа не коиррациональны. Если результатом является иррациональное число, которое хорошо аппроксимируется путем деления относительно небольших целых чисел, числа не являются очень иррациональными. Если результатом является золотое сечение, числа максимально иррациональны.
Если вы хотите увидеть, насколько коиррациональны 3 или более чисел, один из способов — посмотреть на них попарно. Вам придется выяснить, как объединить результаты нескольких тестов, поскольку вы проверяете каждую возможную пару, но это должно дать вам представление о том, насколько они были коиррациональны.
Это также может натолкнуть вас на некоторые мысли о том, как вы могли бы получить набор из N коиррациональных чисел. Возможно, можно было бы использовать градиентный спуск, чтобы найти N чисел, которые при попарном рассмотрении давали результаты, наиболее близкие к золотому сечению, и позволяли равномерно разделить ошибку между парами.
В этом разделе мало доказательств/экспериментов/и т. д., но пост уже становится довольно длинным. Было бы интересно более подробно рассмотреть со-иррациональность в отдельном посте.
д., но пост уже становится довольно длинным. Было бы интересно более подробно рассмотреть со-иррациональность в отдельном посте.
Видимо супер золотое сечение. Изображение ниже взято из этого видео: https://www.youtube.com/watch?v=X9DpdomPRvg
Здесь есть короткое видео, рассказывающее о некоторых его свойствах: https://www.youtube.com/watch?v= A4cN_44VOfQ
Анализируя суперзолотое сечение, оно не так иррационально, как золотое сечение, но мне любопытно, для чего оно может быть полезно. Если вы найдете или придумаете что-нибудь, я буду рад услышать об этом!
Вот код C++ для его вычисления, который вы можете скопировать и вставить
static const double c_superGoldenRatio = ( std::pow((29.0 + 3.0 * std::sqrt(93.0)) / 2.0, 1.0 / 3.0) + std::pow((29.0 - 3.0 * std::sqrt(93.0)) / 2.0, 1.0 / 3.0) + 1,0 ) / 3,0;
Вот цепная дробь:
1,465571 = [1, 2, 6, 1, 3, 5, 4, 22, 1, 1, 4, 1, 2, 83, 1, 1, 1, 25, 11 , 1]
Здесь выполняется тот же тест, что и раньше, для окружности и числовой прямой.
Это действительно отличное чтение Мартина Робертса (https://twitter.com/TechSparx), в котором говорится об обобщении золотого сечения и использовании этого обобщения для многомерных последовательностей с низким расхождением, что конкурирует с Соболем.
http://extremelearning.com.au/unreasonable-efficientness-of-quasirandom-sequences/
Это говорит о том, приводит ли сложение иррациональных чисел или их умножение к иррациональному числу:
https://mathbitsnotebook.com/ Алгебра1/RatIrratNumbers/RNRationalSumProduct.html?s=09
Здесь говорится о том, откуда мы знаем, что e+pi иррационально, или e*pi иррационально, или и то, и другое, но это все, что мы можем сказать об этом:
http://mathforum.org/library/drmath/view/51617. html
Здесь показана связь между простыми числами, треугольником Паскаля и конструируемыми многоугольниками:
https://en.wikipedia.org/wiki/Constructible_polygon
Вот альтернативный способ измерения коиррациональности:
https:/ /twitter. com/R4_Unit/status/1284588140473155585?s=20
com/R4_Unit/status/1284588140473155585?s=20
Легенда гласит, что человек по имени Гиппас был убит пифагорейскими культистами за доказательство существования иррациональных чисел, что разрушило их мировоззрение о том, что все числа рациональны.
Вот видео об этом:
https://www.youtube.com/watch?v=sbGjr_awePE
Вот статья:
https://nrich.maths.org/2671
Вот еще статья:
http://kiwihellenist.blogspot.com/2015/11/were-greeks-scared-of-irrational-numbers.html
И еще:
https://io9.gizmodo.com/did-pythagoras-really-murder -a-guy-1460668208
У Numberphile есть хорошее видео об иррациональности фи: https://www.youtube.com/watch?v=sj8Sg8qnjOg
Нравится:
Нравится Загрузка…
Объяснение урока: Рациональные и иррациональные числа
В этом объяснении мы научимся определять и различать рациональные и иррациональные числа.
Напомним, что множество рациональных чисел ℚ — это множество всех чисел, которые можно записать
как частное целых чисел. Более формально имеем
ℚ=𝑎𝑏∶𝑎,𝑏∈ℤ,𝑏≠0.
Более формально имеем
ℚ=𝑎𝑏∶𝑎,𝑏∈ℤ,𝑏≠0.
Также стоит отметить, что мы можем отменить любые общие факторы между 𝑎 и 𝑏. Этот означает, что мы можем записать любое рациональное число как частное, которое нельзя упростить. Другими словами, мы можем написать любое рациональное число в виде 𝑝𝑞, где наибольший общий делитель 𝑝 и 𝑞 равно 1. Тогда мы можем задать вопрос: все ли числа рациональны?
Ответ на этот вопрос – нет; Примером нерационального числа является √2. Чтобы понять, почему это так, давайте предположим, что √2 — рациональное число. Это означает, что √2=𝑝𝑞 для некоторых целых чисел 𝑝 и 𝑞, где 𝑞 отличен от нуля, а их наибольший общий делитель равен 1. Теперь мы возводим в квадрат обе части уравнения, чтобы получить 2=𝑝𝑞.
Если умножить на 𝑞, получим 2𝑞=𝑝.
Левая часть уравнения четная, поэтому правая тоже должна быть четной. Тем не менее, 𝑝 является
целое число, поэтому 𝑝 должно быть четным. Допустим, 𝑝=2𝑘 для некоторого целого числа 𝑘. Замена
это в уравнение и упрощение дает
2𝑞=(2𝑘),2𝑞=4𝑘𝑞=2𝑘.
Допустим, 𝑝=2𝑘 для некоторого целого числа 𝑘. Замена
это в уравнение и упрощение дает
2𝑞=(2𝑘),2𝑞=4𝑘𝑞=2𝑘.
Теперь правая часть уравнения четная, поэтому левая тоже должна быть четной. Так как 𝑞 является целое число, то 𝑞 должно быть четным. Это означает, что и 𝑝, и 𝑞 имеют общий фактор из 2. Но мы предполагали, что 𝑝 и 𝑞 не имеют общих делителей. Это показывает, что наш исходный предположение, что √2 является рациональным числом, не может быть верным. Следовательно, √2 не рациональный.
Точно такие же рассуждения можно использовать, чтобы показать, что квадратный корень из любого числа, не являющегося полным квадратом, не является рациональный.
Теперь мы можем определить иррациональные числа следующим образом.
Определение: множество иррациональных чисел
Иррациональное число — это число, которое нельзя записать в виде 𝑎𝑏, где 𝑎
и 𝑏 — целые числа, а 𝑏 — ненулевое число. Так как это множество содержит все числа, которые
не рационально, мы можем записать это множество как дополнение к ℚ∶ℚ′.
Таким образом, мы показали следующее свойство, и мы также можем распространить это свойство на кубические корни.
Свойство: Квадратные и кубические корни несовершенных квадратов и несовершенных кубов
Если 𝑛 — натуральное число, а не полный квадрат, то √𝑛 иррационально.
Если 𝑛 — целое число, а не совершенный куб, то √𝑛 иррационально.
В общем, очень трудно определить, является ли число рациональным или иррациональным. Есть несколько свойств рациональные и иррациональные числа, которые мы можем использовать, чтобы определить, является ли число рациональным или иррациональным.
Свойство: свойства рациональных и иррациональных чисел
- Если число имеет конечное (или завершающее) десятичное разложение, то оно рационально.
- Если число имеет повторяющееся десятичное расширение (например, 0.̇12̇3=0.123123…), тогда это рационально.
- Если число имеет десятичное представление, которое не заканчивается и не повторяется, то оно иррационально.

Верно и обратное этому свойству: все рациональные числа имеют либо конечную, либо повторяющуюся десятичную дробь. расширение, и все иррациональные числа имеют бесконечное неповторяющееся десятичное расширение.
Эти свойства позволяют нам определить, являются ли некоторые числа рациональными или иррациональными. Например, известно, что цифры 𝜋 никогда не заканчиваются и не имеют повторяющегося рисунка; следовательно, 𝜋 иррациональный.
Давайте теперь рассмотрим пример определения, является ли число рациональным или иррациональным.
Пример 1. Определение, является ли целое число рациональным или иррациональным
Является ли 7 рациональным или иррациональным числом?
Ответ
Напомним, что рациональные числа — это числа, которые можно записать в виде 𝑎𝑏, где
𝑎 и 𝑏 — целые числа, а 𝑏 не равно нулю. Иррациональные числа
являются не рациональными. Мы видим, что 7=71, значит, это рациональное число. Все
целые числа могут быть записаны таким образом. Следовательно, все целые числа рациональны.
Все
целые числа могут быть записаны таким образом. Следовательно, все целые числа рациональны.
В частности, 7 рационально.
В нашем следующем примере мы рассмотрим возможность того, что число может быть как рациональным, так и иррациональным.
Пример 2. Нахождение пересечения рациональных и иррациональных чисел
Что такое ℚ∩ℚ′?
Ответ
Мы можем ответить на этот вопрос, используя только операции над множествами. Мы знаем, что пересечение любого множества с его дополнение пусто. В частности, ℚ∩ℚ′=∅.
Однако полезно подумать об этом с точки зрения чисел. Напомним, что ℚ это множество рациональных чисел, то есть множество чисел, которые можно записать как частное двух целых чисел. Точно так же напомним, что ℚ′ — это множество иррациональных чисел, т. е. все числа, которые нельзя записать как частное двух целых чисел.
Мы видим, что число не может быть как в ℚ, так и в ℚ′, поскольку
либо число можно записать как частное двух целых чисел, либо нельзя. Следовательно,
ℚ∩ℚ′=∅.
Следовательно,
ℚ∩ℚ′=∅.
Давайте теперь рассмотрим пример определения того, является ли заданное число рациональным или иррациональным.
Пример 3. Определение того, является ли число с повторяющимся десятичным знаком рациональным или иррациональным
Является ли число 0,̇45̇6 рациональным или иррациональным?
Ответ
Напомним, что все числа с повторяющимся десятичным разложением рациональны. С 0.̇45̇6 имеет повторяющееся десятичное разложение, мы можем заключить, что число рационально.
Мы можем найти точное значение рационального числа 0,̇45̇6 с помощью калькулятора. Если мы запишем 0.̇45̇6 в калькулятор, получим 0.̇45̇6=152333.
В следующем примере мы определим, является ли кубический корень заданного числа рациональным или иррациональным.
Пример 4. Определение того, является ли кубический корень рациональным или иррациональным
Является ли √27 рациональным или иррациональным числом?
Ответ
Напомним, что рациональные числа — это числа, которые можно представить как частное двух целых чисел, и что если 𝑛
является целым числом, а не совершенным кубом, то √𝑛 иррационально.
Следовательно, мы должны начать с проверки, является ли 27 совершенным кубом. Мы отмечаем, что 27=3×3×3.
Итак, √27=√3=3.
Поскольку все целые числа рациональны, мы знаем, что 3 рационально.
Следовательно, √27 рационально.
В нашем следующем примере мы определим, является ли решение уравнения рациональным или иррациональным.
Пример 5. Определение того, является ли решение уравнения рациональным или иррациональным
Если 𝑥 является решением уравнения (𝑥+1)=8, определите, является ли 𝑥∈ℚ или 𝑥∈ℚ′.
Ответ
Мы можем решить это уравнение, взяв квадратные корни из обеих частей уравнения, где мы заметим, что мы будем иметь положительный и отрицательный корень. Итак, мы получаем 𝑥+1=√8𝑥+1=−√8.или
В обоих случаях мы можем вычесть 1 из обеих частей уравнения, чтобы получить 𝑥=−1+√8𝑥=−1−√8.or
Тогда мы можем вспомнить, что квадратный корень из любого несовершенного квадрата иррационален. Итак, √8
иррациональный. Это говорит нам о том, что десятичное расширение √8 не повторяется и не заканчивается. Умножение √8 на −1 не изменит десятичного разложения; это будет только
изменить знак. Точно так же вычитание 1 изменит только цифру единицы. Следовательно, оба −1−√8
и −1+√8 имеют неповторяющиеся и не заканчивающиеся десятичные расширения; они оба иррациональны.
Итак, √8
иррациональный. Это говорит нам о том, что десятичное расширение √8 не повторяется и не заканчивается. Умножение √8 на −1 не изменит десятичного разложения; это будет только
изменить знак. Точно так же вычитание 1 изменит только цифру единицы. Следовательно, оба −1−√8
и −1+√8 имеют неповторяющиеся и не заканчивающиеся десятичные расширения; они оба иррациональны.
Стоит отметить, что нам не нужно было находить значение этого решения. Мы могли бы просто отметить, что √8 иррационально, а затем обнаружил, что решение 𝑥 включает только вычитание и умножение на ненулевые рациональные числа до этого иррационального числа. Этого достаточно, чтобы показать, что 𝑥 иррационально.
Другой способ сказать это так: поскольку не существует рационального числа, квадрат которого равен 8, не существует рационального числа мы можем прибавить 1, а затем возвести в квадрат, чтобы получить 8.
Следовательно, 𝑥∈ℚ′.
В нашем последнем примере мы будем использовать площадь квадрата, чтобы определить, является ли его длина рациональной или иррациональной.
Пример 6. Определение того, является ли сторона квадрата иррациональной по площади
Квадрат со стороной 𝑥 см имеет площадь 280 см 2 . Что из следующего верно относительно 𝑥?
- Это целое число.
- Это рациональное число.
- Это иррациональное число.
- Это натуральное число.
- Это отрицательное число.
Ответ
Напомним, что площадь квадрата со стороной 𝑥 определяется выражением area=𝑥.
Нам сказали, что площадь этого квадрата равна 280 см 2 . Подстановка этого значения в уравнение дает 280=𝑥.
Мы можем найти 𝑥, взяв квадратный корень из обеих частей уравнения, где мы заметим, что
𝑥 см — это длина, поэтому она должна быть положительной. Это дает нам
𝑥=√280.
Затем мы вспоминаем, что если 𝑛 — натуральное число, а не полный квадрат, то √𝑛 иррационально. Мы проверяем квадратные числа, чтобы убедиться, что 280 не является идеальным квадратом. Следовательно, √280 иррационально.
Следовательно, ответ C: это иррациональное число.
Давайте закончим повторением некоторых важных моментов из этого объяснения.
Ключевые моменты
- Иррациональное число — это число, которое нельзя записать в виде 𝑎𝑏, где 𝑎 и 𝑏 — целые числа, а 𝑏 не равно нулю.
- Множество иррациональных чисел записывается как ℚ′.
- Число не может быть одновременно рациональным и иррациональным. В частности, ℚ∩ℚ′=∅.
- Если 𝑛 — натуральное число, а не полный квадрат, то √𝑛 иррационально.
- Если 𝑛 — целое число, а не совершенный куб, то √𝑛 иррационально.
- Если число имеет конечное (или завершающее) десятичное разложение, то оно рационально.
- Если число имеет повторяющееся десятичное расширение, то оно рационально.

