Ная производная. Где что искать на других страницах
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Многие удивятся неожиданному расположению этой статьи в моём авторском курсе о производной функции одной переменной и её приложениях. Ведь как оно было ещё со школы: стандартный учебник в первую очередь даёт определение производной, её геометрический, механический смысл. Далее учащиеся находят производные функций по определению, и, собственно, только потом оттачивается техника дифференцирования с помощью таблицы производных .
Но с моей точки зрения, более прагматичен следующий подход: прежде всего, целесообразно ХОРОШО ПОНЯТЬ предел функции , и, в особенности, бесконечно малые величины . Дело в том, что определение производной базируется на понятии предела , которое слабо рассмотрено в школьном курсе. Именно поэтому значительная часть молодых потребителей гранита знаний плохо вникают в саму суть производной. Таким образом, если вы слабо ориентируетесь в дифференциальном исчислении либо мудрый мозг за долгие годы успешно избавился от оного багажа, пожалуйста, начните с
Тот же практический смысл подсказывает, что сначала выгодно научиться находить производные , в том числе производные сложных функций . Теория теорией, а дифференцировать, как говорится, хочется всегда. В этой связи лучше проработать перечисленные базовые уроки, а может и стать мастером дифференцирования , даже не осознавая сущности своих действий.
К материалам данной страницы рекомендую приступать после ознакомления со статьёй Простейшие задачи с производной , где, в частности рассмотрена задача о касательной к графику функции. Но можно и повременить. Дело в том, что многие приложения производной не требуют её понимания, и неудивительно, что теоретический урок появился достаточно поздно – когда мне потребовалось объяснять нахождение интервалов возрастания/убывания и экстремумов функции. Более того, он довольно долго находился в теме «Функции и графики », пока я всё-таки не решил поставить его раньше.
Поэтому, уважаемые чайники, не спешите поглощать суть производной, как голодные звери, ибо насыщение будет невкусным и неполным.
Понятие возрастания, убывания, максимума, минимума функцииМногие учебные пособия подводят к понятию производной с помощью каких-либо практических задач, и я тоже придумал интересный пример. Представьте, что нам предстоит путешествие в город, до которого можно добраться разными путями. Сразу откинем кривые петляющие дорожки, и будем рассматривать только прямые магистрали. Однако прямолинейные направления тоже бывают разными: до города можно добраться по ровному автобану. Или по холмистому шоссе – вверх-вниз, вверх-вниз. Другая дорога идёт только в гору, а ещё одна – всё время под уклон. Экстремалы выберут маршрут через ущелье с крутым обрывом и отвесным подъемом.
Сразу откинем кривые петляющие дорожки, и будем рассматривать только прямые магистрали. Однако прямолинейные направления тоже бывают разными: до города можно добраться по ровному автобану. Или по холмистому шоссе – вверх-вниз, вверх-вниз. Другая дорога идёт только в гору, а ещё одна – всё время под уклон. Экстремалы выберут маршрут через ущелье с крутым обрывом и отвесным подъемом.
Но каковы бы ни были ваши предпочтения, желательно знать местность или, по меньшей мере, располагать её топографической картой. А если такая информация отсутствует? Ведь можно выбрать, например, ровный путь, да в результате наткнуться на горнолыжный спуск с весёлыми финнами. Не факт, что навигатор и даже спутниковый снимок дадут достоверные данные. Поэтому неплохо бы формализовать рельеф пути средствами математики.
Рассмотрим некоторую дорогу (вид сбоку):
На всякий случай напоминаю элементарный факт: путешествие происходит слева направо . Для простоты полагаем, что функция непрерывна
Какие особенности у данного графика?
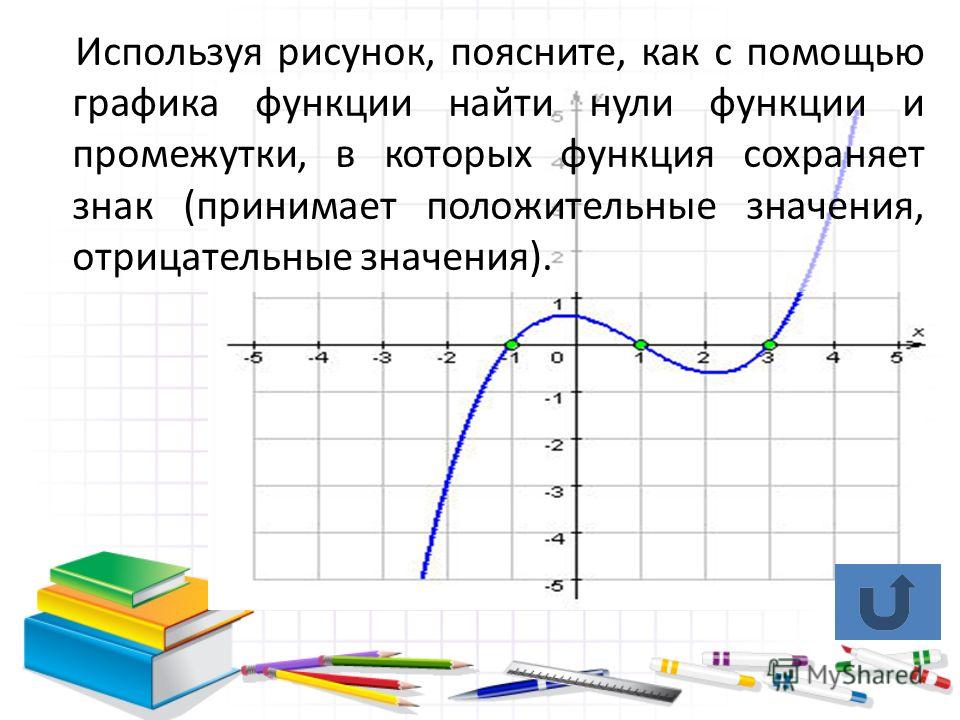
На интервалах функция возрастает , то есть каждое следующее её значение больше предыдущего. Грубо говоря, график идёт снизу вверх (забираемся на горку). А на интервале функция убывает – каждое следующее значение меньше предыдущего, и наш график идёт сверху вниз (спускаемся по склону).
Также обратим внимание на особые точки. В точке мы достигаем максимума , то есть существует такой участок пути, на котором значение будет самым большим (высоким). В точке же достигается минимум , и существует такая её окрестность, в которой значение самое маленькое (низкое).
Более строгую терминологию и определения рассмотрим на уроке об экстремумах функции , а пока изучим ещё одну важную особенность: на промежутках функция возрастает, но возрастает она  Нельзя ли измерить крутизну дороги с помощью математического инструментария?
Нельзя ли измерить крутизну дороги с помощью математического инструментария?
Идея состоит в следующем: возьмём некоторое значение (читается «дельта икс») , которое назовём приращением аргумента , и начнём его «примерять» к различным точкам нашего пути:
1) Посмотрим на самую левую точку: минуя расстояние , мы поднимаемся по склону на высоту (зелёная линия). Величина называется приращением функции , и в данном случае это приращение положительно (разность значений по оси – больше нуля). Составим отношение , которое и будет мерИлом крутизны нашей дороги. Очевидно, что – это вполне конкретное число, и, поскольку оба приращения положительны, то .
Внимание! Обозначение являются ЕДИНЫМ символом, то есть нельзя «отрывать» «дельту» от «икса» и рассматривать эти буквы отдельно. Разумеется, комментарий касается и символа приращения функции.
Исследуем природу полученной дроби содержательнее. Пусть изначально мы находимся на высоте 20 метров (в левой чёрной точке). Преодолев расстояние метров (левая красная линия), мы окажемся на высоте 60 метров. Тогда приращение функции составит метров (зелёная линия) и: . Таким образом, на каждом метре этого участка дороги высота увеличивается в среднем на 4 метра …не забыли альпинистское снаряжение? =) Иными словами, построенное отношение характеризует СРЕДНЮЮ СКОРОСТЬ ИЗМЕНЕНИЯ (в данном случае – роста) функции.
Пусть изначально мы находимся на высоте 20 метров (в левой чёрной точке). Преодолев расстояние метров (левая красная линия), мы окажемся на высоте 60 метров. Тогда приращение функции составит метров (зелёная линия) и: . Таким образом, на каждом метре этого участка дороги высота увеличивается в среднем на 4 метра …не забыли альпинистское снаряжение? =) Иными словами, построенное отношение характеризует СРЕДНЮЮ СКОРОСТЬ ИЗМЕНЕНИЯ (в данном случае – роста) функции.
Примечание : числовые значения рассматриваемого примера соответствуют пропорциям чертежа лишь приблизительно.
2) Теперь пройдём то же самое расстояние от самой правой чёрной точки. Здесь подъём более пологий, поэтому приращение (малиновая линия) относительно невелико, и отношение по сравнению с предыдущим случаем будет весьма скромным. Условно говоря, метров и
3) Маленькое приключение на склоне горы. Посмотрим на верхнюю чёрную точку, расположенную на оси ординат. Предположим, что это отметка 50 метров. Снова преодолеваем расстояние , в результате чего оказываемся ниже – на уровне 30-ти метров. Поскольку осуществлено движение сверху вниз (в «противоход» направлению оси ), то итоговое приращение функции (высоты) будет отрицательным : метров (коричневый отрезок на чертеже). И в данном случае речь уже идёт о скорости убывания функции: , то есть за каждый метр пути этого участка высота убывает в среднем на 2 метра. Берегите одежду на пятой точке.
Теперь зададимся вопросом: какое значение «измерительного эталона» лучше всего использовать? Совершенно понятно, 10 метров – это весьма грубо. На них запросто уместится добрая дюжина кочек. Да что там кочки, внизу может быть глубокое ущелье, а через несколько метров – другая его сторона с дальнейшим отвесным подъёмом. Таким образом, при десятиметровом мы не получим вразумительной характеристики подобных участков пути посредством отношения .
Из проведённого рассуждения следует вывод – чем меньше значение , тем точнее мы опишем рельеф дороги. Более того, справедливы следующие факты:
– Для любой точки подъемов можно подобрать значение (пусть и очень малое), которое умещается в границах того или иного подъёма. А это значит, что соответствующее приращение высоты будет гарантированно положительным, и неравенство корректно укажет рост функции в каждой точке этих интервалов.
– Аналогично, для любой точки склона существует значение , которое полностью уместится на этом склоне. Следовательно, соответствующее приращение высоты однозначно отрицательно, и неравенство корректно покажет убыль функции в каждой точке данного интервала.
– Особо интересен случай, когда скорость изменения функции равна нулю: . Во-первых, нулевое приращение высоты () – признак ровного пути. А во-вторых, есть другие любопытные ситуации, примеры которых вы видите на рисунке. Представьте, что судьба завела нас на самую вершину холма с парящими орлами или дно оврага с квакающими лягушками. Если сделать небольшой шажок в любую сторону, то изменение высоты будет ничтожно мало, и можно сказать, что скорость изменения функции фактически нулевая. В точках наблюдается именно такая картина.
Если сделать небольшой шажок в любую сторону, то изменение высоты будет ничтожно мало, и можно сказать, что скорость изменения функции фактически нулевая. В точках наблюдается именно такая картина.
Таким образом, мы подобрались к удивительной возможности идеально точно охарактеризовать скорость изменения функции. Ведь математический анализ позволяет устремить приращение аргумента к нулю: , то есть сделать его бесконечно малым .
По итогу возникает ещё один закономерный вопрос: можно ли для дороги и её графика найти другую функцию , которая сообщала бы нам обо всех ровных участках, подъёмах, спусках, вершинах, низинах, а также о скорости роста/убывания в каждой точке пути?
Что такое производная? Определение производной.Геометрический смысл производной и дифференциала
Пожалуйста, прочитайте вдумчиво и не слишком быстро – материал прост и доступен каждому! Ничего страшного, если местами что-то покажется не очень понятным, к статье всегда можно вернуться позже. Скажу больше, теорию полезно проштудировать несколько раз, чтобы качественно уяснить все моменты (совет особенно актуален для студентов-«технарей», у которых высшая математика играет значительную роль в учебном процессе).
Скажу больше, теорию полезно проштудировать несколько раз, чтобы качественно уяснить все моменты (совет особенно актуален для студентов-«технарей», у которых высшая математика играет значительную роль в учебном процессе).
Естественно, и в самом определении производной в точке заменим на :
К чему мы пришли? А пришли мы к тому, что для функции по закону ставится в соответствие другая функция , которая называется производной функцией (или просто производной) .
Производная характеризует скорость изменения функции . Каким образом? Мысль идёт красной нитью с самого начала статьи. Рассмотрим некоторую точку области определения функции . Пусть функция дифференцируема в данной точке. Тогда:
1) Если , то функция возрастает в точке . И, очевидно, существует интервал (пусть даже очень малый), содержащий точку , на котором функция растёт, и её график идёт «снизу вверх».
2) Если , то функция убывает в точке . И существует интервал, содержащий точку , на котором функция убывает (график идёт «сверху вниз»).
3) Если , то бесконечно близко около точки функция сохраняет свою скорость постоянной. Так бывает, как отмечалось, у функции-константы и в критических точках функции , в частности в точках минимума и максимума .
Немного семантики. Что в широком смысле обозначает глагол «дифференцировать»? Дифференцировать – это значит выделить какой-либо признак. Дифференцируя функцию , мы «выделяем» скорость её изменения в виде производной функции . А что, кстати, понимается под словом «производная»? Функция произошла от функции .
Термины весьма удачно истолковывает механический смысл производной :
Рассмотрим закон изменения координаты тела , зависящий от времени , и функцию скорости движения данного тела . Функция характеризует скорость изменения координаты тела, поэтому является первой производной функции по времени: . Если бы в природе не существовало понятия «движение тела», то не существовало бы и производного понятия «скорость тела».
Ускорение тела – это скорость изменения скорости, поэтому: . Если бы в природе не существовало исходных понятий «движение тела» и «скорость движения тела», то не существовало бы и производного понятия «ускорение тела».
Производная функции одной переменной.
Введение.
Настоящие методические разработки предназначены для студентов факультета промышленное и гражданское строительство. Они составлены применительно к программе курса математики по разделу «Дифференциальное исчисление функций одного переменного».
Разработки представляют собой единое методическое руководство, включающее в себя: краткие теоретические сведения; «типовые» задачи и упражнения с подробными решениями и пояснениями к этим решениям; варианты контрольной работы.
В конце каждого параграфа дополнительные упражнения. Такая структура разработок делает их пригодными для самостоятельного овладения разделом при самой минимальной помощи со стороны преподавателя.
Механический и геометрический смысл
производной.
Понятие производной является одним из самых важных понятий математического анализа.Оно возникло еще в 17 веке. Формирование понятия производной исторически связано с двумя задачами: задачей о скорости переменного движения и задачей о касательной к кривой.
Эти задачи, несмотря на их различное содержание, приводят к одной и той же математической операции, которую нужно провести над функцией.Эта операция получила в математике специальное название. Она называется операцией дифференцирования функции. Результат операции дифференцирования называется производной.
Итак, производной функцииy=f(x)
в точкеx0 называется
предел (если он существует) отношения
приращения функции
к приращению аргумента
при
.
Производную принято обозначать
так:
.
Таким образом, по определению
Для обозначения производной употребляются
также символы
.
Механический смысл производной.
Если s=s(t)
– закон прямолинейного движения
материальной точки, то
есть скорость этой точки в момент времениt.
Геометрический смысл производной.
Если функция y=f(x)
имеет производную в точке,
то угловой коэффициент касательной к
графику функции в точке
равен
.
Пример.
Найдите производную функции
в точке=2:
1) Дадим точке
=2
приращение
.
Заметим, что.
2) Найдем приращение функции в точке =2:
3) Составим отношение приращения функции к приращению аргумента:
Найдем предел отношения при
:
.
Таким образом,
.
§ 2. Производные от некоторых
простейших функций.
Студенту необходимо научиться вычислять производные конкретных функций: y=x,y=и вообщеy=.
Найдем производную функции у=х.
т.е. (x)′=1.
Найдем производную функции
Производная
Пусть
тогда
Легко заметить закономерность в
выражениях производных от степенной
функции
приn=1,2,3.
Следовательно,
. (1)
Эта формула справедлива для любых
действительных n.
В частности, используя формулу (1), имеем:
;
.
Пример.
Найдите производную функции
.
.
Данная функция является частным случаем функции вида
при
.
Используя формулу (1), имеем
.
Производные функций y=sin x и y=cos x.
Пусть y=sinx.
Разделим на ∆x, получим
Переходя к пределу при ∆x→0, имеем
Пусть y=cosx .
Переходя к пределу при ∆x→0, получим
;
.
(2)
§3. Основные правила дифференцирования.
Рассмотрим правила дифференцирования.
Теорема 1 . Если функцииu=u(x) иv=v(x) дифференцируемы в данной точкеx,то в этой точке дифференцируема и их сумма, причем производная суммы равна сумме производных слагаемых: (u+v)»=u»+v».(3)
Доказательство: рассмотрим функцию y=f(x)=u(x)+v(x).
Приращению ∆x аргумента x соответствуют приращения ∆u=u(x+∆x)-u(x), ∆v=v(x+∆x)-v(x) функций u и v. Тогда функция y получит приращение
∆y=f(x+∆x)-f(x)=
=—=∆u+∆v.
Следовательно,
Итак, (u+v)»=u»+v».
Теорема 2. Если функцииu=u(x) иv=v(x) дифференцируемы в данной точкеx, то в той же точке дифференцируемо и их произведение.При этом производная произведения находится по следующей формуле: (uv)»=u»v+uv». (4)
Доказательство: Пусть y=uv, где u и v – некоторые дифференцируемые функции от x. Дадим x приращение ∆x;тогда u получит приращение ∆u, v получит приращение ∆v и y получит приращение ∆y.
Имеем y+∆y=(u+∆u)(v+∆v), или
y+∆y=uv+u∆v+v∆u+∆u∆v.
Следовательно, ∆y=u∆v+v∆u+∆u∆v.
Отсюда
Переходя к пределу при ∆x→0 и учитывая, чтоuиvне зависят от ∆x, будем иметь
Теорема 3 . Производная частного двух функций равна дроби, знаменатель которой равен квадрату делителя, а числитель- разности между произведением производной делимого на делитель и произведением делимого на производную делителя, т.е.
Если
то
(5)
Теорема 4. Производная постоянной
равна нулю, т. е. если y=C, где С=const, то
y»=0.
е. если y=C, где С=const, то
y»=0.
Теорема 5. Постоянный множитель можно выносить за знак производной, т.е. если y=Cu(x), где С=const, то y»=Cu»(x).
Пример 1.
Найдите производную функции
.
Данная функция имеет вид
,
гдеu=x,v=cosx. Применяя правило
дифференцирования (4), находим
.
Пример 2.
Найдите производную функции
.
Применим формулу (5).
Здесь
;
.
Задачи.
Найдите производные следующих функций:
;
11)
2)
;
12)
;
3)
13)
4)
14)
5)
15)
6)
16)
7 )
17)
8)
18)
9)
19)
10)
20)
{\large\bf Производная функции}
Рассмотрим функцию y=f(x) , заданную на интервале (a, b) . Пусть x — любое фиксированная точка интервала (a, b) , а Δx — произвольное число, такое, что значение x+Δx также принадлежит интервалу (a, b) .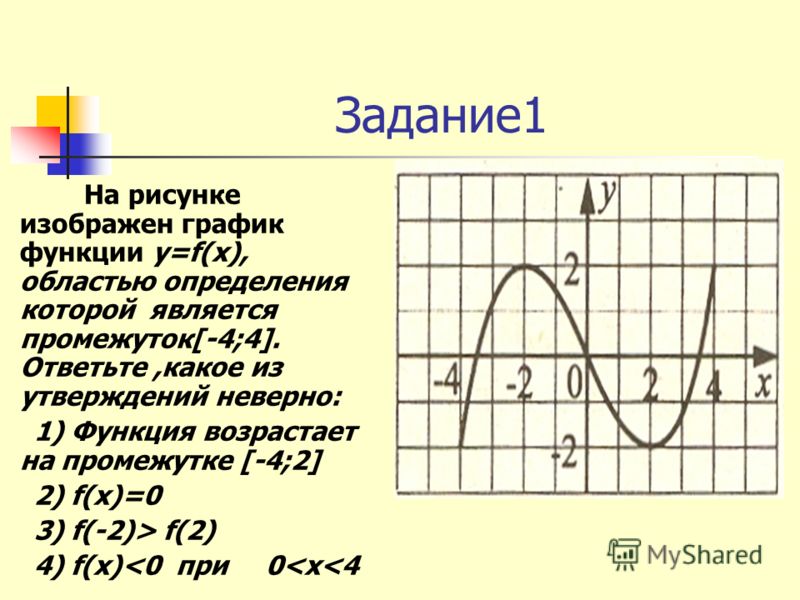 Это число Δx называют приращением аргумента.
Это число Δx называют приращением аргумента.
Определение . Приращением функции y=f(x) в точке x , соответствующим приращению аргумента Δx , назовем число
Δy = f(x+Δx) — f(x) .
Считаем, что Δx ≠ 0 . Рассмотрим в данной фиксированной точке x отношение приращения функции в этой точке к соответствующему приращению аргумента Δx
Это отношение будем называть разностным отношением. Так как значение x мы считаем фиксированным, разностное отношение представляет собой функцию аргумента Δx . Эта функция определена для всех значений аргумента Δx , принадлежащих некоторой достаточно малой окрестности точки Δx=0 , за исключением самой точки Δx=0 . Таким образом, мы имеем право рассматривать вопрос о существовании предела указанной функции при Δx → 0 .
Определение . Производной функции y=f(x) в данной фиксированной точке x называется предел при Δx → 0 разностного отношения, то есть
При условии, что этот предел существует.
Обозначение . y′(x) или f′(x) .
Геометрический смысл производной : Производная от функции f(x) в данной точке x равна тангенсу угла между осью Ox и касательной к графику этой функции в соответствующей точке:
f′(x 0) = \tgα .
Механический смысл производной : Производная от пути по времени равна скорости прямолинейного движения точки:
Уравнение касательной к линии y=f(x) в точке M 0 (x 0 ,y 0) принимает вид
y-y 0 = f′(x 0) (x-x 0) .
Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Если f′(x 0)≠ 0 , то уравнение нормали к линии y=f(x) в точке M 0 (x 0 ,y 0) записывается так:
Понятие дифференцируемости функции
Пусть функция y=f(x) определена на некотором интервале (a, b) , x — некоторое фиксированное значение аргумента из этого интервала, Δx — любое приращение аргумента, такое, что значение аргумента x+Δx ∈ (a, b) .
Определение . Функция y=f(x) называется дифференцируемой в данной точке x , если приращение Δy этой функции в точке x , соответствующее приращению аргумента Δx , может быть представимо в виде
Δy = A Δx +αΔx ,
где A — некоторое число, не зависящее от Δx , а α — функция аргумента Δx , являющая бесконечно малой при Δx→ 0 .
Так как произведение двух бесконечно малых функций αΔx является бесконечно малой более высокого порядка, чем Δx (свойство 3 бесконечно малых функций), то можем записать:
Δy = A Δx +o(Δx) .
Теорема . Для того, чтобы функция y=f(x) являлась дифференцируемой в данной точке x , необходимо и достаточно, чтобы она имела в этой точке конечную производную. При этом A=f′(x) , то есть
Δy = f′(x) Δx +o(Δx) .
Операцию нахождения производной обычно называют дифференцированием.
Теорема . Если функция y=f(x) x , то она непрерывна в этой точке.
Если функция y=f(x) x , то она непрерывна в этой точке.
Замечание . Из непрерывности функции y=f(x) в данной точке x , вообще говоря, не вытекает дифференцируемость функции f(x) в этой точке. Например, функция y=|x| — непрерывна в точке x=0 , но не имеет производной.
Понятие дифференциала функции
Определение . Дифференциалом функции y=f(x) называется произведение производной этой функции на приращение независимой переменной x :
dy = y′ Δx, df(x) = f′(x) Δx .
Для функции y=x получаем dy=dx=x′Δx = 1· Δx= Δx , то есть dx=Δx — дифференциал независимой переменной равен приращению этой переменной.
Таким образом, можем записать
dy = y′ dx, df(x) = f′(x) dx
Дифференциал dy и приращение Δy функции y=f(x) в данной точке x , оба отвечающие одному и тому же приращению аргумента Δx , вообще говоря, не равны друг другу.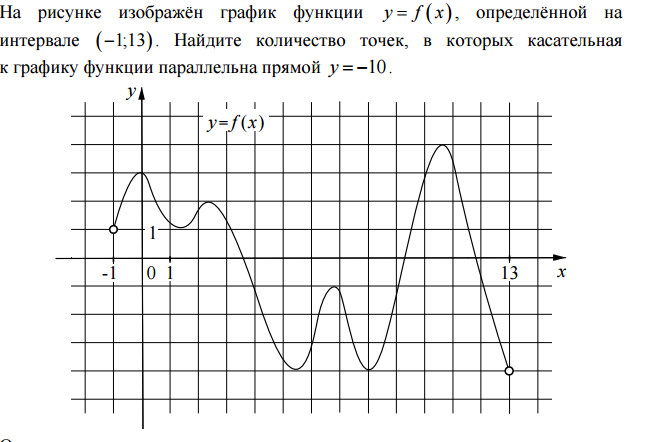
Геометрический смысл дифференциала : Дифференциал функции равен приращению ординаты касательной к графику данной функции, когда аргумент получает приращение Δx .
Правила дифференцирования
Теорема . Если каждая из функций u(x) и v(x) дифференцируема в данной точке x , то сумма, разность, произведение и частное этих функций (частное при условии, что v(x)≠ 0 ) также дифференцируемы в этой точке, причем имеют место формулы:
Рассмотрим сложную функцию y=f(φ(x))≡ F(x) , где y=f(u) , u=φ(x) . В этом случае u называют промежуточным аргументом , x — независимой переменной .
Теорема . Если y=f(u) и u=φ(x) — дифференцируемые функции своих аргументов, то производная сложной функции y=f(φ(x)) существует и равна произведению этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т. е.
е.
Замечание . Для сложной функции, являющейся суперпозицией трех функций y=F(f(φ(x))) , правило дифференцирования имеет вид
y′ x = y′ u u′ v v′ x ,
где функции v=φ(x) , u=f(v) и y=F(u) — дифференцируемые функции своих аргументов.
Теорема . Пусть функция y=f(x) возрастает (или убывает) и непрерывна в некоторой окрестности точки x 0 . Пусть, кроме того, эта функция дифференцируема в указанной точке x 0 и ее производная в этой точке f′(x 0) ≠ 0 . Тогда в некоторой окрестности соответствующей точки y 0 =f(x 0) определена обратная для y=f(x) функция x=f -1 (y) , причем указанная обратная функция дифференцируема в соответствующей точке y 0 =f(x 0) и для ее производной в этой точке y справедлива формула
Таблица производных
Инвариантность формы первого дифференциала
Рассмотрим дифференциал сложной функции. Если y=f(x) , x=φ(t) — дифференцируемы функции своих аргументов, то производная функции y=f(φ(t)) выражается формулой
y′ t = y′ x x′ t .
По определению dy=y′ t dt , тогда получим
dy = y′ t dt = y′ x · x′ t dt = y′ x (x′ t dt) = y′ x dx ,
dy = y′ x dx .
Итак, доказали,
Свойство инвариантности формы первого дифференциала функции : как в случае, когда аргумент x является независимой переменной, так и в случае, когда аргумент x сам является дифференцируемой функцией новой переменной, дифференциал dy функции y=f(x) равен производной этой функции, умноженной на дифференциал аргумента dx .
Применение дифференциала в приближенных вычислениях
Мы показали, что дифференциал dy функции y=f(x) , вообще говоря, не равен приращению Δy этой функции. Тем не менее с точностью до бесконечно малой функции более высокого порядка малости, чем Δx , справедливо приближенное равенство
Δy ≈ dy .
Отношение называют относительной погрешностью равенства этого равенства. Так как Δy-dy=o(Δx) , то относительная погрешность данного равенства становится как угодно малой при уменьшении |Δх| .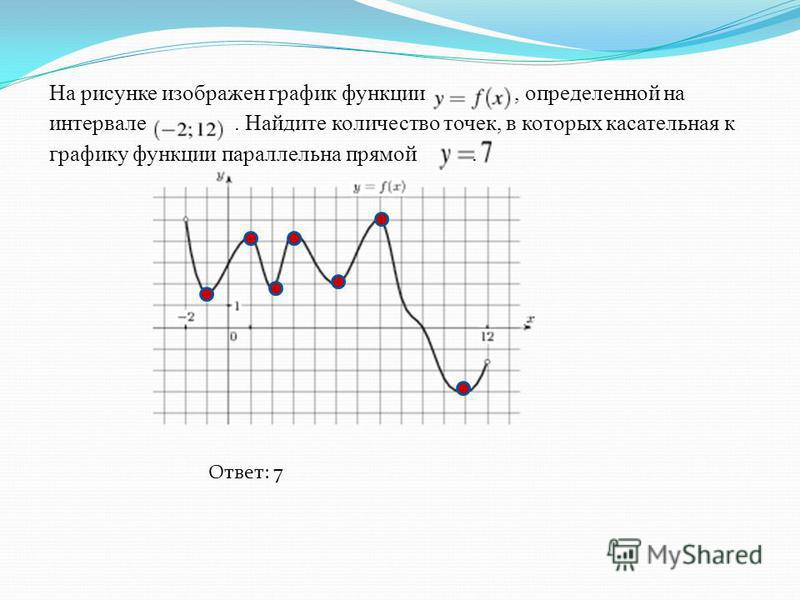
Учитывая, что Δy=f(x+δ x)-f(x) , dy=f′(x)Δx , получим f(x+δ x)-f(x) ≈ f′(x)Δx или
f(x+δ x) ≈ f(x) + f′(x)Δx .
Это приближенное равенство позволяет с ошибкой o(Δx) заменить функцию f(x) в малой окрестности точки x (т.е. для малых значений Δx ) линейной функцией аргумента Δx , стоящей в правой части.
Производные высших порядков
Определение . Второй производной (или производной второго порядка) функции y=f(x) называется производная от ее первой производной.
Обозначение второй производной функции y=f(x) :
Механический смысл второй производной . Если функция y=f(x) описывает закон движения материальной точки по прямой линии, то вторая производная f″(x) равна ускорению движущейся точки в момент времени x .
Аналогично определяется третья, четвертая производная.
Определение . n -й производной (или производной n -го порядка) функции y=f(x) называется производная от ее n-1 -й производной:
y (n) =(y (n-1))′, f (n) (x)=(f (n-1) (x))′ .
Обозначения: y″′ , y IV , y V и т.д.
Определение. Пусть функция \(y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \(x_0 \). Дадим аргументу приращение \(\Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение \(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то указанный предел называют производной функции \(y=f(x) \) в точке \(x_0 \) и обозначают \(f»(x_0) \).
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f»(x_0) $$
Для обозначения производной часто используют символ y». Отметим, что y» = f(x) — это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел. Эту функцию называют так: производная функции у = f(x) .
Геометрический смысл производной состоит в следующем. 2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение \(x \), найти \(f(x) \)
2. Дать аргументу \(x \) приращение \(\Delta x \), перейти в новую точку \(x+ \Delta x \), найти \(f(x+ \Delta x) \)
3. Найти приращение функции: \(\Delta y = f(x + \Delta x) — f(x) \)
4. Составить отношение \(\frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.
Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f»(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \(\Delta y \approx f»(x) \cdot \Delta x \). Если в этом равенстве \(\Delta x \) устремить к нулю, то и \(\Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .
Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику
функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой
точке не существует производная.
Еще один пример. Функция \(y=\sqrt{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \(f»(0) \)
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием .
При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций»,
то есть сложными функциями.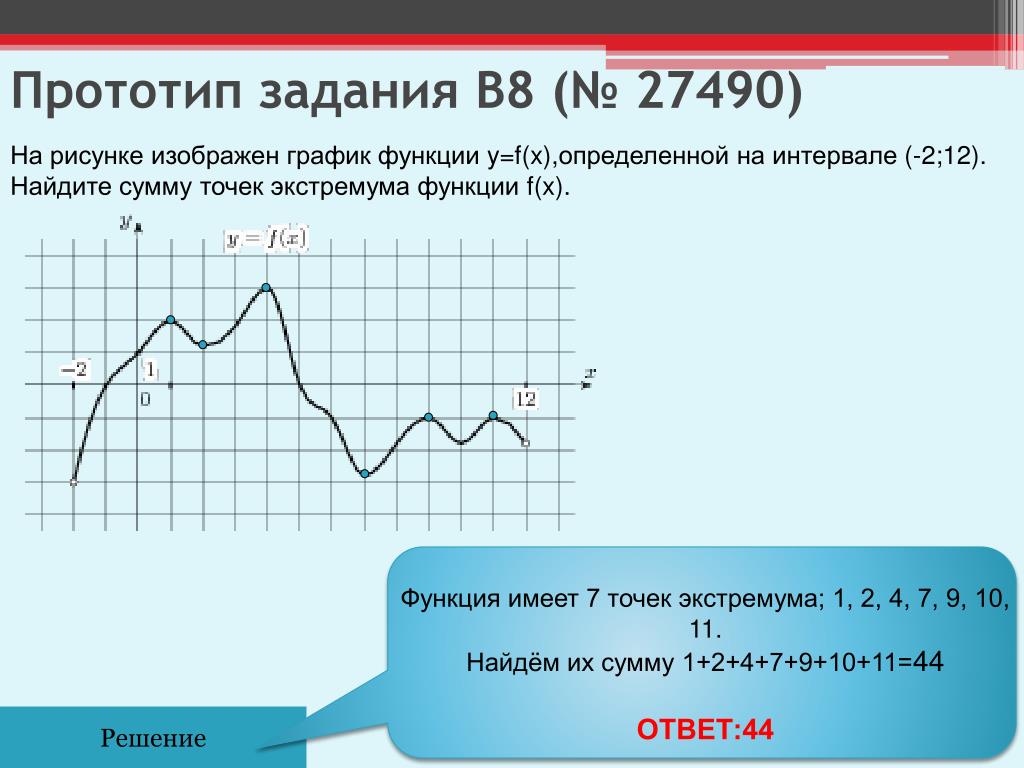 2} $$
2} $$
Производной функции в точке называется. Производная
Многие удивятся неожиданному расположению этой статьи в моём авторском курсе о производной функции одной переменной и её приложениях. Ведь как оно было ещё со школы: стандартный учебник в первую очередь даёт определение производной, её геометрический, механический смысл. Далее учащиеся находят производные функций по определению, и, собственно, только потом оттачивается техника дифференцирования с помощью таблицы производных .
Но с моей точки зрения, более прагматичен следующий подход: прежде всего, целесообразно ХОРОШО ПОНЯТЬ предел функции , и, в особенности, бесконечно малые величины . Дело в том, что определение производной базируется на понятии предела , которое слабо рассмотрено в школьном курсе. Именно поэтому значительная часть молодых потребителей гранита знаний плохо вникают в саму суть производной. Таким образом, если вы слабо ориентируетесь в дифференциальном исчислении либо мудрый мозг за долгие годы успешно избавился от оного багажа, пожалуйста, начните с пределов функций . Заодно освоите/вспомните их решение.
Заодно освоите/вспомните их решение.
Тот же практический смысл подсказывает, что сначала выгодно научиться находить производные , в том числе производные сложных функций . Теория теорией, а дифференцировать, как говорится, хочется всегда. В этой связи лучше проработать перечисленные базовые уроки, а может и стать мастером дифференцирования , даже не осознавая сущности своих действий.
К материалам данной страницы рекомендую приступать после ознакомления со статьёй Простейшие задачи с производной , где, в частности рассмотрена задача о касательной к графику функции. Но можно и повременить. Дело в том, что многие приложения производной не требуют её понимания, и неудивительно, что теоретический урок появился достаточно поздно – когда мне потребовалось объяснять нахождение интервалов возрастания/убывания и экстремумов функции. Более того, он довольно долго находился в теме «Функции и графики », пока я всё-таки не решил поставить его раньше.
Поэтому, уважаемые чайники, не спешите поглощать суть производной, как голодные звери, ибо насыщение будет невкусным и неполным.
Понятие возрастания, убывания, максимума, минимума функцииМногие учебные пособия подводят к понятию производной с помощью каких-либо практических задач, и я тоже придумал интересный пример. Представьте, что нам предстоит путешествие в город, до которого можно добраться разными путями. Сразу откинем кривые петляющие дорожки, и будем рассматривать только прямые магистрали. Однако прямолинейные направления тоже бывают разными: до города можно добраться по ровному автобану. Или по холмистому шоссе – вверх-вниз, вверх-вниз. Другая дорога идёт только в гору, а ещё одна – всё время под уклон. Экстремалы выберут маршрут через ущелье с крутым обрывом и отвесным подъемом.
Но каковы бы ни были ваши предпочтения, желательно знать местность или, по меньшей мере, располагать её топографической картой. А если такая информация отсутствует? Ведь можно выбрать, например, ровный путь, да в результате наткнуться на горнолыжный спуск с весёлыми финнами. Не факт, что навигатор и даже спутниковый снимок дадут достоверные данные. Поэтому неплохо бы формализовать рельеф пути средствами математики.
Не факт, что навигатор и даже спутниковый снимок дадут достоверные данные. Поэтому неплохо бы формализовать рельеф пути средствами математики.
Рассмотрим некоторую дорогу (вид сбоку):
На всякий случай напоминаю элементарный факт: путешествие происходит слева направо . Для простоты полагаем, что функция непрерывна на рассматриваемом участке.
Какие особенности у данного графика?
На интервалах функция возрастает , то есть каждое следующее её значение больше предыдущего. Грубо говоря, график идёт снизу вверх (забираемся на горку). А на интервале функция убывает – каждое следующее значение меньше предыдущего, и наш график идёт сверху вниз (спускаемся по склону).
Также обратим внимание на особые точки. В точке мы достигаем максимума , то есть существует такой участок пути, на котором значение будет самым большим (высоким). В точке же достигается минимум , и существует такая её окрестность, в которой значение самое маленькое (низкое).
Более строгую терминологию и определения рассмотрим на уроке об экстремумах функции , а пока изучим ещё одну важную особенность: на промежутках функция возрастает, но возрастает она с разной скоростью . И первое, что бросается в глаза – на интервале график взмывает вверх гораздо более круто , чем на интервале . Нельзя ли измерить крутизну дороги с помощью математического инструментария?
Скорость изменения функцииИдея состоит в следующем: возьмём некоторое значение (читается «дельта икс») , которое назовём приращением аргумента , и начнём его «примерять» к различным точкам нашего пути:
1) Посмотрим на самую левую точку: минуя расстояние , мы поднимаемся по склону на высоту (зелёная линия). Величина называется приращением функции , и в данном случае это приращение положительно (разность значений по оси – больше нуля). Составим отношение , которое и будет мерИлом крутизны нашей дороги. Очевидно, что – это вполне конкретное число, и, поскольку оба приращения положительны, то .
Внимание! Обозначение являются ЕДИНЫМ символом, то есть нельзя «отрывать» «дельту» от «икса» и рассматривать эти буквы отдельно. Разумеется, комментарий касается и символа приращения функции.
Исследуем природу полученной дроби содержательнее. Пусть изначально мы находимся на высоте 20 метров (в левой чёрной точке). Преодолев расстояние метров (левая красная линия), мы окажемся на высоте 60 метров. Тогда приращение функции составит метров (зелёная линия) и: . Таким образом, на каждом метре этого участка дороги высота увеличивается в среднем на 4 метра …не забыли альпинистское снаряжение? =) Иными словами, построенное отношение характеризует СРЕДНЮЮ СКОРОСТЬ ИЗМЕНЕНИЯ (в данном случае – роста) функции.
Примечание : числовые значения рассматриваемого примера соответствуют пропорциям чертежа лишь приблизительно.
2) Теперь пройдём то же самое расстояние от самой правой чёрной точки. Здесь подъём более пологий, поэтому приращение (малиновая линия) относительно невелико, и отношение по сравнению с предыдущим случаем будет весьма скромным. Условно говоря, метров и скорость роста функции составляет . То есть, здесь на каждый метр пути приходится в среднем пол метра подъёма.
Условно говоря, метров и скорость роста функции составляет . То есть, здесь на каждый метр пути приходится в среднем пол метра подъёма.
3) Маленькое приключение на склоне горы. Посмотрим на верхнюю чёрную точку, расположенную на оси ординат. Предположим, что это отметка 50 метров. Снова преодолеваем расстояние , в результате чего оказываемся ниже – на уровне 30-ти метров. Поскольку осуществлено движение сверху вниз (в «противоход» направлению оси ), то итоговое приращение функции (высоты) будет отрицательным : метров (коричневый отрезок на чертеже). И в данном случае речь уже идёт о скорости убывания функции: , то есть за каждый метр пути этого участка высота убывает в среднем на 2 метра. Берегите одежду на пятой точке.
Теперь зададимся вопросом: какое значение «измерительного эталона» лучше всего использовать? Совершенно понятно, 10 метров – это весьма грубо. На них запросто уместится добрая дюжина кочек. Да что там кочки, внизу может быть глубокое ущелье, а через несколько метров – другая его сторона с дальнейшим отвесным подъёмом.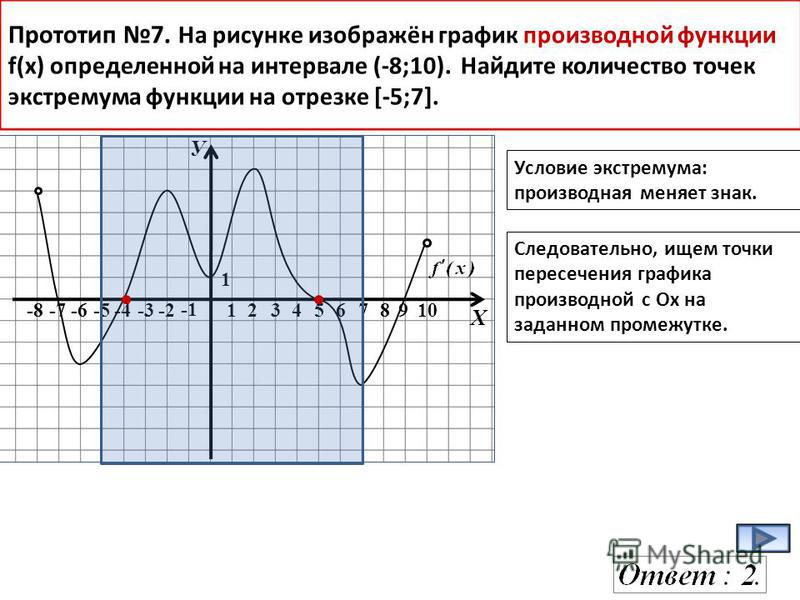 Таким образом, при десятиметровом мы не получим вразумительной характеристики подобных участков пути посредством отношения .
Таким образом, при десятиметровом мы не получим вразумительной характеристики подобных участков пути посредством отношения .
Из проведённого рассуждения следует вывод – чем меньше значение , тем точнее мы опишем рельеф дороги. Более того, справедливы следующие факты:
– Для любой точки подъемов можно подобрать значение (пусть и очень малое), которое умещается в границах того или иного подъёма. А это значит, что соответствующее приращение высоты будет гарантированно положительным, и неравенство корректно укажет рост функции в каждой точке этих интервалов.
– Аналогично, для любой точки склона существует значение , которое полностью уместится на этом склоне. Следовательно, соответствующее приращение высоты однозначно отрицательно, и неравенство корректно покажет убыль функции в каждой точке данного интервала.
– Особо интересен случай, когда скорость изменения функции равна нулю: . Во-первых, нулевое приращение высоты () – признак ровного пути. А во-вторых, есть другие любопытные ситуации, примеры которых вы видите на рисунке. Представьте, что судьба завела нас на самую вершину холма с парящими орлами или дно оврага с квакающими лягушками. Если сделать небольшой шажок в любую сторону, то изменение высоты будет ничтожно мало, и можно сказать, что скорость изменения функции фактически нулевая. В точках наблюдается именно такая картина.
А во-вторых, есть другие любопытные ситуации, примеры которых вы видите на рисунке. Представьте, что судьба завела нас на самую вершину холма с парящими орлами или дно оврага с квакающими лягушками. Если сделать небольшой шажок в любую сторону, то изменение высоты будет ничтожно мало, и можно сказать, что скорость изменения функции фактически нулевая. В точках наблюдается именно такая картина.
Таким образом, мы подобрались к удивительной возможности идеально точно охарактеризовать скорость изменения функции. Ведь математический анализ позволяет устремить приращение аргумента к нулю: , то есть сделать его бесконечно малым .
По итогу возникает ещё один закономерный вопрос: можно ли для дороги и её графика найти другую функцию , которая сообщала бы нам обо всех ровных участках, подъёмах, спусках, вершинах, низинах, а также о скорости роста/убывания в каждой точке пути?
Что такое производная? Определение производной.Геометрический смысл производной и дифференциала
Пожалуйста, прочитайте вдумчиво и не слишком быстро – материал прост и доступен каждому! Ничего страшного, если местами что-то покажется не очень понятным, к статье всегда можно вернуться позже. Скажу больше, теорию полезно проштудировать несколько раз, чтобы качественно уяснить все моменты (совет особенно актуален для студентов-«технарей», у которых высшая математика играет значительную роль в учебном процессе).
Скажу больше, теорию полезно проштудировать несколько раз, чтобы качественно уяснить все моменты (совет особенно актуален для студентов-«технарей», у которых высшая математика играет значительную роль в учебном процессе).
Естественно, и в самом определении производной в точке заменим на :
К чему мы пришли? А пришли мы к тому, что для функции по закону ставится в соответствие другая функция , которая называется производной функцией (или просто производной) .
Производная характеризует скорость изменения функции . Каким образом? Мысль идёт красной нитью с самого начала статьи. Рассмотрим некоторую точку области определения функции . Пусть функция дифференцируема в данной точке. Тогда:
1) Если , то функция возрастает в точке . И, очевидно, существует интервал (пусть даже очень малый), содержащий точку , на котором функция растёт, и её график идёт «снизу вверх».
2) Если , то функция убывает в точке . И существует интервал, содержащий точку , на котором функция убывает (график идёт «сверху вниз»).
3) Если , то бесконечно близко около точки функция сохраняет свою скорость постоянной. Так бывает, как отмечалось, у функции-константы и в критических точках функции , в частности в точках минимума и максимума .
Немного семантики. Что в широком смысле обозначает глагол «дифференцировать»? Дифференцировать – это значит выделить какой-либо признак. Дифференцируя функцию , мы «выделяем» скорость её изменения в виде производной функции . А что, кстати, понимается под словом «производная»? Функция произошла от функции .
Термины весьма удачно истолковывает механический смысл производной :
Рассмотрим закон изменения координаты тела , зависящий от времени , и функцию скорости движения данного тела . Функция характеризует скорость изменения координаты тела, поэтому является первой производной функции по времени: . Если бы в природе не существовало понятия «движение тела», то не существовало бы и производного понятия «скорость тела». nx. Формулы производных высших порядков.
nx. Формулы производных высших порядков.
Производная экспоненты равна самой экспоненте (производная e в степени x равна e в степени x):
(1) (e x )′
= e x
.
Производная показательной функции с основанием степени a
равна самой функции, умноженной на натуральный логарифм от a
:
(2) .
Вывод формулы производной экспоненты, e в степени x
Экспонента — это показательная функция, у которой основание степени равно числу e
,
которое является следующим пределом:
.
Здесь может быть как натуральным, так и действительным числом. Далее мы выводим формулу (1) производной экспоненты.
Вывод формулы производной экспоненты
Рассмотрим экспоненту, e
в степени x
:
y = e x
.
Эта функция определена для всех .
Найдем ее производную по переменной x
.
По определению, производная является следующим пределом:
(3) .
Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам понадобятся следующие факты:
Для этого нам понадобятся следующие факты:
А) Свойство экспоненты :
(4) ;
Б) Свойство логарифма :
(5) ;
В) Непрерывность логарифма и свойство пределов для непрерывной функции:
(6) .
Здесь — некоторая функция, у которой существует предел и этот предел положителен.
Г) Значение второго замечательного предела:
(7) .
Применяем эти факты к нашему пределу (3). Используем свойство (4):
;
.
Сделаем подстановку .
Тогда ;
.
В силу непрерывности экспоненты,
.
Поэтому при ,
.
В результате получаем:
.
Сделаем подстановку .
Тогда .
При ,
.
И мы имеем:
.
Применим свойство логарифма (5):
.
Тогда
.
Применим свойство (6). Поскольку существует положительный предел и логарифм непрерывен, то:
.
Здесь мы также воспользовались вторым замечательным пределом (7). Тогда
.
Тем самым мы получили формулу (1) производной экспоненты.
Вывод формулы производной показательной функции
Теперь выведем формулу (2) производной показательной функции с основанием степени a
.
Мы считаем, что и .
Тогда показательная функция
(8)
Определена для всех .
Преобразуем формулу (8). Для этого воспользуемся свойствами показательной функции
и логарифма
.
;
.
Итак, мы преобразовали формулу (8) к следующему виду:
.
Производные высших порядков от e в степени x
Теперь найдем производные высших порядков. Сначала рассмотрим экспоненту:
(14) .
(1) .
Мы видим, что производная от функции (14) равна самой функции (14). Дифференцируя (1), получаем производные второго и третьего порядка:
;
.
Отсюда видно, что производная n-го порядка также равна исходной функции:
.
Производные высших порядков показательной функции
Теперь рассмотрим показательную функцию с основанием степени a
:
.
Мы нашли ее производную первого порядка:
(15) .
Дифференцируя (15), получаем производные второго и третьего порядка:
;
.
Мы видим, что каждое дифференцирование приводит к умножению исходной функции на .
Поэтому производная n-го порядка имеет следующий вид:
.
Пусть функция y = f(x) определена в промежутке X. Производной функции y = f(x) в точке х o называется предел
= .
Если этот предел конечный, то функция f(x) называется дифференцируемой в точке x o ; при этом она оказывается обязательно и непрерывной в этой точке.
Если же рассматриваемый предел равен (или — ), то при условии, что функция в точке х o непрерывна, будем говорить, что функция f(x) имеет в точке х o бесконечную производную .
Производная обозначается символами
y , f (x o), , .
Нахождение
производной называется дифференцированием функции. Геометрический
смысл производной состоит в том,что
производная есть угловой коэффициент
касательной к кривой y=f(x) в данной точке х o ; физический
смысл — в
том, что производная от пути по времени
есть мгновенная скорость движущейся
точки при прямолинейном движении s =
s(t) в момент t o .
Если с — постоянное число, и u = u(x), v = v(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
1) (с) » = 0, (cu) » = cu»;
2) (u+v)» = u»+v»;
3) (uv)» = u»v+v»u;
4) (u/v)» = (u»v-v»u)/v 2;
5) если y = f(u), u = (x), т.е. y = f((x)) — сложная функция, или суперпозиция , составленная из дифференцируемых функций и f, то , или
6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем 0, то .
На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций.
1. (u )» = u 1 u» ( R ).
2. (a u)» = a u lna u».
3. (e u)» = e u u».
4. (log a u)» = u»/(u ln a).
5. (ln u)» = u»/u.
6. (sin u)» = cos u u».
7. (cos u)» = — sin u u».
8.
(tg u)» = 1/ cos 2 u
u».
9. (ctg u)» = — u» / sin 2 u.
10. (arcsin u)» = u» / .
11. (arccos u)» = — u» / .
12. (arctg u)» = u»/(1 + u 2).
13. (arcctg u)» = — u»/(1 + u 2).
Вычислим производную степенно-показательного выражения y=u v , (u>0), где u и v суть функции от х , имеющие в данной точке производные u» , v» .
Прологарифмировав равенство y=u v , получим ln y = v ln u.
Приравнивая производные по х от обеих частей полученного равенства с помощью правил 3, 5 и формулы для производной логарифмической функции, будем иметь:
y»/y = vu»/u +v» ln u, откуда y» = y (vu»/u +v» ln u).
(u v)»=u v (vu»/u+v» ln u), u > 0.
Например, если y = x sin x , то y» = x sin x (sin x/x + cos x ln x).
Если
функция y = f(x) дифференцируема в точке x ,
т.е. имеет в этой точке конечную
производную y» ,
то
=
y»+,
где 0
при х
0; отсюда
y = y» х
+
x.
Главная часть приращения функции, линейная относительно х, называется дифференциалом функции и обозначается dy: dy = y» х. Если положить в этой формуле y=x, то получим dx = x»х = 1х =х, поэтому dy=y»dx, т. е. символ для обозначения производной можно рассматривать как дробь.
Приращение функции y есть приращение ординаты кривой, а дифференциал dy есть приращение ординаты касательной.
Пусть мы нашли для функции y=f(x) ее производную y = f (x). Производная от этой производной называется производной второго порядка функции f(x), или второй производной, и обозначается .
Аналогично определяются и обозначаются:
производная третьего порядка — ,
производная четвертого порядка —
и вообще производная n-го порядка — .
Пример 3 .15. Вычислить производную функции y=(3x 3 -2x+1)sin x.
Решение. По правилу
3, y»=(3x 3 -2x+1)»sin
x + (3x 3 -2x+1)(sin
x)» =
= (9x 2 -2)sin
x + (3x 3 -2x+1)cos
x.
Пример 3.16 . Найти y», y = tg x + .
Решение. Используя правила дифференцирования суммы и частного, получим: y»=(tgx + )» = (tgx)» + ()» = + = .
Пример 3 .17. Найти производную сложной функции y= , u=x 4 +1.
Решение. По правилу дифференцирования сложной функции, получим: y» x =y » u u» x =()» u (x 4 +1)» x =(2u + . Так как u=x 4 +1,то (2 x 4 +2+ .
Содержание статьи
ПРОИЗВОДНАЯ –производной функции y = f (x ), заданной на некотором интервале (a , b ) в точке x этого интервала, называется предел, к которому стремится отношение приращения функции f в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.
Производную принято обозначать так:
Широко употребляются и другие обозначения:
Мгновенная скорость.
Пусть точка M движется по прямой. Расстояние s движущейся точки, отсчитываемое от некоторого начального ее положения M 0 , зависит от времени t , т.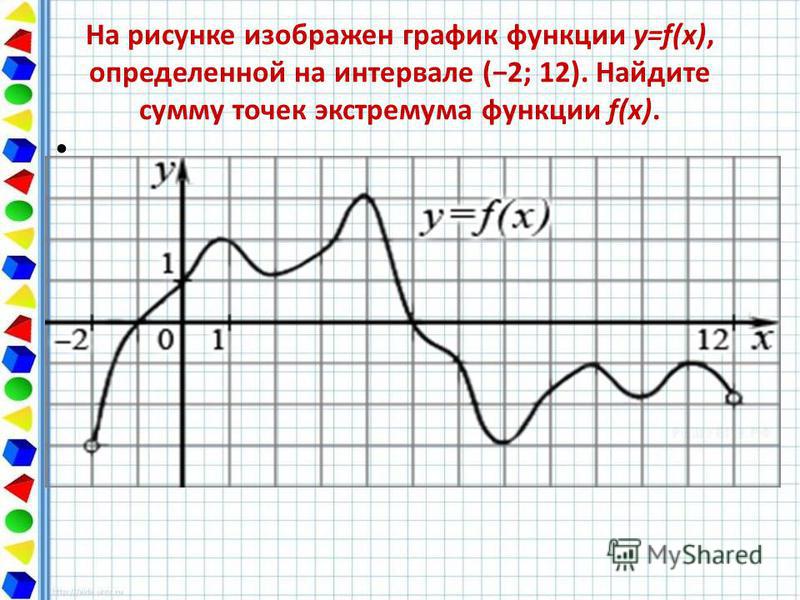 е. s есть функция времени t : s = f (t ). Пусть в некоторый момент времени t движущаяся точка M находилась на расстоянии s от начального положения M 0, а в некоторый следующий момент t + Dt оказалась в положении M 1 – на расстоянии s + Ds от начального положения (см. рис .).
е. s есть функция времени t : s = f (t ). Пусть в некоторый момент времени t движущаяся точка M находилась на расстоянии s от начального положения M 0, а в некоторый следующий момент t + Dt оказалась в положении M 1 – на расстоянии s + Ds от начального положения (см. рис .).
Таким образом, за промежуток времени Dt расстояние s изменилось на величину Ds . В этом случае говорят, что за промежуток времени Dt величина s получила приращение Ds .
Средняя скорость не может во всех случаях точно охарактеризовать быстроту перемещения точки M в момент времени t . Если, например, тело в начале промежутка Dt перемещалось очень быстро, а в конце очень медленно, то средняя скорость не сможет отразить указанных особенностей движения точки и дать представление об истинной скорости ее движения в момент t .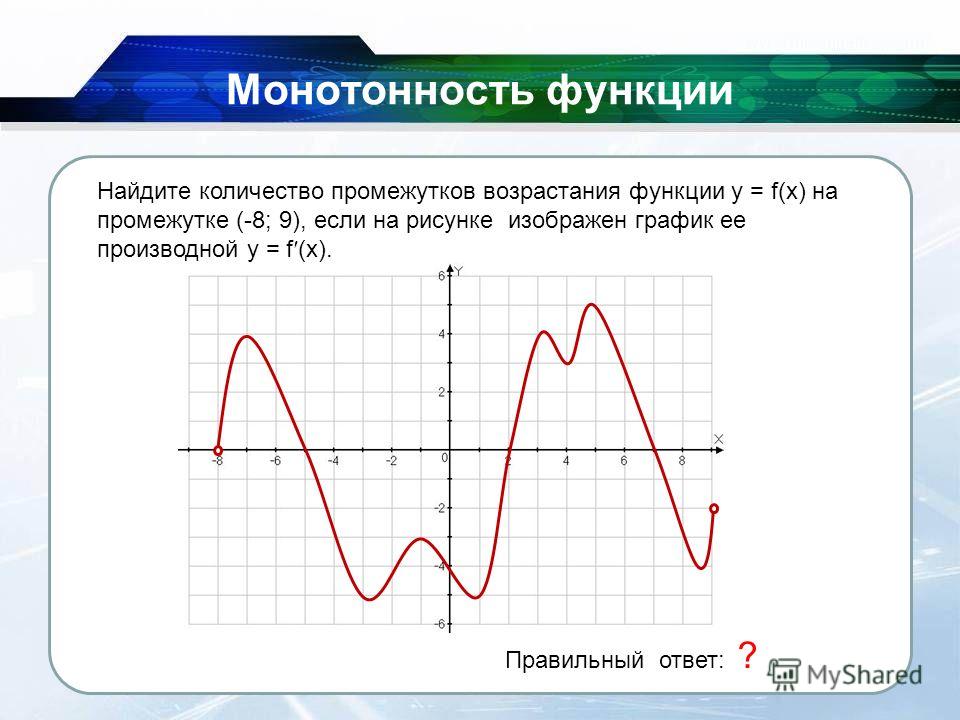 Чтобы точнее выразить истинную скорость с помощью средней скорости, надо взять меньший промежуток времени Dt . Наиболее полно характеризует скорость движения точки в момент t тот предел, к которому стремится средняя скорость при Dt ® 0. Этот предел называют скоростью движения в данный момент:
Чтобы точнее выразить истинную скорость с помощью средней скорости, надо взять меньший промежуток времени Dt . Наиболее полно характеризует скорость движения точки в момент t тот предел, к которому стремится средняя скорость при Dt ® 0. Этот предел называют скоростью движения в данный момент:
Таким образом, скоростью движения в данный момент называется предел отношения приращения пути Ds к приращению времени Dt , когда приращение времени стремится к нулю. Так как
Геометрическое значение производной. Касательная к графику функции.
Построение касательных – одна из тех задач, которые привели к рождению дифференциального исчисления. Первый опубликованный труд, относящийся к дифференциальному исчислению и принадлежащий перу Лейбница, имел название Новый метод максимумов и минимумов, а также касательных, для которого не служат препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления .
Пусть кривая есть график функции y = f (x ) в прямоугольной системе координат (см . рис.).
рис.).
При некотором значении x функция имеет значение y = f (x ). Этим значениям x и y на кривой соответствует точка M 0(x , y ). Если аргументу x дать приращение Dx , то новому значению аргумента x + Dx соответствует новое значение функции y+ Dy = f (x + Dx ). Соответствующей ему точкой кривой будет точка M 1(x + Dx , y + Dy ). Если провести секущую M 0M 1 и обозначить через j угол, образованный секущей с положительным направлением оси Ox , из рисунка непосредственно видно, что .
Если теперь Dx стремится к нулю, то точка M 1 перемещается вдоль кривой, приближаясь к точке M 0, и угол j изменяется с изменением Dx . При Dx ® 0 угол j стремится к некоторому пределу a и прямая, проходящая через точку M 0 и составляющая с положительным направлением оси абсцисс угол a, будет искомой касательной. Ее угловой коэффициент:
Ее угловой коэффициент:
Следовательно, f ´(x ) = tga
т.е. значение производной f ´(x ) при данном значении аргумента x равняется тангенсу угла, образованного касательной к графику функции f (x ) в соответствующей точке M 0(x ,y ) с положительным направлением оси Ox .
Дифференцируемость функций.
Определение. Если функция y = f (x ) имеет производную в точке x = x 0, то функция дифференцируема в этой точке.
Непрерывность функции, имеющей производную. Теорема.
Если функция y = f (x ) дифференцируема в некоторой точке x = x 0, то она в этой точке непрерывна.
Таким образом, в точках разрыва функция не может иметь производной. Обратное заключение неверно, т.е. из того, что в какой-нибудь точке x = x 0 функция y = f (x ) непрерывна не следует, что она в этой точке дифференцируема. Например, функция y = |x | непрерывна для всех x (–Ґ х x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.
Например, функция y = |x | непрерывна для всех x (–Ґ х x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.
Некоторые теоремы о дифференцируемых функциях. Теорема о корнях производной (теорема Ролля). Если функция f (x ) непрерывна на отрезке [a ,b ], дифференцируема во всех внутренних точках этого отрезка и на концах x = a и x = b обращается в нуль (f (a ) = f (b ) = 0), то внутри отрезка [a ,b ] существует, по крайней мере одна, точка x = с , a c b, в которой производная f ў(x ) обращается в нуль, т.е. f ў(c ) = 0.
Теорема о конечных приращениях (теорема Лагранжа). Если функция f (x ) непрерывна на отрезке [a , b ] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a , b ] найдется по крайней мере одна точка с , a c b, что
f (b ) – f (a ) = f ў(c )(b – a ).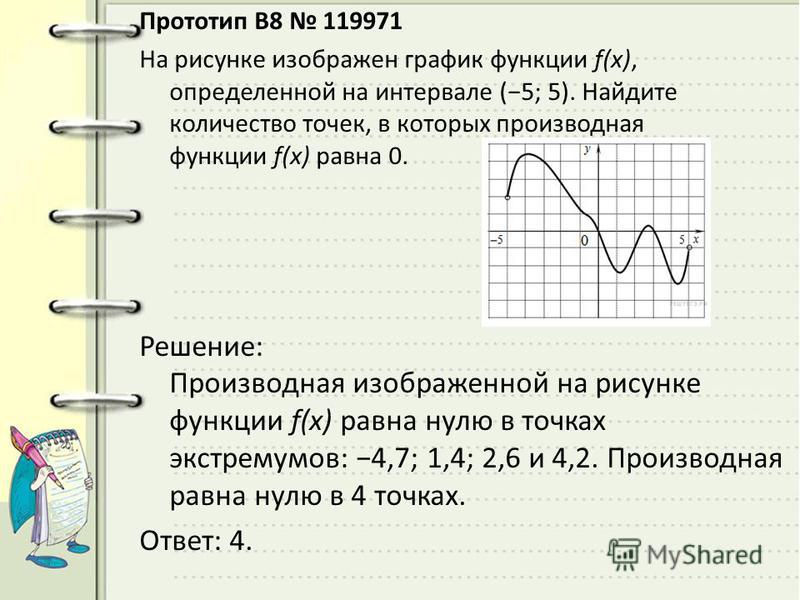
Теорема об отношении приращений двух функций (теорема Коши). Если f (x ) и g (x ) – две функции, непрерывные на отрезке [a , b ] и дифференцируемые во всех внутренних точках этого отрезка, причем g ў(x ) нигде внутри этого отрезка не обращается в нуль, то внутри отрезка [a , b ] найдется такая точка x = с , a c b, что
Производные различных порядков.
Пусть функция y = f (x ) дифференцируема на некотором отрезке [a , b ]. Значения производной f ў(x ), вообще говоря, зависят от x , т.е. производная f ў(x ) представляет собой тоже функцию от x . При дифференцировании этой функции получается так называемая вторая производная от функции f (x ), которая обозначается f ўў (x ).
Производной n- го порядка от функции f (x ) называется производная (первого порядка) от производной n- 1— го и обозначается символом y (n ) = (y (n – 1))ў.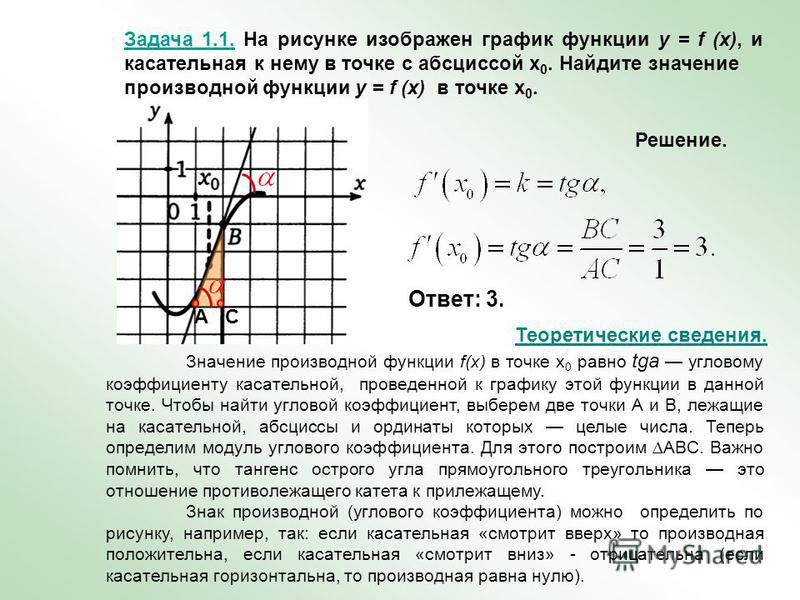
Дифференциалы различных порядков.
Дифференциал функции y = f (x ), где x – независимая переменная, есть dy = f ў(x )dx , некоторая функция от x , но от x может зависеть только первый сомножитель f ў(x ), второй же сомножитель (dx ) является приращением независимой переменной x и от значения этой переменной не зависит. Так как dy есть функция от x , то можно определить дифференциал этой функции. Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d 2y :
d (dx ) = d 2y = f ўў(x )(dx ) 2 .
Дифференциалом n- го порядка называется первый дифференциал от дифференциала n- 1— го порядка:
d n y = d (d n –1 y ) = f (n )(x )dx (n ).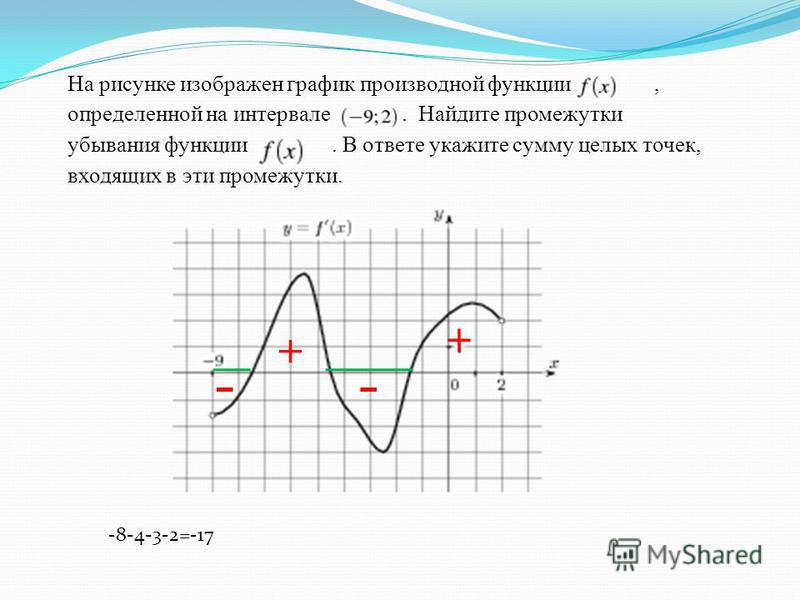
Частная производная.
Если функция зависит не от одного, а от нескольких аргументов x i (i изменяется от 1 до n , i = 1, 2,… n ), f (x 1, x 2,… x n ), то в дифференциальном исчислении вводится понятие частной производной, которая характеризует скорость изменения функции нескольких переменных, когда изменяется только один аргумент, например, x i . Частная производная 1-ого порядка по x i определяется как обычная производная, при этом предполагается, что все аргументы, кроме x i , сохраняют постоянные значения. Для частных производных вводятся обозначения
Определенные таким образом частные производные 1-ого порядка (как функции тех же аргументов) могут, в свою очередь, также иметь частные производные, это частные производные второго порядка и т.д. Взятые по разным аргументам такие производные называются смешанными. Непрерывные смешанные производные одного порядка не зависят от порядка дифференцирования и равны между собой.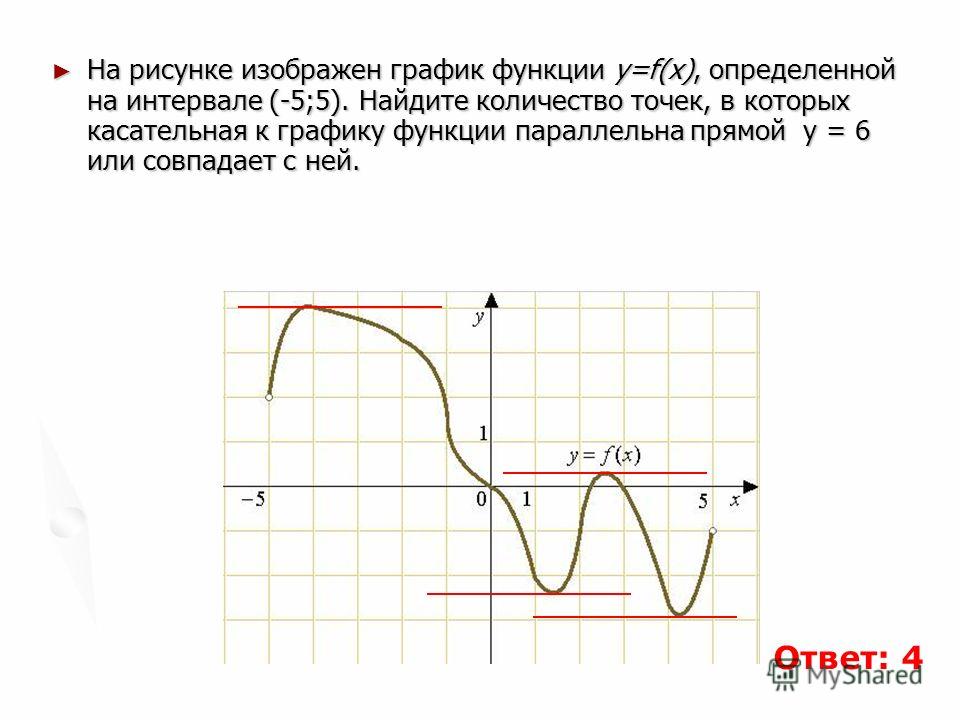
Анна Чугайнова
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Когда производная функции равна. Найти производную: алгоритм и примеры решений
Вычисление производной часто встречается в заданиях ЕГЭ. Данная страница содержит список формул для нахождения производных.
Правила дифференцирования
- (k⋅ f(x))′=k⋅ f ′(x).
- (f(x)+g(x))′=f′(x)+g′(x).
- (f(x)⋅ g(x))′=f′(x)⋅ g(x)+f(x)⋅ g′(x).
- Производная сложной функции.
 Если y=F(u), а u=u(x), то функция y=f(x)=F(u(x)) называется сложной функцией от x. Равна y′(x)=Fu′⋅
ux′.
Если y=F(u), а u=u(x), то функция y=f(x)=F(u(x)) называется сложной функцией от x. Равна y′(x)=Fu′⋅
ux′. - Производная неявной функции. Функция y=f(x) называется неявной функцией, заданной соотношением F(x,y)=0, если F(x,f(x))≡0.
- Производная обратной функции. Если g(f(x))=x, то функция g(x) называется обратной функцией для функции y=f(x).
- Производная параметрически заданной функции. Пусть x и y заданы как функции от переменной t: x=x(t), y=y(t). Говорят, что y=y(x) параметрически заданная функция на промежутке x∈ (a;b), если на этом промежутке уравнение x=x(t) можно выразить в виде t=t(x) и определить функцию y=y(t(x))=y(x).
- Производная степенно-показательной функции. Находится путем логарифмирования по основанию натурального логарифма.
Советуем сохранить ссылку, так как эта таблица может понадобиться еще много раз.
Когда человек сделал первые самостоятельные шаги в изучении математического анализа и начинает задавать неудобные вопросы, то уже не так-то просто отделаться фразой, что «дифференциальное исчисление найдено в капусте». Поэтому настало время набраться решимости и раскрыть тайну появления на светтаблицы производных и правил дифференцирования
. Начало положено в статьео смысле производной
, которую я настоятельно рекомендую к изучению, поскольку там мы как раз рассмотрели понятие производной и начали щёлкать задачи по теме. Этот же урок носит ярко выраженную практическую направленность, более того,
Поэтому настало время набраться решимости и раскрыть тайну появления на светтаблицы производных и правил дифференцирования
. Начало положено в статьео смысле производной
, которую я настоятельно рекомендую к изучению, поскольку там мы как раз рассмотрели понятие производной и начали щёлкать задачи по теме. Этот же урок носит ярко выраженную практическую направленность, более того,
рассматриваемые ниже примеры, в принципе, можно освоить и чисто формально (например, когда нет времени/желания вникать в суть производной). Также крайне желательно (однако опять не обязательно) уметь находить производные «обычным» методом – хотя бы на уровне двух базовых занятий: Как найти производную?и Производная сложной функции.
Но без чего-чего сейчас точно не обойтись, так это безпределов функций . Вы должны ПОНИМАТЬ, что такое предел и уметь решать их, как минимум, на среднем уровне. А всё потому, чтопроизводная
функции в точке определяется формулой:
Напоминаю обозначения и термины: называютприращением аргумента ;
– приращением функции;
– это ЕДИНЫЕ символы («дельту» нельзя «отрывать» от «икса» или «игрека»).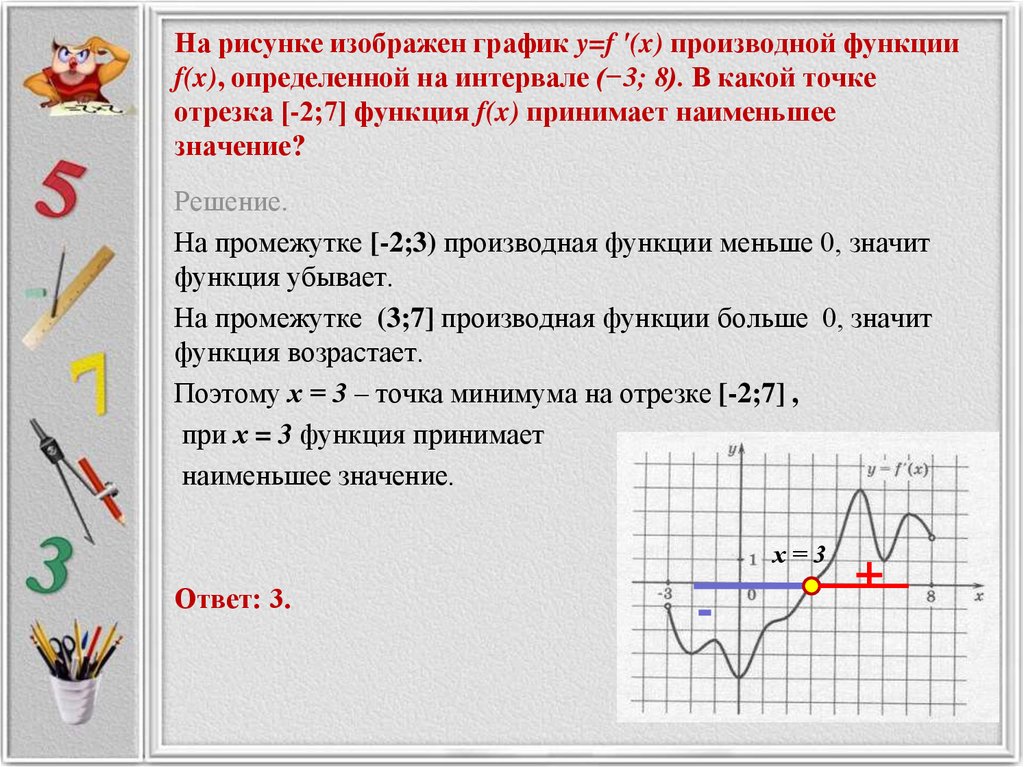
Очевидно, что является «динамической» переменной,– константой и результат вычисления предела– числом(иногда – «плюс» либо «минус» бесконечностью) .
В качестве точки можно рассмотреть ЛЮБОЕ значение, принадлежащееобласти определения функции, в котором существует производная.
Примечание : оговорка «в котором существует производная» –в общем случае существенна ! Так, например, точкахоть и входит в область определения функции, но производной
там не существует. Поэтому формула
не применима в точке,
и укороченная формулировка без оговорки будет некорректна. Аналогичные факты справедливы и для других функций с «обрывами» графика, в частности, для арксинуса и арккосинуса.
Таким образом, после замены , получаем вторую рабочую формулу:
Обратите внимание на коварное обстоятельство, которое может запутать чайника: в данном пределе «икс», будучи сам независимой переменной, исполняет роль статиста, а «динамику» задаёт опять же приращение . Результатом вычисления предела
является производная функция.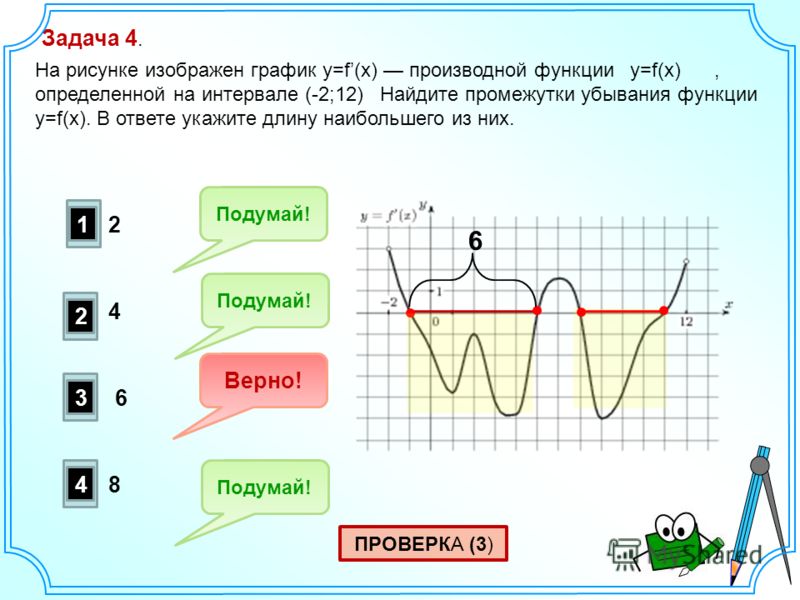
Исходя из вышесказанного, сформулируем условия двух типовых задач:
– Найти производную в точке , используя определение производной.
– Найти производную функцию , используя определение производной. Эта версия, по моим наблюдениям, встречается заметно чаще и ей будет уделено основное внимание.
Принципиальное отличие заданий состоит в том, что в первом случае требуется найти число (как вариант, бесконечность) , а во втором –
функцию . Кроме того, производной может и вовсе не существовать.
Как ?
Составить отношение и вычислить предел.
Откуда появилась таблица производных и правила дифференцирования? Благодаря единственному пределу
Кажется волшебством, но в
действительности – ловкость рук и никакого мошенничества. На уроке Что такое производная? я начал рассматривать конкретные примеры, где с помощью определения нашёл производные линейной и квадратичной функции. В целях познавательной разминки продолжим тревожитьтаблицу производных , оттачивая алгоритм и технические приёмы решения:
По сути, требуется доказать частный случай производной степенной функции, который обычно фигурирует в таблице: .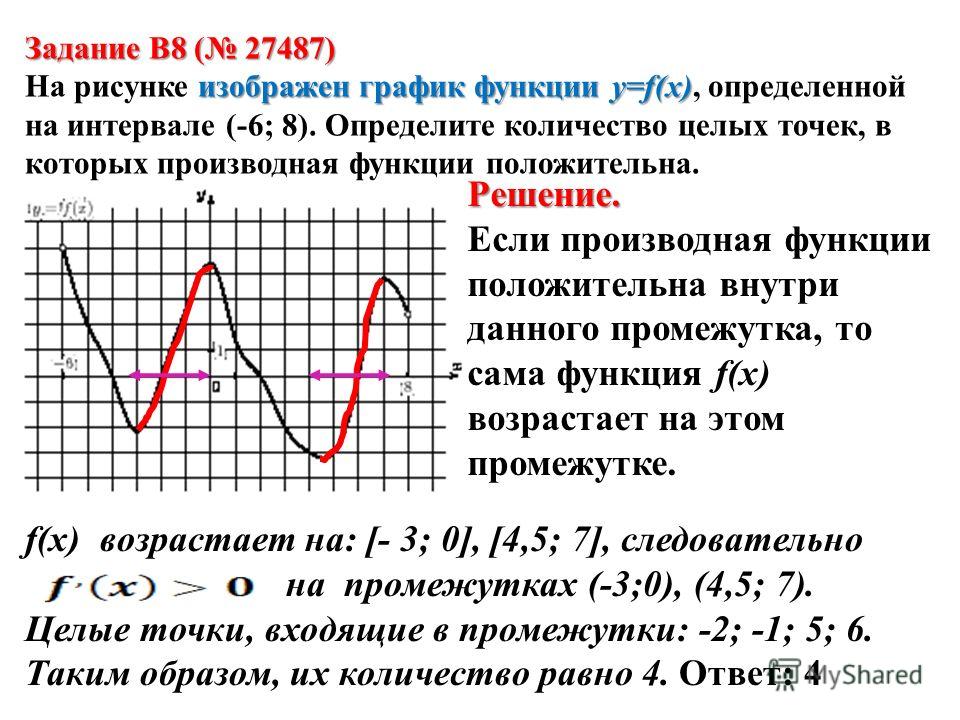
Решение технически оформляется двумя способами. Начнём с первого, уже знакомого подхода: лесенка начинается с дощечки, а производная функция – с производной в точке.
Рассмотрим некоторую (конкретную) точку, принадлежащуюобласти определения функции, в которой существует производная. Зададим в данной точке приращение (разумеется, не выходящее за рамки о/о -я) и составим соответствующее приращение функции:
Вычислим предел:
Неопределённость 0:0 устраняется стандартным приёмом, рассмотренным ещё в первом веке до нашей эры. Домножим
числитель и знаменатель на сопряженное выражение :
Техника решения такого предела подробно рассмотрена на вводном уроке о пределах функций .
Поскольку в качестве можно выбрать ЛЮБУЮ точкуинтервала
То, осуществив замену, получаем:
В который раз порадуемся логарифмам:
Найти производную функции , пользуясь определением производной
Решение
: рассмотрим другой подход к раскрутке той же задачи. Он точно такой же, но более рационален с точки зрения оформления. Идея состоит в том, чтобы в начале решения избавиться от
Идея состоит в том, чтобы в начале решения избавиться от
подстрочного индекса и вместо буквы использовать букву.
Рассмотрим произвольную точку, принадлежащуюобласти определения функции(интервалу), и зададим в ней приращение.А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
Тогда соответствующее приращение функции:
Найдём производную:
Простота оформления уравновешивается путаницей, которая может
возникнуть у начинающих (да и не только). Ведь мы привыкли, что в пределе изменяется буква «икс»! Но тут всё по-другому: – античная статуя, а– живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
Устранение неопределённости закомментирую пошагово:
(1) Используем свойство логарифма .
(2) В скобках почленно делим числитель на знаменатель.
(3) В знаменателе искусственно домножаем и делим на «икс» чтобы
воспользоваться замечательным пределом , при этом в качествебесконечно малой величины
выступает.
Ответ : по определению производной:
Или сокращённо:
Предлагаю самостоятельно сконструировать ещё две табличные формулы:
Найти производную по определению
В данном случае составленное приращение сразу же удобно привести к общему знаменателю. Примерный образец оформления задания в конце урока (первый способ).
Найти производную по определению
А тут всё необходимо свести к замечательному пределу . Решение оформлено вторым способом.
Аналогично выводится ряд других табличных производных . Полный список можно найти в школьном учебнике, или, например, 1- м томе Фихтенгольца. Не вижу особого смысла переписывать из книг и доказательства правил дифференцирования – они тоже порождены
формулой .
Переходим к реально встречающимся заданиям: Пример 5
Найти производную функции , используя определение производной
Решение
: используем первый стиль оформления. Рассмотрим некоторую точку, принадлежащую, и зададим в ней приращение аргумента.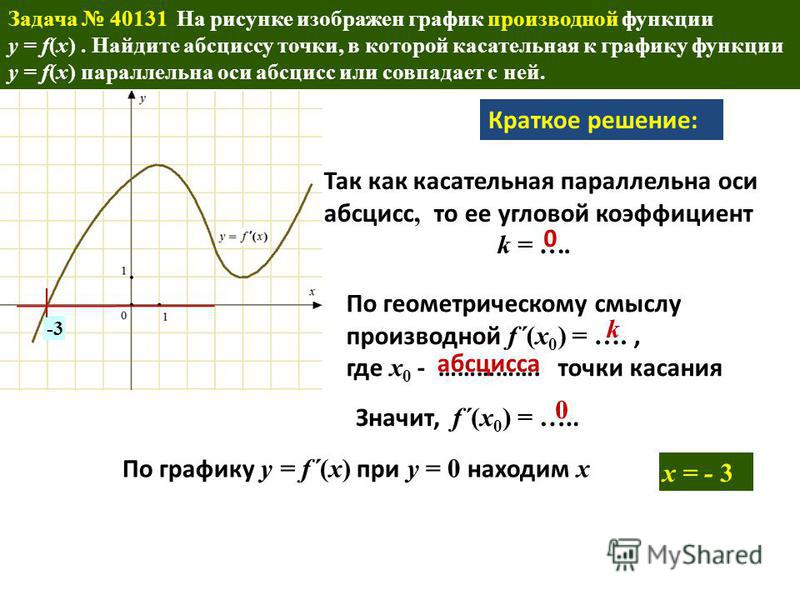 Тогда соответствующее приращение функции:
Тогда соответствующее приращение функции:
Возможно, некоторые читатели ещё не до конца поняли принцип, по которому нужно составлять приращение . Берём точку(число) и находим в ней значение функции:, то есть в функцию
вместо «икса» следует подставить. Теперь берём
Составленное приращение функции бывает выгодно сразу же упростить . Зачем? Облегчить и укоротить решение дальнейшего предела.
Используем формулы , раскрываем скобки и сокращаем всё, что можно сократить:
Индейка выпотрошена, с жаркое никаких проблем:
В итоге:
Поскольку в качестве можно выбрать любое действительное число, то проведём заменуи получим.
Ответ :по определению.
В целях проверки найдём производную с помощью правил
дифференцирования и таблицы:
Всегда полезно и приятно знать правильный ответ заранее, поэтому лучше мысленно либо на черновике продифференцировать предложенную функцию «быстрым» способом в самом начале решения.
Найти производную функции по определению производной
Это пример для самостоятельного решения. Результат лежит на поверхности:
Результат лежит на поверхности:
Вернёмся к стилю №2: Пример 7
Давайте немедленно узнаем, что должно получиться. По правилу дифференцирования сложной функции :
Решение : рассмотрим произвольную точку, принадлежащую, зададим в ней приращение аргументаи составим приращение
Найдём производную:
(1) Используем тригонометрическую формулу
(2) Под синусом раскрываем скобки, под косинусом приводим подобные слагаемые.
(3) Под синусом сокращаем слагаемые, под косинусом почленно делим числитель на знаменатель.
(4) В силу нечётности синуса выносим «минус». Под косинусом
указываем, что слагаемое .
(5) В знаменателе проводим искусственное домножение, чтобы использовать первый замечательный предел . Таким образом, неопределённость устранена, причёсываем результат.
Ответ :по определению Как видите, основная трудность рассматриваемой задачи упирается в
сложность самого предела + небольшое своеобразие упаковки. На практике встречаются и тот и другой способ оформления, поэтому я максимально подробно расписываю оба подхода. Они равноценны, но всё-таки, по моему субъективному впечатлению, чайникам целесообразнее придерживаться 1-го варианта с «икс нулевым».
Они равноценны, но всё-таки, по моему субъективному впечатлению, чайникам целесообразнее придерживаться 1-го варианта с «икс нулевым».
Пользуясь определением, найти производную функции
Это задание для самостоятельного решения. Образец оформлен в том же духе, что предыдущий пример.
Разберём более редкую версию задачи:
Найти производную функции в точке, пользуясь определением производной.
Во-первых, что должно получиться в сухом остатке? Число Вычислим ответ стандартным способом:
Решение : с точки зрения наглядности это задание значительно проще, так как в формулевместо
рассматривается конкретное значение.
Зададим в точке приращениеи составим соответствующее приращение функции:
Вычислим производную в точке:
Используем весьма редкую формулу разности тангенсов и в который раз сведём решение кпервому
замечательному пределу:
Ответ :по определению производной в точке.
Задачу не так трудно решить и «в общем виде» – достаточно заменить наили простов зависимости от способа оформления.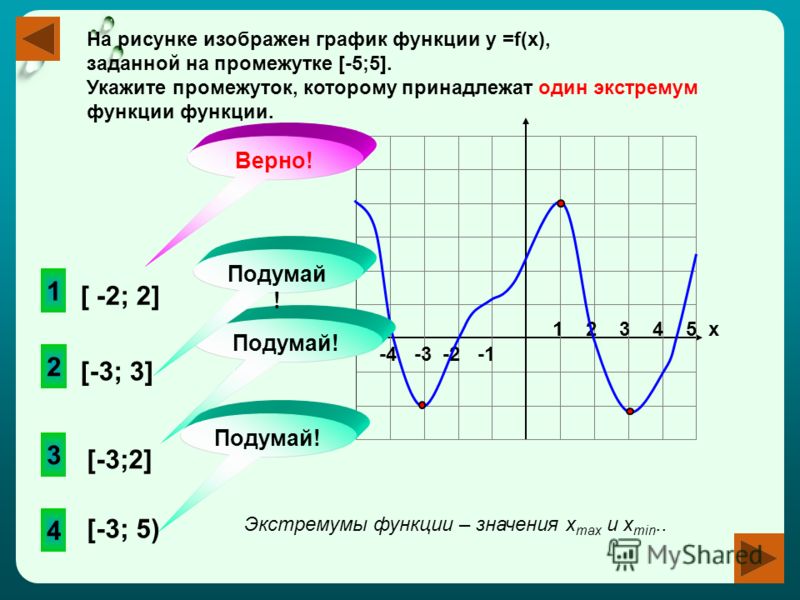 В этом случае, понятно, получится не число, а производная функция.
В этом случае, понятно, получится не число, а производная функция.
Пример 10 Используя определение, найти производную функциив точке
Это пример для самостоятельного решения.
Заключительная бонус-задача предназначена, прежде всего, для студентов с углубленным изучением математического анализа, но и всем остальным тоже не помешает:
Будет ли дифференцируема функция в точке?
Решение : очевидно, что кусочно-заданная функциянепрерывна в точке, но будет ли она там дифференцируема?
Алгоритм решения, причём не только для кусочных функций, таков:
1) Находим левостороннюю производнуюв данной точке: .
2) Находим правостороннюю производнуюв данной точке: .
3) Если односторонние производныеконечны и совпадают:
, то функциядифференцируема в точкеи
геометрически здесь существует общая касательная (см. теоретическую часть урока Определение и смысл производной ).
Если получены два разных значения: (одно из которых может оказаться и бесконечным)
, то функция не дифференцируема в точке.
Если же обе односторонние производные равны бесконечности
(пусть даже разных знаков), то функция не
дифференцируема в точке , но там существует бесконечная производная и общая вертикальная касательная к графику(см. Пример 5 урока Уравнение нормали ) .
Производная — главнейшее понятие математического анализа. Она характеризует изменение функции аргумента x в некоторой точке. При этом и сама производная является функцией от аргумента x
Производной функции в точке называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю.
Наиболее употребительны следующие обозначения производной :
Пример 1. Пользуясь определением производной , найти производную функции
Решение. Из определения производной вытекает следующая схема её вычисления.
Дадим аргументу приращение (дельта) и найдём приращение функции:
Найдём отношение приращения функции к приращению аргумента:
Вычислим предел этого отношения при условии, что приращение аргумента стремится к нулю, то есть требуемую в условии задачи производную:
Физический смысл производной
К понятию производной привело изучение Галилео Галилеем закона свободного падения тел, а в
более широком смысле — задачи о мгновенной скорости неравномерного прямолинейного движения точки.
Пусть камешек поднят и затем из состояния покоя отпущен. Путь s , проходимый за время t , является функцией времени, то есть. s = s (t ). Если задан закон движения точки, то можно определить среднюю скорость за любой промежуток времени. Пусть в момент времени камешек находился в положении A , а в момент — в положении B . За промежуток времени (от t до ) точка прошла путь . Поэтому средняя скорость движения за этот промежуток времени, которую обзначим через , составляет
.
Однако движение свободно падающего тела явно неравномерное. Скорость v падения постоянно возрастает. И средней скорости уже недостаточно для характеристики быстроты движения на различных участках пути. Такая характеристика тем точнее, чем меньше промежуток времени . Поэтому вводится следующее понятие: мгновенной скоростью прямолинейного движения (или скоростью в данный момент времени t ) называется предел средней скорости при :
(при условии, что этот предел существует и конечен).
Так выясняется, что мгновенная скорость есть предел отношения приращения функции s (t ) к приращению аргумента t при Это и есть производная, которая в общем виде записывается так:.
.
Решение обозначенной задачи представляет собой физический смысл производной . Итак, производной функции y=f (x ) в точке x называется предел (если он существует и конечен) приращения функции к приращению аргумента при условии, что последнее стремится к нулю.
Пример 2. Найти производную функции
Решение. Из определения производной вытекает следующая схема для её вычисления.
Шаг 1. Дадим аргументу приращение и найдём
Шаг 2. Найдём приращение функции:
Шаг 3. Найдём отношение приращения функции к приращению аргумента:
Шаг 4. Вычислим предел этого отношения при , то есть производную:
Геометрический смысл производной
Пусть функция определена на интервале и пусть точка М на графике функции соответствует значению аргумента , а точка Р – значению . Проведём через точки М и Р прямую и назовём её секущей . Обозначим через угол между секущей и осью . Очевидно, что этот угол зависит от .
Проведём через точки М и Р прямую и назовём её секущей . Обозначим через угол между секущей и осью . Очевидно, что этот угол зависит от .
Если существует
проходящую через точку , называют предельным положением секущей МР при (или при ).
Касательной к графику функции в точке М называется предельное положение секущей МР при , или, что то же при .
Из определения следует, что для существования касательной достаточно, чтобы существовал предел
,
причём предел равен углу наклона касательной к оси .
Теперь дадим точное определение касательной.
Касательной к графику функции в точке называется прямая, проходящая через точку и имеющая угловой коэффициент , т.е. прямая, уравнение которой
Из этого определения следует, что производная функции равна угловому коэффициенту касательной к графику этой функции в точке с абсциссой x . В этом состоит геометрический смысл производной.
Пусть функция y = f(x) определена в промежутке X. Производной функции y = f(x) в точке х o называется предел
= .
Если этот предел конечный, то функция f(x) называется дифференцируемой в точке x o ; при этом она оказывается обязательно и непрерывной в этой точке.
Если же рассматриваемый предел равен (или — ), то при условии, что функция в точке х o непрерывна, будем говорить, что функция f(x) имеет в точке х o бесконечную производную .
Производная обозначается символами
y , f (x o), , .
Нахождение
производной называется дифференцированием функции. Геометрический
смысл производной состоит в том,что
производная есть угловой коэффициент
касательной к кривой y=f(x) в данной точке х o ; физический
смысл — в
том, что производная от пути по времени
есть мгновенная скорость движущейся
точки при прямолинейном движении s =
s(t) в момент t o .
Если с — постоянное число, и u = u(x), v = v(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
1) (с) » = 0, (cu) » = cu»;
2) (u+v)» = u»+v»;
3) (uv)» = u»v+v»u;
4) (u/v)» = (u»v-v»u)/v 2;
5) если y = f(u), u = (x), т.е. y = f((x)) — сложная функция, или суперпозиция , составленная из дифференцируемых функций и f, то , или
6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем 0, то .
На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций.
1. (u )» = u 1 u» ( R ).
2. (a u)» = a u lna u».
3. (e u)» = e u u».
4. (log a u)» = u»/(u ln a).
5. (ln u)» = u»/u.
6. (sin u)» = cos u u».
7. (cos u)» = — sin u u».
8.
(tg u)» = 1/ cos 2 u
u».
9. (ctg u)» = — u» / sin 2 u.
10. (arcsin u)» = u» / .
11. (arccos u)» = — u» / .
12. (arctg u)» = u»/(1 + u 2).
13. (arcctg u)» = — u»/(1 + u 2).
Вычислим производную степенно-показательного выражения y=u v , (u>0), где u и v суть функции от х , имеющие в данной точке производные u» , v» .
Прологарифмировав равенство y=u v , получим ln y = v ln u.
Приравнивая производные по х от обеих частей полученного равенства с помощью правил 3, 5 и формулы для производной логарифмической функции, будем иметь:
y»/y = vu»/u +v» ln u, откуда y» = y (vu»/u +v» ln u).
(u v)»=u v (vu»/u+v» ln u), u > 0.
Например, если y = x sin x , то y» = x sin x (sin x/x + cos x ln x).
Если
функция y = f(x) дифференцируема в точке x ,
т.е. имеет в этой точке конечную
производную y» ,
то
=
y»+,
где 0
при х
0; отсюда
y = y» х
+
x.
Главная часть приращения функции, линейная относительно х, называется дифференциалом функции и обозначается dy: dy = y» х. Если положить в этой формуле y=x, то получим dx = x»х = 1х =х, поэтому dy=y»dx, т. е. символ для обозначения производной можно рассматривать как дробь.
Приращение функции y есть приращение ординаты кривой, а дифференциал dy есть приращение ординаты касательной.
Пусть мы нашли для функции y=f(x) ее производную y = f (x). Производная от этой производной называется производной второго порядка функции f(x), или второй производной, и обозначается .
Аналогично определяются и обозначаются:
производная третьего порядка — ,
производная четвертого порядка —
и вообще производная n-го порядка — .
Пример 3 .15. Вычислить производную функции y=(3x 3 -2x+1)sin x.
Решение. По правилу
3, y»=(3x 3 -2x+1)»sin
x + (3x 3 -2x+1)(sin
x)» =
= (9x 2 -2)sin
x + (3x 3 -2x+1)cos
x.
Пример 3.16 . Найти y», y = tg x + .
Решение. Используя правила дифференцирования суммы и частного, получим: y»=(tgx + )» = (tgx)» + ()» = + = .
Пример 3 .17. Найти производную сложной функции y= , u=x 4 +1.
Решение. По правилу дифференцирования сложной функции, получим: y» x =y » u u» x =()» u (x 4 +1)» x =(2u + . Так как u=x 4 +1,то (2 x 4 +2+ .
Многие удивятся неожиданному расположению этой статьи в моём авторском курсе о производной функции одной переменной и её приложениях. Ведь как оно было ещё со школы: стандартный учебник в первую очередь даёт определение производной, её геометрический, механический смысл. Далее учащиеся находят производные функций по определению, и, собственно, только потом оттачивается техника дифференцирования с помощью таблицы производных .
Но с моей точки зрения, более прагматичен следующий подход: прежде всего, целесообразно ХОРОШО ПОНЯТЬ предел функции , и, в особенности, бесконечно малые величины . Дело в том, что определение производной базируется на понятии предела , которое слабо рассмотрено в школьном курсе. Именно поэтому значительная часть молодых потребителей гранита знаний плохо вникают в саму суть производной. Таким образом, если вы слабо ориентируетесь в дифференциальном исчислении либо мудрый мозг за долгие годы успешно избавился от оного багажа, пожалуйста, начните с пределов функций . Заодно освоите/вспомните их решение.
Дело в том, что определение производной базируется на понятии предела , которое слабо рассмотрено в школьном курсе. Именно поэтому значительная часть молодых потребителей гранита знаний плохо вникают в саму суть производной. Таким образом, если вы слабо ориентируетесь в дифференциальном исчислении либо мудрый мозг за долгие годы успешно избавился от оного багажа, пожалуйста, начните с пределов функций . Заодно освоите/вспомните их решение.
Тот же практический смысл подсказывает, что сначала выгодно научиться находить производные , в том числе производные сложных функций . Теория теорией, а дифференцировать, как говорится, хочется всегда. В этой связи лучше проработать перечисленные базовые уроки, а может и стать мастером дифференцирования , даже не осознавая сущности своих действий.
К материалам данной страницы рекомендую приступать после ознакомления со статьёй Простейшие задачи с производной , где, в частности рассмотрена задача о касательной к графику функции. Но можно и повременить. Дело в том, что многие приложения производной не требуют её понимания, и неудивительно, что теоретический урок появился достаточно поздно – когда мне потребовалось объяснять нахождение интервалов возрастания/убывания и экстремумов функции. Более того, он довольно долго находился в теме «Функции и графики », пока я всё-таки не решил поставить его раньше.
Но можно и повременить. Дело в том, что многие приложения производной не требуют её понимания, и неудивительно, что теоретический урок появился достаточно поздно – когда мне потребовалось объяснять нахождение интервалов возрастания/убывания и экстремумов функции. Более того, он довольно долго находился в теме «Функции и графики », пока я всё-таки не решил поставить его раньше.
Поэтому, уважаемые чайники, не спешите поглощать суть производной, как голодные звери, ибо насыщение будет невкусным и неполным.
Понятие возрастания, убывания, максимума, минимума функцииМногие учебные пособия подводят к понятию производной с помощью каких-либо практических задач, и я тоже придумал интересный пример. Представьте, что нам предстоит путешествие в город, до которого можно добраться разными путями. Сразу откинем кривые петляющие дорожки, и будем рассматривать только прямые магистрали. Однако прямолинейные направления тоже бывают разными: до города можно добраться по ровному автобану. Или по холмистому шоссе – вверх-вниз, вверх-вниз. Другая дорога идёт только в гору, а ещё одна – всё время под уклон. Экстремалы выберут маршрут через ущелье с крутым обрывом и отвесным подъемом.
Или по холмистому шоссе – вверх-вниз, вверх-вниз. Другая дорога идёт только в гору, а ещё одна – всё время под уклон. Экстремалы выберут маршрут через ущелье с крутым обрывом и отвесным подъемом.
Но каковы бы ни были ваши предпочтения, желательно знать местность или, по меньшей мере, располагать её топографической картой. А если такая информация отсутствует? Ведь можно выбрать, например, ровный путь, да в результате наткнуться на горнолыжный спуск с весёлыми финнами. Не факт, что навигатор и даже спутниковый снимок дадут достоверные данные. Поэтому неплохо бы формализовать рельеф пути средствами математики.
Рассмотрим некоторую дорогу (вид сбоку):
На всякий случай напоминаю элементарный факт: путешествие происходит слева направо . Для простоты полагаем, что функция непрерывна на рассматриваемом участке.
Какие особенности у данного графика?
На интервалах функция возрастает , то есть каждое следующее её значение больше предыдущего. Грубо говоря, график идёт снизу вверх (забираемся на горку). А на интервале функция убывает – каждое следующее значение меньше предыдущего, и наш график идёт сверху вниз (спускаемся по склону).
Грубо говоря, график идёт снизу вверх (забираемся на горку). А на интервале функция убывает – каждое следующее значение меньше предыдущего, и наш график идёт сверху вниз (спускаемся по склону).
Также обратим внимание на особые точки. В точке мы достигаем максимума , то есть существует такой участок пути, на котором значение будет самым большим (высоким). В точке же достигается минимум , и существует такая её окрестность, в которой значение самое маленькое (низкое).
Более строгую терминологию и определения рассмотрим на уроке об экстремумах функции , а пока изучим ещё одну важную особенность: на промежутках функция возрастает, но возрастает она с разной скоростью . И первое, что бросается в глаза – на интервале график взмывает вверх гораздо более круто , чем на интервале . Нельзя ли измерить крутизну дороги с помощью математического инструментария?
Скорость изменения функцииИдея состоит в следующем: возьмём некоторое значение (читается «дельта икс») , которое назовём приращением аргумента , и начнём его «примерять» к различным точкам нашего пути:
1) Посмотрим на самую левую точку: минуя расстояние , мы поднимаемся по склону на высоту (зелёная линия). Величина называется приращением функции , и в данном случае это приращение положительно (разность значений по оси – больше нуля). Составим отношение , которое и будет мерИлом крутизны нашей дороги. Очевидно, что – это вполне конкретное число, и, поскольку оба приращения положительны, то .
Величина называется приращением функции , и в данном случае это приращение положительно (разность значений по оси – больше нуля). Составим отношение , которое и будет мерИлом крутизны нашей дороги. Очевидно, что – это вполне конкретное число, и, поскольку оба приращения положительны, то .
Внимание! Обозначение являются ЕДИНЫМ символом, то есть нельзя «отрывать» «дельту» от «икса» и рассматривать эти буквы отдельно. Разумеется, комментарий касается и символа приращения функции.
Исследуем природу полученной дроби содержательнее. Пусть изначально мы находимся на высоте 20 метров (в левой чёрной точке). Преодолев расстояние метров (левая красная линия), мы окажемся на высоте 60 метров. Тогда приращение функции составит метров (зелёная линия) и: . Таким образом, на каждом метре этого участка дороги высота увеличивается в среднем на 4 метра …не забыли альпинистское снаряжение? =) Иными словами, построенное отношение характеризует СРЕДНЮЮ СКОРОСТЬ ИЗМЕНЕНИЯ (в данном случае – роста) функции.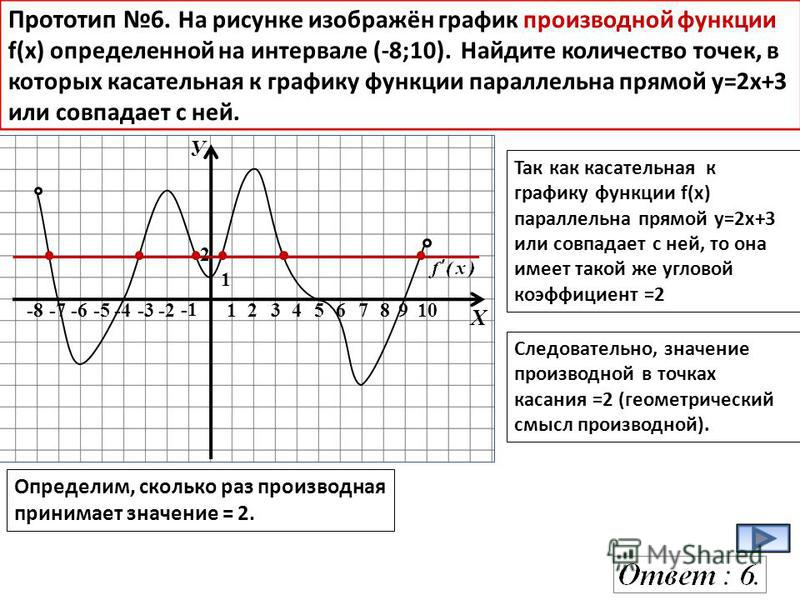
Примечание : числовые значения рассматриваемого примера соответствуют пропорциям чертежа лишь приблизительно.
2) Теперь пройдём то же самое расстояние от самой правой чёрной точки. Здесь подъём более пологий, поэтому приращение (малиновая линия) относительно невелико, и отношение по сравнению с предыдущим случаем будет весьма скромным. Условно говоря, метров и скорость роста функции составляет . То есть, здесь на каждый метр пути приходится в среднем пол метра подъёма.
3) Маленькое приключение на склоне горы. Посмотрим на верхнюю чёрную точку, расположенную на оси ординат. Предположим, что это отметка 50 метров. Снова преодолеваем расстояние , в результате чего оказываемся ниже – на уровне 30-ти метров. Поскольку осуществлено движение сверху вниз (в «противоход» направлению оси ), то итоговое приращение функции (высоты) будет отрицательным : метров (коричневый отрезок на чертеже). И в данном случае речь уже идёт о скорости убывания функции: , то есть за каждый метр пути этого участка высота убывает в среднем на 2 метра. Берегите одежду на пятой точке.
Берегите одежду на пятой точке.
Теперь зададимся вопросом: какое значение «измерительного эталона» лучше всего использовать? Совершенно понятно, 10 метров – это весьма грубо. На них запросто уместится добрая дюжина кочек. Да что там кочки, внизу может быть глубокое ущелье, а через несколько метров – другая его сторона с дальнейшим отвесным подъёмом. Таким образом, при десятиметровом мы не получим вразумительной характеристики подобных участков пути посредством отношения .
Из проведённого рассуждения следует вывод – чем меньше значение , тем точнее мы опишем рельеф дороги. Более того, справедливы следующие факты:
– Для любой точки подъемов можно подобрать значение (пусть и очень малое), которое умещается в границах того или иного подъёма. А это значит, что соответствующее приращение высоты будет гарантированно положительным, и неравенство корректно укажет рост функции в каждой точке этих интервалов.
– Аналогично, для любой точки склона существует значение , которое полностью уместится на этом склоне.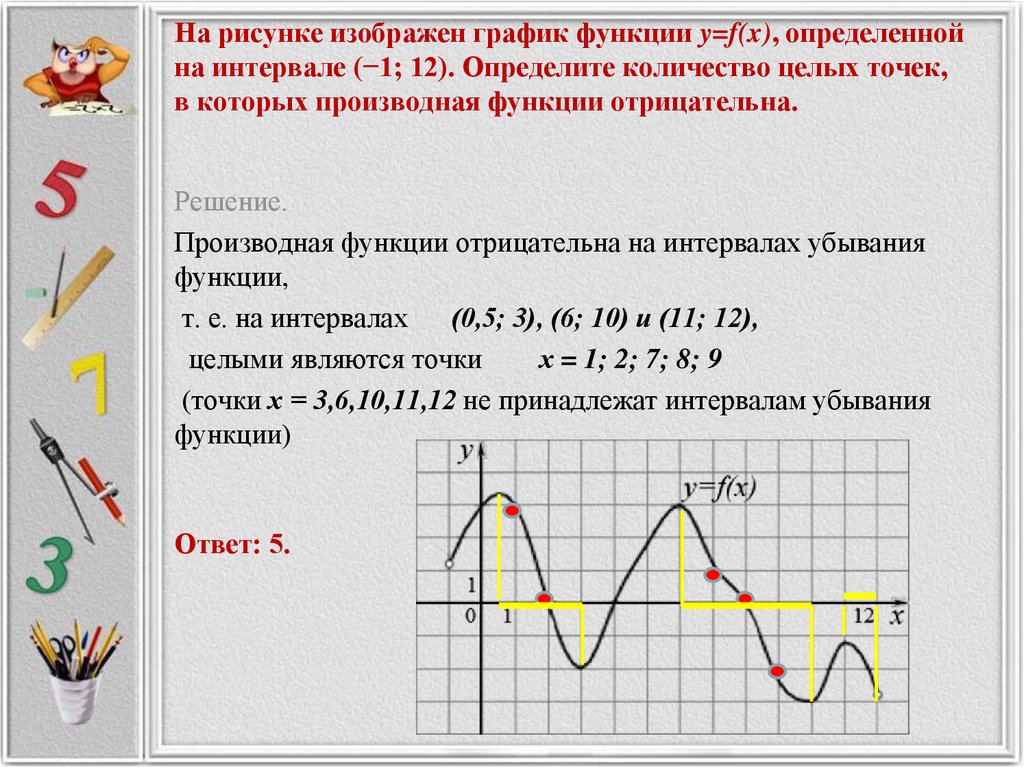 Следовательно, соответствующее приращение высоты однозначно отрицательно, и неравенство корректно покажет убыль функции в каждой точке данного интервала.
Следовательно, соответствующее приращение высоты однозначно отрицательно, и неравенство корректно покажет убыль функции в каждой точке данного интервала.
– Особо интересен случай, когда скорость изменения функции равна нулю: . Во-первых, нулевое приращение высоты () – признак ровного пути. А во-вторых, есть другие любопытные ситуации, примеры которых вы видите на рисунке. Представьте, что судьба завела нас на самую вершину холма с парящими орлами или дно оврага с квакающими лягушками. Если сделать небольшой шажок в любую сторону, то изменение высоты будет ничтожно мало, и можно сказать, что скорость изменения функции фактически нулевая. В точках наблюдается именно такая картина.
Таким образом, мы подобрались к удивительной возможности идеально точно охарактеризовать скорость изменения функции. Ведь математический анализ позволяет устремить приращение аргумента к нулю: , то есть сделать его бесконечно малым .
По итогу возникает ещё один закономерный вопрос: можно ли для дороги и её графика найти другую функцию , которая сообщала бы нам обо всех ровных участках, подъёмах, спусках, вершинах, низинах, а также о скорости роста/убывания в каждой точке пути?
Что такое производная? Определение производной.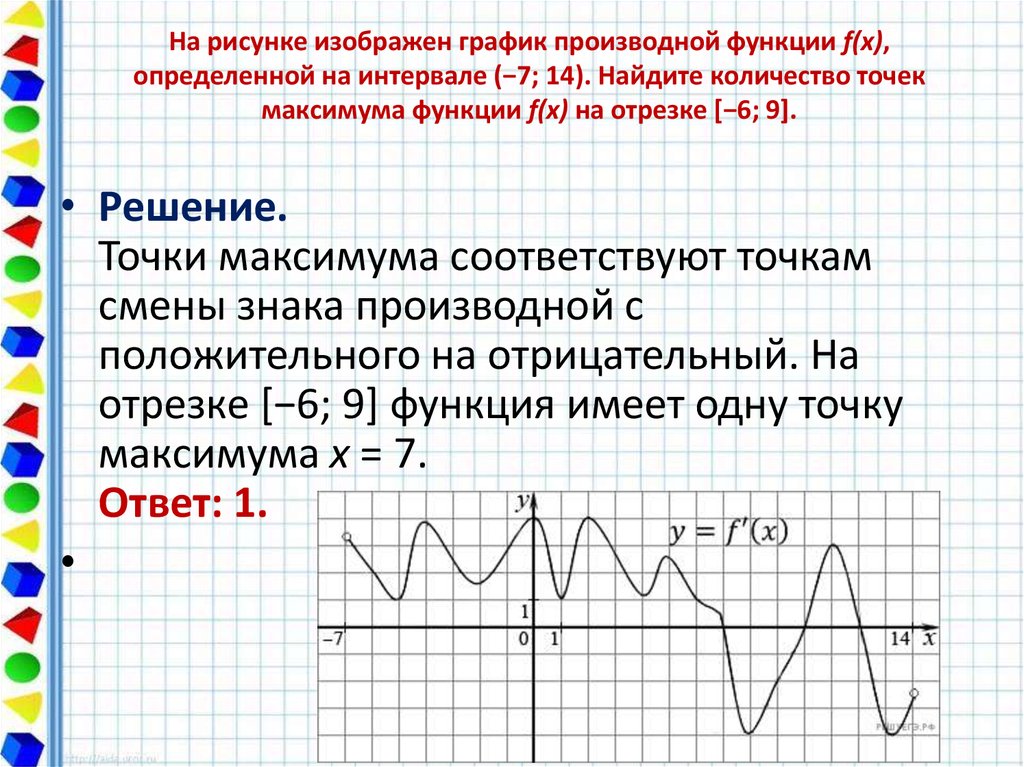
Геометрический смысл производной и дифференциала
Пожалуйста, прочитайте вдумчиво и не слишком быстро – материал прост и доступен каждому! Ничего страшного, если местами что-то покажется не очень понятным, к статье всегда можно вернуться позже. Скажу больше, теорию полезно проштудировать несколько раз, чтобы качественно уяснить все моменты (совет особенно актуален для студентов-«технарей», у которых высшая математика играет значительную роль в учебном процессе).
Естественно, и в самом определении производной в точке заменим на :
К чему мы пришли? А пришли мы к тому, что для функции по закону ставится в соответствие другая функция , которая называется производной функцией (или просто производной) .
Производная характеризует скорость изменения функции . Каким образом? Мысль идёт красной нитью с самого начала статьи. Рассмотрим некоторую точку области определения функции . Пусть функция дифференцируема в данной точке. Тогда:
Тогда:
1) Если , то функция возрастает в точке . И, очевидно, существует интервал (пусть даже очень малый), содержащий точку , на котором функция растёт, и её график идёт «снизу вверх».
2) Если , то функция убывает в точке . И существует интервал, содержащий точку , на котором функция убывает (график идёт «сверху вниз»).
3) Если , то бесконечно близко около точки функция сохраняет свою скорость постоянной. Так бывает, как отмечалось, у функции-константы и в критических точках функции , в частности в точках минимума и максимума .
Немного семантики. Что в широком смысле обозначает глагол «дифференцировать»? Дифференцировать – это значит выделить какой-либо признак. Дифференцируя функцию , мы «выделяем» скорость её изменения в виде производной функции . А что, кстати, понимается под словом «производная»? Функция произошла от функции .
Термины весьма удачно истолковывает механический смысл производной :
Рассмотрим закон изменения координаты тела , зависящий от времени , и функцию скорости движения данного тела .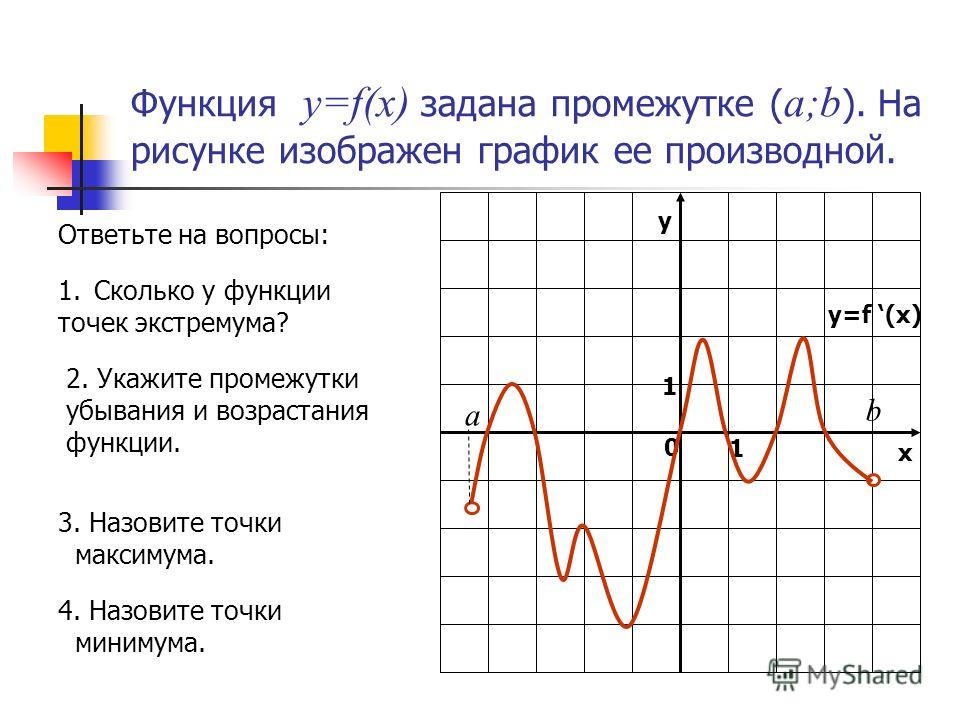 Функция характеризует скорость изменения координаты тела, поэтому является первой производной функции по времени: . Если бы в природе не существовало понятия «движение тела», то не существовало бы и производного понятия «скорость тела».
Функция характеризует скорость изменения координаты тела, поэтому является первой производной функции по времени: . Если бы в природе не существовало понятия «движение тела», то не существовало бы и производного понятия «скорость тела».
Ускорение тела – это скорость изменения скорости, поэтому: . Если бы в природе не существовало исходных понятий «движение тела» и «скорость движения тела», то не существовало бы и производного понятия «ускорение тела».
Производная функции смысл. Правила вычисления производных
Многие удивятся неожиданному расположению этой статьи в моём авторском курсе о производной функции одной переменной и её приложениях. Ведь как оно было ещё со школы: стандартный учебник в первую очередь даёт определение производной, её геометрический, механический смысл. Далее учащиеся находят производные функций по определению, и, собственно, только потом оттачивается техника дифференцирования с помощью таблицы производных .
Но с моей точки зрения, более прагматичен следующий подход: прежде всего, целесообразно ХОРОШО ПОНЯТЬ предел функции , и, в особенности, бесконечно малые величины .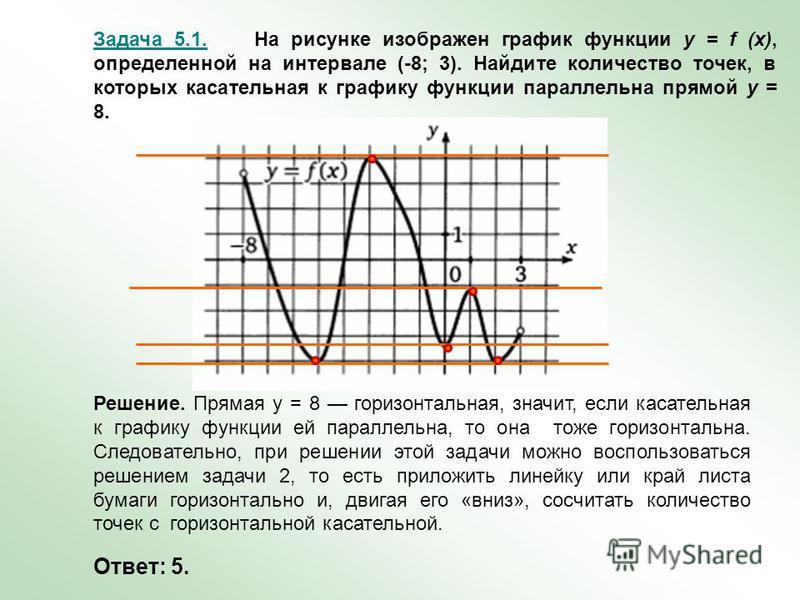 Дело в том, что определение производной базируется на понятии предела , которое слабо рассмотрено в школьном курсе. Именно поэтому значительная часть молодых потребителей гранита знаний плохо вникают в саму суть производной. Таким образом, если вы слабо ориентируетесь в дифференциальном исчислении либо мудрый мозг за долгие годы успешно избавился от оного багажа, пожалуйста, начните с пределов функций . Заодно освоите/вспомните их решение.
Дело в том, что определение производной базируется на понятии предела , которое слабо рассмотрено в школьном курсе. Именно поэтому значительная часть молодых потребителей гранита знаний плохо вникают в саму суть производной. Таким образом, если вы слабо ориентируетесь в дифференциальном исчислении либо мудрый мозг за долгие годы успешно избавился от оного багажа, пожалуйста, начните с пределов функций . Заодно освоите/вспомните их решение.
Тот же практический смысл подсказывает, что сначала выгодно научиться находить производные , в том числе производные сложных функций . Теория теорией, а дифференцировать, как говорится, хочется всегда. В этой связи лучше проработать перечисленные базовые уроки, а может и стать мастером дифференцирования , даже не осознавая сущности своих действий.
К материалам данной страницы рекомендую приступать после ознакомления со статьёй Простейшие задачи с производной , где, в частности рассмотрена задача о касательной к графику функции.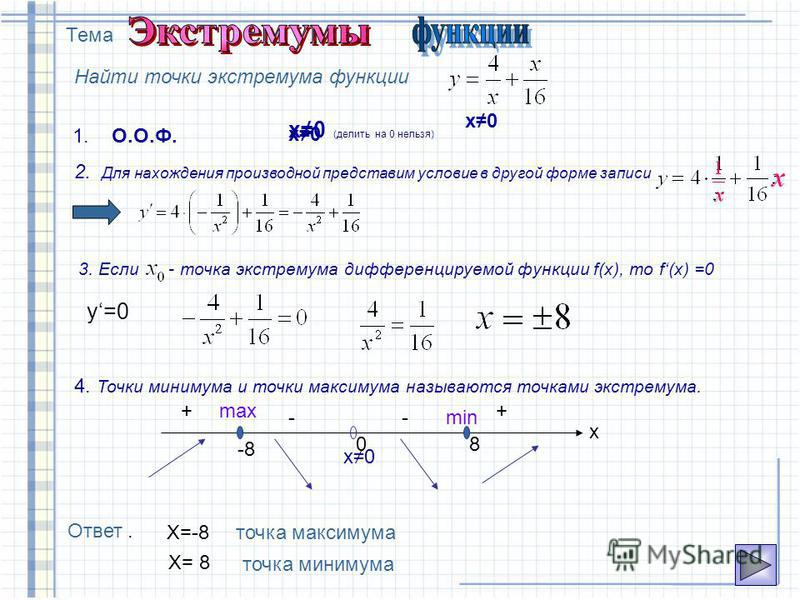 Но можно и повременить. Дело в том, что многие приложения производной не требуют её понимания, и неудивительно, что теоретический урок появился достаточно поздно – когда мне потребовалось объяснять нахождение интервалов возрастания/убывания и экстремумов функции. Более того, он довольно долго находился в теме «Функции и графики », пока я всё-таки не решил поставить его раньше.
Но можно и повременить. Дело в том, что многие приложения производной не требуют её понимания, и неудивительно, что теоретический урок появился достаточно поздно – когда мне потребовалось объяснять нахождение интервалов возрастания/убывания и экстремумов функции. Более того, он довольно долго находился в теме «Функции и графики », пока я всё-таки не решил поставить его раньше.
Поэтому, уважаемые чайники, не спешите поглощать суть производной, как голодные звери, ибо насыщение будет невкусным и неполным.
Понятие возрастания, убывания, максимума, минимума функцииМногие учебные пособия подводят к понятию производной с помощью каких-либо практических задач, и я тоже придумал интересный пример. Представьте, что нам предстоит путешествие в город, до которого можно добраться разными путями. Сразу откинем кривые петляющие дорожки, и будем рассматривать только прямые магистрали. Однако прямолинейные направления тоже бывают разными: до города можно добраться по ровному автобану. Или по холмистому шоссе – вверх-вниз, вверх-вниз. Другая дорога идёт только в гору, а ещё одна – всё время под уклон. Экстремалы выберут маршрут через ущелье с крутым обрывом и отвесным подъемом.
Или по холмистому шоссе – вверх-вниз, вверх-вниз. Другая дорога идёт только в гору, а ещё одна – всё время под уклон. Экстремалы выберут маршрут через ущелье с крутым обрывом и отвесным подъемом.
Но каковы бы ни были ваши предпочтения, желательно знать местность или, по меньшей мере, располагать её топографической картой. А если такая информация отсутствует? Ведь можно выбрать, например, ровный путь, да в результате наткнуться на горнолыжный спуск с весёлыми финнами. Не факт, что навигатор и даже спутниковый снимок дадут достоверные данные. Поэтому неплохо бы формализовать рельеф пути средствами математики.
Рассмотрим некоторую дорогу (вид сбоку):
На всякий случай напоминаю элементарный факт: путешествие происходит слева направо . Для простоты полагаем, что функция непрерывна на рассматриваемом участке.
Какие особенности у данного графика?
На интервалах функция возрастает , то есть каждое следующее её значение больше предыдущего. Грубо говоря, график идёт снизу вверх (забираемся на горку). А на интервале функция убывает – каждое следующее значение меньше предыдущего, и наш график идёт сверху вниз (спускаемся по склону).
Грубо говоря, график идёт снизу вверх (забираемся на горку). А на интервале функция убывает – каждое следующее значение меньше предыдущего, и наш график идёт сверху вниз (спускаемся по склону).
Также обратим внимание на особые точки. В точке мы достигаем максимума , то есть существует такой участок пути, на котором значение будет самым большим (высоким). В точке же достигается минимум , и существует такая её окрестность, в которой значение самое маленькое (низкое).
Более строгую терминологию и определения рассмотрим на уроке об экстремумах функции , а пока изучим ещё одну важную особенность: на промежутках функция возрастает, но возрастает она с разной скоростью . И первое, что бросается в глаза – на интервале график взмывает вверх гораздо более круто , чем на интервале . Нельзя ли измерить крутизну дороги с помощью математического инструментария?
Скорость изменения функцииИдея состоит в следующем: возьмём некоторое значение (читается «дельта икс») , которое назовём приращением аргумента , и начнём его «примерять» к различным точкам нашего пути:
1) Посмотрим на самую левую точку: минуя расстояние , мы поднимаемся по склону на высоту (зелёная линия). Величина называется приращением функции , и в данном случае это приращение положительно (разность значений по оси – больше нуля). Составим отношение , которое и будет мерИлом крутизны нашей дороги. Очевидно, что – это вполне конкретное число, и, поскольку оба приращения положительны, то .
Величина называется приращением функции , и в данном случае это приращение положительно (разность значений по оси – больше нуля). Составим отношение , которое и будет мерИлом крутизны нашей дороги. Очевидно, что – это вполне конкретное число, и, поскольку оба приращения положительны, то .
Внимание! Обозначение являются ЕДИНЫМ символом, то есть нельзя «отрывать» «дельту» от «икса» и рассматривать эти буквы отдельно. Разумеется, комментарий касается и символа приращения функции.
Исследуем природу полученной дроби содержательнее. Пусть изначально мы находимся на высоте 20 метров (в левой чёрной точке). Преодолев расстояние метров (левая красная линия), мы окажемся на высоте 60 метров. Тогда приращение функции составит метров (зелёная линия) и: . Таким образом, на каждом метре этого участка дороги высота увеличивается в среднем на 4 метра …не забыли альпинистское снаряжение? =) Иными словами, построенное отношение характеризует СРЕДНЮЮ СКОРОСТЬ ИЗМЕНЕНИЯ (в данном случае – роста) функции.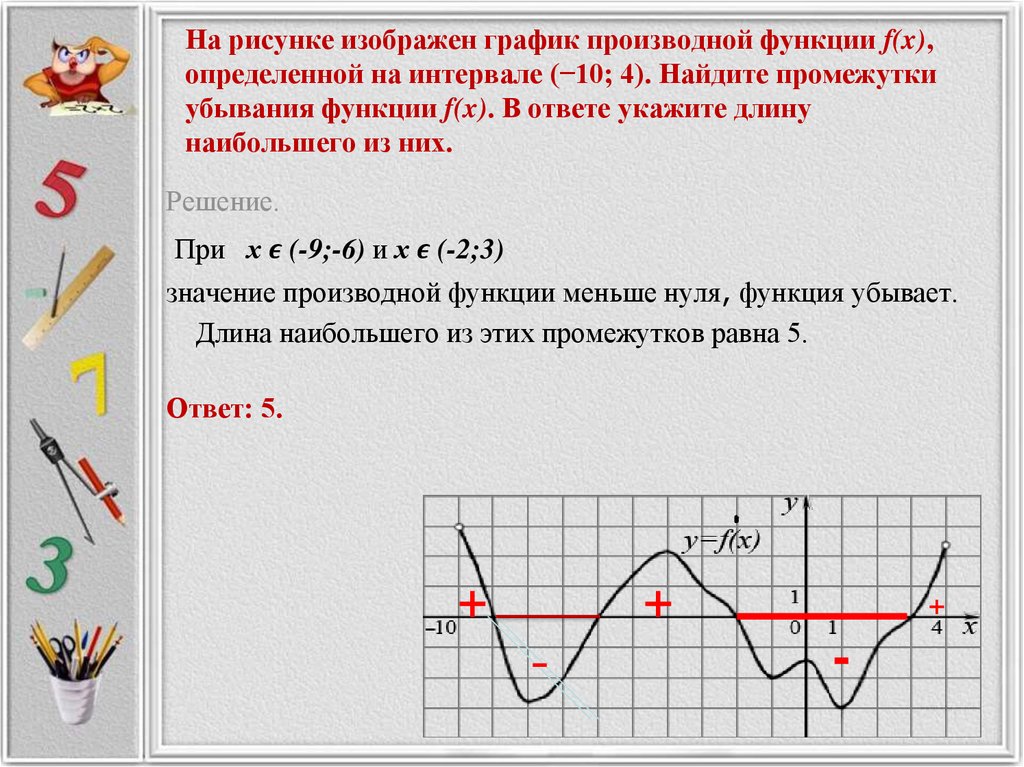
Примечание : числовые значения рассматриваемого примера соответствуют пропорциям чертежа лишь приблизительно.
2) Теперь пройдём то же самое расстояние от самой правой чёрной точки. Здесь подъём более пологий, поэтому приращение (малиновая линия) относительно невелико, и отношение по сравнению с предыдущим случаем будет весьма скромным. Условно говоря, метров и скорость роста функции составляет . То есть, здесь на каждый метр пути приходится в среднем пол метра подъёма.
3) Маленькое приключение на склоне горы. Посмотрим на верхнюю чёрную точку, расположенную на оси ординат. Предположим, что это отметка 50 метров. Снова преодолеваем расстояние , в результате чего оказываемся ниже – на уровне 30-ти метров. Поскольку осуществлено движение сверху вниз (в «противоход» направлению оси ), то итоговое приращение функции (высоты) будет отрицательным : метров (коричневый отрезок на чертеже). И в данном случае речь уже идёт о скорости убывания функции: , то есть за каждый метр пути этого участка высота убывает в среднем на 2 метра.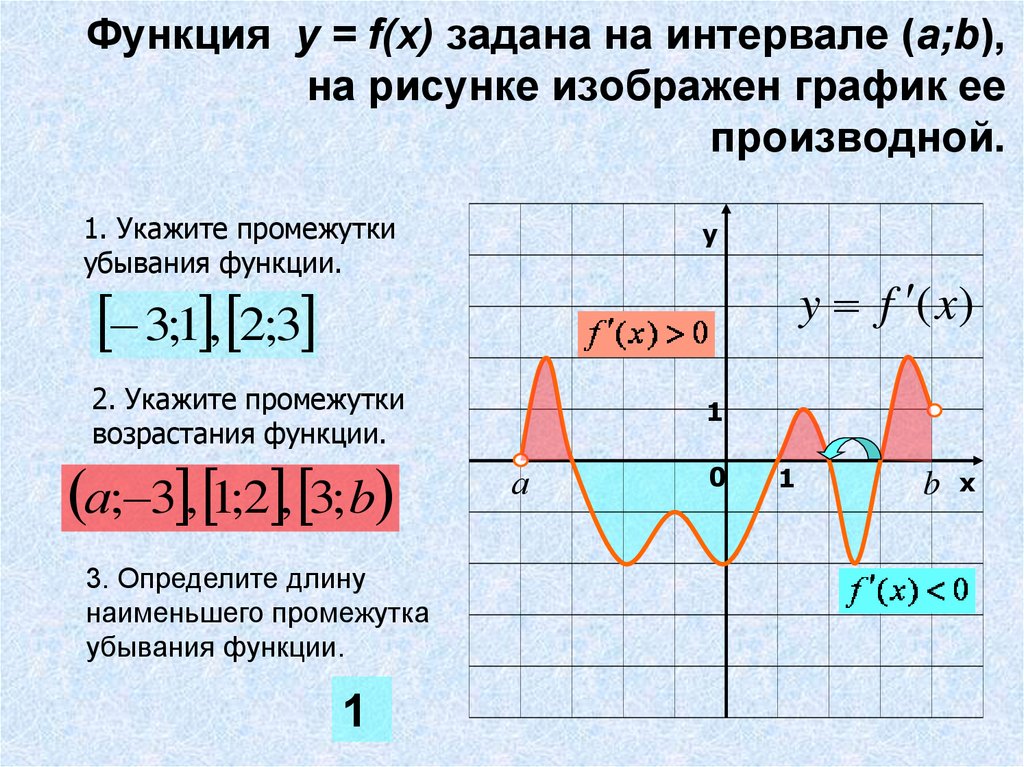 Берегите одежду на пятой точке.
Берегите одежду на пятой точке.
Теперь зададимся вопросом: какое значение «измерительного эталона» лучше всего использовать? Совершенно понятно, 10 метров – это весьма грубо. На них запросто уместится добрая дюжина кочек. Да что там кочки, внизу может быть глубокое ущелье, а через несколько метров – другая его сторона с дальнейшим отвесным подъёмом. Таким образом, при десятиметровом мы не получим вразумительной характеристики подобных участков пути посредством отношения .
Из проведённого рассуждения следует вывод – чем меньше значение , тем точнее мы опишем рельеф дороги. Более того, справедливы следующие факты:
– Для любой точки подъемов можно подобрать значение (пусть и очень малое), которое умещается в границах того или иного подъёма. А это значит, что соответствующее приращение высоты будет гарантированно положительным, и неравенство корректно укажет рост функции в каждой точке этих интервалов.
– Аналогично, для любой точки склона существует значение , которое полностью уместится на этом склоне.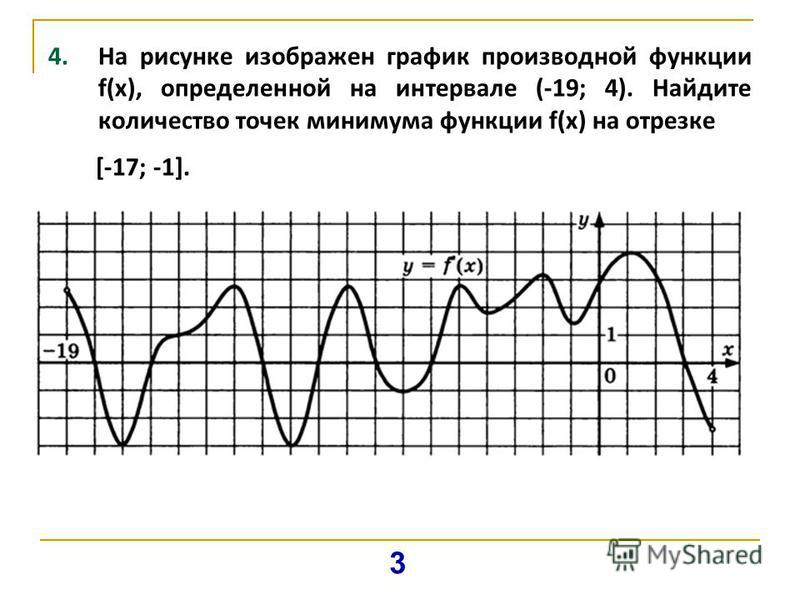 Следовательно, соответствующее приращение высоты однозначно отрицательно, и неравенство корректно покажет убыль функции в каждой точке данного интервала.
Следовательно, соответствующее приращение высоты однозначно отрицательно, и неравенство корректно покажет убыль функции в каждой точке данного интервала.
– Особо интересен случай, когда скорость изменения функции равна нулю: . Во-первых, нулевое приращение высоты () – признак ровного пути. А во-вторых, есть другие любопытные ситуации, примеры которых вы видите на рисунке. Представьте, что судьба завела нас на самую вершину холма с парящими орлами или дно оврага с квакающими лягушками. Если сделать небольшой шажок в любую сторону, то изменение высоты будет ничтожно мало, и можно сказать, что скорость изменения функции фактически нулевая. В точках наблюдается именно такая картина.
Таким образом, мы подобрались к удивительной возможности идеально точно охарактеризовать скорость изменения функции. Ведь математический анализ позволяет устремить приращение аргумента к нулю: , то есть сделать его бесконечно малым .
По итогу возникает ещё один закономерный вопрос: можно ли для дороги и её графика найти другую функцию , которая сообщала бы нам обо всех ровных участках, подъёмах, спусках, вершинах, низинах, а также о скорости роста/убывания в каждой точке пути?
Что такое производная? Определение производной.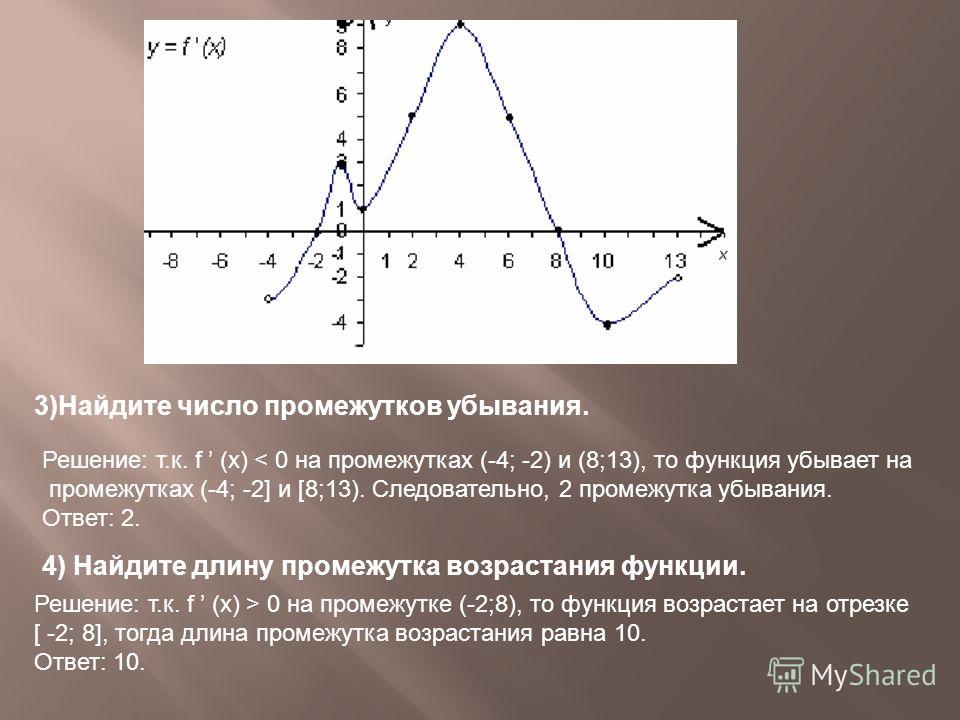
Геометрический смысл производной и дифференциала
Пожалуйста, прочитайте вдумчиво и не слишком быстро – материал прост и доступен каждому! Ничего страшного, если местами что-то покажется не очень понятным, к статье всегда можно вернуться позже. Скажу больше, теорию полезно проштудировать несколько раз, чтобы качественно уяснить все моменты (совет особенно актуален для студентов-«технарей», у которых высшая математика играет значительную роль в учебном процессе).
Естественно, и в самом определении производной в точке заменим на :
К чему мы пришли? А пришли мы к тому, что для функции по закону ставится в соответствие другая функция , которая называется производной функцией (или просто производной) .
Производная характеризует скорость изменения функции . Каким образом? Мысль идёт красной нитью с самого начала статьи. Рассмотрим некоторую точку области определения функции . Пусть функция дифференцируема в данной точке.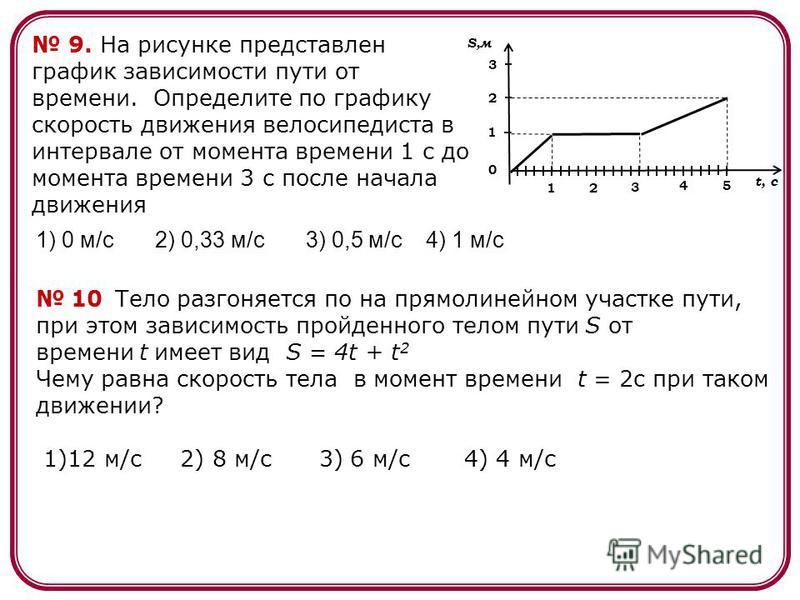 Тогда:
Тогда:
1) Если , то функция возрастает в точке . И, очевидно, существует интервал (пусть даже очень малый), содержащий точку , на котором функция растёт, и её график идёт «снизу вверх».
2) Если , то функция убывает в точке . И существует интервал, содержащий точку , на котором функция убывает (график идёт «сверху вниз»).
3) Если , то бесконечно близко около точки функция сохраняет свою скорость постоянной. Так бывает, как отмечалось, у функции-константы и в критических точках функции , в частности в точках минимума и максимума .
Немного семантики. Что в широком смысле обозначает глагол «дифференцировать»? Дифференцировать – это значит выделить какой-либо признак. Дифференцируя функцию , мы «выделяем» скорость её изменения в виде производной функции . А что, кстати, понимается под словом «производная»? Функция произошла от функции .
Термины весьма удачно истолковывает механический смысл производной :
Рассмотрим закон изменения координаты тела , зависящий от времени , и функцию скорости движения данного тела .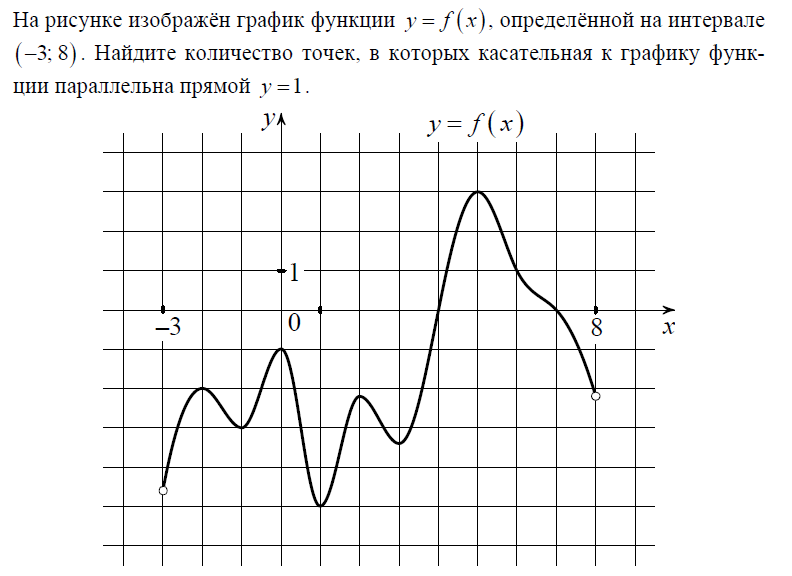 Функция характеризует скорость изменения координаты тела, поэтому является первой производной функции по времени: . Если бы в природе не существовало понятия «движение тела», то не существовало бы и производного понятия «скорость тела».
Функция характеризует скорость изменения координаты тела, поэтому является первой производной функции по времени: . Если бы в природе не существовало понятия «движение тела», то не существовало бы и производного понятия «скорость тела».
Ускорение тела – это скорость изменения скорости, поэтому: . Если бы в природе не существовало исходных понятий «движение тела» и «скорость движения тела», то не существовало бы и производного понятия «ускорение тела».
При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f(x) и обозначают символом
Тот
процесс, с помощью которого из данной
функции f(x) получают новую функцию f
» (x) ,
называют дифференцированием и состоит он из следующих трех шагов:
1)
даем аргументу x приращение x и определяем соответствующее приращение
функции y
= f(x+ x)
-f(x) ;
2)
составляем отношение
3)
считая x постоянным, а x 0,
находим
,
который обозначаем черезf
» (x) ,
как бы подчеркивая тем самым, что
полученная функция зависит лишь от того
значения x ,
при котором мы переходим к
пределу. Определение : Производной
y » =f » (x) данной
функции y=f(x) при
данном x называется предел отношения приращения
функции к приращению аргумента при
условии, что приращение аргумента
стремится к нулю, если, конечно, этот
предел существует, т.е. конечен.
Таким
образом,
Определение : Производной
y » =f » (x) данной
функции y=f(x) при
данном x называется предел отношения приращения
функции к приращению аргумента при
условии, что приращение аргумента
стремится к нулю, если, конечно, этот
предел существует, т.е. конечен.
Таким
образом,
,
или
Заметим,
что если при некотором значении x ,
например при x=a ,
отношение
при x 0
не стремится к конечному пределу, то в
этом случае говорят, что функция f(x) при x=a (или в точке x=a )
не имеет производной или не дифференцируема
в точке x=a .
2. Геометрический смысл производной.
Рассмотрим график функции у = f (х), дифференцируемой в окрестностях точки x 0
f(x)
Рассмотрим
произвольную прямую, проходящую через
точку графика функции — точку А(x 0 ,
f
(х 0))
и пересекающую график в некоторой точке
B(x;f(x)).
Такая прямая (АВ) называется секущей.
Из ∆АВС: АС = ∆x;
ВС =∆у; tgβ=∆y/∆x
.
Так как АС || Ox, то ALO = BAC = β (как соответственные при параллельных). Но ALO — это угол наклона секущей АВ к положительному направлению оси Ох. Значит, tgβ = k — угловой коэффициент прямой АВ.
Теперь будем уменьшать ∆х, т.е. ∆х→ 0. При этом точка В будет приближаться к точке А по графику, а секущая АВ будет поворачиваться. Предельным положением секущей АВ при ∆х→ 0 будет прямая (a), называемая касательной к графику функции у = f (х) в точке А.
Если
перейти к пределу при ∆х → 0 в равенстве
tgβ
=∆y/∆x,
то получим
илиtg
=f
«(x 0),
так как
-угол
наклона касательной к положительному
направлению оси Ох
,
по определению производной. Но tg
= k — угловой коэффициент касательной,
значит, k = tg
= f
«(x 0).
Итак, геометрический смысл производной заключается в следующем:
Производная функции в точке x 0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x 0 .
3.
 Физический смысл производной.
Физический смысл производной.Рассмотрим движение точки по прямой. Пусть задана координата точки в любой момент времени x(t). Известно (из курса физики), что средняя скорость за промежуток времени равна отношению расстояния, пройденного за этот промежуток времени, на время, т.е.
Vср = ∆x/∆t. Перейдем к пределу в последнем равенстве при ∆t → 0.
lim Vср (t) = (t 0) — мгновенная скорость в момент времени t 0 , ∆t → 0.
а lim = ∆x/∆t = x»(t 0) (по определению производной).
Итак, (t) =x»(t).
Физический смысл производной заключается в следующем: производная функции y = f (x ) в точке x 0 — это скорость изменения функции f (х) в точке x 0
Производная применяется в физике для нахождения скорости по известной функции координаты от времени, ускорения по известной функции скорости от времени.
(t) = x»(t) — скорость,
a(f) = »(t) — ускорение, или
Если известен закон движения материальной точки по окружности, то можно найти угловую скорость и угловое ускорение при вращательном движении:
φ = φ(t) — изменение угла от времени,
ω = φ»(t) — угловая скорость,
ε
= φ»(t)
— угловое ускорение, или ε
= φ»(t).
Если известен закон распределения массы неоднородного стержня, то можно найти линейную плотность неоднородного стержня:
m = m(х) — масса,
x , l — длина стержня,
р = m»(х) — линейная плотность.
С помощью производной решаются задачи из теории упругости и гармонических колебаний. Так, по закону Гука
F = -kx, x – переменная координата, k- коэффициент упругости пружины. Положив ω 2 =k/m, получим дифференциальное уравнение пружинного маятника х»(t) + ω 2 x(t) = 0,
где ω = √k/√m частота колебаний (l/c), k — жесткость пружины (H/m).
Уравнение вида у» + ω 2 y = 0 называется уравнением гармонических колебаний (механических, электрических, электромагнитных). Решением таких уравнений является функция
у = Asin(ωt + φ 0) или у = Acos(ωt + φ 0), где
А — амплитуда колебаний, ω — циклическая частота,
φ 0 — начальная фаза.
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной
как предела отношения приращения к приращению аргумента появились таблица производных и
точно определённые правила дифференцирования. Первыми на ниве нахождения производных
потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Первыми на ниве нахождения производных
потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
| 11. Производная арккосинуса | |
| 12. Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
1. Производная суммы или разности Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль.
Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как
производную «икса». Получаем следующие значения производных:
В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль.
Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как
производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где
сплошное нагромождение корней и степеней, как, например, ,
то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6. Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Определение. Пусть функция \(y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \(x_0 \).
Дадим аргументу приращение \(\Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции
\(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение
\(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то
указанный предел называют производной функции \(y=f(x) \) в точке \(x_0 \) и обозначают \(f»(x_0) \).
Пусть функция \(y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \(x_0 \).
Дадим аргументу приращение \(\Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции
\(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение
\(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то
указанный предел называют производной функции \(y=f(x) \) в точке \(x_0 \) и обозначают \(f»(x_0) \).
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f»(x_0) $$
Для обозначения производной часто используют символ y». Отметим, что y» = f(x) — это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел. Эту функцию называют так: производная функции у = f(x) .
Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно
провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
\(k = f»(a) \)
Поскольку \(k = tg(a) \), то верно равенство \(f»(a) = tg(a) \) . 2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение \(x \), найти \(f(x) \)
2. Дать аргументу \(x \) приращение \(\Delta x \), перейти в новую точку \(x+ \Delta x \), найти \(f(x+ \Delta x) \)
3. Найти приращение функции: \(\Delta y = f(x + \Delta x) — f(x) \)
4. Составить отношение \(\frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.
Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f»(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \(\Delta y \approx f»(x) \cdot \Delta x \). Если в этом равенстве \(\Delta x \) устремить к нулю, то и \(\Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .
Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику
функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой
точке не существует производная.
Еще один пример. Функция \(y=\sqrt{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \(f»(0) \)
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием .
При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций»,
то есть сложными функциями. 2} $$
2} $$
Производная функции одной переменной.
Введение.
Настоящие методические разработки предназначены для студентов факультета промышленное и гражданское строительство. Они составлены применительно к программе курса математики по разделу «Дифференциальное исчисление функций одного переменного».
Разработки представляют собой единое методическое руководство, включающее в себя: краткие теоретические сведения; «типовые» задачи и упражнения с подробными решениями и пояснениями к этим решениям; варианты контрольной работы.
В конце каждого параграфа дополнительные упражнения. Такая структура разработок делает их пригодными для самостоятельного овладения разделом при самой минимальной помощи со стороны преподавателя.
Механический и геометрический смысл
производной.
Понятие производной является одним
из самых важных понятий математического
анализа.Оно возникло еще в 17 веке.
Формирование понятия
производной исторически связано с двумя
задачами: задачей о скорости переменного
движения и задачей о касательной к
кривой.
Эти задачи, несмотря на их различное содержание, приводят к одной и той же математической операции, которую нужно провести над функцией.Эта операция получила в математике специальное название. Она называется операцией дифференцирования функции. Результат операции дифференцирования называется производной.
Итак, производной функцииy=f(x)
в точкеx0 называется
предел (если он существует) отношения
приращения функции
к приращению аргумента
при
.
Производную принято обозначать
так:
.
Таким образом, по определению
Для обозначения производной употребляются
также символы
.
Механический смысл производной.
Если s=s(t)
– закон прямолинейного движения
материальной точки, то
есть скорость этой точки в момент времениt.
Геометрический смысл производной.
Если функция y=f(x)
имеет производную в точке,
то угловой коэффициент касательной к
графику функции в точке
равен
.
Пример.
Найдите производную функции
в точке=2:
1) Дадим точке
=2
приращение
. Заметим, что.
Заметим, что.
2) Найдем приращение функции в точке =2:
3) Составим отношение приращения функции к приращению аргумента:
Найдем предел отношения при
:
.
Таким образом,
.
§ 2. Производные от некоторых
простейших функций.
Студенту необходимо научиться вычислять производные конкретных функций: y=x,y=и вообщеy=.
Найдем производную функции у=х.
т.е. (x)′=1.
Найдем производную функции
Производная
Пусть
тогда
Легко заметить закономерность в
выражениях производных от степенной
функции
приn=1,2,3.
Следовательно,
. (1)
Эта формула справедлива для любых действительных n.
В частности, используя формулу (1), имеем:
;
.
Пример.
Найдите производную функции
.
.
Данная функция является частным случаем функции вида
при
.
Используя формулу (1), имеем
.
Производные функций y=sin x и y=cos
x.
Пусть y=sinx.
Разделим на ∆x, получим
Переходя к пределу при ∆x→0, имеем
Пусть y=cosx .
Переходя к пределу при ∆x→0, получим
;
.
(2)
§3. Основные правила дифференцирования.
Рассмотрим правила дифференцирования.
Теорема 1 . Если функцииu=u(x) иv=v(x) дифференцируемы в данной точкеx,то в этой точке дифференцируема и их сумма, причем производная суммы равна сумме производных слагаемых: (u+v)»=u»+v».(3)
Доказательство: рассмотрим функцию y=f(x)=u(x)+v(x).
Приращению ∆x аргумента x соответствуют приращения ∆u=u(x+∆x)-u(x), ∆v=v(x+∆x)-v(x) функций u и v. Тогда функция y получит приращение
∆y=f(x+∆x)-f(x)=
=—=∆u+∆v.
Следовательно,
Итак, (u+v)»=u»+v».
Теорема 2. Если
функцииu=u(x)
иv=v(x)
дифференцируемы в данной точкеx,
то в той же точке дифференцируемо и их
произведение.При этом
производная произведения находится по
следующей формуле: (uv)»=u»v+uv». (4)
(4)
Доказательство: Пусть y=uv, где u и v – некоторые дифференцируемые функции от x. Дадим x приращение ∆x;тогда u получит приращение ∆u, v получит приращение ∆v и y получит приращение ∆y.
Имеем y+∆y=(u+∆u)(v+∆v), или
y+∆y=uv+u∆v+v∆u+∆u∆v.
Следовательно, ∆y=u∆v+v∆u+∆u∆v.
Отсюда
Переходя к пределу при ∆x→0 и учитывая, чтоuиvне зависят от ∆x, будем иметь
Теорема 3 . Производная частного двух функций равна дроби, знаменатель которой равен квадрату делителя, а числитель- разности между произведением производной делимого на делитель и произведением делимого на производную делителя, т.е.
Если
то
(5)
Теорема 4. Производная постоянной равна нулю, т.е. если y=C, где С=const, то y»=0.
Теорема 5. Постоянный множитель можно выносить за знак производной, т.е. если y=Cu(x), где С=const, то y»=Cu»(x).
Пример 1.
Найдите производную функции
.
Данная функция имеет вид
,
гдеu=x,v=cosx. Применяя правило
дифференцирования (4), находим
Применяя правило
дифференцирования (4), находим
.
Пример 2.
Найдите производную функции
.
Применим формулу (5).
Здесь
;
.
Задачи.
Найдите производные следующих функций:
;
11)
2)
;
12)
;
3)
13)
4)
14)
5)
15)
6)
16)
7 )
17)
8)
18)
9)
19)
10)
20)
Конечная производная в точке. Записи с меткой «определение производной»
Главная > Новостройки > Конечная производная в точке. Записи с меткой «определение производной»
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f(x) и обозначают символом
Тот
процесс, с помощью которого из данной
функции f(x) получают новую функцию f
» (x) ,
называют дифференцированием и состоит он из следующих трех шагов:
1)
даем аргументу x приращение x и определяем соответствующее приращение
функции y
= f(x+ x)
-f(x) ;
2)
составляем отношение
3)
считая x постоянным, а x 0,
находим
,
который обозначаем черезf
» (x) ,
как бы подчеркивая тем самым, что
полученная функция зависит лишь от того
значения x ,
при котором мы переходим к
пределу. Определение : Производной
y » =f » (x) данной
функции y=f(x) при
данном x называется предел отношения приращения
функции к приращению аргумента при
условии, что приращение аргумента
стремится к нулю, если, конечно, этот
предел существует, т. е. конечен.
Таким
образом,
е. конечен.
Таким
образом,
,
или
Заметим,
что если при некотором значении x ,
например при x=a ,
отношение
при x 0
не стремится к конечному пределу, то в
этом случае говорят, что функция f(x) при x=a (или в точке x=a )
не имеет производной или не дифференцируема
в точке x=a .
2. Геометрический смысл производной.
Рассмотрим график функции у = f (х), дифференцируемой в окрестностях точки x 0
f(x)
Рассмотрим произвольную прямую, проходящую через точку графика функции — точку А(x 0 , f (х 0)) и пересекающую график в некоторой точке B(x;f(x)). Такая прямая (АВ) называется секущей. Из ∆АВС: АС = ∆x; ВС =∆у; tgβ=∆y/∆x .
Так как АС || Ox, то ALO = BAC = β (как соответственные при параллельных). Но ALO — это угол наклона секущей АВ к положительному направлению оси Ох. Значит, tgβ = k — угловой коэффициент прямой АВ.
Теперь
будем уменьшать ∆х, т. е. ∆х→ 0. При этом
точка В будет приближаться к точке
А по графику, а секущая АВ будет
поворачиваться. Предельным положением
секущей АВ при ∆х→ 0 будет прямая (a),
называемая касательной к графику функции
у = f
(х) в точке А.
е. ∆х→ 0. При этом
точка В будет приближаться к точке
А по графику, а секущая АВ будет
поворачиваться. Предельным положением
секущей АВ при ∆х→ 0 будет прямая (a),
называемая касательной к графику функции
у = f
(х) в точке А.
Если
перейти к пределу при ∆х → 0 в равенстве
tgβ
=∆y/∆x,
то получим
илиtg
=f
«(x 0),
так как
-угол
наклона касательной к положительному
направлению оси Ох
,
по определению производной. Но tg
= k — угловой коэффициент касательной,
значит, k = tg
= f
«(x 0).
Итак, геометрический смысл производной заключается в следующем:
Производная функции в точке x 0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x 0 .
3. Физический смысл производной.
Рассмотрим
движение точки по прямой. Пусть задана
координата точки в любой момент времени
x(t).
Известно (из курса физики), что средняя
скорость за промежуток времени
равна отношению расстояния, пройденного
за этот промежуток времени, на время,
т. е.
е.
Vср = ∆x/∆t. Перейдем к пределу в последнем равенстве при ∆t → 0.
lim Vср (t) = (t 0) — мгновенная скорость в момент времени t 0 , ∆t → 0.
а lim = ∆x/∆t = x»(t 0) (по определению производной).
Итак, (t) =x»(t).
Физический смысл производной заключается в следующем: производная функции y = f (x ) в точке x 0 — это скорость изменения функции f (х) в точке x 0
Производная применяется в физике для нахождения скорости по известной функции координаты от времени, ускорения по известной функции скорости от времени.
(t) = x»(t) — скорость,
a(f) = »(t) — ускорение, или
Если известен закон движения материальной точки по окружности, то можно найти угловую скорость и угловое ускорение при вращательном движении:
φ = φ(t) — изменение угла от времени,
ω = φ»(t) — угловая скорость,
ε
= φ»(t)
— угловое ускорение, или ε
= φ»(t).
Если известен закон распределения массы неоднородного стержня, то можно найти линейную плотность неоднородного стержня:
m = m(х) — масса,
x , l — длина стержня,
р = m»(х) — линейная плотность.
С помощью производной решаются задачи из теории упругости и гармонических колебаний. Так, по закону Гука
F = -kx, x – переменная координата, k- коэффициент упругости пружины. Положив ω 2 =k/m, получим дифференциальное уравнение пружинного маятника х»(t) + ω 2 x(t) = 0,
где ω = √k/√m частота колебаний (l/c), k — жесткость пружины (H/m).
Уравнение вида у» + ω 2 y = 0 называется уравнением гармонических колебаний (механических, электрических, электромагнитных). Решением таких уравнений является функция
у = Asin(ωt + φ 0) или у = Acos(ωt + φ 0), где
А — амплитуда колебаний, ω — циклическая частота,
φ 0 — начальная фаза.
В координатной плоскости хОу рассмотрим график функции y=f (x) . Зафиксируем точку М(х 0 ; f (x 0)) . Придадим абсциссе х 0 приращение Δх . Мы получим новую абсциссу х 0 +Δх . Это абсцисса точки N , а ордината будет равна f (х 0 +Δх ). Изменение абсциссы повлекло за собой изменение ординаты. Это изменение называют приращение функции и обозначают Δy .
Придадим абсциссе х 0 приращение Δх . Мы получим новую абсциссу х 0 +Δх . Это абсцисса точки N , а ордината будет равна f (х 0 +Δх ). Изменение абсциссы повлекло за собой изменение ординаты. Это изменение называют приращение функции и обозначают Δy .
Δy=f (х 0 +Δх) — f (x 0). Через точки M и N проведем секущую MN , которая образует угол φ с положительным направлением оси Ох . Определим тангенс угла φ из прямоугольного треугольника MPN .
Пусть Δх стремится к нулю. Тогда секущая MN будет стремиться занять положение касательной МТ , а угол φ станет углом α . Значит, тангенс угла α есть предельное значение тангенса угла φ :
Предел отношения приращения функции к приращению аргумента, при стремлении последнего к нулю, называют производной функции в данной точке:
Геометрический смысл производной заключается в том, что численно производная функции в данной точке равна тангенсу угла, образованного касательной, проведенной через эту точку к данной кривой, и положительным направлением оси Ох :
Примеры.
1. Найти приращение аргумента и приращение функции y=x 2 , если начальное значение аргумента было равно 4 , а новое —4,01 .
Решение.
Новое значение аргумента х=х 0 +Δx . Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх =4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.
Ответ: приращение аргумента Δх =0,01; приращение функции Δу =0,0801.
Можно было приращение функции найти по-другому: Δy =y (х 0 +Δx) -y (х 0)=у(4,01) -у(4)=4,01 2 -4 2 =16,0801-16=0,0801.
2. Найти угол наклона касательной к графику функции y=f (x) в точке х 0 , если f «(х 0) = 1 .
Решение.
Значение производной в точке касания х 0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f «(х 0) = tgα = 1 → α = 45°, так как tg45°=1.
Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45° .
3. Вывести формулу производной функции y=x n .
Дифференцирование — это действие нахождения производной функции.
При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (x n)» = nx n-1 .
Вот эти формулы.
Таблицу производных легче будет заучить, проговаривая словесные формулировки:
1. Производная постоянной величины равна нулю.
2. Икс штрих равен единице.
3. Постоянный множитель можно вынести за знак производной.
4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.
5. Производная корня равна единице, деленной на два таких же корня.
6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.
7. Производная синуса равна косинусу.
8. Производная косинуса равна минус синусу.
9. Производная тангенса равна единице, деленной на квадрат косинуса.
10. Производная котангенса равна минус единице, деленной на квадрат синуса.
Учим правила дифференцирования .
1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.
2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.
3. Производная «у», деленного на «вэ» равна дроби, в числителе которой «у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».
4. Частный случай формулы 3.
Учим вместе!
Страница 1 из 1 1
Многие удивятся неожиданному расположению этой статьи в моём авторском курсе о производной функции одной переменной и её приложениях. Ведь как оно было ещё со школы: стандартный учебник в первую очередь даёт определение производной, её геометрический, механический смысл. Далее учащиеся находят производные функций по определению, и, собственно, только потом оттачивается техника дифференцирования с помощью таблицы производных .
Но с моей точки зрения, более прагматичен следующий подход: прежде всего, целесообразно ХОРОШО ПОНЯТЬ предел функции , и, в особенности, бесконечно малые величины . Дело в том, что определение производной базируется на понятии предела , которое слабо рассмотрено в школьном курсе. Именно поэтому значительная часть молодых потребителей гранита знаний плохо вникают в саму суть производной. Таким образом, если вы слабо ориентируетесь в дифференциальном исчислении либо мудрый мозг за долгие годы успешно избавился от оного багажа, пожалуйста, начните с пределов функций . Заодно освоите/вспомните их решение.
Заодно освоите/вспомните их решение.
Тот же практический смысл подсказывает, что сначала выгодно научиться находить производные , в том числе производные сложных функций . Теория теорией, а дифференцировать, как говорится, хочется всегда. В этой связи лучше проработать перечисленные базовые уроки, а может и стать мастером дифференцирования , даже не осознавая сущности своих действий.
К материалам данной страницы рекомендую приступать после ознакомления со статьёй Простейшие задачи с производной , где, в частности рассмотрена задача о касательной к графику функции. Но можно и повременить. Дело в том, что многие приложения производной не требуют её понимания, и неудивительно, что теоретический урок появился достаточно поздно – когда мне потребовалось объяснять нахождение интервалов возрастания/убывания и экстремумов функции. Более того, он довольно долго находился в теме «Функции и графики », пока я всё-таки не решил поставить его раньше.
Поэтому, уважаемые чайники, не спешите поглощать суть производной, как голодные звери, ибо насыщение будет невкусным и неполным.
Понятие возрастания, убывания, максимума, минимума функцииМногие учебные пособия подводят к понятию производной с помощью каких-либо практических задач, и я тоже придумал интересный пример. Представьте, что нам предстоит путешествие в город, до которого можно добраться разными путями. Сразу откинем кривые петляющие дорожки, и будем рассматривать только прямые магистрали. Однако прямолинейные направления тоже бывают разными: до города можно добраться по ровному автобану. Или по холмистому шоссе – вверх-вниз, вверх-вниз. Другая дорога идёт только в гору, а ещё одна – всё время под уклон. Экстремалы выберут маршрут через ущелье с крутым обрывом и отвесным подъемом.
Но каковы бы ни были ваши предпочтения, желательно знать местность или, по меньшей мере, располагать её топографической картой. А если такая информация отсутствует? Ведь можно выбрать, например, ровный путь, да в результате наткнуться на горнолыжный спуск с весёлыми финнами. Не факт, что навигатор и даже спутниковый снимок дадут достоверные данные. Поэтому неплохо бы формализовать рельеф пути средствами математики.
Не факт, что навигатор и даже спутниковый снимок дадут достоверные данные. Поэтому неплохо бы формализовать рельеф пути средствами математики.
Рассмотрим некоторую дорогу (вид сбоку):
На всякий случай напоминаю элементарный факт: путешествие происходит слева направо . Для простоты полагаем, что функция непрерывна на рассматриваемом участке.
Какие особенности у данного графика?
На интервалах функция возрастает , то есть каждое следующее её значение больше предыдущего. Грубо говоря, график идёт снизу вверх (забираемся на горку). А на интервале функция убывает – каждое следующее значение меньше предыдущего, и наш график идёт сверху вниз (спускаемся по склону).
Также обратим внимание на особые точки. В точке мы достигаем максимума , то есть существует такой участок пути, на котором значение будет самым большим (высоким). В точке же достигается минимум , и существует такая её окрестность, в которой значение самое маленькое (низкое).
Более строгую терминологию и определения рассмотрим на уроке об экстремумах функции , а пока изучим ещё одну важную особенность: на промежутках функция возрастает, но возрастает она с разной скоростью . И первое, что бросается в глаза – на интервале график взмывает вверх гораздо более круто , чем на интервале . Нельзя ли измерить крутизну дороги с помощью математического инструментария?
Скорость изменения функцииИдея состоит в следующем: возьмём некоторое значение (читается «дельта икс») , которое назовём приращением аргумента , и начнём его «примерять» к различным точкам нашего пути:
1) Посмотрим на самую левую точку: минуя расстояние , мы поднимаемся по склону на высоту (зелёная линия). Величина называется приращением функции , и в данном случае это приращение положительно (разность значений по оси – больше нуля). Составим отношение , которое и будет мерИлом крутизны нашей дороги. Очевидно, что – это вполне конкретное число, и, поскольку оба приращения положительны, то .
Внимание! Обозначение являются ЕДИНЫМ символом, то есть нельзя «отрывать» «дельту» от «икса» и рассматривать эти буквы отдельно. Разумеется, комментарий касается и символа приращения функции.
Исследуем природу полученной дроби содержательнее. Пусть изначально мы находимся на высоте 20 метров (в левой чёрной точке). Преодолев расстояние метров (левая красная линия), мы окажемся на высоте 60 метров. Тогда приращение функции составит метров (зелёная линия) и: . Таким образом, на каждом метре этого участка дороги высота увеличивается в среднем на 4 метра …не забыли альпинистское снаряжение? =) Иными словами, построенное отношение характеризует СРЕДНЮЮ СКОРОСТЬ ИЗМЕНЕНИЯ (в данном случае – роста) функции.
Примечание : числовые значения рассматриваемого примера соответствуют пропорциям чертежа лишь приблизительно.
2) Теперь пройдём то же самое расстояние от самой правой чёрной точки. Здесь подъём более пологий, поэтому приращение (малиновая линия) относительно невелико, и отношение по сравнению с предыдущим случаем будет весьма скромным. Условно говоря, метров и скорость роста функции составляет . То есть, здесь на каждый метр пути приходится в среднем пол метра подъёма.
Условно говоря, метров и скорость роста функции составляет . То есть, здесь на каждый метр пути приходится в среднем пол метра подъёма.
3) Маленькое приключение на склоне горы. Посмотрим на верхнюю чёрную точку, расположенную на оси ординат. Предположим, что это отметка 50 метров. Снова преодолеваем расстояние , в результате чего оказываемся ниже – на уровне 30-ти метров. Поскольку осуществлено движение сверху вниз (в «противоход» направлению оси ), то итоговое приращение функции (высоты) будет отрицательным : метров (коричневый отрезок на чертеже). И в данном случае речь уже идёт о скорости убывания функции: , то есть за каждый метр пути этого участка высота убывает в среднем на 2 метра. Берегите одежду на пятой точке.
Теперь зададимся вопросом: какое значение «измерительного эталона» лучше всего использовать? Совершенно понятно, 10 метров – это весьма грубо. На них запросто уместится добрая дюжина кочек. Да что там кочки, внизу может быть глубокое ущелье, а через несколько метров – другая его сторона с дальнейшим отвесным подъёмом. Таким образом, при десятиметровом мы не получим вразумительной характеристики подобных участков пути посредством отношения .
Таким образом, при десятиметровом мы не получим вразумительной характеристики подобных участков пути посредством отношения .
Из проведённого рассуждения следует вывод – чем меньше значение , тем точнее мы опишем рельеф дороги. Более того, справедливы следующие факты:
– Для любой точки подъемов можно подобрать значение (пусть и очень малое), которое умещается в границах того или иного подъёма. А это значит, что соответствующее приращение высоты будет гарантированно положительным, и неравенство корректно укажет рост функции в каждой точке этих интервалов.
– Аналогично, для любой точки склона существует значение , которое полностью уместится на этом склоне. Следовательно, соответствующее приращение высоты однозначно отрицательно, и неравенство корректно покажет убыль функции в каждой точке данного интервала.
– Особо интересен случай, когда скорость изменения функции равна нулю: . Во-первых, нулевое приращение высоты () – признак ровного пути. А во-вторых, есть другие любопытные ситуации, примеры которых вы видите на рисунке. Представьте, что судьба завела нас на самую вершину холма с парящими орлами или дно оврага с квакающими лягушками. Если сделать небольшой шажок в любую сторону, то изменение высоты будет ничтожно мало, и можно сказать, что скорость изменения функции фактически нулевая. В точках наблюдается именно такая картина.
А во-вторых, есть другие любопытные ситуации, примеры которых вы видите на рисунке. Представьте, что судьба завела нас на самую вершину холма с парящими орлами или дно оврага с квакающими лягушками. Если сделать небольшой шажок в любую сторону, то изменение высоты будет ничтожно мало, и можно сказать, что скорость изменения функции фактически нулевая. В точках наблюдается именно такая картина.
Таким образом, мы подобрались к удивительной возможности идеально точно охарактеризовать скорость изменения функции. Ведь математический анализ позволяет устремить приращение аргумента к нулю: , то есть сделать его бесконечно малым .
По итогу возникает ещё один закономерный вопрос: можно ли для дороги и её графика найти другую функцию , которая сообщала бы нам обо всех ровных участках, подъёмах, спусках, вершинах, низинах, а также о скорости роста/убывания в каждой точке пути?
Что такое производная? Определение производной.Геометрический смысл производной и дифференциала
Пожалуйста, прочитайте вдумчиво и не слишком быстро – материал прост и доступен каждому! Ничего страшного, если местами что-то покажется не очень понятным, к статье всегда можно вернуться позже. Скажу больше, теорию полезно проштудировать несколько раз, чтобы качественно уяснить все моменты (совет особенно актуален для студентов-«технарей», у которых высшая математика играет значительную роль в учебном процессе).
Скажу больше, теорию полезно проштудировать несколько раз, чтобы качественно уяснить все моменты (совет особенно актуален для студентов-«технарей», у которых высшая математика играет значительную роль в учебном процессе).
Естественно, и в самом определении производной в точке заменим на :
К чему мы пришли? А пришли мы к тому, что для функции по закону ставится в соответствие другая функция , которая называется производной функцией (или просто производной) .
Производная характеризует скорость изменения функции . Каким образом? Мысль идёт красной нитью с самого начала статьи. Рассмотрим некоторую точку области определения функции . Пусть функция дифференцируема в данной точке. Тогда:
1) Если , то функция возрастает в точке . И, очевидно, существует интервал (пусть даже очень малый), содержащий точку , на котором функция растёт, и её график идёт «снизу вверх».
2) Если , то функция убывает в точке . И существует интервал, содержащий точку , на котором функция убывает (график идёт «сверху вниз»).
3) Если , то бесконечно близко около точки функция сохраняет свою скорость постоянной. Так бывает, как отмечалось, у функции-константы и в критических точках функции , в частности в точках минимума и максимума .
Немного семантики. Что в широком смысле обозначает глагол «дифференцировать»? Дифференцировать – это значит выделить какой-либо признак. Дифференцируя функцию , мы «выделяем» скорость её изменения в виде производной функции . А что, кстати, понимается под словом «производная»? Функция произошла от функции .
Термины весьма удачно истолковывает механический смысл производной :
Рассмотрим закон изменения координаты тела , зависящий от времени , и функцию скорости движения данного тела . Функция характеризует скорость изменения координаты тела, поэтому является первой производной функции по времени: . Если бы в природе не существовало понятия «движение тела», то не существовало бы и производного понятия «скорость тела».
Ускорение тела – это скорость изменения скорости, поэтому: . Если бы в природе не существовало исходных понятий «движение тела» и «скорость движения тела», то не существовало бы и производного понятия «ускорение тела».
В этой статье дадим основные понятия, на которых будет базироваться вся дальнейшая теория по теме производная функции одной переменной.
Путь x – аргумент функции f(x) и — малое число, отличное от нуля.
(читается «дельта икс») называют приращением аргумента функции . На рисунке красной линией показано изменение аргумента от значения x до значения (отсюда видна суть названия «приращение» аргумента).
При переходе от значения аргумента к значения функции изменяются соответственно от до при условии монотонности функции на отрезке . Разность называют приращением функции f(x) , соответствующем данному приращению аргумента. На рисунке приращение функции показано синей линией.
Рассмотрим эти понятия на конкретном примере.
Возьмем, к примеру, функцию . Зафиксируем точку и приращение аргумента . В этом случае приращение функции при переходе от к будет равно
Отрицательное приращение говорит об убывании функции на отрезке .
Графическая иллюстрация
Определение производной функции в точке .
Пусть функция f(x) определена на промежутке (a; b) , и — точки этого промежутка. Производной функции f(x) в точке называется предел отношения приращения функции к приращению аргумента при . Обозначается .
Когда последний предел принимает конкретное конечное значение, то говорят о существовании конечной производной в точке . Если предел бесконечен, то говорят, что производная бесконечна в данной точке . Если же предел не существует, то и производная функции в этой точке не существует .
Функцию f(x) называют дифференцируемой в точке , когда она имеет в ней конечную производную.
Если функция f(x)
дифференцируема в каждой точке некоторого промежутка (a; b)
, то функцию называют дифференцируемой на этом промежутке. Таким образом, любой точке x
из промежутка (a; b)
можно поставить в соответствие значение производной функции в этой точке , то есть, мы имеем возможность определить новую функцию , которую называют производной функции f(x)
на интервале (a; b) .
Таким образом, любой точке x
из промежутка (a; b)
можно поставить в соответствие значение производной функции в этой точке , то есть, мы имеем возможность определить новую функцию , которую называют производной функции f(x)
на интервале (a; b) .
Операция нахождения производной называется дифференцированием .
Проведем разграничения в природе понятий производной функции в точке и на промежутке: производная функции в точке – это есть число, а производная функции на промежутке – это есть функция.
Давайте разберем это на примерах для ясности картины. При дифференцировании будем пользоваться определением производной, то есть переходить к нахождению пределов. При возникновении трудностей рекомендуем обращаться к разделу теории .
Пример.
Найти производную функции в точке , используя определение.
Решение.
Так как мы ищем производную функции в точке, то в ответе должно быть число. Запишем предел отношения приращения функции к приращению аргумента и воспользуемся формулами тригонометрии:
Карта сайта
Карта сайтаШрифт 18px 20px 22px
Цветовая схема Aa Aa Aa Aa
Показать изображения
Выключить версию для слабовидящих
|
|
Средняя и мгновенная скорость изменения
Средняя скорость изменения представляет собой общее изменение одной переменной по отношению к общему изменению другой переменной. Мгновенная скорость изменения, или производная, измеряет конкретную скорость изменения одной переменной по отношению к конкретному бесконечно малому изменению другой переменной. Средняя скорость изменения функции может быть определена секущими линиями, а мгновенная скорость изменения может быть определена касательными линиями. Как вы узнаете, эти ставки также могут быть определены с помощью специального типа математики, называемого исчислением.
Мгновенная скорость изменения, или производная, измеряет конкретную скорость изменения одной переменной по отношению к конкретному бесконечно малому изменению другой переменной. Средняя скорость изменения функции может быть определена секущими линиями, а мгновенная скорость изменения может быть определена касательными линиями. Как вы узнаете, эти ставки также могут быть определены с помощью специального типа математики, называемого исчислением.
Какова скорость изменения?
Скорость изменения – это изменение одной переменной по отношению к изменению другой переменной. Распространенной скоростью изменения является скорость, которая измеряет изменение пройденного расстояния по отношению к прошедшему времени. Олимпийский чемпион Усэйн Болт стал самым быстрым человеком в мире, разогнавшись до 44,72 км/ч в беге на 100 метров. В среднем его скорость была немного ниже (тем не менее, очень впечатляющей) — 37,58 км/ч. Максимальная скорость Болта — это пример мгновенной скорости изменения, а его средняя скорость — это средняя скорость изменения.
Средняя скорость изменения
Секущие линии получаются путем соединения двух точек на кривой. Наклон секущей между двумя точками представляет среднюю скорость изменения в этом интервале.
Формула:
Средняя скорость изменения = Уклон (м) = △y/△x = =
Как найти среднюю скорость изменения между двумя точками с помощью секущей: 3 Шаг 1: Нарисуйте секущую, соединяющую две точки. Шаг 2: Используйте координаты двух точек для расчета уклона. Уравнение наклона: Среднее изменение функции за заданный интервал времени [x 0 , x 1 ] Наклон секущей представляет среднюю скорость 90 изменения графика на этом интервале. После того, как вы вычислили наклон секущей линии, вы можете использовать наклон, чтобы написать уравнение для его представления. . y 0 = 9 Следовательно, уравнение секущей между x = 2 и x = 9 равно точка находится путем проведения прямой линии, которая касается кривой в этой точке, не пересекая кривую. Другими словами, линия должна локально касаться только одной точки. Наклон касательной в точке представляет собой мгновенную скорость изменения или производную в этой точке. Формула: Мгновенная скорость изменения = Как найти производную в точке с помощью касательной: Шаг 1: Нарисуйте касательную линию в точке. Шаг 2: Используйте координаты любых двух точек на этой линии для расчета уклона. Уравнение наклона: Среднее изменение функции за заданный интервал времени x 0 Наклон касательной в точке представляет После того, как вы вычислили наклон касательной, вы можете написать уравнение для его представления. . = 6 Следовательно, уравнение касательной в точке x = 16 имеет вид В начале 18 века возникли разногласия. между великими математиками Исааком Ньютоном и Готфридом Вильгельмом Лейбницем над тем, кто первым изобрел исчисление. Этот аргумент стал известен как Prioritätsstreit , или «спор о приоритете» на немецком языке. Это разногласие оказало длительное влияние на математический мир, оставив нам два стандартных обозначения производных. Обозначение Лагранжа — еще одно распространенное производное обозначение, установленное французским математиком и философом 9.0005 Жозеф-Луи Лагранж
6
Наклон =
Наклон =
y – 9 = Производные (мгновенная скорость изменения)
Наклон =
Наклон =
мгновенную скорость изменения или производную в этой точке.
y – 16 = \frac{5}{6}(x – 6) Производное обозначение
Если взять функцию y = f(x), то
1. Обозначения Лейбница:
«Первая производная y по x»
⇒«Вторая производная y по x
⇒«Первая производная от y по x
при x = 2″
⇒
Функция 0040 была дифференцирована.
«Первая производная y»
⇒
«Вторая производная Y»
⇒
«Первая производная y при x = 2”
⇒
3. Лагранжа:
Количество апетритов после переменная function
показывает, сколько раз функция
была дифференцирована.
«Первая производная y»
⇒y’
«Первая производная y при x = 2»
⇒y'(2)
«Вторая производная y»
⇒ y ”
4. Обозначение Эйлера
« Первая производная »
⇒ D x F
« Второй производный »
⇒ D x 2F
⇒ D x 2F
⇒ D x 2F
⇒ D x 2F
⇒ D
Примеры задач
Вопрос 1. Найти среднюю скорость изменения на интервале x = 4, x = 6.
Решение: Точка 2: (6, 15)
Наклон =
=
=
Следовательно, средняя скорость изменения =
Вопрос 2. Напишите уравнение тангенсной линии при x = 16.
Напишите уравнение тангенсной линии при x = 16.
Решение
Точка пересечения: (16, 18)
Slope =
=
Уравнение касательной линии:
Вопрос 3. Какова дериватив графика x = 20? Выразите ответ в системе обозначений Лейбница.
Solution:
Given point of intersection: (20, 23)
Slope of tangent line =
=
So, the Leibniz notation:
Вопрос 4. Найдите производную графика при x = 4. Запишите ответ в обозначениях Ньютона.
Решение:
Заданная точка пересечения: (4, 18)
Наклон касательной = =
Итак, ньютоновские обозначения
Вопрос 5. Найдите среднюю скорость изменения на интервале x = 4, x = 25. Как это соотносится с производной при х = 4?
Найдите среднюю скорость изменения на интервале x = 4, x = 25. Как это соотносится с производной при х = 4?
Решение:
Наклон из секущей линии =
=
Средняя скорость изменения по сравнению с x = 4, x = 25 —6/21,
, что меньше, чем x = x = 25 —6/21,
производная от y при x = 4, которую мы нашли равной
быть 7/3.
Вопрос 6. Найдите мгновенную скорость изменения заданной функции f(x) = 2x 2 + 18 при x = 9 ?
Решение:
Дано: F (x) = 2x 2 + 18
F ‘(x) = 4x+ 0
f’ (x) = 4x
Теперь у нас есть найти мгновенную скорость изменения при x = 9
f(9) = 4x
f(9) = 4(9)
f(9) = 36
Вопрос 7. Найти мгновенную скорость изменения заданной функции f(x) = 4x 2 + 12x + 8 при x = 4 ?
Решение:
Дано: f(x) = 4x 2 + 12x + 8
f'(x) = 8x + 12
xТеперь нам нужно найти скорость изменения в момент времени = 4
f(4) = 8x + 12
f(4) = 8(4) + 12
f(4) = 44
Деловой расчет
Мгновенная скорость
Предположим, мы сбрасываем помидор с вершины 100-футового здания и измеряем время его падения.
На некоторые вопросы легко ответить прямо из таблицы:
- Через какое время помидор упал с высоты 100 футов? (2,5 секунды)
- На какое расстояние упал помидор за первую секунду? (100 – 84 = 16 футов)
- На какое расстояние упал помидор за последнюю секунду? (64 – 0 = 64 фута)
- Как далеко помидор упал между \(t = 0,5\) и \(t = 1\)? (96 – 84 = 12 футов)
Некоторые вопросы требуют небольшого расчета:
- Какова была средняя скорость помидора во время его падения? \[\text{Средняя скорость}=\frac{\text{расстояние падения}}{\text{общее время}}=\frac{\Delta\text{позиция}}{\Delta\text{время}}=\ frac{-100 \text{ ft}}{2.5 \text{ s}}=-40 \text{ ft/s}\]
- Какой была средняя скорость между \(t=1\) и \(t=2\) секундами? \[\text{Средняя скорость}=\frac{\Delta\text{позиция}}{\Delta\text{время}}=\frac{36\text{фут}- 84\text{фут}}{2\ text{ s} — 1\text{ s}}=\frac{-48 \text{ ft}}{1 \text{ s}}=-48 \text{ ft/s}\]
Некоторые вопросы сложнее:
С какой скоростью падал помидор через 1 секунду после падения?
Этот вопрос существенно отличается от двух предыдущих вопросов о средней скорости.
 Здесь нам нужна мгновенная скорость , скорость в момент времени. К сожалению, помидор не оснащен спидометром, поэтому придется дать приблизительный ответ.
Здесь нам нужна мгновенная скорость , скорость в момент времени. К сожалению, помидор не оснащен спидометром, поэтому придется дать приблизительный ответ.Одно грубое приближение мгновенной скорости через 1 секунду — это просто средняя скорость за все время падения, -40 футов/с. Но помидор медленно падал в начале и быстро ближе к концу, поэтому оценка «-40 футов/с» может быть или не быть хорошим ответом.
Мы можем получить лучшее приближение к мгновенной скорости при \(t=1\), рассчитав средние скорости за короткий промежуток времени около \(t = 1\). Средняя скорость между \(t = 0,5\) и \(t = 1\) равна \(\dfrac{-12\text{фут}}}{0,5\text{с}} = -24\текст{фут/с }\), а средняя скорость между \(t = 1\) и \(t = 1,5\) равна \(\dfrac{-20\text{ футов}}{0,5\text{с}} = -40\ text{ ft/s}\), поэтому мы можем быть достаточно уверены, что мгновенная скорость находится между -24 ft/s и -40 ft/s.
В целом, чем короче временной интервал, для которого мы вычисляем среднюю скорость, тем лучше средняя скорость будет аппроксимировать мгновенную скорость. Средняя скорость за интервал времени равна \(\dfrac{\Delta\text{position}}{\Delta\text{time}} \), что представляет собой наклон секущей , проходящей через две точки на графике высота против времени. Мгновенная скорость в определенное время и на определенной высоте представляет собой наклон касательной линии на графике в точке, заданной этим временем и высотой.
Средняя скорость за интервал времени равна \(\dfrac{\Delta\text{position}}{\Delta\text{time}} \), что представляет собой наклон секущей , проходящей через две точки на графике высота против времени. Мгновенная скорость в определенное время и на определенной высоте представляет собой наклон касательной линии на графике в точке, заданной этим временем и высотой.
Средняя против мгновенной скорости
Средняя скорость = \( \dfrac{\Delta\text{position}}{\Delta\text{time}} \) = наклон секущей через 2 точки.
Мгновенная скорость = наклон касательной к графику.
Растущие бактерии
Предположим, мы настроили машину для подсчета количества бактерий, растущих на чашке Петри. Сначала бактерий мало, поэтому популяция растет медленно. Затем нужно разделить больше бактерий, чтобы популяция росла быстрее. Позже для растущей популяции становится больше бактерий и меньше места и питательных веществ, поэтому популяция снова растет медленно. Наконец, бактерии израсходовали большую часть питательных веществ, и их популяция сокращается по мере того, как бактерии умирают.
Наконец, бактерии израсходовали большую часть питательных веществ, и их популяция сокращается по мере того, как бактерии умирают.
График населения можно использовать для ответа на ряд вопросов.
Какова численность бактерий в момент времени \(t = 3\) дней?
Из графика при \(t = 3\) популяция составляет около 0,5 тыс. или 500 бактерий.
Чему равен прирост населения от \(t = 3\) до \(t =10\) дней?
При \(t = 10\) популяция составляет около 4,5 тысяч, поэтому прирост составляет около 4000 бактерий.
Какова скорость прироста населения от \(t = 3\) до \(t = 10\) дней?
Скорость роста от \(t = 3\) до \(t = 10\) представляет собой среднее изменение численности населения за это время: \[ \begin{выравнивание*} \text{среднее изменение численности населения}=& \frac{\text{изменение численности населения}}{\text{изменение во времени}}\\ =& \frac{\Delta\text{население}}{\Delta\text{время}} \\ =& \frac{4000\text{ бактерии}}{7\text{ дней}} \\ \прибл& 570\text{ бактерий/день}.
 \end{выравнивание*} \]
\end{выравнивание*} \]Это наклон секущей, проходящей через две точки (3, 500) и (10, 4500).
Чему равен темп прироста населения на третий день в \(t = 3\) ?
Этот вопрос касается мгновенной скорости изменения населения, наклона линии, которая касается кривой населения в точке (3, 500). Если мы нарисуем линию, приблизительно касательную к кривой в точке (3, 500), и выберем две точки рядом с концами отрезка касательной, мы можем оценить, что мгновенная скорость роста популяции составляет примерно 320 бактерий/день.
Касательные линии
Попробуйте это!
График ниже представляет собой график \( y=f(x) \). Мы хотим найти наклон касательной в точке (1, 2).
Сначала проведите секущую между (1, 2) и (2, −1) и вычислите ее наклон.
Теперь проведите секущую между (1, 2) и (1,5, 1) и вычислите ее наклон.
Сравните две нарисованные линии. Что было бы лучшим приближением касательной к кривой в точке (1, 2)?
Что было бы лучшим приближением касательной к кривой в точке (1, 2)?
Теперь проведите секущую между (1, 2) и (1,3, 1,5) и вычислите ее наклон. Является ли эта линия еще лучшим приближением касательной?
Теперь нарисуйте касательную и измерьте ее наклон. Вы видите закономерность на склонах?
Вы должны были заметить, что по мере того, как интервал становился все меньше и меньше, секущая становилась ближе к касательной, а ее наклон приближался к наклону касательной. Это хорошая новость — мы знаем, как найти наклон секущей.
В некоторых приложениях нам нужно знать, где график функции \(f(x)\) имеет горизонтальные касательные линии (наклоны = 0).
Пример 1
Ниже приведен график \(y = g(x)\). При каких значениях \(x\) график \(g(x)\) имеет горизонтальные касательные?
Касательные к графику \(g(x)\) горизонтальны (наклон = 0), когда \(x\приблизительно -1, 1, 2,5, \text{ и } 5\).
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5 92\) в точке (2,4).
Мы могли бы оценить наклон \(L\) по графику, но не будем. Вместо этого мы воспользуемся идеей, что секущие через крошечные промежутки приближаются к касательной.
Мы видим, что линия, проходящая через (2,4) и (3,9) на графике \(f\), является аппроксимацией наклона касательной, и мы можем точно вычислить этот наклон: \( m = \frac{\Delta y}{\Delta x} = \frac{9-4}{3-2} = 5\). Но \(m = 5\) — это только оценка наклона касательной, а не очень хорошая оценка. Это слишком большое. Мы можем получить лучшую оценку, выбрав вторую точку на графике \(f\), которая ближе к (2,4) — точка (2,4) фиксирована, и она должна быть одной из точек, которые мы используем.
Из второго рисунка видно, что наклон прямой, проходящей через точки (2,4) и (2.5,6.25), является лучшим приближением наклона касательной в точках (2,4): \( m = \ frac {\ Delta y} {\ Delta x} = \ frac {6,25 — 4} {2,5 — 2} = \ frac {2,25} {0,5} = 4,5 \), лучшая оценка, но все же приблизительная. Мы можем продолжать выбирать точки все ближе и ближе к (2,4) на графике \(f\), а затем вычислять наклоны линий через каждую из этих точек и точку (2,4):
92\) 2\), наклоны линий, проходящих через точки и (2,4), являются лучшими приближениями наклон касательной, и эти наклоны все ближе и ближе к 4,92 \справа)\). По мере того, как \(h\) становится все меньше и меньше, этот наклон приближается к наклону касательной к графику \(f\) в (2,4).
2\), наклоны линий, проходящих через точки и (2,4), являются лучшими приближениями наклон касательной, и эти наклоны все ближе и ближе к 4,92 \справа)\). По мере того, как \(h\) становится все меньше и меньше, этот наклон приближается к наклону касательной к графику \(f\) в (2,4).Более формально мы могли бы написать: \[\text{Наклон касательной} = \dfrac{\Delta y}{\Delta x} = \lim\limits_{h\to 0} (4+h). \]
Мы можем легко оценить этот предел, используя прямую замену, обнаружив, что по мере того, как интервал \(h\) сжимается до 0, наклон секущей приближается к наклону касательной, 4.
Задача о касательной и задача о мгновенной скорости — это одна и та же задача. В каждой задаче мы хотели знать, насколько быстро что-то было изменяется в момент времени , а ответом оказалось нахождение наклона касательной , которую мы аппроксимировали наклоном секущей . Эта идея является ключом к определению наклона кривой.
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5
Производная
Мы можем рассматривать производную по-разному. Вот три из них:
- Производная функции \(f\) в точке (x, f(x)) представляет собой мгновенную скорость изменения.
- Производная — это наклон касательной к графику \(f\) в точке \((x, f(x))\).
- Производная — это наклон кривой \(f(x)\) в точке \((x, f(x))\).
Функция называется дифференцируемой в точке \((x, f(x))\), если ее производная существует в точке \((x, f(x))\).
Обозначение производной
Производная \(y = f(x)\) по \(x\) записывается как \[f'(x)\] (читается вслух как «\(f\) простое число \(x \)»), или \[y’\] (читается вслух как «почему прайм») или \[\frac{dy}{dx}\] (читается вслух как «ди почему ди экс»), или \[\ frac{df}{dx}.\]
Обозначение, напоминающее дробь, называется обозначением Лейбница . Он отображает не только имя функции (\(f\) или \(y\)), но и имя переменной (в данном случае \(x\)). Это похоже на дробь, потому что производная — это наклон. На самом деле это просто \( \frac{\Delta y}{\Delta x} \), написанное латинскими буквами, а не греческими.
Он отображает не только имя функции (\(f\) или \(y\)), но и имя переменной (в данном случае \(x\)). Это похоже на дробь, потому что производная — это наклон. На самом деле это просто \( \frac{\Delta y}{\Delta x} \), написанное латинскими буквами, а не греческими.
Глагольные формы
Мы находим производную функции, или берем производную функции, или дифференцируем функцию.
Мы используем адаптацию нотации \( \frac{df}{dx} \) для обозначения «найти производную от \(f(x)\):» \[\frac{d}{dx}\left [f(x)\right]=\frac{df}{dx}.\] [В книге используются круглые скобки вместо квадратных скобок — обе формы записи допустимы.]
Формальное алгебраическое определение
\[f'( х)=\lim\limits_{h\to 0} \dfrac{f(x+h)-f(x)}{h}\]
Практическое определение
Производную можно аппроксимировать, глядя на среднюю скорость изменения или наклон секущей на очень маленьком интервале. Чем меньше интервал, тем ближе он к истинной мгновенной скорости изменения, наклону касательной или наклону кривой.
Взгляд в будущее
Скоро у нас будут методы для вычисления точных значений производных по формулам. Если функция дана вам в виде таблицы или графика, вам все равно придется аппроксимировать таким образом.
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5
Это основа для остальной части этой главы. Замечательно, что такая простая идея (наклон касательной) и такое простое определение (для производной \(f'(x)\)) приведет к столь многим важным идеям и приложениям.
Пример 3
Найдите наклон касательной к \( f(x)=\frac{1}{x} \) в точке \(x = 3\).
Наклон касательной равен значению производной \(f'(3)\). \( f(3)=\frac{1}{3}\) и \( f(3+h)=\frac{1}{3+h} \), поэтому, используя формальное предельное определение производной , \[ f'(3)=\lim\limits_{h\to 0}\frac{f(3+h)-f(3)}{h}=\lim\limits_{h\to 0}\frac {\ гидроразрыва {1} {3+ч} — \ гидроразрыва {1} {3}} {ч}. \]
\]
Мы можем упростить, приведя дроби к общему знаменателю: \[ \begin{выравнивание*} \lim\limits_{h\to 0}\frac{\frac{1}{3+h}-\frac{1}{3}}{h}=& \lim\limits_{h\to 0}\frac {\ frac {1} {3 + h} \ cdot \ frac {3} {3} — \ frac {1} {3} \ cdot \ frac {3 + h} {3 + h}} {h} \\ =& \lim\limits_{h\to 0}\frac{\frac{3}}{9+3h}-\frac{3+h}{9+3h}}{h} \\ =& \lim\limits_{h\to 0}\frac{\frac{3-(3+h)}{9+3h}}{h} \\ =& \lim\limits_{h\to 0}\frac{\frac{3-3-h}{9+3h}}{h} \\ =& \lim\limits_{h\to 0}\frac{\frac{-h}{9+3h}}{h} \\ =& \lim\limits_{h\to 0}\frac{-h}{9+3h}\cdot\frac{1}{h} \\ =& \lim\limits_{h\to 0}\frac{-1}{9+3h} \\ \end{align*} \] и оцените с помощью прямой замены: \[\lim\limits_{h\to 0}\frac{-1}{9+3h}=\frac{-1}{9+3( 0)}=-\frac{1}{9}.\]
Таким образом, наклон касательной к \( f(x)=\frac{1}{x} \) в точке \(x = 3\) равен \( -\frac{1}{9} \).
Производная как функция
Теперь мы знаем, как найти (или хотя бы приблизительно) производную функции для любого \(х\)-значения; это означает, что мы также можем думать о производной как о функции. Входные данные те же самые \(x\); выход — это значение производной при этом значении \(x\).
Входные данные те же самые \(x\); выход — это значение производной при этом значении \(x\).
Пример 4
Ниже приведен график функции \( y=f(x) \). Мы можем использовать информацию на графике, чтобы заполнить таблицу, показывающую значения \( f'(x): \)
При различных значениях \(x\) нарисуйте, насколько возможно, касательную и измерьте ее наклон. Возможно, вам придется расширить свои линии, чтобы вы могли прочитать некоторые моменты. В общем, ваша оценка наклона будет лучше, если вы выберете точки, которые легко читаются и находятся далеко друг от друга. Вот оценки для нескольких значений \(x\) (части используемых касательных линий показаны выше на графике):
| \( x \) | \(у=е(х)\) | \( f'(x)= \) оценка наклон касательной к кривой в точке \((x,y)\). |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
| 2 | 0 | -1 |
| 3 | -1 | 0 |
| 3,5 | 0 | 2 |
Мы также можем оценить значения \(f'(x)\) при некоторых нецелочисленных значениях \(x\): \(f'(0,5) \приблизительно 0,5\) и \(f’ (1,3) \приблизительно -0,3\).
Мы можем думать даже о целых интервалах. Например, если \(0 \lt x \lt 1\), то \(f(x)\) возрастает, все наклоны положительны, а значит, \(f'(x)\) положительна.
Значения \(f'(x)\) определенно зависят от значений \(x\), а \(f'(x)\) является функцией \(x\). Мы можем использовать результаты в таблице, чтобы набросать график \(f'(x)\).
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5
Пример 5
Показан график высоты \(h(t)\) ракеты в момент времени \(t\).
Нарисуйте график скорости ракеты за время \(t\). (Скорость — это производная функции высоты, поэтому она представляет собой наклон касательной к графику положения или высоты.) 92-4h}{h} \qquad \text{(Теперь упростим.)}\\ =& \lim\limits_{h\to 0} \frac{h(4x+2h-4)}{h} \qquad \text{(Вынести \( h \), затем отменить.)} \\ =& \lim\limits_{h\to 0} (4x+2h-4) \end{выравнивание*} \] Мы можем найти предел этого выражения прямой подстановкой: \[ f'(x)=\lim\limits_{h\to 0} (4x+2h-4)=4x-4\]
Обратите внимание, что производная зависит на \(x\), и что эта формула сообщит нам наклон касательной к \(f\) при любом значении \(x\). Например, если бы мы хотели узнать наклон касательной \(f\) в точке \(x = 3\), мы бы просто вычислили: \( f'(3)=4(3)-4=8 \).
Например, если бы мы хотели узнать наклон касательной \(f\) в точке \(x = 3\), мы бы просто вычислили: \( f'(3)=4(3)-4=8 \).
Формула для производной функции очень мощная, но, как вы можете видеть, вычисление производной с использованием определения предела занимает очень много времени. В следующем разделе мы определим некоторые шаблоны, которые позволят нам начать создавать набор правил для поиска производных без необходимости определения предела.
Интерпретация производной
До сих пор мы подчеркивали производную как наклон линии, касательной к графику. Эта интерпретация очень наглядна и полезна при изучении графика функции, и мы продолжим ее использовать. Однако производные используются в самых разных областях и приложениях, и в некоторых из этих областей используются другие интерпретации. Ниже приведены несколько интерпретаций производной, которые обычно используются.
Общее
Скорость изменения: \(f ‘(x)\) — это скорость изменения функции в точке \(x\). Если единицами для \(x\) являются годы, а единицами для \(f(x)\) являются люди, то единицами для \(\frac{df}{dx} \) являются \(\frac{\text {люди}}{\text{год}}\), скорость изменения численности населения.
Если единицами для \(x\) являются годы, а единицами для \(f(x)\) являются люди, то единицами для \(\frac{df}{dx} \) являются \(\frac{\text {люди}}{\text{год}}\), скорость изменения численности населения.
Графический
Наклон: \(f ‘(x)\) — это наклон линии, касательной к графику \(f\) в точке \(( x, f(x))\) .
Физический
Скорость: Если \(f(x)\) — положение объекта в момент времени \(x\), то \(f ‘(x)\) — это скорость объекта в момент времени \(x\). ). Если единицами измерения \(x\) являются часы, а \(f(x)\) — расстояние, измеренное в милях, то единицами измерения \(f ‘(x) = \frac{df}{dx}\) являются \ ( \frac{\text{miles}}{\text{hour}} \), миль в час, что является мерой скорости.
Ускорение: Если \(f(x)\) — скорость объекта в момент времени \(x\), то \(f ‘(x)\) — это ускорение объекта в момент времени \(x \). Если единицами для \(x\) являются часы, а \(f(x)\) имеет единицы \(\frac{\text{мили}}{\text{час}} \), то единицы для ускорение \(f ‘(x) = \frac{df}{dx}\) равны \( \frac{\text{мили/час}}{\text{час}} =\frac{\text{мили}} {\text{час}^2} \), миль в час в час.
Бизнес
Предельные затраты, предельный доход и предельная прибыль: мы рассмотрим эти термины более подробно позже в этом разделе. По сути, предельные издержки равны приблизительно 90 635 дополнительным 90 636 затратам на создание еще одного объекта после того, как мы уже сделали \(x\) объектов. Если единицами для \(x\) являются велосипеды, а единицами для \(f(x)\) являются доллары, то единицами для \(f ‘(x) = \frac{df}{dx}\) являются \ ( \frac{\text{доллары}}{\text{велосипед}} \), стоимость одного велосипеда.
В деловом контексте слово » маргинальный номер «обычно означает производную или скорость изменения некоторой величины.
Одной из сильных сторон исчисления является то, что оно обеспечивает единство и экономию идей среди различных приложений. Словарь и задачи могут быть разными, но идеи и даже обозначения исчисления по-прежнему полезны.
Пример 7
Предположим, что кривая спроса на виджеты задается формулой \(D(p)=\frac{1}{p} \), где \(D\) — количество виджетов в тысячах по цене в \(p\) долларов. Интерпретируйте производную \(D\) в точке \(p = \)$3.
Интерпретируйте производную \(D\) в точке \(p = \)$3.
Обратите внимание, что мы вычислили \( D'(3) \) ранее как \( D'(3)=-\frac{1}{9}\приблизительно -0,111 \).
Так как \(D\) имеет единицы тысячи виджетов
, а единицами для \(p\) являются цены в долларах, единицы для \(D’\) будут \( \frac{\text{тысячи виджеты}}{\text{доллар цены}} \). Другими словами, он показывает, как изменится спрос при повышении цены.
В частности, \( D'(3)\приблизительно -0,111 \) говорит нам, что при цене 3 доллара спрос уменьшится примерно на 0,111 тыс. штук на каждый доллар цена увеличивается.
(Примечание. Скриншоты в следующем видео взяты из более ранней версии книги, поэтому номера некоторых разделов или заголовки могут отличаться. Однако большая часть содержания осталась прежней, и комментарии по-прежнему актуальны. )
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5
Обзор вычисленияAP: средняя скорость изменения — Блог Magoosh
By Shaun Ault on 25 января 2018 г. в AP
в AP
Исчисление — это изучение движения и скорости изменения. На самом деле, Исаак Ньютон разработал исчисление (да, как и все остальное) только для того, чтобы помочь ему определить точное влияние гравитации на движение планет! В этой короткой обзорной статье мы поговорим о концепции средней скорости сдачи.
Мы также поговорим о том, как средние ставки приводят к мгновенным ставкам и производным. И мы увидим несколько примеров проблем по пути. Так что пристегнитесь!
Знание скорости изменений имеет решающее значение для планирования миссий на Луну и дальше!
Какова средняя скорость изменения функции
Все сводится к простой формуле из элементарной физики. Предположим, что объект движется с постоянной скоростью (или скоростью , или скоростью ). Затем мы можем найти расстояние, которое он проходит за любой указанный период времени, используя:
Расстояние = Скорость × Время
Однако лучше думать о изменениях в расстоянии и во времени. Например, если я проеду от отметки 25 миль до отметки 35 миль, это расстояние составит 10 миль (это изменение с 25 до 35).
Например, если я проеду от отметки 25 миль до отметки 35 миль, это расстояние составит 10 миль (это изменение с 25 до 35).
(Изменение расстояния) = Скорость × (Изменение во времени)
Скорость можно найти, разделив обе части на Изменение во времени.
Скорость = (изменение расстояния) / (изменение времени)
Различные тарифы
С другой стороны, если скорость объекта не остается постоянной, формула не работает.
Представьте себе автомобильную поездку на 10 миль. Если я скажу вам, что дорога заняла ровно 20 минут, то можете ли вы сказать мне мою скорость в любой точке пути?
Пустынная дорога (Фото Уильяма Уорби)
Конечно нет!
Вы не представляете, если бы я остановился на красный свет через 2 минуты после начала поездки, ускорился, чтобы обогнать другую машину на полпути, или нажал на тормоза, когда дорожный патруль появился ближе к концу поездки.
С другой стороны, если бы вы использовали формулу оценки, вы все равно могли бы получить полезную информацию.
Скорость = (Изменение расстояния) / (Изменение времени) = (10 миль) / (20 минут)
= 0,5 мили/мин.
Умножая на коэффициент пересчета 60 мин/час, находим скорость:
0,5 × 60 = 30 миль в час.
Но что означает это число? Возможно, я не ехал с постоянной скоростью 30 миль в час всю поездку, но если вы сгладите все медленные и быстрые участки, то в среднем Я ехал 30 миль в час.
Вы только что вычислили мою среднюю скорость изменения или среднюю скорость .
Формула средней скорости изменения
Хорошо, теперь поговорим о точной формуле.
В исчислении большинство формул имеют дело с функциями. Итак, пусть f ( x ) будет функцией. Давайте договоримся рассматривать ввод x как умножить на в формуле скорости изменения. Выход, y = f ( x ), будет считаться аналогом расстояния .
Выход, y = f ( x ), будет считаться аналогом расстояния .
Итак, если скорость = расстояние/время, то давайте определим (среднюю) скорость функции как изменение y -значений, деленное на изменение x -значений на заданном интервале. Чтобы упростить формулы, мы часто используем дельту греческой столицы (Δ) для обозначения изменений.
средняя скорость изменения функции f на заданном интервале [ a , б ] это:
Обратите внимание, насколько это близко к другой важной формуле, наклону секущей .
На самом деле, они той же формулы ! Средняя скорость изменения функции на интервале [ a , b ] точно равна наклону секущей между точками x = a и x = b .
Альтернативная формула и производная
Предположим теперь, что мы указываем, что точка b находится точно на h единиц правее a . С точки зрения математики, 90 635 b 90 636 = 90 635 a 90 636 + 90 635 h 90 636. Как это меняет нашу формулу?
С точки зрения математики, 90 635 b 90 636 = 90 635 a 90 636 + 90 635 h 90 636. Как это меняет нашу формулу?
Последняя строка кажется знакомой?
Если вы замените a на x (чтобы сделать его более похожим на функцию) и позволите разности h приблизиться к 0, взяв предел, то вы получите определение производной функции.
После применения предела мы часто называем эту формулу мгновенной скоростью изменения или мгновенной скоростью .
Таким образом, понятие скорости изменения служит стартовой площадкой для изучения пределов и производных, сердцевины дифференциального исчисления!
Связь с теоремой о среднем значении
Существует важный математический результат, называемый теоремой о среднем значении (MVT) . По сути, MVT утверждает, что любая непрерывная и дифференцируемая на интервале функция должна иметь точку внутри этого интервала, в которой мгновенная скорость изменения (производная) должна равняться средней скорости изменения на интервале.
В математической записи для некоторых c таких, что a < c < b .
Чтобы получить хороший обзор MVT, вы можете проверить: AP Calculus Review: Teopeme Mean Value.
Вы можете ожидать пару вопросов о MVT, поэтому хорошо знать, связана ли она со средней скоростью изменений.
Примеры проблем
Давайте рассмотрим пару задач, хорошо?
Проблема 1
Тело движется прямолинейно по формуле х = 3 t 2 – 2 t + 1, для 0 ≤ t ≤ 8. Найти среднюю скорость тела на заданном интервале времени .
Решение
Будьте осторожны! В этой задаче входная переменная равна t , а выходная — x . Поэтому формула средней скорости принимает вид Δx/Δt.
Данный интервал равен [0, 8], поэтому мы используем a = 0 и b = 8 в формуле.
Средняя скорость 22.
Задача 2
Найдите любую точку от 1 до 9 такую, что мгновенная скорость изменения f ( x ) = x 2 в этой точке соответствует средней скорости изменения за интервал [1, 9].
Решение
Это работа для МВТ! Обратите внимание, как мы должны установить производную равной средней скорости изменения.
Гарантированно улучшите свой результат SAT или ACT. Начните свою 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep сегодня!
Автор
Кстати, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT. Нажмите сюда, чтобы узнать больше!
Расчет AP
← Предыдущий
Следующий →
6.4 Длина дуги кривой и площадь поверхности – исчисление, том 1
Цели обучения
- 6.4.1 Определите длину кривой y=f(x),y=f(x) между двумя точками.
- 6.4.2 Определите длину кривой x=g(y),x=g(y) между двумя точками.
- 6.4.3 Найдите площадь поверхности тела вращения.
В этом разделе мы используем определенные интегралы для нахождения длины дуги кривой. Мы можем думать о длине дуги как о расстоянии, которое вы прошли бы, если бы шли по пути кривой. Во многих реальных приложениях используется длина дуги. Если ракета запускается по параболической траектории, мы можем захотеть узнать, как далеко пролетит ракета. Или, если кривая на карте представляет собой дорогу, мы можем захотеть узнать, какое расстояние нам нужно проехать, чтобы добраться до пункта назначения.
Мы можем думать о длине дуги как о расстоянии, которое вы прошли бы, если бы шли по пути кривой. Во многих реальных приложениях используется длина дуги. Если ракета запускается по параболической траектории, мы можем захотеть узнать, как далеко пролетит ракета. Или, если кривая на карте представляет собой дорогу, мы можем захотеть узнать, какое расстояние нам нужно проехать, чтобы добраться до пункта назначения.
Мы начинаем с вычисления длины дуги кривых, определенных как функции x,x, затем мы исследуем тот же процесс для кривых, определенных как функции y.y. (Процесс идентичен, но роли xx и yy поменялись местами.) Методы, которые мы используем для определения длины дуги, можно расширить, чтобы найти площадь поверхности вращения, и мы завершаем раздел рассмотрением этой концепции.
Длина дуги кривой
y = f ( x ) В предыдущих приложениях интеграции мы требовали, чтобы функция f(x)f(x) была интегрируемой или, самое большее, непрерывной. Однако для расчета длины дуги у нас есть более строгие требования к f(x).f(x). Здесь мы требуем, чтобы функция f(x)f(x) была дифференцируемой, и, кроме того, мы требуем, чтобы ее производная f′(x),f′(x) была непрерывной. Такие функции, которые имеют непрерывные производные, называются гладкий . (Это свойство снова появится в следующих главах.)
Однако для расчета длины дуги у нас есть более строгие требования к f(x).f(x). Здесь мы требуем, чтобы функция f(x)f(x) была дифференцируемой, и, кроме того, мы требуем, чтобы ее производная f′(x),f′(x) была непрерывной. Такие функции, которые имеют непрерывные производные, называются гладкий . (Это свойство снова появится в следующих главах.)
Пусть f(x)f(x) — гладкая функция, определенная над [a,b].[a,b]. Мы хотим вычислить длину кривой от точки (a,f(a))(a,f(a)) до точки (b,f(b)).(b,f(b)). Начнем с использования линейных сегментов для аппроксимации длины кривой. Для i=0,1,2,…,n,i=0,1,2,…,n пусть P={xi}P={xi} будет правильным разбиением [a,b].[a, б]. Затем для i=1,2,…,n,i=1,2,…,n построить отрезок из точки (xi−1,f(xi−1))(xi−1,f(xi −1)) в точку (xi,f(xi)).(xi,f(xi)). Хотя может показаться логичным использовать либо горизонтальные, либо вертикальные сегменты линий, мы хотим, чтобы наши сегменты линий как можно точнее аппроксимировали кривую. На рис. 6.37 показана эта конструкция для n=5.n=5.
6.37 показана эта конструкция для n=5.n=5.
Рисунок 6,37 Мы можем аппроксимировать длину кривой, добавляя отрезки.
Чтобы помочь нам найти длину каждого сегмента линии, мы смотрим на изменение расстояния по вертикали, а также изменение расстояния по горизонтали на каждом интервале. Поскольку мы использовали регулярное разбиение, изменение горизонтального расстояния на каждом интервале определяется как Δx.Δx. Однако изменение вертикального расстояния варьируется от интервала к интервалу, поэтому мы используем Δyi=f(xi)−f(xi−1)Δyi=f(xi)−f(xi−1) для представления изменения вертикального расстояния в течение интервал [xi−1,xi],[xi−1,xi], как показано на рис. 6.38. Обратите внимание, что некоторые (или все) ΔyiΔyi могут быть отрицательными.
Рисунок 6,38 Репрезентативный отрезок линии аппроксимирует кривую на интервале [xi−1,xi].[xi−1,xi].
По теореме Пифагора длина отрезка равна (Δx)2+(Δyi)2.(Δx)2+(Δyi)2. Мы также можем записать это как ∆x1+((∆yi)/(∆x))2. ∆x1+((∆yi)/(∆x))2. Теперь по теореме о среднем значении существует точка xi*∈[xi−1,xi]xi*∈[xi−1,xi] такая, что f′(xi*)=(Δyi)/(Δx).f ′(xi*)=(Δyi)/(Δx). Тогда длина отрезка равна ∆x1+[f′(xi*)]2.∆x1+[f′(xi*)]2. Складывая длины всех отрезков, получаем
∆x1+((∆yi)/(∆x))2. Теперь по теореме о среднем значении существует точка xi*∈[xi−1,xi]xi*∈[xi−1,xi] такая, что f′(xi*)=(Δyi)/(Δx).f ′(xi*)=(Δyi)/(Δx). Тогда длина отрезка равна ∆x1+[f′(xi*)]2.∆x1+[f′(xi*)]2. Складывая длины всех отрезков, получаем
Длина дуги≈∑i=1n1+[f′(xi*)]2Δx. Длина дуги≈∑i=1n1+[f′(xi*)]2Δx.
Это сумма Римана. Беря предел при n→∞,n→∞, мы имеем
Длина дуги=limn→∞∑i=1n1+[f′(xi*)]2Δx=∫ab1+[f′(x)]2dx.Длина дуги=limn→∞∑i=1n1+[f′(xi*)] 2∆x=∫ab1+[f′(x)]2dx.
Мы суммируем эти выводы в следующей теореме.
Теорема 6.4
Длина дуги для
y = f ( x )Пусть f(x)f(x) — гладкая функция на интервале [a,b].[a,b]. Тогда длина дуги участка графика f(x)f(x) от точки (a,f(a))(a,f(a)) до точки (b,f(b))( b,f(b)) равно
Длина дуги=∫ab1+[f′(x)]2dx.Длина дуги=∫ab1+[f′(x)]2dx.
(6.7)
Обратите внимание, что мы интегрируем выражение, включающее f′(x),f′(x), поэтому нам нужно убедиться, что f′(x)f′(x) интегрируемо. Вот почему мы требуем, чтобы функция f(x)f(x) была гладкой. В следующем примере показано, как применить теорему.
Пример 6.18
Вычисление длины дуги функции
xПусть f(x)=2×3/2.f(x)=2×3/2. Вычислите длину дуги графика функции f(x)f(x) на интервале [0,1].[0,1]. Округлите ответ до трех знаков после запятой.
Решение
Имеем f′(x)=3×1/2,f′(x)=3×1/2, поэтому [f′(x)]2=9x. [f′(x)]2=9x. Тогда длина дуги равна
Длина дуги=∫ab1+[f′(x)]2dx=∫011+9xdx. Длина дуги=∫ab1+[f′(x)]2dx=∫011+9xdx.
Замените u=1+9x.u=1+9x. Тогда du=9dx.du=9dx. Когда x=0,x=0, то u=1,u=1, а когда x=1,x=1, то u=10.u=10. Таким образом,
Длина дуги=∫011+9xdx=19∫011+9x9dx=19∫110udu=19·23u3/2|110=227[1010−1]≈2,268 единиц. Длина дуги=∫011+9xdx=19∫ 011+9x9dx=19∫110udu=19·23u3/2|110=227[1010−1]≈2,268 ед.
Длина дуги=∫011+9xdx=19∫ 011+9x9dx=19∫110udu=19·23u3/2|110=227[1010−1]≈2,268 ед.
Контрольно-пропускной пункт 6.18
Пусть f(x)=(4/3)x3/2.f(x)=(4/3)x3/2. Вычислите длину дуги графика функции f(x)f(x) на интервале [0,1].[0,1]. Округлите ответ до трех знаков после запятой.
Хотя хорошо иметь формулу для вычисления длины дуги, эта конкретная теорема может генерировать выражения, которые трудно интегрировать. Мы изучаем некоторые методы интеграции во Введении в методы интеграции. В некоторых случаях нам, возможно, придется использовать компьютер или калькулятор для аппроксимации значения интеграла.
Пример 6.19
Использование компьютера или калькулятора для определения длины дуги функции
xПусть f(x)=x2.f(x)=x2. Вычислите длину дуги графика функции f(x)f(x) на интервале [1,3].[1,3].
Решение
Имеем f′(x)=2x,f′(x)=2x, поэтому [f′(x)]2=4×2. [f′(x)]2=4×2. Тогда длина дуги определяется как
[f′(x)]2=4×2. Тогда длина дуги определяется как
Длина дуги=∫ab1+[f′(x)]2dx=∫131+4x2dx. Длина дуги=∫ab1+[f′(x)]2dx=∫131+4x2dx.
Используя компьютер для аппроксимации значения этого интеграла, мы получаем
∫131+4x2dx≈8,26815.∫131+4x2dx≈8,26815.
Контрольно-пропускной пункт 6.19
Пусть f(x)=sinx.f(x)=sinx. Вычислите длину дуги графика функции f(x)f(x) на интервале [0,π].[0,π]. Используйте компьютер или калькулятор, чтобы приблизить значение интеграла.
Длина дуги кривой
x = г ( y )Мы только что видели, как аппроксимировать длину кривой отрезками. Если мы хотим найти длину дуги графика функции y, y, мы можем повторить тот же процесс, за исключением того, что мы разделим ось y вместо оси x. ось x. Рис. 6.39.показывает репрезентативный сегмент линии.
Рисунок
6,39
Репрезентативный отрезок на интервале [yi-1,yi]. [yi-1,yi].
[yi-1,yi].
Тогда длина отрезка равна (Δy)2+(Δxi)2,(Δy)2+(Δxi)2, что также может быть записано как Δy1+((Δxi)/(Δy))2.Δy1+(( Δxi)/(Δy))2. Если мы теперь будем следовать тому же развитию, что и ранее, мы получим формулу для длины дуги функции x=g(y).x=g(y).
Теорема 6,5
Длина дуги для
x = г ( и )Пусть g(y)g(y) — гладкая функция на интервале yy [c,d].[c,d]. Тогда длина дуги графика g(y)g(y) от точки (g(d), d)(g(d), d) до точки (g(c), c)(g( c), c) определяется как
Длина дуги=∫cd1+[g′(y)]2dy. Длина дуги=∫cd1+[g′(y)]2dy.
(6.8)
Пример 6.20
Вычисление длины дуги функции
yПусть g(y)=3y3.g(y)=3y3. Вычислите длину дуги графика g(y)g(y) на интервале [1,2].[1,2].
Решение
Имеем g′(y)=9y2,g′(y)=9y2, поэтому [g′(y)]2=81y4. [g′(y)]2=81y4. Тогда длина дуги равна
[g′(y)]2=81y4. Тогда длина дуги равна
Длина дуги=∫cd1+[g′(y)]2dy=∫121+81y4dy. Длина дуги=∫cd1+[g′(y)]2dy=∫121+81y4dy.
Используя компьютер для аппроксимации значения этого интеграла, мы получаем
∫121+81y4dy≈21,0277.∫121+81y4dy≈21,0277.
Контрольно-пропускной пункт 6.20
Пусть g(y)=1/y.g(y)=1/y. Вычислите длину дуги графика g(y)g(y) на интервале [1,4].[1,4]. Используйте компьютер или калькулятор, чтобы приблизить значение интеграла.
Площадь поверхности вращения
Понятия, которые мы использовали для определения длины дуги кривой, можно расширить, чтобы найти площадь поверхности вращения. Площадь поверхности — это общая площадь внешнего слоя объекта. Для таких объектов, как кубы или кирпичи, площадь поверхности объекта равна сумме площадей всех его граней. Для криволинейных поверхностей ситуация немного сложнее. Пусть f(x)f(x) — неотрицательная гладкая функция на интервале [a,b].[a,b]. Мы хотим найти площадь поверхности вращения, созданную вращением графика y=f(x)y=f(x) вокруг оси xx, как показано на следующем рисунке.
Рисунок 6.40 (a) Кривая, представляющая функцию f(x).f(x). (b) Поверхность вращения, образованная вращением графика f(x)f(x) вокруг оси x.x-ось.
Как мы делали много раз раньше, мы собираемся разбить интервал [a,b][a,b] и аппроксимировать площадь поверхности, вычислив площадь поверхности более простых форм. Мы начнем с использования линейных сегментов для аппроксимации кривой, как мы делали ранее в этом разделе. Для i=0,1,2,…,n,i=0,1,2,…,n пусть P={xi}P={xi} будет правильным разбиением [a,b].[a, б]. Затем для i=1,2,…,n,i=1,2,…,n построить отрезок из точки (xi−1,f(xi−1))(xi−1,f(xi −1)) в точку (xi,f(xi)).(xi,f(xi)). Теперь поверните эти отрезки линии вокруг оси xx, чтобы создать аппроксимацию поверхности вращения, как показано на следующем рисунке.
Рисунок 6.41 (a) Аппроксимация f(x)f(x) отрезками. (b) Поверхность вращения, образованная вращением отрезков линии вокруг оси х.
Обратите внимание, что когда каждый сегмент линии вращается вокруг оси, образуется полоса. Эти полосы на самом деле представляют собой кусочки рожков (представьте себе рожок мороженого с отрезанным заостренным концом). Часть такого конуса называется усеченным конусом.
Эти полосы на самом деле представляют собой кусочки рожков (представьте себе рожок мороженого с отрезанным заостренным концом). Часть такого конуса называется усеченным конусом.
Чтобы найти площадь поверхности полосы, нам нужно найти площадь боковой поверхности, S, S, усеченного конуса (площадь только наклонной внешней поверхности усеченного конуса, не включая площади верхней или нижней граней) . Пусть r1r1 и r2r2 — радиусы широкого и узкого концов усеченного конуса соответственно, а ll — наклонная высота усеченного конуса, как показано на следующем рисунке.
Рисунок 6,42 Усеченный конус может аппроксимировать небольшую часть площади поверхности.
Мы знаем, что площадь боковой поверхности конуса равна
.Площадь боковой поверхности = πrs, Площадь боковой поверхности = πrs,
, где rr — радиус основания конуса, а ss — наклонная высота (см. следующий рисунок).
Рисунок
6,43
Площадь боковой поверхности конуса равна πrs. πrs.
πrs.
Поскольку усеченный конус можно рассматривать как часть конуса, площадь боковой поверхности усеченного конуса равна площади боковой поверхности всего конуса за вычетом площади боковой поверхности меньшего конуса (заостренного кончика), который был срезан. выключено (см. следующий рисунок).
Рисунок 6,44 Вычисление площади боковой поверхности усеченного конуса.
Сечения малого конуса и большого конуса представляют собой подобные треугольники, поэтому мы видим, что
r2r1=s-ls.r2r1=s-ls.
Решая s,s, получаем
r2r1=s-lsr2s=r1(s-l)r2s=r1s-r1lr1l=r1s-r2sr1l=(r1-r2)sr1lr1-r2=s.r2r1=s-lsr2s=r1(s-l)r2s=r1s- r1lr1l=r1s−r2sr1l=(r1−r2)sr1lr1−r2=s.
Тогда площадь боковой поверхности (SA) усеченного конуса равна
S=(Боковая СА большого конуса)−(Боковая СА малого конуса)=πr1s−πr2(s−l)=πr1(r1lr1−r2)−πr2(r1lr1−r2−l)=πr12lr1−r2−πr1r2lr1− r2+πr2l=πr12lr1−r2−πr1r2lr1−r2+πr2l(r1−r2)r1−r2=πr12lr1−r2−πr1r2lr1−r2+πr1r2lr1−r2−πr22lr1−r2=π(r12−r22)lr1−r2=π( r1−r2)(r1+r2)lr1−r2=π(r1+r2)l. S=(Боковая СА большого конуса)−(Боковая СА малого конуса)=πr1s−πr2(s−l)=πr1(r1lr1− r2)−πr2(r1lr1−r2−l)=πr12lr1−r2−πr1r2lr1−r2+πr2l=πr12lr1−r2−πr1r2lr1−r2+πr2l(r1−r2)r1−r2=πr12lr1−r2−πr1r2lr1−r2+πr1r2lr1− r2−πr22lr1−r2=π(r12−r22)lr1−r2=π(r1−r2)(r1+r2)lr1−r2=π(r1+r2)l.
S=(Боковая СА большого конуса)−(Боковая СА малого конуса)=πr1s−πr2(s−l)=πr1(r1lr1− r2)−πr2(r1lr1−r2−l)=πr12lr1−r2−πr1r2lr1−r2+πr2l=πr12lr1−r2−πr1r2lr1−r2+πr2l(r1−r2)r1−r2=πr12lr1−r2−πr1r2lr1−r2+πr1r2lr1− r2−πr22lr1−r2=π(r12−r22)lr1−r2=π(r1−r2)(r1+r2)lr1−r2=π(r1+r2)l.
Теперь воспользуемся этой формулой для расчета площади поверхности каждой из полос, образованных вращением отрезков линии вокруг оси x.x. Репрезентативная полоса показана на следующем рисунке.
Рисунок 6,45 Репрезентативная полоса, используемая для определения площади поверхности.
Обратите внимание, что наклонная высота этой усеченной пирамиды равна длине отрезка, использованного для ее создания. Итак, применяя формулу площади поверхности, мы имеем
S=π(r1+r2)l=π(f(xi−1)+f(xi))Δx2+(Δyi)2=π(f(xi−1)+f(xi))Δx1+(ΔyiΔx)2 .S=π(r1+r2)l=π(f(xi−1)+f(xi))Δx2+(Δyi)2=π(f(xi−1)+f(xi))Δx1+(ΔyiΔx)2 .
Теперь, как и при разработке формулы длины дуги, мы применяем теорему о среднем значении, чтобы выбрать xi*∈[xi−1,xi]xi*∈[xi−1,xi] такое, что f′(xi* )=(Δyi)/Δx. f′(xi*)=(Δyi)/Δx. Это дает нам
f′(xi*)=(Δyi)/Δx. Это дает нам
S=π(f(xi−1)+f(xi))Δx1+(f′(xi*))2.S=π(f(xi−1)+f(xi))Δx1+(f′(xi *))2.
Кроме того, поскольку функция f(x)f(x) непрерывна, по теореме о промежуточном значении существует точка xi**∈[xi−1,xi]xi**∈[xi−1,xi] такая, что f (xi**)=(1/2)[f(xi−1)+f(xi)],f(xi**)=(1/2)[f(xi−1)+f(xi)] , поэтому получаем
S=2πf(xi**)∆x1+(f′(xi*))2.S=2πf(xi**)∆x1+(f′(xi*))2.
Тогда приблизительная площадь всей поверхности вращения равна
Площадь поверхности≈∑i=1n2πf(xi**)Δx1+(f′(xi*))2. Площадь поверхности≈∑i=1n2πf(xi**)Δx1+(f′(xi*))2.
Это почти выглядит как сумма Римана, за исключением того, что у нас есть функции, вычисляемые в двух разных точках, xi*xi* и xi**,xi**, на интервале [xi−1,xi].[xi−1, xi]. Хотя мы не рассматриваем здесь детали, оказывается, что, поскольку f(x)f(x) гладкая, если мы позволим n→∞,n→∞, предел работает так же, как сумма Римана, даже с двумя разными оценочные баллы. Это интуитивно понятно. Оба xi*xi* и xi**xi** находятся в интервале [xi−1,xi],[xi−1,xi], поэтому имеет смысл, что при n→∞,n→∞ оба xi*xi * и xi**xi** приближаются к x.x. Тем из вас, кто интересуется подробностями, следует обратиться к учебнику по продвинутому исчислению.
Оба xi*xi* и xi**xi** находятся в интервале [xi−1,xi],[xi−1,xi], поэтому имеет смысл, что при n→∞,n→∞ оба xi*xi * и xi**xi** приближаются к x.x. Тем из вас, кто интересуется подробностями, следует обратиться к учебнику по продвинутому исчислению.
Принимая предел как n→∞,n→∞, мы получаем
Площадь поверхности=limn→∞∑i=1n2πf(xi**)Δx1+(f′(xi*))2=∫ab(2πf(x)1+(f′(x))2)dx. Площадь поверхности= limn→∞∑i=1n2πf(xi**)∆x1+(f′(xi*))2=∫ab(2πf(x)1+(f′(x))2)dx.
Как и в случае с длиной дуги, мы можем провести аналогичное развитие для функций yy, чтобы получить формулу для площади поверхности поверхностей вращения вокруг оси y.ось y. Эти выводы резюмируются в следующей теореме.
Теорема 6,6
Площадь поверхности вращения
Пусть f(x)f(x) — неотрицательная гладкая функция на интервале [a,b].[a,b]. Тогда площадь поверхности вращения, образованная вращением графика функции f(x)f(x) вокруг оси x , равна
Площадь поверхности=∫ab(2πf(x)1+(f ′(x))2)dx. Площадь поверхности=∫ab(2πf(x)1+(f′(x))2)dx.
Площадь поверхности=∫ab(2πf(x)1+(f′(x))2)dx.
(6.9)
Аналогично, пусть g(y)g(y) — неотрицательная гладкая функция на интервале [c,d].[c,d]. Тогда площадь поверхности вращения, образованная вращением графика g(y)g(y) вокруг оси y, равна
Площадь поверхности=∫cd(2πg(y)1+(g′(y))2)dy. Площадь поверхности=∫cd(2πg(y)1+(g′(y))2)dy.
Пример 6.21
Расчет площади поверхности вращения 1
Пусть f(x)=xf(x)=x на интервале [1,4].[1,4]. Найдите площадь поверхности, полученной путем вращения графика f(x)f(x) вокруг оси x.x-ось. Округлите ответ до трех знаков после запятой.
Решение
График f(x)f(x) и поверхность вращения показаны на следующем рисунке.
Рисунок 6,46 (a) График функции f(x).f(x). (б) Поверхность вращения.
Имеем f(x)=x.f(x)=x. Тогда f′(x)=1/(2x)f′(x)=1/(2x) и (f′(x))2=1/(4x).(f′(x))2=1 /(4x). Тогда
Площадь поверхности = ∫ab(2πf(x)1+(f′(x))2)dx=∫14(2πx1+14x)dx=∫14(2πx+14)dx. Площадь поверхности=∫ab (2πf(x)1+(f′(x))2)dx=∫14(2πx1+14x)dx=∫14(2πx+14)dx.
Площадь поверхности=∫ab (2πf(x)1+(f′(x))2)dx=∫14(2πx1+14x)dx=∫14(2πx+14)dx.
Пусть u=x+1/4.u=x+1/4. Тогда du=dx.du=dx. Когда x=1,x=1,u=5/4,u=5/4 и когда x=4,x=4,u=17/4.u=17/4. Это дает нам
∫14(2πx+14)dx=∫5/417/42πudu=2π[23u3/2]|5/417/4=π6[1717−55]≈30,846,∫14(2πx+14) dx=∫5/417/42πudu=2π[23u3/2]|5/417/4=π6[1717−55]≈30,846.
Контрольно-пропускной пункт 6.21
Пусть f(x)=1−xf(x)=1−x на интервале [0,1/2].[0,1/2]. Найдите площадь поверхности, полученной путем вращения графика f(x)f(x) вокруг оси x.x-ось. Округлите ответ до трех знаков после запятой.
Пример 6.22
Расчет площади поверхности вращения 2
Пусть f(x)=y=3×3.f(x)=y=3×3. Рассмотрим часть кривой, где 0≤y≤2.0≤y≤2. Найдите площадь поверхности, полученной путем вращения графика f(x)f(x) вокруг оси y.ось y.
Решение
Обратите внимание, что мы вращаем кривую вокруг оси y, оси y, а интервал выражен в единицах y, y, поэтому мы хотим переписать функцию как функцию от y . Получаем x=g(y)=(1/3)y3.x=g(y)=(1/3)y3. График g(y)g(y) и поверхность вращения показаны на следующем рисунке.
Получаем x=g(y)=(1/3)y3.x=g(y)=(1/3)y3. График g(y)g(y) и поверхность вращения показаны на следующем рисунке.
Рисунок 6,47 (a) График g(y).g(y). (б) Поверхность вращения.
Имеем g(y)=(1/3)y3,g(y)=(1/3)y3, поэтому g′(y)=y2g′(y)=y2 и (g′(y)) 2=у4.(г'(у))2=у4. Затем
Площадь поверхности=∫cd(2πg(y)1+(g′(y))2)dy=∫02(2π(13y3)1+y4)dy=2π3∫02(y31+y4)dy. Площадь поверхности =∫cd(2πg(y)1+(g′(y))2)dy=∫02(2π(13y3)1+y4)dy=2π3∫02(y31+y4)dy.
Пусть u=y4+1.u=y4+1. Тогда du=4y3dy.du=4y3dy. Когда y=0,y=0,u=1,u=1 и когда y=2,y=2,u=17.u=17. Тогда
2π3∫02(y31+y4)dy=2π3∫11714udu=π6[23u3/2]|117=π9[(17)3/2−1]≈24,118,2π3∫02(y31+y4)dy= 2π3∫11714udu=π6[23u3/2]|117=π9[(17)3/2−1]≈24,118.
Контрольно-пропускной пункт 6.22
Пусть g(y)=9−y2g(y)=9−y2 на интервале y∈[0,2].y∈[0,2]. Найдите площадь поверхности, полученной путем вращения графика g(y)g(y) вокруг оси y.ось y.
Раздел 6.4 Упражнения
Для следующих упражнений найдите длину функций на заданном интервале.
165.
y=5xfromx=0tox=2y=5xfromx=0tox=2
166.
y=−12x+25fromx=1tox=4y=−12x+25fromx=1tox=4
167.
x=4yfromy=-1toy=1x=4yfromy=-1toy=1
168.
Выберите произвольную линейную функцию x=g(y)x=g(y) на любом интервале по вашему выбору (y1,y2).(y1,y2). Определите длину функции, а затем докажите, что длина верна, используя геометрию.
169.
Найдите площадь поверхности объема, образованного, когда кривая y=xy=x вращается вокруг оси xx-ось от (1,1)(1,1) до (4,2),(4,2), как видно здесь.
170.
Найдите площадь поверхности объема, образованного, когда кривая y=x2y=x2 вращается вокруг оси y от (1,1)(1,1) до (3,9).(3,9).
Для следующих упражнений найдите длины функций xx на заданном интервале. Если вы не можете точно вычислить интеграл, используйте технологию для его аппроксимации.
Если вы не можете точно вычислить интеграл, используйте технологию для его аппроксимации.
171.
y=x3/2y=x3/2 от (0,0) до (1,1) (0,0) до (1,1)
172.
y=x2/3y=x2/3 от (1,1) до (8,4) (1,1) до (8,4)
173.
y=13(x2+2)3/2y=13(x2+2)3/2 от x=0tox=1x=0tox=1
174.
y=13(x2−2)3/2y=13(x2−2)3/2 от x=2x=2 до x=4x=4
175.
[T] y=exy=ex от x=0x=0 до x=1x=1
176.
y=x33+14xy=x33+14x из x=1tox=3x=1tox=3
177.
y=x44+18x2y=x44+18×2 из x=1tox=2x=1tox=2
178.
y=2×3/23−x1/22y=2×3/23−x1/22 из x=1tox=4x=1tox=4
179.
y=127(9×2+6)3/2y=127(9×2+6)3/2 от x=0tox=2x=0tox=2
180.
[T] y=sinxy=sinx on x=0tox=πx=0tox=π
Для следующих упражнений найдите длины функций yy на заданном интервале. Если вы не можете точно вычислить интеграл, используйте технологию для его аппроксимации.
181.
y=5−3x4y=5−3×4 от y=0y=0 до y=4y=4
182.
x=12(ey+e-y)x=12(ey+e-y) из y=-1toy=1y=-1toy=1
183.
x=5y3/2x=5y3/2 от y=0y=0 до y=1y=1
184.
[T] x=y2x=y2 от y=0y=0 до y=1y=1
185.
x=yx=y из y=0toy=1y=0toy=1
186.
x=23(y2+1)3/2x=23(y2+1)3/2 от y=1y=1 до y=3y=3
187.
[Т] x=tanyx=tany от y=0y=0 до y=34y=34
188.
[T] x=cos2yx=cos2y от y=−π2y=−π2 до y=π2y=π2
189.
[T] x=4yx=4y от y=0toy=2y=0toy=2
190.
[T] x=ln(y)x=ln(y) от y=1ey=1e до y=ey=e
Для следующих упражнений найдите площадь поверхности объема, образованного, когда следующие кривые вращаются вокруг оси х. Если вы не можете точно вычислить интеграл, воспользуйтесь калькулятором, чтобы аппроксимировать его.
191.
y=xy=x от x=2x=2 до x=6x=6
192.
y=x3y=x3 от x=0x=0 до x=1x=1
193.
y=7xy=7x из x=−1tox=1x=−1tox=1
194.
[T] y=1x2y=1×2 из x=1tox=3x=1tox=3
195.
y=4−x2y=4−x2 из x=0tox=2x=0tox=2
196.
y=4−x2y=4−x2 из x=−1tox=1x=−1tox=1
197.
y=5xy=5x от x=1tox=5x=1tox=5
198.
[T] y=tanxy=tanx из x=−π4tox=π4x=−π4tox=π4
Для следующих упражнений найдите площадь поверхности объема, созданного, когда следующие кривые вращаются вокруг оси y.ось y. Если вы не можете точно вычислить интеграл, воспользуйтесь калькулятором, чтобы аппроксимировать его.
199.
y=x2y=x2 из x=0tox=2x=0tox=2
200.
y=12×2+12y=12×2+12 из x=0tox=1x=0tox=1
201.
y=x+1y=x+1 из x=0tox=3x=0tox=3
202.
[T] y=1xy=1x от x=12x=12 до x=1x=1
203.
y=x3y=x3 из x=1tox=27x=1tox=27
204.
[T] y=3x4y=3×4 от x=0x=0 до x=1x=1
205.
[T] y=1xy=1x от x=1x=1 до x=3x=3
206.
[T] y=cosxy=cosx от x=0x=0 до x=π2x=π2
207.
Основание лампы состоит из вращения четверти окружности y=2x−x2y=2x−x2 вокруг оси y от x=1x=1 до x=2,x=2, как показано здесь. Создайте интеграл для площади поверхности этой кривой и вычислите его.
208.
Лампочка представляет собой сферу радиусом 1/21/2 дюйма с отрезанным дном, чтобы точно соответствовать цилиндру радиусом 1/41/4 дюйма и длиной 1/31/3 дюйма, как показано здесь . Сфера обрезана снизу, чтобы точно соответствовать цилиндру, поэтому радиус разреза составляет 1/41/4 дюйма. Найдите площадь поверхности (не включая верх и низ цилиндра).
209.
[T] Абажур создается вращением y=1/xy=1/x вокруг оси xx от y=1y=1 до y=2,y=2, как показано здесь. Определите, сколько материала вам понадобится для изготовления этого абажура, то есть площадь поверхности, с точностью до четырех знаков после запятой.
Определите, сколько материала вам понадобится для изготовления этого абажура, то есть площадь поверхности, с точностью до четырех знаков после запятой.
210.
[T] Якорь тянется за лодкой в соответствии с функцией y=24e-x/2-24,y=24e-x/2-24, где yy представляет глубину под лодкой, а xx — горизонтальную расстояние от якоря до задней части лодки. Если якорь находится на глубине 2323 фута под лодкой, за какое количество веревки нужно потянуть, чтобы добраться до якоря? Округлите ответ до трех знаков после запятой.
211.
[T] Вы строите мост длиной 1010 футов. Вы собираетесь добавить декоративную веревку в форме y=5|sin((xπ)/5)|,y=5|sin((xπ )/5)|, где xx — расстояние в футах от одного конца моста. Узнайте, сколько веревки вам нужно купить, округлив до ближайшего фута.
Для следующих упражнений найдите точную длину дуги для следующих задач за заданный интервал.
212.
y=ln(sinx)y=ln(sinx) от x=π/4x=π/4 до x=(3π)/4.x=(3π)/4. ( Подсказка: Вспомните тригонометрические тождества.)
213.
Нарисуйте графики y=x2, y=x2, y=x6, y=x6 и y=x10.y=x10. Для y=xn,y=xn при увеличении nn сформулируйте прогноз длины дуги от (0,0)(0,0) до (1,1).(1,1). Теперь вычислите длины этих трех функций и определите, верен ли ваш прогноз.
214.
Сравните длины параболы x=y2x=y2 и прямой x=byx=by от (0,0) до (b2,b) (0,0) и (b2,b) при увеличении bb. Что ты заметил?
215.
Найдите длину x=y2x=y2 от (0,0) до (1,1).(0,0) до (1,1). Покажите, что x=(1/2)y2x=(1/2)y2 от (0,0)(0,0) до (2,2)(2,2) вдвое длиннее. Нарисуйте график обеих функций и объясните, почему это так.
216.
[T] Что длиннее между (1,1)(1,1) и (2,1/2):(2,1/2): гипербола y=1/xy=1/x или график x+2y=3?x+2y=3?
217.
Объясните, почему площадь поверхности бесконечна, когда y=1/xy=1/x вращается вокруг оси xx при 1≤x<∞,1≤x<∞, а объем конечен.
Глава 3, Дифференциация видеорешений, исчисление Томаса
Раздел 1
Производная как функция
Выбрать Раздел 3.1: Производная как функция 3.2: Правила дифференцирования 3.3: Производная как скорость изменения 3.4: Производные тригонометрических функций 3.5: Цепь Правило и параметрические уравнения 3.6: Дифференциация входных данных 3.7: Связанные коэффициенты 3.8: Линеаризация и дифференциалы 9{3}}{2}+1
$$
Кайлер Г.
Преподаватель Numerade
06:03
Задача 9
В упражнениях $7-12,$ найдите указанные производные.
$$
\frac{d s}{d t} \quad \text { if } \quad s=\frac{t}{2 t+1}
$$
Роберт Д.
Numerade Educator
06:44
Задача 10
В упражнениях $7-12,$ найдите указанные производные.
$$
\frac{d v}{d t} \quad \text { if } \quad v=t-\frac{1}{t}
$$
Роберт Д.
Numerade Educator
06:22
Задача 11
В упражнениях $7-12,$ найдите указанные производные.
$$
\frac{d p}{d q} \quad \text { if } \quad p=\frac{1}{\sqrt{q+1}}
$$
Роберт Д.
Numerade Educator
09:32
Задача 12
В упражнениях $7-12,$ найдите указанные производные.
$$
\frac{d z}{d w} \quad \text { if } \quad z=\frac{1}{\sqrt{3 w-2}}
$$
Robert D.
Numerade Educator
07:41
Задача 13
В упражнениях $13-16,$ продифференцируйте функции и найдите наклон касательной при заданном значении независимой переменной.
$$
f(x)=x+\frac{9{x}, \quad x=-3
$$
Роберт Д.
Преподаватель нумерейд
04:07
Задача 14
В упражнениях $13-16,$ продифференцируйте функции и найдите наклон касательной при заданном значении независимой переменной.
$$
k(x)=\frac{1}{2+x}, \quad x=2
$$
Роберт Д.
Numerade Educator
05:36
Задача 15 9{3}, \quad x=-2
$$
Кайлер Г.
Numerade Educator
07:12
Задача 17
В упражнениях $17-18$ продифференцируйте функции. Затем найдите уравнение касательной в указанной точке графика функции.
$$
w=g(z)=1+\sqrt{4-z}, \quad(z, w)=(3,2)
$$
Роберт Д.
Преподаватель-счетчик
11:19
Задача 18
В упражнениях $17-18$ продифференцируйте функции. Затем найдите уравнение касательной в указанной точке графика функции.
Затем найдите уравнение касательной в указанной точке графика функции.
$$
y=f(x)=\frac{8}{\sqrt{x-2}}, \quad(x, y)=(6,4)
$$
Роберт Д.
Numerade Воспитатель
03:10
Задача 19
В упражнениях $19-22$ найдите значения производных. 9{2}
$$
Роберт Д.
Numerade Educator
03:00
Задача 20
В упражнениях $19-22$ найдите значения производных.
$$
\left.\frac{d y}{d x}\right|_{x=\sqrt{3}} \text { if } \quad y=1-\frac{1}{x}
$$
Роберт Д.
Преподаватель нумерейд
06:00
Задача 21
В упражнениях $19-22$ найдите значения производных.
$$
\left.\frac{d r}{d \theta}\right|_{\theta=0} \quad \text { if } \quad r=\frac{2}{\sqrt{4-\ theta}}
$$
Роберт Д.
Преподаватель нумерадов
04:02
Задача 22
В упражнениях $19-22$ найдите значения производных.
$$
\left.\frac{d w}{d z}\right|_{z=4} \quad \text { if } \quad w=z+\sqrt{z} 9{\prime}(x)=\lim _{z \rightarrow x} \frac{f(z)-f(x)}{z-x}
$$
, чтобы найти производную функций в упражнениях $23-26$
$$
g(x)=1+\sqrt{x}
$$
Доркас Аттуабеа А.
Воспитатель Numerade
Задача 27
Сопоставьте функции, изображенные в упражнениях $27-30$, с производными, изображенными на рисунках (a)-(d).
Заходите скорее!
Задача 28
Сопоставьте функции, изображенные в упражнениях $27-30$, с производными, изображенными на рисунках (a)-(d).
Заходите скорее!
Задача 29
Сопоставьте функции, изображенные в упражнениях $27-30$, с производными, изображенными на рисунках (a)-(d).
Заходите скорее!
Задача 30 9{\prime}$ не определено? Обоснуйте свой ответ.
б. Постройте график производной от $f$ . На графике должна быть показана ступенчатая функция.
Мади С.
Преподаватель нумерейд
09:06
Задача 32
Восстановление функции по производной
а. Используйте следующую информацию, чтобы построить график функции $f$ на замкнутом интервале $[-2,5].$
i) График функции $f$ состоит из замкнутых отрезков, соединенных встык.
ii) График начинается в точке $(-2,3)$ .
ii) Производная от $f$ представляет собой ступенчатую функцию на рисунке, показанном здесь.
б. Повторите часть (а), предполагая, что граф начинается с $(-2,0)$ вместо $(-2,3).
05:54
Задача 33
Рост экономики График на прилагаемом рисунке показывает среднегодовое процентное изменение $y=f(t)$ валового национального продукта (ВНП) США за годы $1983-1988$. График dy/dt (где определено). (Источник: Statistical Abstracts of the United States, 110-е издание, Министерство торговли США, стр. 427.)
График dy/dt (где определено). (Источник: Statistical Abstracts of the United States, 110-е издание, Министерство торговли США, стр. 427.)
Доркас Аттуабеа А.
Numerade Educator
05:04
Задача 34
Плодовые мушки $(\text {Продолжение примера } 3, \text {Раздел } 2.1 .)$ Популяции, зародившиеся в замкнутых средах, сначала растут медленно, когда членов относительно мало, а затем быстрее, чем
количество размножающихся особей увеличивается, а ресурсы все еще в изобилии, затем снова медленно, когда популяция достигает пропускной способности окружающей среды.
а. Используйте графическую технику примера 3 для построения графика производной популяции плодовой мухи, представленной в разделе $2.1.$ График популяции воспроизводится здесь.
Доркас Аттуабеа А.
Преподаватель нумерейд
05:06
Задача 35
Сравните правую и левую производные, чтобы показать, что функции в упражнениях $35-38$ не дифференцируемы в точке $P$ .
Доркас Аттуабеа А.
Преподаватель нумерейд
04:40
Задача 36
Сравните правую и левую производные, чтобы показать, что функции в упражнениях $35-38$ не дифференцируемы в точке $P$ .
Доркас Аттуабеа А.
Учитель нумерейд
06:01
Задача 37
Сравните правые и левые производные, чтобы показать, что функции в упражнениях $35-38$ не дифференцируемы в точке $P .$
Доркас Аттуабеа А.
Преподаватель нумерейд
05:06
Задача 38
Сравните правые и левые производные, чтобы показать, что функции в упражнениях $35-38$ не дифференцируемы в точке $P .$
Доркас Аттуабеа А.
Преподаватель нумерейд
04:35
Задача 39
На каждом рисунке в упражнениях $39-44$ показан график функции на замкнутом интервале $D . $ В каких точках области функция оказывается равной
$ В каких точках области функция оказывается равной
а. дифференцируемый?
б. непрерывен, но не дифференцируем?
с. ни непрерывны, ни дифференцируемы?
$$
\begin{array}{l}{y=f(x)} \\ {D :-3 \leq x \leq 2}\end{array}
$$
Доркас Аттуабеа А.
Преподаватель нумерейд
02:56
Задача 40
На каждом рисунке в упражнениях $39-44$ показан график функции на замкнутом интервале $D .$ В каких точках области функция оказывается равной
а. дифференцируемый?
б. непрерывен, но не дифференцируем?
с. ни непрерывны, ни дифференцируемы?
Каждый рисунок в упражнениях $39-44$ показывает график функции на замкнутом интервале $D .$ В каких точках области функция оказывается равной
а. дифференцируемый?
б. непрерывен, но не дифференцируем?
с. ни непрерывны, ни дифференцируемы?
$$
\begin{array}{l}{y=f(x)} \\ {D :-3 \leq x \leq 2}\end{array}
$$
Доркас Аттуабеа А.
Педагог-счетчик
06:06
Задача 41
Каждый рисунок в упражнениях $39-44$ показывает график функции на замкнутом интервале $D .$ В каких точках области функция оказывается равной
а. дифференцируемый?
б. непрерывен, но не дифференцируем?
с. ни непрерывны, ни дифференцируемы?
Каждый рисунок в упражнениях $39-44$ показывает график функции на замкнутом интервале $D .$ В каких точках области функция оказывается равной
а. дифференцируемый?
б. непрерывен, но не дифференцируем?
с. ни непрерывны, ни дифференцируемы?
$$
\begin{array}{l}{y=f(x)} \\ {D :-3 \leq x \leq 3}\end{array}
$$
Доркас Аттуабеа А.
Учитель нумерейд
03:33
Задача 42
На каждом рисунке в упражнениях $39-44$ показан график функции на замкнутом интервале $D .$ В каких точках области функция оказывается равной
а. дифференцируемый?
дифференцируемый?
б. непрерывен, но не дифференцируем?
с. ни непрерывны, ни дифференцируемы?
Каждый рисунок в упражнениях $39-44$ показывает график функции на замкнутом интервале $D .$ В каких точках области функция оказывается равной
а. дифференцируемый?
б. непрерывен, но не дифференцируем?
с. ни непрерывны, ни дифференцируемы?
$$
\begin{array}{l}{y=f(x)} \\ {D :-2 \leq x \leq 3}\end{array}
$$
Суман Саурав Т.
Педагог-счетчик
06:35
Задача 43
Каждый рисунок в упражнениях $39-44$ показывает график функции на замкнутом интервале $D .$ В каких точках области функция оказывается равной
а. дифференцируемый?
б. непрерывен, но не дифференцируем?
с. ни непрерывны, ни дифференцируемы?
Каждый рисунок в упражнениях $39-44$ показывает график функции на замкнутом интервале $D .$ В каких точках области функция оказывается равной
а. дифференцируемый?
дифференцируемый?
б. непрерывен, но не дифференцируем?
с. ни непрерывны, ни дифференцируемы?
$$
\begin{array}{l}{y=f(x)} \\ {D :-1 \leq x \leq 2}\end{array}
$$
Доркас Аттуабеа А.
Учитель нумерейд
06:13
Задача 44
На каждом рисунке в упражнениях $39-44$ показан график функции на замкнутом интервале $D .$ В каких точках области функция оказывается равной
а. дифференцируемый?
б. непрерывен, но не дифференцируем?
с. ни непрерывны, ни дифференцируемы?
Каждый рисунок в упражнениях $39-44$ показывает график функции на замкнутом интервале $D .$ В каких точках области функция оказывается равной 9{\prime}$ положительный? Нуль? Отрицательный?
д. На каких интервалах значений $x$ функция $y=f(x)$ возрастает при увеличении $x$, если они есть? Уменьшаться по мере увеличения $x$? Как это связано с тем, что вы нашли в части (c)? (Более подробно об этой взаимосвязи мы поговорим в главе §4. )$
)$
$$
y=-1 / x
$$
Доркас Аттуабеа А.
Учитель нумерейд
09:36
Задача 47
В упражнениях $45-48$ 9{3}$ когда-либо имели отрицательный наклон? Если да, то где? Обоснуйте свой ответ.
Доркас Аттуабеа А.
Преподаватель нумерейд
05:25
Задача 50
Имеет ли кривая $y=2 \sqrt{x}$ горизонтальные касательные? Если да, то где? Обоснуйте свой ответ.
Доркас Аттуабеа А.
Преподаватель нумерейд
02:05
Задача 51 9{2}-13 x+5$ имеют касательную с наклоном $-1 ?$ Если да, найдите уравнение для прямой и точки касания. Если нет, то почему?
Грегори Х.
Преподаватель числа
01:52
Задача 52
Касательная к $y=\sqrt{x}$ Пересекает ли любая касательная к кривой $y=\sqrt{x}$ ось $x$ в точке $x=-1 ?$ Если да, найдите уравнение для линия и точка касания. Если нет, то почему?
Если нет, то почему?
Грегори Х.
Учитель нумерейд
01:44
Задача 53
Наибольшее целое число в $x$ Имеет ли функция, дифференцируемая на $(-\infty, \infty)$, $y=\operatorname{int} x,$ наибольшее целое число в $x$ (см. рис. производная? Обоснуйте свой ответ.
Юцзянь З.
Преподаватель числа
03:45
Задача 54
Производная от $y=|x|$ Постройте график производной от $f(x)=|x| .$ Тогда граф $y=(|x|-0) /(x-0)=|x| / x .$ Какой вывод можно сделать?
Роберт Д.
Преподаватель нумерейд
01:32
Задача 55
Производная от $-f$ Говорит ли вам что-либо о дифференцируемости функции $f(x)$ в точке $x=x_{0}$ о дифференцируемости функции $-f$ в точке $x=x_{0}? ?$ Обоснуйте свой ответ.
Рунпэн Л.
Преподаватель числа
01:07
Задача 56
Производная кратных Говорит ли вам что-нибудь о дифференцируемости функции $g(t)$ при $t=7$ дифференцируемость функции 3$g$ при $t=7 ?$ Обоснуйте свой ответ.
Грегори Х.
Преподаватель числа
02:15
Задача 57 9{\prime}(0)$
Роберт Д.
Преподаватель нумерадов
07:11
Задача 59
График $y=1 /(2 \sqrt{x})$ в окне с $0 \leq x \leq 2 .$ Затем на том же экране график
$$
y=\frac{\sqrt{ x+h}-\sqrt{x}}{h}
$$
для $h=1,0,5,0,1 .$ Затем попробуйте $h=-1,-0,5,-0,1 .$ Объясните, что происходит.
Роберт Д.
Преподаватель нумерейд
02:11 9{2}+1}, \quad x_{0}=-1
$$
Юйцзянь З.
Преподаватель-счетчик
02:47
Задача 66
Используйте CAS для выполнения следующих шагов для функций в упражнениях $62-67 . $
$
$$
f(x)=\sin 2 x, \quad x_{0}=\pi / 2
$$
Yujian Z.
Преподаватель числа
03:42
Задача 67 9{2} \cos x, \quad x_{0}=\pi / 4
$$
Юйцзянь З.
Преподаватель-счетчик
Нахождение средней скорости изменения полиномов
В математике нахождение средней скорости изменения полиномов является предшественником фундаментальной вычислительной техники дифференцирования. От нахождения средней скорости изменения полиномов до нахождения мгновенной скорости изменения функции всего один маленький шаг. Обе эти концепции являются центральными для физики и науки в целом.
В контексте науки и физики полиномиальные функции будут описывать скорость изменения определенных физических величин. Будь то ускорение из-за свободного падения, скорость, с которой болезнь или вирус распространяются среди населения, или скорость роста населения за тысячи лет. Полиномиальные функции описывают такие явления, потому что полиномиальные функции описывают экспоненциальный рост и затухание.
Полиномиальные функции описывают такие явления, потому что полиномиальные функции описывают экспоненциальный рост и затухание.
Таким образом, между двумя значениями или между двумя моментами времени (что обычно имеет место для измеряемой физической величины) наше значение изменится на определенную величину, что приведет к вычисляемому изменению с .
При работе с полиномами наши переменные (которые могут быть , , , , как вы их называете) возводятся в определенную степень, что означает, что наша скорость изменения не является линейной. Вы уже знаете, что такая функция, как будет параболической кривой, что означает, что увеличение на 1 единицу будет равняться квадрату (). Другими словами, склон становится все круче и круче.
Это говорит нам о том, что скорость изменения между всеми точками на графике не будет одинаковой; другими словами, средняя скорость изменения полиномов будет варьироваться в зависимости от того, в каких двух точках мы измеряем среднюю скорость изменения.
Нахождение скорости изменения полиномов говорит нам об изменении наклона графика на интервале , который мы можем рассматривать как находящийся между значениями и .
Средняя скорость изменения многочленов
Чтобы попрактиковаться в нахождении средней скорости изменения многочленов, я собираюсь составить математическую функцию, которую мы можем использовать для исследования и понимания этого процесса.
Рассмотрим полиномиальную функцию . Вы можете увидеть эту функцию на графике справа, который вы можете увеличить, нажав на изображение. Первая средняя скорость изменения, которую мы собираемся проанализировать, находится на интервале, отмеченном и .
График функции . Просто взглянув на график, вы можете увидеть, что это значение не сильно меняется, хотя между этими точками график резко падает и поднимается, чтобы вернуться к этому уровню. Поскольку линия, проведенная между этими двумя точками, будет относительно плоской и немного направленной вниз (слева направо), это означает, что наклон будет небольшим отрицательным.
При вычислении средней скорости изменения полиномов мы вычисляем наклон на интервале. Для этого воспользуемся выражением наклона. Помните, что 9Уклон 0635 равен подъему над пробегом , что означает, что делится на . Сначала мы должны вычислить два значения y из и :
Итак, две точки, по которым мы вычисляем наклон, это (-1,5,7,125) и (3,6), которые мы вводим в уравнение наклона. Учитывая левую точку, мы получаем
Итак, как я догадался выше, наш наклон небольшой отрицательный. Это означает, что средняя скорость изменения этого полинома представляет собой небольшое уменьшение скорости на этом интервале.
Теперь для той же полиномиальной функции рассмотрим среднюю скорость изменения на интервале [2,5] до . Снова взглянув на график, вы увидите, что при x=2 график близок к локальному минимальному значению для , но при x=5 на графике появляются пики. Мы знаем, что наш средний наклон в этом интервале будет большим положительным средним наклоном/скоростью изменения. Мы находим среднюю скорость изменения полиномов, сначала вычисляя любые неизвестные переменные, в данном случае наши два значения y. Так
Мы находим среднюю скорость изменения полиномов, сначала вычисляя любые неизвестные переменные, в данном случае наши два значения y. Так
Затем мы вычисляем наклон между этими двумя точками и как
Наш наклон очень круто возрастает слева направо, поэтому он положительный. Это говорит нам о том, что средняя скорость изменения за этот интервал очень велика. Отлично, по крайней мере, относительно первого рассчитанного нами уклона, который был небольшим минусом.
Знак средней скорости изменения полиномов
Знак средней скорости изменения полиномов – равен ли он положительный или отрицательный — говорит нам направление скорости изменения. Положительная скорость изменения, как в приведенных выше случаях, означает, что она увеличивается в рассматриваемом интервале, тогда как отрицательная скорость изменения указывает на то, что она уменьшается в течение рассматриваемого интервала.
Поскольку средняя скорость изменения эквивалентна наклону графика за указанный интервал, знак наклона определяет, увеличивается или уменьшается скорость изменения.

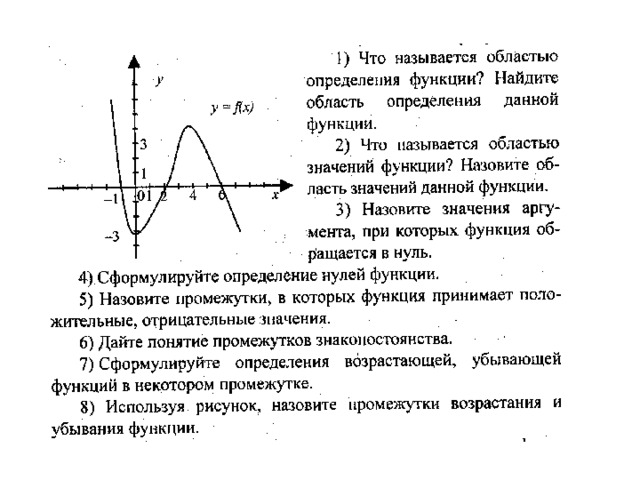
 Если y=F(u), а u=u(x), то функция y=f(x)=F(u(x)) называется сложной функцией от x. Равна y′(x)=Fu′⋅
ux′.
Если y=F(u), а u=u(x), то функция y=f(x)=F(u(x)) называется сложной функцией от x. Равна y′(x)=Fu′⋅
ux′.