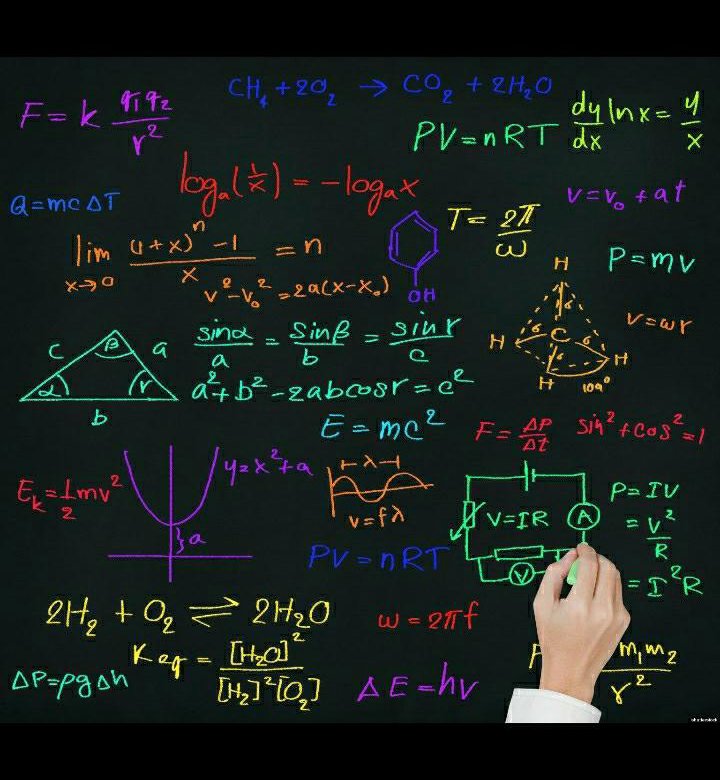
Математические формулы используемые в средних школах. Самые красивые физические и математические формулы
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Голова идёт кругом от множества математических формул, которые необходимо знать. Зубрёжка и шпаргалки — удел слабых. А вот тем, кто хочет стать в математике сильнее, мы подскажем несколько советов, как запоминать формулы по математике так, чтобы они не выветрились из головы до контрольной, экзамена или ЦТ.
Понимай формулу
Если ты будешь заучивать только последовательность переменных, рискуешь «потерять» всю формулу, когда забудешь символ или знак.
Задействуй все виды памяти
Читай формулы вслух, прописывай на листке по нескольку раз, пока не запомнишь.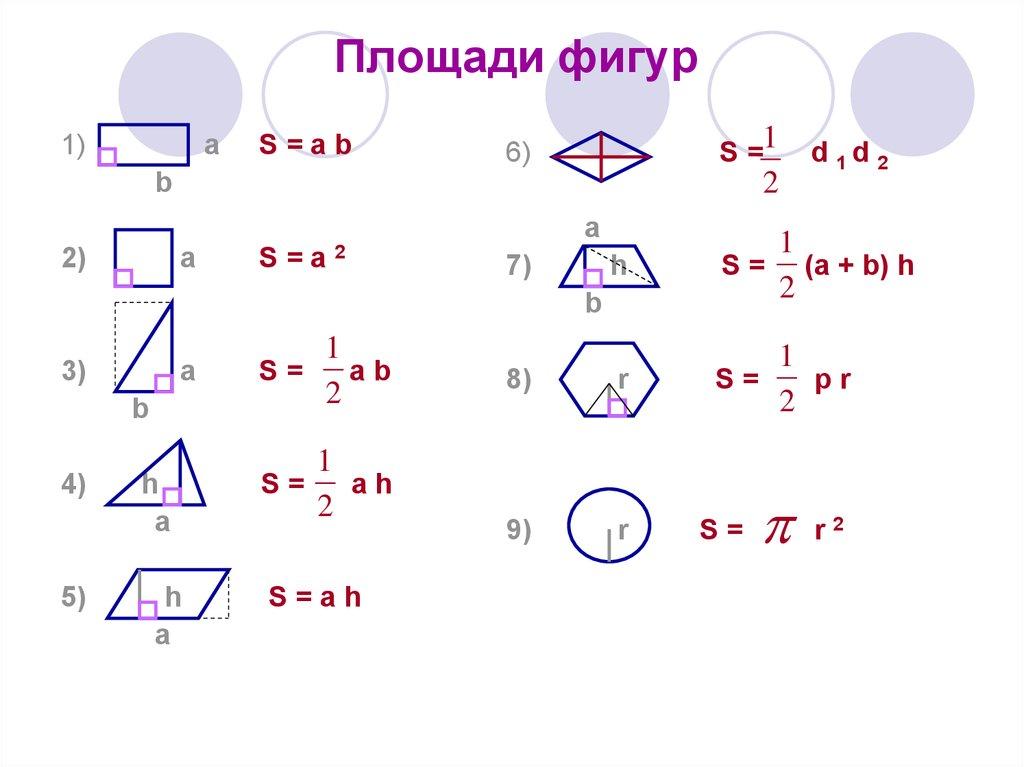
Вот ещё несколько советов, как запомнить формулы
Обязательно делай формулы наглядными: обводи формулу в рамку, пиши её другим цветом. Так будет легче найти в конспекте и запомнить. А лучше выписывай формулы в отдельный блокнот, структурируя их по темам. Помечай, в какого рода задачах та или иная формула пригодится, в чём её особенность. Заведи привычку пополнять список формул. Подобный «дневник наблюдений за формулами» поможет освежить в памяти важную информацию перед контрольной, экзаменом или ЦТ по математике.
Многие школьники ещё вот что делают: когда раздают проштампованные черновики, ты берёшь и сразу же записываешь на них важные формулы, которые тебе тяжело даются. За полчаса до ЦТ ты эти формулы зрительно запомнил, а потом быстренько написал.
Это экономит время. Особенно такой лайфхак хорош в тригонометрии. Чем больше знаешь формул, тем лучше.
Проверяй себя
Нужно постоянно возвращаться к выученному материалу, чтобы не забыть его. Попробуй метод «Две карточки», он подойдёт для запоминания формул приведения, сокращённого умножения, тригонометрических формул. Возьми две стопки карточек разного цвета, на одной напиши левую часть формулы, а на другой — правую. Раздели таким образом все формулы, что тебе нужно запомнить, затем перемешай обе стопки. Тяни по порядку карточку с левой частью формулы и подбирай её продолжение среди «правых» и наоборот.
Карточки хороши и в геометрии
Чтобы запомнить формулы по геометрии, заведи себе карточки по темам («Формулы площади», «Фомулы для треугольника», «Фомулы для квадрата» и т. д.) и записывай в них информацию следующим образом.
Можно фиксировать формулы в отдельном блокноте и всегда был под рукой — как тебе удобно
Будь на позитиве
Если ты учишь что-либо из-под палки, мозг сам желает избавиться от груза знаний.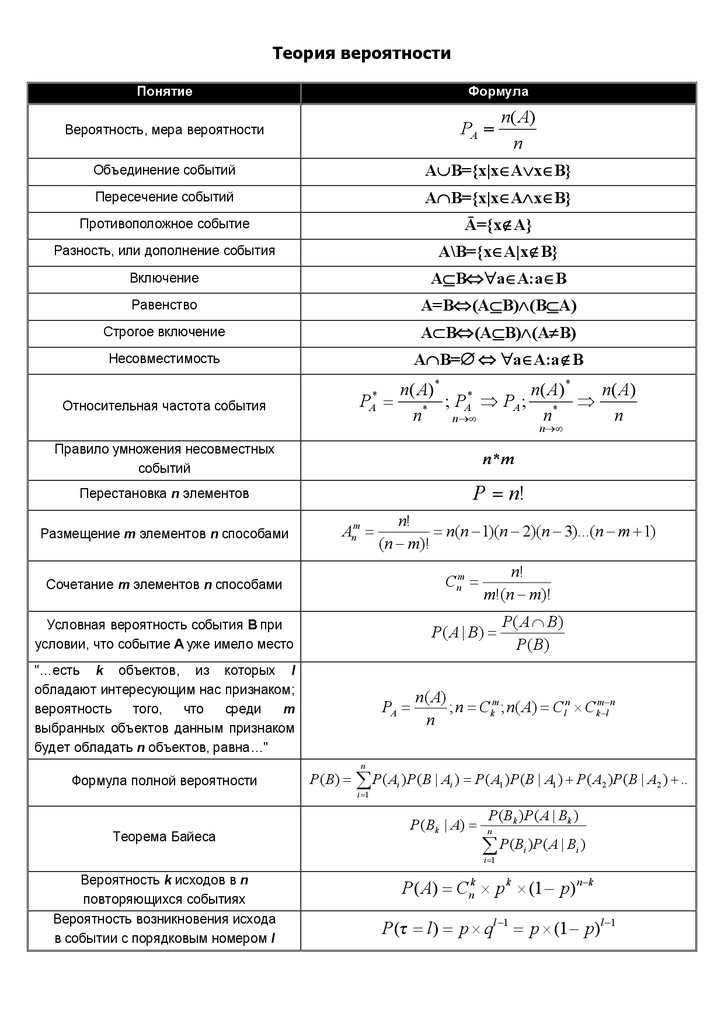 Воспринимай заучивание формул как хорошее упражнение для тренировки памяти. Да и настроение поднимается, когда вспоминаешь нужную формулу для решения.
И конечно же, решай как можно больше тестов и задач для подготовки к контрольной, экзамену или ЦТ!
Воспринимай заучивание формул как хорошее упражнение для тренировки памяти. Да и настроение поднимается, когда вспоминаешь нужную формулу для решения.
И конечно же, решай как можно больше тестов и задач для подготовки к контрольной, экзамену или ЦТ!
ЦТ по математике — это типовые задачи: чем больше тестов решаешь, тем выше шанс встретить что-то похожее на ЦТ. Невозможно подготовиться к ЦТ по одной задаче. Но когда ты прорешал 100 задач, то 101 задача не вызовет затруднений.
Дмитрий Судник, преподаватель математики в
Если материал был для тебя полезен, не забудь поставить «мне нравится» в наших соцсетях
На данной странице Вы можете посмотреть или бесплатно скачать самые востребованные математические формулы, таблицы ,а также справочные материалы по высшей математике. Все математические таблицы составлены лично мной и снабжены дополнительными комментариями. Сделано это в целях преодоления трудностей, с которыми часто сталкиваются студенты-заочники в ходе решения задач. Я не претендую на всеобъемлющую полноту материалов, но то, что ОЧЕНЬ ЧАСТО встречается, Вы найдете.
Я не претендую на всеобъемлющую полноту материалов, но то, что ОЧЕНЬ ЧАСТО встречается, Вы найдете.
Рассмотрим, например, таблицу тригонометрических формул. Тригонометрических формул достаточно много, они давно известны, и нет никакого смысла переписывать справочники. А вот те формулы, которые очень часто используются для решения задач курса высшей математики, собраны воедино, и могут быть очень полезны при выполнении практических заданий. При этом в комментариях я указываю, в каком разделе высшей математики (пределы, производные, интегралы, и т.д.) практически всегда фигурирует та или иная формула.
Итак, прямо сейчас у Вас есть бесплатный доступ к ценным справочным материалам, возможен, как онлайн просмотр, так и скачивание. Удобнее всего сразу распечатать математические таблицы и справочные материалы, которые Вас заинтересуют. Как показывает практика, информация на экране монитора усваивается хуже, чем на бумаге, да и читать с монитора труднее.
Почти все файлы размещены прямо на сайте, а значит, могут быть получены в максимально короткий срок, ограниченный только скоростью Вашего Интернет-подключения.
! В случае некорректного отображения pdf используйте следующие рекомендации
Рекомендую просмотреть всем. Данные формулы встречаются в ходе решения задач по высшей математике буквально на каждом шагу. Без знания этих формул – никуда. С чего начать изучение высшей математики? С повторения этого. Независимо от уровня Вашей математической подготовки на данный момент, крайне желательно СРАЗУ ВИДЕТЬ возможность выполнения элементарных действий, применения простейших формул в ходе решения пределов, интегралов, дифференциальных уравнений и т.д.
В справочнике есть краткая информация о модуле, формулы сокращенного умножения, алгоритм решения квадратного уравнения, правила упрощения многоэтажных дробей, а также важнейшие свойства степеней и логарифмов.
Приведены самые «ходовые» тригонометрические формулы, которые применяются в ходе решения задач по высшей математике. На самом деле таких формул НЕМНОГО, и, собирать десятки других по различным математическим справочникам – пустая трата времени.
При выполнении заданий по математике нередко возникает необходимость заглянуть в тригонометрические таблицы. В данном справочном материале представлена таблица значений тригонометрических функций (синуса, косинуса, тангенса и котангенса) при значениях аргумента от нуля до 360 градусов. Держать в памяти данную информацию нет никакого смысла, но некоторые значения тригонометрических функций хорошо бы знать . Также представлены формулы приведения для вышеуказанных тригонометрических функций, иногда (чаще всего при решении пределов) требуются. По просьбам посетителей сайта в pdf-файл добавлена таблица значений обратных тригонометрических функций и две формулы: формула перевода градусов в радианы, формула перевода радианов в градусы.
Методический материал представляет собой обзор графиков основных элементарных функций и их свойств. Будет полезен при изучении практически всех разделов высшей математики, более того, справочное пособие поможет вам намного  Также вы сможете узнать, какие значения функций следует знать наизусть , чтобы не получить «два автоматом» при ответе на простейший вопрос экзаменатора. Справка выполнена в форме веб страницы и содержит много графиков функций, которые также желательно помнить. По мере развития проекта методичка стала играть роль вводного урока по теме «Функции и графики».
Также вы сможете узнать, какие значения функций следует знать наизусть , чтобы не получить «два автоматом» при ответе на простейший вопрос экзаменатора. Справка выполнена в форме веб страницы и содержит много графиков функций, которые также желательно помнить. По мере развития проекта методичка стала играть роль вводного урока по теме «Функции и графики».
На практике у студентов-заочников практически всегда возникает необходимость использовать первый и второй замечательные пределы, о которых и идет речь в данной справке. Также рассмотрены еще три замечательных предела, которые встречаются значительно реже. Все замечательные пределы снабжены дополнительными важными комментариями. Кроме того, файл дополнен информацией о замечательных эквивалентностях.
В справке приведены правила дифференцирования и таблица производных от основных элементарных функций. Таблица снабжена очень важными примечаниями.
Ваш гид по разделу «Функции и графики». В pdf-ке систематизирована и законспектирована информация об основных этапах исследования функции одной переменной. Руководство сопровождается ссылками, а значит, экономит массу времени. Мануал полезен как чайнику, так и подготовленному читателю.
Руководство сопровождается ссылками, а значит, экономит массу времени. Мануал полезен как чайнику, так и подготовленному читателю.
В общем-то, почти то же самое, что в дифференциальном исчислении. Правила интегрирования и таблица интегралов с моими комментариями.
Справочный материал незаменим при изучении степенных рядов. В таблице представлены разложения в степенной ряд следующих функций: экспоненты, синуса, косинуса, логарифма, арктангенса и арксинуса. Также приведено биномиальное разложение и наиболее распространенные частные случаи биномиального разложения. Разложение функции в ряд является самостоятельным заданием, используется для приближенных вычислений, приближенных вычислений определенного интеграла и в некоторых других задачах.
Основной трудностью при решении неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами является правильный подбор частного решения по виду правой части. Данная методичка, относится, прежде всего, к уроку Как решить неоднородное уравнение второго порядка? и поможет вам легко разобраться в подборе частного решения. Справка не претендует на основательную научную полноту, она написана простым и понятным языком, однако в 99,99% случаев в ней найдется именно тот случай, который вы ищете.
Справка не претендует на основательную научную полноту, она написана простым и понятным языком, однако в 99,99% случаев в ней найдется именно тот случай, который вы ищете.
Справка незаменима в ходе решения прикладных задач комплексного анализа – нахождения частного решения ДУ операционным методом и нахождения частного решения системы ДУ этим же способом. Таблица отличается от аналогов тем, что «заточена» именно под вышеуказанные задания, данная особенность позволяет легко освоить алгоритмы решения. Приведено как прямое, так и обратное преобразование Лапласа для наиболее распространенных функций. В случае если информации окажется недостаточно, рекомендую обратиться к солидному математическому справочнику – полная версия содержит более сотни пунктов.
В справочном материале приведены формулы факториала, количества перестановок, сочетаний, размещений (с повторениями и без повторений), а также содержательные комментарии к каждой формуле, позволяющие понять их суть. + Правила сложения и умножения комбинаций. Кроме того, в pdf-ке есть краткая информация о биноме Ньютона и треугольнике Паскаля с примерами их практического использования.
Кроме того, в pdf-ке есть краткая информация о биноме Ньютона и треугольнике Паскаля с примерами их практического использования.
Файл содержит перечень формул с краткими комментариями по обеим главам тервера – Случайные события и Случайные величины , в том числе приведены формулы и числовые характеристики распространённых дискретных и непрерывных распределений. Справка систематизирует материал и очень удобна для выполнения практических заданий, заглядываем и сразу находим то, что нужно!
Специальные расчётные программы:В данном разделе вы можете найти вспомогательные программы для решения широких и узколокальных математических задач. Они помогут вам быстро выполнить расчёты и оформить решение.
Универсальный калькулятор реализован в рабочей книге MS Excel, которая содержит три листа. Программа может заменить обычный калькулятор с множеством функций. Любые степени, корни, логарифмы, тригонометрические функции, арки – без проблем! Кроме того, калькулятор в автоматическом режиме выполняет основные действия с матрицами , считает определители (до определителя 5 на 5 включительно), мгновенно находит миноры и алгебраические дополнения матриц. За считанные секунды можно решить систему линейных уравнений с помощью обратной матрицы и по формулам Крамера , посмотреть основные этапы решения. Всё это очень удобно для самопроверки. Просто введите свои числа и получите готовый результат!
За считанные секунды можно решить систему линейных уравнений с помощью обратной матрицы и по формулам Крамера , посмотреть основные этапы решения. Всё это очень удобно для самопроверки. Просто введите свои числа и получите готовый результат!
Данная полуавтоматическая программа относится к уроку Формула трапеций, формула Симпсона и помогает рассчитать приближенное значение определенного интеграла на 2, 4, 8, 10 и 20 отрезках разбиения. Прилагается видеоурок по работе с калькулятором. Вычислите ваш определенный интеграл в считанные минуты, и даже секунды!
На данный момент пока всё.
Раздел постепенно пополняется дополнительными материалами и полезными программами. Каждое справочное пособие неоднократно редактировалось и улучшалось, в том числе, с учетом ваших пожеланий и замечаний! Если Вы считаете, что упущено что-то важное, нашли какие-либо неточности, а может быть что-то разъяснено недостаточно понятно, обязательно пишите !
С уважением, Емелин Александр
Математик Анри Пуанкаре в книге «Наука и метод» писал: «Если бы природа не была прекрасна, она не стоила бы того, чтобы ее знать, жизнь не стоила бы того, чтобы ее переживать. Я здесь говорю, конечно, не о той красоте, которая бросается в глаза… Я имею в виду ту более глубокую красоту, которая открывается в гармонии частей, которая постигается только разумом. Это она создает почву, создает каркас для игры видимых красок, ласкающих наши чувства, и без этой поддержки красота мимолетных впечатлений была бы несовершенна как все неотчетливое и преходящее. Напротив красота интеллектуальная дает удовлетворение сама по себе».
Я здесь говорю, конечно, не о той красоте, которая бросается в глаза… Я имею в виду ту более глубокую красоту, которая открывается в гармонии частей, которая постигается только разумом. Это она создает почву, создает каркас для игры видимых красок, ласкающих наши чувства, и без этой поддержки красота мимолетных впечатлений была бы несовершенна как все неотчетливое и преходящее. Напротив красота интеллектуальная дает удовлетворение сама по себе».
П.А.М. Дирак писал: «У теоретической физики есть еще один верный путь развития. Природе присуща та фундаментальная особенность, что самые основные физические законы описываются математической теорией, аппарат которой обладает необыкновенной силой и красотой. Чтобы понять эту теорию, нужно обладать необычайно высокой математической квалификацией. Вы можете спросить: почему природа устроена именно так? На это можно ответить только одно: согласно нашим современным знаниям, природа устроена именно так, а не иначе».
Семь лет назад украинский физик (и художник) Наталия Кондратьева обратилась к ряду ведущих математиков мира с вопросом: «Какие три математические формулы, на ваш взгляд, самые красивые?»
В беседе о красоте математических формул приняли участие сэр Михаэль Атья и Дэвид Элварси из Британии, Яков Синай и Александр Кириллов из США, Фридрих Херцебрух и Юрий Манин из Германии, Давид Рюэль из Франции, Анатолий Вершик и Роберт Минлос из России и другие математики из разных стран. Из украинцев в дискуссии приняли участие академики НАНУ Владимир Королюк и Анатолий Скороход. Часть полученных таким образом материалов и легла в основу изданной Натальей Кондратьевой научной работы «Три самые красивые математические формулы».
Из украинцев в дискуссии приняли участие академики НАНУ Владимир Королюк и Анатолий Скороход. Часть полученных таким образом материалов и легла в основу изданной Натальей Кондратьевой научной работы «Три самые красивые математические формулы».
— Какую цель вы ставили, обращаясь к математикам с вопросом о красивых формулах?
— Каждое новое столетие приносит обновление научной парадигмы. В самом начале века с ощущением, что мы стоим у порога новой науки, ее новой роли в жизни человеческого общества, я обратилась к математикам с вопросом о красоте идей, стоящих за математическими символами, т.е. о красоте математических формул.
Уже сейчас можно отметить некоторые особенности новой науки. Если в науке ХХ века очень важную роль играла «дружба» математики с физикой, то сейчас математика эффективно сотрудничает с биологией, генетикой, социологией, экономикой… Следовательно, наука будет исследовать соответствия. Математические структуры будут исследовать соответствия между взаимодействиями элементов различных областей и планов. И многое, что раньше мы воспринимали на веру как философские констатации, будет утверждено наукой как конкретное знание.
И многое, что раньше мы воспринимали на веру как философские констатации, будет утверждено наукой как конкретное знание.
Этот процесс начался уже в ХХ веке. Так, Колмогоров математически показал, что случайности нет, а есть очень большая сложность. Фрактальная геометрия подтвердила принцип единства в многообразии и т.д.
— Какие же формулы были названы самыми красивыми?
— Сразу скажу, что цели устроить конкурс формулам не было. В своем письме к математикам я писала: «Люди, которые хотят понять, какими законами управляется мир, становятся на путь отыскания гармонии мира. Путь этот уходит в бесконечность (ибо движение вечно), но люди всё равно идут им, т.к. есть особая радость встретить очередную идею или представление. Из ответов на вопрос о красивых формулах, возможно, удастся синтезировать новую грань красоты мира. Кроме того, эта работа может оказаться полезной для будущих ученых как мысль о великой гармонии мира и математики как способе отыскания этой красоты».
Тем не менее среди формул оказались явные фавориты: формула Пифагора и формула Эйлера.
Вслед за ними расположились скорее физические, чем математические формулы, которые в ХХ веке изменили наше преставление о мире, —Максвелла, Шредингера, Эйнштейна.
Также в число самых красивых попали формулы, которые еще находятся на стадии дискуссии, такие, например, как уравнения физического вакуума. Назывались и другие красивые математические формулы.
— Как вы думаете, почему на рубеже второго и третьего тысячелетий формула Пифагора названа одной из самых красивых?
— Во времена Пифагора эта формула воспринималась как выражение принципа космической эволюции: два противоположных начала (два квадрата, соприкасающихся ортогонально) порождают третье, равное их сумме. Можно дать геометрически очень красивые интерпретации.
Возможно, существует какая-то подсознательная, генетическая память о тех временах, когда понятие «математика» означало — «наука», и в синтезе изучались арифметика, живопись, музыка, философия.
Рафаил Хасминский в своем письме написал, что в школе он был поражен красотой формулы Пифагора, что это во многом определило его судьбу как математика.
— А что можно сказать о формуле Эйлера?
— Некоторые математики обращали внимание, что в ней «собрались все», т.е. все самые замечательные математические числа, и единица таит в себе бесконечности! — это имеет глубокий философский смысл.
Недаром эту формулу открыл Эйлер. Великий математик много сделал, чтобы ввести красоту в науку, он даже ввел в математику понятие «градус красоты». Вернее, он ввел это понятие в теорию музыки, которую считал частью математики.
Эйлер полагал, что эстетическое чувство можно развивать и что это чувство необходимо ученому.
Сошлюсь на авторитеты… Гротендик: «Понимание той или иной вещи в математике настолько совершенно, насколько возможно прочувствовать ее красоту».
Пуанкаре: «В математике налицо чувство». Он сравнивал эстетическое чувство в математике с фильтром, который из множества вариантов решения выбирает наиболее гармоничный, который, как правило, и есть верный. Красота и гармония — синонимы, а высшее проявление гармонии есть мировой закон Равновесия. Математика исследует этот закон на разных планах бытия и в разных аспектах. Недаром каждая математическая формула содержит знак равенства.
Математика исследует этот закон на разных планах бытия и в разных аспектах. Недаром каждая математическая формула содержит знак равенства.
Думаю, что высшая человеческая гармония есть гармония мысли и чувства. Может быть, поэтому Эйнштейн сказал, что писатель Достоевский дал ему больше, чем математик Гаусс.
Формулу Достоевского «Красота спасет мир» я взяла в качестве эпиграфа к работе о красоте в математике. И он также обсуждался математиками.
— И они согласились с этим утверждением?
— Математики не утверждали и не опровергали этого утверждения. Они его уточнили: «Осознание красоты спасет мир». Здесь сразу вспомнилась работа Юджина Вигнера о роли сознания в квантовых измерениях, написанная им почти пятьдесят лет назад. В этой работе Вигнер показал, что человеческое сознание влияет на окружающую среду, т.е., что мы не только получаем информацию извне, но и посылаем наши мысли и чувства в ответ. Эта работа до сих пор актуальна и имеет как своих сторонников, так и противников. Я очень надеюсь, что в ХХI веке наука докажет: осознание красоты способствует гармонизации нашего мира.
Я очень надеюсь, что в ХХI веке наука докажет: осознание красоты способствует гармонизации нашего мира.
1. Формула Эйлера. Многие видели в этой формуле символ единства всей математики, ибо в ней «-1 представляет арифметику, i — алгебру, π — геометрию и e — анализ».
2. Это простое равенство показывает, величина 0,999 (и так до бесконечности) эквивалентна единице. Многие люди не верят, что это может быть правдой, хотя существует несколько доказательств, основанных на теории пределов. Тем не менее, равенство показывает принцип бесконечности.
3. Это уравнение было сформулировано Эйнштейном в рамках новаторской общей теории относительности в 1915 году. Правая часть этого уравнения описывает энергию, содержащуюся в нашей Вселенной (в том числе» темную энергию»). Левая сторона описывает геометрию пространства-времени. Равенство отражает тот факт, что в общей теории относительности Эйнштейна, масса и энергия определяют геометрию, и одновременно кривизну, которая является проявлением гравитации. Эйнштейн говорил, что левая часть уравнений тяготения в общей теории относительности, содержащая гравитационное поле, красива и как будто вырезана из мрамора, в то время как правая часть уравнений, описывающая материю, всё ещё уродлива, будто сделана из обыкновенной деревяшки.
Эйнштейн говорил, что левая часть уравнений тяготения в общей теории относительности, содержащая гравитационное поле, красива и как будто вырезана из мрамора, в то время как правая часть уравнений, описывающая материю, всё ещё уродлива, будто сделана из обыкновенной деревяшки.
4. Еще одна доминирующая теория физики — Стандартная модель — описывает электромагнитное, слабое и сильное взаимодействие всех элементарных частиц. Некоторые физики считают, что она отображает все процессы, происходящие во Вселенной, кроме темной материи, темной энергии и не включает в себя гравитацию. В Стандартную модель вписывается и неуловимый до прошлого года бозон Хиггса, хотя не все специалисты уверены в его существовании.
5. Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Ее мы помним еще со школы и считаем, что автор теоремы — Пифагор. На самом деле этой формулой пользовались еще в Древнем Египте при строительстве пирамид.
6. Теорема Эйлера. Эта теорема заложила фундамент нового раздела математики — топологии. Уравнение устанавливает связь между числом вершин, ребер и граней для многогранников, топологически эквивалентных сфере.
7. Специальная теория относительности описывает движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. Эйнштейн составил формулу, которая описывает, что время и пространство не являются абсолютными понятиями, а скорее являются относительными в зависимости от скорости наблюдателя. Уравнение показывает, как расширяется или замедляется время в зависимости от того, как и куда движется человек.
8. Уравнение было получено в 1750-х годах Эйлером и Лагранжем при решении задачи об изохроне. Это проблема определения кривой, по которой тяжелая частица попадает в фиксированную точку за фиксированное время, независимо от начальной точки. В общих словах, если ваша система имеет симметрию, есть соответствующий закон сохранения симметрии.
9. Уравнение Каллана — Симанзика. Оно представляет собой дифференциальное уравнение, описывающее эволюцию н-корреляционной функции при изменении масштаба энергий, при которых теория определена и включает в себя бета-функции теории и аномальные размерности. Это уравнение помогло лучше понять квантовую физику.
10. Уравнение минимальной поверхности. Это равенство объясняет формирование мыльных пузырей.
11. Прямая Эйлера. Теорема Эйлера была доказана в 1765 году. Он обнаружил, что середины сторон треугольника и основания его высот лежат на одной окружности.
12. В 1928 году П.А.М. Дирак предложил свой вариант уравнения Шредингера — которое соответствовало теории А. Эйнштейна. Учёный мир был потрясён — Дирак открыл своё уравнение для электрона путём чисто математических манипуляций с высшими математическими объектами, известными как спиноры. И это было сенсацией — до сих пор все великие открытия в физике должны стоять на прочной базе экспериментальных данных. Но Дирак считал, что чистая математика, если она достаточно красива, является надёжным критерием правильности выводов. «Красота уравнений важнее, чем их соответствие экспериментальным данным. … Представляется, что если стремишься получить в уравнениях красоту и обладаешь здоровой интуицией, то ты на верном пути». Именно благодаря его выкладкам был открыт позитрон — антиэлектрон, и предсказал наличие у электрона «спина» — вращения элементарной частицы.
Но Дирак считал, что чистая математика, если она достаточно красива, является надёжным критерием правильности выводов. «Красота уравнений важнее, чем их соответствие экспериментальным данным. … Представляется, что если стремишься получить в уравнениях красоту и обладаешь здоровой интуицией, то ты на верном пути». Именно благодаря его выкладкам был открыт позитрон — антиэлектрон, и предсказал наличие у электрона «спина» — вращения элементарной частицы.
13. Дж. Максвелл получил удивительные уравнения, объединившие все явления электричества, магнетизма и оптики. Замечательный немецкий физик, один из создателей статистической физики, Людвиг Больцман, сказал об уравнениях Максвелла: «Не Бог ли начертал эти письмена?»
14. Уравнение Шредингера.Уравнение, описывающее изменение в пространстве и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах. Играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона в классической механике.
Образование — то, что остается после того, как забыто все, чему учили в школе.
Игорь Хмелинский, новосибирский учёный, ныне работающий в Португалии, доказывает, что без прямого запоминания текстов и формул развитие абстрактной памяти у детей затруднительно. Приведу выдержки из его статьи » Уроки образовательных реформ в Европе и странах бывшего СССР»
Заучивание наизусть и долговременная памятьНезнание таблицы умножения имеет и более серьезные последствия, чем неспособность обнаружить ошибки в расчетах на калькуляторе. Наша долговременная память работает по принципу ассоциативной базы данных, то есть, одни элементы информации при запоминании оказываются связанными с другими на основе ассоциаций, установленных в момент знакомства с ними. Поэтому, чтобы в голове образовалась база знаний в какой-либо предметной области, например, в арифметике, нужно для начала выучить хоть что-то наизусть. Далее, вновь поступающая информация попадет из кратковременной памяти в долговременную, если в течение короткого промежутка времени (несколько дней) мы столкнемся с нею многократно, и, желательно, в разных обстоятельствах (что способствует созданию полезных ассоциаций). Однако при отсутствии в постоянной памяти знаний из арифметики, вновь поступающие элементы информации связываются с элементами, которые к арифметике никакого отношения не имеют – например, личностью преподавателя, погодой на улице и т.п. Очевидно, такое запоминание никакой реальной пользы учащемуся не принесет – поскольку ассоциации уводят из данной предметной области, то никаких знаний, относящихся к арифметике, учащийся вспомнить не сможет, кроме смутных идей о том, что он вроде бы что-то когда-то об этом должен был слышать. Для таких учащихся роль недостающих ассоциаций обычно выполняют разного рода подсказки – списать у коллеги, воспользоваться наводящими вопросами в самой контрольной, формулами из списка формул, которым пользоваться разрешено, и т.п. В реальной жизни, без подсказок, такой человек оказывается совершенно беспомощным и неспособным применить имеющиеся у него в голове знания.
Однако при отсутствии в постоянной памяти знаний из арифметики, вновь поступающие элементы информации связываются с элементами, которые к арифметике никакого отношения не имеют – например, личностью преподавателя, погодой на улице и т.п. Очевидно, такое запоминание никакой реальной пользы учащемуся не принесет – поскольку ассоциации уводят из данной предметной области, то никаких знаний, относящихся к арифметике, учащийся вспомнить не сможет, кроме смутных идей о том, что он вроде бы что-то когда-то об этом должен был слышать. Для таких учащихся роль недостающих ассоциаций обычно выполняют разного рода подсказки – списать у коллеги, воспользоваться наводящими вопросами в самой контрольной, формулами из списка формул, которым пользоваться разрешено, и т.п. В реальной жизни, без подсказок, такой человек оказывается совершенно беспомощным и неспособным применить имеющиеся у него в голове знания.
Формирование математического аппарата, при котором формулы не заучиваются, происходит медленнее, нежели в противном случае. Почему? Во-первых, новые свойства, теоремы, взаимосвязи между математическими объектами почти всегда используют какие-то особенности ранее изученных формул и понятий. Концентрировать внимание ученика на новом материале будет сложнее, если эти особенности не смогут извлекаться из памяти за короткий промежуток времени. Во-вторых, незнание формул наизусть препятствует поиску решения содержательных задач с большим количеством мелких операций, в которых требуется не только провести определенные преобразования, но и выявить последовательность этих ходов, анализируя применение нескольких формул на два-три шага вперед.
Почему? Во-первых, новые свойства, теоремы, взаимосвязи между математическими объектами почти всегда используют какие-то особенности ранее изученных формул и понятий. Концентрировать внимание ученика на новом материале будет сложнее, если эти особенности не смогут извлекаться из памяти за короткий промежуток времени. Во-вторых, незнание формул наизусть препятствует поиску решения содержательных задач с большим количеством мелких операций, в которых требуется не только провести определенные преобразования, но и выявить последовательность этих ходов, анализируя применение нескольких формул на два-три шага вперед.
Практика показывает, что интеллектуальное и математическое развитие ребенка, формирование его базы знаний и навыков, происходит значительно быстрее, если большая часть используемой информации (свойства и формулы) находиться в голове. И чем прочнее и дольше она там удерживается, тем лучше.
Арифметические формулы в Excel — Формулы и простые математические операции в Excel
Одной из основных возможностей программы Microsoft Excel является возможность работы с формулами. Это значительно упрощает и ускоряет процедуру подсчета общих итогов, и отображения искомых данных. Данный инструмент является своеобразной фишкой приложения. Давайте разберемся, как создать формулы в программе Microsoft Excel, и как работать с ними.
Это значительно упрощает и ускоряет процедуру подсчета общих итогов, и отображения искомых данных. Данный инструмент является своеобразной фишкой приложения. Давайте разберемся, как создать формулы в программе Microsoft Excel, и как работать с ними.
Содержание
Создание простейших формул
Самыми простыми формулами в программе Microsoft Excel являются выражения арифметических действий между данными расположенными в ячейках. Для того, чтобы создать подобную формулу, прежде всего, ставим знак равенства в ту ячейку, в которую предполагается выводить полученный результат от арифметического действия. Либо можно встать на ячейку, и вставить знак равно в строку формул. Эти действия равнозначны, и автоматически дублируются.
Затем выделяем определенную ячейку, заполненную данными, и ставим нужный арифметический знак («+„, “-„, “*»,»/«, и т.д.). Эти знаки называются операторами формул. Выделяем следующую ячейку. Так повторяем до тех пор, пока все ячейки, которые нам требуются, не будут задействованы. После того, как выражение будет, таким образом, введено полностью, для того, чтобы просмотреть результат вычислений, жмем на кнопку Enter на клавиатуре.
После того, как выражение будет, таким образом, введено полностью, для того, чтобы просмотреть результат вычислений, жмем на кнопку Enter на клавиатуре.
Примеры вычислений
Допустим, у нас есть таблица, в которой указано количество товара, и цена его единицы. Нам нужно узнать общую сумму стоимости каждого наименования товара. Это можно сделать путем умножения количества на цену товара. Становимся курсором в ячейку, где должна будет отображаться сумма, и ставим там знак равно (=). Далее, выделяем ячейку с количеством товара. Как видим, ссылка на неё сразу же появляется после знака равно. Затем, после координат ячейки, нужно вставить арифметический знак. В данном случае, это будет знак умножения (*). Далее, кликаем по ячейке, где размещаются данные с ценой единицы товара. Арифметическая формула готова.
Чтобы просмотреть её результат, просто жмем на клавиатуре кнопку Enter.
Для того, чтобы не вводить данную формулу каждый раз для вычисления общей стоимости каждого наименования товара, просто наводим курсор на правый нижний угол ячейки с результатом, и тянем вниз, на всю область строк, в которых расположено наименование товара.
Как видим, формула скопировалось, и общая стоимость автоматически рассчиталась для каждого вида товара, согласно данным о его количестве и цене.
Таким же образом, можно рассчитывать формулы в несколько действий, и с разными арифметическими знаками. Фактически, формулы Excel составляются по тем же принципам, по которым выполняются обычные арифметические примеры в математике. При этом, используется практически тот же синтаксис.
Усложним задачу, разделив количество товара в таблице на две партии. Теперь, чтобы узнать общую стоимость, нам нужно прежде сложить количество обеих партий товара, и, затем, полученный результат умножить на цену. В арифметике подобные действия выполнятся с использованием скобок, иначе первым действием будет выполнено умножение, что приведет к неправильному подсчету. Воспользуемся скобками, и для решения данной задачи в программе Excel.
Итак, ставим знак равно (=) в первой ячейке столбца «Сумма». Затем открываем скобку, кликаем по первой ячейке в столбце «1 партия», ставим знак плюс (+), кликаем по первой ячейки в столбце «2 партия». Далее, закрываем скобку, и ставим знак умножить (*). Кликаем, по первой ячейке в столбце «Цена». Таким образом, мы получили формулу.
Далее, закрываем скобку, и ставим знак умножить (*). Кликаем, по первой ячейке в столбце «Цена». Таким образом, мы получили формулу.
Кликаем на кнопку Enter, чтобы узнать результат.
Таким же образом, как и в прошлый раз, с применением способа перетягивания, копируем данную формулу и для других строк таблицы.
Нужно заметить, что не обязательно все данные формулы должны располагаться в соседних ячейках, или в границах одной таблицы. Они могут находиться в другой таблице, или даже на другом листе документа. Программа все равно корректно подсчитает результат.
Калькулятор
Хотя, основной задачей программы Microsoft Excel является вычисление в таблицах, но приложение можно использовать, и как простой калькулятор. Просто, ставим знак равно, и вводим нужные действия в любой ячейке листа, или действия можно написать в строке формул.
Для получения результата жмем на кнопку Enter.
Основные операторы Excel
К основным операторам вычислений, которые применяются в программе Microsoft Excel, относятся следующие:
- = («знак равенства») — равно;
- + («плюс») — сложение;
- — («минус») — вычитание;
- («звездочка») — умножение;
- / («наклонная черта») — деление;
- ^ («циркумфлекс») — возведение в степень.

Как видим, программа Microsoft Excel предоставляет полный инструментарий пользователю для выполнения различных арифметических действий. Данные действия могут выполняться, как при составлении таблиц, так и отдельно для вычисления результата определенных арифметических операций.
5 самых старых нерешенных задач Математики о простых числах / Хабр
Математика была предметом, который веками бросал вызов величайшим умам в истории человечества. Пожалуй, одной из наиболее исследуемых областей Математики является изучение простых чисел.
Наши размышления о закономерностях в простых числах привели к некоторым сложнейшим проблемам, нерешенным даже величайшими математическими гениями. Сегодня мы рассмотрим 5 старейших математических задач о простых числах, которые интуитивно понятны старшекласснику, но все еще не доказаны даже после упорных попыток в течение 500-2000 лет.
1. Совершенные числа: существуют ли нечетные совершенные числа? Бесконечны ли четные совершенные числа?
Рассмотрим числа 6, 28, 496, 8128…
Что в них особенного? Если вы не знаете, то я бы посоветовал сделать небольшую паузу и попытаться найти красивое свойство, которым обладают эти числа.
Двигаемся дальше….
Если посмотреть на собственные делители этих чисел, то нетрудно заметить то самое «красивое» свойство:
Числа, для которых сумма собственных делителей равна самому числу, называются совершенными числами. Самое раннее исследование совершенных чисел затеряно в истории. Однако, мы знаем, что пифагорейцы 525годдон.э. изучали совершенные числа.
Что мы знаем о таких числах?
Евклид доказал, что для данного n, если — простое число, то — совершенное число. В качестве упражнения попробуйте доказать это самостоятельно.
Окей, краткий экскурс.
Простые числа Мерсенна: простые числа вида для некоторого n. Мерсенн предположил, что все числа вида простые, когда n простое. (Мы знаем, что это неправда. Например, ).
Мерсенн предположил, что все числа вида простые, когда n простое. (Мы знаем, что это неправда. Например, ).
Открытый вопрос: существует ли бесконечно много простых чисел Мерсенна? На данный момент нам известно 47 простых чисел Мерсенна.
Как видите, мы знаем о четных совершенных числах и способах их получения еще со времен Евклида около300годдон.э.. Но нам неизвестно, существую ли нечетные совершенные числа!!! насамомделе,прогрессврешенииэтойпроблемыпрактическиотсутствует.
Подводя итог, можно сказать, что изучение совершенных чисел ставит две давние открытые проблемы, а именно «существование нечетных совершенных чисел» и «существование бесконечно большого числа простых чисел Мерсенна».
Евклид (ок. 300 г. до. н. э.) первым доказал то, что простых чисел бесконечно много.2. Гипотеза о близнецах: простых чисел-близнецов бесконечно много
Простые числа-близнецы — это пара вида (p, p + 2), где p и p + 2 являются простыми числами.
Точное происхождение гипотезы о простых числах-близнецах не установлено. Первая формулировка гипотезы о простых числах-близнецах была дана в 1846 году французским математиком Альфонсом де Полиньяком. Однако греческий математик Евклид дал старейшее из известных доказательств существования бесконечного числа простых чисел. Но он не предполагал, что существует бесконечное число простых чисел-близнецов.
Первая формулировка гипотезы о простых числах-близнецах была дана в 1846 году французским математиком Альфонсом де Полиньяком. Однако греческий математик Евклид дал старейшее из известных доказательств существования бесконечного числа простых чисел. Но он не предполагал, что существует бесконечное число простых чисел-близнецов.
На протяжении 2000 лет в доказательстве этого утверждения практически не было прогресса.
Что мы знаем!
Существует бесконечно много простых пар вида (p, p + k), где k <= 246.
Если допустить истинность гипотезы Эллиота — Халберстама (которая, по нашему мнению, верна), то существует бесконечно много простых пар вида (p, p + k), где k <= 6. Это означает, что множество пар простых чисел, отличающихся на 2 (twin-primes), на 4 (cousin-primes) и на 6 (sexy-primes) бесконечно.
Возможно, величайший из ныне живущих математиков, Теренс Тао, активно работает над этой проблемой. Посмотрите это видео, чтобы познакомиться с этим математическим гением и его работой над простыми числами-близнецами.
3. Какие правильные n-угольники построимы?
Правильный многоугольник считается построимым, если его можно построить с помощью линейки и циркуля. Например, правильный пятиугольник можно построить с помощью линейки и циркуля, а правильный семиугольник нет.
Древние греки знали, как построить правильный многоугольник с 3, 4 и 5 сторонами. Также они умели строить правильные многоугольники с удвоенным числом сторон для данного правильного многоугольника.
Таким образом, они могли построить правильный n-угольник для n = {3, 6, 12, 24… 4, 8, 16… 5, 10, 20…} и так далее.
Естественно задать вопрос, для каких значений n можно построить правильный многоугольник. Первый реальный результат в решении этой проблемы был получен спустя 2000 лет после того, как древние греки впервые начали её изучать. В 1796 году 19-летний подросток построил правильный 17-угольник. Этим ребенком был не кто иной, как Карл Фридрих Гаусс. Несколько лет спустя Гаусс дал ответ на общую проблему.
Что мы знаем!
Гаусс показал, что правильный n-угольник может быть построен с помощью циркуля и линейки тогда и только тогда, когда n является произведением степени двойки и любого количества различных простых чисел Ферма (включая ни одного).
Простое число Ферма — это простое число вида:
Таким образом, проблема поиска всех построимых многоугольников сводится к нахождению всех простых чисел Ферма. Это отдельная нерешенная проблема. Несколько первых чисел Ферма: 3, 5, 17, 257, 65537, 4294967297…
По состоянию на 2021 год единственными известными простыми числами Ферма являются F0=3, F1=5, F2=17, F3=257, F4=65537.
Ферма предположил, что все числа Ферма являются простыми. В 1732 году Эйлер открыл, что F5 делится на 641. С тех пор мы выяснили, что для n = 5, 6…31 числа Ферма составные. Простое число Ферма после F4 неизвестно.
Мы найдем ответ на вопрос о построимых правильных n-угольниках в тот же момент, как только найдем ответ на вопрос о существовании простых чисел Ферма.
4. Гипотеза Гольдбаха (1742)
Сильная гипотеза Гольдбаха:
Каждое чётное число, большее двух, можно представить в виде суммы двух простых чисел.
Слабая гипотеза Гольдбаха:
Каждое нечётное число, большее 5, можно представить в виде суммы трёх простых чисел.
Второе утверждение называется «слабым», потому что в случае истинности «сильной» гипотезы вторая также будет истинной. К сожалению, после значительных усилий поколений математиков, начиная с Эйлера, мы так и не смогли доказать ее.
(Примечание — В 2013 году Харальд Хельфготт опубликовал доказательство слабой гипотезы Гольдбаха. По состоянию на 2018 год доказательство широко принято в математическом сообществе, однако оно еще не было опубликовано в рецензируемом журнале).
В любом случае, все ждут доказательства сильной гипотезы.
Что мы знаем!
В 1930 году было доказано, что любое натуральное число больше 1 может быть записано в виде суммы не более чем C простых чисел, где C < 800 000 [Примечание — мы хотим, чтобы C = 2].

В последнее десятилетие было показано, что каждое четное число n >= 4 на самом деле является суммой не более чем 6 простых чисел (т.е. С <= 6). Позже результат был улучшен до C <= 4.
Забавный факт — гипотеза Гольдбаха является частью сюжета испанского фильма 2007 года «Западня Ферма«.
Отказ от ответственности: название статьи вводит в заблуждение. После рассказа о 4 нерешенных задачах я хотел бы показать одну математическую проблему (пятая проблема), которая была недавно решена (в 2004 году).
5. Тест простоты числа принадлежит классу P (2004)
Допустим, вам дано число n = 10089886811898868001. Вас спрашивают, простое ли это число. Первое, что вам приходит на ум, так это,
Алгоритм A — проверить для каждого числа делится ли n на k. Вы можете оптимизировать этот алгоритм, понимая, что если n не является простым, то n будет иметь такой множитель k, что
Алгоритм B — итак, вы проверяется только
Хорошо, но погодите, что такое «P»?
Говорят, что задача находится в «P», если существует «быстрый» алгоритм, который может решить задачу. В нашем случае задача заключается в том, чтобы определить, является ли заданное n простым числом.
В нашем случае задача заключается в том, чтобы определить, является ли заданное n простым числом.
Итак, что такое быстрый алгоритм?
Для любой заданной проблемы у нас имеется размер ввода (назовем его x). Для нашей задачи размер ввода — это количество цифр в числе n. Итак, x = 20 для указанного выше n. В общем случаем, при заданном n,
Алгоритм называется быстрым (алгоритм с полиномиальным временем), если он решает задачу за f(x) шагов, где f — полиномиальная функция.
Если взглянуть на вышеупомянутые алгоритмы, то получим, что мы имеем n шагов в алгоритме А и шагов в алгоритме B.
Итак, размер ввода в нашем случае —
Обозначим — количество шагов в алгоритме для данного размера ввода x.
Для алгоритма А,
Для алгоритма B,
В обоих случаях алгоритмы имеют экспоненциальное время. В течение 400 лет математики пытались выяснить, можно ли решить задачу определения простоты числа за полиномиальное время. Оказывается, что да. Новость об этом распространилась в математическом сообщество (особенно среди теоретиков чисел) в 2004 году, когда об этом объявили профессор и двое его студентов из IITK.
Новость об этом распространилась в математическом сообщество (особенно среди теоретиков чисел) в 2004 году, когда об этом объявили профессор и двое его студентов из IITK.
Алгоритм (известный как тест простоты AKS) был опубликован в статье под названием «Primes Is In P«, где показывается, что задача (независимо от того, является ли n простым или нет), может быть решена за ~ шагов. Позже были внесены некоторые улучшения, сократившие время до ~ шагов, также выдвигались предположения, что время можно уменьшить и вовсе до ~ шагов (прим. переводчика — предположение оказалось ложным).
Дата-центр ITSOFT — размещение и аренда серверов и стоек в двух дата-центрах в Москве. За последние годы UPTIME 100%. Размещение GPU-ферм и ASIC-майнеров, аренда GPU-серверов, лицензии связи, SSL-сертификаты, администрирование серверов и поддержка сайтов.
Сочинение У математиков существует свой язык – это формулы
- Сочинения
- На свободную тему
- У математиков существует свой язык – это формулы
«У математиков существует свой язык – это формулы» это высказывание знаменитого математика 19 века С. В. Ковалевской. Давайте поразмышляем над этими словами.
В. Ковалевской. Давайте поразмышляем над этими словами.
Математика – любимый школьный предмет многих учеников. Лично мне нравится решать задачи, примеры, искать логический ответ на тот или иной вопрос.
Эта наука привлекает людей, потому что все в ней подчиняется определенным правилам и никак иначе. Эти правила одинаковы для каждого. У математики свои законы, которые не изменились по истечению времени и не зависят от национальности или страны. Люди, увлекающиеся ею, способны обмениваться решениями, примера с другими, даже если те говорят на другом языке. Ведь весь мир использует одни формулы, знаки и это сближает столь разные населения.
Без математики не обойтись ни в одной сфере деятельности. Изо дня в день мы используем навыки обычных арифметических действий для того, чтобы совершить покупки, чтобы распланировать собственное время. Каждая профессия нуждается в использовании тех или иных математических расчетов, даже если на первый взгляд в этом нет необходимости. Многие специальности просто невозможно представить без глубоких математических знаний.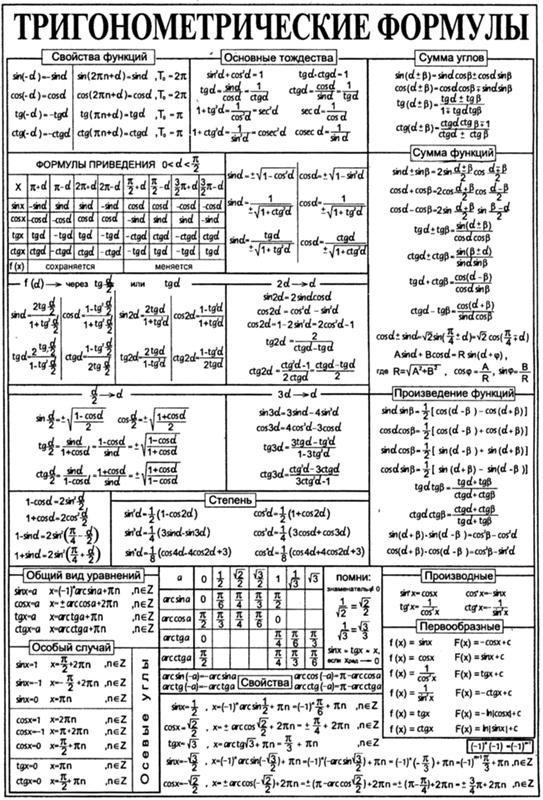
Математика еще миллионы лет назад стала основой для всех наук. Изучить географию, химию, физику не получится без умения выполнять элементарные расчеты. Для достижения успеха и получения отличного образования, необходимо с математикой быть на «ты».
К тому же регулярные занятия математикой способствуют развитию логического мышления. Считается, что люди, имеющие хорошие математические навыки, замечательные игроки в шахматы, умеют разрабатывать стратегические планы. В повседневной жизни не лишним будет умение логично и здраво оценивать ситуацию, находить решение проблем.
Математика еще и отличное хобби. Можно посещать кружки, сообщества, клубы, в которых люди решают непростые математические задачи.
Математика, как и другие науки, имеет свою особенность. В данном случае это ее язык общения – формулы. Именно с их помощью мы и выполняем необходимые действия и получаем желаемое вычисление, решение. Сотни ученых трудились годами, выводя определенные действия, и из этого образовывались формулы. Без них эта наука не смогла бы существовать.
Без них эта наука не смогла бы существовать.
Формулы бывает простые, а бывает замысловатые. Некоторые из них многим из нас никогда и не повстречаются в жизни.
Без математики мир бы остановился на одном месте. Она является основой научно-технического прогресса, а это наше новое будущее.
Вариант 2
«Математика – гуманитарная наука», – сказал однажды Владимир Андреевич Успенский, доктор физико-математических наук и заслуженный профессор Московского университета. Но разве это возможно? Ведь каждый человек знает, что математика относится к точным наукам. Разве есть что-то общее между решением задач и, например, чтением?
Возьмём алгебру, один из разделов математики, и рассмотрим её с точки зрения языковой структуры. Наименьшей частицей языковой системы является буква, которая в свою очередь входит в состав алфавита. Буквы складываются в слова, слова – в предложения и так далее.
В алгебре в качестве алфавита представляются цифры и латинские буквы, некоторые из которых могут обозначать целое слово. Выстраивая формулы, мы получаем предложение, где значение каждого математического «слова» зависит от контекста, то есть задачи. Решение различных упражнений – это своего рода общение на математическом языке с автором учебника.
Выстраивая формулы, мы получаем предложение, где значение каждого математического «слова» зависит от контекста, то есть задачи. Решение различных упражнений – это своего рода общение на математическом языке с автором учебника.
Например, известная всем формула нахождения расстояния: . Расстояние , скорость и время могут принимать для каждой задачи разные значения, но их обозначение латинскими буквами остаётся неизменно. В поисках ответа на вопрос задания мы разговариваем, читаем и пишем на математическом языке.
Другой раздел математики – геометрия – и вовсе является риторическим. Риторика – дисциплина, изучающая искусство речи, основана на богатом словарном запасе, знании правил построения художественной речи, на умении грамотно орудовать фактами.
В геометрии необходимо обладать логикой, знанием правил построения доказательств и большим багажом знаний – теорем, следствий, аксиом. А любая задача на доказательство схожа с дебатами, где требуется отстоять свою позицию, показать истинность или ложность представленных условий.
Если же в целом провести аналогию между изучением математики и иностранного языка, то можно сделать вывод: без знания алфавита, слов и правил построения предложений невозможно понимать чужую речь. Поэтому математика порой так сложно даётся ученикам школы – они не знают и не пытаются понять структуру её языка.
Математику принято относить к точным наукам, так как в этой отрасли науки изучают точные закономерности и применяют строгие методы проверки гипотез. Однако нельзя не заметить её схожесть с лингвистикой, которая в свою очередь является наукой гуманитарной. И также, как разные народы имеют своя речь, у математиков существует язык формул.
Другие сочинения:← Я рожден, и это все, что необходимо, чтобы быть счастливым!↑ На свободную темуСамый холодный материк на Земле Антарктида →
У математиков существует свой язык – это формулы
Несколько интересных сочинений
Введение в формулах (Intro to Formulas)
Lesson 4: Введение в формулах (Intro to Formulas)
/en/tr_ru-misc/-cell-basics/content/
Введение.
Одной из самых главных функций в Excel является возможность вычислить числовую информацию с помощью формул. Также как калькулятор, Excel может выполнять сложение, вычитание, умножение и деление. В этом уроке мы покажем вам как использовать ссылки на ячейки для создания простых формул.
По желанию: загрузите наше практическое учебное пособие .
В приведенном ниже видео вы узнаете больше о создании формул в Excel.
Математические операторы
Excel использует стандартные операторы для формул, такие как: знак плюс для сложения (+), знак минус для вычитания (-), звездочка для умножения (*), косая черта для деления (/) и циркумфлекс (^) для возведения в степень.
Все формулы в Excel должны начинаться со знака равенства (=). Это происходит потому, что данные, содержащиеся в ячейке или в формуле, приравниваются к значению, которое вычисляет формула.
Понятие ссылки на ячейки
Несмотря на то, что вы можете создавать простые формулы в Excel с помощью чисел (например, = 2 + 2 или = 5 * 5), в большинстве случаев для создания формул вы будете использовать адреса ячеек. Это называется созданием ссылки на ячейку. Использование ссылок на ячейки будет гарантировать точность ваших формул, так как вы сможете менять значение ссылочных ячеек без редактирования всей формулы.
В приведенной ниже формуле в ячейке A3 складывается значение ячеек А1 и А2, создавая ссылку на ячейки:
При нажатии кнопки Ввод, формула вычисляет и отображает результат равенства в ячейке A3:
При внесении изменений в указанные ячейки, формула автоматически пересчитывает результат:
Используя математические операторы вместе с ссылками на ячейки, вы можете создавать множество простых формул в Excel. Формулы могут также включать в себя комбинацию ссылок на ячейки и операций, как показано в примерах ниже:
Формулы могут также включать в себя комбинацию ссылок на ячейки и операций, как показано в примерах ниже:
— Разрыв страницы
Создаем формулу в Excel:
В приведенном ниже примере мы будем использовать простую формулу со ссылками на ячейки для расчета бюджета.
- Выделите ячейку, которая будет содержать формулу. В нашем примере мы выделили D12.
- Введите знак равенства (=). Обратите внимание на то, что он появляется как в самой ячейке, так и в строке формул.
- Введите в формуле первую ссылку на ячейку: в нашем примере это ячейка D10. Вокруг ссылки на ячейку отобразится рамка синего цвета.
- Введите математический оператор, который вы хотите применить. В нашем примере, мы введем знак сложения (+).
- Введите в формуле вторую ссылку на ячейку: в нашем примере это ячейка D11.
 Вокруг ссылки на ячейку отобразится рамка красного цвета.
Вокруг ссылки на ячейку отобразится рамка красного цвета. - Нажмите Ввод на клавиатуре. Формула будет рассчитана, а значение отобразится в ячейке. Если вы снова выделите ячейку, то вы заметите, что ячейка показывает результат, в то время как в строке формул отображается формула.
Если результат формулы слишком велик для отображения в ячейке, то вместо значения могут появиться знаки решетки (#######). Это означает, что столбец недостаточно широк для отображения содержимого ячейки. Просто увеличите ширину столбца, чтобы отобразить содержимое ячейки.
Изменение значений в ссылках на ячейки
Главным преимуществом ссылок является возможность обновлять данные на листе Excel без необходимости переписывать формулы. В приведенном ниже примере мы изменили значение ячейки B1 с $ 1200 на $ 1800. Формула в ячейке B3 будет автоматически пересчитана и новый результат отобразится в ячейке B3.
Excel не всегда будет сообщать вам об ошибке формул, поэтому вы должны сами проверять правильность составления всех ваших формул. Чтобы узнать подробней о том, как это сделать, ознакомьтесь с уроком «Перепроверяйте свои формулы» из нашего обучающего курса «Формулы в Excel».
— Разрыв страницы
Создаем формулу в Excel с выделением курсором мыши:
Вместо того, чтобы вводить адреса ячеек вручную, вы можете навести курсор мыши на ячейку, которую вы хотите включить в формулу. Этот метод может сэкономить много времени и усилий при создании формул. В приведенном ниже примере, мы создадим формулу для расчета стоимости заказа нескольких коробок пластиковых столовых приборов.
- Выделите ячейку , которая будет содержать формулу. В нашем примере мы выделили ячейку D4.
- Введите знак равенства (=).
- Введите в формуле первую ссылку на ячейку: в нашем примере это ячейка B4.
 Ссылка на ячейку отобразится в формуле.
Ссылка на ячейку отобразится в формуле. - Введите математический оператор , который вы хотите применить. В нашем примере, мы будем вводить знак умножения (*).
- Введите в формуле вторую ссылку на ячейку: в нашем примере это ячейка С4. Ссылка на ячейку отобразится в формуле.
- Нажмите Ввод на клавиатуре. Формула будет рассчитана, а значение отобразится в ячейке.
Копирование формул с помощью маркера автозаполнения
Формулы также могут быть скопированы в смежные ячейки с помощью маркера автозаполнения, который позволяет сэкономить время и усилия каждый раз, когда вам необходимо выполнять множество вычислений на листе Excel. Маркер автозаполнения выглядит как маленький квадратик в правом нижнем углу выделенной ячейки.
- Выделите ячейку с формулой, которую вы хотите скопировать.
 Нажмите, и удерживая курсором мыши, перетащите маркер автозаполнения по ячейкам, которые нужно заполнить.
Нажмите, и удерживая курсором мыши, перетащите маркер автозаполнения по ячейкам, которые нужно заполнить. - После того, как вы отпустите кнопку мыши, формула будет скопирована в выделенных ячейках.
Как изменить формулу в Excel:
Иногда вам может понадобиться изменить существующую формулу. В приведенном ниже примере, мы ввели в нашу формулу неправильную ссылку на ячейку, и теперь нам нужно это исправить.
- Выделите ячейку с формулой, которую вы хотите изменить. В нашем примере мы выделили ячейки D12.
- Для того, чтобы изменить формулу в ячейке, нажмите на строку формул. Вы можете также дважды щелкнуть по ячейке, чтобы посмотреть и отредактировать формулу непосредственно в самой ячейке.
- Все ячейки, на которые ссылается формула, будут обведены рамкой. В нашем примере мы изменим первую часть формулы, чтобы ссылка вела на ячейку D10, вместо ячейки D9.

- Когда вы закончите, нажмите Ввод на клавиатуре или нажмите на команду Ввод в строке формул.
- Формула будет обновлена и новое значение отобразится в ячейке.
Если вы передумаете, вы можете нажать клавишу Esc на клавиатуре или нажмите на команду Отмена в строке формул, чтобы избежать внесения случайных изменений в формулу.
Чтобы показать все формулы в электронной таблице, нажмите сочетание клавиш Ctrl и `(апостроф). Ключ гравис обычно находится в верхнем левом углу клавиатуры. Чтобы вернуться в обычный режим просмотра, нажмите повторно Ctrl + `.
— Разрыв страницы
Практическое занятие!
- Откройте наше практическое учебное пособие .
- Нажмите на вкладку Вызовы в левом нижнем углу учебного пособия.
- Создайте формулу в ячейке D4 , которая умножит количество товара в ячейке В4 на цену за одну единицу товара в ячейке C4.

- С помощью маркера заполнения скопируйте формулу из ячейки D4 в ячейки D5:D7.
- Измените цену за одну единицу жаренного плода в ячейке С6 и укажите $2,25. Обратите внимание на то, что колонка общей стоимости также будет автоматически изменена.
- Измените формулу для итогового значения в ячейке D8 с прибавлением ячейки D7.
- Когда вы закончите, ваш результат должен выглядеть следующим образом:
Back to Tutorial
Previous: Понятие ячеек (Cell Basics)
Next:Return to Playlist: русский
Электронные ресурсы по предметным дисциплинам
Информатика
Клякс@.net —
информационно-образовательный портал по информатике и ИКТ.
Алгоритмика — вебсайт школы программирования, на котором доступны программы по информатике для учеников младших и средних классов.
Математика
Специализированные математические пакеты и инструменты для изучения математики
Derive и LiveMath, Mathematica или MathCAD – пакеты математических программ. Могут быть использованы в старших классах. Системы используются во многих технических, научных, инженерных, математических и вычислительных областях. Подобные программы позволяют проводить вычисления, работать с функциями, строить графики и пр. В учебном процессе применяются в старших классах, колледжах и вузах при проведении занятий, выполнении курсовых и практических работ по дисциплине «Математика».
Cabri Geometry –
пакет динамической геометрии. Коммерческое программное обеспечение для обучения
и изучения геометрии и тригонометрии. Используется
для преподавания геометрии в средней школе, для обучения на уровне университета
и в качестве инструмента для математиков в их исследовательской работе.
Перечисленные выше пакеты математических программ относятся к достаточно сложным системам, которые требуют специальной подготовки педагога. А есть более простые в освоении системы, которые предназначены именно для использования в учебном процессе. Приложения по математике помогают решить задачи, построить функцию, посмотреть на примеры под новым углом, увлекают учеников игровыми моментами, наглядностью. Например:
Geometryx – это приложение, позволяющее
быстро и удобно рассчитать основные значения и параметры геометрических фигур и
тел. Это современный геометрический калькулятор, который вычисляет необходимые
значения, а при необходимости подскажет, какие данные следует ввести, чтобы
расчеты имели математический и геометрический смысл. Geometryx также содержит
основные формулы и геометрические уравнения, которые могут помочь решить
всевозможные проблемы и задачи по геометрии. Geometryx будет полезным для
учеников, студентов, учителей, ученых, инженеров, техников, а также для всех,
кто имеет дело с геометрией.
Geogebra Classic – приложение для геометрических построений на телефоне. В приложении проще нарисовать ровный прямой угол и заметить все равные углы и стороны, чем на чертеже от руки в тетради. Приложение подходит для помощи школьникам при решении простых и сложных задач и выполнения построений.
Photomath – сервис, который по фотографии, сделанной на телефон из учебника, распознает и решает уравнения, сокращает выражения, строит график функции и многое другое. Есть пошаговый разбор решения задачи.
«Пифагория» – предлагает игры, основанные на математических законах, возможность построения фигур, проведения вычислений. Игра поможет подругому взглянуть на геометрические фигуры, тонкости их построения и закономерности.
Euclidea – это коллекция интерактивных задач по геометрии в виде игры. Рекомендуется школьникам, учителям и всем любителям математики.
MalMath – программа для решения математических задач с пошаговым описанием выполняемых действий и графическим изображением полученного результата.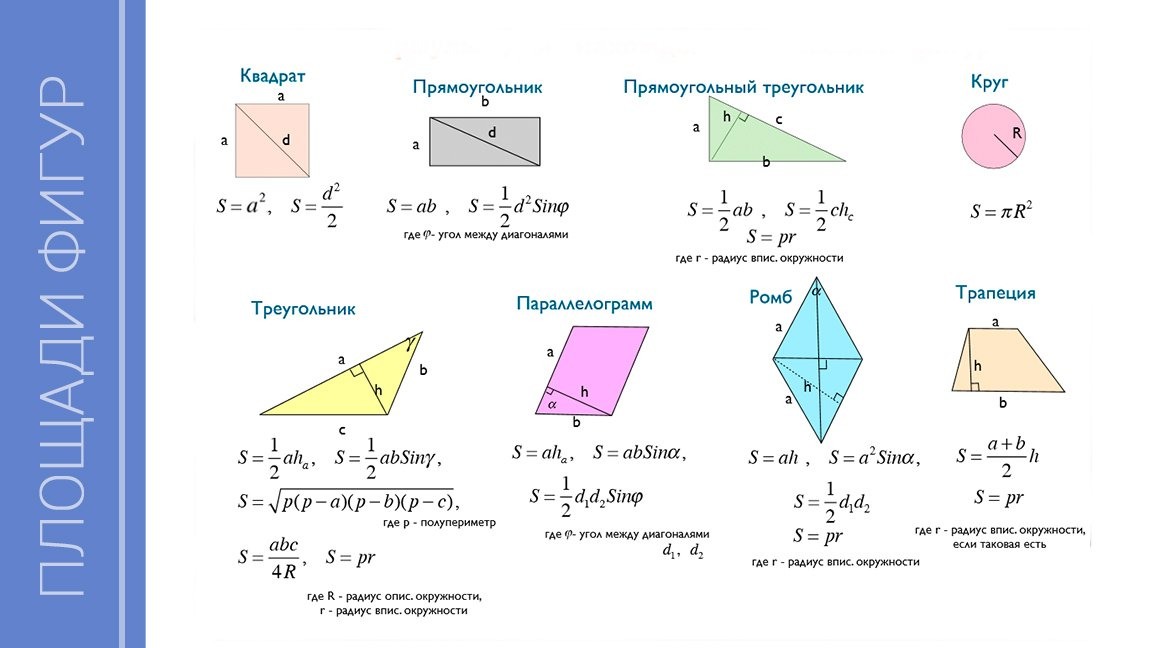 Генерирует случайные математические задачи в нескольких категориях и уровнях сложности. Есть возможность сохранить полученные решения, построенные графики. Полученными решениями и графиками можно поделиться в сообщении или письме. Платформа: Android
Генерирует случайные математические задачи в нескольких категориях и уровнях сложности. Есть возможность сохранить полученные решения, построенные графики. Полученными решениями и графиками можно поделиться в сообщении или письме. Платформа: Android
Advanced Grapher – программа со множеством настроек и функций, содержит все необходимое для решения самых сложных задач, прилагаются примеры простых и сложных графиков. Строит графики в полярных и декартовых координатах, графики с областями, графики, заданные формулой или таблицей значений. Подходит для старших классов.
MathType –интерактивный инструмент для создания математических формул.
Рассмотренные программные продукты рекомендуется использовать в процессе изучения математики для развития цифровых навыков учащихся и навыков исследовательской деятельности.
problems.ru — разработанные
Московским центром непрерывного математического образования (МЦНМО) задачи
по логике и теории множеств, алгебре и арифметике, геометрии,
комбинаторике, вероятности и статистики, математическому анализу и
информатике.
Задачи по геометрии — задачи, разработанные Московским центром непрерывного математического образования.
Math.Ru — сайт МЦНМО для школьников, студентов, учителей и всех, кто интересуется математикой. На сайте имеется библиотека и медиатека, опубликованы задачи и материалы по истории математики.
Etudes.ru — на сайте представлены этюды, выполненные с использованием современной компьютерной 3D графики, рассказывающие о математике и ее приложениях.
Открытая математика — онлайн-учебник, разработанный в рамках проекта “Открытый колледж”.
Euclidea — коллекция интерактивных задач по геометрии в игровом формате. В мобильном версии доступны два приложения — Euclidea и Пифагория, которые можно загрузить с Google Play и App Store.
Photomath — образовательное приложение для смартфона или планшета, которое считывает и решает задачи — от простой арифметики до интегрального исчисления — при помощи камеры на мобильном устройстве. Пошаговые инструкции помогают в решении математических задач, напечатанных в учебнике или записанных от руки.
Desmos – сервис с набором специализированных графических калькуляторов.
MathFight – приложение для проведения математической дуэли, увлекательная образовательная игра для учащихся
Math Playground – бесплатный ресурс с математическими играми и тематическими упражнениями по категориям и уровню подготовки:
Матбюро – сайт с пошаговыми решениями задач по разным математическим дисциплинам. Есть как стандартные примеры высшей математики, так и сложные задачи
Euclidea – коллекция интерактивных задач по геометрии в виде игры. Рекомендуется школьникам, учителям и всем любителям математики
Физика
ЦОР по физике — ресурс содержит учебные материалы по физике и астрономии для 7—11 классов, в т.ч. видеоуроки и тесты,.
Задачник «Кванта» — научно-популярный журнал «Квант», в котором представлена коллекция задач по физике и математике.
Открытая физика — онлайн-учебник, разработанный в рамках проекта «Открытый колледж».
Химия
ChemNet — портал Химического факультета МГУ имени М. В. Ломоносова, на котором размещены электронная библиотека учебных материалов по химии, в т.ч. учебные видеоматериалы, архив заданий и решений школьных олимпиад.
В. Ломоносова, на котором размещены электронная библиотека учебных материалов по химии, в т.ч. учебные видеоматериалы, архив заданий и решений школьных олимпиад.
Основы химии — электронный учебник по общей и неорганической химии для 8—11 классов.
Алхимик — портал Института тонких химических технологий имени М. В. Ломоносова, который содержит электронные пособия, справочник, презентации к лекциям и другие материалы по химии.
Органическая химия — интерактивный мультимедиа учебник по органической химии для средней школы.
Я иду на урок химии — вебсайт, разработанный на основе материалов журнала «Химия» издательского дома «Первое сентября».
Открытая химия — онлайн-учебник, разработанный в рамках проекта «Открытый колледж».
Журнал «Химия и химики» — электронный научно-популярный журнал по химии и физике, публикующий также описания экспериментов по химии и физике с фотографиями и олимпиадные задачи по химии.
Биология
Проект «Вся биология» — научно-образовательный проект, посвященный биологии и смежным дисциплинам.
Биомолекула — проект, направленный на популяризацию современных достижений в области медицины и биологии и продвижение их практического применения в сфере биотехнологий.
Biodat — справочно-информационный ресурс по биологии и экологии, содержащий также инструменты для совместной работы и размещения в интерактивном режиме результатов исследований и наблюдений.
Открытая биология — онлайн-учебник, разработанный в рамках проекта «Открытый колледж».
Биошкола 100 — коллекция видеоматериалов по биологии, объяснение решений задач и подготовка к ЕГЭ и ОГЭ.
География
Русское географическое общество — вебсайт старейшей общественной географической организации России, который содержит достоверные географические сведения, информацию об экспедициях, проектах и выставках.
Вокруг света — научно-популярный и страноведческий журнал Русского географического общества, в котором публикуются материалы по географии, этнографии, биологии, астрономии, медицине, культуре, истории и др.
GeoMan.ru — электронная библиотека, которая содержит материалы по географии для школьников, студентов и преподавателей.
Geo-site.ru — географический портал, на котором представлены статистические данные, словари, географический календарь и информация о географических открытиях.
Мой город — народная энциклопедия городов и регионов России.
Geo.historic.ru — географический справочник и атлас для учителей средней школы.
Бесплатные географические тренажёры
Горные хребты Европы https://online.seterra.com/ru/vgp/3215
Физическая карта https://online.seterra.com/ru/vgp/3459
Россия. Города https://online.seterra.com/ru/vgp/3395
25 самых больших городов в мире https://online.seterra.com/ru/vgp/3127
ОБЖ
Спас Экстрим — портал детской безопасности МЧС России, который содержит тематические интерактивные игры, обучающие видеоролики и мультфильмы, листовки и памятки, учебно-методические материалы.
ОБЖ.рф — коллекция материалов, включающие методические разработки, статьи и справочники, учебные материалы и видеоуроки.
Русский язык и литература
Образование на русском — портал, объединяющий платформу дистанционного обучения русскому языку, систему дистанционного повышения квалификации преподавателей русского языка, систему массовых онлайн-курсов на русском языке для людей разного возраста, изучающих русский язык, и социальную сеть для пользователей портала.
Грамота.ру — справочно-информационный портал, который содержит Единое окно справочных служб русского языка и материалы по всем разделам русской грамматики и орфографии, включая словари, публикации о русском языке, учебники, онлайн-репетитор и игры.
Правила русского языка — справочный вебсайт, на котором размещены правила орфографии и пунктуации.
TextoLogia.ru — интернет-журнал, созданный с целью популяризации русского языка и литературы.
Иностранные языки
Native-english.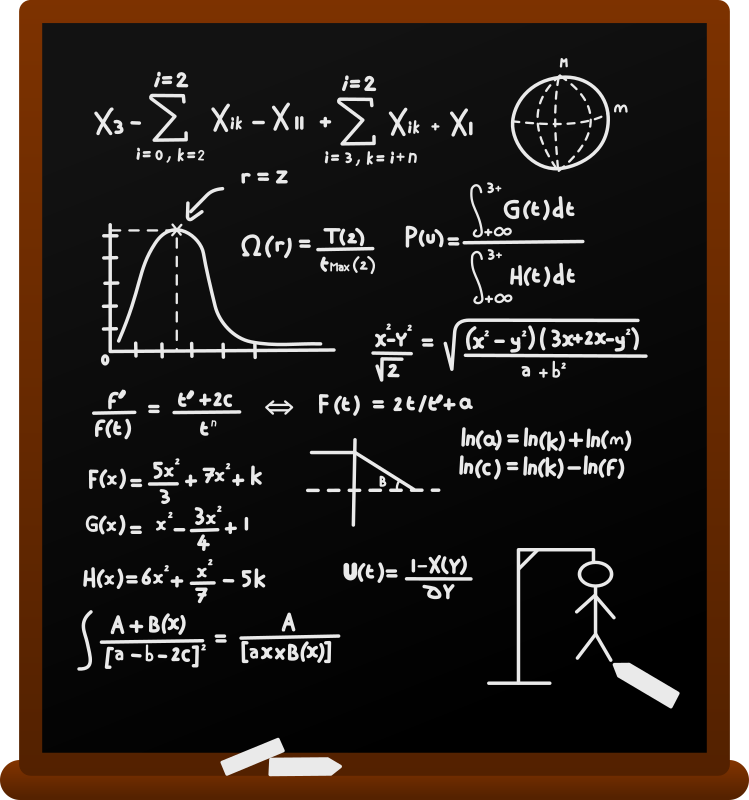 ru — грамматика английского языка, интерактивные тесты, игры, идиомы, тексты песен.
ru — грамматика английского языка, интерактивные тесты, игры, идиомы, тексты песен.
British Council — официальный сайт Британского Совета, на котором представлены возможности для бесплатного изучения английского языка. Материалы, разработанные Британским Советом совместно с BBC, могут также использоваться преподавателями.
EnglishTips.org — ресурсы для изучения и преподавания английского языка.
Goethe Institut — официальный сайт Института Гёте, который содержит информацию как для педагогов, так и для учеников: образцы упражнений, тренировочные тесты для подготовки к экзаменам международного уровня, страноведческую информацию, игры, методические советы
Reverso Context — онлайн-словарь, предоставляющий возможность перевода между различными языковыми парами. Кроме русского, на 2020 год в словаре представлены 13 языков.
Мультитран — онлайн-словарь.
История, обществознание, право
Антропогенез.ру — коллекция научно-просветительских материалов, посвященных эволюции человека.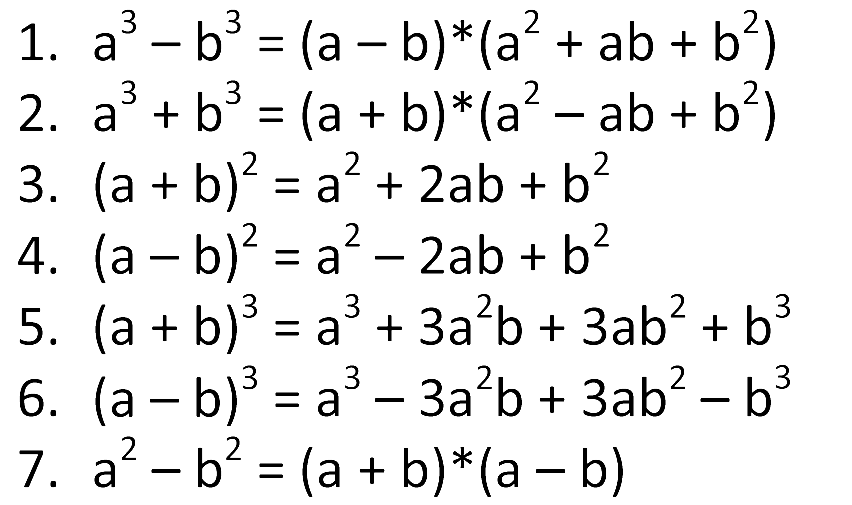
Всемирная история — онлайн-библиотека, содержащая энциклопедии, исторические карты и публикации, посвященные различным периодам человечества от первобытной эпохи до новейшего времени.
Школа обществознания — видеокурсы для подготовки к ЕГЭ и ОГЭ по кодификаторам. Видеоуроки с 6 по 11 классы по учебнику Боголюбова Л.Н.
Обществознание в школе – на сайте собраны материалы по двум разделам: энциклопедии и словари, полезные сайты
Обществознание: изучаем вместе – портал, на котором собраны все самые необходимые материалы по обществознанию, есть даже видеолекции
Учителя.com – разработки, планы и конспекты для проведения уроков, а также сборники заданий
Современный учительский портал – есть отдельный раздел по обществознанию, где собраны различные материалы от презентаций до тестов
«Президент России – гражданам школьного возраста» – сайт, где можно найти ответы на вопросы о президенте, конституции, государственных символах и о многом другом
Искусство и музыка
Google Arts & Culture — коллекции произведений искусства и материалов о событиях, повлиявших на мировую культуру.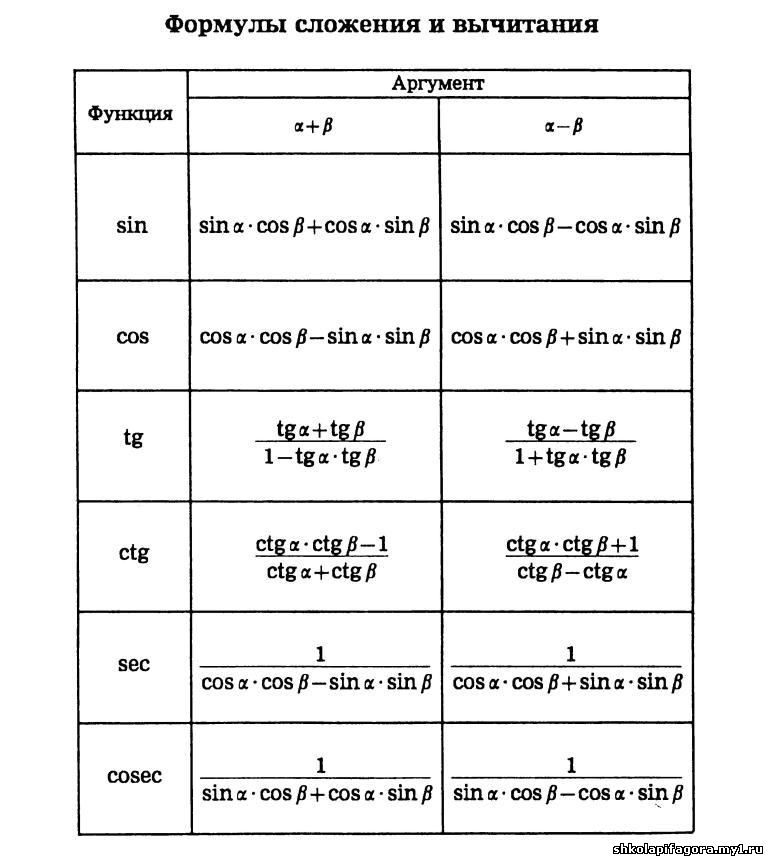
ProstoyKarandash — материалы и видеоуроки по рисованию в различных техниках.
Музыкальная фантазия — коллекции тематических аудиосборников, уроков, детских песен, мультфильмов и нот.
Ресурсы для начального образования
Начальная школа — уроки по математике, русскому языку и окружающему миру для 1—4 классов.
«Детская комната» Arzamas — портал, на котором в открытом доступе размещены книги, фильмы и мультфильмы, игры, музыкальные материалы.
Детский портал «Солнышко»— развивающие компьютерные игры, видеоуроки, мультфильмы и раскраски, занятия по географии, химии, физике, экономике, природоведению, иностранным языкам, макеты развивающих и праздничных стенгазет, сценарии детских праздников, статьи о развитии и обучении детей.
Раздети — библиотека рассказов, сказок, стихов, загадок, поговорок и пословиц, а также уроки, игры, лабиринты и кроссворды, советы по развитию способностей и интеллекта, подготовке к школе, планы уроков, внеклассных занятий, классных часов для начальной школы.
Маам — коллекция учебных материалов для детского сада и начальной школы, в т.ч. конспекты, методические разработки, сценарии, детские поделки, развивающие игры и др.
Учебно-методический кабинет — методические рекомендации, практические материалы, сценарии праздников, развлечений, игры и упражнения.
Страна Мастеров — онлайн-курсы и видео мастер-классы, направленные на развитие творческих способностей учащихся.
Наша сеть — социальная сеть работников образования.
Дошколенок.ру — сценарии мероприятий, методические разработки, мастер-классы, развивающие игры для детского творчества.
Базовые математические формулы — геометрия, вероятности, арифметика и часто задаваемые вопросы
Основная математическая формула обычно используется в базовой математике и используется не только в академических книгах, но и в нашей повседневной жизни. В начальных классах мы все узнали об общем правиле BODMAS. По мере того, как человек продолжает приближаться к более высоким классам от шести до десяти, он столкнется с различными формулами математики, основанными на различных концепциях, таких как алгебра.
Практикуя вопросы и ответы, основанные на различных формулах, можно выучить наизусть каждую формулу, прежде чем явиться на экзамены.
Некоторые из других понятий, которые имеют формулы, приведены ниже:
Основная математическая формула
Основы математики показывают, как можно решить математическую задачу с помощью некоторых уравнений, таких как уравнение сил, ускорений или работы Выполнено. Что еще более важно, они используются для предоставления математических решений реальных проблем в нашей повседневной жизни.
Существует много типов уравнений, и они встречаются во многих областях математики. Но методы, используемые для их изучения, различаются в зависимости от их типа. Это может быть простая формула сложения или сложная, например интегрирование дифференцирования.
Формулы базовой геометрии
Где «a» — длина сторон квадрата
Где «l» — длина, а «b» — ширина
Где «a» — длина сторон квадрата
здесь «l» — длина, а «b» — ширина
Где «b» — основание треугольника, а «h» — высота треугольника
Где b1 и b2 — основания трапеции; h = высота трапеции
Где «r» — радиус окружности
Где «a» — длина сторон куба
The curved surface area of Cylinder = 2πrh
The total surface area of Cylinder = 2πr(r + h)
The volume of Cylinder = V = πr 2 h
Where «r» — радиус основания цилиндра, а «h» — высота цилиндра.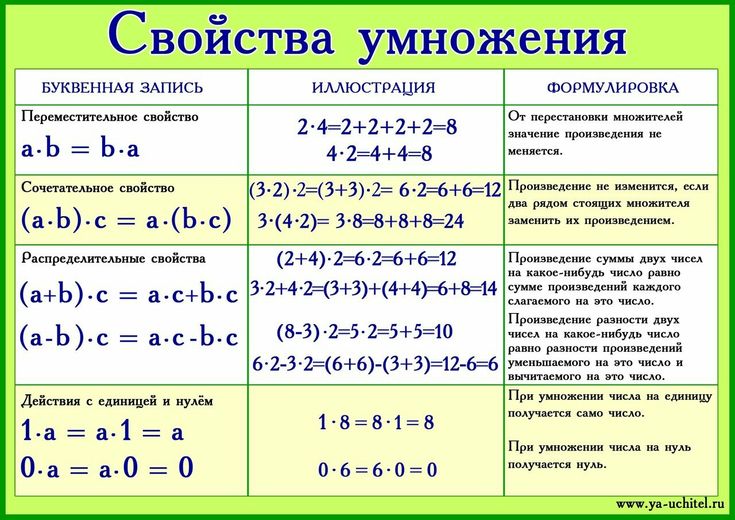 [г + √(ч 2 + г 2 )]
[г + √(ч 2 + г 2 )]
Объем конуса = V = ⅓ × πr2h
Здесь ‘r’ — радиус основания конуса, а h = высота конуса
Где r = радиус сферы
Основная формула вероятности
P(A) = n(A)/n(S) Где
|
Основные арифметические формулы
Простыми словами математическая формула может быть выражена как выражение, которое было получено после того, как исследователи годами изучали конкретную проблему.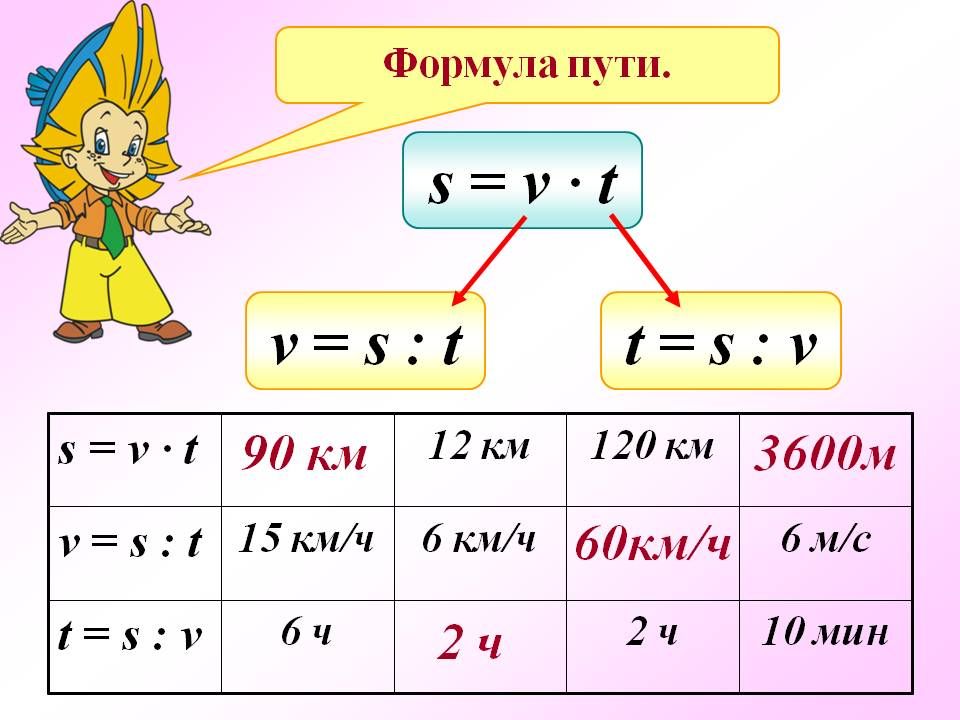 Эти разработанные математические формулы служат для получения правильных ответов в течение нескольких минут или даже секунд. Это позволяет быстрее решать математические задачи и повышает вашу скорость и навыки решения этих задач. Следовательно, Vedantu предоставляет полный список основных математических формул, которые помогут вам хорошо понять проблемы.
Эти разработанные математические формулы служат для получения правильных ответов в течение нескольких минут или даже секунд. Это позволяет быстрее решать математические задачи и повышает вашу скорость и навыки решения этих задач. Следовательно, Vedantu предоставляет полный список основных математических формул, которые помогут вам хорошо понять проблемы.
Эти формулы также пригодятся при подготовке к конкурсным экзаменам, поскольку позволяют решать вопросы всего за несколько секунд. Хотя легко просто складывать или вычитать уравнения, когда дело доходит до решения больших задач по геометрии или алгебре, это становится слишком сложным, если вы не используете эти математические формулы.
Советы по запоминанию основных математических формул — геометрия, вероятность, арифметика:
Существует более сотни формул, которые используются в жизни ученика даже во время учебы в школе, поэтому запомнить их все может быть немного сложно. но вот несколько советов по эффективному запоминанию основных математических формул:
Во-первых, вам нужно понять формулы и то, как они получены
Затем вам нужно попрактиковаться в формулах, применяя их к различным вопросам, как указано в образцах документов Веданту.

Затем сделайте контрольные листы, которые помогут вам взглянуть перед экзаменами.
Более 50 базовых математических формул, которые учащиеся должны выучить в 2021 году
Нужно ли мне изучать базовые математические формулы? Разве это не просто сложение, вычитание, умножение и деление?
Нет, это не так!
Вам необходимо знать основные математические формулы для решения математических задач среднего и продвинутого уровня. Даже математика не ограничивается только сложением и всем остальным. Это намного больше, чем это.
Математические формулы помогают понять реальные проблемы, чтобы их можно было эффективно решать. Предположим, вы хотите измерить, сколько воды вам нужно, чтобы заполнить цилиндрический резервуар. Для этого нужно знать формулу объема цилиндрической формы.
Помимо этого, базовая математика имеет несколько приложений в повседневной жизни, начиная от расчета времени для утренней зарядки и заканчивая расчетом калорий вашего ночного рациона.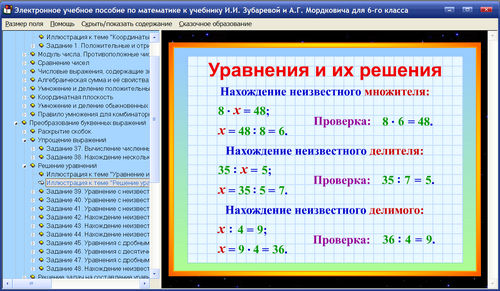
Я знаю, что большинству студентов могут быть трудности с этими формулами. Поэтому я упомянул базовую математическую формулу и дал советы, как легко их выучить. Просто прокрутите страницу вниз, чтобы узнать каждую формулу.
Почему полезно изучать основы математических формул?Содержание
Что ж, изучение формул может принести вам пользу во многих отношениях, например:
- Это поможет вам улучшить свои оценки на экзаменах Совета, а также на вступительных экзаменах.
- Вы можете пересмотреть формулы за короткое время.
- Обучаемые таблицы помогают быстрее решать проблемы.
- Математические формулы необходимы учащимся, готовящимся к высшим олимпиадам.
- Усовершенствованное изучение математических формул позволяет сэкономить время и использовать его для решения задач.
- Когда вы начнете изучать базовые математические формулы, вы сможете укрепить свои математические концептуальные знания.

- Используя математические формулы, вы можете не только легко решать математические задачи, но и эффективно решать реальные задачи.
Дробь означает деление вещей на равные и неравные части. Например, когда вы пошли в ресторан с друзьями, вы разделили общую сумму между всеми своими друзьями.
Некоторые из полезных формул дроби:
Формула на основе потребителяФормула на основе потребителя связана с бизнесом, как формулы, такие как прибыль, убыток, процентная ставка и многое другое. Эти формулы используются не только бизнес-магнатами, но и правительством для разработки финансовой политики.
Вот некоторые из формул, рассчитанных на потребителя:
Читайте также
- Подробное руководство по математическим терминам для начинающих
- Краткие советы по решению математических уравнений
- Подробное руководство о том, что такое статистика в математике
Проценты могут значительно облегчить ваши вычисления. Также довольно просто работать с сотой частью вещи. Например, если вы идете по магазинам и видите скидку или распродажу, вам нужно использовать концепцию процента.
Также довольно просто работать с сотой частью вещи. Например, если вы идете по магазинам и видите скидку или распродажу, вам нужно использовать концепцию процента.
Полезные формулы процентов:
СтатистикаЗнание статистики помогает собирать данные, анализировать данные и представлять результаты. Например, статистика широко используется в открытиях науки и в других областях.
Основные математические формулы для статистики:
ТригонометрияЭто полезно для понимания концепций углов и размеров конкретных форм. Предположим, вы хотите разбить сад на заднем дворе. Тогда вы должны иметь знание угла, чтобы вы могли посадить дерево на правильном расстоянии.
Основные формулы тригонометрической математики:
Алгебра Она помогает улучшить логическое мышление и позволяет человеку разделить задачу. Используя это, вы можете легко решить проблему. Предположим, вы хотите разделить две вещи, возведя их обе в квадрат. Затем вы можете применить формулу алгебры, чтобы выполнить это.
Предположим, вы хотите разделить две вещи, возведя их обе в квадрат. Затем вы можете применить формулу алгебры, чтобы выполнить это.
Основные математические формулы алгебры:
ГеометрияЭто изучение размеров, положения, размеров, форм и позиционных углов вещей. Например, прямоугольное футбольное поле разделено на параллельные линии с шагом в 10 ярдов.
Основные геометрические формулы:
Есть ли какой-нибудь краткий метод решения задач?Да есть!!!
Когда вы решаете математическую задачу, вы должны использовать БОДМАС . Это помогает понять порядок решения математической задачи. Вот полная форма и порядок решения проблемы.
Бонусный балл Лучшие советы для изучения основных математических формул!! Больше практикуйтесь, чтобы улучшить свои знания. Помогает не только выучить математические формулы, но и понятия по другим предметам.
Расслабьте свой мозг короткими перерывами. Всегда необходимо расслабить свой ум; иначе вы не сможете сосредоточиться на учебе.
Практика формул, чтобы запомнить их. «Практика делает человека совершенным» — абсолютно верно. Чем больше вы практикуетесь, тем больше вы изучаете или запоминаете формулы.
Попробуйте решить значения задачи, используя определенную формулу. Это поможет вам выучить формулу в долгосрочной перспективе.
Понимание концепции каждой формулы. Когда ты способен выучить концепции, ты никогда этого не забудешь.
Устраните или уберите все отвлекающие факторы рядом с вами во время изучения формул. Из-за отвлекающих факторов вы не сможете выучить базовые математические формулы.
Придумывайте свои собственные трюки, чтобы выучить формулы. С помощью трюков будет довольно легко выучить понятия формул.
Математика присутствует во всех аспектах жизни, от покупок до экономии денег. Поэтому, если вы хотите с легкостью решать реальные жизненные задачи, изучите базовые формулы математики. Я уже упомянул все необходимые и простые формулы, которые должен выучить студент.
Поэтому, если вы хотите с легкостью решать реальные жизненные задачи, изучите базовые формулы математики. Я уже упомянул все необходимые и простые формулы, которые должен выучить студент.
Если у вас возникли трудности с изучением или использованием этих формул, сообщите нам об этом. Наши специалисты и я обязательно поможем вам с вашими вопросами наилучшим образом.
Нашей основной целью является только помощь студентам с академическими проблемами. Итак, свяжитесь с нами сейчас, чтобы получить лучшую и доступную помощь с вашими заданиями и домашней работой. Получите лучшие услуги по выполнению домашних заданий по исчислению от экспертов.
Часто задаваемые вопросы Кто отец математики?Архимед признан отцом математики.
Какие есть разделы математики? Вот некоторые из основных разделов математики:
Численный анализ.
Матричная алгебра.
Комплексные числа.
Исследование операций.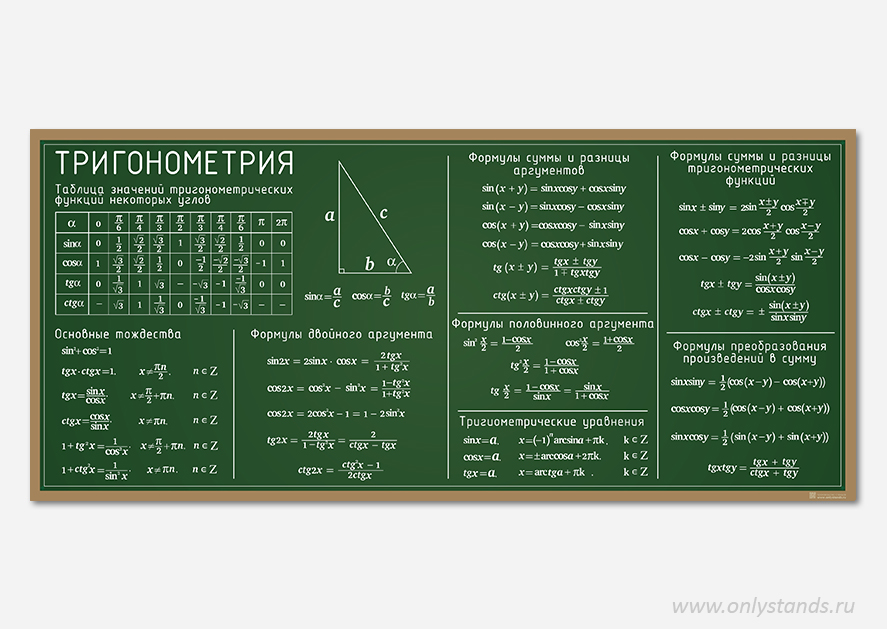
Теория множеств.
Исчисление.
Анализ.
Теория игр.
Три основных типа линейных уравнений: стандартная форма, форма точка-наклон и форма наибольшего уклона.
Математические формулы — примеры, вывод
Математические формулы — это выражения, которые были созданы после нескольких десятилетий исследований и помогают быстро решать вопросы. Легко выполнять простые арифметические вычисления, такие как сложение, вычитание и так далее. Однако, когда дело доходит до алгебраических выражений, геометрии и других тем, вам нужны математические формулы, чтобы упростить процесс достижения ответа и сэкономить время в этом процессе. В Cuemath вы не только найдете формулы для каждой темы, но также получите представление о том, как было разработано это уравнение. Таким образом, вам не придется запоминать формулы, так как вы понимаете лежащую в их основе концепцию.
Используйте эти формулы для творческого решения задач, и вы автоматически заметите улучшение своих математических навыков. Ниже приведен список формул, расположенных в алфавитном порядке для вашего удобства. Следовательно, вы можете легко найти формулы, которые необходимо пересмотреть или на которые нужно сослаться.
Ниже приведен список формул, расположенных в алфавитном порядке для вашего удобства. Следовательно, вы можете легко найти формулы, которые необходимо пересмотреть или на которые нужно сослаться.
Для вашего удобства ссылки на список математических формул, доступных по разным темам, расположены в алфавитном порядке. Так что выбирайте тему и приступайте к обучению!
# | А | Б | С | Д | Е | Ф | Г | Х |
я | Дж | К | л | М | Н | О | Р | В |
Р | С | Т | У | В | Вт | х | Д | З |
Список всех математических формул
В зависимости от того, к какому классу вы принадлежите и какую тему изучаете, вы можете найти все возможные математические формулы. Все доступные варианты математических формул с их доказательствами и выводами приведены ниже. Так чего же ты ждешь? Начните свое обучение уже сегодня!
Все доступные варианты математических формул с их доказательствами и выводами приведены ниже. Так чего же ты ждешь? Начните свое обучение уже сегодня!
Важность математических формул для учащихся
Математические формулы были созданы одними из самых умных людей не просто так. Они помогают детям решать вопросы быстро и точно. Это также помогает значительно упростить процесс достижения решения суммы, а не пытаться с нуля. Преимущества математических формул приведены ниже:
- Ребенок должен следовать учебной программе, установленной школой, которая зависит от времени. Через определенные промежутки времени дети проверяются на свои знания с помощью различных экзаменов, таких как разделы, полугодия и выпускные экзамены. Таким образом, чтобы гарантировать, что студенты подготовили предмет вовремя с буфером для повторения, им нужны математические формулы.
- При повторении ребенок вряд ли решит несколько вопросов с ручкой и бумагой. Таким образом, чтобы иметь быстрый взгляд на суммы и способы их решения, детям необходимо знать формулы, поскольку они являются ключом к получению правильных ответов.

- Во время экзаменов дети не могут позволить себе роскошь выводить всю формулу для решения вопроса, что означает, что они не могут начать с шага 1. Они должны знать и помнить формулы, чтобы заполнить свой вопросник за заданное количество времени, таким образом, помогая их в планировании и организации своего времени.
- Студентам, которые пытаются сдать конкурсные экзамены, необходимо знать не только формулы, но и различные советы и рекомендации, связанные с ними. Поскольку эти экзамены обычно проводятся в форме MCQ, дети должны очень хорошо разбираться в математических формулах.
Важные математические формулы
Прежде чем мы увидим список наиболее важных математических формул, очень важно иметь в виду, что каждая тема в математике взаимосвязана. Если вас не устраивают некоторые формулы, независимо от того, чаще ли они встречаются на экзаменах, вы должны поработать над своими навыками и добиться их четкого понимания. Таким образом, знание всех формул является обязательным; однако данный список дает вам представление о том, какие математические формулы обычно используются для решения экзаменационных вопросов.
1. Алгебра
- Среднее арифметическое или среднее = сумма всех значений/ количество значений
- Квадратичная формула: x = [-b ± (√b 2 — 4ac)]/2a
2. Геометрия координат
- Формула расстояния: d=√[(x₁ — x₂) 2 + (y₁ — y₂ 2 ]
- Пересечение наклона: y = mx + b
- Формула средней точки: [(x₁ + x₂)/2, (y₁ + y₂)/2]
3. Плоская геометрия
- Теорема Пифагора: a 2 + b 2 = c 2
- Площадь треугольника = (1/2) × основание × высота
- Площадь прямоугольника = длина × ширина
4. Тригонометрия
- Синус = перпендикуляр/гипотенуза
- Косинус = основание/гипотенуза
Советы по запоминанию математических формул
Существуют сотни математических формул, которые дети должны выучить на протяжении всей школьной жизни. Таким образом, учащимся важно иметь несколько советов, которые помогут им точно запомнить математические формулы. Ниже приведены несколько приемов:
Таким образом, учащимся важно иметь несколько советов, которые помогут им точно запомнить математические формулы. Ниже приведены несколько приемов:
- Понимание: Очень важно, чтобы ребенок понял концепцию математической формулы. Если он знает вывод и имеет четкое представление о цели, стоящей за математической формулой, то, скорее всего, ребенку даже не придется ее запоминать. Он автоматически узнает, как и когда применить правильную математическую формулу.
- Практика: Пока вы не решите вопрос, который требует использования определенной формулы, вам будет очень трудно оценить ее использование. Решая многочисленные вопросы, вы начинаете запоминать формулу за счет мышечной памяти. Следовательно, вам не нужно прилагать активные усилия для изучения формул, поскольку вы уже знаете их применение.
- Составьте контрольные листы: После того, как вы ознакомитесь с темой и начнете задавать вопросы по ней, сделайте лист со всеми математическими формулами, которые вы используете.
 Продолжайте обновлять его по мере продолжения цикла обучения. Когда вам придет время быстро взглянуть на эти формулы или если вы захотите их запомнить, вы можете обратиться к этому листу. Кроме того, вы также можете воспользоваться помощью Cuemath с математическими формулами, перечисленными выше .
Продолжайте обновлять его по мере продолжения цикла обучения. Когда вам придет время быстро взглянуть на эти формулы или если вы захотите их запомнить, вы можете обратиться к этому листу. Кроме того, вы также можете воспользоваться помощью Cuemath с математическими формулами, перечисленными выше . - Мнемотехника и методы запоминания: Существует множество мнемонических устройств, которые могут помочь вам в изучении математических формул. Например, если вы хотите выучить основные тригонометрические формулы, доступная мнемоника: « S ome P eople H ave, C urly B rown H air, T 90 веревщик B торопится. Таким образом, выделенные буквы помогают запомнить формулы синус = перпендикуляр/гипотенуза и так далее. Если вы воспользуетесь этими техниками запоминания или придумаете свою собственную инновационную мнемонику, вам будет очень легко выучить математические формулы.

Применение математических формул в реальной жизни
При изучении темы учащимся полезно узнать о реальном применении соответствующих математических формул, поскольку это делает предмет более понятным. Ниже перечислены некоторые области, в которых используются математические формулы:
Алгебра:
Алгебраические формулы широко используются в области информатики для выполнения различных аналитических функций. Они также используются в криптографии для защиты финансовой информации. Кроме того, вы используете алгебру ежедневно, сознательно или неосознанно, чтобы планировать свое расписание и выполнять свои задачи.
Исчисление:
Формулы интегрирования и дифференцирования в исчислении широко используются в технике. Он также используется для анализа траектории ракеты, материаловедения, разработки кода физики ударных волн, моделирования воздушного потока над аэродинамическими телами, теплопередачи, распространения сейсмических волн для анализа землетрясений, обработки сигналов и т. д.
д.
Геометрия:
Формулы геометрии широко используются в строительстве и архитектуре для построения различных типов конструкций. Они также используются в моделировании местности, проектировании механических частей, криптологии и схемах воздушного потока.
Вероятность и статистика:
Формулы вероятности и статистики, а также приемы, изученные в школе, можно применить к примерам из реальной жизни. Они используются в таких областях, как моделирование методом Монте-Карло, обработка сигналов, анализ надежности, анализ рисков, модели прогнозирования фондового рынка, проектирование компьютерных сетей, ценообразование в страховании, оценка океанских течений в геостатистике и т. д.
Часто задаваемые вопросы по математическим формулам
Что математическая формула?
Математические формулы можно рассматривать как выражение, которое используется как ключ к быстрому и эффективному решению задач. Они также включают тождества, которые являются утверждениями, которые верны для всех значений конкретной переменной. Таким образом, математические формулы очень важны для изучения и понимания детьми.
Таким образом, математические формулы очень важны для изучения и понимания детьми.
Вам нужно запомнить все математические формулы?
Для детей крайне важно понимать концепцию математической формулы. Как только ребенок овладеет глубокими знаниями, он может переходить к изучению и запоминанию формул, так как ему придется быстро их вспоминать во время экзаменов. Однако, если он знает, как была получена математическая формула и что за ней стоит, ребенок автоматически запомнит формулу.
Какие математические формулы самые важные?
Важные математические формулы относятся к тем формулам, которые часто встречаются на большинстве школьных или конкурсных экзаменов. Однако следует придавать равное значение всем формулам, чтобы получить целостную математическую разработку. Список важных математических формул приведен ниже.
- Среднее = сумма всех значений/общее количество значений
- Площадь треугольника = (1/2)*(основание)*(высота)
- Периметр квадрата = 4 * сторона
- Определитель квадратного уравнения = b 2 — 4ac
Что такое основные математические формулы?
Основные математические формулы могут использоваться для решения простых вопросов или необходимы для построения более сложных формул. Вот список некоторых основных математических формул.
Вот список некоторых основных математических формул.
- Алгебраические тождества: (a + b) 2 = a 2 + b 2 + 2ab, (a — b) 2 = a 2 + b 2 2 — б 2 = (а + б) (а — б)
- Теорема Пифагора: перпендикуляр 2 + основание 2 = гипотенуза 2
- Формула расстояния: d=√(x₁ — x₂) 2 + (y₁ — y₂) 2
- Наклон линии: m = y2 — y1 / x2 — x1
Почему математические формулы так важны?
Математические формулы позволяют детям легко и быстро решать сложные задачи. Все, что нужно сделать детям, это найти правильную формулу для решения вопросов, и они смогут продолжить работу без проблем. Особенно, когда мы рассматриваем сценарий экзамена, рассчитанного по времени, становится необходимым использовать эти математические формулы, чтобы работа могла быть завершена хорошо в заданных пределах.
Нужно ли знать, как работает математическая формула?
Для учащихся очень важно знать, как работают математические формулы. Дети должны начать с развития понимания концепции, лежащей в основе формулы, и построения четкой основы вывода. Если у детей есть эти знания, им не придется запоминать формулы. Даже если они забудут, какую математическую формулу применить к конкретному вопросу во время контрольной работы, они будут знать метод и не застрянут.
Дети должны начать с развития понимания концепции, лежащей в основе формулы, и построения четкой основы вывода. Если у детей есть эти знания, им не придется запоминать формулы. Даже если они забудут, какую математическую формулу применить к конкретному вопросу во время контрольной работы, они будут знать метод и не застрянут.
Как вы учите математические формулы?
Первым шагом в обучении математическим формулам является объяснение учащимся значения формулы. Следующий шаг – познакомить детей с выводом формулы. Наконец, вам нужно показать детям, как применять математическую формулу к вопросам, как простым, так и сложным.
Как мы можем применять математические формулы в повседневной жизни?
Когда мы говорим о такой теме, как дроби или десятичные дроби, мы применяем формулы к таким действиям, как перекрестная проверка правильности квитанции, которую мы получаем от покупки, когда нам нужно разделить такой объект, как пицца, между люди и так далее. Таким образом, сознательно или неосознанно мы используем математические формулы, чтобы эффективно вести свою повседневную жизнь.
Google Sheets: Создание простых формул
Урок 12: Создание простых формул
/en/googlespreadsheets/working-with-multiple-sheets/content/
Введение
При работе с числовой информацией Google Sheets можно использовать для выполнять расчеты. На этом уроке вы узнаете, как создавать простые формулы для сложения, вычитания, умножения и деления значений. Вы также познакомитесь с основами использования ссылок на ячейки в формулах.
Создание простых формул
Удобная и экономящая время функция Google Таблиц — возможность складывать, вычитать, умножать и делить числовую информацию за вас. Google Sheets использует математические выражения, называемые формулами , которые упрощают выполнение этих вычислений. В этом уроке мы сосредоточимся на формулах, содержащих один математический оператор .
Большую часть времени вы будете использовать в формуле адрес ячейки . Это называется использованием номер ячейки . Преимущество использования ссылок на ячейки заключается в том, что вы можете изменить значение в ячейке, на которую указывает ссылка, и формула будет автоматически пересчитана. Использование ссылок на ячейки в формулах гарантирует точность значений в формулах.
Посмотрите видео ниже, чтобы узнать, как работать с простыми формулами в Google Sheets.
Математические операторы
В таблицах Google для формул используются стандартные операторы: знак плюса для сложения ( 9 ) для показателей.
Все формулы должны начинаться со знака равенства ( = ). Это связано с тем, что ячейка содержит или равна формуле и вычисляемому ею значению.
Использование ссылок на ячейки
Когда формула содержит адрес ячейки, она использует ссылку на ячейку . Создание формулы со ссылками на ячейки полезно, поскольку вы можете обновлять числовые значения в ячейках без необходимости переписывать формулу.
Комбинируя математический оператор со ссылками на ячейки, вы можете создавать различные простые формулы в Google Sheets. Формулы также могут включать комбинацию ссылки на ячейку и числа.
Создание формул
В нашем примере мы будем использовать простые формулы и ссылки на ячейки для расчета бюджета.
Чтобы создать формулу:
- Выберите ячейку , которая будет отображать рассчитанное значение.
- Введите знак равенства (=) .
- Введите ячейку адрес ячейки, на которую вы хотите сослаться первой в формуле. Вокруг ячейки, на которую делается ссылка, появится пунктирная рамка.

- Введите оператор вы хотите использовать. Например, введите знак добавления ( + ).
- Введите адрес ячейки ячейки, на которую вы хотите ссылаться второй в формуле.
- Нажмите клавишу Enter на клавиатуре. Формула вычисляет, и Google Sheets отображает результат.
Чтобы увидеть, как пересчитывается формула, попробуйте изменить значение в любой из ячеек. Формула автоматически отображает новое значение.
Google Таблицы не всегда сообщит вам , если ваша формула содержит ошибку, поэтому вы должны проверить все свои формулы. Чтобы узнать, как это сделать, прочитайте нашу статью о том, почему вы должны перепроверять свои формулы.
Чтобы создать формулу методом «укажи и щелкни»:
Вместо ввода адресов ячеек можно указать и щелкнуть ячейки, которые необходимо включить в формулу.
- Выберите ячейку , которая будет отображать рассчитанное значение.

- Введите знак равенства ( = ).
- Щелкните ячейку , на которую вы хотите сослаться первой в формуле. Адрес ячейки появляется в формуле.
Введите оператор , который вы хотите использовать в формуле. Например, введите знак умножения ( * ).
Щелкните ячейку , на которую вы хотите сослаться второй в формуле. Адрес ячейки появляется в формуле.
Нажмите клавишу Enter на клавиатуре. Формула будет рассчитана, и значение появится в ячейке.
Чтобы отредактировать формулу:
Иногда может потребоваться изменить существующую формулу. В нашем примере мы ввели в формулу неверный адрес ячейки, поэтому нам нужно его исправить.
- Дважды щелкните ячейку , содержащую формулу, которую вы хотите изменить. Формула отобразится в ячейке.

- Внесите необходимые изменения в формулу. В нашем примере мы заменим C4 на C5 .
- Когда вы закончите, нажмите клавишу Enter на клавиатуре. Формула пересчитывается, и новое значение отображается в ячейке.
Вызов!
- Откройте файл нашего примера. Убедитесь, что вы вошли в Google, затем нажмите Файл > Сделать копию .
- Выберите лист Challenge .
- В ячейке D4 создайте формулу, которая умножает ячеек B4 и C4. Обязательно используйте ссылки на ячейки.
- Используйте маркер заполнения , чтобы скопировать формулу в ячейки D5 и D6.
- В ячейке D7 создайте формулу, которая добавляет ячеек D4, D5 и D6.
- Измените количество в ячейке B4 на 15. Вы также должны увидеть изменения в ячейках D4 и D7.

- Когда вы закончите, ваша электронная таблица должна выглядеть примерно так:
Предыдущий: Работа с несколькими листами
Далее:Создание сложных формул
/en/googlespreadsheets/creating-complex-formulas/content/
Математические формулы | Важные математические формулы для CBSE от 6 до 12 классов
Математические формулы созданы опытными учителями на основе последних изданий книг. Формулы базовой математики позволяют учащимся завершить учебный план в уникальной схеме обучения «делай-учись-делай». Эти математические формулы помогают учащимся:
- Улучшение результатов на вступительных и вступительных экзаменах.
- Упрощает своевременную полную подготовку.
- Помогает вам сделать ревизию
- Интеллект-карты и таблицы Помогают вам легко вспоминать.

- Знать свои сильные и слабые стороны в формуле математики
- Математические формулы незаменимы для студентов, готовящихся к конкурсным экзаменам и экзаменам.
- Математическая формула расширяет возможности учащихся для практической работы и помогает им получать высокие баллы как на экзаменах в классе, так и на досках. 9{m}} \end{align}\)
Математические формулы
Квадратный корень :
Если x 2 = y, то мы говорим, что квадратный корень из y равен x, и пишем √y = x
Итак , √4 = 2, √9 = 3, √36 = 6Кубический корень:
Кубический корень из заданного числа x — это число, куб которого равен x.
мы можем сказать кубический корень из x как 3 √x- √xy = √x * √y
- √x/y = √x / √y = √x / √y x √y / √y = √xy / y.
Дроби Математические формулы
Что такое дробь ?
Дробь — это название части целого.
Пусть дробное число равно 1 / 8.
Числитель : Количество частей, на которые вы верхнего числа (1)
Знаменатель : Это число равной части целого делится на нижнее число (8).
Мы надеемся, что математические формулы для классов с 6 по 12 помогут вам. Если у вас есть какие-либо вопросы относительно математических формул для классов 6–12, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время.
Часто задаваемые вопросы по математическим формулам
1. Как лучше всего запоминать математические формулы?
Лучший способ запомнить математические формулы, чтобы научиться их выводить. Если вы можете их вывести, то нет необходимости их запоминать.
2. Как выучить математические формулы?
Не пытайтесь выучить формулу, попробуйте изучить логику формулы и интуицию, стоящую за ней.
3. Что такое математическая формула?
Как правило, в каждом виде математики есть формула или несколько формул, которые помогают вам решать определенные задачи, будь то геометрия, статистика, измерения и т.
 д.
д.4. Нужно ли знать, как работает математическая формула?
Действительно необходимо понимать и уметь решать уравнения, если вы хотите работать математиком или в любой другой области, использующей математику, или если вы хотите быть учителем математики или учителем в области, которая использует математика.
Математические выражения — оборотная сторона, онлайн-редактор LaTeX
Содержание
- 1 Введение
- 2 математических режима
- 2.1 Встроенный математический режим
- 2.2 Отображение математического режима
- 3 Другой пример
- 4 Справочник
- 5 Дополнительная литература
Возможности LaTeX для математического набора делают его привлекательным выбором для написания технических документов. В этой статье показаны самые основные команды, необходимые для начала написания математических операций с использованием LaTeX.
Написание основных уравнений в LaTeX очень просто, например:
\documentclass{статья} \начать{документ} Хорошо известная теорема Пифагора \(x^2 + y^2 = z^2\) была оказалось недействительным для других показателей. п \]
\конец{документ}
п \]
\конец{документ}
Открыть этот пример на обратной стороне
Как видите, способ отображения уравнений зависит от разделителя, в данном случае
\[...\]и\(...\).LaTeX допускает два режима записи математических выражений: математический режим inline и математический режим display :
- встроенный математический режим используется для записи формул, которые являются частью абзаца
- дисплей 9Математический режим 0131 используется для написания выражений, которые не являются частью абзаца и поэтому помещаются в отдельные строки
Режим встроенной математики
Вы можете использовать любой из этих «разделителей» для набора математических выражений в встроенном режиме:
-
\(...\) -
$...$ -
\начало{математика}...\конец{математика}.
Все они работают, и выбор — дело вкуса, поэтому давайте рассмотрим несколько примеров.
 2\), открытым в 192\end{math}, открытый в 1905 году Альбертом Эйнштейном.
\конец{цитата}
\конец{документ}
2\), открытым в 192\end{math}, открытый в 1905 году Альбертом Эйнштейном.
\конец{цитата}
\конец{документ} Открыть этот пример на обратной стороне
Режим отображения математики
Используйте одну из этих конструкций для набора математических операций в режиме отображения:
-
\[...\] -
\begin{displaymath}...\end{displaymath} -
\begin{equation}...\end{equation}
Математический режим отображения имеет две версии, которые выводят нумерованные или ненумерованные уравнения. Давайте рассмотрим базовый пример: 92\] открыт в 1905 году Альбертом Эйнштейном. В натуральных единицах ($c$ = 1) формула выражает тождество \begin{уравнение} Е=м \end{уравнение} \конец{документ}
Открыть этот пример на обратной стороне
В следующем примере используется среда
уравнения*, которая предоставляется пакетомamsmath— дополнительные сведения см. 2+1}
\end{уравнение*}
\конец{документ}
2+1}
\end{уравнение*}
\конец{документ} Открыть этот пример на обратной стороне
Ниже приведена таблица с некоторыми распространенными математическими символами. Для более полного списка см. Список греческих букв и математических символов:
описание код примеров Греческие буквы \альфа\бета\гамма\ро\сигма\дельта\эпсилон$$ \alpha \\beta\\gamma\\rho\\sigma\\delta\\epsilon $$ Бинарные операторы \times \otimes \oplus \cup \cap× {\ displaystyle \ times} ⊗ {\ displaystyle \ otimes} ⊕ {\ displaystyle \ oplus} ∪ {\ displaystyle \ cup} ∩ {\ displaystyle \ cap} Операторы отношений < > \подмножество \супсет \супсетек \супсетек< >⊂ ⊃ ⊆ ⊇{\displaystyle <\ >\subset \\supset \\subseteq \\supseteq} Другие \int \oint \sum \prod∫ ∮ ∑ ∏{\displaystyle \int \\oint \\sum \\prod } Различные классы математических символов характеризуются разным форматированием (например, переменные выделены курсивом, а операторы — нет) и разными интервал.




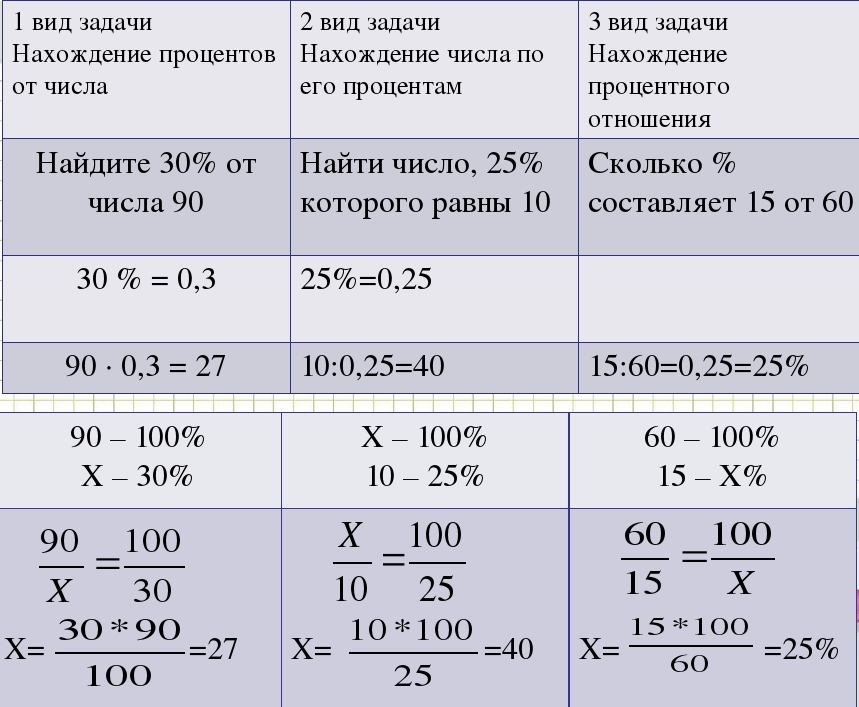
 Вокруг ссылки на ячейку отобразится рамка красного цвета.
Вокруг ссылки на ячейку отобразится рамка красного цвета. Ссылка на ячейку отобразится в формуле.
Ссылка на ячейку отобразится в формуле. Нажмите, и удерживая курсором мыши, перетащите маркер автозаполнения по ячейкам, которые нужно заполнить.
Нажмите, и удерживая курсором мыши, перетащите маркер автозаполнения по ячейкам, которые нужно заполнить.




 Продолжайте обновлять его по мере продолжения цикла обучения. Когда вам придет время быстро взглянуть на эти формулы или если вы захотите их запомнить, вы можете обратиться к этому листу. Кроме того, вы также можете воспользоваться помощью Cuemath с математическими формулами, перечисленными выше
Продолжайте обновлять его по мере продолжения цикла обучения. Когда вам придет время быстро взглянуть на эти формулы или если вы захотите их запомнить, вы можете обратиться к этому листу. Кроме того, вы также можете воспользоваться помощью Cuemath с математическими формулами, перечисленными выше