0 корень из 2: Mathway | Популярные задачи

alexxlab / / Разное
2

Содержание

Решение задач по колористике для парикмахеров

Несколько примеров решения задач по колористике от Elgon. Такие задачи парикмахеру приходится решать ежедневно при работе с клиентами.

Решение задач по колористике – это одновременно и теория, и практика.

Научиться решать колористические задачи после освоения курса колористики для парикмахеров очень важно.

Такие задачи парикмахеру приходится решать ежедневно при работе с клиентами, чтобы гарантировать желаемый цвет волос после окрашивания или тонирования.

Приведем несколько примеров решения задач по колористике для парикмахеров.

ВНИМАНИЕ! Решение задач «по аналогии» скорее всего даст неверный результат. Чтобы изучить все правила для решения колористических задач, необходимо пройти обучение колористике. 
Смотреть расписание курсов от технологов Elgon.

Задача 1

Исходная база волос:

Диаметр волос: нормальный.

Желаемый цвет: 9.2 (бежевый блондин на 9 уровне).

Решение:

1)  В прикорневой зоне использовать:

Краситель Moda&Styling 9/27 + окси-крем 9% (30 Vol.) в пропорции 1:1.

Экспозиция – 35 минут

Красящая смесь с 9% окислителем позволит осветлить натуральный пигмент с 7 уровня глубины тона до желаемого 9-го. При осветлении в результате разрушения натурального пигмента проявится фон осветления желтого цвета (9.3). Чтобы избежать появления желтизны после окрашивания, нужно нейтрализовать ее при помощи фиолетового цвета (противоположного на цветовом круге).

Краситель оттенка 9/27 (очень светлый бежевый фиолетовый блондин) позволит одновременно осветлить волосы на 2 уровня и сформировать косметический цвет бежевого направления с нейтрализацией желтого цвета.

Итоговый цвет в прикорневой зоне – 9/22.

2) Для окрашивания (обновления цвета) по длине использовать:

Краситель Get the Color Dolce (безаммиачный) 9/23 (9/2 + 9/3) + окси-крем 1,5% (5 Vol.) в пропорции 1:2.

Экспозиция – 10-15 минут

Так как красители Elgon бежевого направления содержат большое количество фиолетового пигмента, при умеренной пористости ранее окрашенных волос краска 9.2 может привести к появлению холодных нюансов. Необходимо добавить к желаемому бежевому цвету золотистый оттенок, чтобы нейтрализовать их.

_____________________________________________________________________________

Задача 2

Исходная база волос:

Диаметр волос: нормальный.

Желаемый цвет: 7.44 (яркий насыщенный медный блондин на 8 уровне).

Решение:

1) В прикорневой зоне использовать:

Краситель Moda&Styling 7/44 + Оранжевый корректор Arancio в пропорции 1:1 + окси-крем 6% (20 Vol.) в пропорции 1:1 с красителем.

Экспозиция – 35 минут

Окси-крем 6% (20 Vol.) позволит достичь максимальной яркости. В результате разрушения натурального пигмента 7 уровня проявится оранжево-желтый пигмент (7.43). Чтобы избежать появления желтизны в результате окрашивания, нужно перекрыть ее при помощи оранжевого корректора.

2) Для окрашивания (обновления цвета) по длине использовать:

Тонер Moda&Styling 944 (Chroma Arancio) + окси-крем 1,5% (5 Vol.).

Экспозиция – 10-15 минут

_____________________________________________________________________________

Задача 3

Исходная база волос: 4.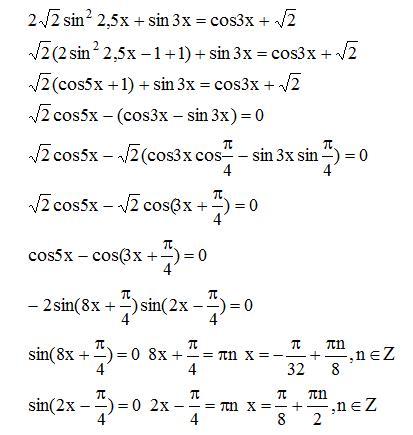 0 по всей длине.

Диаметр волос: нормальный.

Желаемый цвет: 6.8, коричневый нейтральный на 6 уровне.

Решение:

Для окрашивания волос в прикорневой зоне и по длине использовать:

Краситель Moda&Styling 6/81 + окси-крем 9% (30 Vol.) в пропорции 1:1.

Экспозиция: 35 минут

Нужно провести осветление на два уровня глубины тона, поэтому выбран 9% окислитель. При осветлении натурального пигмента до 6 уровня появится фон осветления оранжевого цвета (6.4). Чтобы избежать проявления оранжевых пигментов при окрашивании, этот цвет нужно нейтрализовать при помощи синих цвета (противоположного на цветовом круге).

Таким образом, для получения коричневого нейтрального оттенка нужно использовать краситель с цветовым направлением /81 – с коричневым и синим (пепельным) пигментом.

_____________________________________________________________________________

Задача 4

Исходная база волос: 3.0 по всей длине.

Диаметр волос: нормальный.

Желаемый цвет: 8.23, тёплый бежевый блондин на 8 уровне.

Решение:

Поскольку для получения желаемого цвета требуется осветлить волосы на пять уровней, обработка волос будет проходить в два этапа.

1) Осветление натуральных волос

Краситель Moda&Styling 0/0 + окси-крем 12% (40 Vol.) в пропорции 1:2.

Экспозиция: 35 минут

Краситель 0/0 способен осветлить натуральные волосы до 5 тонов с 12% окислителем. При осветлении натурального пигмента до 8 уровня появится фон осветления желтого цвета (8.3). Наличие этого пигмента нужно учесть при выборе красителя для второго этапа.

2) Окрашивание осветленных волос

Краситель Get the Color Dolce (безаммиачный) 8/2 + окси-крем 1,5% (5 Vol.) в пропорции 1:1.

Экспозиция – 25-35 минут

Чтобы получить желаемый теплый бежевый оттенок на осветлённых до фона осветления 8.3 волосах, необходимо добавить косметический бежевый цвет 8.2. Так как красители Elgon бежевого направления содержат большое количество фиолетового пигмента, он нейтрализует лишнюю желтизну, но сохранит теплый оттенок волос.

Эксперт-колорист: Александр Богданов
Редактор: Марта Губанова

Эта чудо-трава вмиг укрепит иммунитет

https://inosmi.ru/20220928/ekhinatseya-256380808.html

Эта чудо-трава вмиг укрепит иммунитет

Эта чудо-трава вмиг укрепит иммунитет

Эта чудо-трава вмиг укрепит иммунитет

| , 28.09.2022

2022-09-28T00:15

2022-09-28T00:15

2022-09-28T00:15

високий замок

иммунитет

здоровый образ жизни

/html/head/meta[@name=’og:title’]/@content

/html/head/meta[@name=’og:description’]/@content

https://cdnn1. inosmi.ru/img/24687/43/246874366_0:0:2001:1125_1920x0_80_0_0_57f2875f27b47d50177bf859a109cdd2.jpg

Елена РомановаЭхинацея пурпурная – многолетнее растение родом из Северной Америки с красивыми пурпурными соцветиями. Имеет специфический вкус и запах. Культивируют как лечебное и декоративное растение.С лечебной целью используют корни и цветки растения, лучше свежие, а также листья. Во всех частях растения очень много минеральных веществ, в том числе редких, которых нам часто не хватает в питании: это кальций, калий, селен, марганец, цинк, молибден, серебро, кобальт, хлор, железо, алюминий, магний, ванадий, барий, бериллий, никель. Эхинацея оказывает противовоспалительное, противогрибковое, противовирусное, противоаллергическое, противоревматическое и иммуномодулирующее действия.Эхинацея популярна во многих странах: в ФРГ, Франции, США и других. В ФРГ есть средство эхинацин для приема внутрь и в ампулах.Настойка эхинацеи эффективна для лечения, а особенно профилактики, респираторных и вирусных заболеваний.

Ее применяют в случаях простуды, гриппа, инфекций ушей, заболеваниях мочевого пузыря, мононуклеоза, заражения крови, болезней печени, хронических воспалительных процессов, сахарного диабета, последствий воздействия химических веществ – инсектицидов, пестицидов, фунгицидов, тяжелых металлов; после химиотерапии и лучевой терапии, лечения антибиотиками.Благодаря гликозидам кофеиновой кислоты эхинацея существенно ускоряет выздоровление от инфекционных и вирусных заболеваний.Эхинацею используют при психической депрессии, явлениях психического и физического переутомления, а также в случаях инфекционных заболеваний.Настойка: сырой измельченный корень или цветки залить 70%-ым спиртом в соотношении 1:4 и настаивать 1 месяц и дольше. Принимать по 0,5-1 чайной ложке трижды в день, также эту настойку можно использовать наружно для влажных компрессов от ран и ожогов.Другой рецепт: цветки эхинацеи пурпурной сложить в поллитровую банку доверху и залить хорошей водкой до краев. Плотно закрыть крышкой и настаивать в темном месте сорок суток.
Затем слить и употреблять по пятнадцать капель за двадцать-тридцать минут до еды, растворив в небольшом количестве воды или добавив в чай.Настой эхинацеи полезен зимой: защищает нас от простуды, укрепляет иммунитет, избавляет от усталости и стимулирует физическую активность. Одну столовую ложку сухого измельченного сырья (травы) залить одним стаканом кипятка, кипятить на водяной бане десять-пятнадцать минут. Настаивать до остывания, затем процедить. Употреблять по 1/3 стакана трижды в день.Отвар корней: одну столовую ложку сухого измельченного корня залить триста миллилитрами воды, кипятить на водяной бане тридцать минут, настаивать до остывания и процедить. Принимать по одной-две столовых ложки три-четыре раза в день до еды в случае острых инфекционных заболеваний, хронической усталости, гриппа…Отвар листьев: пьют при гриппе и простуде, но он имеет также лечебное действие от отеков, головной боли и болях в суставах, язве желудка; улучшает зрение, возбуждает аппетит, нормализует кровяное давление; оказывает тонизирующее и общеукрепляющее действия.
Свежие или сухие измельченные листья эхинацеи (одну чайную ложку) залить стаканом воды и нагревать на водяной бане около тридцати минут, настоять, процедить и пить по 1/3 стакана трижды в день до еды.Экстракт корней: измельченный свежий корень залить 95%-ым медицинским спиртом так, чтобы он немного покрывал его, настаивать две недели. Процедить, а остатки выжать. Принимать спиртовой настой по двадцать пять-тридцать капель трижды в день за полчаса до еды, запивая водой, как иммуностимулирующее средство, при переутомлении, гриппе (профилактика, лечение)… хранить в холодильнике, срок годности –два-три года.Эхинацея с медом: сырье измельчить в порошок и смешать с медом 1:3; принимать по одной-две чайных ложки два-три раза в день с чаем.Противопоказание. Принимать средства эхинацеи нельзя беременным и кормящим женщинам, больным системной красной волчанкой, ревматоидным артритом, ревматизмом, рассеянным склерозом и туберкулезом. Противопоказанием также является аллергия на само растение. По острой ангине нельзя употреблять настойку. При употреблении эхинацеи в больших дозах может начаться бессонница, человек становится возбудимым, появляются тошнота, рвота, нарушается работа кишечника и почек.

/20220913/immunitet-256072046.html

ИноСМИ

[email protected]

+7 495 645 66 01

ФГУП МИА «Россия сегодня»

2022

ИноСМИ

[email protected]

+7 495 645 66 01

ФГУП МИА «Россия сегодня»

Новости

ru-RU

https://inosmi.ru/docs/about/copyright.html

https://xn--c1acbl2abdlkab1og.xn--p1ai/

ИноСМИ

[email protected]

+7 495 645 66 01

ФГУП МИА «Россия сегодня»

1920

1080

true

1920

1440

true

https://cdnn1.inosmi.ru/img/24687/43/246874366_59:0:1836:1333_1920x0_80_0_0_52a870149e95ea3cf0fd14dede712421.jpg

1920

1920

true

ИноСМИ

[email protected]

+7 495 645 66 01

ФГУП МИА «Россия сегодня»

ИноСМИ

[email protected]

+7 495 645 66 01

ФГУП МИА «Россия сегодня»

високий замок, иммунитет, здоровый образ жизни

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Квадратный корень из 2 — Как найти квадратный корень из 2?

LearnPracticeDownload

Квадратный корень из 2 выражается как √2 в радикальной форме и как (2) ½ или (2) 0,5 в экспоненциальной форме. Квадратный корень из 2, округленный до 10 знаков после запятой, равен 1,4142135624. Это положительное решение уравнения x 2 = 2.

  • Корень квадратный из 2: 1,4142135623730951
  • Квадратный корень из 2 в экспоненциальной форме: (2) ½ или (2) 0,5
  • Квадратный корень из 2 в подкоренной форме: √2
1. Что такое квадратный корень из 2?
2. Является ли квадратный корень из 2 рациональным или иррациональным?
3. Важные замечания по квадратному корню из 2
4. Как найти квадратный корень из 2?
5. Нестандартное мышление!
6. Часто задаваемые вопросы о квадратном корне из 2

Что такое квадратный корень из 2?

Квадратный корень — это просто операция, обратная квадрату. Квадратный корень из 2 представлен как √ 2. Это число, которое при умножении на себя дает нам результат как 2. В древние времена греки нашли число, которое никогда не может быть записано в форме p/q , где p,q — целые числа, а q не равно 0. Это означает, что √ 2 нерационально. √ 2 оказывается очень полезным в геометрии. Допустим, у нас есть квадрат со стороной 1, и вы хотите найти длину диагонали.

Чтобы найти третью сторону, воспользуемся теоремой Пифагора. Третья сторона будет √ 2. Давайте найдем число √ 2   на числовой прямой. Мы будем использовать перенос квадрата, который мы использовали для открытия √ 2. Давайте назовем вершины квадрата, как показано. Держите вершину O в 0. Мы уже обнаружили, что OB= √ 2

С помощью циркуля с центром O и радиусом OB начертите дугу, пересекающую числовую прямую в точке P.

Является ли квадратный корень из 2 рациональным или иррациональным?

Фактическое значение √ 2. не определено. Значение √ 2 до 25 знаков после запятой равно 1,4142135623730950488016887..
. В настоящее время значение √ 2 известно до 1 триллиона знаков после запятой.
Следовательно, √ 2 иррационально.

Важные примечания:

  • √ 2 также называют постоянной Пифагора.
  • √ 2 представляет собой диагональ единичного квадрата.
  • √ 2 было первым числом, которое было открыто как иррациональное.
  • Его десятичное представление не завершается и не повторяется.
  • Отношение более длинного края к более короткому краю листа бумаги формата А4 равно 9.0979 √ 2.

Как найти квадратный корень из 2?

Мы можем найти квадратный корень из 2 следующими двумя способами:

  • Метод длинного деления
  • Метод оценки и приближения

Квадратный корень из 2 методом деления в длину

Значение квадратного корня из 2 методом деления в длину состоит из следующих шагов:

  • Шаг 1 : Найдите наибольшее число, квадрат которого меньше или равен числу 2. Возьмите это число как делитель и частное (в данном случае 1). Разделите и запишите остаток. 909:20
  • Шаг 2 : В частном поставьте запятую после 1. Уберите два нуля справа от остатка. Итак, новый дивиденд равен 100
    • .
  • Шаг 3: Удвойте делитель и введите его с пробелом справа. Угадайте наибольшую возможную цифру, чтобы заполнить пробел, который также станет новой цифрой в частном, так что, когда новый делитель умножается на новое частное, произведение меньше или равно делимому. Разделите и запишите остаток. Повторите этот процесс, чтобы получить нужные десятичные разряды. 909:20

квадратный корень из 2 по оценке и методу приближения

Мы можем использовать формулу Y = √ x, чтобы найти значение √ 2.

. Эта формара может быть написана

. x/y)+y)/2

Формула итерации:

y n+1  = ((x/y n ) + y n )/2

Первые три итерации дают результат как показано ниже. Первый набор y 1 =1

  • Итерация 1: y 1  = (2 + 1)/2 = 1,5
  • Итерация 2:  y 2  = (4/3 + 3/2)/2 = 1,4166
  • Итерация 3:  y 3  = (24/17 + 17/12)/2 = 1,414215…

Вы заметили, что оно начало приобретать вид √ 2 = 1,41421356237309 ?

Изучение квадратного корня с помощью иллюстраций и интерактивных примеров

  • Квадратный корень из 1
  • Квадратный корень из 11 909:20
  • Квадратный корень из 5
  • Квадратный корень из 9
  • Квадратный корень из 8

Аналитический центр:

  • Можете ли вы придумать какое-нибудь квадратное уравнение с корнем √ 2?
  • Поскольку (- √ 2) 2 = 2, можем ли мы сказать, что — √ 2 также является квадратным корнем из 2?

 

Квадратный корень из двух решенных примеров

  1. Пример 1 : Найдите длину диагонали квадрата, состоящего из 4 единичных квадратов.

    Решение

    Мы знаем, что длина диагонали квадрата в 1 единицу равна √ 2 единиц. Чтобы найти диагональ, нам нужно рассмотреть длину диагонали 2 единичных квадратов.
    Диагональ квадрата в 1 единицу = √ 2 единицы
    Сумма диагонали 2 квадратов = 2 √ 2 единицы
    Следовательно, длина диагонали составляет 2 √ 2 единиц.

  2. Пример 2 : Какова длина диагонали квадратного торта, если каждая сторона состоит из 2 единиц? (Запишите ответ в десятичной форме до 3 знаков после запятой)

    Решение

    Дано, Сторона квадратного торта = 2 единицы
    Используя теорему Пифагора,
    Диагональ квадрата =√2a
    Диагональ = √2 × 2 = 2,828 единицы 90 907

  3. Пример: Если площадь равностороннего треугольника равна 2√3 в 2 . Найдите длину одной из сторон треугольника.

    Решение:

    Пусть а будет длиной одной из сторон равностороннего треугольника.
    ⇒ Площадь равностороннего треугольника = (√3/4)a 2 = 2√3 в 2
    ⇒ а = ±√8 в
    Поскольку длина не может быть отрицательной,
    ⇒ а = √8 = 2 √2
    Мы знаем, что квадратный корень из 2 равен 1,414.
    ⇒ а = 2,828 в

перейти к слайдуперейти к слайдуперейти к слайду

 

Как ваш ребенок может освоить математические понятия?

Мастерство в математике приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу Cuemath.

Забронируйте бесплатный пробный урок

Часто задаваемые вопросы о квадратном корне из 2

Каково значение квадратного корня из 2?

Квадратный корень из 2 равен 1,41421.

Почему квадратный корень из 2 является иррациональным числом?

Число 2 простое. Это означает, что число 2 беспарное и не находится в степени двойки. Следовательно, квадратный корень из 2 иррационален.

Если квадратный корень из 2 равен 1,414.

Найдите значение квадратного корня из 0,02.

Представим √0,02 в форме p/q, т.е. √(2/100) = 0,02/10 = 0,141. Следовательно, значение √0,02 = 0,141·

Является ли число 2 идеальным квадратом?

Число 2 простое. Это означает, что квадратный корень из 2 не может быть выражен как произведение двух равных целых чисел. Следовательно, число 2 не является полным квадратом.

Что такое квадратный корень из -2?

Квадратный корень из -2 является мнимым числом. Это можно записать как √-2 = √-1 × √2 = i √2 = 1,414i
где i = √-1 и называется мнимой единицей.

Каково значение 17 квадратного корня из 2?

Квадратный корень из 2 равен 1,414. Следовательно, 17 √ 2 = 17 × 1,414 = 24,042.

Рабочие листы по математике и визуальная программа

Насколько хорошо вы знаете квадратный корень из 2?

Насколько хорошо вы знаете квадратный корень из 2? Возможно, оно не так известно, как число Пи или постоянная Эйлера (е), но оно все же обладает множеством интересных свойств и собственной историей.

Кто открыл квадратный корень из 2?

Одним из лучших свидетельств древнего использования квадратного корня из 2 является вавилонская глиняная табличка, которой более 3500 лет. На изображении ниже он помечен так, что мы можем видеть число 1 24 51 10 по диагонали квадрата. Это число, записанное с основанием 60 и представляющее 9.0907

   

Введите квадратный корень из 2 в свой калькулятор, и вы получите 1,414213562 — вавилоняне работали с точностью до шести знаков после запятой. Это передовое знание квадратного корня из 2, безусловно, предполагает, что это не было новым открытием и использовалось много лет назад.

Квадратный корень из 2 — это иррационально

Иррациональное число — это число, которое нельзя записать в виде простой дроби (отношение двух целых чисел). Если вы выпишете иррациональное число, оно будет иметь десятичное расширение, которое будет продолжаться вечно и всегда без повторения. Считается, что иррациональность квадратного корня из 2 была открыта пифагорейцами, жившими около 2500 лет назад.

Гиппас из Метапонта и страх перед иррациональным

Считается, что иррациональность квадратного корня из 2 расстроила Пифагора и его последователей, которые думали, что все объекты могут быть представлены целыми числами и их отношениями. Существует множество легенд, связанных с судьбой Гиппаса из Метапонта, которому приписывают открытие этой иррациональности. Был ли он утоплен в море или его просто изгнали из пифагорейской секты? Обнаружил ли он вообще иррациональность квадратного корня из 2?

Весьма вероятно, что многое из этого является легендой, но, возможно, эти истории вызывают глубокое беспокойство, которое многие люди до сих пор испытывают в отношении иррациональных чисел.

Откуда взялось слово «сурд»?

Квадратный корень из 2 — это тип surd. Другие примеры сурдов включают или , но не включают, поскольку здесь есть рациональный ответ.

Согласно словарю Merriam-Webster, слово surd в этом математическом контексте впервые было использовано в 1557 году и происходит от латинского слова surdus, означающего глухой, молчаливый или глупый. Кажется, что сурдам все еще не доверяли — даже через 2000 лет после Пифагора.

Доказательство иррациональности квадратного корня из 2

Существует множество различных доказательств иррациональности квадратного корня из 2. Вот один из самых известных:

Шаг 1. Предположим, что это не иррационально и что его можно записать в виде дроби в простейшей форме: где a и b — целые числа (отличные от нуля), а где не может быть сокращена дальше (это означает, что это неприводимая дробь).

Шаг 2. Возведите в квадрат обе части уравнения и переставьте:

   

   

Шаг 3.   Теперь это означает, что это должно быть четное число, а также само должно быть четным числом. Поэтому вы можете переписать с целым числом. Подставив это в строку выше, мы получим:

   

   

По тем же рассуждениям, что и раньше, это означает, что это четное число, и мы можем написать , с целым числом.

Шаг 4. У нас было это , но мы показали, что и то, и другое четно, что означает, что это можно сократить, а это означает, что это не неприводимая дробь. Это противоречит нашему предположению на шаге 1 в его простейшей форме. Это то, что называется доказательством от противного. иррационально!

Чем квадратный корень из 2 отличается от числа Пи?

И число Пи, и корень квадратный из 2 иррациональны, но есть важное отличие: число Пи классифицируется как трансцендентное число, тогда как корень квадратный из 2 не является трансцендентным числом. Если вам нравятся диаграммы Венна, то следующее изображение может оказаться полезным для демонстрации того, что лишь некоторые из иррациональных чисел также являются трансцендентными.


Так что же такое алгебраическое число? Чтобы быть алгебраическим, число должно быть корнем ненулевого полиномиального уравнения с рациональными коэффициентами. Например, если вы решаете , то  является корнем. Вы не можете сделать это с Пи, это Трансцендентно.

Постоянная Гельфонда-Шнайдера

В отличие от квадратного корня из 2, постоянная Гельфонда-Шнайдера является трансцендентным числом (она не является корнем какого-либо ненулевого полиномиального уравнения с рациональными коэффициентами). Если вы возведете постоянную Гельфонда-Шнайдера в степень, то вы вернетесь к целому числу, равному 4!

   

Как компьютеры вычисляют квадратный корень из 2?

Большинство компьютеров используют метод Ньютона-Рафсона, который обычно преподается на уровне A, применяя его для решения . Вот итерационная формула, которая используется:

   

Если мы позволим, то получим:

В течение 5 шагов калькулятор дает нам оценку, которая так же точна, как и полное отображение на стандартном дисплее.

Связь между бумагой формата А4 и квадратным корнем из 2

Самый большой лист бумаги в серии А имеет размер от 1189 мм до 841 мм. Площадь A0 составляет почти ровно 1 квадратный метр. Если разрезать лист бумаги формата А0 пополам, то получится два листа бумаги формата А1, площадь каждого из которых равна половине квадратного метра. После этого схема продолжается — разрежьте лист бумаги формата А1 пополам, и вы получите два листа бумаги формата А2, каждый площадью в четверть квадратного метра. Это удешевляет укладку и воспроизведение документов и делает их более эффективными, но преимуществом этой системы является то, что она также поддерживает постоянное соотношение длины и ширины бумаги. Если вы увеличиваете плакат от А4 до А3, вы хотите, чтобы он точно подходил — вы не хотите обрезать кусочки!

Стандарт ISO для бумаги формата A4 имеет размеры 297 мм на 210 мм. Это соотношение равно или близко к  с и . Это соотношение длины и ширины примерно для всех листов бумаги серии А.

Мэтт Паркер, стендап-математик рассказывает о размерах бумаги

Каково наилучшее приближение для квадратного корня из 2?

Бумага формата A4 использует 99/70 в качестве приближения для квадратного корня из 2. На самом деле, это наиболее точное возможное приближение, которое имеет двузначный знаменатель. Если вы воспользуетесь калькулятором, чтобы вычислить разницу между и квадратным корнем из 2, вы получите 0,000072151 — это довольно точное приближение для простой дроби, которую легко запомнить!

Квадратный корень из 2 как цепная дробь

Непрерывная дробь — это особый тип дроби, в котором вычисление продолжается вечно. Мы можем выразить в виде следующей цепной дроби:

   

На самом деле любую сурд можно записать в виде цепной дроби:

   

Непрерывные дроби обеспечивают еще один способ аппроксимации значения квадратного корня из 2.

Что такое Самый точный расчет квадратного корня из 2?

Текущий рекорд составляет 10 триллионов знаков после запятой — знание квадратного корня из 2 с такой степенью детализации не имеет практического смысла — это скорее проверка вычислительной мощности и самоотверженности. В желающих побить такой рекорд никогда не будет недостатка — для Пи он превысил 30 триллионов знаков после запятой.

День квадратного корня

Пи имеет свой особый день, который широко отмечается 14 марта (3.14 по системе США). Для константы Эйлера (e=2,718…) у вас может быть выбор в зависимости от того, какой формат даты вы хотите использовать – либо пометив его на 7 февраля (7/2) или 2 июля (2/7).

«Квадратный корень из 2 дней» (1.42421…) еще не существует, но у вас может быть выбор между 4 января (4/1) и 1 апреля (1/4) – День смеха! Однако есть дни, называемые «Днями квадратного корня», и они происходят 9 раз в каждом столетии в следующие даты: 1/1/01, 2/2/04, 3/3/09, 4/4/16, 5/5. /25, 6/6/36, 7/7/49, 8/8/64, 9/9/81. Можете ли вы определить закономерность?

Как запомнить квадратный корень из 2 (с помощью мнемоники)

Вот несколько предложений для запоминания квадратных корней (каждое до 3 знаков после запятой):

квадратный корень из 2 :

root of two “

The  square root of 3 :

” O charmed was he
( 1 .     7           3     2 )

to know the root of three “

The  square root of 5 :

”Итак, теперь мы стремимся
(2. 3 2 6)

, чтобы узнать корень пяти«

Квадратный корень из 6 :

”Мы нуждаемся в более высоком уровне. 4 4 9)

, чтобы узнать корень из шести «

Mnemonics от: http://www.eudesign.com/mnems/_mnframe.htm

Содержимое

Содержимое

.

Авторы изображений

Урсия, А., Йельский музей естественной истории Пибоди, http://peabody.yale.edu, http://hdl.handle.net/10079/8931zqj, производная работа, пользователь: Теодор Лангхорн Франклин – Файл: YBC- 7289-OBV.jpg

Paper Size image Sven CC BY-SA 3.0, via Wikimedia Commons

Теги:

квадратный корень

scipy.optimize.root — SciPy v1.9.1 Manual

scipy.optimize.root( fun , x0 , args=() , method=’hybr’ , jac=Нет , tol=Нет , обратный вызов=Нет , options=Нет ) [источник]

Найти корень векторной функции.

Параметры
fun callable

Векторная функция для нахождения корня.

x0 ndarray

Исходное предположение.

args кортеж, необязательный

Дополнительные аргументы, переданные целевой функции и ее якобиану.

метод стр, опционально

Тип решателя. Должен быть один из

  • «гибр» (см. здесь)

  • ‘лм’ (см. здесь)

  • ‘broyden1’ (см. здесь)

  • ‘broyden2’ (см. здесь)

  • «Андерсон» (см. здесь)

  • «линейное смешение» (см. здесь)

  • «диагбройден» (см. здесь)

  • «возбуждающее смешение» (см. здесь)

  • Крылов (см. здесь)

  • ‘df-sane’ (см. здесь)

jac bool или callable, необязательно значение якобиана вместе с целевой функцией. Если Ложь, Якобиан будет оцениваться численно. jac также может быть callable, возвращающим якобиан весело . В в этом случае он должен принимать те же аргументы, что и fun .

tol поплавок, опционально

Допуск на заделку. Для детального контроля используйте специфичный для решателя опции.

функция обратного вызова , дополнительная функция

Дополнительная функция обратного вызова. Он вызывается на каждой итерации как callback(x, f) , где x — текущее решение, а f соответствующий остаток. Для всех методов, кроме «hybr» и «lm».

options dict, необязательный

Словарь опций решателя. Например, xtol или maxiter , см. show_options() для подробностей.

Возвращает
sol OptimizeResult

Решение, представленное как объект OptimizeResult . Важные атрибуты: x массив решений, успех a Логический флаг, указывающий, успешно ли завершен алгоритм и сообщение , в котором описывается причина завершения. Видеть OptimizeResult для описания других атрибутов.

См. также

show_options

Дополнительные опции, принимаемые решателями

Примечания

В этом разделе описываются доступные решатели, которые могут быть выбраны параметр «метод». Метод по умолчанию — hybr .

Метод hybr использует модификацию гибридного метода Пауэлла как реализован в MINPACK [1].

Метод lm решает систему нелинейных уравнений методом наименьших квадратов смысле, используя модификацию алгоритма Левенберга-Марквардта как реализован в MINPACK [1].

Метод df-sane — это спектральный метод без производных. [3]

Методы broyden1 , broyden2 , anderson , linearmixing , диагбройден , возбуждающие смешивания , крылов являются неточными методами Ньютона, с возвратом или полным поиском строки [2]. Каждый метод соответствует конкретным приближениям Якоби.

  • Метод broyden1 использует первое приближение Якоби Бройдена, это известный как хороший метод Бройдена.

  • Метод broyden2 использует второе приближение Якоби Бройдена. известен как плохой метод Бройдена.

  • 9Метод 0906 anderson использует (расширенное) перемешивание по Андерсону.

  • Метод Крылова использует аппроксимацию Крылова для обратного якобиана. Это подходит для масштабной проблемы.

  • Метод diagbroyden использует диагональное приближение Бройдена-Якоби.

  • Метод linearmixing использует приближение скалярного Якоби.

  • Метод excitingmixing использует настроенный диагональный якобиан приближение.

Warning

Алгоритмы реализованы для методов diagbroyden , linearmixing и excitingmixing могут быть полезны для определенных проблем, но будут ли они работать, может сильно зависеть от проблема.

Новое в версии 0.11.0.

Ссылки

1(1,2)

Мор, Хорхе Дж., Бертон С. Гарбоу и Кеннет Э. Хиллстром. 1980. Руководство пользователя для MINPACK-1.

2

К. Т. Келли. 1995. Итерационные методы для линейных и нелинейных Уравнения. Общество промышленной и прикладной математики.

3

  1. Ла Круз, Дж. М. Мартинес, М. Райдан. Мат. Комп. 75, 1429 (2006).

Примеры

Следующие функции определяют систему нелинейных уравнений и ее якобиан.

 >>> забава по определению (x):
... вернуть [x[0] + 0,5 * (x[0] - x[1])**3 - 1,0,
... 0,5 * (x[1] - x[0])**3 + x[1]]
г.
 >>> определение jac(x):
... вернуть np.array([[1 + 1,5 * (x[0] - x[1])**2,
... -1,5 * (х[0] - х[1])**2],
... [-1,5 * (x[1] - x[0])**2,
... 1 + 1,5 * (x[1] - x[0])**2]])

Раствор можно получить следующим образом.

 >>> из Scipy Import Optimize
>>> sol = optimise.root(fun, [0, 0], jac=jac, method='hybr')
>>> сол.х
массив ([0,8411639, 0,1588361])

Большая задача 92\]

с \(P(x,1) = 1\) и \(P=0\) в другом месте на границе квадрат.

Решение можно найти с помощью решателя method='krylov' :

 >>> из Scipy Import Optimize
>>> # параметры
>>> nx, ny = 75, 75
>>> hx, hy = 1./(nx-1), 1./(ny-1)
 
 >>> P_слева, P_справа = 0, 0
>>> P_верх, P_низ = 1, 0
 
 >>> остаток по определению (P):
... d2x = np.zeros_like(P)
... d2y = np.zeros_like(P)
...
... d2x[1:-1] = (P[2:] - 2*P[1:-1] + P[:-2]) / hx/hx
... d2x[0] = (P[1] - 2*P[0] + P_left)/hx/hx
... d2x[-1] = (P_right - 2*P[-1] + P[-2])/hx/hx
...
... d2y[:,1:-1] = (P[:,2:] - 2*P[:,1:-1] + P[:,:-2])/hy/hy
... d2y[:,0] = (P[:,1] - 2*P[:,0] + P_bottom)/hy/hy
... d2y[:,-1] = (P_top - 2*P[:,-1] + P[:,-2])/hy/hy
...
... вернуть d2x + d2y - 10*np.cosh(P).mean()**2
г.
 >>> предположение = np. zeros((nx, ny), float)
>>> sol = optimise.root(остаток, предположение, метод='крылов')
>>> print('Остаток: %g' % абс.(остаток(sol.x)).max())
Остаток: 5.7972e-06 # может отличаться
 
 >>> импортировать matplotlib.pyplot как plt
>>> x, y = np.mgrid[0:1:(nx*1j), 0:1:(ny*1j)]
>>> plt.pcolormesh(x, y, sol.x, shading='gouraud')
>>> plt.colorbar()
>>> plt.show()

Дифференциальные уравнения. Повторяющиеся корни

Онлайн-заметки Пола
Главная / Дифференциальные уравнения / DE второго порядка / Повторяющиеся корни

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 3-4: повторяющиеся корни

9{г\,т}}\]

Это одно и то же решение, и оно НЕ будет «достаточно хорошим», чтобы сформировать общее решение. Мы обещаем, что в конце концов дадим определение «достаточно хороший»! Итак, мы можем использовать первое решение, но нам понадобится второе решение.

Прежде чем найти это второе решение, давайте немного отвлечемся. Причина отъезда со временем станет ясна. Из квадратичной формулы мы знаем, что корни характеристического уравнения равны

9149.2} — 4ac} \right)v} \right) & = 0\end{align*}\]

Теперь, поскольку мы работаем с двойным корнем, мы знаем, что второй член будет равен нулю. Также экспоненты никогда не равны нулю. Следовательно, \(\eqref{eq:eq1}\) будет решением дифференциального уравнения при условии, что \(v(t)\) является функцией, удовлетворяющей следующему дифференциальному уравнению.

\[av» = 0\hspace{0,25 дюйма}{\mbox{ИЛИ}}\hspace{0,25 дюйма}v» = 0\]

: Мы можем отбросить \(a\), потому что знаем, что оно не может быть равно нулю. Если бы это было так, у нас не было бы дифференциального уравнения второго порядка! Итак, теперь мы можем определить наиболее общую возможную форму, допустимую для \(v(t)\).

\[v’ = \int{{v»\,dt}} = c\hspace{0,25 дюйма}v\left( t \right) = \int{{v’\,dt}} = ct + k\ ]

На самом деле это сложнее, чем нам нужно, и на самом деле мы можем удалить из этого обе константы. Чтобы понять, почему это так, давайте продолжим и воспользуемся этим, чтобы получить второе решение. Тогда два решения равны 9. {2t}}\end{выравнивание*}\]

Не забудьте правило продукта для второго члена! Подстановка начальных условий дает следующую систему.

\[\begin{align*}12 & = y\left( 0 \right) = {c_1}\\ — 3 & = y’\left( 0 \right) = 2{c_1} + {c_2}\end{ выровнять*}\]

Эту систему легко решить, чтобы получить \(c_{1} = 12\) и \(c_{2} = -27\). Фактическое решение IVP тогда. 909{\ гидроразрыва {{5 \, т}} {4}}} \ конец {выровнять *} \]

Не забудьте правило продукта для второго члена! Подстановка начальных условий дает следующую систему.

\[\begin{align*}3 = y\left( 0 \right) & = {c_1}\\ — \frac{9}{4} = y’\left( 0 \right) & = \frac{5 }{4}{c_1} + {c_2}\end{выравнивание*}\]

Эту систему легко решить, чтобы получить \(c_{1} = 3\) и \(c_{2} = -6\). Фактическое решение IVP тогда. 9{ — 7\влево( {т + 4} \вправо)}}\конец{выравнивание*}\]

Как найти корни многочлена

Обновлено 08 декабря 2020 г.

Автор Lisa Maloney

равен нулю. Когда дело доходит до фактического поиска корней, в вашем распоряжении есть несколько методов; факторинг — это метод, который вы будете использовать чаще всего, хотя построение графиков также может быть полезным.

Сколько корней?

Исследуйте член высшей степени многочлена, то есть член с наивысшим показателем степени. Этот показатель показывает, сколько корней будет иметь многочлен. Итак, если самый высокий показатель степени в вашем многочлене равен 2, у него будет два корня; если наивысший показатель степени равен 3, у него будет три корня; и так далее.

Предупреждения

  • Есть одна загвоздка: корни многочлена могут быть действительными или мнимыми. «Настоящие» корни входят в набор, известный как действительные числа, которым на данном этапе вашей математической карьеры являются все числа, с которыми вы привыкли иметь дело. Овладение мнимыми числами — это совсем другая тема, так что пока просто запомните три вещи:

    • «Мнимые» корни возникают, когда у вас есть квадратный корень из отрицательного числа. Например, √(-9).
    • Мнимые корни всегда идут парами.
    • Корни многочлена могут быть действительными или мнимыми. Итак, если у вас есть многочлен 5-й степени, у него может быть пять действительных корней, у него может быть три действительных корня и два мнимых корня и так далее. Пример 1 Это имеет гораздо больше смысла, если вы проследите за несколькими примерами. Рассмотрим простой полином x ​ 2 – 4​ x: ​

        Краткое рассмотрение показывает, что вы можете разложить x ​ из обоих членов полинома, что дает:

        x(x — 4 )

        Установить каждый член равным нулю. Это означает решение двух уравнений:

        x = 0

        — первый член, равный нулю, и

        x — 4 = 0

        , — второй член, равный нулю.

        У вас уже есть решение первого члена. Если ​ х ​ = 0, то все выражение равно нулю. Итак, x = 0 — это один из корней или нулей многочлена.

        Теперь рассмотрим второе слагаемое и найдем ​ x ​. Если вы прибавите 4 к обеим сторонам, вы получите:

        x — 4 + 4 = 0 + 4

        , что упрощается до:

        x = 4

        Итак, если x = 4, то второй множитель равен равен нулю, что означает, что весь многочлен тоже равен нулю.

        Поскольку исходный многочлен был второй степени (наивысший показатель степени равен двум), вы знаете, что у этого многочлена есть только два возможных корня. Вы уже нашли их обоих, поэтому все, что вам нужно сделать, это перечислить их:

        x = 0, x = 4

      Поиск корней с помощью факторизации: пример 2

      Вот еще один пример того, как находить корни с помощью факторизации, используя попутно сложную алгебру. Рассмотрим многочлен x 4 – 16. Беглый взгляд на его показатели показывает, что у этого многочлена должно быть четыре корня; теперь пришло время найти их.

        Вы заметили, что этот многочлен можно переписать как разность квадратов? Так что вместо 92+4)

        Теперь пришло время найти нули. Быстро становится ясно, что если x = 2, то первый множитель будет равен нулю, и, таким образом, все выражение будет равно нулю.

        Аналогично, если ​ x ​ = −2, второй множитель будет равен нулю, а значит, и все выражение будет равным нулю.

        Таким образом, x = 2 и x = −2 являются нулями или корнями этого многочлена.

        А как насчет последнего термина? Поскольку у него показатель степени «2», у него должно быть два корня. Но вы не можете разложить это выражение на множители, используя привычные вам действительные числа. Вам придется использовать очень сложную математическую концепцию, называемую мнимыми числами или, если хотите, комплексными числами. Это выходит далеко за рамки вашей текущей математической практики, так что пока достаточно отметить, что у вас есть два действительных корня (2 и −2) и два мнимых корня, которые вы оставите неопределенными.

        No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *