0 в степени х: Степень с показателем 0 — урок. Алгебра, 7 класс.

36Risolvere per ?cos(x)=1/27Risolvere per xsin(x)=-1/28Преобразовать из градусов в радианы2259Risolvere per ?cos(x)=( квадратный корень из 2)/210Risolvere per xcos(x)=( квадратный корень из 3)/211Risolvere per xsin(x)=( квадратный корень из 3)/212Графикg(x)=3/4* корень пятой степени из x 13Найти центр и радиусx^2+y^2=914Преобразовать из градусов в радианы120 град. 2+n-72)=1/(n+9)

помогите пожааалуйста 4 в степени х + 2 в степени х

Помогите пожалуйста составить развёрнутый и вопросный план по этому тексту:

Как известно, небо — это панорама, которая открывается с поверхности планеты, образуя некую видимость, сотканную из света. Причем, если наблюдать из разных точек, небо может выглядеть по-разному. Так, из иллюминатора самолета, поднявшегося над облаками, открывается совсем иной вид, чем с земли в это же время. Ясное небо — голубое, но стоит набежать облакам, и оно становится серым, свинцовым или грязно-белым. Ночное небо — черное. Причина всех подобных изменений — свет и его взаимодействие с воздухом и частичками различных веществ в нем.

Для того чтобы сказать, какой и почему цвет у неба, нужно вспомнить, что цвет — это всего лишь различаемый человеческим глазом участок в довольно узком диапазоне спектра электромагнитных волн. В этом диапазоне граничные позиции занимают красный и фиолетовый цвета постепенно переходя с увеличением длины волны излучения в так называемые инфракрасное и ультрафиолетовое излучения соответственно.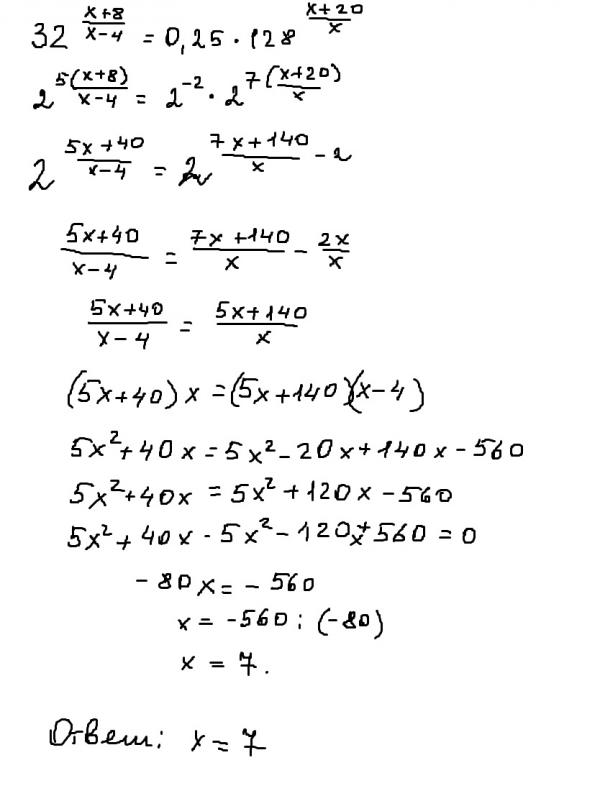 Свет, идущий от Солнца к Земле, видится как белый, но как доказал Ньютон, белый свет представляет собой пучок из семи лучей: красного, оранжевого, желтого, зеленого, голубого, синего и фиолетового. Разложение света на спектр происходит при столкновении его с молекулами различных веществ, при этом часть волн может быть поглощена, а часть — рассеяна.

Многие ученые пытались понять, почему же до нас доходит только голубой цвет при ясном небе. Первые гипотезы предполагали влияние молекул озона и воды. Считалось, что именно они поглощают красный свет и пропускают голубой, что и дает соответствующий цвет небу. Последовавшие за этим подсчеты, однако, показали, что того количества озона, кристаллов льда и молекул водяного пара, которое есть в атмосфере, недостаточно для придания небу голубого цвета.

На следующем этапе исследований Джоном Тиндаллом было высказано предположение, что роль искомых частиц играет пыль. Синий свет обладает наибольшей стойкостью к рассеиванию, а потому способен пройти сквозь все слои пыли и других взвешенных частиц. Тиндалл провел эксперимент, подтвердивший его предположение. Он создал в условиях лаборатории модель смога и осветил ее ярким белым светом. Смог приобрел голубой оттенок. Ученый сделал однозначный вывод из своего исследования: цвет неба определяется частичками пыли, то есть, если бы воздух Земли был чистым, то над головами людей светились не голубые, а белые небеса.

Окончательную точку в вопросе о цвете неба, поставил английский ученый, лорд Д. Рэлей. Он доказал, что не пыль или смог окрашивает пространство над головой в привычный для нас оттенок. Дело в самом воздухе. Молекулы газа поглощают большую часть света и в первую очередь самые длинные волны, эквивалентные красному. Синий при этом рассеивается.

Внимательные люди заметят, что, следуя этой логике, небесный купол над головой должен быть фиолетовым, поскольку именно у этого цвета самая короткая длина волны в видимом диапазоне. Объясняется это просто: при одинаковой яркости человеческий глаз лучше воспринимает именно голубой цвет, а не фиолетовый. Кроме того, зеленый свет, также обладающий некоторой способностью к рассеянию в атмосфере, смешиваясь с отлично рассеивающимся фиолетовым, приводит к тому же голубому. По сути, видимый нами голубой — результат смешения синего с фиолетовым и зеленым.

Можно ли, оперируя этой же логикой, понять ярко красные цвета заката? Конечно, можно даже говорить о том, что солнце на горизонте будет тем краснее, чем толще слой атмосферы лежит между ним и нашим глазом, либо чем беспокойнее и, соответственно, более запылённым будет этот самый слой атмосферы. Так что, чем багровее закат, тем ненастнее и ветренее окажется следующий день. Дело в том, что во время заката и рассвета солнечным лучам приходится преодолевать гораздо больший путь сквозь атмосферу, чем в разгар дня. При этом свет сине-зеленой части спектра сильно рассеиваются или поглощаются атмосферой и облака, расположенные у линии горизонта, становятся окрашенными в оттенки красного.

Когда небо заволакивают облака, картина совершенно меняется. Солнечные лучи не в силах преодолеть плотный слой, и большая часть их просто не достигает земли. Лучи, сумевшие пройти сквозь тучи, встречаются с водными каплями дождя и облаков, которые вновь искажают свет, снова смешивая его. В результате всех этих превращений до земли доходит белый свет, если облака небольшие по размеру, и серый, когда небо закрывают внушительные тучи, вторично поглощающие часть лучей.

Вот так раскрывается причина довольно привычных для нас вещей. Так что теперь мы можем просто получить удовольствие от созерцания уже не таинственного, но по-прежнему бездонного голубого неба и божественного алого заката!

Как можно скорее

Спасибо заранее

Биоматематика: силовые функции

Биологический проект > Biomath > Power Function > Основы Силовые функции Основы Определение Степенная функция — это функция вида ф ( х ) = ах п , , где a ≠ 0 — константа, а p — действительное число. Некоторые примеры силы функции включают в себя: Корневые функции, такие как примеры питания функции. Графически степенные функции могут напоминать экспоненциальные или логарифмические. функции для некоторых значений x . Однако, поскольку x становится очень большим, силовые функции экспоненциальные или логарифмические функции начинают расходиться одна от другой. Экспоненциально растущая функция обгонит растущую мощность функция для больших значений x . С другой стороны, растущие силовые функции будут обгонять логарифмические функции для больших значений x . Домен и диапазон Область определения степенной функции зависит от значения степени стр . Мы будем смотрите каждый случай отдельно. 1 . p — целое неотрицательное число Домен состоит из всех действительных чисел (т. е. (− ∞, ∞)). 2. p — отрицательное целое число Областью определения являются все действительные числа, кроме нуля (т. е. (−∞, 0) ∪ (0, ∞) или { х | x ≠ 0}). Мы вернемся к этому случаю, когда будем изучать рациональные функции. 3 . p — рациональное число, выраженное в наименьших единицах как r / s и s равно даже А . р > 0 Домен неотрицательных действительных чисел (т.е. [0,∞) или { x | x ≥ 0}). Б. р < 0 Домен состоит из положительных действительных чисел (т.е. (0,∞) или { x | x > 0}). 4. p является рациональным числом, выраженным в наименьших единицах как r / s и s равно нечетному А . р > 0 Домен состоит из действительных чисел. Б . р < 0 Домен состоит из всех действительных чисел, кроме нуля. 5. p иррациональное число А . р > 0 Домен состоит из всех неотрицательных действительных чисел. Б. р < 0 Домен состоит из всех положительных действительных чисел.   ***** В следующем разделе мы изучим графики степенных функций. График силовых функций Биологический проект > Биоматематика > Силовые функции > Основы Биологический проект Отделение биохимии и молекулярной биофизики Университет Аризоны апрель 2006 г. Связаться с командой разработчиков http://www.biology.arizona.edu Все права защищены авторским правом © 2006. Все права защищены.

Правило мощности и функция мощности

Содержание:

1. Обзор функции мощности
2. Что такое правило мощности?
3. Примеры
4. Доказательство силы Правило

Функция мощности имеет форму

, где:

• a и p константы,
• p действительное число,
• и a отличны от нуля.

Мы называем a масштабным коэффициентом , а p — показателем степени или степенью . Полиномиальные функции, с которыми мы работаем в большей части алгебры, представляют собой просто комбинации степенных функций.

Иногда силовые функции имеют более узкое определение, например

Согласно этому определению, все степенные функции проходят через точку (1,1). Все степенные функции в нашем более широком определении являются кратными этих более узко определенных функций.

Примеры степенных функций

Простейшей степенной функцией является та, где a = 1 и p = 1; у = х.

Но это только один из многих. y = x ^-1 , y = x ^1/2 и y = x ⁶ также являются степенными функциями.

Приведенные ниже графики представляют собой графики функций мощности.

Показатель p не обязательно должен быть положительным; Ниже приведены все степенные функции:

• y = x ^-1 ,
• у = х ^-1/2 ,
• у = х ^-5

Согласно более широкому определению, y = 2, y = 4x и y = 5x ^1/2 также являются примерами степенных функций.

Форма степенных функций

Предположим для простоты, что масштабный коэффициент a равен единице. Тогда:

• p > 1 Означает, что функция вогнута вверх и растет по мере увеличения x
• p = 1 Означает, что функция представляет собой прямую линию (y = x)
• 0< p< 1 Означает, что функция вогнута вниз и растет по мере увеличения x
• p = 0 Означает, что функция представляет собой прямую линию (y = 1)
• p < 0 Означает, что функция вогнута и приближается к 0 по мере увеличения x

Предел для степенной функции

Предел мощности функции — это степень предела функции, где p — любое действительное число. (См.: Свойства пределов).

Пример : Найдите предел функции f(x) = x ² при x→2.

1. Временно отключить питание: f(x) = x
2. Найдите предел (1) при заданном значении x: lim = 2, используя прямую замену.
3. Включите питание и решите: 2 ² = 4

С правилом степени работать на удивление просто: поместите показатель степени перед «x», а затем вычтите из показателя степени 1. Например, д/дх х ³ = 3x ^{(3 – 1)} = 3x ² .

Формальное определение степенного правила сформулировано так: «Производная x в n-й степени равна n, умноженному на x в n минус одна степень», когда x — моном (одночленное выражение), а n равно реальное число. Условно это выглядит так:
d/dx x ⁿ = nx ^{n – 1} .

Дифференциальные показатели: примеры

Несколько примеров смотрите в видео или читайте ниже:

Правило силы

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

С помощью правила степени вы можете быстро выполнить сложное дифференцирование за считанные секунды без помощи калькулятора. Возьмем, к примеру, производную от x ¹⁰⁰⁰ . Попытка решить (x + h) ¹⁰⁰⁰ потребовала бы много времени, поэтому здесь мы воспользуемся степенным правилом.

Шаг 1: Найдите «n» — показатель степени. Для этой задачи n равно 1000.

Шаг 2: Подставьте значение «n» в начало основания, чтобы получить 1000x ¹⁰⁰⁰ .

Шаг 3: Вычтите 1 из показателя степени:
1000x ^1000-1 = 1000x ⁹⁹⁹

Вот и все!

Чтобы понять, как работает доказательство степенного правила, вы должны быть знакомы с биномиальной теоремой (хотя вы, возможно, сможете обойтись без , а не , зная ее, если хорошо владеете алгеброй). Вы также должны быть знакомы с формальным определением limit . Если у вас есть эти предварительные условия, вам будет очень легко следовать.

Это доказательство степенного правила является доказательством общей формы степенного правила , а именно:

находятся в силовом формате.

Пример задачи: Покажите доказательство правила степени, используя классическое определение производной: предел.

Шаг 1: Вставьте правило мощности в определение предела:

Шаг 2: Используйте биномиальную теорему, чтобы оценить уравнение из шага 1:

Примечание: я включил «…», чтобы указать, что это неполный ряд. Чтобы доказать правило мощности, вам не нужно выписывать всю серию.

Шаг 3: Упростите уравнение из шага 2, используя алгебру. По сути, вы отменяете любые +n ⁿ и -n ⁿ и делите на δx:

Шаг 4: Раскройте уравнение , используя комбинации (n выберите 1):

Обратите внимание, что вы можете удалить любые термины, которые умножаются на Δx (поскольку Δx настолько незначительна, что практически равна нулю).

Шаг 5: Используйте следующие правила для дальнейшего сокращения уравнения :

1. 1! уменьшается до единицы, так что вы можете устранить его. (Символ ! является факториалом).
2. 7! / 6! = 7 или 10!/9!= 10, значит, n! / п – 1! = п

Это уравнение является производной X ⁿ .
Вот и все!

Наверх.

Power Rule: Ссылки

Taba, Kahlil. Конспект лекций: Степенные функции. Колледж Оранжевого побережья. Получено с http://occonline.occ.cccd.edu/online/ktaba/power_functions.htm 23 февраля 2019 г.
Учебные пособия по биоматематике: основы питания. Университет Аризоны. Получено с http://www.biology.arizona.edu/biomath/tutorials/power/Powerbasics.html 23 февраля 2019 г.
Power Functions: Math 251 Lesson Notes. Университет штата Орегон. Получено с https://oregonstate.edu/instruct/mth351/cq/FieldGuide/power/lesson.html 23 февраля 2019 г.

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен .